Применение в жизни

Задачи в курсе физики средней школы требуют знания теоремы Пифагора.

Задача из курса физики за 9 класс:

Когда биатлонист стреляет по мишени, он делает «поправку на ветер». Если ветер дует справа, а спортсмен стреляет по прямой, то пуля уйдёт влево. Чтобы попасть в цель, надо сдвинуть прицел вправо на расстояние смещения пули. Для них составлены специальные таблицы (на основе следствий из т. Пифагора). Биатлонист знает, на какой угол смещать прицел при известной скорости ветра.

Сотовая телефонная связь.

Все понимают, что сейчас мобильный телефон очень важный атрибут жизни современного человека. Каждому абоненту важна качественная сотовая связь. А качество зависит от высоты антенны мобильного оператора. Чтобы рассчитать, в каком радиусе можно принимать передачу, задействуем

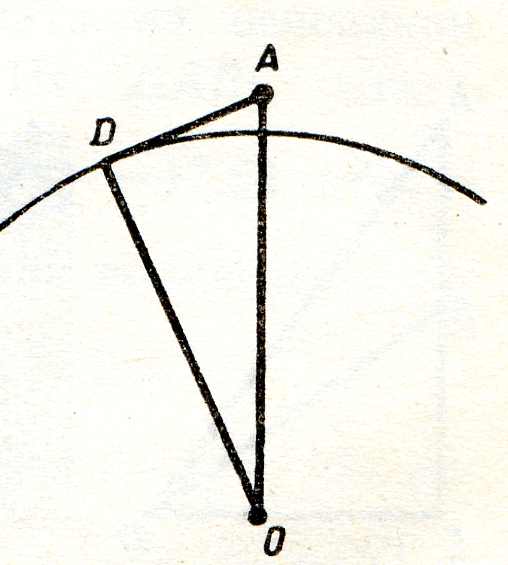
Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)

Решение:

Пусть AB = x, BC=R= 200 км, OC

Теорема Пифагора

Теорема Пифагора по праву является одной из основных теорем математики. Значение этой теоремы заключается в том, что при ее помощи можно вывести большую часть теорем в геометрии. Ценность ее в современном мире также велика, поскольку теорема Пифагора применяется во многих отраслях деятельности человека. Например, ее используют при расположении молниеотводов на крышах зданий, при производстве окон некоторых архитектурных стилей и даже при вычислении высоты антенн операторов мобильной связи. И это далеко не весь перечень практического применения данной теоремы. Вот почему очень важно знать

Для того чтобы разобраться в теореме, названной именем греческого философа, нужно рассмотреть одно из ее доказательств. В настоящее время известно более полутора сотен доказательств теоремы. Мы же остановимся на одном из самых понятных и простых – геометрическом доказательстве теоремы Пифагора.

Итак, изобразим прямоугольный треугольник АВС, прямой угол которого расположен в точке С. АС и ВС – катеты треугольника, а АВ – его гипотенуза.

Далее, опустим на гипотенузу АВ высоту СН с прямым углом и увидим, что точка Н делит гипотенузу на два отрезка АН и НВ. В итоге образуются равные прямые углы АСВ и АНС, а САВ и САН – равные острые углы. Таким образом, мы получаем две пары подобных треугольников АНС и АСВ, ВНС и ВСА.
Отсюда следуют пропорции:

Проводим соответствующее вычисление:

ВС? = ВН*АВ,
АС? = АН*АВ

Получается следующее:

ВС? + АС? = АВ(ВН+АН),

а в связи с тем, что АВ=ВН+АН, получается теорема Пифагора, формула которой такова:

ВС? + АС? = АВ?

Формулировка теоремы Пифагора согласно формуле звучит следующим образом:

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Разобравшись с доказательством, некоторые из вас, несомненно, задались вопросом: почему столь важная теорема в мире математики, называется именем Пифагора? А все потому, что ее создателем ранее считался именно греческий философ Пифагор Самосский. Но на сегодняшний день доказано, что до открытия теоремы Пифагором, информация о ней упоминалась в древнем Китае, Вавилоне, Индии, а самые ранние сведения пришли из Египта. К сожалению, математическая история практически не сохранила достоверных знаний о происхождении одной из важнейших теорем геометрической науки. Тем не менее, Пифагору нужно отдать должное. Несмотря на то, что свойство прямоугольного треугольника он не открыл, но именно Пифагор первым обобщил имеющиеся сведения, благодаря чему каждый из нас без труда сумеет разобраться в теореме Пифагора.

Любите читать? репетитор по литературе (http://nam-pokursu.ru/tutors/repetitor-po-literature.html) поможет повысить ваши навыки во владении литературой.

Практическое применение теоремы Пифагора

МБОУ СОШ № 1 им. С.Соболя г. Ейска МО Ейский район

Практическое применение теоремы Пифагора

Горбаконь Д. А.

Содержание

1. Введение.

2. Способы доказательства теоремы.

3. Применение теоремы на практике.

4. Список литературы.

Введение

Школьные учебники, к сожалению, обычно не объясняют, что в математике важно не только зубрить теоремы, аксиомы и формулы. Важно понимать и чувствовать ее фундаментальные принципы. И при этом попробовать освободить свой ум от штампов и азбучных истин – только в таких условиях рождаются все великие открытия.

К таким открытиям можно отнести и то, которое сегодня мы знаем как теорему Пифагора. С его помощью мы попробуем показать, что математика не только может, но и должна быть увлекательной.

Рассмотрю примеры практического применения теоремы Пифагора. Не буду пытаться привести все примеры использования теоремы — это вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой.

Способы доказательства теоремы.

Приведу несколько простых доказательств теоремы.

Введем обозначения:
A, B, C — углы треугольника, причем, B = 90°,

На приведенном ниже рисунке показана геометрическая интерпретация теоремы Пифагора.

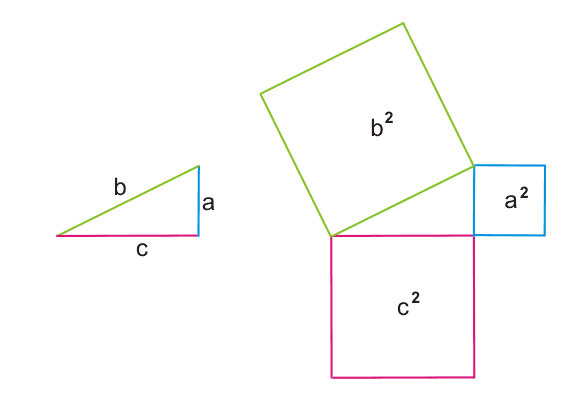
1. Самое простое доказательство теоремы Пифагора.

Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна a + c.

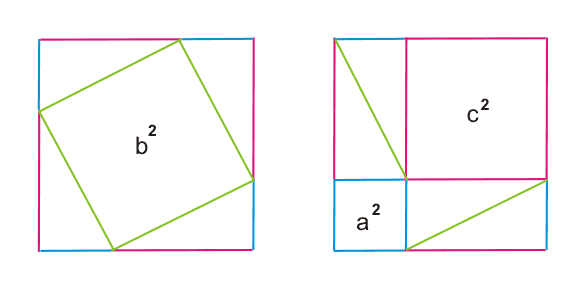
В одном случае (слева) квадрат разбит на квадрат со стороной b и четыре прямоугольных треугольника с катетами a и c.

В другом случае (справа) квадрат разбит на два квадрата со сторонами 

Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.

Кстати, этот чертеж лег в основу многочисленных анекдотов и карикатур, посвященных теореме Пифагора. Самый знаменитый, пожалуй, это «Пифагоровы штаны во все стороны равны»:

2. Доказательство индийского математика Бхаскари.

Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна b, на квадрат наложены 4 исходных треугольника с катетами a и c, как показано на рисунке.

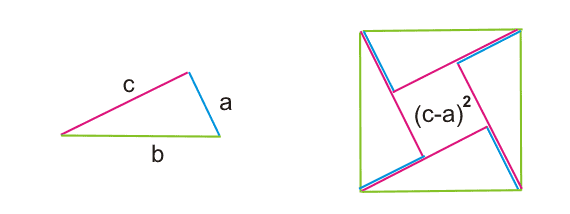
Сторона маленького квадрата, получившегося в центре, равна c — a, тогда:
b² = 4*a*c/2 + (c-a)² =
   = 2*a*c + c² — 2*a*c + a² =
   = a² + c²

Само же древнеиндийское доказательство описано в XII веке в трактате «Венец знания» («Сиддханта широмани») и в качестве главного аргумента автор использует призыв, обращенный к математическим талантам и наблюдательности учеников и последователей: «Смотри!».

Но мы разберем это доказательство более подробно:

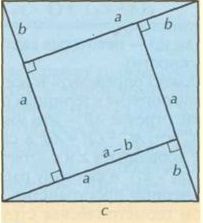
Внутри квадрата постройте четыре прямоугольных треугольника так, как это обозначено на чертеже. Сторону большого квадрата, она же гипотенуза, обозначим с. Катеты треугольника назовем а и b. В соответствии с чертежом сторона внутреннего квадрата это 

Используйте формулу площади квадрата S=c², чтобы вычислить площадь внешнего квадрата. И одновременно высчитайте ту же величину, сложив площадь внутреннего квадрата и площади всех четырех прямоугольных треугольников: (a-b)²2+4*1\2*a*b.

Вы можете использовать оба варианта вычисления площади квадрата, чтобы убедиться: они дадут одинаковый результат. И это дает вам право записать, что c²=(a-b)²+4*1\2*a*b. В результате решения вы получите формулу теоремы Пифагора c²=a²+b². Теорема доказана.

4. «Стул невесты».

Это любопытное древнекитайское доказательство получило название «Стул невесты» — из-за похожей на стул фигуры, которая получается в результате всех построений:

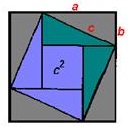
Рис.1.

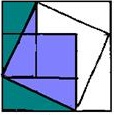
Рис. 2.

В нем используется чертеж, который мы уже видели на рис.3 во втором доказательстве. А внутренний квадрат со стороной с построен так же, как в древнеиндийском доказательстве, приведенном выше.

Если мысленно отрезать от чертежа на рис.1 два зеленых прямоугольных треугольника, перенести их к противоположным сторонам квадрата со стороной с и гипотенузами приложить к гипотенузам сиреневых треугольников, получится фигура под названием «стул невесты» (рис.2). Для наглядности можно то же самое проделать с бумажными квадратами и треугольниками. Вы убедитесь, что «стул невесты» образуют два квадрата: маленькие со стороной b и большой со стороной a.

Эти построения позволили древнекитайским математикам и нам вслед за ними прийти к выводу, что c²=a²+b².

5. Метод Гарфилда.

Постройте прямоугольный треугольник АВС. Нам надо доказать, что ВС²=АС²+АВ².

Для этого продолжите катет АС и постройте отрезок CD, который равен катету АВ. Опустите перпендикулярный AD отрезок ED. Отрезки ED и АС равны. Соедините точки Е и В, а также Е и С и получите чертеж, как на рисунке ниже:

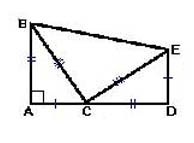
Чтобы доказать терему, мы вновь прибегаем к уже опробованному нами способу: найдем площадь получившейся фигуры двумя способами и приравняем выражения друг к другу.

Найти площадь многоугольника ABED можно, сложив площади трех треугольников, которые ее образуют. Причем один из них, ЕСВ, является не только прямоугольным, но и равнобедренным. Не забываем также, что АВ=CD, АС=ED и ВС=СЕ – это позволит нам упростить запись и не перегружать ее. Итак, S_ABED=2*1/2(AB*AC)+1/2ВС².

При этом очевидно, что ABED – это трапеция. Поэтому вычисляем ее площадь по формуле: S_ABED=(DE+AB)*1/2AD. Для наших вычислений удобней и наглядней представить отрезок AD как сумму отрезков АС и CD.

Запишем оба способа вычислить площадь фигуры, поставив между ними знак равенства: AB*AC+1/2BC²=(DE+AB)*1/2(AC+CD). Используем уже известное нам и описанное выше равенство отрезков, чтобы упростить правую часть записи: AB*AC+1/2BC²=1/2(АВ+АС)². А теперь раскроем скобки и преобразуем равенство: AB*AC+1/2BC²=1/2АС²+2*1/2(АВ*АС)+1/2АВ². Закончив все преобразования, получим именно то, что нам и надо: ВС²=АС²+АВ². Мы доказали теорему.

Конечно, этот список доказательств далеко не полный. Теорему Пифагора также можно доказать с помощью векторов, комплексных чисел, дифференциальный уравнений, стереометрии и т.п. И даже физики: если, например, в аналогичные представленным на чертежах квадратные и треугольные объемы залить жидкость. Переливая жидкость, можно доказать равенство площадей и саму теорему в итоге.

6. Алгебраическое доказательство теоремы Пифагора (доказательство Мёльманна).

Площадь прямоугольного треугольника
S = a*c/2 (3.1)

С другой стороны:
S = r*p, где
r — радиус вписанной окружности, r = (a+c-b)/2.
p — полупериметр.

Таким образом:
S = r*p = (a+b+c)/2 * (a+c-b)/2 =
  = (a²+2*a*c+c²-b²)/4

С учетом (3.1):
a*c/2 = (a²+2*a*c+c²-b²)/4

Приводя к общему знаменателю и перенося в левую часть, получим:
a²+c²-b² = 0, или
a²+c² = b²

Применение теоремы на практике.

Строительство

Окно

В зданиях готического и ромaнского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг и половине ширины (b/2), для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Так как она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоватися вычисления; покажем, как применяется в таких задачах теорема Пифагора.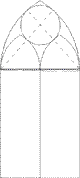

В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p.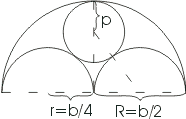

По теореме Пифагора имеем:
(b/4+p)=( b/4)+( b/4-p)
или
b/16+ b*p/2+p=b/16+b/4-b*p+p,
откуда
b*p/2=b/4-b*p.
Разделив на b и приводя подобные члены, получим:
(3/2)*p=b/4, p=b/6.

Крыша

В доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м, и AB=BF.
Решение:
Треугольник ADC — равнобедренный AB=BC=4 м, BF=4 мЕсли предположить, что FD=1,5 м, тогда:

А) Из треугольника DBC: DB=2,5м

Б) Из треугольника ABF: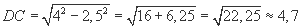

Как рассчитать высоту шкафа-купе?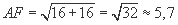

На первый взгляд ничего особенного: снять размеры высоты от пола до потолка в нескольких точках, отнять несколько сантиметров, чтобы шкаф не упирался в потолок. Поступив так, в процессе сборки мебели могут возникнуть трудности. Ведь сборка каркаса мебельщики выполняют, располагая шкаф в горизонтальном положении, а когда каркас собран, поднимают его в вертикальное положение. Рассмотрим боковую стенку шкафа. Высота шкафа должна быть на 10 см меньше расстояния от пола до потолка при условии, что это расстояние не превышает 2500 мм. А глубина шкафа – 700 мм. Почему на 10 см, а не на 5 см или на 7, и причем здесь теорема Пифагора?

Итак: боковая стенка 2500-100=2400(мм)- максимальная высота конструкции.

Боковая стенка в процессе подъема каркаса должна свободно пройти как по высоте, так и по диагонали. По теореме Пифагора

АС= √ АВ² + ВС²

АС= √ 2400²+ 700² = 2500 (мм)

Что произойдет если высоту шкафа уменьшить на 50 мм?

АС= √ 2450²+ 700 ²= 2548 (мм)

Диагональ 2548 мм. Значит, шкаф не поставишь (можно испортить потолок).

Молниеотвод

Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
Решение:
По теореме Пифагора h² ≥ a²+b², значит h ≥ (a²+b²)^½.
Ответ: h ≥ (a²+b²)^½

Астрономия

На этом рисунке показаны точки A и B и путь светового луча от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч — прямой.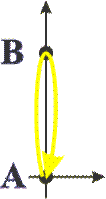

Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равна половина пути, который проходит луч? Если обозначить отрезок AB символом l, половину времени как t, а также обозначив скорость движения света буквой c, то наше уравнение примет вид

c * t = l

Очевидно? Это ведь произведение затраченного времени на скорость!

Теперь попробуем взглянуть на то же самое явление из другой системы отсчета, с другой точки зрения, например, из космического корабля, пролетающего мимо бегающего луча со скоростью v. Раньше мы поняли, что при таком наблюдении скорости всех тел изменятся, причем неподвижные тела станут двигаться со скоростью v в противоположную сторону. Предположим, что корабль движется влево. Тогда две точки, между которыми бегает зайчик, станут двигаться вправо с той же скоростью. Причем, в то время, пока зайчик пробегает свой путь, исходная точка A смещается и луч возвращается уже в новую точку C.

Вопрос: на сколько успеет сместиться точка (чтобы превратиться в точку C), пока путешествует световой луч? Точнее, опять спросим о половине данного смещения! Если обозначить половину времени путешествия луча буквой t’, а половину расстояния AC буквой d, то получим наше уравнение в виде:

v * t’ = d

Буквой v обозначена скорость движения космического корабля. Опять очевидно, не правда ли?

Другой вопрос: какой путь при этом пройдет луч света? (Точнее, чему равна половина этого пути? Чему равно расстояние до неизвестного объекта?)

Если обозначить половину длины пути света буквой s, то получим уравнение:

c * t’ = s

Здесь c — это скорость света, а t’ — это тоже самое время, которые мы рассматривали на формулы выше.

Теперь рассмотрим треугольник ABC. Это равнобедренный треугольник, высота которого равна l. Да-да, тому самому l, которое мы ввели при рассмотрении процесса с неподвижной точки зрения. Поскольку движение происходит перпендикулярно l, то оно не могло повлиять не нее.

Треугольник ABC составлен из двух половинок — одинаковы прямоугольных треуголников, гипотенузы которых AB и BC должны быть связаны с катетами по теореме Пифагора. Один из катетов — это d, которое мы рассчитали только что, а второй катет — это s, который проходит свет, и который мы тоже рассчитали.
Получаем уравнение:

s² = l² + d²

Это ведь просто теорема Пифагора, верно?

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы, которые долгое время считались искусственными) и др. Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора.

Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Мобильная связь

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например радиусе R=200 км?, если известно. что радиус Земли равен 6380 км.)
Решение:
Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB = OA + AB
OB = r + x
Используя теорему Пифагора, получим ответ.
Ответ: 2,3 км.

Список литературы

1. «Успехи математических наук», 1962, т. 17, № 6 (108).

2. Александр Данилович Александров (к пятидесятилетию со дня рождения),

3. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 10 – 11 кл. – М.: Просвещение, 1992.

4. Атанасян Л.С. и др. Геометрия, 10 – 11 кл. – М.: Просвещение, 1992.

5. Владимиров Ю.С. Пространство – время: явные и скрытые размерности. – М.: «Наука», 1989.

6. Волошин А.В. Пифагор. – М.: Просвещение, 1993.

7. Газета «Математика», № 21, 2006.

8. Газета «Математика», № 28, 1995.

9. Геометрия: Учеб. Для 7 – 11 кл. сред.шк./ Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова. – М.: Просвещение, 1992.

10. Геометрия: Учеб.для 7 – 9 кл. общеобразоват. Учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 6-е изд. – М.: Просвещение, 1996.

11. Глейзер Г.И. История математики в школе: IX – Xкл. Пособие для учителей. – М.: Просвещение, 1983.

12. Дополнительные главы к школьному учебнику 8 кл.: Учебное пособие для учащихся шк. и классов с углубл. изуч. математики /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1996.

13. Еленьский Щ. По следам Пифагора. М., 1961.

14. Киселёв А.П., Рыбкин Н.А. Геометрия: Планиметрия: 7 – 9 кл.: Учебник и задачник. – М.: Дрофа, 1995.

15. Клайн М. Математика. Поиск истины: Перевод с англ. / Под ред. и предисл. В.И. Аршинова, Ю.В. Сачкова. – М.: Мир, 1998.

16. Литурман В. Теорема Пифагора. – М., 1960.

17. Математика: Справочник школьника и студента / Б. Франк и др.; Перевод с нем. – 3-е изд., стереотип. – М.: Дрофа, 2003.

18. Пельтуер А. Кто вы Пифагор? – М.: Знание – сила, № 12, 1994.

19. Перельман Я. И. Занимательная математика. – М.: «Наука», 1976.

20. Пономарёва Т.Д. Великие учёные. – М.: ООО «Издательство Астрель», 2002.

21. Свешникова А. Путешествие в историю математики. – М., 1995.

22. Семёнов Е.Е. Изучаем геометрию: Кн. Для учащихся 6 – 8 кл. сред.шк. – М.: Просвещение, 1987.

23. Смышляев В.К. О математике и математиках. – Марийское книжное издательство, 1977.

24. Тучнин Н.П. Как задать вопрос. – М.: Просвещение, 1993.

25. Черкасов О.Ю. Планиметрия на вступительном экзамене. – М.: Московский лицей, 1996.

26. Энциклопедический словарь юного математика. Сост. А.П. Савин. – М.: Педагогика, 1985.

27. Энциклопедия для детей. Т. 11. Математика. /Глав. Ред. М.Д. Аксёнова. – М.: Аванта +, 2001.

Исследовательская работа по математике «Практическое применение теоремы Пифагора»

МОУ «Горская средняя общеобразовательная школа»

Тема: Практическое применение теоремы Пифагора

Автор: Мотченко Руслан Иванович,

ученик 11 класса МОУ «Горская СОШ»

Руководитель: Токорева Галина Петровна

Учитель математики МОУ «Горская СОШ»

Горки 2015 год

Актуальность темы

В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики.

Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой.

По выражению известного ученого Иоганна Кеплера, «геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…».

Теорема Пифагора – одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии.

Цель исследования — выяснить области применения теоремы Пифагора.

Предмет исследования: применение Теоремы Пифагора при решении практических задач.

Гипотеза исследования — с помощью теоремы Пифагора можно решать не только математические задачи.

Исходя из вышеназванной цели, были обозначены следующие задачи:

1. Собрать информацию о практическом применении теоремы Пифагора в различных источниках и определить области применения теоремы.

2. Изучить некоторые исторические сведения о Пифагоре и о его теореме.

3. Показать применение теоремы при решении исторических задач.

Решить прикладные задачи по укреплению недавно посаженных молодых елей и туй и молниеотвода.

Биография Пифагора

Пифагор Самосский (ок. 580 — ок. 500 до н. э.) древнегреческий математик и философ-идеалист. Родился на острове Самос. Получил хорошее образование. По преданию Пифагор, чтобы ознакомиться с мудростью восточных ученых, выехал в Египет и как будто прожил там 22 года. Хорошо овладев всеми науками египтян, в том числе и математикой, он переехал в Вавилон, где прожил 12 лет и ознакомился с научными знаниями вавилонских жрецов. Предания приписывают Пифагору посещение и Индии. Это очень вероятно, так как Иония и Индия тогда имели торговые связи. Возвратившись на родину (ок. 530 г. до н. э.), Пифагор попытался организовать свою философскую школу. Однако по неизвестным причинам он вскоре оставляет Самос и селится в Кротоне (греческая колония на севере Италии). Здесь Пифагору удалось организовать свою школу, которая действовала почти тридцать лет. Школа Пифагора, или, как ее еще называют, пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством. Статут пифагорейского союза был очень суровым. Каждый, кто вступал в него, отказывался от личной собственности в пользу союза, обязывался не проливать крови, не употреблять мясной пищи, беречь тайну учения своего учителя. Членам школы запрещалось обучать других за вознаграждение. По своим философским взглядам Пифагор был идеалистом, защитником интересов рабовладельческой аристократии. Возможно, в этом и заключалась причина его отъезда из Самоса, так как в Ионии очень большое влияние имели сторонники демократических взглядов. В общественных вопросах под «порядком» пифагорейцы понимали господство аристократов. Древнегреческую демократию они осуждали. Пифагорейская философия была примитивной попыткой обосновать господство рабовладельческой аристократии. В конце V в. до н. э. в Греции и ее колониях прокатилась волна демократического движения. Победила демократия В Кротоне. Пифагор вместе с учениками оставляет Кротон и уезжает в Тарент, а затем в Метапонт. Прибытие пифагорейцев в Метапонт совпало со вспышкой там народного восстания. В одной из ночных стычек погиб почти девяностолетний Пифагор. Его школа прекратила свое существование. Ученики Пифагора, спасаясь от преследований, расселились по всей Греции и ее колониям. Добывая себе средства к существованию, они организовывали школы, в которых преподавали главным образом арифметику и геометрию. Сведения об их достижениях содержатся в сочинениях позднейших учёных — Платона, Аристотеля и др.

Открытие того факта, что между стороной и диагональю квадрата не существует общей меры, было самой большой заслугой пифагорейцев. Этот факт вызвал первый кризис в истории математики. Пифагорейское учение о целочисленной основе всего существующего больше нельзя было признавать истинным. Поэтому пифагорейцы пытались сохранить своё открытие в тайне и создали легенду о гибели Гиппаса Мессопотамского, который осмелился разгласить открытие. Пифагору приписывают еще ряд важных в то время открытий, а именно: теорему о сумме внутренних углов треугольника; задачу о делении плоскости на правильные многоугольники (треугольники, квадраты и шестиугольники). Есть сведения, что Пифагор построил «космические» фигуры, т. е. пять правильных многогранников. Но вероятнее, что он знал только три простейших правильных многогранника: куб, четырехгранник, восьмигранник. Школа Пифагора много сделала, чтобы придать геометрии характер науки. Основной особенностью метода Пифагора было объединение геометрии с арифметикой.

Пифагор много занимался пропорциями и прогрессиями и, вероятно подобием фигур, так как ему приписывают решение задачи: «По данным двум фигурам построить третью, равновеликую одной из данных и подобную второй». Пифагор и его ученики ввели понятие о многоугольных, дружественных, совершенных числах и изучали их свойства. Арифметика как практика вычислений не интересовала Пифагора, и он с гордостью заявил, что «поставил арифметику выше интересов торговца». Пифагор одним из первых считал, что Земля имеет форму шара и является центром Вселенной, что Солнце, Луна и планеты имеют собственное движение, отличное от суточного движения неподвижных звезд. Учение пифагорейцев о движении Земли Николай Коперник воспринял как предысторию своего гелиоцентрического учения. Недаром церковь объявила систему Коперника «ложным пифагорейским учением».

История теоремы

Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4». В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.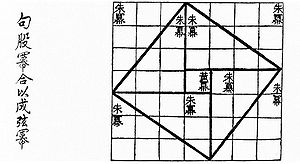

Кантор (крупнейший немецкий историк математики) считает, что равенство 3² + 4² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого . Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.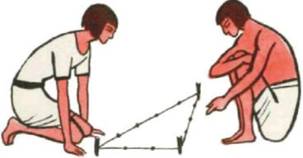

Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой — на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод: «Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку.»

Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.

В первом русском переводе евклидовых «Начал», сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: «В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».

В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих «Начал». С другой стороны, Прокл утверждает, что доказательство в «Началах» принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы. Рассказывают, что в честь этого открытия Пифагор принес в жертву 100 быков.

Теорема Пифагора в древних практических задачах

1.Над озером тихим,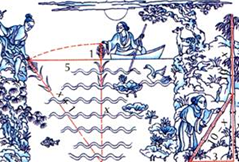

С полфута размером, высился лотоса цвет.

Он рос одиноко. И ветер порывом

Отнёс его в сторону. Нет

Боле цветка над водой.

Нашёл же рыбак его ранней весной

В двух футах от места, где рос.

Итак, предложу я вопрос:

Как озера вода здесь глубока.( 3 3/4 фута)

2. Из учебника»Арифметика» на Руси.

Случися некоему человеку к стене лествицу прибрати, стены же тоя высота есть 117 стоп. И обрете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать.(44 стопы)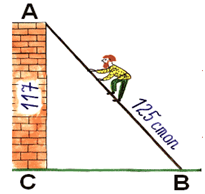

3. Задача индийского математика XII века Бхаскары

На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.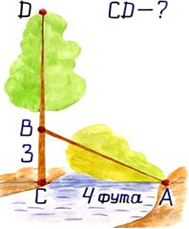

Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в том месте река

В четыре лишь фута была широка.

Верхушка склонилась у края реки.

Осталось три фута всего от ствола,

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота? (3+5 футов)

Строительство

Окно

В зданиях готического и ромaнского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг и половине ширины (b/2), для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Так как она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоватися вычисления; покажем, как применяется в таких задачах теорема Пифагора.

В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны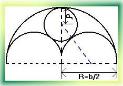

и. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна +p, один катет равен, а другой. По теореме Пифагора имеем: или , откуда Разделив на b и приводя подобные члены, получим: .

Применяется теорема Пифагора при расчете длины стропил при постройке крыши, установке вертикальной мачты. (Приложение 2)

Молниеотвод

Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.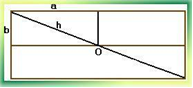

Решение:
По теореме Пифагора h² ≥ a²+b², значит h ≥
Ответ: h ≥

В нашей местности летом часто бывают сильные грозы, поэтому я решил разработать модель молниеотвода для моей времянки. Я измерил высоту и ширину крыши. Известно, что молниеотвод защищает все предметы, расстояние до которых не превышает его удвоенной высоты, т. е. c≤2h, а h≥c/2.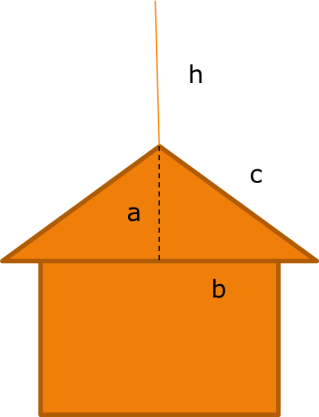

а=5м, b=4 м

с=a²+b²=5²+4²=41 м

h≥√41/2≈6,4 /2=3,2 м

Значит, минимальная высота молниеотвода должна быть 3,2 м

^{Астрономия}

^{12 апреля 1961 года советский гражданин Ю. А. Гагарин на космическом корабле «Восток» был поднят над землей на максимальную высоту 327 км. На каком расстоянии от корабля находились в это время наиболее удаленные от него и видимые космонавтом участки поверхности Земли? (Радиус Земли считать равным 6400 км.)}

^{Решение:} Из прямоугольного следует, AD=

Была рассмотрена задача о прохождении светового луча, где системой отсчета был космический корабль. (Приложение № 3)

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы которые долгое время считались исскуственными) и др. Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора.

Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

^{География}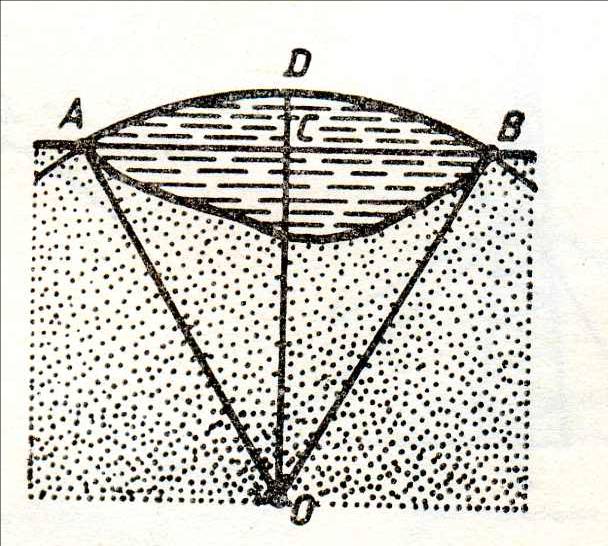

^{Задача 1. Вычислите высоту слоя воды над линией, соединяющей две противоположные точки берега озера Севан, расстояние между которыми 90 км. Замечание. Следует иметь в виду, что поверхность воды озера не плоская, а является частью сферы радиуса 6375 км.}

Решение: Из Тогда DC=0,159

Задача 2. (Приложение № 4)

При проведении токарных и столярных работ

Задача 1. Имеется цилиндрическая заготовка большого диаметра. Как вычислить диаметр этой заготовки, пользуясь штангенциркулем?

Решение: прямоугольный, так как угол СМЕ=, МВ перпендикулярно СЕ, следовательно, МВ²=ВЕ·ВС. Из рисунка видно, что ВМ= BC=h, a BE=D-h. Получаем, что или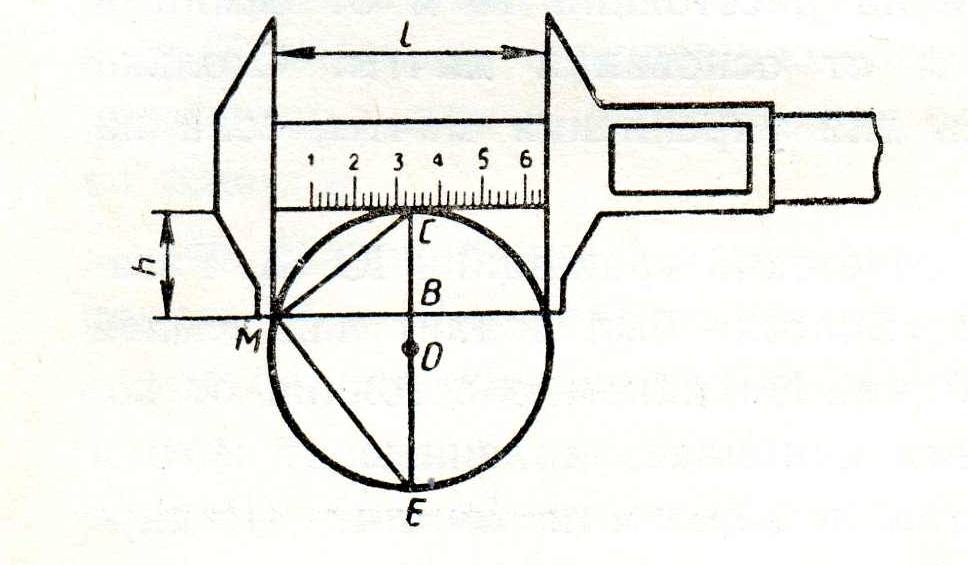

.

Задача 2 (Приложение №5)

В армии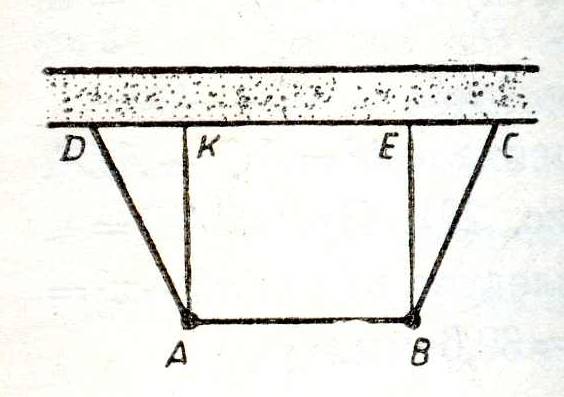

Задача. Параллельно стенду на расстоянии 500 м от него расположена цепь стрелков. Расстояние между крайними стрелками равно 120 м, дальность полета пули равна2,8 км. Какой участок стенда находится под обстрелом этой цепи?

Решение: Пусть АВ – расстояние между крайними стрелками, т.е. АВ=120 м, АК=ВЕ=500 м, AD=BC=2800 м. Из треугольника AKD по теореме Пифагора следует, что DK 2755 м, откуда DC=2DK+AB5630 м.

В сельском хозяйстве

Задача. В дождевальной установке дождеватели расположены по так называемой квадратной схеме.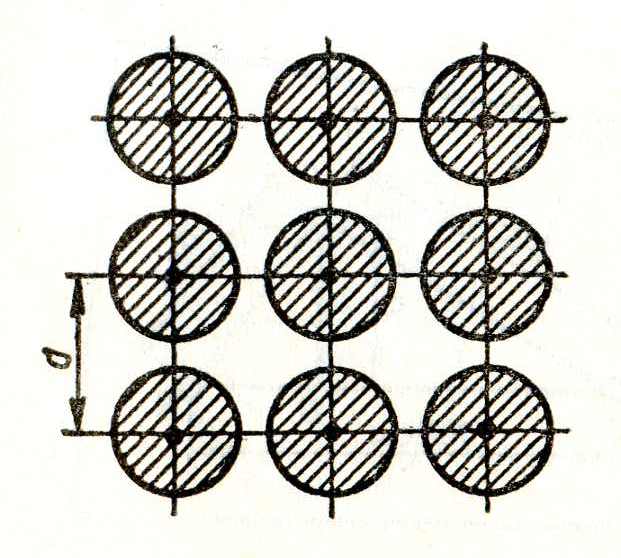

При каком максимальном расстоянии d между дождевателями установка будет орошать все поле, если один дождеватель орошает круг радиуса r?

Решение: На рисунке расстояние слишком велико. Расположим дождеватели так, как показано на следующем рисунке. Это наилучший вариант , поскольку при малейшем удалении дождевателей друг от друга образуются неорошаемые участки, т.е. 2d²=(2r²), откуда d=r.

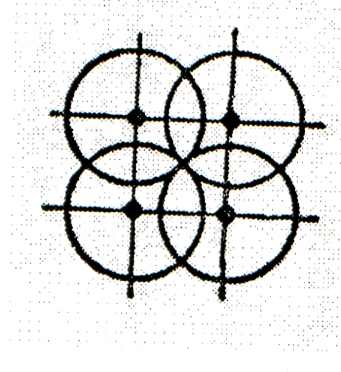
В стереометрии:

1. Куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна а). Отсюда имеем d=, d=a. Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами a, b, с и получить для диагонали выражение d² = a² + b² + c²

2. Исследуем пирамиду, например, такую, в основании которой лежит квадрат и высота которой проходит через центр этого квадрата (правильную пирамиду). Пусть сторона квадрата — а, и высота пирамиды — h. Найдем s (длину боковых ребер пирамиды). Ребра будут гипотенузами прямоугольных треугольников, у которых один из катетов — высота h, а другой — половина диагонали квадрата  Вследствие этого имеем: s=. Затем можем вычислить высоту h₁ боковых граней. h₁= .

Считать эти приложения теоремы Пифагора только теоретическими — большая ошибка. Если, например, рассматривать нашу четырехугольную пирамиду как крышу башни, то в первом нашем вопросе речь идет о том, какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана предписанная высота крыши, а вопрос о величине боковой поверхности должен интересовать, например, кровельщика при подсчете стоимости кровельных работ.

Работы по озеленению школы

Осенью мы возле школы посадили молодые ели и туи. Осень выдалась с сильными ветрами и наши деревца стали наклонятся. Чтобы деревья выросли стройными, мы решили укрепить их с помощью шпагата. Нам нужно было узнать, сколько метров шпагата нужно. Воспользовались задачей об установке вертикальной мачты. Измерили высоту, на которой будем крепить шпагат и расстояние от ствола. ВС=1,5 м, АВ=1,2 м. По теореме Пифагора АС=

Значит, для укрепления одного дерева нужно 1,92 м. Всего мы укрепили 12 деревьев, поэтому 1,9212=23,04 м.

Заключение

Теорема Пифагора — одна из главных и, можно сказать, самая главная теорема геометрии. Теорема Пифагора замечательна тем, что сама по себе она вовсе не очевидна. Например, свойства равнобедренного треугольника можно видеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: c²=a²+b². Уникальна не только теорема Пифагора, но и то, как широко она применяется. Очень интересна и биография Пифагора. Сам факт, что Пифагор — это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор — «убеждающий речью».) Своими речами приобрёл 2000 учеников, которые вместе со своими семьями образовали школу-государство, где действовали законы и правила Пифагора. Хотя это были лишь современники, а что говорить о них, если она уже на протяжении многих веков завораживает всё человечество своей красотой и лаконичностью.

Литература

1. Атанасян Л.С. и др. Геометрия 7-9, М.: Просвещение, 2009, с.383

2. Варданян С.С. История математики в школе. М.: Просвещение, 1989

3. Глейзер Г.И. История математики в школе. М.: Просвещение, 1982

4. Стройк Д.Я. Краткий очерк истории математики. М.: Наука. Главная редакция физико- математической литературы, 1979

5. Поповок Л.М. 1000 проблемных задач по математике. М.: Просвещение, 1995

6. Нагибин Ф.Ф. Математическая шкатулка/ Нагибин Ф.Ф., Канин Е.С., М.: Просвещение, 1988

7. http://encyklopedia.narod.ru/bios/nauka/pifagor.html

8. http:moypifagor.narod.ru/use.htm

Приложения

Приложение № 1

Анкета включала в себя вопросы:

Диаграмма № 1 «Результаты анкетирования учащихся»

Диаграмма № 2 «Результаты анкетирования учителей»

Диаграмма № 3 «Результаты анкетирования родителей»

Приложение № 2

Крыша

В доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м, и AB=BF.
Решение:
Треугольник ADC — равнобедренный AB=BC=4 м, BF=4 м. Если предположить, что DF=1,5 м, тогда: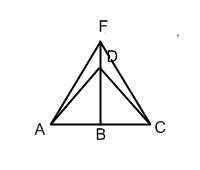

А) Из треугольника DBC: DB=2,5м

м

Б) Из треугольника ABF: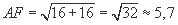

Установка вертикальной мачты

Задача 1. Вертикальная мачта поддерживается четырьмя канатами, прикрепленными к ней на расстоянии 16 м от земли и к земле на расстоянии 12 м от основания мачты. Сколько метров каната потребовалось для укрепления мачты, если на узлы пошло 10 м?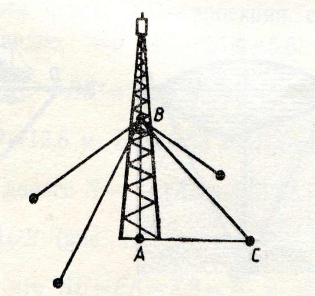

Решение: По теореме Пифагора из ВАС ВС == =20 м. Учитывая, что всего 4 каната и на узлы пошло 10 м, всего потребуется 90 м каната.

Задача 2. Для установки мачты телевизионной антенны изготовлены тросы длиной l = 20,2см. Тросы крепятся к этой мачте на высоте h=18,62 м. На каком расстоянии от основания мачты надо укрепить концы троса?

Решение: Искомое расстояние x=7,8 м.

Приложение № 3

^{Путь светового луча}

На этом рисунке показаны точки A и B и путь светового луча от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч — прямой.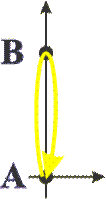

Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равна половина пути, который проходит луч? Если обозначить отрезок AB символом l, половину времени как t, а также обозначив скорость движения света буквой c, то наше уравнение примет вид

c * t = l

Очевидно? Это ведь произведение затраченного времени на скорость!

Теперь попробуем взглянуть на то же самое явление из другой системы отсчета, с другой точки зрения, например, из космического корабля, пролетающего мимо бегающего луча со скоростью v. Раньше мы поняли, что при таком наблюдении скорости всех тел изменятся, причем неподвижные тела станут двигаться со скоростью v в противоположную сторону. Предположим, что корабль движется влево. Тогда две точки, между которыми бегает зайчик, станут двигаться вправо с той же скоростью. Причем, в то время, пока зайчик пробегает свой путь, исходная точка A смещается и луч возвращается уже в новую точку C.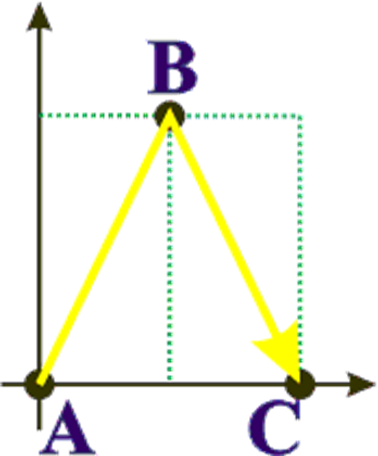

Вопрос: на сколько успеет сместится точка (чтобы превратиться в точку C), пока путешествует световой луч? Точнее, опять спросим о половине данного смещения! Если обозначить половину времени путешествия луча буквой t‘, а половину расстояния AC буквой d, то получим наше уравнение в виде:

v * t‘ = d

Буквой v обозначена скорость движения космического корабля. Опять очевидно, не правда ли?

Другой вопрос: какой путь при этом пройдет луч света?(Точнее, чему равна половина этого пути? Чему равно расстояние до неизвестного объекта?)

Если обозначить половину длины пути света буквой s, то получим уравнение:

c * t‘ = s

Здесь c — это скорость света, а t‘ — это тоже самое время, которые мы рассматривали на формулы выше.

Теперь рассмотрим треугольник ABC. Это равнобедренный треугольник, высота которого равна l. Да-да, тому самому l, которое мы ввели при рассмотрении процесса с неподвижной точки зрения. Поскольку движение происходит перпендикулярно l, то оно не могло повлиять не нее.

Треугольник ABC составлен из двух половинок — одинаковы прямоугольных треуголников, гипотенузы которых AB и BC должны быть связаны с катетами по теореме Пифагора. Один из катетов — это d, которое мы рассчитали только что, а второй катет — это s, который проходит свет, и который мы тоже рассчитали.

Получаем уравнение:

s² = l² + d²

Это ведь просто теорема Пифагора, верно?

Приложение №4

Задача 2. От пристани одновременно отплыли два парохода: один на юг со скоростью 16 морских миль в час, а другой на запад со скоростью 12 морских миль в час. Какое расстояние будет между пароходами через 2,5 ч (1 морская миля=1,85 км.)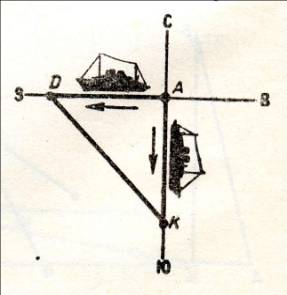

Решение:В прямоугольном AD=12·2,5, AK=16·2,5, KD= откуда KD=50 морских миль92,5 км

Приложение № 5

Задача 2. Две рейки соединены под прямым углом. Как с помощью полученного приспособления найти диаметр круга, центр и большая часть окружности которого находятся вне листа?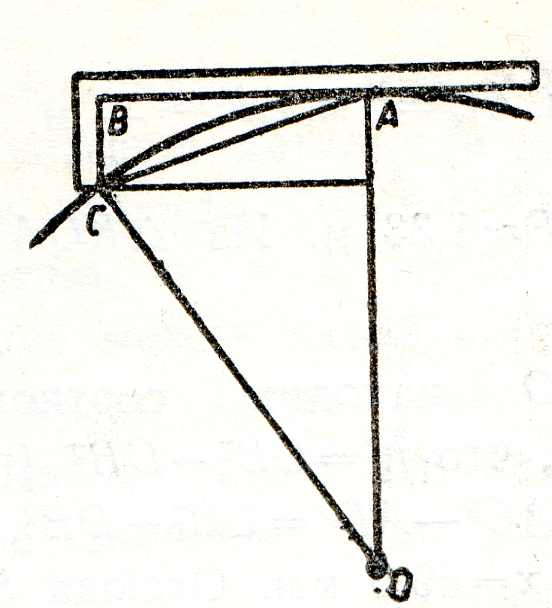

Решение: Пользуясь решением предыдущей задачи, можно написать (d-BC)BC=AB² (d-диаметр круга), откуда d=

Better Explained: удивительные применения теоремы Пифагора / Newtonew: новости сетевого образования

Теорема Пифагора — настоящая знаменитость в мире математики: уж если её формула засветилась в сериале «Симпсоны», она точно известна всем.

Большинство считает, что формула теоремы Пифагора применима только в геометрии и только к треугольникам. Скорее всего, при упоминании этой теоремы вы вспоминаете что-то такое:

Источник: Википедия

А теперь вдумайтесь: теорема Пифагора работает для любых фигур и для всех квадратных уравнений.

Если вы продолжите читать статью, вы узнаете, как эта теорема возрастом в 2,5 тысячи лет может помочь нам разобраться в информационных технологиях, физике и даже в полной мере оценить силу социальных сетей.

Идём к пониманию площади

Всегда увлекательно посмотреть на привычное под новым углом. К примеру, до написания этой статьи я никогда не задумывался о глубинном понятии такого явления, как «площадь фигуры». Да, мы можем помнить формулы, но вот понимаем ли мы саму природу площади?

Удивительно, но площадь любой фигуры может быть вычислена путём возведения в квадрат любого линейного сегмента. Линейный сегмент — это отрезок прямой, который мы выбираем в геометрической фигуре. Например, в качестве линейного сегмента квадрата мы выбрали сторону. Тогда площадью квадрата является квадрат его стороны (сторона = 5, площадь = 25). В качестве линейного сегмента круга можно взять радиус, и тогда площадью круга будет являться число π, умноженное на квадрат его радиуса (радиус = 5, площадь = 25π). Куда проще?

Мы можем взять любой линейный сегмент и с его помощью вычислить площадь: каждый линейный сегмент, возведённый в квадрат, даст нам величину площади фигуры, если его помножить на определённый коэффициент. Так мы получаем универсальную формулу расчёта площади фигуры:

Площадь фигуры = Коэффициент * (линейный сегмент)²

Посмотрите на диагональ d квадрата. Сторона квадрата при этом будет вычисляться как d, поделённая на √2. В этом случае площадь квадрата будет вычисляться как 1/2 d². Если мы хотим использовать диагональ фигуры в качестве линейного сегмента, нашим коэффициентом будет являться число 1/2.

А теперь в качестве линейного сегмента используем периметр p. Сторона квадрата — это p/4, значит, его площадь вычисляется по формуле p²/16. В этом случае коэффициентом для p² будет являться 1/16.

А можно взять вообще любой линейный сегмент?

А как же! Между «традиционным» сегментом (ну, например, стороной квадрата) и любым другим по вашему вкусу (скажем, периметром) всегда существует взаимосвязь (несложно догадаться, что периметр будет равен четырём сторонам квадрата). Если мы можем конвертировать новый сегмент в традиционный, площадь вычисляется легко — изменится лишь коэффициент в уравнении.

А можно взять вообще любую геометрическую фигуру?

Почти. Универсальная формула работает для всех подобных фигур — тех, что являются увеличенными или уменьшенными версиями одной и той же фигуры. Ну, например:

Все квадраты похожи друг на друга (площадь квадрата — всегда квадрат одной его стороны). Все круги похожи друг на друга (площадь круга — всегда π*r²). Треугольники не похожи друг на друга: они бывают вытянутыми или плоскими, «толстенькими» и «тоненькими», и у каждого треугольника — свой коэффициент для вычисления площади в зависимости от того, какой линейный сегмент вы выбрали. Измените форму треугольника, изменится и уравнение.

В целом все треугольники подчиняются правилу «площадь = 1/2 основания * высоту». Но отношения между основанием и высотой зависят от вида треугольника, поэтому и коэффициент в универсальной формуле будет всегда разным.

Почему для сохранения универсальности уравнения необходимы подобные фигуры? Интуитивно понятно, что при масштабировании фигуры вы меняете её размер, но сохраняете пропорции. Периметр квадрата всегда будет вычисляться умножением размера его стороны на 4.

Поскольку коэффициент в формуле площади основывается на отношениях между элементами фигуры, формула будет работать для всех фигур с одинаковыми пропорциями (подобными фигурами). Это как сказать, что полный размах рук человека приблизительно соответствует его росту — вне зависимости от того, кто перед нами, ребёнок или баскетболист.

Источник: Википедия

Так вот, основная концепция расчёта площади фигуры может быть выражена в следующих трёх постулатах:

• Площадь фигуры вычисляется с помощью возведения в квадрат любого её линейного сегмента.
• У каждого линейного сегмента будет свой коэффициент в универсальной формуле.
• Одна и та же формула расчёта площади работает для всех подобных фигур.

Интуитивное понимание теоремы Пифагора

Никто не спорит с тем, что теорема Пифагора работает. Но почти все её доказательства основаны на механических действиях: переставляем местами фигуры, и вуаля! — уравнение всё равно работает. Давайте подумаем: вам правда интуитивно понятно, что уравнение должно выглядеть как a² + b² = c²? А почему не 2a² + b² = c²? Давайте попробуем найти в этом смысл.

Для начала нам понадобится осознать и принять удивительный факт: любой прямоугольный треугольник можно разбить на два подобных прямоугольных треугольника.

Круто, да? Всего один опущенный перпендикуляр, и один треугольник превращается в две свои маленькие копии.

Собственно, этот пример говорит нам об очень простой вещи:

Площадь (чего-то большого) = Площадь (кое-чего среднего) + Площадь (кое-чего поменьше)

Маленькие треугольники были получены из большого, поэтому мы просто складываем их площади. И да, самое главное: поскольку треугольники подобны, для них действует одна и та же формула вычисления площади.

Давайте назовём длинную сторону (с длиной 5) — с, среднюю сторону (с длиной 4) — b, и короткую сторону (с длиной 3) — a. Формула площади для этих треугольников выглядит так:

Площадь = F*гипотенуза²,

где F — это множитель (в этом случае — 6/25 или 0,24). С формулой можно поиграть:

Площадь (чего-то большого) = Площадь (кое-чего среднего) + Площадь (кое-чего поменьше)

Fc² = Fb² + Fa²

Просто уберите F, и вы получите:

c² = b² + a²

Ой, так это же наша любимая теорема! Мы знали, что она нас не подведёт, но теперь мы понимаем, почему:

• Треугольник можно разбить на два маленьких подобных треугольника
• Поскольку площади малых треугольников складываются, квадраты гипотенуз также складываются.

Конечно, теорема Пифагора работает только в Евклидовой геометрии и не может применяться, например, к сферам. Но об этом нужно поговорить в другой раз.

Применение теоремы: Возьмём любую фигуру

Ранее мы использовали простую плоскую фигуру — треугольник. Но ведь линейный сегмент можно извлекать из абсолютно любой фигуры. Возьмём, к примеру, круг. На изображении мы видим три разных круга с радиусами, равными сторонам нашего пифагоровского треугольника.

Можно ли с большим кругом поступить так же, как мы поступили с большим треугольником — сложить площади меньших кругов? При этом мы будем помнить, что площадь каждого маленького круга мы можем высчитать, используя квадрат известного нам линейного сегмента, умноженный на конкретный коэффициент — в данном случае это будет число Пи.

Да-да, всё верно: Площадь круга радиусом 5 = Площадь круга радиусом 4 + Площадь круга радиусом 3.

Мы запросто подставляем в формулу нужный коэффициент, и она всё ещё работает.

Помните, что в качестве линейного сегмента может выступать любой элемент плоской фигуры. Вы могли выбрать радиус, диаметр или длину окружности — изменился бы только коэффициент, но отношения 3-4-5 остались бы неизменными.

Теорема Пифагора позволяет находить соотношение площадей любых подобных фигур. Это то, чему нас не учат в школе.

Применение теоремы: сохранение квадратов

Теорема Пифагора применяется к любому квадратному уравнению. Подобно тому, как вы разбиваете треугольники, вы можете разбить квадрат любого количества чего угодно (c²) на более малые его доли (a²+b²). Этим «чем угодно» может быть расстояние, энергия, человекочасы, время или количество пользователей в социальной сети.

Социальные сети.

Есть такой закон — закон Меткалфа, формулирующий уровень полезности социальной сети: он говорит, что ценность социальной сети растёт в квадратичной зависимости от количества пользователей в ней. Например:

Сеть из 50 млн. пользователей = Сеть из 40 млн. пользователей + Сеть из 30 млн. пользователей

Кажется удивительным, что полезность социальной сети в 50 миллионов человек выражается через полезность двух соцсетей, в сумме имеющих 70 миллионов человек, но это на самом деле так. Социальная сеть растёт нелинейно.

Информационные технологии.

Некоторым программам требуется n² времени для обработки n запросов. Другими словами:

50 запросов = 40 запросов + 30 запросов

Удивительно, но 70 элементов данных, разбитые на две группы, будут обработаны так же быстро, как одна группа из 50 элементов. Именно поэтому имеет смысл сортировать элементы по группам и подгруппам. Эта особенность используется почти во всех алгоритмах сортировки. Теорема Пифагора помогает понять, почему сортировка 50 элементов сразу менее эффективна, чем сортировка этого же количества элементов по отдельности.

Площадь поверхности.

Площадь поверхности сферы определяется как 4πr². Что это значит?

Площадь радиусом 50 = Площадь радиусом 40 + Площадь радиусом 30

В жизни нам встречается не так уж и много сфер, но вот портовым работникам это знание весьма полезно (в конце концов, корпус любого судна — это деформированная сфера). Количеством краски, необходимой для 50-тифутовой яхты, можно окрасить две яхты длиной 40 и 30 футов.

Физика.

Если вспомнить школьные уроки физики, можно привести в пример формулу расчёта кинетической энергии объекта массой m при скорости v: 1/2mv². Применяем теорему Пифагора.

Энергия при скорости в 500 км/ч = Энергия при скорости в 400 км/ч + Энергия при скорости в 300 км/ч

Значит, одного и того же количества энергии хватает либо на запуск одного предмета на скорости 500 км/ч, либо на запуск двух других на меньшей скорости.

Попробуйте сами

В теорему Пифагора можно подставлять абсолютно любые цифры. Она может помочь нам и в повседневной жизни. Например, мы никак не можем выбрать: заказать большую пиццу диаметром 50 см или две диаметром 30 см? Мы с теоремой уже знакомы хорошо и нас не обмануть: площадь одной пиццы в 50 см будет действительно больше, чем площадь двух пицц по 30 см в диаметре (можете проверить, мы не обманываем). Всегда можно подставить другие цифры, а для ленивых есть простой и удобный калькулятор.

Наслаждайтесь

Со школьной скамьи мы уверены, что теорема Пифагора — это что-то о треугольниках и геометрии. Мы с вами вместе убедились, что это не так.

Помните, что стороны прямоугольного треугольника могут превратиться в линейный сегмент любой фигуры, и стать переменными в любом квадратном уравнении. И это ошеломительно.

Спасибо великолепной статье на BetterExplained.

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

Теорема Пифагора в жизни человека

Слайд 1

Слайд 2

« Уделом истины не может быть забвенье, Как только мир её увидит взор, И теорема та, что дал нам Пифагор, Верна теперь , как в день её рожденья.» А.Шамиссо.

Слайд 3

Цель работы Изучить историю теоремы Пифагора Найти различные доказательства теоремы Изучить области её применения Привести примеры решения задач на теорему Пифагора

Слайд 4

Формулировки теоремы «В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол». Евклид «Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол». перевод Г.Клемонского /12век/ «Площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу». « Geometria Culmonensis » /около 1400г/ «В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол». перевод Ф.И.Петрушевского /первый русский перевод/

Слайд 5

Доказательства теоремы Доказательства, основанные на использовании понятия равновеликие фигуры Доказательства методом разложения Доказательства методом построения Алгебраический метод доказательства Доказательства методом дополнения Доказательство, основанное на теории подобия Другие доказательства

Слайд 6

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников , чтобы убедиться в справедливости теоремы. Например, для треугольника ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,- по два. Теорема доказана. Простейшее доказательство

Слайд 7

Доказательство Энштейна Метод разложения Его преимуществом является то, что здесь в качестве составных частей разложения фигурируют исключительно треугольники. Чтобы разобраться в чертеже, заметим, что прямая CD проведена перпендикулярно прямой EF. Разложение на треугольники можно сделать и более наглядным, чем на рисунке.

Слайд 8

Доказательство методом построения Сущность этого метода состоит в том, что к квадратам, построенным на катетах, и к квадрату, построенному на гипотенузе, присоединяют равные фигуры таким образом, чтобы получились равновеликие фигуры. Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ.

Слайд 9

Алгебраический метод доказательства. На рис. 13 ABC – прямоугольный, C – прямой угол, CM принадлежит AB, b1 – проекция катета b на гипотенузу, a1 – проекция катета a на гипотенузу, h – высота треугольника, проведенная к гипотенузе. Из того, что треугольник ABC подобен треугольнику ACM следует b 1 /b = b/c b 2 = cb 1 ; (1) Из того, что треугольник ABC подобен треугольнику BCM следует a 1 /a = a/c a 2 = ca 1 . (2) Складывая почленно равенства (1) и (2), получим a 2 + b 2 = cb 1 + ca 1 = =c(b 1 + a 1 ) = c 2 .

Слайд 10

Доказательство Мёльманна Площадь данного прямоугольного треугольника, с одной стороны, равна ½ а b , с другой ½ р r , где p – полупериметр треугольника, r – радиус вписанной в него окружности r= ½ ( a+b-c) Имеем: ½ а b = ½ р r = ½ ( a+b+c) * ½ ( a+b-c) откуда следует, что c 2 =a 2 +b 2 .

Слайд 11

Доказательство методом дополнения К обычной пифагоровой фигуре приставлены сверху и снизу треугольники 2 и 3, равные исходному треугольнику 1. Прямая DG обязательно пройдет через C. Заметим теперь (далее мы это докажем), что шестиугольники DABGFE и CAJKHB равновелики. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат, построенный на гипотенузе. Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах. Остается доказать, что наши шестиугольники равновелики. Прямая DG делит верхний шестиугольник на равновеликие части; то же можно сказать о прямой CK и нижнем шестиугольнике. Повернем четырехугольник DABG, составляющий половину шестиугольника DABGFE, вокруг точки А по часовой стрелке на угол 90; тогда он совпадет с четырехугольником CAJK, составляющим половину шестиугольника CAJKHB. Поэтому шестиугольники DABGFE и CAJKHB равновелики.

Слайд 12

Иллюстрация теоремы Пифагора. Из двух сосудов в виде квадратов на катетах прямоугольного треугольника вода переливается в один сосуд в виде квадрата на гипотенузе. Убеждаемся — вода в обоих случаях заполняет сосуды «под завязку».

Слайд 13

Применение теоремы Еще в древности возникла необходимость вычислять стороны прямоугольных треугольников по двум известным сторонам. Построение прямых углов египтянами Нахождение высоты объекта и определение расстояния до недоступного предмета.

Слайд 14

Такие задачи решают при проектировании любых строительных объектов. Подобные задачи решаются и в нашей повседневной жизни , например установление ёлки. Покрытие полов паркетом .

Слайд 15

Применение теоремы В планиметрии. Расчёт длинны диагонали квадрата d²=2a² Расчёт длинны диагонали прямоугольника d²=a²+b²

Слайд 16

Применение теоремы Пифагора в строительстве Если рассматривать четырехугольную пирамиду как крышу башни, то речь идет о том, какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана предписанная высота крыши, а вопрос о величине боковой поверхности должен интересовать, кровельщика при подсчете стоимости кровельных работ. Заметим, что расчет площади кровли можно заметно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит: «Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила на перекрываемую площадь.»

Слайд 17

В зданиях романского и готического стиля верхние части окон расчленяются каменными рёбрами, которые не только играют роль орнамента, но и способствуют прочности окон. Радиусы округлых окон рассчитываются с помощью теоремы Пифагора

Слайд 18

Молниеотвод Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту. Решение: По теореме Пифагора h 2 ≥ a 2 +b 2 , значит h ≥ (a 2 +b 2 ) ½ . Ответ: h ≥ (a 2 +b 2 ) ½

Слайд 19

Связь С помощью теоремы Пифагора можно подсчитать какую наибольшую высоту должна иметь телевизионная вышка или антенна телефонной связи.

Слайд 20

В виде сигнала В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора .

Слайд 21

Исторические задачи на теорему « На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?»

Слайд 22

Задача из китайской «Математики в девяти книгах» «Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?»

Слайд 23

Задача из учебника «Арифметика» Леонтия Магницкого «Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.»

Слайд 24

Задача 1: С аэродрома вылетели одновременно два самолёта: один — на запад, другой — на юг. Через два часа расстояние между ними было 2000 км. Найдите скорости самолётов, если скорость одного составляла 75% скорости другого. Решение: По теореме Пифагора: 4x 2 +(0,75x*2) 2 =2000 2 6,25x 2 =2000 2 2,5x=2000 x= 800 0,75x=0,75*800= 600 . Ответ: 800 км/ч.; 600 км/ч.

Слайд 25

Задача 2: Как следовало бы поступить юному математику, чтобы надёжным образом получить прямой угол? Решение: Можно воспользоваться теоремой Пифагора и построить треугольник, придав его сторонам такую длину, чтобы треугольник получился прямоугольный. Проще всего взять для этого планки длиной в 3 , 4 и 5 каких-либо произвольно выбранных равных отрезков.

Слайд 26

Задача 3: Условие: Если каждое ребро куба увеличить на 2см, то его объём увеличится на 98см 3. Найдите ребро куба. Решение: Обозначим ребро куба через х, тогда(x+2) 3 -x 3 =98,т.е. x 2 +2x-15=0. Уравнение имеет два корня: x=3, x=-5. Геометрический смысл имеет только положительный корень. Итак, ребро куба равно 3см.

Слайд 27

Задача 4: Условие: В прямом параллелепипеде стороны основания a и b образуют угол 30 градусов. Боковая поверхность равна S. Найдите его объём. Решение: Обозначим высоту через х. Тогда (2a+2b)x=S, отсюда x=S/2*(a+b). Площадь основания параллелепипеда равна a*b*sin30=a*b/2. Объём равен a*b*S/4*(a+b).

Слайд 28

З а д а ч а 5: Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?

Доклад по теме «Значение теоремы Пифагора»

Слайд 1

Слайд 2

Гипотеза Какое влияние оказала теорема Пифагора на развитие науки и техники многих стран и народов мира. Как могла применяться теорема Пифагора в древности.

Слайд 3

Мы провели исследовательскую работу, привлекая информационные технологии. Определили, что теорема Пифагора имеет огромное значение в развитии науки и техники. Мы заметили, что теорема Пифагора лежит в основе многих общих метрических соотношений на плоскости и в пространстве. Мы определили, что исключительная важность теоремы для геометрии и математики в целом состоит в том, что, благодаря тому что теорема Пифагора позволяет находить длину отрезков(гипотенузы), не измеряя ее непосредственно, она как бы открывает путь с прямой на плоскость, с плоскости в трехмерное пространство. В теореме Пифагора , как в зерне, заключена вся евклидова геометрия.

Слайд 4

История теоремы Пифагора. Интересна история теоремы Пифагора. Хотя эта теорема и связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора, а в Египте это соотношение использовалось для построения прямого угла еще пять тысяч лет назад. Возможно, что тогда еще не знали ее доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений. Пифагор, по-видимому, нашел доказательство этого соотношения. Сохранилось древнее предание, что в честь своего открытия Пифагор принес в жертву богам быка, по другим свидетельствам — даже сто быков. На протяжении последующих веков были найдены различные другие доказательства теоремы Пифагора. В настоящее время их насчитывается более пятисот, в том числе: геометрических, алгебраических, механических и прочих. Благодаря такому количеству доказательств, теорема Пифагора попала в Книгу рекордов Гиннеса, как теорема с наибольшим количеством доказательств.

Слайд 5

Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана. Существует так называемое дерево Пифагора — гипотетическое дерево, которое составлено из соединенных между собой прямоугольных треугольников, с построенными на катетах и гипотенузе квадратами. У теоремы Пифагора есть следствие для произвольного треугольника: Сторона треугольника равна корню квадратному из суммы квадратов двух других ее сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это записывается так: a ² = b ² + c ² — 2bc · cosα Это следствие принято называть теоремой косинусов, но по сути — это теорема Пифагора для произвольного треугольника. Существует три формулировки теоремы Пифагора: 1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах. 3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах. НАЗАД

Слайд 6

Применение теорем Пифагора на практике. Рассмотрим примеры практического применения теоремы Пифагора. Не будем пытаться привести все примеры использования теоремы — это вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой. Определим возможности, которые дает теорема Пифагора для вычисления длин отрезков некоторых фигур на плоскости. Диагональ квадрата. Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом, d²=2a². Диагональ d прямоугольника. Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем d²=a²+b²

Слайд 7

Высота h равностороннего треугольника. Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а другой катет a/2. Таким образом имеем a2 = h3 + (a/2)2, или h3 = (3/4)a2. Отсюда вытекает h =(a√3)/2. Возможности применения теоремы Пифагора к вычислениям не ограничиваются планиметрией. Диагональ куба. На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна a√2). Отсюда имеем d² = a² + 2a², d² = 3a², d = a√3. Теорема Пифагора используется также при построении сечений в объемных фигурах, таких как куб.

Слайд 8

Конус. При построении сечений в конусе также используется теорема Пифагора. Прямоугольный параллелепипед. Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами a, b, с и получить для диагонали выражение d² = a² + b² + c². Пирамида. Исследуем пирамиду, например, такую, в основании которой лежит квадрат и высота которой проходит через центр этого квадрата (правильную пирамиду). Пусть сторона квадрата — а, и высота пирамиды — h. Найдем s (длину боковых ребер пирамиды). Ребра будут гипотенузами прямоугольных треугольников, у которых один из катетов — высота h, а другой — половина диагонали квадрата (1/2*a√2). Вследствие этого имеем: s² = h² + a²/2. Затем можем вычислить высоту h 1 боковых граней. h 1 ² = h 2 + a ² /4.

Слайд 9

В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны 1. ширине окна (b) для наружных дуг 2. половине ширины, (b/2) для внутренних дуг Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора. В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b/2 и r= b/4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4 + p, один катет равен b/4, а другой b/2 — p. По теореме Пифагора имеем: (b/4 + p) ² = (b/4) ² + (b/2 — p) ² или b ² /16 + bp/2 + p ² = b ² /16 +b ² /4 — bp + p ² , откуда bp/2 = b ² /4 — bp. Разделив на b и приводя подобные члены, получим: (3/2)p = b/4, p = b/6

Слайд 10

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы которые долгое время считались исскуственными) и др. Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Слайд 11

Кроме этого, практическое значение теоремы Пифагора и обратной ему теоремы заключается в том, что с их помощью можно найти длины отрезков, не измеряя самих отрезков. Это как бы открывает путь от прямой к плоскости, от плоскости к объемному пространству и дальше. Именно по этой причине теорема Пифагора так важна для человечества, которое стремится открывать все больше измерений и создавать технологии в этих измерениях. Например в Германии недавно открылся кинотеатр, где показывают кино в шести измерениях: первые три даже перечислять не стоит, а также время, запах и вкус. Это наглядно говорит о том, насколько быстро увеличивается количество измерений, используемых человечеством. Ведь еще три года назад никто и не заикался о более чем трех измерениях в кино. Вы спросите: а как связаны между собой теорема Пифагора и запахи, вкусы? А все очень «просто»: ведь при показе кино надо рассчитать куда и какие запахи направлять и т.д. Представьте: на экране показывают джунгли, и вы чувствуете запах листьев, показывают обедающего человека, а вы чувствуете вкус еды… Значение теоремы Пифагора.

Слайд 12

Но не надо думать, что теорема Пифагора больше не имеет других значений. Из того, что я уже сказал, надо сделать вывод, что все эти технологии используются также и в других отраслях. Например, при строительстве любого сооружения, рассчитывают расстояния, центры тяжести, размещение опор, балок и т.д. В целом, значение теоремы, кроме вышесказанного, заключается в том, что она применяется практически во всех современных технологиях, а также открывает простор для создания и придумывания новых.

Слайд 13

Египетский треугольник. Египетский треугольник — это прямоугольный треугольник со сторонами 3, 4 и 5. Он получил такое название. оттого что был известен и широко применялся еще древними египтянами. Они с помощью такого треугольника строили прямые углы на местности, что имело для них огромное значение, так как каждый год разливы Нила размывали границы между полями, и приходилось заново размечать их. Это делалось очень просто: на веревке узлами отмечалось 12 равных отрезков, а потом из этой веревки складывали треугольник, и угол, оказавшийся напротив стороны 5, являлся прямым.

Слайд 14

Исторические задачи . Исторические задачи Предлагаю несколько задач, найденных в исторических книгах. Они настолько легкие, что я не буду объяснять их решение. Задача Бхаскари «На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?» Задача из китайской «Математики в девяти книгах» «Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?».

Слайд 15

Задача из учебника «Арифметика» Леонтия Магницкого «Случился некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать». Задача о бамбуке из древнекитайского трактата «Гоу-гу» Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи). Какова высота бамбука после сгибания?

Слайд 16

Буклет учащихся Практическое значение теоремы Пифагора и обратной ему теоремы заключается в том, что с их помощью можно найти длины отрезков, не измеряя самих отрезков. Это как бы открывает путь от прямой к плоскости, от плоскости к объемному пространству и дальше. Именно по этой причине теорема Пифагора так важна для человечества, которое стремится открывать все больше измерений и создавать технологии в этих измерениях. Заложенная Пифагором вера в красоту и гармонию природы, в мудрую простоту и целесообразность её законов, построенных на единых математических принципах, окрыляла творчество титанов современного естествознания от Иоганна Кеплера (1571 —1630) до Альберта Эйнштейна (1879—1955). Это и есть путеводная звезда современного естествознания, тот вечный кладезь мудрости, который открыл человечеству Пифагор . Ржаксинская сош №2 Группа « теоретиков » Романова Екатерина Гунин Артем Никитина Софья Гаврилин Сергей Значение теоремы Пифагора .

Слайд 17

Выводы по теме проекта Заложенная Пифагором вера в красоту и гармонию природы, в мудрую простоту и целесообразность её законов, построенных на единых математических принципах, окрыляла творчество титанов современного естествознания от Иоганна Кеплера (1571 —1630) до Альберта Эйнштейна (1879—1955). Это и есть путеводная звезда современного естествознания, тот вечный кладезь мудрости, который открыл человечеству Пифагор.

Слайд 18

Используемые ресурсы Акимова С. Занимательная математика, серия «Нескучный учебник». – Санкт-Петербург.: Тригон, 1997. Волошников А.В. Пифагор: союз истины, добра и красоты. – М.: Просвещение, 1993. Я познаю мир: Детская энциклопедия: Математика. – М.: Аванта+, 1997. Еленьский Ш. По следам Пифагора. — М, 1961. Журнал «Квант» № 2, 1992. 8. Журнал «Математика в школе» № 4, 1991. Литцман В. Теорема Пифагора. — М.: Просвещение, 1960. Энциклопедический словарь юного математика / Сост. А.П. Савин. – 3-е изд., испр. и доп. — М.: Педагогика–Пресс, 1997, с. 271. Энциклопедия для детей. Т.11. Математика / Глав. ред. М.Д. Аксёнова. — М.: Аванта+, 1998. Электронные источники: Рефераты и сочинения в помощь школьнику. Дискавери – 2003. Большая энциклопедия Кирилла и Мефодия. – 2004. Электронная энциклопедия: Star World. Internet.