Признаки делимости правило и примеры
Число, которое делится на 2 называется четным, а если не делится — нечетным.
Число делится на 2, если его последняя цифра оканчивается на нуль или чётная.
Пример
Число 7774 делится на 2, так как последняя цифра 4 — чётная.
Число 7775 не делится на 2, так как последняя цифра 5 — нечётная.
На 3 делятся только те числа, у которых сумма всех цифр делится на 3.
Пример
777 делится на 3, так как 7+7+7=21, а 21 делится на 3.
Число делится на 4 в том случае, если две последние его цифры нули или делятся на 4.
Пример
788 делится на 4, так как последние его цифры 88
700 делится на 4, так как последние его цифры нули.
Число делится на 5, если последняя цифра которых оканчивается на 0 или 5.
Пример
775 делится на 5, так как последняя цифра равна 5.
Число делится на 6, если оно делится как на 2, так и на 3.
Пример
786 делится на 6, так как оно делится и на 2 и на 3 одновременно.
Число делится на 7, когда знакочередующаяся сумма трехзначных граней числа делится на 7.
Пример
147700259 делится на 7, так как 147-700+259=-294, а 294 делится на 7.
Число делится на
7, когда утроенное число десятков, сложенное с числом единиц делится на 7.Пример
189 делится на 7, так как 18*3+9=63 делится на 7.
Число делится на 7, когда разность числа десятков и удвоенного числа единиц, взятая по модулю, делится на 7.
Пример
539 делится на 7, так как 53-9*2=35 делится на 7.
Число делится на 8, если три последние цифры его нули или делятся на 8.
Пример
7000 делится на 8, так как три нуля в конце.
7648 делится на 8, так как последние его цифры делятся на 8.
На 9 делятся только те числа, у которых сумма цифр делится на 9.
Пример
774 делится на 9, так как 7+7+4=18, а 18 делится на 9.
На 11 делятся только те числа, у которых сумма цифр с чередующимися знаками по модулю делится на 11
Пример
Число 292919 делится на 11, так как 2-9+2-9+1-9=-22 делится на 11.
Число делится на 12, если оно делится как на 3, так и на 4.
Пример
924 делится на 12, так как оно делится и на 3 и на 4 одновременно.
Число делится на 13, если число десятков, сложенное с учетверенным числом единиц, делится 13.
Пример
572 делится 13, так как 72-4*5=52 делится на
13.На 25 делятся те числа, у которых две последние цифры нули или образуют число, которое делится на 25 (т. е. числа, которые оканчиваются на 00, 25, 50, 75).
Пример
7775 делится на 25, так как оканчивается на 75
На 10 делятся только те числа, последняя цифра которых оканчивается на нуль, на 100 делятся только те числа, у которых две последние цифры нули, на 1000 — только те, у которых три последние цифры нули.
Пример
777 000 делится на 10,100,1000.
Исследовательская работа «Признаки делимости чисел»
муниципальное бюджетное общеобразовательное учреждение «Остерская средняя школа»
Исследовательская работа
Признаки делимости чисел
Аладочкина Нина, Косарева Алина,
обучающиеся 6 класса
Руководитель:
Конохова Г.С., учитель математики
с. Остер, 2016 год
Введение………………………………………………………………………..3
1. Из истории математики о делимости чисел………………………………5
1.1 Признак делимости Паскаля…………………………………………..7
1.2. Признаки делимости………………………………………………… 7
3. Применение признаков делимости при решении цифровых головоломок
и практических задач………………………………………………………….9
4. Заключение………………………………………………………………….10
5.Литература…………………………………………………………………..11
Введение
На уроках математики мы изучали основные признаки делимости чисел на 2, 3, 4, 5, 9, 10 и 25. Но оказывается, признаков делимости гораздо больше. Есть признаки делимости на 6, 7, 8, 11, 13 и другие числа. Неоценимо значение признаков делимости для развития умений устного счета, а также при решении цифровых головоломок и некоторых практических задач.
Мы заинтересовались историей делимости чисел.
Кто из древних учёных занимался делимостью чисел? Кто такой Эратосфен? Что такое решето Эратосфена? Что собой представляет таблица простых чисел? Есть ли последнее простое число?
Старинная восточная притча.
Давным-давно жил-был старик, который, умирая, оставил своим трем сыновьям 19 верблюдов. Он завещал старшему сыну половину, среднему – четвертую часть, а младшему – пятую. Не сумев найти решения самостоятельно (ведь задача в «целых верблюдах» решения не имеет), братья обратились к мудрецу.
— О, мудрец!- сказал старший брат. — Отец оставил нам 19 верблюдов и велел разделить между собой: старшему – половину, среднему – четверть, младшему – пятую часть. Но 19 не делится ни на 2, ни на 4, ни на 5. Можешь ли ты, о, достопочтенный, помочь нашему горю, ибо мы хотим выполнить волю отца?
— Нет ничего проще, — ответил им мудрец. – Возьмите моего верблюда и идите домой.
Братья дома легко разделили 20 верблюдов пополам, на 4 и на 5. Старший брат получил 10, средний – 5, а младший – 4 верблюда. При этом один верблюд остался (10+5+4=19). Раздосадованные, братья вернулись к мудрецу и пожаловались:
— О, мудрец, опять мы не выполнили волю отца! Вот этот верблюд – лишний.
— Это не лишний, — сказал мудрец,- это мой верблюд. Верните его и идите домой.
Изучив тему на уроке, мы решили выполнить исследовательскую работу.
Цель: узнать, не выполняя деления, делится ли число на 6, 7, 8, 11?
Задачи:
Изучить историю математики о делимости чисел.
Узнать признаки делимости на натуральные числа от 2 до 25.
Изучить свойства делимости чисел.
Исследовать применение признаков делимости при решении цифровых головоломок и практических задач.
Значимость: данная работа предназначена для обобщения, расширения и систематизации знаний по теме «Признаки делимости» в курсе математики 6 класса, учебник И.И.Зубарева, А.Г. Мордкович.
Гипотеза: верно ли, что признаки делимости способствуют эффективному и рациональному решению задач.
1. Из истории математики о делимости чисел
Делимость – это способность одного числа делиться на другое без остатка. Признаки делимости были широко известны в эпоху Возрождения, поскольку, пользуясь ими, можно было приводить дроби с большими числителями и знаменателями к несократимому виду.
Эратосфен (около 275–194 до н. э.) — один из самых разносторонних ученых античности. Эратосфен занимался самыми различными вопросами — ему принадлежат интересные исследования в области математики, астрономии и других наук. Трактаты Эратосфена были посвящены решению геометрических и арифметических задач.
Самым знаменитым математическим открытием Эратосфена стало так называемое «решето», с помощью которого находятся простые числа.
Делитель – это число, которое делит данное число без остатка. Все целые числа (кроме 0 и 1) имеют минимум два делителя: 1 и самого себя. Числа, не имеющие других делителей, называются простыми числами. Числа, имеющие другие делители, называются составными (или сложными) числами.
Простых чисел – бесконечное множество. Наименьшим простым числом является 2, это единственное чётное простое число. Все остальные простые числа следует искать среди нечётных чисел, но, разумеется, далеко не всякое нечётное число является простым. Так, например, нечётные числа 3, 5, 7, 11, 13 — простые, а такие нечётные числа как 9, 15, 21 — составные, 9 имеет 3 делителя, число 15 – 4 делителя и т. д. Любое составное число можно разлагать на сомножители до тех пор, пока оно не распадётся на одни только простые числа. Простые числа являются как бы первичными элементами, из которых составляются все числа.
В математике Эратосфена интересовал как раз вопрос о том, как найти все простые числа среди натуральных чисел от 1 до N. Эратосфен считал 1 простым числом. Математики считают 1- числом особого вида, которое не относится ни к простым, ни к составным числам. Эратосфен придумал для этого следующий способ. Сначала вычеркивают все числа, делящиеся на 2 (исключая само число 2). Потом берут первое из оставшихся чисел (а именно 3). Ясно, что это число — простое. Вычеркивают все идущие после него числа, делящиеся на 3. Первым оставшимся числом будет 5. Вычеркивают все идущие после него числа, делящиеся на 5 и т. д. Числа, которые уцелеют после всех вычеркиваний, и являются простыми. Так как во времена Эратосфена писали на восковых табличках и не вычеркивали, а «выкалывали» цифры, то табличка после описанного процесса напоминала решето. Поэтому метод Эратосфена для нахождения простых чисел получил название «решето Эратосфена».
Большой вклад в изучение признаков делимости чисел внес Б. Паскаль.
Блез Паскаль (1623–1662), французский религиозный мыслитель, математик и физик, один из величайших умов 17 столетия. Юный Блез очень рано проявил выдающиеся математические способности, научившись считать раньше, чем читать. Свой первый математический трактат «Опыт теории конических сечений» он написал в 24 года. Примерно в это же время он сконструировал механическую суммирующую машину, прообраз арифмометра. За эти 10 лет разносторонний ученый сделал очень много: он нашел алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, сформулировал способ вычисления биноминальных коэффициентов, изложил ряд основных положений элементарной теории вероятности, впервые точно определил и применил для доказательства метод математической индукции.
Признак делимости Паскаля.
Натуральное число а разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа а на соответствующие остатки, получаемые при делении разрядных единиц на число b, делится на это число. Например: число 2814 делится на 7, так как 2х6 + 8х2 + 1х3 + 4 = 35 делится на 7. (Здесь 6 — остаток от деления 1000 на 7, 2 — остаток от деления 100 на 7 и 3 — остаток от деления 10 на 7).
1.2. Признаки делимости
Признак делимости на 2.
Число делится на 2 в том и только в том случае, если его последняя цифра чётная.
Пример: 124, 200, 152, 68, 406.
Признак делимости на 3.
Число делится на 3 в том и, только в том случае, если сумма его цифр делится на 3.
Пример: 144 на 3, т. к. 1+4+4 =9 делится на 3.
Признак делимости на 4.
Число делится на 4 в том и только в том случае, если две его последние цифры образуют двузначное число, делящееся на 4.
Пример: 724 делится на 4, т. к. 24 делится на 4.
Признак делимости на 5.
Число делится на 5 в том и только в том случае, если оно оканчивается на 0 или на 5.
Пример: 720, 655 делятся на 5.
Признак делимости на 6.
Число делится на 6 в том и только в том случае, если оно чётное и делится на 3.
Пример: 720 делится и на 2 и на 3.
Признак делимости на 7.
Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из числа десятков делится на 7.
Пример: 259 делится на 7, т. к. 25 — (2 х 9) = 7 делится на 7.
Признак делимости на 8.
Число делится на 8 в том и только в том случае, если его последние три цифры образуют число, делящееся на 8.
Пример: 6136 делится на 8, т. к. 136 делится на 8.
Признак делимости на 9.
Число делится на 9 в том и только в том случае, если сумма его цифр делится на 9.
Пример: 6102 делится на 9, т. к. 6+1+0+2 = 9 делится на 9.
Признак делимости на 10.
Число делится на 10 в том и только в том случае, если оно оканчивается на 0.
Пример: 720 делится на 10.
Признак делимости на 11.
Число делится на 11 тогда и только тогда, если модуль разности суммы цифр, стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, делится на 11
Пример: 100397 делится на 11, т. к. 1+0+9=10; 0+3+7=10; 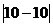 =0 (нумерация идет слева направо).
=0 (нумерация идет слева направо).
Можно проверить делимость числа на 11 другим способом:
испытуемое число разбивают справа налево на группы по две цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.
Пример:15235 делится на 11, т. к. разбивая на группы и складывая их: 1+52+35=88 делится на 11.
Признак делимости на 25.
Число делится на 25 тогда и только тогда, когда две его последние цифры составляют число, которое делится на 25.
Пример: 175делится на 25, т. к. 75 делится на 25.
3. Применение признаков делимости при решении цифровых головоломок и практических задач.
Задача № 1. Туристическое агентство «Дуремар» предложило Карабасу три путевки «в страну Дураков» — две взрослые и одну детскую за 3543 золотые монеты. Известно, что детская путевка на 500 золотых монет дешевле. Каким образом Карабас смог понять, что его обманывают?
Решение. 3543+500= 4043, но 4043 не делится на 3.
Задача № 2. Семеро друзей. У одного гражданина было 7 друзей.
Первый посещал его каждый вечер, второй — каждый второй вечер, третий — каждый третий вечер, четвертый – каждый четвертый вечер и так до седьмого друга, который являлся каждый седьмой вечер. Часто ли случалось, что все семеро друзей встречались у хозяина в один и тот же вечер?
Решение. Задача решается с использованием признаков делимости на 2, на 3, на 4, на 5, на 6, на 7. НОД (2, 3, 4, 5, 6, 7) = 420
Ответ: 1 раз в 420 дней.
Задача № 3. Ваня задумал простое трехзначное число, все цифры которого различны. На какую цифру оно может заканчиваться, если его последняя цифра равна сумме первых двух. Приведите примеры таких чисел.
Решение. Только на 7.
Ответ: 167, 257, 347, 527.
Задача № 4. Найдите наибольшее четырехзначное число, все цифры которого различны и которое делится на 2, 5, 9, 11.
Ответ: 8910.
4. Заключение
В результате выполнения данной работы у нас расширились знания по математике. Мы узнали, что кроме известных нам признаков на 2, 3, 4, 5, 9, 10 и 25 существуют еще признаки делимости на 6, 7, 8, 11. Поняли, что в некоторых случаях без признаков делимости просто невозможно обойтись.
Познакомившись с признаками делимости чисел, мы считаем, что полученные знания сможем использовать в своей учебной деятельности, самостоятельно применить тот или иной признак к определенной задаче, применить изученные признаки в реальной ситуации.
Считаем, что применение признаков делимости чисел в изучении математики является эффективным. Знание их значительно ускоряет решение многих заданий интеллектуальных конкурсов, математического конкурса — игры «Кенгуру». В современном мире тоже используют признаки делимости. Например, в банковском деле, при денежных расчетах в магазине.
5. Литература
Глейзер Г.И. История математики в школе 7 – 8 классы. М.:
Просвещение, 1982.
Депман И.Я. История арифметики. М.: Просвещение, 1965.
Кордемский Б.А. Математическая смекалка. М.: Юнисам, 1994.
Перельман Я.И. Живая математика. М.: Наука, 1978.
Савин А.П. Энциклопедический словарь юного математика. М.: Педагогика, 1989.
1001 вопрос и ответ. Большая книга знаний. М.: Мир книги, 2004.
Признаки делимости
В этой статье мы поговорим о таком понятии, как признаки делимости. Это определенные действия, с помощью которых можно узнать, делится ли целое число a на другое число b, которое в данном случае будет целым положительным. При это само деление не проводится. Очевидно, что для изучения данных признаков необходимо иметь общее представление о делимости чисел.
Когда мы говорим о признаках делимости, чаще всего нам приходится иметь дело не с самим числом, а с цифрами, из которых оно состоит.
С помощью определенных признаков делимости можно заключить, что некое число a можно разделить на другое число. Для одних нам будет нужна последняя цифра в записи: так можно сделать вывод о делимости на 2, 5 и 10. Сформулируем эти признаки.
Определение 1Те числа, в конце которых стоят цифры 0, 2, 4, 6, делятся на 2.
Определение 2На 5 можно разделить те числа, которые заканчиваются на 5 и 0.
Определение 3Все числа, заканчивающиеся на 0, можно разделить на 10.
Приведем примеры.
Пример 1Например, число 34 564 обладает делимостью на 2, поскольку в конце у него стоит 4. Число 567 разделить на 5 нельзя, потому что последняя цифра в нем не удовлетворяет нужным условиям. Число 89 120 мы можем разделить на 10, потому что оно заканчивается нулем.
Другие признаки делимости требуют предварительного анализа не одной, а нескольких последний цифр числа.
Признак делимости на 4 выглядит так:
Определение 4Число можно разделить на 4, если двузначное число, образованное двумя последними цифрами в нем, делится на 4.
Определение 5О признаке делимости на 8 мы говорим, когда число из трех последних цифр можно разделить на 8.
Пример 2Вот примеры таких расчетов: 99 769 775 012 делится на 4, так как в конце у него стоит 12, а 45 907 нельзя разделить на 8: берем три последние цифры, убираем из них 0 и получаем 97. Без остатка на 8 это число разделить нельзя, значит, и
Признаки делимости исследовательская работа
Научно-практическая конференция
Малая академия наук школьников муниципального района Белокатайский район
Секция: Математика
Номинация: Математика
Исследовательская работа
Признаки делимости натуральных чисел
Багаутдинов Данил Русланович
МБОУ СОШ с Ургала, 6 класс,
Руководитель:
Багаутдинова Люция Салимьяновна,
учитель математики МБОУ СОШ с Ургала
Ургала 2017
СОДЕРЖАНИЕ
Введение …………………………………………………….. стр. 3-4
Теоретическая часть
2.1. Признаки делимости на 2, 3. 5, 9, 10 (школьный курс)……..стр. 5
2.2. Признаки делимости натуральных чисел на 4, 25, 50………стр. 6 2.3. Признаки делимости натуральных чисел на 7,11, 13, 17, 19, стр. 7-10
3. Практическая часть
3.1. Применение признаков делимости при решении задач……..стр. 11-12
3.2 Анкетирование ………………………………………………..стр 13
4. Заключение……………………………………………………….стр. 14
Список литературы и интернет-ресурсов………………….….стр. 15
1. Введение
Актуальность: В начале учебного года на уроках математики мы изучали тему: «Признаки делимости натуральных чисел на 2, 3, 5, 9, 10». При изучении этой темы у нас не возникло никаких проблем, выучили признаки, научились их применять при выполнении заданий. При разложении чисел на простые множители мне пришлось делить число на 7. А как узнать, деление получится с остатком или без остатка? Нет ли признаков делимости на 7? А на другие числа?
Так меня заинтересовал вопрос о делимости натуральных чисел на другие числа. Я решил написать исследовательскую работу по данной теме.
Гипотеза: Существуют признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Объект исследования: Делимость натуральных чисел.
Предмет исследования: Признаки делимости натуральных чисел.
Цель: Найти признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Задачи:
Повторить признаки делимости на 2, 3. 5, 9, 10, изученные мною в школе.
Исследовать самостоятельно признаки делимости натуральных чисел на 4, 8, 11, 13, 15, 17, 25, 50 и другие числа.
Изучить дополнительную литературу, подтверждающую правильность гипотезы о существовании других признаков делимости натуральных чисел и правильность выявленных мной признаков делимости.
Провести опрос учащихся 9 и 11 классов
Оформить материал
Представить результаты исследований. Составить буклет «Признаки делимости натуральных чисел».
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Методы исследования: Сбор материала, обработка данных, наблюдение, сравнение, анализ, обобщение, проведение опроса среди учащихся по данной теме.
2 Теоретическая часть
2.1. Признаки делимости натуральных чисел (школьный курс).
При изучении данной темы необходимо знать понятия делитель, кратное, простое и составное числа.
Делителем натурального числа а называют натуральное число b, на которое а делится без остатка.
Часто утверждение о делимости числа а на число b выражают другими равнозначными словами: а кратно b, b — делитель а, b делит а.
Простыми называются натуральные числа, которые имеют два делителя: 1 и само число. Например, числа 5,7,19 – простые, т.к. делятся на 1 и само себя.
Числа, которые имеют более двух делителей, называются составными. Например, число 14 имеет 4 делителя: 1, 2, 7, 14, значит оно составное.

2.2. Признаки делимости натуральных чисел на 4, 25, 50.
Выполняя действия деления, умножения натуральных чисел, наблюдая за результатами действий, я нашел закономерности и получил следующие признаки делимости.
Признак делимости на 4.
25·4=100; 56·4=224; 123·4=492; 125·4=500; 2345·4=9380; 2500·4=10000; …
Умножая натуральные числа на 4, я заметил, что числа образованные из двух последних цифр числа делятся на 4 без остатка.
Признак делимости на 4 читается так:
Натуральное число делится на 4 тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 25.
Выполняя умножение натуральных различных чисел на 25, я увидел такую закономерность: произведения оканчиваются на 00, 25, 50, 75.
Значит, натуральное число делится на 25, если оканчивается цифрами 00, 25, 50, 75.
Признак делимости на 50.
На 50 делятся числа: 50, 100, 150, 200, 250, 300,… Они оканчиваются либо на 50, либо на 00.
Значит, натуральное число делится на 50 тогда и только тогда, когда оканчивается двумя нулями или 50.
2.3. Признаки делимости натуральных чисел на 7, 11, 13, 17, 19.
Из дополнительной литературы я нашел подтверждение правильности сформулированных нами признаков делимости натуральных чисел на 4, 25, 50. Так же я нашел несколько признаков делимости на 7:
1. Натуральное число делится на 7 тогда и только тогда, когда разность числа тысяч и числа, выражаемого последними тремя цифрами, делится на 7.
Примеры:
478009 делится на 7, т.к. 478-9=469, 469 делится на 7.
479345 не делится на 7, т.к. 479-345=134, 134 не делится на 7.
2. Натуральное число делится на 7, если сумма удвоенного числа, стоящего до десятков и оставшегося числа делится на 7.
Примеры:
4592 делится на 7, т.к. 45·2=90, 90+92=182, 182 делится на 7.
57384 не делится на 7, т.к. 573·2=1146, 1146+84=1230, 1230 не делится на 7.
3. Трехзначное натуральное число вида аbа будет делиться на 7, если а+b делится на 7.
Примеры:
252 делится на 7, т.к. 2+5=7, 7/7.
636 не делится на 7, т.к. 6+3=9, 9 не делится на 7.
4. Трехзначное натуральное число вида bаа будет делиться на 7, если сумма цифр числа делится на 7.
Примеры:
455 делится на 7, т.к. 4+5+5=14, 14/7.
244 не делится на 7, т.к. 2+4+4=12, 12 не делится на 7.
5. Трехзначное натуральное число вида ааb будет делиться на 7, если 2а-b делится на 7.
Примеры:
882 делится на 7,т.к. 8+8-2=14, 14/7.
996 не делится на 7, т.к. 9+9-6=12, 12 не делится на 7.
6. Четырехзначное натуральное число вида bаа , где b-двухзначное число, будет делиться на 7, если b+2а делится на 7.
Примеры:
2744 делится на 7, т.к. 27+4+4=35, 35/7.
1955 не делится на 7, т.к. 19+5+5=29, 29 не делится на 7.
7. Натуральное число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
Примеры:
483 делится на 7, т.к. 48-3·2=42, 42/7.
564 не делится на 7, т.к. 56-4·2=48, 48 не делится на 7.
8. Натуральное число делится на 7 тогда и только тогда, когда сумма произведений цифр числа на соответствующие остатки получаемые при делении разрядных единиц на число 7, делится на 7.
Примеры:
10׃7=1 (ост 3)
100׃7=14 (ост 2)
1000׃7=142 (ост 6)
10000׃7=1428 (ост 4)
100000׃7=14285 (ост 5)
1000000׃7=142857 (ост 1) и снова повторяются остатки.
Число 1316 делится на 7, т.к. 1·6+3·2+1·3+6=21, 21/7(6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3- ост. от деления 10 на 7).
Число 354722 не делится на7,т.к. 3·5+5·4+4·6+7·2+2·3+2=81, 81 не делится на 7(5-ост. от деления 100 000 на 7; 4 -ост. от деления 10 000 на 7; 6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3-ост. от деления 10 на 7).
Признаки делимости на 11.
1. Число делится на 11, если разность суммы цифр стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, кратна 11.
Разность может быть отрицательным числом или 0, но обязательно должна быть кратной 11. Нумерация идет слева направо.
Пример:
2135704 2+3+7+4=16, 1+5+0=6, 16-6=10, 10 не кратно 11, значит, это число не делится на 11.
1352736 1+5+7+6=19, 3+2+3=8, 19-8=11, 11 кратно 11, значит, это число делится на 11.
2. Натуральное число разбивают справа налево на группы по 2 цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.
Пример: Определим, делится ли число 12561714 на 11.
Разобьем число на группы по две цифры в каждой: 12/56/17/14; 12+56+17+14=99, 99 делится на 11, значит, данное число делится на 11.
3. Трехзначное натуральное число делится на 11, если сумма боковых цифр числа равна цифре, которая в середине. Ответ будет состоять из тех самых боковых цифр.
Примеры:
594 делится на11, т.к. 5+4=9, 9-в середине.
473 делится на 11, т.к. 4+3=7, 7- в середине.
861 не делится на 11, т.к. 8+1=9, а в середине 6.
Признаки делимости на 13
1. Натуральное число делится на 13, если разность числа тысяч и числа, образованного последними тремя цифрами, делится на 13.
Примеры:
Число 465400 делится на 13, т.к. 465 – 400 = 65, 65 делится на 13.
Число 256184 не делится на 13, т.к. 256 – 184 = 72, 72 не делится на 13.
2. Натуральное число делится на 13 тогда и только тогда, когда результат вычитания последней цифры, умноженной на 9, из этого числа без последней цифры , делится на 13.
Примеры:
988 делится на 13, т.к. 98 — 9·8 = 26, 26 делится на 13.
853 не делится на 13, т.к. 85 — 3·9 = 58, 58 не делится на 13.
Признак делимости на 19
Натуральное число делится на 19 без остатка тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19.
Следует учесть, что число десятков в числе надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.
Примеры:
1534 десятков-153, 4·2=8, 153+8=161, 161 не делится на 19,значит, и 1534 не делится на 19.
1824 182+4·2=190, 190/19, значит, число 1824/19.
Все перечисленные признаки делимости натуральных чисел можно разделить на 4 группы:
1группа- когда делимость чисел определяется по последней(им) цифрой (ми) – это признаки делимости на 2, на 5,на разрядную единицу, на 4, на 8, на 25, на 50;
2 группа – когда делимость чисел определяется по сумме цифр числа – это признаки делимости на3, на 9, на 7(1 признак), на 11, на 37;
3 группа – когда делимость чисел определяется после выполнения каких-то действий над цифрами числа – это признаки делимости на 7, на 11, на 13, на 19;
4 группа – когда для определения делимости числа используются другие признаки делимости — это признаки делимости на 6, на12, на 14, на 15.
Практическая часть
3.1. Применение признаков делимости при решении задач
Рассмотрим применение признаков делимости натуральных чисел на примере
задачи 19 (по теме «Натуральные числа») — КИМ ЕГЭ 2017 года, базовый уровень.
Задача 3
Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Решение.
Раскладываем делитель — число 12 на простые множители. 12 = 3×4. Следователь- но, заданное число после вычеркивания чисел должно делиться на 3 и 4.
Признак делимости на 4: Натуральное число делится на 4 тогда и только тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 3: Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
Признак делимости на 4 утверждает, что на 4 должно делиться двузначное число, образованное последними двумя цифрами. Значит, 181615121 последнюю цифру 1 вычеркиваем сразу. 12:4 = 3, поэтому две последние цифры числа 18161512 вычеркивать нельзя. Они гарантируют делимость числа на 4.
Чтобы число делилось на 3, нужно чтобы на 3 делилась сумма его цифр.
1+8+1+6+1+5+1+2=25
25 = 3×8 + 1 — можно вычеркнуть одну из единиц, но по условию задачи нужно вычеркнуть еще две цифры;
25 = 3×7 + 4 — нет двух цифр для вычеркивания, сумма которых равнялась бы 4, т.к. последние цифры 1 и 2 трогать нельзя;
25 = 3×6 + 7 — сумма двух вычеркнутых цифр будет равна 7, если вычеркнуть 6-ку и любую из единиц, кроме последней.
Итак, возможные ответы: 811512, 181512 или 181152. Выбираем один из них, например Ответ:181512 Замечание: на реальном ЕГЭ нужно сделать проверку своего ответа делением в столбик.
Следующая задача из Открытого банка заданий Федеральнного института педагогических измерений.
Задача 4
Приведите пример пятизначного числа кратного 12, произведение цифр которого равно 40. В ответе укажите ровно одно такое число.
Решение.
Разложим число 40 на простые множители. 40 = 2×2×2×5.
Таких множителей всего четыре, цифр недостаточно для пятизначного числа, но в произведение всегда можно добавить единицу, результат от этого не изменится: 40 = 2×2×2×5×1.
Таким образом, число в ответе можно составить только из этих цифр: 1,2,2,2,5.
Чтобы число было кратным 12 (то же самое, что делилось на 12 без остатка) оно должно удовлетворять признакам делимости на 3 и на 4, так как 12 = 3×4.
Проверим сумму цифр 1+2+2+2+5 = 12. Она делится на 3, поэтому наше число будет делиться на 3 при любых перестановках цифр.
А чтобы оно делилось на 4, в конце нужно поставить две цифры так, чтобы образованное ими число делилось на 4.
Очевидно, что последней цифрой должна быть 2-ка, другие — нечетные. Проверим варианты 12, 22, 52.
12:4 = 3; 22:4 = 5,5 — не делится нацело; 52:4 = 13.
Вывод: число должно быть составлено так, чтобы в конце было 12 или 52, а в начале любые перестановки из оставшихся трёх цифр.
Возможные ответы: 12252, 21252, 22152, 22512, 25212, 52212. В ответ пишем один из них. Например,
Ответ: 21252 Таким образом, мы убедились в применении признаков делимости натуральных чисел при решении задач.
Рассмотрев задачи, мне стало интересно, а знают ли наши выпускники о признаках делимости. И я решил провести опрос.
3.2Анкетирование «Помогают Вам признаки делимости при делении?»
Анкетирование проводилось среди обучающихся 9 и 11-х классов. В опросе приняли участие 29 обучающихся МБОУ СОШ с Ургала. Им было предложено ответить на следующие вопросы:
Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?
Какие вы знаете признаки делимости натуральных чисел?
Помогают ли вам признаки делимости натуральных чисел при делении?
А хотели бы узнать еще о других признаках делимости натуральных чисел?
80% опрошенных считают, что современному человеку нужно уметь считать.
Большинство обучающихся знают признаки делимости, изученные в школе
на 2,3, 5, 10. – это 87%
88 % опрошенных считают, что признаки делимости помогают при делении.
По результатам проведенного анкетирования 76 % опрошенных хотели бы познакомиться с признаками делимости, не изученными в школе.
4. Заключение.
Работая с разными источниками, я убедился в том, что существуют другие признаки делимости натуральных чисел (на 7, 11, 13, 19), что подтвердило правильность гипотезы о существовании других признаков делимости натуральных чисел.
Решая задачи я убедился, что знание и использование выше перечисленных признаков делимости натуральных чисел значительно упрощает многие вычисления, экономит время; исключает вычислительные ошибки, которые можно сделать при выполнении действия деления. Следует отметить, что формулировки некоторых признаков сложны. Может быть, поэтому они не изучаются в школе.
Собранный мной материал я оформил в виде буклета, который можно использовать на уроках математики, на занятиях математического кружка. Учителя математики могут использовать его при изучении данной темы. Также рекомендую ознакомиться со своей работой старшеклассников, которые хотят получить высокие баллы на экзаменах по математике. Перед 11-классниками своей школы я выступил, рассказал о признаках делимости, показал решение задач и раздал им буклеты.
В дальнейшем планирую рассмотреть такие вопросы:
-историю возникновения признаков делимости;
— признак Паскаля.
5. СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ – РЕСУРСОВ
Перельман Я.И. Математика – это интересно ! – М.: ТЕРРА – Книжный клуб, 2006
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 6 класс : учеб. для общеобразоват. учреждений /— 25-е изд., стер. — М. : Мнемозина, 2009. — 288 с.
Internet
Секция: Математика
Номинация: Математика
Признаки делимости натуральных чисел
Автор Багаутдинов Данил Русланович МБОУ СОШ с Ургала, 6 класс,
Руководитель: Багаутдинова Люция Салимьяновна, учитель математики МБОУ СОШ с Ургала
Работа посвящена изучению признаков делимости натуральных чисел, которые не изучаются в школьном курсе математики. Знание этих признаков имеет большое значение при выполнении заданий КИМов ЕГЭ базового уровня.
Проект по математике «Признаки делимости натуральных чисел»
Актуальность.
При изучении на уроках математике темы: «Признаки делимости натуральных чисел» у меня возник интерес к исследованию чисел на делимость.
Не всегда одно натуральное число делится на другое натуральное число без остатка. Деля натуральное число мы получаем остаток, допускаем ошибки, тем самым теряем время. Возникает необходимость, не выполняя деления установить, делится ли одно натуральное число на другое.
Гипотеза
Если можно определить делимость натуральных чисел на 2,3,5,9,10 то должны быть признаки, по которым можно определить делимость натуральных чисел на другое число.
Объект исследования:
Делимость натуральных чисел
Предмет исследования:
Признаки делимости натуральных чисел
Цель:
Дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе.
Задачи исследования:
Повторить признаки делимости натуральных чисел, изучаемые в школе
Исследовать самостоятельно признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Изучить дополнительную литературу о других признаках делимости натуральных чисел.
Систематизировать и обобщать признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Рассмотреть применение признаков делимости натуральных чисел при решении задач.
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Немного из истории:
Признаки делимости на 2,3,5,9,10 были известны с давних времён. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до н.э.
Признаки делимости на 2,3 и 5 были изложены итальянским математиком Леонардо Фибоначчи (1170-1228)
Вопросы делимости чисел рассматривались пифагорейцами в теории чисел ими была проведена большая работа по типологии натуральных чисел. Пифагорейцы делили их на классы:
совершенных чисел (число, равное сумме своих делителей 6=1+2+3)
дружественных чисел ( каждое из ,которых равно сумме делителей другого , например: 220 и 284 (284= 1+2+4+5+10+20+11+22+44+55+110) и(220=1+2+4+71+142)
фигурных чисел
простых чисел и д.р
Признак Паскаля
Выдающийся французский математик и физик Блез Паскаль (1623-1662) еще в раннем возрасте вывел общий признак делимости чисел , из которого следует все частные признаки
Признак Паскаля: натуральное число А разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа А на соответствующие остатки , получаемые при деление разрядных единиц на число b делится на это число .
Признаки делимости натуральных чисел , полученных самостоятельно, изучая дополнительную литературу .
Выполняя действие деления, умножения натуральных чисел, наблюдая за результатами действий , я нашла закономерность и получила следующие признаки делимости:
Признак делимости на 4: если число, образованное двумя последними цифрами данного числа, делится на 4, то и само число делится на 4 без остатка.
Признак делимости на 8: если число, образованное тремя последними цифрами данного числа, делится на 8, то и само число делится на 8 без остатка.
Признак делимости на 6: если число делится и на 3 и на 2 , то и само число делится на 6 без остатка.
Признак делимости на 15: если число одновременно делится на 5 и на 3 и если оно заканчивает на 0 и на 5 и сумма цифр числа делится на 3, то и само число делится на 15.
Признак делимости на 25: если число оканчивается на 00,25,50,75, то и само число делится на 25 без остатка.
Признак делимости на 50: если число заканчивается на 00 или 50, то и само число делится на 50.
Из дополнительной литературы я нашла подтверждения правильности сформулированных мною признаков делимости натуральных чисел на 4,6,8,15,25,50.
Так же я нашла признаки делимости на 7,на 11,на 12,на 13. Все рассмотренные признаки я сформулировала в виде брошюры
Признак делимости на 7
Если последнюю цифру числа умножить на 2 и вычесть из числа, оставшегося без последней цифры и если получившееся число делится на 7, то и само число делится на 7. Число 1102283
1-й шаг: 110228-3*2 = 110222
2-й шаг: 11022-2*2 = 11018
3-й шаг: 1101-8*2 = 1085
4-й шаг: 108-5*2 = 98
5-й шаг: 9-8*2 = -7. Делится на 7
Значит, 1102283 делится на 7
Признак делимости на 11
Если сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо отличается от нее на число, делящееся на 11, то число делится на 11 без остатка.
Пример: 160369 (Сумма цифр, которые стоят на нечётных местах 1+0+6 = 7.
Сумма цифр, которые стоят на чётных местах 6+3+9 = 18.
18 — 7 = 11. Делится на 11. Значит, число 160369 делится на 11).
Признак делимости на 12.
Если две последние цифры числа делятся на 4 и сумма цифр его делится на 3,то всё число делится на 12, без остатка.
Пример:
78864 (Две последние цифры — 64. Число, составленное из них, делится на 4; сумма цифр равна 7+8+8+6+4 = 33-делится на 3.) Значит, всё число делится на 12.
Еще пример:
Число, составленное из них,делится на 4;
сумма цифр равна 7+6+8+1+2=24,
(данное число делится на 3).
Значит, всё число делится на 12.
Признак делимости на 13
Если взять последнюю цифру числа, умножить ее на 4 и прибавить к числу, оставшемуся без последней цифры, и если получившееся число делится на 13, то и само число делится на 13, без остатка.
Пример:
Число 595166.
1-й шаг. 59516 + 6*4 = 59540
2-й шаг. 5954 + 0*4 = 5954
3-й шаг. 595 + 4*4 = 611
4-й шаг. 61 + 1*4 = 65
5-й шаг. 6 + 5*4 = 26. Делится на 13.
Применение признаков делимости при решении задач.
Задача:
Ученики 5 класса купили 203 учебника. Сколько было пятиклассников и сколько учебников купил каждый из них.
Решение:
Обе величины , должны быть целыми числами.
Разложим 203 на простые множители: 203=1*7*29. Учебников не может быть 29, так же число
учебников не может равняться 1,т.к. В этом случае учеников было бы 203. Значит 5 –ов 29 и каждый из них купил по 7 учебников.
Спасибо за внимание.
Онлайн урок: Признаки делимости на 9 и на 3 по предмету Математика 6 класс
Пусть у нас есть 153 конфеты. Нужно раздать их троим детям поровну, используя только признак делимости.
Число 153 можно разложить на 1 сотню, 5 десятков и 3 единицы.
Разделим сначала нашу сотню конфет. Каждый ребенок получит по 33 конфеты, и в остатке одна.
Теперь разделим один десяток конфет на троих. Имеем по 3 конфеты у каждого, и одна в остатке. Значит, для наших пяти десятков каждому ребёнку по 15 (3•5) конфет, и в остатке 5 (1•5) конфет.
По аналогии поступим с количеством конфет в единицах — тут всем достанется 1 конфета.
Мы не смогли разделить 1 конфету из сотен, 5 конфет из десятков. То есть в сумме получим 1 + 5 = 6 конфет, которые можно разделить по 2 конфеты каждому.
В итоге каждому ребёнку получится по 33 + 15 + 1 + 2 = 51 конфете.
Значит, число 153 делится без остатка на 3, а 1 + 5 — это сумма цифр этого числа.
Мы на примере посмотрели, как используется признак делимости на 3.
Если сумма цифр числа делится на 3, то и число делится на 3.
Если сумма цифр числа не делится на 3, то и число не делится на 3.
Пример 1
Выберите среди чисел 75432, 2772825, 5402070 те, которые делятся на 3.
Решение:
По признаку делимости на 3 нужно найти сумму цифр каждого числа и дальше работать с нею.
Для первого: 7 + 5+ 4+ 3+ 2 = 21,а 21 : 3 = 7, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для второго: 2 + 7 + 7 + 2 + 8 + 2 + 5 = 33, а 33 : 3 = 11, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для третьего: 5 + 4 + 0 + 2 + 0 + 7 + 0 = 18, а 18 : 3 = 6, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Пример 2
Замените звёздочки в числах 2*5, 31*, *15, на необходимые цифры, чтобы эти числа стали делиться на 3.

Решение:
Возьмем первое число 2*5. Из признака делимости мы знаем, что нужно, чтобы сумма цифр числа делилась на 3. Значит, 2 + 5 + * должно делиться на 3.
Сумма известных цифр равна 8, значит, вместо звездочки можно взять, например, 1.
Тогда сумма станет 9, и она делится на 3, значит, и получившееся число 215 будет делиться на 3.
Кроме единицы подходят цифры: 4, 7, так как они отличаются от 1 на 3 и 6 каждая.
Возьмем второе число 31*. Сумма первых цифр равна 4, значит, вместо звездочки минимум надо брать 2, чтоб в сумме было 6.
Тогда сумма цифр будет делиться на 3 и само число, 312, будет делиться тоже.
Кроме двойки брать можно и другие цифры, прибавляя по 3: 5 или 8.
Получившиеся числа 315 или 318 будут делиться на 3.
Берём последнее число *15. Сумма последних двух цифр — 6, уже делится на 3. Значит нужно брать вместо первой цифры такие, которые делятся на 3. Это 3, 6 или 9.
Получившиеся числа 315, 615, 915 будут делиться на 3 без остатка.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьИз признака делимости на 3 можно получить интересный признак делимости на 6
Чтобы ваше число делилось на 6, нужно чтоб оно делилось на 2 и на 3 одновременно.
Пример
Делится ли 216 на 6?
Решение:
216— это чётное число, значит, оно делится на 2.
Сумма цифр числа 216 равна 2 + 1+ 6 = 9, значит, оно делится на 3.
Отсюда, делаем вывод, что 216 делится на 6.

1. Введение
Актуальность: В начале учебного года на уроках математики мы изучали тему: «Признаки делимости натуральных чисел на 2, 3, 5, 9, 10». При изучении этой темы у нас не возникло никаких проблем, выучили признаки, научились их применять при выполнении заданий. При разложении чисел на простые множители мне пришлось делить число на 7. А как узнать, деление получится с остатком или без остатка? Нет ли признаков делимости на 7? А на другие числа?
Так меня заинтересовал вопрос о делимости натуральных чисел на другие числа. Я решил написать исследовательскую работу по данной теме.
Гипотеза: Существуют признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Объект исследования: Делимость натуральных чисел.
Предмет исследования: Признаки делимости натуральных чисел.
Цель: Найти признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Задачи:
Повторить признаки делимости на 2, 3. 5, 9, 10, изученные мною в школе.
Исследовать самостоятельно признаки делимости натуральных чисел на 4, 8, 11, 13, 15, 17, 25, 50 и другие числа.
Изучить дополнительную литературу, подтверждающую правильность гипотезы о существовании других признаков делимости натуральных чисел и правильность выявленных мной признаков делимости.
Провести опрос учащихся 9 и 11 классов
Оформить материал
Представить результаты исследований. Составить буклет «Признаки делимости натуральных чисел».
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Методы исследования: Сбор материала, обработка данных, наблюдение, сравнение, анализ, обобщение, проведение опроса среди учащихся по данной теме.
2 Теоретическая часть
2.1. Признаки делимости натуральных чисел (школьный курс).
При изучении данной темы необходимо знать понятия делитель, кратное, простое и составное числа.
Делителем натурального числа а называют натуральное число b, на которое а делится без остатка.
Часто утверждение о делимости числа а на число b выражают другими равнозначными словами: а кратно b, b — делитель а, b делит а.
Простыми называются натуральные числа, которые имеют два делителя: 1 и само число. Например, числа 5,7,19 – простые, т.к. делятся на 1 и само себя.
Числа, которые имеют более двух делителей, называются составными. Например, число 14 имеет 4 делителя: 1, 2, 7, 14, значит оно составное.

2.2. Признаки делимости натуральных чисел на 4, 25, 50.
Выполняя действия деления, умножения натуральных чисел, наблюдая за результатами действий, я нашел закономерности и получил следующие признаки делимости.
Признак делимости на 4.
25·4=100; 56·4=224; 123·4=492; 125·4=500; 2345·4=9380; 2500·4=10000; …
Умножая натуральные числа на 4, я заметил, что числа образованные из двух последних цифр числа делятся на 4 без остатка.
Признак делимости на 4 читается так:
Натуральное число делится на 4 тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 25.
Выполняя умножение натуральных различных чисел на 25, я увидел такую закономерность: произведения оканчиваются на 00, 25, 50, 75.
Значит, натуральное число делится на 25, если оканчивается цифрами 00, 25, 50, 75.
Признак делимости на 50.
На 50 делятся числа: 50, 100, 150, 200, 250, 300,… Они оканчиваются либо на 50, либо на 00.
Значит, натуральное число делится на 50 тогда и только тогда, когда оканчивается двумя нулями или 50.
2.3. Признаки делимости натуральных чисел на 7, 11, 13, 17, 19.
Из дополнительной литературы я нашел подтверждение правильности сформулированных нами признаков делимости натуральных чисел на 4, 25, 50. Так же я нашел несколько признаков делимости на 7:
1. Натуральное число делится на 7 тогда и только тогда, когда разность числа тысяч и числа, выражаемого последними тремя цифрами, делится на 7.
Примеры:
478009 делится на 7, т.к. 478-9=469, 469 делится на 7.
479345 не делится на 7, т.к. 479-345=134, 134 не делится на 7.
2. Натуральное число делится на 7, если сумма удвоенного числа, стоящего до десятков и оставшегося числа делится на 7.
Примеры:
4592 делится на 7, т.к. 45·2=90, 90+92=182, 182 делится на 7.
57384 не делится на 7, т.к. 573·2=1146, 1146+84=1230, 1230 не делится на 7.
3. Трехзначное натуральное число вида аbа будет делиться на 7, если а+b делится на 7.
Примеры:
252 делится на 7, т.к. 2+5=7, 7/7.
636 не делится на 7, т.к. 6+3=9, 9 не делится на 7.
4. Трехзначное натуральное число вида bаа будет делиться на 7, если сумма цифр числа делится на 7.
Примеры:
455 делится на 7, т.к. 4+5+5=14, 14/7.
244 не делится на 7, т.к. 2+4+4=12, 12 не делится на 7.
5. Трехзначное натуральное число вида ааb будет делиться на 7, если 2а-b делится на 7.
Примеры:
882 делится на 7,т.к. 8+8-2=14, 14/7.
996 не делится на 7, т.к. 9+9-6=12, 12 не делится на 7.
6. Четырехзначное натуральное число вида bаа , где b-двухзначное число, будет делиться на 7, если b+2а делится на 7.
Примеры:
2744 делится на 7, т.к. 27+4+4=35, 35/7.
1955 не делится на 7, т.к. 19+5+5=29, 29 не делится на 7.
7. Натуральное число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
Примеры:
483 делится на 7, т.к. 48-3·2=42, 42/7.
564 не делится на 7, т.к. 56-4·2=48, 48 не делится на 7.
8. Натуральное число делится на 7 тогда и только тогда, когда сумма произведений цифр числа на соответствующие остатки получаемые при делении разрядных единиц на число 7, делится на 7.
Примеры:
10׃7=1 (ост 3)
100׃7=14 (ост 2)
1000׃7=142 (ост 6)
10000׃7=1428 (ост 4)
100000׃7=14285 (ост 5)
1000000׃7=142857 (ост 1) и снова повторяются остатки.
Число 1316 делится на 7, т.к. 1·6+3·2+1·3+6=21, 21/7(6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3- ост. от деления 10 на 7).
Число 354722 не делится на7,т.к. 3·5+5·4+4·6+7·2+2·3+2=81, 81 не делится на 7(5-ост. от деления 100 000 на 7; 4 -ост. от деления 10 000 на 7; 6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3-ост. от деления 10 на 7).
Признаки делимости на 11.
1. Число делится на 11, если разность суммы цифр стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, кратна 11.
Разность может быть отрицательным числом или 0, но обязательно должна быть кратной 11. Нумерация идет слева направо.
Пример:
2135704 2+3+7+4=16, 1+5+0=6, 16-6=10, 10 не кратно 11, значит, это число не делится на 11.
1352736 1+5+7+6=19, 3+2+3=8, 19-8=11, 11 кратно 11, значит, это число делится на 11.
2. Натуральное число разбивают справа налево на группы по 2 цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.
Пример: Определим, делится ли число 12561714 на 11.
Разобьем число на группы по две цифры в каждой: 12/56/17/14; 12+56+17+14=99, 99 делится на 11, значит, данное число делится на 11.
3. Трехзначное натуральное число делится на 11, если сумма боковых цифр числа равна цифре, которая в середине. Ответ будет состоять из тех самых боковых цифр.
Примеры:
594 делится на11, т.к. 5+4=9, 9-в середине.
473 делится на 11, т.к. 4+3=7, 7- в середине.
861 не делится на 11, т.к. 8+1=9, а в середине 6.
Признаки делимости на 13
1. Натуральное число делится на 13, если разность числа тысяч и числа, образованного последними тремя цифрами, делится на 13.
Примеры:
Число 465400 делится на 13, т.к. 465 – 400 = 65, 65 делится на 13.
Число 256184 не делится на 13, т.к. 256 – 184 = 72, 72 не делится на 13.
2. Натуральное число делится на 13 тогда и только тогда, когда результат вычитания последней цифры, умноженной на 9, из этого числа без последней цифры , делится на 13.
Примеры:
988 делится на 13, т.к. 98 — 9·8 = 26, 26 делится на 13.
853 не делится на 13, т.к. 85 — 3·9 = 58, 58 не делится на 13.
Признак делимости на 19
Натуральное число делится на 19 без остатка тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19.
Следует учесть, что число десятков в числе надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.
Примеры:
1534 десятков-153, 4·2=8, 153+8=161, 161 не делится на 19,значит, и 1534 не делится на 19.
1824 182+4·2=190, 190/19, значит, число 1824/19.
Все перечисленные признаки делимости натуральных чисел можно разделить на 4 группы:
1группа- когда делимость чисел определяется по последней(им) цифрой (ми) – это признаки делимости на 2, на 5,на разрядную единицу, на 4, на 8, на 25, на 50;
2 группа – когда делимость чисел определяется по сумме цифр числа – это признаки делимости на3, на 9, на 7(1 признак), на 11, на 37;
3 группа – когда делимость чисел определяется после выполнения каких-то действий над цифрами числа – это признаки делимости на 7, на 11, на 13, на 19;
4 группа – когда для определения делимости числа используются другие признаки делимости — это признаки делимости на 6, на12, на 14, на 15.
Практическая часть
3.1. Применение признаков делимости при решении задач
Рассмотрим применение признаков делимости натуральных чисел на примере
задачи 19 (по теме «Натуральные числа») — КИМ ЕГЭ 2017 года, базовый уровень.
Задача 3
Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Решение.
Раскладываем делитель — число 12 на простые множители. 12 = 3×4. Следователь- но, заданное число после вычеркивания чисел должно делиться на 3 и 4.
Признак делимости на 4: Натуральное число делится на 4 тогда и только тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 3: Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
Признак делимости на 4 утверждает, что на 4 должно делиться двузначное число, образованное последними двумя цифрами. Значит, 181615121 последнюю цифру 1 вычеркиваем сразу. 12:4 = 3, поэтому две последние цифры числа 18161512 вычеркивать нельзя. Они гарантируют делимость числа на 4.
Чтобы число делилось на 3, нужно чтобы на 3 делилась сумма его цифр.
1+8+1+6+1+5+1+2=25
25 = 3×8 + 1 — можно вычеркнуть одну из единиц, но по условию задачи нужно вычеркнуть еще две цифры;
25 = 3×7 + 4 — нет двух цифр для вычеркивания, сумма которых равнялась бы 4, т.к. последние цифры 1 и 2 трогать нельзя;
25 = 3×6 + 7 — сумма двух вычеркнутых цифр будет равна 7, если вычеркнуть 6-ку и любую из единиц, кроме последней.
Итак, возможные ответы: 811512, 181512 или 181152. Выбираем один из них, например Ответ:181512 Замечание: на реальном ЕГЭ нужно сделать проверку своего ответа делением в столбик.
Следующая задача из Открытого банка заданий Федеральнного института педагогических измерений.
Задача 4
Приведите пример пятизначного числа кратного 12, произведение цифр которого равно 40. В ответе укажите ровно одно такое число.
Решение.
Разложим число 40 на простые множители. 40 = 2×2×2×5.
Таких множителей всего четыре, цифр недостаточно для пятизначного числа, но в произведение всегда можно добавить единицу, результат от этого не изменится: 40 = 2×2×2×5×1.
Таким образом, число в ответе можно составить только из этих цифр: 1,2,2,2,5.
Чтобы число было кратным 12 (то же самое, что делилось на 12 без остатка) оно должно удовлетворять признакам делимости на 3 и на 4, так как 12 = 3×4.
Проверим сумму цифр 1+2+2+2+5 = 12. Она делится на 3, поэтому наше число будет делиться на 3 при любых перестановках цифр.
А чтобы оно делилось на 4, в конце нужно поставить две цифры так, чтобы образованное ими число делилось на 4.
Очевидно, что последней цифрой должна быть 2-ка, другие — нечетные. Проверим варианты 12, 22, 52.
12:4 = 3; 22:4 = 5,5 — не делится нацело; 52:4 = 13.
Вывод: число должно быть составлено так, чтобы в конце было 12 или 52, а в начале любые перестановки из оставшихся трёх цифр.
Возможные ответы: 12252, 21252, 22152, 22512, 25212, 52212. В ответ пишем один из них. Например,
Ответ: 21252 Таким образом, мы убедились в применении признаков делимости натуральных чисел при решении задач.
Рассмотрев задачи, мне стало интересно, а знают ли наши выпускники о признаках делимости. И я решил провести опрос.
3.2Анкетирование «Помогают Вам признаки делимости при делении?»
Анкетирование проводилось среди обучающихся 9 и 11-х классов. В опросе приняли участие 29 обучающихся МБОУ СОШ с Ургала. Им было предложено ответить на следующие вопросы:
Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?
Какие вы знаете признаки делимости натуральных чисел?
Помогают ли вам признаки делимости натуральных чисел при делении?
А хотели бы узнать еще о других признаках делимости натуральных чисел?
80% опрошенных считают, что современному человеку нужно уметь считать.
Большинство обучающихся знают признаки делимости, изученные в школе
на 2,3, 5, 10. – это 87%
88 % опрошенных считают, что признаки делимости помогают при делении.
По результатам проведенного анкетирования 76 % опрошенных хотели бы познакомиться с признаками делимости, не изученными в школе.
4. Заключение.
Работая с разными источниками, я убедился в том, что существуют другие признаки делимости натуральных чисел (на 7, 11, 13, 19), что подтвердило правильность гипотезы о существовании других признаков делимости натуральных чисел.
Решая задачи я убедился, что знание и использование выше перечисленных признаков делимости натуральных чисел значительно упрощает многие вычисления, экономит время; исключает вычислительные ошибки, которые можно сделать при выполнении действия деления. Следует отметить, что формулировки некоторых признаков сложны. Может быть, поэтому они не изучаются в школе.
Собранный мной материал я оформил в виде буклета, который можно использовать на уроках математики, на занятиях математического кружка. Учителя математики могут использовать его при изучении данной темы. Также рекомендую ознакомиться со своей работой старшеклассников, которые хотят получить высокие баллы на экзаменах по математике. Перед 11-классниками своей школы я выступил, рассказал о признаках делимости, показал решение задач и раздал им буклеты.
В дальнейшем планирую рассмотреть такие вопросы:
-историю возникновения признаков делимости;
— признак Паскаля.
5. СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ – РЕСУРСОВ
Перельман Я.И. Математика – это интересно ! – М.: ТЕРРА – Книжный клуб, 2006
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 6 класс : учеб. для общеобразоват. учреждений /— 25-е изд., стер. — М. : Мнемозина, 2009. — 288 с.
Internet
Секция: Математика
Номинация: Математика
Признаки делимости натуральных чисел
Автор Багаутдинов Данил Русланович МБОУ СОШ с Ургала, 6 класс,
Руководитель: Багаутдинова Люция Салимьяновна, учитель математики МБОУ СОШ с Ургала
Работа посвящена изучению признаков делимости натуральных чисел, которые не изучаются в школьном курсе математики. Знание этих признаков имеет большое значение при выполнении заданий КИМов ЕГЭ базового уровня.
Проект по математике «Признаки делимости натуральных чисел»
Актуальность.
При изучении на уроках математике темы: «Признаки делимости натуральных чисел» у меня возник интерес к исследованию чисел на делимость.
Не всегда одно натуральное число делится на другое натуральное число без остатка. Деля натуральное число мы получаем остаток, допускаем ошибки, тем самым теряем время. Возникает необходимость, не выполняя деления установить, делится ли одно натуральное число на другое.
Гипотеза
Если можно определить делимость натуральных чисел на 2,3,5,9,10 то должны быть признаки, по которым можно определить делимость натуральных чисел на другое число.
Объект исследования:
Делимость натуральных чисел
Предмет исследования:
Признаки делимости натуральных чисел
Цель:
Дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе.
Задачи исследования:
Повторить признаки делимости натуральных чисел, изучаемые в школе
Исследовать самостоятельно признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Изучить дополнительную литературу о других признаках делимости натуральных чисел.
Систематизировать и обобщать признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Рассмотреть применение признаков делимости натуральных чисел при решении задач.
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Немного из истории:
Признаки делимости на 2,3,5,9,10 были известны с давних времён. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до н.э.
Признаки делимости на 2,3 и 5 были изложены итальянским математиком Леонардо Фибоначчи (1170-1228)
Вопросы делимости чисел рассматривались пифагорейцами в теории чисел ими была проведена большая работа по типологии натуральных чисел. Пифагорейцы делили их на классы:
совершенных чисел (число, равное сумме своих делителей 6=1+2+3)
дружественных чисел ( каждое из ,которых равно сумме делителей другого , например: 220 и 284 (284= 1+2+4+5+10+20+11+22+44+55+110) и(220=1+2+4+71+142)
фигурных чисел
простых чисел и д.р
Признак Паскаля
Выдающийся французский математик и физик Блез Паскаль (1623-1662) еще в раннем возрасте вывел общий признак делимости чисел , из которого следует все частные признаки
Признак Паскаля: натуральное число А разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа А на соответствующие остатки , получаемые при деление разрядных единиц на число b делится на это число .
Признаки делимости натуральных чисел , полученных самостоятельно, изучая дополнительную литературу .
Выполняя действие деления, умножения натуральных чисел, наблюдая за результатами действий , я нашла закономерность и получила следующие признаки делимости:
Признак делимости на 4: если число, образованное двумя последними цифрами данного числа, делится на 4, то и само число делится на 4 без остатка.
Признак делимости на 8: если число, образованное тремя последними цифрами данного числа, делится на 8, то и само число делится на 8 без остатка.
Признак делимости на 6: если число делится и на 3 и на 2 , то и само число делится на 6 без остатка.
Признак делимости на 15: если число одновременно делится на 5 и на 3 и если оно заканчивает на 0 и на 5 и сумма цифр числа делится на 3, то и само число делится на 15.
Признак делимости на 25: если число оканчивается на 00,25,50,75, то и само число делится на 25 без остатка.
Признак делимости на 50: если число заканчивается на 00 или 50, то и само число делится на 50.
Из дополнительной литературы я нашла подтверждения правильности сформулированных мною признаков делимости натуральных чисел на 4,6,8,15,25,50.
Так же я нашла признаки делимости на 7,на 11,на 12,на 13. Все рассмотренные признаки я сформулировала в виде брошюры
Признак делимости на 7
Если последнюю цифру числа умножить на 2 и вычесть из числа, оставшегося без последней цифры и если получившееся число делится на 7, то и само число делится на 7. Число 1102283
1-й шаг: 110228-3*2 = 110222
2-й шаг: 11022-2*2 = 11018
3-й шаг: 1101-8*2 = 1085
4-й шаг: 108-5*2 = 98
5-й шаг: 9-8*2 = -7. Делится на 7
Значит, 1102283 делится на 7
Признак делимости на 11
Если сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо отличается от нее на число, делящееся на 11, то число делится на 11 без остатка.
Пример: 160369 (Сумма цифр, которые стоят на нечётных местах 1+0+6 = 7.
Сумма цифр, которые стоят на чётных местах 6+3+9 = 18.
18 — 7 = 11. Делится на 11. Значит, число 160369 делится на 11).
Признак делимости на 12.
Если две последние цифры числа делятся на 4 и сумма цифр его делится на 3,то всё число делится на 12, без остатка.
Пример:
78864 (Две последние цифры — 64. Число, составленное из них, делится на 4; сумма цифр равна 7+8+8+6+4 = 33-делится на 3.) Значит, всё число делится на 12.
Еще пример:
Число, составленное из них,делится на 4;
сумма цифр равна 7+6+8+1+2=24,
(данное число делится на 3).
Значит, всё число делится на 12.
Признак делимости на 13
Если взять последнюю цифру числа, умножить ее на 4 и прибавить к числу, оставшемуся без последней цифры, и если получившееся число делится на 13, то и само число делится на 13, без остатка.
Пример:
Число 595166.
1-й шаг. 59516 + 6*4 = 59540
2-й шаг. 5954 + 0*4 = 5954
3-й шаг. 595 + 4*4 = 611
4-й шаг. 61 + 1*4 = 65
5-й шаг. 6 + 5*4 = 26. Делится на 13.
Применение признаков делимости при решении задач.
Задача:
Ученики 5 класса купили 203 учебника. Сколько было пятиклассников и сколько учебников купил каждый из них.
Решение:
Обе величины , должны быть целыми числами.
Разложим 203 на простые множители: 203=1*7*29. Учебников не может быть 29, так же число
учебников не может равняться 1,т.к. В этом случае учеников было бы 203. Значит 5 –ов 29 и каждый из них купил по 7 учебников.
Спасибо за внимание.
Онлайн урок: Признаки делимости на 9 и на 3 по предмету Математика 6 класс
Пусть у нас есть 153 конфеты. Нужно раздать их троим детям поровну, используя только признак делимости.
Число 153 можно разложить на 1 сотню, 5 десятков и 3 единицы.
Разделим сначала нашу сотню конфет. Каждый ребенок получит по 33 конфеты, и в остатке одна.
Теперь разделим один десяток конфет на троих. Имеем по 3 конфеты у каждого, и одна в остатке. Значит, для наших пяти десятков каждому ребёнку по 15 (3•5) конфет, и в остатке 5 (1•5) конфет.
По аналогии поступим с количеством конфет в единицах — тут всем достанется 1 конфета.
Мы не смогли разделить 1 конфету из сотен, 5 конфет из десятков. То есть в сумме получим 1 + 5 = 6 конфет, которые можно разделить по 2 конфеты каждому.
В итоге каждому ребёнку получится по 33 + 15 + 1 + 2 = 51 конфете.
Значит, число 153 делится без остатка на 3, а 1 + 5 — это сумма цифр этого числа.
Мы на примере посмотрели, как используется признак делимости на 3.
Если сумма цифр числа делится на 3, то и число делится на 3.
Если сумма цифр числа не делится на 3, то и число не делится на 3.
Пример 1
Выберите среди чисел 75432, 2772825, 5402070 те, которые делятся на 3.
Решение:
По признаку делимости на 3 нужно найти сумму цифр каждого числа и дальше работать с нею.
Для первого: 7 + 5+ 4+ 3+ 2 = 21,а 21 : 3 = 7, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для второго: 2 + 7 + 7 + 2 + 8 + 2 + 5 = 33, а 33 : 3 = 11, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для третьего: 5 + 4 + 0 + 2 + 0 + 7 + 0 = 18, а 18 : 3 = 6, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Пример 2
Замените звёздочки в числах 2*5, 31*, *15, на необходимые цифры, чтобы эти числа стали делиться на 3.

Решение:
Возьмем первое число 2*5. Из признака делимости мы знаем, что нужно, чтобы сумма цифр числа делилась на 3. Значит, 2 + 5 + * должно делиться на 3.
Сумма известных цифр равна 8, значит, вместо звездочки можно взять, например, 1.
Тогда сумма станет 9, и она делится на 3, значит, и получившееся число 215 будет делиться на 3.
Кроме единицы подходят цифры: 4, 7, так как они отличаются от 1 на 3 и 6 каждая.
Возьмем второе число 31*. Сумма первых цифр равна 4, значит, вместо звездочки минимум надо брать 2, чтоб в сумме было 6.
Тогда сумма цифр будет делиться на 3 и само число, 312, будет делиться тоже.
Кроме двойки брать можно и другие цифры, прибавляя по 3: 5 или 8.
Получившиеся числа 315 или 318 будут делиться на 3.
Берём последнее число *15. Сумма последних двух цифр — 6, уже делится на 3. Значит нужно брать вместо первой цифры такие, которые делятся на 3. Это 3, 6 или 9.
Получившиеся числа 315, 615, 915 будут делиться на 3 без остатка.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьИз признака делимости на 3 можно получить интересный признак делимости на 6
Чтобы ваше число делилось на 6, нужно чтоб оно делилось на 2 и на 3 одновременно.
Пример
Делится ли 216 на 6?
Решение:
216— это чётное число, значит, оно делится на 2.
Сумма цифр числа 216 равна 2 + 1+ 6 = 9, значит, оно делится на 3.
Отсюда, делаем вывод, что 216 делится на 6.

1. Введение
Актуальность: В начале учебного года на уроках математики мы изучали тему: «Признаки делимости натуральных чисел на 2, 3, 5, 9, 10». При изучении этой темы у нас не возникло никаких проблем, выучили признаки, научились их применять при выполнении заданий. При разложении чисел на простые множители мне пришлось делить число на 7. А как узнать, деление получится с остатком или без остатка? Нет ли признаков делимости на 7? А на другие числа?
Так меня заинтересовал вопрос о делимости натуральных чисел на другие числа. Я решил написать исследовательскую работу по данной теме.
Гипотеза: Существуют признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Объект исследования: Делимость натуральных чисел.
Предмет исследования: Признаки делимости натуральных чисел.
Цель: Найти признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Задачи:
Повторить признаки делимости на 2, 3. 5, 9, 10, изученные мною в школе.
Исследовать самостоятельно признаки делимости натуральных чисел на 4, 8, 11, 13, 15, 17, 25, 50 и другие числа.
Изучить дополнительную литературу, подтверждающую правильность гипотезы о существовании других признаков делимости натуральных чисел и правильность выявленных мной признаков делимости.
Провести опрос учащихся 9 и 11 классов
Оформить материал
Представить результаты исследований. Составить буклет «Признаки делимости натуральных чисел».
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Методы исследования: Сбор материала, обработка данных, наблюдение, сравнение, анализ, обобщение, проведение опроса среди учащихся по данной теме.
2 Теоретическая часть
2.1. Признаки делимости натуральных чисел (школьный курс).
При изучении данной темы необходимо знать понятия делитель, кратное, простое и составное числа.
Делителем натурального числа а называют натуральное число b, на которое а делится без остатка.
Часто утверждение о делимости числа а на число b выражают другими равнозначными словами: а кратно b, b — делитель а, b делит а.
Простыми называются натуральные числа, которые имеют два делителя: 1 и само число. Например, числа 5,7,19 – простые, т.к. делятся на 1 и само себя.
Числа, которые имеют более двух делителей, называются составными. Например, число 14 имеет 4 делителя: 1, 2, 7, 14, значит оно составное.

2.2. Признаки делимости натуральных чисел на 4, 25, 50.
Выполняя действия деления, умножения натуральных чисел, наблюдая за результатами действий, я нашел закономерности и получил следующие признаки делимости.
Признак делимости на 4.
25·4=100; 56·4=224; 123·4=492; 125·4=500; 2345·4=9380; 2500·4=10000; …
Умножая натуральные числа на 4, я заметил, что числа образованные из двух последних цифр числа делятся на 4 без остатка.
Признак делимости на 4 читается так:
Натуральное число делится на 4 тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 25.
Выполняя умножение натуральных различных чисел на 25, я увидел такую закономерность: произведения оканчиваются на 00, 25, 50, 75.
Значит, натуральное число делится на 25, если оканчивается цифрами 00, 25, 50, 75.
Признак делимости на 50.
На 50 делятся числа: 50, 100, 150, 200, 250, 300,… Они оканчиваются либо на 50, либо на 00.
Значит, натуральное число делится на 50 тогда и только тогда, когда оканчивается двумя нулями или 50.
2.3. Признаки делимости натуральных чисел на 7, 11, 13, 17, 19.
Из дополнительной литературы я нашел подтверждение правильности сформулированных нами признаков делимости натуральных чисел на 4, 25, 50. Так же я нашел несколько признаков делимости на 7:
1. Натуральное число делится на 7 тогда и только тогда, когда разность числа тысяч и числа, выражаемого последними тремя цифрами, делится на 7.
Примеры:
478009 делится на 7, т.к. 478-9=469, 469 делится на 7.
479345 не делится на 7, т.к. 479-345=134, 134 не делится на 7.
2. Натуральное число делится на 7, если сумма удвоенного числа, стоящего до десятков и оставшегося числа делится на 7.
Примеры:
4592 делится на 7, т.к. 45·2=90, 90+92=182, 182 делится на 7.
57384 не делится на 7, т.к. 573·2=1146, 1146+84=1230, 1230 не делится на 7.
3. Трехзначное натуральное число вида аbа будет делиться на 7, если а+b делится на 7.
Примеры:
252 делится на 7, т.к. 2+5=7, 7/7.
636 не делится на 7, т.к. 6+3=9, 9 не делится на 7.
4. Трехзначное натуральное число вида bаа будет делиться на 7, если сумма цифр числа делится на 7.
Примеры:
455 делится на 7, т.к. 4+5+5=14, 14/7.
244 не делится на 7, т.к. 2+4+4=12, 12 не делится на 7.
5. Трехзначное натуральное число вида ааb будет делиться на 7, если 2а-b делится на 7.
Примеры:
882 делится на 7,т.к. 8+8-2=14, 14/7.
996 не делится на 7, т.к. 9+9-6=12, 12 не делится на 7.
6. Четырехзначное натуральное число вида bаа , где b-двухзначное число, будет делиться на 7, если b+2а делится на 7.
Примеры:
2744 делится на 7, т.к. 27+4+4=35, 35/7.
1955 не делится на 7, т.к. 19+5+5=29, 29 не делится на 7.
7. Натуральное число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
Примеры:
483 делится на 7, т.к. 48-3·2=42, 42/7.
564 не делится на 7, т.к. 56-4·2=48, 48 не делится на 7.
8. Натуральное число делится на 7 тогда и только тогда, когда сумма произведений цифр числа на соответствующие остатки получаемые при делении разрядных единиц на число 7, делится на 7.
Примеры:
10׃7=1 (ост 3)
100׃7=14 (ост 2)
1000׃7=142 (ост 6)
10000׃7=1428 (ост 4)
100000׃7=14285 (ост 5)
1000000׃7=142857 (ост 1) и снова повторяются остатки.
Число 1316 делится на 7, т.к. 1·6+3·2+1·3+6=21, 21/7(6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3- ост. от деления 10 на 7).
Число 354722 не делится на7,т.к. 3·5+5·4+4·6+7·2+2·3+2=81, 81 не делится на 7(5-ост. от деления 100 000 на 7; 4 -ост. от деления 10 000 на 7; 6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3-ост. от деления 10 на 7).
Признаки делимости на 11.
1. Число делится на 11, если разность суммы цифр стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, кратна 11.
Разность может быть отрицательным числом или 0, но обязательно должна быть кратной 11. Нумерация идет слева направо.
Пример:
2135704 2+3+7+4=16, 1+5+0=6, 16-6=10, 10 не кратно 11, значит, это число не делится на 11.
1352736 1+5+7+6=19, 3+2+3=8, 19-8=11, 11 кратно 11, значит, это число делится на 11.
2. Натуральное число разбивают справа налево на группы по 2 цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.
Пример: Определим, делится ли число 12561714 на 11.
Разобьем число на группы по две цифры в каждой: 12/56/17/14; 12+56+17+14=99, 99 делится на 11, значит, данное число делится на 11.
3. Трехзначное натуральное число делится на 11, если сумма боковых цифр числа равна цифре, которая в середине. Ответ будет состоять из тех самых боковых цифр.
Примеры:
594 делится на11, т.к. 5+4=9, 9-в середине.
473 делится на 11, т.к. 4+3=7, 7- в середине.
861 не делится на 11, т.к. 8+1=9, а в середине 6.
Признаки делимости на 13
1. Натуральное число делится на 13, если разность числа тысяч и числа, образованного последними тремя цифрами, делится на 13.
Примеры:
Число 465400 делится на 13, т.к. 465 – 400 = 65, 65 делится на 13.
Число 256184 не делится на 13, т.к. 256 – 184 = 72, 72 не делится на 13.
2. Натуральное число делится на 13 тогда и только тогда, когда результат вычитания последней цифры, умноженной на 9, из этого числа без последней цифры , делится на 13.
Примеры:
988 делится на 13, т.к. 98 — 9·8 = 26, 26 делится на 13.
853 не делится на 13, т.к. 85 — 3·9 = 58, 58 не делится на 13.
Признак делимости на 19
Натуральное число делится на 19 без остатка тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19.
Следует учесть, что число десятков в числе надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.
Примеры:
1534 десятков-153, 4·2=8, 153+8=161, 161 не делится на 19,значит, и 1534 не делится на 19.
1824 182+4·2=190, 190/19, значит, число 1824/19.
Все перечисленные признаки делимости натуральных чисел можно разделить на 4 группы:
1группа- когда делимость чисел определяется по последней(им) цифрой (ми) – это признаки делимости на 2, на 5,на разрядную единицу, на 4, на 8, на 25, на 50;
2 группа – когда делимость чисел определяется по сумме цифр числа – это признаки делимости на3, на 9, на 7(1 признак), на 11, на 37;
3 группа – когда делимость чисел определяется после выполнения каких-то действий над цифрами числа – это признаки делимости на 7, на 11, на 13, на 19;
4 группа – когда для определения делимости числа используются другие признаки делимости — это признаки делимости на 6, на12, на 14, на 15.
Практическая часть
3.1. Применение признаков делимости при решении задач
Рассмотрим применение признаков делимости натуральных чисел на примере
задачи 19 (по теме «Натуральные числа») — КИМ ЕГЭ 2017 года, базовый уровень.
Задача 3
Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Решение.
Раскладываем делитель — число 12 на простые множители. 12 = 3×4. Следователь- но, заданное число после вычеркивания чисел должно делиться на 3 и 4.
Признак делимости на 4: Натуральное число делится на 4 тогда и только тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 3: Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
Признак делимости на 4 утверждает, что на 4 должно делиться двузначное число, образованное последними двумя цифрами. Значит, 181615121 последнюю цифру 1 вычеркиваем сразу. 12:4 = 3, поэтому две последние цифры числа 18161512 вычеркивать нельзя. Они гарантируют делимость числа на 4.
Чтобы число делилось на 3, нужно чтобы на 3 делилась сумма его цифр.
1+8+1+6+1+5+1+2=25
25 = 3×8 + 1 — можно вычеркнуть одну из единиц, но по условию задачи нужно вычеркнуть еще две цифры;
25 = 3×7 + 4 — нет двух цифр для вычеркивания, сумма которых равнялась бы 4, т.к. последние цифры 1 и 2 трогать нельзя;
25 = 3×6 + 7 — сумма двух вычеркнутых цифр будет равна 7, если вычеркнуть 6-ку и любую из единиц, кроме последней.
Итак, возможные ответы: 811512, 181512 или 181152. Выбираем один из них, например Ответ:181512 Замечание: на реальном ЕГЭ нужно сделать проверку своего ответа делением в столбик.
Следующая задача из Открытого банка заданий Федеральнного института педагогических измерений.
Задача 4
Приведите пример пятизначного числа кратного 12, произведение цифр которого равно 40. В ответе укажите ровно одно такое число.
Решение.
Разложим число 40 на простые множители. 40 = 2×2×2×5.
Таких множителей всего четыре, цифр недостаточно для пятизначного числа, но в произведение всегда можно добавить единицу, результат от этого не изменится: 40 = 2×2×2×5×1.
Таким образом, число в ответе можно составить только из этих цифр: 1,2,2,2,5.
Чтобы число было кратным 12 (то же самое, что делилось на 12 без остатка) оно должно удовлетворять признакам делимости на 3 и на 4, так как 12 = 3×4.
Проверим сумму цифр 1+2+2+2+5 = 12. Она делится на 3, поэтому наше число будет делиться на 3 при любых перестановках цифр.
А чтобы оно делилось на 4, в конце нужно поставить две цифры так, чтобы образованное ими число делилось на 4.
Очевидно, что последней цифрой должна быть 2-ка, другие — нечетные. Проверим варианты 12, 22, 52.
12:4 = 3; 22:4 = 5,5 — не делится нацело; 52:4 = 13.
Вывод: число должно быть составлено так, чтобы в конце было 12 или 52, а в начале любые перестановки из оставшихся трёх цифр.
Возможные ответы: 12252, 21252, 22152, 22512, 25212, 52212. В ответ пишем один из них. Например,
Ответ: 21252 Таким образом, мы убедились в применении признаков делимости натуральных чисел при решении задач.
Рассмотрев задачи, мне стало интересно, а знают ли наши выпускники о признаках делимости. И я решил провести опрос.
3.2Анкетирование «Помогают Вам признаки делимости при делении?»
Анкетирование проводилось среди обучающихся 9 и 11-х классов. В опросе приняли участие 29 обучающихся МБОУ СОШ с Ургала. Им было предложено ответить на следующие вопросы:
Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?
Какие вы знаете признаки делимости натуральных чисел?
Помогают ли вам признаки делимости натуральных чисел при делении?
А хотели бы узнать еще о других признаках делимости натуральных чисел?
80% опрошенных считают, что современному человеку нужно уметь считать.
Большинство обучающихся знают признаки делимости, изученные в школе
на 2,3, 5, 10. – это 87%
88 % опрошенных считают, что признаки делимости помогают при делении.
По результатам проведенного анкетирования 76 % опрошенных хотели бы познакомиться с признаками делимости, не изученными в школе.
4. Заключение.
Работая с разными источниками, я убедился в том, что существуют другие признаки делимости натуральных чисел (на 7, 11, 13, 19), что подтвердило правильность гипотезы о существовании других признаков делимости натуральных чисел.
Решая задачи я убедился, что знание и использование выше перечисленных признаков делимости натуральных чисел значительно упрощает многие вычисления, экономит время; исключает вычислительные ошибки, которые можно сделать при выполнении действия деления. Следует отметить, что формулировки некоторых признаков сложны. Может быть, поэтому они не изучаются в школе.
Собранный мной материал я оформил в виде буклета, который можно использовать на уроках математики, на занятиях математического кружка. Учителя математики могут использовать его при изучении данной темы. Также рекомендую ознакомиться со своей работой старшеклассников, которые хотят получить высокие баллы на экзаменах по математике. Перед 11-классниками своей школы я выступил, рассказал о признаках делимости, показал решение задач и раздал им буклеты.
В дальнейшем планирую рассмотреть такие вопросы:
-историю возникновения признаков делимости;
— признак Паскаля.
5. СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ – РЕСУРСОВ
Перельман Я.И. Математика – это интересно ! – М.: ТЕРРА – Книжный клуб, 2006
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 6 класс : учеб. для общеобразоват. учреждений /— 25-е изд., стер. — М. : Мнемозина, 2009. — 288 с.
Internet
Секция: Математика
Номинация: Математика
Признаки делимости натуральных чисел
Автор Багаутдинов Данил Русланович МБОУ СОШ с Ургала, 6 класс,
Руководитель: Багаутдинова Люция Салимьяновна, учитель математики МБОУ СОШ с Ургала
Работа посвящена изучению признаков делимости натуральных чисел, которые не изучаются в школьном курсе математики. Знание этих признаков имеет большое значение при выполнении заданий КИМов ЕГЭ базового уровня.
Проект по математике «Признаки делимости натуральных чисел»
Актуальность.
При изучении на уроках математике темы: «Признаки делимости натуральных чисел» у меня возник интерес к исследованию чисел на делимость.
Не всегда одно натуральное число делится на другое натуральное число без остатка. Деля натуральное число мы получаем остаток, допускаем ошибки, тем самым теряем время. Возникает необходимость, не выполняя деления установить, делится ли одно натуральное число на другое.
Гипотеза
Если можно определить делимость натуральных чисел на 2,3,5,9,10 то должны быть признаки, по которым можно определить делимость натуральных чисел на другое число.
Объект исследования:
Делимость натуральных чисел
Предмет исследования:
Признаки делимости натуральных чисел
Цель:
Дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе.
Задачи исследования:
Повторить признаки делимости натуральных чисел, изучаемые в школе
Исследовать самостоятельно признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Изучить дополнительную литературу о других признаках делимости натуральных чисел.
Систематизировать и обобщать признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Рассмотреть применение признаков делимости натуральных чисел при решении задач.
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Немного из истории:
Признаки делимости на 2,3,5,9,10 были известны с давних времён. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до н.э.
Признаки делимости на 2,3 и 5 были изложены итальянским математиком Леонардо Фибоначчи (1170-1228)
Вопросы делимости чисел рассматривались пифагорейцами в теории чисел ими была проведена большая работа по типологии натуральных чисел. Пифагорейцы делили их на классы:
совершенных чисел (число, равное сумме своих делителей 6=1+2+3)
дружественных чисел ( каждое из ,которых равно сумме делителей другого , например: 220 и 284 (284= 1+2+4+5+10+20+11+22+44+55+110) и(220=1+2+4+71+142)
фигурных чисел
простых чисел и д.р
Признак Паскаля
Выдающийся французский математик и физик Блез Паскаль (1623-1662) еще в раннем возрасте вывел общий признак делимости чисел , из которого следует все частные признаки
Признак Паскаля: натуральное число А разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа А на соответствующие остатки , получаемые при деление разрядных единиц на число b делится на это число .
Признаки делимости натуральных чисел , полученных самостоятельно, изучая дополнительную литературу .
Выполняя действие деления, умножения натуральных чисел, наблюдая за результатами действий , я нашла закономерность и получила следующие признаки делимости:
Признак делимости на 4: если число, образованное двумя последними цифрами данного числа, делится на 4, то и само число делится на 4 без остатка.
Признак делимости на 8: если число, образованное тремя последними цифрами данного числа, делится на 8, то и само число делится на 8 без остатка.
Признак делимости на 6: если число делится и на 3 и на 2 , то и само число делится на 6 без остатка.
Признак делимости на 15: если число одновременно делится на 5 и на 3 и если оно заканчивает на 0 и на 5 и сумма цифр числа делится на 3, то и само число делится на 15.
Признак делимости на 25: если число оканчивается на 00,25,50,75, то и само число делится на 25 без остатка.
Признак делимости на 50: если число заканчивается на 00 или 50, то и само число делится на 50.
Из дополнительной литературы я нашла подтверждения правильности сформулированных мною признаков делимости натуральных чисел на 4,6,8,15,25,50.
Так же я нашла признаки делимости на 7,на 11,на 12,на 13. Все рассмотренные признаки я сформулировала в виде брошюры
Признак делимости на 7
Если последнюю цифру числа умножить на 2 и вычесть из числа, оставшегося без последней цифры и если получившееся число делится на 7, то и само число делится на 7. Число 1102283
1-й шаг: 110228-3*2 = 110222
2-й шаг: 11022-2*2 = 11018
3-й шаг: 1101-8*2 = 1085
4-й шаг: 108-5*2 = 98
5-й шаг: 9-8*2 = -7. Делится на 7
Значит, 1102283 делится на 7
Признак делимости на 11
Если сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо отличается от нее на число, делящееся на 11, то число делится на 11 без остатка.
Пример: 160369 (Сумма цифр, которые стоят на нечётных местах 1+0+6 = 7.
Сумма цифр, которые стоят на чётных местах 6+3+9 = 18.
18 — 7 = 11. Делится на 11. Значит, число 160369 делится на 11).
Признак делимости на 12.
Если две последние цифры числа делятся на 4 и сумма цифр его делится на 3,то всё число делится на 12, без остатка.
Пример:
78864 (Две последние цифры — 64. Число, составленное из них, делится на 4; сумма цифр равна 7+8+8+6+4 = 33-делится на 3.) Значит, всё число делится на 12.
Еще пример:
Число, составленное из них,делится на 4;
сумма цифр равна 7+6+8+1+2=24,
(данное число делится на 3).
Значит, всё число делится на 12.
Признак делимости на 13
Если взять последнюю цифру числа, умножить ее на 4 и прибавить к числу, оставшемуся без последней цифры, и если получившееся число делится на 13, то и само число делится на 13, без остатка.
Пример:
Число 595166.
1-й шаг. 59516 + 6*4 = 59540
2-й шаг. 5954 + 0*4 = 5954
3-й шаг. 595 + 4*4 = 611
4-й шаг. 61 + 1*4 = 65
5-й шаг. 6 + 5*4 = 26. Делится на 13.
Применение признаков делимости при решении задач.
Задача:
Ученики 5 класса купили 203 учебника. Сколько было пятиклассников и сколько учебников купил каждый из них.
Решение:
Обе величины , должны быть целыми числами.
Разложим 203 на простые множители: 203=1*7*29. Учебников не может быть 29, так же число
учебников не может равняться 1,т.к. В этом случае учеников было бы 203. Значит 5 –ов 29 и каждый из них купил по 7 учебников.
Спасибо за внимание.
Онлайн урок: Признаки делимости на 9 и на 3 по предмету Математика 6 класс
Пусть у нас есть 153 конфеты. Нужно раздать их троим детям поровну, используя только признак делимости.
Число 153 можно разложить на 1 сотню, 5 десятков и 3 единицы.
Разделим сначала нашу сотню конфет. Каждый ребенок получит по 33 конфеты, и в остатке одна.
Теперь разделим один десяток конфет на троих. Имеем по 3 конфеты у каждого, и одна в остатке. Значит, для наших пяти десятков каждому ребёнку по 15 (3•5) конфет, и в остатке 5 (1•5) конфет.
По аналогии поступим с количеством конфет в единицах — тут всем достанется 1 конфета.
Мы не смогли разделить 1 конфету из сотен, 5 конфет из десятков. То есть в сумме получим 1 + 5 = 6 конфет, которые можно разделить по 2 конфеты каждому.
В итоге каждому ребёнку получится по 33 + 15 + 1 + 2 = 51 конфете.
Значит, число 153 делится без остатка на 3, а 1 + 5 — это сумма цифр этого числа.
Мы на примере посмотрели, как используется признак делимости на 3.
Если сумма цифр числа делится на 3, то и число делится на 3.
Если сумма цифр числа не делится на 3, то и число не делится на 3.
Пример 1
Выберите среди чисел 75432, 2772825, 5402070 те, которые делятся на 3.
Решение:
По признаку делимости на 3 нужно найти сумму цифр каждого числа и дальше работать с нею.
Для первого: 7 + 5+ 4+ 3+ 2 = 21,а 21 : 3 = 7, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для второго: 2 + 7 + 7 + 2 + 8 + 2 + 5 = 33, а 33 : 3 = 11, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для третьего: 5 + 4 + 0 + 2 + 0 + 7 + 0 = 18, а 18 : 3 = 6, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Пример 2
Замените звёздочки в числах 2*5, 31*, *15, на необходимые цифры, чтобы эти числа стали делиться на 3.

Решение:
Возьмем первое число 2*5. Из признака делимости мы знаем, что нужно, чтобы сумма цифр числа делилась на 3. Значит, 2 + 5 + * должно делиться на 3.
Сумма известных цифр равна 8, значит, вместо звездочки можно взять, например, 1.
Тогда сумма станет 9, и она делится на 3, значит, и получившееся число 215 будет делиться на 3.
Кроме единицы подходят цифры: 4, 7, так как они отличаются от 1 на 3 и 6 каждая.
Возьмем второе число 31*. Сумма первых цифр равна 4, значит, вместо звездочки минимум надо брать 2, чтоб в сумме было 6.
Тогда сумма цифр будет делиться на 3 и само число, 312, будет делиться тоже.
Кроме двойки брать можно и другие цифры, прибавляя по 3: 5 или 8.
Получившиеся числа 315 или 318 будут делиться на 3.
Берём последнее число *15. Сумма последних двух цифр — 6, уже делится на 3. Значит нужно брать вместо первой цифры такие, которые делятся на 3. Это 3, 6 или 9.
Получившиеся числа 315, 615, 915 будут делиться на 3 без остатка.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьИз признака делимости на 3 можно получить интересный признак делимости на 6
Чтобы ваше число делилось на 6, нужно чтоб оно делилось на 2 и на 3 одновременно.
Пример
Делится ли 216 на 6?
Решение:
216— это чётное число, значит, оно делится на 2.
Сумма цифр числа 216 равна 2 + 1+ 6 = 9, значит, оно делится на 3.
Отсюда, делаем вывод, что 216 делится на 6.

1. Введение
Актуальность: В начале учебного года на уроках математики мы изучали тему: «Признаки делимости натуральных чисел на 2, 3, 5, 9, 10». При изучении этой темы у нас не возникло никаких проблем, выучили признаки, научились их применять при выполнении заданий. При разложении чисел на простые множители мне пришлось делить число на 7. А как узнать, деление получится с остатком или без остатка? Нет ли признаков делимости на 7? А на другие числа?
Так меня заинтересовал вопрос о делимости натуральных чисел на другие числа. Я решил написать исследовательскую работу по данной теме.
Гипотеза: Существуют признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Объект исследования: Делимость натуральных чисел.
Предмет исследования: Признаки делимости натуральных чисел.
Цель: Найти признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Задачи:
Повторить признаки делимости на 2, 3. 5, 9, 10, изученные мною в школе.
Исследовать самостоятельно признаки делимости натуральных чисел на 4, 8, 11, 13, 15, 17, 25, 50 и другие числа.
Изучить дополнительную литературу, подтверждающую правильность гипотезы о существовании других признаков делимости натуральных чисел и правильность выявленных мной признаков делимости.
Провести опрос учащихся 9 и 11 классов
Оформить материал
Представить результаты исследований. Составить буклет «Признаки делимости натуральных чисел».
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Методы исследования: Сбор материала, обработка данных, наблюдение, сравнение, анализ, обобщение, проведение опроса среди учащихся по данной теме.
2 Теоретическая часть
2.1. Признаки делимости натуральных чисел (школьный курс).
При изучении данной темы необходимо знать понятия делитель, кратное, простое и составное числа.
Делителем натурального числа а называют натуральное число b, на которое а делится без остатка.
Часто утверждение о делимости числа а на число b выражают другими равнозначными словами: а кратно b, b — делитель а, b делит а.
Простыми называются натуральные числа, которые имеют два делителя: 1 и само число. Например, числа 5,7,19 – простые, т.к. делятся на 1 и само себя.
Числа, которые имеют более двух делителей, называются составными. Например, число 14 имеет 4 делителя: 1, 2, 7, 14, значит оно составное.

2.2. Признаки делимости натуральных чисел на 4, 25, 50.
Выполняя действия деления, умножения натуральных чисел, наблюдая за результатами действий, я нашел закономерности и получил следующие признаки делимости.
Признак делимости на 4.
25·4=100; 56·4=224; 123·4=492; 125·4=500; 2345·4=9380; 2500·4=10000; …
Умножая натуральные числа на 4, я заметил, что числа образованные из двух последних цифр числа делятся на 4 без остатка.
Признак делимости на 4 читается так:
Натуральное число делится на 4 тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 25.
Выполняя умножение натуральных различных чисел на 25, я увидел такую закономерность: произведения оканчиваются на 00, 25, 50, 75.
Значит, натуральное число делится на 25, если оканчивается цифрами 00, 25, 50, 75.
Признак делимости на 50.
На 50 делятся числа: 50, 100, 150, 200, 250, 300,… Они оканчиваются либо на 50, либо на 00.
Значит, натуральное число делится на 50 тогда и только тогда, когда оканчивается двумя нулями или 50.
2.3. Признаки делимости натуральных чисел на 7, 11, 13, 17, 19.
Из дополнительной литературы я нашел подтверждение правильности сформулированных нами признаков делимости натуральных чисел на 4, 25, 50. Так же я нашел несколько признаков делимости на 7:
1. Натуральное число делится на 7 тогда и только тогда, когда разность числа тысяч и числа, выражаемого последними тремя цифрами, делится на 7.
Примеры:
478009 делится на 7, т.к. 478-9=469, 469 делится на 7.
479345 не делится на 7, т.к. 479-345=134, 134 не делится на 7.
2. Натуральное число делится на 7, если сумма удвоенного числа, стоящего до десятков и оставшегося числа делится на 7.
Примеры:
4592 делится на 7, т.к. 45·2=90, 90+92=182, 182 делится на 7.
57384 не делится на 7, т.к. 573·2=1146, 1146+84=1230, 1230 не делится на 7.
3. Трехзначное натуральное число вида аbа будет делиться на 7, если а+b делится на 7.
Примеры:
252 делится на 7, т.к. 2+5=7, 7/7.
636 не делится на 7, т.к. 6+3=9, 9 не делится на 7.
4. Трехзначное натуральное число вида bаа будет делиться на 7, если сумма цифр числа делится на 7.
Примеры:
455 делится на 7, т.к. 4+5+5=14, 14/7.
244 не делится на 7, т.к. 2+4+4=12, 12 не делится на 7.
5. Трехзначное натуральное число вида ааb будет делиться на 7, если 2а-b делится на 7.
Примеры:
882 делится на 7,т.к. 8+8-2=14, 14/7.
996 не делится на 7, т.к. 9+9-6=12, 12 не делится на 7.
6. Четырехзначное натуральное число вида bаа , где b-двухзначное число, будет делиться на 7, если b+2а делится на 7.
Примеры:
2744 делится на 7, т.к. 27+4+4=35, 35/7.
1955 не делится на 7, т.к. 19+5+5=29, 29 не делится на 7.
7. Натуральное число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
Примеры:
483 делится на 7, т.к. 48-3·2=42, 42/7.
564 не делится на 7, т.к. 56-4·2=48, 48 не делится на 7.
8. Натуральное число делится на 7 тогда и только тогда, когда сумма произведений цифр числа на соответствующие остатки получаемые при делении разрядных единиц на число 7, делится на 7.
Примеры:
10׃7=1 (ост 3)
100׃7=14 (ост 2)
1000׃7=142 (ост 6)
10000׃7=1428 (ост 4)
100000׃7=14285 (ост 5)
1000000׃7=142857 (ост 1) и снова повторяются остатки.
Число 1316 делится на 7, т.к. 1·6+3·2+1·3+6=21, 21/7(6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3- ост. от деления 10 на 7).
Число 354722 не делится на7,т.к. 3·5+5·4+4·6+7·2+2·3+2=81, 81 не делится на 7(5-ост. от деления 100 000 на 7; 4 -ост. от деления 10 000 на 7; 6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3-ост. от деления 10 на 7).
Признаки делимости на 11.
1. Число делится на 11, если разность суммы цифр стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, кратна 11.
Разность может быть отрицательным числом или 0, но обязательно должна быть кратной 11. Нумерация идет слева направо.
Пример:
2135704 2+3+7+4=16, 1+5+0=6, 16-6=10, 10 не кратно 11, значит, это число не делится на 11.
1352736 1+5+7+6=19, 3+2+3=8, 19-8=11, 11 кратно 11, значит, это число делится на 11.
2. Натуральное число разбивают справа налево на группы по 2 цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.
Пример: Определим, делится ли число 12561714 на 11.
Разобьем число на группы по две цифры в каждой: 12/56/17/14; 12+56+17+14=99, 99 делится на 11, значит, данное число делится на 11.
3. Трехзначное натуральное число делится на 11, если сумма боковых цифр числа равна цифре, которая в середине. Ответ будет состоять из тех самых боковых цифр.
Примеры:
594 делится на11, т.к. 5+4=9, 9-в середине.
473 делится на 11, т.к. 4+3=7, 7- в середине.
861 не делится на 11, т.к. 8+1=9, а в середине 6.
Признаки делимости на 13
1. Натуральное число делится на 13, если разность числа тысяч и числа, образованного последними тремя цифрами, делится на 13.
Примеры:
Число 465400 делится на 13, т.к. 465 – 400 = 65, 65 делится на 13.
Число 256184 не делится на 13, т.к. 256 – 184 = 72, 72 не делится на 13.
2. Натуральное число делится на 13 тогда и только тогда, когда результат вычитания последней цифры, умноженной на 9, из этого числа без последней цифры , делится на 13.
Примеры:
988 делится на 13, т.к. 98 — 9·8 = 26, 26 делится на 13.
853 не делится на 13, т.к. 85 — 3·9 = 58, 58 не делится на 13.
Признак делимости на 19
Натуральное число делится на 19 без остатка тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19.
Следует учесть, что число десятков в числе надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.
Примеры:
1534 десятков-153, 4·2=8, 153+8=161, 161 не делится на 19,значит, и 1534 не делится на 19.
1824 182+4·2=190, 190/19, значит, число 1824/19.
Все перечисленные признаки делимости натуральных чисел можно разделить на 4 группы:
1группа- когда делимость чисел определяется по последней(им) цифрой (ми) – это признаки делимости на 2, на 5,на разрядную единицу, на 4, на 8, на 25, на 50;
2 группа – когда делимость чисел определяется по сумме цифр числа – это признаки делимости на3, на 9, на 7(1 признак), на 11, на 37;
3 группа – когда делимость чисел определяется после выполнения каких-то действий над цифрами числа – это признаки делимости на 7, на 11, на 13, на 19;
4 группа – когда для определения делимости числа используются другие признаки делимости — это признаки делимости на 6, на12, на 14, на 15.
Практическая часть
3.1. Применение признаков делимости при решении задач
Рассмотрим применение признаков делимости натуральных чисел на примере
задачи 19 (по теме «Натуральные числа») — КИМ ЕГЭ 2017 года, базовый уровень.
Задача 3
Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Решение.
Раскладываем делитель — число 12 на простые множители. 12 = 3×4. Следователь- но, заданное число после вычеркивания чисел должно делиться на 3 и 4.
Признак делимости на 4: Натуральное число делится на 4 тогда и только тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 3: Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
Признак делимости на 4 утверждает, что на 4 должно делиться двузначное число, образованное последними двумя цифрами. Значит, 181615121 последнюю цифру 1 вычеркиваем сразу. 12:4 = 3, поэтому две последние цифры числа 18161512 вычеркивать нельзя. Они гарантируют делимость числа на 4.
Чтобы число делилось на 3, нужно чтобы на 3 делилась сумма его цифр.
1+8+1+6+1+5+1+2=25
25 = 3×8 + 1 — можно вычеркнуть одну из единиц, но по условию задачи нужно вычеркнуть еще две цифры;
25 = 3×7 + 4 — нет двух цифр для вычеркивания, сумма которых равнялась бы 4, т.к. последние цифры 1 и 2 трогать нельзя;
25 = 3×6 + 7 — сумма двух вычеркнутых цифр будет равна 7, если вычеркнуть 6-ку и любую из единиц, кроме последней.
Итак, возможные ответы: 811512, 181512 или 181152. Выбираем один из них, например Ответ:181512 Замечание: на реальном ЕГЭ нужно сделать проверку своего ответа делением в столбик.
Следующая задача из Открытого банка заданий Федеральнного института педагогических измерений.
Задача 4
Приведите пример пятизначного числа кратного 12, произведение цифр которого равно 40. В ответе укажите ровно одно такое число.
Решение.
Разложим число 40 на простые множители. 40 = 2×2×2×5.
Таких множителей всего четыре, цифр недостаточно для пятизначного числа, но в произведение всегда можно добавить единицу, результат от этого не изменится: 40 = 2×2×2×5×1.
Таким образом, число в ответе можно составить только из этих цифр: 1,2,2,2,5.
Чтобы число было кратным 12 (то же самое, что делилось на 12 без остатка) оно должно удовлетворять признакам делимости на 3 и на 4, так как 12 = 3×4.
Проверим сумму цифр 1+2+2+2+5 = 12. Она делится на 3, поэтому наше число будет делиться на 3 при любых перестановках цифр.
А чтобы оно делилось на 4, в конце нужно поставить две цифры так, чтобы образованное ими число делилось на 4.
Очевидно, что последней цифрой должна быть 2-ка, другие — нечетные. Проверим варианты 12, 22, 52.
12:4 = 3; 22:4 = 5,5 — не делится нацело; 52:4 = 13.
Вывод: число должно быть составлено так, чтобы в конце было 12 или 52, а в начале любые перестановки из оставшихся трёх цифр.
Возможные ответы: 12252, 21252, 22152, 22512, 25212, 52212. В ответ пишем один из них. Например,
Ответ: 21252 Таким образом, мы убедились в применении признаков делимости натуральных чисел при решении задач.
Рассмотрев задачи, мне стало интересно, а знают ли наши выпускники о признаках делимости. И я решил провести опрос.
3.2Анкетирование «Помогают Вам признаки делимости при делении?»
Анкетирование проводилось среди обучающихся 9 и 11-х классов. В опросе приняли участие 29 обучающихся МБОУ СОШ с Ургала. Им было предложено ответить на следующие вопросы:
Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?
Какие вы знаете признаки делимости натуральных чисел?
Помогают ли вам признаки делимости натуральных чисел при делении?
А хотели бы узнать еще о других признаках делимости натуральных чисел?
80% опрошенных считают, что современному человеку нужно уметь считать.
Большинство обучающихся знают признаки делимости, изученные в школе
на 2,3, 5, 10. – это 87%
88 % опрошенных считают, что признаки делимости помогают при делении.
По результатам проведенного анкетирования 76 % опрошенных хотели бы познакомиться с признаками делимости, не изученными в школе.
4. Заключение.
Работая с разными источниками, я убедился в том, что существуют другие признаки делимости натуральных чисел (на 7, 11, 13, 19), что подтвердило правильность гипотезы о существовании других признаков делимости натуральных чисел.
Решая задачи я убедился, что знание и использование выше перечисленных признаков делимости натуральных чисел значительно упрощает многие вычисления, экономит время; исключает вычислительные ошибки, которые можно сделать при выполнении действия деления. Следует отметить, что формулировки некоторых признаков сложны. Может быть, поэтому они не изучаются в школе.
Собранный мной материал я оформил в виде буклета, который можно использовать на уроках математики, на занятиях математического кружка. Учителя математики могут использовать его при изучении данной темы. Также рекомендую ознакомиться со своей работой старшеклассников, которые хотят получить высокие баллы на экзаменах по математике. Перед 11-классниками своей школы я выступил, рассказал о признаках делимости, показал решение задач и раздал им буклеты.
В дальнейшем планирую рассмотреть такие вопросы:
-историю возникновения признаков делимости;
— признак Паскаля.
5. СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ – РЕСУРСОВ
Перельман Я.И. Математика – это интересно ! – М.: ТЕРРА – Книжный клуб, 2006
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 6 класс : учеб. для общеобразоват. учреждений /— 25-е изд., стер. — М. : Мнемозина, 2009. — 288 с.
Internet
Секция: Математика
Номинация: Математика
Признаки делимости натуральных чисел
Автор Багаутдинов Данил Русланович МБОУ СОШ с Ургала, 6 класс,
Руководитель: Багаутдинова Люция Салимьяновна, учитель математики МБОУ СОШ с Ургала
Работа посвящена изучению признаков делимости натуральных чисел, которые не изучаются в школьном курсе математики. Знание этих признаков имеет большое значение при выполнении заданий КИМов ЕГЭ базового уровня.
Проект по математике «Признаки делимости натуральных чисел»
Актуальность.
При изучении на уроках математике темы: «Признаки делимости натуральных чисел» у меня возник интерес к исследованию чисел на делимость.
Не всегда одно натуральное число делится на другое натуральное число без остатка. Деля натуральное число мы получаем остаток, допускаем ошибки, тем самым теряем время. Возникает необходимость, не выполняя деления установить, делится ли одно натуральное число на другое.
Гипотеза
Если можно определить делимость натуральных чисел на 2,3,5,9,10 то должны быть признаки, по которым можно определить делимость натуральных чисел на другое число.
Объект исследования:
Делимость натуральных чисел
Предмет исследования:
Признаки делимости натуральных чисел
Цель:
Дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе.
Задачи исследования:
Повторить признаки делимости натуральных чисел, изучаемые в школе
Исследовать самостоятельно признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Изучить дополнительную литературу о других признаках делимости натуральных чисел.
Систематизировать и обобщать признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Рассмотреть применение признаков делимости натуральных чисел при решении задач.
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Немного из истории:
Признаки делимости на 2,3,5,9,10 были известны с давних времён. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до н.э.
Признаки делимости на 2,3 и 5 были изложены итальянским математиком Леонардо Фибоначчи (1170-1228)
Вопросы делимости чисел рассматривались пифагорейцами в теории чисел ими была проведена большая работа по типологии натуральных чисел. Пифагорейцы делили их на классы:
совершенных чисел (число, равное сумме своих делителей 6=1+2+3)
дружественных чисел ( каждое из ,которых равно сумме делителей другого , например: 220 и 284 (284= 1+2+4+5+10+20+11+22+44+55+110) и(220=1+2+4+71+142)
фигурных чисел
простых чисел и д.р
Признак Паскаля
Выдающийся французский математик и физик Блез Паскаль (1623-1662) еще в раннем возрасте вывел общий признак делимости чисел , из которого следует все частные признаки
Признак Паскаля: натуральное число А разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа А на соответствующие остатки , получаемые при деление разрядных единиц на число b делится на это число .
Признаки делимости натуральных чисел , полученных самостоятельно, изучая дополнительную литературу .
Выполняя действие деления, умножения натуральных чисел, наблюдая за результатами действий , я нашла закономерность и получила следующие признаки делимости:
Признак делимости на 4: если число, образованное двумя последними цифрами данного числа, делится на 4, то и само число делится на 4 без остатка.
Признак делимости на 8: если число, образованное тремя последними цифрами данного числа, делится на 8, то и само число делится на 8 без остатка.
Признак делимости на 6: если число делится и на 3 и на 2 , то и само число делится на 6 без остатка.
Признак делимости на 15: если число одновременно делится на 5 и на 3 и если оно заканчивает на 0 и на 5 и сумма цифр числа делится на 3, то и само число делится на 15.
Признак делимости на 25: если число оканчивается на 00,25,50,75, то и само число делится на 25 без остатка.
Признак делимости на 50: если число заканчивается на 00 или 50, то и само число делится на 50.
Из дополнительной литературы я нашла подтверждения правильности сформулированных мною признаков делимости натуральных чисел на 4,6,8,15,25,50.
Так же я нашла признаки делимости на 7,на 11,на 12,на 13. Все рассмотренные признаки я сформулировала в виде брошюры
Признак делимости на 7
Если последнюю цифру числа умножить на 2 и вычесть из числа, оставшегося без последней цифры и если получившееся число делится на 7, то и само число делится на 7. Число 1102283
1-й шаг: 110228-3*2 = 110222
2-й шаг: 11022-2*2 = 11018
3-й шаг: 1101-8*2 = 1085
4-й шаг: 108-5*2 = 98
5-й шаг: 9-8*2 = -7. Делится на 7
Значит, 1102283 делится на 7
Признак делимости на 11
Если сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо отличается от нее на число, делящееся на 11, то число делится на 11 без остатка.
Пример: 160369 (Сумма цифр, которые стоят на нечётных местах 1+0+6 = 7.
Сумма цифр, которые стоят на чётных местах 6+3+9 = 18.
18 — 7 = 11. Делится на 11. Значит, число 160369 делится на 11).
Признак делимости на 12.
Если две последние цифры числа делятся на 4 и сумма цифр его делится на 3,то всё число делится на 12, без остатка.
Пример:
78864 (Две последние цифры — 64. Число, составленное из них, делится на 4; сумма цифр равна 7+8+8+6+4 = 33-делится на 3.) Значит, всё число делится на 12.
Еще пример:
Число, составленное из них,делится на 4;
сумма цифр равна 7+6+8+1+2=24,
(данное число делится на 3).
Значит, всё число делится на 12.
Признак делимости на 13
Если взять последнюю цифру числа, умножить ее на 4 и прибавить к числу, оставшемуся без последней цифры, и если получившееся число делится на 13, то и само число делится на 13, без остатка.
Пример:
Число 595166.
1-й шаг. 59516 + 6*4 = 59540
2-й шаг. 5954 + 0*4 = 5954
3-й шаг. 595 + 4*4 = 611
4-й шаг. 61 + 1*4 = 65
5-й шаг. 6 + 5*4 = 26. Делится на 13.
Применение признаков делимости при решении задач.
Задача:
Ученики 5 класса купили 203 учебника. Сколько было пятиклассников и сколько учебников купил каждый из них.
Решение:
Обе величины , должны быть целыми числами.
Разложим 203 на простые множители: 203=1*7*29. Учебников не может быть 29, так же число
учебников не может равняться 1,т.к. В этом случае учеников было бы 203. Значит 5 –ов 29 и каждый из них купил по 7 учебников.
Спасибо за внимание.
Онлайн урок: Признаки делимости на 9 и на 3 по предмету Математика 6 класс
Пусть у нас есть 153 конфеты. Нужно раздать их троим детям поровну, используя только признак делимости.
Число 153 можно разложить на 1 сотню, 5 десятков и 3 единицы.
Разделим сначала нашу сотню конфет. Каждый ребенок получит по 33 конфеты, и в остатке одна.
Теперь разделим один десяток конфет на троих. Имеем по 3 конфеты у каждого, и одна в остатке. Значит, для наших пяти десятков каждому ребёнку по 15 (3•5) конфет, и в остатке 5 (1•5) конфет.
По аналогии поступим с количеством конфет в единицах — тут всем достанется 1 конфета.
Мы не смогли разделить 1 конфету из сотен, 5 конфет из десятков. То есть в сумме получим 1 + 5 = 6 конфет, которые можно разделить по 2 конфеты каждому.
В итоге каждому ребёнку получится по 33 + 15 + 1 + 2 = 51 конфете.
Значит, число 153 делится без остатка на 3, а 1 + 5 — это сумма цифр этого числа.
Мы на примере посмотрели, как используется признак делимости на 3.
Если сумма цифр числа делится на 3, то и число делится на 3.
Если сумма цифр числа не делится на 3, то и число не делится на 3.
Пример 1
Выберите среди чисел 75432, 2772825, 5402070 те, которые делятся на 3.
Решение:
По признаку делимости на 3 нужно найти сумму цифр каждого числа и дальше работать с нею.
Для первого: 7 + 5+ 4+ 3+ 2 = 21,а 21 : 3 = 7, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для второго: 2 + 7 + 7 + 2 + 8 + 2 + 5 = 33, а 33 : 3 = 11, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для третьего: 5 + 4 + 0 + 2 + 0 + 7 + 0 = 18, а 18 : 3 = 6, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Пример 2
Замените звёздочки в числах 2*5, 31*, *15, на необходимые цифры, чтобы эти числа стали делиться на 3.

Решение:
Возьмем первое число 2*5. Из признака делимости мы знаем, что нужно, чтобы сумма цифр числа делилась на 3. Значит, 2 + 5 + * должно делиться на 3.
Сумма известных цифр равна 8, значит, вместо звездочки можно взять, например, 1.
Тогда сумма станет 9, и она делится на 3, значит, и получившееся число 215 будет делиться на 3.
Кроме единицы подходят цифры: 4, 7, так как они отличаются от 1 на 3 и 6 каждая.
Возьмем второе число 31*. Сумма первых цифр равна 4, значит, вместо звездочки минимум надо брать 2, чтоб в сумме было 6.
Тогда сумма цифр будет делиться на 3 и само число, 312, будет делиться тоже.
Кроме двойки брать можно и другие цифры, прибавляя по 3: 5 или 8.
Получившиеся числа 315 или 318 будут делиться на 3.
Берём последнее число *15. Сумма последних двух цифр — 6, уже делится на 3. Значит нужно брать вместо первой цифры такие, которые делятся на 3. Это 3, 6 или 9.
Получившиеся числа 315, 615, 915 будут делиться на 3 без остатка.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьИз признака делимости на 3 можно получить интересный признак делимости на 6
Чтобы ваше число делилось на 6, нужно чтоб оно делилось на 2 и на 3 одновременно.
Пример
Делится ли 216 на 6?
Решение:
216— это чётное число, значит, оно делится на 2.
Сумма цифр числа 216 равна 2 + 1+ 6 = 9, значит, оно делится на 3.
Отсюда, делаем вывод, что 216 делится на 6.

1. Введение
Актуальность: В начале учебного года на уроках математики мы изучали тему: «Признаки делимости натуральных чисел на 2, 3, 5, 9, 10». При изучении этой темы у нас не возникло никаких проблем, выучили признаки, научились их применять при выполнении заданий. При разложении чисел на простые множители мне пришлось делить число на 7. А как узнать, деление получится с остатком или без остатка? Нет ли признаков делимости на 7? А на другие числа?
Так меня заинтересовал вопрос о делимости натуральных чисел на другие числа. Я решил написать исследовательскую работу по данной теме.
Гипотеза: Существуют признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Объект исследования: Делимость натуральных чисел.
Предмет исследования: Признаки делимости натуральных чисел.
Цель: Найти признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Задачи:
Повторить признаки делимости на 2, 3. 5, 9, 10, изученные мною в школе.
Исследовать самостоятельно признаки делимости натуральных чисел на 4, 8, 11, 13, 15, 17, 25, 50 и другие числа.
Изучить дополнительную литературу, подтверждающую правильность гипотезы о существовании других признаков делимости натуральных чисел и правильность выявленных мной признаков делимости.
Провести опрос учащихся 9 и 11 классов
Оформить материал
Представить результаты исследований. Составить буклет «Признаки делимости натуральных чисел».
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Методы исследования: Сбор материала, обработка данных, наблюдение, сравнение, анализ, обобщение, проведение опроса среди учащихся по данной теме.
2 Теоретическая часть
2.1. Признаки делимости натуральных чисел (школьный курс).
При изучении данной темы необходимо знать понятия делитель, кратное, простое и составное числа.
Делителем натурального числа а называют натуральное число b, на которое а делится без остатка.
Часто утверждение о делимости числа а на число b выражают другими равнозначными словами: а кратно b, b — делитель а, b делит а.
Простыми называются натуральные числа, которые имеют два делителя: 1 и само число. Например, числа 5,7,19 – простые, т.к. делятся на 1 и само себя.
Числа, которые имеют более двух делителей, называются составными. Например, число 14 имеет 4 делителя: 1, 2, 7, 14, значит оно составное.

2.2. Признаки делимости натуральных чисел на 4, 25, 50.
Выполняя действия деления, умножения натуральных чисел, наблюдая за результатами действий, я нашел закономерности и получил следующие признаки делимости.
Признак делимости на 4.
25·4=100; 56·4=224; 123·4=492; 125·4=500; 2345·4=9380; 2500·4=10000; …
Умножая натуральные числа на 4, я заметил, что числа образованные из двух последних цифр числа делятся на 4 без остатка.
Признак делимости на 4 читается так:
Натуральное число делится на 4 тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 25.
Выполняя умножение натуральных различных чисел на 25, я увидел такую закономерность: произведения оканчиваются на 00, 25, 50, 75.
Значит, натуральное число делится на 25, если оканчивается цифрами 00, 25, 50, 75.
Признак делимости на 50.
На 50 делятся числа: 50, 100, 150, 200, 250, 300,… Они оканчиваются либо на 50, либо на 00.
Значит, натуральное число делится на 50 тогда и только тогда, когда оканчивается двумя нулями или 50.
2.3. Признаки делимости натуральных чисел на 7, 11, 13, 17, 19.
Из дополнительной литературы я нашел подтверждение правильности сформулированных нами признаков делимости натуральных чисел на 4, 25, 50. Так же я нашел несколько признаков делимости на 7:
1. Натуральное число делится на 7 тогда и только тогда, когда разность числа тысяч и числа, выражаемого последними тремя цифрами, делится на 7.
Примеры:
478009 делится на 7, т.к. 478-9=469, 469 делится на 7.
479345 не делится на 7, т.к. 479-345=134, 134 не делится на 7.
2. Натуральное число делится на 7, если сумма удвоенного числа, стоящего до десятков и оставшегося числа делится на 7.
Примеры:
4592 делится на 7, т.к. 45·2=90, 90+92=182, 182 делится на 7.
57384 не делится на 7, т.к. 573·2=1146, 1146+84=1230, 1230 не делится на 7.
3. Трехзначное натуральное число вида аbа будет делиться на 7, если а+b делится на 7.
Примеры:
252 делится на 7, т.к. 2+5=7, 7/7.
636 не делится на 7, т.к. 6+3=9, 9 не делится на 7.
4. Трехзначное натуральное число вида bаа будет делиться на 7, если сумма цифр числа делится на 7.
Примеры:
455 делится на 7, т.к. 4+5+5=14, 14/7.
244 не делится на 7, т.к. 2+4+4=12, 12 не делится на 7.
5. Трехзначное натуральное число вида ааb будет делиться на 7, если 2а-b делится на 7.
Примеры:
882 делится на 7,т.к. 8+8-2=14, 14/7.
996 не делится на 7, т.к. 9+9-6=12, 12 не делится на 7.
6. Четырехзначное натуральное число вида bаа , где b-двухзначное число, будет делиться на 7, если b+2а делится на 7.
Примеры:
2744 делится на 7, т.к. 27+4+4=35, 35/7.
1955 не делится на 7, т.к. 19+5+5=29, 29 не делится на 7.
7. Натуральное число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
Примеры:
483 делится на 7, т.к. 48-3·2=42, 42/7.
564 не делится на 7, т.к. 56-4·2=48, 48 не делится на 7.
8. Натуральное число делится на 7 тогда и только тогда, когда сумма произведений цифр числа на соответствующие остатки получаемые при делении разрядных единиц на число 7, делится на 7.
Примеры:
10׃7=1 (ост 3)
100׃7=14 (ост 2)
1000׃7=142 (ост 6)
10000׃7=1428 (ост 4)
100000׃7=14285 (ост 5)
1000000׃7=142857 (ост 1) и снова повторяются остатки.
Число 1316 делится на 7, т.к. 1·6+3·2+1·3+6=21, 21/7(6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3- ост. от деления 10 на 7).
Число 354722 не делится на7,т.к. 3·5+5·4+4·6+7·2+2·3+2=81, 81 не делится на 7(5-ост. от деления 100 000 на 7; 4 -ост. от деления 10 000 на 7; 6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3-ост. от деления 10 на 7).
Признаки делимости на 11.
1. Число делится на 11, если разность суммы цифр стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, кратна 11.
Разность может быть отрицательным числом или 0, но обязательно должна быть кратной 11. Нумерация идет слева направо.
Пример:
2135704 2+3+7+4=16, 1+5+0=6, 16-6=10, 10 не кратно 11, значит, это число не делится на 11.
1352736 1+5+7+6=19, 3+2+3=8, 19-8=11, 11 кратно 11, значит, это число делится на 11.
2. Натуральное число разбивают справа налево на группы по 2 цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.
Пример: Определим, делится ли число 12561714 на 11.
Разобьем число на группы по две цифры в каждой: 12/56/17/14; 12+56+17+14=99, 99 делится на 11, значит, данное число делится на 11.
3. Трехзначное натуральное число делится на 11, если сумма боковых цифр числа равна цифре, которая в середине. Ответ будет состоять из тех самых боковых цифр.
Примеры:
594 делится на11, т.к. 5+4=9, 9-в середине.
473 делится на 11, т.к. 4+3=7, 7- в середине.
861 не делится на 11, т.к. 8+1=9, а в середине 6.
Признаки делимости на 13
1. Натуральное число делится на 13, если разность числа тысяч и числа, образованного последними тремя цифрами, делится на 13.
Примеры:
Число 465400 делится на 13, т.к. 465 – 400 = 65, 65 делится на 13.
Число 256184 не делится на 13, т.к. 256 – 184 = 72, 72 не делится на 13.
2. Натуральное число делится на 13 тогда и только тогда, когда результат вычитания последней цифры, умноженной на 9, из этого числа без последней цифры , делится на 13.
Примеры:
988 делится на 13, т.к. 98 — 9·8 = 26, 26 делится на 13.
853 не делится на 13, т.к. 85 — 3·9 = 58, 58 не делится на 13.
Признак делимости на 19
Натуральное число делится на 19 без остатка тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19.
Следует учесть, что число десятков в числе надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.
Примеры:
1534 десятков-153, 4·2=8, 153+8=161, 161 не делится на 19,значит, и 1534 не делится на 19.
1824 182+4·2=190, 190/19, значит, число 1824/19.
Все перечисленные признаки делимости натуральных чисел можно разделить на 4 группы:
1группа- когда делимость чисел определяется по последней(им) цифрой (ми) – это признаки делимости на 2, на 5,на разрядную единицу, на 4, на 8, на 25, на 50;
2 группа – когда делимость чисел определяется по сумме цифр числа – это признаки делимости на3, на 9, на 7(1 признак), на 11, на 37;
3 группа – когда делимость чисел определяется после выполнения каких-то действий над цифрами числа – это признаки делимости на 7, на 11, на 13, на 19;
4 группа – когда для определения делимости числа используются другие признаки делимости — это признаки делимости на 6, на12, на 14, на 15.
Практическая часть
3.1. Применение признаков делимости при решении задач
Рассмотрим применение признаков делимости натуральных чисел на примере
задачи 19 (по теме «Натуральные числа») — КИМ ЕГЭ 2017 года, базовый уровень.
Задача 3
Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Решение.
Раскладываем делитель — число 12 на простые множители. 12 = 3×4. Следователь- но, заданное число после вычеркивания чисел должно делиться на 3 и 4.
Признак делимости на 4: Натуральное число делится на 4 тогда и только тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 3: Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
Признак делимости на 4 утверждает, что на 4 должно делиться двузначное число, образованное последними двумя цифрами. Значит, 181615121 последнюю цифру 1 вычеркиваем сразу. 12:4 = 3, поэтому две последние цифры числа 18161512 вычеркивать нельзя. Они гарантируют делимость числа на 4.
Чтобы число делилось на 3, нужно чтобы на 3 делилась сумма его цифр.
1+8+1+6+1+5+1+2=25
25 = 3×8 + 1 — можно вычеркнуть одну из единиц, но по условию задачи нужно вычеркнуть еще две цифры;
25 = 3×7 + 4 — нет двух цифр для вычеркивания, сумма которых равнялась бы 4, т.к. последние цифры 1 и 2 трогать нельзя;
25 = 3×6 + 7 — сумма двух вычеркнутых цифр будет равна 7, если вычеркнуть 6-ку и любую из единиц, кроме последней.
Итак, возможные ответы: 811512, 181512 или 181152. Выбираем один из них, например Ответ:181512 Замечание: на реальном ЕГЭ нужно сделать проверку своего ответа делением в столбик.
Следующая задача из Открытого банка заданий Федеральнного института педагогических измерений.
Задача 4
Приведите пример пятизначного числа кратного 12, произведение цифр которого равно 40. В ответе укажите ровно одно такое число.
Решение.
Разложим число 40 на простые множители. 40 = 2×2×2×5.
Таких множителей всего четыре, цифр недостаточно для пятизначного числа, но в произведение всегда можно добавить единицу, результат от этого не изменится: 40 = 2×2×2×5×1.
Таким образом, число в ответе можно составить только из этих цифр: 1,2,2,2,5.
Чтобы число было кратным 12 (то же самое, что делилось на 12 без остатка) оно должно удовлетворять признакам делимости на 3 и на 4, так как 12 = 3×4.
Проверим сумму цифр 1+2+2+2+5 = 12. Она делится на 3, поэтому наше число будет делиться на 3 при любых перестановках цифр.
А чтобы оно делилось на 4, в конце нужно поставить две цифры так, чтобы образованное ими число делилось на 4.
Очевидно, что последней цифрой должна быть 2-ка, другие — нечетные. Проверим варианты 12, 22, 52.
12:4 = 3; 22:4 = 5,5 — не делится нацело; 52:4 = 13.
Вывод: число должно быть составлено так, чтобы в конце было 12 или 52, а в начале любые перестановки из оставшихся трёх цифр.
Возможные ответы: 12252, 21252, 22152, 22512, 25212, 52212. В ответ пишем один из них. Например,
Ответ: 21252 Таким образом, мы убедились в применении признаков делимости натуральных чисел при решении задач.
Рассмотрев задачи, мне стало интересно, а знают ли наши выпускники о признаках делимости. И я решил провести опрос.
3.2Анкетирование «Помогают Вам признаки делимости при делении?»
Анкетирование проводилось среди обучающихся 9 и 11-х классов. В опросе приняли участие 29 обучающихся МБОУ СОШ с Ургала. Им было предложено ответить на следующие вопросы:
Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?
Какие вы знаете признаки делимости натуральных чисел?
Помогают ли вам признаки делимости натуральных чисел при делении?
А хотели бы узнать еще о других признаках делимости натуральных чисел?
80% опрошенных считают, что современному человеку нужно уметь считать.
Большинство обучающихся знают признаки делимости, изученные в школе
на 2,3, 5, 10. – это 87%
88 % опрошенных считают, что признаки делимости помогают при делении.
По результатам проведенного анкетирования 76 % опрошенных хотели бы познакомиться с признаками делимости, не изученными в школе.
4. Заключение.
Работая с разными источниками, я убедился в том, что существуют другие признаки делимости натуральных чисел (на 7, 11, 13, 19), что подтвердило правильность гипотезы о существовании других признаков делимости натуральных чисел.
Решая задачи я убедился, что знание и использование выше перечисленных признаков делимости натуральных чисел значительно упрощает многие вычисления, экономит время; исключает вычислительные ошибки, которые можно сделать при выполнении действия деления. Следует отметить, что формулировки некоторых признаков сложны. Может быть, поэтому они не изучаются в школе.
Собранный мной материал я оформил в виде буклета, который можно использовать на уроках математики, на занятиях математического кружка. Учителя математики могут использовать его при изучении данной темы. Также рекомендую ознакомиться со своей работой старшеклассников, которые хотят получить высокие баллы на экзаменах по математике. Перед 11-классниками своей школы я выступил, рассказал о признаках делимости, показал решение задач и раздал им буклеты.
В дальнейшем планирую рассмотреть такие вопросы:
-историю возникновения признаков делимости;
— признак Паскаля.
5. СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ – РЕСУРСОВ
Перельман Я.И. Математика – это интересно ! – М.: ТЕРРА – Книжный клуб, 2006
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 6 класс : учеб. для общеобразоват. учреждений /— 25-е изд., стер. — М. : Мнемозина, 2009. — 288 с.
Internet
Секция: Математика
Номинация: Математика
Признаки делимости натуральных чисел
Автор Багаутдинов Данил Русланович МБОУ СОШ с Ургала, 6 класс,
Руководитель: Багаутдинова Люция Салимьяновна, учитель математики МБОУ СОШ с Ургала
Работа посвящена изучению признаков делимости натуральных чисел, которые не изучаются в школьном курсе математики. Знание этих признаков имеет большое значение при выполнении заданий КИМов ЕГЭ базового уровня.
Проект по математике «Признаки делимости натуральных чисел»
Актуальность.
При изучении на уроках математике темы: «Признаки делимости натуральных чисел» у меня возник интерес к исследованию чисел на делимость.
Не всегда одно натуральное число делится на другое натуральное число без остатка. Деля натуральное число мы получаем остаток, допускаем ошибки, тем самым теряем время. Возникает необходимость, не выполняя деления установить, делится ли одно натуральное число на другое.
Гипотеза
Если можно определить делимость натуральных чисел на 2,3,5,9,10 то должны быть признаки, по которым можно определить делимость натуральных чисел на другое число.
Объект исследования:
Делимость натуральных чисел
Предмет исследования:
Признаки делимости натуральных чисел
Цель:
Дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе.
Задачи исследования:
Повторить признаки делимости натуральных чисел, изучаемые в школе
Исследовать самостоятельно признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Изучить дополнительную литературу о других признаках делимости натуральных чисел.
Систематизировать и обобщать признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Рассмотреть применение признаков делимости натуральных чисел при решении задач.
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Немного из истории:
Признаки делимости на 2,3,5,9,10 были известны с давних времён. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до н.э.
Признаки делимости на 2,3 и 5 были изложены итальянским математиком Леонардо Фибоначчи (1170-1228)
Вопросы делимости чисел рассматривались пифагорейцами в теории чисел ими была проведена большая работа по типологии натуральных чисел. Пифагорейцы делили их на классы:
совершенных чисел (число, равное сумме своих делителей 6=1+2+3)
дружественных чисел ( каждое из ,которых равно сумме делителей другого , например: 220 и 284 (284= 1+2+4+5+10+20+11+22+44+55+110) и(220=1+2+4+71+142)
фигурных чисел
простых чисел и д.р
Признак Паскаля
Выдающийся французский математик и физик Блез Паскаль (1623-1662) еще в раннем возрасте вывел общий признак делимости чисел , из которого следует все частные признаки
Признак Паскаля: натуральное число А разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа А на соответствующие остатки , получаемые при деление разрядных единиц на число b делится на это число .
Признаки делимости натуральных чисел , полученных самостоятельно, изучая дополнительную литературу .
Выполняя действие деления, умножения натуральных чисел, наблюдая за результатами действий , я нашла закономерность и получила следующие признаки делимости:
Признак делимости на 4: если число, образованное двумя последними цифрами данного числа, делится на 4, то и само число делится на 4 без остатка.
Признак делимости на 8: если число, образованное тремя последними цифрами данного числа, делится на 8, то и само число делится на 8 без остатка.
Признак делимости на 6: если число делится и на 3 и на 2 , то и само число делится на 6 без остатка.
Признак делимости на 15: если число одновременно делится на 5 и на 3 и если оно заканчивает на 0 и на 5 и сумма цифр числа делится на 3, то и само число делится на 15.
Признак делимости на 25: если число оканчивается на 00,25,50,75, то и само число делится на 25 без остатка.
Признак делимости на 50: если число заканчивается на 00 или 50, то и само число делится на 50.
Из дополнительной литературы я нашла подтверждения правильности сформулированных мною признаков делимости натуральных чисел на 4,6,8,15,25,50.
Так же я нашла признаки делимости на 7,на 11,на 12,на 13. Все рассмотренные признаки я сформулировала в виде брошюры
Признак делимости на 7
Если последнюю цифру числа умножить на 2 и вычесть из числа, оставшегося без последней цифры и если получившееся число делится на 7, то и само число делится на 7. Число 1102283
1-й шаг: 110228-3*2 = 110222
2-й шаг: 11022-2*2 = 11018
3-й шаг: 1101-8*2 = 1085
4-й шаг: 108-5*2 = 98
5-й шаг: 9-8*2 = -7. Делится на 7
Значит, 1102283 делится на 7
Признак делимости на 11
Если сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо отличается от нее на число, делящееся на 11, то число делится на 11 без остатка.
Пример: 160369 (Сумма цифр, которые стоят на нечётных местах 1+0+6 = 7.
Сумма цифр, которые стоят на чётных местах 6+3+9 = 18.
18 — 7 = 11. Делится на 11. Значит, число 160369 делится на 11).
Признак делимости на 12.
Если две последние цифры числа делятся на 4 и сумма цифр его делится на 3,то всё число делится на 12, без остатка.
Пример:
78864 (Две последние цифры — 64. Число, составленное из них, делится на 4; сумма цифр равна 7+8+8+6+4 = 33-делится на 3.) Значит, всё число делится на 12.
Еще пример:
Число, составленное из них,делится на 4;
сумма цифр равна 7+6+8+1+2=24,
(данное число делится на 3).
Значит, всё число делится на 12.
Признак делимости на 13
Если взять последнюю цифру числа, умножить ее на 4 и прибавить к числу, оставшемуся без последней цифры, и если получившееся число делится на 13, то и само число делится на 13, без остатка.
Пример:
Число 595166.
1-й шаг. 59516 + 6*4 = 59540
2-й шаг. 5954 + 0*4 = 5954
3-й шаг. 595 + 4*4 = 611
4-й шаг. 61 + 1*4 = 65
5-й шаг. 6 + 5*4 = 26. Делится на 13.
Применение признаков делимости при решении задач.
Задача:
Ученики 5 класса купили 203 учебника. Сколько было пятиклассников и сколько учебников купил каждый из них.
Решение:
Обе величины , должны быть целыми числами.
Разложим 203 на простые множители: 203=1*7*29. Учебников не может быть 29, так же число
учебников не может равняться 1,т.к. В этом случае учеников было бы 203. Значит 5 –ов 29 и каждый из них купил по 7 учебников.
Спасибо за внимание.
Онлайн урок: Признаки делимости на 9 и на 3 по предмету Математика 6 класс
Пусть у нас есть 153 конфеты. Нужно раздать их троим детям поровну, используя только признак делимости.
Число 153 можно разложить на 1 сотню, 5 десятков и 3 единицы.
Разделим сначала нашу сотню конфет. Каждый ребенок получит по 33 конфеты, и в остатке одна.
Теперь разделим один десяток конфет на троих. Имеем по 3 конфеты у каждого, и одна в остатке. Значит, для наших пяти десятков каждому ребёнку по 15 (3•5) конфет, и в остатке 5 (1•5) конфет.
По аналогии поступим с количеством конфет в единицах — тут всем достанется 1 конфета.
Мы не смогли разделить 1 конфету из сотен, 5 конфет из десятков. То есть в сумме получим 1 + 5 = 6 конфет, которые можно разделить по 2 конфеты каждому.
В итоге каждому ребёнку получится по 33 + 15 + 1 + 2 = 51 конфете.
Значит, число 153 делится без остатка на 3, а 1 + 5 — это сумма цифр этого числа.
Мы на примере посмотрели, как используется признак делимости на 3.
Если сумма цифр числа делится на 3, то и число делится на 3.
Если сумма цифр числа не делится на 3, то и число не делится на 3.
Пример 1
Выберите среди чисел 75432, 2772825, 5402070 те, которые делятся на 3.
Решение:
По признаку делимости на 3 нужно найти сумму цифр каждого числа и дальше работать с нею.
Для первого: 7 + 5+ 4+ 3+ 2 = 21,а 21 : 3 = 7, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для второго: 2 + 7 + 7 + 2 + 8 + 2 + 5 = 33, а 33 : 3 = 11, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для третьего: 5 + 4 + 0 + 2 + 0 + 7 + 0 = 18, а 18 : 3 = 6, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Пример 2
Замените звёздочки в числах 2*5, 31*, *15, на необходимые цифры, чтобы эти числа стали делиться на 3.

Решение:
Возьмем первое число 2*5. Из признака делимости мы знаем, что нужно, чтобы сумма цифр числа делилась на 3. Значит, 2 + 5 + * должно делиться на 3.
Сумма известных цифр равна 8, значит, вместо звездочки можно взять, например, 1.
Тогда сумма станет 9, и она делится на 3, значит, и получившееся число 215 будет делиться на 3.
Кроме единицы подходят цифры: 4, 7, так как они отличаются от 1 на 3 и 6 каждая.
Возьмем второе число 31*. Сумма первых цифр равна 4, значит, вместо звездочки минимум надо брать 2, чтоб в сумме было 6.
Тогда сумма цифр будет делиться на 3 и само число, 312, будет делиться тоже.
Кроме двойки брать можно и другие цифры, прибавляя по 3: 5 или 8.
Получившиеся числа 315 или 318 будут делиться на 3.
Берём последнее число *15. Сумма последних двух цифр — 6, уже делится на 3. Значит нужно брать вместо первой цифры такие, которые делятся на 3. Это 3, 6 или 9.
Получившиеся числа 315, 615, 915 будут делиться на 3 без остатка.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьИз признака делимости на 3 можно получить интересный признак делимости на 6
Чтобы ваше число делилось на 6, нужно чтоб оно делилось на 2 и на 3 одновременно.
Пример
Делится ли 216 на 6?
Решение:
216— это чётное число, значит, оно делится на 2.
Сумма цифр числа 216 равна 2 + 1+ 6 = 9, значит, оно делится на 3.
Отсюда, делаем вывод, что 216 делится на 6.

1. Введение
Актуальность: В начале учебного года на уроках математики мы изучали тему: «Признаки делимости натуральных чисел на 2, 3, 5, 9, 10». При изучении этой темы у нас не возникло никаких проблем, выучили признаки, научились их применять при выполнении заданий. При разложении чисел на простые множители мне пришлось делить число на 7. А как узнать, деление получится с остатком или без остатка? Нет ли признаков делимости на 7? А на другие числа?
Так меня заинтересовал вопрос о делимости натуральных чисел на другие числа. Я решил написать исследовательскую работу по данной теме.
Гипотеза: Существуют признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Объект исследования: Делимость натуральных чисел.
Предмет исследования: Признаки делимости натуральных чисел.
Цель: Найти признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Задачи:
Повторить признаки делимости на 2, 3. 5, 9, 10, изученные мною в школе.
Исследовать самостоятельно признаки делимости натуральных чисел на 4, 8, 11, 13, 15, 17, 25, 50 и другие числа.
Изучить дополнительную литературу, подтверждающую правильность гипотезы о существовании других признаков делимости натуральных чисел и правильность выявленных мной признаков делимости.
Провести опрос учащихся 9 и 11 классов
Оформить материал
Представить результаты исследований. Составить буклет «Признаки делимости натуральных чисел».
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Методы исследования: Сбор материала, обработка данных, наблюдение, сравнение, анализ, обобщение, проведение опроса среди учащихся по данной теме.
2 Теоретическая часть
2.1. Признаки делимости натуральных чисел (школьный курс).
При изучении данной темы необходимо знать понятия делитель, кратное, простое и составное числа.
Делителем натурального числа а называют натуральное число b, на которое а делится без остатка.
Часто утверждение о делимости числа а на число b выражают другими равнозначными словами: а кратно b, b — делитель а, b делит а.
Простыми называются натуральные числа, которые имеют два делителя: 1 и само число. Например, числа 5,7,19 – простые, т.к. делятся на 1 и само себя.
Числа, которые имеют более двух делителей, называются составными. Например, число 14 имеет 4 делителя: 1, 2, 7, 14, значит оно составное.

2.2. Признаки делимости натуральных чисел на 4, 25, 50.
Выполняя действия деления, умножения натуральных чисел, наблюдая за результатами действий, я нашел закономерности и получил следующие признаки делимости.
Признак делимости на 4.
25·4=100; 56·4=224; 123·4=492; 125·4=500; 2345·4=9380; 2500·4=10000; …
Умножая натуральные числа на 4, я заметил, что числа образованные из двух последних цифр числа делятся на 4 без остатка.
Признак делимости на 4 читается так:
Натуральное число делится на 4 тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 25.
Выполняя умножение натуральных различных чисел на 25, я увидел такую закономерность: произведения оканчиваются на 00, 25, 50, 75.
Значит, натуральное число делится на 25, если оканчивается цифрами 00, 25, 50, 75.
Признак делимости на 50.
На 50 делятся числа: 50, 100, 150, 200, 250, 300,… Они оканчиваются либо на 50, либо на 00.
Значит, натуральное число делится на 50 тогда и только тогда, когда оканчивается двумя нулями или 50.
2.3. Признаки делимости натуральных чисел на 7, 11, 13, 17, 19.
Из дополнительной литературы я нашел подтверждение правильности сформулированных нами признаков делимости натуральных чисел на 4, 25, 50. Так же я нашел несколько признаков делимости на 7:
1. Натуральное число делится на 7 тогда и только тогда, когда разность числа тысяч и числа, выражаемого последними тремя цифрами, делится на 7.
Примеры:
478009 делится на 7, т.к. 478-9=469, 469 делится на 7.
479345 не делится на 7, т.к. 479-345=134, 134 не делится на 7.
2. Натуральное число делится на 7, если сумма удвоенного числа, стоящего до десятков и оставшегося числа делится на 7.
Примеры:
4592 делится на 7, т.к. 45·2=90, 90+92=182, 182 делится на 7.
57384 не делится на 7, т.к. 573·2=1146, 1146+84=1230, 1230 не делится на 7.
3. Трехзначное натуральное число вида аbа будет делиться на 7, если а+b делится на 7.
Примеры:
252 делится на 7, т.к. 2+5=7, 7/7.
636 не делится на 7, т.к. 6+3=9, 9 не делится на 7.
4. Трехзначное натуральное число вида bаа будет делиться на 7, если сумма цифр числа делится на 7.
Примеры:
455 делится на 7, т.к. 4+5+5=14, 14/7.
244 не делится на 7, т.к. 2+4+4=12, 12 не делится на 7.
5. Трехзначное натуральное число вида ааb будет делиться на 7, если 2а-b делится на 7.
Примеры:
882 делится на 7,т.к. 8+8-2=14, 14/7.
996 не делится на 7, т.к. 9+9-6=12, 12 не делится на 7.
6. Четырехзначное натуральное число вида bаа , где b-двухзначное число, будет делиться на 7, если b+2а делится на 7.
Примеры:
2744 делится на 7, т.к. 27+4+4=35, 35/7.
1955 не делится на 7, т.к. 19+5+5=29, 29 не делится на 7.
7. Натуральное число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
Примеры:
483 делится на 7, т.к. 48-3·2=42, 42/7.
564 не делится на 7, т.к. 56-4·2=48, 48 не делится на 7.
8. Натуральное число делится на 7 тогда и только тогда, когда сумма произведений цифр числа на соответствующие остатки получаемые при делении разрядных единиц на число 7, делится на 7.
Примеры:
10׃7=1 (ост 3)
100׃7=14 (ост 2)
1000׃7=142 (ост 6)
10000׃7=1428 (ост 4)
100000׃7=14285 (ост 5)
1000000׃7=142857 (ост 1) и снова повторяются остатки.
Число 1316 делится на 7, т.к. 1·6+3·2+1·3+6=21, 21/7(6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3- ост. от деления 10 на 7).
Число 354722 не делится на7,т.к. 3·5+5·4+4·6+7·2+2·3+2=81, 81 не делится на 7(5-ост. от деления 100 000 на 7; 4 -ост. от деления 10 000 на 7; 6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3-ост. от деления 10 на 7).
Признаки делимости на 11.
1. Число делится на 11, если разность суммы цифр стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, кратна 11.
Разность может быть отрицательным числом или 0, но обязательно должна быть кратной 11. Нумерация идет слева направо.
Пример:
2135704 2+3+7+4=16, 1+5+0=6, 16-6=10, 10 не кратно 11, значит, это число не делится на 11.
1352736 1+5+7+6=19, 3+2+3=8, 19-8=11, 11 кратно 11, значит, это число делится на 11.
2. Натуральное число разбивают справа налево на группы по 2 цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.
Пример: Определим, делится ли число 12561714 на 11.
Разобьем число на группы по две цифры в каждой: 12/56/17/14; 12+56+17+14=99, 99 делится на 11, значит, данное число делится на 11.
3. Трехзначное натуральное число делится на 11, если сумма боковых цифр числа равна цифре, которая в середине. Ответ будет состоять из тех самых боковых цифр.
Примеры:
594 делится на11, т.к. 5+4=9, 9-в середине.
473 делится на 11, т.к. 4+3=7, 7- в середине.
861 не делится на 11, т.к. 8+1=9, а в середине 6.
Признаки делимости на 13
1. Натуральное число делится на 13, если разность числа тысяч и числа, образованного последними тремя цифрами, делится на 13.
Примеры:
Число 465400 делится на 13, т.к. 465 – 400 = 65, 65 делится на 13.
Число 256184 не делится на 13, т.к. 256 – 184 = 72, 72 не делится на 13.
2. Натуральное число делится на 13 тогда и только тогда, когда результат вычитания последней цифры, умноженной на 9, из этого числа без последней цифры , делится на 13.
Примеры:
988 делится на 13, т.к. 98 — 9·8 = 26, 26 делится на 13.
853 не делится на 13, т.к. 85 — 3·9 = 58, 58 не делится на 13.
Признак делимости на 19
Натуральное число делится на 19 без остатка тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19.
Следует учесть, что число десятков в числе надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.
Примеры:
1534 десятков-153, 4·2=8, 153+8=161, 161 не делится на 19,значит, и 1534 не делится на 19.
1824 182+4·2=190, 190/19, значит, число 1824/19.
Все перечисленные признаки делимости натуральных чисел можно разделить на 4 группы:
1группа- когда делимость чисел определяется по последней(им) цифрой (ми) – это признаки делимости на 2, на 5,на разрядную единицу, на 4, на 8, на 25, на 50;
2 группа – когда делимость чисел определяется по сумме цифр числа – это признаки делимости на3, на 9, на 7(1 признак), на 11, на 37;
3 группа – когда делимость чисел определяется после выполнения каких-то действий над цифрами числа – это признаки делимости на 7, на 11, на 13, на 19;
4 группа – когда для определения делимости числа используются другие признаки делимости — это признаки делимости на 6, на12, на 14, на 15.
Практическая часть
3.1. Применение признаков делимости при решении задач
Рассмотрим применение признаков делимости натуральных чисел на примере
задачи 19 (по теме «Натуральные числа») — КИМ ЕГЭ 2017 года, базовый уровень.
Задача 3
Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Решение.
Раскладываем делитель — число 12 на простые множители. 12 = 3×4. Следователь- но, заданное число после вычеркивания чисел должно делиться на 3 и 4.
Признак делимости на 4: Натуральное число делится на 4 тогда и только тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 3: Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
Признак делимости на 4 утверждает, что на 4 должно делиться двузначное число, образованное последними двумя цифрами. Значит, 181615121 последнюю цифру 1 вычеркиваем сразу. 12:4 = 3, поэтому две последние цифры числа 18161512 вычеркивать нельзя. Они гарантируют делимость числа на 4.
Чтобы число делилось на 3, нужно чтобы на 3 делилась сумма его цифр.
1+8+1+6+1+5+1+2=25
25 = 3×8 + 1 — можно вычеркнуть одну из единиц, но по условию задачи нужно вычеркнуть еще две цифры;
25 = 3×7 + 4 — нет двух цифр для вычеркивания, сумма которых равнялась бы 4, т.к. последние цифры 1 и 2 трогать нельзя;
25 = 3×6 + 7 — сумма двух вычеркнутых цифр будет равна 7, если вычеркнуть 6-ку и любую из единиц, кроме последней.
Итак, возможные ответы: 811512, 181512 или 181152. Выбираем один из них, например Ответ:181512 Замечание: на реальном ЕГЭ нужно сделать проверку своего ответа делением в столбик.
Следующая задача из Открытого банка заданий Федеральнного института педагогических измерений.
Задача 4
Приведите пример пятизначного числа кратного 12, произведение цифр которого равно 40. В ответе укажите ровно одно такое число.
Решение.
Разложим число 40 на простые множители. 40 = 2×2×2×5.
Таких множителей всего четыре, цифр недостаточно для пятизначного числа, но в произведение всегда можно добавить единицу, результат от этого не изменится: 40 = 2×2×2×5×1.
Таким образом, число в ответе можно составить только из этих цифр: 1,2,2,2,5.
Чтобы число было кратным 12 (то же самое, что делилось на 12 без остатка) оно должно удовлетворять признакам делимости на 3 и на 4, так как 12 = 3×4.
Проверим сумму цифр 1+2+2+2+5 = 12. Она делится на 3, поэтому наше число будет делиться на 3 при любых перестановках цифр.
А чтобы оно делилось на 4, в конце нужно поставить две цифры так, чтобы образованное ими число делилось на 4.
Очевидно, что последней цифрой должна быть 2-ка, другие — нечетные. Проверим варианты 12, 22, 52.
12:4 = 3; 22:4 = 5,5 — не делится нацело; 52:4 = 13.
Вывод: число должно быть составлено так, чтобы в конце было 12 или 52, а в начале любые перестановки из оставшихся трёх цифр.
Возможные ответы: 12252, 21252, 22152, 22512, 25212, 52212. В ответ пишем один из них. Например,
Ответ: 21252 Таким образом, мы убедились в применении признаков делимости натуральных чисел при решении задач.
Рассмотрев задачи, мне стало интересно, а знают ли наши выпускники о признаках делимости. И я решил провести опрос.
3.2Анкетирование «Помогают Вам признаки делимости при делении?»
Анкетирование проводилось среди обучающихся 9 и 11-х классов. В опросе приняли участие 29 обучающихся МБОУ СОШ с Ургала. Им было предложено ответить на следующие вопросы:
Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?
Какие вы знаете признаки делимости натуральных чисел?
Помогают ли вам признаки делимости натуральных чисел при делении?
А хотели бы узнать еще о других признаках делимости натуральных чисел?
80% опрошенных считают, что современному человеку нужно уметь считать.
Большинство обучающихся знают признаки делимости, изученные в школе
на 2,3, 5, 10. – это 87%
88 % опрошенных считают, что признаки делимости помогают при делении.
По результатам проведенного анкетирования 76 % опрошенных хотели бы познакомиться с признаками делимости, не изученными в школе.
4. Заключение.
Работая с разными источниками, я убедился в том, что существуют другие признаки делимости натуральных чисел (на 7, 11, 13, 19), что подтвердило правильность гипотезы о существовании других признаков делимости натуральных чисел.
Решая задачи я убедился, что знание и использование выше перечисленных признаков делимости натуральных чисел значительно упрощает многие вычисления, экономит время; исключает вычислительные ошибки, которые можно сделать при выполнении действия деления. Следует отметить, что формулировки некоторых признаков сложны. Может быть, поэтому они не изучаются в школе.
Собранный мной материал я оформил в виде буклета, который можно использовать на уроках математики, на занятиях математического кружка. Учителя математики могут использовать его при изучении данной темы. Также рекомендую ознакомиться со своей работой старшеклассников, которые хотят получить высокие баллы на экзаменах по математике. Перед 11-классниками своей школы я выступил, рассказал о признаках делимости, показал решение задач и раздал им буклеты.
В дальнейшем планирую рассмотреть такие вопросы:
-историю возникновения признаков делимости;
— признак Паскаля.
5. СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ – РЕСУРСОВ
Перельман Я.И. Математика – это интересно ! – М.: ТЕРРА – Книжный клуб, 2006
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 6 класс : учеб. для общеобразоват. учреждений /— 25-е изд., стер. — М. : Мнемозина, 2009. — 288 с.
Internet
Секция: Математика
Номинация: Математика
Признаки делимости натуральных чисел
Автор Багаутдинов Данил Русланович МБОУ СОШ с Ургала, 6 класс,
Руководитель: Багаутдинова Люция Салимьяновна, учитель математики МБОУ СОШ с Ургала
Работа посвящена изучению признаков делимости натуральных чисел, которые не изучаются в школьном курсе математики. Знание этих признаков имеет большое значение при выполнении заданий КИМов ЕГЭ базового уровня.
Проект по математике «Признаки делимости натуральных чисел»
Актуальность.
При изучении на уроках математике темы: «Признаки делимости натуральных чисел» у меня возник интерес к исследованию чисел на делимость.
Не всегда одно натуральное число делится на другое натуральное число без остатка. Деля натуральное число мы получаем остаток, допускаем ошибки, тем самым теряем время. Возникает необходимость, не выполняя деления установить, делится ли одно натуральное число на другое.
Гипотеза
Если можно определить делимость натуральных чисел на 2,3,5,9,10 то должны быть признаки, по которым можно определить делимость натуральных чисел на другое число.
Объект исследования:
Делимость натуральных чисел
Предмет исследования:
Признаки делимости натуральных чисел
Цель:
Дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе.
Задачи исследования:
Повторить признаки делимости натуральных чисел, изучаемые в школе
Исследовать самостоятельно признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Изучить дополнительную литературу о других признаках делимости натуральных чисел.
Систематизировать и обобщать признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Рассмотреть применение признаков делимости натуральных чисел при решении задач.
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Немного из истории:
Признаки делимости на 2,3,5,9,10 были известны с давних времён. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до н.э.
Признаки делимости на 2,3 и 5 были изложены итальянским математиком Леонардо Фибоначчи (1170-1228)
Вопросы делимости чисел рассматривались пифагорейцами в теории чисел ими была проведена большая работа по типологии натуральных чисел. Пифагорейцы делили их на классы:
совершенных чисел (число, равное сумме своих делителей 6=1+2+3)
дружественных чисел ( каждое из ,которых равно сумме делителей другого , например: 220 и 284 (284= 1+2+4+5+10+20+11+22+44+55+110) и(220=1+2+4+71+142)
фигурных чисел
простых чисел и д.р
Признак Паскаля
Выдающийся французский математик и физик Блез Паскаль (1623-1662) еще в раннем возрасте вывел общий признак делимости чисел , из которого следует все частные признаки
Признак Паскаля: натуральное число А разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа А на соответствующие остатки , получаемые при деление разрядных единиц на число b делится на это число .
Признаки делимости натуральных чисел , полученных самостоятельно, изучая дополнительную литературу .
Выполняя действие деления, умножения натуральных чисел, наблюдая за результатами действий , я нашла закономерность и получила следующие признаки делимости:
Признак делимости на 4: если число, образованное двумя последними цифрами данного числа, делится на 4, то и само число делится на 4 без остатка.
Признак делимости на 8: если число, образованное тремя последними цифрами данного числа, делится на 8, то и само число делится на 8 без остатка.
Признак делимости на 6: если число делится и на 3 и на 2 , то и само число делится на 6 без остатка.
Признак делимости на 15: если число одновременно делится на 5 и на 3 и если оно заканчивает на 0 и на 5 и сумма цифр числа делится на 3, то и само число делится на 15.
Признак делимости на 25: если число оканчивается на 00,25,50,75, то и само число делится на 25 без остатка.
Признак делимости на 50: если число заканчивается на 00 или 50, то и само число делится на 50.
Из дополнительной литературы я нашла подтверждения правильности сформулированных мною признаков делимости натуральных чисел на 4,6,8,15,25,50.
Так же я нашла признаки делимости на 7,на 11,на 12,на 13. Все рассмотренные признаки я сформулировала в виде брошюры
Признак делимости на 7
Если последнюю цифру числа умножить на 2 и вычесть из числа, оставшегося без последней цифры и если получившееся число делится на 7, то и само число делится на 7. Число 1102283
1-й шаг: 110228-3*2 = 110222
2-й шаг: 11022-2*2 = 11018
3-й шаг: 1101-8*2 = 1085
4-й шаг: 108-5*2 = 98
5-й шаг: 9-8*2 = -7. Делится на 7
Значит, 1102283 делится на 7
Признак делимости на 11
Если сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо отличается от нее на число, делящееся на 11, то число делится на 11 без остатка.
Пример: 160369 (Сумма цифр, которые стоят на нечётных местах 1+0+6 = 7.
Сумма цифр, которые стоят на чётных местах 6+3+9 = 18.
18 — 7 = 11. Делится на 11. Значит, число 160369 делится на 11).
Признак делимости на 12.
Если две последние цифры числа делятся на 4 и сумма цифр его делится на 3,то всё число делится на 12, без остатка.
Пример:
78864 (Две последние цифры — 64. Число, составленное из них, делится на 4; сумма цифр равна 7+8+8+6+4 = 33-делится на 3.) Значит, всё число делится на 12.
Еще пример:
Число, составленное из них,делится на 4;
сумма цифр равна 7+6+8+1+2=24,
(данное число делится на 3).
Значит, всё число делится на 12.
Признак делимости на 13
Если взять последнюю цифру числа, умножить ее на 4 и прибавить к числу, оставшемуся без последней цифры, и если получившееся число делится на 13, то и само число делится на 13, без остатка.
Пример:
Число 595166.
1-й шаг. 59516 + 6*4 = 59540
2-й шаг. 5954 + 0*4 = 5954
3-й шаг. 595 + 4*4 = 611
4-й шаг. 61 + 1*4 = 65
5-й шаг. 6 + 5*4 = 26. Делится на 13.
Применение признаков делимости при решении задач.
Задача:
Ученики 5 класса купили 203 учебника. Сколько было пятиклассников и сколько учебников купил каждый из них.
Решение:
Обе величины , должны быть целыми числами.
Разложим 203 на простые множители: 203=1*7*29. Учебников не может быть 29, так же число
учебников не может равняться 1,т.к. В этом случае учеников было бы 203. Значит 5 –ов 29 и каждый из них купил по 7 учебников.
Спасибо за внимание.
Онлайн урок: Признаки делимости на 9 и на 3 по предмету Математика 6 класс
Пусть у нас есть 153 конфеты. Нужно раздать их троим детям поровну, используя только признак делимости.
Число 153 можно разложить на 1 сотню, 5 десятков и 3 единицы.
Разделим сначала нашу сотню конфет. Каждый ребенок получит по 33 конфеты, и в остатке одна.
Теперь разделим один десяток конфет на троих. Имеем по 3 конфеты у каждого, и одна в остатке. Значит, для наших пяти десятков каждому ребёнку по 15 (3•5) конфет, и в остатке 5 (1•5) конфет.
По аналогии поступим с количеством конфет в единицах — тут всем достанется 1 конфета.
Мы не смогли разделить 1 конфету из сотен, 5 конфет из десятков. То есть в сумме получим 1 + 5 = 6 конфет, которые можно разделить по 2 конфеты каждому.
В итоге каждому ребёнку получится по 33 + 15 + 1 + 2 = 51 конфете.
Значит, число 153 делится без остатка на 3, а 1 + 5 — это сумма цифр этого числа.
Мы на примере посмотрели, как используется признак делимости на 3.
Если сумма цифр числа делится на 3, то и число делится на 3.
Если сумма цифр числа не делится на 3, то и число не делится на 3.
Пример 1
Выберите среди чисел 75432, 2772825, 5402070 те, которые делятся на 3.
Решение:
По признаку делимости на 3 нужно найти сумму цифр каждого числа и дальше работать с нею.
Для первого: 7 + 5+ 4+ 3+ 2 = 21,а 21 : 3 = 7, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для второго: 2 + 7 + 7 + 2 + 8 + 2 + 5 = 33, а 33 : 3 = 11, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для третьего: 5 + 4 + 0 + 2 + 0 + 7 + 0 = 18, а 18 : 3 = 6, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Пример 2
Замените звёздочки в числах 2*5, 31*, *15, на необходимые цифры, чтобы эти числа стали делиться на 3.

Решение:
Возьмем первое число 2*5. Из признака делимости мы знаем, что нужно, чтобы сумма цифр числа делилась на 3. Значит, 2 + 5 + * должно делиться на 3.
Сумма известных цифр равна 8, значит, вместо звездочки можно взять, например, 1.
Тогда сумма станет 9, и она делится на 3, значит, и получившееся число 215 будет делиться на 3.
Кроме единицы подходят цифры: 4, 7, так как они отличаются от 1 на 3 и 6 каждая.
Возьмем второе число 31*. Сумма первых цифр равна 4, значит, вместо звездочки минимум надо брать 2, чтоб в сумме было 6.
Тогда сумма цифр будет делиться на 3 и само число, 312, будет делиться тоже.
Кроме двойки брать можно и другие цифры, прибавляя по 3: 5 или 8.
Получившиеся числа 315 или 318 будут делиться на 3.
Берём последнее число *15. Сумма последних двух цифр — 6, уже делится на 3. Значит нужно брать вместо первой цифры такие, которые делятся на 3. Это 3, 6 или 9.
Получившиеся числа 315, 615, 915 будут делиться на 3 без остатка.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьИз признака делимости на 3 можно получить интересный признак делимости на 6
Чтобы ваше число делилось на 6, нужно чтоб оно делилось на 2 и на 3 одновременно.
Пример
Делится ли 216 на 6?
Решение:
216— это чётное число, значит, оно делится на 2.
Сумма цифр числа 216 равна 2 + 1+ 6 = 9, значит, оно делится на 3.
Отсюда, делаем вывод, что 216 делится на 6.

1. Введение
Актуальность: В начале учебного года на уроках математики мы изучали тему: «Признаки делимости натуральных чисел на 2, 3, 5, 9, 10». При изучении этой темы у нас не возникло никаких проблем, выучили признаки, научились их применять при выполнении заданий. При разложении чисел на простые множители мне пришлось делить число на 7. А как узнать, деление получится с остатком или без остатка? Нет ли признаков делимости на 7? А на другие числа?
Так меня заинтересовал вопрос о делимости натуральных чисел на другие числа. Я решил написать исследовательскую работу по данной теме.
Гипотеза: Существуют признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Объект исследования: Делимость натуральных чисел.
Предмет исследования: Признаки делимости натуральных чисел.
Цель: Найти признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Задачи:
Повторить признаки делимости на 2, 3. 5, 9, 10, изученные мною в школе.
Исследовать самостоятельно признаки делимости натуральных чисел на 4, 8, 11, 13, 15, 17, 25, 50 и другие числа.
Изучить дополнительную литературу, подтверждающую правильность гипотезы о существовании других признаков делимости натуральных чисел и правильность выявленных мной признаков делимости.
Провести опрос учащихся 9 и 11 классов
Оформить материал
Представить результаты исследований. Составить буклет «Признаки делимости натуральных чисел».
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Методы исследования: Сбор материала, обработка данных, наблюдение, сравнение, анализ, обобщение, проведение опроса среди учащихся по данной теме.
2 Теоретическая часть
2.1. Признаки делимости натуральных чисел (школьный курс).
При изучении данной темы необходимо знать понятия делитель, кратное, простое и составное числа.
Делителем натурального числа а называют натуральное число b, на которое а делится без остатка.
Часто утверждение о делимости числа а на число b выражают другими равнозначными словами: а кратно b, b — делитель а, b делит а.
Простыми называются натуральные числа, которые имеют два делителя: 1 и само число. Например, числа 5,7,19 – простые, т.к. делятся на 1 и само себя.
Числа, которые имеют более двух делителей, называются составными. Например, число 14 имеет 4 делителя: 1, 2, 7, 14, значит оно составное.

2.2. Признаки делимости натуральных чисел на 4, 25, 50.
Выполняя действия деления, умножения натуральных чисел, наблюдая за результатами действий, я нашел закономерности и получил следующие признаки делимости.
Признак делимости на 4.
25·4=100; 56·4=224; 123·4=492; 125·4=500; 2345·4=9380; 2500·4=10000; …
Умножая натуральные числа на 4, я заметил, что числа образованные из двух последних цифр числа делятся на 4 без остатка.
Признак делимости на 4 читается так:
Натуральное число делится на 4 тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 25.
Выполняя умножение натуральных различных чисел на 25, я увидел такую закономерность: произведения оканчиваются на 00, 25, 50, 75.
Значит, натуральное число делится на 25, если оканчивается цифрами 00, 25, 50, 75.
Признак делимости на 50.
На 50 делятся числа: 50, 100, 150, 200, 250, 300,… Они оканчиваются либо на 50, либо на 00.
Значит, натуральное число делится на 50 тогда и только тогда, когда оканчивается двумя нулями или 50.
2.3. Признаки делимости натуральных чисел на 7, 11, 13, 17, 19.
Из дополнительной литературы я нашел подтверждение правильности сформулированных нами признаков делимости натуральных чисел на 4, 25, 50. Так же я нашел несколько признаков делимости на 7:
1. Натуральное число делится на 7 тогда и только тогда, когда разность числа тысяч и числа, выражаемого последними тремя цифрами, делится на 7.
Примеры:
478009 делится на 7, т.к. 478-9=469, 469 делится на 7.
479345 не делится на 7, т.к. 479-345=134, 134 не делится на 7.
2. Натуральное число делится на 7, если сумма удвоенного числа, стоящего до десятков и оставшегося числа делится на 7.
Примеры:
4592 делится на 7, т.к. 45·2=90, 90+92=182, 182 делится на 7.
57384 не делится на 7, т.к. 573·2=1146, 1146+84=1230, 1230 не делится на 7.
3. Трехзначное натуральное число вида аbа будет делиться на 7, если а+b делится на 7.
Примеры:
252 делится на 7, т.к. 2+5=7, 7/7.
636 не делится на 7, т.к. 6+3=9, 9 не делится на 7.
4. Трехзначное натуральное число вида bаа будет делиться на 7, если сумма цифр числа делится на 7.
Примеры:
455 делится на 7, т.к. 4+5+5=14, 14/7.
244 не делится на 7, т.к. 2+4+4=12, 12 не делится на 7.
5. Трехзначное натуральное число вида ааb будет делиться на 7, если 2а-b делится на 7.
Примеры:
882 делится на 7,т.к. 8+8-2=14, 14/7.
996 не делится на 7, т.к. 9+9-6=12, 12 не делится на 7.
6. Четырехзначное натуральное число вида bаа , где b-двухзначное число, будет делиться на 7, если b+2а делится на 7.
Примеры:
2744 делится на 7, т.к. 27+4+4=35, 35/7.
1955 не делится на 7, т.к. 19+5+5=29, 29 не делится на 7.
7. Натуральное число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
Примеры:
483 делится на 7, т.к. 48-3·2=42, 42/7.
564 не делится на 7, т.к. 56-4·2=48, 48 не делится на 7.
8. Натуральное число делится на 7 тогда и только тогда, когда сумма произведений цифр числа на соответствующие остатки получаемые при делении разрядных единиц на число 7, делится на 7.
Примеры:
10׃7=1 (ост 3)
100׃7=14 (ост 2)
1000׃7=142 (ост 6)
10000׃7=1428 (ост 4)
100000׃7=14285 (ост 5)
1000000׃7=142857 (ост 1) и снова повторяются остатки.
Число 1316 делится на 7, т.к. 1·6+3·2+1·3+6=21, 21/7(6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3- ост. от деления 10 на 7).
Число 354722 не делится на7,т.к. 3·5+5·4+4·6+7·2+2·3+2=81, 81 не делится на 7(5-ост. от деления 100 000 на 7; 4 -ост. от деления 10 000 на 7; 6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3-ост. от деления 10 на 7).
Признаки делимости на 11.
1. Число делится на 11, если разность суммы цифр стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, кратна 11.
Разность может быть отрицательным числом или 0, но обязательно должна быть кратной 11. Нумерация идет слева направо.
Пример:
2135704 2+3+7+4=16, 1+5+0=6, 16-6=10, 10 не кратно 11, значит, это число не делится на 11.
1352736 1+5+7+6=19, 3+2+3=8, 19-8=11, 11 кратно 11, значит, это число делится на 11.
2. Натуральное число разбивают справа налево на группы по 2 цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.
Пример: Определим, делится ли число 12561714 на 11.
Разобьем число на группы по две цифры в каждой: 12/56/17/14; 12+56+17+14=99, 99 делится на 11, значит, данное число делится на 11.
3. Трехзначное натуральное число делится на 11, если сумма боковых цифр числа равна цифре, которая в середине. Ответ будет состоять из тех самых боковых цифр.
Примеры:
594 делится на11, т.к. 5+4=9, 9-в середине.
473 делится на 11, т.к. 4+3=7, 7- в середине.
861 не делится на 11, т.к. 8+1=9, а в середине 6.
Признаки делимости на 13
1. Натуральное число делится на 13, если разность числа тысяч и числа, образованного последними тремя цифрами, делится на 13.
Примеры:
Число 465400 делится на 13, т.к. 465 – 400 = 65, 65 делится на 13.
Число 256184 не делится на 13, т.к. 256 – 184 = 72, 72 не делится на 13.
2. Натуральное число делится на 13 тогда и только тогда, когда результат вычитания последней цифры, умноженной на 9, из этого числа без последней цифры , делится на 13.
Примеры:
988 делится на 13, т.к. 98 — 9·8 = 26, 26 делится на 13.
853 не делится на 13, т.к. 85 — 3·9 = 58, 58 не делится на 13.
Признак делимости на 19
Натуральное число делится на 19 без остатка тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19.
Следует учесть, что число десятков в числе надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.
Примеры:
1534 десятков-153, 4·2=8, 153+8=161, 161 не делится на 19,значит, и 1534 не делится на 19.
1824 182+4·2=190, 190/19, значит, число 1824/19.
Все перечисленные признаки делимости натуральных чисел можно разделить на 4 группы:
1группа- когда делимость чисел определяется по последней(им) цифрой (ми) – это признаки делимости на 2, на 5,на разрядную единицу, на 4, на 8, на 25, на 50;
2 группа – когда делимость чисел определяется по сумме цифр числа – это признаки делимости на3, на 9, на 7(1 признак), на 11, на 37;
3 группа – когда делимость чисел определяется после выполнения каких-то действий над цифрами числа – это признаки делимости на 7, на 11, на 13, на 19;
4 группа – когда для определения делимости числа используются другие признаки делимости — это признаки делимости на 6, на12, на 14, на 15.
Практическая часть
3.1. Применение признаков делимости при решении задач
Рассмотрим применение признаков делимости натуральных чисел на примере
задачи 19 (по теме «Натуральные числа») — КИМ ЕГЭ 2017 года, базовый уровень.
Задача 3
Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Решение.
Раскладываем делитель — число 12 на простые множители. 12 = 3×4. Следователь- но, заданное число после вычеркивания чисел должно делиться на 3 и 4.
Признак делимости на 4: Натуральное число делится на 4 тогда и только тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 3: Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
Признак делимости на 4 утверждает, что на 4 должно делиться двузначное число, образованное последними двумя цифрами. Значит, 181615121 последнюю цифру 1 вычеркиваем сразу. 12:4 = 3, поэтому две последние цифры числа 18161512 вычеркивать нельзя. Они гарантируют делимость числа на 4.
Чтобы число делилось на 3, нужно чтобы на 3 делилась сумма его цифр.
1+8+1+6+1+5+1+2=25
25 = 3×8 + 1 — можно вычеркнуть одну из единиц, но по условию задачи нужно вычеркнуть еще две цифры;
25 = 3×7 + 4 — нет двух цифр для вычеркивания, сумма которых равнялась бы 4, т.к. последние цифры 1 и 2 трогать нельзя;
25 = 3×6 + 7 — сумма двух вычеркнутых цифр будет равна 7, если вычеркнуть 6-ку и любую из единиц, кроме последней.
Итак, возможные ответы: 811512, 181512 или 181152. Выбираем один из них, например Ответ:181512 Замечание: на реальном ЕГЭ нужно сделать проверку своего ответа делением в столбик.
Следующая задача из Открытого банка заданий Федеральнного института педагогических измерений.
Задача 4
Приведите пример пятизначного числа кратного 12, произведение цифр которого равно 40. В ответе укажите ровно одно такое число.
Решение.
Разложим число 40 на простые множители. 40 = 2×2×2×5.
Таких множителей всего четыре, цифр недостаточно для пятизначного числа, но в произведение всегда можно добавить единицу, результат от этого не изменится: 40 = 2×2×2×5×1.
Таким образом, число в ответе можно составить только из этих цифр: 1,2,2,2,5.
Чтобы число было кратным 12 (то же самое, что делилось на 12 без остатка) оно должно удовлетворять признакам делимости на 3 и на 4, так как 12 = 3×4.
Проверим сумму цифр 1+2+2+2+5 = 12. Она делится на 3, поэтому наше число будет делиться на 3 при любых перестановках цифр.
А чтобы оно делилось на 4, в конце нужно поставить две цифры так, чтобы образованное ими число делилось на 4.
Очевидно, что последней цифрой должна быть 2-ка, другие — нечетные. Проверим варианты 12, 22, 52.
12:4 = 3; 22:4 = 5,5 — не делится нацело; 52:4 = 13.
Вывод: число должно быть составлено так, чтобы в конце было 12 или 52, а в начале любые перестановки из оставшихся трёх цифр.
Возможные ответы: 12252, 21252, 22152, 22512, 25212, 52212. В ответ пишем один из них. Например,
Ответ: 21252 Таким образом, мы убедились в применении признаков делимости натуральных чисел при решении задач.
Рассмотрев задачи, мне стало интересно, а знают ли наши выпускники о признаках делимости. И я решил провести опрос.
3.2Анкетирование «Помогают Вам признаки делимости при делении?»
Анкетирование проводилось среди обучающихся 9 и 11-х классов. В опросе приняли участие 29 обучающихся МБОУ СОШ с Ургала. Им было предложено ответить на следующие вопросы:
Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?
Какие вы знаете признаки делимости натуральных чисел?
Помогают ли вам признаки делимости натуральных чисел при делении?
А хотели бы узнать еще о других признаках делимости натуральных чисел?
80% опрошенных считают, что современному человеку нужно уметь считать.
Большинство обучающихся знают признаки делимости, изученные в школе
на 2,3, 5, 10. – это 87%
88 % опрошенных считают, что признаки делимости помогают при делении.
По результатам проведенного анкетирования 76 % опрошенных хотели бы познакомиться с признаками делимости, не изученными в школе.
4. Заключение.
Работая с разными источниками, я убедился в том, что существуют другие признаки делимости натуральных чисел (на 7, 11, 13, 19), что подтвердило правильность гипотезы о существовании других признаков делимости натуральных чисел.
Решая задачи я убедился, что знание и использование выше перечисленных признаков делимости натуральных чисел значительно упрощает многие вычисления, экономит время; исключает вычислительные ошибки, которые можно сделать при выполнении действия деления. Следует отметить, что формулировки некоторых признаков сложны. Может быть, поэтому они не изучаются в школе.
Собранный мной материал я оформил в виде буклета, который можно использовать на уроках математики, на занятиях математического кружка. Учителя математики могут использовать его при изучении данной темы. Также рекомендую ознакомиться со своей работой старшеклассников, которые хотят получить высокие баллы на экзаменах по математике. Перед 11-классниками своей школы я выступил, рассказал о признаках делимости, показал решение задач и раздал им буклеты.
В дальнейшем планирую рассмотреть такие вопросы:
-историю возникновения признаков делимости;
— признак Паскаля.
5. СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ – РЕСУРСОВ
Перельман Я.И. Математика – это интересно ! – М.: ТЕРРА – Книжный клуб, 2006
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 6 класс : учеб. для общеобразоват. учреждений /— 25-е изд., стер. — М. : Мнемозина, 2009. — 288 с.
Internet
Секция: Математика
Номинация: Математика
Признаки делимости натуральных чисел
Автор Багаутдинов Данил Русланович МБОУ СОШ с Ургала, 6 класс,
Руководитель: Багаутдинова Люция Салимьяновна, учитель математики МБОУ СОШ с Ургала
Работа посвящена изучению признаков делимости натуральных чисел, которые не изучаются в школьном курсе математики. Знание этих признаков имеет большое значение при выполнении заданий КИМов ЕГЭ базового уровня.
Проект по математике «Признаки делимости натуральных чисел»
Актуальность.
При изучении на уроках математике темы: «Признаки делимости натуральных чисел» у меня возник интерес к исследованию чисел на делимость.
Не всегда одно натуральное число делится на другое натуральное число без остатка. Деля натуральное число мы получаем остаток, допускаем ошибки, тем самым теряем время. Возникает необходимость, не выполняя деления установить, делится ли одно натуральное число на другое.
Гипотеза
Если можно определить делимость натуральных чисел на 2,3,5,9,10 то должны быть признаки, по которым можно определить делимость натуральных чисел на другое число.
Объект исследования:
Делимость натуральных чисел
Предмет исследования:
Признаки делимости натуральных чисел
Цель:
Дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе.
Задачи исследования:
Повторить признаки делимости натуральных чисел, изучаемые в школе
Исследовать самостоятельно признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Изучить дополнительную литературу о других признаках делимости натуральных чисел.
Систематизировать и обобщать признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Рассмотреть применение признаков делимости натуральных чисел при решении задач.
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Немного из истории:
Признаки делимости на 2,3,5,9,10 были известны с давних времён. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до н.э.
Признаки делимости на 2,3 и 5 были изложены итальянским математиком Леонардо Фибоначчи (1170-1228)
Вопросы делимости чисел рассматривались пифагорейцами в теории чисел ими была проведена большая работа по типологии натуральных чисел. Пифагорейцы делили их на классы:
совершенных чисел (число, равное сумме своих делителей 6=1+2+3)
дружественных чисел ( каждое из ,которых равно сумме делителей другого , например: 220 и 284 (284= 1+2+4+5+10+20+11+22+44+55+110) и(220=1+2+4+71+142)
фигурных чисел
простых чисел и д.р
Признак Паскаля
Выдающийся французский математик и физик Блез Паскаль (1623-1662) еще в раннем возрасте вывел общий признак делимости чисел , из которого следует все частные признаки
Признак Паскаля: натуральное число А разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа А на соответствующие остатки , получаемые при деление разрядных единиц на число b делится на это число .
Признаки делимости натуральных чисел , полученных самостоятельно, изучая дополнительную литературу .
Выполняя действие деления, умножения натуральных чисел, наблюдая за результатами действий , я нашла закономерность и получила следующие признаки делимости:
Признак делимости на 4: если число, образованное двумя последними цифрами данного числа, делится на 4, то и само число делится на 4 без остатка.
Признак делимости на 8: если число, образованное тремя последними цифрами данного числа, делится на 8, то и само число делится на 8 без остатка.
Признак делимости на 6: если число делится и на 3 и на 2 , то и само число делится на 6 без остатка.
Признак делимости на 15: если число одновременно делится на 5 и на 3 и если оно заканчивает на 0 и на 5 и сумма цифр числа делится на 3, то и само число делится на 15.
Признак делимости на 25: если число оканчивается на 00,25,50,75, то и само число делится на 25 без остатка.
Признак делимости на 50: если число заканчивается на 00 или 50, то и само число делится на 50.
Из дополнительной литературы я нашла подтверждения правильности сформулированных мною признаков делимости натуральных чисел на 4,6,8,15,25,50.
Так же я нашла признаки делимости на 7,на 11,на 12,на 13. Все рассмотренные признаки я сформулировала в виде брошюры
Признак делимости на 7
Если последнюю цифру числа умножить на 2 и вычесть из числа, оставшегося без последней цифры и если получившееся число делится на 7, то и само число делится на 7. Число 1102283
1-й шаг: 110228-3*2 = 110222
2-й шаг: 11022-2*2 = 11018
3-й шаг: 1101-8*2 = 1085
4-й шаг: 108-5*2 = 98
5-й шаг: 9-8*2 = -7. Делится на 7
Значит, 1102283 делится на 7
Признак делимости на 11
Если сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо отличается от нее на число, делящееся на 11, то число делится на 11 без остатка.
Пример: 160369 (Сумма цифр, которые стоят на нечётных местах 1+0+6 = 7.
Сумма цифр, которые стоят на чётных местах 6+3+9 = 18.
18 — 7 = 11. Делится на 11. Значит, число 160369 делится на 11).
Признак делимости на 12.
Если две последние цифры числа делятся на 4 и сумма цифр его делится на 3,то всё число делится на 12, без остатка.
Пример:
78864 (Две последние цифры — 64. Число, составленное из них, делится на 4; сумма цифр равна 7+8+8+6+4 = 33-делится на 3.) Значит, всё число делится на 12.
Еще пример:
Число, составленное из них,делится на 4;
сумма цифр равна 7+6+8+1+2=24,
(данное число делится на 3).
Значит, всё число делится на 12.
Признак делимости на 13
Если взять последнюю цифру числа, умножить ее на 4 и прибавить к числу, оставшемуся без последней цифры, и если получившееся число делится на 13, то и само число делится на 13, без остатка.
Пример:
Число 595166.
1-й шаг. 59516 + 6*4 = 59540
2-й шаг. 5954 + 0*4 = 5954
3-й шаг. 595 + 4*4 = 611
4-й шаг. 61 + 1*4 = 65
5-й шаг. 6 + 5*4 = 26. Делится на 13.
Применение признаков делимости при решении задач.
Задача:
Ученики 5 класса купили 203 учебника. Сколько было пятиклассников и сколько учебников купил каждый из них.
Решение:
Обе величины , должны быть целыми числами.
Разложим 203 на простые множители: 203=1*7*29. Учебников не может быть 29, так же число
учебников не может равняться 1,т.к. В этом случае учеников было бы 203. Значит 5 –ов 29 и каждый из них купил по 7 учебников.
Спасибо за внимание.
Онлайн урок: Признаки делимости на 9 и на 3 по предмету Математика 6 класс
Пусть у нас есть 153 конфеты. Нужно раздать их троим детям поровну, используя только признак делимости.
Число 153 можно разложить на 1 сотню, 5 десятков и 3 единицы.
Разделим сначала нашу сотню конфет. Каждый ребенок получит по 33 конфеты, и в остатке одна.
Теперь разделим один десяток конфет на троих. Имеем по 3 конфеты у каждого, и одна в остатке. Значит, для наших пяти десятков каждому ребёнку по 15 (3•5) конфет, и в остатке 5 (1•5) конфет.
По аналогии поступим с количеством конфет в единицах — тут всем достанется 1 конфета.
Мы не смогли разделить 1 конфету из сотен, 5 конфет из десятков. То есть в сумме получим 1 + 5 = 6 конфет, которые можно разделить по 2 конфеты каждому.
В итоге каждому ребёнку получится по 33 + 15 + 1 + 2 = 51 конфете.
Значит, число 153 делится без остатка на 3, а 1 + 5 — это сумма цифр этого числа.
Мы на примере посмотрели, как используется признак делимости на 3.
Если сумма цифр числа делится на 3, то и число делится на 3.
Если сумма цифр числа не делится на 3, то и число не делится на 3.
Пример 1
Выберите среди чисел 75432, 2772825, 5402070 те, которые делятся на 3.
Решение:
По признаку делимости на 3 нужно найти сумму цифр каждого числа и дальше работать с нею.
Для первого: 7 + 5+ 4+ 3+ 2 = 21,а 21 : 3 = 7, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для второго: 2 + 7 + 7 + 2 + 8 + 2 + 5 = 33, а 33 : 3 = 11, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для третьего: 5 + 4 + 0 + 2 + 0 + 7 + 0 = 18, а 18 : 3 = 6, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Пример 2
Замените звёздочки в числах 2*5, 31*, *15, на необходимые цифры, чтобы эти числа стали делиться на 3.

Решение:
Возьмем первое число 2*5. Из признака делимости мы знаем, что нужно, чтобы сумма цифр числа делилась на 3. Значит, 2 + 5 + * должно делиться на 3.
Сумма известных цифр равна 8, значит, вместо звездочки можно взять, например, 1.
Тогда сумма станет 9, и она делится на 3, значит, и получившееся число 215 будет делиться на 3.
Кроме единицы подходят цифры: 4, 7, так как они отличаются от 1 на 3 и 6 каждая.
Возьмем второе число 31*. Сумма первых цифр равна 4, значит, вместо звездочки минимум надо брать 2, чтоб в сумме было 6.
Тогда сумма цифр будет делиться на 3 и само число, 312, будет делиться тоже.
Кроме двойки брать можно и другие цифры, прибавляя по 3: 5 или 8.
Получившиеся числа 315 или 318 будут делиться на 3.
Берём последнее число *15. Сумма последних двух цифр — 6, уже делится на 3. Значит нужно брать вместо первой цифры такие, которые делятся на 3. Это 3, 6 или 9.
Получившиеся числа 315, 615, 915 будут делиться на 3 без остатка.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьИз признака делимости на 3 можно получить интересный признак делимости на 6
Чтобы ваше число делилось на 6, нужно чтоб оно делилось на 2 и на 3 одновременно.
Пример
Делится ли 216 на 6?
Решение:
216— это чётное число, значит, оно делится на 2.
Сумма цифр числа 216 равна 2 + 1+ 6 = 9, значит, оно делится на 3.
Отсюда, делаем вывод, что 216 делится на 6.

1. Введение
Актуальность: В начале учебного года на уроках математики мы изучали тему: «Признаки делимости натуральных чисел на 2, 3, 5, 9, 10». При изучении этой темы у нас не возникло никаких проблем, выучили признаки, научились их применять при выполнении заданий. При разложении чисел на простые множители мне пришлось делить число на 7. А как узнать, деление получится с остатком или без остатка? Нет ли признаков делимости на 7? А на другие числа?
Так меня заинтересовал вопрос о делимости натуральных чисел на другие числа. Я решил написать исследовательскую работу по данной теме.
Гипотеза: Существуют признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Объект исследования: Делимость натуральных чисел.
Предмет исследования: Признаки делимости натуральных чисел.
Цель: Найти признаки делимости натуральных чисел на другие числа, которые не изучаются в школьном курсе математики.
Задачи:
Повторить признаки делимости на 2, 3. 5, 9, 10, изученные мною в школе.
Исследовать самостоятельно признаки делимости натуральных чисел на 4, 8, 11, 13, 15, 17, 25, 50 и другие числа.
Изучить дополнительную литературу, подтверждающую правильность гипотезы о существовании других признаков делимости натуральных чисел и правильность выявленных мной признаков делимости.
Провести опрос учащихся 9 и 11 классов
Оформить материал
Представить результаты исследований. Составить буклет «Признаки делимости натуральных чисел».
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Методы исследования: Сбор материала, обработка данных, наблюдение, сравнение, анализ, обобщение, проведение опроса среди учащихся по данной теме.
2 Теоретическая часть
2.1. Признаки делимости натуральных чисел (школьный курс).
При изучении данной темы необходимо знать понятия делитель, кратное, простое и составное числа.
Делителем натурального числа а называют натуральное число b, на которое а делится без остатка.
Часто утверждение о делимости числа а на число b выражают другими равнозначными словами: а кратно b, b — делитель а, b делит а.
Простыми называются натуральные числа, которые имеют два делителя: 1 и само число. Например, числа 5,7,19 – простые, т.к. делятся на 1 и само себя.
Числа, которые имеют более двух делителей, называются составными. Например, число 14 имеет 4 делителя: 1, 2, 7, 14, значит оно составное.
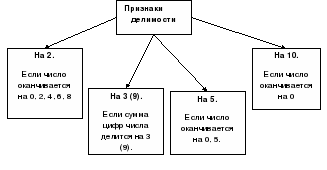
2.2. Признаки делимости натуральных чисел на 4, 25, 50.
Выполняя действия деления, умножения натуральных чисел, наблюдая за результатами действий, я нашел закономерности и получил следующие признаки делимости.
Признак делимости на 4.
25·4=100; 56·4=224; 123·4=492; 125·4=500; 2345·4=9380; 2500·4=10000; …
Умножая натуральные числа на 4, я заметил, что числа образованные из двух последних цифр числа делятся на 4 без остатка.
Признак делимости на 4 читается так:
Натуральное число делится на 4 тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 25.
Выполняя умножение натуральных различных чисел на 25, я увидел такую закономерность: произведения оканчиваются на 00, 25, 50, 75.
Значит, натуральное число делится на 25, если оканчивается цифрами 00, 25, 50, 75.
Признак делимости на 50.
На 50 делятся числа: 50, 100, 150, 200, 250, 300,… Они оканчиваются либо на 50, либо на 00.
Значит, натуральное число делится на 50 тогда и только тогда, когда оканчивается двумя нулями или 50.
2.3. Признаки делимости натуральных чисел на 7, 11, 13, 17, 19.
Из дополнительной литературы я нашел подтверждение правильности сформулированных нами признаков делимости натуральных чисел на 4, 25, 50. Так же я нашел несколько признаков делимости на 7:
1. Натуральное число делится на 7 тогда и только тогда, когда разность числа тысяч и числа, выражаемого последними тремя цифрами, делится на 7.
Примеры:
478009 делится на 7, т.к. 478-9=469, 469 делится на 7.
479345 не делится на 7, т.к. 479-345=134, 134 не делится на 7.
2. Натуральное число делится на 7, если сумма удвоенного числа, стоящего до десятков и оставшегося числа делится на 7.
Примеры:
4592 делится на 7, т.к. 45·2=90, 90+92=182, 182 делится на 7.
57384 не делится на 7, т.к. 573·2=1146, 1146+84=1230, 1230 не делится на 7.
3. Трехзначное натуральное число вида аbа будет делиться на 7, если а+b делится на 7.
Примеры:
252 делится на 7, т.к. 2+5=7, 7/7.
636 не делится на 7, т.к. 6+3=9, 9 не делится на 7.
4. Трехзначное натуральное число вида bаа будет делиться на 7, если сумма цифр числа делится на 7.
Примеры:
455 делится на 7, т.к. 4+5+5=14, 14/7.
244 не делится на 7, т.к. 2+4+4=12, 12 не делится на 7.
5. Трехзначное натуральное число вида ааb будет делиться на 7, если 2а-b делится на 7.
Примеры:
882 делится на 7,т.к. 8+8-2=14, 14/7.
996 не делится на 7, т.к. 9+9-6=12, 12 не делится на 7.
6. Четырехзначное натуральное число вида bаа , где b-двухзначное число, будет делиться на 7, если b+2а делится на 7.
Примеры:
2744 делится на 7, т.к. 27+4+4=35, 35/7.
1955 не делится на 7, т.к. 19+5+5=29, 29 не делится на 7.
7. Натуральное число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
Примеры:
483 делится на 7, т.к. 48-3·2=42, 42/7.
564 не делится на 7, т.к. 56-4·2=48, 48 не делится на 7.
8. Натуральное число делится на 7 тогда и только тогда, когда сумма произведений цифр числа на соответствующие остатки получаемые при делении разрядных единиц на число 7, делится на 7.
Примеры:
10׃7=1 (ост 3)
100׃7=14 (ост 2)
1000׃7=142 (ост 6)
10000׃7=1428 (ост 4)
100000׃7=14285 (ост 5)
1000000׃7=142857 (ост 1) и снова повторяются остатки.
Число 1316 делится на 7, т.к. 1·6+3·2+1·3+6=21, 21/7(6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3- ост. от деления 10 на 7).
Число 354722 не делится на7,т.к. 3·5+5·4+4·6+7·2+2·3+2=81, 81 не делится на 7(5-ост. от деления 100 000 на 7; 4 -ост. от деления 10 000 на 7; 6-ост. от деления 1000 на 7; 2-ост. от деления 100 на 7; 3-ост. от деления 10 на 7).
Признаки делимости на 11.
1. Число делится на 11, если разность суммы цифр стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, кратна 11.
Разность может быть отрицательным числом или 0, но обязательно должна быть кратной 11. Нумерация идет слева направо.
Пример:
2135704 2+3+7+4=16, 1+5+0=6, 16-6=10, 10 не кратно 11, значит, это число не делится на 11.
1352736 1+5+7+6=19, 3+2+3=8, 19-8=11, 11 кратно 11, значит, это число делится на 11.
2. Натуральное число разбивают справа налево на группы по 2 цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.
Пример: Определим, делится ли число 12561714 на 11.
Разобьем число на группы по две цифры в каждой: 12/56/17/14; 12+56+17+14=99, 99 делится на 11, значит, данное число делится на 11.
3. Трехзначное натуральное число делится на 11, если сумма боковых цифр числа равна цифре, которая в середине. Ответ будет состоять из тех самых боковых цифр.
Примеры:
594 делится на11, т.к. 5+4=9, 9-в середине.
473 делится на 11, т.к. 4+3=7, 7- в середине.
861 не делится на 11, т.к. 8+1=9, а в середине 6.
Признаки делимости на 13
1. Натуральное число делится на 13, если разность числа тысяч и числа, образованного последними тремя цифрами, делится на 13.
Примеры:
Число 465400 делится на 13, т.к. 465 – 400 = 65, 65 делится на 13.
Число 256184 не делится на 13, т.к. 256 – 184 = 72, 72 не делится на 13.
2. Натуральное число делится на 13 тогда и только тогда, когда результат вычитания последней цифры, умноженной на 9, из этого числа без последней цифры , делится на 13.
Примеры:
988 делится на 13, т.к. 98 — 9·8 = 26, 26 делится на 13.
853 не делится на 13, т.к. 85 — 3·9 = 58, 58 не делится на 13.
Признак делимости на 19
Натуральное число делится на 19 без остатка тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19.
Следует учесть, что число десятков в числе надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.
Примеры:
1534 десятков-153, 4·2=8, 153+8=161, 161 не делится на 19,значит, и 1534 не делится на 19.
1824 182+4·2=190, 190/19, значит, число 1824/19.
Все перечисленные признаки делимости натуральных чисел можно разделить на 4 группы:
1группа- когда делимость чисел определяется по последней(им) цифрой (ми) – это признаки делимости на 2, на 5,на разрядную единицу, на 4, на 8, на 25, на 50;
2 группа – когда делимость чисел определяется по сумме цифр числа – это признаки делимости на3, на 9, на 7(1 признак), на 11, на 37;
3 группа – когда делимость чисел определяется после выполнения каких-то действий над цифрами числа – это признаки делимости на 7, на 11, на 13, на 19;
4 группа – когда для определения делимости числа используются другие признаки делимости — это признаки делимости на 6, на12, на 14, на 15.
Практическая часть
3.1. Применение признаков делимости при решении задач
Рассмотрим применение признаков делимости натуральных чисел на примере
задачи 19 (по теме «Натуральные числа») — КИМ ЕГЭ 2017 года, базовый уровень.
Задача 3
Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Решение.
Раскладываем делитель — число 12 на простые множители. 12 = 3×4. Следователь- но, заданное число после вычеркивания чисел должно делиться на 3 и 4.
Признак делимости на 4: Натуральное число делится на 4 тогда и только тогда, когда две его последние цифры 0 или образуют число, делящееся на 4.
Признак делимости на 3: Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
Признак делимости на 4 утверждает, что на 4 должно делиться двузначное число, образованное последними двумя цифрами. Значит, 181615121 последнюю цифру 1 вычеркиваем сразу. 12:4 = 3, поэтому две последние цифры числа 18161512 вычеркивать нельзя. Они гарантируют делимость числа на 4.
Чтобы число делилось на 3, нужно чтобы на 3 делилась сумма его цифр.
1+8+1+6+1+5+1+2=25
25 = 3×8 + 1 — можно вычеркнуть одну из единиц, но по условию задачи нужно вычеркнуть еще две цифры;
25 = 3×7 + 4 — нет двух цифр для вычеркивания, сумма которых равнялась бы 4, т.к. последние цифры 1 и 2 трогать нельзя;
25 = 3×6 + 7 — сумма двух вычеркнутых цифр будет равна 7, если вычеркнуть 6-ку и любую из единиц, кроме последней.
Итак, возможные ответы: 811512, 181512 или 181152. Выбираем один из них, например Ответ:181512 Замечание: на реальном ЕГЭ нужно сделать проверку своего ответа делением в столбик.
Следующая задача из Открытого банка заданий Федеральнного института педагогических измерений.
Задача 4
Приведите пример пятизначного числа кратного 12, произведение цифр которого равно 40. В ответе укажите ровно одно такое число.
Решение.
Разложим число 40 на простые множители. 40 = 2×2×2×5.
Таких множителей всего четыре, цифр недостаточно для пятизначного числа, но в произведение всегда можно добавить единицу, результат от этого не изменится: 40 = 2×2×2×5×1.
Таким образом, число в ответе можно составить только из этих цифр: 1,2,2,2,5.
Чтобы число было кратным 12 (то же самое, что делилось на 12 без остатка) оно должно удовлетворять признакам делимости на 3 и на 4, так как 12 = 3×4.
Проверим сумму цифр 1+2+2+2+5 = 12. Она делится на 3, поэтому наше число будет делиться на 3 при любых перестановках цифр.
А чтобы оно делилось на 4, в конце нужно поставить две цифры так, чтобы образованное ими число делилось на 4.
Очевидно, что последней цифрой должна быть 2-ка, другие — нечетные. Проверим варианты 12, 22, 52.
12:4 = 3; 22:4 = 5,5 — не делится нацело; 52:4 = 13.
Вывод: число должно быть составлено так, чтобы в конце было 12 или 52, а в начале любые перестановки из оставшихся трёх цифр.
Возможные ответы: 12252, 21252, 22152, 22512, 25212, 52212. В ответ пишем один из них. Например,
Ответ: 21252 Таким образом, мы убедились в применении признаков делимости натуральных чисел при решении задач.
Рассмотрев задачи, мне стало интересно, а знают ли наши выпускники о признаках делимости. И я решил провести опрос.
3.2Анкетирование «Помогают Вам признаки делимости при делении?»
Анкетирование проводилось среди обучающихся 9 и 11-х классов. В опросе приняли участие 29 обучающихся МБОУ СОШ с Ургала. Им было предложено ответить на следующие вопросы:
Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?
Какие вы знаете признаки делимости натуральных чисел?
Помогают ли вам признаки делимости натуральных чисел при делении?
А хотели бы узнать еще о других признаках делимости натуральных чисел?
80% опрошенных считают, что современному человеку нужно уметь считать.
Большинство обучающихся знают признаки делимости, изученные в школе
на 2,3, 5, 10. – это 87%
88 % опрошенных считают, что признаки делимости помогают при делении.
По результатам проведенного анкетирования 76 % опрошенных хотели бы познакомиться с признаками делимости, не изученными в школе.
4. Заключение.
Работая с разными источниками, я убедился в том, что существуют другие признаки делимости натуральных чисел (на 7, 11, 13, 19), что подтвердило правильность гипотезы о существовании других признаков делимости натуральных чисел.
Решая задачи я убедился, что знание и использование выше перечисленных признаков делимости натуральных чисел значительно упрощает многие вычисления, экономит время; исключает вычислительные ошибки, которые можно сделать при выполнении действия деления. Следует отметить, что формулировки некоторых признаков сложны. Может быть, поэтому они не изучаются в школе.
Собранный мной материал я оформил в виде буклета, который можно использовать на уроках математики, на занятиях математического кружка. Учителя математики могут использовать его при изучении данной темы. Также рекомендую ознакомиться со своей работой старшеклассников, которые хотят получить высокие баллы на экзаменах по математике. Перед 11-классниками своей школы я выступил, рассказал о признаках делимости, показал решение задач и раздал им буклеты.
В дальнейшем планирую рассмотреть такие вопросы:
-историю возникновения признаков делимости;
— признак Паскаля.
5. СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ – РЕСУРСОВ
Перельман Я.И. Математика – это интересно ! – М.: ТЕРРА – Книжный клуб, 2006
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 6 класс : учеб. для общеобразоват. учреждений /— 25-е изд., стер. — М. : Мнемозина, 2009. — 288 с.
Internet
Секция: Математика
Номинация: Математика
Признаки делимости натуральных чисел
Автор Багаутдинов Данил Русланович МБОУ СОШ с Ургала, 6 класс,
Руководитель: Багаутдинова Люция Салимьяновна, учитель математики МБОУ СОШ с Ургала
Работа посвящена изучению признаков делимости натуральных чисел, которые не изучаются в школьном курсе математики. Знание этих признаков имеет большое значение при выполнении заданий КИМов ЕГЭ базового уровня.
Проект по математике «Признаки делимости натуральных чисел»
Актуальность.
При изучении на уроках математике темы: «Признаки делимости натуральных чисел» у меня возник интерес к исследованию чисел на делимость.
Не всегда одно натуральное число делится на другое натуральное число без остатка. Деля натуральное число мы получаем остаток, допускаем ошибки, тем самым теряем время. Возникает необходимость, не выполняя деления установить, делится ли одно натуральное число на другое.
Гипотеза
Если можно определить делимость натуральных чисел на 2,3,5,9,10 то должны быть признаки, по которым можно определить делимость натуральных чисел на другое число.
Объект исследования:
Делимость натуральных чисел
Предмет исследования:
Признаки делимости натуральных чисел
Цель:
Дополнить уже известные признаки делимости натуральных чисел нацело, изучаемые в школе.
Задачи исследования:
Повторить признаки делимости натуральных чисел, изучаемые в школе
Исследовать самостоятельно признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Изучить дополнительную литературу о других признаках делимости натуральных чисел.
Систематизировать и обобщать признаки делимости натуральных чисел на 4,6,7,8,11,12,13,15,18,25,50,100.
Рассмотреть применение признаков делимости натуральных чисел при решении задач.
Новизна:
В ходе выполнения проекта я пополнила свои знания о признаках делимости натуральных чисел.
Немного из истории:
Признаки делимости на 2,3,5,9,10 были известны с давних времён. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до н.э.
Признаки делимости на 2,3 и 5 были изложены итальянским математиком Леонардо Фибоначчи (1170-1228)
Вопросы делимости чисел рассматривались пифагорейцами в теории чисел ими была проведена большая работа по типологии натуральных чисел. Пифагорейцы делили их на классы:
совершенных чисел (число, равное сумме своих делителей 6=1+2+3)
дружественных чисел ( каждое из ,которых равно сумме делителей другого , например: 220 и 284 (284= 1+2+4+5+10+20+11+22+44+55+110) и(220=1+2+4+71+142)
фигурных чисел
простых чисел и д.р
Признак Паскаля
Выдающийся французский математик и физик Блез Паскаль (1623-1662) еще в раннем возрасте вывел общий признак делимости чисел , из которого следует все частные признаки
Признак Паскаля: натуральное число А разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа А на соответствующие остатки , получаемые при деление разрядных единиц на число b делится на это число .
Признаки делимости натуральных чисел , полученных самостоятельно, изучая дополнительную литературу .
Выполняя действие деления, умножения натуральных чисел, наблюдая за результатами действий , я нашла закономерность и получила следующие признаки делимости:
Признак делимости на 4: если число, образованное двумя последними цифрами данного числа, делится на 4, то и само число делится на 4 без остатка.
Признак делимости на 8: если число, образованное тремя последними цифрами данного числа, делится на 8, то и само число делится на 8 без остатка.
Признак делимости на 6: если число делится и на 3 и на 2 , то и само число делится на 6 без остатка.
Признак делимости на 15: если число одновременно делится на 5 и на 3 и если оно заканчивает на 0 и на 5 и сумма цифр числа делится на 3, то и само число делится на 15.
Признак делимости на 25: если число оканчивается на 00,25,50,75, то и само число делится на 25 без остатка.
Признак делимости на 50: если число заканчивается на 00 или 50, то и само число делится на 50.
Из дополнительной литературы я нашла подтверждения правильности сформулированных мною признаков делимости натуральных чисел на 4,6,8,15,25,50.
Так же я нашла признаки делимости на 7,на 11,на 12,на 13. Все рассмотренные признаки я сформулировала в виде брошюры
Признак делимости на 7
Если последнюю цифру числа умножить на 2 и вычесть из числа, оставшегося без последней цифры и если получившееся число делится на 7, то и само число делится на 7. Число 1102283
1-й шаг: 110228-3*2 = 110222
2-й шаг: 11022-2*2 = 11018
3-й шаг: 1101-8*2 = 1085
4-й шаг: 108-5*2 = 98
5-й шаг: 9-8*2 = -7. Делится на 7
Значит, 1102283 делится на 7
Признак делимости на 11
Если сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо отличается от нее на число, делящееся на 11, то число делится на 11 без остатка.
Пример: 160369 (Сумма цифр, которые стоят на нечётных местах 1+0+6 = 7.
Сумма цифр, которые стоят на чётных местах 6+3+9 = 18.
18 — 7 = 11. Делится на 11. Значит, число 160369 делится на 11).
Признак делимости на 12.
Если две последние цифры числа делятся на 4 и сумма цифр его делится на 3,то всё число делится на 12, без остатка.
Пример:
78864 (Две последние цифры — 64. Число, составленное из них, делится на 4; сумма цифр равна 7+8+8+6+4 = 33-делится на 3.) Значит, всё число делится на 12.
Еще пример:
Число, составленное из них,делится на 4;
сумма цифр равна 7+6+8+1+2=24,
(данное число делится на 3).
Значит, всё число делится на 12.
Признак делимости на 13
Если взять последнюю цифру числа, умножить ее на 4 и прибавить к числу, оставшемуся без последней цифры, и если получившееся число делится на 13, то и само число делится на 13, без остатка.
Пример:
Число 595166.
1-й шаг. 59516 + 6*4 = 59540
2-й шаг. 5954 + 0*4 = 5954
3-й шаг. 595 + 4*4 = 611
4-й шаг. 61 + 1*4 = 65
5-й шаг. 6 + 5*4 = 26. Делится на 13.
Применение признаков делимости при решении задач.
Задача:
Ученики 5 класса купили 203 учебника. Сколько было пятиклассников и сколько учебников купил каждый из них.
Решение:
Обе величины , должны быть целыми числами.
Разложим 203 на простые множители: 203=1*7*29. Учебников не может быть 29, так же число
учебников не может равняться 1,т.к. В этом случае учеников было бы 203. Значит 5 –ов 29 и каждый из них купил по 7 учебников.
Спасибо за внимание.
Онлайн урок: Признаки делимости на 9 и на 3 по предмету Математика 6 класс
Пусть у нас есть 153 конфеты. Нужно раздать их троим детям поровну, используя только признак делимости.
Число 153 можно разложить на 1 сотню, 5 десятков и 3 единицы.
Разделим сначала нашу сотню конфет. Каждый ребенок получит по 33 конфеты, и в остатке одна.
Теперь разделим один десяток конфет на троих. Имеем по 3 конфеты у каждого, и одна в остатке. Значит, для наших пяти десятков каждому ребёнку по 15 (3•5) конфет, и в остатке 5 (1•5) конфет.
По аналогии поступим с количеством конфет в единицах — тут всем достанется 1 конфета.
Мы не смогли разделить 1 конфету из сотен, 5 конфет из десятков. То есть в сумме получим 1 + 5 = 6 конфет, которые можно разделить по 2 конфеты каждому.
В итоге каждому ребёнку получится по 33 + 15 + 1 + 2 = 51 конфете.
Значит, число 153 делится без остатка на 3, а 1 + 5 — это сумма цифр этого числа.
Мы на примере посмотрели, как используется признак делимости на 3.
Если сумма цифр числа делится на 3, то и число делится на 3.
Если сумма цифр числа не делится на 3, то и число не делится на 3.
Пример 1
Выберите среди чисел 75432, 2772825, 5402070 те, которые делятся на 3.
Решение:
По признаку делимости на 3 нужно найти сумму цифр каждого числа и дальше работать с нею.
Для первого: 7 + 5+ 4+ 3+ 2 = 21,а 21 : 3 = 7, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для второго: 2 + 7 + 7 + 2 + 8 + 2 + 5 = 33, а 33 : 3 = 11, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Для третьего: 5 + 4 + 0 + 2 + 0 + 7 + 0 = 18, а 18 : 3 = 6, то есть сумма цифр делится на 3, значит, и наше число делится на 3
Пример 2
Замените звёздочки в числах 2*5, 31*, *15, на необходимые цифры, чтобы эти числа стали делиться на 3.
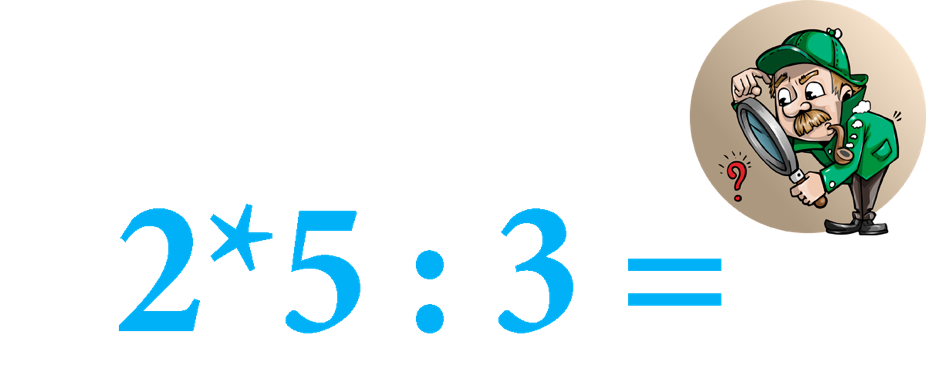
Решение:
Возьмем первое число 2*5. Из признака делимости мы знаем, что нужно, чтобы сумма цифр числа делилась на 3. Значит, 2 + 5 + * должно делиться на 3.
Сумма известных цифр равна 8, значит, вместо звездочки можно взять, например, 1.
Тогда сумма станет 9, и она делится на 3, значит, и получившееся число 215 будет делиться на 3.
Кроме единицы подходят цифры: 4, 7, так как они отличаются от 1 на 3 и 6 каждая.
Возьмем второе число 31*. Сумма первых цифр равна 4, значит, вместо звездочки минимум надо брать 2, чтоб в сумме было 6.
Тогда сумма цифр будет делиться на 3 и само число, 312, будет делиться тоже.
Кроме двойки брать можно и другие цифры, прибавляя по 3: 5 или 8.
Получившиеся числа 315 или 318 будут делиться на 3.
Берём последнее число *15. Сумма последних двух цифр — 6, уже делится на 3. Значит нужно брать вместо первой цифры такие, которые делятся на 3. Это 3, 6 или 9.
Получившиеся числа 315, 615, 915 будут делиться на 3 без остатка.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьИз признака делимости на 3 можно получить интересный признак делимости на 6
Чтобы ваше число делилось на 6, нужно чтоб оно делилось на 2 и на 3 одновременно.
Пример
Делится ли 216 на 6?
Решение:
216— это чётное число, значит, оно делится на 2.
Сумма цифр числа 216 равна 2 + 1+ 6 = 9, значит, оно делится на 3.
Отсюда, делаем вывод, что 216 делится на 6.
