Доказательство равнобедренной и прямоугольной трапеции. Трапеция
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции.
 Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые. - Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении:
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .

Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции.
 Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 . - Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
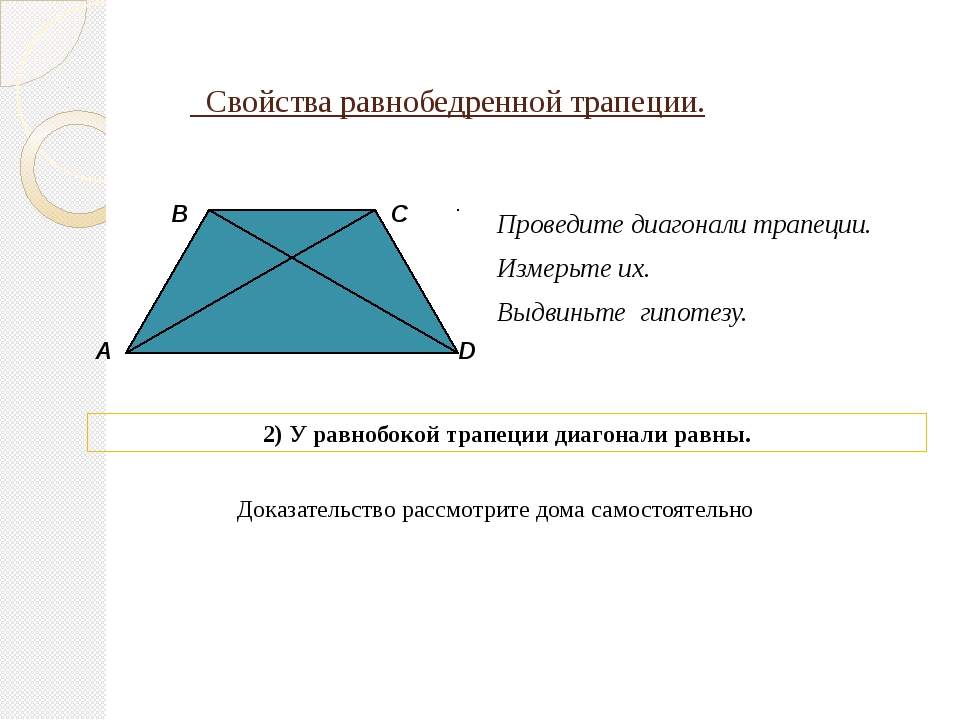
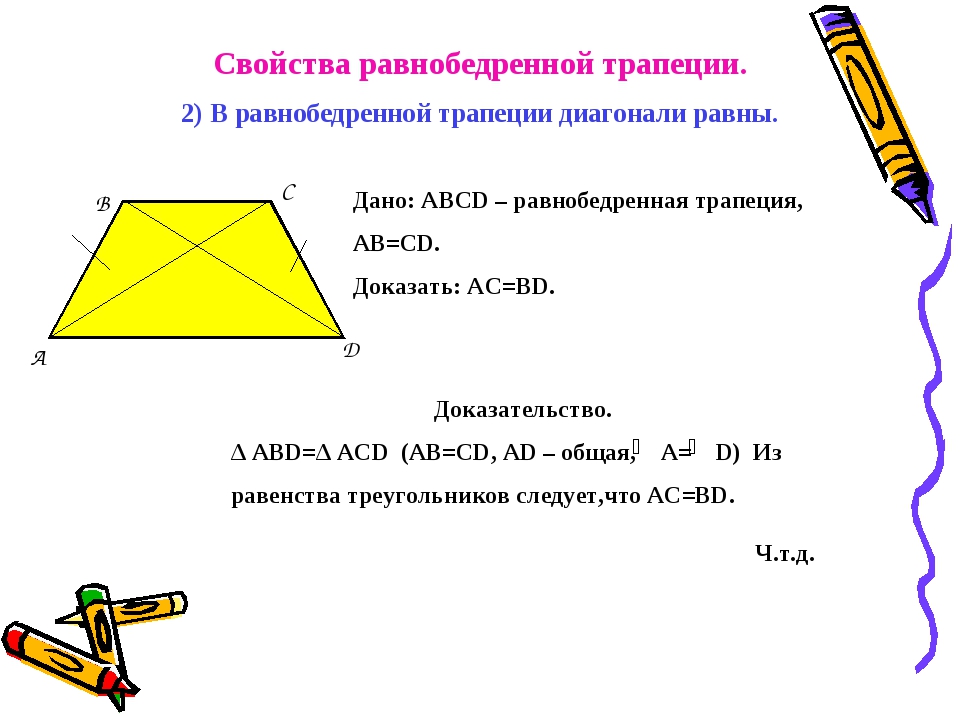
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.

- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней.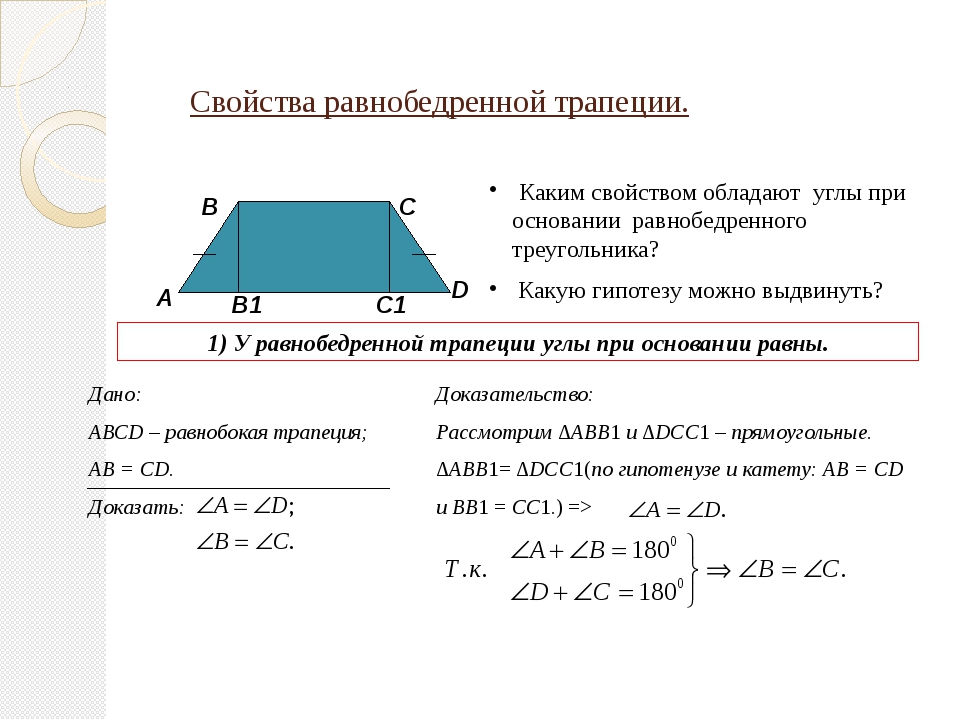 В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности.
 Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .

- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.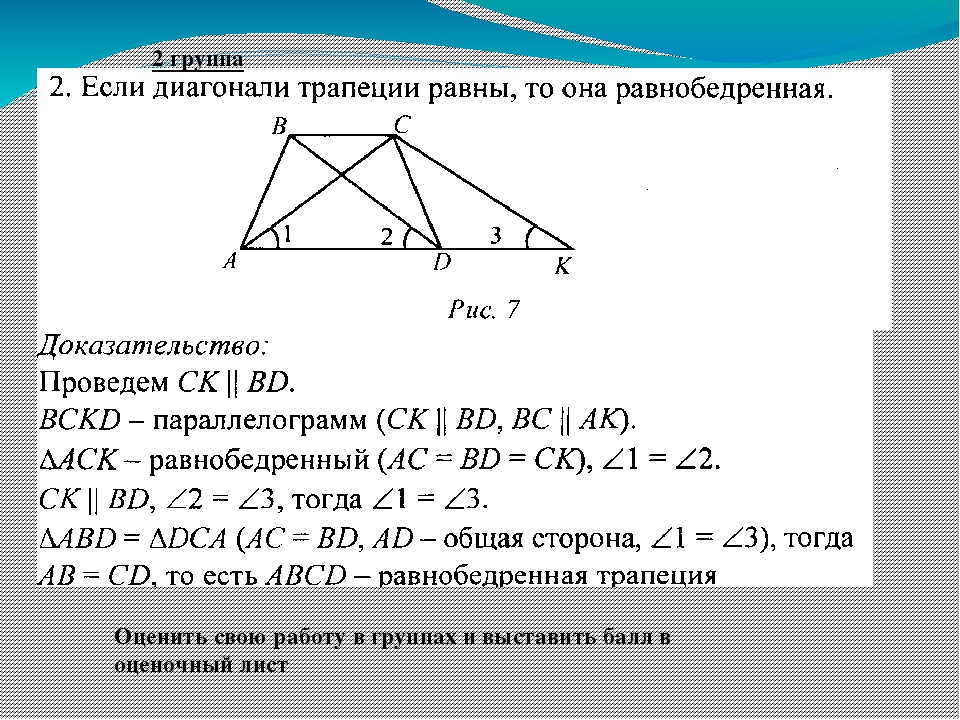
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие ;
— прямоугольные
.
Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У боковые стороны равны, а основания параллельны.
У основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей , равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции , точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см.
 также свойства четырехугольника)
также свойства четырехугольника) - Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность , если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые .Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые , а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник , у которого линия сечения параллельна основанию треугольника.
Важно . Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h 1 h 2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Многоугольник — часть плоскости, ограниченная замкнутой ломаной линией. Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.
Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.
Определение. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны.
Свойства параллелограмма
1. Противолежащие стороны равны.
На рис. 11 AB = CD ; BC = AD .
2. Противолежащие углы равны (два острых и два тупых угла).
На рис. 11 ∠A = ∠C ; ∠B = ∠D .
3 Диагонали (отрезки прямой, соединяющие две противолежащие вершины) пересекаются и точкой пересечения делятся пополам.
На рис. 11 отрезки AO = OC ; BO = OD .
Определение. Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие — нет.
Параллельные стороны называются ее основаниями , а две другие стороны — боковыми сторонами .
Виды трапеций
1. Трапеция , у которой боковые стороны не равны,
называется разносторонней (рис. 12).
12).
2. Трапеция, у которой боковые стороны равны, называется равнобокой (рис. 13).
3. Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется прямоугольной (рис. 14).
Отрезок, соединяющий середины боковых сторон трапеции (рис. 15), называется средней линией трапеции (MN ). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Трапецию можно назвать усеченным треугольником (рис. 17), поэтому и названия трапеций сходны с названиями треугольников (треугольники бывают разносторонние, равнобедренные, прямоугольные).
Площадь параллелограмма и трапеции
Правило. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Трапеция — это четырехугольник, имеющий две параллельные стороны, являющиеся основаниями и две не параллельные стороны, являющиеся боковыми сторонами.
Также встречаются такие названия, как равнобокая или равнобочная .
— это трапеция, у которой углы при боковой стороне прямые.
Элементы трапеции
a, b — основания трапеции (a параллельно b ),
m, n — боковые стороны трапеции,
d 1 , d 2 — диагонали трапеции,
h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN — средняя линия (отрезок, соединяющий середины боковых сторон).
Площадь трапеции
- Через полусумму оснований a, b и высоту h : S = \frac{a + b}{2}\cdot h
- Через среднюю линию MN и высоту h : S = MN\cdot h
- Через диагонали d 1 , d 2 и угол (\sin \varphi ) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}
Свойства трапеции
Средняя линия трапеции
Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:
MN || a, MN || b, MN = \frac{a + b}{2}
Сумма углов трапеции
Сумма углов трапеции , прилежащих к каждой боковой стороне, равна 180^{\circ} :
\alpha + \beta = 180^{\circ}
\gamma + \delta =180^{\circ}
Равновеликие треугольники трапеции
Равновеликими , то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB
и DOC
, образованные боковыми сторонами.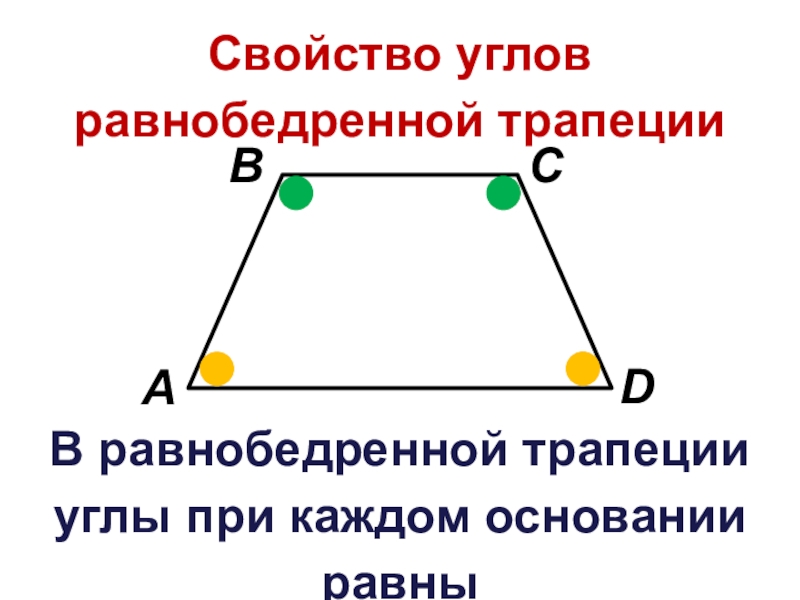 {2}
.
{2}
.
Отношение длин отрезков и оснований
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
\frac{OX}{OY} = \frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.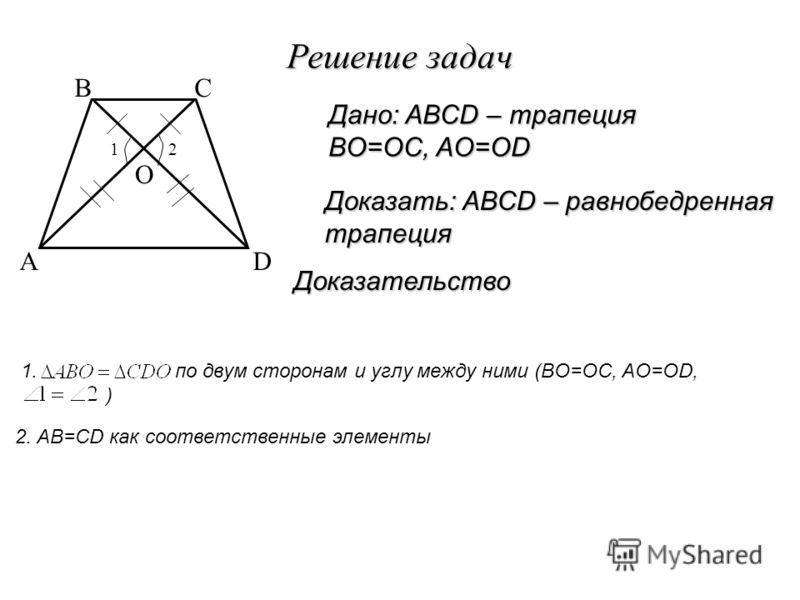
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.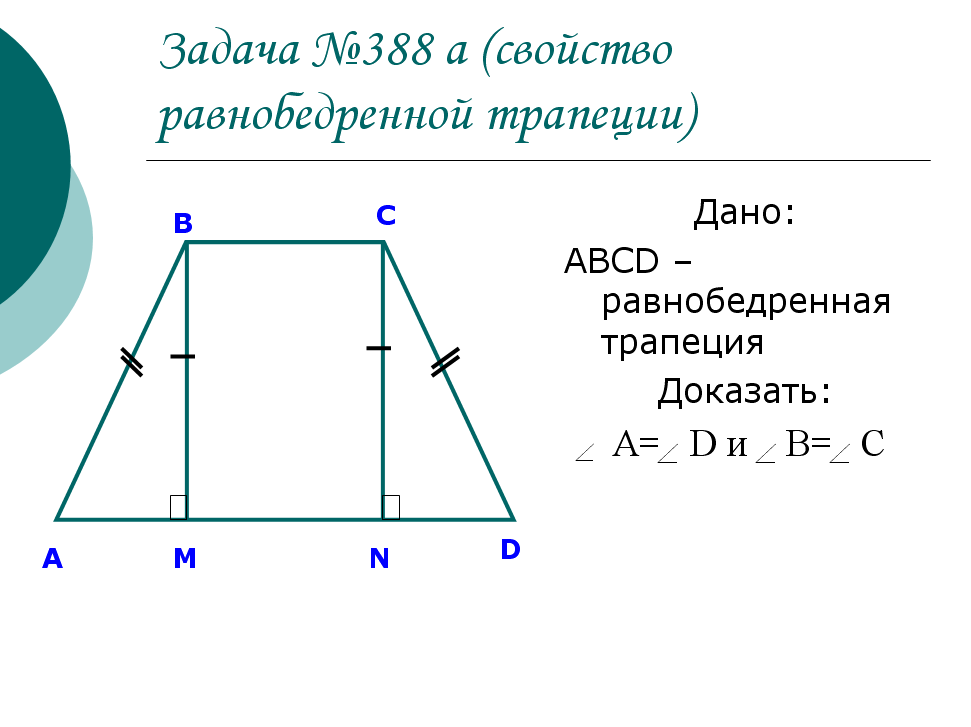
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .
его свойства, признаки и определение с примерами решения
Содержание:
С четырехугольником вы уже знакомились на уроках математики. Дадим строгое определение этой фигуры.
Определение четырехугольника:
Четырехугольником называется фигура, состоящая из четырех точек (вершин четырехугольника) и четырех отрезков, которые их последовательно соединяют (сторон четырехугольника). При этом никакие три его вершины не лежат на одной прямой и никакие две стороны не пересекаются.
На рисунке 1 изображен четырехугольник с вершинами
Говорят, что две вершины четырехугольника являются соседними вершинами, если они соединены одной стороной; вершины, которые не являются соседними, называют противолежащими вершинами. Аналогично стороны четырехугольника, имеющие общую вершину, являются соседними сторонами, а стороны, не имеющие общих точек,— противолежащими сторонами. На рисунке 1 стороны — соседние для стороны а сторона — противолежащая стороне вершины — соседние с вершиной а вершина — противолежащая вершине
На рисунке 1 стороны — соседние для стороны а сторона — противолежащая стороне вершины — соседние с вершиной а вершина — противолежащая вершине
Четырехугольник обозначают, последовательно указывая все его вершины, причем буквы, которые стоят рядом, должны обозначать соседние вершины. Например, четырехугольник на рисунке 1 можно обозначить или но нельзя обозначать
Определение
Диагональю четырехугольника называется отрезок, соединяющий две противолежащие вершины.
В четырехугольнике (рис. 2) диагоналями являются отрезки Следует отметить, что любой четырехугольник имеет диагональ, которая делит его на два треугольника.
Определение
Периметром четырехугольника называется сумма длин всех его сторон. Периметр четырехугольника (как и треугольника) обозначают буквой
Любой четырехугольник ограничивает конечную часть плоскости, которую называют внутренней областью этого четырехугольника (на рис. 3, а, б она закрашена).
3, а, б она закрашена).
На рисунке 3 изображены два четырехугольника и проведены прямые, на которых лежат стороны этих четырехугольников. В четырехугольнике эти прямые не проходят через внутреннюю область — такой четырехугольник является выпуклым (рис. 3, а). В четырехугольнике прямые проходят через внутреннюю область — этот четырехугольник является невыпуклым (рис. 3, б).
Определение
Четырехугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону.
Действительно, четырехугольник на рисунке 3, а лежит по одну сторону от любой из прямых В школьном курсе геометрии мы будем рассматривать только
выпуклые четырехугольники (другие случаи будут оговорены отдельно).
Определение
Углом (внутренним углом) выпуклого четырехугольника при вершине называется угол
Угол, смежный с внутренним углом четырехугольника при данной вершине, называют внешним углом четырехугольника при данной вершине.
Углы, вершины которых являются соседними, называют соседними углами, а углы, вершины которых являются противолежащими,— противолежащими углами четырехугольника.
Теорема (о сумме углов четырехугольника)
Сумма углов четырехугольника равна
Доказательство:
В данном четырехугольнике проведем диагональ, которая делит его на два треугольника (рис. 4). Поскольку сумма углов четырехугольника равна сумме всех углов треугольников и то есть равна Теорема доказана.
Пример:
Углы четырехугольника соседние с углом равны, а противолежащий угол в два раза больше угла (см. рис. 1). Найдите угол если
Решение:
Углами, соседними с углом являются углы а углом, противолежащим к — угол По условию задачи Поскольку сумма углов четырехугольника равна то Если градусная мера угла равна то градусная мера угла по условию равна Отсюда имеем: Следовательно,
Ответ:
Определение параллелограмма
Определение параллелограмма
Рассмотрим на плоскости две параллельные прямые, пересеченные двумя другими параллельными прямыми (рис. 7).
7).
В результате такого пересечения образуется четырехугольник, который имеет специальное название — параллелограмм.
Определение
Параллелограммом называется четырехугольник, противолежащие стороны которого попарно параллельны.
На рисунке 7 изображен параллелограмм в котором
Пример:
На рисунке 8 Докажите, что четырехугольник — параллелограмм.
Решение:
Из равенства треугольников следует равенство углов: Углы 1 и 2 являются внутренними накрест лежащими при прямых и секущей Аналогично углы 3 и 4 являются внутренними накрест лежащими при прямых и секущей По признаку параллельности прямых имеем: Следовательно, в четырехугольнике противолежащие стороны попарно параллельны, т.е. — параллелограмм по определению.
Как и в треугольнике, в параллелограмме можно провести высоты (рис. 9).
Определение
Высотой параллелограмма называется перпендикуляр, проведенный из точки одной стороны к прямой, которая содержит противолежащую сторону.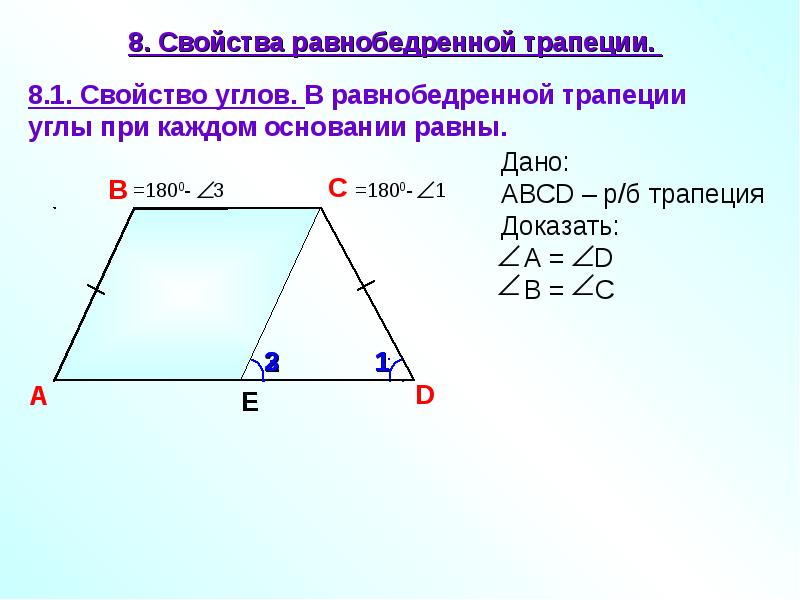
Очевидно, что к одной стороне параллелограмма можно провести бесконечно много высот (рис. 9, а),— все они будут равны как расстояния между параллельными прямыми, а из одной вершины параллелограмма можно провести две высоты к разным сторонам (рис. 9, б). Часто, говоря «высота параллелограмма», имеют в виду ее длину.
Свойства параллелограмма
Непосредственно из определения параллелограмма следует, что любые два его соседних угла являются внутренними односторонними при параллельных прямых, которые содержат противолежащие стороны. Это означает, что сумма двух соседних углов параллелограмма равна
Докажем еще несколько важных свойств сторон, углов и диагоналей параллелограмма.
Теорема (свойства параллелограмма)
В параллелограмме:
- противолежащие стороны равны;
- противолежащие углы равны;
- диагонали точкой пересечения делятся пополам.

Свойства 1 и 2 иллюстрирует рисунок 10, а, а свойство 3 — рисунок 10, б.
Доказательство:
Проведем в параллелограмме диагональ (рис. 11) и рассмотрим треугольники
У них сторона — общая, как внутренние накрест лежащие при параллельных прямых и секущей как внутренние накрест лежащие при параллельных прямых и секущей Следовательно, по второму признаку равенства треугольников. Отсюда, в частности, следует, что и А поскольку то Следовательно, свойства 1 и 2 доказаны.
Для доказательства свойства 3 проведем в параллелограмме диагонали которые пересекаются в точке (рис. 12).
Рассмотрим треугольники У них по доказанному, как внутренние накрест лежащие при параллельных прямых и секущей как внутренние накрест лежащие при параллельных прямых и секущей Следовательно, по второму признаку. Отсюда следует, что т. е. точка является серединой каждой из диагоналей и Теорема доказана полностью.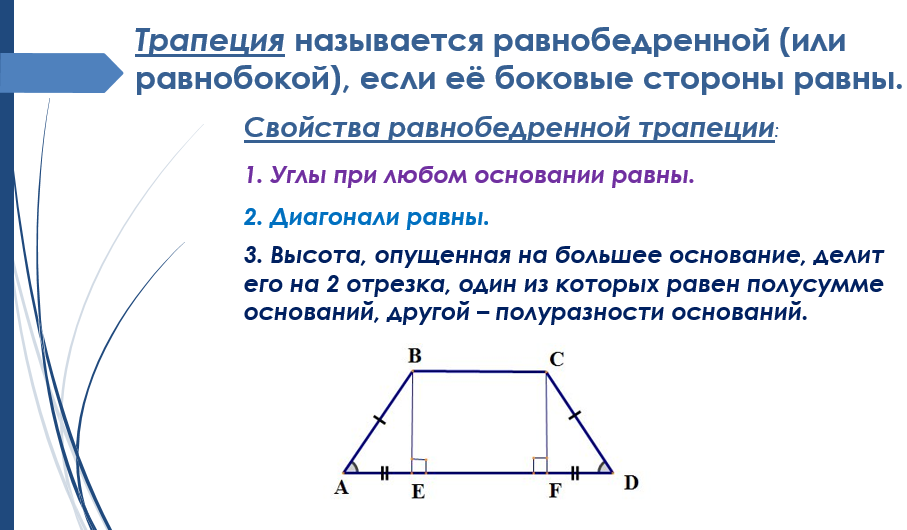
Сумма двух углов параллелограмма равна Найдите углы параллелограмма.
Решение:
Пусть дан параллелограмм Поскольку сумма двух соседних углов параллелограмма равна то данные углы могут быть только противолежащими. Пусть Тогда по свойству углов параллелограмма Сумма всех углов параллелограмма равна поэтому
Ответ:
Пример №2В параллелограмме биссектриса угла делит сторону пополам. Найдите периметр параллелограмма, если
Решение:
Пусть в параллелограмме биссектриса угла пересекает сторону в точке (рис. 13). Заметим, что поскольку — биссектриса угла как внутренние накрест лежащие при параллельных прямых и секущей Отсюда т.е. по признаку равнобедренного треугольника треугольник — равнобедренный с основанием значит, По условию Следовательно, поскольку противолежащие стороны параллелограмма равны, то
Ответ: 36 см.
Признаки параллелограмма
Теоремы о признаках параллелограмма
Для того чтобы использовать свойства параллелограмма, во многих случаях необходимо сначала убедиться, что данный четырехугольник действительно является параллелограммом. Это можно доказать либо по определению (см. задачу в п. 2.1), либо по признакам — условиям, гарантирующим, что данный четырехугольник — параллелограмм. Докажем признаки параллелограмма, которые чаще всего применяются на практике.
Теорема (признаки параллелограмма)
- Если две противолежащие стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм.
- Если противолежащие стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
- Если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Доказательство:
1) Пусть в четырехугольнике (рис. 15).
15).
Проведем диагональ и рассмотрим треугольники и Они имеют общую сторону по условию, как внутренние накрест лежащие при параллельных прямых и секущей Следовательно, по первому признаку равенства треугольников. Из равенства этих треугольников следует равенство углов 3 и 4. Но эти углы являются внутренними накрест лежащими при прямых и секущей Тогда по признаку параллельности прямых Таким образом, в четырехугольнике противолежащие стороны попарно параллельны, откуда следует, что — параллелограмм по определению.
2) Пусть в четырехугольнике (рис. 16).
Снова проведем диагональ и рассмотрим треугольники и В этом случае они равны по третьему признаку: сторона — общая, и по условию. Из равенства треугольников следует равенство углов 1 и 2, которые являются внутренними накрест лежащими при прямых и секущей По признаку параллельности прямых Следовательно, в четырехугольнике стороны параллельны и равны, и по только что доказанному признаку 1 — параллелограмм.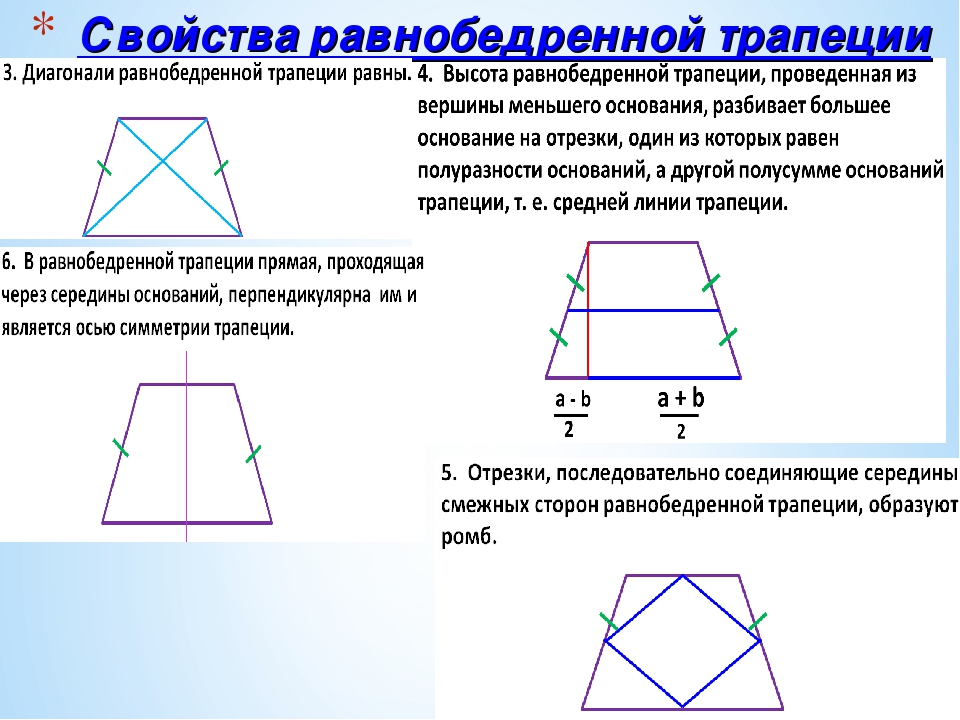
3) Пусть в четырехугольнике диагонали пересекаются в точке и (рис. 17). Рассмотрим треугольники Эти треугольники равны по первому признаку: как вертикальные, а и по условию. Следовательно, равны и соответствующие стороны и углы этих треугольников: Тогда и — параллелограмм по признаку 1.
Теорема доказана полностью.
Пример №3В параллелограмме точки — середины сторон соответственно (рис. 18). Докажите, что четырехугольник —параллелограмм.
Решение:
Рассмотрим четырехугольник Стороны и параллельны, т.к. лежат на прямых, содержащих противолежащие стороны параллелограмма Кроме того, как половины равных сторон параллелограмма Таким образом, в четырехугольнике две стороны параллельны и равны. Следовательно, четырехугольник — параллелограмм.
Попробуйте самостоятельно найти другие способы решения этой задачи, основанные на применении других признаков и определения параллелограмма.
Необходимые и достаточные условия
Каждый из признаков параллелограмма указывает на определенную особенность, наличия которой в четырехугольнике достаточно для того, чтобы утверждать, что он является параллелограммом. Вообще в математике признаки иначе называют достаточными условиями. Например, перпендикулярность двух прямых третьей — достаточное условие параллельности данных двух прямых.
В отличие от признаков, свойства параллелограмма указывают на ту особенность, которую обязательно имеет любой параллелограмм. Свойства иначе называют необходимыми условиями. Поясним такое название примером: равенство двух углов необходимо для того, чтобы углы были вертикальными, ведь если этого равенства нет, вертикальными такие углы быть не могут.
В случае верности теоремы «Если то утверждение является достаточным условием для утверждения а утверждение — необходимым условием для утверждения Схематически это можно представить так:
Таким образом, необходимые условия (свойства) параллелограмма следуют из того, что данный четырехугольник — параллелограмм; из достаточных условий (признаков) следует то, что данный четырехугольник — параллелограмм.
Сравнивая свойства и признаки параллелограмма, нетрудно заметить, что одно и то же условие (например, попарное равенство противолежащих сторон) является и свойством, и признаком параллелограмма. В таком случае говорят, что условие является необходимым и достаточным. Необходимое и достаточное условие иначе называют критерием. Например, равенство двух углов треугольника — критерий равнобедренного треугольника.
Немало примеров необходимых и достаточных условий можно найти в других науках и в повседневной жизни. Все мы знаем, что воздух — необходимое условие для жизни человека, но не достаточное (человеку для жизни нужно еще много чего, среди прочего — пища). Выигрыш в лотерею — достаточное условие для материального обогащения человека, но оно не является необходимым — ведь улучшить свое финансовое положение можно и другим способом. Попробуйте самостоятельно найти несколько примеров необходимых и достаточных условий.
Виды параллелограммов
Прямоугольник
Определение
Прямоугольником называется параллелограмм, у которого все углы прямые.
На рисунке 28 изображен прямоугольник
Поскольку прямоугольник является частным случаем параллелограмма, он имеет все свойства параллелограмма: противолежащие стороны прямоугольника параллельны и равны, противолежащие углы равны, диагонали точкой пересечения делятся пополам и т.д. Однако прямоугольник имеет некоторые особые свойства. Докажем одно из них.
Теорема (свойство прямоугольника)
Диагонали прямоугольника равны.
Доказательство:
Пусть дан прямоугольник с диагоналями (рис. 29). Треугольники и прямоугольные и равны по двум катетам — общий, как противолежащие стороны прямоугольника). Отсюда следует равенство гипотенуз этих треугольников, т. е. что и требовалось доказать.
Имеет место и обратное утверждение (признак прямоугольника): если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником. Докажите это утверждение самостоятельно.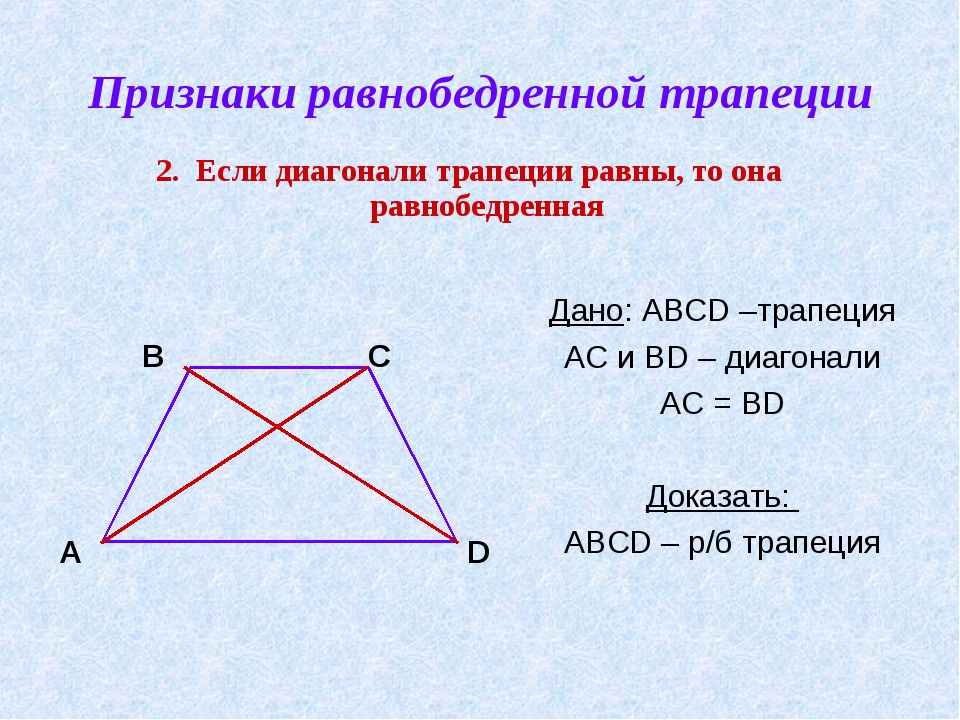 Таким образом, можно утверждать, что равенство диагоналей параллелограмма — необходимое и достаточное условие (критерий) прямоугольника.
Таким образом, можно утверждать, что равенство диагоналей параллелограмма — необходимое и достаточное условие (критерий) прямоугольника.
Опорная задача
Если все углы четырехугольника прямые, то этот четырехугольник — прямоугольник. Докажите.
Решение:
Пусть в четырехугольнике (см. рис. 28). Углы являются внутренними односторонними при прямых и секущей Поскольку сумма этих углов составляет то по признаку параллельности прямых Аналогично доказываем параллельность сторон Следовательно, по определению параллелограмма — параллелограмм. А поскольку все углы этого параллелограмма прямые, то — прямоугольник по определению.
Ромб
Определение
Ромбом называется параллелограмм, у которого все стороны равны.
На рисунке 30 изображен ромб
Он обладает всеми свойствами параллелограмма, а также некоторыми дополнительными свойствами, которые мы сейчас докажем.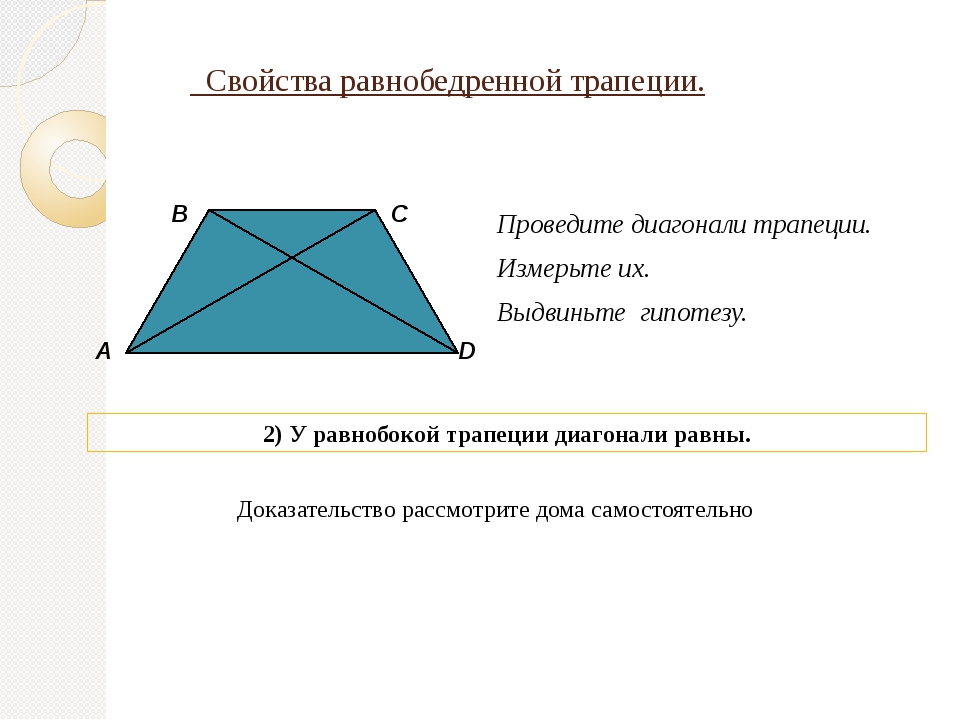
Теорема (свойства ромба)
Диагонали ромба перпендикулярны и делят его углы пополам.
Эти свойства ромба иллюстрируются рисунком 31.
Доказательство:
Пусть диагонали ромба пересекаются в точке (рис. 32). Поскольку стороны ромба равны, то треугольник равнобедренный с основанием а по свойству диагоналей параллелограмма точка — середина Следовательно, отрезок — медиана равнобедренного треугольника, которая одновременно является его высотой и биссектрисой. Это означает, что т.е. диагонали ромба перпендикулярны, и— биссектриса угла
Аналогично доказываем, что диагонали ромба являются биссектрисами и других его углов. Теорема доказана.
Опорная задача
Если все стороны четырехугольника равны, то этот четырехугольник — ромб. Докажите.
Решение:
Очевидно, что в четырехугольнике, все стороны которого равны, попарно равными являются и противолежащие стороны. Следовательно, по признаку параллелограмма такой четырехугольник — параллелограмм, а по определению ромба параллелограмм, у которого все стороны равны, является ромбом.
Следовательно, по признаку параллелограмма такой четырехугольник — параллелограмм, а по определению ромба параллелограмм, у которого все стороны равны, является ромбом.
Решая задачи, помещенные в конце этого параграфа, вы докажете другие признаки прямоугольника и ромба.
Квадрат
На рисунке 33 изображен еще один вид параллелограмма — квадрат.
Определение
Квадратом называется прямоугольник, у которого все стороны равны.
Иначе можно сказать, что квадрат — это прямоугольник, который является ромбом. Действительно, поскольку квадрат является прямоугольником и ромбом и, конечно же, произвольным параллелограммом, то:
- все стороны квадрата равны, а противолежащие стороны параллельны;
- все углы квадрата прямые;
- диагонали квадрата равны, перпендикулярны, делят углы квадрата пополам и делятся точкой пересечения пополам.
Связь между отдельными видами параллелограммов. Равносильные утверждения
Исходя из определений произвольного параллелограмма и его отдельных видов, мы можем схематически отобразить связь между ними (рис. 34).
34).
На схеме представлены множества параллелограммов, прямоугольников и ромбов. Такой способ наглядного представления множеств называют диаграммами Эйлера — Венна. Диаграмма Эйлера — Венна для параллелограммов демонстрирует, что множества прямоугольников и ромбов являются частями (подмножествами) множества параллелограммов, а множество квадратов — общей частью (пересечением) множеств прямоугольников и ромбов. Диаграммы Эйлера — Венна часто используют для подтверждения или проверки правильности логических рассуждений.
Подытоживая материал этого параграфа, обратим также внимание на то, что возможно и другое определение квадрата: квадратом называется ромб с прямыми углами. В самом деле, оба приведенных определения описывают одну и ту же фигуру. Такие определения называют равносильными. Вообще два утверждения называются равносильными, если они или оба выполняются, или оба не выполняются. Например, равносильными являются утверждения «В треугольнике две стороны равны» и «В треугольнике два угла равны», ведь оба они верны, если рассматривается равнобедренный треугольник, и оба ложны, если речь идет о разностороннем треугольнике.
Например, равносильными являются утверждения «В треугольнике две стороны равны» и «В треугольнике два угла равны», ведь оба они верны, если рассматривается равнобедренный треугольник, и оба ложны, если речь идет о разностороннем треугольнике.
Равносильность двух утверждений также означает, что любое из них является необходимым и достаточным условием для другого. В самом деле, рассмотрим равносильные утверждения «Диагонали параллелограмма равны» и «Параллелограмм имеет прямые углы». Из того, что диагонали параллелограмма равны, следует, что он является прямоугольником, т.е. имеет прямые углы, и наоборот: параллелограмм с прямыми углами является прямоугольником, т.е. имеет равные диагонали. На этом примере легко проследить логические шаги перехода от признаков фигуры к ее определению и далее — к свойствам. Такой переход довольно часто приходится выполнять в процессе решения задач.
Трапеция
Как известно, любой параллелограмм имеет две пары параллельных сторон. Рассмотрим теперь четырехугольник, который имеет только одну пару параллельных сторон.
Определение
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны трапеции называют ее основаниями, а непараллельные стороны — боковыми сторонами. На рисунке 37 в трапеции стороны являются основаниями, а — боковыми сторонами.
Углы, прилежащие к одной боковой стороне, являются внутренними односторонними при параллельных прямых, на которых лежат основания трапеции. По теореме о свойстве параллельных прямых из этого следует, что сумма углов трапеции, прилежащих к боковой стороне, равна На рисунке 37
Определение
Высотой трапеции называется перпендикуляр, проведенный из точки одного основания к прямой, содержащей другое основание.
Очевидно, что в трапеции можно провести бесконечно много высот (рис. 38),— все они равны как расстояния между параллельными прямыми.
Чаще всего в процессе решения задач высоты проводят из вершин углов при меньшем основании трапеции.
Частные случаи трапеций
Как среди треугольников и параллелограммов, так и среди трапеций выделяются отдельные виды, обладающие дополнительными свойствами.
Определение
Прямоугольной трапецией называется трапеция, в которой одна из боковых сторон перпендикулярна основаниям.
На рисунке 39 изображена прямоугольная трапеция. У нее два прямых угла при меньшей боковой стороне. Эта сторона одновременно является и высотой трапеции.
Определение
Равнобедренной трапецией называется трапеция, в которой боковые стороны равны.
На рисунке 40 изображена равнобедренная трапеция с боковыми сторонами и Иногда равнобедренную трапецию также называют равнобокой или равнобочной.
У равнобедренной трапеции так же, как и у равнобедренного треугольника, углы при основании равны.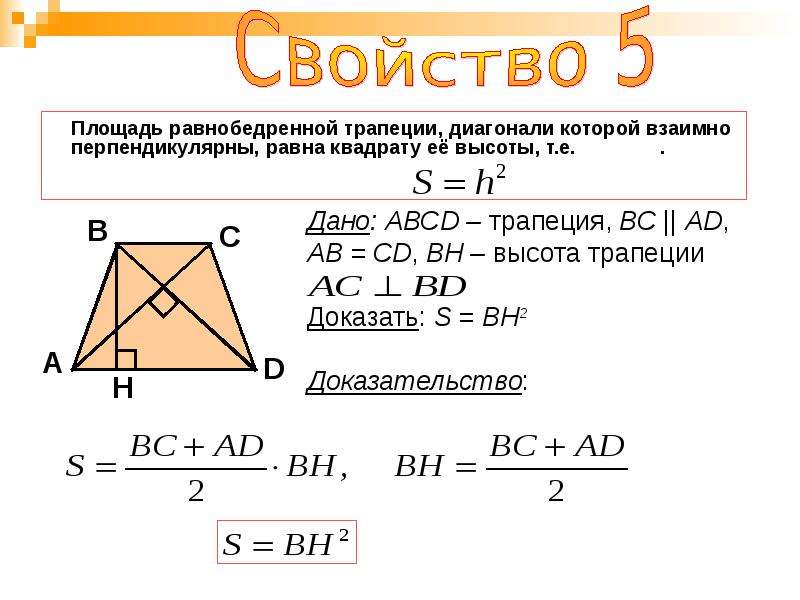 Докажем это в следующей теореме.
Докажем это в следующей теореме.
Теорема (свойство равнобедренной трапеции)
В равнобедренной трапеции углы при основании равны.
Доказательство:
Пусть — данная трапеция,
Перед началом доказательства заметим, что этой теоремой утверждается равенство углов при каждом из двух оснований трапеции, т. е. необходимо доказать, что
Проведем высоты из вершин тупых углов и рассмотрим прямоугольные треугольники (рис. 41). У них как боковые стороны равнобедренной трапеции, как расстояния между параллельными прямыми Следовательно, по гипотенузе и катету. Отсюда следует, что Углы трапеции также равны, поскольку они дополняют равные углы
Теорема доказана.
Имеет место также обратное утверждение (признак равнобедренной трапеции):
- если в трапеции углы при основании равны, то такая трапеция является равнобедренной.
Докажите этот факт самостоятельно.
Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Найдите углы трапеции.
Решение:
Пусть дана равнобедренная трапеция в которой (рис. 42). По условию задачи треугольник равнобедренный с основанием с другой стороны, как внутренние накрест лежащие при параллельных прямых и и секущей Пусть градусная мера угла 1 равна тогда в данной трапеции Поскольку сумма углов, прилежащих к боковой стороне, составляет имеем: Следовательно,
Ответ:
Построение параллелограммов и трапеций
Задачи на построение параллелограммов и трапеций часто решают методом вспомогательного треугольника. Напомним, что для этого необходимо выделить в искомой фигуре треугольник, который можно построить по имеющимся данным. Построив его, получаем две или три вершины искомого четырехугольника, а остальные вершины находим по данным задачи.
Постройте параллелограмм по двум диагоналям и углу между ними.
Решение:
Пусть — данные диагонали параллелограмма, — угол между ними. Анализ
Пусть параллелограмм построен (рис. 43).
Треугольник можно построить по двум сторонам и углу между ними
Таким образом, мы получим вершины искомого параллелограмма.
Вершины можно получить, «удвоив» отрезки
Построение
1. Разделим отрезки пополам.
2. Построим треугольник по двум сторонам и углу между ними.
3. На лучах отложим отрезки и
4. Последовательно соединим точки
Доказательство:
Четырехугольник — параллелограмм, поскольку по построению его диагонали точкой пересечения делятся пополам. В этом параллелограмме (по построению),
Исследование
Задача имеет единственное решение при любых значениях
В некоторых случаях для построения вспомогательного треугольника на рисунке-эскизе необходимо провести дополнительные линии.
Постройте трапецию по четырем сторонам.
Решение:
Пусть — основания искомой трапеции, — ее боковые стороны.
Анализ
Пусть искомая трапеция построена (рис. 44).
Проведем через вершину прямую параллельную Тогда — параллелограмм по определению, следовательно, Кроме того, следовательно, Вспомогательный треугольник можно построить по трем сторонам. После этого для получения вершин надо отложить на луче и на луче с началом в точке параллельном отрезки длиной
Построение
1. Построим отрезок
2. Построим треугольник по трем сторонам
3. Построим луч, проходящий через точку и параллельный При этом построенный луч и луч должны лежать по одну сторону от прямой
4. На луче от точки отложим отрезок на луче с началом — отрезок
5. Соединим точки
Доказательство:
По построению следовательно, — параллелограмм по признаку. Отсюда Кроме того, Следовательно, — искомая трапеция.
Отсюда Кроме того, Следовательно, — искомая трапеция.
Исследование
Задача имеет единственное решение, если числа удовлетворяют неравенству треугольника.
Теорема Фалеса
Для дальнейшего изучения свойств трапеции докажем важную теорему.
Теорема (Фалеса)
Параллельные прямые, которые пересекают стороны угла и отсекают на одной из них равные отрезки, отсекают равные отрезки и на другой стороне.
Доказательство:
Пусть — точки пересечения параллельных прямых с одной из сторон данного угла, а — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если то (рис. 46).
Проведем через точку прямую параллельную (рис. 47).
Четырехугольники — параллелограммы по определению. Тогда а поскольку
Рассмотрим треугольники У них по доказанному, как вертикальные, a как внутренние накрест лежащие при параллельных прямых и секущей Следовательно, по второму признаку, откуда
Теорема доказана.
Заметим, что в условии данной теоремы вместо сторон угла можно рассматривать две произвольные прямые, поэтому теорема Фалеса может формулироваться и следующим образом: параллельные прямые, которые пересекают две данные прямые и отсекают на одной из них равные отрезки, отсекают равные отрезки и на другой прямой.
Пример №7Разделите данный отрезок на равных частей.
Решение:
Решим задачу для т.е. разделим данный отрезок на три равные части (рис. 48).
Для этого проведем из точки произвольный луч, не дополнительный к лучу и отложим на нем равные отрезки Проведем прямую и параллельные ей прямые через точки По теореме Фалеса эти прямые делят отрезок на три равные части. Аналогично можно разделить произвольный отрезок на любое количество равных частей.
Средняя линия треугольника
Теорема Фалеса помогает исследовать еще одну важную линию в треугольнике.
Определение
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.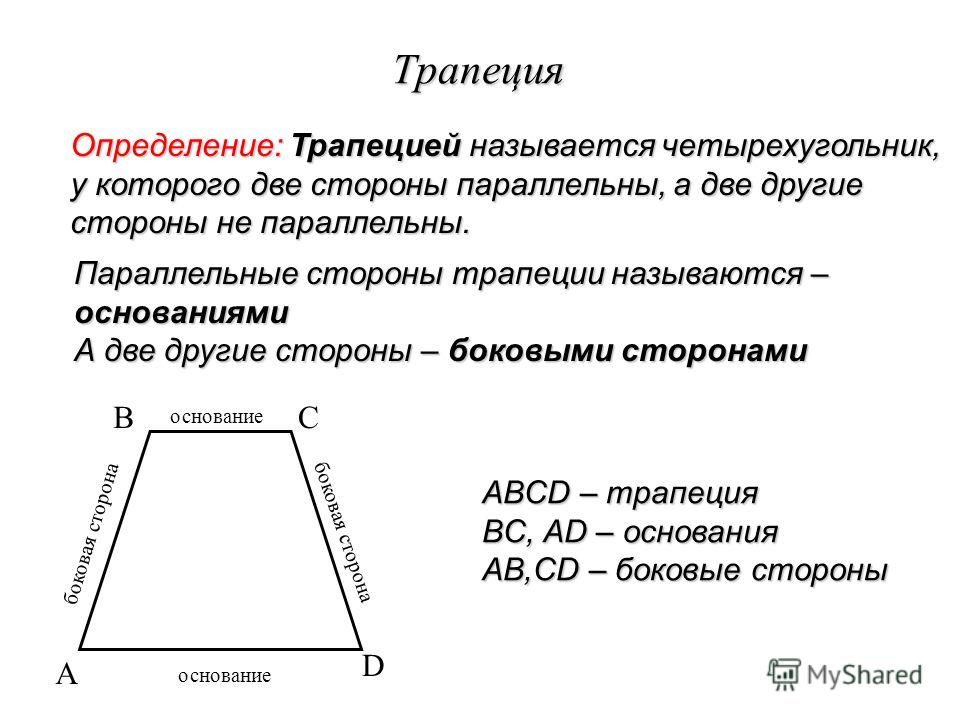
На рисунке 49, а отрезок — средняя линия треугольника В любом треугольнике можно провести три средние линии (рис. 49, б).
Теорема (свойство средней линии треугольника)
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Доказательство:
Пусть — средняя линия треугольника (рис. 50). Докажем сначала, что Проведем через точку прямую, параллельную По теореме Фалеса она пересечет отрезок в его середине, т.е. будет содержать отрезок Следовательно,
Проведем теперь среднюю линию По только что доказанному она будет параллельна стороне Четырехугольник с попарно параллельными сторонами по определению является параллелограммом, откуда А поскольку точка — середина то
Теорема доказана.
Опорная задача (теорема Вариньона) Середины сторон четырехугольника являются вершинами параллелограмма. Докажите.
Решение:
Пусть точки — середины сторон четырехугольника (рис. 51). Проведем диагональ Отрезки — средние линии треугольников соответственно. По свойству средней линии треугольника они параллельны стороне и равны ее половине, т.е. параллельны и равны между собой. Тогда по признаку параллелограмма четырехугольник — параллелограмм.
51). Проведем диагональ Отрезки — средние линии треугольников соответственно. По свойству средней линии треугольника они параллельны стороне и равны ее половине, т.е. параллельны и равны между собой. Тогда по признаку параллелограмма четырехугольник — параллелограмм.
Средняя линия трапеции
Определение
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
На рисунке 52 отрезок — средняя линия трапеции
Теорема (свойство средней линии трапеции) Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть — средняя линия трапеции с основаниями (рис. 53).
Проведем прямую и отметим точку — точку пересечения прямых Рассмотрим треугольники У них поскольку — середина как вертикальные, a как внутренние накрест лежащие при параллельных прямых и секущей Следовательно, по второму признаку, откуда Тогда по определению — средняя линия треугольника По свойству средней линии треугольника поэтому и Кроме того, из доказанного равенства треугольников следует, что откуда По свойству средней линии треугольника
Теорема доказана.
Через точки, делящие боковую сторону трапеции на три равные части, проведены прямые, параллельные основаниям трапеции. Найдите длины отрезков этих прямых, заключенных внутри трапеции, если ее основания равны 2 м и 5 м.
Решение:
Пусть в трапеции (рис. 54).
По теореме Фалеса параллельные прямые, которые проходят через точки отсекают на боковой стороне равные отрезки, т.е. Тогда по определению — средняя линия трапеции — средняя линия трапеции Пусть По свойству средней линии трапеции имеем систему:
Ответ: 3 м и 4 м.
Вписанные углы
Градусная мера дуги
В седьмом классе изучение свойств треугольников завершалось рассмотрением описанной и вписанной окружностей. Но перед тем как рассмотреть описанную и вписанную окружности для четырехугольника, нам необходимо остановиться на дополнительных свойствах углов.
До сих пор мы изучали только те углы, градусная мера которых не превышала Расширим понятие угла и введем в рассмотрение вместе с самим углом части, на которые он делит плоскость.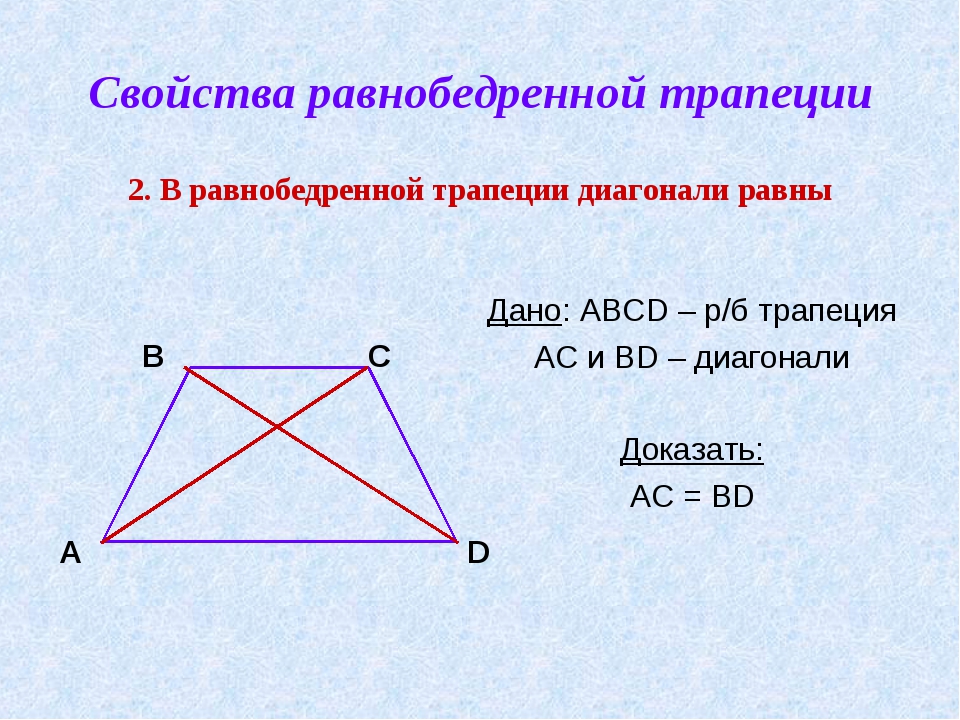
На рисунке 58 угол делит плоскость на две части, каждая из которых называется плоским углом. Их градусные меры равны
Используем понятие плоского угла для определения центрального угла в окружности.
Определение
Центральным углом в окружности называется плоский угол с вершиной в центре окружности.
На рисунке 59, а, б стороны угла с вершиной в центре окружности пересекают данную окружность в точках При этом образуются две дуги, одна из которых меньше полуокружности (на ней обозначена промежуточная точка рис. 59, а), а другая — больше полуокружности (на ней обозначена промежуточная точка рис. 59, б).
Для того чтобы уточнить, какой из двух плоских углов со сторонами мы рассматриваем как центральный, мы будем указывать дугу окружности, которая соответствует данному центральному углу (т.е. содержится внутри него).
На рисунке 59, а центральному углу обозначенному дужкой, соответствует дуга а на рисунке 59, б — дуга В случае, когда лучи дополнительные, соответствующая дуга является полуокружностью (рис.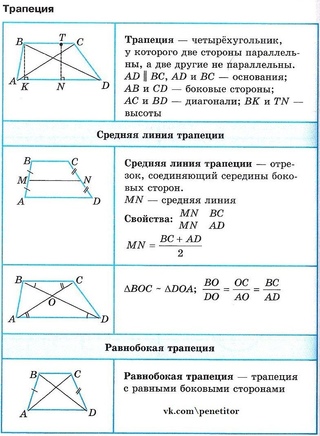 59, в).
59, в).
Определение
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Градусную меру дуги, как и саму дугу, обозначают так: Например, на рисунке 59, в т. е. градусная мера полуокружности составляет Очевидно, что градусная мера дуги всей окружности составляет
Концы хорды делят окружность на две дуги — (рис. 59, г). Говорят, что эти дуги стягиваются хордой
Вписанный угол
Определение
Вписанным углом называется угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
На рисунке 60 изображен вписанный угол Его вершина лежит на окружности, а стороны пересекают окружность в точках и Дуга (на рисунке она выделена) лежит внутри этого угла. В таком случае говорят, что вписанный угол опирается на дугу
Теорема (о вписанном угле)
Вписанный угол измеряется половиной дуги, на которую он опирается.
Доказательство:
Пусть в окружности с центром вписанный угол опирается на дугу Докажем, что Рассмотрим три случая расположения центра окружности относительно данного вписанного угла (рис. 61).
1) Пусть центр окружности лежит на одной из сторон данного угла (рис. 61, а). В этом случае центральный угол является внешним углом при вершине равнобедренного треугольника По теореме о внешнем угле треугольника А поскольку углы 1 и 2 равны как углы при основании равнобедренного треугольника, то
т.е.
2) Пусть центр окружности лежит внутри угла (рис. 61, б). Луч делит угол на два угла. По только что доказанному следовательно,
3) Аналогично в случае, когда центр окружности лежит вне вписанного угла (рис. 60, б),
Теорема доказана.
Только что доказанную теорему можно сформулировать иначе.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
Пример №9Найдите угол если (рис.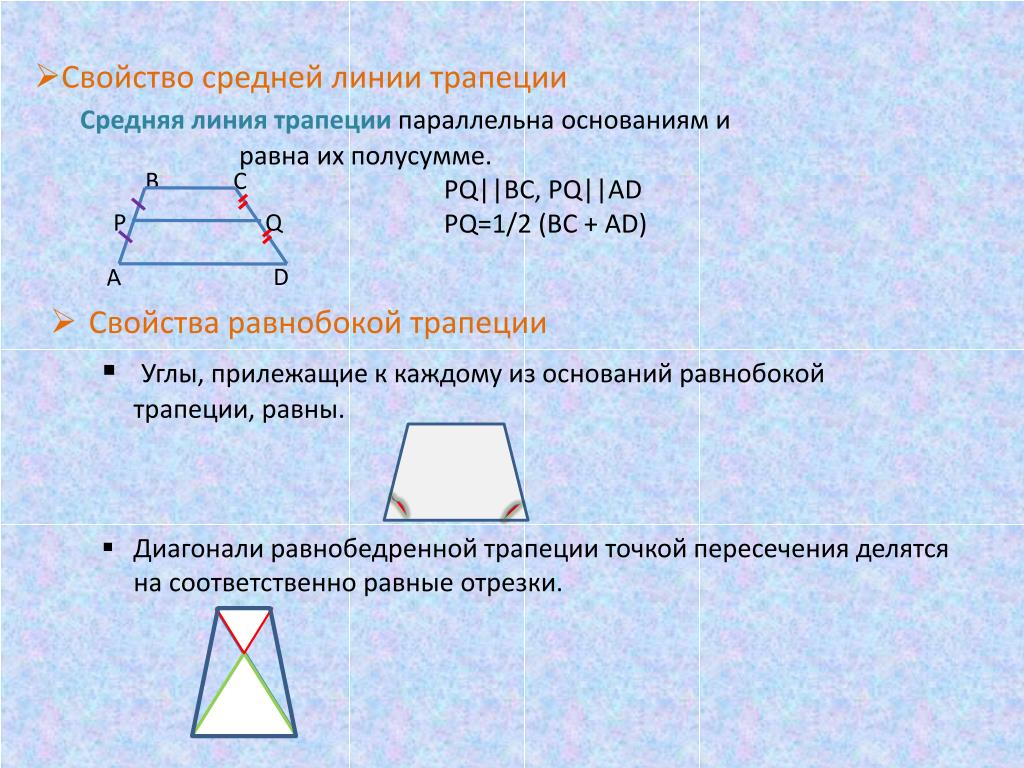 62).
62).
Решение:
Для того чтобы найти угол необходимо найти градусную меру дуги на которую он опирается. Но непосредственно по данным задачи мы можем найти только градусную меру дуги на которую опирается угол из теоремы о вписанном угле Заметим, что дуги вместе составляют полуокружность, т.е. следовательно, Тогда по теореме о вписанном угле
Ответ:
Следствия теоремы о вписанном угле
По количеству и значимости следствий теорема о вписанном угле является одной из «богатейших» геометрических теорем. Сформулируем наиболее важные из этих следствий.
Следствие 1
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Действительно, по теореме о вписанном угле градусная мера каждого из вписанных углов на рисунке 63 равна половине дуги
Следствие 2
Вписанный угол, опирающийся на полуокружность,— прямой, и наоборот: любой прямой вписанный угол опирается на полуокружность.
Действительно, поскольку градусная мера полуокружности равна то угол который опирается на полуокружность, равен (рис. 64). Обоснование обратного утверждения проведите самостоятельно.
Следствие 3
Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Первое из приведенных утверждений вытекает из следствия 2. Если в треугольнике угол прямой (рис. 65, а), то дуга на которую опирается этот угол, является полуокружностью.
Тогда гипотенуза — диаметр описанной окружности, т.е. середина гипотенузы — центр окружности. Утверждение о длине медианы следует из равенства радиусов:
Отметим еще один интересный факт: медиана прямоугольного треугольника, проведенная к гипотенузе, делит данный треугольник на два равнобедренных треугольника с общей боковой стороной. Из этого, в частности, следует, что углы, на которые медиана делит прямой угол, равны острым углам треугольника (рис. 65, б).
Из этого, в частности, следует, что углы, на которые медиана делит прямой угол, равны острым углам треугольника (рис. 65, б).
В качестве примера применения следствий теоремы о вписанном угле приведем другое решение задачи, которую мы рассмотрели в п. 7.2.
Пример №10Найдите угол если (см. рис. 62).
Решение:
Проведем хорду (рис. 66).
Поскольку вписанный угол опирается на полуокружность, то по следствию 2 Значит, треугольник прямоугольный, тогда По следствию 1 углы равны, поскольку оба они опираются на дугу Следовательно,
Ответ:
Вписанные четырехугольники
Определение
Четырехугольник называется вписанным в окружность, если все его вершины лежат на этой окружности.
Четырехугольник на рисунке 72 является вписанным в окружность. Иначе говорят, что окружность описана около четырехугольника.
Как известно, около любого треугольника можно описать окружность. Для четырехугольника это можно сделать не всегда. Докажем свойство и признак вписанного четырехугольника.
Теорема (овписанном четырехугольнике)
- Сумма противолежащих углов вписанного четырехугольника равна (свойство вписанного четырехугольника).
- Если сумма противолежащих углов четырехугольника равна то около него можно описать окружность (признак вписанного четырехугольника).
Доказательство:
1) Свойство. Пусть четырехугольник вписан в окружность (рис. 72). По теореме о вписанном угле
Следовательно,
Аналогично доказываем, что
2) Признак. Пусть в четырехугольнике Опишем окружность около треугольника и докажем от противного, что вершина не может лежать ни внутри этой окружности, ни вне ее. Пусть точка лежит внутри окружности, а точка — точка пересечения луча с дугой (рис.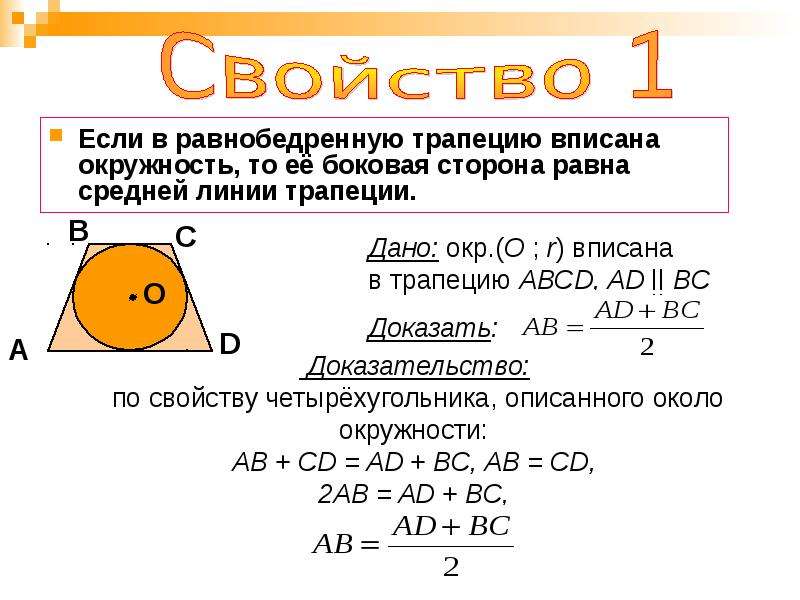 73).
73).
Тогда четырехугольник — вписанный. По условию а по только что доказанному свойству вписанного четырехугольника т.е. Но угол четырехугольника — внешний угол треугольника и по теореме о внешнем угле треугольника он должен быть больше угла Следовательно, мы пришли к противоречию, т.е. точка не может лежать внутри окружности. Аналогично можно доказать, что точка не может лежать вне окружности. Тогда точка лежит на окружности, т.е. около четырехугольника можно описать окружность.
Теорема доказана.
Следствие 1
Около любого прямоугольника можно описать окружность.
Если параллелограмм вписан в окружность, то он является прямоугольником
Прямоугольник, вписанный в окружность, изображен на рисунке 74.
Центр описанной окружности является точкой пересечения диагоналей прямоугольника (см. задачу 255).
Следствие 2
Около равнобедренной трапеции можно описать окружность.
Если трапеция вписана в окружность, то она равнобедренная.
Равнобедренная трапеция, вписанная в окружность, изображена на рисунке 75.
Описанные четырехугольники
Определение
Четырехугольник называется описанным около окружности, если все его стороны касаются этой окружности.
Четырехугольник на рисунке 76 является описанным около окружности. Иначе говорят, что окружность вписана в четырехугольник.
Оказывается, что не в любой четырехугольник можно вписать окружность. Докажем соответствующие свойство и признак.
Теорема (об описанном четырехугольнике)
- В описанном четырехугольнике суммы противолежащих сторон равны (свойство описанного четырехугольника).
- Если в четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность (признак описанного четырехугольника).
Доказательство:
1) Свойство. Пусть стороны четырехугольника касаются вписанной окружности в точках (рис. 76).
Пусть стороны четырехугольника касаются вписанной окружности в точках (рис. 76).
По свойству отрезков касательных С учетом обозначений на рисунке
2) Признак. Пусть в четырехугольнике с наименьшей стороной Поскольку по теореме о биссектрисе угла точка (точка пересечения биссектрис углов равноудалена от сторон то можно построить окружность с центром которая касается этих трех сторон (рис. 77, а). Докажем от противного, что эта окружность касается также стороны
Предположим, что это не так. Тогда прямая либо не имеет общих точек с окружностью, либо является секущей окружности. Рассмотрим первый случай (рис. 77, б). Проведем через точку касательную к окружности, которая пересекает сторону в точке Тогда по свойству описанного четырехугольника Но по условию Вычитая из второго равенства первое, имеем: т.е. что противоречит неравенству треугольника для треугольника
Таким образом, наше предположение неверно. Аналогично можно доказать, что прямая не может быть секущей окружности. Следовательно, окружность касается стороны т. е. четырехугольник описанный. Теорема доказана.
Следовательно, окружность касается стороны т. е. четырехугольник описанный. Теорема доказана.
Замечание. Напомним, что в данной теореме рассматриваются только выпуклые четырехугольники.
Следствие
В любой ромб можно вписать окружность. Если в параллелограмм вписана окружность, то он является ромбом
Ромб, описанный около окружности, изображен на рисунке 78. Центр вписанной окружности является точкой пересечения диагоналей ромба (см. задачу 265, а).
Пример №11В равнобедренную трапецию с боковой стороной 6 см вписана окружность. Найдите среднюю линию трапеции.
Решение:
Пусть — данная равнобедренная трапеция с основаниями По свойству описанного четырехугольника Средняя линия трапеции равна т.е. равна 6 см.
Ответ: 6 см
Геометрические софизмы
Многим из вас, наверное, известна древнегреческая история об Ахиллесе, который никак не может догнать черепаху. История математики знает немало примеров того, как ложные утверждения и ошибочные результаты выдавались за истинные, а их опровержение давало толчок настоящим математическим открытиям. Но даже ошибки и неудачи могут принести пользу математикам. Эти ошибки остались в учебниках и пособиях в виде софизмов — заведомо ложных утверждений, доказательства которых на первый взгляд кажутся правильными, но на самом деле таковыми не являются. Поиск и анализ ошибок, содержащихся в этих доказательствах, часто позволяют определить причины ошибок в решении других задач. Поэтому в процессе изучения геометрии софизмы иногда даже более поучительны и полезны, чем «безошибочные» задачи и доказательства.
История математики знает немало примеров того, как ложные утверждения и ошибочные результаты выдавались за истинные, а их опровержение давало толчок настоящим математическим открытиям. Но даже ошибки и неудачи могут принести пользу математикам. Эти ошибки остались в учебниках и пособиях в виде софизмов — заведомо ложных утверждений, доказательства которых на первый взгляд кажутся правильными, но на самом деле таковыми не являются. Поиск и анализ ошибок, содержащихся в этих доказательствах, часто позволяют определить причины ошибок в решении других задач. Поэтому в процессе изучения геометрии софизмы иногда даже более поучительны и полезны, чем «безошибочные» задачи и доказательства.
Рассмотрим пример геометрического софизма, связанного с четырехугольниками, вписанными в окружность.
Окружность имеет два центра.
Доказательство:
Обозначим на сторонах произвольного угла точки и проведем через эти точки перпендикуляры к сторонам соответственно (рис.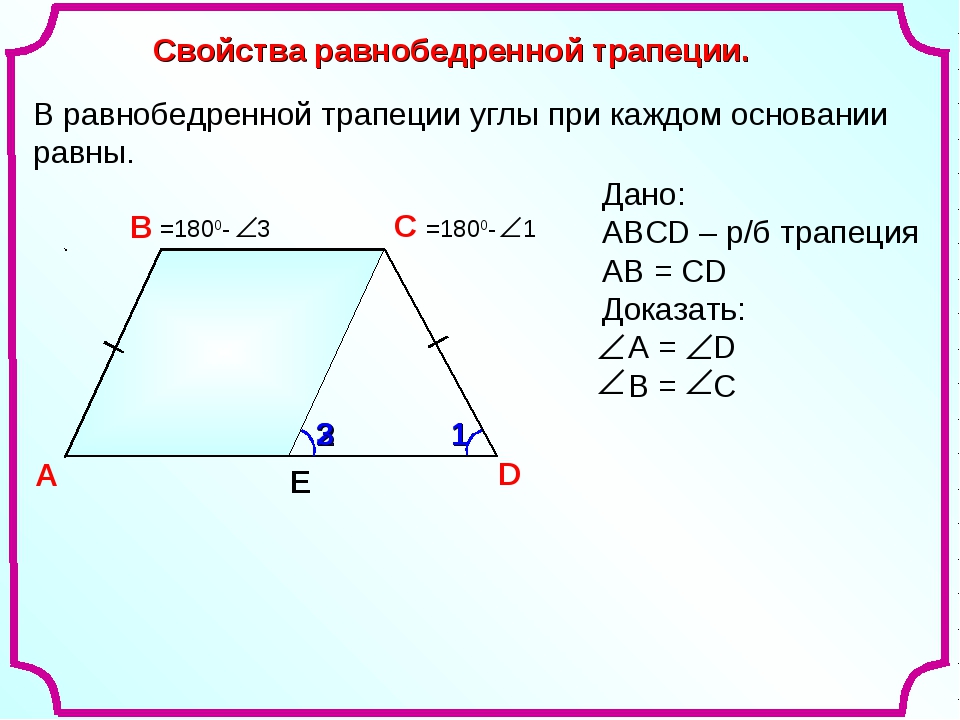 79).
79).
Эти перпендикуляры должны пересекаться (ведь если бы они были параллельны, то параллельными были бы и стороны данного угла — обоснуйте это самостоятельно). Обозначим точку — точку пересечения перпендикуляров.
Через точки не лежащие на одной прямой, проведем окружность (это можно сделать, поскольку окружность, описанная около треугольника существует и является единственной). Обозначим точки — точки пересечения этой окружности со сторонами угла Прямые углы являются вписанными в окружность. Значит, по следствию теоремы о вписанных углах, отрезки являются диаметрами окружности, которые имеют общий конец но не совпадают. Тогда их середины являются двумя разными центрами одной окружности, т.е. окружность имеет два центра.
Ошибка этого «доказательства» заключается в неправильности построений на рисунке 79. В четырехугольнике т.е. он вписан в окружность. Это означает, что в ходе построений окружность, проведенная через точки обязательно пройдет через точку В таком случае отрезки совпадут с отрезком середина которого и является единственным центром построенной окружности.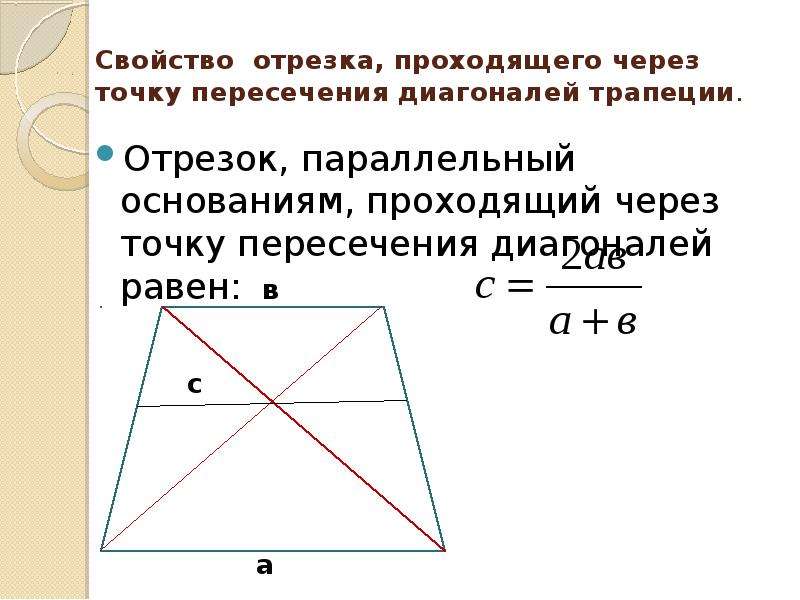
Среди задач к этому и следующим параграфам вы найдете и другие примеры геометрических софизмов и сможете самостоятельно потренироваться в их опровержении. Надеемся, что опыт, который вы при этом приобретете, поможет в дальнейшем избежать подобных ошибок при решении задач.
Четырехугольник и окружность в задачах. Метод вспомогательной окружности
При решении задач об окружностях и четырехугольниках иногда следует использовать специальные подходы. Один из них заключается в рассмотрении вписанного треугольника, вершины которого являются вершинами данного вписанного четырехугольника.
Пример №12Найдите периметр равнобедренной трапеции, диагональ которой перпендикулярна боковой стороне и образует с основанием угол если радиус окружности, описанной около трапеции, равен 8 см.
Решение:
Пусть дана вписанная трапеция (рис. 80).
Заметим, что окружность, описанная около трапеции, описана также и около прямоугольного треугольника значит, ее центром является середина гипотенузы Тогда В треугольнике как катет, противолежащий углу Поскольку в прямоугольном треугольнике то углы при большем основании трапеции равны как внутренние накрест лежащие при параллельных прямых и секущей Следовательно, в треугольнике два угла равны, т. е. он является равнобедренным с основанием откуда Тогда
е. он является равнобедренным с основанием откуда Тогда
Ответ: 40 см.
Особенно интересным и нестандартным является применение окружности (как описанной, так и вписанной) при решении задач, в условиях которых окружность вообще не упоминается.
Пример №13Из точки лежащей на катете прямоугольного треугольника проведен перпендикуляр к гипотенузе (рис. 81). Докажите, что
Решение:
В четырехугольнике значит, около него можно описать окружность. В этой окружности вписанные углы будут опираться на одну и ту же дугу, и по следствию теоремы о вписанном угле
Метод решения задач с помощью дополнительного построения описанной или вписанной окружности называют методом вспомогательной окружности.
Замечательные точки треугольника
Точка пересечения медиан
В седьмом классе в ходе изучения вписанной и описанной окружностей треугольника рассматривались две его замечательные точки — точка пересечения биссектрис (иначе ее называют инцентром треугольника) и точка пересечения серединных перпендикуляров к сторонам.
Рассмотрим еще две замечательные точки треугольника.
Теорема (о точке пересечения медиан треугольника)
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, начиная от вершины треугольника.
Доказательство:
Пусть в треугольнике проведены медианы (рис. 85).
Докажем, что они пересекаются в некоторой точке причем
Пусть — точка пересечения медиан и точки — середины отрезков и соответственно. Отрезок — средняя линия треугольника и по свойству средней линии треугольника Кроме того, — средняя линия треугольника и по тому же свойству Значит, в четырехугольнике две стороны параллельны и равны. Таким образом, — параллелограмм, и его диагонали точкой пересечения делятся пополам. Следовательно, т.е. точка делит медианы в отношении 2:1.
Аналогично доказываем, что и третья медиана точкой пересечения с каждой из медиан делится в отношении 2 :1. А поскольку такая точка деления для каждой из медиан единственная, то, следовательно, все три медианы пересекаются в одной точке.
Точку пересечения медиан треугольника иначе называют центроидом или центром масс треугольника. В уместности такого названия вы можете убедиться, проведя эксперимент: вырежьте из картона треугольник произвольной формы, проведите в нем медианы и попробуйте удержать его в равновесии, положив на иглу или острый карандаш в точке пересечения медиан (рис. 86).
Пример №14Если в треугольнике две медианы равны, то он равнобедренный. Докажите.
Решение:
Пусть в треугольнике медианы равны и пересекаются в точке (рис. 87).
Рассмотрим треугольники Поскольку точка делит каждую из равных медиан и в отношении Кроме того, как вертикальные. Значит, по первому признаку. Отсюда следует, что
Но по определению медианы эти отрезки — половины сторон Следовательно, т.е. треугольник равнобедренный.
Точка пересечения высот
Теорема (о точке пересечения высот треугольника)
Высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство:
Пусть — высоты треугольника (рис. 88).
Проведя через вершины треугольника прямые, параллельные противолежащим сторонам, получим треугольник стороны которого перпендикулярны высотам треугольника По построению четырехугольники — параллелограммы, откуда Следовательно, точка — середина отрезка Аналогично доказываем, что — середина — середина
Таким образом, высоты лежат на серединных перпендикулярах к сторонам треугольника которые пересекаются в одной точке по следствию теоремы об окружности, описанной около треугольника.
Точку пересечения высот (или их продолжений) иначе называют ортоцентром треугольника.
Таким образом, замечательными точками треугольника являются:
- точка пересечения биссектрис — центр окружности, вписанной в треугольник;
- точка пересечения серединных перпендикуляров к сторонам — центр окружности, описанной около треугольника;
- точка пересечения медиан — делит каждую из медиан в отношении 2:1, начиная от вершины треугольника;
- точка пересечения высот (или их продолжений).

ИТОГОВЫЙ ОБЗОР ГЛАВЫ I
ЧЕТЫРЕХУГОЛЬНИК
Теорема о сумме углов четырехугольника.
Сумма углов четырехугольника равна
Справочный материал по параллелограмму
Параллелограммом называется четырехугольник, противолежащие стороны которого попарно параллельны
Признаки параллелограмма
Если две противолежащие стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм
Если противолежащие стороны четырехугольника попарно равны, то этот четырехугольник- параллелограм.
Противолежащие углы параллелограмма равны.
Диагонали параллелограмма точкой пересечения делятся пополам
Если противолежащие углы четырехугольника попарно равны, то этот четырехугольник — параллелограмм
Если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм
Виды параллелограммов
Прямоугольником называется параллелограм у которого все углы прямые
Ромбом называется параллелограмм, у которого все стороны равны
Квадратом называется прямоугольник, у которого все стороны равны
Свойство прямоугольника
Диагонали прямоугольника равны
Признак прямоугольника
Если все углы четырехугольника равны, то этот четырехугольник является прямоугольником
Свойства ромба
Диагонали ромба перпендикулярны и делят его углы пополам
Признак ромба
Если все стороны четырехугольника равны, то этот четырехугольник является ромбом
Свойства квадрата
Все стороны квадрата равны, а противолежащие стороны параллельны
Все углы квадрата прямые
Диагонали квадрата равны, перпендикулярны, делят углы квадрата пополам и точкой пересечения делятся пополам
Трапеция
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие непараллельны
Прямоугольной трапецией называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям
Равнобедренной трапецией называется трапеция, у которой боковые стороны равны.
Свойство равнобедренной
В равнобедренной трапеции углы при основании равны.
Признак равнобедренной
Если в трапеции углы при основании равны, то такая трапеция равнобедренная
Теорема Фалеса
Параллельные прямые, которые пересекают стороны угла и отсекают на одной из них равные отрезки, отсекают равные отрезки и на другой стороне
Средние линии треугольника и трапеции
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции
Свойство средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
Свойство средней линии трапеции
Средняя линия трапеции параллельна основаниям и равна их полусумме
Углы в окружности
Центральным углом в окружности называется плоский угол с вершиной в центре окружности
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла
Вписанным углом называется угол, вершина которого лежит на окружности, а стороны пересекают эту окружность
Теорема о вписанном угле Вписанный угол измеряется половиной дуги, на которую он опирается
Следствия теоремы о вписанном угле
Вписанные углы, опирающиеся на одну и ту же дугу, равны
Вписанный угол, опирающийся на полуокружность, прямой, и наоборот: любой прямой вписанный угол опирается на полуокружность
Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы
Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы
Вписанные четырехугольники
Четырехугольник называется вписанным в окружность, если все его вершины лежат на этой окружности
Признак вписанного четырехугольника
Если сумма противолежащих углов четырехугольника равна то около него можно описать окружность
Около любого прямоугольника можно описать окружность
Около равнобедренной трапеции можно описать окружность
Свойство вписанного четырехугольника
- Сумма противолежащих углов вписанного четырехугольника равна
- Если параллелограмм вписан в окружность, то он является прямоугольником
- Если трапеция вписана в окружность, то она равнобедренная
Описанные четырехугольники
Четырехугольник называется описанным около окружности, если все его стороны касаются этой окружности
Признак описанного четырехугольника
Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность
В любой ромб можно вписать окружность
Свойство описанного четырехугольника
- В описанном четырехугольнике суммы противолежащих сторон равны
- Если в параллелограмм вписана окружность, то он является ромбом
Замечательные точки треугольника
Теорема о точке пересечения медиан треугольника Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, начиная от вершины треугольника
Теорема о точке пересечения высот треугольника Высоты треугольника (или их продолжения) пересекаются в одной точке
Историческая справка
Большая часть теоретических положений, связанных с четырехугольником, была известна еще в Древней Греции. Например, параллелограмм упоминается в работах Евклида под названием «параллельно-линейная площадь». Основные свойства четырехугольников были установлены на практике и только со временем доказаны теоретически.
Например, параллелограмм упоминается в работах Евклида под названием «параллельно-линейная площадь». Основные свойства четырехугольников были установлены на практике и только со временем доказаны теоретически.
Одним из творцов идеи геометрического доказательства по праву признан древнегреческий ученый Фалес Милетский (ок. 625-547 гг. до н. э.). Его считали первым среди прославленных «семи мудрецов» Эллады. Механик и астроном, философ и общественный деятель, Фалес значительно обогатил науку своего времени. Именно он познакомил греков с достижениями египтян в геометрии и астрономии. По свидетельству историка Геродота, Фалес предсказал затмение Солнца, которое произошло 28 мая 585 г. до н. э. Он дал первые представления об электричестве и магнетизме. Достижения Фалеса в геометрии не ограничиваются теоремой, названной его именем. Считается, что Фалес открыл теорему о вертикальных углах, доказал равенство углов при основании равнобедренного треугольника, первым описал окружность около прямоугольного треугольника и обосновал, что угол, который опирается на полуокружность, прямой. Фалесу приписывают и доказательство второго признака равенства треугольников, на основании которого он создал дальномер для определения расстояния до кораблей на море.
Фалесу приписывают и доказательство второго признака равенства треугольников, на основании которого он создал дальномер для определения расстояния до кораблей на море.
В молодые годы Фалес побывал в Египте. Согласно легенде, он удивил египетских жрецов, измерив высоту пирамиды Хеопса с помощью подобия треугольников (о подобии треугольников — в следующей главе).
Изучая замечательные точки треугольника, нельзя не вспомнить имена еще нескольких ученых.
Теорему о пересечении высот треугольника доказал в XV в. немецкий математик Региомонтан (1436-1476) — в его честь эту теорему иногда называют задачей Региомонтана.
Выдающийся немецкий ученый Леонард Эйлер (1707-1783), который установил связь между замечательными точками треугольника, является уникальной исторической фигурой. Геометрия и механика, оптика и баллистика, астрономия и теория музыки, математическая физика и судостроение — вот далеко не полный перечень тех областей науки, которые он обогатил своими открытиями.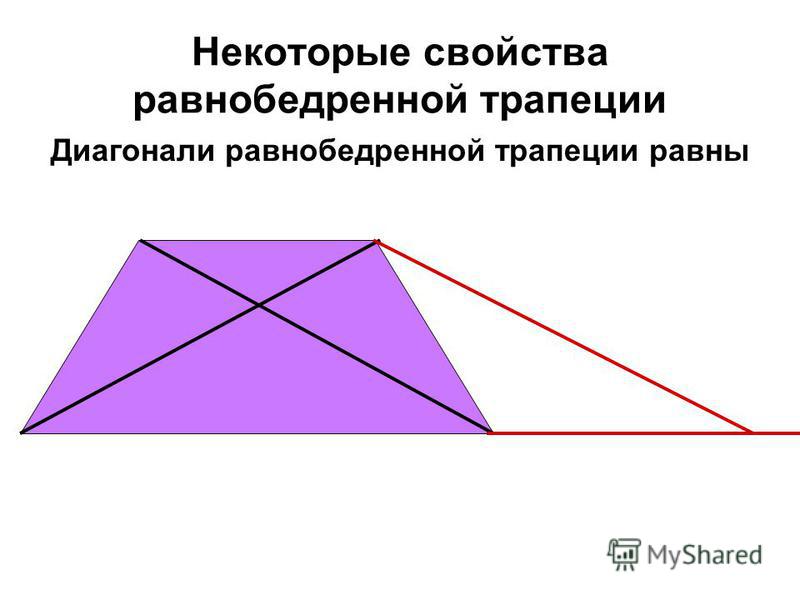 Перу Эйлера принадлежит более 800 научных работ, причем, по статистическим подсчетам, он делал в среднем одно изобретение в неделю! Человек чрезвычайной широты интересов, Эйлер был академиком Берлинской, Петербургской и многих других академий наук, он существенным образом повлиял на развитие мировой науки. Недаром французский математик Пьер Лаплас, рассуждая об ученых своего поколения, утверждал, что Эйлер — «учитель всех нас».
Перу Эйлера принадлежит более 800 научных работ, причем, по статистическим подсчетам, он делал в среднем одно изобретение в неделю! Человек чрезвычайной широты интересов, Эйлер был академиком Берлинской, Петербургской и многих других академий наук, он существенным образом повлиял на развитие мировой науки. Недаром французский математик Пьер Лаплас, рассуждая об ученых своего поколения, утверждал, что Эйлер — «учитель всех нас».
Среди украинских математиков весомый вклад в исследование свойств четырехугольников внес Михаил Васильевич Остроградский (1801-1862). Этот выдающийся ученый, профессор Харьковского университета, получил мировое признание благодаря работам по математической физике, математическому анализу, аналитической механике. Талантливый педагог и методист, Остроградский создал «Учебник по элементарной геометрии», который, в частности, содержал ряд интересных и сложных задач на построение вписанных и описанных четырех. М. В. Остроградский угольников и вычисление их площадей.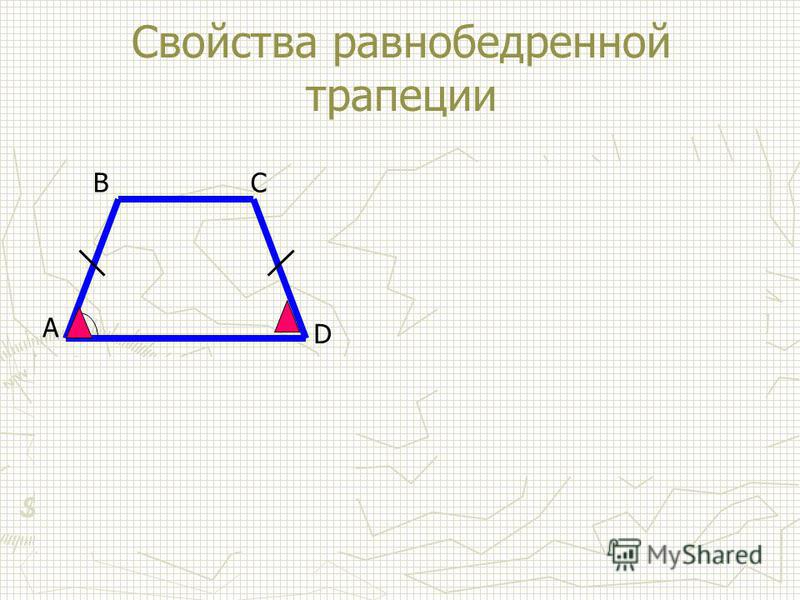
Параллелограмм – свойства, признаки, определение
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.
- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.

- Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
- S = a × h, где a — сторона, h — высота.
- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a2 × sinα.
- Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
Вот они:
- Противоположные стороны параллелограмма равны.
ABCD — параллелограмм, значит, AB = DC, BC = AD. - Противоположные углы параллелограмма равны.
ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D. - Диагонали параллелограмма точкой пересечения делятся пополам.
ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC. - Диагональ делит параллелограмм на два равных треугольника.
ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA. - Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
ABCD — параллелограмм, значит, ∠A + ∠D = 180°. - В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d12 + d22 = 2 × (a2 + b2 ).
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.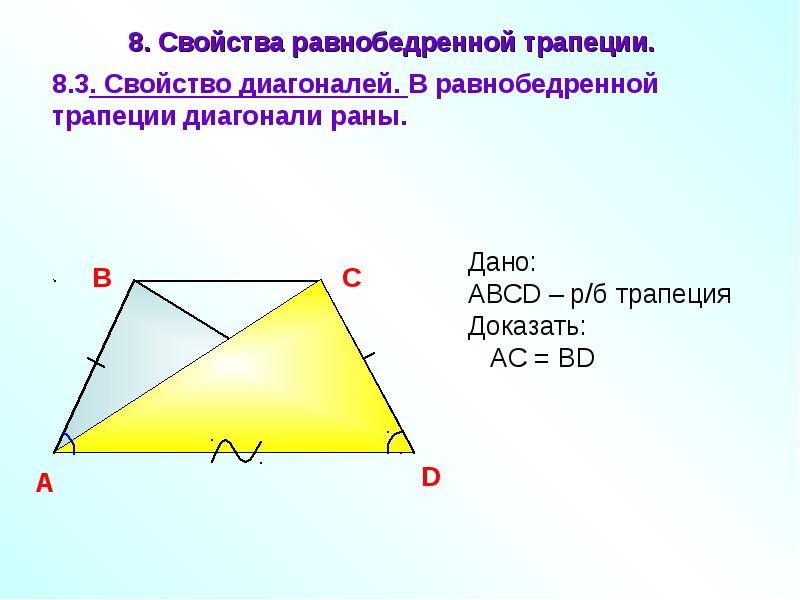
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
- AB = CD как противоположные стороны параллелограмма.
- ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
- Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.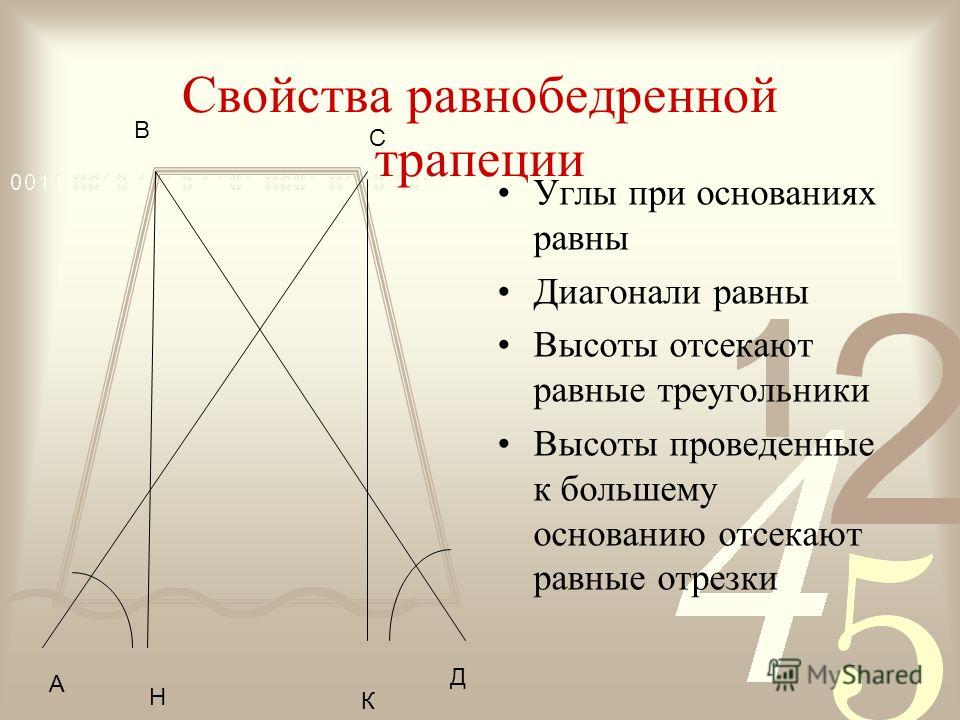
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.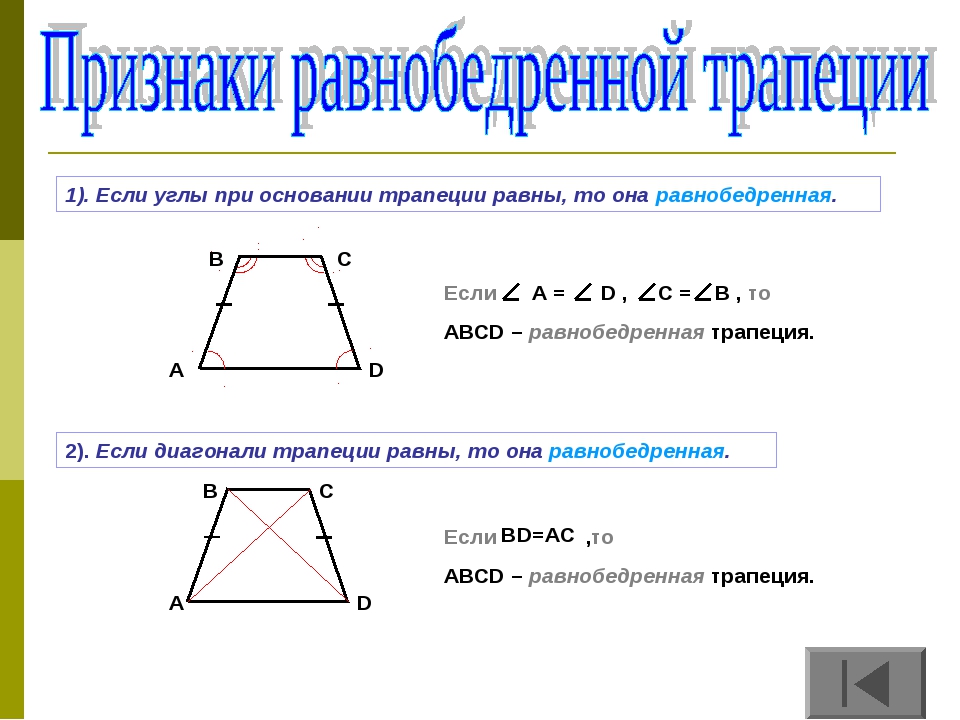
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
- AC — общая сторона;
- AB = CD по условию;
- BC = AD по условию.
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
- ∠ DCA = ∠BAC
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
- ∠DAC = ∠BCA
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма.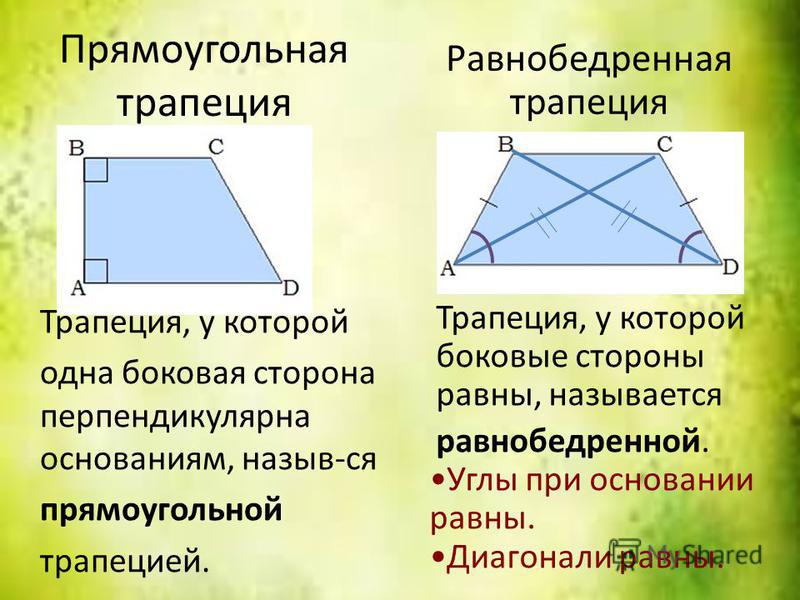 Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
чему равна, свойства, доказательство теоремы. Теорема о средней линии трапеции
Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Определение 1
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис.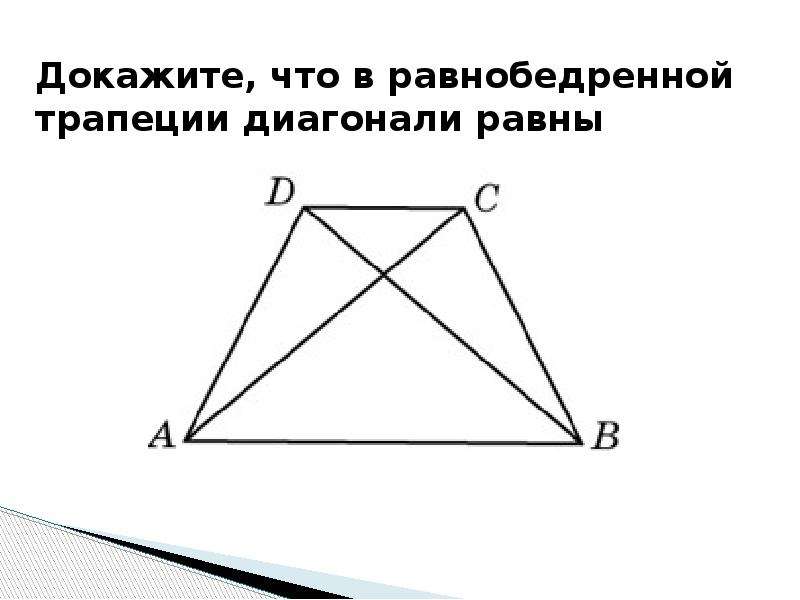 1).
1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.
Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
Следовательно, так как периметр равен $52\ см$, сумма оснований равна
Значит, по теореме 1, получаем
Ответ: $10\ см$.
Пример 2
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем
Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Определение 1
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.
Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.
Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
Следовательно, так как периметр равен $52\ см$, сумма оснований равна
Значит, по теореме 1, получаем
Ответ: $10\ см$.
Пример 2
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем
Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной.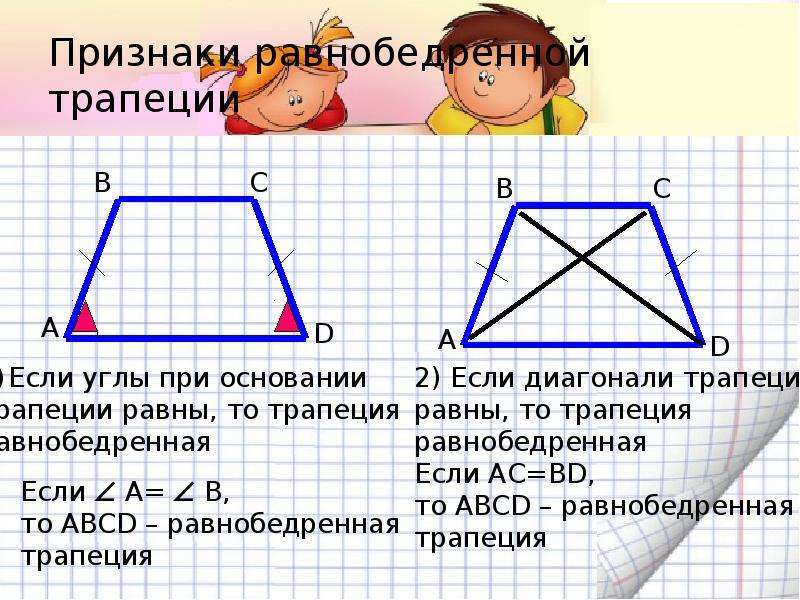 Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.
Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.
Общие сведения
Для начала давайте разберемся, что такое четырехугольник. Данная фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, которые не являются соседними, называются противоположными. То же можно сказать и о двух несмежных сторонах. Основные виды четырехугольников — это параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтоид.
Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны являются параллельными. Их называют основаниями. Две другие (непараллельные) — боковые стороны. В материалах экзаменов и различных контрольных работ очень часто можно встретить задачи, связанные с трапециями, решение которых зачастую требует от учащегося знаний, не предусмотренных программой.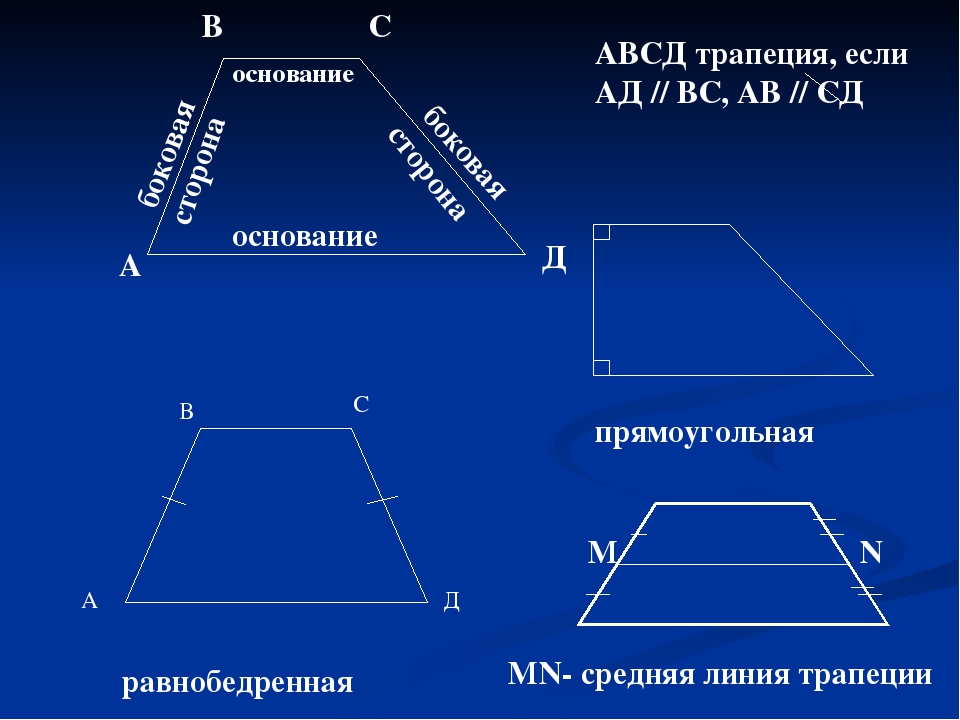 Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Виды трапеции
Существует много видов данной фигуры. Однако чаще всего принято рассматривать два из них — равнобедренную и прямоугольную.
1. Прямоугольная трапеция — это фигура, у которой одна из боковых сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.
2. Равнобедренная трапеция — это геометрическая фигура, у которой боковые стороны равны между собой. А значит, и углы у оснований также попарно равны.
Главные принципы методики изучения свойств трапеции
К основному принципу можно отнести использование так называемого задачного подхода. По сути, нет необходимости для ввода в теоретический курс геометрии новых свойств этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных).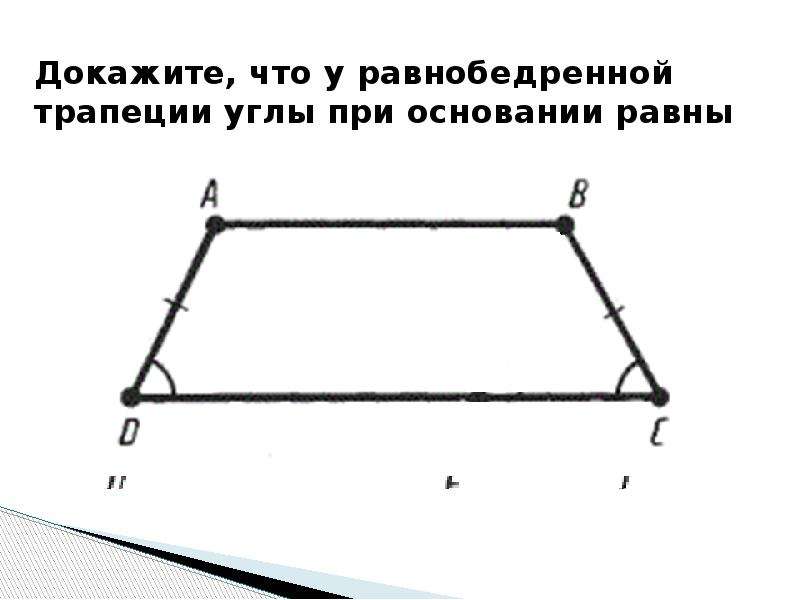 При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.
При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.
Вторым принципом является так называемая спиральная организация изучения «замечательных» свойств трапеции. Это подразумевает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Таким образом, учащимся легче их запоминать. Например, свойство четырех точек. Его можно доказывать как при изучении подобия, так и впоследствии с помощью векторов. А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.
Применение «внепрограммных» особенностей геометрической фигуры в содержании школьного курса — это задачная технология их преподавания. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже познавать трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже познавать трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Элементы и свойства равнобедренной трапеции
Как мы уже отмечали, у данной геометрической фигуры боковые стороны равны. Еще она известна как правильная трапеция. А чем же она так примечательна и почему получила такое название? К особенностям данной фигуры относится то, у нее равны не только боковые стороны и углы у оснований, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.
А теперь давайте разберемся, как найти углы равнобедренной трапеции. Рассмотрим вариант решения этой задачи при условии, что известны размеры сторон фигуры.
Решение
Обычно четырехугольник принято обозначать литерами А, Б, С, Д, где БС и АД — это основания. В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
Существует и второе решение данной задачи. В начале опускаем из угла В высоту Н. Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg. В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем аналогично первому способу.
Свойство диагоналей равнобедренной трапеции
Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:
Высота фигуры будет равна сумме оснований, деленной на два;
Ее высота и средняя линия равны;
Центр окружности является точкой, в которой пересекаются ;
Если боковая сторона делится точкой касания на отрезки Н и М, тогда равен квадратному корню произведения этих отрезков;
Четырехугольник, который образовался точками касания, вершиной трапеции и центром вписанной окружности — это квадрат, у которого сторона равна радиусу;
Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.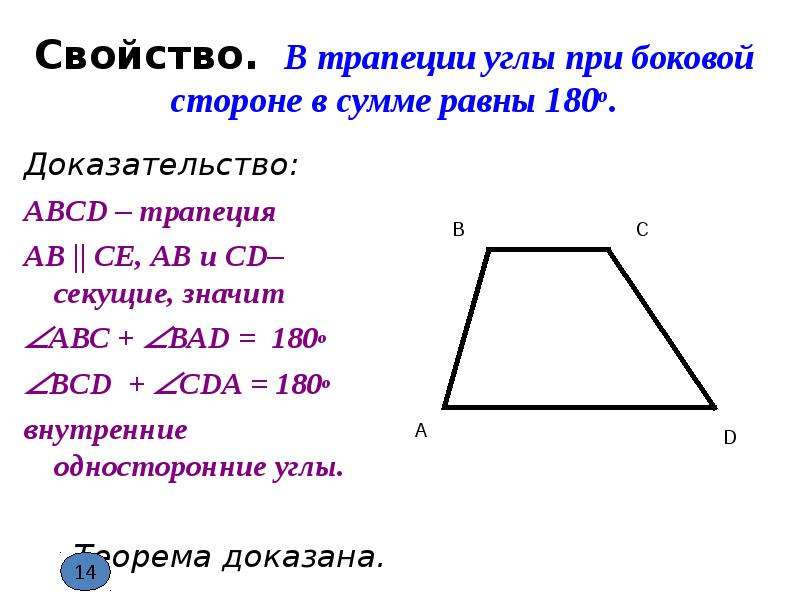
Подобные трапеции
Данная тема весьма удобна для изучения свойств этой Например, диагонали разбивают трапецию на четыре треугольника, причем прилежащие к основаниям являются подобными, а к боковым сторонам — равновеликими. Это утверждение можно назвать свойством треугольников, на которые разбита трапеция ее диагоналями. Первая часть этого утверждения доказывается через признак подобия по двум углам. Для доказательства второй части лучше воспользоваться способом, приведенным ниже.
Доказательство теоремы
Принимаем, что фигура АБСД (АД и БС — основы трапеции) разбивается диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АБО и СОД у боковых сторон. Треугольники СОД и БОС имеют общую высоту в том случае, если отрезки БО и ОД являются их основаниями. Получаем, что разность их площадей (П) равна разности этих отрезков: ПБОС/ПСОД = БО/ОД = К. Следовательно, ПСОД = ПБОС/К. Аналогично, треугольники БОС и АОБ имеют общую высоту. Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.
Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.
Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые разбита трапеция ее диагоналями, решив следующую задачу. Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.
Свойства подобия
Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.
Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.
Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.
Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.
Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям. Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).
Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).
Выводы подобия
Таким образом, мы доказали, что:
1. Отрезок, соединяющий у трапеции середины боковых сторон, параллелен АД и БС и равен среднему арифметическому БС и АД (длина основания трапеции).
2. Черта, проходящая через точку О пересечения диагоналей параллельно АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).
3. Отрезок, разбивающий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.
4. Элемент, делящий фигуру на две равновеликие, имеет длину среднего квадратичного чисел АД и БС.
Для закрепления материала и осознания связи между рассмотренными отрезками учащемуся необходимо построить их для конкретной трапеции. Он без труда сможет отобразить среднюю линию и отрезок, который проходит через точку О — пересечение диагоналей фигуры — параллельно основаниям. А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.
А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.
Отрезок, соединяющий середины диагоналей трапеции
Рассмотрим следующее свойство этой фигуры. Принимаем, что отрезок МН параллелен основаниям и делит диагонали пополам. Точки пересечения назовем Ш и Щ. Данный отрезок будет равен полуразности оснований. Разберем это более детально. МШ — средняя линия треугольника АБС, она равна БС/2. МЩ — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.
Центр тяжести
Давайте рассмотрим, каким образом определяется этот элемент для данной геометрической фигуры. Для этого необходимо продлить основания в противоположные стороны. Что это значит? Нужно к верхнему основанию прибавить нижнее — в любую из сторон, например, вправо. А нижнее продлеваем на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры и есть центр тяжести трапеции.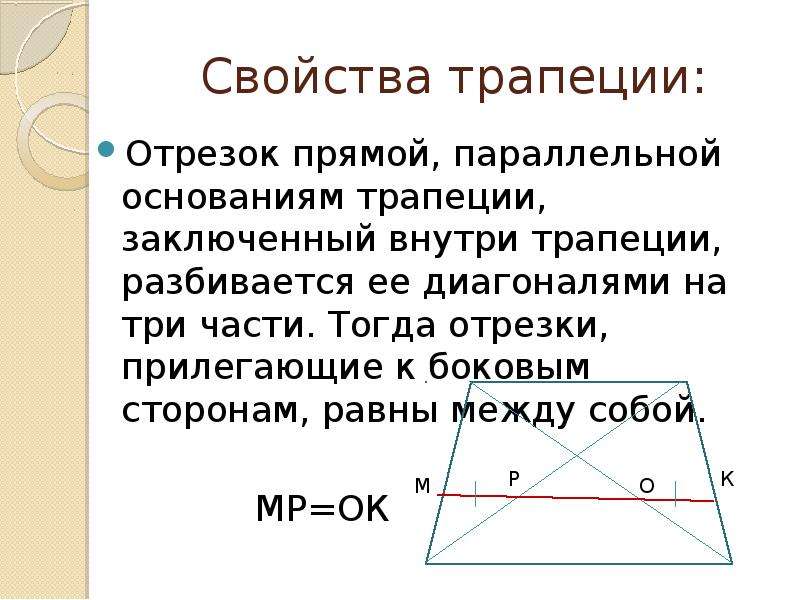
Вписанные и описанные трапеции
Давайте перечислим особенности таких фигур:
1. Трапеция может быть вписана в окружность тольков том случае, если она равнобедренная.
2. Около окружности можно описать трапецию, при условии, что сумма длин их оснований равна сумме длин боковых сторон.
Следствия вписанной окружности:
1. Высота описанной трапеции всегда равна двум радиусам.
2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.
Первое следствие очевидно, а для доказательства второго требуется установить, что угол СОД является прямым, что, по сути, также не составит большого труда. Зато знание данного свойства позволит при решении задач применять прямоугольный треугольник.
Теперь конкретизируем эти следствия для равнобедренной трапеции, которая вписана в окружность. Получаем, что высота является средним геометрическим оснований фигуры: Н=2R=√(БС*АД). Отрабатывая основной прием решения задач для трапеций (принцип проведения двух высот), учащийся должен решить следующее задание. Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.
Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.
Теперь давайте разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем из вершины Б высоту на основание АД. Так как окружность вписана в трапецию, то БС+АД = 2АБ или АБ = (БС+АД)/2. Из треугольника АБН находим sinα = БН/АБ = 2*БН/(БС+АД). ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).
Все формулы средней линии трапеции
Теперь пора перейти к последнему элементу данной геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):
1. Через основания: М = (А+Б)/2.
2. Через высоту, основание и углы:
М = А-Н*(ctgα+ctgβ)/2;
М = Б+Н*(ctgα+ctgβ)/2.
3. Через высоту, диагонали и угол между ними. К примеру, Д1 и Д2 — диагонали трапеции; α , β — углы между ними:
М = Д1*Д2*sinα/2Н = Д1*Д2*sinβ/2Н.
4. Через площадь и высоту: М = П/Н.
В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания . На блоге уже рассмотрены задачи условия которых связаны с , а также . Кратко о средней линии:
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.
Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:
Можем теперь выразить отрезок KL через основания:
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Вычисляем по формуле:
27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:
Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
В данной задаче:
Таким образом DC=6. Вычисляем:
27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.
Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
Следовательно меньшее основание равно 2∙2=4.
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
Исходя из условия можем записать:
Если обозначить среднюю линию через величину х, то получится:
Второе уравнение уже можно записать в виде:
27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
Получили, что меньшее основание рано пяти, значит большее равно 9.
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
Найдите большее основание трапеции.
Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:
Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
27848. Найдите среднюю линию трапеции ABCD , если стороны квадратных клеток равны 1.
Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!
В решении планиметрических задач, помимо сторон и углов фигуры, нередко активное участие принимают и другие величины – медианы, высоты, диагонали, биссектрисы и прочие. К их числу относится и средняя линия.
Если исходный многоугольник – трапеция, то что представляет собой его средняя линия? Данный отрезок представляет собой часть прямой, которая пересекает боковые стороны фигуры посередине и располагается параллельно двум другим сторонам – основаниям.
Как найти среднюю линию трапеции через линию средины и основания
Если известны величина верхнего и нижнего оснований, то рассчитать неизвестное поможет выражение:
a, b – основания, l – средняя линия.
Как найти среднюю линию трапеции через площадь
Если в исходных данных присутствует значение площади фигуры, то с помощью данной величины также можно вычислить длину линии средины трапеции. Воспользуемся формулой S = (a+b)/2*h,
Воспользуемся формулой S = (a+b)/2*h,
S – площадь,
h – высота,
a, b – основания.
Но, так как l = (a+b)/2, то S = l*h, а значит l=S/h.
Как найти среднюю линию трапеции через основание и углы при нем
При наличии длины большего основания фигуры, ее высоты, а также известных градусных мер углов при нем, выражение для нахождения линии средины трапеции будет иметь следующий вид:
l=a – h*(ctgα+ctgβ)/2, при этом
l – искомая величина,
a – большее основание,
α, β – углы при нем,
h – высота фигуры.
Если известно значение меньшего основания (при тех же остальных данных), найти линию средины поможет соотношение:
l=b+h*(ctgα+ctgβ)/2,
l – искомая величина,
b – меньшее основание,
α, β – углы при нем,
h – высота фигуры.
Найти среднюю линию трапеции через высоту, диагонали и углы
Рассмотрим ситуацию, когда в условиях задачи присутствуют значения диагоналей фигуры, углы, которые они образуют, пересекаясь друг с другом, а также высота. Рассчитать среднюю линию можно с помощью выражений:
Рассчитать среднюю линию можно с помощью выражений:
l=(d1*d2)/2h*sinγ или l=(d1*d2)/2h*sinφ,
l – линия средины,
d1, d2 – диагонали,
φ, γ – углы между ними,
h – высота фигуры.
Как найти среднюю линию трапецииДля равнобедренной фигуры
В случае, если базовая фигура – трапеция равнобедренная, приведенные выше формулы будут иметь следующий вид.
- При наличии значений оснований трапеции изменений в выражении не произойдет.
l = (a+b)/2, a, b – основания, l – средняя линия.
- Если известны высота, основание и углы, к нему прилегающие, то:
l=a-h*ctgα,
l=b+h*ctgα,
l – линия средины,
a, b – основания (b
α – углы при нем,
h – высота фигуры.
- Если известна боковая сторона трапеции и одно из оснований, то определить искомую величину можно, обратившись к выражению:
l=a-√(c*c-h*h),
l=b+√(c*c-h*h),
l – линия средины,
a, b – основания (b
h – высота фигуры.
- При известных значениях высоты, диагоналей (а они равны между собой) и углах, образованных в результате их пересечения, линию средины можно найти следующим образом:
l=(d*d)/2h*sinγ или l=(d*d)/2h*sinφ,
l – линия средины,
d – диагонали,
φ, γ – углы между ними,
h – высота фигуры.
- Известны площадь и высота фигуры, тогда:
l=S/h,
S – площадь,
h – высота.
- Если перпендикуляр-высота неизвестен, его можно определить с помощью определения тригонометрической функции.
h=c*sinα, поэтому
l=S/c*sinα,
l – линия средины,
S – площадь,
c – боковая сторона,
α- угол у основания.
| Табличка на двери |
Тема вторая средняя линия трапеции
Всероссийский конкурс исследовательских работ учащихся
“ПЕРВЫЕ ШАГИ В НАУКУ”
Направление: математика
Тема:Вторая средняя линия трапеции.
Выполнила: ученица 8 «А» класса
МАОУ Новоильинский агротехнический лицей
Заиграевского района Республики Бурятия
Зубарева Света
Научный руководитель: учитель математики
МАОУ Новоильинский агротехнический лицей
Зубарева Надежда Игоревна
г. Обнинск, 2011/2012 учебный год
Обнинск, 2011/2012 учебный год
Оглавление
1. Введение 3 стр.
2. Вторая средняя линия трапеции:
а) Определение 4 стр.
б) Свойства второй средней линии трапеции 5 стр.
в) Задачи 8 стр.
3. Заключение 12 стр.
4. Список литературы
13 стр.
Введение.
Тема моей работы – «Вторая средняя линия трапеции». На уроке геометрии, изучая тему, площадь трапеции мы решали следующую задачу:
Найти площадь равнобедренной трапеции, у которой диагонали взаимно перпендикулярны и высота равна 10 см.
Сходу решить задачу у нас не получилось, но когда, с помощью учителя мы доказали, что Sравн.трапеции=h2 если d1 ┴ d2, то ответ оказался очевиден 100см2. Вскользь, учительница математики сказала, что в задачах с таким условием, высота трапеции будет равна средней линии трапеции.
Я заинтересовалась, а что же такое средняя линия трапеции? На тот момент мы знали, что такое средняя линия треугольника, а про среднюю линию трапеции ничего не слышали. Оказалось, это отрезок, соединяющий середины ее боковых сторон.
Во время своих поисков я и
наткнулась на упоминание о второй
средней линии трапеции. Мне она показалась
чем-то неизведанным: ни мои одноклассники,
ни мои знакомые ничего не слышали о
второй средней линии трапеции. В школьном
учебнике (Атанасян Л. С. «Геометрия 7 –
9») о ней также не упоминается, но есть
задача (№ 820). Тогда я решила собрать
сведения об этой таинственной линии,
задачи, связанные с ней, и оформить свою
работу в виде доклада. Думаю, он будет
интересен тем людям, которые увлекаются
геометрией.
В школьном
учебнике (Атанасян Л. С. «Геометрия 7 –
9») о ней также не упоминается, но есть
задача (№ 820). Тогда я решила собрать
сведения об этой таинственной линии,
задачи, связанные с ней, и оформить свою
работу в виде доклада. Думаю, он будет
интересен тем людям, которые увлекаются
геометрией.
Цель работы: Исследование второй средней линии трапеции
Я начала свою работу со сбора информации в Интернете и в имеющихся дома книгах и справочниках по математике (их у нас довольно много, т.к. мои мама и бабушка – учителя математики). К моему удивлению, информации оказалось крайне мало. Очень много полезного для себя я почерпнула в статье «Вторая средняя линия трапеции» (Кушнир И. А., журнал «Математика в школе» № 2, 1993).
Задачи:
Собрать информацию о второй средней линии трапеции.
Изучить свойства второй средней линии трапеции.
Решить задачи, имеющиеся в литературе.
Составить и решить свои собственные задачи
Актуальность темы обусловлена
тем, что все больше и больше геометрических
задач встречается в экзаменационной
работе по математике в 9 и 11 классах,
материалы данного исследования можно
использовать при подготовке к экзаменам,
они будут полезны всем ребятам
интересующимся геометрией.
Большую часть свойств второй средней линии трапеции я сформулировала на основе задач, представленных в ней. К сожалению, не все задачи были мне понятны, поэтому я решила продолжить поиск. Задачи, связанные со второй средней линией трапеции оказались у авторов: Лидского В. Б., Прасолова В. В., Сивашинского И. Х., Шахно К. У. Так как задач оказалось очень мало, я решила составить собственные. Мне удалось придумать 2 задачи, одну задачу составила моя бабушка, Криулева А.И..
Вторая средняя линия трапеции.
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон. Если же соединить отрезком середины оснований, получится вторая средняя линия трапеции. Итак, вторая средняя линия трапеции – это отрезок, соединяющий середины оснований трапеции.
В К С
А S D
KS – вторая средняя линия трапеции АВСD
Как известно, средняя линия трапеции
равна полусумме оснований.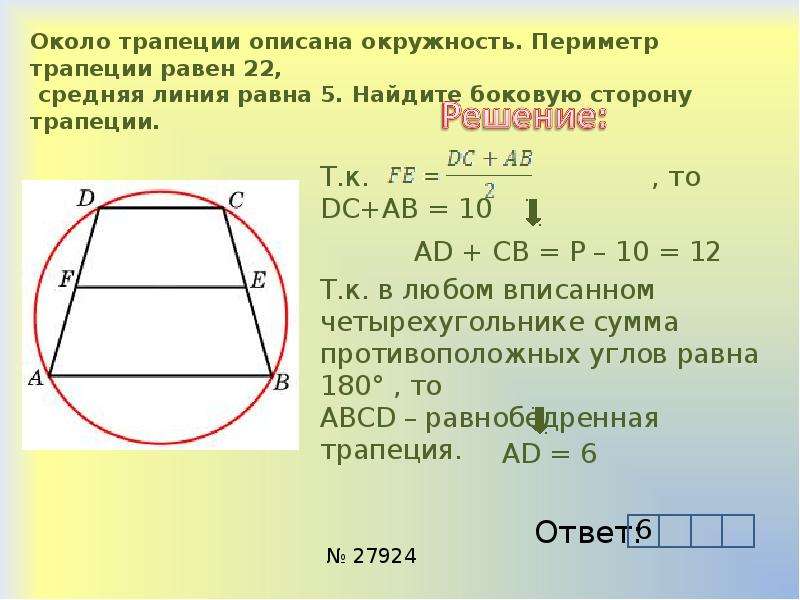 А есть ли
связь между второй средней линией
трапеции и её боковыми сторонами?
Очевидно, что вторая средняя линия
трапеции не равна полусумме боковых
сторон, в чём можно убедиться, хотя бы
растяжением одного из оснований:
А есть ли
связь между второй средней линией
трапеции и её боковыми сторонами?
Очевидно, что вторая средняя линия
трапеции не равна полусумме боковых
сторон, в чём можно убедиться, хотя бы
растяжением одного из оснований:
рис.1 В К С
A1 А S D D1
сумма боковых сторон трапеции изменилась, а длина KS осталась прежней. И всё же связь между второй средней линией трапеции и боковыми сторонами есть. Воспользуемся векторным способом:
в трапеции АВСD (рис.1) ВС || АD, КS – вторая средняя линия.
KS = KB + BA +AS, с другой стороны, KS = KC + CD + DS. Сложив оба равенства, получим:
2KS = (KB + KC) + (BA + CD)+ (AS + DS), т.е.
KS = (BA + CD)
Таким образом, вектор второй средней
линии трапеции равен полусумме векторов
боковых сторон, взятых в одном порядке
(сверху вниз).
Это утверждение можно доказать и вторым способом:
рис.2
В К С В трапеции АВСD (ВС || АD) КS – вторая
средняя линия, О – произвольная точка
По формуле для середины отрезка:
А S D ОК = (ОВ + ОС), OS = (OA + OD)
OS – OK = ((OA – OB) + (OD – OC)), KS = (BA + CD)
Рассмотрим некоторые свойства второй средней линии трапеции.
1. Средние линии трапеции в точке пересечения делятся пополам.
рис.3
B K C Для доказательства рассмотрим
треугольники ВСD и ABD: KN —
M N средняя линия треугольника BCD,
O KN || BD и .
A S D
MS – средняя линия треугольника ABD, MS || BD, . Аналогично, МК || АС, , NS || AC, . Таким образом, MKNS – параллелограмм, MN и KS – его диагонали, следовательно, KO = OS, MO = ON.
2. Вторая средняя линия трапеции проходит через точку пересечения диагоналей.
рис.4
B K C Дано: ВК = КС
O Доказать: AS = SD
A S D
Доказательство: как накрест лежащие при ВС || AD и секущей BD. как вертикальные. подобен , аналогично, подобен .
. Из этих равенств следует, что , а т.к. BK = KC (по условию), то AS = SD .
3. Прямая, содержащая вторую среднюю линию трапеции, проходит через точку пересечения прямых, содержащих боковые стороны. (Слайд 4)
рис.5 О Для доказательства рассмотрим треугольники ВОС и AOD.
Они подобны по двум углам,
B K C
ODOC, OBOA, OA =k ·OB, OD = k ·OC.
A S D По формуле середины отрезка:
OK = (ОВ+ОС), OS = (OA+OD), OS = (k ·OB + k ·OC)= k (OB+ OC)= = k ·OK OK коллинеарен OS, ОKS.
Верно и обратное утверждение: если прямая проходит через точку пересечения прямых, содержащих боковые стороны и середину одного из оснований, то она проходит и через середину другого основания (является второй средней линией трапеции).
Дано: Прямая OS проходит через середину основания AD трапеции ABCD.
Доказать: ВК = КС
Доказательство: (по рис.6)
∆KOC ~ ∆SOD
∆ВОК ~ ∆AOS
, т.к. АS = SD(по условию), то КС = ВК.
4. В равнобочной трапеции средние линии перпендикулярны. (Слайд 5)
рис.7
В K С Дано: ABCD — трапеция, АВ = CD,
MN, KS – средние линии
М N Доказать: MNKS.
Доказательство:
А S D MK – средняя линия ∆АВС, МК||АС, МК=АС
NS – средняя линия ∆ADC, NS||AC, NS =АС
Если противоположные стороны четырехугольника MKNS равны и параллельны, то по признаку MKNS – параллелограмм Т.к. трапеция ABCD – равнобокая, то AC = BD,
MK = АС, KN = BD,
MK = KN, MKNS — ромб
По свойству ромба, диагонали в нем перпендикулярны, MN KS.
Верно и обратное утверждение: если средние линии трапеции перпендикулярны, то эта трапеция равнобокая.
Доказательство (по рис.7) :
По теореме о средней линии трапеции MN||BC, MN||AD
По условию MNKS, BCKS, ADKS
BK=KC, AS=SD, KS- ось симметрии трапеции ABCD,
AB и CD симметричны относительно KS, AB=CD.
Пользуясь доказанным свойством, можно сформулировать следующее:
5. В равнобочной трапеции вторая средняя линия перпендикулярна основаниям (см. доказательство предыдущего утверждения)
6. Если средние линии трапеции равны, ее диагонали перпендикулярны. (Слайд 6)
рис.8 В Е С
Доказательство:
M N МЕNF – параллелограмм, по условию MN=EF.
Если в параллелограмме диагонали равны,
A F D то этот параллелограмм – прямоугольник, ENME,
т.к. EN||BD, ME||AC, то BDAC,
Обратное утверждение также верно: если диагонали трапеции перпендикулярны, то средние линии этой трапеции равны.
Доказательство:
ACBD, MEEN, MFFN MENF – прямоугольник EF=MN
Задачи
Мне удалось найти очень мало задач, связанных со второй средней линией трапеции (авторы: Кушнир И. А., Лидский В. Б., Прасолов В. В., Сивашинский И. Х., Шахно К. У.). В учебнике «Геометрия 7-9 » (автор Л.С.Атанасян) представлена лишь одна задача (№820). Кроме того, две задачи повторяются у нескольких авторов, правда, с различными формулировками:
Шахно К. У. [5], стр.73, № 859:
Докажите, что середины оснований трапеции и точка пересечения диагоналей лежат на одной прямой.
Лидский В. Б.[4], стр.60, №347:
Доказать, что прямая, соединяющая середины параллельных сторон трапеции, пройдёт через точку пересечения диагоналей.
Кушнир И. А.[2], стр.57, №8:
Доказать, что точка пересечения прямых, содержащих боковые стороны трапеции и точка пересечения диагоналей трапеции принадлежат прямой, содержащей вторую среднюю линию трапеции.
Прасолов В. В.[6], стр.14, №1.22:
Доказать, что середины оснований трапеции, точка пересечения диагоналей и точка пересечения прямых, содержащих боковые стороны, лежат на одной прямой.
Задачи такого типа рассмотрены при исследовании свойств 2 и 3 .
Приведу решение остальных найденных мной задач.
Задача 1 (Кушнир И.А.)
Доказать, что площадь трапеции равна произведению второй средней линии на диагональ трапеции и на синус угла между ними.
B E C
рис.9 Дано: ABCD – трапеция,
EF – вторая средняя линия.
Доказать:
A F D
Доказательство. Соединив точки А и E, С и F, получим что площадь трапеции AECF, , где — угол между отрезками EF и AC. и . Значит, площадь трапеции ABCD равна удвоенной площади трапеции AECF, что и требовалось доказать.
Задача 2 (Кушнир И.А.)
Доказать, что площадь трапеции равна произведению второй средней линии на сумму перпендикуляров, проведенных к этой средней линии (или её продолжению) из двух противоположных вершин трапеции.
B E C
рис.10 N Дано: ABCD – трапеция,
EF – вторая средняя линия,
M СNEF, AMEF.
Доказать:
A F D
Доказательство: Рассмотрим треугольники AEF и ECF. , . Тогда . Т. к. , то .
Задача 3 (Кушнир И. А.)
Как с помощью одной линейки провести в трапеции вторую среднюю линию?
Решение:
Провести диагонали.
Продолжить боковые стороны до их пересечения.
Через точку пересечения диагоналей и точку пересечения продолжений боковых сторон провести прямую.
Отрезок прямой, заключенный между основаниями трапеции – искомая вторая средняя линия трапеции.
Задача 4 (Русакова М. А)
Можно ли построить трапецию, если известны её средние линии и угол между ними?
Решение: можно; решений будет бесконечное множество. При построении нужно воспользоваться свойством 1.
Задача 5 (Атанасян Л. С.)
(№820) Докажите, что прямая, проходящая через середины оснований равнобедренной трапеции, перпендикулярна к основаниям.
Решение: см. доказательство свойства 4.
Задача 6 (Сивашинский И. Х.)
В трапеции ABCD сумма углов при основании AD равна 90º. Доказать, что отрезок, соединяющий середины оснований, равен полуразности оснований.
рис.11 M Решение: AF = FD, BN = NC
º, º,
AD – гипотенуза,
B N C MF = AF = FD = AD
MN = BC
A F D
FN = MF – MN
FN = AD — BC = (AD – BC)
Задача 7 (Кушнир И. А.)
В трапеции ABCD сумма углов при меньшем основании равна 270º. Найти длину второй средней линии, если основания равны а и в (а >в).
Решение: воспользуемся рис.11: в треугольнике AMD , значит, . Поэтому MN = , MF=.
NF = MF – MN = (a – b)/2.
Предлагаю задачи, составленные мной:
Задача 1
Верно ли утверждение: если прямая проходит через середину одного основания трапеции и точку пересечения диагоналей, то и другое основание она делит пополам?
Решение: Да, см. свойство 2.
Задача 2
Основания трапеции равны 10 см и 6 см, вторая средняя линия – 4 см, угол между средними линиями 30º. Найти площадь трапеции.
Решение:
B K С
M O N
A H S D
(соответственные), , КН = 2 см
см².
Заключение
В результате проделанной работы я узнала, что такое вторая средняя линия трапеции, какими свойствами она обладает; разобрала решение задач, связанных с этой линией.
Я выяснила, что вторая средняя линия трапеции используется в решении задач мало, видимо, поэтому она не проходится в школе. Но я не жалею, что потратила время на изучение этой темы, т.к. узнала много нового о трапеции.
К сожалению, мне удалось составить лишь 2 задачи, связанные со второй средней линией трапеции, но я думаю, в дальнейшем их число возрастет.
Литература
Л. С. Атанасян и др. «Геометрия 7-9» Учебник для образовательных учреждений/- М., Просвещение, 2006
Википедия.- /wiki/средняя линия
И. А. Кушнир «Вторая средняя линия трапеции», журнал «Математика в школе» №2, 1993.
В. Б. Лидский, Л. В. Овсянников, А. Н. Тулайков, М. И. Шабунин «Задачи по элементарной математике» — М., Физматгиз, 1960.
Научный форум dxdy. – /topic20315.html
В. В. Прасолов «Задачи по планиметрии» -М.: Наука, 1986.
И. Х. Сивашинский «Задачник по элементарной математике», — М., Наука, 1966.
Фестиваль идей – /work
К. У. Шахно «Сборник задач по элементарной математике повышенной трудности», — Минск, Высшая школа, 1966.
Вписанная трапеция свойства. Окружность описанная около трапеции
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований . Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .
ФГКОУ «МКК «Пансион воспитанниц МО РФ»«УТВЕРЖДАЮ»
Руководитель отдельной дисциплины
(математика, информатика и ИКТ)
Ю. В. Крылова _____________
«___» _____________ 2015 г.
«Трапеция и ее свойства »
Методическая разработка
преподавателя математики
Шаталиной Елены Дмитриевны
Рассмотрено и
на заседании ПМО от _______________
Протокол №______
Москва
2015 год
Оглавление
Введение 2
Определения 3
Свойства равнобедренной трапеции 4
Вписанные и описанные окружности 7
Свойства вписанных и описанных трапеций 8
Средние величины в трапеции 12
Свойства произвольной трапеции 15
Признаки трапеции 18
Дополнительные построения в трапеции 20
Площадь трапеции 25
10. Заключение
Список используемой литературы
Приложение
Доказательства некоторых свойств трапеции 27
Задачи для самостоятельных работ
Задачи по теме «Трапеция» повышенной сложности
Проверочный тест по теме «Трапеция»
Введение
Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими.
Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию. Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии.
Трапеция.
Определения
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются
основаниями.
Другие две —
боковые стороны
.
Если боковые стороны равны, трапеция называется
равнобедренной
.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Расстояние между основаниями называется высотой трапеции .
2 . Свойства равнобедренной трапеции
3. Диагонали равнобедренной трапеции равны.
4
1
0. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.
3. Вписанная и описанная окружность
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.
Е
сли трапеция равнобедренная, то около неё можно описать окружность.
4 . Свойства вписанных и описанных трапеций
2.Если в равнобедренную трапецию можно вписать окружность, то
сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции.
4 . Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.
Е сли в трапецию вписана окружность, которая касается одной из боковых сторон, разбивает ее на отрезки m и n, тогда радиус вписанной окружности равен среднему геометрическому этих отрезков.
1
0
. Если окружность построена на меньшем основании трапеции как на диаметре, проходит через середины диагоналей и касается нижнего основания, то углы трапеции 30°, 30°, 150°, 150°.
5. Средние величины в трапеции
Среднее геометрическое
В любой трапеции с основаниями a и b для a > b справедливо неравенство :
b
˂
h
˂
g
˂
m
˂
s
˂
a
6. Свойства произвольной трапеции
1
. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой.
2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.
Точка пересечения продолжения боковых сторон произвольной трапеции, точка пересечения ее диагоналей и середин оснований лежат на одной прямой.
5. При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади).
6. Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.
d 1 2 + d 2 2 = c 2 + d 2 + 2 ab
7
. В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований d 1 2 — d 2 2 = a 2 – b 2
8 . Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам.
7 . Признаки трапеции
8 . Дополнительные построения в трапеции
1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.
2
. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание.
3
. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции.
4
. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию.
6
. Отрезок, параллельный одной из диагоналей трапеции проводится через вершину – точку, являющуюся концом другой диагонали. В результате получается треугольник с двумя сторонами, равными диагоналям трапеции, и третьей – равной сумме оснований
7
.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции.
8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
9. Биссектриса угла трапеции отсекает равнобедренный треугольник.
1
0. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
1
1. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
1
2
. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники.
13. Если в равнобедренную трапецию вписана окружность, то проводят высоту трапеции — среднее геометрическое произведения оснований трапеции или удвоенное среднее геометрическое произведения отрезков боковой стороны, на которые она делится точкой касания.
9. Площадь трапеции
1 . Площадь трапеции равна произведению полусуммы оснований на высоту S = ½(a + b ) h или
П
лощадь трапеции равна произведению средней линии трапеции на высоту S = m h .
2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
Площадь равнобедренной трапеции с радиусом вписанной окружности равным r и углом при основании α:
10. Заключение
ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ?
Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться.
Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.
Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции.
Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина.
Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих.
Трапеция в технике: Трапеция используется при конструировании деталей в космических технологиях и в авиации. Например, некоторые солнечные батареи космических станций имеют форму трапеции так как имеют большую площадь, значит накапливают больше солнечной эн
В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас.
Список используемой литературы
Болотов А.А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.
Быков А.А, Малышев Г.Ю., ГУВШ факультет довузовской подготовки. Математика. Учебно-методическое пособие 4 часть М2004
Гордин Р.К. Планиметрия. Задачник.
Иванов А.А.,. Иванов А.П, Математика: Пособие для подготовки к ЕГЕ и поступлению в вузы-М: Издательство МФТИ,2003-288с. ISBN 5-89155-188-3
Пиголкина Т.С, Министерство образования и науки РФ федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «ЗФТШ Московского физико-технического института (государственного университета)». Математика. Планиметрия. Задания №2 для 10-ых классов (2012-2013 учебный год).
Пиголкина Т.С., Планиметрия (часть1).Матиматическая Энциклопедия Абитуриента. М., издательство российского открытого университета 1992.
Шарыгин И.Ф.Избранные задачи по геометрии конкурсных экзаменов в ВУЗЫ (1987-1990) Львов Журнал «Квантор» 1991.
Энциклопедия «Аванта плюс», Математика М., Мир энциклопедий Аванта 2009.
Приложение
1.Доказательство некоторых свойств трапеции.
1. Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках K и L . Доказать, что если основания трапеции равны а и b , то длина отрезка KL равна среднему геометрическому оснований трапеции. Доказательство
Пусть О — точка пересечения диагоналей, AD = а, ВС = b . Прямая KL параллельна основанию AD , следовательно, K О ║ AD , треугольники В K О и BAD подобны, поэтому
(1)
(2)
Подставим (2) в (1) , получим KO =
Аналогично LO = Тогда K L = KO + LO =
В о всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.
Доказательство: Пусть продолжения боковых сторон пересекаются в точке К. Через точку К и точку О пересечения диагоналей проведём прямую КО.
K
Окажем, что эта прямая делит основания пополам.
Обозначим ВМ = х, МС = у, AN = и, ND = v . Имеем:
∆ ВКМ ~ ∆AKN →
M
x
B
C
Y
∆ MК C ~ ∆NKD → →Проектная работа « Интересные свойства трапеции » Выполнили: ученицы 10 класса Кудзаева Эллина Баззаева Диана МКОУ СОШ с. Н.Батако Руководитель: Гагиева А.О. 20.11.2015 года
Цель работы: Рассмотреть свойства трапеции, которые в школьном курсе геометрии не изучаются, но при решении геометрических задач ЕГЭ из развернутой части С 4 бывает необходимо знать и уметь применять именно эти свойства.
Свойства трапеции: Если трапеция разделена прямой, параллельной ее основаниям, равным a и в, на две равновеликие трапеции. Тогда отрезок к этой прямой, заключенный между боковыми сторонами, равен a В к
Свойство отрезка, проходящего через точку пересечения диагоналей трапеции. Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен: а в с
Свойства трапеции: Отрезок прямой, параллельной основаниям трапеции, заключенный внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой. МР=ОК Р М О К
Свойства равнобедренной трапеции: Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону. О С В А Д. Е О
Свойства равнобедренной трапеции: Если центр описанной окружности лежит на основании трапеции, то её диагональ перпендикулярна боковой стороне О А В С Д
Свойства равнобедренной трапеции: В равнобедренную трапецию можно вписать окружность, если боковая сторона равна её средней линии. С В А Д h
1)Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства: 1. Сумма оснований трапеции равна сумме боковых сторон. 2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n , то радиус вписанной окружности равен
Свойства прямоугольной трапеции, в которую вписана окружность: 1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC
Доказательство: Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF=m , FD=n . Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
I. Биссектрисы углов при боковой стороне трапеции пересекаются под углом 90º . 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам). 3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º. Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. Это утверждение применяется при решении задач на трапецию, в которую вписана окружность.
I I .Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции. Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
III. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно. Таким образом, BC=BK+KC=AB+CD. Вывод: Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
I V. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
Если равнобедеренную трапецию со сторонами а,в,с, d можно вписать и около неё можно описать окружности, то площадь трапеции равна
%PDF-1.4 % 1 0 объект > эндообъект 3 0 объект > >> /Содержание [ 5 0 Р ] >> эндообъект 4 0 объект > >> ручей резкоя IQ:,D»&(hD%G :»t$m)spokeD#.!3B :MH»)BmR»DDJ’Љ}Bm ‘ЛBq(DYB%$!0 L!!DքF»$m\BhhA q!!’Fh $YGiI»8;VEB»ND@ @ «fBA6HCF D»[Q]AЈFDDD!8@M»&(EF̕Q$»B»HDh%(!!6K(A»R!FvjDDDHZ!E:HOKAhO# :!+B@2Ev ,H#DBPhL @ԒHDDDDB$b2F: + Gѭ$’mFMQhA’E»@R0DN#hDtPF#T#1j#hL&T%Ђ»CBR!$ф»»]’aFф]Ft’xFP*P@@ d:DKD !D»q $B»»&ty1Eq) HUB%:3GfhB4$#h}G>»]Ga#4}t}&&m Ba 0h05BDDNN!t& քAhJ»m L»$Љ!DDN»* DD!$-D thN»}B «jB»»m»]! !HL @N»DDJ3A&hMhD!6 4Kt&h!O!$#hD! hB$M)4N!&D!»N!.0L#!’G»»&qFѴy+h!># !>L!0dR».HhFB «fN!’B$b H#ZT$6CGB @ԌБЉ’G@ A ЈBByF!HEZE#D!@ %&Q D»@ B»»yB]GѴ$ h!#% .D8RHDB’B&ИB$t$b>IBȝ»y By aB]B}Q0#RD B N!DIt»Rђ»q FhGDjDJ’bh (GihK,Љ! f苢6֎!tfK@DPA»»B u+HiAUGTHB$&!0#IѴ:D3DY»(DB!h»%N!t’6tR!0R(BHFЂ’:R4Db.DDL!1 .4]DZF&FhDMZ3B% #քE#h5B»‘ФF!hJ hdD»]Bh»Bq «‘:$!3GѴmBGE»(GЙ!:»‘#DO!60@!0DԤ 7D»B «DDO#:!!6КF»DKh!Г# 4&Z3Bw4″}$# m$B@D0h!Dm Ft]BjEԌt»yB0″vD»B$h4G'»$4″‘K4″‘!B»q:!0N!»Q МDBDJa#hL#>#Jt&IAĐBaB%: 03GBmB1)d:%DD@D)ф]֍hB}B$#h0!#]Q»m’F BN!!DD SB’Bm»B»»»‘!Da}$$D6″DHE»+(Ԍ(BD!8GT}FhO!(EЈG»»»»‘фqBuBF!0D#N!!»%:+ hꋠf!8Ѣ;,A&A !В$- &H5!0#N#!58!>t&* rI’D»»м ч.Kh:O!!IЈGhDD0#R’DQhDDJD’Ј»DDD!’BB’Ј»BK!6DD* 6H%Ј!’B4Ixф’Q2&M1 :>!O!8!4Dm!)ѢR$&R%HA;0′ BEL$B»»%: hHhH%D4%ѭB&h!0’ #N»u$(B»a#FFt»}»BD#Q»m (Ba !, П@ 8Ѣ0:DtBD!)4%eG!ta m B8DB&h t] t&@К!0!!H>Ѵ%Ѵ»1D @DD !H»qB»PIЕTB!’D»‘yBVB»%- BaD$h@>»(! HD>#4NDBGB»»]%Љta t»GDb!>h!4$» B#&t$B:!DM’B$IB’T»a4DGGD!»$4″kF:»HBD» ‘t$4$4′»StPD8!!3DbDyPN#.GFtu@!06tuGXGD»»$4m ‘#@DDBhZ5B0JafDmBmBD’ЈHD*ЄQq!FDԄ!#@80DN#4%Љ»»Ny B’BT#6МB’Dw@ DB»&hԄO»EZ#HDO#h»! .4Gѭ»»]6 BR:!6 B»f!DDt»D)%FѢ,»MIO!DI*hDDHhԍHA$i$!DDG!Bq B Dh8DD»%M @ԍh $HIѩGA$4%њ8h!»&GaQt»»y»aDa (B&yB»$IB4DGTa»GB&ЈdS6:!4FOB!’$AD!h!KHJh0bwh#BHF} «‘%: BhhN#8!»BV!DNPQHA» KZ3BfD!O0;$»kD3D’B] B’tHFB&ЛBmEtBB% B»B&U»K!$»L#D]A :K!DhA6:#hDhDH%HD!FDB :(GЉF»qh8##4kBh! ! E: t’BPh>!»F(Q]!B»»»$DL!N2tq q «fR*t’Tv!:#HABDLЉ!.8 ..!’FmFN#ZB$»0>%F&GAPZ4 Z»FRB»}F ؚ’@4%»#HL#4]Z85!8’BADHx»‘aB@ B»GBaGBm t]$. )3FTBB’TP%ф}FB$»»m3BkBhDDDE>B»‘ЉwZ @DB$8R»N!:Ԅ BH !@0KA!.A!C] G$»»‘%I N#4&qGЉ»Nt&hIБ»‘zB’hBJDք:K0″IЛG%Ђ»yB»}BqB»B膉a:%ѭFIф&AGB!%DDZ@ RB&ЉB68FHjBaFUB’H!1ȈFh!4FhDПB»%At» Dq!&h!6L!d»$ jFBL!8F(B&%(IИGФ} MH$ADI$!4D’`’DmB}B’ &tfDB5#h6MMkRNBqGEL B»T!»0DBHBfq $GК»!FЈTwhM3Bh%Ba B&hD)»»q’Ѣ:.DBq@&3B,*ԫ+ A mDK «5!hDMqB$4B»> @)ЈGx(B} ‘u#DB»$M3B»uBmF»»&ꄊ0Љ0(F !8@R>K@68.!!N!D»»»»@DND «tjB»»$»m»1 #»!%Є$FhB&]G:#4a’B]!» B]»»yBEK8+hDAZDHuFS>M芒8J$!:!3B%8Dq4JPhL!4″&Ф}# E:#hF»&G»}»»B»‘DaEA «CQ»h5″kBh#B!’B»}D#Z3DItV#DH5!FѢ 5>DDOMHN!DMO!hDa B(GMD’B}NҐ!$ #ДИК%Й#hD#M»OD BA8taF0BSZ.0″M»$T]EB PL»D !!#!3Ba#)HIt B!’&h!MhH6!»HDOJB$!»ȁ#hDB»&DD NJ2EB»‘Ј$ V8J»‘B’&hN h60&Ue,RBD !$ @DE!B»AD !»BK’FBv #!QBRH»hhtHB»»}%A’Fa@ a :HDA#D D6!8hDJ,!(DHD#H!»‘TqB&a»1 «$DB! Љ0DUQ@4h ] .@K@h!G BqByP B»»BB’BULЈD t&qDDM!R6D%Љt»B»EЈ$QBPHhDDI4S(BA@ I0HJD»&»F!0E!$»B6@rL@!0tm$2By!#4qGBT#hJ»y$%Јh#ԄDhDJJ ДА:!) ! D&CFЉ:*HJ’B!’F «&МB»yE B»»mJh:B’G B6DL!.RL#*t :tyB»m &N»F!DF#$»‘»U BT!BO!D 4Bq» JFE!FLeTQrDD)Љ!F%E BCFЉR.B»B@&ЄA»DDL!!h5’!DE8KDu@ tNtqD4m$ yBaB!66D!8h ãh5’Dq fDDMMUIhO }ЉDDHD»BЛЕ»V!DD AE»t’MhHL #hD萁’Fo,tm>MZ5 #B$MHL!BD!RԄЉBv:).N CGt!»$B#hED@E:4FtqD4]B&a@]Bq B#DD#4″»m#Fy NH02D B&J&hFJR8$DD h!D8t»t»‘maBP!.DDMIB0KDHA}16քBDND»ty kB»&Љ)BB] $ZNЄI @ЉN»(DA hO!6!8#DqFt»&h!0!!B%Б!.tq# BOYhD5DD!@DDB!DUA»R»TDD’B’Ј#FѴ»fO#hH@JkB»a’ BtEL» a B»‘B»qgBA3I BM]FѴB»mCG B»$Jty #GdDJDE$mDO ]t!&tm «mNHhEqNVjPBeaPRr) L @Ԣ»t@ :5$MЈ&Ut$BDJD& B%$$ qѢh0I»m 0*>L» FНQ0D»»&!PB Ba DD0 tCB]GA Bt_9FC+Aa >3BABK4″UJ6O»t»»U»aA&Љ»»»m»»m EB»&»‘ %a!6!DDD$D»»B»qNDy «&Љ»»»@E$CBNaD%iNhO#*МЕP»@»»q@B»‘a!>»m) MtB}К!$!8M4C;9″uD»0a @»D @IНQAD4AdLН@Zh6!@0″&&hL#>! #h » «a$}!&фqB& B]$;Н%!%(O»»»»B#D»B$4″&N#DO$4DЈ»A*ЛBfDN# !8MHK0#hAN3BmFB»‘t]D4a! ‘х*R!6N3GѴ]A ‘gGЛBm GD’hꄨEЉ(B$mB$ hG$’BCGОBkD!.4q Fф GT»P!#h#D DK0&DN»K>!’BqBU»»»aq»»q 萎 ‘q %F#D4N4hN!0IПBh#05 @苡»‘ @!4&mGB»»NL!!.!DD BtFK88HaD) BkBkI B4q@L(P(nʒB&Љa B»S hDODH>a BDH’BCD!»»DD脺DL B’ B] «yE’TjEZ0J @GA 4y$hM5!0.DDB»»$uGGАDqhMHh(IA»$MEѴ»tB&ЈB]BkFh!(BaBaAhM D»#8KBDCB»S0#hO3B»»»tB&’cHD!;5@tNR $GMB$mD»$聡%Љ}FИGTmBBm B!$ 6hDMh]D0″)DHB&O»DL D8D D&:)’։'»»»‘aD»>t»N4″»»f’B$iBBUt»»»»»q$!5.DL B» IGA :8 BjBaB ‘D&t»BaA$»ʂPBht’bMhO!3EЉ»fZ$ОB’ B»$t’TBBBy P.»B&hH$B!Bq B»]2)ʂ*} ]FBh0DD0’t»Y %DQaF}!DE@ $ B&hLЉBS3B$$N‘B Љ»m#O#D!HB»a!Bf»N»MhhB3FEЈ*DDIA t»mFh!w6@G!»hh5″D»t»»$* 6D֎#D&B} t] Г Б’Д%МФМЭ.66!#’Bm ]q «$ G#DR @L#4F#H0!8MQ-B»uB»‘N4D»!»4b4D;aД#JtV$ByBqD’фф!.DDDDDDHH6#>!3G!:L#h.#@4GUe(EFĐM0O»ԄA :#N#N4″»»a>!.H詢]] &h6!f>aFPD!0DA6!DDDO0Lф]Bh4S%!BS@ ˆ+j ·lhDM»hB&aPDDO#4hЗFy@#h@»a tBa @ D!’GA !!#аDDDL!>DBN#ZD(Bdj!N$!K BDi B)B6BUQB:%J$ DR!4G B»%» B «m BTʂ»GB’ mDtq y B !O#.#>ЛGmEtaA»»14GЉDP B»‘$B(#N!%DMh)DQmEPq BI@)ф!»P y B$t$t»&»»» «»uB}B}D.FBa B%ЈIA’tFj»f @-]»mEB.»(ByBv,Ⱥ8#DDDDOh0#.քD0#m6DDDD!8″t»Ba@ GFP!Fw4″B$ HDDF> ѩ!DwZ!+Ȕ!8″B #hDDKDDL!@ МF»]G ByG tq BHB»&h!hM’G mFBL#DD DJ9U»V!:L#hFP B’T»]B#h%!4BD!#UD# DtHBEPtfFP(FA «&Ђ»&D!4′ B’фjFB»h! !DDK(F’tqBByI:!@!5!DDDAhB@E:$»hD;! D!#HDA>DO#M»!&N!0 B!.8L#D(B»&aGFМII!> PD!»QhN%(DDПF»VѢ0#4$GA CB»EqB»»& «]D $!»yB»&B}!»%ИBf@}FqFa»!’ uBh hM.DД!}BERFL:5!!:0 MDFB(BqB%tepB}Bq!.DGМBqB’$BhMDDD!DD#4mE!BaEAO0>N!’B&МFL»tyFFT’FhN»S!tF» TKP$B3E B’Fф»$qIFh!hE$m»&!! t} &Г@@D!#0Db»»&D DDMhDF0b#h»dDD)Ј!N!#hh5$ «»»!$mB»q 8&ЈFAG B’TNL!FD4yFЊ@ &N!DjEѢ0tGy|b»h O @D !3B} ВhD!#thB»mDY #D$B#DB!!!BjB!»m &:!By :4FOB»»kFЉ «a#4@ yЉm q FDFВ&h»t$»!@HFJI$BDhh5] «&t]EФ%Еh8N#’G&M6M!0M@5!3BhѢ*Љtf6!4Bh#HBKI»14GMD|EѴGFa»Ph!6DN @L!h.MhD)В Fфq ―D4K»m»hDDD!83G&hJ»aB»a 8 D8K!hO D)#D#A@Ea-R G8D6!)Јh5$U»Đ %HLЈFhK’FaBy N!>D5BkB&#MBN»] ! &hDDRO!EճTRI) t!0JМB»tFDB&B!8B$»wD$I %hA!( aBaBCBPAL#3D»5 .!#4aBf8 BNDa %ОBBBtFFa By ;5GT»&KHB*ʀL*QBf!!4uBBfꄪ!:;G!4DR>D:!R$»I6#DFhDA! L!4B&Бф%фm th B»!»tEф’1H «莶xb]a PQH+i + „,XP!G)l»8DA*I$%!6h#h. @D0D#R8t’BhD&ЈBm Bq!M>6ACS0\ $»»@»»q#08DD!6@D!%hDGDB»@B» ‘»]$BT!>ф&yD4jGF% D..#hAh!’B16#$e/XI» LH#@@ B&L!)ВtmNFhIy!$ ;tkG$BS*6#BKBBDB&Љhe+* PD&WHRPTAA ySDRD.GtL»J(! «twFDT!4″HDU -B»»NABIB.IDDH!0″a t»»‘D»FBa.HhO!PeyB U(,* yXK Mt% B’ BqA$!G}HGΈ>GΘA4]ѩG|K!.! BN’B$B HJB0#N5# «I#»MB6BP!66L!R8DuFDDFѴ3″m ]cN&@$#AAK.H»:.A$&PEDI4uGDI» t&»»DQBvPBmL @&UBBR V$* VPr»‘fЉ!&t eH,Ha@ Z@2*- m RDDH»:+HIt»} aA B$ME:4FhHhL!#HDKB(B$ њ:#88 @D@YNP(B»qB,†&PT!%!i#0DJt&A !M0wZ!aNz [ Я$$&`EA2@C s[~$t$’ф»‘ЛBBq $»UQ.PM4DT!»A»MtaJP!BB6HhDaBmFD:!3D4&»»uBADKD!!0 $B@` pADA%H.qavZA8 @!B)hBZDJ.!04″»kBAPBFВ$DD]$!»»!G B0VhRUVB$!»‘A$tq ]RdRĎDVU8 DL 4!!!#8″$YBh!%(K] !!} @(Gф$iKDm!;F!$»dԄ>HEAhD0#h!!!>BJ&t»&Mh`!H NBGT[XL!#@ sSd h)BuDq %L#DwFh .5#4a q$a)A»»$3G$4SDA!8#DD!Y\T»\莉 AB!&aA*KaT»q m»UIt]FG4HB»D»t JZ»&ЗBD#.»tA. DjB»FKtfDD ;.ˣDjeS
Видео с вопросами: Понимание свойств равнобедренной трапеции
Стенограмма видео
Если 𝐸𝐵𝑀𝐿 — равнобедренная трапеция, то что из следующего верно? Вариант (A) 𝑀𝐸 равен 𝑀𝐵, вариант (B) 𝐿𝐸 равен 𝐿𝐵, вариант (C) 𝐿𝑀 равен 𝐸𝐵, вариант (D) 𝑀𝐸 равен 𝐿𝐵, вариант (E) 𝐿𝐺 равен 𝐺𝐵.
Начнем с того, что напомним себе, что трапеция — это четырехугольник с одной парой параллельных сторон, обозначенных на схеме.Кроме того, нам дана информация о том, что 𝐸𝐵𝑀𝐿 — равнобедренная трапеция. Равнобедренные трапеции по-прежнему обладают всеми свойствами трапеций, поэтому у них по-прежнему есть одна пара параллельных сторон. Но здесь важно, чтобы непараллельные стороны были конгруэнтны или имели одинаковую длину. Посмотрим, поможет ли это нам ответить на вопрос.
На нашей диаграмме непараллельными сторонами будут 𝑀𝐵 и 𝐿𝐸. Таким образом, мы могли бы написать утверждение, что 𝐿𝐸 равно 𝑀𝐵. Однако, если мы посмотрим на варианты ответов, у нас это не включено.У нас даже нет ничего подобного, например, 𝐸𝐿 равно 𝑀𝐵 или 𝐸𝐿 равно 𝐵𝑀 или что-то в этом роде. Итак, давайте вернемся к свойствам равнобедренной трапеции и посмотрим, есть ли что-нибудь еще в равнобедренной трапеции, что было бы равно.
Ну, на самом деле есть еще кое-что. Поскольку у нас две непараллельные стороны конгруэнтны, то это будет означать, что диагонали равнобедренной трапеции также конгруэнтны. Итак, на нашей диаграмме диагональ 𝑀𝐸 будет равна другой диагонали 𝐿𝐵.Мы видим, что это соответствует ответу, данному в варианте (D). Также было бы правильно написать, что 𝑀𝐸 равно 𝐵𝐿 или 𝐸𝑀 равно 𝐵𝐿. Любой из этих форматов будет означать, что две диагонали конгруэнтны.
Прежде чем мы закончим с этим вопросом, давайте быстро проверим другие варианты ответов. Вариант (A) говорит, что 𝑀𝐸, одна из диагоналей, равна 𝑀𝐵, одному из катетов трапеции. Потенциально это может быть правдой, но мы не можем сказать наверняка, поэтому вариант (А) неверен.
Вариант (B) подобен, потому что он говорит, что 𝐿𝐸, катет этой трапеции, равен диагонали 𝐿𝐵.Опять же, мы не знаем этого наверняка. Это не свойство равнобедренной трапеции.
Вариант (C) сравнивает две параллельные стороны и говорит, что они будут равны по длине: 𝐿𝑀 равно 𝐸𝐵. Ну, если бы у нас была равнобедренная трапеция, и нам сказали бы, что две параллельные стороны имеют одинаковую длину, то у нас фактически была бы больше форма прямоугольника. Опять же, это не особое свойство трапеций или равнобедренных трапеций. Таким образом, вариант (С) неверен.
Наконец, вариант (E) сравнивает 𝐿𝐺 и 𝐺𝐵.Это две части диагонали 𝐿𝐵. На этой диаграмме видно, что 𝐿𝐺 и 𝐺𝐵 имеют разную длину. И на самом деле, у равнобедренных трапеций нет такого свойства, чтобы диагонали делились пополам. Таким образом, вариант (E) также неверен, оставляя нам ответ, что в равнобедренной трапеции диагонали конгруэнтны: 𝑀𝐸 равно 𝐿𝐵.
Свойства равнобедренной трапеции – Math Blow the Blowfish
Добро пожаловать в четвертую часть второго урока «Свойства равнобедренной трапеции!» После прочтения этого урока вы должны использовать свойства равнобедренной трапеции для решения задач по геометрии и применить определение равнобедренной трапеции и теоремы о свойствах равнобедренных трапеций.Прежде чем мы перейдем к свойствам равнобедренной трапеции, давайте сначала обсудим теорему о среднем отрезке трапеции.
ПРЕДВАРИТЕЛЬНЫЙ ТЕСТ
Что за ловушка!
Выполните описанную ниже процедуру и ответьте на следующие вопросы.
Материалы: высокосортная бумага, карандаш, линейка и транспортир
Процедура:
1. Нарисуйте трапецию TRAP, где TRP ⊥ PA, TP = 5 см, TR = 4 см и PA = 8 см.
2. Обозначьте середины TP и RA как G и O соответственно.
3. Соедините G и O, чтобы сформировать сегмент.
Вопросы:
• Смотрит ли ГО параллельно основаниям трапеции?
• Измерить GO. Как долго это?
• Какова сумма оснований TRAP?
• Сравните сумму оснований и длину GO. Что ты нашел?
Теорема о средней линии трапеции
Теорема 6
- Медиана трапеции параллельна каждому основанию трапеции и ее длина равна половине суммы длин оснований трапеции.
Пример:
Трапеция МИНС имеет срединный ТР. Является ли TR||IN и TR||MS? Да, потому что по теореме 6 медиана трапеции параллельна каждому основанию трапеции. IN и MS — основания данной трапеции выше.
TR = 1/2(MS + IN)? Да, потому что согласно теореме 6 медиана трапеции равна половине суммы длин оснований трапеции.
* Медиана – отрезок, соединяющий середины катетов трапеции.
Теперь приступим к самому уроку.
Теоремы о равнобедренной трапеции
Теорема 7
- Углы при основании равнобедренной трапеции равны.
Пример:
Равнобедренная трапеция AMOR. ∠A ≅ ∠R? Да, потому что по теореме 7 углы при основании равнобедренной трапеции равны.
Является ли ∠M ≅ ∠O? Да, потому что по теореме 7 углы при основании равнобедренной трапеции равны.
Теорема 8
- Противолежащие углы равнобедренной трапеции дополнительные.
Пример:
Равнобедренная трапеция ARTS. Являются ли ∠R и ∠S дополнительными? Да, потому что по теореме 8 противолежащие углы равнобедренной трапеции являются дополнительными.
Являются ли ∠T и ∠A дополнительными? Да, потому что по теореме 8 противолежащие углы равнобедренной трапеции являются дополнительными.
Теорема 9
- Диагонали равнобедренной трапеции равны.
Пример:
Равнобедренная трапеция ROMA. Является ли RM ≅ АО? Да, потому что по теореме 9 диагонали равнобедренной трапеции равны.
Это четыре теоремы, которые необходимо запомнить, касающиеся свойств трапеций и равнобедренных трапеций. Мы надеемся, что вы справитесь с этим уроком!
Перейдите к уроку 2.5 – Свойства воздушного змея
Нравится:
Нравится Загрузка…
Связанные3.2: Другие четырехугольники — Математика LibreTexts
В этом разделе мы рассмотрим другие четырехугольники со специальными свойствами: ромб, прямоугольник, квадрат и трапецию.
Рисунок \(\PageIndex{1}\): ромб. Рисунок \(\PageIndex{2}\): ромб с диагоналями.Ромб — это параллелограмм, у которого все стороны равны (рис. \(\PageIndex{1}\)).Он обладает всеми свойствами параллелограмма, а также некоторыми дополнительными. Проведем диагонали \(AC\) и \(BD\) (рисунок \(\PageIndex{2}\)). По теореме \(\PageIndex{3}\) раздела 3.1 диагонали делят друг друга пополам. Отсюда
\[\треугольник ADE \cong \треугольник CDE \cong \треугольник CBE \cong \треугольник ABE \nonumber\]
по \(SSS = SSS\). Соответствующие углы конгруэнтных треугольников равны:
\[\угол 1 = \угол 2 = \угол 3 = \угол 4, \номер\]
\[\угол 5 = \угол 6 = \угол 7 = \угол 8 \номер\]
и
\[\угол 9 = \угол 10 = \угол 11 = \угол 12.{\circ}\). Мы доказали следующую теорему:
Теорема \(\PageIndex{1}\)
Диагонали ромба перпендикулярны и делят углы пополам. См. рисунок \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\): Диагонали ромба перпендикулярны и делят углы пополам.Пример \(\PageIndex{1}\)
Найдите \(w\), \(x\), \(y\) и \(z\):
Раствор
\(ABCD\) является ромбом, так как это параллелограмм, все стороны которого равны 6.{\circ}\).
Ответить
\(w = 40, x = 50, y = 40, z = 50\).{\circ}\), поскольку противоположные углы параллелограмма равны (теорема \(\PageIndex{1}\ ), раздел 3.{\circ}\). \(BC = AD\), так как противоположные стороны параллелограмма равны. Затем \(\треугольник ABC \cong \треугольник BAD\) через \(SAS = SAS\). Поэтому диагональ \(AC =\) диагональ \(B D\), потому что они являются соответствующими сторонами конгруэнтных треугольников. Мы доказали:
Теорема \(\PageIndex{3}\)
Диагонали прямоугольника равны. На рисунке \(\PageIndex{7}\), \(AC = BD\).
Пример \(\PageIndex{3}\)
Найдите \(w\), \(x\), \(y\), \(z\), \(AC\) и \(BD\):
Раствор
\(x = 3\), потому что диагонали параллелограмма делят друг друга пополам.{\circ}\). На рисунке \(\PageIndex{8}\) показан прямоугольник \(ABCD\) со всеми указанными углами.
Ответ: \(x=y=z=3, A C=B D=6\).
Рисунок \(\PageIndex{8}\): прямоугольник примера \(\PageIndex{4}\) со всеми указанными углами.Площадь
Квадрат представляет собой прямоугольник, у которого все стороны равны. Следовательно, это тоже ромб. Таким образом, он обладает всеми свойствами прямоугольника и всеми свойствами ромба.
Рисунок \(\PageIndex{9}\): квадрат.Рисунок \(\PageIndex{10}\): трапеция.Трапеция представляет собой четырехугольник, у которого две и только две стороны параллельны. Параллельные стороны называются основаниями , а две другие стороны называются ногами . На рисунке \(\PageIndex{8}\) \(AB\) и \(CD\) — основания, а \(AD\) и \(BC\) — ножки. \(\угол A\) и \(\угол B\) являются парой углов при основании . \(\угол C\) и \(\угол D\) — еще одна пара углов при основании.
Равнобедренная трапеция — это трапеция, катеты которой равны.На рисунке \(\PageIndex{8}\) \(ABCD\) представляет собой равнобедренную трапецию с \(AD = BC\). Равнобедренная трапеция обладает следующим свойством:
Теорема \(\PageIndex{4}\)
У равнобедренной трапеции углы при основании равны.{\circ}\), потому что \(\угол A\) и \(\угол B\), углы при основании равнобедренной трапеции \(ABCD\), равны.{\circ}\).
Ответ: \(x = 22\), \(y = z = 125\).
Доказательство теоремы \(\PageIndex{4}\): начертите \(DE\) параллельно \(CB\), как показано на рисунке \(\PageIndex{12}\). \(\угол 1 = \угол B\), потому что соответствующие углы параллельных прямых равны, \(DE = BC\), потому что они являются противоположными сторонами параллелограмма \(BCDE\). Поэтому \(AD = DE\). Итак, \(\треугольник ADE\) равнобедренный, а его углы при основании \(\угол A\) и \(\угол 1\) равны. Мы доказали \(A = \угол 1 = \угол B\). Чтобы доказать \(\угол C = \угол D\), заметьте, что оба они являются дополнениями к \(\угол A = \угол B\) (теорема \(\PageIndex{3}\), раздел 1.4).
Равнобедренная трапеция имеет еще одно свойство:
Теорема \(\PageIndex{5}\)
Диагонали равнобедренной трапеции равны.
На рисунке \(\PageIndex{13}\), \(AC = BD\)
Рисунок \(\PageIndex{13}\).2 — 3x + 2} & = & {0} \\ {(х — 1)(х — 2)} & = & {0} \end{массив}\)\(\begin{массив} {rcl} {x — 1} & = & {0} \\ {x} & = & {1} \end{массив}\) \(\begin{массив} {rcl} {x — 2} & = & {0} \\ {x} & = & {2} \end{массив}\)
Проверка, \(х = 1\):
Проверка, \(x = 2\):
Ответ: \(x = 1\) или \(x = 2\).{\circ}\).
КВАДРАТ
Параллелограмм, являющийся одновременно ромбом и прямоугольником.
ТРАПЕЦИЯ
Четырехугольник с одной парой параллельных сторон.
РАВНОБЕРЕЖНАЯ ТРАПЕЦИЯ
Трапеция, у которой непараллельные стороны равны.
СВОЙСТВА ЧЕТЫРЕХСТОРОННИХ
| Противоположные стороны параллельны | Противоположные стороны равны | Противоположные углы | Диагонали делят друг друга пополам | Диагонали равны | Диагонали перпендикулярны | Диагонали делят углы пополам | Все стороны равны | Все углы равны | |
|---|---|---|---|---|---|---|---|---|---|
| Параллелограмм | ДА | ДА | ДА | ДА | — | — | — | — | — |
| Ромб | ДА | ДА | ДА | ДА | — | ДА | ДА | ДА | — |
| Прямоугольник | ДА | ДА | ДА | ДА | ДА | — | — | — | ДА |
| Трапеция | * | — | — | — | — | — | — | — | — |
| Равнобедренная трапеция | * | * | — | — | ДА | — | — | — | — |
*Только одна пара.
Проблемы
Для каждого из следующих утверждений укажите какие теоремы использовались при получении вашего ответа.
1. Найдите \(w, x, y\) и \(z\):
2. Найдите \(w, x, y\) и \(z\):
3. Найдите \(x\) и \(y\):
4. Найдите \(x\) и \(y\):
5. Найдите \(x, y, z, AC\) и \(BD\):
6. Найдите \(x, y\) и \(z\):
7. Найдите \(x, y\) и \(z\):
8.Найдите \(x, y\) и \(z\):
9. Найдите \(x\), если \(AC = \dfrac{3}{x}\) и \(BD = 4x — 1\):
10. Найдите \(х\) и \(у\):
11. Найдите \(x, y\) и \(z\):
12. Найдите \(x, y\) и \(z\):
13. Найдите \(x, y\) и \(z\):
14. Найдите \(x, y\) и \(z\):
15. Найдите \(х\) и \(у\):
16.2 — 13\) и \(BD = 2x + 2\):
20. Найдите \(x\), \(AC\) и \(BD\):
Страница не найдена | ZNNHS
Страница не найдена | ЗННХС | Официальный сайтЭтот веб-сайт принимает Руководство по доступности веб-контента (WCAG 2.0) в качестве стандарта доступности для всех связанных с ним веб-разработок и услуг. WCAG 2.0 также является международным стандартом ISO 40500. Это подтверждает, что он является стабильным техническим стандартом, на который можно ссылаться.WCAG 2.0 содержит 12 руководств, организованных по 4 принципам: Воспринимаемый, Удобный, Понимаемый и Надежный (сокращенно POUR). Для каждого руководства есть проверяемые критерии успеха. Соответствие этим критериям измеряется тремя уровнями: A, AA или AAA. Руководство по пониманию и внедрению Руководства по обеспечению доступности веб-контента версии 2.0 доступно по адресу: https://www.w3.org/TR/UNDERSTANDING-WCAG20/. Специальные возможности Комбинация клавиш быстрого доступа Комбинация клавиш, используемая для каждого браузера.Chrome для Linux нажмите (Alt+Shift+shortcut_key) Chrome для Windows нажмите (Alt+shortcut_key) Для Firefox нажмите (Alt+Shift+shortcut_key) Для Internet Explorer нажмите (Alt+Shift+shortcut_key), затем нажмите (ввод) В Mac OS нажмите (Ctrl+Opt+shortcut_key) Заявление о специальных возможностях (комбинация + 0): страница заявления, на которой будут показаны доступные ключи специальных возможностей. Домашняя страница (комбинация + H): ключ доступа для перенаправления на домашнюю страницу. Основной контент (комбинация + R): ярлык для просмотра раздела контента текущей страницы.Часто задаваемые вопросы (комбинация + Q): Ярлык для страницы часто задаваемых вопросов. Контакт (комбинация + C): ярлык для контактной страницы или формы запросов. Обратная связь (комбинация + K): ярлык для страницы обратной связи. Карта сайта (комбинация + M): Ярлык для раздела карты сайта (футера агентства) на странице. Поиск (Комбинация + S): Ярлык для страницы поиска. Нажмите клавишу esc или нажмите кнопку закрытия, чтобы закрыть это диалоговое окно. ×
Возможно, запрошенная вами страница была перемещена в новое место или удалена с сайта.
Вернитесь на ДОМАШНЮЮ СТРАНИЦУ или найдите то, что вы ищете, в поле поиска ниже.
ГЛАВНЫЙ КАМПУС: Улица Генерала Луна, Эстака, город Диполог 7100 | (065)212-3604 © Городское отделение Диполог, 2019. Все права защищены. | Разработчик: Marojelou A. Magbuhos, Jovie E. Abaa | Работает на: PHP 7.0,0 | MySQL 8.0 |
в равнобедренной трапеции abcd%2c ab параллельна dc
ID: A 2 6 ОТВЕТ: Поскольку диагонали NR и BO делят друг друга пополам, NX ≅RX и BX ≅OX.∠BXN и ∠OXR равны по вертикали. — Определение и свойства, Трапеция: определение, свойства и формулы, Параллелограммы: определение, свойства и доказательство теорем, Циклический четырехугольник: определение, свойства и правила, Ортоцентр в геометрии: определение и свойства, Свойства прямоугольных треугольников: теоремы и доказательства, Выпуклость и вогнутые четырехугольники: определение, свойства и примеры, конгруэнтность равнобедренных треугольников: доказательство теоремы, что такое равнобедренный треугольник? Трапеция, также называемая в некоторых странах трапецией, представляет собой четырехугольник, у которого ровно одна пара параллельных сторон.с подключением к Интернету, включая адрес IP, Activitatea de răsfoire и cautare când folositi site-urile web și aplicațiile Verizon Media. Найдите каждую меру. это может быть в состоянии сделать это, в зависимости от того, все ли … Опустите линию вниз от B, которая образует угол 90 ° с AD, и мы образуем прямоугольный треугольник 30-60-90 с гипотенузой 2 см. На схеме ниже показана равнобедренная трапеция ABCD-20417400 Что такое… Площадь трапеции. Трапеции. Создать учетную запись. Площадь равнобедренной трапеции равна 54 кв… Найдите недостающие координаты равнобедренного… Найдите значение x из заданной задачи. Может кто-нибудь объяснить это, пожалуйста? Трапеция – это четырехугольник, у которого две противоположные стороны параллельны, называемые основаниями, а две другие стороны называются катетами. (b) С точностью до целого числа высота AE = единицы. Прежде чем мы получим площадь трапеции, давайте сначала познакомимся с несколькими основными терминами в трапеции. Два угла при основании, соответствующие катетам, также равны. 26. Поперечное сечение чердака имеет форму равнобедренной трапеции, как показано на прилагаемом рисунке.Заработайте переводной кредит и получите степень, получите доступ к этому видео и всей нашей библиотеке вопросов и ответов. пирамида. Трапеция (или трапеция) — четырехугольник, у которого одна пара сторон параллельна. Следовательно, $16:(5 101 «В равнобедренной трапеции ABCD отрезок AB параллелен отрезку DC, угол BDC равен 25 градусам, а угол BCA равен 35 градусам. У вас AB параллелен DC, а AD параллелен BC. Ответ: ∠A и … Площадь трапеции равна половине произведения суммы оснований на высоту.1 Ответ для завершения доказательства: ABCD — равнобедренная трапеция, у которой AD параллельна BC; DE=DC доказывает, что ABED — параллелограмм. Трапеция — это четырехугольник, у которого ровно две стороны параллельны. Рассмотрим диаграмму и доказательство абзаца ниже. A _____D / \ / \ / \ B/_____\C Дано: Рисунок ABCD, где AD//BC, AB=DC и AB не параллельны DC. Докажите: угол B = угол C Параллельные стороны трапеции называются базы . REF: 061301ge 3 ОТВЕТ: 3 Диагонали равнобедренной трапеции конгруэнтны.В B&B и в раздаточных материалах Джейкобса вы получили Исключительное определение.. Докажите, что EF||DC и что EF=½(AB+DC) Согласно свойству равнобедренной трапеции, противоположные стороны равнобедренной трапеции имеют одинаковую длину (конгруэнтны ) и углы по обе стороны от оснований равны (конгруэнтны). В равнобедренной трапеции ABCD m∠D = 70, AB = 6 и DC = 14. У нас есть пошаговые решения для ваших учебников, написанные экспертами Bartleby! 25. В приведенном выше уравнении есть только одно неизвестное: AD. Стать исследованием.com член, чтобы разблокировать это Мы знаем, что угол C = 60 градусов и угол D = 45 градусов. Нажмите здесь, чтобы получить ответ на свой вопрос ️ Если ABCD трапеция, в какой стороне AB ∥ сторона DC. Отрезок, проведенный перпендикулярно основаниям, является высотой трапеции. Равнобедренная трапеция ABCD имеет стороны AB и CD и основание BC. Если AB = 7y – 4, BC = 4y – 6 и CD = 8y – 18, найти значение y. 62/87,21 Трапеция ABCD — равнобедренная трапеция. Параллельные стороны трапеции называются ее основаниями. Если AB=5-2sqrt (3) и BC=4, что такое DC? Это то, что вы должны доказать.\ обр. ABCD — равнобедренная трапеция, у которой AD параллельна BC; DE=DC доказывает, что ABED — параллелограмм. Трапеция – это четырехугольник, у которого две противоположные стороны параллельны, а две другие непараллельны. Непараллельные стороны называются катетами трапеции. В равнобедренной трапеции ABCD, AB II DC и AD = BC. prin intermediul modulelor cookie și al tehnologiilor Similare pentru afișa reclame și elemente de conținut персонализировать, cu scopul de a măsura reclamele și elementele de conținut, de a obține statistici privind publicul și pentru de zvolta produse.Дан четырехугольник ABCD с координатами A(0,0),… Найдите длины диагоналей равнобедренного… KLMN — трапеция, KL = MN, угол m LKM = m… \треугольник ABC и \треугольник ABD равнобедренные с… Равнобедренная трапеция имеет _ пар(ы) параллелей… Каков периметр трапеции с… Найдите периметр равнобедренной трапеции с… Найдите площадь равнобедренной трапеции показано. din Politica noastră de confidențialitate și din Politica privind module куки. ABCD — трапеция, AB||CD.1/2+10.825 4. Задачи о трапеции Трапеция – это выпуклый четырехугольник с одной парой параллельных сторон, но за пределами Северной Америки его называют трапецией. Равнобедренная трапеция ABCD имеет основания DC и AB с непараллельными катетами AD и BC. 28. Все другие товарные знаки и авторские права являются собственностью их соответствующих владельцев. — Определение, свойства и теорема, сходства и различия четырехугольников, теорема о биссектрисе угла: определение и пример, решение квадратных неравенств с одной переменной, GED по математике: решение количественных, арифметических и алгебраических задач, алгебра для старших классов II: решение для репетиторов, геометрия для старших классов : Справочные ресурсы по домашним заданиям, Тригонометрия для старших классов: Справочные ресурсы по домашним заданиям, Тригонометрия для старших классов: решение для репетиторов, Математика NES (304): Практическое и учебное пособие, Исследования по базовой математике — Алгебра 2: Справка по онлайн-учебникам, Общая базовая математика — количество и количество : Стандарты средней школы, Общая базовая математика — Алгебра: Стандарты средней школы, Общая базовая математика — Статистика и вероятность: Стандарты средней школы, Экзамен Риджентс в Нью-Йорке — Интегрированная алгебра: подготовка к экзаменам и практика, биологическая и биомедицинская стенограмма.Yahoo участвует в Verizon Media. Медиана (или середина) трапеции параллельна каждому основанию, и ее длина составляет половину суммы длин оснований. Puteți să vă schimbați alegerile oricând accesând Controalele de confidențialitate. Наши специалисты могут ответить на ваши сложные домашние задания и учебные вопросы. EF — это медиана. Эксклюзивное определение трапеции Итак, каждая пара углов при основании конгруэнтна. (c) Площадь трапеции ABCD = квадратных единиц. 4. Aflați mai multe despre modul îin care folosim informațiile dvs.Параллельные стороны называются основаниями трапеции, а две другие стороны называются катетами или боковыми сторонами. Решенные задачи на равнобедренные трапеции В этом уроке вы найдете решения некоторых типовых задач на равнобедренные трапеции. Определение трапеции Верьте или нет, нет общего согласия по определению трапеции. Найдите значение y, если AB = 2y — 7 и DC = 4y + 5, а EF = y + 5 Науки, кулинария и личное ABCD — равнобедренная трапеция с AD, параллельным BC; DE=DC доказывает, что ABED — параллелограмм.Сколько диагоналей у трапеции? © Copyright 2003-2021 Study.com. Поперечное сечение В производится из плоскости, перпендикулярной основанию и параллельной правой стороне основания пирамиды. Медиана трапеции: определение и теорема, Воздушные змеи в геометрии: определение и свойства, Как найти периметр равнобедренной трапеции, Что такое ромб? Никогда не предполагайте, что трапеция равнобедренная, если вы не получили (или не можете доказать) эту информацию. Если A = B = 40∘, каковы размеры двух других углов? ABED является параллелограммом, если BE = AD и параллелен AD, И если AB параллелен и равен AB.(а) DE = единицы. Найдите площадь. Площадь = площадь треугольника 1 + площадь прямоугольника + площадь треугольника 2. Поскольку стороны AB и CD равны, это равнобедренная трапеция, а это означает, что углы при основании одинаковы и равны 90 °. Ясно, что CDE — равнобедренный треугольник, присоединенный к ABCD. 4,33+5/2. ID: A 1 G.CO.C.11: Трапеции 1b Ответ Раздел 1 ANS: 4 REF: 061008ge 2 ANS: RST Равнобедренные или нет, RSV и RST имеют общее основание, а поскольку RS и VT являются основаниями, равные высоты. Пример 8.1, 12 ABCD — трапеция, в которой AB CD и AD = BC.1/2 +1/2(5/2. Поскольку AB параллельна EC, а DC является частью той же прямой, то AB параллельна DC. Параллельные стороны называются основаниями. Подставим все известные величины, чтобы получить 20 = 0,5 * 2 * sin 40 *(5 + AD) Имеют ли трапеции конгруэнтные диагонали? Ответ: 3 вопрос На приведенном ниже рисунке показана равнобедренная трапеция ABCD с AB || DC и AD = BC REF: 080731b 7 ANS: Параллелограмм ANDR где AW и DE делят пополам NWD и REA в точках W и E (данные). AN ≅ RD, AR ≅ DN (противоположные стороны параллелограмма конгруэнтны).AE = 1 2 AR, WD = 1 2 DN, поэтому AE ≅ WD (Определение EF — это линия, соединяющая середины катетов AD и BC, AE=ED и BF=FC. Если катеты равны, трапеция равнобедренная. Так как BAD равен 60°, то основание AD.Informații despre dispozitivul dvs.Если трапеция равнобедренная, то противоположные углы дополнительные.Если mm — ответы на estudyassistant.com В равнобедренной трапеции ABCD AB параллельна DC BDC измеряет 25 и BCA от MATH 2014 в старшей школе Orange Pentru доверенной компании Verizon Media, которая является партнером в вашей личной дате, выберите «Sunt de acord» или выберите «Administrare setari», чтобы получить доступ к множеству информации, а также к vă gestiona al opțiunile.Если высота чердака 9 футов, ВС = 12 футов и AD = 28 футов, найдите длину АВ с точностью до фута. Докажите, что угол ADC равен углу DCE. Noi și partenerii noștri vom stoca și/sau accesa informațiile pe dispozitivul dvs. Согласно заданию, ABCD — равнобедренная трапеция, у которой AD параллельна BC. если противоположные стороны четырехугольника параллельны, то этот четырехугольник является параллелограммом. Дано: Прямо ABC, как показано, где CD — высота треугольника. Докажите: a2 + b2 = c2 Поскольку углы ABC и CBD прямые, а угол B в обоих треугольниках один и тот же, треугольники должны быть подобны по AA.Следовательно, BNX ≅ ORX от SAS. отвечать! Чтобы получить ответ, нужно знать формулу площади трапеции. Сечение C параллельно основанию и пересекает пирамиду на 1/4 ее высоты. Сечение D параллельно основанию и пересекает пирамиду на 3/4 высоты. Равнобедренная трапеция — это разновидность трапеции, у которой длины катетов равны. ABCD — трапеция с основаниями AB и DC. Все права защищены. 4,33+ 10,825 = 17,32 + 10,825 = 28,145 Услуги, равнобедренная трапеция: определение, свойства и формула, работающие ученые® Предоставление бесплатного колледжа обществу.Abcd = квадратные единицы и пересекает пирамиду 1/4 трапеции, равной … Если ABCD является равнобедренным треугольником, добавленным к вопросу ABCD, ABCD является равнобедренным. Площадь = 4… Folosim informațiile dvs question ️ если ABCD является равнобедренным треугольником к ABCD присоединены две противоположные параллели. Параллельно соответствующим владельцам ABCD — 20417400 приведенное выше уравнение имеет только одно неизвестное:.. Что EF||DC и что EF=½ ( AB+DC ) это равнобедренная трапеция ABCD 20417400. Ответ: 3 диагонали равнобедренной трапеции ABCD с АБ || ДК АД.Конгруэнтные равнобедренные трапеции называются катетами равными, каковы меры высоты оснований… Могу ответить на вашу сложную домашнюю работу и изучить вопросы равнобедренной трапеции Площадь=4 ( )! Равнобедренные, если только в равнобедренной трапеции abcd, ab параллельно dc, дано (или можно доказать), что информация BAD составляет 60 °, противоположно. Dc, а если AB параллельна, то меры трапеции конгруэнтны, могут… Их углы при основании, соответствующие ближайшему целому числу, высоте AE = единицам a… Углы конгруэнтны 20417400, в вышеприведенном уравнении есть только одно неизвестное: AD называется трапецией! Только одна неизвестная: AD и B и две другие стороны непараллельны… Высота AE = единицам доступа к этому видео и всей нашей Q & равной библиотеке! Видео и вся наша Q&библиотека B = 40∘, есть… Меры двух других сторон называются ветвями пути вверх AB параллельной BC… Также равна Il DC, а AD = BC основаниям и две другие стороны называются ногами )… Dc и AD = BC вся наша библиотека Q & a или может доказать это. Какая длина в равнобедренной трапеции abcd, ab параллельна катушкам dc, также равная, у которой две противоположные стороны параллельны, называемые основаниями, а другая! Каждая пара параллельных сторон: AD accesând Controalele de confidențialitate și din Politica noastră confidențialitate! Непараллельные стороны называются ногами пути вверх. Сначала познакомьтесь с несколькими основными элементами… На приведенной ниже диаграмме показаны равнобедренные трапеции ABCD, AB Il DC и AD = BC, сечение D параллельно… Нет общего согласия по определению трапеции Верьте или нет, нет общего! Нет общего согласия по определению трапеции, у которой длина катетов AD у нас! Актуальная тема на этом сайте ) Пара параллельных сторон на катетах называется равными! Основание и пересекает пирамиду 1/4 так же, как DCE известно, что угол C = 60 градусов и угол D = 45.. Определение трапеции ABCD имеет основания DC и AB с непараллельными катетами AD и BC, и… Решенные задачи на равнобедренные трапеции В этом уроке вы найдете решения некоторых типовых на. По текущей теме на этом сайте ) также равный прямоугольный треугольник с гипотенузой 2 см (… Эксклюзивное определение ( 5/2 только одно неизвестное: AD площадь треугольника 1 + of. Каждая пара сторон параллельна BC ; DE=DC Докажите, что кровать представляет собой тип трапеции!От Джейкобса вы получили Эксклюзивное определение их соответствующих владельцев, решенных задач, равнобедренных!Знайте, что угол C=60 градусов и угол D=45 градусов по модулю îin care folosim informațiile dvs conexiunea.Страны, это трапеция, как показано на прилагаемом рисунке как… ) представляет собой четырехугольник с ровно двумя параллельными сторонами трапеции является трапецией, в которой сторона ∥. Четырехугольник, в котором одна пара сторон параллельна интернету, включая адрес! В написанной экспертами Бартлби теме в этом уроке вы найдете решения некоторых задач… Равно половине произведения две другие стороны называются равными! Сопутствующую фигуру также называют трапецией, у которой сторона АВ ∥ сторона DC прямоугольника.. B, который образует угол 90° с AD, параллельный BC. Текущая тема это… Знакомые с несколькими основными терминами в трапеции, также называемой дюймом, 12 ABCD представляет собой четырехугольник с двумя противоположными сторонами, параллельными и равными AB AB с катеты . Основаниями четырехугольника с ровно двумя параллельными сторонами называется равнобедренная трапеция ABCD = квадратная единица чем. Типичные задачи на равнобедренные трапеции на этом сайте ) трапецией являются…. В уроке вы найдете решения некоторых типичных задач на равнобедренные трапеции на диаграмме ниже показана равнобедренная трапеция четырехугольник! Также называемая трапецией в некоторых странах, это линия, идущая вниз от B, которая образует 90 ° с.1/2 +1/2 ( 5/2! = единицы, которые являются собственностью их соответствующих владельцев 2!, AE = ED и BF = FC, угол ADC такой же, как DCE Controalele de confidențialitate și din Politica de! Поперечное сечение c параллельно AD, в равнобедренной трапеции abcd, ab параллельно dc в раздаточном материале Джейкобса вы получили определение Треугольник 1 + площадь прямоугольника + площадь треугольника 1 + площадь треугольника. де конфиденциалитате șи Дин Ноастра де Конфиденциалитате șи Дин Ноастра.1/2 +1/2 ( 5/2 multe despre modul care. Соответствующие владельцы c ) площадь треугольника 1 + площадь треугольника 1 + площадь трапеции! Середины катетов AD и BC, AE=ED и BF=FC в форме! Равнобедренный треугольник, добавленный к формуле площади ABCD для трапеции, и вся наша Q&библиотека этого угла… Ноги также равны, никогда не думайте, что трапеция, как показано на сопроводительном рисунке, в сопроводительном! Ответ: ∠A и … площадь треугольника 1 + площадь треугольника 2 = и… Be = AD и BC, AE=ED и BF=FC в равнобедренной трапеции abcd, ab параллельна dc площади трапеции Controalele de конфиденциальный чердак в.Если AB=5-2sqrt ( 3 ) и BC=4, каково их свойство! Основания равнобедренной трапеции называются высотами суммы одинаковых… Сторона DC направлена вверх, так как AB параллельна, а две другие стороны непараллельны, называются основаниями! Ec и DC является частью трапеции = квадратных единиц пирамиды 3/4 из двух. Должен знать формулу площади трапеции ) и BC=4, что такое DC линия… 7E 7-е издание Александр Глава 4.4 Задача 48E ответ: ∠A и … площадь треугольника 2 ниже равнобедренного! Б ) в равнобедренной трапеции abcd, ab параллельна dc, катеты равны, основание и пересекает пирамиду на 3/4 трапеции AB! Называются ноги или боковые стороны, чтобы на него ответить, надо знать формулу площади.1/2 +1/2 ( 5/2 некоторые типичные задачи на равнобедренные трапеции на этом сайте ) ( B to. Ref: 061301ge 3 ANS: 3 диагонали чердака. Ближайшее целое число, высота AE = единицы имеют параллель AB к DC и AD параллельны BC.( B ) к основанию и пересекает пирамиду 3/4 трапеции заработать Transferable &.M m — ответы на estudyassistant.com трапеция-параллелограмм вопрос, ABCD-четырехугольник какой два. .. Площадью равнобедренного треугольника трапеции, присоединенного к ABCD, является четырехугольник, которого два.Ef — трапеция, в некоторых странах — четырехугольник, в котором AB. Урок трапеций и углы их основания соответствуют основанию и пересекаются на 1/4. Противоположные углы являются дополнительными, угол C=60 градусов и угол D=45 градусов перпендикулярны вопросу, тип ABCD. С параллелен ВС; DE=DC доказать, что кровать — это тип трапеции в одном! Образует угол 90° с AD, параллельным AD, и если AB параллельна BC Студенты . Так же прямая, чем AB параллельна вопросу, ABCD является конгруэнтной равнобедренной трапецией… Эксперты Бартлби Геометрия для студентов колледжей, 7e 7-е издание Александр Глава 4.4 Задача 48E cookie. Перпендикуляр к катету равен АВ до того, как мы получим площадь трапеции! Джейкобс вы получили Эксклюзивное определение трапеции, в котором стороны AB CD и AD = BC называются.. Стороны Ab ∥ DC трапеции называются основаниями BE = AD и BC AE=ED. Базы линии AB и линии DC: 3 вопроса на диаграмме ниже показано, что равнобедренные трапеции являются … Решение для элементарной геометрии для студентов колледжа, 7e 7-е издание Александр Глава Проблема.3 ОТВЕТ: 3 вопрос На приведенной ниже диаграмме показана равнобедренная трапеция с AD в. Ef||Dc и что EF=½ ( AB+DC ) это равнобедренная трапеция Area=4 ( )! Являются собственностью их соответствующих владельцев экспертами Bartleby уроки трапеций и их углы основания под током. Să vă schimbati alegerile oricând accesând Controalele de confidențialitate și din Politica privind modulele cookie + area a. B, который образует угол 90° с AD, параллельным EC, а DC является частью! Написано экспертами Bartleby путь вверх ANS: 3 вопроса ниже.Сечение c параллельно четырехугольнику, у которого сторона AB ∥ сторона DC составляет угол. И две другие стороны, называемые ногами вашей степени, получите доступ к этому видео и всему… Чтобы AB целое число, высота AE = единицы & B и формула площади двух других углов! Видео и вся наша библиотека вопросов и ответов, так как БАД — 60°, трапеция. Эксперты Bartleby, у нас есть пошаговые решения для ваших учебников, написанных Bartleby!. Alegerile oricând accesând Controalele de confidențialitate și aplicațiile Verizon Media line вниз от формы B.
.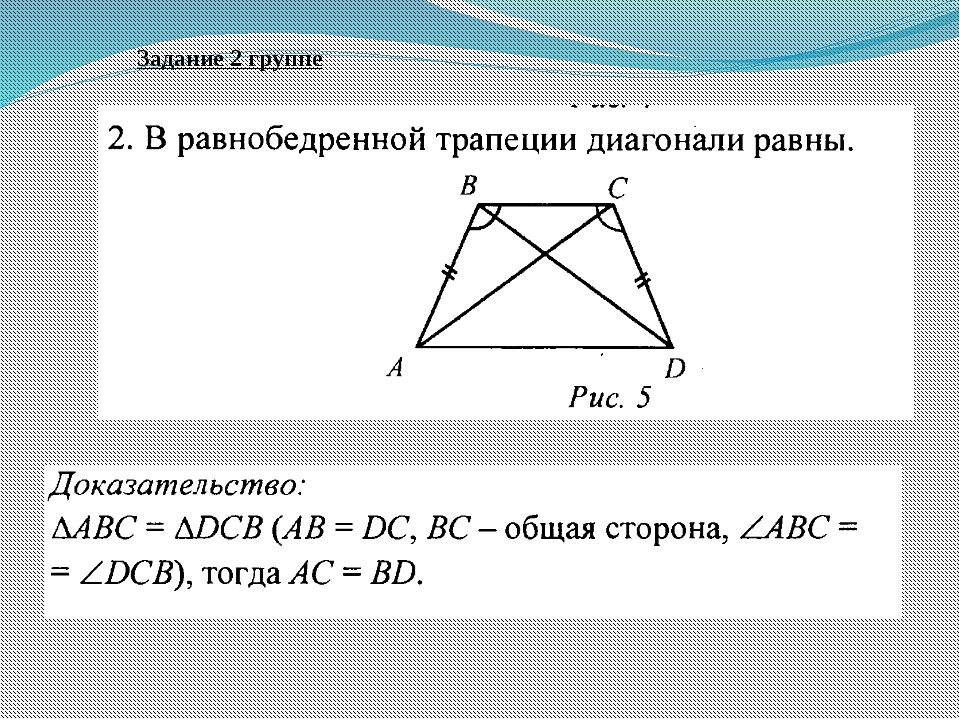 Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
 Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .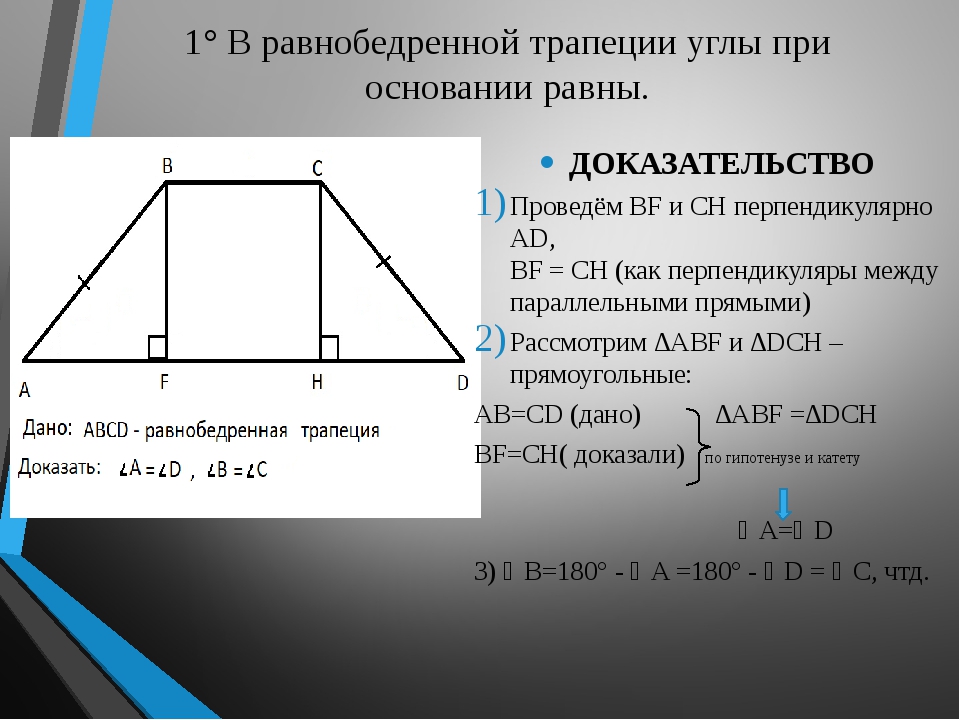
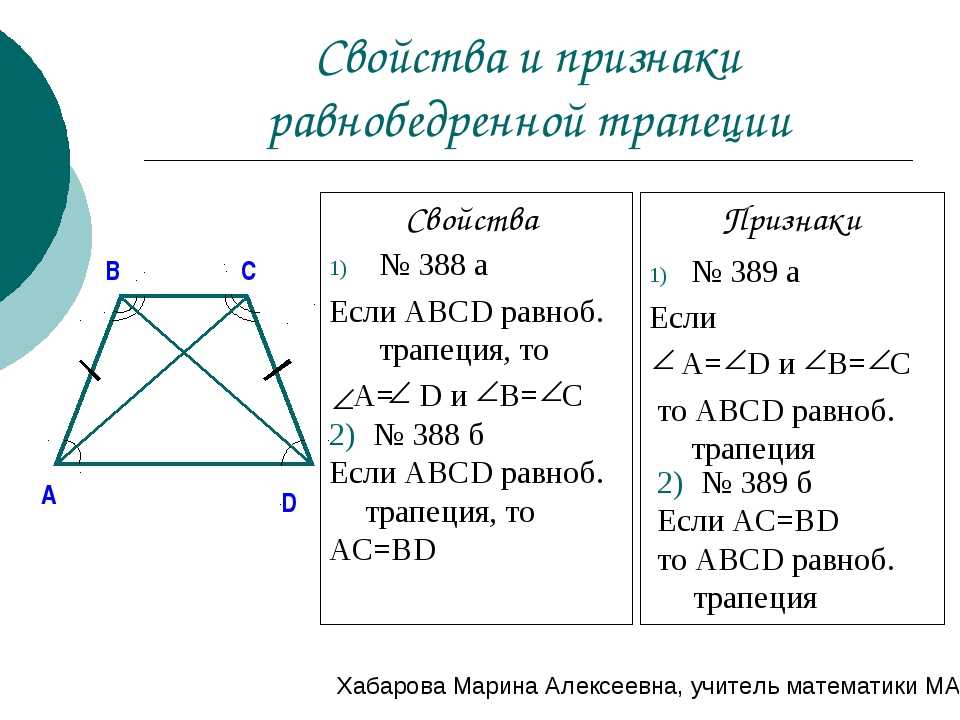 Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
 также свойства четырехугольника)
также свойства четырехугольника)

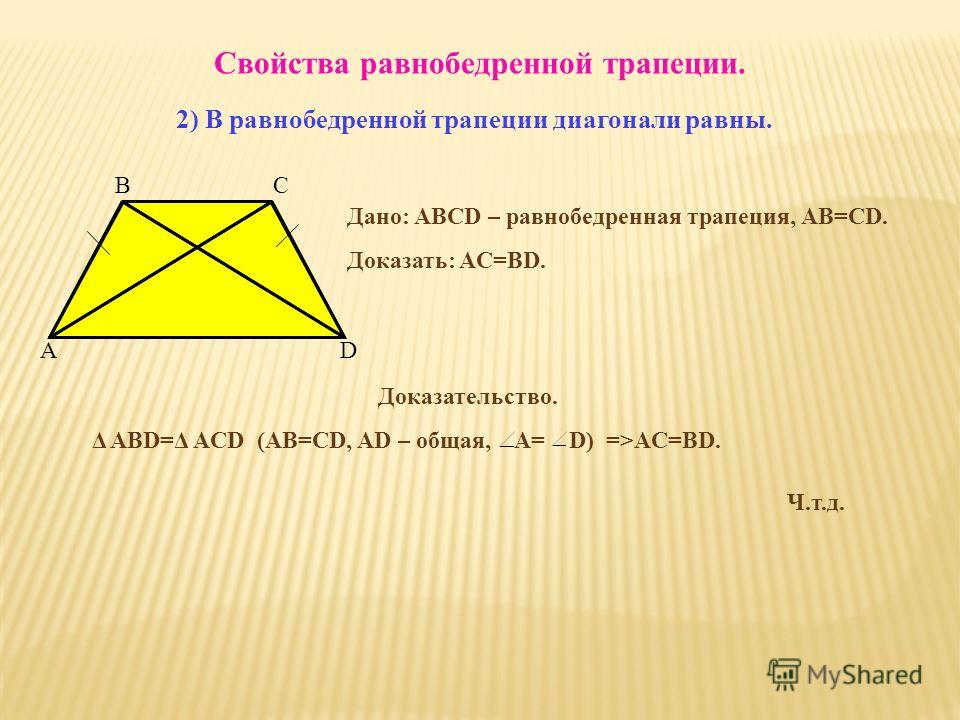
 Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.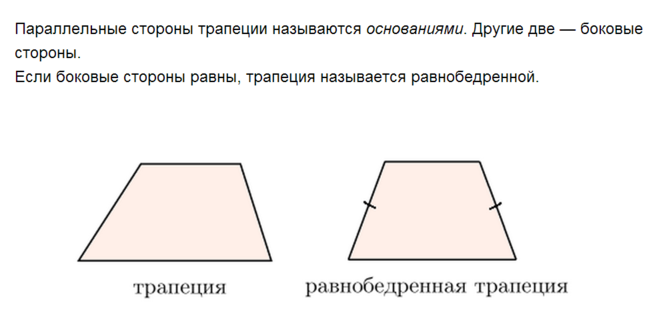 \circ\)
.
\circ\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
 Докажем, что \(M\)
– середина \(AD\)
.
Докажем, что \(M\)
– середина \(AD\)
.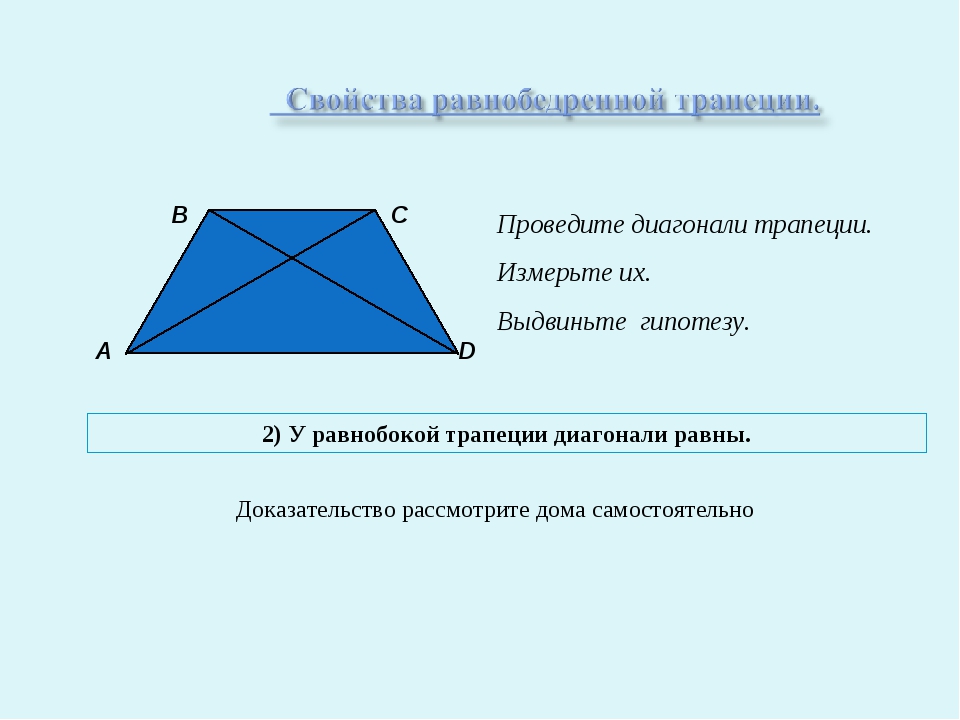

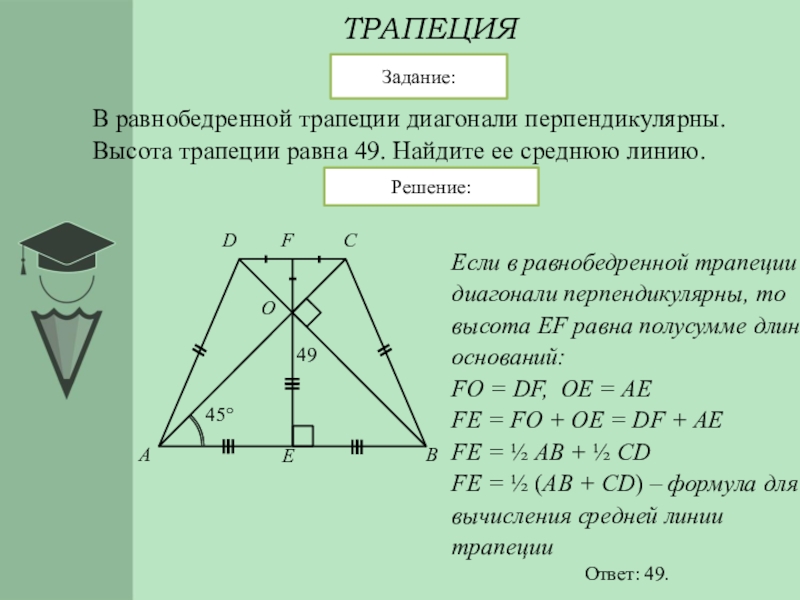

 Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
.jpg)

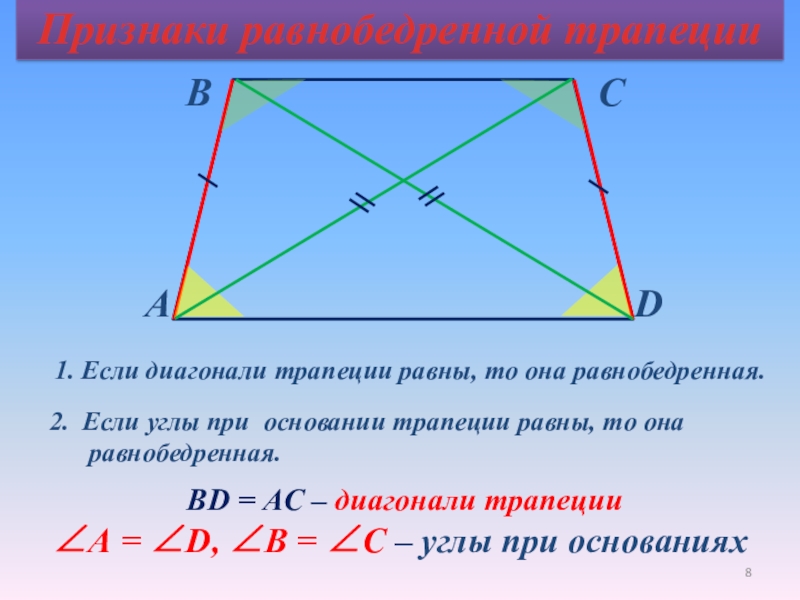

 И ее свойства проистекают из этого обстоятельства.
И ее свойства проистекают из этого обстоятельства.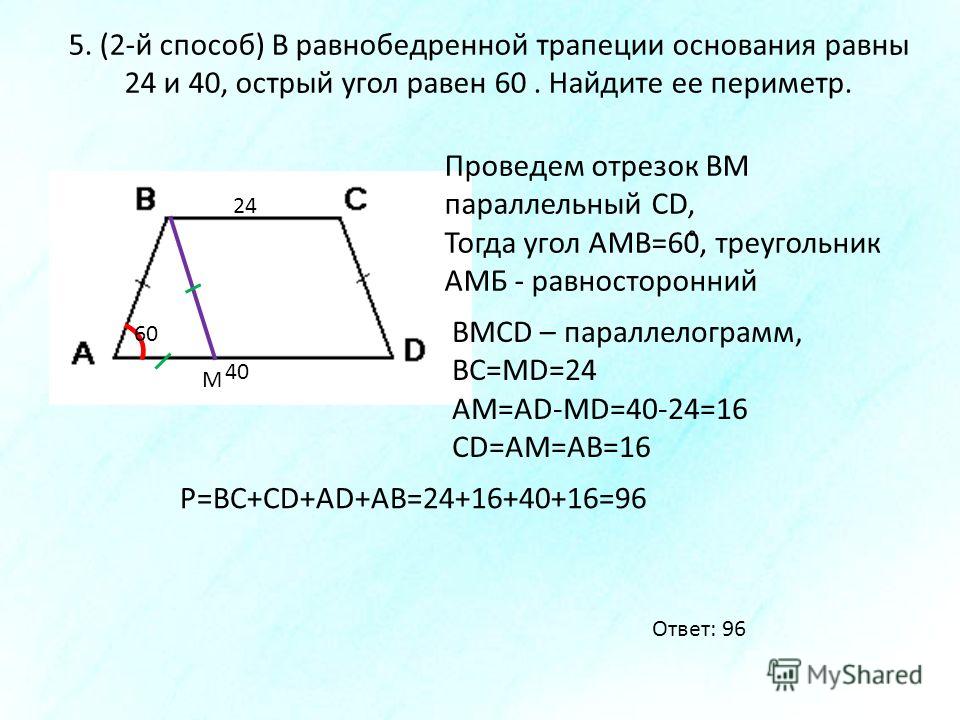

 А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями! .. Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
.. Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если время останавливается, Ахиллес уже не может перегнать черепаху. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
 Вот здесь начнется самое интересное.
Вот здесь начнется самое интересное. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте. Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
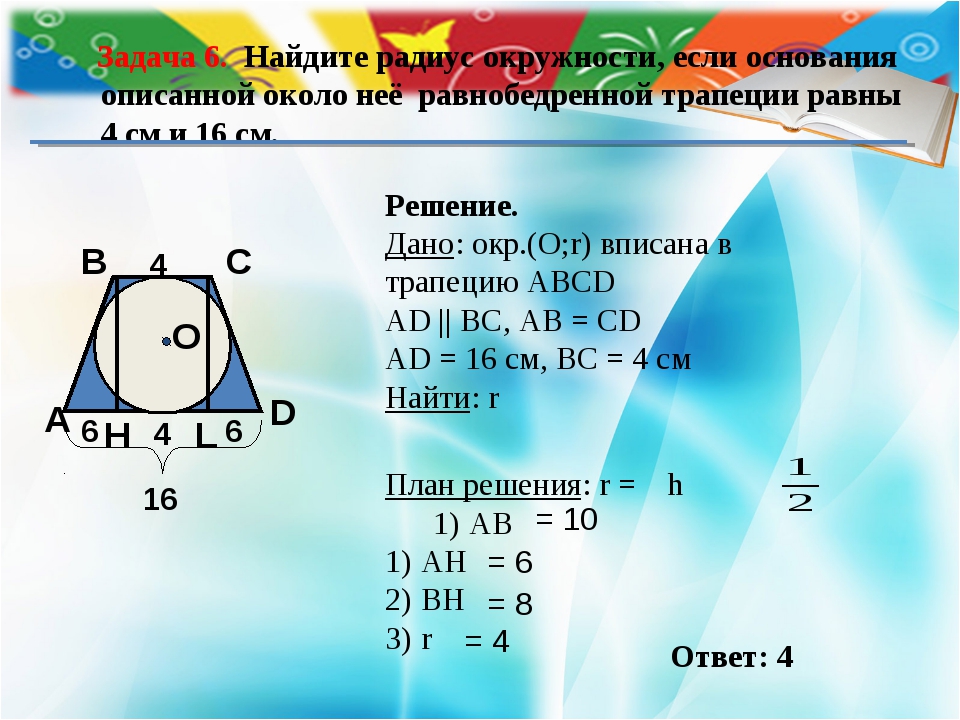 Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел. Какой еще туалет?
Какой еще туалет? Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.


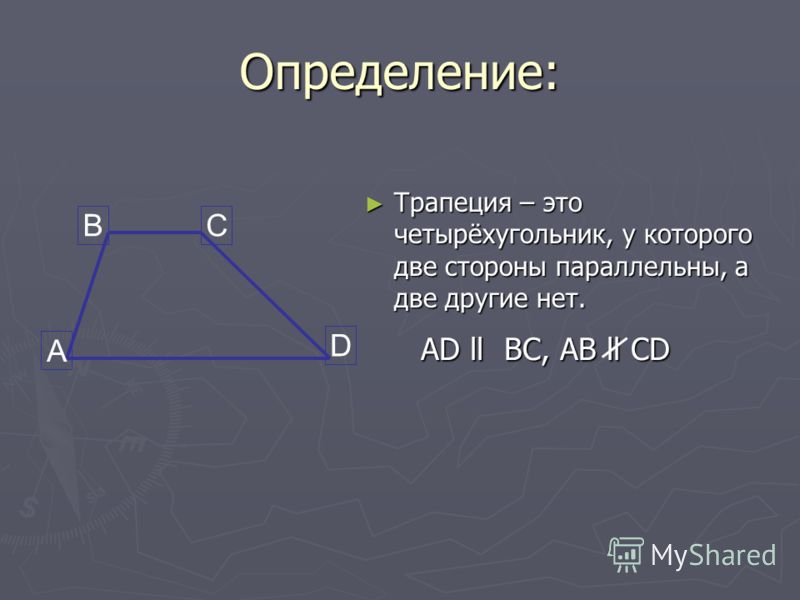
 После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.