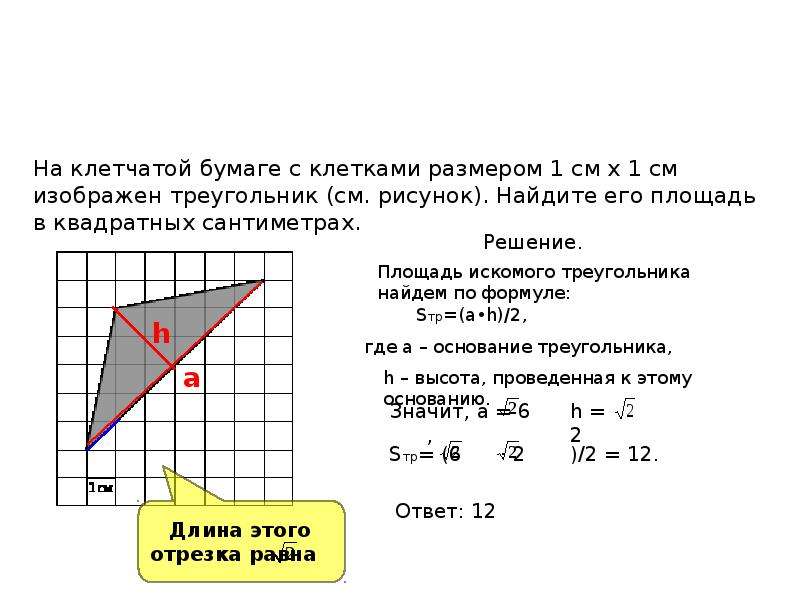
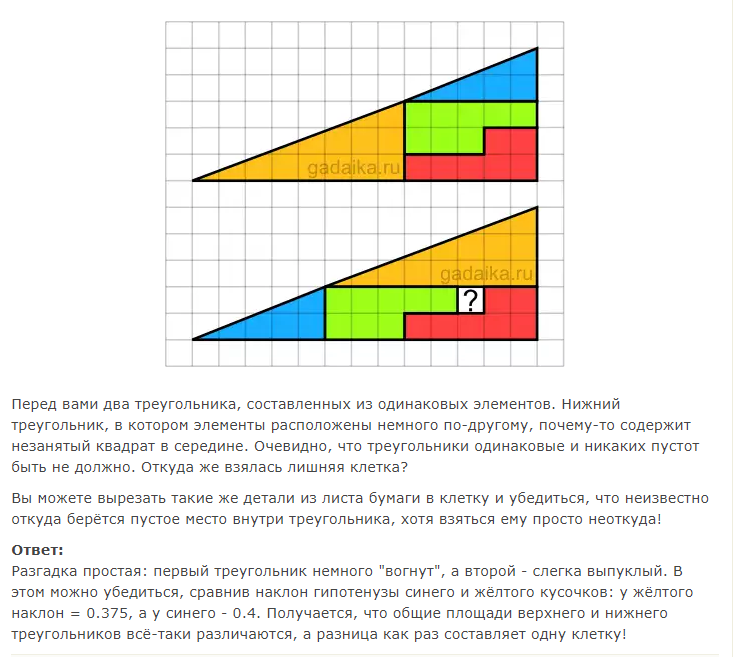
Прямоугольный треугольник. Задачи по геометрии
Задачи на прямоугольный треугольник
Часть 2
к содержанию задачника
- Две стороны треугольника равны 6 и 8. Медианы, проведенные к этим сторонам, пересекаются под прямым углом. Найдите неизвестную сторону треугольника. ответ:
- В прямоугольном треугольнике АВС с гипотенузой АВ медианы СМ и ВР перпендикулярны. Найдите длины всех трех медиан, если АВ равно . ответ:
- Точка на гипотенузе находится на одинаковом расстоянии от катетов и делит гипотенузу на отрезки 15 и 20. Найдите катеты треугольника. ответ: 21; 28
- В прямоугольном треугольнике АВС из вершины С прямого угла проведена высота СD. Точка D находится на расстоянии и от катетов АС и ВС соответственно. Найдите длины катетов. ответ:
- В прямоугольном треугольнике гипотенуза равна 10, высота, проведенная из вершины прямого угла, равна 3. Найдите отрезки, на которые биссектриса прямого угла делит гипотенузу. ответ: 5/2; 15/2
- В прямоугольном треугольнике биссектриса острого угла делит противолежащий катет на отрезки 8 и 10.

- Катеты прямоугольного треугольника равны и . Найдите длину биссектрисы прямого угла треугольника. ответ:
- Катеты прямоугольного треугольника равны 9 и 12. Найдите биссектрисы острых углов треугольника. ответ:
- Внутри прямоугольного треугольника АВС с прямым углом В взята точка D так, что площади треугольников ABD и BDC соответственно в три и четыре раза меньше площади треугольника АВС. Длины отрезков AD и DC равны соответственно и . Найдите длину отрезка BD. ответ:
- Прямоугольный треугольник, периметр которого равен 10, делится высотой, опущенной на гипотенузу, на два треугольника. Периметр одного из них равен 6. Найдите периметр второго треугольника. ответ: 8
- В прямоугольном треугольнике медиана равна и делит прямой угол в отношении 1 : 2. Найдите площадь треугольника. ответ:
- Точка пересечения медиан прямоугольного треугольника находится от катетов на расстоянии 3 и 4 соответственно. Найдите расстояние от этой точки до гипотенузы.
 ответ: 12/5
ответ: 12/5 - В прямоугольном треугольнике длины медиан острых углов равны и . Найдите длину гипотенузы треугольника. ответ: 14
- Площадь прямоугольного треугольника равна 6, а периметр равен 12. Найдите длину перпендикуляра, опущенного из вершины прямого угла на гипотенузу. ответ: 12/5
- Найдите острые углы прямоугольного треугольника, длины сторон которого образуют арифметическую прогрессию. ответ: 2arctg 2; /2-2arctg 2
- Длина одного из катетов прямоугольного треугольника больше длины другого на 10, но меньше длины гипотенузы на 10. Найдите длину гипотенузы. ответ: 50
- В прямоугольном треугольнике BAD с прямым углом А точка К делит катет AD пополам. Найдите угол между медианами ВК и АО, если AD : DO = ответ: 90 градусов
- В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу в отношении 3 : 1. В каком отношении делит гипотенузу высота? ответ: 1 : 9
- Гипотенуза прямоугольного треугольника равна 10, проекция меньшего катета на гипотенузу равна 3,6.
 Найдите радиус окружности, вписанной в этот треугольник. ответ: 2
Найдите радиус окружности, вписанной в этот треугольник. ответ: 2 - В прямоугольном треугольнике острый угол равен 30 градусов, а высота, проведенная из вершины прямого угла. равна . Найдите гипотенузу. ответ: 4
Смотрите еще Прямоугольный треугольник Часть 1
Метки задачи, треугольник. Смотреть запись.
Задачи про несуществующие треугольники | Шевкин.Ru
Известна задача из американского теста.
1. Найдите площадь прямоугольного треугольника, гипотенуза которого равна 10, а высота, проведённая к гипотенузе, равна 6.
Академик В.И. Арнольд рассказывал, что в США не сразу заметили, что учащиеся вычисляли площадь несуществующего треугольника (упомянутая высота не может быть больше половины гипотенузы).
Проколы бывают и в краю родных осин. Похожая ситуация случилась на сайте, где я нашёл такую задачу.
2. В треугольнике ABC провели медиану BM. Оказалось, что AB = MC = 7, а углы AMB и ACB равны соответственно 70 и 50 градусов. Найдите радиус окружности, описанной около треугольника ABC.
Готовимся к ОГЭ и ЕГЭ! Коварные задачи из экзаменационных вариантов!
Эту задачу полезно дать учащимся с заданием: докажите, что треугольник ABC, удовлетворяющий условиям задачи, не существует.
Доказательство.

Учащимся можно предложить найти другой способ доказательства. Вряд ли он будет короче решения, присланного Алексеем Владимировичем.
Если сторона AC треугольника в 2 раза больше стороны AB, то наибольшая величина угла С равна 30 градусам (если угол B прямой). Треугольник с углом C в 50 градусов не существует.
Планиметрия в тезисах и решениях. 9 класс
К задачам на равнобедренный треугольник применимы все формулы п. 1.1 этой главы, разве что во всех формулах b = с, ? = ?.В случае равностороннего треугольника формулы значительно упрощаются, т. к. а = b = с, ? = ? = ? = 60°. Тогда
длины всех медиан, высот и биссектрис равны
Примеры решения задач
18. Один из углов равнобедренного треугольника равен 120°. Найдите отношение сторон треугольника (рис. 134). (1)
Рис. 134.
Решение. Обозначим основание треугольника через b, боковые стороны через а (см. рис.). По теореме косинусов
Тогда отношения сторон треугольника а: а: в = 1:1:?3.
Ответ: 1:1:?3.
19. Найдите площадь круга, описанного вокруг равностороннего треугольника со стороной а (рис. 135). (1)
Рис. 135.
Решение. Обозначим сторону треугольника через а. Тогда по теореме синусов имеем:
Площадь круга:
Ответ:
20. Основание равнобедренного треугольника равно 4?2, медиана боковой стороны равна 5. Найдите длину боковой стороны (рис. 136). (2)
Рис. 136.
Решение. Можно воспользоваться готовой формулой длины медианы:
Обозначим АВ через 2х, тотда ВМ = МС = х (см. рис.).
Имеем:
АВ = ВС = 6.
Задачу можно решить по-другому. Из ?ABC по теореме косинусов:
Далее, по той же теореме косинусов из ?АМВ:
Ответ: 6.
21. На основании равнобедренного треугольника, равном 8 см, как на хорде, построена окружность, касающаяся боковых сторон треугольника. Найдите радиус окружности, если длина высоты, опущенной на основание треугольника, равна 3 см (рис. 137). (2)
Рис. 137.Решение. Пусть данный треугольник ABC, где АВ = ВС; ВК = 3; АК = КС = 4 (см. рис.). Угол ОВС обозначим через ?. Из треугольника ВКС по теореме Пифагора находим:
Из того же треугольника следует: tg ? = 4/3. Радиус окружности R = ОС найдём из треугольника ВСО:
Ответ: 20/3 см.
Задачи для самостоятельного решения
22. В равнобедренном треугольнике боковая сторона равна 12, а угол при вершине – 120°. Определите высоту треугольника. (1)
23. В равнобедренном треугольнике основание и опущенная на него высота равны 4. Найдите площадь описанного круга. (1)
24. В равнобедренном треугольнике высота равна 8, а основание относится к боковой стороне, как 6:5. Найдите радиус вписанной окружности. (1)
Найдите радиус вписанной окружности. (1)
25. Длина окружности, описанной около равностороннего треугольника, равна 4. Найдите площадь заштрихованного сектора (рис. 138). (2)
Рис. 138.
26. Докажите, что сумма расстояний от любой точки равностороннего треугольника до его сторон равна длине высоты треугольника. (2)
Автор легкой математической задачи поставил в тупик интернет-пользователей / AdMe
Существует легенда, согласно которой на двери академии, где Платон учил своих учеников, висела табличка с надписью: «Пусть сюда не входит тот, кто не знает геометрии». Основы этой науки известны каждому школьнику. Но, как выяснилось, геометрическая задачка на внимательность привела в замешательство многих взрослых людей.
Мы в AdMe.ru даже предположить не могли, что головоломка, в которой нужно просто посчитать количество треугольников на картинке, окажется таким крепким орешком.
А началось все с того, что австралиец под ником @thomas_violence опубликовал пост в своем твиттере, где обратил внимание на то, что простая математическая задача вызвала серьезные трудности и разногласия у других пользователей.
«Лечу свое похмелье, наслаждаясь абсурдной уверенностью, с которой люди ошибочно отвечают на этот пост в фейсбуке».
Ответы людей вызвали у автора поста полное недоумение. Ему отправляли самые разные варианты, насчитывая от 5 до 25 треугольников. Томас начал публиковать самые забавные предположения в своем твиттере, удивляясь тому, как такая с виду легкая математическая задача могла вызвать столько споров.
Шутки шутками, но сколько треугольников насчитали вы на этой картинке?
А вот и все треугольники
В конце концов девушка с ником @ProphetOfFlame не просто посчитала нужное количество треугольников, но и проиллюстрировала решение этой задачи в своем твиттере.
Как видим, их целых 18, что, впрочем, не помешало некоторым пользователям найти намного больше: видимо, они посчитали, что трапеции тоже могут сойти за треугольники. Чаще всего в неверных ответах фигурировали значения от 12 до 15.
Чаще всего в неверных ответах фигурировали значения от 12 до 15.
Бонус
Если предыдущая задача показалась вам слишкой легкой, предлагаем ее усложнить. Сколько треугольников вы найдете здесь?
«Сколько треугольников?»
Ответ
На рисунке можно найти 24 треугольника. В верхнем ряду 6 треугольников: 3 одиночных, 2 двойных и 1 тройной. Используя эту же стратегию, можно без проблем найти по 6 треугольников во 2-м, 3-м и 4-м рядах.
Еще один маленький треугольник автор этого рисунка Kumar Ankit спрятал в своей подписи. Как видим, правильный ответ — 25. Особо придирчивые пользователи считают, что необходимо включить в подсчеты слово «треугольники» (triangles) в самом вопросе, а значит, ответ будет равным 26.
А теперь расскажите нам, сколько треугольников насчитали вы на обоих рисунках? Все удалось найти?
Задача 533. Треугольники — 3 | Тренер по программированию
Одна из задач на геометрию с регионального этапа Всероссийской олимпиады школьников 2009 года, в которой используется интересная идея и совсем немного комбинаторики.
Условие задачи с сайта acmp.ru
Точек довольно много, чтобы перебрать все тройки и проверить, составляют ли они равнобедренный треугольник. Такое решение на олимпиаде набирало 40 баллов из 100.
Давайте для начала будем перебирать лишь одну вершину — противоположную основанию. Если теперь выделить множество вершин, равноудалённых от выбранной, то все их попарные комбинации будут образовывать основание равнобедренного треугольника. С одним лишь исключением, что этот треугольник может быть вырожденным, если все три точки окажутся на одной прямой.
В решении будем использовать всю мощь стандартной библиотеки, к тому же удобно сделать подстановку x и y вместо first и second (как мы уже делали в задаче 628):
Подключение библиотек и определение подстановокПодключение библиотек и определение подстановок
Считывание данных благодаря подстановкам очень читаемо:
Считывание данныхСчитывание данных
Основное решение тоже довольно короткое. Стоит обратить внимание на используемый тип long long для результата и для вычисления расстояния между точками (кстати, в очередной раз мы не берём корень, чтобы не возиться с точностью вещественных чисел).
Стоит обратить внимание на используемый тип long long для результата и для вычисления расстояния между точками (кстати, в очередной раз мы не берём корень, чтобы не возиться с точностью вещественных чисел).
Подсчёт количества равнобедренных треугольников
В map для каждой возможной длины бокового ребра (точнее, квадрата его длины) подсчитывается количество точек. А второй вложенный цикл проходит по всем длинам и вычисляет количество пар, которые можно получить, по формуле количества сочетаний из n по 2.
Чтобы посчитать количество вырожденных равнобедренных треугольников переберём все пары точек, тогда координаты третьей вершины однозначно определяются. Проверим, есть ли эта вершина во входных данных, для этого сложим все точки в set:
Подсчёт количества вырожденных равнобедренных треугольниковПодсчёт количества вырожденных равнобедренных треугольников
При выводе количество вырожденных треугольников делим пополам, потому что каждый из них посчитался дважды (для каждой вершины основания):
Вывод ответаВывод ответа
Важным замечанием в этом решении является то, что не существует равносторонних треугольников с целочисленными координатами, потому что в таком случае мы бы посчитали их три раза.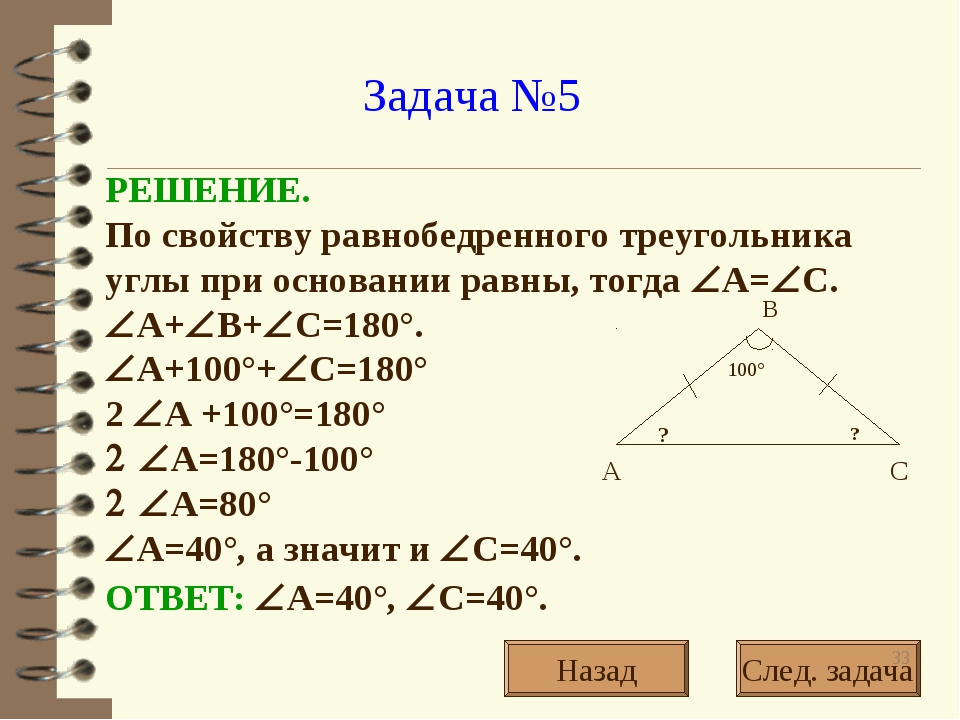 Тогда, аналогично подсчёту вырожденных треугольников, пришлось вычесть и их.
Тогда, аналогично подсчёту вырожденных треугольников, пришлось вычесть и их.
Предыдущий выпуск: Задача 26. Две окружности
Я очень хочу, чтобы мои советы были полезны вам, а для того, чтобы быстрее всех получать новые статьи можно подписаться на мой канал.
Задачи на подобие треугольников
Рассмотрим некоторые задачи на подобие треугольников.
I. В треугольнике проведен отрезок, параллельный стороне. Концы отрезка лежат на других сторонах треугольника.
Рассмотрим треугольники ABC и A1BC1.
Решать задачи на подобие треугольников удобнее, используя цветовую визуализацию, поэтому выделим данные треугольники разными цветами:
1) ∠B — общий;
2)∠ BAC=∠BA1C1 (как соответственные углы при AC∥A1C1 и секущей AB).
Следовательно, треугольники ABC и A1BC1 подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
Задача
Прямая, параллельная стороне АС треугольника АВС, пересекает сторону АВ в точке А1, а сторону ВС — в точке В1. Найти длину отрезка А1С1, если АС=35, АА1: А1В=2:5.
Найти длину отрезка А1С1, если АС=35, АА1: А1В=2:5.
Решение:
Доказываем подобие треугольников ABC и A1BC1.
Ответ: 25.
II. В треугольник вписан ромб.
Рассмотрим треугольники AFK и BFC.
Выделим данные треугольники в цвете.
1) ∠F — общий;
2)∠ FAK=∠FBC (как соответственные углы при AD∥BC и секущей AB).
Следовательно, треугольники AFK и BFC подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
Задача.
В треугольник AFK вписан ромб ABCD так, что угол A у них общий, в вершина C принадлежит стороне FK. Найти сторону ромба, если AF=21 см, AK=24 см.
Решение.
Доказываем подобие треугольников AFK и BFC. Из трех соотношений выбираем те, в которых нам что-либо известно:
Примем сторону ромба за x:
Тогда BF=AF-AB=21-x см. Отсюда
Отсюда
Разделив обе части уравнения на 3, получаем:
Ответ: 11,2 см.
В следующий раз рассмотрим задачи на подобные треугольники в трапеции.
Решение задач по теме «Треугольники» (10 – 11 класс)
Решение задач по теме «Треугольники» (10 – 11 класс)
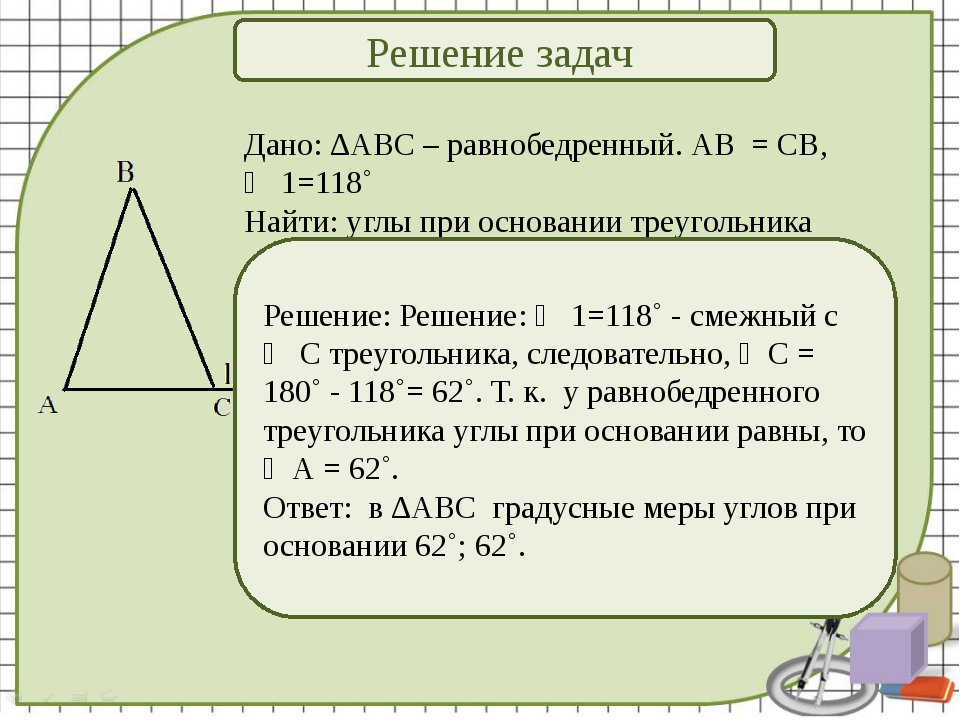
В равнобедренном треугольнике АВС известно, что АВ=ВС, угол В = 480 отрезки АТ и АМ – высота и биссектриса треугольника соответственно. Найдите угол ТАМ.
Один из углов треугольника равен 1000 . Высота и биссектриса, проведенные из вершины этого угла, образуют угол 200. Найдите неизвестные углы треугольника.
E
D
Один из острых углов прямоугольного треугольника равен 210. Найдите угол между биссектрисой и высотой, проведенными из вершины прямого угла.
Параллельные прямые c и d пересекают стороны угла BAC. Найдите длину отрезка DE, если AD=4 см, D1E1=16 см, DE=AD1.
Найдите длину отрезка DE, если AD=4 см, D1E1=16 см, DE=AD1.
Продолжения боковых сторон АВ и CD трапеции ABCD пересекаются в точке F. Найдите АВ, если AF=10 см и BC:AD=2:5.
Катет прямоугольного треугольника равен 6 см, а медиана, проведенная к нему – 5 см. Найдите гипотенузу треугольника.
В треугольнике две стороны равны а и b, а угол между ними – 60°. Найдите длину третьей стороны, если: а) а = 10 см, b = 16 см; б) а = 8 см, b = 15 см.
Шайба находится на льду на расстоянии 7 м и 8 м от оснований штанг ворот, ширина которых равна 1,5 м. Найдите угол α, при котором шайба, скользя по льду, попадает в ворота (рис. 51).
Найдите неизвестные стороны и углы ΔАВС, если: а) АВ = 4 см, ВС = 5 см, ∠В = 110°; б) АВ = = 2 дм, ВС = 5 дм, ∠А = 40°; в) ВС = 17 см, ∠А = 40°, ∠С = 75°; г) АС = 15 мм, ∠А = 30°, ∠С = 50°.
Диагональ прямоугольника равна 7,5 см, а угол между диагоналями равен 48°. Найдите периметр прямоугольника.
Найдите периметр прямоугольника.
Длина гипотенузы прямоугольного треугольника равна 55 см, а длина катета – 5 см. Найдите длину его биссектрисы, проведенной из вершины прямого угла.
13 Найдите х и у 14 Найдите х и у
Решение треугольников
«Решение» означает нахождение недостающих сторон и углов.
Когда мы знаем любые 3 стороны или углы… … мы можем найти остальные 3 | |
| (За исключением только 3 углов, потому что нам нужно по крайней мере одной стороны, чтобы найти размер треугольника.) |
Шесть различных типов
Если вам нужно решить треугольник прямо сейчас выберите один из шести вариантов ниже:
Какие стороны или углы вы уже знаете? (Нажмите на изображение или ссылку)
ААА
Три угла
ААС
Два угла и сторона , а не между
АСА
Два угла и сторона между ними
САС
Две стороны и Угол между
ССА
Две стороны и Угол , а не между
ССС
Три стороны
. .. или читайте дальше, чтобы узнать, как стать экспертом в решении треугольников :
.. или читайте дальше, чтобы узнать, как стать экспертом в решении треугольников :
Ваш набор инструментов для решения
Хотите научиться решать треугольники?
Представьте, что вы « Решатель » …
… тот, кого просят, когда нужно решить треугольник!
В вашем наборе инструментов для решения (вместе с ручкой, бумагой и калькулятором) у вас есть эти 3 уравнения:
1. Сумма углов всегда равна 180°:
А + В + С = 180°
Зная два угла, можно найти и третий.
2. Закон синусов (правило синусов):
a sin(A) = b sin(B) = c sin(C)
Когда против стороны есть угол, на помощь приходит это уравнение.
Примечание: угол A лежит напротив стороны a, B — напротив стороны b, а C — напротив стороны c.
3. Закон косинусов (правило косинусов):
c 2 = a 2 + b 2 − 2ab cos(C)
Это самое сложное в использовании (и запомните), но иногда оно необходимо
, чтобы выручить вас из трудных ситуаций.
Это расширенная версия теоремы Пифагора, которая работает
на любом треугольнике.
Шесть различных типов (подробнее)
Есть ШЕСТЬ различных типов головоломок, которые вам, возможно, придется решить. Ознакомьтесь с ними:
1. ААА
Это означает, что нам даны все три угла треугольника, но нет сторон.
ТреугольникиAAA дальше решать невозможно, т.к. нам нечего показывать размера … мы знаем форму, но не знаем, насколько она велика.
Нам нужно знать хотя бы одну сторону, чтобы идти дальше.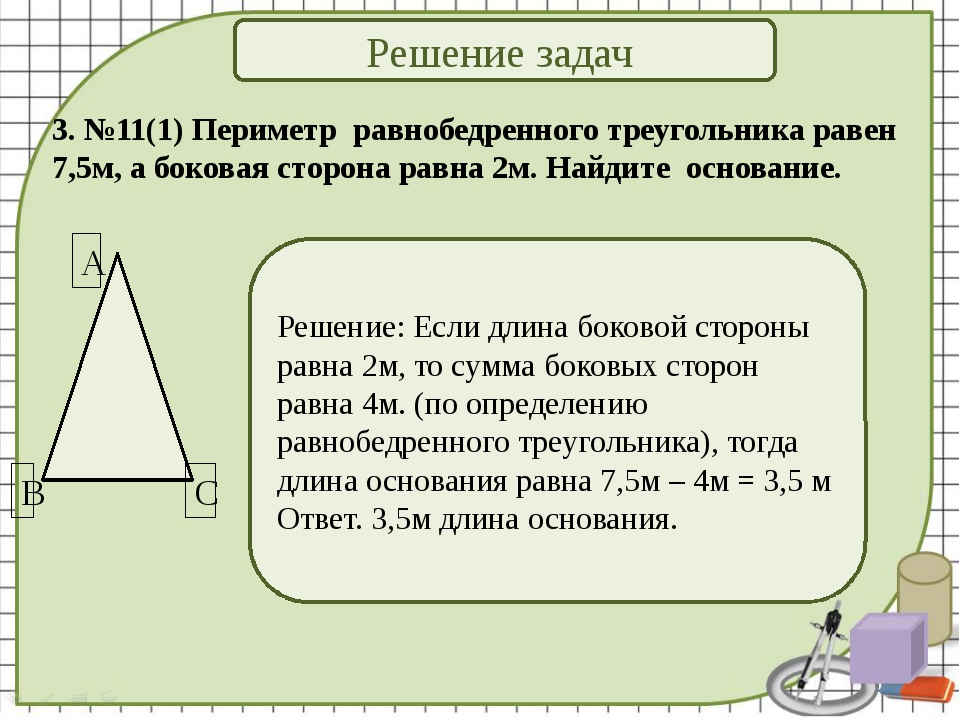 См. Решение треугольников «AAA».
См. Решение треугольников «AAA».
2. ААС
Это означает, что нам даны два угла треугольника и одна сторона, которая не является стороной, примыкающей к двум заданным углам.
Такой треугольник можно решить, используя Углы треугольника, чтобы найти другой угол, и Закон синусов, чтобы найти каждую из двух других сторон.См. раздел «Решение треугольников AAS».
3. АСА
Это означает, что нам даны два угла треугольника и одна сторона, которая равна стороне, прилегающей к двум заданным углам.
В этом случае мы находим третий угол, используя Углы Треугольника, затем используем Закон синусов, чтобы найти каждую из двух других сторон. См. раздел «Решение треугольников ASA».
4. САС
Это означает, что нам даны две стороны и угол между ними.
Для этого типа треугольника мы должны использовать Закон косинусов сначала для вычисления третьей стороны треугольника; затем мы можем использовать закон синусов, чтобы найти один из двух других углов, и, наконец, использовать углы треугольника, чтобы найти последний угол. См. раздел «Решение треугольников SAS».
См. раздел «Решение треугольников SAS».
5. ССА
Это означает, что нам даны две стороны и один угол, который не является внутренним углом.
В этом случае сначала используйте Закон синусов, чтобы найти один из двух других углов, затем используйте Углы треугольника, чтобы найти третий угол, затем снова Закон синусов, чтобы найти последнюю сторону.См. раздел «Решение треугольников SSA».
6. ССС
Это означает, что нам даны все три стороны треугольника, но нет углов.
В этом случае у нас нет выбора. Мы должны сначала использовать закон косинусов, чтобы найти любой из трех углов, затем мы можем использовать закон синусов (или снова использовать закон косинусов), чтобы найти второй угол, и, наконец, углы треугольника, чтобы найти третий угол. См. раздел «Решение треугольников SSS».
Советы по решению
Вот простой совет:
Когда треугольник имеет прямой угол, то использовать его, что обычно гораздо проще.
Когда известны два угла, определите третий, используя Углы треугольника. Прибавьте к 180°.
Попробуйте закон синусов перед законом косинусов, так как он проще в использовании.
Треугольник
: Поиск и устранение неисправностей Треугольник
: Поиск и устранение неисправностей Исправление проблемВ моей выходной сетке нет треугольников!
Если вы используете PSLG, вы, вероятно, не указали правильный набор ограничивающих сегментов, или забыли использовать ключ -c.Или, возможно, вы плохо разместили отверстие, тем самым съев все свои треугольники. Чтобы проверить эти возможности, попробуйте еще раз с помощью ключи -c и -O. В качестве альтернативы все ваши входные вершины могут быть коллинеарны, и в этом случае вы вряд ли сможете их триангулировать.
Треугольник не завершается или просто падает.
Плохие вещи могут случиться, когда треугольники становятся настолько маленькими, что расстояние
между их вершинами не намного больше, чем точность вашего
машинная арифметика. Если вы скомпилировали Triangle для одинарной точности
арифметика, вы могли бы добиться большего успеха, перекомпилировав его для двойной точности.
Опять же, вам, возможно, придется согласиться на более мягкие ограничения.
на минимальный угол и максимальную площадь, чем вы планировали.
Если вы скомпилировали Triangle для одинарной точности
арифметика, вы могли бы добиться большего успеха, перекомпилировав его для двойной точности.
Опять же, вам, возможно, придется согласиться на более мягкие ограничения.
на минимальный угол и максимальную площадь, чем вы планировали.
Вы можете свести к минимуму проблемы с точностью, убедившись, что исходная точка лежит внутри вашего набора вершин или даже внутри самой плотной части вашего сетка. Если вы триангулируете объект, размер которого x координаты все попадают между 6247133 и 6247134, ты не уйдешь большая точность с плавающей запятой для работы с Triangle.
Проблемы с точностью могут возникать скрытно, если входной PSLG содержит два
сегменты, которые встречаются (или пересекаются) под очень большим углом, или если такой
угол вводится ключом -c.
Если вы не понимаете, что
формируется крошечный угол, вы, возможно, никогда не узнаете, почему Треугольник
сбой. Чтобы проверить эту возможность, используйте
-S переключатель (с
соответствующее ограничение на количество точек Штейнера, найденное методом проб и ошибок)
для ранней остановки Triangle и просмотра вывода
. poly файл с
Покажите мне.Внимательно ищите области, где плотные
формируются скопления вершин и при малых углах между сегментами.
Увеличьте масштаб, так как такие сегменты могут выглядеть как один сегмент из
дистанция.
poly файл с
Покажите мне.Внимательно ищите области, где плотные
формируются скопления вершин и при малых углах между сегментами.
Увеличьте масштаб, так как такие сегменты могут выглядеть как один сегмент из
дистанция.
Если некоторые из входных значений слишком велики, Triangle может пострадать. плавающее исключение из-за переполнения при попытке выполнить тест на ориентацию или круговой тест. (прочитайте раздел о Точная арифметика.) Опять же, я рекомендую компилировать Triangle для двойного (скорее чем одинарная) точная арифметика.
Неожиданные проблемы могут возникнуть, если вы используете качественную сетку
(-q,
-а, или
-у)
с входом, который не ограничен сегментом, то есть, если ваш ввод
является набором вершин, или вы используете
-c переключатель. Если выпуклая оболочка
ваши входные вершины имеют коллинеарные вершины на своей границе, входная вершина
что, по вашему мнению, лежит на выпуклой оболочке, на самом деле может лежать прямо внутри
выпуклая оболочка. Если это так, то чрезвычайно тонкий треугольник формируется
вершина и ребро выпуклой оболочки рядом с ней.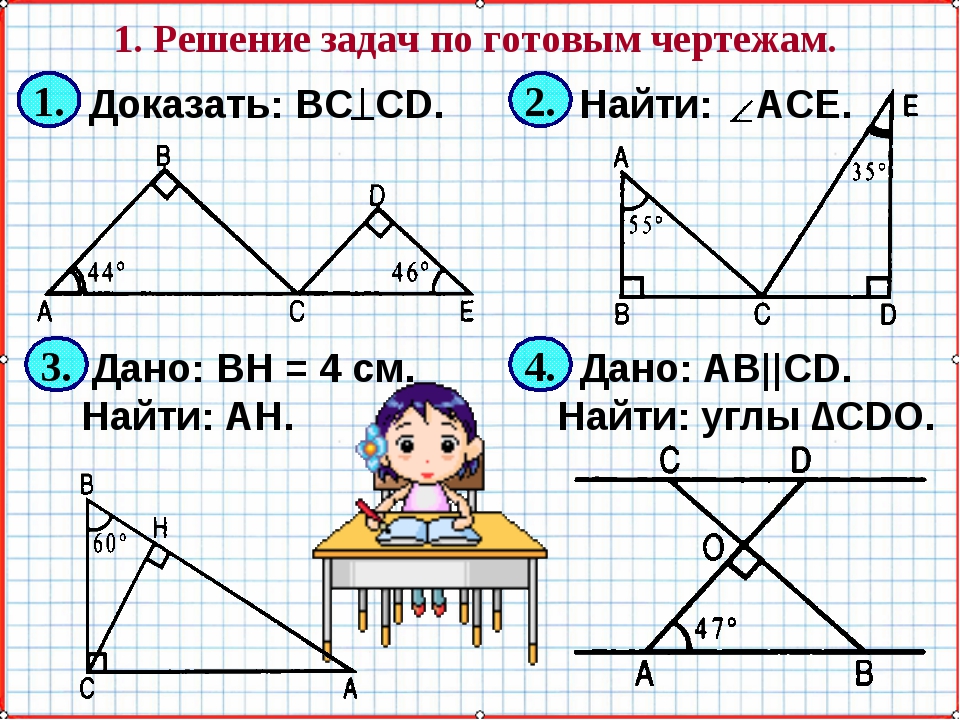 Когда Треугольник пытается
уточните сетку, чтобы применить ограничения угла и площади, очень маленькие
могут образоваться треугольники, или Треугольник может выйти из строя из-за недостаточного
точность с плавающей запятой.
Когда Треугольник пытается
уточните сетку, чтобы применить ограничения угла и площади, очень маленькие
могут образоваться треугольники, или Треугольник может выйти из строя из-за недостаточного
точность с плавающей запятой.
Нумерация выходных вершин не соответствует входной вершины.
Возможно, у вас были дубликаты входных вершин, или вы, возможно, съели некоторые из ваших входных вершин с дырой или поместив их вне области, ограниченной сегментами. В любом случае вы можете решить проблему, не используя ключ -j.
Треугольник выполняется без происшествий, но когда я смотрю на результат сетки, она имеет перекрывающиеся треугольники или другие геометрические несоответствия.
Если вы выберете переключатель -X и тем самым выключите
точная арифметика,
Triangle иногда делает ошибки из-за плавающей запятой
ошибка округления. Хотя эти ошибки случаются редко, не используйте ключ -X.
Если у вас все еще есть проблемы, пожалуйста, сообщите об ошибке.
Странные вещи могут случиться, если вы позволили себе вольности с вашим PSLG. Делать у вас есть вершина, лежащая в середине сегмента? Треугольник иногда плохо справляется с такими вещами. Вы хотите выложить коллинеар ряд равномерно расположенных сегментно-соединенных вершин? Вы просто определили один длинный отрезок, соединяющий крайнюю левую вершину с крайней правой вершиной, и куча вершин лежащих вдоль него? Этот метод иногда работает, особенно с горизонтальными и вертикальными линиями, но часто это не так, и вам придется соединить каждую соседнюю пару вершин с отдельным сегмент.Если не нравится, жестко.
Кроме того, если у вас есть сегменты, которые пересекаются не в их конечные точки, старайтесь не допускать, чтобы пересечения проходили слишком близко к PSLG вершины или друг друга.
Если у вас возникли проблемы с уточнением триангуляции, созданной не Triangle:
Вы уверены, что триангуляция геометрически правильна? Он отформатирован
правильно для треугольника? Все ли треугольники перечислены, поэтому первые три
вершины являются их углами в порядке против часовой стрелки? Все ли
треугольники, ограниченные Делоне? Алгоритм уточнения Делоне треугольника
предполагает, что он начинается с CDT.
Вернуться на домашнюю страницу треугольника.
[email protected]
Формула площади треугольника, примеры, рисунки и интерактивные практические задачи. Найти базу иногда сложно, но..
Площадь треугольника всегда равна половине произведения высоты на основание.
$ Площадь = \frac{1}{2} (высота основания \cdot) $
Так с какой стороны база?
Получение площади треугольника из прямоугольникаПример 1
Какова площадь треугольника, изображенного ниже?
Покажи ответ Используйте приведенную выше формулу.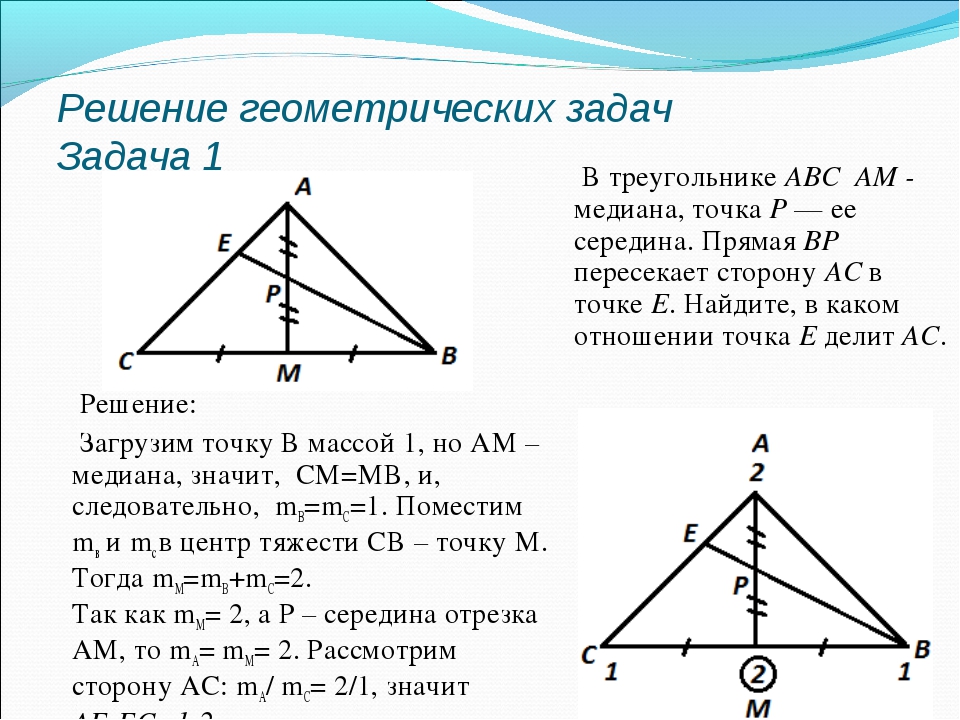
$$ A = \frac{1}{2} (высота основания \cdot) \\ A = \frac{1}{2} (10 \cdot 3) \\ = \frac{1}{2} (30) \\ = \ гидроразрыва {30} {2} = 15 $$
Найдите площадь каждого треугольника ниже.Округлите каждый ответ до ближайшей десятой единицы.
Проблема 1
Какова площадь треугольника на следующем рисунке?
Покажи ответ Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу площади.
$$ Площадь = \frac{1}{2} (высота основания \cdot) \\ =\frac{1}{2} (3 \cdot 3) \\ = \frac{1}{2} (9) \\ =\ гидроразрыв{9}{2} \\ = 4,5 \text{ дюйма в квадрате} $$
Проблема 2
Вычислите площадь треугольника, изображенного ниже.
Покажи ответ Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу площади.
$$ Площадь = \frac{1}{2} (высота основания \cdot) \\ =\frac{1}{2} (24 \cdot 27.6) \\ = 331,2 \text{дюймы в квадрате} $$
Проблема 3
Вычислите площадь треугольника, изображенного ниже.
Покажи ответ Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу площади.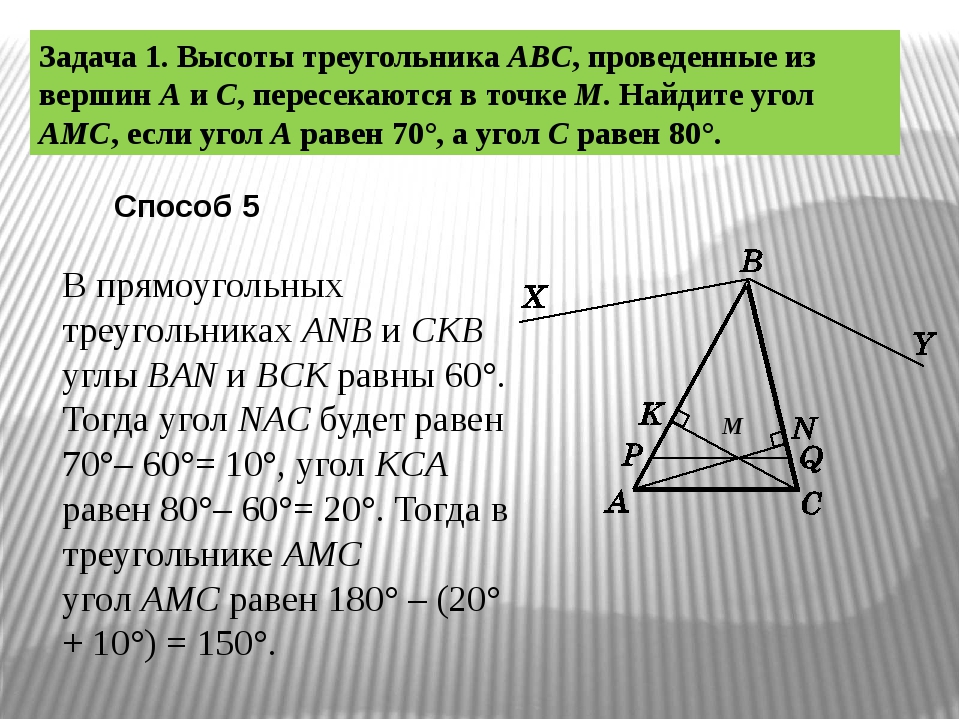
$$ Площадь = \frac{1}{2} (высота основания \cdot) \\ =\frac{1}{2} (12 \cdot 2.5) \\ = 15 \text{ дюймов в квадрате} $$
Проблема 4
Вычислите площадь треугольника, изображенного ниже.
Покажи ответ Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу площади.
$$ Площадь = \frac{1}{2} (высота основания \cdot) \\ =\frac{1}{2} (12 \cdot 3.9) \\ = 23,4 \text{ дюйма в квадрате} $$
Проблема 5
Вычислите площадь треугольника, изображенного ниже.
Покажи ответ Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу площади.
$$ Площадь = \frac{1}{2} (высота основания \cdot) \\ =\frac{1}{2} (14 \cdot 4) \\ = 28 \text{ дюймов в квадрате} $$
Проблема 6
Какова площадь следующего треугольника?
Покажи ответ Эта проблема включает в себя 1 небольшой поворот.Вы должны решить, какую из 3 баз использовать. Только помните, что основание и высота перпендикулярны. Следовательно, основание равно «11», так как оно перпендикулярно высоте 13,4.
Следовательно, основание равно «11», так как оно перпендикулярно высоте 13,4.
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу площади.
$$ Площадь = \frac{1}{2} (высота основания \cdot) \\ =\frac{1}{2} (11 \cdot 13.4) \\ = 73,7 \text{дюймы в квадрате} $$
Проблема 7
Какова площадь следующего треугольника?
Покажи ответ Эта проблема включает в себя 1 небольшой поворот.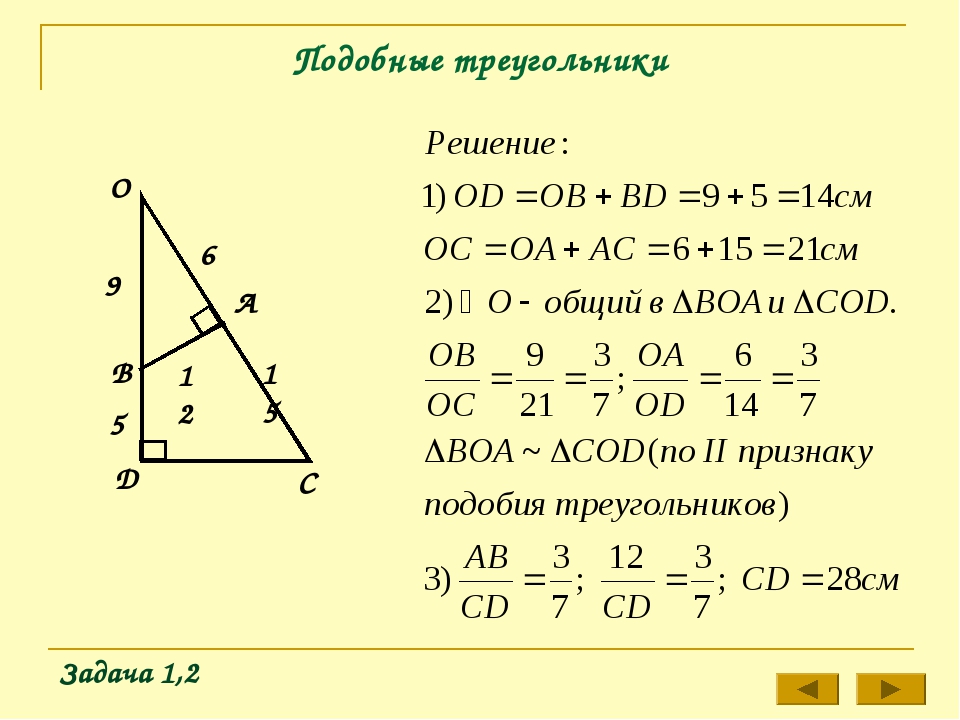 Вы должны решить, какую из 3 баз использовать. Только помните, что основание и высота перпендикулярны. Следовательно, основание равно «12», так как оно перпендикулярно высоте 5,9.
Вы должны решить, какую из 3 баз использовать. Только помните, что основание и высота перпендикулярны. Следовательно, основание равно «12», так как оно перпендикулярно высоте 5,9.
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу площади.
$$ Площадь = \frac{1}{2} (высота основания \cdot) \\ =\frac{1}{2} (12 \cdot 5.9) \\ = 35,4 \text{дюймы в квадрате} $$
Проблема 8
Какова площадь следующего треугольника?
Покажи ответ Как и в последней задаче, вы должны решить, какую из 3 баз использовать. Только помните, что основание и высота перпендикулярны. Следовательно, основание равно «4», поскольку оно перпендикулярно высоте 17,7.
Только помните, что основание и высота перпендикулярны. Следовательно, основание равно «4», поскольку оно перпендикулярно высоте 17,7.
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу площади.
$$ Площадь = \frac{1}{2} (высота основания \cdot) \\ =\frac{1}{2} (4 \cdot 17.7) \\ = 35,4 \text{дюймы в квадрате} $$
Проблема 9
Какова площадь следующего треугольника?
Покажи ответ Опять же, вы должны решить, какую из 3 баз использовать.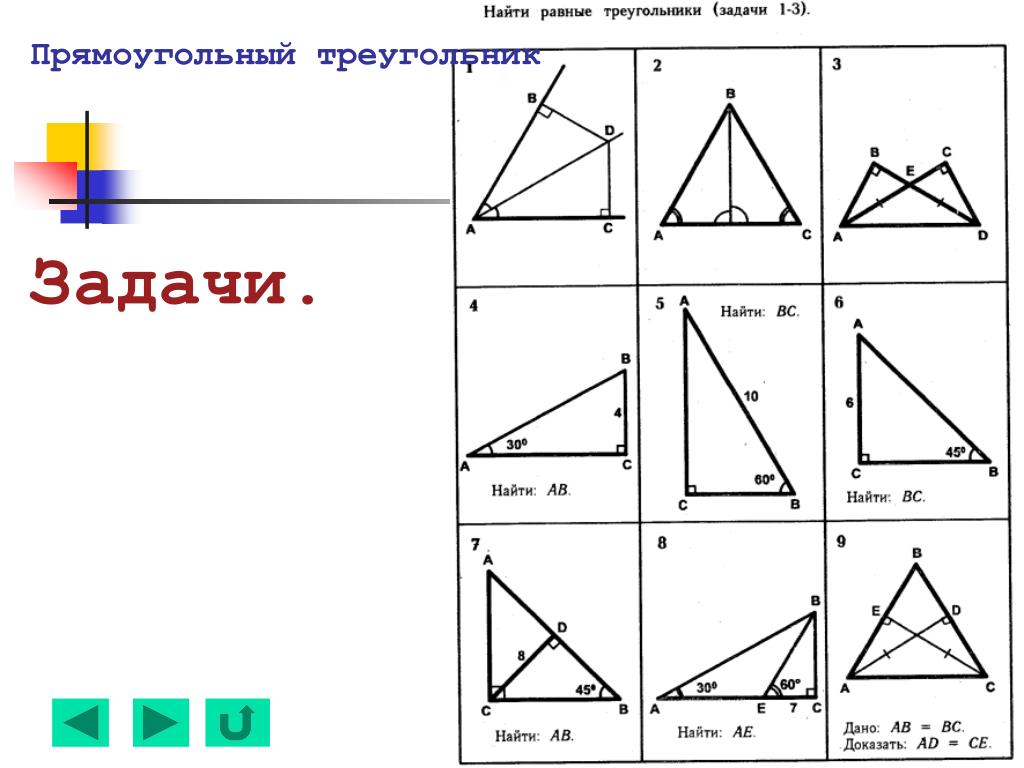 Только помните, что основание и высота перпендикулярны. Следовательно, основание равно «22», так как оно перпендикулярно высоте 26,8.
Только помните, что основание и высота перпендикулярны. Следовательно, основание равно «22», так как оно перпендикулярно высоте 26,8.
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу площади.
$$ Площадь = \frac{1}{2} (высота основания \cdot) \\ =\frac{1}{2} (22 \cdot 26.8) \\ = 294,8 \text{дюймы в квадрате} $$
Геометрические стратегии и практические задачи
Треугольные вопросы составляют менее 10% всех математических вопросов SAT. При этом вы все еще хотите правильно ответить на эти вопросы, поэтому вы должны быть готовы знать все виды треугольников: прямоугольные треугольники, равнобедренные треугольники, равнобедренные прямоугольные треугольники — SAT может проверить вас по любому из них.Поскольку задачи с треугольниками составляют лишь небольшой процент математических вопросов SAT, вам не следует тратить все свое учебное время на треугольники.
При этом вы все еще хотите правильно ответить на эти вопросы, поэтому вы должны быть готовы знать все виды треугольников: прямоугольные треугольники, равнобедренные треугольники, равнобедренные прямоугольные треугольники — SAT может проверить вас по любому из них.Поскольку задачи с треугольниками составляют лишь небольшой процент математических вопросов SAT, вам не следует тратить все свое учебное время на треугольники.
Эта статья должна быть всем, что вам нужно, чтобы подготовиться к ответу на вопросы треугольника SAT. Я расскажу вам о типах треугольников, которые появятся в SAT, их формулах и стратегиях, которые вам нужно будет применять при подходе к вопросу о треугольнике. Я также разберу тренировочные вопросы SAT по математике и объясню, как избавиться от треугольных вопросов.
Что такое треугольники?
Сначала поговорим об основах. Треугольник — это плоская фигура, состоящая из трех прямых линий, которые соединяются под тремя углами. Сумма этих углов равна 180°.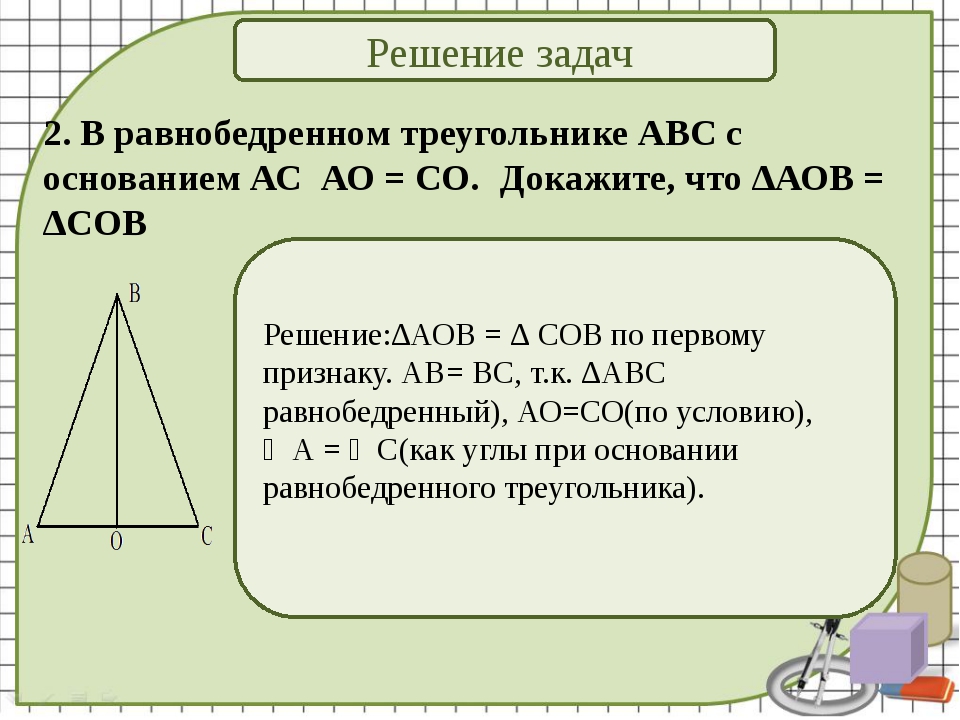
Каждая из трех сторон треугольника называется катетом треугольника, а самый длинный катет прямоугольного треугольника называется гипотенузой. Угол, противолежащий гипотенузе, всегда будет равен 90°, самому большому из трех углов.
Когда мы рассмотрим множество различных типов, вы заметите, что многие категории треугольников будут подмножествами других категорий треугольников, и определения будут продолжать сужаться.
Особые треугольники
Существует несколько различных видов особых треугольников, которые обычно появляются в SAT.
В этом разделе мы определим и опишем все виды треугольников, которые вы увидите в тесте. В следующем разделе мы рассмотрим все формулы, которые вам нужно знать для ваших задач с треугольником SAT, а также способы их использования.
Равносторонние треугольники
Равносторонний треугольник – это треугольник, у которого три равные стороны и три равных угла.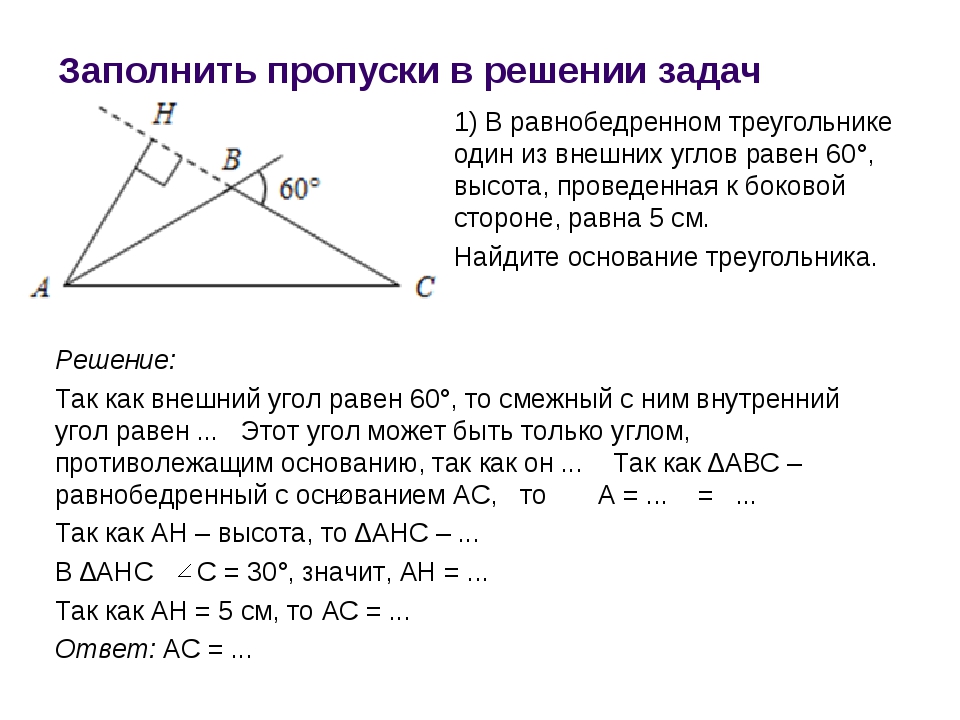 Хотя размеры ног могут быть любыми (при условии, что все они равны), все измерения углов должны равняться 60°. Почему? Потому что углы треугольника всегда должны составлять 180°, а ${180}/{3}=60$.
Хотя размеры ног могут быть любыми (при условии, что все они равны), все измерения углов должны равняться 60°. Почему? Потому что углы треугольника всегда должны составлять 180°, а ${180}/{3}=60$.
Давайте посмотрим на эти типы треугольников в действии. ПРИМЕЧАНИЕ: этот вопрос представляет собой измененный старый вопрос SAT в стиле нового SAT.
На рисунке выше треугольник ABC вписан в окружность с центром O и диаметром AC.Если $\ov{AB}=\ov{AO}$, какова градусная мера ∠ABO?
(А) 15°
(Б) 30°
(С) 45°
(Г) 60°
Ответ Пояснение: Нам сказали, что длины двух сторон круга равны, и мы должны найти неизвестный угол ∠ABO. Если вы знакомы с вашими кругами, то вы знаете, что все радиусы круга равны.
Прямые $\ov{AO}$ и $\ov{OB}$ являются радиусами окружности, поэтому они должны быть равны.
Это означает, что все три стороны окружности BOA — линии $\ov {AO}$, $\ov {OB}$ и $\ov {BA}$ — равны. А мы знаем, что наличие трех равных катетов треугольника означает, что у нас есть равносторонний треугольник.
А мы знаем, что наличие трех равных катетов треугольника означает, что у нас есть равносторонний треугольник.
Мы также знаем, что равносторонние треугольники имеют три равных внутренних угла, каждый из которых равен 60 градусам. Это означает, что угол АВО равен 60 градусов.
Наш окончательный ответ: D, 60°.
Равнобедренные треугольники
Равнобедренный треугольник – это треугольник, у которого две стороны и два угла равны.
Стороны, противоположные равным углам, всегда будут равны, а углы, лежащие напротив равных сторон, всегда будут равны. Это знание часто приведет вас к правильным ответам на многие вопросы SAT, в которых вам дается очень мало информации.
Объяснение ответа: Поскольку вопрос говорит вам, что $180−z=2y$ и $y=75$, мы знаем, что $180−z=(2)(75)$, и решение этого вопроса дает $z=30$. Если $z=30$, то каждый из углов при основании равнобедренного треугольника справа должен быть равен 75°(${180−30}/{2}$).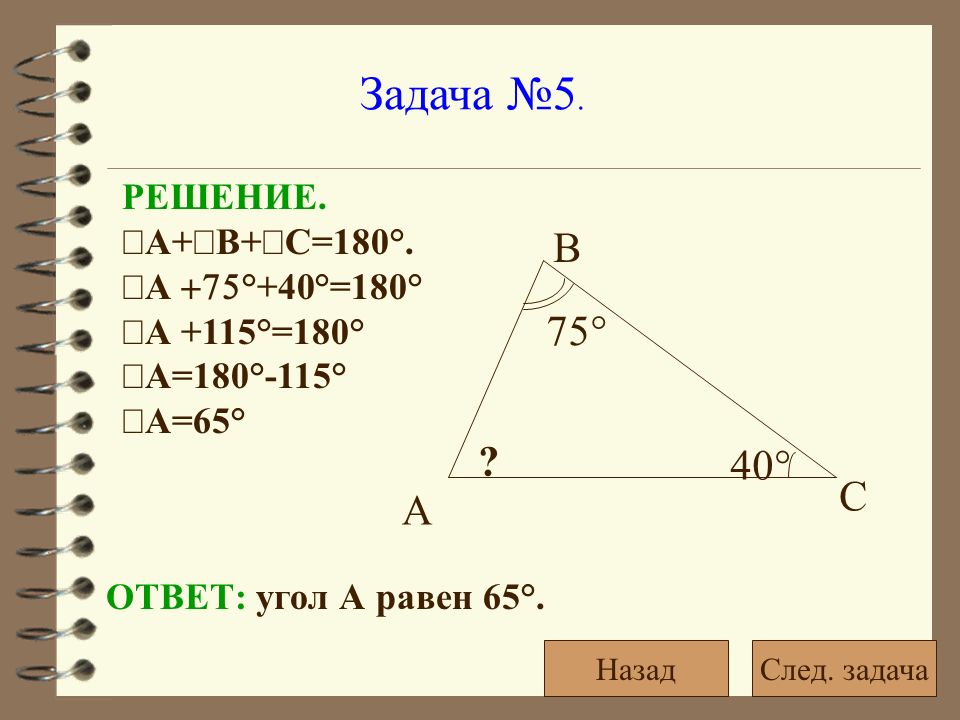 Таким образом, угол, обозначенный $x°$, равен $180°−75°=105°$, поэтому значение $x$ равно 105. Ответ равен 105.
Таким образом, угол, обозначенный $x°$, равен $180°−75°=105°$, поэтому значение $x$ равно 105. Ответ равен 105.
Прямоугольные треугольники
Прямоугольный треугольник — это треугольник, в котором один из углов равен 90° (90° — прямой угол). Это означает, что сумма двух других углов также должна быть 90°, так как сумма углов треугольника всегда равна 180°.
Особые прямоугольные треугольники
Существует множество различных видов прямоугольных треугольников, и некоторые из них считаются «особыми».Это треугольники, у которых установлены углы или длины сторон и соответствующие им формулы. Понимание этих типов треугольников (и их формул) сэкономит вам значительное количество времени на вопросы о треугольниках.
Мы рассмотрим формулы, соответствующие этим типам треугольников, в следующем разделе, а пока давайте пройдемся по их определениям.
Прямоугольный равнобедренный треугольник
Равнобедренный прямоугольный треугольник — это именно то, на что он похож — прямоугольный треугольник, в котором две стороны и два угла равны.
Хотя размеры сторон могут меняться, равнобедренный треугольник всегда будет иметь один угол 90° и два угла 45°. (Почему? Потому что прямоугольный треугольник по определению должен иметь один угол 90°, а сумма двух других углов должна составлять 90°. Таким образом, ${90}/{2}=45$.
30-60-90 Треугольники
Треугольник 30-60-90 — это особый прямоугольный треугольник, определяемый своими углами. Это прямоугольный треугольник из-за угла 90°, а два других угла должны быть равны 30° и 60°.
Это также половина равностороннего треугольника. Как я упоминал ранее, в равностороннем треугольнике три равных угла, каждый из которых равен 60°. Если к этому треугольнику присоединить еще один треугольник 30-60-90 (вдоль катета, противоположного 60°), то получится равносторонний треугольник, все углы которого равны 60°.
Прямоугольные треугольники 3-4-5 и 5-12-13
Треугольники 3-4-5 и 5-12-13 — это особые прямоугольные треугольники, определяемые длинами сторон. Числа 3-4-5 и 5-12-13 описывают длины катетов треугольника, а это означает, что если у вас есть прямоугольный треугольник с длиной катета 4 и длиной гипотенузы 5, то вы автоматически знаете, что третий катет равно 3.
Числа 3-4-5 и 5-12-13 описывают длины катетов треугольника, а это означает, что если у вас есть прямоугольный треугольник с длиной катета 4 и длиной гипотенузы 5, то вы автоматически знаете, что третий катет равно 3.
Любые непротиворечивые множители этих чисел также будут работать одинаково. Таким образом, прямоугольный треугольник может иметь катеты:
3(1)-4(1)-5(1) => 3-4-5
3(2)-4(2)-5(2) => 6-8-10
3(3)-4(3)-5(3) => 9-12-15
И так далее.
Они считаются «особыми» прямоугольными треугольниками, потому что все их стороны являются целыми числами.
Узнаете этого красавца? Потому что Пифагор здесь, чтобы поделиться своей мудростью треугольника.
Формулы треугольников
Теперь, когда вы знаете, как будут выглядеть все ваши треугольники, давайте рассмотрим, как найти недостающие переменные и информацию о них.
Это коробка с формулами, которые вам будут давать на каждом математическом разделе SAT. Хотя все формулы, которые вам нужно знать для треугольников, включены, вы должны понимать, как и почему эти формулы работают, а также когда их использовать. Это также сэкономит ваше время и усилия, чтобы запомнить их, а не переключаться между задачей и полем формулы.
Хотя все формулы, которые вам нужно знать для треугольников, включены, вы должны понимать, как и почему эти формулы работают, а также когда их использовать. Это также сэкономит ваше время и усилия, чтобы запомнить их, а не переключаться между задачей и полем формулы.
Итак, запомните свои формулы, если это возможно, и прочитайте ниже, чтобы увидеть, что эти формулы означают и как их использовать. Все коробки с формулами в мире не стоят бумаги, на которой они напечатаны, если вы не знаете, как их применять при решении своих задач.
Все треугольники
Некоторые формулы применимы ко всем треугольникам, тогда как другие формулы применимы только к особым треугольникам. Итак, давайте сначала рассмотрим формулы треугольника, применимые ко всем без исключения типам треугольников.
Зона
$$a= {1}/{2}bh$$
$b$ — это основание треугольника, равное длине любой из сторон треугольника.
$h$ — высота треугольника, найденная путем проведения прямой линии (под углом 90°) от основания треугольника до угла, противоположного от основания.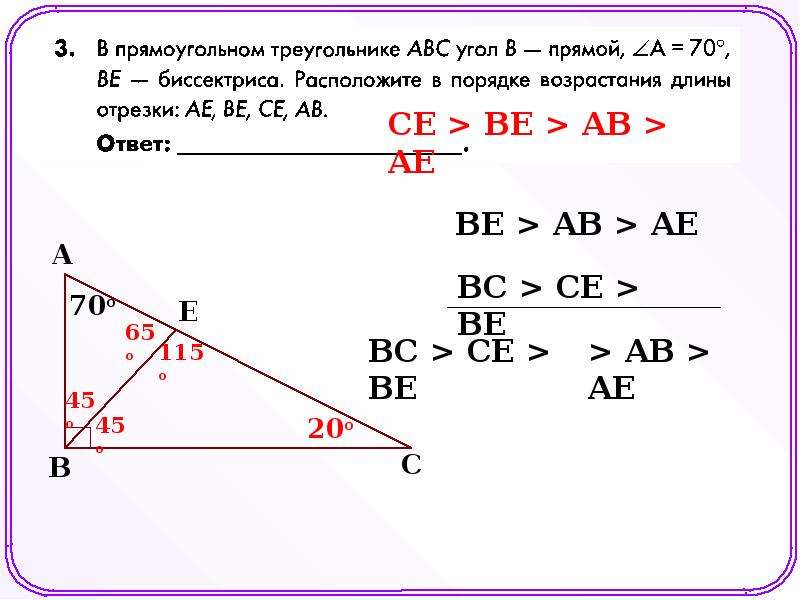
Это означает, что в прямоугольном треугольнике высота равна длине катета, сходящегося под углом 90° к основанию. В непрямоугольном треугольнике вы должны создать новую линию для своего роста.
Периметр
р=11+12+13
Как и в случае любой другой фигуры плоской геометрии, периметр треугольника представляет собой сумму его внешних сторон (трех катетов треугольника).
Прямоугольные треугольники
Существуют также формулы, применимые к прямоугольным треугольникам и к определенным типам прямоугольных треугольников. Давайте взглянем.
Теорема Пифагора
а2+b2=с2
Теорема Пифагора позволяет найти длины сторон прямоугольного треугольника, используя длины других его сторон.a и b обозначают более короткие катеты треугольника, а c всегда является катетом, противоположным углу 90° (гипотенуза).
Треугольники 3-4-5 и 5-12-13 (и их кратные) особенные, потому что вам не нужно работать по теореме Пифагора, чтобы найти меры сторон третьей длины (хотя, конечно, вы всегда может). Помните, если одна сторона прямоугольного треугольника равна 8, а его гипотенуза равна 10, то вы автоматически знаете, что третья сторона равна 6.
Помните, если одна сторона прямоугольного треугольника равна 8, а его гипотенуза равна 10, то вы автоматически знаете, что третья сторона равна 6.
Тригонометрические формулы: синус и косинус
Тригонометрия составляет менее 5% всех математических вопросов, но вы не сможете правильно ответить ни на один вопрос по тригонометрии, не зная формул тригонометрии.Ознакомьтесь с нашим руководством по тригонометрии, чтобы узнать все формулы, которые вам нужно знать, и узнать, как применять формулы к математическим вопросам SAT.
Прямоугольный равнобедренный треугольник
х, х, х√2
Хотя недостающие длины сторон равнобедренного треугольника можно найти с помощью теоремы Пифагора, можно также сократить путь и сказать, что равные длины сторон равны x, а гипотенуза равна $x√2$.
Почему это работает? Ну, представьте себе равнобедренный треугольник с катетом 6.
Мы знаем, что второй катет также должен быть равен 6, потому что в равнобедренном треугольнике оба катета равны. И мы также можем найти гипотенузу, используя теорему Пифагора, потому что это прямоугольный треугольник. Итак:
И мы также можем найти гипотенузу, используя теорему Пифагора, потому что это прямоугольный треугольник. Итак:
62+62=с2
36+36=с2
72=с2
$$c = √72$$
$c = √36 * √2$ (Почему мы смогли разделить наш корень таким образом? Ознакомьтесь с нашим руководством по расширенным целым числам SAT и его разделом, посвященным корням, если этот процесс вам незнаком.)
$c = 6√2$
Итак, у нас остались длины сторон 6, 6 и $6√2$. Или, другими словами, длины наших сторон равны x,x и $x√2$.
30-60-90 Треугольник
$$x, x√3, 2x$$
Как и в случае с равнобедренным прямоугольным треугольником, длина сторон треугольника 30-60-90 определяется набором правил. Опять же, вы можете найти эти длины с помощью теоремы Пифагора, но вы также всегда можете найти их, используя правило: $x, x√3, 2x$, где $x$ — сторона, противоположная 30°, $x√3$ — сторона, противоположная 60°, а $2x$ — сторона, противоположная 90°.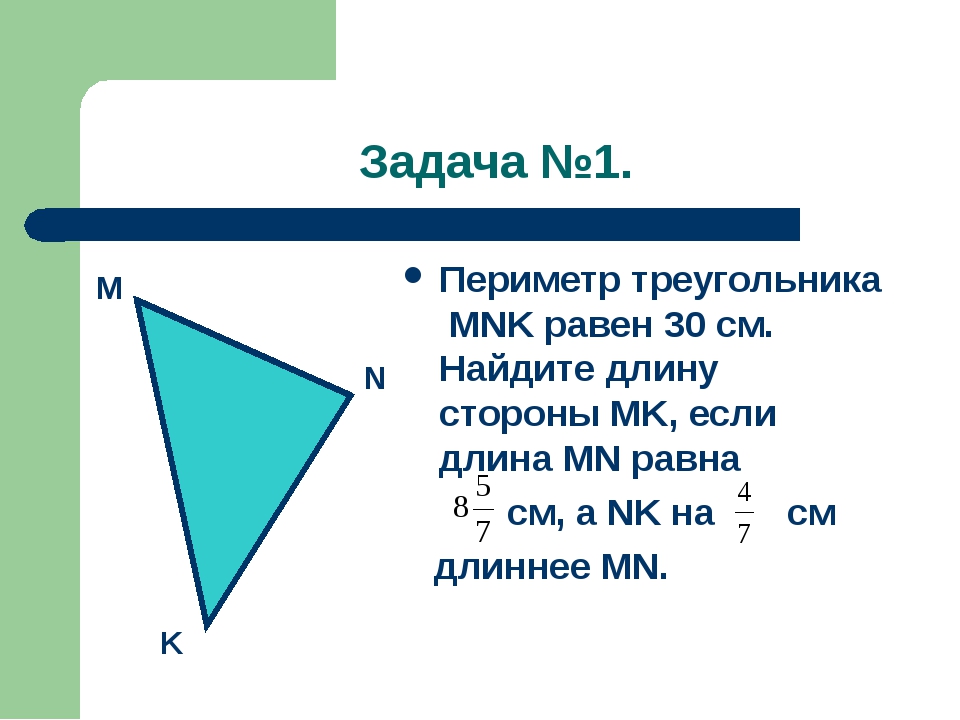
Это знание может помочь вам найти длины сторон при решении более сложной задачи о треугольнике.
Прилежность!Собака сейчас гордится твоей прилежностью. (Столько прилежания.)
Типичные вопросы треугольника
Давайте рассмотрим некоторые стандартные типы вопросов в каждой категории. ПРИМЕЧАНИЕ. Представленные примеры вопросов не относятся к официальным тестам SAT, так как недавно переработанный SAT не начнется до марта 2016 года.Эти вопросы были взяты из новых практических тестов SAT Совета колледжей или адаптированы из других учебных материалов Совета колледжей для нового SAT.
№ 1: поиск пропущенных значений
Большинство задач с треугольниками попадают в эту категорию — вас попросят найти недостающий угол, площадь, периметр или длину стороны (среди прочего) на основе имеющейся информации.
Некоторые из этих вопросов будут более сложными, чем другие, но SAT всегда предоставит вам достаточно информации для решения проблемы, поэтому вам решать, как собрать подсказки вместе.
Давайте рассмотрим пример вопроса такого типа:
Примечание: Рисунок выполнен не в масштабе.
На рисунке выше линия м параллельна линии n , линия d перпендикулярна линии n , а линия e пересекает линию м и линию n 9 Какова длина х?
Ответ Объяснение: Поскольку прямые d и прямые e пересекаются в точке C, >ACB и ∠DCE являются вертикальными углами, а значит, они равны по размеру.Поскольку линия м параллельна линии n , ∠DEC и ∠CAB являются альтернативными внутренними углами параллельных прямых, пересеченных секущей, поэтому меры ∠DEC и ∠CAB равны. По теореме угол-угол треугольник ABC подобен треугольнику EDC с вершинами A, B и C, соответствующими вершинам E, D и C соответственно.
Кроме того, треугольник EDC является прямоугольным, поэтому вы можете использовать либо теорему Пифагора, либо свои знания о прямоугольных треугольниках 3-4-5, чтобы найти, что гипотенуза равна 5.
Поскольку треугольник ABC подобен треугольнику EDC, отношения длин соответствующих сторон двух треугольников одинаковы, поэтому ${CD}/{BC}={3}/{5}={DE}/{AB} ={4}/{x}$.
Решая $x$, мы получаем $3x=20$. Следовательно, $x={20}/{3}$.
#2: Соотношения и (не)равенства
Обычно в таких вопросах вас просят либо найти отношения между частями разных треугольников, либо вам задают вопрос о том, равны или не равны определенные стороны или углы треугольников.
Ответ Пояснение: Углы ABE и DBC являются вертикальными углами (т. е. парами противоположных углов, образованных двумя пересекающимися прямыми), а значит, имеют одинаковую меру. Поскольку отрезок AE параллелен отрезку CD, углы A и D имеют одинаковую меру по теореме об альтернативных внутренних углах. Поскольку в треугольниках ABE и DBC все углы равны, треугольник ABE подобен треугольнику DBC с вершинами A, B и E, соответствующими вершинам D, B и C соответственно. Следовательно,
Следовательно,
Решив это, вы получите CB = 4, и, таким образом, CE = CB + BE = 4 + 8 = 12.
№ 3: Мультифигуры или фигуры внутри фигур
Как вы можете видеть из предыдущих примеров, некоторые задачи на треугольники в SAT будут включать несколько треугольников (или других геометрических фигур), объединенных вместе. Этот метод представления задач предназначен для проверки вашего понимания линий и углов, а также треугольников.
Для этих типов проблем вы должны использовать предоставленную вам информацию и решать для получения дополнительной информации в будущем, пока не найдете именно то, что вам нужно.По сути, это эффект домино при решении проблем.
Объяснение ответа: Вопрос говорит вам, что ∠AEB и ∠CDB имеют одинаковую меру. Поскольку ∠ABE и ∠CBD являются вертикальными углами (то есть представляют собой пары противоположных углов, образованных двумя пересекающимися прямыми), они имеют одинаковую меру. Треугольник EAB подобен треугольнику DCB тем, что треугольники имеют две пары конгруэнтных соответственных углов (угол-угол-критерий подобия треугольников). Поскольку треугольники подобны, соответствующие стороны находятся в одной пропорции:
Треугольник EAB подобен треугольнику DCB тем, что треугольники имеют две пары конгруэнтных соответственных углов (угол-угол-критерий подобия треугольников). Поскольку треугольники подобны, соответствующие стороны находятся в одной пропорции:
$${CD}/{x}={BD}/{EB}$$
Подстановка заданных значений 800 для CD, 700 для BD и 1400 для EB в ${CD}/{x}={BD}/{EB}$ дает ${800}/{x}={700}/ {1400}$
Следовательно, $x={(800)(1400)}/{700}=1600$.
Окончательный ответ: 1600.
#4: Переменные и комбинированные переменные
Наконец, треугольные задачи, которые включают несколько переменных (или только переменных) как в задаче, так и в ответе, обычно находятся где-то в последних трех вопросах любого математического раздела SAT. Это означает, что они являются одними из самых сложных типов математических задач для большинства учащихся.
Хорошая новость заключается в том, что существует множество различных способов решения подобных задач, и что немного времени, организованности и творчества почти всегда помогут вам найти правильный ответ.
Учитывая, что в таких задачах задействовано несколько переменных, вероятно, стоит проверить стратегию подстановки чисел, если вы еще этого не сделали. Это отличная техника, которую можно использовать, если вы сомневаетесь в геометрии и/или алгебре, или просто если вас беспокоит несколько целых чисел.
Давайте рассмотрим пример задачи этого типа и различные методы ее решения.
Что из следующего выражает $z$ через $x$ и $y$?
(А) $2x+3y−180$
(Б) $x+2y−180$
(С) $180-x-y$
(Г) $360−2x−3y$
Как видите, это задача треугольника, в которой используется несколько переменных, поэтому она немного сложна.Давайте рассмотрим все наши варианты решения вопроса:
Метод решения 1: Подставляем собственные числа
В большинстве случаев, когда вам дается несколько переменных в вопросе или в вариантах ответа, безошибочным методом, который вы можете использовать, является подстановка ваших собственных чисел. (Чтобы узнать больше об этой стратегии, ознакомьтесь с нашим руководством по подстановке чисел.)
(Чтобы узнать больше об этой стратегии, ознакомьтесь с нашим руководством по подстановке чисел.)
Нам даны переменные $x$ и $y$ и сказано найти $z$. Итак, давайте выберем некоторые значения для $x$ и $y$, которые кажутся подходящими, и используем их для нахождения $z$.
Давайте просто скажем, что $x=60$ и $y=70$. Почему эти цифры? Почему нет!
Поскольку сумма углов треугольника всегда равна 180°, мы можем найти недостающие значения в наших двух нижних треугольниках, сказав:
$180−60−70=50$$
Это означает, что мы также можем найти значение недостающего угла в нашем верхнем треугольнике, потому что мы знаем, что прямая также должна быть равна 180°. Итак:
$180−50−50=80$$
Это означает, что мы можем, наконец, найти значение z, сказав, что:
$$z=180−80−70$$
$$z=30$$
Теперь давайте воспользуемся теми же значениями для $x$ и $y$, которые мы использовали в нашей задаче, чтобы найти, какой вариант ответа (или варианты) дает нам $z=30$.
Вариант ответа А дает нам:
$$2x+3y−180$$
Что, когда мы заменим наши переменные, будет:
$$2(60)+3(70)−180$$
$120+210−180$$
$150$$
Мы ищем ответ, соответствующий $z=30$, поэтому он слишком велик. Мы можем исключить вариант ответа A.
Давайте попробуем выбрать ответ B:
$$x+2y−180$$
$60+2(70)−180$$
60$+140−180$
$$$20$$
Этот ответ по-прежнему не равен 30, поэтому мы можем исключить вариант ответа B.
Вариант ответа C говорит:
$$180-x-y$$
Но мы уже знаем, что это 50, а не 30, так как мы использовали это уравнение, чтобы найти недостающие компоненты наших треугольников ранее (180−60−70). Мы можем исключить выбор C.
Путем исключения вариант ответа D должен быть правильным. Но давайте перепроверим, чтобы быть уверенным.
$360−2x−3y$$
$360−2(60)−3(70)$$
$360−120−210$$
$30$$
Успех! Мы нашли вариант ответа (и только один вариант ответа), который соответствует тому, что мы нашли для $z$.
Наш окончательный ответ: Д.
Метод решения 2: Алгебраический подход
В качестве альтернативы мы могли бы найти ответ, используя чистую алгебру и свойства треугольников, вместо того, чтобы вводить собственные числа. Для этого мы, по сути, повторяем процесс, который мы использовали для поиска недостающих переменных сверху, но сохраняем переменные нетронутыми.
Каждый из трех треугольников, на которых мы фокусируемся, в сумме дает 180°.У нас есть три разных треугольника и три недостающих угла, поэтому их уравнения будут выглядеть так:
.$$180-x-y$$
$$180-x-y$$
$$180−y−z$$
Мы знаем, что все эти уравнения найдут нам один из трех неотмеченных углов. Мы также знаем, что эти три угла в сумме дают 180°. (Почему? Потому что они лежат на прямой, а прямая равна 180°.)
Таким образом, если мы сложим уравнения и установим их равными 180°, мы получим:
$$(180−x−y)+(180−x−y)+(180−y−z)=180$$
$540−2x−3y−z=180$$
$$−2x−3y−z=−360$$
$$−z=−360+2x+3y$$
$$z=360−2x−3y$$
Итак, снова наш окончательный ответ — D.
(Примечание: есть третий — и даже более быстрый — способ решить эту задачу, связанный с четырехугольниками. Дополнительную информацию см. в нашем руководстве по полигонам SAT!)
Хотя в SAT есть много разных типов задач на треугольники, они выделяются из толпы.
Как решить вопрос о треугольнике
ВопросыTriangle столь же многочисленны (составляя почти 10% всего математического раздела SAT), как и разнообразны.Из-за этого трудно выделить один точный путь для вопросов-треугольников решения проблем.
Тем не менее, ваши самые большие активы и стратегии при решении задач треугольника будут заключаться в следующем:
№ 1: используйте свои формулы (и используйте короткие пути)
Использование ваших формул — самый важный шаг в решении любой задачи с треугольником. И, учитывая, что большинство ваших формул, по сути, действуют как короткие пути (зачем решать с помощью теоремы Пифагора, если вы знаете, что катеты треугольника 30-60-90 равны $x, x√3, 2x$?), вы сэкономит вам много времени и энергии, если вы сможете держать свои формулы под рукой и в порядке.
№ 2: при работе с несколькими фигурами разбивайте их на небольшие шаги
Помните, что решение задачи с многогранным треугольником похоже на работу с домино. Каждая последующая часть информации уступает место для поиска следующей части информации.
Не пугайтесь мысли о том, что у вас недостаточно информации или слишком много фигур или линий, с которыми нужно иметь дело. У вас всегда будет достаточно данных для дальнейшей работы — просто сосредоточьтесь на поиске одной формы и одной части информации за раз, и костяшки домино встанут на свои места.
#3: Нарисуй это
Нарисуйте свои собственные диаграммы, если вам их не предоставили. Нарисуйте сверху ваших диаграмм, когда вы — это заданных картинок. Запишите свои данные и все измерения, которые вы найдете на пути к отсутствующей переменной (или переменным), и отметьте конгруэнтные линии и углы.
Чем больше вы сможете прояснить свои диаграммы, тем меньше вероятность того, что вы сделаете ошибки по невнимательности, перепутав числа и равенства.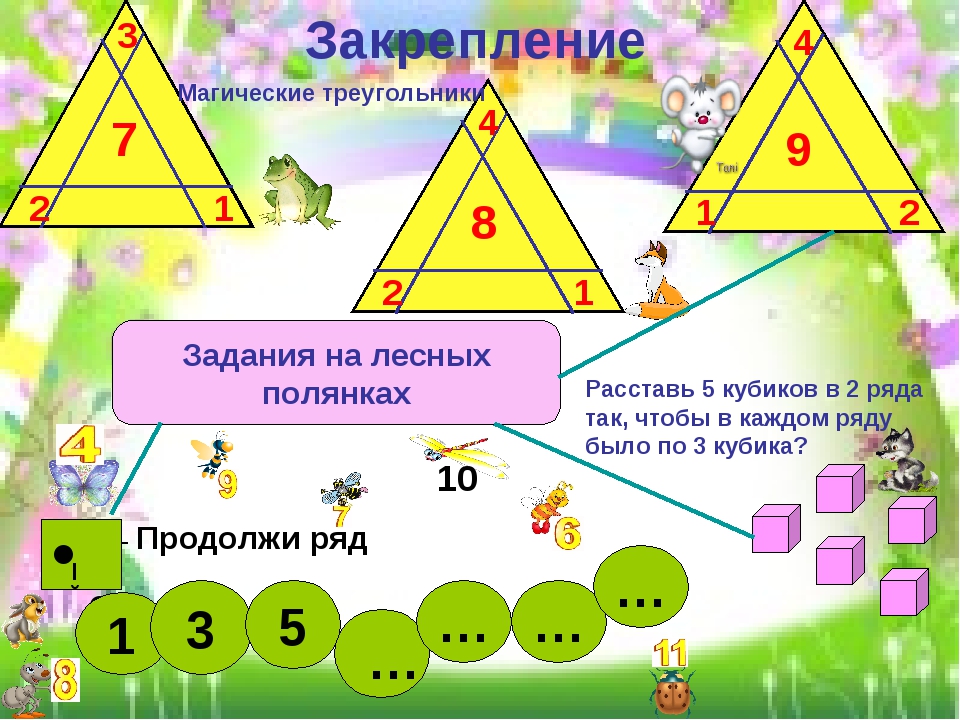
№ 4: Подставляйте свои номера, когда это возможно
Наконец, дайте себе отдохнуть от работы с переменными и сложной алгеброй, если вам это нужно.Слишком легко сделать ошибку, имея дело только с переменными, поэтому, если у вас есть свободное время, попробуйте ввести свои собственные числа!
В вашем распоряжении больше информации и стратегий, чем вы думаете. Просто держите их под рукой и организуйте в голове, и все будет готово.
Проверьте свои знания
А теперь давайте проверим ваши знания о треугольниках на других математических задачах SAT. ПРИМЕЧАНИЕ: эти вопросы не являются официальными вопросами раздела SAT по математике (поскольку в марте 2016 года дебютирует обновленный SAT).Эти вопросы были взяты из практических тестов Совета колледжей для нового SAT или адаптированы из других новых практических вопросов SAT и старых вопросов SAT.
1.
Примечание: Рисунок выполнен не в масштабе.
На рисунке выше правильный многоугольник с 8 сторонами разделен на 8 конгруэнтных равнобедренных треугольников отрезками, проведенными из центра многоугольника к его вершинам. Какова стоимость $x$?
Ответ Пояснение: Сумма углов вокруг точки равна 360°.Так как 8 треугольников равны, то и величины всех 8 углов одинаковы. Следовательно, мера каждого равна ${360°}/{8}=45°$. В любом треугольнике градусная мера внутренних углов равна 180°. Таким образом, в каждом треугольнике сумма мер оставшихся двух углов равна $180°-45°=135°$. Так как треугольники равнобедренные, то и величины двух углов равны. Следовательно, мера каждого из этих углов равна ${135°}/{2}=67,5°$.
2.
Примечание: Рисунок выполнен не в масштабе.
В приведенном выше треугольнике ABC $AB=AC$, E — середина $\ov{AB}$, а D — середина $\ov{AC}$. Если $AE = x$ и $ED = 4$, какова длина $\ov{BC}$?
(А) 6
(Б) 8
(С) $2x$
(Д) $4x$
Объяснение ответа: Как всегда, давайте сначала заполним нашу информацию.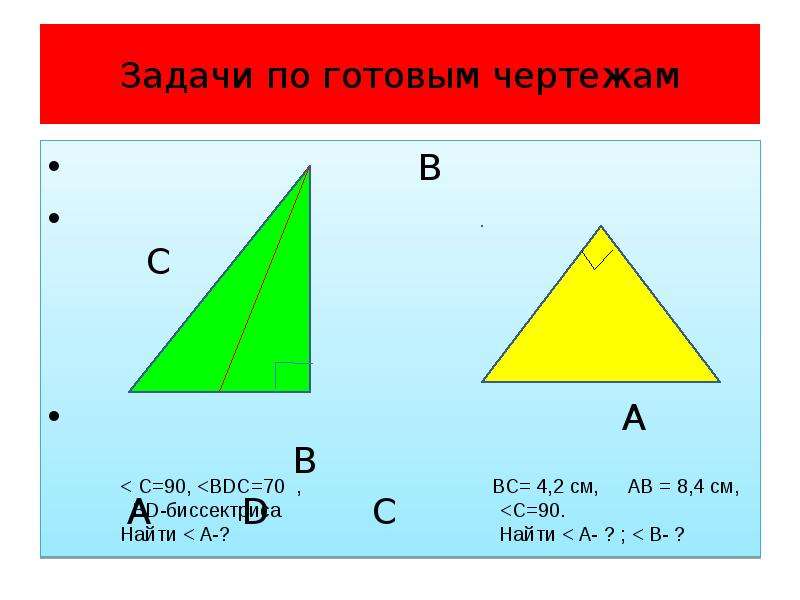
Теперь, хотя это может и не выглядеть так, нам говорят, что E является серединой линии AB. Это означает, что если сегмент AE стоит $x$, то сегмент EB также стоит $x$.Это также означает, что вся длина AB будет стоить $x+x=2x$.
Итак, составим пропорцию.
Участок AE будет соответствовать своему основанию ED, так как участок AB будет соответствовать своему основанию BC. Итак:
$${AE}/{ED}:{AB}/{BC}$$
$${x}/{4}:{2x}/{BC}$$
$$8x=BCx$$
$$8=BC$$
Наш окончательный ответ: B, BC = 8.
3.
Примечание: Рисунок выполнен не в масштабе.
Выше показаны два равнобедренных треугольника. Если $180−x=3y$ и $y=20$, каково значение z?
Объяснение ответа: Поскольку вопрос говорит вам, что $180−x=3y$ и $y=20$, тогда $180−x=3y=60$, и решение дает $x=120$. Если $x=120$, то каждый из углов при основании равнобедренного треугольника справа должен быть равен 30° (${180−120}/{2}$). Таким образом, угол, отмеченный $z°$, равен $180°−30°=150°$, поэтому значение z равно 150. Ответ равен 150.
Таким образом, угол, отмеченный $z°$, равен $180°−30°=150°$, поэтому значение z равно 150. Ответ равен 150.
Мы думаем, что вы заслужили передышку, не так ли?
Еда на вынос
Треугольники обязательно будут появляться по крайней мере несколько раз на каждом SAT (обычно примерно в 1-3 задачах).Хорошей новостью является то, что вам будет предоставлено несколько формул, которые помогут вам ответить на эти типы вопросов, но недостатком является то, что тест рассчитан на время, и поэтому вам следует тратить время на посещение поля с формулами только в том случае, если у вас нет всех вариантов.
Знайте свои определения, старайтесь запоминать формулы и делайте все возможное, чтобы сохранить ясность ума во время прохождения теста. И, как всегда, практика, практика, практика! Чем больше опыта вы приобретете в решении разнообразных вопросов о треугольниках, которые SAT может поставить перед вами, тем лучше вы будете справляться с этими проблемами треугольника.
Что дальше?
Теперь, когда вы выполнили задания по треугольникам, пришло время убедиться, что вы готовы ко всем темам по математике, которые вы увидите на SAT. Все наши руководства по математике познакомят вас со стратегиями и практическими задачами по всем темам, затронутым в математическом разделе, от целых чисел до отношений, от кругов до многоугольников (и многого другого!).
Волнуетесь перед экзаменом? Убедитесь, что вы точно знаете, что делать, и возьмите с собой, чтобы успокоиться и успокоить нервы, прежде чем придет время сдавать SAT.
Не хватает времени на математический раздел SAT? Не ищите ничего, кроме нашего руководства, которое поможет вам побить время и максимизировать свой результат SAT по математике.
Рыбалка, чтобы получить высший балл? Ознакомьтесь с нашим руководством по получению идеальных 800, написанным отличником.
Хотите улучшить свой результат SAT на 160 баллов?
Посетите наши лучшие в своем классе онлайн-курсы по подготовке к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой результат SAT на 160 или более баллов.
Мы гарантируем возврат ваших денег , если вы не улучшите свой результат SAT на 160 или более баллов.
Наши занятия полностью онлайн, и их проводят эксперты SAT. Если вам понравилась эта статья, вам понравятся наши занятия. Наряду с занятиями под руководством экспертов вы получите индивидуальное домашнее задание с тысячами практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно. Мы также предоставим вам пошаговую индивидуальную программу, чтобы вы никогда не запутались в том, что изучать дальше.
Попробуйте сегодня без риска:
Задачи по геометрии с участием углов треугольника
Задачи по геометрии с участием углов треугольника Задачи на геометрию углы треугольникаВо-первых, давайте вспомним некоторые мелочи треугольника:
Равнобедренный треугольник имеет две равные стороны и две равные углы.
Прямоугольный треугольник имеет один угол 90 o .
Если треугольник не равнобедренный и не прямоугольный, мы назовите его общим треугольником.
Мелочи, которые верны для всех треугольников:
Сумма трех углов любого треугольника равна
180 градусов.
Теперь давайте решим задачу.
Наибольший угол треугольника в 5 раз больше самый маленький угол.Третий угол на 12 градусов больше наименьшего угол. Найдите величину всех трех углов.
Что нас просят найти в этой задаче? Посмотрите на последнее предложение задачи, и вы увидите, что мы хотим найти меры всех трех углов треугольника.
Чтобы определить переменные в этой задаче, мы начнем нарисовав изображение общего треугольника:
Так как задача многое говорит нам о наибольшем угле и средний угол но не много про наименьший угол ну назовите наименьший угол х градусов.
Наибольший угол в 5 раз больше наименьшего угла, поэтому наибольший угол равен 5х градусов.

Средний угол на 12 градусов больше наименьшего угол, так что хорошо называть средний угол х +12 градусов. Ну напиши все эта информация на нашей картинке:
Наше уравнение будет исходить из того, что сумма три угла любого треугольника должны быть равны 180 градусам. Это дает нам:
(5х) + (х + 12) + (х) = 180
Теперь решим уравнение:
5х + х + 12 + х = 180
7х + 12 = 180
7х = 168
х = 24
Значит, наименьший угол равен 24 градусам.
Мы решили задачу? Не совсем. Нам все еще нужно найти меры двух других углов. Хорошо вернемся к нашему треугольнику чтобы убедиться, что наибольший угол равен 5x=5(24)=120 o , а средний угол измеряет x+12=24+12=36 o .
Таким образом, три угла имеют размеры 24 o , 36 o , и 120 или .
Прежде чем мы закончим с проблемой, давайте проверим наш ответ с помощью
слова проблемы:
| слов | чек |
Наибольший угол треугольника
в 5 раз больше наименьшего угла. | 120 в пять раз больше 24? Да! |
| Третий угол 12 градусов больше наименьшего угла. | Является ли 36 равным 12 больше, чем 24? Да! |
| Это треугольник: углы все в сумме 180 градусов? | 24 + 36 + 120 = 180 |
Наш ответ проверяет. Были сделаны!
Прямоугольный треугольник Word Проблемы Как только вы узнали о тригонометрии
отношения (и их обратные), вы можете решать треугольники.Естественно, многие
из этих треугольников будут представлены в контексте текстовых задач.
В качестве основы я буду использовать отношение косинуса: Лестница достигает
около 5,20 метров вверх по стене, Примечание. Если вам не велят отдать ответ в десятичной форме, или округлить, или каким-то другим способом не до дать «точный» ответ, вероятно, следует предположить, что «точная» форма — это то, чего они хотят.Например, если они не сказал мне округлить в упражнении выше, мое значение высоты должно было быть значение с радикалом.
Мне дали «наоборот»
и гипотенузу, и спросил у меня значение угла. Угол, который образует лестница с землей около 53° .
Мне нужно найти ширину Солнца. Это только половина ширины; несущий вычисления в моем калькуляторе (чтобы свести к минимуму ошибку округления), я получаю стоимость 919002.8129. Это больше фактического диаметра, который ближе к 864 900 милям, но этого значения будет достаточно для целей этого упражнения. Диаметр около 919 003 миль.
Подшипники указывают мне углы от «строго на север» по часовой стрелке. Поскольку 130 – 40 = 90, эти два подшипника дадут мне прямоугольный треугольник. По временам и ставкам могу найти расстояния: Теперь, когда у меня есть длина двух
ножки, могу поставить треугольник: Я могу найти расстояние, используя теорему Пифагора: 165° находится напротив неизвестного угла, а 143° находится рядом с ним, поэтому я воспользуюсь отношением, обратным тангенсу, чтобы найти угол. мера угла: Но это не «подшипник», поскольку азимут — это угол по отношению к «прямому северу».Мне нужно добавить исходный угол в сорок градусов, чтобы получить ответ: . Самолет находится на расстоянии около 218 миль, по азимуту около 89° . Еще один большой класс прямоугольных слов проблемы, с которыми вы, вероятно, столкнетесь, это углы высота и депрессия…. Топ | Вернуться к индексу
|
|
3.
 4: Применение тригонометрии треугольника
4: Применение тригонометрии треугольникаОсновные вопросы
Следующие вопросы помогут нам изучить материал этого раздела.Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
- Как мы можем использовать закон синусов и закон косинусов для решения прикладных задач, связанных с треугольниками?
- Как определить площадь треугольника?
- Что такое закон Герона для площади треугольника?
В разделе 3.2 мы использовали прямоугольные треугольники для решения некоторых прикладных задач.Поэтому неудивительно, что мы можем использовать закон синусов и закон косинусов для решения прикладных задач, связанных с треугольниками, которые не являются прямоугольными.
В большинстве задач мы сначала получаем грубую диаграмму или изображение, показывающее треугольник или треугольники, задействованные в задаче. Затем нам нужно пометить известные величины. Как только это будет сделано, мы сможем увидеть, достаточно ли информации для использования закона синусов или закона косинусов. Помните, что каждый из этих законов включает четыре величины.Если мы знаем значение трех из этих четырех величин, мы можем использовать этот закон для определения четвертой величины.
Как только это будет сделано, мы сможем увидеть, достаточно ли информации для использования закона синусов или закона косинусов. Помните, что каждый из этих законов включает четыре величины.Если мы знаем значение трех из этих четырех величин, мы можем использовать этот закон для определения четвертой величины.
Начнем с примера из упражнения \(\PageIndex{1}\). Решение этой задачи потребовало сложной работы с прямоугольными треугольниками и некоторой алгебры. Теперь мы решим эту задачу, используя результаты раздела 3.3.
Пример \(\PageIndex{1}\): высота до вершины флагштока
Предположим, что флагшток находится на вершине холма и мы не можем напрямую измерить длину тени от флагштока, как показано на рисунке \(\PageIndex{2}\).\цирк\]
\[d = 22,75 фута\]
Рисунок \(\PageIndex{1}\): Флагшток на холме
Заметим, что если бы мы знали длину \(BC\) или \(BD\) в \(\треугольнике BDC\), то мы могли бы использовать тригонометрию прямоугольного треугольника, чтобы определить длину \(BC\), которая равна час Теперь посмотрите на \(\треугольник ABC\). \circ — 43.\circ)}\]
\circ — 43.\circ)}\]
\[AB \примерно 121,7\]
Мост из точки \(B\) в точку \(A\) будет приблизительно \(121,7\) футов в длину.
Площадь треугольника
Теперь мы разработаем несколько различных способов вычисления площади треугольника. Пожалуй, самая знакомая формула площади такова:
.Треугольники на рисунке \(\PageIndex{2}\) иллюстрируют использование переменных в этой формуле.
Площадь \(A\) треугольника равна \[A = \dfrac{1}{2}bh.\]
, где \(b\) — длина основания треугольника, а \(h\) — длина высоты, перпендикулярной этому основанию.
Рисунок \(\PageIndex{2}\): диаграммы для формулы площади треугольника
Доказательство этой формулы для площади треугольника зависит от формулы для площади параллелограмма и включено в Приложение C.
Упражнение \(\PageIndex{2}\)
Предположим, что длины двух сторон треугольника равны \(5\) метрам и \(7\) метрам, а угол, образованный этими двумя сторонами, равен \(26. \circ) \примерно 7,8085\]
\circ) \примерно 7,8085\]
Площадь треугольника примерно равна \(7,8085\) квадратных метров.
Цель Проверки прогресса 3.21 состояла в том, чтобы проиллюстрировать, что если мы знаем длину двух сторон треугольника и угол, образованный этими двумя сторонами, то мы можем определить площадь этого треугольника.
Площадь треугольника
Площадь треугольника равна половине произведения двух его сторон на синус угла, образованного этими двумя сторонами.
Упражнение \(\PageIndex{3}\)
На диаграмме справа \(b\) — длина основания треугольника, \(a\) — длина другой стороны, а \(\theta\) — угол, образованный этими двумя сторонами. . Пусть \(A\) будет площадью треугольника.
Следуйте процедуре, показанной в разделе Проверка выполнения 3.21, чтобы доказать, что \[A = \dfrac{1}{2}ab\sin(\theta)\]
Объясните, почему это доказывает формулу площади треугольника.
- Ответить
Используя прямоугольный треугольник, мы видим, что \(\sin(\theta) = \dfrac{h}{a}\).
 Итак, \(h = a\sin(\theta\), а площадь треугольника равна \[A = \dfrac{1}{2}b(a\sin(\theta)) = \dfrac{1}{ 2}ab\sin(\theta)\]
Итак, \(h = a\sin(\theta\), а площадь треугольника равна \[A = \dfrac{1}{2}b(a\sin(\theta)) = \dfrac{1}{ 2}ab\sin(\theta)\]
Существует еще одна распространенная формула площади треугольника, известная как формула Герона, названная в честь Герона Александрийского (около 75 г. н.э.). Эта формула показывает, что площадь треугольника можно вычислить, если известны длины трех сторон треугольника.
Формула Герона
Площадь \(A\) треугольника со сторонами длины \(a\), \(b\) и \(c\) находится по формуле
\[A = \sqrt{s(s — a)(s — b)(s — c)} \label{Heron}\]
, где \(s = \dfrac{1}{2}(a+ b + c)\).
Например, предположим, что длины трех сторон треугольника равны \(a = 3ft\), \(b = 5ft\) и \(c = 6ft\). Используя формулу Герона (уравнение \ref{Heron}), мы получаем
\[s = \dfrac{1}{2}(a+ b + c)\]
\[с = 7\]
\[A = \sqrt{s(s — a)(s — b)(s — c)}\]
\[A = \sqrt{7(7 — 3)(7 — 5)(7 — 6)}\]
\[A = \sqrt{42}\]
Эта довольно сложная формула фактически получена из предыдущей формулы площади треугольника и закона косинусов. {2}(\gamma)\) по формуле (1). Это дает формулу для \(\sin(\gamma)\) в терминах \(a\), \(b\) и \(c\). (Не делайте никаких алгебраических упрощений.)
{2}(\gamma)\) по формуле (1). Это дает формулу для \(\sin(\gamma)\) в терминах \(a\), \(b\) и \(c\). (Не делайте никаких алгебраических упрощений.)
Подставьте вместо \(\sin(\gamma)\) формулу из (2). (Не делайте никакого алгебраического упрощения.) Это дает формулу для площади \(A\) в терминах \(a\), \(b\) и \(c\).
Формула, полученная при проверке прогресса 3.{2} = \dfrac{-(a — b — c)(a — b + c)(a + b — c)(a + b + c)}{16}\]
\[= \dfrac{( 2s — 2a)(2s — 2b)(2s — 2c)(2s)}{16}\]
\[= \dfrac{16s(s — a)(s — b)(s — c)}{16} \]
\[= s(s — a)(s — b)(s — c)\]
\[A = \sqrt{s(s — a)(s — b)(s — c)}\ ]
Это завершает доказательство формулы Герона.
Резюме
В этом разделе мы изучили следующие важные концепции и идеи:
- Как использовать тригонометрию прямоугольного треугольника, закон синусов и закон косинусов для решения прикладных задач, связанных с треугольниками.

- Три способа определения площади \(A\) треугольника.
\(A = \dfrac{1}{2}bh\), где \(b\) — длина основания, а \(h\) — длина высоты.
\(A = \dfrac{1}{2}ab\), где \(a\) и \(b\) – длины двух сторон треугольника, а \(\theta\) – угол, образованный стороны длины \(a\) и \(b\).
Формула Герона . Если \(a\), \(b\) и \(c\) — длины сторон треугольника и \(s = \dfrac{1}{2}(a + b + c)\) , то \[A = \sqrt{s(s — a)(s — b)(s — c)}.\]

 ответ: 12/5
ответ: 12/5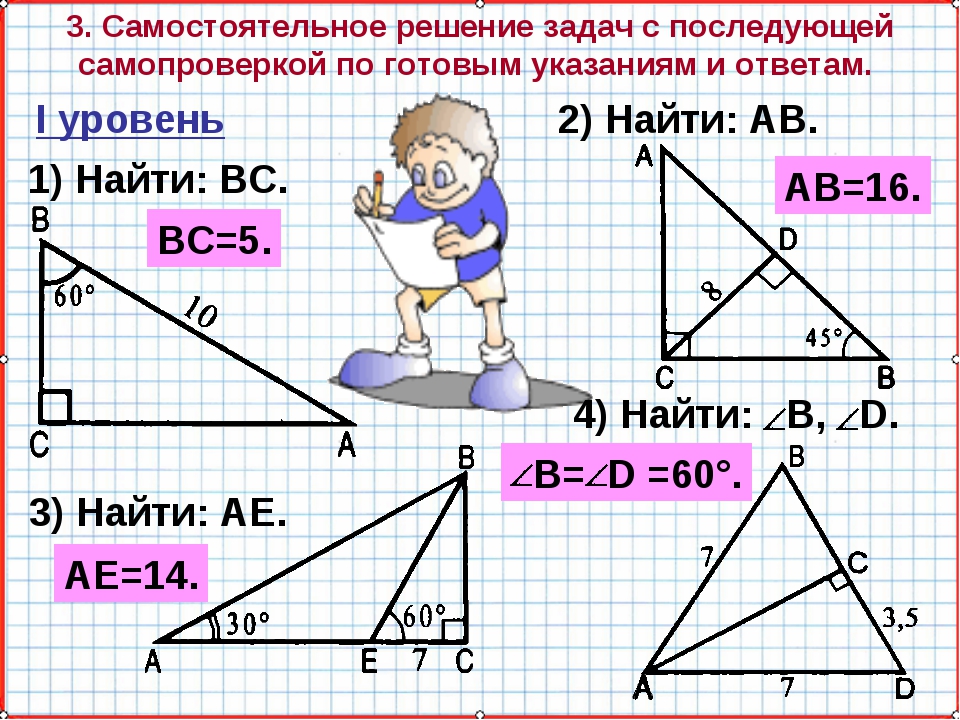 Найдите радиус окружности, вписанной в этот треугольник. ответ: 2
Найдите радиус окружности, вписанной в этот треугольник. ответ: 2
 Хороший первый шаг после прочтения всего упражнения — нарисовать правую
треугольник и попытайтесь понять, как его обозначить. Как только вы получите полезный
диаграмма, математика обычно довольно проста.
Хороший первый шаг после прочтения всего упражнения — нарисовать правую
треугольник и попытайтесь понять, как его обозначить. Как только вы получите полезный
диаграмма, математика обычно довольно проста. 196152423.
196152423. Для этого я
необходимо использовать обратные коэффициенты срабатывания.
Для этого я
необходимо использовать обратные коэффициенты срабатывания. Что, если я добавлю еще одну линию, являющуюся прямой линией
от Земли до центра Солнца?
Что, если я добавлю еще одну линию, являющуюся прямой линией
от Земли до центра Солнца? Эта ширина будет в два раза больше основания одного из прямоугольных треугольников. С участием
что касается моего угла, они дали мне «соседний» и имеют
попросил «противоположное», поэтому я буду использовать отношение тангенса:
Авторское право © Элизабет
Stapel 2010-2011 Все права защищены
Эта ширина будет в два раза больше основания одного из прямоугольных треугольников. С участием
что касается моего угла, они дали мне «соседний» и имеют
попросил «противоположное», поэтому я буду использовать отношение тангенса:
Авторское право © Элизабет
Stapel 2010-2011 Все права защищены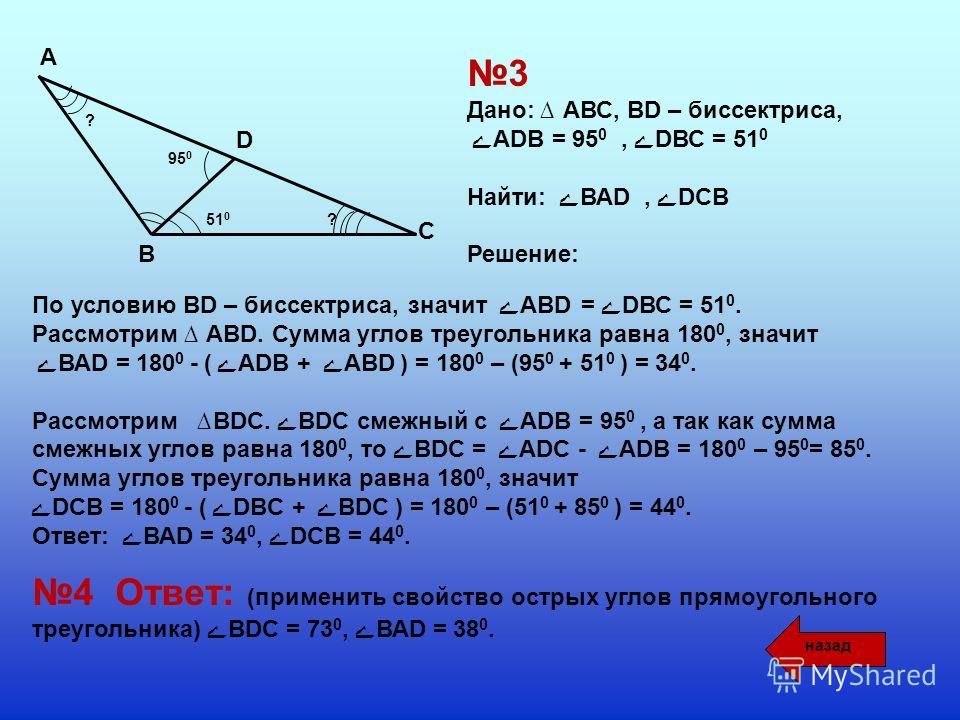 В
в конце этого времени, как далеко самолет от начальной точки?
Каково его отношение к этой отправной точке?
В
в конце этого времени, как далеко самолет от начальной точки?
Каково его отношение к этой отправной точке? 
 Итак, \(h = a\sin(\theta\), а площадь треугольника равна \[A = \dfrac{1}{2}b(a\sin(\theta)) = \dfrac{1}{ 2}ab\sin(\theta)\]
Итак, \(h = a\sin(\theta\), а площадь треугольника равна \[A = \dfrac{1}{2}b(a\sin(\theta)) = \dfrac{1}{ 2}ab\sin(\theta)\]