Обобщённая теорема Фалеса

Основные понятия

Прежде чем сформулировать теорему Фалеса и доказать её, напомним несколько ключевых определений геометрии:

• четырёхугольник;
• параллелограмм;
• трапеция.

Четырёхугольник имеет четыре вершины.

Параллелограмм — это четырёхугольник, противоположные стороны которого попарно параллельны друг другу. В параллелограмме равны противоположные стороны между собой и противоположные углы.

Трапеция — это такой четырёхугольник, у которого две противоположные стороны параллельны друг другу, а две другие противоположные стороны не параллельны друг другу.

В целях понимания, приведём примеры задач с параллелограммом и трапецией.

Пример 1

Задача. Найти углы параллелограмма $ABCD$, если $\angle A=73^{\circ}$.

Решение. Сделаем такой рисунок:

Рисунок 1. Параллелограмм. Автор24 — интернет-биржа студенческих работ

На рисунке проведена прямая, параллельная $AB$ из вершины $B$. Угол, образованный вершиной $B$, проведённой прямой и стороной $BC$ равен $73^{\circ}$ как накрест лежащий относительно $\angle A$. По определению развернутого угла (развёрнутый угол равен $180^{\circ}$) получаем простые вычисления:

$\angle B=180-73=107^{\circ}$. Так как в параллелограмме противоположные углы равны, то $\angle C=\angle A=73^{\circ}, \angle D=\angle B=107^{\circ}$.

Ответ. $73^{\circ}, 73^{\circ}, 107^{\circ}, 107^{\circ}$.

В примере выше можно было решить через свойство четырёхугольников о том, что сумма углов выпуклого четырёхугольника равна $360^{\circ}$. Для этого нужно было бы дополнительно доказать, что параллелограмм — это выпуклый четырёхугольник. Этот простой вопрос останется читателю для размышлений на досуге.

Пример 2

Задача. Найти $\angle B$ и $\angle D$ в трапеции $ABCD$, если $\angle A = 47^{\circ}, \angle C = 108^{\circ}$.

Решение. Сделаем рисунок:

Рисунок 2. Трапеция. Автор24 — интернет-биржа студенческих работ

На рисунке проведена прямая, параллельная $AB$ из вершины $B$. Угол, образованный вершиной $B$, проведённой прямой и стороной $BC$ равен $47^{\circ}$ как накрест лежащий относительно $\angle A$. По определению развернутого угла получаем простые вычисления: $\angle B=180-47=133^{\circ}$.

На рисунке также проведена прямая параллельно $CD$ из вершины $D$. Угол, образованный вершиной $D$, проведённой прямой и стороной $CD$ равен $108^{\circ}$ как накрест лежащий относительно $\angle С$. По определению развернутого угла получаем простые вычисления: $\angle B=180-108=72^{\circ}$.

Ответ. $133^{\circ}, 72^{\circ}$.

Как и в случае параллелограмма, данную задачу можно проверить, сложив все углы данной трапеции. Их сумма должна быть равна $360^{\circ}$. Можно убедиться, что сумма всех углов данной трапеции действительно равна $360$.

Владея ключевыми понятиями, можем перейти к теореме Фалеса и её доказательству.

Теорема Фалеса

Теорема названа в честь древнегреческого ученого Фалеса Милетского. Звучит она следующим образом:

Теорема 1

Если последовательно отложить на прямой несколько равных друг другу отрезков и провести через их концы параллельные прямые, которые пересекают вторую проведённую прямую, то эти параллельные прямые отсекут на ней также равные отрезки.

Доказательство теоремы Фалеса

Докажем эту теорему.

Рассмотрим рисунок:

Рисунок 3. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

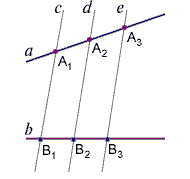
На прямой $a$ отложены следующие отрезки: $A_1 A_2, A_2 A_3, A_3 A_4,…$. Через эти отрезки проведены несколько параллельных прямых, пересекающих прямую $b$ в соответствующих точках $B_1,B_2,B_3,B_4,…$. Докажем, что отрезки $B_1 B_2, B_2 B_3, B_3 B_4,…$ равны между собой. Для начала упростим задачу и докажем следующее: $B_1 B_2 = B_2 B_3$.

На рисунке прямые $a$ и $b$ параллельны. Следовательно, $A_1 B_1 B_2 A_2$ и $A_2 B_2 B_3 A_3$ — параллелограммы. Это означает, что противоположные стороны параллелограммов равны, следовательно, $A_1 A_2 = B_1 B_2, A_2 A_3 = B_2 B_3$. И из $A_1 A_2=A_2 A_3$ следует, что $B_1 B_2= B_2 B_3$.

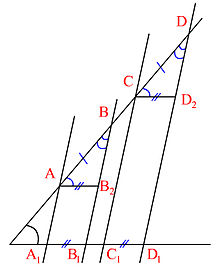
Есть и другой случай, когда прямые $a$ и $b$ не параллельны:

Рисунок 4. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

Проведём такую прямую $c$, которая параллельна $a$:

Рисунок 5. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

Прямая $c$ пересекает $A_2 B_2$ и $A_3 B_3$ соответственно в т. $C_1, C_2$. Так как $A_1 A_2=A_2 A_3$, то, по аналогии в предыдущем случае, $B_1 C_1 = C_1 C_2$.

Рассмотрим $\triangle C_2 B_1 B_3$. $C_1$ — середина $B_1 C_2$. $B_2 C_1$ параллельна $B_3 C_2$.

Проведём через точку $B_3$ такую прямую, которая параллельна $B_1 C_2$.

Рисунок 6. Доказательство теоремы Фалеса. Автор24 — интернет-биржа студенческих работ

Точкой $D$ обозначено пересечение $B_2 C_1$ с проведённой прямой. Получаем параллелограмм $C_1 C_2 B_3 D$. Так как $C_1$ — середина $B_1 C_2$, а $C_1 C_2= B_3 D$ (как противоположные стороны параллелограмма), следовательно, $C_1 B_1 = B_3 D$.

Рассмотрим $\triangle C_1 B_1 B_2$ и $\triangle B_2 B_3 D$ Они равны согласно второму признаку равенства треугольников. То есть так как выполняются равенства $C_1 B_1 = B_3 D$, $\angle C_1 B_1 B_2 = \angle B_2 B_3 D$ и $\angle B_1 C_1 B_2=\angle B_2 D B_3$ (как лежащие накрест углы при пересечении параллельных прямых $B_1 C_2$ и $B_3 D$ секущими $B_1 B_3$ и $C_1 D$).

Следовательно, $B_1 B_2= B_2 B_3$.

Аналогично доказывается равенство $B_2 B_3=B_3 B_4$ и другие.

Таким образом, в данной статье мы полностью разобрали теорему Фалеса, произвели подробное её доказательство, фигурируя известными понятиями.

spravochnick.ru

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

      Теорема Фалеса. Через произвольные точки

A₁,  A₂,  …   A_n–1,  A_n,

лежащие на стороне AO угла AOB (рис.1), проведены параллельные прямые, пересекающие сторону угла OB в точках

B₁,  B₂,  …  B_n–1,  B_n,

соответственно. Тогда справедливы равенства

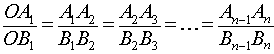
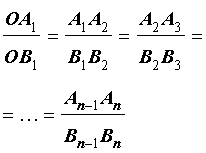
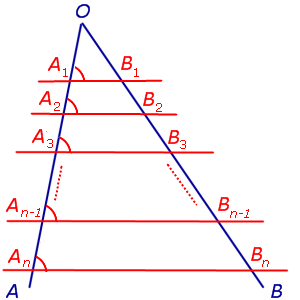
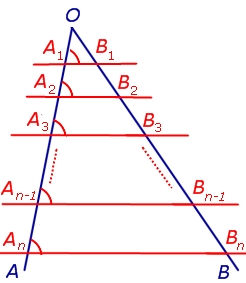
Рис.1

      Доказательство. Докажем сначала следующую лемму.

      Лемма. Через произвольную точку C, лежащую на стороне OA треугольника OAB, проведена прямая, параллельная прямой AB и пересекающая сторону OB в точке D (рис.2).

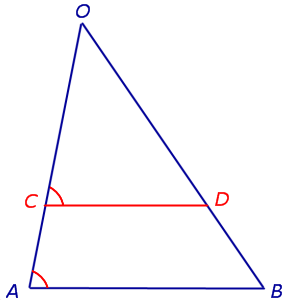
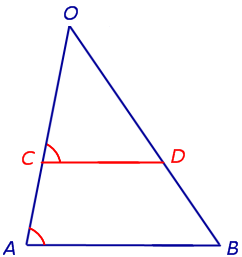
Рис.2

      Тогда справедливо равенство

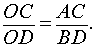(1)

      Доказательство леммы. Опустим из точек A и B перпендикуляры AK и BL на прямую CD (рис.3). Заметим, что эти перпендикуляры равны, поскольку AKLB – прямоугольникпрямоугольник.

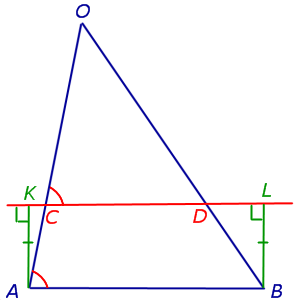
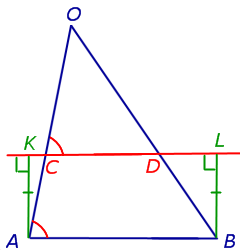
Рис.3

      Из точки D опустим перпендикуляр DF на прямую OA (рис.4).

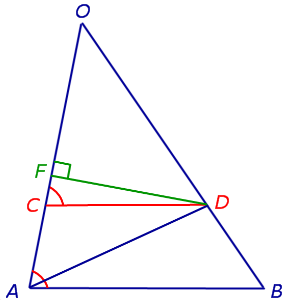
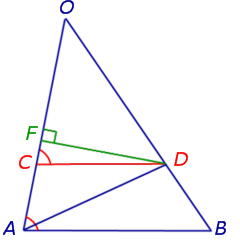
Рис.4

      Из точки C  опустим перпендикуляр CG на прямую OB (рис.5).

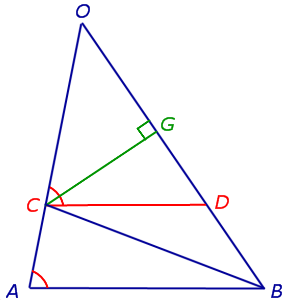
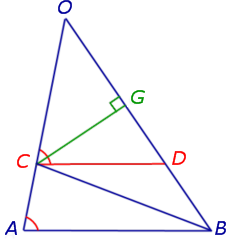
Рис.5

      В соответствии с рисунком 4 площади треугольников OCD и ACD можно вычислить по формулам

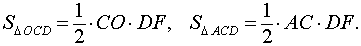
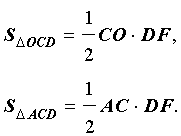
      Следовательно,

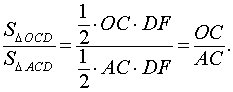
      В соответствии с рисунком 5 площади треугольников OCD и BCD можно вычислить по формулам

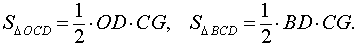
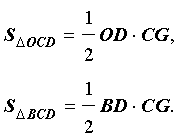
      Следовательно,

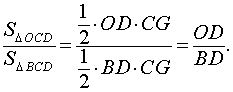
      Кроме того, заметим, что площади треугольников ACD и BCD равны. Действительно, в соответствии с рисунком 3 справедливы формулы

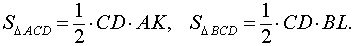
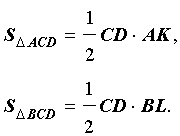
      Следовательно,

S_{Δ ACD} = S_{Δ BCD} ,

откуда получаем цепочку равенств

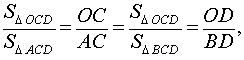
что и завершает доказательство леммы.

      Воспользовавшись леммой, заметим (рис.1), что из равенства (1) вытекают равенства

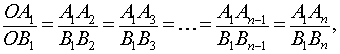
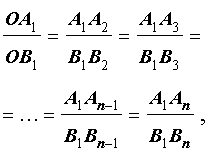
откуда на основе свойств производных пропорций, заключаем, что справедливы равенства

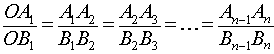
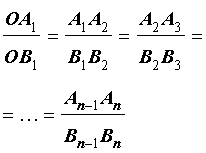
что и завершает доказательство теоремы Фалеса.

      Следствие. Если через точки

A₁,  A₂,  …   A_n–1,  A_n,

лежащие на стороне AO угла AOB (рис.6) и удовлетворяющие условию

A₁A₂ = A₂A₃ = … =
= A_n–2 A_n–1 = A_n–1A_n ,

проведены параллельные прямые, пересекающие сторону угла OB в точках

B₁, B₂,  …   B_{n –1},  B_n ,

соответственно, то справедливы равенства

B₁B₂ = B₂B₃ = … =
= B_n–2B_n–1 = B_n–1B_n ,

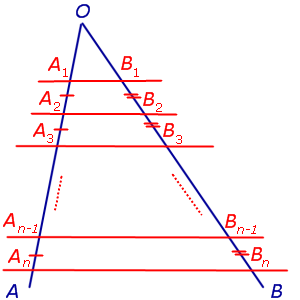
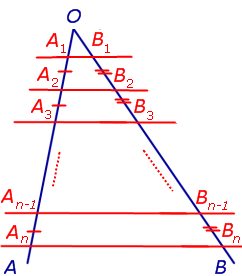
Рис.6

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

www.resolventa.ru

Теорема Фалеса и обобщенная теорема, формула

ТЕОРЕМА

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

На рисунке 1, по теореме Фалеса, если прямые , а отрезки , то .

Обобщение теоремы Фалеса (Теорема о пропорциональных отрезках)

ТЕОРЕМА

Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

На рисунке 2, согласно обобщенной теореме Фалеса, если , то

   

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Теорема Фалеса (8 класс)

Урок геометрии в 8 классе. Дата проведения: _______________

Тема: «Теорема Фалеса»

Цели:

Образовательные:

— рассмотреть теорему Фалеса и её доказательство;

— закрепить теорему Фалеса в процессе решения задач;

— совершенствовать навыки решения задач на применение знаний по теме «Трапеция»

Воспитательные:

— формирование способностей анализировать свои действия, умения внимательно слушать

Развивающие:

Развитие логического мышления, воображения, памяти, кругозора, умения рассуждать и аргументировать.

Оборудование:

доска, циркуль, линейка, треугольник, компьютер, проектор, экран, презентация.

Ход урока.

1. Сообщение темы и целей урока.

Французский писатель XIX столетия Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.

Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.

Тема сегодняшнего урока «Теорема Фалеса». Вы не только познакомитесь с этой теоремой, её доказательством, но также увидите, где можно ее применить.

Предлагаю выполнить такое задание: разделить отрезок на две, четыре, три части с помощью циркуля. (Учащиеся выходят к доске и показывают)

Перед вами стоит проблема деления отрезка на три равные части, а ученые столкнулись с проблемой деления отрезка на равные части много веков назад. И, конечно, они нашли выход из положения.

И чтобы нам сегодня справиться с возникшей задачей, докажем одну из важнейших теорем геометрии, которая называется Теорема Фалеса. Кем же был Фалес, что в его честь даже названа теорема в геометрии?

Фалес Милетский – древнегреческий философ из г. Милета (Малая Азия – территория современной Турции). Сведения о его жизни до сих пор носят противоречивый характер, но считается, что:

— именно он привез геометрию из Египта и познакомил с нею греков; его последователи и ученики основали Милетскую школу;

— именно его греки уже в древности называли «отцом философии»;

— именно он «открыл» для греков созвездие Малой Медведицы как путеводный инструмент;

— именно он ввёл календарь по египетскому образцу, в котором год состоял из 365 дней.

— одна из легенд гласит, что будучи в Египте, Фалес поразил фараона Амасиса тем, что сумел точно измерить высоту пирамиды. Как вы думаете, как он это сделал? Дождался пока длина тени от палки станет равной самой палке, значит и тень от пирамиды равна будет самой пирамиде;

— он предсказал солнечное затмение в мае 585 года до н.э.

Но одна из важнейших заслуг Фалеса в том, что ученый первый стал доказывать геометрические теоремы:

• круг делится диаметром пополам;

• в равнобедренном треугольнике углы при основании равны;

• при пересечении двух прямых образуемые ими вертикальные углы равны;

• два треугольника равны, если два угла и сторона одного из них равны двум углам и соответствующей стороне другого.

Вот такой был Фалес Милетский, в честь которого названа теорема в геометрии и эту теорему мы сегодня и рассмотрим.

2. Изучение нового материала.

Помощь в доказательстве Теоремы Фалеса нам окажет задача № 384, которую мы сейчас решим. (презентация)

Задача. Через середину М стороны АВ

треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC.

Доказательство.

1. Проведем DC║АВ.

2. Рассмотрим Δ AMN и ΔNDC.

1. AM = MВ (по условию), МВ = DC (как противоположные стороны параллелограмма BMDC), поэтому AM = DC.

2. Угол 1 равен углу 2, угол 3 равен углу 4 (как накрест лежащие углы при пересечении параллельных прямых AB и CD секущими AC и MD)

Из 1) и 2) Δ AMN = ΔNDC, значит AN = NC, что и требовалось доказать.

Какой вывод из этой задачи мы можем сделать?

Если в треугольнике через середину одной стороны провести прямую, параллельную одной из двух других сторон, то эта прямая пройдет через середину третьей стороны.

Теорема Фалеса: «Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки».

Доказательство:

Пусть на прямой l₁ отложены равные отрезки А₁А₂, А₂А₃, А₃А₄, … и через их концы проведены параллельные прямые, которые пересекают прямую l₂ в точках В₁, В₂, В₃, В₄, …. Требуется доказать, что отрезки В₁В₂, В₂В₃, В₃В₄, … равны друг другу. Докажем , например, что В₁В₂ = В₂В₃.

1. Пусть l₁║l_2. Тогда А₁А₂ = В₁В₂, А₂

   А₃ = В₂В₃, как противоположные стороны параллелограммов А₁ В₁В₂ А₂ и А₂В₂В₃А₃. Т.к. А₁А₂ = А₂А₃, то и В₁В₂ = В₂В₃.

2. Если l₁ и l₂ не параллельны, то через точку В₁ проведем прямую l║ l₁. Она пересечет прямые А₂В₂ и А₃В₃ в некоторых точках C и D. Так как А₁А₂ = А₂А₃, то по ранее доказанному В₁С = СD. Отсюда получаем В₁В₂ = В₂В₃.

Теорема доказана.

3. Закрепление пройденного материала.

Решение задач на готовых чертежах.

4. Практическая работа.

Разделить отрезок на 5 равных частей.

5. Итоги урока.

— С какой теоремой вы сегодня познакомились?

— На сколько частей вы теперь можете разделить данный отрезок?

Собрать из кусочков Теорему Фалеса.

6. Домашнее задание.

Решить задачу № 391

Выучить доказательство теоремы Фалеса

(см. запись в тетради или задачи № 384, 385)

Выполнить практическую работу:

Разделить отрезок на 11 равных частей.

infourok.ru

Конспект «Теорема Фалеса» (8 класс)

Учебный проект

«Теорема Фалеса» в 8 классе

Учитель Гармаева Ц.Ц.

Цели урока:

Образовательная: доказать теорему Фалеса, научить применять её при решении задач по математике

Развивающая: развивать у учащихся познавательный интерес к учебным дисциплинам, умение применять свои знания на практике.

Воспитательная: воспитывать внимание, аккуратность, расширять кругозор учеников.

Оборудование и материалы:

Компьютер
Проектная работа “Теорема Фалеса”.
Плакат с рисунками 1,2,3.

Приложение

Задачи учителя

Показать практическое применение теоретических знаний учащихся при решении задач по геометрии и информатике.

Выявить глубокие связи между математикой и информатикой.

Название проекта: Теорема Фалеса

Тема проекта: Теорема Фалеса

Вид проекта: учебный.

Типология проекта: практико-ориентированный, индивидуально- групповой.

Предметные области: математика.

Гипотеза: Если человек знает как разделить отрезок на равные части, возникнет ли необходимость их применять в жизни?

Ход урока:

Приветствие и вступительное слово о целях урока.

Фронтальный опрос учащихся:

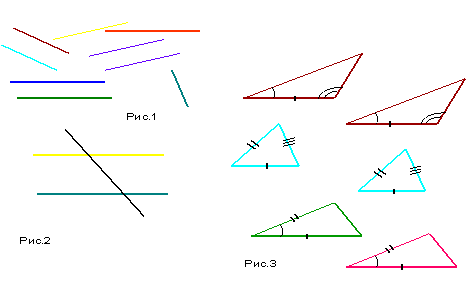
1. Какие отрезки называются равными?

2. Какие прямые называются параллельными? На рис. 1 покажите параллельные прямые.

3. Какие углы называются вертикальными, внутренними накрест лежащими? Покажите их на рис.2

4. Сформулируйте теорему о свойстве параллельных прямых, пересечённых третьей прямой.

5. Сформулируйте признаки равенства треугольников. По каким признакам равны треугольники на рис 3?

Объяснение нового материала (приложение)

Учащиеся вместе с учителем изучают и выполняют работу по новой теме с помощью просмотра презентации «Теорема Фалеса».

Сегодня мы докажем теорему, носящую имя древнегреческого учёного Фалеса, который жил в 624-547г.г. до н.э. Про древнегреческого ученого Фалеса расскажет ученица Дондокова Людмила.

 

• Великий учёный Фалес Милетский основал одну из прекраснейших наук — геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Короче: он был то же для Греции, что Ломоносов для России.

Карьеру он начинал как купец и ещё в молодости попал в Египет. В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Считается, что геометрию и астрономию в Грецию привёз он.

Фалес — математик. Он измерил по тени высоту пирамиды; установил, что окружность диаметром делится пополам, что углы при основании равнобедренного треугольника равны. Ему же принадлежит теорема, что вписанный угол, опирающийся на диаметр окружности- прямой.

Фалес доказал теорему: “Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне”.

При активном участии учащихся разбирается доказательство теоремы с последовательным показом на экране каждого этапа построения чертежа и доказательства теоремы.

Из условия теоремы Фалеса делается вывод, что вместо сторон угла можно взять любые две прямые.

Затем ученики в парах выполняют в тетрадях практическую задачу на деление отрезка длиной в 7см. на 6 равных частей.

Греческие ученые открыли множество геометрических свойств и создали стройную систему геометрических знаний. В ее основу они положили простейшие геометрические свойства, подсказанные опытом. Остальные свойства выводились из простейших с помощью рассуждений.

Все этапы решения задачи учащиеся видят на экране. Это способствует зрительному запоминанию алгоритма решения и выполнения данной практической задачи

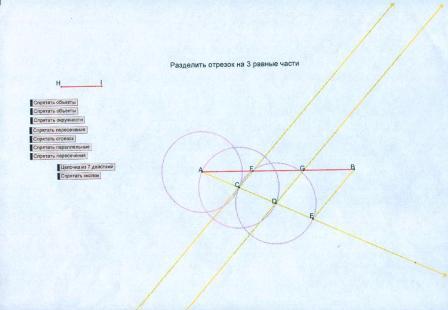
Вторую часть урока ведёт учитель информатики. Ученики вместе с учителем на компьютерах делят отрезок на три равные части.

Выполнение практического задания

Разделить данный отрезок на 3-равные части на компьютере

Используемые ИНСТРУМЕНТЫ

• стрелка;

• линейка (отрезок, луч).

Используемые КОМАНДЫ

• построения;

• правка;

Порядок работы:

1 .Построим данный отрезок АВ.

2.Проведем из т. А полупрямую а, не лежащую на прямой АВ.

3.Отложим на полупрямой а 3 равных отрезка.

Для этого используем команду ПОСТРОЕНИЯ— “окружность по центру и радиусу”; зададим произвольный радиус СО и построим на полупрямой а 3 окружности.

Они отсекают на полупрямой а равные отрезки АЕ=ЕР=РО.

4.Соединим точки В и О.

5. Проведем через точки Е и Р прямые, параллельные прямой ВО.

6. Они пересекают отрезок АВ в точках Н и I , которые делят отрезок АВ на 3 равные части; т.к. по теореме Фалеса:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Домашнее задание.

Задача: Разделить отрезок длиной 5 см. на 7 равных частей. Выучить теорему Фалеса.

Подведение итогов урока.

Общие выводы. Заключение

Осуществление данного учебного проекта позволило учащимся развить свои навыки работы не только с дополнительными источниками по математике, но и с компьютером, сформировать навыки работы в сети Интернет, а также коммуникативные способности учащихся.

Участие в осуществлении проекта позволило углубить знания по применению математики в различных областях, а также закрепить знания по указанной теме. Следует отметить, что полученные в ходе осуществления проекта знания извлекаются с конкретной целью и являются объектом заинтересованности ученика. Это способствует их глубокому усвоению.

В целом работа по проекту прошла успешно, в ней приняли участие практически все ученики 8 класса. Каждый был вовлечен в мыслительную деятельность по данной проблематике, приобрел новые знания путем самостоятельной работы. На защите своего проекта выступал каждый ученик. На заключительном этапе были апробированы практические приемы работы, проведен самоанализ в виде презентации.

Проектная деятельность учащихся способствует истинному обучению, т.к. она:

-Личностно ориентирована.

-Характеризуется возрастанием интереса и вовлеченности в работу по мере её выполнения.

-Позволяет реализовать педагогические цели на всех этапах.

-Позволяет учиться на собственном опыте, на реализации конкретного дела.

-Приносит удовлетворение ученикам, видящим продукт собственного труда.

Презентация.

Приложение

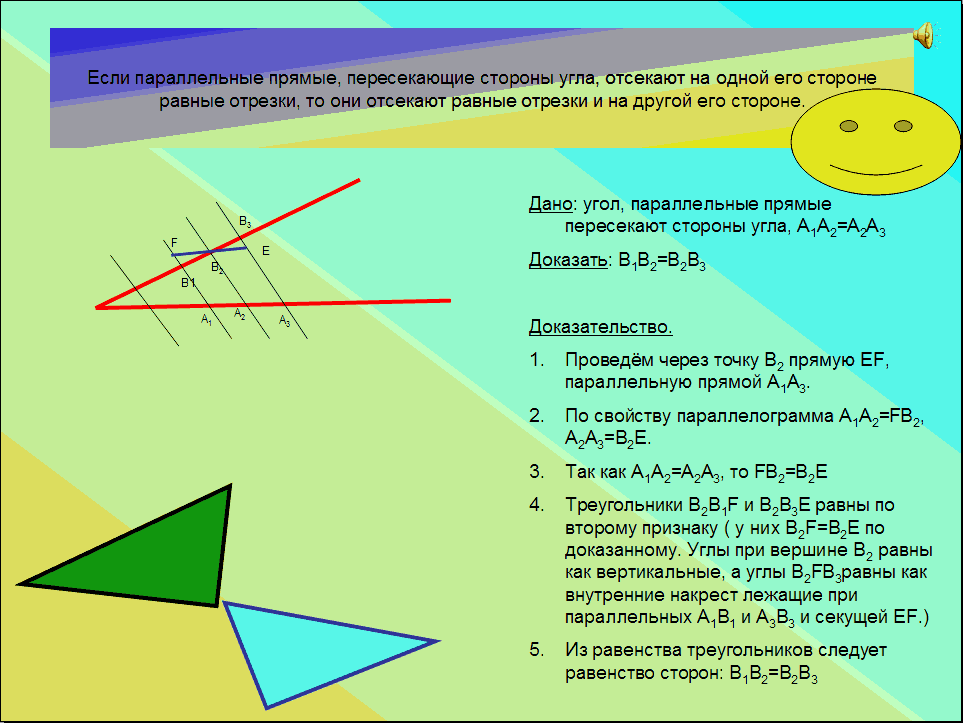
Теорема: если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Дано: угол, параллельные прямые пересекают стороны угла, А₁А₂=А₂А₃

Доказать: В₁В₂=В₂В₃

Доказательство.

1. Проведём через точку В₂ прямую ЕF, параллельную прямой А₁А₃.

2. По свойству параллелограмма А₁А₂=FВ₂, А₂А₃=В₂Е.

3. Так как А₁А₂=А₂А₃, то FВ₂=В₂Е

4. Треугольники В₂В₁F и В₂В₃Е равны по второму признаку ( у них В₂F=В₂Е по доказанному. Углы при вершине В₂ равны как вертикальные, а углы В₂FВ₃равны как внутренние накрест лежащие при параллельных А₁В₁ и А₃В₃ и секущей ЕF.)

5. Из равенства треугольников следует равенство сторон: В₁В₂=В₂В₃

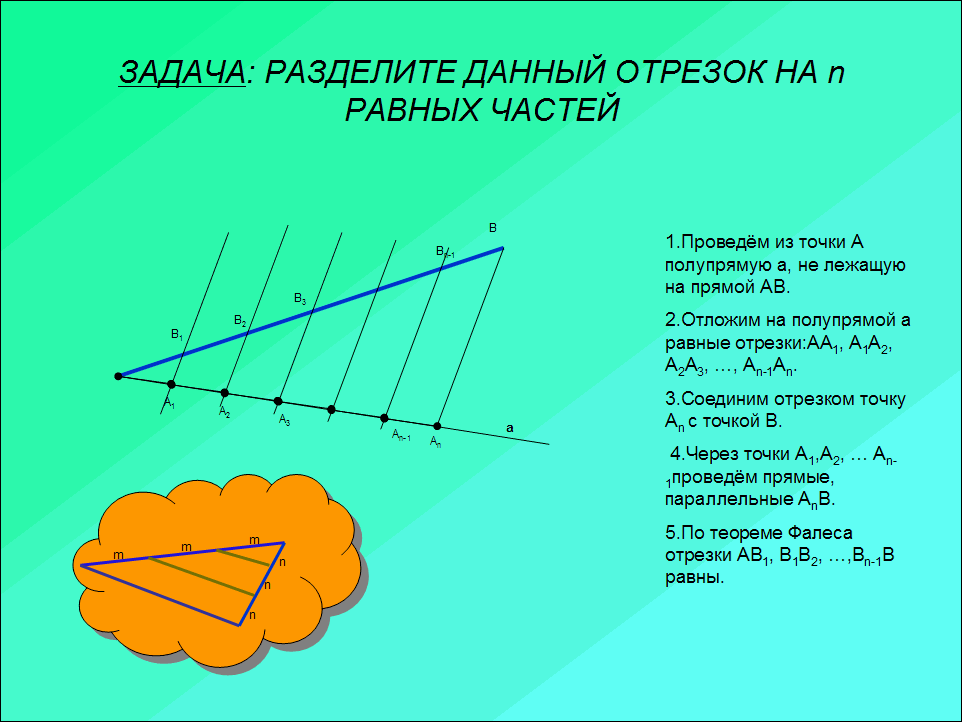
ЗАДАЧА: РАЗДЕЛИТЕ ДАННЫЙ ОТРЕЗОК НА n РАВНЫХ ЧАСТЕЙ

1.Проведём из точки А полупрямую а, не лежащую на прямой АВ.

2.Отложим на полупрямой а равные отрезки:АА₁, А₁А₂, А₂А₃, …, А_n-1А_n.

3.Соединим отрезком точку А_n с точкой В.

4.Через точки А₁,А₂, … А_n-1проведём прямые, параллельные А_nВ.

5.По теореме Фалеса отрезки АВ₁, В₁В₂, …,В_n-1В равны.

infourok.ru

math-public:obobshchenaya_teorema_falesa [Президентский ФМЛ №239]

Лемма

Пусть на сторонах $AB$ и $BC$ треугольника $ABC$ отмечены точки $M$ и $N$ соответственно. Тогда

1. Если $BM:MA=BN:NC$, то $MN\parallel AC$;

2. Если $MN\parallel AC$, то $BM:MA=BN:NC$;

Доказательство

Докажем первый пункт леммы.

Пусть $BM=a, MA=xa, BN=b, NC=xb$.

Тогда $\dfrac{BM}{BA}=\dfrac{a}{a+ax}=\dfrac{1}{1+x}=\dfrac{b}{b+bx}=\dfrac{BN}{BC}$.

Тогда треугольники $BMN$ и $ABC$ подобны по второму признаку подобия треугольников, так как $\angle B$ – общий.

Следовательно, $\angle 1=\angle 2$, а так как это соответственные углы при секущей $AB$, то $MN\parallel AC$.

Докажем второй пункт теоремы.

Так как $MN\parallel AC$, то $\angle 1=\angle 2$, а поскольку $\angle B$ – общий, то треугольники $BMN$ и $ABC$ подобны.

Тогда $\dfrac{BM}{BA}=\dfrac{BN}{BC}$, откуда $\dfrac{BM}{BM+MA}=\dfrac{1}{1+\dfrac{MA}{BM}}=\dfrac{1}{1+\dfrac{NC}{BN}}$.

Следовательно, $\dfrac{MA}{BM}=\dfrac{NC}{BN}$.

Обобщенная теорема Фалеса

Параллельные прямые отсекают на секущих пропорциональные отрезки.

Доказательство

Пусть параллельные прямые $l_1, l_2, l_3$ пересекают прямые $a$ и $b$ в точках $A_1, A_2, A_3$ и $B_1, B_2, B_3$ соответственно.

Пусть при этом $A_1A_2:A_2A_3=x$.

Докажем, что тогда $B1B_2:B_2B_3=x$.

Рассмотрим случай, когда прямые $a$ и $b$ параллельны.

Тогда $A_2A_1B_1B_2$ и $A_3A_2B_2B_3$ – параллелограммы, следовательно, $A_1A_2=B_1B_2$ и $A_2A_3=B_2B_3$, и так как $A_1A_2:A_2A_3=B_1B_2:B_2B_3=x$.

Рассмотрим случай, когда прямые $a$ и $b$ не параллельны.

Проведем через точку $B_1$ прямую $c$, параллельную прямой $a$.

Пусть прямые $l_2,l_3,l_4$ и прямая $c$ пересекаются в точках $C_2, C_3, C_4$.

По первому случаю $B_1C_2:C_2C_3=x$, кроме того $B_2C_2\parallel B_3C_3$.

Тогда по второму пункту леммы $B_1C_2:C_2C_3=B_1B_2:B_2B_3=x$.

Замечание

Следующее утверждение неверно:
пусть прямые $l_1, l_2, l_3$ пересекают прямые $a$ и $b$ в точках $A_1,A_2,A_3$ и $B_1,B_2,B_3$ соответственно. Тогда из того, что $A_1A_2:A_2A_3=B_1B_2:B_2B_3$ следует, что $l_1\parallel l_2\parallel l_3$.

math-public/obobshchenaya_teorema_falesa.txt · Последние изменения: 2016/04/13 23:35 — labreslav

wiki.sch239.net

Теорема Фалеса — Википедия

Материал из Википедии — свободной энциклопедии

Эта теорема о параллельных прямых. Смотри также Теорема Фалеса об угле, опирающемся на диаметр окружности.

Теорема Фалеса — теорема планиметрии о параллельных и секущих.

Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Формулировки

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.

Более общая формулировка, также называемая теорема о пропорциональных отрезках

Параллельные прямые отсекают на секущих пропорциональные отрезки:

A1A2B1B2=A2A3B2B3=A1A3B1B3.{\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}

Замечания

• В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.

• Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Доказательство в случае секущих

Доказательство теоремы Фалеса

Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые AA1||BB1||CC1||DD1{\displaystyle AA_{1}||BB_{1}||CC_{1}||DD_{1}} и при этом AB=CD

wiki2.red