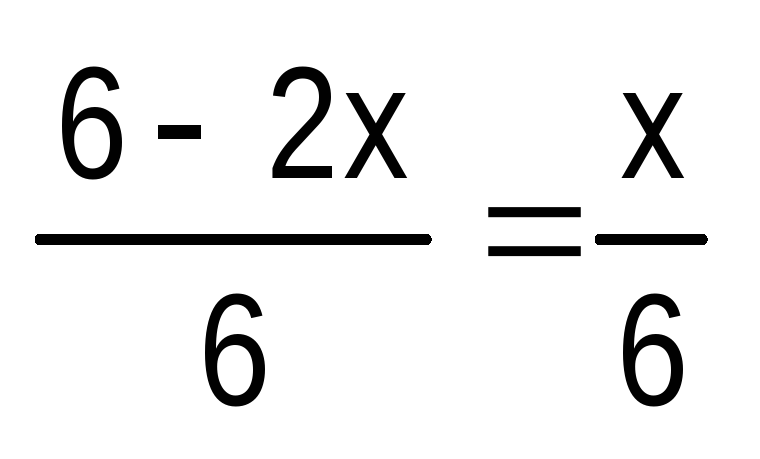Решение уравнений с одной переменной. Уравнение – это равенство.
Что такое уравнение?
Уравнение – это равенство, содержащее одну или несколько переменных, значение которых нужно найти.
Другими словами, уравнение содержит переменную – одну или несколько и знак равенства.
Цель уравнения – найти все возможные значения входящих переменных.
Решенные задачи по математике с одной переменной приводятся ниже с решением.
Давайте еще раз вспомним методы решения линейных уравнений с одной переменной.
- Прочитайте линейную задачу и обратите внимание, что указано в вопросе и что необходимо выяснить.
- Обозначить неизвестное любой переменной, например \(x\) (\(x\) – любая переменная)
- Переведите задачу на язык математики или математических высказываний.
- Перенесите выражения с неизвестными в одну часть уравнения, а числовые слагаемые в другую.
- Сформируйте линейное уравнение с одной переменной, используя условия, приведенные в задаче.
- Решите уравнение для неизвестного.
- Убедитесь, что ответ удовлетворяет условиям задачи, проверьте решение.
Разработанные задачи по математике с одной переменной.
Задача 1. Знаменатель рационального числа больше ее числителя на \(3\). Если числитель увеличивается на \(7\), а знаменатель уменьшается на \(1\), то новое число становится \(\frac{3}{2}\). Найдите исходую дробь.
Решение:
Пусть числитель рационального числа \(=\) \(x\)
Тогда знаменатель рационального числа \(=\) \(x+3\)
Когда числитель увеличивается на 7, то новый числитель \(=\) \(x+7\)
Когда знаменатель уменьшается на 1, то новый знаменатель \(x+3-1\)
Сформировано новое число \(\frac{3}{2}\)
\(\frac{x+7}{x+3-1}\)\(=\)\(\frac{3}{2}\)
\(\frac{x+7}{x+2}\)\(=\) \(\frac{3}{3}\)
\(2\) \((x+7)\) = \(3\)\((x+2)\)
\(2\)\(x+14\) = \(3\)\(\)\(x+6\)
\(3\)\(x-2\)\(x\)= \(14-6\)
\(x\)\(=\)\(8\)
Исходное число: \(\frac{x}{x+3}\) \(=\)\(\frac{8}{8+3}\)= \(\frac{8}{11}\)
Ответ:\(\frac{8}{11}\).
Задача 2. Сумма цифр двузначного числа равна \(7\). Если число, образованное смещением цифр, меньше исходного числа на \(27\), найдите исходное число.
Решение:
Пусть цифра единиц исходного числа \(x\).
Тогда десятичная цифра исходного числа будет \(7-x\)
\(10(7-x)+1x\)
\(70-10x+x=70-9x\)
\(10x+(7-x)1\)
\(10x+7-x=9x+7\)
\(9x+7=70-9x-27\)
\(9x+7=43-9x\)
\(9x+9x=43-7\)
\(18x=36\)
\(x=\frac{36}{18}\)
\(x=2\)
Поэтому \(7-x\):
\(7-2=5\)
Ответ: Исходное число \(52\).
Задача 3. Катер идет по течению реки и проходит расстояние между двумя прибрежными городами за 5 часов. Он проходит это расстояние по течению за 6 часов. Если скорость потока 3 км/ч, найдите скорость лодки в стоячей воде.
Решение:
Пусть скорость лодки в стоячей воде = х км/час.
Скорость лодки вниз по течению\(=(x+3)\) км / ч.
Время, необходимое для покрытия расстояния = \(5\) часов
Таким образом, расстояние, пройденное за \(5\) часов \(=(x+3)*5\)(S(путь) = скорость × время)
Скорость лодки по течению \(=(x-3)\)км/ч
Время, необходимое для покрытия расстояния\(=6\) часов.
Таким образом, расстояние, пройденное за \(6\) часов\(=6*(x-3)\)
Поэтому расстояние между двумя прибрежными городами фиксированное, то есть одинаковое.
\(5(x+3)=6(x-3)\)
\(5x+15=6x-18\)
\(5x-6x=-18-15\)
\(-x=-33\)
\(x=33\)
Необходимая скорость лодки \(33\) км / час.
Задача 4. Разделите \(28\) на две части таким образом, чтобы \(\frac{6}{5}\) одной части было равно \(\frac{2}{3}\) другой.
Решение:
Пусть одна часть будет \(x\)
Затем другая часть \(=28-x\)
Дается \(\frac{6}{5}\) одной части \(=\frac{2}{3}\) другой.
\(\frac{6}{5}x=\frac{2}{3}(28-x)\)
\( \frac{3x}{5}= \frac{1}{3}(28-x)\)
\(9x=5(28-x)\)
\(9x=140-5x\)
\(9x+5x=140\)
\(14x=140\)
\(x=140/14\)
\(x=10\)
Получаем: \(10\) и \(28-10\) \(=18\).
Ответ:18.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
3. Уравнения с одной переменной
Возьмем два выражения с переменной: 4х и 5х + 2. Соединив их знаком равенства, получим предложение 4х = 5х + 2. Оно содержит переменную и при подстановке значений переменной обращается в высказывание.
Например, при х = -2 предложение 4х = 5х + 2 обращается в истинное числовое равенство 4-(-2) = 5-(-2) + 2, а при х = 1 — в ложное 4-1 = 5-1+2. Поэтому предложение 4х = 5х + 2 есть высказывательная форма. Ее называют уравнением с одной переменной.
В общем виде уравнение с одной переменной можно определить так:
Определение. Пусть f(х) и q(х) — два выражения с переменной х и областью определения X. Тогда высказывательная форма вида f(х) = q(х) называется уравнением с одной переменной.
Значение переменной х из множества X, при котором уравнение обращается в истинное числовое равенство, называется корнем уравнения (или его решением). Решить уравнение — это значит найти множество его корней.
Так, корнем уравнения 4х = 5х + 2, если рассматривать его на множестве R действительных чисел, является число -2. Других корней это уравнение не имеет. Значит множество его корней есть {-2}.
Пусть на множестве действительных чисел задано уравнение (х-1)(х+2)=0. Оно имеет два корня — числа 1 и -2. Следовательно, множество корней данного уравнения таково: {-2,- 1}.
Уравнение (3х + 1) 2 = 6х + 2, заданное на множестве действительных чисел, обращается в истинное числовое равенство при всех действительных значениях переменной х: если раскрыть скобки в левой части, то получим 6х + 2 = 6
Уравнение (3х + 1)-2 = 6х + 1, заданное на множестве действительных чисел, не обращается в истинное числовое равенство ни при одном действительном значении х: после раскрытия скобок в левой части получаем, что 6х + 2 = 6х + 1, что невозможно ни при одном х. В этом случае говорят, что данное уравнение не имеет корней и что множество его корней пусто.
Чтобы решить какое-либо уравнение, его сначала преобразовывают, заменяя другим, более простым; полученное уравнение опять преобразовывают, заменяя более простым, и т.д. Этот процесс продолжают до тех пор, пока не получают уравнение, корни которого можно найти известным способом. Но чтобы эти корни были корнями заданного данного уравнения, необходимо, чтобы в процессе преобразований получились уравнения, множества корней которых совпадают. Такие уравнения называют равносильными.
Определение. Два уравнения f1(х) = q1(х) и f2(х) = q2(х) называются равносильными, если множества их корней совпадают.
Например, уравнения х2 — 9 = 0 и (2х + 6)(х — 3) = 0 равносильны так как оба имеют своими корнями числа 3 и -3. Равносильны и уравнения (3х + 1)-2 = 6х + 1 и х2 + 1 = 0, так как оба не имеют корней, т.е. множества их корней совпадают.
Определение. Замена уравнения равносильным ему уравнением называется равносильным преобразованием.
Выясним теперь, какие преобразования позволяют получать равносильные уравнения.
Теорема 1. Пусть уравнение f(х) = q(х) задано на множестве и h(х) — выражение, определенное на том же множестве. Тогда уравнение f(х) = q(х) (1) и f(х) + h(х) = q(х) + h(х) (2) равносильны.
Доказательство. Обозначим через Т1, — множество решений уравнения (1), а через Т2 — множество решений уравнения (2). Тогда уравнения (1) и (2) будут равносильны, если Т1 = Т2. Чтобы убедиться в этом, необходимо показать, что любой корень из Т1 является корнем уравнения (2) и, наоборот, любой корень из Т 2, является корнем уравнения (1).
Пусть число а — корень уравнения (1). Тогда а Т1, и при подстановке в уравнение (1) обращает его в истинное числовое равенство f(а) = q(а), а выражение h(х) обращает в числовое выражение h(а) имеющее смысл на множестве X. Прибавим к обеим частям истинного равенства f(а) = q(а) числовое выражение h(а). Получим, согласно свойствам истинных числовых равенств, истинное числовое равенство f(а) + h(а) = q(а) + h(а), которое свидетельствует о том, что число а является корнем уравнения (2).
Итак, доказано, что каждый корень уравнения (1) является корнем и уравнения (2), т.е. Т1 Т2.
Пусть теперь а — корень уравнения (2). Тогда а Т2, и при подстановке в уравнение (2) обращает его в истинное числовое равенство f(а) + h(а) = q(а) + h(а). Прибавим к обеим частям этого равенства числовое выражение — h(а). Получим истинное числовое равенство f(а) = q(а), что число а — корень уравнения (1).
Итак, доказано, что каждый корень уравнения (2) является и корнем уравнения (1), т.е. Т2 Т1.
Так как Т1 Т2 и Т2 Т1, то по определению равных множеств Т1 = Т2, а значит, уравнения (1) и (2) равносильны.
Данную теорему 1 можно сформулировать иначе: если к обеим частям уравнения с областью определения Х прибавить одно и то же выражение с переменной, определенное на том же множестве, то получим новое уравнение, равносильное данному.
Из этой теоремы вытекают следствия, которые используются при решении уравнений:
1. Если к обеим частям уравнения прибавить одно и то же число, то получим уравнение, равносильное данному.
2. Если какое-либо слагаемое (числовое выражение или выражение с переменной) перенести из одной части уравнения в другую, поменяв знак слагаемого на противоположный, то получим уравнение, равносильное данному.
Теорема 2. Пусть уравнение f(х) = q(х), задано на множестве Х и h(х) — выражение, которое определено на том же множестве и не обращается в нуль ни при каких значениях х из множества X. Тогда уравнения f(х) = q(х) и f(х) h(х) = q(х) h(х) равносильны.
Доказательство этой теоремы аналогично доказательству теоремы 1.
Теорему 2 можно сформулировать иначе: если обе части уравнения с областью определения Х умножить на одно и то же выражение, которое определено на том же множестве и не обращается на нем в нуль, то получим новое уравнение, равносильное данному.
Из этой теоремы вытекает следствие: если обе части уравнения умножить (или разделить) на одно и то же число, отличное от нуля, то получим уравнение, равносильное данному.
Решим
уравнение  ,
х
R,
и обоснуем все преобразования, которые
мы будем выполнять в процессе решения.
,
х
R,
и обоснуем все преобразования, которые
мы будем выполнять в процессе решения.
Преобразования | Обоснование преобразований |
1.
Приведем выражения, стоящие в левой
и правой частях уравнения, к общему
знаменателю: | Выполнили тождественное преобразование выражения в левой части уравнения. |
2. Отбросим общий знаменатель: 6 – 2х = х. | Умножим на 6 обе части уравнения (теорема 2), получили уравнение, равносильное данному. |
3. Выражение – 2х переносим в правую часть уравнения с противоположным знаком: 6=х+2х. | Воспользовались следствием из теоремы 1, получили уравнение, равносильное предыдущему и, значит, данному. |
4. Приводим подобные члены в правой части уравнения: 6=3х. | Выполнили тождественное преобразование выражения. |
5. Разделим обе части уравнения на 3:х=2. | Воспользовались следствием из теоремы 2, получили уравнение, равносильное предыдущему, а значит, и данному. |
Так как все преобразования, которые мы выполняли, решая данное уравнение, были равносильными, то можно утверждать, что 2 — корень этого уравнения.
Если же в процессе решения уравнения не выполняются условия теорем 1 и 2, то может произойти потеря корней или могут появиться посторонние корни. Поэтому важно, осуществляя преобразования уравнения с целью получения более простого, следить за тем, что они приводили к уравнению, равносильному данному.
Рассмотрим,
например, уравнение х(х-1)=2х, х
R.
Разделим обе части на х, получим уравнение
х-1=2, откуда х=3, т.е. данное уравнение
имеет единственный корень — число 3. Но
верно ли это? Нетрудно видеть, что если
в данное уравнение вместо переменной
х подставить 0, оно обратится в истинное
числовое равенство 0(0-1)=20.
А это означает, что 0 — корень данного
уравнения, который мы потеряли, выполняя
преобразования. Проанализируем их.
Первое, что сделали, — это разделили обе
части уравнения на х,
т. е. умножили выражение 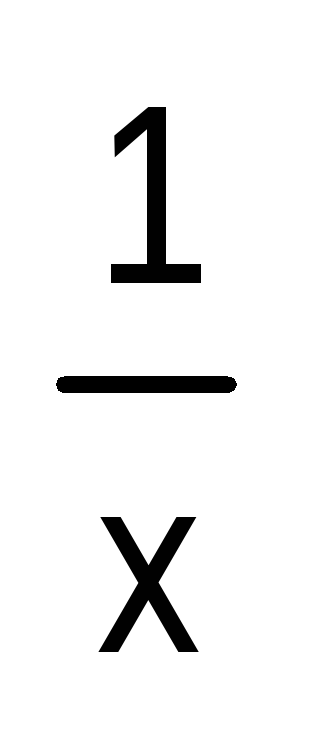 ,
но прих=0
оно не имеет смысла. Следовательно, мы
не выполнили условие теоремы 2, что и
привело к потере корня.
,
но прих=0
оно не имеет смысла. Следовательно, мы
не выполнили условие теоремы 2, что и
привело к потере корня.
Чтобы убедиться в том, что множество корней данного уравнения состоит из двух чисел 0 и 3, приведем другое его решение. Перенесем выражение 2х из правой части в левую: х(х-1)-2х= 0. Вынесем в левой части уравнения за скобки х и приведем подобные члены: х(х–3)=0. Произведение двух множителей равно нулю в том и только в том случае, когда хотя бы один из них равен нулю, поэтому х или х-3 = 0. Отсюда получаем, что корни данного уравнения – 0 и 3.
В начальном курсе математики теоретической основой решения уравнений является взаимосвязь между компонентами и результатами действий. Например, решение уравнения (х9):24=3 обосновывается следующим образом. Так как неизвестное находится в делимом, то, чтобы найти делимое, надо делитель умножить на частное: х 9 =243, или х 9=72.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель: х=72:9, или х=8, следовательно, корнем данного уравнения является число 8.
studfile.net
Рациональные уравнения, решаемые через замену. Основные типы
Рассмотрим ряд сложных рациональных уравнений, которые сводятся к решению простейших уравнений при помощи метода замены переменной.
Задача 1.
Решить уравнение: 
Решение: + показать Замечаем, что уравнение можно переписать следующим образом: Напрашивается замена: Тогда имеем: Тогда обратная замена: Ответ: Можно было бы оформить решение и так, чуть короче: Ответ: 














Задача 2.
Решить уравнение: 
Решение: + показать Перепишем уравнение следующим образом: Тогда напрашивается замена: Имеем: Обратная замена: Ответ: 









Задача 3.
Решить уравнение: 
Решение: + показать
Задача 4.
Решить уравнение:  .
.
Решение: + показать Замена переменной: Имеем: Домножаем обе части равенства на Обратная замена: Первое уравнение совокупности не имеет решений. Решаем второе уравнение: Ответ:  , тогда
, тогда 











Задача 5.
Решить уравнение: 
Решение: + показать Замена: Обратная замена: Ответ: 









Задача 6.
Решить уравнение: 
Решение: + показать Разделим обе части уравнения на Напрашивается замена: Обратная замена: Данная совокупность равносильна следующему уравнению (только второе уравнение имеет корни): Ответ:  (заметим,
(заметим,  ):
):













Задача 7.
Решить уравнение: 
Решение: + показать Перемножим первую скобку и последнюю, вторую и третью: Напрашивается замена: Обратная замена: Совокупность равносильна уравнению: Откуда Ответ: 










Задача 8.
Решить уравнение: 
Решение: + показать Заметим, Замена: Домножаем обе части уравнения на Обратная замена: Совокупность равносильна уравнению: Ответ:  не является корнем уравнения, поэтому разделим числитель и знаменатель каждой дроби из левой части уравнения на
не является корнем уравнения, поэтому разделим числитель и знаменатель каждой дроби из левой части уравнения на  :
:














Задача 9.
Решить уравнение: 
Решение: + показать Перепишем уравнение следующим образом: Замечаем, что первые четыре слагаемые можно свернуть в куб разности: Ответ: 






Задача 10.
Решить уравнение: 
Решение: + показать Прибавим к обеим частям равенства Тогда левую часть уравнения можно свернуть в квадрат разности: Замена: Обратная замена: Откуда Ответ: 















Задача 11.
Решить уравнение: 
Решение: + показать Замена: Пусть Тогда Откуда Обратная замена: Ответ:  .
.








Задача 12.
Решить уравнение: 
Решение: + показать Замена: Обратная замена: Откуда Ответ: 

















Предлагаю задания для самостоятельной работы:
1. 
Ответ: + показать

2. 
Ответ: + показать
-1; 3
3. 
Ответ: + показать

4. 
Ответ: + показать
-3; 1
5. 
Ответ: + показать
нет решений
6. 
Ответ: + показать

7. 
Ответ: + показать

8. 
Ответ: + показать

9. 
Ответ: + показать

10. 
Ответ: + показать
-3
11. 
Ответ: + показать

egemaximum.ru