Формулировка и доказательство теоремы Пифагора. Видеоурок. Геометрия 8 Класс

Мы знаем, что если у двух треугольников равны две стороны и углы между ними тоже равны, то такие треугольники обязательно равны. Это один из признаков равенства треугольников.

Если один из углов треугольника прямой и во втором треугольнике тоже один из углов прямой, то эти углы равны друг другу. И если стороны, заключающие прямые углы (а стороны, которые заключают прямые углы, называются катетами), равны, то равны и сами прямоугольные треугольники. Но это, в свою очередь, означает, что если мы знаем два катета прямоугольного треугольника, то гипотенуза определена одним единственным образом, который мы и рассмотрим.

Еще в Древнем Египте было известно, что если взять прямоугольный треугольник, катеты которого равны 3 и 4 единицы, то гипотенуза обязательно будет равна 5 единицам.

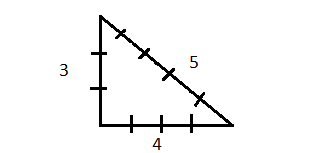
Рис. 1. Египетский треугольник

В Древнем Египте часто пользовались таким треугольником. Он называется египетским треугольником (рис. 1). Это самый маленький из прямоугольных треугольников с целыми сторонами. Вы можете сложить прямоугольные треугольники с помощью спичек и увидеть, что если хотя бы какой-нибудь из катетов будет меньшим числом, то гипотенуза обязательно не будет целым числом.

Мы готовы сформулировать теорему Пифагора и записать формулу, которая позволит вычислить гипотенузу прямоугольного треугольника, если известны катеты этого прямоугольного треугольника:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

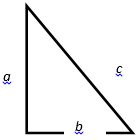
Рис. 2. Прямоугольный треугольник

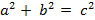 – эта формула и называется теоремой Пифагора (рис. 2).

Теорема Пифагора формула

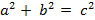—  в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Докажем теорему Пифагора.

Задача № 1. Дано: прямоугольный треугольник АВС, в котором угол С – прямой (90 °). Катет ВС = a, катет АС = b, гипотенуза АВ = с (рис. 3).

Доказать: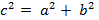

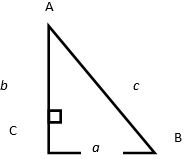
Рис. 3. Иллюстрация к теореме Пифагора

Решение.

В формуле, которую нам необходимо доказать, фигурируют квадраты трех величин: квадраты с, а и

b. В геометрии мы сталкиваемся с квадратами длин отрезков, когда считаем площади фигур. Но и, наверное, самая простая фигура, площадь которого можем посчитать – квадрат. Соответсвенно, первая мысль – достроить эту картинку до квадратов. Достроим треугольник АВС до квадрата со стороной а+b.

Для этого продолжим катет АС на длину катета ВС (+ а), а ВС на длину катета АС (+ b) (рис. 4).

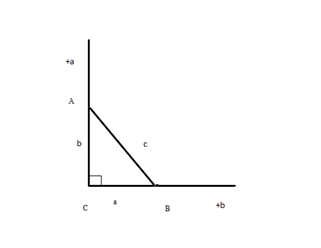
Рис. 4. Иллюстрация к теореме

Достроим получившуюся картинку до прямоугольника (рис. 5).

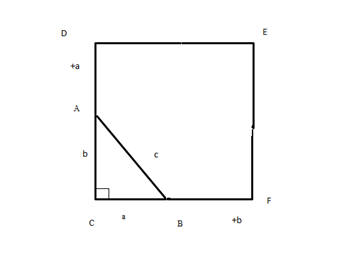
Рис. 5. Иллюстрация к теореме

У этого прямоугольника смежные стоороны равны (а+b). Значит, этот прямоугольник обязательно является квадратом. Обозначим получившиеся точки буквами. Получим квадрат СDEF.

Все стороны этого квадарта равны (а + b). Соответственно, стороны DE и EF тоже можем разделить на отрезки а и b. Обозначим эти точки буквами G и H. Соединим точку А с точкой G, точку G с точкой Н, точку Н с точкой В (рис. 6).

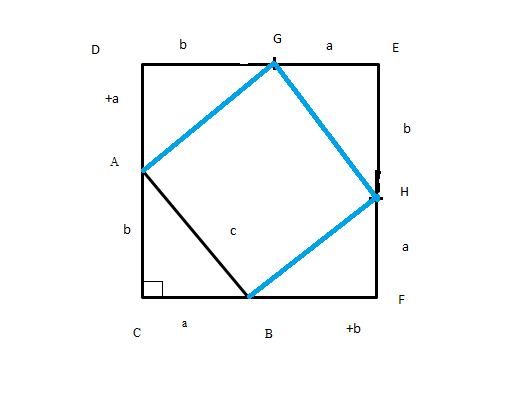
Рис. 6. Иллюстрация к теореме

Квадрат СDEF оказался разрезанным на 5 фигур: 4 треугольника по углам и 1 четырехугольник в центре. Если этот четырехугольник окажется квадратом, то это будет удобно для нас. Но это сначала нужно доказать.

Выясним, что мы знаем про получившуюся фигуру. Все 4 треугольника обязательно являются прямоугольными,потому что каждый из них содержит один из углов квадрата (Ð С = Ð D = Ð Е = Ð F = 90°). Катеты в этих треугольниках равны а и b. Значит, все эти треугольники равны друг другу (по двум сторонам и углу между ними). А если все эти треугольники равны друг другу, то равны все их соответсвенные элементы. Например, все гипотенузы у них обязательно равны с (рис. 7).

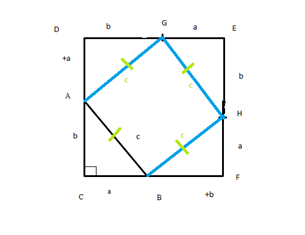
Рис. 7. Иллюстрация к теореме

Значит, четырехугольник АGНВ – ромб. Четырехугольник, у которого все стороны равны, называется ромб. Мы доказали, что все стороны равны, АG = GН = НВ = ВА = с. АGНВ – ромб.

Гипотенуза не единственное, что равно у наших треугольников. Еще у них равны все острые углы. Отметим это на картинке. Во-первых, равны Ð САВ = Ð DGA = Ð EHG = Ð FBH. Зеленым цветом обозначим эти углы, величиной α. И такие углы тоже равны: Ð СВА = Ð DAG = Ð EGH = Ð FHB. Красным цветом обозначим углы величиной b (рис. 8).

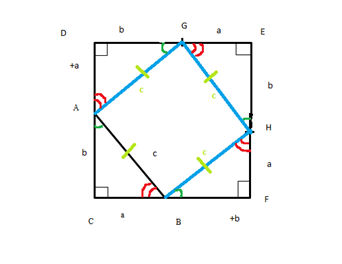
Рис. 8. Иллюстрация к теореме

На нашей картинке отмечено очень много углов, но не все. Остался, например, не отмеченным Ð GАВ. Вычислим его.

Эти три угла вместе, Ð DAG, ÐGAB, Ð CAB, составляют развернутый угол. Соответственно:

Ð GАВ = 180° — Ð CAB — Ð DAG = 180 ° — α — b.

Преобразуем эту формулу следующим образом:

Ð GАВ = 180° — (α + b).

У нас получилась сумма (α + b). Что такое сумма (α + b)? Это сумма острых углов прямоугольного треугольника. В прямоугольном треугольнике сумма острых углов равна 90°. Поэтому получается:

Ð GАВ = 180° — (α + b) = 180° — 90° = 90°. То есть Ð GАВ – прямой. А значит наш ромб АGНВ является квадратом. Если в ромбе один из углов прямой, то этот ромб обязательно квадрат.

Мы получили: большой квадрат СDEF, квадрат меньше АGНВ. Можно начинать записывать площади.

С одной стороны, СDEF – квадрат и его площадь можно посчитать как квадрат стороны:

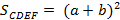
С другой стороны, этот квадрат состоит из 5 фигур: 4 треугольников и квадрата в центре. Площадь квадрата в центре равна с², а четыре треугольника равны друг другу и площадь каждого из них – половина произведения катетов.

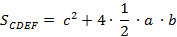
Площадь четырехугольника СDEF не зависит от того, каким образом мы с вами ее считаем. Она всегда одна и та же. Соответственно, мы можем приравнять наши равенства, но сначала их надо преобразовать.

В первом равенстве раскрываем квадрат суммы:

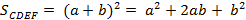
Во втором случае:

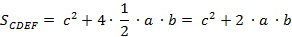
Первое выражение равно второму.

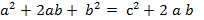
И там, и там есть 2аb. От них легко отказаться – сократим их. И получим: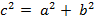

То есть в нашем прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Что и требовалось доказать.

Это доказательство – не единственное доказательство теоремы Пифагора. У нее очень много доказательств. Теорема Пифагора занесена даже в Книгу рекордов Гиннеса за счет того, что у нее так много доказательств. Интересным является тот факт, что многие из них почти не требуют алгебры. Вот, например, в Древней Индии использовали такой способ доказательства.

Рисовали 2 одинаковых квадрата. Один такой, как у нас уже был нарисован (№1). И второй тоже со стороной (а + b). Такой же квадрат, но разрезали его немного по-другому (№2) (рис. 9).

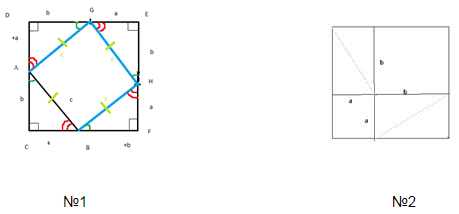
Рис. 9. Иллюстрация к теореме

Сначала его разрезали на 4 фигуры: 2 квадрата. Один со стороной а, второй со стороной b. Соответственно, по углам оставались прямоугольники со сторонами а и b. А дальше каждый из этих прямоугольников со сторонами а и b разрезали пополам на 2 треугольника.

Теперь получается 2 одинаковых квадрата, по-разному разрезанных. И в этих одинаковых квадратах есть одинаковые фигуры. Даже в одном и том же положении. Их равенство выделено одинаковыми цветами на рисунках (рис. 10).

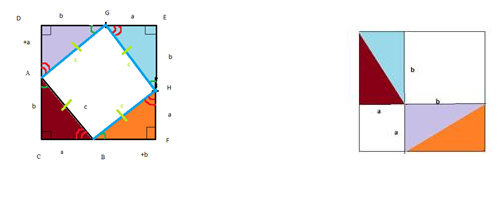
Рис. 10. Иллюстрация к теореме

Если у каждой картинке вырезать эти треугольники, то на одной картинке остается квадрат со стороной с и площадью с²; а на другой картинке остается 2 квадрата со сторонами а и b, сумма площадей этих квадратов – это а² + b².

Такое доказательство использовали в Древней Индии.

 

Также есть другое доказательство, благодаря которому стало известно про «пифагоровы штаны, которые во все стороны равны». Посмотрите на картинку (рис. 11).

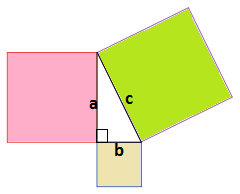
Рис. 11. Иллюстрация к теореме

На катетах прямоугольного треугольника построены квадраты. На гипотенузе тоже построен квадрат. Его вырезали, и осталось пустое место (для удобства окрашен в зеленый цвет). Квадраты, которые образованы на катетах, разрезаны на 5 кусочков. Попробуем сложить из этих кусочков квадрат на гипотенузе. (Из двух маленьких квадратов построили большой на гипотенузе. Каждый кусочек со своей окраской показывает расположение в большом квадрате.)

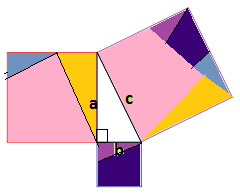
Рис. 12. Иллюстрация к теореме

Мы видим

interneturok.ru

Проект по математике «Интересные доказательства теоремы Пифагора» 8 класс

Проект на тему:

Интересные доказательства теоремы Пифагора

Выполнил:

Ученик 8 класса

МБОУ «Соболевская СОШ»

Доброслов Даниил

Руководитель: учитель математики

Вагапова Ангелина

Тимуровна

2017 год

Математика – увлекательная наука! В 8 классе я познакомился с интересной теоремой – теоремой Пифагора – «Квадрат, построенный на гипотенузе прямоугольного треугольника равновелик сумме квадратов построенных на катетах» или в привычной для нас школьной формулировке: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов . Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника

Данная тема меня заинтересовала. И я решил узнать больше о б авторе, теореме и доказательстве, а оказалось, что их несколько сотен!

Актуальность темы: Несмотря на то, что теорема называется «теоремой Пифагора», сам автор ее не открывал. Особенности прямоугольного треугольника изучались с древнейших времен. Задачи, связанные с прямоугольным треугольником, встречаются в египетских, древнекитайских и древнеиндийских сочинениях. Возможно, что Пифагор нашел первым доказательство теоремы. А о том, что теорема Пифагора очень важна, говорит существование около 400 различных доказательств. В этом не может сравниться с ней ни одна другая теорема! А так же о ее важности можно судить по тому, что из нее выводится много теорем в геометрии, а также она является основой для решения большого количества задач. Великая теорема Пифагора имеет огромное практическое применение. Без теоремы Пифагора нам обойтись при строительстве крыш домов, громоотводов, в астрономии, мобильной связи и многом другом.

Цель моего исследования: Изложить теорему Пифагора, представить разные способы её доказательства.

Задачи:

— узнать некоторые исторические факты;

— познакомиться с классическими и другими интересными доказательствами;

— сделать выводы о значимости теоремы.

1. Биография Пифагора

Великий древнегреческий философ и математик, создатель религиозно-философской школы пифагорейцев Пифагор Самосский родился около 570 г. до н.э. на острове Самосе. Его имя связано с названием теоремы.

Конечно, говорить о достоверности биографических фактов мы не можем, и вот то, что нам известно.

Родителями Пифагора были Мнесарх и Партенида с Самоса. Мнесарх был камнерезом. Партенида, происходила из знатного рода Анкея, основателя греческой колонии на Самосе.

Учителями юного Пифагора были старцы Гермодамант и Ферекид Сиросский. Целые дни проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым — Фалесом. Фалес советует ему отправиться за знаниями в Египет, что Пифагор и сделал. В Египте он жил у жрецов, овладел всею их мудростью, выучил египетский язык с его тремя азбуками – письменной, священной и символической. Научившись всему, что дали ему жрецы, Пифагор, решает убежать от них на родину в Элладу. Однако, проделав часть пути, Пифагор попадает в плен к царю Вавилона — Киру. В Вавилоне Пифагор живет с халдеями, но это не мешает ему изучать науку — Вавилонская математика была, бесспорно, более развитой, чем египетская, и Пифагору было чему поучиться. Но в 530 г. до н.э. Кир двинулся в поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину. А на Самосе в то время царствовал тиран Поликрат. Конечно же, Пифагора не устраивала жизнь придворного полу раба, и он удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена («пифагорейцы»). Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принципов достойны подражания и сейчас.

Диоген, ссылаясь на Гераклида (IV в. до н. э.), писал, что Пифагор мирно скончался в возрасте 80 лет в 490г. до н. э.

2. В своем проекте хочу изучить и представить некоторые интересные и известные доказательства теоремы Пифагора:

Доказательство 1.

Самое простое, на мой взгляд, доказательство – это доказательство, в котором треугольник не только треугольный, но еще и равнобедренный.

Утверждение: «Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах».

Дан равнобедренный прямоугольный треугольник АВС, на гипотенузе построен квадрат равный 4 таким треугольникам, а на катетах по квадрату, содержащих по 2 таких треугольника.

Иллюстрация:

Существует множество карикатур и шуток: «Пифагоровы штаны во все стороны равны».

На основе этого доказательства есть интересный эксперимент: переливая жидкость можно доказать равенство объемов, а затем и равенство площадей.

Доказательство 2.

Вариант древнеиндийского доказательства математика Бхаскари.

Постройте прямоугольный треугольник со сторонами a, b и c (рис.1). Затем постройте два квадрата со сторонами, равными сумме длин двух катетов (a+b). В каждом из квадратов выполните построения, как на рисунках 2 и 3.

В первом квадрате постройте четыре таких же треугольника, как на рисунке 1. В результате получаться два квадрата: один со стороной a, второй со стороной b.

Во втором квадрате четыре построенных аналогичных треугольника образуют квадрат со стороной, равной гипотенузе c.

Сумма площадей построенных квадратов на рис.2 равна площади построенного нами квадрата со стороной с на рис.3. Это легко проверить, высчитав площади квадратов на рис. 2 по формуле. А площадь вписанного квадрата на рисунке 3. путем вычитания площадей четырех равных между собой вписанных в квадрат прямоугольных треугольников из площади большого квадрата со стороной (a+b).

Записав все это, имеем: a2+b2=(a+b)2 – 4*1/2*a*b. Раскройте скобки, проведите все необходимые алгебраические вычисления и получите, что a2+b2= a2+b2. При этом площадь вписанного на рис.3. квадрата можно вычислить и по традиционной формуле S=c2. Т.е. a2+b2=c2 – теорема доказана.

Доказательство 3.

Древнеиндийское доказательство построено в трактате «Венец знания» («Сиддханта широмани»).

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Достроим прямоугольный треугольник до квадрата. Обозначим площадь квадрата S. Квадрат состоит из четырехугольника и четырех равных треугольников. Треугольники равны по двум катетам. Значит, их площади равны. Площадь квадрата равна сумме площади внутреннего квадрата и площадей все треугольников: (a-b)2+4*1\2*a*b, c2=(a-b)2+4*1\2*a*b. После вычислений получим теорему Пифагора, ч.т.д.

Доказательство 4.

Кресло невесты или стул невесты. Необходимо построить внутренний квадрат со стороной с. Мы это уже умеем делать. Если отрезать два зеленых прямоугольных треугольника, приложить их к противоположным сторонам квадрата, чтобы гипотенузы совпадали с гипотенузами сиреневых, получится стул – «стул невесты». Стул невесты образуют два квадрата: со стороной b и стороной а. приходим к выводу, что c2=a2+b2,ч.т.д.

Рис1. Рис.2

Доказательство 5.

Доказательство Хоукинса.

Приведем еще одно доказательство, которое имеет вычислительный характер, однако сильно отличается от всех предыдущих. Оно опубликовано англичанином Хоукинсом в 1909 году; было ли оно известно до этого — трудно сказать.

Прямоугольный треугольник ABC с прямым углом C повернем на 90° так, чтобы он занял положение A’CB’. Продолжим гипотенузу A’В’ за точку A’ до пересечения с линией АВ в точке D. Отрезок В’D будет высотой треугольника В’АВ. Рассмотрим теперь заштрихованный четырехугольник A’АВ’В . Его можно разложить на два равнобедренных треугольника САA’ и СВВ’ (или на два треугольника A’В’А и A’В’В).

SCAA’=b²/2 

SCBB’=a²/2  

SA’AB’B=(a²+b²)/2

Треугольники A’В’А и A’В’В имеют общее основание с и высоты DA и DB, поэтому :

                     SA’AB’B=c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2

Сравнивая два полученных выражения для площади, получим:

a²+b²=c²

Теорема доказана.

Доказательство 6.

«Метод Гарфилда».

или

Еще один геометрический способ. Продолжим один из катетов на величину другого и опустим перпендикуляр, величина которого равна первому катету. Соединим две вершины, получим трапецию. Ясно, что площадь трапеции состоит из площади трех треугольников: 2*1/2(AB*AC)+1/2ВС²

Или по формуле площади трапеции S_ABED=(DE+AB)*1/2AD.

Приравняем, раскроим скобки, получим известную нам формулу ВС²=АС²+АВ²

Выводы:

Теорема Пифагора привлекает к себе внимание не просто на протяжении столетий, а на протяжении тысячелетий. И в этом ее уникальность.

Невозможно привести все или даже только самые красивые доказательства.

Но и доказательства, рассмотренные в проекте, свидетельствуют об огромном интересе к теореме Пифагора.

Существует огромное множество и других интересных доказательств: доказательство Хоукинса, Леонардо да Винчи, доказательство с помощью комплексных чисел, векторов, дифференциальных уравнений и стереометрии, но я с этим еще не знаком, а значит, у меня есть возможность вести проект на эту тему до окончания школы, а. возможно, и дальше…

Несмотря на то, что суть теоремы проста, все же остается возможность для новых исследований.

Использованная литература:

1.Геометрия. 7 – 9 классы: учеб. для общеобразоват. Организаций с прил. на электрон. Носителе / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. — 3-е изд. – М.: Просвещение, 2014. – 383 с.

2.Геометрические миниатюры. З.А. Скопец, изд.: Просвещение, 1990г. – 224с.

3. Мир математики, Том 5, Секта чисел, Теорема Пифагора, Альсина К., М.: Де Агостини, 2014. — 160с.

4.http://www.platonizm.ru/content/porfiriy-o-zhizni-pifagora //ПОРФИРИЙ. ЖИЗНЬ ПИФАГОРА.

5. https://www.livelib.ru/tag/ Пифагор – популярные книги.

infourok.ru

Проект по математике на тему «Различные способы доказательства Теоремы Пифагора» (8 класс)

МБОУ — СОШ «Рязанские сады»

Проект

«Различные способы доказательства теоремы Пифагора»

Выполнила ученица 8 класса

МБОУ- СОШ «Рязанские сады»

Ермилова Екатерина

Учитель I квалификационной категории: Ярославцева Л.Е.

2013-2014

СОДЕРЖАНИЕ.

Обоснование……………………………………………………………3

Цели……………………………………………………………………..3

Задачи……………………………………………………………………3

Введение………………………………………………………………..4

История…………………………………………………………………5

Теорема Пифагора……………………………………………………..6

Анализ доказательств………………………………………………….8

Ученические шаржи………………………………………………….16

Практическое применение……………………………………………17

Заключение……………………………………………………………20

Используемые источники и литература…………………………….20

ОБОСНОВАНИЕ:

Теорема Пифагора является одной из важнейших теорем курса геометрии 8 класса. Она возникла из потребности человека выполнять измерения на местности, применяется при доказательстве других теорем, решении многих задач. Теорема известна с древнейших времен. На уроке мы рассмотрели один из способов ее доказательства. От учителя я узнала, что существует более 300 способов доказательства. Я заинтересовалась и решила найти уже известные способы доказательства этой уникальной теоремы.

ЦЕЛИ ПРОЕКТА:

1. Расширить свои знания по истории математики.

2. Узнать больше информации, легенд, мифов о Пифагоре и о его теореме.

3. Познакомиться с различными способами доказательства теоремы Пифагора.

4. Найти ответ на вопрос: «В чем уникальность теоремы Пифагора?»

5. Овладеть навыками применения ИКТ.

ЗАДАЧИ ПРОЕКТА:

1. Найти исторический материал из биографии Пифагора и о его теореме.

2. Выступить с докладом о Пифагоре перед одноклассниками на кружке «Математический калейдоскоп».

3. Найти и разобрать различные способы доказательства теоремы Пифагора.

4. Рассмотреть применение теоремы Пифагора при решении задач из различных разделов геометрии.

5. Создать презентацию своего проекта.

ВВЕДЕНИЕ.

«Геометрия владеет двумя сокровищами: одно из них — это теорема Пифагора…»

Иоганн Кеплер.

Теорема Пифагора издавна широко применялась в разных областях науки, техники и практической жизни. О ней писали свои произведения великие писатели всего мира. О ней складывалось множество легенд и мифов. Вокруг теоремы ходит много споров: Кто же ее открыл?

Актуальность темы:

1. Мне стала интересна история теоремы, способы доказательства. Я решила найти информацию о теореме и ее открытии.

2. В школьном курсе я нашла 3 способаее доказательства. А их известно более 300, как я узнала от учителя. Я решила найти и другие способы.

Объект исследования: теорема Пифагора.

Предмет исследования: способы доказательства теоремы Пифагора.

Методы исследования:

1. Работа с учебной и научно-популярной литературой, ресурсами интернета.

2. Наблюдение, сравнение, анализ.

3. Решение задач.

Ожидаемые результаты: В ходе изучения данной работы, я реально смогу оценить свой интеллектуальный потенциал, обогатить свои знания историческими сведениями, увлечься математикой, применить полученные знания в дальнейшей учебе, создать проектный продукт по исследуемой теме в форме компьютерной презентации. Изучение данного вопроса позволит мне укрепить свои знания по данной теме.

Считаю свою работу перспективной, так как в дальнейшем этим материалом могут воспользоваться и ученики для повышения математической грамотности,  и учителя на факультативных занятиях.

ИСТОРИЯ.

Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя матери Парфениса. По многим античным свидетельствам, родившийся мальчик был сказочно красив. Мнесарх, как всякий отец, мечтал, что сын будет продолжать его дело — ремесло золотых дел мастера. Жизнь рассудила иначе. Будущий великий математик и философ уже в детстве обнаружил большие способности к наукам. У своего первого учителя Гермодамаса Пифагор получает знания основ музыки и живописи. Для упражнения памяти Гермодамас заставлял его учить песни из «Одиссеи» и «Илиады». Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. Вскоре, неугомонному воображению юного Пифагора стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым — Фалесом. Затем отправляется в путешествие и попадает в плен к вавилонскому царю Киру. В 530 г. до н.э. Кир двинулся в поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину.

А на Самосе в то время царствовал тиран Поликрат. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена («пифагорейцы»), члены которого обязывались вести такназываемый пифагорейский образ жизни.

ИСТОРИЯ ТЕОРЕМЫ.

Измеряй свои желания,

взвешивай свои мысли,

исчисляй свои слова.

Пифагор

Древний Китай:

В древнекитайской книге Чу-пей говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:

«Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4″.

В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.

Древний Вавилон:

Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, то есть к 2000 году до н. э., приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере, в некоторых случаях.

Древняя Индия:

Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.

Древний Египет:

Кантор (крупнейший немецкий историк математики) считает, что равенство: 3² + 4² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I. По мнению Кантора гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12м и привяжем к ней по цветной полоске на расстоянии 3м от одного конца и 4м от другого. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра.

Существует легенда, что когда Пифагор Самосский доказал свою теорему, он отблагодарил богов, принеся в жертву 100 быков. Также о гипнотических способностях учёного ходили легенды: будто он одним своим взглядом мог менять направление полёта птиц. А ещё рассказывали, что этого удивительного человека одновременно видели в разных городах, между которыми было несколько дней пути. И что ему якобы принадлежало «колесо фортуны», вращая которое, он не только предсказывал будущее, но и вмешивался, если это было необходимо, в ход событий.

ФОРМУЛИРОВКИ ТЕОРЕМЫ.

Геометрическая формулировка:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка:

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Формулировка, известная с древности(около 1400 г. до н.э.), в переводе читается так:

» площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу».

СПОСОБЫ ДОКАЗАТЕЛЬСТВА.

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы, она занесена в книгу рекордов Гиннеса. Самые известные методы доказательства: методом площадей, аксиоматические и экзотические доказательства.

Существует несколько основных приемов доказательства теоремы Пифагора:

1. Алгебраический метод.

2. Метод площадей.

3. Подобие треугольников.

4. Тригонометрический.

1. 1. Доказательство методом площадей (школьный метод):

Достроим ΔАВС до квадрата со сторонойа+b

S = 4S_Δ+ S□

S = (a+b)²

S_Δ= ab

∟1 + ∟2 = 90° (по свойству прямоугольного треугольника)

∟1 + ∟2 + ∟3 = 180° (развернутый угол)

∟3 = 90°

Аналогично можно доказать, что все остальные углы ромба равны 90°. Таким образом, внутри — квадрат со стороной с.

(а+b)² = 4 ·аb + с²

а²+ 2аb +b² = 2аb + с²

а²+ b² = с²

1.2Доказательство Басхари «Смотри!»:

Доказательство великого индийского математика Басхари сопровождало лишь одно слово: СМОТРИ!

Внутри – квадрат со сторонойb–a.

(b — a)² = c² — 4 · аb

b² — 2ab + a² = c² – 2ab

b² + a² = c²

1. 1. Доказательство через равнобедренные треугольники:

Рассмотрим прямоугольный равнобедренный треугольник.На его сторонах строят квадраты.

Рассмотрим прямоугольный равнобедренный треугольник. На его сторонах строят квадраты.

Квадраты, построенные на катетах исходного треугольника, содержит по 2 таких треугольника.

Квадрат, построенный на гипотенузе исходного треугольника, содержит четыре таких треугольника.

Получим, что квадрат, построенный на гипотенузе, равен сумме квадратов, построенных на катетах: с² = a² + b²

2.2 Доказательство древних индусов:

На рисунке изображено два разных квадрата со сторонами а+b. Каждый из квадратов разбит на части, состоящие из прямоугольных треугольников и квадратов. Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного треугольника с катетами a и b, то останутся равные площади, т. е. с ²= а²+ b²

2.3 Доказательство методом вычитания:

Знакомый чертеж Пифагора заключим в прямоугольную рамку, направление сторон которой совпадает с направлением катетов прямоугольника. Продолжим некоторые из отрезков фигуры так, как указано на рисунке, при этом прямоугольник разделится на несколько треугольников, прямоугольников и квадратов. Выбросим сначала несколько частей так, чтобы остался лишь квадрат, построенный на гипотенузе. Эти части следующие части:

1. Треугольники 1, 2, 3, 4.

2. Прямоугольник 5.

3. Прямоугольник 6 и квадрат 8.

4. Прямоугольник 7 и квадрат 9.

Затем выбросим из прямоугольника части так, чтобы остались только квадраты, построенные на катетах. Эти части будут:

1. Прямоугольники 6 и 7.

2. Прямоугольник 5.

3. Прямоугольник 1.

4. Прямоугольник 2.

Из рисунков ясно, что:

1. Прямоугольник 5 равен самому себе.

2. Треугольники 1, 2, 3, 4 равны прямоугольникам 6 и 7.

3. Прямоугольник 6 и квадрат 8 (вместе) равновелики прямоугольнику 1.

4. Прямоугольник 7 и квадрат 9 (вместе) равновелики прямоугольнику 2

2.4 Доказательство Леонардо да Винчи:

Рассмотрим чертеж, как видно из симметрии, отрезок CI рассекает квадрат ABHJ на две одинаковые части(т.к. ΔABC = ΔIHJ по построению). Пользуясь поворотами вокруг точки А на 90° мы устраиваем равенство фигур CAJI и DABG. Площадь закрашенной фигуры равна сумме половин площадей маленьких квадратов(построенных на катетах) и площади исходного треугольника ABC. Так же она равна половине площади большого квадрата(построенного на гипотенузе) плюс площади исходного треугольника ABC. Таким образом,

половина суммы меньших квадратов равна половине площади большого квадрата, а следовательно сумма площадей квадратов, построенных на катетах, равна площади квадратов, построенных на гипотенузе, т.е.

+ + S_∆ = + S_∆

+ =

+ b² = c²

2.5 Доказательство Эйнштейна:

Точки Е, С, F лежат на одной прямой, это следует из нескольких несложных расчетов градусной меры угла ECF(он развернутый). Проведем CDEF. Продолжим вверх левую и правую стороны квадрата, построенного на гипотенузе, до пересечения с EF. Продолжим сторону ЕА до пересечения с CD. Соответственно равны треугольники одинаково пронумерованные.

(1+2+3+4)+(5+6+7+8)= (1+2+3+4+5+6+7+8)

b² + а² = с², т.е.

а² + b² = с²

2. 6. Доказательство Евклида:

1. Рассмотрим ΔАВС: ˪С=90°

АВ = с, ВС = а, АС = b.

СН = h, АН = b_с – проекция катета b на гипотенузу.

ВН = а_с – проекция катета a на гипотенузу.

1. На сторонах ΔABC построим квадраты со сторонами а, b, с.

2. Проведем луч СН⟘ АВ – гипотенузе.

Луч СН делит квадрат ABJK на два прямоугольника AHTK и BJTH.

Очевидно, что S□ = S□+ S□ = S□_b+ S□_а

3. Рассмотрим вспомогательные треугольники:

ΔACK и ΔABD

AK = AB = c

AC = AD = b

∟CAK = 90° + ∟CAB = ∟DAB

ΔACK = ΔABD (по двум сторонам и углу между ними).

S_ΔACK = S_∆ABD

c∙b_с = b∙b

S□ = b²

S□ = S□_b

S□= S□_b

4. Аналогично можно доказать, чтоS□ = S□_a

5. S□_c = S□ + S□

S□_c = S□_a +S□_b

с² = a² + b²

2.7Доказательство методом Гофмана:

Построим ΔАВС с ∟С=90°

Построим BF=CB, BF⟘CB

BE=AB, BE⟘AB

AD=AC, AD⟘AC

Получили равнобедренные прямоугольные треугольники, острые углы в них по 45̊. Тогда точкиF, C, D принадлежат одной прямой, т.к. образуется развернутый угол DCF.

Четырехугольники ADFB и ACBE равновелики, т. к. ΔABF = ΔBCE (по двум сторонам и углу между ними).

Отнимем от обоих равновеликих четырехугольников общий для них ΔАВС, получим:

S_ACD+ S_BCF =S_ABE, т.е.

а² + b² = с².

Соответственно: a² + b² = с²

2. 6. Доказательство, основанное на разрезании квадратов («колесо с лопастями» — Перигаль):

Этот метод основан на разрезании квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.

О – центр квадрата, построенного на большем катете (см. рис.)

Через т. О проводят прямую, параллельную гипотенузе и прямую, перпендикулярную гипотенузе.

Квадрат разрезают. Его части и второй квадрат укладывают на квадрат, построенный на гипотенузе.

3.1Доказательство через подобие треугольников:

В ΔАВС ∟С = 90°

1. Проведем высоту СН

2. Рассмотрим ΔАСН и ΔАВС

ΔАСН~ΔАВС (по двум углам)

= =

3. Рассмотрим ΔВСН и ΔАВС

ΔВСН ~ ΔАВС (по двум углам)

= = (по определению).

4. = ; =

а² = с ∙ ВН;

b² = с ∙ АН

а² + b² = с ∙ ВН + с ∙ АН

а² + b² = с ∙ (ВН + АН)

а² + b² = с²

1. 1. Доказательство по косинусу:

1. В ΔАВС: ∟С = 90°. Проведем высоту СН = h.

2. ΔАСН: ∟Н = 90°

=

3. ΔАВС: ∟С = 90°

=

4. =

АС²= АН + АВ

b² = b_с + с

5. ΔВСН: ∟Н = 90°

=

6. ΔАВС: ∟С = 90°

=

7. =

BC² = BD ∙ AB

a^{2 =} a_c ∙ c

а² + b² = b_c ∙ с + а_с ∙ с

а² + b² = с ( b_c + а_с)

а² + b² = с²

Теорема Пифагора получила много различных названий: «теорема бабочки», «теорема невесты», теорема «100 быков», «бегство убогих», «ветреная мельница», «мост ослов». Думаю, только по количеству названий, теорему можно считать уникальной!

УЧЕНИЧЕСКИЕ ШАРЖИ.

В средневековье для легкого запоминания теоремы Пифагора было придумано много стихов, рисовались шаржи.

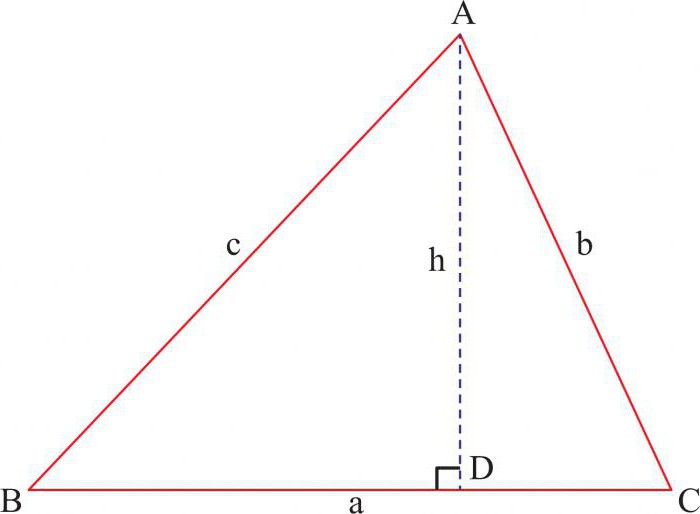
• Отрубил Иван-царевич дракону голову, а у него две новые выросли. На математическом языке это означает: провели в Δ АВС высоту CD, и образовалось два новых прямоугольных треугольника ADC и BDC.

О теореме Пифагора И. Дырченко

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим —

И таким простым путем

К результату мы придем.

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ.

Теорема Пифагора находит применение не только в математике, но и в астрономии и даже литературе. В математике теорему используют для решения задач, для доказательства других теорем. Что касается литературы, то теорема Пифагора вдохновляла писателей со времен античности и продолжает это делать в наше время. А в двадцатом веке советский писатель Евгений Велтистов в книге «Приключения Электроника» доказательствам теоремы Пифагора отвел целую главу. И еще полглавы рассказу о двухмерном мире, какой мог бы существовать, если бы теорема Пифагора стала основополагающим законом и даже религией для отдельно взятого мира. Жить в нем было бы гораздо проще, но и гораздо скучнее: например, там никто не понимает значения слов «круглый» и «пушистый». А еще в книге «Приключения Электроника» автор устами учителя математики Таратара говорит: «Главное в математике – движение мысли, новые идеи». Именно этот творческий полет мысли порождает теорема Пифагора – не зря у нее столько разнообразных доказательств. Она помогает выйти за границы привычного, и на знакомые вещи посмотреть по-новому.

Задача №1

Дано:

ΔАВС

∟С = 90°

АС = 8 см

ВС = 6 см

Найти: АВ

Решение:

а² + b² = с²

ВС² + АС² = АВ²

6² + 8² = АВ²

36 + 64 = АВ²

АВ² = 100

Из курса алгебры известно, что уравнение АВ² = 100 имеет два корня:

АВ = ± 10. АВ = – 10 не удовлетворяет условию задачи, так как длина стороны треугольника всегда положительна. Значит, АВ = 10.

АВ = 10 см

Ответ: 10 см.

Задача 2

Дано:

ΔАВС

∟С = 90°

АВ =13 см

ВС = 12 см

Найти: АС

Решение:

а² + b² = с²

ВС² + АС² = АВ²

12² +АС² = 13²

144 +АС² = 169²

АС² = 25

АС = 5

Из курса алгебры известно, что уравнение АВ² = 100 имеет два корня:

АС = ± 5. АС = – 5 не удовлетворяет условию задачи, так как длина стороны треугольника всегда положительна. Значит, АС= 5

Ответ: АС = 5 см.

ЗАКЛЮЧЕНИЕ.

Теорема Пифагора – одна из главных теорем в геометрии. Значение ее в том, что с ее помощью можно вывести большинство теорем геометрии, например: в стереометрии (10 класс) при доказательстве теоремы о трех перпендикулярах, при доказательстве теоремы о квадрате диагонали прямоугольного параллелепипеда. Она замечательна еще тем, что сама по себе она вовсе не является очевидной. Например, свойства равнобедренного треугольника, ромба можно увидеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что квадрат гипотенузы равен сумме квадратов катетов. Теорема Пифагора популярна по трем причинам:

1. простота;

2. красота;

3. значимость.

Занимаясь теоремой Пифагора, я узнала историю ее открытия, нашла 12 способов доказательства, разобралась в них. Некоторые из них простые, легко воспринимаются. А некоторые сложны в решении.

Вот почему теорему Пифагора считают уникальной.

Используемые источники:

1. http://ru.wikipedia.org/

2. http://rpp.nashaucheba.ru/

infourok.ru

Разные способы доказательства теоремы Пифагора: примеры, описание и отзывы

В одном можно быть уверенным на все сто процентов, что на вопрос, чему равен квадрат гипотенузы, любой взрослый человек смело ответит: «Сумме квадратов катетов». Эта теорема прочно засела в сознании каждого образованного человека, но достаточно лишь попросить кого-либо ее доказать, и тут могут возникнуть сложности. Поэтому давайте вспомним и рассмотрим разные способы доказательства теоремы Пифагора.

Краткий обзор биографии

Теорема Пифагора знакома практически каждому, но почему-то биография человека, который произвел ее на свет, не так популярна. Это поправимо. Поэтому прежде чем изучить разные способы доказательства теоремы Пифагора, нужно кратко познакомиться с его личностью.

Пифагор – философ, математик, мыслитель родом из Древней Греции. Сегодня очень сложно отличить его биографию от легенд, которые сложились в память об этом великом человеке. Но как следует из трудов его последователей, Пифагор Самосский родился на острове Самос. Его отец был обычный камнерез, а вот мать происходила из знатного рода.

Судя по легенде, появление на свет Пифагора предсказала женщина по имени Пифия, в чью честь и назвали мальчика. По ее предсказанию рожденный мальчик должен был принести много пользы и добра человечеству. Что вообще-то он и сделал.

Рождение теоремы

В юности Пифагор переехал с острова Самос в Египет, чтобы встретиться там с известными египетскими мудрецами. После встречи с ними он был допущен к обучению, где и познал все великие достижения египетской философии, математики и медицины.

Вероятно, именно в Египте Пифагор вдохновился величеством и красотой пирамид и создал свою великую теорию. Это может шокировать читателей, но современные историки считают, что Пифагор не доказывал свою теорию. А лишь передал свое знание последователям, которые позже и завершили все необходимые математические вычисления.

Как бы там ни было, сегодня известна не одна методика доказательства данной теоремы, а сразу несколько. Сегодня остается лишь гадать, как именно древние греки производили свои вычисления, поэтому здесь рассмотрим разные способы доказательства теоремы Пифагора.

Теорема Пифагора

Прежде чем начинать какие-либо вычисления, нужно выяснить, какую теорию предстоит доказать. Теорема Пифагора звучит так: «В треугольнике, у которого один из углов равен 90^о, сумма квадратов катетов равна квадрату гипотенузы».

Всего существует 15 разных способов доказательства теоремы Пифагора. Это достаточно большая цифра, поэтому уделим внимание самым популярным из них.

Способ первый

Сначала обозначим, что нам дано. Эти данные будут распространяться и на другие способы доказательств теоремы Пифагора, поэтому стоит сразу запомнить все имеющееся обозначения.

Допустим, дан прямоугольный треугольник, с катетами а, в и гипотенузой, равной с. Первый способ доказательства основывается на том, что из прямоугольного треугольника нужно дорисовать квадрат.

Чтобы это сделать, нужно к катету длиной а дорисовать отрезок равный катету в, и наоборот. Так должно получиться две равные стороны квадрата. Остается только нарисовать две параллельные прямые, и квадрат готов.

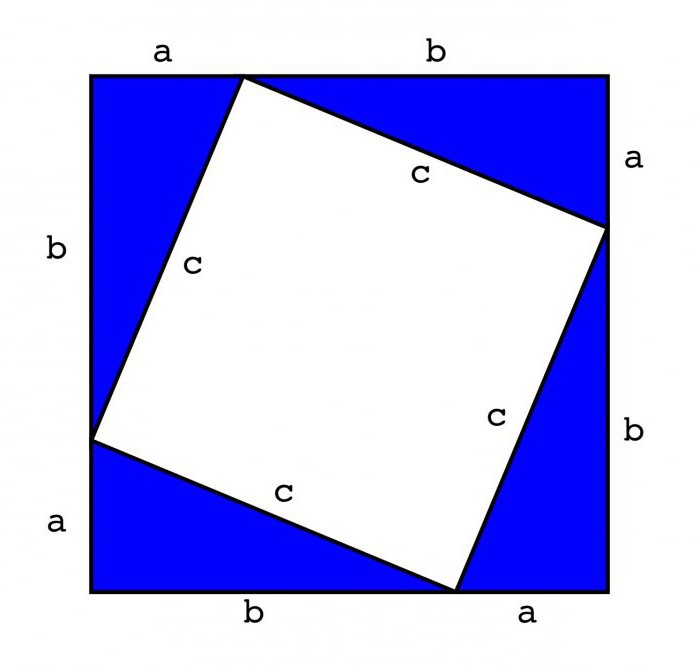
Внутри получившейся фигуры нужно начертить еще один квадрат со стороной равной гипотенузе исходного треугольника. Для этого от вершин ас и св нужно нарисовать два параллельных отрезка равных с. Таким образом, получиться три стороны квадрата, одна из которых и есть гипотенуза исходного прямоугольного треугольники. Остается лишь дочертить четвертый отрезок.

На основании получившегося рисунка можно сделать вывод, что площадь внешнего квадрата равна (а+в)². Если заглянуть внутрь фигуры, можно увидеть, что помимо внутреннего квадрата в ней имеется четыре прямоугольных треугольника. Площадь каждого равна 0,5ав.

Поэтому площадь равна: 4*0,5ав+с²=2ав+с²

Отсюда (а+в)²=2ав+с²

И, следовательно, с²=а²+в²

Теорема доказана.

Способ два: подобные треугольники

Данная формула доказательства теоремы Пифагора была выведена на основании утверждения из раздела геометрии о подобных треугольниках. Оно гласит, что катет прямоугольного треугольника – среднее пропорциональное для его гипотенузы и отрезка гипотенузы, исходящего из вершины угла 90^о.

Исходные данные остаются те же, поэтому начнем сразу с доказательства. Проведем перпендикулярный стороне АВ отрезок СД. Основываясь на вышеописанном утверждении катеты треугольников равны:

АС=√АВ*АД, СВ=√АВ*ДВ.

Чтобы ответить на вопрос, как доказать теорему Пифагора, доказательство нужно проложить возведением в квадрат обоих неравенств.

АС²=АВ*АД и СВ²=АВ*ДВ

Теперь нужно сложить получившиеся неравенства.

АС²+ СВ²=АВ*(АД*ДВ), где АД+ДВ=АВ

Получается, что:

АС²+ СВ²=АВ*АВ

И, следовательно:

АС²+ СВ²=АВ²

Доказательство теоремы Пифагора и различные способы ее решения нуждаются в разностороннем подходе к данной задаче. Однако этот вариант является одним из простейших.

Еще одна методика расчетов

Описание разных способов доказательства теоремы Пифагора могут ни о чем не сказать, до тех самых пор пока самостоятельно не приступишь к практике. Многие методики предусматривают не только математические расчеты, но и построение из исходного треугольника новых фигур.

В данном случае необходимо от катета ВС достроить еще один прямоугольный треугольник ВСД. Таким образом, теперь имеется два треугольника с общим катетом ВС.

Зная, что площади подобных фигур имеют соотношение как квадраты их сходных линейных размеров, то:

S_авс *^{с2— S_авд*в2 =S_авд*а2— S_всд*а2}

S_авс*(с²-в²)=а²*(S_авд-S_всд)

с²-в²=а²

с²=а²+в²

Поскольку из разных способов доказательств теоремы Пифагора для 8 класса этот вариант едва ли подойдет, можно воспользоваться следующей методикой.

Самый простой способ доказать теорему Пифагора. Отзывы

Как полагают историки, этот способ был впервые использован для доказательства теоремы еще в древней Греции. Он является самым простым, так как не требует абсолютно никаких расчетов. Если правильно начертить рисунок, то доказательство утверждения, что а²+в²=с² , будет видно наглядно.

Условия для данного способа будет немного отличаться от предыдущего. Чтобы доказать теорему, предположим, что прямоугольный треугольник АВС – равнобедренный.

Гипотенузу АС принимаем за сторону квадрата и дочерчиваем три его стороны. Кроме этого необходимо провести две диагональные прямые в получившемся квадрате. Таким образом, чтобы внутри него получилось четыре равнобедренных треугольника.

К катетам АВ и СВ так же нужно дочертить по квадрату и провести по одной диагональной прямой в каждом из них. Первую прямую чертим из вершины А, вторую – из С.

Теперь нужно внимательно всмотреться в получившийся рисунок. Поскольку на гипотенузе АС лежит четыре треугольника, равные исходному, а на катетах по два, это говорит о правдивости данной теоремы.

Кстати, благодаря данной методике доказательства теоремы Пифагора и появилась на свет знаменитая фраза: «Пифагоровы штаны во все стороны равны».

Доказательство Дж. Гарфилда

Джеймс Гарфилд – двадцатый президент Соединенных Штатов Америки. Кроме того, что он оставил свой след в истории как правитель США, он был еще и одаренным самоучкой.

В начале своей карьеры он был обычным преподавателем в народной школе, но вскоре стал директором одного из высших учебных заведений. Стремление к саморазвитию и позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения выглядит следующим образом.

Сначала нужно начертить на листе бумаги два прямоугольных треугольника таким образом, чтобы катет одного из них был продолжением второго. Вершины этих треугольников нужно соединить, чтобы в конечном итоге получилась трапеция.

Как известно, площадь трапеции равна произведению полусуммы ее оснований на высоту.

S=а+в/2 * (а+в)

Если рассмотреть получившуюся трапецию, как фигуру, состоящую из трех треугольников, то ее площадь можно найти так:

S=ав/2 *2 + с²/2

Теперь необходимо уравнять два исходных выражения

2ав/2 + с/2=(а+в)²/2

с²=а²+в²

О теореме Пифагора и способах ее доказательства можно написать не один том учебного пособия. Но есть ли в нем смысл, когда эти знания нельзя применить на практике?

Практическое применение теоремы Пифагора

К сожалению, в современных школьных программах предусмотрено использование данной теоремы только в геометрических задачах. Выпускники скоро покинут школьные стены, так и не узнав, а как они могут применить свои знания и умения на практике.

На самом же деле использовать теорему Пифагора в своей повседневной жизни может каждый. Причем не только в профессиональной деятельности, но и в обычных домашних делах. Рассмотрим несколько случаев, когда теорема Пифагора и способы ее доказательства могут оказаться крайне необходимыми.

Связь теоремы и астрономии

Казалось бы, как могут быть связаны звезды и треугольники на бумаге. На самом же деле астрономия – это научная сфера, в которой широко используется теорема Пифагора.

Например, рассмотрим движение светового луча в космосе. Известно, что свет движется в обе стороны с одинаковой скоростью. Траекторию АВ, которой движется луч света назовем l. А половину времени, которое необходимо свету, чтобы попасть из точки А в точку Б, назовем t. И скорость луча – c. Получается, что: c*t=l

Если посмотреть на этот самый луч из другой плоскости, например, из космического лайнера, который движется со скоростью v, то при таком наблюдении тел их скорость изменится. При этом даже неподвижные элементы станут двигаться со скоростью v в обратном направлении.

Допустим, комический лайнер плывет вправо. Тогда точки А и В, между которыми мечется луч, станут двигаться влево. Причем, когда луч движется от точки А в точку В, точка А успевает переместиться и, соответственно, свет уже прибудет в новую точку С. Чтобы найти половину расстояния, на которое сместилась точка А, нужно скорость лайнера умножить на половину времени путешествия луча (t’).

d= t’*v

А чтобы найти, какое расстояние за это время смог пройти луч света, нужно обозначить половину пути новой буковой s и получить следующее выражение:

s=c* t’

Если представить, что точки света С и В, а также космический лайнер – это вершины равнобедренного треугольника, то отрезок от точки А до лайнера разделит его на два прямоугольных треугольника. Поэтому благодаря теореме Пифагора можно найти расстояние, которое смог пройти луч света.

s² =l² + d²

Этот пример, конечно, не самый удачный, так как только единицам может посчастливиться опробовать его на практике. Поэтому рассмотрим более приземленные варианты применения этой теоремы.

Радиус передачи мобильного сигнала

Современную жизнь уже невозможно представить без существования смартфонов. Но много ли было бы от них прока, если бы они не могли соединять абонентов посредством мобильной связи?!

Качество мобильной связи напрямую зависит от того, на какой высоте находиться антенна мобильного оператора. Для того чтобы вычислить, каком расстоянии от мобильной вышки телефон может принимать сигнал, можно применить теорему Пифагора.

Допустим, нужно найти приблизительную высоту стационарной вышки, чтобы она могла распространять сигнал в радиусе 200 километров.

АВ (высота вышки) = х;

ВС (радиус передачи сигнала) = 200 км;

ОС (радиус земного шара) = 6380 км;

Отсюда

ОВ=ОА+АВОВ=r+х

Применив теорему Пифагора, выясним, что минимальная высота вышки должна составить 2,3 километра.

Теорема Пифагора в быту

Как ни странно, теорема Пифагора может оказаться полезной даже в бытовых делах, таких как определение высоты шкафа-купе, например. На первый взгляд, нет необходимости использовать такие сложные вычисления, ведь можно просто снять мерки с помощью рулетки. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все мерки были сняты более чем точно.

Дело в том, что шкаф-купе собирается в горизонтальном положении и только потом поднимается и устанавливается к стене. Поэтому боковина шкафа в процессе подъема конструкции должна свободно проходить и по высоте, и по диагонали помещения.

Предположим, имеется шкаф-купе глубиной 800 мм. Расстояние от пола до потолка – 2600 мм. Опытный мебельщик скажет, что высота шкафа должна быть на 126 мм меньше, чем высота помещения. Но почему именно на 126 мм? Рассмотрим на примере.

При идеальных габаритах шкафа проверим действие теоремы Пифагора:

АС=√АВ²+√ВС²

АС=√2474²+800²=2600 мм – все сходится.

Допустим, высота шкафа равна не 2474 мм, а 2505 мм. Тогда:

АС=√2505²+√800²=2629 мм.

Следовательно, этот шкаф не подойдет для установки в данном помещении. Так как при поднятии его в вертикальное положение можно нанести ущерб его корпусу.

Пожалуй, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что она более чем правдива. Теперь можно использовать полученную информацию в своей повседневной жизни и быть полностью уверенным, что все расчеты будут не только полезны, но и верны.

fb.ru

Урок по геометрии в 8 классе «Теорема Пифагора»

Конспект урока по теме:

« Теорема Пифагора »

ГЕОМЕТРИЯ 8 КЛАСС

учителя математики Мбоу «Партизанская ош»

Республики Крым

Абдулджелиловой НА 2017-2018

Тема урока: Теорема Пифагора.

Тип урока: урок изучения нового материала

Цель урока:

• Знакомство с теоремой Пифагора, формирование навыков решения задач;

• Развитие познавательного интереса, логического мышления учащихся;

• Воспитание нравственных качеств личности.

Задачи урока:

• Познакомить учащихся с древнегреческим математиком Пифагором.

• Сформулировать и доказать теорему  Пифагора.

• Научить применять теорему для нахождения неизвестных сторон прямоугольного треугольника, показать практическое применение теоремы.

Оборудование: компьютер, презентация, плакаты, карточки с высказываниями Пифагора

ХОД УРОКА

I. Организационный момент 

– Сегодня у нас с вами необычный день и необычный урок. 
Необычен тем, что мы  изучим одну из самых известных теорем древности, называемую теоремой Пифагора. Узнаем о жизни Пифагора, познакомимся с его математическими открытиями, докажем теорему и научимся применять её для решения задач.

СЛАЙД 2

На уроке нам предстоит узнать много нового, и поэтому девизом нашего урока я подобрала слова великого педагога Я.А.Коменского: “Считай несчастным тот день или тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию”.

II. Актуализация знаний учащихся в ходе фронтальной беседы по вопросам

СЛАЙД 3

Новые знания нам будет очень трудно осваивать без опоры на предыдущие, поэтому урок начнем с устной работы.

 СЛАЙДЫ 4-15

– Внимание на экран: «ВОПРОС-ОТВЕТ»   

III. Изучение нового материала

СЛАЙД 16

Задача (проблемная): в прямоугольной трапеции угол А равен 90°. Меньшая боковая сторона 4 см. Основания АВ и CD соответственно равны 8см. и 5 см. Найти большую боковую сторону.       

Учитель: Мы не можем довести решение задачи до конца, т.к не знаем зависимости между катетами и гипотенузой в прямоугольном треугольнике.
Для того, чтобы определить большую боковую сторону трапеции ВС нам нужно установить равенство, связывающее длины сторон в прямоугольном треугольнике. И если эта зависимость существует, то как она формулируется.
Давайте попытаемся найти эту зависимость!

СЛАЙД 17

Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

СЛАЙД 18

Историческая справка о Пифагоре

О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.
Родился Пифагор в семье резчика по камню. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове.
Пифагор перебрался в город Милет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет, где сам  когда-то изучал науки.
Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем ему было разрешено познакомиться с многовековыми достижениями египетской науки. Пифагор был чемпионом Олимпийских игр по кулачному бою.
Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу.    Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов.    Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Кротоне.
Там Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю. Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания.
После его смерти ученики окружили имя своего учителя множеством легенд.

Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:   

• теорема о сумме внутренних углов треугольника;

• построение правильных многоугольников и деление плоскости на некоторые из них;

• деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;

• доказательство того, что не является рациональным числом;

• создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.

Доказательство теоремы Пифагора. СЛАЙД 19 

Вопрос: Какие известные определения, формулы  использовались для доказательства теоремы?
Теорема Пифагора одна из основополагающих теорем евклидовой геометрии. Существует около 400 способов её доказательства. 

IV. Закрепление материала

СЛАЙД 20
– А теперь познакомившись с теоремой Пифагора, давайте вернемся  к задаче о нахождении боковой стороны трапеции.  Можем ли мы теперь найти боковую сторону. (Решается задача)   

СЛАЙД 21
– Обратите внимание, мы получили треугольник со сторонами 3, 4, 5; он называется египетским 

Египетский треугольник – это прямоугольный треугольник с соотношением сторон 3 : 4 : 5. Особенностью треугольника, известной ещё со времён античности, является то, что при таком отношении сторон теорема Пифагора даёт целые квадраты как катетов, так и гипотенузы, то есть 9 : 16 : 25. 
Название треугольнику с таким отношением сторон дали эллины. Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами.     Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3 + +4 + 5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.

Пифагоровы тройки

Кроме чисел 3, 4, 5 существует бесчисленное множество целых положительных чисел a, b, c, удовлетворяющих соотношению Пифагора: a² + b² = c². Их называют «Пифагоровыми тройками».
Пифагоровы тройки известны очень давно. В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.
Пифагоровы числа обладают рядом любопытных особенностей, которые мы перечислим без доказательства:
Одно из чисел должно быть кратно трём.
Одно из чисел должно быть кратно четырём.
Одно из пифагоровых чисел должно быть кратно пяти.
Можете удостовериться в наличии этих свойств

Практическое применение теоремы Пифагора.

СЛАЙДЫ 22-23

Рассмотрим примеры практического применения теоремы Пифагора. Не будем пытаться привести все примеры использования теоремы – это вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой. Определим возможности, которые дает теорема Пифагора для вычисления длин отрезков некоторых фигур на плоскости. Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника.
Задача.

СЛАЙД 24

Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?

V. Подведение итогов

– Мы с вами познакомились с одним из способов доказательства теоремы. 
– Что вы знаете о прямоугольных треугольниках на сегодняшний день? (По модели)

1. Определение прямоугольного треугольника.
2. Названия сторон, соотношения между ними.
3. Свойство острых углов прямоугольного треугольника.
4.Свойство прямоугольного треугольника с углом в 30° 
5. Свойство прямоугольного треугольника с углом в 45°.
6. Площадь прямоугольного треугольника
7. Теорема Пифагора

– Анализируем, все ли задачи, поставленные на урок, выполнены.
– Чем необычным был для вас сегодняшний урок?

VI. Заключение

Не только сила личности и мудрость Пифагора, но и высокая нравственность проповедуемых им идей и жизненных принципов притягивала к нему единомышленников.
Система морально-этических правил, завещанная ученикам Пифагора, была собрана в своеобразный моральный кодекс пифагорейцев – «Золотые стихи». Они переписывались и дополнялись на протяжении всей тысячелетней истории античности, а затем и в эпоху средневековья и Возрождения. В 18-19 веках «Золотые стихи» были особенно популярны в России. В 1808 году в Санкт-Петербурге вышла карманного формата книжечка «Пифагоровы законы и нравственные правила», начинавшаяся словами: «Пифагор есть законодатель всего человеческого рода».

Вот некоторые из 325 Пифагоровых заповедей:

Берегите слёзы ваших детей, дабы они могли проливать их на вашей могиле.
Во время гнева не должно ни говорить, ни действовать.
Молчание прекрасно. Молчи, если не можешь изречь то, что было бы прекрасней молчания.
Просыпаясь утром, спроси себя: «Что я  должен сделать?», а, засыпая вечером, спроси: 
Мысль – превыше всего между людьми. 
Сыщи себе верного друга; имея его, ты можешь обойтись без богов.
Юноша! Если ты желаешь себе жизни долгоденственной, то воздержи себя от пресыщения и всякого излишества. 
Юные девицы! Помятуйте, что лицо лишь тогда бывает прекрасным, когда оно изображает изящную душу. 
Не гоняйся за счастьем: оно всегда находится в тебе самом.
Не пекись о скитании великого знания: из всех знаний нравственная наука, может быть, есть самая нужнейшая, но ей не обучаются.
Делай лишь то, что впоследствии не омрачит тебя и не заставит раскаиваться.
Не делай никогда того, чего не знаешь, но научись всему, что нужно знать.
Не пренебрегай здоровьем своего тела.
Научись жить просто и без роскоши.
Через весы не шагай – избегай алчности.
Не садись на хлебную меру – не живи праздно.
Либо молчи, либо говори то, что ценнее молчания.
Ласточек в доме не держи – не принимай гостей болтливых и не сдержанных на язык.
Не закрывай глаза, когда хочешь спать, не разобравши всех своих поступков за день.
По торной дороге не ходи – следуй не мнениям толпы, а мнениям немногих понимающих.

– Сегодня абсолютно невозможно сказать, какие из сотен подобных заповедей восходят к самому Пифагору. Но совершенно очевидно, что все они выражают вечные общечеловеческие ценности, которые остаются актуальными всегда.

(Каждый учащийся сам вытаскивает себе высказывание Пифагора, которые выписаны на специальных карточках)

VII. Домашнее задание: п.54,  № 483, 484

infourok.ru

Урок геометрии в 8-м классе по теме «Теорема Пифагора»

Тип урока:

1-й час — урок ознакомления с новым материалом;
2-й час — первичное закрепление изученного материала.

Учебное пособие: Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. Геометрия 7-9. Учебник для 7-9 классов средней школы. М.: Просвещение, 2004.

Цели и задачи урока:

1. Образовательные: познакомить учащихся с теоремой Пифагора, многообразием способов ее доказательства, применением при решении задач, повторить изученный ранее материал (площадь треугольника, ромба, прямоугольника, квадрата, параллелограмма), выработать умение применять теоретический материал для решения задач и доказательства теоремы.　 Закрепить полученные знания при решении практических задач.
2. Воспитательные: воспитывать познавательную активность, повышать интерес к изучению математики, показывая красоту математических доказательств, их стройность, логичность.
3. Развивающие: развивать умения обнаруживать способ доказательства нового математического утверждения и выполнять его, развивать мышление, память, навыки аргументированной речи, навыки доказательного воспроизведения в процессе деятельности.

Средства обучения (в том числе средства ИКТ): компьютер, мультимедийный проектор, презентация, выполненная при помощи программы PowerPoint (Приложение 1).

Методы и приемы: объяснительно-иллюстративный метод, вопросно-ответный метод, наглядный метод, словесный (рассказ, беседа, диалог), постановка проблемных вопросов, поисковый метод, эвристический метод, использование ИКТ, дифференцированный подход.

Формы организации деятельности учащихся: коллективная форма работы (фронтальный опрос, устная работа), индивидуальная работа (по карточке), письменная работа.

План урока:

1. Организационный момент.
2. Подготовительная работа по готовым чертежам:
3. Проверка домашнего задания.
4. Объяснение нового материала.
5. Различные способы доказательства теоремы Пифагора.
6. Постановка домашнего задания.
7. Первичное закрепление материала.
8. Решение задач.
9. Подведение итогов.

Ход урока

Объявление темы урока, постановка целей и задач перед учащимися: познакомиться с теоремой Пифагора, многообразием способов ее доказательства и ее применением при решении задач, а также повторить изученный ранее материал (площади треугольника, ромба, прямоугольника, квадрата, параллелограмма).

К доске с тетрадями вызываются 2 ученика для проверки на доске домашнего задания (выписывают на доске решения №480(б), №479 (б) – учебное пособие Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина. Геометрия 7-9. Учебник для 7-9 классов средней школы. М.: Просвещение, 2004.). В это время с классом проводится подготовительная работа – решение задач по готовым чертежам. Задачи транслируются учащимся посредством презентации (Приложение 1).

Проверка решений домашних задач:

№480 (б)

Дано: АВСD – трапеция, АВ и СD – основания. = 30^о, АВ=2 см, СD = 10 см, DA = 8 см.

Найти S_АВСD

Решение: так как = 30^о, то АН = 0,5 AD = 4 см.

S_АВСD = (2 + 10)×4 = 24 см².

№479 (б)

Дано:

АВ = 8 см, АС = 3 см, АЕ = 2 см. S_АВС = 10 см², S_АDE = 2 см².

Найти AD.

Решение:

Фронтальная работа с классом по готовым чертежам на слайдах (Приложение 1)

1. По данным рисунка найдите площадь четырехугольника АВСD.

2. Вычислить:

3. По данным рисунков найдите угол

4. По данным рисунка докажите, что четырехугольник КМNР – квадрат (эта задача особенно важна, так как такая же фигура, как на рисунке, используется для доказательства теоремы).

Проверка домашнего задания, выписанного учеником на доске.

— Все согласны с решением задач? Какие есть замечания, дополнения?

— Дополнительный вопрос: какая теорема использовалась при решении задачи № 479, сформулируйте ее? (Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы).

Объяснение нового материала «Теорема Пифагора»

Учитель: Сегодня мы изучаем одну из самых известных геометрических теорем древности, называемую теоремой Пифагора. Ее и сейчас знают практически все, кто когда-либо изучал планиметрию. Теорема Пифагора одна из главных теорем планиметрии. Значение ее состоит в том, что с ее помощью можно доказать многие другие теоремы и решить множество задач.

(Учащиеся записывают в тетрадях тему урока – «Теорема Пифагора»).

Знаменитый греческий философ и математик Пифагор Самосский, именем которого названа теорема, жил около 2,5 тысяч лет тому назад. Он родился в 500 г до нашей эры и прожил 80 лет. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко не достоверны. Пифагор – это не имя, а прозвище, данное　 ему за то, что он высказывал истину так же постоянно, как дельфийский оракул («Пифагор» значит «убеждающий речью»).

Знаменитая теорема Пифагора звучала так: Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов построенных на его катетах.

Про картинку, иллюстрирующую эту теорему, сложена шутливая поговорка: «Пифагоровы штаны на все стороны равны». Что имелось ввиду?

Теореме Пифагора можно дать эквивалентную формулировку, применив понятие равносоставленных фигур.

Попробуйте сформулировать теорему Пифагора по-другому.

— Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.

-Чтобы сформулировать теорему Пифагора в современном изложении, давайте вспомним, как найти площадь квадрата? (сторону квадрата возвести в квадрат). Тогда площадь квадрата, построенного на гипотенузе – это …? (квадрат гипотенузы), а площади квадратов, построенных на катетах – это …? (квадраты катетов). Попробуйте сами дать еще одну, современную формулировку теоремы Пифагора.

— В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

— Давайте в своих тетрадях начертим прямоугольный треугольник, обозначим катеты и гипотенузу буквами а, b, с и запишем формулу, которую нам дает теорема Пифагора (с² = а²+b²), перед формулой запишем слово «Доказать».

— Сейчас известно более трёхсот доказательств теоремы Пифагора. Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т.　е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий. Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике. В самом древнем дошедшем до нас китайском математико-астрономическом сочинении, написанном примерно за 600 лет до Пифагора, среди других предложений, относящихся к прямоугольному треугольнику, содержится и теорема Пифагора. Еще раньше эта теорема была известна индусам. Таким образом, Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым из области практики в область науки. Сегодня мы с вами познакомимся с некоторыми из многочисленных доказательств теоремы Пифагора.

Различные способы доказательства теоремы Пифагора

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы (для треугольника АВС квадрат, построенный на гипотенузе АС содержит 4 исходных треугольника, а квадраты, построенные на катетах – по 2 треугольника) Теорема доказана.

Еще одно наглядное доказательство теоремы Пифагора принадлежит индусам. Посмотрите внимательно на два квадрата, и вам всё станет ясно. Индусы к этому чертежу добавляли лишь одно слово: «СМОТРИ!»

Кому стало ясно? Кто мне сможет объяснить, почему площадь серого квадрата, построенного на гипотенузе равна сумме площадей серых квадратов, построенных на катетах (Выслушать ответы учащихся. Из двух одинаковых квадратов вычитаем по 4 площади одинаковых треугольников).

— Двадцатый президент США Джеймс Гарфилд, который был избран президентом в 1880 году тоже смог привести свое доказательство теоремы Пифагора. Причём сделал он это доселе неизвестным способом. А узнать об этом широкие массы американцев смогли почти через 60 лет после его смерти. Правда, в изданной в 1940 году книге с доказательствами теоремы Пифагора доказательство Гарфилда затерялось, так как всего там было представлено 370 различных способов доказательства теоремы. Сейчас мы повторим путь доказательства Гарфилда и запишем его в тетрадь. Я вам подскажу только чертеж, с помощью которого Гарфилд доказал теорему Пифагора, а вы сейчас сами докажите теорему. При доказательстве используйте формулы для вычисления площади треугольника и площади трапеции. (В качестве повторения тем «Площадь треугольника» и «Площадь трапеции» учащимся будет полезно провести это доказательство письменно. Учитель добивается с помощью наводящих вопросов, чтобы дети сами провели рассуждения лучше, чтобы ученик или учитель записал доказательство на доске).

Доказательство Гарфилда:
На рисунке три прямоугольных треугольника составляют трапецию. Поэтому площадь этой фигуры можно находить по формуле площади прямоугольной трапеции, либо как сумму площадей трех треугольников. В первом случае эта площадь равна

Рассмотрим еще одно доказательство теоремы Пифагора, которое приведено в вашем учебнике. Оно выполнено по следующему рисунку. Вам напоминает что-нибудь этот рисунок? Когда вы это видели? (Задача, решенная вначале урока)

(Учащимся сообщается лишь идея доказательства — достроить треугольник до квадрата со стороной (а + b) и выразить площадь квадрата возможными способами).

Доказательство (на уроке не проговаривается): S_кв. = (а + b)². С другой стороны квадрат составлен из четырех одинаковых треугольников с катетами а и в и квадрата со стороной с. Площади приравниваются:

Учащимся дается задание: дома самостоятельно провести это доказательство и записать полное доказательство в тетрадь, включая доказательства того факта, что внутри квадрат (в учебнике этот факт не доказывается). В классе выполняется только чертеж к доказательству теоремы)

Подводится промежуточный итог:

— Итак, сегодня вы познакомились с самой известной теоремой планиметрии – теоремой Пифагора. Кто сможет напомнить, как же формулируется теорема Пифагора? Кто запомнил? Как еще можно сформулировать?

Первичное закрепление материала.

1. Теорема Пифагора имеет большое практическое применение при решении задач. Она позволяет найти гипотенузу, зная катеты прямоугольного треугольника.

Выразите из формулы гипотенузу с. Почему взяли только положительное значение, ведь данное квадратное уравнение имеет два противоположных решения (речь идет о длине отрезка, который не может быть отрицательным) Выразите катет b; выразите катет а.

2. Дана таблица, в которой а и b катеты, с – гипотенуза.
Заполните пустые ячейки таблицы, произведя вычисления устно (таблица представлена на слайде, приложение 1).

— Треугольник с катетами 3 и 4 и гипотенузой 5 называется египетским треугольником, так как он известен был еще древним египтянам, с помощью такого треугольника египтяне строили прямой угол.

3. Решение задач по готовым чертежам – самостоятельная работа в тетрадях по рядам. Каждый ряд имеет свой рисунок (чертежи заранее выполнены на доске): вычислить длину неизвестного отрезка х по данным рисунка. Затем, один отвечающий от каждого ряда комментирует вслух свое решение.

4. Постановка домашнего задания:

1. провести полное доказательство теоремы Пифагора путем достроения треугольника до квадрата со стороной (а + b).
2. индивидуальное задание сильным учащимся – найти и подготовить другие доказательства теоремы Пифагора.
3. Уметь доказывать теорему одним из способов.
4. Решить задачи: № 483 (а; б), № 484 (б, г), № 487.
5. дополнительное творческое задание (по желанию): придумайте сами чертеж к задаче, где для решения применялась бы теорема Пифагора (можно использовать комбинации различных фигур – прямоугольника, ромба, трапеции, прямоугольного треугольника). Предложите свою задачу классу.

5. Решение задач по учебнику с вызовом учеников к доске.

№ 493, № 494 – решение по вариантам самостоятельно с последующей проверкой– 1 вариант № 493, 2 вариант – № 494, по одному представителю от каждого варианта приглашаются к доске, они решают задачу на отворотах доски самостоятельно, не комментируя, а класс решает самостоятельно в тетрадях, затем крылья доски поворачиваются классу и проверяем ход решения задачи.

Решения:

№ 493

Дано: АВСD-ромб. АС = 10 см, BD = 24 см.

№ 494

Дано: АВСD-ромб. АВ = 10 см, АС = 12 см.

Найти BD, S_ромба

Решение:

BD = 2ВО = 16 см.

Sромба= АС×BD= 96см²

№ 492

(Один ученик вызывается к доске и решает задачу с объяснением).

Дано: АВ = ВС = 10 см, АС = 12 см.

ВН, АN,СМ – высоты.

Найти: ВН, АN,СМ — ?

Решение: АН = 0,5 АС

Подведение итогов:

• Что нового сегодня узнали?
• Как звучит теорема Пифагора?
• Понятны ли были способы доказательства теорем?
• Какую практическую пользу дает нам теорема Пифагора?
• Оценивание ответов учащихся, оглашение оценок за урок.

urok.1sept.ru

Конспект урока по математике на тему «Введение теоремы Пифагора» (8 класс)

Конспект урока по введению теоремы Пифагора с применением ИКТ.

Цели:

1. Образовательные:

познакомить учащихся с теоремой Пифагора, а также с многообразием способов ее доказательства;

2. Воспитательные:

воспитывать познавательную активность, повышать интерес к изучению математики, применяя ИКТ.

3. Развивающие:

развивать умения доказывать новые математические утверждения, развивать мышление, память, навыки аргументированной речи.

Методы обучения: частично-поисковый, объяснительно-иллюстративный

Средства обучения: компьютер, мультимедийный проектор.

Структура урока:

1. Организационный момент. (2 мин)

2. Актуализация опорных знаний.(7 мин)

3. Объяснение нового материала. (15 мин)

4. Различные способы доказательства теоремы Пифагора.(10 мин)

5. Решение задач. (7 мин)

6. Постановка домашнего задания. (2 мин)

7. Подведение итогов.(2 мин)

План урока:

1. Организационный момент. (2 мин)

Приветствие, проверка готовности к уроку, рабочих тетрадей, учебников, письменных принадлежностей.

2. Актуализация опорных знаний.(7 мин)

ТЕСТ (взаимопроверка, задания на слайдах)

1) Треугольник называется прямоугольным, если у него один из углов:

а) 45° б) 180° в) 60° г) 90°

2) Найдите прямоугольный треугольник

3) Назовите прилежащий катет угла B в треугольнике ABC

4) Чем является сторона АВ в треугольнике ABC?

5) Чем являются стороны АС и ВС в треугольнике ABC?

6) Какая сторона прямоугольного треугольника называется гипотенузой?

7) Какие стороны прямоугольного треугольника называются катетами?

8)С помощью, каких формул можно найти площадь квадрата и площадь треугольника?

3. Объяснение нового материала. (15 мин)

I. Создание проблемной ситуации.

СКАЗКА-ЗАДАЧА

«Давным — давно в некоторой стране жила прекрасная принцесса и была она настолько прекрасной, что затмевала красотой всех своих подруг и свою старшую сестру, которая красотой не блистала. Старшая сестра завидовала принцессе и решила ей отомстить. Тогда она пошла к ведьме и попросила её заколдовать принцессу. Ведьма не смогла ей отказать, но все же, ей стало жалко принцессу, поэтому ведьма придумала усыпить принцессу в башне до той поры, пока какой — нибудь принц не посмотрит на окно башни с такого места, чтобы расстояние от глаз принца до окна было 50 шагов.

И вот принцесса заснула крепким сном. Прошло много лет, но никто мне смог расколдовать принцессу, несмотря на то, что отец ее Король пообещал отдать принцессу в жены тому, кто спасет её от пут сна.

В один прекрасный день в этом городе появляется на белом прекрасном коне молодой принц. Узнав, какое несчастье произошло с принцессой, молодой принц берется расколдовать её. Для этого он измеряет длину от основания башни до окна, за которым скрывается принцесса. У него получается 30 шагов. Затем что — то прикидывает в уме и отходит на 40 шагов, поднимает голову и вдруг. . . башня озаряется светом и через мгновенье навстречу принцу выбегает еще более прекрасная принцесса. . .»

— Как вы считаете, как же принц догадался, что от башни надо отойти на 40 шагов?

— Что необходимо было знать принцу, чтобы освободить принцессу?

*Для решения этой задачи необходимо знать соотношение между сторонами прямоугольного треугольника.

Проблема: — найти соотношение между сторонами прямоугольного треугольника.

— Для решения задачи нам нужны специальные формулы, связывающие между собой длины отрезков, площади, величины углов в фигурах. Такие формулы называют метрическими соотношениями.

Об одной из таких формул узнаем из следующего видеофрагмента (мультфильм Алия – 1.30)

II Историческая справка

Сегодня мы изучаем одну из самых известных геометрических теорем древности, называемую теоремой Пифагора. Ее и сейчас знают практически все, кто когда-либо изучал планиметрию. Теорема Пифагора одна из главных теорем планиметрии. Значение ее состоит в том, что с ее помощью можно доказать многие другие теоремы и решить множество задач.

(Учащиеся записывают в тетрадях тему урока – «Теорема Пифагора»).

Пифагор Самосский — знаменитый греческий математик, механик, музыкант, философ, геометр, олимпийский чемпион древности. Он родился в 500г до нашей эры и прожил 80 лет. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко не достоверны. Пифагор – это не имя, а прозвище, данное ему за то, что он высказывал истину так же постоянно, как дельфийский оракул («Пифагор» значит «убеждающий речью»).

• Берегите слёзы ваших детей, дабы они могли проливать их на вашей могиле.

• Во время гнева не должно ни говорить, ни действовать.

• Живи с людьми так, чтобы твои друзья не стали недругами, а недруги стали друзьями.

• Молчание прекрасно. Молчи, если не можешь изречь то, что было бы прекрасней молчания.

• Просыпаясь утром, спроси себя: «Что я должен сделать?», а, засыпая вечером, спроси: «Что я сделал?»

Эти высказывания называют акусмами Пифагора. Как вы думаете, почему?

(Слово созвучно со словом «аксиома» — предложение, не требующее доказательства. Эти нравственные правила также не требуют доказательства.)

Знаменитая теорема Пифагора звучала так: Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов построенных на его катетах.

Про картинку, иллюстрирующую эту теорему, сложена шутливая поговорка: «Пифагоровы штаны на все стороны равны». Что имелось ввиду?

Теореме Пифагора можно дать эквивалентную формулировку, применив понятие равносоставленных фигур. Попробуйте сформулировать теорему Пифагора по-другому.

— Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.

Чтобы сформулировать теорему Пифагора в современном изложении, давайте вспомним, как найти площадь квадрата? (сторону квадрата возвести в квадрат). Тогда площадь квадрата, построенного на гипотенузе – это …? (квадрат гипотенузы), а площади квадратов, построенных на катетах – это …? (квадраты катетов). Попробуйте сами дать еще одну, современную формулировку теоремы Пифагора (в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов).

4. Различные способы доказательства теоремы Пифагора.(10 мин)

— Начертите в тетрадях прямоугольный треугольник;

— Обозначьте катеты и гипотенузу буквами а, b, с4

— Запишите формулу, которую нам дает теорема Пифагора (с² = а²+b²), перед формулой запишите слово «Доказать».

Сейчас известно более трёхсот доказательств теоремы Пифагора. Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т.　е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий. Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике. В самом древнем дошедшем до нас китайском математико-астрономическом сочинении, написанном примерно за 600 лет до Пифагора, среди других предложений, относящихся к прямоугольному треугольнику, содержится и теорема Пифагора. Еще раньше эта теорема была известна индусам. Таким образом, Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым из области практики в область науки. Сегодня мы с вами познакомимся с некоторыми из многочисленных доказательств теоремы Пифагора. А для начала посмотрим отрывок из мини-сериала «Приключения Электроника» (1979 года выпуска). (электроник)

ДОКАЗАТЕЛЬСТВА

1) Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы (для треугольника АВС квадрат, построенный на гипотенузе АС содержит 4 исходных треугольника, а квадраты, построенные на катетах – по 2 треугольника) Теорема доказана.

2) Еще одно наглядное доказательство теоремы Пифагора принадлежит индусам. Посмотрите внимательно на два квадрата, и вам всё станет ясно. Индусы к этому чертежу добавляли лишь одно слово: «СМОТРИ!» (анимация Лиана)

3) Рассмотрим еще одно доказательство теоремы Пифагора, которое приведено в вашем учебнике. Оно выполнено по следующему рисунку.

(Учащимся сообщается лишь идея доказательства — достроить треугольник до квадрата со стороной (а + b) и выразить площадь квадрата возможными способами).

Доказательство (на уроке не проговаривается):

Sкв. = (а + b)². С другой стороны квадрат составлен из четырех одинаковых треугольников с катетами а и в и квадрата со стороной с. Площади приравниваются:

5. Решение задач. (7 мин)

Алгоритм решения задач по теореме Пифагора

1. Внимательно прочитай условие задачи

2. Сделай чертёж

3. Выдели на чертеже прямоугольный треугольник

4. Найди катеты и гипотенузу

5. Запиши теорему Пифагора и соотнеси данные в задаче с ней

6. Выполни подстановку данных

7. Соотнеси полученный ответ с вопросом задачи и смыслом условия

8. Радуйся тому, что задача решена верно!

Древнеиндийская задача.

Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко, 
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”

Решение.
(1 фут = 0,3метра)
АС = х, АВ = х + , АВ² = АС² + СВ²,

, АС = 4 – , АС = (фута).

6. Постановка домашнего задания. (2 мин)

— Уметь доказывать теорему одним из способов.

— Найти одно док-во теоремы (желательно, чтобы док-ва в классе не повторялись, за оригинальность +)

— Придумать рэп или стихотворение на тему «Теорема Пифагора» или её доказательство. (Ералаш)

7. Подведение итогов.(2 мин)

Что нового сегодня узнали?

Как звучит теорема Пифагора?

Понятны ли были способы доказательства теорем?

Какую практическую пользу дает нам теорема Пифагора?

infourok.ru