Точка. Кривая линия. Прямая линия. Отрезок. Луч.
Муниципальное автономное
общеобразовательное учреждение
«Средняя общеобразовательная школа № 7»
городского округа город Стерлитамак
Республики Башкортостан
Конспект урока по математике на тему:
«Точка. Кривая линия. Прямая линия.
Отрезок. Луч».
Учитель начальных классов
Муртазина Эльмира Альбертовна
2015
Тема урока: «Точка. Кривая линия. Прямая линия.
Отрезок. Луч».
Цели:
– формировать представления о фигурах «точка»,«кривая линия»,«прямая линия»,«луч»,«отрезок»;
– учить различать и выполнять построение геометрических фигур: прямая линия, отрезок, луч;
– развивать пространственное воображение;
– воспитывать интерес к геометрическому материалу.
Планируемые результаты: умения: различать геометрические фигуры «точка», «кривая линия», «прямая линия», «луч», «отрезок», отличать их от других фигур и уметь выполнять построение названных геометрических фигур на плоскости.
Оборудование: презентация, сделанная в программеMicrosoftPowerPoint, карточки с фигурами и их названиями, две катушки ниток, ножницы.
Структура урока:
I. Актуализация знаний. Подведение к учебной задаче.
II. Формулировка учебной задачи
III. Решение учебной задачи.
IV. Обобщение по решённой учебной задаче и постановка новой (учебная задача 2).
V. Решение учебной задачи 2.
VI. Применение знаний в новых условиях.
VII. Обобщение. Рефлексия. Перспектива.
VIII. Установление связи с жизнью.
Ход урока
I. Актуализация знаний. Подведение к учебной задаче.
Дети получают карточки с заданием:
– Найдите недостающую фигуру. (Рис.1.)
Рис.1
– Назовите фигуры, которые вы сейчас рассматривали? (Круг, квадрат, треугольник, прямоугольник.)
– Где мы часто встречаемся с этими фигурами? (На уроке математики.)
– Какие из окружающих нас предметов в классе и дома имеют форму треугольника, квадрата, круга и прямоугольника? (Треугольник – крыша дома и школы, квадрат – телевизор, круг – сковородка, прямоугольник – классная доска. )
)
– Сегодня ребята, у нас необычный урок: урок-путешествие в математическую страну, название которой вы прочитаете на воротах этого города.
Слайд № 1
Рис.2
– Верно, это Геометрия, часть великой науки Математики. Посмотрите, а кто живет в этой стране! Вы узнали их? Верно, это наши знакомые: круг, треугольник, квадрат, прямоугольник.
II.Формулировка учебной задачи.
– Открыв ворота, мы познакомимся с новыми фигурами – жителями этой страны.
Слайд № 2
Рис. 3
– Что видите на слайде? (Геометрические фигуры; дом, солнце, дерево.)
– Из каких фигур они состоят? (Квадрат, треугольник, круг, овал, прямоугольник.)
– Какие новые фигуры вы увидели? (Дети задумываются.)
– Сегодня мы познакомимся с новыми фигурами, которые помогли создать рисунок страны Геометрии.
III. Решение учебной задачи.
Практическая работа. Понятие «точка».
– У каждого из вас, на парте есть карандаш и листочек бумаги.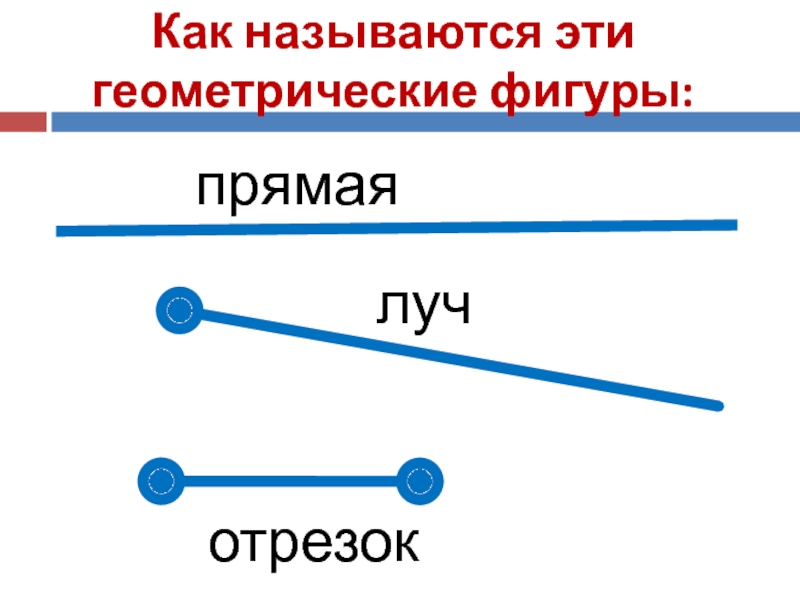 Возьмите карандаш и поставьте его на лист (Учитель то же самое выполняет на доске мелом.)
Возьмите карандаш и поставьте его на лист (Учитель то же самое выполняет на доске мелом.)
– Что сделал карандаш? (Оставил след.)
– Этот след и есть точка – геометрическая фигура.
– В стране Геометрии жила-была точка. Она была маленькой. Её оставил карандаш, когда он дотронулся до листа бумаги своим остро оточенным носиком-грифелем. Но точку никто не замечал. Найдите на рисунке 3 точку. Где она находится? (На дороге.) Так и жила бы она, если бы не попала в гости к линиям.
Рис. 4
– Посмотрите, какие это были линии? (Прямые, искривленные, завитые, неровные, кривые.)
– Сколько на рисунке прямых линий? (Две прямые линии.)
– Сколько изображено кривых линий? (Четыре кривые линии.)
– На что похожи эти линии? Посмотрите на следующий слайд. (Прямые линии похожи на натянутые верёвочки, а верёвочки, которые не натянули, – это кривые линии).
Слайд № 3
Рис. 5
– Определите, у кого из зверей прямая линия, а у кого — кривая линия? (У зайца прямая линия, так как у него натянутая веревочка, а у волка кривая линия, потому что его веревка не натянута. )
)
– Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»
– Как вы, ребята, понимаете, что прямая линия «бесконечна»?
Учитель берет две катушки ниток, держит их в руках, прижав друг к другу. Два ученика разматывают нитки в обе стороны, натягивая их, демонстрируют, что прямую линию можно продолжать в оба конца.
– Как долго можно продолжать прямую линию? (Пока нитки не закончатся.)
– А, если мы возьмем катушки, на которых очень много ниток, выйдем на улицу, размотаем их в две стороны, натянем, то что произойдет с «прямой линией»? (Она станет длиннее, мы ее продолжим.)
– В математике считается, что прямую линию можно продолжать в обе стороны очень долго и что она никогда не кончается. Говорят, что прямая линия бесконечна, т.е. у нее нет концов. Прочитаем стихотворение о прямой линии или короче: прямой.
Вот она какая – линия прямая,
Без начала и без края.
Хоть 100 лет по ней иди,
Не на найдешь конца пути.
– Очень интересно стало точке посмотреть на неё. Сама-то точка малюсенькая. Подошла она, да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг прямая линия превратилась… Что же получилось из прямой?
ЛУЧ ЛУЧ
– Рассмотрите еще раз слайд «Страна Геометрия». На что похожи полученные из прямой ее две части? (На лучи солнца.) Эти фигуры в геометрии называют лучами.
– Каждый луч тоже очень длинный. Но продолжить его можно только в одну сторону. Ведь с другой стороны – точка – начало луча. (На доске учитель прикрепляет рисунок с прямой, разделенной точкой на два луча и еще один луч.)
– Продолжим сказку.Испугалась точка: «Что же я наделала?» Хотела она убежать, да как назло наступила опять на один из лучей.
– И на месте этого луча появилась новая фигура, вот такая:
Р ис. 6
6
– Какое же имя у этой новой фигуры? Как ее называют в стране Геометрии? Как из прямой получилась новая фигура, ограниченная двумя точками? Как из длинной нити получить короткую? (Отрезать ее часть.)
ОТРЕЗОК
Рис. 7
– Можно представить, что для получения отрезка от прямой отрезали часть и отметили ее начало и конец точками. Поэтому и называется эта фигура – отрезок.
IV. Обобщение по решённой учебной задаче и постановка новой (учебная задача 2).
– Вот такая маленькая точка смогла изменить жизнь «больших» линий.
– Какие же еще геометрические фигуры вместе с треугольником, квадратом, прямоугольником и кругом живут в стране геометрии? (Точка, прямая линия, кривая линия, луч, отрезок.)
– Кто догадался, чему нам нужно научиться в стране Геометрии? (Научиться узнавать и чертить прямую линию, луч, отрезок, рисовать кривые линии.)
– Как нарисовать кривые линии? (Дети задумываются. ) Кривую линию удобно моделировать из шнура, веревочек, ниток. Кривые линии могут быть замкнутыми и незамкнутыми.
) Кривую линию удобно моделировать из шнура, веревочек, ниток. Кривые линии могут быть замкнутыми и незамкнутыми.
Незамкнутая кривая линия Замкнутая кривая линия
Рис. 8
Слайд № 4
Рис. 9
V. Решение учебной задачи 2.
– Что вы узнали о прямой линии? (Она не имеет ни начала, ни конца, т.е. она бесконечная.)
– Что узнали о луче? (У него есть начало, но нет конца.)
– Что узнали об отрезке? (Его получили из прямой, у него есть и начало, и конец.)
Слайд № 5
Рис. 10
– Как начертить линию в тетради так, чтобы она была прямой? Какой из имеющихся у вас на парте инструментов нам поможет? (Линейка. Надо провести вдоль линейки линию.)
– Начертим прямую линию. Я – на доске, а вы – тетрадях. Поставьте на прямой линии две точки. Какие фигуры получились? (Прямая линия и отрезок.)
– Как начертить отрезок? (Поставить две точки и соединить их по линейке.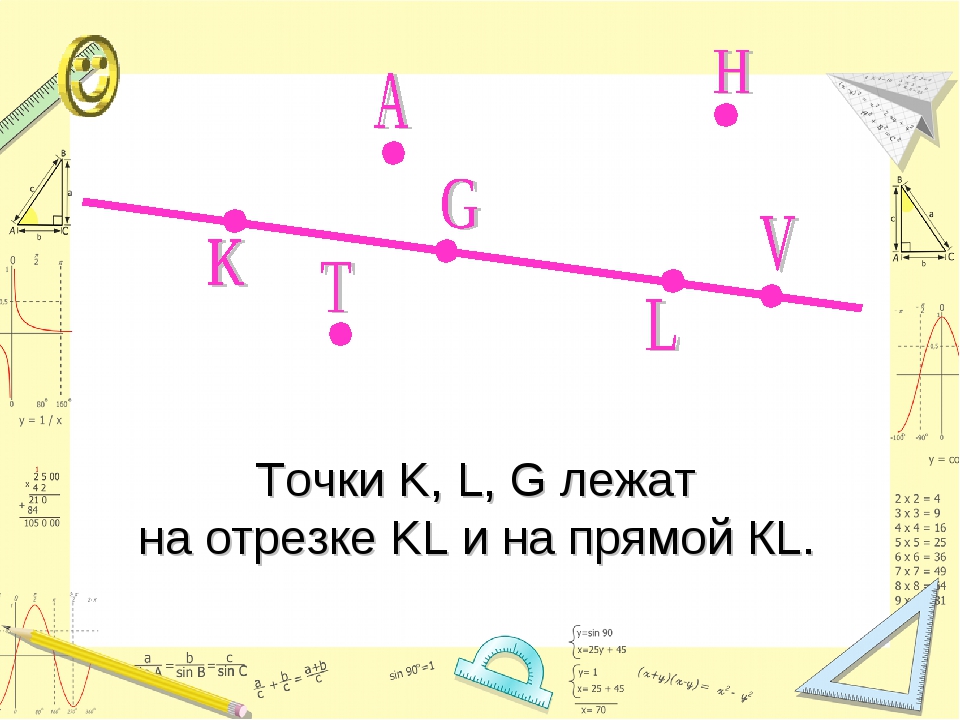 )
)
– Как начертить луч? (Поставить одну точку и провести по линейке прямую линию.)
– Постройте отрезок и луч в тетрадях.
Правило:
Линейку прижать одной рукой.
Другой рукой, направляя карандаш вдоль линейки, провести линию.
Слайд № 6
Рис. 11
VI.Применение знаний в новых условиях.
Работа в парах.
– Посоветуйтесь в парах и ответьте на вопрос: сколько прямых линий можно провести через две точки? (Одну.)
– Для этого выполните задание на листочках, которые лежат у вас на партах.
– Посоветуйтесь в парах: сколько кривых линий можно провести через две точки? (Много.)
– Проверим по слайду.
Слайд № 7
Рис. 12
– Проведите три кривые линии через эти же две точки.
VII. Обобщение. Рефлексия. Перспектива.
– Посмотрите на слайд. Подумайте, на какие группы можно разделить данные геометрические фигуры. (Лучи – 2, 5; отрезки – 1, 3, 4.)
(Лучи – 2, 5; отрезки – 1, 3, 4.)
Слайд № 8
Рис. 13
– Какие жители страны Геометрии Вам были знакомы? (Квадрат, треугольник, прямоугольник и круг.)
– С какими жителями страны Геометрии познакомились?(Точка, кривая линия, прямая линия, отрезок, луч.)
– Какой может быть линия? (Прямая, кривая.)
– Как получить отрезок? (Поставить две точки и соединить их по линейке линией.)
– Как отрезок отличить от прямой линии? (У отрезка есть начало и конец, а прямая линия бесконечна.)
– Понравилось ли вам в стране Геометрия? (Да/Нет.)
– Жители страны Геометрии благодарят вас за дружбу с ними и за ваши правильные ответы.
– Оцените свою работу на уроке с помощью «Светофора».Если вам было интересно, и всё понятно, поднимите вверх зеленый сигнал светофора.
– Если вам понравился урок, но было не всё понятно, поднимите вверх желтый сигнал светофора.
– Если урок вам не понравился, и было ничего не понятно, то поднимите вверх красный сигнал светофора.
VIII. Установление связи с жизнью.
– Ребята, дома с родителями или самостоятельно найдите на предметах, которые вас окружают точки, прямые линии, кривые линии, лучи и отрезки.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/153698-tochka-krivaja-linija-prjamaja-linija-otrezok
Сколько можно сделать лучей из одной точки. Точка, линия, прямая, луч, отрезок, ломанная
Цель: провести исследовательский эксперимент с помощью осязательного метода сравнения выявить отличия плоскости и пространства по размерности
Оборудование: игрушка объемная, альбом, карандаши, тетрадь, ручка, проектор, фонарик
Аннотация: в ходе работы дети отвечают на вопросы:
как получить плоскую фигуру и как
получить объемную фигуру. Возьмите
объемную игрушку, нарисуйте ее в альбоме
и сравните саму игрушку и ее изображение
на бумаге. Проанализируйте отличие
плоскости от пространства на примере
детских игр (настольный хоккей (1 рычаг
управ.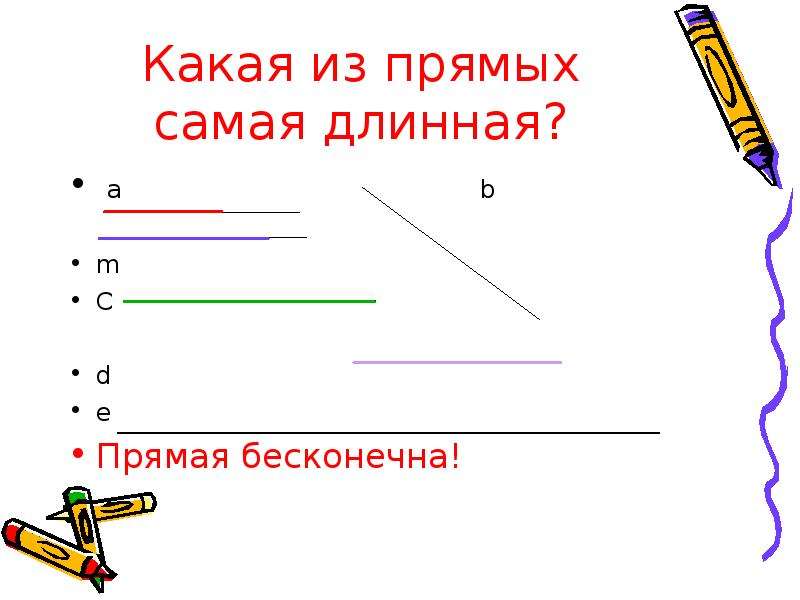 ), машинка на плоскости (2 рычага
управ.), самолет (3 рычага управ.)): линия
(в т.ч. прямая) -1 разм., поверхность – 2
разм., пространство – 3 разм. Нарисуйте
в альбоме рыбку. Раскрасьте ее. Вылепите
такую же из пластилина. Посадите ее в
прозрачную банку. Чем отличаются
изображения рыбок. Можно даже сделать
аквариум с рыбками и проанализировать
эту модель также. Понятие луча можно
рассмотреть на примере луча света, как
абстрактное понятие обладающее св-вами:
прямолинейность и существование начала.
Началом луча будем считать источник
света, прямолинейность определяется
по наличию тени (луч не может обогнуть
препятствие). На примере с солнечными
лучами можно показать еще одно их
свойство – бесконечность. Для этого
фонарик используют как маленькое
солнышко, пуская луч света в сторону
поля или вдоль дороги нельзя сказать
где он заканчивается. Проанализируйте,
что считать лучом, а что отрезком.
Договоримся, что луч имеет начало и
направление, а отрезок – начало и конец.
Как быть с солнечными лучами? Это отрезок
или луч? (часть их попадает на Землю,
часть рассеивается в пространстве, если
на пути луча встречается физический
объект, то это уже не луч, а отрезок).
), машинка на плоскости (2 рычага
управ.), самолет (3 рычага управ.)): линия
(в т.ч. прямая) -1 разм., поверхность – 2
разм., пространство – 3 разм. Нарисуйте
в альбоме рыбку. Раскрасьте ее. Вылепите
такую же из пластилина. Посадите ее в
прозрачную банку. Чем отличаются
изображения рыбок. Можно даже сделать
аквариум с рыбками и проанализировать
эту модель также. Понятие луча можно
рассмотреть на примере луча света, как
абстрактное понятие обладающее св-вами:
прямолинейность и существование начала.
Началом луча будем считать источник
света, прямолинейность определяется
по наличию тени (луч не может обогнуть
препятствие). На примере с солнечными
лучами можно показать еще одно их
свойство – бесконечность. Для этого
фонарик используют как маленькое
солнышко, пуская луч света в сторону
поля или вдоль дороги нельзя сказать
где он заканчивается. Проанализируйте,
что считать лучом, а что отрезком.
Договоримся, что луч имеет начало и
направление, а отрезок – начало и конец.
Как быть с солнечными лучами? Это отрезок
или луч? (часть их попадает на Землю,
часть рассеивается в пространстве, если
на пути луча встречается физический
объект, то это уже не луч, а отрезок).
4. Проект 1-2 класс «Плоское и объемное: угол»
Эта
тема является продолжением предыдущей.
Цель: сформировать представление об угле, научить узнавать и обозначать его.
Аннотация: Эта тема связана с негативным опыт
детей, поэтому учителю следует обратить
внимание на изучаемый предмет, а не
фиксировать воспоминания ребенка.
Рассмотрите разные примеры: стрелки на
часах (у них есть начало и направление
– поэтому это лучи). Стрелки разводятся
на разное расстояние, та часть плоскости,
что нах. между ними наз. углом. Выполните
различные задания на эту тему, которые
показывают, что углы можно сравнивать
между собой (найдите такие задачи сами).
Сравнивать можно так: нарисовать два
угла, перевести на полупрозрачную бумагу
один из углов и сравнить изображения,
изображение на другой угол. Сложите
лист бумаги два раза – получится прямой
угол. Покажите, как можно пользоваться
треугольником для построения разных
углов. Какое время показывают часы, если
стрелки образуют прямой угол, а минутная
стрелка стоит на 12? Подберите рисунок,
на котором учащиеся сосчитают изображенные
там углы.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие? A A A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a b cЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
B AПрямые могут быть
- пересекающимися, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
B AЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B AОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Aпрямая линия AB
B AОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B A ✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого.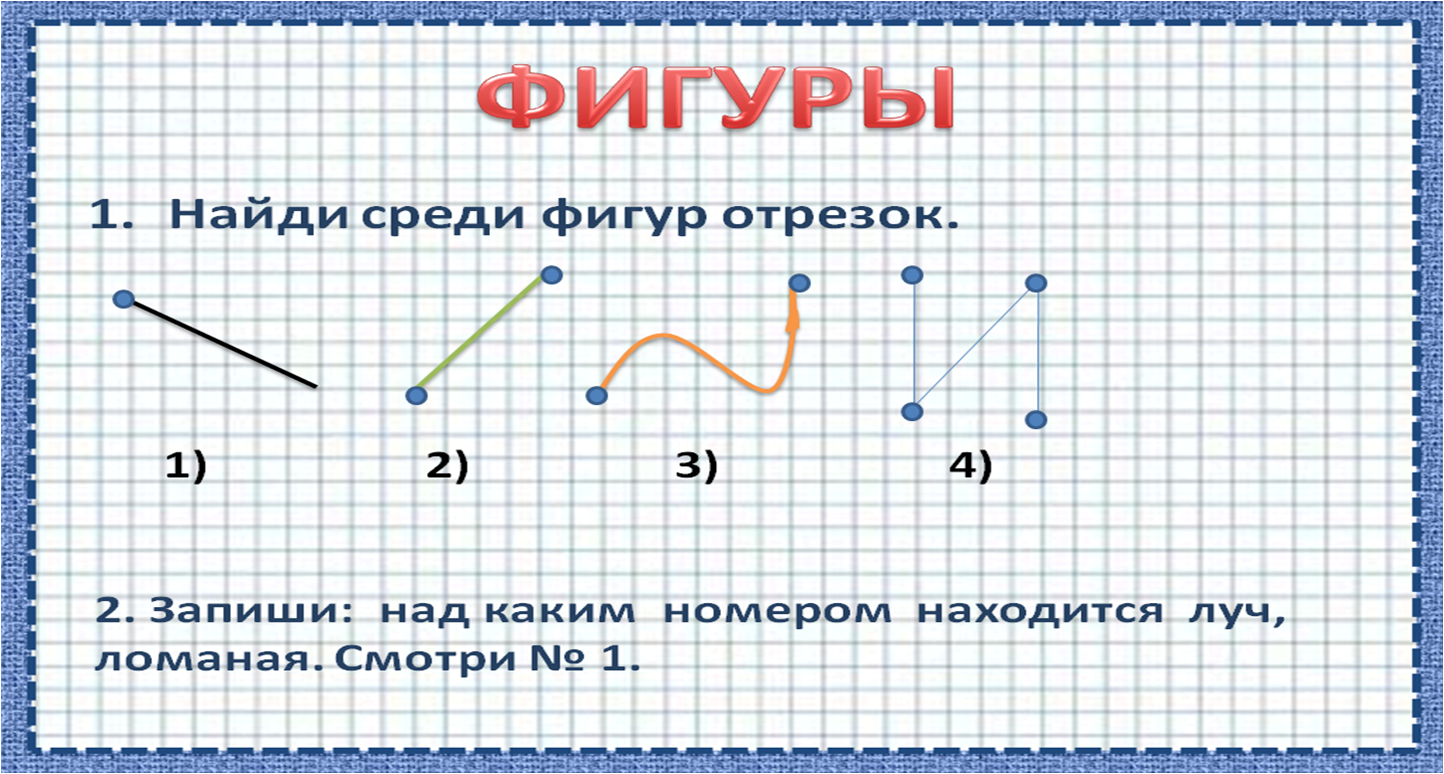
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
Технология: развивающее обучение Л. В. Занкова.
Цели урока:
- создать условия для формирования первичного представления о луче, научить различать прямую линию, отрезок, луч, проверить степень усвоения детьми ранее данной информации;
- развивать память, внимание, мышление, умение наблюдать, сравнивать, классифицировать, анализировать и обобщать, развивать интеллектуальные и практические умения детей;
- воспитывать активную личность.
Ход урока
1. Оргмомент.
Уч: Здравствуйте, ребята. Я очень рада видеть ваши добрые, веселые глаза. Вижу, что вы готовы к работе. И сегодня мы с вами отправляемся в очередное путешествие по Великой стране Математики и побываем в уже известном нам городе Геометрии. Нашим экскурсоводом будет Карандаш.
(рисунок №1)
2. Актуализация базовых знаний.
Уч: Со многими жителями города вы уже знакомы
и сможете без труда их узнать.
Игра: “Узнай меня”.
(На партах у каждого ребенка набор геометрических фигур.)
Я – многоугольник, имею 3 стороны. Как меня зовут?
(Учащиеся выбирают из раздаточного материала треугольник и показывают его учителю. Учитель крепит на доску синий треугольник.)
Я – многоугольник, у меня 4 равные стороны. (квадрат)
А вот я – вообще не многоугольник. Зато у меня можно найти в часах, в машине, в чашке, на меня даже солнышко издали похоже. Кто же я? (круг)
(рисунок №2)
Уч: Чем похожи все фигуры?
Дети: Они все одного цвета.
Уч: Чем отличаются?
Дети: Они имеют разную форму.
Дети: Они разного размера.
Уч: Какая фигура лишняя?
Дети: Лишняя фигура – треугольник, потому что он самый маленький.
Дети: Я согласен, что лишняя фигура
треугольник, потому что квадрат и круг имеют
немножко похожую форму. Если у квадрата обрезать
уголки, то он станет похожим на круг.
Если у квадрата обрезать
уголки, то он станет похожим на круг.
Дети: А я думаю, что лишний круг. Он круглый и у него нет прямых линий.
Дети: А еще у круга нет углов. Я тоже думаю, что круг лишний.
Физминутка .
(Гимнастика для глаз по методу Г. А. Шичко.)
Уч: А теперь нарисуйте данные фигуры, выполнив просьбы букв.
(рисунок №3)
(Ф. – форма, Ц. – цвет, Р. – размер. Дети рисуют геометрические фигуры, меняя форму, цвет и размер по данному заданию.)
Уч: Молодцы. Все с заданием справились. А еще, ребята, у данных фигур был разный характер. Круг был веселее, чем треугольник, а треугольник веселее, чем квадрат. Кто был самый веселый?
Дети: Круг.
Уч: А кто самый грустный?
Дети: Квадрат.
Уч: А теперь продолжим наше путешествие.
Вместе с нашим экскурсоводом Карандашом
отправимся на проспект Линейный. Здесь живут
веселые и добрые наши друзья.
Как вы думаете, кто они?
Дети: В этих домах живут прямые линии.
Дети: Там еще живет отрезок.
Дети: Там живут прямые и кривые линии.
Уч: Молодцы. А теперь я расскажу историю, которая случилась с Карандашом. А вы мне будете помогать. Договорились? Но прежде, чем слушать сказку про Карандаша, я предлагаю вам немножко отдохнуть.
Физминутк а.
(Упражнения, корректирующие осанку.)
Выход на тему урока.
Уч: Вот какая история случилась с Карандашом.
Решил однажды Карандаш прогуляться по Прямой линии. Идет, идет, устал, а конца линии все не видно.
Долго ли мне еще идти? Доберусь ли я до конца? – спрашивает он у Прямой.
Что ему ответит Прямая линия?
Дети: Карандаш, не дойдет до конца линии, потому что у прямой нет конца.
Уч: Правильно.
Эх ты, у меня же нет конца, – ответила Прямая.
Тогда я пойду в другую сторону, — сказал
Карандаш.
Дети: И в другую сторону, Карандаш, не дойдет до конца линии, потому что у прямой нет начала и конца.
Уч: Верно. А Прямая, даже песенку ему спела.
Без конца и края линия прямая,
Хоть сто лет по ней иди,
Не найдешь конца пути.
Уч: Давайте начертим прямую линию в тетрадь.
Расстроился Карандаш.
Что же мне делать? Я не хочу ходить по линии. Я устал.
Что вы, ребята, посоветуете Карандашу?
(Дети дают различные советы.)
Уч: Тогда отметь на мне 2 точки, — посоветовала ему Прямая. Так Карандаш и сделал.
(Учащиеся ставят на прямой две точки.)
Ура! – Закричал Карандаш. – Появились два конца. Теперь я могу гулять от одного конца до другого. Но тут же задумался.
А что же это такое на Прямой получилось?
Ребята, помогите Карандашу.
Дети: Это отрезок.
Уч: А что вы знаете об отрезке?
Дети: Отрезок – это часть прямой. У него есть
начало и конец.
У него есть
начало и конец.
4. Изучение нового материала.
Уч: А однажды Карандаш решил отнять у Прямой отрезок. Взял он с собой ножницы и потихоньку вырезал отрезок. Соединил оставшиеся концы и завязал. Только не понятно ему, что же это такое получилось.
А вы, ребята, знаете? Может это быть новым отрезком?
Дети: Нет, не может. У одной линии нет начала и есть конец, а у другой – есть начало, но нет конца.
Уч: А получилось на прямой 2 луча, выходящих из одной точки. У луча есть начало, а вот конца нет.
5. Практическая часть.
Работа по учебнику. (И. Аргинская, математика, часть 1, стр. 52, №100)
Уч: Сравни линии. Чем они похожи? Чем отличаются? С какими линиями ты уже был знаком?
(рисунок № 4)
Дети: Мы знали прямую линию, отрезок.
Уч: Обведи прямую линию синим карандашом, отрезок – зеленым. Как называется линия, с которой вы познакомились сегодня?
Дети: Эта линия называется лучом.
Уч: Найди луч и обведи его красным карандашом.
Подумай и объясни, чем отличается луч от прямой?. От отрезка?
Начерти два луча.
Уч: Луч приготовил для вас загадку.
Среди поля голубого —
Яркий блеск огня большого.
Не спеша огонь тут ходит,
Землю-матушку обходит,
Светит весело в оконце.
Ну, конечно, это …….
Дети: Солнце.
Физминутка.
(Упражнения для кистей рук.)
Уч: А почему Луч загадал вам загадку про солнышко?
Д: Потому что у солнышка тоже есть лучи.
Уч: Нарисуйте в тетрадках солнышко.
Уч: А сколько лучей у вашего солнышка?
(Дети говорят, сколько лучей они нарисовали у солнышка. Количество лучей разное.)
Уч: Сколько лучей можно провести из одной точки?
(Дети высказывают свое мнение.)
Уч: Молодцы. Действительно, из одной точки
мы можем провести любое количество лучей.
Работа по учебнику. (стр. 54 № 105)
Под каждым рисунком в левой клетке напиши, сколько на нем прямых, а в правой – сколько лучей.
(рисунок №5)
Уч: В тетрадке начерти 3 отрезка и 2 луча.
6. Итог урока.
Уч: Вот и закончилось наше воображаемое путешествие. Мы прощаемся с городом Геометрией, его прекрасными жителями – геометрическими фигурами. Давайте еще раз вспомним, что же мы знает про прямую линию, отрезок и луч.
Дети: У прямой нет начала и нет конца.
Дети: У отрезка есть начало и есть конец.
Дети: А у луча есть начало и нет конца.
Уч: Надеюсь, наше путешествие было
увлекательным и интересным. Давайте улыбнемся на
прощание всем обитателям волшебной страны
Математики, друг другу и порадуемся нашим
успехам. Но это лишь малая часть того, что можно
узнать на уроках математики. Впереди вас ждет еще
много путешествий по Великой стране, название
которой: Математика.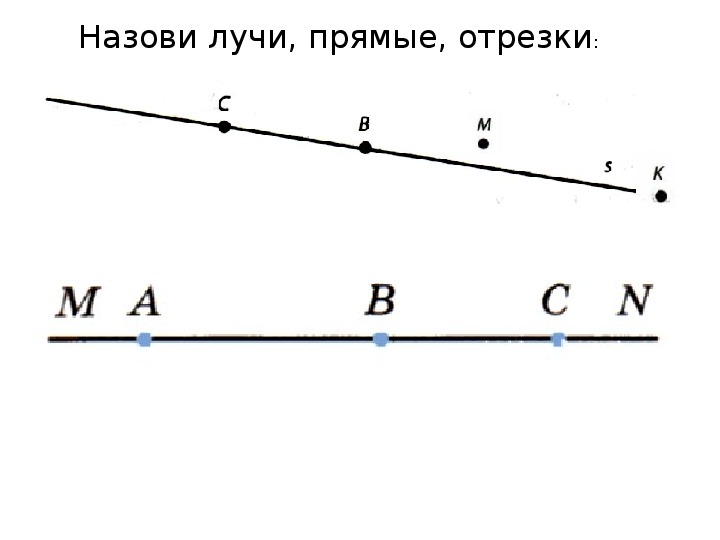
Луч — это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой. Луч также называется полупрямой .
Любой луч имеет начало и направление. Начало луча , начальная точка или вершина луча — это точка, из которой исходит луч. Таким образом, у луча есть начало, но нет конца.
Рассмотрим три луча с общим началом:
Все 3 луча имеют общую начальную точку O , но разные направления. Про каждый из них можно сказать: луч исходит из точки O или луч исходящий из точки O .
Дополнительные лучи
Любая точка, лежащая на прямой линии, делит эту прямую на две полупрямые, то есть на две части. Каждая из этих частей будет называться дополнительным лучом относительно второго луча:
Дополнительные лучи — это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой. Также можно сказать, что дополнительными называются лучи, дополняющие друг друга до прямой линии.
Обозначение лучей
Луч обозначают одной строчной латинской буквой:
луч h .
Также луч можно обозначить двумя точками, лежащими на нём:
При обозначении луча двумя точками, на первом месте ставится буква, обозначающая начало луча, а на втором — буква, обозначающая какую-либо другую его точку: луч BC .
Посмотрим на следующий пример:
Луч с началом в точке A можно обозначить как AB или AC .
Конспект урока по математике для учащихся 1 класса по теме «Точка. Линии прямая, кривая, отрезок, луч, ломаная.»
Конспект урока по математике для учащихся 1 класса по теме
«Точка. Линии: прямая, кривая, отрезок, луч, ломаная.»
Тема: Точка. Линии: прямая, кривая, отрезок, луч, ломаная.
Образовательные цели:
Уточнить геометрические понятия: «точка, прямая, кривая, луч, отрезок, ломаная» через предметно-практическую деятельность.

Упражнять в черчении линий, располагая их в пространстве в разном положении.
Научить измерять длину отрезков разными способами.
Применять сформированные понятия при выполнении различных заданий.
Развивающая цель: Развитие математической речи.
Коррекционная цель: Развитие ориентировки в пространстве, зрительно-моторной координации.
Воспитательная цель: Развитие умения анализировать свои действия и управлять ими.
Тип урока: комбинированный урок, урок-практикум.
Методы, формы, приемы: словесный, практический, наглядный.
Оборудование: тетради, линейки, карандаши, карточки, ленты, домики, табличка с правилом урока, листы бумаги, звоночек.
Ход урока
I – Организационный этап
Учитель: На какой урок нас позвал звонок?
Что мы делаем на уроках математики?
В стране «Математика» есть много разных городов.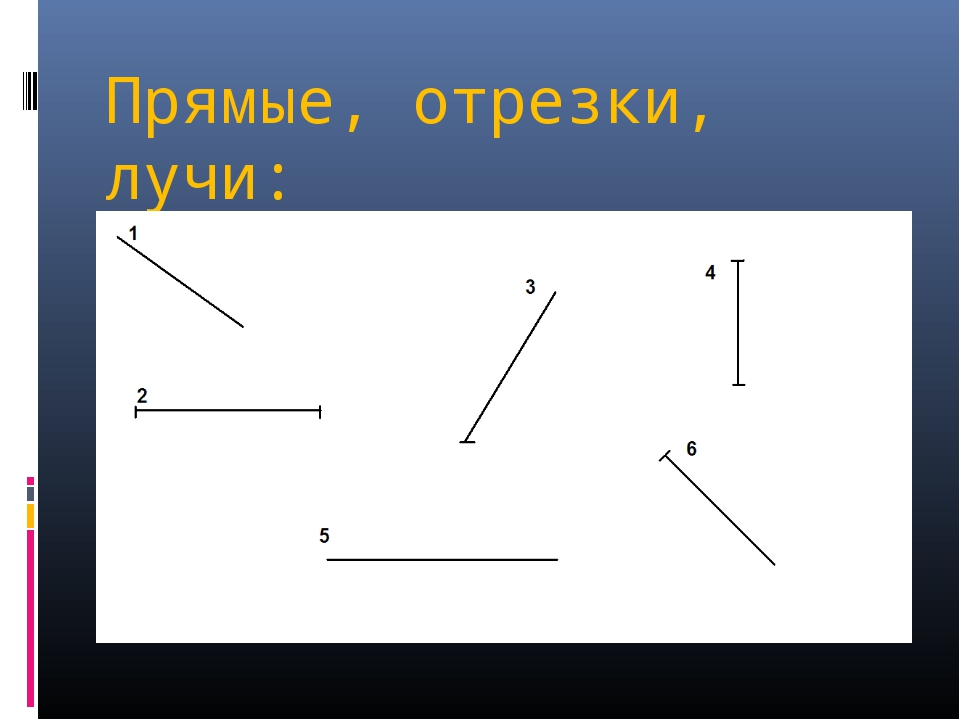
На этом уроке мы посетим город, который называется «ГЕОМЕТРИЯ».
Стихотворение читает ученица
Геометрия – наука про измерение Земли.
Без нее нельзя построить ни дома, ни корабли.
Не скроить костюм и платье, не подстричь в саду кусты.
И, поэтому, друзья, без нее никак нельзя!
Геометрия – наука, которая занимается изучением свойств разных фигур на плоскости и в пространстве.
Учитель: В городе много улиц, но мы посетим только одну. Кто там живет? Это вы сейчас узнаете и назовете тему урока.
II – Мотивация учебной деятельности учащихся. Сообщения темы, цели, задач урока и мотивация учебной деятельности школьников
1) рисование учителем на доске человечка
Точка, точка, запятая, минус рожица кривая,
Палки, палки, огуречик. Вот и вышел человечек.
Вот и вышел человечек.
Учитель: Смотрите, к нам пришел человечек из города «Геометрия». Он хочет подсказать нам тему урока. (Что я использовала, рисуя фигуру смешного человека?)
(Ученики определяют тему урока).
Тема урока: «Точка. Линии».
А какие линии вы знаете? Как вы думаете, чем мы будем сегодня заниматься?
На уроке нам предстоит много строить и чертить. А что нам в этом поможет? (карандаш и линейка)
Стихотворения читают ученики
Я чёрный, красный, желтый, синий,
С начинкой твёрдой в середине,
Я с острым ножиком дружу
И что хочу – изображу. (Карандаш)
Всем ребятам помогаю сделать ровную черту.
Я в тетрадках уважаю чистоту и прямоту. (линейка)
Учитель: Точки и линии окружают нас повсюду. Архитектор чертит дома, используя прямые линии. Художник рисует людей, животных и растения, отражая кривые линии. Многие приборы работают, применяя луч. Посмотрите, у нас в классе многие предметы состоят из линий и точек. Нам тоже нужно хорошо знать эту тему, этим мы и займемся. Кроме того, есть много игр с точками и линиями. Это «Морской бой», «Обводки», «Точки», «Точки и отрезки», «Крестики и нолики». В конце урока научимся играть в игру «Точки».
Архитектор чертит дома, используя прямые линии. Художник рисует людей, животных и растения, отражая кривые линии. Многие приборы работают, применяя луч. Посмотрите, у нас в классе многие предметы состоят из линий и точек. Нам тоже нужно хорошо знать эту тему, этим мы и займемся. Кроме того, есть много игр с точками и линиями. Это «Морской бой», «Обводки», «Точки», «Точки и отрезки», «Крестики и нолики». В конце урока научимся играть в игру «Точки».
Учитель: Проверьте все ли учебные принадлежности на месте? А очки готовы помочь вам в работе? Раз вы готовы, то начинаем. Запишем в тетрадках число. Посмотрите на дома. Как вы думаете, кто там живет? (ответы учеников).
Прочитайте правило урока: «Математику нельзя изучать, наблюдая, как это делает сосед».
Поэтому работаем все дружно, старательно, красиво и внимательно!
III – Восприятие и первичное осознание нового материала
Учитель: Кроме линейки есть и другой способ провести прямую линию – надо просто перегнуть лист. Линия сгиба — это прямая линия.
Линия сгиба — это прямая линия.
Выполним геометрическую разминку.
1. Геометрическая разминка
Учитель: Возьмите в руки лист бумаги. Какая это геометрическая фигура? Перегните ее так, чтобы получилось
1) 2 прямоугольника
2) 2 треугольника
3) треугольник и трапеция
4) 4 квадрата
5) 4 треугольника
Учитель: У вас получались линии на сгибах, которые формировали разные геометрические фигуры. А сейчас прогуляемся по улице, где живут линии.
2. Усвоение новых знаний
А) Точка
Учитель: Пора заглянуть в домик № 1. Кто там живет? (Звенит звоночек, ученица встает и рассказывает свою тему).
Рассказ ученицы про точку.
1.Знаете ли вы, что точка- самая простая геометрическая фигура.
Ее нельзя измерить, у нее нет длины, ширины.
Точку можно назвать буквой, например, точка А.
Все линии и фигуры начинаются с точки и состоят из них.
Точки могут располагаться на прямой или вне прямой.
Через точку можно проводить разные линии.
А еще точка живет в русском языке. Там она заканчивает предложение.
Практическая работа № 1 «Точка»
Учитель: Поработаем с точками. Откройте тетради. Запишите число. Пропустите 3 клетки вниз и 3 клетки справа и карандашом поставьте точку. Назовем ее точка А. Через 8 клеточек поставьте вторую точку М. Мы можем сказать, что обе точки расположены на одной линии? Проверьте линейкой. Поставьте внизу посредине листа третью точку К. Можно сказать, что все 3 точки расположены на одной прямой линии? Если соединить точки А и К, К и М , что получим? А все 3 точки? А если линию замкнуть?
Можно сказать, что все 3 точки расположены на одной прямой линии? Если соединить точки А и К, К и М , что получим? А все 3 точки? А если линию замкнуть?
Упражнение «Точки в жизни»
Учитель: Давайте подумаем, а где в жизни мы встречаемся с точками. В этом вам поможет карточка с картинками. (Ученики приводят примеры. Опираясь на карточку с картинками).
Б) Прямая
Учитель: Давайте заглянем в домик № 2. Кто там живет? (Звенит звоночек, ученица встает и рассказывает свою тему).
Рассказ ученицы про прямую линию.
Знаете ли вы, что прямая линия может быть продолжена сколько угодно в обе стороны, то есть она не имеет концов или границ. Поэтому у нее нет имени.
Через одну точку можно провести сколько угодно прямых линий.
Через две точки можно провести только одну прямую линию.

Прямые могут располагаться вертикально, горизонтально и под углом, т.е. наклонно.
Прямые могут пересекаться, а могут идти параллельно.
Практическая работа №2 «Прямая линия»
Учитель: В тетради проведите через точки А и М линию. Какая это будет линия? Сколько таких линий можно провести через эти 2 точки? А через 1 точку? Проведите через точку К несколько прямых линий.
Практическая работа № 3
Учитель: Возьмите в руки ленты, это ваши линии. Покажите прямую линию.
Кончики свисают, т. к. у нее нет начала и конца. Расположите их горизонтально, а теперь вертикально, наклонно.
Поработайте в парах. Покажите параллельные прямые. А теперь пусть они пересекутся. Точка, где линии встретились называется точкой пересечения.
Упражнение «Прямые в жизни»
Учитель: Давайте подумаем, а где в жизни мы встречаемся с прямыми. В этом вам поможет карточка с картинками. (Ученики приводят примеры, опираясь на карточку с картинками).
В этом вам поможет карточка с картинками. (Ученики приводят примеры, опираясь на карточку с картинками).
В) Луч
Учитель: Отправляемся в домик № 3. (Звенит звоночек, ученик встает и рассказывает свою тему).
Рассказ ученика про луч
Знаете ли вы, что Луч – это часть прямой линии, ограниченной, с одной стороны.
У луча всегда есть начало, и это точка, ее можно назвать буквой.
Из 1 точки можно провести сколько угодно лучей.
А если провести 2 луча из 1 точки, то получится угол. Углы могут быть разные: прямые, острые и тупые.
Практическая работа № 4
Учитель: Возьмите ленточку только за один конец. Какая линия получилась?
Соедините 2 луча, что получили? (угол, ломаную).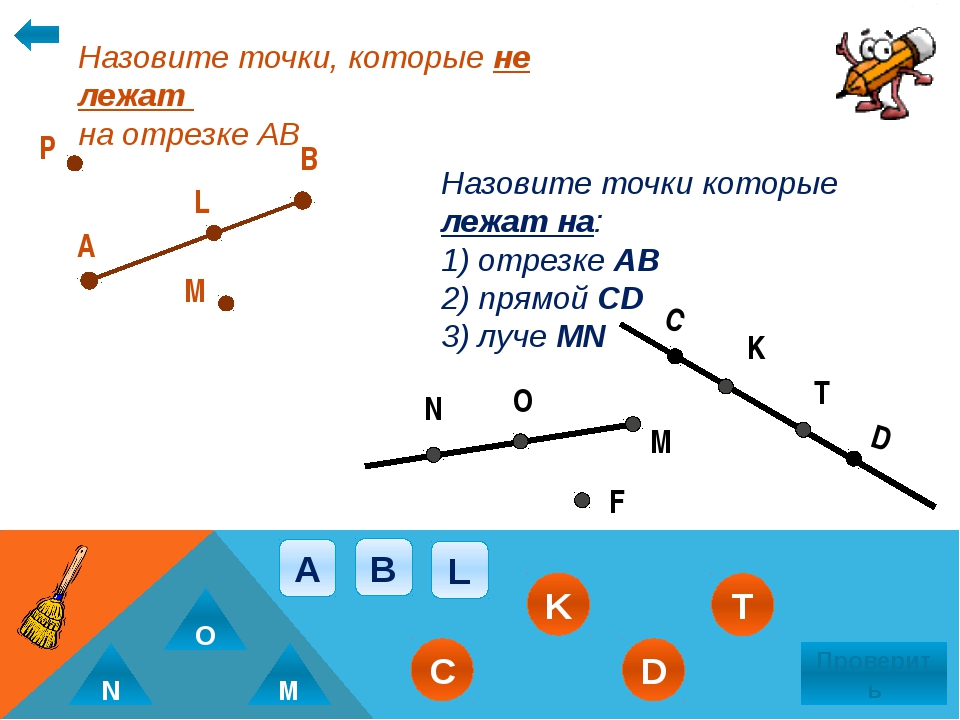 Могу я добавить свою линию? Сколько можно провести лучей из одной точки?
Могу я добавить свою линию? Сколько можно провести лучей из одной точки?
Практическая работа № 5
Учитель: Давайте построим лучик в тетрадях. Что надо поставить? (точку) Назовем ее точкой О. Сколько еще лучей можно провести через эту точку. Проведите. Найдите угол.
Упражнение «Лучи в жизни».
Учитель: Давайте подумаем, а где в жизни мы встречаемся с лучами. В этом вам поможет карточка с картинками. (Ученики приводят примеры, опираясь на карточку с картинками).
Г) Кривая
Учитель: Отправляемся в домик № 4. Кто там живет? (Звенит звоночек, ученик встает и рассказывает свою тему).
Рассказ ученика про кривую линию
Знаете ли вы, что кривые линии тоже состоят из точек?
Их можно проводить без инструмента, от руки.

Они не имеют начала и конца.
Они, могут быть замкнутые и незамкнутые.
Через 1, 2 и более точек можно провести много кривых линий.
Кривые линии живут в круге, овале, геометрических фигурах и других рисунках.
Практическая работа № 6
Учитель: Возьмите ленты за 2 конца, натяните. А теперь расслабьте руки. Какая получилась линия? Бросьте ленту на парту. Какую линию видите?
Практическая работа № 7
Учитель: Поставьте в тетрадях 2 точки и соедините их от руки, без линейки. Что у вас получилось? Можно еще провести кривую линию через эти 2 точки? Проведите. Сколько кривых можно провести через 1 точку? А как вы думаете, можно ли нарисовать кривую линию без точек? (Можно). Нарисуйте.
Упражнение «Кривые линии в жизни»
Учитель: Давайте подумаем, а где в жизни мы встречаемся с кривыми линиями.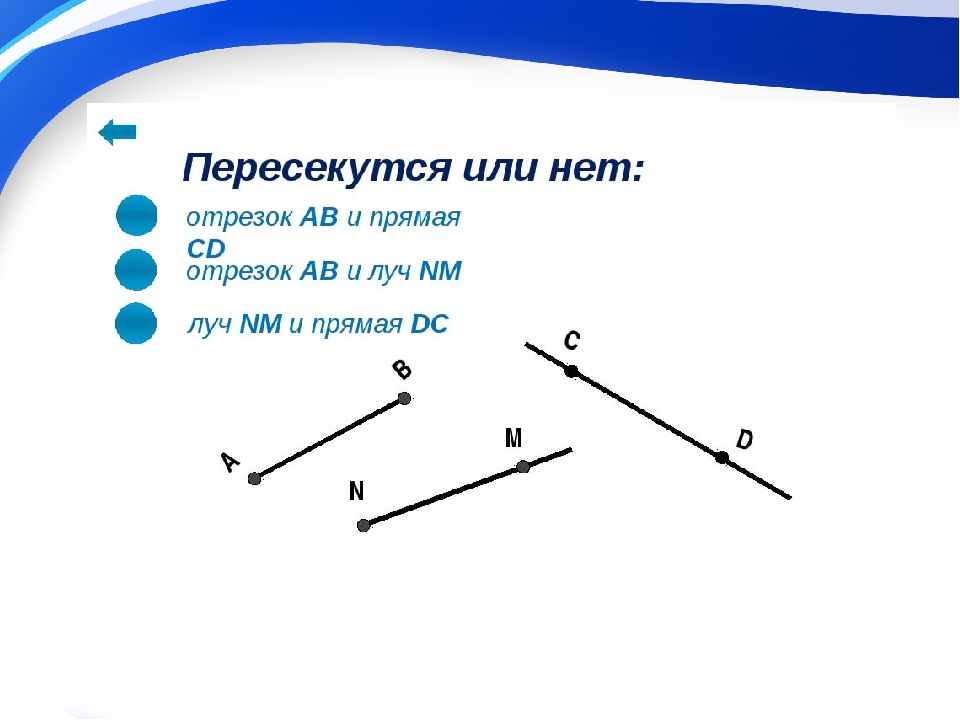
(Ученики приводят примеры, опираясь на карточку с картинками).
Физкультурная пауза с лентами.
Зрительная гимнастика.
Д) Отрезок
Учитель: Чтобы познакомиться еще с одной линией, послушайте сказку.
Жила-была любопытная точка, которая хотела всё знать. Увидит любую линию и непременно спросит: «Какая это линия, длинная или короткая? Замкнутая или нет?» Подумала однажды точка: «Как же я всё смогу узнать, если всегда буду жить в одном месте?» И отправилась точка путешествовать по прямой линии. Шла она шла. Долго шла. Устала и говорит: «Скоро ли будет конец у прямой линии?»
Дайте ответ точке. Почему?
«Что же мне делать, — задумалась точка, — Не могу же я вечно гулять по прямой». «А ты позови на помощь ножницы», — подсказала прямая. Тут, откуда ни возьмись появились ножницы, щёлкнули раз, щёлкнули два, и разрезали прямую.
«Как интересно, что же получилось из моей прямой?» «Это отрезок — сказали ножницы, теперь ты на отрезке прямой.
Учитель: Отрезки прямой живут в доме № 5. (Звенит звоночек, ученик встает и рассказывает свою тему).
Рассказ ученика про отрезок.
Часть прямой, ограниченной с обеих сторон, называется отрезком.
От прямой линии можно в любом месте отрезать кусочек и получится отрезок.
Отрезок имеет начало и конец и его обозначают буквами.
Через одну точку можно провести сколько угодно отрезков прямой линий.
Через две точки можно провести только один отрезок.
Отрезок имеет определенную длину, которую можно измерить. Линейка — инструмент для измерения длин отрезков.
Отрезки могут быть равными и неравными по длине.

Отрезки могут располагаться вертикально, горизонтально и наклонно.
Отрезки прямой могут пересекаться.
Отрезки прямой могут идти параллельно.
Их можно складывать, делить на равные части.
Практическая работа № 8
Учитель: Возьмите ленты и покажите отрезки. Расположите их горизонтально, вертикально и наклонно. Поработайте в парах и покажите параллельные отрезки, а теперь пусть они пересекутся. Как называется их общая точка?
Практическая работа № 9
Учитель: Поставьте точку К. Постройте отрезок КМ=7 см горизонтально. Второй отрезок АС=6см, вертикально. Пусть они пересекутся. Точка О будет называться точкой пересечения. (см. карточку)
Как можно измерять отрезки? (линейкой, наложением, на глаз)
Практическая работа № 10
3) Учитель: У вас на парте полоски. Это три отрезка: красный, синий, желтый. Какой самый большой (маленький?) Как можно определить, какой самый большой, а какой самый маленький? (на глаз, наложением, измерением). Сделайте это. Какой длины самый большой отрезок? Самый маленький?
Это три отрезка: красный, синий, желтый. Какой самый большой (маленький?) Как можно определить, какой самый большой, а какой самый маленький? (на глаз, наложением, измерением). Сделайте это. Какой длины самый большой отрезок? Самый маленький?
Упражнение «Отрезки в жизни».
Учитель: Давайте подумаем, а где в жизни мы встречаемся с отрезками.
(Ученики приводят примеры, опираясь на карточку с картинками).
Е) Ломаная
Учитель: У нас остался еще один домик № 6. Кто там живет?
(Звенит звоночек, ученица встает и рассказывает свою тему).
Рассказ ученицы про ломаную.
Линия, состоящая из нескольких отрезков и лучей, называется ломаной.
Знаете ли вы, что, когда отрезки соединяются, получается ломаная линия.

Она может состоять из 2, 3, 4 и более отрезков. Начало одного отрезка является концом другого отрезка.
Ломаная может быть замкнутой и незамкнутой.
Замкнутая ломаная на плоскости ограничивает многоугольник.
Отрезок ломаной называется звеном, а место соединения 2-х отрезков называется вершиной.
Для нахождения длины ломаной следует измерить длину каждого звена и результаты сложить.
Практическая работа № 11
Учитель: Поработайте в парах. У вас вместе 6 отрезков.
Какую линию можете сложить из них? Сделайте это. Что получилось?
Практическая работа №12
Учитель: Начертите ломаную из 4 отрезков и найдите ее длину. Как называются отрезки ломаной, а места их соединения? А теперь замкните ее. Какую фигуру получили? А из 3-х, 6-ти ломаных какая получится фигура?
Какую фигуру получили? А из 3-х, 6-ти ломаных какая получится фигура?
Упражнение «Ломаные в жизни»
Учитель: Давайте подумаем, а где в жизни мы встречаемся с ломаными.
(Ученики приводят примеры, опираясь на карточку с картинками).
IV – Первичная проверка понимания усвоенного материала
1) фронтальный опрос
Учитель: Подведем итоги работы.
Какая самая простая геометрическая фигура, из которой состоят все остальные?
Какие линии повторили?
Чем отличаются прямая, луч и отрезок?
Из чего состоит ломаная и как называются ее отрезки? А места соединения?
Как получить угол?
Чем отличается прямая от кривой линии?
2) Учитель: Подумаем, где в жизни мы встречаем все эти линии?
Поработаем с карточками.
Карточка № 1 Игра «Найди линию»
Учитель: На карточке под номерами расположены разные предметы. Запишите в тетрадях номера предметов, где есть 1. прямые линии, 2. отрезки, 3. ломаные, 4. кривые, 5. лучи.
Карточка № 2 Игра «Точки и числа»
Учитель: У каждого на столах лежит лист, на котором изображены точки и числа. Ваша задача поочередно соединять данные точки линиями, прямыми или кривыми вы должны решить сами, в порядке возрастания чисел. От меньшего к большему. Кто раньше получит рисунок. Поднимите руку.
VII – Рефлексия
Учитель: Чем мы занимались на уроке?
Повторили: «Какие бывают линии и чем они отличаются друг от друга?»
Узнали, что линии бывают замкнутые и незамкнутые.
Чертили эти линии и показывали.
Учились сравнивать отрезки.
Что нового узнали?
Точка и линии-самые простые геометрические фигуры.
Линии состоят из множества точек.
Линии располагаются на плоскости и в пространстве горизонтально, вертикально, наклонно.
Линии бывают параллельные и могут пересекаться.
VIII – Сообщение домашнего задания
Учитель: Нарисуйте примеры предметов с прямыми, кривыми, ломаными линиями и с лучами по 2-4 примера.
Приложение к уроку
Карточка
Фотографии с урока
Презентация — Математика 1 класс «Линии: кривая, прямая. Луч — Отрезок
Луч — Отрезок
Слайды и текст этой презентации
Слайд 1
2014 год,
13 октября,
понедельник.
Слайд 2
К задуманному числу прибавили 1 и получили 5. Какое число задумали?
Какое число при счёте следует за числом 6?
Число на 1 меньше, чем 8.
Какое число имеет соседей 3 и 4?
Какое число предшествует числу 7?
Слайд 3
1
2
3
4
5
6
7
8
9
10
Слайд 4
Ежик по лесу шел,
На обед грибы нашел:
Два — под березой,
Один — у осины,
Сколько их будет
В плетеной корзине?
2+1=3
Слайд 5
Три ромашки-желтоглазки,
Два веселых василька
Подарили маме дети.
Сколько же цветов в букете?
3+2=5
Слайд 6
1
1
2
Слайд 7
Слайд 8
Слайд 9
Слайд 10
Отдыхай-ка
Слайд 11
Слайд 12
.Линии: кривая, прямая.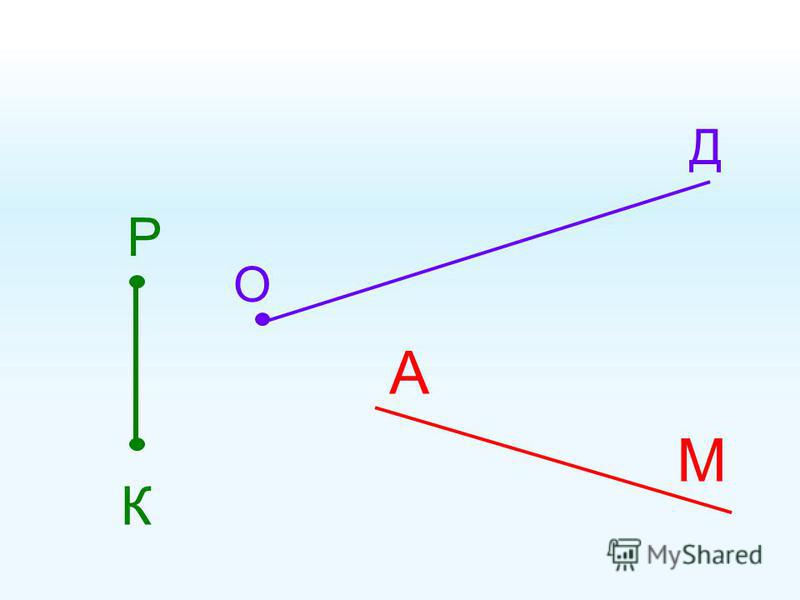 Луч. Отрезок.
Точка.
Луч. Отрезок.
Точка.
Слайд 13
На какие две группы можно разделить эти
линии?
Сколько прямых линий?
Сколько кривых линий?
Каких линий больше?
Слайд 14
Сказка
В стране Геометрии жила-была точка.
Она была маленькой. Её оставил карандаш, когда наступил на лист тетради, и никто её не замечал. Так и жила она, пока не попала в гости к линиям.
Слайд 15
Прямая линия начала хвастаться: «Я самая длинная
У меня ни начала, ни конца! Я бесконечная!»
Очень интересно стало точке посмотреть на неё.
Сама-то она малюсенькая. Вышла она да так
увлеклась, что не заметила и наступила на прямую
линию. И вдруг исчезла прямая линия. На её месте
появился луч.
Слайд 16
Он тоже был длинный, но всё же не такой, как
прямая линия. У него появилось начало.
Испугалась точка: «Что же я наделала!» Хотела она
убежать, да как назло наступила опять на луч.
И на месте луча появился отрезок.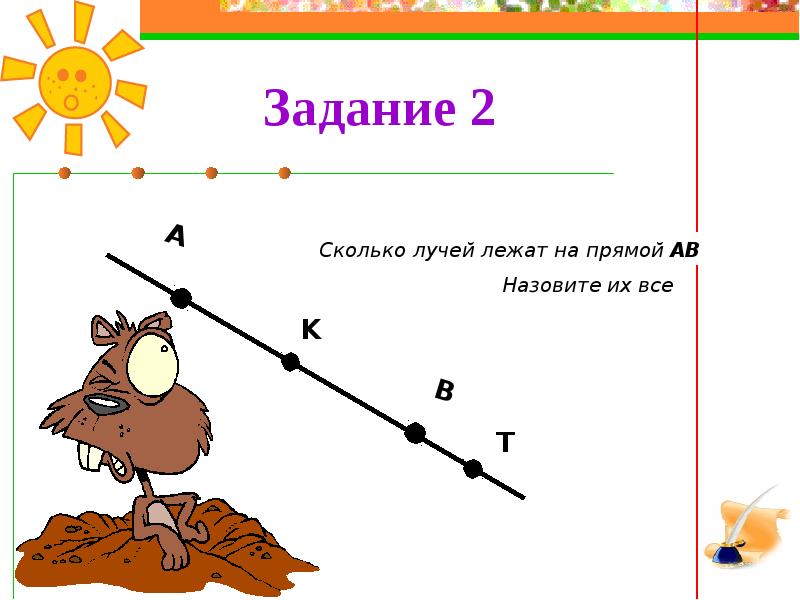 Он не хвастался,
какой он большой, у него уже были и начало и конец.
Он не хвастался,
какой он большой, у него уже были и начало и конец.
Слайд 17
Вот так маленькая точка смогла изменить жизнь
больших линий.
Слайд 18
Слайд 19
Слайд 20
! Прямую линию мы проводим по линейке.
Слайд 21
Сколько линий можно провести через одну точку?
Слайд 22
Сколько линий можно провести через две точки?
Слайд 23
Отдыхай-ка
Слайд 24
Слайд 25
С.15
Слайд 26
Слайд 27
Что мы узнали?
Что повторили?
Слайд 28
Оцени свою работу на уроке.
Слайд 29
Наше настроение
Что такое отрезок прямая луч дополнительные лучи. Прямая луч отрезок правило
Несмотря на то что геометрия относится к числу точных наук, ученые не могут однозначно дать определение термину «прямая». В самом общем виде можно дать такое определение: «Прямая — это линия, путь вдоль которой равен расстоянию между двумя точками».
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности.
К основным понятиям геометрии относятся точка, прямая и плоскость, они даются без определения, но определения других геометрических фигур даются через эти понятия. Плоскость, как и прямая, — это первичное понятие, не имеющее определения. Это утверждение устанавливается следующей аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости. А само утверждение, которое доказывается, называется теоремой. Формулировка теоремы обычно состоит из двух частей.
Задача: где прямая, луч, отрезок, кривая? Вершины ломаной(похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная. Задача: какая ломанная длиннее, а у какой больше вершин? Смежные стороны многоугольника — это смежные звенья ломанной. Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка.
В дальнейшем будут определения для разных фигур кроме двух — точка и прямая. Значит иногда обозначить прямую можем и двумя большими латинскими буквами, например, прямая\(AB\), так как никакая другая прямая через эти две точки не может быть проведена. Символически записываем отрезок \(AB\).
Что такое точка в математике?
Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. С. Вписанный угол, опирающийся на полуокружность, — прямой. Здесь собраны основные определения, теоремы, свойства фигур на плоскости.
Здесь собраны основные определения, теоремы, свойства фигур на плоскости.
Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенно определяется аксиомами геометрии.
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны. Лучом называют часть прямой линии, ограниченную с одной стороны. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
Точка и прямая являются основными геометрическими фигурами на плоскости.
Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др., а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками. Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.
При этом начальная точка ставится на первом месте.
Получается, что прямая бесконечна: у неё нет ни начала, ни конца; у луча есть только начало, но нет конца, а отрезок имеет начало и конец. Поэтому только отрезок мы можем измерить.
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.
Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Конспект урока по математике
в 1 классе.
Тема: Точка. Кривая линия. Прямая линия. Отрезок. Луч.
Составила и провела
Бувайлова Елена Ивановна
Тема: Точка. Кривая линия. Прямая линия. Отрезок. Луч
Цель: в ходе выполнения практических заданий и наблюдений научить различать разные виды линий.
Планируемые результаты: учащиеся научатся различать и называть прямую линию, кривую, отрезок, луч, ломаную; пользоваться линейкой для черчения; соотносить реальные предметы и их элементы с изученными геометрическими линиями и фигурами; выполнять мыслительные операции анализа и синтеза и делать умозаключения; применять полученные ранее знания в измененных условиях; слушать собеседника и вести диалог; слушать учителя и выполнять его требования; оценивать себя, границы своего знания и незнания; работать в паре и оценивать товарища.
Ход урока
1.Организационный момент
Математика зовёт
Первоклашек на урок,
Числа нас ведут вперёд
Будем знать всё «на зубок»
2.Актуализация знаний
К нам сегодня на урок пришел в гости кот Тишка с незнакомыми друзьями, а какие это друзья вы назовете их чуть позже
а) Прямой и обратный счёт в пределах 10.
Индивидуальный опрос.
б) Задачи в стихах:
Тишка – кот такой глупышка,
Очень рыбу любит Тишка.
На рыбалке побывал,
Два пескарика поймал,
Щуки две и два ерша.
Жизнь у Тишки хороша!
Кто быстрее сосчитал,
Сколько рыбок кот поймал? (6)
На забор взлетел петух,
Повстречал ещё там двух.
Сколько стало петухов? (3)
По тропинке в лесок
Покатился колобок.
Встретил серого зайчишку,
Встретил волка, встретил мишку,
Да плутовку лису
Повстречал он в лесу
Отвечай поскорей
Сколько встретил колобок зверей. (4)
Игра «Молчанка»
(Учитель показывает пропуск, учащиеся соответствующую цифру на веере цыфр.)
4 — □ = 2 5 — □= 2
4 — □ = 3 5 — 1 = □
1 + 3 = □ □ — 3=1
□ -4=1 1 + □ = 2
3. Физкультминутка
4. Самоопределение к деятельности
В стране Геометрии жила-была точка. Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям.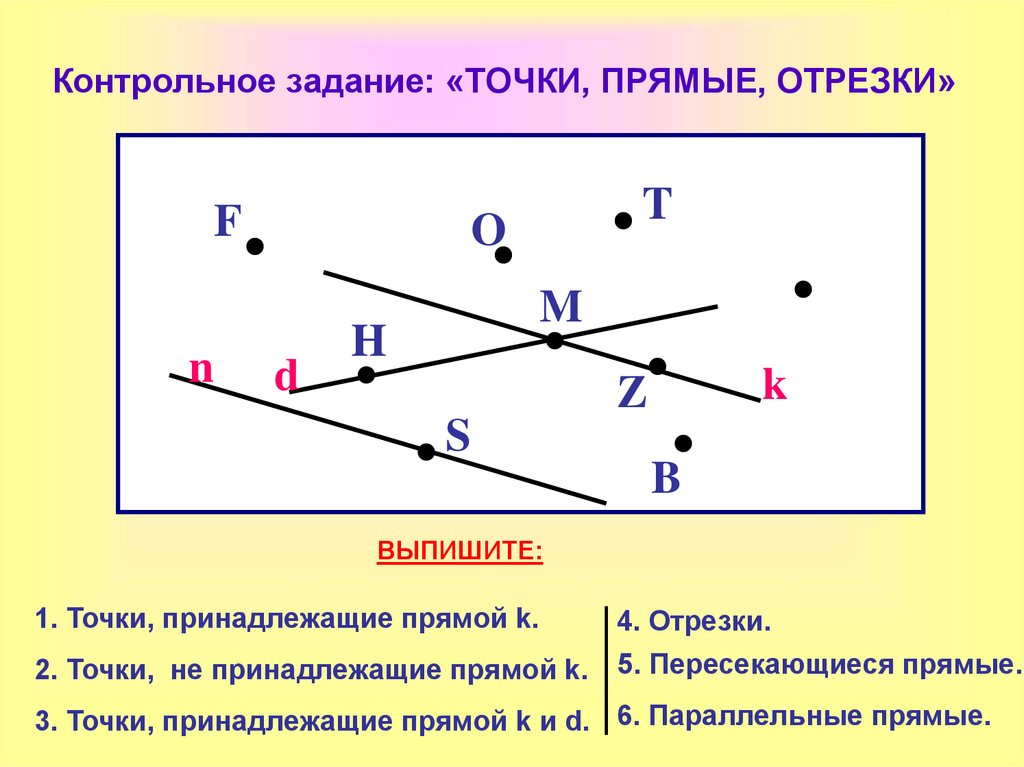 (На доске рисунок.) (Математический планшет)
(На доске рисунок.) (Математический планшет)
Посмотрите, какие это были линии. (Прямые и кривые.)
Прямые линии похожи на натянутые веревочки, а веревочки,
которые не натянули, — это кривые линии.
Сколько прямых линий? (2.)
Сколько кривых? (3.)
Прямая линия начала хвастаться: « Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»
Очень интересно стало точке посмотреть на нее. Сама-то точка малюсенькая. Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч.
Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.
Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч.
И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.
Вот так маленькая точка смогла изменить жизнь больших линий.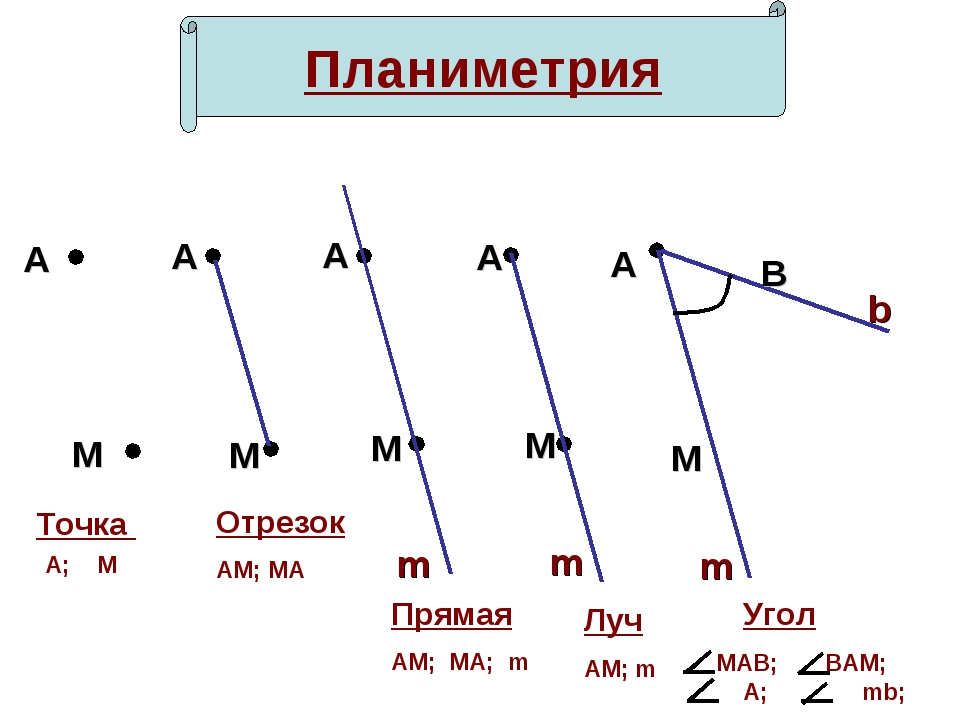
Так кто догадался кто вместе с котиком пришел к нам в гости?( прямая линия, луч, отрезок и точка )
Правильно вместе с котиком пришли прямая линия, луч, отрезок и точка к нам на урок.
Кто догадался, что мы будем делать на этом уроке? (Учиться распознавать и чертить прямую линию, луч, отрезок.)
5. Работа по теме урока
Практическая работа
О каких линиях вы узнали? (О прямой, луче, отрезке.)
Что узнали о прямой линии? (Она не имеет ни начала, ни конца. Она бесконечная.)
(Учитель берет две катушки ниток, натягивает их, изображая прямую линию, и разматывая то одну, то другую, демонстрирует, что прямую можно продолжать в оба конца до бесконечности.)
Что узнали о луче? (У него есть начало, но нет конца.) (Учитель берет ножницы, разрезает нитку. Показывает, что теперь линию можно продолжать только в один конец.)
Что узнали об отрезке? (Унего есть и начало, и конец. ) (Учитель отрезает другой конец нитки и показывает, что нитка
) (Учитель отрезает другой конец нитки и показывает, что нитка
не тянется. У нее есть и начало, и конец.)
6.Работа по учебнику
— Посмотрите на рисунок на с. 40 . Расскажите, чем прямая линия отличается от кривой. (Прямая линия натянута, кривая — нет.)
Что вы запомнили о прямой линии, луче, отрезке? (Ответы детей.)
Как начертить прямую линию? (Провести по линейке линию .)
Как начертить отрезок? (Поставить две точки и соединить их.)
7.Физкультминутка
В понедельник я купался,
(Движения руками, выполняемые при плавании.)
А во вторник рисовал,
(Изобразить рисование.)
В среду долго умывался,
(Изобразить умывание.)
А в четверг в футбол играл.
(Бег на месте.)
В пятницу я бегал, прыгал,
(Прыжки на месте.)
Очень долго танцевал.
(Покружиться. )
)
А в субботу, воскресенье
(Хлопки в ладоши.)
Целый день я отдыхал.
(Сесть на корточки, руки под щеку.)
8.Закрепление изученного материала
Работа в тетради с печатной основой
Откройте тетрадь на с. 15. Рассмотрите линии. На какие группы их можно разделить? (Прямые — 2,3, 5 и кривые -1,4.)
Выполните следующее задание.
Сколько прямых можно провести через две точки? (Одну.)
Сколько кривых можно провести через две точки? (Много.)
Прочитайте следующее задание.
Раскрасьте рисунки самостоятельно.
9. Пальчиковая гимнастика
Работа в тетради
Тишка хочет научиться изображать прямую, отрезок, луч.
А теперь начертите в тетради прямую, отрезок, луч и кривую линию, по которым побежит кот Тишка.
Обсудить в парах начерченные линии.
10.Работа по учебнику
Прочитайте задание на полях на с. 40. Как узнать, какой отрезок самый длинный? (Посчитать, сколько клеточек составляет длина каждого отрезка.)
40. Как узнать, какой отрезок самый длинный? (Посчитать, сколько клеточек составляет длина каждого отрезка.)
Посчитайте и скажите, какой отрезок самый длинный. (Синий.)
Какой отрезок самый короткий? (Красный.)
Рассмотрите рисунок на с. 41. Расскажите соседу по парте, какие линии вы видете.
(Работа в парах.)
Посмотрите на рисунки и записи, приведенные ниже.
Какие записи подходят к рисункам?
Объясните их смысл.
(4 + 1 = 5- к 4 цыплятам прибежал еще один.
Стало 5 цыплят. 5-2 = 3- плавали 5 утят, 2 утенка ушли.
Осталось 3утенка.
Записи 4- 1 = 3и 5- 1 = 4не подходят.)
урок понравился
Было трудно, но интересно
урок не понравился
Подведение итогов урока
Что нового вы узнали о линиях?
Где в жизни встречаются прямые линии? кривые линии?
А, что могут означать для кота: точка, прямая, кривая линия?
(Точка похожа на клубок –он может поиграть, покатать;
Луч – попускать «зайчиков»
Прямая линия на дорогу –где нужно соблюдать правила ПДД;
Кривая линия – на извилистую тропинку, где он может поиграть в догонялки со своими друзьями)
Все мы когда-то изучали в школе геометрию, но далеко не каждый из нас вспомнит, что представляет собой отрезок. А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.
А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.
Определение понятий
Для начала давайте вспомним, что называется геометрией. Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства. К ним относятся треугольник, квадрат, прямоугольник, параллелепипед, круг, овал, ромб, цилиндр и т. п. Простейшая фигура — это прямая. Она является бесконечной и не имеет начала. Две прямые пересекутся только в одной единственной точке. Через одну точку можно проводить бессчетное количество прямых линий. Каждая точка на линии делит ее на два .
Он состоит из точек, расположенных по одну сторону. Все понятия данных подмножеств можно именовать таким образом. Луч обозначают одной строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е) .
В основе геометрической фигуры, имеющей углы, лежат полупрямые. Они начинаются в точке, где пересекаются, но второй стороной направлены в бесконечность. Начало делит прямую на 2 части. На письме его обычно именуют двумя заглавными (OF) или одной буквой латиницы (а, в, с). Если дана прямая, то записывается ОВ в закругленных скобках: (ОВ). Если же это отрезок — в квадратных скобках.
Таким образом, луч — это часть прямой. Через любую точку можно провести множество прямых, но через 2 несовпадающие — только одну. Последние могут быть взаимодействовать только в трех вариантах: пересекаться, скрещиваться, быть параллельными друг другу. Существуют линейные уравнения, которые задают прямую на плоскости.
Обозначения в геометрии
Вариантов для обозначения несколько:
Нужно знать: Что такое и горизонтальное положение?
Отличие световых лучей от геометрических
В геометрии таковые понятия очень схожи. Луч — это линия, но она является энергией света . Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки ,,,, и , а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Как объяснить, что такое луч в геометрии.
Наряду с такими понятиями как точка, отрезок, прямая, в геометрии существует и еще одно понятие. Оно имеет название луч. Луч — это часть прямой, ограниченная с одной стороны точкой, а с другой стороны — бесконечная, т.е. ни чем не ограниченная.
Оно имеет название луч. Луч — это часть прямой, ограниченная с одной стороны точкой, а с другой стороны — бесконечная, т.е. ни чем не ограниченная.
Можно провести аналогию с природой. Например, луч света, который мы можем направить с земли в космос. С одной стороны он ограничен, а с другой стороны — нет. Каждый луч имеет одну крайнюю точку, в которой он начинается. Она называется началом луча .
Если взять произвольную прямую a , и отметим на ней некоторую точку О , то эта точка разобьет нашу прямую на две части. Каждая из которых будем лучом. Точка О будет принадлежать каждому из этих лучей. Точка О будет в данном случае началом этих двух лучей.
Луч обычно обозначают одной латинской буквой. На рисунке ниже представлен луч k .
Также можно обозначать луч двумя большими латинским буквами. При этом первая из них — это точка, в которой лежит начало луча. Вторая — это точка которая принадлежит лучу или другими словами — через которую луч проходит.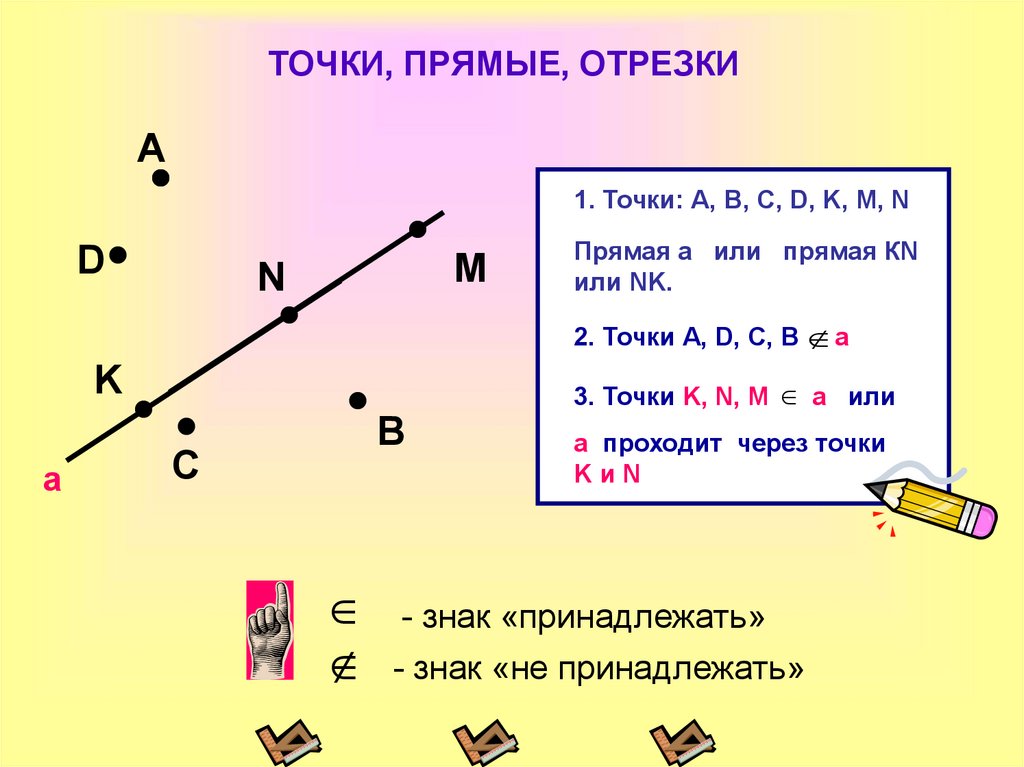
На рисунке представлен луч ОС.
Еще одним способом обозначения луча, является указание начальной точки луча и прямой, которой этот луч принадлежит. Например, на рисунке ниже представлен луч Оk.
Иногда говорят, что луч исходит из точки О. Это значит, что точка О является началом луча. Лучи еще иногда называют полупрямыми .
Задача:
Проведите прямую, и отметьте на ней точки A B и на отрезке AB отметьте точку C. Среди лучей АB, BC, CA, AC и BA найдите пары совпадающих лучей.
Лучи совпадают, если они лежат на одной прямой и имеют общее начало и ни один из них не является продолжением другого луча.
По рисунку видно, что этим условиям удовлетворяют лучи AB и AC, а также лучи BC и BA. Следовательно, они являются совпадающими.
Посещая дополнительные занятия мы поняли, что не умеем оперировать понятиями точка, линия, угол, луч, отрезок, прямая, кривая, замкнутая линии и рисовать их, точнее рисовать можем, но идентифицировать не получается.
Дети должны различать линии, кривые, окружности. Это развивает у них графику и чувство правильности при занятиях рисованием, аппликацией. Важно знать, какие основные геометрические фигуры существую, что из себя представляют. Разложите карточки перед ребенком, попросите нарисовать точно так же как на картинке. Повторите несколько раз.
На занятиях нам выдали следующие материалы:
Небольшая сказка.
В стране Геометрии жила-была точка. Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям. (На доске рисунок.)
Посмотрите, какие это были линии. (Прямые и кривые.)
Прямые линии похожи на натянутые веревочки, а веревочки, которые не натянули, — это кривые линии.
Сколько прямых линий? (2.)
Сколько кривых? (3.)
Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»
Очень интересно стало точке посмотреть на нее. Сама-то точка малюсенькая. Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч.
Сама-то точка малюсенькая. Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч.
Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.
Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч.
И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.
Вот так маленькая точка смогла изменить жизнь больших линий.
Так кто догадался кто вместе с котиком пришел к нам в гости?(прямая линия, луч, отрезок и точка)
Правильно вместе с котиком пришли прямая линия, луч, отрезок и точка к нам на урок.
Кто догадался, что мы будем делать на этом уроке? (Учиться распознавать и чертить прямую линию, луч, отрезок.)
О каких линиях вы узнали? (О прямой, луче, отрезке.)
Что узнали о прямой линии? (Она не имеет ни начала, ни конца. Она бесконечная.)
Она бесконечная.)
(Берем две катушки ниток, натягивает их, изображая прямую линию, и разматывая то одну, то другую, демонстрирует, что прямую можно продолжать в оба конца до бесконечности.)
Что узнали о луче? (У него есть начало, но нет конца.) (Педагог берет ножницы, разрезает нитку. Показывает, что теперь линию можно продолжать только в один конец.)
Что узнали об отрезке? (Унего есть и начало, и конец.) (Педагог отрезает другой конец нитки и показывает, что нитка не тянется. У нее есть и начало, и конец.)
Как начертить прямую линию? (Провести по линейке линию.)
Как начертить отрезок? (Поставить две точки и соединить их.)
И конечно прописи:
Все мы когда-то изучали в школе геометрию, но далеко не каждый из нас вспомнит, что представляет собой отрезок. А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.
Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.
Определение понятий
Для начала давайте вспомним, что называется геометрией. Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства. К ним относятся треугольник, квадрат, прямоугольник, параллелепипед, круг, овал, ромб, цилиндр и т. п. Простейшая фигура — это прямая. Она является бесконечной и не имеет начала. Две прямые пересекутся только в одной единственной точке. Через одну точку можно проводить бессчетное количество прямых линий. Каждая точка на линии делит ее на два .
Он состоит из точек, расположенных по одну сторону. Все понятия данных подмножеств можно именовать таким образом. Луч обозначают одной строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е) .
В основе геометрической фигуры, имеющей углы, лежат полупрямые. Они начинаются в точке, где пересекаются, но второй стороной направлены в бесконечность. Начало делит прямую на 2 части. На письме его обычно именуют двумя заглавными (OF) или одной буквой латиницы (а, в, с). Если дана прямая, то записывается ОВ в закругленных скобках: (ОВ). Если же это отрезок — в квадратных скобках.
Таким образом, луч — это часть прямой. Через любую точку можно провести множество прямых, но через 2 несовпадающие — только одну. Последние могут быть взаимодействовать только в трех вариантах: пересекаться, скрещиваться, быть параллельными друг другу. Существуют линейные уравнения, которые задают прямую на плоскости.
Обозначения в геометрии
Вариантов для обозначения несколько:
Нужно знать: Что такое и горизонтальное положение?
Отличие световых лучей от геометрических
В геометрии таковые понятия очень схожи. Луч — это линия, но она является энергией света . Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие? A A A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a b cЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру.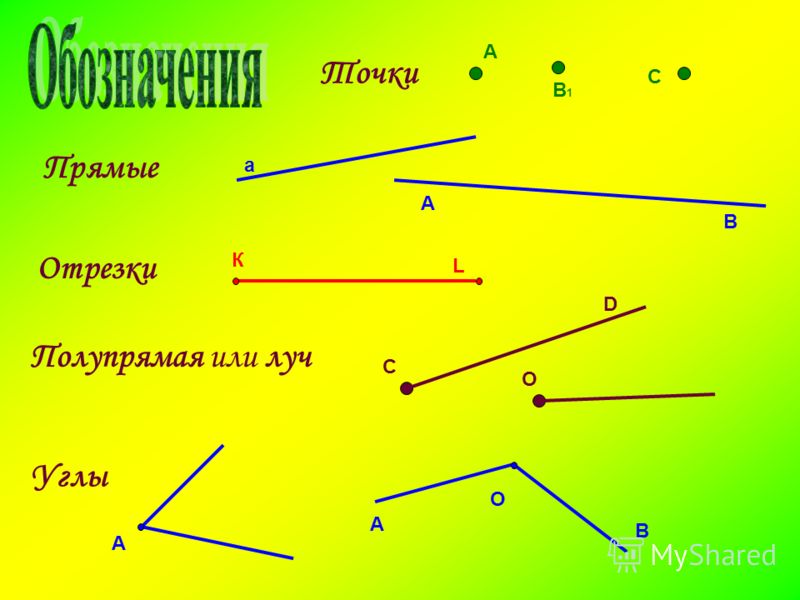 Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
B AПрямые могут быть
- пересекающимися, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
B AЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B AОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Aпрямая линия AB
B AОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B A ✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.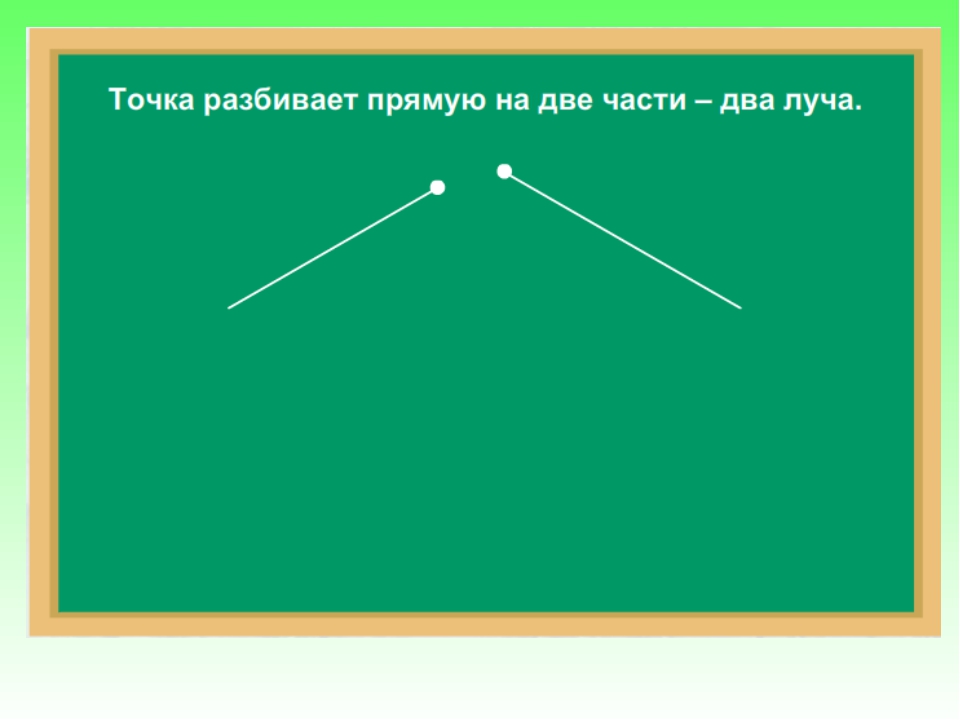 д.
д.
Конспект урока по математике
в 1 классе.
Тема: Точка. Кривая линия. Прямая линия. Отрезок. Луч.
Составила и провела
Бувайлова Елена Ивановна
Тема: Точка. Кривая линия. Прямая линия. Отрезок. Луч
Цель: в ходе выполнения практических заданий и наблюдений научить различать разные виды линий.
Планируемые результаты: учащиеся научатся различать и называть прямую линию, кривую, отрезок, луч, ломаную; пользоваться линейкой для черчения; соотносить реальные предметы и их элементы с изученными геометрическими линиями и фигурами; выполнять мыслительные операции анализа и синтеза и делать умозаключения; применять полученные ранее знания в измененных условиях; слушать собеседника и вести диалог; слушать учителя и выполнять его требования; оценивать себя, границы своего знания и незнания; работать в паре и оценивать товарища.
Ход урока
1.Организационный момент
Математика зовёт
Первоклашек на урок,
Числа нас ведут вперёд
Будем знать всё «на зубок»
2.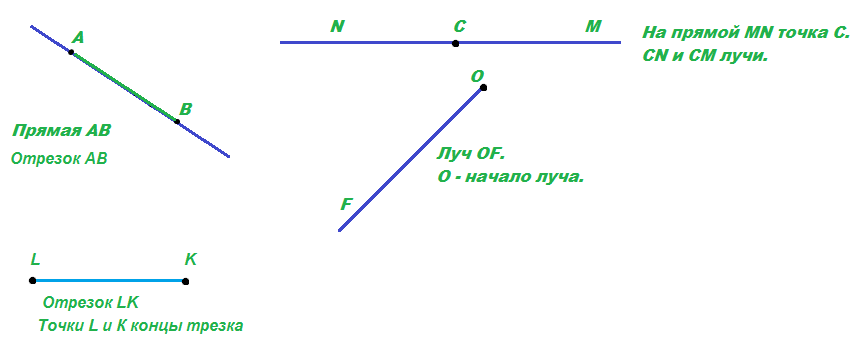 Актуализация знаний
Актуализация знаний
К нам сегодня на урок пришел в гости кот Тишка с незнакомыми друзьями, а какие это друзья вы назовете их чуть позже
а) Прямой и обратный счёт в пределах 10.
Индивидуальный опрос.
б) Задачи в стихах:
Тишка – кот такой глупышка,
Очень рыбу любит Тишка.
На рыбалке побывал,
Два пескарика поймал,
Щуки две и два ерша.
Жизнь у Тишки хороша!
Кто быстрее сосчитал,
Сколько рыбок кот поймал? (6)
На забор взлетел петух,
Повстречал ещё там двух.
Сколько стало петухов? (3)
По тропинке в лесок
Покатился колобок.
Встретил серого зайчишку,
Встретил волка, встретил мишку,
Да плутовку лису
Повстречал он в лесу
Отвечай поскорей
Сколько встретил колобок зверей. (4)
Игра «Молчанка»
(Учитель показывает пропуск, учащиеся соответствующую цифру на веере цыфр. )
)
4 — □ = 2 5 — □= 2
4 — □ = 3 5 — 1 = □
1 + 3 = □ □ — 3=1
□ -4=1 1 + □ = 2
3. Физкультминутка
4. Самоопределение к деятельности
В стране Геометрии жила-была точка. Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям. (На доске рисунок.) (Математический планшет)
Посмотрите, какие это были линии. (Прямые и кривые.)
Прямые линии похожи на натянутые веревочки, а веревочки,
которые не натянули, — это кривые линии.
Сколько прямых линий? (2.)
Сколько кривых? (3.)
Прямая линия начала хвастаться: « Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»
Очень интересно стало точке посмотреть на нее. Сама-то точка малюсенькая. Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия.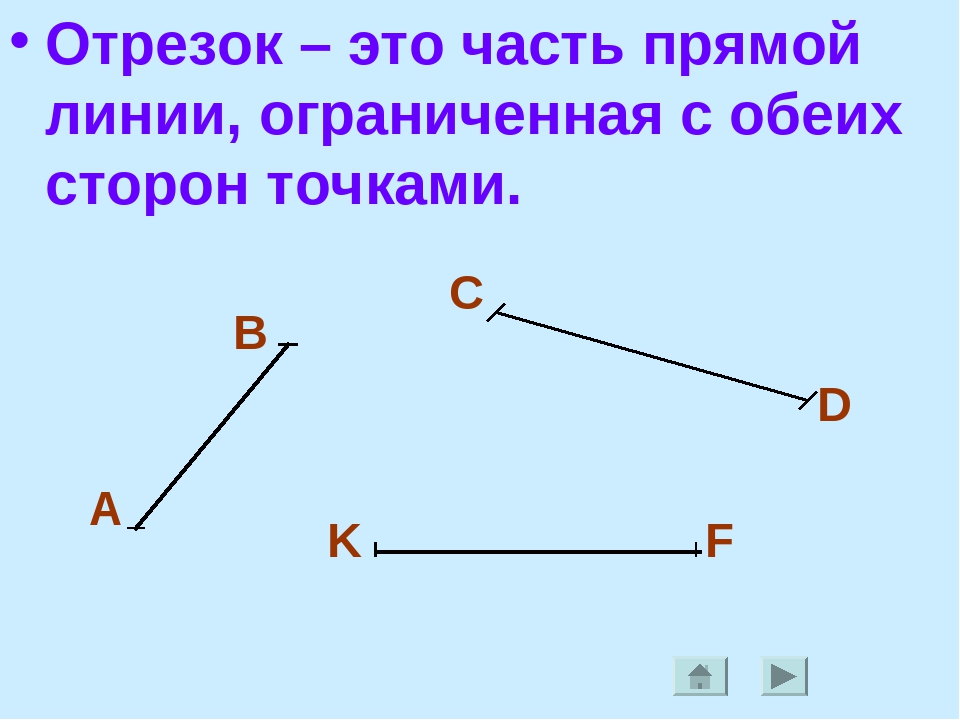 На ее месте появился луч.
На ее месте появился луч.
Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.
Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч.
И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.
Вот так маленькая точка смогла изменить жизнь больших линий.
Так кто догадался кто вместе с котиком пришел к нам в гости?( прямая линия, луч, отрезок и точка )
Правильно вместе с котиком пришли прямая линия, луч, отрезок и точка к нам на урок.
Кто догадался, что мы будем делать на этом уроке? (Учиться распознавать и чертить прямую линию, луч, отрезок.)
5. Работа по теме урока
Практическая работа
О каких линиях вы узнали? (О прямой, луче, отрезке.)
Что узнали о прямой линии? (Она не имеет ни начала, ни конца. Она бесконечная. )
)
(Учитель берет две катушки ниток, натягивает их, изображая прямую линию, и разматывая то одну, то другую, демонстрирует, что прямую можно продолжать в оба конца до бесконечности.)
Что узнали о луче? (У него есть начало, но нет конца.) (Учитель берет ножницы, разрезает нитку. Показывает, что теперь линию можно продолжать только в один конец.)
Что узнали об отрезке? (Унего есть и начало, и конец.) (Учитель отрезает другой конец нитки и показывает, что нитка
не тянется. У нее есть и начало, и конец.)
6.Работа по учебнику
— Посмотрите на рисунок на с. 40 . Расскажите, чем прямая линия отличается от кривой. (Прямая линия натянута, кривая — нет.)
Что вы запомнили о прямой линии, луче, отрезке? (Ответы детей.)
Как начертить прямую линию? (Провести по линейке линию .)
Как начертить отрезок? (Поставить две точки и соединить их.)
7.Физкультминутка
В понедельник я купался,
(Движения руками, выполняемые при плавании. )
)
А во вторник рисовал,
(Изобразить рисование.)
В среду долго умывался,
(Изобразить умывание.)
А в четверг в футбол играл.
(Бег на месте.)
В пятницу я бегал, прыгал,
(Прыжки на месте.)
Очень долго танцевал.
(Покружиться.)
А в субботу, воскресенье
(Хлопки в ладоши.)
Целый день я отдыхал.
(Сесть на корточки, руки под щеку.)
8.Закрепление изученного материала
Работа в тетради с печатной основой
Откройте тетрадь на с. 15. Рассмотрите линии. На какие группы их можно разделить? (Прямые — 2,3, 5 и кривые -1,4.)
Выполните следующее задание.
Сколько прямых можно провести через две точки? (Одну.)
Сколько кривых можно провести через две точки? (Много.)
Прочитайте следующее задание.
Раскрасьте рисунки самостоятельно.
9. Пальчиковая гимнастика
Работа в тетради
Тишка хочет научиться изображать прямую, отрезок, луч.
А теперь начертите в тетради прямую, отрезок, луч и кривую линию, по которым побежит кот Тишка.
Обсудить в парах начерченные линии.
10.Работа по учебнику
Прочитайте задание на полях на с. 40. Как узнать, какой отрезок самый длинный? (Посчитать, сколько клеточек составляет длина каждого отрезка.)
Посчитайте и скажите, какой отрезок самый длинный. (Синий.)
Какой отрезок самый короткий? (Красный.)
Рассмотрите рисунок на с. 41. Расскажите соседу по парте, какие линии вы видете.
(Работа в парах.)
Посмотрите на рисунки и записи, приведенные ниже.
Какие записи подходят к рисункам?
Объясните их смысл.
(4 + 1 = 5- к 4 цыплятам прибежал еще один.
Стало 5 цыплят. 5-2 = 3- плавали 5 утят, 2 утенка ушли.
Осталось 3утенка.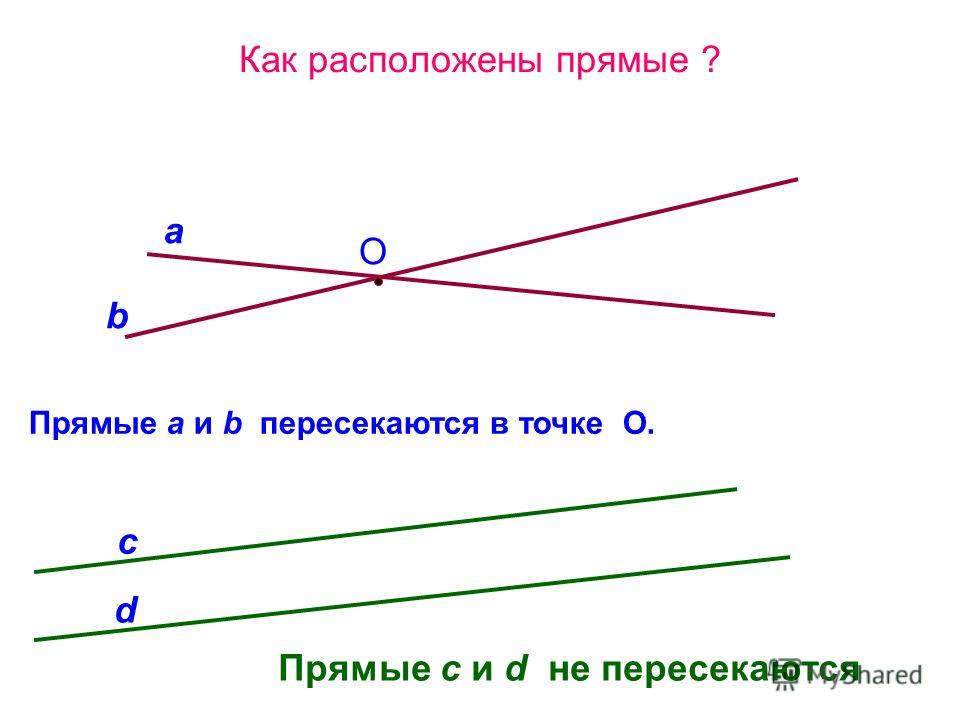
Записи 4- 1 = 3и 5- 1 = 4не подходят.)
урок понравился
Было трудно, но интересно
урок не понравился
Подведение итогов урока
Что нового вы узнали о линиях?
Где в жизни встречаются прямые линии? кривые линии?
А, что могут означать для кота: точка, прямая, кривая линия?
(Точка похожа на клубок –он может поиграть, покатать;
Луч – попускать «зайчиков»
Прямая линия на дорогу –где нужно соблюдать правила ПДД;
Кривая линия – на извилистую тропинку, где он может поиграть в догонялки со своими друзьями)
Прямая линия, отрезок, луч — online presentation
81вычесть 23
?
48
увеличить на19
?
?
уменьшить на 36
40
?
прибавить 7
92
4. 58 67 76 85
58 67 76 85 94 103Прямые линии – красным цветом,
лучи – синим,
отрезки зеленым.
Найдите точки пересечения этих
дорожек
7. Цель урока: научиться различать прямые линии, отрезки, лучи; научиться их обозначать и находить точки их пересечения.
8. Тема: Прямая, луч, отрезок.
ППрямаяОтрезок
Луч
Прямая линия — она натянутая, ее
можно продлить в оба конца, она
бесконечна.
П
Прямая
Отрезок
Луч
Бесконечна
Можно продлить
в оба конца
А
О
М
В
Отрезок — это часть прямой линии,
ограниченной с двух сторон.
П
Прямая
Отрезок
Луч
Бесконечна
Можно продлить
в оба конца
Ограничен с двух Нельзя продлить
сторон
А
О
М
В
Луч – это часть прямой,
ограниченной с одной стороны.
Прямая
Бесконечна Можно
продлить в оба
конца
Отрезок
Часть
прямой
Часть
прямой
Луч
Ограничен с 2
сторон
Ограничен с
одной стороны,
продлить в 1
сторону
18. Найди прямую, луч, отрезок. Начерти в тетради.
ВX
l
P
М
А
Е
Д
К
R N
Y
C
19. Физкультминутка
20. План.
План.
1.Обозначать лучи.2.Распознавать луч, прямую и отрезок.
3.Определять, являются ли лучи
пересекающимися
21. Распредели (устно)
Прямая АБОтрезок АВ
В
Луч АВ
А
А
А
В
В
Прямая АБ
Отрезок АВ
В
А
Луч АВ
А
А
В
В
23. Начерти в тетради.
• Луч МК пересекает луч АВ• Луч СЕ пересекает луч ДС
24. Алгоритм
1.Обозначим вершину луча.2.Построим луч при помощи линейки.
3.Продлим лучи до их пересечения.
4. Проверим, пересекаются ли они.
А
• Д
М
С
26. Домашнее задание
С. 72- №2,№4.Фото отправь учителю в viber.
27. Молодец!!!!
Точка. Кривая линия. Прямая линия. Отрезок. Луч.
Муниципальное автономное
общеобразовательное учреждение
«Средняя общеобразовательная школа № 7»
городского округа город Стерлитамак
Республики Башкортостан
Конспект урока по математике на тему:
«Точка. Кривая линия. Прямая линия.
Кривая линия. Прямая линия.
Отрезок. Луч ».
Учитель начальных классов
Муртазина Эльмира Альбертовна
2015
Тема урока: «Точка.Кривая линия. Прямая линия.
Отрезок. Луч ».
Цели:
— формировать представление о фигурах «точка», «кривая линия», «прямая линия», «луч», «отрезок»;
— учить различать и выполнять геометрических фигур: прямая линия, отрезок, луч;
— установить пространственное воображение;
— воспитывать интерес к геометрическому материалу.
Планируемые результаты: умения: различать геометрические фигуры «точка», «кривая линия», «прямая линия», «луч», «отрезок», отличать их от других фигур и уметь выполнять построение названных геометрических фигур на плоскости.
Оборудование : презентация, сделанная в программеMicrosoftPowerPoint, карточки с фигурами и их названиями, две катушки ниток, ножницы.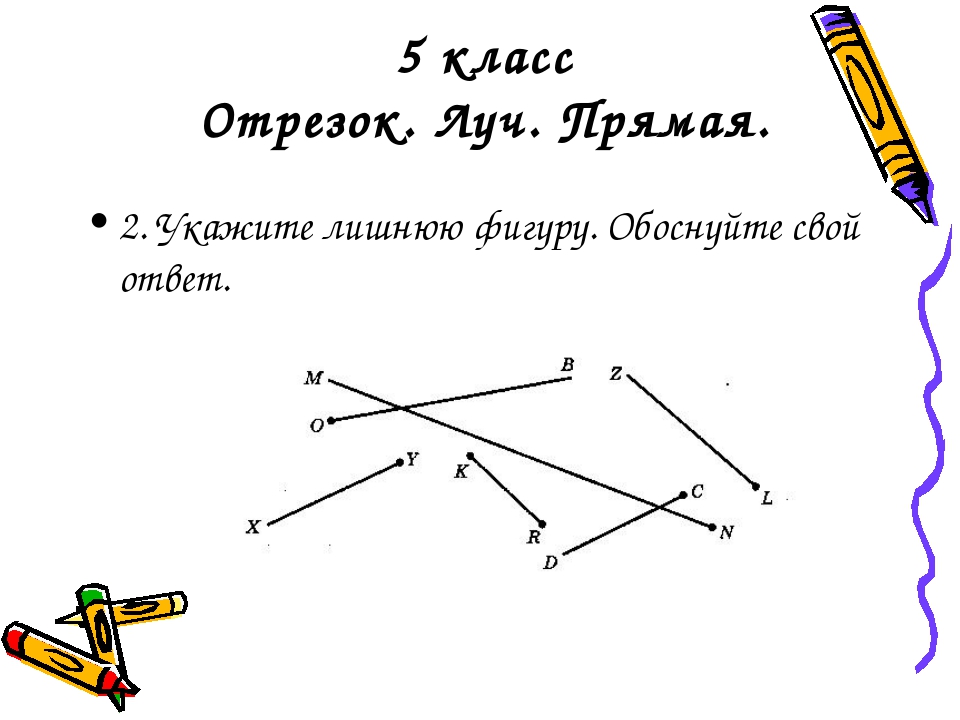
Структура урока:
I. Актуализация знаний. Подведение к учебной задаче.
II. Формулировка учебной задачи
III. Решение учебной задачи.
IV. Обобщение по решённой учебной задаче и постановка новой (учебная задача 2).
V. Решение учебной задачи 2.
VI. Применение знаний в новых условиях.
VII. Обобщение. Рефлексия. Перспектива.
VIII. Установление связи с жизнью.
Ход урока
Я . Актуализация знаний. Подведение к учебной задаче.
Дети получают карточки с заданием:
— Найдите недостающую фигуру.(Рис.1.)
Рис.1
— Назовите фигуры, которые вы сейчас рассматривали? (Круг, квадрат, треугольник, прямоугольник.)
— Где мы часто встречаемся с этим фигурами? (На уроке математики.)
— Какие из окружающих нас предметов в классе и дома имеют форму треугольника, квадрата, круга и прямоугольника? (Треугольник — крыша дома и школы, квадрат — телевизор, круг — сковородка, прямоугольник — классная доска. )
)
— Сегодня ребята, у нас необычный урок: урок-путешествие в математическую страну, название которой вы прочитаете на воротах этого города.
Слайд № 1
Рис.2
— Верно, это Геометрия, часть великой науки Математики. Посмотрите, а кто живет в этой стране! Вы узнали их? Верно, это наши знакомые: круг, треугольник, квадрат, прямоугольник.
II .Формулировка учебной задачи.
— Открыв ворота, мы познакомимся с новыми фигурами — жителями этой страны.
Слайд № 2
Рис. 3
— Что видите на слайде? (Геометрические фигуры; дом, солнце, дерево.)
— Из каких фигур они состоят? (Квадрат, треугольник, круг, овал, прямоугольник.)
— Какие новые фигуры вы увидели? (Дети задумываются.)
— Сегодня мы познакомимся с новыми фигурами, которые помогли создать рисунок страны Геометрии.
III . Решение учебной задачи.
Практическая работа. Понятие «точка».
— У каждого из вас, на парте есть карандаш и листочек бумаги. Возьмите карандаш и поставьте его на лист.)
— Что сделал карандаш? (Оставил след.)
— Этот след и есть точка — геометрическая фигура.
— В стране Геометрии жила-была точка. Она была маленькой. Её оставил карандаш, когда он дотронулся до листа бумаги своим остро оточенным носиком-грифелем. Но точка никто не замечал. Найдите на рисунке 3 точку. Где она находится? (На дороге.) Так и жила бы она, если бы не попала в гости к линиям.
Рис. 4
— Посмотрите, какие это были линии? (Прямые, искривленные, завитые, неровные, кривые.)
— Сколько на рисунке прямых линий? (Две прямые линии.)
— Сколько изображено кривых линий? (Четыре кривые линии.)
— На что похожи эти линии? Посмотрите на следующий слайд. ( Прямые линии похожи на натянутые верёвочки, а верёвочки, которые не натянули, — это кривые линии).
Слайд № 3
Рис. 5
5
— Определите, у кого из зверей прямая линия, а у кого — кривая линия? (У зайца прямая линия, так как у него натянутая веревочка, а у волка кривая линия, потому что его веревка не натянута.)
— Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная! »
— Как вы, ребята, понимаете, что прямая линия «бесконечна»?
Учитель берет катушки ниток, держит их двумя руками, прижав друг к другу. Два ученика разматывают нитки в обе стороны, натягивая их, демонстрируют, что прямую линию можно продолжать в оба конца.
— Как долго можно продолжать прямую линию? (Пока нитки не закончатся.)
— А, если мы возьмем катушки, выйдем на улицу, размотаем их на две стороны, натянем, что произойдет с «прямым линией»? (Она станет длиннее, мы ее продолжим.)
— В математике считается, что прямую линию можно продолжать в обе стороны очень долго и что она никогда не кончается. Говорят, что прямая линия бесконечна, т.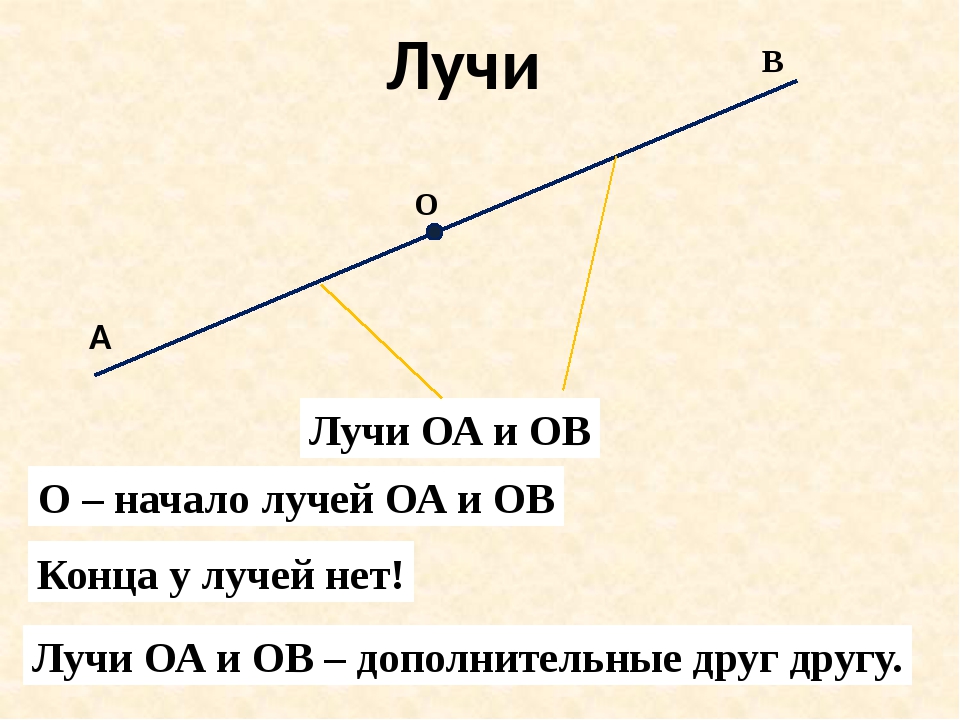 е. у нее нет концов. Прочитаем стихотворение о прямой линии или короче: прямой.
е. у нее нет концов. Прочитаем стихотворение о прямой линии или короче: прямой.
Вот она какая — линия прямая,
Без начала и без края.
Хоть 100 лет по ней иди,
Не на найдешь конца пути.
— Очень интересно стало посмотреть на нее. Сама-то точка малюсенькая. Подошла она, да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг прямая превратилась … Что же получилось из прямой?
ЛУЧ ЛУЧ
— Рассмотрите еще раз слайд «Страна Геометрия».На что похожи получи из прямой ее две части? (На лучи солнца.) Эти фигуры в геометрии называют лучами.
— Каждый луч тоже очень длинный. Но продолжить его можно только в одну сторону. Ведь с другой стороны — точка — начало луча . (На доске учитель прикрепляет рисунок с прямым, разделенной точкой на два луча и еще один луч.)
— Продолжим сказку. Испугалась точка: «Что же я наделала?» Хотела она убежать, да как назло наступила на один из лучей.
— И на месте этого луча появилась новая фигура, вот такая:
Р ис. 6
— Какое же имя у этой новой фигуры? Как ее называют в стране Геометрии? Как из прямого получилась новая фигура, ограниченная двумя точками? Как из длинной нити получить короткую? (Отрезать ее часть.)
ОТРЕЗОК
Рис.7
— Можно представить, что для отрезка от прямого отрезали часть и отметили ее начало и конец точками. Поэтому и называется эта фигура — отрезок.
IV . Обобщение по решённой учебной задаче и постановка новой (учебная задача 2).
— Вот такая маленькая точка смогла изменить жизнь «больших» линий.
— Какие же еще геометрические фигуры вместе с треугольником, прямоугольником и кругом живут в стране геометрии? (Точка, прямая линия, кривая линия, луч, отрезок.)
— Кто догадался, чему нам нужно научиться в стране Геометрии? (Научиться узнавать и чертить прямую линию, луч, отрезок, рисовать кривые линии. )
)
— Как нарисовать кривые линии? (Дети задумываются.) Кривую линию удобно моделировать из шнура, веревочек, ниток. Кривые линии могут быть замкнутыми и незамкнутыми.
Незамкнутая кривая линия Замкнутая кривая линия
Рис. 8
Слайд № 4
Рис.9
В . Решение учебной задачи 2.
— Что вы узнали о прямой линии? (Она не имеет ни начала, ни конца, т.е. она бесконечная.)
— Что узнали о луче? (У него есть начало, но нет конца.)
— Что узнали об отрезке? (Его получили из прямого, у него есть и начало, и конец.)
Слайд № 5
Рис. 10
— Как начертить линию в тетради так, чтобы она была прямой? Какой из инструментов у вас на парте инструментов поможет нам? (Линейка.Надо провести вдоль линейки линии.)
— Начертим прямую линию. Я — на доске, а вы — тетрадях. Поставьте на прямую линию две точки. Какие фигуры получились? (Прямая линия и отрезок.)
Какие фигуры получились? (Прямая линия и отрезок.)
— Как начертить отрезок? (Поставить две точки и соединить их по линейке.)
— Как начертить луч? (Поставить одну точку и провести по линейке прямую линию.)
— Постройте отрезок и луч в тетрадях.
Правило:
Линейку прижать одной рукой.
Другой рукой, направляя карандаш вдоль линейки, провести линию.
Слайд № 6
Рис. 11
VI .Применение знаний в новых условиях.
Работа в парах.
— Посоветуйтесь в парах и ответьте на вопрос: сколько прямых линий можно провести через две точки? (Одну.)
— Для этого выполните задание на листочках, которые лежат у вас на партах.
— Посоветуйтесь в парах: сколько кривых линий можно провести через две точки? (Много.)
— Проверим по слайду.
Слайд № 7
Рис. 12
— Проведите три кривые линии через эти же две точки.
VII . Обобщение. Рефлексия. Перспектива.
— Посмотрите на слайд. Подумайте, на какие группы можно разделить данные геометрические фигуры. (Лучи — 2, 5; отрезки — 1, 3, 4.)
Слайд № 8
Рис.13
— Какие жители страны Геометрии Вам были знакомы? (Квадрат, треугольник, прямоугольник и круг.)
— С какими жителями страны Геометрии познакомились? ( Точка, кривая линия, прямая линия, отрезок, луч.)
— Какой может быть линия? (Прямая, кривая.)
— Как получить отрезок? ( Поставить две точки и соединить их по линейке линией.)
— Как отрезок отличить от прямой линии? (У отрезка есть начало и конец, а прямая линия бесконечна.)
— Понравилось ли вам в стране Геометрия? (Да / Нет.)
— Жители страны Геометрии благодарят вас за дружбу с ними и за ваши правильные ответы.
— Оцените свою работу на уроке с помощью «Светофора». Если вам было интересно, и всё понятно, поднимите вверх зеленый сигнал светофора.
Если вам было интересно, и всё понятно, поднимите вверх зеленый сигнал светофора.
— Если вам понравился урок, но было не всё понятно, поднимите вверх желтый сигнал светофора.
— Если урок вам не понравился, и было ничего не понятно, то поднимите вверх красный сигнал светофора.
VIII . Установление связи с жизнью.
— Ребята, дома с родителями или сами на предметах, которые вас окружают точки, прямые линии, кривые линии, лучи и отрезки.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/153698-tochka-krivaja-linija-prjamaja-linija-otrezok
| Организационный момент . Актуализация знаний Учебная ситуация Открытие детей нового знания. Физкультминутка Закрепление новых знаний Итог урока | Быть всегда в порядке: Ручки, книжки и тетрадки. А девиз у нас такой: «Все, что надо, — под рукой!» — Посмотрите ка внимательно на солнышко. Какое солнышко вам больше нравится? — Я рада, что вызывает у вас хорошее настроение. Надеюсь, что к концу урока хорошее настроение будет у всех. — Верным помощником на уроке будет самая маленькая геометрическая фигура — веселая точка. Устный счет. А) Какая операция переводит первое число во второе? 12______________24. 67_____________54 Б) Выполните операцию, результат запишите. 24 _______ + 6_________ ______ 20 _______- 13_________ _______ 35 _______ + 6__________ ________ 72 _______- 15_________ ________ В) На доске запись. 567. — Расскажите про это число — Кроме точки у нас на уроке еще 1 гость. А кто это, узнаем с вами, выполнив задание. Решите примеры и расшифруйте имя гостя. -Ребята, а как вы думаете, какое любимое занятие у карандаша? -Совершенно верно. Рассмотрите фигуру на доске. — На какие группы их можно разбить? — Возникает вопрос: куда можно отнести фигуру? — Можно ли эту фигуру назвать отрезком? Почему? — Можем включить ее в прямую прямую? Почему? — Чему же нам надо научиться? Итак цель нашего урока — выявить признаки прямой, луча и отрезка, научиться их распознавать. Поэтому тема нашего урока «Прямая. Отрезок. Луч». — А теперь послушайте загадку. Все бежит куда-то и зовет вперед. Хочешь видеть друга? К другу приведет. — Как вы догадались, что это дорога, какие слова вам помогли? -Построим красивую дорожку. Растянем нить двух катушек в разные стороны -Какая получилась линия? (учитель ослабляет нить) 9000 прямой2 — А вот такая линия будет?— А дальше продолжить прямую линию можно? До каких пор? Без конца и края, линия прямая. Хоть сто лет по ней иди, не найдешь конца пути. — У людей есть имена, у животных клички. А прямую линию можно обозначить одной или двумя буквами. — Какой вывод можно с вами сделать? ВЫВОД. У прямой линии нет ни начала, ни конца. Ее можно продолжить. — Ребята, а теперь давайте с вами посмотрим вокруг и найдём прямую среди предметов, которые нас окружают. — Какие прямые линии вы знаете? -Наша веселая точка поможет нам еще поработать с прямой линией.Поставьте точку, проведите через нее прямую линию. — Можно ли еще провести линию через эту точку? Сколько прямых линий можно провести через одну точку? -Поставьте 2 точки. Через эти точки проведите прямую линию. Можно ли еще провести? ВЫВОД. Через одну точку можно провести сколько угодно точек, а через точки только одну линию. -Теперь на прямую, я помещаю солнышко точку. На сколько частей разбилась наша прямая? -Что они напоминают? Как их назовем? (учитель разрезает нить в обозначенной точке, к месту разреза прикрепляются точки) — Сколько получилось лучей? О новой фигуре разносится весть. Конца в ней пусть нет, Начало то есть! И солнце тихонько, Взойдя из -за туч. Сказало: «Друзья, назовем его луч!» -Можно ли продолжить луч со стороны разреза? -А с другой стороны? -Луч обозначается двумя буквами, причем на первом месте всегда указывается начало луча. — Чем похожи и чем отличаются луч и прямая? Вывод: Луч — прямая линия ограниченная с одной стороны.Из одной точки можно провести бесконечное множество лучей. -Молодцы, вы нашли признак луча. А теперь сделаем на одном из лучей еще один разрез. Что получилось? Я прикрепляю еще одну точку. -Сравните луч и отрезок. -Отрезок обозначается двумя буквами. — А можно из одной прямой сделать несколько отрезков? ВЫВОД. Отрезок это прямая, ограниченная с двух сторон. — Для закрепления выполним задание №6 стр.8 Включаю видео Работа по учебнику Стр.7 №2. Отметь цветным карандашом начало каждого луча и обозначь их. Стр. 7 №3. Соедини фигуры с их названиями. Стр. 7 №4. Определи, какие лучи на рисунке пересекаются? -Что нового вы сегодня узнали? — Какой вывод мы сделали с вами о прямой? — А о луче? — Отрезке? Целью этого урока было выявить признаки прямого луча и отрезка, научиться их распознавать.Мы достигли этой цели? — Молодцы. Мы сегодня с вами очень хорошо поработали. Урок окончен, спасибо всем за внимание! | — которое улыбается Ответы детей трехзначное, 5с., 6д, 7 е. Предыдущее 566, последнее 568. Сумма разрядных слагаемых 500 + 60 + 7, сумма цифр. 5 + 6 + 7 = 18 и т.д. — решают примеры и в ходе решения получают ответ КАРАНДАШИК. — рисовать, чертить «прямые» и «отрезки» — эту фигуру нельзя отрезком. , потому что она не имеет 2 точки -Нет. -Не знаем -правильно определять где прямая, где отрезок, а где луч; правильно их называть — дорога -бежит, вперед два ребенка растягивают нить — Прямая -Нет — бесконечно Прямую линию можно продолжить — ответы детей — ответы детей параллельные, наклонные дети работают в тетрадях — Множество — больше нельзя -на две -лучами -2 — нет, мешает точка — можно до бесконечности луч это прямая часть линии, ограниченная с одной стороны — отрезок -У луча есть только начало, а отрезок имеет и начало и конец. -Можно дети обводят прямыми линиями красным карандашом, лучи — синим, отрезки — зеленым повторяют движения — выполняют задание -О прямом, луче, отрезке. -У прямая линия нет ни начала, ни конца. — Луч — прямая линия ограниченная с одной стороны. Из одной точки можно провести бесконечное множество лучей. -Отрезок это прямая, ограниченная с двух сторон. На прямой линии может быть несколько отрезков. — да. | на доске 3 солнышка с разными изображениями настроения Слайд 2 Слайд 3 Слайд 4 Слайд 5 Появление на экране Слайд 6 Слайд 7 Слайд 7 Слайд 7Слайд 10 Слайд 11 |
Презентация — Математика 1 класс «Линии: кривая, прямая.Луч — Отрезок
Слайды и текст этой презентации
Слайд 1
2014 год,
13 октября,
понедельник.
Слайд 2
К задуманному числу прибавили 1 и получили 5. Какое число задумали?
Какое число при счёте следует за номером 6?
Число на 1 меньше, чем 8.
Какое число имеет соседей 3 и 4?
Какое число предшествует ядру 7?
Слайд 3
1
2
3
4
5
6
7
8
9
10
Слайд 4
Ежик по лесу шел,
На обед грибы нашел:
Два — под березой,
Один — у осины,
Сколько их будет
В плетеной корзине?
2 + 1 = 3
Слайд 5
Три ромашки-желтоглазки,
Два веселых василька
Подарили маме дети. Сколько же цветов в букете?
Сколько же цветов в букете?
3 + 2 = 5
Слайд 6
1
1
2
Слайд 7
Слайд 8
Слайд 9
Слайд 10
Отдыхай-ка
Слайд 11
Слайд 12
. Линии: кривая, прямая.
Луч. Отрезок.
Точка.
Слайд 13
На какие две группы можно разделить эти
линии?
Сколько прямых линий?
Сколько кривых линий?
Каких линий больше?
Слайд 14
Сказка
В стране Геометрии жила-была точка.
Она была маленькой. Её оставил карандаш, когда наступил на лист тетради, и никто её не замечал. Так и жила она, пока не попала в гости к линиям.
Слайд 15
Прямая линия начала хвастаться: «Я самая длинная
У меня ни начала, ни конца! Я бесконечная! »
Очень интересно стало посмотреть на нее.
Сама-то она малюсенькая. Вышла она да так
увлеклась, что не заметила и наступила на прямую
линию. И вдругла прямая линия. На её месте
появился луч.
Слайд 16
Он тоже был длинный, но всё же не такой, как
прямая линия. У него появилось начало.
Испугалась точка: «Что же я наделала!» Хотела она
убежать, да как назло наступила опять на луч.
И на месте луча появился отрезок. Он не хвастался,
какой он большой, у него уже были и начало и конец.
Слайд 17
Вот так маленькая точка смогла изменить жизнь
больших линий.
Слайд 18
Слайд 19
Слайд 20
! Прямую линию мы проводим по линейке.
Слайд 21
Сколько линий можно провести через одну точку?
Слайд 22
Сколько линий можно провести через две точки?
Слайд 23
Отдыхай-ка
Слайд 24
Слайд 25
С.15
Слайд 26
Слайд 27
Что мы узнали?
Что повторили?
Слайд 28
Оцени свою работу на уроке.
Слайд 29
Наше настроение
Урок математики «Точка. Кривая линия. Прямая линия. Отрезок. Луч ». | План-конспект урока по математике (1 класс) на тему:
Кривая линия. Прямая линия. Отрезок. Луч ». | План-конспект урока по математике (1 класс) на тему:
Тема урока: «Точка. Кривая линия. Прямая линия. Отрезок. Луч ».
Цели: уточнить и обобщить геометрические представления детей, полученных ими в дошкольном возрасте; расширить геометрические представления школьников; сформировать представление о понятиях «прямая», «кривая», «отрезок», «луч»; объемное воображение; внимание учащихся, наблюдательность, стремление к точности и аккуратности.
Тип урока: изучение нового материала.
Технологии: игровая, групповая, ИКТ технология, здоровьесберегающая.
Личностные умения: проявлять интерес к изучению темы; осознание собственной успешности при изучении темы; умение выслушивать своего товарища при работе в паре.
Метапредметные умения
Познавательные: определять геометрическую фигуру: точка, прямая и кривая линии и обосновывать свое мнение; сравнивать геометрические фигуры и обосновывать свое мнение; использовать приобретенные знания при выполнении заданий.
Регулятивные: выполнять учебные задания в соответствии с целью; оценивать правильность выполнения действий; соотносить поставленную цель и полученный результат деятельности.
Коммуникативные: формулировать высказывание, используя математические термины, в рамках учебного диалога; оформлять речевое высказывание, представляя свою позицию; адекватно использовать речевые средства для представления результата деятельности; умение работать в паре.
Предметные умения: называть геометрическую фигуру; распознавать геометрическую фигуру на плоскости; выполнять построение геометрической фигуры: точка, кривая линия, прямая линия, отрезок, луч.
Оборудование: у учителя: счетный материал, клубок с нитками, презентация к уроку. У учащихся: листочек бумаги, карандаш для практической работы.
Ход урока.
1. Организационный момент.
2. Актуализация знаний.
Устный счёт:
1) Счет предметов.
— Игра «Курочка» Учитель читает стихотворение:
— Вышла курочка гулять, свежей травки пощипать. А за ней ребятки, желтые цыплятки (ребенок с простым карандашом в руке стучит по столу…).раз в пределах 10. Дети отвечаю же раз: цып, цып, цып ..);
А за ней ребятки, желтые цыплятки (ребенок с простым карандашом в руке стучит по столу…).раз в пределах 10. Дети отвечаю же раз: цып, цып, цып ..);
— Молодцы!
— Назовите правила счета.
2) — Посмотрите на рисунки и записи, приведённые ниже.
— Какие записи подходят к рисункам? (4 + 1 = 5 — к 4 цыплятам прибежал ещё один. Стало 5 цыплят. 5-2 = 3 — плавали 5 утят, 2 утёнка ушли. Осталось 3 утёнка.
-Проверим
3) — С какими числами мы уже познакомились?
Игра «Засели домики».
— Вспомним состав числа 4 и5
— Для чего нужно знать состав числа?
(чтобы без ошибок решать примеры)
— Правильно! Решим примеры:
4) Решение примеров.(на доске)
Физминутка
3. Самоопределение к деятельности.
— Назовите фигуры, которые вы сейчас рассматривали? (круг, квадрат. треугольник). Как их можно сказать по другому?
— А где мы часто встречаемся с этим фигурами? (в математике)
— Сегодня ребята, у нас необычный урок: урок-путешествие в математическую страну, название которой вы прочитаете на воротах этого города. (Слайд 2). — Кто может прочитать?
(Слайд 2). — Кто может прочитать?
— Верно, это Геометрия, часть великой науки Математики.Посмотрите-ка, а кто живет в этой стране! Вы узнали их? Верно, это наши знакомые: круг, треугольник, квадрат. На этом уроке мы познакомимся и подружимся с другими жителями этой страны.
Практическая работа: Понятие «точка».
— У каждого из вас, на парте есть карандаш и листочек бумаги. Возьмите карандаш и поставьте его на лист (учитель то же самое на доске мелом).
— что сделал карандаш? (оставил след).
— Этот след и есть точка — геометрическая фигура.(Слайд 3)
— В стране Геометрии жила-была точка. Она была маленькой. Её оставил карандаш, когда наступил на лист тетради, и никто её не замечал. Так и жила она, пока не попала в гости к линиям. (Слайд 3)
-Посмотрите, какие это были линии. (Прямые и кривые)
-На что похожи прямые линии? (похожи на натянутые верёвочки, а верёвочки)
-Сколько прямых линий? (2)
— На что похожи кривые линии? (которые не натянули, — это кривые линии)
— Сколько кривых? (3)
Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная! » (Слайд 4)
-Очень интересно сталь точку посмотреть на нее. Сама-то точка малюсенькая. Вышла она, да так увлеклась, что не заметила, как наступила на прямую линию. И вдругла прямая линия. На её месте появился луч. (Слайд 4)
Сама-то точка малюсенькая. Вышла она, да так увлеклась, что не заметила, как наступила на прямую линию. И вдругла прямая линия. На её месте появился луч. (Слайд 4)
-Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.
-Испугалась точка: «Что же я наделала?» Хотела она убежать, да как назло наступила опять на луч. (Слайд 4)
-И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.
-Вот так маленькая точка смогла изменить жизнь больших линий.
-Ребята, какие же геометрические фигуры живут в стране геометрии? (точка, прямая линия, кривая линия, луч, отрезок) (Слайд 5)
-Кто назовет тему урока?
— Кто догадался, чему мы будем учиться в стране Геометрии? (учиться распознавать и чертить прямую линию, луч, отрезок)
4. Работа по теме урока.
1) Практическая работа 2.
— Что вы узнали о прямой линии? (она не имеет ни начала, ни конца). Она бесконечная) (Слайд 6)
Она бесконечная) (Слайд 6)
(Учитель берёт две катушки ниток, натягивает их, изображает прямую линию, и разматывает одну, другую, демонстрируя, что прямую можно продолжать в оба конца до бесконечности).
Без начала и без края
Линия прямая.
Хоть сто лет по ней иди,
Не найдёшь конца пути.
— Что о луче? (у него есть начало, но нет конца). (Слайд 6)
(Учитель берёт ножницы, разрезает нитку. Показывает, что теперь можно продолжать только в один конец).
— Что об отрезке? (у него есть и начало, и конец) (Слайд 7)
(Учитель отрезает другой конец нитки и показывает, что нитка не тянется. У нее есть и начало, и конец).
2) Работа по учебнику.
— Откройте учебник:
— Посмотрите на рисунок на стр.40. Расскажите, чем прямая линия отличается от кривой. (Прямая линия натянута, кривая — нет.)
-Что вы запомнили о прямой линии, луче, отрезке?
— Как начертить прямую линию? (провести по линейке линию) (Слайд 8)
— Как начертить отрезок? (поставить две точки и соединить их) (Слайд 9)
— Прочитайте задание на полях на стр. 40. Как узнать, какой отрезок самый длинный. (Посчитать, сколько клеточек составляет длина каждого отрезка.)
40. Как узнать, какой отрезок самый длинный. (Посчитать, сколько клеточек составляет длина каждого отрезка.)
— Посчитайте и скажите, какой отрезок самый длинный. (Синий)
— Какой отрезок самый короткий? (красный)
Работа в парах.
— Рассмотрите рисунок на стр.41. Расскажите по парте, какие линии вы видите.
Физминутка.
5. Закрепление изученного материала.
1) Работа в тетради
Работа в парах.
— Выполните следующее задание.
— Посоветуйтесь в парах и ответьте на вопрос: сколько прямых линий можно провести через две точки? (одну) (Слайд 10)
— Проведите линию с помощью карандаши и линейки.
— Посоветуйтесь в парах: сколько кривых линий можно провести через две точки? (Много)
6. Рефлексия.
— Посмотрите на слайд. (Слайд 11). Подумайте, на какие группы можно разделить данные геометрические фигуры. (Лучи — 2,5; отрезки — 1,3,4)
— Что нового узнали о линиих?
— Где в жизни прямые прямые линии? Кривые линии?
— Оцените свою работу на уроке с помощью «Светофора»:
зеленый — поняли новый материал, урок понравился;
желтый — поняли новый материал, но испытывали трудности;
красный — ничего не поняли.
7. Подведение итогов урока.
— Жители страны Геометрии благодарят вас за дружбу с ними, за активную работу на уроке.
Прямая линия, отрезок, луч — презентация онлайн
81вычесть 23
?
48
увеличить на19
?
?
уменьшить на 36
40
?
прибавить 7
92
4. 58 67 76 85
58 67 76 85 94 103Прямые линии красным цветом,
лучи — синим,
отрезки зеленым.
Найдите точки пересечения этих
дорожек
7.Цель урока: научиться различать прямые линии, отрезки, лучи; научиться их обозначать и находить точки их пересечения.
8. Тема: Прямая, луч, отрезок.
ППрямаяОтрезок
Луч
Прямая линия — она натянутая, ее
можно продлить в оба конца, она
бесконечна.
П
Прямая
Отрезок
Луч
Бесконечна
Можно продлить
в оба конца
А
О
М
В
Отрезок — это часть прямой линии,
ограничена с двух сторон.

П
Прямая
Отрезок
Луч
Бесконечна
Можно продлить
в оба конца
Ограничен с двух Нельзя продлить
сторон
А
О
М
В
Луч — это часть прямой,
ограничен с одной стороны.
Прямая
Бесконечна Можно
продлить в оба
конца
Отрезок
Часть
прямой
Часть
прямой
Луч
Ограничен с 2
сторон
Ограничен с
одной стороны,
продлить в 1
сторону
18.Найди прямую, луч, отрезок. Начерти в тетради.
Вх л
П
М
А
Е
Д
К
R N
Y
C
19. Физкультминутка
20. План.
1.Обозначать лучи.2.Распознавать луч, прямую и отрезок.
3.Определять, являются ли лучи
пересекаются
21. Распредели (устно)
Прямая АБОтрезок АВ
В
Луч АВ
А
А
А
В
В
Прямая АБ
Отрезок АВ
В
А
Луч АВ
А
А
В
В
23. Начерти в тетради.
Начерти в тетради.
• Луч МК пересекает луч АВ • Луч СЕ пересекает луч ДС
24. Алгоритм
1.Обозначим вершину луча.2.Построим луч при помощи линейки.
3.Продлим лучи до их пересечения.
4. Проверим, пересекаются ли они.
А
• Д
М
С
26. Домашнее задание
С. 72- №2, №4.Фото отправь учителю в viber.
27. Молодец !!!!
«Точка. Кривая линия. Прямая линия. Отрезок. Луч ». — me-po.ru
Конспект урока на тему: «Точка.Кривая линия. Прямая линия. Отрезок. Луч ».
Тип урока : комбинированный.
Цель : познакомить с точкой, кривой линией, отрезком, лучом.
Планируемые результаты (в соответствии с ФГОС).
Понятия : Геометрические фигуры: точка, прямые, кривые линии, отрезки, лучи.
Предметные результаты.
Научатся: различать понятия «линия», «точка», «прямая», «отрезок», и умение находить на чертеже геометрические фигуры.
УУД.
Регулятивные: формировать умение работать в группе: конструирование геометрических фигур поцу образ, описанию, рисунку.
Познавательные: первоначальное умение практического исследования математических объектов: распознавание, называние геометрических фигур, создание моделей.
Коммуникативные: задавать вопросы, просить о помощи одноклассников, учителя, формулировать свои затруднения.
Личностные результаты : Мотивация учебной деятельности.
Оборудование: учебник, тетради, плакаты, мультимедийный проектор, ноутбук.
1.Ход урока. Вступление. Здравствуйте, ребята! Сегодня мы поговорим с Вами о линии в нашей жизни. Но сначала повторим те цифры, которые уже изучили. На доске написаны стихи (озвучивает хорошо читающий ученик):
Красиво вышила Татьяна
2 лилии и 2 тюльпаны,
Какие чудные цветы!
А сколько их нам скажешь ты.
(2 + 2 = 4)
В кормушке сидели лишь 3 только птицы,
Но к ним прилетели еще 2 синицы.
Так сколько же птиц на кормушке у нас
Напишет сейчас пусть каждый из вас.
(2 + 3 = 5)
Молодцы, ребята. С этим заданием справились.
2. На доске начертили точку, кривую линию, прямую линию, отрезок, луч. Я предлагаю вам окунуться в сказочной атмосфере и послушать сказку о линиях.
-В стране Геометрии жила-была точка.(Показываю указкой на изображение точки на доске). Она была маленькой. Ее никто не оставил, когда наступил на лист тетради. Так и жила она, пока не попала в гости к линиям. (Линии на доске).
-Какие это линии? Ответы детей.
-Прямые линии, ребята, похожие на натянутые веревочки, а веревочки, которые не натянули — это кривые линии. Сколько прямых на доске? (2). Сколько кривых? (3).
-Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца.Я бесконечная! » (Показываю изображение прямой на доске).
-Очень интересно стало точкой посмотреть. Сама-то точка малюсенькая. Вышла она, да так увлеклась, что не заметила, как наступила на прямую линию. И вдругла прямая линия. На ее месте появился луч (Показываю изображение луча).
И вдругла прямая линия. На ее месте появился луч (Показываю изображение луча).
Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало. Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч.И на месте луча появился отрезок. У него уже были начало и конец (Показываю изображение отрезка).
-Понравилась сказка? (Ответы детей). Что о прямой линии? (Она бесконечная). Сейчас я возьму катушку ниток и размотаю ее. Посмотрите, это прямая? (Ответы детей).
-Что узнали о луче? (У него есть начало, но нет конца). Я отрезаю кусок нитки. Теперь линию можно продолжить только в 1 конец.
-Что узнать об отрезке? (У него есть начало и конец). Попрошу одного из ребят отрезать еще кусочек нити.
А теперь отдохнем. Физминутка отображается через проектор. Первоклассники напрягали зрение, выбрана физминутка «Рыбки в аквариуме», следим за движением рыбок.
-А теперь сядем все правильно, спинку держимровно, откроем тетради под наклоном вправо, возьмем правильно карандаш, линейку в руки.
Начертите луч, отрезок, прямую. Не забывайте, ребята, что у луча должна быть точка в начале, а отрезок с двух сторон должен быть ограничен точками. Теперь он никуда не убежит.
Физминутка.
Хомка, Хомка, хомячок,
Полосатенький бочок.
Хомка раненько встает,
Шейку моет, щечки трет.
Подметает Хомка хатку
И выходит на зарядку.
Раз, два, три, четыре, пять
Хомка сильным хочет стать.
Ребята, как Вы думаете, как можно определите прямую? (Ответы детей). Что значит определить «на глаз»? (Не измеряя). К доске выходят 1 девочка и1 мальчик. Измерим длины класса шагами.Посмотрите, количество шагов разное. Есть разные мерки. Здесь это — шаг. Для того, чтобы не было путаницы, люди придумали общую мерку — сантиметр. Проговорите это хором. Пишем (см), а читаем сантиметр. На следующем уроке мы продолжим эту тему и узнаем, как измерить и начертить отрезки с помощью линейки.
3. Итоги. Рефлексия. Вопросы по уроку.
Какую тему мы изучили сегодня? (Ответы детей). Оцените свою работу на уроке с помощью светофора (Зеленый — отлично, желтый — хорошо, красный — плохо).
Объявление домашнего задания: найти в прямых линиях, кривые линии, озвучить в классе.
Правило что такое луч. Точка, линия, прямая, луч, отрезок, ломанная
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи только важно его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
А B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А».Но как понять через какие? А А А
Линия — это множество точек. У нее измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия а, линия б, линия с
а б cЛиния может быть
- замкнутой, если ее начало и конец находятся в одной точке,
- разомкнутой, если ее начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обеих сторонах
Даже когда виден небольшой прямой юридический вопрос, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой.Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия а
апрямая линия АБ
B AПрямые могут быть
- пересекающиеся, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.- перпендикулярными, если пересекаются под прямым углом (90 °).
- параллельные, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, ее можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча А A
Луч обозначается строчной (маленькой) латинской буквой.Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч а
алуч АБ
BЛучи начинаются, если
- расположены прямо на одной и той же,
- идут в одной точке,
- движутся в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B А Отрезок — это часть прямого, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить ее длину. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Апрямая линия АБ
B AОт прямого «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B А ✂
Отрезок обозначается двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, имеющая отрезок
отрезок AB
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединенных отрезков не под углом 180 °
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из состоящих из ломаной.Смежные звенья — это звенья, у которых один конец звена является началом другого.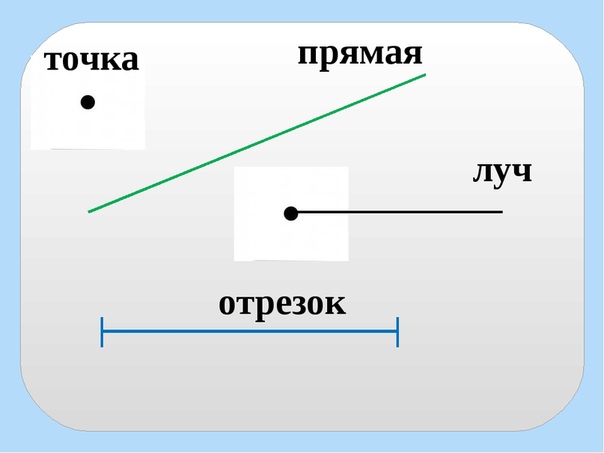 Смежные звенья не должны лежать на одной прямой.
Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, которые соединяются отрезками, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются дополнительными
звено BC и звено CD являются дополнительными
звено CD и звено DE являются дополнительными
А B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см.У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Сторона многоугольника (поможет запомнить выражение: «пойти на все четыре стороны дома», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это дополнительные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точка конца одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и
вершина A и вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC имеют смежные
сторона BC и сторона CD соответствуют друг другу
CD и сторона DE соответствуют
сторона DE и сторона EF имеют смежными
сторона EF и сторона FA являются собственными
А
B
C
D
E
F
120
60
58
122
98
141 Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
Луч и прямая связь к геометрическим элементам. Сведения о них даются уже на первом этапе надлежащем разделе математики. Чем отличается луч от прямой? Информация об этом изложена ниже.
Определение
Луч — это полупрямая, с одной стороны исходящая из конкретной точки, с другой — ничем не ограниченная.
Прямая — это бесконечная с обеих сторон линия, проходящая через две точки и не меняющее свое направление (отличие от кривой или ломаной).
Прямая Сравнение
Из определений, что кардинальное отличие луча от прямого видно в том, ограничены ли они в пространстве. Так, луч обязательно имеет начало и продолжается только с одной стороны. У прямой, в свою очередь, нет предела ни с того, ни с другого края. В связи с этим начертить можно лишь ее часть, что, впрочем, относится и к лучу.
Если взять на прямую произвольную точку, то отходящая от нее бесконечная линия будет проходить лучом.В этом смысле луч можно назвать частью прямой. Справедливо и то, что избранная точка будет служить в качестве исходной сразу для двух противоположно лучей.
Справедливо и то, что избранная точка будет служить в качестве исходной сразу для двух противоположно лучей.
Сравнивая луч и прямую, следует сказать о способах их обозначения. Каждый из геометрических объектов может называться латинской строчной буквой: луч a (с, d, t) или прямая b (a, h, c). Также в том и другом случае используется обозначение двумя заглавными буквами: луч NK или прямая OD.
Однако в последнем случае имеются отличия.Буквы в названии прямой, помечающие точки, через которые она проведена, при чтении и записи можно менять местами. Между тем относительно луча первым указывается строго его начало, а точка расположенная на определенном расстоянии от исходной.
Кроме того, луч имеет собственный вариант обозначения. В этом случае после заглавного символа, называющего начальную точку, с помощью строчной буквы указывается прямая. Таким образом, обозначение Bo трактуется так: луч с начала в точке B принадлежит прямой o.
В чем разница между лучом и прямой, кроме сказанного? В том, что лучи могут образовывать угол. Для этого они должны исходить из одной точки. Прямые угловые не образуют.
Для этого они должны исходить из одной точки. Прямые угловые не образуют.
Цели:
- Познакомить учащихся с понятием луча как бесконечной фигуры;
- Учить показывать луч с помощью указки;
- Продолжить формирование вычислительных навыков;
- Совершенствовать умение решать задачи;
- Развивать умение анализировать и обобщать.
Ход урока
я . Организационный момент.
Ребята, вы готовы к уроку? ( Да . )
На вас надеюсь я, друзья!
Вы хороший дружный класс.
Всё получится у вас!
II . Мотивация учебной деятельности.
Я очень хочу, чтобы урок получился интересным, чтобы мы вместе повторили и закрепили то, что мы уже знаем и постарались открыть для себя что-то новое.
III. Актуализация знаний.
- Прочтите число и назовите «лишнее» число в каждом ряду:
а) 90, 30, 40, 51,60;
б) 88, 64,55,11, 77, 33;
с) 47, 27, 87, 74, 97, 17; - Назовите числа по порядку:
а) от 20 до 30;
б) от 46 до 57;
в) от 75 до 84; - Как вы думаете, будут ли эти тексты задачами?
Измените вопрос второго текста так, чтобы он стал желаемым.
Измените условие так, чтобы стал обещанием.
Решите полученные задачи.
IV . Первичное усвоение новых знаний.
Начертите такую линию.
Как она называется?
Начертите такую линию.
Как она называется? Чем отличается отрезок от прямого?
Начертите такую линию.
Кто знает, как она называется?
Посмотрите на картинку, вы видите похожие линии, что это?
Вот и эта линия называется луч.Чем он отличается от прямого и отрезка?
Это очень интересная фигура: у нее есть начало и нет конца.
А изображают её так. ( Работа на доске и в тетрадях. ) Отметим на точку, приложим к ней линейку и по линейке проведём линию.
Какой бы длинной ни была линейка, весь луч мы всё равно не сможем начертить. На рисунке мы изобразили лишь часть луча, которая показывает направление луча.
Луч можно начертить в любом направлении:
Начертите три разных луча у себя в тетради.
, чтобы отличать один луч от другого, договоримся обозначать луч двумя буквами латинского алфавита так, чтобы мы обозначали с вами отрезки. Писать буквы нужно в строго определенном порядке: первая пишется та буква, которая обозначает начало луча, вторая пишется над или под лучом.
Посмотрите на рисунок в учебнике. Луч красного цвета обозначен двумя буквами. Какой буквой обозначено начало луча?
Прочитаем все вместе запись: «Луч АВ»
Теперь прочитайте следующие записи: луч ВС, луч МК, луч ВА, луч ОХ.
Важно научиться правильно показывать луч. Мы будем делать это концом указки. ( Показ учителем. )
Теперь посмотрите на плакат. ( Подготавливается заранее, на нём 3 луча .) На нём изображены 3 луча. Прочитайте название каждого из них. Называя луч, показывайте его указкой.
Физминутка
1, 2, 3, 4, 5
Все умеем мы считать.
Отдыхать умеем тоже:
Руки за спину положим,
Голову поднимем выше
И легко-легко подышим.
Раз, два — выше голова,
Три, — ноги шире,
, Пять шесть — тихо сеть.
Раз — подняться, потянуться.
Два — согнуться, разогнуться.
Три — в ладоши три хлопка,
Головою три кивка.
На четыре — руки шире.
Пять — руками помахать.
Шесть — за парту тихо сесть.
В. Первичная проверка понимания.
1) Работа с учебником.
Можно ли нарисовать весь луч?
В каком направлении можно начертить луч?
Учащиеся называют каждый луч, сначала читая букву, соответствующую началу луча.
Учащиеся чертят в тетради луч, обозначают его буквами.
Поставьте в тетради точку О. Проведите через нее прямую линию. Сколько получилось лучей?
Проведите ещё одну прямую линию через эту точку. Сколько теперь лучей?
VI . Организация усвоения способов деятельности.
1) Работа в тетради на печатной основе.
Дифференцированное задание.
1-я группа — № 19
2-я группа — № 20
3-я группа — № 21
2) Физминутка — офтальмотренажёр.
3) Работа по учебнику
Прочитайте, какие способы сложения придумал Знайка?
Найдите результаты сложения такими же методами.
Что известно в задаче?
Что надо узнать?
Короче — это больше или меньше?
Как узнать длину карандаша?
Запишите ответ.
VII . Рефлексия.
Что узнали нового на уроке?
Что такое луч?
Как начертить луч?
Сколько лучей можно провести через одну точку?
Сегодня на уроке мне помогали…..
VIII . Домашнее задание.
Все мы когда-то изучали в школе геометрию, но далеко не каждый из нас вспомнит, что представляет собой отрезок. А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.
А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.
Определение понятий
Для начала вспомним, что называется геометрией.Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства. Квадрат треугольник, прямоугольник, параллелепипед, круг, овал, ромб, цилиндр и т. п. Простейшая фигура — это прямая. Она является бесконечной и не имеет начала. Две прямые пересекутся только в одной единственной точке. Через одну точку можно проводить бессчетное количество прямых линий. Каждая точка на линии делит ее на два .
Он состоит из точек, располаг по одной стороне.Все понятия данных подмножеств можно именовать таким образом. Лучше обозначают одну строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е).
В основе геометрической фигуры, лежащей углы, лежат полупые. Они начинаются в точке, где пересекаются, но второй стороной в бесконечность. Начало делит прямую на 2 части. На письме его обычно именуют двумя заглавными (OF) или одной буквой латиницы (а, в, с).Если дана прямая, то записывается ОВ в закругленных скобках: (ОВ). Если же это отрезок — в квадратных скобках.
Таким образом, луч — это часть прямой. Через 2 несовпадающие — только одну точку. Последние могут быть пересмотрены только в трех вариантах: параллельные друг другу. Существуют линейные уравнения, которые задают прямую на плоскости.
Обозначения в геометрии
Вариантов для обозначения несколько:
Нужно знать: Что такое и горизонтальное положение?
Отличие световых лучей от геометрических
В геометрии таковые понятия очень схожи. Луч — это линия, но она является энергией света . Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Из курса школьной геометрии мало у кого остались точные сведения о том, что представляет собой отрезок, как он обозначается, что такое ломаная линия, прямая, точка и как обозначаются лучи.Если вы не можете вспомнить начальный курс геометрии, ознакомьтесь с этой статьей.
Что такое геометрия? Это математический раздел, в котором школьник знакомится с геометрическими фигурами и их свойствами. Информации много, иногда недостаточно времени для того, чтобы все охватить и запомнить. Некоторые знания необходимо освежить спустя несколько месяцев и даже лет. Например, вспомнить, что такое лучи и как они обозначаются.
Что такое луч в геометрии
Луч — это прямая, с одной стороны ограниченная точка, а с другой стороны — свободная, то есть не имеющая ограничений. Чтобы быстрее запомнить, как обозначаются лучи и как они выглядят, можно простой пример: мы ведь можем направить лучи света из фонарика в небо? С одной стороны луч ограничен — с того места, откуда он выходит, то есть — из фонарика. С другой стороны — он не имеет ограничений. Получается, что крайняя точка начала луча только одна, она и называется «начало». Вторая точка не существует, потому что луч уходит в бесконечность.
Чтобы быстрее запомнить, как обозначаются лучи и как они выглядят, можно простой пример: мы ведь можем направить лучи света из фонарика в небо? С одной стороны луч ограничен — с того места, откуда он выходит, то есть — из фонарика. С другой стороны — он не имеет ограничений. Получается, что крайняя точка начала луча только одна, она и называется «начало». Вторая точка не существует, потому что луч уходит в бесконечность.
Чтобы понимать, как обозначить луч на листке бумаги, нужно начертить прямую линию.Например, пусть это будет отрезок, равный 10 см. С правой стороны поставим ограничение — точка, это начало луча. Вторая точка на конце отрезка не будет.
Как обозначаются лучи
Продолжим вспоминать, что представляет собой луч и как его обозначить.
Вариантов обозначения несколько:
- Начертим в тетрадке прямую, обозначим точку начала луча. И присвоим ей имя. Например, пусть это будет луч «С». Первая точка — это начало луча, вторая точка, как вы уже вспомнили, не существует.
 Это классическая схема обозначения лучей.
Это классическая схема обозначения лучей. - Второй вариант поинтереснее: лучи можно использовать посредством буквами. Например, на одном луче может быть 2 буквы. Первая — это начало луча, пусть это будет буква А, а вторая может располагаться с определенным шагом. Допустим, на отрезке длиной 10 см начало луча обозначено буквой А, а на расстоянии 4 см от начала луча имеется вторая точка, точка В. Тогда луч нужно обозначить, как луч «АВ». Чтобы было понятнее, можно так: вторая точка В — это точка, через которую читать луч.
- Лучи еще можно обозначить и третьим способом, когда начальная точка будет находиться не в начале луча, а с небольшим отступлением. Например, чертимую прямую длиной 10 см, отступаем от левого края 1 см, ставим точку — это будет начало луча. Обозначаем, например, буквой О. Посередине луча точку не ставим, но обозначаем эту часть луча буквой К. В данном случае буква О, будет началом этого луча, он исходит из этой точки. Читается луч так: «ОК», он является полупрямым.

вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC имеют смежные
сторона BC и сторона CD соответствуют друг другу
CD и сторона DE соответствуют
сторона DE и сторона EF имеют смежными
сторона EF и сторона FA являются собственными
А B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
Луч и прямая связь к геометрическим элементам. Сведения о них даются уже на первом этапе надлежащем разделе математики. Чем отличается луч от прямой? Информация об этом изложена ниже.
Определение
Луч — это полупрямая, с одной стороны исходящая из конкретной точки, с другой — ничем не ограниченная.
Прямая — это бесконечная с обеих сторон линия, проходящая через две точки и не меняющее свое направление (отличие от кривой или ломаной).
Прямая
Сравнение
Из определений, что кардинальное отличие луча от прямого видно в том, ограничены ли они в пространстве. Так, луч обязательно имеет начало и продолжается только с одной стороны. У прямой, в свою очередь, нет предела ни с того, ни с другого края. В связи с этим начертить можно лишь ее часть, что, впрочем, относится и к лучу.
Если взять на прямую произвольную точку, то отходящая от нее бесконечная линия будет проходить лучом.В этом смысле луч можно назвать частью прямой. Справедливо и то, что избранная точка будет служить в качестве исходной сразу для двух противоположно лучей.
Справедливо и то, что избранная точка будет служить в качестве исходной сразу для двух противоположно лучей.
Сравнивая луч и прямую, следует сказать о способах их обозначения. Каждый из геометрических объектов может называться латинской строчной буквой: луч a (с, d, t) или прямая b (a, h, c). Также в том и другом случае используется обозначение двумя заглавными буквами: луч NK или прямая OD.
Однако в последнем случае имеются отличия.Буквы в названии прямой, помечающие точки, через которые она проведена, при чтении и записи можно менять местами. Между тем относительно луча первым указывается строго его начало, а точка расположенная на определенном расстоянии от исходной.
Кроме того, луч имеет собственный вариант обозначения. В этом случае после заглавного символа, называющего начальную точку, с помощью строчной буквы указывается прямая. Таким образом, обозначение Bo трактуется так: луч с начала в точке B принадлежит прямой o.
В чем разница между лучом и прямой, кроме сказанного? В том, что лучи могут образовывать угол. Для этого они должны исходить из одной точки. Прямые угловые не образуют.
Для этого они должны исходить из одной точки. Прямые угловые не образуют.
Цели:
- Познакомить учащихся с понятием луча как бесконечной фигуры;
- Учить показывать луч с помощью указки;
- Продолжить формирование вычислительных навыков;
- Совершенствовать умение решать задачи;
- Развивать умение анализировать и обобщать.
Ход урока
я . Организационный момент.
Ребята, вы готовы к уроку? ( Да . )
На вас надеюсь я, друзья!
Вы хороший дружный класс.
Всё получится у вас!
II . Мотивация учебной деятельности.
Я очень хочу, чтобы урок получился интересным, чтобы мы вместе повторили и закрепили то, что мы уже знаем и постарались открыть для себя что-то новое.
III. Актуализация знаний.
- Прочтите число и назовите «лишнее» число в каждом ряду:
а) 90, 30, 40, 51,60;
б) 88, 64,55,11, 77, 33;
с) 47, 27, 87, 74, 97, 17; - Назовите числа по порядку:
а) от 20 до 30;
б) от 46 до 57;
в) от 75 до 84; - Как вы думаете, будут ли эти тексты задачами?
Измените вопрос второго текста так, чтобы он стал желаемым.
Измените условие так, чтобы стал обещанием.
Решите полученные задачи.
IV . Первичное усвоение новых знаний.
Начертите такую линию.
Как она называется?
Начертите такую линию.
Как она называется? Чем отличается отрезок от прямого?
Начертите такую линию.
Кто знает, как она называется?
Посмотрите на картинку, вы видите похожие линии, что это?
Вот и эта линия называется луч.Чем он отличается от прямого и отрезка?
Это очень интересная фигура: у нее есть начало и нет конца.
А изображают её так. ( Работа на доске и в тетрадях. ) Отметим на точку, приложим к ней линейку и по линейке проведём линию.
Какой бы длинной ни была линейка, весь луч мы всё равно не сможем начертить. На рисунке мы изобразили лишь часть луча, которая показывает направление луча.
Луч можно начертить в любом направлении:
Начертите три разных луча у себя в тетради.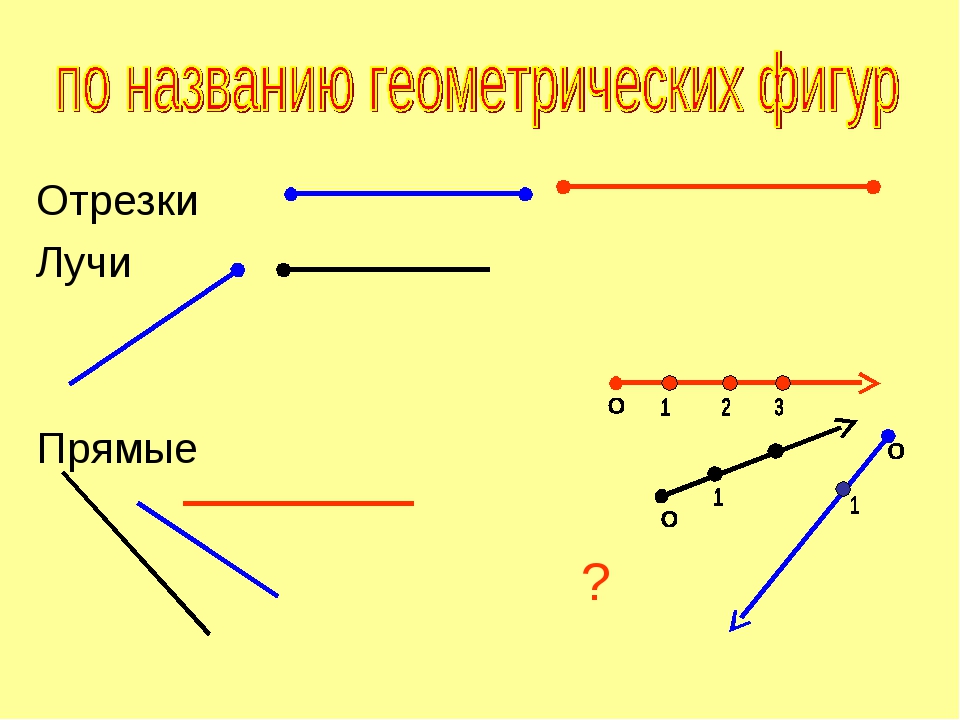
, чтобы отличать один луч от другого, договоримся обозначать луч двумя буквами латинского алфавита так, чтобы мы обозначали с вами отрезки. Писать буквы нужно в строго определенном порядке: первая пишется та буква, которая обозначает начало луча, вторая пишется над или под лучом.
Посмотрите на рисунок в учебнике. Луч красного цвета обозначен двумя буквами. Какой буквой обозначено начало луча?
Прочитаем все вместе запись: «Луч АВ»
Теперь прочитайте следующие записи: луч ВС, луч МК, луч ВА, луч ОХ.
Важно научиться правильно показывать луч. Мы будем делать это концом указки. ( Показ учителем. )
Теперь посмотрите на плакат. ( Подготавливается заранее, на нём 3 луча .) На нём изображены 3 луча. Прочитайте название каждого из них. Называя луч, показывайте его указкой.
Физминутка
1, 2, 3, 4, 5
Все умеем мы считать.
Отдыхать умеем тоже:
Руки за спину положим,
Голову поднимем выше
И легко-легко подышим.
Раз, два — выше голова,
Три, — ноги шире,
, Пять шесть — тихо сеть.
Раз — подняться, потянуться.
Два — согнуться, разогнуться.
Три — в ладоши три хлопка,
Головою три кивка.
На четыре — руки шире.
Пять — руками помахать.
Шесть — за парту тихо сесть.
В. Первичная проверка понимания.
1) Работа с учебником.
Можно ли нарисовать весь луч?
В каком направлении можно начертить луч?
Учащиеся называют каждый луч, сначала читая букву, соответствующую началу луча.
Учащиеся чертят в тетради луч, обозначают его буквами.
Поставьте в тетради точку О. Проведите через нее прямую линию. Сколько получилось лучей?
Проведите ещё одну прямую линию через эту точку. Сколько теперь лучей?
VI . Организация усвоения способов деятельности.
1) Работа в тетради на печатной основе.
Дифференцированное задание.
1-я группа — № 19
2-я группа — № 20
3-я группа — № 21
2) Физминутка — офтальмотренажёр.
3) Работа по учебнику
Прочитайте, какие способы сложения придумал Знайка?
Найдите результаты сложения такими же методами.
Что известно в задаче?
Что надо узнать?
Короче — это больше или меньше?
Как узнать длину карандаша?
Запишите ответ.
VII . Рефлексия.
Что узнали нового на уроке?
Что такое луч?
Как начертить луч?
Сколько лучей можно провести через одну точку?
Сегодня на уроке мне помогали…..
VIII . Домашнее задание.
Все мы когда-то изучали в школе геометрию, но далеко не каждый из нас вспомнит, что представляет собой отрезок. А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.
А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.
Определение понятий
Для начала вспомним, что называется геометрией.Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства. Квадрат треугольник, прямоугольник, параллелепипед, круг, овал, ромб, цилиндр и т. п. Простейшая фигура — это прямая. Она является бесконечной и не имеет начала. Две прямые пересекутся только в одной единственной точке. Через одну точку можно проводить бессчетное количество прямых линий. Каждая точка на линии делит ее на два .
Он состоит из точек, располаг по одной стороне.Все понятия данных подмножеств можно именовать таким образом. Лучше обозначают одну строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е).
В основе геометрической фигуры, лежащей углы, лежат полупые. Они начинаются в точке, где пересекаются, но второй стороной в бесконечность. Начало делит прямую на 2 части. На письме его обычно именуют двумя заглавными (OF) или одной буквой латиницы (а, в, с).Если дана прямая, то записывается ОВ в закругленных скобках: (ОВ). Если же это отрезок — в квадратных скобках.
Таким образом, луч — это часть прямой. Через 2 несовпадающие — только одну точку. Последние могут быть пересмотрены только в трех вариантах: параллельные друг другу. Существуют линейные уравнения, которые задают прямую на плоскости.
Обозначения в геометрии
Вариантов для обозначения несколько:
Нужно знать: Что такое и горизонтальное положение?
Отличие световых лучей от геометрических
В геометрии таковые понятия очень схожи. Луч — это линия, но она является энергией света . Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Из курса школьной геометрии мало у кого остались точные сведения о том, что представляет собой отрезок, как он обозначается, что такое ломаная линия, прямая, точка и как обозначаются лучи.Если вы не можете вспомнить начальный курс геометрии, ознакомьтесь с этой статьей.
Что такое геометрия? Это математический раздел, в котором школьник знакомится с геометрическими фигурами и их свойствами. Информации много, иногда недостаточно времени для того, чтобы все охватить и запомнить. Некоторые знания необходимо освежить спустя несколько месяцев и даже лет. Например, вспомнить, что такое лучи и как они обозначаются.
Что такое луч в геометрии
Луч — это прямая, с одной стороны ограниченная точка, а с другой стороны — свободная, то есть не имеющая ограничений.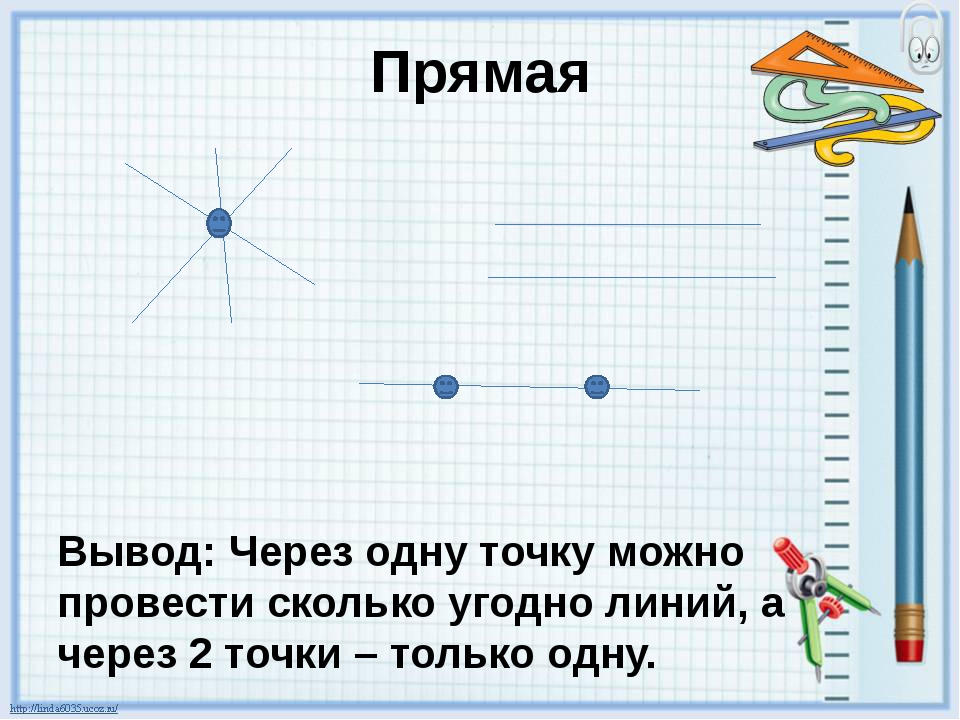 Чтобы быстрее запомнить, как обозначаются лучи и как они выглядят, можно простой пример: мы ведь можем направить лучи света из фонарика в небо? С одной стороны луч ограничен — с того места, откуда он выходит, то есть — из фонарика. С другой стороны — он не имеет ограничений. Получается, что крайняя точка начала луча только одна, она и называется «начало». Вторая точка не существует, потому что луч уходит в бесконечность.
Чтобы быстрее запомнить, как обозначаются лучи и как они выглядят, можно простой пример: мы ведь можем направить лучи света из фонарика в небо? С одной стороны луч ограничен — с того места, откуда он выходит, то есть — из фонарика. С другой стороны — он не имеет ограничений. Получается, что крайняя точка начала луча только одна, она и называется «начало». Вторая точка не существует, потому что луч уходит в бесконечность.
Чтобы понимать, как обозначить луч на листке бумаги, нужно начертить прямую линию.Например, пусть это будет отрезок, равный 10 см. С правой стороны поставим ограничение — точка, это начало луча. Вторая точка на конце отрезка не будет.
Как обозначаются лучи
Продолжим вспоминать, что представляет собой луч и как его обозначить.
Вариантов обозначения несколько:
- Начертим в тетрадке прямую, обозначим точку начала луча. И присвоим ей имя. Например, пусть это будет луч «С». Первая точка — это начало луча, вторая точка, как вы уже вспомнили, не существует.
 Это классическая схема обозначения лучей.
Это классическая схема обозначения лучей. - Второй вариант поинтереснее: лучи можно использовать посредством буквами. Например, на одном луче может быть 2 буквы. Первая — это начало луча, пусть это будет буква А, а вторая может располагаться с определенным шагом. Допустим, на отрезке длиной 10 см начало луча обозначено буквой А, а на расстоянии 4 см от начала луча имеется вторая точка, точка В. Тогда луч нужно обозначить, как луч «АВ». Чтобы было понятнее, можно так: вторая точка В — это точка, через которую читать луч.
- Лучи еще можно обозначить и третьим способом, когда начальная точка будет находиться не в начале луча, а с небольшим отступлением. Например, чертимую прямую длиной 10 см, отступаем от левого края 1 см, ставим точку — это будет начало луча. Обозначаем, например, буквой О. Посередине луча точку не ставим, но обозначаем эту часть луча буквой К. В данном случае буква О, будет началом этого луча, он исходит из этой точки. Читается луч так: «ОК», он является полупрямым.

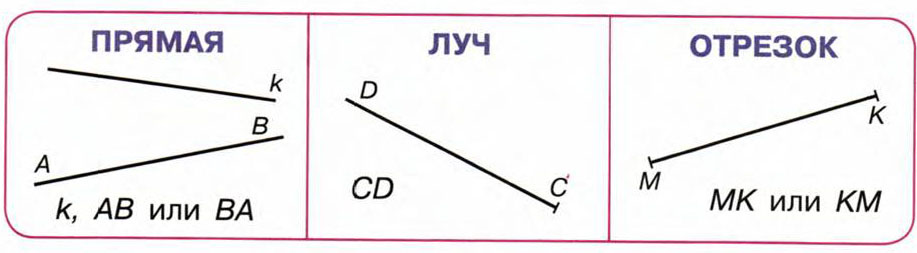 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
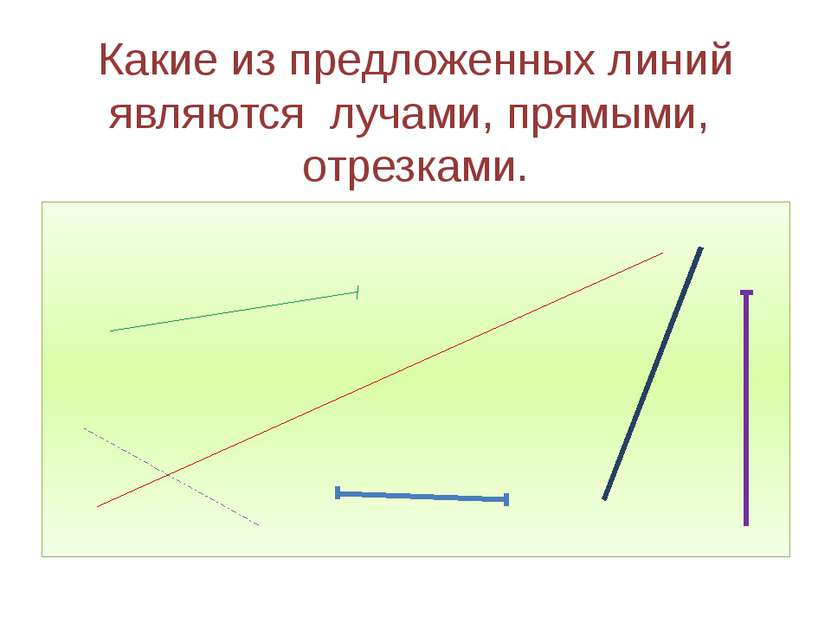

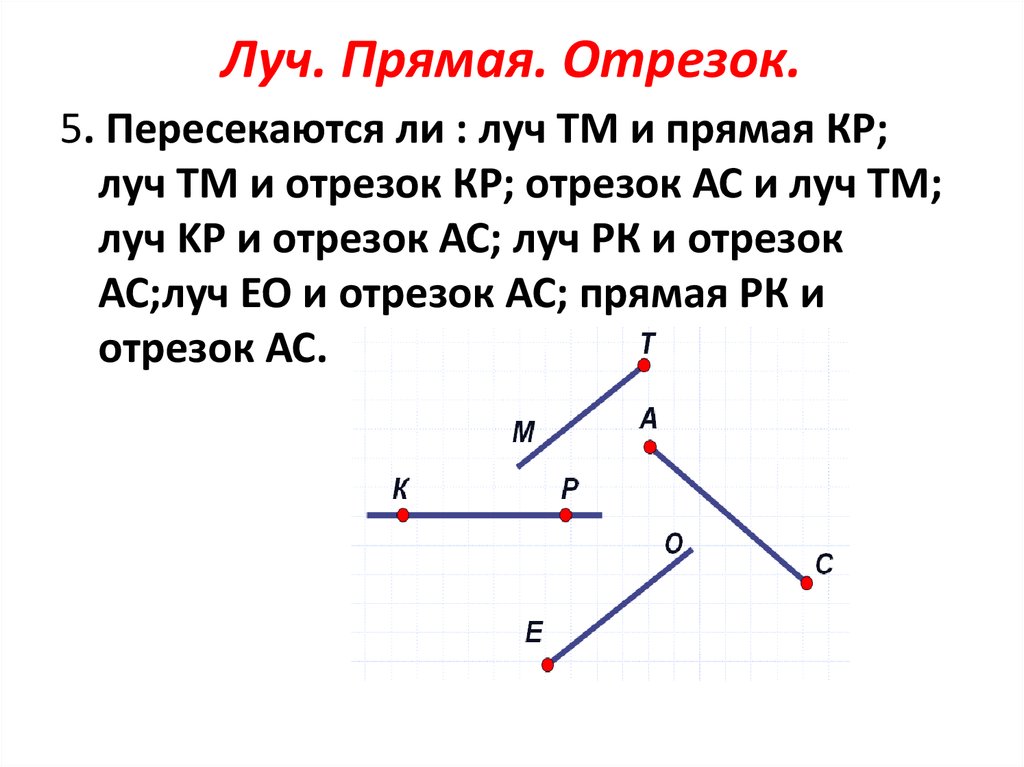

 Луч — Отрезок
Луч — Отрезок Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками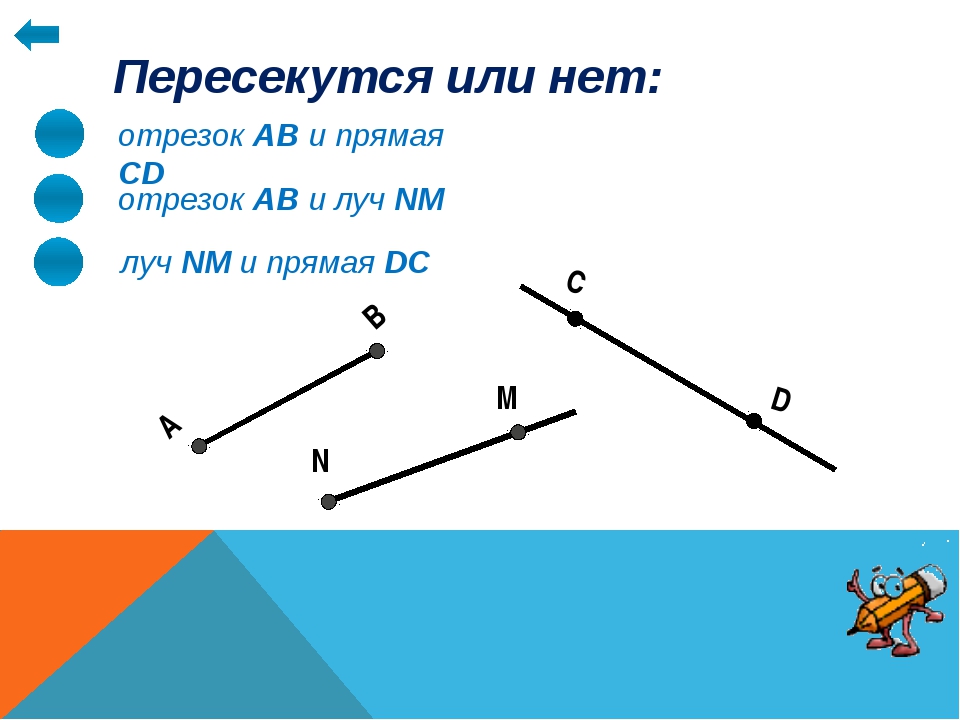
 План.
План.
 Чертить и рисовать Карандаш очень любит. А больше всего он любит изображать различные линии.
Чертить и рисовать Карандаш очень любит. А больше всего он любит изображать различные линии.

 На прямой линии может быть несколько отрезков.
На прямой линии может быть несколько отрезков.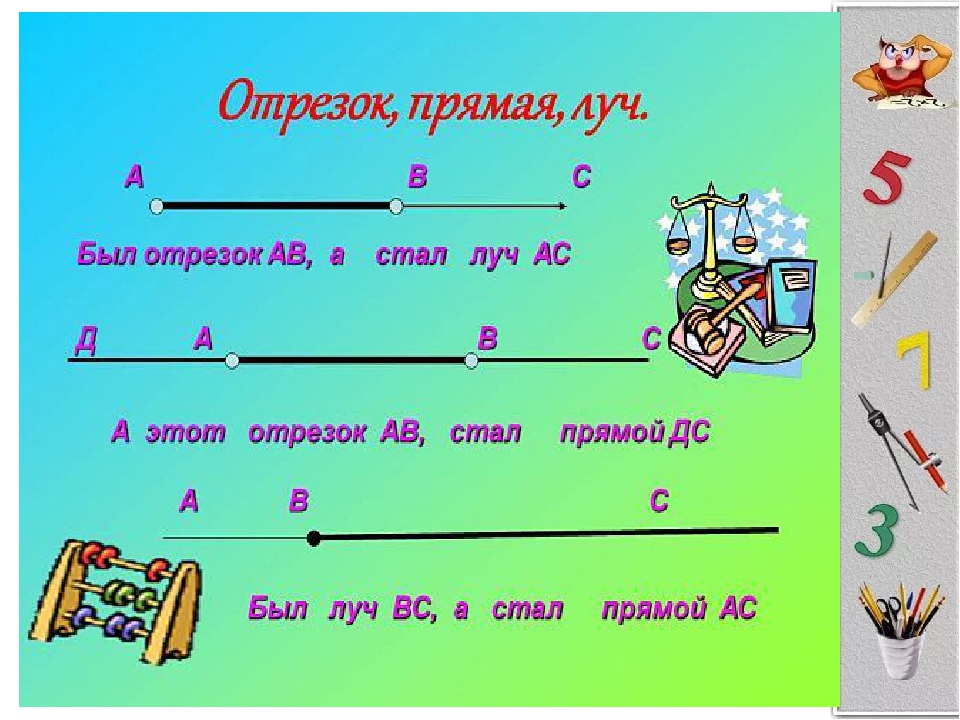
 Ее можно продолжить
Ее можно продолжить Кривая линия. Прямая линия. Отрезок. Луч ». | План-конспект урока по математике (1 класс) на тему:
Кривая линия. Прямая линия. Отрезок. Луч ». | План-конспект урока по математике (1 класс) на тему:  Начерти в тетради.
Начерти в тетради. 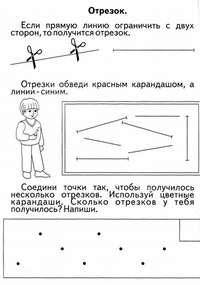 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками 
 Это классическая схема обозначения лучей.
Это классическая схема обозначения лучей.