Дроби 5 класс задачи – Задачи на тему дроби математика 5 класс — Детская игровая комната «Волшебный лес»

Posted on 15.09.202025.12.2019 by alexxlab

Содержание

Методическая разработка по математике (5 класс) на тему: Проверочная работа по математике для 5 класса по теме «Задачи на дроби. Нахождение части целого и целого по части»

СПЕЦИФИКАЦИЯ

проверочной работы по математике для 5 класса

по теме «Задачи на дроби. Нахождение части целого

и целого по части»

Разработка Зинченко Т.В.

1. Назначение проверочной работы

Работа предназначена для проведения процедуры тематического контроля индивидуальных достижений учащихся по математике по теме «Задачи на дроби. Нахождение части целого и целого по части». Основной целью работы является проверка и оценка способности обучающихся 5 класса применять полученные в процессе изучения математики знания для решения разнообразных задач учебного и практического характера.

2. Документы, определяющие содержание и характеристики проверочной работы

Содержание и основные характеристики проверочных материалов разработаны на основе следующих документов:

Федеральный компонент государственного стандарта основного общего образования по математике (Приказ МО от 5 марта 2004 г. № 1089).
О сертификации качества педагогических тестовых материалов (Приказ Минобразования России от 17.04.2000 г. № 1122).

3. Условия и время проведения проверочной работы.

На выполнение диагностической работы отводится 30 минут.

Дополнительных материалов и оборудования не требуется.

4. Содержание и структура проверочной работы

Каждый вариант диагностической работы состоит из 1 заданий: 5 заданий с выбором одного правильного ответа, 4 задания с кратким ответом и 2 задания с развёрнутым ответом.

В каждом варианте представлены как задания базового уровня сложности, так и задания повышенного уровня сложности (до 30% заданий).

Содержание диагностической работы охватывает основные элементы курса математики 5 класса. Работа может использоваться для контроля знаний при обучении по учебнику «Математика.5 класс» (авторы С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин)

Распределение заданий по проверяемым умениям представлено в таблице 1:

Таблица 1

№ п/п	Перечень проверяемых знаний и умений	Число заданий
1	Формулировать определение делителя и кратного	2
2	Формулировать определение простого и составного числа	2
3	Знать и использовать в решении признаки делимости чисел	4
4	Классифицировать натуральные числа по признакам делимости	2
5	Доказывать утверждения о делимости чисел	1
6	Решать задачи с использованием чётности и с делимостью чисел	1

5. Система оценивания отдельных заданий и работы в целом

За правильное выполнение каждого из заданий 1-10 — ставится 1 балл.

За выполнение заданий 11,12 — ставятся 2 балла.

Всего – 14 баллов.

В Приложении 1 приведен план проверочной работы.

В Приложении 2 приведен календарно-тематический план.

Приложение 1

План проверочной работы

по математике в 5 классе

по теме «Признаки делимости. Простые и составные числа»

Используются следующие условные обозначения:

ВО – задание с выбором ответа, КО – задание с кратким ответом, РО – задание с развёрнутым ответом.

Б – базовый уровень сложности, П – повышенный уровень сложности.

Коды проверяемых умений приведены в соответствии с кодификатором МЦКО по математике для 5 класса.

№ зада-ния	Контролируемые элементы содержания	Проверяемые умения	Тип зада- ния	Время (мин)	Уро-вень слож-ности	Макс. балл
1			ВО	1	Б	1
2			ВО	1	Б	1
3			ВО	2	Б	1
4			ВО	2	Б	1
5			ВО	2	Б	1
6			ВО	2	Б	1
7			КО	2	Б	1
8			КО	2	Б	1
9			КО	2	П	1
10			КО	2	П	1
11			РО	5	П	2
12			РО	5	П	2

Приложение 2

Математика 5 класс

к учебнику С.М. Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин «Математика 5» для общеобразовательных организаций

№ п/п	Раздел программы	количество часов	Характеристика основных учебных действий
1	Натуральные числа и нуль	52	Описывать свойства натурального ряда. Читать и записывать натуральные чмсла, сравнивать их. Выполнять вычисления с натуральными числами; вычислять значения степеней. Формулировать законы арифметических действий, записывать их с помощью букв, применять их для рационализации вычислений. Анализировать и осмысливать текст задачи, извлекать необходимую информацию, моделировать условие с помощью схем, строить логическую цепочку рассуждений. Осуществлять самоконтроль, проверяя ответ на соответствие условию. Уметь решать задачи на понимание отношений «больше на…», «меньше на…», «больше в…», «меньше в…», а также понимание стандартных ситуаций, в которых используются слова «всего», «осталось» и т.п.; типовые задачи «на части», на нахождение двух чисел по их сумме и разности.
1.1	Ряд натуральных чисел.	1
1.2	Десятичная система записи натуральных чисел.	2
1.3	Сравнение натуральных чисел.	2
1.4	Сложение. Законы сложения.	3
1.5	Вычитание.	2
1.6.	Решение текстовых задач с помощью сложения и вычитания	3
1.7	Умножение. Законы умножения.	2
1.8	Распределительный закон.	3
1.9	Сложение и вычитание столбиком	3
	Контрольная работа №1.	1
1.10	Умножение чисел столбиком.	3
1.11	Степень с натуральным показателем.	2
1.12	Деление нацело.	2
1.13	Решение текстовых задач с помощью умножения и деления	3
1.14	Задачи на «части»	5
1.15	Деление с остатком.	3
1.16	Числовые выражения.	2
	Контрольная работа №2.	1
1.17	Задачи на нахождение двух чисел по их сумме и разности.	5
1.18	Дополнительный материал Вычисление с помощью калькулятора. Исторические сведения Занимательные задачи	1 3
2	Измерение величин	38	Измерять с помощью линейки и сравнивать длины отрезков. Строить отрезки заданной длины с помощью циркуля и линейки. Выражать одни единицы измерения длины через другие. Представлять натуральные числа на координатном луче. Распознавать геометрические фигуры и приводить примеры аналогов из окружающего мира. Измерять с помощью транспортира и сравнивать величины углов. Строить углы заданной величины с помощью транспортира. Выражать одни единицы измерения углов через другие. Вычислять площади квадратов и прямоугольников, объёмы кубов и параллелепипедов, используя соответствующие формулы. Решать задачи на движение, на движение по реке.
2.1.	Прямая. Луч. Отрезок.	2
2.2	Измерение отрезков.	2
2.3	Метрические единицы длины.	2
2.4	Представление натуральных чисел на координатном луче.	2
	Контрольная работа №3.	1
2.5	Окружность и круг. Сфера и шар.	1
2.6	Углы. Измерение углов.	3
2.7	Треугольники.	3
2.8	Четырехугольники	3
2.9	Площадь прямоугольника. Единицы площади.	3
2.10	Прямоугольный параллелепипед	2
2.11	Объем прямоугольного параллелепипеда. Единицы объема.	3
2.12	Единицы массы	1
2.13	Единицы времени	1
2.14	Задачи на движение	4
	Контрольная работа №4	1
3	Делимость натуральных чисел	25	Формулировать определение делителя и кратного, простого и составного числа, свойства и признаки делимости чисел, классифицировать натуральные числа (четные и нечетные, по остаткам от деления), Решать задачи, связанные с использованием четности и делимости чисел.
3.1	Свойства делимости	3
3.2	Признаки делимости	4
3.3	Простые и составные числа.	2
3.4	Делители натурального числа.	3
3.5	Наибольший общий делитель	4
3.6	Наименьшее общее кратное	4
	Контрольная работа №5	1
	Дополнительный материал 1.Использование четности и нечетности при решении задач 2.Исторические сведения 3.Занимательные задачи	2 2
4	Обыкновенные дроби	75	Преобразовывать обыкновенные дроби с помощью основного свойства дроби. Приводить дроби к общему знаменателю, сравнивать и упорядочивать их. Выполнять вычисления с обыкновенными дробями, использовать законы арифметических действий и уметь записывать их с помощью букв, применять их для рационализации вычислений. Решать задачи на дроби, на все действия с дробями, на совместную работу. Выражать с помощью дробей одни единицы измерения через другиеВыполнять вычисления со смешанными дробями, в том числе площадь и объем. Представлять дроби на координатном луче.
4.1	Понятие дроби.	1
4.2	Равенство дробей.	3
4.3	Задачи на дроби	5
4.4	Приведение дробей к общему знаменателю.	4
4.5	Сравнение дробей	3
4.6	Сложение дробей	3
4.7	Законы сложения	4
4.8	Вычитание дробей.	4
	Контрольная работа № 6	1
4.9	Умножение дробей	4
4.10	Законы умножения.	2
4.11	Деление дробей	4
4.12	Нахождение части целого и целого по части	2
	Контрольная работа № 7	1
4.13	Задачи на совместную работу	5
4.14	Понятие смешанной дроби	3
4.15	Сложение смешанных дробей	3
4.16	Вычитание смешанных дробей	4
4.17	Умножение и деление смешанных дробей	5
	Контрольная работа №8	1
4.18	Представление дробей на координатном луче	4
4.19	Площадь прямоугольника. Объём прямоугольного параллелепипеда	3
	Дополнительный материал 1.Сложные задачи на движение по реке 2.Исторические сведения 3.Занимательные задачи	2 4
5	Повторение курса математики 5 класса.	14
	Повторение	13
	Итоговая контрольная работа №9	1
	Итого	204

nsportal.ru

Формулы для решения задач на дроби для 5 класса

В 5 классе на уроках математики ученики знакомятся с дробями и процентами. В 6 классе эта тема повторяется, но изучается более глубоко. А встречаться дроби и проценты продолжат вплоть до задач внешнего тестирования (ЗНО) для 11 класса.

Обыкновенная дробь — это пара чисел, записанных через черту.
Число под чертой (знаменатель), показывает, на сколько частей разделили целое.
Число над чертой (числитель) показывает, сколько этих частей выбрано.

То есть дробь $\frac{3}{8}$ (три восьмых) означает, что целое было разделено на 8 частей, а взято из них три.

Существуют три класса задач на дроби: нахождение дроби от числа, нахождение числа по его дроби и выражение отношения чисел в виде дроби.

Как найти дробь от числа

В задачах на дробь от числа известно само число и дробь, которая от него взята. А найти требуется, какую величину составит эта дробь. Рассмотрим такую задачу

Пример 1.1.
В самолёте 120 пассажиров. $\frac{2}{5}$ (две пятых) из них летят в самолёте в первый раз. Сколько пассажиров летит в первый раз?

Это задача на нахождение дроби от числа.
Есть число: 120.
Есть дробь: $\frac{2}{5}$
Нужно найти, чему равны две пятых от 120.

Решаются задачи на нахождение дроби от числа так.

Решение
Задаём себе два вопроса:
1. Чему равна $\frac{1}{5}$ (одна пятая) от 120?
Для этого 120 делим на 5, получаем 24.
2. Чему равны $\frac{2}{5}$ (две пятых) от 120?
Результат 24, корый мы получили, нужно умножить на 2.
Получаем 48.

Значит, $\frac{2}{5}$ от 120 составляет 48.
Ответ: 48 пассажиров летят впервые.

Попробуем решить ещё одну задачу на нахождение дроби от числа.
Пример 1.2.
В городе живут 1 500 000 человек. Из них $\frac{3}{25}$ — школьники. Сколько в городе школьников?

Решение
1. Чему равна $\frac{1}{25}$ от 1 500 000?
1 500 000:25 = 60 000
2. Чему равны $\frac{2}{25}$ от 1 500 000?
60 000*3 = 180 000

Ответ: 180 000 школьников.

Когда вы набрались опыта решать такие задачи по вопросам, эти два вопроса можно свести в одно действие и использовать правило:
Чтобы найти дробь от числа, нужно это число умножить на дробь
Или, что то же самое:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на её числитель

Пример 1.3.
В автосалон завезли 14 автомобилей. За месяц продали 2/7 этого количества. Сколько автомобилей продали?

Решение
Умножим 14 на $\frac{2}{7}$:
$14\cdot \frac{2}{7} = \frac{14\cdot 2}{7} = 2\cdot 2 = 4$

Ответ: 4 автомобиля.

Теперь рассмотрим задачи второго типа:

Как найти число по дроби

В задачах этого типа исходное число неизвестно. Зато известна величина некоторой части от этого числа и какую дробь составляет эта часть от исходного числа. Для удобства рассмотрим, как бы выглядели эти же три задачи, если бы в них требовалось найти число по дроби.

Пример 2.1.
В самолёте сидят пассажиры (сколько их неизвестно!). Известно, что 48 пассажиров или $\frac{2}{5}$ (две пятых) от их количества летят впервые. Нужно найти: сколько всего пассажирова в самолёте?

Решение
Эти 48 пассажиров, которые летят впервые, составляют две пятых ($\frac{2}{5}$) от общего количества пассажиров в салоне. Мы можем найти одну пятую?
Да, нужно 48 разделить на 2.
48:2 = 24.
Мы узнали, что одна пятая часть от всех пассажиров — это 24 человека. Сколько всего пассажиров? В пять раз больше, то есть 24х5 = 120.

Ответ: 120 пассажиров всегов самолёте

Понятно? Давайте разберём ещё одну задачу.
Пример 2.2.
Три двадцать пятых ($\frac{3}{25}$) населения города составляют школьники. Школьников в городе 180 000. Каково общее население города?

Решение
Опять само число (то есть население города) на неизвестно, зато известно, чему равны $\frac{3}{25}$ от него.Значит, можно сначала найти, чему равна $\frac{1}{25}$ от населения города. Разделим 180 000 на 3:

180 000:3 = 60 000

Зная одну двадцать пятую, можно найти и целое, умножив 60 000 на 25.
60 000х25 = 1 500 000

Ответ: в городе 1 500 000 жителей

Когда будете уверенно решать задачи на нахождение числа по его дроби по вопросам, можно будет заменить эти вопросы одним действием и использовать правило:

Чтобы найти число по его дроби, известную величину нужно разделить на эту дробь
Или, что то же самое:
Чтобы найти число по его дроби, известную величину нужно разделить на числитель дроби и умножить на её знаменатель

Пример 2.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4, что составляет 2/7 всех автомобилей. Сколько автомобилей завезли в салон?

Решение
Разделим 4 на $\frac{2}{7}$:
$4: \frac{2}{7} = \frac{4\cdot 7}{2} = 2\cdot 7 = 14$

Ответ: 14 автомобилей завезли в салон.

И перейдём теперь к третьему типу задач на дроби, которые изучаются в математике 5 класса:

Как найти отношение двух чисел и выразить его в виде дроби

В задачах на нахождение отношения оба числа известны, а нужно найти, какую дробь второе число составляет от первого. Решаются они проще всего

Пример 3.1.
В самолёте 120 пассажиров. Из них 48 человек летят в первый раз. Какая часть пассажиров летит в первый раз?

Решение
Чтобы найти, какую дробь 48 составляет от общего количества пассажиров (120), нужно 48 разлелить на 120 и затем скоратить, что возможно.
Доля летящих впервые пассажиров составляет $\frac{48}{120}$.

И числитель, и знаменатель делятся на 2, значит, можно сократить на 2.
$\frac{48}{120}=\frac{24}{60}$

Сократим ещё раз на 2:
$\frac{24}{60} = \frac{12}{30}$

И ещё раз:
$\frac{12}{30} = \frac{6}{15}$

Теперь можно сократить на 3:

$\frac{6}{15} = \frac{2}{5}$

Больше сокращать не на что — это и можно записать как окончательный ответ задачи.
Ответ: $\frac{2}{5}$ пассажиров летят впервые.

Так что правило для решения задач на нахождение отношения чисел самое простое:
Чтобы найти, в виде какой дроби выражается отноешние двух чисел, нужно сначала записать дробь, в которой числитель и знаменатель — эти числа, а затем сократить её.

Обратите внимание, что дробь $\frac{A}{B}$ обозначает, какую долю величина А составляет от величины В и правильно записывайте величины в числитель и знаменатель.

Разберём ещё два примера.

Пример 3.2.
В городе с населением 1 500 000 жителей живут 180 000 школьников. Какую часть населения города составляют школьники?

Решение
Нужно найти, какую часть 180 000 составляет от 1 500 000?
Записываем дробь и сокращаем:
$\frac{180000}{1500000}=\frac{18}{150}=\frac{9}{75}=\frac{3}{25}$

Ответ: школьники составляют $\frac{3}{25}$ от общего населения города

Пример 3.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4. Какую часть от всех автомобилей это составляет, если всегов автомалон завезли 14 машин?

Решение
Точно так же, берём дробь $\frac{4}{14}$ и сокращаем:
$\frac{4}{14}=\frac{2}{7}$

Ответ: продали $\frac{2}{7}$ от общего количества автомобилей.

Вот как решаются задачи на дроби. Вы найдёте справочники по формулам математики 5, 6 и других классов в разделе «Математика в школе».

evolventa.blogspot.com

Репетитор по математике о задачах на дроби в 5-6 классе

Задачи на части (на дроби) в 5 — 6 классе, безусловно, тяжелейшая тема для преподавания. Возможно даже самая тяжелая за весь школьный курс. Как может построить свою работу с ней репетитор по математике? Рассмотрим некоторые приемы обучения решению таких задач, опишем связанные с темой проблемы и поговорим о ее дидактике.

Причиной большинства обращений к репетитору в 5 классе является повальное непонимание законов разделения на части. Это естественно, ибо задачи, на которых формируется представление о долях, предъявляют достаточно высокие (для этого возраста) требования к уровню развития ученика, часто связанные с его физиологией. Этот обстоятельство часто не позволяет репетитору математики действовать стандартно, опираясь на традиционые объяснения.

Несмотря на влияние физиогогии родители ребенка обычно стараются повлиять на ситуацию как можно быстрее. Большинству из них нужен репетитор по математике для скорейшего исправления текущей отметки. Иногда это мешает планомерно и неспешно объяснять математические законы и выстраивать темы в логически правильном порядке.

Долгое время я не решался написать об этих задачах. И дело не только в сложности восприятия материала школьниками. В изучении темы выделяется несколько этапов с различными ограничениями в использовании чисел. Не случайно дроби проходят не один год. Программа 5 класса переплетается с программой 6-го класса (а по Петерсону еще и с четвертым). Поэтому даже при одном и том же характере работы преподавателя с дробями разница в индивидуальных особенностях учеников и программах не позволяют описать методы работы репетитора по математике с темой точно и коротко. Более того, в разных учебниках «доли» изучаются в разное время, по-разному «обкладываются» задачами и по-разному интегрируются в дидактику смежных тем. Поэтому очень сложно охватить все проблемы. Надеюсь, что

репетиторы по математике со стажем меня понимают.

Много раз я сталкивался с проблемами задач на дроби и уяснил для себя главное: тема требуют постепенного и долгого изучения. Ее нельзя проработать за один-два урока. Поэтому первое, что я делаю, — объясняю родителям ситуацию и прошу предоставить дополнительные часы для занятий. Не менее двух раз в неделю. Для репетитора по математике это стандартный график, позволяющий в большинстве случаев полноценно заниматься пробелами.

Репетитор по математике о своей методике

Формально мой подход не отличается от того, что предлагают другие репетиторы, а именно — решение задач в большом количестве. Однако к ним еще нужно поготовить ученика, предложить ему некий план или даже алгоритм подбора пути решения. К сожалению, его точность и прозрачность не всегда соответствует желаемому. Репетитор по математике должен понимать, какие задачи и с каким учеником следует разбирать, в каком порядке и в каком количестве. Подходы разных преподавателей могут отличаться порядком разбора задач, пояснениями, терминологией, сопровождениями в рисунках, схемах и даже их полным отсутствием. Я использую собственную базу типовых примеров и наводящих вопросов, систему записей, оформлений и обозначений (немного схожую с Петерсоновской). Оптимизирую краткие записи к задачам, делаю их удобными, информативными и ориентированными на поиск решения.

Попробую изложить …

Разбор элементарных задач

Первый этап работы репетитора — знакомство ученика с базовыми задачами, обучение составлению для них кратких записей. Очень важно вложить в ученика мысль о том, что сложная задача на дроби состоит из нескольких упакованных в нее простых, с определенной последовательных элементарных операций. Их выделением и проработкой репетитор по математике занимается на первом уроке.

Выделяется 3 типа простейших задач на дроби:
1) Целая величина известна
2) Целая величина неизвестна
3) Неизвестна дробь

Для каждой из них подбирается реальная ситуация, которую удобно моделировать рисунком. Распространены примеры деления яблока или плошади. Например: Яблоко имеет массу 160 грамм, найдите вес 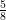$\frac{5}{8}$ яблока. Пример стандартный, но подходит не всех ученикам, ибо для проверки правильности демонстрируемых репетитором ариметических действий приходится делить то, что нельзя взять в руки, именно вес. При низком интеллектуальном уровене развития ученика репетитор по математике оказывается бессильным что-либо ему объяснить, ибо проблемы уходят далеко от темы «дроби». Если такое происходит, я использую пример с полом:

Пол выложен одинаковыми плитками как показано на рисунке. На каждую плитку положили по шарику. Сколько шариков лежит на 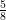$\frac{5}{8}$ пола?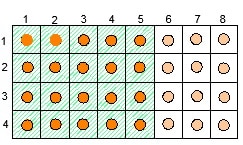
Преимущество этого примера в том, что ребенок может не только выделить (закрасить) 5/8 пола, но и пересчитать количество шариков непосредственно. При этом репетитор по математике указывает на возможность ответить на вопрос через простые арифметические действия (на рядах и колонках).

Наводящие вопросы репетитора по математике

Cлабого ребенку можно еще и полдвести к выполнению действий. Для этого репетитор по математике задает ему систему наводящих вопросов, например:

Репетитор: сколько колонок на рисунке?
Ученик: 8 колонок
Репетитор: сколько шариков расположено в одной колонке?
Ученик: 4 шарика
Репетитор: Каким действием это можно найти?
Ученик: 32:8=4
Репетитор: сколько колонок в 5/8 пола?
Ученик: 5 колонок
Рептитор: Если в одной колонке 32:8=4 шарика, то в пяти колонках шаров будет …
Ученик: 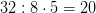$32:8 \cdot 5 =20$ шариков.
Привильно !!!!!

Главное преимущество задачи на плитки и шарики состоит в использовании арифметических действий, каждое из которых удается проверить простым пересчетом. После того, как репетитор по математике убедился в понимании действий, он диктует ученику проверенное правило: «делим на знаменатель и умножаем на числитель».

Несмотря на то, что можно пересчитывать количество не шариков, а самих плиток, я намеренно оставляю шары в сюжете задачи. Почему? На их примере изучается ситуация, когда какой-нибудь целый объект удерживает внутри себя (или на себе) мелкие объекты (в нашем случае пол удерживает шарики). Это широко распространено в дидактике математики 5-6 класса. Часто что-то куда-то засыпается, заливается, вкладывается и равномерно распределяется по объекту. В мешки засыпают сахар, в бидоны заливают молоко и т.д. Репетитор по математике на примере шариков помогает ребенку быстрее разобраться в числовых особеннностях этих ситуаций и понять законы измерения частей объектов.

Далее … На том же рисунке с шариками нужно поставить обратную задачу: Допустим, мы знаем, что на 5/8 пола лежит 20 шаров. Как найти их общее количество? И здесь репетитору по математике тоже помогает рисунок, на котором можно просто пересчитать кружочки. Легко подбирать и комментировать выполняемые действия: $20:5 \cdot 8=32$ . Все ясно и прозрачно. Наводящие вопросы (если они нужны) аналогичны первому случаю.

Репетитору по математике важно остановиться на терминологии и оформлении краткой записи.От того, насколько как она будет зависит идентификация правил. Ученик должен усвоить, что целый объект — это такая же величина, как и его часть, измеряемая двумя единицами: привычной (метрами, сантиметрами, килограммами, литрами, страницами, деревьями, шариками и т.д.) и «особой». В роли последней выступает целая величина. Рядом с ней в кратких записях можно поставить 1ед. Все участники элементарной задачи получают названия. То, от чего ищется часть называется целой величиной, сама дробь так и остается дробью, а часть, которую находят от целого репетитор по математике называет «частью» или «значением» дроби». Я предпочитаю второй вариант.

Как правило, к репетитору обращаются в момент, когда тема набрала обороты и в классе решают в перемешку задачи на разные базовые правила. Поэтому, их приходится включать в один урок. Если ребенок не самый слабый, то вместо плиток я применяю яблоко, причем с одним и тем же набором значений величин для всех типов задач. Выписываю из образцы в отведенную для этого теоретическую тетрадь (или на форзац рабочей тетради). Каждую запись отдельно комментирую и специальным образом оформляю:
Задача 1-го типа: целая величина известна.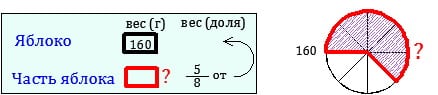
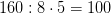$160:8\cdot 5=100$ (г) -вес части яблока.
Чтобы найти значение дроби нужно целую величину разделить на знаменатель и умножить на числитель.

Задача 2-го типа: целая величина неизвестна.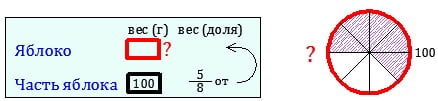
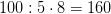$100:5 \cdot 8=160$ (г) — вес яблока.
Чтобы найти целую величину нужно значение дроби разделеить на числитель и умножить на знаменатель.

Задача 3-го типа: неизвестна дробь.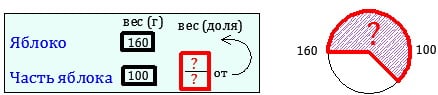
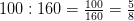$100:160=\frac{100}{160}=\frac{5}{8}$ (яблока) -вес его части

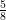В третьей задаче для 5 класса репетитором по математике должны быть выбраны другие числа, ибо сократить дробь $\frac{100}{160}$ пятиклашки еще не могут. Обратите внимание на то, что обыгрывается один и тот же комплект чисел. В первой задаче репетитор по математике находит $\frac{5}{8}$ целого яблока, а во второй выполняет обратные действия: по той же дроби 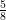$\frac{5}{8}$ и найденному ранее значению 100 восстановливает число 160 (его даже можно в определенный помент стереть ластиком). Прием обратных действий полезен для работы с невнимательными школьниками. Он позволяет быстро сконцентрироваться на правилах, а не на изучении нового условия новой задачи. Более того, при заранее изветном ответе ребенок убеждается в правильности выбора этих действий. Действительно, как можно в них усомниться, если репетитор по математике получает в ответе то, что и должно получиться?

Под каждой краткой записью оформляется решение и записывается правило:

1) чтобы найти значение дроби, нужно целую величину разделить на знаменатель и умножить на числитель.
2) Чтобы найти целую величну нужно разделить на числитель и умножить на знаменатель.
3) Чтобы найти дробь нужно разделить ее значение на целую величину.

Как репетитор математики работает с комбинированными задачами

Чаще всего они встречаются в 6 классе, хотя в учебнике Петерсона сочетания двух и даже трех типов задач предлагаются уже в 5 классе. Прежде всего ученик должен знать с чего начинать исследование задачи. Важно отработать каждый его этап в отдельности.

Краткая запись

Краткая запись к задаче — важнейший и незаменимый элемент методики любого хорошего репетитора по математике. Она является одновременно и опорой и средством заставить ученика перечитывать условие как минимум — два три раза. Правильно составленная краткая запись в сочетании с четкими правилами «трех типов» позволяют разложить комбинированную задачу на несколько элементарных. Поэтому репетитору чрезвычайно важно научить правильно ее составлять.

Как репетитор по математике работает с текстами?
Главной проблемой составления краткой записи является проблема анализа текста задачи. Практика показывает, что дети крайне невнимательно и низкоэффективно с ним работают. Не умеют выделять ценную информацию о величинах и сами величины, сортировать главное и второстепенное. Для борьбы с такими проблемами репетитор математики может взять на вооружение метод слежения. Что такое краткая запись? — всего лишь короткий текст условия, из которого выброшены лишние слова, а названия величин и их значения записаны отдельными строками. Что мешает репетитору по математике выделять эти слова в тексте? Особенно важно научить поиску целых величин, на которые в краткой записи будут указывать стрелки. Репетитор должен обратить внимание ученика на то, что слово или фраза, написанная сразу после дроби, указывает на единицу измерения дроби, то есть на ее целую величину. Репетитору по математике никто не запрещает выделить ее в тексте (подчеркнуть или записать другим цветом) и поставить к ней стрелочку. Пример оформления:

Если внимание ребенка ослаблено, на первых порах ему лучше предлагать уже размеченные тексты, с выделенными целыми величинами и стрелочками.

Для того, чтобы не пропустить ни одну из участвующих величин репетитору по математике нужно задать вопрос: Что в задаче можно измерить? Пок ученик думато, репетитор подчеркивает в тексте соответствующие им слова. В нашем случае это показано синим цветом.

Важно отработать поиск и применение типовых задач внутри комбинированной. Дети часто путают когда им делить на знаменатель, а когда на числитель. В 6 классе путают умножать ли на дробь или делить на нее. Проблема усугубляется когда в задачу встревает еще и сумма (разность) величин. Ребенок пытается запомнить эти ситуации, но от их многообразия пухнет голова. Чем может помочь ему репетитор по математике? Самое эффективное запоминание — зрительное. При многократном зрительрном анализе ребенок «фотографирует» расположение известных и неизвестных компонент выделенных репетитором строк (связанных «дробной стрелкой») и распознает эту же комбинацию величин в другой задаче. по нему в другой задаче что именно надо лелать. Для увеличения числа обращений к правилам типовых задач я рекоментдую репетиторам по математике использовать визуальные образы задач (без текстов). Репетитор подает ученику задачу ее краткой записью с полной информацией о всех известных взаимосвязях между величинами . Сложности возникают с суммами нескольких величин. В таком случае репетитору по математике приходится искать дополнительные обозначения для суммы. Я решил это пробьлему так: поле суммы закрашивается, а поля ее слагаемых обводятся тем же цветом по периметру. Очень удобно. Если какое-то из слагаемых тоже равно сумме других, более мелких величин, то его внутренняя частсь закрашивается другим цветом, а поля слагаемых этим же цветом обводятся по контуру. И таких вложений может быть сколько угодно.

Например, краткая запись к задаче про вишню может быть следующей:

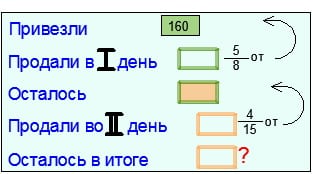
Попрбуйте составить краткую запись к олимпиадной задачке: мама испекла булочки. Аня съеха 2/3 всех булочек и еще 2. Петр съел 2/3 остатка и еще 2 булочки, а Денис съел 2/3 последнего остатки и последние 2 булочки. Сколько булочек испекла мама?

Александр Николаевич, репетитор по математике Москва (м.Щукинская, Строгино)

Метки: Работа репетитора, Репетиторам по математике

ankolpakov.ru

Разработка урока по математике «Задачи на дроби» (5 класс)

Разработка урока по математике

«Задачи на дроби»

для 5 класса

в условиях реализации ФГОС

Учитель: Попова Ирина Геннадьевна

МБОУ Мурзицкая школа

Технологическая карта урока

Предмет: математика

Класс: 5

Тип урока: урок обобщения и закрепления знаний (путешествие в страну сказочных задач)

Образовательные: Формирование умения решать задачи на дроби, совершенствовать вычислительные навыки
Развивающие: Развивать умение анализировать, сравнивать, делать выводы, развивать устную речь
Воспитательные: Воспитывать умение высказывать свою точку зрения, слушать других, принимать участие в диалоге, формировать способность к позитивному сотрудничеству

УУД

осуществляют контроль и самоконтроль

Регулятивные УУД: различают способ и результат действия
Коммуникативные УУД: контролируют действия партнера
Познавательные УУД: ориентируются на разнообразие способов решения задач

Планируемые результаты

Предметные: учащиеся должны

Знать способы решения задач на нахождение части числа от целого и целого числа по его части
Уметь воспроизводить изученную информацию; подбирать аргументы, соответствующие решению; правильно оформлять работу. Решать задачи разными способами, выбирать наиболее рациональный способ решения.

Личностные: уметь ясно, точно и грамотно излагать свои мысли в устной и письменной речи,

применять креативность мышления, инициативу, находчивость, активность при решении математических задач.

Метапредметные: самостоятельно формулировать познавательную цель и строить свои действия в соответствии с ней.

планировать собственную деятельность, определять средства для её осуществления.
уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;

находить ответы на вопросы, используя учебник, интернет технологии, свой жизненный опыт и информацию, полученную на уроке

регулировать собственную деятельность посредством речевых действий, уметь слушать и вступать в диалог, воспитывать чувство взаимопомощи;
уважительно относиться к чужому умению, культуру учебного труда, требовательно относиться к себе и своей работе.

Основные понятия

Обыкновенная дробь. Нахождение части числа от целого и целого числа по его части

Межпредметные связи

Литература

Ресурсы:

1. «Математика» 5 класс, учебник для общеобразовательных учреждений/С.М. Никольский, М.К..Потапов, Н.Н Решетников, А.В.Шевкин, М. Просвещение. 2015г

2.Планируемые результаты. Система заданий. Математика 5-6 класс. Ред. Г.С. Ковалевой, О.Б.Логиновой. М. «Просвещение», 2013г

3.КИМы «Математика. 5 класс», М. ВАКО, 2016

4.http://testedu.ru/test/matematika/5-klass/obyiknovennyie-drobi-5.html

Формы урока

фронтальная, И – индивидуальная, П – парная, Г – групповая Фронтальный опрос, индивидуальная, парная и с применением активных методов обучения, тестирование

Технология

технология проблемного обучения,
уровневая дифференциация,
технология сотрудничества,
компьютерные технологии
здоровьесберегающие технологии.

Деятельность учеников

Деятельность учителя

Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов

Планируемые результаты

Предметные

УУД

(Познавательные УУД).

(Коммуникативные УУД).

(Регулятивные УУД).

Организационный момент

Время: 3 мин

Основные этапы:

1 Приветствие учителя и друг друга.

2. Разгадывание ребуса.

3. Формулировка цели урока

4. Ознакомление с оценочным листом.

Приветствуют учителя.

Настраиваются на урок.

Формулируют цель урока

— повторить решение задач на дроби;

· — решать задачи разными способами;

· — составлять задачи;

— использовать умение решать задачи в нестандартных ситуациях.

Организует включение учащихся в учебную деятельность на личностно значимом уровне

1. Приветствие. АМО «Энергизатор».

Здравствуйте, ребята! Я рада видеть вас, надеюсь, что вы рады видеть меня. Давайте улыбнемся друг другу и начнем урок

Запись темы. Сегодня у нас необычный урок, мы с вами совершим путешествие в «Страну сказочных задач». Во время путешествия мы посетим городок «Устный», побываем в домике «Повторения и обобщения», заглянем на станцию «Физкультурная», а затем прокатимся на карусели «Сказочные задачки»

2. Урок начнем с разгадывания ребуса, получив билет на путешествие. Кто справился? Мы решали много различных задач на дроби. Подошли к концу изучения этой темы. Какую цель вы поставили бы перед собой на этот урок-путешествие. Хочется чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата. Получил хорошую оценку, которая будет складываться из самооценки, оценки друга(друзей) и оценки учителя. (С- , Д- , У- )-

1. Ребус

Формулирование проблемы и способа решения

Познавательные: ставят перед собой цель: «Что я хочу получить сегодня от урока»

Регулятивные: самоопределяются, настраиваются на урок

Коммуникативные: планируют учебное сотрудничество с учителем и одноклассниками

Актуализация знаний

Фронтально

Время: 5мин

Этапы:

1.Задача на внимание

2.Считаем устно

3.Логическая задача

4. Оценивание деятельности на данном этапе (самооценка, взаимооценка)

Участвуют в устной работе

Организует с учащимися работу по готовности мышления и осознанию потребности к построению способа действия.

Задает вопросы.

Городок «Устный» 1.Задача на внимание (показывается на несколько минут, затем убирается и ребята по памяти отвечают на вопросы учителя)

Вопросы:

Какие геометрические фигуры вы запомнили?
Назовите дробь, записанную в окружности
Каков цвет окружности?
Есть ли среди дробей дробь с числителем 1?
В какой фигуре она записана?
Назовите эту дробь.
Каков цвет квадрата?
Каков цвет треугольника?
Назовите дробь, записанную в нём.

2.Устно:

3.Логическая задача

Закрепляют умение считать устно, тренируют вычислительные навыки, вспоминают понятие дроби как части целого

Познавательные: анализируя и сравнивая предлагаемые задания, извлекают необходимую информацию для построения речевого высказывания

Регулятивные: выполняют тренировочное учебное действие

Коммуникативные: выражают свои мысли с достаточной полнотой и точностью, обосновывают своё суждение

Физкультминутка

Время: 2 мин

Повторяют за учителем упражнения

Нас встречает станция «Физкультурная». Небольшая разминка перед основным этапом нам не помешает.

Все умеем мы считать

Раз, два, три, четыре, пять! (Шагаем на месте.)

Все умеем мы считать, (Хлопаем в ладоши.)

Отдыхать умеем тоже (Прыжки на месте.)

Руки за спину положим, (Руки за спину.)

Голову поднимем выше (Подняли голову выше.)

И легко-легко подышим. (Глубокий вдох-выдох.)

Формирование потребности к ЗОЖ

Познавательные: сопоставление текста и действия

Регулятивные: осуществляют пошаговый контроль своих действий, ориентируясь на показ движений, а затем самостоятельно оценивают правильность выполнения действий на уровне адекватной ретроспективной оценки

Коммуникативные: выполнение действия в группе

Обобщение и закрепление изученного материала

Время: 30 мин

Этапы:

1 Решение задачи у доски (2 ученика) №777б, 781б с закреплением правил нахождения части числа и числа по по известной части (8-10 мин)

2. ИНФО-карусель по сказкам (работа в парах) (20-22 мин)

1. Отвечают на вопросы. Определяют правило. Решают задачи. Проговаривают правила:

1).Если часть целого выражена дробью, то, чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на ее числитель.

2).Если часть искомого целого выражена дробью, то, чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на ее знаменатель.

2. Работают в группах. Ориентируются в тексте задачи, видят связь математики с литературой.

Определяют тип задачи, применяют правило.

Организует работу по фиксации полученных знаний и применения их в решении задач.

Задает вопросы:

— О чем задача?

— Что требуется найти?

— Что известно в задаче- Какое правило здесь можно применить?

— Существует ли другой способ решения?

2. Организует работу в группах, применяя АМО «Инфо-карусель».

Побываем в домике «Повторения и обобщения»1.№777(б), №871(б) («Математика» 5 класс, /С.М. Никольский и др)

2.Карусель «Сказочные задачки». АМО «Инфо-карусель» (работа в группах)

Проведение: на столе лежат листки с заданиями. Каждая пара за своим столом выполняет сначала первое задание, выбрав из него одну задачу, закончив его по истечении отведенного времени, подходит и берет другое (по кругу), пока не попробует каждое (или не менее 3-х). Проверить правильность выполнения задания можно по компьютеру или у учителя.

Задания (дифференцированные) для групп:

1группа.Сказки А.С. Пушкина

Королевич Елисей ехал за невестой со скоростью 18 км/ч, и эта скорость составляла 2/3 от скорости ветра, который подсказал Елисею местонахождение царевны. Какова скорость ветра? (1 балл)
Масса одного богатыря равна 90 кг и составляет 9/10 от массы дядьки Черномора. Какова общая масса 33 богатырей и дядьки Черномора? (2 балла)
Ручная белка разгрызает в день 48 кг орехов, отделяя золотые скорлупки от ядер-изумрудов. Масса изумрудов составляет 5/8 от общей массы орехов. Сколько золота получится у белки за 5 дней? (3 балла)

2 группа. Приключения Буратино А.Толстой

Черепахе Тортилле 200 лет, а возраст Дуремара составляет 8/50 возраста Тортиллы. Сколько лет Дуремару? (1 балл)
Буратино закопал на Поле Чудес в Стране Дураков 4 золотых монеты, что составило 2/19 количества монет, которые он хотел потом откопать. Сколько монет хотел откопать Буратино? (2 балла
Папа Карло подарил Буратино азбуку. В азбуке 350 страниц и 6/7 всех страниц были с картинками. Сколько в азбуке страниц без картинок? (3 балла)

3 группа. Сказки Шарля Перро

Хрустальную туфельку, потерянную Золушкой, по приказу принца примерило 248 принцесс, герцогинь и придворных дам, что составило 4/7 всех женщин в королевстве. Сколько всего женщин в королевстве? (1 балл)

Скорость движения Красной Шапочки составляет 2/3 от скорости дровосеков, а скорость движения дровосеков составляет 3/5 от скорости волка. Найти скорость Красной Шапочки и скорость дровосеков, если скорость волка 15 км/ч. (3 балла)

4 группа. Сказки русских писателей

Д.Н. Мамин-Сибиряк Сказка про славного царя Гороха и его прекрасных дочерей царевну Кутафью и царевну Горошинку

Царь Горох построил для своей дочери, царевны Кутафьи, башню высотой 34 м, а для себя- царские палаты, высота которых составила 2/17 от высоты башни. Какова высота царских палат? (1 балл)

В. Одоевский «Мороз Иванович»

Мороз Иванович подарил за работу Рукодельнице ведерко с горстью серебряных монет, а Ленивице сундук с ледяными сосульками. Монет было 63 и это составило 7/10 от числа сосулек. Сколько сосулек получила Ленивица? (2 балла)

С.Т. Аксаков «Аленький цветочек»

На первом этаже дворца чудища лесного Настенька, дочь купеческая, насчитала 64 комнаты, что составляет 8/57 всех комнат дворца. Сколько комнат во дворце лесного чудища? (3 балла)

5 группа. Тест на компьютере. (Образовательные тесты, математика 5 класс)

http://testedu.ru/test/matematika/5-klass/obyiknovennyie-drobi-5.html

Фиксирование умений выполнять алгоритм решения задач на дроби и применения их в решении задач.

Осознанно воспринимают математическое понятие задачи с дробями.

Познавательные: поиск и извлечение нужной информации из прочитанного или услышанного условия задачи;

умение ориентироваться в своей системе знаний;

свободная ориентация в условии задачи и её восприятие;

подведение задачи под понятие

Регулятивные УУД:

самостоятельно формулируют познавательную цель и строят свои действия в соответствии с ней.

планируют собственную деятельность, определяют средства для выполнения;

— контроль в форме сличения способа действия и его результата с заданным эталоном

Коммуникативные УУД:

регулируют собственную деятельность посредством речевых действий, умение слушать и вступать в диалог, воспитывать чувство взаимопомощи;

уважительное отношение к чужому умению, культуру учебного труда, требовательное отношение к себе и своей работе

Контроль

Время:2 мин

Самооценка, взвимооценка

Заполняют оценочные листы:

-самооценка,

-взаимооценка

Подсчитывается количество баллов.

Оценивает работу учащихся. Комментирует оценку

Заполнение оценочных листов

Проводят самооценку результатов своей деятельности и деятельности своей группы

Познавательные: проводят рефлексию способов и условий своих действий

Регулятивные: проводят самооценку, учатся адекватно принимать причины успеха (неуспеха)

Коммуникативные: планируют сотрудничество, используют критерии для обоснования своих суждений

Рефлексия

Время:2 мин

Анализируют:

Я узнал …
Я научился…
Мне понравилось…
Я бы хотел…

Обеспечивает осознание учащимися своей учебной деятельности на уроке

Организует обсуждение: Какова была тема урока? Какую задачу ставили? Каким способом решали поставленную задачу?

Что удалось? Задачи по каким сказкам вам понравились более всего?

Анализ своей деятельности на уроке

Осознание своей учебной деятельности на уроке

Познавательные: проводят рефлексию способов и условий своих действий

Регулятивные: проводят самооценку, учатся адекватно принимать причины успеха (неуспеха)

Коммуникативные: планируют сотрудничество, используют критерии для обоснования своих суждений

Домашнее задание

Время: 1 мин

Записывают домашнее задание

Комментирует домашнее задание

Домашнее задание на выбор АМО «Выбери сам». :

1 уровень-№782(б),788(а)

2 уровень-№788(б), 791

Творч.з.:

1.Кроссворд по изученному материалу.

2.Составить задачи для Книжки-малышки «Задачи на дроби»

Закрепляют навыки решения задач на дроби, учатся применять их в решении творческих задач

Познавательные: учатся применять знания в решении творческих задач.

Регулятивные: в соответствии со своей самооценкой, выбирают домашнее задание

Задания по группам

1группа.Сказки А.С. Пушкина

Королевич Елисей ехал за невестой со скоростью 18 км/ч, и эта скорость составляла 2/3 от скорости ветра, который подсказал Елисею местонахождение царевны. Какова скорость ветра? (1 балл)
Масса одного богатыря равна 90 кг и составляет 9/10 от массы дядьки Черномора. Какова общая масса 33 богатырей и дядьки Черномора? (2 балла)
Ручная белка разгрызает в день 48 кг орехов, отделяя золотые скорлупки от ядер-изумрудов. Масса изумрудов составляет 5/8 от общей массы орехов. Сколько золота получится у белки за 5 дней? (3 балла)

2 группа. Приключения Буратино А.Толстой

Черепахе Тортилле 200 лет, а возраст Дуремара составляет 8/50 возраста Тортиллы. Сколько лет Дуремару? (1 балл)
Буратино закопал на Поле Чудес в Стране Дураков 4 золотых монеты, что составило 2/19 количества монет, которые он хотел потом откопать. Сколько монет хотел откопать Буратино? (2 балла
Папа Карло подарил Буратино азбуку. В азбуке 350 страниц и 6/7 всех страниц были с картинками. Сколько в азбуке страниц без картинок? (3 балла)

3 группа. Сказки Шарля Перро

Хрустальную туфельку, потерянную Золушкой, по приказу принца примерило 248 принцесс, герцогинь и придворных дам, что составило 4/7 всех женщин в королевстве. Сколько всего женщин в королевстве? (1 балл)

Скорость движения Красной Шапочки составляет 2/3 от скорости дровосеков, а скорость движения дровосеков составляет 3/5 от скорости волка. Найти скорость Красной Шапочки и скорость дровосеков, если скорость волка 15 км/ч. (3 балла)

4 группа. Сказки русских писателей

Царь Горох построил для своей дочери, царевны Кутафьи, башню высотой 34 м, а для себя- царские палаты, высота которых составила 2/17 от высоты башни.

Какова высота царских палат? (1 балл)

В. Одоевский «Мороз Иванович»

Мороз Иванович подарил за работу Рукодельнице ведерко с горстью серебряных монет, а Ленивице сундук с ледяными сосульками. Монет было 63 и это составило 7/10 от числа сосулек. Сколько сосулек получила Ленивица? (2 балла)

С.Т. Аксаков «Аленький цветочек»

На первом этаже дворца чудища лесного Настенька, дочь купеческая, насчитала 64 комнаты, что составляет 8/57 всех комнат дворца. Сколько комнат во дворце лесного чудища? (3 балла)

5 группа. Тест на компьютере. (Образовательные тесты, математика 5 класс)

http://testedu.ru/test/matematika/5-klass/obyiknovennyie-drobi-5.html

Оценочный лист

Я(самооценка)

Друг (взаимооценка))

Учитель

Итого

Устная работа

Решение задач у доски

ИНФО-карусель (работа в паре)

Оценка работы группы

15-17 баллов – «5»

11-14 баллов – «4»

7-10 баллов – «3»

Общая оценка за урок

Список используемой литературы

3.КИМы «Математика. 5 класс», М. ВАКО, 2016

4.http://testedu.ru/test/matematika/5-klass/obyiknovennyie-drobi-5.html

Сказки и подсказки (задачи для математического кружка)/ Е.Г.Козлова. – М.: МЦНМО, 2008. – 165 с. КомКнига, 2005. – 208 с

5. Задачи на смекалку/ С.Н.Олехник, ЮВ.Нестеренко, М.К.Потапов. – М.: Дрофа, 2005. – 233 с.,

6.http://project.1september.ru/works/599961 Задачи с дробями с сюжетами из сказок

infourok.ru

План-конспект урока изучение нового материала по теме «Обыкновенные дроби. Задачи на дроби» (5 класс)

Урок изучение нового материала по теме

«Обыкновенные дроби. Задачи на дроби» в 5 классе

Медведевой Ксении Сергеевны

Учитель математики

МОУ «СОШ № 100»

Г. Саратов

Обыкновенные дроби. Задачи на дроби

Цели урока:

1. Обучающая:

дальнейшее ознакомление учащихся с понятием «Обыкновенные дроби»;
отрабатывать навыки нахождения части от целого числа;
ознакомить учащихся с понятиями «Задачи на дроби »;
начать отрабатывать навыки по решению задач на дроби.

2. Развивающая:

продолжить формирование ряда умений частично-поисковой познавательной деятельности: осознать проблему, делать выводы и обобщения.

3. Воспитательная:

пробудить у учащихся интерес к учебному материалу и познавательным действиям;
формировать умения, аккуратность, грамотность математической речи.

Ход урока

1 этап. Организационный момент.

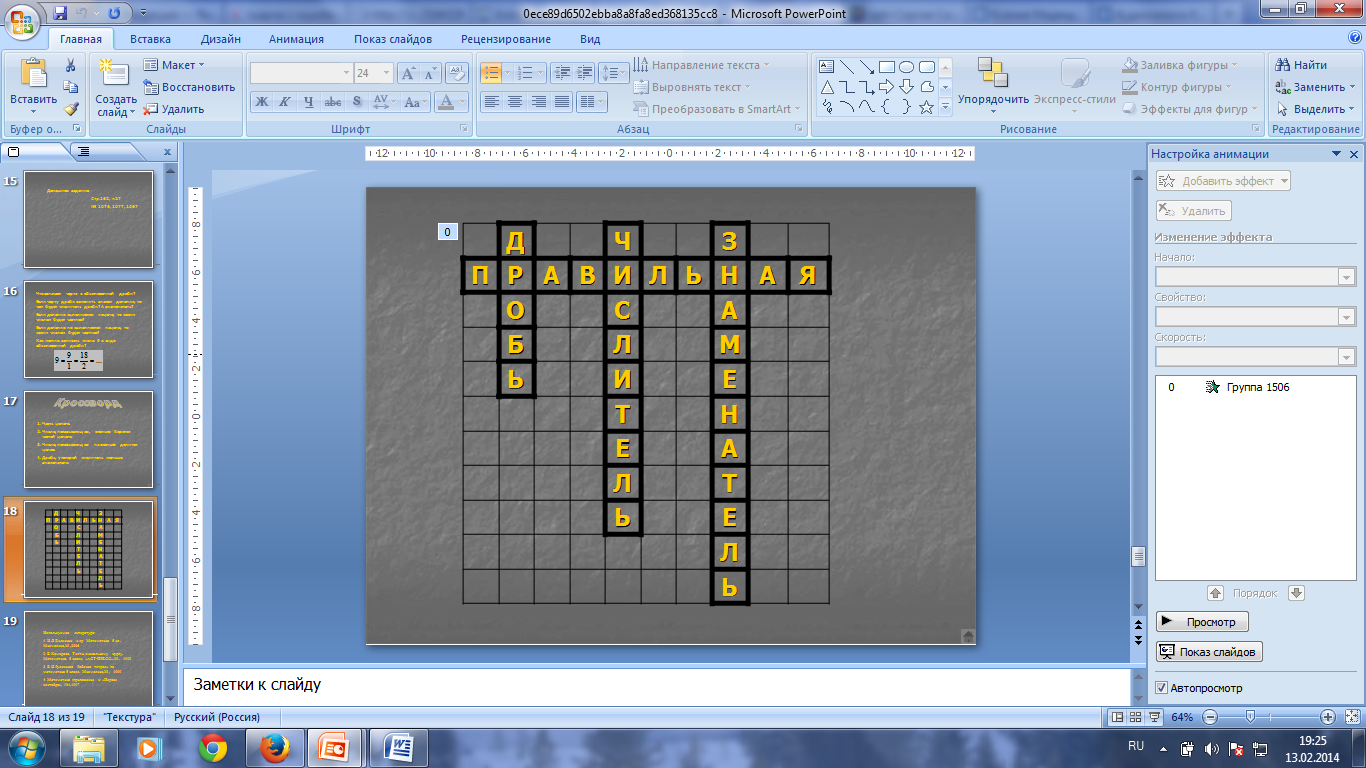
2 этап. Работа устно.(на слайдах)

Кроссворд: дробь, числитель, знаменатель, правильная.

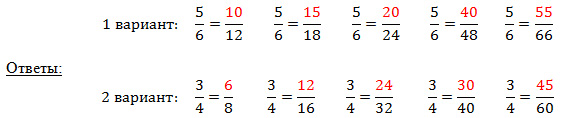
3 этап. Объяснение нового материала.

Задача 1 (нахождение дроби от числа/части числа)

В магазин завезли 800 книг. 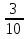этих книг было куплено. Сколько книг купили?

Решение. Дробь три десятых указывает на то, что 800 книг разделили на 10 равных частей. Давайте найдем одну десятую от всех книг, а затем три десятых.

800:10=80(книг)
80∙3=240(книг)

Есть запись короче 800:10∙3=240(книг)

Ответ: 240 книг было куплено.

Задача 2 нахождение числа по дроби

Ученики купили 70 тетрадей. Это составило семь восьмых всех тетрадей в магазине. Сколько тетрадей было в магазине?

Рассмотрим дробь семь восьмых. Что она показывает?

Что искомое число было разделено на 8 частей. По условию семь восьмых этого числа равно 70. Сначала найдем одну восьмую первоначального числа тетрадей в магазине, а потом семь восьмых.

1)70:7=10(тетрадей)

2)10∙8=80(тетрадей)

Или 70:7∙8=80(тетрадей) Ответ: 80 тетрадей.

Задача 3 (нахождение отношения чисел)

Стакан вмещает 200 грамм молока. Какую часть стакана нужно наполнить, чтобы в нем оказалось 160 грамм молока?

Решение

По условию мы должны получить в виде дроби. У дроби есть числитель и знаменатель. В нашей задачи числитель –160, знаменатель 200. Получаем

Решая задачи на дроби, мы должны помнить, что существует 3 типа задач на дроби:

1)нахождение части от числа

2)нахождение числа по дроби

3)отношение чисел

5 этап. Работа у доски.

6 этап. Домашнее задание.

Выучить теорию пункта 4.3, № 766. 770, 784, 787

infourok.ru

Презентация к уроку по математике (5 класс): Презентация «Задачи на дроби»

Слайд 1

Задачи на дроби

Слайд 2

Из трехлитрового бидона с молоком взяли 2 л молока. Какую часть всего молока взяли?

Слайд 3

В гараже стояло 9 машин. Какую часть всех машин составляли красные машины? Какую часть всех машин составляли грузовые машины? Какую часть всех машин составляли синие машины?

Слайд 4

Какую часть всех лошадей составляют черные?

Слайд 5

Какую часть всех птиц составляют белые лебеди?

Слайд 6

Какую часть всех домашних птиц составляют петухи?

Слайд 7

9 м 4 м От доски длиной 9 м отпилили 4 м. Какую часть доски отпилили? Какая часть доски осталась?

Слайд 8

А В С О D Какая часть четырехугольника ABCD закрашена? Какая часть осталась незакрашенной?

Слайд 9

А В С О К Е D Какую часть составляет: а) треугольник АВО от четырехугольника АВСО; б) треугольник АВО от четырехугольника АВС D ; в) четырехугольник АВСО от четырехугольника АВС D ; г) четырехугольник АВСО от шестиугольника АВС D ЕК.

Слайд 10

Сколько молока в бидоне, если этого бидона составляет 13 л? 13 л 13•5=65 (л)

Слайд 11

Купили кусок ткани длиной 2м 50 см и из куска сшили платье для куклы. Сколько сантиметров ткани ушло на платье? 250:5=50

Слайд 12

Длина дороги 20 км. Заасфальтировали дороги Сколько километров дороги заасфальтировали? Сколько осталось заасфальтировать? 20 км 4 км 4 км 4 км 4 км 4 км 1) 20:5=4(км) составит 2) 4*2=8(км) составят

Слайд 13

От дыни массой 2 кг 400 г Ване отрезали дыни, а Маше дыни. Сколько граммов дыни осталось? 1 кг 520 г

Слайд 14

Велосипедист проехал дороги. Какова длина дороги, если он проехал 40 км? 40 км 1) 40:2=20(км) составит дороги 2) 20*9=180(км) вся дорога 20км 20км

Слайд 15

Купили 5 кг 600 г сахара и израсходовали на варенье всего сахара. Сколько сахара пошло на варенье? Сколько сахара осталось? 1) 5600:8=700(г) составит 700 г 700 г 700 г 700 г 700 г 700 г 700 г 700 г 2) 700*7=4900(г) составит

Слайд 16

В аквариум налили 6 л воды, заполнив его объема. Сколько литров воды вмещает аквариум? 6 л 7 л

Слайд 17

Андрей гулял 2 ч. этого времени он играл. Сколько времени Андрей играл? 1) 120:3=40(мин) составит часть от 2 часов 2) 40*2=80(мин) играл Андрей

Слайд 18

Человек прошел дороги. Какова длина всей дороги, если он прошел 4 км? 4 км 1) 4:2=2(км) составит дороги 2) 2*3=6(км) вся дорога 2 км 2 км

Слайд 19

40 м 2 Дом занимает всего садового участка. Найдите площадь участка, если площадь земли под домом 40 м 2 600 м 2

Слайд 20

56км/ч I 420 км 4ч С одной станции одновременно в противоположных направлениях вышли два поезда. Скорость первого 56км/ч, а скорость второго составляет скорости первого. Через сколько времени расстояние между ними станет равно 420км? II

nsportal.ru

Обыкновенные дроби. Математика, 5 класс: уроки, тесты, задания.

Вход Вход Регистрация Начало Поиск по сайту ТОПы Учебные заведения Предметы Проверочные работы Обновления Новости Переменка Отправить отзыв
Предметы

Математика

5 класс

Деление с остатком. Понятие обыкновенной дроби

Основное свойство дроби

Правильные и неправильные дроби. Смешанные числа

Сравнение дробей

Сложение и вычитание обыкновенных дробей и смешанных чисел

Умножение и деление обыкновенной дроби на натуральное число

Нахождение части от целого и числа по его части

Геометрические понятия: окружность и круг

Отправить отзыв Нашёл ошибку? Сообщи нам! Copyright © 2019 ООО ЯКласс Контакты Пользовательское соглашение
www.yaklass.ru