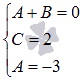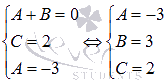Разложение дробей при интегрировании — Википедия
В интегрировании, разложение дробей позволяет интегрировать рациональные функции. Любая рациональная функция может быть представлена в виде суммы некоторого многочлена и некоторого числа дробных функций. Каждая дробь имеет знаменатель в виде многочлена первой или второй степени, причём многочлен в знаменателе, в свою очередь, также может быть возведён в некоторую положительную целую степень. (В случае комплексной переменной, знаменатели являются многочленами первой степени, и эти многочлены могут быть возведены в целую положительную степень). Если знаменатель является многочленом первой степени, возведённым в некоторую целую положительную степень, то числитель дроби является постоянным числом. Если знаменатель является многочленом второй степени (или некоторой целой положительной степенью такого многочлена), то числитель является многочленом первой степени.
Решение Исаака Барроу для интеграла от секанса было первым случаем использования разложения дробей в интегрировании.
Известно, что многочлен n-й степени в общем случае имеет n комплексно-сопряжённых корней (некоторые корни могут совпадать). Например, многочлен x2 − 6x + 8 имеет два корня; многочлен x3 − 6x2 + 8x + 7 имеет три корня и т. д.
Соответственно, любой многочлен может быть разложен по формуле
axn+bxn−1+…+k=a(x−x1)(x−x2)(x−x3)…(x−xn){\displaystyle ax^{n}+bx^{n-1}+…+k=a(x-x_{1})(x-x_{2})(x-x_{3})…(x-x_{n})}
где x1{\displaystyle x_{1}}, x2{\displaystyle x_{2}}…xn{\displaystyle x_{n}} — корни многочлена.
Например, многочлен x2 − 6x + 8 можно разложить следующим образом:
x2 − 6x + 8 = (x — 2)(x — 4)
где 2 и 4 — корни квадратного уравнения x2 − 6x + 8=0
Следовательно, дробь, знаменателем которой является многочлен, может быть разложена следующим образом:
1axn+bxn−1+…+k=Aa+B(x−x1)+C(x−x2)+D(x−x3)+…+K(x−xn){\displaystyle {\frac {1}{ax^{n}+bx^{n-1}+…+k}}={\frac {A}{a}}+{\frac {B}{(x-x_{1})}}+{\frac {C}{(x-x_{2})}}+{\frac {D}{(x-x_{3})}}+…+{\frac {K}{(x-x_{n})}}}
Эта операция разложения дроби в некотором смысле обратна операции приведения дробей общему знаменателю, с той разницей, что здесь ставится обратная задача — не привести дроби к общему знаменателю, а разложить дробь, имеющую общий знаменатель, на несколько дробей, имеющих разные знаменатели.
В качестве примера, разложим дробь
1×2−6x+8{\displaystyle {\frac {1}{x^{2}-6x+8}}}
Согласно написанному выше, разложение этой дроби таково
1×2−6x+8=Ax−2+Bx−4{\displaystyle {\frac {1}{x^{2}-6x+8}}={\frac {A}{x-2}}+{\frac {B}{x-4}}}
Начнём приводить две дроби, расположенные в правой части равенства, к общему знаменателю, и очевидно, что числитель получившейся дроби будет равен числителю исходной дроби
1×2−6x+8{\displaystyle {\frac {1}{x^{2}-6x+8}}}
то есть, числитель получившейся дроби будет равен единице.
Имеем
1×2−6x+8=A(x−4)(x−2)(x−4)+B(x−2)(x−4)(x−2){\displaystyle {\frac {1}{x^{2}-6x+8}}={\frac {A(x-4)}{(x-2)(x-4)}}+{\frac {B(x-2)}{(x-4)(x-2)}}}
Записывая две дроби справа под одну дробную черту, получим
1×2−6x+8=A(x−4)+B(x−2)(x−2)(x−4){\displaystyle {\frac {1}{x^{2}-6x+8}}={\frac {A(x-4)+B(x-2)}{(x-2)(x-4)}}}
или раскрыв скобки в знаменателе, получим
1×2−6x+8=A(x−4)+B(x−2)x2−6x+8{\displaystyle {\frac {1}{x^{2}-6x+8}}={\frac {A(x-4)+B(x-2)}{x^{2}-6x+8}}}
Учитывая, что знаменатели одинаковы, то числители дробей справа и слева можно приравнять; тогда получим
1=A(x−4)+B(x−2){\displaystyle 1=A(x-4)+B(x-2)}
Раскроем скобки в правой части равенства и сгруппируем слагаемые:
1=(A+B)x+(−4A−2B){\displaystyle 1=(A+B)x+(-4A-2B)}
В левой части множитель при переменной х равен нулю (переменная х отсутствует), а свободный член равен 1. В правой части равенства множитель при х равен (А+В), а свободный член равен (-4A — 2B). Приравнивая множители при х в правой и левой части получаем уравнение:
(A+B)=0{\displaystyle (A+B)=0}
Аналогично приравниваем свободные члены, и получаем второе уравнение
(−4A−2B)=1{\displaystyle (-4A-2B)=1}
Объединяем эти два уравнения в систему:
- {A+B=0−4A−2B=1{\displaystyle \left\{{\begin{matrix}A+B=0\\-4A-2B=1\end{matrix}}\right.}
Решая эту систему, находим
A=−12{\displaystyle A=-{\frac {1}{2}}}
B=12{\displaystyle B={\frac {1}{2}}}
Итак, имеем разложение
1×2−6x+8=−1/2x−2+1/2x−4{\displaystyle {\frac {1}{x^{2}-6x+8}}={\frac {-1/2}{x-2}}+{\frac {1/2}{x-4}}}
Тогда, интеграл от дроби
∫1×2−6x+8dx{\displaystyle \int {\frac {1}{x^{2}-6x+8}}\,dx}
будет равен сумме интегралов от двух дробей
∫1×2−6x+8dx=∫−1/2x−2dx+∫1/2x−4dx{\displaystyle \int {\frac {1}{x^{2}-6x+8}}\,dx=\int {\frac {-1/2}{x-2}}\,dx+\int {\frac {1/2}{x-4}}\,dx}
Учитывая, что под знаком дифференциала к переменной можно прибавить любую постоянную, запишем
∫1×2−6x+8dx=∫−1/2x−2d(x−2)+∫1/2x−4d(x−4){\displaystyle \int {\frac {1}{x^{2}-6x+8}}\,dx=\int {\frac {-1/2}{x-2}}\,d(x-2)+\int {\frac {1/2}{x-4}}\,d(x-4)}
Сделаем две замены
(x-2)=z
(x-4)=y
Тогда интеграл примет вид
∫1×2−6x+8dx=−12∫1zd(z)+12∫1yd(y){\displaystyle \int {\frac {1}{x^{2}-6x+8}}\,dx=-{\frac {1}{2}}\int {\frac {1}{z}}\,d(z)+{\frac {1}{2}}\int {\frac {1}{y}}\,d(y)}
Эти два интеграла не составит труда найти по таблицам интегралов. Тогда окончательно получаем:
∫1×2−6x+8dx=−12ln|z|+12ln|y|+constant{\displaystyle \int {\frac {1}{x^{2}-6x+8}}\,dx=-{\frac {1}{2}}\ln |z|+{\frac {1}{2}}\ln |y|+{\text{constant}}}
или
∫1×2−6x+8dx=−12ln|x−2|+12ln|x−4|+constant{\displaystyle \int {\frac {1}{x^{2}-6x+8}}\,dx=-{\frac {1}{2}}\ln |x-2|+{\frac {1}{2}}\ln |x-4|+{\text{constant}}}
Многочлен первой степени в знаменателе[править | править код]
Подстановка u = ax + b, du = a dx позволяет упростить интеграл
- ∫1ax+bdx{\displaystyle \int {1 \over ax+b}\,dx}
до
- ∫1udua=1a∫duu=1aln|u|+C=1aln|ax+b|+C.{\displaystyle \int {1 \over u}\,{du \over a}={1 \over a}\int {du \over u}={1 \over a}\ln \left|u\right|+C={1 \over a}\ln \left|ax+b\right|+C.}
Многочлен первой степени в знаменателе, возведённый в некоторую целую положительную степень[править | править код]
Та же самая подстановка упрощает интеграл, подобный следующему
- ∫1(ax+b)8dx{\displaystyle \int {1 \over (ax+b)^{8}}\,dx}
до
- ∫1u8dua=1a∫u−8du=1a⋅u−7(−7)+C=−17au7+C=−17a(ax+b)7+C.{\displaystyle \int {1 \over u^{8}}\,{du \over a}={1 \over a}\int u^{-8}\,du={1 \over a}\cdot {u^{-7} \over (-7)}+C={-1 \over 7au^{7}}+C={-1 \over 7a(ax+b)^{7}}+C.}
В знаменателе многочлен второй степени, не имеющий действительных корней[править | править код]
Рассмотрим интеграл
- ∫x+6×2−8x+25dx.{\displaystyle \int {x+6 \over x^{2}-8x+25}\,dx.}
Самый простой путь увидеть, что знаменатель x2 − 8x + 25 не имеет действительных корней, состоит в том, чтобы вычислить его дискриминант, и увидеть, что этот дискриминант отрицательный. По-другому, можно выделить полный квадрат в знаменателе:
- x2−8x+25=(x2−8x+16)+9=(x−4)2+9{\displaystyle x^{2}-8x+25=(x^{2}-8x+16)+9=(x-4)^{2}+9}
и можно увидеть, что знаменатель представляет собой сумму квадратов двух чисел, и эта сумма никогда не может быть равна 0 или меньше 0, если x — действительное число.
Используя подстановку
- u=x2−8x+25du=(2x−8)dxdu/2=(x−4)dx{\displaystyle {\begin{aligned}u&=x^{2}-8x+25\\du&=(2x-8)\,dx\\du/2&=(x-4)\,dx\end{aligned}}}
нам нужно выделить выражение x − 4 в числителе. Тогда мы сможем записать числитель x + 6 в виде суммы (x − 4) + 10, и тогда интеграл будет записан в виде
- ∫x−4×2−8x+25dx+∫10×2−8x+25dx.{\displaystyle \int {x-4 \over x^{2}-8x+25}\,dx+\int {10 \over x^{2}-8x+25}\,dx.}
Выше приведённая подстановка позволяет взять первый из этих двух интегралов:
- ∫x−4×2−8x+25dx=∫du/2u=12ln|u|+C=12ln(x2−8x+25)+C.{\displaystyle \int {x-4 \over x^{2}-8x+25}\,dx=\int {du/2 \over u}={1 \over 2}\ln \left|u\right|+C={1 \over 2}\ln(x^{2}-8x+25)+C.}
Заметим, что причина, по которой мы можем опустить модульные скобки, состоит в том, что, как мы заметили ранее, выражение (x − 4)2 + 9 не может иметь отрицательных значений.
Далее следует взять интеграл
- ∫10×2−8x+25dx.{\displaystyle \int {10 \over x^{2}-8x+25}\,dx.}
В первую очередь, выделим полный квадрат в знаменателе, после чего проведём несложные алгебраические преобразования:
- ∫10×2−8x+25dx=∫10(x−4)2+9dx=∫10/9(x−43)2+1dx=103∫1(x−43)2+1(dx3){\displaystyle {\begin{aligned}&{}\quad \int {10 \over x^{2}-8x+25}\,dx=\int {10 \over (x-4)^{2}+9}\,dx\\[9pt]&=\int {10/9 \over \left({x-4 \over 3}\right)^{2}+1}\,dx={10 \over 3}\int {1 \over \left({x-4 \over 3}\right)^{2}+1}\,\left({dx \over 3}\right)\end{aligned}}}
Теперь используем следующую подстановку
- w=(x−4)/3{\displaystyle w=(x-4)/3}
- dw=dx/3{\displaystyle dw=dx/3}
что позволяет найти
- 103∫dww2+1=103arctgw+C=103arctg(x−43)+C.{\displaystyle {10 \over 3}\int {dw \over w^{2}+1}={10 \over 3}\operatorname {arctg} \,w+C={10 \over 3}\operatorname {arctg} \left({x-4 \over 3}\right)+C.}
Складывая оба найденных выражения, запишем окончательный результат интегрирования
- ∫x+6×2−8x+25dx=12ln(x2−8x+25)+103arctg(x−43)+C.{\displaystyle \int {x+6 \over x^{2}-8x+25}\,dx={1 \over 2}\ln(x^{2}-8x+25)+{10 \over 3}\operatorname {arctg} \left({x-4 \over 3}\right)+C.}
Использование комплексного разложения[править | править код]
В ряде случаев, при определённом навыке, удобнее использовать комплексное разложение многочлена. Так, в вышеприведённом примере:
- ∫x+6×2−8x+25dx{\displaystyle \int {x+6 \over x^{2}-8x+25}\,dx}
Разлагаем знаменатель на два комплексных множителя:
- x2−8x+25=(x−4+3i)(x−4−3i){\displaystyle x^{2}-8x+25=(x-4+3i)(x-4-3i)}
После чего ищем разложение подынтегрального выражения на два слагаемых:
- x+6×2−8x+25=Ax−4+3i+Bx−4−3i{\displaystyle {\frac {x+6}{x^{2}-8x+25}}={\frac {A}{x-4+3i}}+{\frac {B}{x-4-3i}}}
Решив несложную систему линейных уравнений, получаем:
- A=12+53i,B=12−53i{\displaystyle A={\tfrac {1}{2}}+{\tfrac {5}{3}}i,B={\tfrac {1}{2}}-{\tfrac {5}{3}}i}
- ∫x+6×2−8x+25dx=(12+53i)∫1x−4+3idx+(12−53i)∫1x−4+3idx{\displaystyle \int {\frac {x+6}{x^{2}-8x+25}}\,dx=({\tfrac {1}{2}}+{\tfrac {5}{3}}i)\int {\frac {1}{x-4+3i}}\,dx+({\tfrac {1}{2}}-{\tfrac {5}{3}}i)\int {\frac {1}{x-4+3i}}\,dx}
После очевидного интегрирования имеем:
- (12+53i)ln(x−4+3i)+(12−53i)ln(x−4−3i)+C{\displaystyle \left({\tfrac {1}{2}}+{\tfrac {5}{3}}i\right)\ln(x-4+3i)+\left({\tfrac {1}{2}}-{\tfrac {5}{3}}i\right)\ln(x-4-3i)+C}
Сгруппируем отдельно действительные и мнимые слагаемые:
- 12(ln(x−4+3i)+ln(x−4−3i))+53i(ln(x−4+3i)−ln(x−4−3i))+C{\displaystyle {\tfrac {1}{2}}\left(\ln(x-4+3i)+\ln(x-4-3i)\right)+{\tfrac {5}{3}}i\left(\ln(x-4+3i)-\ln(x-4-3i)\right)+C}
- 12ln((x−4+3i)(x−4−3i))+53ilnx−4+3ix−4−3i+C{\displaystyle {\tfrac {1}{2}}\ln \left((x-4+3i)(x-4-3i)\right)+{\tfrac {5}{3}}i\ln {\frac {x-4+3i}{x-4-3i}}+C}
- 12ln(x2−8x+25)+53iln1−ix−431+ix−43+C{\displaystyle {\tfrac {1}{2}}\ln(x^{2}-8x+25)+{\tfrac {5}{3}}i\ln {\frac {1-i{\frac {x-4}{3}}}{1+i{\frac {x-4}{3}}}}+C}
Как известно, арктангенс комплексного переменного выражается через логарифм:
- arctgz=12iln1−iz1+iz{\displaystyle \operatorname {arctg} \,z={\tfrac {1}{2}}i\ln {\frac {1-i\,z}{1+i\,z}}}
Это даёт нам возможность переписать второе слагаемое через арктангенс:
- 12ln(x2−8x+25)+103arctgx−43+C{\displaystyle {\tfrac {1}{2}}\ln(x^{2}-8x+25)+{\tfrac {10}{3}}\operatorname {arctg} {\frac {x-4}{3}}+C}
В знаменателе многочлен второй степени, возведённый в целую положительную степень[править | править код]
Рассмотрим интеграл
- ∫x+6(x2−8x+25)8dx.{\displaystyle \int {x+6 \over (x^{2}-8x+25)^{8}}\,dx.}
Так же, как это делалось выше, можно представить числитель x + 6 в виде суммы (x − 4) + 10, и взять ту часть, которая содержит выражение x − 4, с помощью подстановки
- u=x2−8x+25,du=(2x−8)dx,du/2=(x−4)dx.{\displaystyle {\begin{aligned}u&=x^{2}-8x+25,\\du&=(2x-8)\,dx,\\du/2&=(x-4)\,dx.\end{aligned}}}
Нам остаётся лишь найти интеграл
- ∫10(x2−8x+25)8dx.{\displaystyle \int {10 \over (x^{2}-8x+25)^{8}}\,dx.}
Как это делалось выше, сначала выделим полный квадрат, после чего произведём несложные математические преобразования
- ∫10(x2−8x+25)8dx=∫10((x−4)2+9)8dx=∫10/98((x−43)2+1)8dx.{\displaystyle \int {10 \over (x^{2}-8x+25)^{8}}\,dx=\int {10 \over ((x-4)^{2}+9)^{8}}\,dx=\int {10/9^{8} \over \left(\left({x-4 \over 3}\right)^{2}+1\right)^{8}}\,dx.}
После этого можно использовать подстановку:
- tgθ=x−43,{\displaystyle tg\theta ={x-4 \over 3},}
Разложение дроби на простейшие
Информация предоставлена с сайта www.cleverstudents.ru
Разложение дроби на простейшие.
Для начала разберем теорию, далее решим парочку примеров для закрепления материала по разложению дробно рациональной функции на сумму простейших дробей. Подробно остановимся на методе неопределенных коэффициентов и методе частных значений, а также на их комбинации. Простейшие дроби часто называют элементарными дробями. Различают следующие виды простейших дробей:
где A, M, N, a, p, q – числа, а дискриминант знаменателя в дробях 3) и 4) меньше нуля. Называют их соответственно дробями первого, второго, третьего и четвертого типов. Для чего вообще дробь раскладывать на простейшие? Приведем математическую аналогию. Часто приходится заниматься упрощением вида выражения, чтобы можно было проводить какие-то действия с ним. Так вот, представление дробно рациональной функции в виде суммы простейших дробей примерно то же самое. Применяется для разложения функций в степенные ряды, ряды Лорана и, конечно же, для нахождения интегралов. К примеру, требуется взять интеграл от дробно рациональной функции
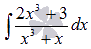 .
После разложения подынтегральной
функции на простейшие дроби, все сводится
к достаточно простым интегралам
.
После разложения подынтегральной
функции на простейшие дроби, все сводится
к достаточно простым интегралам 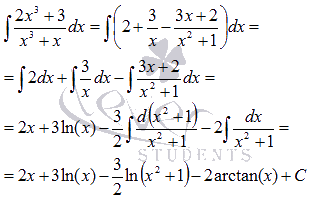 Но
об интегралах в другом
разделе. Пример. Разложить
дробь
Но
об интегралах в другом
разделе. Пример. Разложить
дробь 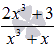 на
простейшие. Решение. Вообще
отношение многочленов раскладывают на
простейшие дроби, если степень многочлена
числителя меньше степени многочлена в
знаменателе. В противном случае сначала
проводят деление
многочлена числителя на многочлен
знаменателя,
а уже затем проводят разложение правильной
дробно рациональной функции. Выполним
деление столбиком (уголком):
на
простейшие. Решение. Вообще
отношение многочленов раскладывают на
простейшие дроби, если степень многочлена
числителя меньше степени многочлена в
знаменателе. В противном случае сначала
проводят деление
многочлена числителя на многочлен
знаменателя,
а уже затем проводят разложение правильной
дробно рациональной функции. Выполним
деление столбиком (уголком): 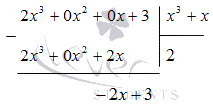 Следовательно,
исходная дробь примет вид:
Следовательно,
исходная дробь примет вид: 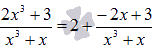
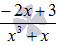 Алгоритм
метода неопределенных коэффициентов.
Алгоритм
метода неопределенных коэффициентов. Во-первых, раскладываем знаменатель на множители. Здесь все методы хороши – от вынесения за скобки, применения формул сокращенного умножения, до подбора корня и последующего деления столбиком (при знаменателе в виде многочлена с рациональными коэффициентами степени выше второй). Об этом подробнее в разделе теории – разложение многочлена на множители. В нашем примере все просто – выносим х за скобки.

Во-вторых, раскладываемую дробь представляем в виде суммы простейших дробей с неопределенными коэффициентами
. Здесь стоит рассмотреть виды выражений, которые могут быть у Вас в знаменателе.Если в знаменателе что-то вроде этого
 ,
количество линейных множителей роли
не играет, (будь их 2 или 22),
то дробь представится в виде суммы
простейших дробей первого типа:
,
количество линейных множителей роли
не играет, (будь их 2 или 22),
то дробь представится в виде суммы
простейших дробей первого типа:  a, b, c и d — числа, A, B, C и D — неопределенные коэффициенты.
a, b, c и d — числа, A, B, C и D — неопределенные коэффициенты.
Если в знаменателе что-то вроде этого
 количество
множителей роли не играет и не играют
роли степени этих множителей (хоть
221ая степень), то дробь представится в
виде суммы простейших дробей первого
и второго типов:
количество
множителей роли не играет и не играют
роли степени этих множителей (хоть
221ая степень), то дробь представится в
виде суммы простейших дробей первого
и второго типов: 
 —
неопределенные коэффициенты. Возьмите
на заметку: какая степень – столько и
слагаемых.
—
неопределенные коэффициенты. Возьмите
на заметку: какая степень – столько и
слагаемых.
Если в знаменателе что-то вроде этого
 количество
квадратичных выражений роли не играет,
то дробь представится в виде суммы
простейших дробей третьего типа:
количество
квадратичных выражений роли не играет,
то дробь представится в виде суммы
простейших дробей третьего типа:  p, q, r и s — числа, P, Q, R и S — неопределенные коэффициенты.
p, q, r и s — числа, P, Q, R и S — неопределенные коэффициенты.
Если в знаменателе что-то вроде этого
количество множителей роли не играет и не играют роли степени этих множителей, то дробь представится в виде суммы простейших дробей третьего и четвертого типов:
 p, q, r и s — числа,
p, q, r и s — числа,  —
неопределенные коэффициенты. ОБЫЧНО
ВСТРЕЧАЕТСЯ КОМБИНАЦИЯ ЭТИХ ВАРИАНТОВ
(как правило, довольно простая).
—
неопределенные коэффициенты. ОБЫЧНО
ВСТРЕЧАЕТСЯ КОМБИНАЦИЯ ЭТИХ ВАРИАНТОВ
(как правило, довольно простая).
Хватит
теории, на практике все равно
понятнее. Пришло время вернуться к
примеру. Дробь раскладывается в сумму
простейших дробей первого и третьего
типов с неопределенными коэффициентами A, B и C. 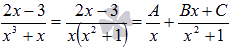
В-третьих, приводим полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях
 То
есть, пришли к равенству:
То
есть, пришли к равенству:  При x отличных от нуля это равенство сводится
к равенству двух многочленов
При x отличных от нуля это равенство сводится
к равенству двух многочленов  А
два многочлена являются равными тогда
и только тогда, когда коэффициенты при
одинаковых степенях совпадают.
А
два многочлена являются равными тогда
и только тогда, когда коэффициенты при
одинаковых степенях совпадают.
В-четвертых, приравниваем коэффициенты при одинаковых степенях х. При этом получаем систему линейных алгебраических уравнений с неопределенными коэффициентами в качестве неизвестных:

В-пятых, решаем полученную систему уравнений любым способом (при необходимости смотрите статью решение систем линейных алгебраических уравнений, методы решения, примеры), который нравится Вам, находим неопределенные коэффициенты. О решении систем линейных уравнений подробнее в разделе – решение систем линейных алгебраических уравнений.

P.S. Пожалуйста,
не ленитесь, проверяйте ответ, приводя
к общему знаменателю полученное
разложение. 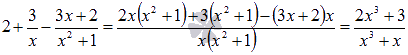 Метод
неопределенных коэффициентов является универсальным способом при
разложении дроби на простейшие. Очень
удобно использовать метод частных
значений, если знаменатель представляет
собой произведение линейных множителей,
то есть имеет вид схожий с
Метод
неопределенных коэффициентов является универсальным способом при
разложении дроби на простейшие. Очень
удобно использовать метод частных
значений, если знаменатель представляет
собой произведение линейных множителей,
то есть имеет вид схожий с 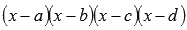 Рассмотрим
на примере, чтобы показать плюсы этого
метода.
Рассмотрим
на примере, чтобы показать плюсы этого
метода.
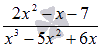 на
простейшие. Решение. Так
как степень многочлена в числителе
меньше степени многочлена в знаменателе,
то производить деление нам не придется.
Переходим к разложению знаменателя на
множители. Для начала выносим х за скобки.
на
простейшие. Решение. Так
как степень многочлена в числителе
меньше степени многочлена в знаменателе,
то производить деление нам не придется.
Переходим к разложению знаменателя на
множители. Для начала выносим х за скобки. 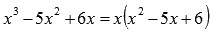 Находим
корни квадратного трехчлена
Находим
корни квадратного трехчлена 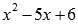 (например,
по теореме Виета):
(например,
по теореме Виета):  Следовательно,
квадратный трехчлен можно записать как
Следовательно,
квадратный трехчлен можно записать как 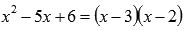 То
есть, знаменатель примет вид
То
есть, знаменатель примет вид 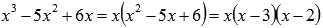 При
данном знаменателе, исходная дробь
раскладывается в сумму трех простейших
дробей первого типа с неопределенными
коэффициентами:
При
данном знаменателе, исходная дробь
раскладывается в сумму трех простейших
дробей первого типа с неопределенными
коэффициентами: 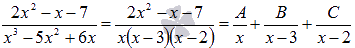 Полученную
сумму приводим к общему знаменателю,
но в числителе при этом скобки не
раскрываем и не приводим подобные при А, В и С (на этом этапе как раз отличие от метода
неопределенных коэффициентов):
Полученную
сумму приводим к общему знаменателю,
но в числителе при этом скобки не
раскрываем и не приводим подобные при А, В и С (на этом этапе как раз отличие от метода
неопределенных коэффициентов): 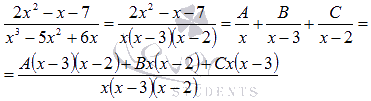 Таким
образом, пришли к равенству:
Таким
образом, пришли к равенству: 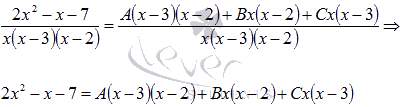 А
теперь, для нахождения неопределенных
коэффициентов, начинаем подставлять в
полученное равенство «частные значения»,
при которых знаменатель обращается в
ноль, то есть х=0, х=2 и х=3 для нашего примера: При х=0 имеем:
А
теперь, для нахождения неопределенных
коэффициентов, начинаем подставлять в
полученное равенство «частные значения»,
при которых знаменатель обращается в
ноль, то есть х=0, х=2 и х=3 для нашего примера: При х=0 имеем: 
 При х=3 имеем:
При х=3 имеем:  Ответ:
Ответ: 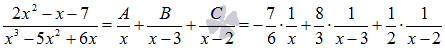 Как
видите, различие метода неопределенных
коэффициентов и метода частных значений
лишь в способе нахождения неизвестных.
Эти методы можно совмещать для упрощения
вычислений. Рассмотрим
пример. Пример. Разложить
дробно рациональное выражение
Как
видите, различие метода неопределенных
коэффициентов и метода частных значений
лишь в способе нахождения неизвестных.
Эти методы можно совмещать для упрощения
вычислений. Рассмотрим
пример. Пример. Разложить
дробно рациональное выражение 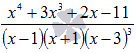 на
простейшие дроби. Решение. Так
как степень многочлена числителя меньше
степени многочлена знаменателя и
знаменатель уже разложен на множители,
то исходное выражение представится в
виде суммы простейших дробей следующего
вида:
на
простейшие дроби. Решение. Так
как степень многочлена числителя меньше
степени многочлена знаменателя и
знаменатель уже разложен на множители,
то исходное выражение представится в
виде суммы простейших дробей следующего
вида: 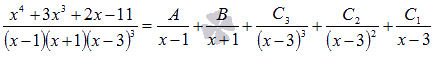 Приводим
к общему знаменателю:
Приводим
к общему знаменателю: 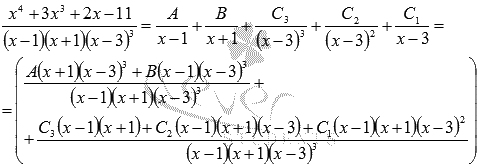 Приравниваем
числители.
Приравниваем
числители. 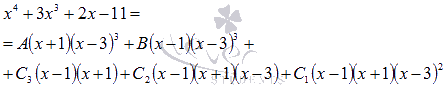 Очевидно,
что нулями знаменателя являются значения х=1, х=-1 и х=3.
Используем метод частных значений. При х=1 имеем:
Очевидно,
что нулями знаменателя являются значения х=1, х=-1 и х=3.
Используем метод частных значений. При х=1 имеем:  При х=-1 имеем:
При х=-1 имеем:  При х=3 имеем:
При х=3 имеем:  Осталось
найти неизвестные
Осталось
найти неизвестные 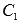 и
и 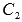 Для
этого подставляем найденные значения
в равенство числителей:
Для
этого подставляем найденные значения
в равенство числителей: 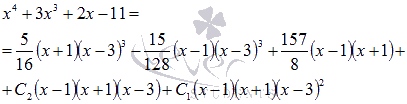 После
раскрытия скобок и приведения подобных
слагаемых при одинаковых степенях х
приходим к равенству двух
многочленов:
После
раскрытия скобок и приведения подобных
слагаемых при одинаковых степенях х
приходим к равенству двух
многочленов: 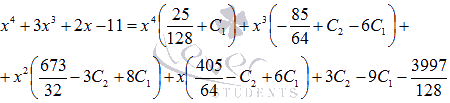 Приравниваем
соответствующие коэффициенты при
одинаковых степенях, тем самым составляем
систему уравнений для нахождения
оставшихся неизвестных
Приравниваем
соответствующие коэффициенты при
одинаковых степенях, тем самым составляем
систему уравнений для нахождения
оставшихся неизвестных 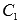 и
и 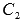 .
Получаем систему из пяти уравнений с
двумя неизвестными:
.
Получаем систему из пяти уравнений с
двумя неизвестными: 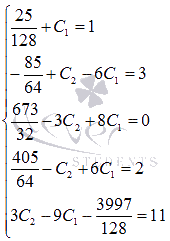 Из
первого уравнения сразу находим
Из
первого уравнения сразу находим 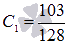 ,
из второго уравнения
,
из второго уравнения 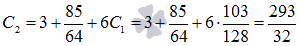 В
итоге получаем разложение на простейшие
дроби:
В
итоге получаем разложение на простейшие
дроби: 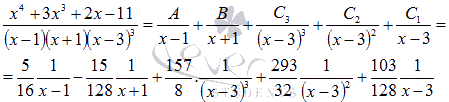 Примечание. Если
бы мы сразу решили применить метод
неопределенных коэффициентов, то
пришлось бы решать систему пяти линейных
алгебраических уравнений с пятью
неизвестными. Применение метода частных
значений позволило легко отыскать
значения трех неизвестных из пяти, что
значительно упростило дальнейшее
решение. Удачных решений!
Примечание. Если
бы мы сразу решили применить метод
неопределенных коэффициентов, то
пришлось бы решать систему пяти линейных
алгебраических уравнений с пятью
неизвестными. Применение метода частных
значений позволило легко отыскать
значения трех неизвестных из пяти, что
значительно упростило дальнейшее
решение. Удачных решений!1.7.2. Интегрирование рациональных дробей с помощью разложения на простейшие дроби
Интегрирование
рациональной дроби 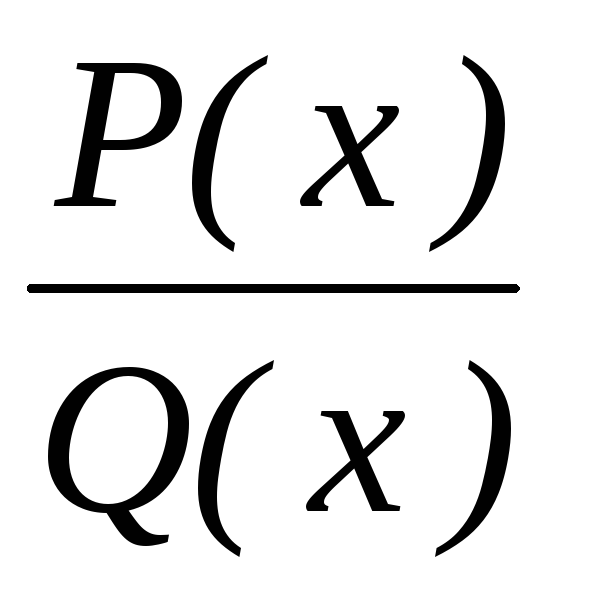 проводится по следующему алгоритму:
проводится по следующему алгоритму:
если дана неправильная рациональная дробь, то необходимо выделить из нее целую часть, т. е. представить в виде
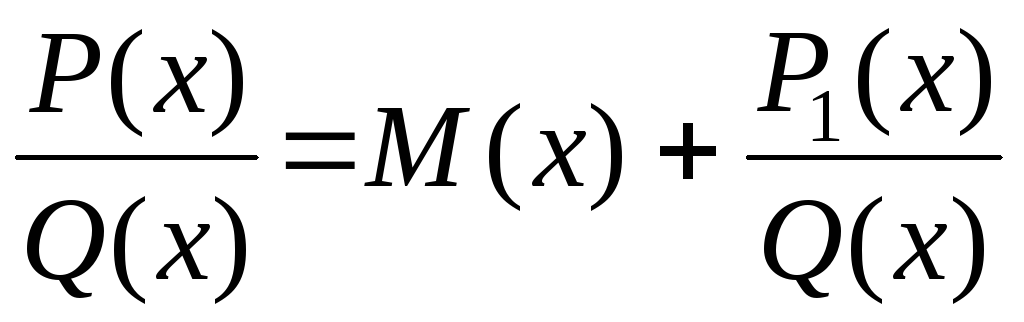 ,
,
где M(x) – многочлен, а 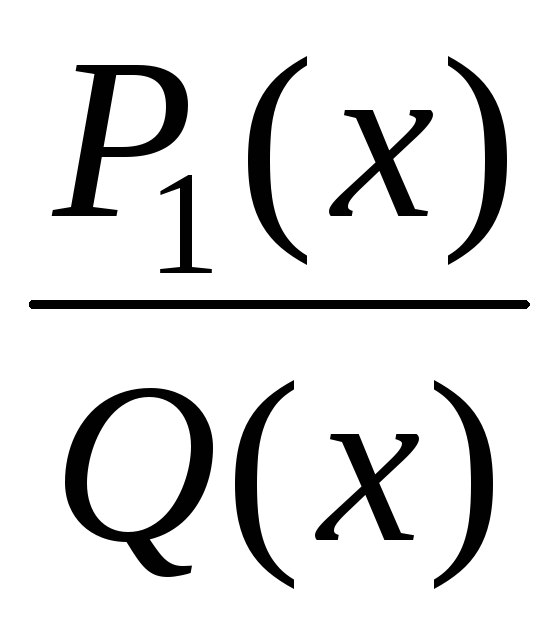 – правильная рациональная дробь;
– правильная рациональная дробь;
2) разложить знаменатель дроби на линейные и квадратичные множители:
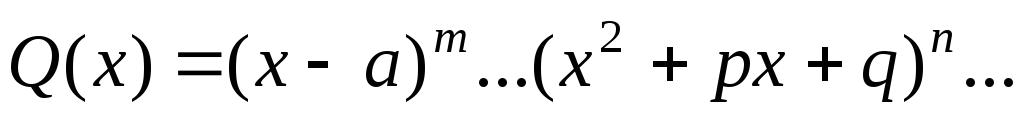 ,
,
где 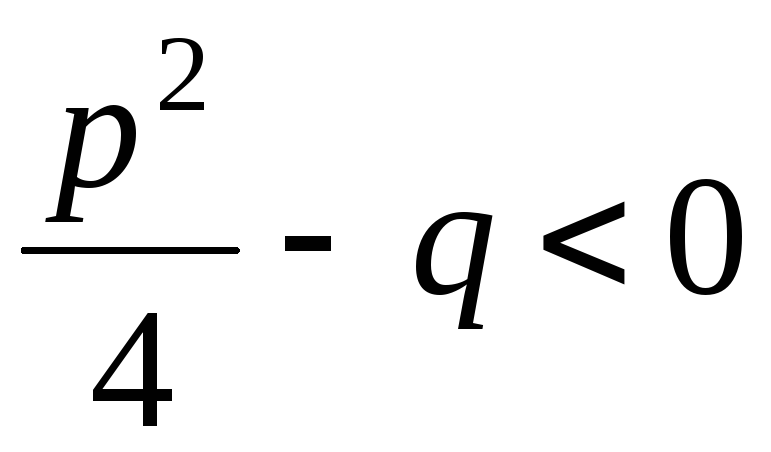 ,
т. е. трехчлен
,
т. е. трехчлен 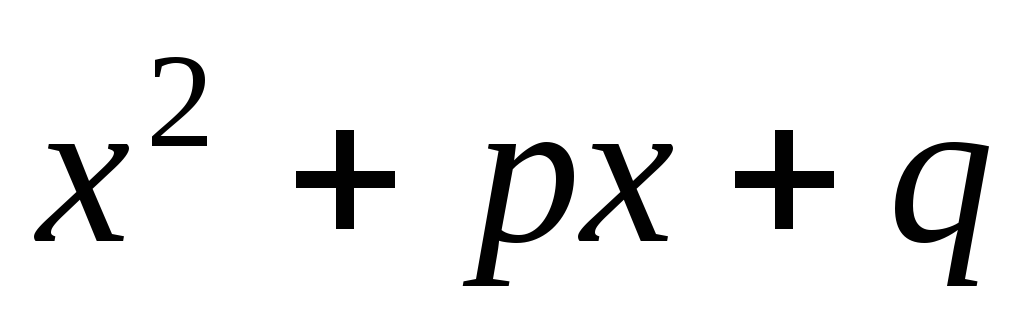 имеет комплексные сопряженные корни;
имеет комплексные сопряженные корни;
3) правильную рациональную дробь разложить на простейшие дроби:
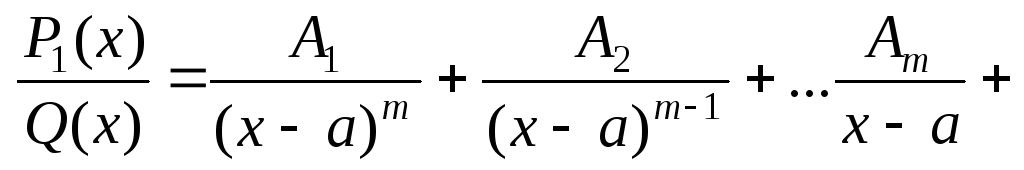

4) вычислить
неопределенные коэффициенты  .
Для этого привести последнее равенство
к общему знаменателю, приравнять
коэффициенты при одинаковых степенях х в левой и правой частях полученного
тождества и решить систему линейных
уравнений относительно искомых
коэффициентов. Можно определить
коэффициенты и другим способом, придавая
в полученном тождестве переменной х произвольные числовые значения.
.
Для этого привести последнее равенство
к общему знаменателю, приравнять
коэффициенты при одинаковых степенях х в левой и правой частях полученного
тождества и решить систему линейных
уравнений относительно искомых
коэффициентов. Можно определить
коэффициенты и другим способом, придавая
в полученном тождестве переменной х произвольные числовые значения.
В результате интегрирование рациональной дроби сведется к нахождению интегралов от многочлена и от простейших рациональных дробей.
Случай 1. Знаменатель имеет только действительные различные корни.
Пример. Вычислить интеграл
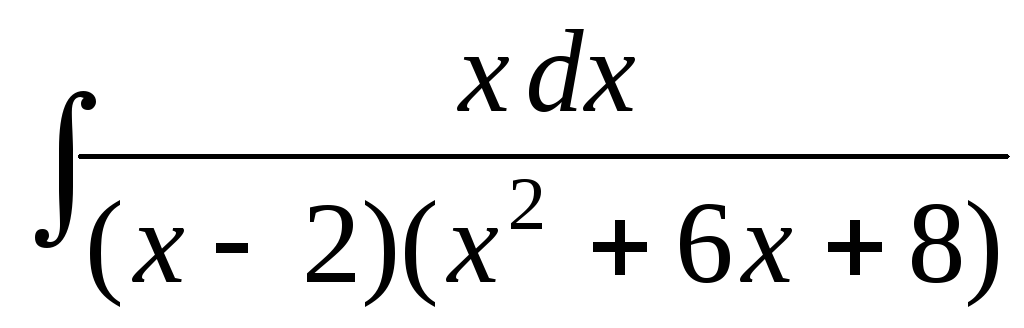 .
.
Решение
Рассмотрим
подынтегральную функцию 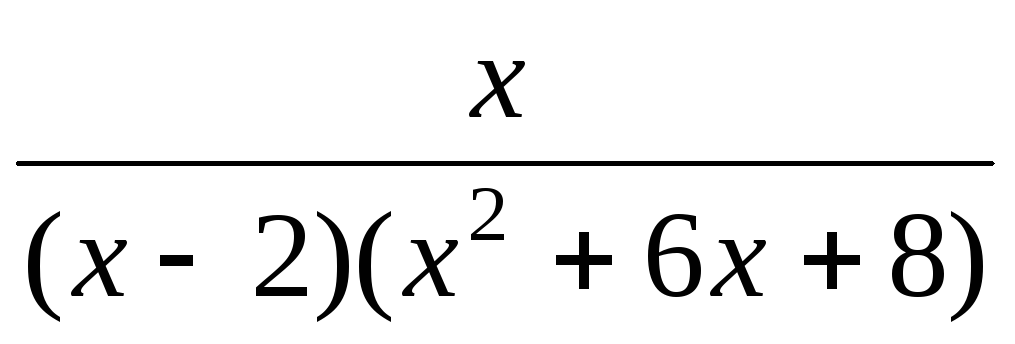 – правильная рациональная дробь.
Представим ее в виде суммы простейших
дробей, разложив знаменатель на
множители:
– правильная рациональная дробь.
Представим ее в виде суммы простейших
дробей, разложив знаменатель на
множители:
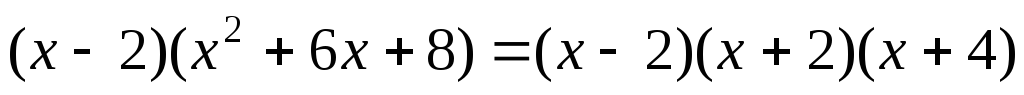 ;
;
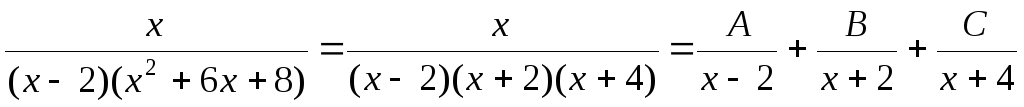 .
.
Приведем к общему знаменателю и рассмотрим числители дробей
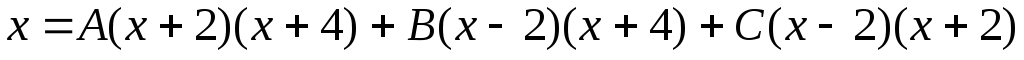 .
.
Полагая,
что 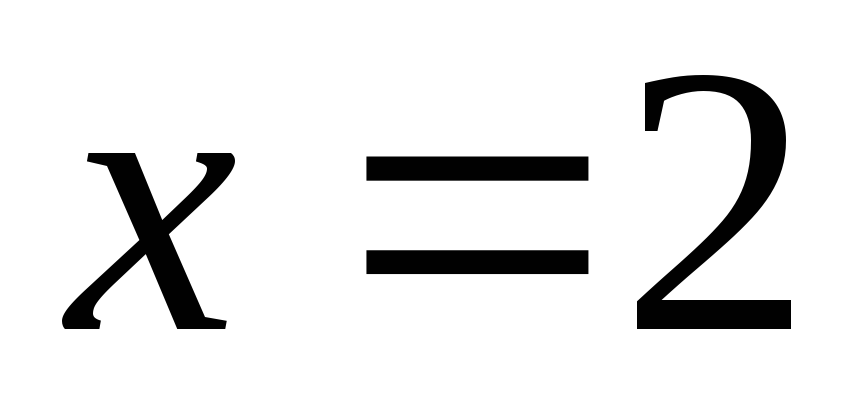 ,
найдем
,
найдем 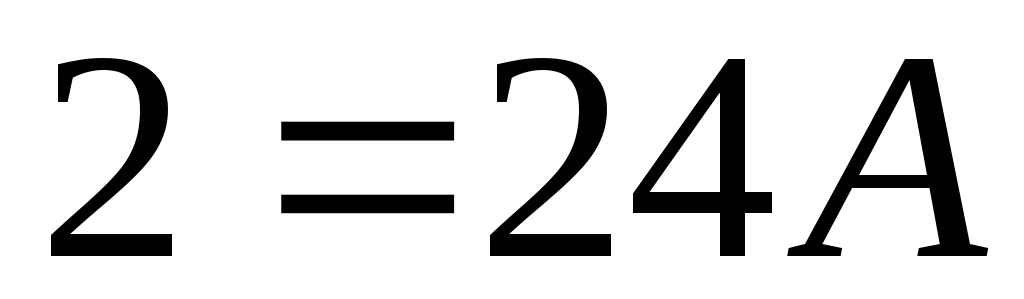 ,
т. е.
,
т. е. 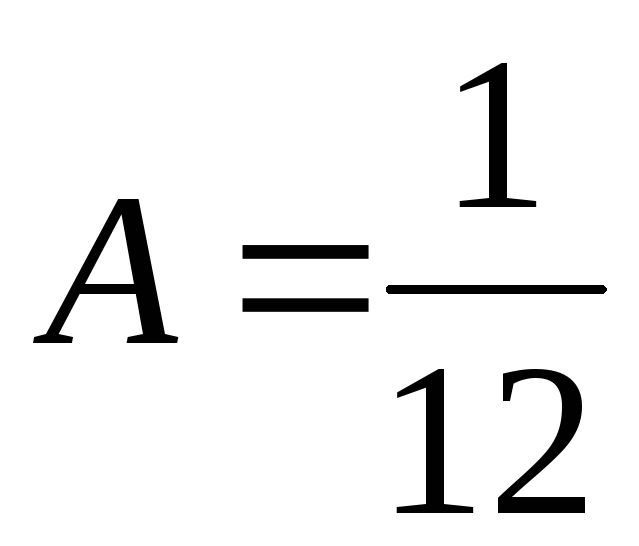 .
Если
.
Если 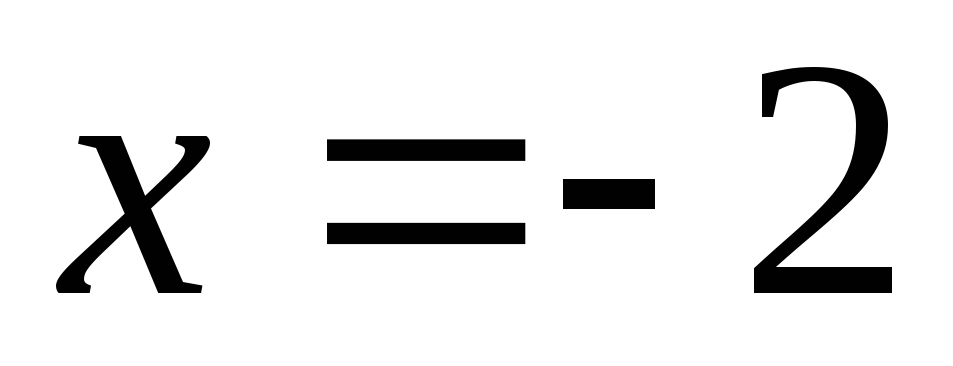 ,
то получим
,
то получим 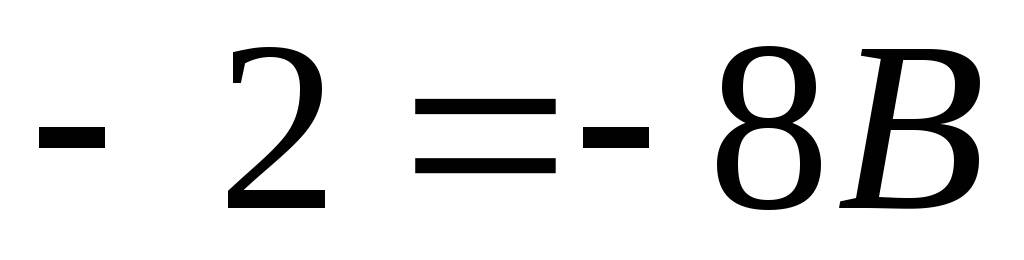 ,
т. е.
,
т. е. 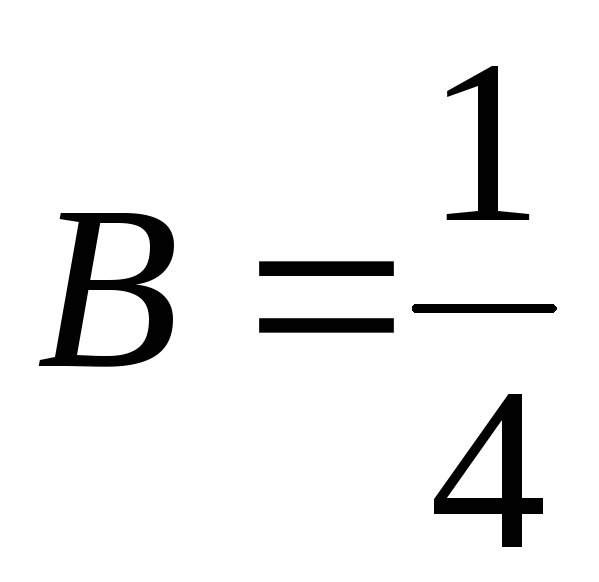 .
При
.
При 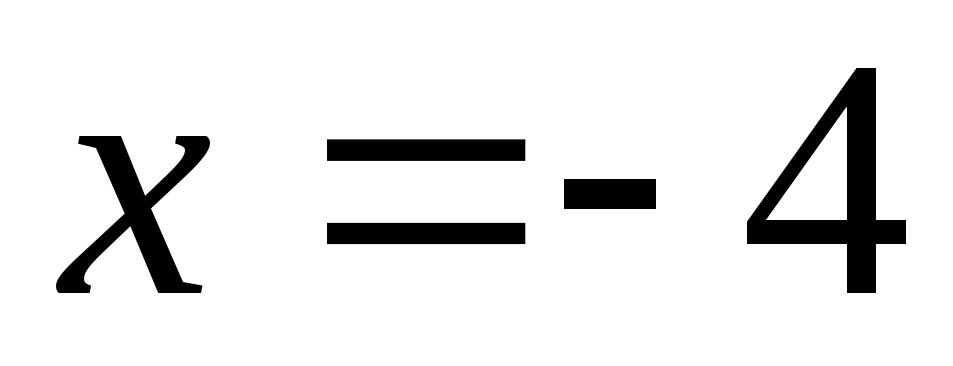 получим
получим 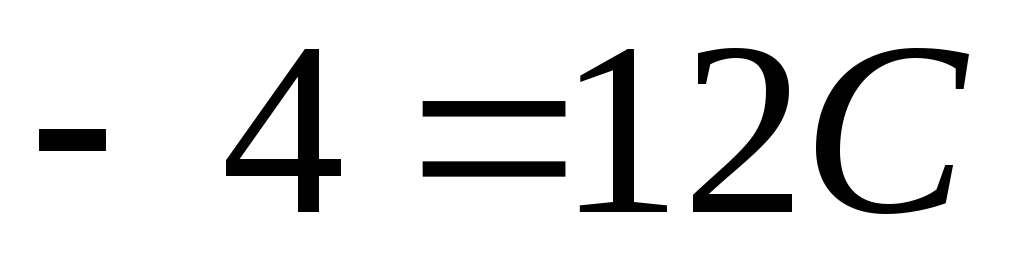 ,
т. е.
,
т. е. 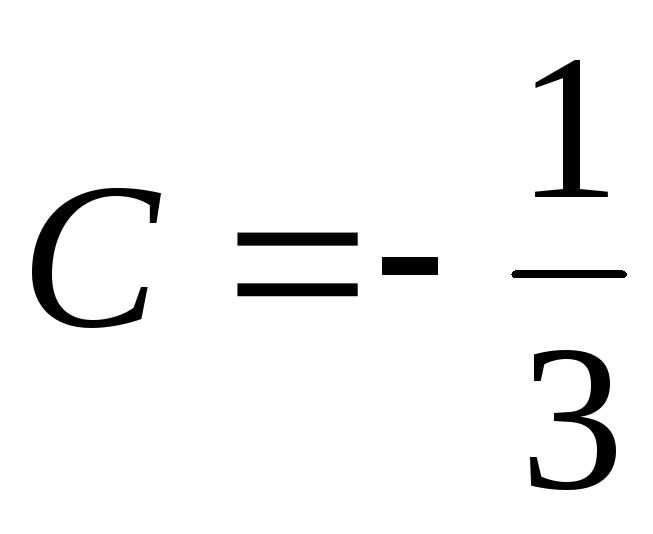 .
.
Итак,

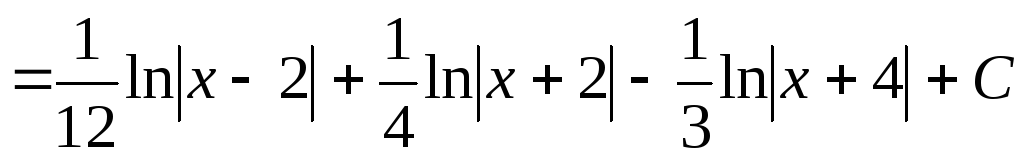 .
.
Случай 2. Знаменатель имеет только действительные корни, причем некоторые из них – кратные.
Пример. Вычислить интеграл
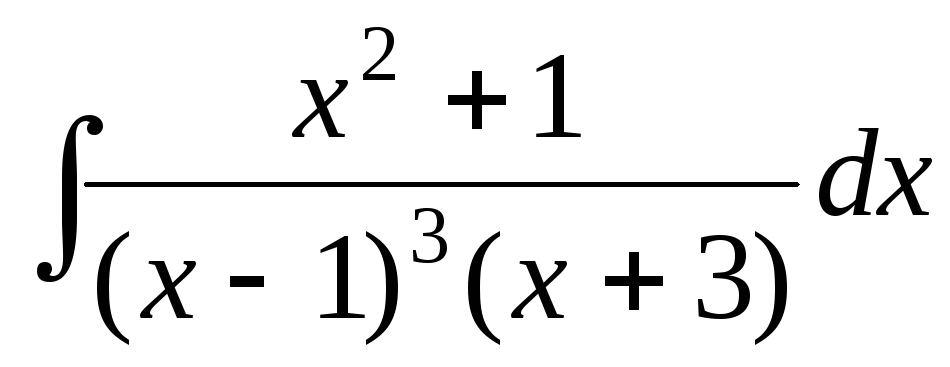 .
.
Решение
Рассмотрим
подынтегральную функцию 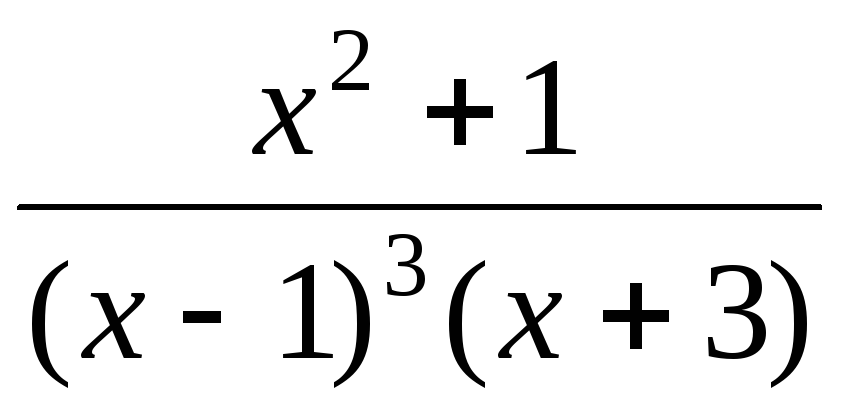 – правильная рациональная дробь.
Представим ее в виде суммы простейших
дробей. Корни знаменателя – действительные
числа, среди них есть кратные (выражению
– правильная рациональная дробь.
Представим ее в виде суммы простейших
дробей. Корни знаменателя – действительные
числа, среди них есть кратные (выражению 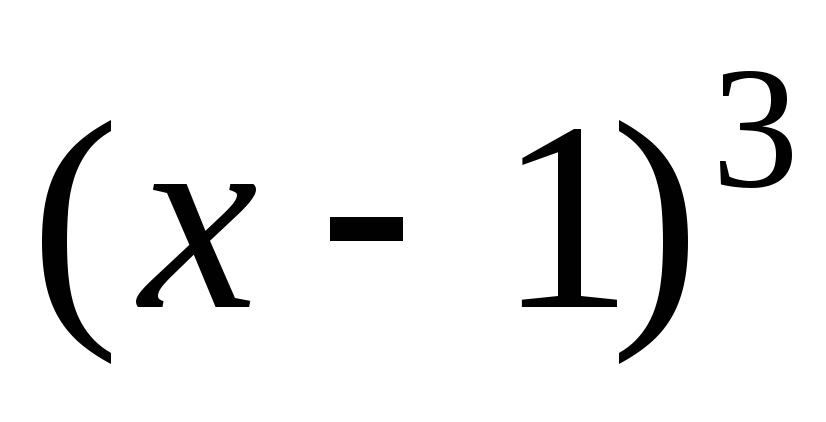 соответствует сумма трех простейших
дробей).
соответствует сумма трех простейших
дробей).
Таким образом,
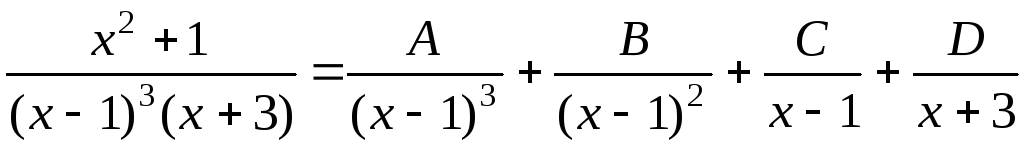 .
.
Приведем к общему знаменателю и рассмотрим числители дробей:
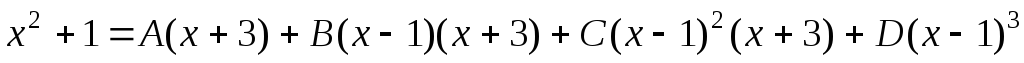 .
.
Сравним коэффициенты при одинаковых степенях x:
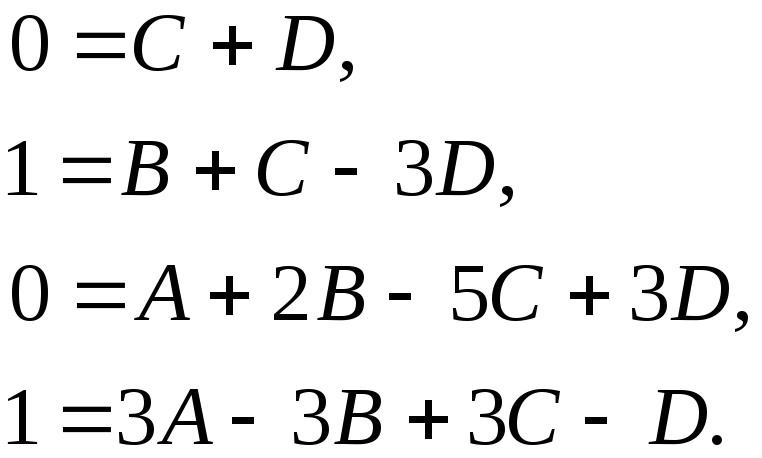
Решая полученную систему уравнений, находим неизвестные коэффициенты
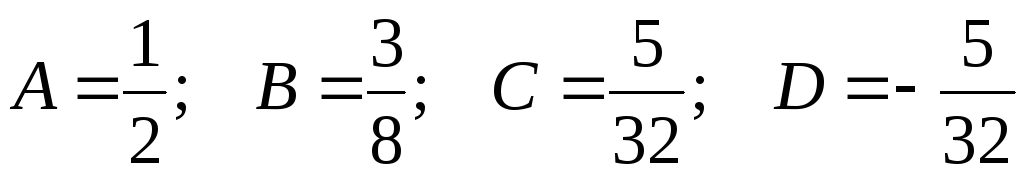 .
.
Итак,
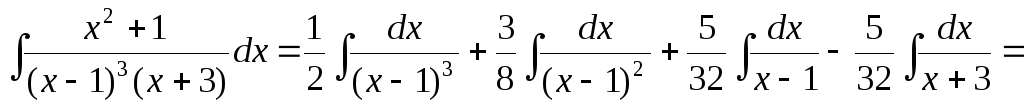
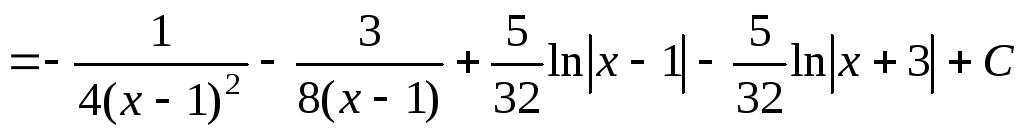 .
.
Случай 3. Среди корней имеются простые комплексные корни.
Пример 1. Вычислить интеграл
 .
.
Решение
Рассмотрим
подынтегральную функцию 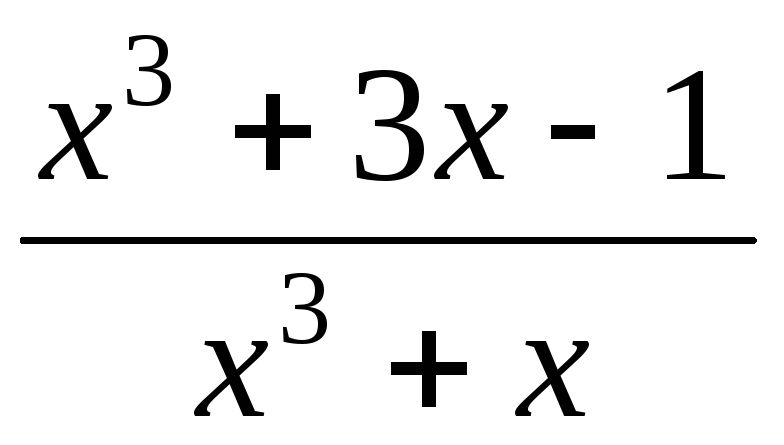 – неправильная рациональная дробь.
Выделим целую часть
– неправильная рациональная дробь.
Выделим целую часть
 .
.
Представим дробь в виде суммы простейших дробей, разложив знаменатель на множители
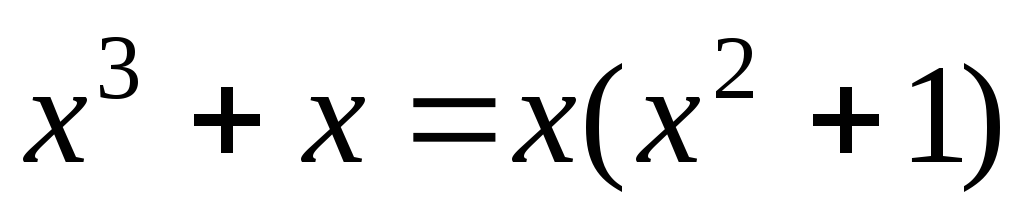 .
.
Тогда
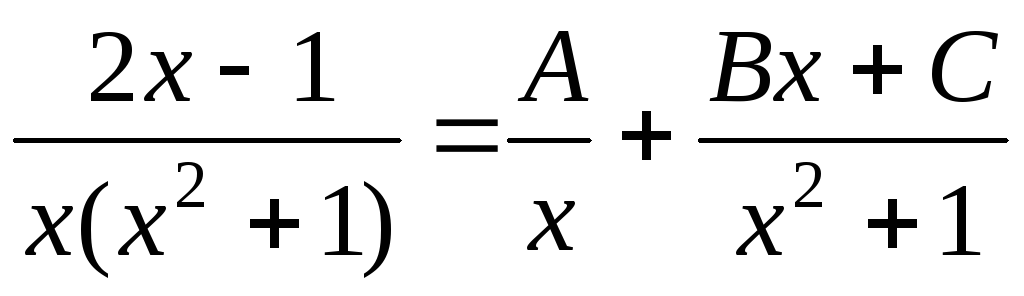 .
.
Приведем к общему знаменателю и рассмотрим числители дробей
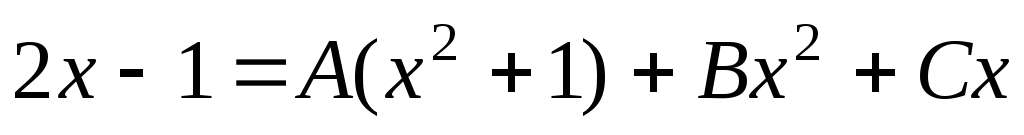 .
.
Сравним коэффициенты при одинаковых степенях x:
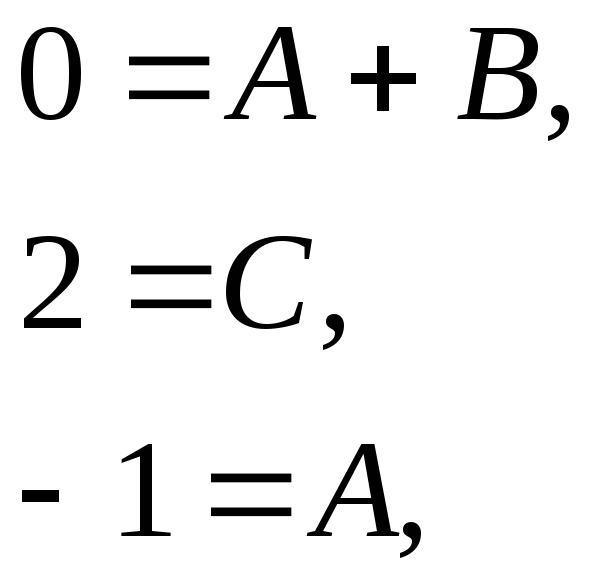
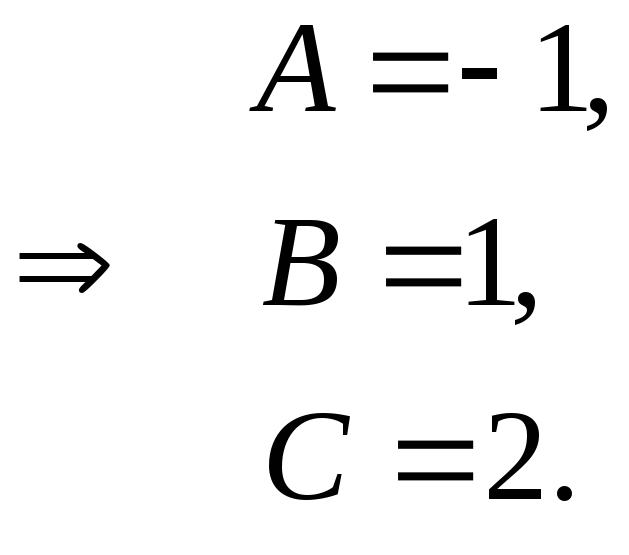
Итак,
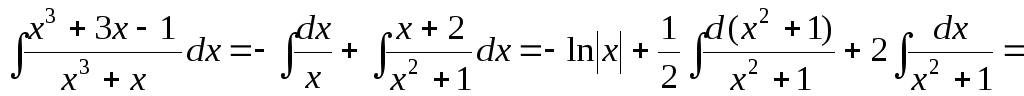
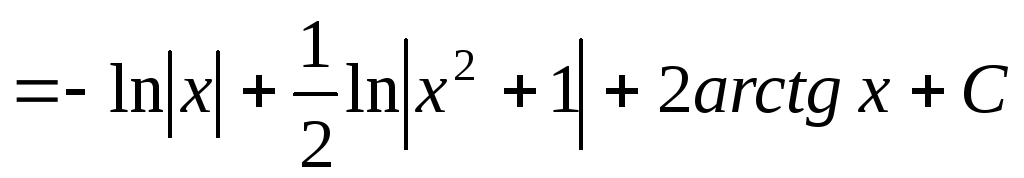 .
.
Пример 2. Найти интеграл
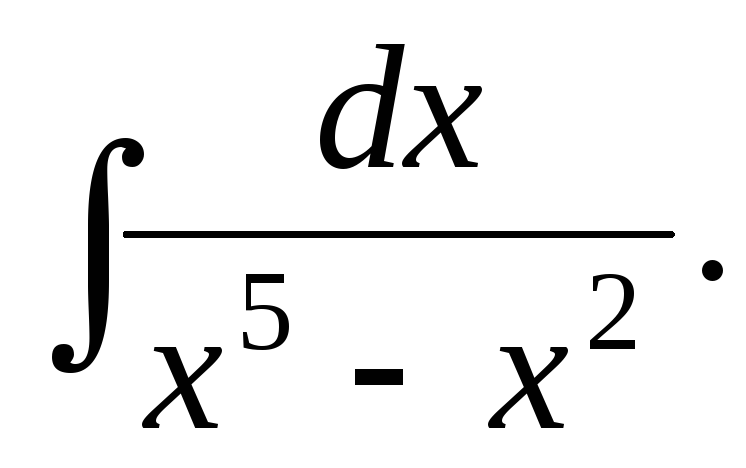
Решение
Рассмотрим
подынтегральную функцию 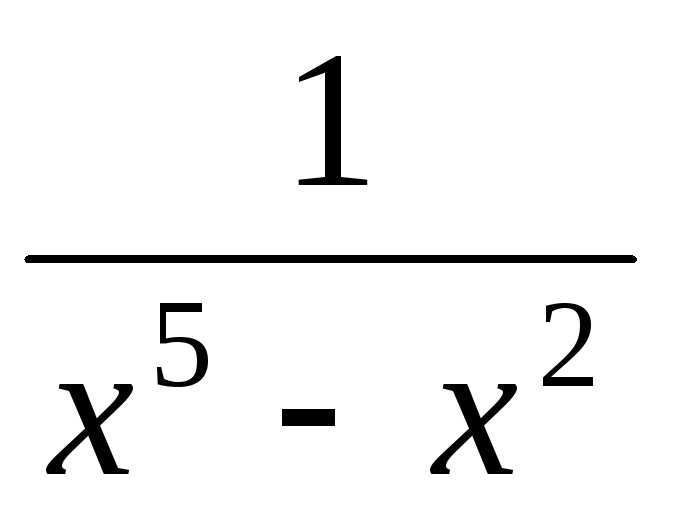 – правильная рациональная дробь.
Представим в виде суммы простейших
дробей. Разложим знаменатель на множители
– правильная рациональная дробь.
Представим в виде суммы простейших
дробей. Разложим знаменатель на множители
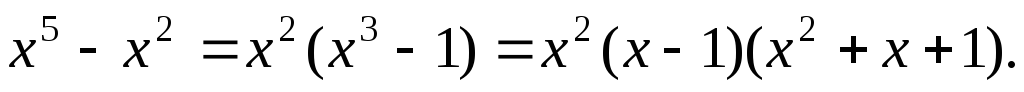
Тогда
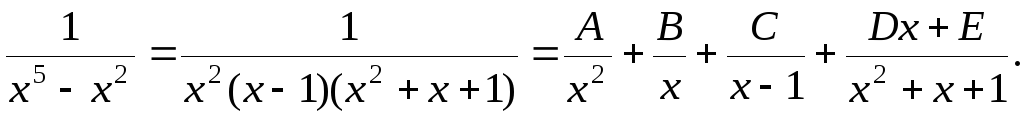
Приведем к общему знаменателю и рассмотрим числители дробей
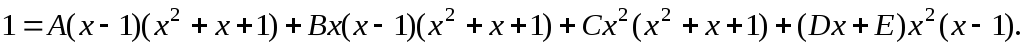
Воспользуемся комбинированным способом определения коэффициентов. Перепишем предыдущее равенство в виде
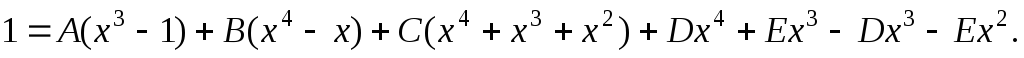
Сравнивая
коэффициенты при соответствующих
степенях и придавая значение  ,
получаем систему:
,
получаем систему:
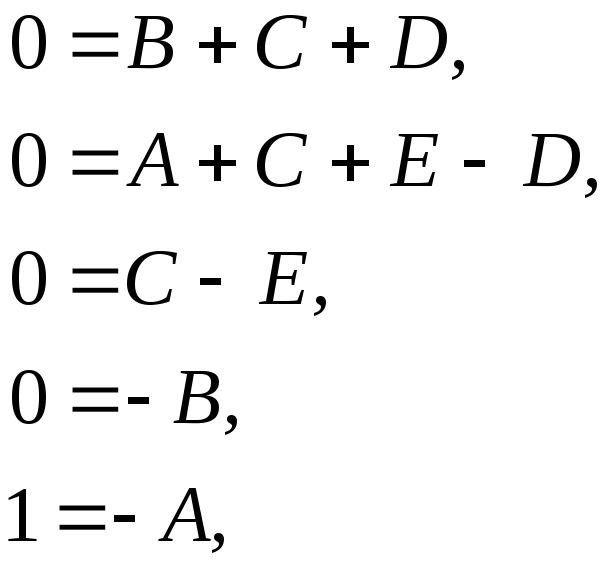 при
при 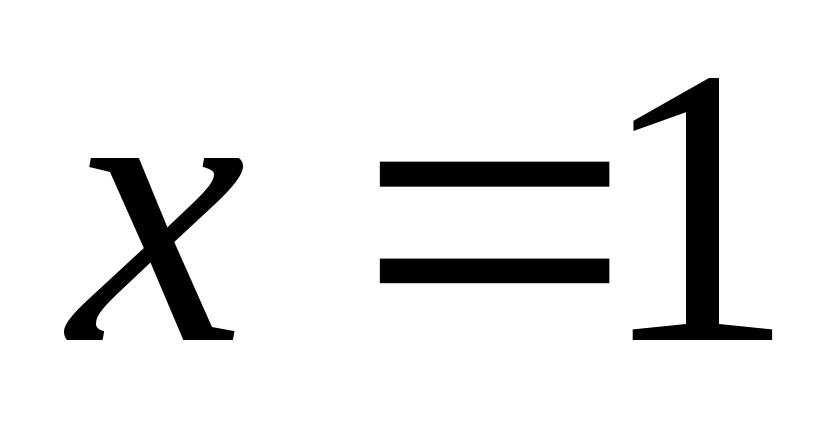 ,
, 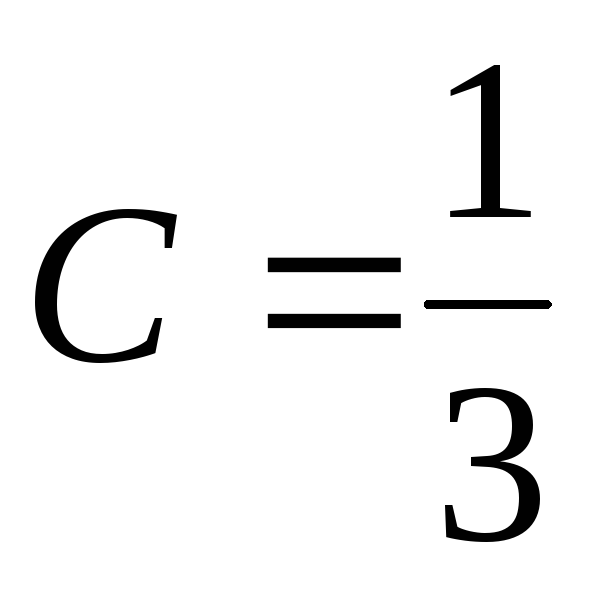 ;
; 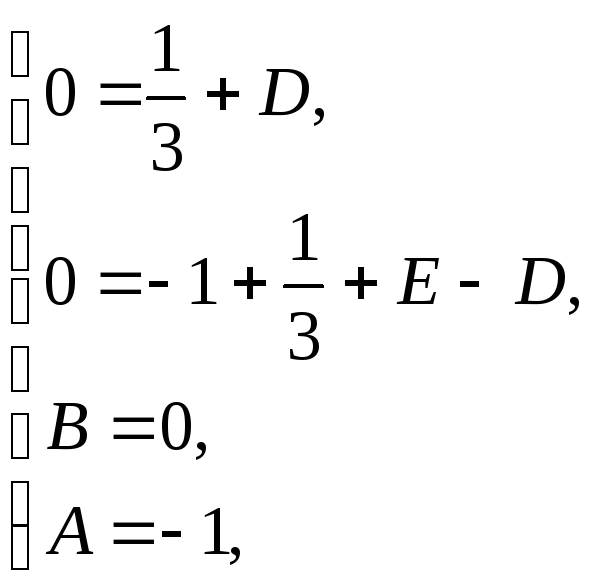
т. е. 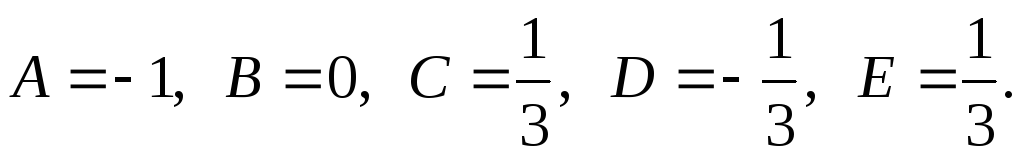
Следовательно,
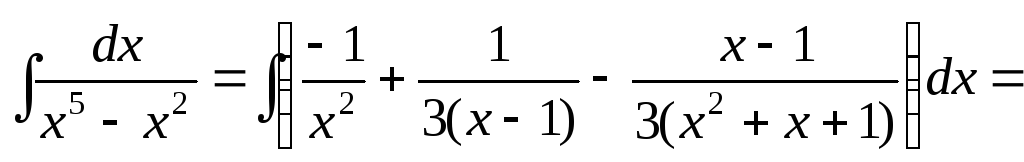
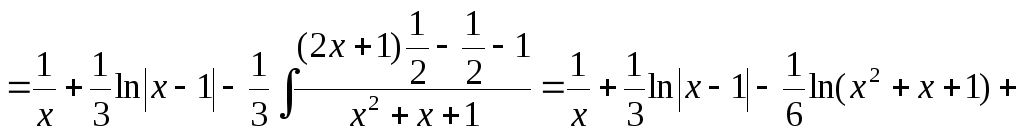
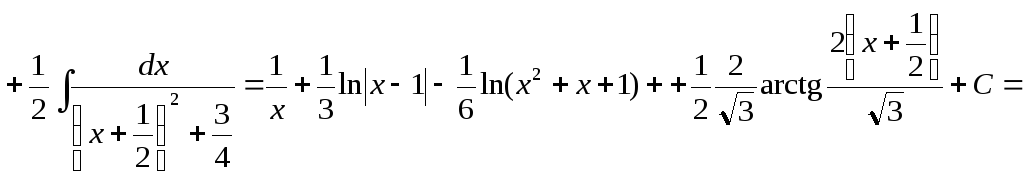
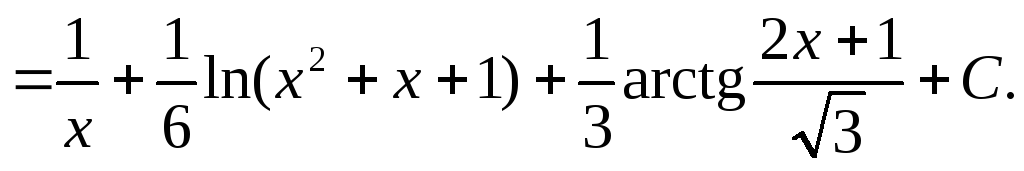
Случай 4. Среди корней знаменателей имеются кратные комплексные корни, т. е. разложение знаменателя содержит повторяющиеся квадратичные множители.
Пример 1. Найти интеграл
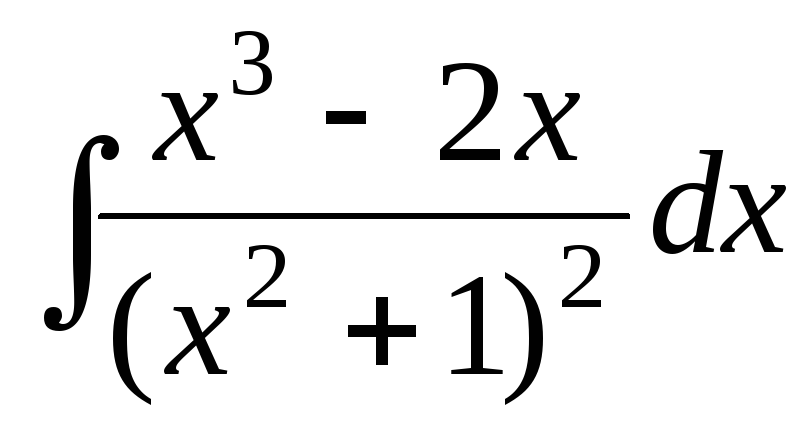 .
.
Решение
Так как есть двукратный множитель, то
 .
.
Приведем к общему знаменателю и рассмотрим числители дробей
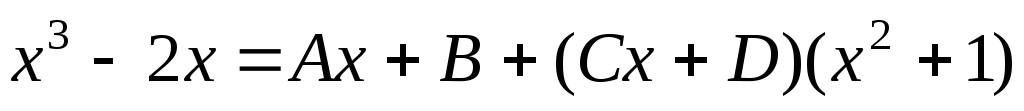 .
.
Приравняем коэффициенты при одинаковых степенях x

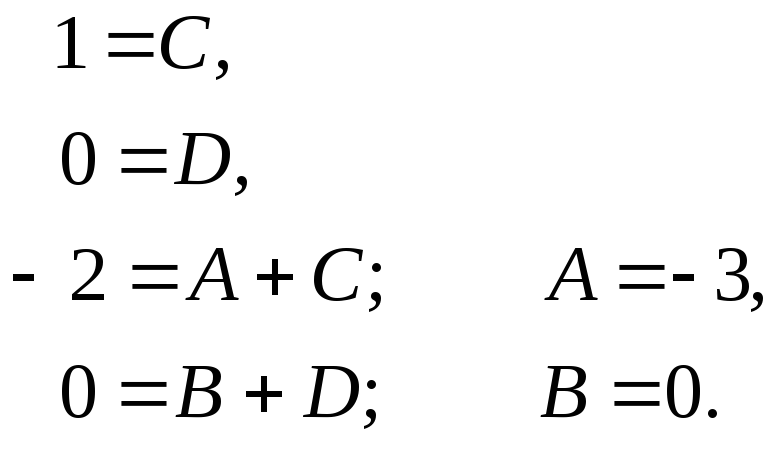
Следовательно,
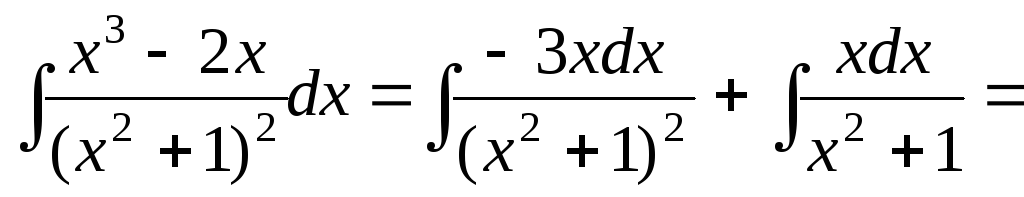
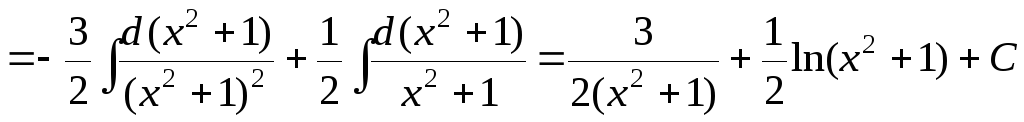 .
.
Заметим,
что данный интеграл можно было найти
проще с помощью подстановки 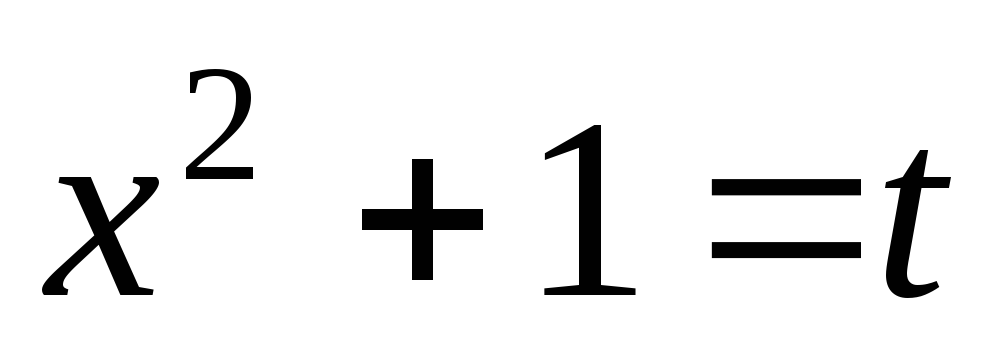 .
.
Пример 2. Вычислить интеграл
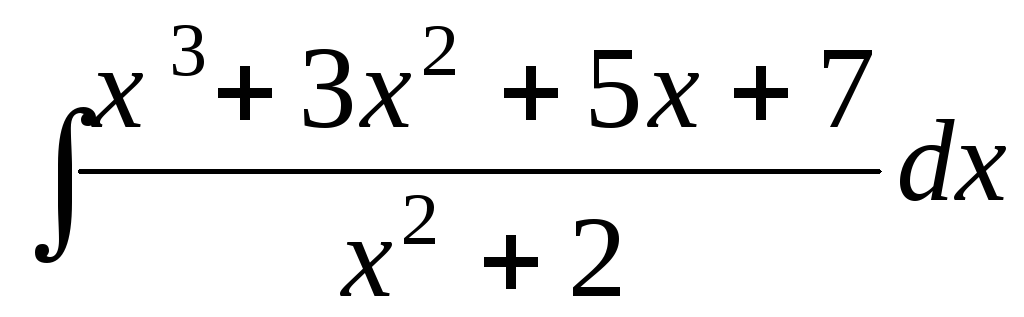 .
.
Решение
Выделим
целую часть данной неправильной
рациональной дроби. Для этого разделим
многочлен 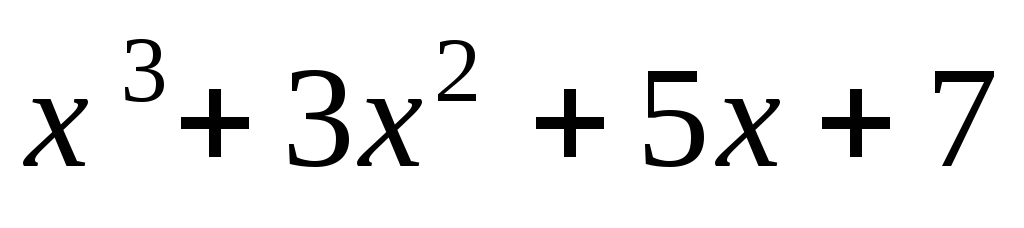 на многочлен
на многочлен  :
:
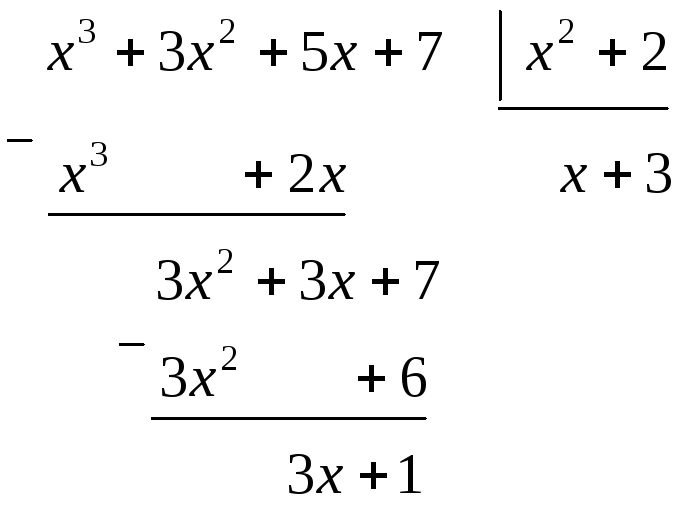
Тогда
подынтегральную функцию можно представить
в виде суммы целой части  и дроби, в числителе которой стоит
остаток от деления
и дроби, в числителе которой стоит
остаток от деления 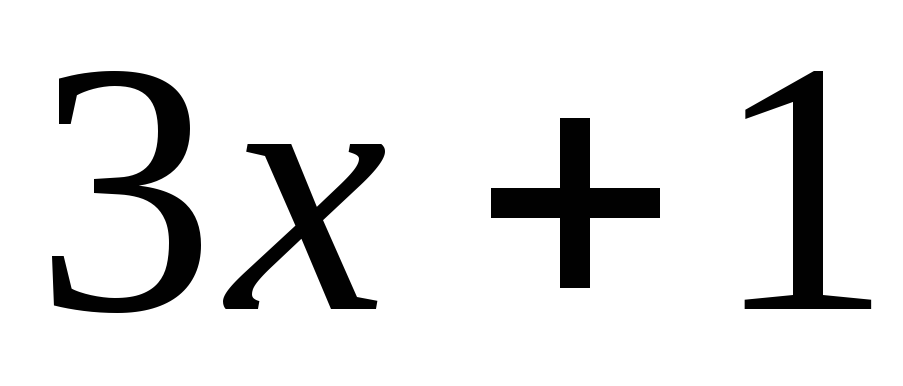 :
:
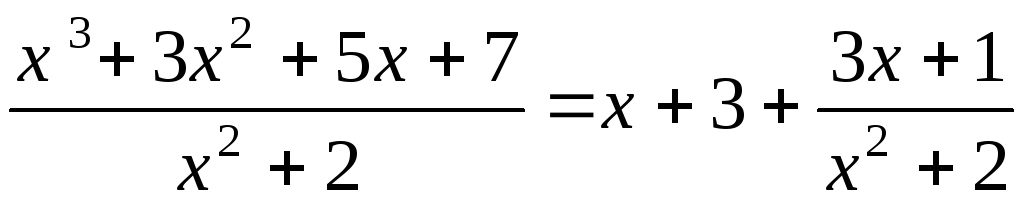 .
.
Тогда
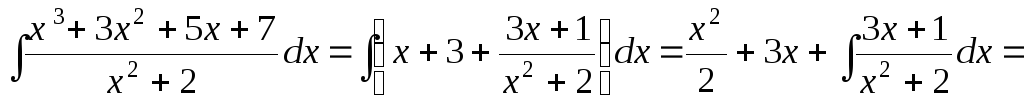
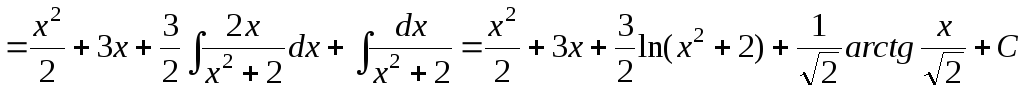 .
.
Что такое разложение многочленов на множители и зачем оно нужно
Нам известно распределительное свойство умножения, которое называется распределительным законом. Выглядит этот закон следующим образом:
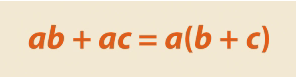
То есть существует сумма, которая преобразуется в произведение – это называется разложение на множители.
Распределительный закон справедлив и для вычитания, и для нескольких чисел:

Задача 1
Вычислите значение выражения 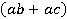 при
при 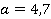 ;
; 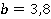 ;
; 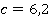 .
.
Решение
Для вычисления значения данного выражения можно подставить известные нам числа и умножить 4,7 на 3,8, затем умножить 4,7 на 6,2, далее полученные в результате умножения числа сложить:
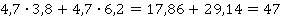
Однако для упрощения вычисления значения данного выражения применим распределительный закон:
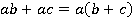
Таким образом, необходимо выполнить всего два действия – сложение и умножение:
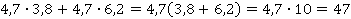
Ответ: 47.
С помощью разложения на множители можно доказывать, что некоторое буквенное выражение делится на число.
Задача 2
Докажите, что 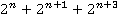 делится на 11.
делится на 11.
Доказательство
Для доказательства необходимо разложить данное выражение на множители, при этом один из множителей в полученном выражении должен быть равен 11.
По свойству степеней:
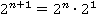

Таким образом, данное в условие выражение можно представить в виде:
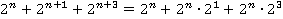
Вынесем общий множитель 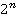 за скобку:
за скобку:
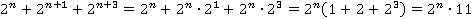
Данное выражение делится на 11, так как один из его сомножителей равен 11. Что и требовалось доказать.
Алгебраические дроби – дроби, у которых числитель и знаменатель могут быть алгебраическими выражениями (содержать в себе переменные).
Для сокращения таких дробей необходимо разложить числитель и знаменатель на множители, сократив после этого общий множитель.
Задача 3
Сократите дробь: 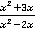 .
.
Решение
Для выражений в числителе есть общий множитель 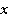 , который можно вынести за скобку. Также можно вынести за скобку
, который можно вынести за скобку. Также можно вынести за скобку 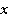 и в знаменателе:
и в знаменателе:
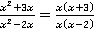
Следовательно, можно сократить данную дробь на 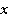 :
:
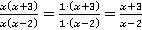
Ответ: 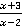 .
.
С помощью разложения на множители можно решать весьма непростые уравнения, например уравнения в целых или натуральных числах.
Задача 4
Найти все пары целых 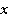 и
и 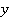 , таких, что
, таких, что 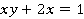 , где
, где 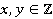 .
.
Решение
Вынесем общий множитель в левой части уравнения за скобку:
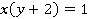
Следовательно, в левой части данного уравнения находится произведение целых чисел, а в правой части единица.
Какие целые числа в произведении могут давать 1? Либо 1 на 1, либо -1 на -1. Получаем два случая:
а) 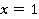

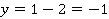
б) 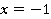
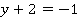
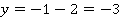
Ответ: 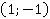 ,
, 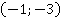 .
.
Пример
Решите уравнение: 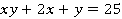 , где
, где 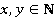 (
(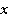 и
и 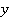 – натуральные числа).
– натуральные числа).
Решение
Вынесем 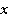 из первых двух слагаемых выражения в левой части уравнения:
из первых двух слагаемых выражения в левой части уравнения:
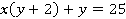
Прибавим к обеим частям данного выражения число 2:
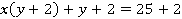

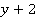 возьмем в скобки и умножим на 1:
возьмем в скобки и умножим на 1:
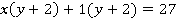
Видно, что 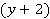 является общим множителем для левой части уравнения. Вынесем этот общий множитель за скобку.
является общим множителем для левой части уравнения. Вынесем этот общий множитель за скобку.
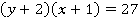
Какие натуральные числа в произведении дают 27? 1 и 27 либо 9 и 3. Первый вариант не подходит, так как 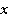 и
и 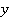 натуральные и каждая скобка будет больше 1. Следовательно, если выражение
натуральные и каждая скобка будет больше 1. Следовательно, если выражение 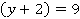 , то
, то 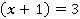 , или наоборот, если
, или наоборот, если 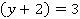 , то
, то 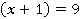 .
.
Разберем два возможных случая:
а) 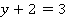 ,
, 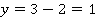
 ,
, 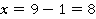
б) 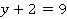 ,
, 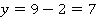
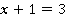 ,
, 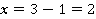
Ответ: 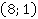 ,
, 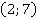 .
.
На этом уроке мы познакомились с понятием разложения на множители алгебраических выражений. С помощью различных примеров мы узнали, где разложение на множители может быть применено.
Список литературы
1. Мордкович А.Г. Алгебра 7 кл. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
2. Мордкович А.Г., Н.П. Николаев. Алгебра 7 кл. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
3. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. – М.: Просвещение. 2010.
4. Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др. Алгебра 7. – М.: Просвещение. 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Видеохостинг «YouTube» (Источник)
2. Интернет портал «МетаШкола» (Источник)
3. Интернет портал «Intemodino Group» (Источник)
Домашнее задание
1. Задания 540, 547, 586, 671 (стр. 67-78) – Мордкович А.Г. Задачник для учащихся общеобразовательных учреждений (см. список рекомендованной литературы)
2. Разложить многочлен на множители 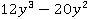 .
.
3. Решите уравнение

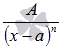
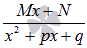
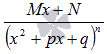
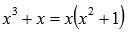
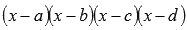 ,
количество линейных множителей роли
не играет, (будь их 2 или 22),
то дробь представится в виде суммы
простейших дробей первого типа:
,
количество линейных множителей роли
не играет, (будь их 2 или 22),
то дробь представится в виде суммы
простейших дробей первого типа:  a, b, c и d — числа, A, B, C и D — неопределенные коэффициенты.
a, b, c и d — числа, A, B, C и D — неопределенные коэффициенты.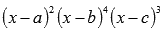 количество
множителей роли не играет и не играют
роли степени этих множителей (хоть
221ая степень), то дробь представится в
виде суммы простейших дробей первого
и второго типов:
количество
множителей роли не играет и не играют
роли степени этих множителей (хоть
221ая степень), то дробь представится в
виде суммы простейших дробей первого
и второго типов: 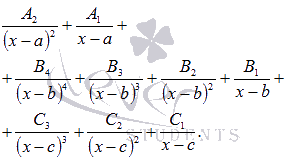
 —
неопределенные коэффициенты. Возьмите
на заметку: какая степень – столько и
слагаемых.
—
неопределенные коэффициенты. Возьмите
на заметку: какая степень – столько и
слагаемых.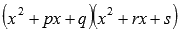 количество
квадратичных выражений роли не играет,
то дробь представится в виде суммы
простейших дробей третьего типа:
количество
квадратичных выражений роли не играет,
то дробь представится в виде суммы
простейших дробей третьего типа: 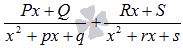 p, q, r и s — числа, P, Q, R и S — неопределенные коэффициенты.
p, q, r и s — числа, P, Q, R и S — неопределенные коэффициенты.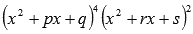
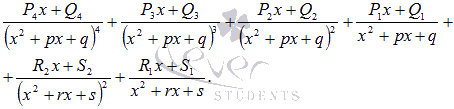 p, q, r и s — числа,
p, q, r и s — числа, 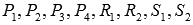 —
неопределенные коэффициенты. ОБЫЧНО
ВСТРЕЧАЕТСЯ КОМБИНАЦИЯ ЭТИХ ВАРИАНТОВ
(как правило, довольно простая).
—
неопределенные коэффициенты. ОБЫЧНО
ВСТРЕЧАЕТСЯ КОМБИНАЦИЯ ЭТИХ ВАРИАНТОВ
(как правило, довольно простая).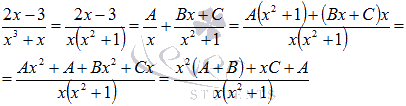 То
есть, пришли к равенству:
То
есть, пришли к равенству: 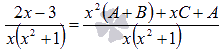 При x отличных от нуля это равенство сводится
к равенству двух многочленов
При x отличных от нуля это равенство сводится
к равенству двух многочленов 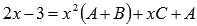 А
два многочлена являются равными тогда
и только тогда, когда коэффициенты при
одинаковых степенях совпадают.
А
два многочлена являются равными тогда
и только тогда, когда коэффициенты при
одинаковых степенях совпадают.