Дробно-рациональная функция
Пример 1. Построим график функции.
Преобразуем функцию с выделением целой части:
Дробно-линейная функция имеет две асимптоты: горизонтальную и вертикальную.
y=2 горизонтальная асимптота
x=1 вертикальная асимптота, т.к. D(y)=(-∞;0)∪(0;∞)
Точки пересечения графика с осями координат:
при x=0 , точка (0;3)
при y=0 , точка (1,5;0)
Получаем график:
Пример 2. Построить график функции .
Чтобы раскрыть модуль, надо рассмотреть два случая:
1)x>0, тогда модуль раскроется со знаком «+» =
2)x=
Построим график для первого случая.
Отбросим часть графика, где x
Построим график для второго случая и аналогично отбросим часть, где x>0, в итоге получим.
Соединим два графика и получим окончательный.
Пример 3. Построить график функции .
Построим сначала график функции .Для этого удобно выделить целую часть, получим . Строя по таблице значений, получаем график.
Применим операцию модуль (часть графика, расположенная ниже оси OX симметрично отражается относительно оси OX). Получаем окончательный график
tofmal.ru
7. Интегрирование дробно-рациональных функций.
Определение 3. Дробно-рациональной функцией (или рациональной дробью) будем называть частное от деления двух многочленов. Общий вид рациональной дроби таков
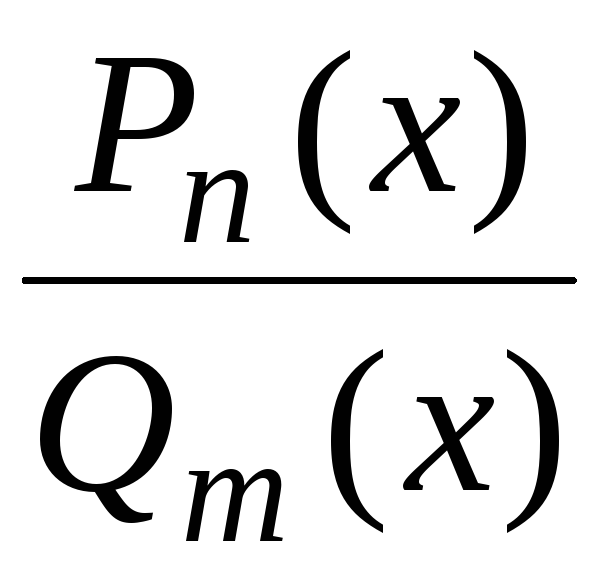 ,
,
где 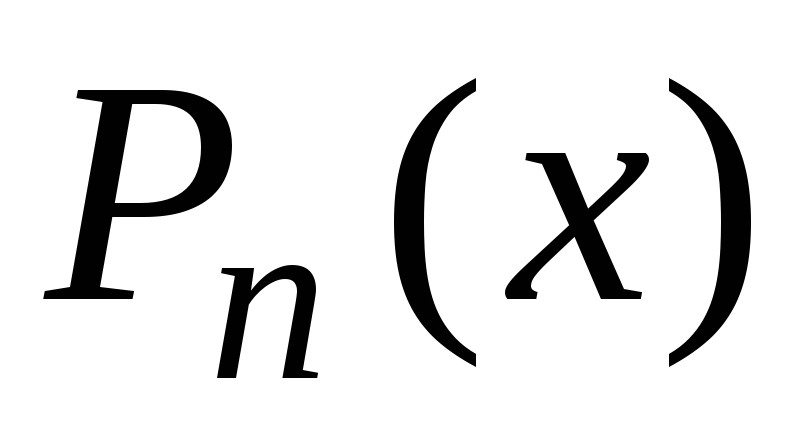 – многочлен степени
– многочлен степени ,
а
,
а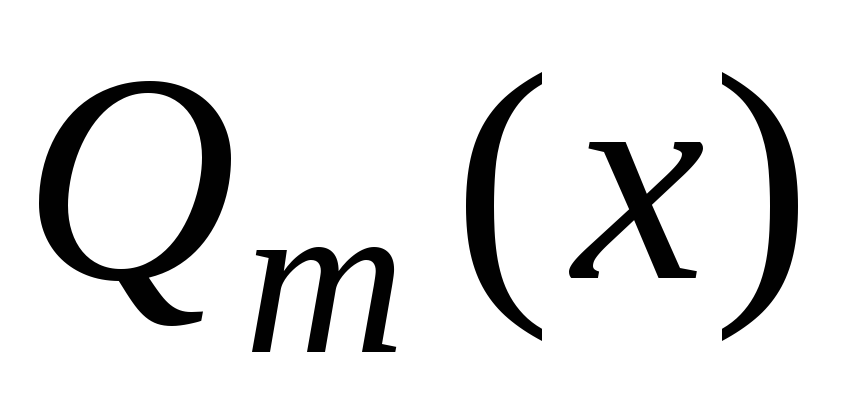 – многочлен степени
– многочлен степени 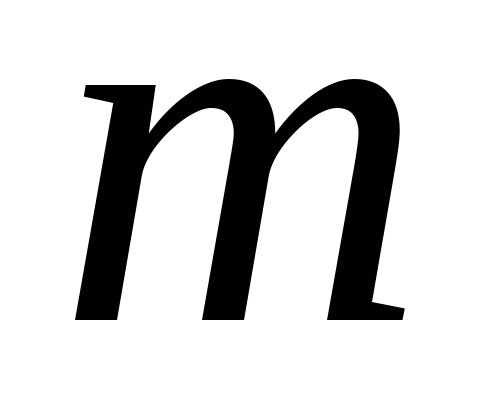 .
.
Если  ,
то рациональная дробь называетсяправильной,
если
,
то рациональная дробь называетсяправильной,
если 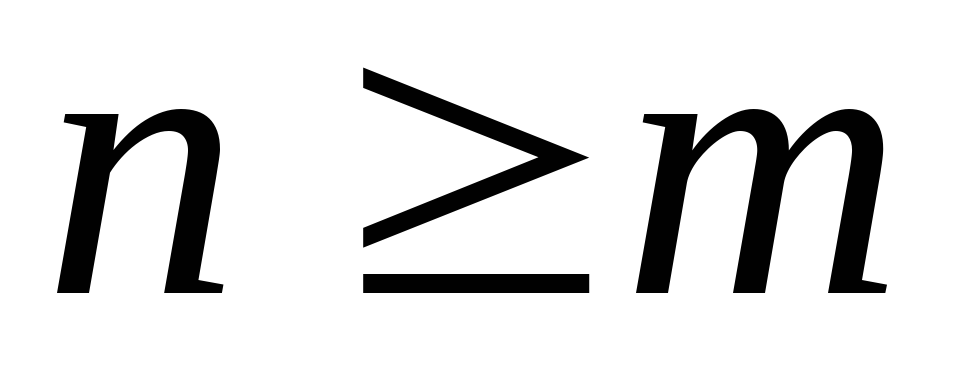 ,
то рациональная дробь называетсянеправильной.
Из общей совокупности правильных дробей
выделяются четыре специальных типа
дробей, называемых простейшими
,
то рациональная дробь называетсянеправильной.
Из общей совокупности правильных дробей
выделяются четыре специальных типа
дробей, называемых простейшими
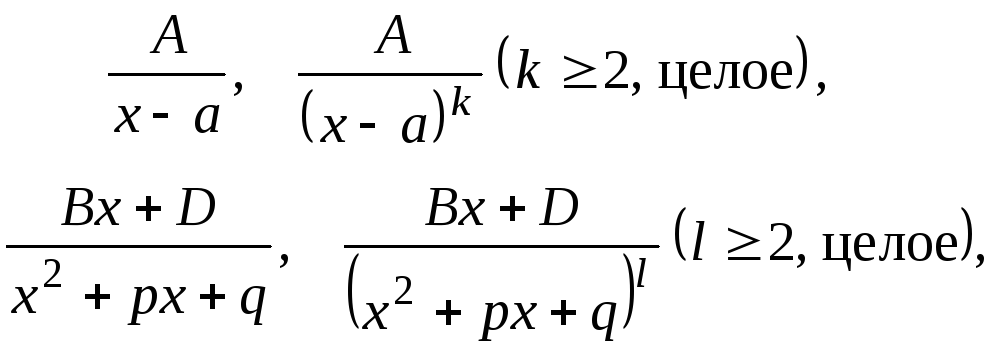
где A, B, D, a, p, q – действительные числа, а трехчлен 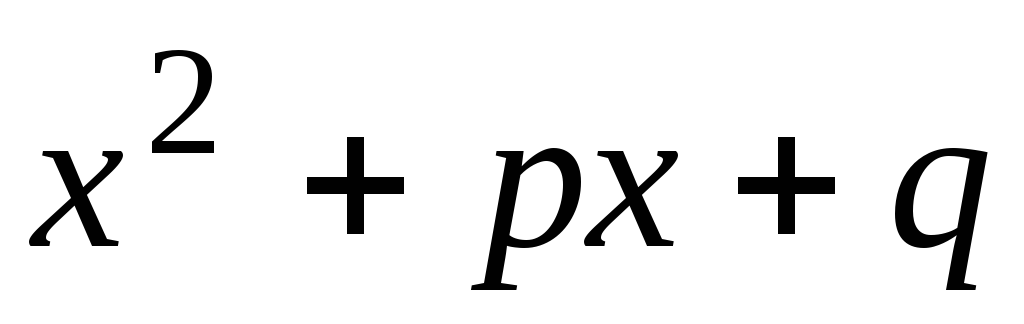 не имеет действительных корней (
не имеет действительных корней (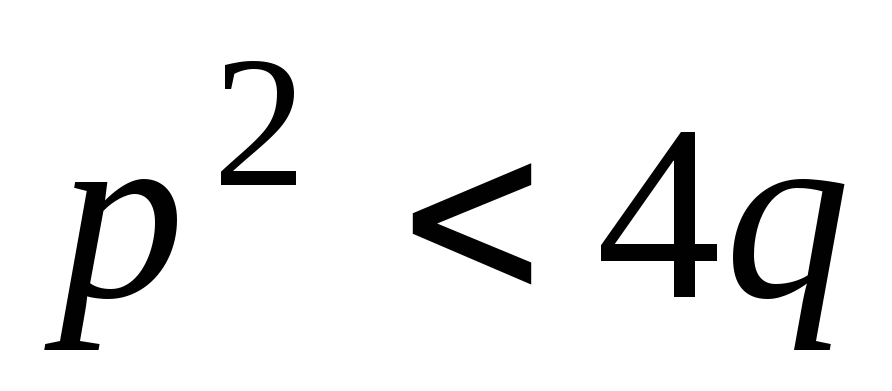 ),
т.е. не раскладывается на множители
первой степени.
),
т.е. не раскладывается на множители
первой степени.
В целом классификацию рациональных дробей можно представить следующим образом.
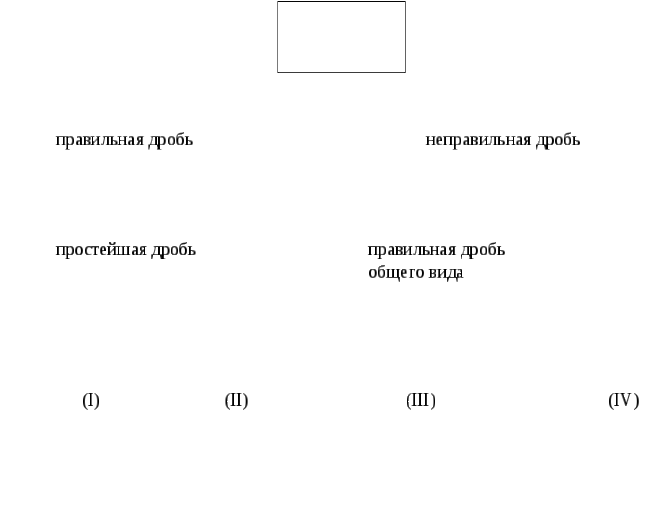
Интегралы от рациональных дробей всегда являются берущимися. Покажем это, двигаясь по приведённой здесь схеме, поднимаясь с нижнего уровня на верхний уровень.
Интегрирование простейших дробей.Интеграл типа (I) берется с использованием формулы (3.3) таблицы 1 и линейной замены.
 .
.
Интеграл типа (II) берется с использованием формулы (3.2) таблицы 1 и линейной замены.
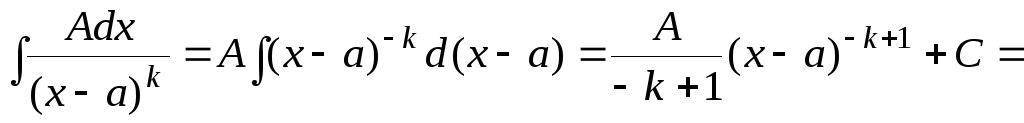
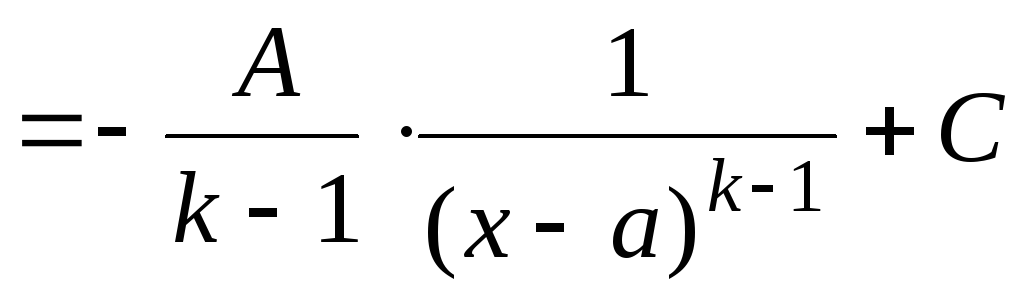 .
( Здесь
.
( Здесь 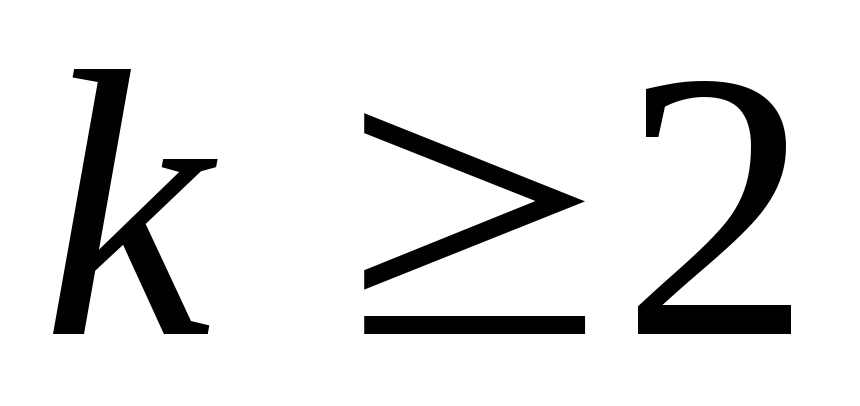 .)
.)
Рассмотрим интеграл типа (III)
 ,
где
,
где
Чтобы вычислить
интеграл 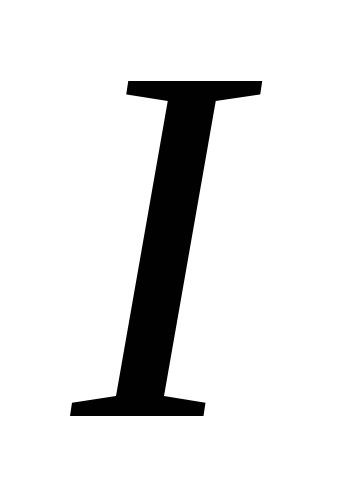 ,
найдём сначала производную знаменателя
подынтегральной функции:
,
найдём сначала производную знаменателя
подынтегральной функции:
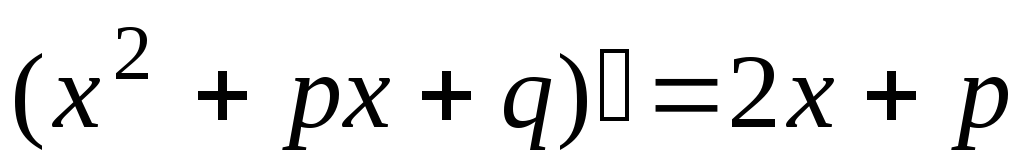 .
.
Далее представим числитель как сумму двух слагаемых:
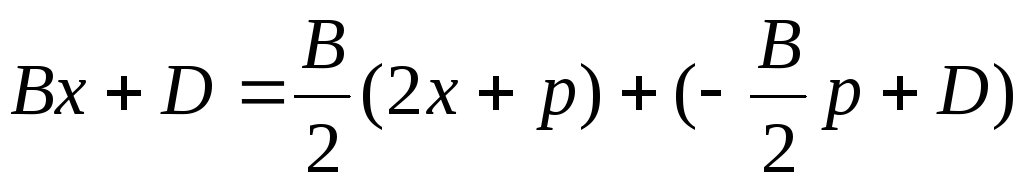 ,
,
т.е. “выделим” в
числителе производную знаменателя.
Теперь 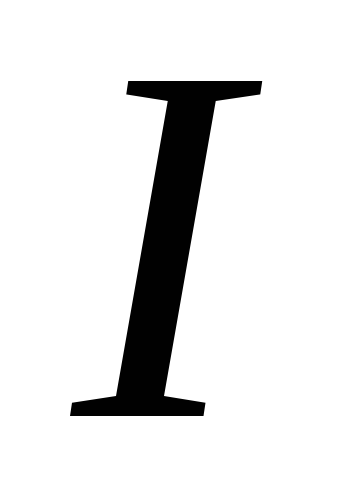 можно представить как сумму двух
слагаемых:
можно представить как сумму двух
слагаемых:
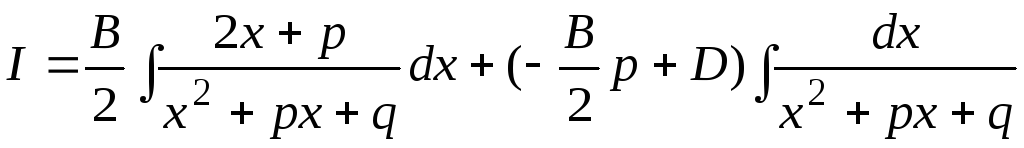 .
(7.1)
.
(7.1)
Вычислим каждый из интегралов, стоящих в правой части (7.1), отдельно:
 ,
,
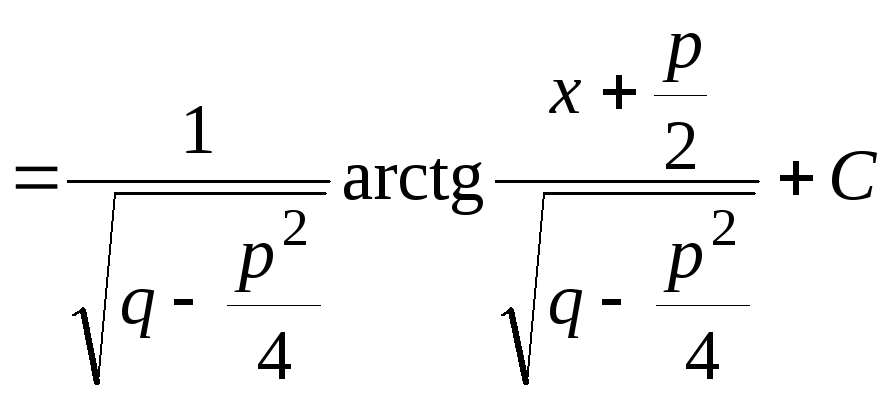 .
.
Таким образом,
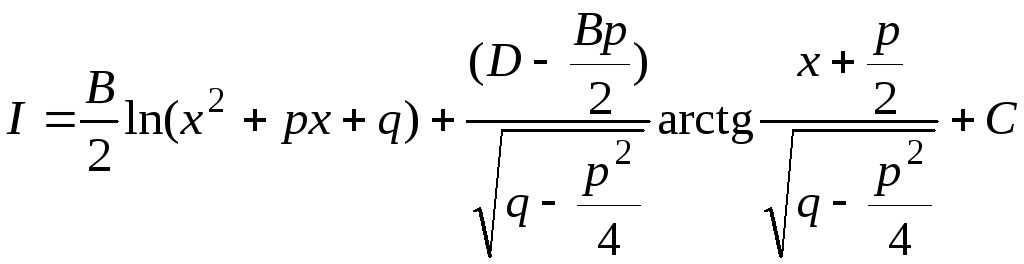 .
(7.2)
.
(7.2)
Заметим, что 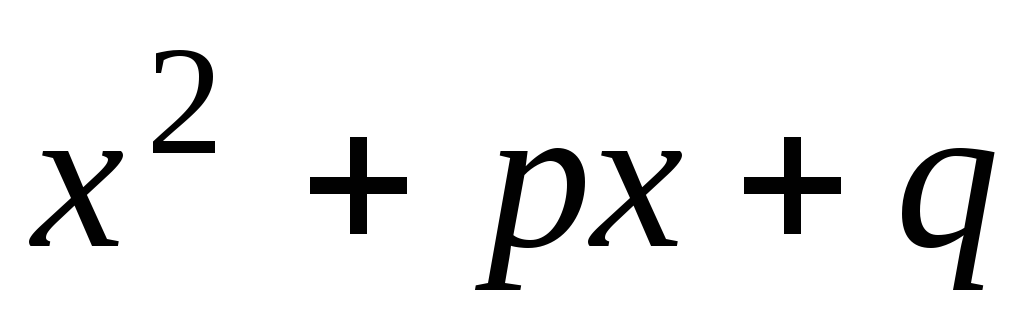 всегда можно представить как сумму
квадратов в силу того, что
всегда можно представить как сумму
квадратов в силу того, что .
.
Формула (7.2) сложна для запоминания. Как правило, ею не пользуются, а непосредственно применяют к конкретному интегралу изложенный здесь метод.
Приведём примеры.
Пример
7.1. 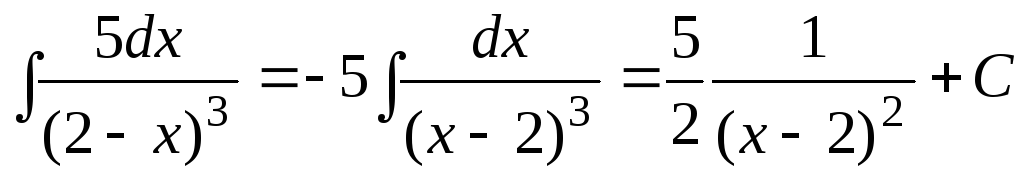 .
.
Пример
7.2. 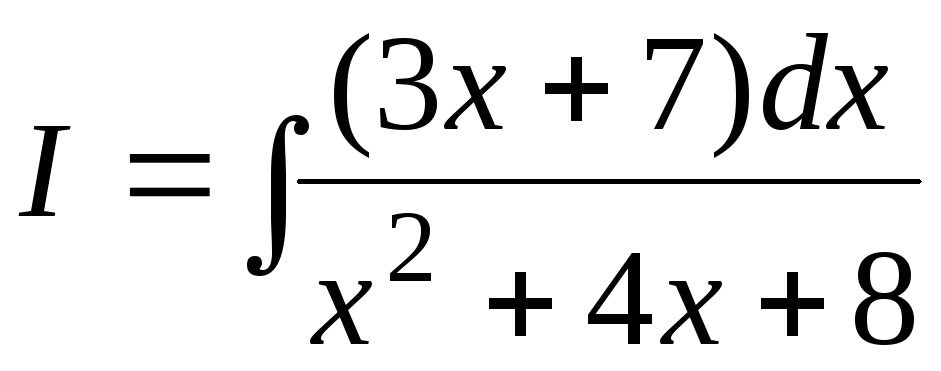 .
Найдем производную знаменателя
.
Найдем производную знаменателя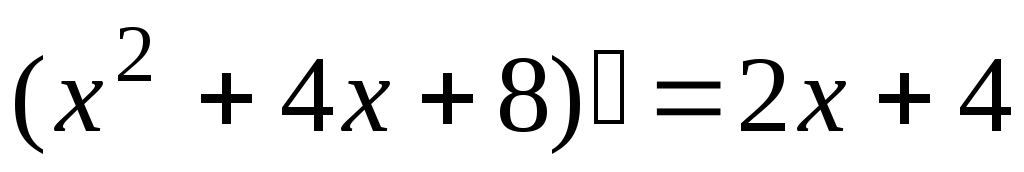 .
Выделим эту производную в числителе
.
Выделим эту производную в числителе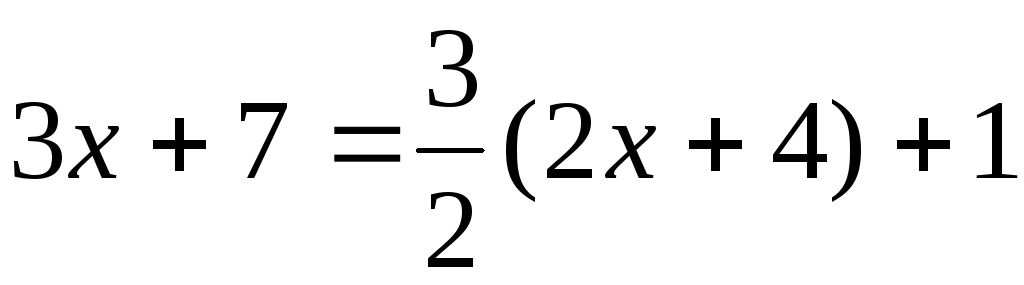 .
Тогда
.
Тогда
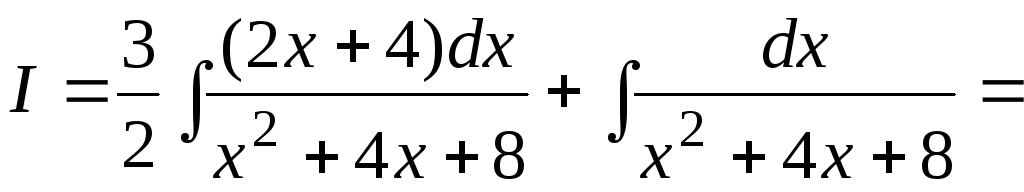
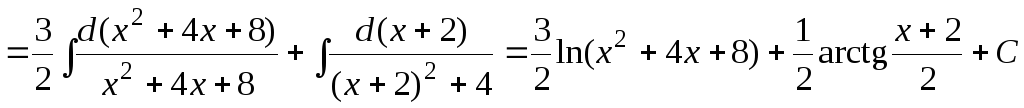 .
.
Пример
7.3. 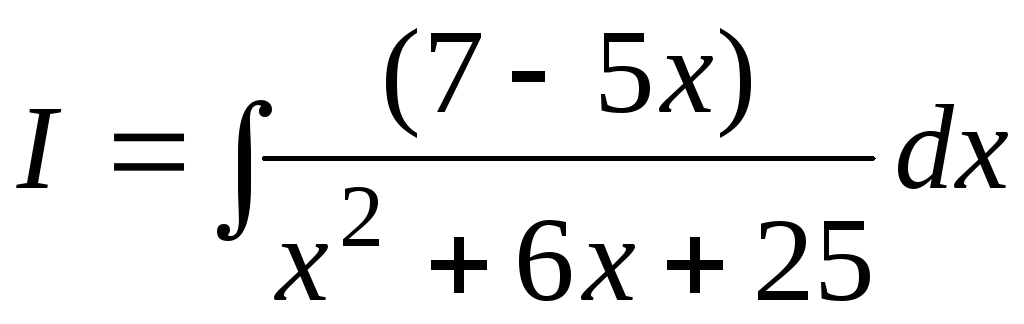 .
Воспользуемся формулами
.
Воспользуемся формулами
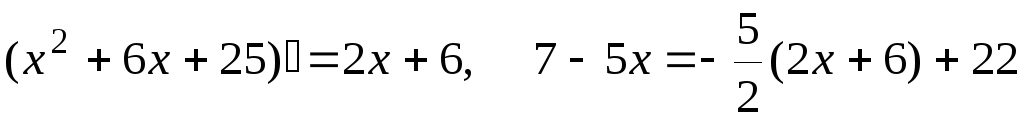 .
Тогда
.
Тогда
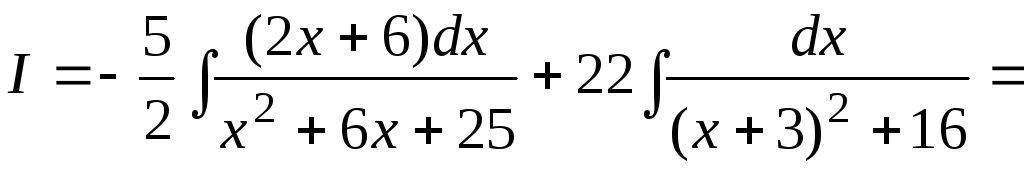

Для интеграла типа (IV)
 ,
где
,
где ,
, ,
непосредственное интегрирование
является столь громоздким, что следует
пользоваться справочником.
,
непосредственное интегрирование
является столь громоздким, что следует
пользоваться справочником.
Интегрирование правильных дробей общего вида.
Рассмотрим
правильную дробь 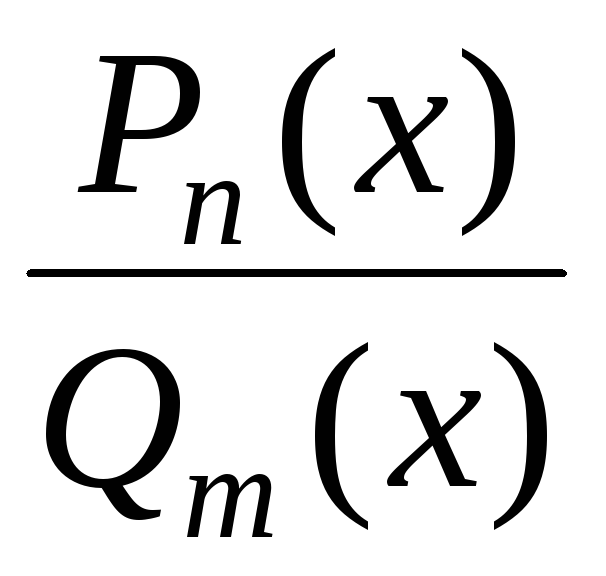
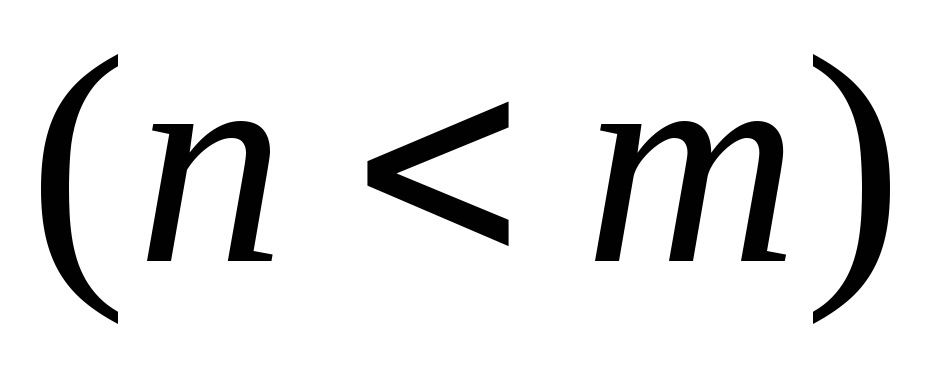 ,
которая не является простейшей дробью.
Чтобы проинтегрировать такую функцию,
её нужно представить в виде суммы
простейших дробей.
,
которая не является простейшей дробью.
Чтобы проинтегрировать такую функцию,
её нужно представить в виде суммы
простейших дробей.Представление правильной дроби в виде суммы простейших дробей осуществляется по следующему правилу.
Знаменатель
 следует разложить на множители вида
следует разложить на множители вида
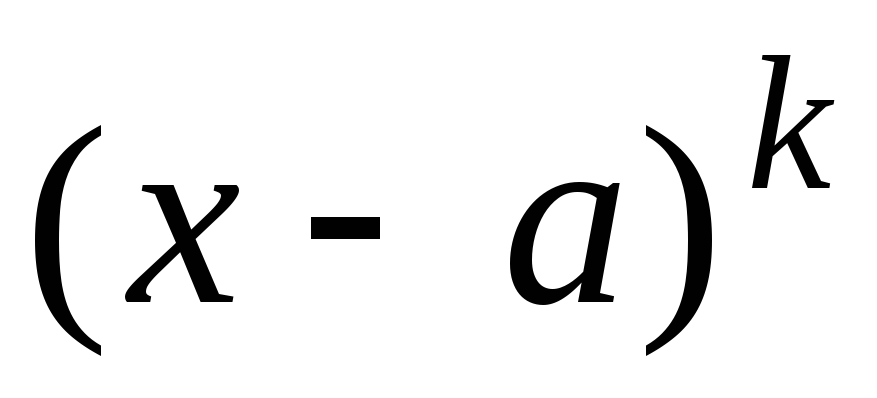 и
и 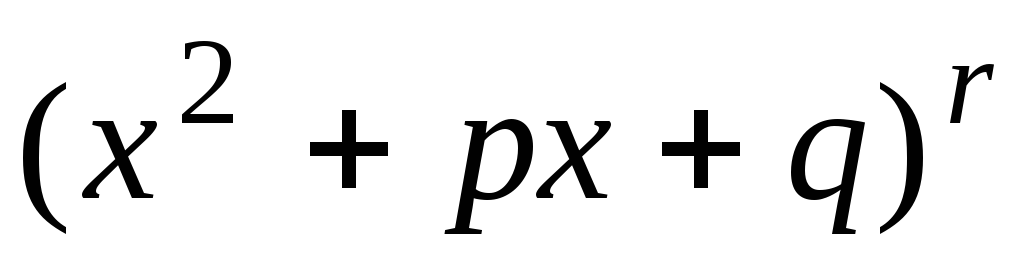 ,
,
где 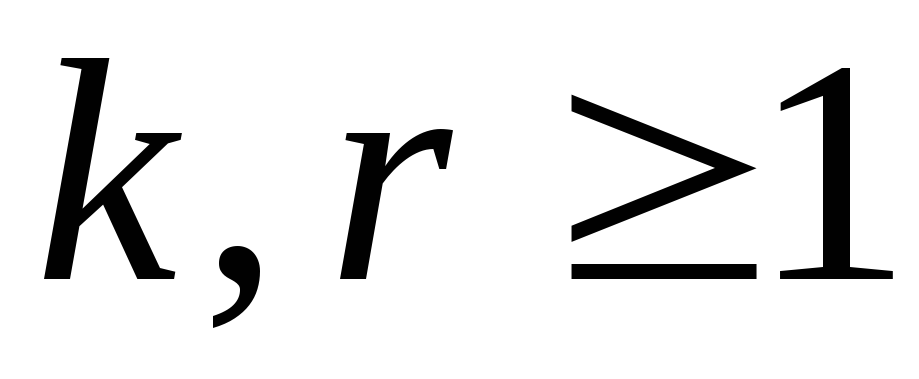 ,
а
,
а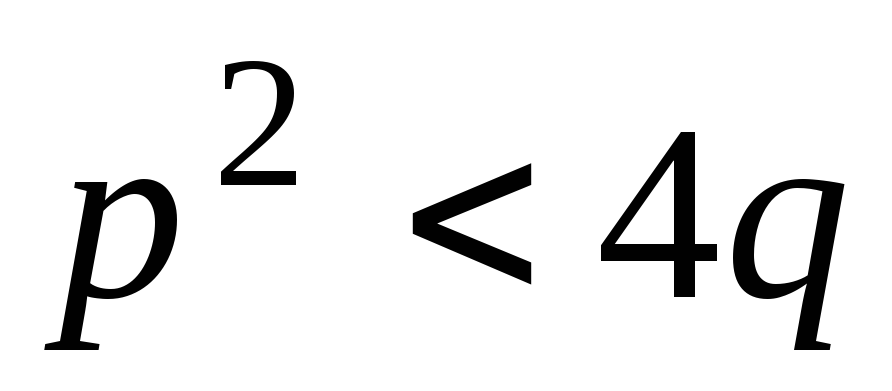 .
Заметим, что
.
Заметим, что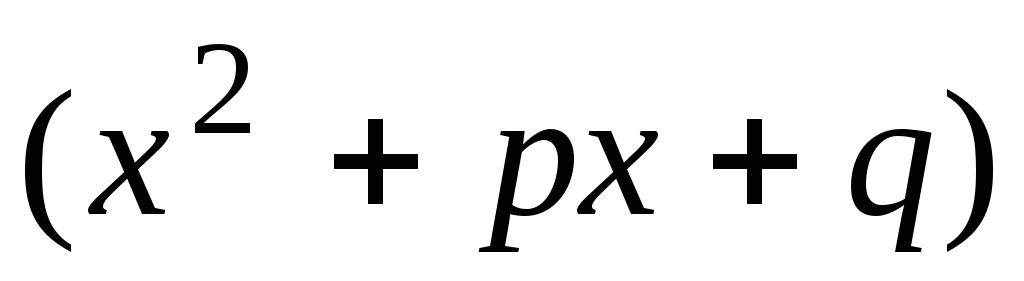
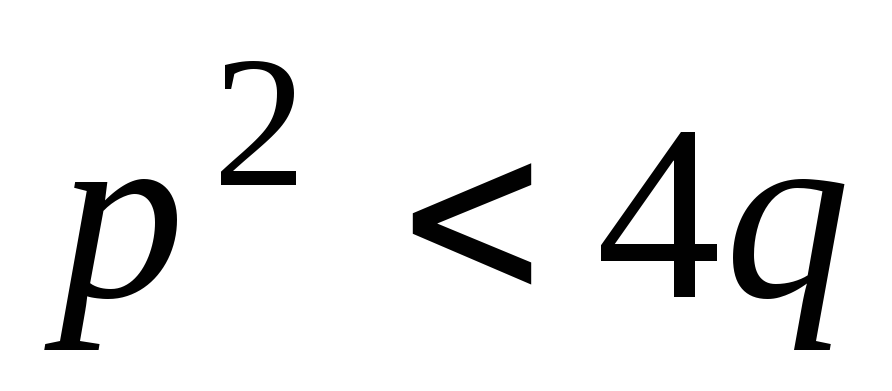 на множители разложить нельзя.
на множители разложить нельзя.Следует построить “общий вид” представления с неопределёнными пока коэффициентами. При этом каждому множителю
 должна соответствовать сумма дробей
должна соответствовать сумма дробей
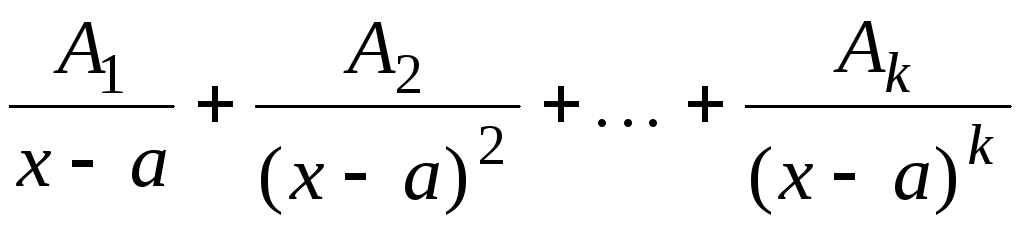 ,
(7.3)
,
(7.3)
а каждому множителю 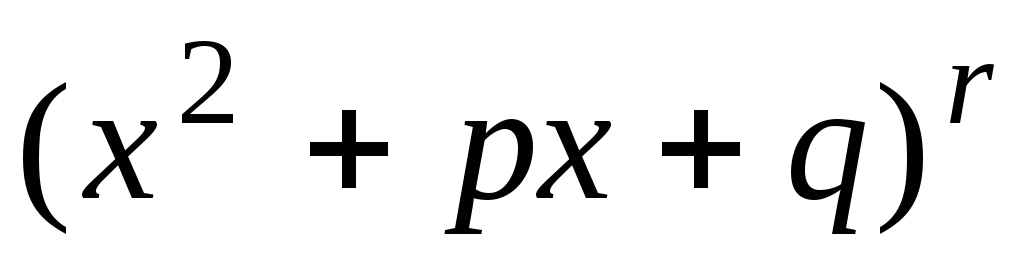 должна соответствовать сумма дробей
должна соответствовать сумма дробей
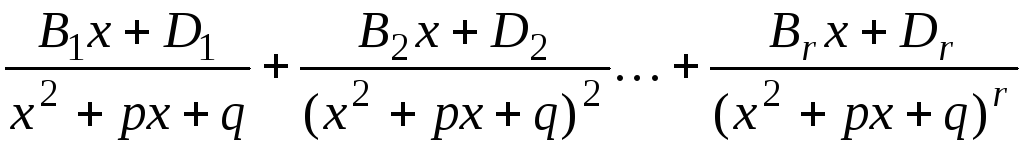 ,
(7.4)
,
(7.4)
где коэффициенты 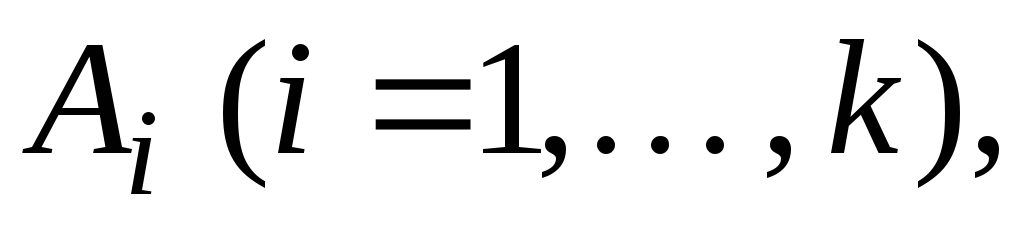
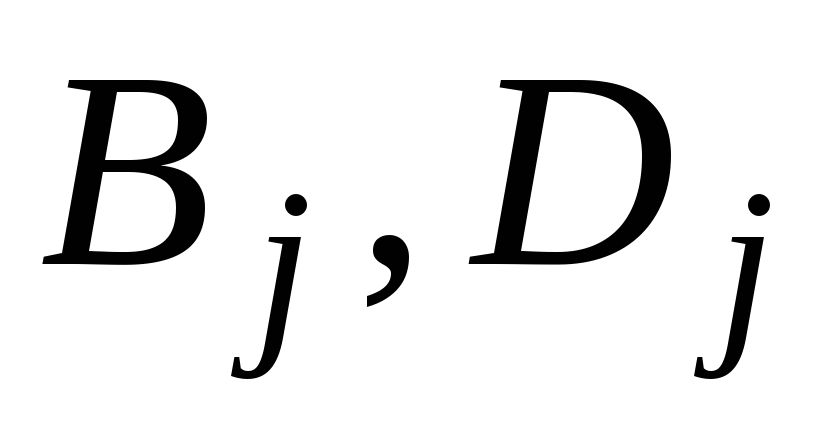
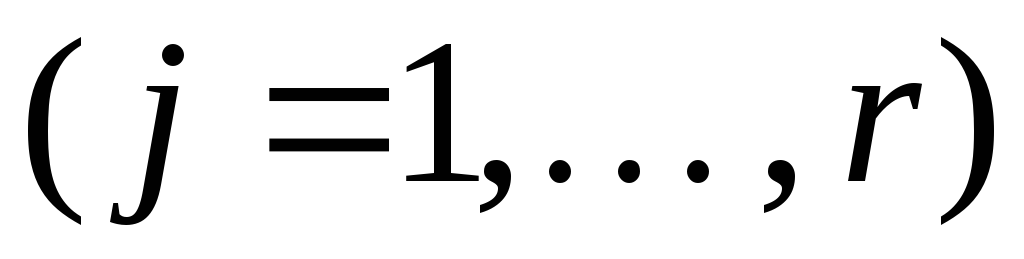 пока неизвестны и представлены буквами.
В суммах (7.3) и (7.4) должны обязательно
присутствовать все перечисленные выше
слагаемые (
пока неизвестны и представлены буквами.
В суммах (7.3) и (7.4) должны обязательно
присутствовать все перечисленные выше
слагаемые ( слагаемых в сумме (7.3) и
слагаемых в (7.4)) . Общий вид представления
содержит в себе все суммы (7.3) и (7.4).
слагаемых в сумме (7.3) и
слагаемых в (7.4)) . Общий вид представления
содержит в себе все суммы (7.3) и (7.4).Следует определить коэффициенты представления, полученного в пункте 2, исходя из тождественного равенства правильной дроби и суммы простейших дробей, полученной в пункте 2.
Покажем на конкретных примерах, как пользоваться данным правилом.
Пример
7.4. 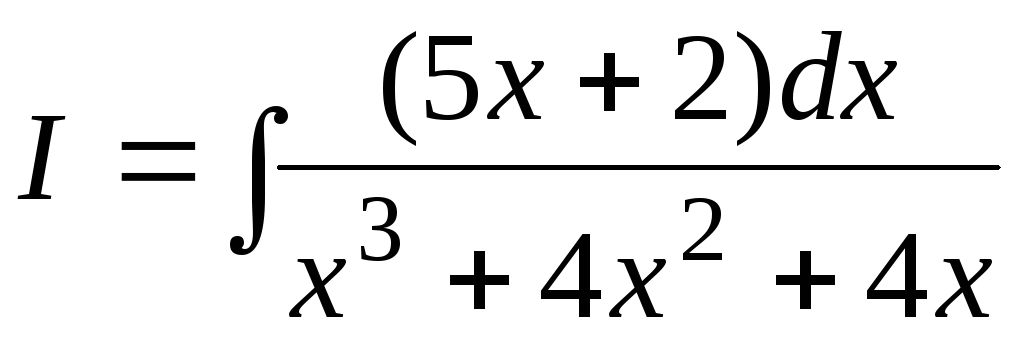 .
.
Применим сформулированное выше правило.
1) Разложим знаменатель дроби, стоящей под знаком интеграла, на множители:
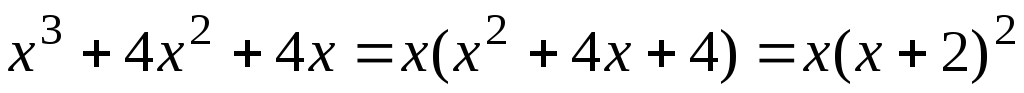 .
.
2) Построим для дроби, стоящей под знаком интеграла, представление в виде суммы простейших дробей с неизвестными пока коэффициентами
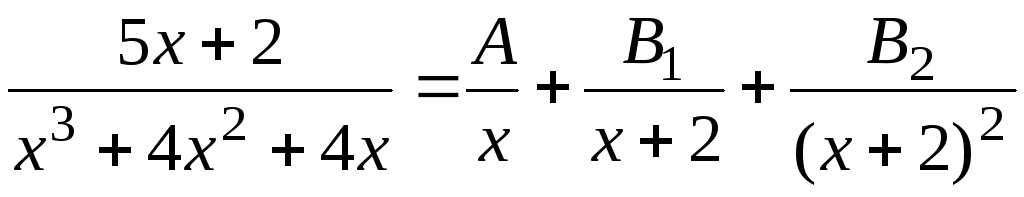 .
(7.5)
.
(7.5)
Множитель 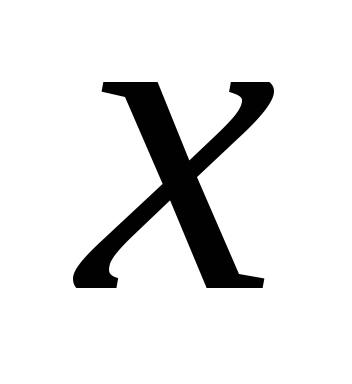 имеет степень 1, и ему соответствует в
сумме одно слагаемое, множитель
имеет степень 1, и ему соответствует в
сумме одно слагаемое, множитель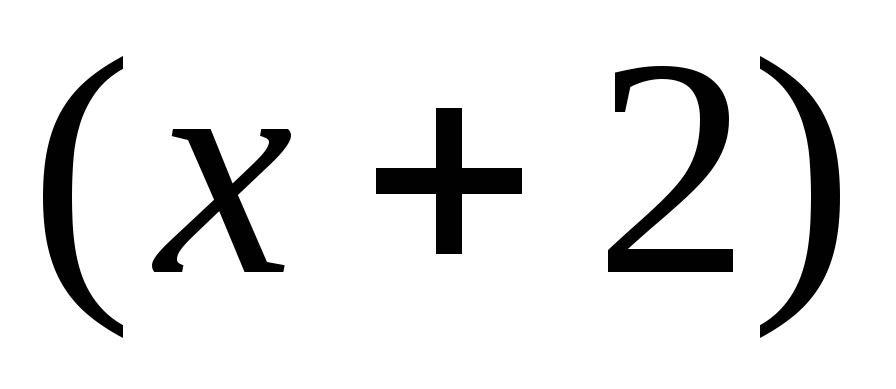 имеет степень 2, и ему в сумме соответствуют
два слагаемых.
имеет степень 2, и ему в сумме соответствуют
два слагаемых.
3) Приведём правую часть равенства (7.5) к общему знаменателю. Получим
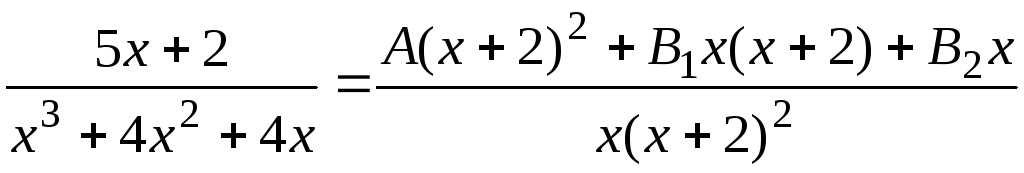 .
(7.6)
.
(7.6)
Равенство (7.6)
должно выполняться при всех значениях 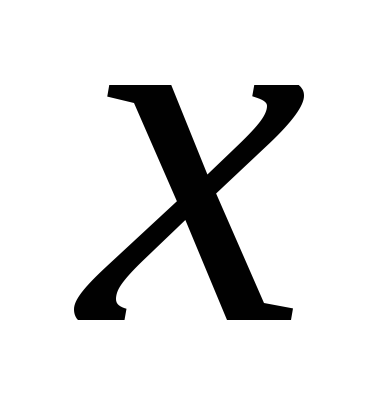 .
Поскольку знаменатели дробей, стоящих
в левой и правой частях (7.6), одинаковы,
числители этих дробей должны быть
тождественно равными. Таким образом,
.
Поскольку знаменатели дробей, стоящих
в левой и правой частях (7.6), одинаковы,
числители этих дробей должны быть
тождественно равными. Таким образом,
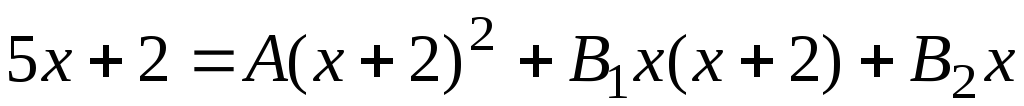 (7.7)
(7.7)
при всех значениях 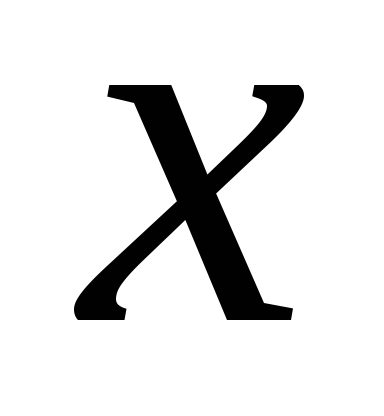 .
Чтобы определить
.
Чтобы определить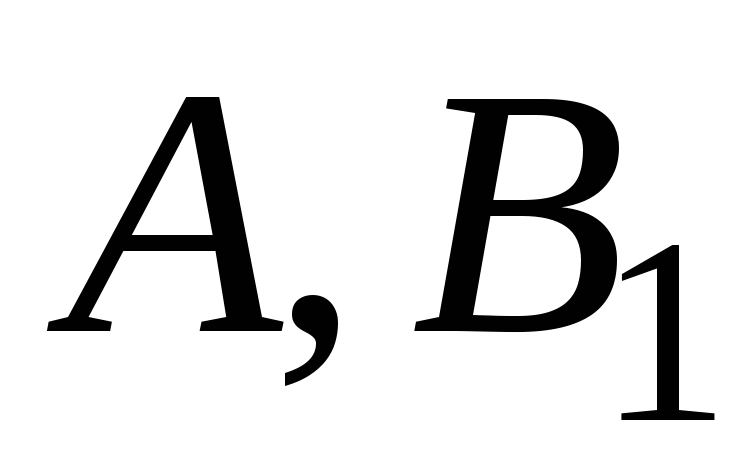 и
и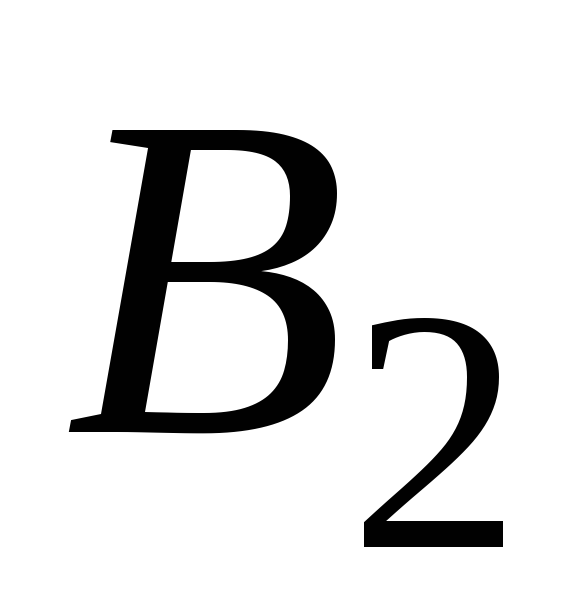 ,
подставим в (7.7) три каких-либо значения
,
подставим в (7.7) три каких-либо значения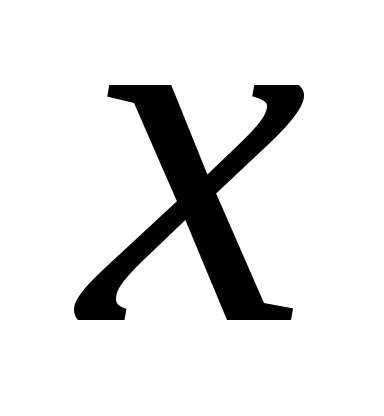 и получим систему трёх уравнений
относительно неизвестных
и получим систему трёх уравнений
относительно неизвестных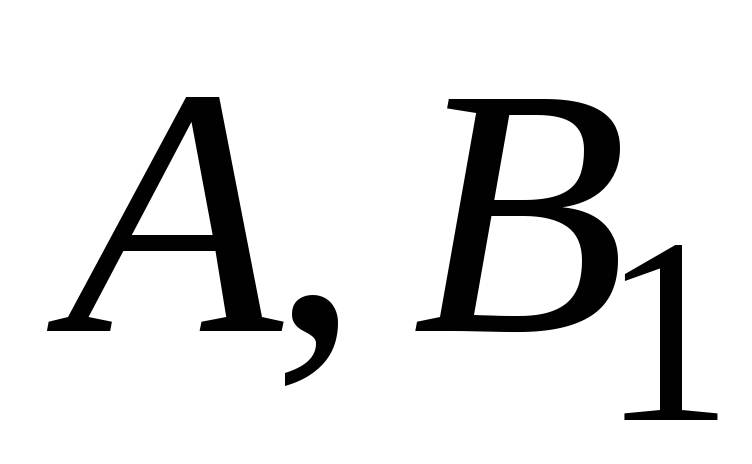 и
и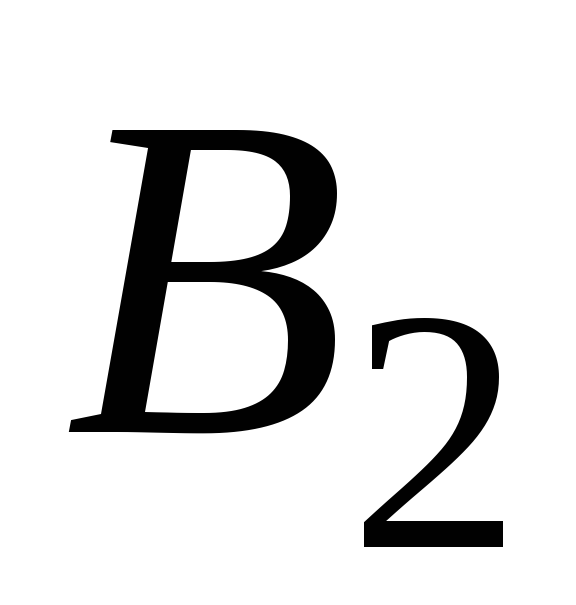 .
Если представление правильной дроби в
виде суммы простейших дробей составлено
правильно, то эта система имеет
единственное решение. Значения
.
Если представление правильной дроби в
виде суммы простейших дробей составлено
правильно, то эта система имеет
единственное решение. Значения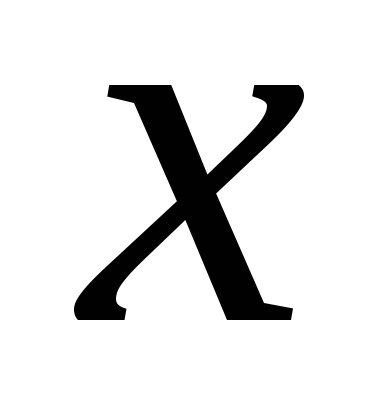 обычно выбирают так, чтобы расчеты были
как можно более простыми. В нашем случае
выгодно выбрать
обычно выбирают так, чтобы расчеты были
как можно более простыми. В нашем случае
выгодно выбрать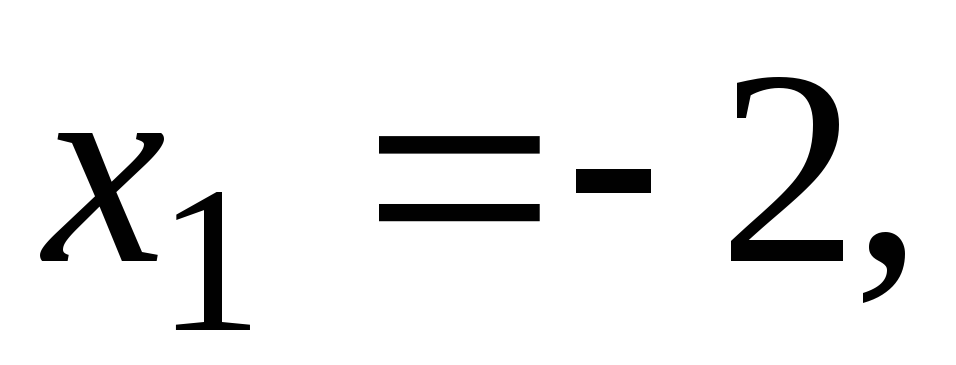
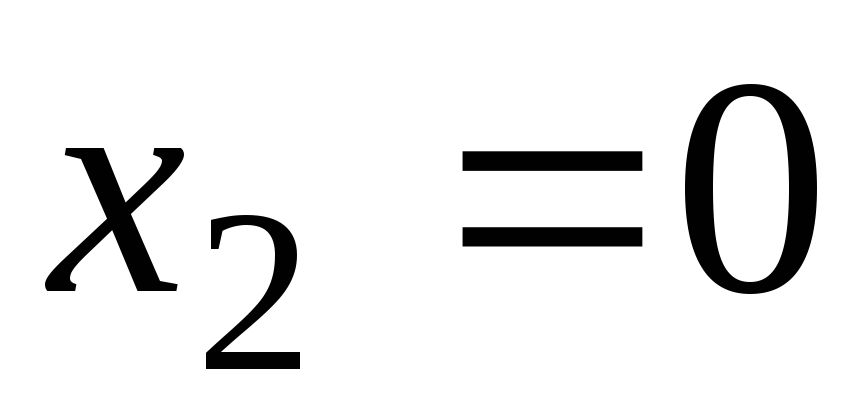 и
и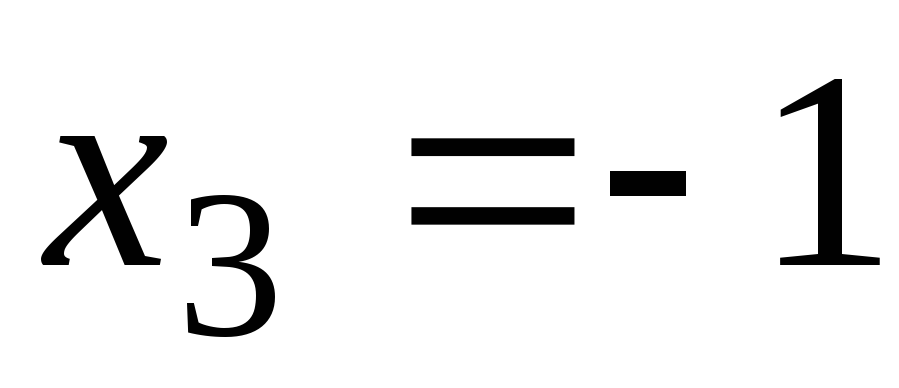 .
Последовательно подставляя эти значения
.
Последовательно подставляя эти значения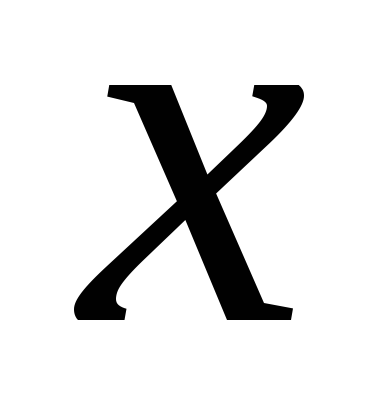 в тождество (7.7), получим систему
в тождество (7.7), получим систему
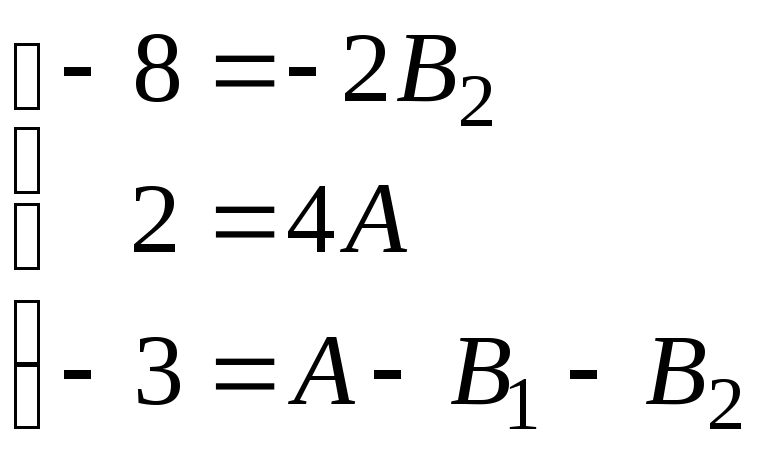 (7.8)
(7.8)
Система (7.8) имеет решение:
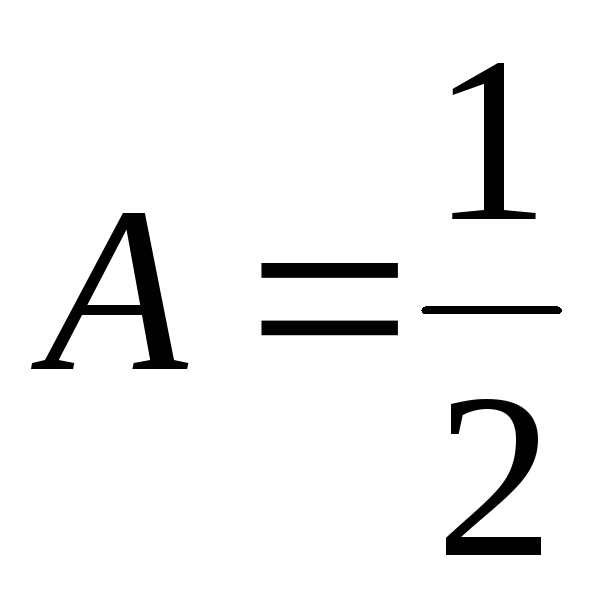 ;
; 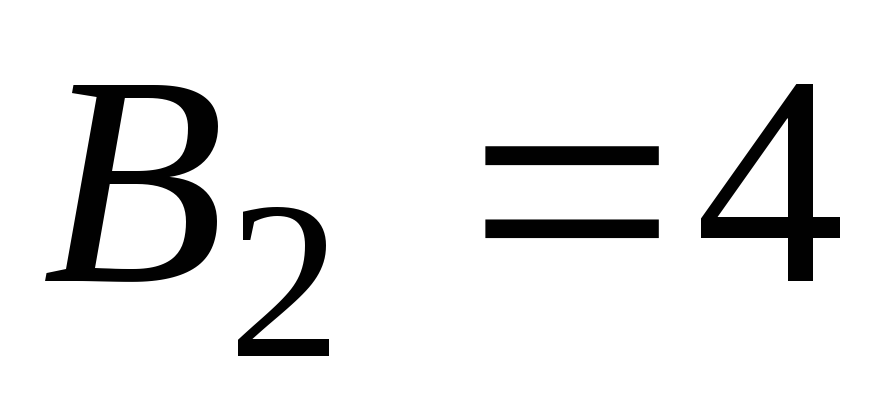 ;
;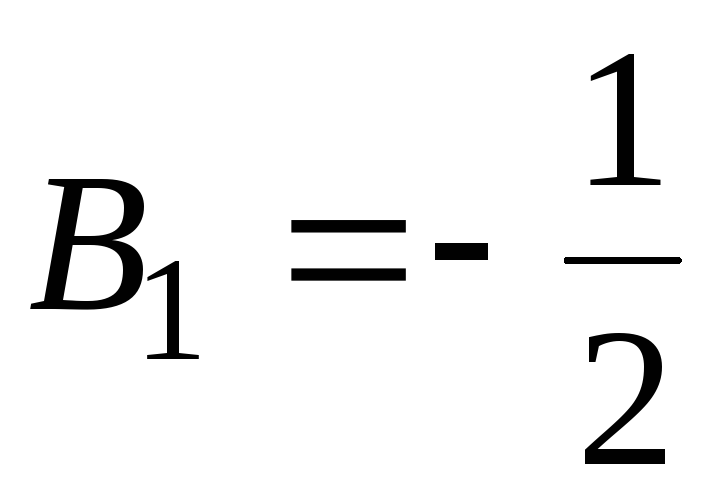 .
.
Замечание. Если коэффициенты 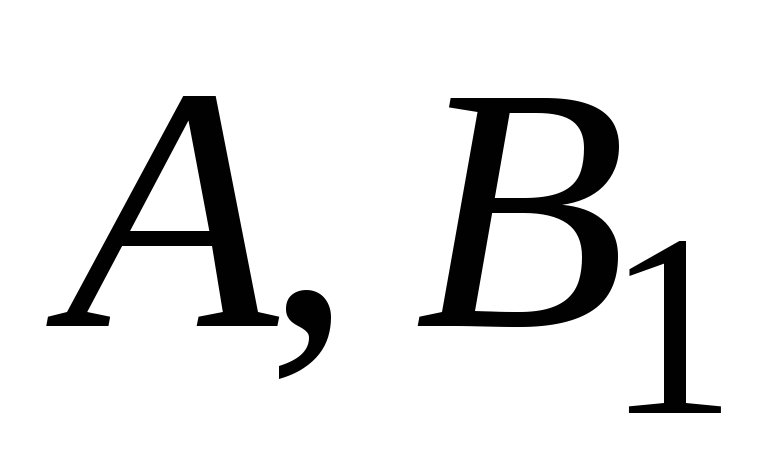 ,
,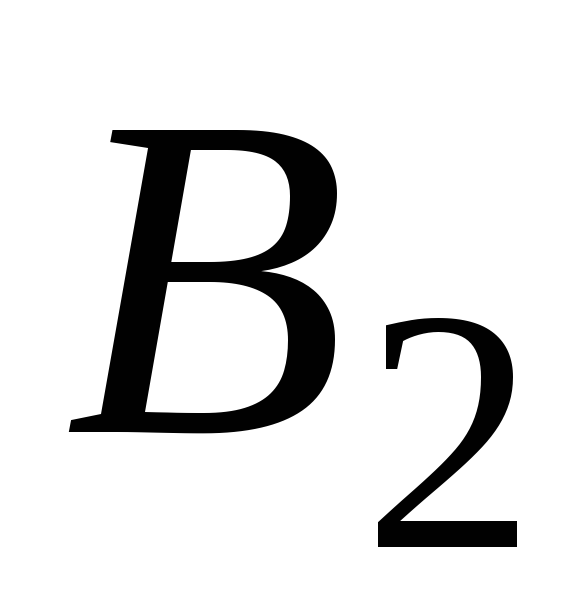 найдены верно, то слева и справа в (7.7)
стоят одинаковые многочлены. Следовательно,
их коэффициенты при одинаковых степенях
должны быть равны. Установим это:
найдены верно, то слева и справа в (7.7)
стоят одинаковые многочлены. Следовательно,
их коэффициенты при одинаковых степенях
должны быть равны. Установим это:

Таким образом, коэффициенты найдены верно. Итак, мы получили тождество
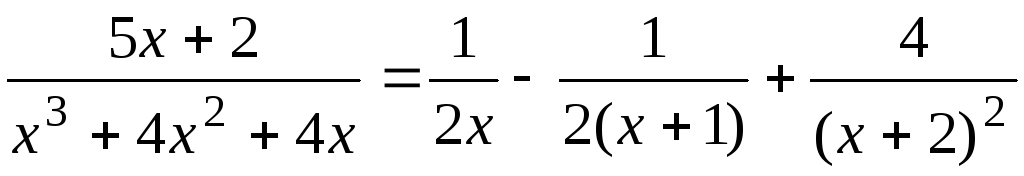 .
.
Тогда
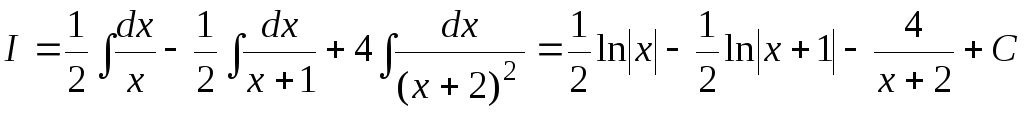 .
.
Пример
7.5. 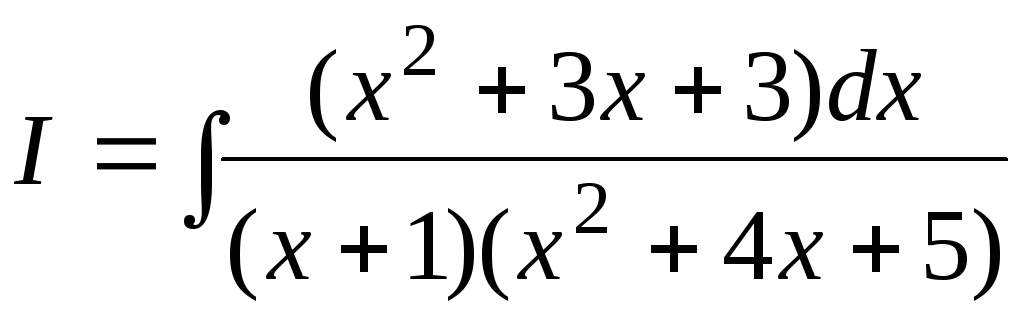 .
.
Представим дробь, стоящую под знаком интеграла, в виде суммы простейших дробей. Так как оба множителя, стоящих в знаменателе, имеют степень 1, представление будет иметь вид
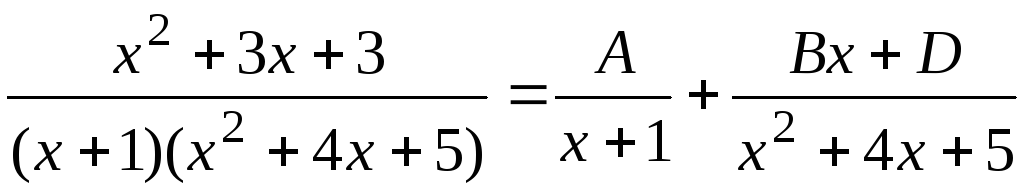 .
(7.9)
.
(7.9)
Заметим, что если
в знаменателе стоит квадратный трёхчлен 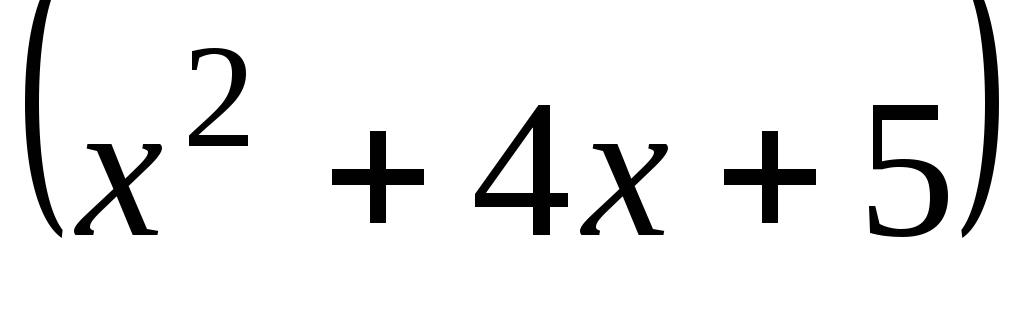 ,
то в числителе обязательно должен стоять
многочлен первой степени
,
то в числителе обязательно должен стоять
многочлен первой степени 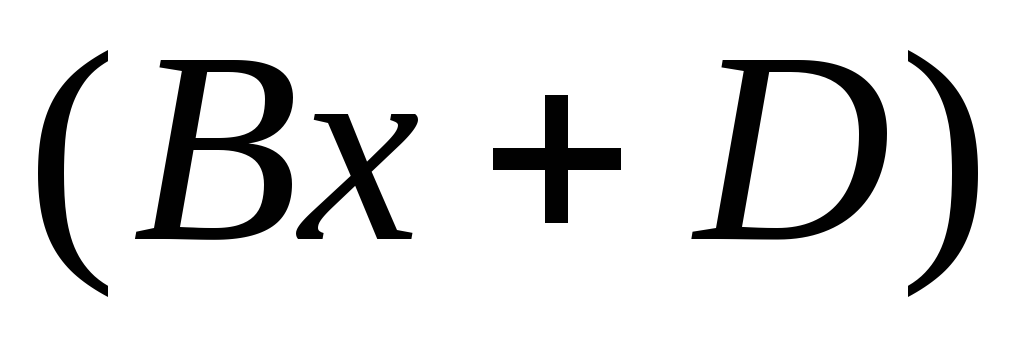 .
.
Приводим правую часть (7.9) к общему знаменателю. Тогда
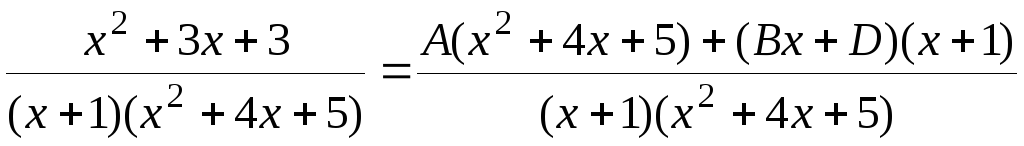 ,
,
откуда следует
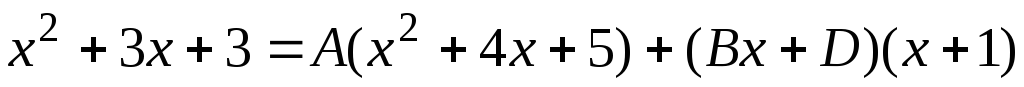 .
(7.10)
.
(7.10)
Нужно определить
три коэффициента 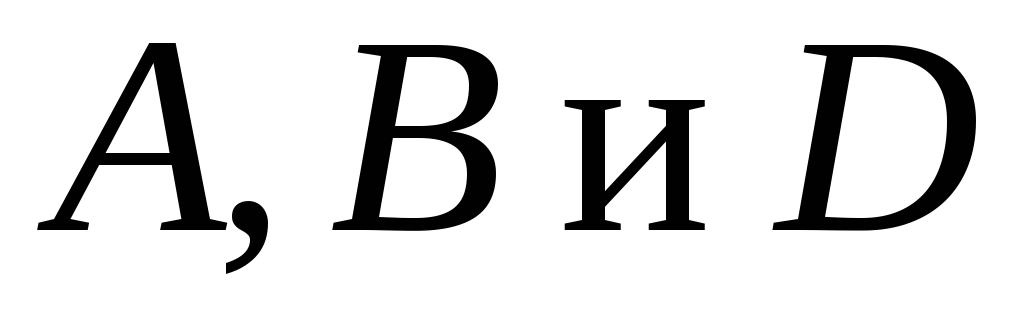 .
Используем удобные значения:
.
Используем удобные значения: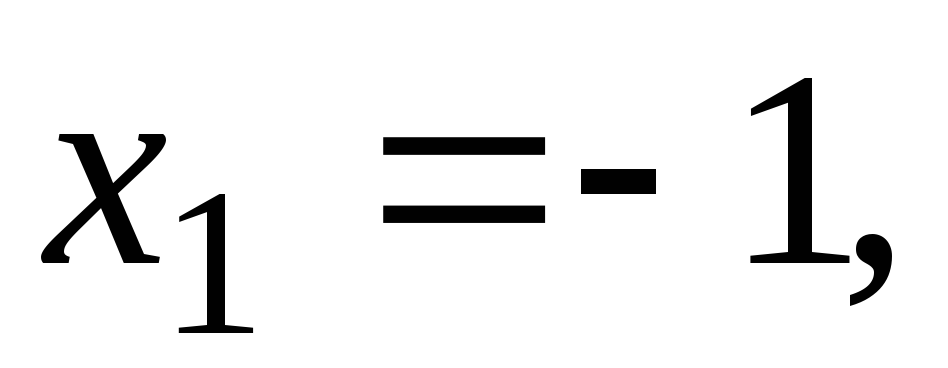
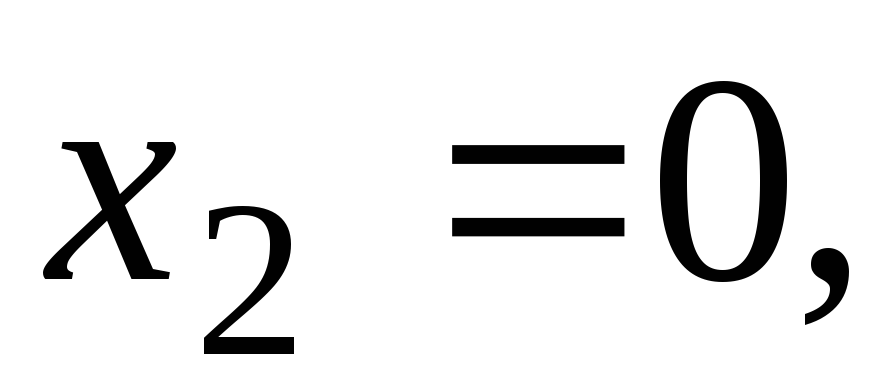
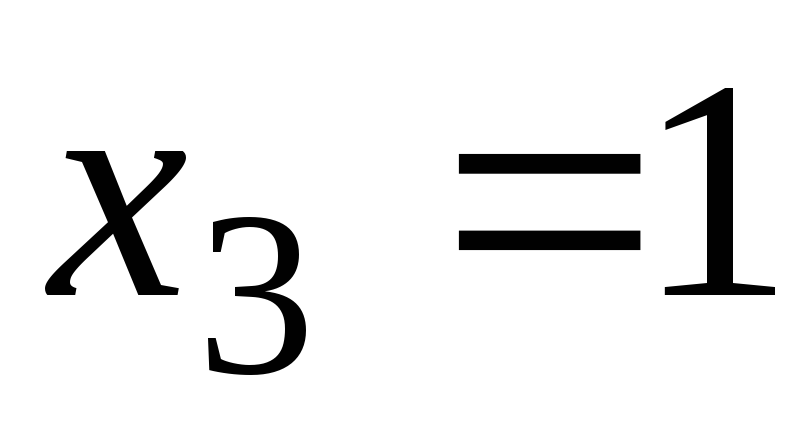 .
Подставим их последовательно в (7.10).
Получим
.
Подставим их последовательно в (7.10).
Получим
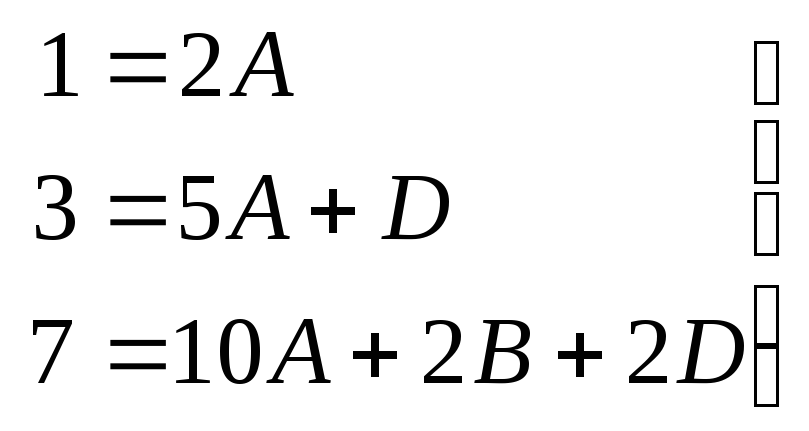 .
(7.11)
.
(7.11)
Система (7.11) имеет решение:
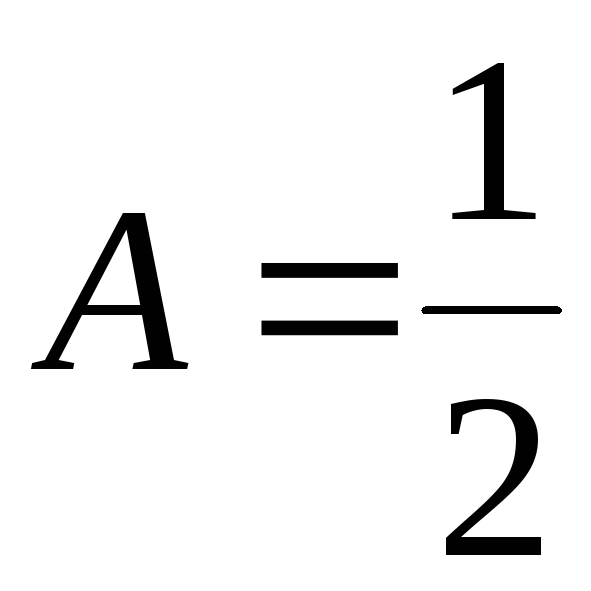 ;
; 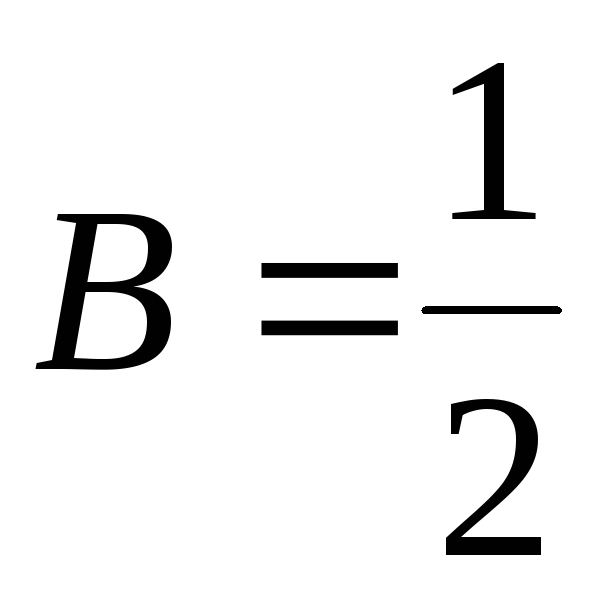 ;
;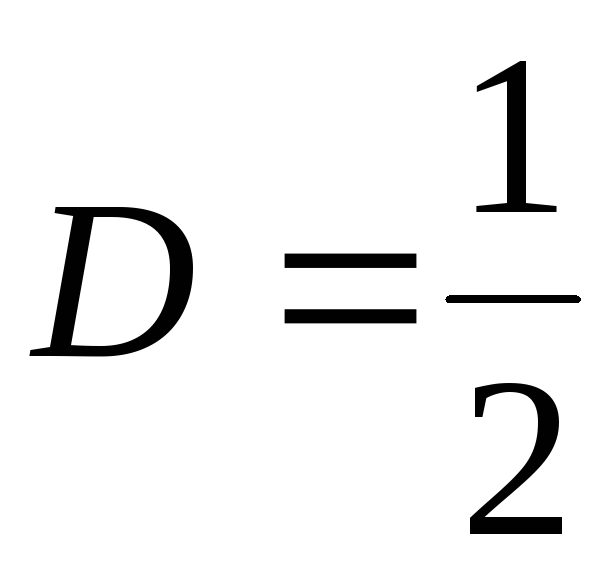 .
.
Проверим полученный результат.
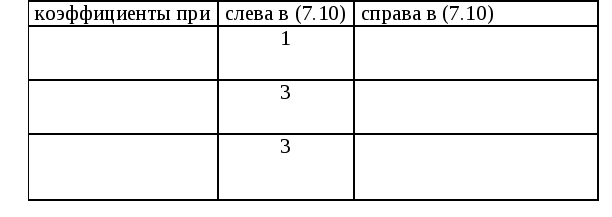
Получено тождество
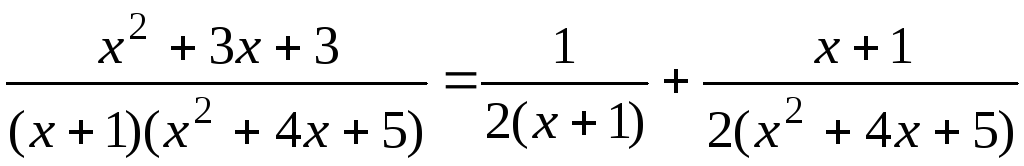 .
.
Следовательно,
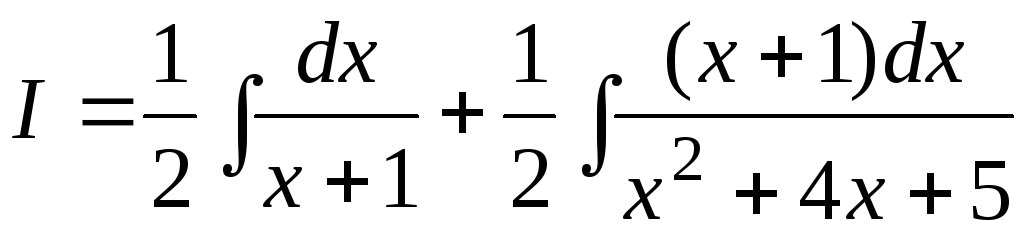 .
.
Отдельно вычислим 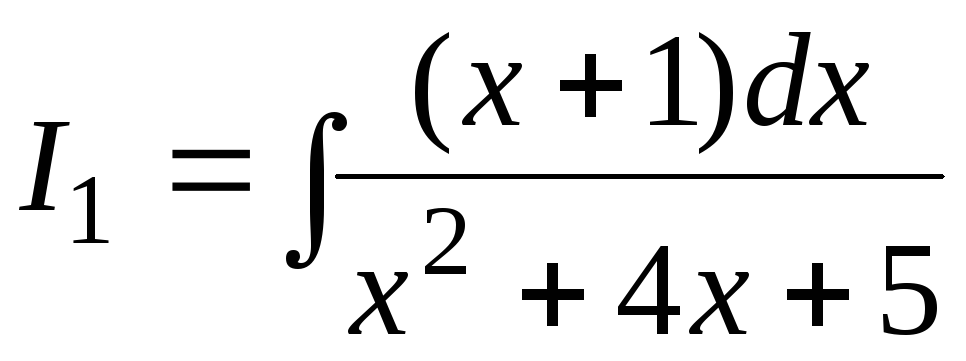 ,
используя формулы
,
используя формулы
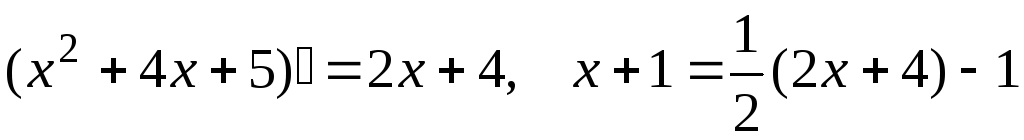 .
.
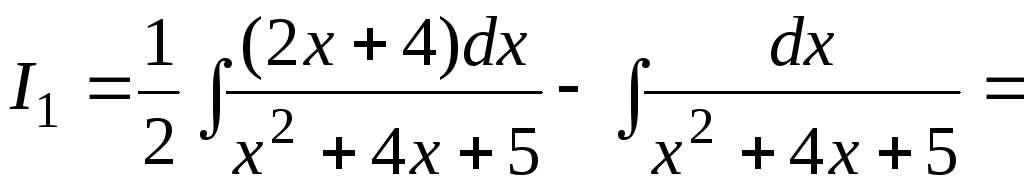
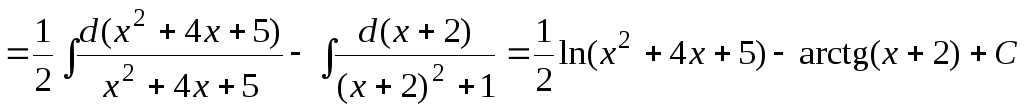 .
.
Итак,
 .
.
Пример
7.6. 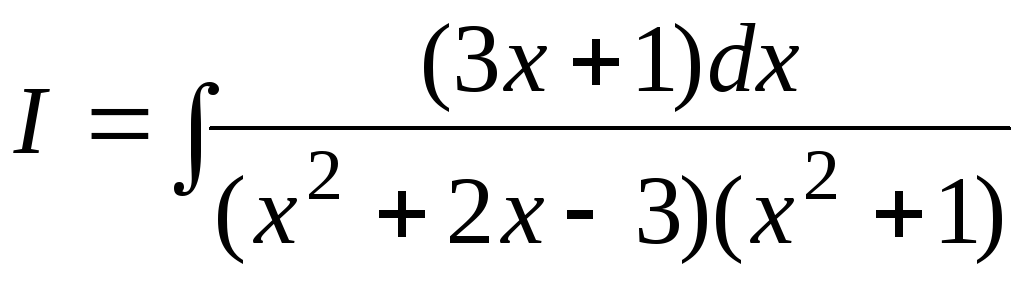 .
.
Разлагаем знаменатель на множители:
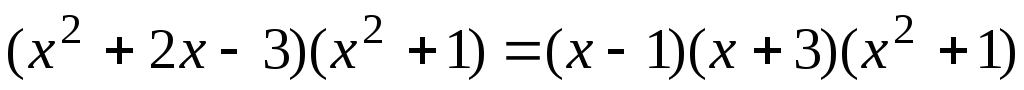 .
.
Выписываем общий вид представления дроби в виде суммы простейших дробей и сразу же приводим сумму дробей к общему знаменателю:
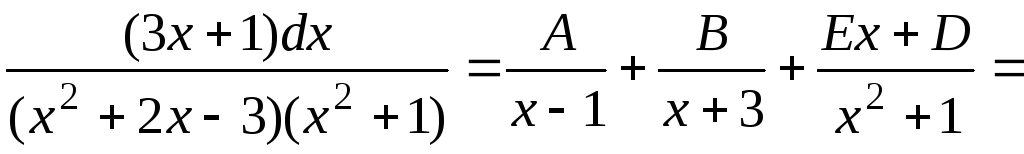
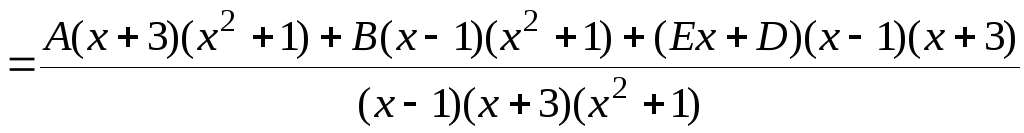 .
.
Составляем равенство числителей двух равных дробей с одинаковыми знаменателями:
 .
(7.12)
.
(7.12)
Выбираем удобные
значения 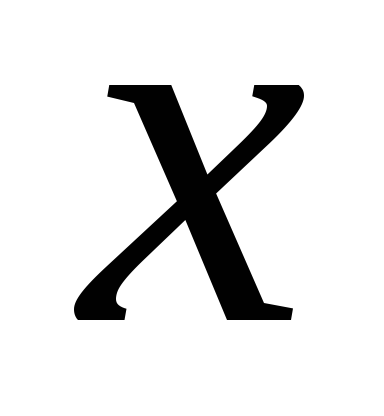 :
: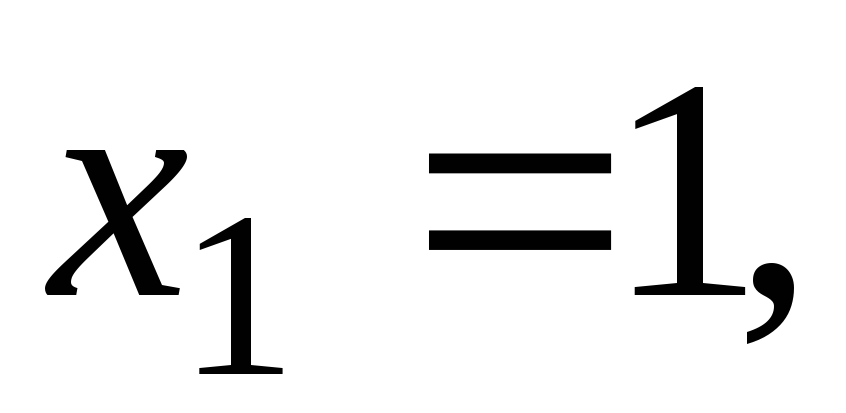
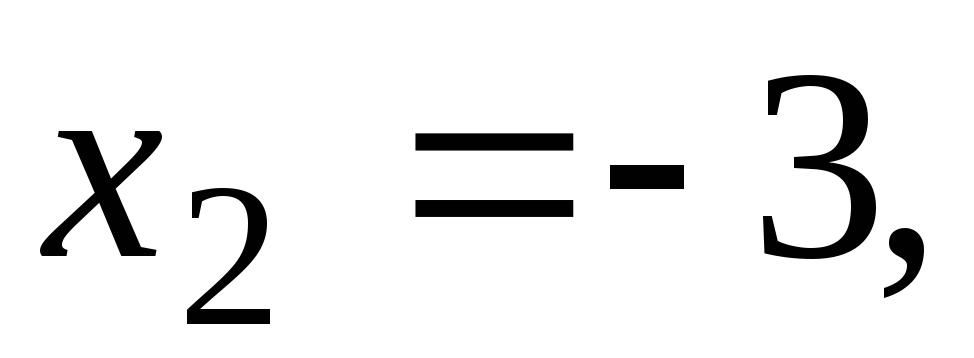
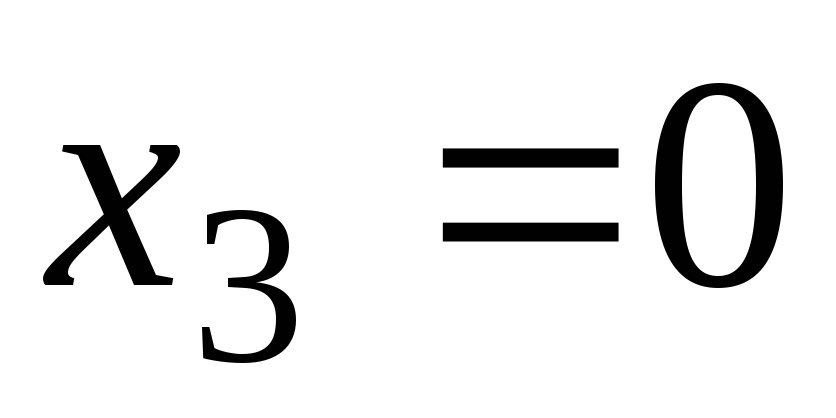 ,
, и составляем систему уравнений для
определения четырёх коэффициентов:
и составляем систему уравнений для
определения четырёх коэффициентов: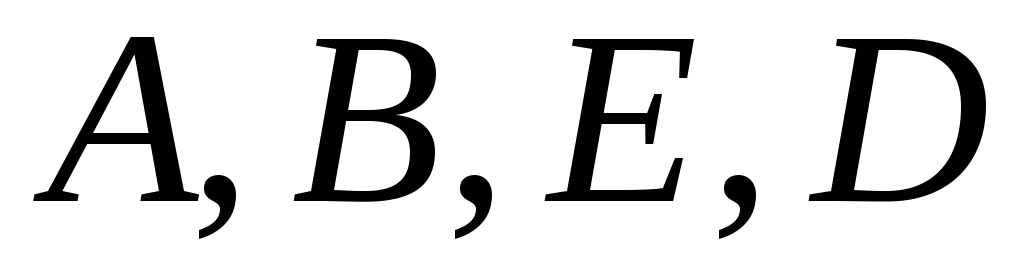 .
.
 .
(7.13)
.
(7.13)
Решаем систему
(7.13): 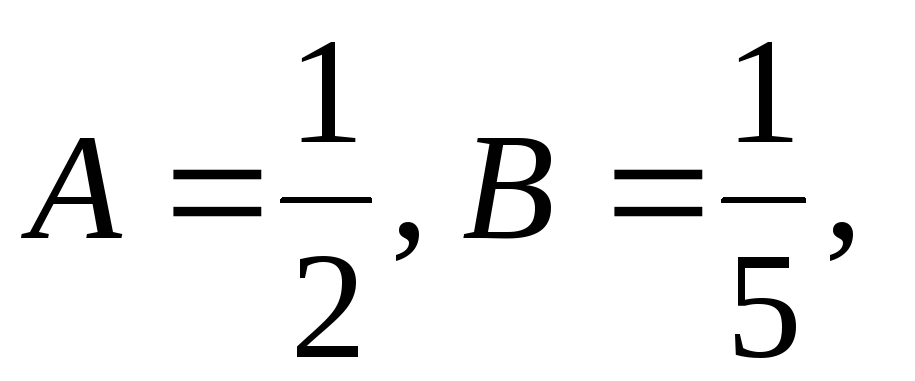
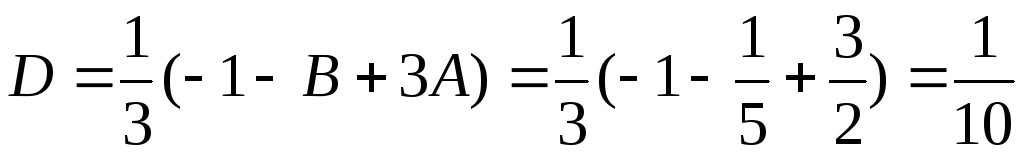 ,
, 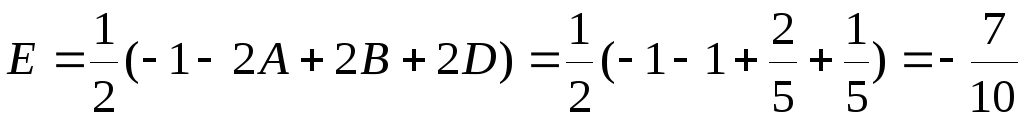 .
.
Проверим полученные значения.
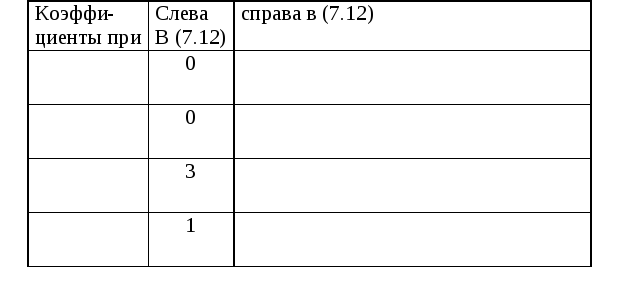
Таким образом,
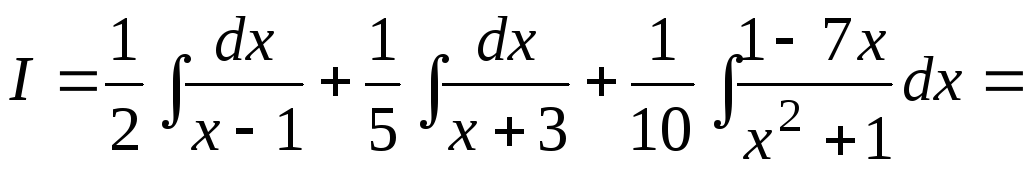
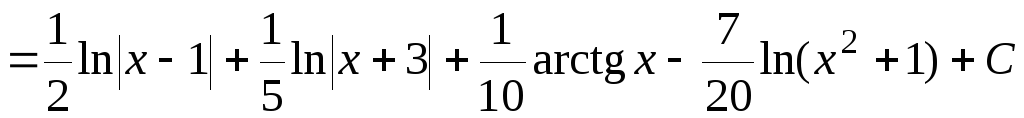 .
.
Интегрирование неправильных дробей.
Чтобы проинтегрировать
неправильную дробь  ,
где
,
где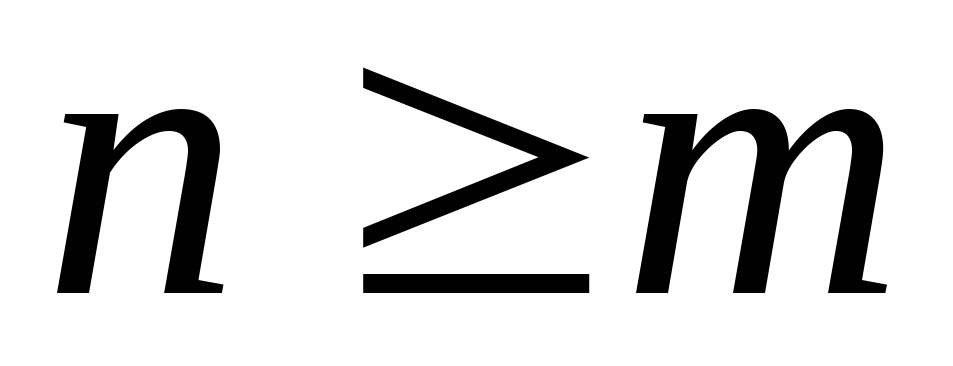 ,
её следует представить в виде суммы
многочлена и правильной дроби. Для этого
сначала следует представить
,
её следует представить в виде суммы
многочлена и правильной дроби. Для этого
сначала следует представить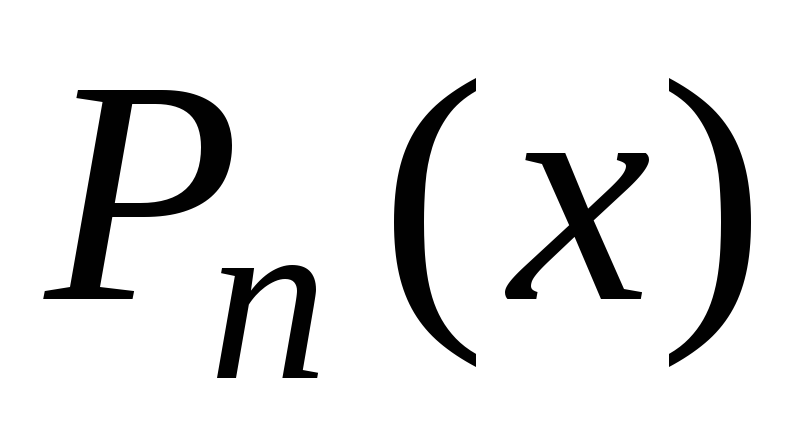 в виде
в виде
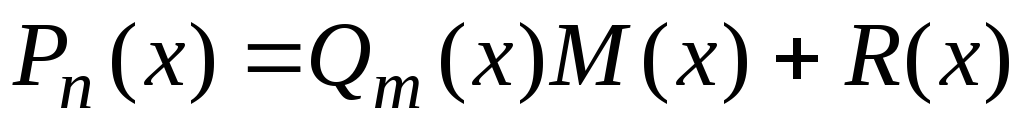 ,
(7.14)
,
(7.14)
где степень
многочлена 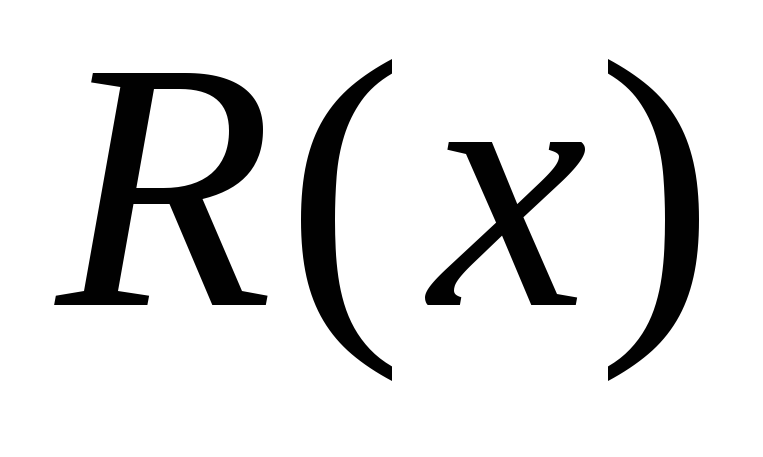 меньше, чем степень многочлена
меньше, чем степень многочлена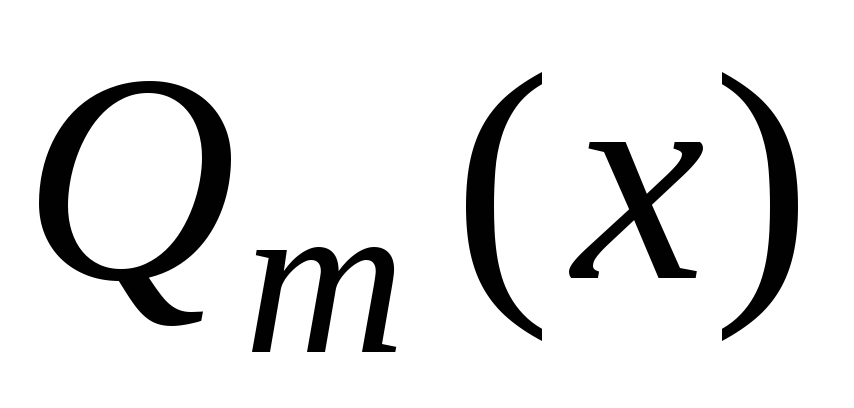 .
Представление (7.14) равносильно делению
многочлена
.
Представление (7.14) равносильно делению
многочлена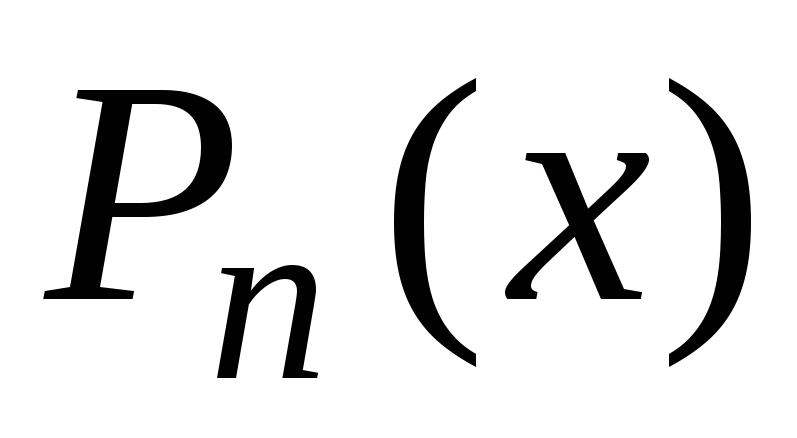 на многочлен
на многочлен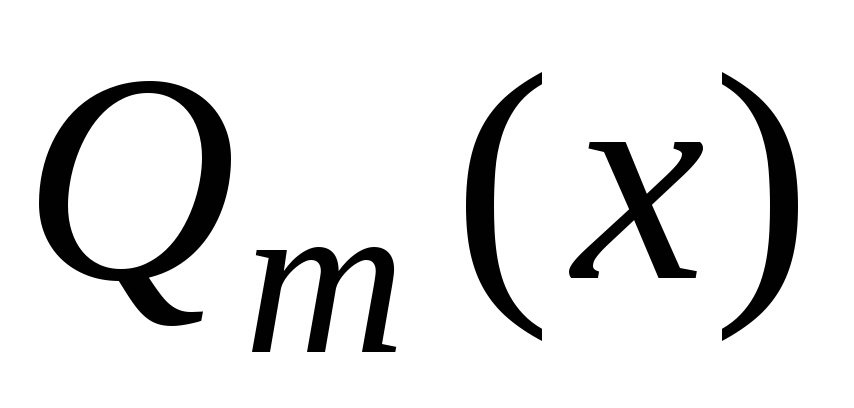 с остатком. В формуле (7.14) многочлен
с остатком. В формуле (7.14) многочлен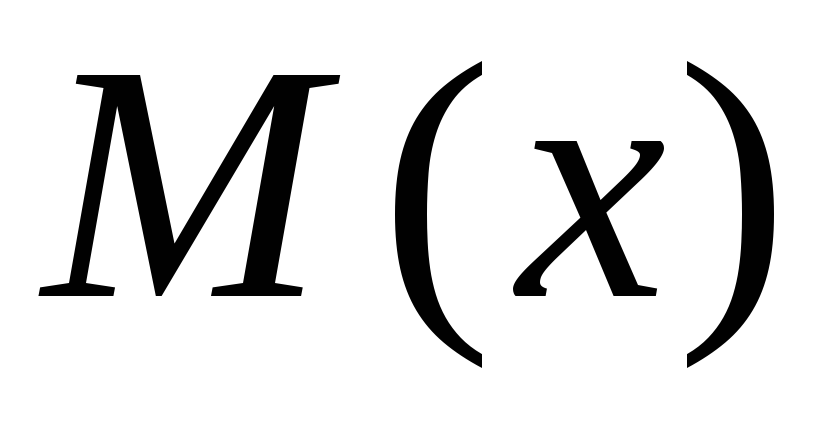 является частным, а многочлен
является частным, а многочлен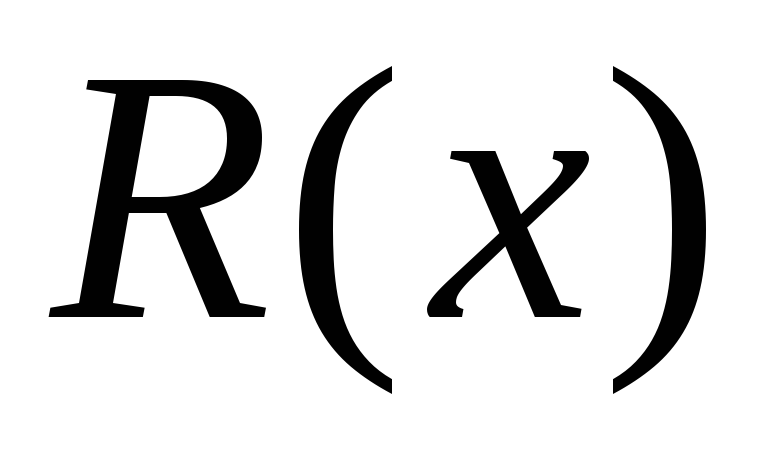 является остатком. Затем равенство
(7.14) следует почленно поделить на
является остатком. Затем равенство
(7.14) следует почленно поделить на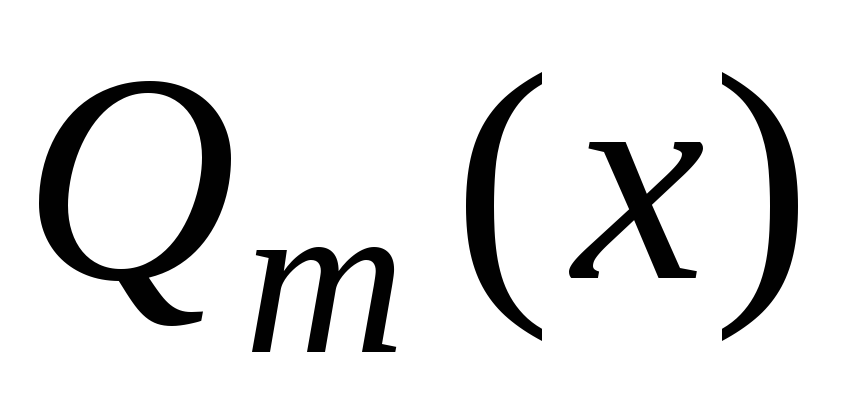 .
Мы получим
.
Мы получим
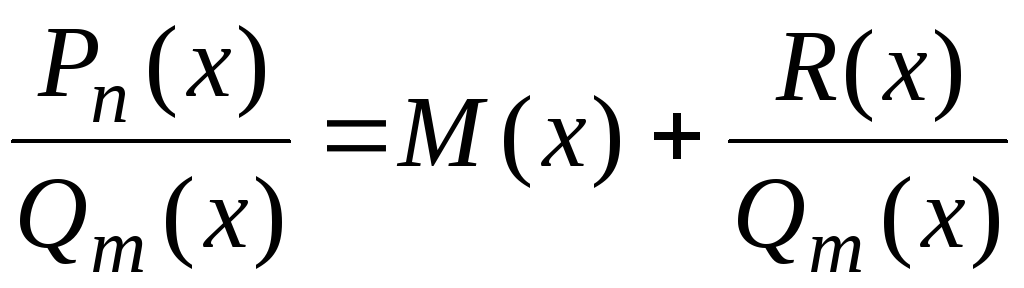 .
.
Здесь 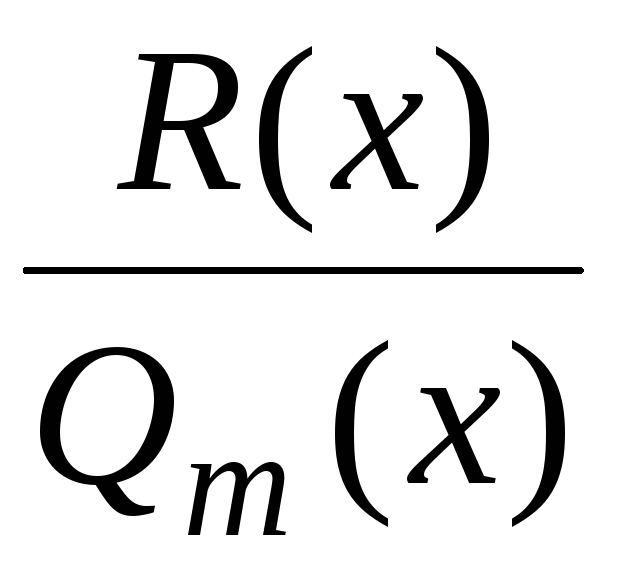 – правильная дробь.
– правильная дробь.
Представление
(7.14) иногда легко угадать (если  и
и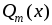 имеют достаточно простой вид), но, как
правило, оно получается в результате
деления
имеют достаточно простой вид), но, как
правило, оно получается в результате
деления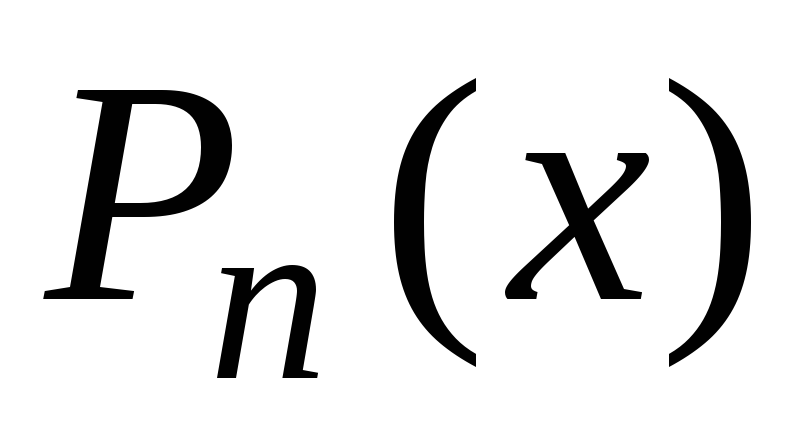 на
на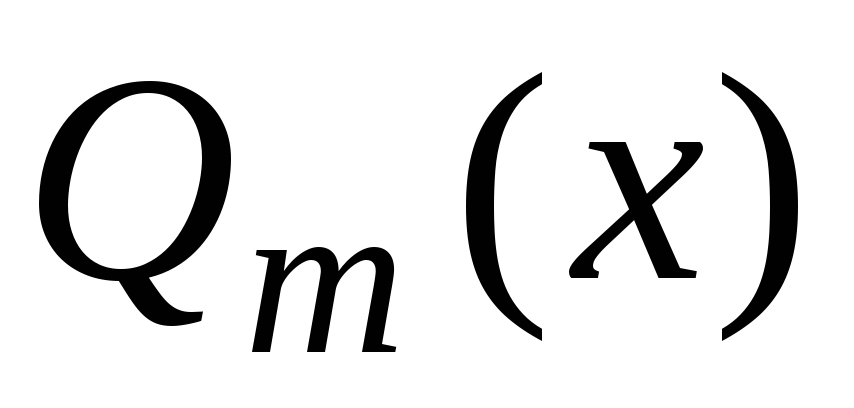 “уголком”.
“уголком”.
Приведём примеры.
Пример
7.7. 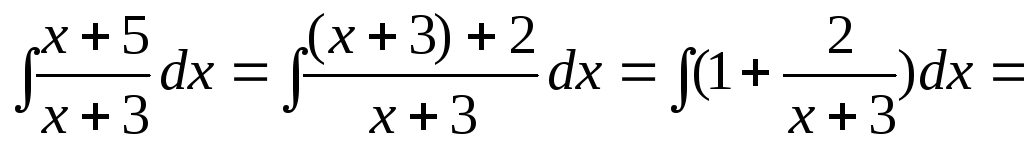
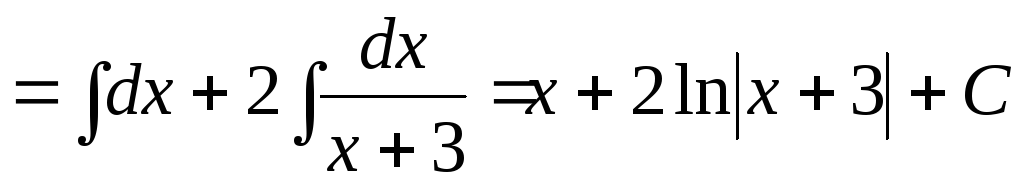 .
.
Пример
7.8. 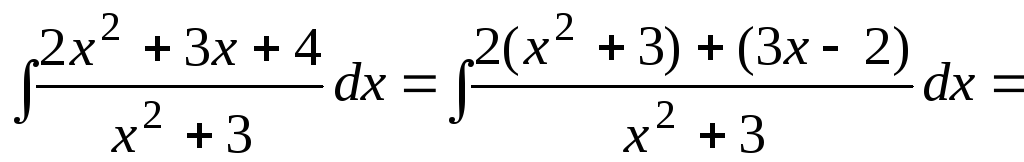
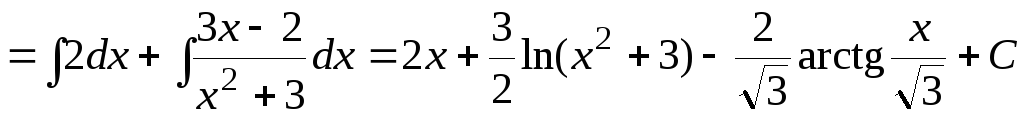 .
.
Пример
7.9. 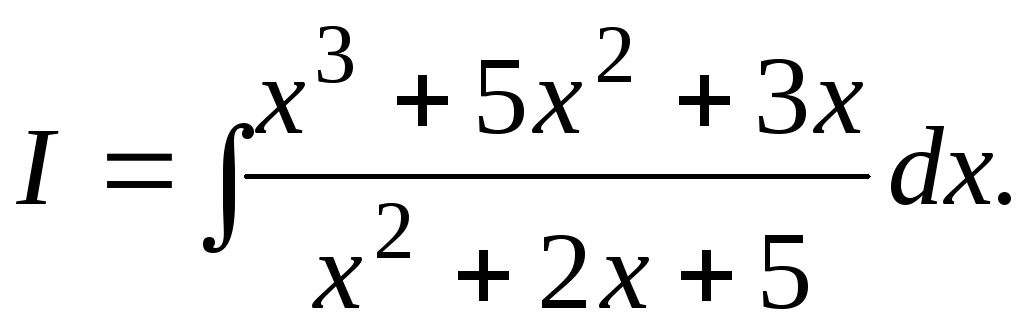 Подынтегральная функция является
неправильной рациональной дробью.
Разделим числитель этой дроби на
знаменатель с остатком.
Подынтегральная функция является
неправильной рациональной дробью.
Разделим числитель этой дроби на
знаменатель с остатком.
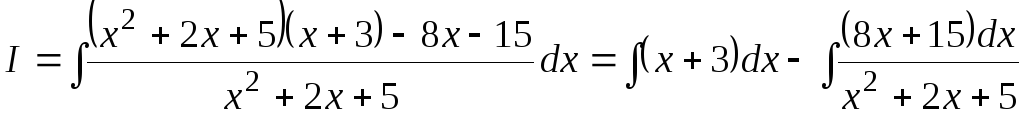 .
.
Вычислим отдельно
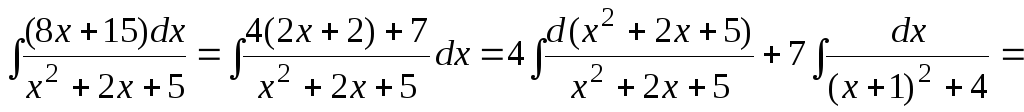
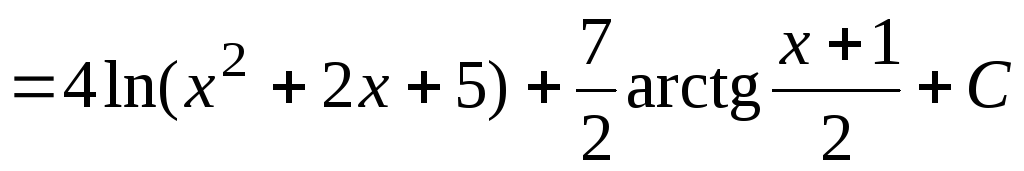 .
.
Окончательно,
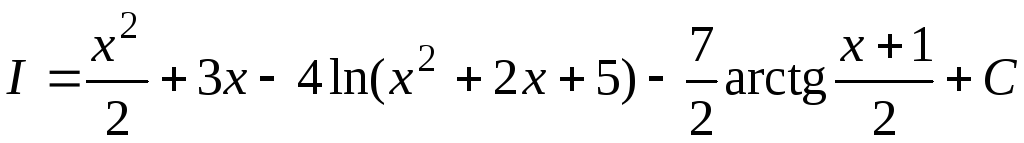 .
.
Пример
7.10. 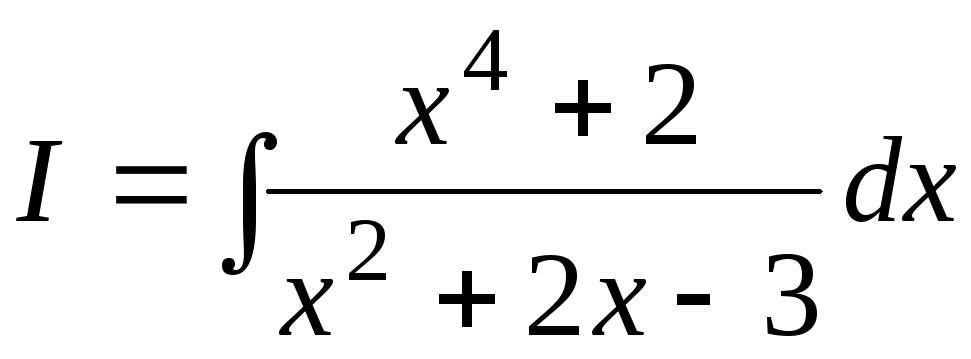 .
Поделим числитель на знаменатель с
остатком.
.
Поделим числитель на знаменатель с
остатком.
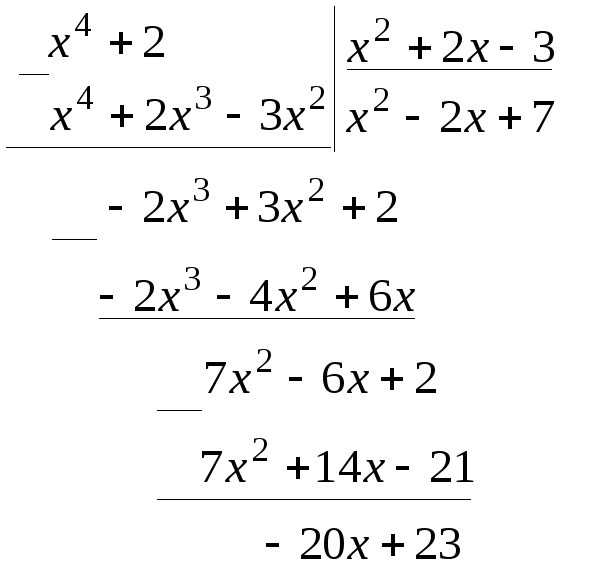
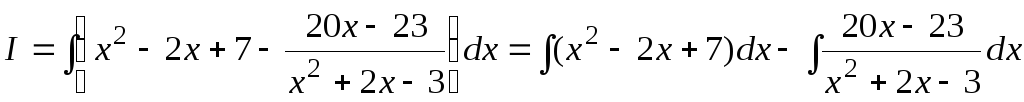 .
.
Вычислим отдельно 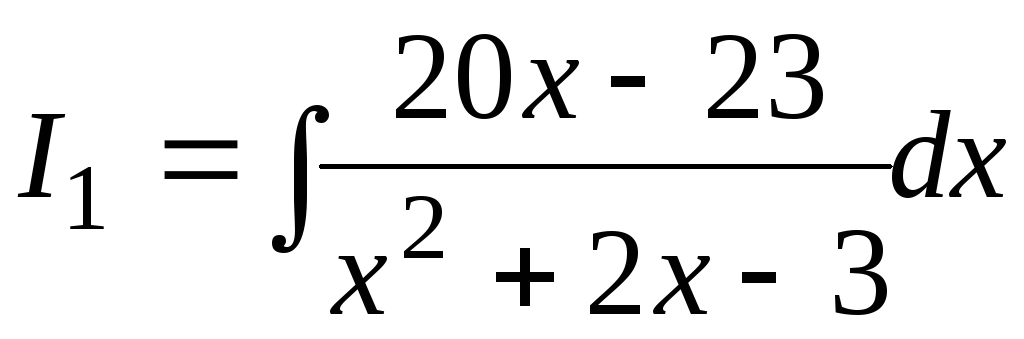 .
Разложим правильную дробь на простейшие
дроби.
.
Разложим правильную дробь на простейшие
дроби.
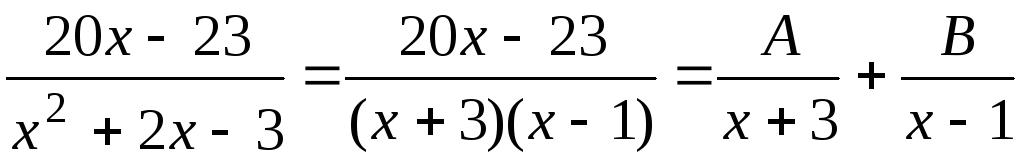 .
.
 .
.
Подставим в
полученное тождество последовательно
значения переменной 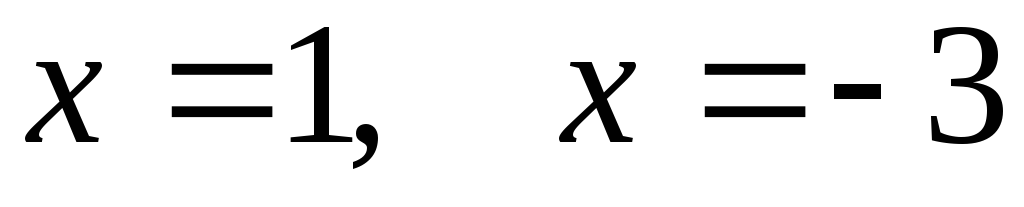 .
Тогда
.
Тогда
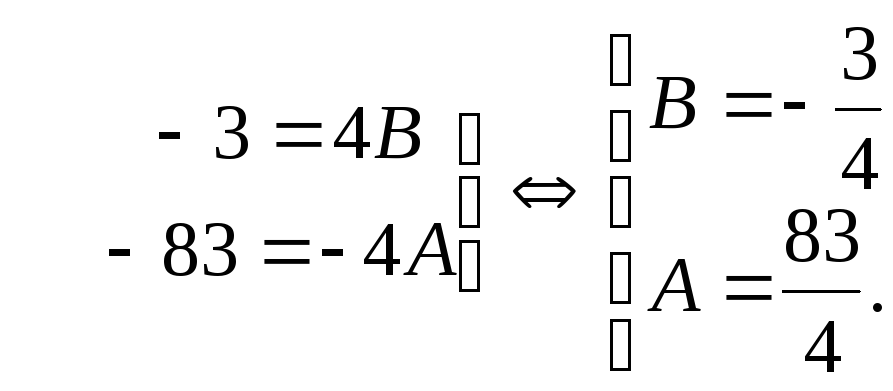
Получим 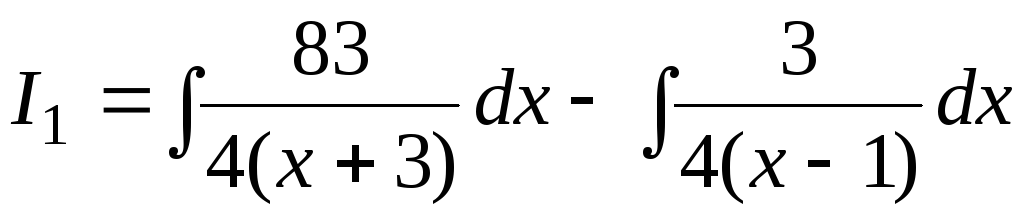 .
.
Окончательно,
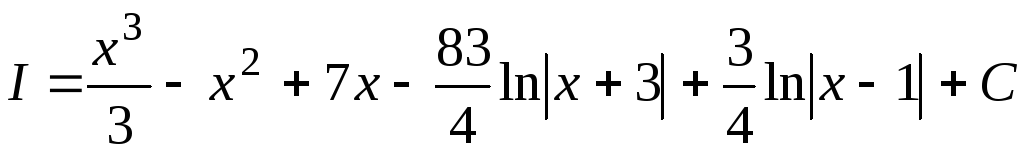 .
.
studfile.net
6. Понятия о рациональных функциях
Многочлен (некоторые сведения справочного характера)
Функция вида
Рn(х)= aохn+a1xn-l+• • •+аn-1х+аn, (31.1)
где n — натуральное число, αi (i=0,1,.., n) — постоянные коэффициенты, называется многочленом (или целой рациональной функцией). Число n называется степенью многочлена.
Корнем многочлена (31.1) называется такое значение х0 (вообще говоря, комплексное) переменной х, при котором многочлен обpaщaeтcя в нуль, т. е. Рn(хо)=0.
Теорема 31.1. Если х1 есть корень многочлена Рn(х), то многочлен делится без остатка на х-х1, т. е.
Pn(x)=(x-x1)*Pn -1(x), (31.2)
где Рn-1(х) — многочлен степени (n-1).
Возникает вoпpос: всякий ли многочлен имеет корень? Положительный ответ на этот вoпpос дает следующее утверждение.
Теорема 31.2 (основная теорема алгебры). Всякий многочлен n-й степени (n > 0) имеет по крайней мере один корень, действительный или комплексный.
Доказательство этой теоремы мы не пpивoдим.
Пользуясь основной теоремой алгебры, докажем теорему о разложе-нии многочлена на линейные множители.
Теорема 31.3. Всякий многочлен Рn(х) можно представить в виде
Рn(x)= αо(х-х1)(х-х2)… (х-хn), (31.3)
где х1, х2,…,хn — корни многочлена, αо — коэффициент многочлена при хn.
▲Рассмотрим многочлен (31.1). По теоpeмe 31.2 он имеет корень. Обозначим его через х1. Тогда имеет место соотношение (31.2). А так как Рn-1(х) — также многочлен, то он имеет корень. Обозначим его через Х2.Тогда Рn-1(х)=(х-x2)•Рn-2(х), где Рn-2(х) — многочлен (n-2)-й степени. Cлeдoвaтельнo, Рn(х)=(х-х1)(х-х2)Рn-2(х). Продолжая этот процесс, получим в итоге:
Рn(х)=αо(х-х1)(х-х2)… (х-хn). ▲
Mнoжители (х-xi) в равенстве (31.3) называются линейными множителями.
Пpимep 31.1. Разложить многочлен Рз(х)=х3-2x2-х+2 на мнoжители.
Решение: Многочлен Рз(х)=х3-2х2-x+2 обpaщaeтcя в нуль при х=-1, х=1, х=2. Следовательно, х3-2х2-х+2=(х+1)(х-1)(х-2).
7. Дробно-рациональная функция
Функция вида y = P(x) / Q(x), где P(x) и Q(x) – многочлены, называется дробно-рациональной функцией.
Если 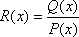 —
правильная рациональная дробь, знаменатель
P(x) которой представлен в виде произведения
линейных и квадратичных множителей, то
она может быть разложена на элементарные
по следующей схеме:
—
правильная рациональная дробь, знаменатель
P(x) которой представлен в виде произведения
линейных и квадратичных множителей, то
она может быть разложена на элементарные
по следующей схеме:
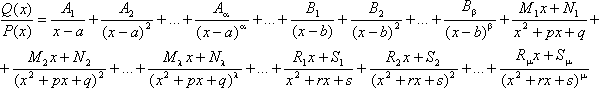
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
Метод неопределенных коэффициентов
Для нахождения неизвестных коэффициентов в разложении
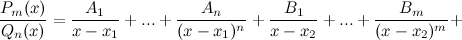
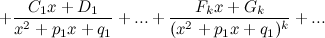
метод неопределенных коэффициентов, суть которого состоит в следующем:
правую часть записанного равенства приводим к общему знаменателю, который совпадает со знаменателем дроби, стоящей в левой части этого равенства —
 ,
в числителе левой части получим некоторый
многочлен
,
в числителе левой части получим некоторый
многочлен с
неизвестными коэффициентами;
с
неизвестными коэффициентами;используем тот факт, что две дроби равны, когда равны их числители и знаменатели. Из того, что знаменатели левой и правой частей равенства равны, то значит, равны и числители:
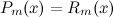
два многочлена равны, если равны коэффициенты при соответствующих степенях переменной, поэтому приравниваем коэффициенты при одинаковых степенях переменной
 .
В результате получаем систему для
определения неизвестных коэффициентов.
.
В результате получаем систему для
определения неизвестных коэффициентов.
Пример
Задание. Разложить
рациональную дробь 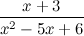 на
простые дроби.
на
простые дроби.
Решение. Так
как корнями знаменателя являются
значения 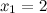 ,
,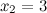 ,
то его можно разложить на множители
следующим образом:
,
то его можно разложить на множители
следующим образом:
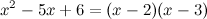
А тогда

Искомое разложение имеет вид:
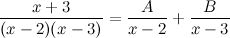
Приводим к общему знаменателю в правой части равенства и приравниваем числители:
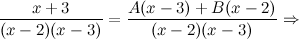
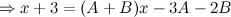
Приравнивая коэффициенты, при соответствующих степенях, получаем:
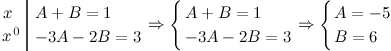
Отсюда, искомое разложение:
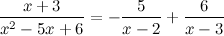
Ответ. 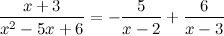
studfile.net
Дробно-рациональная функция (задание №23 ОГЭ)
Дробно-рациональная функция — это функция вида  , где f(x) и g(x) — некоторые функции.
, где f(x) и g(x) — некоторые функции.
График дробно-рациональной функции представляет собой гиперболу.
Функция имеет две асимптоты — вертикальную и горизонтальную.
Определение.Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность:
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты
Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь  , у которой числитель и знаменатель представляют собой линейные функции.
, у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
Построим график функции y=1/x:
D(y): х≠0
E(y): у≠0
y = k/x — нечетная


Построим график функции y=k/x:
При k=2 y=-2/x:
ООФ: х≠0
МЗФ: у≠0
y=k/x – нечетная


Пример1 . Построим график функции  , т.е. представим ее в виде
, т.е. представим ее в виде  : выделим целую часть дроби, разделив числитель на знаменатель, мы получим:
: выделим целую часть дроби, разделив числитель на знаменатель, мы получим:
 .
.
Итак,  . Мы видим, что график этой функции может быть получен из графика функции у=5/х с помощью двух последовательных сдвигов: сдвига гиперболы у=5/х вправо на 3 единицы, а затем сдвига полученной гиперболы
. Мы видим, что график этой функции может быть получен из графика функции у=5/х с помощью двух последовательных сдвигов: сдвига гиперболы у=5/х вправо на 3 единицы, а затем сдвига полученной гиперболы  вверх на 2 единицы.
вверх на 2 единицы.
При этих сдвигах асимптоты гиперболы у=5/х также переместятся: ось х на 2 единицы вверх, а ось у на 3 единицы вправо.
Для построения графика проведем в координатной плоскости пунктиром асимптоты: прямую у=2 и прямую х=3. Так как гипербола состоит из двух ветвей, то для построения каждой из них составим две таблицы: одну для х3 (т. е. первую слева от точки пересечения асимптот, а вторую справа от нее):
x | -7 | -2 | -1 | 0 | 1 | 2 | 2,5 |
y | 1,5 | 1 | 0,75 | 0,33 | -0,5 | -3 | -8 |
x | 3,5 | 4 | 5 | 6 | 7 | 8 | 13 |
y | 12 | 7 | 4,5 | 3,33 | 3,25 | 3 | 2,52 |
Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной линией, получим одну ветвь гиперболы. Аналогично (используя вторую таблицу) получим вторую ветвь гиперболы. График функции  изображен на рисунке 3.
изображен на рисунке 3.

Любую дробь  можно записать аналогичным образом, выделив ее целую часть. Следовательно, графики всех дробно-линейных функций являются гиперболами, различным образом сдвинутыми параллельно координатным осям и растянутыми по оси Оу.
можно записать аналогичным образом, выделив ее целую часть. Следовательно, графики всех дробно-линейных функций являются гиперболами, различным образом сдвинутыми параллельно координатным осям и растянутыми по оси Оу.
Пример 2.
Построим график функции  .
.
Поскольку мы знаем, что график есть гипербола, достаточно найти прямые, к которым приближаются ее ветви (асимптоты), и еще несколько точек.
Найдем сначала вертикальную асимптоту. Функция не определена там, где 2х+2=0, т.е. при х=-1. Стало быть, вертикальной асимптотой служит прямая х=-1.
Чтобы найти горизонтальную асимптоту, надо посмотреть, к чему приближаются значения функций, когда аргумент возрастает (по абсолютной величине), вторые слагаемые в числителе и знаменателе дроби  относительно малы. Поэтому
относительно малы. Поэтому
 .
.
Стало быть, горизонтальная асимптота – прямая у=3/2.
Определим точки пересечения нашей гиперболы с осями координат. При х=0 имеем у=5/2. Функция равна нулю, когда 3х+5=0, т.е. при х=-5/3.
Отметив на чертеже точки (-5/3;0) и (0;5/2) и проведя найденные горизонтальную и вертикальную асимптоты, построим график (рис.4).

Вообще, чтобы найти горизонтальную асимптоту, надо разделить числитель на знаменатель, тогда y=3/2+1/(x+1), y=3/2 – горизонтальная асимптота.
Алгоритм построения графика дробно-рациональной функции, содержащей квадратный трехчлен.
Найти область определения функции.
Разложить на множители квадратный трехчлен.
Сократить дробь.
Построить график (параболу, гиперболу, кубическую параболу).
Исключить из графика точки, не входящие в область определения («выколотые» точки).
Найти значение функции в «выколотых» точках.
Определить, при каких значениях b прямая y=b имеет с графиком ровно одну общую точку.
ЗАДАНИЕ
Построить график функции (D(y), на графике – выколотые точки):
multiurok.ru
Дробно-рациональная функция Википедия
 Пример рациональной функции от одной переменной: f(x)=x2−3x−2×2−4{\displaystyle f(x)={\frac {x^{2}-3x-2}{x^{2}-4}}}
Пример рациональной функции от одной переменной: f(x)=x2−3x−2×2−4{\displaystyle f(x)={\frac {x^{2}-3x-2}{x^{2}-4}}} 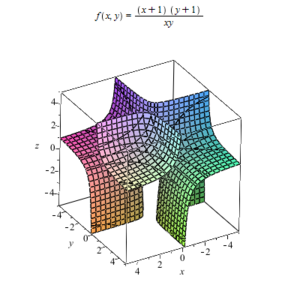 Пример рациональной функции от двух переменных
Пример рациональной функции от двух переменныхРациональная функция — это дробь, числителем и знаменателем которой являются многочлены.
Определение[ | ]
Рациональной функцией называется функция вида
- Pn(x1,…,xn)Qm(x1,…,xm){\displaystyle {\frac {P_{n}(x_{1},\dots ,x_{n})}{Q_{m}(x_{1},\dots ,x_{m})}}}
где Pn(x1,…,xn){\displaystyle P_{n}(x_{1},\dots ,x_{n})}, Qm(x1,…,xm){\displaystyle Q_{m}(x_{1},\dots ,x_{m})} — многочлены от любого числа переменных.
Такая функция определена во всех точках, кроме тех, в которых знаменатель Qm(x1,…,xm){\displaystyle Q_{m}(x_{1},\dots ,x_{m})} обращается в ноль.
Частным случаем являются рациональные функции одной переменной:
- R(x)=P(x)Q(x){\displaystyle R(x)={\frac {P(x)}{Q(x)}}}, где P(x){\displaystyle P(x)} и Q(x){\displaystyle Q(x)} — многочлены.
Другим частным случаем является отношение двух линейных функций —
ru-wiki.ru
Рациональная функция — это… Что такое Рациональная функция?
Рациональная функция — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид
где , — многочлены от любого числа переменных.
Частным случаем являются рациональные функции одного переменного:
- , где P(x) и Q(x) — многочлены.
Другим частным случаем является отношение двух линейных функций — дробно-линейная функция.
Свойства
Правильные дроби
Различают правильные и неправильные рациональные дроби, по аналогии с обычными числовыми дробями. Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если наоборот.
Любую неправильную рациональную дробь можно преобразовать в сумму некоторого многочлена и правильной рациональной дроби
Любую рациональную дробь многочленов с вещественными коэффициентами можно представить как сумму рациональных дробей, знаменателями которых являются выражения (a — вещественный корень Q(x)) либо (где не имеет действительных корней), причём степени k не больше кратности соответствующих корней в многочлене Q(x). На основании этого утверждения основана теорема об интегрируемости рациональной дроби. Согласно ей, любая рациональная дробь может быть интегрирована в элементарных функциях, что делает класс рациональных дробей весьма важным в математическом анализе.
C этим связан метод выделения рациональной части в первообразной от рациональной дроби, который был предложен в 1844 году М. В. Остроградским.
См. также
dic.academic.ru
Непрерывность дробно-рациональных функций
Дробно-рациональные функции терпят разрыв только в тех точках, где знаменатель обращается в 0, при этом разрыв – либо устранимый, либо бесконечный скачок (частный случай разрыва 2-го рода).
Пример 9. Исследуем на непрерывность функцию 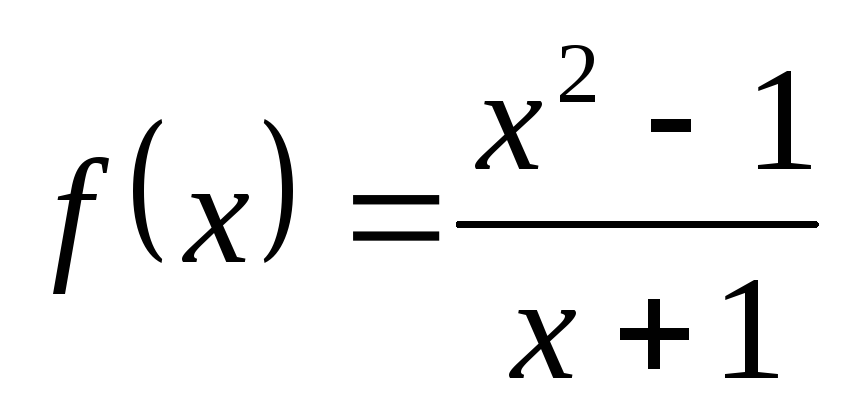 .
.
Знаменатель
обращается в 0 в точке 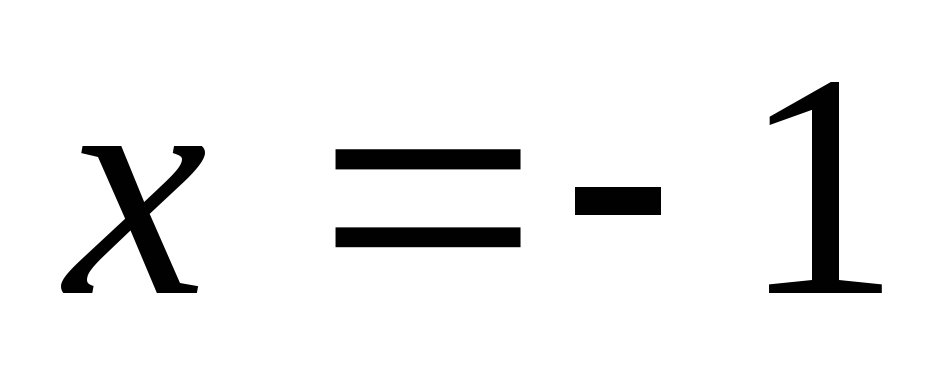 ,
при подстановке получаем неопределённость
,
при подстановке получаем неопределённость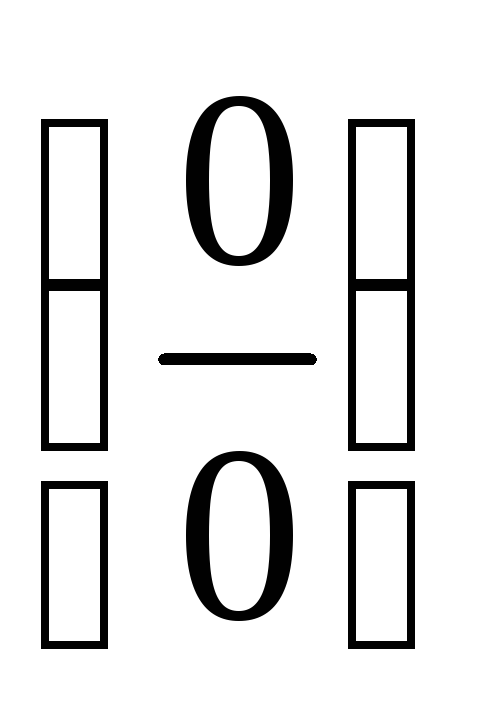 .
Раскроем её:
.
Раскроем её:
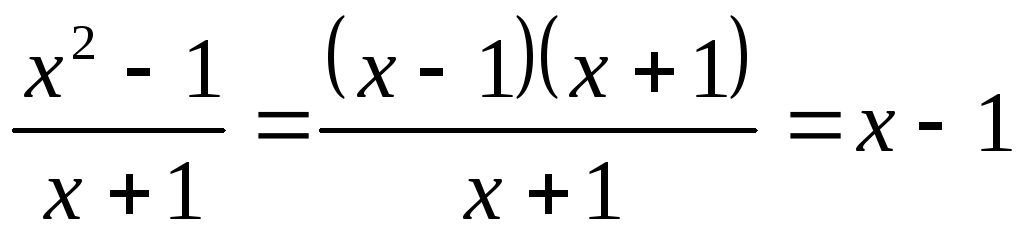 ,
,
тогда 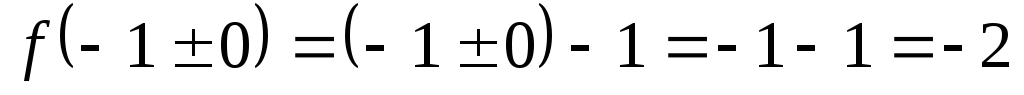 .
.
В точке  имеет место устранимый разрыв, на графике
получается прямая
имеет место устранимый разрыв, на графике
получается прямая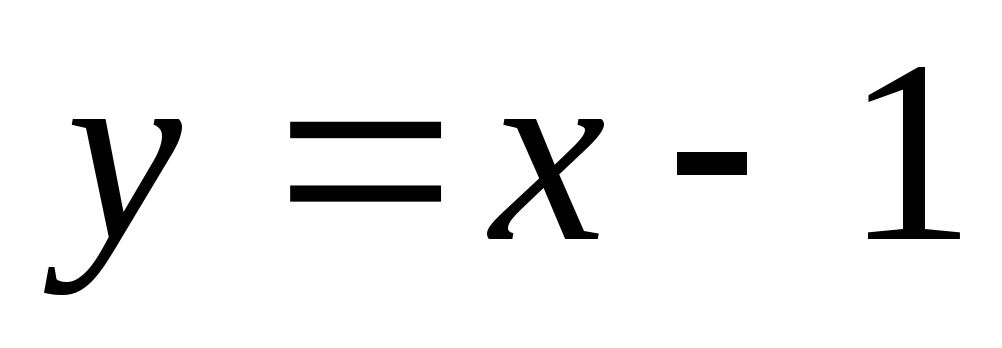 ,
из которой удалена точка с координатами
,
из которой удалена точка с координатами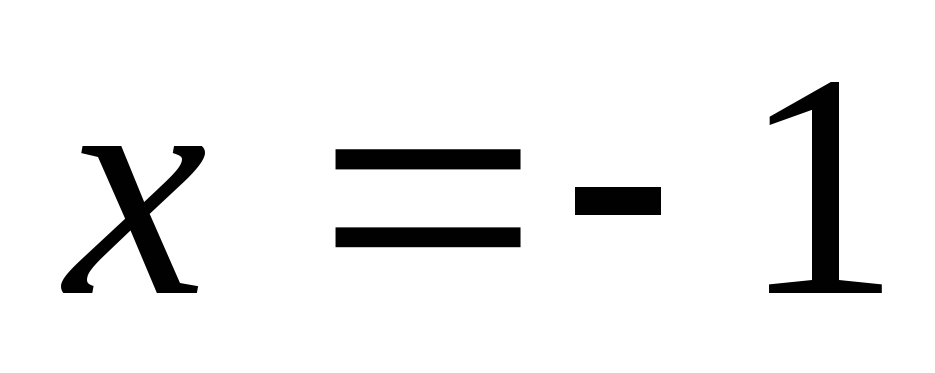 и
и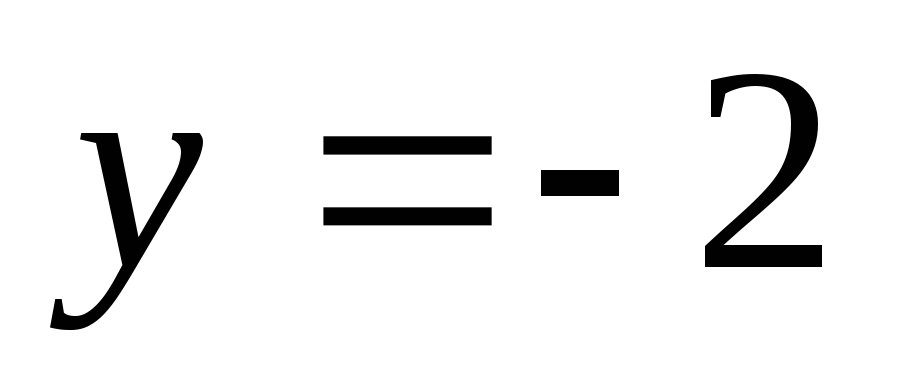 .
.
НФ7. Исследуйте на непрерывность функции и постройте их графики:
1) а) 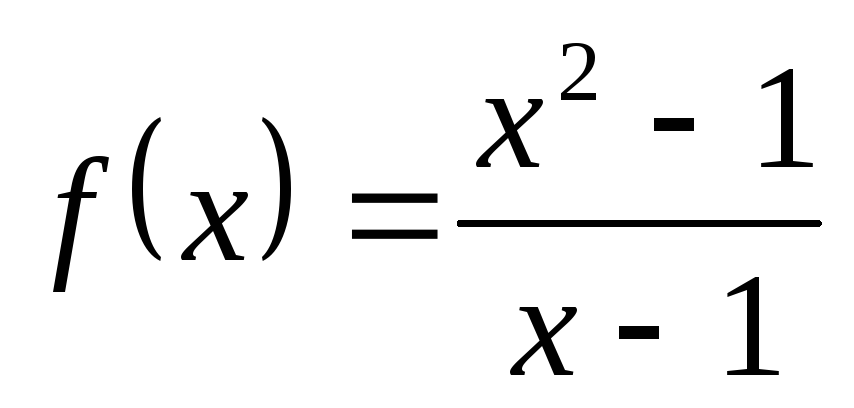 ; б)
; б)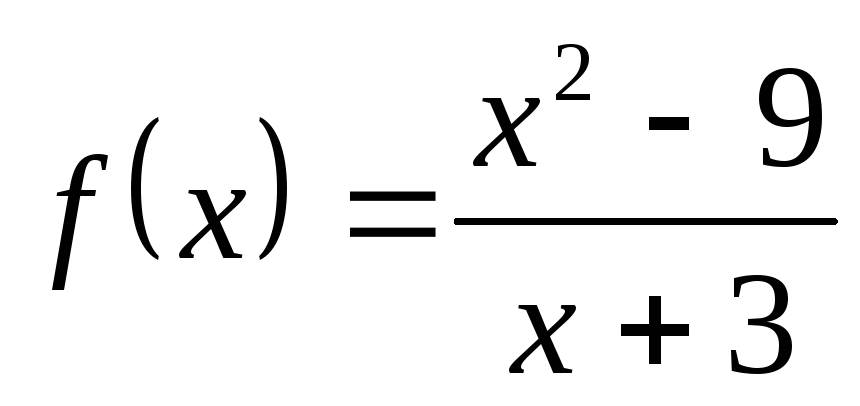 ; в)
; в)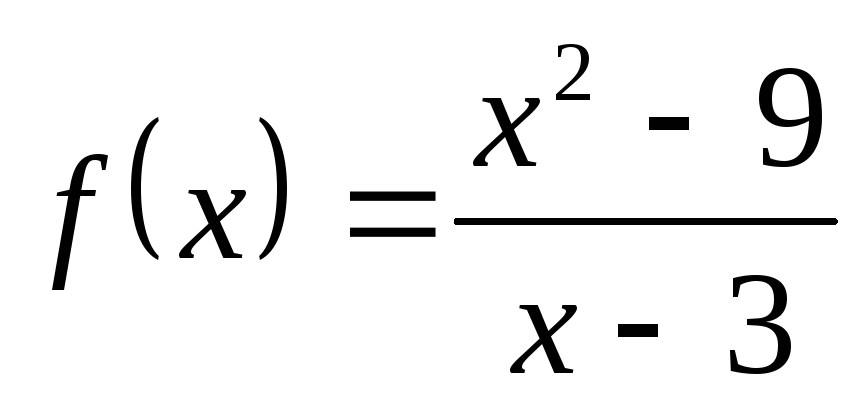 ; г)
; г)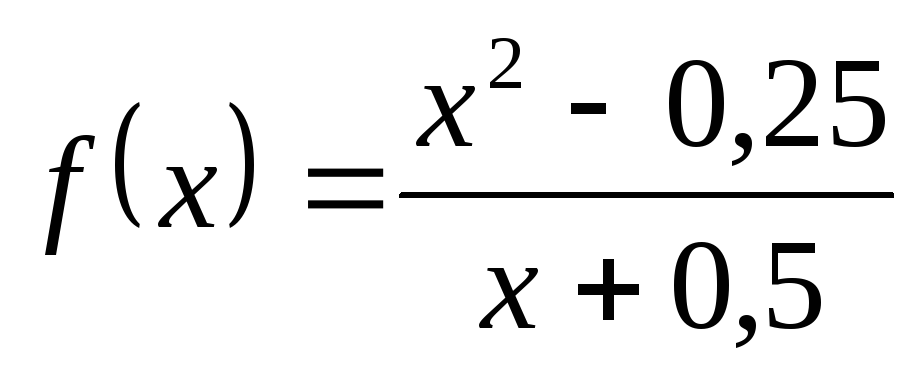 ;
;
2) а) 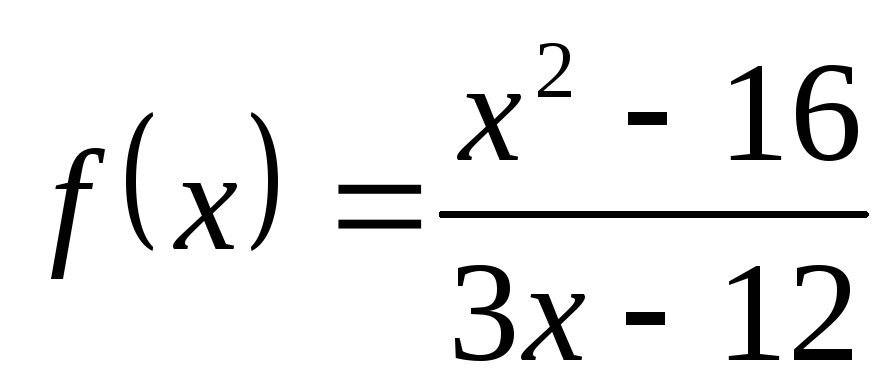 ; б)
; б)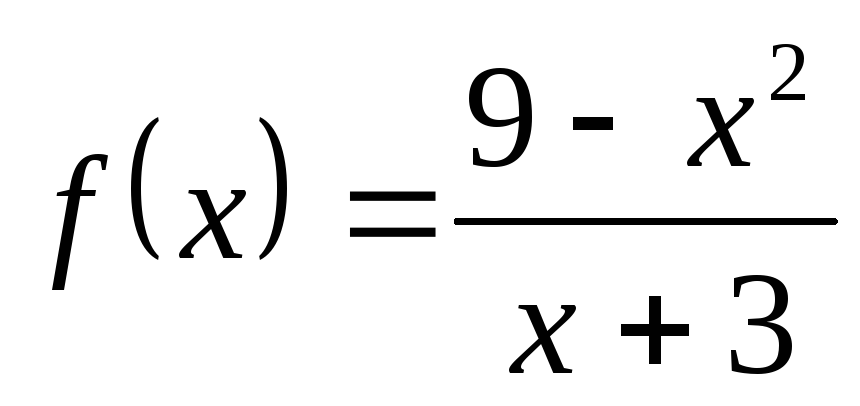 ; в)
; в)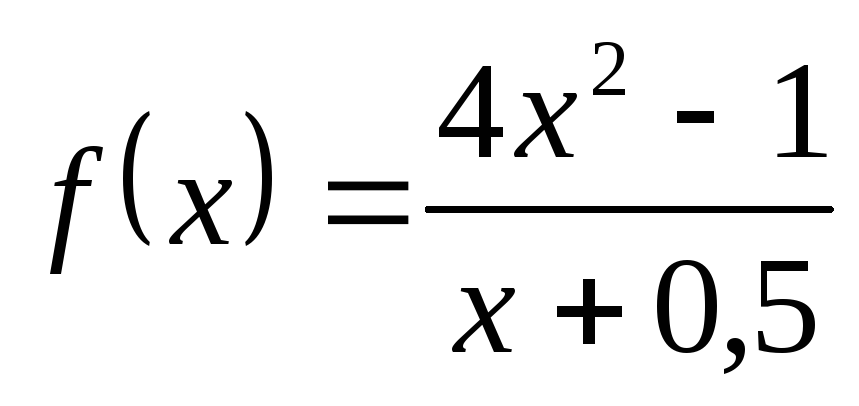 ; г)
; г) ;
;
3) а) 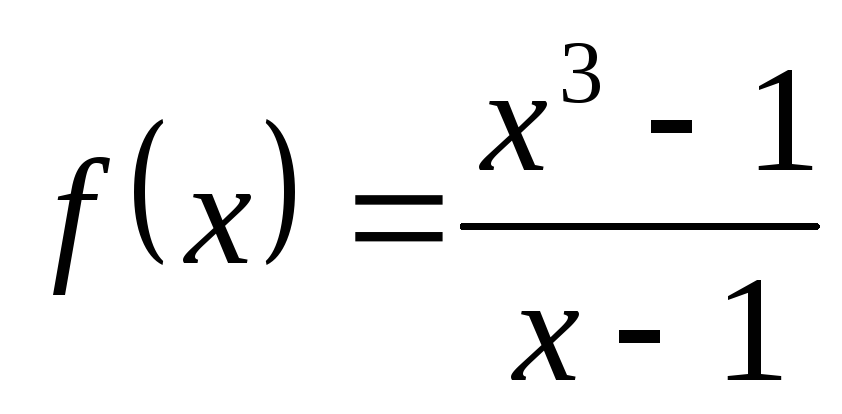 ; б)
; б)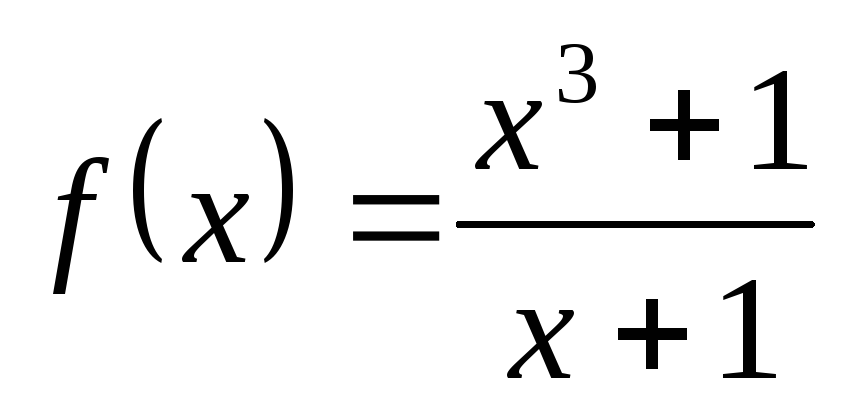 ; в)
; в)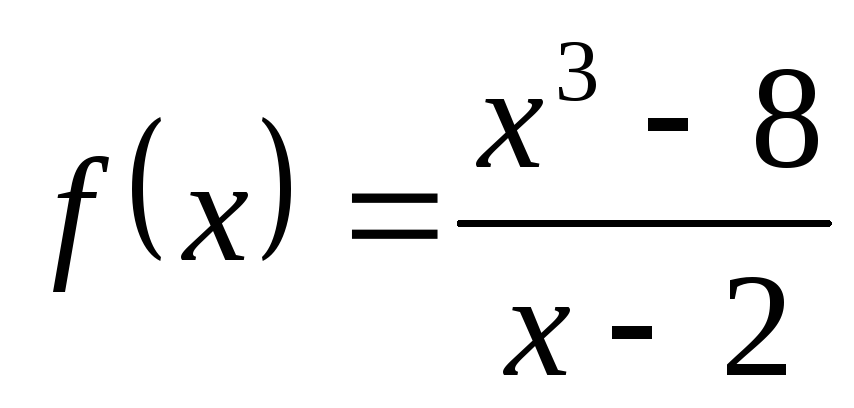 ; г)
; г)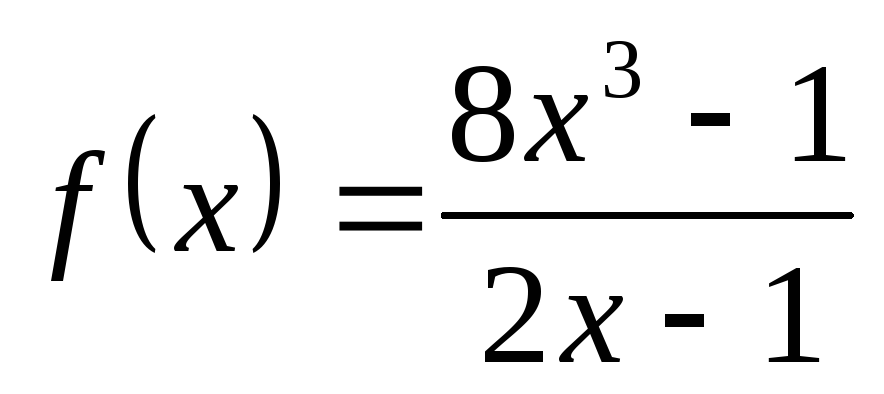 .
.
НФ8. Исследуйте на непрерывность дробно-рациональные функции. Покажите схематично поведение графика функции вблизи точки разрыва:
1) а) 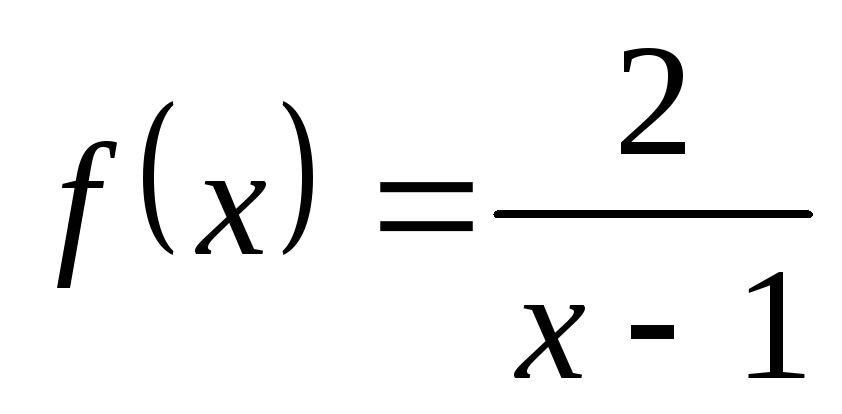 ; б)
; б)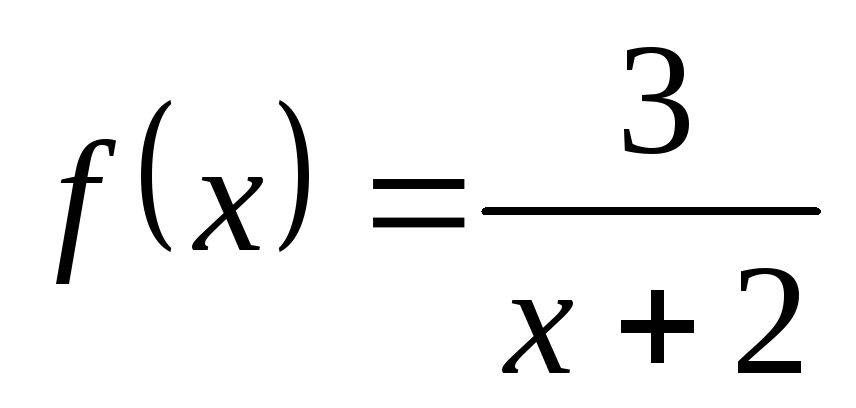 ; в)
; в)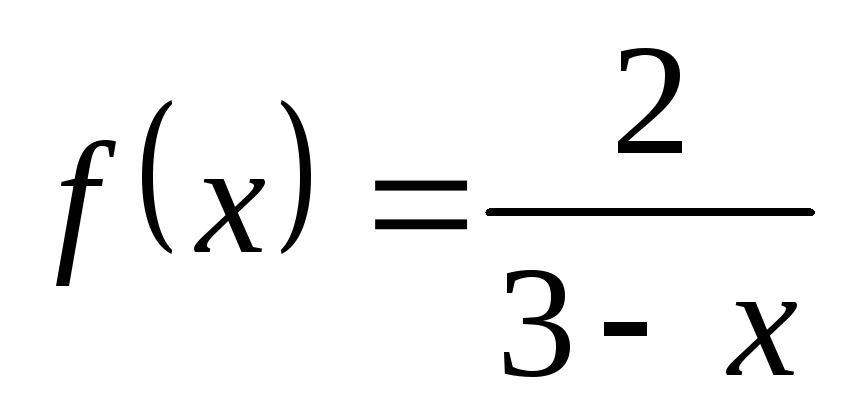 ; г)
; г)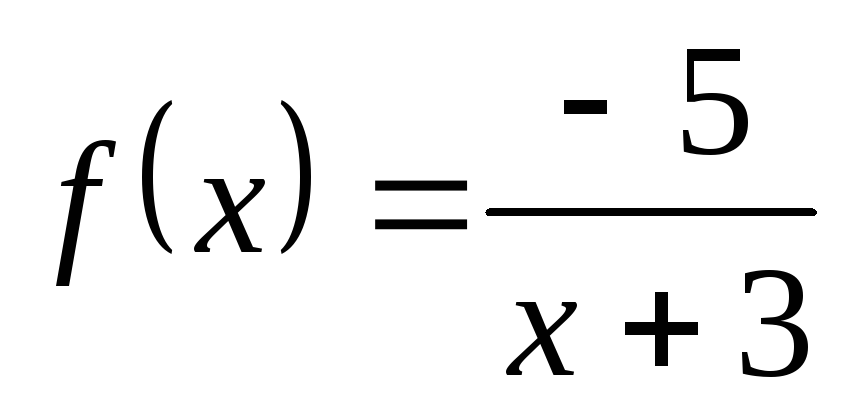 ;
;
2) а) 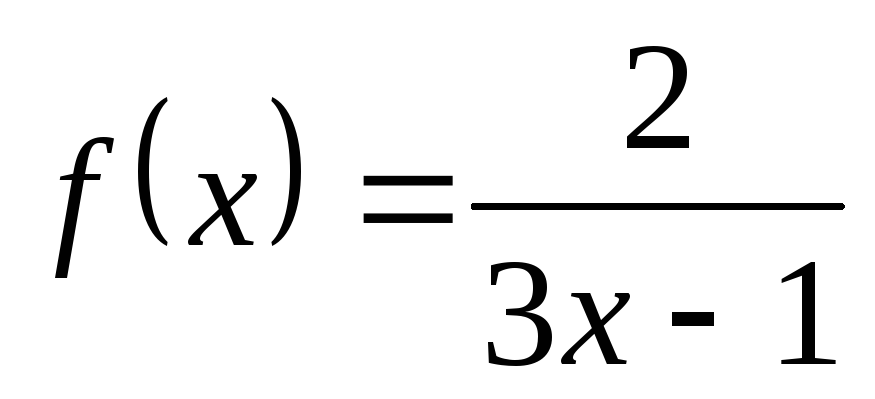 ; б)
; б)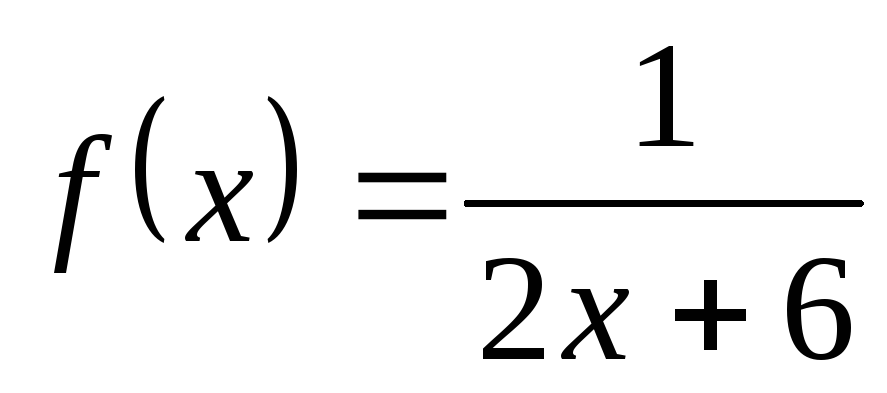 ; в)
; в)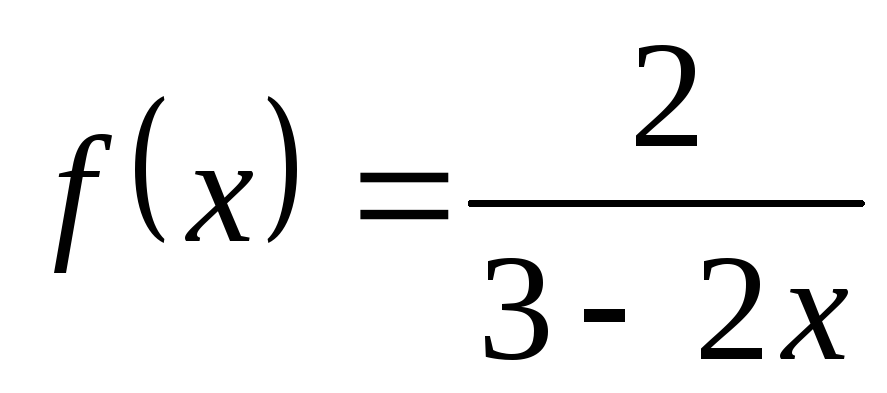 ; г)
; г)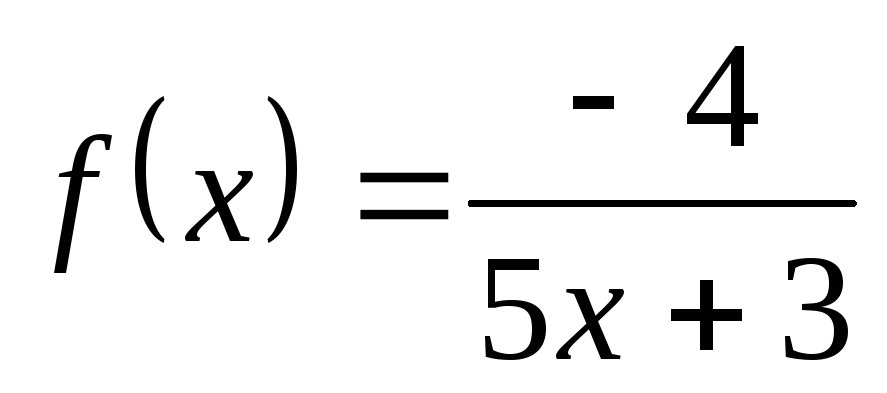 ;
;
3) а) 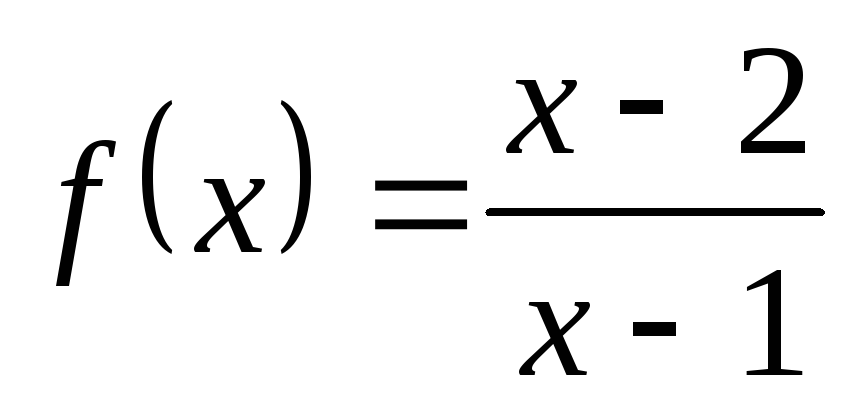 ; б)
; б)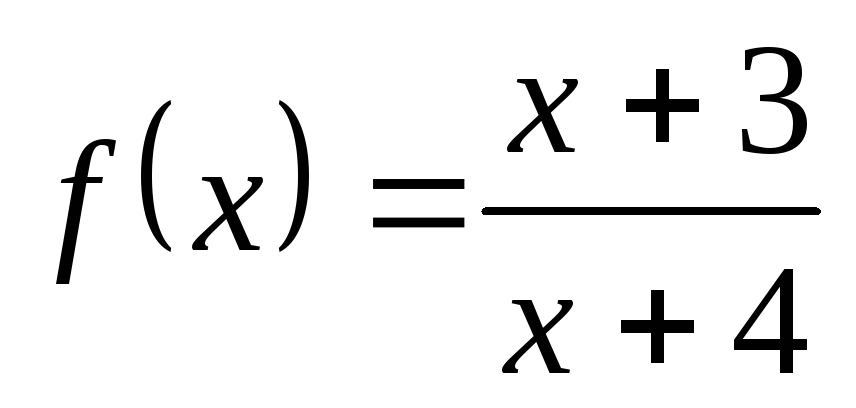 ; в)
; в)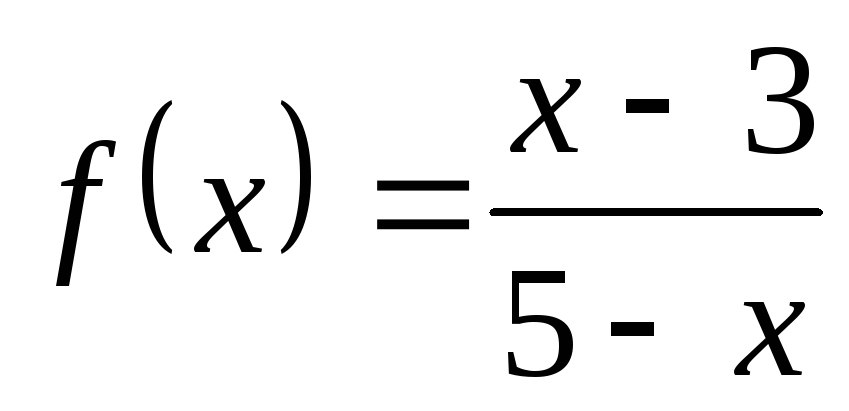 ; г)
; г)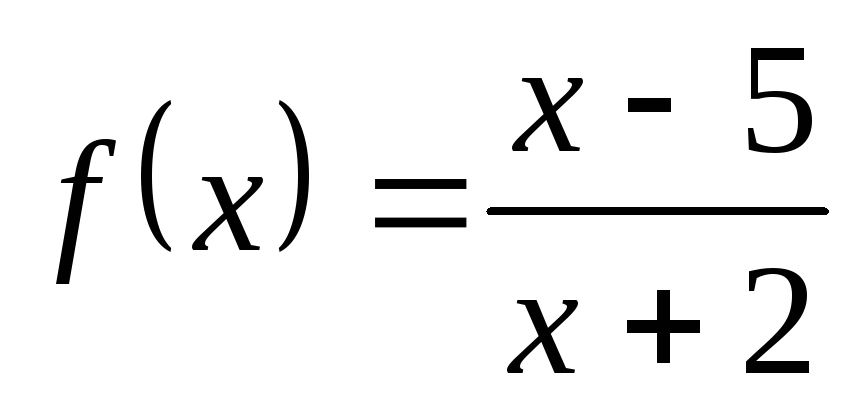 ;
;
4) а) 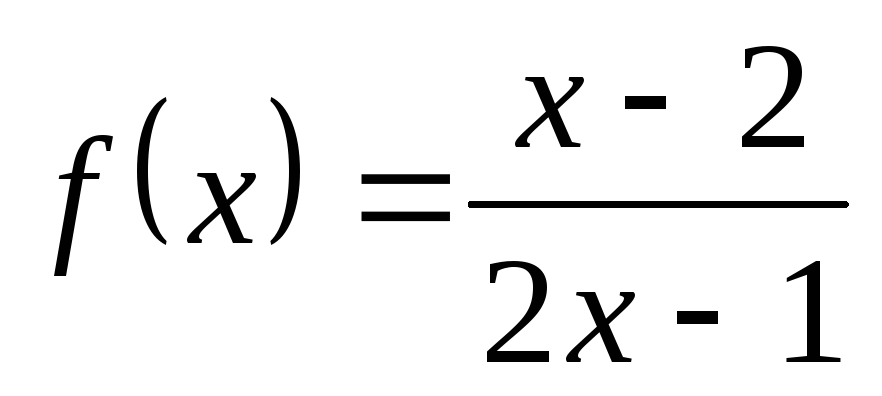 ; б)
; б)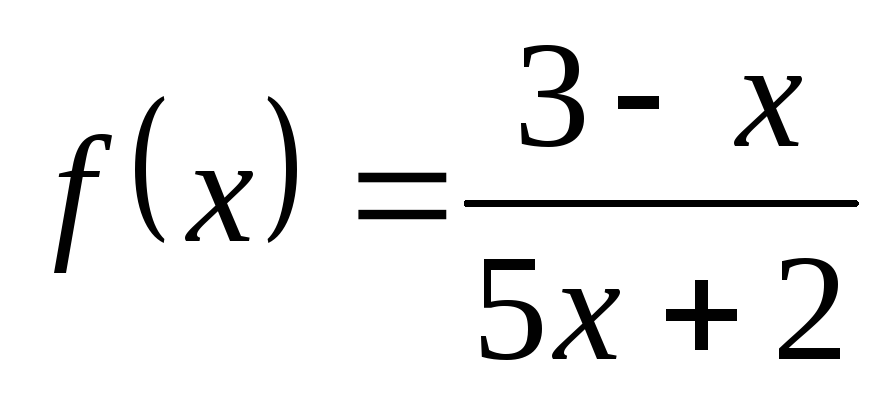 ; в)
; в)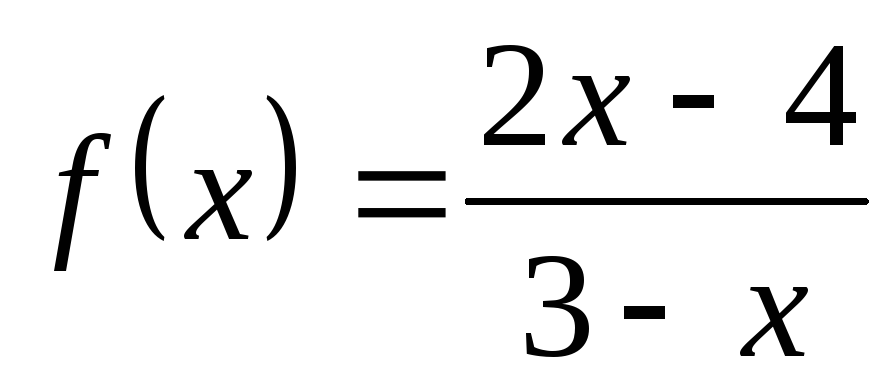 ; г)
; г)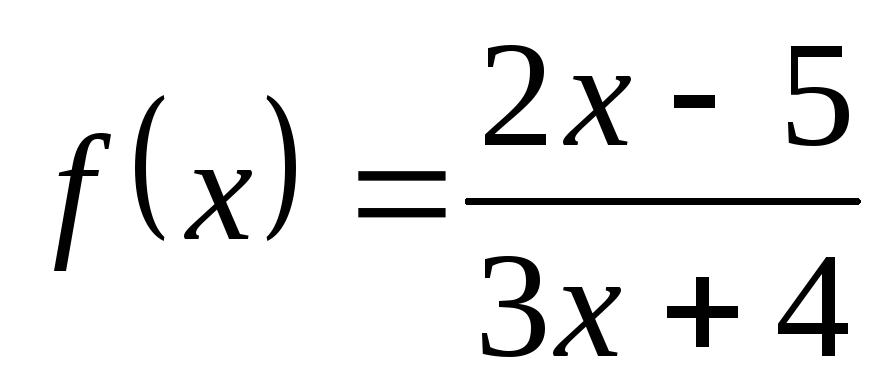 .
.
Пример
10. Пусть 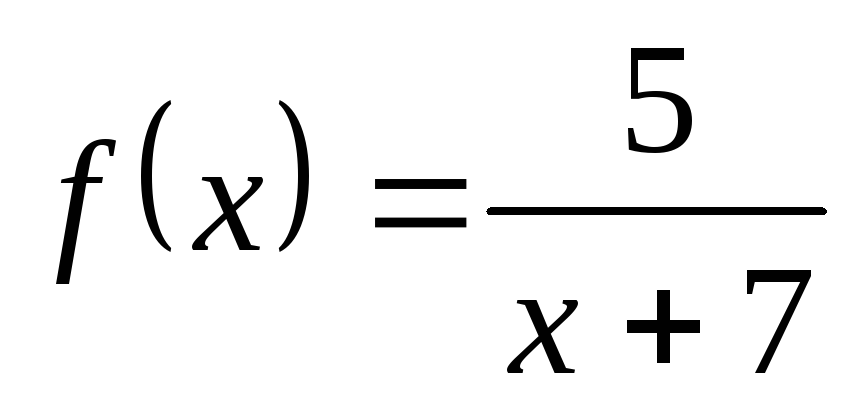 .
Эта функция не определена в точке
.
Эта функция не определена в точке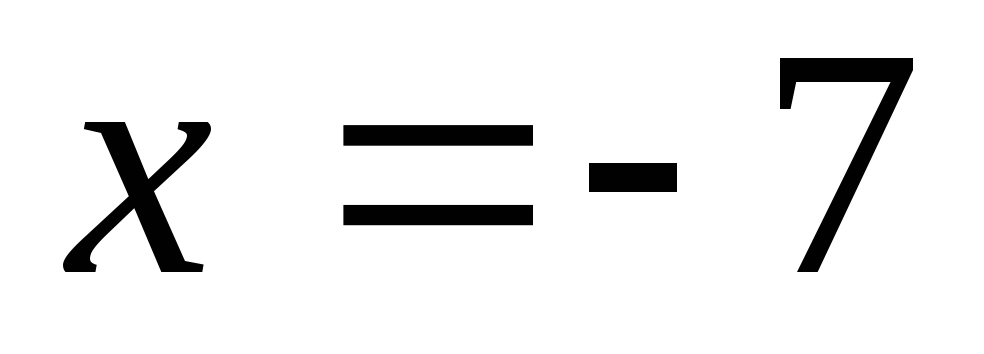 ,
где знаменатель равен 0. Во всех других
точках она определена и потому непрерывна
по свойству элементарных функций.
,
где знаменатель равен 0. Во всех других
точках она определена и потому непрерывна
по свойству элементарных функций.
Проверим точку 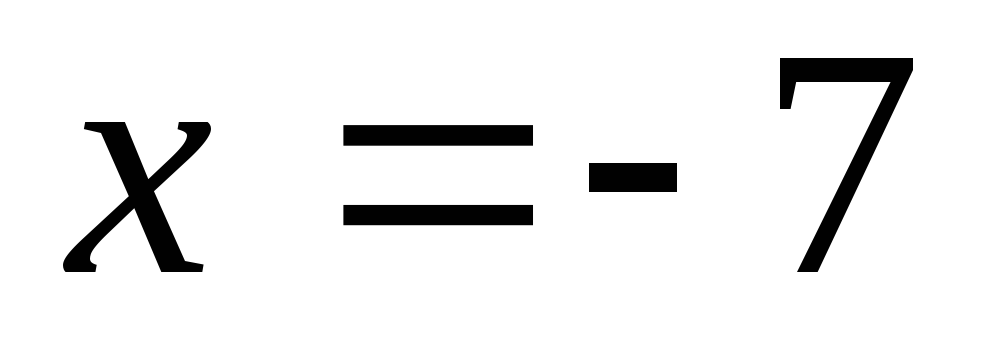 .
При подстановке её в функцию число 5
делится на бесконечно малую величину,
получается бесконечность, и тогда
.
При подстановке её в функцию число 5
делится на бесконечно малую величину,
получается бесконечность, и тогда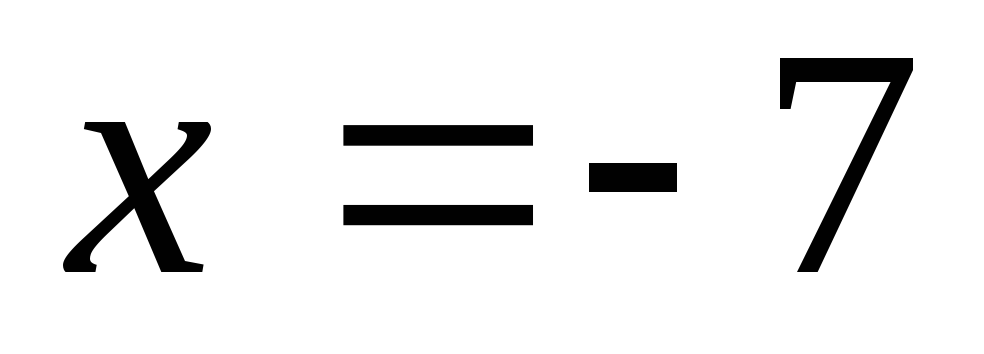 –точка
разрыва 2-го рода.
Для построения схематичного графика
находим пределы слева и справа:
–точка
разрыва 2-го рода.
Для построения схематичного графика
находим пределы слева и справа:
а) 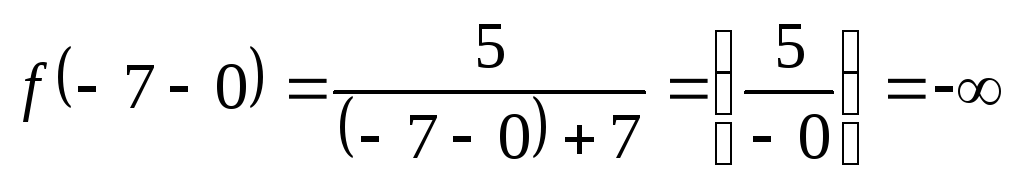 ;
;
б) 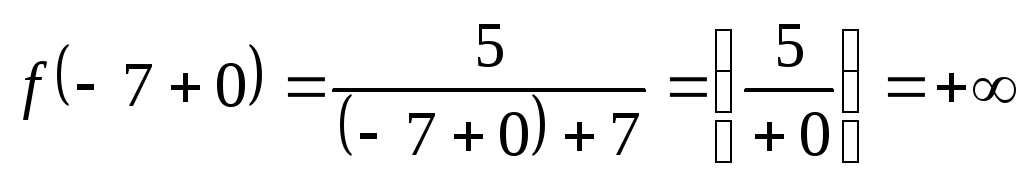 .
.
Если подходить к
точке 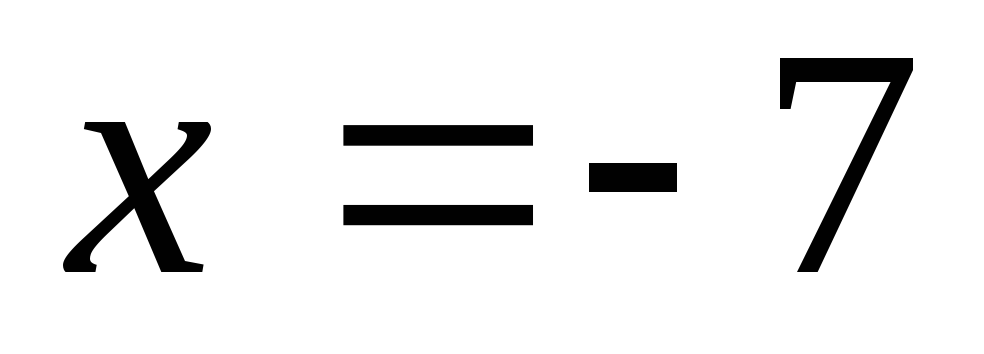 слева, график падает круто вниз вдоль
вертикальной прямой
слева, график падает круто вниз вдоль
вертикальной прямой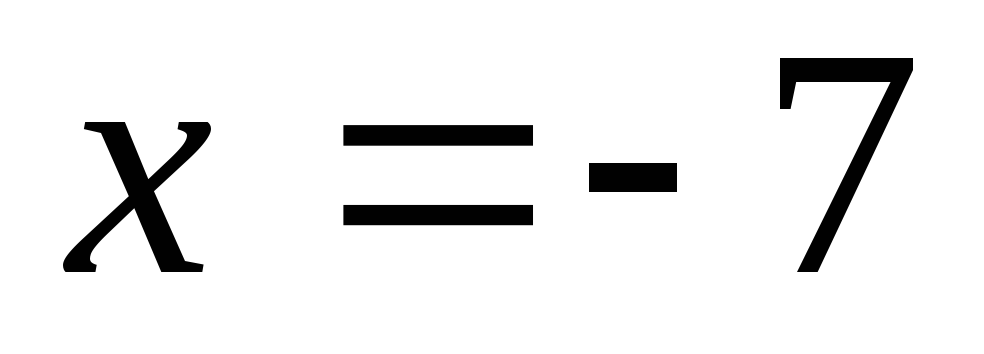 ,
а при подходе справа – круто поднимается
вверх.
,
а при подходе справа – круто поднимается
вверх.
Пример
11. Пусть 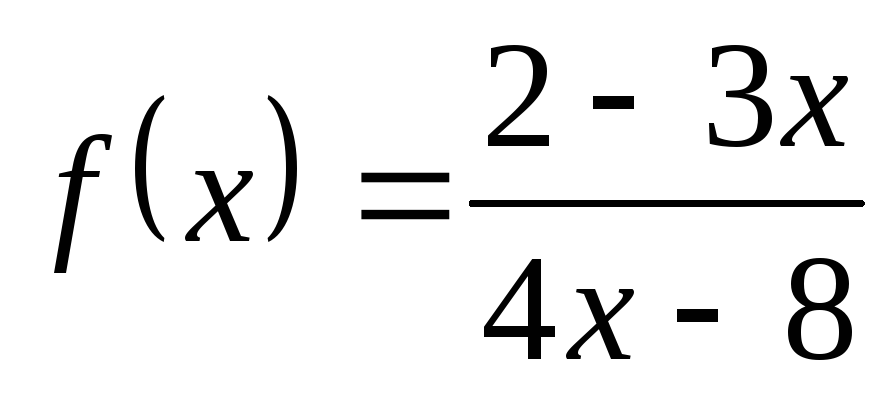 .
Функция непрерывна во всех точках, кроме
той, где
.
Функция непрерывна во всех точках, кроме
той, где ,
т.е. кроме точки
,
т.е. кроме точки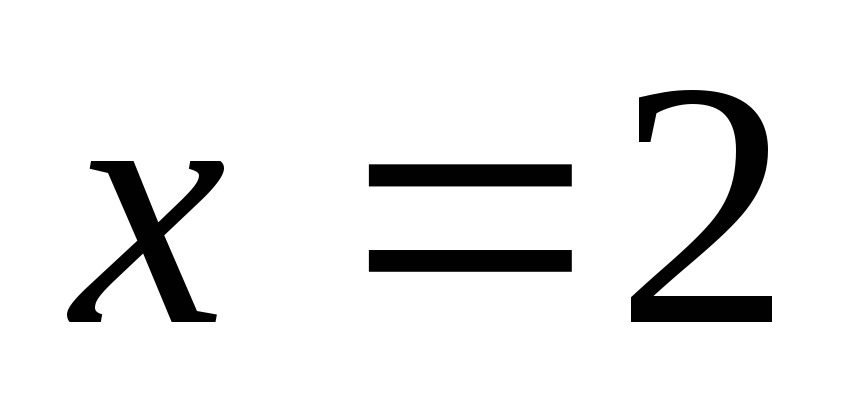 .
.
При подстановке 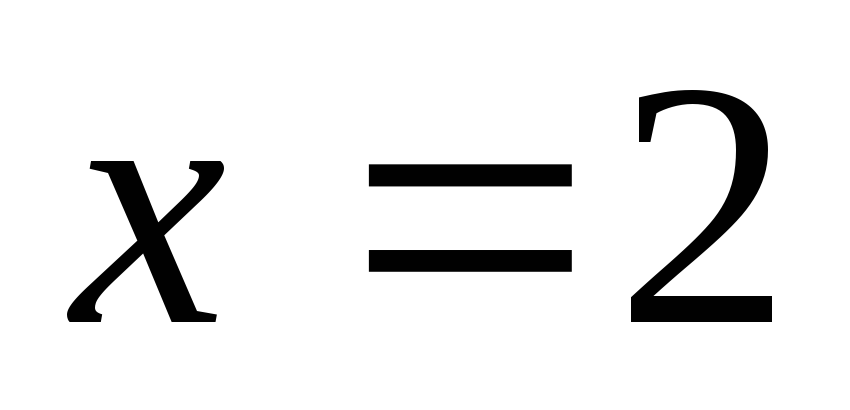 получим
получим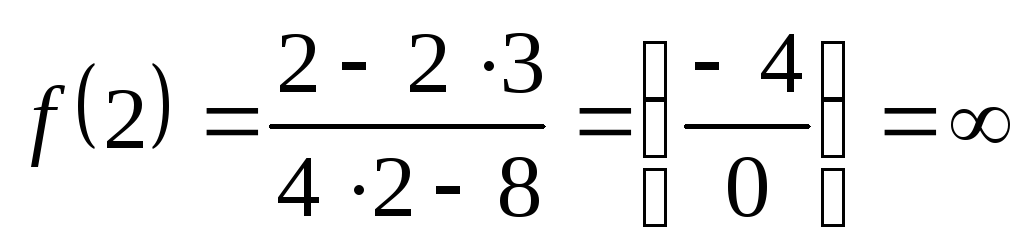 ,
и потому
,
и потому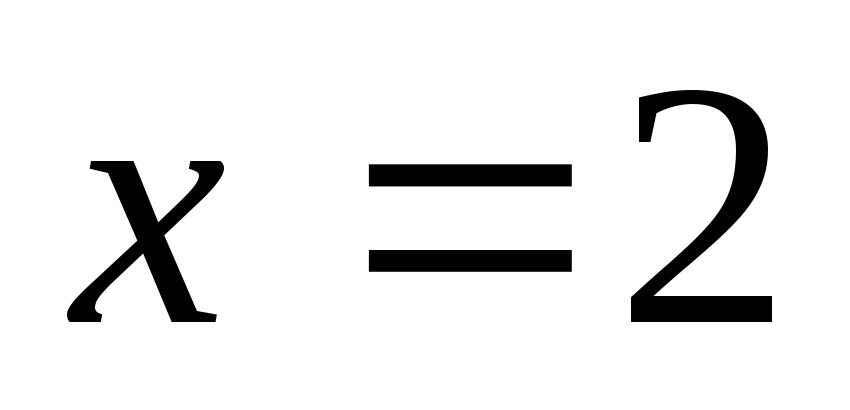 – точка разрыва 2-го рода. Найдём пределы
слева и справа:
– точка разрыва 2-го рода. Найдём пределы
слева и справа:
а) 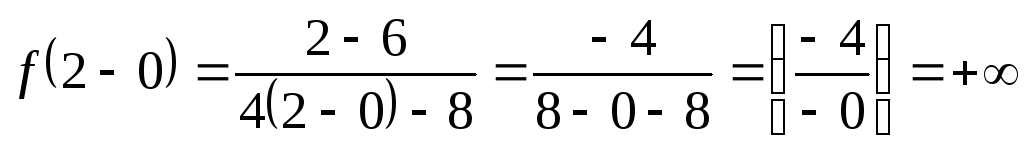 ;
;
б) 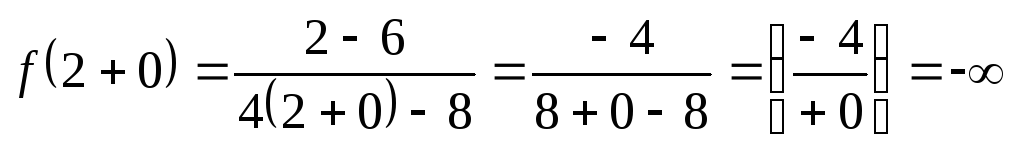 .
.
При подходе
аргумента x слева к точке 2 график поднимается вдоль
вертикальной прямой  ,
а при подходе справа – круто падает.
,
а при подходе справа – круто падает.
НФ9. Исследуйте на непрерывность дробно-рациональные функции. Покажите схематично поведение графика функции вблизи точки разрыва:
1) а) 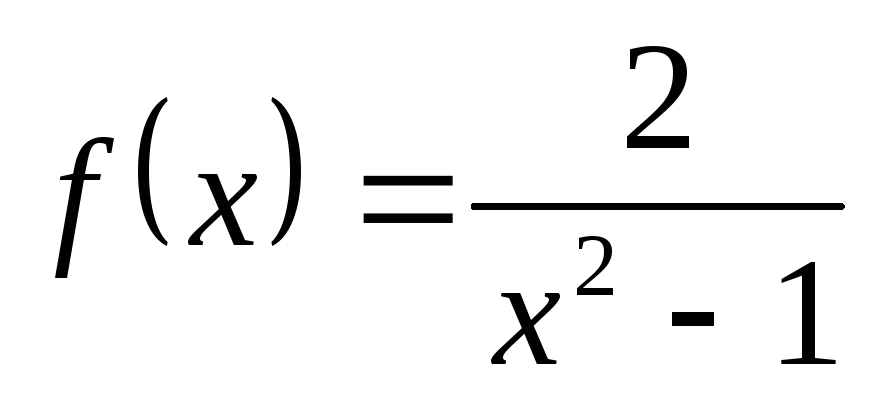 ; б)
; б)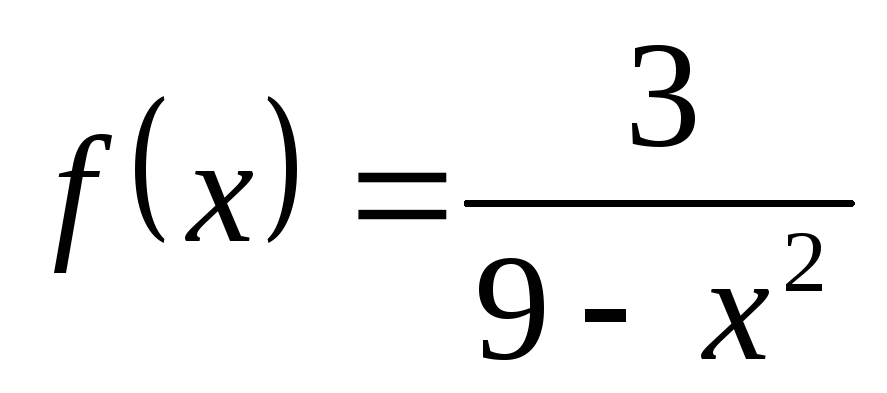 ; в)
; в)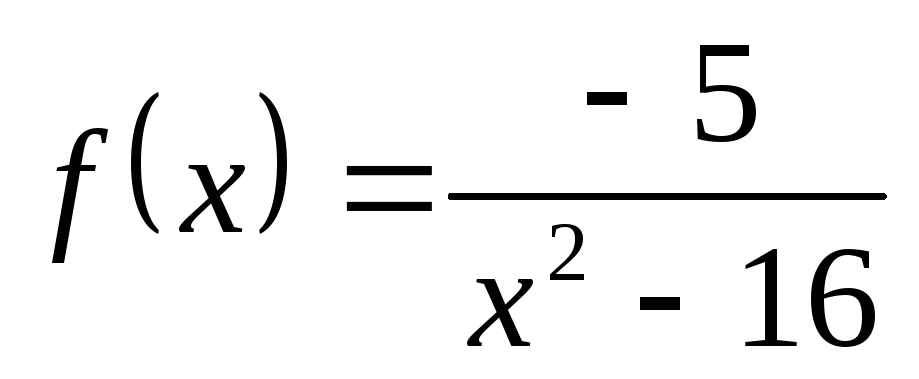 ;
;
2) а) 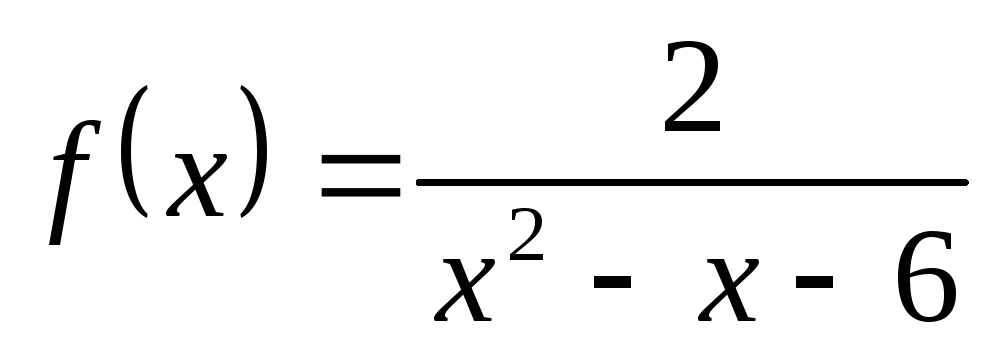 ; б)
; б)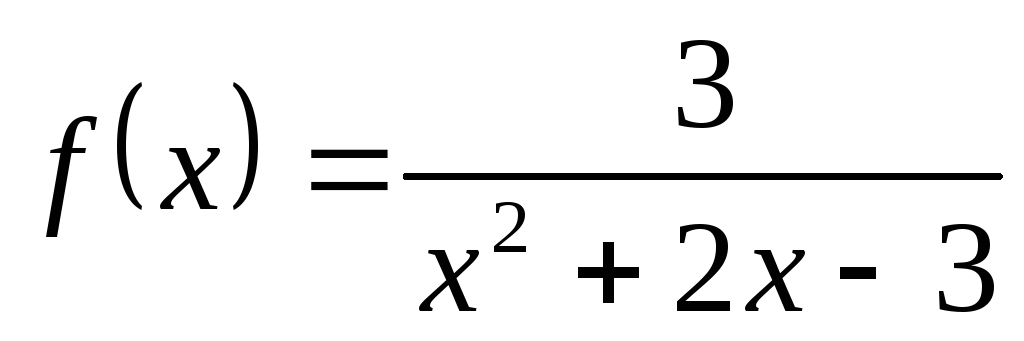 ; в)
; в)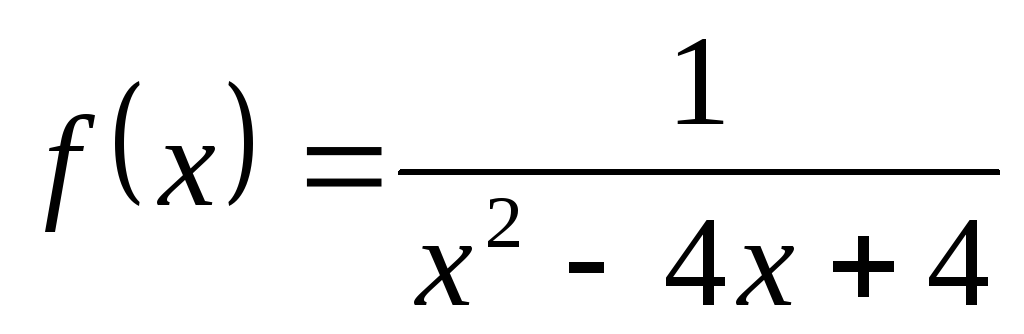 ;
;
3) а) 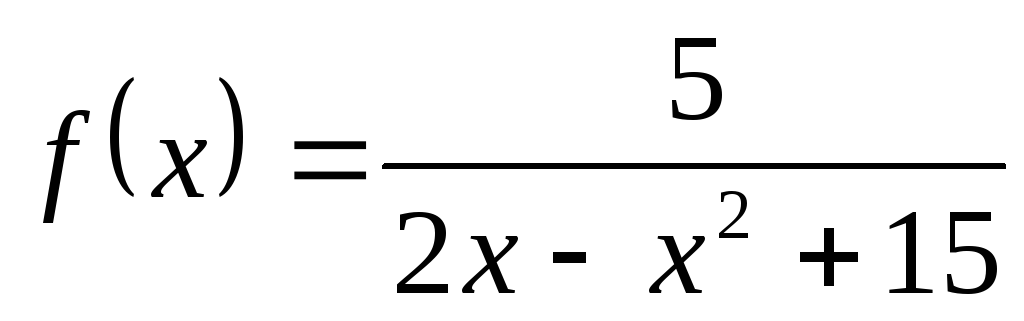 ; б)
; б)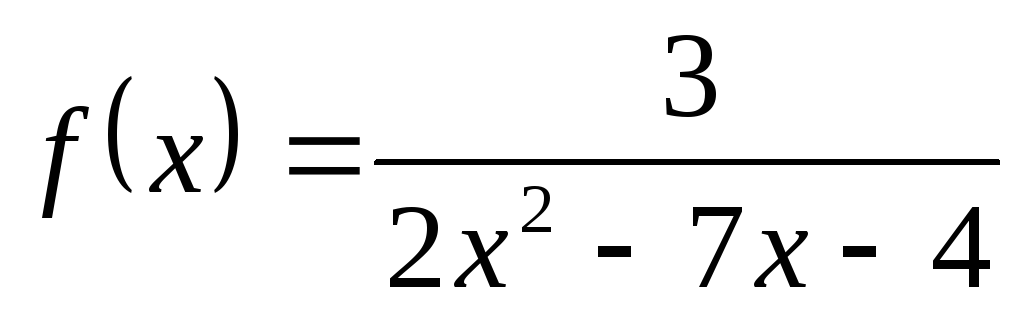 ; в)
; в)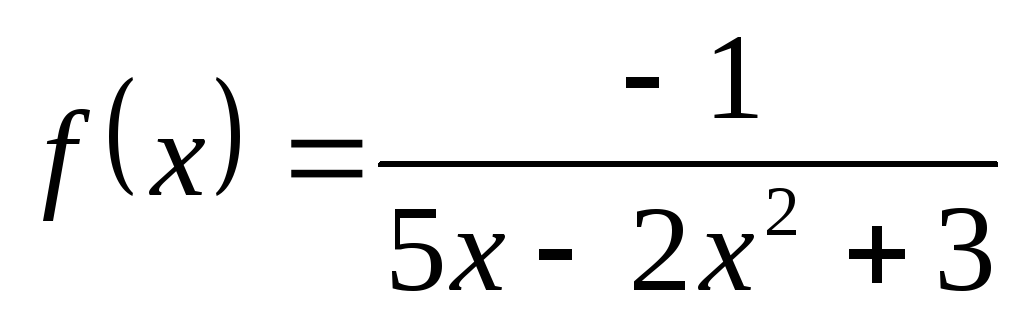 ;
;
4) а) 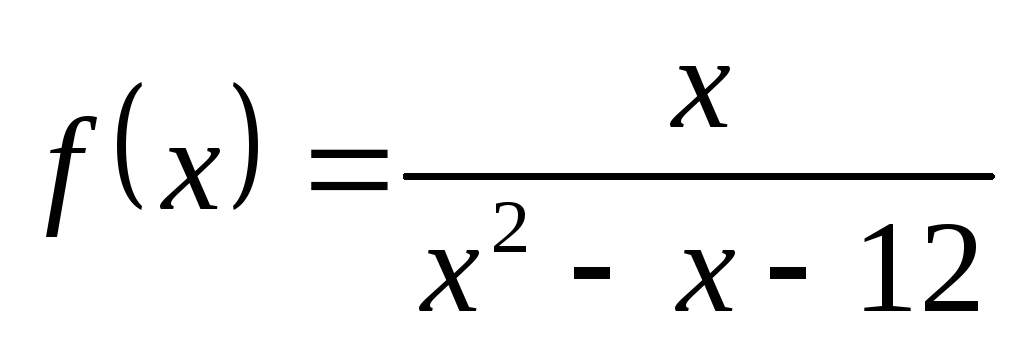 ; б)
; б)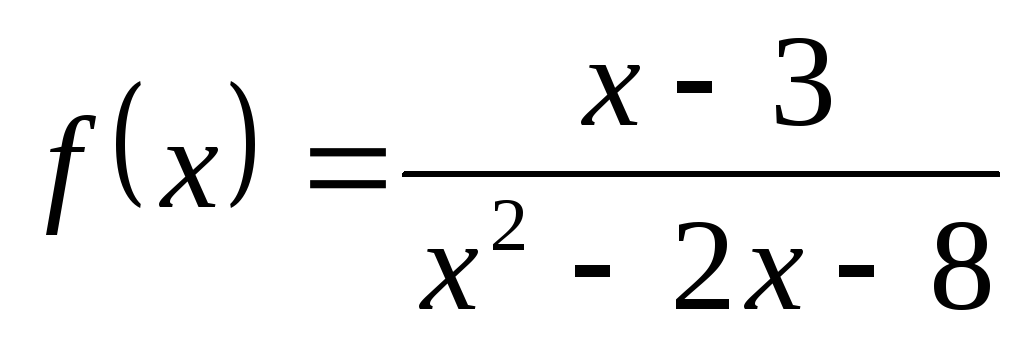 ; в)
; в)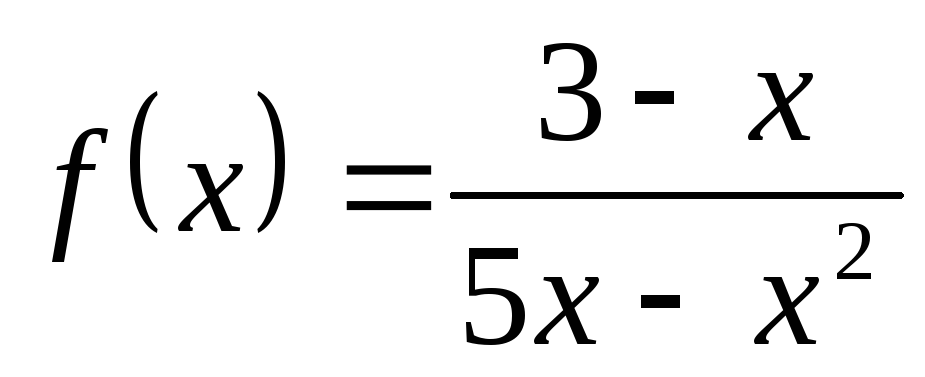 .
.
Пример
12. Пусть 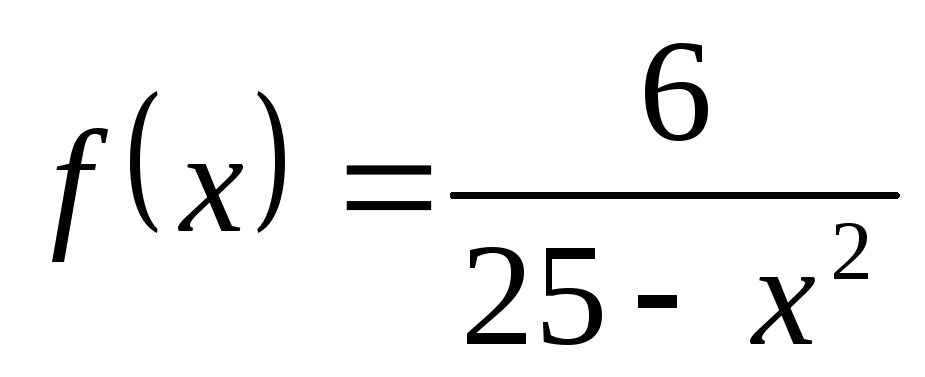 .
Функция не определена при
.
Функция не определена при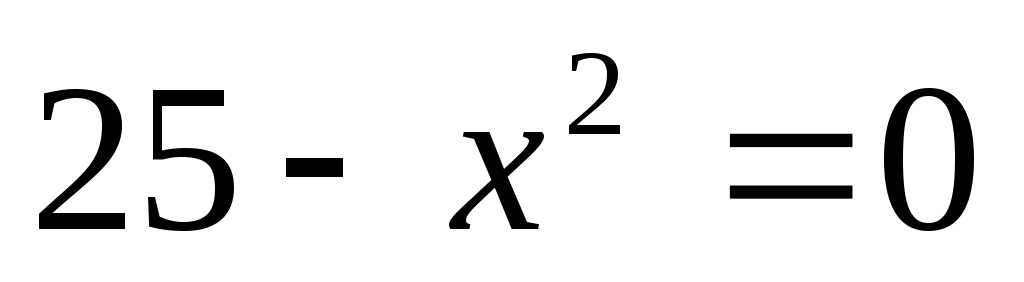 .
Корни знаменателя – числа
.
Корни знаменателя – числа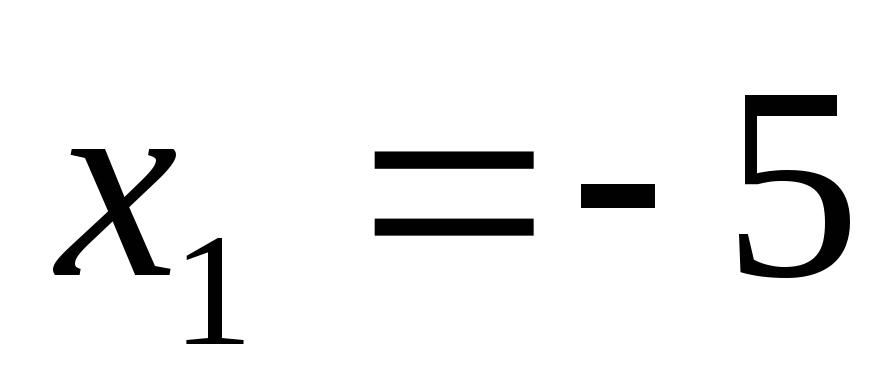 и
и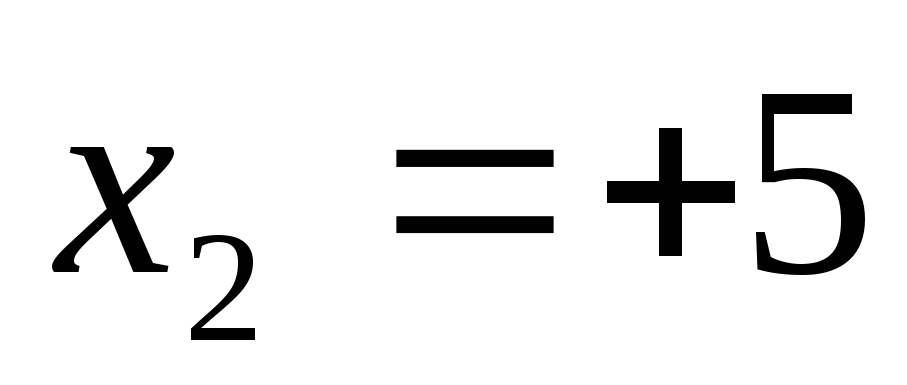 .
Во всех других точках функция определена
и потому непрерывна как элементарная.
.
Во всех других точках функция определена
и потому непрерывна как элементарная.
При 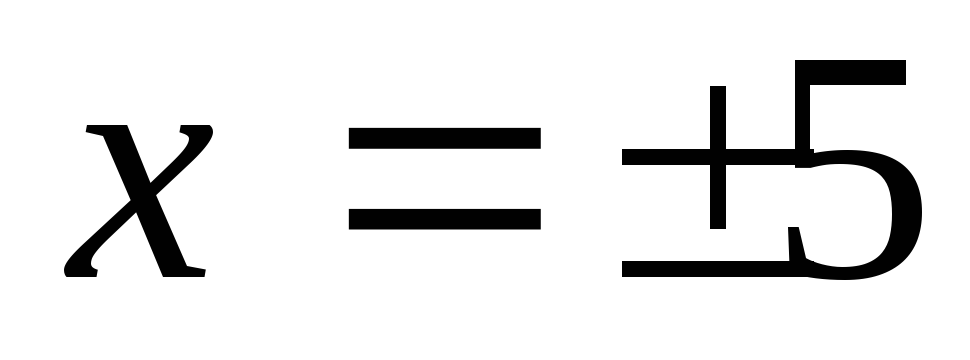 получим
получим ,
и поэтому обе точки – точки разрыва
2-го рода. Дальнейшие действия лишь
уточняют знак бесконечности при подходе
к точкам с конкретных сторон. При
вычислении воспользуемся «методом
близкой точки». Его идея – узнать знак
функции в точках,близких к тем, что нас интересуют.
,
и поэтому обе точки – точки разрыва
2-го рода. Дальнейшие действия лишь
уточняют знак бесконечности при подходе
к точкам с конкретных сторон. При
вычислении воспользуемся «методом
близкой точки». Его идея – узнать знак
функции в точках,близких к тем, что нас интересуют.
Пусть 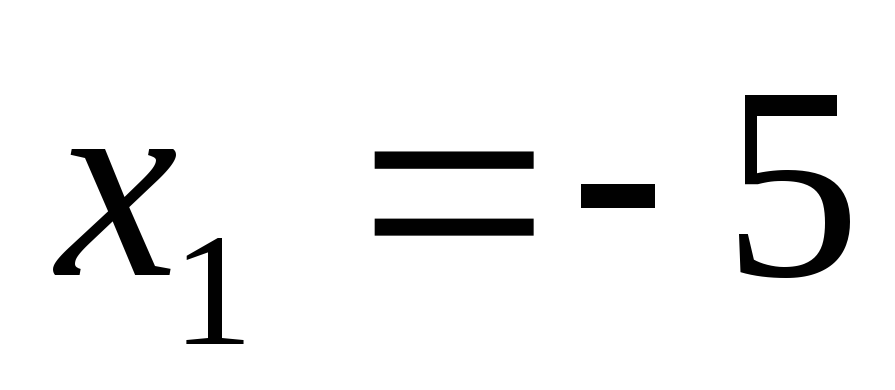 .
Вместо точек –5–0 и –5+0 возьмём
соответственно –5,1 и –4,9:
.
Вместо точек –5–0 и –5+0 возьмём
соответственно –5,1 и –4,9:
а) 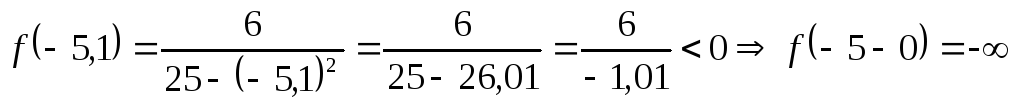 ;
;
б) 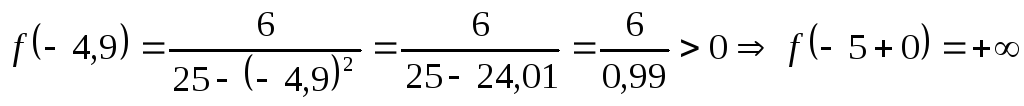 .
.
При подходе слева к точке –5 график падает, при подходе справа – поднимается.
Пусть 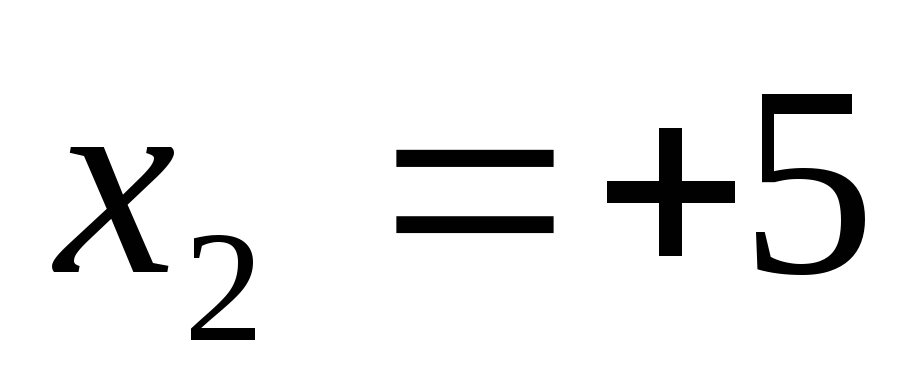 .
Вместо точек 5–0 и 5+0 возьмём соответственно
4,9 и 5,1:
.
Вместо точек 5–0 и 5+0 возьмём соответственно
4,9 и 5,1:
а)  .
.
б) 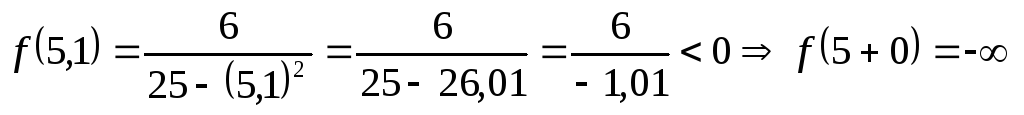 ;
;
При подходе слева к точке 5 график поднимается, при подходе справа – падает.
Пример
13. Пусть 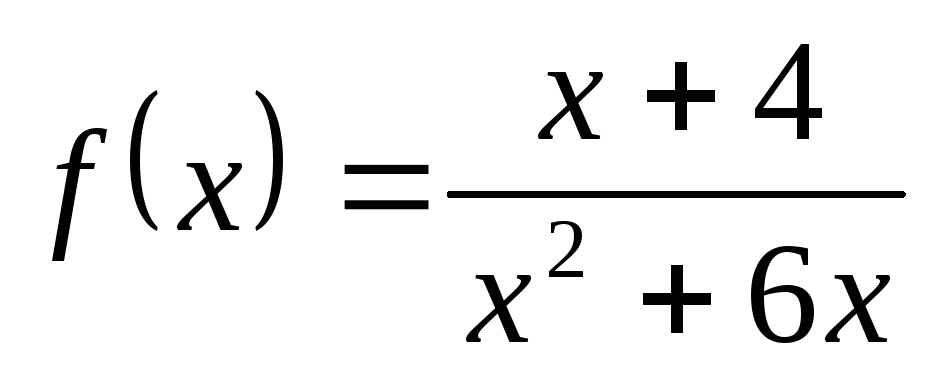 .
Корни знаменателя – числа
.
Корни знаменателя – числа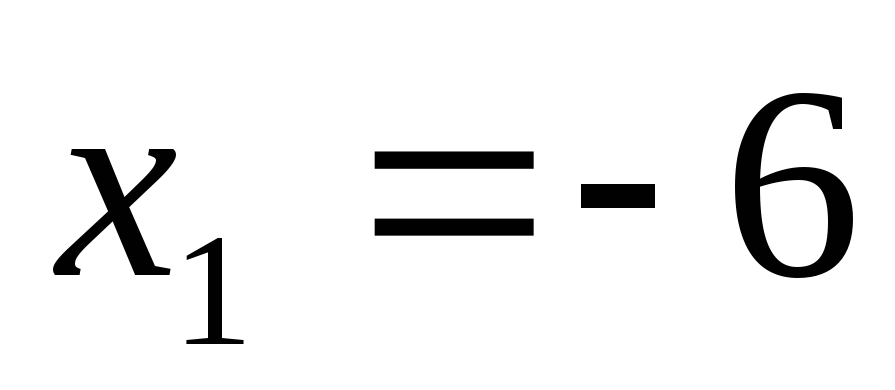 и
и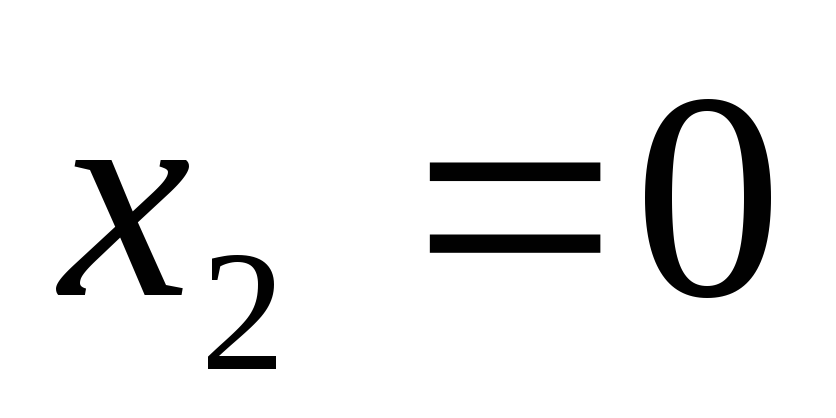 .
В остальных точках функция непрерывна.
.
В остальных точках функция непрерывна.
Подставив, получим 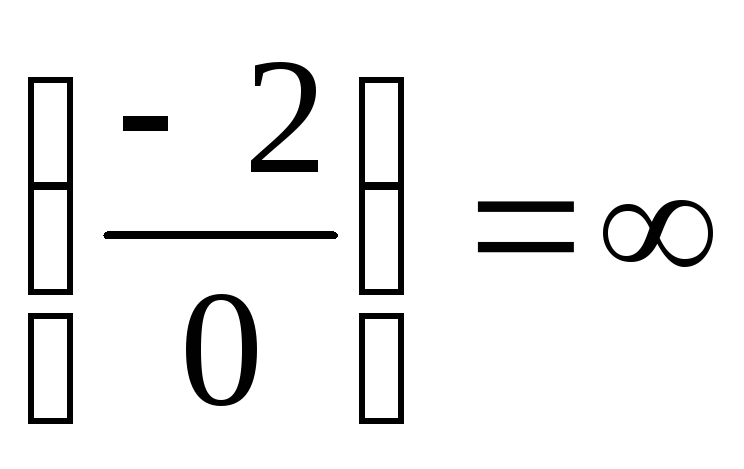 и
и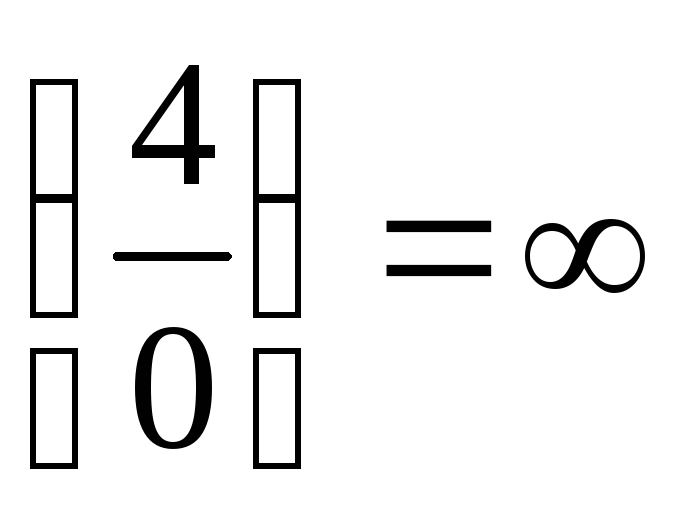 – перед нами точки разрыва 2-го рода.
Для уточнения знаков бесконечности
применяем «метод близкой точки».
– перед нами точки разрыва 2-го рода.
Для уточнения знаков бесконечности
применяем «метод близкой точки».
Для 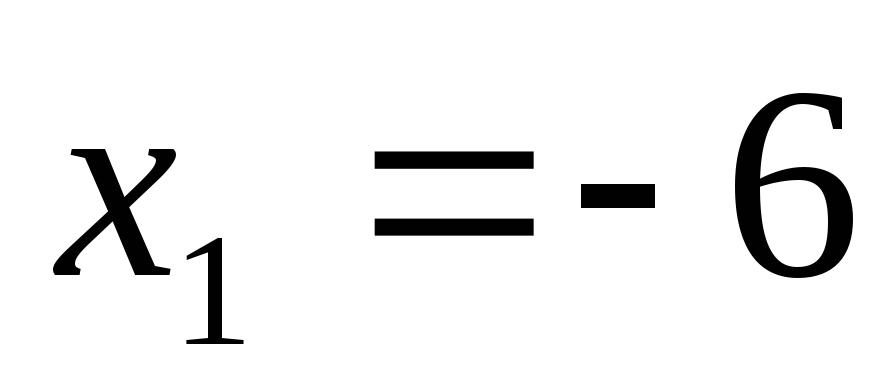 в качестве –6–0 и –6+0 берём соответственно
–6,1 и –5,9:
в качестве –6–0 и –6+0 берём соответственно
–6,1 и –5,9:
а) 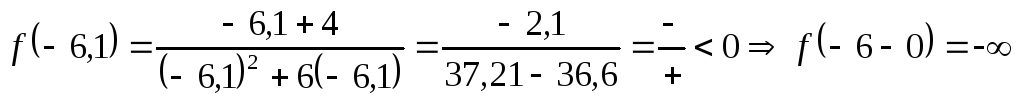 ;
;
б) 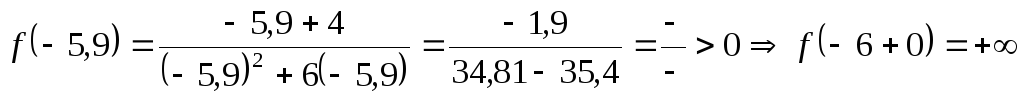 .
.
Для 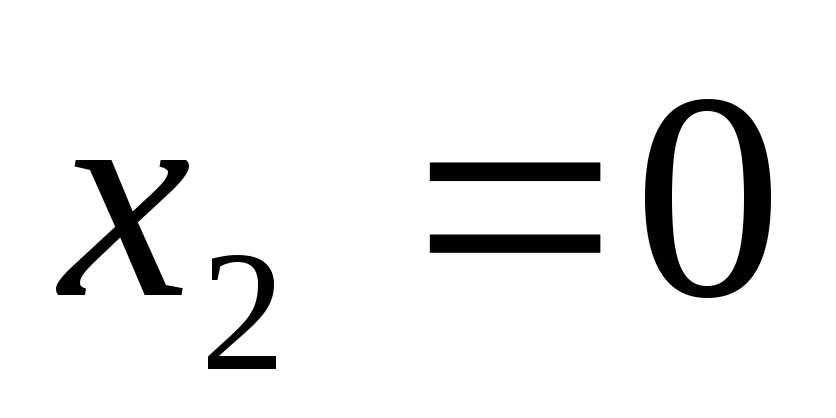 в качестве –0 и +0 возьмём соответственно
–0,1 и +0,1:
в качестве –0 и +0 возьмём соответственно
–0,1 и +0,1:
а) 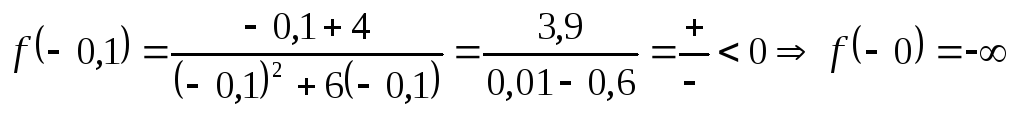 ;
;
б) 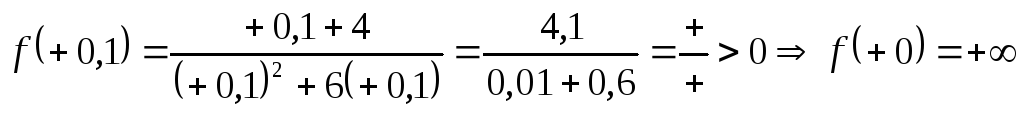 .
.
Вблизи точек –6 и 0 график ведёт себя одинаково – слева падает, справа растёт.
НФ10. Исследуйте на непрерывность дробно-рациональные функции. Покажите схематично поведение графика функции вблизи точки разрыва:
1) а) 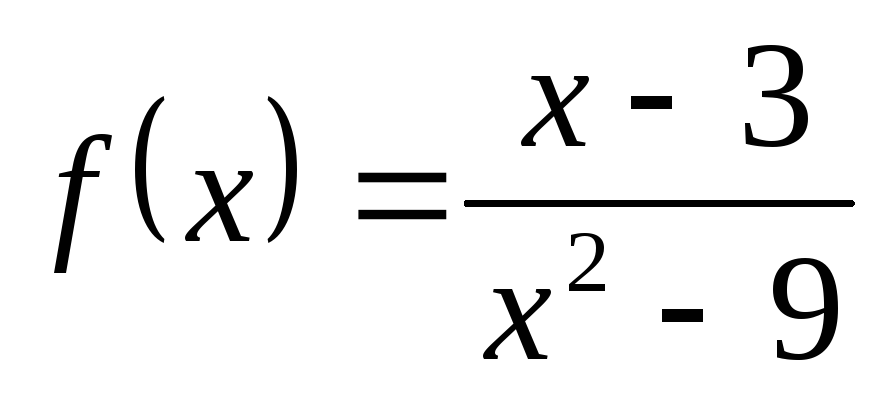 ; б)
; б)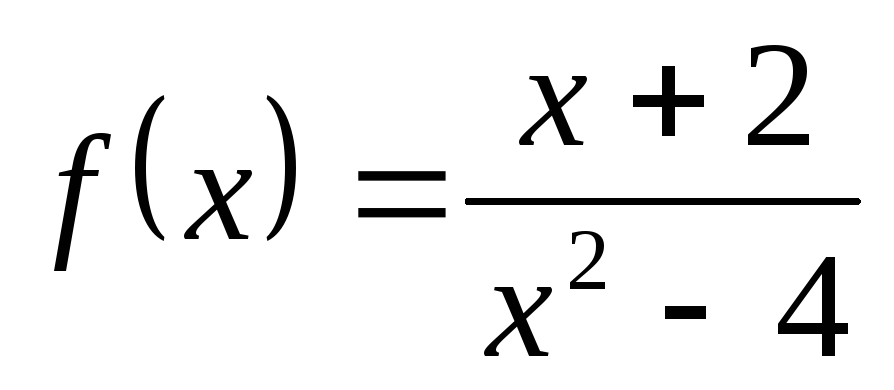 ; в)
; в)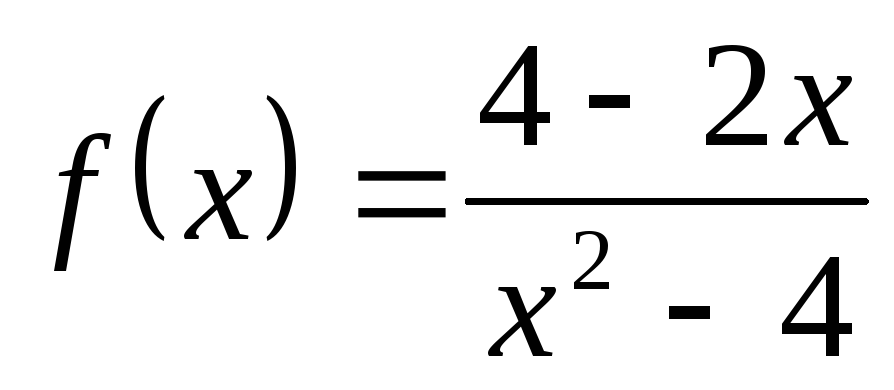 ;
;
2) а) 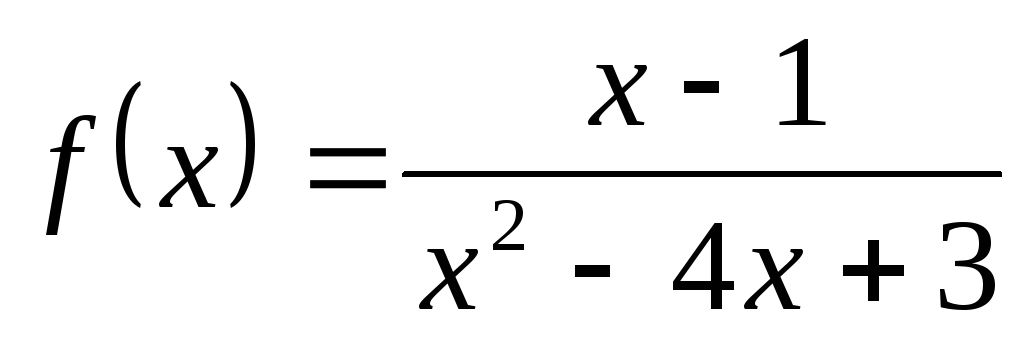 ; б)
; б)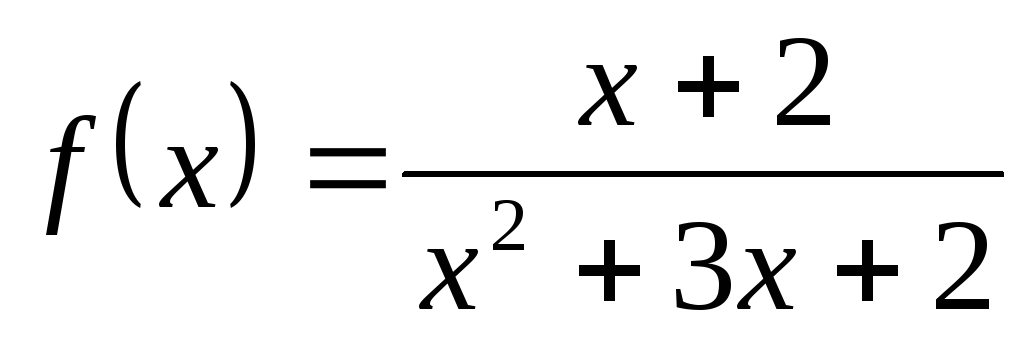 ; в)
; в)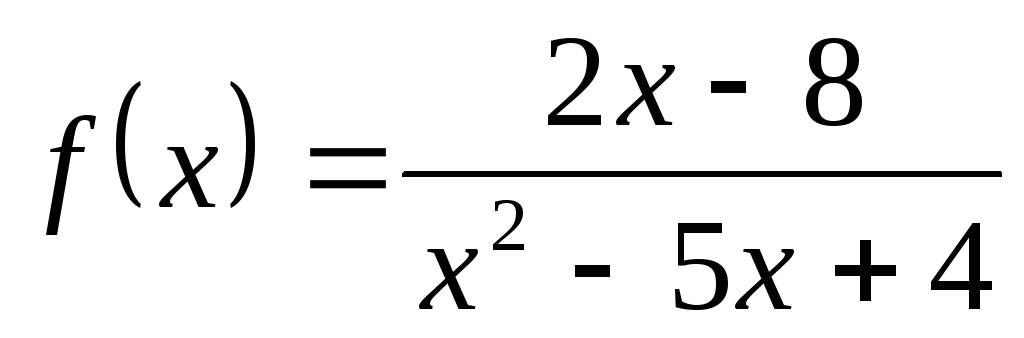 ;
;
3) а) 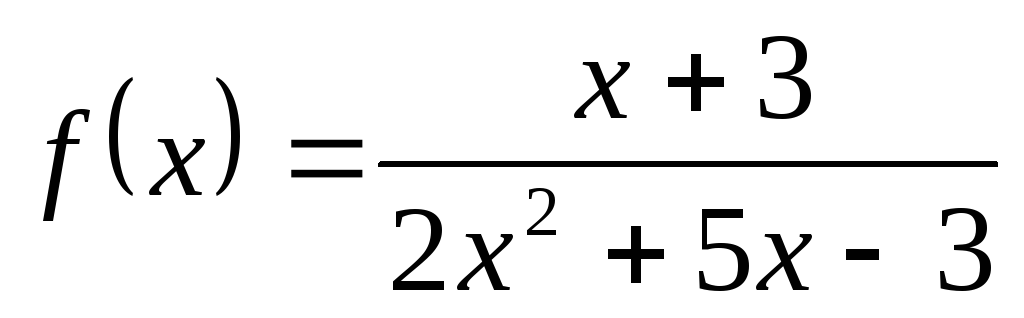 ; б)
; б)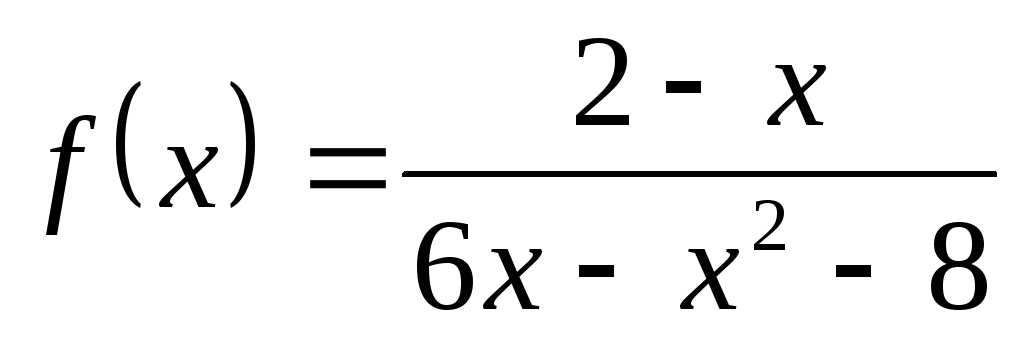 ; в)
; в) ;
;
4) а) 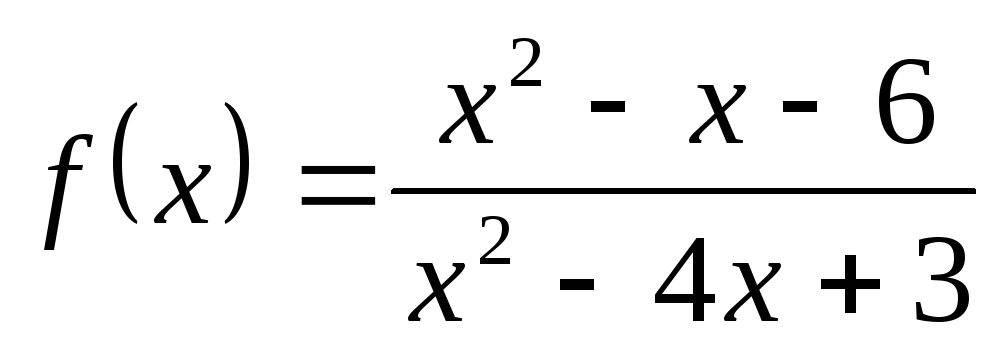 ; б)
; б)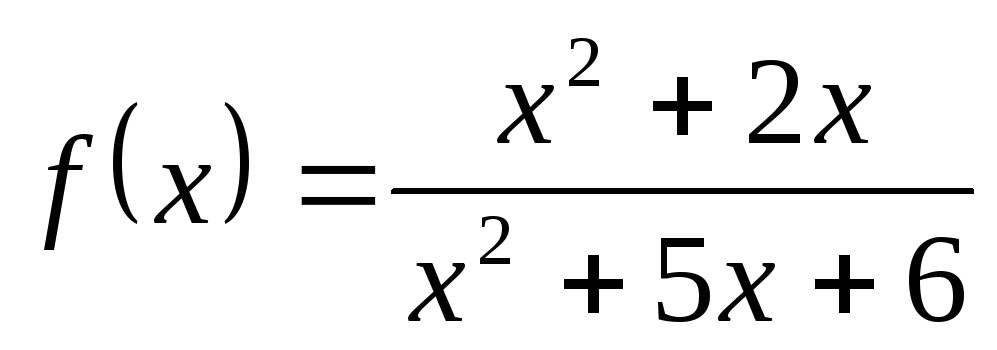 ; в)
; в)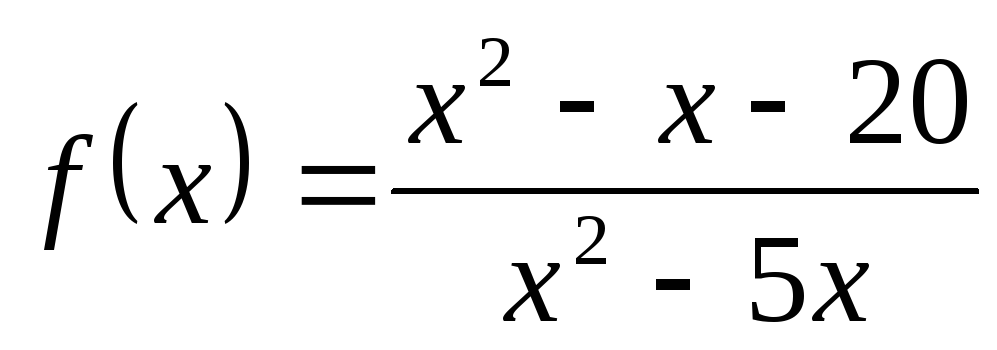 .
.
Пример
14. Пусть 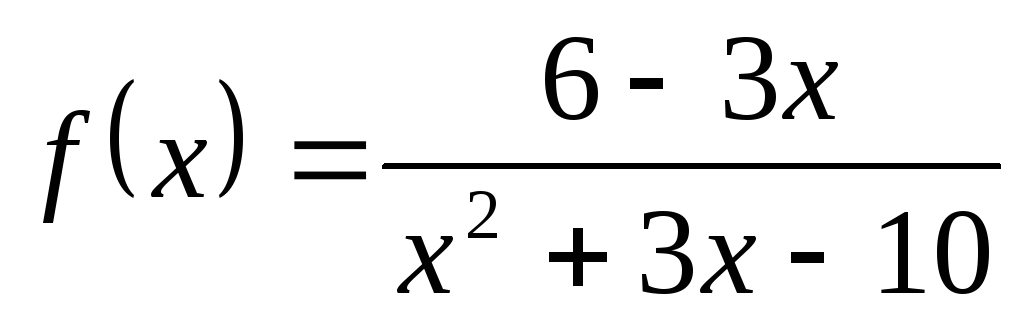 .
Решив уравнение
.
Решив уравнение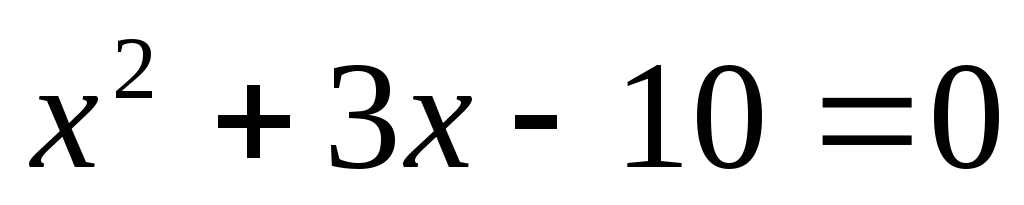 ,
получаем корни
,
получаем корни и
и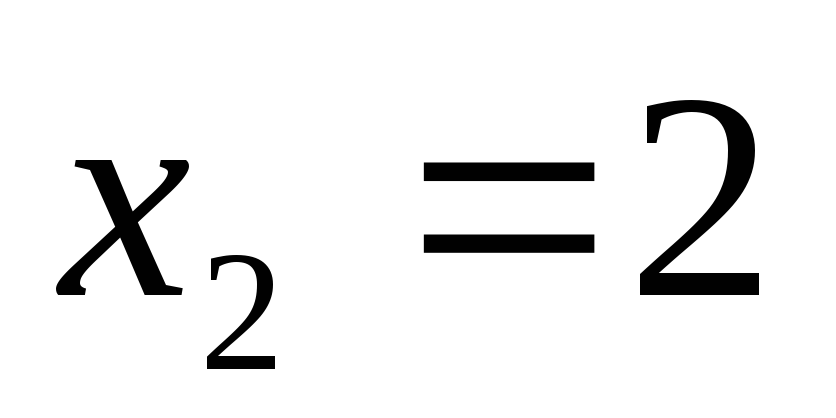 .
В остальных точках функция непрерывна.
.
В остальных точках функция непрерывна.
Подставив 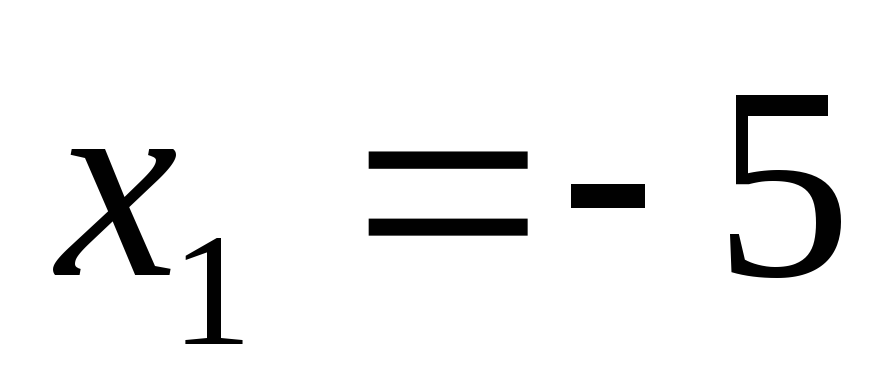 ,
получим
,
получим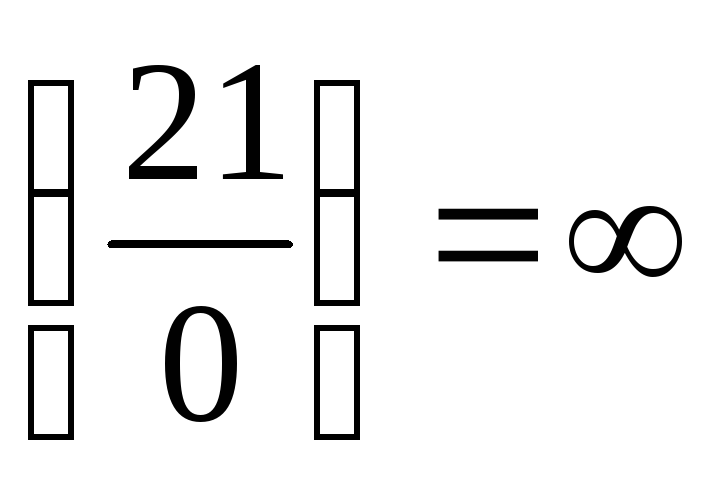 .
Значит,
.
Значит,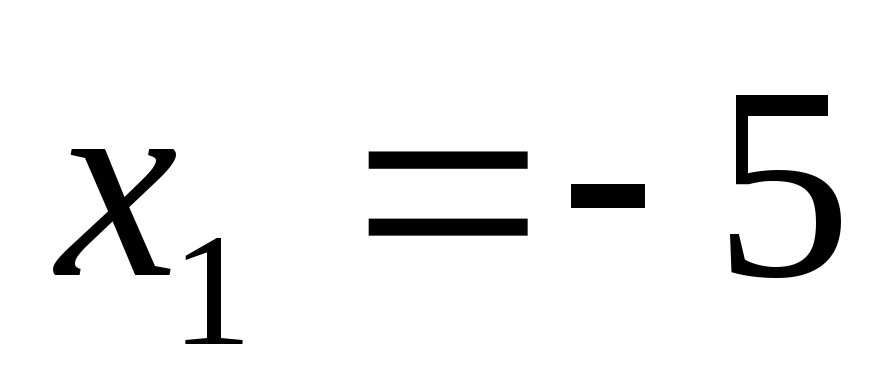 – точка разрыва 2-го рода. Уточним знак
бесконечности:
– точка разрыва 2-го рода. Уточним знак
бесконечности:
а) 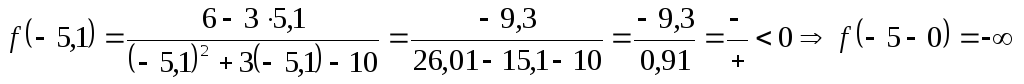 ;
;
б) 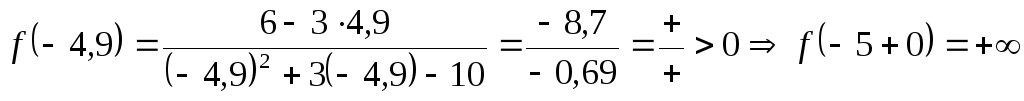 .
.
Подставив 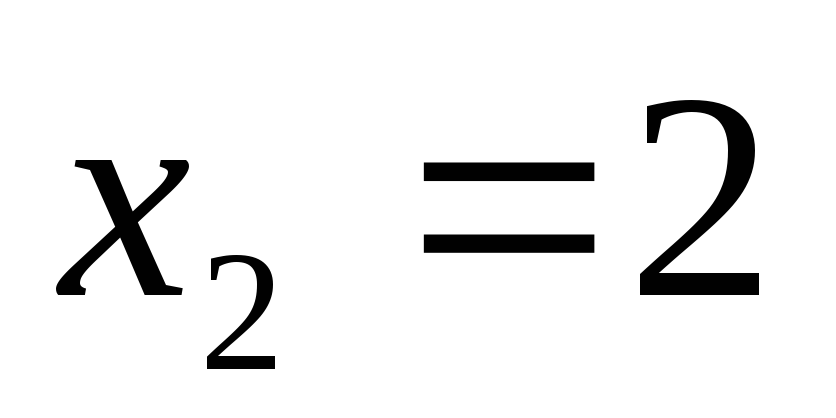 ,
получим
,
получим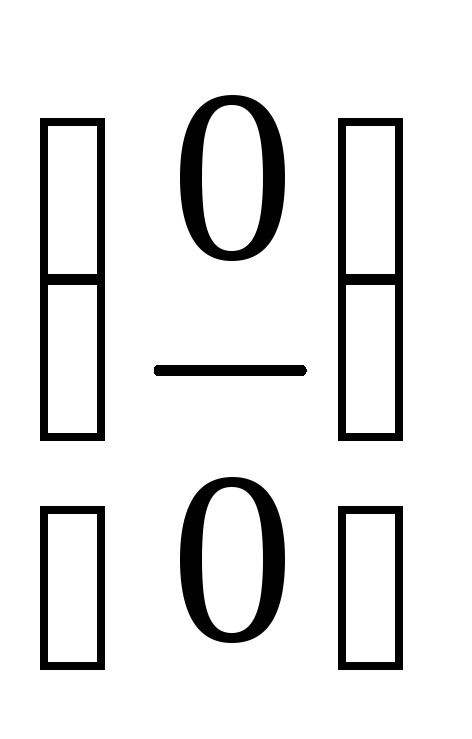 .
В этом случае, как известно, надо упростить
дробь, разложив на скобки и сократив
одинаковые:
.
В этом случае, как известно, надо упростить
дробь, разложив на скобки и сократив
одинаковые:
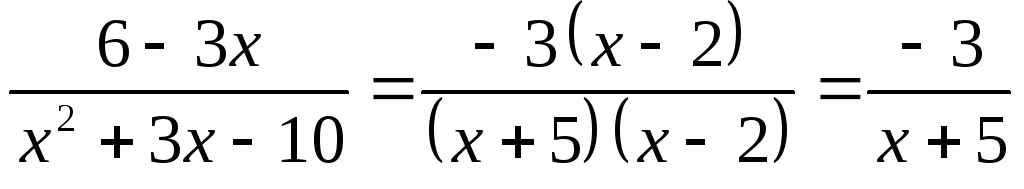 ,
,
тогда 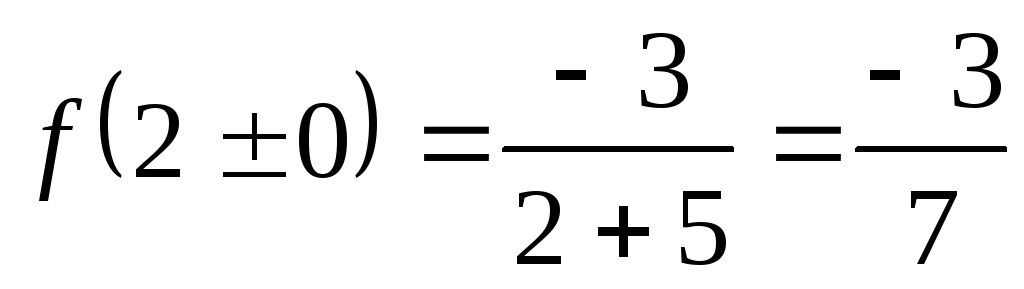 независимо от того, как подходить к
точке
независимо от того, как подходить к
точке .
.
Итак, 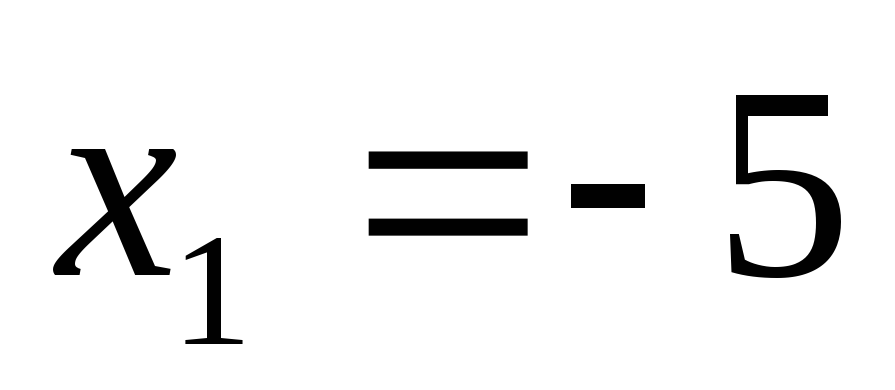 – точка разрыва 2-го рода, в которой знак
бесконечности меняется с «–» на «+»;
– точка разрыва 2-го рода, в которой знак
бесконечности меняется с «–» на «+»; – точка устранимого разрыва, в которой
функция стремится к значению
– точка устранимого разрыва, в которой
функция стремится к значению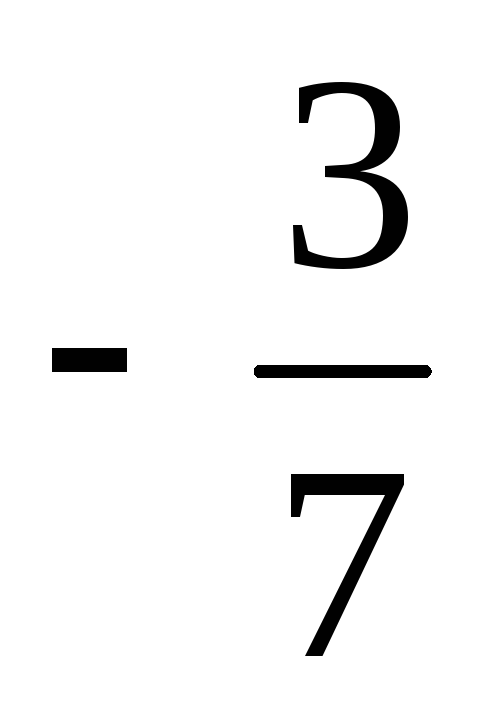 .
.
Замечание 3. Метод близкой точки требует осторожности.
Например, подставив в функцию 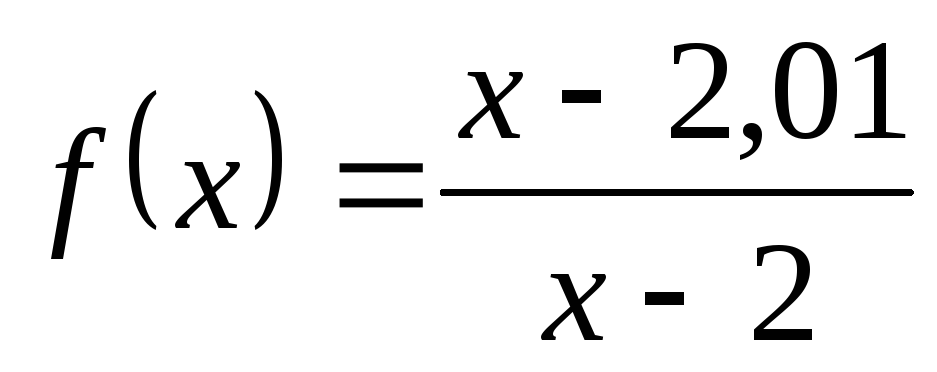 в качестве
в качестве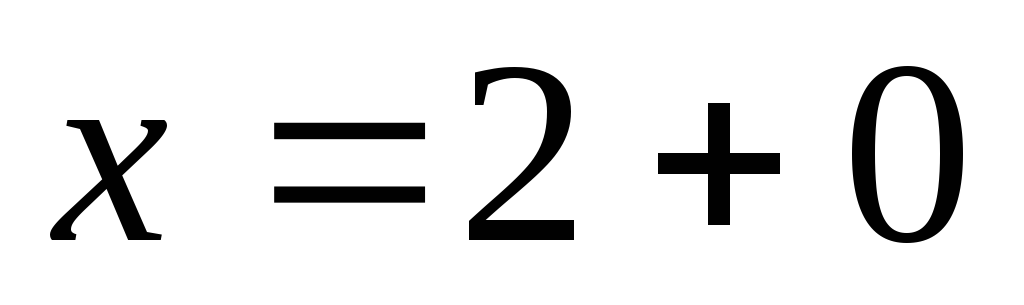 число
число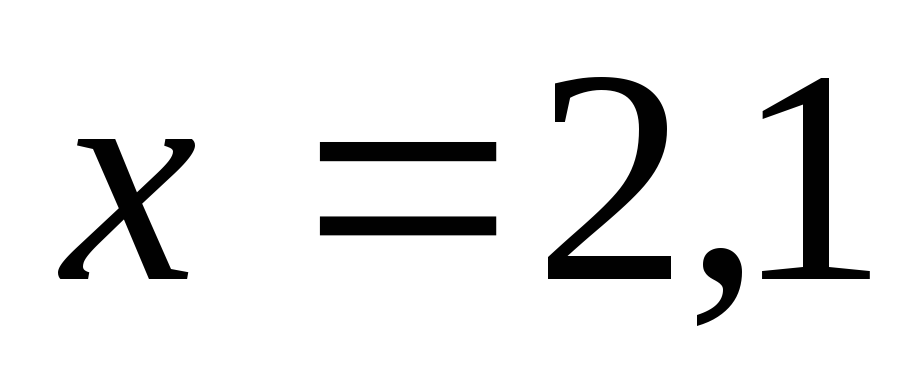 ,
получим, что
,
получим, что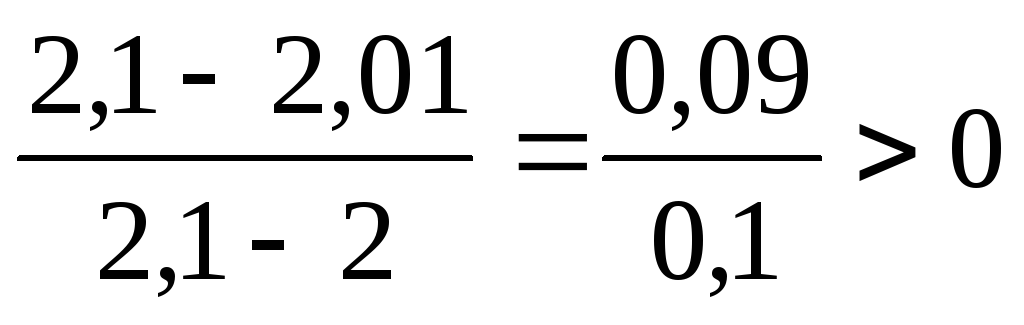 ,
тогда как на самом деле
,
тогда как на самом деле .
Дело в том, что между 2 и 2,1 находится
корень числителя – число 2,01.
.
Дело в том, что между 2 и 2,1 находится
корень числителя – число 2,01.
Лучше усложнить
вычисления, взяв лишние 0 после запятой
– в данном случае можно взять 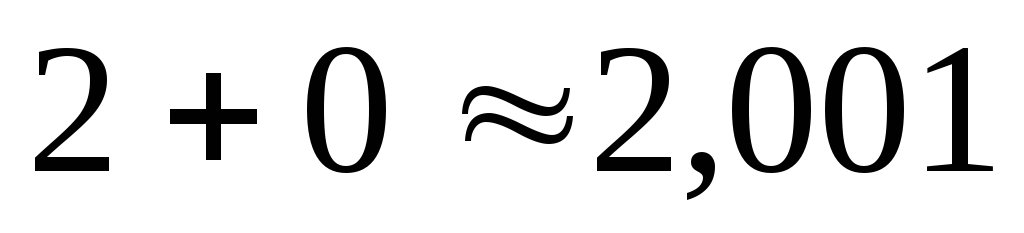 ,
тогда
,
тогда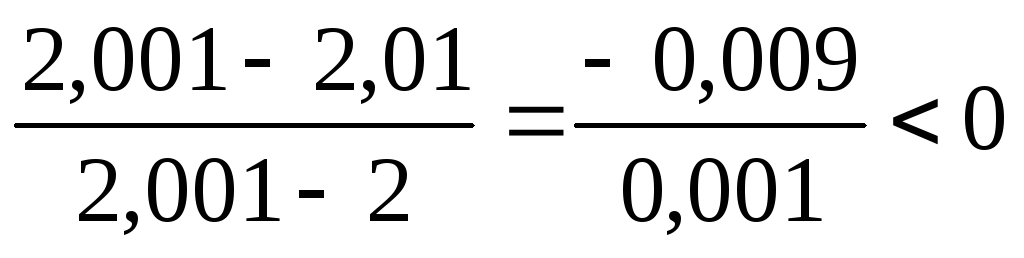 даёт верный вывод.
даёт верный вывод.
studfile.net
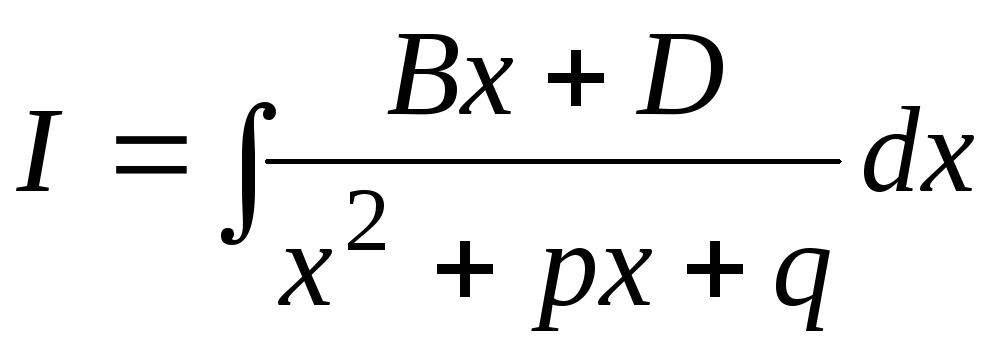 ,
где
,
где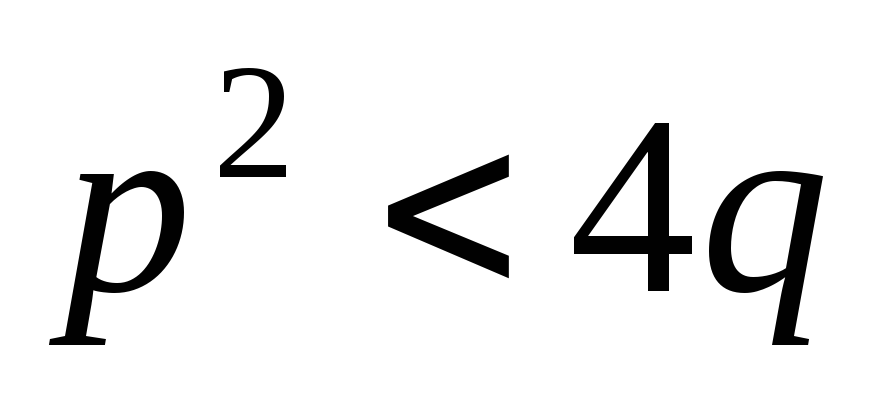
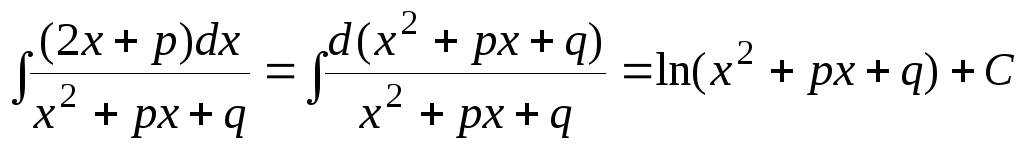 ,
,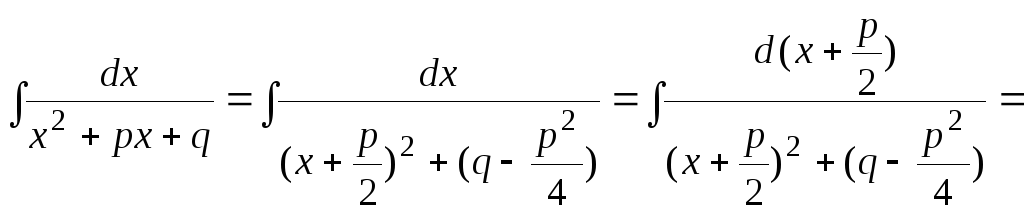
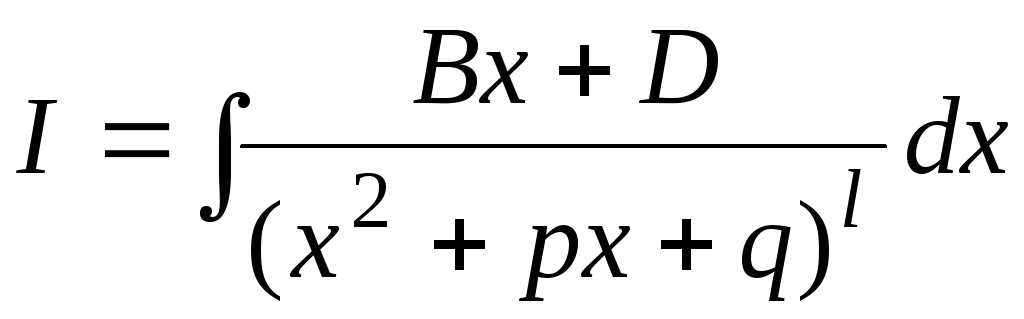 ,
где
,
где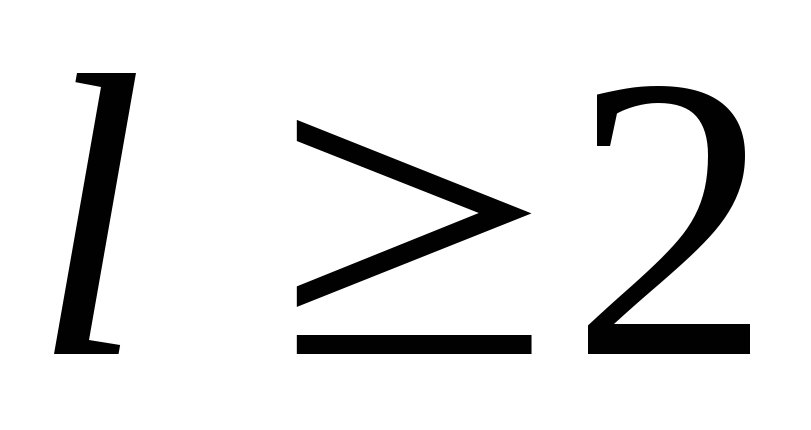 ,
,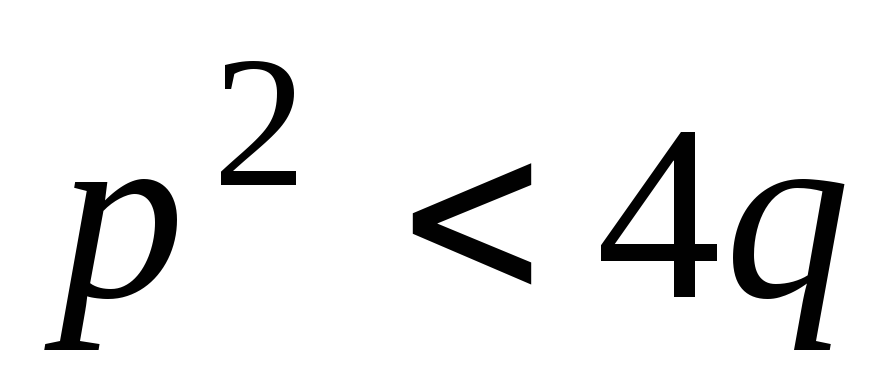 ,
непосредственное интегрирование
является столь громоздким, что следует
пользоваться справочником.
,
непосредственное интегрирование
является столь громоздким, что следует
пользоваться справочником.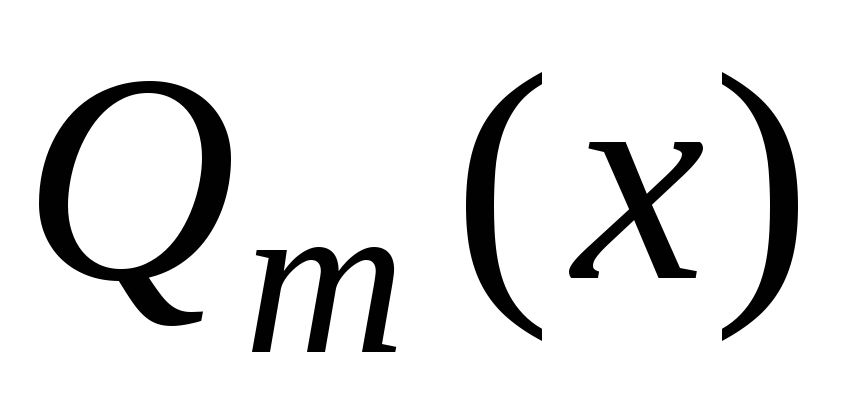 следует разложить на множители вида
следует разложить на множители вида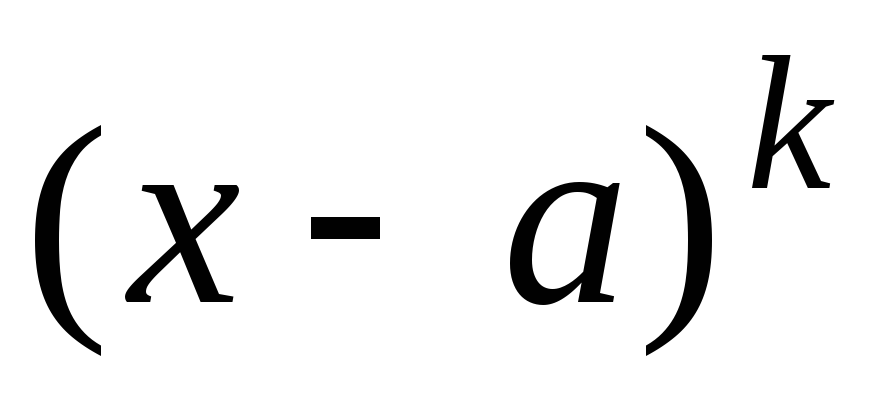 должна соответствовать сумма дробей
должна соответствовать сумма дробей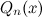 ,
в числителе левой части получим некоторый
многочлен
,
в числителе левой части получим некоторый
многочлен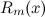 с
неизвестными коэффициентами;
с
неизвестными коэффициентами; .
В результате получаем систему для
определения неизвестных коэффициентов.
.
В результате получаем систему для
определения неизвестных коэффициентов.





