Преобразование выражений. Подробная теория.

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Привет!

Часто мы слышим эту неприятную фразу: «упростите выражение». Обычно при этом перед нами какое-то страшилище типа этого:

 

«Да куда уж проще» – говорим мы, но такой ответ обычно не прокатывает.

Сейчас я научу тебя не бояться никаких подобных задач.

Более того, в конце занятия ты сам упростишь этот пример до (всего лишь!) обычного числа   (да-да, к черту эти буквы).

Но прежде чем приступить к этому занятию, тебе необходимо уметь

обращаться с дробями и раскладывать многочлены на множители.

Поэтому, если ты этого не сделал раньше, обязательно освой темы «Дроби, рациональные числа» и «Разложение на множители».

Прочитал? Если да, то теперь ты готов.

Let’s go! (Поехали!)

СОДЕРЖАНИЕ СТАТЬИ

---

 

Базовые операции упрощения выражений

Сейчас разберем основные приемы, которые используются при упрощении выражений.

Самый простой из них – это

 

1. Приведение подобных

Что такое подобные? Ты проходил это в 7 классе, как только впервые в математике появились буквы вместо чисел.

Подобные – это слагаемые (одночлены) с одинаковой буквенной частью.

Например, в сумме   подобные слагаемые – это   и  .

Вспомнил?

Привести подобные – значит сложить несколько подобных слагаемых друг с другом и получить одно слагаемое.

А как же нам сложить друг с другом буквы? – спросишь ты.

Это очень легко понять, если представить, что буквы – это какие-то предметы.

Например, буква   – это стул. Тогда чему равно выражение  ?

Два стула плюс три стула, сколько будет? Правильно,   стульев:  .

А теперь попробуй такое выражение:  .

Чтобы не запутаться, пусть разные буквы обозначают разны предметы.

Например,   – это (как обычно) стул, а   – это стол.

Тогда:

 стула стола стул столов стульев стульев столов 

Числа, на которые умножаются буквы в таких слагаемых называются коэффициентами.

Например, в одночлене   коэффициент равен  .

А в   он равен  .

Итак, правило приведения подобных: 

Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и приписать буквенную часть.

Примеры:

Приведите подобные:

1.  

2.  

3.  

Ответы:

1.  .

2.   (  и   подобны, так как  , следовательно у этих слагаемых одинаковая буквенная часть).

3.  .

 

2. Разложение на множители

Это обычно самая важная часть в упрощении выражений.

После того как ты привел подобные, чаще всего полученное выражение нужно разложить на множители, то есть представить в виде произведения.

Особенно это важно в дробях: ведь чтобы можно было сократить дробь, числитель и знаменатель должны быть представлены в виде произведения.

Подробно способы разложения выражений на множители ты проходил в теме «Разложение на множители», поэтому здесь тебе остается только вспомнить выученное.

Для этого реши несколько примеров (нужно разложить на множители)

Примеры:

1.  

2.  

3.  

4.  

Решения:

1.  

2.  

3.  

4.  .

3. Сокращение дроби.

Ну что может быть приятнее, чем зачеркнуть часть числителя и знаменателя и забыть о них навсегда?

В этом вся прелесть сокращения.

Все просто:

 

 

Если числитель и знаменатель содержат одинаковые множители, их можно сократить, то есть убрать из дроби.

Это правило вытекает из основного свойства дроби:

Числитель и знаменатель дроби можно умножать или делить на одно и то же ненулевое число, от чего величина дроби не изменяется.

То есть суть операции сокращения в том, что числитель и знаменатель дроби делим на одно и то же число (или на одно и то же выражение).

Чтобы сократить дробь, нужно:

1) числитель и знаменатель разложить на множители

2) если в числителе и знаменателе есть общие множители, их можно вычеркнуть.

Примеры:

 .

 

 

Принцип, я думаю, понятен?

Хочу обратить внимание на одну типичную ошибку при сокращении.

Хоть эта тема и простая, но очень многие делают все неправильно, не понимая, что сократить – это значит поделить числитель и знаменатель на одно и то же число.

Сокращать можно только множители.

Никаких сокращений, если в числителе или знаменателе сумма.

Например: надо упростить  .

Некоторые делают так:  , что абсолютно неверно.

Еще пример: сократить  .

«Самые умные» сделают так:

 .

Скажи мне, что здесь неверно? Казалось бы:   – это множитель, значит можно сокращать.

Но нет:   – это множитель только одного слагаемого в числителе, но сам числитель в целом на множители не разложен.

Вот другой пример:

 .

  – это выражение разложено на множители, значит, можно сократить, то есть поделить числитель и знаменатель на  , а потом и на  :

  – верно.

Можно и сразу поделить на  :

 .

Чтобы не допускать подобных ошибок, запомни…

Легкий способ как определить, разложено ли выражение на множители

 

Арифметическое действие, которое выполняется последним при подсчете значения выражения, является «главным».

То есть, если ты подставишь вместо букв какие-нибудь (любые) числа, и попытаешься вычислить значение выражения, то если последним действием будет умножение – значит, у нас произведение (выражение разложено на множители).

Если последним действием будет сложение или вычитание, это значит, что выражение не разложено на множители (а значит, сокращать нельзя).

Для закрепления реши самостоятельно несколько примеров:

Примеры:

1.  

2.  

3.  

4.  

Решения:

1. Надеюсь, ты не бросился сразу же сокращать   и  ? Еще не хватало «сократить» единицы типа такого:

 

Первым действием должно быть разложение на множители:

 .

2.  

3.  

4.  .

 

4. Сложение и вычитание дробей. Приведение дробей к общему знаменателю.

Сложение и вычитание обычных дробей – операция хорошо знакомая: ищем общий знаменатель, домножаем каждую дробь на недостающий множитель и складываем/вычитаем числители.

Давай вспомним:

1.  

2.  

3.  

Ответы:

1. Знаменатели   и   – взаимно простые, то есть у них нет общих множителей. Следовательно, НОК этих чисел равен их произведению. Это и будет общий знаменатель:

 

2. Здесь общий знаменатель равен  :

 .

3. Здесь первым делом смешанные дроби превращаем в неправильные, а дальше – по привычной схеме:

 .

Совсем другое дело, если дроби содержат буквы, например:

  или  .

Начнем с простого:

a) Знаменатели не содержат букв

Здесь все то же, что и с обычными числовыми дробями: находим общий знаменатель, домножаем каждую дробь на недостающий множитель и складываем/вычитаем числители:

 

теперь в числителе можно приводить подобные, если есть, и раскладывать на множители:

 .

Попробуй сам:

1.  

2.  

3.  

Ответы:

 

1.  

2.  .

3.  .

 

b) Знаменатели содержат буквы

Давай вспомним принцип нахождения общего знаменателя без букв:

· в первую очередь мы определяем общие множители;

· затем выписываем все общие множители по одному разу;

· и домножаем их на все остальные множители, не общие.

Пример:  .

Чтобы определить общие множители знаменателей, сперва разложим их на простые множители:

 ;

 .

 ;

 .

Подчеркнем общие множители:

Теперь выпишем общие множители по одному разу и допишем к ним все необщие (не подчеркнутые) множители:

  – это и есть общий знаменатель.

Вернемся к буквам. Знаменатели приводятся по точно такой же схеме:

· раскладываем знаменатели на множители;

· определяем общие (одинаковые) множители;

· выписываем все общие множители по одному разу;

· домножаем их на все остальные множители, не общие.

Пример:  .

Итак, по порядку:

1) раскладываем знаменатели на множители:

 

 

2) определяем общие (одинаковые) множители:

 

 

3) выписываем все общие множители по одному разу и домножаем их на все остальные (неподчеркнутые) множители:

 .

Значит, общий знаменатель здесь  . Первую дробь нужно домножить на  , вторую – на  :

 

Кстати, есть одна хитрость:

Если в разных знаменателях есть один и тот же множитель в разной степени, то в общем знаменателе такой множитель будет в максимальной из этих степеней.

Например:  .

Видим в знаменателях одни и те же множители, только все с разными показателями. В общий знаменатель пойдут:

  в степени  

  в степени  

  в степени  

  в степени  .

Получим:

 .

Усложним задание:

 .

Как сделать у дробей одинаковый знаменатель?

Если ты сейчас бросился вычитать в первой дроби из   единицу, то ты очень и очень неправ!

Давай вспомним основное свойство дроби:

Числитель и знаменатель дроби можно умножать или делить на одно и то же ненулевое число, от чего величина дроби не изменяется.

Нигде не сказано, что из числителя и знаменателя дроби можно вычитать (или прибавлять) одно и то же число. Потому что это неверно!

Убедись сам: возьми любую дробь, например,   , и прибавь к числителю и знаменателю какое-нибудь число, например,  . Что поучилось?

 .

Итак, очередное незыблемое правило:

Когда приводишь дроби к общему знаменателю, пользуйся только операцией умножения!

Но на что же надо домножить  , чтобы получить  ?

Вот на   и домножай. А   домножай на  :

 .

Выражения, которые невозможно разложить на множители будем называть «элементарными множителями».

Например,   – это элементарный множитель.   – тоже. А вот   – нет: он раскладывается на множители  .

Это как в физике: элементарная частица – это неделимая частица, то есть она не состоит ни из каких других частиц. Например, молекула – это не элементарная частица, так как она состоит из нескольких атомов. Атом – тоже не элементарная, так как состоит из протонов, нейтронов и электронов. А вот эти протоны, нейтроны и электроны поделить нельзя. Значит, они – элементарные частицы.

Что скажешь насчет выражения

ТК М-6 Дробные выражения

Технологических карт урока М-6. У-70. Дробные выражения (1 урок по теме)

Тип урока: Урок изучения нового материала

1.Цели: ввести понятие дробного выражения, разобрать решение дробных выражений; повторить правила действий с обыкновенными дробями.

УУД:

Коммуникативные: формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы.

Регулятивные: осознавать учащимся уровень и качество усвоения результата.

Познавательные: уметь осуществлять анализ объектов с выделением существенных и несущественных признаков.

Личностные: формирование устойчивой мотивации к обучению

2. Задачи:

— образовательные (формирование познавательных УУД):

научить в процессе реальной ситуации использовать определения дробных выражений

— воспитательные (формирование коммуникативных и личностных УУД):

умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.

— развивающие (формирование регулятивных УУД)

1. умение обрабатывать информацию и ранжировать ее по указанным основаниям; формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

3.Формы работы учащихся:Фронтальная, парная, индивидуальная

4.Необходимое техническое оборудование:Компьютер, проектор, интерактивная доска, учебники по математике, электронная презентация, выполненная в программе PowerPoint

Л: самоопределение.

Р: целеполагание.

Определение темы и целей урока

Учитель: Мы знакомы с буквенными выражениями и с числовыми, а теперь познакомимся с дробными.

Подумайте, что означает этот термин, и выполните следующее задание

Дети слушают, думают

 К: постановка вопросов, инициативное сотрудничество.

П: самостоятельное выделение проблемы, решение проблемы, построение логической цепи рассуждение, доказательство

Формирование новых понятий учащихся

На доске: 7ав; 5/8 *х-4; а=в/а-в; 15/5+7у; 6/11*5с;

3/0,8; (3х+у):5; 0,5х/3у; 0,2*0,7/0,2+0,7.

Разделите эти выражения на дробные и надгробные.

Теперь откройте учебник прочитайте пункт и проверите правильно вы разделили или нет.

Как называется выражение стоящее над чертой? Под чертой. Чем являются знаменатели дробных выражений? Сделайте вывод.

С дробными выражениями можно выполнять действия по тем же правилам, что и с обыкновенными дробями. В некоторых случаях особенно удобно применять основное свойство дроби.

Кто может дать это свойство- тот заработает себе балл

 Разделяют как могут.

Читают пункт и проверяют верно ли разделили.

Вывод: дробным называется частное двух чисел или выражений, в котором знак деления обозначен чертой.

 К: постановка вопросов, инициативное сотрудничество.

П: самостоятельное выделение проблемы, решение проблемы, построение логической цепи рассуждение, доказательства

Р: контроль, коррекция

Закрепление изученного материала

 №693; №695(г, и, К)

692 устно

  Решают примеры, если верно выполнили ставят себе балл на полях в своих тетрадях, в конце урока, баллы обмениваются на оценки

самопроверка

 Р: контроль и коррекция, выделение осознание того что уже усвоено.

Л: самоопределение

Повторение

Решение задач

№703,706 (а)

Самостоятельно решают задачи с последующей проверкой

Р: контроль и коррекция

Л: самоопределение

Домашнее задание

П.19. . Стр 116 историческая справка, -один ученик делает эту творческую работу решить № 710,716(а,е), 705

Записывают домашнее задание

Рефлексия

 -Что вы узнали сегодня на уроке?

Какое выражение называют дробным? Как называют выражение, находящееся над чертой? под чертой?

-Оцените свою работу на уроке. У

 

Каждый оценивает свою работу.

 К: умение с достаточной полнотой и точностью выражать свои мысли

П: рефлексия

Технологических карт урока М-6. У-71. Дробные выражения (2 урок по теме)
Тип урока: Урок изучения и углубления новых знаний

Цели: упражнять учащихся в нахождении значений дробных выражений; закрепить знания, умения и навыки решения задач на нахождение числа по его дроби и нахождение дроби от числа. УУД: Коммуникативные: развивать умение точно и грамотно выражать свои мысли, отстаивать свою точку зрения в процессе дискуссии. Регулятивные: оценивать весомость приводимых доказательств и рассуждений. Познавательные: уметь строить рассуждения в форме связи простых суждений об объекте, его строения, свойствах и связях. Личностные: формирование навыка осознанного выбора наиболее эффективного способа решения.

Л: самоопределение.

Р: целеполагание.

Определение темы и целей урока

Двое на доске записывают решения домашнего задания, двое работают по карточкам. Остальные дети показывают модели фигур выполненных дома.

Как называются эти фигуры?

Покажите их боковые грани, что является боковой гранью прямой призмы?

Что лежит в основании призмы?

Где кроме математики встречается слово «призма»

Дети слушают, думают, показывают, отвечают

 К: постановка вопросов, инициативное сотрудничество.

П: самостоятельное выделение проблемы, решение проблемы, построение логической цепи рассуждение, доказательство

Устная работа.

1. Решить устно № 701 (а; в) и № 703 (в).

2. Составить задачу по уравнению № 706 (б).

 

 

Закрепление изученного материала

II. Выполнение упражнений.

1. Решить № 695 (б; е) самостоятельно, № 695 (и) решить на доске.

2. Решить № 696 (а; k) на доске и в тетрадях, № 696 (д; б; л) с комментированием на месте.

3. Решить № 697 (а; в) на доске и в тетрадях.

Разделяют как могут.

Читают пункт и проверяют верно ли разделили.

Вывод: дробным называется частное двух чисел или выражений, в котором знак деления обозначен чертой.

К: постановка вопросов, инициативное сотрудничество.

П: самостоятельное выделение проблемы, решение проблемы, построение логической цепи рассуждение, доказательства

Р: контроль, коррекция

Повторение

Решение задач

а) Решить задачу № 710 с комментированием на месте.

б) Решить задачу № 714 на доске и в тетрадях.

Самостоятельно решают задачи с последующей проверкой

Р: контроль и коррекция

Л: самоопределение

Домашнее задание

изучить п. 19; решить № 712, 716 (б; д; ж), № 703.

Записывают домашнее задание

Рефлексия

1. Привести свои примеры дробного выражения. Назвать числитель и знаменатель дробного выражения.

2. По каким правилам можно выполнять действия с дробными выражениями?

-Оцените свою работу на уроке. У

 

Каждый оценивает свою работу.

 К: умение с достаточной полнотой и точностью выражать свои мысли

П: рефлексия

Технологических карт урока М-6. У-72. Дробные выражения (3 урок по теме)
Тип урока: Урок закреплена новых знаний

Цели: проверить знания учащихся в ходе выполнения самостоятельной работы; подготовить к контрольной работе; развивать логическое мышление учащихся. УУД: Коммуникативные: уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. Регулятивные: осознавать учащимся уровень и качество усвоения результата. Познавательные: владеть общим приемом решения учебных задач. Личностные: формирование познавательного интереса к изучению нового, способам обобщения и систематизации знаний.

Л: самоопределение.

Р: целеполагание.

Актуализация опорных знаний учащихся

1. Решить устно № 701 (б; г; д).

2. Устно решить № 702 по рисунку 30 учебника на с. 113

3. Повторить правила нахождения дроби от числа и нахождения числа по его дроби. Привести свои примеры на доске.

4. Повторить правила умножения и деления дробей. Привести свои примеры.

Дети слушают, думают, показывают, отвечают

 К: постановка вопросов, инициативное сотрудничество.

П: самостоятельное выделение проблемы, решение проблемы, построение логической цепи рассуждение, доказательство

Закрепление изученного материала

II. Тренировочные упражнения.

1. Решить № 695 (в; д; з) на доске и в тетрадях.

2. Решить № 696 (в; ж).

3. Решить № 699 (а) на доске и в тетрадях

Разделяют как могут.

Читают пункт и проверяют верно ли разделили.

Вывод: дробным называется частное двух чисел или выражений, в котором знак деления обозначен чертой.

К: постановка вопросов, инициативное сотрудничество.

П: самостоятельное выделение проблемы, решение проблемы, построение логической цепи рассуждение, доказательства

Р: контроль, коррекция

Самостоятельная работа

Самостоятельная работа (15 мин).

КИМ

Самостоятельно решают задачи с последующей проверкой

Р: контроль и коррекция

Л: самоопределение

Домашнее задание

повторить правила п. 18 и 19; решить № 711 ,716(в,г,з), 632(3,4)

Записывают домашнее задание

Рефлексия

Вы поняли что надо повторить для успешного выполнения контрольной?

-Оцените свою работу на уроке.

 Каждый оценивает свою работу.

 П: рефлексия

6 класс. Математика. Дробные выражения — Дробные выражения

Комментарии преподавателя

При­ме­ры дроб­ных вы­ра­же­ний:

Сна­ча­ла пред­ста­вим сме­шан­ные числа в виде непра­виль­ных дро­бей:

;      .

За­ме­ним дроб­ную черту зна­ком де­ле­ния, а затем умно­жим де­ли­мое на число об­рат­ное де­ли­те­лю, т.е. умно­жим   на  .

 

Сна­ча­ла пред­ста­вим сме­шан­ное число в виде непра­виль­ной дроби:

.

Из­ба­вим­ся от за­пя­тых в пер­вой дроби, умно­жив чис­ли­тель и зна­ме­на­тель на 10.     .

Вы­пол­ним  умно­же­ние обык­но­вен­ных дро­бей.

Из­ба­вим­ся от за­пя­тых, умно­жив чис­ли­тель и зна­ме­на­тель каж­дой дроби на 10.   

        

При­ве­дем дроби к об­ще­му зна­ме­на­те­лю 14, умно­жив чис­ли­тель и зна­ме­на­тель пер­вой дроби на 2.

Вы­пол­ним сло­же­ние дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми.

За­ме­ним  де­ся­тич­ной дро­бью 2,5. Далее из­ба­вим­ся от за­пя­тых в чис­ли­те­ле и зна­ме­на­те­ле,  умно­жив дробь на 1000.   .

Далее по­сте­пен­но со­кра­тим по­лу­чен­ную дробь. Сна­ча­ла со­кра­тим на 11.

.

Потом со­кра­тим на 4, затем на 25. Пред­ста­вим  дробь    в виде де­ся­тич­ной дроби

В самых древ­них до­шед­ших до нас пись­мен­ных ис­точ­ни­ках встре­ча­ют­ся не толь­ко на­ту­раль­ные числа, но и дроби.

Дроби были нужны, чтобы вы­ра­зить ре­зуль­тат из­ме­ре­ния длины, массы, пло­ща­ди в слу­ча­ях, когда еди­ни­ца из­ме­ре­ния не укла­ды­ва­лась в из­ме­ря­е­мой ве­ли­чине целое число раз.

На­при­мер, чтобы из­ме­рить длину дан­но­го от­рез­ка тре­бу­ет­ся еди­ни­ца из­ме­ре­ния 1 см. Эта еди­ни­ца из­ме­ре­ния не укла­ды­ва­ет­ся в из­ме­ря­е­мом от­рез­ке целое число раз.

Тогда вво­ди­ли новую, мень­шую еди­ни­цу из­ме­ре­ния. На­зва­ния этих новых еди­ниц из­ме­ре­ния и стали пер­вы­ми на­зва­ни­я­ми дро­бей.

 — «по­ло­ви­на»

 — «унция»

У рим­лян  слово «унция» сна­ча­ла было на­зва­ни­ем две­на­дца­той доли еди­ни­цы массы, но потом стала обо­зна­чать одну две­на­дца­тую долю любой ве­ли­чи­ны.

В Древ­нем Ва­ви­лоне дроби были ше­сти­де­ся­те­рич­ны­ми. Ис­поль­зуя со­вре­мен­ные обо­зна­че­ния, число можно было, на­при­мер, за­пи­сать так.

За­пись дро­бей с по­мо­щью чис­ли­те­ля и зна­ме­на­те­ля по­яви­лась в Древ­ней Гре­ции, толь­ко греки зна­ме­на­тель за­пи­сы­ва­ли свер­ху, а чис­ли­тель – снизу. Дроби в при­выч­ном для нас виде впер­вые стали за­пи­сы­вать ин­ду­сы около 1500 лет назад, но они не ис­поль­зо­ва­ли черту между чис­ли­те­лем и зна­ме­на­те­лем. Черта дроби стала об­ще­упо­тре­би­тель­ной лишь с 16 века.

 

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/umnozhenie-i-delenie-obyknovennyh-drobej/drobnye-vyrazheniya

источник видео — http://www.youtube.com/watch?v=-AiSSyt6J5Q

источник видео — http://www.youtube.com/watch?v=qkdmHyim82A

источник видео — http://www.youtube.com/watch?v=wcy7hC1bXvU

источник видео — http://www.youtube.com/watch?v=p_AW0V4OcOg

источник презентации — http://ppt4web.ru/matematika/drobnye-vyrazhenija-klass0.html

Онлайн урок: Дробные выражения по предмету Математика 6 класс

Пока что во всех предыдущих случаях мы находили значения дробных выражений «в лоб», по достаточно простому алгоритму.

Но, как это часто бывает в математике, в некоторых случаях можно упростить себе подсчеты, вовремя заметив определенные вещи.

Вы уже наверняка хорошо освоили сокращение дробей.

Напомним, в чем его суть: если числитель представляет из себя произведение, и знаменатель также является произведением, и в этих произведениях есть одинаковый множитель, то мы можем сократить дробь на этот множитель.

Как же это относится к дробным выражениям?

Дело в том, что в некоторых случаях числитель и знаменатель могут быть произведениями или же могут стать произведениями в процессе подсчетов.

Тогда почему бы не сокращать их по возможности?!

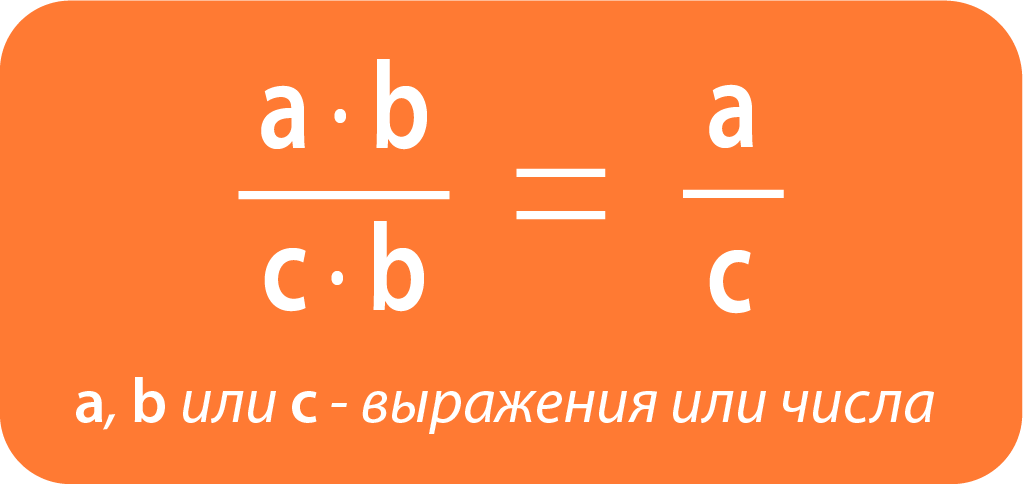
Пример:

\(\mathbf{\frac{7\cdot(123+4)}{3\cdot(120+7)}}\)

Начнем считать выражение и посмотрим, что получается.

\(\mathbf{\frac{7\cdot(123+4)}{3\cdot(120+7)}=\frac{7\cdot127}{3\cdot127}}\)

Числитель и знаменатель дробного выражения после первых преобразований превратились в произведения.

Также можно заметить, что в этих произведениях есть общий множитель: 127

Тогда мы можем поделить числитель и знаменатель дробного выражения на это число, тем самым значительно упростив выражение.

\(\mathbf{\frac{7\cdot127}{3\cdot127}=\frac{7}{3}=2\frac{1}{3}}\)

Это и будет значением этого выражения.

 

Также мы можем быть еще более хитрыми и внимательными.

Найдем значение выражения \(\mathbf{\frac{2\cdot(478569-145236)}{(478569-145236)\cdot3}}\)

Конечно же, можно начать вычислять сначала числитель, потом знаменатель. Для этого мы будем вычислять разность шестизначных чисел.

Но можно сделать проще: заметим, что числитель и знаменатель являются произведениями.

Числитель является произведением 2-х и выражения (478569-145236)

Знаменатель же является произведением выражения (478569-145236) и 3-х.

Выражение (478569-145236) является множителем и можно утверждать, что это один и тот же множитель в числителе и в знаменателе.

Значит, мы можем уверенно сокращать дробное выражение на это выражение.

\(\mathbf{\frac{2\cdot(478569-145236)}{(478569-145236)\cdot3}=\frac{2}{3}}\)

В данном случае мы сразу получили правильную дробь, это и будет являться значением выражения.

 

Отдельно стоит упомянуть работу с многоэтажными дробями.

Мы всегда можем идти по алгоритму с последовательным вычислением числителя и знаменателя — это гарантированно дает результат.

Но также можно запомнить два правила, которые существенно экономят время.

Первое правило говорит о том, что, если в числителе дробного выражения находится дробь (или же дробное выражение), мы можем домножить дробное выражение на знаменатель дроби (или дробного выражения), стоящей в числителе, тем самым уменьшив «этажность» дробного выражения.

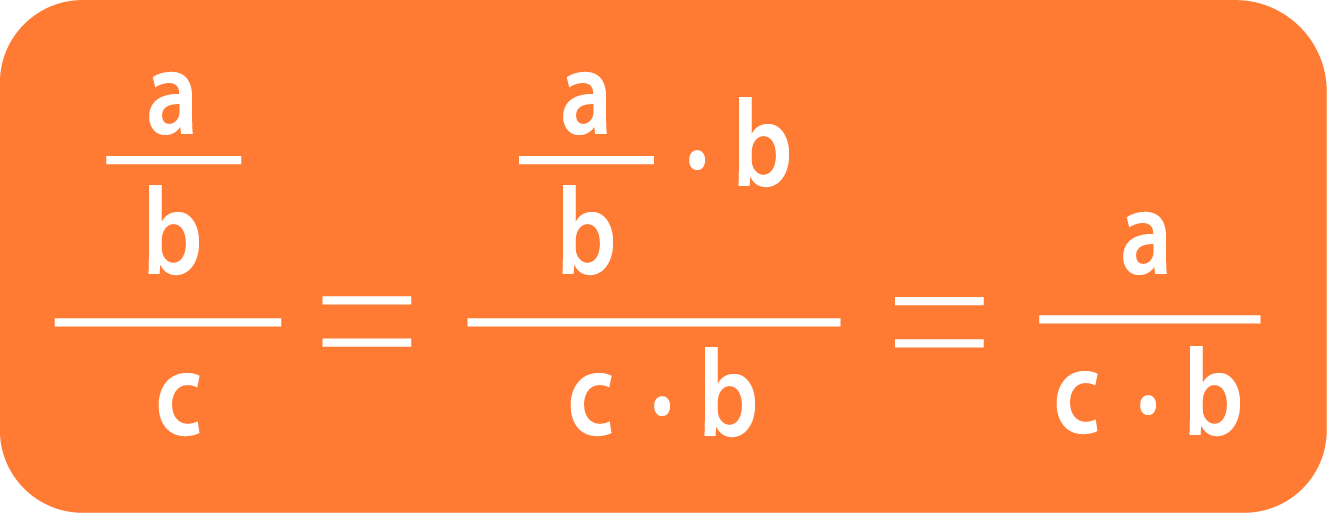
Парочка примеров:

\(\mathbf{\frac{\frac{2}{3}}{4}=\frac{\frac{2}{3}\cdot3}{4\cdot3}=\frac{2}{12}=\frac{1}{6}}\)

\(\mathbf{\frac{\frac{3}{7+13}}{5}=\frac{\frac{3}{7+13}\cdot(7+13)}{5\cdot(7+13)}=}\)

\(\mathbf{=\frac{3}{5\cdot20}=\frac{3}{100}=0.03}\)

 

Второе правило рассматривает случай, когда дробь (или дробное выражение) находится в знаменателе дробного выражения.

В таком случае уменьшить «этажность» дробного выражения поможет домножение всего дробного выражения на знаменатель дроби (или дробного выражения), стоящей в знаменателе.

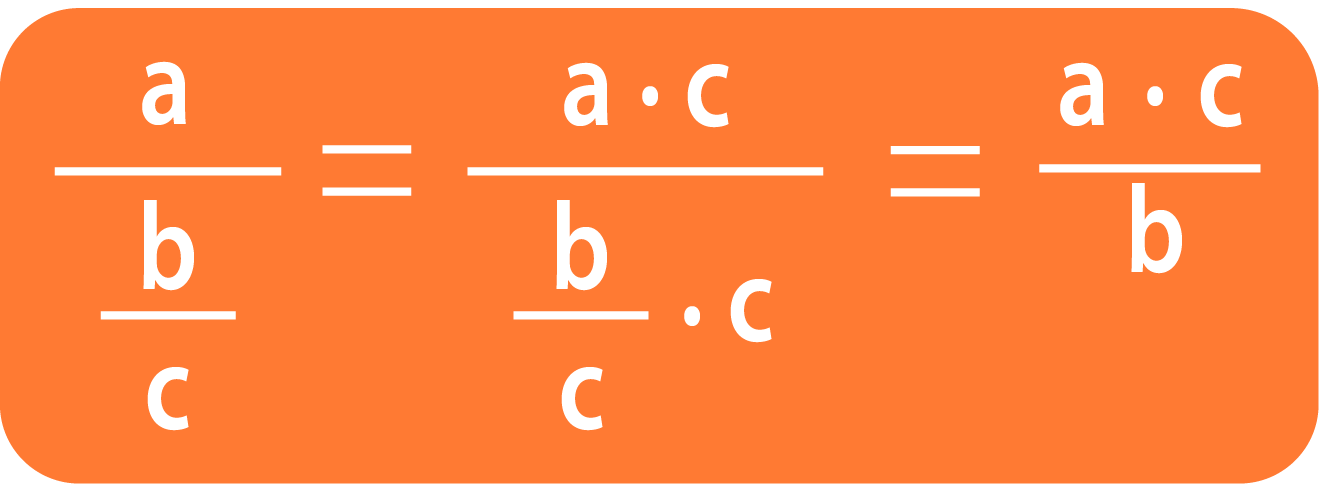
И парочка примеров на этот случай:

\(\mathbf{\frac{3}{\frac{2}{7}}=\frac{3\cdot7}{\frac{2}{7}\cdot7}=\frac{21}{2}=10\frac{1}{2}}\)

\(\mathbf{\frac{11}{\frac{3}{1+7}}=\frac{11\cdot(1+7)}{\frac{3}{1+7}\cdot(1+7)}=}\)

\(\mathbf{=\frac{11\cdot(1+7)}{3}=\frac{11\cdot8}{3}=\frac{88}{3}=29\frac{1}{3}}\)

 

И в завершение еще дам такой пример:

\(\mathbf{\frac{\frac{3}{4+1}}{\frac{7-2}{4}}=\frac{\frac{3}{5}}{\frac{5}{4}}=}\)

\(\mathbf{=\frac{\frac{3}{5}\cdot5}{\frac{5}{4}\cdot5}=\frac{3}{\frac{25}{4}}=\frac{3\cdot4}{\frac{25}{4}\cdot4}=\frac{12}{25}}\)

дробных (рациональных) экспонентов | Purplemath

Purplemath

Вам уже известна одна взаимосвязь между экспонентами и радикалами: соответствующий радикал «отменяет» показатель степени, а правильная сила «отменяет» корень. Например:

Но есть еще одно соотношение, которое, кстати, может значительно упростить вычисления, подобные приведенным выше.

MathHelp.com

Для квадратного (или «второго») корня мы можем записать его как половинную степень, например:

…или:

Кубический (или «третий») корень — это степень одной трети:

Корень четвертой степени равен четвертой степени:

Корень пятой степени равен одной пятой степени; и так далее.

Глядя на первые примеры выше, мы можем переписать их так:

Вы можете ввести дробные показатели на вашем калькуляторе для оценки, но не забудьте использовать круглые скобки.Если вы пытаетесь вычислить, скажем, 15 ^(4/5) , вы должны заключить в круглые скобки «4/5», потому что в противном случае ваш калькулятор будет думать, что вы имеете в виду «(15 ⁴ ) ÷ 5».

---

Дробные показатели обеспечивают большую гибкость (вы часто это увидите в исчислении), их часто проще написать, чем эквивалентный радикальный формат, и они позволяют выполнять вычисления, которые вы не могли раньше. Например:

Всякий раз, когда вы видите дробную экспоненту, помните, что верхнее число — это степень, а нижнее число — это корень (если вы конвертируете обратно в радикальный формат).Например:

Кстати, некоторые десятичные степени могут быть записаны и в виде дробных показателей. Если вы получили что-то вроде «3 ^5.5 «, вспомните, что 5.5 = 11/2, поэтому:

---

Однако, как правило, когда вы получаете десятичную степень (что-то другое, кроме дроби или целого числа), вы должны просто оставить ее как есть или, если необходимо, вычислить ее в своем калькуляторе.Например, 3 π , где π — число, о котором вы узнали в геометрии, и приблизительно равно 3,14159, не может быть упрощено или преобразовано в радикал.

---

Технический момент: когда вы имеете дело с этими показателями с переменными, вам, возможно, придется принять во внимание тот факт, что вы иногда получаете ровные корни. Подумайте об этом: предположим, вы начали с числа –2. Тогда:

Другими словами, вы ввели отрицательное число и получили положительное число! Это официальное определение абсолютной величины:

.

Да, я знаю: они никогда не говорили вам этого, но они ожидают, что вы каким-то образом узнаете, поэтому я говорю вам сейчас.

Итак, если они дадут вам, скажем, x ^3/6 , тогда x лучше не быть отрицательным, потому что x ³ все равно будет отрицательным, и вы попытаетесь извлечь шестой корень отрицательного числа. Если они дадут вам x ^4/6 , тогда отрицательное значение x станет положительным (из-за четвертой степени) и затем будет корнем шестой степени, поэтому оно станет | x | ^2/3 (за счет уменьшения дробной мощности).С другой стороны, если они выдадут что-то вроде x ^4/5 , тогда вам не нужно заботиться о том, является ли x положительным или отрицательным, потому что корень пятой степени не имеет проблем с отрицательными. (Кстати, эти соображения не имеют значения, если в вашей книге указано, что вы должны «предполагать, что все переменные неотрицательны».)

---

Технологический момент: калькуляторы и другое программное обеспечение не вычисляют вещи так, как это делают люди; они используют заранее запрограммированные алгоритмы.Иногда конкретный метод, который использует калькулятор, может создать трудности в контексте дробных показателей.

Например, вы знаете, что кубический корень из –8 равен –2, а квадрат –2 равен 4, поэтому (–8) ^(2/3) = 4. Но некоторые калькуляторы возвращают комплексное значение или сообщение об ошибке, как в случае с одним из моих графических калькуляторов:

Ясно, что это не ожидаемый результат, особенно если вы еще не изучали комплексные числа.(2/3) «в ячейку, электронная таблица Microsoft» Excel «возвращает ошибку» # ЧИСЛО! «, Еще один бесполезный ответ.

Некоторые калькуляторы и программы будут выполнять вычисления, как ожидалось, как показано справа от моего другого графического калькулятора:

Разница связана с заранее запрограммированными вычислительными алгоритмами. Эти алгоритмы обычно пытаются выполнять вычисления способами, требующими наименьшего количества «операций», чтобы обработать введенные вами данные как можно быстрее.

Но иногда самый быстрый метод не всегда самый полезный, и ваш калькулятор «давится».

К счастью, проблему можно обойти. Разделив числитель и знаменатель дробной степени, вы можете ввести выражение, чтобы ваш калькулятор получил правильное значение. Получив бесполезный ответ в моем первом калькуляторе, я повторно ввел число с разбитой на части степенью:

Как вы можете видеть выше, не имело значения, возьму ли я сначала кубический корень из отрицательной восьмерки, а затем возведу в квадрат или сначала возведу в квадрат, а затем получу кубический корень; в любом случае, подавая числитель и знаменатель в калькулятор по отдельности, я смог заставить калькулятор возвращать правильное значение «4».

---

URL: https://www.purplemath.com/modules/exponent5.htm

.

Common Core для 7 класса (решения, примеры, уроки, рабочие листы, игры)

7.SP.A.1 Поймите, что статистику можно использовать для получения информацию о популяции путем изучения выборки население; обобщения о популяции из образец действителен, только если образец является репрезентативным это население. Поймите, что случайная выборка имеет тенденцию производить репрезентативные образцы и поддерживать действительные выводы.

7.SP.A.2 Используйте данные из случайной выборки, чтобы сделать выводы о население с неизвестной интересующей характеристикой. Создайте несколько образцов (или смоделированных образцов) того же размера, чтобы оценить разницу в оценках или предсказания. Например, оцените среднее слово длины книги путем случайной выборки слов из книга; предсказать победителя школьных выборов на основе случайно выбранные данные опроса.Измерьте, как далеко от оценка или прогноз может быть .

7.SP.B.3 Неформально оценить степень визуального перекрытия двух распределения числовых данных с аналогичной изменчивостью, измеряя разницу между центрами, выражая это как кратная мера изменчивости. Для Например, средний рост игроков в баскетбол на 10 см больше среднего роста игроков на футбольной команды, примерно вдвое больше вариабельности (среднее абсолютное отклонение) в любой команде; на точечном графике разделение между двумя распределениями высот равно Заметный .

7.СП.Б.4 Используйте меры центра и меры изменчивости для числовые данные из случайных выборок для рисования неформальных сравнительные выводы о двух популяциях. Для Например, решить, будут ли слова в главе научные книги для седьмого класса обычно длиннее, чем слова в главе учебника для четвертого класса .

7.SP.C.5 Поймите, что вероятность случайного события число от 0 до 1, которое выражает вероятность происходящее событие. Большие числа указывают на большее вероятность. Вероятность около 0 указывает на маловероятный событие, вероятность около 1/2 указывает на событие, которое ни маловероятно, ни вероятно, а вероятность около 1 указывает на вероятное событие.

7.SP.C.6 Примерно вероятность случайного события сбор данных о случайном процессе, который их производит, и наблюдая его долгосрочную относительную частоту, и предсказать приблизительная относительная частота с учетом вероятность. Например, при катании числа куб 600 раз, предсказываем, что выпадет 3 или 6 примерно 200 раз, но, вероятно, не точно 200 раз .

7.SP.C.7 Разработайте вероятностную модель и используйте ее, чтобы найти вероятности событий. Сравните вероятности из модель для наблюдаемых частот; если соглашение не хорошо, объясните возможные источники несоответствия. 7.SP.C.7a 7.SP.C.7b Разработайте единую вероятностную модель, приписав равные вероятность всех исходов, и использовать модель для определить вероятности событий. Например, если учащийся выбран случайным образом из класса, найдите вероятность того, что Джейн будет выбрана, и вероятность того, что девушку выберут . Разработайте вероятностную модель (которая может быть неоднородной) с помощью наблюдение частот в данных, полученных случайно обработать. Например, найти приблизительный вероятность того, что вращающийся пенни выпадет один на один или что брошенный бумажный стаканчик приземлится открытым концом вниз.Сделайте результаты для вращающегося пенни кажутся одинаковыми скорее всего на основе наблюдаемых частот?

7.SP.C.8 Найдите вероятности сложных событий, используя организованные списки, таблицы, древовидные диаграммы и моделирование. 7.SP.C.8a Поймите, что, как и в случае с простыми событиями, вероятность сложного события — это доля результаты в пространстве выборки, для которых составное событие происходит.

7.SP.C.8b Представление пробелов для составных событий с помощью методов такие как организованные списки, таблицы и древовидные диаграммы. Для событие, описанное повседневным языком (например, опрос двойные шестерки, идентифицируйте результаты в пространстве выборки которые составляют событие.

7.SP.C.8c Разработайте и используйте моделирование для генерации частот для сложные события. Например, используйте случайные цифры как инструмент моделирования, чтобы приблизить ответ на вопрос: Если у 40% доноров кровь группы А, то какая вероятность того, что потребуется не менее 4 доноров, чтобы найти человека с кровью типа А?

.

Бесплатные задания по математике для 7-го класса

Вы здесь: Главная → Задания → 7 класс

Это исчерпывающая коллекция бесплатных распечатываемых заданий по математике для 7 класса и для предварительной алгебры, организованных по таким темам, как выражения, целые числа, одношаговые уравнения, рациональные числа, многоступенчатые уравнения, неравенства, скорость, время и расстояние, графики, наклон, соотношения, пропорции, процент, геометрия и пи. Они генерируются случайным образом, их можно распечатать в вашем браузере и включать в себя ключ ответа.Рабочие листы поддерживают любые программы седьмого класса по математике и предалгебре, но были специально разработаны для соответствия учебной программе 7 класса по математике Mammoth.

Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на ссылки ниже. Вы также можете получить новый, другой, просто обновив страницу в своем браузере (нажмите F5).

Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре».Если рабочий лист не умещается на странице, настройте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера. Другой вариант — настроить «масштаб» на 95% или 90% в предварительном просмотре печати. В некоторых браузерах и принтерах есть опция «Печатать по размеру», которая автоматически масштабирует рабочий лист по размеру области печати.

Все рабочие листы содержат ключ ответа, расположенный на 2-й странице файла.

В седьмом классе ученики будут изучать предалгебраические темы, такие как целочисленная арифметика, упрощение выражений, свойство распределения, а также решение уравнений и неравенств.Они продолжают изучать соотношение и проценты и узнают о пропорциях. Обратите внимание, что эти бесплатные рабочие листы не охватывают все темы 7-го класса; в первую очередь, они не включают решение проблем.

Введение в алгебру

Рабочие листы в этом вводном разделе соответствуют главе 1 по математике «Мамонт 7 класс» и не содержат отрицательных чисел.

Порядок работы

Выражения

.

7 класс Математика Модуль 3, Тема C, Обзор

В теме C учащиеся продолжают работать с геометрией, используя уравнения и выражения для изучения площади, периметра, площади поверхности и объема. Эта последняя тема начинается с моделирования круга с помощью велосипедной шины и сравнения его периметра (один оборот шины) с длиной в поперечнике (измеренной с помощью веревки), чтобы позволить учащимся найти наиболее известное соотношение из всех, пи. Упражнения по сравнению окружности и диаметра специально разработаны для учащихся, чтобы они узнали, что этот символ имеет определенное значение и может быть приблизительно равен 22/7 или 3.14, чтобы дать студентам интуитивное представление о существующих отношениях. В дополнение к представлению этого значения символом пи, дробное и десятичное приближения позволяют студентам продолжать практиковать свою работу с операциями с рациональными числами. Все задачи составлены таким образом, чтобы позволить учащимся отработать навыки сокращения в рамках задачи, например, использовать 22/7 для нахождения окружности с заданной длиной диаметра 14 см, и понять, какое значение будет лучше всего приближать решение.Такое понимание позволяет студентам точно оценивать работу на предмет разумности ответов. После открытия и понимания значения этого особого соотношения учащиеся продолжат использовать число Пи при решении задач площади и окружности (7.G.B.4).

В этой теме учащиеся выводят формулу площади круга, разделив круг радиусом r на части пи и переставив части так, чтобы они выстроились в линию, меняя направление и образовав форму, напоминающую прямоугольник.Этот «прямоугольник» имеет длину, равную половине окружности, и ширину r . Учащиеся определяют, что площадь этого прямоугольника (реконфигурированного из круга той же площади) является произведением его длины и ширины: 1/2 ( C ) ( r ) = 1/2 2 (pi) ( r ) ( r ) = pi ( r ) ² ( 7.GB4 ). Точные определения диаметра, окружности, пи и круговой области или диска будут разработаны в рамках этой темы, при этом значительное время будет посвящено пониманию учащимся каждого термина.

Учащиеся основывают свою работу в 6 классе с площадью поверхности и сетками, чтобы понять, что площадь поверхности — это просто сумма площади боковых сторон и основания (я) (6.G.A.4). В 7 классе они продолжают решать реальные и математические задачи, касающиеся площади двумерных форм, площади поверхности и объема призм, например прямоугольных, треугольных, уделяя особое внимание задачам, которые включают дробные значения длины ( 7.GB6 ). Дополнительная работа (примеры) с площадью поверхности будет произведена в Модуле 6 после того, как будет дано формальное определение прямоугольной пирамиды.

.