Обыкновенные дифференциальные уравнения 1-го порядка.
Обыкновенным дифференциальным уравнением 1-го порядка называется уравнение, связывающее независимую переменную, неизвестную искомую функцию, зависящую от этой переменной, и ее производную 1-го порядка.
В
неявной форме записи дифференциальное
уравнение 1-го порядка выглядит следующим
образом:  ,
(3)
,
(3)
где F – известная функция своих аргументов;
х – независимая переменная;
у – искомая неизвестная функция, зависящая от х;
или
(в разрешенном относительно у/ виде): 
где f – известная функция своих аргументов.
Заметим, что функция F в уравнении (3) может не содержать х или у (или оба этих аргумента), но непременно должна включать у/.
Дифференциальное
уравнение 1-го порядка имеет бесчисленное
множество решений. Так, например, решением
уравнения  будет являться не только функция
будет являться не только функция  ,
но и всякая функция вида
,
но и всякая функция вида  (где С – произвольная постоянная), в чем
можно убедиться непосредственной
проверкой.
(где С – произвольная постоянная), в чем
можно убедиться непосредственной
проверкой.
Одной из важных задач теории дифференциальных уравнений является задача Коши (Коши Огюстен Луи (1789-1857) – французский математик).
Для
уравнения (4) (или (3)) задача
Коши формулируется следующим образом: «среди
всевозможных решений указанного
уравнения найти такие, которые
удовлетворяют заданному условию:  ,
(5)
,
(5)
где х0, у0 – заданные действительные числа»
Условие (5) называется начальным условием.
Геометрическая интерпретация задачи Коши заключается в следующем: среди всех интегральных кривых уравнения (4) (или (3)) найти такие, которые проходят через наперед заданную точку с координатами (х0, у0) плоскости Оху.
Общим
решением дифференциального уравнения 1-го порядка
называется однопараметрическое семейство
функций: 
удовлетворяющее следующим условиям:
а) функция (6) является решением данного дифференциального уравнения при любом допустимом значении параметра С;
б)
при любом допустимом начальном условии  найдется такое значение С0 параметра С, при котором функция
найдется такое значение С0 параметра С, при котором функция  будет удовлетворять указанному начальному
условию, т.е. будет иметь место равенство:
будет удовлетворять указанному начальному
условию, т.е. будет иметь место равенство: 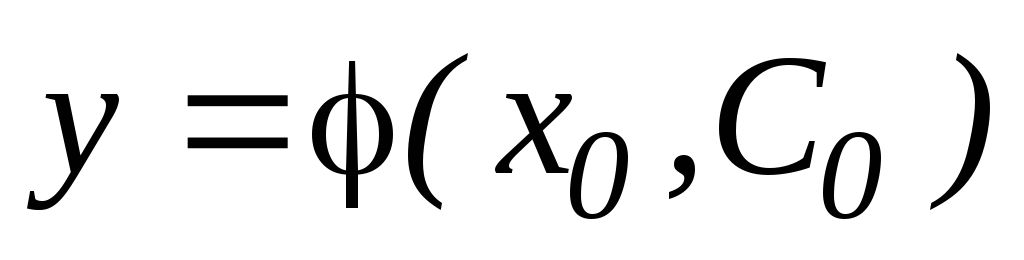 .
.
Всякое
решение  дифференциального уравнения 1-го порядка,
которое получается из общего решения
(6) при конкретном, и вполне определенном
значении С = С 0,
называется частным
решением.
дифференциального уравнения 1-го порядка,
которое получается из общего решения
(6) при конкретном, и вполне определенном
значении С = С 0,
называется частным
решением.
Таким
образом, общему решению (6) дифференциального
уравнения 1-го порядка на плоскости Оху
соответствует семейству интегральных
кривых; а частному решению, удовлетворяющую
начальному условию — кривая этого семейства  ,
проходящая через точку
,
проходящая через точку  .
.
Общее
решение дифференциального уравнения
1-го порядка, выраженное в неявной форме,
т.е. в виде  ,
называется общим
интегралом.
,
называется общим
интегралом.
Дифференциальные уравнения с разделяющимися переменными.
Простейшими дифференциальными уравнениями 1-го порядка являются дифференциальные уравнения с разделяющимися переменными.
Дифференциальным уравнением с разделяющимися переменными
 (7)
(7)(или приводящееся к указанному виду).
Характерной особенностью уравнения (7) является то, что коэффициенты при дифференциалах dx, dy представляют собой произведение функций, зависящих только от х, или только от у.
Преобразуем
дифференциальное уравнение (7) таким
образом, чтобы при dx
множителем была функция, зависящая
только от х, а при dy
– функция, зависящая только от у. С этой
целью разделим обе части уравнения (7)
на функцию  (предполагая, что
(предполагая, что  ,
в результате чего получаем:
,
в результате чего получаем:

При
этом могли быть потеряны решения
уравнения (7), которые одновременно
являются и решениями уравнениями  .
Эти решения записываются в ответ в том
случае, если их нельзя будет получить
из общего решения ни при каком конкретном
значении параметра С.
.
Эти решения записываются в ответ в том
случае, если их нельзя будет получить
из общего решения ни при каком конкретном
значении параметра С.
Почленное интегрирование уравнения (8) приводит к соотношению:
 ,
(9)
,
(9)
(где С – произвольная постоянная, всегда возникающая при применении операции неопределенного интегрирования), которое и определяет общее решение исходного уравнения (7) в неявной форме (общий интеграл).
Пример
2. Для
дифференциального уравнения  найти:
найти:
все его решения;
частное решение, удовлетворяющее условию
 .
.
Решение. 1) Заданное уравнение представляет собой дифференциальное уравнение 1-го порядка с разделяющимися переменными. Запишем его в виде:
 .
.
Умножив
обе части этого уравнения на dx,
получаем:  .
.
Разделив
обе части последнего уравнения на 
 ),
имеем:
),
имеем:  (10)
(10)
Проинтегрируем
обе части уравнения (10):  ;
;
 ,
где С =сonst;
,
где С =сonst; 
 ;
;

Откуда  (11)
(11)
Итак,
соотношение (11) определяет общее решение
исходного уравнения. В процессе перехода
к уравнению (10) при делении на функцию  ,
могло быть потеряно решение заданного
уравнения, которое одновременно является
и решением уравнения
,
могло быть потеряно решение заданного
уравнения, которое одновременно является
и решением уравнения  ,
т.е. у = 0. Непосредственной проверкой
убеждаемся, что функция у = 0 действительно
является решением заданного уравнения
(так как, если у = 0, то у/ = 0 и при их подстановки в исходное
уравнение
,
т.е. у = 0. Непосредственной проверкой
убеждаемся, что функция у = 0 действительно
является решением заданного уравнения
(так как, если у = 0, то у/ = 0 и при их подстановки в исходное
уравнение 
 ).
Однако, решение у = 0 невозможно получить
из общего решения (11) ни при каком числовом
значении параметра С,
следовательно, оно утрачено.
).
Однако, решение у = 0 невозможно получить
из общего решения (11) ни при каком числовом
значении параметра С,
следовательно, оно утрачено.Таким образом, совокупность всех решений заданного уравнения имеет вид:

2) Чтобы найти частное исходного уравнения, удовлетворяющее начальному условию у (-1) = 1, подставим х0 = -1 и у0 = 1 в общее решение (11):
1 = (-1 + С)-3;
(С – 1)3 = 1;
С – 1 = 1;
С = 2.
Подставив полученное выше значение параметра С в общее решение (11), находим частное решение, удовлетворяющее заданному начальному условию: у = (х +2)3.
С геометрической точки зрения, мы нашли ту интегральную кривую (кубическую параболу), которая на плоскости Оху проходит через точку М0 (-1; 1) (рис. 1).
Общему решению (11) на плоскости Оху соответствует семейство кубических парабол, смещающихся вдоль оси ОХ при изменении постоянной интегрирования С.
При С = 0 из (11) имеем: у = х3
С = 1 у = (х + 1)3;
С = 2 у = (х + 2)3;
С = 3 у = (х + 3)3;
С = -1 у = (х — 1)3;
С = -2,5 у = (х – 2,5)3.
Пример 3. Решить дифференциальное уравнение: у2 – 4 – 2хуу/ = 0 (12)
Решение. Уравнение (12) представляет собой дифференциальное уравнение с разделяющимися переменными. Запишем его в виде:
 ,
откуда
,
откуда  .
.
Умножив обе части последнего уравнения на dx, получим:
 (13)
(13)
Преобразуем
уравнение (13) таким образом, чтобы
множителем при dx
являлась функция, зависящая только от
х, а при dy
– функция, зависящая только от у. С этой
целью, разделив обе части уравнения
(13) на 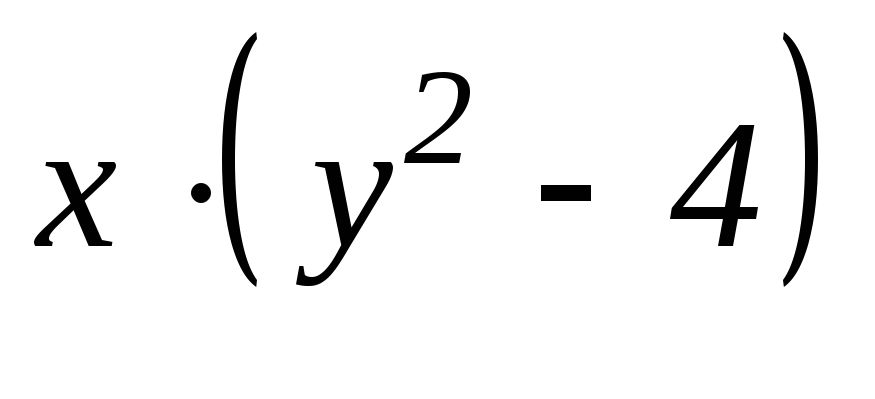 ,
будем иметь:
,
будем иметь:
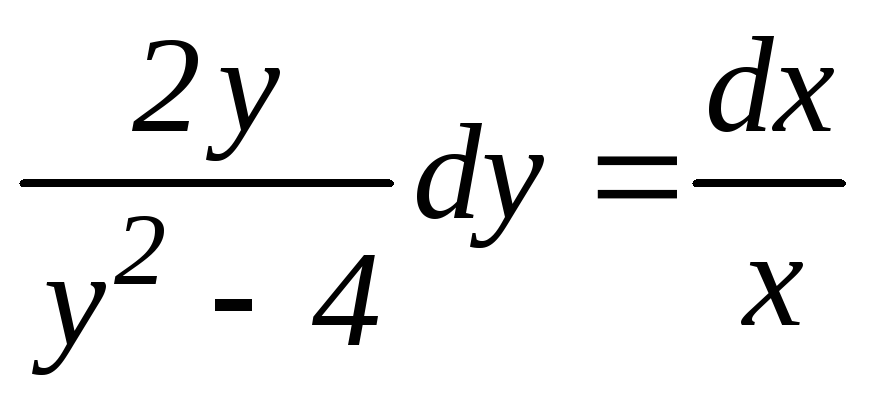 (14)
(14)
Проинтегрируем
обе части равенства (14). Имея в виду
дальнейшие преобразования, обозначим
произвольную постоянную через  ,
что допустимо, так как, если С – константа,
то и
,
что допустимо, так как, если С – константа,
то и  — тоже константа, принимающая любое
значение от
— тоже константа, принимающая любое
значение от  до
до 

 ,
где С – const; С ≠ 0
,
где С – const; С ≠ 0


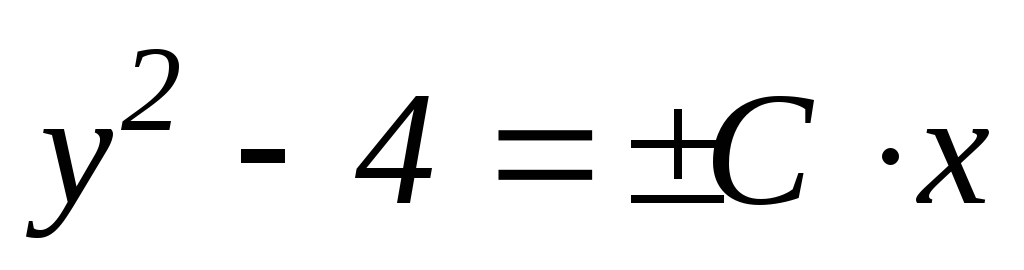
Положим
С0 = ± С (где С0 = const,
причем  ),
тогда
),
тогда
 ;
;
 ,
где С0 = const;
С ≠ 0 (15)
,
где С0 = const;
С ≠ 0 (15)
Таким образом, функция (15) определяет общее решение заданного уравнения (12).
В
процессе преобразований при переходе
от уравнения (13) к уравнению (14) могли
быть потеряны решения заданного уравнения
(12), которые одновременно являются и
решениями уравнения  (т.е. х = 0, у =
(т.е. х = 0, у =  2)
2)
Непосредственной
проверкой убеждаемся, что х = 0 не является
решением уравнения (12), а у = ± 2 являются
его решениями (действительно при
подстановке у = ± 2 в уравнение (12) получаем
тождество  ).
).
Заметим, что решение у = ± 2 можно получить из общего решения (15), если допустить, что постоянна С0 в (15) может принимать значение равное нулю (т.е. С0 = 0).
Таким
образом, все решения исходного уравнения
(12) определяется формулой (15), в которой
постоянная  .
.
Ответ: 
25. Д.У первого порядка, классификация ду
Уравнение
F(x, y, y ‘) = 0,
где y ‘= f(x,y) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.
Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ‘) = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y ‘(x)) ≡ 0 для всех x из (a,b) .
Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия. Чтобы найти частное решение, нужно воспользоваться задачей Коши
Уравнения с частными производными можно классифицировать по многим признакам.
Классификация уравнений важна потому, что для каждого класса существует своя общая теория и методы решения уравнений.
Можно выделить шесть методов классификации уравнений.
1.Порядок уравнения. Порядком уравнения называется наивысший порядок частных производных, входящих в уравнение.
2.Линейность .Дифференциальное уравнение вида

где a(x) и b(x) − непрерывные функции x, называется линейным неоднородным дифференциальным уравнением первого порядка.
26. Ур-я с разделяющимися переменными
Уравнение
вида  ,
в котором коэффициенты при дифференциалах
распадаются на множители, зависящие
только от
,
в котором коэффициенты при дифференциалах
распадаются на множители, зависящие
только от и
только от
и
только от ,
называетсяуравнением
с разделяющимися переменными.
,
называетсяуравнением
с разделяющимися переменными.
Путем
деления на произведение 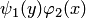 оно
приводится к уравнению с разделенными
переменными:
оно
приводится к уравнению с разделенными
переменными:

Общий интеграл этого уравнения имеет вид

27.Однородные дифференциальные уравнения первого порядка
Однородные
дифференциальные уравнения первого
порядка – это
уравнения вида 
Как распознать однородное дифференциальное уравнение
Для
того, чтобы распознать однородное
дифференциальное уравнение, нужно
ввести постоянную t и сделать замену y
→ ty, x → tx. Если, в результате такого
преобразования, постоянная t сократится,
то это однородное
дифференциальное уравнение.
Производная y′ при таком
преобразовании не меняется: 
28. Линейное дифференциальное уравнение первого порядка
Определение линейного дифференциального уравнения первого порядка. Рассмотрен способ решения линейных дифференциальных уравнений первого порядка методом интегрирующего множителя. Дан пример подробного решения линейного дифференциального уравнения.
Линейное
дифференциальное уравнение первого
порядка – это
уравнение вида 
Линейное
однородное дифференциальное уравнение
первого порядка – это
уравнение вида 
Линейное
неоднородное дифференциальное уравнение
первого порядка – это
уравнение вида 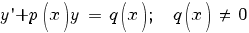
Член q(x) называется неоднородной частью уравнения.
29. Интегрирование по частям в определенном интеграле
Осуществление определенных условий или действий для выявления рассматриваемого события носит название опыта или эксперимента.
Событие называется случайным, если в результате опыта оно может произойти или не произойти.
Событие называется достоверным, если оно обязательно появляется в результате данного опыта, и невозможным, если оно не может появиться в этом опыте.
Например, выпадение снега в Москве 30 ноября является случайным событием. Ежедневный восход Солнца можно считать достоверным событием. Выпадение снега на экваторе можно рассматривать как невозможное событие.
Одной из главных задач в теории вероятностей является задача определения количественной меры возможности появления события.
Каждый
из равновозможных результатов испытаний
(опытов) называется элементарным исходом.
Их обычно обозначают буквами  .
Например, бросается игральная кость.
Элементарных исходов всего может быть
шесть по числу очков на гранях.
.
Например, бросается игральная кость.
Элементарных исходов всего может быть
шесть по числу очков на гранях.
Из элементарных исходов можно составить более сложное событие. Так, событие выпадения четного числа очков определяется тремя исходами: 2, 4, 6.
Количественной мерой возможности появления рассматриваемого события является вероятность.
Наиболее широкое распространение получили два определения вероятности события: классическое и статистическое.
Классическое определение вероятности связано с понятием благоприятствующего исхода.
Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление этого события.
В приведенном примере рассматриваемое событие — четное число очков на выпавшей грани, имеет три благоприятствующих исхода. В данном случае известно и общее количество возможных исходов. Значит, здесь можно использовать классическое определение вероятности события.
Классическое
определение.
Вероятность события  равняется
отношению числа благоприятствующих
исходов к общему числу возможных исходов
равняется
отношению числа благоприятствующих
исходов к общему числу возможных исходов
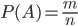 (1.1)
(1.1)
где  —
вероятность события
—
вероятность события ,
, —
число благоприятствующих событию
—
число благоприятствующих событию исходов,
исходов, —
общее число возможных исходов.
—
общее число возможных исходов.
В рассмотренном примере

Статистическое
определение вероятности связано с
понятием относительной частоты появления
события  в
опытах.
в
опытах.
Относительная
частота появления события  вычисляется
по формуле
вычисляется
по формуле
 (1.2)
(1.2)
где  —
число появления события
—
число появления события  в
серии из
в
серии из опытов
(испытаний).
опытов
(испытаний).
Статистическое
определение.
Вероятностью события  называется
число, относительно которого стабилизируется
(устанавливается) относительная
частота
называется
число, относительно которого стабилизируется
(устанавливается) относительная
частота при
неограниченном увеличении числа опытов.
при
неограниченном увеличении числа опытов.
В
практических задачах за вероятность
события  принимается
относительная частота
принимается
относительная частота при
достаточно большом числе испытаний.
при
достаточно большом числе испытаний.
Из
данных определений вероятности
события 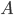 видно,
что всегда выполняется неравенство
видно,
что всегда выполняется неравенство

Для определения вероятности события на основе формулы (1.1) часто используются формулы комбинаторики, по которым находится число благоприятствующих исходов и общее число возможных исходов.
Пример. Известно, что в поступившей партии из 30 швейных машинок 10 имеют внутренний дефект. Определить вероятность того, что из партии в 5 наудачу взятых машинок 3 окажутся бездефектными.
Решение. Для
решения данной задачи введем обозначения.
Пусть  —
общее число машинок,
—
общее число машинок, —
число бездефектных машинок,
—
число бездефектных машинок, —
число отобранных в партию машинок,
—
число отобранных в партию машинок, —
число бездефектных машинок в отобранной
партии.
—
число бездефектных машинок в отобранной
партии.
Общее
число комбинаций по  машинок,
т.е. общее число возможных исходов будет
равно числу сочетаний из
машинок,
т.е. общее число возможных исходов будет
равно числу сочетаний из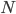 элементов
по
элементов
по ,
т.е.
,
т.е. .
Но в каждой отобранной комбинации должно
содержаться по три бездефектные машинки.
Число таких комбинаций равно числу
сочетаний из
.
Но в каждой отобранной комбинации должно
содержаться по три бездефектные машинки.
Число таких комбинаций равно числу
сочетаний из элементов
по
элементов
по ,
т.е.
,
т.е. .
.
С
каждой такой комбинацией в отобранной
партии оставшиеся дефектные элементы
тоже образуют множество комбинаций,
число которых равно числу сочетаний
из  элементов
по
элементов
по ,
т.е.
,
т.е. .
.
Это
значит, что общее число благоприятствующих
исходов определяется произведением  .
Откуда получаем
.
Откуда получаем

Подставим в эту формулу численные значения данного примера

2.01. Дифференциальные уравнения первого порядка. Основные понятия, связанные с ДУ 1-го порядка
Дифференциальное уравнение 1-го порядка имеет вид
. (1)
Если уравнение (1) можно разрешить относительно производной, то его записывают в виде
. (2)
При этом функция задана на плоскости В некоторой области D, как правило, непрерывна вместе с частной производной .
Определение 1. Решением или частным решением уравнения (1) на некотором промежутке называется функция , имеющая на этом промежутке производную и удовлетворяющая уравнению (1), т. е.
.
Определение 2. Oбщим интегралом или общим решением уравнения (1) называется равенство
Ф . (3)
Где — произвольная постоянная, а функция непрерывно-дифференцируемая в некоторой области и обладает свойством: если продифференцировать равенство (3) по
. (4)
И исключить из (3) и (4) константу , то получится уравнение эквивалентное уравнению (1).
Если уравнение (3) можно разрешить относительно , то
. (5)
Как следует из этого равенства, геометрически общее решение ДУ 1-го порядка представляет собой однопараметрическое семейство кривых на плоскости . Их называют интегральными кривыми уравнения (1) или (2).
Связь между общим и частным решениями ДУ (1) или (2) сформулируем в виде
Определение 3. Совокупность всех частных решений ДУ (1) образует его общее решение и наоборот, любое частное решение следует из общего при некотором значении постоянной в общем решении.
Это определение следует из теоремы:
Теорема. Пусть функция непрерывно-дифференцируемая в некоторой области и является общим решением ДУ (1). Тогда, функция есть решение ДУ (1) при некотором , и обратно, всякое решение ДУ (1) удовлетворяет уравнению при некотором .
Необходимость. Пусть представляет собой общее решение ДУ (1). Зафиксируем : . Обозначим левую часть . Дифференцируем это тождество по , найдем . Подставим эти значения в (4), получим
,
т. е. есть решение ДУ (1).
Достаточность. Пусть есть решение ДУ (1), следовательно, оно есть решение уравнения (4), т. e. . Интегрируя это тождество по в пределах от до , получим
Откуда, есть решение уравнения.
| < Предыдущая | Следующая > |
|---|
порядок ДУ, общее и частное решение. Задача Коши и ее геометрический смысл.
Стр 1 из 5Следующая ⇒ДУ: порядок ДУ, общее и частное решение. Задача Коши и ее геометрический смысл.
Определение д.у. Порядок д.у. Общее и частное решение д.у.
1.Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию y = f(x) и ее производные yʹ, yʹʹ,…y(n).Символическая запись ДУ:F=( yʹ, yʹʹ,…y(n))=0 .
Д.у.-ур-е в кот неизвестная ф-ция y нах под знаком производной (№: yʹ+5y=3x)
2.Порядком д.у. наз-ся порядок наивысшей производной, входящей в ур-е.
Если искомая функция у = f(x) есть функция одной независимой переменной, то ДУ называется обыкновенным ДУ (иначе ДУ называется ДУ в частных производных).
Решением или интегралом ДУ называется всякая дифференцируемая функция y = j(x), которая, будучи подставлена в уравнение, обращает его в тождество.
График решения ДУ (график функции у = f(x)) называется интегральной кривой.
Все д.у. делятся на 2 класса:
1)обыкновенные-ур-я в кот искомая неизв ф-ция y явл-ся функцией одного аргумента y=f(x)
2)д.у.в частных производных- -//- нескольких аргументов z=f(x,y)
3.Решением д.у. явл-ся любая ф-ция y=j (x), кот при подстановке в ур-е обращает его в строгое рав-во.
№: y=x3; yʹ=3x2
3y-xyʹ=0; 3x3-x3x2=0; 0=0
Поскольку реш-е д.у связано с операцией интегрирования,то это приводит к появлению произвольной постоянной С.
При реш-и д.у. первого порядка появл-ся одна произвольная постоянная С.
-//- n-ного порядка интегрирование повторяется n раз, поэтому в реш-и будет содержаться n произв пост С С1, С2, С3,… Сn,
Общим решением д.у. n-ого порядка называется функция: y= j (x, С1, С2, С3,… Сn), кот зависит от n-произвольных постоянных и удовл д.у. при любых значениях С1, С2, С3,… Сn,
Частным реш-ем д.у. n-ого порядка называется любая функция, полученная из общего решения д.у. при конкретных значениях произвольных постоянных.
Для нахождения частного из общего необх исп заданные заранее начальные усл-я.
№: нач усл-я: при х=х0→у=у0, yʹ= у0ʹ, yʹʹ= у0ʹʹ
y(n)—порядок производной
yn-степень
Задача КОШИ. Теорема о существовании и единственности решения задачи Коши.
Задача отыскивания частного решения д.у. наз-ся решением задачи Коши.
Геометрически общее решение д.у. предст собой семейство кривых, кот назыв ИНТЕГРАЛЬНЫМИ КРИВЫМИ
y0
x0
Частное решение предст собой одну интегр кривую, прох через точку, заданную начальным условием.
Замечание. Решение ДУ, которое не может быть получено из общего решения ни при каких начальных условиях, называется особым.
Решить (проинтегрировать) ДУ – значит найти его общее решение и/или частное решение, удовлетворяющее заданным начальным условиям.
Геометрический смысл теоремы Коши. Существует, и притом единственная функция yʹ=j(x), график которой проходит через заданную точку (х0, у0) (единственная интегральная кривая, проходящая через заданную точку).
Рассмотрим решение простейшего ДУ первого порядка yʹ=f(x)
Решение такого уравнения сводится к интегрированию функции, стоящей в правой части уравнения
y=∫ f(x)dx+C
Пример. Общее решение дифференциального уравнения
y¢ – 3y = 0 имеет вид y(x) = Ce3x. Найти его частное решение, удовлетворяющее начальным условиям y(1) = e3.
Решение.
Значение произвольной постоянной С, соответствующее искомому частному решению, получается в результате подстановки в общее решение заданных начальных условий: e3 = C×e3, откуда С = 1. Подставляя полученное значение С = 1 в общее решение, найдем частное решение y = e3x, удовлетворяющее заданным начальным условиям.
ДУ первого порядка: определение, типы, общее и частное решения.
Д.у.-ур-е в кот неизвестная ф-ция y нах под знаком производной (№: yʹ+5y=3x)
ДУ первого порядка – уравнение вида: F(x,y, yʹ)=0 где х – независимая переменная; у – искомая функция; у¢ – ее производная.
Решением д.у. первого порядка назыв функция y=j(x,С) зависящая от одной произвольной постоянной С и кот при подстановке в ДУ обращает его в верное равенство. (и удовлетворяющая ДУ при любом конкретном значении С)
Частным реш-ем ДУ первого порядка является функция y=j(x,С0) получаемая из общего решения при конкретном значении произвольной постоянной.
Соотношение вида Ф(х,у,С)=0называется частным интегралом ДУпервого порядка.
Если ДУ первого порядка разрешено относительно производной yʹ=f(x,у), оно называется ДУ решенным относительно производной.
Другие формы записи ДУ первого порядка: dy/dx=f(x,у), P(x,y)dx+ Q(x,y)dy=0
Равенство вида Ф(х,у,С)=0 неявно задающее общее решение ДУ, называется общим интегралом ДУ.
Решение ДУ в виде общего интеграла получают, когда выразить у из соотношения Ф(х,у,С)=0в элементарных функциях не представляется возможным.
Однородные ДУ первого порядка
О. Уравнение первого порядка yʹ=f(x,у), называется однороднымотносительно x и y, если функцию f(x,у) можно представить как функцию отношения y/х , т.е. в виде f(x,у)=j( y/х),
Существует еще один признак однородного уравнения. Если уравнение yʹ=f(x,у) или уравнение P(x,y)dx+ Q(x,y)dy=0 не меняется при замене x на λx и у на λу, то такие уравнения называются однородными.
Подстановка y/х=t→y=tx→ yʹ=tʹx+tприводит однородное уравнение к уравнению с разделяющимися переменными: tʹx+t=j(t)
Разделив переменные, получим:dt/(j(t)-t)=dx/х
Интегрируя последнее уравнение, найдем: ∫dt/(j(t)-t)=∫dx/х
Подставляя после интегрирования вместо t отношение у/х, получим интеграл уравнения.
Линейные ДУ первого порядка
1.О. Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции y и ее производной yʹ, т.е. уравнение вида:
yʹ+ P(x) ×y=Q(x),
где P(x) и Q(x)– заданные непрерывные функции от х (или постоянные).
Если правая часть данного ур-я =0, т.е. Q(x)=0, то такое ДУ yʹ+ P(x) ×y=0 называется однородным линейным ДУ первого порядка.
yʹ+ P(x) ×y=Q(x)— неоднородное ЛДУ первого порядка
Линейным данное ур-е называется потому что искомая функция у и ее производная yʹ входят в первую степень и не содержат членов содержащих y×yʹ
Решение ЛДУ 1ого порядка.
2.1.Метод вариации произвольной постоянной (метод Лагранжа)
Последовательность решения ЛНДУ методом Лагранжа заключ в следующем:
В начале решается соответствующее исходному неоднородному ДУ однородное ДУ
yʹ+ P(x) ×y=0
dy/dx=- P(x) ×y |×dx |:y
∫dy/y=- ∫P(x) ×dx
ln|y|=-lne P(x) ×dx+ln|C|
|y|=| C×e-∫P(x) ×dx|
y= ±C×e-∫P(x) ×dx ±C=C1
y= C1×e-∫P(x) ×dx
с этого момента начинается вариация произвольной С1
С1=С1(х)-т.к. С1-любое значение
Тогда: y= C1(х)×e-∫P(x) ×dx
Будем полагать что данное решение является решением иходного неоднородного ДУ, подставим его в yʹ+ P(x) ×y=Q(x) и определим закон изм-я произв постоянной С1(х).
Для этого найдем производную yʹ
yʹ=производная первого на второе+производная второго на первое(y= C1(х)×e-∫P(x) ×dx)
yʹ= C1ʹ(х)×e-∫P(x) ×dx— C1(х)×Р(х)×e-∫P(x) ×dx
подставим полученные выражения в yʹ+ P(x) ×y=Q(x)
yʹ= C1ʹ(х)×e-∫P(x) ×dx— C1(х)×Р(х)×e-∫P(x) ×dx
y= C1(х)×e-∫P(x) ×dx , тогда:
C1ʹ(х)×e-∫P(x) ×dx— C1(х)×Р(х)×e-∫P(x) ×dx+ P(x)×C1(х)×e-∫P(x) ×dx =Q(x)
C1ʹ(х)×e-∫P(x) ×dx=Q(x) |× e∫P(x) ×dx
C1ʹ(х)= Q(x)× e∫P(x) ×dx
d C1(х)/dx= Q(x)× e∫P(x) ×dx |×dx
∫d C1(х)= ∫Q(x)× e∫P(x) ×dx×dx
C1(х)= ∫Q(x)× e∫P(x) ×dx×dx +C2
Подставим полученное выражение в выражение y= C1×e-∫P(x) ×dx
y=( ∫Q(x)× e∫P(x) ×dx×dx +C2)×e-∫P(x) ×dx
пример:
1) уʹ+3у=е2х
1. уʹ+3у=0
у=С1×е-3х (это реши сам)
2. пусть С1 изм по вариации С1=С1(х), тогда реш-е однородного ур-я можно записать в виде:
у=С1(х)×е-3х-будем полагать что это общее решение исходного неоднородного ду.
3. Подставим его в исходное неоднор ур-е и найдем закон изменения С1(х).
уʹ= С1ʹ(х)×е-3х-3 С1(х)×е-3х
4. подставим значения у и уʹ в исходное:
С1ʹ(х)×е-3х-3 С1(х)×е-3х+3 С1(х)×е-3х=е2х
С1ʹ(х)×е-3х=е2х |×е3х
С1ʹ(х)= е5х
5. Разделим переменные:
d C1(х)/dx= е5х |×dx
∫d C1(х)= ∫ е5х ×dx
C1(х)=1/5 е5х +С2
6. Подставим значение C1(х) в у=С1(х)×е-3х. получим:
у=(1/5 е5х +С2) ×е-3х
Метод Якова-Бернулли
Будем искать решение уравнения yʹ+ P(x) ×y=Q(x) в виде произведения двух функций y=uv, где u=u(x), v=v(x)-непрерывные ф-ции
Подберем такие функции u=u(x) и v=v(x), чтобы их произведение удовлетворяло исходному уравнению, т.е. превращало бы его в тождество.
Подставим в уравнение y=uv, yʹ=uʹv+ uvʹ:
uʹv+ uvʹ+Р(х)uv= Q(x)
или
uʹv+ u(vʹ+Р(х)v)= Q(x)
Выберем функцию v такой, чтобы vʹ+Р(х)v=0 из чего автоматически следует, что uʹv= Q(x)
Эти два условия превращают уравнение в тождество, поэтому для решения уравнения достаточно решить простую систему двух дифференциальных уравнений с разделяющимися переменными:

Решая первое уравнение системы, найдем функцию v (при интегрировании будем считать С = 0).
Подставив во второе уравнение системы найденную функцию v=v(x), решим дифференциальное уравнение с разделяющимися переменными относительно u, общее решение которого u=u(x,С). Следовательно, искомое общее решение уравнения будет иметь вид: y=v(x)×u(x,С).
Замечание. В ряде случаев дифференциальное уравнение первого порядка является линейным не относительно у, а относительно х, т.е. имеет вид: dy/dx+ P(у) ×х= Q(x)
Для интегрирования такого уравнения используется описанный выше метод, где неизвестной функцией является х=х(у)
Виды случайных событий
Основные понятия ТВ: испытание, случайное событие и вероятность случайного события.
Испытание – опыт, эксперимент, наблюдение явления.
Событие – результат (исход) испытания.
Определение Случайное событие – всякое событие, которое в результате испытания(опыта) может произойти, либо не произойти.
Обозначение: A, B, C, D…
Случайные события. Классификация событий.
Событие-результат опыта(№:стрельба)
Событие назыв ДОСТОВЕРНЫМ,если в результате опыта оно обязат произойдет (№:при бросании 2 кубиков выпадет сумма >=2)
Невозможное событие-которое в рез-те опыта не сможет произойти(№:при выбрасывании 1 игральной кости сумма будет >6)
D-достоверное событие
U-невозможное событие
2 события называются совместными, ели при испытании появление одного из них не исключает появление другого(№:при однократ бросании игральн кости выпадение цифры 2 и событие выпадения четного числа – СОВМЕСТНЫ)
Несовместные события- ели при испытании появление одного из событий исключает появление другого(№:выстрел-попадание и промах)
Полной группой событий называют неск событий,таких что в рез-те опыта непременно произойдет одно из них.(№:игральная кость: A-«1», B-«2», C-«3», D-«4», T-«5», F-«6»,)
Вероятность события-число характеризующее степень объективной возможности появл-я событий в опыте.
Классический
Если исходы опыта можно представить в виде полной группы событий кот несовместны и равновозможны,то вероятность события А м.б. вычислена по формуле:
Р(А)=m:n
m-общее число возможных случаев(общ число случаев)
n-число исходов благоприятствующих событию А(общ число благопр случаев)
благоприятствующий случай-если его появление влечет за собой событие
пример:
1) №:в урне 3 белых и 4 черных шара
А-событие вынуть белый шар.
Р(А)=m:n=3:7-0,43(43%)
m=3,n=3+4
2) Вероятность появл-я четного числа очков при однокр брос кости
А-событие выпад-я четн числа очков
Р(А)=m:n=3:6=0,5(50%)
m-благопр случай 3(2,4,6-четн цифры на кости)
n=6(всего цифр)
Геометрический
Исп-ся д/вычисл вероятностей события в том случае,когда рез-т испыт-я определ-ся случайным полож-ем точек в некот обл-ти,причем любые полож-я точек в этой обл-ти равновозможны.
Р(А)=Wm:Wn
Wm-размер всей площади
Wn-мера обл-ти,попад в кот благоприятствует событию А.
Примечание:
Единицы измерения обл-тей м.б. самые различн,в завис-ти от смысла задачи(S,V,t)
пример:
1) В некот точке С телеф линии АВ длиной L. Определ вероятность того,что С удал от А на расст не <,чем l
А-событие,что произошло в т.С→Р(А)
Р(А)= Wm:Wn=(L-l):L
Статистический
Частотой появл-я события А назыв отношение числа его появл-й к числу произвед опытов
F(A)=m:n
P(A)=lim f(A) (внизу под lim n→∞)=lim m:n(внизу под lim n→∞)
Перестановка
Перестановками из n элементов назыв всевозм комбинации из этих элементов,отлич друг от друга порядком располож-я элементов.
Рn=1×2×3…×n=n!(эн-факториал)
Пример:
1) 1,2,3
123; 321; 231; 213; 132; 312
Р3=3!=1×2×3=6 Ответ:6
2) В ауд 5 столов. Сколькими способами м рассад 5 чел.
Р5=5!=120. Ответ: 120
Размещение
Размещениями из n элементов по m элементов называются все возможные комбинации (группы) из этих элементов, содержащие по m элементов в каждой и различающиеся между собой элементами или их расположением.
Аnm=n(n-1)(n-2)…(n-m+1)
Аnm=Pn😛m—n
Пример:
1) Информация кодируется словами из 4 цифр,цифры в словах не повтор. Сколько м сост слов д/кодир-я информ.
n=10 (0,1,2..9), m=4
A104=10!:(10-4+1!)=10×9×8×7=5040
Ответ: 5040
3. Сочетания
Сочетаниями из n элементов по m элементов (m<n) называются все возможные комбинации (группы) из этих элементов, содержащие по m элементов в каждой и отличающиеся друг от друга, по крайней мере, одним элементом.
Сnm= Аnm: Pm=n!:(m!×(n-m)!)
n!-кол-во чисел
m!×(n-m)!-кол-во групп
пример:
1) в урне 3 белых и 7 черных шаров.Скольк сущ возм-тей вынуть из урны 2 шара одного цвета?
m=2
C32-число возм-тей вытянуть 2 белых шара
C32=3!:(2!1!)=3
C72-число возм-тей вытянуть 2 черных шара
C72=21
С=C32+C72=21+3=24. Ответ: 24
Теорема сложения.
Суммой 2х событий А и В называют событие С состоящее в появлении хотя бы одного из событий А ИЛИ В
Пример:
1) А-событие вынуть из колоды красную карту
В-событие вынуть туза
(рисуются 2 раза 2 кружка, первый раз события несовпад и кружки не пересек, второй раз вынут красный туз-кружки пересек)
С=А+В
Теорема 1.Сложение вероятностей 2х несовместных событий
Вероятность суммы двух несовм событий А и В равна сумме вероятностей этих событий.
Р(А+В)=Р(А)+Р(В)
Если число несовм событий не 2, а более,то данная теорема справедлива,т.е.:
РS(сверху n,снизу i=1)Аi=S(сверху n,снизу i=1) Р(Аi)
Пример:
1) Произв выстрел по мешени сост из 3х зон
Вероятность попадания в первую зону-0,1
Во вторую-0,3
В третью – 0,4
Определ вероятность попадания в мешень.
1. Обозначение событий и их вероятностей.
А1-событие попадания в первую зону
А2-во вторую
А3-в третью
А-событие попадания в мешень
2. Составим расчетную формулу:
А=А1+А2+А3
А1,А2,А3-несовместные события
Р(А)= Р(А1)+Р(А2)+Р(А3)
3. Расчет:
Р(А)=0,1+0,3+0,4=0,8(80%)
Противоположные события-если они несовместные и образуют полную группу.
А(с – сверху)-противоположное событие
Следствие 1 из теоремы 1:
Сумма вероятностей противоположных событий равна еденице: А(с – сверху)=1
Док-во:
Р(А+А с черточкой)=Р(U)=1 (как вероятность достоверного события)
* Событие назыв достоверным ,если в результате опыта оно обязат произойдет (№:при бросании 2 кубиков выпадет сумма >=2)
События А и А с черточкой – несовместны, тогда по теореме 1:
Р(А+А с черточкой)=Р(А)+Р(А с черточкой)=1
Запись формулы Р(А)+Р(А с черточкой)=1 Р(А)+Р(А с черточкой)=1 в других обозначениях:
p+q=1,
где р— вероятность того, что событие А произошло; q — вероятность того, что событие А не произошло.
Следствие 2 из теоремы 1:
Если событие А1,А2, … Аn образуют полную несовм группу событий, то сумма их вероятностей:
Р(А1)+Р(А2)+…+Р(Аn)=1
S(сверху n,снизу- i=1) Р(Аi)=1
* сумма вероятностей несовместных событий, образующих полную группу, равна единице
Пример:
1) Определить вероятность промаха в условия предудущ задачи:
Р(А с -)=1-Р(А)=1-0,8=0,2(20%)
Теорема 2. Сложение вероятностей 2 совместных событий.
Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления (т.е. вероятность произведения)
Р(А+В)=Р(А)+Р(В)-Р(АВ)
Произведением (∩) 2х событий А и В называется событие С,состоящее в проявлении А И В одновременно.
Следствие 1
Если события А1,А2, … Аn-равновероятны, т.е. вероятность
Р(А1)=Р(А2)=…=Р(Аn)=Ру, то
Р(∩-сверху n снизу i=1 ×Аi)=Рn
Следствие 1 (совместны)
Если события А1,А2, … Аn-независимы, но м.б. совместны, то вероятность появл хотя бы одного из них определ формулой:
Р>=1=1-(1-Р(А1))(1-Р(А2))…(1-Р(Аn))
Р(А1)=Р(А2)=…=Р(Аn)=Р
Р>=1=1-(1-Р)n
Пример:
1) Определить вероятность исправной работы цепочки состоящей из 2х элементов.
а) случай параллельного соединения
б) последовательного
если вероятность исправной работы первого 0.5, второго 0,6
решение:
1. Обозн событий:
А1-событие исправной работы 1ого элемента
А2-второго
2. Расчет формулы:
а) А=А1+А2(или 1 или 2 событие, события совсм могут произойти одноврем) необх применить формулу вероятности суммы 2х совм событий:
Р(А)=Р(А1)+Р(А2)-Р(А1×А2)
Вероятность двух независ событий равна произведению их вероятностей.
б) А=А1×А2
Р(А)=Р(А1)×Р(А2)
3. Расчеты:
а) Р(А)=0,5+0,6-0,5*0,6=0,8(80%)
б) Р(А)=0,5*0,6=30%
Формула полной вероятности.
*Событие – результат (исход) испытания.
*Вероятность события-число характеризующее степень объективной возможности появл-я событий в опыте.
Пусть треб определ вероятность события А,кот может произойти только вместе с одним из событий:Н1,Н2, … Hn образующих полную группу несовместных событий
Данные события называются ГИПОТЕЗЫ поэтому формула полн вер им вид:
Р(А)=S(сверху n,снизу i=1) Р(Нi)× Р(А/Нi)
Полн вероятность события А равна сумме произведения вероятностей гипотез на условные вероятности событий.
По данным событиям требования к гипотезам: несовместные,сост полн группу
Пример:
1) Имеется 3 урны. В первой-4 белых,6 черных шаров,во второй-3 и 5,в третьей только белые. К одной из урн подх и выним шар. Какова вероятность вытащить белый?
1. Обозн событий:
А-событие, что вынутый шар белый
Н1— гипотеза,шар вынут из 1 урны, Н2-из второй, Н3-из третьей.
2. Расчет формула:
Р(А)=S(сверху 3,снизу i=1) Р(Нi)× Р(А/Нi) *3-т.к. 3 урны
3. Расчеты:
Р(Н1)= Р(Н2)= Р(Н3)=1/3- вероятность что он подойдет к урне
Р(А/Н1)=4:(4+6)=0,4(40%)
Р(А/Н2)=3/8
Р(А/Н3)=1
Р(А)=1/3*4/10+1/3*3/8+1/3*1=59%
*59% означают,что при проведении достаточно большого кол-ва опятов в одинак условиях в средем в 59 случаях из 100 будет вынут белый шар.
2) Из 2х швейных фабрик поступ на базу внешне одинак изделия. С 1ой фабрики поступ втрое больше изделий,чем со второй. Вероятность брака изд с первой фабрике 0,1, со второй 0,05. Найти вероятность того, что наудачу взятое изделии окаж НЕ браков.
1. А-событие, что изделие вытащ из урны БЕЗ брака
Н1-гипотеза,что изд будет с первой фабрики, Н2-со второй
2. Расчетная формула: Р(А)=S(сверху 2,снизу i=1) Р(Нi)× Р(А/Нi) *2-т.к. 2 фабрики
3. Р(Н1)* Р(Н2)=3/4*1/4
Р(А/Н1)=1-0,1=0,9 – вероятность без брака, а нам дан брак, значит 1-…
Р(А/Н2)=1-0,05=0,95
Р(А)=9/10*3/4+1/4*95/100=91%
3) Предприятие выпуск за смену изделие 3х видов в кол-ве 160,430,360 шт. каждого вида. ОТК ставит штамп «Брак» или «Экспорт». Найти вероятность того,что наудачу взятое изделие пойдет на экспорт,если вероятность этого для каждого изделия вида 1,2,3=0.9, 0,8 и 0,6 соотв-но.
1. А-событие, что изделие пойдет на экспорт
Н1-гипотеза,изделие 1ого вида Н2-2ого вида Н3-3его вида
2. Р(А)=S(сверху 3,снизу i=1) Р(Нi)× Р(А/Нi) *3-т.к. 3 вида изделий
3. Р(Н1)=160/950
Р(Н2)= 430/950
Р(Н3)=360/950
Р(А)= 160/950*0,9+430/950*0,8+360/950*0,6=74%
Теорема гипотез (формула Байеса)
*Событие – результат (исход) испытания.
*Вероятность события-число характеризующее степень объективной возможности появл-я событий в опыте.
Формула Байеса исп д/определ вероятности гипотезы после испытания,когда событие А УЖЕ имело место.
Если событие А уже произошло,какие-то гипотезы отпадут,значит уменьшится их кол-во. А след-но каким-то образом изменятся их вероятности.
Теорема. Вероятность гипотезы после испытания собятия А,кот уже произошло опред по формуле:
Р(Нi /А)= (Р(Нi)× Р(А/Нi)):(S(сверху n,снизу i=1) Р(Нi)× Р(А/Нi))
Вероятность равна произведению вероятности до испытания на условную вероятность события делить на полную вероятность события.
Пример:
1) В пирамиде 5 винтовок.3-с оптикой,2-без.Вероятность попад из оптич винт-0,95,без-0,7. После выстрела из наугад взятой винтовки мишень оказалась поражена. Что вероятнее: стреляли из винт с оптикой или без?
1. Обозн событий и их вероятностей:
А-событие попадания в цель
Н1-гипотеза,из опт винтовки
Н2-без оптики
2. Расчетн формулы:
Вероятность гипотезы Нi до испытания на условную вероятность события,делить на полн вероятность события:
Р(Н1 /А)= (Р(Н1)× Р(А/Н1)):(S(сверху 2,снизу i=1) Р(Нi)× Р(А/Нi))
Р(Н2 /А)= (Р(Н2)× Р(А/Н2)):(S(сверху 2,снизу i=1) Р(Нi)× Р(А/Нi))
3. Расчеты:
Р(Н1)=3/5 *3-винт с оптикой,5-всего винтовок
Р(Н2)=2/5
Р(А/Н1)=95/100
Р(А/Н2)=70/100
Р(Н1 /А)=(3/5*95/100):( 3/5*95/100+2/5*70/100)=57/85
Р(Н2 /А)=( 2/5*70/100):( 3/5*95/100+2/5*70/100)=28/85
Ответ:Вероятнее что стреляли из оптич винтовки.
2) С 3х конвееров поступ на склад детали в кол-ве 150,300,350 шт. вероятность брака 0,3 0,2 0,2. Наудачу взятая дет НЕбрак. Найти вероятность того,что деталь с третьего конвеера.
1. А-событие что деталь небрак
Н1-гипотеза,что с первого конвеера
Н2-со второго
Н3-с третьего.
2. Р(Н3 /А)= (Р(Н3)× Р(А/Н3)):(S(сверху 2,снизу i=1) Р(Нi)× Р(А/Нi))
3. Р(Н1)=m/n=150/(150+300+350)=150/800
Р(Н2)= 300/800
Р(Н3)=350/800
Р(Н1)+Р(Н2)+Р(Н3)=1
Р(А/Н1)=1-0,3=0,7
Р(А/Н2)=1-0,2=0,8
Р(А/Н3)=1-0,2=0,8 *0,7 0,8 0,8-имела место та или иная гипотеза.
Р(Н3 /А)=(7/16*8/10):(3/16*7/10+3/8*8/10+7/16*8/10)=44,8%
Следствие 1
Вероятность появл-я события хотя бы 1 раз в серии из n испытаний определяется по формуле:
Pn(m>=1)=1-(1-p)n
Р-вероятность попадания при 1 выстреле
1-р-вероятность промаха -//-
Следствие 2
Кол-во испытаний, опытов n необходимых д/появления события А хотя бы 1 раз с задан вероятностью опред по формуле:
(1-p)n =1-Pn(m>=1)
Pn(m>=1)-надежность
n×lg(1-p)=lg(1-Pn(m>=1))
n=(lg(1-Pn(m>=1)): lg(1-p)
Ряд распределения
| Х | х1 | Х2 | … | хn |
| pi | p1 | p2 | … | pn |
-возможные значения вероятностей
-событий
2. Многоугольник распределения-графическое изображение выражения ряда распределения.

3. Функция распределения-вероятность события сост в том, что случайная величина Х примет значение меньшее фиксируемого значения х.
*вероятность не м.б. >1

Свойства:
1. Возрастающая по своему физическому смыслу
2. F(-∞)=0
F(+∞)=1
3. F(x1)= P(Х<x1)=Р(-∞<X<х1)
F(x2)= P(Х<x2)=Р(-∞<X<х2)
Р(х1<=X<x2)= F(x2)-F(x1)
Закон Пуассона
Распределение Пуассона-предельное распределение,к кот стремится биномиальное распределение. При увел числа n опытов и одновременном уменьшении вероятности появления события в одном опыте.
n→∞, p→0
закон Пуассона часто называют ЗАКОНОМ РЕДКИХ СОБЫТИЙ, т.к. вероятность столь мала.
СВ X имеет распределение Пуассона если ее возможные значения в серии из n испытаний: X 0,1,2,…m, … а соответствующие им вероятности: Рm= P(X=m)=(am:m!)×e—a
a-параметр закона Пуассона a=n*p
e-иррац число (2ой замечат предел) 2<e<3
n-число которое примет х
Хар-ки закона:
M(x)=a-мат ожидание
Dx=a-дисперсия
σч=√ a-среднее квадратическое отклонение
на практике данный закон применяется при многократном контроле продукции прибором высокой надежности (многокр контроль m→∞, p→0, вероятность отказа стрм к 0)
Характеристики положения СВ
Хар-ки рассеивания CВ
Характеристики положения характеризуют положение центра рассеивания СВ
В качестве этих хар-к исп-ся:
а) математическое ожидание СВ
б) медиана СВ
в) мода СВ *все они имеют размерность.кот характеризуют величины
математическое ожидание СВ-среднее ожидаемое СВ относительно которого происх разброс всех возможных значений СВ.
M[x], M(x) mx
Мат ожидание равно сумме произведений всех возможных значений СВ на соотв им вероятность.
M[x]=S(сверху n, снизу i=1)xi*pi -дискретная СВ
mx=∫(сверху +∞, снизу -∞)×хf(x)dx –непрерывная СВ
f(x)-плотность распределения СВ
f(x)dx-элемент вероятности попадания на прямую шириной dx
Свойства мат ожидания:
1) Мат ожидание суммы СВ равно сумме их ожиданий:
M[X+Y]= M[X]+ M[Y]
2) Общий множитель можно выносить за скобки:
M[сY]= с*M[X], с=const
Медиана СВ-значения СВ,при кот вероятность события что СВ примет значение равное Х меньше медианы равна вероятности события что СВ Х примет значение больше медианы.
Обозначение Ме(Х) Ме[Х]

Мода СВ-наиб вероятное значение СВ,т.е. такое знач-е СВ,которому соответствует большая вероятность.
Обоз-е: Мо(Х)

Дисперсия
ДУ: порядок ДУ, общее и частное решение. Задача Коши и ее геометрический смысл.
 .
.