Презентация «Признаки равенства прямоугольных треугольников»
Инфоурок › Геометрия ›Презентации›Презентация «Признаки равенства прямоугольных треугольников»Описание презентации по отдельным слайдам:
1 слайд Описание слайда: 2 слайд
Описание слайда: 2 слайд  Описание слайда:
Описание слайда: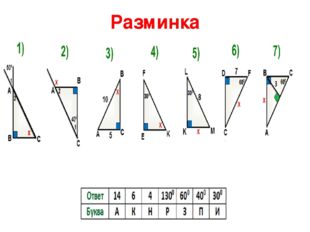 Описание слайда:
Описание слайда:Разминка
4 слайд Описание слайда:
Описание слайда:Признак 1. Примета, знак, по которому можно узнать, определить что-либо 2. Отличительное свойство, качество.
5 слайд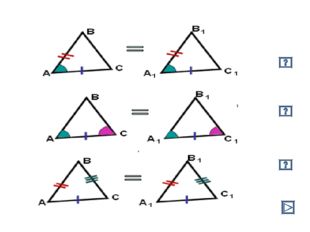 Описание слайда: 6 слайд
Описание слайда: 6 слайд  Описание слайда:
Описание слайда:1 признак Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника , то такие треугольники равны.
 Описание слайда:
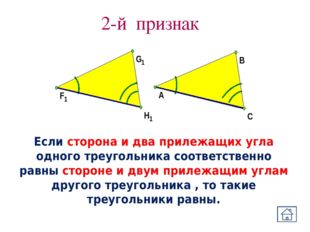
Описание слайда:2-й признак Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника , то такие треугольники равны.
8 слайд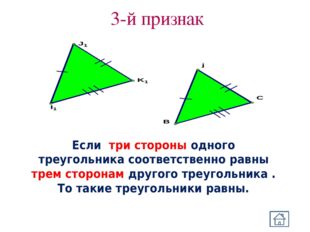 Описание слайда:
Описание слайда: 3-й признак Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника . То такие треугольники равны.
9 слайд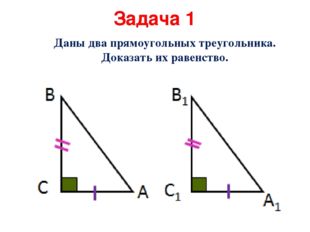 Описание слайда:
Описание слайда:Задача 1 Даны два прямоугольных треугольника. Доказать их равенство.
10 слайд
Признак равенства прямоугольных треугольников (по двум катетам) Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого треугольника, то такие треугольники равны.
11 слайд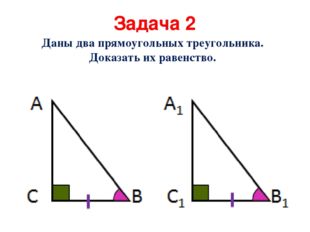 Описание слайда:
Описание слайда:Задача 2 Даны два прямоугольных треугольника. Доказать их равенство.
12 слайд Описание слайда:
Описание слайда:Признак равенства прямоугольных треугольников (по катету и прилежащему углу) Если катет и прилежащий угол одного прямоугольного треугольника соответственно равны катету и прилежащему углу другого треугольника, то такие треугольники равны
13 слайд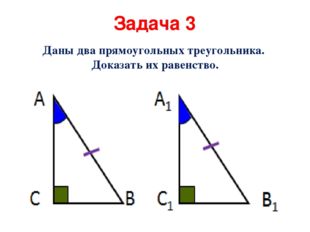 Описание слайда:
Описание слайда:Задача 3 Даны два прямоугольных треугольника. Доказать их равенство.
 Описание слайда:
Описание слайда:Признак равенства прямоугольных треугольников ( по гипотенузе и острому углу) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны
15 слайд Описание слайда:
Описание слайда:Признак равенства прямоугольных треугольников (по гипотенузе и катету) Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.
16 слайд Описание слайда:
Описание слайда:Признак равенства прямоугольных треугольников (по катету и противолежащему углу) Если катет и противолежащий угол одного прямоугольного треугольника соответственно равны катету и противолежащему углу другого треугольника, то такие треугольники равны
 Описание слайда: 18 слайд
Описание слайда: 18 слайд  Описание слайда: 19 слайд
Описание слайда: 19 слайд  Описание слайда: 20 слайд
Описание слайда: 20 слайд 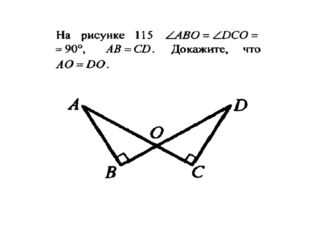 Описание слайда: 21 слайд
Описание слайда: 21 слайд 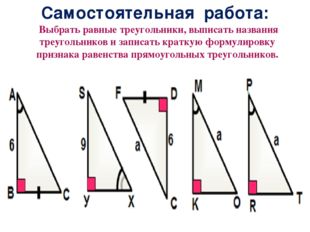 Описание слайда:
Описание слайда:Самостоятельная работа: Выбрать равные треугольники, выписать названия треугольников и записать краткую формулировку признака равенства прямоугольных треугольников.
22 слайд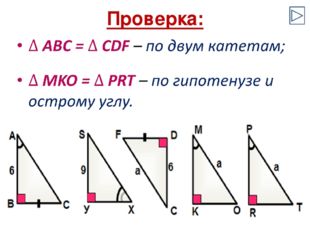
Проверка:
23 слайд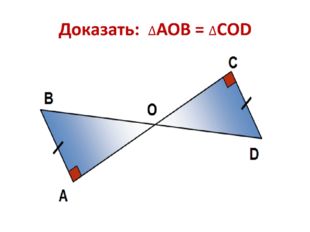 Описание слайда: 24 слайд
Описание слайда: 24 слайд 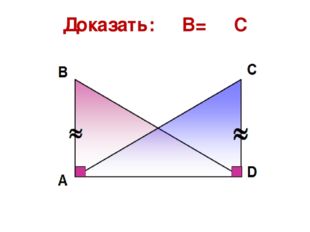 Описание слайда:
Описание слайда:Доказать: ∠ В= ∠ С
25 слайд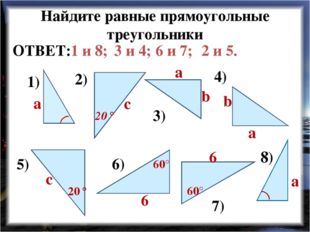 Описание слайда:
Описание слайда:Найдите равные прямоугольные треугольники 1) 2) 3) 4) 5) 6) 7) 8) с a a с a a b b 6 6 60° 60° 20° 20° 1 и 8; 3 и 4; 6 и 7; 2 и 5. ОТВЕТ:
26 слайд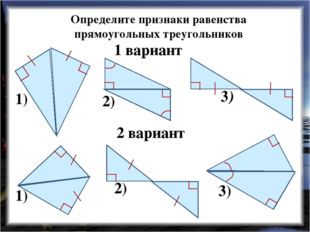 Описание слайда:
Описание слайда:Определите признаки равенства прямоугольных треугольников 1 вариант 2 вариант 1) 2) 3) 1) 2) 3)
27 слайд Описание слайда:
Описание слайда: 
Курс профессиональной переподготовки
Учитель математики

Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-1362975
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийМетодическая разработка по геометрии (7 класс) на тему: Урок геометрии в 7 классе «Признаки равенства прямоугольных треугольников»
7 класс
геометрия
Признаки равенства прямоугольных треугольников
I Организация начала урока
Здравствуйте! Проверьте, пожалуйста, наличие раздаточного материала у вас на парте: маршрутный лист, треугольники, карточки с числами, а также свою готовность к уроку.
II Сообщение темы , цели и задач урока.
На прошлых уроках мы с вами говорили о свойствах прямоугольного треугольника. Сегодня мы продолжим разговор о прямоугольных треугольниках. Чтобы определить тему урока, вам необходимо выполнить два задания.
Первое задание – ребус:
СЛАЙД 1
Второе задание: Решите задачи и найдите х. В соответствии с ключом составьте слово:
МЛ2
СЛАЙД 2
СЛАЙД 3
Вы получили слово – признак.
Кто готов назвать тему урока, в соответствии с изучаемой темой «Прямоугольные треугольники» и полученными словами «равенство» и «признак» ?
Признаки равенства прямоугольных треугольников.
СЛАЙД 4
Запишите тему урока.
Составим план урока, который будем дополнять по ходу урока.
— повторение:
— определение прямоугольного треугольника
— свойства прямоугольного треугольника
— определение равных фигур
— признаки равенства треугольников
— свойства равнобедренного треугольника
— признак равнобедренного треугольника
— сумма углов треугольника
— признаки равенства прямоугольных треугольников
— решение задач
— применение в математике
— применение в жизни
III Актуализация знаний учащихся. Подготовка к активной учебно-познавательной деятельности на основном этапе урока.
Обсудите с соседом понятия, определенные в плане урока
— Кто готов задать вопросы, связанные с прошлой темой?
— Какой треугольник называется прямоугольным?
— Чему равна сумма углов треугольника?
— Чему равна сумма острых углов прямоугольного треугольника?
— Чему равен катет, лежащий против угла в 300?
— Чему равны углы прямоугольного треугольника, если один из катетов равен половине гипотенузы?
— Первый признак равенства треугольников
— Второй признак равенства треугольников
— Третий признак равенства треугольников
— Какие треугольники называются равными?
— Свойство углов равнобедренного треугольника
— Свойство биссектрисы равнобедренного треугольника?
— Признак равнобедренного треугольника
СЛАЙД 5
Ответьте на мои вопросы:
Если мы доказали равенство
— одной стороны в треугольниках, какой признак можно применить? (1,2,3)
— одного угла (1,2)
— двух сторон (1,3)
— двух углов (2)
— стороны и угла (1,2)
Как вы думаете, зачем мы повторили эти понятия?
— Они помогут нам при изучении новой темы.
МЛ1 БЛИЦ – ОПРОС Поставьте баллы.
Чем отличается прямоугольный треугольник от всех остальных?
Нам известна градусная мера одного угла — 900
Какие признаки равенства треугольников мы можем применить к прямоугольным треугольникам, если нам известно, что один угол у них прямой? (1 и 2)
IV Усвоение новых знаний.
СЛАЙД 6,7,8,9,10
МЛ3
3. | ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
| 1 1 2 1 3 |
П.3а) маршрутного листа:
— покажите, что треугольники прямоугольные
— отметьте элементы, чтобы треугольники были равны по первому признаку равенства треугольников (учитывая прямой угол).
— вспомните название сторон прямоугольных треугольников и сформулируйте признак.
— по двум катетам. Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого треугольника, то такие треугольники равны.
П. 3б)
— покажите, что треугольники прямоугольные
— отметьте элементы, чтобы треугольники были равны по второму признаку равенства треугольников (учитывая прямой угол).
— сформулируйте признак.
— по катету и прилежащему острому углу. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углы другого треугольника, то такие треугольники равны
Подумайте, обязательно ли это должен быть прилежащий угол? Отметьте в п. 3в) катет и противолежащий ему угол.
Продолжите фразу: если в треугольниках равны два угла, то …..
— равны и третьи углы равны.
Докажите, что треугольники равны. Сформулируйте признак.
— по катету и противолежащему острому углу.
Можно ли утверждать, что прямоугольные треугольники могут быть равны по катету и острому углу? Докажите на примере, что нет.
Итак, мы сформулировали 2 признака равенства прямоугольных треугольников. Какие элементы в них задействованы?
— катеты и острые углы
Какой элемент не задействован?
— гипотенуза
В п.3г) по аналогии с п.3в) сформулируйте признак — по гипотенузе и острому углу. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Какой вариант мы не рассмотрели?
— гипотенуза и катет
Отметьте эти элементы на чертеже как на экране.
Можем ли мы что-нибудь сказать об острых углах этих треугольников?
— нет. Только, что сумма острых углов равна 900.
Чтобы доказать этот признак, нужно использовать определение равных треугольников.
— треугольники называются равными, если при наложении они совпадают.
Значит, что нужно сделать?
— наложить треугольники друг на друга.
Наложим один треугольник на другой, таким образом, чтобы совпали прямые углы, и равные катеты. Катеты совпадут, т.к. они равны.
Предположим, что треугольники не равны и вторые катеты не совпадают. СЛАЙД 11
Чтобы доказать признак, необходимо воспользоваться свойством равнобедренного треугольника и теоремой о сумме углов треугольника.
Получается равнобедренный треугольник¸ у которого боковые стороны являются гипотенузами данных треугольников (гипотенузы равны по условию). Значит углы при основании равны. А этого быть не может, т.к. удин угол острый, а другой тупой.
Физминутка??? Равные п/у треугольники
На каждой парте лежит один треугольник с известными сторонами и углами.
Задаются вопросы:
— встаньте у кого в треугольнике углы равны 300 и 600.
Обращаясь к одной парте:
Назовите длину гипотенузы ( 7)
Чей треугольник равен – останьтесь стоять, остальные сядьте. И т.п.
V Первичное закрепление знаний
Мы выяснили, что существует четыре признака равенства прямоугольных треугольников. ТАБЛИЦА НА МАГНИТНОЙ ДОСКЕ.
Найдите пары равных треугольников и запишите их номера в таблицу:
4. | см. приложение Найди пары равных треугольников и запишите их номера в таблицу:
| 5 |
VI Закрепление знаний.
5.
| Задача:
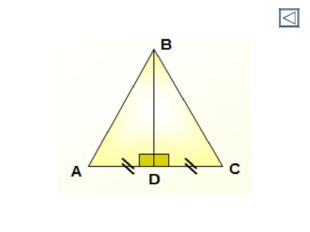
Дано: АВС – равнобедренный АС — основание BD — высота. Доказать: ABD = BCD Доказательство: Рассмотрим _____ и _____ — _______________, т.к. BD — ______________
______ и _____ равны по ___________________ Дано: АВС – равнобедренный АС — основание АD и CЕ — высоты. Доказать: ADC = CЕА Доказательство: Рассмотрим _____ и _____ — _______________, т.к. _____________________________
______ и _____ равны по __________________
____________________________________________ ____________________________________________ ____________________________________________ | 3 5 9 |
VII Обобщение и систематизация.
МЛ7 СЛАЙД 10
VIII Контроль и самопроверка знаний
МЛ9 Графический диктант
Верно ли что:
- прямоугольные треугольники равны, если равны их гипотенузы?
- прямоугольные равнобедренные треугольники равны?
- прямоугольные треугольники равны, если у них равны гипотенуза и острый угол?
- треугольники равны
- треугольники равны
- прямоугольные равнобедренные треугольники равны, если их гипотенузы равны по 8 см?
7.
8. для доказательства равенства прямоугольных треугольников достаточно доказать равенство двух пар соответствующих элементов?
СЛАЙД 11. Взаимопроверка
IX Подведение итогов урока.
Подведем итог.
Что вы нового узнали на уроке? Чему научились?
X Информация о домашнем задании и инструктаж по его выполнению
Урок по геометрии на тему «Признаки равенства прямоугольных треугольников» (7 класс)














 Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
(комбинированный урок геометрии в 7 классе
по учебнику Атанасян Л.С., Бутузов В.Ф. и др. «Геометрия» 7 – 9)
Учитель математики МОУ СОШ № 11: Мелёшина В.В.
г. Орехово – Зуево, Московской области
Тип урока: комбинированный урок.
Цели урока:
повторение основных понятий и свойств по теме «Прямоугольный треугольник»;
формирование знаний по теме «Признаки равенства прямоугольных треугольников»;
научить учащихся решать задачи на применение признаков равенства
прямоугольных треугольников;
развитие математического мышления;
развитие умения правильно и грамотно излагать свои мысли;
повышение мотивации учения и интереса к математике за счет включения в урок элементов проблемного обучения и за счет привлечения ИКТ.
Необходимое оборудование и материалы:
компьютер;
мультимедиапроектор;
интерактивная доска;
набор карточек трех цветов для каждого ученика.
Ход урока
Орг. момент.
Здравствуйте, садитесь. Сегодня мы будем говорить о прямоугольном треугольнике, о его свойствах, познакомимся с признаками равенства прямоугольных треугольников, посмотрим применение этих признаков при решении задач и выполним самостоятельную работу по этой теме.
А начнем наш урок с проверки домашнего задания.
Проверка домашнего задания.
Двое учащихся готовят у доски чертежи и условие домашних задач.
Таблица с возможными решениями домашних задач.
№ 255
1 ученик

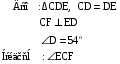 Дано: ∆CDE, CD = DE
Дано: ∆CDE, CD = DE
CF 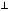 ED
ED
 D=54o
D=54o
Найдите:  ECF
ECF
Решение
∆CDE – равнобедренный, т.к. CD = DE

 С =
С =  Е = (180о – 54о) : 2 = 63о( свойство углов при основании равнобедренного треугольника).
Е = (180о – 54о) : 2 = 63о( свойство углов при основании равнобедренного треугольника).
∆CFЕ – прямоугольный, т.к. CF
 ED
ED 
 ЕCF = 90o —
ЕCF = 90o —  Е (по свойству острого угла в прямоугольном треугольнике)
Е (по свойству острого угла в прямоугольном треугольнике)
 ECF = 90о – 63о = 27о
ECF = 90о – 63о = 27о
Ответ: 27о
№ 257
2 ученик
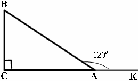
Дано: ∆АВС,  С = 90o
С = 90o
 ВАК = 120o
ВАК = 120o
АС + АВ = 18 см
Найдите: АС, АВ
Решение
 ВАК – внешний угол
ВАК – внешний угол 
 ВАК =
ВАК =  В +
В + С =120о (свойство
С =120о (свойство
внешнего угла треугольника)
Т.к.  С = 90o
С = 90o 
 В = 120о – 90о = 30о
В = 120о – 90о = 30о
Т.к.
 В = 30o, то АС =
В = 30o, то АС =  АВ (свойство катета, лежащего напротив угла равного 30о)
АВ (свойство катета, лежащего напротив угла равного 30о)Т.к. АС + АВ = 18 см (по условию)
 АВ + АВ =18
АВ + АВ =18 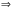 АВ = 12см, АС = 6 см
АВ = 12см, АС = 6 см
Ответ: АС = 6 см, АВ = 12 см
Игра «Ты мне, я тебе»:
(Учащиеся задают друг другу вопросы, выслушивают и оценивают ответы)
Возможные вопросы.
Какой треугольник называется прямоугольным?
Как называются стороны прямоугольного треугольника?
Может ли иметь треугольник два прямых угла? Ответ объясните.
Докажите, что в прямоугольном треугольнике гипотенуза больше катета.
Каким свойством обладают острые углы прямоугольного треугольника?
Каким свойством обладает катет, лежащий напротив угла 30о?
Найдите острые углы в равнобедренном прямоугольном треугольнике.
Каким свойством обладает медиана, проведенная к гипотенузе?
Заслушать решение домашних задач.
Дополнительный вопрос.
Какие геометрические утверждения были применены при решении задач?
Решение задач по готовым чертежам. (Слайды 2 – 6)
(Работа с сигнальными карточками.)
Ребята, у каждой задачи есть три ответа, которые записаны в прямоугольники разного цвета. Перед вами лежат цветные карточки. Вы должны устно решить задачу и по моей команде поднять карточку того цвета, на которой записан правильный ответ.
№
Задачи для тестовой работы
Ответы
Слайд 2
Найдите второй острый угол прямоугольного треугольника, если один из них равен 37о.
53о
Слайд 3
Найдите острый угол прямоугольного треугольника, если гипотенуза равна
10 см, а катет, лежащий напротив этого угла, равен 5 см
30о
Слайд 4
Чему равна гипотенуза, если катет, лежащий напротив угла 30о, равен 4 см?
8 см
Слайд 5
Найдите величину медианы, проведенной из вершины прямого угла к гипотенузе, если гипотенуза равна 10 см.
5 см
Слайд 6
Определите вид треугольника, если медиана, проведенная из вершины одного из углов треугольника, равна половине противоположной стороны
прямоугольный
Объяснение нового материала.
Запишите в рабочих тетрадях тему урока «Признаки равенства прямоугольных треугольников. (Слайд 7)
Сегодня мы самостоятельно попытаемся вывести признаки равенства прямоугольных треугольников, опираясь на ранее изученные теоремы. Нам потребуются признаки равенства треугольников.
Какие признаки равенства треугольников вы знаете?
А теперь решим задачу.
№
Задача 1
Слайд 8
Дано: ∆АВС,
ВН АС
АС
АН = НС
Доказать: ∆АВН = ∆СВН
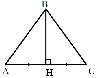
Доказательство
АН = НС (по условию)
 АНВ =
АНВ =  ВНС = 90о, т.к. ВН
ВНС = 90о, т.к. ВН АС
АС  ∆АВН = ∆СВН
∆АВН = ∆СВНВН – обшая
Слайд 9
Беседа
Примерные ответы
1.По какому признаку равны треугольники?
2. Какие это треугольники?
По I признаку
прямоугольные
3.Давайте сравним и проведем аналогию между первым признаком равенства треугольников и равенством данных прямоугольных треугольников.
4.Какой элемент всегда присутствует у любого прямоугольного треугольника?
Прямой угол
5.Равенство, каких элементов нам известно?
Два катета
6.Как можно сформулировать признак равенства для прямоугольного треугольника?
Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
№
Задача 2
Слайд 10
Дано: АC = BD
 B =
B =  C = 90o
C = 90o
 1 =
1 =  2
2
Доказать: ∆АВD = ∆ACD
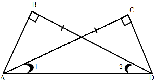
Доказательство
Рассмотрим ∆АВD и ∆ACD
 B =
B =  C = 90o
C = 90oАC = BD (по условию)
 ∆АВD = ∆ACD
∆АВD = ∆ACD  1 =
1 =  2
2
Слайд 11
Беседа
Примерные ответы
1.По какому признаку равны треугольники?
2. Какие это треугольники?
По II признаку
прямоугольные
3.Давайте сравним и проведем аналогию.
4.Какой элемент всегда присутствует у любого прямоугольного треугольника?
Прямой угол
5.Равенство, каких элементов нам известно?
Катет и прилежащий к нему острый угол
6.Как можно сформулировать признак равенства для прямоугольного треугольника?
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
№
Задача 3
Слайд 12
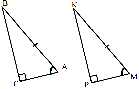 Дано: ∆АВС и ∆МКР
Дано: ∆АВС и ∆МКР
 С =
С = Р = 90о
Р = 90о
 А =
А =  М
М
АВ = МК
Доказать:∆ АВС = ∆ МКР
Доказательство
∆АВС – прямоугольный и ∆МКР – прямоугольный
 В =90о —
В =90о —  А по свойству острых углов
А по свойству острых углов
 К = 90о —
К = 90о —  М прямоугольного треугольника
М прямоугольного треугольника 
 А =
А = М – по условию
М – по условию
 В =
В =  К
К
Итак,
 В =
В = К
К
 А =
А = М – по условию
М – по условию  ∆ АВС = ∆ МКР
∆ АВС = ∆ МКР
АВ = МК – по условию
Слайд 12
Беседа по слайду
Примерные ответы
1.По какому признаку равны треугольники?
2. Какие это треугольники?
По II признаку
прямоугольные
3.Какой элемент всегда присутствует у любого прямоугольного треугольника?
Прямой угол
5. Какие элементы треугольника были известны?
гипотенуза и острый угол
Сформулируйте новый признак равенства прямоугольных треугольников
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Ребята, мы смогли доказать три признака равенства прямоугольных треугольников, но существует еще один признак. (Слайд 13)
Теорема. Если гипотенуза и катет одного прямоугольного треугольника
соответственно равны гипотенузе и катету другого, то такие
треугольники равны.
(Доказательство этого признака проводит сам учитель)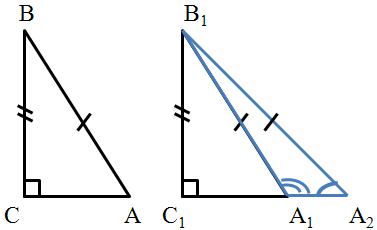
Дано: ∆ АВС и ∆А1В1С1,  С =
С =  С1 = 90о
С1 = 90о
ВС =В1С1
АВ = А1В1
Доказать: ∆ АВС = ∆ А1В1С1
Доказательство
Доказательство проведем методом наложения.
Т.к.  С =
С =  С1 =90о, то ∆ АВС можно наложить на ∆ А1В1С1:
С1 =90о, то ∆ АВС можно наложить на ∆ А1В1С1:
1. Вершина С совместится с вершиной С1
2. Сторона СА и СВ наложатся соответственно на лучи С1А1 и С1В1
3. Вершина В совместится с вершиной В1, т.к. ВС =В1С1
4. Тогда и вершина А совместится с вершиной А1.Это утверждение надо
доказать.
Предположим, что А совместится с точкой А2,
тогда ∆ А1В1А2 – равнобедренный (А1В1 = А2В1)
 А2 – острый,
А2 – острый,  В1А1А2 – тупой, т.к. смежный с острым углом ∆ А1В1С1 .
В1А1А2 – тупой, т.к. смежный с острым углом ∆ А1В1С1 .
 А2 ≠
А2 ≠  В1А1А2 – углы при основании, но это невозможно,
В1А1А2 – углы при основании, но это невозможно,
значит вершины А и А1 совместятся, а, следовательно, ∆ АВС полностью совместится с ∆ А1В1С1  ∆ АВС = ∆ А1В1С1
∆ АВС = ∆ А1В1С1
Мы рассмотрели все признаки равенства прямоугольных треугольников. А теперь давайте еще раз вспомним эти признаки. (Слайд 14)
(Учащиеся дают формулировки признаков равества прямоугольных треугольников).
Запишите в тетрадь признаки равенства прямоугольных треугольников
и сделайте соответствующие чертежи.
Слайд 14
1
По двум катетам
2
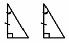
По катету и прилежащему к нему острому углу
3
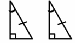
По гипотенузе и острому углу
4
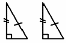
По гипотенузе и катету
Закрепление изученного материала
Устно решить задачи по готовым чертежам.
Слайд 15
Задача 1
Дано: AB║CD
АB = CD
 F =
F =  D = 90o
D = 90o Доказать: BF = ED
Доказать: BF = EDДоказательство
∆ АВF и ∆ CDE:
 F =
F =  D = 90o(по условию)
D = 90o(по условию)АB = CD (по условию)
 АВF =
АВF =  ECD ( внутренние накрест лежащие углы
ECD ( внутренние накрест лежащие углы  при AB║CD и АС – секущей)
при AB║CD и АС – секущей)
 ∆ АВF = ∆ CDE( по гипотенузе и острому углу)
∆ АВF = ∆ CDE( по гипотенузе и острому углу) BF = ED
BF = EDСлайд 15
Задача 2

Дано: О(r)- окружность
 МОВ = 90o
МОВ = 90oМО = ОЕ
Доказать: АЕ = МВ
Доказательство
∆ АОЕ и ∆ МОВ:
 МОВ =
МОВ =  АОЕ = 90o(по условию)
АОЕ = 90o(по условию)МО = ОЕ (по условию)
 ∆ АОЕ = ∆ МОВ (по
∆ АОЕ = ∆ МОВ (поАО = ОВ = r двум катетам)
 АЕ = МВ (соответствующие элементы)
АЕ = МВ (соответствующие элементы)
Решить задачу № 263 письменно у доски и в тетрадях.
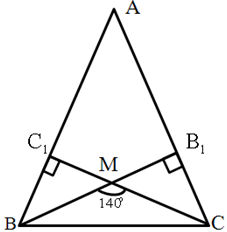
Дано: ∆ АВС, АВ = ВС
СС1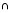 ВВ1 = М
ВВ1 = М
СС1 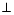 АВ, ВВ1
АВ, ВВ1 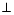 АС
АС
 МВС = 140о
МВС = 140о
Найти:  А,
А,  В,
В,  С
С
Решение
∆ АВС – равнобедренный, т.к. АВ = ВС

 В =
В =  С
С∆ ВВ1С = ∆ С1СВ по гипотенузе и острому углу (
 В1 =
В1 =  С1 =90о,
С1 =90о,
ВС – общая гипотенуза , В =
В =  С – острые углы)
С – острые углы) 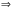
 ВВ1С =
ВВ1С =  СС1В
СС1В
значит ∆ ВМС – равнобедренный 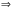
 ВВ1С = (180о – 140о) : 2 = 20о
ВВ1С = (180о – 140о) : 2 = 20о
Из ∆ ВВ1С

 В = 90о – 20о = 70о (по свойству острых углов прямоугольных треугольников)
В = 90о – 20о = 70о (по свойству острых углов прямоугольных треугольников) А = 180о – (70о +70о) = 40о
А = 180о – (70о +70о) = 40о
Ответ: 40о, 70о, 70о
Самостоятельная работа. Решите самостоятельно задачу (Слайд 16)
Вариант 1
Вариант 2
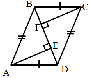
Доказать: AE =FC, BF = ED
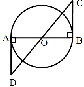
Доказать: О – середина отрезка СD
Взаимопроверка (Слайд 16)
Обменяйтесь тетрадями и проверьте решение задач друг у друга.
Вариант 1
Вариант 2
Доказательство
1.Рассмотрим ∆ АBD и ∆ CBD
AD = BC
AB = CD
 ∆ АBD = ∆ CBD
∆ АBD = ∆ CBD DB – обшая ( по III признаку)

 CBF =
CBF =  ADЕ
ADЕ2.∆ АED и ∆ BFC
ВС = AD
 CBF =
CBF =  ADЕ
ADЕ 
∆ АED = ∆ BFC (по
гипотенузе и острому углу)
3. AE = CF, BF = ED (как соответствующие элементы)
Доказательство
Рассмотрим ∆ АBD = ∆ CBD
(AO = OB – радиус окружности,
 АОD =
АОD = СОВ – вертикальные углы)
СОВ – вертикальные углы) А =
А =  В = 90o
В = 90o
 ∆ АBD = ∆ CBD (по катету и прилежащему к нему острому углу)
∆ АBD = ∆ CBD (по катету и прилежащему к нему острому углу) DO = OC ( как соответствующие элементы)
DO = OC ( как соответствующие элементы) точка О — середина DC
точка О — середина DC
Критерии оценивания:
Доказательство в целом верное
5
Допущены неточности в формулировках геометрических утверждений
4
Пропущено хотя бы одно обоснование геометрических утверждений
3
Отсутствуют формулировки геометрических утверждений
2
Кто верно решил задачу? Поднимите зеленую карточку.
Итоги урока
Наш урок подошел к концу. Что нового вы узнали на уроке?
Сформулируйте признаки равенства прямоугольных треугольников.
Для чего нужны признаки равенства прямоугольных треугольников?
Домашнее задание
Запишите домашнее задание:
п.35, вопросы 12,13.
решите задачи: № 262, № 265.
Спасибо за урок.
Презентация «Прямоугольный треугольник. Признаки равенства прямоугольных треугольников» 7 класс
- . 7 класс. Урок геометрии.
- Тема урока: Прямоугольный треугольник. Признаки равенства прямоугольных треугольников.
- Повторение. Тест.
- Домашние задачи у доски.
- Признаки равенства прямоугольных треугольников.
- Решение задач.
- Сколько существует внешних углов при одной вершине ?
- Прямоугольный треугольник
- Треугольник называется прямоугольным, если у него есть прямой угол.
- ABC – прямоугольный
- C = 90°
- A + B = 90°
- Сумма острых углов прямоугольного треугольника равна 90°.
- Сторона прямоугольного треугольника, противолежащая прямому углу называется гипотенузой.
- Две другие стороны называются катетами.
- Назовите гипотенузу и катеты
- в KBO;
- в KOM.
- Определите вид KBO.
- Признаки равенства прямоугольных треугольников
- по двум катетам
- по двум сторонам и углу между ними
- по гипотенузе и
- острому углу
- по стороне и двум
- прилежащим к ней углам
- по катету и прилежащему острому углу
- по стороне и двум прилежащим к ней углам
- по катету и противолежащему острому углу
- по стороне и двум прилежащим углам
- по гипотенузе и катету
- Домашнее задание
- Вопросы №14,15,16.
- Формулировки признаков.
- Задачи №40, 41(2).
- Урок №2 по теме
- «Прямоугольный
- треугольник».
- по двум катетам
- по гипотенузе и острому углу
- по катету и
- прилежащему
- острому углу
- по катету и
- противолежащему
- острому углу
- по гипотенузе и катету
- Выбери правильное завершение определения.
- Катетом называется…
- Любая сторона треугольника;
- Сторона, лежащая против прямого угла треугольника;
- Перпендикуляр из вершины угла на противолежащую сторону;
- Сторона, примыкающая к вершине прямого угла.
- Выбери правильное завершение определения.
- Гипотенузой называется…
- Любая сторона треугольника;
- Сторона, лежащая против прямого угла треугольника;
- Перпендикуляр из вершины угла на противолежащую сторону;
- Сторона, примыкающая к вершине прямого угла.
- Выбери правильное завершение определения.
- Сумма острых углов прямоугольного треугольника равна …
- Чему равны углы при основании в равнобедренном
- прямоугольном треугольнике?
- Могут ли в равнобедренном прямоугольном
- треугольнике углы при основании быть равными 90?
- Дано: B = D = 90°
- BC || AD
- Доказать: ABC = CDA.
- Доказательство.
- 1) Рассмотрим ABC и CDA
- — треугольники прямоугольные по условию;
- — AC — общая гипотенуза;
- BCA = CAD — т. к. они внутренние накрест лежащие
- при параллельных прямых BC и AD и секущей AC.
- по гипотенузе и острому углу
- Дано: AD — биссектриса A
- DB AB, DC AC.
- Доказать: ADB = ADC.
- Доказательство.
- 1) Рассмотрим ADB и ADC.
- — треугольники прямоугольные т. к. DBAB, DCAC.
- 2) ADB = ADC по гипотенузе и острому углу.
- — BAD = CAD т. к. AD — биссектриса A.
- — AD — общая гипотенуза.
- Дано: C = D = 90°
- AD = BC
- Доказать: ABC = BAD.
- Задача №3. Самостоятельно.
- Доказательство.
- Рассмотрим ABC и BAD.
- — треугольники прямоугольные т. к. C=D=90°.
- — AD = BC
- — AB — общая гипотенуза
- 2) ABC = BAD
- по гипотенузе и катету
- Дано: AB BC; CD BC;
- O — середина AD;
- AB = 3 см.
- Найти: CD.
- 1) Рассмотрим ABO и DCO.
- 2) ABO = DCO по гипотенузе и острому углу.
- 3) Из равенства треугольников следует AB = CD = 3 см.
- • AOB = DOC как вертикальные.
- • AO = OD т. к. O — середина AD.
- • треугольники прямоугольные т. к. ABBC и CDBC.
- Дано: DA AB
- FB AB
- BD = AF
- Доказать: ABD = BAF
- Устно: формулировки признаков.
- №2. Докажите, что два равнобедренных прямоугольных треугольника равны, если равны их гипотенузы.
- №3 Докажите равенство прямоугольных треугольников по катету и высоте, опущенной на гипотенузу.
- Cвойство катета,
- лежащего против угла
- в 30 градусов.
- Катет, лежащий против угла в 30, равен половине гипотенузы.
- Свойство катета, лежащего против угла в 30.
- Дано: ABC
- C = 90°, B = 30°.
- Доказать: АС = АВ.
- Докажите, что в прямоугольном треугольнике с углом 30° катет, противолежащий этому углу, равен половине гипотенузы.
- Доказательство.
- 1) Построим DBC = ABC, как показано на рисунке.
- 2) ABC — равносторонний, так как все его углы равны
- 60° и AB = BD = AD.
- 3) AC = AD или AC = AB.
- Дано: ABC — равнобедренный
- с основанием AC;
- B =120°;
- BD — медиана; BD = 3 см.
- Найти: A, C, AB и BC.
- В равнобедренном треугольнике угол, противолежащий основанию, равен 120°, а медиана, проведенная к основанию, равна 3 см. Найдите углы при основании и боковые стороны треугольника.
- 1) ABC — равнобедренный по условию.
- BD — медиана, биссектриса и высота.
- ABC – равнобедренный
- по условию.
- BD — медиана, биссектриса и высота.
- 3) ABD — прямоугольный т. к. ADB = 90°.
- 5) BD = AB по свойству катета, лежащего против угла в 30°.
- AB = 3 • 2 = 6 см. AB = BC = 6 см.
- 6) A = C = 30° как углы при основании равнобедренного
- треугольника.
- A = C = 30°; AB = BC = 6 см.
- 2) ABD = CBD = 120° : 2 = 60° т. к. BD — биссектриса.
- 4) A + ABD = 90° как острые углы прямоугольного треугольника.
- A = 90° — 60° = 30°.
- по двум катетам
- по гипотенузе и острому углу
- по катету и
- прилежащему
- острому углу
- по катету и
- противолежащему
- острому углу
- по гипотенузе и катету
- Дано: ABC = A1B1C1
- BD AC, B1D1 A1C1
- Доказать: BD = B1D1.
- Доказательство.
- Рассмотрим ABD и A1B1D1.
- треугольники прямоугольные т. к. BDAC и B1D1A1C1.
- 2) ABD = A1B1D1 по гипотенузе и острому углу.
- 3) Из равенства треугольников следует BD = B1D1.
- AB = A1B1 из равенства
- A = A1 ABC = A1B1C1
- Докажите, что сумма трех внешних углов треугольника, взятых по одному при каждой вершине, равна 360º.
- Устно: формулировки признаков и формулировка
- задачи №43.
- №2. Докажите, что равносторонние треугольники равны, если равны их высоты.
- №3. Докажите равенство остроугольных треугольников по двум углам и высоте, проведенной из вершины третьего угла.
- Дано: a | | b; с – секущая; ∠3 больше суммы ∠1 + ∠2 в 4 раза.
- Найти все образовавшиеся углы.
- Катет, лежащий против угла в 30, равен половине гипотенузы.
- Свойство катета, лежащего против угла в 30.
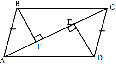 Доказать: BF = ED
Доказать: BF = ED