Тема: «Площади простых фигур».
Тема: «Площади простых фигур». Тема: «Площади простых фигур».Основные задачи:
Дать формулы для вычисления площадей параллелограмма, треугольника, трапеции и доказать их. Привести примеры решения задач с применением данных формул.
Ход урока:I. Организационный момент:
Проверить готовность класса к уроку: наличие чертежных инструментов, дневников. Проверить чистоту класса, готовность доски к уроку.II. Поставить задачу урока.
Записать тему урока и план изучения нового материала:1. Площадь параллелограмма.
2. Площадь треугольника.
3. Площадь трапеции.
(план урока на доске)
III. Словарная работа.
Обратите внимание на написание данных слов: (стенд «Словарь»)треугольник
прямоугольник
параллелограмм
трапеция
площадь
V.
 Повторение пройденного, необходимого для изучения нового материала.
1. Определение трапеции, параллелограмма, треугольника. (Данные фигуры и их высоты натянуты на стенде.)
Повторение пройденного, необходимого для изучения нового материала.
1. Определение трапеции, параллелограмма, треугольника. (Данные фигуры и их высоты натянуты на стенде.)Треугольником называется фигура, которая состоит из трех точек, не лежащих на однойпрямой, и трех отрезков, попарно соединяющих эти точки.
Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны.
Посмотрите на стенд с иголочками. Здесь с помощью резинок натянуты данные фигуры. Показываю на высоту треугольника: что это такое? (высота треугольника).
Вспомнить определение высоты треугольника:
Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенной из этой вершины к прямой, содержащую противолежащую сторону треугольника.
Даю понятие высоты параллелограмма и трапеции.

2. Свойство сторон и углов параллелограмма.
У параллелограмма противолежащие стороны равны, противолежащие углы равны.
3. Признаки равенства треугольника.
а) по двум сторонам и углу между ними;
б) по сторонам и прилежащим к ней углам;
в) по трем сторонам.
4. Признаки равенства прямоугольных треугольников.
а) по гипотенузе и острому углу;
б) по катету и противолежащему углу;
в) по гипотенузе и катету.
5. Свойства площади.
а) Каждая простая фигура при заданной единице измерения имеет определенную площадь.
б) Равные фигуры имеют равные площади.
в) Если фигура разбивается на чести, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей.
6. Повторить формулу для вычисления площади прямоугольника.
S = a*b
(Обратите внимание на стенд «Повторение».)
VI. Объяснение нового материала.

1.Площадь параллелограмма.
Прочитать по плакату: Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.Доказать: SABCD = aha
Доказательство:
1. Дополнительное постороение перпендикуляра CE на продолжение прямой AD.
2. Как называется фигура ABCE? (трапеция) На какие фигуры разбивает трапецию высота BF? (сторона параллелограмма CD)
(Вернуться к свойству площади)
SABCE=SABF+SFBCE=SDCE+SABCD
3. Рассмотрим треугольники ABF и DCE. Какие они? (прямоугольные)
Доказываем их равенство.
AB=DC — противолежащие стороны параллелограмма.
BF=CE — противолежащие стороны прямоугольника.
Следовательно:
Треугольник ABF равен треугольнику DCE — по гипотенузе и катету, значит их площади тоже равны.

4.Из 2 и 3 пункта следует, что S ABCD = SFBCE
SFBCE = BC * BF, следовательно SABCD = aha, что и требовалось доказать.
Повторить устно план доказательства:
1. достроить параллелограмм до трапеции;
2. рассмотреть разбиение площади трапеции на площади параллелограмма и треугольника; прямоугольника и треугольника;
3. доказываем равенство треугольников ABF и DCE и равенство их площадей;
4. равенство площади прямоугольника и параллелограмма.
Записать доказательство в тетрадь по готовой записи.
Задачи (устно) по готовому чертежу:
1. Дана трапеция ABCD с высотой BE. Сторона AD равна 10см, а высота BE — 5см. Найти площадь?
Ответ: 50см2
2. Дан параллелограмм ABCD с высотой BF и CE. CE равна 6см, а BC — 8см. Найти площадь?
Ответ: 48см2
Какие данные лишние?
Вывод по плакату.
2.Площадь треугольника.
Прочитать по плакату: Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.Дано: ABC — треугольник, BК — высота, AС = a, BК = ha.
Доказать: SABC =1/2aha
Доказательство:
1. Достроим треугольник ABC до параллелограмма ABCD.
2. На какие фигуры диагональ ВС делит параллелограмм ABCD?
SABCD = SABC + SDCB
3. Рассмотрим треугольники ABC и DCB.
AB=DC, AC=DB — противоположные стороны параллелограмма.
ВC — общая.
Следовательно: треугольники ABC и DCB равны по трем сторонам, значит (по свойству площади)SABC = SDCB 4. Из пункта 2 и 3 следует, что SABC = 1/2SABDC, значит SABC =1/2aha, что и следовало доказать.
Повторить устно план доказательства:
1.
 достроить до параллелограмма;
достроить до параллелограмма;2. площадь параллелограмма разбивается на площади двух треугольников;
3. доказываем их равенство;
4. площадь треугольника равна половине площади параллелограмма.
Доказательство записать самостоятельно, проверить по готовой записи.
Задача (устно) по готовому чертежу:
1. Дан треугольник АВС с высотой СК. Сторона АВ равна 8 см, а высота СК — 5см. Найти площадь треугольника?
Ответ: 20см2
2. Дан треугольник АВС с высотой СК. Сторона Ас равна 7 см, АК — 4см, а высота СК — 6см. Найти площадь треугольника?
Ответ: 24см2
Какие данные лишние?
Вывод по плакату.
3.Площадь трапеции.
Прочитать по плакату: Площадь трапеции равна произведению полусуммы ее оснований на высоту.Доказать: SABCD =(a+b)/2h
Доказательство:
1.
 На площади каких фигур разобьется площадь трапеции диагональю?
На площади каких фигур разобьется площадь трапеции диагональю?SABCD = SABC + SАCD
2.SABC = 1/2ВС*AF
SACD = 1/2AD*CE
3. Из 1 и 2 пункта следует, что SABCD=1/2BC*AF+1/2AD*CE=1/2BC*CE+1/2AD*CE=1/2CE(BC+AD)=1/2h(a+b)=(a+b)/2*h
SABCD =(a+b)/2h, что и следовало доказать.
Повторить устно план доказательства:
1. SABCD = SABC + SАCD
2. SABC, SАCD — ?
3. Из 1 и 2 пункта следует, что SABCD=(a+b)/2h
Дома записать доказательство данного условия по плану.
Задачи (устно) по готовому чертежу:
1. Дана трапеция АВСD с высотой СЕ. Сторона ВС равна 8 см, AD — 10см, а высота СЕ — 4см. Найти площадь трапеции?
Ответ: 36см2
2. Дана трапеция АВСD с высотой СЕ. Сторона ВС равна 6 см, AD — 10см, АВ — 3см, а высота СЕ — 4см.
 Найти площадь трапеции?
Найти площадь трапеции?Ответ: 32см2
Какие данные лишние?
Вывод по плакату.
VII. Итог урока.
Ратота с формулами на стенде «К уроку».1) S=1/2aha
2) S=(a+b)/2h
3) S=aha
Какая из формул является формулой параллелограмма, трапеции, треугольника?
Объясните значение каждой буквы.
Прочитать еще раз по плакатам.
VIII. Домашнее задание.
1. Вопросы №3, 4 и 5 на стр.176;2. Упражнение №18 на стр.177 (разобрать условие задачи по готовому чертежу)
Заключительное слово учителя:
Спасибо Вам ребята за ваши знания. С задачей урока Вы справились.
Спасибо, все свободны. Сайт создан в системе uCoz
Площадь многоугольника — определение и вычисление с примерами решения
Содержание:
Математика, отделяя линию от площади и площадь от тела, утверждает, что реально только тело, а линия и площадь — абстракции.
До настоящего времени в теоремах и задачах рассматривались лишь числовые характеристики отдельных элементов геометрических фигур — длины сторон, градусные меры углов и т. п. В отличие от них площадь характеризует фигуру в целом, т. е. зависит как от ее формы, так и от размеров.
В повседневной жизни человек имеет дело с площадями каждый день — измеряет жилые помещения и приусадебные участки, лесные массивы и сельскохозяйственные угодья и т.д. Вычислением площадей вы занимались и на уроках математики в младших классах. Тем не менее, дать строгое с научной точки зрения определение площади не так просто, и соответствующая математическая теория была создана значительно позже многих известных теорем.
В этой главе мы обобщим сведения о многоугольниках и их площадях. Благодаря этому ваш математический багаж пополнится немалым количеством новых формул, которые необходимо знать и уметь применять. В этой связи дадим вам совет: усвоить какую-либо формулу значительно проще, если понять и запомнить способ ее получения. Более того, откроем вам маленькую профессиональную тайну: иногда даже профессиональные математики не запоминают формулы, а выводят их в уме в случае необходимости. Будет очень здорово, если такую математическую эрудицию удастся приобрести и вам.
Более того, откроем вам маленькую профессиональную тайну: иногда даже профессиональные математики не запоминают формулы, а выводят их в уме в случае необходимости. Будет очень здорово, если такую математическую эрудицию удастся приобрести и вам.
Многоугольник и его элементы
Определение многоугольника
Рассмотрим фигуру, которая состоит из отрезков
В зависимости от количества вершин многоугольник называют треугольником, четырехугольником, пятиугольником и т.д. Многоугольник, который имеет вершин (а следовательно, сторон), называют
Многоугольник обозначают по его вершинам. При этом буквы, которые стоят в названии многоугольника рядом, должны обозначать вершины, которые принадлежат одной стороне (соседние вершины). Например, пятиугольник на рисунке 136, б можно обозначить или но нельзя обозначать
Определение
Периметром многоугольника называется сумма длин всех его сторон.
Диагональю многоугольника называется отрезок, соединяющий две несоседние вершины.
Например, на рисунке 136, б отрезки и являются диагоналями пятиугольника выходящими из вершины Периметр этого многоугольника вычисляется по формуле
Любой многоугольник делит плоскость на две части. Одна из них (на рисунке 136, а она закрашена) является внутренней областью многоугольника. Фигуру, состоящую из многоугольника и его внутренней области, называют плоским многоугольником, или, в некоторых случаях, просто многоугольником. Определение
Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, которая содержит его сторону.
На рисунке 137, а изображен выпуклый многоугольник, а на рисунке 137, б — невыпуклый. Далее мы будем рассматривать только выпуклые многоугольники.
Рассмотрим выпуклый многоугольник (рис. 138). Углы …, (на рисунке они закрашены) называют углами (внутренними углами) многоугольника В частности, угол данного многоугольника при вершине на рисунке обозначен одной дужкой. Углы, смежные с данным внутренним углом, являются внешними углами многоугольника при вершине (на рисунке они обозначены двумя дужками).
Углы …, (на рисунке они закрашены) называют углами (внутренними углами) многоугольника В частности, угол данного многоугольника при вершине на рисунке обозначен одной дужкой. Углы, смежные с данным внутренним углом, являются внешними углами многоугольника при вершине (на рисунке они обозначены двумя дужками).
Любой внутренний угол выпуклого многоугольника меньше
Определение
Многоугольник называется вписанным в окружность, если все его вершины лежат на этой окружности. Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности.
На рис. 139, а изображен вписанный многоугольник, а на рис. 139, б — описанный.
Сумма углов выпуклого многоугольника
Как известно, сумма углов треугольника равна а сумма углов четырехугольника — Нетрудно предположить, что сумма углов выпуклого многоугольника должна зависеть от количества его сторон. Эта зависимость выражается следующей теоремой.
Эта зависимость выражается следующей теоремой.
Теорема (о сумме углов выпуклого -угольника)
Сумма углов выпуклого «-угольника равна
Доказательство:
Пусть дан выпуклый -угольник (рис. 140). Обозначим внутри него произвольную точку и соединим ее с вершинами При этом образуется треугольников. Обратим внимание на то, что сумма углов данного многоугольника равна сумме всех углов этих треугольников, кроме углов при вершине Поскольку сумма углов составляет то искомая сумма углов многоугольника равна
Пример:
Докажите, что сумма внешних углов выпуклого -угольника, взятых по одному при каждой вершине, равна
Решение:
Поскольку внешний угол многоугольника по определению является смежным с соответствующим внутренним углом, то сумма этих двух углов равна Таким образом, сумма всех внутренних и внешних углов равна Чтобы получить сумму внешних углов, вычтем из этой суммы сумму внутренних углов:
Понятие площади многоугольника
Понятие площади хорошо известно нам из повседневного опыта: мы измеряем площадь спортивной площадки или садового участка, рассчитываем по площади количество обоев или коврового покрытия для ремонта комнаты и т. д. Попробуем придать представлениям о площади определенную математическую строгость.
д. Попробуем придать представлениям о площади определенную математическую строгость.
Условимся, что под площадью многоугольника мы будем понимать площадь его внутренней области. Как и в случае измерения длин отрезков, измерение площадей основывается на сравнении данной фигуры с фигурой, площадь которой принята за единицу измерения. За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
Например, если за единицу измерения отрезков приняты 1 мм, 1 см или 1 м, то за единицу измерения площади принимают площадь квадрата со стороной 1 мм, 1 см или 1 м. Площадь такого квадрата называется квадратным миллиметром квадратным сантиметром или квадратным метром соответственно. Из курса математики известны и другие единицы площади: ар (площадь квадрата со стороной 10 м), гектар (площадь квадрата со стороной 100 м) и др.
При выбранной единице измерения площадь каждого многоугольника выражается положительным числом, которое показывает, сколько раз единица измерения площади и ее части укладываются в данном многоугольнике. Обычно площадь обозначается буквой
Обычно площадь обозначается буквой
Для определения приближенного значения площади можно использовать палетку — прозрачную пленку с квадратной сеткой (рис. 141).
Наложив палетку на фигуру, площадь этой фигуры определяют обычным подсчетом количества единичных квадратов, которые вместились в данной фигуре. Однако на практике применять такой способ неудобно. Поэтому для определения площади многоугольника обычно измеряют лишь некоторые связанные с ним отрезки, а потом вычисляют площадь по соответствующим формулам. Вывод этих формул основывается на свойствах площадей, которые мы рассмотрим ниже.
Прежде всего заметим, что когда два многоугольника равны, то единица измерения площади и ее части укладываются в каждом из них одинаковое количество раз, т. е. имеет место следующее свойство.
1. Равные многоугольники имеют равные площади.
Далее, пусть многоугольник состоит из нескольких частей — других многоугольников, которые не имеют общих внутренних точек (рис. 142). Если эти части имеют площади то площадь всего многоугольника равна их сумме: В этом заключается второе свойство площадей.
142). Если эти части имеют площади то площадь всего многоугольника равна их сумме: В этом заключается второе свойство площадей.
2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Третье свойство площадей связано с единицей их измерения.
3. Площадь квадрата со стороной, равной единице длины, равна единице площади.
Три приведенных свойства называют аксиомами площадей. Итак, площадь многоугольника — это положительная величина, численное значение которой удовлетворяет аксиомам площадей.
Из этого, в частности, следует, что каждый многоугольник имеет некоторую площадь, которая однозначно определяется в заданных единицах измерения.
Определение
Две фигуры называются равновеликими, если они имеют равные площади.
Очевидно, что по первой аксиоме площадей любые два равных многоугольника равновеликие. Однако не любые два равновеликих многоугольника равны.
Однако не любые два равновеликих многоугольника равны.
Если рассмотреть два равных прямоугольных треугольника (рис. 143, а), то, прикладывая их равными сторонами друг к другу, можно получить равнобедренный треугольник (рис. 143, б), параллелограмм (рис. 143, в), прямоугольник (рис. 143, г) или четырехугольник с попарно равными соседними сторонами — дельтоид (рис. 143, д). Все эти фигуры равносоставленные, т. е. составлены из одних и тех же многоугольников.
По второй аксиоме площадей все образованные таким способом фигуры имеют равные площади. Следовательно, любые равносоставленные многоугольники являются равновеликими. Интересно, что имеет место и обратное утверждение (теорема Бойяи — Гервина): два равновеликих многоугольника являются равносоставленными (приводим этот факт без доказательства).
Какие фигуры называются равными. Две геометрические фигуры называются равными, если их можно совместить
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».
Ход урока
I. Повторение.1) Устно по готовому чертежу вывести формулу площади параллелограмма.
2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?
(по готовому чертежу)
зависимость обратно пропорциональная.
3) Найти вторую высоту (по готовому чертежу)
4) Найти площадь параллелограмма по готовому чертежу.
Решение:
5) Сравните площади параллелограммов S1, S2, S3 . (Они имеют равные площади, у всех основание a и высота h).
Определение: Фигуры, имеющие равные площади, называются равновеликими.
II. Решение задач.
Решение задач. 1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.
Решение:
2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.
3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?
Решение: Можно. Все треугольники равновеликие.
4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.
Решение:
5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше.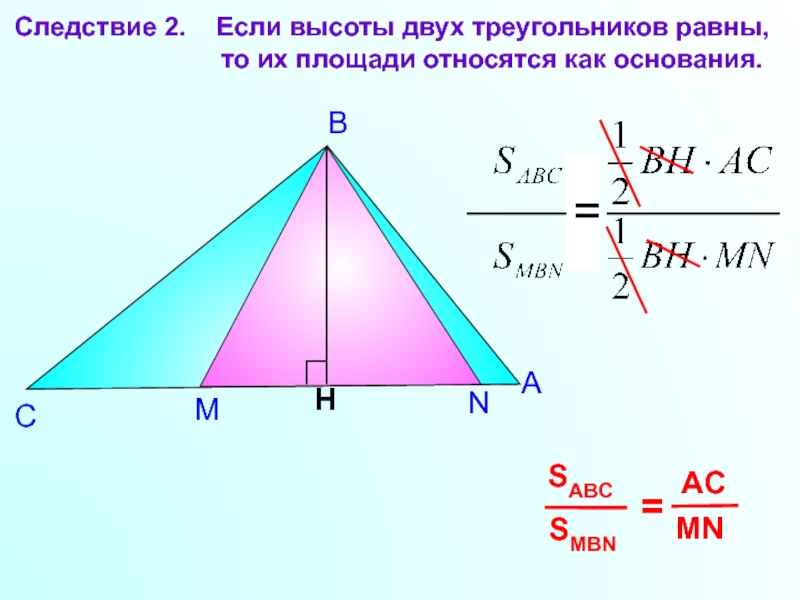 Где Малыш должен поставить точку?
Где Малыш должен поставить точку?
Решение: В точке пересечения диагоналей.
6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.
Решение:
III. Изучение темы «Площадь треугольника»начать с задачи:
«Найти площадь треугольника, у которого основание a, а высота h».
Ребята, используя понятие равновеликих фигур, доказывают теорему.
Достроим треугольник до параллелограмма.
Площадь треугольника равна половине площади параллелограмма.
Задание: Начертите равновеликие треугольники.
Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).
Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».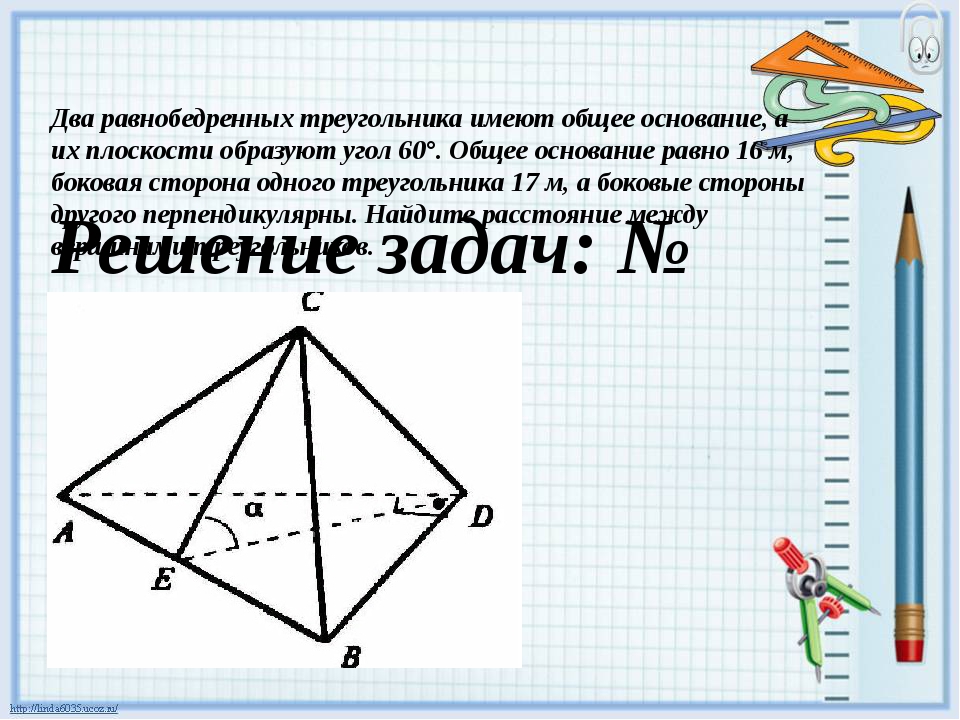
У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь
Вывод: Фигуры, имеющие равные площади, называются равновеликими.
Вопросы к классу:
- Равновелики ли равные фигуры?
- Сформулируйте обратное утверждение. Верно ли оно?
- Верно ли:
а) Равносторонние треугольники равновелики?
б) Равносторонние треугольники с равными сторонами равновелики?
в) Квадраты с равными сторонами равновелики?
г) Докажите, что параллелограммы, образованные при пересечении двух полос одинаковой ширины под разными углами наклона друг к другу, равновелики. Найдите параллелограмм наименьшей площади, образующийся при пересечении двух полос одинаковой ширины. (Показать на модели: полоски одинаковой ширины)
На доске написаны задания по выбору:
1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».
Решение:
2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».
Решение:
3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .
Решение:
Ответ:
3. Из олимпиадных задач:
«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.
Решение: провести диагональ BD.
Упражнение №475.
«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».
Использовать теорему Фалеса (разделить АC на 3 равные части).
Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).
«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».
Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.
Дополнительные задачи (из олимпиадных задач):
1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».
Найти площадь трапеции ABCD».
Решение:
Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S ∆ABK = 2m, ∆BCM = ∆MDK, S ABCD = S ∆ABK = 2m.
Ответ: S ABCD = 2m.
2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».
Решение:
S ∆BCD = S ∆ABC , т.к. у них общее основание BC и одинаковая высота .
3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?
Решение:
В треугольнике МВС : МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ : ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР.
В треугольнике АРС : АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК : ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК : ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,
Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.
4) Сцепленные параллелограммы.
2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.
Решение:
и , значит,
Список использованной литературы :
- Учебник «Геометрия 7-9» (авторы Л.
 С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003).
С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003). - Олимпиадные задачи разных лет, в частности из учебного пособия «Лучшие задачи математических олимпиад» (составитель А.А. Корзняков, Пермь, «Книжный мир», 1996).
- Подборка задач, накопленных за много лет работы.
Фигуры называют равными, если совпадает их форма и размеры. Из этого определения следует, например, что если заданные прямоугольник и квадрат имеют равные площади, то они всё-равно не становятся равными фигурами, так как это разные фигуры по форме. Или, два круга однозначно имеют одну и туже форму, но если их радиусы различны, то это тоже не равные фигуры, так как не совпадают их размеры. Равными фигурами являются, например, два отрезка одинаковой длины, два круга с одинаковым радиусом, два прямоугольника с попарно равными сторонами (короткая сторона одного прямоугольника равна короткой стороне другого, длинная сторона одного прямоугольника равна длинной стороне другого).
На глаз бывает трудно определить, равны ли фигуры, имеющие одинаковую форму. Поэтому для определения равенства простых фигур их измеряют (с помощью линейки, циркуля). У отрезков длину, у кругов радиус, у прямоугольников длину и ширину, у квадратов только одну любую сторону. Тут следует отметить, что не все фигуры можно сравнивать. Нельзя, например, определить равенство прямых, т. к. любая прямая бесконечна и, следовательно, все прямые, можно сказать, равны между собой. То же самое касается лучей. Хотя у них есть начало, но нет конца.
Если же мы имеем дело со сложными (произвольными) фигурами, то бывает даже сложно определить, имеют ли они одинаковую форму. Ведь фигуры могут быть перевернуты в пространстве. Посмотрите на рисунок ниже. Трудно сказать, одинаковые ли это по форме фигуры или нет.
Таким образом, нужно иметь надежный принцип сравнения фигур. Он таков: равные фигуры при наложении друг на друга совпадают .
Чтобы сравнить две изображенные фигуры наложением, на одну из них накладывают кальку (прозрачную бумагу) и копируют (срисовывают) на нее форму фигуры. Копию на кальке пытаются наложить на вторую фигуру так, чтобы фигуры совпали. Если это удастся, то заданные фигуры равные. Если нет, то фигуры не равные. При наложении кальку можно поворачивать как угодно, а также переворачивать.
Копию на кальке пытаются наложить на вторую фигуру так, чтобы фигуры совпали. Если это удастся, то заданные фигуры равные. Если нет, то фигуры не равные. При наложении кальку можно поворачивать как угодно, а также переворачивать.
Если можно вырезать сами фигуры (или они представляют собой отдельные плоские объекты, а не нарисованы) то калька не нужна.
При изучении геометрических фигур можно заметить множество их особенностей, связанных с равенством их частей. Так, если сложить круг вдоль диаметра, то две его половинки окажутся равными (они совпадут наложением). Если разрезать прямоугольник по диагонали, то получится два прямоугольных треугольника. Если один из них повернуть на 180 градусов по часовой или против часовой стрелки, то он совпадет со вторым. То есть диагональ разбивает прямоугольник на две равные части.
Цель: формирование понятия “равные фигуры”.
- сформировать способность к фиксированию понятия “равные фигуры”, к фиксированию умения нахождения равных фигур;
- развивать математическую речь, геометрическое мышление; тренировать мыслительные операции;
- совершенствовать навыка счета в пределах 9;
- воспитывать в учащихся дисциплинированность,
умение совместной деятельности.

Ход урока
1. Организационный момент
Вступительное слово учителя.
Пираты — это морские разбойники, главной их цель всегда была поиск клада. Мы будем добрыми пиратами и отправимся в морское путешествие на поиски нашего клада. Мне в руки попала старинная пиратская карта.
Она очень запутанная, на ней отмечено множество островов, чтобы запутать искателей, но нужно попасть на остров, на котором спрятаны сокровища. Чтобы его найти, нам нужно будет преодолеть множество препятствий. Вы готовы? Тогда в путь.
Путешествовать мы будем на корабле.
Отправляемся на первый остров.
2. Устные счет
Итак, следуя нашей карте, мы оказались на острове под названием “Устный счет”. И чтобы двинуться дальше, нам необходимо выполнить задания:
Назови соседей чисел: 3, 6, 8;
Заполни пропуски:
7,….,….,….,…, 12
10,…,…., 7,….,…,….,…., 2
Реши пример по числовому отрезку.
3. Актуализация знаний
Актуализация знаний
Следующий остров, встретившийся нам на пути, это “Геометрический остров”. Он таит в себе свои тайны и загадки, которые нам необходимо раскрыть!
Ребята нужно вспомнить и нарисовать все известные нам геометрические фигуры. (Круг, квадрат, ромб, овал, прямоугольник)
Посмотрите на рисунок, какие фигуры изображены?
По каким признакам можно разбить все фигуры на группы? (Цвет, форма, размер) . Назови эти группы.
4. Ознакомление с новым материалом
Мы удачно справились с заданием и можем отправиться на следующий остров. На третьем острове я нашла тайные послания для нас с вами. У каждого на парте есть конверт. Давайте откроем их и посмотрим, какое на этот раз испытание нас ждёт. (В каждом конверте находятся большой и маленький зеленый квадрат, большой и маленький синий треугольник, большой и маленький желтый прямоугольник, два красных круга одинакового размера)
Ребята, вспомним, по каким признакам делятся все фигуры? (Цвет, форма, размер)
Задание: разбейте по парам фигуры,
находящиеся в конверте, так, чтобы менялся только
один признак – размер.
Смогли ли вы разбить все предметы по парам? (Нет)
Почему? (Потому что два круга одинаковы по размеру, цвету и форме)
Докажите, что эти фигуры одинаковы. (Наложением)
Давайте подумаем, как можно такие фигуры назвать? (Из предложенных вариантов учитель выбирает понятие “равные фигуры”)
Итак, ребята, тема нашего урока “Равные фигуры”. (Тема фиксируется на доске)
Давайте поближе познакомимся с ними. Для этого нам нужно отправиться на следующий остров, который так и называется: “Равные фигуры”.
Прибыв на остров, я сразу заметила на песке различные фигуры, зарисовала их, так как волна могла в любой момент их смыть.
Посмотрите на доску, вот эти фигуры:
Если среди них равные? (Дети сначала определяют визуально равные фигуры, затем к доске вызывается ученик)
Как мы узнаем, действительно эти фигуры равны
или нет? (Путем наложения одной фигуры на
другую). Выполняется практическое действие.
Итак, какие же фигуры мы можем назвать равными? (Равными фигурами являются те, которые совпадают при наложении).
Определим, какие признаки у равных фигур должны совпадать.
Под темой урока на доске фиксируется краткая запись рассуждений детей.
(Равные фигуры всегда одинаковой формы и одинакового размера, а цвет может различаться)
Как вы считаете, 1 и 2 фигуры – равные?
Как мы это проверим? (Ученики совмещают фигуры и убеждаются, что они равны)
А как вы думаете, 2 и 3 фигуры равны? (Выполняется аналогичная работа)
Ребята, а 1 и 3 фигура равны?
Почему? (Они обе равны фигуре 2, значит, равны друг другу)
Давайте проверим наложением.
Ребята делают вывод, учитель кратко фиксирует на доске 1=2 и 2=3, то 1=3 (Если первая фигура равна второй, а вторая третьей, то первая фигура равна третьей)
У меня возникла проблема, а если я не могу наложить фигуры, например, они нарисованы в тетради, как проверить, равны они или нет? (Можно посчитать по клеткам)
Отправляемся на следующий остров.
5. Первичное закрепление
Работа с учебником.
1) Стр. 36 №1. Найди равные фигуры и раскрась их одинаковым цветом. Работа выполняется по вариантам:
1 вариант — №1 а)
2 вариант — №1 б)
Ребята, и с этим заданием вы справились, но продолжить наше путешествие мы не можем, корабль наткнулся на риф, нам необходимо его снова собрать. Потому что по карте последний остров именно тот, который нам нужен!
2) Стр. 36 №2.
6. Повторение пройденного
Вы сегодня были храбры и не боялись сложных испытаний, которые встречались нам на островах. И в награду за это вы можете стать учителями-капитанами корабля. Но быть капитаном не просто, вам нужно многое знать и уметь, поэтому постарайтесь справиться со следующими заданиями:
1) Учащимся предлагается стать учителем: придумать задание к рисунку, проконтролировать выполнение, оценить.
2) Раздаются карточки. Нужно найти все ошибки.
Взаимопроверка по парам.
8=8 4+3=8 8-2>8-3
7>4 3+1
3
7. Итог урока, рефлексия
Мы прибыли на последний остров, а вот и клад! Наш путь оказался не напрасным, ведь нам в награду достались такие сокровища!
Ребята, как вы понимаете фразу “Знания — наше богатство”?
Перед вами на столе два смайлика — грустный и веселый. Если у вас хорошее настроение, приклейте к кораблю желтый веселый смайлик, если плохое — красный.
Мы с вами теперь опытные путешественники и кладоискатели, и в следующий раз нас будут ждать новые приключения! Спасибо за работу на уроке!
какой угол называется развернутым? Какие фигуры называются равными? Обьясните как сравнить два отрезка? какая точка называетсясерединой отрезка?
Какой луч называется биссектрисой угла?
что такое градусная мера угла?
Какая фигура называется треугольником?Какие треугольники называются равными?Какой отрезок называют медианой треугольника?Какой отрезок называютбиссектрисой треугольника?Какой отрезок называют высотой треугольника?Какой треугольник называется равнобедренным?Какой треугольник называется равносторонним?Что такое окружность? Определение радиуса, диаметра, хорды. Дайте определение параллельных прямых.Какой угол называется внешним углом треугольника?Какой треугольник называется остроугольным, какой треугольник называется тупоугольным, какой прямоугольным. Как называются стороны прямоугольного треугольника?Свойство двух прямых, параллельных третьей.Теорема о прямой, пересекающей одну из параллельных прямых.Свойство двух прямых перпендикулярных к третьей
Дайте определение параллельных прямых.Какой угол называется внешним углом треугольника?Какой треугольник называется остроугольным, какой треугольник называется тупоугольным, какой прямоугольным. Как называются стороны прямоугольного треугольника?Свойство двух прямых, параллельных третьей.Теорема о прямой, пересекающей одну из параллельных прямых.Свойство двух прямых перпендикулярных к третьей
Объясните какая ломанная называется многоугольником. Что такое вершины, стороны, периметр и диагонали многоугольника? Какой многоугольник называется выпуклым?
Объясните какие углы называются выпуклыми углами многоугольника. Выведите формулу для вычисления суммы углов выпуклого n-угольника. Докажите, что сумма внешних углов выпуклого многоугольника. ВЗЯТЫХ по одному прикаждой вершине, равна 360 градусов.
Чему равна сумма углов выпукого четырехугольника?
2)Что такое вершины,углы стороны диагонали периметр четырехугольника?
3)Какие углы стороны четырехугольник называется выпуклым?
4)чему равна сумма углов выпуклого четырехугольника?
5)какой четырех угольник называется выпуклым?
6)какой четырех угольник называют параллелограмм?
7)какими свойствами обладает параллелограмм?
8)назовите признаки параллелограмма.
9)сформулируйте свойства прямоугольника.
10)какой четырехугольник называется квадратом?
11)сформулируйте свойства ромба.
12)какой четырехугольник называется ромбом?
13)какой четырехугольник называется прямоугольником?
14)какими свойствами обладает квадрат? ответьте пожалуйста кратко…
называется треугольником.
2. Что такое периметр треугольника?
3. Какие треугольники называются равными?
4. Что такое теорема и доказательство теоремы?
5. Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой.
6. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
7. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?
8. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
9.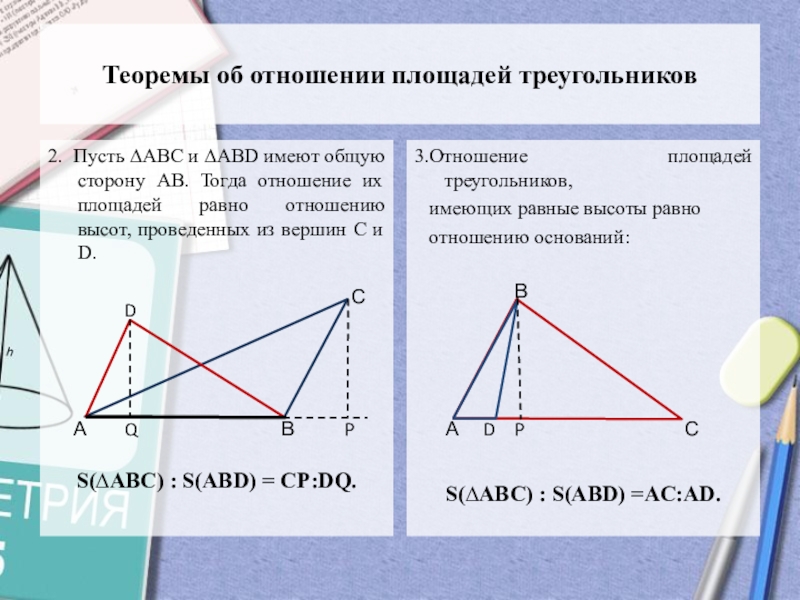 Какой треугольник называется равнобедренным?
Какой треугольник называется равнобедренным?
10. Как называются стороны равнобедренного треугольника?
11. Какой треугольник называется равносторонним?
12. Сформулируйте свойство углов при основании равнобедренного треугольника.
13. Сформулируйте теорему о биссектрисе равнобедренного треугольника.
14. Сформулируйте первый признак равенства треугольников.
15. Сформулируйте второй признак равенства треугольников.
16. Сформулируйте третий признак равенства треугольников.
17. Дайте определение окружности.
18. Что такое центр окружности?
19. Что называется радиусом окружности?
20. Что называется диаметром окружности?
21. Что называется хордой окружности?
Какие фигуры называются равными?
Равными называют фигуры , которые совпадают при наложении.
Частой ошибкой на этот вопрос является ответ, в котором упоминаются равные стороны и углы геометрической фигуры. Однако при этом не принимается в учет, что стороны геометрической фигуры не обязательно бывают прямыми. Поэтому только совпадение геометрических фигур при наложении может быть признаком их равенства.
Поэтому только совпадение геометрических фигур при наложении может быть признаком их равенства.
На практике это легко проверить с помощью наложения, они должны совпасть.
Все очень просто и доступно, обычно равные фигуры видно сразу.
Равными называются те фигуры, у которых совпадают параметры геометрии. Эти параметры: длина сторон, величина углов, толщина.
Проще всего понять что фигуры равны можно с помощью наложения. Если величины фигур одинаковы — их называют равными.
Равными называют только те геометрические фигуры, которые имеют абсолютно одинаковые параметры:
1) периметр;
2) площадь;
4) размеры.
То есть, если одну фигуру наложить на другую, то они совпадут.
Ошибочно полагать, что если фигуры имеют одинаковые периметр или площадь, то они равны. На самом деле, геометрические фигуры, у которых равна площадь называются равновеликими.
Фигуры называются равными, если они совпадают при наложении друг на друга. Равные фигуры имеют одинаковые размеры, форму, площадь и периметр. А вот равные по площади фигуры могут быть и не равными между собой.
Равные фигуры имеют одинаковые размеры, форму, площадь и периметр. А вот равные по площади фигуры могут быть и не равными между собой.
В геометрии, по правилам, равные фигуры должны иметь одинаковую площадь и периметр, то есть у них должны быть абсолютно одиноковые формы и размеры. И они должны полностью совпадать при их наложении друг на друга. Если же есть какие-то расхождения, то эти фигуры уже нельзя будет назвать равными.
Фигуры можно назвать равными при условии, если они полностью совпадают при наложении друг на друга, т.е. они имеют одинаковые размеры, форму и следовательно площадь и периметр, а также другие характеристики. В противном случае говорить о равности фигур нельзя.
В самом слове равные заложена суть.
Это фигуры которые полностью идентичные друг другу. То есть полностью совпадают. Если фигуру положить одну на одну тогда фигуры будут перекрывать себя со всех сторон.
Они одинаковые то есть равные.
В отличие от равных треугольников (для определения которых достаточно выполнения одного из условий — признаков равенства), равными фигурами называют такие, которые имеют одинаковую не только форму, но и размеры.
Определить, равна ли одна фигура другой, можно методом наложения. При этом фигуры должны совпасть и сторонами и углами. Это и будут равные фигуры.
Равными могут быть только такие фигуры, которые при их наложении полностью совпадут сторонами и углами. На самом деле для всех простейших многоугольников равенство их площади свидетельствует и о равенстве самих фигур. Пример: квадрат со стороной а всегда будет равен другому квадрату с той же стороной а. Тоже касается и прямоугольников и ромбов — если их стороны равны сторонам другого прямоугольника, они равны. Более сложный пример: треугольники будут равными, если у них равны стороны и соответствующие углы. Но это только частные случаи. В более общих случаях, равенство фигур доказывается все-таки наложением, а это наложение в планиметрии высокопарно именуют движением.
Как найти площадь многоугольника? Как узнать площадь многоугольника? Как найти площадь разностороннего многоугольника
Тема «Площади многоугольников» является неотъемлемой частью школьного курса математики, что вполне естественно. Ведь исторически само возникновение геометрии связано с потребностью сравнения земельных участков той или иной формы. Вместе с тем следует отметить, что образовательные возможности раскрытия этой темы в средней школе используются далеко не полностью.
Ведь исторически само возникновение геометрии связано с потребностью сравнения земельных участков той или иной формы. Вместе с тем следует отметить, что образовательные возможности раскрытия этой темы в средней школе используются далеко не полностью.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования.
Наряду с решением основной задачи углубленное изучение математики предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к обучению в вузе.
Квалификационная работа включает содержание курса математики общеобразовательной школы и ряд дополнительных вопросов, непосредственно примыкающих к этому курсу и углубляющих его по основным идейным линиям.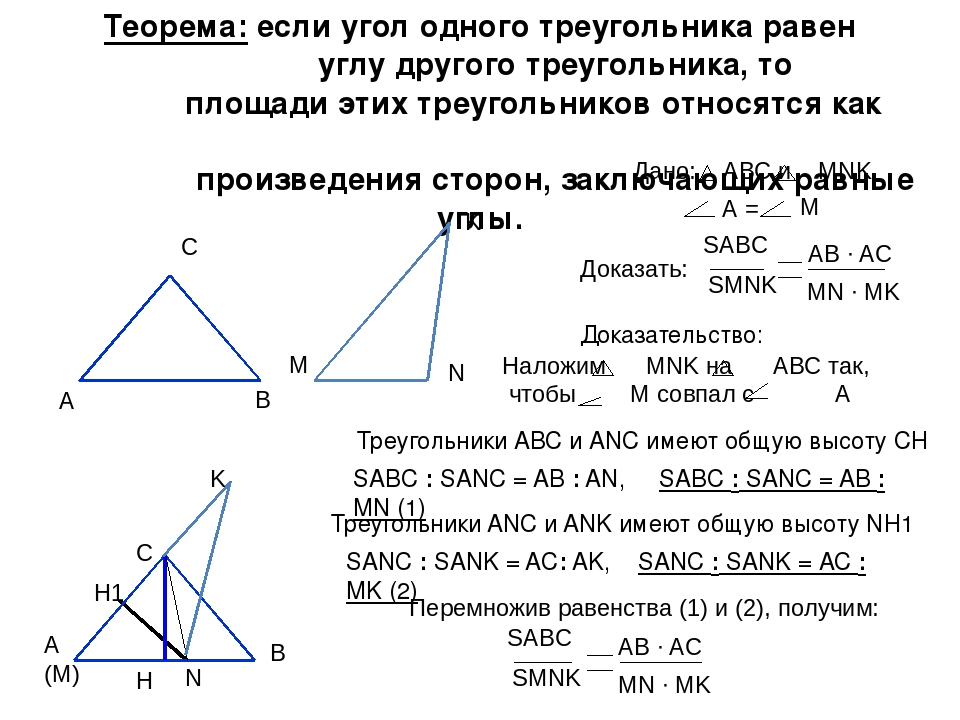
Включение дополнительных вопросов преследует две взаимосвязанные цели. С одной стороны, это создание в совокупности с основными разделами курса базы для удовлетворения интересов и развития способностей учащихся, имеющих склонность к математике, с другой – выполнение содержательных пробелов основного курса, придающее содержанию углубленного изучения необходимую целостность.
Квалификационная работа состоит из введения, двух глав, заключения и цитируемой литературы. В первой главе рассматриваются теоретические основы изучения площадей многоугольников, а во второй главе – непосредственно уже методические особенности изучения площадей.
1.1Вычисление площадей в древности
Зачатки геометрических знаний, связанных с измерением площадей, теряются в глубине тысячелетий.
Еще в 4 – 5 тысяч лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Квадрат издавна служит эталоном при измерении площадей благодаря многим своим замечательным свойствам: равные стороны, равные и прямые углы, симметричность и общее совершенство формы. Квадраты легко строить, или можно заполнить плоскость без пробелов.
Квадраты легко строить, или можно заполнить плоскость без пробелов.
В древнем Китае мерой площади был прямоугольник. Когда каменщики определяли площадь прямоугольной стены дома, они перемножали высоту и ширину стены. Таково принятое в геометрии определение: площадь прямоугольника равна произведению его смежных сторон. Обе эти стороны должны быть выражены в одних и тех же линейных единицах. Их произведение и составит площадь прямоугольника, выраженную в соответствующих квадратных единицах. Скажем, если высота и ширина стены измерены в дециметрах, то произведение обоих измерений будет выражено в квадратных дециметрах. И если площадь каждой облицовочной Плотки составляет квадратный дециметр, то полученное произведение укажет число плиток, нужное для облицовки. Это вытекает из утверждения, положенного в основу измерения площадей: площадь фигуры, составленной из непересекающихся фигур, равна сумме их площадей.
Древние египтяне 4000 лет назад пользовались почти теми же приемами, что и мы, для измерения площади прямоугольника, треугольника и трапеции: основание треугольника делилось пополам, и умножалась на высоту; для трапеции же сумма параллельных сторон делилась пополам и умножалась на высоту и т. п. Для вычисления площади
п. Для вычисления площади
т.е. умножались полусуммы противоположных сторон.
Эта формула явно неверна для любого четырехугольника, из нее вытекает, в частности, что площади всех ромбов одинаковы. Между тем, очевидно, что у таких ромбов площади зависят от величины углов при вершинах. Данная формула верна только для прямоугольника. С ее помощью можно вычислить приближенно площадь четырехугольников, у которых углы близки к прямым.
Для определения площади
равнобедренного треугольника (рис. 1.2), в котором , египтяне пользовались приближенной формулой:(1.2) Рис. 1.2Совершаемая при этом ошибка тем меньше, чем меньше разность между стороной и высотой треугольника, иными словами, чем ближе вершина (и ) к основанию высоты из . Вот почему приближенная формула (1.2) применима лишь для треугольников с сравнительно малым углом при вершине.
Но уже древние греки умели правильно находить площади многоугольников. В своих «Началах» Евклид не употребляет слова «площадь», так как он под самим словом «фигура» понимает часть плоскости, ограниченную той или иной замкнутой линией. Евклид не выражает результат измерения площади числом, а сравнивает площади разных фигур между собой.
В своих «Началах» Евклид не употребляет слова «площадь», так как он под самим словом «фигура» понимает часть плоскости, ограниченную той или иной замкнутой линией. Евклид не выражает результат измерения площади числом, а сравнивает площади разных фигур между собой.
Как и другие ученые древности, Евклид занимается вопросами превращения одних фигур в другие, им равновеликие. Площадь составной фигуры не изменится, если ее части расположить по-другому, но без пересечения. Поэтому, например, можно, исходя из формул площади прямоугольника, находить формулы площадей других фигур. Так, треугольник разбивается на такие части, из которых затем можно составить равновеликий ему прямоугольник. Из этого построения следует, что площадь треугольника равна половине произведения его основания на высоту. Прибегая к подобной перекройке, находят, что площадь параллелограмма равна произведению основания на высоту, площадь трапеции – произведению полусуммы оснований на высоту.
Когда каменщикам приходится облицовывать стену сложной конфигурации, они могут определить площадь стены, подсчитав число пошедших на облицовку плиток.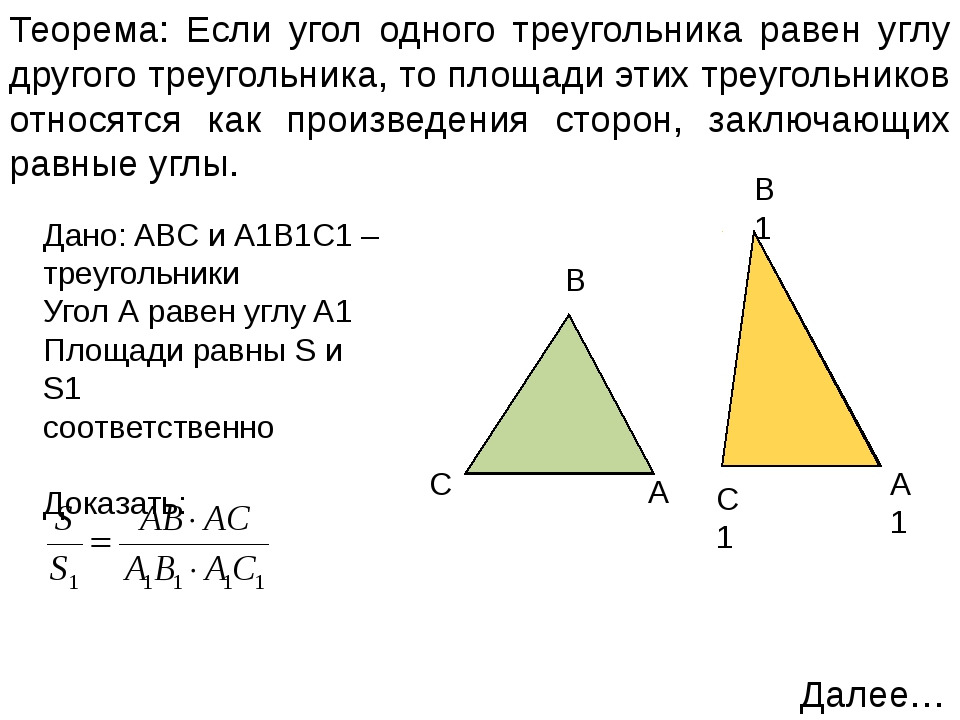 Некоторые плитки, естественно, придется обкалывать, чтобы края облицовки совпали с кромкой стены. Число всех пошедших в работу плиток оценивает площадь стены с избытком, число необломанных плиток – с недостатком. С уменьшением размеров клеток количество отходов уменьшается, и площадь стены, определяемая через число плиток, вычисляется все точнее.
Некоторые плитки, естественно, придется обкалывать, чтобы края облицовки совпали с кромкой стены. Число всех пошедших в работу плиток оценивает площадь стены с избытком, число необломанных плиток – с недостатком. С уменьшением размеров клеток количество отходов уменьшается, и площадь стены, определяемая через число плиток, вычисляется все точнее.
Одним из поздних греческих математиков – энциклопедистов, труды которого имели главным образом прикладной характер, был Герон Александрийский, живший в 1 в. н. э. Будучи выдающимся инженером, он был назван также «Герон Механик». В своем произведении «Диоптрика» Герон описывает разные машины и практические измерительные инструменты.
Одна из книг Герона была названа им «Геометрика» и является своего рода сборником формул и соответствующих задач. Она содержит примеры на вычисление площадей квадратов, прямоугольников и треугольников. О нахождении площади треугольника по его сторонам Герон пишет: « Пусть, например, одна сторона треугольника имеет в длину 13 мерных шнуров, вторая 14 и третья 15.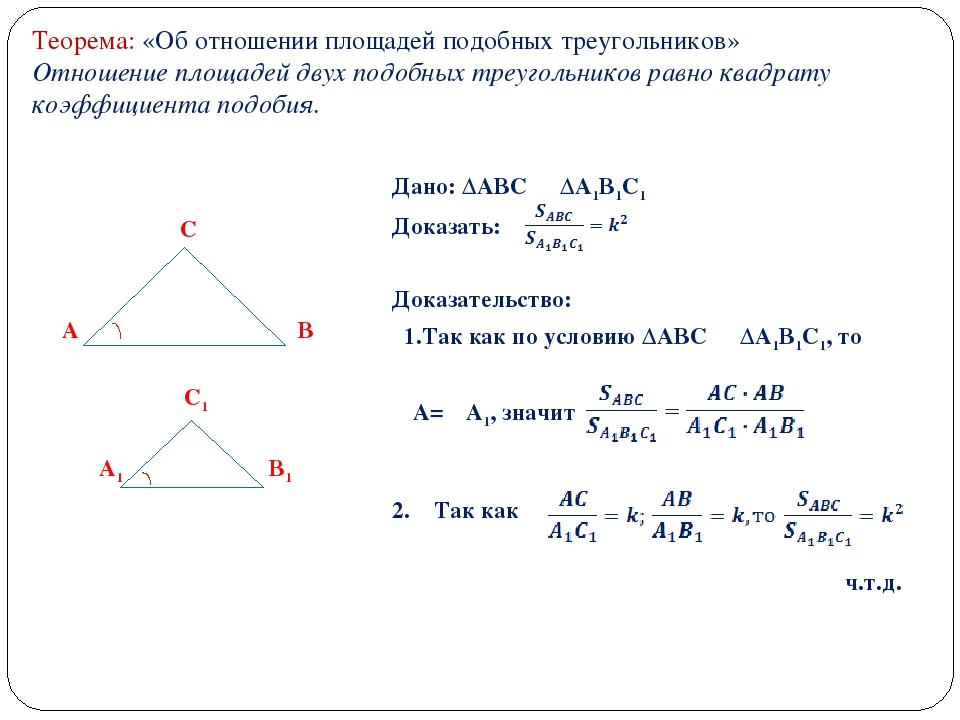 Чтобы найти площадь, поступают вот как. Сложи 13, 14 и 15; получится 42. Половина этого будет 21. Вычти из этого три стороны одну за другой; сперва вычти 13 – останется 8, затем 14 – останется 7 и, наконец, 15 – останется 6. А теперь перемножь их: 21раз по 8 даст 168, возьми это 7 раз – получится 1176, а это еще 6 раз – получится 7056. Отсюда квадратный корень будет 84. Вот сколько мерных шнуров будет в площади треугольника».
Чтобы найти площадь, поступают вот как. Сложи 13, 14 и 15; получится 42. Половина этого будет 21. Вычти из этого три стороны одну за другой; сперва вычти 13 – останется 8, затем 14 – останется 7 и, наконец, 15 – останется 6. А теперь перемножь их: 21раз по 8 даст 168, возьми это 7 раз – получится 1176, а это еще 6 раз – получится 7056. Отсюда квадратный корень будет 84. Вот сколько мерных шнуров будет в площади треугольника».
- обучающие: научить учащихся находить площадь многоугольника, используя выбранные ими способы, сформировать начальные представления
- многоугольнике, графические и измерительные навыки;
- развивающие: развитие способов умственной деятельности учащихся при выполнении заданий от наблюдения, расчетов до выяснения закономерностей вычисления площади многоугольника;
- воспитывающие: раскрытие субъективного опыта учащихся, поощрение действий, стремлений учащихся как основы воспитания положительных качеств личности;
- методическая: создание условий для проявления
познавательной активности учащихся.

Оснащение урока:
- Оформление доски: слева — фигуры многоугольника, справа — чистое полотно доски для записи на уроке, в центре – многоугольник-прямоугольник.
- Листок “К исследованию”.
- Инструментарии учителя и учащихся (мел, указка, линейка, листок исследования, фигуры, ватман, маркер).
Метод урока:
- По взаимодействию учителя и учащихся – диалог-общение;
- По способу решения задач – частично-поисковый;
- По способу умственной деятельности — (СУД) развивающее обучение.
Форма урока — фронтальная, в парах, индивидуальная.
Тип урока — урок усвоения новых знаний, умений и навыков.
Структура урока — постепенное углубление в тему, гибкая, диалогическая.
Ход урока
Приветствие.
Урок прекрасен и приносит радость, когда мы
мыслим, дружно работаем. Сегодня мы будем
рассматривать фигуры, определять их названия,
думать, искать и находить решения. Пожелаем друг
другу успешной работы.
Актуализация знаний.
Рассмотрите фигуры (на доске многоугольники).
Они все вместе. Почему? Какой у них общий признак? (Многоугольники).
Назовите этот многоугольник (5-угольник, 6-угольник…)
Может быть, вы знаете, что такое площадь многоугольника?
Тогда покажите на одной из фигур.
(Обобщение учителем: площадь — часть плоскости внутри замкнутой геометрической фигуры.)
В русском языке это слово имеет несколько значений.
(Ученик по словарю знакомит со значениями.)
- Часть плоскости внутри замкнутой геометрической фигуры.
- Большое незастроенное и ровное место.
- Помещение для какой-либо цели.
Какое из значений используется в математике?
В математике используется первое значение.
(На доске фигура).
Это многоугольник? Да.
Назовите фигуру по-другому. Прямоугольник.
Покажи длину, ширину.
Как найти площадь многоугольника?
Запишите при помощи букв и знаков формулу.
Если длина нашего прямоугольника 20 см, ширина 10см. Чему равна площадь?
Площадь равна 200 см 2
Подумайте, как приложить линейку, чтобы фигура разделилась на:
Увидели, из каких частей состоит фигура? А теперь, наоборот, по частям соберем целое.
(Части фигуры лежат на партах. Дети собирают из них прямоугольник).
Сделайте вывод по наблюдениям.
Целую фигуру можно разделить на части и из частей составить целую.
Дома на основе треугольников и четырехугольников составляли фигуры, силуэты. Вот какие они получились.
(Демонстрация рисунков, выполненных дома учащимися. Одна из работ анализируется).
Какие фигуры использовал? У тебя получился сложный многоугольник.
Постановка учебной задачи.
На уроке мы должны ответить на вопрос: как найти площадь сложного многоугольника?
Для чего человеку нужно находить площадь?
(Ответы детей и обобщение учителем).
Задача определения площади возникла из
практики.
(Показывается план школьного участка).
Для того чтобы построить школу, сначала создали план. Потом разбивалась территория на участки определенной площади, размещались строения, клумбы, стадион. При этом участок имеет определенную форму — форму многоугольника.
Решение учебной задачи.
(Раздаются листы для исследования).
Перед вами фигура. Назовите ее.
Многоугольник, шестиугольник.
Найдем площадь многоугольника. Что для этого надо делать?
Разделить на прямоугольники.
(При затруднении будет другой вопрос: “Из каких фигур состоит многоугольник?”).
Из двух прямоугольников.
С помощью линейки и карандаша разделите фигуру на прямоугольники. Обозначьте цифрами 1 и 2 полученные части.
Проведем измерения.
Найдем площадь первой фигуры.
(Учащиеся предлагают следующие варианты решений и записывают их на доске).
- S 1 = 5 ? 2 = 10 см 2
- S 2 = 5 ? 1 = 5 см 2
Зная площадь частей, как найти площадь целой фигуры?
S = 10 + 5 = 15 см 2
- S 1 = 6 ? 2 = 12 см 2
- S 2 = 3 ? 1 = 3 см 2
- S = 12 + 3 = 15 см 2 .

Сравните результаты и сделайте вывод.
Проследим наши действия
Как находили площадь многоугольника?
Составляется и записывается на плакате алгоритм:?
1. Делим фигуру на части
2. Находим площади частей этих многоугольников (S 1 , S 2).
3. Находим площадь целого многоугольника (S 1 + S 2).
Проговорить алгоритм.
(Несколько учащихся проговаривают алгоритм).
Мы нашли два способа, а может, есть еще?
А можно фигуру достроить.
Сколько прямоугольников получилось?
Обозначим части 1 и 2. Проведем измерения.
Найдите площадь каждой части многоугольника.
- S 1= 6? 5=30см 2
- S 2 = 5 ? 3 = 15 см 2
Как найти площадь нашего шестиугольника?
S = 30 – 15 = 15 см 2
Составим алгоритм:
Достроили фигуру до прямоугольника
Нашли S 1 и S 2 .
Нашли разность S 1 – S 2 .
Сравните два алгоритма. Сделайте вывод. Какие действия одинаковые? Где разошлись наши действия?
Закройте глазки, опустите головки. Мысленно
повторите алгоритм.
Мысленно
повторите алгоритм.
Мы провели исследовательскую работу, рассмотрели разные способы и теперь можем находить площадь любого многоугольника.
Проверка результативности.
Проверьте себя.
Перед вами многоугольники.
Найти площадь одной фигуры по выбору, при этом можете пользоваться разными способами.
Работа выполняется самостоятельно. Дети выбирают фигуру. Находят площадь одним из способов. Проверка – ключ на доске.
Что можно сказать о форме? (Форма разная)
А какова площадь этих многоугольников? (Площади этих многоугольников равны)
Оценивают результаты.
У кого правильно – поставь “+”.
У кого сомнения, затруднения – “?”
Консультанты оказывают помощь ребятам, ищут ошибки, помогают исправить.
Домашнее задание:
Составить свои листки исследования, вычислить площадь многоугольника разными способами.
Итог урока.
Итак, ребята, что вы расскажите родителям, о том
как найти площадь геометрической фигуры –
многоугольника.
Урок из серии «Геометрические алгоритмы »
Здравствуйте, дорогой читатель.
Решения многих задач вычислительной геометрии основывается на нахождении площади многоугольника . На этом уроке мы выведем формулу для вычисления площади многоугольника через координаты его вершин, напишем функцию для вычисления этой площади.
Задача. Вычислить площадь многоугольника , заданного координатами своих вершин, в порядке их обхода по часовой стрелке.
Сведения из вычислительной геометрии
Для вывода формулы площади многоугольника нам понадобятся сведения из вычислительной геометрии, а именно, понятие ориентированной площади треугольника.
Ориентированная площадь треугольника – это обычная площадь, снабженная знаком. Знак ориентированной площади треугольника АВС такой же, как у ориентированного угла между векторами и. То есть ее знак зависит от порядка перечисления вершин.
На рис. 1 треугольник АВС – прямоугольный.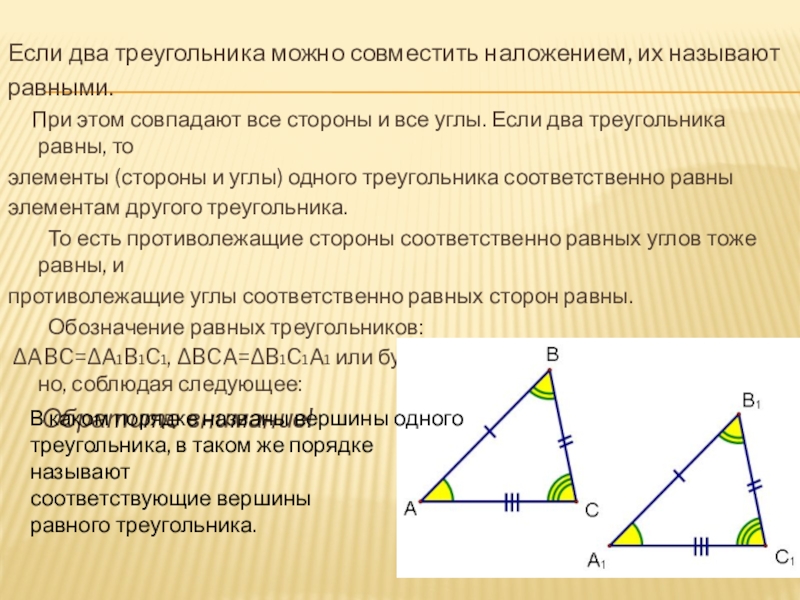 Его ориентированная площадь равна (она больше нуля, так как пара, ориентирована положительно). Эту же величину можно вычислить другим способом.
Его ориентированная площадь равна (она больше нуля, так как пара, ориентирована положительно). Эту же величину можно вычислить другим способом.
Пусть О – произвольная точка плоскости. На нашем рисунке площадь треугольника ABC получится, если из площади треугольника OBC вычесть площади OAB и OCA. Таким образом, нужно просто сложить ориентированные площади треугольников OAB, OBC и OCA. Это правило работает при любом выборе точки О .
Точно так же для вычисления площади любого многоугольника нужно сложить ориентированные площади треугольников
В сумме получится площадь многоугольника, взятая со знаком плюс, если при обходе ломаной многоугольника находится слева (обход границы против часовой стрелки), и со знаком минус, если он находится справа (обход по часовой стрелке).
Итак, вычисление площади многоугольника свелось к нахождению площади треугольника. Посмотрим, как выразить ее в координатах.
Векторное произведение двух векторов на плоскости есть площадь параллелограмма, построенного на этих векторах. 2 \Rightarrow
S_{\text{пр-к}}=ab \end{multline*}\)
2 \Rightarrow
S_{\text{пр-к}}=ab \end{multline*}\)
Определение
Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота \(BK\)
падает на сторону \(AD\)
, а высота \(BH\)
— на продолжение стороны \(CD\)
:
Теорема: площадь параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.
Доказательство
Проведем перпендикуляры \(AB»\) и \(DC»\) , как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма \(ABCD\) .
Тогда \(AB»C»D\) – прямоугольник, следовательно, \(S_{AB»C»D}=AB»\cdot AD\) .
Заметим, что прямоугольные треугольники \(ABB»\) и \(DCC»\) равны. Таким образом,
\(S_{ABCD}=S_{ABC»D}+S_{DCC»}=S_{ABC»D}+S_{ABB»}=S_{AB»C»D}=AB»\cdot AD.\)
\[{\Large{\text{Площадь треугольника}}}\]
Определение
Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.
Теорема
Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.
Доказательство
Пусть \(S\) – площадь треугольника \(ABC\) . Примем сторону \(AB\) за основание треугольника и проведём высоту \(CH\) . Докажем, что \ Достроим треугольник \(ABC\) до параллелограмма \(ABDC\) так, как показано на рисунке:
Треугольники \(ABC\) и \(DCB\) равны по трем сторонам (\(BC\) – их общая сторона, \(AB = CD\) и \(AC = BD\) как противоположные стороны параллелограмма \(ABDC\)), поэтому их площади равны. Следовательно, площадь \(S\) треугольника \(ABC\) равна половине площади параллелограмма \(ABDC\) , то есть \(S = \dfrac{1}{2}AB\cdot CH\) .
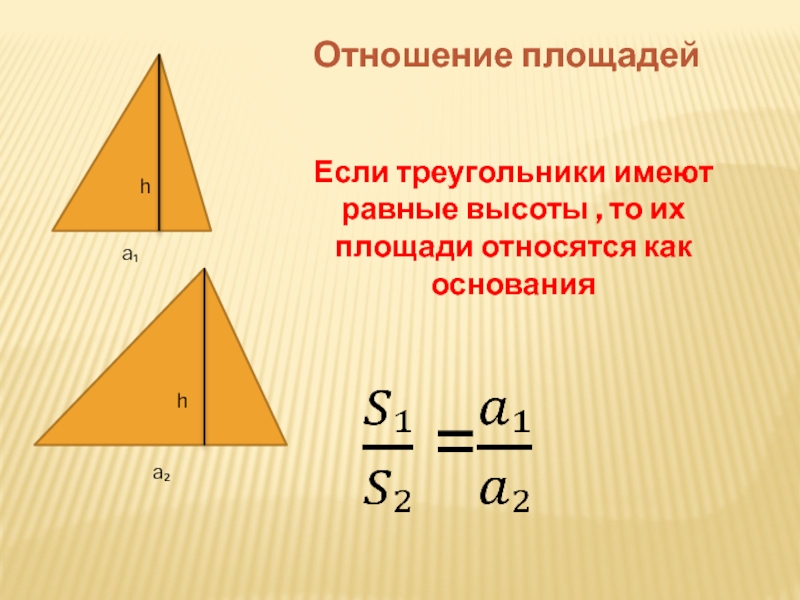
Теорема
Если два треугольника \(\triangle ABC\) и \(\triangle A_1B_1C_1\) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.
Следствие
Медиана треугольника делит его на два треугольника, равных по площади.
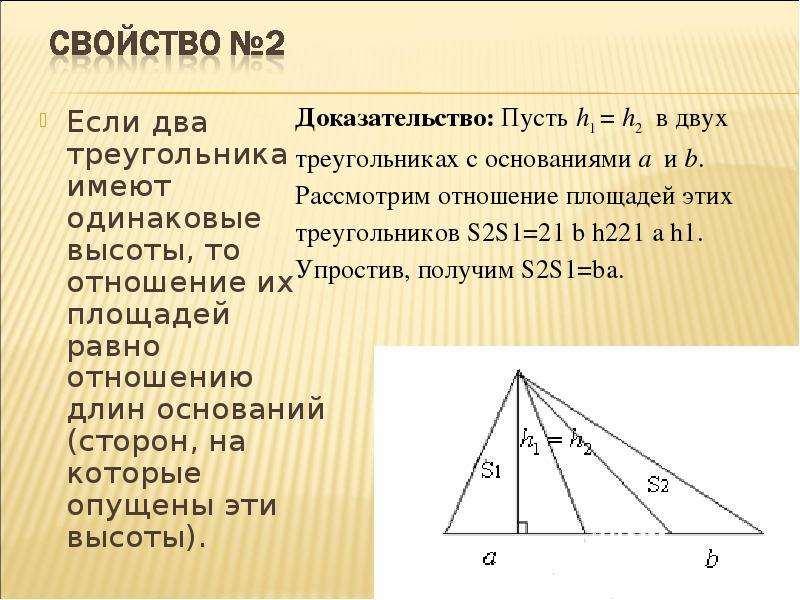
Теорема
Если два треугольника \(\triangle ABC\) и \(\triangle A_2B_2C_2\) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.
Доказательство
Пусть \(\angle A=\angle A_2\) . Совместим эти углы так, как показано на рисунке (точка \(A\) совместилась с точкой \(A_2\)):
Проведем высоты \(BH\) и \(C_2K\) .
Треугольники \(AB_2C_2\) и \(ABC_2\) имеют одинаковую высоту \(C_2K\) , следовательно: \[\dfrac{S_{AB_2C_2}}{S_{ABC_2}}=\dfrac{AB_2}{AB}\]
Треугольники \(ABC_2\) и \(ABC\) имеют одинаковую высоту \(BH\) , следовательно: \[\dfrac{S_{ABC_2}}{S_{ABC}}=\dfrac{AC_2}{AC}\]
Перемножая последние два равенства, получим: \[\dfrac{S_{AB_2C_2}}{S_{ABC}}=\dfrac{AB_2\cdot AC_2}{AB\cdot AC} \qquad \text{ или } \qquad \dfrac{S_{A_2B_2C_2}}{S_{ABC}}=\dfrac{A_2B_2\cdot A_2C_2}{AB\cdot AC}\]
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.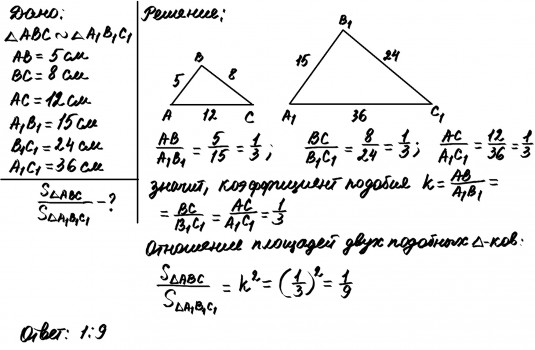
Теорема
Площадь прямоугольного треугольника равна половине произведения катетов.
Теорема: формула Герона
Пусть \(p\) – полупериметр треугольника, \(a\) , \(b\) , \(c\) – длины его сторон, тогда его площадь равна \
\[{\Large{\text{Площадь ромба и трапеции}}}\]
Замечание
Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.
Теорема
Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.
Доказательство
Рассмотрим четырехугольник \(ABCD\) . Обозначим \(AO=a, CO=b, BO=x, DO=y\) :
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников , следовательно, его площадь равна сумме площадей этих треугольников:
\(\begin{multline*} S_{ABCD}=\frac12ax+\frac12xb+\frac12by+\frac12ay=\frac12(ax+xb+by+ay)=\\ \frac12((a+b)x+(a+b)y)=\frac12(a+b)(x+y)\end{multline*}\)
Следствие: площадь ромба
Площадь ромба равна половине произведения его диагоналей: \
Определение
Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.
Теорема: площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Доказательство
Рассмотрим трапецию \(ABCD\) с основаниями \(BC\) и \(AD\) . Проведем \(CD»\parallel AB\) , как показано на рисунке:
Тогда \(ABCD»\) – параллелограмм.
Проведем также \(BH»\perp AD, CH\perp AD\) (\(BH»=CH\) – высоты трапеции).
Тогда \(S_{ABCD»}=BH»\cdot AD»=BH»\cdot BC, \quad S_{CDD»}=\dfrac12CH\cdot D»D\)
Т.к. трапеция состоит из параллелограмма \(ABCD»\) и треугольника \(CDD»\) , то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:
\ \[=\dfrac12 CH\left(BC+AD»+D»D\right)=\dfrac12 CH\left(BC+AD\right)\]
Каждый, кто изучал в школе математику и геометрию, хотя бы поверхностно знает эти науки. Но со временем, если в них не практиковаться, познания забываются. Многие даже считают, что только зря потратили своё время, изучая геометрические расчёты. Однако они ошибаются. Технические работники выполняют повседневную работу, связанную с геометрическими расчётами. Что касается расчета площади многоугольника, то и эти знания находят своё применение в жизни. Понадобятся они хотя бы для того, чтобы рассчитать площадь земельного участка . Итак, давайте узнаем, как найти площадь многоугольника.
Технические работники выполняют повседневную работу, связанную с геометрическими расчётами. Что касается расчета площади многоугольника, то и эти знания находят своё применение в жизни. Понадобятся они хотя бы для того, чтобы рассчитать площадь земельного участка . Итак, давайте узнаем, как найти площадь многоугольника.
Определение многоугольника
Сначала определимся с тем, что такое многоугольник. Это плоская геометрическая фигура, которая образовалась в результате пересечения трех или более прямых. Другое простое определение: многоугольник — это замкнутая ломаная. Естественно, при пересечении прямых образуются точки пересечения, их количество равно количеству прямых, образовывающих многоугольник. Точки пересечения называют вершинами, а отрезки, образованные от прямых, — сторонами многоугольника. Смежные отрезки многоугольника находятся не на одной прямой. Отрезки, являющиеся несмежными, — это те, которые не проходят через общие точки.
Сумма площадей треугольников
Как находить площадь многоугольника? Площадь многоугольника — это внутренняя часть плоскости, которая образовалась при пересечении отрезков или сторон многоугольника. Поскольку многоугольник — это сочетание таких фигур, как треугольник, ромб, квадрат, трапеция, то универсальной формулы для вычисления его площади просто нет. На практике наиболее универсальным является метод разбиения многоугольника на более простые фигуры, нахождение площади которых не вызывают затруднений. Сложив суммы площадей этих простых фигур , получают площадь многоугольника.
Поскольку многоугольник — это сочетание таких фигур, как треугольник, ромб, квадрат, трапеция, то универсальной формулы для вычисления его площади просто нет. На практике наиболее универсальным является метод разбиения многоугольника на более простые фигуры, нахождение площади которых не вызывают затруднений. Сложив суммы площадей этих простых фигур , получают площадь многоугольника.
Через площадь окружности
В большинстве случаев многоугольник имеет правильную форму и образует фигуру с равными сторонами и углами между ними. Рассчитать площадь в этом случае очень просто при помощи вписанной или описанной окружности. Если известна площадь окружности, то её необходимо умножить на периметр многоугольника, а затем полученное произведение поделить на 2. В итоге получается формула расчёта площади такого многоугольника: S = ½∙P∙r., где P — площадь окружности, а r — периметр многоугольника.
Метод разбиения многоугольника на «удобные» фигуры — самый популярный в геометрии, он позволяет быстро и правильно найти площадь многоугольника. 4 класс средней школы обычно изучает такие методы.
4 класс средней школы обычно изучает такие методы.
Площадь, одна из основных величин, связанных с геометрическими фигурами . В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П. было уже в древности… …
У этого термина существуют и другие значения, см. Площадь (значения). Площадь плоской фигуры аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное… … Википедия
I Площадь одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П.… … Большая советская энциклопедия
У этого термина существуют и другие значения, см. Площадь (значения). Площадь Размерность L² Единицы измерения СИ м² … Википедия
Ж. 1. Часть земной поверхности , пространство, естественно ограниченное или специально выделенное для какой либо цели.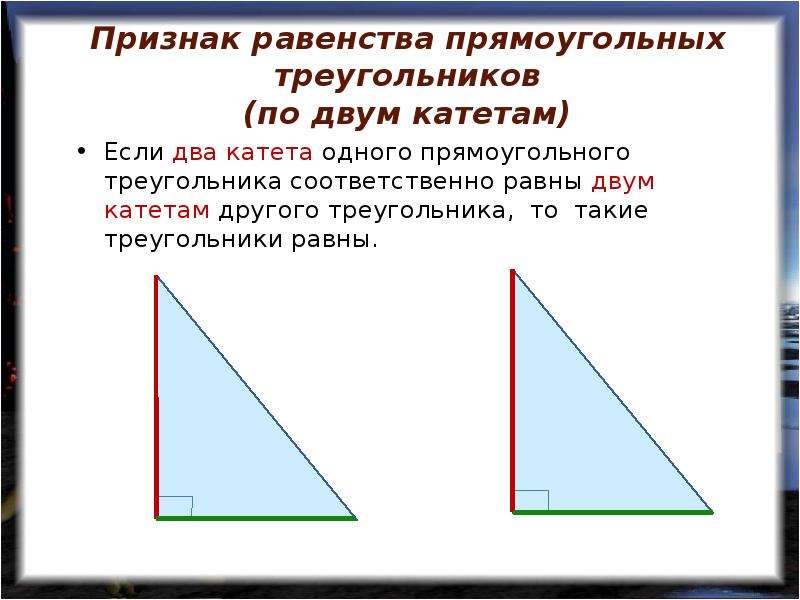 отт. Водное пространство. отт. Большое, ровное место, пространство. 2. Ровное незастроенное пространство общественного… … Современный толковый словарь русского языка Ефремовой
отт. Водное пространство. отт. Большое, ровное место, пространство. 2. Ровное незастроенное пространство общественного… … Современный толковый словарь русского языка Ефремовой
Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/2 сентября 2012. Пока процесс обсуждения не завершён, статью можно попытаться улучшить, однако следует… … Википедия
Две фигуры в R2, имеющие равные площади и соответственно два многоугольника M1 и М 2 такие, что их можно разрезать на многоугольники так, что части, составляющие М 1, соответственно конгруэнтны частям, составляющим М 2. Для, равновеликость… … Математическая энциклопедия
В=7, Г=8, В + Г/2 − 1= 10 Теорема Пика классический результат комбинаторной геометрии и геометрии чисел. Площадь многоугольника с целочисле … Википедия
У этого термина существуют и другие значения, см. Теорема Пика. В = 7, Г = 8, В + Г/2 − 1 = 10 Формула Пика (или теорема Пика) классический результат комбинаторной геометрии и геометрии чисел. Площадь … Википедия
Площадь … Википедия
Область (связное открытое множество) на границе выпуклого тела в евклидовом пространстве Е 3. Вся граница выпуклого тела наз. полной В. п. Если тело конечно, то полная В. п. наз. замкнутой. Если тело бесконечно, то полная В. п. наз. бесконечной.… … Математическая энциклопедия
В задачах по геометрии часто требуется вычислить площадь многоугольника. Причем он может иметь довольно разнообразную форму — от всем знакомого треугольника до некоторого n-угольника с каким-то невообразимым числом вершин. К тому же эти многоугольники бывают выпуклыми или вогнутыми. В каждой конкретной ситуации полагается отталкиваться от внешнего вида фигуры. Так получится выбрать оптимальный путь решения задачи. Фигура может оказаться правильной, что существенно упростит решение задачи.
Немного теории о многоугольниках
Если провести три или более пересекающихся прямых, то они образуют некоторую фигуру. Именно она является многоугольником. По количеству точек пересечения становится ясно, сколько вершин у него будет. Они дают название получившейся фигуре. Это может быть:
Они дают название получившейся фигуре. Это может быть:
Такая фигура непременно будет характеризоваться двумя положениями:
- Смежные стороны не принадлежат одной прямой.
- У несмежных отсутствуют общие точки, то есть они не пересекаются.
Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.
Какие их виды существуют?
Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника. В выпуклом всегда все вершины лежат с одной стороны от такой прямой.
В школьном курсе геометрии большая часть времени уделяется именно выпуклым фигурам. Поэтому в задачах требуется узнать площадь выпуклого многоугольника. Тогда существует формула через радиус описанной окружности, которая позволяет найти искомую величину для любой фигуры. В других случаях однозначного решения не существует. Для треугольника формула одна, а для квадрата или трапеции совершенно другие. В ситуациях, когда фигура неправильная или вершин очень много, принято разделять их на простые и знакомые.
Тогда существует формула через радиус описанной окружности, которая позволяет найти искомую величину для любой фигуры. В других случаях однозначного решения не существует. Для треугольника формула одна, а для квадрата или трапеции совершенно другие. В ситуациях, когда фигура неправильная или вершин очень много, принято разделять их на простые и знакомые.
Как поступить, если фигура имеет три или четыре вершины?
В первом случае он окажется треугольником, и можно воспользоваться одной из формул:
- S = 1/2 * а * н, где а — сторона, н — высота к ней;
- S = 1/2 * а * в * sin (А), где а, в — сторон\ы треугольника, А — угол между известными сторонами;
- S = √(p * (p — а) * (p — в) * (p — с)), где с — сторона треугольника, к уже обозначенным двум, р — полупериметр, то есть сумма всех трех сторон, разделенная на два.
Фигура с четырьмя вершинами может оказаться параллелограммом:
- S = а * н;
- S = 1/2 * d 1 * d 2 * sin(α), где d 1 и d 2 — диагонали, α — угол между ними;
- S = a * в * sin(α).

Формула для площади трапеции: S = н * (a + в) / 2, где а и в — длины оснований.
Как поступить с правильным многоугольником, у которого больше четырех вершин?
Для начала такая фигура характеризуется тем, что в ней все стороны равны. Плюс к этому, у многоугольника одинаковые углы.
Если вокруг такой фигуры описать окружность, то ее радиус совпадет с отрезком от центра многоугольника до одной из вершин. Поэтому для того чтобы вычислить площадь правильного многоугольника с произвольным числом вершин, потребуется такая формула:
S n = 1/2 * n * R n 2 * sin (360º/n), где n — количество вершин многоугольника.
Из нее легко получить такую, которая пригодится для частных случаев:
- треугольника: S = (3√3)/4 * R 2 ;
- квадрата: S = 2 * R 2 ;
- шестиугольника: S = (3√3)/2 * R 2 .
Ситуация с неправильной фигурой
Выходом для того, как узнать площадь многоугольника, если он не является правильным и его нельзя отнести ни к одной из известных ранее фигур, является алгоритм:
- разбить его на простые фигуры, например, треугольники, чтобы они не пересекались;
- вычислить их площади по любой формуле;
- сложить все результаты.

Что делать, если в задаче даны координаты вершин многоугольника?
То есть известен набор пар чисел для каждой точки, которые ограничивают стороны фигуры. Обычно они записываются как (x 1 ; y 1) для первой, (x 2 ; y 2) — для второй, а n-ая вершина имеет такие значения (x n ; y n). Тогда площадь многоугольника определяется, как сумма n слагаемых. Каждое из них выглядит так: ((y i+1 +y i)/2) * (x i+1 — x i). В этом выражении i изменяется от единицы до n.
Стоит отметить, что знак результата будет зависеть от обхода фигуры. При использовании указанной формулы и движении по часовой стрелке ответ будет получаться отрицательным.
Пример задачи
Условие. Координаты вершин заданы такими значениями (0.6; 2.1), (1.8; 3.6), (2.2; 2.3), (3.6; 2.4), (3.1; 0.5). Требуется вычислить площадь многоугольника.
Решение. По формуле, указанной выше, первое слагаемое будет равно (1.8 + 0.6)/2 * (3.6 — 2.1). Здесь нужно просто взять значения для игрека и икса от второй и первой точек. Несложный расчет приведет к результату 1.8.
Несложный расчет приведет к результату 1.8.
Второе слагаемое аналогично получается: (2.2 + 1.8)/2 * (2.3 — 3.6) = -2.6. При решении подобных задач не стоит пугаться отрицательных величин. Все идет так, как нужно. Это планомерно.
Подобным образом получаются значения для третьего (0.29), четвертого (-6.365) и пятого слагаемых (2.96). Тогда итоговая площадь равна: 1.8 + (-2.6) + 0.29 + (-6.365) + 2.96 = — 3.915.
Совет по решению задачи, для которой многоугольник изображен на бумаге в клетку
Чаще всего озадачивает то, что в данных имеется только размер клеточки. Но оказывается, что больше сведений не нужно. Рекомендацией к решению такой задачи является разбивание фигуры на множество треугольников и прямоугольников. Их площади довольно просто сосчитать по длинам сторон, которые потом легко сложить.
Но часто есть более простой подход. Он заключается в том, чтобы дорисовать фигуру до прямоугольника и вычислить значение его площади. Потом сосчитать площади тех элементов, которые оказались лишними.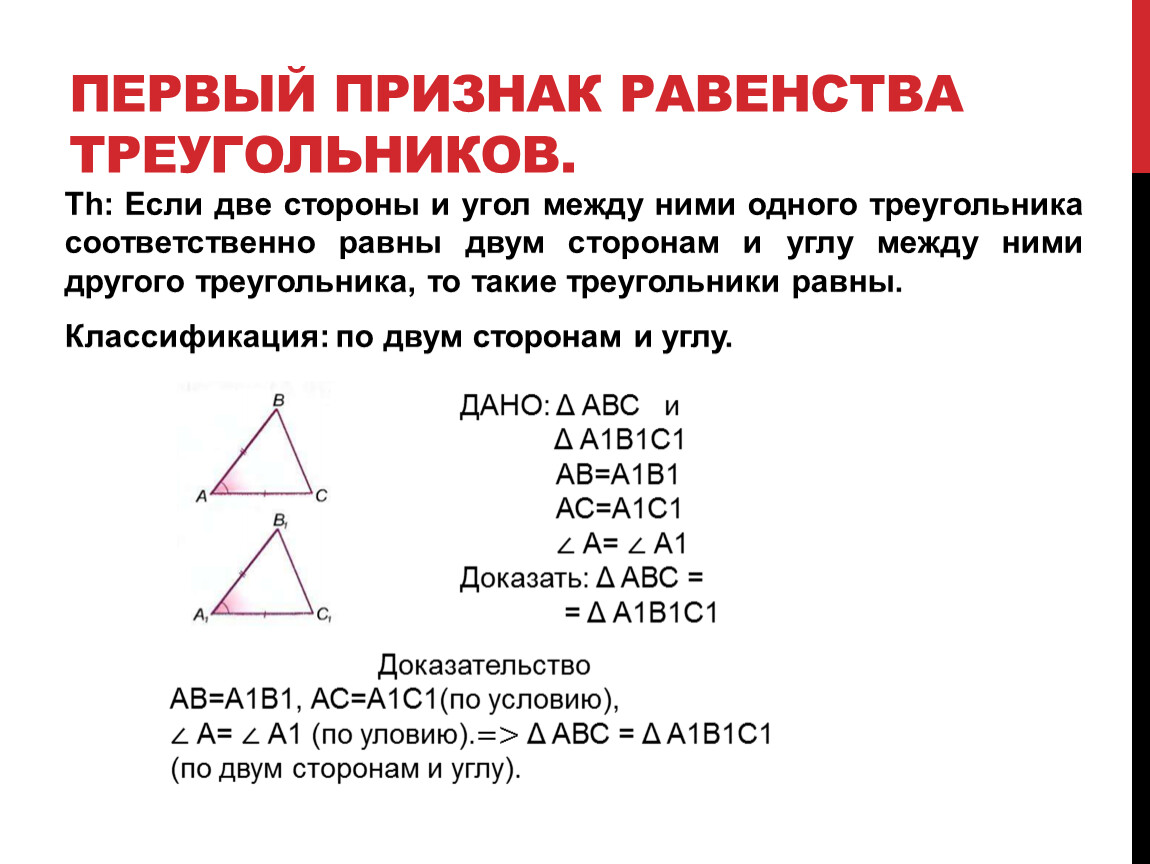 Вычесть их из общего значения. Этот вариант порой предполагает несколько меньшее число действий.
Вычесть их из общего значения. Этот вариант порой предполагает несколько меньшее число действий.
- обучающие: научить учащихся находить площадь многоугольника, используя выбранные ими способы, сформировать начальные представления
- многоугольнике, графические и измерительные навыки;
- развивающие: развитие способов умственной деятельности учащихся при выполнении заданий от наблюдения, расчетов до выяснения закономерностей вычисления площади многоугольника;
- воспитывающие: раскрытие субъективного опыта учащихся, поощрение действий, стремлений учащихся как основы воспитания положительных качеств личности;
- методическая: создание условий для проявления познавательной активности учащихся.
Оснащение урока:
- Оформление доски: слева — фигуры многоугольника, справа — чистое полотно доски для записи на уроке, в центре – многоугольник-прямоугольник.
- Листок “К исследованию”.
- Инструментарии учителя и учащихся (мел, указка,
линейка, листок исследования, фигуры, ватман,
маркер).

Метод урока:
- По взаимодействию учителя и учащихся – диалог-общение;
- По способу решения задач – частично-поисковый;
- По способу умственной деятельности — (СУД) развивающее обучение.
Форма урока — фронтальная, в парах, индивидуальная.
Тип урока — урок усвоения новых знаний, умений и навыков.
Структура урока — постепенное углубление в тему, гибкая, диалогическая.
Ход урока
Приветствие.
Урок прекрасен и приносит радость, когда мы мыслим, дружно работаем. Сегодня мы будем рассматривать фигуры, определять их названия, думать, искать и находить решения. Пожелаем друг другу успешной работы.
Актуализация знаний.
Рассмотрите фигуры (на доске многоугольники).
Они все вместе. Почему? Какой у них общий признак? (Многоугольники).
Назовите этот многоугольник (5-угольник, 6-угольник…)
Может быть, вы знаете, что такое площадь многоугольника?
Тогда покажите на одной из фигур.
(Обобщение учителем: площадь — часть плоскости внутри замкнутой геометрической фигуры.)
В русском языке это слово имеет несколько значений.
(Ученик по словарю знакомит со значениями.)
- Часть плоскости внутри замкнутой геометрической фигуры.
- Большое незастроенное и ровное место.
- Помещение для какой-либо цели.
Какое из значений используется в математике?
В математике используется первое значение.
(На доске фигура).
Это многоугольник? Да.
Назовите фигуру по-другому. Прямоугольник.
Покажи длину, ширину.
Как найти площадь многоугольника?
Запишите при помощи букв и знаков формулу.
Если длина нашего прямоугольника 20 см, ширина 10см. Чему равна площадь?
Площадь равна 200 см 2
Подумайте, как приложить линейку, чтобы фигура разделилась на:
Увидели, из каких частей состоит фигура? А теперь, наоборот, по частям соберем целое.
(Части фигуры лежат на партах. Дети собирают из
них прямоугольник).
Дети собирают из
них прямоугольник).
Сделайте вывод по наблюдениям.
Целую фигуру можно разделить на части и из частей составить целую.
Дома на основе треугольников и четырехугольников составляли фигуры, силуэты. Вот какие они получились.
(Демонстрация рисунков, выполненных дома учащимися. Одна из работ анализируется).
Какие фигуры использовал? У тебя получился сложный многоугольник.
Постановка учебной задачи.
На уроке мы должны ответить на вопрос: как найти площадь сложного многоугольника?
Для чего человеку нужно находить площадь?
(Ответы детей и обобщение учителем).
Задача определения площади возникла из практики.
(Показывается план школьного участка).
Для того чтобы построить школу, сначала создали план. Потом разбивалась территория на участки определенной площади, размещались строения, клумбы, стадион. При этом участок имеет определенную форму — форму многоугольника.
Решение учебной задачи.
(Раздаются листы для исследования).
Перед вами фигура. Назовите ее.
Многоугольник, шестиугольник.
Найдем площадь многоугольника. Что для этого надо делать?
Разделить на прямоугольники.
(При затруднении будет другой вопрос: “Из каких фигур состоит многоугольник?”).
Из двух прямоугольников.
С помощью линейки и карандаша разделите фигуру на прямоугольники. Обозначьте цифрами 1 и 2 полученные части.
Проведем измерения.
Найдем площадь первой фигуры.
(Учащиеся предлагают следующие варианты решений и записывают их на доске).
- S 1 = 5 ? 2 = 10 см 2
- S 2 = 5 ? 1 = 5 см 2
Зная площадь частей, как найти площадь целой фигуры?
S = 10 + 5 = 15 см 2
- S 1 = 6 ? 2 = 12 см 2
- S 2 = 3 ? 1 = 3 см 2
- S = 12 + 3 = 15 см 2 .
Сравните результаты и сделайте вывод.
Проследим наши действия
Как находили площадь многоугольника?
Составляется и записывается на плакате алгоритм:?
1. Делим фигуру на части
Делим фигуру на части
2. Находим площади частей этих многоугольников (S 1 , S 2).
3. Находим площадь целого многоугольника (S 1 + S 2).
Проговорить алгоритм.
(Несколько учащихся проговаривают алгоритм).
Мы нашли два способа, а может, есть еще?
А можно фигуру достроить.
Сколько прямоугольников получилось?
Обозначим части 1 и 2. Проведем измерения.
Найдите площадь каждой части многоугольника.
- S 1= 6? 5=30см 2
- S 2 = 5 ? 3 = 15 см 2
Как найти площадь нашего шестиугольника?
S = 30 – 15 = 15 см 2
Составим алгоритм:
Достроили фигуру до прямоугольника
Нашли S 1 и S 2 .
Нашли разность S 1 – S 2 .
Сравните два алгоритма. Сделайте вывод. Какие действия одинаковые? Где разошлись наши действия?
Закройте глазки, опустите головки. Мысленно повторите алгоритм.
Мы провели исследовательскую работу,
рассмотрели разные способы и теперь можем
находить площадь любого многоугольника.
Проверка результативности.
Проверьте себя.
Перед вами многоугольники.
Найти площадь одной фигуры по выбору, при этом можете пользоваться разными способами.
Работа выполняется самостоятельно. Дети выбирают фигуру. Находят площадь одним из способов. Проверка – ключ на доске.
Что можно сказать о форме? (Форма разная)
А какова площадь этих многоугольников? (Площади этих многоугольников равны)
Оценивают результаты.
У кого правильно – поставь “+”.
У кого сомнения, затруднения – “?”
Консультанты оказывают помощь ребятам, ищут ошибки, помогают исправить.
Домашнее задание:
Составить свои листки исследования, вычислить площадь многоугольника разными способами.
Итог урока.
Итак, ребята, что вы расскажите родителям, о том как найти площадь геометрической фигуры – многоугольника.
Многоугольник – это плоская или выпуклая фигура, которая состоит из пересеченных прямых (больше 3-х) и образует большое количество точек пересечения линий. Еще многоугольник можно определить как ломаную линию, которая замыкается. По-другому точки пересечения можно назвать вершинами фигуры. В зависимости от количества вершин фигура может называться пятиугольником, шестиугольником и так далее. Угол многоугольника – это угол, который образовывается сторонами, сходящимися в одной вершине. Угол находится внутри многоугольника. Причем углы могут быть разными, вплоть до 180 градусов. Есть также и внешние углы, которые обычно являются смежными внутренним.
Еще многоугольник можно определить как ломаную линию, которая замыкается. По-другому точки пересечения можно назвать вершинами фигуры. В зависимости от количества вершин фигура может называться пятиугольником, шестиугольником и так далее. Угол многоугольника – это угол, который образовывается сторонами, сходящимися в одной вершине. Угол находится внутри многоугольника. Причем углы могут быть разными, вплоть до 180 градусов. Есть также и внешние углы, которые обычно являются смежными внутренним.
Прямые линии, которые впоследствии пересекаются, называются сторонами многоугольника. Они могут быть соседними, смежными и не смежными. Очень важной характеристикой представленной геометрической фигуры является то, что несмежные ее стороны не пересекаются, а значит, не имеют общих точек. Смежные стороны фигуры не могут находиться на одной прямой.
Те вершины фигуры, которые принадлежат одной и той же прямой, можно назвать соседними. Если провести линию между двумя вершинами, не являющимися соседними, то получится диагональ многоугольника. Что касается площади фигуры, — это внутренняя часть плоскости геометрической фигуры с большим количеством вершин, которая создается разделяющими ее отрезками многоугольника.
Что касается площади фигуры, — это внутренняя часть плоскости геометрической фигуры с большим количеством вершин, которая создается разделяющими ее отрезками многоугольника.
Какого-либо одного решения для определения площади представленной геометрической фигуры нет, так как вариантов фигуры может быть бесконечное множество и для каждого варианта существует свое решение. Однако некоторые самые частые варианты нахождения площади фигуры все же нужно рассмотреть (они чаще всего используются на практике и включены даже в школьную программу).
Прежде всего, рассмотрим правильный многоугольник, то есть такую фигуру, в которой все углы, образованные равными сторонами, являются также равными. Итак, как найти площадь многоугольника в конкретном примере? Для этого случая нахождение площади многоугольной фигуры возможно, если дан радиус окружности, вписанной в фигуру или описанной вокруг нее. Для этого можно воспользоваться следующей формулой:
S = ½∙P∙r, где r – радиус окружности (вписанной или описанной), а P – является периметром геометрической многоугольной фигуры, которую можно узнать, умножив количество сторон фигуры на их длину.
Как находить площадь многоугольника
Чтобы ответить на вопрос, как находить площадь многоугольника, достаточно следовать следующему интересному свойству многоугольной фигуры, в свое время нашел известный австрийский математик – Георг Пик. Например, по формуле S = N + M/2 -1 можно найти площадь такого многоугольника, вершины которого размещены в узлах квадратной сетки. При этом S – это, соответственно, площадь; N – количество узлов квадратной сетки, которые разместились внутри фигуры с множеством углов; M – количество тех узлов квадратной сетки, которые разместились на вершинах и сторонах многоугольника. Однако, несмотря на свою красоту, формула Пика практически не применяется в практической геометрии.
Самым простым и известным методом определения площади, который изучают в школе, является разделение многоугольной геометрической фигуры на более простые части (трапеции, прямоугольники, треугольники). Найти площадь этих фигур не трудно. В этом случае площадь многоугольника определяется просто: нужно найти площади всех тех фигур, на которые разделен многоугольник.
В основном определение площади многоугольника определяется в механике (размеры деталей).
Прямые параллельны они равны. Как доказать параллельность прямых
Признаки параллельности двух прямых
Теорема 1. Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна 180°, то
прямые параллельны (рис.1).
Доказательство. Ограничимся доказательством случая 1.
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Следствие 1 . Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны (рис.2).
Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное) тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.
Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).
Затем проводим через точку М прямую b
перпендикулярно прямой р. Прямая b
параллельна прямой а согласно следствию из
теоремы 1.
Прямая b
параллельна прямой а согласно следствию из
теоремы 1.
Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной .
Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны;
соответственные углы равны;
сумма односторонних углов равна 180°.
Следствие 2.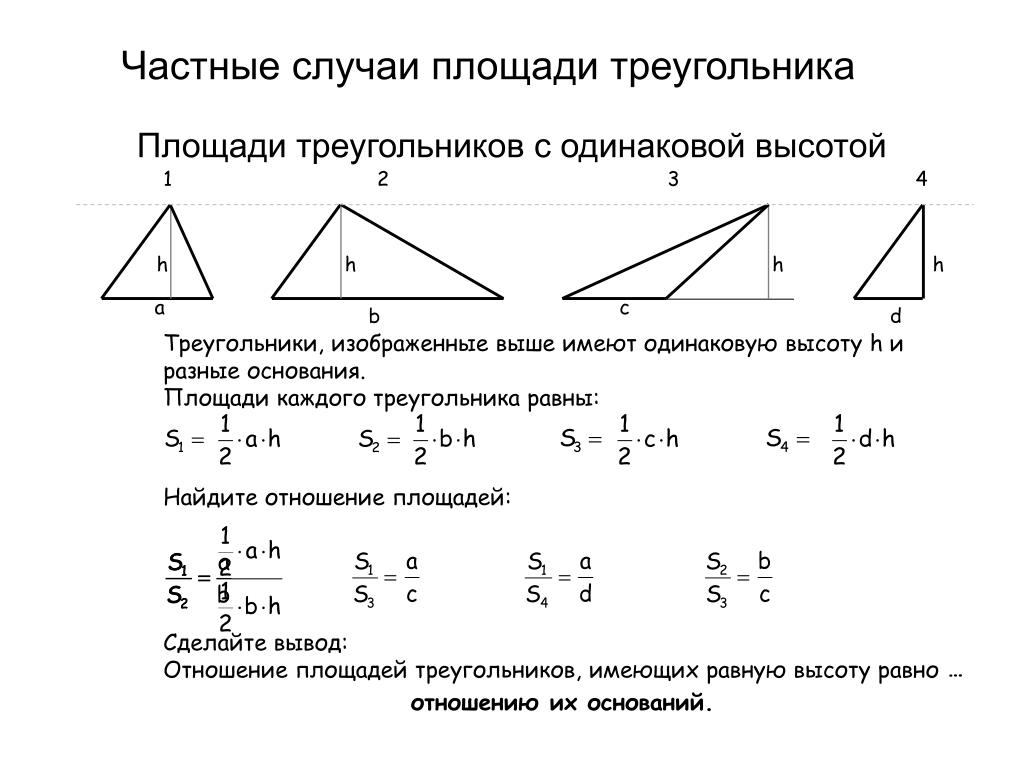 Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).
Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.
Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.
Эта глава посвящена изучению параллельных прямых. Так называются две прямые на плоскости, которые не пересекаются. Отрезки параллельных прямых мы видим в окружающей обстановке — это два края прямоугольного стола, два края обложки книги, две штанги троллейбуса и т. д. Параллельные прямые играют в геометрии очень важную роль. В этой главе вы узнаете о том, что такое аксиомы геометрии и в чём состоит аксиома параллельных прямых — одна из самых известных аксиом геометрии.
Отрезки параллельных прямых мы видим в окружающей обстановке — это два края прямоугольного стола, два края обложки книги, две штанги троллейбуса и т. д. Параллельные прямые играют в геометрии очень важную роль. В этой главе вы узнаете о том, что такое аксиомы геометрии и в чём состоит аксиома параллельных прямых — одна из самых известных аксиом геометрии.
В п. 1 мы отмечали, что две прямые либо имеют одну общую точку, т. е. пересекаются, либо не имеют ни одной общей точки, т. е. не пересекаются.
Определение
Параллельность прямых а и b обозначают так: а || b.
На рисунке 98 изображены прямые а и b, перпендикулярные к прямой с. В п. 12 мы установили, что такие прямые а и b не пересекаются, т. е. они параллельны.
Рис. 98
Наряду с параллельными прямыми часто рассматривают параллельные отрезки. Два отрезка называются параллельными , если они лежат на параллельных прямых. На рисунке 99, а отрезки АВ и CD параллельны (АВ || CD), а отрезки MN и CD не параллельны. Аналогично определяется параллельность отрезка и прямой (рис. 99, б), луча и прямой, отрезка и луча, двух лучей (рис. 99, в).
Аналогично определяется параллельность отрезка и прямой (рис. 99, б), луча и прямой, отрезка и луча, двух лучей (рис. 99, в).
Рис. 99 Признаки параллельности двух прямых
Прямая с называется секущей по отношению к прямым а и b, если она пересекает их в двух точках (рис. 100). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 100 обозначены цифрами. Некоторые пары этих углов имеют специальные названия:
накрест лежащие углы : 3 и 5, 4 и 6;
односторонние углы : 4 и 5, 3 и 6;
соответственные углы : 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Рис. 100
Рассмотрим три признака параллельности двух прямых, связанные с этими парами углов.
Теорема
Доказательство
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны: ∠1 = ∠2 (рис. 101, а).
Докажем, что а || b. Если углы 1 и 2 прямые (рис. 101, б), то прямые а и b перпендикулярны к прямой АВ и, следовательно, параллельны.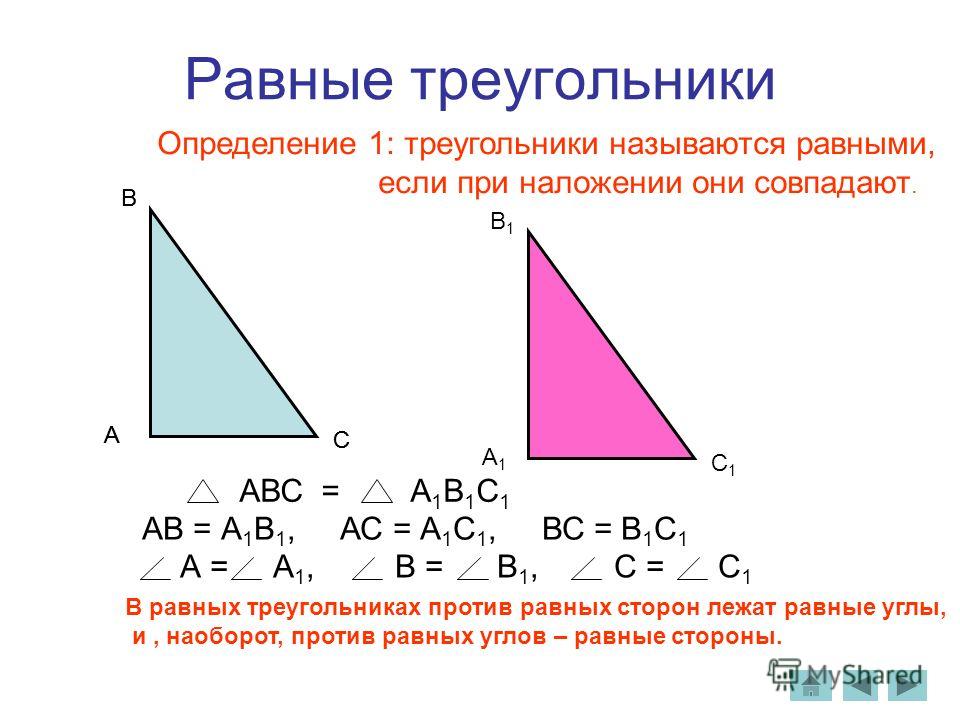
Рис. 101
Рассмотрим случай, когда углы 1 и 2 не прямые.
Из середины О отрезка АВ проведём перпендикуляр ОН к прямой а (рис. 101, в). На прямой b от точки В отложим отрезок ВН 1 , равный отрезку АН, как показано на рисунке 101, в, и проведём отрезок ОН 1 . Треугольники ОНА и ОН 1 В равны по двум сторонам и углу между ними (АО = ВО, АН = ВН 1 , ∠1 = ∠2), поэтому ∠3 = ∠4 и ∠5 = ∠6. Из равенства ∠3 = ∠4 следует, что точка Н 1 лежит на продолжении луча ОН, т. е. точки Н, О и Н 1 лежат на одной прямой, а из равенства ∠5 = ∠6 следует, что угол 6 — прямой (так как угол 5 — прямой). Итак, прямые а и b перпендикулярны к прямой HH 1 поэтому они параллельны. Теорема доказана.
Теорема
Доказательство
Пусть при пересечении прямых а и b секущей с соответственные углы равны, например ∠1 =∠2 (рис. 102).
Рис. 102
Так как углы 2 и 3 — вертикальные, то ∠2 = ∠3. Из этих двух равенств следует, что ∠1 = ∠3.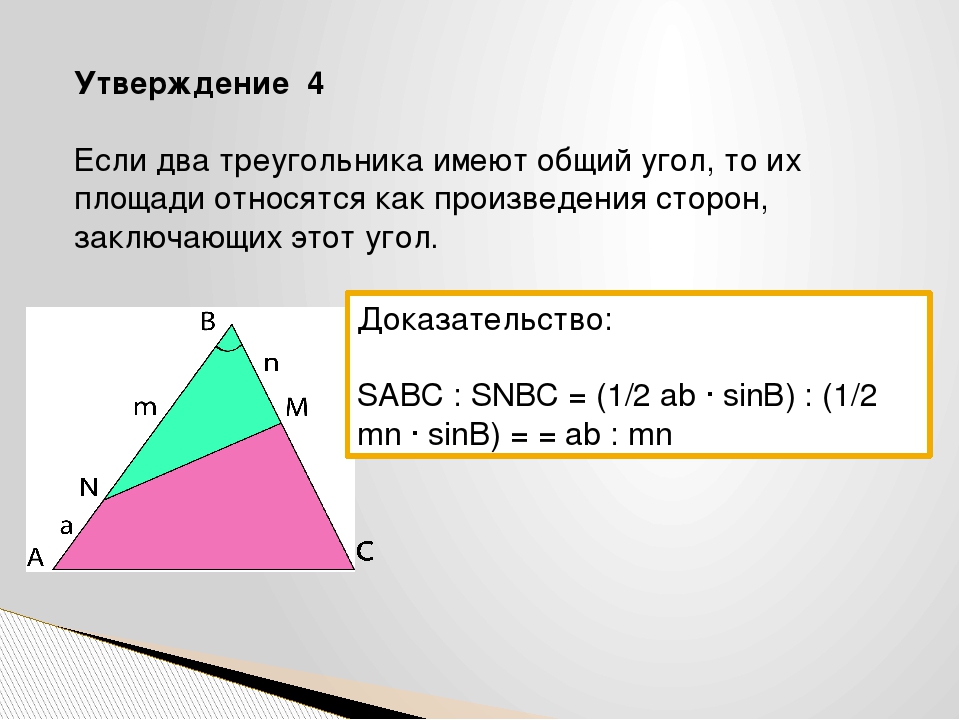 Но углы 1 и 3 — накрест лежащие, поэтому прямые а и b параллельны. Теорема доказана.
Но углы 1 и 3 — накрест лежащие, поэтому прямые а и b параллельны. Теорема доказана.
Теорема
Доказательство
Пусть при пересечении прямых а и b секущей с сумма односторонних углов равна 180°, например ∠1 + ∠4 = 180° (см. рис. 102).
Так как углы 3 и 4 — смежные, то ∠3 + ∠4 = 180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые а и b параллельны. Теорема доказана.
Практические способы построения параллельных прямых
Признаки параллельности прямых лежат в основе способов построения параллельных прямых с помощью различных инструментов, используемых на практике. Рассмотрим, например, способ построения параллельных прямых с помощью чертёжного угольника и линейки. Чтобы построить прямую, проходящую через точку М и параллельную данной прямой а, приложим чертёжный угольник к прямой а, а к нему линейку так, как показано на рисунке 103. Затем, передвигая угольник вдоль линейки, добьёмся того, чтобы точка М оказалась на стороне угольника, и проведём прямую b. Прямые а и b параллельны, так как соответственные углы, обозначенные на рисунке 103 буквами α и β, равны.
Прямые а и b параллельны, так как соответственные углы, обозначенные на рисунке 103 буквами α и β, равны.Рис. 103 На рисунке 104 показан способ построения параллельных прямых при помощи рейсшины. Этим способом пользуются в чертёжной практике.
Рис. 104 Аналогичный способ применяется при выполнении столярных работ, где для разметки параллельных прямых используется малка (две деревянные планки, скреплённые шарниром, рис. 105).
Рис. 105
Задачи
186. На рисунке 106 прямые а и b пересечены прямой с. Докажите, что а || b, если:
а) ∠1 = 37°, ∠7 = 143°;
б) ∠1 = ∠6;
в) ∠l = 45°, а угол 7 в три раза больше угла 3.
Рис. 106
187. По данным рисунка 107 докажите, что АВ || DE.
Рис. 107
188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АС и BD параллельны.
189. Используя данные рисунка 108, докажите, что ВС || AD.
Рис. 108
190. На рисунке 109 АВ = ВС, AD = DE, ∠C = 70°, ∠EAC = 35°. Докажите, что DE || АС.
Рис. 109
191. Отрезок ВК — биссектриса треугольника АВС. Через точку К проведена прямая, пересекающая сторону ВС в точке М так, что ВМ = МК. Докажите, что прямые КМ и АВ параллельны.
192. В треугольнике АВС угол А равен 40°, а угол ВСЕ, смежный с углом АСВ, равен 80°. Докажите, что биссектриса угла ВСЕ параллельна прямой АВ.
193. В треугольнике ABC ∠A = 40°, ∠B = 70°. Через вершину В проведена прямая BD так, что луч ВС — биссектриса угла ABD. Докажите, что прямые АС и BD параллельны.
194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертёжного угольника и линейки проведите прямую, параллельную противоположной стороне.
195. Начертите треугольник АВС и отметьте точку D на стороне АС. Через точку D с помощью чертёжного угольника и линейки проведите прямые, параллельные двум другим сторонам треугольника.
Параллельность двух прямых можно доказать на основе теоремы, согласно которой, два проведенных перпендикуляра по отношению к одной прямой, будут параллельны. Существуют определенные признаки параллельности прямых – всего их три, и все их мы рассмотрим более конкретно.
Первый признак параллельности
Прямые параллельны, если при пересечении их третьей прямой, образуемые внутренние углы, лежащие накрест, будут равны.
Допустим, при пересечении прямых АВ и СD прямой линией ЕF, были образованы углы /1 и /2. Они равны, так как прямая линия ЕF проходит под одним уклоном по отношению к двум остальным прямым. В местах пересечения линий, ставим точки Ки L – у нас получился отрезок секущей ЕF. Находим его середину и ставим точку О (черт. 189).
На прямую АВ опускаем перпендикуляр из точки О. Назовем его ОМ. Продолжаем перпендикуляр до тех пор, пока он не пересечется с прямой СD. В результате, первоначальная прямая АВ строго перпендикулярна МN, а это значит, что и СD_|_МN, но это утверждение требует доказательства. В результате проведения перпендикуляра и линии пересечения, у нас образовалось два треугольника. Один из них – МОЕ, второй – NОК. Рассмотрим их более подробно. признаки параллельности прямых 7 класс
В результате проведения перпендикуляра и линии пересечения, у нас образовалось два треугольника. Один из них – МОЕ, второй – NОК. Рассмотрим их более подробно. признаки параллельности прямых 7 класс
Данные треугольники равны, поскольку, в соответствии с условиями теоремы, /1 =/2, а в соответствии с построением треугольников, сторона ОK = стороне ОL. Угол МОL =/NОК, поскольку это вертикальные углы. Из этого следует, что сторона и два угла, прилежащие к ней одного из треугольников соответственно равны стороне и двум углам, прилежащим к ней, другого из треугольников. Таким образом, треугольник МОL =треугольникуNОК, а значит, и угол LМО = углу КNО, но нам известно, что/LМО прямой, значит, и соответствующий ему, угол КNО тоже прямой. То есть, нам удалось доказать, что к прямой МN, как прямая АВ, так и прямая СD перпендикулярны. То есть, АВ и СD по отношению друг к другу являются параллельными. Это нам и требовалось доказать. Рассмотрим остальные признаки параллельности прямых (7 класс), которые отличаются от первого признака по способу доказательства.
Второй признак параллельности
Согласно второму признаку параллельности прямых, нам необходимо доказать, что углы, полученные в процессе пересечения параллельных прямых АВ и СD прямой ЕF, будут равны. Таким образом, признаки параллельности двух прямых, как первый, так и второй, основывается на равности углов, получаемых при пересечении их третьей линией. Допускаем, что /3 = /2, а угол 1 = /3, поскольку он вертикален ему. Таким образом, и /2 будет равен углу1, однако следует учитывать, что как угол 1, так и угол 2 являются внутренними, накрест лежащими углами. Следовательно, нам остается применить свои знания, а именно то, что два отрезка будут параллельными, если при их пересечении третьей прямой образованные, накрест лежащие углы будут равными. Таким образом, мы выяснили, что АВ || СD.
Нам удалось доказать, что при условии параллельности двух перпендикуляров к одной прямой, согласно соответствующей теореме, признак параллельности прямых очевиден.
Третий признак параллельности
Существует еще и третий признак параллельности, который доказывается посредством суммы односторонних внутренних углов. Такое доказательство признака параллельности прямых позволяет сделать вывод, что две прямые будут параллельны, если при пересечении их третье прямой, сумма полученных односторонних внутренних углов, будет равна 2d. См. рисунок 192.
Такое доказательство признака параллельности прямых позволяет сделать вывод, что две прямые будут параллельны, если при пересечении их третье прямой, сумма полученных односторонних внутренних углов, будет равна 2d. См. рисунок 192.
1. Аксиома параллельных. Через данную точку можно провести не более одной прямой, параллельной данной.
2. Если две прямые параллельны одной и той же прямой, то они параллельны между собой.
3. Две прямые, перпендикулярные одной и той же прямой, параллельны.
4. Если две параллельные прямые пересечь третьей, то образованные при этом внутренние накрест лежащие углы равны; соответственные углы равны; внутренние односторонние углы в сумме составляют 180°.
5. Если при пересечении двух прямых третьей образуются равные внутренние накрест лежащие углы, то прямые параллельны.
6. Если при пересечении двух прямых третьей образуются равные соответственные углы, то прямые параллельны.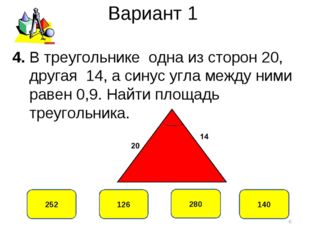
7. Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Теорема Фалеса . Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие вторую сторону угла, то на второй стороне угла отложатся также равные отрезки.
Теорема о пропорциональных отрезках . Параллельные прямые, пересекающие стороны угла, высекают на них пропорциональные отрезки.
Треугольник. Признаки равенства треугольников .
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.
3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то треугольники равны.
Признаки равенства прямоугольных треугольников
1. По двум катетам.
2. По катету и гипотенузе.
3. По гипотенузе и острому углу.
4. По катету и острому углу.
Теорема о сумме углов треугольника и следствия из неё
1. Сумма внутренних углов треугольника равна 180°.
2. Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.
3. Сумма внутренних углов выпуклого n-угольника равна
4. Сумма внешних углов га-угольника равна 360°.
5. Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые.
6. Угол между биссектрисами смежных углов равен 90°.
7. Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.
Основные свойства и признаки равнобедренного треугольника
1. Углы при основании равнобедренного треугольника равны.
2. Если два угла треугольника равны, то он равнобедренный.
3. В равнобедренном треугольнике медиана, биссектриса и высота, проведенные к основанию, совпадают.
В равнобедренном треугольнике медиана, биссектриса и высота, проведенные к основанию, совпадают.
4. Если в треугольнике совпадает любая пара отрезков из тройки — медиана, биссектриса, высота, то он является равнобедренным.
Неравенство треугольника и следствия из него
1. Сумма двух сторон треугольника больше его третьей стороны.
2. Сумма звеньев ломаной больше отрезка, соединяющего начало
первого звена с концом последнего.
3. Против большего угла треугольника лежит большая сторона.
4. Против большей стороны треугольника лежит больший угол.
5. Гипотенуза прямоугольного треугольника больше катета.
6. Если из одной точки проведены к прямой перпендикуляр и наклонные, то
1) перпендикуляр короче наклонных;
2) большей наклонной соответствует большая проекция и наоборот.
Средняя линия треугольника.
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Теорема о средней линии треугольника .
Средняя линия треугольника параллельна стороне треугольника и равна её половине.
Теоремы о медианах треугольника
1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2: 1, считая от вершины.
2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный.
3. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Свойство серединных перпендикуляров к сторонам треугольника . Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.
Теорема о высотах треугольника . Прямые, содержащие высоты треугольника, пересекаются в одной точке.
Теорема о биссектрисах треугольника . Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
Свойство биссектрисы треугольника . Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
Признаки подобия треугольников
1. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны, то треугольники подобны.
3. Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.
Площади подобных треугольников
1. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
2. Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.
В прямоугольном треугольнике
1. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.
2. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к этому катету острого угла.
3. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
4. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30°.
5. R = ; г = , где а, b — катеты, а с — гипотенуза прямоугольного треугольника; г и R — радиусы вписанной и описанной окружности соответственно.
Теорема Пифагора и теорема, обратная теореме Пифагора
1. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
2. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный.
Средние пропорциональные в прямоугольном треугольнике.
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.
Метрические соотношения в треугольнике
1. Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
2. Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
3. Формула для медианы треугольника. Если m — медиана треугольника, проведенная к стороне с, то m = , где а и b — остальные стороны треугольника.
4. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.
5. Обобщённая теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.
Формулы площади треугольника
1. Площадь треугольника равна половине произведения основания на высоту.
2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
3. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.![]()
4. Площадь треугольника равна произведению трёх его сторон, делённому на учетверённый радиус описанной окружности.
5. Формула Герона: S=, где p — полупериметр; а, b, с — стороны треугольника.
Элементы равностороннего треугольника . Пусть h, S, r, R — высота, площадь, радиусы вписанной и описанной окружностей равностороннего треугольника со стороной а. Тогда
Четырёхугольники
Параллелограмм. Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма .
1. Диагональ разбивает параллелограмм на два равных треугольника.
2. Противоположные стороны параллелограмма попарно равны.
3. Противоположные углы параллелограмма попарно равны.
4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.
Свойство середин сторон четырёхугольника . Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.
Прямоугольник. Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника.
1. Диагонали прямоугольника равны.
2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.
Квадрат. Квадратом называется прямоугольник, все стороны которого равны.
Ромб. Ромбом называется четырёхугольник, все стороны которого равны.
Свойства и признаки ромба.
1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его углы пополам.
3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
Трапеция. Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Замечательное свойство трапеции . Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция . Трапеция называется равнобедренной, если её боковые стороны равны.
Свойства и признаки равнобедренной трапеции.
1. Углы при основании равнобедренной трапеции равны.
2. Диагонали равнобедренной трапеции равны.
3. Если углы при основании трапеции равны, то она равнобедренная.
4. Если диагонали трапеции равны, то она равнобедренная.
5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.
Формулы площади четырёхугольника
1. Площадь параллелограмма равна произведению основания на высоту.
2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
3. Площадь прямоугольника равна произведению двух его соседних сторон.
4. Площадь ромба равна половине произведения его диагоналей.
5. Площадь трапеции равна произведению полусуммы оснований на высоту.
6. Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
7. Формула Герона для четырёхугольника, около которого можно описать окружность:
S = , где а, b, с, d — стороны этого четырёхугольника, p — полупериметр, а S — площадь.
Подобные фигуры
1. Отношение соответствующих линейных элементов подобных фигур равно коэффициенту подобия.
2. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Правильный многоугольник .
Пусть а n — сторона правильного n-угольника, а г n и R n — радиусы вписанной и описанной окружностей. Тогда
Окружность.
Окружностью называется геометрическое место точек плоскости, удаленных от данной точки, называемой центром окружности, на одно и то же положительное расстояние.
Основные свойства окружности
1. Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею дуги пополам.
2. Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
3. Серединный перпендикуляр к хорде проходит через центр окружности.
4. Равные хорды удалены от центра окружности на равные расстояния.
5. Хорды окружности, удалённые от центра на равные расстояния, равны.
6. Окружность симметрична относительно любого своего диаметра.
7. Дуги окружности, заключённые между параллельными хордами, равны.
8. Из двух хорд больше та, которая менее удалена от центра.
9. Диаметр есть наибольшая хорда окружности.
Касательная к окружности . Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.
1. Касательная перпендикулярна радиусу, проведённому в точку касания.
2. Если прямая а, проходящая через точку на окружности, перпендикулярна радиусу, проведённому в эту точку, то прямая а — касательная к окружности.
3. Если прямые, проходящие через точку М, касаются окружности в точках А и В, то MA = MB и ﮮАМО = ﮮВМО, где точка О — центр окружности.
4. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Касающиеся окружности . Говорят, что две окружности касаются, если они имеют единственную общую точку (точку касания).
1. Точка касания двух окружностей лежит на их линии центров.
2. Окружности радиусов г и R с центрами О 1 и О 2 касаются внешним образом тогда и только тогда, когда R + г = O 1 O 2 .
3. Окружности радиусов г и R (г
4. Окружности с центрами О 1 и O 2 касаются внешним образом в точке К. Некоторая прямая касается этих окружностей в различных точках А и В и пересекается с общей касательной, проходящей через точку К, в точке С. Тогда ﮮАК В = 90° и ﮮО 1 СО 2 = 90°.
5. Отрезок общей внешней касательной к двум касающимся окружностям радиусов г и R равен отрезку общей внутренней касательной, заключённому между общими внешними. Оба эти отрезка равны .
Углы, связанные с окружностью
1. Величина дуги окружности равна величине центрального угла, на неё опирающегося.
2. Вписанный угол равен половине угловой величины дуги, на которую он опирается.
3. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
4. Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
5. Угол между двумя секущими, пересекающимися вне круга, равен полуразности дуг, высекаемых секущими на окружности.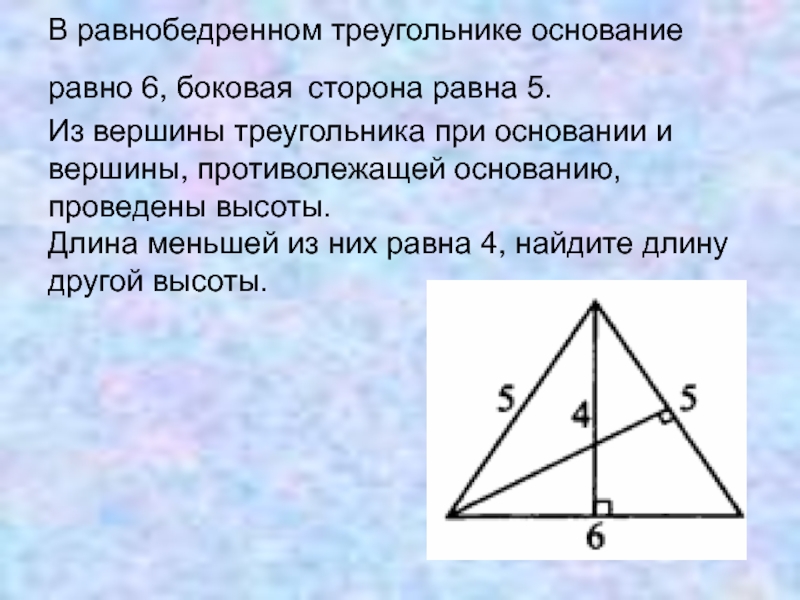
6. Угол между касательной и хордой, проведённой из точки касания, равен половине угловой величины дуги, высекаемой на окружности этой хордой.
Свойства хорд окружности
1. Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.
2. Произведения длин отрезков хорд АВ и CD окружности, пересекающихся в точке Е, равны, то есть АЕ ЕВ = СЕ ED.
Вписанные и описанные окружности
1. Центры вписанной и описанной окружностей правильного треугольника совпадают.
2. Центр окружности, описанной около прямоугольного треугольника, — середина гипотенузы.
3. Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны.
4. Если четырёхугольник можно вписать в окружность, то сумма его противоположных углов равна 180°.
5. Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
6. Если в трапецию можно вписать окружность, то боковая сторона трапеции видна из центра окружности под прямым углом.
7. Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону.
8. Если в многоугольник можно вписать окружность, то его площадь равна произведению полупериметра многоугольника на радиус этой окружности.
Теорема о касательной и секущей и следствие из неё
1. Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной.
2. Произведение всей секущей на её внешнюю часть для данной точки и данной окружности постоянно.
Длина окружности радиуса R равна C= 2πR
1. Если две прямые параллельны третьей прямой, то они являются параллельными:
Если a ||c и b ||c , то a ||b .
2. Если две прямые перпендикулярны третьей прямой, то они параллельны:
Если a ⊥c и b ⊥c , то a ||b .
Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.
3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:
Если ∠1 + ∠2 = 180°, то a ||b .
4. Если соответственные углы равны, то прямые параллельны:
Если ∠2 = ∠4, то a ||b .
5. Если внутренние накрест лежащие углы равны, то прямые параллельны:
Если ∠1 = ∠3, то a ||b .
Свойства параллельных прямых
Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.
1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:
Если a ||b , то ∠1 + ∠2 = 180°.
2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:
Если a ||b , то ∠2 = ∠4.
3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:
Если a ||b , то ∠1 = ∠3.
Следующее свойство является частным случаем для каждого предыдущего:
4. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:
Если a ||b и c ⊥a , то c ⊥b .
Пятое свойство — это аксиома параллельности прямых:
5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
Онлайн урок: Площадь. Площадь прямоугольника по предмету Математика 5 класс
Во всех выше рассмотренных примерах мы имели дело с плоскими геометрическими фигурами (прямоугольником и квадратом).
Вспомним, что называют прямоугольником, а что квадратом.
Прямоугольник- это плоская геометрическая фигура, образованная замкнутой ломаной линией, состоящей из четырех звеньев, и плоскостью, которая располагается внутри этой линии.
У прямоугольника противоположные стороны равны и все четыре угла одинаковые.
Обычно прямоугольник обозначают четырьмя заглавными латинскими буквами, записывая их по порядку следования.
Пример: прямоугольник АВDС
Отрезки АВ, ВD, DC, СА называются сторонами прямоугольника АВDС.
Причем АВ = СD и АС = ВD.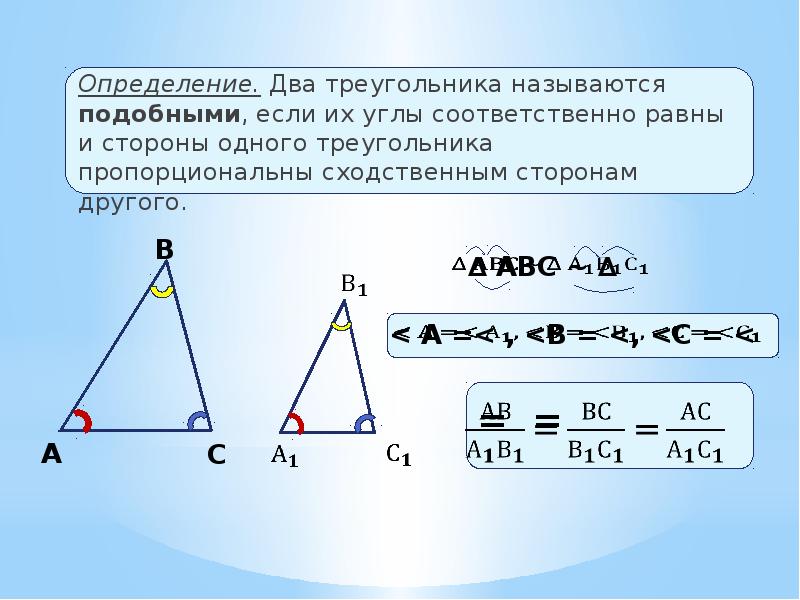
Точки А, В, С, D называют вершинами прямоугольника АВDС.
Углы, образованные сторонами АС и АВ, АВ и ВD, ВD и DC, DC и СА, называют углами прямоугольника АВDС.
Отрезки СВ и АD, соединяющие вершины С и В, А и D, — это диагонали прямоугольника АВDС.
В любом прямоугольнике можно провести две диагонали, и они будут равны СВ = АD.
Диагонали пересекаются в точке пересечения диагоналей (точка О— точка пересечения диагоналей СВ и АD).
Она делит диагонали на равные отрезки:
Точка O делит диагональ СВ на равные отрезки СО и ОB.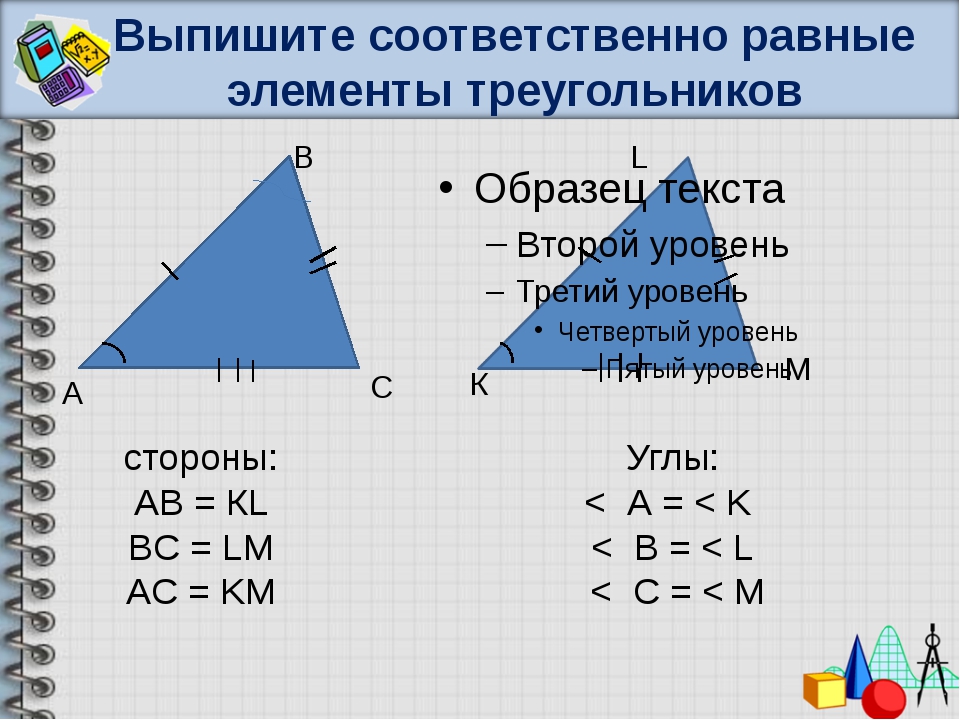
Точка O делит диагональ АD на равные отрезки AО и ОD.
Каждая диагональ делит прямоугольник на два равных треугольника.
Диагональ СВ делит прямоугольник АВDС на равные треугольники САВ и СDВ.
Диагональ АD делит прямоугольник АВDС на равные треугольники АСD и АВD.
Квадрат- это прямоугольник, у которого все стороны равны.
Пример:
Квадрат АВDС.
Отрезки АВ, ВD, DC, СА— называются сторонами квадрата АВDС.
Причем АВ = СD = АС = ВD.
Точки А, В, С, D называют вершинами квадрата АВDС.
Углы, образованные сторонами АС и АВ, АВ и ВD, ВD и DC, DC и СА, называют углами квадрата АВDС.
Отрезки СВ и АD, соединяющие вершины С и В, А и D, — это диагонали квадрата АВDС.
Все свойства прямоугольника характерны и для квадрата.
Чтобы найти площадь прямоугольника, можно разделить его на одинаковые единичные квадраты и сосчитать их количество. Такой способ нахождения площади фигуры мы рассмотрели ранее.
Пример:
Найдем площадь прямоугольника ABCD.
Прямоугольник ABCD разобьем на квадраты со стороной 1 см, значит в нашем случае единицей измерения площади будет квадратный сантиметр (см2).
Посчитаем сколько раз помещается квадратный сантиметр в фигуру ABCD.
В прямоугольнике ABCD содержится 15 квадратов, следовательно, его площадь равна 15 квадратных сантиметров (15 см2).
Если внимательно посмотреть на прямоугольник ABCD, то можно заметить, что он разбит на 3 строчки и каждая строчка содержит 5 квадратов со сторонами 1 см каждый.
Тогда количество таких квадратов в прямоугольнике ABCD можно определить выражением (3 ∙ 5).
Найдем значение данного выражения:
3 ∙ 5 = 15
Значит площадь прямоугольника ABCD равна 15 см2.
Пересчитав по порядку каждый квадратный сантиметр прямоугольника ABCD, мы получили такой же результат.
Этот же прямоугольник можно разбить на 5 полос по 3 квадрата со сторонами 1 см каждый.
Найдем площадь прямоугольника ABCD.
В этом случае площадь прямоугольника ABCD будет определяться выражением (5 ∙ 3).
Как нам уже известно, от перестановки множителей произведение не изменяется:
5 ∙ 3 = 15.
Площадь прямоугольника получается равной 15 см2 Результат, как мы видим, не изменился.
Важно заметить, что сторона АВ прямоугольника ABCD- это ширина данного прямоугольника (равная 3 см), а сторона ВС — это его длина (равная 5 см).
Таким образом, для того, чтобы найти площадь прямоугольника ABCD, не обязательно разбивать его на квадратные единицы, необходимо просто знать длину и ширину этого прямоугольника.
Правило: чтобы найти площадь прямоугольника, нужно его длину умножить на ширину (в одинаковых единицах).
Единицы измерения длины и ширины должны совпадать.
Если меры не совпадают, их необходимо перевести, т.е. свести к единой единице измерения.
Запишем правило в виде формулы.
Площадь прямоугольника обозначим латинской буквой S, ширину прямоугольника обозначим буквой а, длину буквой b.
Формула площади прямоугольника выглядит так:
Рассмотрим некоторые свойства площади.
1. Площади равных фигур равны.
Периметры таких фигур также равны.
Фигуры, имеющие равные площади называются равновеликими.
У меня есть дополнительная информация к этой части урока!
ЗакрытьНе следует путать такие понятия, как периметр и площадь геометрических фигур.
Периметр- это замкнутая ломаная или кривая линия (контур) геометрической фигуры, которая ограничивает внутреннюю область этой фигуры.
По сути, периметр- это длина контура фигуры (для многоугольника это сумма длин всех сторон многоугольника).
Периметр часто обозначают заглавной латинской буквой Р.
Периметр измеряется в линейных единицах длины: мм, см, дм и т.д.
Площадь же- это часть плоскости, которая ограничена периметром.
Площадь измеряется только в квадратных единицах длины: мм2, см2, дм2 и т. д.
д.
Пример:
На рисунке периметр обозначен красной линией, площадь фигуры выделена на рисунке штриховкой.
Р = 2 см + 6 см + 2 см + 6 см = 2 (2 + 6) = 16 (см) периметр фигуры (прямоугольника).
S = 2 см∙ 6 см = 12 (см2) площадь фигуры (прямоугольника)
2. Площадь всей фигуры равна сумме площадей ее частей.
Рассмотрим пример, иллюстрирующий данное свойство.
Разделим прямоугольник ABCD на две части ломаной линией KOMN.
Одна из частей- ABNMОK имеет площадь, равную 10 см2.
S1 = 10 см2.
Вторая часть- KОMNCD имеет площадь 8 см2.
S2 = 8 см2.
Площадь всего прямоугольника равна сумме его частей:
S = S1 + S2
S = 10 см2 + 8 см2 = 18 см2.
Вычислив площадь прямоугольника по формуле S = a ∙ b,
где а = АВ = 3 см, b = ВС = 6 см.
S = 3 ∙ 6 = 18 см2.
Площадь всей фигуры равна 18 см2, такой же результат был получен при сложении площадей двух частей, на которые эта фигура была разделена.
Первое и второе свойства- это основные свойства площадей.
3. Диагональ прямоугольника (квадрата), делит его на два равных треугольника.
Диагональ прямоугольника (квадрата), делит его на два равных треугольника.
Пусть отрезок BD делит прямоугольник ABCD на два равных треугольника:
∆ ABD = ∆ BCD
Сумма площадей каждого треугольника равна площади всего прямоугольника, следовательно, площадь каждого треугольника равна половине площади прямоугольника.
SABD = SABCD ÷ 2.
SBCD = SABCD ÷ 2.
4. Площадь квадрата.
Квадрат- это прямоугольник, у которого все четыре стороны равны.
Изобразим квадрат со стороной 2 см (это выражение означает, что все четыре стороны у квадрата будут 2 см).
Площадь квадрата рассчитывается таким же образом, как и площадь прямоугольника:
S = a ∙ b— произведение длины и ширины прямоугольника.
Известно, что в квадрате все стороны между собой равны, значит, длина квадрата равна ширине этого квадрата.
В таком случае, умножив длину на ширину, получим произведение двух равных по значению множителей, каждый равен длине стороны квадрата (а).
Получаем формулу площади квадрата:
S = a ∙ a
Число, умноженное само на себя, представляет собой квадрат этого числа.
Формула площади квадрата будет выглядеть так:
Число возводится во вторую степень, т.е. возводится в квадрат.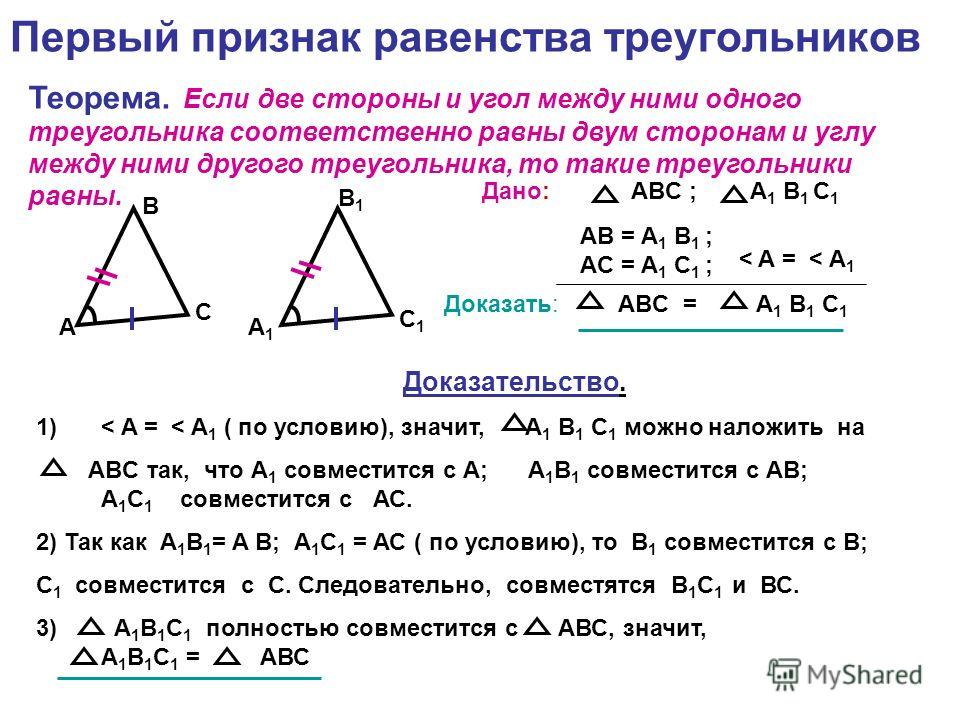
Правило: площадь квадрата равна квадрату его стороны.
Рассмотрим такой пример.
Вычислим площадь квадрата со стороной 4 см.
Решение данной задачи:
Открытая Математика. Планиметия. Площади многоугольников
Площадь прямоугольника равна произведению его сторон (рис. 13.2.1): S = a ċ b.
Пусть ABCD и AB1C1D – два прямоугольника с общим основанием AD (рис. 13.2.1).
К теореме 13.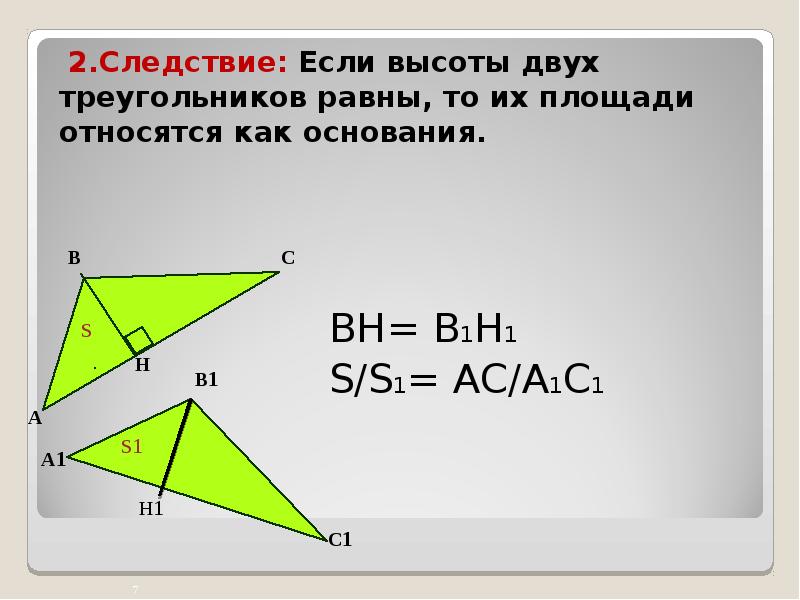 2 2 | К теореме 13.2 |
Пусть S и S1 – их площади. Докажем, что SS1=ABAB1. Разобьем сторону AB прямоугольника на некоторое число n равных частей, каждая из которых равна ABn. Пусть m – число точек деления, которые лежат нa стороне AB1. Тогда (ABn)m≤AB1≤(ABn)(m+1). Отсюда, разделив на AB, получим mn≤AB1AB≤mn+1n. (*)
Проведем через точки деления прямые, параллельные основанию AD. Они разобьют прямоугольник ABCD на n равных прямоугольников. Каждый из них имеет площадь
Sn.
Прямоугольник AB1C1D
содержит первые m прямоугольника, считая от стороны AD, и содержится в m + 1 прямоугольниках. Поэтому
(Sn)m≤S1≤(Sn)(m+1).
Отсюда
mn≤S1S≤mn+1n. (**)
(**)
Сравнивая неравенства (*) и (**), заключаем, что 0≤|S1S-AB1AB|≤1n. При этом S1S и AB1AB – фиксированные числа, а n может быть выбрано сколь угодно большим. Следовательно, неравенство возможно только при S1S=AB1AB. Возьмем теперь единичный квадрат, прямоугольник со сторонами 1, a и прямоугольник со сторонами a, b (рис. 13.2.2). Площадь прямоугольника со сторонами 1 и a обозначим S′. Сравнивая их площади, по доказанному будем иметь S′1=a1 и SS′=b1. Перемножая эти равенства почленно, получим S = a ċ b. Теорема доказана.
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне (рис. 13.2.5):
S = a ċ h.
Пусть ABCD – данный параллелограмм. Если он не является прямоугольником, то один из его углов A или B острый. Пусть для определенности A острый (рис. 13.2.3).
Опустим перпендикуляр AE из вершины A на прямую CB. Площадь трапеции AECD равна сумме площадей параллелограмма ABCD и треугольника AEB. Опустим перпендикуляр DF из вершины D на прямую CD. Тогда площадь трапеции AECD равна сумме площадей прямоугольника AEFD и треугольника DFC. Прямоугольные треугольники AEB и DFC равны, а значит, имеют равные площади. Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника AEFD, т.е. равна AE ċ AD. Отрезок AE – высота параллелограмма, соответствующая стороне AD, и, следовательно, S = a ċ h. Теорема доказана.
Площадь треугольника равна половине произведения его стороны на проведенную к ней высоту (рис.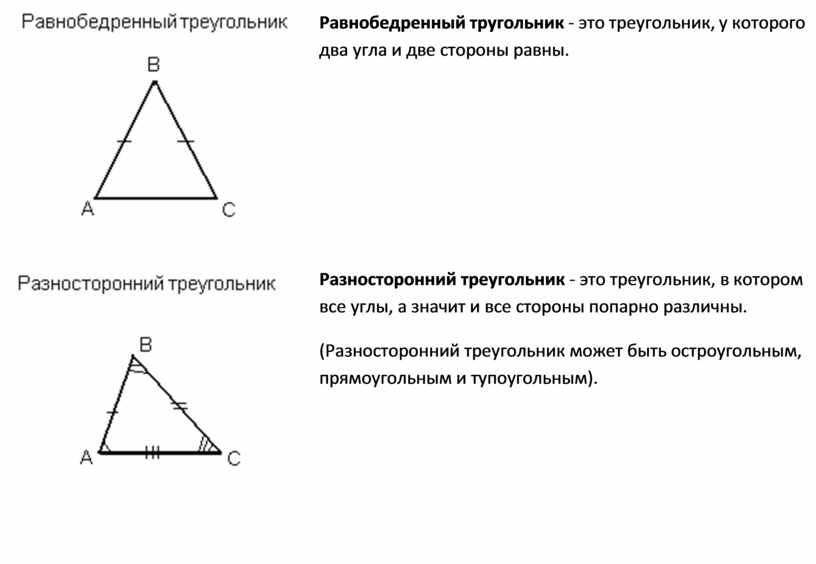 13.2.6):
S=12aċh.
13.2.6):
S=12aċh.
Пусть ABC – данный треугольник (рис. 13.2.7). Дополним его до параллелограмма ABCD, как показано на рисунке.
Площадь параллелограмма равна сумме площадей треугольников ABC и CDA. Так как эти треугольники равны, то площадь параллелограмма равна удвоенной площади треугольника ABC. Высота параллелограмма, соответствующая стороне CB, равна высоте треугольника, проведенной к стороне CB. Отсюда следует утверждение теоремы, и S=12hAċa. Теорема доказана.
Площадь трапеции равна произведению полусуммы его оснований на высоту (рис. 13.2.8). S=a+b2ċh.
Пусть ABCD – данная трапеция (рис. 13.2.9).
 5
5Диагональ AC трапеции разбивает ее на два треугольника: ABC и CDA. Следовательно, площадь трапеции равна сумме площадей этих треугольников. Площадь треугольника ACD равна 12ADċCE, площадь треугольника ABC равна 12BCċAF. Высоты AF и CE этих треугольников равны расстоянию h между параллельными прямыми BC и AD, т.е. высоте трапеции. Следовательно, S=12BCċAF+12ADċCE=(12b+12a)h=a+b2ċh. Теорема доказана.
Треугольники и четырехугольники – Математика для учителей начальных классов
Подумай / Пара / Поделись
Следуйте этим инструкциям самостоятельно:
- Нарисуйте любой треугольник на бумаге.
- Нарисуйте второй треугольник, который чем-то отличается от первого. Запишите предложение или два, чтобы сказать, как это отличается.

- Нарисуйте третий треугольник, отличный от двух других. Опишите, чем он отличается.
- Нарисуйте еще два треугольника, отличных от всех предыдущих.
Сравните свои треугольники и описания с партнером. Чтобы сделать «другие» треугольники, вам нужно изменить некоторые свойства треугольника. Составьте список функций, которые вы или ваш партнер изменили.
Треугольники классифицируются по разным свойствам. Цель изучения геометрии не в том, чтобы выучить много словарного запаса, а в том, чтобы использовать правильные термины для объектов, чтобы мы могли ясно общаться. Вот краткий словарь некоторых типов треугольников.
Классификация по сторонам
| разносторонний | равнобедренный | равносторонний |
|---|---|---|
| все стороны имеют разную длину | две стороны имеют одинаковую длину | все три стороны имеют одинаковую длину |
Классификация по углам
| острый | тупой |
|---|---|
| все внутренние углы меньше 90° | один внутренний угол больше 90° ° |
| справа | равноугольный |
| один внутренний угол равен 90° ° | все внутренние углы имеют одинаковую меру |
Помните, что «геометрия — это искусство делать хорошие выводы из плохих рисунков. Это означает, что вы не всегда можете доверять своим глазам. Если вы посмотрите на изображение треугольника и увидите, что одна сторона длиннее другой, это может означать, что рисунок был сделан немного небрежно.
Это означает, что вы не всегда можете доверять своим глазам. Если вы посмотрите на изображение треугольника и увидите, что одна сторона длиннее другой, это может означать, что рисунок был сделан немного небрежно.
Обозначение: засечки
Математики либо записывают измерения, либо используют галочки, чтобы указать, когда стороны и углы должны быть равны.
Если две стороны имеют одинаковый размер или одинаковое количество делений, вы должны поверить, что они равны, и решить задачу соответствующим образом, даже если это не выглядит так на ваш взгляд .
Примеры можно увидеть на некоторых рисунках выше. Другим примером является маленький квадрат, используемый для обозначения прямого угла на изображении прямоугольного треугольника.
СамостоятельноВыполните следующие упражнения самостоятельно или с партнером.
1. Какие стороны на рисунке ниже понимаются как имеющие одинаковую длину (даже если на рисунке это не выглядит так)?
2. Какие углы на рисунке ниже понимаются как имеющие одинаковую меру (даже если на рисунке это не выглядит так)?
Какие углы на рисунке ниже понимаются как имеющие одинаковую меру (даже если на рисунке это не выглядит так)?
3.Вот разносторонний треугольник. Нарисуйте еще два разносторонних треугольника, каждый из которых чем-то отличается от показанного здесь.
4. Вот остроугольный треугольник. Нарисуйте еще два остроугольных треугольника, каждый из которых чем-то отличается от показанного здесь.
5. Вот тупоугольный треугольник. Нарисуйте еще два тупоугольных треугольника, каждый из которых чем-то отличается от показанного здесь.
6. Вот прямоугольный треугольник. Нарисуйте еще два прямоугольных треугольника, каждый из которых чем-то отличается от показанного здесь.Обязательно укажите, какой угол равен 90°.
7. Вот равнобедренный треугольник. Нарисуйте еще два равнобедренных треугольника, каждый из которых чем-то отличается от показанного здесь. Используйте галочки, чтобы указать, какие стороны равны.
Подумай / Пара / Поделись
К настоящему моменту вы нарисовали на бумаге несколько разных треугольников. Выберите один из ваших треугольников и следуйте этим указаниям:
Выберите один из ваших треугольников и следуйте этим указаниям:
- С помощью ножниц вырежьте треугольник.
- Оторвите (не срезайте) углы и соедините три вершины вместе. У вас должно получиться что-то похожее на эту картинку:
Что вы заметили? Что это говорит об углах треугольника?
Возможно, вы помните, что сумма углов любого треугольника равна 180°. В вашем классе теперь есть много примеров треугольников, в которых сумма углов равна 180°. Но помните, наши рисунки не точны.Как мы можем быть уверены, что наши глаза нас не обманывают? Как мы можем быть уверены, что сумма углов в треугольнике не равна 181° или 178°, а действительно равна 180° на носу в каждом случае?
Подумай / Пара / Поделись
Что могло бы убедить вас вне всяких сомнений в том, что сумма углов любого треугольника равна 180°? Будет ли достаточно тестирования множества случаев? Сколько достаточно? Сможете ли вы когда-нибудь протестировать каждый возможный треугольник?
Часто школьные учителя геометрии доказывают, что сумма углов треугольника равна 180°, обычно используя некоторые факты о параллельных прямых.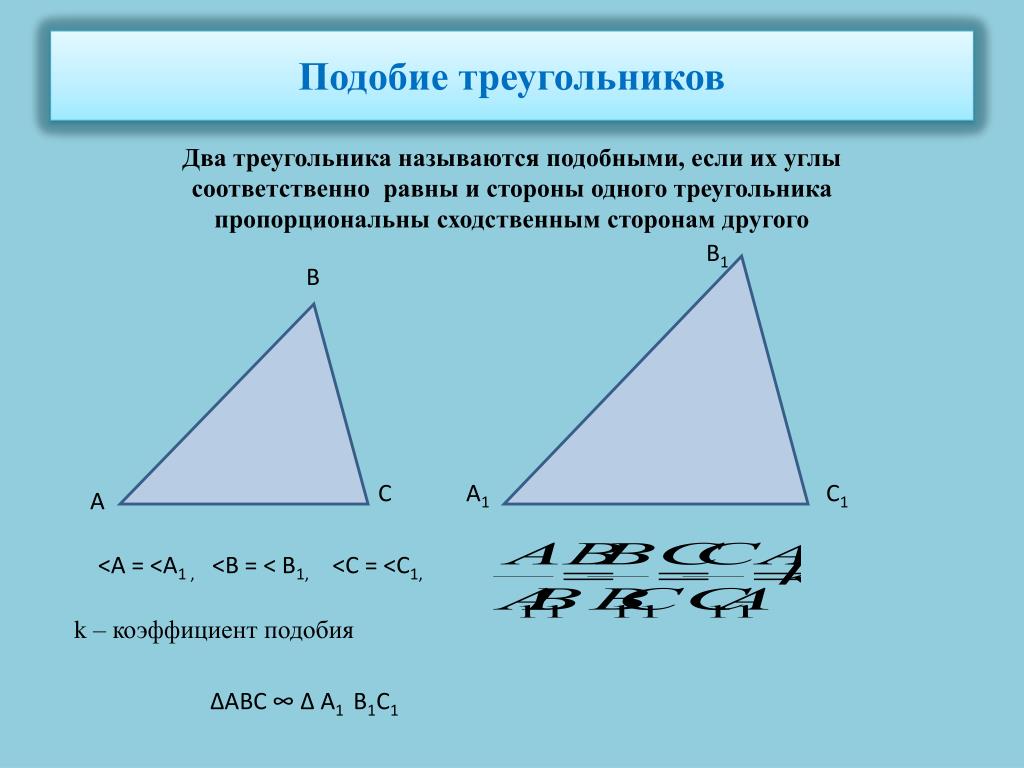 Но (может быть, это удивительно?) столь же хорошо принять это как аксиому , как данный факт о том, как работает геометрия, и исходить из этого. Возможно, это менее удовлетворительно, чем доказательство из какого-либо другого утверждения, и если вам интересно, вы наверняка сможете найти доказательство или ваш инструктор может поделиться им с вами.
Но (может быть, это удивительно?) столь же хорошо принять это как аксиому , как данный факт о том, как работает геометрия, и исходить из этого. Возможно, это менее удовлетворительно, чем доказательство из какого-либо другого утверждения, и если вам интересно, вы наверняка сможете найти доказательство или ваш инструктор может поделиться им с вами.
Приблизительно в 300 г. до н.э. Евклид был первым математиком (насколько нам известно), который попытался тщательно записать аксиомы, а затем построить из этих аксиом строгие доказательства математических истин.
ЕвклидУ Евклида было пять аксиом геометрии, первые четыре из которых казались математикам довольно очевидными. Люди считали, что это разумные предположения, из которых можно построить геометрические истины:
1. Даны две точки, их можно соединить отрезком прямой.
2. Получив отрезок, вы можете продлить его как угодно далеко в любом направлении, образуя линию.
3. Имея отрезок прямой, вы можете нарисовать окружность, используя этот отрезок в качестве радиуса.
4. Все прямые углы равны.
Немного больше беспокоил людей пятый постулат. Первоначально это было сказано более цветистым языком, но это было эквивалентно этому утверждению:
.5. Сумма углов треугольника равна 180°.
Легко понять, почему эта пятая аксиома вызвала такой шум в математике. Это казалось гораздо менее очевидным, чем остальные четыре, и математики чувствовали, что они каким-то образом обманывают, если они просто предполагают это, а не доказывают, что это должно быть правдой.Многие математики потратили много-много лет, пытаясь доказать эту пятую аксиому из других аксиом, но им это не удалось. И не без оснований: есть и другие виды геометрий, в которых первые четыре аксиомы верны, а пятая — нет!
Например, если вы выполняете геометрию на сфере — например, на баскетбольном мяче или, что более важно, на поверхности Земли — а не на плоской плоскости, первые четыре аксиомы верны. Но треугольники немного странные на поверхности земли. Каждый треугольник, который вы можете нарисовать на поверхности земли, имеет сумму углов строго на больше, чем 180°. На самом деле, вы можете нарисовать на Земле треугольник с тремя прямыми углами, дающими в сумме 270°.
На самом деле, вы можете нарисовать на Земле треугольник с тремя прямыми углами, дающими в сумме 270°.
На сфере, подобной Земле, сумма углов не постоянна среди всех треугольников. У больших треугольников сумма углов больше, а у меньших треугольников сумма углов меньше, но даже у крошечных треугольников сумма углов больше 180°.
Геометрия, которую вы изучаете в школе, называется Евклидова геометрия ; это геометрия плоской плоскости, плоского мира.Это довольно хорошее приближение для маленького кусочка Земли, который мы видим в любой момент времени, но это не единственная существующая геометрия!
Сделайте копию этих полосок бумаги и вырежьте их. Они имеют длину от 1 единицы до 6 единиц. Вы можете раскрасить полоски, написать на них цифры или сделать что-то, что позволит легко отслеживать разную длину.
Проблема 3
Повторите следующий процесс несколько раз (не менее 10) и следите за результатами (для вас запущена таблица).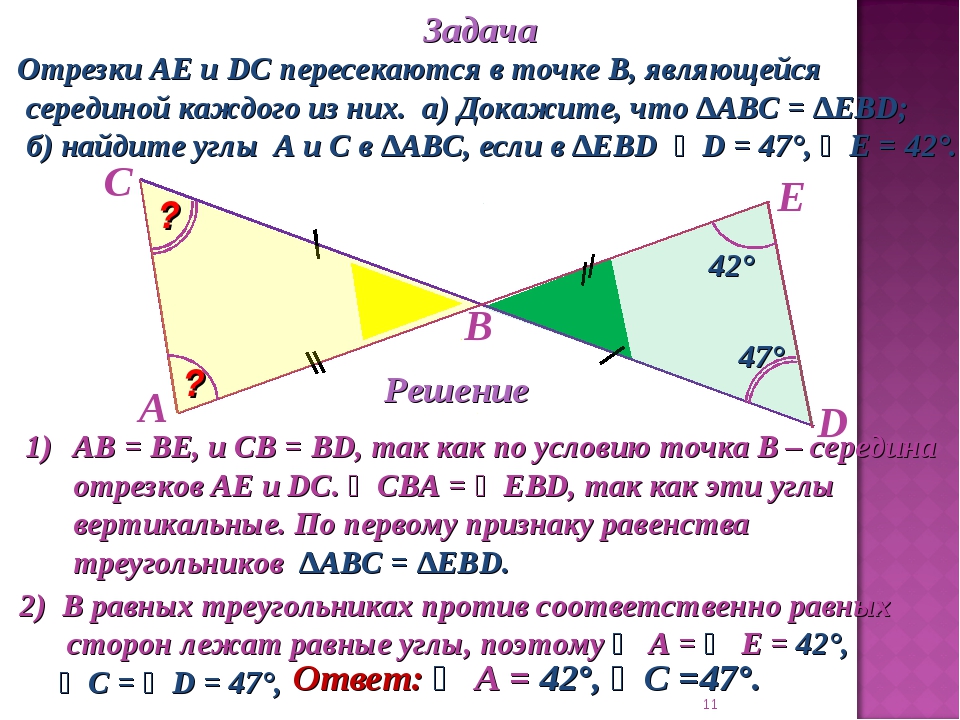
- Возьмите три полоски бумаги. (Длины не обязательно должны отличаться друг от друга, поэтому у вас есть несколько копий каждой длины.)
- Попробуйте сделать из этих трех полосок треугольник и решите, возможно это или нет. (Не накладывайте полоски друг на друга, не обрезайте и не сгибайте их. Длина полосок должна быть равна длине сторон треугольника.)
| Длина 1 | Длина 2 | Длина 3 | Треугольник? |
|---|---|---|---|
| 4 | 3 | 2 | да |
| 4 | 2 | 1 | нет |
| 4 | 2 | 2 | ?? |
Ваша цель — составить правило , описывающее, когда три длины образуют треугольник , а когда нет.Запишите правило своими словами.
Подумай / Пара / Поделись
Сравните свое правило с другими учениками. Затем используйте свое правило, чтобы ответить на следующие вопросы.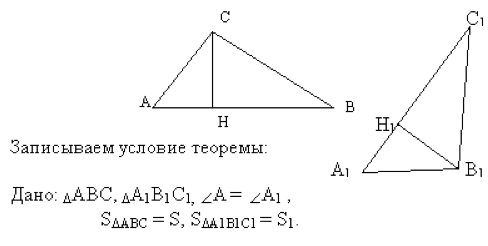 Имейте в виду, что цель состоит не в том, чтобы попытаться построить треугольник, а в том, чтобы предсказать результат на основе вашего правила.
Имейте в виду, что цель состоит не в том, чтобы попытаться построить треугольник, а в том, чтобы предсказать результат на основе вашего правила.
- Предположим, вас попросили построить треугольник со сторонами 40 единиц, 40 единиц и 100 единиц длины. Как вы думаете, вы могли бы это сделать? Поясните свой ответ.
- Предположим, вас попросили составить треугольник со сторонами 2.5 единиц, 2,6 единицы и 5 единиц в длину. Как вы думаете, вы могли бы это сделать? Поясните свой ответ.
Вероятно, вы придумали какую-то версию этого утверждения:
Теорема: неравенство треугольника
Сумма длин двух сторон треугольника больше длины третьей стороны.
Конечно, мы знаем, что в геометрии нельзя верить своим глазам. Вам нужно искать объяснение . Почему ваше утверждение имеет смысл?
Помните, что «геометрия — это искусство хороших рассуждений из плохих рисунков.«Наши материалы были не очень точными, так как же мы можем быть уверены, что это правило, которое мы придумали, верно?
Ну, в этом случае правило действительно то же самое, что и поговорка «Кратчайшее расстояние между двумя точками — прямая». Собственно, это именно то, что мы подразумеваем под словами прямая в геометрии.
Собственно, это именно то, что мы подразумеваем под словами прямая в геометрии.
Мы говорим, что два треугольника (или любые два геометрических объекта) конгруэнтны , если они имеют одинаковую форму и одинаковый размер. Это означает, что если бы вы могли взять одну из них и переместить ее, чтобы положить на другую, они точно перекрылись бы.
Проблема 4
Повторите следующий процесс несколько раз и отслеживайте результаты.
- Выберите три полоски бумаги, которые обязательно образуют треугольник.
- Попробуйте сделать два различных (неконгруэнтных) треугольника из одинаковых трех полосок бумаги. Запишите, смогли ли вы это сделать.
Проблема 5
Повторите следующий процесс несколько раз и отслеживайте результаты.
- Возьмите четыре полоски бумаги и сформируйте из них четырехугольник.(Если ваши четыре полоски не образуют четырехугольник, возьмите еще четыре полоски.
 )
) - Попробуйте составить два различных (неконгруэнтных) четырехугольника из одних и тех же четырех полосок бумаги. Запишите, смогли ли вы это сделать.
Подумай / Пара / Поделись
Что вы заметили в задачах 4 и 5? Можете ли вы сделать общее заявление, чтобы описать, что происходит? Можете ли вы объяснить, почему ваше утверждение имеет смысл?
Вероятно, вы придумали какую-то версию этого утверждения:
Теорема: SSS (сторона-сторона-сторона) Конгруэнтность
Если два треугольника имеют одинаковые длины сторон, то треугольники равны.
Это, безусловно, неверно для четырехугольников. Например, если выбрать четыре полоски одинаковой длины, получится квадрат:
Но вы также можете раздавить этот квадрат в неквадратном ромбе. (Попробуйте!)
Если вы не выберете четыре одинаковые длины, помимо «сжатия» формы, вы можете переставить стороны, чтобы получились разные (неконгруэнтные) формы.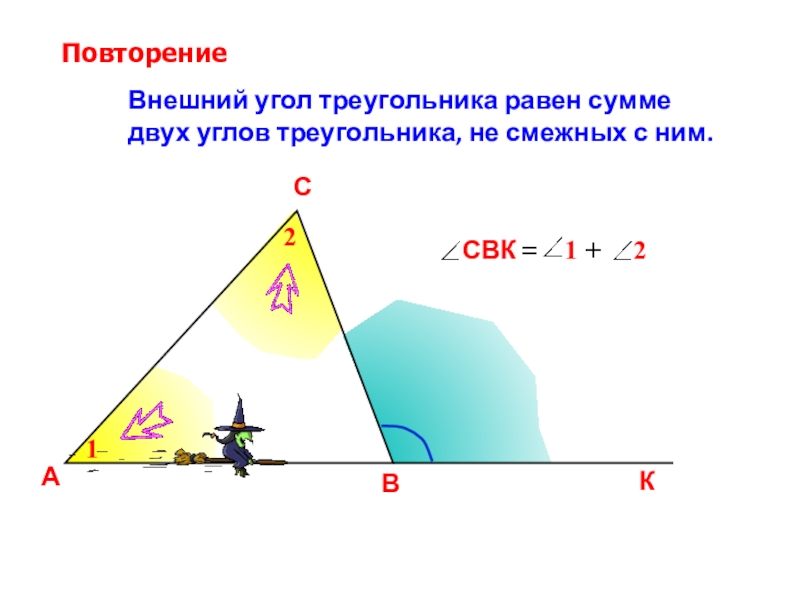 (Попробуйте!)
(Попробуйте!)
| Эти два четырехугольника имеют одинаковые длины четырех сторон в том же порядке. | |
|---|---|
Эти два четырехугольника имеют те же четыре длины сторон, что и два приведенных выше, , но стороны в другом порядке. | |
|---|---|
Но с треугольниками такого не может быть. Почему нет? Ну уж точно три стороны не переставишь. Это было бы то же самое, что вращать треугольник или переворачивать его, но не создавать новую форму.
Почему треугольники не могут «сжиматься», как четырехугольник (и другие фигуры)? Вот один из способов понять это.Представьте, что вы выбираете две из трех длин и кладете их друг на друга, закрепив их в одном углу.
Здесь показан более длинный фиолетовый пунктирный сегмент и более короткий зеленый сегмент. Два сегмента шарнирно соединены с красной точкой слева. |
Теперь представьте, что шарнир открывается понемногу.
Когда петля открывается, две нешарнирные конечные точки отдаляются все дальше и дальше друг от друга.Какой бы ни была ваша третья длина (при условии, что вы действительно можете сделать треугольник из ваших трех длин), есть ровно одно положение шарнира, где он точно подойдет, чтобы закрыть треугольник. Никакая другая позиция не подойдет.
конгруэнтных треугольников
Треугольники, которые имеют одинаковые размеры и форму, называются конгруэнтными треугольниками. Символ конгруэнтности ≅. Два треугольника равны, если три стороны и три угла одного треугольника имеют те же размеры, что и три стороны и три угла другого треугольника.Треугольники на рисунке 1 являются конгруэнтными треугольниками.
Рисунок 1 Конгруэнтные треугольники.
Части двух треугольников, имеющие одинаковые размеры (конгруэнтные), называются соответствующими частями.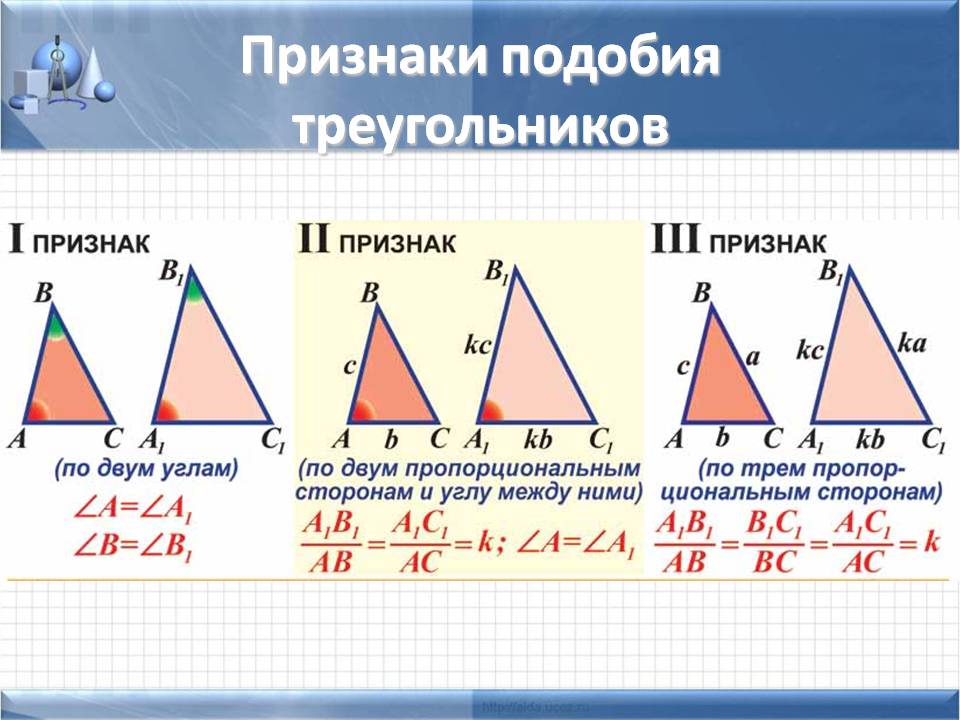 Это означает, что соответствующие части конгруэнтных треугольников конгруэнтны (CPCTC). Конгруэнтные треугольники называются путем перечисления их вершин в соответствующем порядке. На рисунке Δ BAT ≅ Δ ICE .
Это означает, что соответствующие части конгруэнтных треугольников конгруэнтны (CPCTC). Конгруэнтные треугольники называются путем перечисления их вершин в соответствующем порядке. На рисунке Δ BAT ≅ Δ ICE .
Эти части равны, потому что соответствующие части конгруэнтных треугольников конгруэнтны.
Чтобы показать, что два треугольника конгруэнтны, нет необходимости доказывать, что все шесть пар соответствующих частей равны. Следующие постулаты и теоремы являются наиболее распространенными методами доказательства конгруэнтности (или равенства) треугольников.
Постулат 13 (постулат SSS): Если каждая сторона одного треугольника конгруэнтна соответствующей стороне другого треугольника, то треугольники конгруэнтны (рис. 2).
Рисунок 2 Соответствующие стороны (SSS) двух треугольников конгруэнтны.
Постулат 14 (постулат SAS): Если две стороны и угол между ними в одном треугольнике конгруэнтны соответствующим частям в другом треугольнике, то эти треугольники конгруэнтны (рис. 3).
3).
Рисунок 3 Две стороны и угол между ними (SAS) одного треугольника равны
соответствующих частей другого треугольника.
Постулат 15 (Постулат АСА): Если два угла и сторона между ними в одном треугольнике конгруэнтны соответствующим частям в другом треугольнике, то такие треугольники конгруэнтны (рис. 4).
Рисунок 4 Два угла и их общая сторона (ASA) в одном треугольнике равны
соответствующих частей другого треугольника.
Теорема 28 (Теорема ААС): Если два угла и сторона, не заключенная между ними в одном треугольнике, конгруэнтны соответствующим сторонам в другом треугольнике, то такие треугольники конгруэнтны (рис. 5).
Рисунок 5 Два угла и сторона, противолежащая одному из этих углов (ААС) в одном треугольнике
равны соответствующим частям другого треугольника.
Постулат 16 (постулат HL): Если гипотенуза и катет одного прямоугольного треугольника конгруэнтны соответствующим частям другого прямоугольного треугольника, то эти треугольники конгруэнтны (рис. 6).
Рисунок 6 Гипотенуза и катет (HL) первого прямоугольного треугольника равны
соответствующих частей второго прямоугольного треугольника.
Теорема 29 (Теорема HA): Если гипотенуза и острый угол одного прямоугольного треугольника конгруэнтны соответствующим частям другого прямоугольного треугольника, то эти треугольники конгруэнтны (рис. 7).
Рисунок 7 Гипотенуза и острый угол (HA) первого прямоугольного треугольника равны
к соответствующим частям второго прямоугольного треугольника.
Теорема 30 (Теорема LL): Если катеты одного прямоугольного треугольника конгруэнтны соответствующим частям другого прямоугольного треугольника, то эти треугольники конгруэнтны (рис.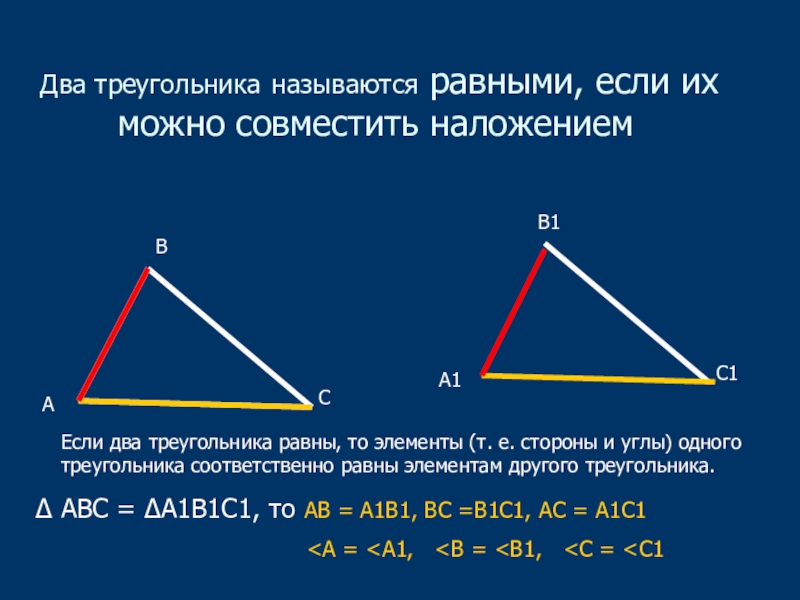 8).
8).
Рисунок 8 Катеты (LL) первого прямоугольного треугольника конгруэнтны соответствующим частям
второго прямоугольного треугольника.
Теорема 31 (теорема LA): Если один катет и острый угол одного прямоугольного треугольника равны соответствующим частям другого прямоугольного треугольника, то такие треугольники равны (рис. 9).
Рисунок 9 Один катет и острый угол (LA) первого прямоугольного треугольника равны
соответствующих частей второго прямоугольного треугольника.
Пример 2: Основываясь на маркировке на рисунке 10, завершите оператор сравнения Δ ABC ≅Δ .
Рисунок 10 Конгруэнтные треугольники.
Δ YXZ , поскольку A соответствует Y, B соответствует X , а C соответствует Z .
Пример 3: Каким методом будет доказана конгруэнтность каждого из треугольников на рисунках с 11 (а) по 11 (i)?
Рисунок 11 Методы доказательства конгруэнтности пар треугольников.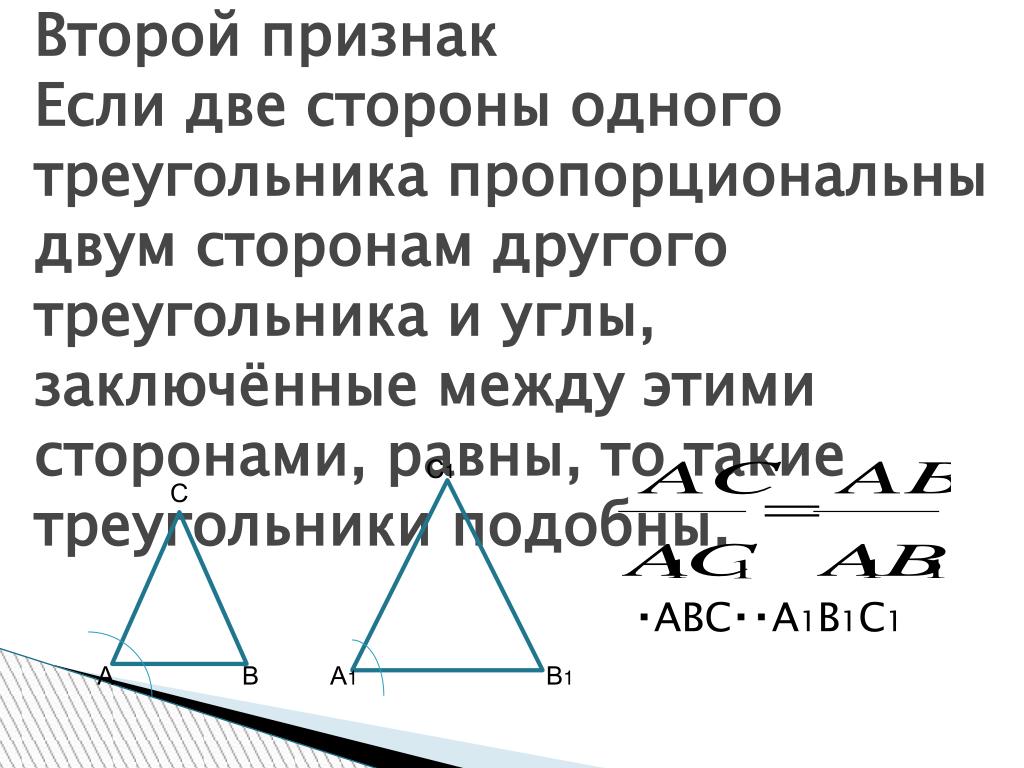
- (б) Нет. Метода AAA не существует.
- (е) ССС. Третья пара конгруэнтных сторон — это сторона, общая для двух треугольников.
- (i) Нет. Метода SSA не существует.
Пример 4: Назовите дополнительные равные соответствующие части, необходимые для доказательства конгруэнтности треугольников на рисунках с 12 (a) по 12 (f) согласно указанному постулату или теореме.
Рисунок 12 Дополнительная информация, необходимая для доказательства конгруэнтности пар треугольников.
- (a) BC = EF или AB = DE (, но не AC = DF , потому что эти две стороны лежат между равными углами).
- (e) м ∠ T = м ∠ E и м ∠TOW = m ∠ EON.
- (f) IX = EN или SX = TN (но не IS = ET , поскольку они являются гипотенузами).

Подобные треугольники — формулы, свойства, теоремы, доказательства
Подобные треугольники — это треугольники, у которых соответствующие стороны пропорциональны друг другу, а соответствующие углы равны друг другу. Подобные треугольники выглядят одинаково, но размеры могут быть разными. В общем, подобные треугольники отличаются от конгруэнтных треугольников. Существуют различные методы, с помощью которых мы можем определить, подобны два треугольника или нет. Давайте узнаем больше о подобных треугольниках и их свойствах вместе с несколькими решенными примерами.
Что такое подобные треугольники?
Подобные треугольники — это треугольники, которые выглядят похожими друг на друга, но их размеры могут не совпадать. Два объекта можно назвать похожими, если они имеют одинаковую форму, но могут различаться по размеру. Это означает, что похожие формы при увеличении или уменьшении накладываются друг на друга. Это свойство подобных фигур называется «сходством».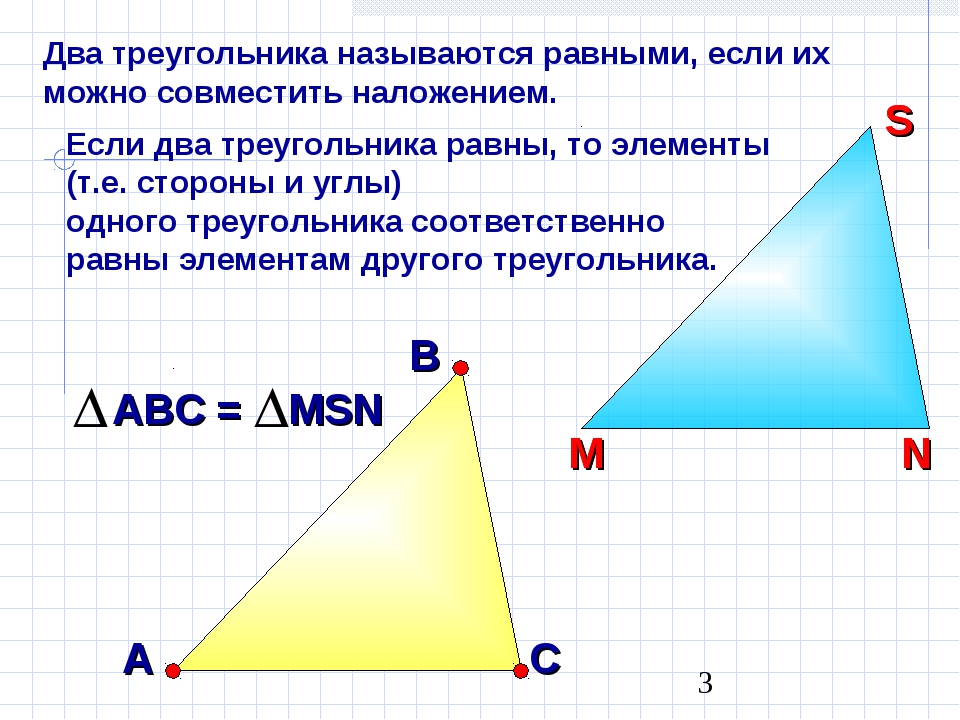
Определение подобных треугольников
Два треугольника будут подобны, если углы равны (соответствующие углы) и стороны находятся в одинаковом отношении или пропорции (соответствующие стороны).Подобные треугольники могут иметь разные индивидуальные длины сторон треугольников, но их углы должны быть равны, и их соответствующее отношение длин сторон должно быть одинаковым. Если два треугольника подобны, значит,
- Все соответствующие пары углов треугольников равны.
- Все соответствующие стороны треугольников пропорциональны.
Мы используем символ «∼» для обозначения сходства. Итак, если два треугольника подобны, мы показываем это как △QPR ∼ △XYZ
.Примеры подобных треугольников
Подобные треугольники — это треугольники, у которых соответствующие пары углов равны.Это означает, что равноугольные треугольники подобны. Следовательно, все равносторонние треугольники являются примерами подобных треугольников. На следующем изображении показаны похожие треугольники, но мы должны заметить, что их размеры различаются.
Формулы подобных треугольников
В предыдущем разделе мы видели, что есть два условия, с помощью которых мы можем проверить, подобны ли данный набор треугольников или нет. Эти условия гласят, что два треугольника можно назвать подобными, если их соответствующие углы равны или конгруэнтны, или если их соответствующие стороны пропорциональны.Следовательно, два треугольника △ABC и △EFG могут быть доказаны подобными (△ABC ∼ △EFG), используя любое условие из следующего набора формул подобных треугольников,
Формула для подобных треугольников в геометрии:
- ∠A = ∠E, ∠B = ∠F и ∠C = ∠G
- AB/EF = BC/FG = AC/EG
Теоремы о подобных треугольниках
Мы можем узнать или доказать, подобны ли два треугольника, используя теоремы подобия. Мы используем эти критерии подобия, когда у нас нет меры всех сторон треугольника или меры всех углов треугольника.Эти теоремы о подобных треугольниках помогают нам быстро выяснить, подобны два треугольника или нет. Существует три основных типа правил подобия, как указано ниже:
Существует три основных типа правил подобия, как указано ниже:
- AA (или AAA) или теорема подобия углов
- SAS или теорема о сходстве стороны-угла-стороны
- SSS или теорема о сходстве сторон
Давайте разберемся в этих теоремах о подобных треугольниках и их доказательствах.
AA (или AAA) или Критерий сходства углов
Критерий подобия AA утверждает, что если любые два угла в треугольнике соответственно равны любым двум углам другого треугольника, то они должны быть подобными треугольниками.Правило подобия AA легко применить, когда мы знаем только меру углов и не имеем никакого представления о длине сторон треугольника. На изображении, приведенном ниже, если известно, что ∠B = ∠G и ∠C = ∠F.
И мы можем сказать, что по критерию сходства АА △ABC и △EGF подобны или △ABC ∼ △EGF.
⇒AB/EG = BC/GF = AC/EF и ∠A = ∠E.
Нажмите здесь, чтобы подробно ознакомиться с критерием подобия AA — критерий сходства AA
SAS или Критерий сходства стороны-угла-стороны
Согласно теореме подобия SAS, если любые две стороны первого треугольника находятся в точной пропорции к двум сторонам второго треугольника, а угол, образованный этими двумя сторонами отдельных треугольников, равен, то они должны быть подобными треугольниками.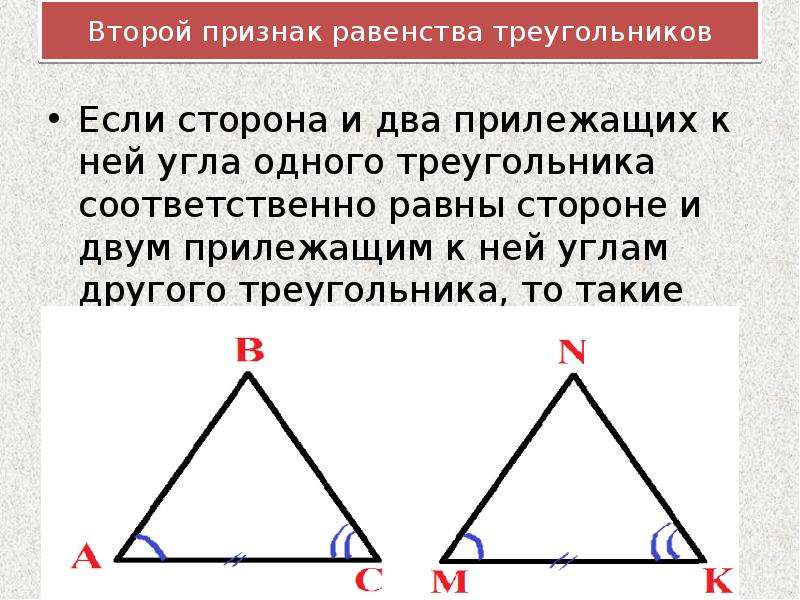 .Это правило обычно применяется, когда мы знаем только меру двух сторон и угол, образованный между этими двумя сторонами в обоих треугольниках соответственно.
.Это правило обычно применяется, когда мы знаем только меру двух сторон и угол, образованный между этими двумя сторонами в обоих треугольниках соответственно.
На изображении ниже, если известно, что AB/DE = AC/DF и ∠A = ∠D
И мы можем сказать, что по критерию подобия SAS △ABC и △DEF подобны или △ABC ∼ △DEF.
SSS или Критерий сходства между сторонами
Согласно теореме подобия SSS, два треугольника будут подобны друг другу, если соответствующие отношения всех сторон двух треугольников равны.Этот критерий обычно используется, когда у нас есть только мера сторон треугольника и меньше информации об углах треугольника.
На изображении ниже, если известно, что PQ/ED = PR/EF = QR/DF
И мы можем сказать, что по критерию подобия SSS △PQR и △EDF подобны или △PQR ∼ △EDF.
Свойства подобных треугольников
Если два треугольника подобны или доказаны подобными по любому из вышеприведенных критериев, то они обладают немногими свойствами подобных треугольников. Свойства подобных треугольников приведены ниже,
Свойства подобных треугольников приведены ниже,
- Подобные треугольники имеют одинаковую форму, но разные размеры.
- В подобных треугольниках соответствующие углы равны.
- Соответствующие стороны подобных треугольников находятся в одинаковом отношении.
- Отношение площадей подобных треугольников равно отношению квадратов любой пары их соответствующих сторон.
Как найти подобные треугольники?
Два заданных треугольника могут быть доказаны как подобные треугольники, используя приведенные выше теоремы.Мы можем выполнить шаги, указанные ниже, чтобы проверить, подобны ли данные треугольники,
- Шаг 1: Запишите заданные размеры треугольников (соответствующие стороны или соответствующие углы).
- Шаг 2: Проверьте, соответствуют ли эти размеры условиям теорем о подобных треугольниках (AA, SSS, SAS).
- Шаг 3: Данные треугольники, если они удовлетворяют любой из теорем подобия, могут быть представлены с использованием «∼» для обозначения подобия.

Давайте лучше разберем эти шаги на примере.
Пример: Проверьте, являются ли △ABC и △PQR подобными треугольниками или нет, используя данные: ∠A = 65°, ∠B = 70º и ∠P = 70°, ∠R = 45°.
Решение:
Используя данное измерение углов, мы не можем сделать вывод, соответствуют ли данные треугольники критерию подобия AA или нет. Найдем меру третьего угла и оценим.
Мы знаем, используя свойство суммы углов треугольника, ∠C в △ABC = 180° — (∠A + ∠B) = 180° — 135° = 45°
Точно так же ∠Q в △PQR = 180° — (∠P + ∠R) = 180° — 115° = 65°
Следовательно, мы можем заключить, что в △ABC и △PQR ∠A = ∠Q, ∠B = ∠P и ∠C = R
⇒ △ABC ∼ △QPR
Разница между подобными треугольниками и конгруэнтными треугольниками
Подобие и конгруэнтность — два разных свойства треугольников.Следующая таблица помогает отличить подобные треугольники от конгруэнтных треугольников:
| Подобные треугольники | Конгруэнтные треугольники |
Подобные треугольники имеют одинаковую форму, но могут быть разными по размеру. Они накладываются друг на друга при увеличении или уменьшении. Они накладываются друг на друга при увеличении или уменьшении. | Конгруэнтные треугольники одинаковы по форме и размеру. Они накладываются друг на друга в своей первоначальной форме. |
| Они представлены с помощью символа «~». Например, подобные треугольники ABC и XYZ будут представлены как △ABC ∼ △XYZ | .Они представлены с помощью символа « ≅». Например, конгруэнтные треугольники ABC и XYZ будут представлены как △ABC ≅ △QPR |
| Отношение всех соответствующих сторон равно в подобных треугольниках. Это общее отношение также называется «масштабным коэффициентом» в подобных треугольниках. | Отношение соответствующих сторон равно 1 для конгруэнтных треугольников. |
☛ Темы, относящиеся к подобным треугольникам:
Важные примечания о подобных треугольниках:
- Отношение площадей подобных треугольников равно квадрату отношения их соответствующих сторон.

- Все конгруэнтные треугольники подобны, но не все подобные треугольники обязательно могут быть конгруэнтны.
- Подобные треугольники обозначаются символом «~».
Часто задаваемые вопросы о подобных треугольниках
Что понимают под подобными треугольниками в геометрии?
Подобные треугольники в геометрии — это треугольники, имеющие одинаковую форму, но не равные по размеру. Все равносторонние треугольники являются примерами подобных треугольников.
Какой символ используется для подобных треугольников?
Подобные треугольники можно выразить с помощью символа «~».Этот символ означает, что данные две фигуры имеют одинаковую форму, но не обязательно одинаковый размер.
Что такое формула подобных треугольников?
Формула, используемая для проверки того, подобны ли два треугольника или нет, зависит от условия подобия. Для двух треугольников △PQR и △XYZ сходство можно доказать с помощью любого из следующих условий:
- ∠P = ∠X, ∠Q = ∠Y и ∠R = ∠Z
- PQ/XY = QR/YZ = PR/XZ
Каковы 3 теоремы о подобных треугольниках?
Три теоремы подобия, используемые для проверки подобия треугольников, приведены ниже:
- AA (или AAA) или теорема подобия углов
- SAS или теорема о сходстве стороны-угла-стороны
- SSS или теорема о сходстве сторон
Каковы свойства подобных треугольников?
Важные свойства двух подобных треугольников можно представить как.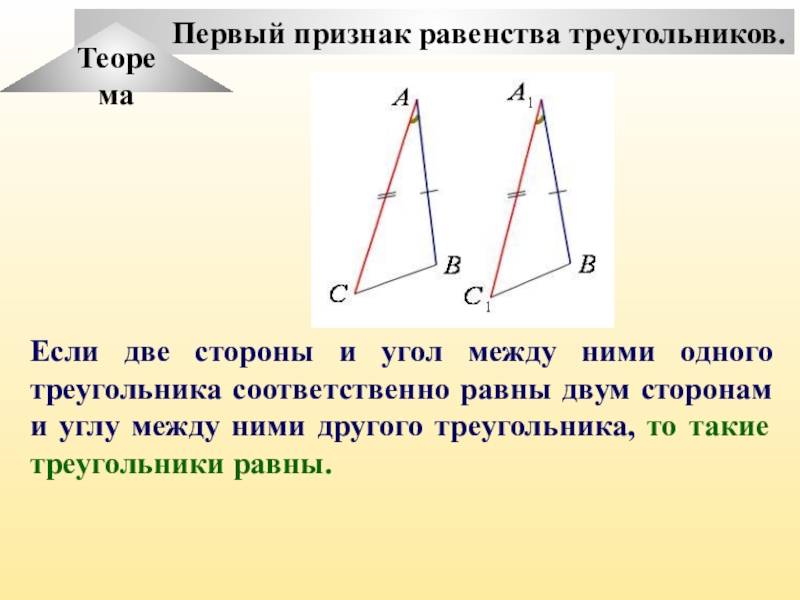
- Форма двух одинаковых треугольников одинакова, но их размеры могут быть разными.
- В подобных треугольниках соответствующие углы равны.
- В подобных треугольниках соответствующие стороны находятся в одинаковом отношении.
Каковы правила для подобных треугольников?
Правила или условия, используемые для проверки того, подобны ли данный набор треугольников или нет, как указано,
- Все пары соответствующих углов треугольников должны быть одинаковыми.
- Все соответствующие стороны треугольников находятся в одной пропорции.
Как узнать, подобны ли два треугольника?
Два треугольника подобны, если их соответствующие углы равны и их соответствующие стороны находятся в одном и том же отношении. Подобные треугольники — это треугольники, которые выглядят одинаково, но могут быть разными по размеру.
Как найти долю подобных треугольников?
Для подобных треугольников пары соответствующих сторон пропорциональны. Это отношение / пропорциональность соответствующих сторон можно использовать для нахождения длины недостающей стороны фигуры, учитывая аналогичную фигуру, для которой известны соответствующие измерения.
Это отношение / пропорциональность соответствующих сторон можно использовать для нахождения длины недостающей стороны фигуры, учитывая аналогичную фигуру, для которой известны соответствующие измерения.
Как найти недостающие стороны подобных треугольников?
Недостающие стороны подобного треугольника можно узнать, сравнив отношения последовательных соответствующих сторон треугольника. Сравниваем отношения и находим длину неизвестной стороны треугольника.
Могут ли два треугольника быть подобными и конгруэнтными?
Все конгруэнтные треугольники также являются подобными треугольниками, но не все подобные треугольники являются конгруэнтными треугольниками.Таким образом, два подобных треугольника могут быть равны, но не всегда. Чтобы два подобных треугольника были равны, они должны иметь одинаковый размер, одинаковую форму и одинаковую меру соответствующих углов.
Какой тип треугольников всегда похож?
Равносторонние треугольники всегда подобны. Любые два равносторонних треугольника всегда подобны независимо от длины сторон равностороннего треугольника. Два равнобедренных прямоугольных треугольника также всегда подобны.
Любые два равносторонних треугольника всегда подобны независимо от длины сторон равностороннего треугольника. Два равнобедренных прямоугольных треугольника также всегда подобны.
Могут ли быть подобны два равнобедренных треугольника?
Два равнобедренных треугольника могут быть подобны тогда и только тогда, когда их соответствующие углы равны и их соответствующие стороны находятся в одном и том же отношении.Следовательно, не всегда верно, что равнобедренные треугольники подобны.
Как ввести подобные треугольники?
Подобные треугольники могут быть представлены как треугольники, имеющие одинаковую форму, но не обязательно одинаковый размер. Подобные треугольники — это треугольники, которые выглядят одинаково, но могут быть разными по размеру.
Как найти отношение площадей двух подобных треугольников?
Если два треугольника подобны, то отношение площадей обоих треугольников пропорционально квадрату отношения их соответствующих сторон. Если два подобных треугольника имеют две соответствующие длины сторон, равные a и b, то отношение их площадей равно a2:b2.
Если два подобных треугольника имеют две соответствующие длины сторон, равные a и b, то отношение их площадей равно a2:b2.
Что нужно знать о конгруэнтных фигурах в геометрии
В геометрии конгруэнтные фигуры имеют одинаковый размер и форму. Это означает, что стороны и сегменты или две фигуры имеют одинаковую длину. И углы имеют одинаковые измерения. При работе с треугольниками существуют постулаты и теоремы, которые можно использовать для доказательства конгруэнтности фигур. Вот те, которые вы должны знать.
Постулат ASA
Постулат ASA утверждает, что когда два треугольника имеют два равных угла и когда сторона между этими углами также имеет одинаковую длину, два треугольника имеют конгруэнтную форму. Например, посмотрите на эти два треугольника:
Здесь у нас есть два равных острых угла, обозначенных буквой А. Есть также два равных тупых угла, обозначенных буквой В. Стороны между углами А и В отмечены двумя черточками, показывающими, что эти стороны также равны. Следовательно, мы знаем, что эти треугольники следуют постулату АСА. Следовательно, они конгруэнтны.
Следовательно, мы знаем, что эти треугольники следуют постулату АСА. Следовательно, они конгруэнтны.
Постулат SAS
Для постулата SAS два треугольника должны иметь две одинаковые стороны и одинаковый угол. Одинаковый угол должен располагаться между одинаковыми сторонами. Давайте посмотрим на следующий пример:
В этом примере треугольники перечислили измерения для сравнения. Длинная сторона каждого треугольника имеет размер 5, а более короткая сторона имеет размер 3 в обоих треугольниках.Угол между этими сторонами равен 45 градусов. Из-за этого мы можем предположить, что треугольник следует постулату SAS.
Постулат SSS
Постулат SSS просто утверждает, что все стороны двух треугольников равны. Итак, если вы можете измерить каждую сторону треугольника и в итоге получить три равные соответствующие стороны, вы знаете, что два треугольника конгруэнтны. Посмотрите на следующий пример и обратите внимание на то, что все три стороны имеют одинаковую длину:
С измерениями трех сторон в первом треугольнике, соответствующими измерениям второго треугольника, мы можем использовать постулат SSS, чтобы определить, что треугольники равны.
Теорема AAS
С помощью теоремы AAS вы можете доказать, что два треугольника равны, проверив измерение двух углов. Если два угла в каждом треугольнике равны, и сторона, которая не лежит между этими углами, также равна, то треугольники равны.
В следующем примере тупые углы в каждом треугольнике имеют одинаковую величину 110 градусов. Один из острых углов имеет размер 30 градусов. И есть сторона, которая не находится между этими углами с измерением 8.Поскольку эти измерения одинаковы для обоих треугольников, мы можем использовать теорему AAS, чтобы сказать, что эти треугольники конгруэнтны.
Теорема о катете гипотенузы
Теорема о катете гипотенузы работает только для прямоугольных треугольников. Если у вас два прямоугольных треугольника, то проверьте измерение гипотенузы и одного из катетов. Если эти длины одинаковы в каждом треугольнике, то эти два треугольника конгруэнтны. Помните, что гипотенуза является наибольшей стороной и расположена напротив прямого угла. Стороны, соприкасающиеся с прямым углом, называются катетами. Выберите одну из этих сторон при оценке треугольников.
Стороны, соприкасающиеся с прямым углом, называются катетами. Выберите одну из этих сторон при оценке треугольников.
Например, в следующем примере у нас есть два прямоугольных треугольника. Следовательно, вы можете посмотреть длины сторон гипотенузы (20) и одного из катетов (16). Поскольку эти длины одинаковы в обоих треугольниках, с помощью теоремы о гипотенузе-ноге можно сделать вывод, что треугольники конгруэнтны.
Хотя два треугольника могут показаться конгруэнтными фигурами, важно использовать один из этих постулатов или теорем, чтобы убедиться, что они действительно конгруэнтны.Когда у вас есть некоторые измерения углов и длин сторон, подтверждающие вашу теорию, вы действительно можете определить, конгруэнтны треугольники или нет.
Джейми окончила Университет имени Бригама Янга в Айдахо по специальности «Английское образование». Она провела несколько лет, обучая и репетиторству студентов в начальной, средней школе и колледже. В настоящее время она работает составителем контрактов и разработчиком учебных программ для курсов онлайн-обучения.
 В свободное время она любит бегать и проводить время со своими мальчиками!
В свободное время она любит бегать и проводить время со своими мальчиками!Посмотреть все сообщения
Подобные треугольники — математический способ
В евклидовой геометрии два объекта подобны, если они имеют одинаковую форму, независимо от их размера.
Два треугольника подобны тогда и только тогда, когда их углы конгруэнтны (равны) и их соответствующие стороны пропорциональны (гомологичны). Другими словами, два треугольника подобны, если разница только в размере.
Гомологичные стороны – это противоположные стороны, находящиеся под равными углами.
Здесь мы имеем пример, где гомологичные элементы (углы и стороны) видны при равенстве или конгруэнтности их углов и пропорциональности их сторон:
В подобных треугольниках выполняются следующие условия:
Чтобы определить, подобны ли два треугольника, не обязательно знать их три угла и три стороны.Помните, что мы знаем, подобны ли два треугольника, когда их соответствующие углы конгруэнтны, а их соответствующие стороны пропорциональны.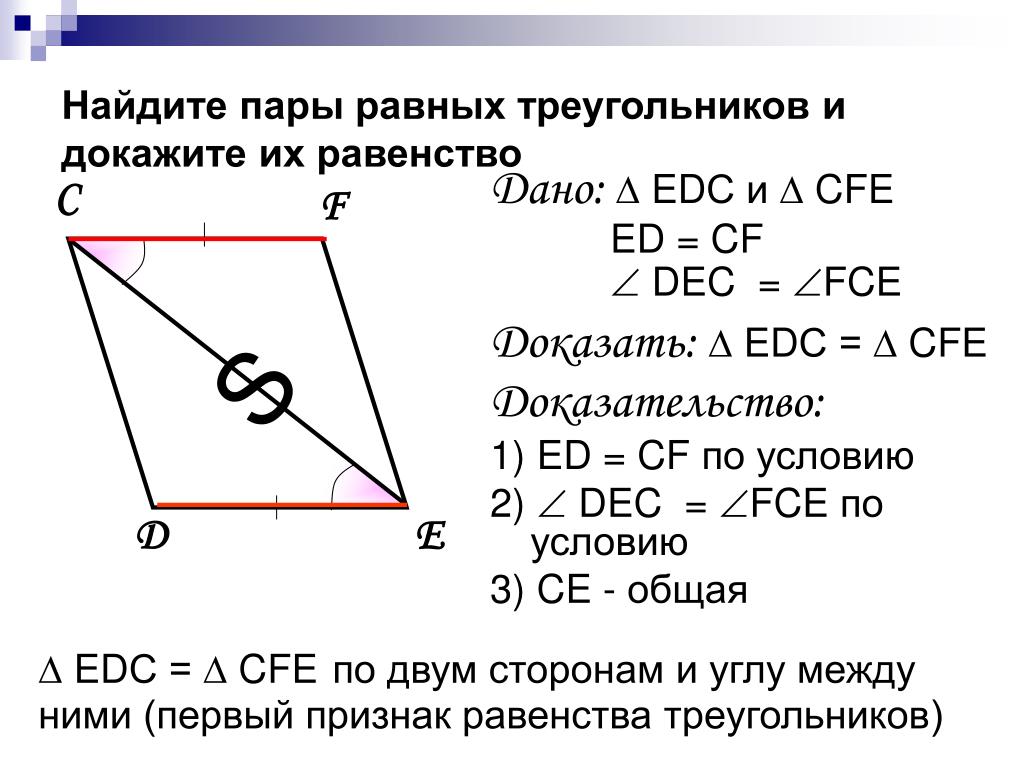 Есть три утверждения или теоремы, каждая из которых необходима и достаточна для того, чтобы два треугольника были подобны:
Есть три утверждения или теоремы, каждая из которых необходима и достаточна для того, чтобы два треугольника были подобны:
Теоремы подобия треугольников
- АА Теорема . Треугольники имеют два равных угла. Третий угол также будет потому, что они должны добавить 180 °.
Если α = α’ и β = β’, то ABC и A’B’C’ подобны.
Критерий равных углов:
- Гомологичные стороны представляют собой параллельные линии (см. рисунок выше).
- Три стороны треугольника перпендикулярны гомологичным сторонам другого треугольника.
- SAS Теорема . Два треугольника имеют две пропорциональные стороны и угол между ними равен.
Тогда:
Следовательно, ABC и A’B’C’ равны.
- SSS Теорема .У двух треугольников три стороны пропорциональны.
Тогда:
Таким образом, ABC и A’B’C’подобны.
Треугольники в позиции Фалеса
Два треугольника находятся в положении Фалеса , если они имеют общий угол и противоположные стороны параллельны. Как и в случае с остальными многоугольниками, если два треугольника можно разместить в положении Фалеса, то они подобны.
Как и в случае с остальными многоугольниками, если два треугольника можно разместить в положении Фалеса, то они подобны.
Это утверждение устанавливает теорему о перехвате (также называемую теоремой Фалеса).Итак, теорему о пересечении можно использовать для доказательства свойств подобных треугольников.
Тогда верно, что:
Упражнение 1
Даны два треугольника со всеми мерами сторон, определить, подобны ли эти треугольники или нет.
Длины сторон первого треугольника: 7,6 см, 4,18 см и 6,65 см.
Длины сторон второго треугольника: 4 см, 2,2 см и 3,5 см.
РЕШЕНИЕ:
Поскольку мы знаем длины сторон треугольника, мы можем применить теорему подобия сторона-сторона-сторона (SSS) :
Затем мы можем определить масштабный коэффициент и выяснить, пропорциональны ли все стороны.
Как мы видим, соотношение между соответствующими сторонами двух треугольников одинаково (коэффициент подобия или масштабный коэффициент = 1,9). Итак, два треугольника подобны .
Итак, два треугольника подобны .
Упражнение 2
Имеем два треугольника: в большем две стороны 10 см и 5,5 см сходятся под углом γ 70°, а у меньшего три стороны 4 см, 2,2 см и 3,5 см. Определите, подобны ли эти треугольников .
РЕШЕНИЕ:
В этом случае три известных данных каждого треугольника не соответствуют одному и тому же критерию из трех представленных выше.Чтобы найти неизвестную сторону c в большем треугольнике, мы прибегаем к процедуре, изложенной в решении треугольников, в разделе «знание двух сторон и угла, который они образуют», в котором мы должны применить закон косинусов.
Применение теоремы косинусов:
Сторона c 9,64 см.
Поскольку мы уже знаем длину трех сторон каждого треугольника, мы можем вычислить отношение между каждой парой гомологичных сторон.
Мы используем теорему SSS,
И потом, проверяем, что коэффициенты не все одинаковые. Соотношения 2,5, 2,5 и 2,75. Следовательно, эти два треугольника не подобны .
Соотношения 2,5, 2,5 и 2,75. Следовательно, эти два треугольника не подобны .
Как найти площадь равностороннего треугольника
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как
в виде
ChillingEffects. org.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
Гиперболическая геометрия — треугольники, углы и площади
Модель полуплоскости Пуанкаре является конформной, что означает, что гиперболические углы в модели полуплоскости Пуанкаре точно такие же, как евклидовы углы, причем углы между двумя пересекающимися окружностями представляют собой угол между их касательными линиями в точке пересечения.
 .Гиперболический треугольник — это всего лишь три точки, соединенные (гиперболическими) отрезками. Несмотря на все эти сходства, гиперболические треугольники сильно отличаются от евклидовых треугольников.
.Гиперболический треугольник — это всего лишь три точки, соединенные (гиперболическими) отрезками. Несмотря на все эти сходства, гиперболические треугольники сильно отличаются от евклидовых треугольников.Поскольку отрезки гиперболической линии (обычно) искривлены, сумма углов гиперболического треугольника строго меньше 180 градусов. Поскольку четырехугольник всегда можно разрезать на два треугольника, сумма углов четырехугольника должна быть меньше 360 градусов, поэтому в гиперболической геометрии нет квадратов, что затрудняет определение площади в квадратных единицах.Однако оказывается, что существует единственная функция (с точностью до умножения на масштабный коэффициент), удовлетворяющая обычным аксиомам площади:
- Площадь неотрицательна.
- Если вы разрежете фигуру на конечное число частей и переставите их, чтобы сформировать вторую фигуру, то две фигуры должны иметь одинаковую площадь.
Для треугольника эта функция дефект , определенная как
, где углы альфа, бета и гамма измеряются в радианах.
В дополнение к меньшей сумме углов между гиперболическими треугольниками и евклидовыми треугольниками есть еще два существенных отличия:
- Хотя стороны гиперболических треугольников могут быть сколь угодно большими, площадь любого треугольника меньше числа пи.
- Не существует понятия подобных треугольников — если два треугольника имеют одинаковые углы, то они конгруэнтны. (В модели они могут выглядеть по-разному, поскольку длины кажутся разными в зависимости от того, насколько они близки к краю, и это касается и площади.)
Апплет
Чтобы помочь вам познакомиться с гиперболическими треугольниками, я подготовил апплет, который позволит вам поэкспериментировать с ними. Для запуска апплета вам потребуется браузер с поддержкой Java (Netscape 3.0 или более поздней версии или Internet Explorer 3.0 или более поздней версии в Windows 95 или Mac). Прочитав следующие инструкции, щелкните ссылку ниже, чтобы запустить апплет в новом окне. Если разрешение вашего монитора 640×480, вы, вероятно, захотите развернуть окно. Если разрешение вашего монитора 800×600 или больше, вы должны видеть все так, как оно выглядит само по себе.
Если разрешение вашего монитора 800×600 или больше, вы должны видеть все так, как оно выглядит само по себе.В апплете у вас будет красная точка, синяя точка и черная точка. Точки соединяются (гиперболическими) отрезками, образуя треугольник. Углы треугольника указаны ниже края полуплоскости. Они имеют цветовую кодировку, поэтому угол в красной точке указан красным цветом и т. д. Под этими углами находится сумма трех углов и площадь треугольника. Щелкните мышью точку и перетащите ее (удерживая кнопку мыши нажатой), чтобы переместить точку. Треугольник будет следовать за точкой, как и в других апплетах.( Предупреждение об ошибке: Иногда, когда окно закрыто, а затем открыто другими окнами на мониторе компьютера, апплет не перерисовывается полностью. Если щелкнуть точку и переместить ее, или если свернуть, а затем восстановить окно , апплет снова правильно перерисует себя.)
Что попробовать
- Переместите точки, чтобы проверить, как ведут себя суммы углов.
 Обратите внимание, что чем меньше треугольник, тем ближе сумма углов к 180 градусам.
Обратите внимание, что чем меньше треугольник, тем ближе сумма углов к 180 градусам. - Какую самую большую область вы можете создать в этом апплете? Поскольку точки показаны с шириной и высотой, поэтому вы можете щелкнуть по ним мышью, вы не можете раздвинуть их до бесконечности, но вы можете развести их достаточно далеко друг от друга, чтобы получить площадь более 3. Куда вы перемещаете точки получить наибольшую площадь?
- Какую наименьшую сумму углов можно составить в этой модели. Как и выше, вы не сможете достичь теоретического минимума, но вы можете приблизиться к нему.
Щелкните здесь, чтобы запустить апплет. (Откроется новое окно.)
.
 В треугольнике АРС : АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК : ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК : ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,
В треугольнике АРС : АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК : ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК : ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,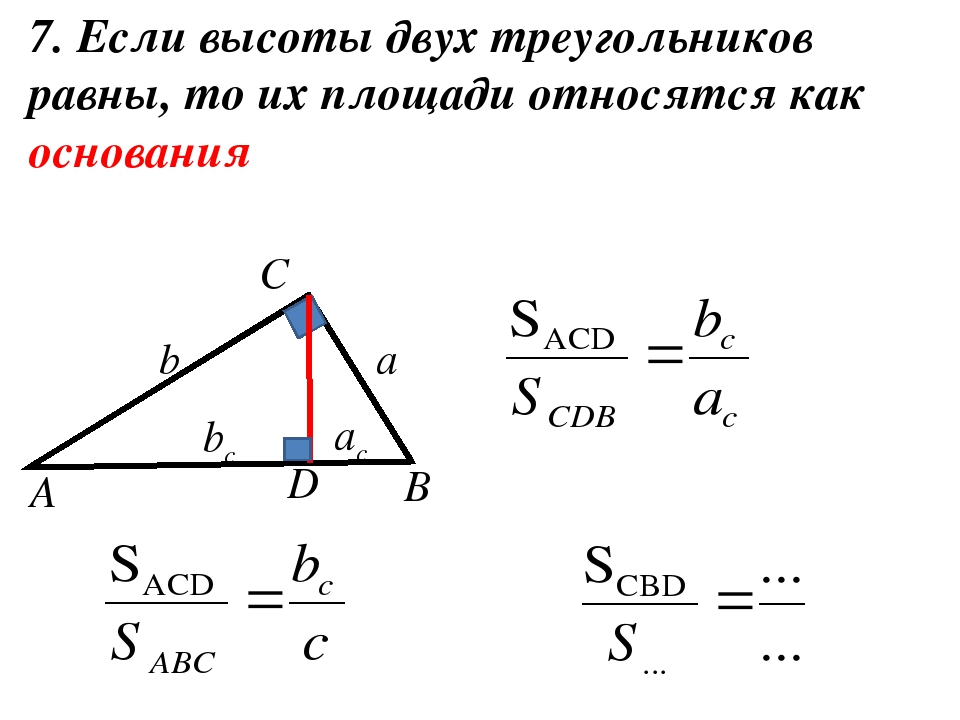 С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003).
С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003).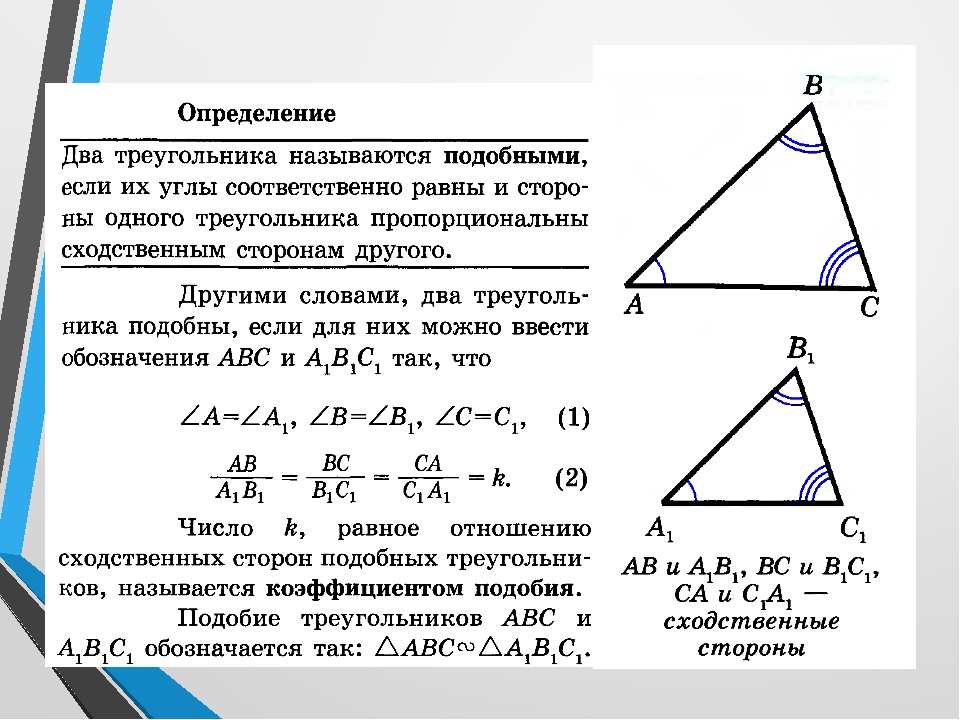

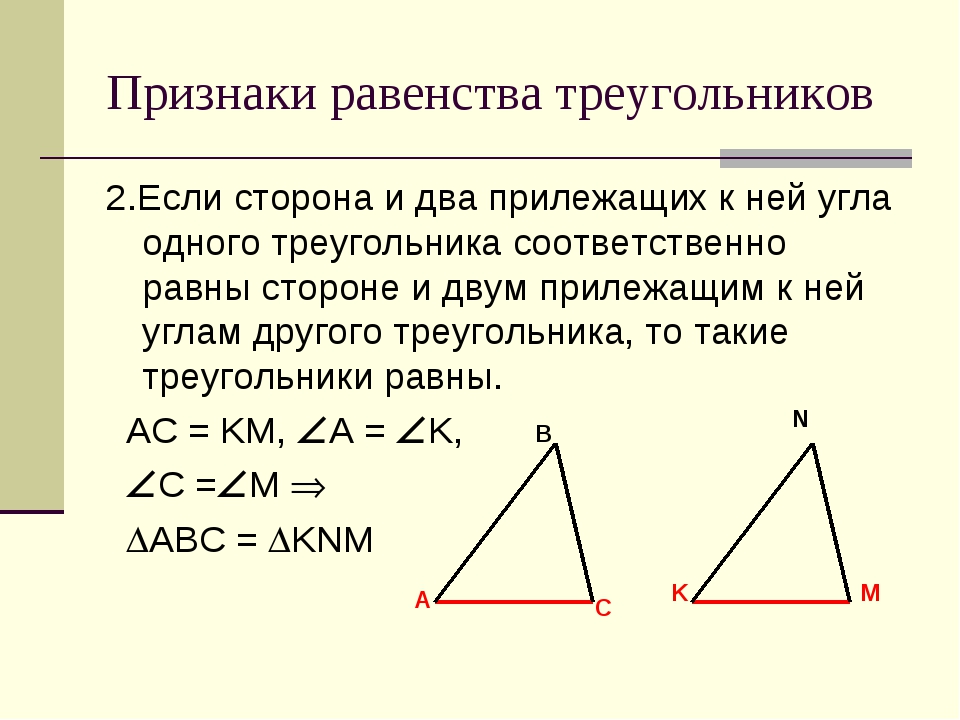



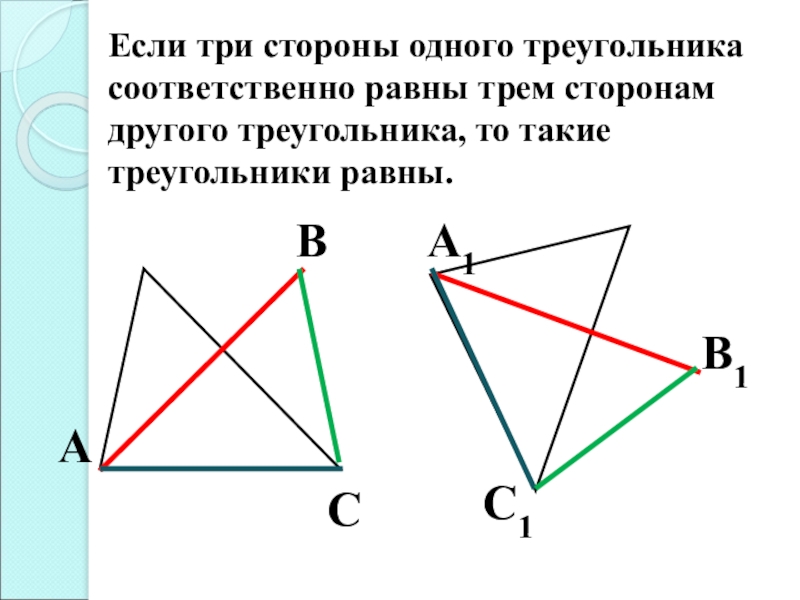
 )
)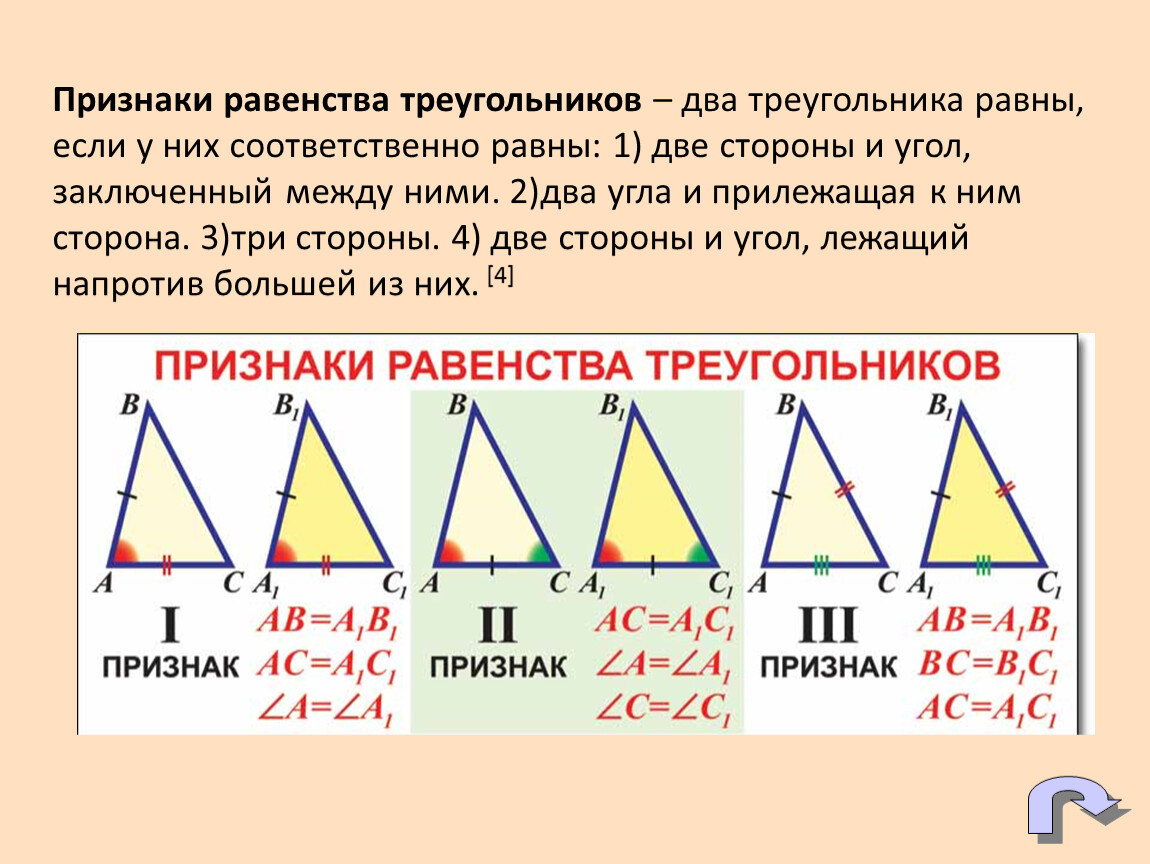



 В свободное время она любит бегать и проводить время со своими мальчиками!
В свободное время она любит бегать и проводить время со своими мальчиками! Обратите внимание, что чем меньше треугольник, тем ближе сумма углов к 180 градусам.
Обратите внимание, что чем меньше треугольник, тем ближе сумма углов к 180 градусам.