Двойные неравенства. 2 способа решения

Например:

\(5<11<17\)
\(-2\leq3x+5\leq2\)
\(2x-5\leq3x+7\leq8x\)

Двойное неравенство по своей сути – это система из двух неравенств, записанных в одну строку. Поэтому  их всегда можно представить в виде системы.

Например:

\(-2\leq3x+5\leq2\Leftrightarrow\begin{cases}-2\leq3x+5\\3x+5\leq2\end{cases}\)
\(2x-5\leq3x+7\leq8x\Leftrightarrow\begin{cases}2x-5\leq3x+7\\3x+7\leq8x\end{cases}\)

Но делать это нужно не всегда.

2 способа решения двойного неравенства

1) Если в крайней левой и крайней правой частях двойного неравенства нет неизвестных, то удобнее оставить его как есть. При этом в процессе решения стремится равносильными преобразованиями привести неравенство к виду \([число]\)\(<\)\(x\)\(<\)\([число]\).

Пример: Решите двойное неравенство:

\(-2\leq3x+5\leq2\)    \(|-5\)		Здесь нет неизвестных по краям, поэтому к системе переходить не будем. Вместо этого делаем такие преобразования, чтоб в центре остался голый икс, а по краям — числа. Для того чтобы «оголить» икс нужно избавиться от пятерки и тройки. Вычтем \(5\) из всего неравенства.
\(-7≤3x≤-3\)   \(|:3\)		Теперь нам мешает \(3\). Поделим все три части неравенства на \(3\).
\(-\)\(\frac{7}{3}\)\(\leq x \leq-1\)		Готово, наш икс «голый». Можно записывать ответ.

Ответ: \([-\)\(\frac{7}{3}\)\(;-1]\)

2) Если в крайних частях двойного неравенства есть неизвестные лучше перевести неравенство в систему и решать его как обычную систему неравенств.

Пример: Решите двойное неравенство:

\(2x-5<3x+7≤8x\)	В крайней левой и крайней правой частях есть неизвестные –значит переходим к системе.
\(\begin{cases}2x-5<3x+7\\3x+7\leq8x\end{cases}\)	Решаем обычные линейные неравенства: все, что с иксами переносим в левую сторону, все что без иксов — в правую.
\(\begin{cases}2x-3x<7+5\\3x-8x\leq-7\end{cases}\)	Приводим подобные слагаемые
\(\begin{cases}-x<12   \\-5x\leq-7   \end{cases}\)	«Оголим» иксы, поделив верхнее неравенство на \((-1)\), нижнее на \((-5)\). Не забываем при этом перевернуть знаки сравнения, так как мы делим на отрицательное число.
\(\begin{cases}x>-12   \\x\geq \frac{7}{5}\end{cases}\)	Отметим на числовой оси оба решения
	Так как у нас система, то мы ищем значения иксов, которые подойдут обоим неравенствам, т.е. интервал, где есть двойная штриховка: и сверху, и снизу. Его и запишем ответ.

Ответ:

\([\)\(\frac{7}{5}\)\(;\infty)\)

Скачать статью

cos-cos.ru

Материалы к уроку «Решение двойных неравенств»

Решение двойных неравенств

Знакомство с двойными неравенствами с одной переменной начинается в 8 классе, а в 9 классе мы уже рассматриваем более сложные неравенства с двумя переменными. Комплекс заданий, который я опишу ниже, подойдет для итоговых уроков алгебры, а также для подготовки к экзамену.

Простейшее двойное неравенство
Рассмотрим ряд примеров:

1

 

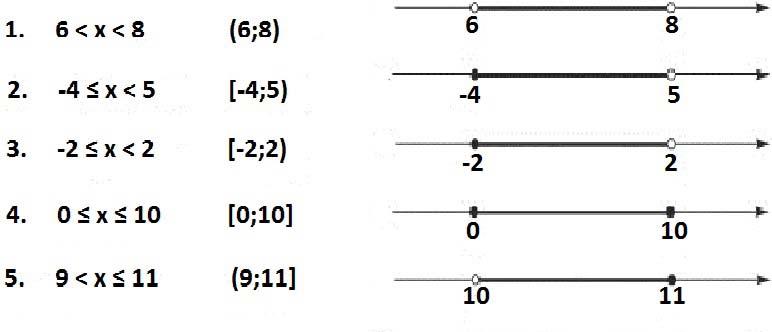
1. 6 < х < 8 .
Решение этого двойного неравенства сводится к решению системы двух неравенств:

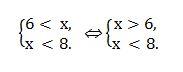
Решение данной системы изображено на числовой оси ОХ рисунка 1. Ответом является интервал, так как неравенство строгое, (6;8).

2. – 4 ≤ х < 5.

На рисунке приведено графическое исполнение решения данного двойного или системы неравенств. Обращает на себя внимание различие в отображении на рисунке концов искомого ответа: левая точка «полная», а правая — «выколотая». Такое различие обусловлено условиями, налагаемыми на переменную х: левое нестрогое – меньше или равно, а правое строгое – строго больше. Отсюда и результат, по которому левая точка х = — 4 является решение неравенства и поэтому точка на графическом изображении «полная», а правая точка х = 5 не является решение и поэтому на графике она изображена «пустой» или, как еще принято называть, «выколотой». Ответом искомого неравенства будет полуинтервал [- 4;5).

Самостоятельно рассмотрим остальные варианты решений простейших двойных неравенств на рисунке 1.

Задание№1.
Решите двойное неравенство самостоятельно.

1. -1 < x ≤ 5;

2. 2 ≤ x ≤ 10. 

Двойное неравенство. Алгебраические действия над ним

Стоит отметить, что для решения двойных неравенств действуют все те же правила, которые применимы и для обычных неравенств, только теперь действие должно применяться сразу к обеим частям неравенства.

1. Без смены знака можно прибавлять/отнимать любое действительное число к обеим сторонам неравенства.

2. Без смены знака можно умножать/делить на любое действительное (отличное от нуля) положительное число. 

3. Сменив знаки на противоположные, можно обе стороны неравенства умножать/делить на любое отрицательное число (кроме нуля).

Более сложное двойное неравенство с двумя переменными.

Решим неравенство:  3x – 8 < y ≤ -x + 4.

Чтобы решить это двойное неравенство нужно решить систему двух неравенств с двумя неизвестными. А именно:

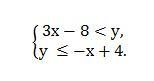
Приведем первое неравенство системы к более удобному для восприятия виду у > 3x – 8 , тогда система будет иметь вид

 

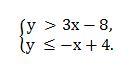
Графическая интерпретация неравенства показана на рисунке 2.

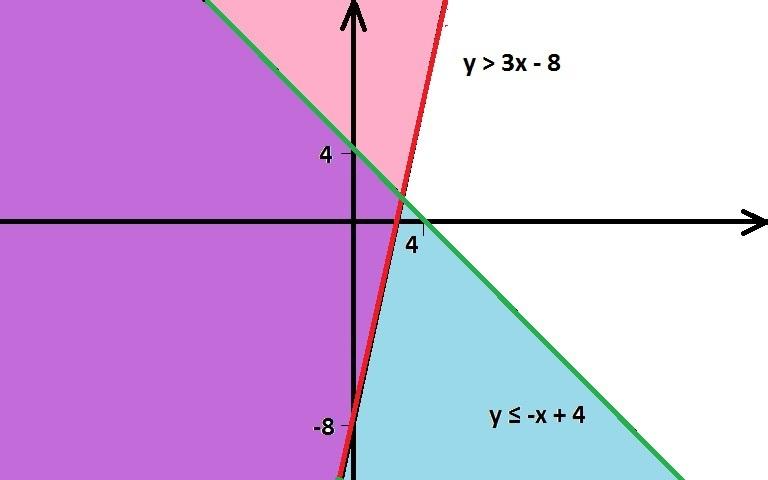
2

 

 

Чтобы найти искомую зону ответов, удовлетворяющих данным условиям, сначала строим две прямые у = 3х — 8 и у = — х + 4. Построение прямых проще всего выполнять по контрольным точкам. Контрольные точки первой прямой (0; -8) и (8/3; 0), через них проводим прямую. На рисунке она красного цвета. Для построения второй прямой достаточно прямую у = х сместить на четыре единичных отрезка вверх по оси ОУ и симметрично отобразить ее относительно оси ОУ. Можно построить вторую прямую по контрольным точкам: (0 ; 4) и (4;0). На рисунке эта прямая зеленого цвета.

Для нахождения области решения двойного неравенства на координатной плоскости изображают области, которые являются решениями каждого неравенства отдельно, зона пересечения этих областей и будет решением первоначального двойного неравенства. На рисунке розовым цветом обозначена область решений 3х – 8 < у, причем прямая у = 3х — 8 не является решением строгого неравенства. Голубая — область решений неравенства у ≤ -х + 4, причем, все точки принадлежащие прямой у = — х + 4 удовлетворяют неравенству и, следовательно, является его решением. Пересечение розовой и зеленой зон и будет решением искомого двойного неравенства с двумя неизвестными.

Задание №2. Решите двойное неравенство:

2х +4 < у ≤ — х;

– х ≤ 4у + 1 ≤ 2х — 1.

 

Определите, графическое решение какого двойного
a) 2х – 5 ≤ у < 5х;

b) Х + 1 < у ≤ — х + 5 неравенства изображено на рисунке 3?

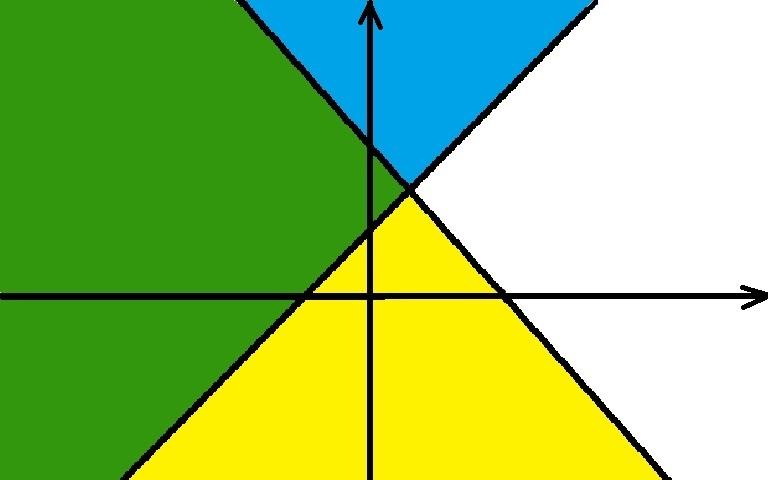
3

xn--j1ahfl.xn--p1ai

Линейные неравенства. Решение линейных неравенств

Линейные неравенства – такие неравенства, которые можно привести к одному из видов:

\(ax>b\),         \(ax<b\),         \(ax \geq b\),         \(ax \leq b\),

где \(a\) и \(b\) любые числа (причем \(a\neq0\)), а \(x\) — неизвестная переменная.

Проще можно сказать, что это такие неравенства, в которых есть переменная только в первой степени, и она не находится в знаменателе дроби.

Примеры:

\(3x>-2\)

\(\frac{3y-4}{5}\)\(\leq1\)

\(5(x-1)-2x>3x-8\)

Примеры не линейных неравенств:

\(3>-2\) – здесь нет переменных, только лишь числа, значит это числовое неравенство
\(\frac{-14}{(y-3)^{2}-5}\) \(\leq0\) – есть переменная в знаменателе, это

дробно-рациональное неравенство
\(5(x-1)-2x>3x^{2}-8\) — есть переменная во второй степени, это квадратное неравенство

Решение линейных неравенств

Решением неравенства будет любое число, подстановка которого вместо переменной сделает неравенство верным. Решить неравенство – значит найти все такие числа.

Например, для неравенства \(x-2>0\) число \(5\) будет решением, т.к. при подстановке пятерки вместо икса мы получим верное числовое: \(3>0\). А вот число \(1\) решением не будет, так как при подстановке получится неверное числовое неравенство:\(-1>0\) . Но решением неравенства будут не только пятерка, но и \(4\), \(7\), \(15\), \(42\), \(726\) и еще бесконечное множество чисел: любое число, больше двойки.

Поэтому линейные неравенства не решают перебором и подстановкой значений. Вместо этого их с помощью равносильных преобразований приводят к одному из видов:

\(x<c\),        \(x>c\),        \(x\leqс\),        \(x\geqс\),       где \(с\) — любое число

После чего ответ отмечается на числовой оси и записывается в виде промежутка (также называемого интервалом).

Вообще, если вы умеете решать линейные уравнения, то и линейные неравенства вам под силу, потому что процесс решения очень схож. Есть лишь одно важное дополнение: 

При умножении или делении неравенства на любое отрицательное число (или выражение) нужно менять знак сравнения на противоположный (почему так – смотри здесь).

Пример. Решить неравенство \(2(x+1)-1<7+8x\)
Решение:

\(2(x+1)-1<7+8x\)		Раскроем скобки
\(2x+2-1<7+8x\)		Перенесем \(8x\) влево, а \(2\) и \(-1\) вправо, не забывая при этом менять знаки
\(2x-8x<7-2+1\)		Приведем подобные слагаемые
\(-6x<6\)        \(|:(-6)\)		Поделим обе части неравенства на \(-6\), не забыв поменять знак сравнения
\(x>-1\)		Отметим на оси числовой промежуток. Неравенство строгое, поэтому само значение \(-1\) «выкалываем» и в ответ не берем
		Запишем ответ в виде интервала

Ответ: \(x\in(-1;\infty)\)

Особый случай №1: решение неравенства – любое число

В линейных неравенствах возможна ситуация, когда ему в качестве решения пойдет абсолютно любое число – целое, дробное, отрицательное, положительное, ноль… Например, вот такое неравенство \(x+2>x\) будет верным при любом значении икса. Ну, а как же может быть иначе, ведь слева к иксу прибавили двойку, а справа – нет. Естественно, что слева будет получаться большее число, какой бы икс мы не взяли.

Пример. Решить неравенство \(3(2x-1)+5<6x+4\)
Решение:

\(3(2x-1)+5<6x+4\)		Раскроем скобки
\(6x-3+5<6x+4\)		Приведем подобные слагаемые
\(6x+2<6x+4\)		Перенесем  члены с иксом влево, а числа вправо, не забывая при этом менять знаки
\(6x-6x<4-2\)		Приведем подобные слагаемые
\(0<2\)		Получили верное числовое неравенство. Причем оно будет верным при любом иксе, ведь он никак не влияет на получившееся неравенство. Значит, любое значение икса будет решением

Ответ: \(x\in(-\infty;\infty)\)

Особый случай №2: неравенство не имеет решений

Возможна и обратная ситуация, когда у линейного неравенства вообще нет решений, то есть никакой икс не сделает его верным. Например, \(x-2>x\) не будет верным никогда, ведь слева из икса вычитают двойку, а справа – нет. Значит, слева всегда будет меньше, а не больше.

Пример. Решить неравенство \(\frac{x-5}{2}\)\(>\) \(\frac{3x+2}{6}\)\(-1\)
Решение:

\(\frac{x-5}{2}\)\(>\) \(\frac{3x+2}{6}\)\(-1\)		Нам мешают знаменатели. Сразу же избавляемся от них, умножая всё неравенство на общий знаменатель всех дробей, то есть – на 6
\(6\cdot\)\(\frac{x-5}{2}\)\(>\)\(6\cdot\)\((\frac{3x+2}{6}\)\(-1\)\()\)		Раскроем скобки
\(6\cdot\)\(\frac{x-5}{2}\)\(>\)\(6\cdot\)\(\frac{3x+2}{6}\)\(-6\)		Сократим то, что можно сократить
\(3\cdot(x-5)>3x+2-6\)		Слева раскроем скобку, а справа приведем подобные слагаемые
\(3x-15>3x-4\)		Перенесем \(3x\) влево, а \(-15\) вправо, меняя знаки
\(3x-3x>-4+15\)		Вновь приводим подобные слагаемые
\(0>11\)		Получили неверное числовое неравенство. И оно будет неверным при любом иксе, ведь он никак не влияет на получившееся неравенство. Значит, любое значение икса решением не будет.

Ответ: \(x\in\varnothing\)

Смотрите также:  
Системы линейных неравенств
Строгие и нестрогие неравенства

Скачать статью

cos-cos.ru