Урок математики на тему «Двойное неравенство» (5 класс)
Дата _____________
Урок № 9
Двойное неравенство
Цель:
Выявить и осмыслить получение двойных неравенств, их запись и решение.
Задачи:
Научиться записывать и решать двойные неравенства
повысить познавательную активность.
Развивать внимание, мышление, речь учащихся, умение обобщать, делать выводы.
Воспитать ответственное отношение к учебе.
Ход урока
Организационный момент
Актуализация знаний
Чему мы научились на прошлом уроке?
Какие правила сравнения чисел мы повторили?
Как сравнить числа с разным количеством цифр?
Как сравнить числа с одинаковым количеством цифр?
Постановка проблемы и “открытие” детьми нового знания.
— Говорят, что математика – это искусство называть разные вещи одним именем. Попробуем и мы.
А) Слова – короче, легче, меньше в математике обозначают знаком …
Слова – длиннее, тяжелее, дольше. Обозначают знаком …
Ставлю знаки в высказывания.
1.726 км ‹ 2.273 км ‹ 4.400км
р.Индигирка р.Алдан р.Лена
— Что же у нас получилось?
— Чем эти записи отличаются от уже привычных нам неравенств?
— Как бы вы назвали эти неравенства?
— А в математике принято называть такие неравенства двойные.
— Кто может назвать тему нашего урока?
Запишем число и тему урока «Двойное наравенство».
Первичное закрепление знаний
1. Отметь на числовом луче множество чисел, которое одновременно больше 3 и меньше 7. Предложи свой вариант записи этого множества с помощью знаков неравенства.
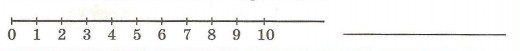
2. При взвешивании арбуза оказалось, что он тяжелее одной 5-килограммовой гири, но легче двух таких гирь. Обозначив массу арбуза х кг, можно записать:
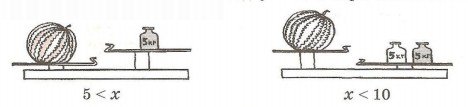
Значит, масса арбуза заключена в промежутке от 5 кг до 10 кг. Вместо двух неравенств 5 < х и х < 10 пишут одно двойное неравенство: 5 < х < 10. Его читают так: «х больше пяти и меньше десяти».
Решениями неравенства 5 < х < 10 являются числа 6, 7, 8 и 9, расположенные между числами 5 и 10:
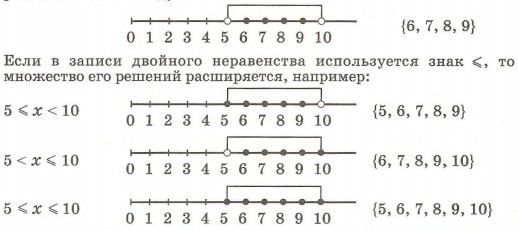
3. Прочитай неравенства
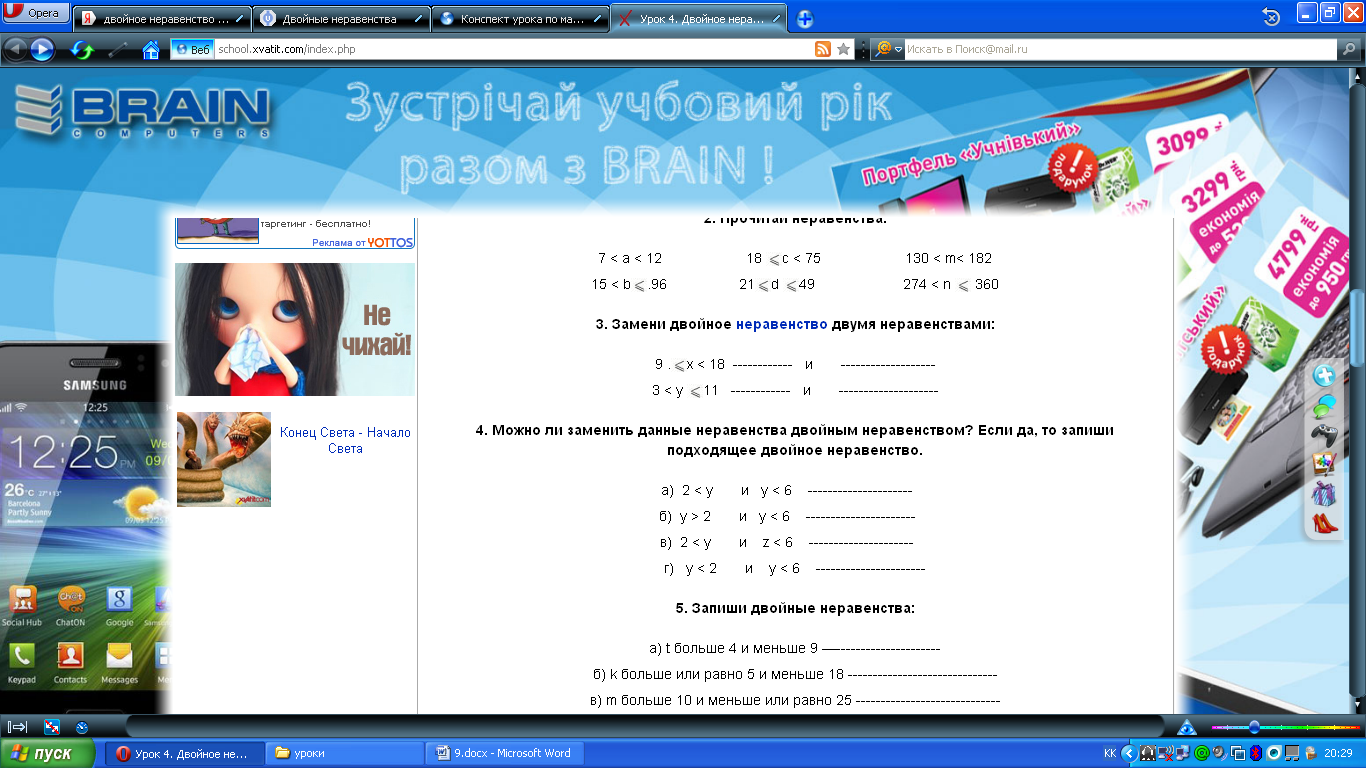
4.Можно ли заменить данные неравенства двойным неравенством? Если да, то запиши подходящее двойное неравенство.
а) 2 < у и у < 6 ———————
б) у > 2 и у < 6 ———————-
в) 2 < у и z < 6 ———————
г) у < 2 и у < 6 ———————
5. Запиши двойные неравенства:
а) t больше 4 и меньше 9 ————————
б) k больше или равно 5 и меньше 18 ——————————
в) m больше 10 и меньше или равно 25 ——————————
г) n больше или равно 6 и меньше или равно 15 —————————-
6. Отметь на луче множество решений двойного неравенства и запиши его с помощью фигурных скобок.
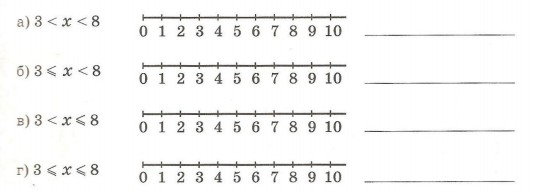
7. Напиши двойные неравенства, множество решений которых совпадает с множеством чисел, отмеченных на луче:
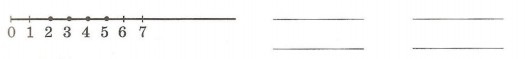
8. Реши уравнения. Что ты замечаешь?
х + 389 = 2076 х — 1687 = 389 2076 -х = 1687
Подведение итогов. Рефлексия.
Д/з
Запиши двойным неравенством.А)2 < у и у < 6
б) у > 2 и у < 6
в) 2 < у и z < 6
г) у < 2 и у < 6
Отметь на луче множество решений двойного неравенства и запиши его с помощью фигурных скобок
Замени двойное неравенство двумя неравенствами
infourok.ru
Алгебра 7-9 классы. 26. Линейные неравенства. Решение линейных неравенств
Алгебра 7-9 классы. 26. Линейные неравенства. Решение линейных неравенств
- Подробности
- Категория: Алгебра 7-9 классы
РЕШЕНИЕ ЛИНЕЙНЫХ НЕРАВЕНСТВ
Свойства числовых равенств помогали нам решать уравнения, т. е. находить те значения переменной, при которых уравнение обращается в верное числовое равенство. Точно так же свойства числовых неравенств помогут нам решать неравенства с переменной, т. е. находить те значения переменной, при которых неравенство с переменной обращается в верное числовое неравенство. Каждое такое значение переменной называют обычно решением неравенства с переменной.
Рассмотрим, например, неравенство
2х + 5 < 7.
Подставив вместо х значение 0, получим 5 < 7 — верное неравенство; значит, х = 0 — решение данного неравенства. Подставив вместо х значение 1, получим 7 < 7 — неверное неравенство; поэтому х = 1 не является решением данного неравенства. Подставив вместо х значение -3, получим -6 + 5 < 7, т.е. — 1 < 7 — верное неравенство; следовательно, х = -3 — решение данного неравенства. Подставив вместо х значение 2,5, получим 2 — 2,5 + 5 < 7, т. е. 10 < 7 — неверное неравенство. Значит, х = 2,5 не является решением неравенства.
Но вы же понимаете, что это — тупиковый путь: ни один математик не станет так решать неравенство, ведь все числа невозможно перебрать! Вот тут-то и нужно использовать свойства числовых неравенств, рассуждая следующим образом.
Нас интересуют такие числа х, при которых 2х + 5 < 7
Что это значит? Это значит, что решением неравенства является любое число х, которое меньше 1. Эти числа заполняют открытый луч (-∞, 1). Обычно говорят, что этот луч — решение неравенства 2х + 5 < 7 (точнее было бы говорить о множестве решений, но математики, как всегда, экономны в словах). Таким образом, можно использовать два варианта записи решений данного неравенства: х < 1 или (-∞, 1).
Свойства числовых неравенств позволяют руководствоваться при решении неравенств следующими правилами:
Правило 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не изменив при этом знак неравенства.
Правило 2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства.
Правило 3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Применим эти правила для решения линейных неравенств, т. е. неравенств, сводящихся к виду ах + b > 0 (или ах + b < 0),
где а и b — любые числа, за одним исключением: а ≠ 0.
Пример 1.
Решить неравенство Зх — 5 ≥ 7х — 15.
Р е ш е н и е.
Перенесем член 7х в левую часть неравенства, а член — 5 — в правую часть неравенства, не забыв при этом изменить знаки и у члена 7х, и у члена -5 (руководствуемся правилом 1). Тогда получим
Зх — 7х ≥ — 15 + 5, т. е. — 4х ≥ — 10.
Разделим обе части последнего неравенства на одно и то же отрицательное число — 4, не забыв при этом перейти к неравенству противоположного смысла (руководствуясь правилом 3). Получим х < 2,5. Это и есть решение заданного неравенства.
Как мы условились, для записи решения можно использовать обозначение соответствующего промежутка числовой прямой: (-∞, 2,5].
О т в е т: х < 2,5, или (-∞, 2,5].
Для неравенств, как и для уравнений, вводится понятие равносильности. Два неравенства f(x) < g(x) и r(x) < s(x) называют равносильными, если они имеют одинаковые решения (или, в частности, если оба неравенства не имеют решений).
Обычно при решении неравенства стараются заменить данное неравенство более простым, но равносильным ему. Такую замену называют равносильным преобразованием неравенства. Эти преобразования как раз и указаны в сформулированных выше правилах 1—3.
Пример 2.
Решить неравенство
Р е ш е н и е.
Умножим обе части неравенства на положительное число 15, оставив знак неравенства без изменения (правило 2), Это позволит нам освободиться от знаменателей, т. е. перейти к более простому неравенству, равносильному данному:
Воспользовавшись для последнего неравенства правилом 1, получим равносильное ему более простое неравенство:
О т в е т: или
В заключение заметим, что, используя свойства числовых неравенств, мы, конечно, сможем решить не любое неравенство с переменной, а только такое, которое после ряда простейших преобразований (типа тех, что были выполнены в примерах из этого параграфа) принимает вид ах > b (вместо знака > может быть, разумеется, любой другой знак неравенства, строгого или нестрогого).
forkettle.ru
Тема урока: «Решение двойных неравенств».
Тема урока:Решение двойных неравенств.
Тип урока: урок изучения нового материала.
Цели урока:
Образовательная: Формировать умение учащихся применять алгоритм решения систем линейных неравенств и свойства числовых неравенств для решения двойных неравенств.
Развивающая:
способствовать формированию умений наблюдать, сравнивать, анализировать, строить гипотезы и делать выводы,
совершенствовать устную математическую речь.
Воспитательная: воспитывать чувство товарищества, чувство ответственности, побуждать учеников к само – взаимоконтролю.
Ожидаемые результаты:
знают алгоритм решения систем линейных неравенств с одной переменной;
понимают и применяют свойства числовых неравенств для решения систем неравенств и двойных неравенств.
Методы и приемы обучения (стратегии): психологический настрой, деление на группы по принципу «Молекулы», работа в группах, взаимопроверка, самопроверка, взаимооценивание, «Выберите одно из предложение».
Оборудование: стикеры, плакат А-4, презентация, раздаточный материал.
План урока:
Организационный момент
Актуализация опорных знаний по теме: «Неравенства и системы неравенств»
Сообщение темы урока и совместное целеполагание
Сообщение темы урока и совместное целеполагание
Решение практических задач
Рефлексия учебной деятельности
Ход урока.
Организационный момент.
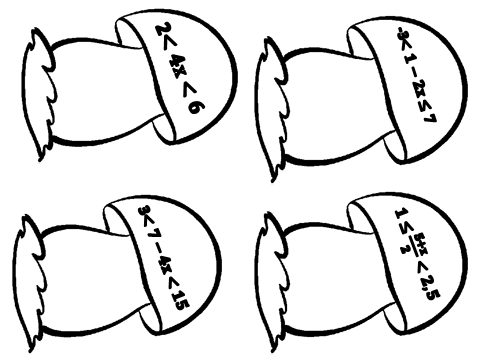
Для работы я предлагаю вам позитивно настроится на урок. Для этого я предлагаю вам сыграть в игру «Молекулы». Тем самым вы разделились на 3 группы. В каждой группе выбираете лидера, тайм менеджера, секретаря ,спикера. (На столах у учащихся находятся грибки, материал для разрезки)
Актуализация знаний.
Работа в группах.
«Корзина идей» (приложение 1)
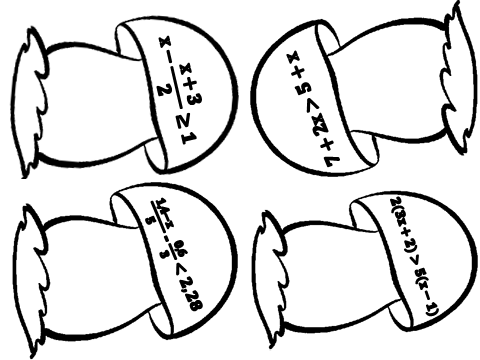
Каждой группе предлагается набор грибов. Ученикам необходимо поместить грибы в «корзину» по заданной проблеме.
1 группа: Неравенства.
2 группа: Системы неравенств.
3 группа: Двойные неравенства.
«Карусель»
Учащиеся совместно дают ответ на каждый проблемный вопрос.
«Галерея». (приложение 2)
После «карусели» вывешиваются работы учащихся на доске. Каждый ученик отдает свой голос за наиболее точный ответ на каждый вопрос. Таким образом, можно определить, какая группа дала лучший ответ.
«Определение темы урока и целеполагание».
Учащиеся формулируют тему урока и чему они должны научиться на уроке.
«
 Мозговой штурм», фронтальная работа.
Мозговой штурм», фронтальная работа.
Эффективные вопросы.
1. Как можно записать иначе двойное неравенство? Для этого прочтите внимательно данное неравенство.(в виде системы неравенств)
2.Сделайте вывод.(Учащиеся делают вывод, что двойное неравенство можно решить с помощью решения системы неравенств)
3. Что значит решить неравенство? ( значит найти множество всех х, для которых данное неравенство выполняется)
4.С помощью, каких свойств неравенств можно найти значения переменной? Учащиеся формулируют второй способ решения двойных неравенств.
Записывают в тетрадь способы решения двойных неравенств.
5.Обсуждают вопрос о выборе наиболее перспективных решений.
Динамическая пауза.
Если верное неравенство – встают руки вверх. Выпадает неверное неравенство – встают руки в стороны: 7<9, -3>5, 0,5<0,75, -2,7>2,7, 987>986, 0,03 < 0,003.
Решение заданий по теме» (приложение 3)
Индивидуальная дифференцированная работа. Учащиеся самостоятельно решают задачи, затем анализируют и оценивают работы друг друга.
(приложение 4)
Решить задачу: Количество яблок, собранных Антоном в саду, больше 15, но меньше 21. Сколько одноклассников он может угостить, если каждому даст по 3 яблока?
Подведение итогов урока.
«Сегодня на уроке я узнал …»
Трудным при решении двойных неравенств для меня было…»
«Больше всего мне понравилось решать двойные неравенства способом …»
«Завтра я буду более успешным, потому что…»
Домашнее задание.
Составить алгоритм решения двойных неравенств, №1577.
Рефлексия (выберите одно из предложений).
Урок был полезным и плодотворным для меня. Я получил заслуженную оценку, и понял весь материал.
Урок был интересен и полезен, я принимал активное участие, мне было легко и комфортно.
Пользы от урока я получил мало, я не очень понимаю материал, мне это не интересно и не понятно
Приложение 1


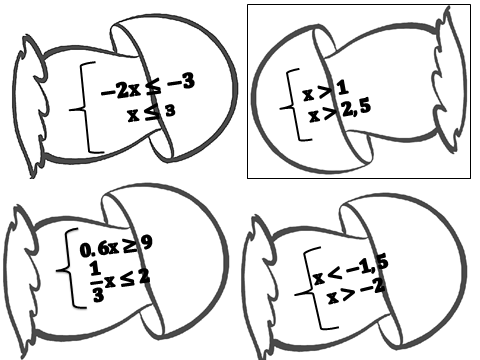

Приложение 2
Алгоритм решения линейных неравенств
Алгоритм решения
систем линейных неравенств
Приложение 3
-2<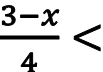 0
0-2,5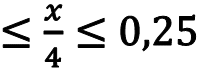


















infourok.ru