Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия
Биссекторная плоскость. Основное свойство биссекторной плоскости
Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).
Рис.1
Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.
Доказательство. Рассмотрим произвольную точку O, расположенную внутри двугранного угла, и проведем через эту точку плоскость δ, перпендикулярную к ребру AB двугранного угла (рис. 2).
Рис.2
Плоскость δ пересекает ребро AB двугранного угла в точке C, а грани двугранного угла α и β по лучам CD и CE соответственно. Угол DCE является линейным углом двугранного угла. Биссекторная плоскость γ пересекает плоскость δ по биссектрисе CF линейного угла DCE .
Поскольку плоскости α и β проходят через перпендикуляр AB к плоскости δ, то плоскости α и β перпендикулярны к плоскости δ. Поскольку плоскости α и β проходят через перпендикуляр AB к плоскости δ, то плоскости α и β перпендикулярны к плоскости δ. Из свойств прямой, перпендикулярной к плоскости, свойств прямой, перпендикулярной к плоскости, следует, что и перпендикуляры, опущенные из точки O на грани двугранного угла α и β, лежат в плоскости δ.
Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла. Доказано.
Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис.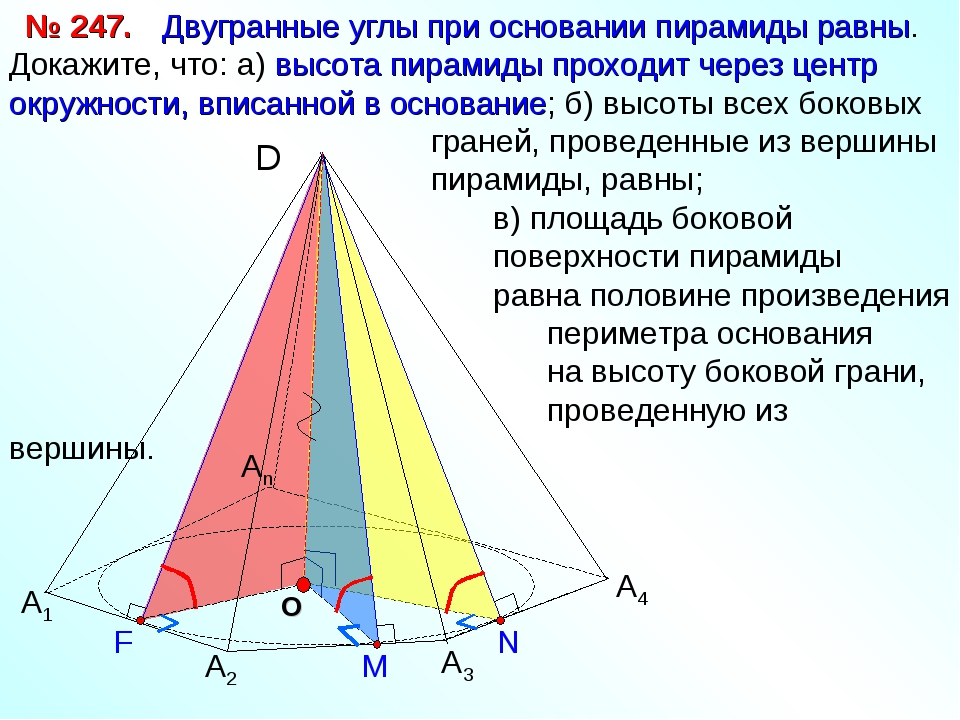 3).
3).
Рис.3
Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы
Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).
Рис.4
Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.
Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.
Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.
Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.
Рассмотрим несколько типов пирамид, в которые можно вписать сферу.
Утверждение 2. Если у пирамиды SA1A2 … An основание O перпендикуляра, опущенного из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A1A2 ..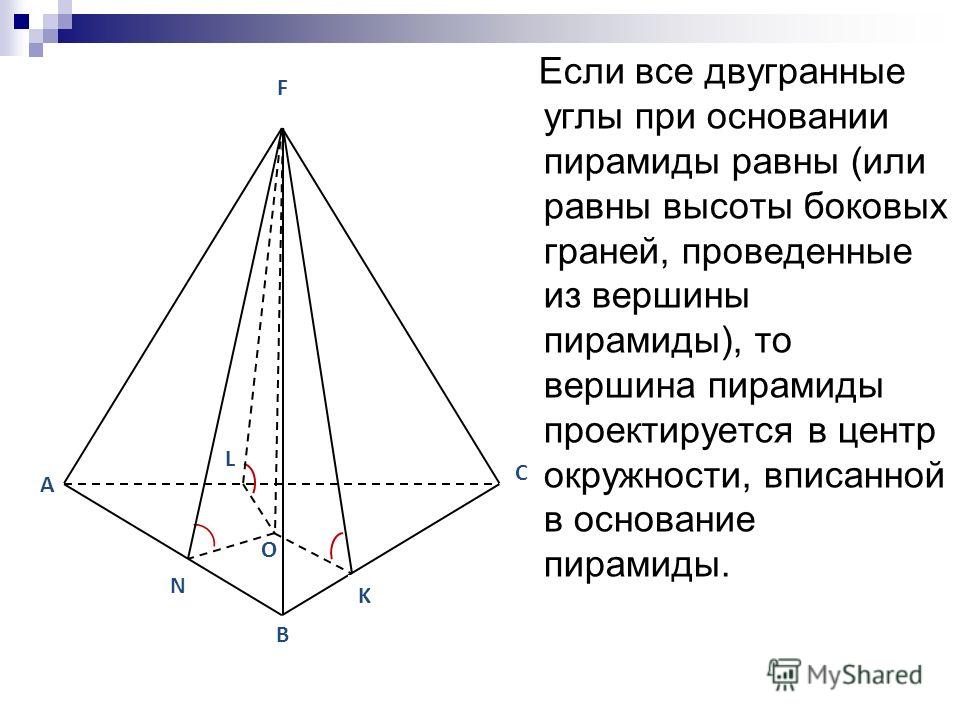 . An , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.
. An , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.
Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом φ , а высота пирамиды равна h. Рассмотрим, например, боковую грань SA1A2 и проведем в ней высоту SB (рис. 5).
Рис.5
По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A1A2. Следовательно, угол SBO является линейным углом двугранного угла между боковой гранью SA1A2 и плоскостью основания пирамиды и равен φ. Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке O’ (рис. 6).
Рис.6
Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле
OB = h ctg φ .
Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле
Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке O’, которая и является центром вписанной в пирамиду сферы.
Доказательство утверждения 2 завершено.
Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо
Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле
| (1) |
Радиус сферы, вписанной в правильную n — угольную пирамиду
Задача. Высота правильной n — угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, вписанной в пирамиду.
Высота правильной n — угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, вписанной в пирамиду.
Решение. Рассмотрим правильную n — угольную пирамиду SA1A2 … An и обозначим символом O’ центр вписанной в пирамиду сферы, а буквой O – центр основания пирамиды. Проведем плоскость через высоту пирамиды SO и апофему SB какой-либо боковой грани (рис. 7).
Рис.7
Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем
| (2) |
В силу следствия 2 из формул (1) и (2) получаем
| (3) |
Поскольку радиус вписанной в правильный n — угольник окружности выражается через сторону этого многоугольника по формуле радиус вписанной в правильный n — угольник окружности выражается через сторону этого многоугольника по формуле
из формулы (3) получаем соотношение
Ответ.
Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой h и ребром основания a, равен
Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром a, равен
Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой h и ребром основания a, равен
Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой h и ребром основания a, равен
Сфера, вписанная в треугольную пирамиду.

Формула для радиуса вписанной сферы
Утверждение 3. В любую треугольную пирамиду можно вписать сферу.
Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.
Действительно, пусть SABC – произвольный тетраэдр. Биссекторная плоскость внутреннего двугранного угла с ребром AC и биссекторная плоскость внутреннего двугранного угла с ребром AB пересекаются по некоторой прямой, проходящей через вершину A. Биссекторная плоскость внутреннего двугранного угла в ребром BC пересекает эту прямую в единственной точке O , которая и является центром вписанной сферы (рис. 8).
Рис.8
Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр SABC сферы. Для этого заметим, что объем пирамиды SABC равен сумме объемов пирамид OABC, OSCA, OSAB, OSCB, причем высота каждой из пирамид OABC, OSCA, OSAB, OSCB равна радиусу R вписанной в пирамиду SABC сферы. Если обозначить площади граней тетраэдра SABC символами
SABC , SASC , SASB , SBSC ,
а объемы пирамид SABC, OABC, OSCA, OSAB, OSCB – символами
VABC , V ASC , V ASB , V BSC ,
то справедливы следующие равенства:
где символом Sполн обозначена площадь полной поверхности пирамиды SABC.
Следовательно,
Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы
где символами Vпир и Sполн обозначены объем и площадь полной поверхности пирамиды соответственно.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Пирамида-2
Решение задач по стереометрии в общем виде – это наиболее трудно. Когда возможно провести промежуточные вычисления – всегда бывает проще. Но в трудностях как раз и закрепляются знания.
Задача 1. В правильной треугольной пирамиде сторона основания равна , высота равна . Найдите: а) боковое ребро пирамиды; б) плоский угол при вершине пирамиды; в) угол между боковым ребром и плоскостью основания пирамиды; г) угол между боковой гранью и основанием пирамиды; д) двугранный угол при боковом ребре пирамиды.
Решение.
К задаче 1
Высота треугольника основания и его медиана
Точка делит в отношении , считая от вершины . Поэтому
а) Тогда определим боковое ребро:
б) Зная его, можно определить плоский угол при вершине по теореме косинусов для любой грани:
в) Угол между боковым ребром и плоскостью основания пирамиды – угол . Поскольку нам известны все стороны треугольника , то можно определить любую функцию этого угла, например, тангенс.
г) Угол между боковой гранью и основанием пирамиды – угол . Также определим тангенс этого угла:
д) Двугранный угол при боковом ребре – угол , где , . Определим длину через площадь треугольника .
Теперь запишем теорему косинусов для треугольника :
Ответ: а) ; б) ; в) ; г) ; д) .
Задача 2. В правильной треугольной пирамиде сторона основания равна 8 см, а плоский угол при вершине равен . Найдите высоту этой пирамиды.
Решение.
К задаче 2
Высота треугольника основания и его медиана
Точка делит в отношении , считая от вершины . Поэтому
Поэтому
Пусть ребро основания , боковое ребро равно , тогда
Теперь можно найти высоту пирамиды по теореме Пифагора:
Ответ: .
Задача 3. В правильной четырехугольной пирамиде сторона основания равна , а плоский угол при вершине равен . Найдите: а) высоту пирамиды; б) боковое ребро пирамиды; в) угол между боковой гранью и плоскостью основания; г) двугранный угол при боковом ребре пирамиды.
К задаче 3
Решение:
Пусть боковое ребро равно , тогда
Диагональ основания пирамиды равна . Ее половина . Таким образом,
Теперь можно определить угол между боковой гранью и плоскостью основания. Для этого нужна апофема пирамиды. Пусть она равна :
Определим косинус угла между боковой гранью и основанием:
Осталось определить двугранный угол при боковом ребре.
Теперь запишем теорему косинусов для треугольника :
Ответ: а) ; б) ; в) ; г) .
Апофема правильной пирамиды
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».Теоретические материалы и формулы см. в главе «Правильная пирамида».
Задача
Апофема правильной треугольной пирамиды равна 4см, а двугранный угол при основании равен 60 градусов. Найдите объем пирамиды.
Найдите объем пирамиды.
Решение.
Поскольку пирамида правильная, учтем следующее:
- Высота пирамиды проецируется на центр основания
- Центр основания правильной пирамиды по условию задачи — равносторонний треугольник
- Центр равностороннего треугольника является одновременно центром вписанной и описанной окружности
- Высота пирамиды образует с плоскостью основания прямой угол
V = 1/3 Sh
Поскольку апофема правильной пирамиды образует вместе с высотой пирамиды прямоугольный треугольник, для нахождения высоты используем теорему синусов. Кроме того, примем во внимание:
- Первый катет рассматриваемого прямоугольного треугольника является высотой, второй катет — радиусом вписанной окружности (в правильном треугольнике центр одновременно является центром вписанной и описанной окружности), гипотенуза является апофемой пирамиды
- Третий угол прямоугольного треугольника равен 30 градусам ( сумма углов треугольника — 180 градусов, угол 60 градусов дан по условию, второй угол — прямой по свойствам пирамиды, третий 180-90-60 = 30 )
- синус 30 градусов равен 1/2
- синус 60 градусов равен корню из трех пополам
- синус 90 градусов равен 1
4 / sin( 90 ) = h / sin ( 60 ) = r / sin( 30 )
4 = h / ( √3 / 2 ) = 2r
откуда
r = 2
h = 2√3
В основании пирамиды лежит правильный треугольник, площадь которого можно найти по формуле:
S правильного треугольника = 3√3 r2.
S = 3√3 22 .
S = 12√3 .
Теперь найдем объем пирамиды:
V = 1/3 * 12√3 * 2√3
V = 24 см3 .

Ответ: 24 см3 .
Задача
Высота и сторона основания правильной четырехугольной пирамиды соответственно равны 24 и 14. найдите апофему пирамиды.Решение.
Поскольку пирамида правильная, то в ее основании лежит правильный четырехугольник — квадрат. Кроме того, высота пирамиды проецируется в центр квадрата. Таким образом, катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды.
Откуда по теореме Пифагора длина апофемы будет найдена из уравнения:
72 + 242 = x2
x2 = 625
x = 25
Ответ: 25 см
Геометрия
— вычисление двугранного угла правильной пирамиды
Короткий ответ: $ DG $ лежит в плоскости $ BCD $, перпендикулярной $ AB $, и, следовательно, (параллельно прямой) перпендикулярной $ AB $. $ DG $ также лежит в плоскости $ DFG $, перпендикулярной $ AC $, и, следовательно, (параллельно прямой) перпендикулярно $ AC $. Будучи перпендикулярным как к $ AB $, так и к $ AC $, $ DG $ перпендикулярно каждой прямой в плоскости $ ABC $, которую он пересекает, включая как $ FG $, так и $ BC $.
Давайте подробно рассмотрим вывод всех трех формул.Следуя связанной статье, мы видим:
Сначала из равнобедренного треугольника со скошенной гранью $ \ треугольник CAD $, используя прямоугольный треугольник с высотой $ AE, $ и $ AC = s, $ получаем $ EC = s \ sin (\ alpha / 2). $
Высота $ AB $ перпендикулярна плоскости $ CAD, $ поэтому треугольник $ ABC $ прямоугольный, а $ BC = AC \ cos \ gamma = s \ cos \ gamma. $ Из базового равнобедренного треугольника $ \ треугольник CBD $ имеем $ EC = s \ cos \ gamma \ sin (\ beta / 2).
$
Приравнивание двух выражений дает $$ \ cos \ gamma = \ frac {\ sin \ left (\ frac \ alpha2 \ right)} {\ sin \ left (\ frac \ beta2 \ right)} \ tag {1} \ label {1}.$
Далее, почему $ FG $ и $ BC $ (то есть плоскость $ ABC $) перпендикулярны $ DG $?
Уловка состоит в том, чтобы понять, что перпендикуляр к плоскости, проходящей через вершину треугольника, ортогонален всем линиям в этой плоскости, включая два ребра, которые встречаются с ним, а также (параллельную линию) противоположному краю.
По построению плоскость $ DFG $ перпендикулярна $ AC $. Следовательно, $ AC $ перпендикулярен любой прямой в $ DFG $, следовательно, $ AC $ перпендикулярен $ FG $ и $ FD $.
Кроме того, прямая $ DG $ лежит в плоскости $ BCD $, поэтому она (или прямая, параллельная ей) перпендикулярна $ AB $, поскольку $ AB $ перпендикулярна плоскости $ BCD. $ Линия $ DG $ также находится в плоскость $ DFG, $ так перпендикулярна $ AC $. Следовательно, она перпендикулярна плоскости $ ABC. $ И, следовательно, также и $ FG. $ Углы $ \ angle DGF $ и $ \ angle DGC $ являются прямыми углами (прямая $ BC $ также находится в плоскости $ ABC $ и поэтому перпендикулярна $ DG $).
Следовательно, глядя на прямоугольный треугольник $ \ треугольник FGD $, мы имеем $ GD = s \ sin \ alpha \ sin \ delta.$
И глядя на прямоугольный треугольник $ \ Triangle BGD $, мы видим $ GD = s \ cos \ gamma \ sin \ beta. $
Приравнивание дает $$ \ sin \ delta = \ frac {\ cos \ gamma \ sin \ beta} {\ sin \ alpha} \ stackrel {\ eqref {1}} = \ frac {\ sin \ left (\ frac \ alpha2 \ right) \ cdot2 \ sin \ left (\ frac \ beta2 \ right) \ cos \ left (\ frac \ beta2 \ right)} {\ sin \ left (\ frac \ beta2 \ right) \ cdot2 \ sin \ left ( \ frac \ alpha2 \ right) \ cos \ left (\ frac \ alpha2 \ right)} = \ frac {\ cos \ left (\ frac \ beta2 \ right)} {\ cos \ left (\ frac \ alpha2 \ right) } \ tag {2} \ label {2}. $$
Глядя на прямоугольный треугольник $ \ треугольник ABE $, мы имеем $ BE = AE \ cos \ epsilon.
 $
$Из треугольника $ \ треугольник AEC $ имеем $ AE = s \ cos \ left (\ frac \ alpha2 \ right). $
И из треугольника $ \ треугольник BEC $ имеем $ BE = s \ cos \ left (\ gamma \ right) \ cos \ left (\ frac \ beta2 \ right). $
Таким образом, $$ \ cos \ epsilon = \ frac {\ sin \ left (\ frac \ alpha2 \ right) \ cos \ left (\ frac \ beta2 \ right)} {\ cos \ left (\ frac \ alpha2 \ right) \ sin \ left (\ frac \ beta2 \ right)} = \ frac {\ tan \ left (\ frac \ alpha2 \ right)} {\ tan \ left (\ frac \ beta2 \ right)} \ tag {3} \ этикетка {3}. $$
Итак, учитывая угол при вершине $ \ alpha $ и проекцию этого угла в основание $ \ beta $, у нас есть угол ребра $ \ gamma $, двугранный угол $ \ delta $ между $ ABC $ и $ ACD $. , и двугранный угол $ \ epsilon $ между $ ACD $ и $ BCD $.
Применяя это к правильной пирамиде, где $ CAD $ — боковая грань, а $ \ треугольник ABC $ — вертикальное (перпендикулярное основанию) поперечное сечение ребра между смежными гранями, тогда двугранный угол между смежными боковыми гранями равен $ 2. \ delta. $
В терминах числа сторон пирамиды $ n $, поскольку вокруг вершины плоскости есть $ n $ углов измерения $ \ beta $, мы имеем $$ \ beta = \ frac {2 \ pi} { n}. $$ И с точки зрения длины наклонной кромки $ AC = s $ и длины базовой стороны $ CD = \ ell $ имеем $$ \ ell = 2s \ sin \ left (\ frac \ alpha2 \ right) .2}}. \ End {align} $$
Например, если положить $ n = 4 $, $ s = \ ell $, мы получим правильную квадратную пирамиду с $ \ gamma = \ frac {\ pi} {4}, $ $ \ sin \ delta = \ sqrt {\ frac {2} {3}}, $ и $ \ cos \ epsilon = \ frac {1} {\ sqrt {3}}. $ Что соответствует углам правильного октаэдра в таблице двугранных твердотельных углов Платона.
Или с $ n = 3 $, $ s = \ ell $ мы получаем $ \ cos \ gamma = 1 / \ sqrt {3} $ и $ \ cos (2 \ delta) = \ cos \ epsilon = 1/3, $ снова соглашаясь с известной геометрией правильного тетраэдра.
Для неплатонического примера правильная шестиугольная пирамида с высотой $ h = \ sqrt {3} \ ell $ и длиной наклонного ребра $ s = 2 \ ell $ будет иметь $ \ cos (2 \ delta) = — 3 / 5 $, угол треугольника $ 3 $ — 4 $ — 5 $.
— Размеры, Углы, Объем — Анимированные интерактивные диаграммы
| Пирамида Установите угол скоса циркулярной пилы, когда вы разрезаете основание сегментов треугольника, чтобы выровнять основание. Убедитесь, что вы выполняете резку в правильном направлении, чтобы скос на был направлен внутрь, на от внешних краев пирамиды. Если смотреть на каждый треугольный сегмент лица (как на диаграмме боковых сегментов выше) от за пределами , с основанием внизу, обрежьте Против часовой стрелки вокруг треугольника — правая сторона снизу вверх, левая сторона сверху вниз, а основание слева направо. | База (Этаж) Цоколь (Этаж) |
Щелкните и перетащите 3D-модель, чтобы переориентировать. Основание Повернуть ↔ Повернуть & varr;
Шаблоны для печати бумажных пирамид
Распечатайте, вырежьте и сложите бумажную пирамиду, чтобы увидеть пропорции и углы введенной пирамиды — размеры, отмеченные на шаблоне.
Надрежьте бумагу вдоль линий сгиба тупым лезвием (ножом для масла) и линейкой, затем согните бумагу вниз от линии надреза для получения хорошего прямого сгиба.

Табуляция соединения печатного размера
Что-то построили с помощью наших калькуляторов? Пожалуйста, пришлите фотографии! Посмотреть примеры
Калькулятор составной торцовочной пилы
Калькулятор составной торцовочной пилы Эта страница использует JavaScript, который недоступен вашему браузеру.Настольная пила или составная торцовочная пила может резать заготовки с двумя установками угла; скос и митра. Такая пила полезна при строительстве, например, ящиков со скошенными сторонами или бетонных форм для столбов. На удивление сложно вычислить настройки составного угла. На этой странице я собрал несколько калькуляторов составных углов, которые помогут вычислить составные углы.
Определения:
Эти определения поясняют концепции, обсуждаемые на этой странице.
- Составной пропил состоит из двух углов: угла скоса и угла скоса .
- Угол наклона Угол (или наклон полотна) — это наклон полотна пилы от вертикали на столе пилы. Это означает, что у обычного квадратного среза скос равен 0 °. Обычно пилы имеют максимальный угол наклона 45 °.
- Угол скоса (или угол поперечного пропила) — это горизонтальный угол, видимый на столе пилы, от линии, перпендикулярной длинному краю доски.Угол скоса устанавливается на ширине резки настольной пилы. Угол наклона перпендикулярного среза равен 0 °.
- Некоторые пилы маркируют угол скоса по-другому, с перпендикулярным разрезом, обозначенным как 90 °. Это угловой элемент с угловым дополнением .
- Двугранный угол — угол между двумя плоскостями поверхности. В частности, мы вычисляем внутренний двугранный угол, который всегда составляет ≤180 °.
 Блок, который плотно прилегает к двум поверхностям, можно разрезать с углом скоса, установленным на двугранный угол минус 90 °, и с нулевым наклоном лезвия.
Блок, который плотно прилегает к двум поверхностям, можно разрезать с углом скоса, установленным на двугранный угол минус 90 °, и с нулевым наклоном лезвия. - Угловой стык соединяет обрезанные концы двух досок.
- Стыковое соединение соединяет обрезанный конец одной доски (стык) с неотрезанной стороной второй доски (колпачок).
- Отрицательный угол показывает, что этот угол противоположен положительному углу, например, лезвие наклоняется вправо, а не влево. Это происходит в основном в стыковых соединениях, поскольку лезвие обычно наклоняется в направлении, противоположном наклонным соединениям.
Соединения под углом и стыки имеют одинаковые углы наклона; отличается только угол скоса. Мы можем видеть это на картинке справа; линии разреза на лицевой стороне доски параллельны.
Точность угла: Выберите количество десятичных цифр, до которого вы хотите округлить угловые результаты.
Доска с уклоном в длинном направлении пересекает вертикальную стойку, повернутую на определенный угол.
Если ваш наклон или вращение идет в направлении, противоположном показанному, используйте отрицательный угол.
Если угол поворота доски равен 0 °, то резку можно производить без математических расчетов. Установите угол наклона полотна на угол поворота стойки, а измеритель угла наклона — на угол наклона, затем положите доску на край (поверните доску на 90 °) на пилу.
Двусторонняя коробка состоит из одинаковых по боковых частей и дна. Коробка может иметь скошенные наружу стороны.Внешний угол — это боковой угол.
Обратите внимание, что этот калькулятор также работает с прямоугольными прямоугольниками.
Вывод
Двусторонняя пирамида построена из n идентичных треугольных боковых частей, не включая основание. Радиус основания — это расстояние от центра основания пирамиды до одного из углов основания. Высота — это расстояние от центра основания до вершины.
Радиус основания — это расстояние от центра основания пирамиды до одного из углов основания. Высота — это расстояние от центра основания до вершины.
Боковой уклон измеряется от горизонтали и может использоваться для расчета любых разрезов, необходимых в нижней части сторон пирамиды.
Пирамиды с стыковыми швами — это какие-то странные животные. Справа показаны несколько более-менее реалистичных примеров.
Прямоугольная пирамида — это пирамида с прямоугольным основанием.
Бетонная форма для отливки крышек столбов может быть выполнена в виде пирамиды. Пирамида может иметь квадратное или прямоугольное основание.
Боковые откосы измеряются от горизонтали и могут использоваться для расчета любых разрезов, необходимых в основании пирамиды.
В случае бетонной формы нам нужно, чтобы внутренние поверхности формы совпадали. В других случаях вы можете захотеть, чтобы внешние поверхности выровнялись, но при той же толщине доски и прямоугольной основе мы не можем выровнять как внутреннюю, так и внешнюю поверхности с этой моделью. Для этого особого случая посмотрите модель Rectangular Frustum ниже.
По геометрии усеченная пирамида похожа на призму, но стороны не параллельны. В этом примере есть основание и верх с разными пропорциями.
Боковые откосы измеряются от горизонтали и могут использоваться для расчета любых разрезов, необходимых в основании и вершине усеченной вершины.
В этой модели внутренняя и внешняя поверхности совпадают, так как угол скоса одинаков для всех деталей.Это хорошо работает, если наверху есть отверстие. Как только это отверстие закроется, мы должны сделать дополнительные разрезы, чтобы устранить помехи между частями. Модель прямоугольной пирамиды со скосом под углом не имеет этого ограничения. Если вы хотите попробовать эту модель с пирамидой, установите оба верхних размера на ноль.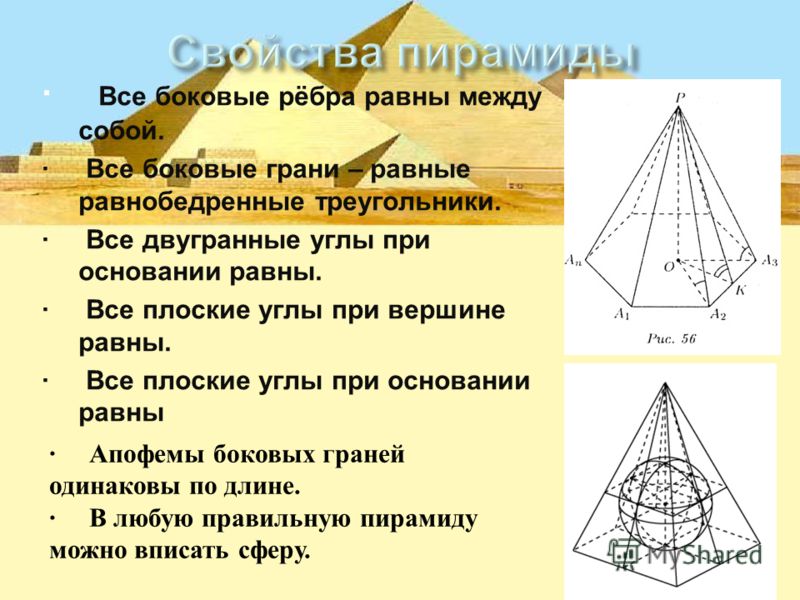
Платоновы тела представляют собой группу из пяти многогранников, построенных с одинаковыми сторонами.
| Стороны | 4 | 6 | 8 | 12 | 20 |
| Имя | Тетраэдр | Куб | Октаэдр | Додекаэдр | Икосаэдр |
| Боковая форма | Равносторонний треугольник | Площадь | Равносторонний треугольник | Пентагон | Равносторонний треугольник |
| Наклон отвала, косое соединение: | 54.736 ° | 45 и | 35,264 ° | 31,717 ° | 20,905 ° |
| Угол скоса: | 30 ° | 0 ° | 30 ° | 18 ° | 30 ° |
| Комплект митры: | 60 ° | 90 ° | 60 ° | 72 ° | 60 ° |
| Двугранный угол: | 70.529 ° | 90 ° | 109,471 ° | 116,565 ° | 138,190 ° |
В общем случае мы имеем две пересекающиеся плоскости поверхности. Определив четыре точки, от 0 до 3 , на поверхностях в трехмерном пространстве мы можем найти углы скоса и скоса сторон A и B.
На рисунке справа показаны две детали в сборе.Пунктирные линии показывают, как определяются координаты XYZ для точки 1 .
Точки 0 и 1 лежат на стыке между двумя поверхностями. Точка 1 может располагаться в любом месте этого шва, кроме начала координат (точка 0 ).
Точка 1 может располагаться в любом месте этого шва, кроме начала координат (точка 0 ).
Граница между точками 0 и 2 является опорным ребром для угла скоса поверхности А в. Точка 2 может располагаться где угодно вдоль этого края, кроме начала координат.Линия 0 — 3 аналогично для поверхности B.
Для соединения со скосом, для простоты наклоны лезвия для деталей A и B одинаковы, но вы можете изменить их, если их сумма одинакова. Это повлияет на пересечение A и B вверху и внизу. Для стыкового соединения наклоны полотна должны быть одинаковыми.
Две доски соединены под произвольным углом. Ориентируем стыкованные доски так, чтобы их края были параллельны горизонтальной плоскости.Теперь мы указываем три угла:
Таблица
В калькуляторах на этой странице предполагается, что доски лежат на столе пилы ровно. Иногда нам нужно вместо этого положить доску узкой стороной вниз. В частности, мы переворачиваем доску так, чтобы поверхность, которая была обращена от нас, теперь была обращена вверх.См. Пример справа, чтобы узнать, как определяются знаки углов.
Чтобы использовать этот калькулятор, либо сначала используйте другой калькулятор, указанный выше, и вводимые данные будут заполнены автоматически, либо введите значения в поля ввода вручную. В простейшем случае требуется всего один наклон лезвия и угол скоса.
Таблица
Следующие методы могут быть полезны для ориентирования доски по сложным углам.
- A (-bevel, -miter): Поворот доски на 180 ° (вращение доски вокруг своей оси), знак изменения наклона лезвия и угла скоса.Это полезно, например, если пила может наклонять полотно только в одном направлении.

- B (-miter): Переворачивание платы встык меняет знак только угла скоса, но также перемещает отходы на другую сторону лезвия. Это может быть или не быть практичным в зависимости от ситуации.
- C (-bevel): При повороте доски на 180 ° по горизонтали (той же стороной вверх) изменяется только знак наклона лезвия, а отходы перемещаются на другую сторону лезвия.
Пропил — ширина паза, прорезанного пильным диском. Когда мы делаем резку компаундом, ширина прорези увеличивается на поверхности доски. Фаска влияет на ширину прорези на верхней поверхности, а фаска и угол наклона влияют на ширину прорези в продольном направлении доски.
Если мы хотим разложить на доске несколько деталей для резки, то нам нужно знать эффективный продольный пропил, который будет значительно увеличиваться для нескольких деталей.
Ссылки
Большинство рисунков на этой странице были созданы с помощью программы для 3D-рисования Sketchup. Sketchup полезен для рисования проекта, а затем измерения составных углов. Тем не менее, довольно сложно измерить угол скоса. Помните, что измерение фаски должно быть перпендикулярно краю на обеих поверхностях. Нарисуйте две короткие линии, чтобы облегчить измерение, и проверьте перпендикулярность краю с помощью транспортира (см. Белые квадраты).Возможно, вам потребуется совместить оси с краем. — это очень просто , чтобы немного изменить размер скоса, не свернув его в квадрат. Переместите или скопируйте линии на открытом воздухе и проведите линию между конечными точками. Это создает поверхность треугольника, на которой мы можем измерить угол между линиями. Тогда угол скоса равен минус 90 °.
Благодарим Криса Глэда за то, что он первым предоставил онлайн-калькулятор для стыковых суставов. Стоит взглянуть на его калькулятор.
Стоит взглянуть на его калькулятор.
(PDF) Хорошо центрированность пентаэдра и пирамидизация простых трехмерных форм с P-хорошо центрированными пентаэдрами
1396 А. Бхаттачарья и Б. Пал
[3] Д. Эппштейн, Дж. М. Салливан и А. ¨
Унг Or, Пространство мозаики и плиты с острыми тетраэдрами
, Computational Geometry: Theory and Application 27,3 (2004),
237-255.
[4] С. Коротов, Н. Крижек, Острое уточнение типа тетраэдрических перегородок
многогранных доменов, SIAM J.Нумер. Анальный. 39 (2): 724-733, 2001.
[5] M.S. Кламкин, Г.А. Цинцифас, Неравенство окружности радиуса и радиуса
для симплекса, Mathematics Magazine 52, 1 (январь 1979), 20-22.
[6] Х. Маэхара, Острая триангуляция многоугольников. European Journal of Com-
binatorics 23, 1 (2002), 45-55.
[7] В. Раджан, Оптимальность триангуляции Делоне в Rd, Dis-
crete и Computational Geometry 12 (1) (декабрь 1994) 189-202,
doi: 10.1007 / BF02574375.
[8] С. Сараф, Острые и нетупорные триангуляции многогранной поверхности
, Европейский журнал комбинаторики 30 (4) (2009) 833-840,
DOI: 10.1016 / j.ejc.2008.08.004.
[9] Э. Вандерзи, А.Н. Хирани, Д. Гой и Э. Рамос, Хорошо центрированное изгибание треугольника
, Tech. Представитель UIUCDCS-R-2008-2936, Департамент компьютеров
Наука, Иллинойский университет в Урбане-Шампейн, февраль 2008 г. Также
доступен в виде препринта в arXiv как arXiv: 0802.2108v1 [cs.CG]. Доступно по номеру
по адресу: http: //arxiv.org/abs/0802.2108.
[10] Э. Вандерзи, А.Н. Хирани, Д. Гой, Э. Рамос и В. Жарницкий, Условия для благополучия, Tech. Res. UIUCDCS-R-2008-2971, Департамент
компьютерных наук, Университет Иллинойса в Урбане-Шампейн, 2008.
[11] Э. Вандерзи, А.Н. Хирани, В. Жарницкий и Д. Гой, Двугранная острая триангуляция куба
, Computational Geometry: Theory and Application Accepted (2009), Также имеется в виде препринта arXiv: 0905. 3715v3 [cs.CG]
3715v3 [cs.CG]
на arxiv.org.
[12] Э. Вандерзи, А.Н. Хирани, Д. Гой, Триангуляция простых трехмерных форм
с хорошо центрированными тетраэдрами, в: RVGarimella (Ed.), Продолжение 17-го Международного круглого стола по построению сетки
, Питтсбург, Пенсильвания,
12-15 октября 2008 г., Springer, Гейдельберг, 2008 г., стр. 19-35. Также доступен в виде препринта
arXiv: 0806.2332v2 [cs.CG].
[13] Л. Юань, Острая триангуляция многоугольников, дискретные и вычислительные
Геометрия 34, 4 (2005), 697-706.
Поступило: декабрь 2010 г.
Задание 1/18 Часть 2: Приложения к многогранникам
Задание 1/18 Часть 2: Приложения к многогранникам
(подавать индивидуально в среду 18.01)
Для каждой задачи 1-3 ответьте на все вопросы, но это в виде пояснения в абзацах без буквенного обозначения вопросы (или даже обязательно строго придерживаясь их порядка). Вместо этого должно быть объяснение в полные предложения, возможно, с рисунками.Объяснение должно быть понятным для читателя, который знает инструменты части 1, но не посещали курс или читали эти задачи.
Задача 1. Куб и тетраэдр
а) Четко объясните, как можно выбрать 4 вершины куба. образовать правильный тетраэдр.
б) Если длина ребра куба равна s, то какова длина край тетраэдра?
в) Предположим s = 2 и запишем координаты всех 8 вершин куб, если куб находится в пространстве (x, y, z), так что центр находится в O = (0,0,0) и каждое ребро параллельно оси координат.
г) В этом случае каковы координаты вершин тетраэдр?
е) Каковы уравнения плоскостей 4-х граней тетраэдр?
е) Используйте скалярное произведение и векторы нормали к этим плоскостям, чтобы вычислить двугранный угол между любыми двумя гранями. (Вы можете объяснить это в кстати, чтоб хватило один раз сделать?)
Задача 2. Тетраэдр и октаэдр и куб
Продолжая ситуацию в Вопросе 1, тетраэдр
можно разложить на четыре меньших «угловых» тетраэдра с ребрами
половина длины исходного ребра и правильный октаэдр посередине, как в
Лаборатория 2.
а) Найдите координаты всех вершин октаэдра.
б) Найдите уравнения плоскостей всех граней октаэдр. Какие бывают самолеты параллельно?
в) Используйте скалярное произведение и нормали (перпендикулярные направления), чтобы плоскости, чтобы найти двугранный угол между двумя гранями.
г) Судя по тому, как октаэдр сидит рядом с углом тетраэдров, как двугранный угол правильного тетраэдра связан с двугранный угол правильного октаэдра? Это согласуется с вашим ответом?
Задача 3.Объемы пирамид
Ссылка: http://www.mathaware.org/mam/00/master/essays/B3D/2/volume.html
а) Постройте сетку для картонной модели куба с квадратным основанием. ABCD.
б) Также постройте сеть для пирамиды с вершинами ABCDE, где E одна из четырех других вершин куба.
в) Постройте 3 совпадающие модели этой пирамиды и покажите, как они могут быть соединенными вместе, чтобы сформировать куб, соответствующий исходному кубу. Сделайте вывод, что объем куба равен равный (1/3) объему площади его основания, умноженному на его высоту.
г) Сделайте вывод, что для ЛЮБОЙ пирамиды или конуса объем = (1/3) (базовая площадь) * высота.
е) Примените это, чтобы найти объем куба, тетраэдра и октаэдр в задачах 1 и 2.
На страницах Whistler Alley, посвященных Платоновым телам, неоднократно используются несколько формул. Эти формулы и их производные более подробно объясняются ниже. Двугранный уголДвугранный угол — угол пересечения двух плоскостей.Это мера угла, вершина которого находится на пересекающемся ребре, а одна сторона — в каждой из плоскостей. Стороны угла перпендикулярны пересекающейся кромке. В контексте многогранников двугранный угол — это угол пересечения двух смежных граней. Для каждого из Платоновых тел существует только один двугранный угол, потому что все пары смежных граней пересекаются под одним углом.
В этом примере будет вычислен двугранный угол на кромке AB, . Снова сложите его в плоскую сетку.Когда грани сложены, вершина в точке D вращается вокруг оси AB и пересекает точку P . Это означает, что точки D , P и Q лежат в плоскости, перпендикулярной прямой AB . Отсюда следует, что точка Q лежит на линии, проходящей через D , перпендикулярной AB .
В треугольнике AFG используйте закон косинусов, чтобы найти FG . Теперь найдите cos∠ AGF . Используйте закон синусов, чтобы найти FQ . Возвращаясь к загнутым граням, мы видим, что FP и FQ оба перпендикулярны AB , поэтому угол, обозначенный как θ , является двугранным углом. Из прямоугольного треугольника PQF получаем: Другие чемоданы Необходимо рассмотреть некоторые другие случаи.Наверху указано, что α и γ являются острыми. В первой версии этого вывода этого условия не было. Двенадцать лет спустя внимательный читатель заметил, что замены AF = cos α и AG = cos γ действительны только для острых углов α и γ . К счастью, формула все еще актуальна, несмотря на этот промах. В тупых случаях AF и AG могут быть приняты как направленные расстояния по отношению к AB и AC . Другая проблема возникает посередине. Хотя с окончательной формулой проблем нет, некоторые промежуточные выражения могут иметь деление на ноль. Это происходит, когда один или несколько углов многоугольника являются прямыми углами. Такой случай вовсе не редкость, когда строятся многогранники с правильными гранями многоугольника.Обратите внимание, что окончательная форма формулы включает знаменатель, который не может быть равен нулю. Этот случай еще должен быть доказан отдельно (кем-то другим). Формула применима только к случаям, когда ровно три грани пересекаются в вершине. Не может быть общей формулы для случая, когда встречаются более трех граней, потому что эти грани сами по себе не могут образовывать жесткую структуру. Апофема, площадь многоугольника и площадь поверхностиИмея достаточно размеров, можно вычислить площадь любого многоугольника, потому что многоугольник можно разрезать на треугольники и затем применить формулу площади элементарного треугольника.Для любого правильного многоугольника площадь может быть вычислена только по длине стороны. Рассмотрим правильный многоугольник ниже со стороной s . Это семиугольник (имеющий 7 сторон), но поскольку мы хотим вывести общую формулу, назовем его n -угольником (имеющим n сторон). Проведя радиалы от центра к каждой вершине, n -угольник разрезается на n равнобедренных равнобедренных треугольников. Теперь нарисуйте радиалы от центра к середине каждой стороны.Это разрежет угольник n на 2 конгруэнтных прямоугольных треугольника n . Возьмите один из прямоугольных треугольников (желтый) и внимательно посмотрите на него. Его база s /2. Угол при вершине при вершине равен π / n , потому что это полный круг, деленный на 2 n . Это дает нам высоту прямоугольного треугольника, который ведет нас к его площади. Есть 2 n этих треугольников в n -угольнике. Для Платонового тела все грани являются конгруэнтными правильными n -угольниками. Чтобы получить общую площадь поверхности ( A ), умножьте площадь n -угольника на f , количество граней. Inradius и Circumradiusinradius твердого тела — это радиус вписанной сферы.Все платоновые тела имеют вписанную сферу. Других многогранников, как правило, нет. На этих иллюстрациях используемое твердое тело является додекаэдром, но концепции и формулы применимы ко всем Платоновым телам. Рассмотрим треугольник OTM . Точка O — центр твердого тела. Точка T — это центр основания, который также является точкой, в которой вписанная сфера касается этой грани. Точка M — это середина одной из базовых кромок. Ясно, что отрезок OM делит двугранный угол пополам, поэтому ∠ OMT = θ /2, половина двугранного угла. Также должно быть ясно, что ∠ OTM — прямой угол. Эти два последних утверждения следуют из симметрии твердого тела. Теперь у нас есть прямоугольный треугольник с одной известной стороной и одним известным острым углом. Описанный радиус — это радиус описанной сферы.Это расстояние от центра до вершины. Все платоновые тела имеют окружной радиус. Продолжая тот же пример с додекаэдром, пусть точка U будет вершиной на том же ребре, которое занимает точка M . Окружной радиус составляет OU . Точки O и U также являются противоположными вершинами прямоугольной призмы, показанной здесь. ОбъемЧтобы получить общую формулу объема Платонова тела, изобразите пирамиду, построенную на одной грани, с центром Платонова тела в качестве вершины пирамиды.Для объема пирамиды нам понадобятся ее площадь основания и высота. Оба этих значения уже вычислены. Базовая область — это площадь одной грани Платонового тела, а высота — это внутренний радиус Платонового тела. Таким же образом можно построить пирамиду на любой грани. Пирамиды будут конгруэнтными и вместе они заполнят твердое тело. Для получения общего объема ( V ) умножьте объем пирамиды на f , количество граней в Платоновом теле. В этой упрощенной формуле объем выражается через площадь поверхности и внутренний радиус. Назад к платоновым телам Последнее обновление: 21 января 2016 г. … Пол Кункель [email protected] Чтобы электронная почта доходила до меня, в теле сообщения должно появиться слово geometry . |
пятиугольная пирамида — PolyhedraMath
Усеченный икосаэдр В течение многих лет меня интересовали различные геометрические формы, от простых кубов, призм и пирамид, сделанных в средней школе, до геодезических куполов, используемых для строительства домов.
Я вырезал и склеил множество листов бумаги почти во все правильные многогранники.
Один из проектов, который я хотел сделать в течение некоторого времени, — это построить усеченный икосаэдр в виде каркаса, иначе известный как бакибол или общая форма футбольного мяча. Сложить бумагу и приклеить края, где они встречаются, — легкая задача даже для детей. Склеивание деревянных дюбелей или пайка проволоки под определенными углами, как правило, немного сложнее, особенно если вы не знаете, какие углы должны быть.
Для любого правильного многогранника существуют сотни Интернет-сайтов и десятки книг, в которых подробно описано, как найти двугранный угол для каждого грани-грани. Проблема в том, что у каркасов нет «граней», каждое ребро соединяет два или более ребра в одной точке и расходится под равными или неравными углами, которые никогда не находятся в одной плоскости. Я искал повсюду, но пока не нашел ни одного веб-сайта, который дает эти углы.
Я предпринял мучительные шаги по вычислению этих углов для усеченного икосаэдра.Используя эти шаги, вы затем можете найти угол для любого другого правильного многогранника.
Сначала давайте определим несколько элементов. Усеченный икосаэдр состоит из 12 пятиугольников и 20 шестиугольников с одинаковой длиной стороны. Поскольку все они имеют одинаковые размеры сторон, мы будем определять любое другое измерение в терминах длины стороны и назовем его 1. Это может быть 1 дюйм, 1 см, 1 миля или 1 световой год, это не имеет значения.
Каждый пятиугольник окружен 5 шестиугольниками. Каждый шестиугольник окружен 3-мя пятиугольниками и 3-мя шестиугольниками, чередующимися.\ circ \).
Как я уже сказал, существует множество источников, где можно найти расшифровку математических расчетов, использованных для получения этих результатов. Я добавляю их сюда только для вашего удобства.
Диаметр можно «развернуть», чтобы показать повторение (рис. 1) от P1 до P2 и P3. P3 будет той же точкой, что и P1.
1) от P1 до P2 и P3. P3 будет той же точкой, что и P1.
Таким образом получается десятиугольник (10-сторонняя фигура), движущийся по граням 4 пятиугольников, 4 шестиугольников и 2 ребер HH. Это дает нам десятиугольник с углами 4 HP и углами 2 HH, но мы не знаем остальных 4 углов между пятиугольником и пятиугольником (Pent-Pent).
Все декагоны имеют общий внутренний угол 1440 ° по формуле для любого N-угольника: (N-2) x180 . Если мы затем воспользуемся небольшой алгеброй, то получим:
1440 = 4 * угол HP + 2 * угол HH + 4 * угол скошенной кромки
Подставляем известные значения:
1440 = 4 x 142,622632 + 2 x 138,189685 + 4 x скошенный угол кромки 1440 = 570,4 + 276,379370 + 4 x Угол Pent-Pent 1440 = 846,869898 + 4 x угол наклона кромки Pent-Pent 1440 - 846 гг.869898 = 4 x угол закругления кромки 593.130102 = 4 x угол наклона Pent-Pent 148.2825255 = Угол наклона Pent-Pent
Итак, если я хочу создать каркас усеченного икосаэдра, мне просто нужно соединить два провода под углом 108 °, внутренний угол для пятиугольника, и добавить третий, торчащий прямо и поднимающийся примерно под углом 31 ° (180 ° -148 °).
Но это правильно? Как это проверить? Есть ли способ найти «точные» измерения?
Нахождение углов вершины пятиугольника, шестиугольника и шестиугольника
Взяв область с красным контуром на рис. 1 и повернув, мы получим рис 2.\ circ = 2 · \ frac {\ sqrt3} {2} = \ sqrt3 \).
На рисунке 4ΔNML (рис. 5) показана длина LM, нам не нужны точные цифры, на данный момент достаточно 2 · sin 54 °. Линии GL и GM имеют угол 54 °.
На рис. 5ΔKML (рис. 6) использует теорему Пифагора для определения длины линии KG. Нам не нужно вычислять фактическую длину, так как мы все равно собираемся выровнять ее.
На рисунке 6 ΔNKG (рис. 7) показан угол η, который мы ищем. Примечание. Я нарисовал это изображение, хотя знал, что η тупое. 2 (60)}} {\ color {Blue} {cos (54)}} & \ text {factor out 2} \\
2 (60)}} {\ color {Blue} {cos (54)}} & \ text {factor out 2} \\
& = \ frac {\ color {yellow} {\ cos (2 \ cdot 60)}} {\ color {Blue} {cos (54)}} & \ text {Используя тождество cos 2α = 1-2 · sin² α} \\
& = \ frac {\ color {yellow} {cos (120)}} {\ color {Blue} {cos (54)}} \\
& = \ frac {- \ frac12} {\ sqrt {\ frac {5- \ sqrt {5}} {8}}} \\
& = \ frac {-1} {2} \ cdot \ frac {\ sqrt {8} } {\ sqrt {5- \ sqrt {5}}} & \ text {invert} \\
& = \ frac {-2 \ sqrt2} {2 \ sqrt {5- \ sqrt {5}}} \ cdot \ frac {\ sqrt {5+ \ sqrt {5}}} {\ sqrt {5+ \ sqrt {5}}} & \ text {Умножить на сопряжение} \\
& = \ frac {- \ sqrt2 \ sqrt {5 + \ sqrt {5}}} {\ sqrt {25-5}} \\
& = \ frac {- \ sqrt2 \ sqrt {5+ \ sqrt {5}}} {\ sqrt {20}} \\
& = \ frac {- \ sqrt2 \ sqrt {5+ \ sqrt {5}}} {\ sqrt {4 \ cdot 5}} \\
& = \ frac {- \ sqrt2 \ sqrt {5+ \ sqrt {5 }}} {2 \ sqrt5} \\
& = \ frac {- \ sqrt2 \ sqrt {5+ \ sqrt {5}}} {2 \ sqrt5} \ cdot \ frac {\ sqrt5} {\ sqrt5} \\
& = \ frac {- \ sqrt2 \ sqrt5 \ sqrt {5+ \ sqrt {5}}} {20} \\
& = — \ sqrt {\ frac {5+ \ sqrt5} {10}}
\ end {align} $$
∠η = 148.2825255… °
Ура! Оно соответствует найденному нами ранее значению.
Нахождение углов правильной пятиугольной пирамиды
Усеченный икосаэдр получают путем усечения (отсечения) правильной пятиугольной пирамиды от каждого из концов икосаэдра, отсюда и название.
Угол грани пятиугольника к любому из ребер треугольника будет 180 ° минус угол ребра Pent-Pent.
Рис. 8a, 8b, 8c Чтобы найти желаемые углы, мы должны сначала найти высоту пятиугольника (рис. 8a).2 (72)} \ color {limegreen} {- \ frac34}} {2 \ cdot1 \ cdot \ color {skyblue} {\ frac12 \ cdot tan (72)}} \\
& = \ frac {\ frac44 \ color {limegreen} {- \ frac34} + \ color {skyblue} {\ frac14 \ cdot (5 + 2 \ sqrt {5})}} {2 \ cdot \ color {skyblue} {\ frac12 \ sqrt {5 + 2 \ sqrt {5}}}} \\
& = \ frac {\ frac14 + \ frac14 (5 + 2 \ sqrt5)} {\ sqrt {5 + 2 \ sqrt5}} \\
& = \ frac {1+ \ quad 5 + 2 \ sqrt5} {4 \ sqrt {5 + 2 \ sqrt5}} \\
& = \ frac {6 + 2 \ sqrt5} {4 \ sqrt {5 + 2 \ sqrt5}} \\
& = \ гидроразрыв {3 + \ sqrt {5}} {2 \ sqrt {5 + 2 \ sqrt {5}}} \\
& = \ frac {3 + \ sqrt {5}} {2 \ sqrt {5 + 2 \ sqrt {5}}} \ cdot \ frac {\ sqrt {5-2 \ sqrt {5}}} {\ sqrt {5-2 \ sqrt {5}}} & \ text {умножить на сопряжение} \\
& = \ frac {(3 + \ sqrt {5}) \ sqrt {5-2 \ sqrt5}} {2 \ sqrt {25-20}} \\
& = \ frac {\ color {yellow} {(3 + \ sqrt {5})} \ sqrt {5-2 \ sqrt5}} {2 \ sqrt5} \\
& = \ frac {\ color {желтый} {\ sqrt {14 + 6 \ sqrt {5}}} \ sqrt {5-2 \ sqrt5}} {2 \ sqrt5} & \ color {желтый} {(3 + \ sqrt {5}) ^ 2 = 14 + 6 \ sqrt5} \\
& = \ frac {\ sqrt { 70 — 60 + 30 \ sqrt5 -28 \ sqrt5}} {2 \ sqrt5} \\
& = \ frac {\ sqrt {10 + 2 \ sqrt5}} {2 \ sqrt5} \\
& = \ frac {\ s qrt {10 + 2 \ sqrt5}} {2 \ sqrt5} \ cdot \ frac {\ sqrt5} {\ sqrt5} \\
& = \ frac {\ sqrt {50 + 10 \ sqrt5}} {10} \\
& = \ frac {\ sqrt {10} \ sqrt {5 + \ sqrt5}} {10} \\
& = \ sqrt {\ frac {5 + \ sqrt5} {10}} \ end {align} $$
∠θ = 31.

 $
$ Блок, который плотно прилегает к двум поверхностям, можно разрезать с углом скоса, установленным на двугранный угол минус 90 °, и с нулевым наклоном лезвия.
Блок, который плотно прилегает к двум поверхностям, можно разрезать с углом скоса, установленным на двугранный угол минус 90 °, и с нулевым наклоном лезвия.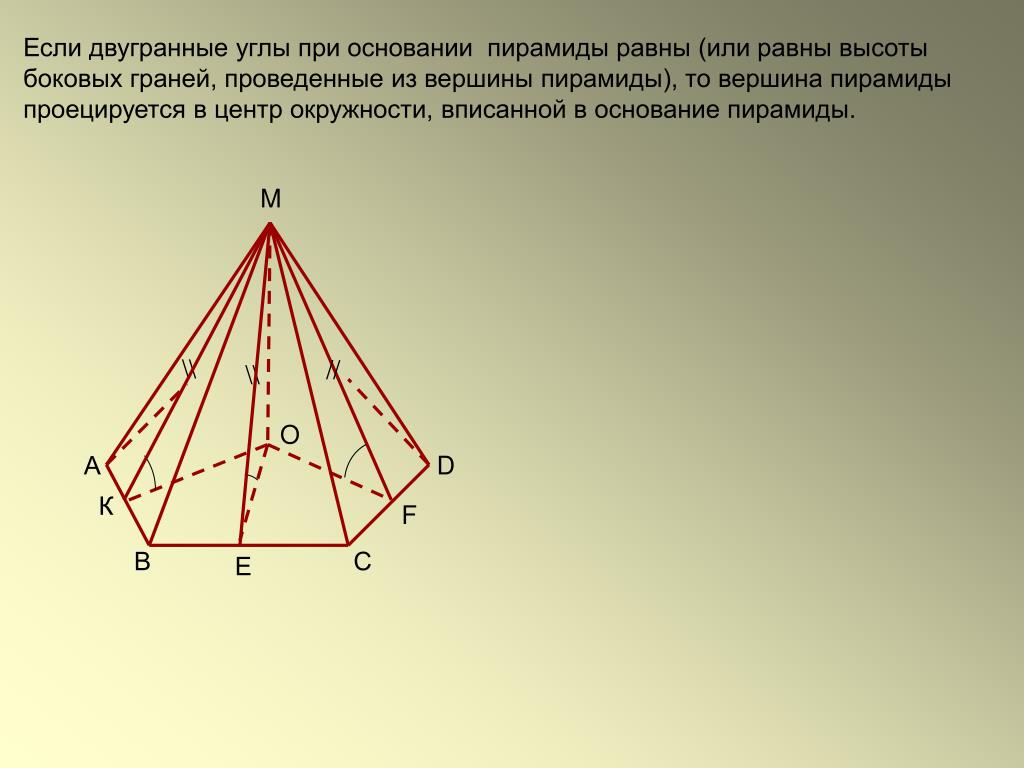

 По тем же соображениям, Q лежит на линии, проходящей через E , перпендикулярной AC .
По тем же соображениям, Q лежит на линии, проходящей через E , перпендикулярной AC .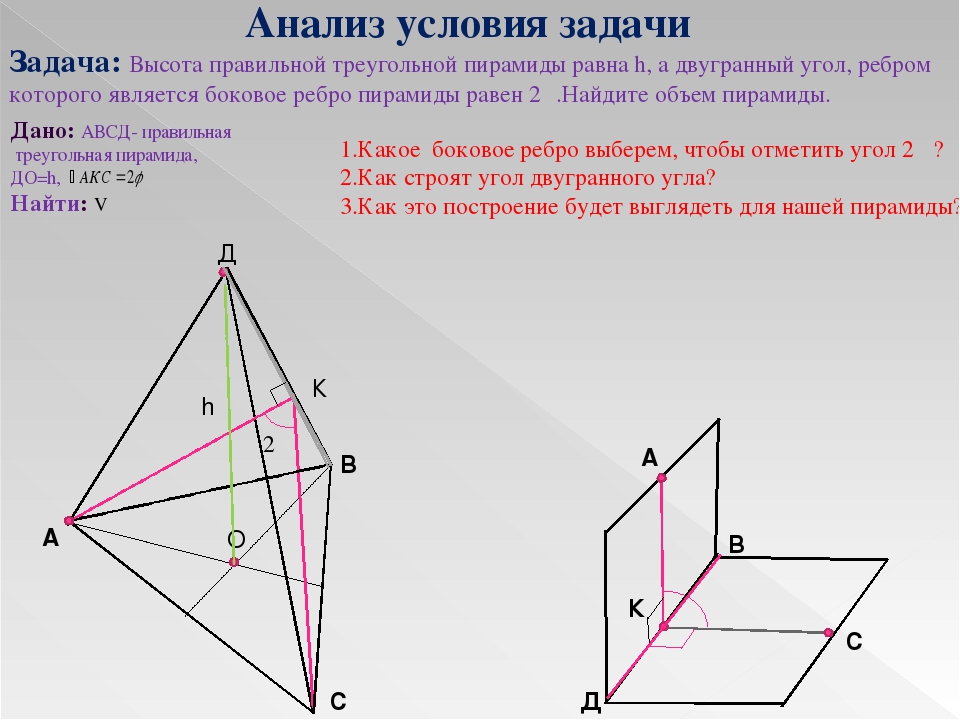 Любой из них может быть отрицательным или нулевым. В результате FQ является направленным расстоянием относительно DQ . Если FQ отрицательное, двугранный угол θ тупой.
Любой из них может быть отрицательным или нулевым. В результате FQ является направленным расстоянием относительно DQ . Если FQ отрицательное, двугранный угол θ тупой. Высота на . Это апофема из n -угольника. Апофема правильного многоугольника — это расстояние от центра до середины стороны.Это также радиус вписанной окружности. Мы можем найти апофему по длине стороны и количеству сторон.
Высота на . Это апофема из n -угольника. Апофема правильного многоугольника — это расстояние от центра до середины стороны.Это также радиус вписанной окружности. Мы можем найти апофему по длине стороны и количеству сторон. Формула для inradius, r i , следует.
Формула для inradius, r i , следует.