Эдс самоиндукции прямо пропорциональна – Самоиндукция простыми словами: определение, формулы, примеры

Posted on by alexxlab

Самоиндукция простыми словами: определение, формулы, примеры

Явление электромагнитной индукции очень часто наблюдается в электротехнике. Взаимное влияние электрических и магнитных полей иногда приводит к интересным результатам. Самоиндукция – частный случай электромагнитной индукции.

Общеизвестно, что причиной порождения электрического тока является переменное магнитное поле. Именно этот принцип реализован в конструкциях современных генераторов. Природа самоиндукции также связана с электромагнетизмом, но это явление проявляется она по-другому.

Определение

Рассмотрим схему катушки, по обмоткам которой протекает электрический ток (рис. 1). Так как вокруг проводника, который находится под током, всегда существует связанное с ним магнитное поле, то силовые линии этого поля пронизывают плоскости витков. В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.

Магнитное поле катушки
Рис. 1. Магнитное поле катушки

Частным случаем катушки является замкнутый контур (один виток). В нём, как и в катушке, образуется собственное магнитное поле (см. рис. 2). Если ток постоянный, то в контуре никаких изменений не происходит.

Но при изменении параметров, например, в результате размыкания цепи, изменяется магнитный поток, создаваемый электрическим полем, что является причиной возникновения ЭДС индукции. Аналогичное изменение произойдёт и в случае замыкания цепи.

Изменение параметров магнитного поля вызывает появление вихревого электрического поля, что в свою очередь приводит к возбуждению индуктивной электродвижущей силы. Возникновение ЭДС индукции, в результате изменения ток в замкнутом контуре, называется самоиндукцией.

Магнитный поток, ограниченный поверхностью контура, меняется прямо пропорционально изменению тока, циркулирующего в нём.

Явление самоиндукции
Рис. 2. Явление самоиндукции

Направление вектора ЭДС самоиндукции не совпадает с направлением тока в период его возрастания (при замыкании цепи), но он сонаправлен с ним в период убывания (разъединения цепи). Такое действие проявляется в замедлении появления тока в соленоиде при замыкания цепи, или в его задержке на какое-то время после разрыва цепи.

Описанное явление можно наблюдать на опыте с лампочками, одна из которых подключена последовательно с индуктивностью (см. рис. 3).

Схема опыта с лампочкамиРис. 3. Схема опыта с лампочками

Как видно на рисунке слева, ток от источника питания, проходящий через лампочку 2, при замыкании контактов встретит сопротивление вихревых токов, поскольку они противоположно направлены. Поэтому зажигание этой лампочки произойдёт с задержкой.

На время включения лампочки 1 вихревые токи повлияют, но сила тока в её цепи уменьшится после зажигания лампы 2. При отключении цепи от источника питания произойдёт обратный процесс: лампочка в цепи индуктивности некоторое время будет медленно угасать, а вторая лампа потухнет сразу после разъединения контактов.

График на рисунке 4 красноречиво объясняет эффект задержки.

Иллюстрация задержки изменения тока в цепи индуктивностиРис. 4. Иллюстрация задержки изменения тока в цепи индуктивности

Обратите внимание на нелинейность изменения силы тока по времени.

Аналогичные процессы происходят в цепи, состоящей из одной катушки. На рисунке 5 изображена такая схема и график изменения силы тока.

Возникновение самоиндукции
Рис. 5. Возникновение самоиндукции

Остаётся добавить, что скорость изменение величины ЭДС зависит от количества витков соленоида. Чем больше витков, тем больше влияние вихревых токов, на параметры цепи.

В случае с переменным током амплитуда ЭДС самоиндукции пропорциональна амплитуде синусоиды питания, её частоте и индуктивности катушки.

Синусоидальный ток, проходя через катушку индуктивности, сдвигается по фазе на величину π/2. Именно этот сдвиг является причиной отставания собственного тока катушки от тока, вырабатываемого источником питания.

Формулы

Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.

При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:

ЭДС самоиндукции

где Eсамоинд. – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.

Индуктивность

Выше мы отметили, что индуктивность контура зависит от его геометрии и размеров, а также от магнитной проницаемости среды. Если речь идёт о катушке, то эти утверждения справедливы и для неё. На индуктивность катушки влияет её диаметр и количество витков. Индуктивность существенно повышается, если в катушку добавить ферромагнитный сердечник.

Магнитные поля отдельных витков катушки складываются. Если витков достаточно много, то ток, протекающий через катушку, образует вокруг неё сильное магнитное поле, реагирующее на изменения электрического поля. Индуктивность является той величиной, которая характеризует то, насколько сильно проводник, из которого состоят витки, противодействует электрическому току.

Чем больше индуктивность катушки и чем выше скорость прерывания её цепи, тем больший всплеск ЭДС произойдёт в цепи. При этом полярность вихревых токов на выводах катушки противоположна направлению тока источника питания.

Индуктивность (то есть коэффициент пропорциональности) является важной характеристикой катушек, дросселей и других контурных элементов. Этот параметр можно сравнить с ёмкостью конденсаторов. Тем более что действие катушки индуктивности и конденсатора в электрических цепях очень похожи. RL и RC цепочки часто используют для сглаживания всплесков напряжений в различных фильтрах.

Единицей измерения индуктивности в международной системе СИ является генри. Величина размеров в 1 Гн – это такая индуктивность, при которой ЭДС составляет 1 В, при скорости изменения тока на 1 А за секунду.

Индуктивность определяет количество энергии, выделяющейся в результате действия собственного магнитного поля при самоиндукции. Эту энергию легко рассчитать по формуле: Wм = LI2/2.

Собственная энергия катушки численно равна работе, которую необходимо выполнить источником питания при преодолении ЭДС самоиндукции.

Важно знать, что в результате резкого разрыва цепи с большой индуктивностью, энергия высвобождается в виде искры или даже с образованием дугового разряда.

Примеры использования на практике

Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.

Работает этот важный узел следующим образом:

  1. На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
  2. Электрическая цепь резко обрывается специальным прерывателем.
  3. Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
  4. Искровой разряд зажигает топливную смесь, приводя в движение поршень.

В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.

Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.

В блоках питания электронной аппаратуры таким же способом убирают:

  • шумы:
  • пульсации;
  • нежелательные частоты.

Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.

Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.

В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.

В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.

Видео в помощь

Самоиндукция — Википедия

Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре [1] при изменении протекающего через контур тока.

При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем).

Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока[4].

При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с силой инерции.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока(переменного) i{\displaystyle i}:

E=−Ldidt{\displaystyle {\mathcal {E}}=-L{\frac {di}{dt}}}.

Коэффициент пропорциональности L{\displaystyle L} называется коэффициентом самоиндукции или индуктивностью контура (катушки).

Самоиндукция и синусоидальный ток

В случае синусоидальной зависимости тока, текущего через катушку, от времени, ЭДС самоиндукции в катушке отстает от тока по фазе на π/2{\displaystyle \pi /2} (то есть на 90°), а амплитуда этой ЭДС пропорциональна амплитуде тока, частоте и индуктивности (E0=LωI0{\displaystyle {\mathcal {E}}_{0}=L\omega I_{0}}). Ведь скорость изменения функции — это её первая производная, а dsin⁡ωtdt=ωcos⁡ωt=ωsin⁡(ωt+π/2){\displaystyle {\frac {d\sin \omega t}{dt}}=\omega \cos \omega t=\omega \sin(\omega t+\pi /2)}.

Для расчета более или менее сложных схем, содержащих индуктивные элементы, то есть витки, катушки и т.п. устройства, в которых наблюдается самоиндукция, (особенно, полностью линейных, то есть не содержащих нелинейных элементов[5]) в случае синусоидальных токов и напряжений применяют метод комплексных импедансов или, в более простых случаях, менее мощный, но более наглядный его вариант — метод векторных диаграмм.

Заметим, что всё описанное применимо не только непосредственно к синусоидальным токам и напряжениям, но и практически к произвольным, поскольку последние могут быть практически всегда разложены в ряд или интеграл Фурье и таким образом сведены к синусоидальным.

В более или менее непосредственной связи с этим можно упомянуть о применении явления самоиндукции (и, соответственно, катушек индуктивности) в разнообразных колебательных контурах, фильтрах, линиях задержки и других разнообразных схемах электроники и электротехники.

Видео по теме

Самоиндукция и скачок тока

За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи, при этом (при резком размыкании) величина ЭДС самоиндукции может в этот момент значительно превышать ЭДС источника.

Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение зажигания при напряжении питающей батареи 12В составляет 7-25 кВ. Впрочем, превышение ЭДС в выходной цепи над ЭДС батареи здесь обусловлено не только резким прерыванием тока, но и коэффициентом трансформации, поскольку чаще всего используется не простая катушка индуктивности, а катушка-трансформатор, вторичная обмотка которой как правило имеет во много раз большее количество витков (то есть, в большинстве случаев схема несколько более сложна, чем та, работа которой полностью объяснялось бы через самоиндукцию; однако физика её работы и в таком варианте отчасти совпадает с физикой работы схемы с простой катушкой).

Это явление применяется и для поджига люминесцентных ламп в стандартной традиционной схеме (здесь речь идет именно о схеме с простой катушкой индуктивности — дросселем).

Кроме того, его надо учитывать всегда при размыкании контактов, если ток течет по нагрузке с заметной индуктивностью: возникающий скачок ЭДС может приводить к пробою межконтактного промежутка и/или другим нежелательным эффектам, для подавления которых в этом случае, как правило, необходимо принимать разнообразные специальные меры.

См. также

Примечания

  1. ↑ Контур может быть и многовитковым — то есть, в частности, катушкой. В этом случае, так же как и в случае одиночного контура, строго говоря, контур должен быть замкнутым (например, через вольтметр, измеряющий ЭДС), но на практике при (очень) большом количестве витков различие ЭДС в полностью замкнутом контуре и в контуре с разрывом (геометрически даже большим по сравнению с размером катушки) может быть пренебрежимым.
  2. ↑ Поскольку магнитный поток через контур пропорционален току в контуре. Для тонкого жесткого контура (для какового случая это утверждение и является точным) точная пропорциональность очевидна исходя из закона Био-Савара, так как исходя из него вектор магнитной индукции просто пропорционален току, а поток этого вектора (что и называется магнитным потоком) через фиксированную (она не меняется при жестком контуре) поверхность тогда тоже пропорционален току. Формально это записывается в виде равенства: магнитный поток = коэффициент самоиндукции• ток в контуре.
  3. ↑ В случае сложной формы контура, например, если контур многовитковый (катушка), поверхность, ограниченная контуром (или, как говорят, «натянутая на контур») оказывается достаточно сложной, что ничуть не меняет сути описываемого явления. Для упрощения понимания случая многовитковых контуров (катушек) можно (приближенно) считать поверхность, натянутую на такой контур, состоящей из множества (стопки) поверхностей, каждая из которых натянута на свой отдельный единичный виток.
  4. ↑ Калашников С. Г., Электричество, М., ГИТТЛ, 1956, гл. IX «Электромагнитная индукция», п. 107 «Исчезновение и установление тока», с. 221 — 224;
  5. ↑ Сами индуктивные элементы являются линейными, то есть подчиняются линейному дифференциальному уравнению, приведенному в статье выше. Впрочем, это уравнение в реальности выполняется лишь приближенно, так что индуктивные элементы являются линейными также лишь приближенно (хотя иногда и с крайне хорошей точностью). Также в реальности встречаются отклонения от идеального уравнения, носящие линейный характер (например, связанные с упругими деформациями катушки в линейном приближении).

Ссылки

3.4.6 Индуктивность. Самоиндукция. ЭДС самоиндукции

Видеоурок: Индуктивность контура (катушки). Явление самоиндукции

Лекция: Индуктивность. Самоиндукция. ЭДС самоиндукции

Самоиндукция

Считается, что индуктивный ток действует сам на себя некоторым образом. Так как индуктивный ток достаточно нестабилен, то он вызывает собственное изменение магнитного потока, а это значит, что в таком проводнике должен бежать ток, в результате изменения потока. Такое явление называется самоиндукцией.

Итак, давайте представим некоторый проводник в виде кольца. Если ток индукции в нем течет против часовой стрелки (он увеличивается), то магнитное поле будет направлено вертикально вверх (оно увеличивается).

Это значит, что появляется некоторое вихревое поле, направленное в противоположном направлении относительно направления движения тока. Таким образом, оно пытается тормозить ток. Однако моментально ток затормозить не может, поэтому магнитное поле изменяется на протяжении некоторого времени.

Если же ток в проводнике будет уменьшаться, что также приводит к уменьшению магнитного поля, то вихревое электрическое поле наоборот начнет ускорять ток в проводнике.

Таким образом, можно сделать вывод, что любое изменение тока и поля будет приводить к появлению внутреннего ЭДС, которое будет либо тормозить, либо ускорять индукционный ток.

Индуктивность

Итак, нам уже известно, что поток описывает магнитное поле, значит, величина потока пропорциональна индукции. Коэффициент, связывающий индукцию и поток, называется индуктивностью.

Определяется индуктивность с помощью геометрических размеров проводника, а также материалом, из которого он создан.

Единицами измерения индуктивности являются Генри (Гн).

Если использовать данную формулу для ЭДС индукции, можно получить:

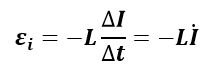
То есть ЭДС пропорционально производной силы тока.


Самоиндукция

Задачи разные, последняя – довольно непростая. Обращаю ваше внимание на необходимость подсчеты вести в системе СИ: то есть переводить длины в м, площади-  в м^2, различные мили- и микро- величины не забывать представлять с помощью соответствующих степеней 10-ки.

Задача 1. Через соленоид индуктивностью L=0,2 мГн и площадью поперечного сечения S=10 см^2 проходит ток силой I=0,5 А. Какова индукция магнитного поля внутри соленоида, если он содержит N=200 витков?

    \[\Phi=NBS=LI\]

Откуда

    \[B=\frac{LI}{NS}=\frac{0,2\cdot10^{-3}\cdot0,5}{200\cdot10\cdot10^{-4}}=5\cdot10^{-4}\]

Ответ: 500 мкТл

Задача 2. Плоская прямоугольная рамка со сторонами 5 см и 15 см находится в магнитном поле с индукцией B=0,2 Тл, перпендикулярной плоскости рамки. По рамке течет ток I=1 А. Эту рамку превращают в окружность, не изменяя периметра и ориентации плоскости рамки. При этом сила тока также не изменяется.  Найти величину работы по изменению формы рамки.

При изменении формы рамки изменится ее площадь. Поэтому

    \[A=I\Delta\Phi=IB\Delta S\]

Периметр прямоугольной рамки равен 40 см, а ее площадь – 75 см^2. Тогда длина окружности тоже равна 40 см, а ее радиус

    \[2 \pi R=40\]

    \[R=\frac{40}{2\pi}=\frac{20}{\pi}\]

А площадь рамки будет

    \[S=\pi R^2=\frac{400}{\pi}\]

Изменение площади (в см^2):

    \[\Delta S=\frac{400}{\pi}-75=52\]

Работа равна

    \[A=IB\Delta S=1\cdot0,2\cdot52\cdot10^{-4}=0,001\]

Ответ: 1 мДж

Задача 3. Катушка сопротивлением R=10 Ом и индуктивностью L=0,02 Гн находится в переменном магнитном поле. Когда создаваемый этим полем поток увеличился на \Delta \Phi=4\cdot10^{-3} Вб, ток в катушке возрос на \Delta I=10 мА. Какой заряд прошел за это время по катушке?

С одной стороны,

    \[E=-\frac{\Delta \Phi}{\Delta t}\]

С другой стороны, она будет складываться из падения напряжения на резисторе и ЭДС самоиндукции на катушке:

    \[E=IR+L\frac{\Delta I}{\Delta t}=\frac{\Delta q}{\Delta t}R+ L\frac{\Delta I}{\Delta t}\]

То есть, приравнивая, имеем:

    \[\Delta \Phi=\Delta q\cdot R+L \Delta I\]

Тогда

    \[\Delta q=\frac{\Delta \Phi - L \Delta I }{R}=\frac{4\cdot10^{-3}-0,02\cdot10^{-2}}{10}=3,8\cdot10^{-4}\]

Ответ: 0,38 мКл

Задача 4. Два одинаковых конденсатора емкостью C=8 мкФ каждый и катушка индуктивности (L=10 мТл) соединены по схеме (см. рис.). В начальный момент ключ K разомкнут, левый конденсатор заряжен до напряжения U=1 В. Правый конденсатор не заряжен, и ток в катушке отсутствует. Определите максимальное значение силы тока в катушке после замыкания ключа. Сопротивлением катушки пренебречь.

самоиндукция

Рисунок 1 к задаче 4

На первом конденсаторе заряд равен q_1=C_1U_1, и он им поделится со вторым, когда ключ замкнется. «Дележ» произойдет таким образом, что напряжения на обоих конденсаторах будут равны: пополам, ведь емкости тоже одинаковые. Тогда:

    \[q_1

Новое напряжение будет равно

    \[U_2=\frac{q_1

Так как конденсаторы соединены параллельно, их емкости можно сложить, получив эквивалентный конденсатор:

    \[C_2=2C=16\cdot10^{-6}\]

Тогда энергия поля такого конденсатора равна

    \[W_e=\frac{C_2U_2^2}{2}\]

Эта энергия перейдет в энергию магнитного поля:

    \[W_e=W_m=\frac{LI^2}{2}\]

Откуда

    \[C_2U_2^2= LI^2\]

    \[I=\sqrt{\frac{2W_e}{L}}=U_2\sqrt{\frac{ C_2}{L}}=0,5\sqrt{\frac{16\cdot10^{-6}}{10^{-2}}}=0,02\]

Ответ: 0,02 А.

Задача 5. Две катушки индуктивностями L_1=5 мГн и L_2=1 мГн подключены через ключи K_1 и K_2 к конденсатору емкости C=20 нФ. В начальный момент времени оба ключа разомкнуты, а конденсатор заряжен до напряжения U_0=30 В. Сначала замыкают ключ K_1 и, когда напряжение на конденсаторе станет равным нулю, замыкают ключ 2. Определите минимальный ток, протекающий через катушку L_1 после замыкания ключа K_2. Сопротивлением катушек пренебречь.

самоиндукция

Рисунок 2 к задаче 5

В тот момент, когда замыкают второй ключ, вся энергия сосредоточилась в первой катушке:

    \[\frac{L_1I_m^2}{2}=\frac{CU^2}{2}\]

Откуда

    \[I_m=U\sqrt{\frac{C}{L_1}}\]

Но это – максимальное значение тока, а нас просят найти минимальное. Когда замкнут второй ключ, напряжение на катушках равное: E_1=E_2, и, следовательно,

    \[L_1\frac{dI_1}{dt}= L_2\frac{dI_2}{dt}\]

То есть

    \[L_1\Delta I_1= L_2\Delta I_2\]

Тогда разность между фактическим током в первой катушке и максимальным в любой момент времени равна I_1(t)-I_m, и это позволяет записать:

    \[L_1(I_1(t)-I_m)=L_2 I_2(t)\]

В момент времени, когда \frac{dI_1}{dt}=0, E_1=0, то есть заряд на конденсаторе равен нулю (вся энергия сосредоточена в катушках). Для такого момента времени можно записать закон сохранения энергии:

    \[\frac{L_1I_1^2}{2}+\frac{L_2I_2^2}{2}=\frac{L_1I_m^2}{2}\]

Решим систему уравнений:

    \[\begin{Bmatrix}{ L_1(I_1(t)-I_m)=L_2 I_2(t)}\\{ L_1I_1^2+L_2I_2^2=L_1I_m^2}\end{matrix}\]

    \[I_2=\frac{ L_1(I_m-I_1(t))}{L_2}\]

Тогда

    \[L_1I_1^2+\frac{ L_1^2(I_m-I_1(t))^2}{L_2}=L_1I_m^2\]

    \[I_1+I_m=\frac{L_1}{L_2}(I_m-I_1)\]

    \[I_1(\frac{L_1}{L_2}+1)=I_m(\frac{L_1}{L_2}-1)\]

    \[I_1=I_m\frac{L_1-L_2}{L_2+L_1}\]

А если подставить I_m=U\sqrt{\frac{C}{L_1}}, то

    \[I_1=U\sqrt{\frac{C}{L_1}}\cdot\frac{L_1-L_2}{L_2+L_1}\]

ЭДС самоиндукции — это… Что такое ЭДС самоиндукции?


ЭДС самоиндукции

Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока.

При изменении тока в контуре меняется поток магнитной индукции через поверхность, ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи эдс препятствует возрастанию тока, а при уменьшении тока — убыванию.

Величина ЭДС пропорциональна скорости изменения силы тока I и индуктивности контура L:

\mathcal E = -L \frac{dI}{dt}.

За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи, при этом величина ЭДС самоиндукции может значительно превышать ЭДС источника. Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение самоиндукции при напряжении питающей батареи 12В составляет 7-25кВ.

Wikimedia Foundation. 2010.

Смотреть что такое «ЭДС самоиндукции» в других словарях:

  • эдс самоиндукции — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN self induced emfFaraday voltageinductance voltageself induction… …   Справочник технического переводчика

  • Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре [1]при изменении протекающего через контур тока. При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение… …   Википедия

  • ИНДУКТИВНОСТЬ — (от лат. inductio наведение, побуждение), величина, характеризующая магн. св ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо… …   Физическая энциклопедия

  • реактивная мощность — Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… …   Справочник технического переводчика

  • ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ — раздел физики, охватывающий знания о статическом электричестве, электрических токах и магнитных явлениях. ЭЛЕКТРОСТАТИКА В электростатике рассматриваются явления, связанные с покоящимися электрическими зарядами. Наличие сил, действующих между… …   Энциклопедия Кольера

  • электрический трансформатор — электрический машина, не имеющая подвижных частей и преобразующая переменный ток одного напряжения в переменный ток другого напряжения. В простейшем случае состоит из магнитопровода (сердечника) и расположенных на нём двух обмоток  первичной и… …   Энциклопедический словарь

  • Импульсный стабилизатор напряжения — Импульсный стабилизатор напряжения  это стабилизатор напряжения, в котором регулирующий элемент работает в ключевом режиме[1], то есть большую часть времени он находится либо в режиме отсечки, когда его сопротивление максимально, либо в… …   Википедия

  • Катушка индуктивности — У этого термина существуют и другие значения, см. Катушка (значения). Катушка индуктивности (дроссель) на материнской плате компьютера …   Википедия

  • Индуктивность — Размерность L2MT−2I−2 Единицы измерения СИ Гн СГС …   Википедия

  • Диод — У этого термина существуют и другие значения, см. Диод (значения). Четыре диода и диодный мост. Диод (от др. греч …   Википедия

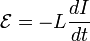Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *