Текстовые задачи: смеси и сплавы
Задание 11 ЕГЭ по математике, 22 ОГЭ по математике. Практика.Шаблон: sm-cs-shab.pdf
С решениями: sm-cs.pdf
Источник: vk.com/math_for_100
Алгоритм решения
Прототипы
Прототип 1: Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 18-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Прототип 2: Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Прототип 3: Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Прототип 4: Имеется два сплава. Первый сплав содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Прототип 5: В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Прототип 6: Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси.
Прототип 7: Имеются два сосуда с растворами кислоты различной концентрации. Первый содержит 30 кг раствора, а второй – 20 кг раствора. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Прототип 8: Виноград содержит 90% влаги, а изюм – 5%. Сколько килограммов винограда требуется для получения 20 кг изюма?
Сколько килограммов винограда требуется для получения 20 кг изюма?
Решение задач на смеси, сплавы и растворы для ЕГЭ по математике
Хочу продолжить тему, начатую одним из моих коллег – решение задач на смеси, сплавы и растворы.
Подобные задачи довольно часто встречаются в реальных и демонстрационных вариантах ОГЭ и ЕГЭ. В обычных школах таким задачам не уделяется должного внимания и даже у учеников 11 классов возникают сложности при их решении.
Рассмотрим решение на примере не сложной задачи.
Имеется два сплава. Первый содержит 10% никеля, второй – 25% никеля. Из этих двух сплавов получили третий сплав массой 105 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Обозначим: m1 — масса первого сплава. Если третий сплав, получившийся из двух, равен 105 кг, то масса второго сплава (105-m1)кг.
Главная идея решения – равенство масс чистого вещества в начале и после соединения сплавов.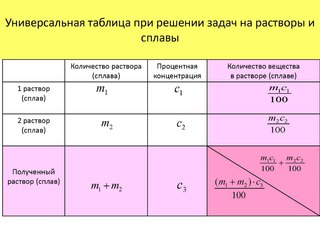
Найдём количество чистого никеля в первом сплаве — 0,1 m1
Количество чистого никеля во втором сплаве — 0,25(105-m1).
Тогда общая масса чистого никеля в обоих сплавах – (0,1 m1+0,25(105-m1))кг. (1)
После соединения сплавов общая масса 105кг, а содержание никеля 20%, тогда в новом славе чистого никеля будет – 0,20*105кг. (2).
Чистый никель никуда не исчез и нового чистого никеля не добавлено, значит величины (1) и (2) равны.
Запишем уравнение ( 0,1 m1+0,25(105-m1))= 0,20*105, решая его находим m1=35,
масса второго сплава 105 -35 = 70кг. И в итоге 70 – 35=35кг — масса первого сплава больше массы второго на 35кг. Ответ: 35
Решим ещё задачу.
Имеется два сосуда. Первый содержит 100кг., а второй -20кг. раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 72% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 78% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение.
Пусть к – концентрация первого раствора, р – концентрация второго раствора. Чистой кислоты в первом растворе – 100к кг., во втором – 20р кг. и всего в двух растворах – (100к +20р) кг.
Если смешать растворы, то вес нового раствора -120кг. и концентрация 72%., при том же количестве, что и в начале, чистой кислоты, т.е (100к +20р) = 0,72*120 (1).
Возьмём теперь равные массы растворов, для простоты возьмём по 10кг.
Определим начальное количество чистой кислоты в обоих растворах. В первом растворе 10к чистой кислоты, во втором 10р чистой кислоты. Тогда всего вначале чистой кислоты было (10к +10р) кг. Масса нового раствора 10+10 =20 кг и по условию его концентрация 0,78. Чистой кислоты в новом растворе – 0,78*20. По условию равенства чистого вещества (10к +10р)= 0,78*20 (2).
Решая совместно (1) и (2) получаем к = 0,69, тогда чистой кислоты в первом растворе – 69кг. Отв.: 69
Теперь посмотрим как легко решается известная задача про изюм и виноград.
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 14 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
Решение.
Если в винограде 90% воды, значит 10% чистого изюма (название образное).
В изюме (магазинном) должно быть 95% чистого изюма. В 14кг. магазинного изюма чистого изюма будет чуть меньше — 14*0,95= 13,3кг. Это количество необходимо набрать из винограда, где только 10% чистого изюма. Значит 13,3 кг в винограде, должны составлять десятую часть, тогда необходимо взять 133 кг. винограда. В 133кг. винограда будет 13,3 чистого изюма, что позволит иметь 14 кг магазинного изюма. Ответ: 133
При решении всех простых задачах на сплавы, смеси, и растворы применяют условие равенства чистых масс вещества в начале и после соединения. В более сложных, это условие помогает найти ходы решения.
В завершении приведу решение сложной задачи, решение которой опирается на понятие «концентрация». Такая задача может быть в задании 11 профильного ЕГЭ. Обычно такого рода задачи прорешивают заранее, чтобы на экзамене не возникла тревога при виде сложного и на первый взгляд, запутанного условия.
Такая задача может быть в задании 11 профильного ЕГЭ. Обычно такого рода задачи прорешивают заранее, чтобы на экзамене не возникла тревога при виде сложного и на первый взгляд, запутанного условия.
В сосуде было 20 литров соляной кислоты. Часть кислоты отлили, и сосуд дополнили водой. Затем отлили в два раза большую (чем в первый раз) часть полученной смеси и снова дополнили сосуд водой. В результате получился 28% раствор кислоты. Сколько литров кислоты отлили в первый раз?
Редакция не несет ответственности за наполнение блогов, они есть персональным мнением автора
Решение задачи на растворы
Я уже объясняла принцип решения задач на растворы здесь. В этой статье я приведу пример решения чуть более сложной задачи.
Решим задачу: из Открытого банка заданий для подготовки к ЕГЭ по математике:
Задание B13 (№ 99577)
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Вспомним, что процентное содержание выражается формулой: . В этой формуле
Р — процентное содержание;
m — масса чистого вещества;
M — масса раствора или сплава.
Тогда
Чтобы решить эту задачу, составим таблицу:
Поскольку в задаче не дана масса каждого раствора, примем массу первого раствора за , а второго за , и, исходя из этого, найдем массу чистого вещества в каждом растворе:
Теперь будем заносить в таблицу все действия, которые описаны в условии задачи. По условию в раствор добавили 10 кг чистой воды. При этом масса раствора увеличилась на 10 кг, а масса чистого вещества не изменилась. В результате получили 36-процентный раствор кислоты:
Теперь у нас достаточно данных, чтобы составить первое уравнение системы. (Поскольку у нас две неизвестных величины, мы должны составить два уравнения. )
)
Читаем условие дальше:
Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты…Добавляем в таблицу эти данные:
то получили бы 41-процентный раствор кислоты:
Можем записать второе уравнение системы:
Получили систему уравнений:
Решим ее.
В ответе нужно записать, сколько килограммов 30-процентного раствора использовали для получения смеси, то есть х.
Ответ: 60.
И.В. Фельдман, репетитор по математике.
Задача на растворы.
Задание B13 (№ 99572) из Открытого банка заданий для подготовки к ЕГЭ по математике:
Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
В задачах на сплавы и растворы используется одна единственная формула:
%, где
P — процентное содержание чистого вещества в сплаве или растворе,
m — масса чистого вещества
M — масса сплава или раствора.
Задачи на сплавы и растворы удобно решать с помощью таблицы. Порядок заполнения таблицы такой:
1. Сначала решаем, какую величину мы примем за неизвестное, и заполняем тот столбец таблицы, в котором речь идет об этой величине.
2. Заполняем тот столбец, параметры которого даны.
3. Параметры третьего столбца выражаем через параметры первых двух.
Поясню алгоритм решения задачи на сплавы и растворы на примере данной задачи.
1. Поскольку в условии масса первого раствора не указана, примем ее за х. Масса второго раствора равна массе первого и тоже равна х. После того, как растворы смешали, мы получила раствор, масса которого равна 2х.
Начнем заполнять таблицу:
2. В условии задачи дано процентное содержание вещества в каждом растворе. Внесем эти условия в соответствующий столбец таблицы:
3. Параметры второго столбца, то есть массу чистого вещества выразим через параметры первых двух. Для этого воспользуемся формулой:
:
Процентное содержание вещества в получившемся растворе равно
массе вещества:
разделить
на массу раствора: ,
и умножить на 100%
Получим:
%%
Ответ: 17%.
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачатьFirefox
Задачи на растворы и смеси с решениями. Для ЕГЭ.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА РАСТВОРЫ И СМЕСИ
Для решения задач этого типа удобно использовать таблицу
|
Раствор (смесь) |
Масса раствора (смеси) |
1-й компонент |
2-компонент |
||
|
% концентрации |
масса |
% концентрации |
масса |
||
Примеры задач
- 1.
 Имеется 40 литров 0,5 % раствора и 50 литров 2% раствора уксусной кислоты. Сколько нужно взять того и другого, чтобы получить 30 литров 1,5% — го раствора уксусной кислоты.
Имеется 40 литров 0,5 % раствора и 50 литров 2% раствора уксусной кислоты. Сколько нужно взять того и другого, чтобы получить 30 литров 1,5% — го раствора уксусной кислоты.
Решение:
|
Раствор (смесь) |
Объем (масса) раствора (смеси) |
Уксусная кислота |
Вода |
||
|
% концентрации |
масса |
% концентрации |
масса |
||
|
1 |
40 л |
0,5 % |
|||
|
2 |
50 л |
2 % |
|||
|
1 |
х |
0,5 % |
0,005х |
||
|
2 |
30-х |
2 % |
0,02(30-х) |
||
3 |
30 |
1,5 % |
0,015*30 |
||
0,005х + 0,02(30-х) = 30*0,015
х = 10 литров
Ответ: 10 литров, 20 литров.
- 2. Имеется два сосуда, содержащие 4 кг и 6 кг раствора кислоты разной концентрации. Если их слить, то получится 35 % раствор. Если слить равные массы этих растворов, то получится 36% раствор. Найти концентрацию каждого раствора?
Решение:
|
Раствор (смесь) |
Объем (масса) раствора (смеси) |
кислота |
Вода |
||
|
% концентрации |
масса |
% концентрации |
масса |
||
|
1 |
4 кг |
|
4*0,01х |
||
|
2 |
6 кг |
y |
6*0,01у |
||
|
3 |
10 кг |
35 % |
0,35*10 |
||
|
4 |
1+1 |
36 % |
0,36*2х |
||
4*0,01х + 6*0,01у = 10*0,35
0,01х + 0,01у = 2*0,36
Ответ: 41%, 31%.
- 3. Влажность сухого цемента на складе 18 %. Во время дождей влажность повысилась на 2 %. Какова стала масса цемента, если его было 400 кг.
Решение:
|
Раствор (смесь) |
Объем (масса) раствора (смеси) |
вода |
Сухое вещество |
||
|
% концентрации |
масса |
% концентрации |
масса |
||
|
1 |
400 кг |
18% |
82% |
400*0,82 |
|
|
2 |
х кг |
20% |
80% |
х*0,8 |
|
400*0,82 = 0,8х
Ответ: 410 кг.
- 4. Из 38 тонн руды, содержащей 25% примесей, получили 30 тонн металла. Сколько процентов примесей содержит металл?
Решение:
|
Раствор (смесь) |
Объем (масса) раствора (смеси) |
примесь |
Основное вещество |
||
|
% концентрации |
масса |
% концентрации |
масса |
||
|
1 |
38 т |
25% |
75% |
38*0,75 |
|
|
2 |
30 т |
х |
30*0,01х |
||
38*0,75 = 30*0,01х
Ответ: 95% — содержание металла, 5% — содержание примесей.
- 5. В 4 кг сплава меди и олова содержится 40 % олова. Сколько кг олова надо добавить к этому сплаву, чтобы его процентное содержание было 70%?
Решение:
|
сплав |
Масса сплава |
медь |
олово |
||
|
% |
масса |
% |
масса |
||
|
1 |
4 кг |
40% |
4*0,4 |
||
|
2 |
х |
100 % |
х |
||
|
3 |
4+х |
70% |
0,7*(4+х) |
||
4*0,4 +х = 0,7(4+х)
Ответ: х=4
- 6.
 Имеется два сплава золота и серебра. В одном эти металлы находятся в отношении 2:3, в другом 3:7. Сколько нужно взять каждого сплава, чтобы получить 8 кг нового сплава, в котором эти металлы были бы в отношении 5:11?
Имеется два сплава золота и серебра. В одном эти металлы находятся в отношении 2:3, в другом 3:7. Сколько нужно взять каждого сплава, чтобы получить 8 кг нового сплава, в котором эти металлы были бы в отношении 5:11?
Решение:
|
сплав |
Масса сплава |
золото |
серебро |
||
|
% |
масса |
% |
масса |
||
|
1 |
х |
2 |
2/5х |
3 |
|
|
2 |
8-х |
3 |
(3/10) (8-х) |
7 |
|
|
3 |
8 |
5 |
8 * 5/16 |
11 |
|
2/5x+3/10(8-x)=8*5/16
х = 1
Ответ: золота – 1 кг, серебра – 7 кг.
как сдать часть 2 ЕГЭ по математике — Учёба.ру
Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно
Татьяна Петрова,
аспирантка механико-математического факультета МГУ им. Ломоносова,
преподаватель математики учебного центра Challenge
Задание № 9
Что требуетсяВыполнить вычисления и преобразования.
ОсобенностиЭто задача на вычисление значения числового или буквенного выражения. Здесь достаточно уметь выполнять действия с числами и знать определение и простейшие свойства степеней с рациональным показателем, тригонометрических функций, корней n-степени и логарифмов.
СоветыНужно знать базовые формулы и уметь их применять.
Задание № 10
Что требуетсяРешить задачу с прикладным содержанием.
Здесь предлагаются задачи прикладного характера, связанные с такими областями науки, как физика, химия, биология. В этом задании можно встретить все типы уравнений и неравенств: линейные, квадратные, степенные, рациональные, иррациональные, показательные, логарифмические и тригонометрические. Ваша задача — выразить требуемую величину из заданной формулы.
СоветыВнимательно читайте условие и старайтесь его понять. Следите, чтобы единицы измерения были приведены к одному виду. Выражайте ту или иную переменную в общем виде и только потом подставляйте числовые значения. Не спешите считать в лоб, пробуйте сокращать.
Задание № 11
Что требуетсяРешить текстовую задачу.
ОсобенностиВсего существует шесть типов текстовых задач. Они могут быть на движение, на совместную работу, на проценты, на смеси, растворы и сплавы, на прогрессии, на оптимальный выбор и целые числа. Соответственно, нужно знать основные законы и формулы для каждого типа. Традиционная текстовая задача сводится к составлению уравнения и его решению.
Соответственно, нужно знать основные законы и формулы для каждого типа. Традиционная текстовая задача сводится к составлению уравнения и его решению.
| Задачи на движение | \(S = V \cdot t\) |
| Задачи на совместную работу | \(A = p \cdot t\) |
| Задачи на смеси, растворы и сплавы | \(C = \frac{V_{1}}{ V} \cdot 100\%\) |
Обратите внимание, что формулы в задачах на движение и на работу очень похожи. Производительность — это аналог скорости. Для задач на смеси и растворы не забывайте формулу концентрации. В качестве неизвестной выбирайте искомую величину. Составленное уравнение будет рациональным и в основном сводится к линейному или квадратному.
Задание № 12
Что требуетсяНайти наибольшее или наименьшее значение функции.
ОсобенностиЗдесь требуется уметь находить производную функции, а также исследовать функцию с помощью производной. Вопрос может быть двух типов: найти точку минимума/максимума функции или найти наибольшее/наименьшее значение функции. Многие школьники не различают этих понятий, а ведь ответ будет совершенно разный. Еще в этом задании мы сталкиваемся с задачей нахождения минимума/максимума на отрезке или на всей действительной прямой. Если вас ограничивают отрезком, то не забывайте находить значения на его концах и сравнивать их с локальными минимумами/максимумами функции на отрезке.
Вопрос может быть двух типов: найти точку минимума/максимума функции или найти наибольшее/наименьшее значение функции. Многие школьники не различают этих понятий, а ведь ответ будет совершенно разный. Еще в этом задании мы сталкиваемся с задачей нахождения минимума/максимума на отрезке или на всей действительной прямой. Если вас ограничивают отрезком, то не забывайте находить значения на его концах и сравнивать их с локальными минимумами/максимумами функции на отрезке.
Выучите базовую таблицу производных, а также формулы производной произведения, частного и композиции функций. Помните, что если производная положительна, то функция растет, если производная отрицательна — функция убывает. Когда производная меняет свой знак с плюса на минус, это значит, что мы попали в точку максимума. Если производная поменяла свой знак с минуса на плюс, значит, мы попали в точку минимума.
Задание № 13
Что требуетсяРешить тригонометрическое, рациональное, показательное, логарифмическое уравнение, уравнение с радикалом или смешанное уравнение, содержащее одновременно логарифмы, модули, радикалы.
Для решения любого уравнения существует два основных правила. Во-первых, решение всегда должно начинаться с нахождения ОДЗ — области допустимых значений, то есть всех значений переменной, при которых это уравнение имеет смысл. Во-вторых, нужно помнить основные методы решения уравнений и уметь применять их. Как правило, решение данной задачи требует замены, позволяющей свести уравнение к квадратному.
СоветыДля решения тригонометрических уравнений важно знать формулы приведения и знаки тригонометрических функций на четвертях окружности. Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций к аргументам первой четверти. Помните про мнемоническое правило («правило лошади»), которое позволит вам не заучивать все многообразие формул приведения: если вы откладываете угол от вертикальной оси, то «лошадь говорит вам „да“», то есть кивает головой вдоль оси ординат, тем самым вы меняете функцию. Если вы откладываете угол от горизонтальной оси, то «лошадь говорит вам „нет“», то есть кивает головой вдоль оси абсцисс, следовательно, приводимая функция не меняет своего названия (не забудьте про знак, он совпадает со знаком исходной функции!).
Если вы откладываете угол от горизонтальной оси, то «лошадь говорит вам „нет“», то есть кивает головой вдоль оси абсцисс, следовательно, приводимая функция не меняет своего названия (не забудьте про знак, он совпадает со знаком исходной функции!).
Задание № 14
Что требуетсяРешить стереометрическую задачу.
ОсобенностиЭто задача на построение сечения многогранника и нахождение его площади, а также на нахождение расстояний и углов в пространстве, нахождение объемов различных многогранников и круглых тел (цилиндр, конус, шар). Здесь нужно хорошо владеть формулировками аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства, знать формулы площадей и объемов. Также в этом задании нужно понимать, что такое угол между прямыми, угол между скрещивающимися прямыми, угол между прямой и плоскостью и угол между плоскостями (вспомните, что такое линейный угол двугранного угла).
СоветыВ этой задаче, как правило, два пункта. В первом пункте нужно либо что-то построить, либо доказать. Для доказательства очень часто используются признаки подобия треугольников и теорема Фалеса. Во втором пункте нужно найти угол, расстояние или площадь. Вспомните основные формулы расстояний: расстояние от точки до прямой, от точки до плоскости, между двумя плоскостями. Вы должны знать основные тригонометрические функции, теорему синусов и косинусов, теорему Пифагора и теорему о трех перпендикулярах. Нужно уметь проводить дополнительные построения и владеть координатным и векторным методами.
В первом пункте нужно либо что-то построить, либо доказать. Для доказательства очень часто используются признаки подобия треугольников и теорема Фалеса. Во втором пункте нужно найти угол, расстояние или площадь. Вспомните основные формулы расстояний: расстояние от точки до прямой, от точки до плоскости, между двумя плоскостями. Вы должны знать основные тригонометрические функции, теорему синусов и косинусов, теорему Пифагора и теорему о трех перпендикулярах. Нужно уметь проводить дополнительные построения и владеть координатным и векторным методами.
Задание № 15
Что требуетсяРешить тригонометрическое, рациональное, показательное, логарифмическое (в том числе с переменным основанием) неравенство, неравенство с радикалом, смешанное неравенство, содержащее одновременно логарифмы, модули, радикалы.
ОсобенностиЗдесь необходимо свести сложное неравенство к простейшему. Часто для этого используются замены показательных и тригонометрических функций (не забывайте про ограничения!). Также нужно знать метод интервалов и метод рационализации для логарифмических, показательных неравенств и неравенств, содержащих модуль.
Также нужно знать метод интервалов и метод рационализации для логарифмических, показательных неравенств и неравенств, содержащих модуль.
Метод решения логарифмических неравенств опирается на монотонность логарифмической функции. Помните, что если у логарифма переменное основание, то нужно рассматривать два случая: а) основание лежит в диапазоне от 0 до 1 (функция убывает), б) основание больше единицы (функция возрастает). Если основание переменное, то можно избавиться от перебора случаев, перейдя к новому, постоянному основанию.
В логарифмических неравенствах внимательно следите за областью допустимых значений, применяя формулы действий с логарифмами, она может как расширяться, так и сужаться. И если первую ситуацию легко исправить, то вторая приведет к потере решений, что недопустимо.
Задание № 16
Что требуетсяРешить планиметрическую задачу.
ОсобенностиПод этим номером может быть два варианта задания. Первый вариант: в задаче два пункта — а и b. В пункте a требуется что-то доказать, в пункте b — что-то найти. Могу сказать, что чаще всего надо начинать решать эту задачу именно с пункта b, а уже решение этого пункта поможет доказать пункт а. Как правило, абитуриентам проще что-то найти, чем доказать.
Первый вариант: в задаче два пункта — а и b. В пункте a требуется что-то доказать, в пункте b — что-то найти. Могу сказать, что чаще всего надо начинать решать эту задачу именно с пункта b, а уже решение этого пункта поможет доказать пункт а. Как правило, абитуриентам проще что-то найти, чем доказать.
Второй вариант: задача без подпунктов. Здесь чаще всего скрыт подводный камень: задача требует рассмотрения двух случаев и приводит к двум разным ответам. Например, в условии задачи сказано, что окружности касаются в точке A, но не сказано каким образом, внешним или внутренним. Часто бывает так, что выпускник рисует один рисунок и возможно даже находит правильный ответ. А второй случай он не рассматривает, в результате чего получает ровно половину баллов за это задание.
СоветыНеобходимое условие для решения этой задачи — хорошее владение теоретическим материалом, например, из классического учебника по геометрии для 7-9 классов (Л.С. Атанасян). Необходимо знать формулировки аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства и формулы. Изучите дополнительные методы: метод дополнительного построения, метод подобия, метод замены, метод введения вспомогательного неизвестного, метод удвоения медианы, метод вспомогательной окружности, метод площадей.
Изучите дополнительные методы: метод дополнительного построения, метод подобия, метод замены, метод введения вспомогательного неизвестного, метод удвоения медианы, метод вспомогательной окружности, метод площадей.
Также здесь важен рисунок. 80% успеха геометрической задачи — это правильно нарисованный рисунок. Сделайте большой, хороший, наглядный рисунок, не экономьте на нем место.
И последнее, лайфхак для абитуриента — для решения задач по планиметрии выучите пять формул площади треугольника: через высоту и основание, через две стороны и угол между ними, через радиус вписанной окружности, через радиус описанной окружности и формулу Герона.
| Площадь треугольника через высоту и основание | \(S = \frac{1}{2}a \cdot h_{a}\) |
| Площадь треугольника через две стороны и угол между ними | \(S = \frac{1}{2}a \cdot b \cdot \sin \alpha\) |
| Площадь треугольника через радиус вписанной окружности | \(S = p \cdot r\), где \(p = \frac{a+b+c}{2}\), \(r\) — радиус вписанной окружности |
| Площадь треугольника через радиус описанной окружности | \(S = \frac{a \cdot b \cdot c}{4R}\), где \(R\) — радиус описанной окружности |
| Формула Герона | \(S = {\sqrt{p(p-a)(p-b)(p-c)}}\), где \(p = \frac{a+b+c}{2}\) |
Задание № 17
Что требуетсяРешить текстовую задачу преимущественно экономического содержания на кредиты, вклады и оптимальный выбор.
Задача на злобу дня, которая появилась на ЕГЭ только в последние годы. Задания на банковские проценты могут быть двух типов: задачи на проценты по вкладам (депозитам) и задачи на проценты по кредитам. Помимо них под этим номером на ЕГЭ могут дать задачу на оптимизацию производства товаров и услуг, в которой необходимо будет либо использовать графическую интерпретацию, либо решать аналитически с помощью производной, чтобы понять, как минимизировать расходы или максимизировать прибыль.
СоветыВнимательно читайте условие задачи, вникайте в процедуры выдачи кредита или открытия вклада, которые там описываются. Каждый пункт условия сразу переводите в уравнение. Таким образом вы получите уравнение или систему уравнений, которые вам останется только решить. Чтоб подготовиться, изучите основные схемы кредитования с дифференцированными и аннуитетными платежами. В задачах оптимизации нужно уметь работать с линейными/нелинейными целевыми функциями с целочисленными/нецелочисленными точками экстремумов.
Задание № 18
Что требуетсяРешить уравнение или неравенство с параметрами, систему уравнений или неравенств с параметрами.
ОсобенностиЭти задачи сложно классифицировать и дать общий алгоритм решения, поскольку каждая из них является нестандартной, но можно изучить основные приемы и методы. Не забывайте про особенности функций: монотонность, непрерывность, четность/нечетность, ограниченность, инвариантность и т. д. Для того чтобы осилить задачу с параметром, необходимо произвести несложные, но последовательные рассуждения и составить логическую схему решения. Самое главное в этом задании — логика.
СоветыЧтобы подготовиться к заданиям с параметрами, я рекомендую решать задачи из учебников С.А. Шестакова «Задачи с параметрами», А.И. Козко и В.Г. Чирского «Задачи с параметрами для абитуриентов». Также хочется дать лайфхак для уравнений с двумя неизвестными: как правило, там спрятана геометрическая фигура, построй ее и получишь честное графическое решение.
Задание № 19
Что требуетсяРешить задачу на числа и их свойства.
ОсобенностиЭто самая сложная задача экзамена, олимпиадного уровня, она оценивается в четыре первичных балла. Тем не менее материал для ее решения школьники проходят еще в 6-8 классе. Задание требует хорошего логического мышления и математической культуры.
СоветыПовторите основные признаки делимости целых чисел, вспомните понятия «НОК/НОД», выучите формулы арифметической и геометрической прогрессии. «Прорешайте» типовые задания из сборника Г.И. Вольфсона и М.Я. Пратусевича «Арифметика и алгебра». Последние два задания (№ 18 и № 19) — это прямая заявка на 100 баллов.
Метод Пирсона в решении задач на смеси и сплавы
Среди текстовых задач нередки задачи типа приготовления растворов с заданной массовой долей растворенного вещества, смешением 2-х растворов разной концентрации или разбавлением раствора водой. Такие задачи решаются с помощью сложных арифметических расчётов. Но этот способ не рационален. Проще применить правило Пирсона (правило креста). Данный способ сводит решение задач к простейшему варианту, основанному на понятии пропорции. Такие задачи решаются с помощью сложных арифметических расчётов. Но этот способ не рационален. Проще применить правило Пирсона (правило креста). Данный способ сводит решение задач к простейшему варианту, основанному на понятии пропорции.В презентации, состоящей из 18 слайдов, содержится 2 части: теоретическая и практическая. В практической части приведено решение 6 задач, даны 5 задач с ответами и подборка из 7 задач для самостоятельного решения. © Наталия Михайловна Чичерова Наталия Михайловна ЧичероваПонравилось? Сохраните и поделитесь: По кнопке ниже вы можете скачать методическую разработку «Метод Пирсона в решении задач на смеси и сплавы» категории «ЕГЭ по математике» бесплатно. Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте. Характеристики документа: «презентация». Скачать материал 495.9 Kb Загрузка началась.  .. Понравился сайт? Получайте ссылки .. Понравился сайт? Получайте ссылкина лучшие материалы еженедельно! Подарок каждому подписчику! | Рекомендации:Порядок вывода комментариев: По умолчаниюСначала новыеСначала старые
| ||||||||||||||||||||||||||||||||||||||||
Патнэм | Математическая ассоциация Америки
Математическое соревнование имени Уильяма Лоуэлла Патнэма — это выдающееся соревнование по математике для студентов бакалавриата в США и Канаде. Конкурс Патнэма проводится ежегодно в первую субботу декабря. Соревнования состоят из двух 3-часовых сессий, одна утренняя и одна дневная. Во время каждого занятия участники индивидуально работают над 6 сложными математическими задачами.
Патнэм начался в 1938 году как соревнование между математическими факультетами колледжей и университетов. Теперь конкурс превратился в ведущий экзамен по математике университетского уровня в мире. Хотя участники работают над задачами самостоятельно, в соревновании присутствует и командный аспект. Призы присуждаются участникам с наивысшими баллами и математическим факультетам пяти вузов, сумма трех лучших баллов которых наибольшая.
Теперь конкурс превратился в ведущий экзамен по математике университетского уровня в мире. Хотя участники работают над задачами самостоятельно, в соревновании присутствует и командный аспект. Призы присуждаются участникам с наивысшими баллами и математическим факультетам пяти вузов, сумма трех лучших баллов которых наибольшая.
Соревнование в этом году вернулось к своему стандартному формату после года, сокращенного из-за пандемии, и включает индивидуальное соревнование и командное соревнование с наградами и призами.
Соревнования проходили в субботу, 4 декабря , под личным наблюдением в кампусах США и Канады. Участники (студенты бакалавриата) зарегистрировались для участия в конкурсе после регистрации научного руководителя из их учебного заведения. При регистрации участникам был присвоен идентификационный номер Патнэма (PIN), который им был необходим для участия в конкурсе 4 декабря. Любой колледж или университет в Соединенных Штатах или Канаде, желающий предложить конкурс своим студентам, должен назначить штатного преподавателя, который будет руководить конкурсом на местном уровне.
Проблемы и решения 82-го конкурса Патнэма
Задачи и решения 82-го конкурса Уильяма Лоуэлла Патнэма теперь доступны для загрузки. Перейдите по ссылкам ниже, чтобы получить доступ к файлам PDF. Проблемы и решения, начиная с 2017 года, можно найти на странице Архива соревнований Патнэма.
82-й конкурс задач Патнэма Сессия
82-е соревнование по задачам Патнэма, сессия B
82-я сессия Putnam Competition Solutions A Session
82nd Putnam Competition Solutions B Session
2019 Putnam Competition Проблемы и решения
Нажмите здесь , чтобы получить доступ к Объявлению победителей 2019 года, в которое входят стипендиаты Патнэма, следующие по рейтингу лица, почетные упоминания, лауреаты премии Элизабет Лоуэлл Патнэм, команды-победители и команды, заслужившие почетные упоминания.
Нажмите здесь, чтобы получить доступ к пресс-релизу Математического конкурса Уильяма Лоуэлла Патнэма 2019 года.
Результаты прошедших математических соревнований Уильяма Лоуэлла Патнэма также можно найти здесь.
Подготовка к Патнэму
Конкурс Патнэма охватывает ряд материалов по математике бакалавриата, включая элементарные понятия из линейной алгебры, современной алгебры, анализа и теории чисел.Ниже приведены некоторые доступные для покупки книги, которые могут помочь учащимся подготовиться к этому экзамену:
- Математические соревнования Уильяма Лоуэлла Патнэма. Задачи и решения, 1938–1964 гг. А. М. Глисон, Р. Э. Гринвуд и Л. М. Келли, редакторы
- Математические соревнования Уильяма Лоуэлла Патнэма Проблемы и решения 1965-1984 Джеральд Л. Александерсон, Леонард Ф. Клосински и Лорен С.
 Ларсон, редакторы
Ларсон, редакторы - Математическое соревнование Уильяма Патнэма 1985-2000: задачи, решения и комментарии Киран С.Кедлая, Бьорн Пунен и Рави Вакил
- Математическое соревнование Уильяма Патнэма 2001-2016 гг.: задачи, решения и комментарии
ИНФОРМАЦИЯ ДЛЯ ЗАРЕГИСТРИРОВАННЫХ УЧАСТНИКОВ НА 82-Й СОРЕВНОВАНИЕ PUTNAM
Соревнования проводятся в две сессии (А и В). Каждое занятие длится ровно три часа.Участники могут начать сессию А 4 декабря во время, указанное в таблице в этом документе. После завершения сессии А у участников будет 2-часовой перерыв. Сеанс B должен начинаться во время, указанное в той же таблице.
Для каждой из 12 задач участники должны написать свою работу от руки на обычных листах нелинованной бумаги размером 8,5 на 11. Вся работа по обоснованию решения и все необходимые этапы доказательства должны быть представлены. При работе над одной проблемой участники не должны ссылаться на работу над другой проблемой.Письменные принадлежности, чистая бумага и ластики разрешены, но другие материалы, такие как книги, калькуляторы, компьютеры, линейки, компас, разлинованная бумага или миллиметровая бумага, запрещены.
При работе над одной проблемой участники не должны ссылаться на работу над другой проблемой.Письменные принадлежности, чистая бумага и ластики разрешены, но другие материалы, такие как книги, калькуляторы, компьютеры, линейки, компас, разлинованная бумага или миллиметровая бумага, запрещены.
Участникам запрещено делиться или обсуждать конкурсную задачу до 20:00. 4 декабря по восточному поясному времени. Копирование, публикация или распространение экзамена до истечения этого времени запрещены.
Часто задаваемые вопросы по 82-му Патнэму
В.Когда состоится 82-й конкурс Патнэма?
A. 82-й конкурс Патнэма состоится в субботу, 4 декабря 2021 г.
В. Является ли 82-й конкурс Патнэма официальным?
О. Да, в этом году конкурс Патнэма вернется к своему стандартному формату. У нас снова будут индивидуальные соревнования и командные соревнования с наградами, призами и почетными грамотами.
 Соревнование состоится в субботу, 4 декабря, под личным наблюдением в кампусах США и Канады.
Соревнование состоится в субботу, 4 декабря, под личным наблюдением в кампусах США и Канады.В. Когда открывается регистрация руководителей?
А. Регистрация супервайзеров открывается 1 сентября 2021 г.
В. Как студенты регистрируются?
A. Участникам необходимо предварительно зарегистрироваться для участия в конкурсе. Они могут сделать это с начала 8 сентября 2021 года при условии, что местный руководитель их учреждения уже зарегистрировался. Обратите внимание, что утверждение супервайзером может занять до 5 рабочих дней.На этой странице будет ссылка.
В. У меня есть степень бакалавра. Могу ли я участвовать?
A. Нет. Конкурс Патнэма открыт только для активно зачисленных студентов бакалавриата, которые еще не получили степень бакалавра.
В.
 Могу ли я участвовать в конкурсе Патнэма без связи с учреждением?
Могу ли я участвовать в конкурсе Патнэма без связи с учреждением? А. №Если вы регулярно не зачислены в учебное заведение в США или Канаде, вы не имеете права участвовать. Если вы соответствуете квалификационным требованиям, но в вашем учреждении нет местного руководителя Патнэма, попросите преподавателя (возможно, заведующего кафедрой математики) стать местным руководителем Патнэма в вашем учреждении. Если никто из преподавателей не желает играть эту роль, вы не сможете участвовать.
В. Я являюсь соискателем степени в одном учебном заведении, но временно работаю в другом.Могу ли я участвовать?
A. Да, и вы можете конкурировать за любое учебное заведение.
В. Должен ли я иметь аттестат о среднем образовании для участия?
A. Нет. Учащиеся, которые одновременно учатся в средней школе, но регулярно посещают занятия в колледже или университете США или Канады, считаются «регулярно зачисленными» студентами.
 Обратите внимание, что студент может участвовать в официальном конкурсе Патнэма не более четырех раз.Как правило, мы не рекомендуем учащимся старших классов исчерпать свои права. Если вы регулярно не зачислены на бакалавриат в высшее учебное заведение, то вы не имеете права.
Обратите внимание, что студент может участвовать в официальном конкурсе Патнэма не более четырех раз.Как правило, мы не рекомендуем учащимся старших классов исчерпать свои права. Если вы регулярно не зачислены на бакалавриат в высшее учебное заведение, то вы не имеете права.В. Ограничено ли количество раз, когда студент может участвовать в конкурсе?
А. Да. Ограничение — четыре, не считая 81-го (неофициального) соревнования Патнэма, состоявшегося в феврале 2021 года.
В.Я иностранный студент, который в настоящее время обучается в учебном заведении США или Канады. Могу ли я участвовать?
А. Да.
В. Я регулярно учусь в учебном заведении США или Канады, но беру годичный отпуск. Я намерен вернуться в свое учреждение в следующем году. Могу ли я участвовать?
А. Да.
В.
 4 декабря меня не будет в родном учреждении.Могу ли я еще участвовать в конкурсе?
4 декабря меня не будет в родном учреждении.Могу ли я еще участвовать в конкурсе? А. Возможно. Иногда можно договориться о сдаче экзамена в другом зарегистрированном учреждении. Обсудите это с вашим местным руководителем.
В. Я зарегистрировался. Что мне нужно взять с собой в экзаменационную комнату?
A. Возьмите с собой карандаши или ручки (с синими или черными чернилами) и PIN-код, который вам дали на платформе регистрации. Больше ничего не нужно.Супервайзеры предоставляют чистую белую бумагу. Калькуляторы, компьютеры, справочные материалы и инструменты для рисования не допускаются, а мобильные телефоны должны быть выключены и убраны во время экзамена.
В. Каков крайний срок регистрации руководителей и учреждений?
A. Крайний срок для надзорных органов для регистрации своих учреждений — 15 ноября
В.
 Каков крайний срок регистрации студентов?
Каков крайний срок регистрации студентов? А.Участникам необходимо будет зарегистрироваться онлайн до начала соревнований по местному времени, чтобы получить свой идентификационный номер Патнэма (PIN).
В. Будут ли задачи к экзамену появляться на портале участника?
A. Нет. Экзамен в этом году будет проходить под наблюдением на территории кампуса, а руководители будут предоставлять задачи на бумаге.
15 самых сложных математических вопросов SAT
Хотите проверить себя, ответив на самые сложные математические вопросы SAT? Хотите знать, что делает эти вопросы такими сложными и как лучше всего их решить? Если вы готовы по-настоящему погрузиться в математический раздел SAT и нацелиться на идеальный результат, то это руководство для вас.
Мы собрали то, что мы считаем 15 самыми сложными вопросами для текущего SAT , со стратегиями и объяснениями ответов для каждого. Все это сложные вопросы SAT по математике из практических тестов SAT College Board, а это означает, что их понимание — один из лучших способов учиться для тех из вас, кто стремится к совершенству.
Все это сложные вопросы SAT по математике из практических тестов SAT College Board, а это означает, что их понимание — один из лучших способов учиться для тех из вас, кто стремится к совершенству.
Изображение: Соня Севилья/Викимедиа
Краткий обзор SAT Math
Третий и четвертый разделы SAT всегда будут математическими разделами .Первый математический подраздел (обозначенный цифрой 3) позволяет использовать калькулятор , а не , а второй математический подраздел (обозначенный цифрой 4) разрешает использование калькулятора. Однако не беспокойтесь слишком сильно о разделе без калькулятора: если вам не разрешено использовать калькулятор для вопроса, это означает, что вам не нужен калькулятор, чтобы ответить на него.
Каждый математический подраздел расположен в порядке возрастания сложности (где чем больше времени требуется для решения задачи и чем меньше людей правильно отвечают на нее, тем она сложнее). В каждом подразделе вопрос 1 будет считаться «легким», а вопрос 15 — «сложным». Тем не менее, возрастающая сложность сбрасывается с легкой на сложную в сетке.
В каждом подразделе вопрос 1 будет считаться «легким», а вопрос 15 — «сложным». Тем не менее, возрастающая сложность сбрасывается с легкой на сложную в сетке.
Таким образом, вопросы с несколькими вариантами ответов расположены в порядке возрастания сложности (вопросы 1 и 2 будут самыми простыми, вопросы 14 и 15 — самыми сложными), но уровень сложности сбрасывается для раздела сетки (это означает, что вопросы 16 и 17 снова быть «легким», а вопросы 19 и 20 будут очень сложными).
Таким образом, за очень немногими исключениями, самые сложные математические задачи SAT будут сгруппированы в конце сегментов с несколькими вариантами ответов или во второй половине вопросов сетки. Тем не менее, помимо места в тесте, эти вопросы также имеют несколько других общих черт. Через минуту мы рассмотрим примеры вопросов и способы их решения, а затем проанализируем их, чтобы выяснить, что общего у этих типов вопросов.
Но сначала: стоит ли вам сейчас сосредоточиться на самых сложных математических вопросах?
Если вы только начинаете подготовку к учебе (или если вы просто пропустили этот первый важный шаг), обязательно остановитесь и пройдите полный практический тест, чтобы оценить свой текущий уровень баллов. Ознакомьтесь с нашим руководством по всем бесплатным практическим тестам SAT, доступным в Интернете, а затем сядьте, чтобы пройти тест сразу.
Ознакомьтесь с нашим руководством по всем бесплатным практическим тестам SAT, доступным в Интернете, а затем сядьте, чтобы пройти тест сразу.
Абсолютно лучший способ оценить свой текущий уровень — это просто пройти тренировочный тест SAT, как если бы он был настоящим, соблюдая строгое время и работая без перерыва только с разрешенными перерывами (мы знаем — возможно, это не ваш любимый способ провести субботу). . Получив хорошее представление о своем текущем уровне и рейтинге в процентах, вы можете установить вехи и цели для своего окончательного результата SAT по математике.
Если в настоящее время вы набираете 200-400 или 400-600 баллов по SAT по математике, вам лучше всего сначала ознакомиться с нашим руководством по улучшению вашего результата по математике , чтобы постоянно быть на уровне 600 или выше, прежде чем начать в попытке решить самые сложные математические задачи на тесте.
Если, однако, вы уже набрали более 600 баллов по математике и хотите проверить свои силы для настоящего SAT, обязательно переходите к остальной части этого руководства. Если вы стремитесь к идеальному результату (или близкому к нему), вам нужно знать, как выглядят самые сложные математические вопросы SAT и как их решать.И, к счастью, именно это мы и сделаем.
Если вы стремитесь к идеальному результату (или близкому к нему), вам нужно знать, как выглядят самые сложные математические вопросы SAT и как их решать.И, к счастью, именно это мы и сделаем.
ПРЕДУПРЕЖДЕНИЕ: Поскольку существует ограниченное количество официальных практических тестов SAT, вы можете подождать, чтобы прочитать эту статью, пока вы не попытаетесь выполнить все или большую часть первых четырех официальных практических тестов (поскольку большинство приведенных ниже вопросов были из этих тестов). Если вы боитесь испортить эти тесты, прекратите читать это руководство прямо сейчас; вернуться и прочитать его, когда вы завершили их.
Теперь давайте перейдем к нашему списку вопросов (ууу)!
Изображение: Niytx/DeviantArt
15 самых сложных вопросов SAT по математике
Теперь, когда вы уверены, что должны ответить на эти вопросы, давайте приступим! Ниже мы подготовили для вас 15 самых сложных вопросов по математике SAT, а также пошаговые инструкции о том, как получить ответ (если вы в тупике).
Нет вопросов по математике SAT с калькулятором
Вопрос 1
$$C=5/9(F-32)$$
Приведенное выше уравнение показывает, как температура $F$, измеренная в градусах Фаренгейта, связана с температурой $C$, измеренной в градусах Цельсия. Исходя из уравнения, какое из следующих утверждений должно быть верным?
- Повышение температуры на 1 градус Фаренгейта эквивалентно повышению температуры на $5/9$ градусов Цельсия.
- Повышение температуры на 1 градус Цельсия эквивалентно повышению температуры на 1.8 градусов по Фаренгейту.
- Повышение температуры на $5/9$ градусов по Фаренгейту эквивалентно повышению температуры на 1 градус Цельсия.
A) Только I
B) Только II
C) Только III
D) Только I и II
ПОЯСНЕНИЕ ОТВЕТА: Думайте об уравнении как об уравнении для линии
$$y=mx+b$$
, где в данном случае
$$C= {5}/{9} (F−32)$$
или
$$C={5}/{9}F −{5}/{9}(32)$$
Вы можете видеть, что наклон графика составляет ${5}/{9}$, что означает, что при увеличении на 1 градус Фаренгейта увеличение составляет ${5}/{9}$ на 1 градус Цельсия.
$$C= {5}/{9} (F)$$
$$C= {5}/{9} (1)= {5}/{9}$$
Следовательно, утверждение I верно. Это эквивалентно утверждению, что увеличение на 1 градус Цельсия равно увеличению на ${9}/{5}$ градусов по Фаренгейту.
$$C= {5}/{9} (F)$$
$$1= {5}/{9} (F)$$
$$(F)={9}/{5}$$
Поскольку ${9}/{5}$ = 1,8, утверждение II верно.
Единственным ответом, в котором и утверждение I, и утверждение II являются истинными, является D , но если у вас есть время и вы хотите быть абсолютно тщательным, вы также можете проверить, соответствует ли утверждение III (увеличение на ${5}/{ 9}$ градусов по Фаренгейту равно повышению температуры на 1 градус Цельсия) верно:
$$C= {5}/{9} (F)$$
$$C= {5}/{9} ({5}/{9})$$
$$C= {25}/{81} (\что \равно 1)$$
Увеличение на $5/9$ градусов по Фаренгейту приводит к увеличению на ${25}/{81}$, а не на 1 градус Цельсия, поэтому утверждение III неверно.2$-термин должен быть равен в обеих частях уравнения, $−8a = 24$ или $a = −3$. 2$
2$
D) Стоимость не может быть определена на основании предоставленной информации.12$$
Окончательный ответ А.
Вопрос 4
Точки A и B лежат на окружности радиуса 1, а дуга ${AB}↖⌢$ имеет длину $π/3$. Какую часть длины окружности составляет длина дуги ${AB}↖⌢$?
ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы найти ответ на этот вопрос, вам сначала нужно знать формулу для нахождения длины окружности.
Длина окружности $C$ равна $C = 2πr$, где $r$ — радиус окружности.Для данного круга с радиусом 1 длина окружности равна $C = 2(π)(1)$ или $C = 2π$.
Чтобы найти долю длины окружности в ${AB}↖⌢$, разделите длину дуги на длину окружности, что даст $π/3 ÷ 2π$. Это деление можно представить как $π/3 * {1/2}π = 1/6$.
Дробь $1/6$ также может быть переписана как $0,166$ или $0,167$.
Окончательный ответ: 1/6$, 0,166$ или 0,167$.
Вопрос 5
$${8-i}/{3-2i}$$
Если приведенное выше выражение переписать в виде $a+bi$, где $a$ и $b$ — действительные числа, каково значение $a$? (Примечание: $i=√{-1}$)
ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы преобразовать ${8-i}/{3-2i}$ в стандартную форму $a + bi$, нужно умножить числитель и знаменатель ${8-i}/{3- 2i}$ сопряжением $3 + 2i$. 2=-1$, эту последнюю дробь можно упростить до
2=-1$, эту последнюю дробь можно упростить до
$$ {24+16i-3i+2}/{9-(-4)}={26+13i}/{13}$$
, что еще больше упрощается до $2 + i$. Следовательно, когда ${8-i}/{3-2i}$ переписывается в стандартной форме a + bi, значение a равно 2,
.Окончательный ответ А.
Вопрос 6
В треугольнике $ABC$ мера $∠B$ равна 90°, $BC=16$ и $AC$=20. Треугольник $DEF$ подобен треугольнику $ABC$, где вершинам $D$, $E$ и $F$ соответствуют вершины $A$, $B$ и $C$ соответственно, а каждой стороне треугольника $ DEF$ равен $1/3$ длины соответствующей стороны треугольника $ABC$.2}=√{400-256}=√{144}=12$$
Так как треугольник DEF подобен треугольнику ABC с вершиной F, соответствующей вершине C, мера $\angle ∠ {F}$ равна мере $\angle ∠ {C}$. Следовательно, $sin F = sin C$. От длин сторон треугольника ABC
$$sinF ={\противоположная \сторона}/{\гипотенуза}={AB}/{AC}={12}/{20}={3}/{5}$$
Следовательно, $sinF ={3}/{5}$.
Окончательный ответ ${3}/{5}$ или 0,6.
Вопросы SAT по математике, разрешенные калькулятором
Вопрос 7
В приведенной выше неполной таблице указано количество левшей и правшей в разбивке по полу среди учащихся восьмого класса средней школы Кейзеля.Студенток-правшей в 5 раз больше, чем студенток-левшей, а студентов-правшей в 9 раз больше, чем студентов-левшей. если в школе 18 учеников-левшей и 122 ученика-правши, что из следующего ближе всего к вероятности того, что случайно выбранный ученик-правша — девочка? (Примечание: предположим, что ни один из восьмиклассников не является одновременно правшой и левшой.)
А) 0.410
Б) 0,357
В) 0,333
Г) 0,250
ПОЯСНЕНИЕ ОТВЕТА: Чтобы решить эту задачу, вы должны составить два уравнения, используя две переменные ($x$ и $y$) и предоставленную вам информацию. Пусть $x$ будет количеством студентов-левшей, а $y$ будет количеством студентов-левшей. Используя информацию, приведенную в задаче, количество праворуких студентов будет $5x$, а количество праворуких студентов-мужчин будет $9y$. Поскольку общее количество учеников-левшей равно 18, а общее количество учеников-правшей равно 122, следующая система уравнений должна быть верной:
Поскольку общее количество учеников-левшей равно 18, а общее количество учеников-правшей равно 122, следующая система уравнений должна быть верной:
$$х + у = 18$$
$$5x + 9y = 122$$
Когда вы решаете эту систему уравнений, вы получаете $x = 10$ и $y = 8$. Таким образом, 5*10, или 50, из 122 студентов-правшей — женщины. Таким образом, вероятность того, что случайно выбранный студент-правша является женщиной, составляет ${50}/{122}$, что с точностью до тысячных равно 0,410.
Окончательный ответ А.
Вопросы 8 и 9
Используйте следующую информацию как для вопроса 7, так и для вопроса 8.
Если покупатели входят в магазин со средней скоростью $r$ покупателей в минуту и каждый остается в магазине в среднем $T$ минут, среднее количество покупателей в магазине, $N$, в любой момент равно задается формулой $N=rT$. Это соотношение известно как закон Литтла.
Владелец магазина Good Deals подсчитал, что в рабочее время в магазин заходит в среднем 3 покупателя в минуту и каждый из них остается в нем в среднем на 15 минут. Владелец магазина использует закон Литтла, чтобы оценить, что в любой момент времени в магазине находится 45 покупателей.
Владелец магазина использует закон Литтла, чтобы оценить, что в любой момент времени в магазине находится 45 покупателей.
Вопрос 8
Закон Литтла можно применить к любой части магазина, например к отдельному отделу или к кассам. Владелец магазина определяет, что в рабочее время примерно 84 покупателя в час совершают покупку, и каждый из этих покупателей тратит в среднем 5 минут в очереди к кассе. Сколько покупателей в среднем стоит в очереди на кассе, чтобы совершить покупку в магазине Good Deals в любое время в рабочее время?
ОБЪЯСНЕНИЕ ОТВЕТА: Поскольку в вопросе говорится, что закон Литтла может быть применен к любой отдельной части магазина (например, только к кассе), то среднее число покупателей, $N$, в очереди к кассе в любой время составляет $N = rT$, где $r$ — количество покупателей, входящих в очередь к кассе в минуту, а $T$ — среднее количество минут, которое каждый покупатель проводит в очереди к кассе.
Поскольку 84 покупателя в час совершают покупку, 84 покупателя в час встают в очередь на кассе. Однако это необходимо преобразовать в количество покупателей в минуту (чтобы использовать его с $T = 5$). Поскольку в одном часе 60 минут, ставка составляет ${84 \покупателей\в\час}/{60\минут} = 1,4$ покупателей в минуту. Использование данной формулы с $r = 1,4$ и $T = 5$ дает
$$N = rt = (1,4)(5) = 7$$
Таким образом, среднее количество покупателей, $N$, в очереди к кассе в любое время в рабочее время равно 7.
Окончательный ответ 7.
Вопрос 9
Владелец магазина «Хорошие предложения» открывает новый магазин на другом конце города. Владелец подсчитал, что в новом магазине в рабочее время в магазин заходят в среднем 90 покупателей в час, и каждый из них остается в нем в среднем на 12 минут. Среднее количество покупателей в новом магазине в любое время на сколько процентов меньше среднего числа покупателей в исходном магазине в любое время? (Примечание: при вводе ответа игнорируйте символ процента. Например, если ответ 42,1%, введите 42,1)
Например, если ответ 42,1%, введите 42,1)
ОБЪЯСНЕНИЕ ОТВЕТА: В соответствии с предоставленной исходной информацией расчетное среднее количество покупателей в исходном магазине в любое время (N) равно 45. В вопросе говорится, что в новом магазине менеджер оценивает количество в магазин заходят в среднем 90 покупателей в час (60 минут), что эквивалентно 1,5 покупателям в минуту (r). Менеджер также подсчитал, что каждый покупатель находится в магазине в среднем 12 минут (T).Таким образом, по закону Литтла в каждый момент времени в новом магазине находится в среднем $N = rT = (1,5)(12) = 18$ покупателей. это
$${45-18}/{45} * 100 = 60$$
Напроцента меньше, чем среднее количество покупателей в исходном магазине в любое время.
Окончательный ответ: 60.
Вопрос 10
В плоскости $xy$ точка $(p,r)$ лежит на прямой с уравнением $y=x+b$, где $b$ — константа. Точка с координатами $(2p, 5r)$ лежит на прямой с уравнением $y=2x+b$. Если $p≠0$, каково значение $r/p$?
Если $p≠0$, каково значение $r/p$?
А) $2/5$
Б) $3/4$
В) $4/3$
Г) $5/2$
ПОЯСНЕНИЕ ОТВЕТА: Поскольку точка $(p,r)$ лежит на прямой с уравнением $y=x+b$, она должна удовлетворять уравнению. Подстановка $p$ вместо $x$ и $r$ вместо $y$ в уравнении $y=x+b$ дает $r=p+b$ или $\bi b$ = $\bi r-\bi p $.
Аналогично, поскольку точка $(2p,5r)$ лежит на прямой с уравнением $y=2x+b$, точка должна удовлетворять уравнению.Подстановка $2p$ вместо $x$ и $5r$ вместо $y$ в уравнении $y=2x+b$ дает:
$5r=2(2p)+b$
$5r=4p+b$
$\bi b$ = $\bo 5 \bi r-\bo 4\bi p$.
Далее мы можем приравнять два уравнения, равные $b$, и упростить:
$b=r-p=5r-4p$
$3p=4r$
Наконец, чтобы найти $r/p$, нам нужно разделить обе части уравнения на $p$ и на $4$:
$3p=4r$
$3={4r}/p$
$3/4=r/p$
Правильный ответ: B , $3/4$.
Если вы выбрали варианты A и D, возможно, вы неправильно сформировали свой ответ из коэффициентов в пункте $(2p, 5r)$. 2h$$
2h$$
можно использовать для определения общего объема силоса.2)(5)=({4}/{3})(250)π$$
, что примерно равно 1047,2 кубических фута.
Окончательный ответ D.
Вопрос 12
Если $x$ — это среднее (среднее арифметическое) $m$ и $9$, $y$ — это среднее между $2m$ и $15$, а $z$ — это среднее между $3m$ и $18$, то что является средним значением $x$, $y$ и $z$ в пересчете на $m$?
A) $m+6$
B) $m+7$
C) $2m+14$
D) $3m + 21$
ПОЯСНЕНИЕ ОТВЕТА: Поскольку среднее (среднее арифметическое) двух чисел равно сумме двух чисел, деленной на 2, уравнения $x={m+9}/{2}$, $y={2m +15}/{2}$, $z={3m+18}/{2}$ соответствуют действительности.2-x-{11}/{4}$$
и
$$y = k$$
Вещественное решение системы двух уравнений соответствует точке пересечения графиков двух уравнений в плоскости $xy$.
Графиком $y = k$ называется горизонтальная линия, содержащая точку $(0,k)$ и трижды пересекающая график кубического уравнения (поскольку оно имеет три действительных решения). На графике единственная горизонтальная линия, которая трижды пересекает кубическое уравнение, — это линия с уравнением $y = −3$ или $f(x) = −3$.2$$
На графике единственная горизонтальная линия, которая трижды пересекает кубическое уравнение, — это линия с уравнением $y = −3$ или $f(x) = −3$.2$$
Динамическое давление $q$, создаваемое жидкостью, движущейся со скоростью $v$, можно найти по приведенной выше формуле, где $n$ — постоянная плотность жидкости. Авиационный инженер использует формулу для нахождения динамического давления жидкости, движущейся со скоростью $v$, и той же жидкости, движущейся со скоростью 1,5$v$. Каково отношение динамического давления более быстрой жидкости к динамическому давлению более медленной жидкости?
ОБЪЯСНЕНИЕ ОТВЕТА: Чтобы решить эту задачу, вам нужно составить уравнения с переменными.2 = (2,25)q_1$$
Следовательно, коэффициент динамического давления более быстрой жидкости равен
$${q2}/{q1} = {2,25 q_1}/{q_1}= 2,25$$
Окончательный ответ 2,25 или 9/4.
Вопрос 15
Для многочлена $p(x)$ значение $p(3)$ равно $-2$. Что из следующего должно быть верно относительно $p(x)$?
Что из следующего должно быть верно относительно $p(x)$?
A) $x-5$ является множителем $p(x)$.
B) $x-2$ является множителем $p(x)$.
C) $x+2$ является множителем $p(x)$.
D) Остаток от деления $p(x)$ на $x-3$ равен $-2$.1$ и без более высоких показателей), остаток является действительным числом.
Следовательно, $p(x)$ можно переписать как $p(x) = (x + k)q(x) + r$, где $r$ — вещественное число.
В вопросе указано, что $p(3) = -2$, поэтому должно быть верно, что
$$-2 = p(3) = (3 + k)q(3) + r$$
Теперь мы можем подставить все возможные ответы. Если ответ A, B или C, $r$ будет $0$, а если ответ D, $r$ будет $-2$.
A. $-2 = p(3) = (3 + (-5))q(3) + 0$
$-2=(3-5)q(3)$
$-2=(-2 )q(3)$
Это может быть правдой, но только если $q(3)=1$
Б.$-2 = p(3) = (3 + (-2))q(3) + 0$
$-2 = (3-2)q(3)$
$-2 = (-1)q( 3)$
Это может быть правдой, но только если $q(3)=2$
C. $-2 = p(3) = (3 + 2)q(3) + 0$
$-2 = p(3) = (3 + 2)q(3) + 0$
$-2 = (5)q(3)$
Это может быть правдой, но только если $q(3)={-2}/{5}$
D. $-2 = p(3) = (3 + (-3))q(3) + (-2)$
$-2 = (3 — 3)q(3) + (-2)$
$-2 = (0)q(3) + (-2)$
Это всегда будет истинным независимо от того, что такое $q(3)$.
Из вариантов ответа единственный, что должно быть верным относительно $p(x)$, это D, что остаток от деления $p(x)$ на $x-3$ равен -2.
Окончательный ответ D.
Хотите улучшить свой результат SAT на 160 баллов? Мы написали руководство о 5 лучших стратегиях, которые вы должны использовать, чтобы попытаться улучшить свой результат. Загрузите его бесплатно прямо сейчас:
Вы заслужили вздремнуть после того, как ответили на эти вопросы.
Что общего у самых сложных математических вопросов SAT?
Важно понять, что делает эти трудные вопросы «сложными». Таким образом, вы сможете понять и решить похожие вопросы, когда увидите их в день экзамена, а также у вас будет лучшая стратегия для выявления и исправления ваших предыдущих математических ошибок SAT.
Таким образом, вы сможете понять и решить похожие вопросы, когда увидите их в день экзамена, а также у вас будет лучшая стратегия для выявления и исправления ваших предыдущих математических ошибок SAT.
В этом разделе мы рассмотрим, что общего у этих вопросов, и приведем примеры каждого типа.Некоторые из причин, по которым самые сложные математические вопросы являются самыми сложными математическими вопросами, заключаются в том, что они:
#1: Проверка нескольких математических концепций одновременно
Здесь мы должны иметь дело с мнимыми числами и дробями одновременно.
Секрет успеха: Подумайте, какую применимую математику вы могли бы использовать для решения задачи, выполняйте один шаг за раз и пробуйте каждый метод, пока не найдете тот, который работает!
№ 2. Много шагов
Помните: чем больше шагов вам нужно сделать, тем легче где-нибудь напортачить!
Мы должны решить эту задачу поэтапно (выполняя несколько средних значений), чтобы разблокировать остальные ответы в результате эффекта домино. Это может сбивать с толку, особенно если вы находитесь в состоянии стресса или у вас мало времени.
Это может сбивать с толку, особенно если вы находитесь в состоянии стресса или у вас мало времени.
Секрет успеха: Делайте это медленно, шаг за шагом и перепроверяйте свою работу, чтобы не делать ошибок!
№ 3: Концепции тестирования, с которыми вы мало знакомы
Например, многие учащиеся менее знакомы с функциями, чем с дробями и процентами, поэтому большинство вопросов о функциях считаются задачами «высокой сложности».
Если вы не разбираетесь в функциях, это будет непростой задачей.
Секрет успеха: Повторите математические понятия, с которыми вы не так хорошо знакомы, например функции. Мы предлагаем использовать наши замечательные бесплатные руководства по обзору SAT Math.
№ 4: сформулированы необычным или запутанным образом
Может быть трудно понять, какие именно вопросы задают , а тем более понять, как их решать. Это особенно актуально, когда вопрос находится в конце раздела, а у вас мало времени.
Поскольку этот вопрос содержит так много информации без диаграммы, может быть трудно разобраться в нем за ограниченное время.
Секрет успеха: Не торопитесь, проанализируйте, что от вас требуется, и нарисуйте схему, если она вам поможет.
№ 5: используйте много разных переменных
С таким количеством разных переменных очень легко запутаться.
Секрет успеха: Не торопитесь, проанализируйте, что от вас спрашивают, и подумайте, является ли подстановка чисел хорошей стратегией для решения проблемы (это не относится к приведенному выше вопросу, но подходит ко многим другим). переменные вопросы SAT).
Еда на вынос
SAT — это марафон, и чем лучше вы к нему подготовитесь, тем лучше вы будете себя чувствовать в день экзамена. Знание того, как ответить на самые сложные вопросы, которые может задать вам тест, сделает сдачу настоящего SAT намного менее сложной задачей.
Если вы чувствовали, что эти вопросы были легкими, не стоит недооценивать влияние адреналина и усталости на вашу способность решать проблемы. Продолжая учиться, всегда придерживайтесь правильного времени и старайтесь проходить полные тесты, когда это возможно. Это лучший способ воссоздать реальную среду тестирования, чтобы вы могли подготовиться к реальной сделке.
Если вы считаете, что эти вопросы кажутся вам сложными, обязательно укрепите свои математические знания, ознакомившись с нашими отдельными руководствами по математике для SAT. Там вы увидите более подробные объяснения рассматриваемых тем, а также более подробную разбивку ответов.
Что дальше?
Почувствовали, что эти вопросы сложнее, чем вы ожидали? Просмотрите все темы, затронутые в математическом разделе SAT, а затем отметьте, какие разделы вызвали у вас особую трудность.Затем взгляните на наши отдельные руководства по математике, которые помогут вам укрепить любую из этих слабых сторон.
Недостаточно времени на математическом разделе SAT? Наш путеводитель поможет вам выиграть время и увеличить свой счет.
Стремитесь к идеальному результату? Ознакомьтесь с нашим руководством о том, как получить идеальные 800 баллов по математическому разделу SAT, написанным отличником.
Хотите улучшить свой результат SAT на 160 баллов?
Посетите наши лучшие в своем классе онлайн-курсы по подготовке к SAT.Мы гарантируем возврат ваших денег , если вы не улучшите свой результат SAT на 160 или более баллов.
Наши занятия полностью онлайн, и их проводят эксперты SAT. Если вам понравилась эта статья, вам понравятся наши занятия. Наряду с занятиями под руководством экспертов вы получите индивидуальное домашнее задание с тысячами практических задач, организованных по индивидуальным навыкам, чтобы вы могли учиться наиболее эффективно. Мы также предоставим вам пошаговую индивидуальную программу, чтобы вы никогда не запутались в том, что изучать дальше.
Попробуйте без риска сегодня:
Стратегии решения проблем GRE (для сдающих тест)
Вопросы из раздела «Количественное мышление» общего теста GRE® требуют от вас моделирования и решения задач с использованием количественных или математических методов. Как правило, решение математической задачи состоит из трех основных шагов:
- Шаг 1. Понимание проблемы
- Шаг 2. Разработайте стратегию решения проблемы
- Шаг 3. Проверьте свой ответ
Вот описание трех шагов, за которым следует список полезных стратегий для решения математических задач.
Шаг 1. Понимание проблемы
Первый шаг — внимательно прочитать описание проблемы, чтобы убедиться, что вы понимаете предоставленную информацию и проблему, которую вам предлагается решить.
Некоторая информация может описывать определенные количества. Количественная информация может быть представлена словами или математическими выражениями, или их комбинацией. Кроме того, в некоторых задачах вам может понадобиться прочитать и понять количественную информацию в представлениях данных, геометрических фигурах или системах координат.Другая информация может принимать форму формул, определений или условий, которым должны удовлетворять величины. Например, условия могут быть уравнениями или неравенствами, или могут быть словами, которые можно перевести в уравнения или неравенства.
Кроме того, в некоторых задачах вам может понадобиться прочитать и понять количественную информацию в представлениях данных, геометрических фигурах или системах координат.Другая информация может принимать форму формул, определений или условий, которым должны удовлетворять величины. Например, условия могут быть уравнениями или неравенствами, или могут быть словами, которые можно перевести в уравнения или неравенства.
Помимо понимания информации, которую вы получаете, важно понимать, что вам нужно сделать, чтобы решить проблему. Например, какие неизвестные величины необходимо найти? В какой форме они должны быть выражены?
Шаг 2. Разработайте стратегию решения проблемы
Решение математической задачи требует большего, чем понимание описания задачи, то есть большего, чем понимание величин, данных, условий, неизвестных и всех других математических фактов, связанных с задачей.Это требует определения того, какие математические факты использовать, когда и как использовать эти факты для разработки решения проблемы. Это требует стратегии.
Это требует стратегии.
Математические задачи решаются с использованием самых разных стратегий. Кроме того, могут быть разные способы решения данной проблемы. Таким образом, вы должны разработать репертуар стратегий решения проблем, а также понять, какие стратегии лучше всего подходят для решения конкретных проблем. Попытка решить проблему без стратегии может привести к большой работе без получения правильного решения.
После того, как вы определите стратегию, вы должны ее выполнить. Если вы застряли, проверьте свою работу, чтобы увидеть, не допустили ли вы ошибку в своем решении. Важно иметь гибкий, открытый образ мышления. Если вы проверяете свое решение и не можете найти ошибку или если ваша стратегия решения просто не работает, поищите другую стратегию.
Шаг 3: проверьте свой ответ
Когда вы получите ответ, вы должны убедиться, что он разумен и корректен с точки зрения вычислений.
- Вы ответили на заданный вопрос?
- Является ли ваш ответ разумным в контексте вопроса? Проверить правильность ответа можно так же просто, как вспомнить базовый математический факт и проверить, согласуется ли ваш ответ с этим фактом.
 Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. В других случаях вы можете использовать оценку, чтобы проверить, является ли ваш ответ разумным. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть в диапазоне от 300 до 600.
Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. В других случаях вы можете использовать оценку, чтобы проверить, является ли ваш ответ разумным. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть в диапазоне от 300 до 600. - Вы допустили ошибку в вычислениях при ответе? Ошибка при вводе ключа с помощью калькулятора? Вы можете проверить наличие ошибок на каждом этапе вашего решения.Или вы можете напрямую проверить правильность вашего решения. Например, если вы решили уравнение для x и получили ответ, вы можете проверить свой ответ, подставив в уравнение, чтобы увидеть, что .
Стратегии
Не существует установленных правил, применимых ко всем математическим задачам, для определения наилучшей стратегии. Способность определить стратегию, которая будет работать, растет по мере того, как вы решаете все больше и больше проблем. Далее следует краткое описание полезных стратегий.Вместе с каждой стратегией даны один или два примерных вопроса, на которые вы можете ответить с помощью стратегии. Эти стратегии не образуют полного списка, и, кроме группировки первых четырех стратегий, они не представлены в каком-либо определенном порядке.
Далее следует краткое описание полезных стратегий.Вместе с каждой стратегией даны один или два примерных вопроса, на которые вы можете ответить с помощью стратегии. Эти стратегии не образуют полного списка, и, кроме группировки первых четырех стратегий, они не представлены в каком-либо определенном порядке.
Первые четыре стратегии являются стратегиями перевода, когда одно представление математической задачи переводится в другое.
Математические олимпиады Лихай 1999-2021
Математические олимпиады Лихай 1999-2021Математические олимпиады Лихай 1999-2021
Вот проблемы и решения по математике средней школы Университета Лихай. конкурса на 1999-2021 годы.Вопросы в конкурсе нужно ответить за 2 часа без использования калькулятора. Экзамен2021 и решения, аннотированные количеством студентов, ответивших правильно на каждое. Экзамен
2020 и решения, аннотированные числом 82 лучших учащихся, ответивших на них правильно. Экзамен
2019 и решения, аннотированные количеством 54 лучших людей, ответивших на них правильно.
Экзамен 2018 и аннотированные решения
Экзамен 2017 г. и аннотированные решения Экзамен
2016 и решения, аннотированные числом 54 лучших людей, ответивших на них правильно.
Экзамен 2015 и решения, аннотированные количеством 49 лучших людей, ответивших на них правильно.
2014 экзамен и решения, аннотированные количество лучших 49 человек, ответивших на них правильно.
2013 экзамен и решения, аннотированные количество 72 лучших людей, ответивших на них правильно.
2012 экзамен и решения, аннотированные с участием количество людей, ответивших на них правильно.
2011 экзамен и решения, с примечанием количество лучших 46 человек, ответивших на них правильно.
2010 экзамен и решения, аннотированные количество лучших 54 человек, ответивших на них правильно.
2009 экзамен и решения, аннотированные количество людей, ответивших на них правильно.
Экзамен 2008 г. и решения, аннотированные
количество людей, ответивших на них правильно.
2007 экзамен и решения.
2006 экзамен и решения.
2005 экзамен и решения.
2004 экзамен и решения.(две задачи говорить о затененных областях, которые не затенены на экране.В под номером 32 есть своего рода крестообразная фигура, которая должна быть заштрихованным, а на номере 40 маленький внутренний треугольник должен быть заштрихованным.)
2003 экзамен и решения.
2002 экзамен и решения.
2001 экзамен и решения.
2000 экзамен и решения.
1999 экзамен и решения.
Вернуться на главную страницу конкурса
Примеры вопросов по математике | Testing Services
Все учащиеся начинают с теста Accuplacer’s Elementary Algebra Test.Тест адаптивный. Если вы хорошо сдадите тест по элементарной алгебре, вы автоматически перейдете к тесту по математике для колледжа. Результаты этих двух тестов поместят вас где-то между средним уровнем алгебры и исчислением. Если вы не так хорошо сдадите элементарную алгебру, вы автоматически перейдете к тесту по арифметике и окажетесь где-то между арифметикой и алгеброй колледжа.
Центр онлайн-обзоров, настоятельно рекомендуемый MCC для вступительного теста по математике, — это вход в Академию Хана. Инструкции по входу в систему можно найти по адресу: https://www.monroecc.edu/go/khan. Учащиеся могут пользоваться обширной библиотекой контента, включая интерактивные задания, тесты и видеоролики, с любого компьютера, имеющего доступ к Интернету. Учащиеся могут заниматься математикой в своем собственном темпе в адаптивной среде оценивания Khan Academy. Вы можете начать с 1 + 1 и перейти к исчислению или перейти сразу к любой теме, которую нужно немного освежить. Войдите в систему и начните проверку сегодня перед тестированием!
Вот несколько шагов, которые вы можете предпринять, чтобы подготовиться к тестам:
- Перейдите на страницу веб-сайта Accuplacer для студентов.http://accuplacer.collegeboard.org/students и щелкните ссылку «Бесплатные примеры вопросов». Прокрутите вниз тесты по чтению и письму, чтобы найти тесты по математике.
- Попробуйте решить все задачи арифметического теста.
 Обязательно проверьте свои ответы, прокрутив документ вниз.
Обязательно проверьте свои ответы, прокрутив документ вниз. - Для ответов на любые вопросы, которые вы пропустили в тесте по арифметике, просмотрите похожие задачи из учебника по арифметике или воспользуйтесь одним из ресурсов, перечисленных ниже. Чтобы просмотреть список всех тем для проверки по арифметике, посетите веб-сайт http://accuplacer.Collegeboard.org/students, перейдите на вкладку Accuplacer Tests, а затем на Arithmetic, чтобы развернуть список тем теста.
- Когда вы освоитесь с арифметикой, попробуйте решить задачи из теста по элементарной алгебре. Проверьте свои ответы и просмотрите задачи, похожие на те, которые вы пропустили, используя учебник по элементарной алгебре или один из ресурсов, перечисленных ниже. Чтобы просмотреть список всех тем для проверки по элементарной алгебре, перейдите на страницу http://accuplacer.collegeboard.org/students, щелкните вкладку «Тесты Accuplacer», а затем — «Элементарная алгебра», чтобы развернуть список тем теста.
- Когда вы освоитесь с задачами по элементарной алгебре, посмотрите тест по математике для колледжа.
 Задачи, вероятно, будут незнакомы учащимся, которые не изучали продвинутую алгебру и тригонометрию, и если да, то нет необходимости пытаться их решить. Если вы успешно завершили курс «Продвинутая алгебра и тригонометрия», решите все задачи, которые кажутся вам знакомыми, и проверьте свои ответы. Просмотрите проблемы, подобные тем, которые вы пропустили, используя учебник по продвинутой алгебре и тригонометрии или предварительному исчислению или один из ресурсов, перечисленных ниже.Чтобы просмотреть список всех тем, которые необходимо просмотреть для теста по математике на уровне колледжа, перейдите на страницу http://accuplacer.collegeboard.org/students, щелкните вкладку «Тесты Accuplacer», а затем — «Математика на уровне колледжа», чтобы развернуть список тем. на тесте.
Задачи, вероятно, будут незнакомы учащимся, которые не изучали продвинутую алгебру и тригонометрию, и если да, то нет необходимости пытаться их решить. Если вы успешно завершили курс «Продвинутая алгебра и тригонометрия», решите все задачи, которые кажутся вам знакомыми, и проверьте свои ответы. Просмотрите проблемы, подобные тем, которые вы пропустили, используя учебник по продвинутой алгебре и тригонометрии или предварительному исчислению или один из ресурсов, перечисленных ниже.Чтобы просмотреть список всех тем, которые необходимо просмотреть для теста по математике на уровне колледжа, перейдите на страницу http://accuplacer.collegeboard.org/students, щелкните вкладку «Тесты Accuplacer», а затем — «Математика на уровне колледжа», чтобы развернуть список тем. на тесте. - Когда вы закончите обзор, вы можете попробовать дополнительные тренировочные тесты, которые можно найти в ресурсах, перечисленных ниже.
Ресурсы Mathematics Review Печатные материалы:
- Математика Боба Миллера для Accuplacer, Bob Miller, Research & Education Association, Inc.
 2010. Эта книга включает обзор тем трех экзаменов по математике Accuplacer, а также дополнительные практические тесты для каждого экзамена.
2010. Эта книга включает обзор тем трех экзаменов по математике Accuplacer, а также дополнительные практические тесты для каждого экзамена. - GED Review Book по арифметике
- SAT I Review Books (издатели: Arco, Kaplan, Nova and Barrons) по арифметике и элементарной алгебре
Экзамены | Расчет с одной переменной | Математика
Формат
Учащимся понадобятся учебники по курсу ( Симмонс, Джордж Ф. Исчисление с аналитической геометрией .2-е изд. Нью-Йорк, штат Нью-Йорк: McGraw-Hill, 1 октября 1996 г., ISBN: 9780070576421) и читатель курса (18.01/18.01A Дополнительные примечания, упражнения и решения; Джерисон, Д. и А. Маттак. Исчисление 1) до выполнить заданные наборы задач. Читатель курса — это место, где можно найти упражнения, обозначенные 1A, 1B и т. д.
Наборы задач состоят из двух частей, I и II
Часть I состоит из упражнений, приведенных в учебнике и решенных в разделе S учебника. Он будет быстро оцениваться, проверяя, что все есть и решения не скопированы.
Часть II состоит из задач, для которых не дано решений; это стоит больше очков. Некоторые из этих задач представляют собой более длинные упражнения, состоящие из нескольких частей, потому что они не подходят для экзамена или формата краткого ответа. Ознакомьтесь с приведенными ниже рекомендациями о том, какое сотрудничество является приемлемым, и следуйте им.
Чтобы побудить вас не отставать от лекций, в Части I и Части II для каждой задачи указано, в какой день занятия у вас будет необходимая база для ее решения.
Правила домашнего задания
Совместная работа над наборами задач приветствуется, но
- Попробуйте выполнить каждую часть каждой задачи самостоятельно. Прежде чем обращаться за помощью, прочитайте каждую часть задачи. Если вы не понимаете, о чем вас спрашивают, попросите помощи в интерпретации проблемы, а затем честно попытайтесь ее решить.
- Запишите каждую задачу отдельно. В упражнениях части A и B вы должны написать ответ своими словами.

- Напишите на наборе задач, с кем вы консультировались и какие источники использовали. Если вы этого не сделаете, вас могут обвинить в плагиате и подвергнуть серьезным санкциям.
- Незаконно просматривать материалы предыдущих семестров.
Ключ к обозначению
2.1 = Раздел 2.1 книги Симмонса
Примечания G = раздел G Примечаний (Course Reader)
1A-3 = Упражнение 1A-3 в Разделе E (Упражнения) Примечаний (решено в Разделе S)
2.4/13; 81/4 = по Симмонсу, соответственно, п. 2.4, задача 13; стр. 81 Проблема 4
Домашние задания
Набор задач 1 (PDF)
Набор задач 2 (PDF 1) (PDF 2)
Набор задач 3 (PDF)
Набор задач 4 (PDF)
Набор задач 5 (PDF)
Набор задач 6 (PDF)
Набор задач 7 (PDF)
Набор задач 8 (PDF 1) (PDF 2)
Экзамены состоялись в сессиях, указанных в таблице.
«>| СЭС № | ЭКЗАМЕН № | ИНФОРМАЦИЯ ОБ ЭКЗАМЕНЕ | ПРАКТИЧЕСКИЕ ЭКЗАМЕНЫ | ЭКЗАМЕНЫ |
|---|---|---|---|---|
| 8 | 1 | Чехлы Ses #1-7 Обзорный лист (PDF) | Практические вопросы к экзамену 1 (PDF) Решения (PDF 1) (PDF 2) Практический экзамен 1 (PDF) Решения (PDF) | Экзамен (PDF) Решение (PDF) |
| 17 | 2 | Чехлы Ses #8-16 Обзорный лист (PDF) | Практические вопросы к экзамену 2 (PDF) Решения (PDF) Практический экзамен 2 (PDF) Решения (PDF) | Экзамен (PDF) Решение (PDF) |
| 26 | 3 | Чехлы Ses #18-24 Обзорный лист (PDF) | Практические вопросы к экзамену 3 (PDF) Решения (PDF) Практический экзамен 3 (PDF) Решения (PDF) | Экзамен (PDF) Решение (PDF) |
| 33 | 4 | Чехлы Ses #26-32 Обзорный лист (PDF) | Лист формул, которые будут предоставлены на экзамене 4 (PDF) Практические вопросы к экзамену 4 (PDF) Решения (PDF) Практический экзамен 4 (PDF) Решения (PDF) | Экзамен (PDF) Решение (PDF) |
| Финал | Охватывает работу за весь семестр, включая весь материал, начиная с экзамена 4 | Информация об окончании срока (PDF) Финал практики (PDF) Решения (PDF) |
прошлых экзаменов | Прикладная математика
Прошлые экзамены | Прикладная математика перейти к содержанию Перейти к навигацииСписок курсов
Список курсов с экзаменами
Математика 21: Расчет одной переменной I
- Осень 2005 г.
 (90-минутный формат экзамена)
(90-минутный формат экзамена) - Весна 2006 г. (90-минутный формат экзамена)
- Осень 2006 г. (90-минутный формат экзамена)
- Весна 2007 г. (50-минутный формат экзамена)
- Осень 2007 г. (50-минутный формат экзамена)
- Весна 2008 г. (50-минутный формат экзамена)
- Осень 2008 г. (50-минутный формат экзамена)
- Весна 2009 г. (50-минутный формат экзамена)
Наверх
Математика 22: Расчет одной переменной II
- Осень 2005 г. (90-минутный формат экзамена)
- Весна 2006 г. (90-минутный формат экзамена)
- Осень 2006 г. (90-минутный формат экзамена)
- Весна 2007 г. (50-минутный формат экзамена)
- Осень 2007 г. (50-минутный формат экзамена)
- Весна 2008 г. (50-минутный формат экзамена)
- Осень 2008 г. (50-минутный формат экзамена)
Наверх
Математика 23: векторное исчисление
- Осень 2005 г.
 (90-минутный формат экзамена)
(90-минутный формат экзамена) - Осень 2006 г. (90-минутный формат экзамена)
- Весна 2007 г. (50-минутный формат экзамена)
- Осень 2007 г. (50-минутный формат экзамена)
- Весна 2008 г. (50-минутный формат экзамена)
- Осень 2008 г. (50-минутный формат экзамена)
Наверх
Математика 24: Введение в линейную алгебру и дифференциальные уравнения
- Весна 2006 г. (90-минутный формат экзамена)
- Осень 2006 г. (90-минутный формат экзамена)
- Весна 2007 г. (50-минутный формат экзамена)
- Осень 2007 г. (50-минутный формат экзамена)
- Весна 2008 г. (50-минутный формат экзамена)
- Осень 2008 г. (50-минутный формат экзамена)
- Весна 2009 г. (50-минутный формат экзамена)
Наверх
Математика 30: Исчисление II для биологических наук
- Осень 2006 г. (90-минутный формат экзамена)
- Осень 2007 г.
 (50-минутный формат экзамена)
(50-минутный формат экзамена) - Весна 2008 г. (50-минутный формат экзамена)
- Осень 2008 г. (50-минутный формат экзамена)
Наверх
Математика 32: Вероятность и статистика
- Осень 2007 г.
- Осень 2008 г.
- Весна 2009 г.
Наверх
Пожалуйста, убедитесь, что Javascript включен для обеспечения доступности веб-сайта .
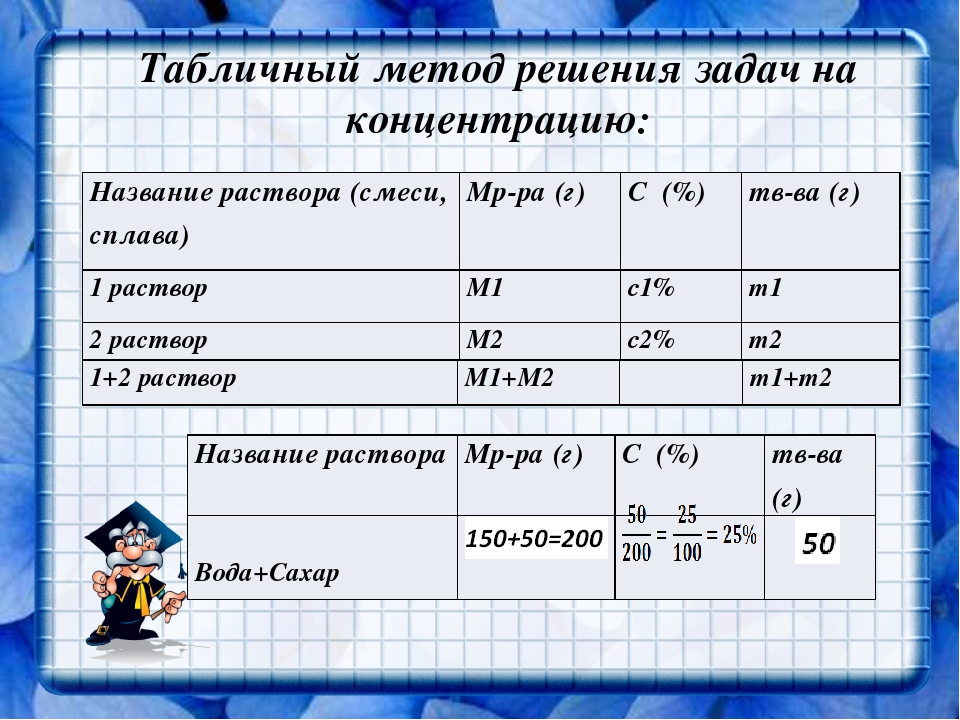 Имеется 40 литров 0,5 % раствора и 50 литров 2% раствора уксусной кислоты. Сколько нужно взять того и другого, чтобы получить 30 литров 1,5% — го раствора уксусной кислоты.
Имеется 40 литров 0,5 % раствора и 50 литров 2% раствора уксусной кислоты. Сколько нужно взять того и другого, чтобы получить 30 литров 1,5% — го раствора уксусной кислоты. Имеется два сплава золота и серебра. В одном эти металлы находятся в отношении 2:3, в другом 3:7. Сколько нужно взять каждого сплава, чтобы получить 8 кг нового сплава, в котором эти металлы были бы в отношении 5:11?
Имеется два сплава золота и серебра. В одном эти металлы находятся в отношении 2:3, в другом 3:7. Сколько нужно взять каждого сплава, чтобы получить 8 кг нового сплава, в котором эти металлы были бы в отношении 5:11? А, именно, разность массовых долей позволяет вычислить не массовую долю, А МАССОВЫЕ ЧАСТИ ПЕРВОГО И ВТОРОГО РАСТВОРОВ, которые впоследствии можно перевести в массы растворов. Во-вторых, зачем такое громоздкое решение, когда подобные задачи можно решить в 2-3 действия, без введения всяких переменных. И использовать при решении данных задач «конверт Пирсона» не всегда логично: чаще приходится пользоваться правилом смешения растворов, формула которого в работе приведена. Поэтому я бы удалила этот ресурс, так как много неточностей с профессиональной точки зрения.
А, именно, разность массовых долей позволяет вычислить не массовую долю, А МАССОВЫЕ ЧАСТИ ПЕРВОГО И ВТОРОГО РАСТВОРОВ, которые впоследствии можно перевести в массы растворов. Во-вторых, зачем такое громоздкое решение, когда подобные задачи можно решить в 2-3 действия, без введения всяких переменных. И использовать при решении данных задач «конверт Пирсона» не всегда логично: чаще приходится пользоваться правилом смешения растворов, формула которого в работе приведена. Поэтому я бы удалила этот ресурс, так как много неточностей с профессиональной точки зрения.
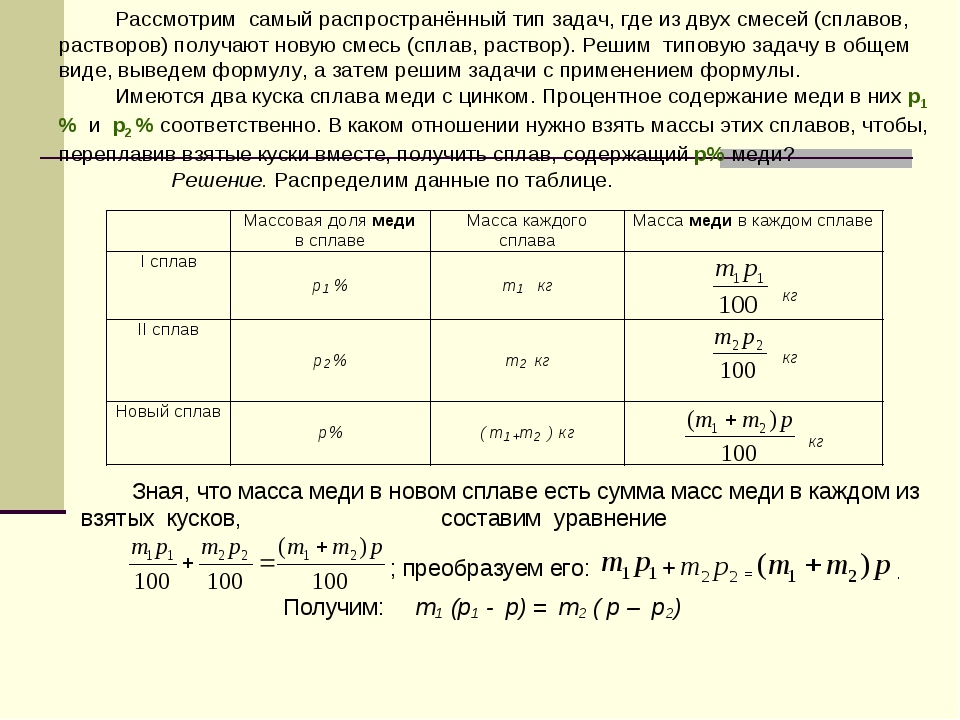 Но для ученика, который не умеет решать уравнения(а такие попадаются и в 11 классе)этот метод -спасение, т.к. решается методом простейших вычислений. А что касается данного ресурса, да, есть ошибки, но куда смотрели эксперты, разве в их обязанности не входит проверка ресурса, прежде чем он появится на СУПе ? Хотя, вопрос, наверное, не по адресу.
Но для ученика, который не умеет решать уравнения(а такие попадаются и в 11 классе)этот метод -спасение, т.к. решается методом простейших вычислений. А что касается данного ресурса, да, есть ошибки, но куда смотрели эксперты, разве в их обязанности не входит проверка ресурса, прежде чем он появится на СУПе ? Хотя, вопрос, наверное, не по адресу. Спасибо
Спасибо Ларсон, редакторы
Ларсон, редакторы  Соревнование состоится в субботу, 4 декабря, под личным наблюдением в кампусах США и Канады.
Соревнование состоится в субботу, 4 декабря, под личным наблюдением в кампусах США и Канады. Могу ли я участвовать в конкурсе Патнэма без связи с учреждением?
Могу ли я участвовать в конкурсе Патнэма без связи с учреждением?  Обратите внимание, что студент может участвовать в официальном конкурсе Патнэма не более четырех раз.Как правило, мы не рекомендуем учащимся старших классов исчерпать свои права. Если вы регулярно не зачислены на бакалавриат в высшее учебное заведение, то вы не имеете права.
Обратите внимание, что студент может участвовать в официальном конкурсе Патнэма не более четырех раз.Как правило, мы не рекомендуем учащимся старших классов исчерпать свои права. Если вы регулярно не зачислены на бакалавриат в высшее учебное заведение, то вы не имеете права. 4 декабря меня не будет в родном учреждении.Могу ли я еще участвовать в конкурсе?
4 декабря меня не будет в родном учреждении.Могу ли я еще участвовать в конкурсе?  Каков крайний срок регистрации студентов?
Каков крайний срок регистрации студентов?  Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. В других случаях вы можете использовать оценку, чтобы проверить, является ли ваш ответ разумным. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть в диапазоне от 300 до 600.
Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. В других случаях вы можете использовать оценку, чтобы проверить, является ли ваш ответ разумным. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть в диапазоне от 300 до 600. Обязательно проверьте свои ответы, прокрутив документ вниз.
Обязательно проверьте свои ответы, прокрутив документ вниз. Задачи, вероятно, будут незнакомы учащимся, которые не изучали продвинутую алгебру и тригонометрию, и если да, то нет необходимости пытаться их решить. Если вы успешно завершили курс «Продвинутая алгебра и тригонометрия», решите все задачи, которые кажутся вам знакомыми, и проверьте свои ответы. Просмотрите проблемы, подобные тем, которые вы пропустили, используя учебник по продвинутой алгебре и тригонометрии или предварительному исчислению или один из ресурсов, перечисленных ниже.Чтобы просмотреть список всех тем, которые необходимо просмотреть для теста по математике на уровне колледжа, перейдите на страницу http://accuplacer.collegeboard.org/students, щелкните вкладку «Тесты Accuplacer», а затем — «Математика на уровне колледжа», чтобы развернуть список тем. на тесте.
Задачи, вероятно, будут незнакомы учащимся, которые не изучали продвинутую алгебру и тригонометрию, и если да, то нет необходимости пытаться их решить. Если вы успешно завершили курс «Продвинутая алгебра и тригонометрия», решите все задачи, которые кажутся вам знакомыми, и проверьте свои ответы. Просмотрите проблемы, подобные тем, которые вы пропустили, используя учебник по продвинутой алгебре и тригонометрии или предварительному исчислению или один из ресурсов, перечисленных ниже.Чтобы просмотреть список всех тем, которые необходимо просмотреть для теста по математике на уровне колледжа, перейдите на страницу http://accuplacer.collegeboard.org/students, щелкните вкладку «Тесты Accuplacer», а затем — «Математика на уровне колледжа», чтобы развернуть список тем. на тесте. 2010. Эта книга включает обзор тем трех экзаменов по математике Accuplacer, а также дополнительные практические тесты для каждого экзамена.
2010. Эта книга включает обзор тем трех экзаменов по математике Accuplacer, а также дополнительные практические тесты для каждого экзамена.
 (90-минутный формат экзамена)
(90-минутный формат экзамена) (90-минутный формат экзамена)
(90-минутный формат экзамена)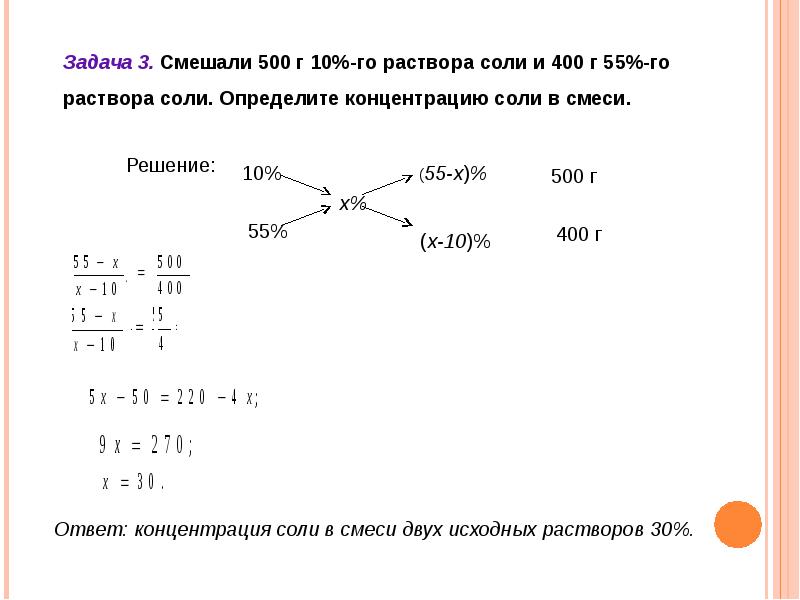 (50-минутный формат экзамена)
(50-минутный формат экзамена)