§ 9. Экстремумы функции. Необходимые условия существования экстремума
Определение 1. Точка х0 из области определения функции f называется точкой минимума этой функции, если найдется такая -окрестность ]х0-; х0 +[ точких0, что для всех хх0 из этой окрестности выполняется неравенство
f(x)>f(x0).
Определение 2. Точка х0 из области определения функции f называется точкой максимума этой функции, если найдется такая -окрестность ]х -; х +[ точких0, что для всех хх0 из этой окрестности выполняется неравенство
f(x)<f(x0).
Точки минимума и максимума называются точками экстремума, а значения функции в этих точках называются
Рассмотрим график функции y = f(x), х [а; b] (рис. 6). Точки хи х3 являются точками максимума, а х2 и — точками минимума. Из рис. 6 видно, что
Рис 6 Рис 7
минимум в точке хбольше максимума данной функции в точке х.Это объясняется тем, что экстремум функции связан с определенной -окрестностью точки экстремума, а не со всей областью определения функции. По этой причине употребляется термин «локальный экстремум», т. е. экстремум, связанный с данным местом. Этим же объясняется и тот факт, что точки а иb не относятся к точкам экстремума. Для них не существуют -окрестности, принадлежащие области определения функции.
Необходимые условия существования экстремума дает теорема Ферма, которая известна по школьному курсу, поэтому мы приводим лишь ее формулировку.
Теорема Ферма. Если точка х
0 является точкой экстремума функции у = f(x) и в этой точке существует производная f (х0), то = 0.Эта теорема имеет простой геометрический смысл: касательная к графику функции у = f(x) в точке, удовлетворяющей условиям теоремы Ферма, параллельна оси абсцисс (рис. 7).
Напомним, что точки, в которых производная функции обращается в нуль или не существует, называются критическими точками (первого рода).
Теорема Ферма дает лишь необходимое условие существования экстремума, но не достаточное.
Пример 1. Производная функции f(x)=x3 в точке х0 = 0 обращается в нуль, а экстремума в этой точке функция не имеет (рис. 8).
Рис 8
Можно показать, что и в тех критических точках, в которых производная не существует, функция
Пример 2. Функция f(x) = |x| в точке х0 = 0 не имеет производной (см. § 1) Однако, как видно из
рис. 3, в точке она имеет экстремум (минимум)
Пример 3. Рассмотрим функцию f(x) = (рис. 9). По графику видно, что в точке х0 = 0
данная функция экстремума не имеет. Производная в рассматриваемой точке не существует.
Рис 9
Таким образом, экстремум функции, если он существует, может быть только в критических точках. Но это не означает, что во всякой критической точке функция имеет экстремум.
Чтобы выяснить, в каких критических точках функция имеет экстремум, рассмотрим достаточные условия существования экстремума.
§ 10. Достаточные условия существования экстремума
1. Первое достаточное условие.
Теорема 1. Пусть функция y = f(x) непрерывна в
точке х0 и в ее-окрестности имеет производную, кроме, быть может, самой точке х0. Тогда:1) если производная f (х) при переходе через точку х0 меняет знак с плюса на минус, то х0 является точкой максимума;
2) если производная f (х) при переходе через точку х0 меняет знак с минуса на плюс, то х0 является точкой минимума;
3) если производная f‘(x) при переходе через точку х0 не меняет знак, то в точке х0 функция f(x) не имеет экстремума.
С доказательством первой части этой теоремы читатель знаком по школьному курсу. Доказательство остальных частей проводится аналогично, поэтому мы его не приводим.
При исследовании функции на экстремум с помощью первой производной применяют правило (первое), которое мы сформулируем, решая конкретный пример.
Пример 1. Исследовать на экстремум функцию
f (х) = (2х + 1).
Решение.
1. Находим производную данной функции:
2. Находим критические точки: а) решая уравнение
получим х =1.
б) f‘(x) не существует при х = 2. Следовательно, критические точки: = 1 и х= 2.
3. Методом пробных точек определяем знак производной в каждом из интервалов: ]-; 1 [, ]1; 2[, ]2; +[ (рис. 10). Имеем:
при
при
при
Таким образом, = 1 — точка максимума, а = 2 — точка минимума.
Рис 10
4. Вычисляем значения данной функции в точках экстремума:
;
Второй признак экстремума функции.
Пусть  ,
,
если
 ,
то
,
то  —
точка минимума;
—
точка минимума;если
 ,
то
,
то  —
точка максимума.
—
точка максимума.
Как
видите, этот признак экстремума функции
требует существования производной как
минимум до второго порядка в точке 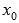 .
.
Пример.
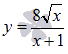 .
.Решение.
Начнем
с области определения: 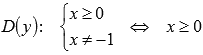
Продифференцируем
исходную функцию: 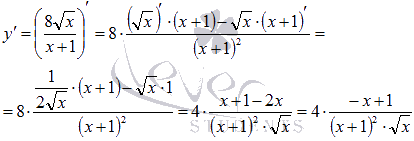
Производная
обращается в ноль при x=1,
то есть, это точка возможного экстремума.
Находим вторую производную функции
и вычисляем ее значение при x
= 1: 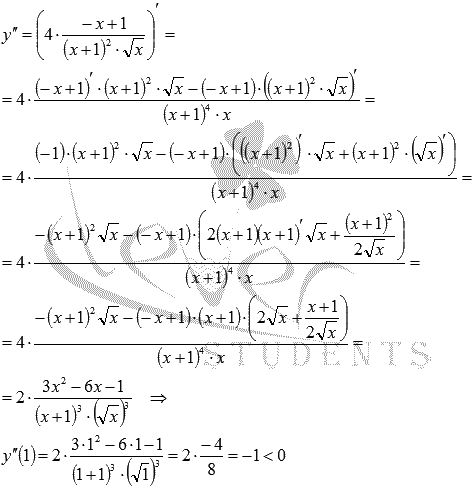
Следовательно,
по второму достаточному условию
экстремума, x=1 —
точка максимума. Тогда 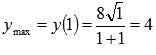 —
максимум функции.
—
максимум функции.
Графическая иллюстрация.

Ответ:
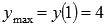
Третье достаточное условие экстремума функции.
Пусть
функция y=f(x) имеет
производные до n-ого
порядка в 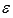 -окрестности
точки
-окрестности
точки 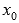 и
производные до n+1-ого
порядка в самой точке
и
производные до n+1-ого
порядка в самой точке 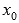 .
Пусть
.
Пусть  и
и  .
.
Тогда,
Пример.
Найти
точки экстремума функции 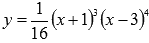 .
.
Решение.
Исходная функция является целой рациональной, ее областью определения является все множество действительных чисел.
Продифференцируем
функцию: 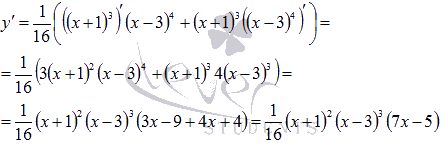
Производная
обращается в ноль при 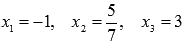 ,
следовательно, это точки возможного
экстремума. Воспользуемся третьим
достаточным условием экстремума.
,
следовательно, это точки возможного
экстремума. Воспользуемся третьим
достаточным условием экстремума.
Находим
вторую производную и вычисляем ее
значение в точках возможного экстремума
(промежуточные вычисления опустим): 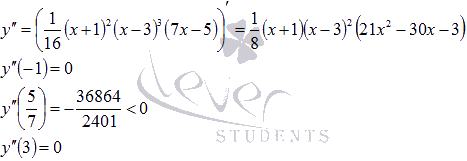
Следовательно, 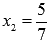 —
точка максимума (для третьего достаточного
признака экстремума имеем n=1 и
—
точка максимума (для третьего достаточного
признака экстремума имеем n=1 и 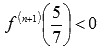 ).
).
Для
выяснения характера точек 

Следовательно, 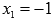 —
точка перегиба функции (n=2 и
—
точка перегиба функции (n=2 и 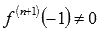 ).
).
Осталось
разобраться с точкой 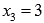 .
Находим четвертую производную и вычисляем
ее значение в этой точке:
.
Находим четвертую производную и вычисляем
ее значение в этой точке: 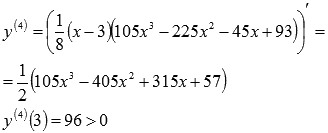
Следовательно, 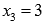 —
точка минимума функции.
—
точка минимума функции.
Графическая иллюстрация.
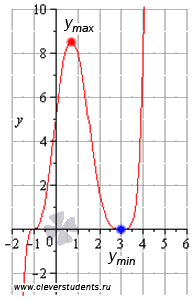
Ответ:
 —
точка максимума,
—
точка максимума, 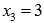 —
точка минимума функции.
—
точка минимума функции.
10. Экстремумы функции Определение экстремума
Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство (f(x1) < f (x2) (f(x1) > f(x2)).
Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ‘(x) 0
(f ‘ (x) 0).
Точка xо называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки xо, для всех точек которой верно неравенство f(x) ≤ f(xо) (f(x) ≥ f(xо)).
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках — ее экстремумами.
Точки экстремума
Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f ‘(xо) = 0, либо f (xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
Первое достаточное условие. Пусть xо — критическая точка. Если f ‘ (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе
достаточное условие. Пусть
функция f(x)
имеет производную
f ‘ (x)
в окрестности точки xо и
вторую производную 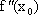 в
самой точке xо.
Если f ‘ (xо)
= 0,
в
самой точке xо.
Если f ‘ (xо)
= 0, 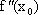 >0
(
>0
( <0),
то точка xо является
точкой локального минимума (максимума)
функции f(x).
Если же
<0),
то точка xо является
точкой локального минимума (максимума)
функции f(x).
Если же 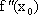 =0,
то нужно либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
=0,
то нужно либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Пример 3.22. Найти экстремумы функции f(x) = 2x3 — 15x2+ 36x — 14.
Решение. Так как f ‘(x) = 6x2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x1 = 2 и x2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x2 = 3 производная меняет знак минус на плюс, поэтому в точке x2 = 3 у функции минимум. Вычислив значения функции в точках x1 = 2 и x2 = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.
Лекция 16. Монотонность функции и точки экстремума
Монотонность функций и точки экстремума. Лекция 16.
Монотонность функций и точки экстремума.
Одним из приложений производной является ее применение к исследованию функций.
Возрастание и убывание функций.
По поведению производной функции на промежутках можно судить о ее монотонности на них.
Необходимые условия возрастания (убывания) функции.
Теорема
32. Если
дифференцируемая на некотором интервале  функция
функция 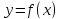 возрастает (убывает) на нем, то
возрастает (убывает) на нем, то 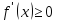 (
( )
для всех
)
для всех 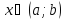 .
.
Доказательство.
Пусть функция 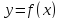 возрастает интервале
возрастает интервале  .
Выберем произвольные точки
.
Выберем произвольные точки 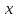 и
и 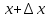 на этом интервале и рассмотрим отношение
на этом интервале и рассмотрим отношение 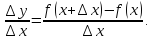
Функция 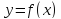 возрастает, поэтому при
возрастает, поэтому при 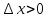 будет
будет 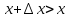 и
и 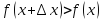 ,
а при
,
а при 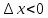 будет
будет  и
и 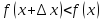 .
В обоих случаях
.
В обоих случаях 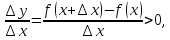
так
как числитель и знаменатель дроби будут
иметь одинаковые знаки. Следовательно, 
Аналогично
рассматривается случай, когда функция 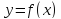 убывает на интервале
убывает на интервале 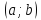 .
.
Замечание
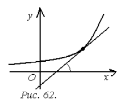
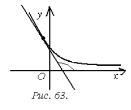
1. Геометрически
теорема 32 означает, что касательные к
графику возрастающей функции имеют
острые углы с положительным направлением
оси 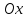 (рис. 62), а убывающие – тупые (рис. 63).
(рис. 62), а убывающие – тупые (рис. 63).
Достаточные условия возрастания (убывания) функции.
Теорема
33. Если
функция  дифференцируема на интервале
дифференцируема на интервале 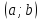 и
и 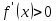 (
(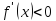 )
для всех
)
для всех 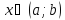 ,
то функция
,
то функция 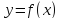 возрастает (убывает) на этом интервале.
возрастает (убывает) на этом интервале.
Доказательство.
Пусть  на
интервале
на
интервале 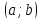 .
Возьмем точки
.
Возьмем точки 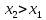 .
Применим к отрезку
.
Применим к отрезку 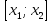 теорему Лагранжа
теорему Лагранжа
 ,
,
где 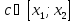 .
Так как
.
Так как  и
и 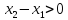 ,
то
,
то 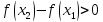 и
и 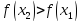 .
Следовательно, функция
.
Следовательно, функция 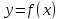 возрастает на интервале
возрастает на интервале 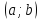 .
.
Максимум и минимум функции.
Основные понятия.
Точка 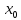 называется точкой
максимума (минимума) функции
называется точкой
максимума (минимума) функции 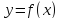 ,
если существует такая
,
если существует такая  – окрестность точки
– окрестность точки 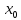 ,
что для всех
,
что для всех 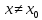 из этой окрестности выполняется
неравенство
из этой окрестности выполняется
неравенство  (
(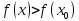 )
(рис. 64).
)
(рис. 64).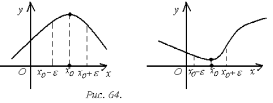
Значение функции в точке максимума (минимума) называется ее максимумом (минимумом).
Максимум и минимум функции называются ее экстремумами.
Точки, в которых производная функции не существует или равна нулю, называют критическими.
Необходимое условие экстремума.
Теорема
34. Если
дифференцируемая функция 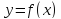 имеет экстремум в точке
имеет экстремум в точке 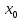 ,
то ее производная в этой точке равна
нулю,
,
то ее производная в этой точке равна
нулю,  .
.
Доказательство.
Пусть 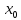 – точка максимума. Следовательно, в
окрестности точки
– точка максимума. Следовательно, в
окрестности точки  выполняется неравенство
выполняется неравенство 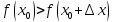 .
Тогда
.
Тогда 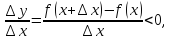 если
если  и
и
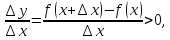
Если  . По условию теоремы производная функции
. По условию теоремы производная функции 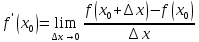
существует.
Переходя к пределу при 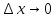 ,
получим
,
получим 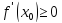 ,
если
,
если 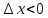 и
и  ,
если
,
если  .
Это возможно лишь в случае
.
Это возможно лишь в случае 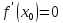 .
.
Аналогично
можно показать утверждение теоремы
если 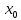 – точка минимума.
– точка минимума.
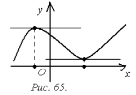
Замечание
1. Геометрически
утверждение теоремы означает, что в
точках экстремума касательные к графику
функции параллельны оси 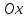 (рис. 65). Обратная теорема не верна. Если
(рис. 65). Обратная теорема не верна. Если  ,
то это не всегда означает, что точка
,
то это не всегда означает, что точка 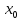 – точка экстремума. Действительно, для
функции
– точка экстремума. Действительно, для
функции 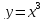 в точке
в точке 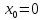 производная
производная 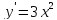 ,
, 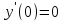 ,
но точка
,
но точка 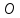 не является ни минимумом, ни максимумом
(рис. 66). Существуют так же функции,
которые в точках экстремума не имеют
производных. Так функция
не является ни минимумом, ни максимумом
(рис. 66). Существуют так же функции,
которые в точках экстремума не имеют
производных. Так функция 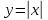 в точке
в точке 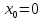 не имеет производной, но эта точка
является ее минимумом (рис. 67).
не имеет производной, но эта точка
является ее минимумом (рис. 67).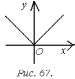

Достаточное условие экстремума.
Теорема
35. Если
непрерывная функция 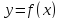 дифференцируема в некоторой
дифференцируема в некоторой  – окрестности критической точки
– окрестности критической точки 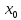 и при переходе через нее (слева направо)
производная
и при переходе через нее (слева направо)
производная  меняет знак с плюса на минус (с минуса
на плюс), то точка
меняет знак с плюса на минус (с минуса
на плюс), то точка 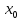 есть точка максимума (минимума).
есть точка максимума (минимума).
Доказательство.
Рассмотрим 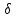 – окрестность точки
– окрестность точки 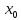 .
Пусть выполняется условия:
.
Пусть выполняется условия: 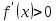 ,
для любого
,
для любого 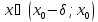 и
и 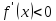 ,
для любого
,
для любого 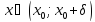 .
Тогда функция
.
Тогда функция 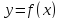 возрастает на интервале
возрастает на интервале
 и
убывает на интервале
и
убывает на интервале  .
Следовательно, значение функции
.
Следовательно, значение функции 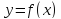 в точке
в точке 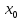 является наибольшим значением на
интервале
является наибольшим значением на
интервале  ,
т. е.
,
т. е.  для всех
для всех 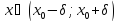 .
Это означает, что
.
Это означает, что 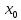 – точка максимума. Аналогично доказывается
случай для точки минимума (рис. 68).
– точка максимума. Аналогично доказывается
случай для точки минимума (рис. 68).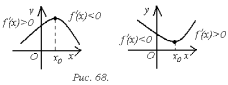
Теорема
36. Если
в точке 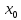 первая производная функции равна нулю
первая производная функции равна нулю  ,
а вторая производная в точке
,
а вторая производная в точке  существует и отлична от нуля
существует и отлична от нуля 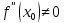 ,
то при
,
то при 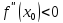 в точке
в точке 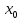 функция
функция 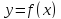 имеет максимум, а при
имеет максимум, а при  – минимум.
– минимум.
Доказательство.
Пусть 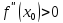 .
Так как
.
Так как
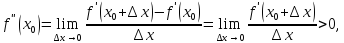
то
в достаточно малой окрестности точки 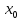 выполняется неравенство
выполняется неравенство
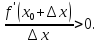
Если  ,
то
,
то 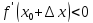 ,
а если
,
а если  ,
то
,
то 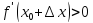 .
.
Таким
образом, при переходе через точку 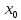 первая производная меняет знак с минуса
на плюс. Следовательно, по теореме 35
достаточных условий экстремума, точка
первая производная меняет знак с минуса
на плюс. Следовательно, по теореме 35
достаточных условий экстремума, точка  есть точка минимума. Аналогично
доказывается случай для точки максимума.
есть точка минимума. Аналогично
доказывается случай для точки максимума.
Пример 60. Исследовать монотонность функции
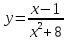
и найти ее точки экстремума.
Решение. Найдем производную функции и приравняем ее к нулю


Отсюда: 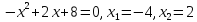 .
Построим числовую ось и на ней отметим
методом интервалов знаки производной.
Там, где производная меняет знак с (+) на
(-), будет точка максимума (
.
Построим числовую ось и на ней отметим
методом интервалов знаки производной.
Там, где производная меняет знак с (+) на
(-), будет точка максимума (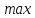 ),
где с (-) на (+) – точка минимума (
),
где с (-) на (+) – точка минимума ( ).
Из рисунка видно, что минимум достигается
в точке
).
Из рисунка видно, что минимум достигается
в точке  ,
максимум — в точке
,
максимум — в точке 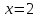 ,
причем
,
причем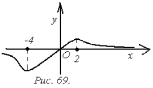


Функция
убывает на интервалах 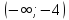 и
и  ,
возрастает на интервале
,
возрастает на интервале  (рис. 69).
(рис. 69).
Наибольшее и наименьшее значения функции на отрезке.
Пусть
функция 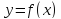 непрерывна на отрезке
непрерывна на отрезке 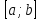 .
Такая функция достигает на этом отрезке
своего наибольшего и наименьшего
значений. Эти значения она может принимать
либо во внутренней точке отрезка
.
Такая функция достигает на этом отрезке
своего наибольшего и наименьшего
значений. Эти значения она может принимать
либо во внутренней точке отрезка 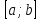 ,
либо на границе отрезка, т. е. в точках
,
либо на границе отрезка, т. е. в точках  и
и 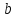 .
.
Если 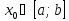 ,
то наибольшее и наименьшее значения
следует искать среди критических точек
функции
,
то наибольшее и наименьшее значения
следует искать среди критических точек
функции  .
.
Таким
образом, можно сформулировать следующее
правило нахождения наибольшего и
наименьшего значений функции 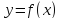 на отрезке
на отрезке  :
:
1)
найти критические точки функции на
интервале  ;
;
2) вычислить значения функции в найденных точках;
3)
вычислить значения функции на концах
отрезка, т. е. в точках 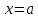 и
и 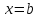 ;
;
4) среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
Замечание
1. Если функция 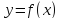 имеет лишь одну критическую точку и она
является точкой максимума (минимума),
то в этой точке функция принимает свое
наибольшее (наименьшее) значение (рис.
70).
имеет лишь одну критическую точку и она
является точкой максимума (минимума),
то в этой точке функция принимает свое
наибольшее (наименьшее) значение (рис.
70). 
Замечание
2. Если функция 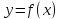 не имеет на отрезке
не имеет на отрезке 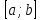 критических точек, то на нем функция
либо монотонно возрастает, либо монотонно
убывает. Свои наибольшее и наименьшее
значения функция принимает в этом случае
на концах отрезка (рис. 71).
критических точек, то на нем функция
либо монотонно возрастает, либо монотонно
убывает. Свои наибольшее и наименьшее
значения функция принимает в этом случае
на концах отрезка (рис. 71). 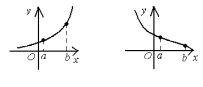
Пример 61. Найти наибольшее и наименьшее значение функции
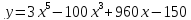
на
отрезке 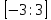 .
.
Решение. Найдем производную функции и приравняем ее к нулю
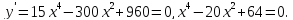
Откуда 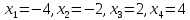 .
Точки
.
Точки 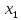 и
и 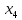 не лежат на отрезке
не лежат на отрезке 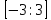 ,
поэтому находим значения функции в
точках
,
поэтому находим значения функции в
точках 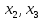 и на границе отрезка — в точках
и на границе отрезка — в точках 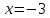 и
и 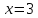 :
:

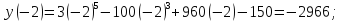
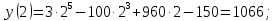

Выбираем наименьшее и наибольшее из этих значений.
Ответ: 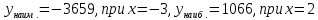 .
.
94
5. Экстремумы функции двух переменных Основные определения
Определение 1. Точка М(x0; у0) называется точкой максимума (минимума) функции z = f(x; y), если существует окрестность точки М, такая, что для всех точек (x; y) из этой окрестности выполняется неравенство:
f(x0;
y0)
f(x; y), 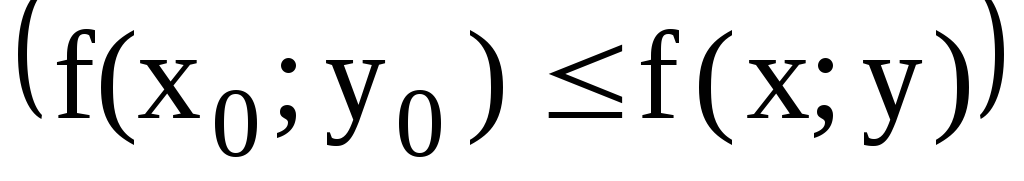 .
.
Теорема 1 (необходимое
условие существования экстремума).
Если дифференцируемая функция z =
f(x; y) достигает экстремума в точке М(x0;
y0),
то ее частные производные первого
порядка в этой точке равны нулю, т.е. 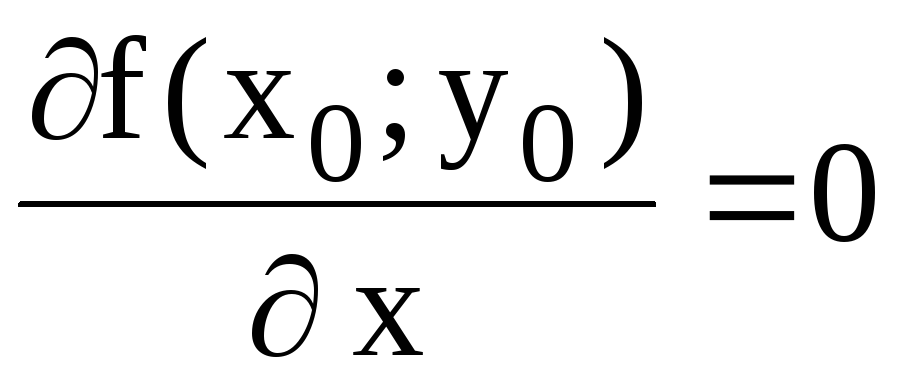 ;
;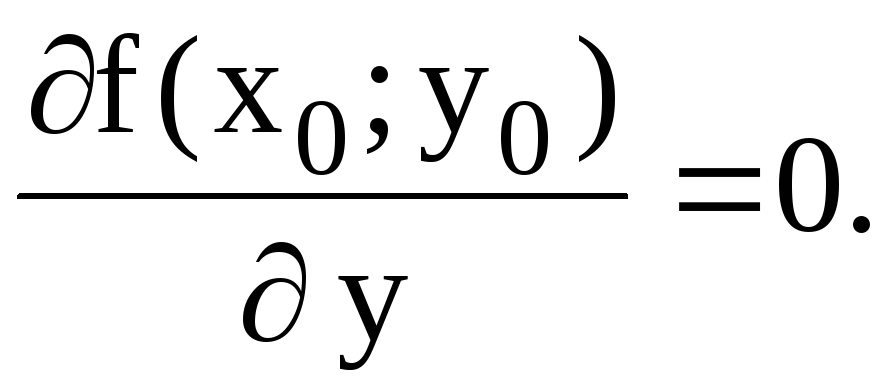
Точки, в которых частные производные равны нулю, называются стационарными или критическими точками.
Теорема 2 (достаточное условие существования экстремума)
Пусть функция z = f(x; y):
а) определена в
некоторой окрестности точки (x0;
y0),
в которой 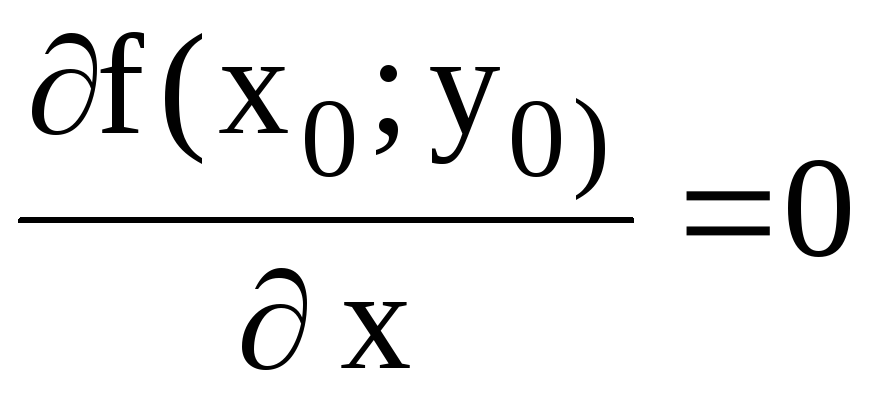 и
и ;
;
б) имеет в этой точке непрерывные частные производные второго порядка
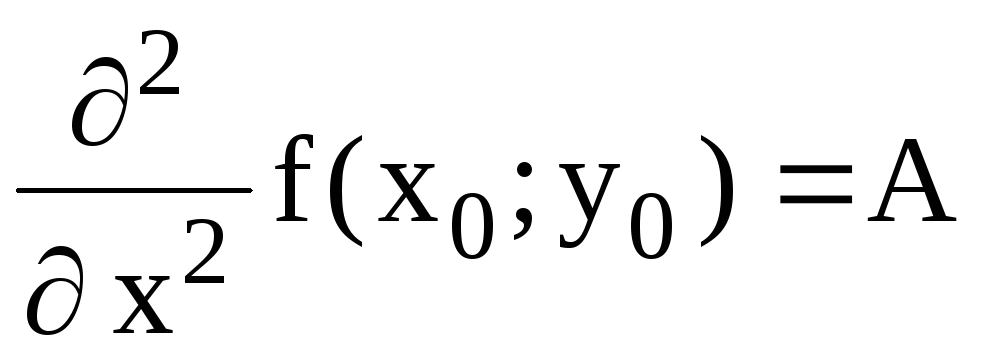 ;
;
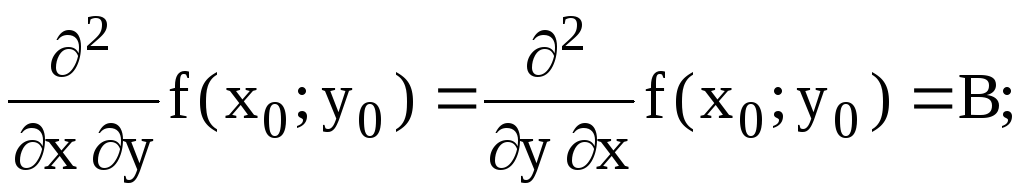

Тогда, если = АС B2 > 0, то в точке (x0; y0) функция z = f(x; y) имеет экстремум, причем, если А < 0 (или С < 0) – максимум, если А > 0 (или С > 0) – минимум. В случае = АС В2 < 0, функция z = f(x; y) экстремума не имеет. Если = AC B2 = 0, то требуется дальнейшее исследование (сомнительный случай).
Пример 1. Найти экстремум функции z = x2 + xy + y2 3x 6y.
Решение. Найдем частные производные первого порядка:

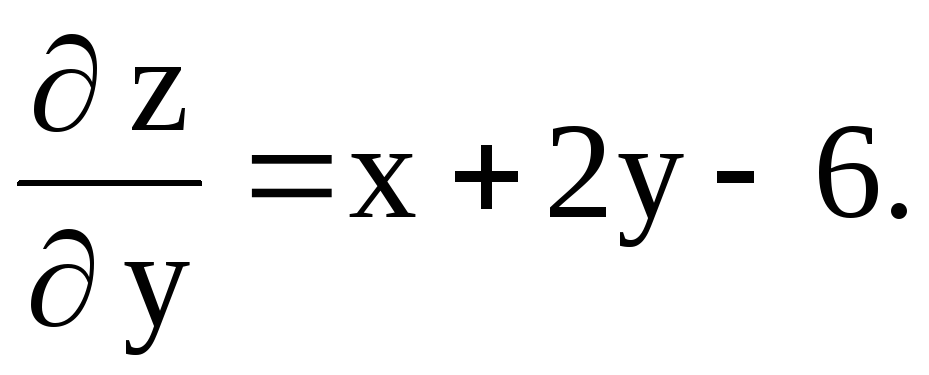
Воспользуемся необходимым условием существования экстремума:

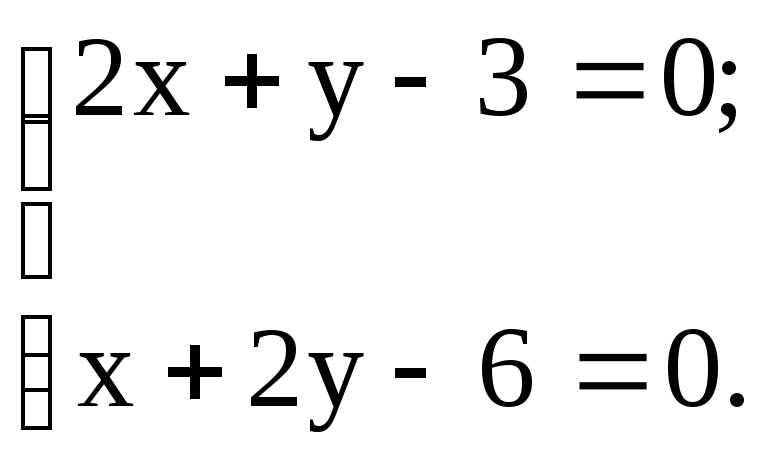
Решая систему уравнений, находим координаты x и y стационарных точек: x = 0; y = 3, т. е. М(0; 3).
Вычислим частные производные второго порядка и найдем их значения в точке М.
А
= 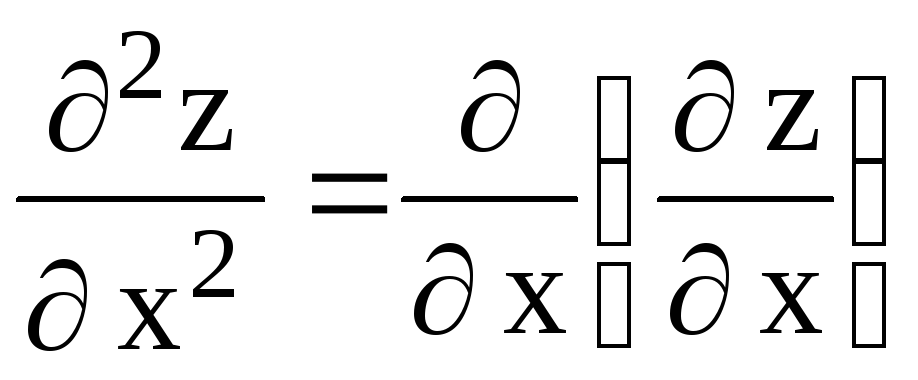 = 2; С =
= 2; С =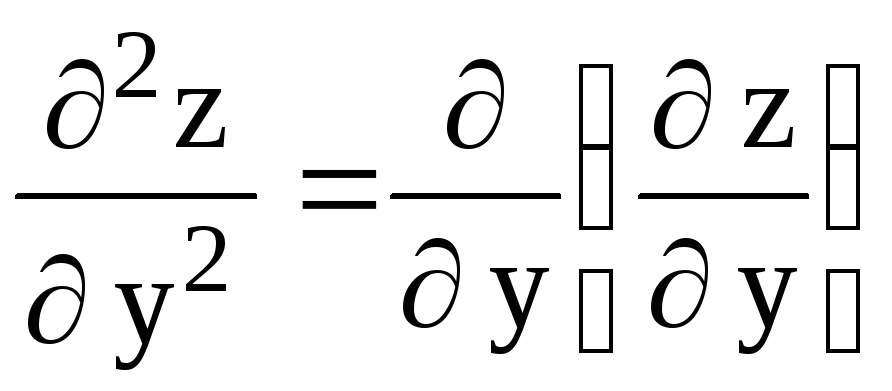 = 2;
= 2;
В
= 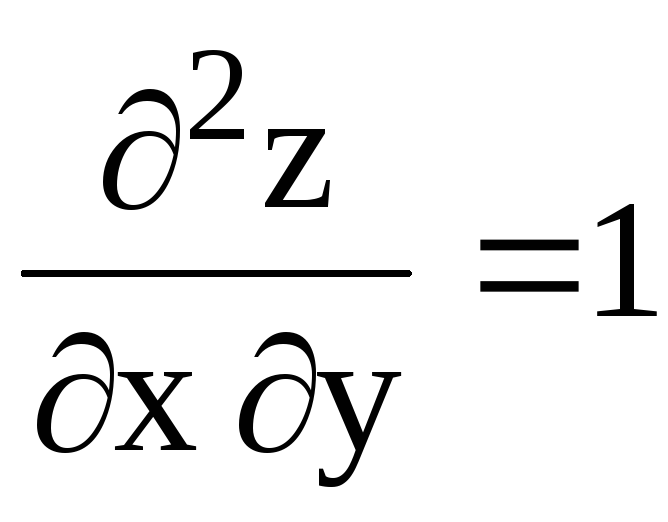 .
.
Составим дискриминант = АС В2 = 2 2 1 > 0, A = 2 > 0. Следовательно, в точке М(0; 3) заданная функция имеет минимум. Значение функции в этой точке zmin = 9.
Найти экстремумы функций
322. z = x2 + y2 + xy 4x 5y 323. z = y3 x3 3xy
324.
z = x2
2xy + 4y3 325.
z =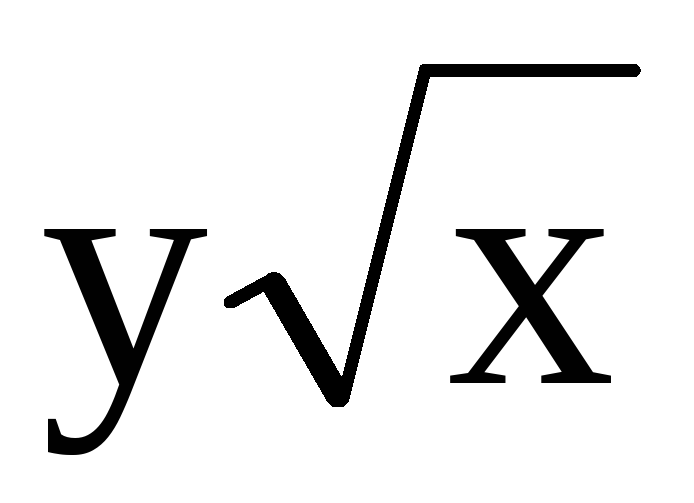
y2
x + 6y
y2
x + 6y
326. z = x y (1 x y) 327. z = 2xy 4x 2y
328. z = ex/2(x + y2) 329. z = x3 + 8y3 6xy + 1
330. z = 3x2y x3 y4 331. z = 3x + 6y x2 xy + y2
Наибольшее и наименьшее значения функции двух переменных в замкнутой области
Для того, чтобы найти наибольшее и наименьшее значения функции в замкнутой области, надо:
1) найти критические точки, расположенные в данной области, и вычислить значения функции в этих точках;
2) найти критические точки на границе области и вычислить наибольшее и наименьшее значения функций в них;
3) из всех найденных значений выбрать наибольшее и наименьшее.
Пример
2. Найти
наибольшее и наименьшее значения функции
z =  в круге x2 + y2
1.
в круге x2 + y2
1.
Решение. Найдем координаты критических точек, расположенных внутри рассматриваемой области, для чего вычислим частные производные первого порядка функции z и приравняем их к нулю.
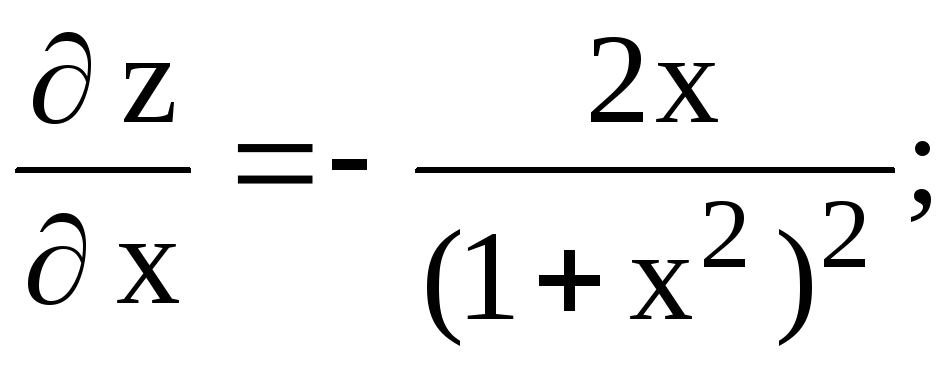

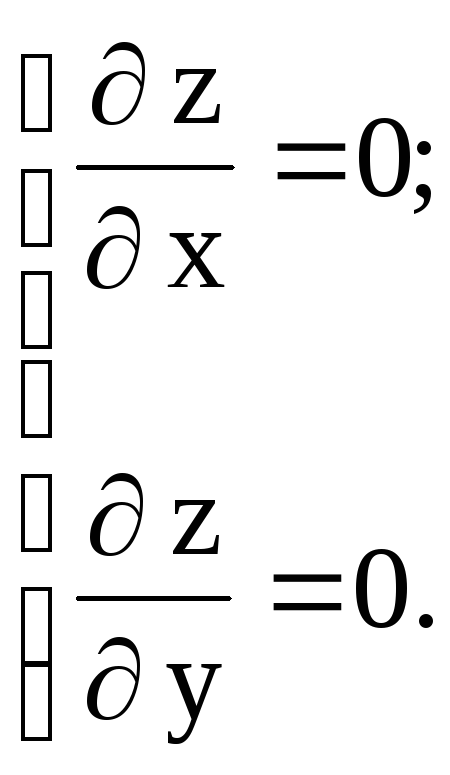
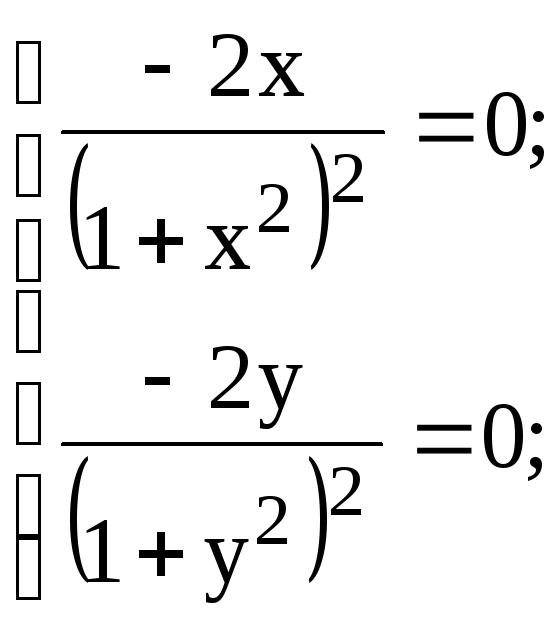
откуда x = 0, y = 0 и, следовательно, М(0; 0) – критическая точка.
Вычислим значение функции z в точке М(0; 0): z(0; 0) = 2.
Найдем критические точки на границе области окружности, заданной уравнением x2 + y2 = 1. Подставляя у2 = 1 x2 в функцию z = z(x; y), получим функцию одной переменной
z
= 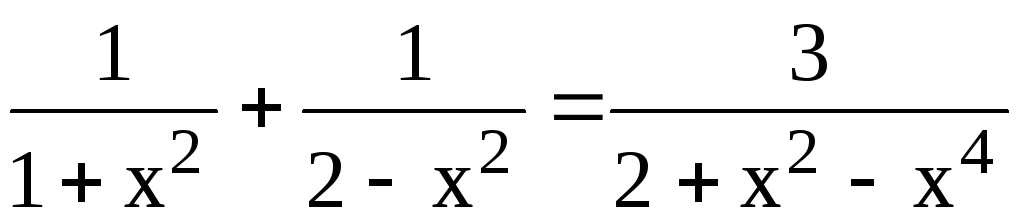 ;
;
причем x[1; 1].
Вычислив
производную 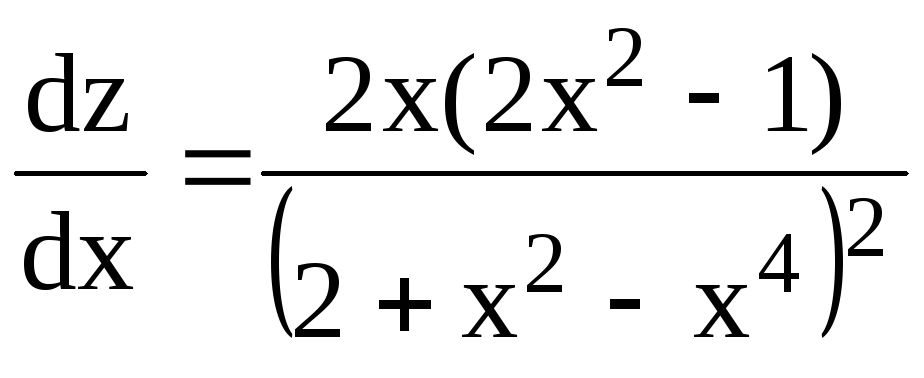 и приравняв ее нулю, получим критические
точки на границе области x1 =
0, x2 =
и приравняв ее нулю, получим критические
точки на границе области x1 =
0, x2 =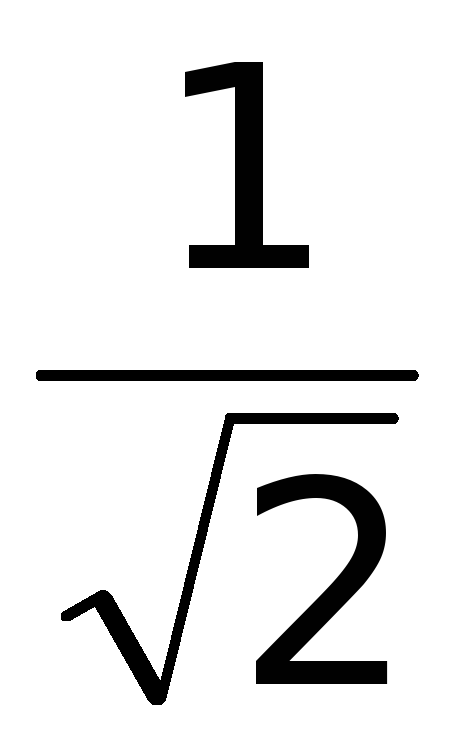 ,
x3 =
,
x3 = 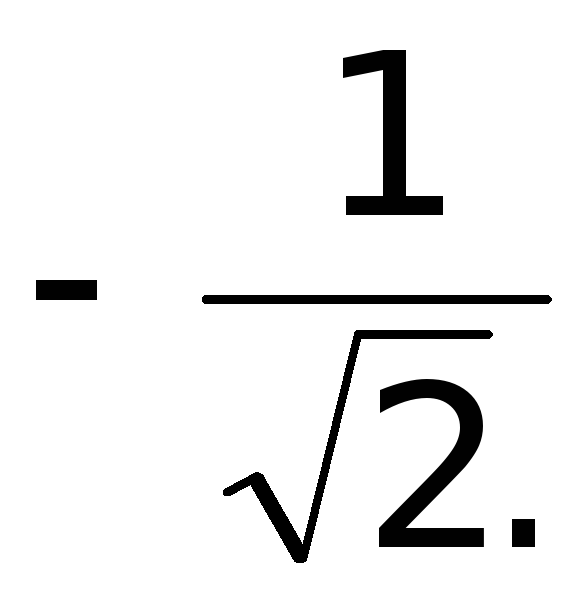
Найдем
значение функции z(x) = 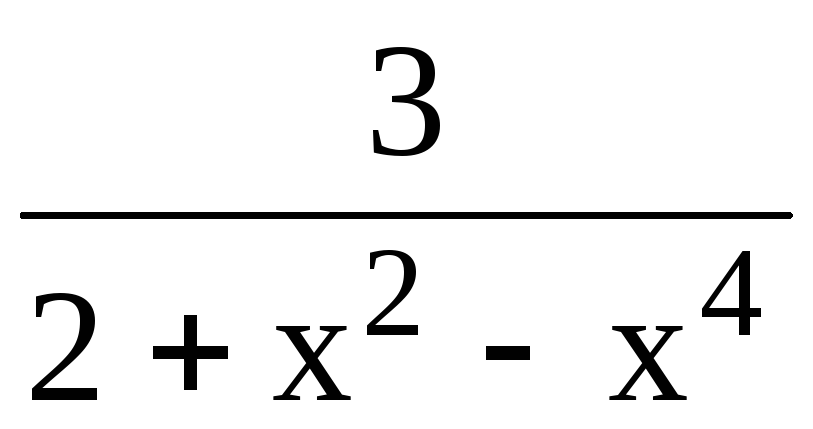 в критических точках и на концах отрезка
[1;
1]: z(0) =
в критических точках и на концах отрезка
[1;
1]: z(0) = 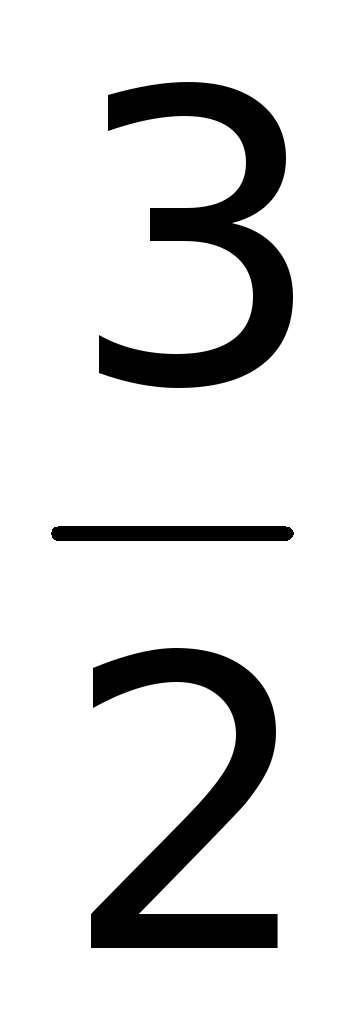 ;
;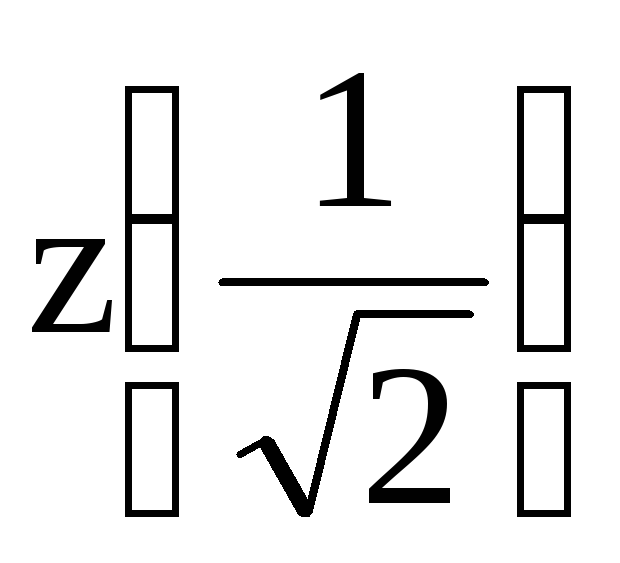 =
=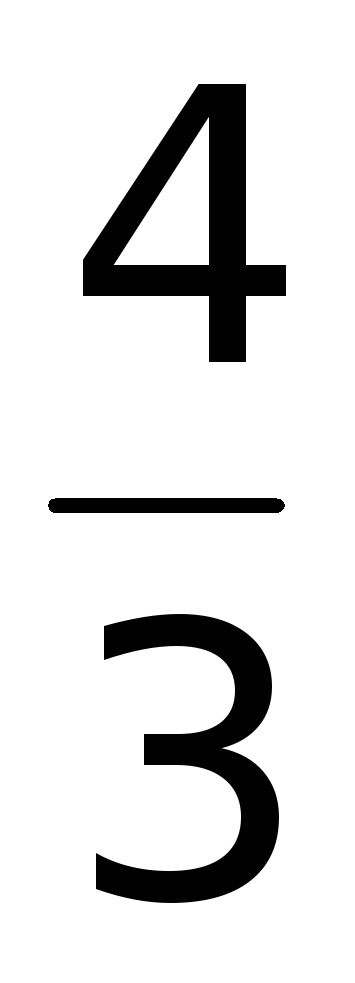 ;
; ;
z(1)
=
;
z(1)
= 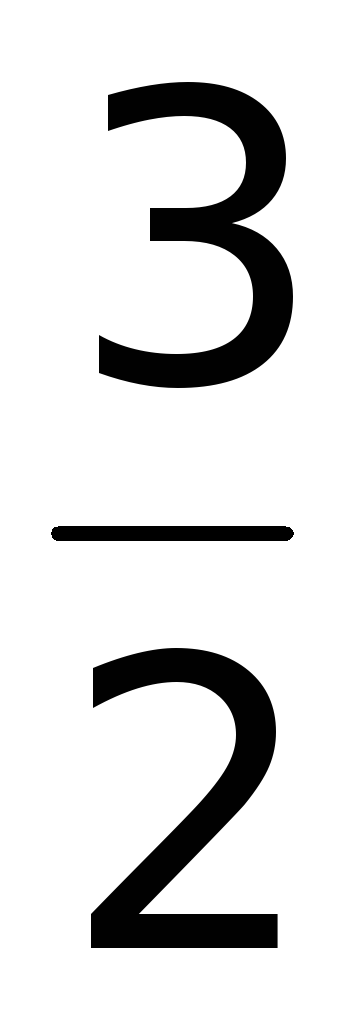 ;
z(1) =
;
z(1) =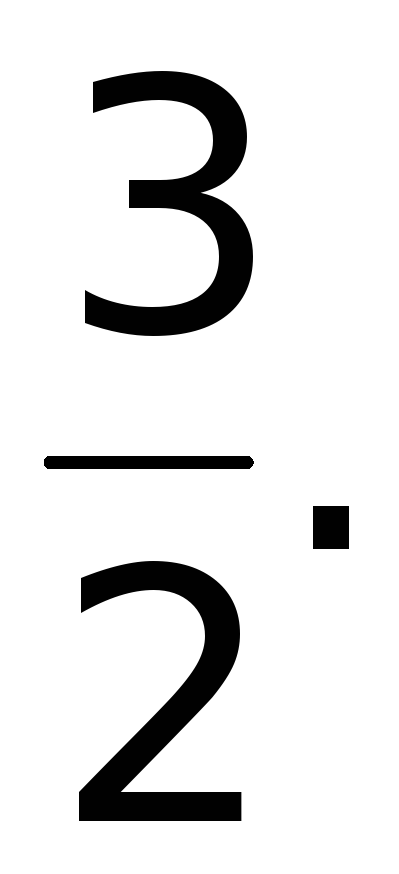
Выберем наибольшее и наименьшее среди значений функции z в критических точках, расположенных внутри и на границе круга.
Итак, zнаиб. = z(0; 0) = 2
и
zнаим. = z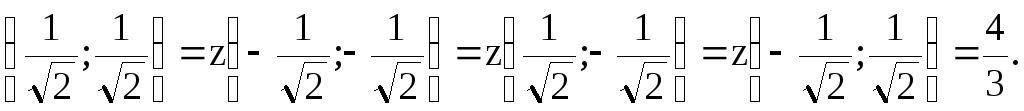
Лекция 13. Необходимое и достаточные условия локального экстремума функции План
Стационарные точки функции. Необходимое условие локального экстремума функции
Первое достаточное условие локального экстремума
Второе и третье достаточные условия локального экстремума
Наименьшее и наибольшее значения функции на сегменте
Выпуклые функции и точки перегиба
1. Стационарные точки функции. Необходимое условие локального экстремума функции
Определение 1. Пусть функция  определена на
определена на 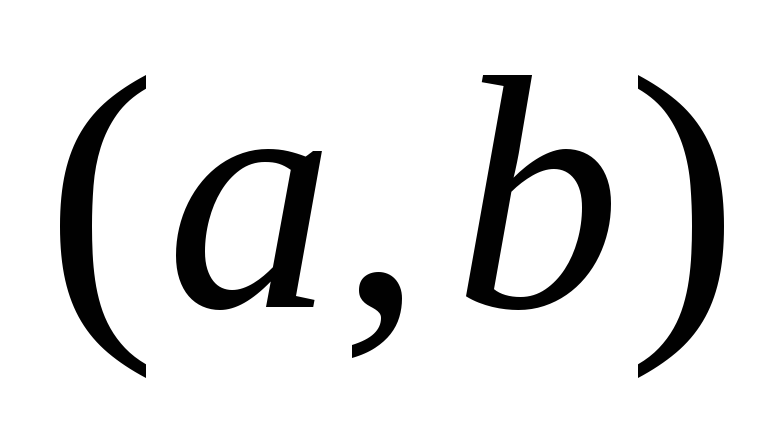 .
Точка
.
Точка 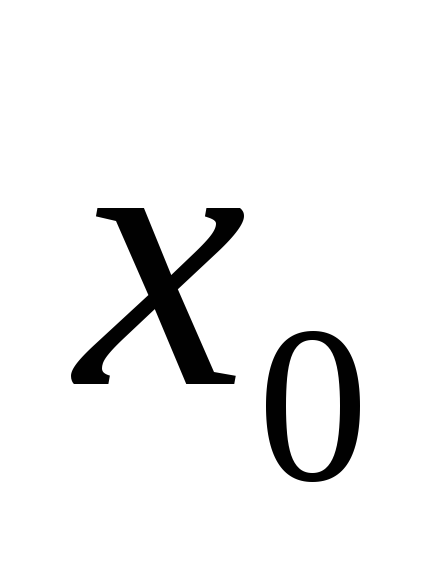 называется стационарной точкой функции
называется стационарной точкой функции 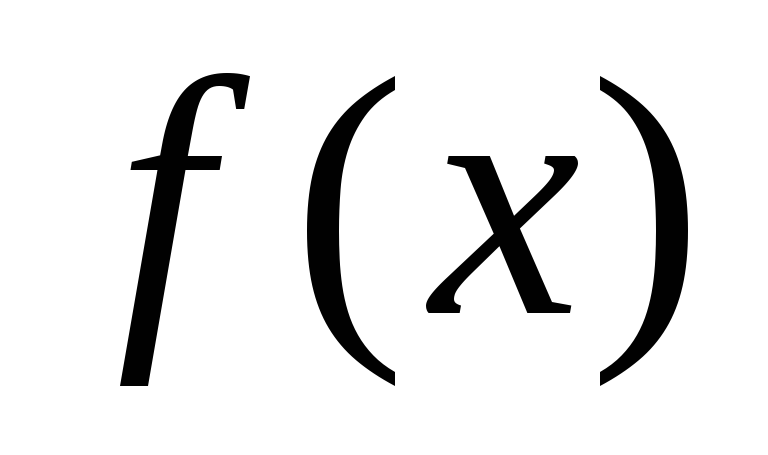 ,
если
,
если  дифференцирована в точке
дифференцирована в точке 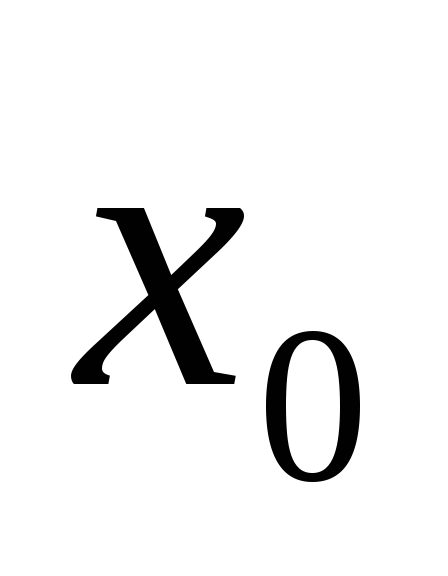 и
и 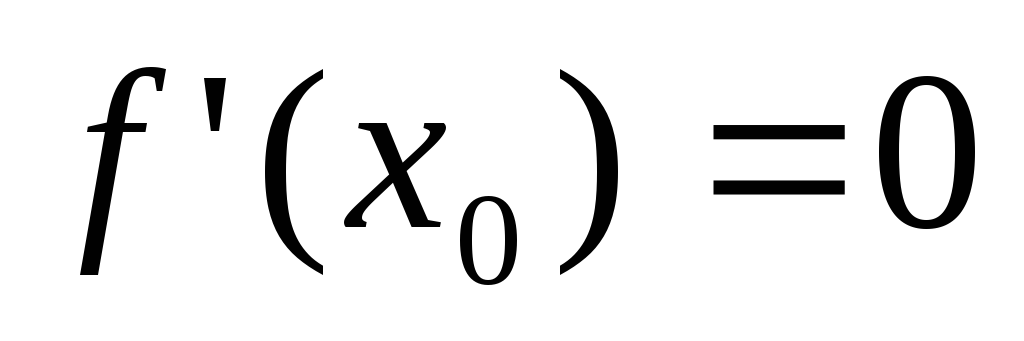 .
.
Теорема 1 (необходимое
условие локального экстремума функции).
Пусть функция  определена на
определена на 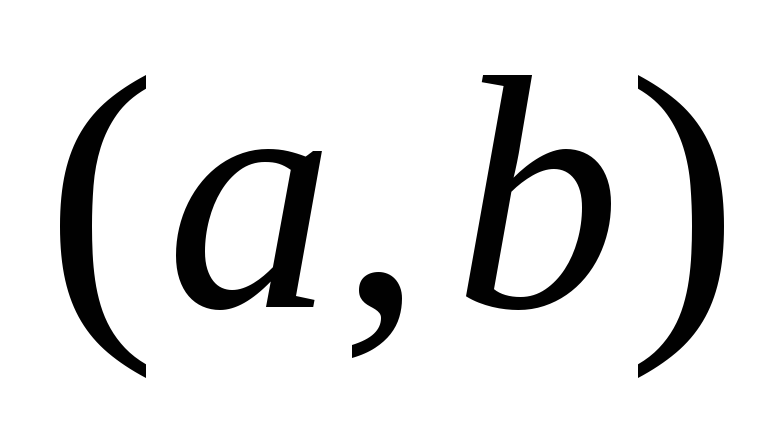 и имеет в точке
и имеет в точке 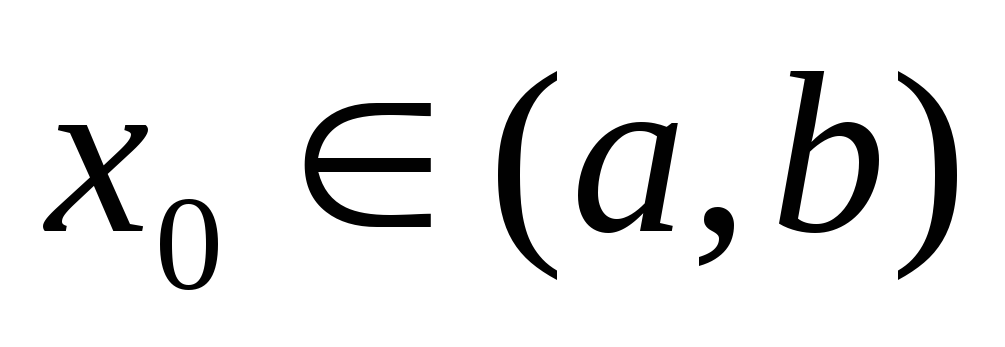 локальный экстремум. Тогда выполняется
одно из условий:
локальный экстремум. Тогда выполняется
одно из условий:
функция
 не имеет в точке
не имеет в точке  производной;
производной;функция
 имеет в точке
имеет в точке  производную и
производную и  .
.
Таким образом, для того, чтобы найти точки, которые являются подозрительными на экстремум, надо найти стационарные точки функции и точки, в которых производная функции не существует, но которые принадлежат области определения функции.
Пример.
Пусть 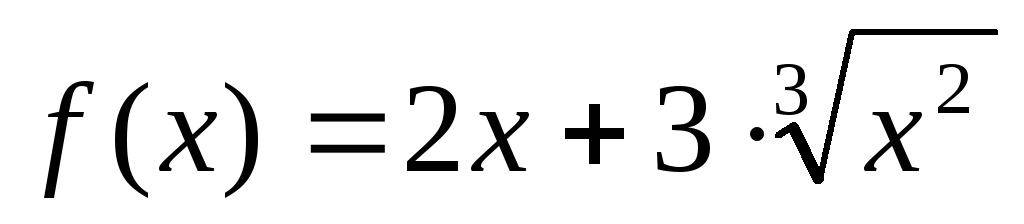 .
Найти для нее точки, которые являются
подозрительными на экстремум. Для
решения поставленной задачи, в первую
очередь, найдем область определения
функции:
.
Найти для нее точки, которые являются
подозрительными на экстремум. Для
решения поставленной задачи, в первую
очередь, найдем область определения
функции:  .
Найдем теперь производную функции:
.
Найдем теперь производную функции:
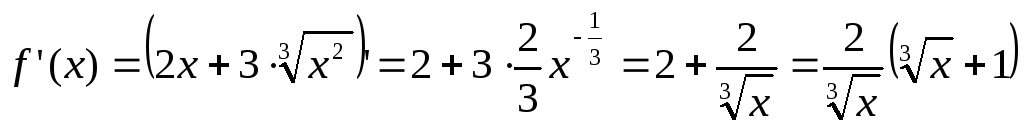 .
.
Точки, в которых производная
не существует:  .
Стационарные точки функции:
.
Стационарные точки функции:
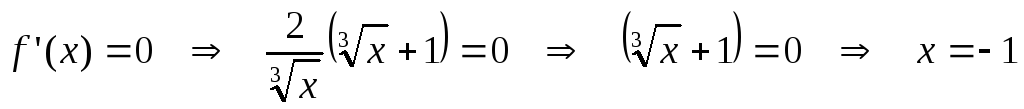 .
.
Поскольку и  ,
и
,
и 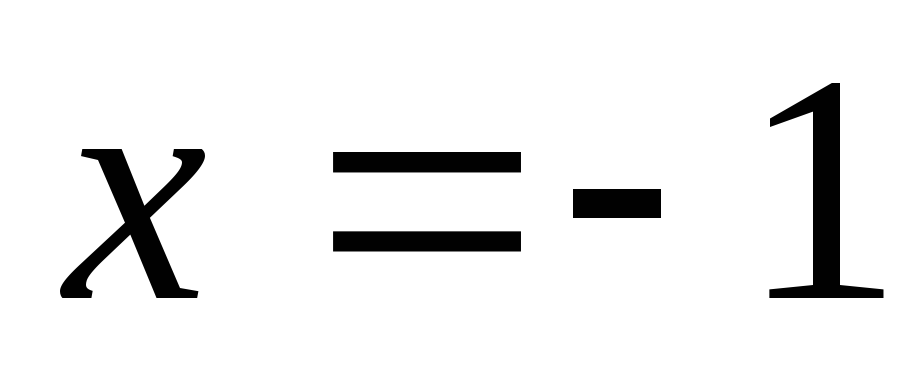 принадлежат области определения функции,
то они обе будут подозрительными на
экстремум. Но для того, чтобы сделать
вывод, будет ли там действительно
экстремум, надо применять достаточные
условия экстремума.
принадлежат области определения функции,
то они обе будут подозрительными на
экстремум. Но для того, чтобы сделать
вывод, будет ли там действительно
экстремум, надо применять достаточные
условия экстремума.
2. Первое достаточное условие локального экстремума
Теорема 1 (первое достаточное
условие локального экстремума).
Пусть функция 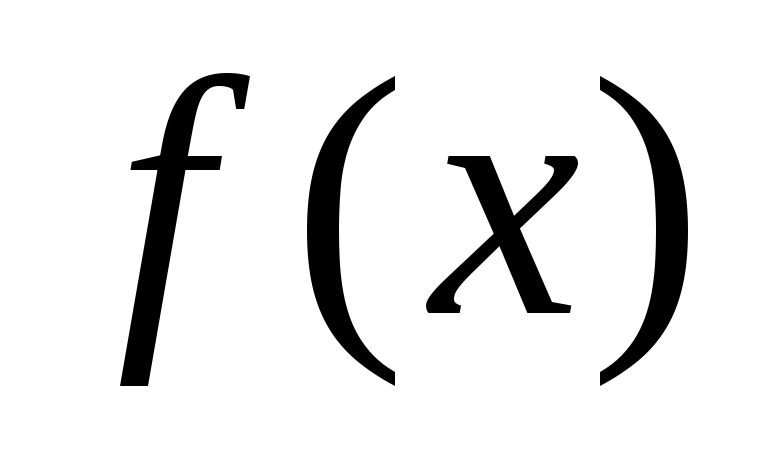 определена на
определена на 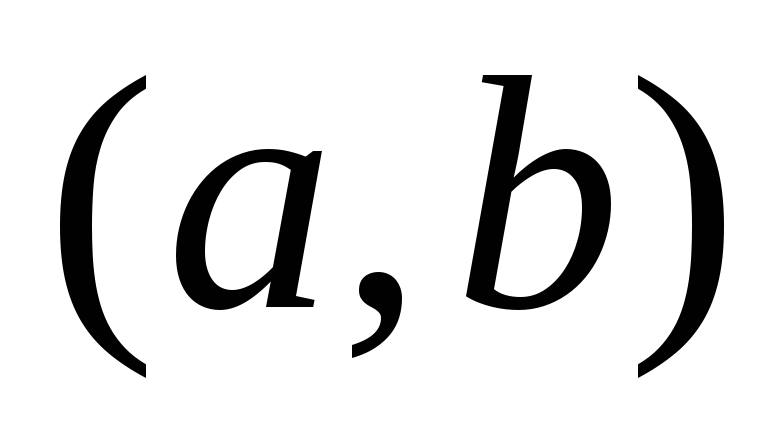 и дифференцирована на этом интервале
везде за исключением, возможно, точки
и дифференцирована на этом интервале
везде за исключением, возможно, точки  ,
но в этой точке
,
но в этой точке 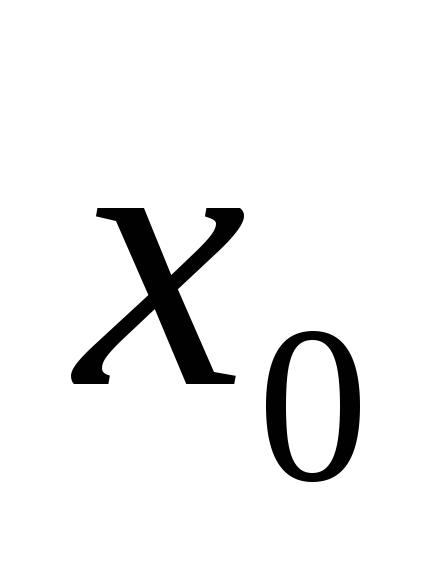 функция
функция 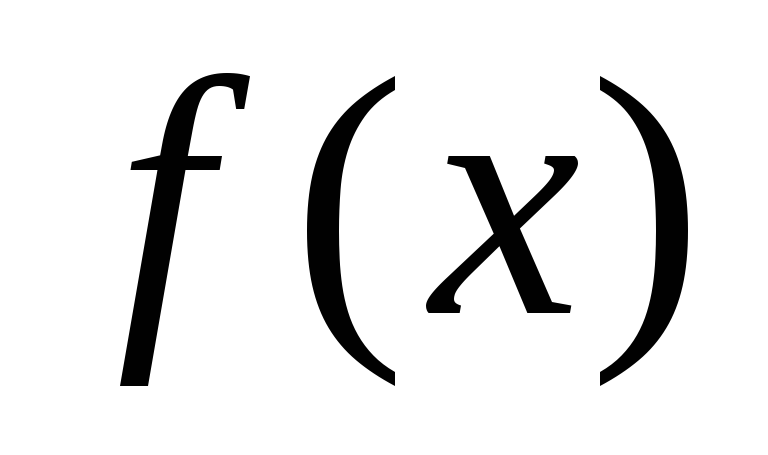 является
непрерывной. Если
существуют такие правая и левая
полуокрестности точки
является
непрерывной. Если
существуют такие правая и левая
полуокрестности точки 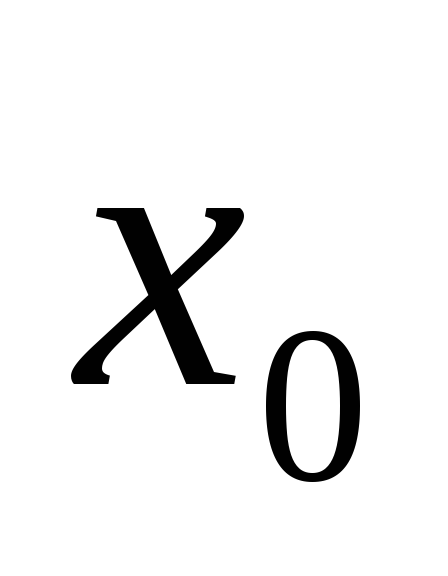 ,
в каждой из которых
,
в каждой из которых 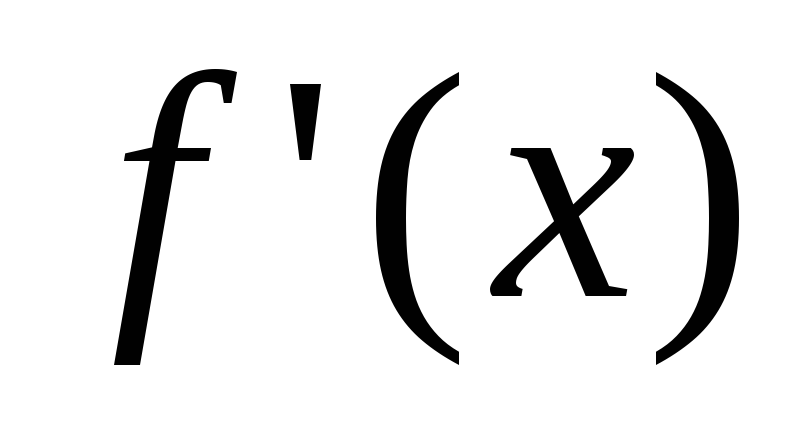 сохраняет определенный знак, то
сохраняет определенный знак, то
1) функция  имеет локальный экстремум в точке
имеет локальный экстремум в точке 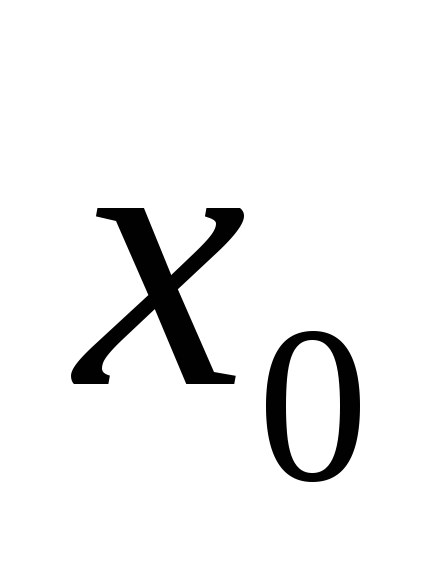 ,
если
,
если 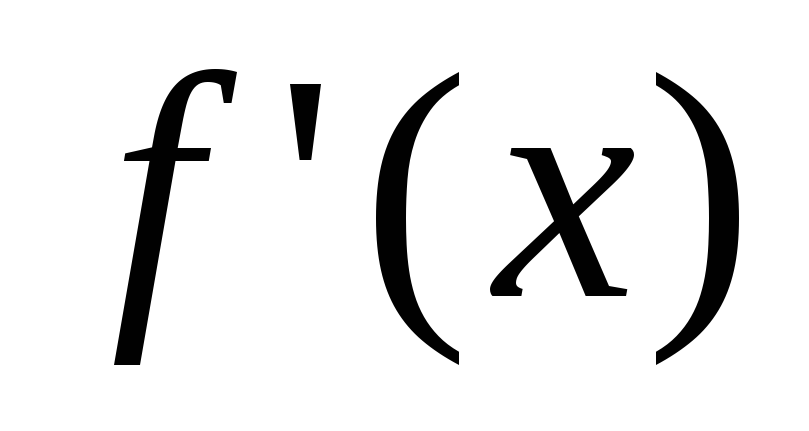 принимает значения разных знаков в
соответствующих полуокрестностях;
принимает значения разных знаков в
соответствующих полуокрестностях;
2) функция  не имеет локальный экстремум в точке
не имеет локальный экстремум в точке 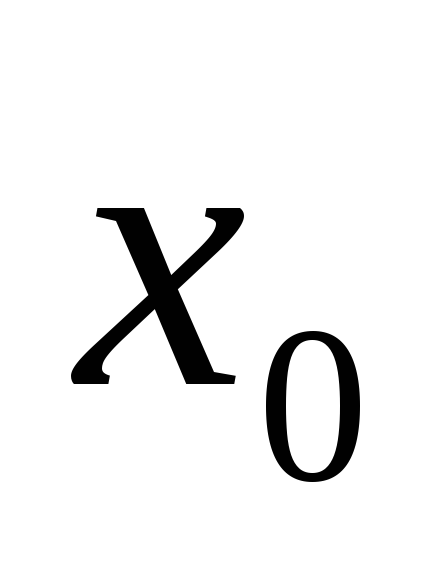 ,
если справа и слева от точки
,
если справа и слева от точки 
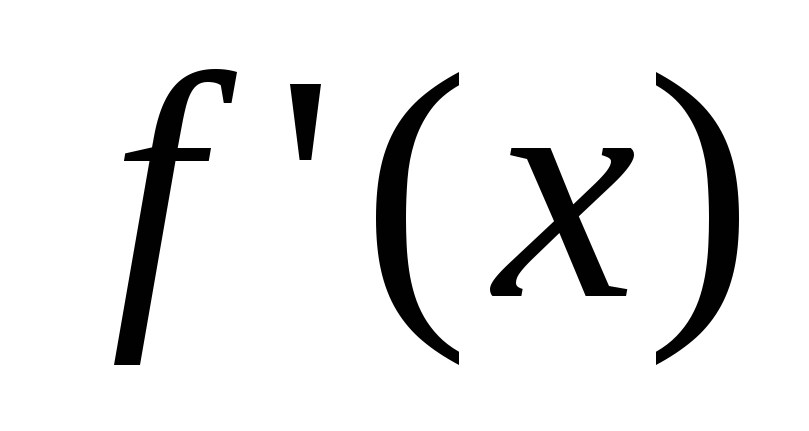 имеет одинаковый знак.
имеет одинаковый знак.
Доказательство.
1) Предположим, что в полуокрестности 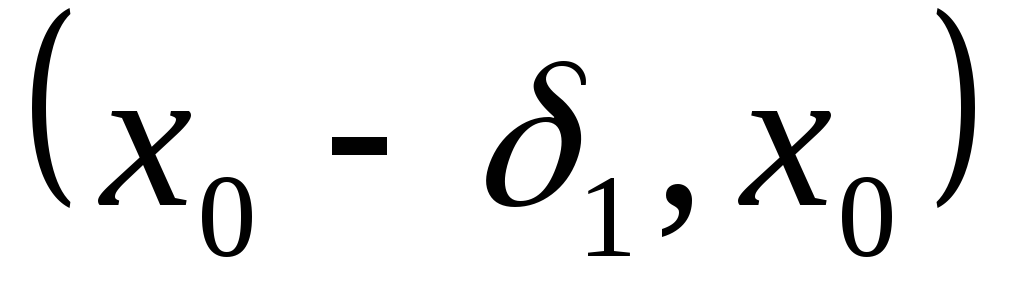 производная
производная  ,
а в
,
а в 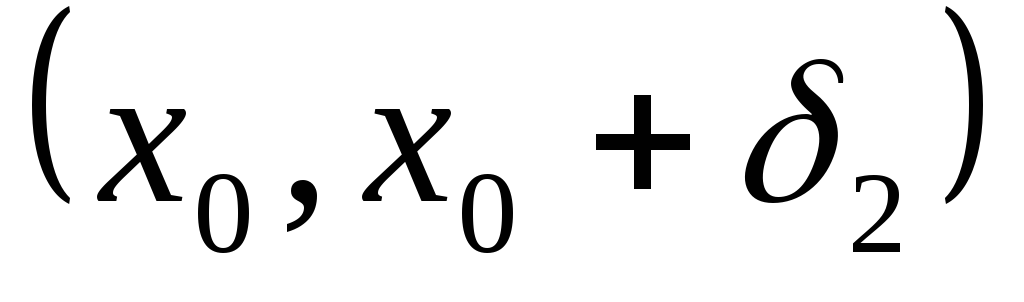
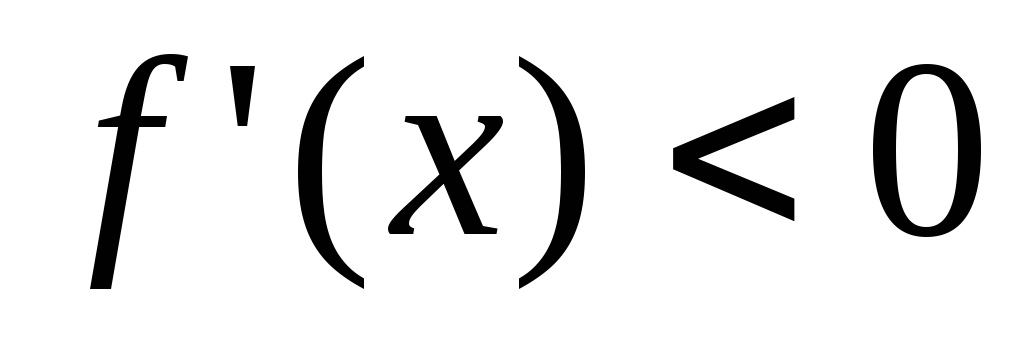 .
.

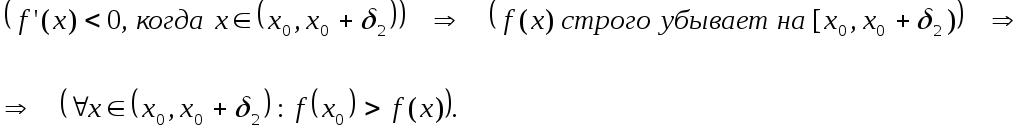
Таким образом в точке 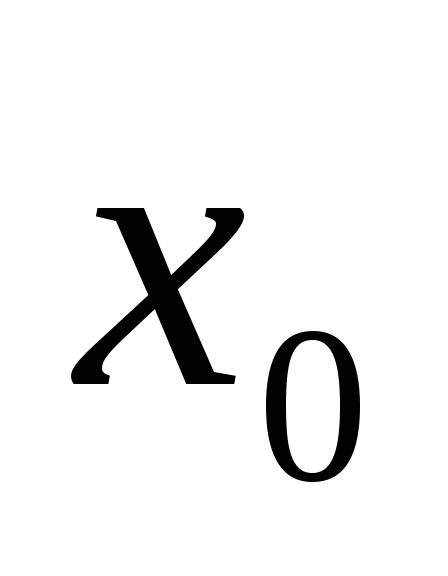 функция
функция  имеет локальный экстремум, а именно —
локальный максимум, что и нужно было
доказать.
имеет локальный экстремум, а именно —
локальный максимум, что и нужно было
доказать.
2) Предположим, что слева
и справа от точки 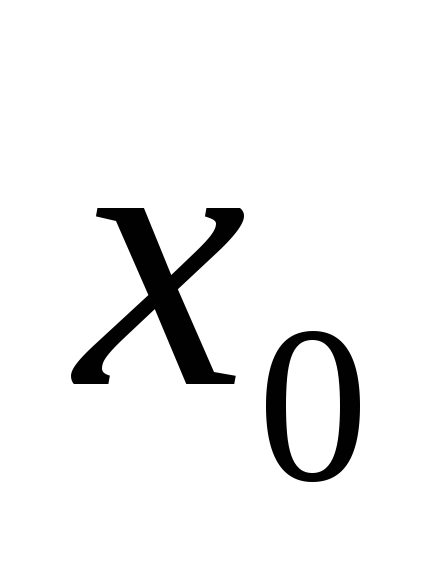 производная сохраняет свой знак,
например,
производная сохраняет свой знак,
например, 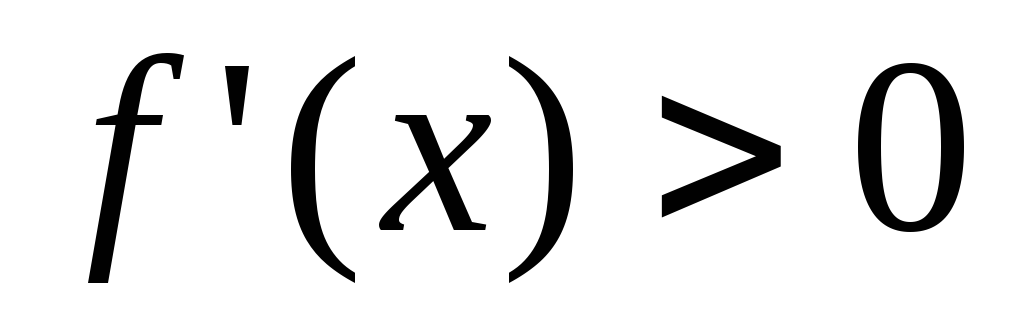 .
Тогда на
.
Тогда на  и
и 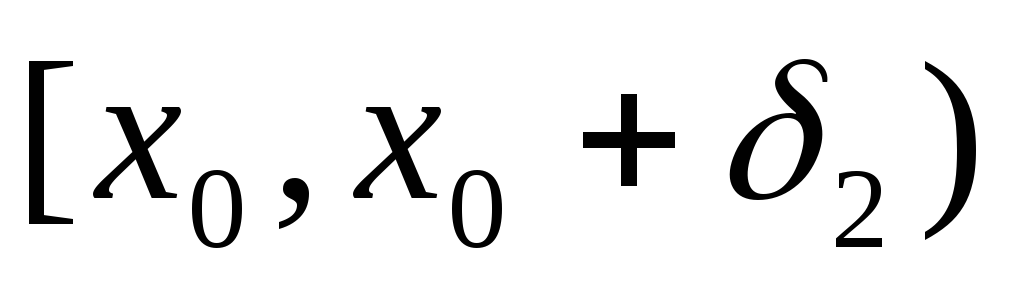 функция
функция  строго монотонно возрастает, то есть:
строго монотонно возрастает, то есть:
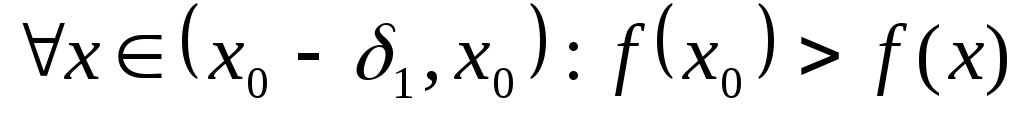 ,
,
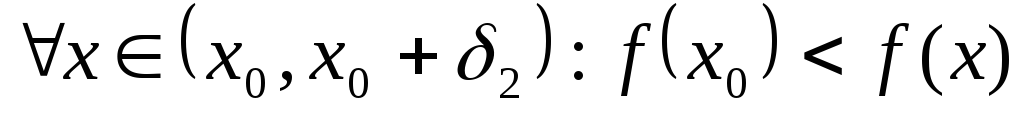 .
.
Таким образом экстремума
в точке 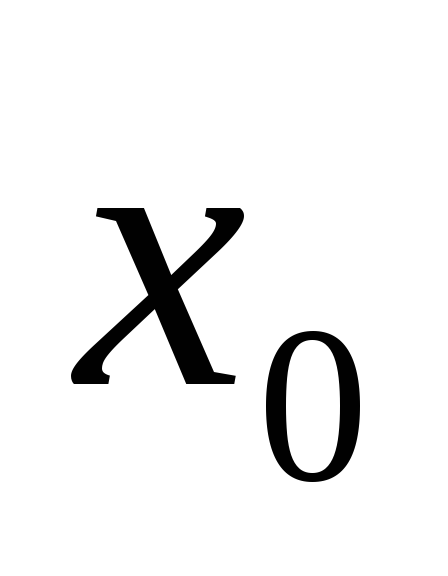 функция
функция 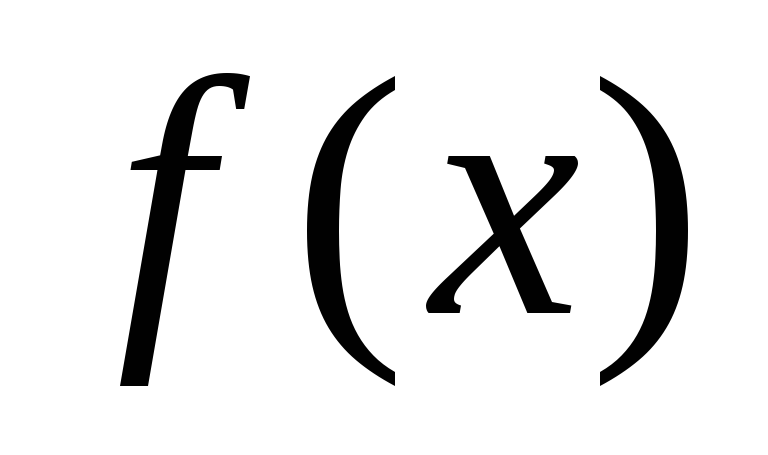 не имеет, что и нужно было доказать.
не имеет, что и нужно было доказать.
Замечание 1.
Если производная 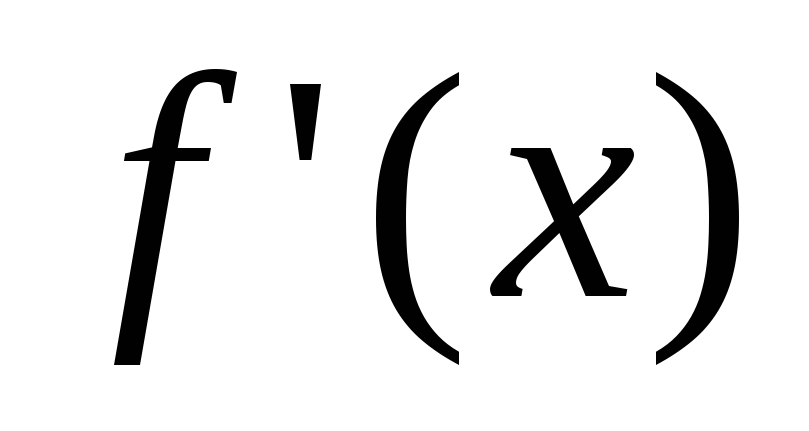 при прохождении через точку
при прохождении через точку  меняет знак с «+» на «-», то в точке
меняет знак с «+» на «-», то в точке 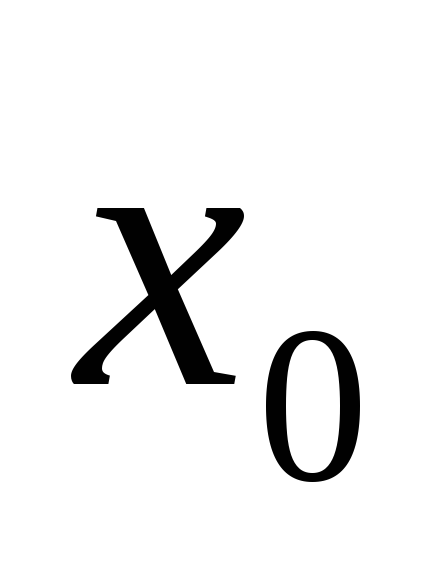 функция
функция 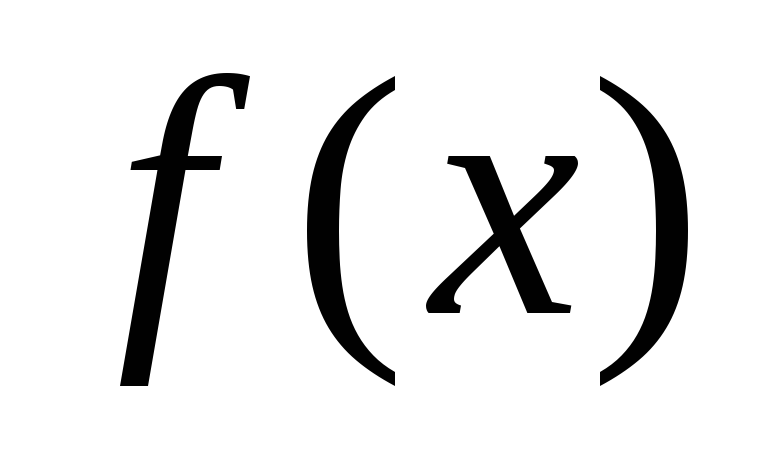 имеет локальный максимум, а если знак
меняется с «-» на «+», то локальный
минимум.
имеет локальный максимум, а если знак
меняется с «-» на «+», то локальный
минимум.
Замечание 2.
Важным является условие непрерывности
функции 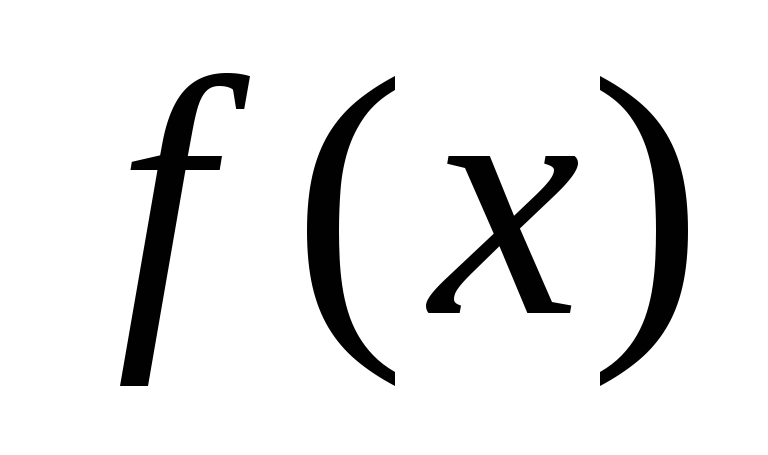 в точке
в точке 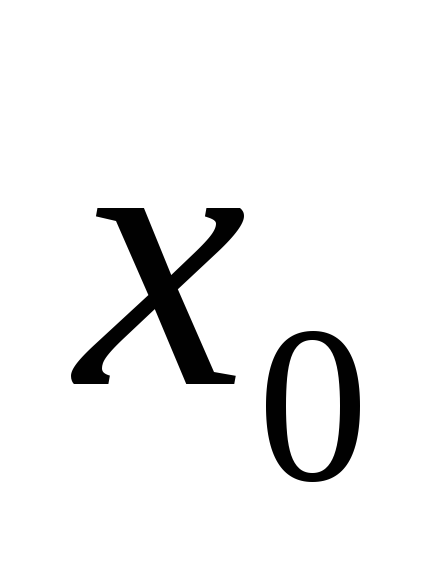 .
Если это условие не выполняется, то
теорема 1 может не иметь места.
.
Если это условие не выполняется, то
теорема 1 может не иметь места.
Пример. Рассматривается функция (рис.1):

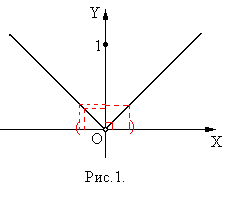
Эта функция определена на 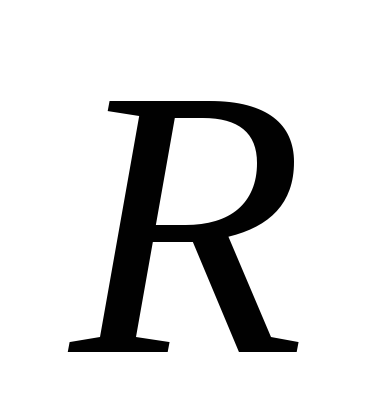 и непрерывна везде, кроме точки
и непрерывна везде, кроме точки 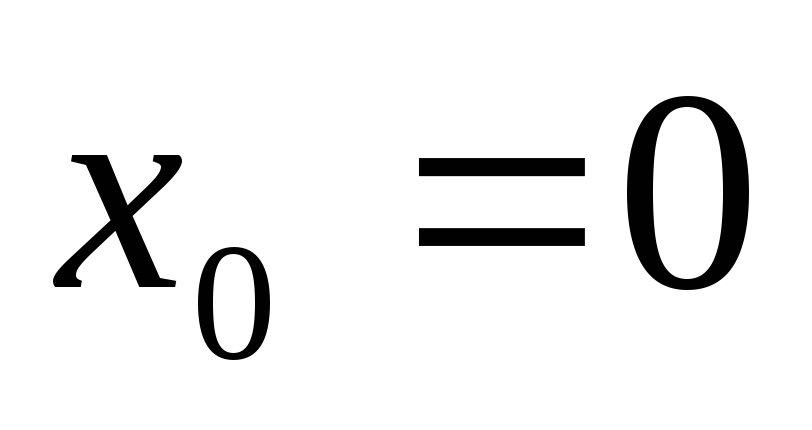 ,
где она имеет устранимый разрыв. При
прохождении через точку
,
где она имеет устранимый разрыв. При
прохождении через точку 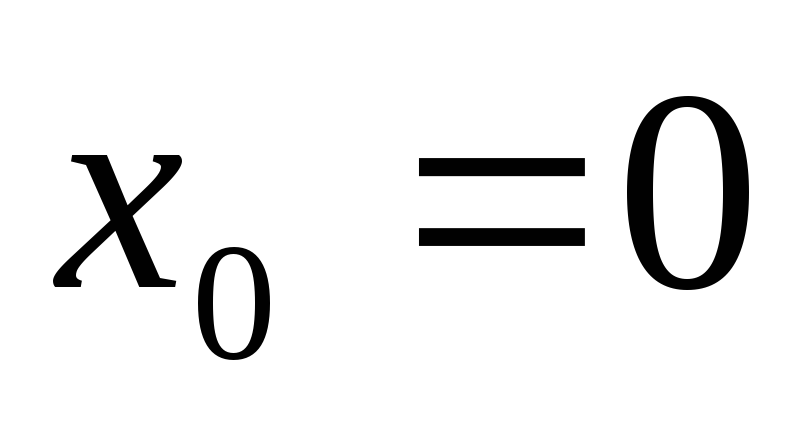
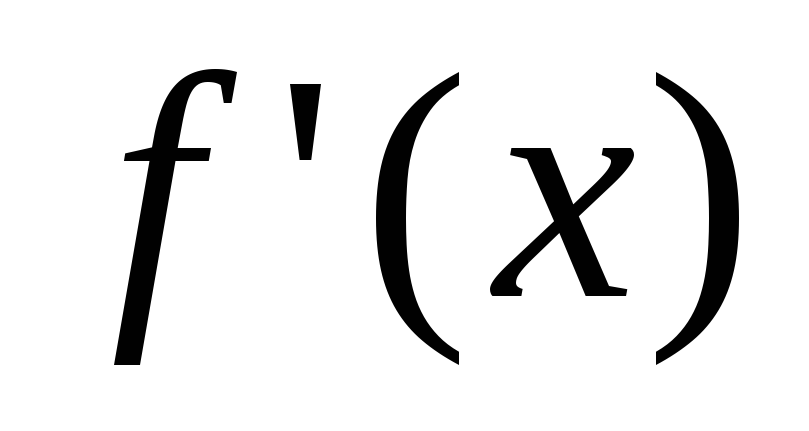 меняет знак с «-» на «+», но локального
минимума в этой точке функция не имеет,
а имеет локальный максимум по определению.
Действительно, около точки
меняет знак с «-» на «+», но локального
минимума в этой точке функция не имеет,
а имеет локальный максимум по определению.
Действительно, около точки 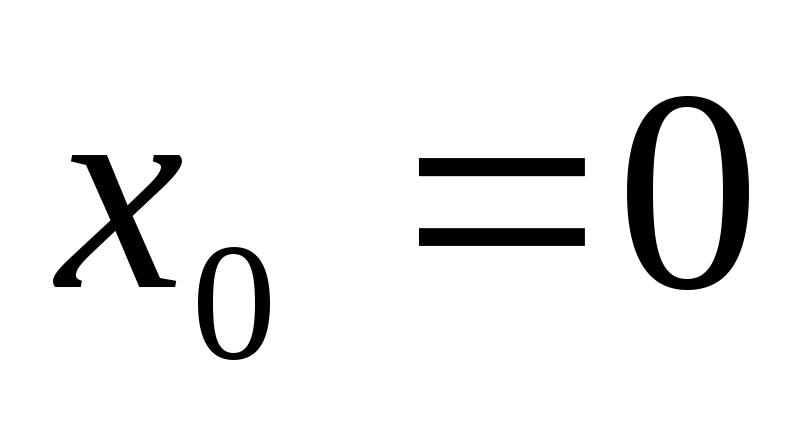 можно построить такую окрестность, что
для всех аргументов из этой окрестности
значения функции будут меньше, чем
значение
можно построить такую окрестность, что
для всех аргументов из этой окрестности
значения функции будут меньше, чем
значение 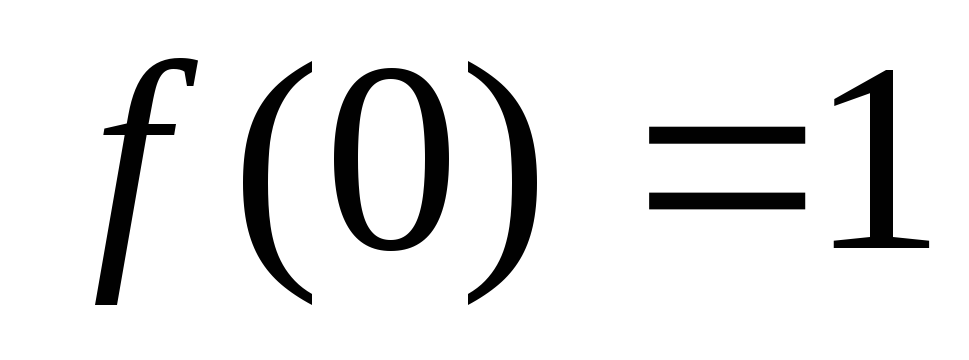 .
Теорема 1 не сработала потому, что в
точке
.
Теорема 1 не сработала потому, что в
точке 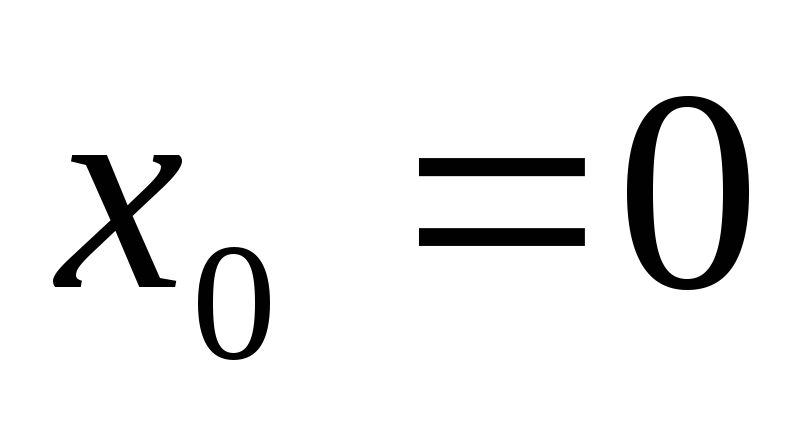 функция имела разрыв.
функция имела разрыв.
Замечание 3.
Первое достаточное условие локального
экстремума не может быть использовано,
когда производная функции  меняет свой знак в каждой левой и каждой
правой полуокрестности точки
меняет свой знак в каждой левой и каждой
правой полуокрестности точки 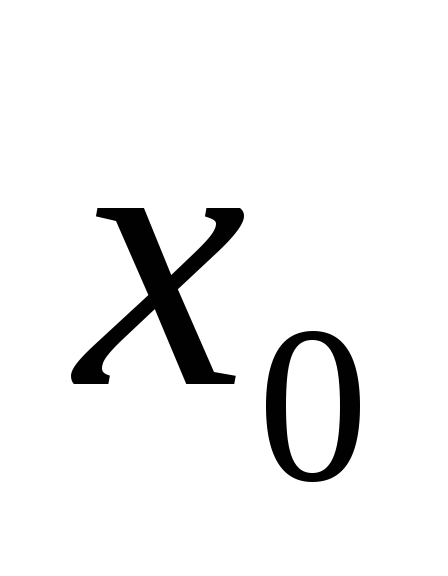 .
.
Пример. Рассматривается функция:
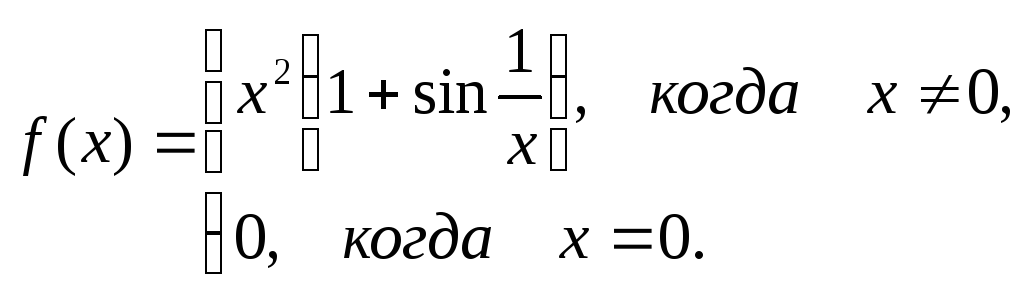
Поскольку 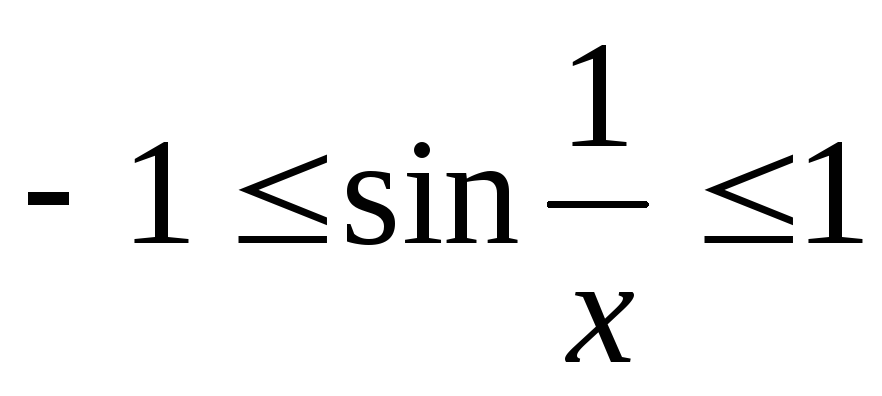 ,
то
,
то 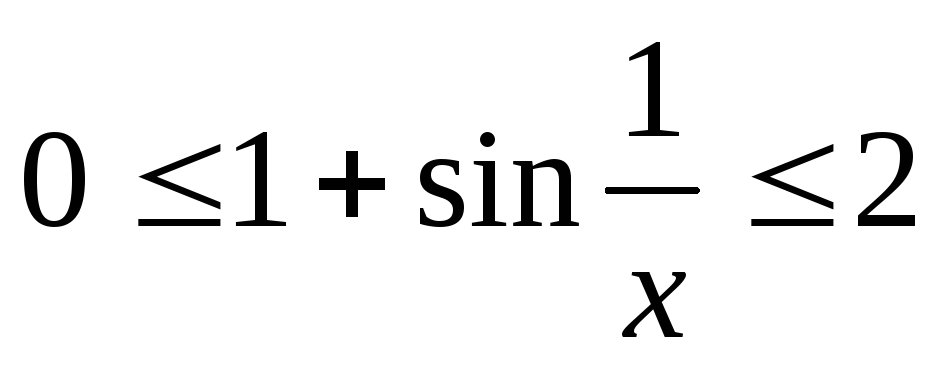 ,
а потому
,
а потому  ,
но
,
но 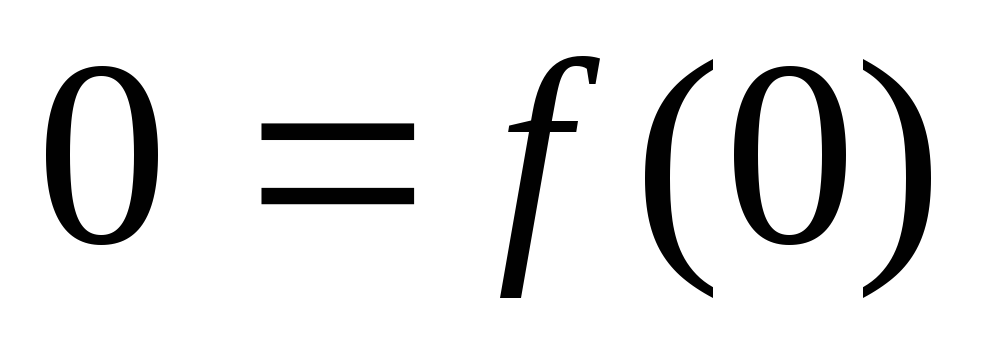 .
Таким образом:
.
Таким образом:
 ,
,
т.е. в точке 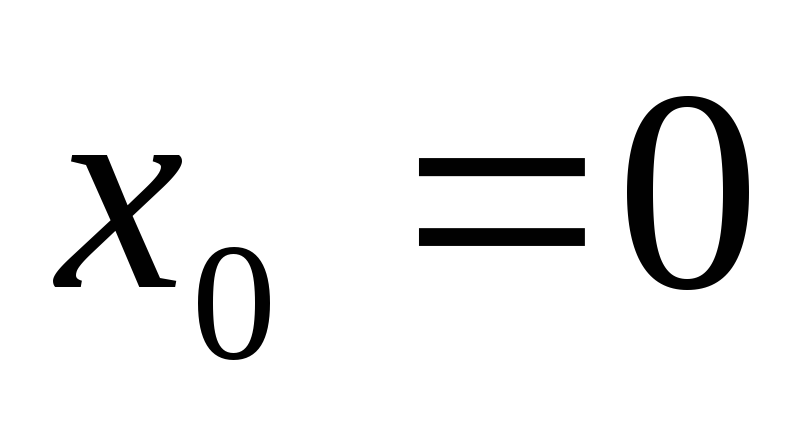 функция
функция 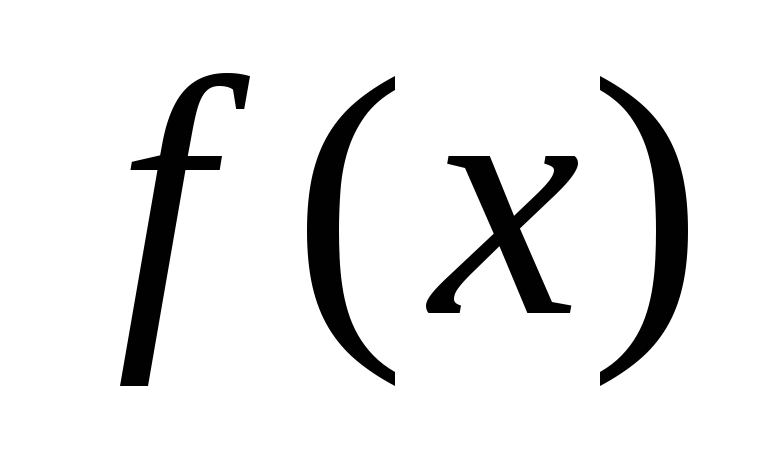 имеет локальный минимум по определению.
Посмотрим, сработает ли здесь первое
достаточное условие локального
экстремума.
имеет локальный минимум по определению.
Посмотрим, сработает ли здесь первое
достаточное условие локального
экстремума.
Для 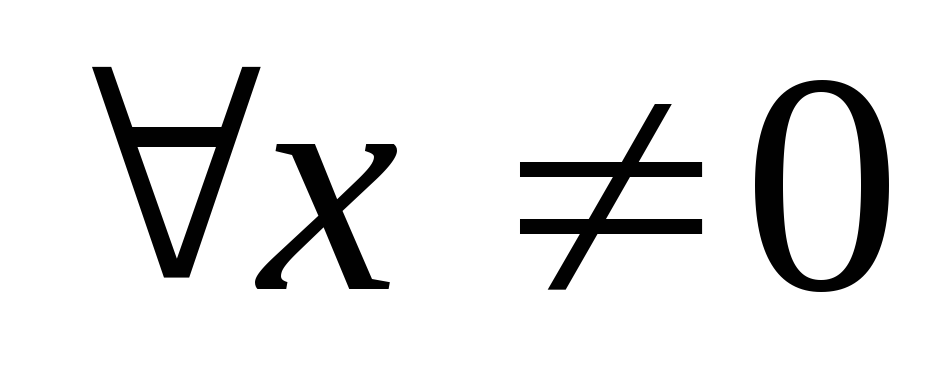 :
:
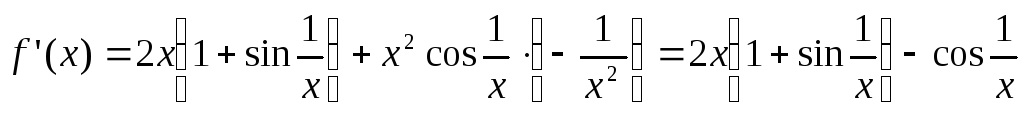 .
.
Для первого слагаемого правой части полученной формулы имеем:
 ,
,
а потому в малой окрестности
точки 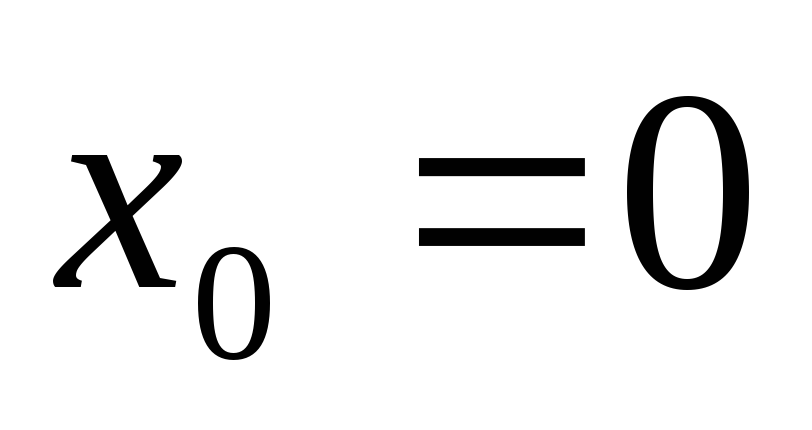 знак производной определяется знаком
второго слагаемого, то есть:
знак производной определяется знаком
второго слагаемого, то есть:
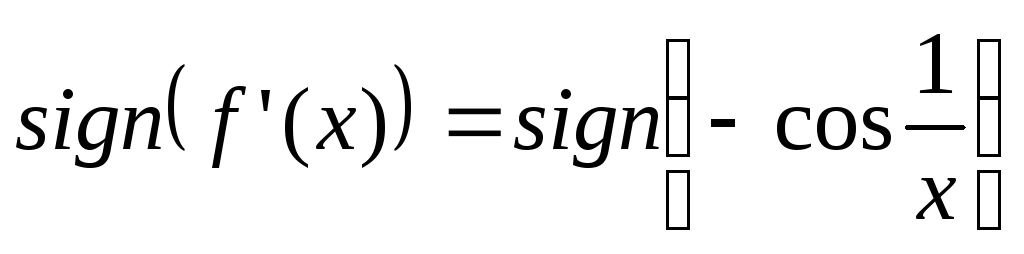 ,
,
а это означает, что в любой
окрестности точки 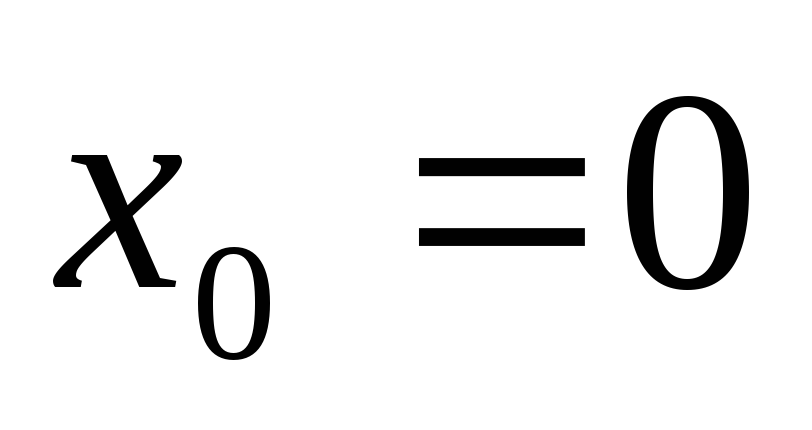
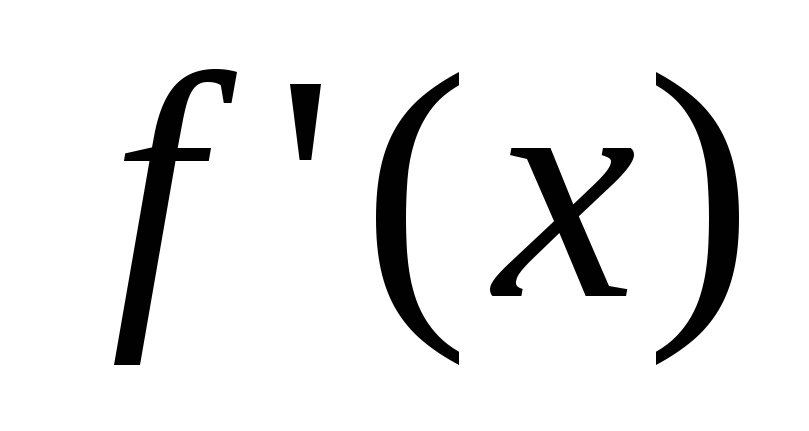 будет принимать как положительные, так
и отрицательные значения. Действительно,
рассмотрим произвольную окрестность
точки
будет принимать как положительные, так
и отрицательные значения. Действительно,
рассмотрим произвольную окрестность
точки 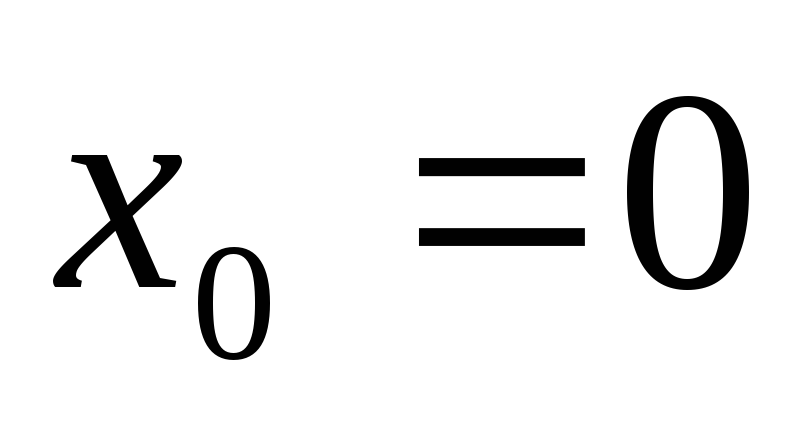 :
: 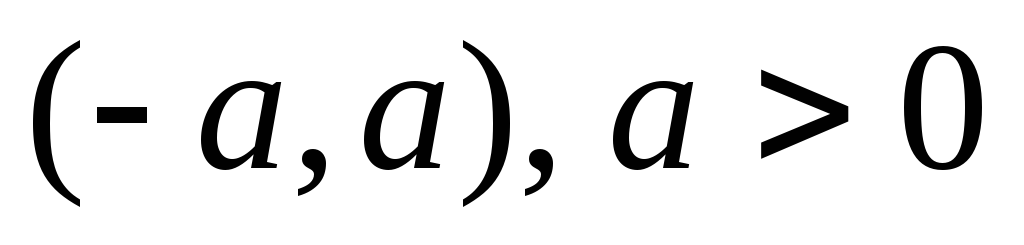 .
Когда
.
Когда
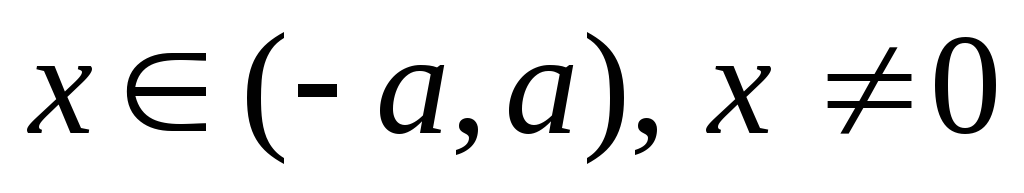 ,
,
то 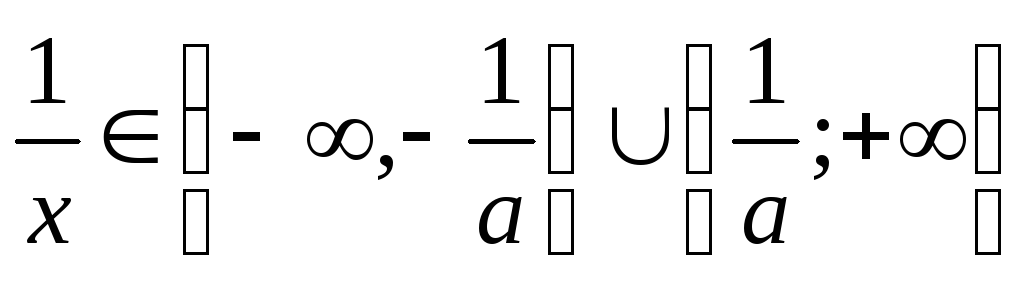
(рис.2), а  меняет свой знак здесь бесконечно много
раз. Таким образом, нельзя использовать
в приведенном примере первое достаточное
условие локального экстремума.
меняет свой знак здесь бесконечно много
раз. Таким образом, нельзя использовать
в приведенном примере первое достаточное
условие локального экстремума.

матан коллоквиум / 12.Понятие экстренума.Определение максиимума,минимума,понятие критической точки,графическая иллюстрация критических точек
Экстре́мум (лат. extremum — крайний) в математике —максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Определения
Пусть
дана функция 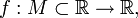 и
и 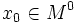 —
внутренняя точка области определения
—
внутренняя точка области определения 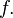 Тогда
Тогда
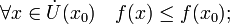

Если
неравенства выше строгие, то  называется
точкой строгого локального максимума
или минимума соответственно.
называется
точкой строгого локального максимума
или минимума соответственно.

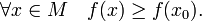
Значение
функции 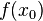 называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
Достаточные условия существования локальных экстремумов
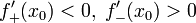
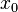 является
точкой строгого локального максимума.
А если
является
точкой строгого локального максимума.
А если

то 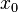 является
точкой строгого локального минимума.
является
точкой строгого локального минимума.
Заметим,
что при этом функция не дифференцируема
в точке 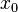
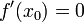 и
и 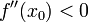
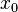 является
точкой локального максимума. А если
является
точкой локального максимума. А если
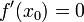 и
и 
то  является
точкой локального минимума.
является
точкой локального минимума.
Если  чётно
и
чётно
и 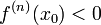 ,
то
,
то 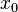 —
точка локального максимума. Если
—
точка локального максимума. Если 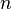 чётно
и
чётно
и 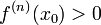 ,
то
,
то 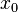 —
точка локального минимума. Если
—
точка локального минимума. Если  нечётно,
то экстремума нет.
нечётно,
то экстремума нет.
Максимум и минимум функции.
Приведем
точные определения точек
экстремума. Определение. Точка
x0 называется
точкой минимума функции f, если для всех
x из некоторой окрестности x0 выполняется
неравенство f(x) ≥ f(x0. Это
наглядно показано на рисунке 1: 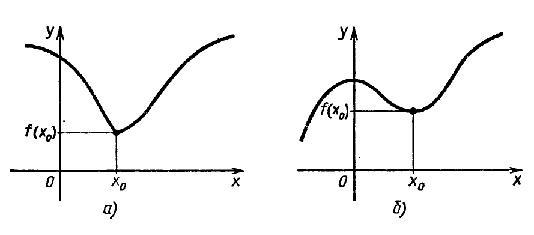 рисунок
1 Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0. Это
наглядно показано на рисунке 2:
рисунок
1 Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0. Это
наглядно показано на рисунке 2: 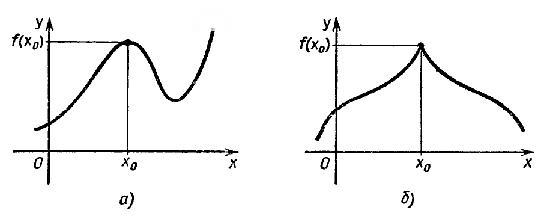 рисунок
2 По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно). В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно). Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже:
рисунок
2 По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно). В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно). Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже: 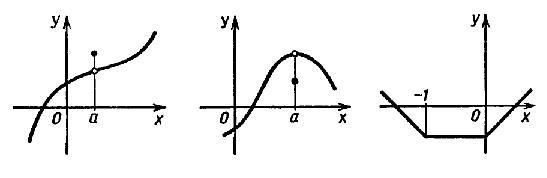 Слева
направо: a — точка максимума; a — точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума. Для
точек минимума и максимума функции есть
общее определение — точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название — экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума — xmin.
Слева
направо: a — точка максимума; a — точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума. Для
точек минимума и максимума функции есть
общее определение — точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название — экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума — xmin.
Критической
точкой дифференцируемой
функции 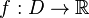 ,
где
,
где 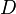 —
область в
—
область в  ,
называется точка, в которой все её частные
производные обращаются
в ноль. Это условие эквивалентно обращению
в ноль дифференциала функции
в данной точке, а также равносильно
горизонтальности касательной гиперплоскости
к графику
функции.
Это условие является необходимым (но
не достаточным) для того, чтобы внутренняя
точка области
могла быть точкой локального
минимума или
максимума функции.
,
называется точка, в которой все её частные
производные обращаются
в ноль. Это условие эквивалентно обращению
в ноль дифференциала функции
в данной точке, а также равносильно
горизонтальности касательной гиперплоскости
к графику
функции.
Это условие является необходимым (но
не достаточным) для того, чтобы внутренняя
точка области
могла быть точкой локального
минимума или
максимума функции.
Необходимое и достаточные условия существования экстремумов функции одной переменной
Из теоремы Ферма следует, что если х = х0 точка экстремума, то производная в этой точке равна нулю
f /(x0) =0.
Следует также отметить, что, иногда, в точке экстремума функция может быть недифференцируемой, т.е. в этой точке производная не существует.
Необходимое условие существования экстремума функции: если х = х0 — точка экстремума, то f /(x0) =0 или f /(x0) не существует.
Точки, в которых f /(x0) обращается в нуль или не существует, называется критическими.
Достаточное условие существования экстремума функции: если функция y=f(x) непрерывна в точке х = х0 и ее окрестности, дифференцируема в этой окрестности, кроме, быть может, самой точки, и производная
 при переходе через
точку х = х0 меняет
свой знак, то функция имеет экстремум
при х = х0
.
при переходе через
точку х = х0 меняет
свой знак, то функция имеет экстремум
при х = х0
.
При этом х = х0 — точка максимума, если знак меняется с « + » на « — », и х = х0 — точка минимума, если знак меняется с « — » на « + » .
2.3.6. Точки перегиба, Выпуклость, вогнутость линии
Дуга кривой называется выпуклой, если она пересекается с любой своей секущей не более, чем в двух точках.Выпуклость дуги может быть направлена или вверх (в направлении оси Оу), или внизЛинии, обращенные выпуклостью вверх, условились называть выпуклыми, а обращенные выпуклостью вниз – вогнутыми.
Необходимое
условие выпуклости дуги: есть дуга линии y=f(x) выпукла на (a, b), то  при
при  .
.
Необходимое условие
вогнутости дуги: если дуга линии y=f(x) вогнута на (a, b),то 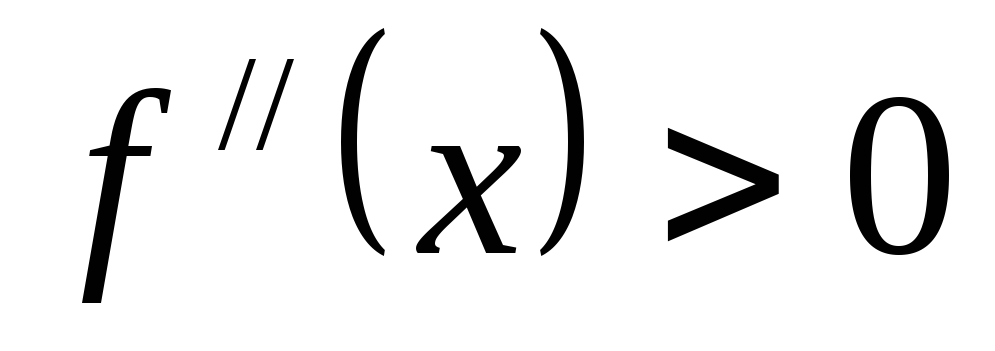 при
при 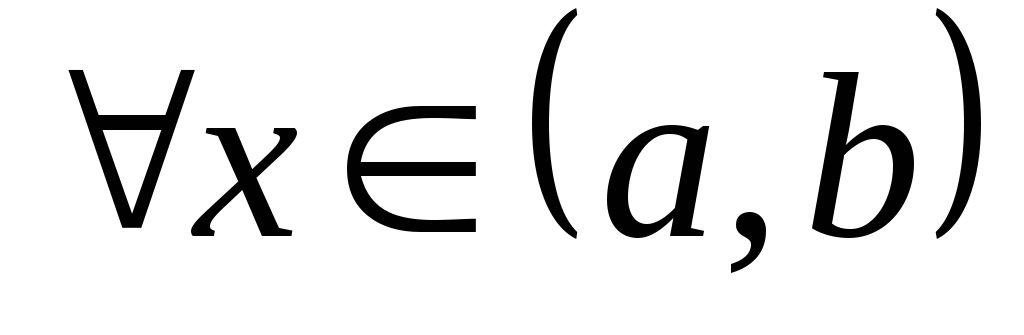 .
.
Достаточное условие
выпуклости, вогнутости дуги: если 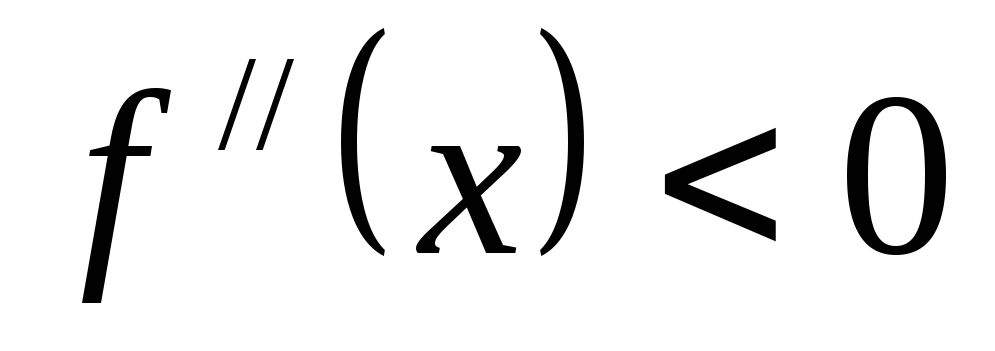 при
при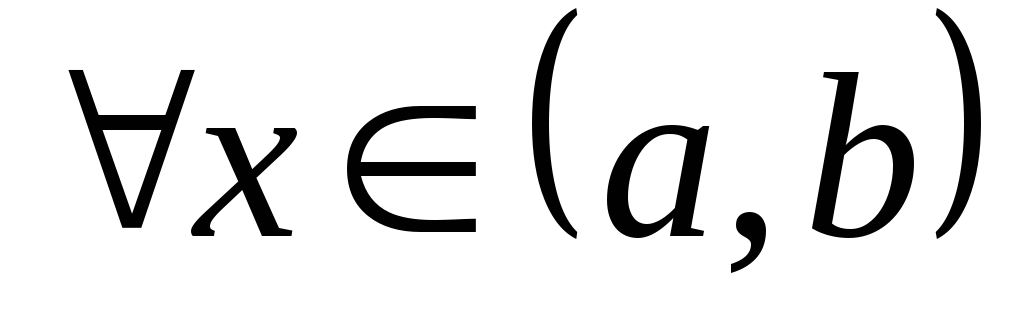 ,
то дуга кривойy=f(x) выпукла на (a, b);
если
,
то дуга кривойy=f(x) выпукла на (a, b);
если 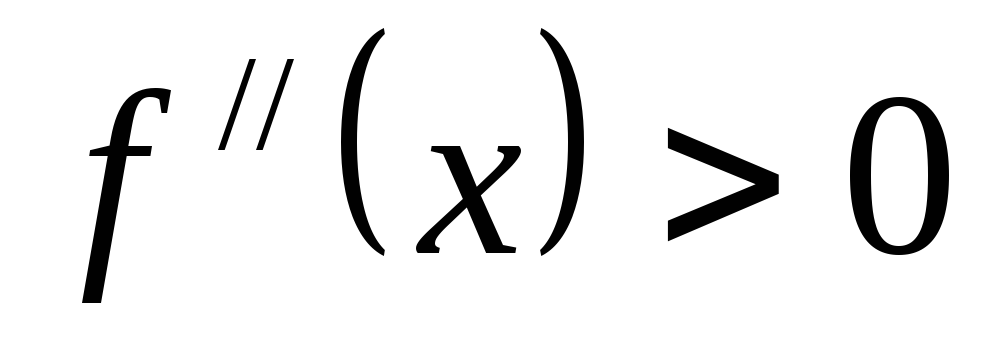 при
при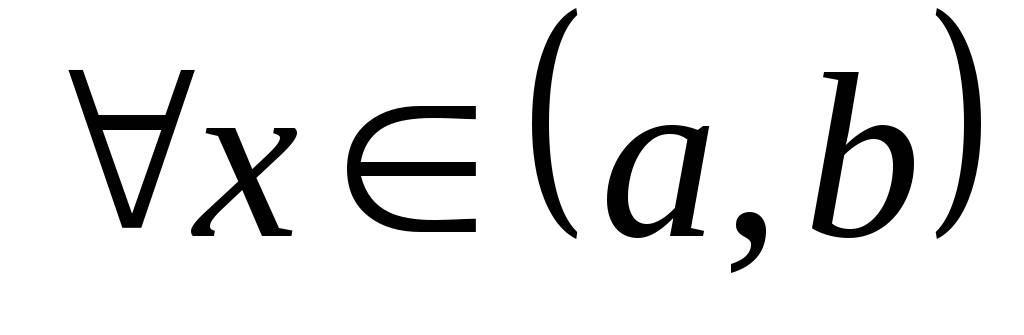 ,
то дуга кривойy=f(x) вогнута на (a, b).
,
то дуга кривойy=f(x) вогнута на (a, b).
Точка С линии, отделяющая выпуклую дугу от вогнутой или наоборот, называется точкой перегиба.
Предполагается, что в точке перегиба можно провести касательную к данной линии, которая лежит при этом по обе стороны от касательной
Cлева
от х = х0 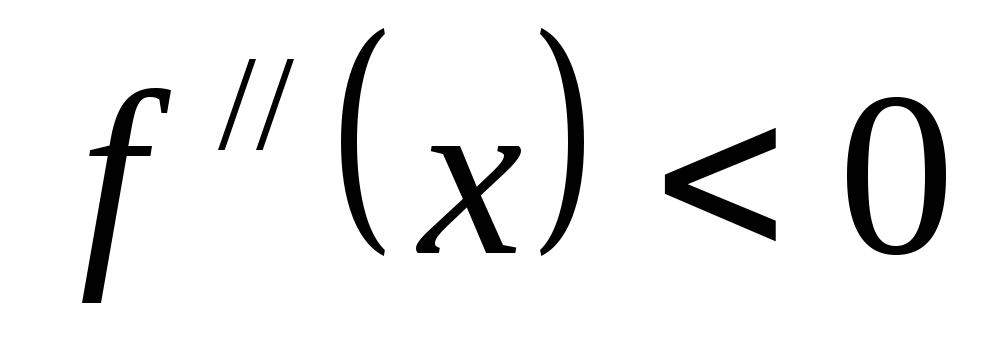 ,
а справа
,
а справа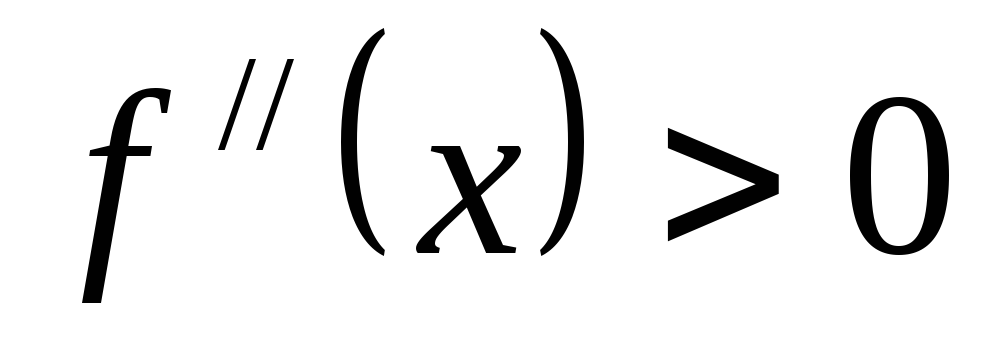 .
Это значит, что слева функция
.
Это значит, что слева функция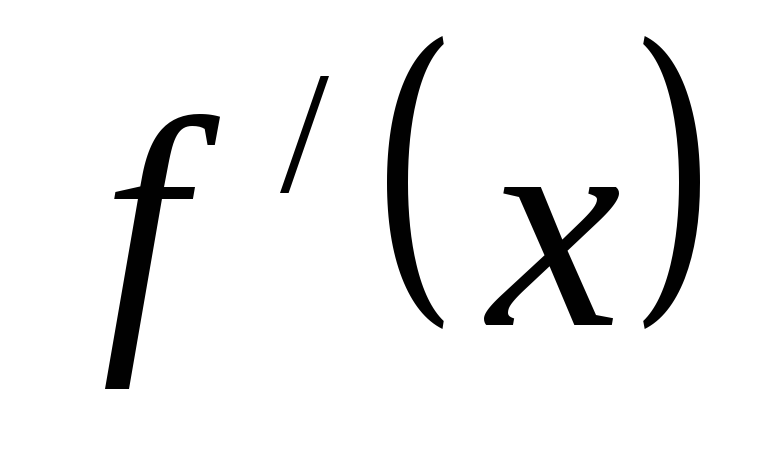 убывает, а справа возрастает. Интервалы
монотонности меняются в точке, в которой
производная функция равна нулю
убывает, а справа возрастает. Интервалы
монотонности меняются в точке, в которой
производная функция равна нулю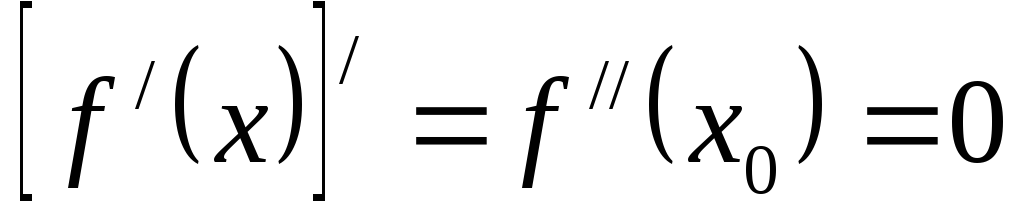 или
или 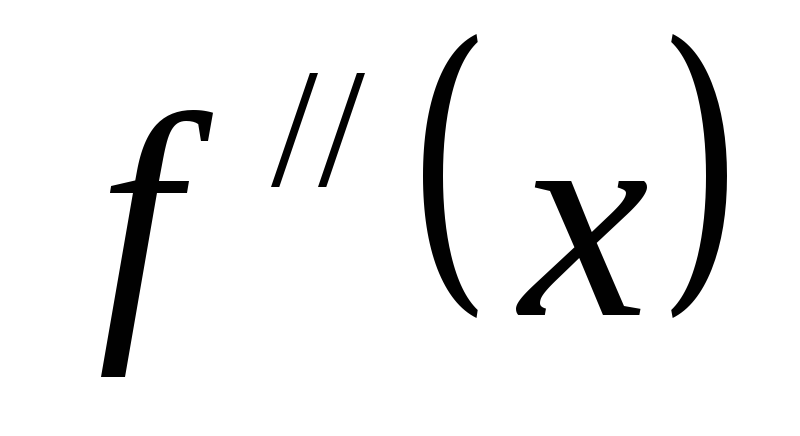 не существует. Точках
= х0 называется
при этом критической.
не существует. Точках
= х0 называется
при этом критической.
Рассмотренное
условие является лишь необходимым
условием существования точки
перегиба.Достаточное условие существования
точки перегиба: если  меняет свой знак при переходе через
критическую точкух
= х0 , то точка
меняет свой знак при переходе через
критическую точкух
= х0 , то точка 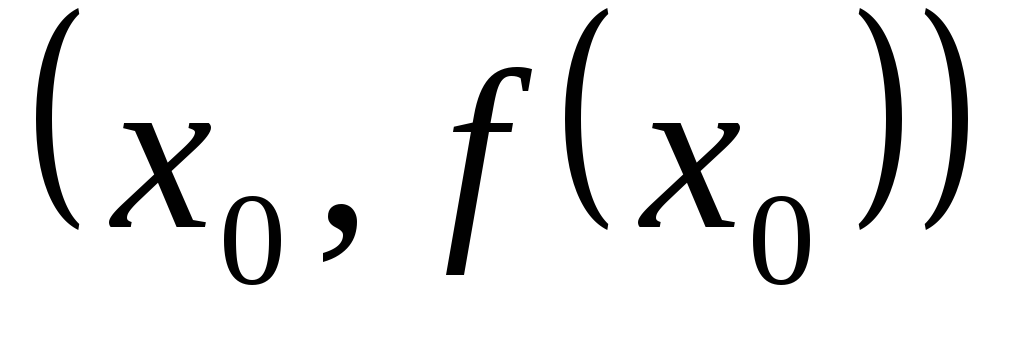 — точка
перегиба кривой y = f(x). Знаки
— точка
перегиба кривой y = f(x). Знаки 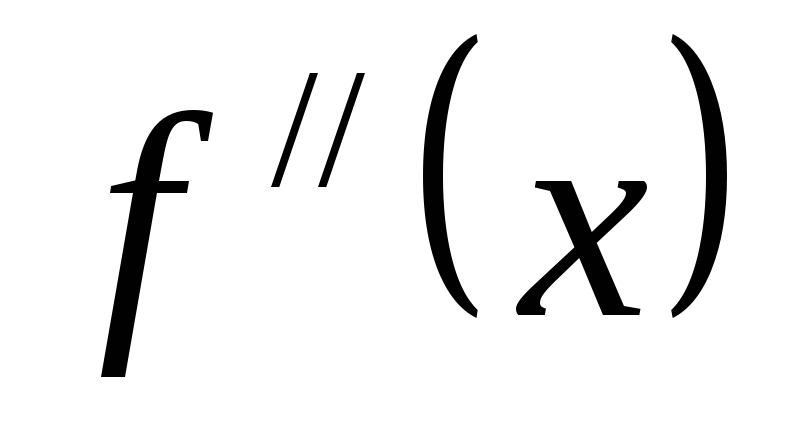 слева и справа отх
= х0 показывают,
как направлена выпуклость кривой при x < x0 и x > x0.
слева и справа отх
= х0 показывают,
как направлена выпуклость кривой при x < x0 и x > x0.
9.6. Асимптоты функции
Если расстояние от точки М линии y=f(x) до прямой l неограниченно уменьшается при неограниченном удалении точки М от начала координат, то такая прямая называется асимптотой линии.
Различают вертикальные и наклонные асимптоты.
1)если х = х0 – точка
разрыва второго рода функции y = f(x),
то эта функция имеет вертикальную
асимптоту х
= х0 ,в этом случае 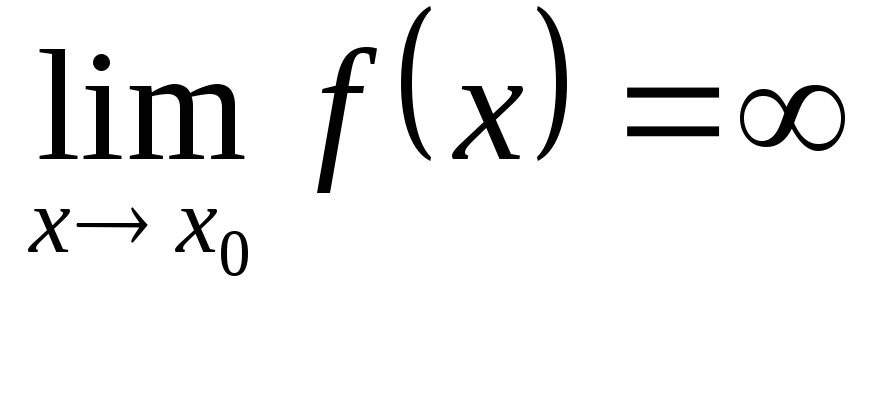 .
.
2)если y=kx+b – наклонная асимптота функции y=f(x),
то 
Чтобы функция y=f(x) имела наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы, определяющие k и b.
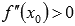 ,
то
,
то 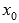 —
точка минимума;
—
точка минимума; ,
то
,
то  —
точка максимума.
—
точка максимума.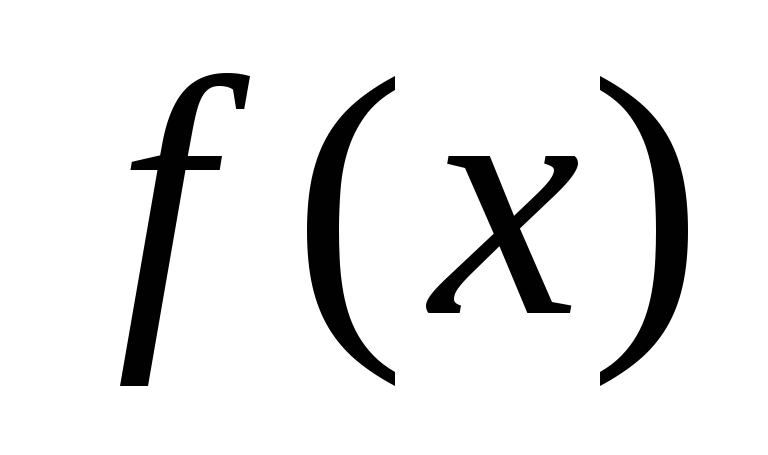 не имеет в точке
не имеет в точке 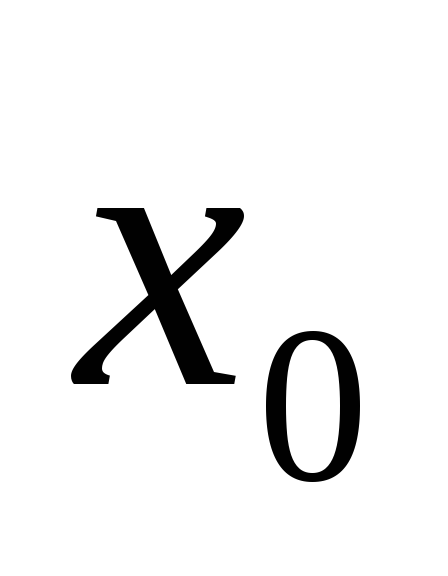 производной;
производной; имеет в точке
имеет в точке 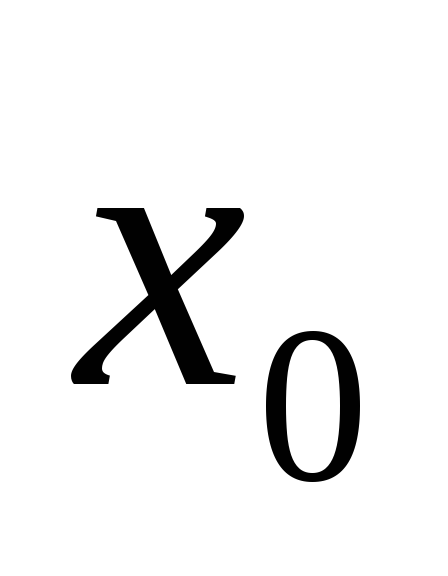 производную и
производную и  .
.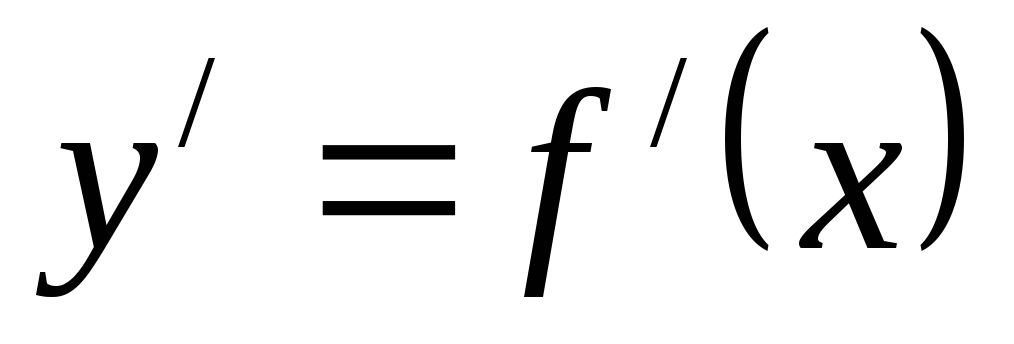 при переходе через
точку х = х0 меняет
свой знак, то функция имеет экстремум
при х = х0
.
при переходе через
точку х = х0 меняет
свой знак, то функция имеет экстремум
при х = х0
.