Построение графиков функций с модулем примеры: Построение графиков функций с модулем

Posted on by alexxlab

График функции с модулем | Алгебра

Построить график функции с модулем — один из видов задания 23 ОГЭ по математике.

Рассмотрим примеры таких заданий.

1) Постройте график функции

   

и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.

Решение:

Область определения функции D(y): x∈R.

1)Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:

x-2=0,  x=2.

Найдём значение функции при x=2.

y(2)=5·0-2²+5∙2-3∙0-6=0.

Получили точку (2;0).

2) Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает положительные значения.

Если x-2>0, то есть при x>2, |х-2|=x-2,

y=5|х-2|-x²+5x-6=5(х-2)-x²+5x-6=5х-10-x²+5x-6=-x²+10x-16.

y=-x²+10x-16 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).

Координаты вершины параболы

   

   

то есть вершина параболы — точка (5;9). От вершины строим график функции y=-x² (так как a=-1).

3)Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает отрицательные значения.

Если x-2<0, то есть при x<2, |х-2|=-(x-2),

y=5|х-2|-x²+5x-6=-5(х-2)-x²+5x-6=-5х+10-x²+5x-6=-x²+4.

y=-x²+4 — квадратичная функция. График — парабола ветвями вниз.

Координаты вершины параболы

   

   

то есть вершина параболы — точка (0;4). От вершины строим график функции y=-x².

Прямая x=2 разбивает координатную плоскость на две полуплоскости. Слева от неё, для x<2,  строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16:

График функции с модулем можно рассматривать и как график кусочной функции:

   

   

   

Прямая y=m имеет с графиком ровно три общие точки при m=0 и m=4:

Ответ: 0; 4.

2) Постройте график функции

   

и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:

   

   

   

|6x+1|=6x+1 и y=x²-(6x+1)=x²-6x-1.

y=x²-6x-1 — квадратичная функция. График — парабола ветвями вверх (поскольку a=1>0).

Координаты вершины параболы

   

   

Так как a=1, от вершины (3;-10) строим график y=x².

   

|6x+1|=-(6x+1) и y=x²+(6x+1)=x²+6x+1.

y=x²+6x+1 — квадратичная функция. График — парабола ветвями вверх.

Координаты вершины параболы

   

   

от вершины (-3;-8)  строим график y=x².

Или:

   

   

 

Прямая y=m имеет с графиком ровно три общие точки при m=1/30 и m=-8:

Ответ: -8; 1/36.

3) Постройте график функции

   

и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Если x=0, y=|0|·0+3·|0|-5·0=0.

2) Если x>0, |x|=x, y=x·x+3·x-5·x=x²-2x.

y=x²-2x — квадратичная функция. График — парабола ветвями вверх (a=1>0).

Координаты вершины параболы

   

   

От вершины (1;-1) строим параболу y=x² (так как a=1).

3) Если x<0, |x|=-x, y=-x·x+3·(-x)-5·x=-x²-8x.

y=-x²-8x — квадратичная функция. График — парабола ветвями вниз (a=-1<0).

Координаты вершины параболы

   

   

От вершины (-4;16) строим параболу y=-x² (так как a=-1).

Таким образом, график данной функции представляет собой комбинацию двух парабол: справа от прямой x=0 (оси Oy) — y=x²-2x, слева — y=-x²-8x:

Альтернативный вариант:

   

   

   

Прямая y=m имеет с графиком ровно две общие точки, когда она проходит через вершины парабол, то есть при m=-1 и m=16:

Ответ: -1; 16.

4) Построить график функции y=|x²+2x-3|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

Решение:

Область определения функции D(y): x∈R.

Построим график функции y=x²+2x-3.

Эта функция — квадратичная. Её графиком является парабола, ветви которой направлены вверх.

Координаты вершины параболы

   

   

, то есть вершина параболы — точка (-1;-4).

От вершины строим график функции y=x²:

График функции y=|x²+2x-3| может быть получен из графика функции y=x²+2x-3 следующим образом: часть графика, расположенную выше оси Ox, сохраняем. Часть, расположенную ниже оси Ox, отображаем симметрично относительно оси Ox.

Или y=|x²+2x-3|

   

   

Вершина параболы (-1;-4) при этом переходит в точку (-1;4):

Наибольшее число общих точек, которое график данной функции может иметь с прямой, параллельной оси абсцисс, равно 4 (например, прямая y=3 пересекает график в четырёх точках).

Ответ: 4.

График функции с модулем и дробью

График функции с модулем и дробью — ещё одна группа заданий номера 23 ОГЭ по математике.

Подобно функциям с переменной в знаменателе, графики таких функций могут содержать выколотую точку. Как и при построении графиков функций с модулем, рассматриваем два варианта раскрытия модуля.

1) Построить график функции

   

и определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:

Так как x²=|х|², формулу, задающую функцию, перепишем в виде

   

В знаменателе общий множитель |х| вынесем за скобки

   

Найдём область определения функции.

|х|(|х|-1)≠0

|х|≠0; |х|-1≠0

x≠0; |х|≠1

x≠0, x≠±1.

D(y):x∈(-∞;-1)∪(-1;0)∪(0;1)∪(1;∞).

Сократив дробь на (|х|-1), получаем

   

При x>0 |х|=x,

   

— функция обратной пропорциональности. График — гипербола. Для построения гиперболы возьмём несколько точек (включая выколотую x=1):

   

При x<0 |х|=-x,

   

— функция обратной пропорциональности.

   

Прямая y=kx не имеет с графиком общих точек, если она проходит через выколотые точки либо совпадает с осью Ox, то есть при k=±1 и k=0:

Ответ: -1; 0; 1.

2)Постройте график функции

   

и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.

Решение:

В числителе вынесем за скобки общий множитель 0,25x:

   

Ищем область определения функции.

x+2≠0

x≠-2.

D(y):x∈(-∞;-2)∪(-2;∞).

Сокращаем дробь на (x+2):

   

Получили функцию, содержащую переменную под знаком модуля (при условии x≠-2).

При x=0, y=0,25·0·|0|=0.

При x>0 |х|=x, y=0,25·x·|x|= y=0,25·x·x=0,25x².

y=0,25x² или

   

— квадратичная функция. График — парабола, полученная из параболы y=x² сжатием к оси Ox в 4 раза.

При x<0 |х|=-x, y=0,25·x·|x|= y=0,25·x·(-x)=-0,25x².

   

— квадратичная функция. График — парабола, полученная из параболы y=-x² сжатием к оси абсцисс в 4 раза.

Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку, то есть при m=-1:

Ответ: -1.

3) Построить график функции

   

и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.

Решение:

Найдём область определения функции: x≠0.

D(y):x∈(-∞;0)∪(0;∞).

Если

   

   

   

то есть при x∈[-4;0)∪[4;∞), то

   

   

   

y=x/4 -функция прямой пропорциональности. График — прямая, проходящая через начало координат.

Для построения прямой достаточно взять одну точку, например, при x=4 y=4/4=1. Вторая точка — точка O — на графике выколотая, так как x≠0. Для более точного построения прямой лучше взять ещё одну точку: при x=-4 y=-4/4=-1.

Если

   

то есть при x∈(-∞;-4)∪(0;4), то

   

   

   

y=4/x — функция обратной пропорциональности. График — гипербола.

Для построения гиперболы возьмём несколько точек из промежутков (-∞;-4)∪(0;4) (-4 и 4 также лучше взять для уточнения построения графика).

Прямая y=m имеет с графиком ровно одну общую точку при m=1 и m=-1:

Ответ: -1; 1.

Построение графиков, содержащих модуль — Студопедия

Построение графика функции 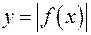по графику функции

Известно, что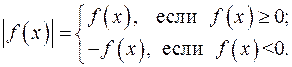

Область определения функции 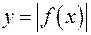такая же, как и у функции , поэтому график функции 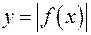получают из графика функции следующим образом.

Все точки графика функции , лежащие на оси Ох и выше ее остаются на месте. Все точки графика

, лежащие ниже оси Ох, симметрично отображают относительно оси Ох.

Пример. Построим этим способом график функции .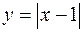

Решение. Строим график функции 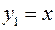. Сдвигаем точки графика 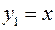на одну единицу масштаба вниз вдоль оси Оу. Получаем график функции 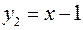. Затем точки графика 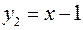, лежащие ниже оси Ох, и те значения, для которых у<0 отбрасываем (Рис. 75). Получили график функции

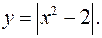
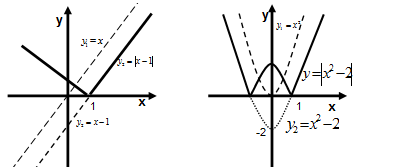
Рис. 75 Рис. 76

Аналогично строят график функции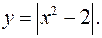

Строим график функции 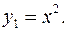Сдвигаем график функции 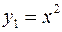,как жесткое тело, на 2 единицы масштаба, вниз вдоль оси Оу, получим график функции 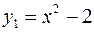. График функции 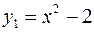, лежащие ниже оси Ох, симметрично отображаем относительно оси Ох, те значения х, для которых у<0 отбрасываем (Рис. 76).

Построение графика функции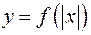

по графику функции

Функция 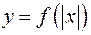четная, так как 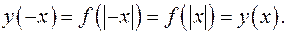График четной функции симметричен относительно оси Ох. Строят данный график следующим образом:

− строят график функции для всех х 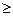0;

− точки, лежащие слева от оси Оу отбросывают;

− все точки графика функции, лежащие на оси Оу и справа от нее оставляют на месте;

− отображают правую часть графика симметрично относительно оси Оу.

Пример. Построим график функции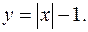

Решение. Строим график функции у=х–1. Часть графика, которая лежит левее оси Оу, отображаем. Часть графика, лежащую правее Оу зеркально отобразим относительно оси Оу (Рис. 77).


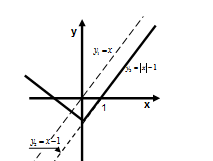Рис. 77 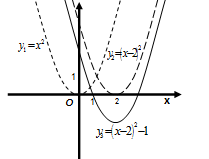Рис. 78

Пример. Построим график функции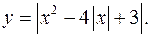

Решение. Построим график функции Для этого для квадратного трехчлена 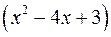выделим полный квадрат:

Строим график функции (Рис. 78)

Далее строим график функции Ту часть графика, которая расположена ниже оси Ох, отображаем, для нее у<0 и строим часть графика симметричную отображенной части относительно оси Ох (Рис. 79).

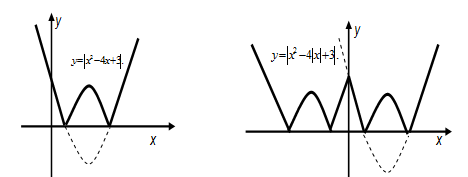
Рис. 79 Рис. 80

Ту часть графика, которая расположена левее оси Оу, отбрасываем и строим кривую симметрично оставшейся части относительно оси Оу (Рис. 80).

Пример. Построение графика квадратичной функции с помощью графика функции Выясним, какие преобразования необходимо выполнить, чтобы построить график функции путем преобразования графика функции


Решение. Выделим полный квадрат:

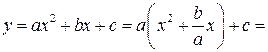
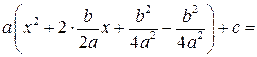
Функция 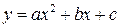представлена в виде . Рассмотрим случай 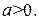Необходимо выполнить следующие преобразования:

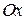− осуществить параллельный перенос графика функции вдоль оси на 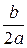единичных отрезков влево, если 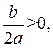вправо, если получим график вспомогательной функции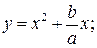

− осуществить параллельный перенос графика функции 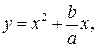вдоль оси , на 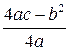единичных отрезков вверх, если 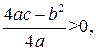вниз, если 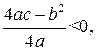получим график вспомогательной функции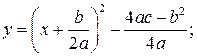

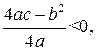− осуществить растяжение (сжатие) графика функции с коэффициентом получим график функции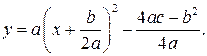

Если необходимо еще осуществить симметричное отображение графика функции относительно оси .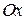

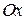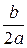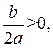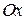Заметим, что вместо параллельного переноса графика функции вдоль оси на единичных отрезков влево, если вправо, если можно осуществить перенос оси на 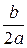единичных отрезков вправо, если 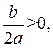влево, если вместо параллельного переноса графика функции 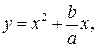вдоль оси , можно осуществить перенос оси на 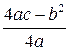единичных отрезков вниз, если 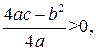вверх, если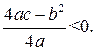

Пример. Построим график функции 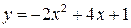путем преобразования графика функции

Решение. Выделим полный квадрат:

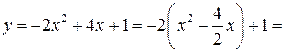
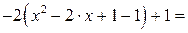
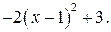
Функция 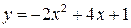представлена нами в виде 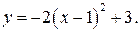Необходимо выполнить следующие преобразования:

− осуществить параллельный перенос графика функции вдоль оси 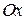на 1 единичный отрезок вправо;

− осуществить параллельный перенос графика функции 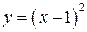вдоль оси , на единичных отрезка вверх;

− осуществить растяжение (сжатие) графика функции 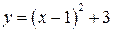с коэффициентом 2;

− осуществить симметричное отображение графика функции относительно оси .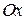

Таким образом,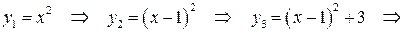

. Построение графика функции 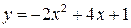показано на рисунках 81-85.

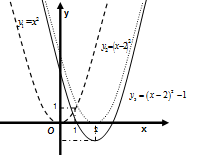
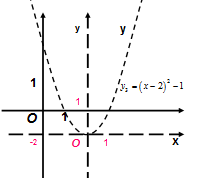Рис. 82

Рис. 81

Заметим, что вместо параллельного переноса графика функции вдоль оси на 2 единичных отрезка вправо, можно осуществить перенос оси на 2 единичных отрезка влево, вместо параллельного переноса графика функции вдоль оси , можно осуществить перенос оси на 1 единичный отрезок вверх.

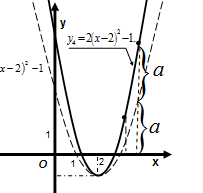
Рис. 83 Рис. 84 Рис. 85

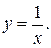Пример. Построение графика дробно-линейной функции по графику функции Выясним, какие преобразования необходимо выполнить, чтобы построить график функции путем преобразования графика функции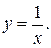

Решение. Выполним следующие преобразования:

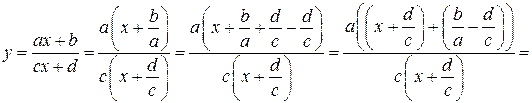
Функция представлена в виде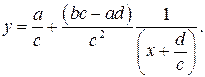

Необходимо выполнить следующие преобразования:

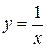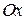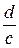− осуществить параллельный перенос графика функции вдоль оси на единичных отрезков влево, если 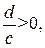вправо, если 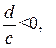получим график вспомогательной функции

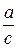− осуществить параллельный перенос графика функции вдоль оси , на единичных отрезков вверх, если 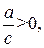вниз, если 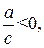получим график вспомогательной функции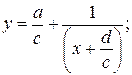

− осуществить растяжение (сжатие) графика функции с коэффициентом получим график функции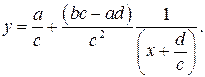

Если 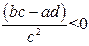необходимо осуществить симметричное отображение графика функции 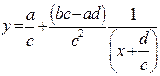относительно оси .

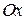Заметим, что вместо параллельного переноса графика функции 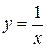вдоль оси 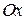на 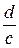единичных отрезков, можно осуществить перенос оси 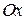на единичных отрезков вправо, если 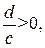влево, если 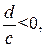вместо параллельного переноса графика функции вдоль оси , можно осуществить перенос оси на единичных отрезков вниз, если 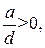вверх, если

Пример. Построим график функции путем преобразования графика функции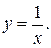

Решение. Выполним следующие преобразования:

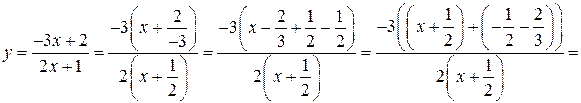
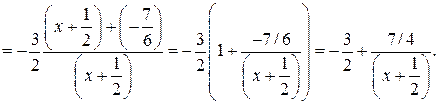
Функция 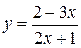представлена нами в виде 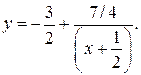Необходимо выполнить следующие преобразования:

− осуществить параллельный перенос графика функции 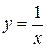вдоль оси 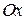на 0,5 единичного отрезка влево, либо осуществить параллельный перенос оси 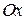на 0,5 единичного отрезка вправо;

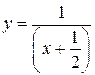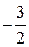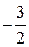− осуществить параллельный перенос графика функции вдоль оси , на единичных отрезка вниз, либо осуществить параллельный перенос оси на единичных отрезка вверх;

− осуществить растяжение (сжатие) графика функции с коэффициентом .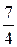

Таким образом,

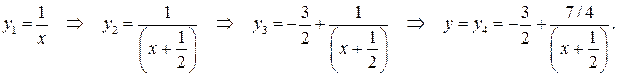
Построение графика функции 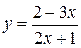показано на рисунке 86.

Рис. 86

Графики функций с модулем — Студопедия

Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.

Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.

Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.

Правило: график функции 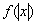получается из графика функции следующим образом: при 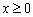график функции сохраняется, а при 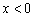«сохранённая часть» отображается симметрично относительно оси .

Пример 22

Построить график функции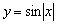

И снова вечная картина: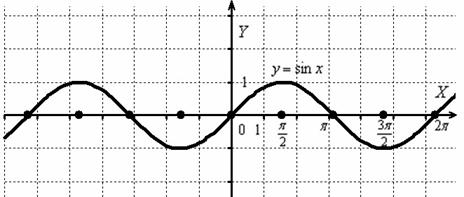

Согласно правилу, при 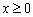график сохраняется: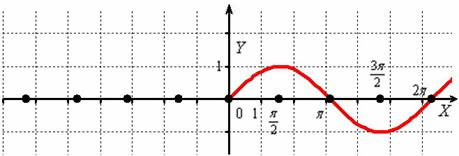

И сохранившаяся часть отображается симметрично относительно оси в левую полуплоскость: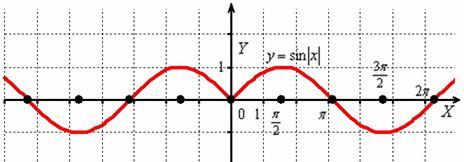

Действительно, функция 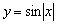– чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на 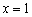и 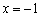. А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.

Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае:

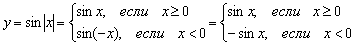
То есть, правая волна графика 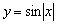задаётся функцией , а левая волна – функцией 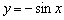(см. Пример 13).


Пример 23

Построить график функции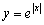

Аналогично, ветвь «обычной» экспоненты правой полуплоскости отображаем симметрично относительно оси в левую полуплоскость: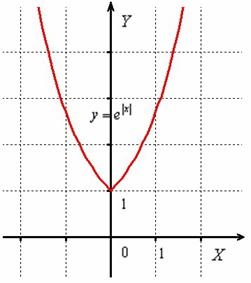

Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .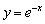

Модуль не имеет смысл «навешивать» на аргумент чётной функции: 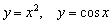и т.п. (проанализируйте, почему).

И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.

Правило: график функции 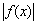получается из графика функции следующим образом: часть графика , лежащая НАД осью 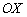сохраняется, а часть графика , лежащаяПОД осью 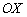отображается симметрично относительно данной оси.

Странно, что широко известный график модуля «икс» оказался на 24-ой позиции, но факт остаётся фактом =)

Пример 24

Построить график функции

Сначала начертим прямую, известную широкому кругу лиц: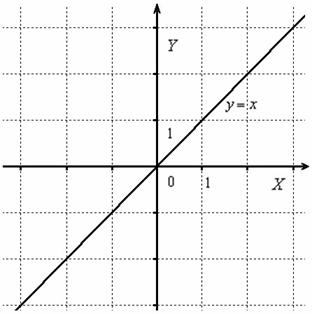

Часть графика, которая ВЫШЕ оси 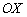, остаётся неизменной, а часть графика, которая НИЖЕ оси 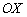– отображается симметрично в верхнюю полуплоскость: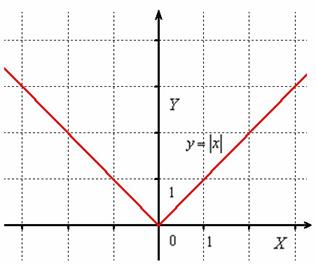


Модуль функции также раскрывается аналитически в кусочном виде: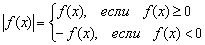

Внимание! Формула отличается от формулы предыдущего пункта!

В данном случае: 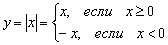, действительно, правый луч задаётся уравнением 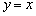, а левый луч – уравнением .

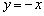Кстати, 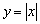– редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: 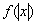, так и к самой функции: 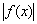. Изучим более «жизненную» ситуацию:

Пример 25

Построить график функции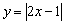

Сначала изобразим график линейной функции :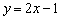

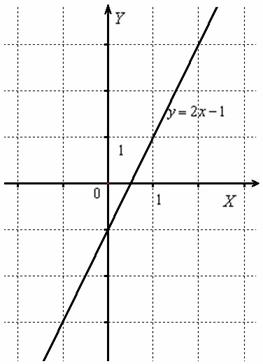
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси 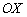в верхнюю полуплоскость:

Согласно формуле 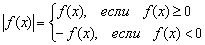, распишем функцию аналитически в кусочном виде: .

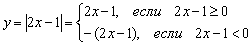Или, упрощая оба этажа: 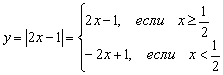, то есть правый луч задаётся функцией 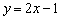, а левый луч – функцией 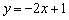. Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.

На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: 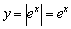. Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .

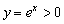Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:

Пример 26

Построить график функции .

Изобразим сами знаете что =)

И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :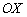

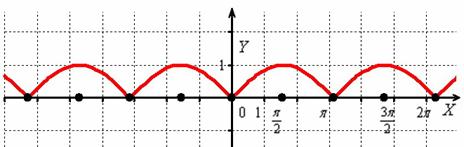
Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.

Распишем функцию в кусочном виде: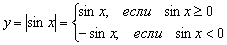

Решив два простейших школьных неравенства 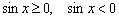, получаем:
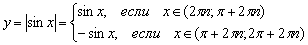, где 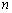– любое целое число.

Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)

Желаю успехов!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Непрерывность функции. Точки разрыва.
Как исследовать функцию на непрерывность?

Идет бычок, качается, вздыхает на ходу:
– Ох, доска кончается, сейчас я упаду!

На данном уроке мы разберём понятие непрерывности функции, классификацию точек разрыва и распространённую практическую задачу исследования функции на непрерывность. Из самого названия темы многие интуитивно догадываются, о чём пойдёт речь, и думают, что материал довольно простой. Это правда. Но именно несложные задачи чаще всего наказывают за пренебрежение и поверхностный подход к их решению. Поэтому рекомендую очень внимательно изучить статью и уловить все тонкости и технические приёмы.

Что нужно знать и уметь?Не очень-то и много. Для качественного усвоения урока необходимо понимать, что такое предел функции. Читателям с низким уровнем подготовки достаточно осмыслить статью Пределы функций. Примеры решений и посмотреть геометрический смысл предела в методичке Графики и свойства элементарных функций. Также желательно ознакомиться с геометрическими преобразованиями графиков, поскольку практика в большинстве случаев предполагает построение чертежа. Перспективы оптимистичны для всех, и даже полный чайник сумеет самостоятельно справиться с задачей в ближайший час-другой!

образцов участков в Matplotlib — Matplotlib 3.1.2, документация

Здесь вы найдете множество примеров графиков с кодом, который сгенерировал их.

Линия Участок

Вот как создать линейный график с текстовыми метками, используя участок () .

Простой участок

Несколько сюжетов на одной фигуре

Несколько осей (т. Е. Вспомогательных участков) создаются с помощью subplot () Функция :

Участок

Картинки

Matplotlib может отображать изображения (при условии одинакового расстояния горизонтальные размеры) с помощью функции imshow () .

Пример использования imshow () для отображения компьютерной томографии

Контурное и псевдоцветное

Функция pcolormesh () может сделать цветной представление двумерного массива, даже если горизонтальные размеры расположены неравномерно contour () Функция — это еще один способ представления те же данные:

гистограмм

Функция hist () автоматически генерирует гистограммы и возвращает количество бинов или вероятности:

Особенности гистограммы

дорожек

Вы можете добавить произвольные пути в Matplotlib, используя матплотлиб.модуль пути :

Path Patch

Трехмерное изображение

Инструментарий mplot3d (см. Начало и 3D-графики) имеет поддержку простых 3D-графиков включая поверхность, каркас, точечные и гистограммы.

Surface3d

Спасибо Джону Портеру, Джонатону Тейлору, Рейниру Хиерсу и Бену Руту за набор инструментов mplot3d . Этот инструментарий включен во все стандартные Matplotlib устанавливает.

Стремплот

Функция streamplot () отображает линии тока векторное поле.Помимо простого построения линий тока, он позволяет отобразить цвета и / или ширину линий линий тока в отдельный параметр, такие как скорость или локальная интенсивность векторного поля.

Streamplot с различными вариантами построения.

Эта функция дополняет функцию quiver () для построение векторных полей. Спасибо Тому Фланнагану и Тони Ю за добавление функция стримплота.

Эллипсы

В поддержку Феникса миссия на Марс (который использовал Matplotlib для отображения наземного отслеживания космический корабль), Майкл Droettboom построен на работе Чарли Моада, чтобы обеспечить чрезвычайно точное 8-сплайновое приближение к эллиптическим дугам (см. Arc ), которые нечувствительны к уровню масштабирования.

Ellipse Demo

Гистограмма

Используйте функцию bar () для создания гистограмм, которые включает в себя настройки, такие как ошибки:

Barchart Demo

Вы также можете создавать сложенные бары (Bar_stacked.py), или горизонтальные гистограммы (

.

Python Plotting с Matplotlib (Руководство) — Настоящий Python