Если дискриминант отрицательный сколько корней: Дискриминант — Детская игровая комната «Волшебный лес»

Posted on 17.11.197431.01.2022 by alexxlab

Содержание

Если в квадратном уравнении дискриминант равен 0. Решение квадратных уравнений

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b 2 – 4ас.

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .

Например. Решить уравнение х 2 – 4х + 4= 0.

D = 4 2 – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х 2 + х + 3 = 0.

D = 1 2 – 4 · 2 · 3 = – 23

Ответ: корней нет .

Решить уравнение 2х 2 + 5х – 7 = 0 .

D = 5 2 – 4 · 2 · (–7) = 81

х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1 .

Итак представим решение полных квадратных уравнений схемой на рисунке1.

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня.

А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.

Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид

х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .

На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х 2 + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3

х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27

√(D 1) = √27 = √(9 · 3) = 3√3

х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.

D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 · 3) = 2√3

х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.

О каких уравнениях пойдет речь?

На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.

Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.

Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.

Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.

Способы решения уравнений второго порядка

Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:

с помощью факторизации;
используя формулу для полного квадрата;
применяя график соответствующей квадратичной функции;
используя уравнение дискриминанта.

Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким.

Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.

Формула для получения корней уравнения

Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).

Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.

В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).

В примере выше a = 6, b=4, c=-8.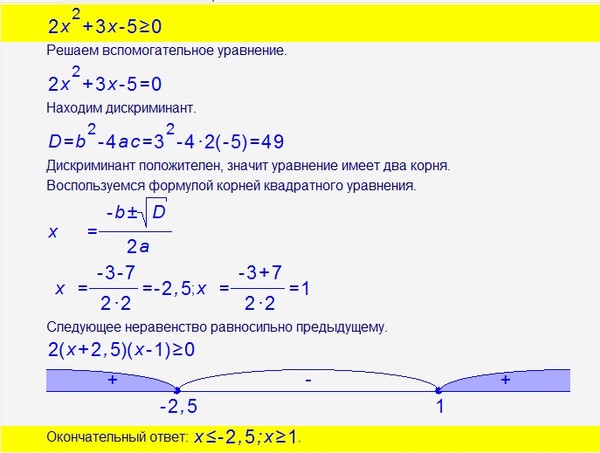 Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.

Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.

Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»). Для этого в него достаточно подставить коэффициенты b, c, и a.

Понятие о дискриминанте

В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.

Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:

D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
D=0: у уравнения всего один корень, и он является действительным числом.

Задача на определение дискриминанта

Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.

Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.

Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.

Пример неравенства через дискриминант

Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.

В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.

Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.

Пример решения уравнения

Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.

В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.

Геометрическая задача

Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.

У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.

Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.

Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.

Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см. 2 + j * w + k равный 0, где «i» и «j» — первый и второй коэффициент соответственно, «k» — константа, которую иногда именуют «свободным членом», а «w» — переменная. Его корнями окажутся все значения переменной, при которых оно превращается в тождество. Такое равенство допустимо переписать, как произведение i, (w — w1) и (w — w2) равное 0. В этом случае очевидно, что если коэффициент «i» не обращается в ноль, то функция в левой части станет нулевой только в случае, если x принимает значение w1 или w2. Эти значения являются результатом приравнивания многочлена к нулю.

Для нахождения значения переменной, при котором квадратный многочлен обращается в ноль, используется вспомогательная конструкция, построенная на его коэффициентах и названная дискриминантом. Эта конструкция рассчитывается согласно формуле D равняется j * j — 4 * i * k. Зачем она используется?

Она говорит, имеются ли действительные результаты.
Она помогает их высчитать.

Как это значение показывает наличие вещественных корней:

Если оно положительное, то можно найти два корня в области действительных чисел. (1/2).
Нахождение результата в соответствии с формулой (-j +/- d) / (2 * i).
Подстановка полученного результата в исходное равенство для проверки.

Некоторые частные случаи

В зависимости от коэффициентов решение может несколько упрощаться. Очевидно, что если коэффициент перед переменной во второй степени равен нулю, то получается линейное равенство.

Когда коэффициент перед переменной в первой степени нулевой, то возможны два варианта:

многочлен раскладывается в разность квадратов при отрицательном свободном члене;
при положительной константе действительных решений найти нельзя.

Если свободный член нулевой, то корни будут {0; -j}

Но есть и другие частные случаи, упрощающие нахождение решения.

Приведенное уравнение второй степени

Приведенным именуют такой квадратный трёхчлен, где коэффициент перед старшим членом — единица. Для данной ситуации применима теорема Виета, гласящая, что сумма корней равняется коэффициенту при переменной в первой степени, помноженному на -1, а произведение соответствует константе «k». 2 + 18 * i * j * k * m.

Допустим, дискриминант превосходит ноль

Видео

Наше видео подробно расскажет о вычислении дискриминанта.

Не получили ответ на свой вопрос? Предложите авторам тему.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:
x 2 − 8x + 12 = 0;
5x 2 + 3x + 7 = 0;
x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

x 2 − 2x − 3 = 0;
15 − 2x − x 2 = 0;
x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x 2 + 9x = 0;
x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:
x 2 − 7x = 0;
5x 2 + 30 = 0;
4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Квадратные уравнения изучают в 8 классе

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

Определение
Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.

Если D Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Задача

Сколько корней имеют квадратные уравнения:

x2 − 8x + 12 = 0;
5×2 + 3x + 7 = 0;
x2 − 6x + 9 = 0.

Решение

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.
Ответ

1) 2 корня; 2) нет корней; 3) один корень.

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Формула корней квадратного уравнения

Задача

Решить квадратные уравнения:

x2 − 2x − 3 = 0;
15 − 2x − x2 = 0;
x2 + 12x + 36 = 0.

Решение

Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:
Решение простого квадратного уравнения

Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их:
Квадратное уравнение: два корня

Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Случай с нулевым дискриминантом
Ответ

1) x1 = 3; x2 = -1; 2) x1 = −5; x2 = 3; 3) x = −6.

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x2 + 9x = 0;
x2 − 16 = 0.

Определение
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
Решение неполного квадратного уравнения

Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
Если же (−c/a)

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Разложение уравнения на множители

Задача

Решить квадратные уравнения:

x2 − 7x = 0;
5×2 + 30 = 0;
4×2 − 9 = 0.

Решение

x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.

5×2 + 30 = 0 ⇒ 5×2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4×2 − 9 = 0 ⇒ 4×2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Ответ

1) x1 = 0; x2 = 7; 2) корней нет; 3) x1 = 1,5; x2 = 1,5.

Что необходимо отметить на координатной плоскости. Старт в науке

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Если D
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Задача. Сколько корней имеют квадратные уравнения:
x 2 − 8x + 12 = 0;
5x 2 + 3x + 7 = 0;
x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

x 2 − 2x − 3 = 0;
15 − 2x − x 2 = 0;
x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x 2 + 9x = 0;
x 2 − 16 = 0.

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. 2 + b*x + c = 0 ,где x — переменная, a,b,c – константы; a0 . Задача состоит в отыскании корней уравнения.

Геометрический смысл квадратного уравнения

Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х) . Из этого следует, что есть три возможных случая:
1) парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).

2) парабола имеет одну точку пересечения с осью Ох . Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).

3) Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс. 2 и осуществим преобразование

Отсюда находим

Формула дискриминанта и корней квадратного уравнения

Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0 При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле

Теорема Виета

Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p , взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q . Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета. 2+x-6=0 .

Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения

С второго условия получаем, что произведение должно быть равно -6 . Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2} . С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равны

Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см 2 .

Решение: Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х – большую сторону, тогда 18-x меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;
или
х 2 -18х+77=0.
Найдем дискриминант уравнения

Вычисляем корни уравнения

Если х=11 , то 18-х=7 , наоборот тоже справедливо (если х=7 , то 21-х=9 ).

Задача 6. Разложить квадратное 10x 2 -11x+3=0 уравнения на множители.

Решение: Вычислим корни уравнения, для этого находим дискриминант

Подставляем найденное значение в формулу корней и вычисляем

Применяем формулу разложения квадратного уравнения по корнями

Раскрыв скобки получим тождество. 2+(2а+6)х-3а-9=0 имеет более одного корня?

Решение: Рассмотрим сначала особые точки, ими будут значения а=0 и а=-3 . При а=0 уравнение упростится до вида 6х-9=0; х=3/2 и будет один корень. При а= -3 получим тождество 0=0 .
Вычислим дискриминант

и найдем значения а при котором оно положительно

С первого условия получим а>3 . Для второго находим дискриминант и корни уравнения

Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0 получим 3>0 . Итак, за пределами промежутка (-3;1/3) функция отрицательная. Не стоит забывать о точке а=0 , которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи

Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

D = b 2 – 4ас.

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .

Например. Решить уравнение х 2 – 4х + 4= 0.

D = 4 2 – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х 2 + х + 3 = 0.

D = 1 2 – 4 · 2 · 3 = – 23

Ответ: корней нет .

Решить уравнение 2х 2 + 5х – 7 = 0 .

D = 5 2 – 4 · 2 · (–7) = 81

х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1 .

Итак представим решение полных квадратных уравнений схемой на рисунке1.

а = 1, b = 3 и с = 2. Тогда

D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .

Пример. Решить уравнение

3х 2 + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3

х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

√(D 1) = √27 = √(9 · 3) = 3√3

х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 · 3) = 2√3

х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Поработаем с квадратными уравнениями . Это очень популярные уравнения! В самом общем виде квадратное уравнение выглядит так:

Например:

Здесь а =1; b = 3; c = -4

Здесь а =2; b = -0,5; c = 2,2

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

Как решать квадратные уравнения? Если перед вами квадратное уравнение именно в таком виде, дальше уже всё просто. Вспоминаем волшебное слово дискриминант . Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении. Итак, формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня – и есть тот самый дискриминант . Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в это формулу и считаем. Подставляем со своими знаками! Например, для первого уравнения а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Вот и всё.

Какие случаи возможны при использовании этой формулы? Всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых . Но это играет роль в неравенствах, там мы поподробнее вопрос изучим.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Итак, как решать квадратные уравнения через дискриминант мы вспомнили. Или научились, что тоже неплохо. Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

Однако частенько квадратные уравнения выглядят слегка иначе. Например, вот так:

Это неполные квадратные уравнения . Их тоже можно решать через дискриминант. Надо только правильно сообразить, чему здесь равняются a, b и с .

Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всякого дискриминанта. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х = 0 , или х = 4

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем через дискриминант.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х = +3 и х = -3 .

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку. Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в предыдущем разделе. При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Дробные уравнения. ОДЗ.

Продолжаем осваивать уравнения. Мы уже в курсе, как работать с линейными уравнениями и квадратными. Остался последний вид – дробные уравнения . Или их ещё называют гораздо солиднее – дробные рациональные уравнения . Это одно и то же.

Дробные уравнения.

Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе . Хотя бы в одном. Например:

Напомню, если в знаменателях только числа , это линейные уравнения.

Как решать дробные уравнения ? Прежде всего – избавиться от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы знаем, что делать… В некоторых случаях оно может превратиться в тождество, типа 5=5 или неверное выражение, типа 7=2. Но это редко случается. Ниже я про это упомяну.

Но как избавиться от дробей!? Очень просто. Применяя всё те же тождественные преобразования.

Нам надо умножить всё уравнение на одно и то же выражение. Так, чтобы все знаменатели посокращались! Всё сразу станет проще. Поясняю на примере. Пусть нам требуется решить уравнение:

Как учили в младших классах? Переносим все в одну сторону, приводим к общему знаменателю и т.д. Забудьте, как страшный сон! Так нужно делать, когда вы складываете или вычитаете дробные выражения. Или работаете с неравенствами. А в уравнениях мы сразу умножаем обе части на выражение, которое даст нам возможность сократить все знаменатели (т.е., в сущности, на общий знаменатель). И какое же это выражение?

В левой части для сокращения знаменателя требуется умножение на х+2 . А в правой требуется умножение на 2. Значит, уравнение надо умножать на 2(х+2) . Умножаем:

Это обычное умножение дробей, но распишу подробно:

Обратите внимание, я пока не раскрываю скобку (х + 2) ! Так, целиком, её и пишу:

В левой части сокращается целиком (х+2) , а в правой 2. Что и требовалось! После сокращения получаем линейное уравнение:

А это уравнение уже решит всякий! х = 2 .

Решим ещё один пример, чуть посложнее:

Если вспомнить, что 3 = 3/1, а 2х = 2х/ 1, можно записать:

И опять избавляемся от того, что нам не очень нравится – от дробей.

Видим, что для сокращения знаменателя с иксом, надо умножить дробь на (х – 2) . А единицы нам не помеха. Ну и умножаем. Всю левую часть и всю правую часть:

Опять скобки (х – 2) я не раскрываю. Работаю со скобкой в целом, как будто это одно число! Так надо делать всегда, иначе ничего не сократится.

С чувством глубокого удовлетворения сокращаем (х – 2) и получаем уравнение безо всяких дробей, в линеечку!

А вот теперь уже раскрываем скобки:

Приводим подобные, переносим всё в левую часть и получаем:

Классическое квадратное уравнение. Но минус впереди – нехорош. От него можно всегда избавиться, умножением или делением на -1. Но если присмотреться к примеру, можно заметить, что лучше всего это уравнение разделить на -2! Одним махом и минус исчезнет, и коэффициенты посимпатичнее станут! Делим на -2. В левой части – почленно, а в правой – просто ноль делим на -2, ноль и получим:

Решаем через дискриминант и проверяем по теореме Виета. Получаем х = 1 и х = 3 . Два корня.

Как видим, в первом случае уравнение после преобразования стало линейным, а здесь – квадратным. Бывает так, что после избавления от дробей, все иксы сокращаются. Остаётся что-нибудь, типа 5=5. Это означает, что икс может быть любым . Каким бы он не был, всё равно сократится. И получится чистая правда, 5=5. Но, после избавления от дробей, может получиться и совсем неправда, типа 2=7. А это означает, что решений нет ! При любом иксе получается неправда.

Осознали главный способ решения дробных уравнений ? Он прост и логичен. Мы меняем исходное выражение так, чтобы исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. Точно так же мы будем поступать и со всякими сложными примерами с логарифмами, синусами и прочими ужасами. Мы всегда будем от всего этого избавляться.

Однако менять исходное выражение в нужную нам сторону надо по правилам , да… Освоение которых и есть подготовка к ЕГЭ по математике. Вот и осваиваем.

Сейчас мы с вами научимся обходить одну из главных засад на ЕГЭ ! Но для начала посмотрим, попадаете вы в неё, или нет?

Разберём простой пример:

Дело уже знакомое, умножаем обе части на (х – 2) , получаем:

Напоминаю, со скобками (х – 2) работаем как с одним, цельным выражением!

Здесь я уже не писал единичку в знаменателях, несолидно… И скобки в знаменателях рисовать не стал, там кроме х – 2 ничего нет, можно и не рисовать. Сокращаем:

Раскрываем скобки, переносим всё влево, приводим подобные:

Решаем, проверяем, получаем два корня. х = 2 и х = 3 . Отлично.

Предположим в задании сказано записать корень, или их сумму, если корней больше одного. Что писать будем?

Если решите, что ответ 5, – вы попали в засаду . И задание вам не засчитают. Зря трудились… Правильный ответ 3.

В чём дело?! А вы попробуйте проверку сделать. Подставить значения неизвестного в исходный пример. И если при х = 3 у нас всё чудненько срастётся, получим 9 = 9, то при х = 2 получится деление на ноль! Чего делать нельзя категорически. Значит х = 2 решением не является, и в ответе никак не учитывается. Это так называемый посторонний или лишний корень. Мы его просто отбрасываем. Окончательный корень один. х = 3 .

Как так?! – слышу возмущённые возгласы. Нас учили, что уравнение можно умножать на выражение! Это тождественное преобразование!

Да, тождественное. При маленьком условии – выражение, на которое умножаем (делим) – отлично от нуля . А х – 2 при х = 2 равно нулю! Так что всё честно.

И что теперь делать?! Не умножать на выражение? Каждый раз проверку делать? Опять непонятно!

Спокойно! Без паники!

В этой тяжелой ситуации нас спасут три магических буквы. Я знаю, о чем вы подумали. Правильно! Это ОДЗ . Область Допустимых Значений.

5х (х — 4) = 0

5 х = 0 или х — 4 = 0

х = ± √ 25/4

Научившись решать уравнения первой степени, безусловно, хочется работать с другими, в частности, с уравнениями второй степени, которые по-другому называются квадратными.

Квадратные уравнения — это уравнения типа ах ² + bx + c = 0, где переменной является х, числами будут — а, b, с, где а не равняется нулю.

Если в квадратном уравнении один или другой коэффициент (с или b) будет равняться нулю, то это уравнение будет относиться к неполному квадратному уравнению.

Как решить неполное квадратное уравнение, если ученики до сих пор умели решать только уравнения первой степени? Рассмотрим неполные квадратные уравнения разных видов и несложные способы их решения.

а) Если коэффициент с будет равен 0, а коэффициент b не будет равен нулю, то ах ² + bх + 0 = 0 сводится к уравнению вида ах ² + bх = 0.

Чтобы решить такое уравнение, нужно знать формулу решения неполного квадратного уравнения, которая заключается в том, чтобы левую часть его разложить на множители и позже использовать условие равенства произведения нулю.

Например, 5х ² — 20х = 0. Раскладываем левую часть уравнения на множители, при этом совершая обычную математическую операцию: вынос общего множителя за скобки

5х (х — 4) = 0

Используем условие, гласящее, что произведения равны нулю.

5 х = 0 или х — 4 = 0

Ответом будет: первый корень — 0; второй корень — 4.

б) Если b = 0, а свободный член не равен нулю, то уравнение ах ² + 0х + с = 0 сводится к уравнению вида ах ² + с = 0. Решают уравнения двумя способами: а) раскладывая многочлен уравнения в левой части на множители; б) используя свойства арифметического квадратного корня. Такое уравнение решается одним из методов, например:

х = ± √ 25/4

х = ± 5/2. Ответом будет: первый корень равен 5/2; второй корень равен — 5/2.

в) Если b будет равен 0 и с будет равен 0, то ах ² + 0 + 0 = 0 сводится к уравнению вида ах ² = 0. В таком уравнении x будет равен 0.

Как видите, неполные квадратные уравнения могут иметь не более двух корней.

Числовой математический диктант по темам «Квадратные уравнения», «Квадратные неравенства». 8 класс.

1	Неполное квадратное уравнение, где с = 0	1	Один корень
2	Приведённое квадратное уравнение	2
3	Полное квадратное уравнение	3	ax² + bx = 0
4	Сколько корней в квадратном уравнении, если дискриминант равен 0	4
5	Формула разложения на множители квадратного трёхчлена	5	x² + px +q = 0
6	Неполное квадратное уравнение, где в = 0	6	ax² + bx +c
7	Сколько корней в квадратном уравнении, если дискриминант отрицательный	7	ax² = 0
8	Квадратный трёхчлен	8	Не имеет корней
9	Формула корней квадратного уравнения	9	b² – 4ac
10	Сколько корней в квадратном уравнении, если дискриминант положительный	10	а(х – х₁)(х – х₂)
11	Формула корней по теореме Виета	11	ax² + c = 0
12	Неполное квадратное уравнение, где в = 0 и с = 0	12	Два корня
13	Основное условие квадратного уравнения и квадратного трёхчлена	13	ax² + bx +c = 0
14	Формула дискриминанта	14

Чему равно значение дискриминанта, дающего два мнимых решения? — Ответы на все

Чему равно значение дискриминанта, дающего два мнимых решения?

Решения не могут быть мнимыми, так как число под радикалом не отрицательно. Если положительное значение дискриминанта является полным квадратом, у нас будет два рациональных решения. Если значение дискриминанта не является идеальным квадратом, у нас будет два иррациональных решения.

Почему дискриминант определяет количество решений?

Дискриминант определяет количество решений, потому что это часть квадратного уравнения, которая находится под корнем.Поскольку мы знаем кое-что о квадратных корнях, мы можем применить эти знания для определения того, что мы знаем о решениях квадратного уравнения.

Сколько решений, если дискриминант отрицательный?

Дискриминант — это термин под квадратным корнем в квадратной формуле, который сообщает нам количество решений квадратного уравнения. Если дискриминант положительный, мы знаем, что у нас есть 2 решения. Если он отрицателен, решений нет, а если дискриминант равен нулю, решение одно.

Что означает, когда дискриминант представляет собой отрицательное целое число?

Дискриминант отрицателен, т. е. реальных решений нет.

Как получить отрицательный дискриминант?

Наличие отрицательного дискриминанта означает, что b2−4ac<0 и многочлен не имеет действительных решений.

Что значит, если дискриминант равен 16?

Все решения — рациональные числа Все решения — действительные числа Все решения — i. Вопрос 1031995: Если квадратное уравнение имеет дискриминант 16, что НЕ верно в отношении его решений? Дискриминант положителен, поэтому «Все решения — вещественные числа» и «Есть два решения» верны.

Сколько корней, если дискриминант отрицательный?

Если дискриминант положительный, то у вас есть , что приводит к двум действительным числовым ответам. Если он отрицательный, у вас есть , что дает два сложных результата. А если b2 – 4ac равно 0, то у вас есть , так что у вас есть только одно решение.

Сколько корней, если дискриминант отрицательный?

Сколько корней имеет отрицательный дискриминант?

Как определить, является ли дискриминант рациональным или иррациональным?

Если дискриминант — полный квадрат, то решения уравнения не только вещественны, но и рациональны. Если дискриминант положителен, но не является точным квадратом, то решения уравнения действительны, но иррациональны.

Является ли квадратный корень из 3 мнимым числом?

Квадратный корень из −9 — мнимое число. Квадратный корень из 9 равен 3, поэтому квадратный корень из минус 9 равен 3start text, 3, end text воображаемые единицы или 3 i 3i 3i …. Упрощение чисто мнимых чисел.

Упрощенная форма	Упрощенная форма
− − 144 −\sqrt{-144} −−144	− 12i -12i −12i

Сколько нулей у положительного дискриминанта?

два нуля
Когда дискриминант положительный, он будет иметь как положительный, так и отрицательный квадратный корень.Как указано знаком плюс или минус, это приведет к двум нулям. Когда дискриминант равен 0, будет только один ноль, а когда он отрицателен, нулей не будет.

Как выглядит график, если дискриминант отрицательный? – Реабилитацияроботикс.нет

Как выглядит график, если дискриминант отрицательный?

Если дискриминант отрицательный, это означает, что корни квадратичной функции не являются действительными числами. Другими словами, на графе нет пересечений по оси x.Если дискриминант отрицателен, то корни комплексные. Следовательно, парабола не пересекает ось абсцисс.

Какой график квадратного уравнения имеет отрицательный дискриминант?

Ответ D. Пошаговое объяснение: если дискриминант отрицателен, график не проходит через ось x, то есть пересечений по оси x нет.

Когда дискриминант отрицательный, уравнение имеет 2?

Это соотношение всегда верно: если вы получите отрицательное значение внутри квадратного корня, тогда не будет действительного числового решения и, следовательно, не будет пересечений по оси x.Другими словами, если дискриминант (являющийся выражением b2 – 4ac) имеет отрицательное значение, то у вас не будет графически отображаемых нулей.

Как узнать, является ли дискриминант положительным отрицательным или нулевым?

Положительный дискриминант указывает на то, что квадратичная функция имеет два различных решения в виде действительных чисел. Дискриминант, равный нулю, указывает на то, что квадратичная функция имеет повторяющееся действительное числовое решение. Отрицательный дискриминант указывает на то, что ни одно из решений не является действительным числом.

Сколько корней, если дискриминант отрицательный?

Как узнать, положительна парабола или отрицательна?

Давайте рассмотрим несколько ключевых моментов об этих паттернах:

Если х в квадрате, парабола вертикальна (открывается вверх или вниз).Если y в квадрате, он горизонтальный (открывается влево или вправо).
Если a положительно, парабола раскрывается вверх или вправо. Если он отрицательный, он открывается вниз или влево.
Вершина находится в точке (h, k).

Что происходит с параболой, когда a отрицательно?

Если a отрицательно, график параболы открывается вниз, а не вверх. Значение b параболы помогает определить скорость увеличения и уменьшения параболы, а также помогает определить положение вершины параболы.

Каков минимум или максимум параболы?

Вертикальные параболы дают важную информацию: когда парабола раскрывается, вершина является самой нижней точкой на графике, называемой минимумом или мин. Когда парабола открывается вниз, вершина является самой высокой точкой на графике, называемой максимумом или макс.

Что такое C в квадратном уравнении?

Стандартное квадратное уравнение выглядит так: ax2+bx+c = 0. Где a, b, c — числа, а a≥1. a, b называются коэффициентами x2 и x соответственно, а c называется константой.

Что означает Y ax2 BX C?

График квадратного уравнения с двумя переменными (y = ax2 + bx + c) называется параболой. Мы говорим, что первая парабола открывается вверх (это U-образная форма), а вторая парабола открывается вниз (это перевернутая U-образная форма). Чтобы нарисовать параболу, нам нужно найти ее точки пересечения, вершину и направление, в котором она открывается.

Что представляет Y ax 2 bx c?

Итак, для квадратичной функции y = ax2 + bx + c, когда «а» положительно, парабола открывается вверх, а вершина является минимальным значением.С другой стороны, если «а» отрицательно, график открывается вниз, а вершина является максимальным значением. Теперь вернемся к нашему исходному графику, y = x2, где «a» равно 1,

Каковы значения AB и C в квадратном уравнении?

Хотя факторинг не всегда может быть успешным, квадратичная формула всегда может найти решение. Квадратичная формула использует «a», «b» и «c» из «ax2 + bx + c», где «a», «b» и «c» — просто числа; это «числовые коэффициенты» квадратного уравнения, которое они дали вам решить.

Что представляют собой AB и C в стандартной форме?

Стандартная форма: стандартная форма строки имеет вид Ax + By = C, где A — положительное целое число, а B и C — целые числа. Стандартная форма линии — это просто еще один способ записи уравнения линии.

Как найти на графике ax 2 bx C?

Координата вершины квадратного уравнения стандартной формы (y = ax2 + bx + c) равна (-b/2a, f(-b/2a)), где x = -b/2a и y = f( -б/2а). Это означает, что для нахождения значения x вершины в уравнении y = -3×2 + x + 1 используйте формулу x = -b/2a.

Полезны ли значения AB и C для определения корней квадратного уравнения, почему бы и нет?

Ответ: Значения a, b и c помогают определить корни. Это потому, что для того, чтобы найти корни, вам нужно разложить квадратное уравнение на множители.

Как найти квадратное уравнение по графику?

Как найти квадратное уравнение на графике:

Шаг 1. Определите точки.
Шаг 2: Подставьте точки в форму вершины и найдите «а»
Шаг 3: Запишите квадратное уравнение.
Шаг 1: Определите точки.
Шаг 2: Подставьте точки в форму вершины и найдите «а»
Шаг 3: Запишите квадратное уравнение.

Что такое корень отличного? – М.В.Организинг

Что такое корень отличного?

отличный (прил.) 1300) «отличать одну вещь от другой; различать», от старофранцузского «отличить», от латинского «отличить», причастие прошедшего времени от «отличить», «отделять между, отделять, отмечать» (см. различать).Значение «простой и понятный для ума» происходит от c.

Что такое реальный и отличный корень?

Если дискриминант больше нуля, это означает, что квадратное уравнение имеет два действительных, различных (разных) корня. Если дискриминант равен нулю, это означает, что квадратное уравнение имеет два действительных одинаковых корня.

Является ли 0 настоящим корнем?

1. b2 −4ac < 0 Действительных корней нет. 2. b2 −4ac = 0 Существует один действительный корень.

Что делать, если дискриминант равен нулю?

Что делать, если b2 4ac отрицательно?

Дискриминант – это выражение b2 – 4ac, которое определено для любого квадратного уравнения ax2 + bx + c = 0. Если вы получите 0, квадратное уравнение будет иметь ровно одно решение – двойной корень. Если вы получите отрицательное число, у квадратного уравнения не будет действительных решений, а только два мнимых.

Если b2 4ac равно нулю, то корни равны?

1. Если b2 – 4ac = 0, то корни будут x = −b±02a = −b−02a, −b+02a = −b2a, −b2a. Ясно, что −b2a — действительное число, потому что b и a — вещественные числа. Таким образом, корни уравнения ax2 + bx + c = 0 действительны и равны, если b2 – 4ac = 0,

Что вам говорит B 2 4ac?

Квадратичные многочлены Величина b2−4ac называется дискриминантом многочлена. Если b2−4ac < 0, уравнение не имеет действительных решений, но имеет комплексные решения.Если b2−4ac = 0, уравнение имеет повторяющийся действительный корень. Если b2−4ac > 0, уравнение имеет два различных действительных корня.

Как узнать, что квадратное уравнение не имеет решения?

Если дискриминант меньше 0, уравнение не имеет действительного решения. Глядя на график квадратного уравнения, если парабола не пересекает или не пересекает ось x, то уравнение не имеет действительного решения. И отсутствие реального решения не означает, что решения нет, а то, что решения не являются действительными числами.

Что означает уравнение, которое не имеет решения?

Иногда уравнения не имеют решения. Это означает, что независимо от того, какое значение подставлено для переменной, вы ВСЕГДА получите противоречие. Посмотрите этот урок и узнайте, что нужно, чтобы уравнение не имело решения.

Сколько существует решений, если дискриминант равен 0?

Если дискриминант положительный, существует 2 действительных решения. Если это 0 , существует 1 реальное повторяющееся решение.Если дискриминант отрицателен, есть 2 комплексных решения (но нет действительных решений).

Чему равен дискриминант 3x 2 10x = — 2?

Дискриминант равен 76.

Сколько корней, если дискриминант отрицателен?

Это отрицательное значение, поэтому у этого уравнения два комплексных корня.

Что значит, если дискриминант больше 0?

Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень.2 – 4 а в. Когда дискриминант больше нуля, корни неравны и действительны. Когда дискриминант равен нулю, корни равны и действительны.

Что такое повторяющееся решение действительного числа?

Когда левая часть делится на два линейных уравнения с одним и тем же решением, говорят, что квадратное уравнение имеет повторяющееся решение. Мы также называем это решение корнем кратности 2 или двойным корнем. РЕШЕНИЕ КВАДРАТОМ.

Имеет ли уравнение x x 5 0 различные действительные корни?

Таким образом, x2+x-5=0 имеет два различных действительных корня.Таким образом, уравнение имеет действительные и равные корни. ∴ Корни уравнения не действительны. Следовательно, корни уравнения не действительны.

Могут ли действительные корни быть отрицательными?

Отрицательные числа не имеют действительных квадратных корней, поскольку квадрат либо положителен, либо равен 0. Квадратные корни чисел, не являющихся полными квадратами, являются членами иррациональных чисел. Иррациональные числа вместе с рациональными числами составляют действительные числа.

Как узнать, имеет ли граф действительные корни?

Корни из графиков Корни квадратного уравнения называются действительными корнями, если график пересекает ось x или касается ее.Эти корни являются действительными числами. Если график НЕ пересекает ось x, уравнение не имеет действительных корней.

Что такое отрицательный дискриминант?

Что такое отрицательный дискриминант? Дискриминант может быть положительным, нулевым или отрицательным, и это определяет, сколько решений есть у данного квадратного уравнения. Дискриминант, равный нулю, указывает на то, что квадратичная функция имеет повторяющееся действительное числовое решение. Отрицательный дискриминант указывает на то, что ни одно из решений не является действительным числом.

Что происходит, когда дискриминант меньше 0? Если дискриминант квадратичной функции меньше нуля, эта функция не имеет действительных корней, а парабола, которую она представляет, не пересекает ось x.

Сколько корней имеет отрицательный дискриминант? Если дискриминант положительный, то у вас есть , что приводит к двум действительным числовым ответам. Если он отрицательный, у вас есть , что дает два сложных результата. А если b2 – 4ac равно 0, то у вас есть , так что у вас есть только одно решение.

Является ли отрицательный дискриминант иррациональным? Дискриминант отрицательный, поэтому уравнение имеет два невещественных решения. Если дискриминант — полный квадрат, то решения уравнения не только вещественны, но и рациональны. Если дискриминант положителен, но не является точным квадратом, то решения уравнения действительны, но иррациональны.

Что такое отрицательный дискриминант? – Часто задаваемые вопросы

Что значит различать в математике?

дискриминант, в математике параметр объекта или системы, вычисляемый для помощи в его классификации или решении.Дискриминант может быть найден для общего квадратного или конического уравнения ax2 + bxy + cy2 + dx + ey + f = 0; он указывает, является ли представленная коника эллипсом, гиперболой или параболой.

Какова природа корней, если дискриминант равен 3?

Если дискриминант квадратного уравнения отрицательный, то квадратный корень из дискриминанта будет неопределенным.

Если дискриминант равен нулю, то корни равны?

Ясно, что дискриминант данного квадратного уравнения равен нулю.2 – 4 а в. Когда дискриминант больше нуля, корни неравны и действительны. Когда дискриминант равен нулю, корни равны и действительны.

Чему равен дискриминант числа 76?

Дискриминант равен 76, что положительно. Это означает, что существует два реальных решения.

Сколько корней в уравнении?

Чтобы вычислить количество корней квадратного числа ax2+bx+c=0, вам нужно вычислить дискриминант (b2-4ac). Если дискриминант меньше 0, то квадратное уравнение не имеет действительных корней.Если дискриминант равен нулю, то у квадратика равные насесты. Если дискриминант больше нуля, то он имеет 2 различных корня.

Как узнать, отрицателен ли дискриминант на графике?

Квадратный корень из отрицательного числа включает мнимое число i. Это означает, что если у вас есть отрицательный дискриминант, вы получите два сложных решения. Если оба решения сложные, вы не увидите их на графике. График будет либо слишком высоким, либо слишком низким и не будет пересекать ось x.

Является ли число 16 правильным квадратом?

Неофициально: когда вы умножаете целое число («целое» число, положительное, отрицательное или нулевое) на себя, полученное произведение называется квадратным числом, или полным квадратом, или просто «квадратом». Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — все квадратные числа.

Какое другое слово означает дискриминант?

дискриминационный, дискриминационный, дискриминационный.

Сколько корней, если дискриминант меньше нуля?

Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня.В этом случае имеется ровно один действительный корень. Это значение x является единственным действительным корнем данного уравнения.

Что такое дискриминантный класс 10?

Дискриминант. Для квадратного уравнения формы ax2+bx+c=0 выражение b2−4ac называется дискриминантом (обозначается D) квадратного уравнения. Дискриминант определяет характер корней квадратного уравнения на основе коэффициентов квадратного уравнения.

Как по графику узнать, положительный ли дискриминант?

Корни/нули/решения — это значения x, которые делают уравнение равным 0.На графике это будет пересечение параболы с осью X. Каждый раз, когда дискриминант положителен, график дважды пересекает ось X. Дискриминант не даст вам реальных ответов.

Чему равен дискриминант квадратного уравнения 3 4x =- 6×2?

Данное квадратное уравнение имеет вид 3 – 4x = -6×2. Стандартное квадратное уравнение имеет вид ax2 + bx + c= 0. Следовательно, дискриминант квадратного уравнения 3 – 4x = -6×2 равен – 56,

Два отрицательных числа равняются положительному?

Когда у вас есть два отрицательных знака, один переворачивается, и они складываются вместе, чтобы получить положительный.Если у вас есть положительный и отрицательный, остается одна черточка, и ответ отрицательный.

Какой дискриминант имеет иррациональные корни?

Если дискриминант положителен и не является полным квадратом (например, 84,52,700), корни иррациональны. Положительный дискриминант имеет два действительных корня (эти действительные корни могут быть иррациональными или рациональными).

Что такое иррациональные корни?

Теорему об иррациональном корне можно сформулировать следующим образом: Теорема об иррациональном корне утверждает, что если иррациональная сумма a плюс квадратный корень из b является корнем многочлена с рациональными коэффициентами, то a минус квадратный корень из b, который равен также иррациональное число, также является корнем этого многочлена.

Как узнать, иррациональны ли корни?

Действительные числа имеют две категории: рациональные и иррациональные. Если квадратный корень не является полным квадратом, то он считается иррациональным числом. Эти числа нельзя записать в виде дроби, потому что десятичная дробь не заканчивается (не завершается) и не повторяет шаблон (не повторяется).

Что такое действительные и различные корни?

Если уравнение имеет действительные корни, то решения или корни уравнения принадлежат множеству действительных чисел.Если уравнение имеет различные корни, то говорят, что все решения или корни уравнений не равны. Если квадратное уравнение имеет дискриминант больше 0, то оно имеет действительные и различные корни.

Что такое основная теорема алгебры?

основная теорема алгебры, Теорема уравнений, доказанная Карлом Фридрихом Гауссом в 1799 году. Она утверждает, что каждое полиномиальное уравнение степени n с комплексными числовыми коэффициентами имеет n корней или решений в комплексных числах.

Как написать ось симметрии?

Для квадратичной функции в стандартной форме y=ax2+bx+c осью симметрии является вертикальная линия x=−b2a . Пример 1: Найдите ось симметрии изображенной параболы. Координата x вершины есть уравнение оси симметрии параболы.

дискриминантных формул — что такое дискриминантные формулы? Примеры

Формулы дискриминанта используются для нахождения дискриминанта полиномиального уравнения.В частности, дискриминант квадратного уравнения используется для определения количества и характера корней. Дискриминант полинома – это функция, состоящая из коэффициентов полинома. Давайте изучим формулы дискриминанта вместе с несколькими решенными примерами.

Что такое дискриминантные формулы?

Дискриминантные формулы дают нам общее представление о природе корней. Дискриминант квадратного уравнения получается из квадратной формулы.Дискриминант обозначается D или Δ. Дискриминантные формулы для квадратного уравнения и кубического уравнения:

Дискриминантная формула квадратного уравнения

Дискриминантная формула квадратного уравнения ax ² + bx + c = 0 есть, Δ (или) D = b ² — 4ac. Мы знаем, что квадратное уравнение имеет максимум 2 корня, так как его степень равна 2. Мы знаем, что квадратная формула используется для нахождения корней квадратного уравнения: ax ² + bx + c = 0.Согласно квадратичной формуле, корни можно найти, используя x = [-b ± √ (b ² — 4ac) ] / [2a]. Здесь b ² — 4ac — это дискриминант D, который находится внутри квадратного корня. Таким образом, квадратичная формула становится x = [-b ± √D] / [2a]. Здесь D может быть либо > 0, = 0, (или) < 0. Определим характер корней в каждом из этих случаев.

Если D > 0, то квадратная формула принимает вид x = [-b ± √(положительное число)] / [2a], и, следовательно, в этом случае квадратное уравнение имеет два различных действительных корня.
Если D = 0, квадратная формула принимает вид x = [-b] / [2a], и, следовательно, в этом случае квадратное уравнение имеет только один действительный корень.
Если D < 0, то квадратная формула принимает вид x = [-b ± √(отрицательное число)] / [2a], и, следовательно, в этом случае квадратное уравнение имеет два различных комплексных корня (это связано с тем, что квадратный корень из отрицательного число приводит к мнимому числу. Например, √(-4) = 2i).

Дискриминантная формула кубического уравнения

Дискриминантная формула кубического уравнения − 27a ² d ² + 18abcd.Мы знаем, что кубическое уравнение имеет максимум 3 корня, так как его степень равна 3. Здесь

Если D > 0, все три корня действительны и различны.
Если D = 0, то вещественными являются все три корня, из которых хотя бы два равны между собой.
Если D < 0, то два его корня — комплексные числа, а третий корень — вещественный.

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила.Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Забронируйте бесплатный пробный урок

Мы можем увидеть применение дискриминантных формул в следующем разделе.

Примеры использования дискриминантных формул

Пример 1: Определить дискриминант квадратного уравнения 5x ² + 3x + 2 = 0. Также определить природу его корней.

Решение:

Данное квадратное уравнение имеет вид 5x ² + 3x + 2 = 0.

Сравнивая это с ax ² + bx + c = 0, мы получаем a = 5, b = 3 и c = 2.

Используя дискриминантную формулу,

D = b ² — 4ac

= 3 ² — 4(5)(2)

= 9–40

= -31

Ответ: Дискриминант равен -31. Это отрицательное число, поэтому данное квадратное уравнение имеет два комплексных корня.

Пример 2: Определить дискриминант квадратного уравнения 2x ² + 8x + 8 = 0.Также определите характер его корней.

Решение:

Данное квадратное уравнение имеет вид 2x ² + 8x + 8 = 0,

Сравнивая это с ax ² + bx + c = 0, мы получаем a = 2, b = 8 и c = 8.

Используя дискриминантную формулу,

Д = б ² — 4ас

= 8 ² — 4(2)(8)

= 64 — 64

= 0

Ответ: Дискриминант равен 0 и, следовательно, данное квадратное уравнение имеет два комплексных корня.

Пример 3: Определить природу корней кубического уравнения x ³ — 4x ² + 6x — 4 = 0.

Решение:

Данное кубическое уравнение равно x ³ — 4x ² + 6x — 4 = 0,

Сравнивая это с ax ³ + bx ² + cx + d = 0, мы получаем a = 1, b = -4, c = 6 и d = -4.

Используя дискриминантную формулу,

D = b ² c ² − 4ac ³ − 4b ³ d − 27a ² d ² + 18abcd

= (-4) ² (6) ² − 4(1)(6) ³ − 4(-4) ³ (-4) − 27(1) ² (-4) ) ² + 18(1)(-4)(6)(-4)

= -16

Ответ: Поскольку дискриминант является отрицательным числом, данное кубическое уравнение имеет два комплексных корня и один действительный корень.

Часто задаваемые вопросы о дискриминантных формулах

Что такое дискриминантные формулы?

Дискриминант полиномиального уравнения – это функция, выраженная через его коэффициенты.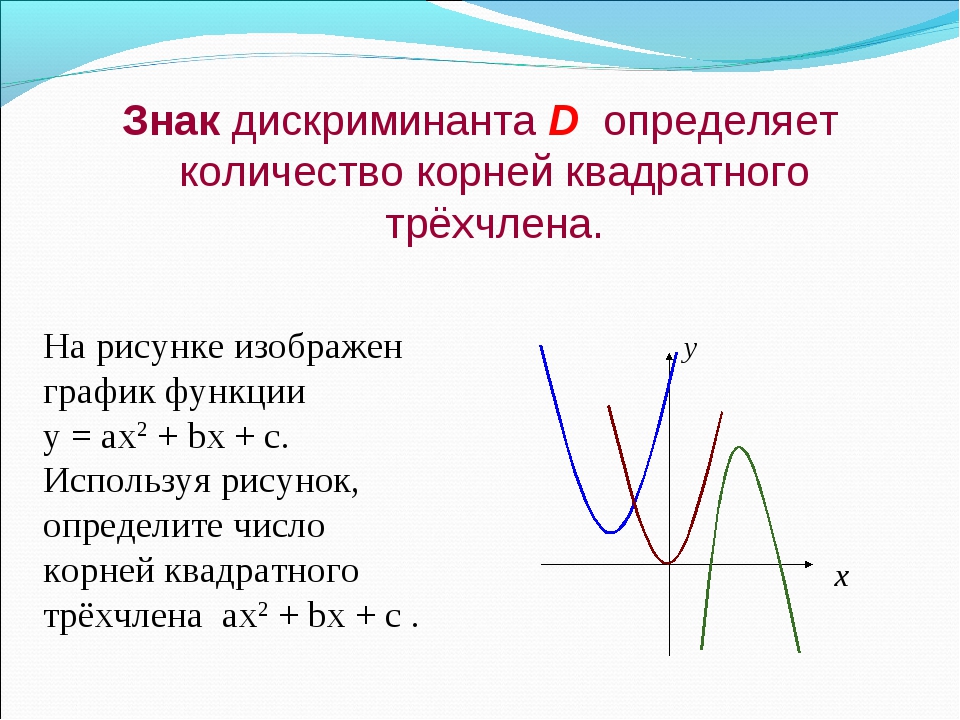 Дискриминант уравнения используется для определения характера его корней. Дискриминантные формулы следующие:

Дискриминантная формула квадратного уравнения ax ² + bx + c = 0 есть, Δ (или) D = b ² — 4ac.
Дискриминантная формула кубического уравнения − 27a ² d ² + 18abcd.

Как вывести дискриминантную формулу квадратного уравнения?

Выведем дискриминантную формулу квадратного уравнения ax ² + bx + c = 0. По квадратной формуле решения этого уравнения находятся с помощью x = [-b ± √ (b ² — 4ac) ] / [2а]. Здесь b ² — 4ac находится внутри квадратного корня, и, следовательно, мы можем определить природу корней, используя свойства квадратного корня (например, квадратный корень из положительного числа является действительным числом, квадратный корень из a отрицательное число является мнимым числом, а квадратный корень из 0 равен 0).Таким образом, дискриминант квадратного уравнения равен b ² — 4ac.

Каковы применения формулы дискриминанта?

Формула дискриминанта используется для определения характера корней квадратного уравнения. Дискриминант квадратного уравнения ax ² + bx + c = 0 равен D = b ² — 4ac.

Если D > 0, то уравнение имеет два действительных различных корня.
Если D = 0, то уравнение имеет только один действительный корень.
Если D < 0, то уравнение имеет два различных комплексных корня.

Что такое дискриминантная формула кубического уравнения?

Дискриминантная формула кубического уравнения ax ³ + bx ² + cx + d = 0 обозначается Δ (или) D и находится по формуле Δ (или) D = b ² c ² − 4ac ³ − 4b ³ d − 27a ² d ² + 18abcd.

3. Квадратичная формула

В конце последнего раздела (Завершение квадрата) мы получили общая формула решения квадратных уравнений. 2-4(6)(-1)))/(2(6))`

`=(6+-кв.(36+24))/12`

`=(6+-sqrt60)/12`

`=(6-2кв.15)/12 или (6+2кв.15)/12`

`=(3-кв.15)/6 или (3+кв.15)/6`

Так

`r=-0,145 или 1,145`

Сколько X-перехватов, если дискриминант отрицательный? – Theburningofrome.com

Сколько X-отрезков, если дискриминант отрицательный?

Если значение дискриминанта равно нулю, существует одно действительное решение для x, что означает, что график решения имеет одну точку пересечения с x.Если внутри квадратного корня находится отрицательное число, пересечений по оси x нет.

Что делать, если дискриминант отрицательный?

Если дискриминант отрицательный, это означает, что под квадратным корнем в квадратной формуле стоит отрицательное число. Возможно, в прошлом вы узнали, что «нельзя извлечь квадратный корень из отрицательного числа». Правда в том, что вы можете извлечь квадратный корень из отрицательного числа, но ответ нереален.

Как узнать, отрицательный ли дискриминант?

Как узнать, равен ли дискриминант нулю?

Если дискриминант равен нулю, это означает, что квадратное уравнение имеет два действительных одинаковых корня. Таким образом, квадратное уравнение x2 + 2x + 1 имеет два действительных одинаковых корня. D > 0 означает два действительных различных корня. D < 0 означает отсутствие действительных корней.

Что такое точка пересечения по оси x в квадратном уравнении?

Х-пересечения — это точки, в которых график функции или уравнения пересекает или «касается» оси х декартовой плоскости. Вы можете думать об этом как о точке с нулевым значением y. Чтобы найти x-отрезки уравнения, пусть y = 0 y = 0 y=0, затем найдите x. В точечной нотации это записывается как (x, 0).

Является ли дискриминант FFF положительным нулем или отрицательным?

Ответ положительный.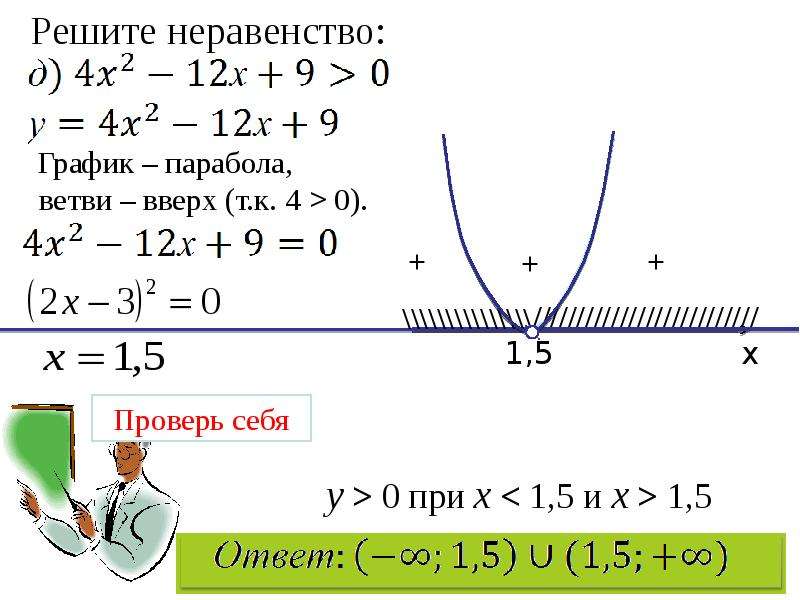

Что произойдет, если дискриминант равен 0?

Дискриминант, равный нулю, указывает на то, что квадратичная функция имеет повторяющееся действительное числовое решение.Отрицательный дискриминант указывает на то, что ни одно из решений не является действительным числом.

Сколько мнимых решений, если дискриминант отрицательный?

Определяет количество и тип решений квадратного уравнения. Если дискриминант положительный, то существует 2 действительных решения. Если это 0 , существует 1 реальное повторяющееся решение. Если дискриминант отрицателен, есть 2 комплексных решения (но нет действительных решений).

Как определяются точки пересечения x квадратного уравнения?

Решения квадратного уравнения вида a x 2 + b x + c = 0 находятся по квадратной формуле.Здесь выражение b 2 − 4 a c называется дискриминантом. Дискриминант можно использовать для подтверждения количества отрезков x и типа решений квадратного уравнения.

Может ли квадратное уравнение иметь отрицательный дискриминант?

Квадратичная формула с отрицательным дискриминантом также известна как отрицательная квадратичная. Эти квадратные уравнения в принципе не имеют действительных решений. В случае, когда квадратное уравнение имеет мнимый дискриминант, говорят, что квадратное уравнение не имеет решений.

Когда использовать дискриминант для подтверждения количества пересечений по оси x?

Дискриминант можно использовать для подтверждения количества пересечений по оси x и типа решений квадратного уравнения. Значение типа дискриминанта и количество пересечений x (корней) Пример графика связанной функции b2−4ac>0; b2−4ac является полным квадратом 2, вещественным и рациональным f(x)=x2−x−6 b2−4ac>0; b2−4ac не является идеальным полем

Каковы x пересечения функции f ( x )?

Х-пересечения функции f (x) = a x 2 + b x + c, a ≠ 0 являются решениями квадратного уравнения a x 2 + b x + c = 0.Решения квадратного уравнения вида a x 2 + b x + c = 0 задаются квадратичной формулой. x = − b ± b 2 − 4 a c 2 a Здесь выражение b 2 − 4 a c называется дискриминантом.