Деление чисел с остатком: формулы, примеры и правила

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Деление с остатком целых положительных чисел

Деление — это разбиение целого на равные части.

Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.

Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!

Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.

Самый удобный способ деления — это столбик.

Попрактикуемся в решении.

Пример

Разделить 14671 на 54.

Как решаем:

Выполним деление столбиком:

Неполное частное равно 271, остаток — 37.

Ответ: 14671 : 54 = 271(остаток 37).

Деление с остатком положительного числа на целое отрицательное

Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:

В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.

Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.

Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».

Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.

Алгоритм деления положительного числа на целое отрицательное (с остатком):

• найти модули делимого и делителя;
• разделить модуль делимого на модуль делителя
• получить неполное частное и остаток;
• записать число противоположное полученному.

Пример

Разделить 17 на −5 с остатком.

Как решаем:

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.

Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.

Ответ: 17 : (− 5) = −3 (остаток 2).

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.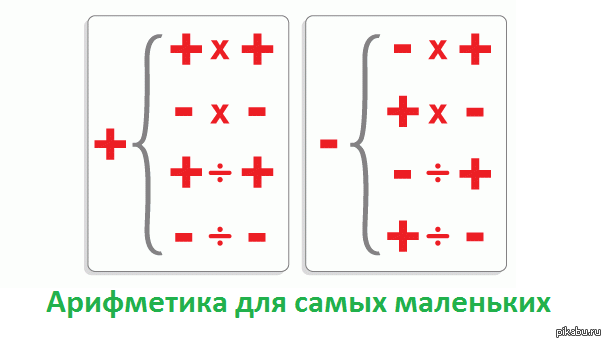

Деление с остатком целого отрицательного числа на целое положительное

Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:

Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле: d = a − b * c

Из правила делаем вывод, что при делении получается целое неотрицательное число.

Для точности решения применим алгоритм деления а на b с остатком:

• найти модули делимого и делителя;
• разделить по модулю;
• записать противоположное данному число и вычесть 1;
• использовать формулу для остатка d = a − b * c.

Рассмотрим пример, где можно применить алгоритм.

Пример

Найти неполное частное и остаток от деления −17 на 5.

Как решаем:

Разделим заданные числа по модулю.

Получаем, что при делении частное равно 3, а остаток 2.

Так как получили 3, противоположное ему −3.

Необходимо отнять единицу: −3 − 1 = −4.

Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:

d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.

Значит, неполным частным от деления является число −4 с остатком 3.

Ответ: (−17) : 5 = −4 (остаток 3).

Деление с остатком целых отрицательных чисел

Сформулируем правило деления с остатком целых отрицательных чисел:

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле: d = a − b * c

Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.

Алгоритм деления с остатком целых отрицательных чисел:

• найти модули делимого и делителя;
• разделить модуль делимого на модуль делителя;
• получить неполное частное и остаток;
• прибавить 1 к неполному частному;
• вычислить остаток, исходя из формулы d = a − b * c.

Пример

Найти неполное частное и остаток при делении −17 на −5.

Как решаем:

Применим алгоритм для деления с остатком.

Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.

Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.

Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.

Получилось, что остаток равен 3, а неполное частное равно 4.

Ответ: (−17) : (−5) = 4 (остаток 3).

Деление с остатком с помощью числового луча

Деление с остатком можно выполнить и на числовом луче.

Пример 1

Рассмотрим выражение: 10 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.

Решение: 10 : 3 = 3 (остаток 1).

Пример 2

Рассмотрим выражение: 11 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.

Решение: 11 : 3 = 3 (остаток 2).

Проверка деления с остатком

Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.

Формула деления с остатком a = b * c + d, где a — делимое, b — делитель, c — неполное частное, d — остаток.

Эту формулу можно использовать для проверки деления с остатком.

Пример

Рассмотрим выражение: 15 : 2 = 7 (остаток 1).

В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.

Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:

• 7 * 2 + 1 = 15;
• 2 * 7 + 1 = 15.

Теорема о делимости целых чисел с остатком

Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.

Теорема Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом: a = b * q + r, где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.

Докажем возможность существования a = b * q + r .

Доказательство:

Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.

Если посчитать, что b — целое положительное число, тогда, следует выбрать целое q так, чтобы произведение b * q не было больше значения числа а , а произведение b * (q + 1) было больше, чем a.

Тогда необходимо взять q такое, чтобы данное неравенством b * q < a < b * (q + 1) было верным. Необходимо вычесть b * q из всех частей выражения. Тогда придем к неравенству такого вида: 0 < a − b * q < b.

Имеем, что значение выражения a − b * q больше нуля и не больше значения числа b, отсюда следует, что r = a − b * q. Получим, что число а можем представить в виде a = b * q + r.

Теперь необходимо рассмотреть возможность представления a = b * q + r для отрицательных значений b.

Модуль числа получается положительным, тогда получим a = b * q1 + r, где значение q1 — некоторое целое число, r — целое число, которое подходит условию 0 ≤ r < b. Принимаем q = −q1, получим, что a = b * q + r для отрицательных b.

Урок 55. название чисел при делении — Математика — 2 класс

Математика, 2 класс

Урок № 55. Название чисел при делении

Перечень вопросов, рассматриваемых в теме:

1. Как называются числа при делении?

2. Как называется числовое выражение со знаком деление?

Глоссарий по теме:

Деление — это арифметическое действие, обратное умножению. С помощью деления по произведению и одному из множителей определяется второй множитель.

Делимое — это число стоящее слева от знака деления, которое делим.

Делитель — это число стоящее справа от знака деления, число на которое делим делимое. (какими частями делим, дробим)

Частное — это число стоящее после знака равно, результат деления, числовое выражение со знаком деление.

Обязательная литература и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 2 класс. Учебник для общеобразовательных организаций. М.; Просвещение, 2017. – с. 62.
2. С. И. Волкова. Математика 2 класс. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – с. 44-47.

Теоретический материал для самостоятельного изучения

Запишем равенство, используя необходимое арифметическое действие:

10 яблок разложили на две тарелки поровну.

10 : 2 = 5

9 конфет раздали трём детям поровну.

9 : 3 = 3

8 тетрадей раздали четырём ученикам поровну.

8 : 4 = 2

Для того, чтобы выполнит задание, нам понадобилось действие деление.

Вы уже знаете, как называются числа при сложении и вычитании, недавно вы познакомились с названиями чисел при умножении.

Вы умеете называть выражения со знаками «плюс», «минус», со знаком умножения. Сегодня вы узнаете, как называются числа при делении. Выражение со знаком деления тоже имеет своё название. Хотите узнать? Вперёд!

Числа при делении имеют свои названия.

Рассмотрим рисунок.

8 листьев раздали детям, по 2 листа каждому.

8 : 2 = 4

4 человека получили листья.

Число, которое делят, называется делимым. 8 – это делимое. Число, на которое делят делимое, называется делитель. 2 – это делитель Результат действия деления называется частным. 4 – это частное. Выражение 8 разделить на 2 тоже называется частным.

Компоненты деления: делимое, делитель, частное.

Найдите частное, если делимое – 6, делитель – 3.

Проверьте: 6 : 3 = 2

Найдите частное чисел 12 и 6. Проверьте: 12 : 6 = 2

Решим задачу: 12 клубничек раздали 4 детям поровну. По сколько клубничек получил каждый ребёнок?

Для решения задачи выберем действие деление, так как надо узнать, сколько раз по 4 содержится в числе 12.

12 : 4 = 3 (кл.)

Ответ: по 3 клубнички получил каждый ребёнок.

Вспомним название чисел при делении. 12 – делимое, 4 – делитель. 3 – частное. 12 : 4 – это частное.

Вывод: компоненты действия деление – делимое, делитель, результат деления – частное.

Ответим на вопросы, поставленные в начале урока.

Число, которое делят, называется делимое.

Число, на которое делят делимое, называется делитель.

Результат деления – частное.

Числа, которые соединены знаком деления, тоже называются частное.

Выполним несколько тренировочных заданий.

1. По рисунку составьте задачи на деление. Запишите решение. Назовите компоненты действия деление.

а) 15 яблок разложили в 3 вазы, в каждую вазу поровну. Сколько яблок положили в одну вазу?

Проверьте: 15 : 3 = 5 (яб.).

Ответ: 5 яблок.

15 – делимое. 3 – делитель. 5 – частное. Выражение 15:3 – частное.

б) 15 яблок разложили в вазы, по 5 штук в каждую. Сколько ваз заняты яблоками?

15 : 5 = 3 (в.)

Ответ: 3 вазы.

15 – делимое. 5 – делитель. 3 – частное. Выражение 15:5 – частное.

2. Запишите выражение и найдите их значения:

Частное чисел 12 и 2.

Делитель 4, делимое 20.

Делимое 8, делитель 4.

Произведение 5 и 3.

Сумма чисел 6 и 4.

Проверьте.

12 : 2 = 6

20 : 4 = 5

8 : 4 = 2

5 ∙ 3 = 15

6 + 4 = 10

Как рассчитать цену на товар. Маржа и наценка

24 июня 2020 Пригодится для: Предприниматели

Что закладывать в цену, как быть с комиссией посредников, как рассчитать наценку и маржу, и чем они отличаются.

Себестоимость и наценка

У цены на товар и услуги две основные составляющие — себестоимость и наценка.

Запомните формулу: цена за ед. = себестоимость + наценка

Что включает в себя себестоимость единицы товара — затраты на производство единицы продукции: материалы, запчасти, комплектующие. Ещё это все переменные расходы, которые напрямую зависят от объёма проданной/произведённой продукции. Сдельная оплата работы сотрудников, расходы на логистику, упаковку, рекламу.

Если у вас пекарня, в себестоимость продукции вы включаете аренду помещения, зарплаты сотрудников, стоимость продуктов, упаковки, расходы на доставку, если доставляете на точки продажи, и пр.

Себестоимость услуг и работ тоже можно рассчитать. По сути это стоимость произведённых затрат на оказание услуги.

К примеру, ФЛП-стилист продаёт консультации по разбору и подбору гардероба. Товар не закупает, а себестоимость его услуги — время работы с клиентом, доставка одежды и обуви для подбора образов, возврат одежды, которая не подошла.

Наценка. Это надбавка к себестоимости товара/услуги, она и формирует валовый доход бизнеса (цена минус себестоимость).

Вот формула, по которой считаем наценку:

Наценка = постоянные расходы + налоги + комиссия посредника + прибыль

Вы обязательно включаете в наценку все постоянные (или операционные) расходы, если не учли их в себестоимости — затраты на логистику, аренду, содержание сотрудников и пр. , иначе вам придётся оплачивать эти расходы за счёт своей прибыли.

Постоянные расходы на единицу продукции легко посчитать, если ведёте управленческий учёт, в частности составляете отчёты о доходах и расходах. Прочитайте нашу статью, мы на примерах показали, как их составлять.

Управленческий отчёт о доходах и расходах

Если кратко: нужно разделить общую сумму постоянных расходов за период на количество произведённой продукции или продаж за это же время.

Если работаете с посредниками, их комиссию надо учитывать в наценке — увеличить розничную цену на величину комиссионного вознаграждения, чтобы платить комиссию со «сверхприбыли», не уменьшая свою.

Если хотите, чтобы ваш товар продавался по единой цене и у вас, и у посредника — придётся выплачивать комиссионное вознаграждение с прибыли.

Можете рассчитать наценку одним из способов:

• в себестоимости учитываете полностью все расходы на товар (переменные и постоянные), тогда наценка будет равна чистой прибыли;
• разделяете расходы — часть относите на себестоимость, а операционные (постоянные) фиксируете в наценке.

Маржа и наценка

Наценка и маржа не одно и то же, но их часто путают. Маржа всегда меньше, а наценка ограничивается только здравым смыслом ФЛП.

Наценка — это то, что мы нацениваем на себестоимость товара, показывает, насколько увеличилась стоимость продукта по сравнению с его закупочной ценой, затратами на производство и пр.

Рассчитывают наценку на этапе формирования цены. Зная себестоимость и норму наценки, легко рассчитать цену реализации товара: она измеряется в процентах или в стоимостном выражении.

А вот маржа показывает рентабельность или прибыльность продаж, сколько прибыли содержится в цене продажи. Может иметь стоимостное и процентное выражение.

Маржа всегда соотносится с ценой реализации товара, показывает прибыльность товара или группы товаров. Даёт понимание, сколько прибыли содержится в 1 грн выручки.

Маржа не может превышать 100%, это всегда какой-то процент от розничной цены. Маржу обычно рассчитывают за отчётный период, чтобы отследить прибыльность работы компании.

Маржинальность в процентах показывает разницу между ценой и себестоимостью к конечной цене.

К примеру, вы продаёте услуги по разработке сайтов, взяли в работу проекты — за 50 тыс. грн, исполнителям заплатили 25 тыс. грн, маржинальность проекта — 50%.

У вас нет физического офиса и сотрудников в штате, все работают за сдельную оплату на удалёнке, из постоянных затрат — только налоги и зарплата бухгалтера — 15 тыс. грн в месяц. Маржинальный доход с одного проекта покрывает постоянные затраты, ваш заработок — 10 тыс. грн.

Маржа может быть валовая и чистая.

Валовая маржа — показывает, сколько валовой, «грязной» прибыли содержится в цене продукта/услуги.

Чистая маржа — это доля чистой прибыли в цене продукта.

Закрепим на примере:

ФЛП продаёт единицу товара за 1400 грн: купил его за 800 грн (себестоимость, в т. ч. закупочная стоимость товара, 700 грн), ставит наценку — 600 грн, в наценке 200 грн — это его прибыль.

Наценка в грн = цена продажи − себестоимость

Наценка в грн = 1400 − 800 = 600 грн

Наценка в % = (Наценка / Себестоимость) × 100% = (600 / 800) × 100% = 75%

Маржа в грн = цена продажи − себестоимость

В стоимостном выражении валовая маржа как наценка. У нас это 600 грн.

Маржа вал. в % = (Маржа вал. / Цена реализации) × 100% = (600 / 1400) × 100% = 43%

Маржа чист. в % = (Маржа чист. / Цена реализации) × 100% = (200 / 1400) × 100% = 14%

Выходит, что в цене реализации сидит 57% себестоимости и 43% валовой прибыли.

В 1 гривне выручки от продажи содержится 43 копейки «грязной» прибыли или 14 копеек чистой.

Зная валовую маржу, можно посчитать наценку, и наоборот.

Пример:

Наценка = маржа / (100 % − маржа) = 43 / (100% − 43) = 75%
Маржа = наценка / (100 % + наценка) = 75 / (100% + 75)= 43%

Наценка показывает добавочную стоимость продукта, а маржа — прибыльность товара и эффективность работы. Чем больше наценка, тем больше маржа, но маржа всегда ниже наценки.

Минимальный уровень наценки. Чтобы покрыть все затраты и понимать, при каком уровне цены бизнес начнёт зарабатывать, рассчитайте минимальный уровень наценки. Точка безубыточности в отношении цены. Это та наценка, которая полностью покрывает расходы, а прибыль равна 0.

Цена минимальная = Себестоимость + Постоянные расходы

В нашем примере цена минимальная = 800 + 400 = 1200 грн, установите цену больше — начнёте получать прибыль.

Считайте наценку и прогнозируйте маржинальность на старте

Подруги решили открыть свой бизнес: пошив и продажа женской одежды.

Решено запустить продажи через Инстаграм, потом открыть шоурум, подключить продажи через посредников.

Промониторив рынок, предпринимательницы пришли к выводу, что в Инстаграме лучше всего продаются вещи стоимостью 500–700 грн.

Запустили собственное производство, на одно изделие уходит материалов на 150 грн, зарплата швеи — 100 грн, зарплата продавца — 35 грн. Всего себестоимость изделия — 285 грн.

Постоянные расходы — аренда помещения под шоурум, фирменная упаковка, налоги, реклама в Инстаграме всех товаров, не конкретного изделия, для которого рассчитываете себестоимость. Общая стоимость на единицу — 220 грн.

То есть продавать единицу нужно не дешевле 505 грн, чтобы окупить затраты. А ещё нужно учесть прибыль на единицу продукции, к примеру, наши предпринимательницы хотят на одной единице зарабатывать 300 грн.

Значит, розничная цена должна быть: 285 + 220 + 300 = 805 грн за одно изделие.

Если ФЛП решат подключить посредника, нужно учесть его комиссию, к примеру 10% от розничной цены товара — 80,5 грн. Комиссию можно включить в стоимость изделия и продавать его дороже или платить из своей прибыли, не увеличивая стоимость изделия, но это значит, что ФЛП заработают меньше.

Если решат делать доставку за свой счёт, придётся либо увеличить стоимость изделия, либо уменьшить свою прибыль.

Наценка = 805 − 285 = 520 грн или (520 / 285) × 100% = 182%

Маржа вал. = (520 / 805) × 100% = 65%

Маржа чист. = (300 / 805) × 100% = 37%

Когда наши ФЛП начнут работать через посредника и делиться частью своей прибыли, то чистая маржа = (300 − 80,5) / 805) × 100% = 27% или 219,5 грн.

На что ориентироваться при формировании цены

Бизнес вправе самостоятельно определять цену и наценку на свою продукцию, товары и услуги (ст. 11 ЗУ «О ценах»). Исключение — только социально значимые товары, цены на них подлежат госрегулированию, в основном это продукты питания (соль, картошка, гречка и пр.), а ещё топливо, услуги ЖКХ и пр.

Как делать правильно: учесть все расходы, посчитать наценку и исходя из этого установить цену.

В цену закладывают себестоимость товара/услуги, постоянные расходы бизнеса, желаемые показатели по прибыли и всё, что можно просчитать по данным учёта — доставку, упаковку и пр.

Обязательно рассчитайте минимальную цену, ниже которой продавать нецелесообразно, потому что уйдёте в минус.

Опыт и узнаваемость бренда влияет на ценообразование. Поэтому, к примеру, рекламное агентство с кейсами для известных компаний может установит цены на свои услуги выше, чем агентство без звёзд в портфолио.

Имеет значение, в каком регионе и городе вы работаете, в конкурентной нише или нет.

Ещё есть факторы, которые от вас не зависят, но их надо учитывать при формировании цен: уровень цен в отрасли, спрос, популярность продукта, если закупаете товары или материалы за границей, учитывайте возможные колебания курса.

Анализируйте цены по отрасли, сколько стоит такой же товар у конкурентов. И помните, что бездумным демпингом вы снижаете свою прибыль, и не факт, что получите лояльных клиентов. Скорее наоборот — получите охотников за скидкой.

Способ продажи: продаёте сами или через посредников, а возможно, посредник — вы. Ведь процент посредника также закладывается в цену.

Автор: Александра Джурило, финансовый аналитик

Тригонометрические тождества и преобразования

Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:

Простейшие тригонометрические тождества

Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств. 
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).

Преобразование отрицательных углов тригонометрических функций (четность и нечетность)

Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.

Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.

Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.

Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)

Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:

Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:

Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла

Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла

Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица

Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла

Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.

Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла

Формулы универсальной тригонометрической подстановки

Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем  α/2 .

Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.

Тригонометрические тождества преобразования половины угла

Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.

Тригонометрические формулы сложения углов

cos (α — β) = cos α · cos β + sin α · sin β

sin (α + β) = sin α · cos β + sin β · cos α 

sin (α — β) = sin α · cos β — sin β · cos α 
cos (α + β) = cos α · cos β — sin α · sin β 

Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:

Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.

Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.

Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.

Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.

Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.

Формулы преобразования суммы или разности тригонометрических функций

Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:

Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα

Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:

Формулы преобразования произведения тригонометрических функций

Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:

В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.

Формулы приведения тригонометрических функций

Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90)  = cos α .

См. также Полный список формул приведения тригонометрических функций.

Угол	α + 90 α + π/2	α + 180 α + π	α + 270 α + 3π/2	90 — α π/2- α	180 — α π- α	270 — α 3π/2- α	360 — α 2π- α
sin	cos α	-sin α	-cos α	cos α	sin α	-cos α	-sin α
cos	-sin α	-cos α	sin α	sin α	-cos α	-sin α	cos α
tg	-ctg α	tg α	-ctg α	ctg α	-tg α	ctg α	-tg α
ctg	-tg α	ctg α	-tg α	tg α	-ctg α	tg α	-ctg α

Содержание главы:
 Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120) | Описание курса | Пояснение (доказательство) простейших тригонометрических тождеств 

   

Как складывать / вычитать / умножать / делить отрицательные числа

Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.

Чтобы подать уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.

Отправьте жалобу нашему назначенному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

 

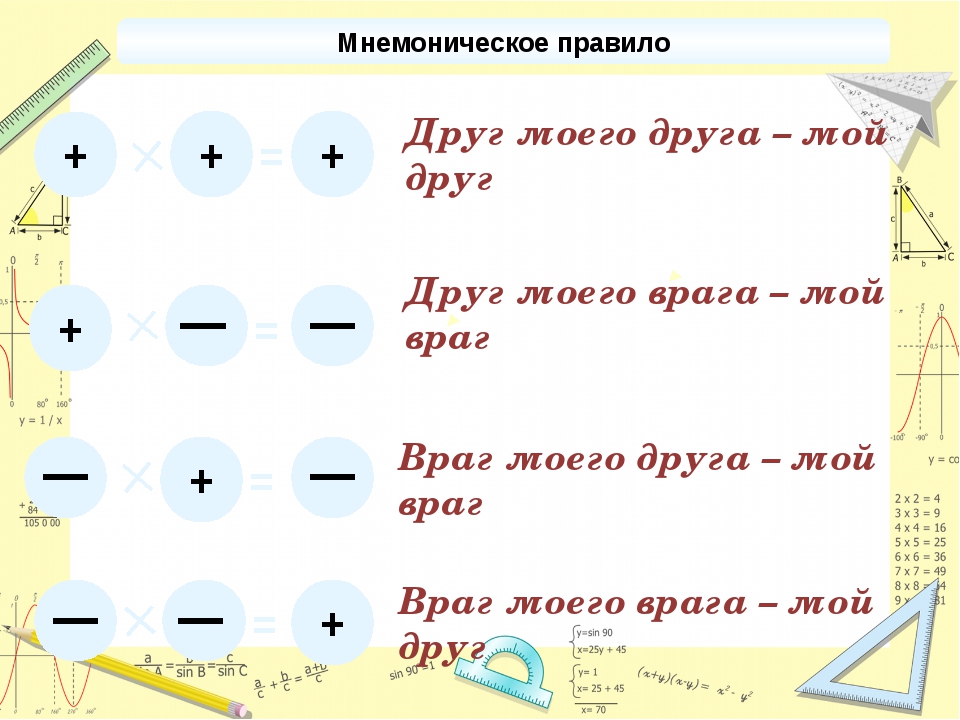
Умножение и деление положительных и отрицательных чисел

Правила умножения и деления чисел очень похожи. Ключ в том, чтобы определить, являются ли знаки данных двух чисел одинаковыми или разными, потому что это определит окончательный знак ответа.

Правила умножения и деления чисел со знаком

---

Примеры того, как найти произведение или частное чисел со знаком

Пример 1 : Найдите произведение (3)(6) и частное 12 ÷ 6 .

• Найдите произведение (3)(6):

Поскольку числа 3 и 6 имеют одинаковые знаки (оба положительные), их произведение положительно.

(3)(6) = 18

• Найдите частное 12 ÷ 6:

Поскольку числа 12 и 6 имеют одинаковые знаки (оба положительные), их частное положительно.

12 ÷ 6 = 2

---

Пример 2 : Найдите произведение (–5)(–3) и частное от – 21 ÷ (–7) .

• Найдите произведение (–5)(–3):

Числа −5 и −3 имеют отрицательные знаки. Наличие одного и того же знака означает, что их произведение также должно быть положительным.

(–5)(–3) = 15

• Найдите частное от – 21 ÷ (–7) :

Оба числа -5 и -3 имеют отрицательные знаки.Частное двух чисел с одинаковым знаком положительно.

– 21 ÷ (–7) = 3

---

Пример 3 : Умножьте числа (9)(–3) и разделите числа 18 ÷ (–9) .

Число 9 имеет положительный знак, а число -3 имеет отрицательный знак. Умножение этих двух чисел с разными знаками должно дать отрицательный ответ.

(9)(–3) = –27

 Число 9 положительное, а −3 отрицательное.Деление двух чисел с разными знаками должно дать отрицательный ответ.

18 ÷ (–9) = –2

---

Пример 4 : Упростите числовое выражение .

Мы можем упростить числитель, перемножив два числа. Проделайте то же самое со знаменателем.

Числа в числителе имеют разные знаки, поэтому мы ожидаем, что их произведение будет отрицательным. Между тем в знаменателе есть два числа с одинаковым знаком (оба отрицательные), поэтому их произведение должно быть положительным.

Завершаем это делением числителя на знаменатель. Не забывайте и о правиле деления. Числитель отрицательный, а знаменатель положительный, при разных знаках ответ должен быть отрицательным.

---

Пример 5 : Умножьте числа (–1)(–2)(–3)(–4) .

До сих пор мы умножали числа по два. На этот раз у нас возникла ситуация, когда нужно найти произведение трех или более чисел.

Мы можем решить это путем умножения двух чисел за раз, потому что мы знаем, как это сделать.

Но есть быстрый способ вычислить знак без необходимости умножать их по два за раз.

Обратите внимание, что у нас есть четное число отрицательных знаков , то есть четыре отрицательных числа. Если вы столкнулись с чем-то подобным, используйте правило:

Четное количество отрицательных знаков означает, что мы ожидаем, что ответ будет положительным.

(–1)(–2)(–3)(–4) = +24

---

Пример 6 : Умножьте числа ) (–1) (–1) .

Эта задача не предназначена для того, чтобы обмануть вас. Вместо этого подумайте об этом как о еще одной возможности научиться правильно решать вопросы. Ваш учитель может добавить что-то подобное в ваш тест, чтобы проверить, хорошо ли вы знаете тему.

Не обращая внимания на знаки, все числа просто единицы. Поэтому мы предсказываем, что ответ может быть либо +1 , либо -1 .

Подсчитав количество отрицательных знаков, мы имеем в общей сложности девять (9), что нечетно!

Помните правило,

Нечетное количество отрицательных знаков означает, что наш окончательный ответ должен быть отрицательным.

(–1) (–1) (–1) (–1) (–1) (–1) (–1) 36 (–336 (–1)= –1

---

Пример 7 : Разделите числа  (–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1) .

Правило нечетного и четного числа отрицательных чисел также работает при делении чисел.

Так как мы имеем семь (7) отрицательных знаков, нечетное число, ответ должен быть отрицательным.

(–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1)= –1

Операции с целыми числами: сложение, вычитание, умножение и деление — видео и расшифровка урока

Сложение

Сложение целых чисел довольно просто. Если это поможет, вы можете думать о своих целых числах как о долларовых купюрах.Или, если вас устраивает ваша числовая линия, вы можете использовать ее вместо нее. Таким образом, 3 будет равняться 3 долларам или 3 пробелам справа от 0 в числовой строке. Помните, что положительные целые числа идут вправо, а отрицательные — влево.

Например, если вы добавите 2 к 3, вы переместитесь на 2 деления вправо. Вы окажетесь под номером 5. Если вы думаете в денежном выражении, вы добавляете еще 2 доллара к своим нынешним 3 долларам. Итак, теперь у вас будет 5 долларов.

Поскольку ваши целые числа могут быть как положительными, так и отрицательными, возможно, вас попросят добавить отрицательное целое число, например:

нужно идти влево по числовой строке. Итак, вы идете на 2 пробела влево и в итоге получаете 1. Взгляните на изображение ниже, чтобы увидеть правила знаков для целых чисел.

Правила целочисленного знака для сложения и вычитания

Это отличная идея запомнить эти правила, и вот простой способ сделать это:

• Знаки лайка = дополнение
• Различие знаков = вычитание

Вычитание

Вышеприведенное можно записать и как задачу на вычитание.Используя наши правила знаков для сложения и вычитания, вы можете видеть, что когда у вас есть знак сложения и отрицательный знак, они объединяются для задачи на вычитание (помните, в отличие от знаков, равных вычитанию). Итак, в приведенной выше задаче 3 + ( -2 ), знак сложения и знак минус объединяются для задачи на вычитание и могут быть переписаны как 3 — 2.

Вы также можете расширить задачу на вычитание и переписать ее как задачу на сложение. :

Теперь вы можете продолжить и оценить, как вы делаете для сложения.Вы начинаете с числа 4 и вычитаете 5 или прибавляете минус 5, поэтому вам нужно пройти 5 пробелов слева от числовой строки. Это приведет вас к -1.

Теперь давайте посмотрим на вычитание отрицательного числа:

Используя наши правила знаков для сложения и вычитания, мы видим, что когда у нас есть два одинаковых знака, они объединяются, чтобы создать задачу на сложение (помните, подобные знаки равны при сложении). Итак, нашу задачу можно переписать так:

И вы решите ее, как любую задачу на сложение.

Умножение

Когда дело доходит до умножения, думайте об этом как о сложении равных групп одинакового количества.Итак, подумайте о 2 * 3 как о суммировании двух групп по 3 в каждой. Это дает вам 6.

Если вы вычислите умножение для всех ваших чисел от 1 до 9, вы можете создать таблицу умножения, которую вы можете использовать для справки.

Чем больше вы его используете, тем лучше и быстрее вы будете выполнять умножение. Скоро вам вообще не придется к нему обращаться.

Когда вы умножаете положительные и отрицательные целые числа, вы сначала умножаете, не обращая внимания на свои положительные и отрицательные знаки.Когда вы закончите умножать и получите ответ, вы вернетесь и вычислите свой знак, используя очень простое правило, показанное в таблице ниже:

Непохожие знаки = минус

Целочисленные знаковые правила для умножения и деления

Согласно этим правилам, если вы умножите два положительных или два отрицательных целых числа (как знаки), ваш ответ будет положительным, но если одно из ваших целых чисел положительное, а другое отрицательное (в отличие от знаков), то ваш ответ будет отрицательным.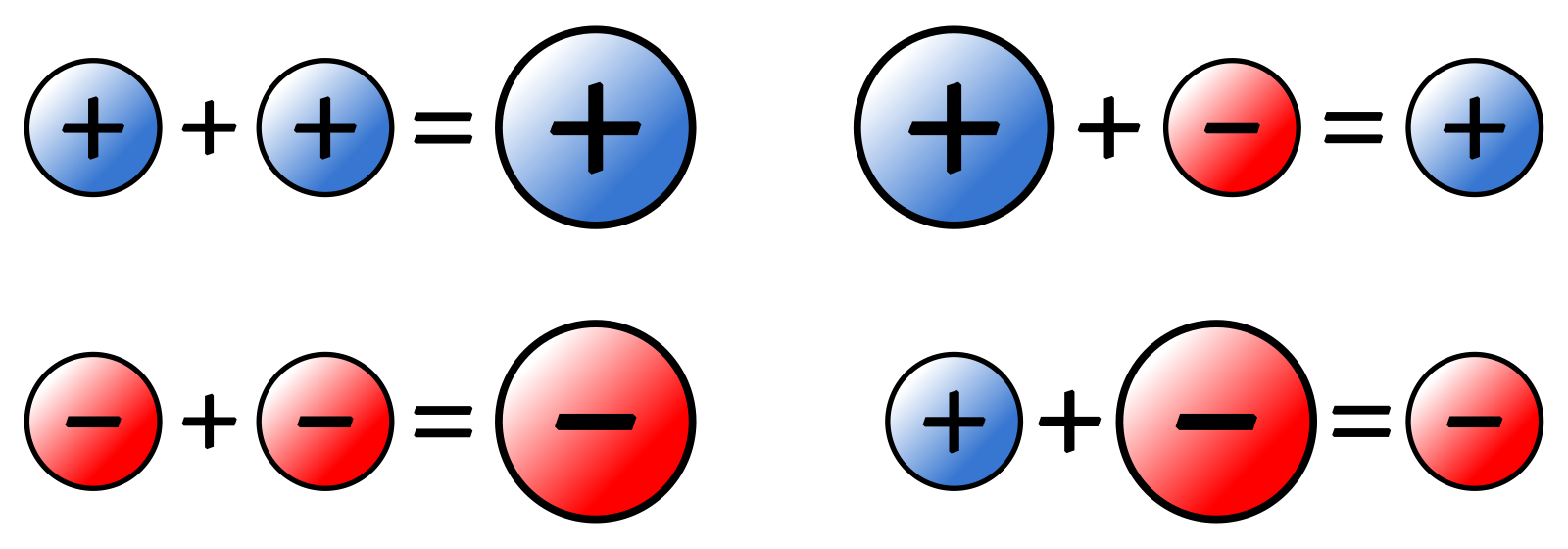 Довольно легко, правда?

• 2 * 2 = 4
• 3 * -2 = -6
• -5 * — 2 = 10

Деление

Думайте о делении как о разделении ряда предметов на более мелкие равные группы. Если вы видите проблему 4/2, она просит вас разделить 4 на 2 небольшие группы. Вы получите ответ: сколько предметов в каждой группе.

И, как мы уже сказали, правила знаков также применимы к делению. Итак,

• 12/-3 = -4
• -18 / -6 = 3

Резюме урока

Целые числа — это целые числа, как положительные, так и отрицательные.С ними можно выполнять четыре основных математических действия: сложение, вычитание, умножение и деление.

При сложении целых чисел помните, что положительные целые числа перемещают вас вправо по числовой строке, а отрицательные целые числа перемещают вас влево по числовой строке.

Вычитание — это то же самое, что сложение отрицательного числа.

Умножение — это сложение нескольких одинаковых групп. 3 * 2 просит вас сложить три группы по 2.

Деление противоположно умножению.При делении вы берете целую группу предметов и делите их на более мелкие группы, каждая из которых имеет одинаковое количество. Например, 24/8 говорит вам разделить 24 предмета поровну на 8 групп и спрашивает, сколько предметов будет в каждой группе — в этом случае ответ равен 3.

Для всех четырех математических операций очень важно, чтобы вы обратите внимание на знаки, чтобы убедиться, что ваш окончательный ответ правильный.

Каков порядок операций? [Видео и практика]

«Пожалуйста, извините, моя дорогая тетя Салли.

Теперь я знаю, о чем вы думаете: «Что на самом деле означает эта фраза?» На самом деле довольно много, потому что это высказывание дает ключ к запоминанию важного математического понятия: порядка операций.

Порядок операций — одно из наиболее важных математических понятий, которое вы изучите, поскольку оно диктует, как мы вычисляем задачи. Он дает нам шаблон, чтобы все решали математические задачи одинаково.

Начнем с простого вопроса. Что такое операция?

Операция — это математическое действие.Сложение, вычитание, умножение, деление и вычисление корня — все это примеры математических операций. Давайте посмотрим на эту задачу:

\(7\times 4-6=?\)

Выглядит просто, правда? Что ж, это было бы не так просто, если бы мы не понимали порядок, в котором выполняются математические операции. Если бы у нас не было правил, определяющих, какие вычисления мы должны произвести в первую очередь, мы бы пришли к другим ответам.

Следует ли начать с вычитания 4 минус 6, а затем умножения на 7?

№Порядок операций говорит нам, как решить математическую задачу. И это возвращает нас к тете Салли.

Каков порядок операций?

Операции имеют определенный порядок, и это то, что «Пожалуйста, извините, моя дорогая тетя Салли» помогает нам понять. Это аббревиатура, которая говорит нам, в каком порядке мы должны решать математическую задачу.

«Пожалуйста» означает « Скобки », поэтому мы сначала решаем все, что внутри скобок.

Затем «Извините», что означает « Экспоненты ».Мы решаем это после того, как решим все в скобках.

Умножение , то есть «Мое», и это происходит слева направо.

А затем деление , то есть «Дорогой», что тоже бывает слева направо.

А потом у нас есть сложение и вычитание , что тоже происходит слева направо, а это «тетя» и «Салли».

Порядок операций Примеры

Итак, теперь, когда мы знаем порядок операций, давайте применим его к нашей задаче и решим ее.

\(7\times 4-6=?\)

У нас нет круглых скобок и у нас нет показателей степени, но у нас есть умножение, поэтому мы делаем это до того, как будем выполнять сложение или вычитание. Давайте продолжим и умножим \(7\х4\). Это дает нам 28.

\(28-6\)

А теперь мы вычитаем 6, что дает нам 22.

\(28-6=22\)

Теперь давайте посмотрим при другой проблеме.

\(7+7\умножить на 3\)

Без операций эту задачу можно вычислить как \(7+7=14\умножить на 3=42\).

И это было бы неправильно!

Помните, вы умножаете, прежде чем складывать. Таким образом, уравнение должно выглядеть так:

\(7+(7\умножить на 3)\)

\(=7+21\)

\(=28\)

Итак, когда мы решаем задачи таким образом, мы можем использовать круглые скобки, чтобы сгруппировать наши числа, которые будут занимать первое место. Так что в этом случае это \(7\умножить на 3\), и когда мы это сделаем, мы получим 21, и у нас останется 7. Если сложить их вместе, получится 28, и это наш ответ!

Давайте рассмотрим более сложные задачи.{2})\)

\(=6\умножить на 9\)

\(=54\)

Видите? Решение уравнения в правильном порядке дает правильный ответ.

Давайте попробуем еще одну задачу. Этот немного сложнее, но он прекрасно иллюстрирует порядок операций.

\(5\умножить на 10-(8\умножить на 6\)\(-15)+4\умножить на 20\дел 4\)

Запомнить порядок. Что мы делаем в первую очередь? Цифры в скобках. Итак, \(8\times 6=48\), затем мы вычитаем 15, и это дает нам 33.Вот как теперь выглядит задача:

\(5\times 10-33+4\times 20\div 4\)

Итак, наш следующий шаг — умножение и деление, поэтому давайте решим все наши задачи на умножение и деление и тогда посмотрим, что у нас осталось.

\(50-33+80\дел 4\)

\(50-33+20\)

Теперь закончим со сложением и вычитанием, вот что у нас есть:

\(50- 33+20\)

\(=50-13\)

\(=37\)

И наш ответ 37!

Есть исключение.Если уравнение имеет только одно выражение, вам не нужно соблюдать порядок операций.

Вот несколько примеров одиночных выражений.

\(10+10\): Ну, других операций нет, так что просто сложите их и получите 20. То же самое с вычитанием, умножением и делением. Все это единичные выражения.

Итак, ребята, это наше видео о порядке действий. Я надеюсь, что это было полезно!

Увидимся в следующий раз!

Сложение, вычитание, умножение и деление значений в элементе управления

Вы можете помочь своим пользователям заполнять формы на основе шаблона формы, используя формулы для вычисления значения элемента управления на основе данных, которые пользователь вводит в другие элементы управления .Вычисления могут включать сложение, вычитание, умножение и деление значений. Например, если вы разрабатываете шаблон формы, который подрядчики по электроснабжению будут использовать для подачи заявок на получение разрешений, вы можете добавить формулу в элемент управления, который автоматически вычисляет общую стоимость, которую подрядчик должен заплатить за заявку, путем умножения количества разрешений в приложение по цене каждого разрешения.

В этой статье

Что такое формула?

Формула — это выражение XPath, состоящее из значений, полей или групп, функций и операторов, используемых для вычисления и отображения других значений.Формулы можно использовать для решения следующих задач:

• Расчет математических значений на основе значений, указанных при разработке шаблона формы, или значений, которые пользователи вводят в элементы управления при заполнении форм на основе вашего шаблона формы.

• Показать определенные даты и время.

• Отображение значений, которые пользователи вводят в один элемент управления, в другой элемент управления.

• Установите значение по умолчанию для поля или элемента управления.

• Запустить правило на основе значения, рассчитанного по формуле.

Каждое выражение XPath, используемое в формуле, представляет собой комбинацию значений, функций и операторов, результатом которой является одно значение. Формула может содержать несколько выражений. Вы можете думать о формуле как о предложении, состоящем из одной или нескольких фраз, где каждая фраза представляет одно выражение в формуле.

На следующем рисунке показана связь между формулой и выражением.

Функция — это выражение, возвращающее значение на основе результатов вычисления. Значения, используемые в функциях, называются аргументами. Вы можете использовать стандартные функции XPath 1.0, включенные в InfoPath, а также некоторые функции, специфичные для InfoPath. Найдите ссылки на дополнительные сведения о функциях InfoPath в разделе См. также .

Верх страницы

Использование двух или более операторов в формуле

Если формула содержит два или более математических оператора, InfoPath выполняет расчет в соответствии с приоритетом оператора. В следующем списке показан порядок выполнения операций:

1. Вычисления в скобках

2. Вычисления умножения и деления

3. Вычисления сложения и вычитания

Если формула содержит два оператора с одинаковым приоритетом, вычисления выполняются слева направо.

Например, представьте, что вы создаете шаблон формы заявки на получение разрешения, в котором есть текстовое поле, отображающее общую стоимость всех разрешений, представленных в заявке. Значения, требуемые этой формулой, берутся из других текстовых полей формы. Текстовое поле, отображающее общую стоимость, содержит следующую формулу:

.

txtPermit1Qty * txtPermitCost1 + txtPermit2Qty * txtPermitCost2 /txtNumberOfPermits

Эта формула включает операторы сложения (+), умножения (*) и деления (/). В соответствии с приоритетом операторов вычисления умножения и деления выполняются перед вычислением сложения. Поскольку операторы умножения и деления имеют одинаковый приоритет, вычисление умножения выполняется перед оператором деления, поскольку оператор умножения расположен слева от оператора деления. Формула рассчитывается таким образом:

1. Значение в txtPermit1Qty умножается на значение в txtPermitCost1 .

2. Значение в txtPermit2Qty умножается на значение в txtPermitCost2 , а затем этот результат делится на значение в txtNumberOfPermits .

3. Результат расчета на шаге 1 добавляется к результатам расчета на шаге 2.

Чтобы управлять порядком вычислений, заключите вычисление, которое вы хотите выполнить первым, в круглые скобки.Вычисления в скобках выполняются перед вычислениями вне скобок. Помещайте вычисления со скобками слева от вычислений без скобок. Вычисления во вложенных скобках выполняются от внутренних к внешним скобкам.

Например, рассмотрим следующую формулу:

((txtPermit1Qty * txtPermitCost1) + (txtPermit2Qty * txtPermitCost2))/txtNumberOfPermits

В этом расчете значение, полученное в результате умножения значений в txtPermit1Qty и txtPermitCost1 , добавляется к значению, полученному в результате умножения значений в txtPermit2Qty и txtPermitCost2 .Затем сумма этого вычисления делится на значение txtNumberOfPermits .

Верх страницы

Вставка математической формулы в элемент управления

1. Дважды щелкните элемент управления или поле, для которого вы хотите создать формулу.

2. Перейдите на вкладку Данные .

3. Щелкните Вставить формулу .

4. Чтобы вставить значение или математический оператор в формулу, введите значение или символ математической операции в поле Формула .

   Список математических операций

   Операция	Символ
   Добавить	+
   Вычесть	—
   Умножить	*
   Разделить	/

   Примечание. Если в формуле используется оператор деления (/), убедитесь, что перед ним и после него есть пробел.Если перед оператором деления и после него нет пробела, InfoPath может интерпретировать «/» как разделитель шагов расположения XPath, а не как оператор деления.

   Совет:  Математические формулы обычно используют в качестве аргументов целые или десятичные значения. Чтобы избежать использования пустых значений в формуле, установите флажок Считать пустые значения равными нулю в категории Расширенные в диалоговом окне Параметры формы .

5. Чтобы проверить правильность синтаксиса формулы, в диалоговом окне Вставить формулу щелкните Проверить формулу .

   Моя формула содержит ошибки

   Щелкните Показать подробности в диалоговом окне Microsoft Office InfoPath , чтобы просмотреть ошибки в формуле. Ниже приведены некоторые предложения по устранению этих ошибок:

   • Если вы используете функцию в своей формуле, убедитесь, что вы используете правильные аргументы для функции.Некоторым функциям требуются поля или группы, в то время как другим функциям требуются указанные значения в качестве аргументов. Найдите ссылки на дополнительную информацию о функциях в разделе См. также .

   • Удалите формулу и введите ее заново, чтобы убедиться, что она введена правильно.

6. Чтобы протестировать изменения, щелкните Preview на панели инструментов Standard или нажмите CTRL+SHIFT+B.

Верх страницы

Сложение, вычитание, умножение и деление степеней

Сложение и вычитание степеней

Очевидно, что степени можно складывать, как и другие величины, , соединяя их одну за другой с их знаками.

Таким образом, сумма a ³ и b ² равна a ³ + b.
А сумма a ³ — b ⁿ и h ⁵ -d ⁴ равно a ³ — b ⁿ + h ^{5 7} — 9 3d 4 90.

90 789 одинаковых степеней одних и тех же букв подобны числам 90 790, и их коэффициенты можно складывать или вычитать.

Таким образом, сумма 2а ² и 3а ² равна 5а ² .

Очевидно, что дважды квадрат а и три раза квадрат а в пять раз больше квадрата а, как дважды а и три раза в пять раз больше а.

Но степени разных букв и разных степеней одной и той же буквы , надо сложить, записав их с их знаками.

Сумма ² и ³ равна ² + ³ .

Очевидно, что квадрат а и куб а не вдвое больше квадрата а и не вдвое больше куба а.

Сумма ³ b ⁿ и 3a ⁵ b ⁶ равна ³ b ⁿ + 3a ⁵ b ^{6 90.}

Вычитание степеней производится так же, как сложение, за исключением того, что меняются знаки вычитаемого.

Из	2а 4	3 ч 2 б 6	5(а — з) 6
Доп.	-6а 4	4ч 2 б 6	2(а — з) 6
Дифференц.	8а 4	-ч 2 б 6	3(а — з) 6

ИЛИ: 2a ⁴ — (-6A ⁴ ) = 8a ) = 8a
4
3H ² — 4H ⁶ — 4H ² B ⁶ = -H ² B ⁶
5 (A — з) ⁶ — 2(а — з) ⁶ = 3(а — з) ⁶

Умножение сил

Степени можно умножать, как и другие величины, записывая множители один за другим, со знаком умножения между ними или без него.

Таким образом, произведение a ³ на b ² равно a ³ b ² или aaabb.

Мульти.	х -3	3а 6 у 2	а 2 б 3 у 2
В	а м	-2x	а 3 б 2 у
Товар.	a м x -3	-6а 6 ху 2	а 2 б 3 у 2 а 3 б 2 у

или:
x ^{-3 9} × ^м = 9 ^м x
3 -3
3A ⁶ × (-2x) = -6A ⁶ XY ²
9 ² B ³ y ² × A ² × A ³ B ² y = A ² B ³ Y ² A ³ B ² y

Произведение в последнем примере можно сократить, объединив повторяющиеся буквы.
Затем он станет ⁵ b ⁵ y ³ .

Причина этого станет очевидной, если вернуться к ряду полномочий в ст. 204, т.е.

Сравнивая несколько членов друг с другом, можно увидеть, что если любые два или более из них перемножить вместе, их произведение будет степенью, показатель которой равен сумме показателей показателей множителей.

Таким образом, a ² ⋅a ³ = aa⋅aaa = aaaaa = a ⁵ .

Здесь 5, показатель произведения, равен 2 + 3, сумме показателей сомножителей.

Таким образом, a ⁿ ⋅a ^m = a ^m+n .

Для ⁿ берется за множитель столько раз, сколько единиц в n;

А ^m берется за множитель столько раз, сколько единиц в m;

Следовательно, произведение должно быть взято в качестве множителя столько раз, сколько единиц как в m, так и в n.Следовательно,

Степени одного и того же основания можно умножать путем сложения их показателей.

Это ² ⋅a ⁶ = a ²⁺⁶ = a ⁸ . И х ³ ⋅х ² ⋅х = х ³⁺²⁺¹ = х ⁶ .

Умножение	4а п	б 2 у 3	(б + з — у) п
В	2а п	б 4 у	(б+ч-у)
Продукт	8а 2н	б 6 у 4	(б + з — у) н+1

или:
4A ^N × 2A ^N = 8A ^2N
B ² y ³ × B ⁴ y = B ⁶ Y ⁴
(B + H — Y ) ⁿ × (b + h — y) = (b + h — y) ⁿ⁺¹

Мульт.х ³ + х ² у + ху ² + у ³ в х — у.
Ответ: х ⁴ — у ⁴ .
Мульт. х ³ + х — 5 в 2х ³ + х + 1.

Правило в равной степени применимо к степеням, показатели которых равны минус .

1. Таким образом, a ^-2 .a ^-3 = a ^-5 . Это $\frac{1}{aa}\cdot \frac{1}{aaa}=\frac{1}{aaaaa}$.

2. у ^-н ⋅у ^-м = у ^-н-м .

3. а ^-n ⋅а ^m = a ^m-n .

Если a + b умножить на a — b, произведение будет a ² — b ² : то есть

Произведение суммы и разности двух величин равно разности их квадратов.

Если сумму квадратов и разность умножить, то произведение будет равно разности четвертых степеней.

Таким образом, (a — y)⋅(a + y) = a ² — y ² .
(а ² — у ² )⋅(а ² + у ² ) = а ⁴ — у ⁴ .
(а ⁴ — у ⁴ )⋅(а ⁴ + у ⁴ ) = а ⁸ — у ⁸ .

Разделение полномочий

Полномочия можно разделить, как и другие количества, отбрасывая от делимого множитель, равный делителю; или подставив под делимое делитель в виде дроби.

Таким образом, частное a ³ b ² , деленное на b ² , равно ³ .

Разделить	9а 3 у 4	а 2 по + 3а 2 у 2	д⋅(а — ч + у) 3
По	-3а 3	а 2 у	(а — ч + у) 3
Частное	-3 года 4	б + 3 года	д

Частное ⁵ , деленное на ³ , равно ⁵ / ³ .Но это равно ² . Ведь в сериале
A ⁺⁴ , ⁺³ , ⁺² , ⁺¹ , ⁺¹ , ⁰ , ^-1 , ^-2 , ^-3 , ^-4 .
, если любой член разделить на другой, показатель степени частного будет равен разности между показателями делимого и показателями делителя.

Степень можно разделить на другую степень того же основания путем вычитания показателя степени делителя из числа делимого .

Таким образом, у ³ :у ² = у ^3-2 = у ¹ . То есть гггг/гг = у.

И ⁿ⁺¹ :a = ^n+1-1 = ⁿ . Это аа ^н / а = а ^н .

Разделить	г 2 м	8а н+м	12(б + у) п
По	г м	4а м	3(б + у) 3
Кот.	г м	2а п	4(б+у) н-3

Правило в равной степени применимо к степеням, показатели которых равны минус .
Частное ^-5 на ^-3 равно ^-2 .
Это $\frac{1}{aaaaa}:\frac{1}{aaa} = \frac{1}{aaaaa} \cdot \frac{aaa}{1} = \frac{aaa}{aaaaa} = \frac{1}{aa}$.

3. ч ² :ч ^-1 = ч ²⁺¹ = ч ³ .То есть ч ² :(1/ч) = ч ² ⋅(ч/1) = ч ³

Умножение и разделение полномочий путем сложения и вычитания их индексов должно быть хорошо знакомо; поскольку они имеют многочисленные и важные приложения в высших разделах алгебры.

Примеры дробей, содержащих степени

В разделе о дробях были опущены следующие примеры, чтобы избежать предвосхищения субъекта полномочий.

1.Сократите 5a ⁴ /3a ² до меньших значений. Ответ: 5а ² /3.

2. Сократите 6x ⁶ /3x ⁵ до меньших значений. Ответ: 2x/1 или 2x.

3. Привести числа ² / ³ и ^-3 / ^-4 к общему знаменателю.
a ² ⋅a ^-4 есть ^-2 первый числитель. (Статья 146.)
а ³ ⋅а ^-3 есть ⁰ = 1, второй числитель.
a ³ ⋅a ^-4 есть ^-1 , общий знаменатель.
Таким образом, приведенные дроби равны а ^-2 /а ^-1 и 1/а ^-1 .

4. Приведите 2a ⁴ /5a ³ и a ² /a ⁴ к общему знаменателю.
Ответ: 2а ³ /5а ⁷ и 5а ⁵ /5а ⁷ или 2а ³ /5а ² и 5/5а ^{2. (Статья 142.)}

5. Умножьте (a ³ + b)/b ⁴ на (a — b)/3.

6.Умножьте (a ⁵ + 1)/x ² на (b ² — 1)/(x + a).

7. Умножьте b ⁴ /a ^-2 на h ^-3 /x и a ⁿ /y ^-3 .

8. Разделите ⁴ /г ³ на ³ /г ² . Ответ: а/у.

9. Разделите (h ³ — 1)/d ⁴ на (d ⁿ + 1)/h.

Уравнения и неравенства — Неравенства

Решение Неравенство очень похоже на решение уравнения.Вы выполняете те же шаги, за исключением одного очень важного отличия. Когда вы умножаете или делите каждый сторону неравенства на отрицательное число, необходимо обратить неравенство символ! Давайте попробуем пример:

-4x > 24

С этого неравенство включает в себя умножение, мы должны использовать обратное, или деление, чтобы решить это. Мы разделим обе части на –4, чтобы оставить х в покое. с левой стороны.

Когда мы упрощаем, поскольку мы делим на отрицательное число, мы должны помнить об обратном символ. Это дает «x меньше –6», а не «x равно больше –6″.

х < -6

Почему мы перевернуть символ? Посмотрим, что будет, если мы этого не сделаем. Подумайте о простое неравенство –3 < 9. Очевидно, это верное утверждение.

-3 < 9

Для демонстрации что произойдет, если мы разделим на отрицательное число, давайте разделим обе части на –3.Если мы оставим символ неравенства прежним, наш ответ, очевидно, будет неверно, так как 1 не меньше –3.

Мы должны перевернуть символ, чтобы найти правильный ответ, то есть «1 больше, чем –3».

Давай вернемся к исходной задаче и нарисуйте решение x < –6 на числе линия. Чтобы построить график решения неравенства, вы начинаете с определения точку в неравенстве.Здесь -6. Затем вы рисуете все точки которые есть в растворе.

Красная стрела показывает, что все значения на числовой прямой, меньшие –6, находятся в решение. Незаштрихованный кружок на -6 показывает нам, что -6 не находится в решение. Если бы решение было «x меньше или равно –6», круг был бы темным или заполненным кругом.

Как мы можем проверить наш ответ? Мы не можем использовать –6 для подстановки в неравенстве, потому что он лежит вне нашего решения.Для проверки можем выбрать любое значение что лежит в решении. Возьмем –7.

-4x > 24
-4(-7) > 24
28 > 24 Верно!

Наша замена дал верный результат, значит решение верное.

назад до

.