заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

2. Выбрать платежную систему.
3. Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
4. Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

Квадратичная функция, как построить Параболу

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax² + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

a — старший коэффициент, который отвечает за ширину параболы. Большое значение a — парабола узкая, небольшое — парабола широкая. b — второй коэффициент, который отвечает за смещение параболы от центра координат. с — свободный член, который соответствует координате пересечения параболы с осью ординат.

График квадратичной функции — парабола, которая имеет следующий вид для y = x²:

 

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x², нужно составить таблицу:

x	-2	-1	0	1	2
y	4	1	0	1	4

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x² при любых значениях остальных коэффициентов.

График функции y = –x² выглядит, как перевернутая парабола:

 

Зафиксируем координаты базовых точек в таблице:

x	-2	-1	0	1	2
y	-4	-1	0	-1	-4

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ.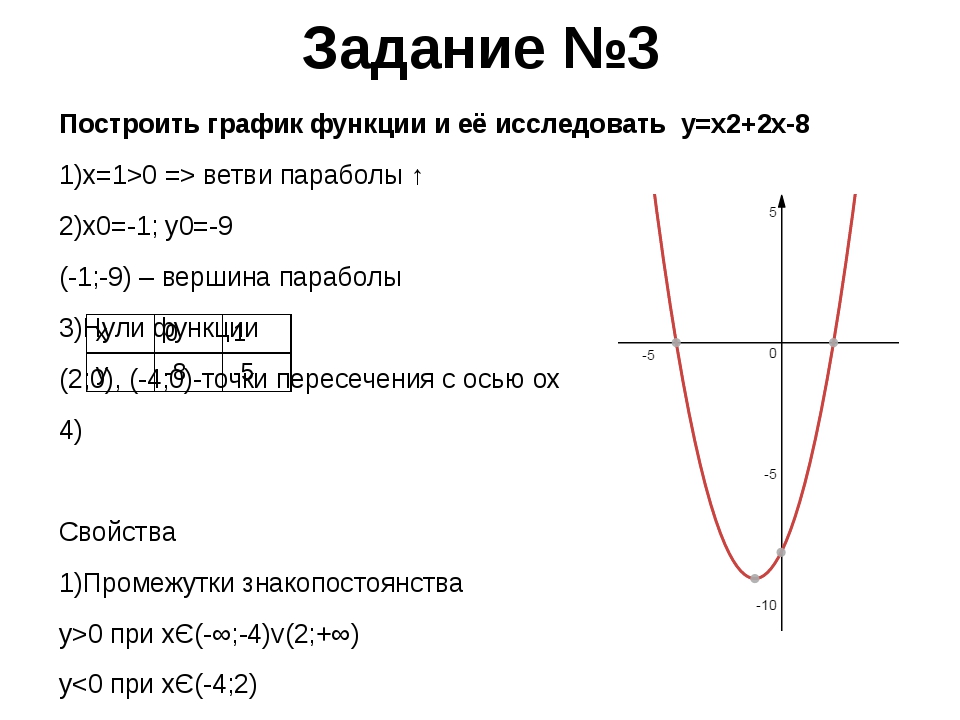 Отметим важные выводы:

• Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.

Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.

Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.

Для наглядности возьмем функцию y = ax² + bx + c, для построения которой нужно решить квадратное уравнение ax² + bx + c = 0. В процессе найдем дискриминант D = b² — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1.  Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ.
   Если a > 0,то график выглядит так:
   

2. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
3. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:



Если a > 0, то график выглядит как-то так:

 

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax² + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

 

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax

² + bx + c.

Разберем общий алгоритм на примере y = 2x² + 3x — 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x ² + 3x — 5.

D = b² — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

√D = 7

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

2x² + 3x — 5 = 0

3. Координаты вершины параболы:

4. Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
5. Нанести эти точки на координатную плоскость и построить график параболы:
   

Уравнение квадратичной функции имеет вид y = a * (x — x₀)

² + y₀

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x² + 3x — 5 при а = 1, то второй коэффициент является четным числом.

Рассмотрим пример: y = 2 * (x — 1)² + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить y = x²,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

2. Построить график параболы для каждого случая.

Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)

Рассмотрим следующий пример: y = (x — 2) * (x + 1).

Как строим:

1. Данный вид уравнения позволяет быстро найти нули функции:

(x — 2) * (x + 1) = 0, отсюда х₁ = 2, х₂ = -1.

2. Определим координаты вершины параболы:

3. Найти точку пересечения с осью OY:

с = ab =(-2) * (1)= -2 и ей симметричная.

4. Отметим эти точки на координатной плоскости и соединим плавной прямой.

Чтобы не запутаться во всех графиках, приходите вместе с ребенком на бесплатный урок математики в современную школу Skysmart: порисуем параболы на интерактивной онлайн-доске, разберемся в самых коварных формулах и покажем, что математика может быть увлекательным путешествием.

1 2 производная

Вы искали 1 2 производная? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 2x 2 производная, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 2 производная».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 1 2 производная,1 2x 2 производная,1 2x производная,1 3 х 3 производная,1 3x 3 производная,1 4 x производная,1 sin 2x производная,1 x 2 производная,1 x 3 производная,1 x 5 производная,1 x производная,1 найти производную функции 1 2,1 х 2 производная,1 х 3 производная,1 х производная,2 3 x производная,2 4x производная,2 x sinx производная,2 x sqrt x производная,2 x производная,2 производная от,2 х производная,2x 1 2 производная,2x 2 2x 1 производная,2x 2 производная,2x 3 производная,2x производная,2х производная,3 2x производная,3 sin x производная,3 sinx производная,3 x 2 производная,3 x производная,3 в степени x производная,3 производная,3 х 2 производная,3 х производная,3sinx производная,3x 2 производная,3x производная,3х производная,4 x 2 производная,4 x производная,4 в степени х производная,4 производная,4 х 2 производная,4 х производная,4x 2 производная,4x производная,4х производная,5 x производная,5 в степени х производная,5 х производная,5x производная,5х производная,6 x производная,7 x производная,8 x производная,a x производная,arccos x производная,arcsin 2 x производная,arcsin 2x производная,arcsin x 2 производная,ctg 2 x производная,ctg 2x производная,ctg x 2 производная,e x 1 производная,f x 1 x решение,f x 2x 2 y 2 x,f x y x 2,f x как найти,f x калькулятор,f x калькулятор онлайн,f x корень x 3,f x найти,f x производная,f x производная функции,f х 2 х,ln y x производная,mathsolution производная,sin x 3 производная,sinx 3 производная,sinx x 2 производная,tg 3 2x производная,x 1 2 x 4 производная,x 1 2 производная,x 1 3 производная,x 1 в квадрате производная,x 2 1 производная,x 2 3 производная,x 2 4 x производная,x 2 4 производная,x 2 sinx производная,x 2 sqrt x производная,x 2 производная,x 2x 2 производная,x 3 2 x производная,x 3 2 производная,x 3 4 производная,x 3 производная,x 4 2 производная,x 4 производная,x 5 производная,x 7 производная,x 8 производная,x sqrt x производная,x y производная,x в 3 степени производная,x в степени 3 производная,x производная,y 1 x 1 2x 3 производная,y 1 x 2 найти производную,y 1 x 2 производная,y 1 x 3 производная,y 1 x производная,y 2 x производная,y 2x 3 производная,y 3 2x производная,y 3 x производная,y 5 x производная,y 6 x производная,y cos 2x найти производную,y x 1 x найти производную функции,y x 1 x производная,y x 1 производная,y x 2 1 найти производную,y x 2 ln x производная,y x 2 корень из x производная,y x 2 найти производную,y x 2 производная,y x 3 2x 2 x 2 производную,y x 3 x производная,y x 3 производная,y x 4 x производная,y x 5 найдите производную функции,y x 5 производная,y x 6 производная,y x arcsin x найти производную,y x arcsin x производная,y x arctg x производная,y x cos x производная,y x e x найти производную,y x e x производная,y x sin x найти производную,y x производная,y производная,а х производная,бесплатно найти производную функции онлайн с подробным решением бесплатно,взятие производной онлайн,взять производную,взять производную онлайн,вычисление производной,вычисление производной онлайн,вычисление производной онлайн функции,вычисление производной функции,вычисление производной функции онлайн,вычисление производных,вычисление производных онлайн,вычисление производных функций,вычисление производных функций онлайн,вычисление функции производной онлайн,вычисления производных,вычисления производных калькулятор,вычислите значение производной функции,вычислите производную функции,вычислить производную,вычислить производную онлайн,вычислить производную онлайн с подробным решением бесплатно,вычислить производную с подробным решением онлайн,вычислить производную функции,вычислить производную функции онлайн,вычислить производную функции онлайн с подробным решением,вычислить производные функции онлайн с решением,дифференциация онлайн,дифференцирование калькулятор онлайн,дифференцирование онлайн,дифференцирование онлайн калькулятор,дифференцирование сложной функции онлайн,дифференцирование функции онлайн,знайти похідну,знайти похідну онлайн,знайти похідну функції,знайти похідну функції онлайн калькулятор,икс производная,как найти производную функции калькулятор онлайн,как найти производную функции онлайн калькулятор,калькулятор f x,калькулятор дифференцирования,калькулятор найти производную,калькулятор найти производную функции,калькулятор онлайн найти производную функции,калькулятор онлайн найти с решением производную функции,калькулятор онлайн похідних,калькулятор онлайн приращение функции,калькулятор онлайн производная с решением,калькулятор онлайн производной,калькулятор онлайн производной функции,калькулятор онлайн производных,калькулятор онлайн производных с решением,калькулятор онлайн производных функций,калькулятор онлайн производных функций с решением,калькулятор онлайн решение производных,калькулятор похідних,калькулятор похідних онлайн,калькулятор производная,калькулятор производная сложной функции,калькулятор производная функции,калькулятор производной,калькулятор производной онлайн,калькулятор производной онлайн с решением,калькулятор производной сложной функции,калькулятор производной функции,калькулятор производной функции онлайн,калькулятор производной функции онлайн с решением,калькулятор производные,калькулятор производные функции,калькулятор производные функции онлайн,калькулятор производный,калькулятор производных,калькулятор производных онлайн,калькулятор производных онлайн решение,калькулятор производных онлайн с подробным решением,калькулятор производных онлайн с решением,калькулятор производных решение онлайн,калькулятор производных с решением,калькулятор производных с решением онлайн,калькулятор производных сложных,калькулятор производных сложных функций,калькулятор производных функций,калькулятор производных функций онлайн,калькулятор производных функций онлайн с подробным решением,калькулятор производных функций онлайн с решением,калькулятор производных функций с решением,калькулятор производных функций с решением онлайн,калькулятор решение производных онлайн,калькулятор с решением производных,калькулятор сложной производной функции,калькулятор сложной функции производная,калькулятор сложных производных,калькулятор сложных производных функций,калькулятор сложных функций онлайн,логарифмическое дифференцирование онлайн калькулятор с решением,найдите производную,найдите производную заданной функции y x корень из x,найдите производную функции,найдите производную функции f x,найдите производную функции f x 1 3x 3 x 2 2x,найдите производную функции f x 2 3x 3 2x 2 x,найдите производную функции f x 3 2x x,найдите производную функции f x 3 x,найдите производную функции f x 3 x 2 3,найдите производную функции h x ex 4×2,найдите производную функции x sin x,найдите производную функции y,найдите производную функции y 3 x,найдите производную функции y 4 x,найдите производную функции y 5 x,найдите производную функции y x 2 x,найдите производную функции y x 3,найдите производную функции y x 3 cosx,найдите производную функции y x6 4sinx,найдите производную функции в точке х0,найдите производную функции онлайн,найдите производную функции онлайн с решением,найдите производную функцию,найдите производную функцию f x,найдите производные следующих функций,найдите производные функций,найти f x,найти f от x онлайн,найти y,найти y производную онлайн,найти значение производной,найти значение производной функции,найти значение производной функции в точке онлайн,найти значение производной функции в точке х0 онлайн,найти онлайн,найти онлайн производную функцию,найти первую производную функции,найти первую производную функции онлайн,найти первые производные функций онлайн,найти приращение функции онлайн калькулятор,найти производная,найти производная онлайн,найти производную,найти производную 3 x,найти производную x 1 x,найти производную x 3,найти производную x e x,найти производную x sin x,найти производную y 1 x 2,найти производную y sinx cosx,найти производную y x 3 x 2 x 1,найти производную y x e x,найти производную y x корень из x,найти производную y онлайн,найти производную в точке,найти производную и дифференциал функции онлайн,найти производную калькулятор,найти производную калькулятор онлайн,найти производную онлайн,найти производную онлайн y,найти производную онлайн калькулятор,найти производную онлайн с подробным решением,найти производную онлайн с решением,найти производную от функции онлайн,найти производную сложной функции онлайн,найти производную сложной функции онлайн с подробным решением,найти производную функции,найти производную функции x 2 x,найти производную функции x 3 x,найти производную функции y,найти производную функции y x 2 x,найти производную функции y x 3 y,найти производную функции в точке,найти производную функции в точке x0,найти производную функции в точке онлайн,найти производную функции калькулятор,найти производную функции калькулятор онлайн с решением,найти производную функции онлайн,найти производную функции онлайн в точке,найти производную функции онлайн калькулятор,найти производную функции онлайн калькулятор с подробным решением,найти производную функции онлайн калькулятор с подробным решением бесплатно,найти производную функции онлайн калькулятор с решением,найти производную функции онлайн с подробным решением бесплатно,найти производную функции онлайн с подробным решением бесплатно калькулятор,найти производную функции онлайн с решением,найти производную функции с решением онлайн,найти производную функции сложной онлайн с подробным решением,найти производную функцию,найти производную функцию онлайн,найти производные,найти производные данных функций,найти производные данных функций решение онлайн калькулятор,найти производные онлайн,найти производные следующих функций,найти производные следующих функций онлайн калькулятор с решением,найти производные функции,найти производные функции онлайн,найти производные функции онлайн с подробным решением,найти производные функций,найти производные функций калькулятор онлайн,найти производные функций онлайн,найти производные функций онлайн калькулятор,найти функцию,нахождение производной,нахождение производной онлайн,нахождение производной онлайн с подробным решением,нахождение производной сложной функции онлайн с решением,нахождение производной функции,нахождение производной функции онлайн,нахождение производных онлайн,нахождения производной калькулятор,онлайн взятие производной,онлайн вычисление производной,онлайн вычисление производной функции,онлайн вычисление производных,онлайн вычисление производных функций,онлайн дифференцирование,онлайн дифференцирование сложной функции,онлайн дифференцирование функции,онлайн калькулятор дифференцирование,онлайн калькулятор знайти похідну функції,онлайн калькулятор найти производную,онлайн калькулятор найти производную функции,онлайн калькулятор найти производную функции с подробным решением бесплатно,онлайн калькулятор похідних,онлайн калькулятор приращение функции,онлайн калькулятор производная функции,онлайн калькулятор производная функция,онлайн калькулятор производной,онлайн калькулятор производной функции,онлайн калькулятор производной функции с решением,онлайн калькулятор производные,онлайн калькулятор производные сложных функций,онлайн калькулятор производных,онлайн калькулятор производных решение,онлайн калькулятор производных с подробным решением,онлайн калькулятор производных с решением,онлайн калькулятор производных функций,онлайн калькулятор производных функций с подробным решением,онлайн калькулятор производных функций с решением,онлайн калькулятор решение производных,онлайн калькулятор сложных функций,онлайн найти производную функцию,онлайн найти производные,онлайн нахождение производной,онлайн нахождение производной функции,онлайн похідна,онлайн продифференцировать функцию,онлайн производная от функции,онлайн производная решение,онлайн производная с решением,онлайн производная сложной функции,онлайн производная функция,онлайн производные решение,онлайн производные с подробным решением,онлайн производные с решением,онлайн производные сложных функций,онлайн производные функции,онлайн расчет производной,онлайн расчет производных,онлайн решение производной,онлайн решение производной функции,онлайн решение производные,онлайн решение производных,онлайн решение производных калькулятор,онлайн решение производных с подробным решением,онлайн решение производных функций,онлайн решение производных функций с подробным решением,онлайн сложная производная,онлайн считать производную,первая производная онлайн,поиск производной,поиск производной онлайн,посчитать производную,посчитать производную онлайн,похідна,похідна онлайн,похідна функції калькулятор онлайн,похідна функції онлайн калькулятор,приращение функции калькулятор онлайн,приращение функции онлайн калькулятор,продифференцировать функцию онлайн,продифференцировать функцию онлайн с решением,производная 1,производная 1 2,производная 1 2 x,производная 1 2 х,производная 1 2x,производная 1 2x 2,производная 1 3 х,производная 1 3 х 3,производная 1 3x 3,производная 1 sqrt x,производная 1 x,производная 1 x 2,производная 1 x 3,производная 1 x 4,производная 1 x 5,производная 1 x в квадрате,производная 1 делить на х,производная 1 х,производная 1 х 2,производная 1 х 3,производная 1 х в квадрате,производная 10 в 10 степени,производная 2,производная 2 1,производная 2 2x,производная 2 3x,производная 2 arcsin x,производная 2 x,производная 2 x 2 2x,производная 2 x 3,производная 2 х,производная 2 х 3,производная 2 х у х,производная 2x,производная 2x 1,производная 2x 1 2,производная 2x 2,производная 2x 3,производная 2х,производная 3,производная 3 2 x,производная 3 2x,производная 3 sinx,производная 3 x,производная 3 x 2,производная 3 x cosx,производная 3 в степени x,производная 3 в степени х,производная 3 х,производная 3 х 1,производная 3 х 2,производная 3x,производная 3x 2,производная 3х,производная 4,производная 4 3 x,производная 4 x,производная 4 x 2,производная 4 x 3,производная 4 в степени х,производная 4 х,производная 4 х 2,производная 4 х корень из х,производная 4x,производная 4x 2,производная 5 2 x,производная 5 x,производная 5 x y,производная 5 в степени х,производная 5 х,производная 5x,производная 5х,производная 6 x,производная 6 х,производная 7 x,производная 8 x,производная a b x,производная a x,производная arcsin 2 x,производная arcsin 2x,производная arcsin x 2,производная cosx x,производная ctg 2x,производная ctg x 2,производная e 1 x,производная e 2x,производная e x 2,производная e x sinx,производная f x,производная f x 2 x,производная sin 1 x,производная sin x 1,производная sin x 3,производная sin x 3 x,производная sin корень из 2 на икс,производная sinx 2 x,производная sinx 3,производная sinx e x,производная x,производная x 1,производная x 1 2,производная x 1 3,производная x 1 в квадрате,производная x 2,производная x 2 1,производная x 2 2x,производная x 2 3,производная x 2 4,производная x 2 4 x,производная x 2 ctg x,производная x 2 e x,производная x 2 sinx,производная x 2 sqrt x,производная x 2 x 3,производная x 2 y,производная x 2 в квадрате,производная x 3,производная x 3 1,производная x 3 2,производная x 3 4,производная x 3 sin x,производная x 3 y,производная x 3 корень x,производная x 3 корень из x,производная x 4,производная x 4 2,производная x 4 3 x,производная x 5,производная x 6,производная x 7,производная x 8,производная x a,производная x arctg x,производная x sin x 3,производная x sqrt x,производная x sqrt x 2,производная x y,производная x y 2,производная x в квадрате 1,производная x в степени 2,производная x в степени 3,производная x корень из 2,производная x корень из x 3,производная y,производная y 1 x,производная y 1 x 2,производная y 1 x 3,производная y 2 x,производная y 2x 3,производная y 3 2x,производная y 3 x,производная y 4 x,производная y 5 x,производная y e y,производная y x,производная y x 2 1,производная y x 3,производная y x 5,производная y x 6,производная y x arcsin x,производная y x cos x,производная y x e x,производная y x lnx,производная а х,производная в точке онлайн,производная дроби онлайн,производная калькулятор,производная калькулятор онлайн,производная калькулятор онлайн с решением,производная квадратного уравнения,производная корень из 3 x 3,производная найти,производная найти онлайн,производная онлайн,производная онлайн в точке,производная онлайн в точке онлайн,производная онлайн дроби,производная онлайн калькулятор,производная онлайн калькулятор с подробным,производная онлайн калькулятор с подробным решением,производная онлайн калькулятор с решением,производная онлайн найти,производная онлайн решение,производная онлайн с подробным решением,производная онлайн с подробным решением калькулятор,производная онлайн с решением,производная онлайн с решением калькулятор,производная онлайн сложная,производная от,производная от 1,производная от 1 x,производная от 1 x 2,производная от 1 x 2 1,производная от 1 х,производная от 1 х 2,производная от 2,производная от 2 x,производная от 2 x 2,производная от 2 x 3,производная от 2 х,производная от 2x,производная от 2х,производная от 3,производная от 3 x,производная от 3 x 2,производная от 3 x 3,производная от 3x,производная от 3х,производная от 4 x,производная от 5 x,производная от 5x,производная от x,производная от x 1,производная от x 1 2,производная от x 2,производная от x 2 1,производная от x 2 3,производная от x 3,производная от x 3 2,производная от x 4,производная от x 5,производная от x sinx,производная от x в степени x 2,производная от y,производная от икса,производная от у,производная от функции онлайн,производная от х,производная от х 1,производная от х 1 2,производная от х 2,производная от х 2 1,производная от х в 2 степени,производная от х в степени 3,производная от х равна,производная от х синус х,производная отрицательного числа,производная решение онлайн,производная с,производная сложная онлайн,производная сложной функции калькулятор,производная сложной функции калькулятор онлайн,производная сложной функции онлайн,производная сложной функции онлайн калькулятор,производная сложной функции онлайн калькулятор с подробным решением,производная у,производная у х 1 х,производная функции 1 x 1,производная функции f x,производная функции y 2x в точке x0 1 равна,производная функции калькулятор,производная функции калькулятор онлайн,производная функции калькулятор онлайн с решением,производная функции онлайн,производная функции онлайн калькулятор,производная функции онлайн калькулятор с подробным решением,производная функции онлайн калькулятор с решением,производная функции онлайн решение,производная функции равна,производная функции решение онлайн,производная функция калькулятор онлайн,производная функция онлайн,производная функция онлайн калькулятор,производная х,производная х 1,производная х 1 2,производная х 1 в квадрате,производная х 2,производная х 2 1,производная х 2 3,производная х 2 х 3,производная х 3,производная х 3 1,производная х 3 2,производная х 4,производная х 5,производная х 6,производная х а,производная х в 5 степени,производная х в степени 1 х,производная х в степени 3,производная х в степени 4,производная х в степени 5,производная х по х,производная х3,производной сложной функции калькулятор,производной функции калькулятор,производной функции онлайн калькулятор,производной функции решение онлайн,производную,производную взять,производную онлайн,производную посчитать,производные калькулятор,производные калькулятор онлайн,производные онлайн,производные онлайн калькулятор,производные онлайн калькулятор с подробным решением,производные онлайн решение,производные онлайн с подробным решением,производные онлайн с решением,производные первого порядка онлайн калькулятор,производные решение онлайн,производные с решением онлайн,производные сложные онлайн,производные сложных функций онлайн,производные сложных функций онлайн калькулятор,производные функции калькулятор,производные функции онлайн,производные функции онлайн калькулятор,производные функции онлайн калькулятор с подробным решением,производные функций калькулятор онлайн,производные функций онлайн калькулятор,производный калькулятор,производных,рассчитать производную онлайн,расчет производной,расчет производной онлайн,расчет производных онлайн,решение онлайн производная,решение онлайн производной функции,решение онлайн производных функций,решение производная онлайн,решение производная функции онлайн,решение производной онлайн,решение производной онлайн с подробным решением бесплатно,решение производной функции онлайн,решение производные онлайн,решение производных,решение производных калькулятор онлайн,решение производных онлайн,решение производных онлайн бесплатно с подробным решением,решение производных онлайн калькулятор,решение производных онлайн с подробным решением,решение производных онлайн с подробным решением бесплатно,решение производных онлайн с подробным решением онлайн,решение производных функций,решение производных функций онлайн,решение производных функций онлайн с подробным решением,решение сложных производных онлайн,решить производную,решить производную онлайн,решить производную онлайн с подробным решением,решить производную функции онлайн с решением,решить функцию онлайн с решением,сложные производные онлайн,у производная,х 1 2 производная,х 1 3 производная,х 2 3 производная,х 2 производная,х 3 производная,х 5 в 5 степени производная,х 5 производная,х 6 производная,х в 3 степени производная,х в 4 степени производная,х в 5 степени производная,х в квадрате 1 производная,х в степени 4 производная,х в степени 5 производная,х3 производная. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 1 2 производная. Просто введите задачу в окошко и нажмите «решить» здесь (например, 1 2x производная).

Где можно решить любую задачу по математике, а так же 1 2 производная Онлайн?

Решить задачу 1 2 производная вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

квадратичных функций

квадратичных функций

---

Содержание : Эта страница соответствует § 3. 1 (стр. 244) текста.

Предлагаемые задачи из текста:

с. 251 # 1-8, 10, 11, 15, 16, 18, 19, 21, 23, 24, 30, 33, 37, 38, 75

Графики

Стандартная форма

Приложения

---

Графики

Квадратичная функция имеет вид f (x) = ax ² + bx + c , где a , b и c — числа, где a не равны нулю.

График квадратичной функции — это кривая, называемая параболой . Параболы могут открываться вверх или вниз и различаются по «ширине» или «крутизне», но все они имеют одинаковую базовую U-образную форму. В На рисунке ниже показаны три графика, и все они являются параболами.

Все параболы симметричны относительно линии, называемой осью симметрии . Парабола пересекает его ось симметрии находится в точке, называемой вершиной параболы.

Вы знаете, что две точки определяют линию. Это означает, что если вам даны любые две точки на плоскости, то есть одна и только одна линия, содержащая обе точки. Аналогичное утверждение можно сделать относительно точек и квадратичных функции.

Учитывая три точки на плоскости, которые имеют разные первые координаты и не лежат на одной прямой, существует ровно одна квадратичная функция f, график которой содержит все три точки. Апплет ниже иллюстрирует этот факт.График содержит три точки и параболу, проходящую через все три. Соответствующая функция показана в тексте поле под графиком. Если вы перетащите любую из точек, функция и парабола обновятся.

Многие квадратичные функции можно легко изобразить вручную, используя методы растяжения / сжатия и сдвига. (перевод) парабола y = x ² . (См. Раздел о работе с графики.)

Пример 1 .

Нарисуйте график y = x ² /2. Начиная с графика y = x ² , мы сокращаемся в раз половины. 2-5.Начнем с графика y = x ² , сдвинем на 4 единицы вправо, затем 5 единиц вниз.

Упражнение 1 :

(a) Нарисуйте график y = (x + 2) ² — 3. Ответ

(b) Нарисуйте график y = — (x — 5) ² + 3. Ответ

Вернуться к содержанию

Стандартная форма

Функции в частях (a) и (b) упражнения 1 являются примерами квадратичных функций в стандартной форме .Когда квадратичная функция имеет стандартную форму, ее график легко построить, отражая, сдвигая и растяжение / сжатие параболы y = x ² .

Квадратичная функция f (x) = a (x — h) ² + k, не равная нулю, считается в стандартной форме . Если а положительно, график открывается вверх, а если отрицательно, то открывается вниз. Линия симметрии — это вертикальная линия x = h, а вершина — это точка (h, k).

Любую квадратичную функцию можно переписать в стандартной форме с помощью , завершившего квадрат . (См. Раздел о решая уравнения алгебраически, чтобы просмотреть завершение квадрата.) Шаги, которые мы используем в этом разделе для завершения квадрата, будут выглядеть немного иначе, потому что наш главный цель здесь не в решении уравнения.

Обратите внимание, что когда квадратичная функция имеет стандартную форму, ее нули также легко найти с помощью квадратного корня. принцип.

Пример 3 .

Запишите функцию f (x) = x ² — 6x + 7 в стандартной форме. Нарисуйте график функции f и найдите его нули и вершина.

f (x) = x ² — 6x + 7.

= (x ² — 6x) + 7. Сгруппируйте члены x ² и x и затем заполните квадрат на этих условиях.

= (x ² — 6x + 9 — 9) + 7.

Нам нужно добавить 9, потому что это квадрат половины коэффициента при x, (-6/2) ² = 9. Когда мы решая уравнение, мы просто добавляли 9 к обеим частям уравнения. В этой настройке мы добавляем и вычитаем 9 так что мы не меняем функцию.

= (x ² — 6x + 9) — 9 + 7. Мы видим, что x ² — 6x + 9 — это полный квадрат, а именно (x — 3) ² .

f (x) = (x — 3) ² — 2.Это стандартная форма .

Из этого результата легко найти, что вершина графа f равна (3, -2).

Чтобы найти нули f, мы устанавливаем f равным 0 и решаем относительно x.

(x — 3) ² — 2 = 0.

(x — 3) ² = 2.

(x — 3) = ± sqrt (2).

х = 3 ± sqrt (2).

Чтобы набросать график f, сдвинем график y = x ² на три единицы вправо и на две единицы вниз.

Если коэффициент при x ² не равен 1, то мы должны вынести этот коэффициент из x ² и x, прежде чем продолжить.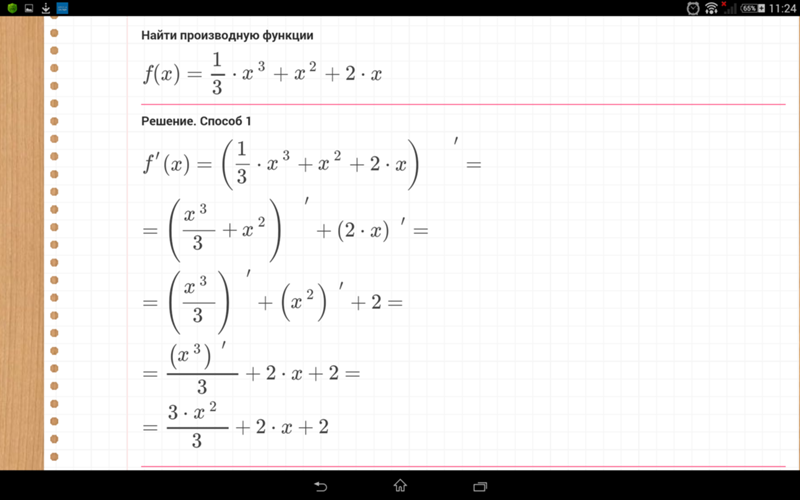

Пример 4 .

Запишите f (x) = -2x ² + 2x + 3 в стандартной форме и найдите вершину графика f.

f (x) = -2x ² + 2x + 3.

= (-2x ² + 2x) + 3.

= -2 (x ² — x) + 3.

= -2 (x ² — x + 1/4 — 1/4) + 3.

Мы складываем и вычитаем 1/4, потому что (-1/2) ² = 1/4, а -1 — коэффициент при x.

= -2 (x ² — x + 1/4) -2 (-1/4) + 3.

Обратите внимание, что все в круглых скобках умножается на -2, поэтому, когда мы убираем -1/4 из круглых скобок, мы необходимо умножить на -2.

= -2 (x — 1/2) ² + 1/2 + 3.

= -2 (х — 1/2) ² + 7/2.

Вершина — это точка (1/2, 7/2). Поскольку граф открывается вниз (-2 <0), вершина является высшей точкой на графике.

Упражнение 2 :

Запишите f (x) = 3x ² + 12x + 8 в стандартной форме. Нарисуйте график функции f, найдите его вершину и найдите нули f. Ответ

Альтернативный метод поиска вершины

В некоторых случаях завершение квадрата — не самый простой способ найти вершину параболы. Если график квадратичная функция имеет два пересечения по оси x, тогда линия симметрии — это вертикальная линия, проходящая через среднюю точку х-перехватчиков.

Х-точки пересечения на графике выше находятся в точках -5 и 3.Линия симметрии проходит через -1, что является средним -5 и 3. (-5 + 3) / 2 = -2/2 = -1. Как только мы узнаем, что линия симметрии x = -1, мы узнаем первую координату вершины -1. Вторую координату вершины можно найти, вычислив функцию при x = -1.

Пример 5 .

Найдите вершину графика функции f (x) = (x + 9) (x — 5).

Поскольку формула для f разложена на множители, легко найти нули: -9 и 5.

Среднее значение нулей (-9 + 5) / 2 = -4/2 = -2. Итак, линия симметрии x = -2 и первая координата вершины -2.

Вторая координата вершины: f (-2) = (-2 + 9) (- 2-5) = 7 * (- 7) = -49.

Следовательно, вершина графика f равна (-2, -49).

Вернуться к содержанию

Приложения

Пример 6 .

У владельца ранчо есть 600 метров забора, чтобы ограждать прямоугольный загон с другим забором, разделяющим его посередине. как на схеме ниже.

Как показано на схеме, каждая из четырех горизонтальных секций забора будет иметь длину х метров, а три каждая вертикальная секция будет иметь длину y метров.

Цель владельца ранчо — использовать весь забор, а оградить как можно большую площадь .

Каждый из двух прямоугольников имеет площадь xy, поэтому мы имеем

Общая площадь: A = 2xy.

Мы мало что можем сделать с величиной A, если она выражается как произведение двух переменных. Тем не мение, Тот факт, что у нас есть только 1200 метров забора, приводит к уравнению, которому должны удовлетворять x и y.

3г + 4х = 1200.

3y = 1200 — 4x.

y = 400 — 4x / 3.

Теперь у нас есть y, выраженный как функция от x, и мы можем заменить это выражение на y в формулу для общего площадь А.

A = 2xy = 2x (400 -4x / 3).

Нам нужно найти значение x, которое делает A как можно большим. A — квадратичная функция от x, а график открывается вниз, поэтому наивысшая точка на графике A — вершина. Поскольку A разложено на множители, самый простой способ найти вершина — найти пересечения по оси x и усреднить.

2x (400 -4x / 3) = 0,

2x = 0 или 400 -4x / 3 = 0.

x = 0 или 400 = 4x / 3.

x = 0 или 1200 = 4x.

х = 0 или 300 = х.

Следовательно, линия симметрии графика A равна x = 150, среднему от 0 до 300.

Теперь, когда мы знаем значение x, соответствующее наибольшей площади, мы можем найти значение y, вернувшись назад. уравнению, связывающему x и y.

y = 400 — 4x / 3 = 400-4 (150) / 3 = 200.

Вернуться к содержанию

---

Нахождение обратной функции: другие примеры

В поисках Обратная функция (стр. 5 из 7) Разделы: Определение / Обращение графика, является ли обратным функция ?, Нахождение обратных, Доказательство обратных Найти обратное f ( x ) = ( x 2) / ( x + 2) , где x не равно 2. Is обратная функция? Во-первых, я узнаю что f ( x ) является рациональной функцией. Вот его график: Ограничение на домен исходит из того факта, что я не могу делить на ноль, поэтому x не может быть равным 2.Обычно я бы не стал записывать ограничение, но это полезно здесь, потому что мне нужно знать домен и диапазон обратного. Примечание с картинки (и вспоминая концепцию горизонтального асимптоты), что л никогда не будет равным 1. Тогда домен будет « x не равно 2 «и диапазон составляет « y не равно 1 «.Для наоборот, они поменяются местами: домен будет « x не равно 1 «и диапазон будет « y не равно 2 «. Вот алгебра: The исходная функция: Я переименовать « f ( x )» как « y «: Тогда Я решаю для « x знак равно Я получить x -материал с одной стороны: Вот Уловка: я исключил x ! Тогда Я переключаюсь x и y : А переименовать « y » как « f -инверсия»; ограничение домена связано с тем, что это рациональная функция. Поскольку обратное это просто рациональная функция, тогда обратная функция действительно является функцией. Вот график: Затем обратное — y = (2 x 2) / ( x 1) , и обратное тоже функция, с областью всех x не равно на номер 1 и ассортимент всех y не равно на номер 2 . Найти обратное из f ( x ) = x 2 3 x + 2, x < 1,5 С доменом ограничение, график выглядит так: Насколько я знаю о построении графиков квадратики вершина находится в ( x , y ) = (1.5, 0,25), так что этот график — левая «половина» параболы. Эта половина параболы проходит тест горизонтальной линии, поэтому (ограниченная) функция обратима. Но как найти обратное? Авторские права Элизабет Стапель 2000-2011 Все права защищены The исходная функция: f ( x ) = x 2 3 x + 2 Я переименовать « f ( x )» как « y «: y = x 2 3 x + 2 Сейчас Я решаю для « x = «с помощью квадратичный Формула: 0 = x 2 3 x + 2 y 0 = x 2 3 x + (2 y ) Начиная с x < 1.5, тогда мне нужен отрицательный квадратный корень: Сейчас Я переключаюсь x и y : А переименовать « y » как « f -инверсия»; ограничение домена связано с тем, что это рациональная функция. << Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Вернуться к указателю Далее >> Цитируйте эту статью как: Стапель, Елизавета.«Нахождение обратной функции». Фиолетовый Математик . Доступно по номеру https://www.purplemath.com/modules/invrsfcn5.htm . Дата обращения [Дата] [Месяц] 2016 г.

Как найти решение системы уравнений

Пояснение:

Во-первых, нам нужно найти точки A и B, которые, как нам сказали, образуют точки пересечения между графиками y = 9 — x ² и y = 3 — x .Чтобы решить эти два уравнения, мы можем установить значение y в первом уравнении равным значению y во втором, а затем решить для x .

9-90 843 x ² = 3-90 843 x

Добавьте x ² с обеих сторон.

9 = 3 — x + x ²

Вычтем 9 с обеих сторон. Затем переставьте так, чтобы степени x были в порядке убывания.

-6 — x + x ² = x ² — x — 6 = 0

Разложите на множители x ² — x — 6, думая о двух числах, которые умножаются, чтобы получить –6, и складывать, чтобы получить –1. Эти два числа — –3 и 2.

x ² — x — 6 = ( x — 3) ( x + 2) = 0

Установите каждый коэффициент равным нулю и решите.

x — 3 = 0

х = 3

х + 2 = 0

x = –2

Таким образом, встречаются точки пересечения, где x = –2 и 3.Мы можем найти значения y точек пересечения, подставив –2 и 3 в любое уравнение. Воспользуемся уравнением y = 3 — x .

Когда x = –2, y = 3 — (–2) = 5. Одна точка пересечения равна (–2,5).

Когда x = 3, y = 3 — 3 = 0. Другая точка пересечения — (3,0).

Предположим, что точка A находится в точке (–2,5), а точка B находится в точке (3,0). Нам говорят, что C находится по адресу ( p , 0), где p <0.Нарисуем треугольник ABC с информацией, которая у нас есть.

На рисунке выше оранжевая линия представляет высоту от стороны BC до A .

Площадь любого треугольника равна (1/2) bh , где b — длина основания, а h — длина высоты. Мы будем использовать BC для обозначения основания и оранжевую линию для обозначения высоты.

Длина BC будет равна 3 — p , так как обе точки лежат на оси x .Длина оранжевой линии — это расстояние от CB до точки A , то есть 5. Теперь мы можем найти формулу для площади и установить ее равной 50.

Площадь ABC = (1/2) (3 — p ) (5) = 50

Умножьте обе стороны на 2.

(3 — п ) (5) = 100

Разделить на 5.

3 — р = 20

Вычтем 3 с обеих сторон.

–p = 17

Умножьте обе стороны на –1.

p = –17.

Ответ –17.

Инверсия функции — объяснение и примеры

Что такое обратная функция?

В математике обратная функция — это функция, отменяющая действие другой функции.

Например, , сложение и умножение являются инверсией соответственно вычитания и деления.

Обратную функцию можно рассматривать как отражение исходной функции по линии y = x.Проще говоря, обратная функция получается заменой (x, y) исходной функции на (y, x).

Мы используем символ f ^{— 1} для обозначения обратной функции. Например, если f (x) и g (x) противоположны друг другу, то мы можем символически представить это утверждение как:

g (x) = f ^{— 1} (x) или f (x) = g ⁻¹ (x)

Следует отметить, что обратная функция — это не то же самое, что обратная функция, т.е.е., f ^{— 1} (x) ≠ 1 / f (x). В этой статье мы обсудим, как найти обратную функцию.

Поскольку не все функции имеют инверсию, важно проверить, есть ли у функции инверсия, прежде чем приступать к определению инверсии.

Мы проверяем, есть ли у функции инверсия, чтобы не тратить время на поиск чего-то, чего не существует.

Индивидуальные функции

Итак, как мы можем доказать, что данная функция имеет обратную? Функции, у которых есть обратные, называются взаимно однозначными функциями.

Функция называется взаимно однозначной, если для каждого числа y в диапазоне f существует ровно одно число x в области определения f такое, что f (x) = y.

Другими словами, домен и диапазон однозначной функции имеют следующие отношения:

• Область f ⁻¹ = Диапазон f.

• Диапазон f ⁻¹ = Область f.

Например, чтобы проверить, является ли f (x) = 3x + 5 взаимно однозначной заданной функцией, f (a) = 3a + 5 и f (b) = 3b + 5.

⟹ 3a + 5 = 3b + 5

⟹ 3a = 3b

⟹ а = б.

Следовательно, f (x) является взаимно однозначной функцией, поскольку a = b.

Рассмотрим другой случай, когда функция f задается формулой f = {(7, 3), (8, –5), (–2, 11), (–6, 4)}. Эта функция взаимно однозначна, потому что ни одно из ее значений y не встречается более одного раза.

А что насчет этой другой функции h = {(–3, 8), (–11, –9), (5, 4), (6, –9)}? Функция h не является взаимно однозначной, потому что значение y, равное –9, встречается более одного раза.

Вы также можете графически проверить взаимно однозначную функцию, проведя вертикальную и горизонтальную линии через график функции. Функция взаимно однозначна, если и горизонтальная, и вертикальная линии проходят через график один раз.

Как найти обратную функцию?

Найти инверсию функции — несложный процесс, хотя нам действительно нужно быть осторожными с парой шагов. В этой статье мы будем предполагать, что все функции, с которыми мы будем иметь дело, относятся друг к другу.

Вот процедура нахождения обратной функции f (x):

• Заменить обозначение функции f (x) на y.
• Поменять местами x на y и наоборот.
• Начиная с шага 2, решите уравнение относительно y. Будьте осторожны с этим шагом.
• Наконец, измените y на f ⁻¹ (x). Это обратная функция.
• Вы можете проверить свой ответ, проверив, верны ли следующие два утверждения:

⟹ (f ∘ f ⁻¹ ) (x) = x

⟹ (f ⁻¹ ∘ f) (x) = x

Давайте поработаем пару примеров.

Пример 1

Найдите функцию f (x) = 3x — 2, обратную ей.

Решение

f (x) = 3x — 2

Заменить f (x) на y.

⟹ у = 3х — 2

Поменять местами x на y

⟹ x = 3y — 2

Решить для y

х + 2 = 3 года

Разделим на 3, чтобы получить;

1/3 (х + 2) = у

х / 3 + 2/3 = у

Наконец, заменим y на f ⁻¹ (x).

f ⁻¹ (x) = x / 3 + 2/3

Проверить (f ∘ f ⁻¹ ) (x) = x

(f ∘ f ⁻¹ ) (x) = f [f ⁻¹ (x)]

= е (х / 3 + 2/3)

⟹ 3 (х / 3 + 2/3) — 2

⟹ x + 2 — 2

= х

Следовательно, f ⁻¹ (x) = x / 3 + 2/3 — правильный ответ.

Пример 2

Дано f (x) = 2x + 3, найдите f ⁻¹ (x).

Решение

f (x) = y = 2x + 3

2x + 3 = y

Поменять местами x и y

⟹2y + 3 = х

Теперь решите для

у.

⟹2y = х — 3

⟹ у = х / 2 — 3/2

Наконец, заменим y на f ⁻¹ (x)

⟹ f ​​ ⁻¹ (x) = (x– 3) / 2

Пример 3

Задайте функцию f (x) = log ₁₀ (x), найдите f ⁻¹ (x).

Решение

f (x) = log₁₀ (x)

Заменено f (x) на y

⟹ y = журнал ₁₀ (x) ⟹ 10 ^y = x

Теперь поменяйте местами x на y, чтобы получить;

⟹ y = 10 ^x

Наконец, заменим y на f ⁻¹ (x).

f ^-1 (x) = 10 ^x

Следовательно, обратное значение f (x) = log ₁₀ (x) равно f ^-1 (x) = 10 ^x

Пример 4

Найдите обратную функцию следующей функции g (x) = (x + 4) / (2x -5)

Решение

г (x) = (x + 4) / (2x -5) ⟹ y = (x + 4) / (2x -5)

Обмен y с x и наоборот

y = (x + 4) / (2x -5) ⟹ x = (y + 4) / (2y -5)

⟹ х (2у − 5) = у + 4

⟹ 2xy — 5x = y + 4

⟹ 2xy — y = 4 + 5x

⟹ (2x — 1) y = 4 + 5x

Разделите обе части уравнения на (2x — 1).

⟹ у = (4 + 5x) / (2x — 1)

Заменить y на g ^{— 1} (x)

= г ^{— 1} (x) = (4 + 5x) / (2x — 1)

Проба:

(г г ^-1 ) (x) = г [г ^-1 (x)]

= г [(4 + 5x) / (2x — 1)]

= [(4 + 5x) / (2x — 1) + 4] / [2 (4 + 5x) / (2x — 1) — 5]

Умножьте числитель и знаменатель на (2x — 1).

⟹ (2x — 1) [(4 + 5x) / (2x — 1) + 4] / [2 (4 + 5x) / (2x — 1) — 5] (2x — 1).

⟹ [4 + 5x + 4 (2x — 1)] / [2 (4 + 5x) — 5 (2x — 1)]

⟹ [4 + 5x + 8x − 4] / [8 + 10x — 10x + 5]

⟹13x / 13 = x
Следовательно, g ^{— 1} (x) = (4 + 5x) / (2x — 1)

Пример 5

Определите обратную функцию следующей функции f (x) = 2x — 5

Решение

Заменить f (x) на y.

f (x) = 2x — 5⟹ y = 2x — 5

Переключите x и y, чтобы получить;

⟹ х = 2у — 5

Изолировать переменную y.

2у = х + 5

⟹ у = х / 2 + 5/2

Измените y обратно на f ^–1 (x).

⟹ f ​​ ^–1 (x) = (x + 5) / 2

Пример 6

Найти обратную функцию к функции h (x) = (x — 2) ³ .

Решение

Измените h (x) на y, чтобы получить;

h (x) = (x — 2) ³ ⟹ y = (x — 2) ³

Поменять местами x и y

⟹ х = (у — 2) ³

Изолятор ул.

y ³ = x + 2 ³

Найдите кубический корень из обеих частей уравнения.

³ √y ³ = ³ √x ³ + ³ √2 ³

y = ³ √ (2 ³ ) + 2

Заменить y на h ^{— 1} (x)

ч ^{— 1} (x) = ³ √ (2 ³ ) + 2

Пример 7

Найти обратную величину h (x) = (4x + 3) / (2x + 5)

Решение

Заменить h (x) на y.

h (x) = (4x + 3) / (2x + 5) ⟹ y = (4x + 3) / (2x + 5)

Поменять местами x и y.

⟹ х = (4у + 3) / (2у + 5).

Решите относительно y в приведенном выше уравнении следующим образом:

⟹ х = (4у + 3) / (2у + 5)

Умножить обе стороны на (2y + 5)

⟹ х (2у + 5) = 4у + 3

Распределить x

⟹ 2xy + 5x = 4y + 3

Изолятор ул.

⟹ 2xy — 4y = 3 — 5x

⟹ y (2x — 4) = 3-5x

Разделим на 2x — 4, чтобы получить;

⟹ у = (3 — 5x) / (2x — 4)

Наконец, замените y на h ^{— 1} (x).

⟹ ч ^{— 1} (x) = (3 — 5x) / (2x — 4)

Практические вопросы

Найдите обратное значение для следующих функций:

1. г (x) = (2x — 5) / 3.
2. h (x) = –3x + 11.
3. г (x) = — (x + 2) ² — 1.
4. г (х) = (5/6) х — 3/4
5. f (x) = 3 x — 2.
6. h (x) = x ² + 1.
7. г (x) = 2 (x — 3) ² -5
8. f (x) = x ² / (x ² + 1)
9. h (x) = √x — 3.
10. f (x) = (x — 2) ⁵ + 3
11. f (x) = 2 x ³ — 1
12. f (x) = x ² — 4 x + 5
13. г (x) = ⁵ √ (2x + 11)
14. h (x) = 4x / (5 — x)

Предыдущий урок | Главная страница | Следующий урок

Математическая сцена — Уравнения III — Урок 3

Математическая сцена — Уравнения III — Урок 3 — Квадратные уравнения

2008 Rasmus ehf и Jhann sak

Уравнения III

Урок 3 Пересечение точек графиков

---

Как приступить к поиску точек, в которых два графика y = f (x) и y = g (x) пересекаются?

Мы уже знаем, где найти график f (x) пересекает ось x.Здесь y = 0. Мы вычисляем его, решая уравнение f (x) = 0.
Когда графики y = f (x) и y = g (x) пересекаются, оба графа имеют точно такие же значения x и y. Итак, мы можем найти точку или точки пересечения путем решения уравнения f (x) = g (x). Решение этого уравнения даст нам значение (я) x точка (и) пересечения. Затем мы можем найти значение y, поместив значение для x, который мы нашли в одном из исходных уравнений.То есть путем расчета либо f (x), либо g (x).

Пример 1

Рассчитать точку пересечение двух прямых f (x) = 2x — 1 и g (x) = x + 1. Сначала давайте посмотрим на график двух функций. Мы видим смысл пересечение есть (2, 3).

Рассчитываем точку пересечения по решение уравнения f (x) = g (x). То есть:

2х — 1 = х + 1

2х — х = 1 + 1

х = 2

Координата Y теперь может быть найдена вычисление f (2):

f (2) = 2 × 2 — 1 = 3

Точка пересечения (2, 3) .

Пример показывает, что мы можем найти точку пересечения двумя способами.
Либо графически, нарисовав два графика в одной системе координат, либо алгебраически, решив уравнение, подобное тому, которое приведено в приведенном выше примере.

Решить уравнение графически легко с помощью графический калькулятор или компьютерная программа, например Excel.
Некоторые уравнения нельзя решить алгебраически, но мы можем найти решения, которые исправляем до любого количества значащих цифр, используя компьютеры и калькуляторы.

Пример 2

Решите уравнение x ² — 2x — 3 = 2x — 3 сначала графически, а затем алгебраически.

Рисуем графики f (x) = x ² — 2x — 3 и g (x) = 2x — 3, составив таблицу значений и построив график точки. Как из графика, так и из таблицы значений видно, что графики пересекаются при x = 0 и x = 4 .

Решает алгебраически:

x ² — 2x — 3 = 2x — 3

x ² — 4x = 0

х (х — 4) = 0

Даем решения x = 0 и x = 4 .

Пример 3

Решите уравнение x ² — 1 = 2x — 3

Сначала переместите все термины перейдите к левой части уравнения и упростите.

Это дает x ² — 2x + 2 = 0

Используем формулу корней квадратного уравнения с a = 1, b = −2 и c = 2.

Число под знаком квадратного корня: отрицательный, что означает, что это уравнение не имеет решения.
Чтобы понять, почему это так, мы рисуем графики левой части оригинала. уравнение

f (x) = x ² — 1 и правая часть g (x) = 2x — 3.

Мы видим, что парабола f (x) и прямая g (x) не пересекаются.Легко видеть, что мы не может вычислить точку пересечения просто потому, что такой точки нет.

Пример 4

Решите уравнение x ³ — 3x + 2 = x ² — 2x + 1

Как и в предыдущем примере, мы перемещаем все слагаемые в левую часть уравнения.

x ³ — 3x + 2 = x ² — 2x + 1

x ³ — x ² — x + 1 = 0

(x ³ — x ² ) — (x — 1) = 0

x ² (x — 1) — (x — 1) = 0

(х — 1) (х ² — 1) = 0

(х — 1) (х — 1) (х + 1) = 0

Расчеты показывают, что их всего два решений, x = 1 и x = −1, но кубическое уравнение может иметь три решения.График показывает нам, что происходит.

Графики f (x) = x ² — 2x + 1 и g (x) = x ³ — 3x + 2 пересекаются только в двух местах, где x = −1 и x = 1, которые были решениями уравнение.

Пример 5

Решите уравнение x ² = x

Легко видеть, что x = 0 и x = 1 являются решения уравнения, но есть ли еще решения? Это не очень вероятно, но давайте посмотрим на графики.

Назовите левую часть f (x) = x ² и правую часть g (x) = x. Помните, что g (x) не может принимать отрицательные значения x, поэтому не может быть никаких отрицательные точки пересечения.

На графике видно, что точек всего две пересечения и, следовательно, только два решения уравнения. х = 0 и х = 1.
Вот как решить уравнение расчетом:

x 2 = x х 4 = х х 4 — х = 0 x (x 3 — 1) = 0

Квадрат обе стороны уравнения, чтобы избавиться от квадратного корня .

Это дает решение x = 0 и x = 1 .

Пример 6

Решите уравнение ln x = x ² — 1

Это уравнение не так-то просто решить. Если мы вспомните определение логарифма, мы видим, что x = 1 делает обе стороны уравнение равно 0 и, следовательно, является одним решением уравнения. Мы рисуем графики, чтобы увидеть, есть ли другие решения.

График показывает нам, что есть два решения. Одно решение — ровно x = 1, поскольку e ⁰ = 1.

Обратите внимание, что мы выбираем значения x так, чтобы значения y становятся все ближе и ближе друг к другу в таблице значений. Таким образом мы можем выбрать значение x, чтобы получить желаемую точность.

Пример 7

EXCEL

Если мы воспользуемся графическим калькулятором, мы сможем найти решение уравнения ln x = x ² — 1 намного проще.

Рисуем графики обеих сторон уравнение и используйте Zoom (сдвиг F2), а затем Trace (сдвиг F1), чтобы найти точка пересечения.

Еще проще использовать G-Solve (F5) и затем функция пересечения ISCT (F5). Это дает нам первую точку зрения пересечение. Затем нажимаем стрелку вправо, и калькулятор переходит к вторая точка пересечения. 2-ln (B2)

Теперь выберите Инструменты а затем «Поиск цели» в строке меню.В на экране появляется следующее:

Пишем D2, 1 и B2 в промежутках, как показано. Мы просим Excel сделать значение ячейки D2 равным к значению 1, изменив значение в B2.

Когда нажимаем ОК, появляется следующая информация.

Это говорит нам о том, что аппроксимация x ≈ 0,45, которую мы нашли графически в примере 6, довольно хорошо, решение x ≈ 0.2-х-6

Уравнение y = 2x ² — x — 6

a) Чтобы найти точку пересечения y, подставьте x = 0 в y = 2x ² — x — 6.

у = 2 (0) ² -0-6

y перехват — 6.

b) Чтобы найти точку пересечения с x, подставьте y = 0 в y = 2x ² — x — 6

2x ² — x — 6 = 0

2x ² — 4x + 3x — 6 = 0

2x (x — 2) + 3 (x — 2) = 0

(х — 2) (2x + 3) = 0

х — 2 = 0 и 2x = — 3

х = 2 и х = — 3/2

х перехватов 2 и -3/2.

в) y = 2x ² — x — 6

Сравните это с y = ax ² + bx + c

а = 2, б = — 1, в = — 6

Найти вершину оси симметрии x = — b / 2a

х = — (- 1) / 2 (2)

х = 1/4

Чтобы найти координату y вершины, подставьте x = 1/4 в y = 2x ² — x — 6.

у = 2 (1/4) ² — (1/4) — 6

у = 1/8 — 1/4 — 6

у = (1-2-48) / 8

у = — 49/8

Вершина равна (x, y) = (1/4, -49/8) или (0.25, — 6,125).

График

Выберите случайные значения для y и найдите соответствующие значения для x .

х	y = 2x 2 — x — 6	(х, у)
1	у = 2 (1) 2 -1-6	(1, — 5)
— 1	у = 2 (-1) 2 + 1-6	(-1, — 3)
— 2	у = 2 (-2) 2 + 2-6	(-2, 4)
2.5	у = 2 (2,5) 2 — 2,5 — 6	(7, — 3)

1. Нарисуйте координатную плоскость.

2. Постройте пересечения осей симметрии x, y и координаты точек, найденных в таблице.

3. Затем нарисуйте график, соединив точки плавной кривой.

Частные производные

Частичная производная — это производная, в которой некоторые переменные остаются постоянными.Как в этом примере:

Пример: функция для поверхности, которая зависит от двух переменных

x и y

Когда мы находим наклон в направлении x (при фиксированном y ), мы нашли частную производную.

Или мы можем найти наклон в направлении y (при сохранении фиксированного x ).

Давайте сначала подумаем о функции одной переменной (x):

f (x) = x ²

Мы можем найти его производную, используя правило мощности:

f ’(x) = 2x

А как насчет функции двух переменных (x и y):

f (x, y) = x ² + y ³

Мы можем найти его частную производную по x , если рассматривать y как константу (представьте, что y — это число вроде 7 или что-то в этом роде):

f ’ _x = 2x + 0 = 2x

Пояснение:

• производная x ² (по x) равна 2x
• мы рассматриваем y как константу , поэтому y ³ также является константой (представьте, что y = 7, тогда 7 ³ = 343 также является константой), а производная константы равна 0

Чтобы найти частную производную по y , мы рассматриваем x как константу :

f ’ _y = 0 + 3y ² = 3y ²

Пояснение:

• мы теперь обрабатываем x как константу , поэтому x ² также является константой, а производная константы равна 0
• производная y ³ (по y) равна 3y ²

Вот и все.Просто не забудьте рассматривать со всеми другими переменными, как если бы они были константами .

Сохраняет переменную константу

Так как же выглядит «сохранение переменной-константы»?

Пример: объем цилиндра V = π r

² ч

Мы можем записать это в «многопеременной» форме как

f (r, h) = π r ² h

Для частной производной по r мы держим h постоянной , а r изменяется:

f ’ _r = π (2r) h = 2πrh

(Производная r ² по r равна 2r, а π и h являются константами)

В нем говорится: «Поскольку изменяется только радиус (на минимальную величину), объем изменяется на 2πrh»

Это как если бы мы добавляли скин с окружностью круга (2πr) и высотой h.

Для частной производной по h мы держим r постоянной :

f ’ _h = π r ² (1) = πr ²

(π и r ² — константы, а производная h по h равна 1)

В нем говорится, что «при изменении только высоты (на минимальную величину) объем изменяется на πr ² »

Это похоже на то, как будто мы добавляем сверху самый тонкий диск с площадью круга πr ² .

Давайте посмотрим на другой пример.

Пример: Площадь поверхности квадратной призмы.

Поверхность включает верхнюю и нижнюю части площадью x ² каждая и 4 стороны области xy каждая:

f (x, y) = 2x ² + 4xy

f ’ _x = 4x + 4y

f ’ _y = 0 + 4x = 4x

Три или более переменных

У нас может быть 3 или более переменных.Просто найдите частную производную каждой переменной по очереди, рассматривая всех остальных переменных как константы .

Пример: Объем куба с вырезанной из него квадратной призмой.

f (x, y, z) = z ³ — x ² y

f ’ _x = 0 — 2xy = −2xy

f ’ _y = 0 — x ² = −x ²

f ’ _z = 3z ² — 0 = 3z ²

Когда имеется много x и y, это может сбивать с толку, поэтому мысленный трюк состоит в том, чтобы заменить «постоянные» переменные на буквы, такие как «c» или «k», чтобы выглядело как константы.

Пример: f (x, y) = y

³ sin (x) + x ² tan (y)

У него повсюду крестики и у! Итак, давайте попробуем трюк со сменой букв.

Что касается x, мы можем изменить «y» на «k»:

f (x, y) = k ³ sin (x) + x ² tan (k)

f ’ _x = k ³ cos (x) + 2x tan (k)

Но не забудьте снова повернуть его обратно!

f ’ _x = y ³ cos (x) + 2x tan (y)

Аналогично по отношению к y мы превращаем «x» в «k»:

f (x, y) = y ³ sin (k) + k ² tan (y)

f ’ _y = 3y ² sin (k) + k ² sec ² (y)

f ’ _y = 3y ² sin (x) + x ² sec ² (y)

Но делайте это только в том случае, если у вас проблемы с запоминанием, поскольку это небольшая дополнительная работа.

Обозначение : мы использовали f ’ _x , чтобы обозначить« частную производную по x », но еще одно очень распространенное обозначение — это использование забавного обратного d (∂), например:

∂f ∂x = 2x

Это то же самое, что:

f ’ _x = 2x

∂ называется «дель», «ди» или «кудрявый ди»

Так ∂f ∂x можно сказать «del f del x»

Пример: найти частные производные

f (x, y, z) = x ⁴ — 3xyz , используя обозначение curly dee

f (x, y, z) = x ⁴ — 3xyz

∂f ∂x = 4x ³ — 3yz

∂f ∂y = −3xz

∂f ∂z = −3xy

Возможно, вы предпочтете такую ​​нотацию, она определенно выглядит круто.