Фибоначчи числа золотое сечение – «Можете объяснить по-простому, что такое золотое сечение и почему его так часто везде используют?» – Яндекс.Знатоки — Детская игровая комната «Волшебный лес»

Posted on 20.06.202013.01.2020 by alexxlab

Содержание

Золотое сечение — Википедия

1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362

Первая тысяча знаков значения Φ^[1].

Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин a{\displaystyle a} и b{\displaystyle b}, при котором бо́льшая величина относится к меньшей так же как сумма величин к бо́льшей, то есть: ab=a+ba.{\displaystyle {\frac {a}{b}}={\frac {a+b}{a}}.} Исторически изначально в древнегреческой математике золотым сечением именовалось деление отрезка AB{\displaystyle AB} точкой C{\displaystyle C} на две части так, что бо́льшая часть относится к меньшей, как весь отрезок к большей: BCAC=ABBC{\displaystyle {\frac {BC}{AC}}={\frac {AB}{BC}}}. Позже это понятие было распространено на произвольные величины.

Число, равное отношению a/b{\displaystyle a/b}, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия

[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства (например, представляя a или даже a/b независимой переменной и решая выводимое из исходного равенства квадратное уравнение) нетрудно получить, что число

Φ=5+12{\displaystyle \Phi ={\frac {{\sqrt {5}}+1}{2}}}

Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }^[2],

φ=1Φ=5−12≈0.61803{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {{\sqrt {5}}-1}{2}}\approx 0.61803}

Отсюда следует, что

φ=Φ−1{\displaystyle \varphi =\Phi -1}.

Число Φ{\displaystyle \Phi } называется также золотым числом.

Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.

Иллюстрация к определению

Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства^[3]^[4]^[5].

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа^[6].

Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке^[7] или относят появление этого термина к XVI веку^[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»

[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам^[10]^[11], хотя некоторые авторы утверждают обратное^[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги^[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.^[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.^[15] В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.^[16]

1Φ=φ=tg⁡(arctg⁡(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}

Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:
Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}
Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби
Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}

подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,

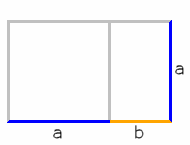${\frac {F_{n+1}}{F_{n}}}$ Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения

Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.

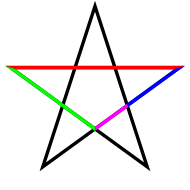$\Phi = (a+b)/a$ Золотое сечение в пятиконечной звезде

В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.

$\Phi$ Построение золотого сечения

Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}

Другой способ построить отрезок, равный по длине числу золотого сечения

Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }^[17].

Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны^[18].
∑n=1∞(−1)n+1n2(2nn)=2ln2⁡φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }

Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}^{[источник не указан 1452 дня]}

Общее сопротивление этой бесконечной цепи равно Фr.

Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке, имеет общее сопротивление (между двумя левыми концами) Ф·r.

Отношение амплитуд колебаний и частот ~ Ф.

Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).

Полностью эти две задачи рассматриваются в книге «В поисках пятого порядка», глава «Две простые задачки»^[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.

Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию^[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.7⁰ , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н⁺(Н₂0)₂₁, который представляет из себя ион Н₃0⁺, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра^[21]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра^[22]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды^[23].

Золотое сечение и гармония в искусстве[править | править код]

Золотое сечение и зрительные центры

Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:

Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»^{[источник не указан 3820 дней]}.
Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.

Примеры сознательного использования[править | править код]

Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах^[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)^{[источник не указан 1045 дней]}.

Современными примерами применения золотого сечения может служить мозаика Пенроуза и пропорции государственного флага Того.

Золотое сечение в биологии и медицине[править | править код]

$\sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}$

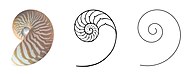Золотое сечение в природе

Живые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов^[25]^{[неавторитетный источник?]} и др.

↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits Архивная копия от 6 марта 2015 на Wayback Machine
↑ ¹ ² Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
↑ Радзюкевич А. В. Красивая сказка о «золотом сечении»
↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
↑ Devlin’s Angle, The Myth That Will Not Go Away
↑ В. Лаврус, Золотое сечение
↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76.
↑ Boyer, Carl B. (англ.)русск.. A History of Mathematics (неопр.). — Second Edition. — John Wiley & Sons, Inc., 1991. — С. 50. — ISBN 0-471-54397-7.
↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
↑ Herz-Fischler, 2013, p. 168.
↑ Livio, 2008, p. 6-7.
↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77—6567, публ. 16335.
↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
↑ Herz-Fischler, 2013, p. 169.
↑ Livio, 2008, p. 7.
↑ Herz-Fischler, 2013, p. 169-170.
↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700.
↑ Системы счисления (неопр.).
↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
↑

Спираль Фибоначчи: фото, построение спирали Фибоначчи

Природа всегда решает задачи самым простым и элегантным путем, какой только можно придумать. Золотое сечение, или, по-другому, спираль Фибоначчи, является наглядным отражением гениальности этих решений.

Следы этой пропорции обнаруживают в древних строениях и великих картинах, человеческом теле и небесных объектах. Вот уже несколько веков Золотое сечение и коэффициент Фи находятся под пристальным вниманием ученых различных областей.

«Сын счастливчика»

Именно так, по мнению ученых, можно назвать Леонардо Пизанского по прозвищу Фибоначчи. Это прозвище означает, что он — сын Боначчи («Боначчи» переводится как «счастливчик»). Весьма забавный факт, учитывая, скольких людей он сделал счастливыми косвенно, способствуя развитию математики, экономики и других областей знаний, в которых сейчас широко используется его открытие.

Этот средневековый итальянец внес настолько большой вклад в развитие современной науки, что переоценить его очень сложно. Ежедневно все большее количество научных исследований только подтверждает принцип, который он наглядно показал всему миру в виде цифр.

Леонардо Пизанский знаменит тем, что представил свой последовательный ряд чисел, который постоянно стремится к золотому сечению.

Золотое сечение

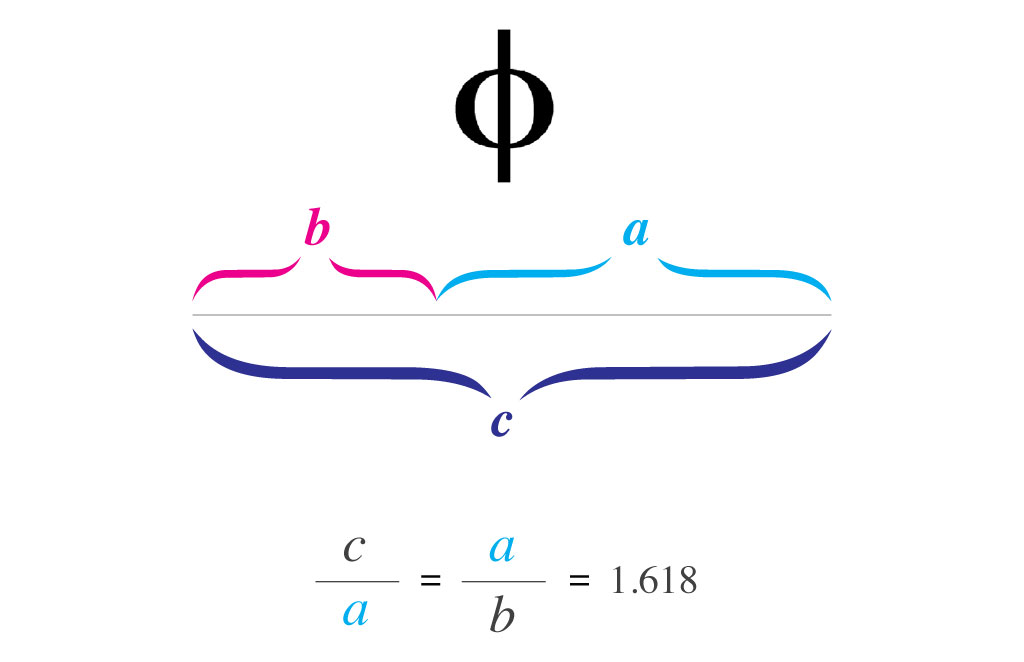
Это пропорция, которую можно графически изобразить в качестве отрезка, разделенного точкой на две части. Самое главное правило деления: весь отрезок относится к его большей части так же, как большая часть относится к меньшей.

То есть точка разделит отрезок таким образом, что если разделить всю длину (сумму частей) на величину большей части, получим то же число, что и при делении большей части на меньшую.

В результате деления всегда получается один и тот же результат — 1,618. Он получил название коэффициента Фи.

Числа Фибоначчи

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и далее — именно эти цифры играют огромную роль в науке вот уже несколько веков.

Их назвали «ряд Фибоначчи» или «числа Фибоначчи». Самым главным свойством последовательности является то, что каждое новое число равно сумме двух предыдущих. Отражением именно этой последовательности стала так называемая золотая спираль Фибоначчи. Это она принесла ему большую известность.

Но мало кто знает, что на одной лишь спирали Фибоначчи вклад ученого не завершился. Этот средневековый математик научил Европу использовать в математике арабские цифры, что значительно ускорило развитие науки. Удивительно, но до написания им трактата об арабских цифрах вся Европа пользовалась исключительно римской системой.

Кто знает, как развивалась бы наука, если бы не его светлый ум.

Коэффициент «Фи»

Самое главное число в золотом сечении — 1,618. Присутствует оно и в последовательности Фибоначчи. Именно к этому коэффициенту стремится отношение каждого следующего числа к предыдущему. Вот почему открытие ряда Фибоначчи так повлияло на все научное сообщество. С появлением математического точного выражения человечество получило способ применять один из самых важных законов окружающего мира в новых изобретениях и исследованиях.

Это совершенное число, золотая середина и гениальное решение, которое повсеместно использует сама природа.

Как построить спираль Фибоначчи

Вполне логично, что узнав так много про этот замечательный «завиток», кому-то наверняка захочется собственноручно создать его аналог.

Сделать это достаточно просто. Достаточно иметь под рукой циркуль и тетрадь в клеточку или миллиметровую бумагу (либо линейку, которая поможет построить симметричные, аккуратные квадраты).

Начать построение спирали Фибоначчи нужно с изображения двух одинаковых квадратов с длиной стороны в одну единицу длины. Дуга, соединяющая два противоположных угла первого квадрата, и станет началом золотой спирали. По мере раскручивания последней к ней присоединяется все большее количество пропорциональных фигур, до тех пор, пока не будет достигнут нужный размер спирали. Самое важное – соблюдать правило, где длина стороны каждого следующего квадрата всегда равна сумме длин сторон двух предыдущих.

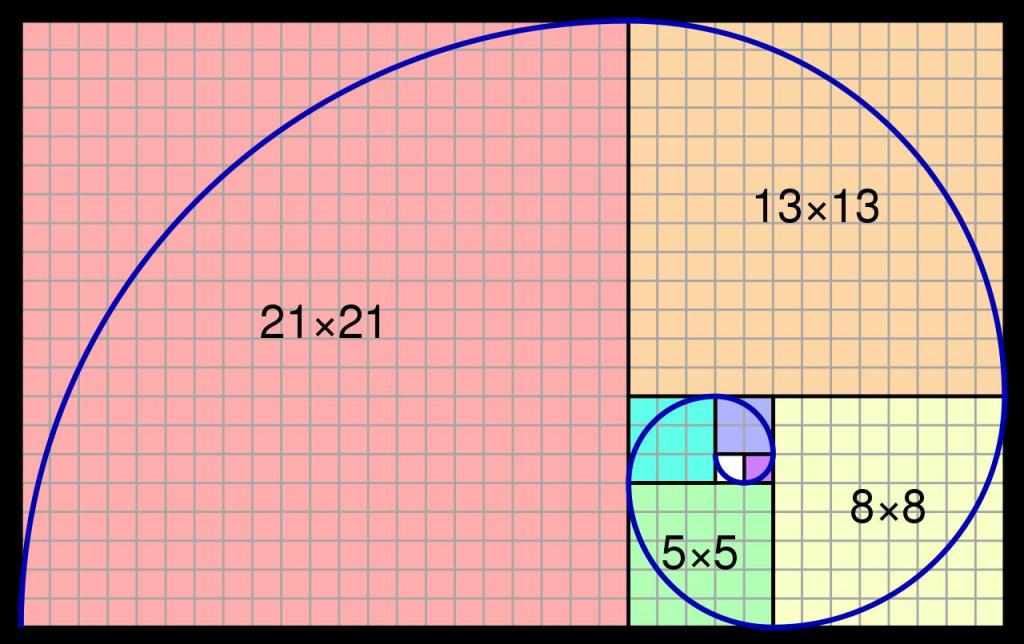
Золотой прямоугольник

Идеальный, с точки зрения спирали Фибоначчи, прямоугольник имеет стороны, длина которых пропорциональна друг к другу именно по коэффициенту фи. Иными словами, при делении одной стороны на другую обязательно должно получиться 1,618 либо 0,618 (число, обратное коэффициенту фи).

Такие прямоугольники довольно распространены в архитектуре и композиции. Интересно также то,что именно их большинство людей считают «идеальными» или «правильными» с визуальной точки зрения. Иными словами, человек интуитивно воспринимает эти пропорции более красивыми и естественными, приятным глазу. Даже если дело касается геометрических фигур.

В искусстве

Если отметить точками или линиями основные элементы в картинах и поделить полотно на множество мелких прямоугольников Фибоначчи, то можно заметить интересный факт. На огромном количестве произведений искусства фигуры размещены таким образом, что явные контрасты и важные элементы непременно будут находиться на гранях прямоугольников или располагаться непосредственно на самой спирали Фибоначчи.

Более того, уважающие себя современные архитекторы и дизайнеры тоже верны этому принципу. И в этом нет ничего удивительного. Спираль отражает закон самой природы, а она – гениальный творец.

Несколько поразительных и интересных фактов

Совсем недавно в социальных сетях даже была определенного рода мода на снимки девушек, которые откидывают волосы в воде, получая множество красивых брызг в форме спирали Фибоначчи.
Многие трейдеры считают принцип очень значимым, основывая на числах ряда Фибоначчи стратегии по продаже и покупке валюты.
Соотношение пиков кардиограммы также попадает под действие золотого сечения.
В металлургии давно известен факт, что сплавы различных металлов обладают лучшими свойствами стойкости, если удельный вес элементов относится друг к другу согласно коэффициенту Фи.
Пропорции различных веществ в гемоглобине подчинены этому закону.
Существует даже официально зарегистрированный Институт золотого сечения.
Помимо прямого коэффициента фи, существует еще обратно пропорциональное ему число 0,618, которое тоже часто используется в различных расчетах.

Все основополагающие знания человечество получило, наблюдая за миром вокруг. Раз за разом люди отмечали закономерности в смене сезонов, находили взаимосвязь между громом и молнией, изучали звезды и создавали календари.

Закон золотого сечения находится совсем на поверхности. И спирали Фибоначчи в природе, как отражение принципа, которому соответствует все живое, встречаются в огромном количестве явлений, в растительном и животном мирах.

Именно так, по принципу золотого сечения, наиболее гармонично развиваются живые организмы. Каждый следующий шаг — лишь сумма двух предыдущих. Каждый следующий виток спирали нарастает постепенно, раскрываясь все больше, но повторяя общее направление.

Это один из самых великих законов мироздания.

Золотая спираль — Википедия

Материал из Википедии — свободной энциклопедии

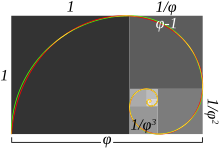Спираль Дюрера и золотая спираль, вписанные в последовательность вложенных друг в друга золотых прямоугольников: зелёная спираль — спираль Дюрера — составлена из четвертинок окружностей внутри квадратов, в то время как красная спираль является золотой спиралью, особым видом логарифмической спирали. Перекрывающиеся секции показаны жёлтым цветом. Длина части спирали внутри большего квадрата находится к длине спирали внутри следующего квадрата в золотой пропорции

Золотая спираль или спираль Фибоначчи — логарифмическая спираль, коэффициент роста которой равен φ⁴, где φ — золотое сечение. Коэффициент роста логарифмической спирали показывает во сколько раз изменился полярный радиус спирали при повороте на угол 360°.^[1] Свое название эта спираль получила из-за связи с последовательностью вложенных друг в друга прямоугольников с отношением сторон, равным φ, которые принято называть золотыми. Золотую спираль можно как вписать в систему таких прямоугольников, так и описать вокруг нее. Популярность золотая спираль приобрела из-за того, что известная с начала XVI века и применяющаяся в искусстве^[2] спираль, построенная по методу Дюрера^[3]^[4], оказалась хорошей аппроксимацией для золотой спирали (см. рисунок)

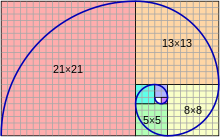Спираль Фибоначчи аппроксимирует золотую спираль с использованием четвертинок окружности в квадратах с размерами квадратов, равных числам Фибоначчи. На рисунке показаны квадраты с размерами 1, 1, 2, 3, 5, 8, 13, 21.

Уравнение для золотой спирали в полярной системе координат то же самое, что и для других логарифмических спиралей, но со специальным значением коэффициента роста — φ⁴:

r=aφ±2θπ{\displaystyle r=a\varphi ^{\pm {\frac {2\theta }{\pi }}}},

где a — произвольная положительная вещественная константа, а φ=5+12{\displaystyle \varphi ={\frac {{\sqrt {5}}+1}{2}}} — золотое сечение.

Основное свойство логарифмической спирали: угол между радиус-вектором, исходящим из полюса, и касательной к спирали — μ — постоянен, и для золотой спирали определяется формулой:

tg⁡μ=rr′=π2ln⁡φ{\displaystyle \operatorname {tg} \mu ={\dfrac {r}{r’}}={\dfrac {\pi }{2\ln \varphi }}}, где r′=drdθ{\displaystyle r’={\dfrac {dr}{d\theta }}}.

Откуда μ≈73∘{\displaystyle \mu \approx 73^{\circ }}.

Литовская монета

Существует несколько похожих спиралей, которые близки, но не совпадают в точности с золотой спиралью^[5], с которой их часто путают.

Как уже было написано выше, при вписывании золотой спирали в последовательность вложенных друг в друга золотых прямоугольников, она аппроксимируется спиралью, построенной по методу Дюрера. Золотой прямоугольник можно разделить на квадрат и подобный ему прямоугольник, его, в свою очередь, разделить тем же образом, и продолжать этот процесс произвольное число раз. Если в эти квадраты вписать соединенные между собой четвертинки окружностей, то получается спираль, изображенная на первом рисунке.

Ещё одной аппроксимацией является спираль Фибоначчи, которая строится подобно вышеописанной спирали, за исключением того, что начинают с прямоугольника из двух квадратов и добавляют потом к большей стороне прямоугольника квадрат такой же длины. Поскольку отношение между соседними числами Фибоначчи стремится к золотой пропорции, спираль всё больше приближается к золотой спирали по мере добавления квадратов (см. второй рисунок).

В природе встречаются приближения к логарифмическим спиралям с коэффициентом роста равным φ^k. Так раковины моллюсков Nautilus pompilius и окаменелых аммонитов хорошо описываются при k = 2, а раковины некоторых улиток при k = 1.^[6] Отношение длин трех витков спирали уха у человека равно φ^[7], что соответствует спирали с k = 1. Рукава спиральных галактик, несмотря на существующие утверждения^[8], если и описываются логарифмической, то не золотой спиралью. В данном случае, описание ею является проявлением случайной близости. Недавний анализ спиралей, встречающихся в роговичном эпителии мышей, показал, что там встречаются как золотая, так и другие логарифмические спирали.^[9]

↑ Выгодский М. Я. Справочник по высшей математике. М.: Наука, 1977, с. 884.
↑ Прохоров А. Золотая спираль, Квант, 1984, №9.
↑ Аракелян. Г. Математика и история золотого сечения, М.: Логос, 2014, с. 50.
↑ Albrecht Durer (1525): Unterweysung der Messung mit dem Zirkel und Richtscheyt, in Linien Ebnen und gantzen Corporen. Verlag Dr. Alfons Uhl (Reprint 2000), Nordlingen, ISBN 3 921503 65 5 (Engl. Transl.: The Painter’s Manual, Abaris Books, New York 1977).
↑ Madden, 1999, с. 14–16.
↑ А.Н. Ковалев, Еще раз о золотых спиралях // Академия Тринитаризма, М., Эл № 77-6567, публ.23545, 13.07.2017 http://www.trinitas.ru/rus/doc/0016/001f/3352-kv.pdf
↑ Петухов С. В. Матричная генетика, алгебры генетического кода, помехоустойчивость. — Москва: Регулярная и хаотическая динамика, 2008. — С. 107.
↑ Gazale, 1999, с. 3.
↑ Rhee, 2015, с. 22–38.

David Darling. The Universal Book of Mathematics: From Abracadabra to Zeno’s Paradoxes. — John Wiley & Sons, 2004. — ISBN 9780471270478.
Ivars Peterson. Sea Shell Spirals. — Society for Science & the Public, 2005-04-01.
Keith Devlin. The myth that will not go away. — May 2007.
Jerry Rhee, Talisa Mohammad Nejad , Olivier Comets, Sean Flannery, Eine Begum Gulsoy, Philip Iannaccone , Craig Foster. Promoting convergence: The Phi spiral in abduction of mouse corneal behaviors // Complexity. — 2015. — Т. 20, вып. 3. — С. 22–38. — DOI:10.1002/cplx.21562.
Midhat Gazale. Gnomon: From Pharaohs to Fractals. — Princeton University Press, 1999. — ISBN 9780691005140.
Charles B. Madden. Fractals in Music: introductory mathematics for musical analysis. — High Art Press, 1999. — ISBN 0-9671727-6-4.
Klaus Mainzer. Symmetries of Nature: A Handbook for Philosophy of Nature and Science. — Walter de Gruyter, 1996. — ISBN 3-11-012990-6.
Priya Hemenway. Divine Proportion: Φ Phi in Art, Nature, and Science. — Sterling Publishing Co, 2005. — ISBN 1-4027-3522-7.

Метод золотого сечения — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 февраля 2018; проверки требуют 5 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 февраля 2018; проверки требуют 5 правок.

Метод золотого сечения — метод поиска экстремума действительной функции одной переменной на заданном отрезке. В основе метода лежит принцип деления отрезка в пропорциях золотого сечения. Является одним из простейших вычислительных методов решения задач оптимизации. Впервые представлен Джеком Кифером в 1953 году.

Пусть задана функция f(x):[a,b]→R,f(x)∈C([a,b]){\displaystyle f(x):\;[a,\;b]\to \mathbb {R} ,\;f(x)\in \mathrm {C} ([a,\;b])}. Тогда для того, чтобы найти неопределённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точки x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}} такие, что:

Иллюстрация выбора промежуточных точек метода золотого сечения.

b−ab−x1=b−ax2−a=Φ=1+52=1.618…{\displaystyle {\frac {b-a}{b-x_{1}}}={\frac {b-a}{x_{2}-a}}=\Phi ={\frac {1+{\sqrt {5}}}{2}}=1.618\ldots }, где Φ{\displaystyle \Phi } — пропорция золотого сечения.

Таким образом:

x1=b−(b−a)Φx2=a+(b−a)Φ{\displaystyle {\begin{array}{ccc}x_{1}&=&b-{\frac {(b-a)}{\Phi }}\\x_{2}&=&a+{\frac {(b-a)}{\Phi }}\end{array}}}

То есть точка x1{\displaystyle x_{1}} делит отрезок [a,x2]{\displaystyle [a,\;x_{2}]} в отношении золотого сечения. Аналогично x2{\displaystyle x_{2}} делит отрезок [x1,b]{\displaystyle [x_{1},\;b]} в той же пропорции. Это свойство и используется для построения итеративного процесса.

Алгоритм[править | править код]

На первой итерации заданный отрезок делится двумя симметричными относительно его центра точками и рассчитываются значения в этих точках.
После чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поиска минимума), отбрасывают.
На следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку.
Процедура продолжается до тех пор, пока не будет достигнута заданная точность.

Формализация[править | править код]

Шаг 1. Задаются начальные границы отрезка a,b{\displaystyle a,\;b} и точность ε{\displaystyle \varepsilon }.
Шаг 2. Рассчитывают начальные точки деления: x1=b−(b−a)Φ,x2=a+(b−a)Φ{\displaystyle x_{1}=b-{\frac {(b-a)}{\Phi }},\quad x_{2}=a+{\frac {(b-a)}{\Phi }}} и значения в них целевой функции: y1=f(x1),y2=f(x2){\displaystyle y_{1}=f(x_{1}),\;y_{2}=f(x_{2})}.
- Если y1≥y2{\displaystyle y_{1}\geq y_{2}} (для поиска max изменить неравенство на y1≤y2{\displaystyle y_{1}\leq y_{2}}), то a=x1{\displaystyle a=x_{1}}
- Иначе b=x2{\displaystyle b=x_{2}}.
Шаг 3.
- Если |b−a|<ε{\displaystyle |b-a|<\varepsilon }, то x=a+b2{\displaystyle x={\frac {a+b}{2}}} и останов.
- Иначе возврат к шагу 2.

Алгоритм взят из книги Мэтьюза и Финка «Численные методы. Использование MATLAB».

Реализация данного алгоритма на языке F#, в которой значения целевой функции используются повторно:

let phi = 0.5 * (1.0 + sqrt 5.0)
let minimize f eps a b = 
    let rec min_rec f eps a b fx1 fx2 = 
        if b - a < eps then 
            0.5 * (a + b)
        else 
            let t = (b - a) / phi
            let x1, x2 = b - t, a + t
            let fx1 = match fx1 with Some v -> v | None -> f x1
            let fx2 = match fx2 with Some v -> v | None -> f x2
            if fx1 >= fx2 then
                min_rec f eps x1 b (Some fx2) None
            else
                min_rec f eps a x2 None (Some fx1)
    min_rec f eps (min a b) (max a b) None None

// Примеры вызова:
minimize cos 1e-6 0.0 6.28 |> printfn "%.10g"
// = 3.141592794; функция f вызвана 34 раза.
minimize (fun x -> (x - 1.0)**2.0) 1e-6 0.0 10.0 |> printfn "%.10g"
// = 1.000000145; функция f вызвана 35 раз.

В силу того, что в асимптотике Φ=limn→∞Fn+1Fn{\displaystyle \Phi =\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}}, метод золотого сечения может быть трансформирован в так называемый метод чисел Фибоначчи. Однако при этом в силу свойств чисел Фибоначчи количество итераций строго ограничено. Это удобно, если сразу задано количество возможных обращений к функции.

Алгоритм[править | править код]

Шаг 1. Задаются начальные границы отрезка a,b{\displaystyle a,\;b} и число итераций n{\displaystyle n}, рассчитывают начальные точки деления: x1=a+(b−a)Fn−2Fn,x2=a+(b−a)Fn−1Fn{\displaystyle x_{1}=a+(b-a){\frac {F_{n-2}}{F_{n}}},\quad x_{2}=a+(b-a){\frac {F_{n-1}}{F_{n}}}} и значения в них целевой функции: y1=f(x1),y2=f(x2){\displaystyle y_{1}=f(x_{1}),\;y_{2}=f(x_{2})}.

Шаг 2. n=n−1{\displaystyle n=n-1}.
- Если y1>y2{\displaystyle y_{1}>y_{2}}, то a=x1,x1=x2,x2=b−(x1−a),y1=y2,y2=f(x2){\displaystyle a=x_{1},\;x_{1}=x_{2},\;x_{2}=b-(x_{1}-a),\;y_{1}=y_{2},\;y_{2}=f(x_{2})}.
- Иначе b=x2,x2=x1,x1=a+(b−x2),y2=y1,y1=f(x1){\displaystyle b=x_{2},\;x_{2}=x_{1},\;x_{1}=a+(b-x_{2}),\;y_{2}=y_{1},\;y_{1}=f(x_{1})}.
Шаг 3.
- Если n=1{\displaystyle n=1}, то x=x1+x22{\displaystyle x={\frac {x_{1}+x_{2}}{2}}} и остановка.
- Иначе возврат к шагу 2.

Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. —
М.: Мир, 1985.
Коршунов Ю. М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
Максимов Ю. А., Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
Максимов Ю. А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575—576.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1973. — С. 832 с илл..
Джон Г. Мэтьюз, Куртис Д. Финк. Численные методы. Использование MATLAB. — 3-е издание. — М., СПб.: Вильямс, 2001. — С. 716.

«Можете объяснить по-простому, что такое золотое сечение и почему его так часто везде используют?» – Яндекс.Знатоки

Золотое сечение — правило пропорции, не случайно его еще называют божественной гармонией.

Коротко эта пропорция определяется так: «меньшая часть относится к большей, как большая ко всему целому «.

В математике золотое сечение называют «асимметричной симметрией», оно выражается вполне конкретной формулой. Само понятие впервые использовал Пифагор, а число золотого сечения получило «имя» древнегреческого архитектора Фидия — число «фи» (греческая буква φ). Равно это число (с округлением) 1,62, а в процентном выражении золотое сечение выглядит, как 62% и 38%.

По канонам этой пропорции создавались произведения искусства еще древними египтянами, так что можно сказать, что золотое сечение сопровождает человеческую цивилизацию на протяжении всего ее развития.

Пропорции, если не совсем точные, то все же максимально близкие к золотому сечению, присутствуют везде — в искусстве, в природе и в самом человеке. Поэтому не совсем верно говорить, что его используют искуственно, оно просто является своеобразным маркером того, что красиво и гармонично.

Вот, например, можете и Вы убедиться, если измерите сами себя 🙂

Число «фи» или близкое к нему получится, если вычислить отношение расстояния от плеч до макушки к размеру головы; отношение расстояния от пупка до коленок и от коленок до ступней. И лицо воспринимается как более красивое, чем ближе его пропорции к идеальным: от подбородка до крайней точки верхней губы и от нее до носа пропорция близка к 1:1,62.

По правилу божественной гармонии «устроены» шишки, раковины моллюсков, чешуйки на плодах ананаса. Его обнаружили в молекуле ДНК и в спиралевидных галактиках.

Настоящие произведения искусства, которые человек подсознательно воспринимает, как прекрасные, тоже основаны на этой пропорции — будь это живопись, музыка, скульптура, архитектура и так далее.

Гармония в нашей жизни рулит! А гармония — это и есть золотое сечение 🙂

Гармонии и Вам!

Золотое сечение и числа Фибоначчи

Законы природы и законы Жизни до сих пор не разгаданы. И каждый новый взгляд на обычные вещи отображается новым открытием или новыми изобретениями. Жизнь интересная штука! И каждый раз узнаешь о чем-то новом.

Для меня было большим открытием узнать о золотом сечение и числах Фибоначчи. Я до сих пор под впечатлением. И спешу рассказать Вам об этом обычном (для мира) и уникальном (для человечества) явлении.

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами.

В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:

Месяцы 0 1 2 3 4 5 6 7 8 9 10 11 12 … и т.д.
Пары кроликов 0 1 1 2 3 5 8 13 21 34 55 89 144 … и т.д.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … и т.д.

Набор этих чисел известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф.

Последовательность Фибоначчи — это числовой ряд, в котором каждый последующий член представляет собой сумму двух предыдущих:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т.д.

каждое последующее число в числовом ряду приблизительно в 1.618 раз больше предыдущего, а каждое предыдущее составляет приблизительно 0.618 от следующего.
Отношение через одно число составляет 0.382, а обратное ему число = 2.618. За исключением нескольких первых чисел последовательности.

Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.

Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.

Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы.

Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения.

Понравилась статья? Расскажи о ней своим друзьям в социальных сетях, жми соответствующую кнопку ниже!

Tags: Законы Успеха, Золотое сечение, Колесо Жизненного Баланса, Правила Жизни, ряд Фибоначчи

«Можете объяснить по-простому, что такое золотое сечение и почему его так часто везде используют?» – Яндекс.Кью

Золотое сечение — правило пропорции, не случайно его еще называют божественной гармонией.

Коротко эта пропорция определяется так: «меньшая часть относится к большей, как большая ко всему целому «.

Вот, например, можете и Вы убедиться, если измерите сами себя 🙂

Гармония в нашей жизни рулит! А гармония — это и есть золотое сечение 🙂

Гармонии и Вам!