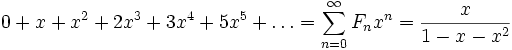Лекция № 8. Числа фибоначчи и простые числа
Задача Фибоначчи
Итальянский математик Леонардо Фибоначчи жил в 13 столетии и одним из первых в Европе стал использовать арабские (индийские) цифры. Он придумал несколько искусственную задачу о кроликах, которых выращивают на ферме, причем все они считаются самками, самцы игнорируются. Кролики начинают размножаться после того, как им исполняется два месяца, а потом каждый месяц рожают по кролику. Кролики никогда не умирают.
Нужно определить, сколько кроликов будет на ферме через n месяцев, если в начальный момент времени был только один новорожденный кролик.
Очевидно, что фермер имеет одного кролика в первый месяц и одного кролика – во второй месяц. На третий месяц будет уже два кролика, на четвертый – три и т.д. Обозначим количество кроликов в
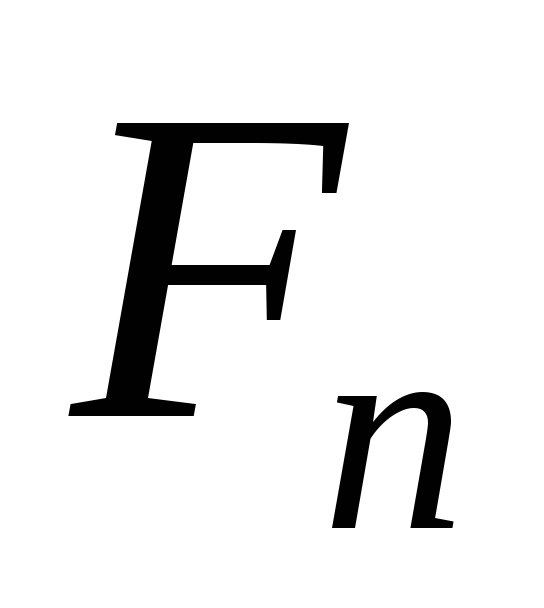 .
Таким образом,
.
Таким образом,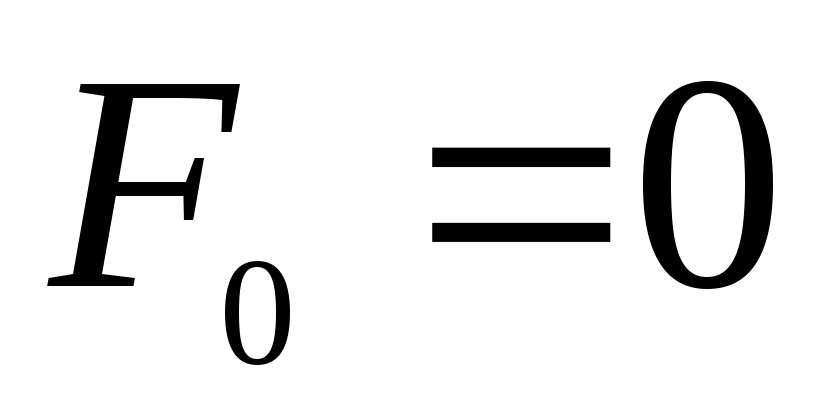 ,
,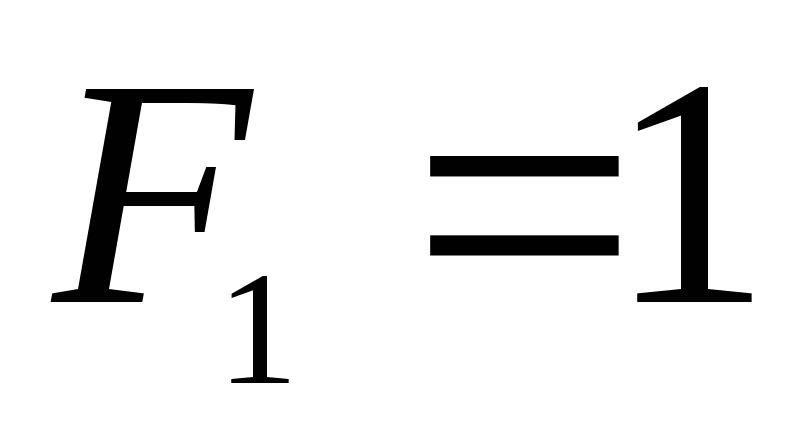 ,
, ,
, ,
, ,
…
,
… Можно построить
алгоритм, позволяющий найти 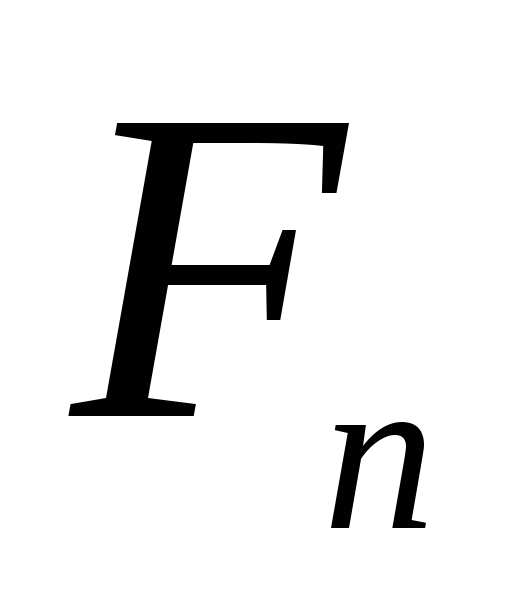 при любомn.
при любомn.
Согласно условию
задачи общее количество кроликов  вn+1
месяце раскладывается на три составляющие:
вn+1
месяце раскладывается на три составляющие:
одномесячные кролики, не способные к размножению, в количестве
 ;
;
кролики, способные к размножению, в количестве
 ;
;новорожденные кролики, их количество также равно
 .
.
Таким образом, получим
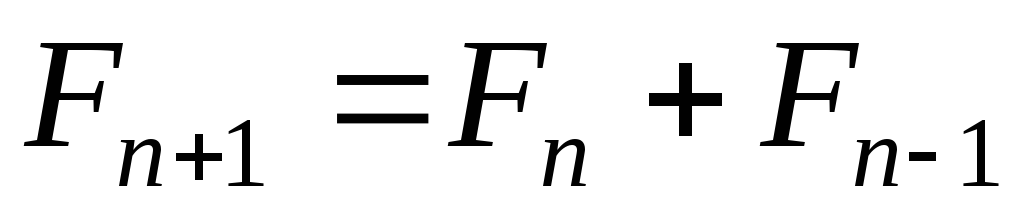 . (8.1)
. (8.1)
Формула (8.1) позволяет вычислить ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, …
Числа в данной последовательности называются числами Фибоначчи
Если
принять 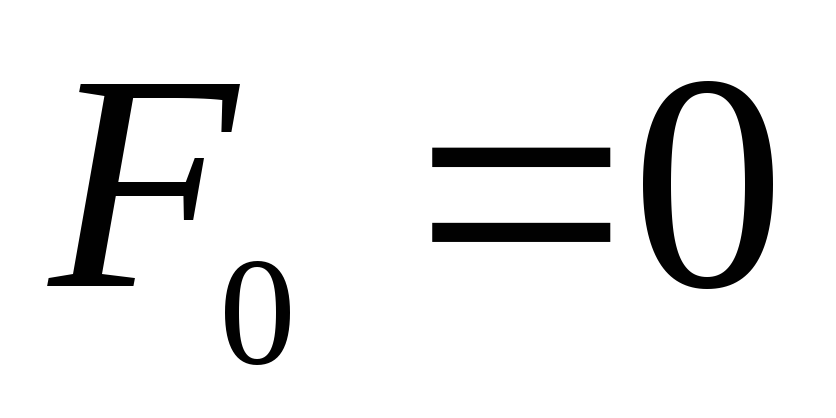 и
и  ,
то с помощью формулы (8.1) можно определить
все остальные числа Фибоначчи. Формула
(8.1) называется рекуррентной формулой (recurrence – «возвращение» на латыни).
,
то с помощью формулы (8.1) можно определить
все остальные числа Фибоначчи. Формула
(8.1) называется рекуррентной формулой (recurrence – «возвращение» на латыни).
Пример 8.1. Предположим, что имеется лестница в n ступенек. Мы можем подниматься по ней с шагом в одну ступеньку, либо – с шагом в две ступеньки. Сколько существует комбинаций различных способов подъема?
Если n = 1, имеется только один вариант решения задачи. Для n = 2 существует 2 варианта: два единичных шага либо один двойной. Для n = 3 существует 3 варианта: три единичных шага, либо один единичный и один двойной, либо один двойной и один единичный.
В следующем случае
n = 4, имеем 5 возможностей (1+1+1+1, 2+1+1, 1+2+1, 1+1+2, 2+2). Для
того чтобы ответить на заданный вопрос
при произвольном n,
обозначим количество вариантов как  ,
и попробуем определить
,
и попробуем определить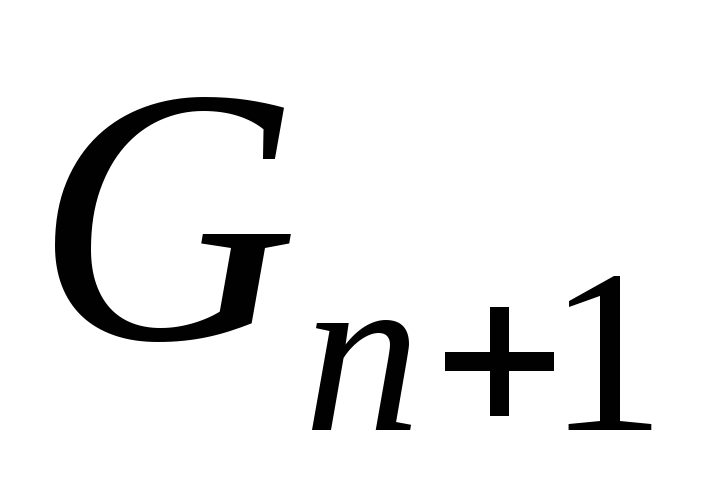 по известным
по известным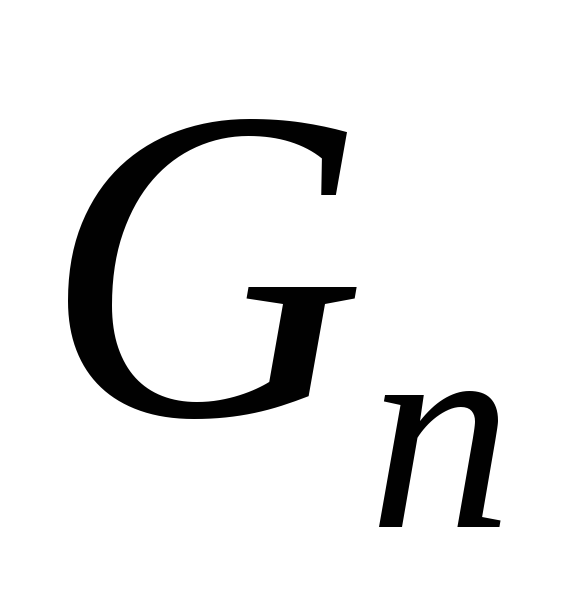 и
и 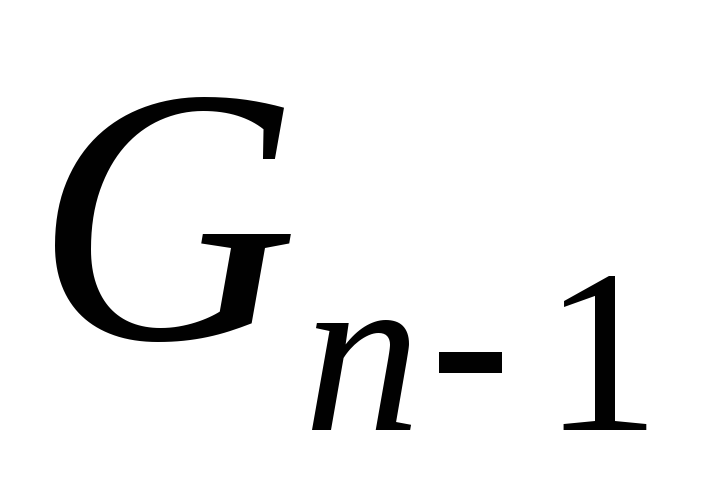 .
Если мы стартуем с единичного шага, то
имеем
.
Если мы стартуем с единичного шага, то
имеем 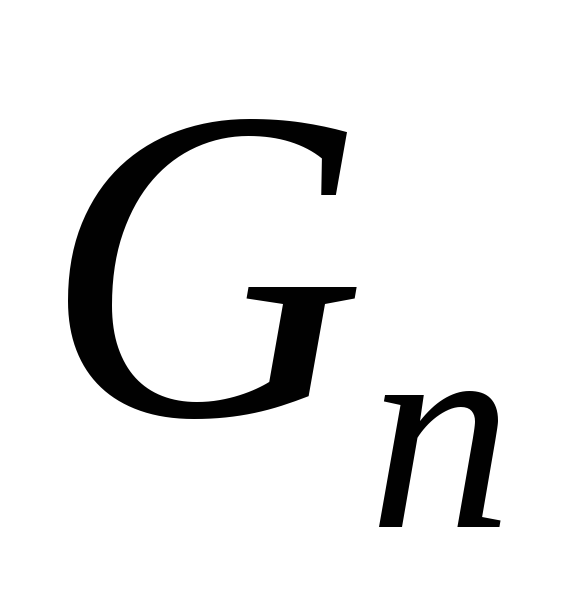 комбинаций для оставшихсяn ступенек. Если стартуем с двойного шага,
то имеем
комбинаций для оставшихсяn ступенек. Если стартуем с двойного шага,
то имеем 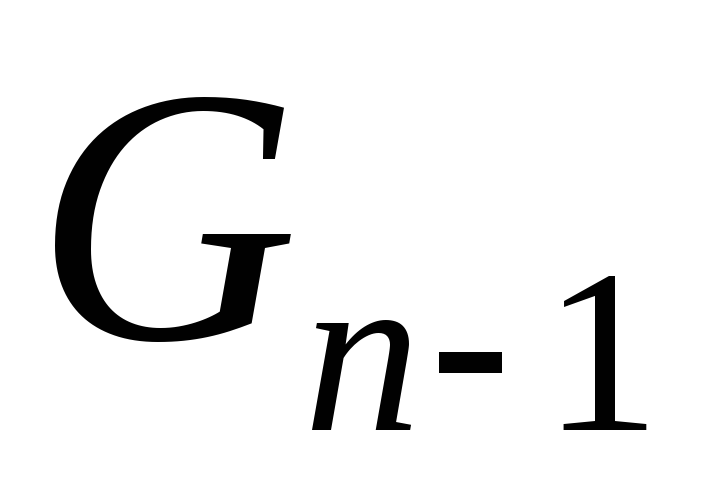 комбинаций для оставшихсяn–1
ступенек. Общее количество вариантов
для
комбинаций для оставшихсяn–1
ступенек. Общее количество вариантов
для
 . (8.2)
. (8.2)
Полученная
формула как близнец напоминает формулу
(8.1). Тем не менее, это не позволяет
отождествлять количество комбинаций 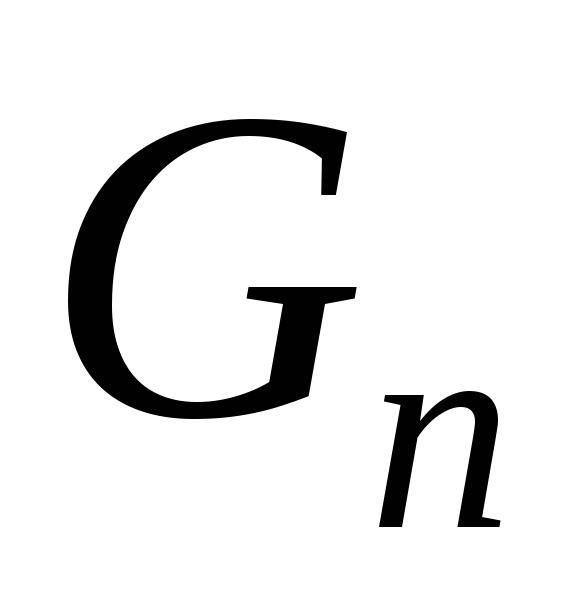 с числами Фибоначчи
с числами Фибоначчи .
Мы видим, например, что
.
Мы видим, например, что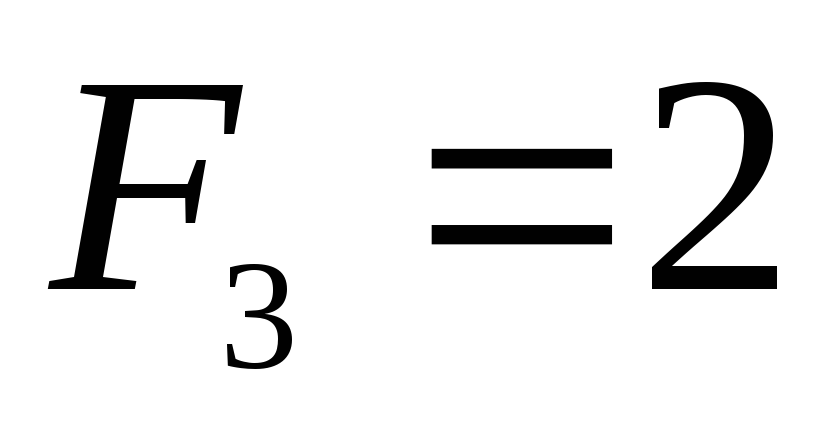 ,
но
,
но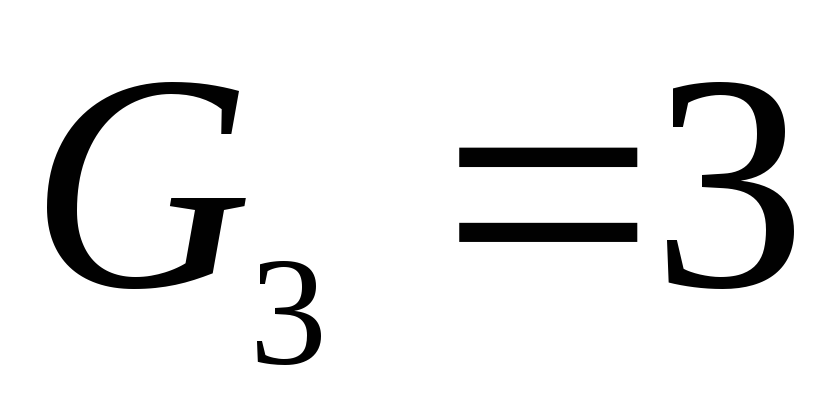 .
Однако имеет место следующая зависимость:
.
Однако имеет место следующая зависимость:
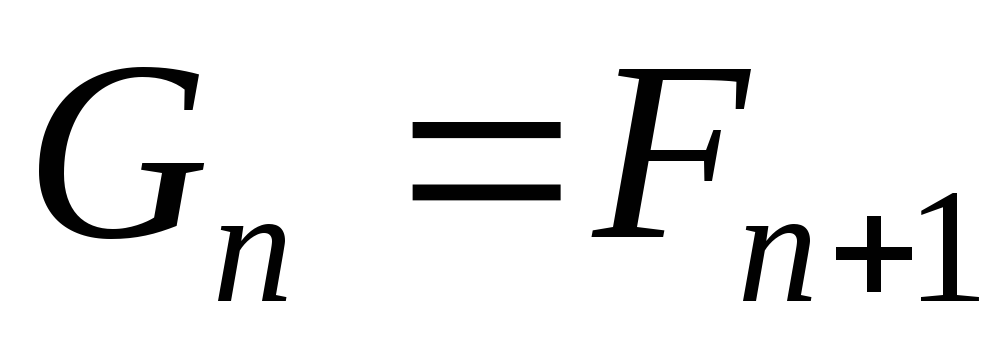 .
.
Это
справедливо для n = 1, 2, и также справедливо для каждого n.
Числа Фибоначчи и количество комбинаций 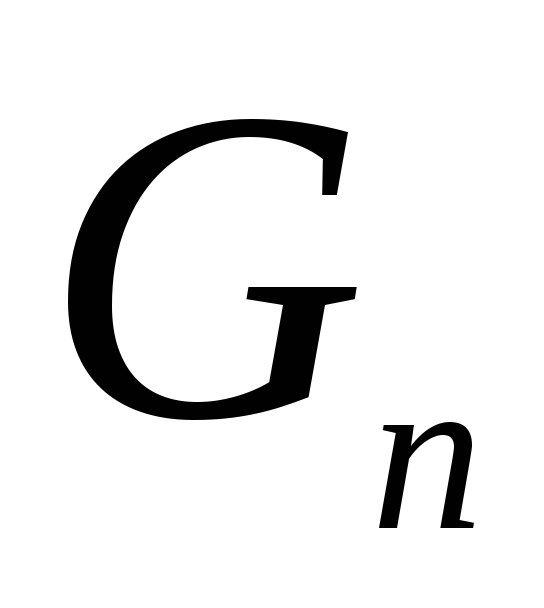
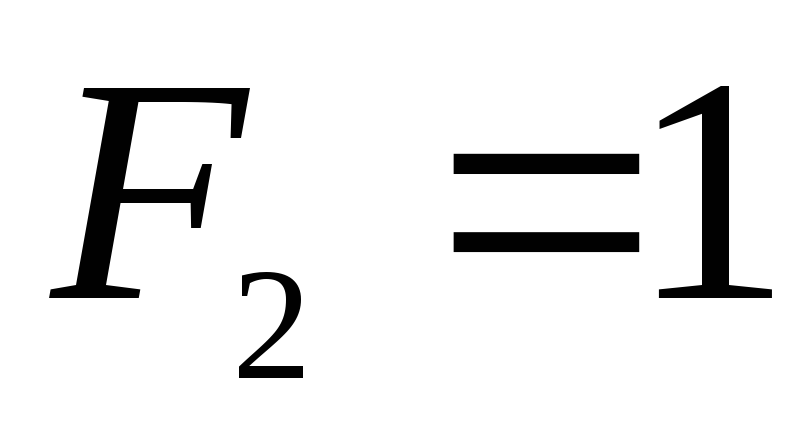 и
и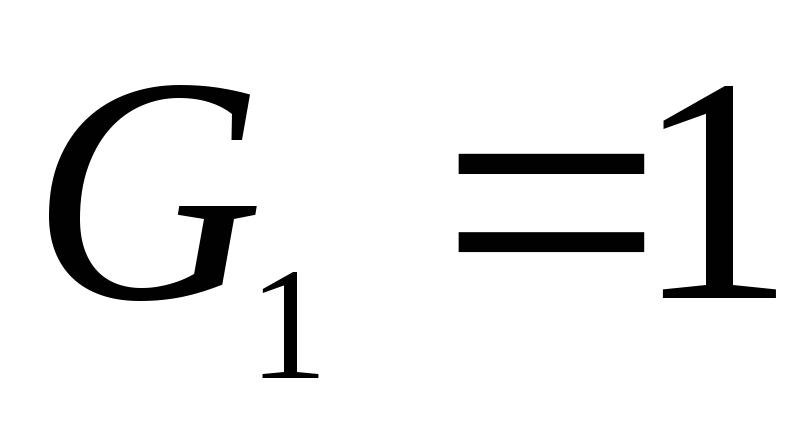 ,
,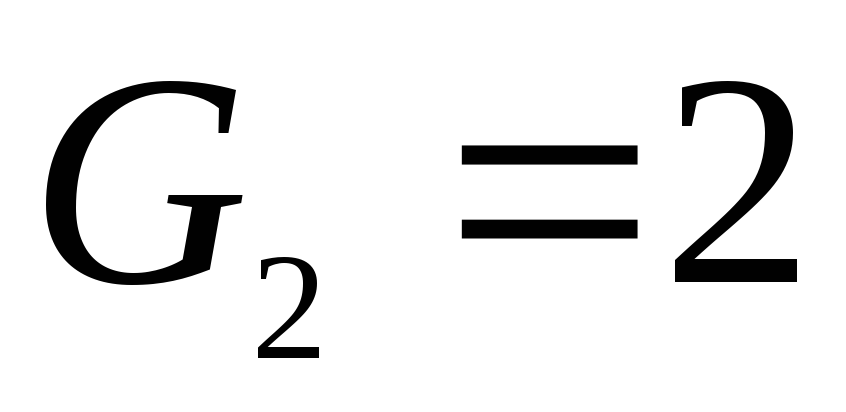 у них различаются.
у них различаются. Пример 8.2. Этот пример имеет
практическое
значение для задач помехоустойчивого
кодирования. Найдем число всех двоичных
слов длины n,
не содержащих несколько нулей подряд.
Обозначим это число через 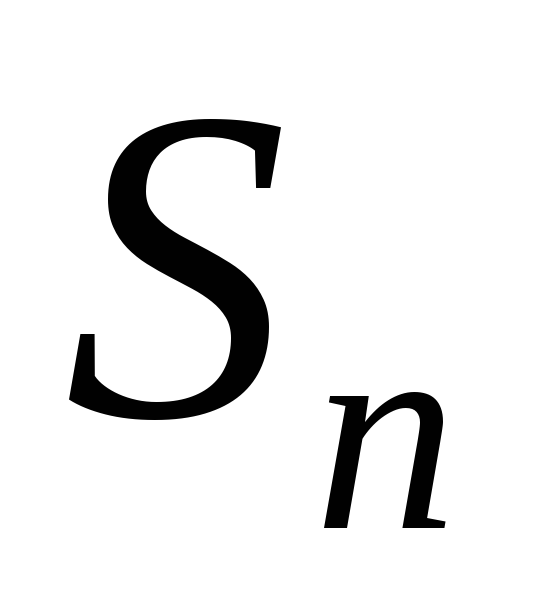 .
Очевидно,
.
Очевидно,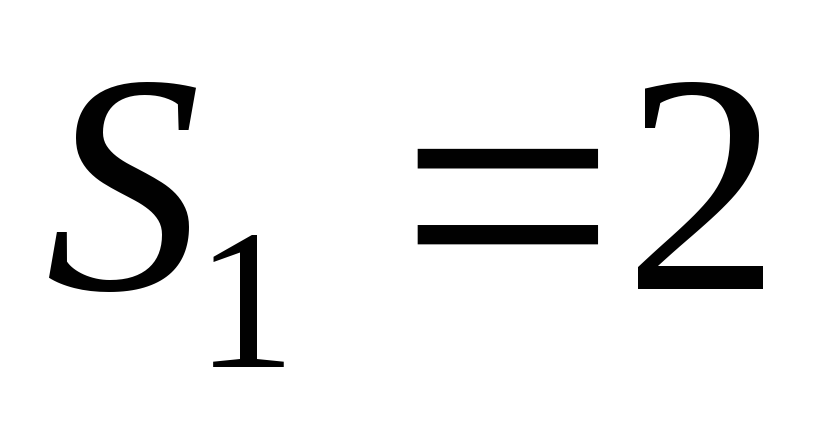 ,
а слова длины 2, удовлетворяющие нашему
ограничению, таковы: 10, 01, 11, т.е.
,
а слова длины 2, удовлетворяющие нашему
ограничению, таковы: 10, 01, 11, т.е.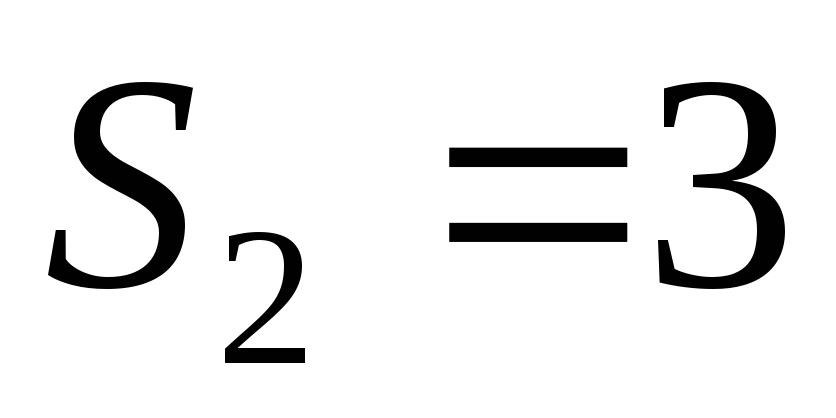
 – такое слово изn символов. Если символ
– такое слово изn символов. Если символ 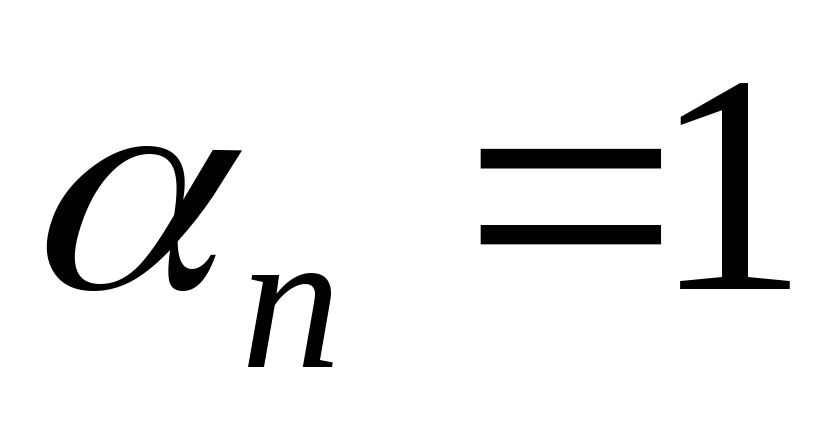 ,
то
,
то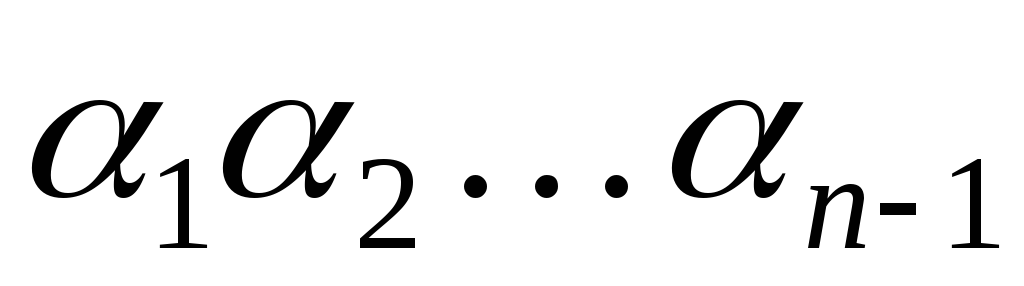 может быть произвольным (
может быть произвольным (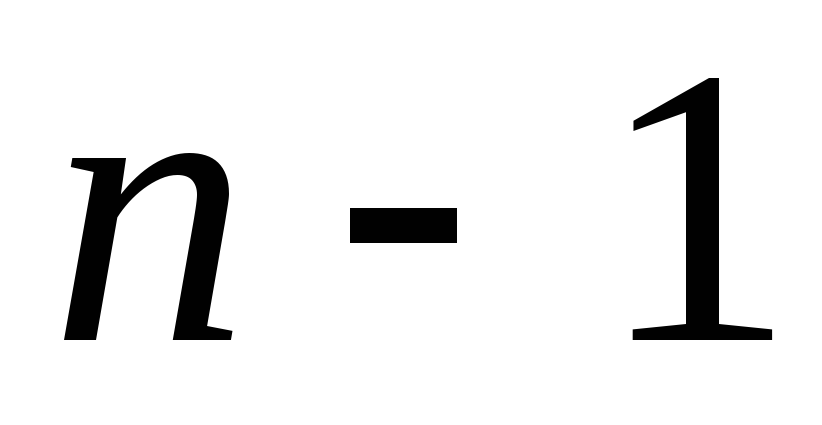 )-буквенным
словом, не содержащим несколько нулей
подряд. Значит, число слов с единицей
на конце равно
)-буквенным
словом, не содержащим несколько нулей
подряд. Значит, число слов с единицей
на конце равно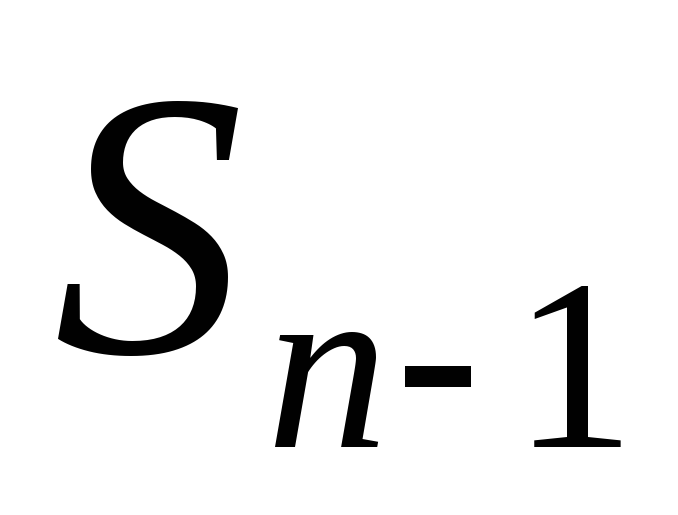 .
. Если же символ 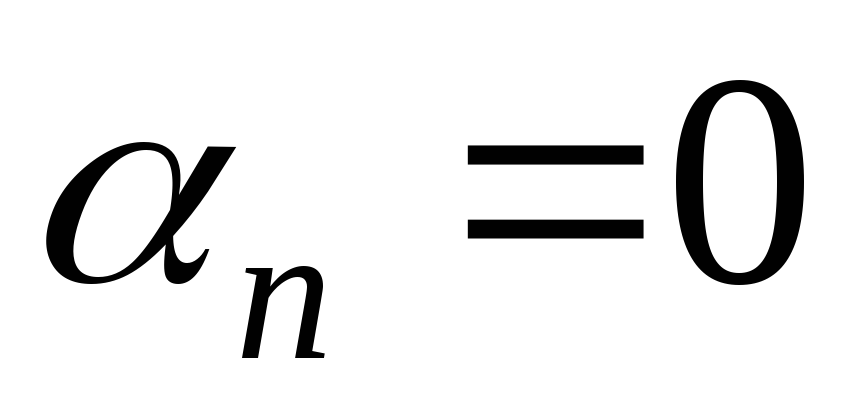 ,
то обязательно
,
то обязательно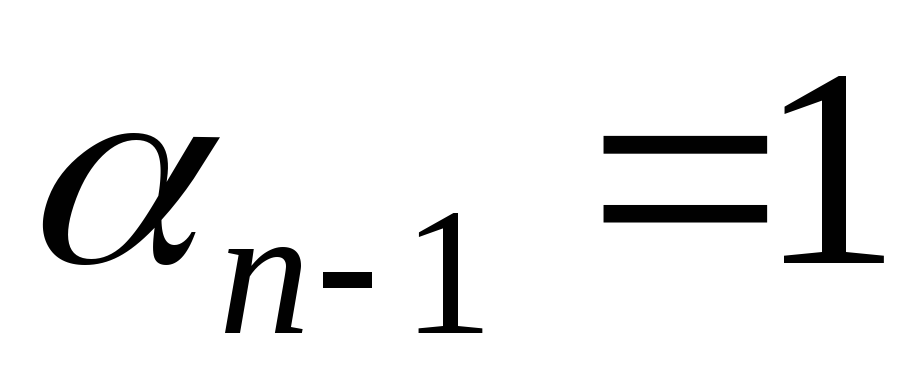 ,
а первые
,
а первые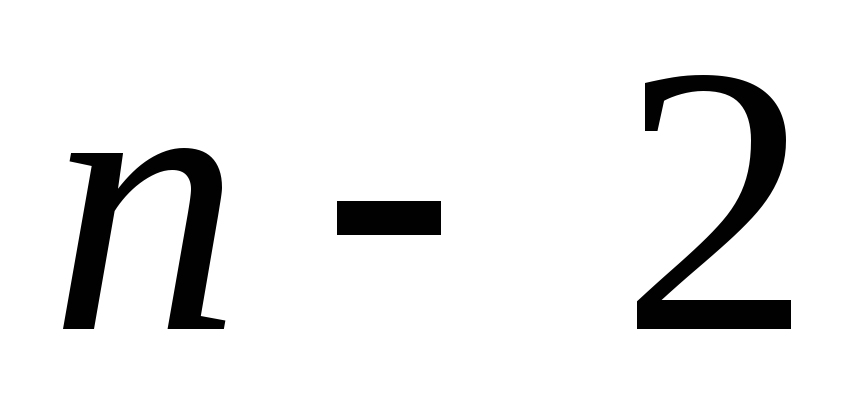
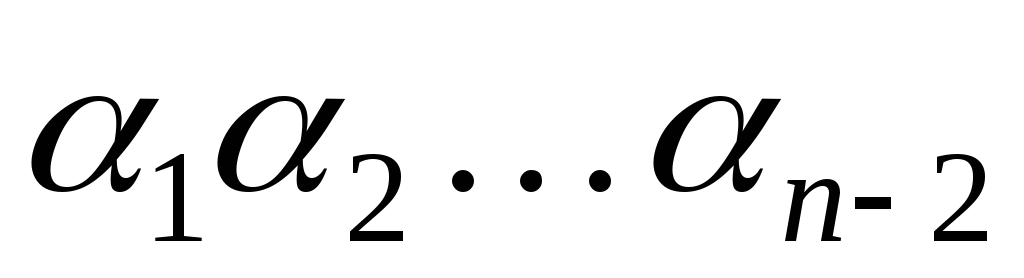 могут быть произвольными с учетом
рассматриваемых ограничений. Следовательно,
имеется
могут быть произвольными с учетом
рассматриваемых ограничений. Следовательно,
имеется слов длины n с нулем на конце. Таким образом, общее
число интересующих нас слов равно
слов длины n с нулем на конце. Таким образом, общее
число интересующих нас слов равно 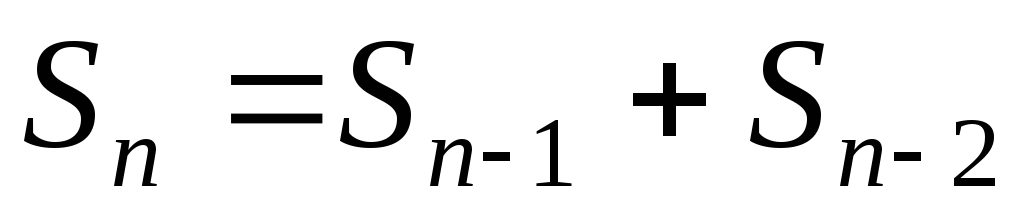 .
.
С учетом того, что 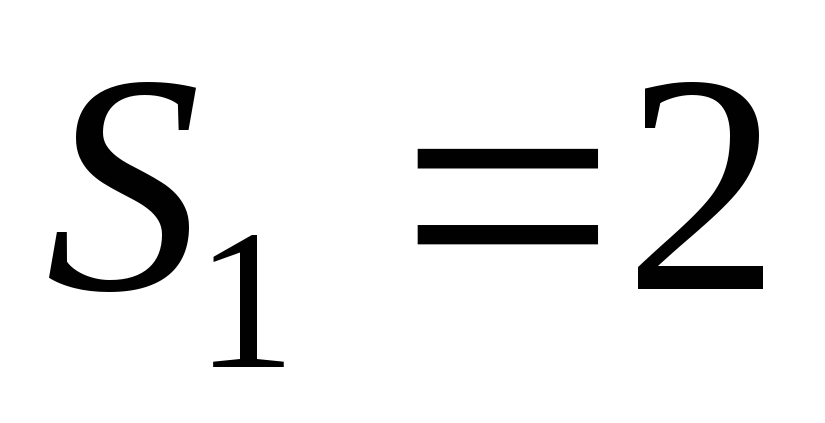 и
и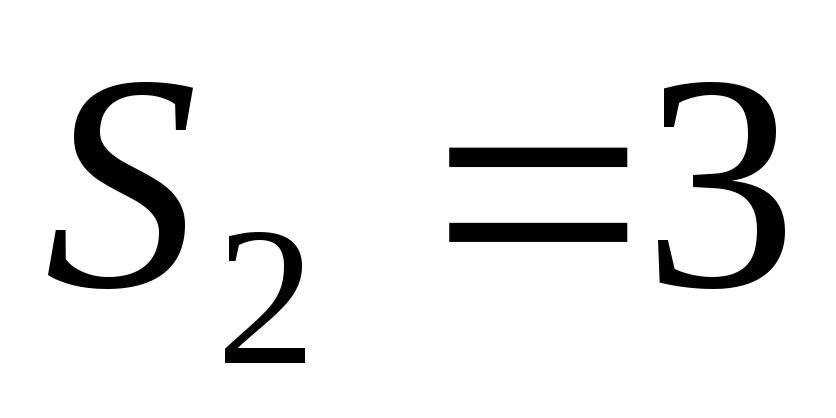 ,
полученная последовательность чисел
– это числа Фибоначчи.
,
полученная последовательность чисел
– это числа Фибоначчи.
Пример 8.3. В
примере 7.6 мы нашли, что число двоичных
слов постоянного веса t (и длиной k)
равно 
Рассуждать можно
так. Пусть 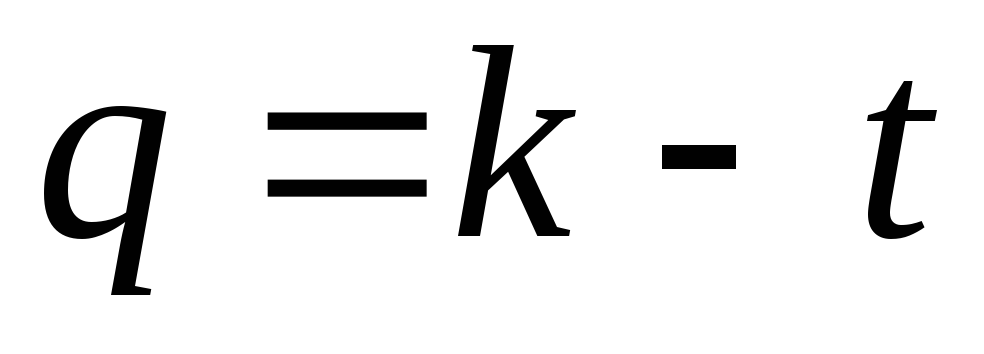 число нулей в рассматриваемых словах.
В любом слове имеется
число нулей в рассматриваемых словах.
В любом слове имеется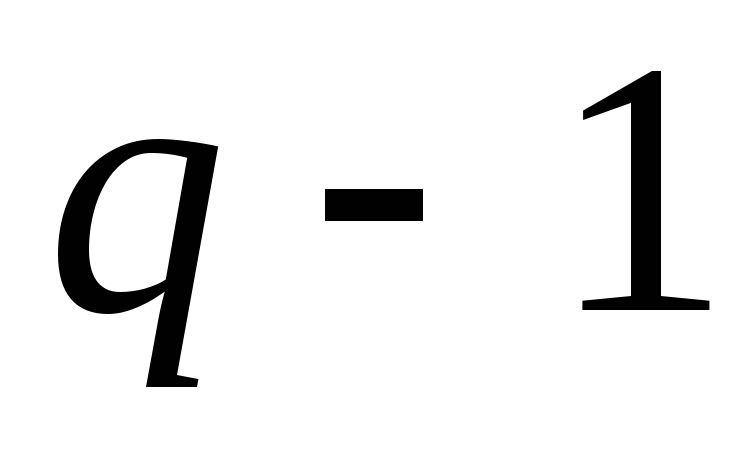 промежутков между ближайшими нулями,
в каждом из которых находится одна или
несколько единиц. Предполагается, что
промежутков между ближайшими нулями,
в каждом из которых находится одна или
несколько единиц. Предполагается, что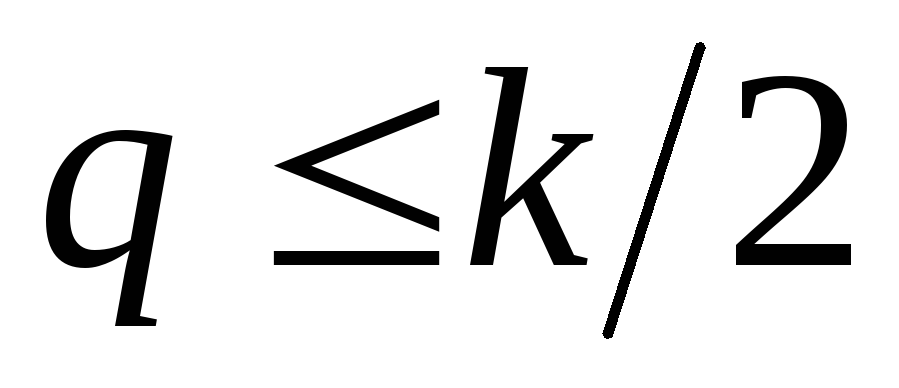 .
В противном случае нет ни одного слова
без рядом стоящих нулей.
.
В противном случае нет ни одного слова
без рядом стоящих нулей.
Если из каждого
промежутка удалить ровно по одной
единице, то получим слово длины 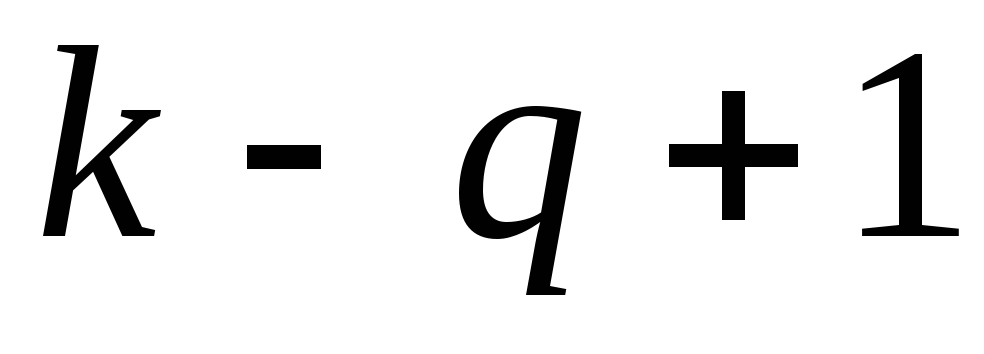 ,
содержащее
,
содержащее
 нулей, никакие два из которых не стоят
рядом. Значит, искомое число совпадает
с числом всех слов длины
нулей, никакие два из которых не стоят
рядом. Значит, искомое число совпадает
с числом всех слов длины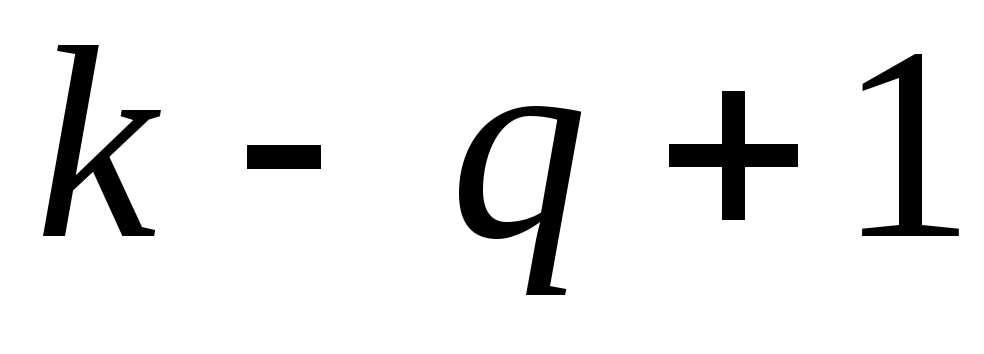 ,
содержащих ровно
,
содержащих ровно нулей, т.е. равно
нулей, т.е. равно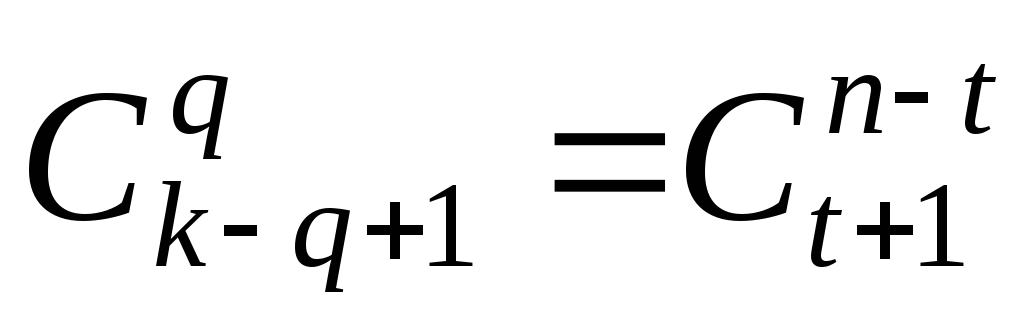 .
. Пример 8.4. Докажем, что сумма 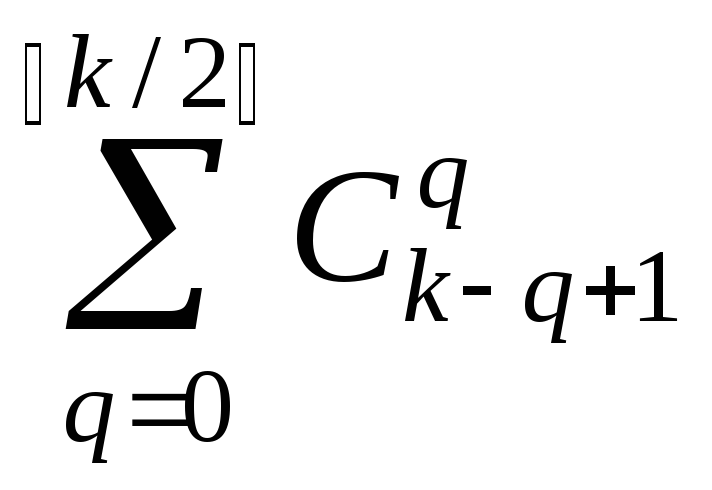 равна числам Фибоначчи для любого целого
равна числам Фибоначчи для любого целого .
Символ
.
Символ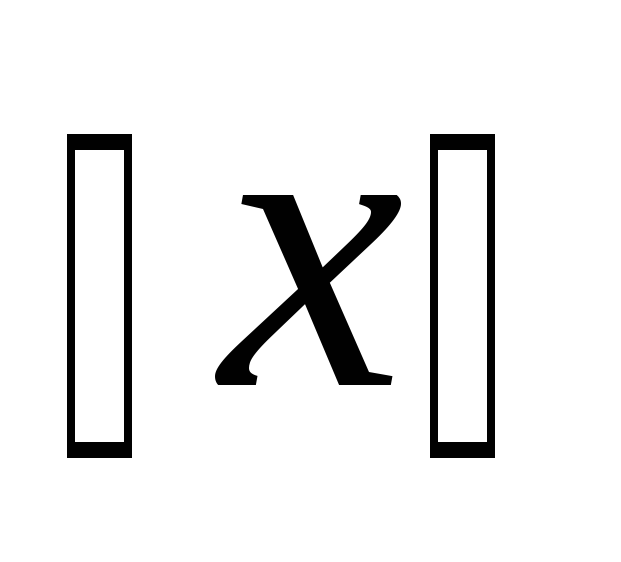
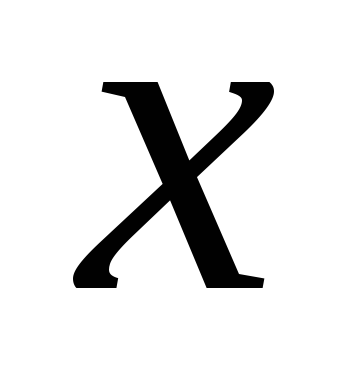 .
Например, если
.
Например, если ,
то
,
то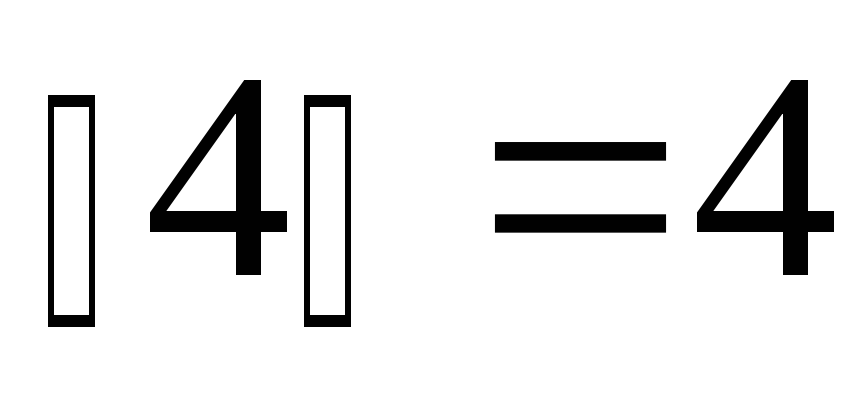 ;
а если
;
а если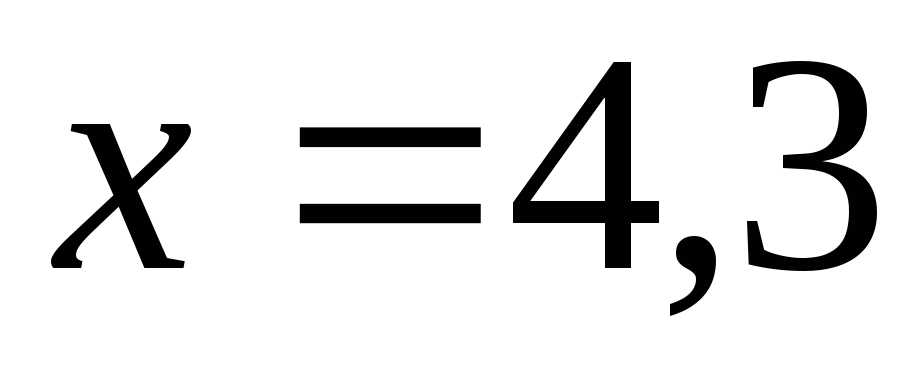 ,
то
,
то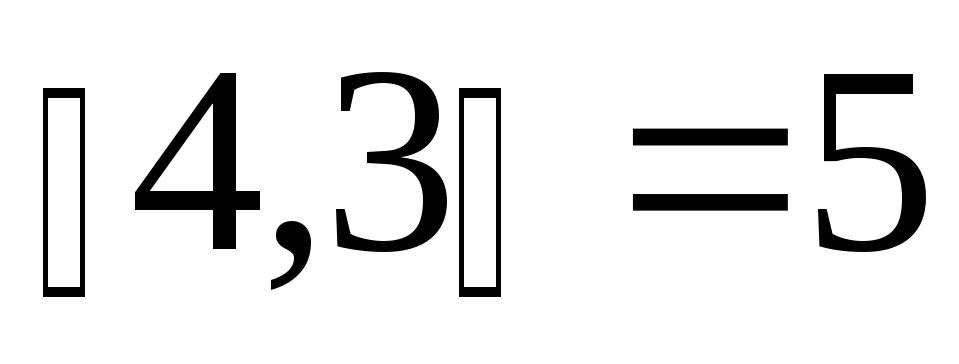 .
По-английски эту операцию называютceil («потолок»). Также встречается символ
.
По-английски эту операцию называютceil («потолок»). Также встречается символ 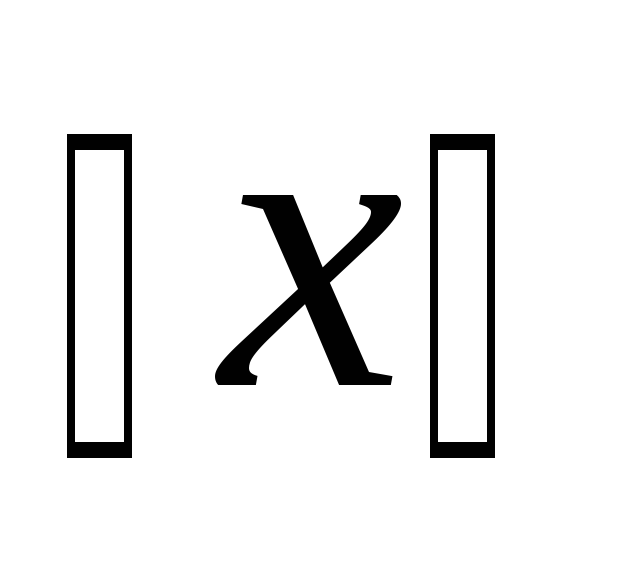 ,
который обозначаетнаибольшее
целое число, меньшее или равное
,
который обозначаетнаибольшее
целое число, меньшее или равное 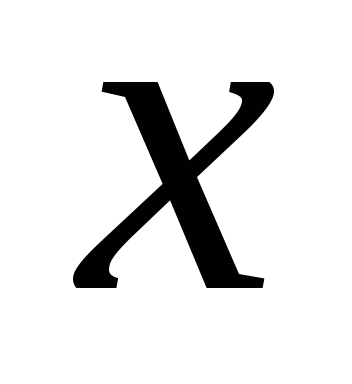 .
По-английски эту операцию называютfloor («пол»).
.
По-английски эту операцию называютfloor («пол»). Если 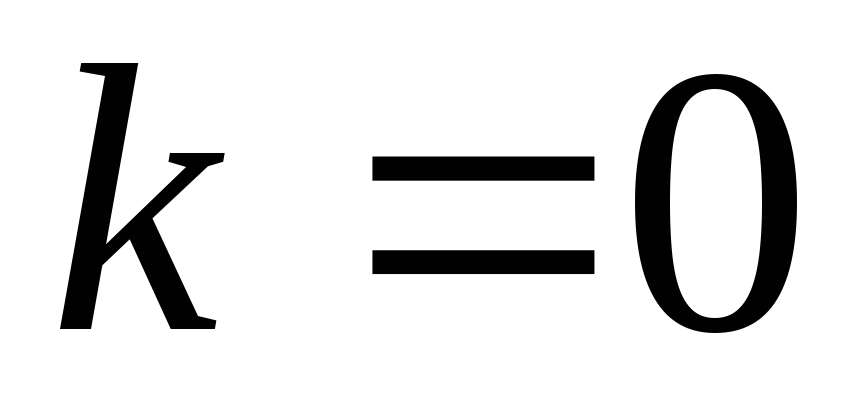 ,
то
,
то .
Если
.
Если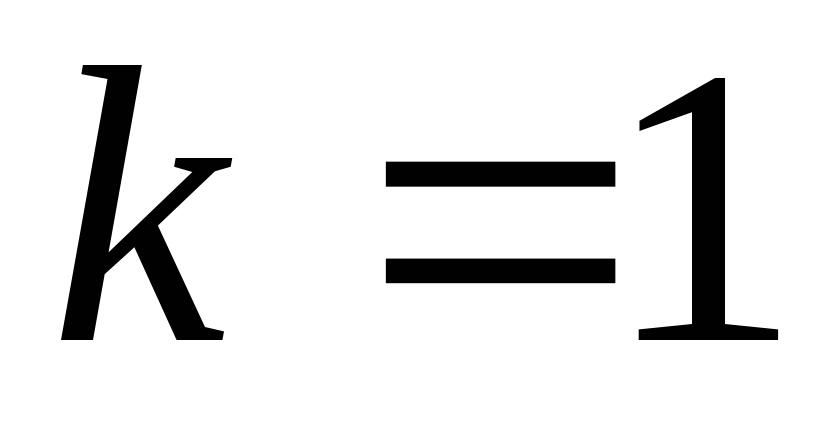 ,
то
,
то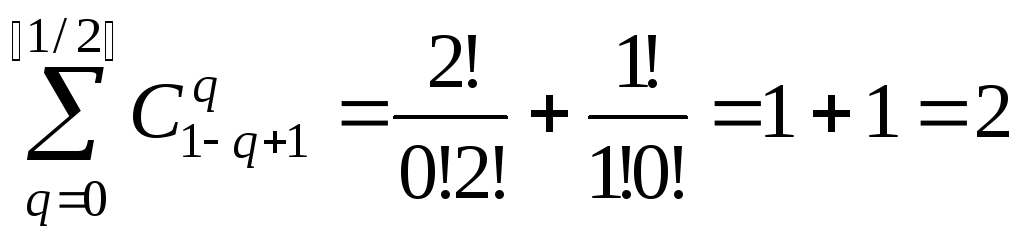 .
Если
.
Если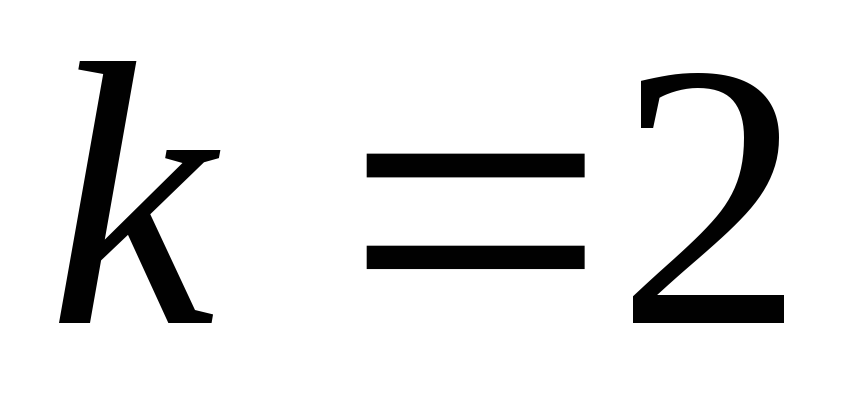 ,
то
,
то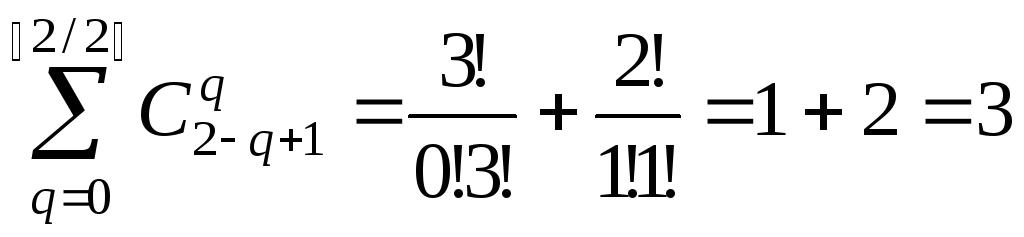 .
.
Таким образом, для рассмотренных случаев сумма действительно равна числам Фибоначчи. Теперь приведем доказательство для общего случая. Поскольку числа Фибоначчи можно получить с помощью рекуррентного уравнения (8.1), то должно выполняться равенство:
 .
.
И оно действительно выполняется:
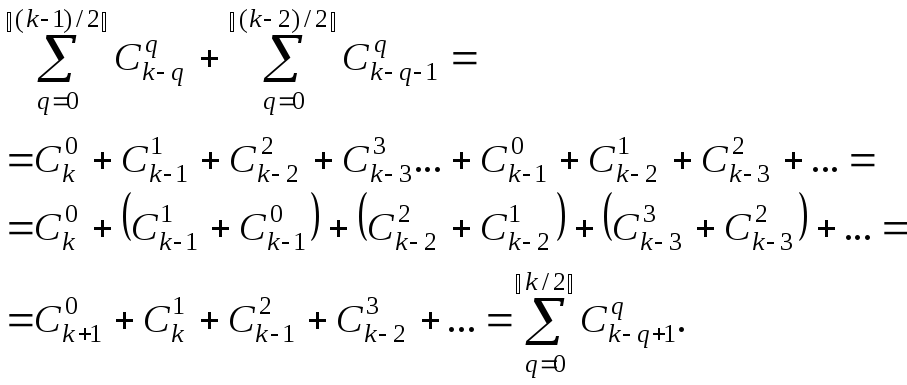
Здесь мы использовали
полученную ранее формулу (4.4): 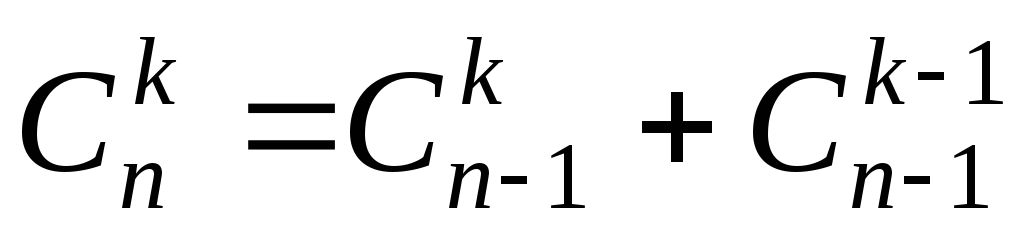 .
.
Сумма чисел Фибоначчи
Определим сумму первых n чисел Фибоначчи.
0 = 0,
0+1 = 1,
0+1+1 = 2,
0+1+1+2 = 4,
0+1+1+2+3 = 7,
0+1+1+2+3+5 = 12,
0+1+1+2+3+5+8 = 20,
0+1+1+2+3+5+8+13 = 33.
Легко заметить, что прибавлением к правой части каждого уравнения единицы мы снова получаем число Фибоначчи. Общая формула для определения суммы первых n чисел Фибоначчи имеет вид:
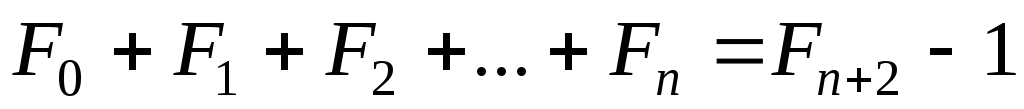 .
.
Докажем это, используя метод математической индукции. Для этого запишем:
 .
.
Эта
сумма должна быть равна 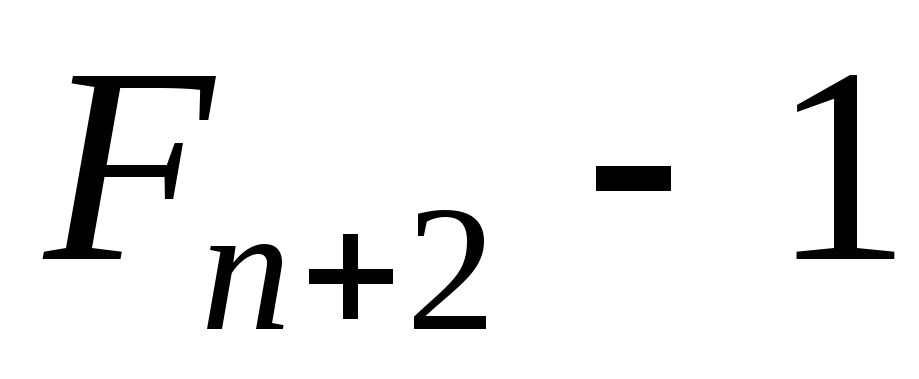 .
.
 .
.
Сократив левую и правую часть уравнения на –1, получим уравнение (6.1).
Формула для чисел Фибоначчи
Теорема 8.1. Числа Фибоначчи можно рассчитать по формуле
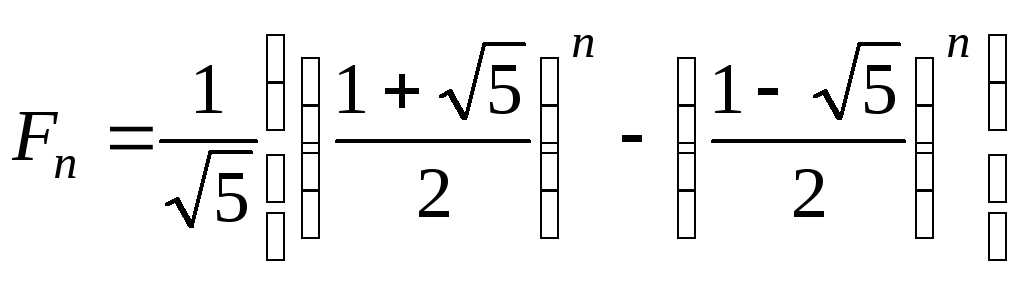 .
.
Доказательство. Убедимся в справедливости этой формулы для n = 0, 1, а затем докажем справедливость данной формулы для произвольного n по индукции. Вычислим отношение двух ближайших чисел Фибоначчи:
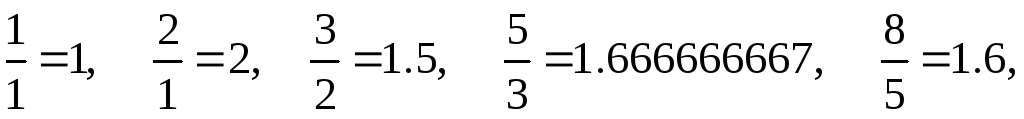
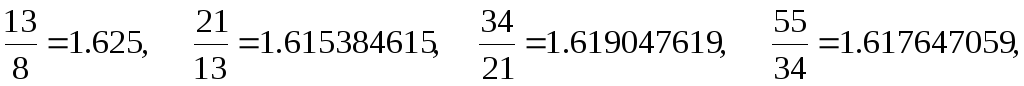
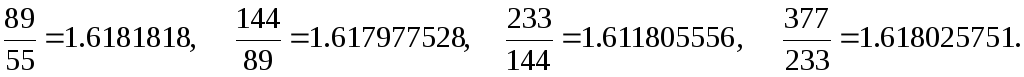
Мы
видим, что отношение этих чисел колеблется
около значения 1.618 (если игнорировать
несколько первых значений). Этим свойством
числа Фибоначчи напоминают члены
геометрической прогрессии. Примем  ,
(
,
(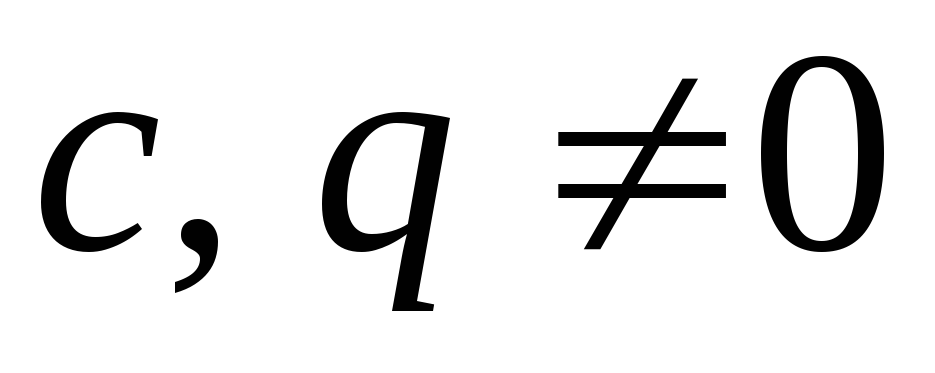 ).
Тогда выражение
).
Тогда выражение
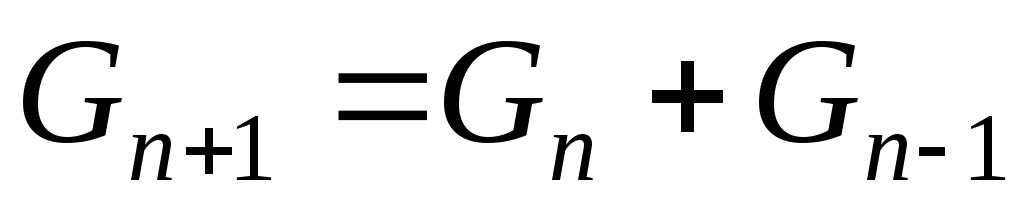
преобразуется в
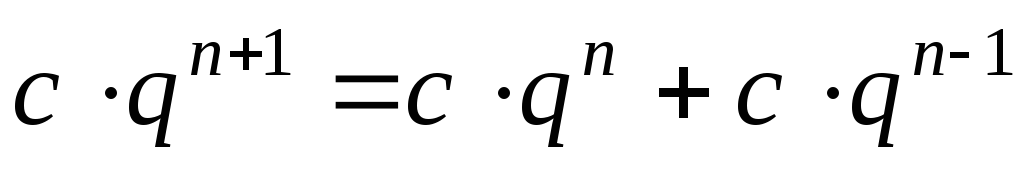 ,
,
которое после упрощений выглядит так
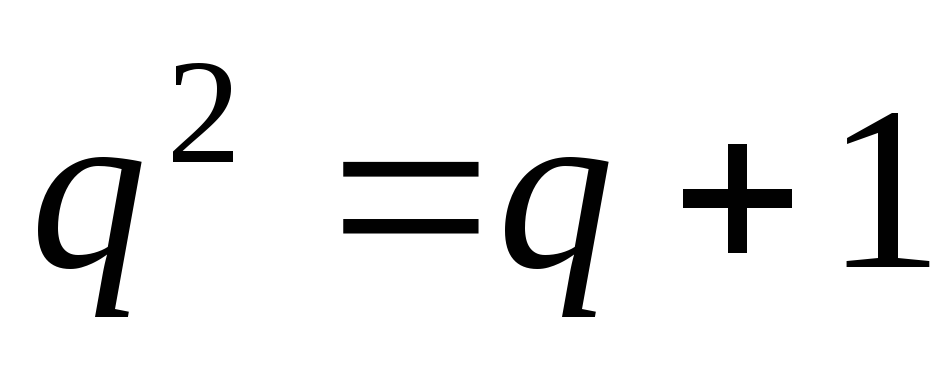 .
.
Мы получили квадратное уравнение, корни которого равны:
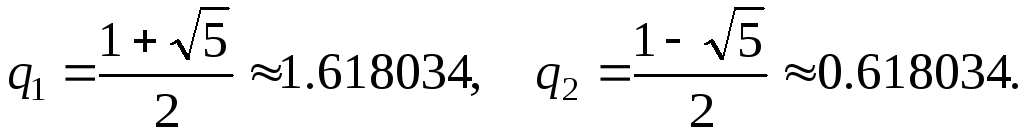
Теперь можем записать:
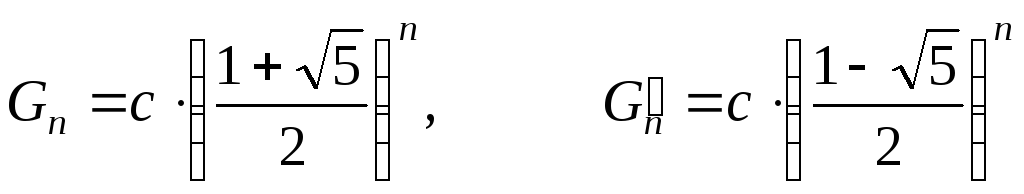
(где c является константой). Оба члена 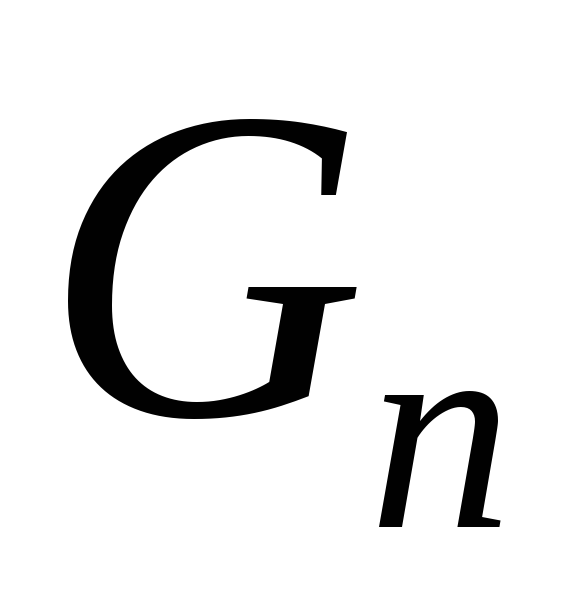 и
и 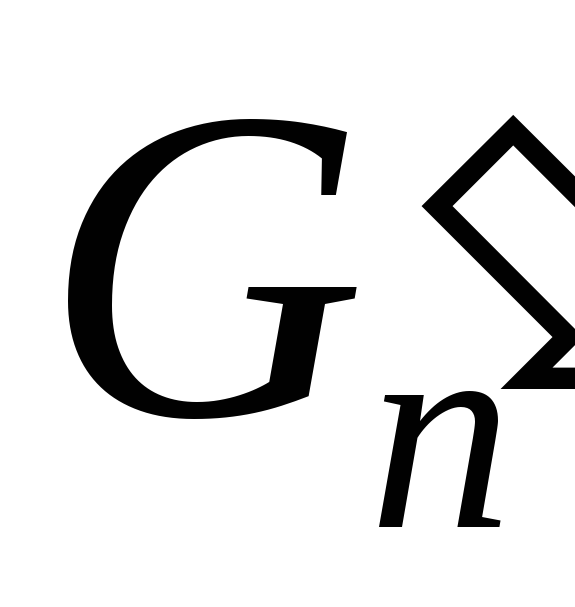 не дают чисел Фибоначчи,
например
не дают чисел Фибоначчи,
например 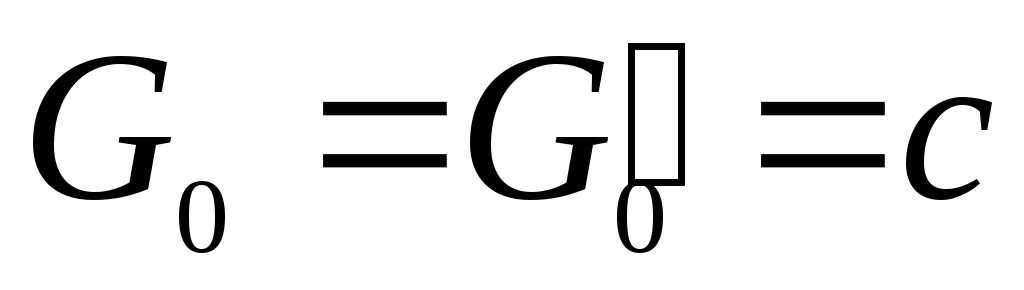 ,
в то время как
,
в то время как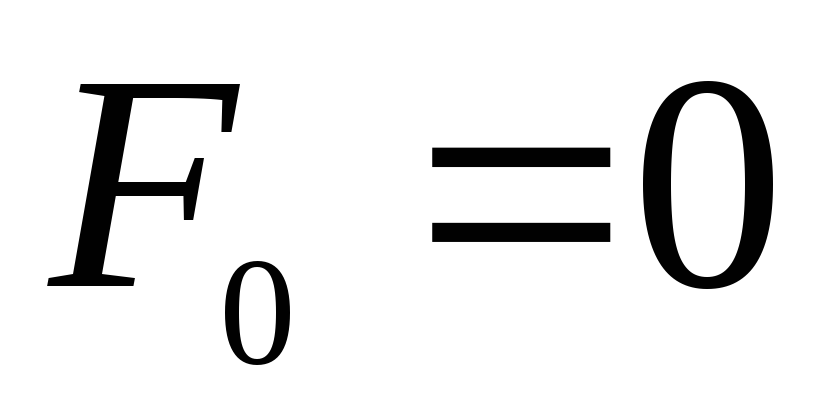 .
Однако разность
.
Однако разность 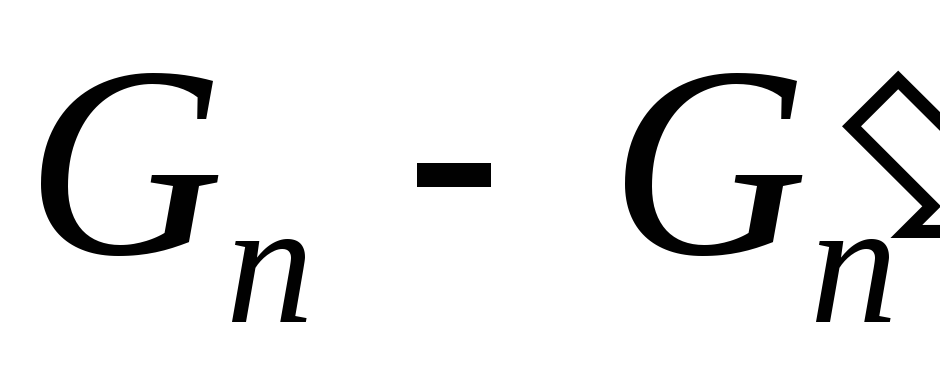 удовлетворяет
рекуррентному уравнению:
удовлетворяет
рекуррентному уравнению:
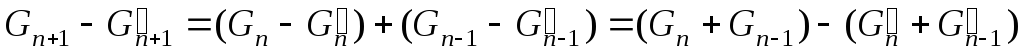 .
.
Для n=0
эта разность дает ,
то есть:
,
то есть:  .
Однако при n=1
мы имеем
.
Однако при n=1
мы имеем 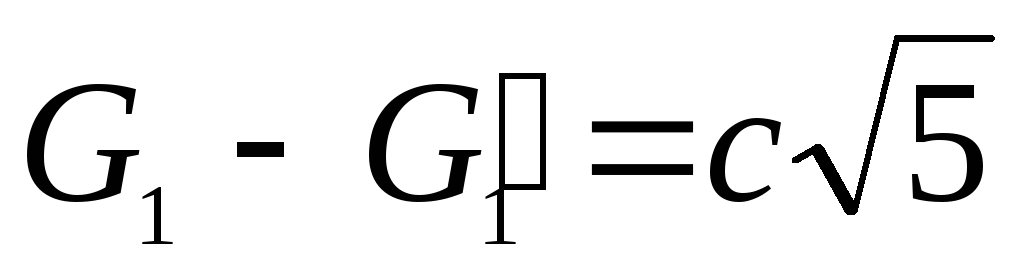 .
Чтобы получить
.
Чтобы получить  ,
необходимо принять:
,
необходимо принять: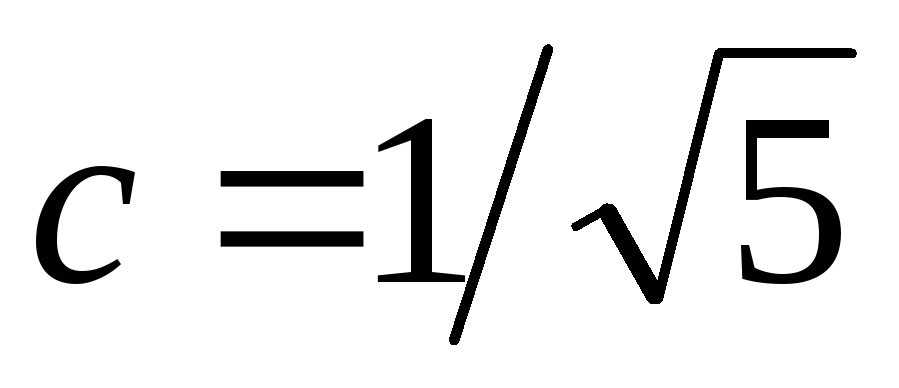 .
.
Теперь
мы имеем две последовательности:  и
и  ,
которые начинаются с одинаковых двух
чисел и удовлетворяют одной и той же
рекуррентной формуле. Они должны быть
равны:
,
которые начинаются с одинаковых двух
чисел и удовлетворяют одной и той же
рекуррентной формуле. Они должны быть
равны: 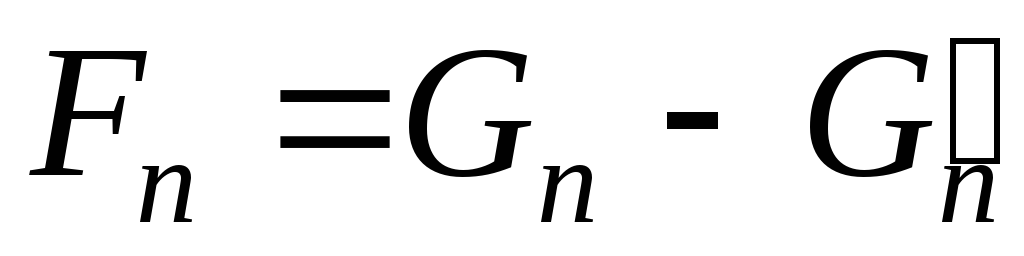 .
Теорема доказана.
.
Теорема доказана.
При
возрастании n член 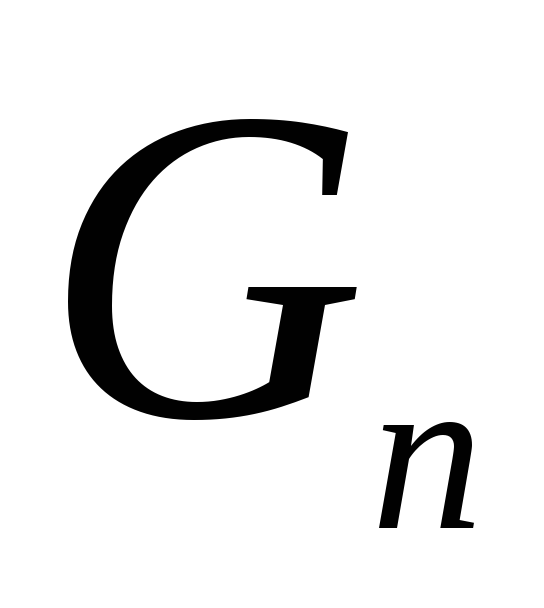 становится очень большим, в то время
как
становится очень большим, в то время
как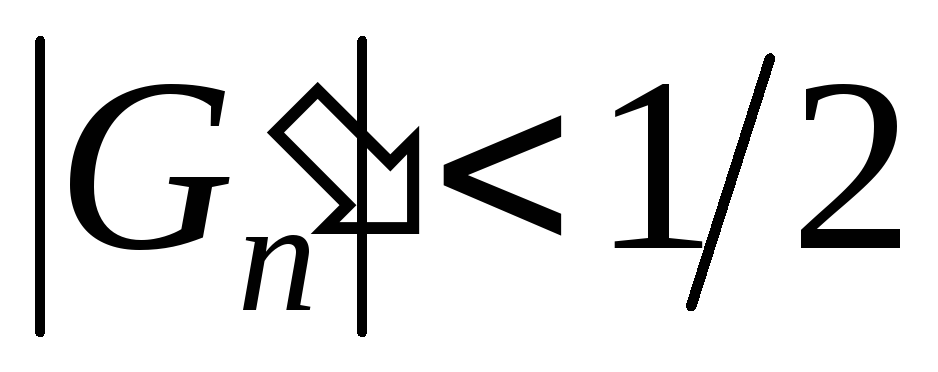 ,
и роль члена
,
и роль члена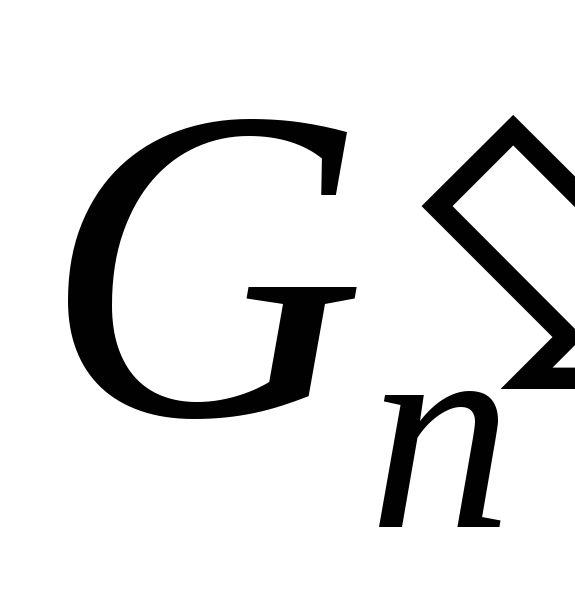 в разности сокращается.
Поэтому при больших n приближенно можем записать
в разности сокращается.
Поэтому при больших n приближенно можем записать
 .
.
Мы игнорируем 1/2 (поскольку числа Фибоначчи возрастают до бесконечности при росте n до бесконечности).
Отношение  называется золотым
сечением,
его используют за пределами математики
(например, в скульптуре и архитектуре).
Золотым сечением является отношение
между диагональю и стороной правильного
пятиугольника (рис. 8.1).
называется золотым
сечением,
его используют за пределами математики
(например, в скульптуре и архитектуре).
Золотым сечением является отношение
между диагональю и стороной правильного
пятиугольника (рис. 8.1).
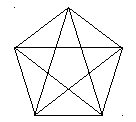
Рис. 8.1. Правильный пятиугольник и его диагонали
Для обозначения
золотого сечения принято использовать
букву 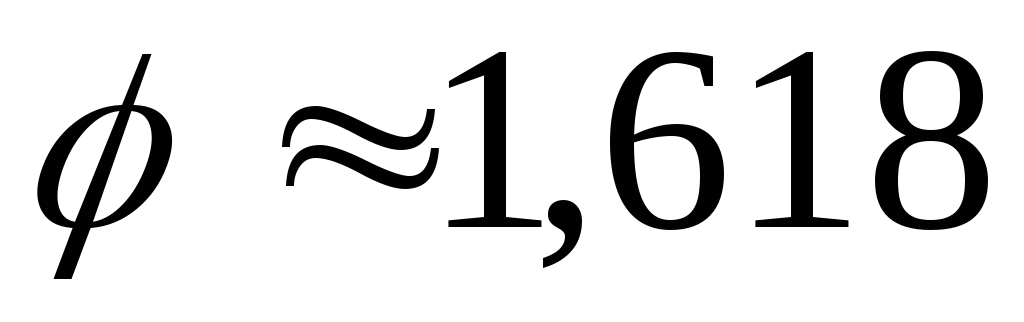 в честь известного афинского скульптора
Фидия.
в честь известного афинского скульптора
Фидия.
Простые числа
Все натуральные числа, большие единицы, распадаются на два класса. К первому относятся числа, имеющие ровно два натуральных делителя, единицу и самого себя, ко второму – все остальные. Числа первого класса называют простыми, а второго – составными. Простые числа в пределах первых трех десятков: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …
Свойства простых чисел и их связь со всеми натуральными числами изучалась Евклидом (3 век до нашей эры). Если выписывать простые числа подряд, то можно заметить, что относительная плотность их убывает. На первый десяток их приходится 4, т. е. 40%, на сотню – 25, т.е. 25%, на тысячу – 168, т.е. меньше 17%, на миллион – 78498, т.е. меньше 8%, и т.д.. Тем не менее, их общее число бесконечно.
Среди простых чисел попадаются пары таких, разность между которыми равна двум (так называемые простые близнецы), однако конечность или бесконечность таких пар не доказана.
Евклид считал очевидным, что с помощью умножения только простых чисел можно получить все натуральные числа, причем каждое натуральное число представимо в виде произведения простых чисел единственным образом (с точностью до порядка множителей). Таким образом, простые числа образуют мультипликативный базис натурального ряда.
Изучение распределения
простых чисел привело к созданию
алгоритма, позволяющего получать таблицы
простых чисел. Таким алгоритмом является решето
Эратосфена (3 век до нашей эры). Этот метод заключается
в отсеивании (например, путем зачеркивания)
тех целых чисел заданной последовательности  ,
которые делятся хотя бы на одно из
простых чисел, меньших
,
которые делятся хотя бы на одно из
простых чисел, меньших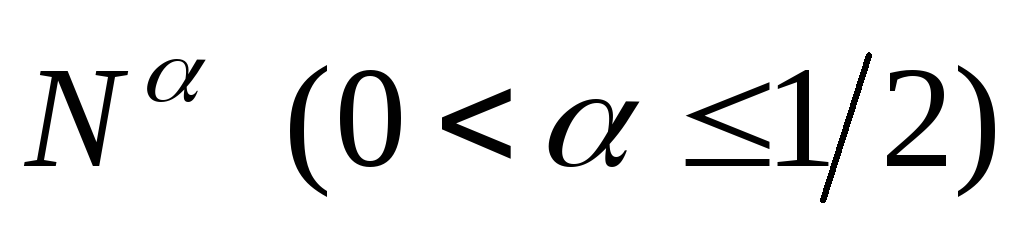 .
.
Теорема 8.2. (теорема Евклида). Число простых чисел бесконечно.
Доказательство. Теорему Евклида о бесконечности числа простых чисел докажем способом, предложенным Леонардом Эйлером (1707–1783). Эйлер рассмотрел произведение по всем простым числам p:

при 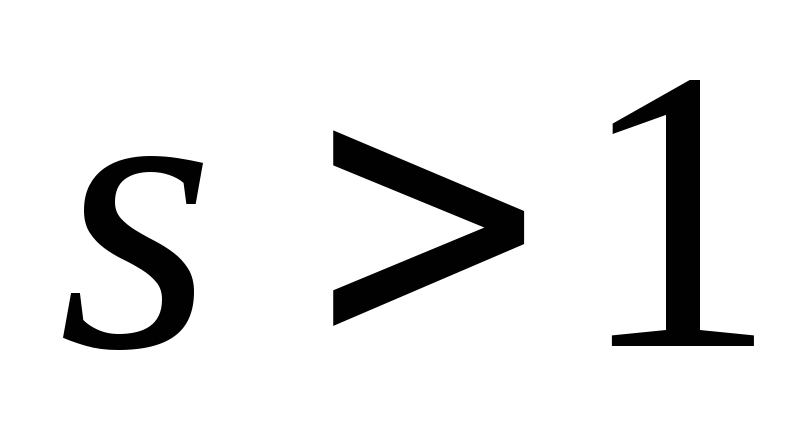 .
Это произведение сходится, и если его
раскрыть, то в силу однозначности
разложения натуральных чисел на простые
сомножители получается, что оно равняется
сумме ряда
.
Это произведение сходится, и если его
раскрыть, то в силу однозначности
разложения натуральных чисел на простые
сомножители получается, что оно равняется
сумме ряда ,
откуда следует тождество Эйлера:
,
откуда следует тождество Эйлера:
 .
.
Так как при 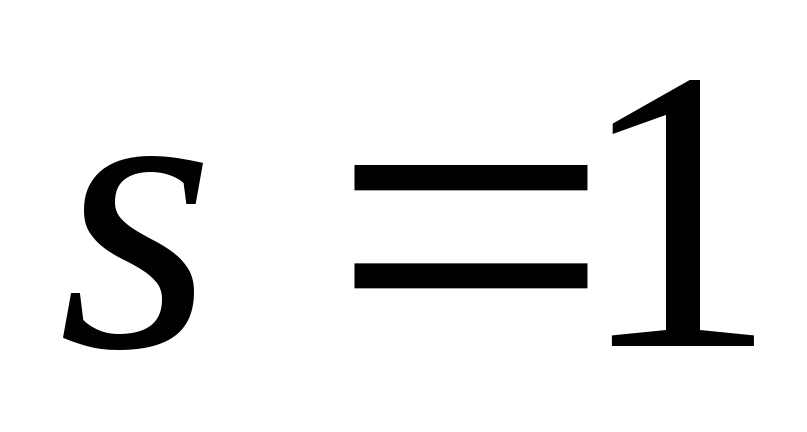 ряд справа расходится (гармонический
ряд), то из тождества Эйлера следует
теорема Евклида.
ряд справа расходится (гармонический
ряд), то из тождества Эйлера следует
теорема Евклида.
Русский математик
П.Л. Чебышев (1821–1894) вывел формулу,
определяющую пределы, в которых заключено
число простых чисел  ,
не превосходящихX:
,
не превосходящихX:
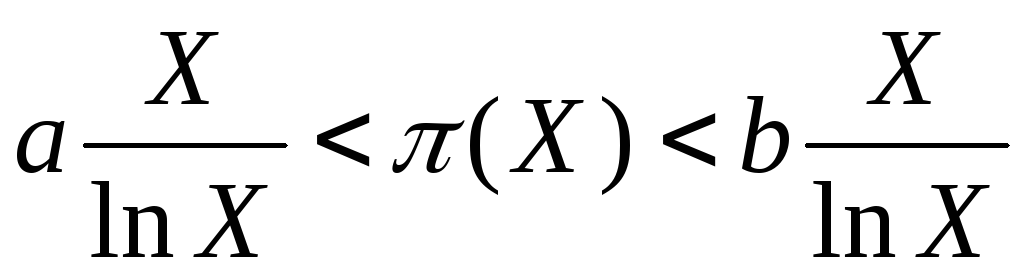 ,
,
где  ,
,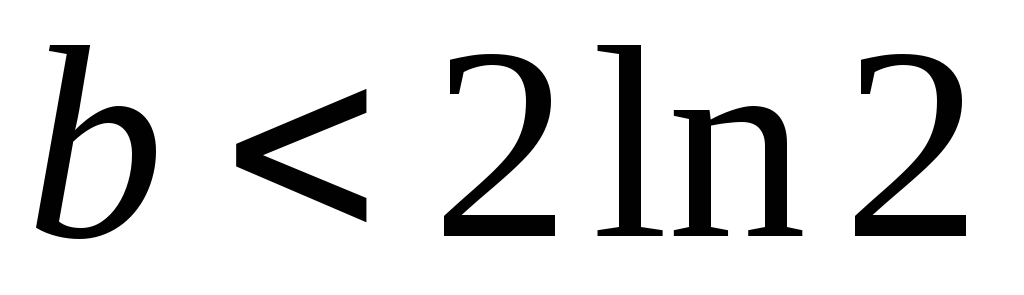 .
.
studfile.net
Последовательность Фибоначчи — это… Что такое Последовательность Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) [1].
Более формально, последовательность чисел Фибоначчи 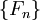 задается рекуррентным соотношением:
задается рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1:
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fn | −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко видеть, что F − n = ( − 1)n + 1Fn. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце, имеется пара кроликов (0 новых пар).
- В первом месяце, первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце, обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
- В третьем месяце, вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц n будет равна F(n). В это время, только кролики которые жили в месяце n-2 являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n — 1) + F(n — 2).
Формула Бине
Формула Бине выражает в явном виде значение Fn как функцию от n:
 ,
,
где 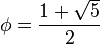 — золотое сечение. При этом
— золотое сечение. При этом 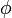 и
и 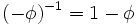 являются корнями квадратного уравнения
являются корнями квадратного уравнения 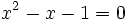 .
.
Из формулы Бине следует, что для всех 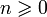 , Fn есть ближайшее к
, Fn есть ближайшее к 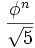 целое число, то есть
целое число, то есть 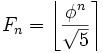 . В частности, справедлива асимптотика
. В частности, справедлива асимптотика 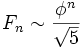 .
.
Тождества
И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц:
 , то есть
, то есть
 , а также
, а также  ,
,
- где матрицы имеют размер
 , i — мнимая единица.
, i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример —
 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
 .
.
- В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144. При этом для n=0,1,12 верно утверждение Fn = n2.
- Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y [2].
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т. д.
Вариации и обобщения
В других областях
- В природе
- Расстояния между листьями (или ветками) на стволе растения относятся примерно как числа Фибоначчи.
- В культуре
См. также
Литература
Ссылки
Примечания
- ↑ [1] БСЭ]
- ↑ P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p. 193.
Wikimedia Foundation. 2010.
dic.academic.ru
Число Фибоначчи — это… Что такое Число Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) [1].
Более формально, последовательность чисел Фибоначчи  задается рекуррентным соотношением:
задается рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1:
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fn | −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко видеть, что F − n = ( − 1)n + 1Fn. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце, имеется пара кроликов (0 новых пар).
- В первом месяце, первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце, обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
- В третьем месяце, вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц n будет равна F(n). В это время, только кролики которые жили в месяце n-2 являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n — 1) + F(n — 2).
Формула Бине
Формула Бине выражает в явном виде значение Fn как функцию от n:
 ,
,
где  — золотое сечение. При этом
— золотое сечение. При этом  и
и  являются корнями квадратного уравнения
являются корнями квадратного уравнения  .
.
Из формулы Бине следует, что для всех  , Fn есть ближайшее к
, Fn есть ближайшее к  целое число, то есть
целое число, то есть  . В частности, справедлива асимптотика
. В частности, справедлива асимптотика  .
.
Тождества
И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц:
 , то есть
, то есть
 , а также
, а также  ,
,
- где матрицы имеют размер
 , i — мнимая единица.
, i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример —
 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
 .
.
- В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144. При этом для n=0,1,12 верно утверждение Fn = n2.
- Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y [2].
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т. д.
Вариации и обобщения
В других областях
- В природе
- Расстояния между листьями (или ветками) на стволе растения относятся примерно как числа Фибоначчи.
- В культуре
См. также
Литература
Ссылки
Примечания
- ↑ [1] БСЭ]
- ↑ P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p. 193.
Wikimedia Foundation. 2010.
partners.academic.ru
Числа Фибоначчи — это… Что такое Числа Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи)[1]. Иногда число 0 не рассматривается как член последовательности.
Более формально, последовательность чисел Фибоначчи задается линейным рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: :
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко заметить, что .
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце имеется пара кроликов (1 новая пара).
- В первом месяце первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (2 новые пары).
- В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (3 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц будет равна . В это время только те кролики, которые жили в месяце , являются способными к размножению и производят потомков, тогда пар прибавится к текущей популяции . Таким образом общее количество пар будет равно:
Формула Бине
Формула Бине выражает в явном виде значение как функцию от n:
- ,
где — золотое сечение. При этом и являются корнями характеристического уравнения .
Из формулы Бине следует, что для всех , есть ближайшее к целое число, то есть . В частности, при справедлива асимптотика .
Формула Бине может быть аналитически продолжена следующим образом:
При этом соотношение выполняется для любого комплексного числа z.
Тождества
Геометрическое доказательство формулы для суммы квадратов первых n чисел Фибоначчи[2].И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц: , то есть
- , а также ,
- где матрицы имеют размер , i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. . Следствия:
- Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен имеет корни и .
- Отношения являются подходящими дробями золотого сечения и, в частности,
- Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы
- .
- В 1964 году Дж. Кон (J. H. E. Cohn) доказал,[3] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:
- , , , .
- Производящей функцией последовательности чисел Фибоначчи является:
- Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена
- на множестве неотрицательных целых чисел x и y.[4]
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:
- 1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)
- В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.
- Натуральное число N является числом Фибоначчи тогда и только тогда, когда или является квадратом.[5]
- Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.[6]
- Число Фибоначчи равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних нулей. При этом равно количеству таких кортежей, начинающихся с нуля, а — начинающихся с единицы.
Вариации и обобщения
В других областях
Следует отметить, что существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространенный миф, который почти всегда оказывается неточной подгонкой под желаемый результат[7][8].
В природе
В культуре
- Американский писатель-фантаст Дэн Браун в книге «Код да Винчи» описал анаграмму на основе последовательности Фибоначчи.
- Светящиеся числа Фибоначчи от 1 до 55 прикреплены на дымовой трубе Turku Energia в Турку[14] и главном вокзале Цюриха[15].
- В фильме «Двадцать одно» (англ. 21) последовательность Фибоначчи представлена в виде надписи на торте.
- «Ряд Фибоначчи» — дополнительное название песни 2012 года «Новый сигнал из космоса» российской рок-группы «Сплин».
- В java-игре Doom RPG для мобильных телефонов в «Проходе» после прохождения 7 сектора есть секретная дверь, кодом которой являются числа Фибоначчи
- Числам Фибоначчи посвящён один их шуточных лимериков Джеймса Линдона[16]:
Плотная пища жён Фибоначчи
Только на пользу им шла, не иначе.
Весили жёны, согласно молве,
Каждая — как предыдущие две.
См. также
Примечания
Литература
Ссылки
dikc.academic.ru
Число Фибоначчи — это… Что такое Число Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) [1].
Более формально, последовательность чисел Фибоначчи 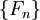 задается рекуррентным соотношением:
задается рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1:
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fn | −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко видеть, что F − n = ( − 1)n + 1Fn. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце, имеется пара кроликов (0 новых пар).
- В первом месяце, первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце, обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
- В третьем месяце, вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц n будет равна F(n). В это время, только кролики которые жили в месяце n-2 являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n — 1) + F(n — 2).
Формула Бине
Формула Бине выражает в явном виде значение Fn как функцию от n:
 ,
,
где 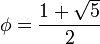 — золотое сечение. При этом
— золотое сечение. При этом 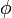 и
и 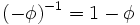 являются корнями квадратного уравнения
являются корнями квадратного уравнения 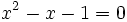 .
.
Из формулы Бине следует, что для всех 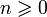 , Fn есть ближайшее к
, Fn есть ближайшее к 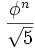 целое число, то есть
целое число, то есть 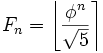 . В частности, справедлива асимптотика
. В частности, справедлива асимптотика 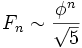 .
.
Тождества
И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц:
 , то есть
, то есть
 , а также
, а также  ,
,
- где матрицы имеют размер
 , i — мнимая единица.
, i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример —
 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
 .
.
- В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144. При этом для n=0,1,12 верно утверждение Fn = n2.
- Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y [2].
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т. д.
Вариации и обобщения
В других областях
- В природе
- Расстояния между листьями (или ветками) на стволе растения относятся примерно как числа Фибоначчи.
- В культуре
См. также
Литература
Ссылки
Примечания
- ↑ [1] БСЭ]
- ↑ P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p. 193.
Wikimedia Foundation. 2010.
veter.academic.ru
Числа Фибоначчи Википедия
Черепица с квадратами, длина сторон которых является последовательными числами Фибоначчи: 1, 1, 2, 3, 5, 8, 13 и 21.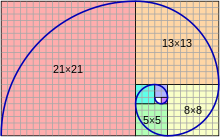 Спираль Фибоначчи: приближение золотой спирали, созданной путём рисования круговых дуг, соединяющих противоположные углы квадратов в мозаике Фибоначчи;[1] (см. предыдущее изображение)
Спираль Фибоначчи: приближение золотой спирали, созданной путём рисования круговых дуг, соединяющих противоположные углы квадратов в мозаике Фибоначчи;[1] (см. предыдущее изображение)Чи́сла Фибона́ччи (иногда пишут Фибона́чи[2]) — элементы числовой последовательности
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, … (последовательность A000045 в OEIS),
в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел[3]. Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи)[4].
Более формально, последовательность чисел Фибоначчи {Fn}{\displaystyle \{F_{n}\}} задаётся линейным рекуррентным соотношением:
- F0=0,F1=1,Fn=Fn−1+Fn−2, n⩾2, n∈Z.{\displaystyle F_{0}=0,\quad F_{1}=1,\quad F_{n}=F_{n-1}+F_{n-2},\ n\geqslant 2,\ n\in \mathbb {Z} .}
В некоторых книгах, особенно в старых, F0{\displaystyle F_{0}}, равное нулю опускается, и последовательность Фибоначчи начинается с F1=F2=1{\displaystyle F_{1}=F_{2}=1}[6].
Иногда числа Фибоначчи рассматривают и для отрицательных значений n{\displaystyle n}, как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: Fn=Fn+2−Fn+1{\displaystyle F_{n}=F_{n+2}-F_{n+1}}:
| n | … | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fn{\displaystyle F_{n}} | … | −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | … |
Легко заметить, что F−n=(−1)n+1Fn{\displaystyle F_{-n}=(-1)^{n+1}F_{n}}.
ru-wiki.ru
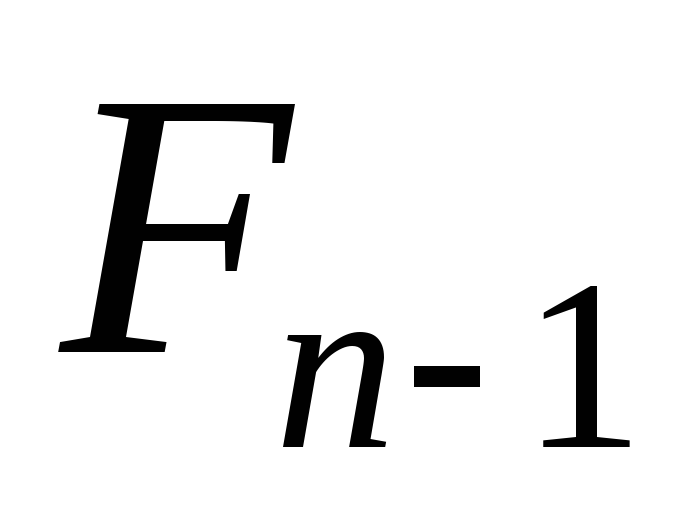 ;
;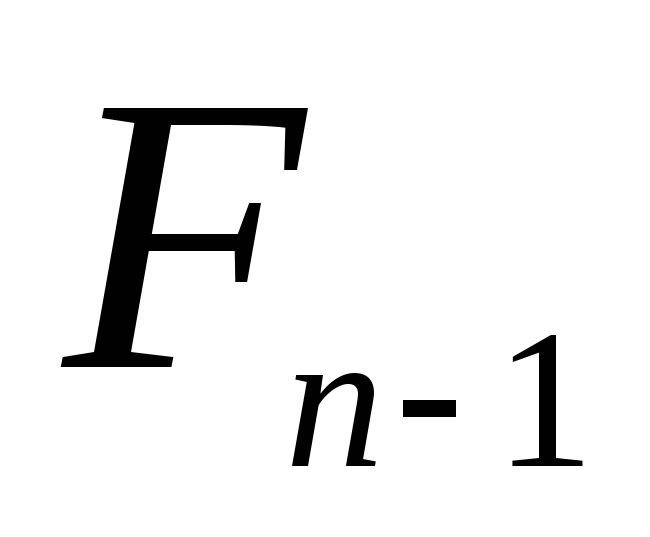 .
.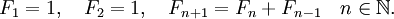
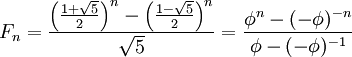 ,
,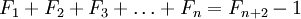
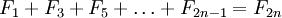
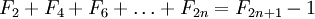
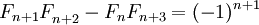

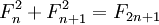
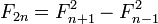
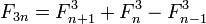
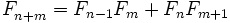
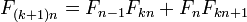
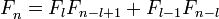
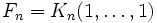 , то есть
, то есть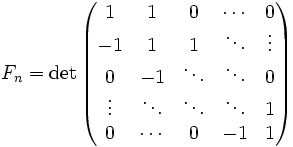 , а также
, а также 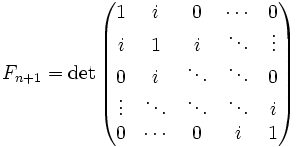 ,
,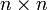 , i — мнимая единица.
, i — мнимая единица.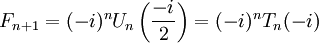
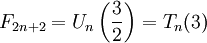
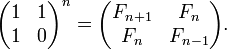
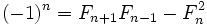
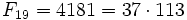 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.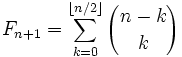 .
.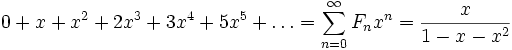

 ,
,










 , то есть
, то есть , а также
, а также  ,
, , i — мнимая единица.
, i — мнимая единица.



 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми. .
.
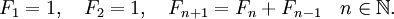
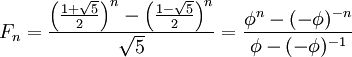 ,
,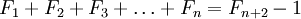
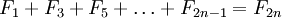
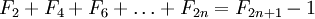
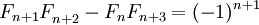

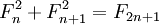
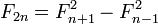
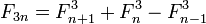
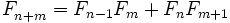
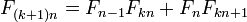
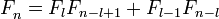
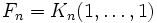 , то есть
, то есть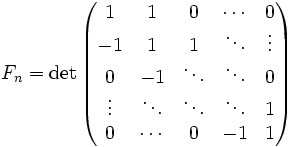 , а также
, а также 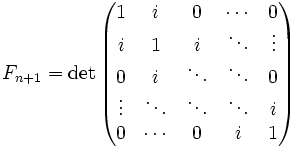 ,
,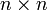 , i — мнимая единица.
, i — мнимая единица.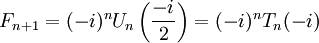
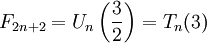
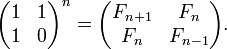
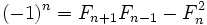
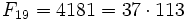 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.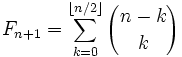 .
.