Метод Фибоначчи с запаздываниями — Википедия
Запаздывающие генераторы Фибоначчи (англ. lagged Fibonacci generator) — генераторы псевдослучайных чисел, также называемые аддитивными генераторами.
В отличие от генераторов, использующих линейный конгруэнтный алгоритм, фибоначчиевы генераторы можно использовать в статистических алгоритмах, требующих высокого разрешения.
В связи с этим линейный конгруэнтный алгоритм постепенно потерял свою популярность и его место заняло семейство фибоначчиевых алгоритмов, которые могут быть рекомендованы для использования в алгоритмах, критичных к качеству случайных чисел.
Последовательность, в которой Xn+1{\displaystyle X_{n+1}} зависит более, чем от одного из предшествующих значений, и которая определяется следующей формулой:
- Xn+1=(Xn+Xn−1)mod(2m),{\displaystyle X_{n+1}=(X_{n}+X_{n-1})\mod (2^{m}),}
носит название последовательность Фибоначчи.
В начале 50-х годов изучался данный алгоритм, однако, исследования показали, что этот генератор, как источник случайных чисел, был неэффективен. Грин (Green), Смит (Smith) и Клем (Klem) предложили доработанную формулу последовательности Фибоначчи в виде:
- Xn+1=(Xn+Xn−k)mod(2m).{\displaystyle X_{n+1}=(X_{n}+X_{n-k})\mod (2^{m}).}
Однако, положительный результат получался лишь при k≥16{\displaystyle k\geq 16}.
В 1958 году Митчел Дж. Ж. (Mitchell G. J.) и Мур Д. Ф. (Moore D. P.) вывели последовательность[1]:
- Xn=(Xn−24+Xn−55)mod(2m),{\displaystyle X_{n}=(X_{n-24}+X_{n-55})\mod (2^{m}),} (1){\displaystyle (1)}
где n≥55{\displaystyle n\geq 55}, m{\displaystyle m} — чётное число, X0,X1,…,X54{\displaystyle X_{0},X_{1},…,X_{54}} — произвольные целые не все чётные числа. Числа 24 и 55 выбраны так, чтобы определялась последовательность, младшие значащие двоичные разряды (Xnmod(2)){\displaystyle (X_{n}\mod (2))} которой имеют длину периода 255−1{\displaystyle 2^{55}-1}.
Очевидными преимуществами данного алгоритма являются его быстрота, поскольку он не требует умножения чисел, а также, длина периода, однако, случайность, полученных с помощью него чисел, мало исследована.
Числа 24 и 55 обычно называют запаздыванием, а числа Xn{\displaystyle X_{n}}, определённые в (1) — последовательностью Фибоначчи с запаздыванием[2].
Впоследствии, на основе этих работ было подобрано множество запаздываний, которые приводят к длинным периодам по модулю 2.
Аддитивные генераторы генерируют вместо случайных битов случайные слова.
Для работы аддитивному генератору требуется некое начальное состояние, которое является ключом — набор n-битовых слов: 16-битовых, 32-битовых, 64-битовых слов и т. д. — X1,X2,…,Xk{\displaystyle X_{1},X_{2},…,X_{k}}.
Зная начальное состояние, можно вычислить i-е слово генератора по формуле[3]:
- Xi=(Xi−a+Xi−b+…+Xi−k)mod(2m),{\displaystyle X_{i}=(X_{i-a}+X_{i-b}+…+X_{i-k})\mod (2^{m}),}
причём период генератора должен быть более или равен 2m−1{\displaystyle 2^{m}-1}.
Примеры алгоритмов, на основе аддитивных генераторов[править | править код]
Основной источник: [4]1) Один из широко распространённых фибоначчиевых генераторов основан на следующей итеративной формуле:
- Xk={Xk−a−Xk−b,if Xk−a≥Xk−b;Xk−a−Xk−b+1,if Xk−a<Xk−b;{\displaystyle X_{k}={\begin{cases}X_{k-a}-X_{k-b},&{\text{if }}X_{k-a}\geq X_{k-b};\\X_{k-a}-X_{k-b}+1,&{\text{if }}X_{k-a}<X_{k-b};\end{cases}}}
где Xk{\displaystyle X_{k}} — вещественные числа из диапазона [0,1){\displaystyle [0,1)}, a,b{\displaystyle a,b} — целые положительные числа, называемые лагами. При реализации через целые числа достаточно формулы Xk=Xk−a−Xk−b{\displaystyle X_{k}=X_{k-a}-X_{k-b}} (при этом будут происходить арифметические переполнения). Для работы фибоначчиеву генератору требуется знать max{a,b}{\displaystyle \max\{a,b\}} предыдущих сгенерированных случайных чисел. При программной реализации для хранения сгенерированных случайных чисел используется конечная циклическая очередь на базе массива. Для старта фибоначчиевому генератору требуется max{a,b}{\displaystyle \max\{a,b\}} случайных чисел, которые могут быть сгенерированы простым конгруэнтным методом.
Получаемые случайные числа обладают хорошими статистическими свойствами, причём все биты случайного числа равнозначны по статистическим свойствам. Период фибоначчиева генератора может быть оценён по следующей формуле:
- T=(2max{a,b}−1)⋅2ℓ,{\displaystyle T=(2^{\max\{a,b\}}-1)\cdot 2^{\ell },}
где ℓ{\displaystyle \ell } — число битов в мантиссе вещественного числа.
Выбор параметров[править | править код]
Лаги a и b — «магические» и их не следует выбирать произвольно. Рекомендуются следующие значения лагов: (a,b)=(55,24){\displaystyle (a,b)=(55,24)}, (17,5){\displaystyle (17,5)} или (97,33){\displaystyle (97,33)}. Качество получаемых случайных чисел зависит от значения константы, a чем оно больше, тем выше размерность пространства, в котором сохраняется равномерность случайных векторов, образованных из полученных случайных чисел. В то же время, с увеличением величины константы a увеличивается объём используемой алгоритмом памяти.
Значения (a,b)=(17,5){\displaystyle (a,b)=(17,5)} можно рекомендовать для простых приложений, не использующих векторы высокой размерности со случайными компонентами. Значения (a,b)=(55,24){\displaystyle (a,b)=(55,24)} позволяют получать числа, удовлетворительные для большинства алгоритмов, требовательных к качеству случайных чисел. Значения (a,b)=(97,33){\displaystyle (a,b)=(97,33)} позволяют получать очень качественные случайные числа и используются в алгоритмах, работающих со случайными векторами высокой размерности. Описанный фибоначчиев генератор случайных чисел (с лагами 20 и 5) используется в широко известной системе Matlab (автором первой версии этой системы был Д. Каханер).
В настоящее время подобрано достаточно много пар чисел a и b, приведём некоторые из них:
- (24,55),(38,89),(37,100),(30,127),(83,258),(107,378),(273,607),(1029,2281),(576,3217),(4178,9689),…{\displaystyle (24,55),(38,89),(37,100),(30,127),(83,258),(107,378),(273,607),(1029,2281),(576,3217),(4178,9689),…}
2) Брюс Шнайер в своей работе «Прикладная криптография» приводит примеры 3-х алгоритмов на основе аддитивных генераторов[5]:
Алгоритм Fish[править | править код]
«Fish — это аддитивный генератор, основанный на методах, используемых в прореживаемом генераторе. Он выдает поток 32-битовых слов, которые могут быть использованы (с помощью XOR) с потоком открытого текста для получения шифротекста или с потоком шифротекста для получения открытого текста. Название алгоритма представляет собой сокращение от Fibonacci shrinking generator — прореживаемый генератор Фиббоначи.
Во первых используйте два следующих аддитивных генератора. Ключом является начальные состояния этих генераторов.
- Ai=(Ai−55+Ai−24)mod(232){\displaystyle A_{i}=(A_{i-55}+A_{i-24})\mod (2^{32})}
- Bi=(Bi−52+Bi−19)mod(232){\displaystyle B_{i}=(B_{i-52}+B_{i-19})\mod (2^{32})}
Эти последовательности прореживаются попарно в зависимости от младшего значащего бита Bi{\displaystyle B_{i}}: если его значение равно 1, то пара используется, если 0 — игнорируется. Cj{\displaystyle C_{j}} — это последовательность используемых слов Ai{\displaystyle A_{i}}, a Dj{\displaystyle D_{j}} — это последовательность используемых слов Bi{\displaystyle B_{i}}. Для генерации двух 32-битовых слов-результатов K2j{\displaystyle K_{2j}} и K2j+1{\displaystyle K_{2j+1}} эти слова используются парами — C2j,C2j+1,D2j,D2j+1{\displaystyle C_{2j},C_{2j+1},D_{2j},D_{2j+1}}.
- E2j=C2j⊕(D2j∧D2j+1){\displaystyle E_{2j}=C_{2j}\oplus (D_{2j}\land D_{2j+1})}
- F2j=D2j+1⊕(E2j∧C2j+1){\displaystyle F_{2j}=D_{2j+1}\oplus (E_{2j}\land C_{2j+1})}
- K2j=E2j⊕F2j{\displaystyle K_{2j}=E_{2j}\oplus F_{2j}}
- K2j+1=C2j+1⊕F2j{\displaystyle K_{2j+1}=C_{2j+1}\oplus F_{2j}}
Этот алгоритм быстр, на процессоре i486/33 реализация Fish на языке С шифрует данные со скоростью 15-Мбит/с. К сожалению он также не безопасен, порядок вскрытия составляет около 240.»
Алгоритм Pike[править | править код]
«Pike — это обедненная и урезанная версия Fish, предложенная Россом Андерсоном, тем, кто взломал Fish . Он использует три аддитивных генератора. Например:
- Ai=(Ai−55+Ai−24)mod(232){\displaystyle A_{i}=(A_{i-55}+A_{i-24})\mod (2^{32})}
- Bi=(Bi−57+Bi−7)mod(232){\displaystyle B_{i}=(B_{i-57}+B_{i-7})\mod (2^{32})}
- Ci=(Ci−58+Ci−19)mod(232){\displaystyle C_{i}=(C_{i-58}+C_{i-19})\mod (2^{32})}
Для генерации слова потока ключей взгляните на биты переноса при сложении. Если все три одинаковы (все нули или все единицы), то тактируются все три генератора. Если нет, то тактируются только два совпадающих генератора. Сохраните биты переноса для следующего раза. Окончательным выходом является XOR выходов трех генераторов.
Pike быстрее Fish, так как в среднем для получения результата нужно 2.75 действия, а не 3. Он также слишком нов, чтобы ему доверять, но выглядит очень неплохо».
Алгоритм Mush[править | править код]
«Mush представляет собой взаимно прореживающий генератор. Его работу объяснить легко. Возьмем два аддитивных генератора: А и В. Если бит переноса А установлен, тактируется В. Если бит переноса В установлен, тактируется А.Тактируем А и при переполнении устанавливаем бит переноса. Тактируем В и при переполнении устанавливаем бит переноса. Окончательным выходом является XOR выходов А и В. Проще всего использовать те же генераторы, что и в Fish:
- Ai=(Ai−55+Ai−24)mod(232){\displaystyle A_{i}=(A_{i-55}+A_{i-24})\mod (2^{32})}
- Bi=(Bi−52+Bi−19)mod(232){\displaystyle B_{i}=(B_{i-52}+B_{i-19})\mod (2^{32})}
В среднем для генерации одного выходного слова нужно три итерации генератора. И если коэффициенты аддитивного генератора выбраны правильно и являются взаимно простыми, длина выходной последовательности будет максимальна.»
- ↑ Кнут Д. Искусство программирования. — том 2. — 3-е издание. — 2001 г. — гл.3.2.2.
- ↑ Кнут Д. Искусство программирования. — том 2. — 3-е издание — 2001 г. — C.39.
- ↑ Шнайер Б. Прикладная криптография. Протоколы, алгоритмы и исходные тексты на языке C. — 2002 г. — С. 291.
- ↑ Bruce, Schneier. 16.9 Additive Generators // Applied cryptography: protocols, algorithms, and source code in C. John Wiley & Sons, Inc., New York (1996).
- ↑ Шнайер Б. Прикладная криптография. Протоколы, алгоритмы и исходные тексты на языке C. — 2002 г. — гл.16.9.
- Фергюсон Н., Шнайер Б. Практическая криптография. — Диалектика, 2005. — 418 с.
- Лифшиц Ю. №9 // Современные задачи криптографии. — Курс лекций.. — Лаборатория мат. логики ПОМИ РАН, 2005.
- Жельников В. Криптография от папируса до компьютера. — 1996. — 325 с.
- William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Numerical Recipes in C: The Art of Scientific Computing. — 1992.
- Ross Anderson. On Fibonacci Keystream Generators. — Computer Laboratory,. Pembroke Street, Cambridge CB2 3QG.
Числа трибоначчи — Википедия
Материал из Википедии — свободной энциклопедии
Чи́сла трибона́ччи — последовательность целых чисел {tn}{\displaystyle \left\{t_{n}\right\}}, заданная с помощью линейного рекуррентного соотношения:
- t0=0,t1=0,t2=1,tn+3=tn+2+tn+1+tn{\displaystyle t_{0}=0,\quad t_{1}=0,\quad t_{2}=1,\quad t_{n+3}=t_{n+2}+t_{n+1}+t_{n}}.
Название является вариацией «чисел Фибоначчи» — с добавкой «три» (лат. tri-), обозначающей количество суммируемых чисел.
Последовательность чисел трибоначчи начинается так:
- 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, 121415, 223317, 410744, 755476, 1389537, 2555757, 4700770, 8646064, 15902591, 29249425, 53798080, 98950096, 181997601, 334745777, … (последовательность A000073 в OEIS)
- C=13[(19+333)1/3+4(19+333)−1/3+1]=1,839286755….{\displaystyle C={\frac {1}{3}}\left[\left(19+3{\sqrt {33}}\right)^{1/3}+4\left(19+3{\sqrt {33}}\right)^{-1/3}+1\right]=1{,}839286755\ldots .}
- Десятичные цифры C{\displaystyle C} образуют последовательность A058265 в OEIS.
- Любой член ряда трибоначчи можно определить из соотношения, аналогичного формуле Бине для чисел Фибоначчи.
- tn=⌊3b(13(a++a−+1))nb2−2b+4⌉,{\displaystyle t_{n}=\left\lfloor 3\,b{\frac {\left({\frac {1}{3}}\left(a_{+}+a_{-}+1\right)\right)^{n}}{b^{2}-2b+4}}\right\rceil ,}
- где a±=(19±333)1/3{\displaystyle a_{\pm }=\left(19\pm 3{\sqrt {33}}\right)^{1/3}}, b=(586+10233)1/3{\displaystyle b=\left(586+102{\sqrt {33}}\right)^{1/3}}, а ⌊⋅⌉{\displaystyle \lfloor \cdot \rceil } — округление до ближайшего целого (англ.).
Числа Фибоначчи — это… Что такое Числа Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи)[1]. Иногда число 0 не рассматривается как член последовательности.
Более формально, последовательность чисел Фибоначчи задается линейным рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: :
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко заметить, что .
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце имеется пара кроликов (1 новая пара).
- В первом месяце первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (2 новые пары).
- В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (3 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц будет равна . В это время только те кролики, которые жили в месяце , являются способными к размножению и производят потомков, тогда пар прибавится к текущей популяции . Таким образом общее количество пар будет равно:
Формула Бине
Формула Бине выражает в явном виде значение как функцию от n:
- ,
где — золотое сечение. При этом и являются корнями характеристического уравнения .
Из формулы Бине следует, что для всех , есть ближайшее к целое число, то есть . В частности, при справедлива асимптотика .
Формула Бине может быть аналитически продолжена следующим образом:
При этом соотношение выполняется для любого комплексного числа z.
Тождества
Геометрическое доказательство формулы для суммы квадратов первых n чисел Фибоначчи[2].И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц: , то есть
- , а также ,
- где матрицы имеют размер , i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. . Следствия:
- Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен имеет корни и .
- Отношения являются подходящими дробями золотого сечения и, в частности,
- Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы
- .
- В 1964 году Дж. Кон (J. H. E. Cohn) доказал,[3] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:
- , , , .
- Производящей функцией последовательности чисел Фибоначчи является:
- Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена
- на множестве неотрицательных целых чисел x и y.[4]
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:
- 1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)
- В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.
- Натуральное число N является числом Фибоначчи тогда и только тогда, когда или является квадратом.[5]
- Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.[6]
- Число Фибоначчи равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних нулей. При этом равно количеству таких кортежей, начинающихся с нуля, а — начинающихся с единицы.
Вариации и обобщения
В других областях
Следует отметить, что существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространенный миф, который почти всегда оказывается неточной подгонкой под желаемый результат[7][8].
В природе
В культуре
- Американский писатель-фантаст Дэн Браун в книге «Код да Винчи» описал анаграмму на основе последовательности Фибоначчи.
- Светящиеся числа Фибоначчи от 1 до 55 прикреплены на дымовой трубе Turku Energia в Турку[14] и главном вокзале Цюриха[15].
- В фильме «Двадцать одно» (англ. 21) последовательность Фибоначчи представлена в виде надписи на торте.
- «Ряд Фибоначчи» — дополнительное название песни 2012 года «Новый сигнал из космоса» российской рок-группы «Сплин».
- В java-игре Doom RPG для мобильных телефонов в «Проходе» после прохождения 7 сектора есть секретная дверь, кодом которой являются числа Фибоначчи
- Числам Фибоначчи посвящён один их шуточных лимериков Джеймса Линдона[16]:
Плотная пища жён Фибоначчи
Только на пользу им шла, не иначе.
Весили жёны, согласно молве,
Каждая — как предыдущие две.
См. также
Примечания
Литература
Ссылки
Простое число Фибоначчи — Вифериха — Википедия
Материал из Википедии — свободной энциклопедии

Простое число Фибоначчи — Вифериха (также простое число Уолла — Суня — Суня, англ. Wall – Sun – Sun) — одно из предположительно существующих простых чисел определённого вида, связанных с числами Фибоначчи. По состоянию на 2013 год ни одного такого числа не найдено.
Простое p>5{\displaystyle p>5} называется простым числом Фибоначчи — Вифериха, если p2{\displaystyle p^{2}} делит число Фибоначчи Fp−(p5){\displaystyle F_{p-\left({\frac {p}{5}}\right)}}, где символ Лежандра (p5){\displaystyle \left({\tfrac {p}{5}}\right)} определяется как:
- (p5)={1,if p≡±1(mod5)−1,if p≡±2(mod5){\displaystyle \left({\frac {p}{5}}\right)={\begin{cases}1,&{\text{if}}\ p\equiv \pm 1{\pmod {5}}\\-1,&{\text{if}}\ p\equiv \pm 2{\pmod {5}}\end{cases}}}
Эквивалентное определение: простое p{\displaystyle p} называется простым числом Фибоначи — Вифериха, если Lp≡1(modp2){\displaystyle L_{p}\equiv 1{\pmod {p^{2}}}}, где Lp{\displaystyle L_{p}} — p{\displaystyle p}-ое число Люка.[1]:42
Существует гипотеза, что простых чисел Фибоначчи — Вифериха бесконечно много[2], однако по состоянию на 2013 год ни одно такое простое число не обнаружено.
В 2007 году Ричард Макинтош (Richard J. McIntosh) и Эрик Рётгер (Eric L. Roettger) показали, что если они существуют, то должны быть больше 2⋅1014[3], в 2010 году Франсуа Дорэ (François G. Dorais) и Доминик Клайв (Dominic Klyve) довели границу до 9,7⋅1014[4]. В декабре 2011 года был начат поиск в проекте PrimeGrid[5], в декабре 2012 года PrimeGrid дошёл до границы 1,5⋅1016[6]. По состоянию на апрель 2014 года PrimeGrid дошёл до границы 2.8⋅1016 и продолжает поиск[6].
Простые числа Уолла — Суня — Суня названы в честь Дональда Уолла (Donald Dines Wall)[7], Сунь Чжихуна (Sūn Zhìhóng) и Сунь Чживэя (Sūn Zhìwěi), которые в 1992 году показали, что если первый случай великой теоремы Ферма неверен для некоторого простого p,{\displaystyle p,} то p{\displaystyle p} должно быть простым числом Фибоначи — Вифериха[8]. Таким образом, до доказательства великой теоремы Ферма Эндрю Уайлсом, поиск простых Фибоначчи — Вифериха преследовал цель найти потенциальный контрпример.
Простое (число) трибоначчи — Вифериха (англ. Tribonacci-Wieferich prime)[9] — простое число, удовлетворяющее условию
- h(p)=h(p2),{\displaystyle h(p)=h(p^{2}),}
где h(m){\displaystyle h(m)} — наименьшее положительное целое, для которого выполняется условие
- [Th,Th+1,Th+2]≡[T0,T1,T2](modm),{\displaystyle \left[T_{h},T_{h+1},T_{h+2}\right]\equiv \left[T_{0},T_{1},T_{2}\right]{\pmod {m}},}
Tn{\displaystyle T_{n}} — число трибоначчи с номером n, определённое как
- Tn+3=Tn+2+Tn+1+Tn,{\displaystyle T_{n+3}=T_{n+2}+T_{n+1}+T_{n},}
- T0=0,T1=0,T2=1.{\displaystyle T_{0}=0,T_{1}=0,T_{2}=1.}
Простых трибоначчи — Вифериха, меньших 1011, не существует[9].
- ↑ Vladica, A. On Fibonacci powers (неопр.) // Univ. Beograd Publ. Elektrotehn. Fak. Ser. Mat.. — 2006. — Т. 17. — С. 38—44. — DOI:10.2298/PETF0617038A.
- ↑ Klaška, Jiří (2007), «Short remark on Fibonacci−Wieferich primes», Acta Mathematica Universitatis Ostraviensis Т. 15 (1): 21–25, <http://dml.cz/dmlcz/137492>
- ↑ McIntosh, R. J.; Roettger, E. L. A search for Fibonacci−Wieferich and Wolstenholme primes (англ.) // Mathematics of Computation (англ.)русск. : journal. — 2007. — Vol. 76, no. 260. — P. 2087—2094. — DOI:10.1090/S0025-5718-07-01955-2.
- ↑ Dorais, F. G.; Klyve, D. W. Near Wieferich primes up to 6.7 × 1015 (англ.) : journal. — 2010. Архивировано 6 августа 2011 года.
- ↑ PrimeGrid Announcement of Wieferich and Wall-Sun-Sun searches
- ↑ 1 2 Wall-Sun-Sun Prime Search project at PrimeGrid
- ↑ Wall, D. D. (1960), «Fibonacci Series Modulo m», American Mathematical Monthly Т. 67 (6): 525–532, DOI 10.2307/2309169
- ↑ Sun, Zhi-Hong & Sun, Zhi-Wei (1992), «Fibonacci numbers and Fermat’s last theorem», Acta Arithmetica Т. 60 (4): 371–388, <http://matwbn.icm.edu.pl/ksiazki/aa/aa60/aa6046.pdf>
- ↑ 1 2 Klaška, Jiří. A search for Tribonacci–Wieferich primes (неопр.) // Acta Mathematica Universitatis Ostraviensis. — 2008. — Т. 16, № 1. — С. 15—20.
- Crandall, Richard E. & Pomerance, Carl (2001), Prime Numbers: A Computational Perspective, Springer, с. 29, ISBN 0-387-94777-9
Число Фибоначчи — это… Что такое Число Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) [1].
Более формально, последовательность чисел Фибоначчи 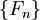 задается рекуррентным соотношением:
задается рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1:
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fn | −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко видеть, что F − n = ( − 1)n + 1Fn. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце, имеется пара кроликов (0 новых пар).
- В первом месяце, первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце, обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
- В третьем месяце, вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц n будет равна F(n). В это время, только кролики которые жили в месяце n-2 являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n — 1) + F(n — 2).
Формула Бине
Формула Бине выражает в явном виде значение Fn как функцию от n:
 ,
,
где 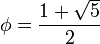 — золотое сечение. При этом
— золотое сечение. При этом 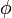 и
и 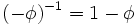 являются корнями квадратного уравнения
являются корнями квадратного уравнения 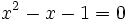 .
.
Из формулы Бине следует, что для всех 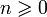 , Fn есть ближайшее к
, Fn есть ближайшее к 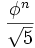 целое число, то есть
целое число, то есть 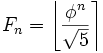 . В частности, справедлива асимптотика
. В частности, справедлива асимптотика 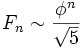 .
.
Тождества
И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц:
 , то есть
, то есть
 , а также
, а также  ,
,
- где матрицы имеют размер
 , i — мнимая единица.
, i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример —
 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
 .
.
- В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144. При этом для n=0,1,12 верно утверждение Fn = n2.
- Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y [2].
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т. д.
Вариации и обобщения
В других областях
- В природе
- Расстояния между листьями (или ветками) на стволе растения относятся примерно как числа Фибоначчи.
- В культуре
См. также
Литература
Ссылки
Примечания
- ↑ [1] БСЭ]
- ↑ P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p. 193.
Wikimedia Foundation. 2010.
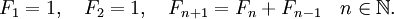
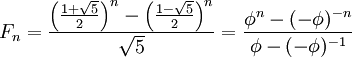 ,
,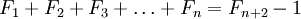
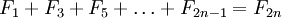
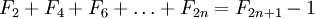
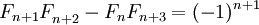

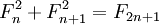
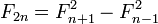
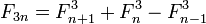
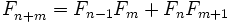
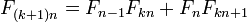
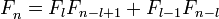
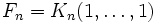 , то есть
, то есть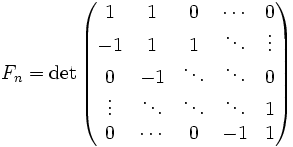 , а также
, а также 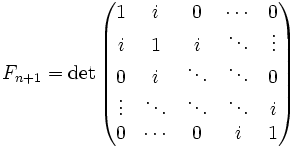 ,
,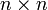 , i — мнимая единица.
, i — мнимая единица.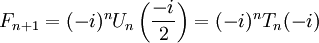
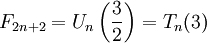
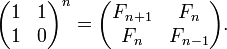
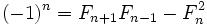
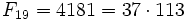 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.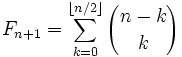 .
.