Фигур уравнения: Глава 3. Уравнения фигур — МАТВОКС — Детская игровая комната «Волшебный лес»

Posted on 12.10.197509.02.2022 by alexxlab

Содержание

Добавление математических формул к документам Pages, Numbers и Keynote

Вы можете добавлять математические формулы и уравнения к документам Pages, Numbers и Keynote при использовании команд LaTeX и элементов MathML.

Добавление уравнений к документам Pages, Numbers и Keynote

Нажмите или щелкните место в документе, текстовом поле или фигуре, где следует добавить уравнение,^{затем следуйте инструкциям для вашего устройства: На iPhone, iPad или iPod touch нажмите кнопку «Вставить» , затем кнопку «Медиа» , а затем кнопку «Уравнение».
На компьютере Mac на панели меню выберите «Вставить» > «Уравнение».}
Введите уравнение с помощью команд LaTeX или элементов MathML.¹ На iPhone и iPad можно также использовать символы быстрого доступа, расположенные над клавиатурой. По завершении ввода откроется предварительный просмотр формулы.²
Нажмите кнопку «Вставить».³.

Использование MathType

MathType также можно использовать в приложениях Pages, Numbers и Keynote для Mac, если на компьютере установлен редактор MathType 6.7d или более поздней версии. При первой вставке уравнения выберите пункт «Использовать MathType» или включите этот параметр в разделе «Настройки».

Откройте приложение Pages, Numbers и Keynote.
Выберите [приложение] > «Настройки».
Установите флажок «Вставлять и редактировать уравнения с помощью MathType».

Дополнительная информация

Узнайте, какие команды LaTeX и элементы MathML можно использовать в приложениях Pages, Numbers и Keynote.

1. С целью упрощения создания формул редактор формул по умолчанию работает в математическом режиме, поэтому нет необходимости добавлять в формулы команды математического режима.

2. Если в окне предварительного просмотра ничего нет или отображается ошибка, убедитесь, что формула правильная.

3. Если формула находится в отдельной строке текста, она выравнивается таким образом, чтобы в центре находился знак равенства. Чтобы поместить в центр строки середину формулы, добавьте пробел перед формулой или после нее.

Информация о продуктах, произведенных не компанией Apple, или о независимых веб-сайтах, неподконтрольных и не тестируемых компанией Apple, не носит рекомендательного или одобрительного характера. Компания Apple не несет никакой ответственности за выбор, функциональность и использование веб-сайтов или продукции сторонних производителей.

Компания Apple также не несет ответственности за точность или достоверность данных, размещенных на веб-сайтах сторонних производителей. Обратитесь к поставщику за дополнительной информацией.

Дата публикации: 27 июля 2021 г.

Математики разрезают фигуры в поисках частей уравнений

Новая работа над задачей о «равносоставленности» объясняет, когда имеется возможность разрезать одну фигуру и собрать из неё другую

Если у вас есть две плоские фигуры из бумаги и ножницы, можете ли вы разрезать одну фигуру и переставить кусочки так, чтобы получить другую? Если можете, тогда две эти фигуры «ножнично конгруэнтны» [равносоставлены].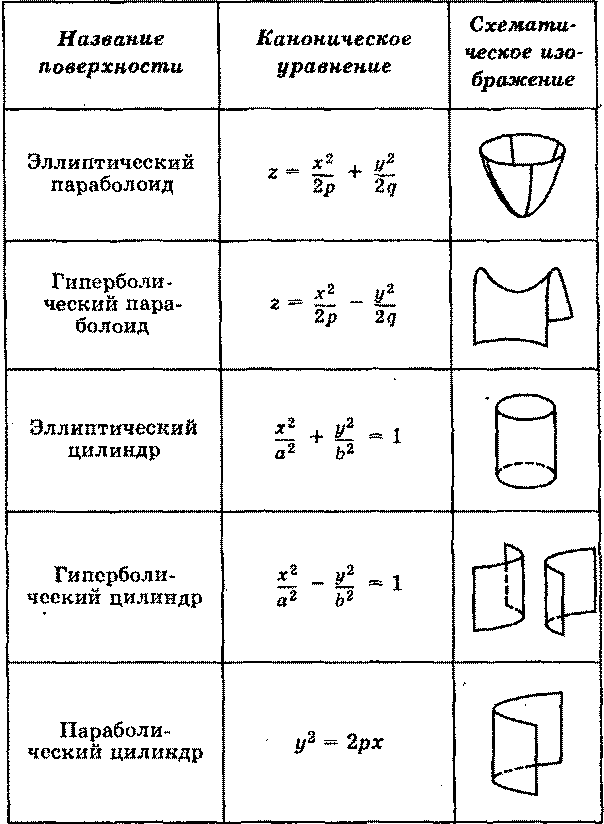

Однако математиков интересует, можно ли обнаружить такое взаимоотношение у фигур, не используя ножницы? Иначе говоря, есть ли у этих фигур такие характеристики, которые можно было бы измерить заранее и определить, конгруэнтны ли они?

Для двумерных фигур ответ прост. Нужно просто измерить их площади; если они совпадают, то фигуры ножнично конгруэнтны.

Но для фигур в высших измерениях – к примеру, для трёхмерного мяча или одиннадцатимерного пончика, который невозможно себе представить – вопрос разрезания и пересборки в другом виде становится гораздо сложнее. И несмотря на века попыток, математики не могли определить характеристик, подтверждающих равносоставленность для большинства фигур высшей размерности.

Однако этой осенью два математика совершили наиболее значимый прорыв в решении этой задачи за несколько десятилетий. В работе, представленной в Чикагском университете 6 октября, Джонатан Кэмпбел из университета Дьюка и Инна Захаревич из Корнеллского университета совершили значимый шаг по направлению к доказательству ножничной конгруэнтности для форм любых размерностей.

Но не только. Как и большинство важных задач математики, равносоставленность – это кроличья нора: скромное заявление, затягивающее математиков в глубокую нору сложной математики. В попытках понять ножничную конгруэнтность, Кэмпбелл и Захаревич, возможно, показали новый способ рассуждать о совершенно другой области этой науки: об алгебраических уравнениях.

Первый разрез

Равносоставленность может показаться простой задачей. Более 2000 лет назад Евклид догадался, что две двумерные фигуры одной площади можно переставлять из одной в другую. Разумно предположить, что фигуры высших измерений одинакового объёма можно переделывать аналогично.

Но в 1900-м году Давид Гильберт предположил, что эта задача на самом деле не так проста.

В том году, выступая на международном математическом конгрессе в Париже, он определил 23 открытых задачи, которые, по его мнению, будут направлять математическую мысль в ближайшее столетие. Третья из них касалась ножничной конгруэнтности [равносоставленность равновеликих многогранников].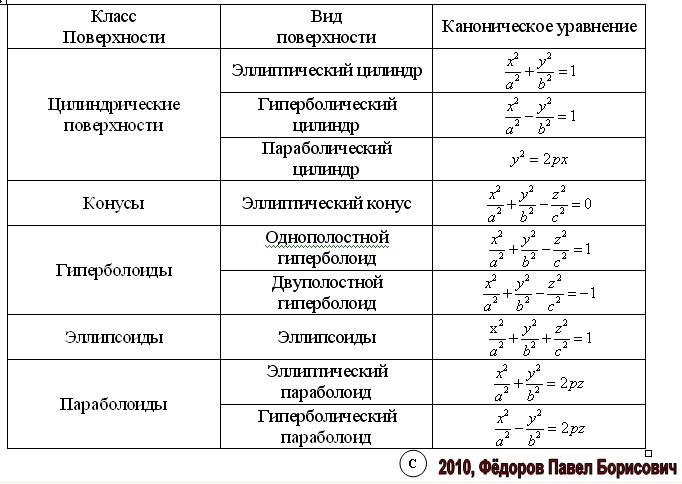 Гильберт предположил, что не все трёхмерные фигуры одного объёма конгруэнтны – и бросил математикам вызов, предложив найти пару фигур, доказывающих это.

Через год после речи ученик Гильберта, Макс Ден, так и сделал. Такой срок показался математикам подозрительным. «Некоторые считают, что Гильберт включил эту задачу в список только потому, что её уже решил его ученик», — сказала Захаревич.

Был ли это заговор или нет, результат Дена перевернул представление математиков о равносоставленности. Он доказал, что тетраэдр единичного объёма не является равносоставленным кубу того же объёма. Неважно, как вы разрежете первый, вы никогда не сможете собрать из кусочков второй.

Кроме демонстрации того, что равенства объёмов недостаточно для определения равносоставленности, Ден предложил новый способ измерения фигур. Он доказал, что любые трёхмерные фигуры, равносоставленные друг другу, должны иметь одинаковый объём, а также совпадать по новой мере.

Ден сконцентрировался на внутренних углах между двумя гранями трёхмерной фигуры.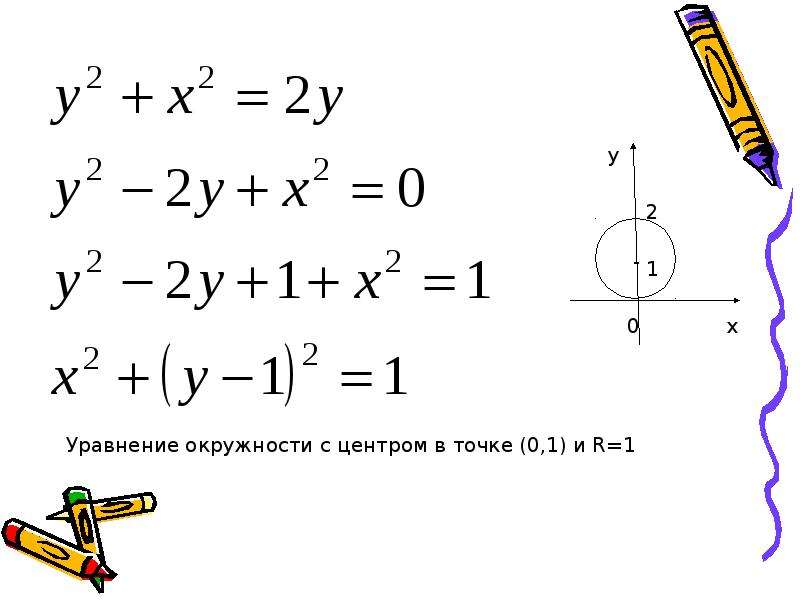 К примеру, внутри куба все грани встречаются под прямыми углами. Но в более сложных формах углы бывают разными и имеют разную важность. Углы между более длинными рёбрами больше влияют на форму фигуры, чем углы между более короткими рёбрами, поэтому Ден присвоил углам веса на основе длин формирующих их рёбер. Он скомбинировал эту информацию в сложную формулу, выдававшую в итоге единственное число – «инвариант Дена» – для заданной фигуры.

Математики хотят знать, когда фигуру можно разрезать и собрать из неё другую.
Двумерные фигуры равносоставлены, если у них одинаковая площадь.
Трёхмерные фигуры равносоставлены, если у них одинаковые объём и инвариант Дена.
Куб и тетраэдр не равносоставлены – у них одинаковый объём, но разный инвариант Дена.
Фигуры можно резать на кусочки, а графики уравнений – на подграфики. Математики ищут аналог инварианта Дена, который показывает, что два уравнения состоят из одинаковых кусочков.

Ден доказал, что любые трёхмерные фигуры, равносоставленные друг другу, должны иметь одинаковый объём и инвариант Дена.

Но он не смог ответить на более сложный вопрос: если у трёхмерных фигур одинаковый объём и инвариант Дена, значит ли это, что они обязательно равносоставлены? Жан-Пьер Сидлер, наконец, доказал это в 1965. Через три года Бьёрг Джессен показал, что эти же две характеристики определяют равносоставленность в четырёх измерениях.

Результаты Сидлера и Джессена были серьёзными шагами вперёд, но математики – народ жадный: достаточно ли объёма и инварианта Дена для определения равносоставленности фигур во всех измерениях? Достаточно ли этих измерений в других геометрических пространствах, кроме Евклидового – в сферической геометрии (представьте себе широту и долготу на поверхности Земли) или седловидной вселенной гиперболической геометрии?

В конце XX века математик Александр Борисович Гончаров предложил подход, который, по его мнению, мог решить всю задачу раз и навсегда – и при этом связать равносоставленность с совершенно другой областью математики.

Странные связи

Математика полна неожиданных связей. Захаревич говорит, что заниматься математикой – это как наткнуться на нечто странное в природе, и попытаться понять, почему оно такое.

«Если вы встретите в лесу кольцо из грибов, и не будете знать, как грибы растут, вы задумаетесь, откуда им известно, как расти кругом? – сказала она. – Причина же в том, что грибы имеют грибницу, растущую под землёй».

В 1996 году Гончаров сформулировал набор гипотез, говорящих о существовании математической структуры, также скрытой под поверхностью. Если эта структура существует, она сможет объяснить, почему некоторые математические явления – включая равносоставленность – работают именно так.

Одна из гипотез утверждает, что объёма фигуры и её инварианта Дена достаточно для определения равносоставленности фигур любой размерности и в любом пространстве.

«Гончаров сказал, что те же принципы, что применяются в трёх измерениях, применимы во всех», — сказал Чарльз Вейбель из университета Рутгерса.

Но Гончаров, ныне работающий в Йельском университете, также предсказал, что эта скрытая структура объяснит гораздо больше этого. Он сказал, что равносоставленность – это концепция более универсальная, и что она применима не только к разрезанию геометрических фигур, но и к разрезанию форм, порождаемых решениями алгебраических уравнений – к примеру, графика уравнения x² + y² + z² = 1. А информация, необходимая для классификации по равносоставленности, отражает информацию, необходимую для классификации алгебраических уравнений – такую, при которой уравнения одного класса будут составлены из одинаковых кусочков.

Связь была шокирующей, будто бы принцип, подходящий для систематизации животных каким-то образом позволял бы вам систематизировать ещё и химические элементы. Многие математики считают эту идею настолько же странной, насколько она кажется на первый взгляд.

«Это совершенно загадочно. На первый взгляд, эти вещи вообще не должны быть связаны», — сказал Кэмпбелл.

Разрезая уравнения

Чтобы понять, как могут быть аналогичными геометрические фигуры и алгебраические уравнения, сначала полезно будет понять, как можно разбить решения уравнений на части. Для этого давайте вернёмся к нашему предыдущему примеру и нарисуем график уравнения x² + y² + z² = 1.

Это будет сфера. Однако эта поверхность является не только набором решений этого уравнения: это также набор множества более мелких графиков, или подграфиков, решений других уравнений. К примеру, на поверхности сферы можно нарисовать окружность на манер земного экватора. Это один подграфик, представляющий решения алгебраического уравнения x² + y² = 1. Или можно изолировать единственную точку на северном полюсе сферы, соответствующую уравнению z = 1. Изучая различные подграфики, которые можно нарисовать в рамках более крупного графика – нечто вроде его составных частей – вы можете узнать какие-то свойства более крупного графика.

Более 50 лет математики разрабатывали теорию подграфиков алгебраических уравнений. Как обычная материя состоит из атомов, так и, по мнению математиков, алгебраические уравнения состоят из фундаментальных частей под названием «мотивы».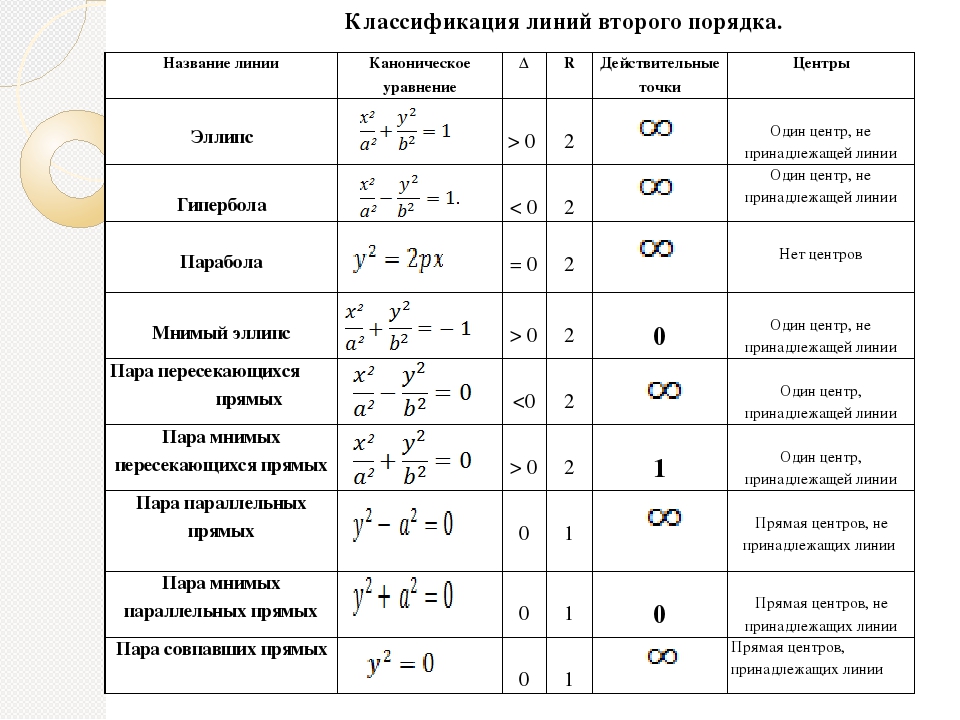 Термин происходит от французского слова motif, обозначающего базовые элементы мелодии.

Инна Захаревич из Корнеллского университета

«Мотивы – это фундаментальные составные части. Они расскажут обо всём, из чего состоят алгебраические уравнения, как мелодия, состоит из различных составных частей», — сказала Захаревич. Сфера, к примеру, состоит из окружностей, точек и плоскостей. Каждая из них состоит из составных частей (проявляющихся в результате математических действий над ними), и так далее, всё ниже и ниже, пока мы не придём к мотивам, предполагаемому фундаменту алгебраических уравнений.

Математикам нужно классифицировать алгебраические уравнения по их мотивам, чтобы получить полную и систематическую картину уравнений, принадлежащих к важнейшим математическим объектам. Это сложная и незаконченная задача. Но в 1996 году Гончаров предположил, что сортировка фигур по равносоставленности и сортировка алгебраических уравнений по мотивам являются двумя сторонами одной задачи – то есть, классификация одной даст вам принцип, по которому можно классифицировать и другую.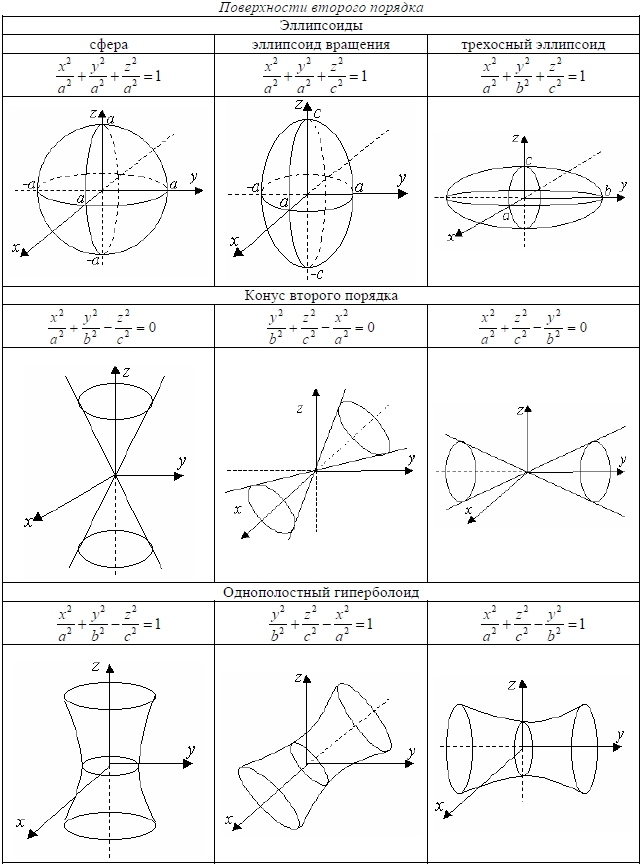

Он предположил, что эта связь имеет в основе аналог инварианта Дена. Только вместо того, чтобы появляться из простейших геометрических подсчётов, этот аналог должен возникнуть из похожего расчёта мотивов алгебраических уравнений («мотивное копроизведение»).

«Идея в том, что задача инварианта Дена параллельна другой задаче, связанной с мотивами», — сказал Вейбель.

Но чтобы обнаружить такую связь, математикам сначала нужно доказать, что инвариант Дена действительно сортирует фигуры по равносоставленным группам. Сам Ден показал, что любые равносоставленные трёхмерные фигуры имеют равные объёмы и инвариант Дена. Однако Ден, и все остальные после него, не опровергли возможность того, что существуют некие фигуры высших измерений одинакового объёма и с одинаковым инвариантом Дена, не являющиеся при этом равносоставленными. В своей новой работе Кэмпбелл и Захаревич попытались навсегда закрыть эту возможность.

Два по цене одного

В июне 2018 года Кэмпбелл и Захаревич три недели работали вместе в Институте передовых исследований в Принстоне, Нью-Джерси.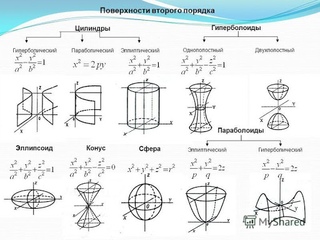 Они давно интересовались равносоставленностью, но Захаревич считала, что гипотезы Гончарова были слишком сложными, чтобы с ними можно было разобраться за такое короткое время. А Кэмпбелл всё равно хотел попытаться, и Захаревич не пришлось долго уговаривать.

«Джонатан сказал: ’У нас есть три недели, давай попробуем подступиться к этому и посмотрим, что у нас получилось, к концу первой’», — сказала Захаревич. Через две недели они разработали многие ключевые идеи, лежащие в основе их новой работы.

В работе они проводят контринтуитивный мысленный эксперимент. Чтобы понять его представьте, что у вас есть гостиница со множеством комнат. Вам нужно расположить все равносоставленные друг с другом фигуры в одной комнате. Нам неизвестно, как определять, что фигуры являются равносоставленными – в этом и есть корень проблемы. Однако для нашего мысленного эксперимента давайте представим, что это возможно. Или, как говорит Захаревич, «Мы притворимся, что существует некая всезнающая личность, которой известно, равносоставлены две фигуры или нет».

Рассортировав фигуры по комнатам, мы проверим, что у всех фигур в одной комнате одинаковый объём и одинаковый инвариант Дена. Также важно проверить, что все фигуры одинакового объёма и с одинаковым инвариантом Дена оказались в нужной комнате – что в баре гостиницы не ошиваются отбившиеся от коллектива фигуры. Цель мысленного эксперимента доказать наличие идеального взаимно однозначного соответствия между группами равносоставленных фигур и группами фигур, имеющих одинаковый объём и одинаковый инвариант Дена. Существование такого соответствия докажет, что для определения равносоставленности фигур вам действительно будет достаточно только объёма и инварианта Дена.

Гончаров предсказал существование такого соответствия, и Кэмпбелл с Захаревич доказали его наличие – при выполнении одного условия. Соответствие существует, если верен ещё один недоказанный результат, связанный с гипотезами Бейлинсона.

Две гипотезы Гончарова – классификация равносоставленных фигур по объёму и инварианту Дена, а также классификация алгебраических уравнений по аналогу инварианта Дена – не доказываются работой Кэмпбелла и Захаревич полностью. Однако их работа всё же обеспечивает математиков более чётким представлением о том, как доказать их все: если у вас получится доказать гипотезы Бейлинсона, тогда, благодаря работе Кэмпбелла и Захаревич, вы бесплатно получите в придачу и равносоставленность.

«Их работа действительно переосмысливает эту задачу, — сказал Вейбель. – Когда вы связываете таким образом две гипотезы, это проливает свет на структуру изучаемого объекта».

Кэмпбелл и Захаревич сейчас работают ещё с одним математиком, Даниилом Руденко из Чикагского университета, пытаясь определить связь между разрезанием фигур и разбором на части уравнений, предложенным Гончаровом. Руденко до этого уже несколько продвинулся в этом направлении. Теперь, совместно с Кэмпбеллом и Захаревич, он надеется продвинуться гораздо дальше.

«Думаю, у нас есть все шансы достичь значительного прогресса. Может быть, таким способом даже получится доказать гипотезы Гончарова», — сказал Руденко.

Автор: SLY_G

Источник

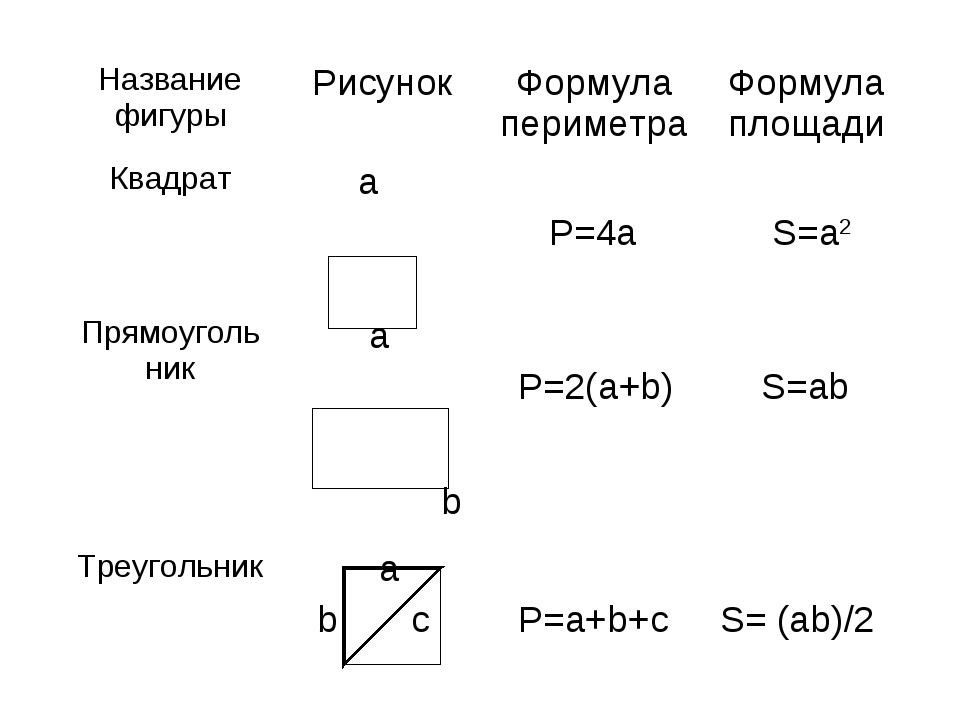
Уравнение фигуры.

Уравнение окружности.

Уравнение фигуры. Уравнение окружности

составила учитель математики Веселова С.М.

1.Как называется геометрическая фигура, состоящая из множества всех точек, равноудаленных от данной точки?

2. Как называется точка равноудаленная от всех точек окружности?

1. Окружность

2. Центр окружности

3.Как называется хорда, проходящая через центр окружности?

3. Диаметр

4. Как называется отрезок, соединяющий центр окружности с точкой на окружности?

4. Радиус

5.Чему равно расстояние между точками А и В?

Какая фигура является графиком уравнения?

С. у = 2х-1

А. у =

В. у =

Рис. 2

Рис. 3

Рис. 1

Уравнение у=2х-1 является уравнением прямой

т. А (0;-1) и т. В(2;3) лежат на прямой

т. С (2;2) не лежит на прямой

Уравнением фигуры F, заданной на плоскости xy, называют уравнение с двумя переменными x и y, обладающее следующими свойствами: 1) если точка принадлежит фигуре F, то ее координаты являются решением данного уравнения; 2) любое решение (x; y) данного уравнения является координатами точки, принадлежащей фигуре F.

уравнение окружности

пример

А (2;4) – центр, R = 3, то

( х – 2 ) 2 + ( у – 4 ) 2 = 3 2 ;

( х – 2 ) 2 + ( у – 4 ) 2 = 9 .

Пример 1:

Напишите уравнение окружности

(0;0) – центр окружности, R- радиус

( х – а ) 2 + ( у – b ) 2 = R 2 .

( х – 0 ) 2 + ( у – 0 ) 2 = R 2 ,

х 2 + у 2 = R 2 − уравнение окружности с центром в начале координат.

Пример: 2

О (0;0) – центр, R = 5, тогда

х 2 + у 2 = 5 2 ;

х 2 + у 2 = 25 .

Для того чтобы составить уравнение окружности, нужно:

1) узнать координаты центра;

2) узнать длину радиуса;

3) подставить координаты центра ( а ; b ) и длину радиуса R в уравнение окружности

( х – а ) 2 + ( у – b ) 2 = R 2 .

(Задание выполняется Устно)

Уравнение окружности

Центр

( x – 3 ) 2 + ( y – 2) 2 = 16

радиус

C(3; 2)

( x – 1 ) 2 + ( y + 2) 2 = 4

C(1;-2)

r = 4

( x + 5 ) 2 + ( y – 3) 2 = 25

x 2 + ( y + 2) 2 = 2

r = 2

C(-5; 3)

C(0;-2)

r = 5

x 2 + y 2 = 9

C(0; 0)

r = 3

Уравнение окружности

Центр

( x – 1 ) 2 + ( y – 2) 2 = 64

радиус

C(1; 2)

( x – 1 ) 2 + ( y + 2) 2 = 0,64

C(1;-2)

( x + 5 ) 2 + y 2 = 1,44

r = 8

x 2 + y 2 = 5

C(-5; 0)

r = 0,8

C(0; 0)

r = 1,2

( x + 6) 2 + ( y + 2) 2 = 7

C(-6;-2)

Решение задач с записью в тетради № 330 (а,б), № 332

Что называют уравнением фигуры, заданной на плоскости ху?
Какой вид имеет уравнение окружности с центром в точке (а;b) и радиусом R?
Какой вид имеет уравнение окружности с центром в начале координат и радиусом R?

П. 9 читать, знать все определения и формулы наизусть,

№ 329, № 331, № 333

Уравнения плоского движения твердого тела. Уравнения движения

Содержание:

Уравнения плоского движения твердого тела. Уравнения движения точки плоской фигуры

Уравнение плоского движения твердого тела. Уравнения движения точек в плане этажа 1 Определите плоские уравнения движения твердого тела и плоские точки F и r движения. Плоскость (плоскопараллельная) — это движение последней цели, и траектория всех ее точек находится в плоскости, параллельной некоторой неподвижной плоскости. С этим ходом Все точки твердого тела, лежащие на приподнятом перпендикуляре к этой плоскости, имеют одинаковую траекторию, скорость и ускорение.

Поэтому при изучении плоского движения твердых тел достаточно изучить движение плоской фигуры. Движение плоской фигуры можно разложить на поступательное движение вместе с произвольно выбранной точки 0 [}, называемой полюсом, и вращение фигуры вокруг этой точки(рис. 6.1).

Плоская фигура-это сечение твердого грунта плоскостью, параллельной неподвижному грунту. Людмила Фирмаль

О Система координат, в которой находится уравнение Выберите фиксированные системы координат xy и nat и подключитесь строго к плану. Плоское движение твердого тела： xoi = Ф \ второй)> йот = л(0″ 9 = Дж.* И Х / г \ ч. 1. 1 Дж. 1 1-й- Рисунок 6.1. О) 0） К задаче 6.3. Решение. Соедините центр o колеса и начальное и конечное положения 0{прямая линия (рисунок B).Нарисуйте линию между точками A и Ax. Эти линии пересекаются и становятся точками, обозначенными C. OA, OAj. OiAh 0 \ A (рисунок Tf), a} a {- параллелограмм.

Прямые OOt и AAX являются диагоналями этого parallelogram. As в результате их пересечение C делит отрезки 00 \и AA {пополам. Если восстановить точки перпендикулярно к]и AA \в точках C, то единственной точкой их пересечения будет C. Таким образом, C является центром конечного вращения при перемещении колеса из первого положения во 2-е положение.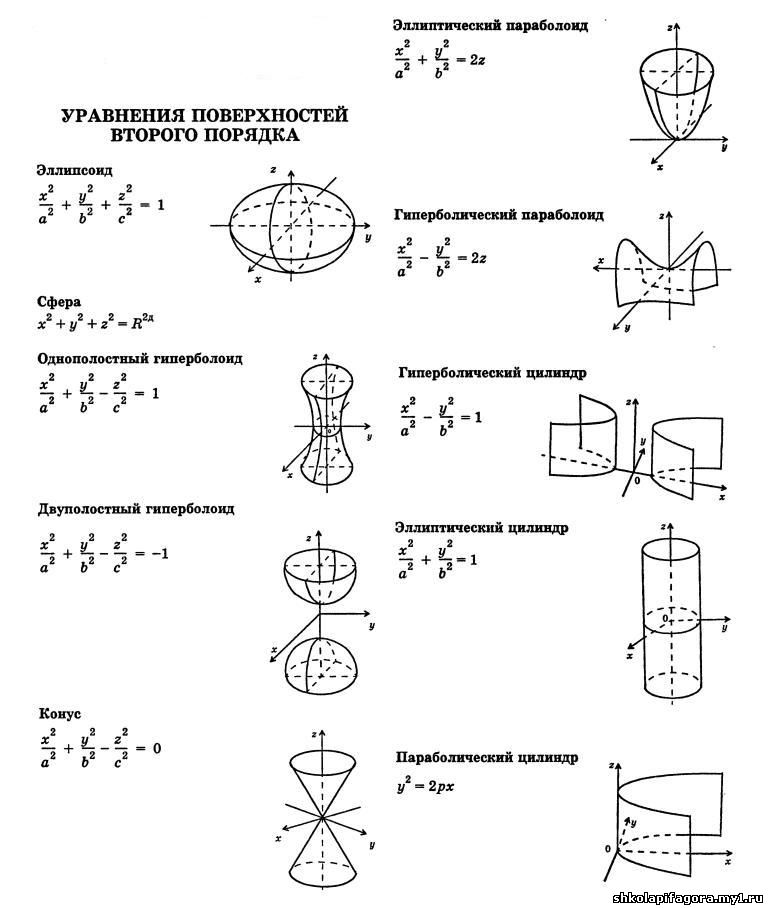

Задача 6.4.Движение звена кривошипно-шагового механизма определяется углом, — [ — ’<] с COS <Р-СР МВ, г = yolJ7 Мп? «!» В этих уравнениях x, y-координаты точки M и фиксированная система координат. hoch> J’o, — координаты полюса O;; x, y {система координат X {y \координаты точки M, плотно связанной с плоской фигурой. 9-угол поворота подвижной системы координат. вый\, внизу константа, не меняется, но это время движения числа, которое определяет точку с учетом плоской фшуры. Оставшаяся сумма Формулы (2*) является функцией времени и определяется по центральной формуле

Задача 6.1.In кривошипно-шатунный механизм, центр вращения кривошипа О находится на расстоянии а от горизонтальной траектории ползуна В. угол поворота кривошипа изменяется по закону. 0 = hi, где k-постоянный / пятый коэффициент. Длина Кривошип () A = g, шатун AB-L О11 с треском замахнулся на меня плоско-плоскостным кругом движения на шатуне.

Поэтому точка а шатуна(начало координат движущейся системы координат) является полюсом. Людмила Фирмаль

К задаче 0.1. D e n c e. выберите 11C в качестве координаты координаты с точкой O в качестве начала координат. Возьмем начальную точку и движущуюся систему координат, содержащую точку А, которая принадлежит как кривошипу, так и Шатуну. .нарисуйте вдоль оси v, шатуна AB, оси y, перпендикулярно ей.

Форма уравнения движения полюсов имеет вид ХЛ = ОА что-то J = р потому что КТ, я = ОА грех или грех ХТ. Спроектировать отрезок AN по оси y, чтобы найти 3-е уравнение движения, то есть временную зависимость угла поворота шатуна. углы между j-осями обозначаются цифрой 9 ми » ж И Л -, найти： An sin 9 = OA sinO — ’ * а、 Или AN=/, OA = r, O-kt, так что это выглядит так: г. и… Фундамент? = 7 грехов?/-;- Отсюда возникает угол o как функция времени.

Задача 6.2.Жесткий прямой угол / GC перемещается так, что точка A всегда остается на оси y! Когда противоположная сторона угла L1C проходит через неподвижную точку N, мы знаем, что это AM-OH = a и определяем траекторию движения точки M. The solution. To определите траекторию движения точки M, выберите ту систему координат, которая начинается с точки N. укажите радиус К выпуску 62.

Вектор VM через r и угол OBM через a、 Я грех-Ф-БМ потому что = Обь、 Или грех Г, потому что А-А. Г. я-Силл А. И потому что а-р -» а-1•(•sifl Р (1) от： Или г 1-л грех «» л г _ ы ы а-1-зта г 1-СМЭВ в Отсюда, после простого преобразования, это выглядит так: _ * ля а + — р-2- Это уравнение траектории точки / и-станоид полярного координатного уравнения. 2°.Определение местоположения центра конечной плоскости плоского фщ-ИПУ.

Прерывистые движения плоских фигур могут быть выполнены вращением вокруг точки, называемой центром конечного вращения. Да. 6.} Рисунок. >’_>. Чтобы построить положение центра конечного вращения, нужно выбрать любые 2 точки плоскости фигур а и Н(рис.6.！2, а).После перемещения этих точек мы находимся в точке Aj, и если соединить точки A и Ait Hn прямой линией, то будем считать, что точки D и f найдены. .Их точка пересечения будет центром вращения объекта. Однако если (рис.6.2, c), средняя точка [) и/::соединяет точку A с точкой B и точкой Bb, то множество перпендикуляров к прямой является параллельным, то центра конечного вращения нет. II определение и исследование состояния вращения печи также recommended. In л 1)

Выберите 2 точки в исходном положении плоской формы. 2)найти положение той же точки после окончательного перемещения фигуры. 3) соедините начальное и конечное положения каждой из 2 точек на рисунке прямой линией. 4) в центре этих отрезков восстановите перпендикуляр к этим прямым линиям и пересечение этих перпендикуляров, найдите нужный центр конечного поворота вида в плане. Задача 6.3.Колесо вращается на прямом рельсе без скольжения. Если колесо перемещается так, что точка соприкосновения колеса и рельса является самой дальней точкой от рельса, найдите положение центра последнего оборота (рисунок а).

Смотрите также:

Предмет теоретическая механика

Уравнения движения плоской фигуры — Энциклопедия по машиностроению XXL

Уравнения движения плоской фигуры [c. 115]

Уравнения (50), определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела. [c.128]

Третье дифференциальное уравнение движения плоской фигуры получают из уравнения (85.4) [c.233]

Составление уравнений плоскопараллельного движения твердого тела (уравнений движения плоской фигуры). [c.169]

УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ (задачи 492—500) [c.169]

Уравнения (74) называются уравнениями движения плоской фигуры, пли уравнениями плоскопараллельного движения твердого тела. Из этих уравнений следует, что движение плоской фигуры можно разложить на два движения 1) поступательное движение, определяемое первыми двумя уравнениями (74), и 2) вращательное движение вокруг полюса, определяемое третьим из уравнений (74). [c.170]

Для приобретения навыков в решении задач на составление уравнения движения плоской фигуры и ее точек рекомендуется решить следующие задачи из Сборника задач по теоретической механике И. В. Мещерского, издания 1950 г. и более поздних лет 492, 493, 495, 498, 500. [c.371]

Аналитический метод. При аналитическом методе должны быть заданы уравнения движения плоской фигуры (рис. 6.3) [c.372]

Формулами (13 ), (14 ), (15 ) целесообразно пользоваться, когда заданы уравнения движения плоской фигуры (1 ). [c.377]

Уравнениями движения плоской фигуры в неподвижной системе координат являются [c.190]

Эти уравнения являются уравнениями движения плоской фигуры в ее плоскости, следовательно, они определяют плоское движение твердого тела. [c.216]

Движение вместе с полюсом и вокруг полюса. Уравнения (112 ) и (112″) представляют поступательное движение плоской фигуры. Вместе с тем они выражают координаты полю.са Е в функции времени. Следовательно, поступательное движение фигуры определяется движением полюса. Если бы за полюс мы выбрали какую-нибудь другую точку фигуры, то уравнения (112 ) и (112″) были бы иными, а следовательно, изменилось бы и описываемое этими уравнениями движение плоской фигуры. [c.217]

Эти функциональные зависимости называются уравнениями движения плоской фигуры. [c.198]

Дифференцированием по времени уравнений движения плоской фигуры [c.48]

Как по уравнениям движения плоской фигуры найти скорость полюса и угловую скорость [c.62]

Как и в случае определения скоростей, уравнения движения плоской фигуры XA = fi(i), yA = h(t), Ф = /з(г) позволяют найти лишь ускорение точки А, выбранной за полюс, угловую скорость и [c.62]

Если заданы уравнения движения плоской фигуры, то модуль угловой скорости определяется как производная от угла поворота по времени [c. 539]

Аналитический метод определения скоростей целесообразно применять, если известны по условию или могут быть без особых затруднений составлены уравнения движения плоской фигуры (1 )- Аналитический метод позволяет, вообще говоря, найти скорость точки плоской фигуры как функцию времени. Однако получить такое решение в обозримом виде не всегда возможно. [c.539]

Предположим, что твердое тело совершает плоское движение. Совместим с плсЗскостью чертежа плоскость, в которой движется центр масс тела, показав плоскую фигуру, полученную от сечения тела этой плоскостью (рис. 196). В динамике за полюс принимают не произвольную точку фигуры, а центр масс тела. Тогда уравнения движения плоской фигуры имеют вид [c.232]

Для задания положения плоской фигуры на плоскости относительно систе.мы координат О х у , лежащей в плоскости фигуры, достаточно задать на этой плоскости положение отрезка ОМ (рис. 42), скрепленного с фигурой. Положение отрезка ОМ относительно системы координат О х у онределгггся заданием координат какой-либо точк1Г этого отрезка и его направления. Например, для точки О нужно задать к( ординаты х , у , а направление задать углом ), который образует отрезок ОМ с какой-либо осью, например О1Х1 или ей параллельной осью 0х[. Вместо угла ф можно взять угол между любой другой осью или отрезком, скрепленными с плос-кой фигурой, и осью O Xl, например угол ф. Тогда 5 = ф -Ь а, где а не зависит от времени Таким образо.м, уравнения движения плоской фигуры в ее плоскости, а следовательно, н плоского движения твердого тела относительно системы координат О х у имеют вид [c.139]

Если функции f ii) и fg t) известны, то для каждого момента t можно из уравнений (62) найти соответствующие значения хо, Уоуравнения (62) вполне определяют движение плоской фигуры и называются уравнениями движения плоской фигуры, движущейся в своей плоскости, или, что то же, уравнениями плоскопараллелъного движения твердого тела. [c.301]

Уравнения движения плоской фигуры относительно некоторой неподвижной системы координат Оху имеют следуюпщй вид ( 77) [c.326]

«Знакомство с пространственными фигурами» (6-й класс). «Уравнения» (математический турнир, 5-й класс)

Математический турнир по темам:

“Уравнения” и “Математическая — гимнастика ума”

Девиз:

1) Набирайся ума в ученье, храбрости в сраженье.

2) Ум хорошо, а два лучше.

Цель:

Проверить умения и навыки при решении уравнений.

Познакомить с историческим материалом по изучаемой темам.

Активизация работы учащихся на уроке через вовлечение в игру помочь приобрести и выработать собственную систему приёмов, которая позволяет решать незнакомые задачи.

План урока
Разминка.

Приветствие команд:

а) Трифонова К.
б) Калашников Ж
в) Булычева О.
3. Задание командам.
4. Конкурс капитанов.
а) Теоретический конкурс
б) Математическая эстафета

5. Домашнее задание /историческая справка/
6. Занимательная страничка.
7. Подведение итогов.
Сколько яиц можно съесть натощак? (Одно)

Из какой посуды не едят? (Из пустой)

Какую траву и слепые узнают? (Крапиву)

В доме 100 квартир. Сколько раз на табличках написана цифра 9? (20)

Како месяц короче всех? (Май)

Хорошо видит, а слепой? (Неграмотный)

Какое целое число делится без остатка на любое целое число? (0)

Сумма, каких двух натуральных чисел равна их произведению? (2+2=2х2)

Сколько пальцев на 10 руках? (50)

Одно яйцо варится минуты. Сколько минут будут вариться 5 яиц? (4)

К однозначному числу приписали такую же цифру. Во сколько раз увеличилось число? (В 11 раз)

Приветствие команд:
“Умники и умницы”

Этот турнир ждали мы
По нему истосковались умы.
Дружно будем задачи решать –
Мы хотим математику знать.

Не крутите пестрый глобус
Не найдете вы на нем
Той страны, страны загадок,
Но мы живем ведь в ней.

“Смекалка”

Пусть смекалка нам поможет:
Сил прибавит, знания умножит.
Ох, полным полно болельщиков,
Негде яблоку упасть.

Помогите нам, пожалуйста, место 1 занять.
Вы похлопайте в ладоши,
Напишите лозунг нам,
И тогда команда наша, благодарна, будет Вам.

“ Крепкий орешек ”

Считать, умножать, вычитать и делить
Иначе нельзя математиком быть.
В сегодняшнем турнире
Мы участвовать хотим.

И победу просто так,
Мы не отдадим.
За каждое очко мы будем драться
Придется хорошо нам постараться.

Задание командам:
1.
а)95+х=125

б)300-х=272

в)t-28=136

а)m-34=106

б)81-7=59

в)х+48=131

а)к-28=112

б)93-g=29

в)у+3=125

В первый день ученик отремонтировал
несколько книг, во 2 день на 22 книги

больше, а в3 день 48. Всего отремонтировал 200 книг.

Сколько книг отремонтировал в 1 день?
5б посадил несколько березок, 5а на 8 березок больше, чем 5б, 5в на 3 березы меньше, чем 5б.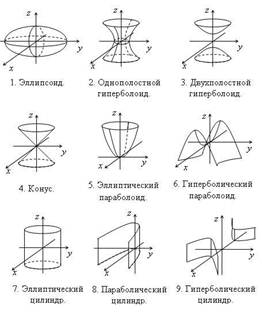
(Сколько березок посадили все классы?)

Вместе они посадили 450 березок. Сколько берез посадил 5а.
Школьники отправились в поход. В 1 день они прошли несколько километров, во 2 день на 7 км меньше, чем в 1, а в 3 день на 2 км больше, чем в 1 день. Всего они прошли 34 км. Сколько прошли во 2 день?
(х-8)-24=42 48-(а+5)=16 (24-х)+37=49
Задание капитанам:
Капитаны получают в красивых конвертах задания командам.
Пока команды работают, капитаны участвуют в теоретическом конкурсе.
Какое равенство называется уравнением?

Какое число называется корнем уравнения?

Что, значит, решить уравнение?

Как найти неизвестное слагаемое?

Как найти неизвестное уменьшаемое?

Как найти неизвестное вычитаемое?

Как проверить, верно ли решено уравнение?

При чтении уравнений или буквенных выражений, кА правильно произнести х=25?

У=17

Р=5

Мир, в котором живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нем, открывать новое, понимать красоту окружающего мира помогает геометрия.
Геометрия – это не только раздел математики, это, прежде всего феномен общечеловеческой культуры, являющийся носителем собственного метода познания мира.
Геометрическое мышление в своей основе является разновидностью образного, чувственного мышления, по мере развития геометрического мышления происходит возрастание логической составляющей. Отсюда важность изучения геометрии в возрасте 10-12 лет. Занятия геометрией в таком возрасте способствует развитию интуиции, воображения и др. важнейших качеств, лежащих в основе любого творческого процесса. В повседневной жизни ребенка окружают разнообразные по форме предметы быта. Манипулируя ими, он замечает, что мяч легко катается, а кубик – устойчив, из них можно построить башенки. Ребенок способен отличить куб и квадрат, давая оригинальное определение (кубик похож на шарик, но только у него есть углы). Уровень этих ощущений позволяет говорить об у него чутье формы, размера, объёма окружающих его предметов.
Эти наблюдения позволяют делать вывод о том, что необходимо изучать геометрию уже с 5 класса. Многие видные методисты страны считают, что целесообразно начинать изучение геометрии с 1 класса.
Я проводила уроки “Наглядная геометрия” в 5 классе, продолжаю проводить и в 6 классе, поэтому могу сделать вывод. Те учащиеся, которые проявляют усидчивость, аккуратность, трудолюбие добиваются успеха, а те, кто как бы созерцают со стороны, не умеют, долгое время трудиться научились хорошо чертить, рисовать. Это пока небольшой вклад в художественное воспитание и развитие у них изобразительной культуры. Ребята просто научились восторгаться красотой окружающего мира, у них лучше развит глазомер, умеют рассуждать, доказывать.
Предлагаю Вашему вниманию один из уроков.
Тема: “Фигуры в пространстве”
Такие уроки провожу раз в месяц (6класс).

Цели.
Развивающие – расширить кругозор (историческая справка), учить грамотно, использовать математические термины в ходе рассуждений, учить делать аккуратные, “умные” чертежи, а также дополнять готовые чертежи.

Воспитательные – Учить преодолевать трудности, воспитывать стремление к совершенствованию знаний.

Тип урока. “Урок ознакомления с новым материалом”.
План
Великий итальянский ученый Галилео Галилей однажды сказал: “Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».
В классе 28 учащихсяся, делим их на группы в зависимости от тог, какую из плоских фигур они выбрали.
В каждой группе выбирается ведущий, выбирают сами ребята.
Группы:
Треугольник

Прямоугольник

Круг

Трапеция

Квадрат

Ромб

Параллелограмм

1. Проверка домашнего задания.
Ведущие групп проверяют домашнее задание (составить модель, придумать игру, сказку, историю)
Затем, после того как ребята посоветуются в группах, защищается лучший проект.
Например, команда под номером 2 представила рассказ “Полезный прямоугольник”, рассказ сопровождался рисунками.
Прямоугольник постоянно завидовал квадрату.
– Я такой неуклюжий. Если поднимусь во весь рост, то стану узким и длинным.
А если лягу набок, то буду низким и толстым.
– А ты всегда остаешься одинаковым – продолжал он, обращаясь к квадрату.
Квадрат от гордости нос задрал.
Но однажды случилось помочь заблудившемуся через реку перебраться, вот тут-то и пригодился прямоугольник. Квадрат в воду плюхнулся, а прямоугольник в мостик превратился.
Команда “Треугольник” предлжила показ фокусов, превращая треугольники:
в горку, колпак, палатку.
Группе победительнице выпало право отгадать пословицу (об учебе)
(на доске карточки, на обратной стороне написаны буквы)

Корень учения горек, да плод его сладок.
2. Изучение новой темы.
Вниманию ребят предлагаются модели: призмы, прямоугольного параллелепипеда, пирамиды, куба.
Проводится небольшая беседа.
Назовите фигуры в пространстве, которые знакомы.
Как познакомились с ними впервые.
Форму пирамиды имели гробницы фараонов в Древнем Египте. Они сохранились до наших времен. Одна из них, самая знаменитая – пирамида Хеопса, высота которой достигает – 147м. Спичечная коробка, кирпич, холодильник и многие другие окружающие нас предметы имеют форму прямоугольного параллелепипеда. Название параллелепипеда произошло от греческих слов параллелос – идущие рядом и епипедон – плоскости (грани).
3. Закрепление
1) Из каких плоских фигур состоят многогранники?
На столе приготовлены равносторонние треугольники. Разделите стороны пополам. Середины соедините отрезками.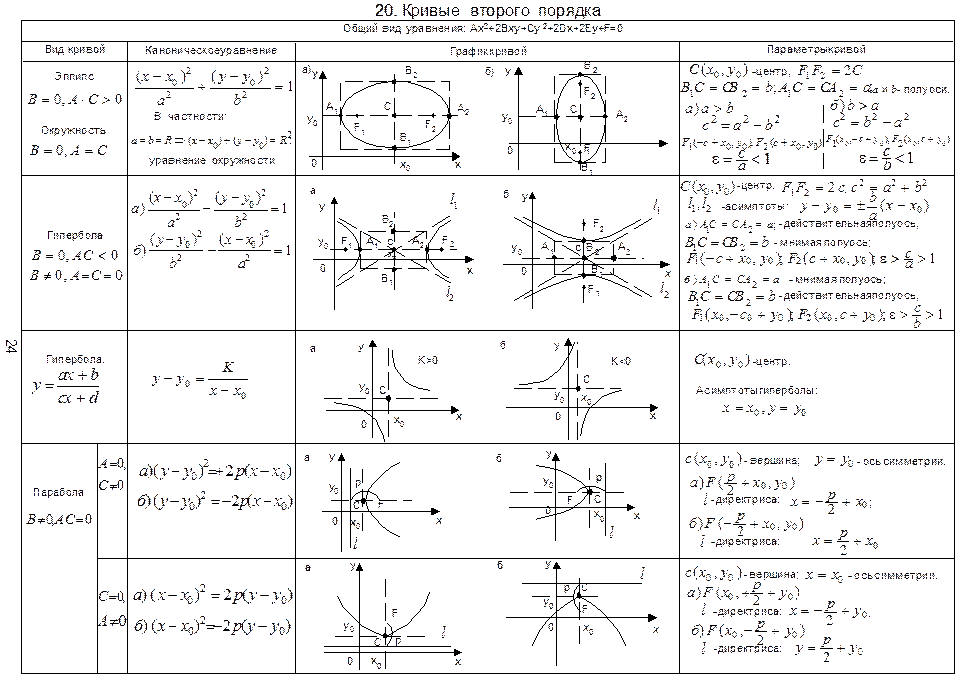 Если согнуть по отрезкам, какой многогранник получится? (Индивидуальная работа)

2) Работа в группах.

Из 6 спиц составить 4 равных треугольника.

4. Знакомство с новыми понятиями.
Учитель:
А) Сделайте 2 квадрата из спиц, теперь соедините между собой эти квадраты еще 4-мя спицами, что получилось? (соединяют шариками из пластилина)
Посчитайте шарики, которыми соединяли, сколько их получилось?

Ученики: 8
Учитель: 8 – это вершины
А сколько потребовалось спиц?

Ученики: 12
Учитель: 12 – это ребра
Посчитайте, из скольких квадратов состоит куб?

Ученики: 6
Учитель : 6 – это грани
Б) Закрепление:

Работа в парах с использованием раздаточного материала

5. Итог урока:
Закрыли глаза, мысленно вспоминаем все многогранники, которые приходили к нам в гости. Вспоминаем их название. Вот пирамида, в жизни встречается очень редко. А вдруг опять Дед Мороз принесет конфеты в “пирамидке”.
А вот этой геометрической фигурой ты играл, когда был совсем маленьким – это кубик. Все его грани квадраты. Сразу вспоминается лето, солнце, подруги. Мы все вместе играем в “классики”. И вообще, когда мы все вместе, нам под силу любая наука.
Урок окончен. Всем спасибо.
В геометрии очень важно уметь смотреть и видеть, замечать различные особенности геометрических фигур, делать выводы.
Эти умения необходимо тренировать и развивать.
Дерзайте! Желаю творческих успехов!
Литература

1.Заниматика. Г Юдин
2. Наглядная геометрия И.Ф. Шарыгин
3. “Путешествие в сообразилию или как стать ребенку смышленым”. Москва, НПО и АЛТА
4. Математика – приложение к газете «Первое сентября».

Уравнения поверхностей второго порядка

Эллипсоид
a, b, c — полуоси

Сфера (частный случай эллипсоида)

Однополостный гиперболоид
c — действительная полуось,
a и b — мнимые полуоси

Двуполостный гиперболоид
c — действительная полуось,
a и b — мнимые полуоси

Конус
Вершина конуса в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат

Эллиптический параболоид

Гиперболический параболоид

Эллиптический цилиндр
a и b — полуоси

Гиперболический цилиндр

Параболический цилиндр
p — фокальный параметр

Глава 4.
Уравнения, рисунки и таблицы Данные, вымученные достаточно долго, почти всегда признаются.
— The Economist, 16 мая 1998 г.
Чтобы подчеркнуть важность хорошего дизайна рисунка и подписи, я хотел бы использовать следующий пример. Обратите внимание на эту сомнительно известную неотесанную фигуру без подписи:
.

Держу пари, что немногие зрители этой фигуры смогут понять, что она должна изображать, а те, кто угадает правильно, скорее всего, сделают это только потому, что видели фигуру раньше с соответствующей подписью.
Теперь рассмотрим рисунок с добавленной подписью:
Рисунок 1. Корабль, прибывший слишком поздно
, чтобы спасти тонущую ведьму (Заппа, 1982).
Без подписи — хотя мы все видели простые рисунки, корабли и шляпы ведьм — мы вряд ли поймем значение рисунка. Однако с помощью полезной, тщательно сформулированной подписи мы можем легко понять (и быть в восторге) от предполагаемой цели рисунка. И с цитатой в конце подписи мы можем перейти на страницу «Ссылки», чтобы обнаружить, что этот рисунок является обложкой обложки альбома Фрэнка Заппы 1982 года.Этот пример представляет собой простую демонстрацию того, насколько важно писать полезные подписи к рисункам, и показывает, как даже самая простая графика может быть загадочной для читателя (особенно если она нарисована не в масштабе, как на рисунке Заппы), когда эффективны подсказки о ее значении. отсутствуют.
Рисунки, уравнения и таблицы должны быть представлены так, чтобы читатели могли быстро понять их назначение в вашей работе. Они предоставляют возможность представить ваши идеи, объяснения и результаты экспериментов в профессиональной, эстетичной и, по правде говоря, даже в забавной форме.Компьютер произвел для нас настоящую революцию в наборе уравнений и представлении графиков. Однако некоторые профессора тоскуют по дням, когда фигуры приходилось кропотливо рисовать вручную, потому что стоимость и трудозатраты делали привлекательным сведение рисунков и таблиц к минимуму. Теперь графическое излишество является обычным явлением, особенно среди продвинутых студентов; некоторые профессора называют это менталитетом USA Today . Мы должны помнить, что графика — это средство для достижения цели, а не самоцель.
Кроме того, поскольку читатели могут сразу перейти к таблице или рисунку во время чтения статьи, крайне важно, чтобы каждая таблица или рисунок были осмысленно представлены и работали как независимо, так и как часть текста.Внимательно изучите таблицы и рисунки, опубликованные в лучших журналах в вашей области, и применяйте те же правила представления к своей собственной работе.
Цель этой главы не в том, чтобы облегчить вам создание уравнений, рисунков или таблиц (компьютерное программное обеспечение сделало их создание достаточно простым), а в том, чтобы научить вас, как сделать их презентацию профессиональной. Для более подробной информации о том, как представлять таблицы и рисунки, а также для отличного обзора различных типов, я настоятельно рекомендую Paul V. Техническое письмо Андерсона : подход, ориентированный на читателя . Я просмотрел более 40 учебников, в которых есть место для этого предмета, и главы Андерсона — лучшие из тех, что я видел.
Калькулятор значащих цифр
Использование калькулятора
Сложение, вычитание, умножение и деление значащих цифр. Введите числа, экспоненциальное представление или электронное обозначение и выберите оператор. Калькулятор вычисляет и округляет ответ до нужного числа значащих цифр (значащих цифр).3 и 3.5e3.
Осторожно: См. примечание относительно расчета значащих цифр.
Что такое значимые цифры?
Значащие цифры — это цифры числа, которые имеют значение с точки зрения точности или прецизионности. Эти цифры предоставляют важную информацию о точности расчета или измерения.
Значащие цифры Правила
Ненулевые цифры всегда значащие
Нули между ненулевыми цифрами всегда значащие
Ведущие нули никогда не являются значащими
Нули в конце имеют значение только в том случае, если число содержит десятичную точку
Примеры значащих цифр
Чтобы узнать больше об округлении значащих цифр, см. Калькулятор округления значащих цифр.
Чтобы попрактиковаться в определении значащих цифр в числах, см. Счетчик значимых цифр.
Примечание. Выполнение математических операций со значащими цифрами
Если вы вводите постоянное или точное значение, которое может встречаться в формуле, обязательно укажите правильное количество значащих цифр.
Например, рассмотрим формулу диаметра круга d = 2r, где диаметр в два раза больше длины радиуса.Если вы измерили радиус 2,35, умножьте на 2, чтобы найти диаметр круга: 2 * 2,35 = 4,70
Если вы используете этот калькулятор для расчета и введете только «2» для значения радиуса, калькулятор будет читать 2 как одну значащую цифру. Ваш результирующий расчет будет округлен от 4,70 до 5, что явно не является правильным ответом на расчет диаметра d=2r.
Вы можете думать, что константы или точные значения имеют бесконечно много значащих цифр или, по крайней мере, столько значащих цифр, сколько наименее точное число в вашем вычислении.В этом примере вы хотите ввести 2,00 в качестве постоянного значения, чтобы оно имело то же количество значащих цифр, что и запись радиуса. Полученный ответ будет 4,70, который имеет 3 значащих цифры.
Ссылки
Раздел 7 Заголовки и перекрестные ссылки
Если вы включаете в свои документы таблицы, рисунки и уравнения, они должны быть правильно пронумерованы и снабжены перекрестными ссылками. По соглашению подписи к таблицам располагаются над таблицей; подписи к рисункам находятся под рисунком, а номера уравнений — справа от уравнения.
В этом упражнении мы будем добавлять подписи и перекрестные ссылки к таблице, рисунку и уравнению.
Загрузите и откройте документ captions.docx. Он содержит одну таблицу, одно изображение и одно уравнение.
Подписи к таблицам
R-щелкните виджет выбора таблицы в левом верхнем углу таблицы.
Во всплывающем меню выберите Вставить заголовок
Поскольку это таблица, выберите Таблица в качестве метки .Введите текст подписи после метки в элементе управления Caption . Убедитесь, что заголовок установлен над таблицей.
Нажмите OK , чтобы добавить заголовок.
Если вы хотите изменить стиль подписи, щелкните правой кнопкой мыши стиль и выберите Изменить .
Здесь мы не указываем пробел после абзаца …
… Калибри 12 пт …
… черный шрифт…
Другой способ обновления стиля заключается в выделении текста и изменении его свойств (т.g., абзац, шрифт), а затем правой кнопкой мыши щелкните стиль и выберите Обновить [стиль], чтобы он соответствовал выделенному .
Подписи к рисункам
Подписи к рисункам добавляются таким же образом; R-щелкните изображение и выберите Insert Caption .
Для рисунков обязательно поместите легенду под изображением.
Перекрестные ссылки
После создания титров на них можно легко ссылаться. Чтобы добавить перекрестные ссылки, в меню References выберите Cross-reference .
Это открывает диалоговое окно для вставки перекрестной ссылки. Выберите тип ссылки, которую вы хотите использовать, что ограничит список заголовков этого типа. Нажмите на нужную надпись. Чтобы включить обычную метку и номер, выберите Only label и number из Insert reference to control.
Щелкните Вставить , а затем Отменить .
Вставьте также перекрестные ссылки для рисунка и уравнения.
Наконец, обновите основной текст, включив в него нужные формулировки в качестве ссылок на заголовки.
Поскольку все они управляются формами Word, если вы когда-нибудь измените порядок подписей в тексте, номера будут обновлены автоматически. Чтобы принудительно обновить любой полученный из поля текст в Word, выберите весь документ ( Ctrl-A ) и нажмите клавишу F9 .
Например, здесь мы добавили еще одно уравнение.
Изменение порядка уравнений, неправильный числовой порядок
Итак, мы выделяем весь текст в документе ( Ctrl-A ) и нажимаем F9
Добавление, форматирование или удаление подписей в Word
Вы можете добавлять подписи к рисункам, уравнениям и другим объектам. Подпись — это пронумерованная метка, например «Рисунок 1», которую можно добавить к рисунку, таблице, уравнению или другому объекту. Он состоит из настраиваемого текста («Рисунок», «Таблица», «Уравнение» или что-то еще, что вы вводите), за которым следует упорядоченная цифра или буква («1, 2, 3…» или «a, b, c. ..», как правило), за которым может следовать какой-либо дополнительный описательный текст, если хотите.
1. Текст, который вы выбираете или создаете.
2.Номер, который Word вставляет для вас
Если вы позже добавите, удалите или переместите подписи, вы можете легко обновить номера всех подписей сразу.
Вы также можете использовать эти подписи для создания таблицы элементов с подписями, например, таблицы рисунков или таблицы уравнений.
Что ты хочешь сделать?
Нажмите тему или темы ниже, которые вас интересуют.
Добавить подписи
Совет: Если вы хотите иметь возможность перемещать рисунок и подпись как один объект или оборачивать текст вокруг рисунка и подписи, следуйте приведенным ниже инструкциям по добавлению подписей к плавающим объектам.
Выберите объект (таблицу, формулу, рисунок или другой объект), к которому вы хотите добавить подпись.
На вкладке Ссылки в группе Заголовки щелкните Вставить заголовок .
В списке Этикетка выберите метку, которая лучше всего описывает объект, например рисунок или уравнение.Если в списке нет нужной метки, щелкните New Label , введите новую метку в поле Label и нажмите OK .
Введите любой текст, включая знаки препинания, который должен отображаться после метки.
Щелкните OK .
Примечание: Word вставляет порядковый номер подписи в качестве поля. Если ваша подпись похожа на «Рисунок {SEQ Table \* ARABIC}», Word отображает коды полей вместо результатов полей. Чтобы увидеть заголовок в обычном режиме, нажмите ALT+F9.
Добавить подпись к плавающему объекту
Если вы хотите иметь возможность оборачивать текст вокруг объекта и подписи или хотите иметь возможность перемещать объект и подпись как единое целое, вам необходимо сгруппировать объект и подпись вместе.
Вставьте свою фигуру.
Выберите Параметры макета и выберите один из вариантов С переносом текста .
Важно: Вы должны выполнить этот шаг до того, как вставите подпись. Если вы уже вставили подпись, удалите ее, выполните этот шаг, а затем снова добавьте подпись.
Добавьте подпись, выполнив действия, описанные в разделе «Добавить подписи» выше.
Выберите свою подпись, затем, удерживая нажатой клавишу Shift, выберите свою фигуру.
Щелкните правой кнопкой мыши любой элемент и выберите Группа > Группа .
Теперь текст должен обтекать рисунок и подпись, как и ожидалось, а рисунок и подпись останутся вместе, если вы переместите их в другое место на странице или в документе.
Примечание: Если вы перемещаете рисунок, рекомендуется обновить номера подписей (см. ниже), чтобы убедиться, что нумерация по-прежнему в правильном порядке.
Обновить номера заголовков
Если вы вставите новую подпись, Word автоматически обновит номера подписей. Однако при удалении или перемещении подписи необходимо вручную запустить обновление подписи.
Щелкните в любом месте документа и нажмите CTRL+A, чтобы выбрать весь документ.
Щелкните правой кнопкой мыши и выберите Обновить поле в контекстном меню. Все подписи в документе теперь должны быть обновлены.
Совет: Вы также можете обновить подписи, выбрав весь документ и нажав F9.
Формат подписей
После добавления хотя бы одной подписи к документу в галерее стилей должен отображаться новый стиль под названием «Подпись».Чтобы изменить форматирование подписей во всем документе, просто щелкните правой кнопкой мыши этот стиль в галерее и выберите Изменить . Здесь вы можете установить размер шрифта, цвет, тип и другие параметры, которые будут применяться к вашим подписям.
Дополнительные сведения об изменении стилей в Word см. в разделе Настройка стилей в Word
.
Удалить заголовок
Чтобы удалить подпись, выделите ее мышью и нажмите Удалить. Если у вас есть дополнительные подписи в документе, когда вы закончите удаление тех, которые хотите удалить, вам следует обновить их. Нажмите CTRL+A, чтобы выделить весь текст в документе, а затем нажмите F9, чтобы обновить все. Это гарантирует, что ваши номера подписей будут правильными после того, как вы удалите те, которые вам не нужны.
См. также
У вас есть вопрос о подписях в Word, на который мы не ответили?
Задайте вопрос на форуме Word Answers.
Помогите нам улучшить Word
У вас есть предложения по улучшению подписей (или любой другой функции) Word? Если это так, дайте нам знать, предоставив нам обратную связь. См. раздел Как оставить отзыв о Microsoft Office? Чтобы получить больше информации.
Вы получите математическое уравнение в слове, отлично нарисуете цифры и графики
привет, я Дипак, я хочу поделиться своими навыками и опытом с моими клиентами.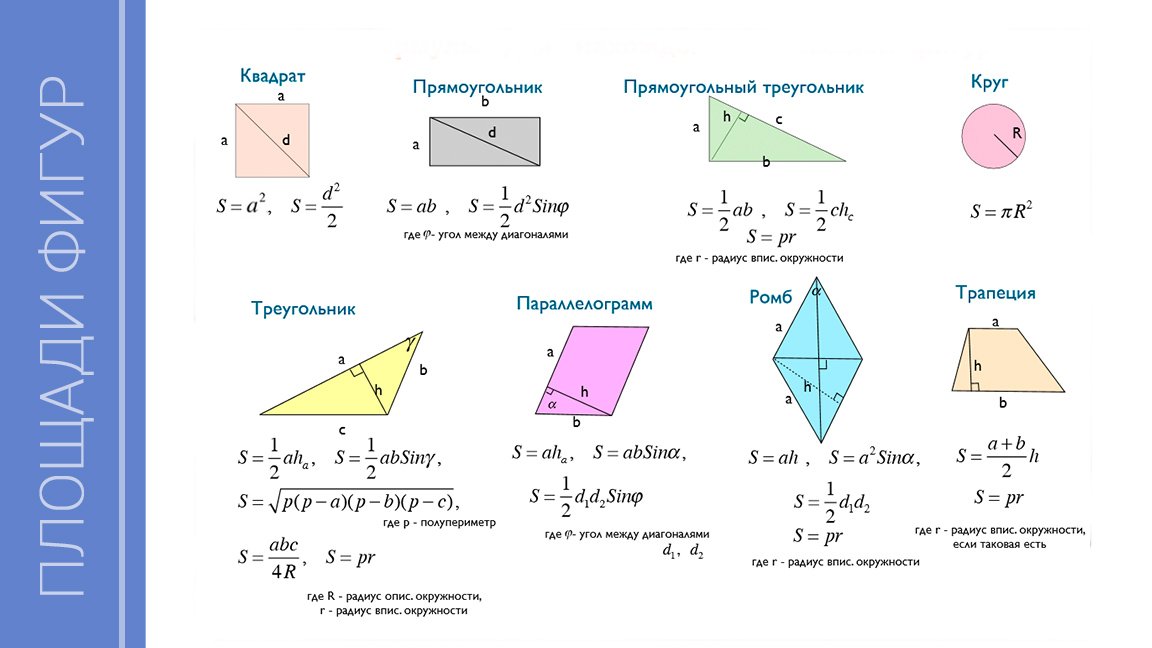
✔ очень ответственный человек и готов взять на себя ответственность за каждую поставленную передо мной задачу.
✔ Выкладываюсь по максимуму в каждом проекте.
✔ обладать необходимыми навыками для успешного выполнения работы и превосходить ожидания.
Сталкивались ли вы с трудностями при работе с PDF-документами?
Вы хотите преобразовать, отредактировать текст, улучшить свой PDF-файл?
Нужна машинистка для быстрого и точного ввода данных без ошибок?
Ищете эксперта для создания заполняемой формы PDF?
Да, вы в правильном месте.Позвольте мне сделать это для вас, это моя работа, чтобы предоставить вам полное решение
мои предложения услуг:
✔Преобразование документов:
преобразование отсканированных pdf. в слово
конвертировать PDF в Word, Excel, PowerPoint, текст, изображения, HTML, Epub.
конвертировать PDF в doc, docx, xls, xlsx, ppt, pptx, txt, jpg, HTML.
конвертировать в PDF-превратить практически любой файл в pdf
конвертировать в Editable TexT
✔Enhance Pdf:
Убрать фоновый шум, изменить фон
Добавить пароль, страницы, номер страницы, текст, изображения, водяной знак
✔Управление PDF-файлы:
Создать PDF, Объединить, Разделить, Объединить, Сжать, Связать, Извлечь
✔Дополнительно:
Измените размер PDF по вашему выбору
Увеличьте качество P. Д.Ф. (300 dpi)
Извлечение изображений из файлов
Изменение размера, обрезка страниц
Редактирование текста в файлах
Готов внести любые изменения в соответствии с вашими инструкциями
✔Заполняемая PDF-форма Особенности:
Добавление текста и изображений, Флажки, Радиокнопки, Поле со списком, раскрывающийся список, пункт меню, поле со списком и кнопка
Добавить поле изображения, поле данных, текстовые поля
Добавить кнопки, такие как «Отправить», «Сохранить», «Сбросить», «Печать», «Очистить»
Поле с ограниченным набором символов
✔Ввод:
Идеальный ввод уравнений по математике, химии, физике и всех символов в MS-word
Быстрый ввод на английском, хинди, языках маратхи
Преобразование рукописных/отсканированных pdf/изображений в редактируемый текст
Редактирование и форматирование документа.
✔Программное обеспечение/инструменты, с которыми я работаю:
Adobe Acrobat DC
Microsoft Office
Photoshop
✔ЗАЧЕМ пользоваться этой услугой?
Навык решения проблем
Быстрое время отклика
Хорошая коммуникация
Знание продукта
Желание учиться
Быстрый оборот
Гарантия максимальной удовлетворенности
Свяжитесь с нами сегодня, чтобы воспользоваться нашими лучшими услугами.
Спасибо, что посетили нас!🙂
Попробуй! Игра «Построение уравнений»
Подумай! это математическая карточная игра, которая была разработана, чтобы сделать математику интересной для всех!
Интервью с создателем игр Алоном Ниром

Что заставило вас создать эту игру?
Когда я был маленьким, мы с братом играли в «Монополию» практически день и ночь.Мой папа не был высокого мнения о «Монополии», поэтому он разработал свои собственные игры. С ними было очень весело, но они никогда не выходили за пределы нашего кухонного стола.
Некоторое время назад мы с отцом собрались вместе и попытались улучшить одну из его игр. Мы провели день, возясь. Посреди ночи я не мог уснуть, потому что все еще думал об этом, и я придумал концепцию Go Figure!. На следующее утро я создал прототип. Я играл в нее со своими детьми и их друзьями. Всем понравилось.Родители стали просить меня сделать им игры. Одно привело к другому, и теперь игра стала хитом более чем в десяти странах мира.

Каковы основные преимущества игр в школе?
«O В среднем использование академических игр в классе связано с увеличением успеваемости учащихся на 20 процентилей » (Marzano – 2010).
Существует серьезное исследование, которое поддерживает использование игр для улучшения успеваемости.На мой взгляд, на это есть несколько причин. Основная причина в том, что в игры весело играть! Когда детям весело, их мотивация и вовлеченность повышаются, они становятся более внимательными и обретают уверенность.
Кроме того, игры улучшают социальные навыки (учась изящно проигрывать) и улучшают исполнительные навыки (такие как планирование и обдумывание, прежде чем действовать).

Как Go Figure улучшает беглость чтения по математике?
Когда дети играют Поди разберись! они даже не замечают, что изучают и практикуют математические навыки. Для них они просто играют в забавную игру, хотя занимаются математикой 100% времени. Каждому игроку раздаются карты, которые он использует для построения уравнений. Каждый ход игроки используют карты в руке, чтобы добавить их в стопки, чтобы изменить уравнение. Они одновременно практикуют беглость математики и творческое решение задач.
Могут ли ученики разного уровня играть в игру «Го-фигурка»?
Одна вещь, которая мне нравится в , поди разберись! заключается в том, что он подходит как отличному математику, так и студенту, которому не помешало бы больше практики.Игроки с разным уровнем мастерства могут играть вместе. Когда игроки по очереди составляют уравнения с сыгранными картами, есть элемент удачи, основанный на картах, которые вам сдали. Это означает, что иногда игрок, который является лучшим в математике, не обязательно выигрывает.
В то же время игру можно легко дифференцировать для разных уровней. Для младших школьников используйте только символы сложения и вычитания. Для более продвинутых детей добавьте символы умножения и деления.
Для старших школьников: Пойми! Advanced включает карты с дробями, квадратным и квадратным корнем, которые можно использовать для отработки более сложных уравнений.

Можно ли играть в Go Figure дома?
Абсолютно! Это веселая игра для всей семьи. Правила просты, и родители могут быстро научиться играть.
Важно укреплять математические навыки. Мы все обеспокоены потерями в обучении, которые произошли за последний год. Играя в такие игры, как Go Figure! дома — это интересный способ закрепить математические навыки для всех учащихся.

Что бы вы назвали ключевыми преимуществами игры в Go Figure?
Что бы вы назвали основными преимуществами игры Go Figure! ?
Игроки связывают математику с развлечением. Это самый важный элемент и может оказать длительное влияние на остальную часть жизни.
Игроки становятся более изобретательными с числами
Игроки лучше разбираются в комбинациях чисел
Игроки обретают уверенность в математике

Получите скидку 10 % на все игры Go Figure с промокодом:
GoFigure10

Предложение действительно до 1 октября 2021 г., 11:59 по восточному поясному времени.

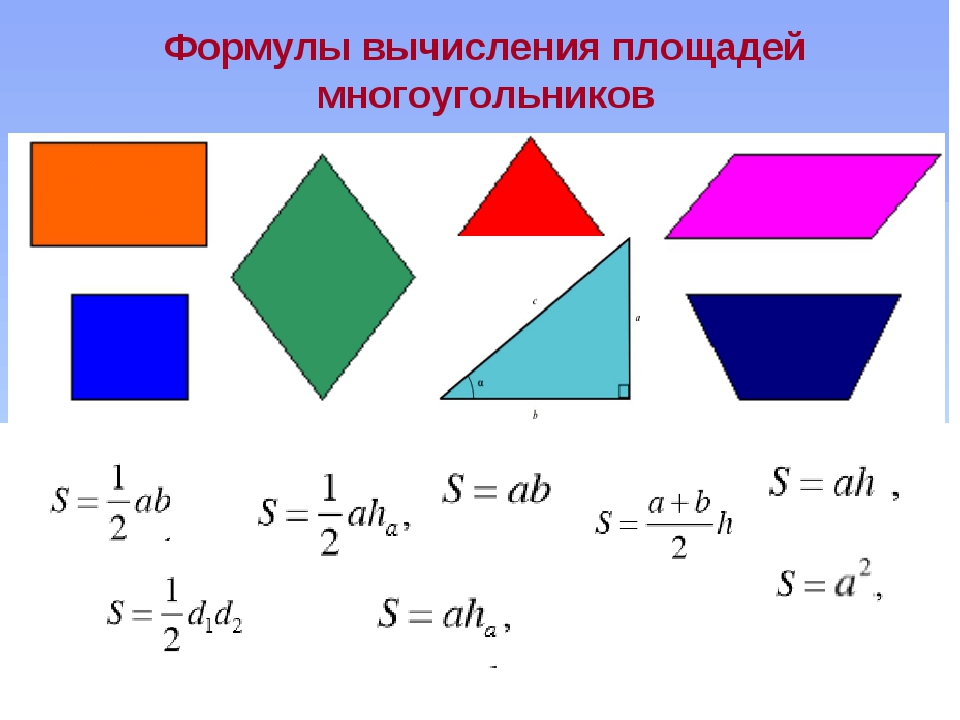
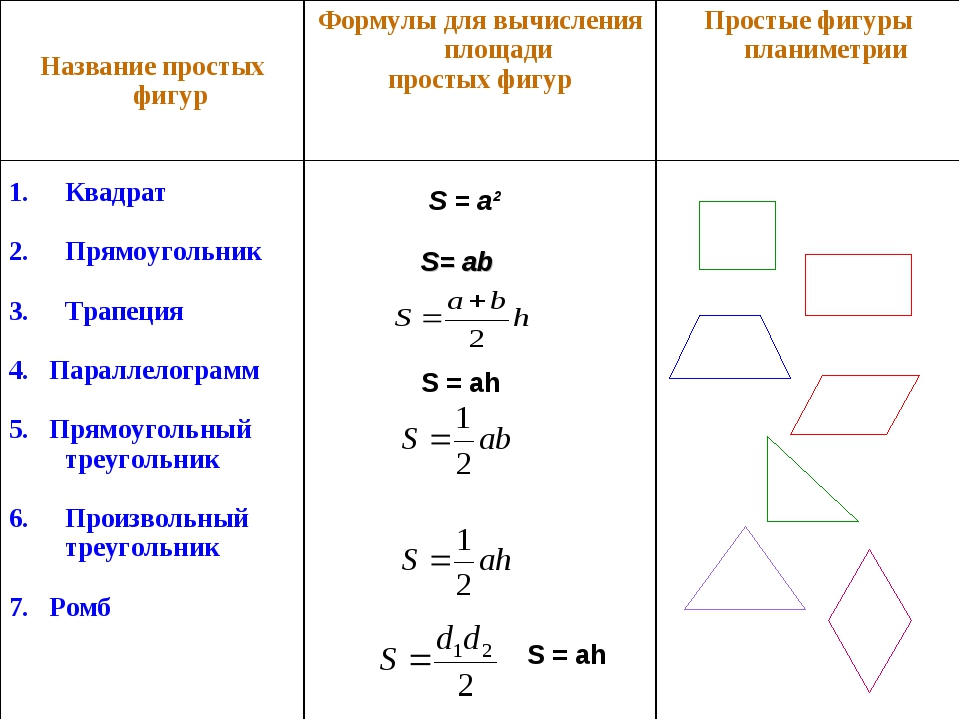
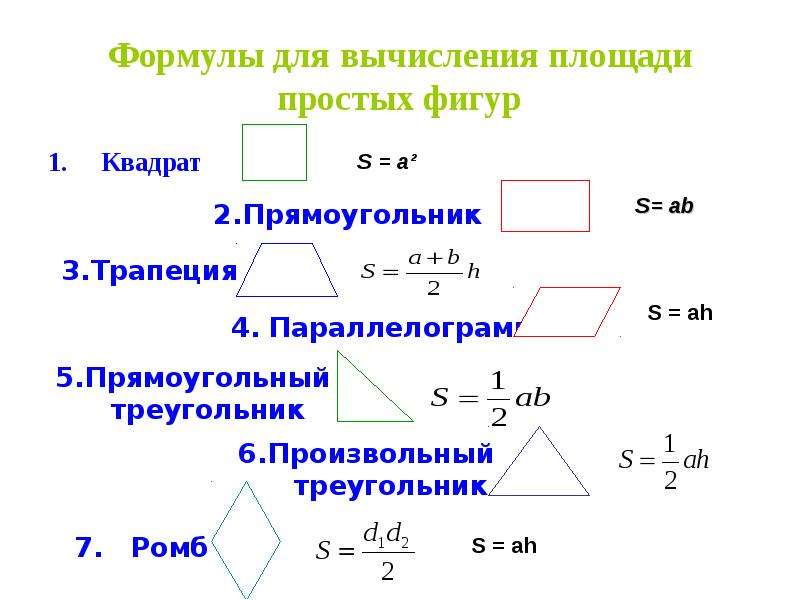
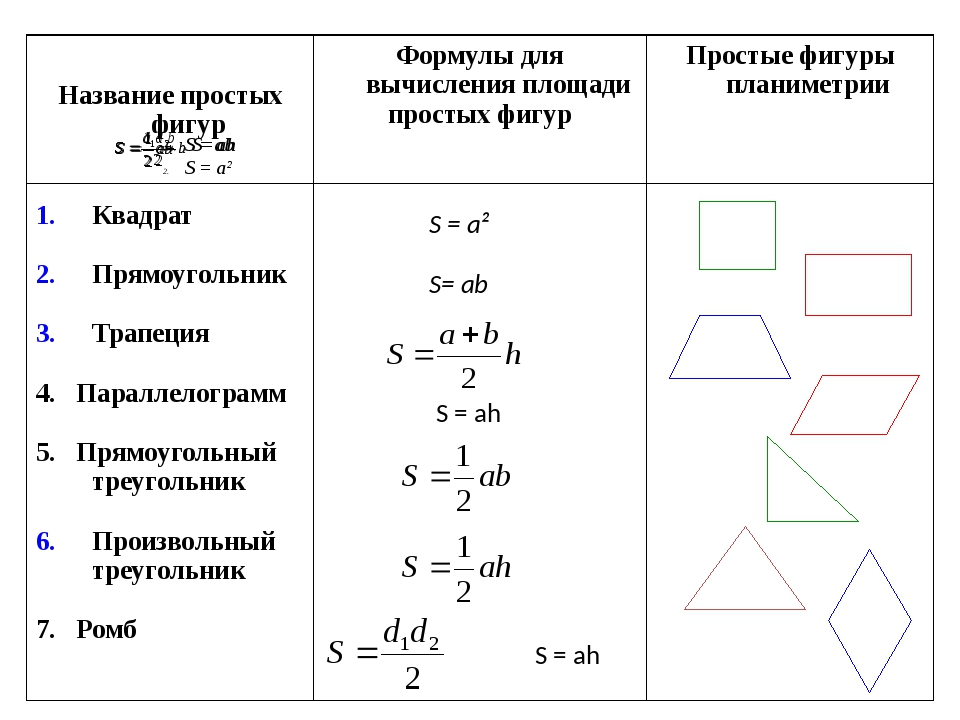
Площадь составных фигур – формула, примеры, определение
Площадь составных фигур — это площадь, покрываемая любой составной фигурой. Составная форма — это форма, в которой несколько полигонов соединяются вместе, чтобы сформировать требуемую форму. Эти формы или фигуры могут состоять из комбинации треугольников, квадратов, четырехугольников и т. д. Разделите составную фигуру на основные формы, такие как квадрат, треугольник, прямоугольник, шестиугольник и т. д.для определения площади составных фигур.
В основном, составная фигура состоит из основных фигур, соединенных вместе. Его также называют «составной» или «сложной» формой. В этом мини-уроке объясняется область составной формы вместе с решенными примерами и практическими вопросами.
Какова площадь составных фигур?
Площадь составных фигур — это площадь объединенных фигур одного или нескольких простых многоугольников и кругов. Чтобы вычислить площадь составных фигур, мы можем сложить площади всех основных фигур вместе.Чтобы найти площадь составных фигур, просто найдите площадь каждой фигуры и сложите их вместе. Следующий рисунок даст представление о том, как найти площадь составной фигуры. Единица площади составных фигур выражается в м ², см ², в ² или в футах ² и т. д.
Как найти площадь составных фигур?
Площадь составных фигур представляет собой комбинацию основных форм.С помощью следующих шагов, упомянутых ниже, мы можем вычислить площадь составных фигур.
Шаг 1 : Разбейте составную фигуру на основные формы.
Шаг 2 : Найдите площадь каждой базовой формы.
Шаг 3 : Сложите все области основных фигур вместе.
Шаг 4 : Представьте ответ в квадратных единицах.
Чтобы разложить любую составную фигуру, мы должны уметь вычислять площадь некоторых основных фигур, таких как квадраты, треугольники, прямоугольники и т. д.Проверьте таблицу ниже, содержащую площадь основных фигур.
Пример: Найдите площадь составной фигуры, образованной соединением квадрата и треугольника. Длина стороны квадрата равна 5 единицам. Основание и высота треугольника равны 6 единицам и 7 единицам соответственно.
Решение: Длина стороны квадрата = 5 единиц, основание треугольника = 6 единиц и высота треугольника = 7 единиц
Площадь составной фигуры = площадь квадрата + площадь треугольника
⇒ А = (5) ² + [(1/2) × 6 × 7]
⇒ A = 25 + 21 = 46 квадратных единиц
Площадь составной фигуры 46 квадратных единиц.
Часто задаваемые вопросы по области составных форм
Какова площадь составных фигур?
Площадь составных фигур определяется как площадь, покрываемая любой составной фигурой. Составная форма состоит из основных фигур, соединенных вместе. Таким образом, площадь составной фигуры находится путем сложения по отдельности всех основных фигур.
Что такое формула площади составных фигур?
Не существует фиксированной формулы для определения площади составных фигур.Площадь составных фигур можно рассчитать, разделив составную фигуру на основные формы, такие как квадрат, треугольник, круг, прямоугольник, многоугольник и т. д., и сложив их площади.
Какова единица площади составных фигур?
Площадь составных фигур можно узнать, сложив площади всех фигур вместе. Единица площади составных фигур выражается в квадратных единицах, таких как м 90 539 2 90 540, см 90 539 2 90 540, 90 539 2 90 540 или фут 90 539 2 90 540 и т. д.
Как найти площадь составной фигуры?
Шаги для нахождения площади составных фигур:
Шаг 1 : Разделите составную фигуру на основные формы.
Шаг 2 : Найдите площадь каждой базовой формы отдельно.
Шаг 3 : Сложите все области основных фигур вместе.
Шаг 4 : Теперь запишите ответ в квадратных единицах.
Как найти площадь составной фигуры, если известны площади всех входящих в нее основных фигур?
Площадь составных фигур, если известны площади всех основных фигур в ней, находится с помощью следующих шагов:
Шаг 1 : Определите отдельные области всех основных фигур.
Шаг 2 : Сложите площади всех основных фигур вместе.
Шаг 3 : Теперь запишите ответ в квадратных единицах.
Что произойдет с площадью составных фигур, если увеличить размеры всех основных фигур?
Если размеры всех основных форм увеличиваются, площадь составных фигур также увеличивается.