Окружность и круг — геометрия и искусство
В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении.
В школе изучается много полезных свойств окружности. Одной из самых красивых теорем является следующая: проведем через заданную точку прямую, пересекающую заданную окружность, тогда произведение расстояний от этой точки до точек пересечения окружности с прямой не зависит от того, как именно была проведена прямая. Этой теореме около двух тысяч лет.
На рис. 2 изображены две окружности и цепочка окружностей, каждая из которых касается этих двух окружностей и двух соседей по цепочке. Швейцарский геометр Якоб Штейнер около 150 лет назад доказал следующее утверждение: если при некотором выборе третьей окружности цепочка замкнется, то она замкнется и при любом другом выборе третьей окружности.
Вначале мы упомянули о колесе, но еще до колеса люди использовали круглые бревна — катки для перевозки тяжестей.
А можно ли использовать катки не круглой, а какой-нибудь другой формы? Немецкий инженер Франц Рело обнаружил, что таким же свойством обладают катки, форма которых изображена на рис. 3. Эта фигура получается, если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие вершины. Если провести к этой фигуре две параллельные касательные, то расстояние между ними будет равно длине стороны исходного равностороннего треугольника, так что такие катки ничем не хуже круглых. В дальнейшем были придуманы и другие фигуры, способные выполнять роль катков.
Энц. «Я познаю мир. Математика», 2006
Круг. Круг — геометрическая фигура
Форма круга является интересной с точки зрения оккультизма, магии и древних значений, придаваемых ей людьми. Все мельчайшие составляющие вокруг нас – атомы и молекулы – имеют круглую форму. Солнце круглое, Луна круглая, наша планета тоже круглая. Молекулы воды – основы всего живого – тоже имеют круглую форму. Даже природа создает свою жизнь в кругах. Например, можно вспомнить про птичье гнездо – птицы вьют его также в этой форме.
Данная фигура в древних помыслах культур
Круг – это символ единства. Он присутствует в разных культурах во многих мельчайших деталях. Мы даже не придаем столько значения этой форме, как это делали наши предки.
Издавна круг – это знак бесконечной линии, который символизирует время и вечность. В дохристианскую эпоху он был древним знаком колеса солнца. Все точки в этой фигуре эквивалентны, линия круга не имеет ни начала, ни конца.
А центр круга был источником бесконечного вращения пространства и времени для масонов. Круг – конец всех фигур, недаром в нем была заключена тайна творения, по мнению масонов. Форма циферблата часов, имеющая тоже такую форму, обозначает собой непременное возвращение в точку отправления.
Эта фигура имеет глубокий магический и мистический состав, которым его наделили многие поколения людей из разных культур. Но что собой представляет круг как фигура в геометрии?
Что такое окружность
Часто понятие круга путают с понятием окружности. Это немудрено, ведь они между собой очень тесно взаимосвязаны. Даже названия их схожи, что вызывает много путаницы в незрелых умах школьников. Чтобы разобраться, «кто есть кто», рассмотрим эти вопросы подробнее.
По определению, окружностью является такая кривая, которая замкнута, и каждая точка которой находится равноудалённо от точки, именуемой центром окружности.
Что необходимо знать и чем уметь пользоваться, чтобы построить окружность
Чтобы построить окружность, достаточно выбрать произвольную точку, которую можно обозначить как О (именно так в большинстве источников именуются центр окружности, не будем отходить от традиционных обозначений). Следующим этапом идет использование циркуля – инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.
Следующим этапом идет использование циркуля – инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.
Эти две части соединены между собой шарниром, что позволяет выбирать произвольный радиус в определенных границах, связанных с длиной этих самых частей. С помощью данного прибора в произвольную точку О устанавливается остриё циркуля, а карандашом уже очерчивается кривая, которая из итоге получается окружностью.
Какими величинами характеризуется окружность
Если соединить при помощи линейки центр окружности и любую произвольную точку на кривой, полученной в результате работы циркулем, мы получим радиус окружности. Все такие отрезки, именуемые радиусами, будут равны. Если же соединить при помощи линейки прямой линией две точки на окружности и центр, мы получим ее диаметр.
Для окружности также характерно вычисление ее длины. Чтобы ее найти, необходимо знать либо диаметр, либо радиус окружности и воспользоваться формулой, представленной на рисунке ниже.
В этой формуле С – длина окружности, r – радиус окружности, d – диаметр, а число Пи – константа со значением 3,14.
Кстати, константа Пи была вычислена как раз из окружности.
Оказалось, что независимо от того, каков диаметр круга, соотношение длины окружности и диаметра одинаковое, равное примерно 3,14.
В чем же главное отличие круга от окружности
По сути, окружность – это линия. Она не является фигурой, она является кривой замкнутой линией, не имеющей ни конца, ни начала. А то пространство, что расположено внутри нее – это пустота. Простейшим примером окружности выступает обруч или, по-иному, хула-хуп, который дети используют на занятии физической культуры или же взрослые, для того чтобы создать себе стройную талию.
Теперь мы подошли к понятию того, что такое круг. Это в первую очередь фигура, то есть некое множество точек, ограниченных линией. В случае круга этой линией выступает окружность, рассмотренная выше. Выходит, что круг – это окружность, в середине которой не пустота, а множество точек пространства. Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью – его пустота замещена тканью, куском пространства.
Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью – его пустота замещена тканью, куском пространства.
Перейдем непосредственно к понятию круга
Круг – геометрическая фигура, которая является частью плоскости, ограниченной окружностью. Для него также характерны такие понятия, как радиус и диаметр, рассмотренные выше при определении окружности. И вычисляются они точно таким же образом. Радиус круга и радиус окружности являются идентичными по размеру. Соответственно, длина диаметра тоже аналогична в обоих случаях.
Так как круг является частью плоскости, то для него характерно наличие площади. Вычислить ее можно снова-таки при помощи радиуса и числа Пи. Формула выглядит следующими образом (см. рисунок ниже).
В данной формуле S – площадь, r – радиус круга. Число Пи – снова та же константа, равная 3,14.
Формула круга, для вычисления которой возможно также использовать диаметр, изменяется и принимает вид, представленный на следующем рисунке.
Одна четвертая появляется из того, что радиус – это 1/2 диаметра. Если радиус в квадрате, выходит, что соотношение преобразуется до вида:
r*r = 1/2*d*1/2*d;
r*r = 1/ d*d.
Круг – это фигура, в которой можно выделить отдельные части, например сектор. Выглядит он как часть круга, которая ограничена отрезком дуги и его двумя радиусами, проведенными из центра.
Формула, которая позволяет вычислить площадь данного сектора, представлена на нижеследующем рисунке.
Использование фигуры в задачах с многоугольниками
Также круг – геометрическая фигура, которая часто используется в комплекте с другими фигурами. Например, такими как треугольник, трапеция, квадрат или ромб. Нередко встречаются задачи, где нужно найти площадь вписанного круга или, наоборот, описанного вокруг определенной фигуры.
Вписанный круг является таким, который соприкасается со всеми сторонами многоугольника. С каждой стороной любого многоугольника у окружности должна быть точка соприкосновения.
Для определенного вида многоугольника определение радиуса вписанной окружности вычисляется по отдельным правилам, которые доступно объясняются в курсе геометрии.
Можно привести для примера несколько из них. Формула круга, вписанного в многоугольники, может вычисляться следующим образом (ниже на фото приведено несколько примеров).
Несколько простых примеров из жизни, для того чтобы закрепить понимание разницы между кругом и окружностью
Перед нами канализационный люк. Если он открыт, то железная каемка люка – это окружность. Если он закрыт, то крышка выступает в роли круга.
Окружностью также можно назвать любое кольцо – золотое, серебряное или бижутерию. Кольцо, которое держит на себе связку ключей, – тоже окружность.
А вот круглый магнит на холодильнике, тарелка или блинчики, испеченные бабушкой, –это круг.
Горлышко бутылки или банки при виде сверху – это окружность, а вот крышка, которая закроет это горлышко, при том же виде сверху является кругом.
Таких примеров можно привести множество, и для усвоения такого материала их нужно приводить, чтобы дети лучше улавливали связь теории с практикой.
Геометрические фигуры для детей. Круг.
Сегодня мы будем делать цыплёнка. Каким цветом цыпленок? Правильно, жёлтый. Из всех кругов выбери только желтые круги. Потом отложи отдельно голубые круги и зеленые.
Сначала просто выкладываем цыплёнка на бумаге без клея, чтобы у малыша было понимание того, что мы делаем, это также поможет избежать ошибок при работе с клеем.
Большой жёлтый круг будет туловищем цыпленка. Куда мы его положим? (предлагаем ребенку самому выбрать место на листе бумаги).
Кружок поменьше будет головой. Где у нашего цыплёнка будет голова? (ребёнок пусть снова сам выберет место, в какую сторону будет смотреть цыплёнок: вверх на небо и солнце или вниз на травку, может он будет клевать зернышки. Помогайте малышу фантазировать, предлагайте варианты. Маленьким можно подсказать, посоветовать, но не настаивайте, пусть он сам сделает выбор)
Где маленький чёрный кружок? Это будет глаз. Маленький треугольник — клюв, два одинаковых треугольника — лапки. Разложи фигуры на свои места.
Маленький треугольник — клюв, два одинаковых треугольника — лапки. Разложи фигуры на свои места.
Чего не хватает нашему цыпленку? Правильно, крыльев! У нас есть ещё 2 жёлтых круга, один мы отложим — это будет солнце, а из второго сделаем крылья. Как ты думаешь, как из одного круга сделать два крыла? (с этим справятся дети от трёх лет. Пусть ребёнок подержит круг в руках, повертит, приложит к бумаге, возможно, у него появится ответ).
Мы разрежем круг напополам. Для этого давай найдем центр круга. Где центр (середина) у круга? (можно дать ребенку карандаш и предложить самому найти и отметить центр с тыльной (не цветной!) стороны листа. Даже если точка не в центре, а где-то рядом, ничего страшного, похвалите кроху! Если ребёнок мал, сделайте все сами, объясняя каждое действие).
Через центр теперь проведем прямую линию, которая разделит круг напополам. По этой линии мы разрежем наш круг на две части. Получилось два крыла (обязательно разрезайте через точку (центр), указанную ребёнком, во-первых, ребёнок будет чувствовать, что его мнение важно для вас и вы прислушиваетесь к нему, а во-вторых — аппликация будет более художественной)
В ходе занятия для детей постарше можно объяснить, что такое полукруг (или вспомнить эту фигуру)
Посмотри, какие фигуры у нас получились. Это фигура называется полукруг. Пол круга — полукруг (повторяем несколько раз и предлагаем повторить название)
Это фигура называется полукруг. Пол круга — полукруг (повторяем несколько раз и предлагаем повторить название)
Где будут крылышки у нашего цыплёнка?
Цыплёнка выложили на бумаге, теперь можно приклеить его.
Цыплёнок готов.
Давай возьмём большие зелёные круги (или 1 круг) — это будет наша травка. Как ты думаешь, как из круга сделать травку? Правильно, снова разрезать напополам (повторяем шаги, как с крылышками: даём ребёнку отметить центр, разрезаем и приклеиваем снизу). Чтобы травка была натуральнее, можно сделать небольшие надрезы по округлой стороне.
На небо приклеиваем солнышко.
Облака можно сделать разными способами:
1. Наклеить кружки внахлёст, формируя облако. Разный размер кружков сделает форму облака более натуральной.
2. Разрезать круги напополам и также наклеивать внахлёст.
У нас получилось по-другому: Поля захотела сложить круги напополам и приклеить только одну половину круга. Таким образом мы уже делали другие поделки и этот вариант ей понравился.
Когда бумага окончательно высохнет, можно дорисовать солнечные лучи и цветы на травке карандашом. Можно сделать это пластилином. Пусть малыш выбирает сам.
Что общего у окружности и круга. Чем отличается круг от шара
На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга.
Выводы сайт
- Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
- Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.
Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку.
Что такое окружность?
Окружность — это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.
Что такое круг?
Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые — кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг — это часть поверхности, очерченная окружностью.
У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый — это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).
Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).
Ну и наконец, третья характеристика, присущая кругу — это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий. В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.
Примеры круга в реальной жизни
На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга — это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.
Да, сама звезда Солнце — это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.
Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.
Отличия окружности от круга
Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.
Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность — круга.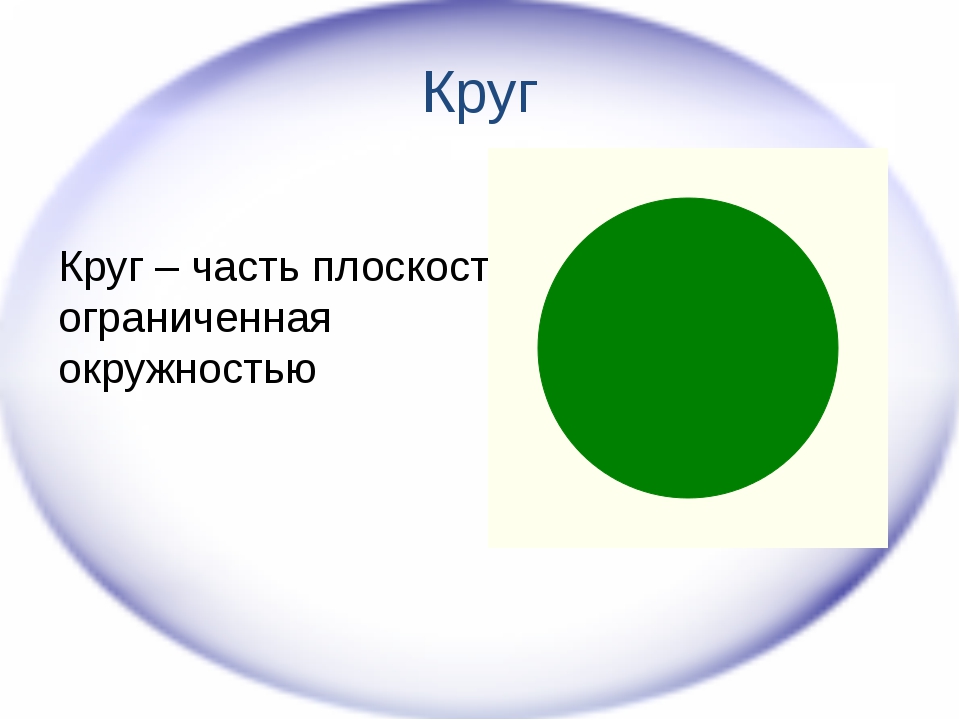 Вот чем отличается окружность от круга.
Вот чем отличается окружность от круга.
Что такое сектор?
Сектор — это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.
Предмет, отображаемый этим понятием, может иметь только круг. тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.
Выводы
Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг — фигура капризная. Но, как говорится, тяжело в учении — легко в бою. Да, геометрия — наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.
Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.
Школьные годы для большого количества взрослых – синоним беззаботной поры детства. Вполне понятно, почему многие дети и подростки не горят желанием каждый день ходить в школу – но именно в ее стенах они получают общие знания о мире и навыки социальной жизни, которые становятся незаменимыми после получения аттестата зрелости.
Одним из таких вопросов, таких общих понятий является тема сходств и различий круга и шара. Спутать рассматриваемые понятия одновременно просто и сложно – потому что различий между кругом и шаром не так много, как кажется малоопытному ребенку.
Итак, в чем же несходства между шаром и кругом? Чем они похожи?
Что такое круг?
Начертание круга начинается с окружности.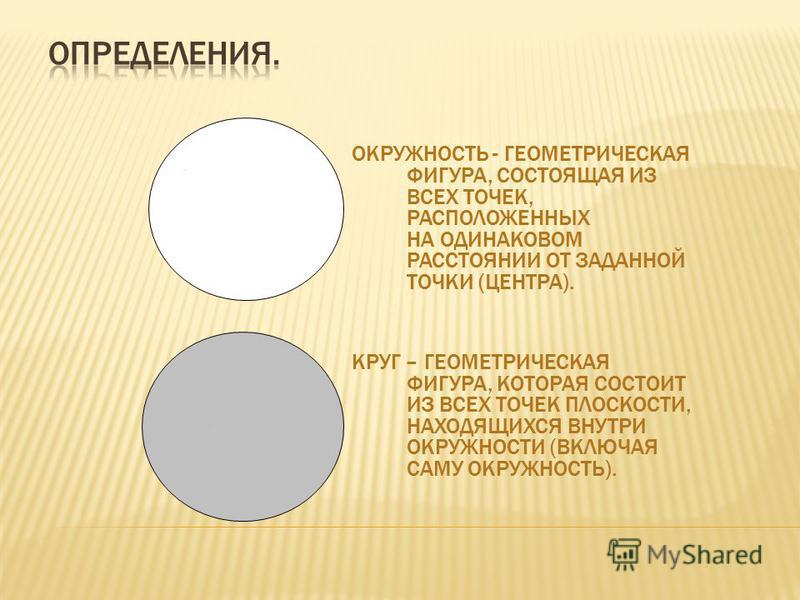 Окружность – это замкнутая черта без конца и начала , каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.
Окружность – это замкнутая черта без конца и начала , каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.
Круг получится, если начертить окружность, например, на бумаге – и потом разукрасить ее. Любыми красками: желтой, синей, зеленой – какая больше нравится. Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.
Круг обладает некоторыми важными для понимания его сущности параметрами. Кстати, часть данных параметров присуща и окружности.
- Радиус – расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
- Диаметр – важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.

- Площадь – свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.
Круг в реальной жизни
В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.
Другой пример круга – . Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.
Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.
Сектор
Что такое круг внимательный читатель ужен разобрался. Но вот что за «зверь» этот сектор, о котором упоминалось немного выше? Сектор – это часть круга, отделенная от остальной поверхности парой начерченных радиусов. Для наглядности можно примести такой пример: все когда-нибудь видели нарезанную пиццу. Кусочки – это сектора круга, которым является все это аппетитное блюдо.
Секторы не обязательно должны быть равной величины. К примеру, если пицца разрезана пополам, обе ее половины тоже будут секторами круга.
Что такое шар?
тело, ограниченное сферической поверхностью . То есть, это не двухмерная фигура, как круг, а трехмерная. Сферическая поверхность – это геометрическое сочетание поверхности точек, расположенных на неотрицательном расстоянии от некоей центральной точки. Расстояние, на которое удалены все точки поверхности шара от его центра, называется радиусом. И оно не должно превышать некие заданные цифры. Таким образом, круг – это та же сферическая поверхность, расположенная в другом пространстве.
И оно не должно превышать некие заданные цифры. Таким образом, круг – это та же сферическая поверхность, расположенная в другом пространстве.В этом проявляются сходства и главное различие шара и круга. Круг – это двухмерная фигура, точки которой ограничены окружностью. Шар – это фигура трехмерная, а ее точки ограничены сферической поверхностью.
Разновидности шара
В метрическом и векторном пространствах рассматриваются два понятия, имеющие связь со сферической поверхностью. Шар, который включает в себя данную сферу, именуют замкнутым . Шар, который не включает в себя сферу, называют открытым .
Характеристики шара
Шар, как и круг, имеет диаметр и радиус. Обе эти величины в шаре вычисляются по вышеописанным принципам (как для круга). Радиус шара – это отрезок между любой точкой на сферической поверхности, ограничивающей фигуру, и ее центром. Диаметр соединяет две точки на сферической поверхности шара, проходя через его центр.
Интересное дополнение: круг может быть частью шара. Точнее, шар состоит из очень большого количества кругов различного диаметра. Называются эти круги сечениями сферы. Когда сечение пролегает через центр шара, его именуют большим кругом. Все остальные сечения именуются малыми кругами. Такого рода сечений, проходящих через пару точек на поверхности шара, возможно начертить поистине бесконечное множество.
Точнее, шар состоит из очень большого количества кругов различного диаметра. Называются эти круги сечениями сферы. Когда сечение пролегает через центр шара, его именуют большим кругом. Все остальные сечения именуются малыми кругами. Такого рода сечений, проходящих через пару точек на поверхности шара, возможно начертить поистине бесконечное множество.
Выводы
Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).
Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.
Альбина Сергеева
Урок математики во 2 классе. Тема «Окружность. Круг»
Тема : «Окружность . Круг »
Цель : познакомить уч-ся с новыми геометрическими фигурами : окружностью , кругом и их элементами (диаметр, радиус, центр) .
Задачи : 1) познакомить с историей возникновения математических понятий ;
2) научить уч-ся пользоваться циркулем для вычеркивания окружностей ;
3) развивать внимание, пространственное мышление, память, воображение, кругозор , словарный запас детей;
4) провести инструктаж по технике безопасности о правилах пользования циркулем;
5) воспитывать любовь к математике , трудолюбие, дисциплинированность, товарищество.
6) аккуратность и осторожность при применении циркуля.
6) воспитывать духовно-нравственные ценности. Уважение к традициям народа.
Вид урока : объяснение нового материала .
Образовательные технологии :
1. Здоровьесберегающие технологии.
3. Технология предметного проектирования.
4. Технология развивающего обучения.
5. Технология личностно-ориентированного обучения.
Место проведения урока : кабинет информатики.
Оборудование для уч-ся :
1. рабочая тетрадь
рабочая тетрадь
2. циркуль
3. цветные карандаши
4. линейка
Оборудование для учителя :
1. Плакат «Сиди правильно»
2. тренажёр для глаз
3. тестовая работа
4. циркуль
5. линейка
6. набор геометрических фигур
7. компьютеры
9. музыкальная шкатулка с геометрическими фигурами
10. раздаточный материал
11. таблица
12. цветные мелки
Ход урока
I. Организация класса
1. У : Прозвенел звонок для нас,
Всех ребят позвал он в класс
Чтобы дети не ленились
С удовольствием трудились,
Всем здоровья пожелаем
И урок наш начинаем
Друг на друга посмотрели
Улыбнулись друг другу
Пожелали добрым взглядом
Отличных отметок
И за парты тихо сели.
2. У : На уроке у нас присутствует много гостей – это учителя нашей школы. Давайте у них поинтересуемся для чего они к нам пришли на урок (ответ учителей) .
3. Желаю вам успехов в работе, я обязательно буду помогать, кто будет затрудняться. Наша помощница и хозяйка кабинета это Кавинская Н. А.
Девиз нашей работы : «Все помогают каждому, каждый помогает всем» . (слайд №1)
II. Проверка домашнего задания
1. Ребята, как этот девиз связан с домашним заданием? (Нужно было решить примеры, сопоставить ответ с буквой и отгадать загадку – «Возле елок из иголок, летним днём построен дом, за травой не виден он, а жильцов в нём миллион» — муравей).
2. Муравьи очень большие труженики. Они работают дружно, слажено, активно помогают друг другу. Вот так и мы должны с вами работать.
3. 6000 видов муравьев : муравьи бывают лесные, медовые, садовые, портные, листорезы и другие.
III. Актуализация знаний.
1. Посмотри внимательно на геометрические фигуры (открываю доску) .
(треугольник, квадрат, круг , пятиугольник)
2. Назови, что это за фигуры?
3. Некоторые их точки обозначены буквами. Где располагаются точки? (внутри, на границе) .
Некоторые их точки обозначены буквами. Где располагаются точки? (внутри, на границе) .
4. Посмотри внимательно на фигуры и скажи . Какая фигура лишняя?
Треугольник — одна точка на границе;
Квадрат — точка находится не в центре;
Круг — остальные многоугольники.
5. Составьте 2 слова : 1) из букв, которые находятся на границе фигуры (окружность ) ; 2) из букв, которые находятся внутри фигур (круг )
6. Сегодня на уроке мы подробно и поговорим об окружности и круге .
IV. Тема урока : «Окружность . Круг » (слайд №2)
1. Сейчас, ребята, вместе с вами попробуем определить цель нашего урока (если затрудняются, спросить : Что нужно для того, чтобы понять эту тему)
2. Один мудрый человек сказал : «Окружность – душа геометрии » .
(слайд №3)
3. Почему окружность называют душой геометрии нам расскажет Буйлова Алёна (Алёна выступает за кафедрой) .
«Окружность »
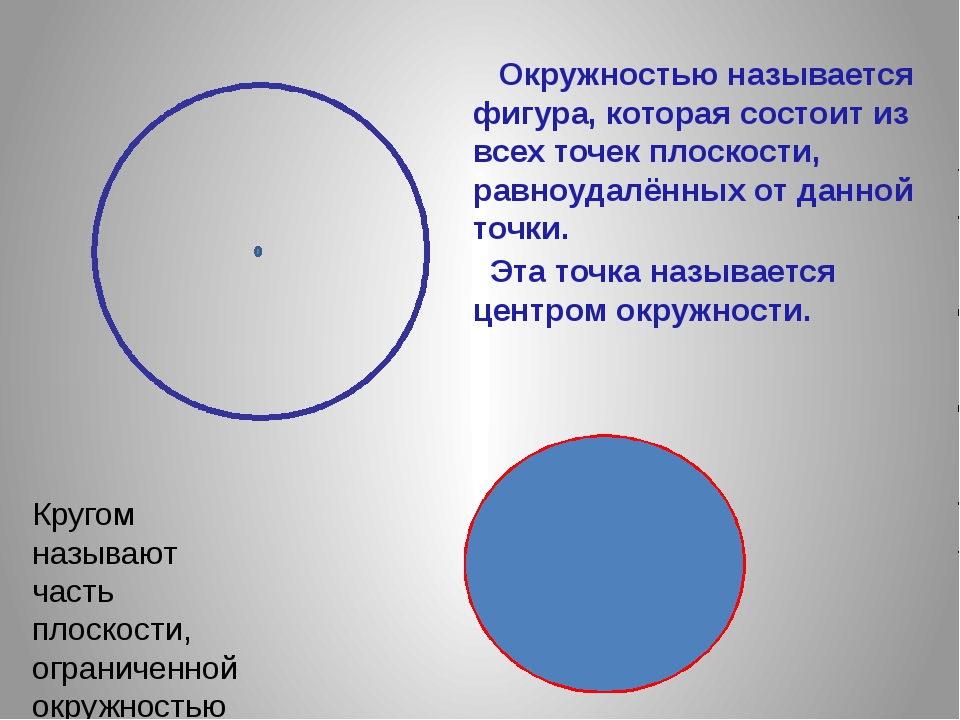
Окружность – замкнутая линия , все точки которой, равноудалены от центра.
Окружность – удивительная фигура, древние греки её считали самой совершенной. Почему не бывает треугольных колес? Представьте себе, нашелся чудак, сделал велосипед с треугольными колёсами. Только нет таких чудаков, люди давно поняли, что колёса должны быть круглыми .
Ось колеса находится в центре, спицы – радиусы, обод – окружность .
Как ни повернётся колесо, расстояние между землёй и осью остаётся одинаковое, поэтому и катится колесо плавно.
Колесо было изобретено давным – давно. С тех пор сделано много открытий и изображений, но и теперь в основе приборов и машин лежит круг .
Окружность всегда привлекала к себе внимание художников и архитекторов. Арки, полукруглые окна придают торжественность. При использовании окружности получатся очень красивые узоры.
В некоторых приборах шкалы располагаются на окружностях или её дугах .
Вот почему окружность – душа геометрии .
Окружность действительно обладает красотой и изяществом, и в этом мы с вами убедимся, когда будем чертить окружности , решать задачи. Где преобладает окружность ? (ответы детей)
V. Работа в тетрадях.
1. Открыли тетради, записали число, классная работа (опереться на плакат «Сиди правильно» ).
2. К доске попрошу выйти двух учеников. Один ученик нам нарисует окружность , другой ученик круг .
Вы ребята работаете в тетрадях : 1в. — поднимите правую руку – рисуете окружность , 2в. — поднимите левую руку – рисуете круг .
3. Были даны разные задания, а фигуры получились похожие. Чем круг отличается от окружности ? Вот эту проблему мы будем решать на уроке . (слайд №4)
4. Почему фигуры получились неточные – (не было инструмента, а от руки не проведёшь.
5. – Приготовьте циркуль. Посмотрите на него внимательно (у учителя большой циркуль) .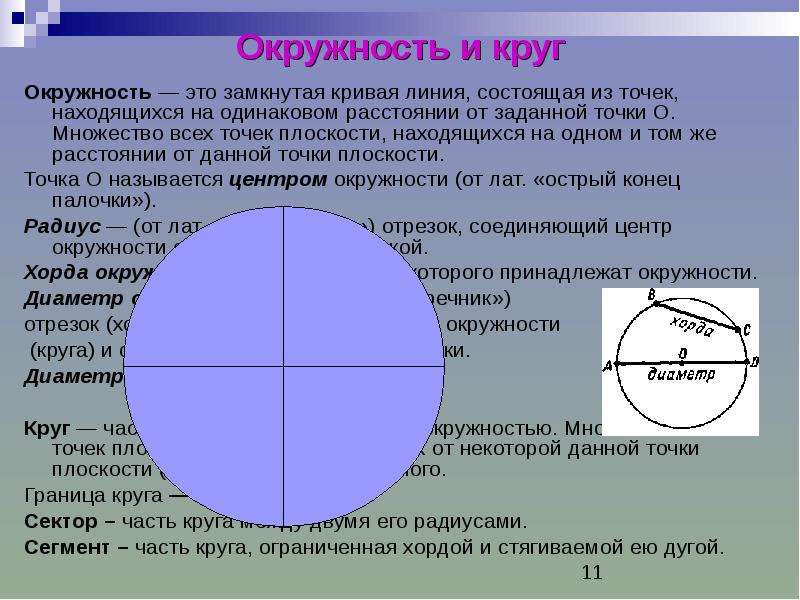
Из чего он состоит (2 ножки, на конце первой иголочка, на конце второй – грифель – это карандаш).
Циркуль – это чертёжный инструмент для вычеркивания окружностей . В переводе с латинского обозначает круг — циркус (если дети не ответят на вопрос, учитель помогает) .
С циркулем нужно работать очень осторожно.
6. Назовите правила как пользоваться циркулем (нельзя подносить к лицу, глазам; нельзя передавать циркуль соседу иглой вперёд; не играть; циркуль должен находиться в специальном футляре).
7. — Продемонстрируйте как нужно передавать циркуль соседу по парте (1в. передает, потом 2в., при этом сосед должен сказать волшебные слова).
Какая ножка циркуля стоит в центре окружности (с иглой) . Почему? (грифелем рисуем) .
VI. Тренировочная работа.
1. Сейчас мы с вами будем тренироваться строить окружности .
2. Любая работа выполняется по….(алгоритму) .
3. Что такое алгоритм? (порядок выполнения) .
4. Мы будем учиться строить окружность по алгоритму .
5. Внимание на экран (слайд №5)
1) — Отступите вниз 10 клеток
Отметить точку О
Поставить иглу в центр
Провели замкнутую линию
Эта замкнутая линия и называется окружность , а О – центр окружности . (кентрон – палка с заостренным концом, которым погоняли животных в упряжке). (слайд №6)
2) Расстояние между ножками циркуля – радиус, обозначается буквой r карточка r.
3) Сами попробуйте сформулировать определение радиуса (r – это отрезок, соединяет центр окружности с точкой на окружности ).
4) Провели несколько радиусов. Одинаковые ли они по длине? (да)
(слайд №7)
5) Окружность делит плоскость на 2 части. Как называется часть внутри окружности (круг ) —закрасить. (слайд №8)
6) Вывод : Чем же окружность отличается от круга ? Окружность – это граница круга . Круг – часть внутри окружности .
Круг – часть внутри окружности .
VII. Тренажер для глаз (физпауза) .
VIII. Практическая работа.
1) Приступаем к практической работе.
2) – Возьмите круг (слайд №9)
Сложите пополам
Нашли линию сгиба
Обведите её любым цветным карандашом
Эта линия называется диаметром и обозначается буквой d (показываю карточку)
Сами сформулируйте определение диаметра (отрезок, соединяющий две точки окружности , и проходит через центр).
IX. Работа в группах. (слайд №10)
1) Первая группа работает на компьютерах, выполняет задание.
2) Вторая группа выполняет творческое задание на местах.
3) Прошу 1 группу сесть за компьютеры, включить их и познакомиться с заданиями.
Творческое задание (2 группа)
1. Обведи окружность красным карандашом
2. Закрась внутреннюю часть фигуры
3. Проведи r
4. Проведи d
5. Из данных фигур выбери овал и раскрась его как пасхальное яйцо
4) Прочитайте внимательно задание , какие затруднения.
5) Работаем самостоятельно.
6) Работа по алгоритму
Начертите 2 окружности разных размеров
Выполни заливку
Обведи границу
Начерти диаметр
На какую фигуру похож вытянутый круг .
Попробуйте и вы оформить яйцо.
С помощью чего можно оформить его? (ластика, заливки, распылителя, карандаша) .
7) Попросим гостей посмотреть работы.
8) Информация о пасхе.
Ребята не зря мы с вами раскрашивали яйца.
Когда раскрашивают яйца?
На пасху яйца раскрашивают разными цветами, но основное место принадлежит красному цвету. Яйцо является символом жизни. В скорлупе находится скрытая жизнь, потом появляется желтый цыпленок. Мария Магдалина (святая) пришла к императору, в руке у неё было яйцо, и сказала, что Иисус Христос воскрес. Император рассмеялся и говорит : «Этого не может быть так же как белое яйцо станет вдруг красным» , не успел он это сказать, как яйцо стало красным. С тех пор это событие символизирует веру в Господа, и мы красим яйца.
С тех пор это событие символизирует веру в Господа, и мы красим яйца.
X. Итог урока . (слайд №11)
1. На протяжении всего урока мы были активны , внимательны , трудились как муравьи.
2. Достигли ли мы с вами цель урока ?
3. Решили ли мы проблемные вопросы?
XI. Домашнее задание (раздаю листочки)
Составьте аппликацию из кругов разных размеров , добавляя другие геометрические фигуры.
XII. Психологическая игра (волшебный сундучок)
1. Выбрать из сундучка (я подношу сундучок, любую фигуру (треугольник, квадрат, круг ) .
2. — Хлопайте в ладоши те, кто выбрал круг .
Круг – эти люди добрые , общительные
Попрыгайте, кто выбрал треугольник.
Треугольник – это лидер, настойчивый, упорный
Выполняйте наклоны вправо, влево, кто выбрал квадрат.
Квадрат – люди спокойные, дружелюбные.
Вывод : несмотря на то, что вы все по характеру разные, но порадовали меня своей работой. Молодцы! Умнички! Спасибо за урок , а гостям спасибо за внимание. (слайд №12)
Молодцы! Умнички! Спасибо за урок , а гостям спасибо за внимание. (слайд №12)
В память о нашем уроке уч-ся преподносят вербу (дарят вербу) .
NMitra В Opera есть баг: у вложенного элемента углы не закругляются. Это можно подправить, дописав
#ball:after {
content: «»;
position: absolute;
top: 0; bottom: 0; right: 0; left: 0;
box-shadow: 0 0 0 100px #fff;
border-radius: 100%;
}
Но тогда тень в Гугл Хром «обрезанная» получается. Поскольку Опера переезжает на движок Google, то я сделала выбор в пользу его браузера.
Космо Мизраил
Прикольно.
Сейчас делаю дизайн как раз с планетами, но аватарки и другие изображения приходится делать плоскими, потому что img не применишь box-shadow: inset.
NMitra
Сделайте фоном background. Скоро благодаря поддержки трансформации CSS можно будет добавлять объём. Предвестники http://codepen.io/html5web/pen/pnbwo
Космо Мизраил
Мдо, вроде-бы для вебкита, а не работает х) Это будет вступать лет пять ещё, до этого надо ещё дожить 🙂
Фоны сделать не всегда получится, а вот наложить поверх изображения элемент с заданными стилями очень даже можно. Но это если известны размеры изображения.
Но это если известны размеры изображения.
Пример: http://jsfiddle.net/9qzm6/
Ещё нашёл скрипт, который выполняет эту работу самостоятельно:
http://www.htmldrive.net/items/demo/1156/Multiple-CSS3-Image-Styles
Здесь он сам определяет размер, если изображение загрузилось. Нужен jQuery.
Это так, на заметку 🙂 NMitra Там нужны настройки какие-то устанавливать.. Это сильно вперёд:))
Пжалст 🙂 я ваш постоянный читатель уже год как минимум 🙂
Анонимный
IE 11
Все анимировано))
NMitra
Молодцом IE, дотянулось. Осталась Хрому убрать -webkit-, он теперь в числе отстающих.
Что такое круг?
Начертание круга начинается с окружности. Окружность – это замкнутая черта без конца и начала , каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.
Круг получится, если начертить окружность, например, на бумаге – и потом разукрасить ее. Любыми красками: желтой, синей, зеленой – какая больше нравится. Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.
Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.
Круг обладает некоторыми важными для понимания его сущности параметрами. Кстати, часть данных параметров присуща и окружности.
- Радиус – расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
- Диаметр – важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.
- Площадь – свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.
Круг в реальной жизни
В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.
К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.
Другой пример круга – Солнце . Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.
Сектор
Что такое круг внимательный читатель ужен разобрался. Но вот что за «зверь» этот сектор, о котором упоминалось немного выше? Сектор – это часть круга, отделенная от остальной поверхности парой начерченных радиусов. Для наглядности можно примести такой пример: все когда-нибудь видели нарезанную пиццу. Кусочки – это сектора круга, которым является все это аппетитное блюдо.
Кусочки – это сектора круга, которым является все это аппетитное блюдо.
Секторы не обязательно должны быть равной величины. К примеру, если пицца разрезана пополам, обе ее половины тоже будут секторами круга.
Что такое шар?
Шар – тело, ограниченное сферической поверхностью . То есть, это не двухмерная фигура, как круг, а трехмерная. Сферическая поверхность – это геометрическое сочетание поверхности точек, расположенных на неотрицательном расстоянии от некоей центральной точки. Расстояние, на которое удалены все точки поверхности шара от его центра, называется радиусом. И оно не должно превышать некие заданные цифры. Таким образом, круг – это та же сферическая поверхность, расположенная в другом пространстве.
В этом проявляются сходства и главное различие шара и круга. Круг – это двухмерная фигура, точки которой ограничены окружностью. Шар – это фигура трехмерная, а ее точки ограничены сферической поверхностью.
Разновидности шара
В метрическом и векторном пространствах рассматриваются два понятия, имеющие связь со сферической поверхностью.![]() Шар, который включает в себя данную сферу, именуют замкнутым . Шар, который не включает в себя сферу, называют открытым .
Шар, который включает в себя данную сферу, именуют замкнутым . Шар, который не включает в себя сферу, называют открытым .
Характеристики шара
Шар, как и круг, имеет диаметр и радиус. Обе эти величины в шаре вычисляются по вышеописанным принципам (как для круга). Радиус шара – это отрезок между любой точкой на сферической поверхности, ограничивающей фигуру, и ее центром. Диаметр соединяет две точки на сферической поверхности шара, проходя через его центр.
Интересное дополнение: круг может быть частью шара. Точнее, шар состоит из очень большого количества кругов различного диаметра. Называются эти круги сечениями сферы. Когда сечение пролегает через центр шара, его именуют большим кругом. Все остальные сечения именуются малыми кругами. Такого рода сечений, проходящих через пару точек на поверхности шара, возможно начертить поистине бесконечное множество.
Выводы
Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).
Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).
Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.
Публикации по теме:
Детско-родительский игровой сеанс «Круг» для детей ОВЗ Игровое занятие КРУГ для детей ОВЗ Тема «Осень. Природные явления» Цели и задачи занятия КРУГ Главная цель занятия КРУГ – дать каждому ребенку.
Конкурс профессионального мастерства «Солнечный круг» (фотоотчет) С 12 по 26 октября 2015 года в нашем детском саду проходил конкурс профессионального мастерства «Воспитатель года». Цель конкурса: выявление.
Конспект НОД по ФЭМП «Знакомьтесь: круг» Конспект НОД по ФЭМП во второй младшей группе «Знакомьтесь- круг» Цель: развитие познавательных интересов детей Задачи: Познакомить.
НОД по математике «Круг и квадрат» (младшая группа) Тема: «Круг и квадрат» (младшая группа) Образовательная область: познание Цель: Продолжать учить находить один и много предметов в специально.
Поделки в технике «объемный квиллинг» Здравствуйте, коллеги! Недавно открыла для себя технику объемного квиллинга. Искусство, которое на русском языке называют «бумагокручением»,.
Проект по математическому развитию «Круг, квадрат и треугольник-фигуры важные, фигуры нужные» Номинация проекта – «Дошкольный возраст» Вид проекта: долгосрочный, фронтальный. Участники проекта: подгруппа детей средней группы, воспитатель.
«Снежинка 3-D». Объемный модуль для украшения интерьера Приближаются Новогодние праздники и перед нами, как воспитателями опять стоит вопрос «Чем же удивить детей и взрослых?». Просторы Интернета.
Совместная образовательная деятельность по ФЭМП «Круг и квадрат» Совместная образовательная деятельность взрослого и детей ФЭМП «Круг и квадрат». Цель: закреплять умение различать и называть круг и квадрат.
Весенний объемный тюльпан на открытке в подарок маме Не за горами прекрасный весенний праздник 8 Марта. И уже сейчас многие педагоги задумались над тем, что бы смастерить с детьми мамам в.
Виды геометрических фигур / Бери и делай
Множество точек дает линию, а из нескольких соединенных между собой линий можно получить различные геометрические фигуры на плоскости и в пространстве. Таким образом, произвольное множество точек позволяет нам создавать геометрическую фигуру. Это может быть квадрат или куб, круг или шар, а также более сложные и неоднозначные фигуры, например икосаэдр, который может быть представлен двумя разными формами.
«Бери и Делай» предлагает узнать, чем отличаются разные виды геометрических фигур.
Плоские геометрические фигуры
Плоская геометрическая фигура располагается в двумерном пространстве, где объекты характеризуются только длиной и шириной. Различают следующие фигуры:
- Круг — это фигура, у которой нет углов и в которой все точки по окружности находятся на равном расстоянии от центра.

- Овал — это фигура, похожая на яйцо. У нее также нет углов.
- Квадрат — это фигура, у которой 4 равные стороны и 4 прямых угла.
- Прямоугольник — это фигура, похожая на квадрат: у нее 4 стороны и они пересекаются под прямым углом. В отличие от квадрата, у прямоугольника только противолежащие стороны равны. Если с помощью отрезка соединить любой угол с противоположным, получится диагональ. И у квадрата, и у прямоугольника диагонали равны.
- Ромб — это фигура, у которой 4 равные стороны, но пересекаются они не под прямыми углами. У ромба противоположные углы ромба равны. Ромб, так же как квадрат и прямоугольник, является четырехугольником.
- Треугольник — это фигура, у которой 3 угла и 3 стороны. Точки, в которых пересекаются стороны треугольника, принято называть его вершинами.
Виды треугольников в зависимости от размера углов:
🔷 остроугольный — все углы острые (каждый равен менее 90°)
🔷 тупоугольный — один угол является тупым (равным более 90°)
🔷 прямоугольный — один угол является прямым (равным 90°)
Различают также виды треугольников по соотношению их сторон:
🔶 равносторонний имеет 3 равные стороны
🔶 равнобедренный — 2 равные стороны
🔶 разносторонний — 3 разные стороны
Выше мы рассмотрели основные геометрические фигуры на плоскости. Но существует множество других, например:
Но существует множество других, например:
- Трапеция — это четырехугольник, у которого как минимум 2 стороны параллельны. Таким образом, квадрат, ромб и прямоугольник можно рассматривать как частные случаи трапеции.
- Параллелограмм — четырехугольник, у которого противолежащие стороны попарно параллельны. Так, прямоугольник, квадрат и ромб считаются частными случаями параллелограмма.
- Пентагон — фигура, представляющая собой правильный многоугольник с 5 сторонами. У пентагона все стороны и углы равны.
- Гексагон — это правильный многоугольник, у которого 6 равных сторон, а углы образуют 6 равносторонних треугольников.
- Крест — это фигура, которая состоит из 2 пересекающихся линий или прямоугольников.
- Звезда — плоский невыпуклый многоугольник, по форме напоминающий звезду. Звезда может быть трехконечной, четырехконечной, пятиконечной (как на картинке выше) и так далее.

Геометрическая фигура может быть выпуклой, если ей целиком принадлежат все точки отрезка, соединяющего любые ее две точки. Круг, шар, овал и треугольник являются выпуклыми фигурами. А четырехугольники могут быть как выпуклыми, так и невыпуклыми. К примеру, на картинке выше изображена одна и та же фигура — дельтоид. Это четырехугольник, стороны которого можно сгруппировать в две пары равных смежных сторон. Слева — дельтоид выпуклый, а справа — невыпуклый.
Пространственные геометрические фигуры
Если фигура располагается в трехмерном пространстве, где объекты характеризуются длиной, шириной и высотой, а также имеют глубину или толщину, ее называют пространственной. Чаще всего различают следующие пространственные фигуры:
- Шар можно назвать аналогом круга в пространстве. Все точки, располагающиеся на поверхности шара, находятся на равном расстоянии от его центра.
- Конус образован множеством лучей, которые соединяют все точки некоторой плоской кривой с единой точкой пространства (вершиной конуса).
 Конусы различаются между собой: например, если основанием конуса является круг, то это может быть прямой круговой конус.
Конусы различаются между собой: например, если основанием конуса является круг, то это может быть прямой круговой конус. - Цилиндр по своей форме напоминает валик. В его основании находятся круги, а между ними — часть цилиндрической поверхности.
- Куб — это многогранная фигура, каждая грань которой представляет собой квадрат. При этом у него 6 граней, 12 ребер и 8 вершин. Куб также можно назвать правильным гексаэдром, или шестигранником.
- Пирамида — это многогранник, у которого в основании находится многоугольник, а грани представлены треугольниками, имеющими общую вершину.
- Призма — это многогранник, 2 грани которого являются равными многоугольниками, располагающимися в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. На картинке выше частный пример — шестиугольная призма. У нее 8 граней, 18 ребер и 12 вершин.
Если выпуклый многогранник состоит из одинаковых правильных многоугольников и обладает пространственной симметрией, то его называют правильным многогранником, или платоновым телом.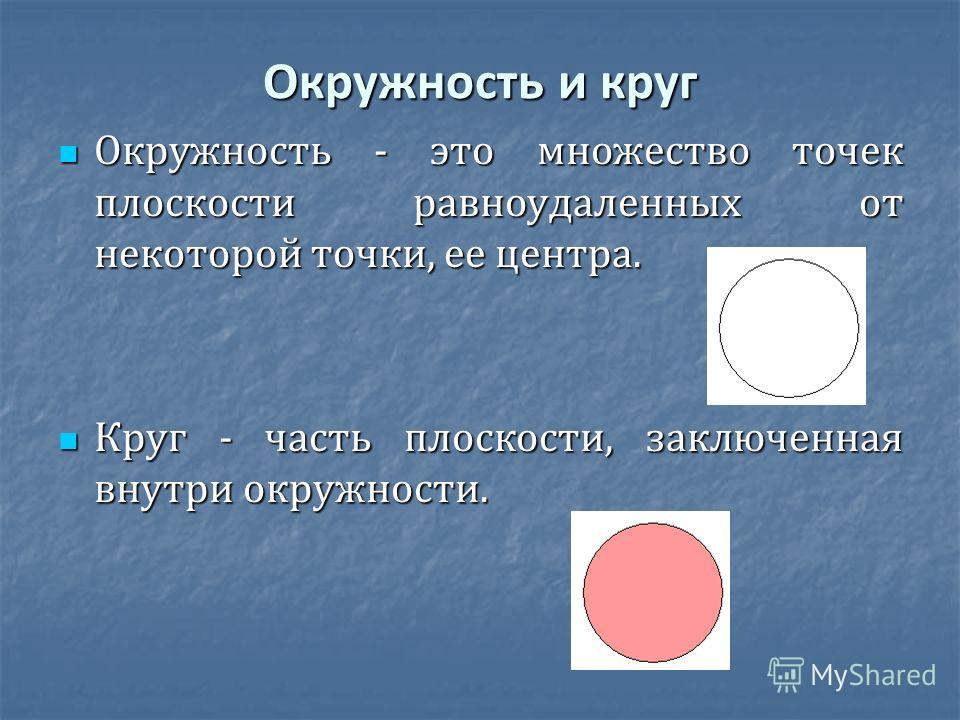 В трехмерном пространстве различают 5 таких правильных многогранников. Название каждого из них происходит от греческого наименования количества его граней:
В трехмерном пространстве различают 5 таких правильных многогранников. Название каждого из них происходит от греческого наименования количества его граней:
- Тетраэдр, или треугольная пирамида. У этого многогранника гранями являются 4 треугольника.
- Гексаэдр, или куб.
- Октаэдр — многогранник, чьими гранями являются 8 равносторонних треугольников. Если разрезать октаэдр пополам, можно получить две одинаковые пирамиды.
- Додекаэдр — многогранник, у которого 12 граней и все они правильные пятиугольники.
- Икосаэдр — многогранник, гранями которого являются 20 правильных треугольников.
При этом правильный икосаэдр может быть как выпуклым, так и невыпуклым. Но термин «правильный икосаэдр» чаще относится к выпуклому виду, а невыпуклая форма называется большим икосаэдром.
ОСНОВЫ КОМПОЗИЦИИ: Геометрия в фотографии
09 Февраля 2016
Фотография — это то, чем становятся живопись, композиция, пластический ритм, геометрия, размещенные в считанных долях секунды (Анри Картье-Брессон).
Фото: Ronald Koster
Когда мы думаем о композиции в фотографии, первое, что приходит в голову — это золотое сечение, правило третей, формат кадра, контраст, точка съемки…
Но есть еще один важный элемент в композиции – геометрия. Геометрия в фотографии — это простые формы, такие как квадрат, треугольник, круг, прямые и кривые линии.
Геометрические объекты обычно вспомогательные, они усиливают восприятие и могут объединять отдельные элементы фотографии в единое целое. Выбирая ту или иную геометрическую форму в фотографии, автор может заранее акцентировать внимание будущего зрителя на его определенных зонах. Установлено, например, что углы квадрата оказываются очень активными зонами, а для круга или овала – это центр. Не случайно, с давних времен сложилась традиция портретов в овале. Углы не отвлекали внимание от главного — изображения лица. Наиболее распространенный и наиболее разносторонний геометрический инструмент – это линии. Более подробно о них читайте в нашей отдельной статье.
Более подробно о них читайте в нашей отдельной статье.
Фактически, любой объект окружающей среды можно сравнить с какой-либо геометрической фигурой, но все они пробуждают у зрителя разные эмоции и чувства. Простые геометрические формы, такие как круг и квадрат, намного быстрее фиксируются нашим глазом и воспринимаются мозгом, а следовательно и лучше запоминаются, нежели сложные и неправильные. Вообще выделяют три базовых фигуры. Это прямоугольник, треугольник и круг. Всё остальное – овал, квадрат, трапеция, эллипс, ромб всего лишь их вариации. Все они отличаются как графически, так и (не удивляйтесь) эмоционально.
КВАДРАТ В КОМПОЗИЦИИ
Квадрат — это самая устойчивая, законченная форма, готовая вызывать утверждающие образы. Он ассоциируется с такими понятиями, как порядок, стабильность, надежность, прочность. В то же время, квадрат воспринимается несколько приземленно и тяжеловесно.
Фото: Robertino Nikolic. “Свет играет с геометрией или геометрия со светом?”. Победитель конкурса Black & White Spider Awards, 2007.
Победитель конкурса Black & White Spider Awards, 2007.
Фото: Alma (источник — 1510.deviantart.com)
Фото: G. Diaz Deleon
ПРЯМОУГОЛЬНИК В КОМПОЗИЦИИ
Прямоугольник, расположенный̆ большей̆ стороной̆ по горизонтали вызывает ощущение стабильности, покоя, основательности.
Фото: Guerel Sahin
Фото: Guerel Sahin
Особенно гармонично смотрится, если он выполнен в пропорциях «золотого сечения». Прямоугольник, расположенный̆ большей̆ стороной̆ вдоль вертикали, создаёт ощущение лёгкости, воздушности.
Фото: Joe McNally
ТРЕУГОЛЬНИК В КОМПОЗИЦИИ
Треугольник — наиболее часто встречающаяся в природе форма. Треугольник — самая динамичная, неустойчивая форма, которая ассоциируется с движением, развитием, скоростью. В положении «вершиной вверх» вызывает образы устойчивости, стабильности (пирамида). Несколько треугольников — позитивное динамическое движение. В положении «вершиной вниз» – шаткое равновесие, балансировка. В отличие от прямоугольника, стороны не противостоят друг другу, а меняют направление развития. Это может быть использовано для создания конкретных образов. Треугольник естественным образом вносит в композицию ощущение глубины пространства.
В положении «вершиной вниз» – шаткое равновесие, балансировка. В отличие от прямоугольника, стороны не противостоят друг другу, а меняют направление развития. Это может быть использовано для создания конкретных образов. Треугольник естественным образом вносит в композицию ощущение глубины пространства.
Фото: Josh Johnson
КРУГ В КОМПОЗИЦИИ
В форме круга более чем, в какой̆ — либо, выражена идея природы, земли, мироздания. Круги изобилуют как в природе, так и в мире рукотворных предметов. Поэтому такие понятия как «добро», «жизнь», «счастье», «процветание» ассоциируются у человека именно с этой̆ формой̆. Данная форма направляет взгляд внутрь кадра. Круг ассоциируется с чем-то легким, воздушным и при этом – уравновешенным. Но, в отличие от квадрата, это равновесие ближе к физическому понятию «неустойчивое равновесие». Круги — самые приятные глазу фигуры, которые можно смело использовать в кадре. Они сразу приковывают внимание зрителя и, благодаря своей идеальной симметричности, привносят в изображение гармонию.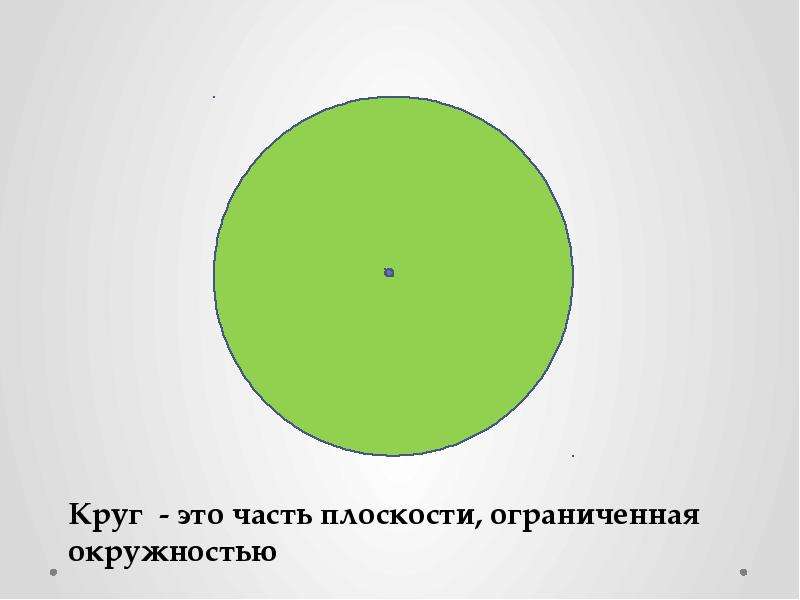 Поскольку у круга нет углов, он прекрасно контрастирует с прямоугольным обрезом кадра.
Поскольку у круга нет углов, он прекрасно контрастирует с прямоугольным обрезом кадра.
Фото: Steve McCurry
Фото: Georgios Karamanis
Фото: Elia Locardi
Как и треугольник, круг — очень эффектная геометрическая фигура, которую можно с пользой применить в композиции кадра, хотя и с другим смыслом. В отличие от диагоналей, заряжающих кадр динамикой и напряжением, кривые линии создают гармонию. Таким образом, можно создавать выразительные и информативные композиции, основанные на простых геометрических фигурах.
Фото: William Morris Kahn
Фото: Joe McNally
Фото: Joe McNally
Геометрические объекты можно условно разделить на три группы по их функциям: направляющие линии, разделители пространства и обрамление. Разделители пространства делят снимок на отдельные зоны, несущие свою смысловую нагрузку, но работающие вместе для создания единой композиции. Примером, простейшего разделителя пространства может послужить линия горизонта, отделяющая небо от поверхности моря. Очень хорошо смотрятся в качестве разделителя пространства треугольники, но и такие элементы, как диагонали и незамкнутые линии, тоже уверенно можно использовать.
Примером, простейшего разделителя пространства может послужить линия горизонта, отделяющая небо от поверхности моря. Очень хорошо смотрятся в качестве разделителя пространства треугольники, но и такие элементы, как диагонали и незамкнутые линии, тоже уверенно можно использовать.
Фото: Вадим Докторов
Обрамления носят функцию притяжения взгляда зрителя и его фокусировку на основном объекте. В качестве обрамляющих элементов отлично работают дверные проемы, арки, окна. Кроме того, великолепно с этой функцией справляются и естественные элементы, например, ветви деревьев. Важно чтобы обрамление присутствовало, как минимум, с двух сторон снимка и было выполнено в спокойной тональности, желательно более темной, чем главный объект, чтобы не отвлекать зрителя. Обрамляющий элемент должен иметь интересный цвет, форму, текстуру или иные примечательные характеристики, но стоит помнить, что обрамляющие элементы должны направлять, а не отвлекать. Особенно хорошо в этом плане работают треугольники или арки. Арка способна создать интересную динамичную композицию.
Арка способна создать интересную динамичную композицию.
Фото: Guerel Sahin
Фото: Ian Plant
Фото: Tom La
Пробуйте, экспериментируйте и не забывайте, что в одном снимке вы можете использовать сразу несколько геометричских фигур для построения композиции.
Другие статьи о композиции в фотографии:
Золотое сечение в фотографии
Сила линий в фотографии
Формат кадра в фотографии
Контраст в фотографии (Часть 1)
Контраст в фотографии (Часть 2)
Точка съемки и выбор плана
Ракурс
Равновесие в композиции
Тест. Психогеометрия личности – Психология – Домашний
тест
Психогеометрия – сравнительно молодая система анализа личности, позволяющая прогнозировать и оценивать некоторые черты характера, модель поведения и стиль жизни человека с помощью простейших геометрических фигур. Она была разработана в США доктором психологии Сьюзен Деллингер, которая много лет проработала с персоналом и обобщила свой опыт в психогеометрии.
В чем суть:
В основе психогеометрии лежит пять типов личности, которым соответствуют геометрические фигуры. Посмотрите на фото внизу в течение 10 секунд и из предложенных фигур (квадрат, треугольник, прямоугольник, круг и загзаг) выберите ту, с которой ассоциируете себя. Оставшиеся фигуры пронумеруйте в порядке убывания предпочтения. Выбранная фигура и определяет основные черты характера. А последняя фигура, в вашем пронумерованном списке, может обозначать персоны, контакты с которой будут наиболее затруднительными для вас. Следует отметить, что речь идет не столько о типах личности, сколько о привычных для человека установках и способах поведения. Также имейте ввиду, что результат работает «здесь и сейчас», а не на протяжении всей жизни.
фигуры
Интерпретация результатов:
Главная черта характера тех, кто выбрал квадрат – трудолюбие в сочетании с организованностью, упорством, терпением и твердостью, а также пунктуальностью, чистоплотностью и практичностью.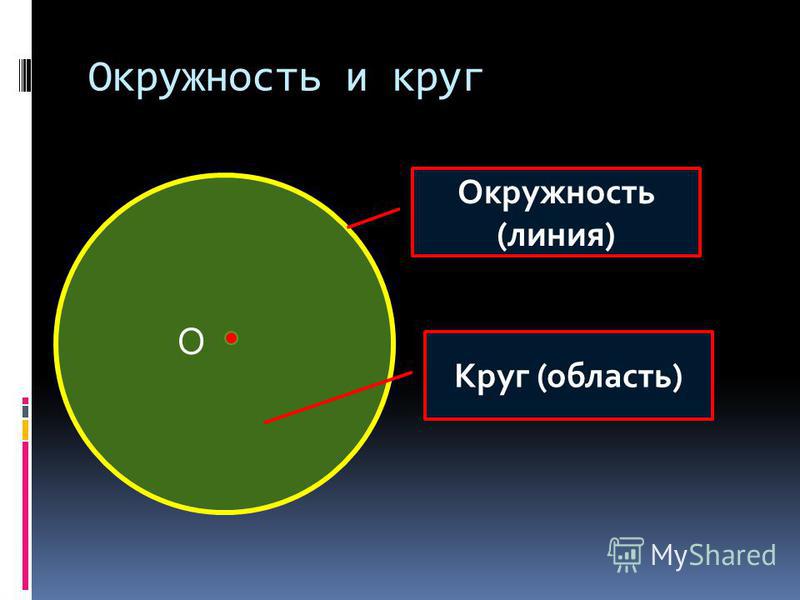 Выбор квадрата в качестве основной фигуры может свидетельствовать о склонности к аналитическому мышлению и рациональности. Такой человек все свои дела стремится сделать максимально хорошо и эффективно. А поскольку умеет управлять собой и организовывать других, то может занимать руководящие должности.
Выбор квадрата в качестве основной фигуры может свидетельствовать о склонности к аналитическому мышлению и рациональности. Такой человек все свои дела стремится сделать максимально хорошо и эффективно. А поскольку умеет управлять собой и организовывать других, то может занимать руководящие должности.
Человек-квадрат отличается консерватизмом, строгим соблюдением правил и норм, и отсутствием спонтанности и креативности. Стремится упорядочить и систематизировать все вокруг себя – пространство, вещи, любую информацию, с которой работает. Ему нравится, когда информация подается в соответствии с жесткой логикой. Выбравший квадрат человек любит, чтобы речь изобиловала фактами, цифрами и тезисами, желательно, со ссылками на источник, из которых взята. Предпочитает порядок, распланированную жизнь. Разборчив в знакомствах, не любит шумных вечеринок. В конфликтах часто уходит от прямого столкновения. Это хороший администратор и исполнитель. Проигрывает в оперативности действий, контактности с разными лицами.
Женщины, выбравшие квадрат, организованны, пунктуальны, придирчивы, внимательны к деталям. Они терпеливы, трудолюбивы, настойчивы в достижении цели, тверды в решениях и склонны к строгому соблюдению правил и инструкций. Не любят выделяться.
Люди-квадраты говорят, как правило, тихо, предпочитая не повышать голос без надобности. И не терпят повышенных тонов и у других. При этом их речь отличается ясностью, точностью, логичностью и обстоятельностью. Она бывает, как правило, несколько монотонной, «механической». Для них характерно употребление речевых штампов.
Педантичность, скрупулезность и последовательность проявляются и в выборе одежды. Эти люди предпочитают строгий, классический стиль, сдержанные, неяркие тона. Они опрятны, сухощавы. Нежелание выделяться проявляется и в жестах, которые скупы и невыразительны.
ТреугольникТе, кто ассоциирует себя с треугольником, безусловно, сильные личности, весьма уверенные в себе и деятельные. Они не любят сидеть на месте, стремятся всегда находиться в гуще событий. Выбор треугольника в качестве основной фигуры может свидетельствовать о развитом честолюбии и власти любой ценой. Они прирожденные лидеры. Нетерпеливость – одна из главных черт их характера. Треугольники могут прервать вас на полуслове, но лишь потому, что уже уловили суть ваших мыслей.
Они не любят сидеть на месте, стремятся всегда находиться в гуще событий. Выбор треугольника в качестве основной фигуры может свидетельствовать о развитом честолюбии и власти любой ценой. Они прирожденные лидеры. Нетерпеливость – одна из главных черт их характера. Треугольники могут прервать вас на полуслове, но лишь потому, что уже уловили суть ваших мыслей.
Эти люди решительны, энергичны, неудержимы, умеют ставить ясные цели и достигать их, концентрируясь на главном, глубоко и быстро анализировать ситуацию. Это прекрасные менеджеры и политики. Жаждут быть первыми и управлять положением дел, решать не только за себя, но и за других, побеждать конкурентов. Хорошо чувствуют выгоду. Треугольники любят риск, бывают нетерпеливы и нетерпимы, с трудом признают ошибки. Эгоцентричны, но люди тянутся к ним и идут за ними.
Женщины, выбравшие треугольник, сконцентрированы на достижении цели, уверены в себе, решительны и импульсивны. Для них характерны высокий уровень самооценки, склонность к риску, бьющая через край энергия, высокая работоспособность и тяга к развлечениям.
Люди-треугольники весьма контактны и, не испытывая никакого дискомфорта, могут с любым завязать беседу. Их речь отличается логичностью, доходчивостью и афористичностью. Она бывает, как правило, эмоциональной, красочной, быстрой и четкой. Им дано умение задеть собеседника «за живое». Для них характерны громкий голос и низкий тембр, употребление жаргонных слов и выражений, анекдотов. Соответственно и жестикуляция тех, кто ассоциирует себя с треугольником, довольно непринужденная.
Предпочитают модную, элегантную одежду, выдержанную в классическом стиле. Отличаются ухоженностью, умением следить за собой и любовью к дорогим вещам. Походка – уверенная и раскованная, с плавными движениями.
КругОсновная ценность для этого типа – люди и общение с ними. Это крайне контактные и доброжелательные представители рода человеческого, занимающие позицию миротворца в любых конфликтах. Даже в деловых переговорах они не могут удержаться, чтобы не задать оппоненту личный вопрос.
Выбор круга в качестве основной фигуры может свидетельствовать о доверчивости, общительности, ориентации на мнение окружающих и нерешительности. Человек-круг прекрасный слушатель, ему всегда можно «поплакаться в жилетку». Он переживает чужую боль, как собственную, потому как в нем развито эмоциональное восприятие. И порадоваться, разделить счастье может как никто другой. Кстати, благодаря тонкой душевной организации «круги» прямо-таки ходячие детекторы лжи, тонко чувствуют, когда их обманывают.
Те, кто выбрал круг сторонятся ответственности, предпочитая ее перекладывать на других. Боясь испортить отношения, не умеют отказывать, дают расплывчатые обещания.
Женщины, выбравшие круг, доброжелательны, щедры, чувствительны. Для них характерны склонность к сопереживанию и стремление к заботе о других. Они отличаются меланхоличностью, сентиментальностью и устремленностью в прошлое.
Люди круга любят задушевные беседы и теплую атмосферу. Их речь характеризуется непоследовательностью, нелогичностью и частыми отступлениями от главной темы. Она бывает, как правило, эмоциональной, плавной и несколько замедленной. Эти люди обожают шутки, веселы, порой до легкомысленности, щедры. Им свойственен сочный, густой голос низкого тембра, употребление восторженных оценок и комплиментов.
Она бывает, как правило, эмоциональной, плавной и несколько замедленной. Эти люди обожают шутки, веселы, порой до легкомысленности, щедры. Им свойственен сочный, густой голос низкого тембра, употребление восторженных оценок и комплиментов.
Предпочитают неофициальный стиль одежды. Склонны к полноте, женственны и обаятельны. Походка легкая, плавная, с расслабленными телодвижениями.
ЗигзагВыбор зигзага в качестве основной фигуры может свидетельствовать об импульсивности мышления, непостоянстве взглядов, изменчивости настроения и отношений с окружающими. Это творцы, генераторы идей, одним словом, творческие и креативные личности. Они предпочитают мыслить образами и опираться на внезапные прозрения, начисто лишенные логики. Последовательность чужда таким людям от природы. Экспрессивность, несдержанность, эксцентричность – вот черты их характера. А еще они идеалисты, непрактичные и наивные. Впрочем, бывают остроумны, порой даже язвительны.
Зигзаги нуждаются в высокой стимуляции деятельности. Генерируя идеи в большом количестве, довольно часто отдают их на откуп другим, так как сами не способны довести дело до конца. Не терпят субординацию, любят свободу и независимость, и не поддаются организации, ни в быту, ни в деятельности. Хаос – вот органичное состояние людей-зигзагов. А еще это самая сексапильная фигура.
Генерируя идеи в большом количестве, довольно часто отдают их на откуп другим, так как сами не способны довести дело до конца. Не терпят субординацию, любят свободу и независимость, и не поддаются организации, ни в быту, ни в деятельности. Хаос – вот органичное состояние людей-зигзагов. А еще это самая сексапильная фигура.
Им характерна резкая смена настроения. Сегодня человек-зигзаг может вам улыбаться, а завтра не заметит. Игнорирует условности и принятые нормы. Крайне нетерпим к чужим слабостям. При этом сам падок на лесть.
Женщины, выбравшие зигзаг, мечтательны, восторженны, непрактичны и непосредственны. Для них характерны позитивная установка на все новое, устремленность в будущее, бунтарская жажда переустройства. Они отличаются отсутствием самодисциплины, безалаберностью в финансовых вопросах и самодостаточностью.
Речь образна, ярка, непоследовательна и ассоциативна. Она бывает, как правило, эмоциональной, торопливой и зажигательной. Голос имеет много оттенков, его тембр варьируется от очень высокого до низкого. Лексика богата и разнообразна, характеризуется употреблением оценочных слов и выражений.
Лексика богата и разнообразна, характеризуется употреблением оценочных слов и выражений.
Отдают предпочтение модным экстравагантным нарядам. Склонны к смешению стилей и небрежности в одежде. Могут появиться в обществе в мятом костюме и чувствовать при этом себя комфортно. Стремительны, манерны, с оживленной мимикой и жестикуляцией.
ПрямоугольникПрямоугольник часто выбирают люди, которые находятся на этапе перехода из одного состояния в другое. Эта ситуация, отражающая некий личностный кризис, как правило, не длится долго, и человек выбирает более определенный тип поведения, описанный из четырех выше представленных. Словом, это тот, кто ищет лучшее положение или только что изменил его, или предчувствует изменения. Но бывают индивиды, для которых оно затягивается на долгое время.
Характерной чертой, присущей человеку этого типа, является выраженная внутренняя неудовлетворенность тем, как складывается его жизнь на текущий момент, и желание что-то изменить. Часто такое положение дел осложняется состоянием замешательства, путанностью мыслей, непониманием собственных желаний и отсутствием ориентиров в дальнейшем движении.
Часто такое положение дел осложняется состоянием замешательства, путанностью мыслей, непониманием собственных желаний и отсутствием ориентиров в дальнейшем движении.
Выбор прямоугольника в качестве основной фигуры может свидетельствовать о непоследовательности, склонности к принятию импульсивных решений, непунктуальности и нервозности. Настроение человека-прямоугольника может многократно меняться даже в течении одного дня, что влечет за собой и изменение его поведения.
Те, кто предпочел прямоугольник, как правило, непоследовательны, не уверены в себе и имеют низкую самооценку. Они остро нуждаются в общении. При этом эти люди смелы, пытливы. Открыты для новых идей, ценностей, способов мышления и жизни, легко усваивают все новое. Чувство собственного несовершенства побуждает их искать способы саморазвития и изменений: больше читать, посещать различные курсы.
Женщины, выбравшие прямоугольник, болезненно любознательны, внушаемы, доверчивы и наивны. Часто становятся жертвой чужих манипуляций. Для них характерна поспешность в решении вопросов.
Для них характерна поспешность в решении вопросов.
Речь прямоугольников отличается неуверенностью, невнятностью и сбивчивостью. Она бывает, как правило, эмоциональной и аритмичной: то убыстряется до скороговорки, то замедляется вплоть до пауз. Поэтому эти люди предпочитают простую манеру разговора. Они не способны ясно и четко донести свою мысль. Для них характерны колебания громкости голоса и высоты тона, употребление междометий и «слов-паразитов». Неуверенность проявляется и в движении. Жесты неуклюжи и невыразительны.
Особых предпочтений в одежде нет. Люди-прямоугольники не отличаются аккуратностью и характеризуются полнейшим отсутствием стиля.
Калькулятор окружности
Укажите любое значение ниже, чтобы вычислить оставшиеся значения круга.
В то время как круг символически представляет множество различных вещей для многих различных групп людей, включая такие понятия, как вечность, вневременность и тотальность, круг по определению представляет собой простую замкнутую форму. Это множество всех точек на плоскости, которые равноудалены от данной точки, называемой центром. Его также можно определить как кривую, прочерченную точкой, где расстояние от данной точки остается постоянным по мере движения точки.Расстояние между любой точкой окружности и центром окружности называется ее радиусом, а диаметр окружности определяется как наибольшее расстояние между любыми двумя точками на окружности. По сути, диаметр в два раза больше радиуса, так как наибольшее расстояние между двумя точками на окружности должно быть отрезком прямой, проходящим через центр окружности. Окружность круга может быть определена как расстояние вокруг круга или длина цепи по кругу. Все эти значения связаны через математическую константу π или пи, которая представляет собой отношение длины окружности к ее диаметру и составляет приблизительно 3.14159. π — иррациональное число, означающее, что оно не может быть выражено точно в виде дроби (хотя оно часто приближается к 22/7), и его десятичное представление никогда не заканчивается или имеет постоянно повторяющийся образец.
Это множество всех точек на плоскости, которые равноудалены от данной точки, называемой центром. Его также можно определить как кривую, прочерченную точкой, где расстояние от данной точки остается постоянным по мере движения точки.Расстояние между любой точкой окружности и центром окружности называется ее радиусом, а диаметр окружности определяется как наибольшее расстояние между любыми двумя точками на окружности. По сути, диаметр в два раза больше радиуса, так как наибольшее расстояние между двумя точками на окружности должно быть отрезком прямой, проходящим через центр окружности. Окружность круга может быть определена как расстояние вокруг круга или длина цепи по кругу. Все эти значения связаны через математическую константу π или пи, которая представляет собой отношение длины окружности к ее диаметру и составляет приблизительно 3.14159. π — иррациональное число, означающее, что оно не может быть выражено точно в виде дроби (хотя оно часто приближается к 22/7), и его десятичное представление никогда не заканчивается или имеет постоянно повторяющийся образец. Это также трансцендентное число, что означает, что оно не является корнем любого ненулевого многочлена с рациональными коэффициентами. Интересно, что доказательство, проведенное Фердинандом фон Линдеманном в 1880 году, что число π трансцендентно, наконец положило конец тысячелетнему поиску, начатому древними геометрами «квадратуры круга».«Это включало попытку построить квадрат с той же площадью, что и данный круг, за конечное число шагов, используя только циркуль и линейку. Хотя теперь известно, что это невозможно, и представляя себе ревностные усилия взволнованных древних геометров, пытающихся невозможное при свете свечи может вызвать смехотворный образ, важно помнить, что именно благодаря таким людям сегодня хорошо определены многие математические понятия.
Это также трансцендентное число, что означает, что оно не является корнем любого ненулевого многочлена с рациональными коэффициентами. Интересно, что доказательство, проведенное Фердинандом фон Линдеманном в 1880 году, что число π трансцендентно, наконец положило конец тысячелетнему поиску, начатому древними геометрами «квадратуры круга».«Это включало попытку построить квадрат с той же площадью, что и данный круг, за конечное число шагов, используя только циркуль и линейку. Хотя теперь известно, что это невозможно, и представляя себе ревностные усилия взволнованных древних геометров, пытающихся невозможное при свете свечи может вызвать смехотворный образ, важно помнить, что именно благодаря таким людям сегодня хорошо определены многие математические понятия.
Круговые формулы
Д = 2R С = 2πR А = πR 2 | где: R: Радиус |
Калькулятор окружности круга
Объяснение расчета окружности
Понимание того, что такое окружность окружности и как ее вычислить, имеет решающее значение при переходе на более высокий уровень математики. В этой статье вы узнаете ответы на следующие вопросы.
- Какова длина окружности?
- Как рассчитать длину окружности?
Окружность окружности — это расстояние по внешней стороне окружности.Это похоже на периметр других форм, таких как квадраты. Вы можете думать об этом как о линии, определяющей форму. Для фигур, состоящих из прямых краев, эта линия называется периметром , а для кругов эта определяющая линия называется окружностью.
На этом рисунке показана длина окружности.
На окружности есть два других важных расстояния: радиус (r) и диаметр (d). Радиус, диаметр и длина окружности являются тремя определяющими аспектами каждого круга.Зная радиус или диаметр и число пи, вы можете рассчитать длину окружности. Диаметр — это расстояние от одной стороны круга до другой в его самых широких точках. Диаметр всегда будет проходить через центр окружности. Радиус равен половине этого расстояния. Вы также можете думать о радиусе как о расстоянии между центром круга и его краем.
Радиус, диаметр и длина окружности являются тремя определяющими аспектами каждого круга.Зная радиус или диаметр и число пи, вы можете рассчитать длину окружности. Диаметр — это расстояние от одной стороны круга до другой в его самых широких точках. Диаметр всегда будет проходить через центр окружности. Радиус равен половине этого расстояния. Вы также можете думать о радиусе как о расстоянии между центром круга и его краем.
На этой диаграмме показаны длина окружности, диаметр, центр и радиус окружности.
Как рассчитать длину окружности?Если вы знаете диаметр или радиус круга, вы можете вычислить длину окружности.Для начала вспомним, что пи — иррациональное число, записываемое через символ π. π примерно равно 3,14.
Формула для расчета длины окружности:
Длина окружности = π x Диаметр окружности
Обычно это записывается как C = πd. Это говорит нам о том, что длина окружности в три «с небольшим» раза больше диаметра. Мы можем видеть это на графике ниже:
Мы можем видеть это на графике ниже:
Вы также можете вычислить длину окружности, если знаете ее радиус.Помните, что диаметр в два раза больше длины радиуса. Мы уже знаем, что C = πd. Если r — радиус окружности, то d = 2r. Итак, C = 2πr.
Пример 1Если диаметр круга 10 см, какова его окружность?
ОтветМы знаем, что C = πd. Поскольку диаметр равен 10 см, мы знаем, что C = π x 10 см = 31,42 см (с точностью до 2 знаков после запятой).
Пример 2Если круг имеет радиус 3 м, какова его длина окружности?
ОтветМы знаем, что C = 2πr.Поскольку радиус равен 3 м, мы знаем, что C = π x 6 м = C = 18,84 м (с точностью до 2 знаков после запятой).
Пример 3Найдите недостающую длину (отмеченную знаком ?) на диаграмме ниже:
Ответ Недостающая длина — это длина окружности. Зная, что диаметр на диаграмме равен 4,3 м, и зная, что C = πd, мы можем вычислить длину окружности. Немного подумав, мы можем легко понять, что C = π x 4,3 м = 13,51 м (с точностью до 2 знаков после запятой).Недостающая длина составляет 13,51 м.
Немного подумав, мы можем легко понять, что C = π x 4,3 м = 13,51 м (с точностью до 2 знаков после запятой).Недостающая длина составляет 13,51 м.
Задумывались ли вы, насколько велика Земля? Что ж, с помощью пи можно вычислить окружность Земли! Ученые установили, что диаметр Земли составляет 12 742 км. Учитывая эту информацию, какова окружность Земли? Возьмите лист бумаги и калькулятор и посмотрите, сможете ли вы решить это самостоятельно.
Опять же, мы знаем, что C = πd и что диаметр Земли равен 12 742 км.Используя эту информацию, мы можем рассчитать окружность Земли как C = π x 12 742 км = 40 030 км.
Формула длины окружности и площади кругаФорма: круг – элементарная математика
Значение
Неформальное значение: Слово «круг» знакомо большинству детей очень рано, но оно имеет лишь неформальное значение слова «круглый». Мы сидим «в кругу», не особо задумываясь о том, насколько он круглый, и не представляя себе геометрический объект, связанный со словом.
По мере того как учащиеся изучают геометрию, мы помогаем им уточнить значение из неформального смысла — формы кольца, колеса или фрисби — и принять более формальное математическое значение. Во-первых, круг — это двумерная фигура: то есть фотография мяча может быть круглой, но сам мяч — нет (мяч трехмерен). И «круглого» недостаточно: все приведенные ниже фигуры «круглые», но чтобы что-то было кругом, каждая его точка должна быть на одинаковом расстоянии от центра.
Некоторые точки эллипса и яйцевидной формы находятся дальше от центра (красные), чем другие; все точки окружности находятся на одинаковом расстоянии от центра.
Формальн центр, чем точки на самой окружности. Когда студентов просят указать на круг, они часто указывают внутри круга и могут называть круговой «обод» этой формы окружностью.В точном использовании замкнутая кривая сама по себе является окружностью, а термин окружность относится к длине кривой. (Слово «диск» используется для обозначения области, заключенной в круглую границу. Но даже математики могут сказать «разрезать круг пополам» вместо «разрезать диск пополам», когда контекст делает значение достаточно ясным.)
Но даже математики могут сказать «разрезать круг пополам» вместо «разрезать диск пополам», когда контекст делает значение достаточно ясным.)
Один из способов прояснить язык — представить картинку, на которой круг и его внутренняя часть окрашены по-разному. На этой картинке круг красный; его внутренняя часть желтая.Внешний вид круга — это вся оставшаяся плоскость, не находящаяся на круге и не заключенная в нем. На этом рисунке показана небольшая квадратная область этой плоскости, а внешняя сторона круга окрашена в синий цвет.
Измерения на окружностях
Для нахождения длины окружности и площади круга можно использовать две важные формулы:
- Окружность: C = πd = 2πr
- Площадь: A = πr 2
В каждой формуле r представляет длину радиуса окружности, а d представляет длину диаметра или удвоенную длину радиуса.Число пи (π) — иррациональное число, определяемое как отношение C/d — отношение длины окружности к длине его диаметра — хотя точные вычисления значения π никогда не основываются на измерениях. Его значение примерно равно 3,14159265…
Его значение примерно равно 3,14159265…
Открытие формулы длины окружности
Поскольку это определение числа пи, «формула» для длины окружности на самом деле не является чем-то новым, это просто переформулировка или повторное использование определения числа пи.
Если , то .
Открытие формулы площади
Мы не можем точно измерить площадь круга, нанеся на него квадраты; они не подойдут, независимо от того, какой размер мы выберем. Итак, чтобы найти формулу площади круга, мы «рассекаем» его, разрезаем на части, площади которых можем измерить. (См. Формулы площади для примеров рассечения параллелограммов и треугольников.)
Сектора круга немного похожи на треугольники, особенно если разделить круг на достаточное количество таких секторов. Если мы разделим круг на восьмые части (левый круг на рисунке ниже), разница (показана розовым цветом) между полным сектором и треугольником, который он содержит (показан синим цветом), будет довольно существенной. Мы могли бы вычислить площадь этого синего треугольника, умножить на 8, а затем просто удовлетвориться этой заниженной оценкой площади круга.
Мы могли бы вычислить площадь этого синего треугольника, умножить на 8, а затем просто удовлетвориться этой заниженной оценкой площади круга.
Но мы могли бы добиться большего. Если мы разделим круг на двенадцатые части (в центре вверху), ошибка — количество оставшегося розового — будет значительно меньше. А если разрезать круг на 24 части (справа вверху), то остаток будет еще меньше, даже с учетом того, что таких остатков теперь 24.
Что еще более важно, мы замечаем кое-что еще.По мере того, как круг делится на большее количество секторов — и различие между «сектором» и «треугольником» все больше и больше испаряется — размеры каждого треугольника теперь легче соотносить с размерами круга. Если мы разделили круг на 24 сектора, короткая сторона треугольника будет (почти) 1/24 длины окружности круга, а высота этого треугольника будет (почти) радиусом круга. Итак, используя эти приближения, площадь треугольника равна
. Но в круге 24 таких треугольника, поэтому площадь круга будет и мы знаем, что C = 2πr, поэтому Еще немного заботы. Наша окончательная формула предполагала, что основание и высота треугольника равны 90 201 — ровно 90 202, что мы и хотели — 90 201 — ровно 90 202 длины окружности и 90 201 — ровно 90 202 радиуса, — что, как мы знали, было неверным. Что спасает рассуждения, так это то, что мы можем сделать приближение сколь угодно точным. Если бы мы разбили круг на 1000 секторов — чертить совершенно бессмысленно — основание и высота треугольника были бы еще ближе к 1/1000 длины окружности круга и точно радиусу.Поскольку рассуждения и всегда дают один и тот же результат, и мы можем получить приближение, поддерживающее это рассуждение, сколь угодно точное — разрезать круг на миллиард секторов или миллиард миллион секторов — результат является общим.
Наша окончательная формула предполагала, что основание и высота треугольника равны 90 201 — ровно 90 202, что мы и хотели — 90 201 — ровно 90 202 длины окружности и 90 201 — ровно 90 202 радиуса, — что, как мы знали, было неверным. Что спасает рассуждения, так это то, что мы можем сделать приближение сколь угодно точным. Если бы мы разбили круг на 1000 секторов — чертить совершенно бессмысленно — основание и высота треугольника были бы еще ближе к 1/1000 длины окружности круга и точно радиусу.Поскольку рассуждения и всегда дают один и тот же результат, и мы можем получить приближение, поддерживающее это рассуждение, сколь угодно точное — разрезать круг на миллиард секторов или миллиард миллион секторов — результат является общим.Еще одно изображение, которое иногда используется, чтобы получить представление о площади круга, показано ниже. Там все сектора раздвинуты, как дольки апельсина.
Затем их можно собрать вместе, чтобы получился параллелограмм.
Опять же, чем больше секторов, тем больше этот параллелограмм аппроксимирует прямоугольник, размеры которого равны r и . Тот же результат.
Тот же результат.
Другие размеры на окружности
Обобщения формул площади и окружности можно использовать для нахождения длины дуги на окружности или площади сектора окружности:
- Площадь сектора:
- Длина дуги:
В каждой формуле x представляет меру дуги в градусах.
Этимология
От латинского circulus, уменьшительного от circus, что означает «кольцо», возможно, от индоевропейского корня ker- или sker- означает поворачиваться или сгибаться.
Индоевропейское ker- также дает начало Кривой, Кривизне и короне, коронату, солнечной короне и т. д.
Связанные математические термины
Корень окружность дает начало многим терминам, используемым в математических и случайных значениях.
Окружность, Окружность
Другие родственные слова
циркулировать, цирк, обход, кругосветное плавание, обстоятельство, корона, корона и т. д.
кругов, вписанных в квадраты
Когда
круг
вписан в
квадратный
,
диаметр
стороны круга равна длине стороны квадрата.
Вы можете найти периметр и площадь квадрата, когда дана хотя бы одна мера круга или квадрата.
Для квадрата со стороной с , используются следующие формулы.
Периметр = 4 с
Площадь = с 2
Диагональ = с 2
Аналогичным образом можно найти длина окружности и площадь круга , когда дана хотя бы одна мера круга или квадрата.
Для окружности с радиусом р , используются следующие формулы.
Окружность = 2 π р
Площадь = π р 2
Пример 1:
Найдите периметр квадрата.
Когда круг вписан в квадрат, диаметр круга равен длине стороны квадрата.
Значит, длина стороны квадрата
6
см.
Периметр п квадрата со стороной с дан кем-то п знак равно 4 с .
Заменять 6 за с в п знак равно 4 с .
п знак равно 4 ( 6 ) знак равно 24
Периметр квадрата 24 см.
Пример 2:
Чему равна площадь круга, вписанного в квадрат площади 64 квадратные единицы?
Когда круг вписан в квадрат, длина каждой стороны квадрата равна диаметру круга. То есть диаметр вписанной окружности равен 8 единиц, поэтому радиус равен 4 единицы.
Площадь круга радиуса
р
единиц
А
знак равно
π
р
2
.
Заменять р знак равно 4 в формуле.
А знак равно π ( 4 ) 2 знак равно 16 π ≈ 50.24
Следовательно, площадь вписанного круга примерно 50,24 квадратных единиц.
Column Pi (отношение длины окружности к ее диаметру)
Что касается значения π, то древние цивилизации использовали свое собственное. Так как правильный шестиугольник, вписанный в окружность радиусом 1, имеет периметр 6, то получается, что число Пи больше 3. В Древнем Египте получили приближение
(примерно 3.16)
путем размещения правильного восьмиугольника на окружности, а в древней Вавилонии использовали
.
Архимед в своей работе Kyklu metresis (мера окружности) пришел к выводу, что Пи удовлетворяет
.
В древней Индии мы можем найти пример использования =3,1622776 или
.
В Китае использовали
или
или
для Пи.
В период Эдо в Японии Jinkoki (1627) Ёсида Мицуёси использовал 3,16 для числа Пи, но, поскольку люди признали, что это значение было неточным, появилось поле под названием Enri ( en означает круг, а ri означает теорию), в которой рассчитывались более точные значения числа Пи. Ученые-васан, такие как Мурамацу Шигекио, Секи Такаказу, Камата Тошикиё, Такебе Катахиро и Мацунага Йошисуке, рассчитали более точные значения числа Пи и достигли результатов, которые можно сравнить с европейской математикой.
В Европе Виете (1540-1603) открыл первую формулу, выражающую число π:
После этого Wallis (1616-1703) Формула:
Григорий (1638-1675) и Лейбниц (1646-1716) Формула:
Кроме того, Ньютон (1642-1727) и Эйлер (1707-1783) открыли ряд, который сходится быстрее, что позволило им вычислять значения числа Пи с большим числом знаков после запятой. Если мы используем соотношение
Если мы используем соотношение
, обнаруженный Дж.Мачин (1680-1752),
мы можем получить значение 3,14159 для π с точностью до пяти знаков после запятой с первыми 4 членами разложения Тейлора tan -1 . В недавнем компьютерном расчете использовались следующие уравнения:
или
* tan -1 : Арктангенс. Обратная функция тангенса.
Расчет числа Пи в васане
Генри Мур — Лежащая фигура: круг
Китай ADAMSAI WEIWEIDOUG AITKENDIANA АЛ-HADIDJOSEF ALBERSGERTRUDE Партингтон ALBRIGHTBRIAN ALFREDHERB ALPERTMICAELA AMATODAVID AMICOJOE ANDOECARL ANDREPETER ANTONRICHARD ANUSZKIEWICZRON ARADRICHARD ARTSCHWAGERMAURICE ASKENAZYLUIS КРУШ AZACETAZALIKO BACHANASHVILLCESAR BALDACCINIROBERT BATEMANWILLIAM BAZIOTESPETER BEARDKARL BENJAMINLAUREN BENRIMONLUC BERNARDHARRY BERTOIADAVIS BIRKSROSS BLECKNERNORMAN BLUHMFERNANDO BOTEROJESSIE ARMS BOTKETATIANA BOTTONLOUISE BOURGEOISGEORGE BRANDRIFFDAVID BREUER-WEILWILLIAM Теофилус BROWNOSVALDO BUDETDEBORAH BUTTERFIELDMATTY BYLOOSALEXANDER CALDERFERNANDO CANOVASSANTIAGO CARBONELLLEONORA CARRINGTONLAWRENCE CARROLLFELIPE CASTANEDABRUNO CECCOBELLIFRANCIS CELENTANOMARC CHAGALLGENIA CHEFDALE CHIHULYCHINESECHUCK CLOSEGEORGE CONDOLINDA CONNERJOSEPH CORNELLMARY CORSECHARLES-Жан-Луи COURTRYMARTIN CREEDJERRY CROWLEYAARON CURRYALLAN D’ARCANGELOSALVADOR DALILYNN DAVISWILLEM ДЕ KOONINGELAINE ДЕ KOONINGTONY ДЕ ЛОС REYESNIKI ДЕ СЕНТ PHALLEED DEANMICHAEL ПАТРИК Д EEEDGAR DEGASROBYN DENNYRICHARD DIEBENKORNJIM DINEGASPARD DUGHET (ПОСЛЕ)LEANDRO ERLICHMERION ESTESSHEPARD FAIREYJAVIER FERNANDEZKELTIE FERRISCHARLES FINEPERLE FINESAM FRANCISSHINGO FRANCISHELEN FRANKENTHALERFREDERIC FRIESEKELEON GASPARDTTHASTER GATESTER. GERAKARISKARL GERSTNERGILBERT & GEORGESAM GILLIAMJUDITH GODWINANTONY GORMLEYPENELOPE GOTTLIEBADOLPH GOTTLIEBPAUL GRIMMJiang GuofangSUBODH GUPTAPHILIP GUSTONZAHA HADIDPETER HALLEYJANE HAMMONDKEITH HARINGGRACE HARTIGANCHILDE HASSAMTIM HAWKINSONRUEHL ФРЕДЕРИК HECKMANANTON HENNINGJOHN HENRYARNE HIERSOUXJENE HIGHSTEINCLINTON HILLCLARENCE HINKLEDAMIEN HIRSTHANS HOFMANNSAKAI HOITSUERIC JON HOLSWADEJENNY HOLZERWINSLOW HOMERVOLKER HUELLERMARINE HUGONNIERELLIOTT HUNDLEYKYOKO IBEROBERT INDIANAVALERIE JAUDONPAUL JENKINSZENG JIANYONGLUIS JIMENEZMATT JOHNSONFRIDA KAHLOKRISJANIS Кактиньш-GORSLINESAUL KAMINERJUN KANEKORYOKO KATOALEX KATZSETH KAUFMANJOSEPH KLEITSCHJEFF KOONSLEE KRASNERTADAAKI KUWAYAMATADASUKE (Tadasky) KUWAYAMATSENG Kwong CHICHET Л.А. MORELEONID LAMMANNIE LAPINLAWRENCE Leeroy LICHTENSTEINBESSIE LIDDLEJACQUES LIPCHITZRICHARD LONGMORRIS LOUISRICHARD ATTILA LUKACSCARLOS LUNADANNY LYONDAVID MACHALEX MACLEANRICARDO MAFFEIRENE MAGRITTECONSTANCE MALLINSONPAUL MANESHENRI MANGUINJEAN MANNHEIMKAOR U MANSOURYANG MAOYUANROBERT MARCMARINO MARINIMELVIN MARTINEZRICARDO MARTINEZROBERTO MATTAMERCEDES MATTERSTEVEN MCCALLUMTHOMAS MCGLYNNRODNEY MCMILLIANJOHN MILLEIJOAN MIROANDREA MODICAALISON MOFFETTMATTHEW MONAHANCLAUDE MONETHENRY MOOREROBERT MOOREMARY DENEALE MORGANCARL MORRISDAVID MORRISED MOSESROBERT MOTHERWELLSADAMASA MOTONAGAVIK MUNIZTAKASHI MURAKAMIFORREST MYERSDAN NAMINGHAROBERT NATKINJOAN NELSONMANUEL NERILOUISE NEVELSONBARNETT NEWMANMARC NEWSONHELMUT NEWTONLILLIE МАЙ NICHOLSONKENNETH NOLANDIRVING NORMANNot VitalDAVID NOVROSTHOMAS NOZKOWSKIGEORGIA O’KEEFFEJULES OLITSKINATHAN OLIVEIRAJULIAN OPIEDENNIS OPPENHEIMDEBORAH OROPALLOGEORGE ORTMANMARUYAMA OSHINDAN OSTERMILLERARTHUR OUMIMMO PALADINOJAE KON PARKDEWITT PARSHALLEDGAR Alwin PAYNEMAX PECHSTEINMAX PELLEGRINIENOC PEREZROLAND PETERSENJOHN PFAHLFRANCIS PICABIAPABLO PICASSOOTTO PIENECAMILLE PISSARROJACKSON POLLOCKELIOT PORTERKATHERINE PORTERRICHARD POUSETTE-DARTROBERT RAUSCHENBERGRON REIHELAD REINHARDTCLARE RICHARDSONDIEGO RIVERALAR Ry Riversnorman Rockwellchristian Rosajames Rosenquistjack Jenmarkhn RothoDavid Rowsandra Mendelsohn Rothinling Rusyed Ruschalawrence Schillermary Jane Schmidjulian Schnabeldonna Schustzzeulgore Segalgeorge Segideneckedgar Serranopeter Sheltonjose Maria Siciliaamy Sillmanalfred Sisleyg.
GERAKARISKARL GERSTNERGILBERT & GEORGESAM GILLIAMJUDITH GODWINANTONY GORMLEYPENELOPE GOTTLIEBADOLPH GOTTLIEBPAUL GRIMMJiang GuofangSUBODH GUPTAPHILIP GUSTONZAHA HADIDPETER HALLEYJANE HAMMONDKEITH HARINGGRACE HARTIGANCHILDE HASSAMTIM HAWKINSONRUEHL ФРЕДЕРИК HECKMANANTON HENNINGJOHN HENRYARNE HIERSOUXJENE HIGHSTEINCLINTON HILLCLARENCE HINKLEDAMIEN HIRSTHANS HOFMANNSAKAI HOITSUERIC JON HOLSWADEJENNY HOLZERWINSLOW HOMERVOLKER HUELLERMARINE HUGONNIERELLIOTT HUNDLEYKYOKO IBEROBERT INDIANAVALERIE JAUDONPAUL JENKINSZENG JIANYONGLUIS JIMENEZMATT JOHNSONFRIDA KAHLOKRISJANIS Кактиньш-GORSLINESAUL KAMINERJUN KANEKORYOKO KATOALEX KATZSETH KAUFMANJOSEPH KLEITSCHJEFF KOONSLEE KRASNERTADAAKI KUWAYAMATADASUKE (Tadasky) KUWAYAMATSENG Kwong CHICHET Л.А. MORELEONID LAMMANNIE LAPINLAWRENCE Leeroy LICHTENSTEINBESSIE LIDDLEJACQUES LIPCHITZRICHARD LONGMORRIS LOUISRICHARD ATTILA LUKACSCARLOS LUNADANNY LYONDAVID MACHALEX MACLEANRICARDO MAFFEIRENE MAGRITTECONSTANCE MALLINSONPAUL MANESHENRI MANGUINJEAN MANNHEIMKAOR U MANSOURYANG MAOYUANROBERT MARCMARINO MARINIMELVIN MARTINEZRICARDO MARTINEZROBERTO MATTAMERCEDES MATTERSTEVEN MCCALLUMTHOMAS MCGLYNNRODNEY MCMILLIANJOHN MILLEIJOAN MIROANDREA MODICAALISON MOFFETTMATTHEW MONAHANCLAUDE MONETHENRY MOOREROBERT MOOREMARY DENEALE MORGANCARL MORRISDAVID MORRISED MOSESROBERT MOTHERWELLSADAMASA MOTONAGAVIK MUNIZTAKASHI MURAKAMIFORREST MYERSDAN NAMINGHAROBERT NATKINJOAN NELSONMANUEL NERILOUISE NEVELSONBARNETT NEWMANMARC NEWSONHELMUT NEWTONLILLIE МАЙ NICHOLSONKENNETH NOLANDIRVING NORMANNot VitalDAVID NOVROSTHOMAS NOZKOWSKIGEORGIA O’KEEFFEJULES OLITSKINATHAN OLIVEIRAJULIAN OPIEDENNIS OPPENHEIMDEBORAH OROPALLOGEORGE ORTMANMARUYAMA OSHINDAN OSTERMILLERARTHUR OUMIMMO PALADINOJAE KON PARKDEWITT PARSHALLEDGAR Alwin PAYNEMAX PECHSTEINMAX PELLEGRINIENOC PEREZROLAND PETERSENJOHN PFAHLFRANCIS PICABIAPABLO PICASSOOTTO PIENECAMILLE PISSARROJACKSON POLLOCKELIOT PORTERKATHERINE PORTERRICHARD POUSETTE-DARTROBERT RAUSCHENBERGRON REIHELAD REINHARDTCLARE RICHARDSONDIEGO RIVERALAR Ry Riversnorman Rockwellchristian Rosajames Rosenquistjack Jenmarkhn RothoDavid Rowsandra Mendelsohn Rothinling Rusyed Ruschalawrence Schillermary Jane Schmidjulian Schnabeldonna Schustzzeulgore Segalgeorge Segideneckedgar Serranopeter Sheltonjose Maria Siciliaamy Sillmanalfred Sisleyg. Е. SMITHHASSEL SMITHJOHN КРИСТОФЕР SMITHJESUS РАФАЭЛЬ SOTODANIEL SPRICKEARL STALEYTHEODOROS STAMOSEDWARD STEICHENJENNIFER STEINKAMPFRANK STELLAJOSEPH STELLAJOHN STEZAKERRAY СТЭНФОРД STRONGTHOMAS STRUTHKUMI SUGAISE ОК SUHDONALD SULTANSUMATRAGREGORY SUMIDARAY SWANSONLINO TAGLIAPIETRARUFINO TAMAYOPAULETTE TAVORMINAANDREW TAYLORFELANDUS THAMESGERT И УВЕ TOBIASSEIJU TODAFRANCISCO TOLEDOTIMOTHY TOMPKINSGEORGE TOOKERWILLIAM TUCKERRICHARD TUTTLEMANUEL VALENCIAVINCENT VAN GOGHJAN JOSEPHSZOON VAN GOYENSALOMON VAN RUYSDAELCHRISTIAN VINCENTMASSIMO VITALITOMAS VUANDY УОРХОЛНЕЛ УОКЕР УОРНЕРАБЕЛЬ ДЖОРДЖ УОРШАВСКИРАЛФ УОТЕРХАУСУИЛЬЯМ ВЭГМАНУИЛЬЯМ ВЭНДТТОМ ВЕССЕЛЬМАННДЭВИД УОРТОНРЭЙЧЕЛ УАЙТРИДУИЛЬЯМ Т.WILEYPAUL WONNERJAMIE WYETN.C. WYETHXIAOZE XIEHIRO YAMAGATATERUKO YOKOIZHU Yi YongRUSSELL YOUNGHIKARU YUMURANORMAN ZAMMITTZHANG HUANFRANCESCO ZUNIGA
Е. SMITHHASSEL SMITHJOHN КРИСТОФЕР SMITHJESUS РАФАЭЛЬ SOTODANIEL SPRICKEARL STALEYTHEODOROS STAMOSEDWARD STEICHENJENNIFER STEINKAMPFRANK STELLAJOSEPH STELLAJOHN STEZAKERRAY СТЭНФОРД STRONGTHOMAS STRUTHKUMI SUGAISE ОК SUHDONALD SULTANSUMATRAGREGORY SUMIDARAY SWANSONLINO TAGLIAPIETRARUFINO TAMAYOPAULETTE TAVORMINAANDREW TAYLORFELANDUS THAMESGERT И УВЕ TOBIASSEIJU TODAFRANCISCO TOLEDOTIMOTHY TOMPKINSGEORGE TOOKERWILLIAM TUCKERRICHARD TUTTLEMANUEL VALENCIAVINCENT VAN GOGHJAN JOSEPHSZOON VAN GOYENSALOMON VAN RUYSDAELCHRISTIAN VINCENTMASSIMO VITALITOMAS VUANDY УОРХОЛНЕЛ УОКЕР УОРНЕРАБЕЛЬ ДЖОРДЖ УОРШАВСКИРАЛФ УОТЕРХАУСУИЛЬЯМ ВЭГМАНУИЛЬЯМ ВЭНДТТОМ ВЕССЕЛЬМАННДЭВИД УОРТОНРЭЙЧЕЛ УАЙТРИДУИЛЬЯМ Т.WILEYPAUL WONNERJAMIE WYETN.C. WYETHXIAOZE XIEHIRO YAMAGATATERUKO YOKOIZHU Yi YongRUSSELL YOUNGHIKARU YUMURANORMAN ZAMMITTZHANG HUANFRANCESCO ZUNIGA
АфроамериканскийКитайскийКлассическийСовременныйДизайнЕвропейскийИмпрессионизм и модернЯпонскийЮвелирныйКорейскийЛатиноамериканскийОкеаническийСтарые мастераИскусство аутсайдеровПослевоенныйДоколумбовыйЮго-Восточная АзияТибетский
Минимальная цена:
Максимальная цена:
Вписанные и описанные фигуры: определение и построение — видео и расшифровка урока
Вписанные и описанные фигуры
Что это за путь? Это круг. Поскольку он находится внутри такого пятиугольника, он называется вписанной фигурой. Вписанная фигура — это фигура, нарисованная внутри другой фигуры. Мы говорим, что окружность вписана в пятиугольник.
Поскольку он находится внутри такого пятиугольника, он называется вписанной фигурой. Вписанная фигура — это фигура, нарисованная внутри другой фигуры. Мы говорим, что окружность вписана в пятиугольник.
В перерывах Эмма любит бегать. Обычно у нее не так много времени, поэтому она бегает по зданию кратчайшим путем. Ее путь выглядит так. Теперь наша окружность находится вне пятиугольника, и теперь она не вписана, а описана. Описанная фигура — это фигура, нарисованная вне другой фигуры.
Подождите. Какая разница? Не могли бы вы сказать, что пятиугольник вписан в окружность, а не окружность описана в пятиугольнике? Да! Разница между вписанным и описанным просто заключается в том, какая фигура описывается в терминах другой.
Помните, что вписанная фигура находится внутри другой. А «обведенная» фигура «обводит» другую.Это верно даже здесь, когда пятиугольник описывает окружность.
Вписанные многоугольники
В конце концов, Эмма уходит из Пентагона и устраивается на работу в Капитолий. Люди в Конгрессе любят проводить импровизированные встречи под ротондой. Так что Эмма часто перемещается в этой круглой области.
Каждая встреча образует уголок на нашей фигуре.И каждый угол также известен как вершина . Когда у нас есть более одной вершины, мы говорим вершины. Кажется причудливым, верно? Ну, это Конгресс.
Вот треугольник, показывающий путь, по которому Эмма проходит три встречи с сенаторами, которые не любят находиться рядом друг с другом. Это важно, так как для того, чтобы фигура была вписана в круг, все ее вершины должны быть на круге.
Если бы сенаторы были более дружелюбны, и треугольник выглядел бы так, мы бы не говорили, что треугольник вписан в окружность.Вершины не касаются окружности.
И не всякую фигуру можно вписать в круг. Треугольники и пятиугольники могут. Вот квадрат. А вот и прямоугольник. Это оба параллелограмма, которые работают. Как насчет любого параллелограмма? Не этот. Только две стороны касаются круга. Так что не каждый параллелограмм можно вписать, только квадрат или прямоугольник. Для любой формы просто убедитесь, что все вершины касаются круга.
Вписанные круги
Когда Эмма находится на полу квадратного дома, она движется по кругу, уклоняясь от представителей.
Когда мы говорим об окружностях, мы ищем, чтобы окружность касалась сторон фигуры. Имея здесь наш квадрат, обратите внимание, что окружность касается всех четырех сторон квадрата. Тангенс просто означает, что он касается только в одном месте.
Имея здесь наш квадрат, обратите внимание, что окружность касается всех четырех сторон квадрата. Тангенс просто означает, что он касается только в одном месте.
Как и прежде, это будет работать только с некоторыми формами. Возьмите треугольник. Некоторые круги могут быть вписаны в некоторые треугольники, как вы видите здесь. А как же здесь? Круг не касается каждой стороны, так что нет.
Практические задачи
Но когда круг вписан, мы можем сделать несколько изящных вещей.2) или 81pi.
А как насчет этого надоедливого квадрата? Если радиус круга равен 9, то диагональ квадрата равна 18. Знаете ли вы, что можно найти площадь, используя только это число? Помните, что квадрат — это всего лишь два сложенных прямоугольных треугольника. Итак, основание нашего треугольника равно 18. А высота треугольника? Это радиус круга, или 9. Это означает, что площадь каждого треугольника равна 1/2 bh или 1/2*18*9, что равно 81.2/2? Это 324/2, или, да, 162. Таким образом, площадь заштрихованной области составляет 81pi — 162. Это примерно 92.
Итак, основание нашего треугольника равно 18. А высота треугольника? Это радиус круга, или 9. Это означает, что площадь каждого треугольника равна 1/2 bh или 1/2*18*9, что равно 81.2/2? Это 324/2, или, да, 162. Таким образом, площадь заштрихованной области составляет 81pi — 162. Это примерно 92.
Резюме урока
Таким образом, вписанная фигура — это фигура, нарисованная внутри другой фигуры. Описанная фигура — это фигура, нарисованная вне другой фигуры.
Чтобы многоугольник вписался в круг, все его углы, также известные как вершины, должны касаться круга. Если какая-либо вершина не касается окружности, то это не вписанная фигура.
Окружность, вписанная в многоугольник, должна касаться или касаться всех сторон фигуры.
Что касается Эммы, то все эти перемещения довольно утомительны. Иногда ей кажется, что она пытается воткнуть квадратный колышек в круглое отверстие. О, юмор с вписанными фигурами…
Результаты обучения
Посмотрите это видео, чтобы:
- Распознавать вписанные или описанные фигуры
- Обратите внимание на объекты, которые не вписаны
- Решите для области
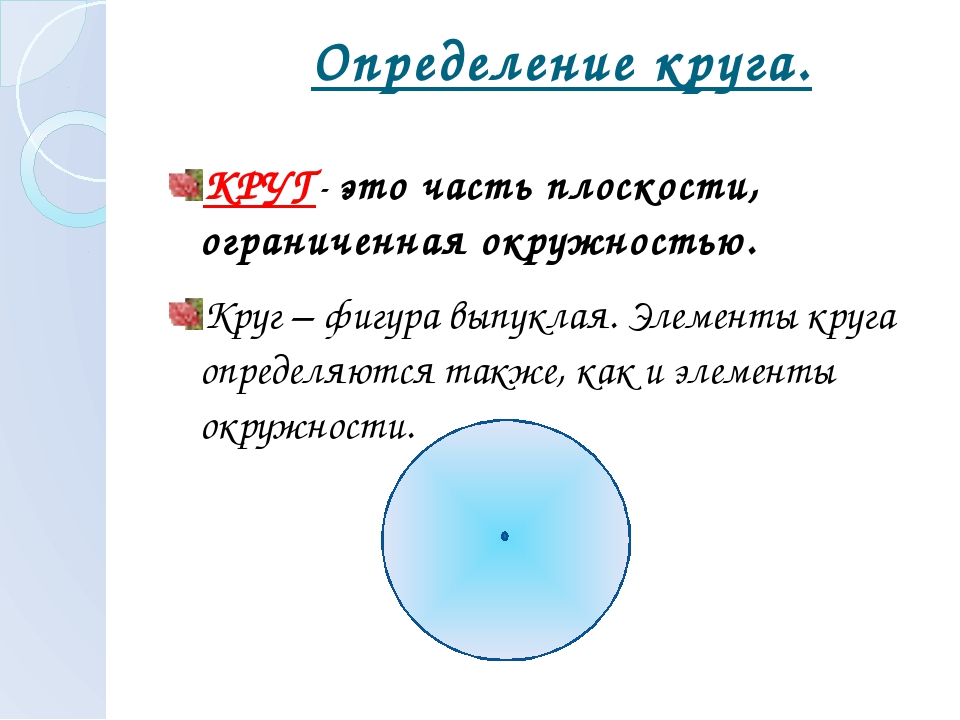


 Конусы различаются между собой: например, если основанием конуса является круг, то это может быть прямой круговой конус.
Конусы различаются между собой: например, если основанием конуса является круг, то это может быть прямой круговой конус. 14159
14159