«Почему говорят, что круг — идеальная форма?» – Яндекс.Кью

Правило золотого сечения — это изумительный закон гармонии и развития всех живых систем в пространстве и времени. Так уж заложено, что оно упорядочивает структуру мироздания и задает правильный курс движения жизни. В целом заключается оно в том, что меньшая часть относится к большей, как большая ко всему целому. Этот закон встречается в природе начиная от строения цветка или шишки, заканчивая движением косяка рыб или траекторией образования вихря. Эту пропорцию наглядно можно проследить, если, например, провести условную линию вдоль само широкой части куриного яйца. При всей хрупкости яичной скорлупы курица не раздавливает его своим весом, благодаря совершенной его форме, основанной на принципе золотого сечения.

Привлекательность такой пропорции для нас объясняется законом эволюции. Человек всегда инстинктивно стремился стабилизировать и улучшить окружающую его реальность, в том числе и самого себя как биологический вид. Именно золотое сечение в лице и телосложении другого человека дает нам сигнал: этот индивид гармоничен, его развитие идет без сбоев, он готов к переходу на следующий этап.

На мужчин это правило распространяется бОльшим образом: их ноги длиннее, чем у женщин, отчего отношение расстояния от пола до пупка к расстоянию от пупка до макушки более приближено к «божественной пропорции», нежели чем у женщин. От этого многие женщины носят обувь на каблуках или подчеркивают линию талии, чтобы граница между верхней и нижней частями была более заметна.

В некоторых случаях, смотря на лица разных людей, человек не может точно объяснить, почему одно нравится ему больше, чем другое. Просто природные пропорции одного лица ближе к золотому сечению, чем пропорции другого. Для определения этого не нужно каждый раз хвататься за линейку и калькулятор, достаточно довериться своему инстинкту. Природа оставила нам множество подсказок и инструкций, как выживать и эволюционировать: травоядным — есть растения; хищникам — охотиться за травоядными; гнилое плохо пахнет — есть нельзя; пресная вода — без соли, можно пить, и т.д. И всё это выполняется без размышлений и доказательств, а просто в гармонии с природными законами. Хочешь эволюционировать — следуй за гармонией, а о встроенном «чипе» стремления к этой гармонии природа позаботилась с самого начала.

http://n-t.ru/tp/iz/zs.htm

План-конспект урока по математике (1 класс) по теме: Геометрическая фигура: круг.

Урок математики в 1 классе с ГУО на тему: «Геометрическая фигура: круг»

   

           

 

Цель: Познакомить с геометрической фигурой – кругом. Учить отличать круг от других геометрических фигур и правильно его называть. Закрепить названия цветов. Воспитывать уважительное отношение друг к другу.

I Организационный момент.

1.  Кто ходит в гости по утрам,

     Тот поступает мудро!

     Тарам-парам, тарам-парам,

     На то оно и утро!

-Дети, какое сейчас время суток?  (утро)

-Следом за утром приходит … (день)

-Часто из гостей возвращаются, когда наступает….(вечер) (С помощью картинок)

2. Посмотрите внимательно на картинки, что на них общее? Чем они все похожи?  (на всех картинках нарисовано солнце)

II. Сообщение темы.

Солнце круглое. Сегодня на уроке мы познакомимся с геометрической фигурой – кругом. Поучимся отличать его от других фигур, будем находить предметы круглой формы.

III. Знакомство с фигурой.

1.К нам на урок пришёл гость – Винни-Пух. Он прилетел на воздушных шарах. (Детям раздаются воздушные шары) Шар круглый. (Предложить обвести шар ладонью, пальцем.)

2. Посмотрите на Винни-Пуха, какие части тела у него круглые?

3. Вини-Пух очень любит покушать, и поэтому принёс с собой набор посуды (плоскостные изображения посуды круглой и квадратной формы). Но Вини-Пух любит есть только из посуды круглой формы. Помогите выбрать посуду круглой формы.

4. Пока Вини-Пух добирался до нас, у него разбилось несколько тарелок. Помогите, склейте их! (Дети собирают разрезную картинку)

-Какой формы тарелка?

5. Посмотрите вокруг, найдите круглые предметы в нашем классе.

IV. Физ. минутка (хороводная игра)

     Ровным кругом друг за другом

     Мы идём за шагом шаг.

     Дружно вместе все на месте

     Делаем вот так!

(Водящий выбирается по очереди)

V. Закрепление изученного

1. У Вини-Пуха много друзей. Он принёс их портреты. ( Изображения из геометрических фигур. Рассматриваем, обговариваем, кто это).

-Скажите, что у них круглое?

2. Детям раздаются наборы геом.фигур. Найдите круг. (Тактильное обследование, прокатить круг по столу). Обговорить цвет и размер фигур.

-Почему круг катится? (потому что нет углов)

-Почему колёса круглые? (потому что нет углов, они могут катиться)

3. Выкладывание по образцу изображения из набора геом. фигур. (Друг Винни)

VI. Работа в тетради.

1. Пальчиковая гимнастика.
2. Объяснение задания.
3.  Работа в тетради.

VII. Итог: С какой фигурой познакомились? Чем занимались на уроке?

VIII. Объяснение домашнего задания.

IX. Оценка деятельности детей.

 

 

Кольцо (геометрия) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Кольцо.

Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.

Открытое кольцо является топологическим эквивалентом цилиндра S1×(0,1){\displaystyle S^{1}\times (0,1)} и проколотой плоскости.

Площадь кольца, ограниченного окружностями радиусов R и r, определяется как разность площадей кругов с такими радиусами:

A=π(R2−r2){\displaystyle A=\pi (R^{2}-r^{2})}

Площадь кольца также может быть вычислена путём умножения числа пи на квадрат половины длины самого большого отрезка, лежащего внутри кольца. Это можно доказать через теорему Пифагора — такой отрезок будет являться касательной к кругу меньшего радиуса. Половина длины отрезка с радиусами r и R образуют прямоугольный треугольник.

Kольцо ann(a;r,R){\displaystyle \mathrm {ann} (a;r,R)} на комплексной плоскости определяется следующим образом:

ann(a;r,R)={z∈C∣r<|z−a|<R}.{\displaystyle \mathrm {ann} (a;r,R)=\{\,z\in \mathbb {C} \mid r<|z-a|<R\,\}.}

Kольцо является открытым множеством Если r равно 0, область называется проколотым диском радиуса R вокруг точки a.

Как подмножество комплексной плоскости кольцо может рассматриваться в качестве Римановой поверхности. Комплексная структура кольца зависит только от отношения r/R. Каждое кольцо ann(a; r, R) может быть голоморфно отображено в расположенное в начале координат стандартное кольцо с внешним радиусом 1 с помощью отображения:

z↦z−aR.{\displaystyle z\mapsto {\frac {z-a}{R}}.}

Внутренний радиус тогда будет r/R < 1.

Свойства[править | править код]

Компактные поверхности и их погружения в трёхмерное пространство
Класс гомеоформности компактной триангулируемой поверхности определяется ориентируемостью, числом компонент границы и эйлеровой характеристикой.
Без границы
С границей
Связанные понятия

Большой круг — Википедия

Материал из Википедии — свободной энциклопедии

Большой круг делит сферу на две полусферы

Большой круг — круг, получаемый при сечении шара плоскостью, проходящей через его центр. Диаметр любого большого круга совпадает с диаметром сферы, поэтому все большие круги имеют одинаковый периметр и один центр, совпадающий с центром шара. Иногда под термином «большой круг» подразумевают большую окружность, то есть окружность, получаемую при сечении сферы плоскостью, проходящей через её центр^[1].

Для любых двух точек на сфере, не являющихся диаметрально противоположными, существует ровно один большой круг, проходящий через них. Через две противоположные точки можно провести бесконечно много больших кругов. Меньшая дуга большого круга между двумя точками является кратчайшим путём между ними по поверхности сферы. В этом смысле большие круги выполняют роль прямых линий в сферической геометрии. Длина этой дуги берётся за расстояние между точками в геометрии Римана. Большие круги являются геодезическими линиями сферы.

Также большой круг — путь с наименьшей кривизной, которая является постоянной величиной, определяемой соотношением κ=1R{\displaystyle \kappa ={\frac {1}{R}}}.

Примеры больших кругов на небесной сфере включают горизонт, небесный экватор и эклиптику.

Приплюснутый около полюсов сфероид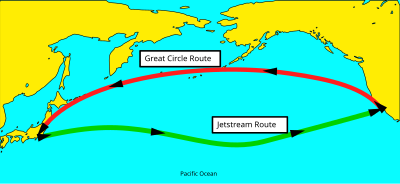

Говоря точно, форма Земли — не идеальная сфера. Это приплюснутый около полюсов эллипсоид. Поэтому кратчайший путь между двумя точками на поверхности Земли (геодезическая линия) не является, строго говоря, дугой окружности. Однако форма Земли не сильно отличается от шарообразной, поэтому сферу можно брать как приближение земной поверхности с погрешностью меньше процента.

Большими кругами Земли среди бесконечного множества являются, например, меридианы и самая длинная параллель — экватор (другие параллели образуют малые круги). В XVIII веке метр был введён как ¹/_{40 000 000} часть парижского меридиана на основе данных Жан-Батиста Деламбра, соответственно, можно считать, что все большие круги планеты имеют длину приблизительно 4⋅10⁷ метров. В дальнейшем длина экватора была рассчитана как 40 075 км.

Отрезки больших кругов используются морскими и воздушными судами как маршруты, когда течения и ветры не оказывают значительного влияния. Длина полёта часто может быть оценена ортодромой между двумя аэропортами. При этом для самолётов, которые в северном полушарии двигаются между континентами на запад, оптимальный путь пролегает севернее ортодромы, соответственно для движения на восток оптимальные пути будут чуть южнее.

Когда длинные авиационные или морские маршруты изображают на плоской карте (например, в проекции Меркатора), они часто выглядят кривыми. Маршрут, соответствующий прямому отрезку на карте, будет более длинным. Дело в том, что в таких проекциях большие круги не соответствуют прямым. Лучше отображают ситуации карты в гномонической проекции, где прямые линии являются проекциями больших кругов.

Какая геометрическя фигура идеальна?Почему? Срочно…

Следует напомнить, что куб — идеальная геометрическая фигура, символизирующая вершину творения человека, в отличие от второй идеальной фигуры — шара — вершины творения Природы. Соответственно и их N-мерные проекции Впрочем, геометрически «более идеален» шар, поскольку обладает всеми возможными видами симметрии и на любое (n-1)-мерное пространство n-мерный шар проецируется одинаково

Шар, т.к. прицепиться не к чему. Или точка в бесконечности — у нее бесконечные перспективы

круг, потому что все в мире стремится к равновесию

Шар, почему объяснить научно не могу)))

Круг.Это вечность,заполненная пониманием и дружелюбием.

Пирамида так как ученые утверждают что в ней есть какоето особое свойство, на пример не портятся долгое время продукты.

Правильная пирамида. Ведь неспроста в них хоронили настоящих фараонов!

Круг, потому что без углов, обтекаемая, по ней можно двигаться непрерывно и бесконечно. И земля круглая, все планеты, солнечная система.

шар,куб,точка(но это не фигура)

Если фигура, то круг. Если тело, то шар. У этих объектов максимально возможное число симметрий. Не существует геометрических фигур и тел с большим, чем у них числом элементов симметрии.

Самой идеальной плоской фигурой считается круг. Это объясняется его свойствами. 1. Все точки окружности полностью идентичны (равноправны, одинаковы). Невозможно выделить ни одной точки. Таким же свойством обладает только бесконечная прямая линия, но она не ограничивает никакой фигуры. 2. Окружность ограничивает на плоскости наибольшую площадь по сравнению с другими замкнутыми линиями с тем же периметром. 3. Отношение длины окружности к ее диаметру — число пи — входит как основная математическая константа во многие разделы математики и физики. В этом с ней может посоревноваться лишь число е.