Фигура, ограниченная кривой линией яйцеобразной формы 4 буквы
Ad
Ответы на сканворды и кроссворды
Овал
Фигура, ограниченная кривой линией яйцеобразной формы 4 буквы
НАЙТИ
Похожие вопросы в сканвордах
- Фигура, ограниченная кривой линией яйцеобразной формы 4 буквы
- Фигура яйцеобразной формы 4 буквы
- В геометрии — часть плоскости, ограниченная замкнутой ломанной или кривой линией 6 букв
Похожие ответы в сканвордах
- Овал — Замкнутое яйцевидное очертание чего-нибудь 4 буквы
- Овал — Остров России 4 буквы
- Овал — Геометрическая фигура 4 буквы
- Овал — Выпуклая замкнутая плоская кривая без изломов 4 буквы
- Овал — Выпуклая плоская замкнутая кривая 4 буквы
 «яйцо 4 буквы
«яйцо 4 буквы
- Овал — Замкнутая окружность 4 буквы
- Овал — Лицевая геометрия 4 буквы
- Овал — На что похож эллипс 4 буквы
- Овал — Округлая форма лица вице-премьера 4 буквы
- Овал — Округлая форма лица 4 буквы
- Овал — Окружность яйца 4 буквы
- Овал — Проекция дыни 4 буквы
- Овал — Сдавленный круг 4 буквы
- Овал — Синоним эллипс 4 буквы
- Овал — Фигура, ограниченная кривой линией яйцеобразной формы 4 буквы
- Овал — Форма яйца 4 буквы
- Овал — Яйцевидное очертание 4 буквы
- Овал — плоская замкнутая выпуклая C-гладкая кривая 4 буквы
- Овал — Абрис яйца 4 буквы
- Овал — Форма лица, стадиона и яйца 4 буквы
- Овал — Геометрическая форма лица 4 буквы
- Овал — Окосевшая окружность 4 буквы
- Овал — Форма мяча для регби 4 буквы
- Овал — Форма лица и стадиона 4 буквы
- Овал — Приплюснутый круг 4 буквы
- Овал — Нелюбимый Маяковским эллипс 4 буквы
- Овал — Круг в подавленном состоянии 4 буквы
- Овал — Родственник круга 4 буквы
- Овал — Контур регбийного мяча 4 буквы
- Овал — Эллипс 4 буквы
- Овал — Контур яйца 4 буквы
- Овал — Сплюснутый круг 4 буквы
- Овал — Выпуклая гладкая кривая 4 буквы
- Овал — Силуэт яйца 4 буквы
- Овал — Яйцеподобная фигура 4 буквы
- Овал — И лицо, и яйцо 4 буквы
- Овал — Обычная форма медальона 4 буквы
- Овал — Фигура на срезе колбасы 4 буквы
-
Овал — «Я с детства не любил .
 ..» 4 буквы
..» 4 буквы
- Овал — Форма лица 4 буквы
- Овал — Растянутая окружность 4 буквы
- Овал — Круг всмятку 4 буквы
- Овал — «Помятый» круг 4 буквы
- Овал — Вытянутый круг 4 буквы
- Овал — Пришлёпнутый круг 4 буквы
- Овал — Сплющенный круг 4 буквы
- Овал — «Окосевшая» окружность 4 буквы
- Овал — Скособоченный круг 4 буквы
- Овал — Геометрия буквы «О» 4 буквы
- Овал — «Сжатый» круг 4 буквы
- Овал — Яйцевидный абрис 4 буквы
- Овал — Контур мяча для регби 4 буквы
- Овал — Родич круга 4 буквы
- Овал — Контур рабочей части ракетки 4 буквы
- Овал — Вытянутый «круг» 4 буквы
- Овал — Форма кабинета Барака Обамы 4 буквы
- Овал — Замкнутая кривая 4 буквы
-
Овал — Фигура Кассини (матем.
 ) 4 буквы
) 4 буквы
- Овал — Продолговатый «круг» 4 буквы
- Овал — Яйцевидный силуэт 4 буквы
- Овал — Контур стадиона 4 буквы
- Овал — Очертание яйца 4 буквы
- Овал — Фигура яйцеобразной формы 4 буквы
- Овал — Чуть «помятый» круг 4 буквы
- Овал — Геометрическая форма яйца 4 буквы
- Овал — Контур куриного яйца 4 буквы
- Овал — «Круг» стадиона. 4 буквы
- Овал — Исхудавший круг. 4 буквы
- Овал — Похудевший круг. 4 буквы
- Овал — Вытянутая окружность 4 буквы
- Овал — Форма красивого лица 4 буквы
- Овал — Форма велотрека 4 буквы
- Овал — Правильная форма лица 4 буквы
- Овал — Форма лица и форма яйца 4 буквы
- Овал — Фигура без углов 4 буквы
- Овал — Замкнутое яйцевидное очертание чего–нибудь 4 буквы
- Овал — Форма кабинета президента в Белом доме 4 буквы
- Овал — Геометрическая форма зеркальца под лицо 4 буквы
- Овал — Какую форму имеет земная орбита 4 буквы
- Овал — Круг на который присели 4 буквы
Линии — геометрия и искусство
Кандинский систематизировал свои взгляды на живопись в книге «Точка и линия на плоскости» (1926). Изучая геометрические формы, художник нашёл, что с их помощью можно усиливать или ослаблять свойства цвета. Для этой картины он использовал приглушённую палитру, смещённую к цветам, расположенным в одной части спектра.
Изучая геометрические формы, художник нашёл, что с их помощью можно усиливать или ослаблять свойства цвета. Для этой картины он использовал приглушённую палитру, смещённую к цветам, расположенным в одной части спектра.
Цитаты из книги:
ЛИНИЯ
Геометрическая линия – это невидимый объект. Она – след перемещающейся точки, то есть ее произведение. Она возникла из движения – а именно вследствие уничтожения высшего, замкнутого в себе покоя точки. Здесь произошел скачок из статики в динамику.
ВОЗНИКНОВЕНИЕ
Силы, приходящие извне, преобразовавшие точку в линию, могут быть различными. Разнообразие линий зависит от числа этих сил и их комбинаций.
В конце концов [происхождение] всех форм линий можно свести к двум случаям:
1. приложение одной силы и
2. приложение двух сил:
а) одно- или многократное поочередное воздействие обеих сил,
б) одновременное воздействие обеих сил.

ПРЯМАЯ
Если одна приходящая извне сила перемещает точку в каком-либо направлении, то возникает первый тип линии, причем выбранное направление остается неизменным, и сама линия стремится двигаться по прямому пути бесконечно.
Это – прямая, представляющая в своем напряжении самую сжатую форму бесконечной возможности движения.
…
Среди прямых мы выделяем три типа, по отношению к которым все прочие прямые – лишь отклонения.
1. Простейшая форма прямой – это горизонталь. В человеческом представлении она соответствует линии или поверхности, на которой человек стоит или передвигается. Итак, горизонталь – это холодная несущая основа, которая может быть продолжена на плоскости в различных направлениях. Холод и плоскостность – это основные звучания данной линии, она может быть определена как кратчайшая форма неограниченной холодной возможности движения.
2. Полностью противоположна этой линии и внешне, и внутренне стоящая к ней под прямым углом вертикаль, в которой плоскостность заменяется высотой, то есть холод – теплом.

3. Третий типичный вид прямой – это диагональ, которая схематичным образом под равным углом отклоняется от обеих вышеназванных и тем самым имеет к обеим равное тяготение, что и определяет ее внутреннее звучание, равномерное соединение холода и тепла. Итак: кратчайшая форма неограниченной тепло-холодной возможности движения…
Какая линия ограничивает фигуру круг. Рэмп «геометрическая фигура круг
Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..
Давайте сначала рассмотрим, какие у круга бывают части и как они называются.
- Окружность — линия, ограничивающая круг.
- Дуга — часть окружности.

- Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
- Хорда — отрезок, соединяющий две точки окружности.
- Сегмент — часть круга, ограниченная хордой и дугой.
- Сектор — часть круга, ограниченная двумя радиусами и дугой.
Интересующие нас величины и их обозначения:
Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.
- Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
- Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
- Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных.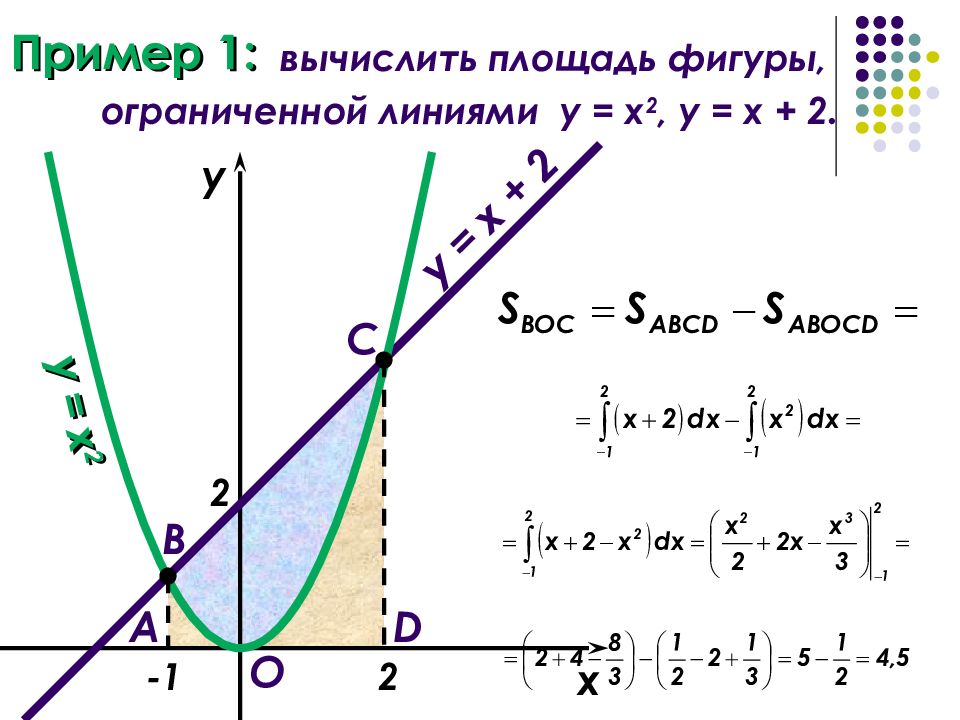 Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).
И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.
И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
1. Даны диаметр D и длина дуги L
; длина хорды ;
высота сегмента ; центральный угол .
2. Даны диаметр D и длина хорды X
; длина дуги ;
высота сегмента ; центральный угол .
Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол .
3. Даны диаметр D и центральный угол φ
; длина дуги ;
длина хорды ; высота сегмента .
4. Даны диаметр D и высота сегмента H
; длина дуги ;
длина хорды ; центральный угол .
6. Даны длина дуги L и центральный угол φ
; диаметр ;
длина хорды ; высота сегмента .
8. Даны длина хорды X и центральный угол φ
; длина дуги ;
диаметр ; высота сегмента .
9. Даны длина хорды X и высота сегмента H
; длина дуги ;
диаметр ; центральный угол .
10. Даны центральный угол φ и высота сегмента H
; диаметр ;
длина дуги ; длина хорды .
Внимательный читатель не мог не заметить, что я пропустил два варианта:
5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H
Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?
Задача эта сводится к решению уравнений:
; — в варианте 5
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем . Всё то, что я тут длинно рассказываю, она делает за микросекунды.
Всё то, что я тут длинно рассказываю, она делает за микросекунды.
Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:
длина окружности ;
площадь круга ;
площадь сектора ;
площадь сегмента ;
И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.
Урок математики в 1 классе с ГУО на тему: «Геометрическая фигура: круг»
Цель: Познакомить с геометрической фигурой – кругом. Учить отличать круг от других геометрических фигур и правильно его называть. Закрепить названия цветов. Воспитывать уважительное отношение друг к другу.
I Организационный момент.
1. Кто ходит в гости по утрам,
Тот поступает мудро!
Тарам-парам, тарам-парам,
На то оно и утро!
Дети, какое сейчас время суток? (утро)
Следом за утром приходит … (день)
Часто из гостей возвращаются, когда наступает….(вечер) (С помощью картинок)
2. Посмотрите внимательно на картинки, что на них общее? Чем они все похожи? (на всех картинках нарисовано солнце)
II. Сообщение темы.
Солнце круглое. Сегодня на уроке мы познакомимся с геометрической фигурой – кругом. Поучимся отличать его от других фигур, будем находить предметы круглой формы.
III. Знакомство с фигурой.
1.К нам на урок пришёл гость – Винни-Пух. Он прилетел на воздушных шарах. (Детям раздаются воздушные шары) Шар круглый. (Предложить обвести шар ладонью, пальцем.)
2. Посмотрите на Винни-Пуха, какие части тела у него круглые?
3. Вини-Пух очень любит покушать, и поэтому принёс с собой набор посуды (плоскостные изображения посуды круглой и квадратной формы). Но Вини-Пух любит есть только из посуды круглой формы. Помогите выбрать посуду круглой формы.
Но Вини-Пух любит есть только из посуды круглой формы. Помогите выбрать посуду круглой формы.
4. Пока Вини-Пух добирался до нас, у него разбилось несколько тарелок. Помогите, склейте их! (Дети собирают разрезную картинку)
Какой формы тарелка?
5. Посмотрите вокруг, найдите круглые предметы в нашем классе.
IV. Физ. минутка (хороводная игра)
Ровным кругом друг за другом
Мы идём за шагом шаг.
Дружно вместе все на месте
Делаем вот так!
(Водящий выбирается по очереди)
V. Закрепление изученного
1. У Вини-Пуха много друзей. Он принёс их портреты. (Изображения из геометрических фигур. Рассматриваем, обговариваем, кто это).
Скажите, что у них круглое?
2. Детям раздаются наборы геом.фигур. Найдите круг. (Тактильное обследование, прокатить круг по столу). Обговорить цвет и размер фигур.
Почему круг катится? (потому что нет углов)
Почему колёса круглые? (потому что нет углов, они могут катиться)
3. Выкладывание по образцу изображения из набора геом. фигур. (Друг Винни)
Выкладывание по образцу изображения из набора геом. фигур. (Друг Винни)
VI. Работа в тетради.
- Пальчиковая гимнастика.
- Объяснение задания.
- Работа в тетради.
VII. Итог: С какой фигурой познакомились? Чем занимались на уроке?
Сегодня мы будем делать цыплёнка. Каким цветом цыпленок? Правильно, жёлтый. Из всех кругов выбери только желтые круги. Потом отложи отдельно голубые круги и зеленые.
Сначала просто выкладываем цыплёнка на бумаге без клея, чтобы у малыша было понимание того, что мы делаем, это также поможет избежать ошибок при работе с клеем.
Большой жёлтый круг будет туловищем цыпленка. Куда мы его положим? (предлагаем ребенку самому выбрать место на листе бумаги).
Кружок поменьше будет головой. Где у нашего цыплёнка будет голова? (ребёнок пусть снова сам выберет место, в какую сторону будет смотреть цыплёнок: вверх на небо и солнце или вниз на травку, может он будет клевать зернышки. Помогайте малышу фантазировать, предлагайте варианты.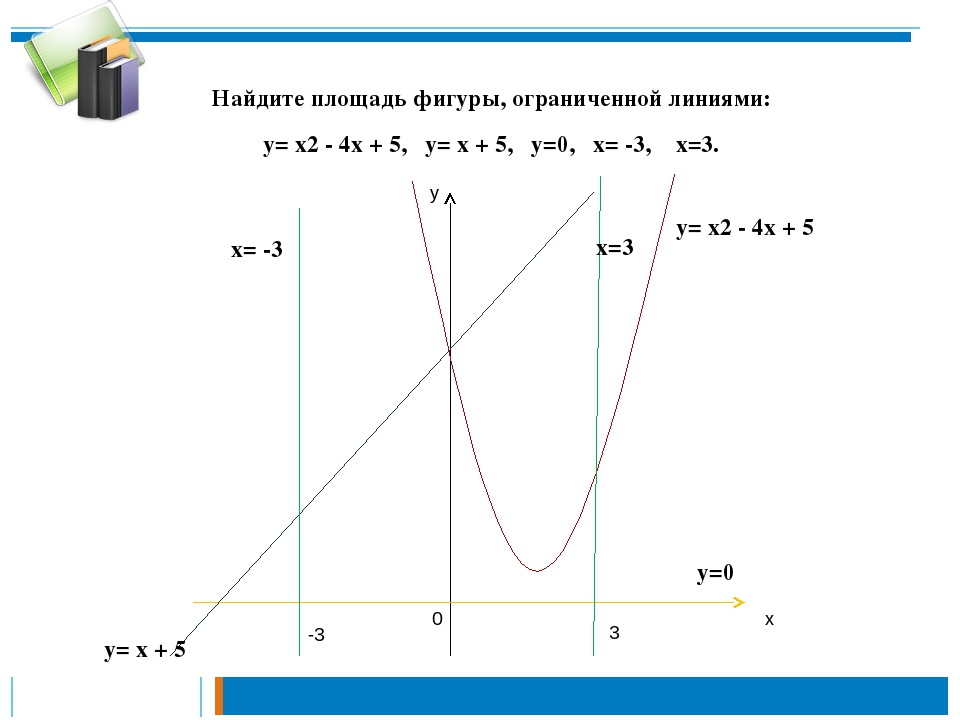 Маленьким можно подсказать, посоветовать, но не настаивайте, пусть он сам сделает выбор)
Маленьким можно подсказать, посоветовать, но не настаивайте, пусть он сам сделает выбор)
Где маленький чёрный кружок? Это будет глаз. Маленький треугольник — клюв, два одинаковых треугольника — лапки. Разложи фигуры на свои места.
Чего не хватает нашему цыпленку? Правильно, крыльев! У нас есть ещё 2 жёлтых круга, один мы отложим — это будет солнце, а из второго сделаем крылья. Как ты думаешь, как из одного круга сделать два крыла? (с этим справятся дети от трёх лет. Пусть ребёнок подержит круг в руках, повертит, приложит к бумаге, возможно, у него появится ответ).
Мы разрежем круг напополам. Для этого давай найдем центр круга. Где центр (середина) у круга? (можно дать ребенку карандаш и предложить самому найти и отметить центр с тыльной (не цветной!) стороны листа. Даже если точка не в центре, а где-то рядом, ничего страшного, похвалите кроху! Если ребёнок мал, сделайте все сами, объясняя каждое действие).
Через центр теперь проведем прямую линию, которая разделит круг напополам. По этой линии мы разрежем наш круг на две части. Получилось два крыла (обязательно разрезайте через точку (центр), указанную ребёнком, во-первых, ребёнок будет чувствовать, что его мнение важно для вас и вы прислушиваетесь к нему, а во-вторых — аппликация будет более художественной)
По этой линии мы разрежем наш круг на две части. Получилось два крыла (обязательно разрезайте через точку (центр), указанную ребёнком, во-первых, ребёнок будет чувствовать, что его мнение важно для вас и вы прислушиваетесь к нему, а во-вторых — аппликация будет более художественной)
В ходе занятия для детей постарше можно объяснить, что такое полукруг (или вспомнить эту фигуру)
Посмотри, какие фигуры у нас получились. Это фигура называется полукруг. Пол круга — полукруг (повторяем несколько раз и предлагаем повторить название)
Где будут крылышки у нашего цыплёнка?
Цыплёнка выложили на бумаге, теперь можно приклеить его.
Цыплёнок готов.
Давай возьмём большие зелёные круги (или 1 круг) — это будет наша травка. Как ты думаешь, как из круга сделать травку? Правильно, снова разрезать напополам (повторяем шаги, как с крылышками: даём ребёнку отметить центр, разрезаем и приклеиваем снизу). Чтобы травка была натуральнее, можно сделать небольшие надрезы по округлой стороне.
На небо приклеиваем солнышко.
Облака можно сделать разными способами:
1. Наклеить кружки внахлёст, формируя облако. Разный размер кружков сделает форму облака более натуральной.
2. Разрезать круги напополам и также наклеивать внахлёст.
У нас получилось по-другому: Поля захотела сложить круги напополам и приклеить только одну половину круга. Таким образом мы уже делали другие поделки и этот вариант ей понравился.
Когда бумага окончательно высохнет, можно дорисовать солнечные лучи и цветы на травке карандашом. Можно сделать это пластилином. Пусть малыш выбирает сам.
Форма круга является интересной с точки зрения оккультизма, магии и древних значений, придаваемых ей людьми. Все мельчайшие составляющие вокруг нас — атомы и молекулы — имеют круглую форму. Солнце круглое, Луна круглая, наша планета тоже круглая. Молекулы воды — основы всего живого — тоже имеют круглую форму. Даже природа создает свою жизнь в кругах. Например, можно вспомнить про птичье гнездо — птицы вьют его также в этой форме.
Данная фигура в древних помыслах культур
Круг — это символ единства. Он присутствует в разных культурах во многих мельчайших деталях. Мы даже не придаем столько значения этой форме, как это делали наши предки.
Издавна круг — это знак бесконечной линии, который символизирует время и вечность. В дохристианскую эпоху он был древним знаком колеса солнца. Все точки в эквивалентны, линия круга не имеет ни начала, ни конца.
А центр круга был источником бесконечного вращения пространства и времени для масонов. Круг — конец всех фигур, недаром в нем была заключена тайна творения, по мнению масонов. Форма циферблата часов, имеющая тоже такую форму, обозначает собой непременное возвращение в точку отправления.
Эта фигура имеет глубокий магический и мистический состав, которым его наделили многие поколения людей из разных культур. Но что собой представляет круг как фигура в геометрии?
Что такое окружность
Часто понятие круга путают с понятием окружности. Это немудрено, ведь они между собой очень тесно взаимосвязаны. Даже названия их схожи, что вызывает много путаницы в незрелых умах школьников. Чтобы разобраться, «кто есть кто», рассмотрим эти вопросы подробнее.
Это немудрено, ведь они между собой очень тесно взаимосвязаны. Даже названия их схожи, что вызывает много путаницы в незрелых умах школьников. Чтобы разобраться, «кто есть кто», рассмотрим эти вопросы подробнее.
По определению, окружностью является такая кривая, которая замкнута, и каждая точка которой находится равноудалённо от точки, именуемой центром окружности.
Что необходимо знать и чем уметь пользоваться, чтобы построить окружность
Чтобы построить окружность, достаточно выбрать произвольную точку, которую можно обозначить как О (именно так в большинстве источников именуются центр окружности, не будем отходить от традиционных обозначений). Следующим этапом идет использование циркуля — инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.
Эти две части соединены между собой шарниром, что позволяет выбирать произвольный радиус в определенных границах, связанных с длиной этих самых частей.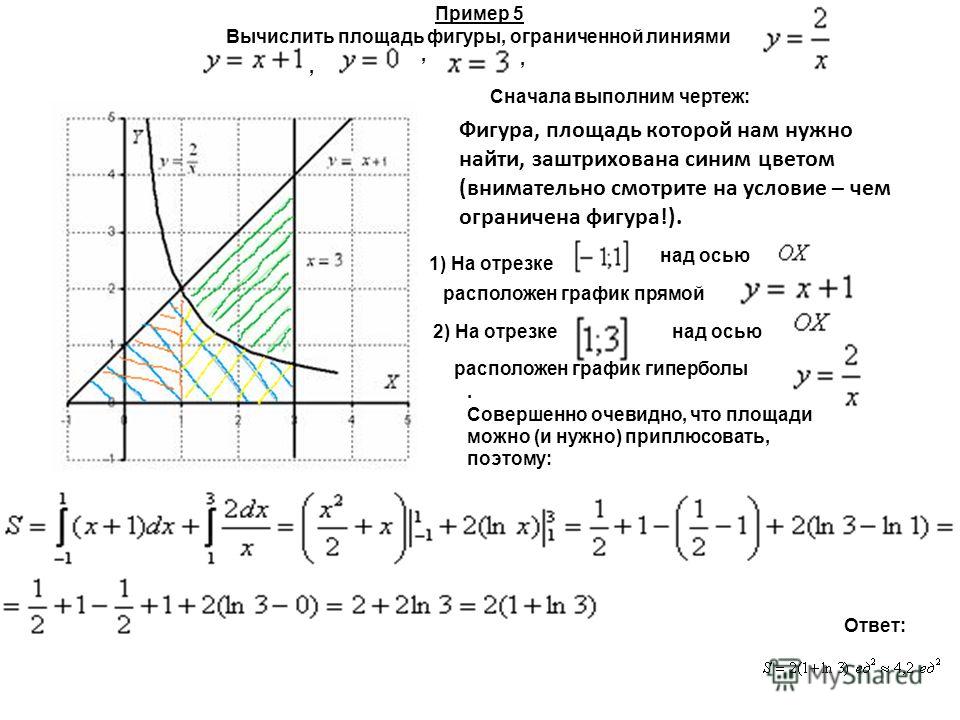 С помощью данного прибора в произвольную точку О устанавливается остриё циркуля, а карандашом уже очерчивается кривая, которая из итоге получается окружностью.
С помощью данного прибора в произвольную точку О устанавливается остриё циркуля, а карандашом уже очерчивается кривая, которая из итоге получается окружностью.
Какими величинами характеризуется окружность
Если соединить при помощи линейки центр окружности и любую произвольную точку на кривой, полученной в результате работы циркулем, мы получим Все такие отрезки, именуемые радиусами, будут равны. Если же соединить при помощи линейки прямой линией две точки на окружности и центр, мы получим ее диаметр.
Для окружности также характерно вычисление ее длины. Чтобы ее найти, необходимо знать либо диаметр, либо радиус окружности и воспользоваться формулой, представленной на рисунке ниже.
В этой формуле С — длина окружности, r — радиус окружности, d — диаметр, а число Пи — константа со значением 3,14.
Кстати, константа Пи была вычислена как раз из окружности.
Оказалось, что независимо от того, каков диаметр круга, соотношение длины окружности и диаметра одинаковое, равное примерно 3,14.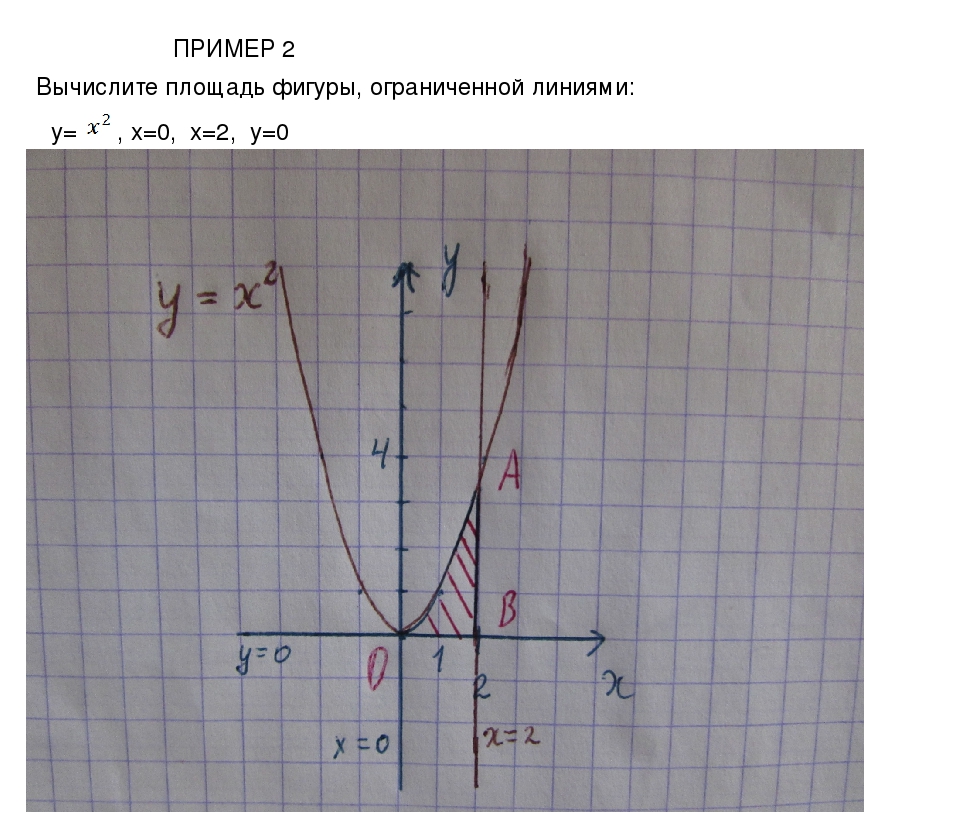
В чем же главное отличие круга от окружности
По сути, окружность — это линия. Она не является фигурой, она является кривой замкнутой линией, не имеющей ни конца, ни начала. А то пространство, что расположено внутри нее — это пустота. Простейшим примером окружности выступает обруч или, по-иному, хула-хуп, который дети используют на занятии физической культуры или же взрослые, для того чтобы создать себе стройную талию.
Теперь мы подошли к понятию того, что такое круг. Это в первую очередь фигура, то есть некое множество точек, ограниченных линией. В случае круга этой линией выступает окружность, рассмотренная выше. Выходит, что круг — это окружность, в середине которой не пустота, а множество точек пространства. Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью — его пустота замещена тканью, куском пространства.
Перейдем непосредственно к понятию круга
Круг — геометрическая фигура, которая является частью плоскости, ограниченной окружностью. Для него также характерны такие понятия, как радиус и диаметр, рассмотренные выше при определении окружности. И вычисляются они точно таким же образом. Радиус круга и радиус окружности являются идентичными по размеру. Соответственно, длина диаметра тоже аналогична в обоих случаях.
Для него также характерны такие понятия, как радиус и диаметр, рассмотренные выше при определении окружности. И вычисляются они точно таким же образом. Радиус круга и радиус окружности являются идентичными по размеру. Соответственно, длина диаметра тоже аналогична в обоих случаях.
Так как круг является частью плоскости, то для него характерно наличие площади. Вычислить ее можно снова-таки при помощи радиуса и числа Пи. Формула выглядит следующими образом (см. рисунок ниже).
В данной формуле S — площадь, r — радиус круга. Число Пи — снова та же константа, равная 3,14.
Формула круга, для вычисления которой возможно также использовать диаметр, изменяется и принимает вид, представленный на следующем рисунке.
Одна четвертая появляется из того, что радиус — это 1/2 диаметра. Если радиус в квадрате, выходит, что соотношение преобразуется до вида:
r*r = 1/2*d*1/2*d;
Круг — это фигура, в которой можно выделить отдельные части, например сектор. Выглядит он как часть круга, которая ограничена отрезком дуги и его двумя радиусами, проведенными из центра.
Формула, которая позволяет вычислить площадь данного сектора, представлена на нижеследующем рисунке.
Использование фигуры в задачах с многоугольниками
Также круг — геометрическая фигура, которая часто используется в комплекте с другими фигурами. Например, такими как треугольник, трапеция, квадрат или ромб. Нередко встречаются задачи, где нужно найти площадь вписанного круга или, наоборот, описанного вокруг определенной фигуры.
Вписанный круг является таким, который соприкасается со всеми сторонами многоугольника. С каждой стороной любого многоугольника у окружности должна быть точка соприкосновения.
Для определенного вида многоугольника определение радиуса вписанной окружности вычисляется по отдельным правилам, которые доступно объясняются в курсе геометрии.
Можно привести для примера несколько из них. Формула круга, вписанного в многоугольники, может вычисляться следующим образом (ниже на фото приведено несколько примеров).
Несколько простых примеров из жизни, для того чтобы закрепить понимание разницы между кругом и окружностью
Перед нами Если он открыт, то железная каемка люка — это окружность. Если он закрыт, то крышка выступает в роли круга.
Окружностью также можно назвать любое кольцо — золотое, серебряное или бижутерию. Кольцо, которое держит на себе связку ключей, — тоже окружность.
А вот круглый магнит на холодильнике, тарелка или блинчики, испеченные бабушкой, -это круг.
Горлышко бутылки или банки при виде сверху — это окружность, а вот крышка, которая закроет это горлышко, при том же виде сверху является кругом.
Таких примеров можно привести множество, и для усвоения такого материала их нужно приводить, чтобы дети лучше улавливали связь теории с практикой.
Тема урока
Геометрические фигуры
Что такое геометрическая фигура
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Точка и прямая — это основные геометрические фигуры, расположенные на плоскости.
К самым простым геометрическим фигурам на плоскости принадлежат — отрезок, луч и ломаная линия.
Что такое геометрия
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике. Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д. , и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
, и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
Какая ломаная линия называется незамкнутой?
Как обозначается прямая?
Как называется ломаная линия, у которой четыре замкнутых звена?
Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Угол
Фигура, которая имеет два луча и вершину, называется углом.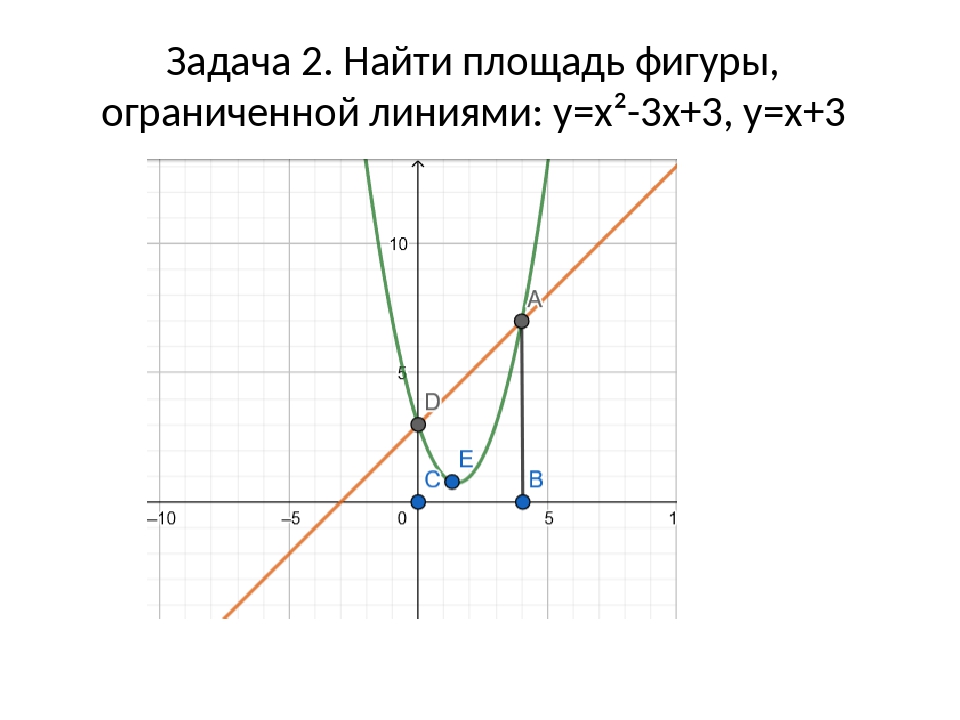 Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Задание:
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм
Параллелограмм — это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.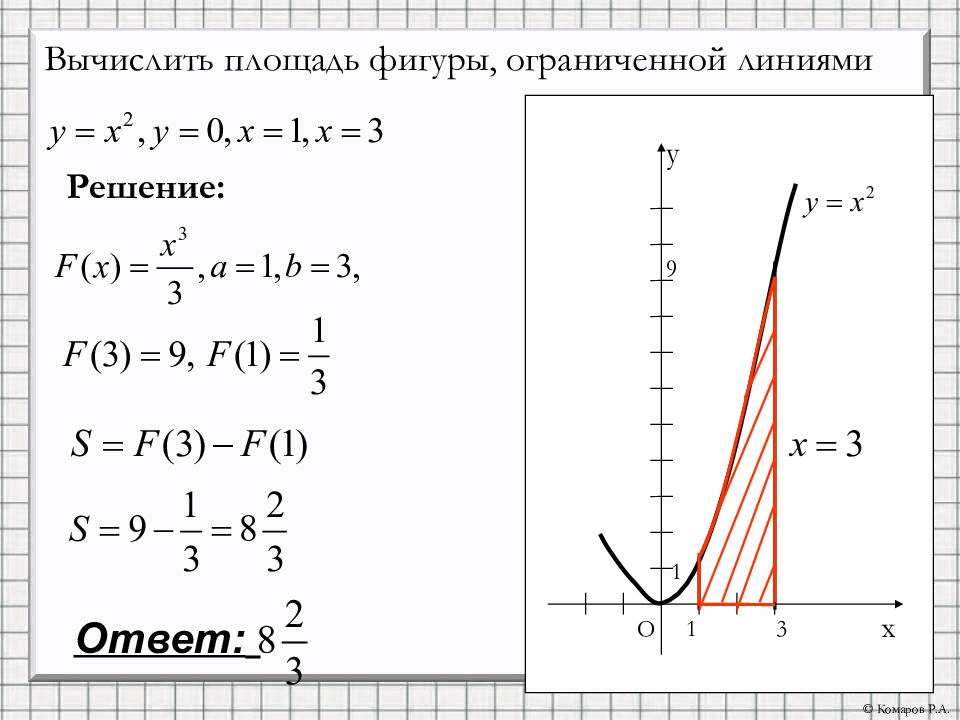
Окружность и круг
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром.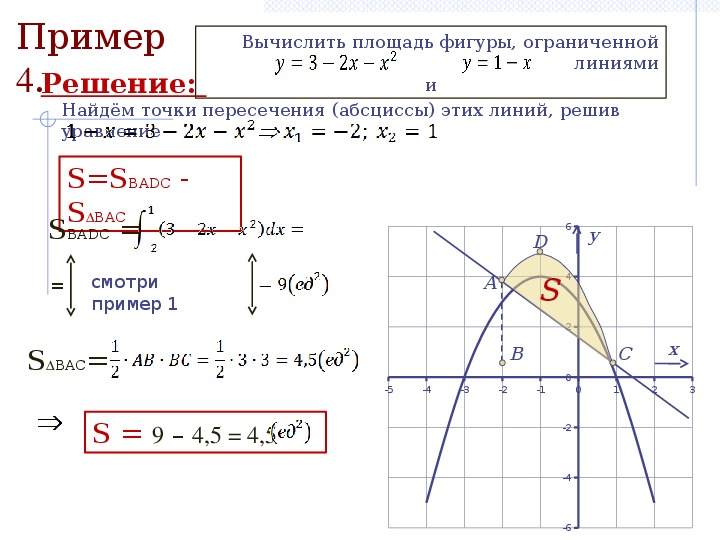 Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
«Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
«Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
| A | B |
|---|---|
| Остроугольный треугольник | Треугольник, в котором только углы меньше 90 градусов. |
| Угол | Величина поворота, необходимая для совмещения одной линии или плоскости с другой, обычно измеряется в радианах или градусах. |
| Площадь | Количество квадратных единиц, необходимых для покрытия поверхности. |
| Ось | 1.Воображаемая линия, проходящая через тело, вокруг которого оно вращается. 2. Воображаемая линия, вокруг которой симметрично расположена правильная фигура. 3. Фиксированная опорная линия для измерения координат. |
| Центр тяжести | Трехмерная точка, в которой можно считать сосредоточенным общий вес тела. |
| Центроид | Трехмерная точка, определяющая геометрический центр твердого тела. |
| Окружность | Круглая плоская фигура, граница которой состоит из точек, равноудаленных от центра |
| Описанная окружность | 1. Треугольник, расположенный вокруг многоугольника, например окружности. 2 Нарисовать фигуру вокруг другой, касаясь ее в точках, но не разрезая. Треугольник, расположенный вокруг многоугольника, например окружности. 2 Нарисовать фигуру вокруг другой, касаясь ее в точках, но не разрезая. |
| Цилиндр | Тело, состоящее из двух конгруэнтных окружностей в параллельных плоскостях, их внутренностей и всех прямых отрезков, параллельных оси с концами на двух окружностях. |
| Плотность | Мера массовой плотности – это мера массы на единицу объема. |
| Диаметр | Прямая линия, проходящая из стороны в сторону через центр круга или сферы. |
| Эллипс | Форма, образованная точкой, движущейся по плоскости так, что сумма расстояний от нее до двух других точек (фокусов) постоянна и равна большой оси |
| Скругление | Кривая на внутреннем пересечении двух или более поверхностей. |
| Вписать | Начертить фигуру внутри другой так, чтобы их границы соприкасались, но не пересекались. |
| Масса | Количество материи в объекте или количество инерции объекта. |
| Мениск | Изогнутая верхняя поверхность столба жидкости, которая вогнута, когда содержащиеся в ней стенки смачиваются жидкостью, и выпукла, когда нет. |
| Тупоугольный треугольник | Треугольник, один из углов которого больше 90 градусов. |
| Параллелограмм | Четырехсторонний многоугольник, у которого обе пары противоположных сторон параллельны. |
| Пи (π) | Числовое значение отношения длины окружности к ее диаметру приблизительно равное 3. 14159. 14159. |
| Многоугольник | Любая плоская фигура, ограниченная прямыми линиями. |
| Главные оси | Линии пересечения, созданные из трех взаимно перпендикулярных плоскостей, с точкой пересечения трех плоскостей в центре тяжести детали. |
| Призма | Объемная геометрическая фигура, два конца которой представляют собой подобные, равные и параллельные прямолинейные фигуры, а стороны — параллелограммы. |
| Четырехугольник | Четырехсторонний многоугольник. |
| Радиус | Прямая линия от центра к окружности круга или сферы. |
| Прямоугольник | Параллелограмм с углами 90 градусов. Квадрат также является прямоугольником. |
| Правильный многоугольник | Многоугольник с равными углами и равными сторонами. |
| Прямоугольный треугольник | Треугольник с углом 90 градусов. |
| Круглый | Две или более наружных поверхностей, закругленных в местах их пересечения. |
| Квадрат | Правильный многоугольник с четырьмя равными сторонами и четырьмя углами по 90 градусов. |
| Площадь поверхности | Размеры внешней поверхности в квадрате |
| Касательная | Прямая или изогнутая линия, пересекающая окружность или дугу только в одной точке. |
| Основная надпись | Таблица, расположенная в правом нижнем углу технического чертежа, в которой систематизировано указана вся необходимая информация, отсутствующая на самом чертеже. Также называется титульной полосой. Также называется титульной полосой. |
| Треугольник | Многоугольник с тремя сторонами. |
| Вершина | Каждая угловая точка многоугольника, многогранника или другой фигуры. |
| Объем | Объем трехмерного пространства, занимаемого объектом или заключенного в контейнере. |
| Четырехугольник | Четырехсторонний многоугольник. |
Простая плоская замкнутая фигура, ограниченная тремя отрезками прямой 9 класс математики CBSE
Подсказка:Здесь нам нужно завершить данное утверждение правильным вариантом.Мы будем использовать определения угла, треугольника, круга и квадрата, чтобы проверить, какой из вариантов является правильным.
Полное пошаговое решение:
Мы проверим определения каждого из вариантов один за другим, чтобы найти правильный вариант.
Угол – это фигура, образованная двумя лучами, имеющими общую вершину.
Например: Угол \[\угол BAC\] образован двумя лучами \[\overrightarrow {AB} \] и \[\overrightarrow {AC} \] с общей вершиной \[A\].
Угол не является замкнутой фигурой.
Следовательно, вариант (а) не является правильным вариантом.
Треугольник — это замкнутая фигура, образованная тремя отрезками, соединенными вершиной с вершиной.
Например: треугольник ABC образован отрезками AB, BC и AC.
Таким образом, вариант (б) является правильным вариантом.
Мы также проверим определение варианта (c) и варианта (d).
Окружность — это замкнутая фигура, образованная путем взятия точки в качестве центра и проведения ее геометрического места на постоянном расстоянии, называемом радиусом.
Линейные сегменты всегда прямые.
Мы знаем, что окружность не строится ни с одной прямой.
Таким образом, вариант (в) неверен.
Квадрат – это четырехугольник, у которого все стороны равны, а внутренние углы прямые.
Поскольку квадрат является четырехугольником, он представляет собой замкнутую фигуру, состоящую из четырех отрезков.
Таким образом, вариант (г) неверен.
Следовательно, мы можем сказать, что только вариант (а) завершает данное предложение и, следовательно, является ответом.
Примечание:
Плоская замкнутая фигура, построенная из прямых линий, называется многоугольником.Многоугольник, имеющий только три стороны, называется треугольником. Многоугольник, у которого всего четыре стороны, называется четырехугольником. Квадрат — это, скорее, частный случай четырехугольника. Круг — это замкнутая фигура, но это не многоугольник, так как он не образован прямыми линиями.
Элементарность некоторых кратных интегралов, связанных с фигурами, ограниченными плоскостями и сферами на JSTOR
Перейти к основному содержанию Есть доступ к библиотеке? Войдите через свою библиотекуВесь контент Картинки
Поиск JSTOR Регистрация Вход- Поиск
- Расширенный поиск
- Поиск изображений
- Просматривать
- от Субъекта
- по названию
- по коллекциям
- от издателя
- Инструменты
- Рабочее пространство
- Анализатор текста
- Серия JSTOR Understanding
- Данные для исследований
Некоторые теоремы планиметрии.
 Темы по тригонометрии.
Темы по тригонометрии.Темы | Дом
ВОТ НЕСКОЛЬКО ТЕОРЕМ, которые должен знать каждый, кто изучает тригонометрию.
Начнем с того, что теорема — это утверждение, которое можно доказать. Однако мы не будем доказывать теоремы здесь. (Те, что из Первой книги Евклида, доказываются здесь.) Скорее, мы представим каждое из них с его изложением и спецификацией. Изложение формулирует теорему в общих чертах. Спецификация повторяет теорему по отношению к конкретной фигуре.(См. теорему 1 ниже.)
Прежде всего, вот несколько основных определений.
11. Угол — это угол наклона друг к другу двух пересекающихся прямых.
12. Точка, в которой встречаются две прямые, называется вершиной угла; множественное число, вершины.
13. Если прямая, лежащая на другой прямой, делает смежные углы равными, то каждый из этих углов называется прямым углом; а прямая, лежащая на другой, называется перпендикуляром к ней.
14. Острый угол меньше прямого. Тупой угол больше прямого.
Острый угол меньше прямого. Тупой угол больше прямого.
| 5. Углы являются дополнительными (или дополняют друг друга), если вместе они составляют прямой угол. Углы являются дополнительными (или дополнениями друг друга), если вместе они равны двум прямым углам. |
16. Прямолинейные фигуры — это фигуры, ограниченные прямыми линиями.Треугольник ограничен тремя прямыми линиями, четырехугольник — четырьмя, а многоугольник — более чем четырьмя прямыми линиями.
17. Правильный многоугольник имеет равные стороны и равные углы.
18. У равностороннего треугольника три равные стороны. У равнобедренного треугольника две равные стороны. У разностороннего треугольника три неравные стороны.
19. Угол при вершине треугольника — это угол, противолежащий основанию.
10. Высотой треугольника называется прямая, проведенная из вершины перпендикулярно основанию.
11. Прямоугольный треугольник – это треугольник с прямым углом.
Прямоугольный треугольник – это треугольник с прямым углом.
| 12. Фигуры конгруэнтны, если положить одну из них на другую, и они точно совпадут. (Таким образом, конгруэнтные фигуры равны друг другу во всех отношениях.) |
| 13. Параллельные линии — это прямые, лежащие в одной плоскости и не пересекающиеся, как бы далеко они ни простирались в любом направлении. |
14. Окружность — это плоская фигура, ограниченная одной линией, называемой окружностью, так что все прямые, проведенные из определенной точки фигуры к окружности, равны друг другу.
15. И эта точка называется центром круга.
16. Прямая линия от центра к окружности называется радиусом. Диаметр окружности – это прямая линия, проходящая через центр и заканчивающаяся в обоих направлениях на окружности.
17. Хорда окружности – это прямая линия, соединяющая любые две точки на окружности.
18. Секущая – это прямая, пересекающая окружность.
19. Касательная – это прямая линия, которая касается окружности, но не пересекает ее, несмотря на то, что она может быть продолжена.
20. Центральный угол имеет вершину в центре окружности.
Вот наша первая теорема. Он утверждает условие равенства треугольников.Изложение выделено курсивом. Далее следует спецификация.
Теорема 1. (Евклид, I. 4.) Если у двух треугольников две стороны равны двум сторонам соответственно, и если углы, заключенные между этими сторонами, также равны, то треугольники будут равны во всех отношениях.
. Пусть у треугольников ABC, DEF две стороны AB, BC равны двум сторонам DE, EF соответственно;
и пусть угол ABC равен углу DEF;
, то оставшаяся сторона AC будет равна оставшейся стороне DF;
сами треугольники будут равновеликими;
и угол при A (противоположный стороне BC) будет равен углу при D (против равной стороне EF), а угол при C (противоположный стороне AB) будет равен углу при F (против равной стороне DE) .
*
Выражение равно «соответственно» означает каждый к каждому. Это в отличие от «вместе» равных, что означало бы, что сумма АВ, ВС равна сумме DE, EF.
Эта теорема кратко известна как «S.A.S.» (Сторона-Угол-Сторона). Это одно из четырех достаточных условий равенства треугольников. Другие — «S.S.S.» (Сторона-Сторона-Сайда. Евклид, I. 8.) и «А. С. А.» (Угол-Сторона-Угол. Евклид, I. 26.).
Еще одно условие, Side-Side-Angle, известно как неоднозначный случай.
*
Теорема 2 является простым следствием теоремы 1, и учащийся должен легко ее доказать.
Теорема 2. Прямая, которая делит пополам угол при вершине равнобедренного треугольника, является серединным перпендикуляром к основанию.
Пусть прямая AD делит пополам угол при вершине равнобедренного треугольника BAC, так что углы BAD, DAC равны между собой. Тогда AD — серединный перпендикуляр к основанию BC.То есть углы ADB, ADC прямые, а прямая BD равна прямой DC.
Чтобы увидеть доказательство, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Треугольники BAD, CAD равны: S.A.S. Следовательно, угол ADB равен углу ADC, а значит, они прямые (по опр. 3). А BD равен DC, потому что они противолежащие равным углам BAD, DAC. Таким образом, AD является серединным перпендикуляром к основанию.
Теорема 3. (Евклид, I. 5.) В равнобедренном треугольнике углы при основании равны .
Пусть ABC — равнобедренный треугольник с равными сторонами AB, AC; тогда углы при основании, углы при В и С, равны.
Теорема 4. (Евклид, I.6.) Если два угла треугольника равны, то равны и стороны, опирающиеся на эти углы.
Со ссылкой на рисунок выше, если углы при B и C равны, то стороны, которые опираются или противоположны этим углам, будут равны, а именно стороны AB, AC.
(Мы говорим в геометрии, что сторона стягивает — буквально тянется под — углом. )
)
*
Эта теорема называется обратной предыдущей. То есть, когда теорема имеет вид «Если p , то q », то предложение p называется гипотезой, а предложение q называется заключением. Обратное имеет вид «Если q , то p .» Гипотеза и заключение меняются местами.
Теорема 5. (Евклид, I. 13.) Когда прямая, лежащая на другой прямой, образует углы, она либо образует два прямых угла, либо образует углы, которые вместе равны двум прямым углам.
Пусть любая прямая AB лежит на прямой CD, образуя углы ABD, ABC; то либо углы ABC, ABD являются двумя прямыми углами, либо вместе они равны двум прямым углам.
Теорема 6.(Евклид, I. 19.) Больший угол треугольника лежит против большей стороны.
. Пусть ABC — треугольник, в котором угол при B больше, чем угол при C; тогда сторона СА больше стороны АВ.
Теорема 7. (Евклид, I. 27.) Если прямая, пересекающая две прямые, делает противоположные углы равными, то две прямые параллельны.
Пусть прямая EF пересекает две прямые AB, CD и образует равные углы AEF, EFD; тогда AB параллельна CD.(Определение альтернативных углов см. в предложении I.27 плоской геометрии.)
Теорема 8. (Евклид, I. 29.) Когда прямая пересекает две параллельные прямые, противоположные углы становятся равными, а внешний угол равен противоположному внутреннему углу той же стороны.
Если прямые AB, CD параллельны, а прямая GEF пересекает их, то противоположные углы AEF, EFD будут равны друг другу, а внешний угол GEA будет равен противолежащему внутреннему углу EFC.
Эта теорема частично обратна предыдущей.
Теорема 9. (Евклид, I. 32.) Три угла любого треугольника будут равны двум прямым углам.
Пусть ABC будет любым треугольником; тогда три угла при A, B и C вместе будут равны двум прямым углам.
Доказательство Пифагора настолько простое, что мы быстро покажем его:
Через точку A провести прямую PQ, параллельную BC, образующую
углы 1, 2, 3.
Теперь углы 1, 2, 3 вместе равны двум прямым углам. Теорема 5.
Но угол при B равен углу 1, потому что AB пересекает параллельные прямые PQ, BC, что делает противоположные углы равными. Теорема 8.
По той же причине угол при С равен углу 3. Следовательно, три угла треугольника А, В, С вместе равны углам 1, 2, 3. Они равны двум прямым углам.
Теорема 10.(Евклид, I. 47. Теорема Пифагора.) В прямоугольном треугольнике квадрат, проведенный на стороне, противоположной Прямой угол будет равен квадратам, нарисованным на сторонах, образующих прямой угол.
. Пусть ABC — прямоугольный треугольник, в котором угол CAB — прямой; тогда квадрат, нарисованный на ВС против прямого угла, будет равен двум квадратам вместе на СА, АВ.
(Подробнее см. в разделе 32 книги «Алгебра: формула расстояния Пифагора».)
Теорема 11. (Следствие Евклида, III. 1.) Центр окружности лежит на серединном перпендикуляре к любой хорде.
В окружности DAB пусть AB — любая хорда, а прямая CD — ее биссектриса; тогда центр окружности лежит на прямой CD.
(Значит, чтобы найти центр окружности, проведите две хорды, проведите их биссектрисы, тогда центр окружности будет точкой их пересечения.)
Теорема 12. (Евклид, III. 3.) Угол, вписанный в полуокружность, является прямым углом.
Пусть угол ABC вписан в полуокружность ABC; то есть пусть AC будет диаметром и пусть вершина B лежит на окружности; тогда угол АВС прямой.
Теорема 13. (Евклид, III. 16.) Прямая, проведенная под прямым углом к диаметру окружности от ее конца, является касательной к окружности.
Пусть AB диаметр окружности, и пусть прямая CD проведена под прямым углом к AB от ее конца B; тогда прямая CD касается окружности.
Следующая теорема является обратной.
Теорема 14. (Евклид, III. 18.) Если прямая касается окружности, то радиус, проведенный к точке касания, будет перпендикулярен касательной.
Пусть прямая DE касается окружности ABC в точке C; пусть F будет центром круга, и нарисуйте радиус FC; тогда FC будет перпендикулярно DE.
*
Следующая теорема показывает, что для того, чтобы треугольника были подобны, достаточно, чтобы они были равноугольными. Это основа тригонометрии. (Тема 3: Тригонометрия прямоугольных треугольников.)
Теорема 15. (Евклид, VI. 4.) Если два треугольника равноугольные, то стороны, содержащие равные углы, пропорциональны, а соответствующие стороны лежат против равных углов.
Пусть ABC, DEB — равноугольные треугольники с углом ABC, равным углу DEB, углом BCA, равным углу EBD, и, наконец, углом CAB, равным углу BDE;
, то в этих треугольниках стороны, содержащие эти равные углы, пропорциональны,
и сторона AB (противолежащая углу BCA) соответствует стороне DE (противолежащей равному углу EBD) и так далее для каждой пары соответствующих сторон.
Следующая и последняя теорема связывает дуги окружностей, которые являются длинами, с углами.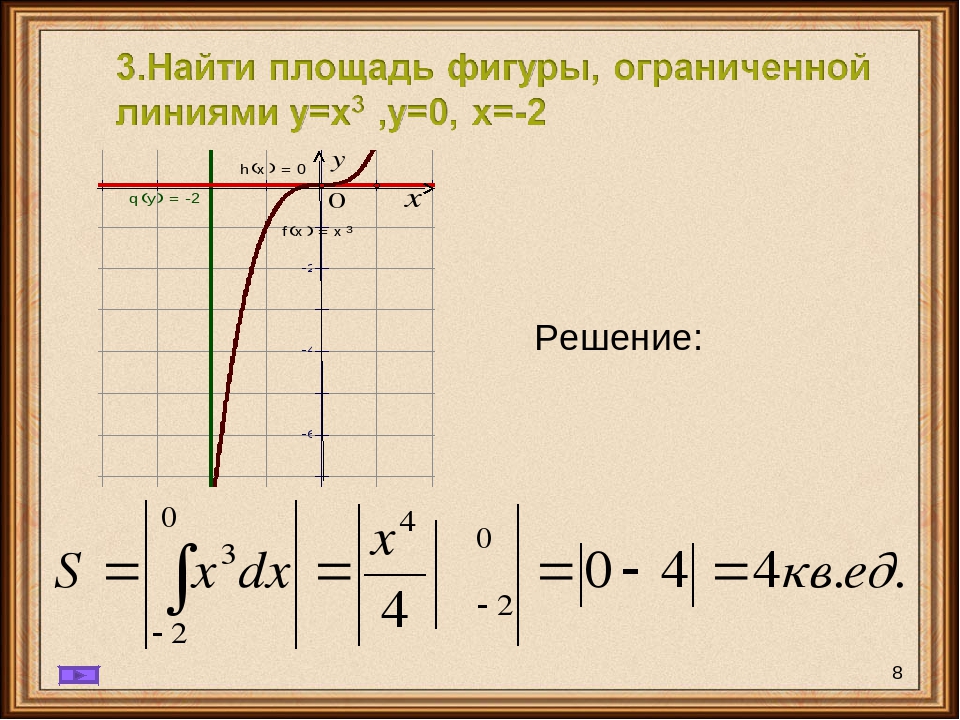 Это величины разных видов . Эта теорема обеспечивает, среди прочего, основу для измерения в радианах (тема 12).
Это величины разных видов . Эта теорема обеспечивает, среди прочего, основу для измерения в радианах (тема 12).
Теорема 16. (Евклид, VI. 33.) В одинаковых или равных окружностях центральные углы имеют такое же отношение друг к другу, как дуги, которые их стягивают.
(В геометрии мы говорим, что дуга «стягивает» угол; буквально «протягивается под ним».»)
Пусть окружности с центрами A и D равны, а углы BAC, EDF — углы при центре; затем пропорционально
Угол BAC относится к углу EDF так же, как дуга BC относится к дуге EF .
Другими словами, если дуга BC составляет, скажем, треть дуги EF, то угол BAC также составляет треть угла EDF. Этот факт лежит в основе измерения углов, потому что на самом деле мы измеряем дугу. Ибо мы считаем всю окружность дугой и в градусной мере говорим, что ее длина равна 360°.Следовательно, дуга, составляющая шестую часть окружности, будет стягивать центральный угол, равный шестой части 360°; будет 60°.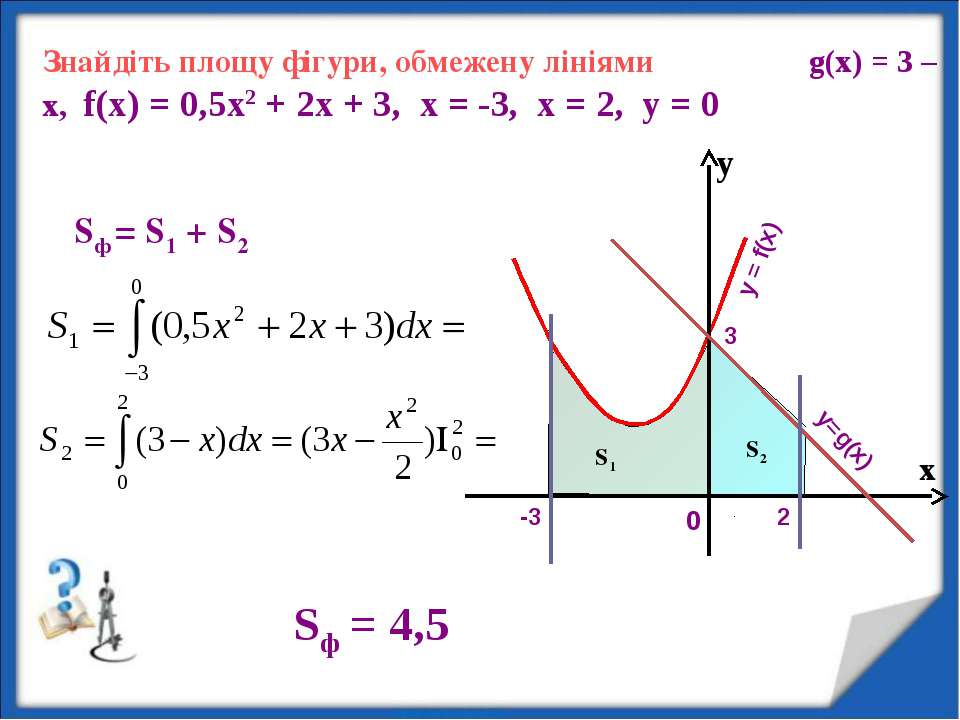
См. раздел 11.
Хотя сам факт теоремы может быть очевиден, доказательство — это совсем другое дело, потому что оно требует удовлетворительного определения «иметь одинаковое отношение». Принятие такого определения было одним из величайших математических достижений древности.
Непосредственно из теоремы 16 можно доказать следующее:
В любых кругах одинаковое отношение длины дуги к радиусу
определяет уникальный центральный угол, на который опираются дуги.
Это основа для определения меры в радианах. Мы докажем эту теорему в теме 13 «Длина дуги».
Темы | Главная
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Геометрические фигуры и прямые линии
Прямые линии являются ключом к распознаванию форм, которые мы часто видим в реальном мире: геометрические фигуры .
В сегодняшнем посте мы будем классифицировать геометрические фигуры, образованные прямыми линиями, и подумаем, где их можно найти.
Начнем с самого простого:
Две прямые линииМожно ли составить фигуру из двух прямых линий?
Ну конечно можно! Однако мы не называем эту фигуру геометрической фигурой. Чтобы быть геометрической фигурой, она должна быть «замкнутой». То есть, если мы поместим шарик внутрь фигуры, он не сможет вырваться.На сделанном нами рисунке мяч мог улететь!
Если вы попытаетесь сдвинуть две линии, то увидите, что их никоим образом нельзя замкнуть. Можно взять два прямых предмета, например, две палочки для еды, и попробовать.
Базовые геометрические фигуры
А теперь попробуем с тремя прямыми…
Готово! Теперь вы можете сделать фигуру, от которой мяч не сможет убежать.
Каждая из прямых линий, которые мы использовали, теперь действует как часть фигуры.
Будем называть каждую прямую стороной фигуры . Итак, эта фигура имеет три стороны и называется треугольником. Когда мы говорим «треугольник», мы имеем в виду либо расположение трех линий, либо окружающее их пространство.
Итак, эта фигура имеет три стороны и называется треугольником. Когда мы говорим «треугольник», мы имеем в виду либо расположение трех линий, либо окружающее их пространство.
Представляете, где мы можем найти вокруг себя треугольники? Я нашел несколько в Smartick , посмотрим, узнаете ли вы их!
4-сторонние геометрические фигуры
Давайте посмотрим, что мы можем сделать с 4 прямыми линиями…
Мы могли бы сделать, например,
Мы называем эти фигуры четырехугольниками.Есть несколько особых четырехугольников, у которых есть пары параллельных сторон. То есть есть две стороны, которые параллельны друг другу, и две другие тоже. Кроме того, параллельные стороны равны. Как мы могли сделать это? Получаем две равные стороны и ставим их параллельно друг другу:
Как расположить две другие стороны так, чтобы они тоже были параллельны? Вот и все! Просто объединив их вместе.
На данный момент у нас есть три возможности:
- Все стороны равны, образуя ромб.

Где найти алмазы?
Я нашел два!
- Если четыре угла фигуры прямые, то мы создали прямоугольник.
Мы можем найти много прямоугольников вокруг себя… Я уверен, что вы можете придумать множество!
- Если мы создадим геометрическую фигуру, которая удовлетворяет обоим вышеуказанным условиям, а также имеет все равные стороны и четыре прямых угла, это будет квадрат.
Геометрические фигуры, имеющие более 4 сторон
Мы можем продолжать добавлять все линии, которые хотим, чтобы создать разные фигуры с разным количеством сторон. Они особенно важны, когда у них равные стороны. Например, следующим будет пятиугольник (5-сторонний).
Мы можем найти их, например, в рисунке футбольных мячей.
И затем у нас есть шестигранник (6-гранный).
Мы можем найти их… в ульях! Откуда пчелы умеют делать такие идеальные геометрические фигуры?
А потом семиугольники, восьмиугольники, эннагоны, нонагоны… чего не хватает? Конечно! Что мы можем сделать с изогнутыми линиями? Кривые линии не имеет смысла классифицировать, потому что они различаются гораздо больше… но я могу сказать вам, что есть очень, очень важная изогнутая фигура, о которой, я уверен, вы уже знаете… круг !
Мы получаем круг, когда сохраняем расстояние от точки. Например, с помощью компаса мы устанавливаем точку с помощью стрелки. Затем, сохраняя отверстие, рисуем карандашом окружность. Вы можете найти множество кругов вокруг себя, на колесах вашего автомобиля или на теннисном мяче.
Например, с помощью компаса мы устанавливаем точку с помощью стрелки. Затем, сохраняя отверстие, рисуем карандашом окружность. Вы можете найти множество кругов вокруг себя, на колесах вашего автомобиля или на теннисном мяче.
Если вы хотите, вы можете продолжить изучение элементарной математики со Smartick!
Узнать больше:
Веселье — любимый способ обучения нашего мозга
Дайан Акерман
Smartick — увлекательный способ изучения математики- 15 минут веселья в день
- Адаптируется к уровню вашего ребенка
- Миллионы учеников с 2009 года
Группа создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
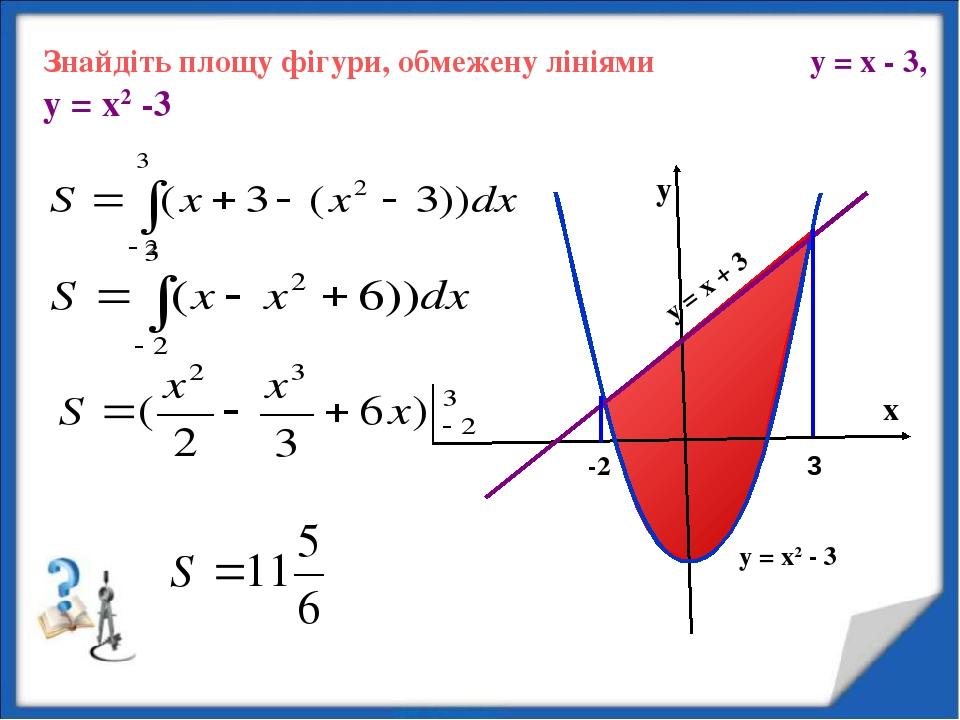
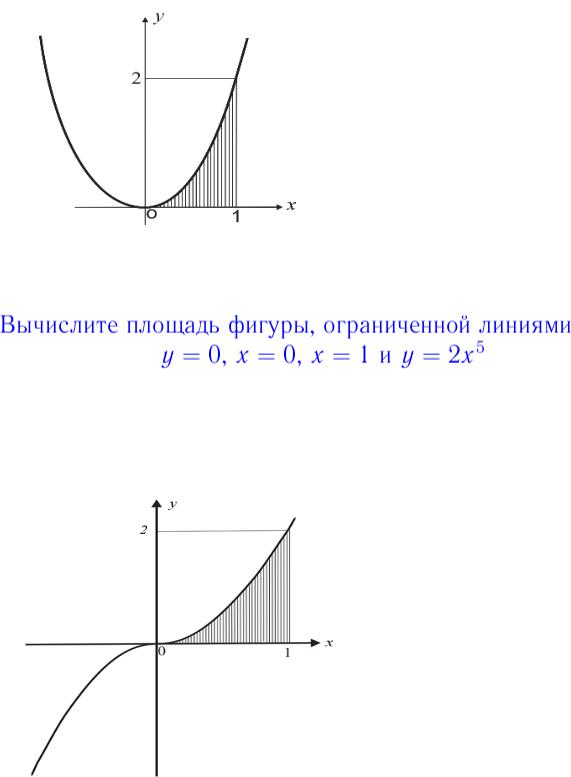
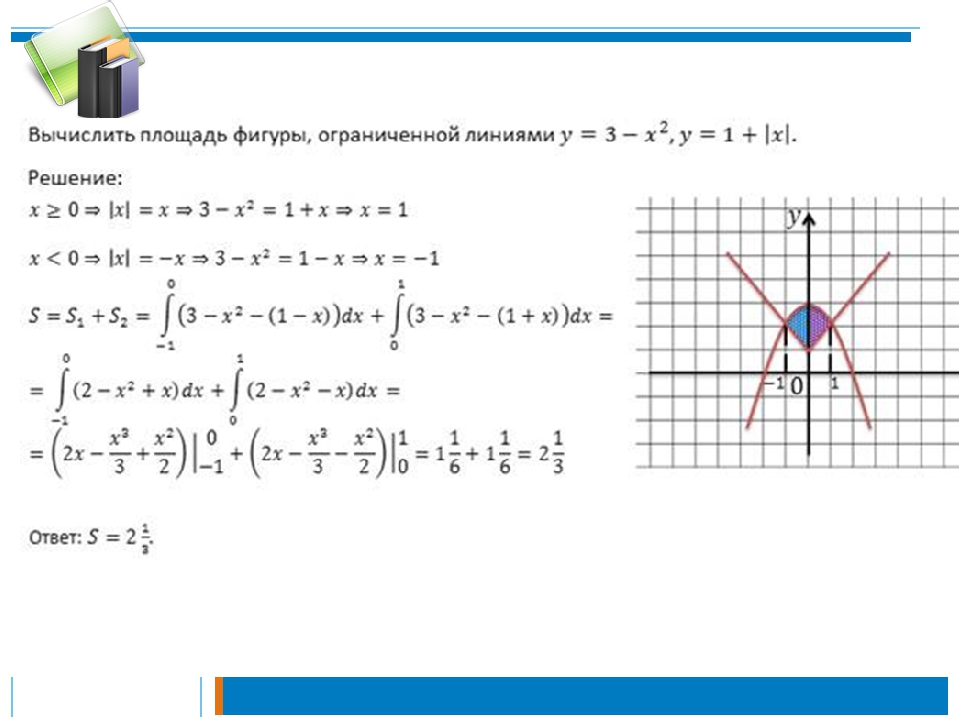
6.1: Площади между кривыми — Mathematics LibreTexts
В разделе «Введение в интегрирование» мы разработали концепцию определенного интеграла для вычисления площади под кривой на заданном интервале.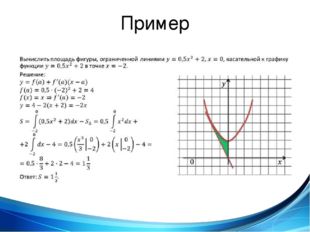 В этом разделе мы расширим эту идею, чтобы вычислить площадь более сложных регионов. Начнем с нахождения площади между двумя кривыми, являющимися функциями \(\displaystyle x\), начиная с простого случая, когда значение одной функции всегда больше другого.Затем рассмотрим случаи, когда графики функций пересекаются. Наконец, мы рассмотрим, как вычислить площадь между двумя кривыми, которые являются функциями \(\displaystyle y\).
В этом разделе мы расширим эту идею, чтобы вычислить площадь более сложных регионов. Начнем с нахождения площади между двумя кривыми, являющимися функциями \(\displaystyle x\), начиная с простого случая, когда значение одной функции всегда больше другого.Затем рассмотрим случаи, когда графики функций пересекаются. Наконец, мы рассмотрим, как вычислить площадь между двумя кривыми, которые являются функциями \(\displaystyle y\).
Площадь области между двумя кривыми
Пусть \(\displaystyle f(x)\) и \(\displaystyle g(x)\) — непрерывные функции на интервале \(\displaystyle [a,b]\) такие, что \(\displaystyle f(x) ≥g(x)\) на \(\displaystyle [a,b]\). Нам нужно найти площадь между графиками функций, как показано на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): Площадь между графиками двух функций, \(\displaystyle f(x)\) и \(\displaystyle g(x)\), на интервале \(\ displaystyle [a,b]\) Как и раньше, мы собираемся разбить интервал по оси x и аппроксимировать площадь между графиками функций прямоугольниками. ∗_i)\).b_a[f(x)−g(x)]dx.\]
∗_i)\).b_a[f(x)−g(x)]dx.\]
Эти результаты резюмируются в следующей теореме.
Нахождение площади между двумя кривыми
Пусть \(\displaystyle f(x)\) и \(\displaystyle g(x)\) — непрерывные функции такие, что \(\displaystyle f(x)≥g(x)\) на интервале [\(\ стиль отображения a,b]\). Обозначим через R область, ограниченную сверху графиком \(\displaystyle f(x)\), снизу графиком \(\displaystyle g(x)\), а слева и справа линиями \(\ displaystyle x=a\) и \(\displaystyle x=b\) соответственно.b_a[f(x)−g(x)]dx.\]
Применим эту теорему в следующем примере.
Пример \(\PageIndex{1}\): нахождение площади области между двумя кривыми I
Если \(\textbf{R}\) — область, ограниченная сверху графиком функции \(\displaystyle f(x)=x+4\), а снизу графиком функции \(\displaystyle g( x)=3−\dfrac{x}{2}\) на интервале \(\displaystyle [1,4]\), найти площадь области \(\textbf{R}\).
Раствор
Область изображена на следующем рисунке. 2\).
2\).
Упражнение \(\PageIndex{1}\)
Если \(\textbf{R}\) является областью, ограниченной графиками функций \(\displaystyle f(x)=\dfrac{x}{2}+5\) и \(\displaystyle g(x )=x+\dfrac{1}{2}\) на интервале \(\displaystyle [1,5]\), найти площадь области \(\textbf{R}\).
- Подсказка
Нарисуйте графики функций, чтобы определить, график какой функции формирует верхнюю границу, а график нижней границы, затем выполните процесс, описанный в примере.
- Ответить
\(\displaystyle 12\) единиц 2
В примере \(\PageIndex{1}\) мы определили интересующий интервал как часть условия задачи. Однако довольно часто мы хотим определить интересующий нас интервал на основе того, где пересекаются графики двух функций. Это показано в следующем примере.
Пример \(\PageIndex{2}\): нахождение площади области между двумя кривыми II
Если \(\textbf{R}\) является областью, ограниченной сверху графиком функции \(\displaystyle f(x)=9−(x/2)^2\), а снизу графиком функции \(\displaystyle g(x)=6−x\), найти площадь области \(\textbf{R}\). 4\), найдите площадь области \(\textbf{R}\).
4\), найдите площадь области \(\textbf{R}\).
- Подсказка
Используйте процесс из примера \(\PageIndex{2}\).
- Ответить
\(\displaystyle \dfrac{3}{10}\) ед. 2
Площади составных регионов
До сих пор нам требовалось \(\displaystyle f(x)≥g(x)\) на всем интересующем интервале, но что, если мы хотим посмотреть на области, ограниченные графиками пересекающихся функций? В этом случае мы модифицируем процесс, который мы только что разработали, используя функцию абсолютного значения.b_a|f(x)−g(x)|dx.\]
На практике применение этой теоремы требует от нас разбить интервал \(\displaystyle [a,b]\) и вычислить несколько интегралов в зависимости от того, какое из значений функции больше на данной части интервала. Изучим этот процесс на следующем примере.
Пример \(\PageIndex{3}\): нахождение площади области, ограниченной пересекающимися функциями
Если \(\textbf{R}\) является областью между графиками функций \(\displaystyle f(x)=\sin x \) и \(\displaystyle g(x)=\cos x\) над интервал \(\displaystyle [0,π]\), найти площадь области \(\textbf{R}\).
Раствор
Область изображена на следующем рисунке.
Рисунок \(\PageIndex{5}\): Область между двумя кривыми может быть разбита на две подобласти. Графики функций пересекаются в точке \(\displaystyle x=π/4\). Для \(\displaystyle x∈[0,π/4], \cos x≥\sin x,\) поэтому\(\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\cos x−\sin x .\)
С другой стороны, для \(\displaystyle x∈[π/4,π], \sin x ≥\cos x,\), поэтому
\(\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\sin x −\cos x.π_{π/4} \\[4pt] =(\sqrt{2}−1)+(1+\sqrt{2})=2\sqrt{2}. \конец{выравнивание*}\]
Площадь региона составляет \(\displaystyle 2\sqrt{2}\) единиц 2 .
Упражнение \(\PageIndex{3}\)
Если \(\textbf{R}\) является областью между графиками функций \(\displaystyle f(x)=\sin x \) и \(\displaystyle g(x)=\cos x\) над интервал \(\displaystyle [π/2,2π]\), найти площадь области \(\textbf{R}\).
- Подсказка
Две кривые пересекаются в точке \(\displaystyle x=(5π)/4.
 \)
\)
- Ответить
\(\displaystyle 2+2\sqrt{2}\) единиц 2
Пример \(\PageIndex{4}\): нахождение площади сложной области
Рассмотрим область, изображенную на рисунке \(\PageIndex{6}\). Найдите площадь \(\textbf{R}\).
Рисунок \(\PageIndex{6}\): Для вычисления площади этой области требуются два интеграла.Раствор
Как и в примере \(\PageIndex{3}\), нам нужно разделить интервал на две части.2_1=\dfrac{1}{2}.\)
Складывая эти площади вместе, получаем
\(\displaystyle A=A_1+A_2=\dfrac{1}{3}+\dfrac{1}{2}=\dfrac{5}{6}.\)
Площадь области составляет \(\displaystyle 5/6\) единиц 2 .
Упражнение \(\PageIndex{4}\)
Рассмотрим область, изображенную на следующем рисунке. Найдите площадь \(\textbf{R}\).
- Подсказка
Две кривые пересекаются в точке x=1
- Ответить
\(\displaystyle \dfrac{5}{3}\) единиц 2
Области, определенные относительно y
В примере \(\PageIndex{4}\) нам пришлось вычислить два отдельных интеграла для вычисления площади области. 2\) как функция \(\displaystyle y\). Однако на основе графика становится ясно, что нас интересует положительный квадратный корень.) Точно так же правый график представлен функцией \(\displaystyle y=g(x)=2−x\), но мог бы просто легко представить функцией \(\displaystyle x=u(y)=2−y\). Когда графики представлены как функции \(\displaystyle y\), мы видим, что область ограничена слева графиком одной функции и справа графиком другой функции. Следовательно, если мы интегрируем по \(\displaystyle y\), нам нужно вычислить только один интеграл.Разработаем формулу для этого типа интеграции.
2\) как функция \(\displaystyle y\). Однако на основе графика становится ясно, что нас интересует положительный квадратный корень.) Точно так же правый график представлен функцией \(\displaystyle y=g(x)=2−x\), но мог бы просто легко представить функцией \(\displaystyle x=u(y)=2−y\). Когда графики представлены как функции \(\displaystyle y\), мы видим, что область ограничена слева графиком одной функции и справа графиком другой функции. Следовательно, если мы интегрируем по \(\displaystyle y\), нам нужно вычислить только один интеграл.Разработаем формулу для этого типа интеграции.
Пусть \(\displaystyle u(y)\) и \(\displaystyle v(y)\) — непрерывные функции на интервале \(\displaystyle [c,d]\) такие, что \(\displaystyle u(y) ≥v(y)\) для всех \(\displaystyle y∈[c,d]\). Мы хотим найти площадь между графиками функций, как показано на рисунке \(\PageIndex{7}\).
Рисунок \(\PageIndex{7}\): мы можем найти площадь между графиками двух функций, \(\displaystyle u(y)\) и \(\displaystyle v(y)\).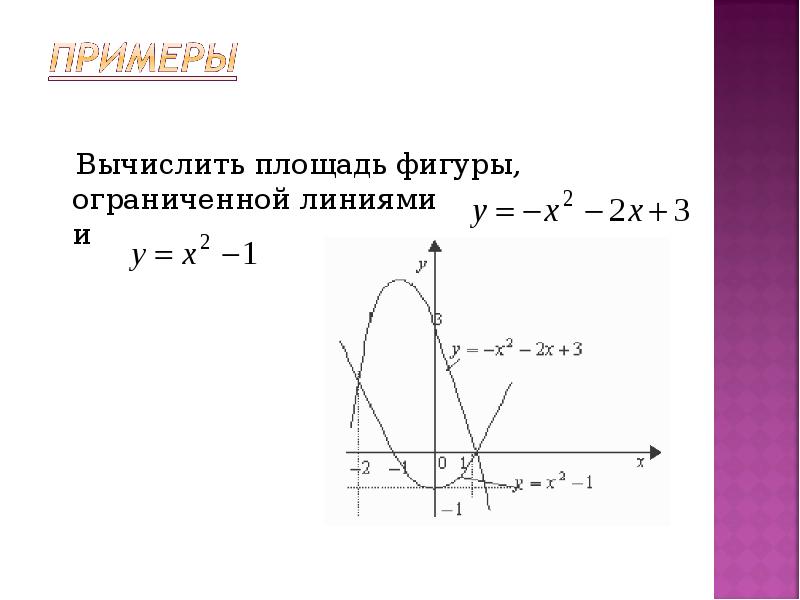 d_c[u(y)−v(y)]dy. \конец{выравнивание*}\]
d_c[u(y)−v(y)]dy. \конец{выравнивание*}\]Эти результаты резюмируются в следующей теореме.
Нахождение площади между двумя кривыми, интегрирование по оси Y
Пусть \(\displaystyle u(y)\) и \(\displaystyle v(y)\) — непрерывные функции такие, что \(\displaystyle u(y)≥v(y) \)для всех \(\displaystyle y ∈[c,d]\). Пусть \(\textbf{R}\) обозначает область, ограниченную справа графиком \(\displaystyle u(y)\), слева графиком \(\displaystyle v(y)\ ), а сверху и снизу строками \(\displaystyle y=d\) и \(\displaystyle y=c\) соответственно.d_c[u(y)−v(y)]dy.\]
Пример \(\PageIndex{5}\): интеграция с учетом y
Вернемся к примеру \(\PageIndex{4}\), только на этот раз интегрируем по \(\displaystyle y\). Пусть \(\textbf{R}\) будет регионом, изображенным на рисунке \(\PageIndex{9}\). Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\).
Рисунок \(\PageIndex{9}\): площадь области \(\textbf{R}\) можно рассчитать с помощью одного интеграла, только если кривые рассматриваются как функции \(\displaystyle y\).
Раствор
Сначала мы должны представить графики как функции \(\displaystyle y\). Как мы видели в начале этого раздела, кривая слева может быть представлена функцией \(\displaystyle x=v(y)=\sqrt{y}\), а кривая справа может быть представлена функцией функция \(\displaystyle x=u(y)=2−y\).
Теперь нам нужно определить пределы интегрирования. Область ограничена снизу осью x, поэтому нижний предел интегрирования равен \(\displaystyle y=0\).1_0\\[4pt] =\dfrac{5}{6}. \конец{выравнивание*}\]
Площадь региона составляет \(\displaystyle 5/6\) единиц 2 .
Упражнение \(\PageIndex{5}\)
Давайте вернемся к контрольной точке, связанной с примером \(\PageIndex{4}\), только на этот раз проинтегрируем по \(\displaystyle y\). Пусть \(\textbf{R}\) будет областью, изображенной на следующем рисунке. Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\).
- Подсказка
Повторите процесс из предыдущего примера.

- Ответить
\(\displaystyle \dfrac{5}{3}\) единиц 2
Как называется фигура, ограниченная более чем четырьмя прямыми линиями?
Прямолинейные фигуры состоят из фигур, ограниченных прямыми линиями . Треугольник ограничен тремя прямыми , четырехугольник четырьмя , а многоугольник ограничен четырьмя прямыми .
Сколько прямых линий имеет следующий рисунок?
Вертикальные строки — это AE, LF и KG, т.е. 3 в количестве. Наклонные линии — это LC, CF, FI, LI, EK и AG, т.е. 6 в количестве. Таким образом, в фигуре 5 + 3 + 6 = 14 прямых .
что такое плоская фигура с четырьмя равными сторонами? Параллелограмм – это четырехугольник (плоская фигура с четырьмя сторонами), у которого противоположные стороны параллельны и имеют одинаковую длину.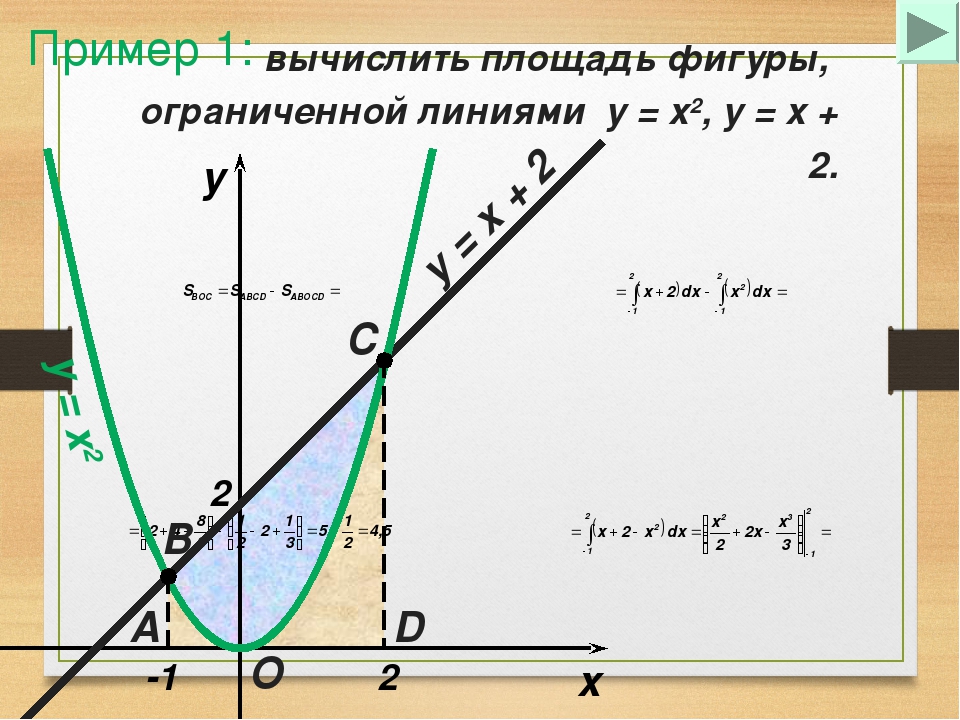 Противолежащие углы параллелограмма также равны. В случае, когда все углов прямые углов параллелограмм является прямоугольником, а когда все стороны равны — ромбом. что такое геометрические фигуры и примеры?
Противолежащие углы параллелограмма также равны. В случае, когда все углов прямые углов параллелограмм является прямоугольником, а когда все стороны равны — ромбом. что такое геометрические фигуры и примеры? Геометрические фигуры — это фигуры, которые мы встречаем в математике под разными названиями. Треугольник, круг, трапеция, квадрат, , прямоугольник , куб, сердце, ромб и т. д. — вот некоторые из геометрических фигур.Некоторые из названий фигур, таких как многоугольники, были описаны на основе количества их сторон.
Какая фигура не имеет прямой линии?Круг. С другой стороны, круг, который является другой формой геометрии, не имеет прямых линий . Это скорее комбинация кривых, которые все связаны. В окружности не найти углов.
Какое минимальное количество прямых линий необходимо, чтобы нарисовать замкнутую фигуру?
минимальное количество линий, необходимое для создания замкнутой фигуры, равно 3.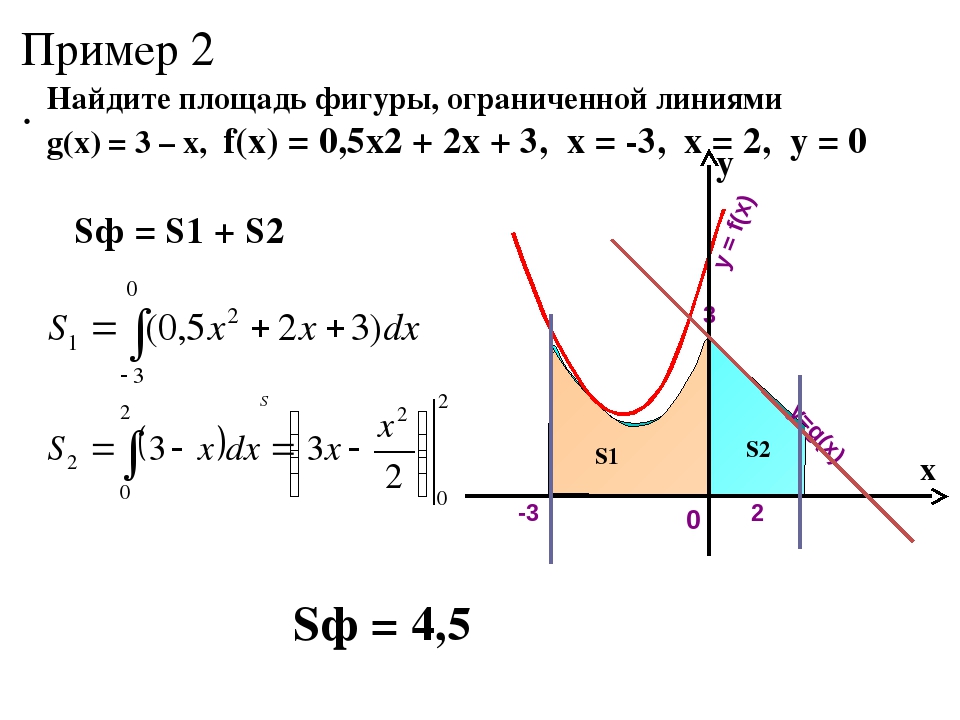 потому что, используя 3 линии, мы можем сделать треугольник.
потому что, используя 3 линии, мы можем сделать треугольник.Сколько прямых в треугольнике?
Таким образом, на рисунке 2 + 3 + 4 = 9 прямых. Теперь посчитаем количество треугольников на рисунке.Какие 16 основных фигур?
квадрат, прямоугольник, треугольник, круг, пятиугольник, шестиугольник, семиугольник, восьмиугольник, девятиугольник, десятиугольник, параллелограмм, ромб, воздушный змей, четырехугольник, трапеция.Как называются фигуры?
Больше четырех сторон Пятиугольник называется пятиугольником.Шестиугольник — это шестиугольник, семиугольник — семиугольник, а восьмиугольник имеет восемь сторон… Многоугольники имеют разные названия, и обычно количество сторон важнее, чем название формы.Что такое закрытая фигура?
В геометрии замкнутая форма может быть определена как замкнутая форма или фигура, сегменты линий и/или кривые которых соединены или встречаются. Они начинаются и заканчиваются в одной и той же точке. Вот несколько примеров закрытых форм. Забавные факты.
Забавные факты.Как называются фигуры с разными сторонами?
2D-фигуры Треугольник – 3 стороны Квадрат – 4 стороны Пятиугольник – 5 сторон Шестиугольник – 6 сторон Семиугольник – 7 сторон Восьмиугольник – 8 сторон Многоугольник – 9 сторон Десятиугольник – 10 сторон ЕщеЧто такое базовая форма?
Основные формы включают квадрат, круг и треугольник.У вас может быть нос в форме лыжного склона. Когда вы восхищаетесь чьей-то формой, вы восхищаетесь их формой или телом. Когда вы не в форме или обещаете вернуться в форму, вы используете форму для обозначения своей физической выносливости или общего состояния здоровья.Что такое положительная форма?
Положительные и отрицательные формы Положительные формы — это форма фактического объекта (например, оконной рамы). Негативные формы — это промежутки между объектами (например, пространство внутри оконной рамы).Что имеет форму треугольника?
Треугольник — это фигура или часть двумерного пространства.У него три прямые стороны и три вершины.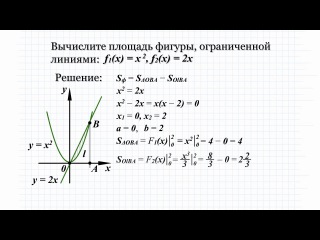
 «яйцо 4 буквы
«яйцо 4 буквы
 ..» 4 буквы
..» 4 буквы
 ) 4 буквы
) 4 буквы

 \)
\)