Решение уравнений с параметрами содержащие модуль решением. Решение уравнений с модулем и параметром план-конспект занятия по алгебре (10 класс) на тему
К задачам с параметром можно отнести, например, поиск решения линейных и квадратных уравнений в общем виде, исследование уравнения на количество имеющихся корней в зависимости от значения параметра.
Не приводя подробных определений, в качестве примеров рассмотрим следующие уравнения:
у = kx, где x, y – переменные, k – параметр;
у = kx + b, где x, y – переменные, k и b – параметр;
аx 2 + bх + с = 0, где x – переменные, а, b и с – параметр.
Решить уравнение (неравенство, систему) с параметром это значит, как правило, решить бесконечное множество уравнений (неравенств, систем).
Задачи с параметром можно условно разделить на два типа:
а) в условии сказано: решить уравнение (неравенство, систему) – это значит, для всех значений параметра найти все решения. Если хотя бы один случай остался неисследованным, признать такое решение удовлетворительным нельзя.
Если хотя бы один случай остался неисследованным, признать такое решение удовлетворительным нельзя.
б) требуется указать возможные значения параметра, при которых уравнение (неравенство, система) обладает определенными свойствами. Например, имеет одно решение, не имеет решений, имеет решения, принадлежащие промежутку и т. д. В таких заданиях необходимо четко указать, при каком значении параметра требуемое условие выполняется.
Параметр, являясь неизвестным фиксированным числом, имеет как бы особую двойственность. В первую очередь, необходимо учитывать, что предполагаемая известность говорит о том, что параметр необходимо воспринимать как число. Во вторую очередь, свобода обращения с параметром ограничивается его неизвестностью. Так, например, операции деления на выражение, в котором присутствует параметр или извлечения корня четной степени из подобного выражения требуют предварительных исследований. Поэтому необходима аккуратность в обращении с параметром.
Например, чтобы сравнить два числа -6а и 3а, необходимо рассмотреть три случая:
1) -6a будет больше 3a, если а отрицательное число;
2) -6а = 3а в случае, когда а = 0;
3) -6а будет меньше, чем 3а, если а – число положительное 0.
Решение и будет являться ответом.
Пусть дано уравнение kx = b. Это уравнение – краткая запись бесконечного множества уравнений с одной переменной.
При решении таких уравнений могут быть случаи:
1. Пусть k – любое действительное число не равное нулю и b – любое число изR, тогда x = b/k.
2. Пусть k = 0 и b ≠ 0, исходное уравнение примет вид 0 · x = b. Очевидно, что у такого уравнения решений нет.
3. Пусть k и b числа, равные нулю, тогда имеем равенство 0 · x = 0. Его решение – любое действительное число.
Алгоритм решения такого типа уравнений:
1. Определить «контрольные» значения параметра.
2. Решить исходное уравнение относительно х при тех значениях параметра, которые были определены в первом пункте.
3. Решить исходное уравнение относительно х при значениях параметра, отличающихся от выбранных в первом пункте.
4. Записать ответ можно в следующем виде:
1) при … (значения параметра), уравнение имеет корни …;
2) при … (значения параметра), в уравнении корней нет.
Пример 1.
Решить уравнение с параметром |6 – x| = a.
Решение.
Легко видеть, что здесь a ≥ 0.
По правилу модуля 6 – x = ±a, выразим х:
Ответ: х = 6 ± a, где a ≥ 0.
Пример 2.
Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.
Решение.
Раскроем скобки: aх – а + 2х – 2 = 0
Запишем уравнение в стандартном виде: х(а + 2) = а + 2.
В случае, если выражение а + 2 не нуль, т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.
В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое действительное число.
Ответ: х = 1 при а ≠ -2 и х € R при а = -2.
Пример 3.
Решить уравнение x/a + 1 = а + х относительно переменной х.
Решение.
Если а = 0, то преобразуем уравнение к виду а + х = а 2 + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.
Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.
Если а ≠ 1, то последнее уравнение примет вид х = -а.
Данное решение можно проиллюстрировать на координатной прямой (рис. 1)
Ответ: нет решений при а = 0; х – любое число при а = 1; х = -а при а ≠ 0 и а ≠ 1.
Графический метод
Пример 4.
Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?
Решение.
Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2) .
На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.
Ответ: корней у уравнения не будет, если а 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0
Пример 5.
При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?
Решение.
Изобразим графики функций y = 2|x| + |x – 1| и y = a. Для y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:
{-3x + 1, при x
y = {x + 1, при 0 ≤ x ≤ 1,
{3x – 1, при x > 1.
На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.
Ответ: а = 1.
Пример 6.
Определить число решений уравнения |x + 1| + |x + 2| = a в зависимости от параметра а?
Решение.
График функции y = |x + 1| + |x + 2| будет представлять собой ломаную. Ее вершины будут располагаться в точках (-2; 1) и (-1; 1) (рисунок 4) .
Ответ: если параметр a будет меньше единицы, то корней у уравнения не будет; если а = 1, то решение уравнения является бесконечное множество чисел из отрезка [-2; -1]; если значения параметра а будут больше одного, то уравнение будет иметь два корня.
Остались вопросы? Не знаете, как решать уравнения с параметром?
Чтобы получить помощь репетитора – зарегистрируйтесь .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Занятие «Решение линейных уравнений с параметром, содержащих модуль».
Цель: сформировать умение решать линейные уравнения с параметром, содержащие модуль; развивать логическое мышление и навыки самостоятельной работы.
Оборудование: презентация.
Ход урока.
1.Для актуализации знаний учащихся необходимо повторить понятие модуля и решить несколько уравнений с модулем: |х|=3; |х|= — 5; |х|=0.
Затем предложить учащимся ответить на вопрос: Сколько корней может иметь уравнение с модулем и от чего это зависит?
Вывод содержится на 2 слайде. Его записывают в тетради.
Разбор решения уравнения |х — 2 |= 3
Фронтальная работа с классом: решение уравнения 1.
Самостоятельное решение уравнений:
2. |х — 3 |= 5; 3. |4 — х |= 7; 4. |5 — х |= — 9. Проверка.
Разбор решения задание 1 :
Определите число корней уравнения
||х| +5 — а |= 2. (слайд 3)
Комментарии учителя: это уравнение с параметром, т.е. с переменной а. В зависимости от значения этой переменной будет изменяться вид уравнения. А значит, и число корней уравнения зависит от а.
Предложить учащимся ответить на вопрос задания «Найдите все значения а, при каждом из которых уравнение ||х| +5 — а |= 2 имеет ровно 3 корня. (Если значений а более одного, то в бланке ответов запишите их сумму). Ответ: 7. (слайд 4)
Решить у доски задание 2: Найдите все значения а, при каждом из которых уравнение ||х| — 3 + а |= 4 имеет ровно 3 корня. Ответ: — 1.
Самостоятельная работа. Задание 3 .Найдите все значения а, при каждом из которых уравнение ||х| -4+ а |= 3 имеет ровно 1 корень. Ответ: 7.
Задание 4 . При каких значениях а уравнение
|а — 5 — |х||= 3 имеет нечетное число корней (если значений а более одного, то в бланке ответов запишите их сумму). Ответ: 10.
Предложить учащимся разобрать способ решения задания, используя свойство четности функции и графический способ.
7. Итог урока. Над чем вы сегодня работали на уроке? Было ли для вас что-то нового и познавательного? Над чем бы вы хотели поработать на следующем уроке?
«Линейное уравнение с двумя переменными» — Равенство, содержащее две переменные, называется уравнением с двумя переменными. -Что называется уравнением с двумя переменными? Приведите примеры. -Какое уравнение с двумя переменными называется линейным? Линейное уравнение с двумя переменными. Определение: Алгоритм доказательства, что данная пара чисел является решением уравнения:
«Решение показательных уравнений» — Сведение к одному основанию. Вынесение за скобки. Т. Виета. Графический способ. Показательным уравнением называют уравнение, содержащее переменную в показателе степени. Решение показательных уравнений. Устная работа. ab+ac=a(b+c). Степени. 2.Решить уравнение: Свойство. Виды и способы решения показательных уравнений.
Показательным уравнением называют уравнение, содержащее переменную в показателе степени. Решение показательных уравнений. Устная работа. ab+ac=a(b+c). Степени. 2.Решить уравнение: Свойство. Виды и способы решения показательных уравнений.
«Графический способ решения уравнений» — Ответ: один корень, х=-1. Два корня. Решить графически уравнение (х+1)/(х-2)=2. Построить график функции y=x?+6x+8. Практикум по решению уравнений графическим способом Подготовка к зачету. Построить графики функций. Построить график функции y=(x+1)/(x-2). 1. Перенесем 8 в правую часть уравнения. Корней нет.
«Решение целых уравнений» — «Уравнения, в которых скопом Корни, степень, неравенств бездна. Три великих математика. Удачи в дальнейшем изучении методов решения уравнений. Осевая симметрия присуща большинству видов растений и животных. Центральная. В животном мире 2 вида симметрии. Диктант. Осевая. Определите методы решения уравнений.
«Уравнения с логарифмами» — Логарифмические уравнения. Реши устно уравнения. Формулы преобразования логарифмов. Уравнение. Определение. Таблицы логарифмов. Определение логарифма. Определение и свойства логарифма. Логарифмическая линейка. Функция. Наушники или колонки. Область определения. Подходы к решению. Решить уравнение. Гимназия.
Формулы преобразования логарифмов. Уравнение. Определение. Таблицы логарифмов. Определение логарифма. Определение и свойства логарифма. Логарифмическая линейка. Функция. Наушники или колонки. Область определения. Подходы к решению. Решить уравнение. Гимназия.
«Иррациональные уравнения» — На контроль д/з выполнили: №419 (в,г) Сафиуллина, №418(в,г) Кульмухаметов, №420(в,г)Шагеев. 2 урок Решение систем уравнений. Урок 1 Тема: Решение иррациональных уравнений. 1.Какие из следующих уравнений являются иррациональными: Цели: Познакомить учащихся с решениями некоторых видов иррациональных уравнений.
Всего в теме 49 презентаций
1. Системы линейных уравнений с параметром
Системы линейных уравнений с параметром решаются теми же основными методами, что и обычные системы уравнений: метод подстановки, метод сложения уравнений и графический метод. Знание графической интерпретации линейных систем позволяет легко ответить на вопрос о количестве корней и их существовании.
Пример 1.
Найти все значения для параметра а, при которых система уравнений не имеет решений.
{х + (а 2 – 3)у = а,
{х + у = 2.
Решение.
Рассмотрим несколько способов решения данного задания.
1 способ . Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а 1 = b/b 1 ≠ c/c 1). Тогда имеем:
1/1 = (а 2 – 3)/1 ≠ а/2 или систему
{а 2 – 3 = 1,
{а ≠ 2.
Из первого уравнения а 2 = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.
Ответ: а = -2.
2 способ . Решаем методом подстановки.
{2 – у + (а 2 – 3)у = а,
{х = 2 – у,
{(а 2 – 3)у – у = а – 2,
{х = 2 – у.
После вынесения в первом уравнении общего множителя у за скобки, получим:
{(а 2 – 4)у = а – 2,
{х = 2 – у.
Система не имеет решений, если первое уравнение не будет иметь решений, то есть
{а 2 – 4 = 0,
{а – 2 ≠ 0.
Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.
Ответ: а = -2.
Пример 2.
Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.
{8х + ау = 2,
{ах + 2у = 1.
Решение.
По свойству, если отношение коэффициентов при х и у одинаковое, и равно отношению свободных членов системы, то она имеет бесконечное множество решений (т. е. а/а 1 = b/b 1 = c/c 1). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.
Ответ: а = 4.
2. Системы рациональных уравнений с параметром
Пример 3.
{3|х| + у = 2,
{|х| + 2у = a.
Решение.
Умножим первое уравнение системы на 2:
{6|х| + 2у = 4,
{|х| + 2у = a.
Вычтем из первого второе уравнение, получим 5|х| = 4 – а. Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а 4).
Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а 4).
Ответ: а = 4.
Пример 4.
Найти все значения параметра а, при которых система уравнений имеет единственное решение.
{х + у = а,
{у – х 2 = 1.
Решение.
Данную систему решим с использованием графического метода. Так, графиком второго уравнения системы является парабола, поднятая по оси Оу вверх на один единичный отрезок. Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1) . Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а:
1,25 = 0,5 + а;
Ответ: а = 0,75.
Пример 5.
Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.
{ах – у = а + 1,
{ах + (а + 2)у = 2.
Решение.
Из первого уравнения выразим у и подставим во второе:
{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.
Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:
ах + а 2 х – а 2 – а + 2ах – 2а – 2 = 2;
а 2 х + 3ах = 2 + а 2 + 3а + 2.
Квадратный трехчлен а 2 + 3а + 2 представим в виде произведения скобок
(а + 2)(а + 1), а слева вынесем х за скобки:
(а 2 + 3а)х = 2 + (а + 2)(а + 1).
Очевидно, что а 2 + 3а не должно быть равным нулю, поэтому,
а 2 + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.
Ответ: а ≠ 0; ≠ -3.
Пример 6.
Используя графический метод решения, определите, при каком значении параметра а, система имеет единственное решение.
{х 2 + у 2 = 9,
{у – |х| = а.
Решение.
Исходя из условия, строим окружность с центром в начале координат и радиусом 3 единичных отрезка, именно ее задает первое уравнение системы
х 2 + у 2 = 9. Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2 рассматриваем все возможные случаи ее расположения относительно окружности. Легко видеть, что а = 3.
Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2 рассматриваем все возможные случаи ее расположения относительно окружности. Легко видеть, что а = 3.
Ответ: а = 3.
Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как решать выражения с модулем. Модуль числа. Учебник по ЕГЭ и ГИА
Модуль числа a — это расстояние от начала координат до точки А (a ).
Чтобы понять это определение, подставим вместо переменной a любое число, например 3 и попробуем снова прочитать его:
Модуль числа 3 — это расстояние от начала координат до точки А (3 ).
Становится ясно, что модуль это ни что иное, как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3 )
Давайте попробуем увидеть расстояние от начала координат до точки А(3 )
Расстояние от начала координат до точки А(3 ) равно 3 (трём единицам или трём шагам).
Модуль числа обозначает двумя вертикальными линиями, например:
Модуль числа 3 обозначается так: |3|
Модуль числа 4 обозначается так: |4|
Модуль числа 5 обозначается так: |5|
Мы искали модуль числа 3 и выяснили, что он равен 3. Так и записываем:
Читается как: «Модуль числа три равен три»
Теперь попробуем найти модуль числа -3. Опять же возвращаемся к определению и подставляем в него число -3. Только вместо точки A используем новую точку B . Точку A мы уже использовали в первом примере.
Модулем числа —3 называют расстояние от начала координат до точки B (—3 ).
Расстояние от одного пункта до другого не может быть отрицательным. Поэтому и модуль любого отрицательного числа, будучи являясь расстоянием тоже не будет отрицательным. Модуль числа -3 будет число 3. Расстояние от начала координат до точки B(-3) равно также трём единицам:
Модуль числа -3 будет число 3. Расстояние от начала координат до точки B(-3) равно также трём единицам:
Читается как: «Модуль числа минус три равен три»
Модуль числа 0 равен 0, та как точка с координатой 0 совпадает с началом координат, т.е. расстояние от начала координат до точки O(0) равно нулю:
«Модуль нуля равен нулю»
Делаем выводы:
- Модуль числа не может быть отрицательным;
- Для положительного числа и нуля модуль равен самому числу, а для отрицательного – противоположному числу;
- Противоположные числа имеют равные модули.
Противоположные числа
Числа, отличающиеся только знаками называют противоположными . Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числа −2 знак минуса, а у 2 знак плюса, но мы его не видим, потому что плюс, как мы говорили ранее, по традиции не пишут.
Еще примеры противоположных чисел:
Противоположные числа имеют равные модули. Например, найдём модули для −2 и 2
Например, найдём модули для −2 и 2
На рисунке видно, что расстояние от начала координат до точек A(−2) и B(2) одинаково равно двум шагам.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Базовые сведения о модуле
Определение модуля может быть дано следующим образом: Абсолютной величиной числа a (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат. Из определения следует, что:
Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать.
Основные свойства модуля:
Некоторые методы решения уравнений с модулями
Существует несколько типов уравнений с модулем, для которых имеется предпочтительный способ решения. При этом данный способ не является единственным. Например, для уравнения вида:
При этом данный способ не является единственным. Например, для уравнения вида:
Предпочтительным способом решения будет переход к совокупности:
А для уравнений вида:
Также можно переходить к почти аналогичной совокупности, но так как модуль принимает только положительные значения, то и правая часть уравнения должна быть положительной. Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:
Оба этих типа уравнений можно решать и другим способом: раскрывая соответствующим образом модуль на промежутках где подмодульное выражение имеет определённый знак. В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше:
Для решения уравнений в которых содержится более чем один модуль применяется метод интервалов , который состоит в следующем:
- Сначала находим точки на числовой оси, в которых обращается в ноль каждое из выражений, стоящих под модулем.

- Далее делим всю числовую ось на интервалы между полученными точками и исследуем знак каждого из подмодульных выражений на каждом интервале. Заметьте, что для определения знака выражения надо подставить в него любое значение x из интервала, кроме граничных точек. Выбирайте те значения x , которые легко подставлять.
- Далее на каждом полученном интервале раскрываем все модули в исходном уравнении в соответствии с их знаками на данном интервале и решаем полученное обычное уравнение. В итоговый ответ выписываем только те корни этого уравнения, которые попадают в исследуемый промежуток. Еще раз: такую процедуру проводим для каждого из полученных интервалов.
- Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ.
 После этого Вам останется подумать только над самыми сложными задачами.
После этого Вам останется подумать только над самыми сложными задачами. - Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
В математике, как и в жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла: например, мы не можем проехать на машине километров (мы проедем километров, неважно, в каком направлении), как и не можем купить килограммов апельсинов. Эти значения всегда должны быть положительными. Именно поэтому в математике существует специальный термин — модуль.
Что же такое модуль числа?
Представь, что это ты.
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления.
Итак, ты делаешь шага вперёд и оказываешься в точке с координатой.
Это означает, что ты удалился от места, где стоял на шага (единичных отрезка). То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно.
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой сделать шага в обратную сторону, то окажешься в точке с координатой.
Какое расстояние было пройдено в первом и во втором случае? Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (и), в которых ты оказался одинаково удалены от точки, из которой было начато движение ().
Таким образом, мы приблизились к понятию модуля . Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа будет. Модуль числа также равен, потому что расстояние не может быть отрицательным !
Модуль — это абсолютная величина
Обозначается модуль просто:
(- любое число).
Итак, найдём модуль числа и:
Основные свойства модуля
Вот мы и приблизились к первому свойству модуля: модуль не может быть выражен отрицательным числом.
То есть, если — число положительное, то его модуль будет равен этому же числу.
если то.
Если — отрицательное число, то его модуль равен противоположному числу:
если то
А если? Ну, конечно! Его модуль также равен:
если, то, или.
Из этого следует, что модули противоположных чисел равны, то есть:
А теперь потренируйся:
Ответы:9;3;16;8;17.
Довольно легко, правда?
А если перед тобой вот такое число:
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию. Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль :
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим:
(Забыл, что такое корень? )
Если, то какой знак имеет? Ну конечно, ! А, значит, знак модуля раскрываем, меняя знак у выражения:
Разобрался? Тогда попробуй сам:
Ответы:
Какими же ещё свойствами обладает модуль?
Во-первых, если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел. То есть:
То есть:
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
Например:
А что, если нам нужно разделить два числа (выражения) под знаком модуля? Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
при условии, что (так как на ноль делить нельзя).
Стоит запомнить ещё одно свойство модуля: модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:
Почему так? Всё очень просто! Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное. Допустим, что числа и оба положительные. Тогда левое выражение будет равно правому выражению. Рассмотрим на примере:
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
Вроде с этим свойством все ясно, рассмотрим еще парочку полезных свойств модуля.
Что если перед нами такое выражение:
Что мы можем сделать с этим выражением? Значение x нам неизвестно, но зато мы уже знаем, что, а значит. Число больше нуля, а значит можно просто записать:
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
А чему равно такое выражение:
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак? Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему . И что же получается? А вот что:
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
Ну, и почему сомнения? Действуем смело!
Во всем разобрался? Тогда вперед тренироваться на примерах!
1. Найдите значение выражения, если.
2. У каких чисел модуль равен?
3. Найдите значение выражений:
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Решение 1 :
Итак, подставим значения и в выражение Получим:
Решение 2:
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное имеют два числа: и.
Значит, значение модуля, равное имеют два числа: и.
Решение 3:
а)
б)
в)
г)
Все уловил? Тогда пора перейти к более сложному!
Попробуем упростить выражение
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу. Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «-»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
Получается, значение первого выражения под модулем.
Следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Среди примеров на модули часто встречаются уравнения где нужно найти корни модуля в модуле , то есть уравнение вида
||a*x-b|-c|=k*x+m
.
Если k=0
, то есть правая сторона равна постоянной (m)
то проще искать решение уравнения с модулями графически. Ниже приведена методика раскрытия двойных модулей на распространенных для практики примерах. Хорошо разберите алгоритм вычисления уравнений с модулями, чтобы не иметь проблем на контрольных, тестах, и просто, чтобы знать.
Пример 1. Решить уравнение модуль в модуле |3|x|-5|=-2x-2.
Решение:
Всегда начинают раскрывать уравнения с внутреннего модуля
|x|=0
x=0.
В точке x=0
уравнения с модулем разделяется на 2
.
При x |-3x-5|=-2x-2.
При x>0
или равно, раскрывая модуль получим
|3x-5|=-2x-2
.
Решим уравнение для отрицательных переменных (x
Из первого уравнения получим что решение не должно превышать (-1) , т.е.
Это ограничение полностью принадлежит области в которой решаем. Перенесем переменные и постоянные по разные стороны равенства в первой и второй системе
и найдем решение
Оба значения принадлежат промежутку что рассматривается, то есть являются корнями.
Рассмотрим уравнение с модулями при положительных переменных
|3x-5|=-2x-2.
Раскрывая модуль получим две системы уравнений
Из первого уравнения, которое является общим для двух сиcтем, получим знакомое условие
которое в пересечении с множеством, на котором ищем решение дает пустое множество (нет точек пересечения). Итак единственными корнями модуля с модулем являются значения
x=-3; x=-1,4.
Пример 2. Решить уравнение с модулем ||x-1|-2|=3x-4.
Решение:
Начнем с раскрытия внутреннего модуля
|x-1|=0
x=1.
Подмодульная функция меняет знак в единице. При меньших значениях она отрицательная, при больших — положительная. В соответствии с этим при раскрытии внутреннего модуля получим два уравнения с модулем
x |-(x-1)-2|=3x-4;
x>=1 -> |x-1-2|=3x-4.
Обязательно проверяем правую сторону уравнения с модулем, она должна быть больше нуля.
3x-4>=0 ->
x>=4/3.
Это означает, что первое из уравнений нет необхидноcти решать, поcкольку оно выпиcано для x|x-3|=3x-4 ->
x-3=3x-4
или x-3=4-3x;
4-3=3x-x
или x+3x=4+3;
2x=1
или 4x=7;
x=1/2
или x=7/4.
Получили два значения, первое из которых отвергаем, поскольку не принадлежит нужному интервалу. Окончательно уравнение имеет одно решение x=7/4.
Пример 3. Решить уравнение с модулем ||2x-5|-1|=x+3.
Решение:
Раскроем внутренний модуль
|2x-5|=0
x=5/2=2,5.
Точка x=2,5
разбивает числовую ось на два интервала. Соответственно, подмодульная функция меняет знак при переходе через 2,5.
Выпишем условие на решение с правой стороны уравнения с модулем.
x+3>=0 ->
x>=-3
.
Итак решением могут быть значения, не меньше (-3)
. Раскроем модуль для отрицательного значения внутреннего модуля
|-(2x-5)-1|=x+3;
|-2x+4|=x+3.
Этот модуль также при раскрытии даст 2 уравнения
-2x+4=x+3
или 2x-4=x+3;
2x+x=4-3
или 2x-x=3+4;
3x=1; x=1/3
или x=7
.
Значение x=7
отвергаем, поскольку мы искали решение на промежутке [-3;2,5].
Теперь раскрываем внутренний модуль для x>2,5
. Получим уравнение с одним модулем
|2x-5-1|=x+3;
|2x-6|=x+3.
При раскрытии модуля получим следующие линейные уравнения
-2x+6=x+3
или 2x-6=x+3;
2x+x=6-3
или 2x-x=3+6;
3x=3; x=1
или x=9
.
Первое значение x=1
не удовлетворяет условие x>2,5.
Так что на этом интервале имеем один корень уравнения с модулем x=9,
а всего их два (x=1/3)
.Подстановкой можно проверять правильность выполненных вычислений
Ответ:
x=1/3; x=9.
Пример 4. Найти решения двойного модуля ||3x-1|-5|=2x-3.
Решение:
Раскроем внутренний модуль уравнения
|3x-1|=0
x=1/3.
Точка x=2,5
делит числовую ось на два интервала, а заданное уравнение на два случая. Записываем условие на решение, исходя из вида уравнения с правой стороны
2x-3>=0 ->
x>=3/2=1,5.
Отсюда следует, что нас интересуют значения >=1,5
. Таким образом модульное уравнения рассматриваем на двух интервалах
,
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
Полученный модуль при раскрытии делится на 2 уравнения
-3x-4=2x-3
или 3x+4=2x-3;
2x+3x=-4+3
или 3x-2x=-3-4;
5x=-1; x=-1/5
или x=-7
.
Оба значения не попадают в промежуток
, то есть не являются решениями уравнения с модулями. Далее раскроем модуль для x>2,5
. Получим следующее уравнение
|3x-1-5|=2x-3;
|3x-6|=2x-3
.
Раскрывая модуль, получим 2 линейные уравнения
3x-6=2x-3
или –(3x-6)=2x-3;
3x-2x=-3+6
или 2x+3x=6+3;
x=3
или 5x=9; x=9/5=1,8.
Второе значение из найденных не соответствует условию x>2,5
, его мы отвергаем.
Наконец имеем один корень уравнения с модулями x=3
.
Выполняем проверку
||3*3-1|-5|=2*3-3 3=3
.
Корень уравнения с модулем вычислено правильно.
Ответ:
x=1/3; x=9.
Примеров с модулями где есть один или несколько вложенных модулей в интернете или методичке можно найти немало. Схема их вычислений ничем не отличается от приведенной выше. Для проверки знаний прошу решить следующие задачи.
Равнение на модуль в модуле:
- ||3x-3|-2|=5-2x;
- ||5x-3|-3|=3x-1;
- ||2x-7|-4|=x-2;
- ||5x-4|-8|=x+4;
- ||2x-2|-3|=1;
- ||x-2|-3|=4-x.

Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 5 является 5, модулем числа –5 тоже является 5.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |5|, |х |, |а | и т.д.
Правило :
Пояснение :
|5| = 5
Читается так: модулем числа 5 является 5.
|–5| = –(–5) = 5
Читается так: модулем числа –5 является 5.
|0| = 0
Читается так: модулем нуля является ноль.
Свойства модуля:
1) Модуль числа есть неотрицательное число: |а | ≥ 0 2) Модули противоположных чисел равны: |а | = |–а | 3) Квадрат модуля числа равен квадрату этого числа: |а | 2 = a 2 4) Модуль произведения чисел равен произведению модулей этих чисел: |а · b | = |а | · |b | 6) Модуль частного чисел равен отношению модулей этих чисел: |а : b | = |а | : |b | 7) Модуль суммы чисел меньше или равен сумме их модулей: |а + b | ≤ |а | + |b | 8) Модуль разности чисел меньше или равен сумме их модулей: |а – b | ≤ |а | + |b | 9) Модуль суммы/разности чисел больше или равен модулю разности их модулей: |а ± b | ≥ ||а | – |b || 10) Постоянный положительный множитель можно вынести за знак модуля: |m · a | = m · |а |, m >0 11) Степень числа можно вынести за знак модуля: |а k | = |а | k , если а k существует 12) Если |а | = |b |, то a = ± b |
Геометрический смысл модуля.
Модуль числа – это величина расстояния от нуля до этого числа.
Для примера возьмем снова число 5. Расстояние от 0 до 5 такое же, что и от 0 до –5 (рис.1). И когда нам важно знать только длину отрезка, то знак не имеет не только значения, но и смысла. Впрочем, не совсем верно: расстояние мы измеряем только положительными числами – или неотрицательными числами. Пусть цена деления нашей шкалы составляет 1 см. Тогда длина отрезка от нуля до 5 равна 5 см, от нуля до –5 тоже 5 см.
На практике часто расстояние отмеряется не только от нуля – точкой отсчета может быть любое число (рис.2). Но суть от этого не меняется. Запись вида |a – b| выражает расстояние между точками а и b на числовой прямой.
Пример 1 . Решить уравнение |х – 1| = 3.
Решение .
Смысл уравнения в том, что расстояние между точками х и 1 равно 3 (рис.2). Поэтому от точки 1 отсчитываем три деления влево и три деления вправо – и наглядно видим оба значения х :
х 1 = –2, х 2 = 4.
Можем и вычислить.
│х – 1 = 3
│х – 1 = –3
│х = 3 + 1
│х = –3 + 1
│х = 4
│ х = –2.
Ответ : х 1 = –2; х 2 = 4.
Пример 2 . Найти модуль выражения:
Решение .
Сначала выясним, является ли выражение положительным или отрицательным. Для этого преобразуем выражение так, чтобы оно состояло из однородных чисел. Не будем искать корень из 5 – это довольно сложно. Поступим проще: возведем в корень 3 и 10. Затем сравним величину чисел, составляющих разность:
3 = √9. Следовательно, 3√5 = √9 · √5 = √45
10 = √100.
Мы видим, что первое число меньше второго. Значит, выражение отрицательное, то есть его ответ меньше нуля:
3√5 – 10
Но согласно правилу, модулем отрицательного числа является это же число с противоположным знаком. У нас отрицательное выражение. Следовательно, надо поменять его знак на противоположный. Выражением, противоположным 3√5 – 10, является –(3√5 – 10). Раскроем в нем скобки – и получим ответ:
Раскроем в нем скобки – и получим ответ:
–(3√5 – 10) = –3√5 + 10 = 10 – 3√5.
Ответ .
Решение уравнений с модулем — презентация онлайн
1. Решение уравнений с модулем
Учителя МОУ СОШ №23Сурмалян Л.М.
Кущевский район.
2. Обучение- это ремесло, использующее бесчисленное количество маленьких трюков.
3. Задание 1. IХ-3I=5 Отметьте точки, координаты которых удовлетворяют указанному условию. Запишите их координаты.
Отметим точки, удаленные от точки А на 5 единичныхотрезков. Запишем их координаты.
4. Геометрическая интерпретация
Уравнение Iх – аI = b, где b > 0, допускает простуюгеометрическую интерпретацию.
Решить уравнение Iх – 1I = 3 – значит найти все
точки числовой оси, которые отстоят от точки с
координатой (1) на расстоянии 3.
Ответ: -2 ; 4.
5. Геометрическая интерпретация
Решить уравнение Iх + 2I = 3 – значит найти всеточки числовой оси, которые отстоят от точки
с координатой (-2) на расстоянии 3.

Ответ: -5 ; 1.
6. Задание 2. Решите уравнения
IХ – 4I = 3I х + 2 I= 7
ответ 1; 7
5; -9
7. Метод интервалов
Уравнение вида:b1I x – a1I + … + bnI x – anI = b,
где a1
решается методом интервалов.
Суть: точки a1 , a2 , …, an числовую ось делят на
непересекающиеся промежутки знакопостоянства.
Решаем уравнение на каждом промежутке;
совокупность решений на всех промежутках и
составит решение исходного уравнения.
8. Решение уравнений.
Ⅰx
-x+2-x-3=7
X=-4
Iх — 2I + Iх + 3I = 7
Ⅱ
-3
-x+2+x+3=7
решений нет
Ответ: -4; 3.
Ⅲ
x>2
x-2+x+3=7
x=3
9. Решение уравнений.
Ⅰx
-x+5+x-2=3
X
Iх — 5I — Iх — 2I = 3
Ⅱ
2
-x+5-x+2=3
x=2
Ответ: x
Ⅲ
x>5
x-5-x+2=3
решений нет
10. Геометрическая интерпретация
УравненияIx – aI + Ix – bI =c и Ix – aI — Ix – bI =c
имеют простую геометрическую интерпретацию.

Вернемся к предыдущим уравнениям.
11. Пример 1.
Решить уравнениеIх — 2I + Iх + 3I = 7 – это
значит найти все точки на числовой оси Ох, для
каждой из которых сумма расстояний до точек с
координатами (2) и (-3) равна 7. Внутри отрезка
таких точек нет, так как длина меньше семи, значит
точки вне отрезка.
Ответ: -4; 3.
12. Пример 2.
Решить уравнениеIх — 5I — Iх — 2I = 3 – это
значит найти все точки на числовой оси Ох, для
каждой из которых разность расстояний от нее до
точки с координатой (5) и расстояний от нее до
точки с координатой (2) равнялось 3. Длина отрезка
равна 3 следовательно любая точка левее (2) будет
решением уравнения.
Ответ: x
13. Пример 3.
IX — 1I + IX — 2I + IX — 3I =2Построим графики функций:
Y=IX — 1I +
y
4
0
2
4
IX — 3I и Y= 2 — IX — 2I
пересечение графиков
точка (2;2)
Ответ: 2.
6
x
14.
 Обобщение. Если в уравнении Ix – aI + Ix – bI =c,
Обобщение. Если в уравнении Ix – aI + Ix – bI =c,Iа – bI
отрезка [a;b];
а если Ia – bI=c, то отрезок [a;b] будет
решением уравнения;
если Ia – bI>c, то уравнение решений иметь
не будет.
15. Обобщение.
Если в уравнении Ix – aI — Ix – bI =c,Iа – bI = c, то при a b
a > b, x
если Ia – bI
если Ia – bI>c, то решение лежит внутри
отрезка [a;b].
16. Домашняя работа.
IX + 3I + IX — 3I =6IX — 1I + IXI = 9
IX — 3I + IX — 1I =3
IX + 6I + IX + 4I =5
IX — 1I – IX + 1I = 3
I5 + XI – Iх – 8I = 13
IX — 3I + 2IX + 1I =4
IX — 4I + IX — 2I = IX+ 1I
IX+1I +IX-2I+IX-5I=6
Алгебраическое и графическое решение уравнений, содержащих модули реферат по математике
Алгебраическое и графическое решение уравнений, содержащих модули Цель работы: хотя уравнения с модулями ученики начинают изучать уже с 6-го – 7-го класса, где они проходят самые азы уравнений с модулями. Я выбрал именно эту тему, потому что считаю, что она требует более глубокого и досканального исследования. Я хочу получить более широкие знания о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины. 1. Введение: Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово(омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, програмировании и других точных науках. В архитектуре-это исходная еденица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов. В технике-это термин, применяемый в различных облостях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п. Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению.
Я выбрал именно эту тему, потому что считаю, что она требует более глубокого и досканального исследования. Я хочу получить более широкие знания о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины. 1. Введение: Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово(омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, програмировании и других точных науках. В архитектуре-это исходная еденица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов. В технике-это термин, применяемый в различных облостях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п. Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению. 2. Понятия и определения Чтобы глубоко изучать данную тему, необходимо познакомиться с простейшими определениями, которые мне будут необходимы: Уравнение-это равенство, сродержащее переменные. Уравнение с модулем-это уравнение, содержащие переменную под знаком абсолютной величины(под знаком модуля).Например: |x|=1 Решить уравнение-это значит найти все его корни, или доказать, что корней нет. В математике модуль имеет несколько значений, но в моей исследовательской работе я возьму лишь одно: Модуль-абсолютная величина числа, равная расстоянию от начала отсчета до точки на числовой прямой. 3. Доказательство теорем Определение. Модуль числа a или абсолютная величина числа a равна a, если a больше или равно нулю и равна -a, если a меньше нуля: Из определения следует, что для любого действительного числа a, Теорема 1. Абсолютная величина действительного числа равна большему из двух чисел a или -a. Доказательство 1. Если число a положительно, то -a отрицательно, т. е. -a < 0 < a. Отсюда следует, что — a < a.
2. Понятия и определения Чтобы глубоко изучать данную тему, необходимо познакомиться с простейшими определениями, которые мне будут необходимы: Уравнение-это равенство, сродержащее переменные. Уравнение с модулем-это уравнение, содержащие переменную под знаком абсолютной величины(под знаком модуля).Например: |x|=1 Решить уравнение-это значит найти все его корни, или доказать, что корней нет. В математике модуль имеет несколько значений, но в моей исследовательской работе я возьму лишь одно: Модуль-абсолютная величина числа, равная расстоянию от начала отсчета до точки на числовой прямой. 3. Доказательство теорем Определение. Модуль числа a или абсолютная величина числа a равна a, если a больше или равно нулю и равна -a, если a меньше нуля: Из определения следует, что для любого действительного числа a, Теорема 1. Абсолютная величина действительного числа равна большему из двух чисел a или -a. Доказательство 1. Если число a положительно, то -a отрицательно, т. е. -a < 0 < a. Отсюда следует, что — a < a. Например, число 5 положительно, тогда -5 — отрицательно и -5 < 0 < 5, отсюда -5 < 5. В этом случае |a| = a, т. е. |a| совпадает с большим из двух чисел a и — a. 2. Если a отрицательно, тогда -a положительно и a < — a, т. е. большим числом является — a. По определению, в этом случае, |a| = -a — снова, равно большему из двух чисел -a и a. Следствие 1. Из теоремы следует, что |-a| = |a|. В самом деле, как , так и равны большему из чисел -a и a, а значит равны между собой. Следствие 2. Для любого действительного числа a справедливы неравенства Умножая второе равенство на -1 (при этом знак неравенства изменится на противоположный), мы получим следующие неравенства: справедливые для любого действительного числа a. Объединяя последние два неравенства в одно, получаем: Теорема 2. Абсолютная величина любого действительного числа a равна арифметическому квадратному корню из В самом деле, если то, по определению модуля числа, будем иметь С другой стороны, при значит |a| = Если a < 0, тогда |a| = -a и и в этом случае |a| = Эта теорема дает возможность при решении некоторых задач заменять |a| на Геометрически |a| означает расстояние на координатной прямой от точки, изображающей число a, до начала отсчета.
Например, число 5 положительно, тогда -5 — отрицательно и -5 < 0 < 5, отсюда -5 < 5. В этом случае |a| = a, т. е. |a| совпадает с большим из двух чисел a и — a. 2. Если a отрицательно, тогда -a положительно и a < — a, т. е. большим числом является — a. По определению, в этом случае, |a| = -a — снова, равно большему из двух чисел -a и a. Следствие 1. Из теоремы следует, что |-a| = |a|. В самом деле, как , так и равны большему из чисел -a и a, а значит равны между собой. Следствие 2. Для любого действительного числа a справедливы неравенства Умножая второе равенство на -1 (при этом знак неравенства изменится на противоположный), мы получим следующие неравенства: справедливые для любого действительного числа a. Объединяя последние два неравенства в одно, получаем: Теорема 2. Абсолютная величина любого действительного числа a равна арифметическому квадратному корню из В самом деле, если то, по определению модуля числа, будем иметь С другой стороны, при значит |a| = Если a < 0, тогда |a| = -a и и в этом случае |a| = Эта теорема дает возможность при решении некоторых задач заменять |a| на Геометрически |a| означает расстояние на координатной прямой от точки, изображающей число a, до начала отсчета. Если то на координатной прямой существует две точки a и -a, равноудаленной от нуля, модули которых равны. Если a = 0, то на координатной прямой |a| изображается точкой 0 (см. рис.) Рис 4.Способы решения уравнений, содержащих модуль. Для решения уравнений, содержащих знак абсолютной величины, мы будем основыватся на определении модуля числа и свойствах абсолютной величины числа. Мы решим несколько примеров одним и тем же способом и посмотрим, какой из способов окажется проще для решения уравнений, содержащих модуль. Пример 1. Решитм аналитически и графически уравнение |x — 2| = 3. Решение Аналитическое решение 1-й способ Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем неотрицательно, т. е. x — 2 0, тогда оно «выйдет» из под знака модуля со знаком «плюс» и уравнение примет вид: x — 2 = 3. Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: или x — 2=-3 Таким образом, получаем, либо x — 2 = 3, либо x — 2 = -3.
Если то на координатной прямой существует две точки a и -a, равноудаленной от нуля, модули которых равны. Если a = 0, то на координатной прямой |a| изображается точкой 0 (см. рис.) Рис 4.Способы решения уравнений, содержащих модуль. Для решения уравнений, содержащих знак абсолютной величины, мы будем основыватся на определении модуля числа и свойствах абсолютной величины числа. Мы решим несколько примеров одним и тем же способом и посмотрим, какой из способов окажется проще для решения уравнений, содержащих модуль. Пример 1. Решитм аналитически и графически уравнение |x — 2| = 3. Решение Аналитическое решение 1-й способ Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем неотрицательно, т. е. x — 2 0, тогда оно «выйдет» из под знака модуля со знаком «плюс» и уравнение примет вид: x — 2 = 3. Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: или x — 2=-3 Таким образом, получаем, либо x — 2 = 3, либо x — 2 = -3. Решая полученные уравнения, находим: Рис. 11 Графики не пересекаются, значит уравнение не имеет решений (см. рис. 11). Ответ: нет решений. Пример 3. Решите аналитически и графически уравнение |-x + 2| = 2x + 1. Решение: Аналитическое решение 1-й способ Прежде следует установить область допустимых значений переменной. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости делать этого, а сейчас она возникла. Дело в том, что в этом примере в левой части уравнения модуль некоторого выражения, а в правой части не число, а выражение с переменной, — именно это важное обстоятельство отличает данный пример от предыдущих. Поскольку в левой части — модуль, а в правой части, выражение, содержащее переменную, необходимо потребовать, чтобы это выражение было неотрицательным, т. е. Таким образом, область допустимых значений модуля Теперь можно рассуждать также, как и в примере 1, когда в правой части равенства находилось положительной число. Получим две смешанных системы: (1) и (2) Решим каждую систему: (1) входит в промежуток и является корнем уравнения.
Решая полученные уравнения, находим: Рис. 11 Графики не пересекаются, значит уравнение не имеет решений (см. рис. 11). Ответ: нет решений. Пример 3. Решите аналитически и графически уравнение |-x + 2| = 2x + 1. Решение: Аналитическое решение 1-й способ Прежде следует установить область допустимых значений переменной. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости делать этого, а сейчас она возникла. Дело в том, что в этом примере в левой части уравнения модуль некоторого выражения, а в правой части не число, а выражение с переменной, — именно это важное обстоятельство отличает данный пример от предыдущих. Поскольку в левой части — модуль, а в правой части, выражение, содержащее переменную, необходимо потребовать, чтобы это выражение было неотрицательным, т. е. Таким образом, область допустимых значений модуля Теперь можно рассуждать также, как и в примере 1, когда в правой части равенства находилось положительной число. Получим две смешанных системы: (1) и (2) Решим каждую систему: (1) входит в промежуток и является корнем уравнения. (2) x = -3 не входит в промежуток и не является корнем уравнения. Ответ: 2-й способ Установим, при каких значениях x модуль в левой части уравнения обращается в нуль: Получим два промежутка, на каждом из которых решим данное уравнение (см. рис. 12): Рис. 12 В результате будем иметь совокупность смешанных систем: Решая полученные системы, находим: (1) входит в промежуток и является корнем уравнения. (2) не входит в промежуток и x=-3 не является корнем уравнения Ответ: 4.1.Решение при помощи зависимостей между числами a и b, их модулями и квадратами этих чисел. Помимо приведенных мною выше способов существует определенная равносильность, между числами и модулями данных чисел, а также между квадратами и модулями данных чисел: |a|=|b| F 0D B a=b или a=-b a2=b2 F 0D B a=b или a=-b (1) Отсюда в свою очередь получим, что F 0 D B|a|=|b| a2=b2 (2) Пример 4. Решим уравнение |x + 1|=|2x – 5| двумя различными способами. 1.Учитывая соотношение (1), получим: x + 1=2x – 5 или x + 1=-2x + 5 x – 2x=-5 – 1 x + 2x=5 – 1 -x=-6|(:1) 3x=4 x=6 x=11/3 Корень первого уравнения x=6, корень второго уравнения x=11/3 Таким образом корни исходного уравнения x1=6, x2=11/3 2.
(2) x = -3 не входит в промежуток и не является корнем уравнения. Ответ: 2-й способ Установим, при каких значениях x модуль в левой части уравнения обращается в нуль: Получим два промежутка, на каждом из которых решим данное уравнение (см. рис. 12): Рис. 12 В результате будем иметь совокупность смешанных систем: Решая полученные системы, находим: (1) входит в промежуток и является корнем уравнения. (2) не входит в промежуток и x=-3 не является корнем уравнения Ответ: 4.1.Решение при помощи зависимостей между числами a и b, их модулями и квадратами этих чисел. Помимо приведенных мною выше способов существует определенная равносильность, между числами и модулями данных чисел, а также между квадратами и модулями данных чисел: |a|=|b| F 0D B a=b или a=-b a2=b2 F 0D B a=b или a=-b (1) Отсюда в свою очередь получим, что F 0 D B|a|=|b| a2=b2 (2) Пример 4. Решим уравнение |x + 1|=|2x – 5| двумя различными способами. 1.Учитывая соотношение (1), получим: x + 1=2x – 5 или x + 1=-2x + 5 x – 2x=-5 – 1 x + 2x=5 – 1 -x=-6|(:1) 3x=4 x=6 x=11/3 Корень первого уравнения x=6, корень второго уравнения x=11/3 Таким образом корни исходного уравнения x1=6, x2=11/3 2. В силу соотношения (2), получим (x + 1)2=(2x – 5)2, или x2 + 2x + 1=4×2 – 20x + 25 x2 – 4×2 +2x+1 + 20x – 25=0 -3×2 + 22x – 24=0|(:-1) 3×2 – 22x + 24=0 F 0 B 4 F 0 D ED/4=121-3 24=121 – 72=49>0 уравнение имеет 2 различных корня. x1=(11 – 7 )/3=11/3 x2=(11 + 7 )/3=6 Как показывает решение, корнями данного уравнения также являются числа 11/3 и 6 Ответ: x1=6, x2=11/3 Пример 5. Решим уравнение (2x + 3)2=(x – 1)2. Учитывая соотношение (2), получим, что |2x + 3|=|x – 1|, откуда по образцу предыдущего примера(и по соотношению (1)): 2х + 3=х – 1 или 2х + 3=-х + 1 2х – х=-1 – 3 2х+ х=1 – 3 х=-4 х=-0,(6) Таким образом корнями уравнения являются х1=-4, и х2=-0,(6) Ответ: х1=-4, х2=0,(6) Пример 6. Решим уравнение |x – 6|=|x2 – 5x + 9| Пользуясь соотношением (1), получим: х – 6=х2 – 5х + 9 или х – 6 = -(х2 – 5х + 9) -х2 + 5х + х – 6 – 9=0 |(-1) x – 6=-x2 + 5x — 9 x2 — 6x + 15=0 x2 – 4x + 3=0 F 0 2 A F 0 D E F 0 2 A F 0 D ED=36 – 4 15=36 – 60= -24 <0 D=16 – 4 3=4 >0 2 р.к. F 0 D E корней нет.
В силу соотношения (2), получим (x + 1)2=(2x – 5)2, или x2 + 2x + 1=4×2 – 20x + 25 x2 – 4×2 +2x+1 + 20x – 25=0 -3×2 + 22x – 24=0|(:-1) 3×2 – 22x + 24=0 F 0 B 4 F 0 D ED/4=121-3 24=121 – 72=49>0 уравнение имеет 2 различных корня. x1=(11 – 7 )/3=11/3 x2=(11 + 7 )/3=6 Как показывает решение, корнями данного уравнения также являются числа 11/3 и 6 Ответ: x1=6, x2=11/3 Пример 5. Решим уравнение (2x + 3)2=(x – 1)2. Учитывая соотношение (2), получим, что |2x + 3|=|x – 1|, откуда по образцу предыдущего примера(и по соотношению (1)): 2х + 3=х – 1 или 2х + 3=-х + 1 2х – х=-1 – 3 2х+ х=1 – 3 х=-4 х=-0,(6) Таким образом корнями уравнения являются х1=-4, и х2=-0,(6) Ответ: х1=-4, х2=0,(6) Пример 6. Решим уравнение |x – 6|=|x2 – 5x + 9| Пользуясь соотношением (1), получим: х – 6=х2 – 5х + 9 или х – 6 = -(х2 – 5х + 9) -х2 + 5х + х – 6 – 9=0 |(-1) x – 6=-x2 + 5x — 9 x2 — 6x + 15=0 x2 – 4x + 3=0 F 0 2 A F 0 D E F 0 2 A F 0 D ED=36 – 4 15=36 – 60= -24 <0 D=16 – 4 3=4 >0 2 р.к. F 0 D E корней нет. x1=(4- 2 ) /2=1 x2=(4 + 2 ) /2=3 F 0 2 A F 0 2 AПроверка: |1 – 6|=|12 – 5 1 + 9| |3 – 6|=|32 – 5 3 + 9| 5 = 5(И) 3 = |9 – 15 + 9| 3 = 3(И) Ответ: x1=1; x2=3 4.2.Использование геометрической интерпритации модуля для решения уравнений. Геометрический смысл модуля разности величин-это расстояние между ними. Например, геометрический смысл выражения |x – a | -длина отрезка координатной оси, соединяющей точки с абсцисами а и х . Перевод алгеб-раической задачи на геометрический язык часто позволяет избежать громоздких решений. Пример7. Решим уравнение |x – 1| + |x – 2|=1 с использованием геометрической интерпритации модуля. Будем рассуждать следующим образом: исходя из геометрической интерпри-тации модуля, левая часть уравнения представляет собой сумму расстояний от некторой точки абсцисс х до двух фиксированных точек с абсциссами 1 и 2. Тогда очевидно, что все точки с абсциссами из отрезка [1; 2] обладают требуемым свойством, а точки, расположенные вне этого отрезка- нет. Отсюда ответ: множеством решений уравнения является отрезок [1; 2].
x1=(4- 2 ) /2=1 x2=(4 + 2 ) /2=3 F 0 2 A F 0 2 AПроверка: |1 – 6|=|12 – 5 1 + 9| |3 – 6|=|32 – 5 3 + 9| 5 = 5(И) 3 = |9 – 15 + 9| 3 = 3(И) Ответ: x1=1; x2=3 4.2.Использование геометрической интерпритации модуля для решения уравнений. Геометрический смысл модуля разности величин-это расстояние между ними. Например, геометрический смысл выражения |x – a | -длина отрезка координатной оси, соединяющей точки с абсцисами а и х . Перевод алгеб-раической задачи на геометрический язык часто позволяет избежать громоздких решений. Пример7. Решим уравнение |x – 1| + |x – 2|=1 с использованием геометрической интерпритации модуля. Будем рассуждать следующим образом: исходя из геометрической интерпри-тации модуля, левая часть уравнения представляет собой сумму расстояний от некторой точки абсцисс х до двух фиксированных точек с абсциссами 1 и 2. Тогда очевидно, что все точки с абсциссами из отрезка [1; 2] обладают требуемым свойством, а точки, расположенные вне этого отрезка- нет. Отсюда ответ: множеством решений уравнения является отрезок [1; 2]. F 0 C EОтвет: х [1; 2] Пример8. Решим уравнение |x – 1| — |x – 2|=1 1 с использованием геометрической интерпритации модуля. Будем рассуждать аналогично предыдущему примеру, при этом получим, что разность расстояний до точек с абсциссами 1 и 2 равна единице только для точек, расположенных на координатной оси правее числа 2. Следовательно решением данного уравнения будет являтся не отрезок, заключенный между точками 1 и 2, а луч, выходящий из точки 2, и направленный в положительном направлении оси ОХ. F 0 C E F 0 A 5Ответ: х [2; + ) Обобщением вышеприведенных уравнений являются следующие равносильные переходы: |x – a| + |x – b|=b – a, где b F 0B 3 a F 0 D B a F 0 A 3 x F 0 A 3 b |x – a| — |x – b|=b – a, где b F 0B 3 a F 0 D B x F 0 B 3 b 4.3. Графики простейших функций, содержащих знак абсолютной величины Под простейшими функциями понимают алгебраическую сумму модулей линейных выражений. Сформулируем утверждение, позволяющее строить графики таких функций, не раскрывая модули ( что особенно важно, когда модулей достаточно много ): «Алгебраическая сумма модулей n линейных выражений представляет собой кусочно- линейную функцию, график которой состоит из n +1 прямолинейного отрезка.
F 0 C EОтвет: х [1; 2] Пример8. Решим уравнение |x – 1| — |x – 2|=1 1 с использованием геометрической интерпритации модуля. Будем рассуждать аналогично предыдущему примеру, при этом получим, что разность расстояний до точек с абсциссами 1 и 2 равна единице только для точек, расположенных на координатной оси правее числа 2. Следовательно решением данного уравнения будет являтся не отрезок, заключенный между точками 1 и 2, а луч, выходящий из точки 2, и направленный в положительном направлении оси ОХ. F 0 C E F 0 A 5Ответ: х [2; + ) Обобщением вышеприведенных уравнений являются следующие равносильные переходы: |x – a| + |x – b|=b – a, где b F 0B 3 a F 0 D B a F 0 A 3 x F 0 A 3 b |x – a| — |x – b|=b – a, где b F 0B 3 a F 0 D B x F 0 B 3 b 4.3. Графики простейших функций, содержащих знак абсолютной величины Под простейшими функциями понимают алгебраическую сумму модулей линейных выражений. Сформулируем утверждение, позволяющее строить графики таких функций, не раскрывая модули ( что особенно важно, когда модулей достаточно много ): «Алгебраическая сумма модулей n линейных выражений представляет собой кусочно- линейную функцию, график которой состоит из n +1 прямолинейного отрезка. Тогда график может быть построен по n +2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна — произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя — с абсциссой, большей большего из корней. Например: 1)f(x)=|x — 1| Вычисляя функции в точках 1, 0 и 2, получаем график, состоящий из двух отрезков(рис.1) Уравнение равносильно системе Ответ: Пример12.Решить уравнение х2 — 4х +|x — 3| +3=0 Для освобождения от знака абсолютной величины разобьем числовую прямую на две области и будем искать решения исходного уравнения в каждой из этих областей отдельно: F 0 B 3__________x 3__________________|____________x<3_________________ |x – 3|=x – 3 |x – 3|=-x + 3 x2 — 4x + x – 3 + 3=0 x2 – 4x – x + 3 + 3=0 x2 – 3x=0 x2 – 5x + 6=0 x(x – 3) x1=0 или F 02 A F 0 D Ex2=3 D=25 – 4 6=1> 0 два различ. корня x=0 –посторонний корень, так как x1= (5- 1 )/2 =2 не удовлетворяет промежутку. x2=(5 + 1)/2=3 x=3 — посторонний корень, так как не удовлетворяет промежутку.
Тогда график может быть построен по n +2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна — произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя — с абсциссой, большей большего из корней. Например: 1)f(x)=|x — 1| Вычисляя функции в точках 1, 0 и 2, получаем график, состоящий из двух отрезков(рис.1) Уравнение равносильно системе Ответ: Пример12.Решить уравнение х2 — 4х +|x — 3| +3=0 Для освобождения от знака абсолютной величины разобьем числовую прямую на две области и будем искать решения исходного уравнения в каждой из этих областей отдельно: F 0 B 3__________x 3__________________|____________x<3_________________ |x – 3|=x – 3 |x – 3|=-x + 3 x2 — 4x + x – 3 + 3=0 x2 – 4x – x + 3 + 3=0 x2 – 3x=0 x2 – 5x + 6=0 x(x – 3) x1=0 или F 02 A F 0 D Ex2=3 D=25 – 4 6=1> 0 два различ. корня x=0 –посторонний корень, так как x1= (5- 1 )/2 =2 не удовлетворяет промежутку. x2=(5 + 1)/2=3 x=3 — посторонний корень, так как не удовлетворяет промежутку. Значит, исходное уравнение имеет два решения х1=2 и х2=3 Ответ: х1=2, х2=3 Пример13. Решить уравнение | 2x + 8 | – | x – 5 | = 12. Решение. Раскрытие пары модулей приводит к трем случаям (без F 0A 3 F 0 2 0 F 0 B 3x + 4 0, x – 5 0). Ответ: {– 25; 3}. Пример 14. Решить уравнение . Решение: Напишем равносильную смешанную систему: Ответ: х=-4 Пример 15 Решить графически уравнение |1 – x| — |2x + 3| + x + 4=0 Решение: Представим уравнение в виде |1 – x| — |2x + 3| =-х – 4 Построим два графика у=|1 – x| — |2x + 3| и у=-х – 4 1) у=|1 – x| — |2x + 3| Критические точки: х=1, х=-1.5 (1 – х) ________+________|______ +____________|_____-______ > (2х +3) — -1.5 + 1 + а) х< -1.5, (1– x)>0 и (2х + 3)<0, т.е функция примет вид у=1 – х + 2х + 3, у=х + 4 –графиком является прямая, проходящая через две точки (0; 4), (-4; 0) F 0 2 0 F 0 A 3б)При -1.5 x <1, (1 – х)>0 и (2x +3 F 0 B 3) 0, т.е функция примет вид у=1 – х – 2х -3, у=-3х – 2 –графиком является прямая, проходящая через две точки (0; -2), (-1; 1).
Значит, исходное уравнение имеет два решения х1=2 и х2=3 Ответ: х1=2, х2=3 Пример13. Решить уравнение | 2x + 8 | – | x – 5 | = 12. Решение. Раскрытие пары модулей приводит к трем случаям (без F 0A 3 F 0 2 0 F 0 B 3x + 4 0, x – 5 0). Ответ: {– 25; 3}. Пример 14. Решить уравнение . Решение: Напишем равносильную смешанную систему: Ответ: х=-4 Пример 15 Решить графически уравнение |1 – x| — |2x + 3| + x + 4=0 Решение: Представим уравнение в виде |1 – x| — |2x + 3| =-х – 4 Построим два графика у=|1 – x| — |2x + 3| и у=-х – 4 1) у=|1 – x| — |2x + 3| Критические точки: х=1, х=-1.5 (1 – х) ________+________|______ +____________|_____-______ > (2х +3) — -1.5 + 1 + а) х< -1.5, (1– x)>0 и (2х + 3)<0, т.е функция примет вид у=1 – х + 2х + 3, у=х + 4 –графиком является прямая, проходящая через две точки (0; 4), (-4; 0) F 0 2 0 F 0 A 3б)При -1.5 x <1, (1 – х)>0 и (2x +3 F 0 B 3) 0, т.е функция примет вид у=1 – х – 2х -3, у=-3х – 2 –графиком является прямая, проходящая через две точки (0; -2), (-1; 1). F 0 2 0 F 0 B 3 F 0 2 0 F 0 A 3в)При х 1, (1 – х) 0 и (2х + 3)>0, т.е. функция примет вид у= -1 + х – 2х – 3, у= -х – 4 –графиком является прямая, проходящая через две точки (0; -4), (-4; 0). График функции у= — х – 4 совпадает с графиком у=|1 – x| — |2x + 3|, F 02 0 F 0 B 3при х 1, F 0 2 0 F 0 B 3Поэтому решением являются все х 1 и х= -4 F 0 2 0 F 0 B 3Ответ: х 1,х= -4 Аналитическое решение. y=|1 – x| — |2x + 3| y=-x – 4 Построим числовую прямую так, чтобы по определению модуля знак абсолютной величины числа можно будет снять. Для этого найдем критические точки: 1- х=0 и 2х – 3 =0, х=1 х=-1,5 F 0 A 3___________х<-1,5_____|_______-1,5 F 0 B 3x <1_____|_________x 1__________ |1 – x|=1 – x |1 – x|=1 – x |1 – x|=-1 + x |2x + 3|=-2x – 3 |2x + 3|=2x + 3 |2x + 3|=2x + 3 1 – x + 2x + 3 + x + 4=0 1 – x – 2x – 3 + x +4=0 -1 + x – 2x – 3 + x + 4=0 2x=-8 -2x=-2 0x=0 F 0 D Ex=-4 x=1 x – любое число. F 0 D EУдовлетворяет данному Не удовлетворяет F 0 C E F 0 A 5x [1; + ) F 0 D E F 0 D Eпромежутку является данному промежут- F 0 B 3x 1 корень уравнения F 0 D Eкорнем уравнения.
F 0 2 0 F 0 B 3 F 0 2 0 F 0 A 3в)При х 1, (1 – х) 0 и (2х + 3)>0, т.е. функция примет вид у= -1 + х – 2х – 3, у= -х – 4 –графиком является прямая, проходящая через две точки (0; -4), (-4; 0). График функции у= — х – 4 совпадает с графиком у=|1 – x| — |2x + 3|, F 02 0 F 0 B 3при х 1, F 0 2 0 F 0 B 3Поэтому решением являются все х 1 и х= -4 F 0 2 0 F 0 B 3Ответ: х 1,х= -4 Аналитическое решение. y=|1 – x| — |2x + 3| y=-x – 4 Построим числовую прямую так, чтобы по определению модуля знак абсолютной величины числа можно будет снять. Для этого найдем критические точки: 1- х=0 и 2х – 3 =0, х=1 х=-1,5 F 0 A 3___________х<-1,5_____|_______-1,5 F 0 B 3x <1_____|_________x 1__________ |1 – x|=1 – x |1 – x|=1 – x |1 – x|=-1 + x |2x + 3|=-2x – 3 |2x + 3|=2x + 3 |2x + 3|=2x + 3 1 – x + 2x + 3 + x + 4=0 1 – x – 2x – 3 + x +4=0 -1 + x – 2x – 3 + x + 4=0 2x=-8 -2x=-2 0x=0 F 0 D Ex=-4 x=1 x – любое число. F 0 D EУдовлетворяет данному Не удовлетворяет F 0 C E F 0 A 5x [1; + ) F 0 D E F 0 D Eпромежутку является данному промежут- F 0 B 3x 1 корень уравнения F 0 D Eкорнем уравнения. ку не является кор- нем уравнения. Объеденив данные промежутки, получим, что решением данного уравнения являются: x=-4 и F 0B 3x 1 Ответ: F 0B 3x=-4, x 1
ку не является кор- нем уравнения. Объеденив данные промежутки, получим, что решением данного уравнения являются: x=-4 и F 0B 3x 1 Ответ: F 0B 3x=-4, x 1
Решение уравнений и неравенств содержащие модули
Управление образования администрации г. Чебоксары
Муниципальное образовательное учреждение
«Средняя общеобразовательная школа №55»
Решение уравнений и неравенств, содержащие модули.
Учитель математики
Морозова Галина Сергеевна.
.
Чебоксары 2010 г
Пояснительная записка.
Существенной характеристикой числа, как в действительной, так и в комплексной области является понятие его абсолютной величины (модуля).
Это понятие имеет широкое распространение
в различных отделах физико-математических
наук. Так, в математическом анализе одно
из первых и фундаментальных понятий –
понятие предела – в своем определении
содержит понятие абсолютной величины
числа. В теории приближенных вычислений
первым, важнейшим понятием, является
понятие абсолютной погрешности
приближенного числа. В механике основным
первоначальным понятием является
понятие вектора, важнейшей характеристикой
которого служит его абсолютная величина
(модуль).
В теории приближенных вычислений
первым, важнейшим понятием, является
понятие абсолютной погрешности
приближенного числа. В механике основным
первоначальным понятием является
понятие вектора, важнейшей характеристикой
которого служит его абсолютная величина
(модуль).
С понятием модуля (абсолютной величины) действительного числа учащиеся знакомятся еще в 6 классе. Однако в программах общеобразовательных школ и соответствующих учебниках в дальнейшем это понятие ни в теоретических материалах, ни в задачах и упражнениях почти не применяется. Возможность решения уравнений и неравенств, содержащих неизвестные под знаком модуля, имеют учащиеся классов или школ с углубленным изучением математики и некоторых других альтернативных школ, однако и в учебниках для этих школ задач подобного рода до обидного мало. В то же время на ЕГЭ задачи с модулем предлагаются все чаще и чаще.
Несмотря на кажущуюся простоту определения
модуля числа, решение уравнений и
неравенств, содержащих неизвестные под
знаком модуля, вызывает у учащихся
определенные трудности. По-видимому,
они связаны с тем, что решение задач
подобного рода предполагает элементарные
навыки исследования, логического
мышления, заключающиеся в переборе
различных возможных случаев, так как в
подавляющем большинстве задач одно
уравнение или неравенство с модулем
равносильно совокупности или системе
нескольких уравнений и неравенств,
освобожденных от знака модуля.
По-видимому,
они связаны с тем, что решение задач
подобного рода предполагает элементарные
навыки исследования, логического
мышления, заключающиеся в переборе
различных возможных случаев, так как в
подавляющем большинстве задач одно
уравнение или неравенство с модулем
равносильно совокупности или системе
нескольких уравнений и неравенств,
освобожденных от знака модуля.
Цели курса:
классификации способов решений уравнений и неравенств, содержащих неизвестную под знаком модуля;
систематизации и обобщении различной информации о модуле и решении задач с модулем, содержащихся в многочисленной литературе;
рассмотрение некоторых методов при решении задач с модулем.
Задачами данной методической разработки стали:
ввести определение модуля и показать геометрический смысл модуля; рассмотреть свойства модуля;
рассмотреть решения основных видов уравнений, содержащих переменную под знаком модуля;
показать решения основных видов неравенств, содержащих переменную под знаком модуля;
расширить сферу математических знаний, общекультурный кругозор у учащихся.

Методические рекомендации.
Разработанный курс может быть использован учителями математики при подготовке к математическим олимпиадам, ЕГЭ, централизованному тестированию и вступительным экзаменам в ВУЗ.
Для реализации целей и задач этого курса предполагаются следующие формы занятий: лекции учителя, доклады учеников, самостоятельная работа по разборке решенных уравнений и неравенств.
Успешность усвоения курса определяется преобладанием самостоятельной творческой работы ученика в содружестве с учителем.
Содержание
Введение
Определение модуля. Свойства модуля.
Определение модуля.
Геометрический смысл модуля.
Формула расстояния между двумя точками числовой прямой.

Свойства модуля.
Решение уравнений с модулем.
Уравнения вида |f(x)|=a.
Уравнения вида |f(x)|=|g(x)|
Уравнения вида |f(x)|= g(x)
Уравнения вида .
Решение неравенств с модулем.
Неравенства вида |f(x)|a
Неравенства вида
Неравенства вида и .
Метод интервалов.
План урока по теме «Решение уравнений, содержащих знак абсолютной величины (модуля)»(8 класс)
Примерные тесты для подготовки к ЕГЭ.
Заключение.
Литература
Урок по теме:
«Решение уравнений, содержащих знак абсолютной величины (модуля)»
(9 класс)
Цель урока: Обобщение и
систематизация знаний учащихся , развитие
навыка решения уравнений и логического
мышления учащихся.
Оборудование урока: таблица “Модуль”, плакаты с изображением уравнений содержащих переменную под знаком модуля и с графическим способом решения уравнений.
План урока
Вступительное слово учителя.
Некоторые способы решения уравнений, содержащих переменную под знаком модуля. (Сообщения учащихся).
а)Метод интервалов.
б)Графический метод.
в)Раскрытие модуля по определению
Решение уравнения, в котором под знаком модуля находится выражение, тоже содержащее модуль. (Сообщение учителя).
Подведение итогов урока.
Ход урока.
Вступительное слово учителя. Сообщается план семинара и почему именно эта тема выбрана.
Вступительное слово учителя.
Математика за 2500 лет своего существования
накопила богатейший инструмент для
исследования окружающего нас мира. Однако, как заметил один из ведущих
математиков, кораблестроителей академик
Крылов, человек обращается к математике
не затем, чтобы любоваться неисчислимыми
сокровищами, ему, прежде всего, необходимо
ознакомиться со столетними испытанными
инструментами, научится ими искусно
владеть.
Однако, как заметил один из ведущих
математиков, кораблестроителей академик
Крылов, человек обращается к математике
не затем, чтобы любоваться неисчислимыми
сокровищами, ему, прежде всего, необходимо
ознакомиться со столетними испытанными
инструментами, научится ими искусно
владеть.
Существенной характеристикой действительного числа является абсолютная величина. Это понятие имеет широкое распространение в различных отделах физико-математических и технических наук. Так в математическом анализе одно из первых и фундаментальных понятий – понятие предела – в своем определении содержит понятие абсолютной величины числа. В теории приближенных вычислений первым важнейшим понятием является понятие абсолютной погрешности приближенного числа. В механике основным первоначальным понятием является понятие вектора, важнейшей характеристикой которого служит его абсолютная величина.
При решении уравнений, содержащих
переменную под знаком модуля, чаще всего
применяются следующих методы: 1) раскрытие
модуля по определению, 2) возведение
обоих частей в квадрат, 3) метод разбиения
на промежутки, 4) графический метод.
Сообщение №1 «Некоторые способы решения уравнений с модулями». Напомним сначала определение числа x:
Приведем также основные свойства модуля, часто применяемых в решение задач:
|ab|=|a||b|;
|a|n=|an|;
|a|=0, если a=0
Поговорим о некоторых способах решения задач с модулем. Среди них один занимает самое главное место, так как он является самым общим, однако, иногда не самым рациональным. Заключается он в следующем.
Метод интервалов.
Предположим, что имеется уравнение или неравенство, в которое входят один или несколько модулей.
Первым делом нужно отделить критические точки. Под этим мы понимаем все значения переменной, при которых один из модулей обращается в нуль.

Нанесите полученное множество значений на ось данной переменной, например Ox. Прямая разобьется на несколько конечных и два бесконечных интервала. Каждый интервал соответствует знакопостоянству подмодульных выражений.
Рассмотреть столько случаев решения, сколько получилось интервалов. При этом освобождаться от модулей нужно, проверяя знак подмодульного выражения. Т.е. изменять его на противоположный, если выражение отрицательно и оставлять его прежним в противном случае. Важно не забыть, что частным ответом в каждом из полученных случаев является пересечение интервала и найденного решения.
Объединить полученные в каждом интервале ответы в один.
Рассмотрим подробнее этот метод на следующем примере.
|x + 2| + |x — 3| = 5
Нанесем
на числовую прямую значение x, при котором
x + 2 = 0 и значение x, при котором x – 3 = 0. Числовая прямая разобьется на промежутки
(-;
-2), [-2; 3], (3; +).
Числовая прямая разобьется на промежутки
(-;
-2), [-2; 3], (3; +).
Решим уравнений на каждом из этих интервалов.
х | (-; -2) | [-2;3] | (3; +) |
х+2 | — | + — + | + |
x-3 | — | — — | + |
Рассмотрим первый промежуток, чтобы
определить знак подмодульного выражения,
возьмем контрольную точку x = 3, подставим
ее в наше уравнение –3 + 2 < 0 и во второе
-3 – 3 < 0. Аналогично рассмотрим знаки
подмодульных выражений на втором и
третьем промежутках.
Решим уравнение на каждом из этих промежутков, т.е. решим равносильную уравнению совокупность смешанных систем:
1) –х –
2 – х + 3 = 5 х =
–2 Не может быть корнем. | 2) х + 2
– х + 3 = 5 3) х + 2 + х – 3 = 5, x = 3 |
Вывод: Решение второй системы является объединением решений 3-х систем.
Ответ: x принадлежит [-2;3] или все значения сегмента [-2;3].
Сообщение №2 Графический метод.
Этот способ уже не столь универсален,
но им нельзя пренебрегать, если он
применим. Часто уравнение или неравенства
с модулем содержит только линейные
выражения относительно переменной. В
этом случае существует очень простой
рецепт построения графиков с модулями,
что часто существенно облегчает решение
задачи. Он базируется на простом замечании
– графики таких выражений состоят из
кусков линий, т.е. являются ломаными.
Метод состоит в следующем:
Он базируется на простом замечании
– графики таких выражений состоят из
кусков линий, т.е. являются ломаными.
Метод состоит в следующем:
Найти, как и раньше, все критические точки и нанести их на ось абсцисс. Найти непосредственно значения заданной функции в этих точках (это удобно делать с помощью отдельной таблицы) и нанести их на координатную плоскость.
В каждой из конечных интервалов, получаемых после разбиения критическими точками, график является прямой и может быть простым соединением нанесенных в предыдущем пункте точек на координатной плоскости.
Выбрать две удобные для вычисления точки, расположенные в левом и правом бесконечных интервалах и аналогично п.1 найти значения функций в них. Окончательно, соединяя построенный участок графика с оставшимися двумя точками, получим требуемый график.
Проиллюстрируем
это на примере построения графика
|x+2|+|x-3|=5. Построим график функции
Построим график функции
у = |x + 2| + |x – 3| и y = 5
х + 2 = 0, x –3 = 0
x1 = –2 x2 = 3
Наносим на ось корни линейных функций стоящих под знаком модуля. На каждом из трех промежутков знаки этих линейных функций постоянны и мы можем избавиться от знака модуля.
если x
< – 2, то y =-(x + 2) – (x – 3) = –2x + 1
если –2
< x < 3, то y = +(x + 2) – (x – 3) = x + 2 – x + 3 =
5
если x > 3, то y = +(x + 2) + (x – 3) = 2x – 1
При построении графика провести вертикальные прямые x = –2 и x = 3, которые разобьют плоскость на три части. В левой части надо провести прямую y=–2x + 1, в центральной полосе y = 5 и в правой y = 2x – 1: (для контроля надо следить, чтобы ломаная была непрерывной, т.е. чтобы значения в разделяющих точках изломах, вычисленные по соседним формулам совпали). В нашем случае при x — 2 значение функции y = –2x + 1 совпадает со значением y = 5, точно так же при x=3 совпадают значения функции y = 5 и y=2x – 1
Строим график 1) y = –2x + 1 | 2) у = 5 | 3) y = 2x – 1 |
Графики и
y = 5 пересекаются на промежутке, если .
Ответ
Сообщение №3 Раскрытие модуля по определению .
Решить уравнение
Решение.
.
Проверим справедливость неравенства для найденных значений х:
верное неравенство, значит 0 – корень данного уравнения.
неверное неравенство, значит — посторонний корень.
верное неравенство, значит – корень данного уравнения
Ответ: ; 0.
Решение уравнения, в котором под знаком модуля находится выражение содержащее модуль.
Решить уравнение
Решение.
.
Ответ: .
Итоги урока. Домашнее задание.
Всем учащимся даются задания для самостоятельного решения:
Записать в тетради решения уравнений вида:
1. |2x-3|=11
2. |2x-5|=5-4x
3. |4x-3|=4x-3
4. |x+2|+|x-3|=5
5. |x+1|-|x-2|+|3x+6|=5
6. 2u+v=7, |u-v|=2
7. 3|x+1|+2|y-2|=20, x+2y=4
8. x+1|+|y+1|=8, 2x-|y+1|=5
9. |x+1|-|x|+3|x-1|-2|x-2|=x+2
10. Найти все значения, при которых система уравнения ах+(а–1)y = 2+4а 3|x|+2у=а-5.
Имеет единственное решение. Найти это решение.
Примерные тесты для подготовки к ЕГЭ.
Тест №1
Тест №2
Заключение.
В практике преподавания математики в средней школе и других средних учебных заведениях понятие абсолютной величины числа (модуля числа) встречаются неоднократно.
В VI классе, в курсе приближенных вычислений, при уяснении понятия абсолютной погрешности приближенного числа формируется понятие абсолютной величины числа. Во втором полугодии VI класса вводится определение абсолютной величины числа, с помощью этого понятия формулируются правила действий над рациональными числами.
В VIII классе при рассмотрении свойств арифметического квадратного корня находит свое новое приложение понятие абсолютной величины числа.
В VIII классе при рассмотрении свойств арифметического квадратного корня находит свое новое приложение понятие абсолютной величины числа. Например: , и другие.
В IX классе в теме “Степень с рациональным
показателем” рассматриваются свойства
корней n – й степени, где также используется
понятие абсолютной величины числа; так,
например, , если m – нечетное.
В X классе понятие абсолютной величины числа встречается при изучении предела функций, при исследование функций на ограниченность и при изучение комплексных чисел, где понятие абсолютной величины получает свое дальнейшее развитие в более общей числовой области.
Таким образом, во всех классах, в соответствии с учебной программой, следует включать и рассматривать упражнения, содержащие знак абсолютной величины числа.
В VI классе можно решать уравнения вида:k · |x| + b = k1 · |x| + b1 и |k·x+b|=a.
В VII классе имеется возможность рассматривать решения уравнений вида |k·|x|+b|=c; |kx+b|=ax+c и т.п., систем уравнений вида:|2x-y|=1, |x+2y|=2x-4, а так же построение графиков функций вида: y=k·|x|+b; y=|k·x+b|; y=|k·|x|+b|; y=1/|x| и др.
В VIII классе приложения понятия абсолютной
величины распространяются на квадратные
уравнения, график квадратного трехчлена
и др. Можно решать уравнения вида:
Можно решать уравнения вида:
ax2+b·|x|+c=0;
Можно рассмотреть построение графиков функций:
y=ax2+b·|x|+c; y=|ax2+bx+c|; y=|ax2+b·|x|+c|;
; ;
y=||||x|-2|+1|-3| и др.
При построении графиков целесообразно пользоваться методом преобразования графиков (Параллельный перенос, симметрия и др.).
В IX-X классе решение уравнений, систем уравнений, неравенств и построение графиков функций, аналитические выражения которых содержат знак абсолютной величины, рассматриваются для трансцендентных функций и уравнений, изучаемых в школе.
Таким образом, поставленные и решённые задачи в данной методической разработке имеют большое значение при составлении промежуточного контроля и при подготовке к ЕГЭ.
Литература
Гайдуков И.
 И. Абсолютная величина. М., Просвещение,
1966.
И. Абсолютная величина. М., Просвещение,
1966.Гусев В.А. и др. 300 задач. М., Просвещение, 1993.
Литвиненко В.Н, Мордкович А.Г. Практикум по решению задач. Алгебра. Тригонометрия. М., Просвещение, 1991.
Сидоров Н.Н. Модуль числа. Уравнения и неравенства: Учебное пособие. Чебоксары:1998.
Как решать линейные сравнения
Числа конгруэнтны, если они обладают тем свойством, что разница между ними полностью делится на число (целое число). Число называется модулем, и утверждение рассматривается как конгруэнтное модулю. Математически это можно выразить как b = c (mod m)
.Как правило, линейное сравнение — это задача нахождения целого числа x, удовлетворяющего уравнению ax = b (mod m). Таким образом, линейное сравнение — это сравнение в виде ax = b (mod m), где x – неизвестное целое число.В линейном сравнении, где x0 – решение, все целые числа x1 равны x1 = x0 (mod m).
Различные методы решения линейных сравнений
Вы можете использовать несколько методов для решения линейных сравнений. Наиболее часто используемые методы – метод алгоритма Евклида и метод Эйлера.
Наиболее часто используемые методы – метод алгоритма Евклида и метод Эйлера.
Пример: Решить линейное сравнение ax = b (mod m)
Решение: ax = b (mod m) _____ (1)
a, b и m — целые числа, такие что m > 0 и c = (a, m).
Если c не может делить b, линейное сравнение ax = b (mod m) не имеет решения.
Если c может делить b, сравнение ax = b(mod M) имеет неконгруэнтное решение по модулю m.
Как уже упоминалось, ax = b (mod m) равно ax — my = b. Если мы применим теорему 19, вы поймете, что c не может делить b; таким образом, невозможно получить решение уравнения ax — my = b.
В качестве альтернативы, если c может делить b, это означает, что существует несколько решений, переменная x которых обозначается как x = x0 + (m/c)t _____ (2)
Таким образом, значения x становятся решением сравнения ax = b (mod m).Теперь вы можете легко найти количество всех неконгруэнтных решений.
Предположим, что два решения несовместимы, так что:
x0 + (m/c)t1 = x0 + (m/c)t2 (mod m) _____ (3)
(м/с)t1 = (м/с)t2 (mod m) _____ (4)
Теперь вы понимаете, что (m, m/c) = m/c
Таким образом, t1 = t2 (mod c) _____ (5)
Теперь у вас есть набор неконгруэнтных решений, заданный формулой X = X0 + (M/C)T, где T задается как модуль C.
Математически, если C = (A, M) = 1, всегда существует определенное единственное решение для модуля M в линейном сравнении AX = B(mod M).
Решение линейных сравнений с использованием метода алгоритма Евклида
Метод алгоритма Евклида — один из простейших методов решения линейных сравнений. Техника работает таким образом, что если d является наибольшим общим делителем двух положительных целых чисел, скажем, a и b, d делит напоминание (r). Этот остаток (r) получается в результате деления меньшего из a и b на большее.
Метод алгоритма Евклида позволяет находить золотую середину простых чисел при решении линейных сравнений.
Пример: Решите линейное сравнение 3x = 12 (mod 6)
Решение:
3x = 12 (мод. 6)
(3, 6) = 3 и 3/12
Таким образом, вы получаете три несовместимых решения по модулю 6.
Вы должны использовать метод алгоритма Евклида, чтобы найти решение результирующего линейного диофантова уравнения 3x — 6y = 12, чтобы получить x0 = 0.
Три неконгруэнтных решения находятся по формуле:
x1 = 6 (мод. 6)
х1 = 6+2 = 2 (мод. 6)
х2 = 6+4 = 4 (мод 6)
Иллюстрация
НОД чисел 24 и 16 равен 8.
Таким образом; 24 = 1(16) + 8
Следовательно, при делении 24 на 16, которое делится на 8, остаток равен 8.
Примеры
Чтобы лучше понять, как использовать метод алгоритма Евклида, мы будем использовать уравнение 11x = 1 mod 23.
Пример: Решите линейное сравнение 11x = 1 по модулю 23
Решение: Найти наибольший общий делитель алгоритма.
23 = 2(11) +1
11 = 1(11) + 0
Следовательно, НОД равен 1.
Из уравнения видно, что 1 = (1)(23) + (-2)11 (mod 23)
(-2)(11) = 1 мод 23
Таким образом, x = -2
Чтобы записать ответ как значение от 0 до 22, вы понимаете, что -2 = 21 по модулю 23; таким образом, решение x = 21,
Пример: Рассмотрим линейное сравнение 16x = 5 mod 29
Решение:
Сначала решите сравнение 16x = 1 по модулю 29
29 = 1(16) +13 (2)
16 = 1(13) + 3 (3)
13 = 4(3) + 1 (4)
Отсюда получаем:
1 = 1(13) + (-4)(3).
Подставляем в уравнение 1 = 1(13) + (-4)(3), учитывая, что из (3) 3 = 16 -1(13) получаем:
1 = 1(13) + (-4)(16-1(13)) = 5(13) + (-4)(16) (5)
Теперь вы можете использовать (2), зная, что 13 = 29 -1(16), чтобы заменить 13 в (5).
1 = 5(29-1(16)) + (-4)(16) = (-9)(16) +(5)(29)
Следовательно, последнее уравнение по модулю 29 дает результат:
(-9)(16) = 1 по модулю 29
Таким образом, значение x равно -9, что в данном случае соответствует модулю от 29 до 30.
Но это еще не все.
Теперь, когда вы знаете, что 16(20) сравнимо с 1 по модулю 29, умножьте обе части уравнения на 5, чтобы получить 100(16), сравнимое по модулю 29. А поскольку 100 сравнимо с 13 по модулю 29, решение уравнения линейное сравнение 16x = 5 по модулю 29 равно 13,
.Наконец, убедитесь, что 16(13)-5 оставляет нулевой остаток при делении на 29.
Как решать линейные сравнения с помощью метода Эйлера
Этот метод применяется для решения линейного диофантова уравнения.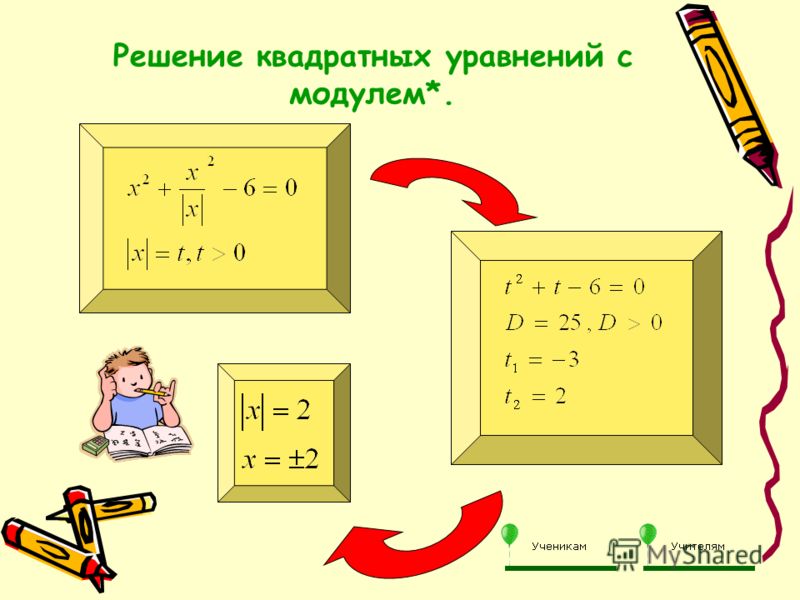 Линейное диофантово уравнение — это любое уравнение, выраженное как ax + by = c. Метод Эйлера применяет знания о решении линейных диофантовых уравнений для решения линейных сравнений.
Линейное диофантово уравнение — это любое уравнение, выраженное как ax + by = c. Метод Эйлера применяет знания о решении линейных диофантовых уравнений для решения линейных сравнений.
Важно отметить, что существует тесная связь между линейными диофантовыми уравнениями и линейными сравнениями.
Это так, потому что в уравнении a = b (mod n) n делит (a-b) или a-b = nt для некоторого t, или a= b + nt.
Кроме того, уравнение a = b + nt можно преобразовать по модулю n:
а = б + нт
а = b + 0t мод n
Следовательно, a = b mod n
Пример:
Вы можете легко преобразовать линейное сравнение 13x = 4 по модулю 37 в диофантово уравнение 13x = 4 + 37y.
Решение линейных сравнений с использованием метода Эйлера включает преобразование сравнений в уравнения. Затем вы изменяете уравнение на сравнение по модулю, используя наименьший коэффициент.
Пример:
Решите следующее диофантово линейное уравнение.
23х + 49у = 102
Решение:
23x + 49y = 102 _____ (1)
Сначала преобразуем диофантово уравнение в линейное сравнение. Вы понимаете из уравнения, что по модулю 23 наименьший коэффициент.
Вы понимаете из уравнения, что по модулю 23 наименьший коэффициент.
49y = 101 mod 23
Теперь упростим уравнение, чтобы получить:
3 года = 10 мод 23
Теперь используйте метод Эйлера, чтобы преобразовать уравнение в равенство.
3 года +10 + 23 года _____ (2)
Теперь уменьшите уравнение до сравнения по модулю 3, что является наименьшим коэффициентом.
0 = 10 + 2a mod 3 или 0 = эквивалент 1+ 2a mod 3.
Упростите это уравнение, чтобы получить:
0 = 1 + 2а + 3б _____ (3)
Прежде чем перейти к следующему шагу, обратите внимание на введение новой переменной (b).
Далее, давайте возьмем режим 2, чтобы получить:
0 = 1 +3b мод 2
Упростите дальше, чтобы получить:
0 = 1 + б мод 2
Результат:
б-1 мод 2
Теперь, когда у вас есть b по модулю 2, выберите любое целое число b, удовлетворяющее этому сравнению, например, b = -1.
Вернитесь к уравнению x (2), чтобы получить:
1 + 2а + 3(-1) = 0,
1 + 2а — 3 = 0
Затем перейдите к y в уравнении (2), чтобы получить:
3г = 10 + 23а = 10 + 23 = 33
Следовательно, у = 11
Вернитесь к исходному уравнению (1), чтобы получить:
23x + 49 11 = 102
23х = 102 — 539 = 437
х = 19
Следовательно, окончательное решение:
х = 19
г = 11
Последние мысли
Понимание алгоритма Евклида и методов Эйлера упрощает решение линейных сравнений. Эти два метода позволяют нам расширить модульную арифметику за пределы простого сложения, умножения и вычитания, чтобы освободить место для деления. Он закрепил фундаментальную связь между целочисленной линейной комбинацией чисел и их НОД.
Эти два метода позволяют нам расширить модульную арифметику за пределы простого сложения, умножения и вычитания, чтобы освободить место для деления. Он закрепил фундаментальную связь между целочисленной линейной комбинацией чисел и их НОД.
Не торопитесь, изучите два метода и начните с легкостью решать линейные сравнения.
Все еще нужна помощь?
Найти репетитора
Будьте первым, кто оставит комментарий ниже.
китайская теорема об остатках | Блестящая математика и естественные науки вики
Когда система содержит относительно небольшое количество сравнений, существует эффективный процесс применения китайской теоремы об остатках.
Решить систему сравнений
{x≡1(mod3)x≡4(mod5)x≡6(mod7).\begin{случаи}\begin{выровнены} х &\экв 1 \pmod{3} \\ х &\ эквив 4 \pmod{5} \\ х &\эквив 6 \pmod{7}. \end{выровнено}\end{cases}⎩⎪⎨⎪⎧xxx≡1(mod3)≡4(mod5)≡6(mod7).
Начните с сравнения с наибольшим модулем, x≡6(mod7).
x \equiv 6 \pmod{7}.x≡6(mod7). Перепишите это сравнение как эквивалентное уравнение:
x=7j+6, для некоторого целого числа j.x=7j+6, \text{ для некоторого целого числа }j.x=7j+6, для некоторого целого числа j.
Подставьте это выражение вместо xxx в сравнение со следующим наибольшим модулем:
x≡4(mod5) ⟹ 7j+6≡4(mod5).x \equiv 4 \pmod{5} \ подразумевает 7j+6 \equiv 4 \pmod{5}.x≡4(mod5)⟹7j+6 ≡4(mod5).
Затем решите это сравнение для j:j:j:
j≡4(mod5).j \equiv 4 \pmod{5}.j≡4(mod5).
Перепишите это сравнение как эквивалентное уравнение:
j=5k+4, для некоторого целого числа k.j=5k+4, \text{ для некоторого целого числа }k.j=5k+4, для некоторого целого числа k.
Подставьте это выражение для jjj в выражение для x:x:x:
x=7(5k+4)+6x=35k+34.\begin{выровнено} х &= 7(5k+4)+6 \\ х &= 35k+34. \\ \end{выровнено}xx=7(5k+4)+6=35k+34.
Теперь подставьте это выражение для xxx в окончательное сравнение и решите сравнение для k:k:k:
35k+34≡1(mod3)k≡0(mod3).
\begin{выровнено} 35k+34 &\экв 1 \pmod{3} \\ k &\equiv 0 \pmod{3}. \end{выровнено}35k+34k≡1(mod3)≡0(mod3).
Запишите это сравнение в виде уравнения, а затем подставьте выражение для kkk в выражение для x:x:x:
k=3l, для некоторого целого числа l.x=35(3l)+34x=105l+34.\begin{выровнено} k &= 3l, \text{ для некоторого целого числа }l. \\ х &= 35(3l)+34 \\ х &= 105l+34. \end{aligned}kxx=3l, для некоторого целого l.=35(3l)+34=105l+34.
Из этого уравнения следует сравнение
x≡34(mod105).x \эквив 34 \pmod{105}.x≡34(mod105).
Это решение системы сравнений. □\ _\квадрат □
Процесс решения систем сравнений с китайской теоремой об остатках:
Для системы сравнений с взаимно простыми модулями процесс выглядит следующим образом:
Начните с сравнения с наибольшим модулем x≡ak(modnk).x \equiv a_k \pmod{n_k}.x≡ak(modnk). Перепишите этот модуль в виде уравнения x=nkjk+ak,x=n_kj_k+a_k,x=nkjk+ak для некоторого положительного целого числа jk.
j_k.jk.
Подставьте выражение для xxx в сравнение со следующим по величине модулем x≡ak(modnk) ⟹ nkjk+ak≡ak−1(modnk−1).x \equiv a_k \pmod{n_k} \имплицитно n_kj_k+a_k \equiv a_{k-1} \pmod{n_{k-1}}.x≡ak(modnk)⟹nkjk+ak≡ak−1(modnk−1).
Решите это сравнение для jk.j_k.jk.
Запишите полученное сравнение в виде уравнения, а затем подставьте это выражение для jkj_kjk в уравнение для x.х.х.
Продолжайте подставлять и решать сравнения до тех пор, пока уравнение для xxx не будет давать решение системы сравнений.
В коробке золотые монеты.
Если монеты поровну разделить между шестью друзьями, останется четыре монеты.
Если монеты поровну разделить между пятью друзьями, останется три монеты.
Если в коробке находится наименьшее количество монет, удовлетворяющее этим двум условиям, сколько монет останется, если разделить поровну между семью друзьями?
Китайская теорема об остатках может быть применена к системам с не взаимно простыми модулями, но решение такой системы не всегда существует.
Решить систему сравнений
{х≡5(mod6)x≡3(mod8).\begin{случаи}\begin{выровнены} х &\эквив 5 \pmod{6} \\ х &\эквив 3 \pmod{8}. \\ \end{выровнено}\end{cases}{xx≡5(mod6)≡3(mod8).
Обратите внимание, что наибольший общий делитель модулей равен 2. Из первого сравнения следует, что x≡1(mod2)x \equiv 1\pmod {2}x≡1(mod2), а из второго сравнения также следует x≡1(mod2 ).x \equiv 1 \pmod{2}.x≡1(mod2). Следовательно, между этими двумя совпадениями нет противоречия. На самом деле систему сравнений можно свести к более простой системе сравнений, выделив НОД модулей из модуля первого сравнения:
{х≡2(mod3)x≡3(mod8).
\begin{случаи}\begin{выровнены} х &\ эквив 2 \pmod{3} \\ х &\эквив 3 \pmod{8}. \\ \end{выровнено}\end{cases}{xx≡2(mod3)≡3(mod8).
Запишите второе сравнение в виде уравнения:
х=8j+3.x=8j+3.x=8j+3.
Подставить в первое сравнение и найти j:j:j:
8j+3≡2(mod3)j≡1(mod3).\begin{выровнено} 8j+3 &\equiv 2 \pmod{3} \\ j &\equiv 1 \pmod{3}. \end{выровнено}8j+3j≡2(mod3)≡1(mod3).
Запишите это сравнение в виде уравнения, а затем подставьте в уравнение для x:x:x:
j=3k+1x=8(3k+1)+3x=24k+11.\begin{выровнено} j &= 3k+1 \\ х &= 8(3k+1)+3 \\ х &= 24k+11. \end{выровнено}jxx=3k+1=8(3k+1)+3=24k+11.
Это дает x≡11(mod24)x \equiv 11 \pmod{24}x≡11(mod24) как решение системы сравнений. Обратите внимание, что lcm(6,8)=24.\text{lcm}(6,8)=24.lcm(6,8)=24. □_\квадрат□
Отправьте свой ответ
Количество учеников в школе от 500 до 600. Если мы сгруппируем их в группы по 12, 20 или 36 человек в каждой, всегда останется 7 студентов. Сколько учеников в этой школе?
Если мы сгруппируем их в группы по 12, 20 или 36 человек в каждой, всегда останется 7 студентов. Сколько учеников в этой школе?
Имеет ли система сравнений решения, зависит от того, есть ли конфликты между парами сравнений.
Покажите, что нет решений системы сравнений:
.{x≡2(mod6)x≡5(mod9)x≡7(mod15).\begin{случаи}\begin{выровнены} х &\эквив 2 \pmod{6} \\ х &\эквив 5 \pmod{9} \\ х &\экв 7 \pmod{15}.\end{выровнено}\end{cases}⎩⎪⎨⎪⎧xxx≡2(mod6)≡5(mod9)≡7(mod15).
Обратите внимание, что каждый модуль делится на 3. Из первого и второго сравнений следует, что x≡2(mod3).x \equiv 2 \pmod{3}.x≡2(mod3). Однако из третьего сравнения следует, что x≡1(mod3).x \equiv 1 \pmod{3}.x≡1(mod3). Поскольку оба они не могут быть истинными, у системы сравнений нет решений. □_\квадрат□
Система линейных сравнений имеет решения тогда и только тогда, когда для каждой пары сравнений внутри системы
{x≡ai(modni)x≡aj(modnj),ai≡aj (mod gcd(ni,nj)).
\begin{выровнено} \begin{случаи} х \ эквив a_i \ pmod {n_i} \\ х \ эквив a_j \ pmod {n_j}, \ qquad \end{случаи} a_i &\equiv a_j\\\big(\text{mod}\ {\gcd(n_i,n_j)}\big). \end{выровнено} {x≡ai(modni)x≡aj(modnj),ai≡aj (mod gcd(ni,nj)).
Более того, если решения существуют, то они имеют вид
x≡b (mod lcm(n1,n2,…,nk))x \equiv b\ \\big(\text{mod}\ {\text{lcm}(n_1,n_2, \ldots , n_k)}\ big)x≡b (mod lcm(n1,n2,…,nk))
для некоторого целого числа b.b.b.
Отправьте свой ответ
У Брахмагупты есть корзина, полная яиц.Когда он вынимает яйца из корзины по 2 за раз, остается 1 яйцо. Когда он вынимает их по 3 за раз, остается 2 яйца. Точно так же, когда он вынимает яйца по 4, 5 и 6 за раз, он находит остатки 3, 4 и 5 соответственно. Однако, когда он вынимает яйца по 7 за раз, яиц не остается.
Точно так же, когда он вынимает яйца по 4, 5 и 6 за раз, он находит остатки 3, 4 и 5 соответственно. Однако, когда он вынимает яйца по 7 за раз, яиц не остается.
Какое наименьшее количество яиц могло быть в корзине Брахмагупты?
Найдите общее решение данного уравнения линейного сравнения
#include
int inverse(int a, int b)
{
int inv = -1;
int q, r, r1 = a, r2 = b, t, t1 = 0, t2 = 1;
пока (r2 > 0)
{
q = r1 / r2;
r = r1 — q * r2;
r1 = r2;
r2 = r;
t = t1 — q * t2;
t1 = t2;
t2 = t;
}
if (r1 == 1) {
inv = t1;
}
if (inv < 0) {
inv = inv + a;
}
возврат инв;
}
int gcd(int a, int b)
{
int q, r;
пока (b > 0)
{
q = a / b;
r = a — q * b;
а = б;
b = r;
}
возврат a;
}
// Программа на C для поиска общего решения заданного уравнения линейного сравнения х0;
char ch;
инв инв;
в то время как (!feof(stdin))
{
fscanf(stdin, «%dx», &a);
ch = getc(stdin);
if (ch == ‘+’)
{
fscanf(stdin, «%d=%d(mod %d)\n», &c, &b, &n);
fprintf(stdout, «%dx+%d=%d(mod %d)\n», a, c, b, n);
b = b — c;
если (b < 0) {
b = b + n;
}
}
else {
fscanf(stdin, «%d(mod %d)\n», &b, &n);
fprintf(stdout, «%dx=%d(mod %d)\n», a, b, n);
}
fprintf(stdout, «Сокращенное уравнение: %dx=%d(mod %d)\n», a, b, n);
d = gcd(a, n);
fprintf(stdout, «GCD(%d, %d) = %d\n», a, n, d);
if ((n % b == 0) || (d % b == 0))
{
fputs(«Заданное уравнение не имеет решения. \ n «, stdout);
\ n «, stdout);
продолжение;
}
a1 = a / d;
b1 = b / d;
n1 = n / d;
FPRINTF (STDOUT,« уменьшен Уравнение: %dx=%d(mod %d)\n», a1, b1, n1);
inv = inverse(n1, a1);
fprintf(stdout, «inv(%d) = % d\n», a1, inv);
x0 = (b1 * inv) % n1;
fprintf(stdout, «General Solution: »
% %, любое целое число\n\n», x0, n / d);
}
return 0;
}
Модульное линейное уравнение | bartleby
Решение модульной линейной задачи 9000 решение данного уравнения,
ax ≡ b (mod n)
Чтобы решить уравнение ax ≡ b (mod n), для печати e решения данного уравнения.Входные данные как n, так и a являются произвольными положительными целыми числами, тогда как b будет произвольным целым числом.
Алгоритм
РЕШЕНИЕ МОДУЛЬНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ (a, b, n)
- (d, x′, y′) ← EXTENDED-EUCLIDALG(a, n)
- , если d | b
- then x0 ← x’ bd mod n
- for i ← 0 to d — 1
- do print x0 + i nd mod n
- else print «нет решений»
Рассмотрим следующие примеры
1
14x≡30(mod100), где b = 30, n = 100 и a = 14. Вызвав EXTENDED_EUCLIDALG в строке 1, пользователь может просто получить (d, x, y) = (2, -7, 1). Однако 2 | 30, то выполняются строки с 3 по 5. В строке 3 вычислить x0 = (-7)(15) mod 100 и x0 = 95. Цикл в строках с 4 по 5 выводит два разных решения, таких как 45 и 95.
Вызвав EXTENDED_EUCLIDALG в строке 1, пользователь может просто получить (d, x, y) = (2, -7, 1). Однако 2 | 30, то выполняются строки с 3 по 5. В строке 3 вычислить x0 = (-7)(15) mod 100 и x0 = 95. Цикл в строках с 4 по 5 выводит два разных решения, таких как 45 и 95.
Из теоремы 1 уравнение ax≡ b(mod n) имеет решение тогда и только тогда, когда gcd (a, n) | б. Решение уравнения уникально тогда и только тогда, когда gcd (a, n) = 1.
Пример 2: Решите 3x ≡ 5 (mod 6). Обратите внимание, что gcd (3, 6) = 3 и 3 — 5 .Таким образом, это уравнение не имеет решения.
Процедура MODULARLINEAREQUATIONSOLVE работает следующим образом:
Строка 1 вычисляет значение d как gcd(a, n), а также два других значения, таких как x’ и y’, такие, что d = ax’ + ny’, при этом демонстрируя, уравнение ax′ ≡ d (mod n) приводит к x′. Если d не может делить b, то ax ≡ b (mod n) не будет иметь никакого решения. Строка 2 проверяет, если d | б; если нет, то строка 6 сообщит, что решений нет. В противном случае в строке 3 вычисляется решение от x0 до ax ≡ b (mod n).Другое решение d — 1 можно получить, просто добавив много nd по модулю n. Цикл for в строках с 4 по 5 выводит все решения, связанные с d, начиная с x0 и разделенные интервалом nd по модулю n.
В противном случае в строке 3 вычисляется решение от x0 до ax ≡ b (mod n).Другое решение d — 1 можно получить, просто добавив много nd по модулю n. Цикл for в строках с 4 по 5 выводит все решения, связанные с d, начиная с x0 и разделенные интервалом nd по модулю n.
MODULARLINEAREQUATIONSOLVE выполняет арифметические операции O(lg n + gcd (a, n)), так как EXTENDED-EUCLIDALG выполняет арифметические операции O(lg n), и каждая итерация цикла for в строках с 4 по 5 выполняет постоянное число арифметические операции.
3.1 Конгруэнтность
$\def\iff{\mbox{iff}}$
Как и многие концепции, которые мы увидим, конгруэнтность прост, возможно, вам знаком,
но чрезвычайно полезным и мощным в изучении теории чисел.Если
$n$ — натуральное число, мы говорим, что целые числа $a$ и $b$ равны конгруэнтно по модулю $n$, и писать $a\equiv b\pmod n$, если
они имеют одинаковый остаток от деления на $n$. (по остатку из
разумеется, имеется в виду уникальное число $r$, определяемое
Алгоритм деления. ) Это обозначение и многое другое
элементарной теории конгруэнтности, обязан знаменитому немецкому
математик Карл Фридрих Гаусс, конечно
выдающийся математик своего времени и, пожалуй, величайший
математик всех времен.
) Это обозначение и многое другое
элементарной теории конгруэнтности, обязан знаменитому немецкому
математик Карл Фридрих Гаусс, конечно
выдающийся математик своего времени и, пожалуй, величайший
математик всех времен.
Пример 3.1.1 $\{…,-6,1,8,15,…\}$ конгруэнтны по модулю 7, потому что их остатки при делении на 7 равно 1. $\{…,-4,4,12,20,…\}$ — все конгруэнтны по модулю 8, так как их остатки от деления на 8 равны 4. $\квадрат$
Вот удивительно полезный результат.
Лемма 3.1.2 $a\equiv b\pmod n$ тогда и только тогда, когда $n|(a-b)$.
Доказательство. Разобьем доказательство на две части:
(только если) Если $a\equiv b\pmod n$, то существуют целые числа $q$, $q’$ и $r$, где $a=qn+r$ и $b=q’n+r$.Так $a-b=(qn+r)-(q’n+r)=(q-q’)n$, что означает $n|a-b$.
(if) Предположим, что $n|a-b$, поэтому существует $x$ с
$a-b=xn$, то есть $a=b+xn$. Предположим, что $r$ — остаток от деления
$n$ в $b$; нам нужно показать, что $r$ также является остатком на
деление $n$ на $a$. Поскольку $b=qn+r$, имеем
$a=b+xn=qn+r+xn=(q+x)n+r$. Таким образом, когда $n$ делится на $a$,
остаток равен $r$ по желанию.$\qed$
Поскольку $b=qn+r$, имеем
$a=b+xn=qn+r+xn=(q+x)n+r$. Таким образом, когда $n$ делится на $a$,
остаток равен $r$ по желанию.$\qed$
Если значение $n$ ясно из контекста, мы часто пишем просто $а\экв б$.Конгруэнтность целых чисел имеет много общих свойств с равенством; мы перечисляем несколько здесь.
Теорема 3.1.3 Сравнение по модулю $n$ удовлетворяет следующему:
1. $a\equiv a$ для любого $a$;
2. Из $a\equiv b$ следует $b\equiv a$;
3. Из $a\equiv b$ и $b\equiv c$ следует $a\equiv c$;
4. $a\equiv 0$ тогда и только тогда, когда $n|a$;
5. $a\equiv b$ и $c\equiv d$ влекут $a+c \equiv b+d$;
6. $a\equiv b$ и $c\equiv d$ влекут $a-c \equiv b-d$;
7.j$. Убедитесь, что вы заметили, как часто мы использовали лемма 3.1.2.$\qed$
Части 5–8 можно обобщить, сказав, что в любом выражении
включая $+,-,\cdot$ и положительные целые показатели (т. е. любые
«полиномиальный»), если отдельные термины заменить на
другие члены, конгруэнтные им по модулю $n$, в результате
выражение соответствует оригиналу. 2$ — некоторый совершенный квадрат.2\экв 1$,
поэтому он никогда не конгруэнтен $2$ или $3$.
$\квадрат$
2$ — некоторый совершенный квадрат.2\экв 1$,
поэтому он никогда не конгруэнтен $2$ или $3$.
$\квадрат$
Пример 3.1.5 Найдите все целые числа $x$ такие, что $3x-5$ делится на $11$. Ставить в несколько более привычных терминах, мы пытаются решить конгруэнтность $3x\equiv 5\pmod {{11}}$ для $x$, как бы мы ни пытались решить уравнение для неизвестного. Предположим, что $3x\equiv 5$ и посмотрим, что это говорит нам о $x$. Так как $4\cdot 3=12\экв 1$, $$ 3x\equiv 5 \подразумевается 4\cdot 3 x\equiv 4\cdot 5\подразумевается 12x\экв 20 \подразумевает х\экв 9.$$ Итак, если $3x\equiv 5$, то $x\equiv 9$ или $x\in\{…, -13, -2, 9, 20, …\}$. Мы также хотим знать, что на самом деле все эти значения являются решениями, то есть если $x\equiv 9$, то $3x\equiv 5$. Это легкий. (Правильно?) $\квадрат$
Пример 3.1.6 Вы, вероятно, знакомы
со старым правилом («отбрасывание девяток»), согласно которому целое число делится на 9, если и
только если сумма его цифр делится на 9. Вот доказательство.
Предположим, что $x$ — некоторое положительное целое число, и когда мы записываем его в десятичной форме
форма выглядит как $d_kd_{k-1}… d_1d_0$ (где каждый $d_i$ находится между
0 и 9).i=1\pmod 9$ за каждый
$я$. Это означает, что
$$
х\эквив d_k+d_{k-1}+… +d_1+d_0 \pmod 9.
$$
На самом деле это доказывает больше, чем нам нужно. Он говорит, что целое число
и сумма его цифр конгруэнтна по модулю 9. В частности,
одно конгруэнтно 0 (то есть делится на 9) тогда и только тогда, когда другое.
$\квадрат$
Вот доказательство.
Предположим, что $x$ — некоторое положительное целое число, и когда мы записываем его в десятичной форме
форма выглядит как $d_kd_{k-1}… d_1d_0$ (где каждый $d_i$ находится между
0 и 9).i=1\pmod 9$ за каждый
$я$. Это означает, что
$$
х\эквив d_k+d_{k-1}+… +d_1+d_0 \pmod 9.
$$
На самом деле это доказывает больше, чем нам нужно. Он говорит, что целое число
и сумма его цифр конгруэнтна по модулю 9. В частности,
одно конгруэнтно 0 (то есть делится на 9) тогда и только тогда, когда другое.
$\квадрат$
Карл Фридрих Гаусс. Гаусс (1777–1855) был
вундеркинд и, возможно, величайший математик всех времен
(если такие рейтинги что-то значат; конечно, он был бы почти в
всеобщий список пяти лучших математиков по таланту,
достижения и влияние).Пожалуй, самая известная история о
Гаусс рассказывает о своей победе над рутинной работой. Как рассказывает Карл Бойер
История: «Однажды, чтобы занять класс, учительница
учащиеся складывают все числа от одного до ста,
инструкции, что каждый должен положить свой планшет на стол, как только он
выполнил задание. Почти сразу же Карл положил планшет на
стол, говоря: «Вот он!» учитель посмотрел на него пренебрежительно
в то время как другие работали усердно. Когда инструктор, наконец, посмотрел
в результате сланец Гаусса был единственным, кто имел
правильный ответ, 5050, без дальнейших вычислений.Десятилетний
мальчик, очевидно, вычислил в уме сумму арифметического
прогрессия $1+2+\cdots+100$, предположительно по формуле
$м(м+1)/2$.»
Почти сразу же Карл положил планшет на
стол, говоря: «Вот он!» учитель посмотрел на него пренебрежительно
в то время как другие работали усердно. Когда инструктор, наконец, посмотрел
в результате сланец Гаусса был единственным, кто имел
правильный ответ, 5050, без дальнейших вычислений.Десятилетний
мальчик, очевидно, вычислил в уме сумму арифметического
прогрессия $1+2+\cdots+100$, предположительно по формуле
$м(м+1)/2$.»
К тому времени, когда Гауссу было около 17 лет, он разработал и обосновал
метод наименьших квадратов, но не решил, стоит ли становиться
математик или филолог. Незадолго до своего девятнадцатилетия,
он выбрал математику, когда ему удалось построить (под
древнее ограничение на циркуль и линейку) семнадцатигранный
правильный многоугольник, первый многоугольник с простым числом сторон
построен более 2000 лет; Раньше только равносторонний
треугольник и правильный пятиугольник были построены.п}+1$
для некоторого $n$. К сожалению, неизвестно, существуют ли
бесконечное число простых чисел Ферма. )
)
Гаусс опубликовал относительно немного своих работ, но с 1796 по 1814 гг. вел небольшой дневник, всего девятнадцать страниц, содержащий 146 кратких заявления. Этот дневник оставался неизвестным до 1898 года. во многом широта его гения и его приоритет во многих открытия. Снова цитируя Бойера: «Неопубликованные меморандумы Гаусса висела, как дамоклов меч, над математикой первой половины девятнадцатого века.Когда произошло важное новое событие объявлено другими, часто оказывалось, что Гаусс идею ранее, но разрешил ей остаться неопубликованной».
Диапазон вклада Гаусса поистине ошеломляющий, в том числе некоторые
глубокие и все еще стандартные результаты, такие как Quadratic Reciprocity
Теорема и Основная теорема алгебры . Он посвятил
большую часть своей дальнейшей жизни посвятил астрономии и статистике и сделал
значительный вклад во многие другие области.Его зовут
прилагается ко многим математическим объектам, методам и теоремам; ученики
физики лучше всего его знают как тезку стандартной единицы магнитного поля. интенсивность, Гс .
интенсивность, Гс .
Информация здесь взята из A History of Mathematics , by Карл Бойер, Нью-Йорк: John Wiley & Sons, 1968.
Упражнения 3.1
Пример 3.1.1 Для заданных значений $n$ и $a$ найдите число $b\in \{0,1,… , n-1\}$, для которых $a\equiv b\pmod n.$
а) $n=7$, $a=30$
б) $n=9$, $a=69$
в) $n=2$, $a=123{,}472{,}461$
г) $n=6$, $a=-60$
д) $n=11$, $a=-63$
е) $n=17$, $a=-38$
Пример 3.1.2 Если $a=nq+r$, то не обязательно, что $r$ остаток от деления $a$ на $n$; например, $20=6\cdot2+8$, но 8$, конечно, не остаток, когда мы делим 20$ на 6$. В лемме 3.1.2 мы показал, что $a=(q+x)n+r$, и сделал из этого вывод, что остаток на деление $a$ на $n$ равно $r$.Объясните, почему этот вывод оправдан.
Пример 3.1.3 Докажите части (5) и (7) в теорема 3.1.3. (Для части 7 вы можете докажите $ac\equiv bc\equiv bd$.)
Пример 3.

 После этого Вам останется подумать только над самыми сложными задачами.
После этого Вам останется подумать только над самыми сложными задачами.
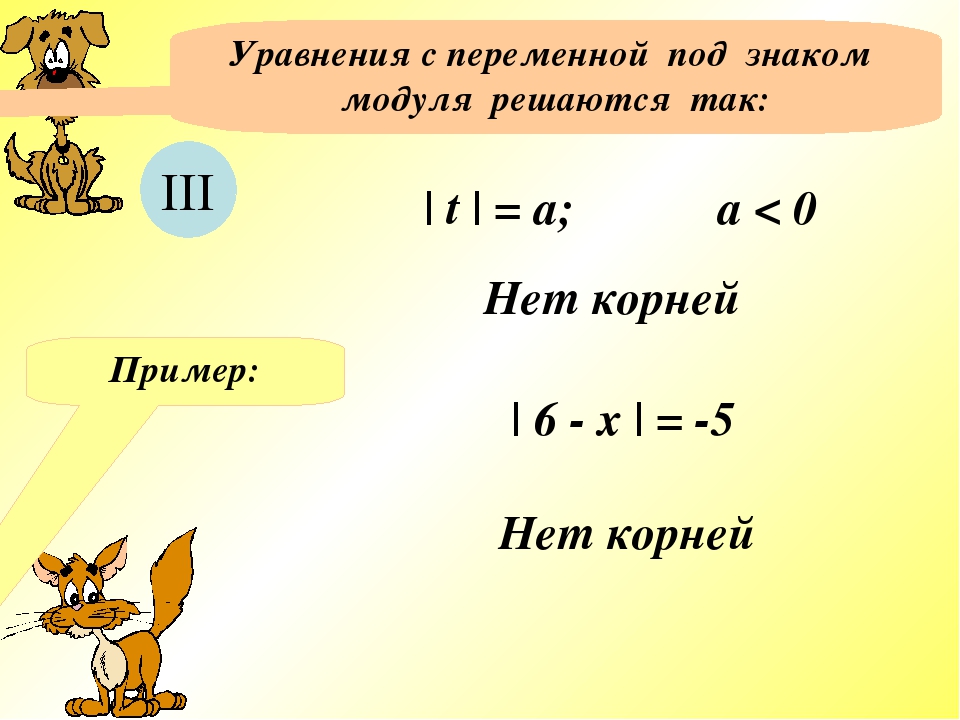


 И. Абсолютная величина. М., Просвещение,
1966.
И. Абсолютная величина. М., Просвещение,
1966. x \equiv 6 \pmod{7}.x≡6(mod7). Перепишите это сравнение как эквивалентное уравнение:
x \equiv 6 \pmod{7}.x≡6(mod7). Перепишите это сравнение как эквивалентное уравнение: \begin{выровнено}
35k+34 &\экв 1 \pmod{3} \\
k &\equiv 0 \pmod{3}.
\end{выровнено}35k+34k≡1(mod3)≡0(mod3).
\begin{выровнено}
35k+34 &\экв 1 \pmod{3} \\
k &\equiv 0 \pmod{3}.
\end{выровнено}35k+34k≡1(mod3)≡0(mod3). j_k.jk.
j_k.jk. \begin{случаи}\begin{выровнены}
х &\ эквив 2 \pmod{3} \\
х &\эквив 3 \pmod{8}. \\
\end{выровнено}\end{cases}{xx≡2(mod3)≡3(mod8).
\begin{случаи}\begin{выровнены}
х &\ эквив 2 \pmod{3} \\
х &\эквив 3 \pmod{8}. \\
\end{выровнено}\end{cases}{xx≡2(mod3)≡3(mod8). \begin{выровнено}
\begin{случаи}
х \ эквив a_i \ pmod {n_i} \\
х \ эквив a_j \ pmod {n_j}, \ qquad
\end{случаи}
a_i &\equiv a_j\\\big(\text{mod}\ {\gcd(n_i,n_j)}\big).
\end{выровнено}
{x≡ai(modni)x≡aj(modnj),ai≡aj (mod gcd(ni,nj)).
\begin{выровнено}
\begin{случаи}
х \ эквив a_i \ pmod {n_i} \\
х \ эквив a_j \ pmod {n_j}, \ qquad
\end{случаи}
a_i &\equiv a_j\\\big(\text{mod}\ {\gcd(n_i,n_j)}\big).
\end{выровнено}
{x≡ai(modni)x≡aj(modnj),ai≡aj (mod gcd(ni,nj)).