Формулы — Оптика

Основные формулы

• Радиус k—ой. зоны Френеля:

для сферической волны

,

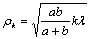где а — расстояние диафрагмы с круглым отверстием от точечного источника света; b — расстояние диафрагмы от экрана, на котором ведется наблюдение дифракционной картины; k — номер зоны Фре­неля; λ — длина волны;

для плоской волны

.

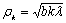• Дифракция света на одной щели при нормальном падении лучей. Условие минимумов интенсивности света

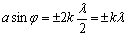, k=1,2,3,…,

где а — ширина щели; φ— угол дифракции; k — номер минимума;

λ — длина волны.

Условие максимумов интенсивности света

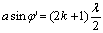, k=l, 2, 3,…,

где φ’ — приближенное значение угла дифракции.

• Дифракция света на дифракционной решетке при нормальном падении лучей. Условие главных максимумов интенсивности

d sinφ=±kλ, k=0,1,2,3,…,

где d — период (постоянная) решетки; k — номер главного макси­мума; φ —угол между нормалью к поверхности решетки и нап­равлением дифрагированных волн.

• Разрешающая сила дифракционной решетки

,

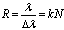где Δλ — наименьшая разность длин волн двух соседних спектраль­ных линий (λ и λ+Δλ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N — число штрихов решетки; k — порядковый номер дифракцион­ного максимума.

• Угловая дисперсия дифракционной решетки

,

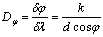линейная дисперсия дифракционной решетки

.

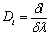Для малых углов дифракции

,

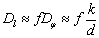
где f — главное фокусное расстояние линзы, собирающей на экра­не дифрагирующие волны.

• Разрешающая сила объектива телескопа

,

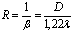где β — наименьшее угловое расстояние между двумя светлыми точками, при котором изображения этих точек в фокальной плос­кости объектива могут быть видны раздельно; D — диаметр объек­тива; λ — длина волны.

• формула Вульфа — Брэгга

2d sin 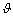=kλ,

где d — расстояние между атомными плоскостями кристалла; 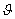 — угол скольжения (угол между направлением пучка параллель­ных лучей, падающих на кристалл, и гранью кристалла), опре­деляющий направление, в котором имеет место зеркальное отраже­ние лучей (дифракционный максимум).

Лекции по оптике — Кафедра общей физики

КУРС ЛЕКЦИЙ 

ПО ОПТИКЕ:

Лекция №1 «Геометрическая оптика» от 9 февраля 2019 г.

Содержание лекции: Обзор литературы к курсу «Оптика». Энергия кванта света. Геометрическая оптика. Принцип Ферма. Закон преломления, закон отражения. Оптические Аберрации. Формула тонкой линзы. Условие синусов Аббе. Микроскоп.

Лекция №2 «Волновая оптика» от 16 февраля 2019 г.

Содержание лекции: Телескоп. Элементы фотометрии. Волновая оптика. Волновое уравнение, монохроматические волны, комплексная амплитуда, уравнение Гельмгольца, плоские и сферические волны, показатель преломления, фазовая скорость распространения, комплексная диэлектрическая проницаемость и комплексный показатель преломления, связь мнимой части с поглощением света средой. Угол Брюстера.

Лекция №3 «Дисперсия» от 2 марта 2019 г.

Содержание лекции: Теория дисперсии. Коэффициент преломления. Коэффициент поглощения. Связь коэффициента преломления с поглощением среды. Аномальная дисперсия, нормальная дисперсия. Особенные случаи преломления. Поляризация в плотных средах. Формула Лоренца-Лоренца. Связь векторов E, H и k. Метаматериалы. Фазовая и групповая скорости. Волновой пакет. Формула Рэлея. Размытие волнового пакета. Эффект Доплера.

Лекция №4 «Интерференция» от 9 марта 2019 г.

Содержание лекции: Принцип суперпозиции. Интенсивность световой волны. Метод векторных диаграмм. Интерференция плоских монохроматических волн. Разность хода. Видность. Кольца Ньютона. Временная когерентность. Спектральный подход. Корреляционная функция.

Лекция №5 «Пространственная когерентность. Дифракция» от 16 марта 2019 г.

Содержание лекции: Временная когерентность (продолжение). Функция когерентности. Видность. Средняя интенсивность интерференционной картины. Теорема Винера-Хинчина. Пространственная когерентность. Радиус когерентности. Звездный интерферометр Майкельсона. Условие наблюдения интерференции. Дифракция. Основная задача теории дифракции. Дифракция на тонком экране.

Лекция №6 «Дифракция Френеля» от 23 марта 2019 г.

Содержание лекции: Граничные условия Киргофа. Принцип Гюйгенса-Френеля. Дифракция Френеля. Задачи с осевой симметрией. Приближение Френеля. Зоны Френеля. Пятно Пуассона. Зонные пластинки. Линза Френеля. Дифракция Френеля на щели. Спираль Корню.

Лекция №7 «Дифракция Фраунгофера» от 30 марта 2019 г.

Содержание лекции: Дифракция Фраунгофера. Интеграл Френеля. Приближение Френеля. Дифракция на одной щели. Дифракция на круглом и квадратном отверстии. Разрешение оптического прибора. Волновой параметр. Демонстрация переходов между геометрической оптикой и дифракцией. Спектральные приборы.

Лекция №8 «Спектральные приборы» от 6 апреля 2019 г.

Содержание лекции: Спектральные приборы. Спектральные характеристики дифракционной решетки (дисперсия, дисперсионная область, разрешающая способность). Интерферометр Фабри-Перо. Спектральные характеристики интерферометра Фабри-Перо. Призма. Сравнение спектральных приборов. Лазеры. Дифракция Рентгеновских лучей. Условие Брегга-Вульфа.

Лекция №9 «Фурье-оптика» от 13 апреля 2019 г.

Содержание лекции: Элементы Фурье-оптики. Плоская волна. Дифракция на синусоидальной решетке. Теория Аббе формирования оптического изображения. Частотная характеристика свободного пространства. Голограммы.

Лекция №10 «Голограммы. Поляризация» от 20 апреля 2019 г.

Содержание лекции: Голограммы. Голограмма точечного источника (голограмма Габора). Объемная голограмма. Метод Денисюка. Поляризация. Эллиптическая, линейная, круговая поляризация. Монохроматическая волна. Естественный свет. Как получить поляризованный свет? Закон Малюса.

Лекция №11 «Поляризация. Оптика анизотропных сред» от 27 апреля 2019 г.

Содержание лекции: Поляризация. Линейная поляризация. Круговая поляризация. Эллиптическая поляризация. Поляризация естественного света. Поляроиды. Оптика анизотропных сред. Взаимная ориентация векторов k, E, D, B, направление вектора Пойнтинга. Модель осциллятора. Фазовые пластинки (λ/4, λ/2).

Лекция №12 «Анизотропия. Рассеяние света» от 4 мая 2019 г.

Содержание лекции: Двойное лучепреломление в одноосных кристаллах. Принцип Гюйгенса-Френеля для обыкновенной и необыкновенной волн. Явление Керра. Эффект Поккельса. Ячейка Поккельса. Эффект Фарадея. Рассеяние света. Рассеяние Рэлея. Поляризация рассеянного света. Рассеяние Ми. Закон Бугера-Ламберта-Бера.

Лекция №13 «Нелинейные эффекты» от 11 мая 2019 г.

Содержание лекции: Элементы нелинейной оптики. Нелинейная поляризация среды. Метод последовательных приближений. Генерация второй гармоники. Инверсия координат. Учет кубической поправки к поляризации. Самофокусировка. Гауссовы пучки. Радиус кривизны луча. Световоды. Градиентные оптоволокна. Одномодовое волокно.

Законы геометрической оптики — ГЕОМЕТРИЧЕСКАЯ ОПТИКА — ФИЗИКА

ФИЗИКА

 

ГЕОМЕТРИЧЕСКАЯ ОПТИКА

 

Законы геометрической оптики

 

Закон отражения

α = γ

 

 

α — угол падения;

γ — угол отражения;

— перпендикуляр к границе раздела двух сред.

 

Закон преломления

 

 

β — угол преломления.

 

Относительный показатель преломления

n₂₁ — относительный показатель преломления;

υ₁,_{υ2— скорость света в данных средах, [м/c].}

 

Абсолютный показатель преломления

n₂₁ — абсолютный показатель преломления;

с — скорость света в вакууме, c = 2,998 10⁸м/c.

 

Оптическая плотность среды.

Луч из среды с большей оптической плотностью переходит в среду с меньшей оптической плотностью

n₁, n₂ — показатели преломления среды каждого.

 

 

Оптическая плотность среды.

Луч из среды с меньшей оптической плотностью переходит в среду с большей оптической плотностью

 

 

Предельный угол полного отражения

 

 

α_в — угол падения, при котором наступает полное отражение света.

 

Построение изображения в плоском зеркале

 

 

Изображение предмета в плоском зеркале является мнимым

 

Построение изображения в вогнутом зеркале

 

 

Построение изображения в выпуклом зеркале

 

 

Прохождение света сквозь плоскопараллельную пластинку

 

 

α — смещение луча.

 

Прохождение света сквозь треугольную призму

 

 

Если нет полного отражения.

 

При полном отражении. Применяется в перископе

 

 

При полном отражении. Применяется в отражателях

 

 

При полном отражении. Применяется в биноклях

 

 

Собирательная линза

F > 0, d > 0

 

 

Рассеивающую линза

F < 0, d > 0

 

 

Формула линзы

 

 

d — расстояние от линзы до источника, [м];

f — расстояние от линзы до изображения, [м];

F — фокусное расстояние, [м].

Главная оптическая ось

 

 

Оптический центр

 

 

Побочная оптическая ось

 

 

Фокус

 

 

Фокусное расстояние

 

 

Фокальная плоскость

 

 

Увеличение линзы

 

 

Г — увеличение линзы;

Н — линейный размер изображения, [м];

h — линейный размер предмета, [м].

 

Оптическая сила линзы

D — оптическая сила линзы, [дптр].

Изображения действительное f > 0.

Изображения мнимое f < 0.

 

Луч, проходящий через оптический центр

 

 

Луч, параллельный главной оптической оси

 

 

Луч, проходящий через фокус

 

 

Изображение точки, не лежащей на главной оптической оси

 

 

Ход пучка параллельных лучей, что идут вдоль побочной оптической оси

 

определение, описание, формула и решение

Существуют объекты, которые способны изменять плотность падающего на них потока электромагнитного излучения, то есть либо увеличивать его, собирая в одну точку, либо уменьшать его путем рассеивания. Эти объекты называются линзами в физике. Рассмотрим подробнее этот вопрос.

Что представляют собой линзы в физике?

Под этим понятием подразумевают абсолютно любой объект, который способен изменять направление распространения электромагнитного излучения. Это общее определение линз в физике, под которое попадают оптические стекла, магнитные и гравитационные линзы.

В данной статье главное внимание будет уделено именно оптическим стеклам, которые представляют собой объекты, изготовленные из прозрачного материала, и ограниченные двумя поверхностями. Одна из этих поверхностей обязательно должна иметь кривизну (то есть являться частью сферы конечного радиуса), в противном случае объект не будет обладать свойством изменения направления распространения световых лучей.

Принцип работы линзы

Суть работы этого незамысловатого оптического объекта заключается в явлении преломления солнечных лучей. В начале XVII века знаменитый голландский физик и астроном Виллеброрд Снелл ван Ройен опубликовал закон преломления, который в настоящее время носит его фамилию. Формулировка этого закона следующая: когда солнечный свет переходит через границу раздела двух оптически прозрачных сред, то произведение синуса угла падения между лучом и нормалью к поверхности на коэффициент преломления среды, в которой он распространяется, является величиной постоянной.

Для пояснения вышесказанного приведем пример: пусть свет падает на поверхность воды, при этом угол между нормалью к поверхности и лучом равен θ₁. Затем, световой пучок преломляется и начинает свое распространение в воде уже под углом θ₂ к нормали к поверхности. Согласно закону Снелла получим: sin(θ₁)*n₁ = sin(θ₂)*n₂, здесь n₁ и n₂ — коэффициенты преломления для воздуха и воды, соответственно. Что такое коэффициент преломления? Это величина, показывающая, во сколько раз скорость распространения электромагнитных волн в вакууме больше таковой для оптически прозрачной среды, то есть n = c/v, где c и v — скорости света в вакууме и в среде, соответственно.

Физика возникновения преломления заключается в выполнении принципа Ферма, согласно которому свет движется таким образом, чтобы за наименьшее время преодолеть расстояние от одной точки к другой в пространстве.

Виды линз

Вид оптической линзы в физике определяется исключительно формой поверхностей, которые ее образуют. От этой формы зависит направление преломления падающего на них луча. Так, если кривизна поверхности будет положительной (выпуклой), то по выходе из линзы световой пучок будет распространяться ближе к ее оптической оси (см. ниже). Наоборот, если кривизна поверхности является отрицательной (вогнутой), тогда пройдя через оптическое стекло, луч станет удаляться от его центральной оси.

Отметим еще раз, что поверхность любой кривизны преломляет лучи одинаково (согласно закону Стелла), но нормали к ним имеют разный наклон относительно оптической оси, в результате получается разное поведение преломленного луча.

Линза, которая ограничена двумя выпуклыми поверхностями, называется собирающей. В свою очередь, если она образована двумя поверхностями с отрицательной кривизной, тогда она называется рассеивающей. Все остальные виды оптических стекол связаны с комбинацией указанных поверхностей, к которым добавляется еще и плоскость. Каким свойством будет обладать комбинированная линза (рассеивающим или собирающим), зависит от суммарной кривизны радиусов ее поверхностей.

Элементы линзы и свойства лучей

Для построения в линзах в физике изображений необходимо познакомиться с элементами этого объекта. Они приведены ниже:

• Главная оптическая ось и центр. В первом случае имеют в виду прямую, проходящую перпендикулярно линзе через ее оптический центр. Последний, в свою очередь, представляет собой точку внутри линзы, проходя через которую, луч не испытывает преломления.
• Фокусное расстояние и фокус — дистанция между центром и точкой на оптической оси, в которую собираются все падающие на линзу параллельно этой оси лучи. Это определение верно для собирающих оптических стекол. В случае рассеивающих линз собираться в точку будут не сами лучи, а мнимое их продолжение. Эта точка называется главным фокусом.
• Оптическая сила. Так называется величина, обратная фокусному расстоянию, то есть D = 1/f. Измеряется она в диоптриях (дптр.), то есть 1 дптр. = 1 м^-1.

Ниже приводятся основные свойства лучей, которые проходят через линзу:

• пучок, проходящий через оптический центр, не изменяет направления своего движения;
• лучи, падающие параллельно главной оптической оси, изменяют свое направление так, что проходят через главный фокус;
• лучи, падающие на оптическое стекло под любым углом, но проходящие через его фокус, изменяют свое направление распространения таким образом, что становятся параллельными главной оптической оси.

Приведенные выше свойства лучей для тонких линз в физике (так их называют, потому что не важно, какими сферами они образованы, и какой толщиной обладают, имеют значение только оптические свойства объекта) используются для построения изображений в них.

Изображения в оптических стеклах: как строить?

Ниже приведен рисунок, где подробно разобраны схемы построения изображений в выпуклой и вогнутой линзах объекта (красной стрелки) в зависимости от его положения.

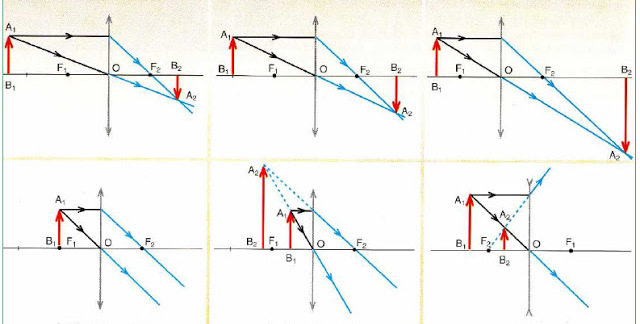
Из анализа схем на рисунке следуют важные выводы:

• Любое изображение строится всего на 2-х лучах (проходящем через центр и параллельном главной оптической оси).
• Собирающие линзы (обозначаются со стрелками на концах, направленными наружу) могут давать как увеличенное, так и уменьшенное изображение, которое в свою очередь может быть реальным (действительным) или мнимым.
• Если предмет расположен в фокусе, то линза не образует его изображения (см. нижнюю схему слева на рисунке).
• Рассеивающие оптические стекла (обозначаются стрелками на их концах, направленными внутрь) дают независимо от положения предмета всегда уменьшенное и мнимое изображение.

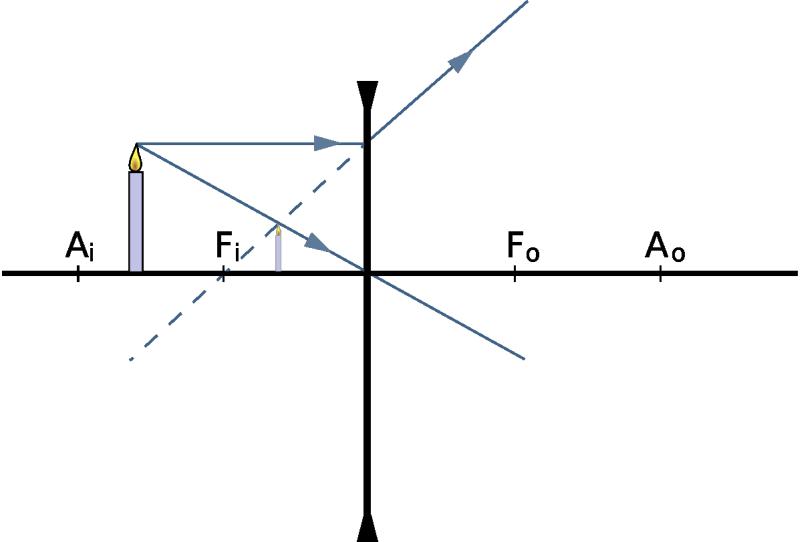
Нахождение расстояния до изображения

Чтобы определять, на каком расстоянии появится изображение, зная положение самого предмета, приведем формулу линзы в физике: 1/f = 1/d_o + 1/d_i, где d_o и d_i — расстояние до предмета и до его изображения от оптического центра, соответственно, f — главный фокус. Если речь идет о собирающем оптическом стекле, тогда число f будет положительным. Наоборот, для рассеивающей линзы f — отрицательное.

Воспользуемся этой формулой и решим простую задачу: пусть предмет находится на расстоянии d_o = 2*f от центра собирающего оптического стекла. Где появится его изображение?

Из условия задачи имеем: 1/f = 1/(2*f)+1/d_i. Откуда: 1/d_i = 1/f — 1/(2*f) = 1/(2*f), то есть d_i = 2*f. Таким образом, изображение появится на расстоянии двух фокусов от линзы, но уже с другой стороны, чем сам предмет (об этом говорит положительный знак величины d_i).

Краткая история

Любопытно привести этимологию слова «линза». Оно ведет происхождение от латинских слов lens и lentis, что означает «чечевица», поскольку оптические объекты по своей форме действительно похожи на плод этого растения.

Преломляющая способность сферических прозрачных тел была известна еще древним римлянам. Для этой цели они применяли круглые стеклянные сосуды, наполненные водой. Сами же стеклянные линзы начали изготавливаться только в XIII веке в Европе. Использовались они в качестве инструмента для чтения (современные очки или лупа).

Активное использование оптических объектов при изготовлении телескопов и микроскопов относится к XVII (в начале этого века Галилей изобрел первый телескоп). Отметим, что математическая формулировка закона преломления Стелла, без знания которой невозможно изготавливать линзы с заданными свойствами, была опубликована голландским ученым в начале того же XVII века.

Другие виды линз

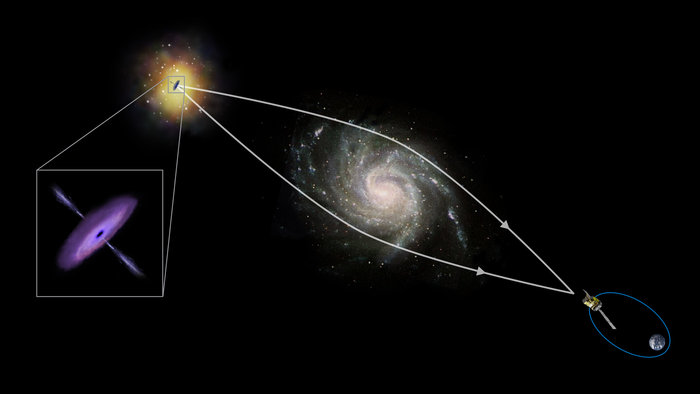
Как было отмечено выше, помимо оптических преломляющих объектов, существуют также магнитные и гравитационные. Примером первых являются магнитные линзы в электронном микроскопе, яркий пример вторых заключается в искажении направления светового потока, когда он проходит вблизи массивных космических тел (звезд, планет).