Как найти диагональ равнобокой трапеции
1. Формулы длины диагонали равнобедренной трапеции через ее стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагональ трапеции
Формула диагонали трапеции ( d ):
2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагональ трапеции
Формулы диагонали трапеции ( d ):
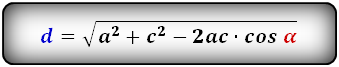
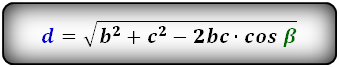
3. Формула длины диагонали равнобедренной трапеции
a — нижнее основание
b — верхнее основание
α , β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d — диагональ трапеции
Формулы диагонали трапеции ( d ):
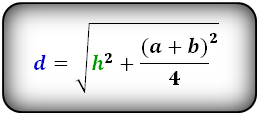
Справедливо для данного случая :
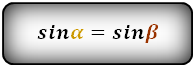
4. Формулы длины диагонали трапеции через высоту и стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
h — высота трапеции
α — угол при нижнем основании
d — диагональ трапеции
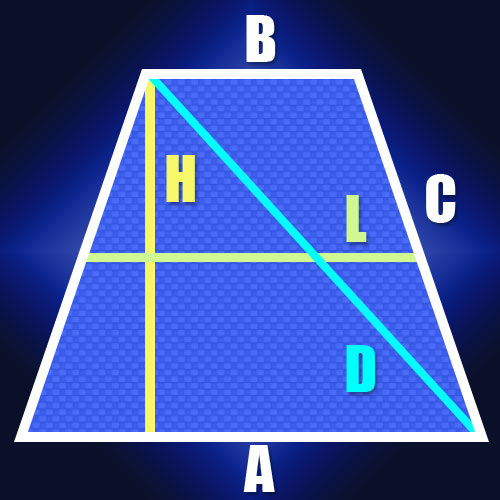
- Как найти диагональ равнобедренной трапеции
- Как найти площадь трапеции, если известны диагонали
- Как доказать, что диагонали в трапеции равны
- диагональ в равнобедренной трапеции
Если известны длины оснований равнобедренной трапеции (A и B) и длина ее боковой стороны (C), то для определения длин диагоналей (D) можно воспользоваться тем, что сумма квадратов длин всех сторон равна сумме квадратов длин диагоналей. Это свойство вытекает из того факта, что каждая из диагоналей трапеции является гипотенузой треугольника, катетами в котором служат боковая сторона и основание. А согласно теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы. Так как боковые стороны в равнобедренной трапеции равны, как и ее диагонали, то это свойство можно записать в таком виде: A² + B² + 2C² = 2D². Из этой формулы вытекает, что длина диагонали равна квадратному корню из половины суммы квадратов длин оснований, сложенной с квадратом длины боковой стороны: D = √((A² + B²)/2 + C²).»
Это утверждение является неверным. Не вводите в заблуждение. Откуда Вы взяли, что:»сумма квадратов длин всех сторон равна сумме квадратов длин диагоналей».
(lacktriangleright) Равнобедренная трапеция – трапеция, у которой боковые стороны равны.
Свойства равнобедренной трапеции:
(lacktriangleright) Углы при каждом основании равны;
(lacktriangleright) Диагонали равны;
(lacktriangleright) Два треугольника, образованные диагоналями и одним из оснований, являются равнобедренными;
(lacktriangleright) Два треугольника, образованные диагоналями и боковой стороной, равны.
В трапеции (ABCD) : (AB = CD) , (angle C — angle A = 80^<circ>) . Найдите (angle D + angle B — angle C) . Ответ дайте в градусах.
У равнобедренной трапеции углы при одном основании равны, тогда (angle B = angle C) и, следовательно, (angle D + angle B — angle C = angle D = angle A) .
У равнобедренной трапеции сумма противоположных углов равна (180^<circ>) (так как (angle C = angle B) , а (angle A + angle B = 180^<circ>) , как сумма односторонних при параллельных прямых и секущей).
(angle A + angle C = 180^<circ>) ,
(angle C — angle A = 80^<circ>)
тогда, вычитая из верхнего равенства нижнее, получаем (2cdot angle A = 100^<circ>) . В итоге имеем: (angle D + angle B — angle C = angle A = 50^<circ>) .
Диагонали в равнобедренной трапеции (ABCD) перпендикулярны. Найдите площадь трапеции, если диагональ (AC) равна (2) .
В равнобедренной трапеции диагонали равны, поэтому (AC = BD = 2) . Пускай (O) – точка пересечения диагоналей.
[egin S_ = S_ < riangle ABC>+ S_ < riangle CDA>= frac<1><2>cdot AC cdot BO + frac<1><2>cdot AC cdot OD =\ =frac<1><2>cdot AC cdot(BO + OD) = frac<1><2>cdot AC cdot BD = frac<1> <2>cdot 2 cdot 2 = 2end]
Найдите диагонали равнобедренной трапеции, если они перпендикулярны, а площадь трапеции равна (8) .
Пусть (ABCD) — трапеция с диагоналями (AC) и (BD) , (O) – точка их пересечения, тогда
(S_ = S_ < riangle ABC>+ S_ < riangle CDA>= frac<1><2>cdot AC cdot BO + frac<1><2>cdot AC cdot OD = )
(frac<1><2>cdot AC cdot(BO + OD) = frac<1><2>cdot AC cdot BD = frac<1><2>cdot AC^2 = 8) (Rightarrow) (AC = 4) .
В равнобедренной трапеции (ABCD) основание (AD) вдвое длиннее основания (BC) и боковой стороны. Найдите острый угол трапеции.
Если опустить высоты (BH) и (CK) на основание (AD) , то они отсекут равные отрезки (AH) и (KD) , причем (AB = BC = HK) (Rightarrow) (AH = frac <2>= frac <2>= frac<2>) (Rightarrow) (angle ABH = 30^circ) , как угол в прямоугольном треугольнике, противолежащий катету, равному половине гипотенузы (Rightarrow) (angle BAK = 90^circ — 30^circ = 60^circ) .
(ABCD) – трапеция с основаниями (AD) и (BC) . При этом (AB = CD = 6) , (BC = 4) , один из углов трапеции (ABCD) равен (60^<circ>) . Найдите (AD) .
Пусть (angle A = 60^<circ>) , (BE) – высота в треугольнике (ABD) . (angle ABE = 90^ <circ>- 60^ <circ>= 30^<circ>) . Катет, лежащий против угла в (30^<circ>) , равен половине гипотенузы, тогда (AE = 0,5cdot 6 = 3) .
У равнобедренной трапеции углы при одном основании равны, тогда (angle D = 60^<circ>) . Пусть (CF) – высота в треугольнике (ACD) , тогда аналогично тому, как находили (AE) , находим, что (FD = 3) . (EF = BC) , так как (BCFE) – прямоугольник. Тогда (AD = AE + EF + FD = 3 + 4 + 3 = 10) .
Диагонали в равнобедренной трапеции (ABCD) перпендикулярны. (O) – точка пересечения диагоналей, причем (AO:OC = 7:1) . Найдите периметр трапеции, если меньшее основание равно (1) .
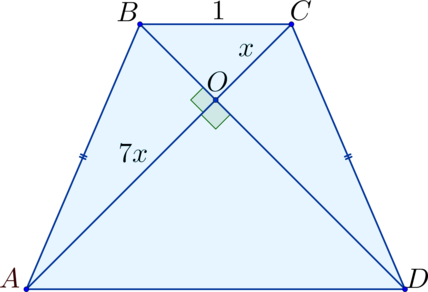
(BC) – меньшее основание, треугольники ( riangle BOC) и ( riangle AOD) подобны и их стороны относятся как (1:7) (Rightarrow) (BC:AD = 1:7) (Rightarrow) (AD = 7) ; (OB = OC) , (OB^2 + OC^2 = 1^2) (Rightarrow) (OB = OC = frac<1><sqrt2>) (Rightarrow) (AO = frac<7><sqrt2>) . В ( riangle ABO) : (AO^2 + OB^2 = AB^2) (Rightarrow) (AB = 5) . Тогда (P_ = AB + BC + CD + AD = 1 + 7 + 5 + 5 = 18) .
В равнобедренной трапеции (ABCD) биссектриса (angle ABC) параллельна боковой стороне (CD) и пересекает основание (AD) в точке (K) , которая делит (AD) в отношении (AK:KD = 1:2) . Найдите периметр трапеции, если меньшее основание равно (4) .
(BCDK) – параллелограмм, т.к. противоположные стороны попарно параллельны; (angle AKB = angle KBC) , т.к. накрест лежащие при параллельных (BC) и (AD) ; (angle BAK = angle CDK = angle KBC) (Rightarrow) ( riangle ABK) – равносторонний треугольник. (BC = KD = 4) (Rightarrow) (AK = 2 = AB = CD) (Rightarrow) (P_ = AB + BC + CD + KD + AK = 2 + 4 + 2 + 4 + 2 = 14) .
Учащимся старших классов, которые готовятся сдавать ЕГЭ по математике, в обязательном порядке стоит повторить тему «Равнобедренная трапеция» и освежить в памяти ее основные свойства и признаки. Многолетняя практика показывает, что подобные задания ежегодно встречаются в программе аттестационного испытания. Поэтому, если вы хотите успешно решить задачи ЕГЭ на применение основных свойств диагоналей или углов равнобедренной трапеции, вам непременно стоит разобраться в этой теме.
Образовательный портал «Школково» предлагает новый подход к подготовке к аттестационному испытанию. Наш ресурс позволяет учащимся определить наиболее сложные темы и ликвидировать имеющиеся пробелы в знаниях. Специалисты «Школково» подготовили и изложили весь материал в максимально доступной форме.
Чтобы выпускники могли успешно справляться с геометрическими задачами, мы рекомендуем вспомнить определение равнобедренной трапеции, свойства ее сторон, углов и диагоналей, а также формулу для вычисления площади. Эта информация представлена в разделе «Теоретическая справка».
Вспомнив основные свойства углов, диагоналей и сторон равнобедренной трапеции, учащиеся имеют возможность закрепить усвоенный материал, выполнив практические задания. Упражнения различного уровня сложности представлены в разделе «Каталог». В каждом из них вы найдете подробный алгоритм решения и правильный ответ.
Практиковаться в выполнении заданий по теме «Трапеция» при подготовке к ЕГЭ выпускники могут в режиме онлайн, находясь не только в Москве, но и в любом другом городе России. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
Равнобедренная трапеция — Википедия
В евклидовой геометрии равнобедренная трапеция — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон. Этот четырёхугольник является частным случаем трапеций. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (боковые) имеют одинаковые длины (свойство, которому удовлетворяет также параллелограмм). Диагонали также имеют одинаковые длины. Углы при каждом основании равны и углы при разных основаниях являются смежными (в сумме дающие 180º).
Прямоугольники и квадраты обычно считаются специальными случами равнобедренных трапеций, хотя в некоторых источниках они таковыми не считаются.
Другим специальным случаем является трапеция с 3 равными сторонами. В англоязычной литературе её называют
Самопересечения[править | править код]
Любой несамопересекающийся четырёхугольник с единственной осью симметрии должен быть либо равнобедренной трапецией, либо дельтоидом[3]. Однако, если разрешить самопересечение, множество симметричных четырёхугольников нужно расширить включением в него самопересекающиеся равнобедренные трапеции, в которых пересекающиеся стороны равны, а две другие стороны параллельны, и антипараллелограммы, у которых противоположные стороны имеют равные длины.
У любого антипараллелограмма выпуклая оболочка является равнобедренной трапецией и антипараллелограмм может быть получен из диагоналей равнобедренной трапеции[4].
 |  |  |
| Выпуклая равнобедренная трапеция | Самопересекающаяся равнобедренная трапеция | антипараллелограмм |
|---|
Если четырёхугольник является трапецией, не обязательно проверять, равны ли боковые стороны (и недостаточно, поскольку ромбы, являющиеся специальными случаями трапеций с боковыми сторонами равной длины, но у него нет осевой симметрии через середины оснований). Любое из следующих свойств выделяет равнобедренную трапецию от других трапеций:
- Диагонали имеют одинаковую длину.
- Углы при основании равны.
- Отрезок, соединяющий середины параллельных сторон, перпендикулярен им.
- Противоположные углы дополнительны (до 180º), из чего, в свою очередь, следует, что равнобедренные трапеции являются вписанными четырёхугольниками.
- Диагонали делятся точкой пересечения на попарно равные отрезки. В терминах рисунка ниже, AE = DE, BE = CE (и AE ≠ CE, если хотят исключить прямоугольники).
Если прямоугольники включаются в класс трапеций, то можно определить равнобедренную трапецию как «вписанный четырёхугольник с равными диагоналями» [5], как «вписанный четырёхугольник с парой параллельных сторон», или как «выпуклый четырёхугольник с осью симметрии, проходящей через середины противоположных сторон».
В равнобедренной трапеции углы при основаниях попарно равны. На рисунке ниже углы ∠ ABC и ∠DCB являются одинаковыми тупыми углами, а углы ∠BAD и ∠CDA являются одинаковыми острыми углами.
Поскольку прямые AD и BC параллельны, углы, принадлежащие противоположным основаниям, являются дополнительными, то есть ∠ABC + ∠BAD = 180°.
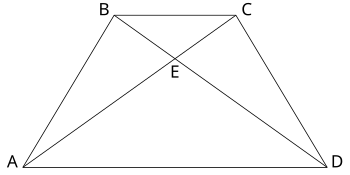Другая равнобедренная трапеция.Диагонали равнобедренной трапеции равны. То есть любая равнобедренная трапеция является равнодиагональным четырёхугольником. Однако диагонали равнобедренной трапеции делятся в одной и той же пропорции. На рисунке диагонали AC и BD имеют одинаковую длину (AC = BD) и делят друг друга на отрезки той же длины (AE = DE и BE = CE).
Отношение, в котором делятся диагонали, равно отношению длин параллельных сторон, то есть
- AEEC=DEEB=ADBC.{\displaystyle {\frac {AE}{EC}}={\frac {DE}{EB}}={\frac {AD}{BC}}.}
Длина каждой диагонали, согласно теореме Птолемея, задаётся формулой
- p=ab+c2{\displaystyle p={\sqrt {ab+c^{2}}}},
где a и b — длины параллельных сторон AD и BC, а c — длина каждой боковой стороны AB и CD.
Высота, согласно теореме Пифагора, задаётся формулой
- h=p2−(a+b2)2=124c2−(a−b)2.{\displaystyle h={\sqrt {p^{2}-\left({\frac {a+b}{2}}\right)^{2}}}={\tfrac {1}{2}}{\sqrt {4c^{2}-(a-b)^{2}}}.}
Расстояние от точки E до основания AD задаётся формулой
- d=aha+b{\displaystyle d={\frac {ah}{a+b}}},
где a и b — длины оснований AD и BC, а h — высота трапеции.
Площадь равнобедренной (а также любой) трапеции равна половине произведения суммы оснований на высоту. На рисунке, если мы примем AD = a, BC = b, а высота h равна длине отрезка между прямыми AD и BC (перпендикулярного им), то площадь K задаётся формулой:
- K=h3(a+b).{\displaystyle K={\frac {h}{2}}\left(a+b\right).}
Если вместо высоты трапеции известны длины боковых сторон AB =CD = c, то площадь можно вычислить по формуле Брахмагупты площади вписанных четырёхугольников. Равенство двух боковых сторон упрощает формулу до
- K=(s−a)(s−b)(s−c)2,{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)^{2}}},}
где s=12(a+b+2c){\displaystyle s={\tfrac {1}{2}}(a+b+2c)} — полупериметр трапеции. Эта формула аналогична формуле Герона вычисления площади треугольника. Эту же формулу можно переписать в виде
- K=14(a+b)2(a−b+2c)(b−a+2c).{\displaystyle K={\frac {1}{4}}{\sqrt {(a+b)^{2}(a-b+2c)(b-a+2c)}}.}
Радиус описанной окружности задаётся формулой[6]
- R=cab+c24c2−(a−b)2.{\displaystyle R=c{\sqrt {\frac {ab+c^{2}}{4c^{2}-(a-b)^{2}}}}.}
Для прямоугольника, в котором a = b, формула упрощается до R=12a2+c2{\displaystyle R={\tfrac {1}{2}}{\sqrt {a^{2}+c^{2}}}}.
- George Bruce Halsted. Elementary Synthetic Geometry. — J. Wiley & sons, 1896..
- William Dwight Whitney, Benjamin Eli Smith. The Century Dictionary and Cyclopedia. — The Century co., 1911..
Диагональ равнобедренной трапеции
1. Формулы длины диагонали равнобедренной трапеции через ее стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагональ трапеции
Формула диагонали трапеции (d ):
2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α, β — углы трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
3. Формула длины диагонали равнобедренной трапеции
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через высоту и стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
h — высота трапеции
α — угол при нижнем основании
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии