Кинетическая энергия | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! 
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Кинетическая энергия — скалярная физическая величи­на, равная половине произведения массы тела на квадрат его скорости.

Что бы понять, что же такое кинетическая энергия тела, рассмотрим случай, когда тело массой m под действием постоянной силы (F=const) движется прямолинейно равноускоренно (а=const). Определим работу силы, приложенной к телу, при изменении модуля скорости этого тела от v1 до v2.

Как мы знаем, работа постоянной силы вычисляют по формуле . Так как в рассматриваемом нами случае направление силы F и перемещения s совпадают, то , и тогда у нас получается, что работа силы равна А=Fs. По второму закону Ньютона найдем силу F=ma. Для прямолинейного равноускоренного движения справедлива формула:

Из это формулы мы выражаем перемещение тела:

Подставляем найденные значения F и S в формулу работы, и получаем:

Из последней формулы видно, что работа силы, приложенной к телу, при изменении скорости этого тела равна разности двух значений некоторой величины . А механическая работа это и есть мера изменения энергии. Следовательно, в правой части формулы стоит разность двух значений энергии данного тела. Это значит, что величина представляет собой энергию, обусловленную движением тела. Эту энергию называют кинетической. Она обозначается Wк.

Если взять выведенную нами формулу работы, то у нас получится

Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии этого тела

Так же есть :

Потенциальная энергия :

В формуле мы использовали :

— Кинетическая энергия

— Масса тела

— Скорость движения тела

— Начальная скорость тела

— Конечная скорость тела

— Работа тела

— Ускорение тела

— Сила, действующая на тело

— Перемещение тела

xn--b1agsdjmeuf9e.xn--p1ai

Формула кинетической и потенциальной видов энергии: в чем она измеряется и чему равна

Окружающий мир пребывает в постоянном движении. Любое тело (объект) способно выполнить определенную работу, даже если оно в состоянии покоя. Но для совершения любого процесса требуется приложить некоторые усилия, порой немалые.

В переводе с греческого языка этот термин означает «деятельность», «сила», «мощь». Все процессы на Земле и за пределами нашей планеты происходят благодаря этой силе, которой обладают окружающие объекты, тела, предметы….

Виды энергии

Среди большого разнообразия выделяют несколько основных видов данной силы, отличающихся прежде всего своими источниками:

• механическая – данный вид характерен для движущихся в вертикальной, горизонтальной или другой плоскости тел,
• тепловая – выделяется в результате неупорядоченного движения молекул в веществах,
• электрическая – источником этого вида является движение заряженных частиц в проводниках и полупроводниках,
• световая – переносчиком ее являются частицы света – фотоны,
• ядерная – возникает вследствие самопроизвольного цепного деления ядер атомов тяжелых элементов.

В этой статье пойдет речь о том, что собой представляет механическая сила предметов, из чего она состоит, от чего зависит и как преобразуется во время различных процессов.

Благодаря этому виду предметы, тела могут находиться в движении либо в состоянии покоя. Возможность такой деятельности объясняется присутствием двух основных составляющих:

• кинетической (Ек),
• потенциальной (Еп).

Именно сумма кинетической и потенциальной энергий определяет общий численный показатель всей системы. Теперь о том, какие формулы используются для расчетов каждой из них, и в чем измеряется энергия.

Как рассчитать энергию

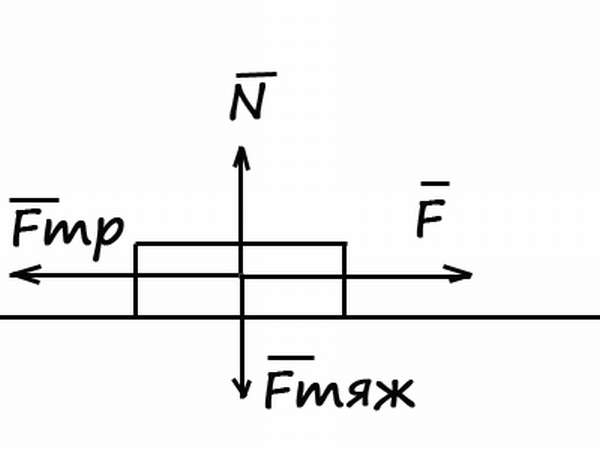Кинетическая энергия – это характеристика любой системы, которая находится в движении. Но как найти кинетическую энергию?

Сделать это несложно, так как расчетная формула кинетической энергии весьма проста:

Конкретное значение определяется двумя основными параметрами: скоростью перемещения тела (V) и его массой (m). Чем больше данные характеристики, тем большей значением описываемого явления обладает система.

Но если объектом не совершаются перемещения (т.е. v = 0), то и кинетическая энергия равна нулю.

Потенциальная энергия – это характеристика, зависящая от положения и координат тел.

Любое тело подвержено земному притяжению и воздействию сил упругости. Такое взаимодействие объектов между собой наблюдается повсеместно, поэтому тела находятся в постоянном движении, меняют свои координаты.

Установлено, чем выше от поверхности земли находится предмет, чем больше его масса, тем большим показателем данной величины оно обладает.

Таким образом, зависит потенциальная энергия от массы (m) , высоты (h). Величина g – ускорение свободного падения, равное 9,81 м/сек2. Функция расчета ее количественного значения выглядит так:

Eп = mgh, (2)

Единицей измерения этой физической величины в системе СИ считается джоуль (1 Дж). Именно столько нужно затратить сил, чтобы переместить тело на 1 метр, приложив при этом усилие в 1 ньютон.

Важно! Джоуль как единица измерения утвержден на Международном конгрессе электриков, который проходил в 1889 году. До этого времени эталоном измерения была Британская термическая единица BTU, используемая в настоящее время для определения мощности тепловых установок.

Основы сохранения и превращения

Из основ физики известно, что суммарная сила любого объекта, независимо от времени и места его пребывания, всегда остается величиной постоянной, преобразуются лишь ее постоянные составляющие (Еп) и (Ек).

Переход потенциальной энергии в кинетическую и обратно происходит при определенных условиях.

Например, если предмет не перемещается, то его кинетическая энергия равна нулю, в его состоянии будет присутствовать только потенциальная составляющая.

И наоборот, чему равна потенциальная энергия объекта, например, когда он находится на поверхности Земли (h=0)? Конечно, она нулевая, а Е тела будет состоять только из ее составляющей Ек.

Но потенциальная энергия – это мощность движения. Стоит только системе приподняться на какую- то высоту, после чего его Еп сразу начнет увеличиваться, а Ек на такую величину, соответственно, уменьшаться. Эта закономерность просматривается в вышеуказанных формулах (1) и (2).

Для наглядности приведем пример с камнем либо мячом, которые подбрасывают. В процессе полета каждый из них обладает и как потенциальной, так и кинетической составляющей. Если одна увеличивается, то другая на такую же величину уменьшается.

Полет предметов вверх продолжается лишь до тех пор, пока хватит запаса и сил у составляющей движения Ек. Как только она иссякла, начинается падение.

А вот чему равна потенциальная энергия предметов в самой верхней точке, догадаться нетрудно, она максимальная.

При их падении происходит все наоборот. При касании с землей уровень кинетической энергии равен максимуму.

Действие этого закона наблюдается не только в обычной жизни, но и в научных теориях. Кратко об одной из них.

Так как между многочисленными частицами идеального газа отсутствует какое-либо взаимодействие, то потенциальная составляющая описываемого явления молекул постоянно нулевая. Значит, вся внутренняя сила частиц идеального газа определяется, как средняя кинетическая, и рассчитывается по приведенной выше формуле (1).

Внимание! В наше время на письменных столах можно увидеть сувенир, называемый «маятником Ньютона». Этот прибор прекрасно демонстрирует процесс преобразования. Если крайний шарик отвести в сторону, а затем его отпустить, он после столкновения передает свой энергетический заряд следующему шарику, а тот своему соседу.

Виды энергии в физике

Кинетическая и потенциальная энергии, формулы

Вывод

На вопрос, например, как найти кинетическую энергию, ученые давно дали ответ. Уже в середине XIX в. английский механик Уильям Томсон использовал в своих опытах определение «кинетическая». Но современная жизнь заставила проводить глубокие исследования по части преобразования одного вида в другой.

Это интересно! Что показывает скорость при равномерном прямолинейном движении: формула

tvercult.ru

Формула кинетической энергии — интернет энциклопедия для студентов

ОПРЕДЕЛЕНИЕ

Кинетическая энергия — это энергия, которую тело обладает благодаря ее движению.

T — кинетическая энергия движущегося тела, m — его масса, v — его скорость движения.

Символ — T

Единицей измерения энергии является Дж (джоуль).

Кинетическая энергия характеризует движение тела. Это векторная физическая величина. Он равен нулю, когда тело неподвижно. Кинетическая энергия делится на энергию поступательного и вращательного движения. Эта формула имеет смысл только для поступательного движения.

Примеры решения задач на тему «Кинетическая энергия»

ПРИМЕР 1

Задача

Корпус весом 1 кг движется постепенно со скоростью 50 км / ч. Найдите его кинетическую энергию.

Решение.

Переведем скорость тела в единицах СИ:

Замените исходные данные в формуле:

Ответ

Кинетическая энергия тела составляет приблизительно 0,966 Дж

ПРИМЕР 2

Задание

Найдите формулу для скорости поступательного движения тела, если известны ее масса и общая кинетическая энергия, а энергия ее вращательного и поступательного движения связана как 2: 1

Решение

Заметим, что величина энергии вращательного движения не влияет на скорость ее поступательного движения, это означает:

Мы выполняем алгебраические преобразования с формулой для кинетической энергии:

Ответ

sciterm.ru

Кинетическая и потенциальная энергия ℹ️ определение, теоремы, обозначение и единицы измерения, формулы, различие, взаимодействие, примеры вычислений

Концепция и классификация

Ещё в древности энергию определяли как свойство или способность, которые тела и вещества должны производить вокруг себя и которые во время преобразований обмениваются через два механизма: в форме работы или тепла. Правда, тогда еще не знали, что таким образом выполняется закон сохранения энергии. Но кроме физических изменений, проявляющихся, например, в подъёме объекта, его транспортировке, деформации или нагревании, энергия также присутствует в химических изменениях, таких как сжигание куска дерева или разложение воды электрическим током.

Энергия — это способность тела работать, а также сила, которая выполняет работу. Она может быть представлена в виде различных переходных форм:

• тепловой;
• механической;
• химической;
• электрической;
• ядерной.

В физике самая важная форма называется механической энергией. Это сумма и определение потенциальной и кинетической энергии, формула которой: E = Ek + Wp.

Энергия движения

Кинетическая энергия тела — это та, которой тело обладает благодаря своему движению. Её определяют как силу, необходимую для ускорения тела определённой массы от покоя до максимальной указанной скорости.

Как только достигается ускорение, тело сохраняет энергию, если скорость не изменяется. Чтобы тело вернулось в состояние покоя, необходима отрицательная работа той же величины.

Единица измерения кинетической энергии — джоуль. Обычно она обозначается буквой E c или E k. Расчёт мощности измеряется по-разному. Для того чтобы найти её количество можно использовать онлайн-калькулятор.

История и определение

Прилагательное «кинетический» в названии произошло от древнегреческого слова кίνησις kinēsis, что означает «движение».

Идею связи классической механики и кинематической энергии впервые выдвинули Готфрид Вильгельм Лейбниц и Даниэль Бернулли. Учёный Грейвсанд из Нидерландов предоставил экспериментальное подтверждение этой связи.

Но первые теоретические выкладки этих идей приписаны Гаспар-Гюстав Кориолису, который в 1829 году опубликовал статью, где была изложена математика этого процесса. Сам термин появился в 1849 году благодаря Уильяму Томсону, более известному как лорд Кельвин.

Теорема о кинетической энергии гласит: изменение кинетической силы тела равно работе равнодействующей всех сил, действующих на тело. Эта теорема справедлива независимо от того, какие силы действуют на тело.

Часто различают кинетическую силу поступательного и вращательного движения. Как и любая физическая величина, которая является функцией скорости, она не только зависит от внутренней природы этого объекта, но также зависит от отношений между объектом и наблюдателем (в физике наблюдатель формально определяется классом определённая система координат, называемая инерциальной системой отсчёта).

Эта энергия деградирует и сохраняется в каждой трансформации, теряя способность совершать новые трансформации, но она не может быть создана или разрушена, только трансформирована, поэтому её сумма во вселенной всегда постоянна.

Кинематика системы частиц

Для частицы или для твёрдого тела, которое не вращается, кинетическая энергия падает до нуля, когда тело останавливается. Однако для систем, которые содержат много частиц с независимыми движениями, это не совсем верно.

Для твёрдого тела, которое вращается, полная кинетическая сила может быть разбита на две суммы: энергия перемещения, связанная со смещением центра масс тела в пространстве, и вращения (с вращательным движением с определённой угловой скоростью).

Потенциальная энергия

Этот термин был введён в XIX веке учёным Уильямом Ренкином и связан с механической энергией, которая зависит от расположения тела в силовом поле (гравитационное, электростатическое и т. д. ) или с наличием силового поля внутри тела.

Теорема о потенциальной энергии утверждает, что она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.

Независимо от силы, её порождающей, потенциальная энергия, которой обладает физическая система, хранится благодаря своему положению и / или конфигурации, в чём и заключается её различие с кинетической энергией.

Значение потенциала всегда зависит от нахождения или конфигурации, выбранной для её измерения, поэтому иногда говорят, что физически имеет значение только его изменение отношений между двумя конфигурациями.

Потенциальная энергия присутствует не только в классической физике, но также в релятивистской и квантовой физике. Эта концепция также была распространена на физику элементарных частиц.

Смысл потенциальной силы связан с работой, выполняемой силами физической системы для перемещения её из одного состояния в другое. А её функция будет существенно зависеть от типа силового поля или взаимодействия, действующего на систему.

Это относится, например, к атомной физике при получении электронных состояний атома или к молекулярной физике для получения таких состояний молекулы, как:

• электронных;
• вибрационных;
• вибрационно-вращательных;
• вращательных.

В других более общих формулировках физики потенциальная функция также играет важную роль. Среди них лагранжева и гамильтонова формулировки механики.

Гравитационная сила

Потенциальной гравитацией обладают тела в силу того, что они имеют массу и находятся на определённом взаимном расстоянии. Среди огромных масс действуют силы притяжения. Применительно, например, к планетарному движению, основная масса солнечной системы состоит из массы Солнца, которая создаёт гравитационное силовое поле, воздействующее на малые массы планет. В свою очередь, каждая планета создаёт такое же поле, которое воздействует на второстепенные тела, находящиеся на её поверхности. Зависимость силы тяжести от высоты можно изобразить на графике. При увеличении массы тела линейно увеличивается и она.

Энергия упругой деформации

Эластичность — это свойство определённых материалов, благодаря которому, будучи деформированными, растянутыми или отделёнными от своего исходного положения, они могут восстановить своё первоначальное состояние или равновесие. Восстановительными силами, ответственными за восстановление, являются силы упругости, как в случае пружин, резиновых полос или струн музыкальных инструментов.

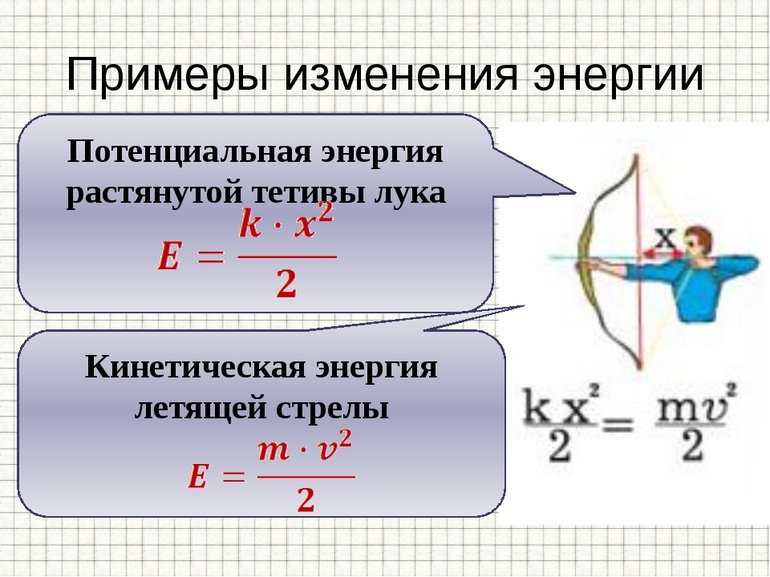
Многие древние военные машины использовали эти силы для запуска объектов на расстоянии, таких как дуга, которая стреляет стрелой, арбалет или катапульта. Вибрации или колебания материальных объектов, вызванные упругими силами, являются источником звуковых волн. Силы восстановления, когда объект восстанавливает свою первоначальную форму практически без какого-либо демпфирования или деформации, являются консервативными, и может быть получена упругая сила.

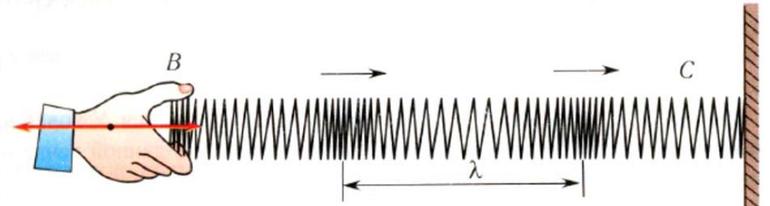
Пружина является примером упругого объекта, который точно восстанавливает первоначальную форму: при растяжении он создаёт упругую силу, стремящуюся вернуть его к первоначальной длине. Экспериментально подтверждено, что эта восстановительная сила пропорциональна растянутой длине пружины. Способ выразить эту пропорциональность между силой и растянутой суммой — через закон Гука.

Коэффициент пропорциональности при этой деформации зависит от типа материала и рассматриваемой геометрической формы. Для твёрдых тел сила упругости обычно описывается в терминах величины деформации, вызванной растягивающей силой, возникающей в результате этого растяжения, называемого упругостью или модулем Юнга. Для жидкостей и газов это выражается изменением давления, способного вызвать изменение объёма, и называется модулем сжимаемости.

Одним из свойств упругости твёрдого тела или жидкости при растяжении или деформации является то, что растяжение или деформация пропорциональны приложенному усилию. То есть для создания двойного растяжения потребуется двойная сила. Эта линейная зависимость смещения от приложенной силы известна как закон Гука.

Прикладное значение

Потенциальная электростатическая энергия может храниться с помощью конденсаторов. Конденсатор — это устройство, которое накапливает её внутри. Чтобы сохранить электрический заряд, он использует две проводящие поверхности, как правило, в форме листов или пластин, разделённых диэлектрическим материалом (изолятором). Эти платы являются электрически заряженными при подключении к источнику питания.

Две пластины имеют одинаковую величину, но с разными знаками, причём величина нагрузки пропорциональна приложенной разности потенциалов. Константа пропорциональности между зарядом, приобретённым конденсатором, и разностью потенциалов, достигнутой между двумя пластинами, называется ёмкостью конденсатора:

Области применения конденсаторов многочисленны в области электроники, и, следовательно, они также предназначены для бытовых приборов. В современных технологических приложениях их используют:

• в компьютерах;
• в средствах связи;
• в видео, аудиоплеерах и т. д.

В этих применениях современной технологии конденсаторы способны накапливать электростатическую энергию в течение коротких периодов времени и с не слишком высокими значениями.

nauka.club

Работа, мощность, энергия — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Механическая работа

К оглавлению…

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Работой, совершаемой постоянной силой F, называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S:

Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.

Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:

Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (F_упр = kx).

 

Мощность

К оглавлению…

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность P (иногда обозначают буквой N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

По этой формуле рассчитывается средняя мощность, т.е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:

По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.

КПД – коэффициент полезного действия, равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:

Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.

Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).

В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:

 

Кинетическая энергия

К оглавлению…

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения):

То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Е_к = 100 кДж и способен совершить работу в 100 кДж. Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.

Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т.е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.

Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью v, то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.

Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:

Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.

 

Потенциальная энергия

К оглавлению…

Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.

Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.

Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:

Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:

Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.

Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.

Потенциальная энергия растянутой пружины рассчитывается по формуле:

где: k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x₁, тогда при переходе в новое состояние с удлинением x₂ сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):

Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы). Понятие потенциальной энергии для силы трения вводить нельзя.

 

Коэффициент полезного действия

К оглавлению…

Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).

КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.

В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.

В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т.д.

Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т.п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.

Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.

 

Закон сохранения механической энергии

К оглавлению…

Полной механической энергией называется сумма кинетической энергии (т.е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):

Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:

Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах. Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.

Алгоритм решения задач на закон сохранения энергии:

1. Найти точки начального и конечного положения тела.
2. Записать какой или какими энергиями обладает тело в данных точках.
3. Приравнять начальную и конечную энергию тела.
4. Добавить другие необходимые уравнения из предыдущих тем по физике.
5. Решить полученное уравнение или систему уравнений математическими методами.

Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.

В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.

При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.

Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.

 

Разные задачи на работу

К оглавлению…

Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:

1. Работу можно найти по формуле: A = FS∙cosα. Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
2. Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
3. Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh, где h – высота, на которую поднимается центр тяжести тела.
4. Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt.
5. Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.

 

Закон сохранения энергии и динамика вращательного движения

К оглавлению…

Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:

1. Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).
2. Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
3. Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
4. В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
5. Провести остальные необходимые математические операции для получения окончательного результата.

При решении задач надо помнить, что:

• Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0. Такое же условие выполняется при прохождении верхней точки мертвой петли.
• При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
• Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.

 

Неупругие соударения

К оглавлению…

Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).

 

Абсолютно упругий удар

К оглавлению…

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.

Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.

 

Законы сохранения. Сложные задачи

К оглавлению…

Несколько тел

В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.

Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:

1. выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
2. записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
3. учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
4. при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.

Разрыв снаряда

В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.

Столкновения с тяжёлой плитой

Пусть навстречу тяжёлой плите, которая движется со скоростью v, движется лёгкий шарик массой m со скоростью u_н. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты. В таком случае, для конечной скорости шарика получим:

Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены. Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:

Задачи о максимальных и минимальных значениях энергии сталкивающихся шаров

В задачах такого типа главное понять, что потенциальная энергия упругой деформации шаров максимальна, если кинетическая энергия их движения минимальна – это следует из закона сохранения механической энергии. Сумма кинетических энергий шаров минимальна в тот момент, когда скорости шаров будут одинаковы по величине и направлены в одном направлении. В этот момент относительная скорость шаров равна нулю, а деформация и связанная с ней потенциальная энергия максимальна.

educon.by

Релятивистская кинетическая энергия

Физика > Релятивистская кинетическая энергия

 

Изучите формулу для кинетической энергии релятивистской частицы. Узнайте, как определить релятивистскую кинетическую энергию, связь с импульсом, полная энергия.

В виде формулы релятивистская кинетическая энергия задается как: (m – масса покоя, v – скорость, c – скорость света).

Задача обучения

• Сопоставьте классическую и кинетическую релятивистские энергии для объектов, чья скорость меньше или приближается к световой.

Основные пункты

• В формуле видно, что энергия объекта близится к бесконечности, если скорость приближается к световой. Поэтому нельзя ускорить объект на границе.
• Расчеты кинетической энергии проводят по формуле: E_покоя = E₀ = mc².
• При низком скоростном показателе релятивистская кинетическая энергия может быть аппроксимирована классической. Поэтому полная энергия делится на энергию массы в состоянии покоя с добавлением традиционной кинетической.

Термины

• Коэффициент Лоренца – фактор для определения степени временного замедления, сокращения длины и релятивистской массы перемещающегося объекта.
• Классическая механика – все физические законы природы, характеризующие поведение обычного мира.
• Специальная теория относительности: скорость света остается стабильной в любой системе отсчета.

Кинетическая энергия основывается на массе тела и скорости. Задается формулой: (m – масса, v – скорость тела).

Классическая кинетическая энергия связана с импульсом уравнением:

(р – импульс).

Если скорость объекта составляет примечательную часть световой, то для определения кинетической энергии нужно воспользоваться специальной теорией относительности. Здесь необходимо изменить выражение для линейного импульса. Формула:

p = mγv, где γ – коэффициент Лоренца:

Кинетическая энергия обладает связью с импульсом, поэтому релятивистское выражение отличается от классического:

Из формулы видно, что энергия объекта подходит к бесконечности, когда скорость приближается к световой. Поэтому нельзя ускорить объект на этой черте.

Математическим побочным результатом выступает уравнение эквивалентности массы-энергии. Тело в позиции покоя обязано обладать энергией:

Популярную связь между Эйнштейном, E = mc² и атомной бомбой отобразили на обложке журнала

E_покоя = E₀ = mc².

Общая формула для энергии объекта, не пребывающего в позиции покоя:

KE = mc² — m₀c² (m – релятивистская масса объекта, а m₀ – масса объекта в состоянии покоя).

При низких скоростях релятивистская кинетическая энергия может аппроксимироваться классической. Это показывают на разложении Тейлора:

E_к ≈ mc² (1 + 0.5 v²/с²) — mc² = 0.5 mv².

Выходит, что полную энергию можно поделить на энергию массы покоя с добавлением классический кинетической при небольших скоростных показателях.

---

v-kosmose.com

Максимальная кинетическая энергия груза: формула

Кинетическая энергия

Определение 1

Кинетическая энергия — внутренняя энергия движущегося тела, обусловленная его инертностью (массой) и скоростью. Она равна энергии, которую нужно затратить, чтобы снизить скорость этого тела до нуля.

Например, движущийся автомобиль невозможно остановить мгновенно. Для остановки необходимо затратить энергию трения тормозных колодок о тормозные диски колес и шин об асфальт.

Замечание 1

Кинетическая и потенциальная энергия измеряются в джоулях ($1 Дж = Н \cdot м$).

В некоторых физических системах происходят циклические преобразования потенциальной (запасенной) энергии в кинетическую и обратно. Такие системы называются маятниками. Например, для груза, подвешенного на нити, потенциальная энергия максимальна, когда он отклонен на максимальный угол от вертикали. Мгновенная скорость груза в этот момент равна нулю и, следовательно, нулю равна и кинетическая энергия. По мере движения вниз под действием силы тяжести, скорость груза нарастает и достигает максимума в нижней точке, после чего снова начинает запасаться по мере движения вверх.

Проще всего изучать переход кинетической и потенциальной энергий друг в друга на примере пружинного маятника, где действует, если пренебречь силой трения, лишь сила упругости. Когда пружину сжимают, энергия запасается. Когда отпускают — потенциальная энергия, сохраненная в кристаллической решетке материала, высвобождается и превращается в кинетическую, разгоняя груз. Когда скорость груза достигает максимума, он продолжает движение по инерции, растягивая пружину в противоположном направлении, вновь запасая энергию и снижая скорость. Характеристики такого колебательного движения зависят только от материала пружины, толщины проволоки, из которой она намотана, диаметра и количества витков. Все эти факторы описываются единым параметром — коэффициентом упругости.

Максимальная кинетическая энергия груза

Для простого пружинного маятника полную энергию груза в любой момент времени можно выразить как

$E = E_p + E_k = \frac{m \cdot v^2}{2} + \frac{k \cdot x^2}{2}$, где:

• $E_p$ — потенциальная энергия,
• $E_k$ — кинетическая энергия,
• $m$ — масса,
• $v$ — моментальная скорость,
• $k$ — коэффициент упругости,
• $x$ — приращение длины пружины в данный момент.

Максимальную кинетическую энергию можно вычислить как

$(E_k)_{max} = \frac{m \cdot v_{max}^2}{2}$,

где $v_{max}$ — максимальная скорость груза. Однако измерить ее на практике сложно. Проще, опираясь на постоянство суммы кинетической и потенциальной энергий, определить максимальную потенциальную (когда кинетическая равна нулю). Поскольку справедливо и обратное, можно записать:

$(E_k)_{max} = (E_p)_{max} = \frac{k \cdot x_{max}^2}{2}$,

где $x_{max}$ — максимальное приращение растяжения пружины. Его легко измерить, а коэффициент упругости посмотреть в справочнике.

Пример 1

Компактный груз, массой 0,5 кг прикреплен к движущейся горизонтально пружине. Ее коэффициент упругости равен 2000 $\frac{Н}{м}$. Каково было начальное приращение длины пружины, если его максимальная скорость во время колебаний составляет 1 $\frac{м}{с}$?

Из условий задачи можно найти максимальную кинетическую энергию груза:

$(E_k)_{max} = \frac{0,5 \cdot 1^2}{2} = 0,25 Дж$

Выразив максимальную потенциальную энергию через приращение длины пружины, составим равенство:

$0,25 = \frac{2000 \cdot x_{max}^2}{2} \implies x_{max} = \sqrt{\frac{2 \cdot 0,25}{2000}} \approx 0,016 м$.

Ответ: $\approx 1,6 мм$.

spravochnick.ru