Химическая формула — Минералогический музей имени А. Е. Ферсмана РАН
Химическая формула минерала выражает его химический состав в виде последовательности символов химических элементов, снабженных подстрочными стехиометрическими индексами, указывающими относительные количества атомов различных сортов, входящих в его состав. Химизм минерала тесно связан с особенностями его строения с (кристаллической структурой), вместе они составляют особое единство, определяемой как конституция минерала. Формулы минералов по возможности отражают их конституцию, что достигается распределением по определенным группам символов химических элементов, атомы которых находятся в идентичных позициях кристаллической структуры. Такие формулы называются кристаллохимическими. Стехиометрические индексы пропорциональны количеству атомов каждого элемента в элементарной ячейке кристаллической структуры минерала. Спецификой минерального вещества является непостоянство его химического состава и обилие примесей, что сказывается и на характере химических формул, применяемых в минералогии.
Различаются эмпирические и идеализированные (обобщенные, генерализованные, теоретические) формулы минералов. Эмпирические формулы детально характеризуют химический состав отдельных минеральных индивидов, реже их множеств, отобранных в одинаковой обстановке (в одном минеральном агрегате, в определенном участке горной породы или рудного тела). Идеализированные формулы относятся к минеральным видам или группам, они могут различаться степенью абстрагирования от конкретных особенностей химизма данного минерала.
Эмпирическая формула минерала получается в результате интерпретации результатов конкретного химического анализа, сводящейся к некоторой процедуре пересчета. Относится такая формула к конкретному минеральному индивиду или к группе индивидов близкого состава. Содержания примесных элементов, находящихся в минерале в количествах ниже определенного порога (требующих применения в формуле значений стехиометрических коэффициентов, меньших 0,01), в эмпирических формулах минералов обычно не отражаются.
Результатом обобщения эмпирических формул минералов являются идеализированные, обобщенные формулы, называемые также теоретическими. Идеализированная формула минерала относится обычно к минеральному виду, она носит абстрактный характер и отражает главнейшие, повторяющиеся от индивида к индивиду особенности химического состава всех минеральных индивидов, относящихся к данному виду. Такая формула содержит обычно лишь присутствующие во всех без исключения индивидах данного вида элементы, определяющие видовую принадлежность минерала, при этом второстепенные особенности состава часто (но не всегда полностью) игнорируются. Правила, рекомендованные ИЮПАК, в формулах этого типа обычно удается соблюдать, однако, отличительной особенностью многих таких формул является перечисление символов изоморфных атомов через запятую, без стехиометрических индексов. Теоретическая формула собственно минерального вида отражает зачастую состав гипотетического чистого вещества (минала), являющегося крайним членом ряда твердых растворов. Состав реальных минеральных индивидов очень редко отвечает таким идеализированным формулам. Идеализированные формулы могут охватывать и целые группы минералов, отражая особенности изоморфных замещений с помощью переменных величин стехиометрических индексов, а также и путем использования переменных, заменяющих символы химических элементов.
Такая формула содержит обычно лишь присутствующие во всех без исключения индивидах данного вида элементы, определяющие видовую принадлежность минерала, при этом второстепенные особенности состава часто (но не всегда полностью) игнорируются. Правила, рекомендованные ИЮПАК, в формулах этого типа обычно удается соблюдать, однако, отличительной особенностью многих таких формул является перечисление символов изоморфных атомов через запятую, без стехиометрических индексов. Теоретическая формула собственно минерального вида отражает зачастую состав гипотетического чистого вещества (минала), являющегося крайним членом ряда твердых растворов. Состав реальных минеральных индивидов очень редко отвечает таким идеализированным формулам. Идеализированные формулы могут охватывать и целые группы минералов, отражая особенности изоморфных замещений с помощью переменных величин стехиометрических индексов, а также и путем использования переменных, заменяющих символы химических элементов.
Рассмотрим в качестве иллюстрации варианты формул минералов, относящихся к минеральным видам, объединенным в группу оливина. Эмпирические формулы некоторых минеральных индивидов группы оливина (отнесенных к определенным видам этой группы) выглядят следующим образом:
Эмпирические формулы некоторых минеральных индивидов группы оливина (отнесенных к определенным видам этой группы) выглядят следующим образом:
| ФОРМУЛА | МИНЕРАЛЬНЫЙ ВИД |
| (Mg1,34Fe2+0,56Ca0,06Mn0,04)2,00[SiO4] | форстерит |
| (Fe2+1.48Mg0.32Mn0.17Fe3+0.03)2.00[(Si0.97Al0.03)O4] | фаялит |
| (Mn1,25Fe2+0,65Mg 0,06Ca0,02)1,98[SiO4] | тефроит |
Идеализированные формулы минеральных видов этой группы таковы:
| ФОРМУЛА | МИНЕРАЛЬНЫЙ ВИД |
| Mg2[SiO4] | форстерит |
| Fe2[SiO4] | фаялит |
| Mn2[SiO4] | тефроит |
С учетом обычных изоморфных компонентов этой группы эти же формулы можно несколько уточнить:
| ФОРМУЛА | МИНЕРАЛЬНЫЙ ВИД |
| (Mg,Fe,Mn)2[SiO4] | форстерит |
| (Fe,Mg,Mn)2[SiO4] | фаялит |
| (Mn,Fe,Mg)2[SiO4] | тефроит |
Количественные связи между содержаниями главных изоморфных компонентов этой группы можно выразить, с использованием переменных индексов, так:
(Mg2-x-yFexMny)2[SiO4]
Обобщенная формула минералов группы оливина, с использованием переменных символов, выражается следующим образом:
A2[SiO4],
где А=Mg,Fe2+.
Важным является следующий момент. Стехиометрические индексы, завершающие собой скобки, содержащие символы изоморфных элементов, представляют собой не множители, а суммы индексов в скобках.
Проведение химического анализа минерала представляет собой экспериментальное исследование, которое имеет целью определение химического состава минерала, как вещества. Химический состав минералов сильно варьирует от одного минерального индивида к другому, даже если эти индивиды относятся к одному минеральному виду, что сказывается и на различиях в результатах анализа, помимо ошибок элементоопределения. В процессе химического анализа по возможности проводится испытание конкретного минерального индивида, более того, современные локальные методы анализа (электронно-зондовый, например) позволяют определять состав весьма малых участков вещества (объемом порядка 1-10 мкм
3). Составы таких участков в пределах даже одного минерального индивида могут существенно различаться, что определяется его зональностью. Химическая и фазовая неоднородность минералов нередко проявляется в таких тонких масштабах (порядка 1-10 нм), при которых даже наиболее локальные методы анализа доставляют минералогу сведения о химическом составе, усредненном по объему опробования. Именно к таким объемам относятся эмпирические формулы минералов.
Химическая и фазовая неоднородность минералов нередко проявляется в таких тонких масштабах (порядка 1-10 нм), при которых даже наиболее локальные методы анализа доставляют минералогу сведения о химическом составе, усредненном по объему опробования. Именно к таким объемам относятся эмпирические формулы минералов.Пересчет результатов химических анализов на кристаллохимическую формулу представляет собой не простую задачу. Для разных минералов используются различные методы пересчета, применимость которых зависит от полноты анализа, возможного наличия примесей других фаз, что определяется методом анализа. Результаты химического анализа, как и результаты всякого другого измерения, не свободны от погрешностей, которые переходят и в эмпирические формулы минералов. В теоретических формулах такие ошибки, в большинстве случаев, устраняются, благодаря обобщению множества эмпирических формул.
Таблица Менделеева online — Mn
| Относительная электроотрицательность (по Полингу): | 1,60 |
| Температура плавления: | 271,3°C |
| Температура кипения: | 1560°C |
| Теплопроводность: | 8 |
| Плотность: | 9,8 г/см3 |
| Открыт: | Известен с глубокой древности |
| Цвет в твёрдом состоянии: | Блестящий красновато-белый |
| Тип: | Металл |
| Орбитали: | 1s22s22p63s23p63d104s24p64d104f145s25p65d105f06s26p3 |
| Электронная формула: |
Mn — 1s2 2s2 2p6 3s2 3p6 4s2 3d5 Mn — [Ar] 4s2 3d5 |
| Валентность: | +2, (+3), +4, (+6), +7 |
| Степени окисления: | 0, +II, IV, VI, VIII |
| Сверхпроводящее состояние при температуре: | 6,154 К |
| Потенциалы ионизации: | 7,237 В 16,687 В |
Электропроводность в тв. фазе: фазе: |
0,92*106 при 273K |
| Ковалентный радиус: | 1,46 Å |
| Атомный объем: | 21,3 см3/моль |
| Атомный радиус: | 1,63 Å |
| Теплота распада: | 11,3 Кдж/моль |
| Теплота парообразования: | 104,8 Кдж/моль |
| Кристаллическая структура: | Ромбоэдрическая. Все углы разные. Высота, ширина, длина не равны. В каждой вершине имеется атом |
Формулы и Задачи (Информатика 10)
Формулы
N = 2i
N — мощность алфавита (количество знаков в алфавите)
i — информационный вес символа алфавита (количество информации в одном символе)
I = K * i
I — количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K — число символов в сообщении
i — информационный вес символа (количество информации в одном символе)
Q = NL
Q — количество разных сообщений
N — количество символов
L — длина сообщения
Формула Хартли:
I = log2N
I — количество информации, содержащееся в выбранном сообщении
N — количество сообщений
Римская система счисления
I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)
Перевод чисел из других систем счисления в десятичную систему счисления
Развернутая запись целого числа:
a3a2a1a0 = a3 * p3 + a2 * p2 + a1 * p1 + a0 * p0
Правило перевода числа из любой системы счисления в десятичную систему счисления — умножаем каждую цифру исходного числа на основание системы счисления в степени разряда, в котором находится эта цифра, а затем всё складываем.
Запись через схему Горнера:
a3a2a1a0 = ((a3 * p + a2) * p + a1) * p + a0
p — основание системы счисления в котором представлено число.
Пример:
637510 = 6 * 103 + 3 * 102 + 7 * 101 + 5 * 100
637510 = ((6 * 10 + 3) * 10 + 7) * 10 + 5
12345 = 1 * 53 + 2 * 52 + 3 * 51 + 4 * 50 = 19410
12345 = ((1 * 5 + 2) * 5 + 3) * 5 + 4 = 19410
Развернутая запись дробного числа:
0,a1a2a3a4 = a1*p-1 + a2*p-2 + a3*p-3 + a4*p-4
Запись через схему Горнера:
0,a1a2a3a4 = p-1 * (a1 + p-1 * (a2 + p-1 * (a3 + p-1 * a4)))
p * (0,a1a2a3a4) = a1 + p-1 * (a2 + p-1 * (a3 + p-1 * a4))
p — основание системы счисления в котором представлено число.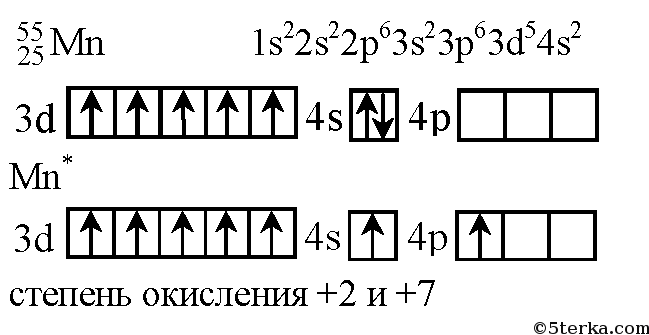
Пример:
0,6375 = 6 * 10-1 + 3 * 10-2 + 7 * 10-3 + 5 * 10-4
0,6375 = 10-1 * (6 + 10-1 * (3 + 10-1 * (7 + 10-1 * 5)))
0,12345 = 1 * 5-1 + 2 * 5-2 + 3 * 5-3 + 4 * 5-4
0,12345 = 5-1 * (1 + 5-1 * (2 + 5-1 * (3 + 5-1 * 4)))
Задачи
Алфавитный подход к измерению количества информации
Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.
- информационная ёмкость символа: 256 = 28 =>> i = 8 бит = 1 байт
-
количество символов на странице:
32 * 64 = 25 * 26 = 211 -
общее количество символов:
L = 10 * 211 -
информационный объём сообщения:
I = L * i = 10 * 211 * 1 байт = 20 Кбайт
Системы счисления
X10 X16 X8 X2 0 0 0 0 1 1 1 1 2 2 2 10 3 3 3 11 4 4 4 100 5 5 5 101 6 6 6 110 7 7 7 111 8 8 10 1000 9 9 11 1001 10 A 12 1010 11 B 13 1011 12 C 14 1100 13 D 15 1101 14 E 16 1110 15 F 17 1111 16 10 20 10000 17 11 21 10001 18 12 22 10010 19 13 23 10011 20 14 24 10100 21 15 25 10101 22 16 26 10110 23 17 27 10111 24 18 30 11000 25 19 31 11001 26 1A 32 11010 27 1B 33 11011 28 1C 34 11100 29 1D 35 11101 30 1E 36 11110 31 1F 37 11111 32 20 40 100000
Логические операции
Логической операцией называется выбор решения (действия), исходя из заданной ситуации, определяемой набором факторов (условий).
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.
Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.
Таблица истинности для операции НЕ имеет вид:
| A | |
| 0 | 1 |
| 1 | 0 |
Действие, связанное с операцией НЕ можно записать следующим образом:
Логическая операция И (конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия). B
B
Логическая операция ИЛИ (дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.
Таблица истинности для операции ИЛИ имеет вид:
| A | B | X=A v B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Действие, связанное с операцией ИЛИ можно записать следующим образом:
X = A + B = A v B
Логическая операция Исключающее ИЛИ. Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.
Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.
Таблица истинности имеет вид:
| A | B | X=AB |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:
X = A B
Действие, связанное с операцией Импликации можно записать следующим образом:
X = A → B
Таблица истинности Импликации имеет вид:
| A | B | A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операция тождество. Операция тождество определяет тождественность аргументов.
Операция тождество определяет тождественность аргументов.
Таблица истинности для операции тождество имеет вид:
| A | B | A Ξ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Действие, связанное с операцией тождество можно записать следующим образом:
X = A Ξ B
Диаграммы Венна (круги Эйлера)
Поиск номера сети
Необходимо найти номер сети по IP-адресу 12. 16.196.10 и маске 255.255.224.0.
16.196.10 и маске 255.255.224.0.
| маска сети | 255. | 255. | 224. | 0 | |
| IP-адрес | 12. | 16. | 196. | 10 | — ip-адрес (узла, компьютера и т.п.) |
| IP-адрес | 0000 1100. | 0001 0000. | 1100 0100. | 0000 1010 | |
| маска сети | 1111 1111. | 1111 1111. | 1110 0000. | 0000 0000 | |
| адрес сети | 0000 1100. | 0001 0000. | 110x xxxx. | xxxx xxxx | — эта часть относится к адресу сети — она взята из ip-адреса, но взяты те цифры, напротив которых стоят единицы остальные цифры справа надо дополнить нулями, чтобы общее число цифр стало равным 32. Получится следующее: |
| адрес сети | 0000 1100.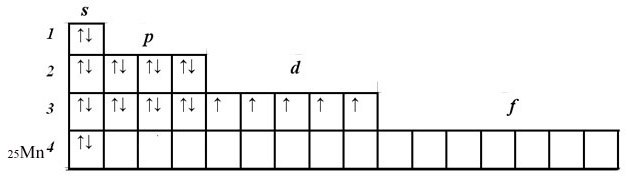 | 0001 0000. | 1100 0000. | 0000 0000 | — полный адрес сети теперь каждую октаду (последовательность из 8 цифр, разделены точками) переводим в десятичный вид. Получаем: |
| адрес сети | 12. | 16. | 192. | 0 | — полный адрес сети (в десятичном виде) |
Публикация математических текстов в Web с помощью MathML
Публикация математических текстов в Web с помощью MathML(перевод статьи «Putting mathematics on the Web with MathML»)
В этой статье Вы узнаете, как включать MathML в веб-страницы для просмотра в большинстве современных браузеров. Вы также узнаете, как настроить браузеры для поддержки MathML. На настоящий момент веб-страницы, созданные с использованием описанной ниже техники, можно просматривать в следующих браузерах (знак ‘+’ означает, что более новые версии тоже работают):
- Windows:
- IE 5.
 0 с плагином Techexplorer
0 с плагином Techexplorer - IE 5.5 с плагинами MathPlayer или Techexplorer
- IE 6.0+ (необязательно) с плагинами MathPlayer или Techexplorer
- Netscape 6.1 с плагином Techexplorer
- Netscape 7.0+
- Amaya, все версии (только Presentation MathML)
- Mozilla 0.9.9+
- IE 5.
- Macintosh:
- IE 5.0+ с плагином Techexplorer
- Mozilla 0.9.9+
- Linux/Unix:
- Netscape 6.1 с плагином Techexplorer
- Netscape 7.0+
- Mozilla 0.9.9+
- Amaya, все версии (только Presentation MathML)
Для тестирование своего браузера загрузите простой пример, использующий Presentation MathML, или более сложный пример, демонстрирующий Content MathML (генерация страницы может занять некоторое время).
Руководство предназначено для авторов веб-страниц, желающих включить в них
математические формулы, а также для тех, кто хочет читать такие страницы.
Подробное техническое описание происходящего можно посмотреть на странице, посвященной XSLT-таблицам для MathML. Смотрите также слайды с выступления David’а Carlisle на конференции, посвященной MathML.
Вставка MathML в страницу
Чтобы документ можно было просмотреть на максимальном числе платформ, он должен быть написан по описанным ниже правилам. Заметьте, что при использовании редактора, следующего стандартам W3C (например, Amaya), все описанное произойдет автоматически.
1. Создайте XHMTL-страницу со встроенным MathML
Веб-страница должна быть написана в формате XHTML со встроенной в нее разметкой MathML. Например:
<?xml version="1.0"?>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>...</head>
<body>
<h2>Пример</h2>
....
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>x</mi><mo>+</mo><mn>3</mn>
</math>
</body>
</html>Разметка MathML не должна находиться внутри тэга <object> и не должна быть в отдельном файле, подключаемом из тэга <embed>.
2. Добавьте обработку с помощью таблицы стилей
Выделенную жирным шрифтом строку нужно вставить в начало XHTML-страницы,
перед открытием тэга <html>, но после XML-объявления <?xml...?> (если оно есть, конечно):
<?xml version="1.0"?> <?xml-stylesheet type="text/xsl" href="http://www.w3.org/Math/XSL/mathml.xsl"?> <html xmlns="http://www.w3.org/1999/xhtml"> ...
Это будет работать не во всех случаях (Например, Internet Explorer, в связи с обеспечением безопасности, не позволяет выполнять XSLT-таблицу, если она находится на сервере, отличном от сервера с XHTML-страницей. В этом случае следуйте инструкциям в пункте «Режим оффлайн» (ниже). Также в конце документа есть дополнительная информация о безопасности в Internet Explorer). Поэтому есть альтернативы:
Режим оффлайн: Чтобы документ с формулами можно было просматривать локально, без интернет-соедининия, объявление должно выглядеть иначе:
<?xml-stylesheet type="text/xsl" href="mathml.
 xsl"?>
xsl"?>И копии следующих файлов нужно поместить на локальный компьютер, вместе с основным документом: mathml.xsl, pmathml.xsl, ctop.xsl and pmathmlcss.xsl.
Presentation MathML: если в документе используется только Presentation MathML, то достаточно только двух файлов:
pmathml.xslиpmathml-css.xsl. В этом случае страница будет обрабатываться быстрее.
Вот и все. Дополнительную информацию смотрите ниже.
Указание предпочтений
Возможна ситуация, когда в браузере есть несколько способов обработать
разметку MathML (например, Internet Explorer с плагином Techexplorer
может еще отображать формулы с помощью CSS). Для таких случаев предоставляется
возможность указать предпочтительный метод обработки, изменяя значение
атрибута renderer. Например:
<?xml-stylesheet type="text/xsl" href="pmathml.xsl"?> <html xmlns="http://www.w3.org/1999/xhtml" xmlns:pref="http://www.w3.org/2002/Math/preference" pref:renderer="css"> <head>...</head> <body>...</body> </html>
Здесь указывается, что предпочтителен метод с использованием CSS.
Значения атрибута renderer:
css: отображать формулы с помощью CSS (плагин не требуется).mathplayer-dl: в случае необходимости запросить установку плагина MathPlayer.mathplayer: использовать MathPlayer.techexplorer-plugin: использовать плагин Techexplorer.techexplorer: использовать Techexplorer.
Безопасность Microsoft Internet Explorer
По умолчанию, Internet Explorer не позволяет применять XSLT-таблицу к документу, если она находится на сервере, отличном от сервера с документом. Поэтому так работать не будет:
<?xml-stylesheet type="text/xsl"
href="http://www.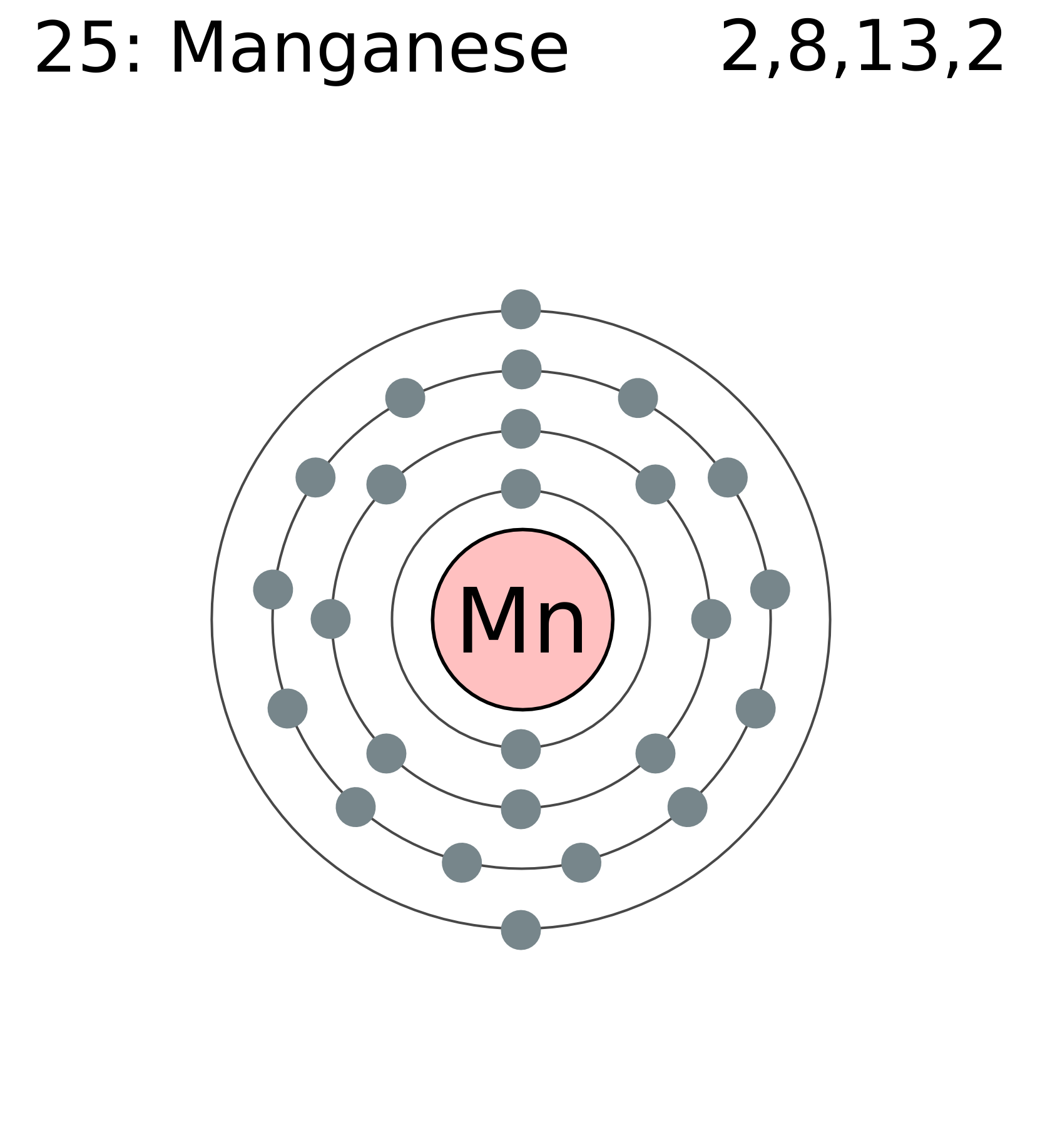 w3.org/Math/XSL/mathml.xsl"?>
w3.org/Math/XSL/mathml.xsl"?>
Вместо этого необходимо скопировать таблицы стилей на тот же сервер, где находится документ (как описано выше). В качестве альтернативы можно изменить настройки безопасности Internet Explorer, но такой способ нельзя порекомендовать, так как изменение настроек повлияет на всю работу браузера, а не только на загрузку таблицы стилей.
Презентация на MathML конференции
Эта таблица стилей была представлена на 2-ой Международной MathML конференции. Там были продемонстрированы примеры использования таблиц стилей для просмотра в полноэкранном режиме браузера. Для показа примеров одновременно использовались IE6, Mozilla 1.0, Amaya 6.1, и Netscape 7.0PR1.
В дополнение к MathML был также продемонстрирован небольшой пример расширения этой таблицы стилей для использования с SVG.
The W3C Math Working Group. Send comments, questions and fixes to www-math@w3.org
Translated by Alexey Shamrin
Формулы в ePub 3 | Та самая читалка
Можно ли читать на мобильных устройствах тексты с формулами – статьи, учебники? В принципе можно, если у устройства достаточно большой экран. На 10-дюймовом планшете типичные PDF-файлы выглядят неплохо. Но уже на 7-дюймовом устройстве (скажем, на популярном Kindle последних моделей) чтение обычного PDF превращается в муку. Приходится либо уменьшать текст до неразличимого размера, либо поворачивать электронную книгу набок и читать сперва верхнюю половинку текста, потом нижнюю. Всё от того, что PDF заранее разбит на страницы и прорисован.
На 10-дюймовом планшете типичные PDF-файлы выглядят неплохо. Но уже на 7-дюймовом устройстве (скажем, на популярном Kindle последних моделей) чтение обычного PDF превращается в муку. Приходится либо уменьшать текст до неразличимого размера, либо поворачивать электронную книгу набок и читать сперва верхнюю половинку текста, потом нижнюю. Всё от того, что PDF заранее разбит на страницы и прорисован.
Думаю, это важное свойство настоящей электронной книги, отличающее её от файла, подготовленного для печати. Электронная книга разбивается на страницы прямо на устройстве для чтения, в зависимости от размера экрана и того, какого размера шрифт предпочитает читатель.
Для обычной художественной книги проблема форматирования текста стоит не слишком остро. Есть наборы правил хорошего тона, которые хотелось бы соблюдать (отсутствие висячих строк, неразрывные пробелы, и т.п.). Их реализация сравнительно проста, а для многих читателей не слишком и важна. Другое дело «сложные тексты», например, содержащие математические формулы. Нарисовать правильно какой-нибудь хитрый интеграл – работа нетривиальная, а разбивать длинные выражения на строки абы как – значит сделать их непонятными (а иногда и вовсе неверными).
Нарисовать правильно какой-нибудь хитрый интеграл – работа нетривиальная, а разбивать длинные выражения на строки абы как – значит сделать их непонятными (а иногда и вовсе неверными).
В «классическом» ePub 2 единственное решение «проблемы формул» – вставлять картинки. Это неудобно для авторов, часто некрасиво выглядит, к тому же такие формулы никак не реагируют на изменение размера шрифта.
Я знаю средство, позволяющее набирать формулы для печати на бумаге. Средство называется TeX, и за 30 с лишком лет, прошедших с момента его рождения, никакая другая программа не смогла предложить что-нибудь близкое по удобству, скорости, и качеству отображения. Но вот беда, TeX нужно компилировать, чтобы получить готовый текст. И этот готовый текст окажется в столь нелюбимом мною формате PDF (или ничуть не более удобных DVI и PostScript).
Мне придется ещё немножко уйти в сторону, и рассказать про ещё один язык. Это громоздкий, совершенно неприменимый для написания формул MathML – формат разметки математических текстов.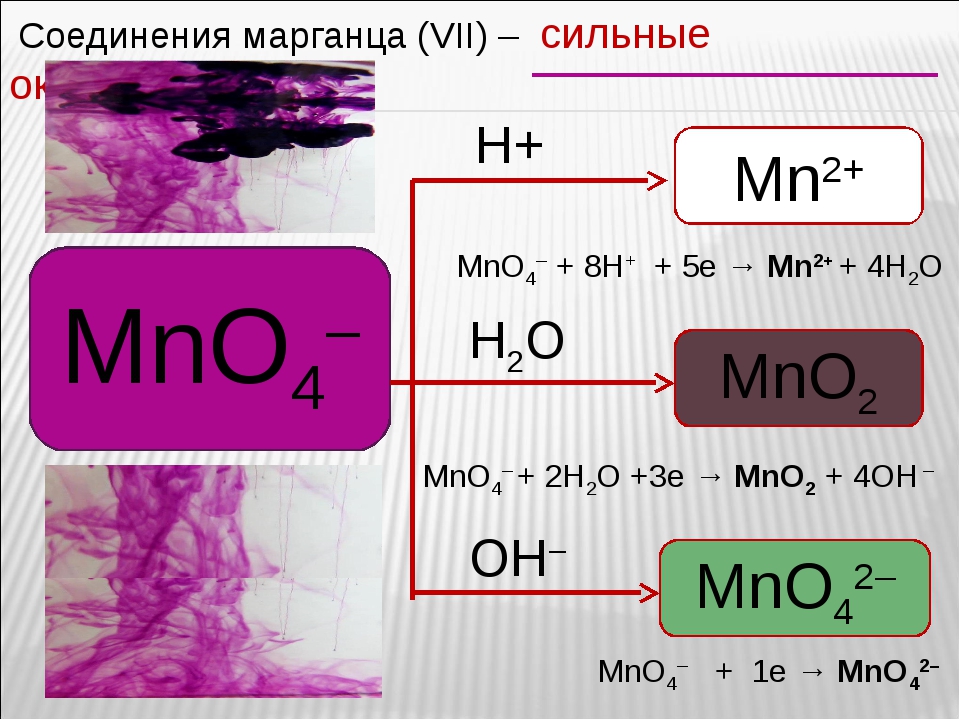 2+1}
2+1}
<math mode="display">
<mi>a</mi>
<mspace/>
<mi>t</mi>
<mspace/>
<mi>a</mi>
<mspace/>
<mi>n</mi>
<mo lspace="0" rspace="0" stretchy="false">(</mo>
<mi>x</mi>
<mo lspace="0" rspace="0.278em" stretchy="false">)</mo>
<mo lspace="0" rspace="0.278em">=</mo>
<msubsup>
<mo lspace="0" rspace="0.167em" stretchy="false">∫</mo>
<mn>0</mn>
<mi>x</mi>
</msubsup>
<mfrac>
<mrow>
<mi>d</mi>
<mspace/>
<mi>t</mi>
</mrow>
<mrow>
<msup>
<mi>t</mi>
<mn>2</mn>
</msup>
<mo lspace="0" rspace="0">+</mo>
<mn>1</mn>
</mrow>
</mfrac>
</math>
Надеюсь, вы не подумали, что я своими руками написал этот XML? Разумеется, он создан автоматически – из TeX-овской записи, программой blahtexml. А формула в самом начале нарисована вашим браузером из этого XML с помощью программы (java script’а) MatJax. Фуф, вот теперь я рассказал всё, что необходимо знать, чтобы понять, как можно решить проблему формул в электронных книгах.
А формула в самом начале нарисована вашим браузером из этого XML с помощью программы (java script’а) MatJax. Фуф, вот теперь я рассказал всё, что необходимо знать, чтобы понять, как можно решить проблему формул в электронных книгах.
Новый формат ePub 3 разрешает вставлять в текст отрывки в формате MathML. Вы можете взять статью в обычном LaTeX, и скомпилировать её прямо в ePub 3 со вставками в MathML. После этого любая читалка электронных книг должна показать вам формулу в книге. Дело за малым: программы, понимающей любой ePub 3, или хотя бы MathML-вставки, пока не существует. Собственно, поводом для этой заметки послужил анонс читалки с поддержкой MathML под названием eqate. По ссылке можно посмотреть видео, но попробовать программу пока невозможно. Авторы обещают, что eqate будет работать на устройствах с iOS и Android, а MathML она отображает с помощью упоминавшегося выше MathJax.
Не знаю, окажется ли решение с вызовом java script из программы-читалки оптимальным. Если бы у меня было бесконечно много времени, я бы непременно потратил маленький его кусочек, чтобы обучить FBReader читать MathML. Но пока ограничусь этим постом.
Но пока ограничусь этим постом.
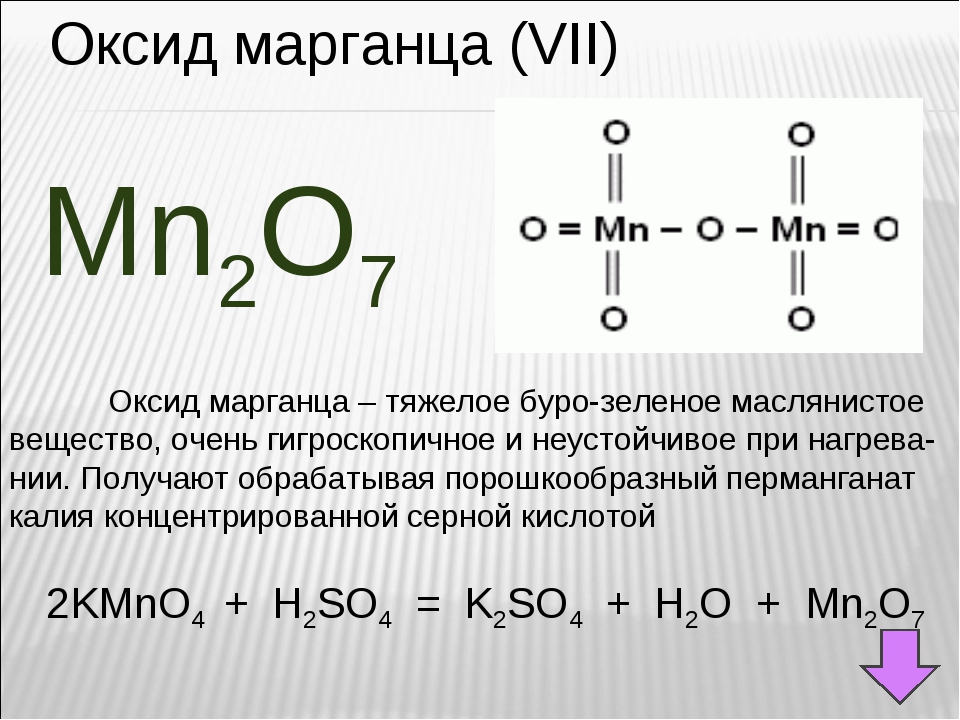
Тримарганца тетраоксид. Высокотемпературный пигмент для керамики.
Mn3O4
Cреди пигментов на основе синтетического тетраоксида марганца (Mn3O4) выделяются продукты линии Color K (K/S, K/P, K/C) компании Kimpe (Франция). Отличительной особенностью марганцевых красителей Color K являются высокое содержание марганца, однородность, низкий уровень пыления и стабильное качество. Тримарганца тетраоксид Color K предназначен для объемного окрашивания керамических изделий из белой и красной обжигаемой глины высокотемпературной обработки от 800° С до 1200° С. Благодаря высокому качеству продукции, пигменты Kimpe не уступают аналогам, продуктам Brickmax (Prince Minerals, Великобритания), так Color K-P является полным аналогом Brickmax P. Благодаря гибкой ценовой политике производителя и высоким стандартам качества марганцевая продукция Kimpe – это лучший выбор производителей облицовочного керамического кирпича и черепицы.
Благодаря гибкой ценовой политике производителя и высоким стандартам качества марганцевая продукция Kimpe – это лучший выбор производителей облицовочного керамического кирпича и черепицы.
Тонкий коричневый порошок.Торговое название: COLOR K/C, COLOR K/P, COLOR K/S
Плотность: 4,8 г/см3
Синонимы: Тримарганца тетраоксид, оксид марганца (II, III), синтетический гаусманнит
Международное название: Trimanganese tetraoxide, Manganese (II,III) oxide, Manganese oxide, Manganomanganic oxide
Формула: Mn3O4
Молекулярная масса: 228.
 81
81 CAS 1317-35-7
EINECS 215-266-5
RTECS OP0895000
Классификация ЕС
R:36/37/38
S26;S36
Символ: Xi
Паспорт безопасности (MSDS)
Транспортная информация
Код ТНВЭД 2820909000
Код ГНГ 282090
Классификация ООН
Группа упаковки ООН: III
1.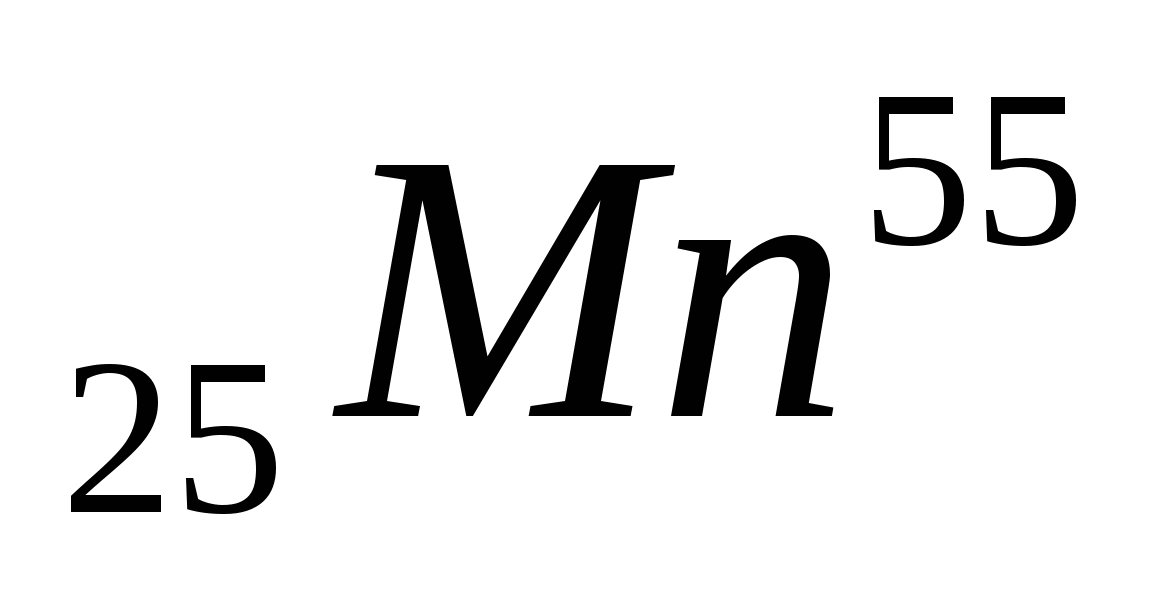 25$
25$
по курсу ЦБ РФ на день оплаты
цена за кг включая НДС 18%
Тримарганца тетраоксид COLOR K (K/S, K/P, K/C) компании Kimpe (Франция), представляет собой синтетический гаусманнит, содержащий не менее 67% Mn или 95% Mn3O4. Продукт не содержит MnO2 (четырехвалентного марганца). Отличительными особенностями марганцевых красителей COLOR K являются:
- высокая концентрация марганца,
- однородность,
- низкий уровень пыления
- стабильное качество.
Пигменты линии COLOR K хорошо растворяются в шихте, быстро и эффективно реагируют с глиной при обжиге глины в печи при температуре от 800 до 1200°C. В настоящее время это самый эффективный коричневый пигмент для окрашивания, пригодный для любой линии по обжигу керамики. COLOR K используется для производства светло-коричневых, желто-коричневых, коричневых, темно-коричневых кирпичей и керамической плитки. Тримарганца тетраоксид COLOR K предназначен для объемного окрашивания керамических изделий из желто-жгущихся и красно-жгущихся глин. Применение COLOR K имеет ряд серьёзных преимуществ по сравнению с процессом на основе MnO2:
В настоящее время это самый эффективный коричневый пигмент для окрашивания, пригодный для любой линии по обжигу керамики. COLOR K используется для производства светло-коричневых, желто-коричневых, коричневых, темно-коричневых кирпичей и керамической плитки. Тримарганца тетраоксид COLOR K предназначен для объемного окрашивания керамических изделий из желто-жгущихся и красно-жгущихся глин. Применение COLOR K имеет ряд серьёзных преимуществ по сравнению с процессом на основе MnO2:
- Резкое повышение экономичности процесса:
- Снижение брака по цвету с 10-50% до 0,5-5%.
- Снижение необходимого объёма пигмента (по информации различных производителей экономия составляет от 43 до 73%)
- Более экономичное потребление электроэнергии при обжиге
- Существенное снижение вредности процесса для персонала и окружающей среды за счёт практического отсутствия пыли, характерной для процесса с MnO2.

- Снижение трудоёмкости процесса:
- За счёт отсутствия пыли значительно облегчается очистка оборудования (трубопроводов, насосов, дозаторов).
- Повышение качества конечного продукта:
- Использование продукта COLOR K снижает водопоглощение окрашенного кирпича по сравнению с красным кирпичом,
- Улучшается структура поверхности – она становится более гладкой и однородной, без обгорелых пузырей.
Красители COLOR K можно добавлять в линию подачи шихты в виде порошка или суспензии. Продукт легко диспергируется в воде, образуя насыщенную суспензию. Суспензия стабильна, проста в работе и легко дозируется в шихту с высокой точностью, что позволяет добиться её эффективного растворения в шихте. На предприятиях, которые используют глины с повышенной влажностью или предпочитают из практических соображений добавлять COLOR K в виде порошка, также выиграют от использования продукта. Благодаря мелкому помолу порошок COLOR K чуть более склонен к слипанию, чем пигменты на основе MnO2, но вместе с тем, как сообщают потребители, образует намного меньше пыли.
На предприятиях, которые используют глины с повышенной влажностью или предпочитают из практических соображений добавлять COLOR K в виде порошка, также выиграют от использования продукта. Благодаря мелкому помолу порошок COLOR K чуть более склонен к слипанию, чем пигменты на основе MnO2, но вместе с тем, как сообщают потребители, образует намного меньше пыли.
Сравнительная таблица
упаковка
Упаковка: биг-беги по 1000 кг
Отгрузка: Автомашинами, контейнерами, крытыми вагонами по 60 т и полувагонами с верхней загрузкой до 67 т.
Нитрат марганца
| Нитрат марганца | |
|---|---|
| Систематическое наименование | Нитрат марганца |
| Традиционные названия | Нитрат марганца II, азотнокислый марганец |
Хим. формула формула | Mn(NO3)2 |
| Состояние | светло-розовые кристаллы |
| Молярная масса | 178,95 г/моль |
| Температура | |
| • плавления | разл. 180 °C |
| Энтальпия | |
| • образования | -574,6 кДж/моль |
| Растворимость | |
| • в воде | 1020; 15725; 42850; 49975 г/100 мл |
| Рег. номер CAS | 10377-66-9 |
| PubChem | 61511 |
| Рег. номер EINECS | 233-828-8 |
| SMILES |
[N+](=O)([O-])[O-].[N+](=O)([O-])[O-].[Mn+2] |
| InChI |
1S/Mn.2NO3/c;2*2-1(3)4/q+2;2*-1 MIVBAHRSNUNMPP-UHFFFAOYSA-N |
| Номер ООН | 2724 |
| ChemSpider | 55431 |
Приведены данные для стандартных условий (25 °C, 100 кПа), если не указано иное. | |
Нитрат марганца — неорганическое соединение, соль металла марганца и азотной кислоты с формулой Mn(NO3)2, светло-розовые кристаллы, растворимые в воде, образует кристаллогидраты.
Получение
- Действие разбавленной азотной кислоты на гидроксид или карбонат марганца:
- Mn(OH)2 + 2 HNO3 → Mn(NO3)2 + 2 H2O
- MnCO3 + 2 HNO3 → Mn(NO3)2 + CO2 ↑ + H2O
Физические свойства
Нитрат марганца образует светло-розовые кристаллы, хорошо растворимые в воде. Также растворим в диоксане, тетрагидрофуране, ацетонитриле.
Образует кристаллогидраты состава Mn(NO3)2•n H2O, где n = 1, 2, 3, 4 и 6. Кристаллогидрат Mn(NO3)2•6H2O плавится при 28,5 °С в собственной кристаллизационной воде, имеет плотность 1,82 г/см³.
С аммиаком образует аддукт вида Mn(NO3)2•9NH3.
Химические свойства
- Разлагается при нагревании:
- Mn(NO3)2 →180−195oC MnO2 + 2 NO2 ↑
Применение
- Для получения высокочистого оксида марганца IV.
- В оксидных катализаторах.
- Компонент микроудобрений.
- Сиккатив.
Соединения марганца | |
|---|---|
| |
Молярная масса mn (ko) 3
Ошибка
| |||||
Публикация математических текстов в Web с помощью MathML
Публикация математических текстов в Web с помощью MathML(перевод статьи «Putting математика в Интернете с помощью MathML «)
В этой статье Вы узнаете. MathML в веб-страницы
для просмотра в большинстве современных браузеров.Вы также узнаете, как настроить браузеры для поддержки MathML.
На настоящий момент веб-страницы, созданные с использованием описанной
ниже техники, можно просмотреть в следующих браузерах (знак ‘+’ означает, что
более новые версии тоже работают):
MathML в веб-страницы
для просмотра в большинстве современных браузеров.Вы также узнаете, как настроить браузеры для поддержки MathML.
На настоящий момент веб-страницы, созданные с использованием описанной
ниже техники, можно просмотреть в следующих браузерах (знак ‘+’ означает, что
более новые версии тоже работают):
- Окна:
- IE 5.0 с плагином Techexplorer
- IE 5.5 с плагинами MathPlayer или Techexplorer
- IE 6.0+ (необязательно) с плагинами MathPlayer или Techexplorer
- Netscape 6.1 с плагином Techexplorer
- Netscape 7.0+
- Amaya, все версии (только Presentation MathML)
- Mozilla 0.9.9+
- Macintosh:
- IE 5.0+ с плагином Techexplorer
- Mozilla 0.9.9+
- Linux / Unix:
- Netscape 6.1 с плагином Techexplorer
- Netscape 7.0+
- Mozilla 0.
 9.9+
9.9+ - Amaya, все версии (только Presentation MathML)
Для тестирования своего загрузите простой пример, использующий Presentation MathML, или более сложный пример, представляющий Content MathML (генерация страницы может занять некоторое время).
Руководство предназначено для авторов веб-страниц, желающих включить в них математические формулы, а также для тех, кто хочет читать такие страницы.
Подробное техническое описание происходящего можно посмотреть на странице, посвященной XSLT-таблицам для MathML. Смотрите также слайды с выступления David’а Карлайла на конференции, посвященной MathML.
Вставка MathML в страницу
Чтобы документ можно было просмотреть на максимальном числе платформ, он должен быть написан по описанным ниже правилам.Заметьте, что при использовании редактора, следующего стандарта W3C (например, Amaya), все описанное автоматически автоматически.
1. Создайте XHMTL-страницу со встроенным MathML
Веб-страница должна быть написана в формате XHTML со встроенной в нее
разметкой MathML. Например:
Например:
...
Пример
....
Разметка MathML не должна находиться внутри тэга <объект> и не должна быть в отдельном файле, подключаемым из тэга <вставка> .
2. Добавьте обработку с помощью таблицы стилей
Выделенную жирным шрифтом нужно вставить в начало XHTML-страницы,
перед открытием тэга , но после XML-объявления (если оно есть, конечно):
...
Это будет работать не во всех случаях
( Например, Internet Explorer, в связи с национальной безопасностью,
не позволяет выполнять XSLT-таблицу, если она находится на сервере,
отличном от сервера с XHTML-страницей. В этом случае следуйте инструкциям в предложении «Режим оффлайн» (ниже).Также в конце документа есть дополнительная информация о безопасности
в Internet Explorer ). Поэтому есть альтернативы:
В этом случае следуйте инструкциям в предложении «Режим оффлайн» (ниже).Также в конце документа есть дополнительная информация о безопасности
в Internet Explorer ). Поэтому есть альтернативы:
Режим оффлайн : Чтобы документ с формулами можно было просматривать локально, без интернет-соедининия, объявление должно выглядеть иначе:
И копии следующих файлов нужно на локальный компьютер, вместе с основным документом: mathml.xsl, pmathml.xsl, ctop.xsl и pmathmlcss.xsl.
Presentation MathML : если в документе используется только Презентация MathML, то достаточно только двух файлов:
pmathml.xslиpmathml-css.xsl. В этом случае страница будет обрабатываться быстрее.
Вот и все. Дополнительную информацию смотрите ниже.
Указание предпочтений
Возможна ситуация, когда в браузере есть несколько способов обработать
разметку MathML (например, Internet Explorer с плагином Techexplorer
может еще отображать формулы с помощью CSS). Для таких случаев предоставляется
возможность указать предпочтительный метод обработки, изменяя значение
атрибута
Для таких случаев предоставляется
возможность указать предпочтительный метод обработки, изменяя значение
атрибута рендерер . Например:
xmlns: pref = "http://www.w3.org/2002/Math/preference"
pref: renderer = "css" >
...
...
Здесь указывается, что предпочтителен метод с использованием CSS.Значения атрибута средство визуализации :
-
css: отображать формулы с помощью CSS (плагин не требуется). -
mathplayer-dl: в случае необходимости запросить установить плагина MathPlayer. -
mathplayer: использовать MathPlayer. -
techexplorer-plugin: использовать плагин Techexplorer. -
techexplorer: использовать Techexplorer.
Безопасность Microsoft Internet Explorer
По умолчанию, Internet Explorer не позволяет применять XSLT-таблицу к документу, если она находится на сервере, отличном от сервера с документом.Поэтому так работать не будет:
Вместо этого необходимо скопировать таблицы стилей на тот же сервер, где находится документ (как описано выше). В качестве альтернативы можно изменить настройки безопасности Internet Explorer, но такой способ нельзя порекомендовать, так как изменение настроек повлияет на всю работу Google, а не только на загрузку таблицы стилей.
Презентация на MathML конференции
Эта таблица стилей была представлена на
2-ой Международной MathML
конференции.Там были настроены
примеры использования
таблиц стилей для просмотра в полноэкранном режиме.
Для показа использовались одновременно IE6, Mozilla 1.0, Amaya 6.1,
и Netscape 7. 0PR1.
0PR1.
В дополнение к MathML был также установлен небольшой пример расширения этой таблицы стилей для использования с SVG.
Рабочая группа W3C по математике. Отправляйте комментарии, вопросы и исправления по адресу www-math@w3.org
Перевод Алексея Шамрина
Химическая формула — Минералогический музей имени А.Е. Ферсмана РАН
Химическая формула минерала выражает его химический состав в виде символов химических элементов, снабженных подстрочными стехиометрическими индексами, следующими относительными количествами различных элементов сортов, входящих в его. Химизм соединяется с особенностями его строения с (кристаллической структурой). Формулы минералов по возможности отражают их конституцию, что достигается распределением по определенным группам символов химических элементов, которые находятся в идентичных позициях кристаллической структуры.Такие формулы называются кристаллохимическими. Стехиометрические индексы элемента измерения количества элементов каждого элемента в элементарной ячейке кристаллической структуры минерала. Спецификой минерального вещества является непостоянство его химического состава и обилие примесей, что сказывается на характере химических формул, применяемых в минералогии. Так, в частности, стехиометрические индексы могут не быть целочисленными.
Спецификой минерального вещества является непостоянство его химического состава и обилие примесей, что сказывается на характере химических формул, применяемых в минералогии. Так, в частности, стехиометрические индексы могут не быть целочисленными.
Различаются эмпирические и идеализированные (обобщенные, генерализованные, теоретические) формулы минералов.Эмпирические формулы детально характеризуют химический состав отдельных минеральных индивидов, реже их множеств, отобранных в одинаковой обстановке (в одном минеральном агрегате, в определенном участке горной породы или рудного тела). Идеализированные формулы к минеральным видам или группам, они могут различаться по степени абстрагирования конкретных химизма данного минерала.
Эмпирическая формула минерала получается в результате интерпретации результатов конкретного химического анализа, сводящейся к некоторой процедуре пересчета.Относится такая формула к конкретному минеральному индивиду или к группе индивидов близкого состава. Содержания примесных элементов, находящихся в минерале в количестве ниже определенного порога (требующие применения в формуле значений стехиометрических коэффициентов, меньших 0,01), в эмпирических формулах минералов обычно не отражаются. Особенность эмпирических формул минералов, как различных составов (бертоллидов), отличающих их от химических веществ постоянного состава (дальтонидов), является порядок перечисления элементов, иногда измененно отличающийся от порядка рекомендованного ИЮПАК (Международный союз по чистой и прикладной химии).Так, в частности, элементы-катионы, согласно которым перечисляются в порядке возрастания их степени окисления или электроотрицательности, составляет перечисление в эмпирической формуле в понижении их содержаний.
Содержания примесных элементов, находящихся в минерале в количестве ниже определенного порога (требующие применения в формуле значений стехиометрических коэффициентов, меньших 0,01), в эмпирических формулах минералов обычно не отражаются. Особенность эмпирических формул минералов, как различных составов (бертоллидов), отличающих их от химических веществ постоянного состава (дальтонидов), является порядок перечисления элементов, иногда измененно отличающийся от порядка рекомендованного ИЮПАК (Международный союз по чистой и прикладной химии).Так, в частности, элементы-катионы, согласно которым перечисляются в порядке возрастания их степени окисления или электроотрицательности, составляет перечисление в эмпирической формуле в понижении их содержаний.
Результатом обобщения эмпирических формул минералов являются идеализированные обобщенные формулы, называемые также теоретическими. Идеализированная формула минерала относится обычно к минеральному виду, она носит абстрактный характер и отражает главнейшие, повторяющиеся от индивида к особенностям химического состава всех минеральных индивидов, относящихся к данному виду. Такая формула содержит обычно лишь присутствующие во всех без исключения индивидах данного вида элементы, определяющие определяющую принадлежность минерала, при этом второстепенные особенности состава (но не всегда полностью) игнорируются. Правила, рекомендованные ИЮПАК, в формулах этого типа обычно помогает, однако, отличительной особенностью многих таких формул перечисление символов изоморфных элементов через запятую, без стехиометрических индексов. Теоретическая формула собственно минерального вида отражает часто состав гипотетического чистого (минала), являющегося крайним частным рядом твердых решений.Состав реальных минеральных индивидов очень редко соответствует таким идеализированным формулам. Идеализированные формулы могут охватывать и целые группы минералов, отражающие особенности изоморфных замен с помощью числовых величин стехиометрических индексов, а также путем использования переменных, заменяющих символы химических элементов.
Такая формула содержит обычно лишь присутствующие во всех без исключения индивидах данного вида элементы, определяющие определяющую принадлежность минерала, при этом второстепенные особенности состава (но не всегда полностью) игнорируются. Правила, рекомендованные ИЮПАК, в формулах этого типа обычно помогает, однако, отличительной особенностью многих таких формул перечисление символов изоморфных элементов через запятую, без стехиометрических индексов. Теоретическая формула собственно минерального вида отражает часто состав гипотетического чистого (минала), являющегося крайним частным рядом твердых решений.Состав реальных минеральных индивидов очень редко соответствует таким идеализированным формулам. Идеализированные формулы могут охватывать и целые группы минералов, отражающие особенности изоморфных замен с помощью числовых величин стехиометрических индексов, а также путем использования переменных, заменяющих символы химических элементов.
Рассмотрим в качестве варианта формул минералов, относящихся к минеральным, объединенным в группу оливина. Эмпирические формулы некоторых минеральных индивидов группы оливина (отнесенных к определенным видам этой группы) выглядят следующим образом:
Эмпирические формулы некоторых минеральных индивидов группы оливина (отнесенных к определенным видам этой группы) выглядят следующим образом:
| ФОРМУЛА | МИНЕРАЛЬНЫЙ ВИД |
| (Mg 1 , 3 4 Fe 2 + 0 , 5 6 Ca 0 , 0 6 0277 Mn 0 4 ) 2 , 0 0 [SiO 4 ] | форстерит |
(Fe 2 + 1 . 4 8 Мг 0 . 3 2 Mn 0 . 1 7 Fe 3 + 0 . 0 3 ) 2 . 0 0 [(Si 0 . 9 7 Al 0 . 0 3 ) O 4 ] 9 7 Al 0 . 0 3 ) O 4 ] | фаялит |
| (Mn 1 , 2 5 Fe 2 + 0 , 6 5 Mg 0 , 0 9027 Ca 0 2 ) 1 , 9 8 [SiO 4 ] | тефроит |
Идеализированные формулы минеральных видов этой группы таковы:
| ФОРМУЛА | МИНЕРАЛЬНЫЙ ВИД |
| мг 2 [SiO 4 ] | форстерит |
| Fe 2 [SiO 4 ] | фаялит |
| Mn 2 [SiO 4 ] | тефроит |
С учетом обычных изоморфных компонентов группы эти же формулы можно несколько уточнить:
| ФОРМУЛА | МИНЕРАЛЬНЫЙ ВИД |
| (Mg, Fe, Mn) 2 [SiO 4 ] | форстерит |
| (Fe, Mg, Mn) 2 [SiO 4 ] | фаялит |
| (Mn, Fe, Mg) 2 [SiO 4 ] | тефроит |
Количественные связи между элементами основных изоморфных компонентов можно выразить, с использованием этого индексов, так:
(Mg 2-x-y Fe x Mn y ) 2 [SiO 4 ]
Обобщенная формула минералов группы оливина, с использованием чисел, выражается следующим образом:
A 2 [SiO 4 ],
где А = Mg, Fe 2 + .
Важным является следующий момент. Стехиометрические индексы, завершающие собой скобки, содержащие изоморфных элементов, представляют собой не множители, а суммы индексов в скобках.
Проведение химического анализа минерала представляет собой экспериментальное исследование, которое имеет целью определение химического состава, как вещество. Химический состав минералов сильно отличается от минерального индивида к другому, даже если эти индивиды относятся к одному минеральному виду, что сказывается и на различных результатах анализа, помимо ошибокентоопределения.В процессе химического анализа по возможности проводит испытание конкретного минерального индивида, более того, современные локальные методы анализа (электронно-зондовый, например) определяют состав весьма малых участков (объем порядка 1-10 мкм 3 ). Составы таких участков в пределах одного минерального индивида. Химическая и фазовая неоднородность минералов нередко проявляется в таких тонких масштабах (порядка 1–10 нм), при которых даже наиболее локальные методы анализа доставляют минералогу сведения о химическом составе, усредненном по объему опробования.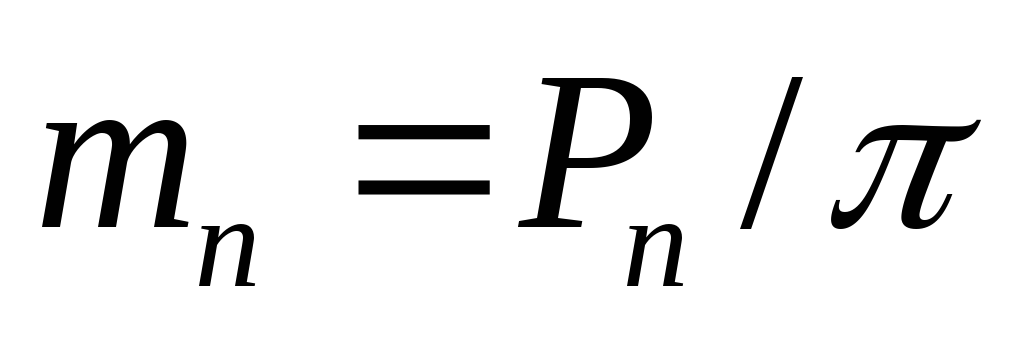 Именно к таким объемам эмпирические формулы минералов.
Именно к таким объемам эмпирические формулы минералов.
Пересчет результатов химической анализов на кристаллохимическую формулу представляет собой не простую задачу. Для разных минералов используются различные методы пересчета, применимость которых зависит от полноты анализа, возможного наличия примесей других фаз, что определяется методом анализа. Результаты химического анализа, как и результаты всякого другого измерения, не свободны от погрешностей, которые переходят и в эмпирические формулы минералов.В теоретических формулах такие ошибки, в большинстве случаев, устраняются, обобщению множества эмпирических формул.
Расчет молекулярной формулы по массовому доле элементов
способ
Найти молекулярную формулу вещества, содержащего 75% углерода, 25% водорода. Молярная масса равна 16.
Решение:
Исходим из формулы расчета доли элемента:
ω = масса компонента / масса целого,
где ω — массовая доля
Для расчета доли элемента в сложном веществе будет иметь следующий вид:
ω = Ar • n / Mr ,
где Ar — относительная атомная масса,
n — число атомов в молекуле,
Mr — относительная молекулярная масса (численно равна M — молярной массе)
n = ω • Mr / Ar
n (C) = 0,75 • 16/12 = 1
n (H) = 0,25 • 16/1 = 4
Ответ: CH 4 (метан)
II способ
За основу необходимо найти молекулярную формулу вещества, молярная масса которого неизвестна. Расчет молекулярной формулы через простейшую формулу позволяет решать задачи и в этом случае.
Расчет молекулярной формулы через простейшую формулу позволяет решать задачи и в этом случае.
Найти молекулярную формулу гидроксида:
Mn — 61,8%
O — 36,0%
H — 2,2%
Решение:
- Найдем простейшую формулу неизвестного вещества (соотношение элементов в молекуле):
(в следующем выражении косая черта деление, двоеточие (:) — соотношение элементов, делить не нужно!)
Mn: O: H = ω (Mn) / Ar (Mn): ω (O) / Ar (O): ω (H) / Ar (H) = 61,8% / 55: 36,0% / 16: 2,2% / 1 = 1,12 : 2.25: 2,2 = (делим на наименьшее) 1,12 / 1,12: 2,25 / 1,12: 2,2 / 1,12 = 1: 2: 2
Простейшая формула Mn (OH) 2Ответ : Mn (OH) 2
- Если получаются дробные индексы, например, PO 2,5 — умножаем все индексы на 2 (или другое подходящее число): P 2 O 5
- Если дана молярная масса, плотность по водороду или и возможность рассчитать молярную (молекулярную) массу, сравниваем её с массой простейшей формулы, как в данном примере: https: // staminaon.
 com / ru / chemistry / chemistry_9-45.htm
com / ru / chemistry / chemistry_9-45.htm
Обратите внимание, что расчет простейшей формулы доле и по продуктам сгорания ведётся аналогично: в числителе дроби содержания элемента в веществе, в знаменателе — атомная масса.
автор: Владимир Соколов
Поддержка LaTeX и MathML в программах Pages, Numbers, Keynote и iBooks Author
В этой статье рассказывается об использовании LaTeX и MathML вместе с Pages, Numbers, Keynote и iBooks Author, а также приводятся примеры формул.
LaTeX и MathML поддерживаются всеми тремя программами iWork (Pages, Numbers и Keynote) и iBooks Author. iWork и iBooks Автор все команды LaTeX, которые можно преобразовать в MathML с blahtex. Дополнительные поддерживаемые расширения LaTeX ниже.
iWork и iBooks Автор все команды LaTeX, которые можно преобразовать в MathML с blahtex. Дополнительные поддерживаемые расширения LaTeX ниже.
Узнайте, как формулы с использованием LaTex и MathML в документы iWork или книгу iBooks Author.
В время LaTeX и MathML не поддерживаются в настоящее время программы iWork для веб-сайта iCloud.com.
Команды LaTeX
Для LaTeX, как правило, формулы должны быть заключены в команды математического режима, см. приведенные ниже примеры. С помощью упрощения создания формул редакторы формул в iWork и iBooks Автор по умолчанию работают в математическом режиме, с необходимостью добавления в формулы математического режима.
- \ begin {math}… \ end {math}
- \ begin {displaymath}… \ end {displaymath}
- \ begin {уравнение}… \ end {уравнение}
- $… $
- $$… $$
- \ (… \)
- \ [… \]
Если в iWork или iBooks Author требуется добавить в формулу текст, который наследует стиль абзаца, використовуйте \ text {…}. Формулы, вложенные в \ text {…}, не поддерживаются.
Формулы, вложенные в \ text {…}, не поддерживаются.
В математическом режиме blahtex принимает только символы ASCII, но в текстовом режиме принимает полный набор символов Unicode.Дополнительные сведения о конкретных символах, таких как авторские права и символы с диакритическими знаками, см. в игре по blahtex, 2.22.
Ниже представлены поддерживаемые команды LaTeX (расширяющие blahtex), а также элементы и атрибуты MathML.
Команды LaTeX, поддерживаемые в iWork
| Команда или символ |
|---|
| \ фантом {} |
| \ цвет |
| \ отменить |
| \ underrightarrow, \ underleftarrow, \ underleftrightarrow |
| \ lneq, \ gneq, \ lvertneq, \ gvertneq |
| \ thinspace, \ medspace, \ Thickspace, \ negthinspace, \ negmedspace, \ negthickspace |
| «\:», «\,», «\;», «\!», «\» |
| \ lmoustache, \ rmoustache |
| \ lgroup, \ rgroup |
| \ скоба, \ скоба |
| \ xleftarrow, \ xrightarrow |
| \ dddot, \ ddddot |
| \ copyright |
| \ фунт |
| \ diagup, \ diagdown |
| \ dag, \ ddag, \ dagger, \ ddagger |
| \ владеет, \ ni |
| {split} |
Команды LaTeX, не поддерживаемые в iWork
| Команда или символ | Заметки |
|---|---|
| \ mathring {} | |
| \ ae, \ AE | |
| \ smallint | |
| \ идоцинт | |
| \ евро | Символ Unicode; работает только в текстовом режиме |
| \ varGamma | |
| \ кал | Используйте \ mathcal {} |
| \ mathml {} | |
| \ центр | |
| [lrc] в \ выровнено | |
| \ заполнить | |
| \ стойка | |
| \ вфантом | |
| \ hphantom | |
| \ разбить | |
| \ hпространство | Используйте «\:», «\,», «\;» или \ phantom {} |
| \ м пространство | |
| \ сантернот | |
| \ buildrelover | Используйте \ overset, \ underset |
| Среды, связанные с \ tabular | Поддержка \ матрица и \ выровнена ограничена |
| \ sideset | |
| \ pmb, \ boldmath, \ unboldmath | Используйте \ boldsymbol |
Команды LaTeX, поддерживаемые программой iBooks Author
| Команда или символ |
|---|
| \ фантом {} |
| \ цвет |
| \ отменить |
| \ underrightarrow, \ underleftarrow, \ underleftrightarrow |
| \ lneq, \ gneq, \ lvertneq, \ gvertneq |
| \ thinspace, \ medspace, \ Thickspace, \ negthinspace, \ negmedspace, \ negthickspace |
| «\:», «\,», «\;», «\!», «\» |
| \ lmoustache, \ rmoustache |
| \ lgroup, \ rgroup |
| \ скоба, \ скоба |
| \ xleftarrow, \ xrightarrow |
| \ dddot, \ ddddot |
Команды LaTeX, не поддерживаемые программой iBooks Author
| Команда или символ | Заметки |
|---|---|
| \ mathring {} | |
| \ copyright | Символ Unicode; работает только в текстовом режиме |
| \ фунт | Символ Unicode; работает только в текстовом режиме |
| \ ae, \ AE | |
| \ smallint | |
| \ diagup, \ diagdown | |
| \ идоцинт | |
| \ евро | Символ Unicode; работает только в текстовом режиме |
| \ varGamma | |
| \ кал | Используйте \ mathcal {} |
| \ mathml {} | |
| \ центр | |
| [lrc] в \ выровнено | |
| \ заполнить | |
| \ стойка | |
| \ вфантом | |
| \ hphantom | |
| \ разбить | |
| \ dag, \ ddag | \ dagger, \ ddagger поддерживается |
| {split} | |
| \ hпространство | Используйте «\:», «\,», «\;» или \ phantom {} |
| \ м пространство | |
| \ сантернот | |
| \ buildrelover | Используйте \ overset, \ underset |
| \ владеет | Используйте \ ni |
| Среды, связанные с \ tabular | Поддержка \ матрица и \ выровнена ограничена |
| \ sideset | |
| \ pmb, \ boldmath, \ unboldmath | Используйте \ boldsymbol |
Пакеты LaTeX
Следующие пакеты LaTeX не поддерживаются:
| Пакет | Заметки |
|---|---|
| отменить | Используйте \ отменить |
| АМС | Используйте \ underrightarrow, \ underleftarrow, \ underleftrightarrow |
| центернот |
Элементы MathML
Используйте приведенные ниже таблицы для получения сведений об элементе MathML, поддерживаемых в iWork и iBooks Author.
Поддерживаемые элементы MathML
| Элемент | Заметки |
|---|---|
| мес | |
| миль | |
| млн | |
| мров | |
| мужчины закрыть | Поддерживаются не все формы включения |
| м Таблица | Поддерживаются не все атрибуты |
| мтр | |
| мтд | |
| МРП | |
| MSUP | |
| мсуб | |
| msubsup | |
| мундер | |
| грузчик | |
| мандереровер | |
| mstack | |
| ряд | |
| группа MS | |
| mscarries | |
| mscarry | |
| msline | |
| млонгдив | |
| mpдобавлено | |
| мпространство | |
| maction | iWork и iBooks Автор включает первый дочерний элемент MathML и игнорируют все остальные |
| мфантом | |
| м огорожен | |
| корень | |
| MSQRT | |
| нет | |
| стиль | |
| mtext | |
| мс | |
| maligngroup | |
| злокачественное образование |
Частично поддерживаемые элементы MathML
| Элемент | Заметки |
|---|---|
| mlabeledtr | Обрабатывается как |
| семантика | Обрабатывается как строка |
| аннотация | На самом деле игнорируется |
Неподдерживаемые элементы MathML
Атрибуты MathML
Используйте приведенные ниже таблицы для получения сведений об атрибутах MathML, поддерживаемых в iWork и iBooks Author.
Поддерживаемые атрибуты MathML
В iWork и iBooks Author поддерживаются следующие атрибуты MathML:
Номинал| Элемент | Атрибут | Значение по умолчанию наследуется от | Значения (Синтаксис значения, если это поднабор спецификаций) |
|---|---|---|---|
| * | mathcolor | да | |
| стиль | уровень сценария | № | |
| стиль | дисплей | № | |
| стиль | скрипт, минимальный размер | № | |
| стиль | scriptsizemultiplier | № | |
| стиль | <заданные атрибуты с наследуемым значением по умолчанию> | отсутствует | |
| мес | lspace | да | |
| мес | rspace | да | |
| мес | большой топ | да | |
| мес | минимальный размер | да | |
| мес | макс. Размер Размер | да | |
| мес | акцент | да | |
| мес | подвижных лимитов | да | |
| мес | симметричный | да | |
| мес | эластичный | да | |
| мес | форма | да | |
| мпространство | ширина | да | |
| мпространство | высота | да | |
| мпространство | глубина | да | |
| мс | lqoute | да | |
| мс | rqoute | да | |
| МРП | толщина линии | да | |
| МРП | число | да | |
| МРП | да | ||
| грузчик | акцент | да | |
| грузчик | выровнять | да | |
| мандереровер | акцент | да | |
| мандереровер | неопытный | да | |
| мундер | акцентпод | да | |
| мундер | выровнять | да | |
| м Таблица | rowalign | да | |
| м Таблица | columnalign | да | |
| м Таблица | столбца между | да | |
| м Таблица | стиль отображения | да | |
| мтр | rowalign | да | |
| мтр | columnalign | да | |
| мтд | rowalign | да | |
| мтд | columnalign | да | |
| mstack | выровнять | да | сверху | внизу | центр | исходный уровень | ось |
| ряд | позиция | да | |
| группа MS | позиция | да | |
| группа MS | смена | да | |
| mscarries | позиция | да | |
| mscarries | crossout | да | восходящий удар | downdiagonalstrike | горизонтальный удар | verticalstrike |
| mscarry | crossout | да | восходящий удар | downdiagonalstrike | горизонтальный удар | verticalstrike |
| msline | длина | да | |
| msline | позиция | да | |
| mpдобавлено | высота | № | |
| mpдобавлено | глубина | № | |
| mpдобавлено | ширина | № | |
| mpдобавлено | lspace | № | |
| mpдобавлено | voffset | № | |
| м огорожен | открыто | да | |
| м огорожен | закрыть | да | |
| м огорожен | сепараторы | да | |
| maligngroup | groupalign | да | |
| злокачественное образование | край | да |
Частично поддерживаемые атрибуты MathML
В iWork и iBooks Author частично поддерживаются атрибуты MathML:
| Элемент | Атрибут | Значение по умолчанию наследуется от | Значения (Синтаксис значения, если это поднабор спецификаций) | Заметки |
|---|---|---|---|---|
мес. , Мин., Мили , Мин., Мили | математический вариант | да | Не поддерживаются начальные, растянутые, зацикленные, хвостовые | |
| м Таблица | выровнять | № | сверху | внизу | центр | исходный уровень | ось | rownumber не поддерживается |
| мужчины закрыть | обозначение | да | восходящий удар | downdiagonalstrike | горизонтальный удар | verticalstrike | Дополнительная информация |
| млонгдив | longdivstyle | № | слева вверху |
Неподдерживаемые атрибуты MathML
| Элемент | Атрибут | Заметки |
|---|---|---|
| * | математический фон | |
| стиль | infixlinebreakstyle | |
| стиль | veryverythinmathspace, verythinmathspace, thinmathspace, mediummathspace, Thickmathspace, verythickmathspace, veryverythickmathspace | Игнорируется в MathML 3. |
| mi, mn, mo, ms, mstyle, mtext | математический размер | |
| mi, mn, mo, ms, mstyle, mtext | дирек | |
| mi, mn, mo, ms, mstyle, mtext | семейство шрифтов, вес шрифта, стиль шрифта, размер шрифта, цвет, фон | Игнорируется в MathML 3. |
| мес | разрыв линии | |
| мес | линейный | |
| мес | linebreakstyle | |
| мес | linebreakmultchar | |
| мес | иденталин | |
| мес | идентшифт | |
| мес | identitytarget | |
| мес | identalignfirst | |
| мес | identshiftfirst | |
| мес | иденталигнласт | |
| мес | identshiftlast | |
| мес | забор | Не влияет на визуальную компоновку |
| мес | сепаратор | Не влияет на визуальную компоновку |
| мпространство | разрыв линии | |
| МРП | скошенная | |
| м Таблица | groupalign | |
| м Таблица | прицел | |
| м Таблица | ширина столбца | |
| м Таблица | ширина | |
| м Таблица | междурядье | |
| м Таблица | строки | |
| м Таблица | столбцов | |
| м Таблица | рама | |
| м Таблица | интервал кадров | |
| м Таблица | равных | |
| м Таблица | равных столбца | |
| м Таблица | сторона | |
| м Таблица | мин. Интервал между этикетками Интервал между этикетками | |
| мтр | groupalign | |
| мтд | пролет между рядами | |
| мтд | размах колонн | |
| мтд | groupalign | |
| mstack | stackalign | |
| mstack | charalign | |
| mstack | знаков | |
| млонгдив | позиция | |
| млонгдив | смена | |
| mscarries | место | |
| mscarries | scriptsizemultiplier | |
| mscarry | место | |
| msline | остаток | |
| msline | правый край | |
| msline | м, толщина | |
| мсуб | смещение индекса | |
| MSUP | надстрочный сдвиг | |
| msubsup | надстрочный сдвиг | |
| msubsup | смещение индекса | |
| мров | л | |
| maction | выбор | |
| maction | тип действия |
Информация о продуктах, произведенных не компанией Apple, неподконтрольных и не тестируемых компанией Apple, не носит рекомендательного или одобрительного характера. Компания Apple не несет ответственности за выбор, функциональность и использование веб-сайтов или продукции сторонних производителей. Компания Apple также несет ответственность за точность или достоверность данных, размещенных на веб-сайтах сторонних производителей. Обратитесь к поставщику за дополнительную дополнительную.
Компания Apple не несет ответственности за выбор, функциональность и использование веб-сайтов или продукции сторонних производителей. Компания Apple также несет ответственность за точность или достоверность данных, размещенных на веб-сайтах сторонних производителей. Обратитесь к поставщику за дополнительную дополнительную.
Дата публикации:
блокчейн — Объясните пожалуйста мне эту задачу. Почему h, m, r находятся именно так
Задача:
Блокчейн (блокчейн) переводится как «цепочка блоков». Это способ хранения данных, защищённый от подделки, в частности, криптовалютой биткоин.
Блокчейн действительно представляет собой последовательность блоков. Каждый блок представляет некоторую полезную информацию (в частности, в случае биткоина этого списка транзакций за установленный период времени — кто кому когда сколько денег передал) от остальной части блока и хэша предыдущего блока.
Хэш должен быть меньше определенного числа. При этом формула вычисляется так, чтобы получить достаточно маленький хэш иначе, чем перебирая различные значения случайного числа. Поэтому если злоумышленник решит подделать блокчейн (и, допустим, вставить в его середину блок с записью о том, что все люди передают ему все свои деньги), то ему придётся подобрать новое число в новое поддельном блоке и всех блока зависит от хэша предыдущего), что потребует невозможно больших вычислительных мощностей.
Поэтому блокчейн в целом защищён от подобных атак.
Напишите программу, которая проводит проверку правильности хэшей в модельном блокне с простым хэш-функцией.
Блок bn с номером n включает полезную информацию mn, представленную натуральным числом, rn — случайное число от 0 до 255 и hn — хеш (целое число от 0 до 255). У каждого блока хэш вычисляется по формуле hn = 37 × (mn + rn + hn-1) (по модулю 256), при вычислении хэша начального блока h0 вместо хэша блока предыдущего берётся ноль.
При этом каждый блок представлен одним числом bn = hn + rn × 256 + mn × 2562. При этом требуется, чтобы хэш был меньше 100.
Формат ввода В первой строке вводится натуральное число N — количество блоков. Далее следуют N чисел, каждую в отдельной строке.
Формат вывода Следует вывести номер первого блока, у которого неправильный хэш (не меньше 100 или не совпадает с вычисленным по заданному в условии формуле), или -1, если все хэши в блокчейне правильные.Нумерация блоков идёт с нуля, т. е. они имеют номера от 0 до N-1.
Пример 1
Ввод
5
6122802
14406496
15230209
2541121
1758741
Вывод: -1
Пример 2
Ввод Вывод
5
1865535
13479687
16689153
1839958
5214020
Вывод: 3
Тримарганца тетраоксид. Высокотемпературный пигмент для керамики.
Высокотемпературный пигмент для керамики.
Mn 3 O 4
Cреди пигментов на основе синтетического тетраоксида марганца (Mn 3 O 4 ) выделяются продукты линии Color K (K / S, K / P, K / C) компании Kimpe (Франция).Отличительной особенностью марганцевых красителей Цвет Высокое высокое содержание марганца, однородность, низкий уровень пыления и стабильное качество. Тримаганца тетраоксид Color предназначен для окрашенного окрашивания керамических изделий из белой и красной обжигаемой глины высокотемпературной обработки от 800 ° С до 1200 ° С. Благодаря высокому качеству продукции, пигменты Kimpe не уступают аналогам, продуктам Brickmax (Prince Minerals, Великобритания), так Color K-P является полным аналогом Brickmax P.Благодаря гибкой продукции марганцевая продукция Kimpe — это лучший выбор производителей облицовочного керамического кирпича и черепицы.
Тонкий коричневый порошок.Торговое название: COLOR K / C, COLOR K / P, COLOR K / S
Плотность: 4,8 г / см 3
Синонимы: Тримарганца тетраоксид, оксид марганца (II, III), синтетический гаусманнит
Международное название: Тетраоксид триманганца, Оксид марганца (II, III), Оксид марганца, Оксид марганца
Формула: Mn 3 O 4
Молекулярная масса: 228.81 год
CAS 1317-35-7
EINECS 215-266-5
RTECS OP0895000
Классификация ЕС
R: 36/37/38
S26; S36
Символ: Xi
Паспорт безопасности (MSDS)
Транспортная информация
Код ТНВЭД 28200
Код ГНГ 282090
Классификация ООН
Группа упаковки ООН: III
1. 25 долларов США
25 долларов США
по курсу ЦБ РФ на день оплаты
цена за кг включая НДС 18%
Тримарганца тетраоксид COLOR K (K / S, K / P, K / C) компании Kimpe (Франция) представляет собой синтетический гаусманнит, обеспечивающий не менее 67% Mn или 95% Mn 3 O 4 . Продукт не содержит MnO 2 (четырехвалентного марганца).Отличительными особенностями марганцевых красителей COLOR K являются:
- высокая степень марганца,
- однородность,
- низкий уровень пыления
- стабильное качество.
Пигменты линии COLOR K хорошо растворяются в шихте, быстро и эффективно реагируют с глиной при обжиге глины в печи при температуре от 800 до 1200 ° C. В настоящее время это самый эффективный коричневый пигмент для окрашивания, пригодный для любой линии по обжигу керамики. COLOR K используется для производства светло-коричневых, желто-коричневых, коричневых, темно-коричневых кирпичей и керамической плитки. Тримарганца тетраоксид COLOR Предназначен для объемного окрашивания керамических изделий из желто-жгущихся и красно-жгущихся глин. Применение COLOR K имеет ряд серьёзных преимуществ по сравнению с процессом на основе MnO 2 :
В настоящее время это самый эффективный коричневый пигмент для окрашивания, пригодный для любой линии по обжигу керамики. COLOR K используется для производства светло-коричневых, желто-коричневых, коричневых, темно-коричневых кирпичей и керамической плитки. Тримарганца тетраоксид COLOR Предназначен для объемного окрашивания керамических изделий из желто-жгущихся и красно-жгущихся глин. Применение COLOR K имеет ряд серьёзных преимуществ по сравнению с процессом на основе MnO 2 :
- Резкое повышение экономичности процесса:
- Снижение брака по цвету с 10-50% до 0,5-5%.
- Снижение необходимого объёма пигмента (по различных производителей экономия составляет от 43 до 73%)
- Более экономичное потребление электроэнергии при обжиге
- Существенное снижение вредности процесса для персонала и окружающей среды за счёт практического выброса пыли, характерной для процесса с MnO2.

- Снижение трудоёмкости процесса:
- За счёт пыли облегчается очистка оборудования (трубопроводов, насосов, дозаторов).
- Повышение качества конечного продукта:
- Использование продукта COLOR K снижает водопоглощение окрашенного кирпича по сравнению с красным цветом,
- Улучшается структура поверхности — она становится более гладкой и однородной, без обгорелых пузырей.
Красители COLOR K можно добавить в линию подачи шихты в виде порошка или суспензии. Продукт легко диспергируется в воде, образуя насыщенную суспензию. Суспензия стабильна, проста в работе и легко дозируется в шихту с высокой точностью, что позволяет использовать ее эффективное решение в шихте. На предприятиях которые используют глины с повышенной влажностью или используют из практических соображений добавки COLOR K в виде порошка, также выиграют от использования.Благодаря мелкому помолу порошок COLOR K чуть более склонен к слипанию, чем пигменты на основе MnO 2 , но вместе с тем, как сообщают использование, образует намного меньше пыли.
На предприятиях которые используют глины с повышенной влажностью или используют из практических соображений добавки COLOR K в виде порошка, также выиграют от использования.Благодаря мелкому помолу порошок COLOR K чуть более склонен к слипанию, чем пигменты на основе MnO 2 , но вместе с тем, как сообщают использование, образует намного меньше пыли.
Сравнительная таблица
упаковка
Упаковка: биг-беги по 1000 кг
Отгрузка: Автомашинами, контейнерами, крытыми вагонами по 60 т и полувагонами с верхней загрузкой до 67 т.

 0 с плагином Techexplorer
0 с плагином Techexplorer xsl"?>
xsl"?>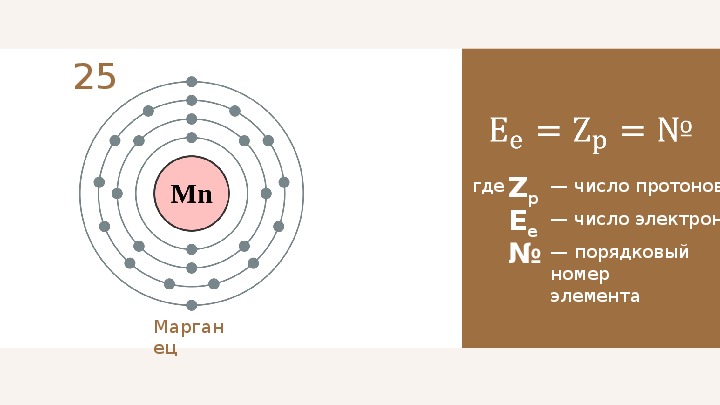 w3.org/1999/xhtml"
xmlns:pref="http://www.w3.org/2002/Math/preference"
pref:renderer="css">
<head>...</head>
<body>...</body>
</html>
w3.org/1999/xhtml"
xmlns:pref="http://www.w3.org/2002/Math/preference"
pref:renderer="css">
<head>...</head>
<body>...</body>
</html>
 В формуле, вы можете использовать:
В формуле, вы можете использовать:
 9.9+
9.9+
 com / ru / chemistry / chemistry_9-45.htm
com / ru / chemistry / chemistry_9-45.htm  Высокотемпературный пигмент для керамики.
Высокотемпературный пигмент для керамики. 