Все про ромб – Ромб. Формулы, признаки и свойства ромба

Posted on by alexxlab

Содержание

Ромб — Википедия

Материал из Википедии — свободной энциклопедии

Rhombus.svg

Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны[1].

Этимология

Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Видео по теме

Свойства

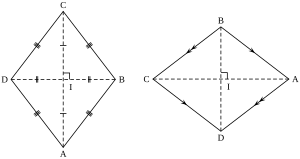
  1. Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны, АВ || CD, AD || ВС.
  2. Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника.
  3. Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
  4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
  5. Середины четырех сторон ромба являются вершинами прямоугольника.
  6. Диагонали ромба являются перпендикулярными осями его симметрии.
  7. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Признаки

Параллелограмм ABCD{\displaystyle ABCD} является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[2]:

  1. Две его смежные стороны равны (отсюда следует, что все стороны равны, AB=BC=CD=AD{\displaystyle AB=BC=CD=AD}).
  2. Его диагонали пересекаются под прямым углом (AC ⊥ BD).
  3. Одна из диагоналей делит содержащие её углы пополам.

Предположим, что заранее не известно, что четырёхугольник является параллелограммом, но дано, что все его стороны равны. Тогда этот четырёхугольник есть ромб[1].

Квадрат, как частный случай ромба

Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.

Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[3][4][5].

Rhombus1.svg
  • Площадь ромба равна половине произведения его диагоналей.
S=AC⋅BD2{\displaystyle S={\frac {AC\cdot BD}{2}}}
  • Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.
S=AB⋅HAB{\displaystyle S=AB\cdot H_{AB}}
  • Кроме того, площадь ромба может быть вычислена по формуле:
S=AB2⋅sin⁡α{\displaystyle S=AB^{2}\cdot \sin \alpha },

где α{\displaystyle \alpha } — угол между двумя смежными сторонами ромба.

  • Также площадь ромба можно рассчитать по формуле, где присутствует радиус вписанной окружности и угол α{\displaystyle \alpha }:
S=4r2sin⁡α{\displaystyle S={\frac {4r^{2}}{\sin \alpha }}}

Радиус вписанной окружности

Радиус вписанной окружности r может быть выражен через диагонали p и q в виде:[6]

r=p⋅q2p2+q2.{\displaystyle r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}}.}

В геральдике

Ромб является простой геральдической фигурой.

  • {\displaystyle r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}}.}

    Червлёный ромб в серебряном поле

  • {\displaystyle r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}}.}

    В червлёном поле 3 сквозных ромба: 2 и 1

  • {\displaystyle r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}}.}

    Просверленный червлёный ромб в серебряном поле

  • В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

Симметрия

Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.

  • {\displaystyle r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}}.}

    Ромбический орнамент

  • {\displaystyle r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}}.}

    Ромбические звёзды

  • {\displaystyle r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}}.}

    Более сложный орнамент

  • {\displaystyle r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}}.}

    Орнамент из ромбов и квадратов

См. также

Литература

  • Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.

Примечания

  1. ↑ 1 2 Элементарная математика, 1976, с. 435..
  2. ↑ Элементарная математика, 1976, с. 435—436..
  3. ↑ Ромб // Малый академический словарь. — М.: Институт русского языка Академии наук СССР. Евгеньева А. П.. 1957—1984.
  4. ↑ Ромб // Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910
  5. ↑ Ромб // Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней. Михельсон А.Д., 1865
  6. ↑ Weisstein, Eric W. Rhombus (англ.) на сайте Wolfram MathWorld.

wiki2.red

Ромб — Википедия

Материал из Википедии — свободной энциклопедии

Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны[1].

Этимология

Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Свойства

  1. Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны, АВ || CD, AD || ВС.
  2. Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника.
  3. Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
  4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
  5. Середины четырех сторон ромба являются вершинами прямоугольника.
  6. Диагонали ромба являются перпендикулярными осями его симметрии.
  7. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Признаки

Параллелограмм ABCD{\displaystyle ABCD} является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[2]:

  1. Две его смежные стороны равны (отсюда следует, что все стороны равны, AB=BC=CD=AD{\displaystyle AB=BC=CD=AD}).
  2. Его диагонали пересекаются под прямым углом (AC ⊥ BD).
  3. Одна из диагоналей делит содержащие её углы пополам.

Предположим, что заранее не известно, что четырёхугольник является параллелограммом, но дано, что все его стороны равны. Тогда этот четырёхугольник есть ромб[1].

Квадрат, как частный случай ромба

Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.

Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[3][4][5].

  • Площадь ромба равна половине произведения его диагоналей.
S=AC⋅BD2{\displaystyle S={\frac {AC\cdot BD}{2}}}
  • Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.
S=AB⋅HAB{\displaystyle S=AB\cdot H_{AB}}
  • Кроме того, площадь ромба может быть вычислена по формуле:
S=AB2⋅sin⁡α{\displaystyle S=AB^{2}\cdot \sin \alpha },

где α{\displaystyle \alpha } — угол между двумя смежными сторонами ромба.

  • Также площадь ромба можно рассчитать по формуле, где присутствует радиус вписанной окружности и угол α{\displaystyle \alpha }:
S=4r2sin⁡α{\displaystyle S={\frac {4r^{2}}{\sin \alpha }}}

Радиус вписанной окружности

Радиус вписанной окружности r может быть выражен через диагонали p и q в виде:[6]

r=p⋅q2p2+q2.{\displaystyle r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}}.}

В геральдике

Ромб является простой геральдической фигурой.

  • Червлёный ромб в серебряном поле

  • В червлёном поле 3 сквозных ромба: 2 и 1

  • Просверленный червлёный ромб в серебряном поле

  • В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

Симметрия

Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.

  • Ромбический орнамент

  • Ромбические звёзды

  • Более сложный орнамент

  • Орнамент из ромбов и квадратов

См. также

Литература

  • Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.

Примечания

  1. ↑ 1 2 Элементарная математика, 1976, с. 435..
  2. ↑ Элементарная математика, 1976, с. 435—436..
  3. ↑ Ромб // Малый академический словарь. — М.: Институт русского языка Академии наук СССР. Евгеньева А. П.. 1957—1984.
  4. ↑ Ромб // Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910
  5. ↑ Ромб // Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней. Михельсон А.Д., 1865
  6. ↑ Weisstein, Eric W. Rhombus (англ.) на сайте Wolfram MathWorld.

wikipedia.green

Ромб Википедия

Rhombus.svg

Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны[1].

Этимология[ | ]

Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Свойства[ | ]

  1. Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны, АВ || CD, AD || ВС.
  2. Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника.
  3. Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
  4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
  5. Середины четырех сторон ромба являются вершинами прямоугольника.
  6. Диагонали ромба являются перпендикулярными осями его симметрии.
  7. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Признаки[ | ]

Параллелограмм ABCD{\displaystyle ABCD} является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[2]:

  1. Две его смежные стороны равны (отсюда следует, что все стороны равны, AB=BC=CD=AD{\displaystyle AB=BC=CD=AD}).
  2. Его диагонали пересекаются под прямым углом (AC ⊥ BD).
  3. Одна из диагоналей делит содержащие её углы пополам.

Предположим, что заранее не известно, что четырёхугольник является параллелограммом, но дано, что все его стороны равны. Тогда этот четырёхугольник есть ромб[1].

Квадрат, как частный случай ромба[ | ]

Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.

Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[3][4][5].

ru-wiki.ru

Формула площади ромба

Что такое Ромб? Ромб — это параллелограмм, у которого все стороны равны.

РОМБ, фигура на плоскости, четырехугольник с равными сторонами. Ромб — частный случай ПАРАЛЛЕЛОГРАММА, у которого или две смежные стороны равны, или диагонали пересекаются под прямым углом, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.

Классической формулой площади ромба считается расчет значения через высоту. Площадь ромба равна произведению стороны на высоту, проведенную к этой стороне.

1. Площадь ромба равна произведению стороны на высоту, проведенную к этой стороне :

\[ S = a \cdot h \]

2. Если известна сторона ромба (у ромба все стороны равны) и угол между сторонами, то площадь можно найти по следующей формуле:

\[ S = a^{2} \cdot sin(\alpha) \]

3. Площадь ромба также равна полупроизведению диагоналей, то есть:

\[ S = \dfrac{d_{1} \cdot d_{2} }{2} \]

4. Если известен радиус r окружности, вписанной в ромб , и сторона ромба a, то его площадь вычисляется по формуле:

\[ S = 2 \cdot a \cdot R \]

Свойства ромба

На рисунке выше \( ABCD \) — ромб, \( AC = DB = CD = AD \) . Так как ромб — это параллелограмм, то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.

В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности равен половине высоты ромба:

\[ r = \frac{ AH }{2} \]

Свойства ромба

Диагонали ромба перпендикулярны;

Диагонали ромба являются биссектрисами его углов.

Признаки ромба

Параллелограмм, диагонали которого пересекаются под прямым углом, есть ромб;

Параллелограмм, диагонали которого являются биссектрисами его углов, есть ромб.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

calcsbox.com

Ромб Википедия

Этимология

Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Свойства

  1. Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны, АВ || CD, AD || ВС.
  2. Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника.
  3. Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
  4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
  5. Середины четырех сторон ромба являются вершинами прямоугольника.
  6. Диагонали ромба являются перпендикулярными осями его симметрии.
  7. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Признаки

Параллелограмм ABCD{\displaystyle ABCD} является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[2]:

  1. Две его смежные стороны равны (отсюда следует, что все стороны равны, AB=BC=CD=AD{\displaystyle AB=BC=CD=AD}).
  2. Его диагонали пересекаются под прямым углом (AC ⊥ BD).
  3. Одна из диагоналей делит содержащие её углы пополам.

Предположим, что заранее не известно, что четырёхугольник является параллелограммом, но дано, что все его стороны равны. Тогда этот четырёхугольник есть ромб[1].

Квадрат, как частный случай ромба

Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.

Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[3][4][5].

Rhombus1.svg
  • Площадь ромба равна половине произведения его диагоналей.
S=AC⋅BD2{\displaystyle S={\frac {AC\cdot BD}{2}}}
  • Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.
S=AB⋅HAB{\displaystyle S=AB\cdot H_{AB}}
  • Кроме того, площадь ромба может быть вычислена по формуле:
S=AB2⋅sin⁡α{\displaystyle S=AB^{2}\cdot \sin \alpha },

где

ruwikiorg.ru

Ромб — Вікіпедія

Ромб (грец. ρομβος) — це паралелограм, у якого всі сторони рівні.

Ромб, сторони якого утворюють прямий кут, називають квадратом.

Діагоналі ромба перетинаються під прямим кутом. Діагоналі ромба є бісектрисами його кутів.

Слово «ромб» походить від грецького слова ῥόμβος (ромбос), що означає щось що обертається[1], що в свою чергу утворене від дієслова ῥέμβω (рембо), що означає «обертатися довкола»[2]. Слово використовувалося Евклідом і Архімедом, які використовували термін «об’ємний суцільний ромб» для двох круглих конусів із спільною основою[3].

Та пласка фігура, яку ми називаємо ромбом сьогодні є поздовжнім перетином того суцільного ромба, що проходить крізь вершини кожного з двох конусів.

Паралелограм ABCD буде ромбом, якщо виконується хоча б одна із наступних умов:

1. Дві його суміжні сторони рівні (звідси випливає, що всі сторони рівні): АВ = ВС = СD = AD

2. Його діагоналі перетинаються під прямим кутом: AC┴BD

3. Одна із діагоналей (бісектриса) ділить кути навпіл:

∠BAC = ∠CAD або ∠BDA = ∠BDC

4. Якщо всі висоти рівні: BN = DL = BM = DK

5. Якщо діагоналі ділять паралелограм на чотири рівні прямокутні трикутники:

Δ ABO = Δ BCO = Δ CDO = Δ ADO

6. Якщо в паралелограм можна вписати коло.

Кожен ромб має дві діагоналі, що з’єднують пари протилежних вершин, і має дві пари паралельних сторін. Використовуючи правила конгруентних трикутників, можна довести, що ромб є симетричним відносно кожної з його діагоналей. Звідси випливає, що ромб має наступні властивості:

  • Це паралелограм, діагоналі якого розділяють внутрішній кут
  • Протилежні кути ромба рівні.
  • Діагоналі ромба перетинаються під прямим кутом, точка перетину є серединою кожної діагоналі.
  • Діагоналі ромба є бісектрисами кутів, з яких вони проведені.
  • Сторони ромба попарно паралельні.
  • Точка перетину діагоналей називається центром симетрії ромба.
  • В будь-який ромб можна вписати коло.
  • Центром кола, вписаного в ромб, є точка перетину його діагоналей.
  • Сума квадратів діагоналей дорівнює квадрату сторони, помноженому на чотири: AC2 + BD2 = 4AB2

Однією із основних властивостей є те, що ромб це паралелограм. Внаслідок чого, ромб також має усі властивості, що має паралелограм: наприклад, протилежні сторони паралельні; прилеглі кути є комплементарними; дві діагоналі поділяють одна одну навпіл; будь-яка пряма, що проходить через центр поділяє площу навпіл; а сума квадратів сторін дорівнює сумі квадратів діагоналей (правило паралелограма). Таким чином, якщо позначити сторону як a, а діагоналі як d1 і d2, для кожного ромба

4a2=d12+d22.{\displaystyle \displaystyle 4a^{2}=d_{1}^{2}+d_{2}^{2}.}

Не кожен паралелограм є ромбом, але кожен паралелограм, у якого діагоналі є перпендикулярними, є ромбом. В загальному випадку, будь-який чотирикутник з перпендикулярними діагоналями, одна з яких є лінією симетрії, це дельтоїд.

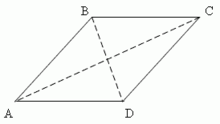
{\displaystyle \displaystyle 4a^{2}=d_{1}^{2}+d_{2}^{2}.}

Формули визначення довжини сторони ромба[ред. | ред. код]

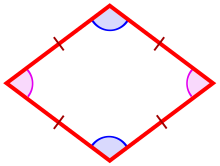
{\displaystyle \displaystyle 4a^{2}=d_{1}^{2}+d_{2}^{2}.}

1. Формула сторони ромба через площу і висоту:

a=Sh{\displaystyle a={\frac {S}{h}}}

2. Формула сторони ромба через площу і синус кута:

a=Ssin⁡α{\displaystyle a={\frac {\sqrt {S}}{\sqrt {\sin {\alpha }}}}}
a=Ssin⁡β{\displaystyle a={\frac {\sqrt {S}}{\sqrt {\sin {\beta }}}}}

3. Формула сторони ромба через площу і радіус вписаного кола:

a=S2r{\displaystyle a={\frac {S}{2r}}}

4. Формула сторони ромба через дві діагоналі:

a=d12+d222{\displaystyle a={\frac {\sqrt {d_{1}^{2}+d_{2}^{2}}}{2}}}

5. Формула сторони ромба через діагональ і косинус гострого кута (cos α) або косинус тупого кута (cos β):

a=d12+2cos⁡α{\displaystyle a={\frac {d_{1}}{\sqrt {2+2\cos {\alpha }}}}}
a=d22−2cos⁡β{\displaystyle a={\frac {d_{2}}{\sqrt {2-2\cos {\beta }}}}}

6. Формула сторони ромба через більшу діагональ і половинний кут:

a=d12cos⁡α2{\displaystyle a={\frac {d_{1}}{2\cos {\frac {\alpha }{2}}}}}
a=d12sin⁡β2{\displaystyle a={\frac {d_{1}}{2\sin {\frac {\beta }{2}}}}}

7. Формула сторони ромба через малу діагональ і половинний кут:

a=d22cos⁡β2{\displaystyle a={\frac {d_{2}}{2\cos {\frac {\beta }{2}}}}}
a=d22sin⁡α2{\displaystyle a={\frac {d_{2}}{2\sin {\frac {\alpha }{2}}}}}

8. Формула сторони ромба через периметр:

a=P4{\displaystyle a={\frac {P}{4}}}
{\displaystyle a={\frac {P}{4}}}

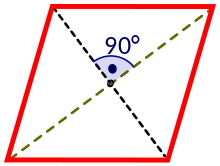
Діагональ ромба — це довільний відрізок, що з’єднує дві вершини протилежних кутів ромба.

Ромб має дві діагоналі — більшу d1, та меншу — d2

Формули визначення довжини діагоналі ромба[ред. | ред. код]

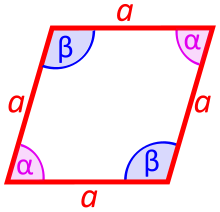
{\displaystyle a={\frac {P}{4}}}

1. Формули більшої діагоналі ромба через сторону і косинус гострого кута (cosα) або косинус тупого кута (cosβ)

d1=a2+2cos⁡α{\displaystyle d_{1}=a{\sqrt {2+2\cos \alpha }}}
d1=a2−2cos⁡β{\displaystyle d_{1}=a{\sqrt {2-2\cos \beta }}}

2. Формули меншої діагоналі ромба через сторону і косинус гострого кута (cosα) або косинус тупого кута (cosβ)

d2=a2+2cos⁡β{\displaystyle d_{2}=a{\sqrt {2+2\cos \beta }}}
d2=a2−2cos⁡α{\displaystyle d_{2}=a{\sqrt {2-2\cos \alpha }}}

3. Формули більшої діагоналі ромба через сторону і половинний кут:

d1=2a⋅cos⁡(α/2){\displaystyle d_{1}=2a\cdot \cos(\alpha /2)}
d1=2a⋅sin⁡(β/2){\displaystyle d_{1}=2a\cdot \sin(\beta /2)}

4. Формули меншої діагоналі ромба через сторону і половинний кут:

d2=2a⋅sin⁡(α/2){\displaystyle d_{2}=2a\cdot \sin(\alpha /2)}
d2=2a⋅cos⁡(β/2){\displaystyle d_{2}=2a\cdot \cos(\beta /2)}

5. Формули діагоналей ромба через сторону і другу діагональ:

d1=4a2−d22{\displaystyle d_{1}={\sqrt {4a^{2}-d_{2}^{2}}}}
d2=4a2−d12{\displaystyle d_{2}={\sqrt {4a^{2}-d_{1}^{2}}}}

6. Формули діагоналей через тангенс гострого tgα або тупого tgβ кута і другу діагональ:

d1=d2⋅tan⁡(β/2){\displaystyle d_{1}=d_{2}\cdot \tan(\beta /2)}
d2=d1⋅tan⁡(α/2){\displaystyle d_{2}=d_{1}\cdot \tan(\alpha /2)}

7. Формули діагоналей через площу і другу діагональ:

d1=2Sd2{\displaystyle d_{1}={\frac {2S}{d_{2}}}}
d2=2Sd1{\displaystyle d_{2}={\frac {2S}{d_{1}}}}

8. Формули діагоналей через синус половинного кута і радіус вписаного кола:

d1=2rsin⁡(α/2){\displaystyle d_{1}={\frac {2r}{\sin(\alpha /2)}}}
d2=2rsin⁡(β/2){\displaystyle d_{2}={\frac {2r}{\sin(\beta /2)}}}

Периметром ромба називається сума довжин всіх сторін ромба.

Формула периметра ромба через сторону ромба:

P=4⋅a{\displaystyle P=4\cdot a}
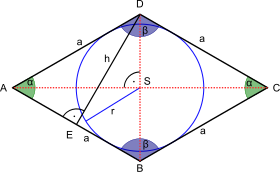
{\displaystyle P=4\cdot a} Ромб. Кожен кут, який відмічений чорною точкою є прямим кутом. Висота h є перпендикуляром між двома протилежними сторонами, яка дорівнює діаметру вписаного кола. Діагоналі з довжиною відміченими червоними пунктирними відрізками.

Площа ромба — це простір, обмежений сторонами ромба, тобто в межах периметра ромба.

Формули визначення площі ромба[ред. | ред. код]

1. Формула площі ромба через сторону і висоту:

S=a⋅h{\displaystyle S=a\cdot h}

2. Формула площі ромба через сторону і синус будь-якого кута:

S=a2⋅sin⁡α=a2⋅sin⁡β{\displaystyle S=a^{2}\cdot \sin \alpha =a^{2}\cdot \sin \beta }

3. Формула площі ромба через сторону і радіус:

S=2a⋅r{\displaystyle S=2a\cdot r}

4. Формула площі ромба через дві діагоналі:

S=d1⋅d22{\displaystyle S={\frac {d_{1}\cdot d_{2}}{2}}}

5. Формула площі ромба через синус кута і радіус вписаного кола:

S=4⋅r2sin⁡α{\displaystyle S={\frac {4\cdot r^{2}}{\sin \alpha }}}

6. Формули площі через більшу діагональ і тангенс гострого кута (tgα) або малу діагональ і тангенс тупого кута (tgβ):

S=12d12⋅tan⁡(α2),{\displaystyle S={\frac {1}{2}}d_{1}^{2}\cdot \tan({\frac {\alpha }{2}}),}
S=12d22⋅tan⁡(β2){\displaystyle S={\frac {1}{2}}d_{2}^{2}\cdot \tan({\frac {\beta }{2}})}
{\displaystyle S={\frac {1}{2}}d_{2}^{2}\cdot \tan({\frac {\beta }{2}})} Коло, вписане у ромб

Колом, вписаним у ромб, називається коло, що дотикається до всіх сторін ромба та має центр на перетині діагоналей ромба.

Формули визначення радіуса кола, вписаного в ромб[ред. | ред. код]

1. Формула радіуса кола, вписаного в ромб, через висоту ромба:

r=h3{\displaystyle r={\frac {h}{2}}}

2. Формула радіуса кола, вписаного в ромб, через площу та сторону ромба:

r=S2a{\displaystyle r={\frac {S}{2a}}}

3. Формула радіуса кола, вписаного в ромб, через площу та синус кута:

r=S⋅sin⁡α2{\displaystyle r={\frac {\sqrt {S\cdot \sin \alpha }}{2}}}

4. Формули радіуса кола, вписаного в ромб, через сторону і синус будь-якого кута:

r=a⋅sin⁡α2{\displaystyle r={\frac {a\cdot \sin \alpha }{2}}}
r=a⋅sin⁡β2{\displaystyle r={\frac {a\cdot \sin \beta }{2}}}

5. Формули радіуса кола, вписаного в ромб, через діагональ та синус кута:

r=d1⋅sin⁡(α/2)2{\displaystyle r={\frac {d_{1}\cdot \sin(\alpha /2)}{2}}}
r=d2⋅sin⁡(β/2)2{\displaystyle r={\frac {d_{2}\cdot \sin(\beta /2)}{2}}}

6. Формула радіуса кола, вписаного в ромб, через дві діагоналі:

r=d1⋅d22d12+d22{\displaystyle r={\frac {d_{1}\cdot d_{2}}{2{\sqrt {d_{1}^{2}+d_{2}^{2}}}}}}

7. Формула радіуса кола, вписаного в ромб, через дві діагоналі та сторону:

r=d1⋅d24a{\displaystyle r={\frac {d_{1}\cdot d_{2}}{4a}}}

Сторони ромба, центр якого суміщено з центром координат із діагоналями, що знаходяться на осях, будуть складатися із точок (x, y), що задовільняють рівняння

|xa|+|yb|=1.{\displaystyle \left|{\frac {x}{a}}\right|\!+\left|{\frac {y}{b}}\right|\!=1.}

Вершини знаходитимуться в точках (±a,0){\displaystyle (\pm a,0)} і (0,±b).{\displaystyle (0,\pm b).} Це є особливим випадком супереліпса, із експонентою 1.

uk.wikipedia.org

Ответы@Mail.Ru: ромб. определение, свойства?

Ромб — четырёхугольник, у которого все стороны равны. Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов.

ромб — это четырёхугольник, у которого все стороны равны. Ромб является параллелограммом. Ромб с прямыми углами называется квадратом. Ромб является параллелограммом. Его противолежащие стороны попарно параллельны, Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам. Диагонали ромба являются биссектрисами его углов Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма) . Площадь ромба равна половине произведения его диагоналей. Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.

па-мм у которого все стороны равны называется ромб диагонали взаимо перпендикулярны и делят углы пополам

Ромб – четырёхугольник, у которого все стороны равны между собой. У ромба есть две диагонали, соединяющие несмежные вершины. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.

touch.otvet.mail.ru

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *