Длина и свойства биссектрисы параллелограмма
Свойства биссектрисы параллелограмма
— Биссектриса по определению делит угол пополам
— Биссектриса отсекает равнобедренный треугольник (в данном случае треугольники ABF и DKC)
— Биссектрисы смежных углов, пересекаются под прямым углом (90°)
— Биссектрисы противоположных углов, равны и параллельны
 AF — биссектриса из острого угла
AF — биссектриса из острого угла
DK — биссектриса из тупого угла
α — острый угол
β — тупой угол
a — меньшая сторона
b — большая сторона
Так как треугольники ABF и DKC, равнобедренные, следовательно справедливы тождества:


Длина биссектрисы параллелограмма

L — биссектриса параллелограмма
a, b — стороны
α, β — углы
Формулы длины биссектрисы через сторону и углы, (L):


Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
- Автор: Administrator

Биссектриса параллелограмма | Треугольники
Как решать задачи, в которых биссектриса параллелограмма делит противолежащую сторону на отрезки? Решение основано на доказанном свойстве биссектрисы параллелограмма.
Это свойство (биссектриса параллелограмма отсекает от него равнобедренный треугольник) после доказательства можно использовать при решении задач. Я предпочитаю доказывать этот факт в каждой задаче (полезное упражнение для отработки навыков).
Задача 1.
Биссектриса острого угла параллелограмма делит противоположную сторону на отрезки 3 см и 2 см, считая от вершины тупого угла. Найти периметр параллелограмма.
Дано: ABCD — параллелограмм,
AF — биссектриса ∠BAD,
F ∈ BC, BF=3 см, FC=2 см.
Найти:
Решение:
1) ∠BAF=∠DAF (так как AF — биссектриса ∠BAD по условию).
2) ∠BFA=∠DAF (как внутренние накрест лежащие углы при BC ∥ AD и секущей AF).
3) Следовательно, ∠BAF=∠BFA.
4) Следовательно, треугольник ABF — равнобедренный с основанием AF (по признаку).
5) Следовательно, AB=BF=3 см.
6) BC=BF+FC, BC=3+2=5 см.
Ответ: 16 см.
Задача 2.
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 1:3, считая от вершины острого угла. Периметр параллелограмма равен 90 см. Найти его стороны.
Дано: ABCD — параллелограмм, BK- биссектриса ∠ABC,
K ∈ AD, AK:KD=1:3,
Найти: AB, AD, CD, BC.
Решение:
1) Пусть k — коэффициент пропорциональности. Тогда AK=k см, KD=3k см, AD=AK+KD=k+3k=4k см.
2) ∠ABK=∠CBK (так как BK — биссектриса ∠ABC по условию).
3) ∠CBK=∠AKB (как внутренние накрест лежащие углы при BC ∥ AD и секущей BK).
4) Следовательно, ∠ABK=∠AKB.
5) Следовательно, треугольник ABK — равнобедренный с основанием BK (по признаку равнобедренного треугольника).
6) Следовательно, AB=AK=k см.
Составляем и решаем уравнение:
Значит, AB=9 см, AD=4∙9=36 см.
8) CD=AB=9 см, BC=AD=36 см (как противоположные стороны параллелограмма).
Ответ: 9 см, 9 см, 36 см, 36 см.
Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.
Высота — перпендикуляр исходящий из вершины угла на противоположенную сторону
 a, b — стороны параллелограмма
a, b — стороны параллелограмма
Hb — высота на сторону b
H
a — высота на сторону aα, β — углы параллелограмма
Формулы длины высоты параллелограмма, через сторону и угол, ( Hb, Ha):


Острый угол пересечения высот, равен острому углу параллелограмма.
Тупой угол пересечения высот, равен тупому углу параллелограмма.
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства биссектрисы параллелограмма
— Биссектриса по определению делит угол пополам
— Биссектриса отсекает равнобедренный треугольник (в данном случае треугольники ABF и DKC)
— Биссектрисы смежных углов, пересекаются под прямым углом (90°)
— Биссектрисы противоположных углов, равны и параллельны
 AF — биссектриса из острого угла
AF — биссектриса из острого угла
DK — биссектриса из тупого угла
α — острый угол
β — тупой угол
a — меньшая сторона
b — большая сторона
Так как треугольники ABF и DKC, равнобедренные, следовательно справедливы тождества:


Длина биссектрисы параллелограмма

L — биссектриса параллелограмма
a, b — стороны
α, β — углы
Формулы длины биссектрисы через сторону и углы, (L


Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства углов между диагоналями параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
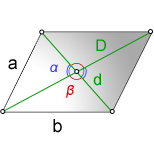
a
, b — стороны параллелограммаD — большая диагональ
d — меньшая диагональ
α — острый угол между диагоналями
β — тупой угол между диагоналями
Формулы косинуса острого и тупого углов между диагоналями, через стороны и диагонали (по теореме косинусов):

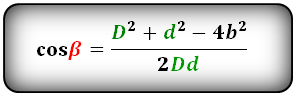
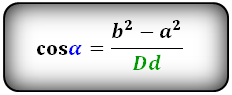
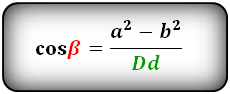
Формула синуса острого и тупого углов через площадь (S) и диагонали:
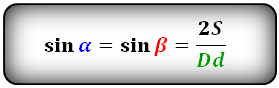
Формулы соотношения острого и тупого углов между диагоналями:
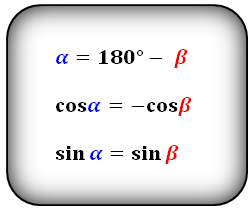
Для определения величины угла в градусах или радианах, используем функции arccos и arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства углов параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0

a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов):


Формула синуса острого и тупого углов через площадь (S) и стороны:
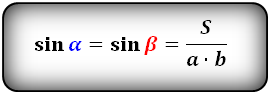
Формулы соотношения острого и тупого углов:
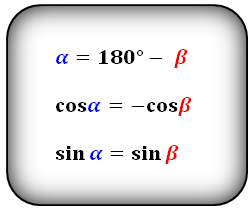
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.

a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
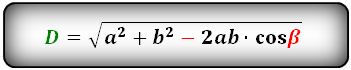

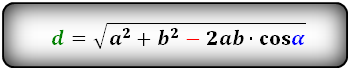

Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
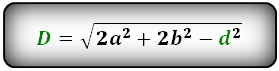
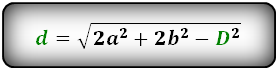
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
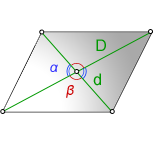
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
S — площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
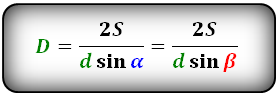
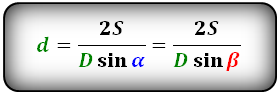
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Формулы длины сторон через диагонали и угол между ними.

a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):




Формулы сторон параллелограмма через диагонали и сторону, (a, b):


Формулы сторон параллелограмма , (a, b):


2. Формулы длины сторон параллелограмма через высоту.

a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
α, β — углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):


3. Дополнительные, интересные формулы параллелограмма:

a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол между диагоналями
Формула суммы квадратов диагоналей:

Формула разности квадратов сторон:

Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Периметр параллелограмма | Треугольники
Что называется периметром параллелограмма? Как найти периметр параллелограмма?
Определение
Периметром параллелограмма называется сумма длин всех его сторон.
Например, периметр параллелограмма ABCD равен
сумме длин сторон AB, BC, CD и AD.
Но так как противоположные стороны параллелограмма равны, чтобы найти периметр параллелограмма, нужно сумму длин его не противоположных сторон умножить на два.
Таким образом,
формула периметра параллелограмма:
Задача.
Периметр параллелограмма равен 38 см. Найти стороны параллелограмма, если одна из них на 5 см длиннее другой.
Рисунок — выше.
Дано: ABCD — параллелограмм, AD на 5 см больше AB,
Найти: AB, AD.
Решение:
Пусть AB=x см, тогда AD=(x+5) см.
что по условию равно 38 см. Составляем уравнение:
Значит, AB=7 см, AD= 7+5=12 см.
Ответ: 7 см, 12 см.
Все формулы биссектрисы в треугольнике

L— биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):


Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
- Подробности
- Автор: Administrator

Высоты параллелограмма и угол между нимиТреугольники
Как найти стороны параллелограмма, если даны высоты параллелограмма и угол между ними? Как найти периметр и площадь параллелограмма по его высотам и углу между высотами?
Задача.
Высоты параллелограмма равны m и n, а угол между ними — . Найти стороны параллелограмма, его периметр и площадь.
I. Так как угол между высотами параллелограмма, проведёнными из вершины тупого угла, равен острому углу параллелограмма,
Рассмотрим прямоугольный треугольник ABM.
По определению синуса,
следовательно,
Аналогично, из треугольника BCN
Периметр параллелограмма
Площадь параллелограмма
II. Так как угол между высотами параллелограмма, проведёнными из вершины острого угла, равен тупому углу параллелограмма,
Рассмотрим прямоугольный треугольник BKC.
(как смежные).
Так как
Аналогично, из треугольника DCF
Вывод:
чтобы найти стороны параллелограмма, надо его высоты разделить на синус угла между высотами;
периметр параллелограмма равен частному от деления удвоенной суммы высот на синус угла между ними;
площадь параллелограмма равна произведению высот, деленному на синус угла между ними.

