Теорема Пифагора — Википедия
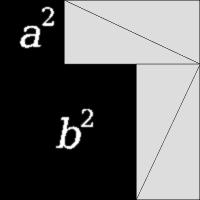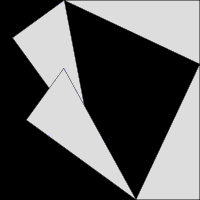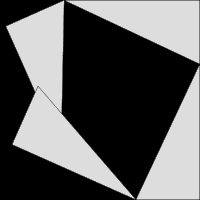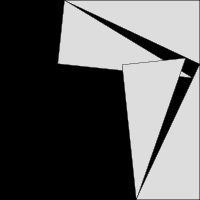 Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость[⇨]
Схема, объясняющая доказательство теоремы Пифагора через равнодополняемость[⇨]Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору. Утверждение появляется как Предложение 47 в «Началах» Евклида[⇨].
Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение[⇨]: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третьей стороны, является прямоугольным.
Существует ряд обобщений данной теоремы[⇨] — для произвольных треугольников, для фигур в пространствах высших размерностей. В неевклидовых геометриях теорема не выполняется[⇨].
По мнению историка математики Морица Кантора, в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок»[1]. В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы[2]. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.
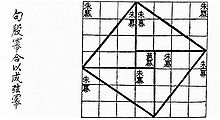
В древнекитайской книге «Чжоу би суань цзин», относимой к периоду V—III веков до н. э., приводится треугольник со сторонами 3, 4 и 5, притом изображение можно трактовать как графическое обоснование соотношения теоремы [3]. В китайском сборнике задач «Математика в девяти книгах» (X—II веков до н. э.) применению теоремы посвящена отдельная книга.
Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (412—485 н. э.), что Пифагор использовал алгебраические методы, чтобы находить пифагоровы тройки[⇨][4], но при этом в течение пяти веков после смерти Пифагора прямых упоминаний о доказательстве его авторства не находится. Однако когда такие авторы, как Плутарх и Цицерон, пишут о теореме Пифагора, из содержания следует, будто авторство Пифагора общеизвестно и несомненно[5][6]. Существует предание, сообщённое Диогеном Лаэртским, согласно которому Пифагор якобы отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков[7].
Приблизительно в 400 году до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Около 300 года до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора
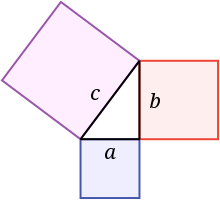 Сумма площадей квадратов, опирающихся на катеты a{\displaystyle a} и b{\displaystyle b}, равна площади квадрата, построенного на гипотенузе c{\displaystyle c}
Сумма площадей квадратов, опирающихся на катеты a{\displaystyle a} и b{\displaystyle b}, равна площади квадрата, построенного на гипотенузе c{\displaystyle c}Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике, длины катетов которого равны a{\displaystyle a} и b{\displaystyle b}, а длина гипотенузы — c{\displaystyle c}, выполнено соотношение:
- a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}.
Возможна и эквивалентная геометрическая формулировка, прибегающая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В таком виде теорема сформулирована в Началах Евклида.
Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}. Как следствие, для всякой тройки положительных чисел a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c}, такой, что a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}, существует прямоугольный треугольник с катетами a{\displaystyle a} и b{\displaystyle b} и гипотенузой c{\displaystyle c}.
В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора[9], что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия[⇨]), метод площадей[⇨], существуют также различные экзотические доказательства (например, с помощью дифференциальных уравнений).
Через подобные треугольники[править | править код]
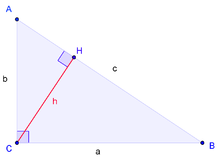
Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры. В нём для треугольника △ABC{\displaystyle \triangle ABC} с прямым углом при вершине C{\displaystyle C} со сторонами a,b,c{\displaystyle a,b,c}, противолежащими вершинам A,B,C{\displaystyle A,B,C} соответственно, проводится высота CH{\displaystyle CH}, при этом (согласно признаку подобия по равенству двух углов) возникают соотношения подобия: △ABC∼△ACH{\displaystyle \triangle ABC\sim \triangle ACH} и △ABC∼△CBH{\displaystyle \triangle ABC\sim \triangle CBH}, из чего непосредственно следуют соотношения:
- ac=|HB|a{\displaystyle {\frac {a}{c}}={\frac {|HB|}{a}}}; bc=|AH|b{\displaystyle {\frac {b}{c}}={\frac {|AH|}{b}}}.
При перемножении крайних членов пропорций выводятся равенства:
- a2=c⋅|HB|{\displaystyle a^{2}=c\cdot |HB|}; b2=c⋅|AH|{\displaystyle b^{2}=c\cdot |AH|},
покомпонентное сложение которых даёт требуемый результат:
- a2+b2=c⋅(|HB|+|AH|)=c2⇔a2+b2=c2{\displaystyle a^{2}+b^{2}=c\cdot \left(|HB|+|AH|\right)=c^{2}\,\Leftrightarrow \,a^{2}+b^{2}=c^{2}}.
Доказательства методом площадей[править | править код]
Большое число доказательств задействуют понятие площади. Несмотря на видимую простоту многих из них, такие доказательства используют свойства площадей фигур, доказательства которых сложнее доказательства самой теоремы Пифагора.
Доказательство через равнодополняемость[править | править код]
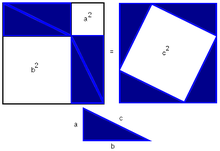 Схема доказательства через равнодополняемость.
Схема доказательства через равнодополняемость.Доказательство через равнодополняемость использует четыре копии прямоугольного треугольника с катетами a,b{\displaystyle a,b} и гипотенузой c{\displaystyle c}, расположенные таким образом, чтобы образовывать квадрат со стороной a+b{\displaystyle a+b} и внутренний четырёхугольник со сторонами длиной c{\displaystyle c}. Внутренний четырёхугольник в этой конфигурации является квадратом, так как сумма двух противоположных прямому острых углов — 90°, а развёрнутый угол — 180°. Площадь внешнего квадрата равна (a+b)2{\displaystyle (a+b)^{2}}, он состоит из внутреннего квадрата площадью c2{\displaystyle c^{2}} и четырёх прямоугольных треугольников, каждый площадью ab2{\displaystyle {\frac {ab}{2}}}, в результате из соотношения (a+b)2=4⋅ab2+c2{\displaystyle (a+b)^{2}=4\cdot {\frac {ab}{2}}+c^{2}} при алгебраическом преобразовании следует утверждение теоремы.
Доказательство Евклида[править | править код]
Чертёж к доказательству Евклида. Основное направление доказательства — установление конгруэнтности △ACK≅△ABD{\displaystyle \triangle ACK\cong \triangle ABD}, площадь которых составляет половину площади прямоугольников AHJK{\displaystyle AHJK} и ACED{\displaystyle ACED} соответственно.Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами.
Конструкция, используемая для доказательства следующая: для прямоугольного треугольника △ABC{\displaystyle \triangle ABC} с прямым углом C{\displaystyle C}, квадратов над катетами ACED{\displaystyle ACED} и BCFG{\displaystyle BCFG} и квадрата над гипотенузой ABIK{\displaystyle ABIK} строится высота CH{\displaystyle CH} и продолжающий её луч s{\displaystyle s}, разбивающий квадрат над гипотенузой на два прямоугольника AHJK{\displaystyle AHJK} и BHJI{\displaystyle BHJI}. Доказательство нацелено на установление равенства площадей прямоугольника AHJK{\displaystyle AHJK} с квадратом над катетом AC{\displaystyle AC}; равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом устанавливается аналогичным образом.
Равенство площадей прямоугольника AHJK{\displaystyle AHJK} и ACED{\displaystyle ACED} устанавливается через конгруэнтность треугольников △ACK{\displaystyle \triangle ACK} и △ABD{\displaystyle \triangle ABD}, площадь каждого из которых равна половине площади прямоугольников AHJK{\displaystyle AHJK} и ACED{\displaystyle ACED} соответственно в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если у фигур есть общая сторона, а высота треугольника к общей стороне является другой стороной прямоугольника. Конгруэнтность треугольников следует из равенства двух сторон (стороны квадратов) и углу между ними (составленного из прямого угла и угла при A{\displaystyle A}.
Таким образом, доказательством устанавливается, что площадь квадрата над гипотенузой, составленного из прямоугольников AHJK{\displaystyle AHJK} и BHJI{\displaystyle BHJI}, равна сумме площадей квадратов над катетами.
Доказательство Леонардо да Винчи[править | править код]
Чертёж к доказательству Леонардо да ВинчиК методу площадей относится также доказательство, найденное Леонардо да Винчи. Пусть дан прямоугольный треугольник △ABC{\displaystyle \triangle ABC} с прямым углом C{\displaystyle C} и квадраты ACED{\displaystyle ACED}, BCFG{\displaystyle BCFG} и ABHJ{\displaystyle ABHJ} (см. рисунок). В этом доказательстве на стороне HJ{\displaystyle HJ} последнего во внешнюю сторону строится треугольник, конгруэнтный △ABC{\displaystyle \triangle ABC}, притом отражённый как относительно гипотенузы, так и относительно высоты к ней (то есть JI=BC{\displaystyle JI=BC} и HI=AC{\displaystyle HI=AC}). Прямая CI{\displaystyle CI} разбивает квадрат, построенный на гипотенузе на две равные части, поскольку треугольники △ABC{\displaystyle \triangle ABC} и △JHI{\displaystyle \triangle JHI} равны по построению. Доказательство устанавливает конгруэнтность четырёхугольников CAJI{\displaystyle CAJI} и DABG{\displaystyle DABG}, площадь каждого из которых, оказывается, с одной стороны, равной сумме половин площадей квадратов на катетах и площади исходного треугольника, с другой стороны — половине площади квадрата на гипотенузе плюс площадь исходного треугольника. Итого, половина суммы площадей квадратов над катетами равна половине площади квадрата над гипотенузой, что равносильно геометрической формулировке теоремы Пифагора.
Через площади подобных треугольников[править | править код]
Следующее доказательство основано на том, что площади подобных треугольников относятся как квадраты соответственных сторон.
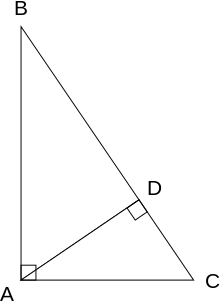
Пусть ABC{\displaystyle ABC} есть прямоугольный треугольник, AD{\displaystyle AD} — перпендикуляр, опущенный на гипотенузу из вершины прямого угла. Треугольники ABC{\displaystyle ABC}, DBA{\displaystyle DBA} подобны, так как имеют по прямому углу и ещё общий угол B{\displaystyle B}. Значит
- площадь DBAплощадь ABC=AB2BC2.{\displaystyle {\frac {{\text{площадь}}~DBA}{{\text{площадь}}~ABC}}={\frac {AB^{2}}{BC^{2}}}.}
Точно также получаем, что
- площадь DACплощадь ABC=AC2BC2.{\displaystyle {\frac {{\text{площадь}}~DAC}{{\text{площадь}}~ABC}}={\frac {AC^{2}}{BC^{2}}}.}
Поскольку треугольники DBA{\displaystyle DBA} и DAC{\displaystyle DAC} вместе составляют △ABC{\displaystyle \triangle ABC}, сумма площадей △DBA{\displaystyle \triangle DBA} и △DAC{\displaystyle \triangle DAC} равна площади △ABC{\displaystyle \triangle ABC}. Отсюда
- AB2+AC2BC2=1{\displaystyle {\frac {AB^{2}+AC^{2}}{BC^{2}}}=1}
или AB2+AC2=BC2.{\displaystyle AB^{2}+AC^{2}=BC^{2}.}
Доказательство методом бесконечно малых[править | править код]
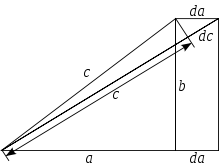 Доказательство методом бесконечно малых
Доказательство методом бесконечно малыхСуществует несколько доказательств, прибегающих к технике дифференциальных уравнений. В частности, Харди приписывается доказательство, использующее бесконечно малые приращения катетов a{\displaystyle a} и b{\displaystyle b} и гипотенузы c{\displaystyle c}. Например, приращение катета da{\displaystyle da} при постоянном катете b{\displaystyle b} приводит к приращению гипотенузы dc{\displaystyle dc}, так что
- dadc=ca{\displaystyle {\frac {da}{dc}}={\frac {c}{a}}}
Методом разделения переменных из них выводится дифференциальное уравнение c dc=ada{\displaystyle c\ dc=a\,da}, интегрирование которого даёт соотношение c2=a2+Const{\displaystyle c^{2}=a^{2}+\mathrm {Const} }. Применение начальных условий a=0,c=b{\displaystyle a=0,c=b} определяет константу как b2{\displaystyle b^{2}}, что в результате даёт утверждение теоремы.
Квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.
Подобные геометрические фигуры на трёх сторонах[править | править код]
Обобщение для подобных треугольников, площадь зелёных фигур равны площади синей. Теорема Пифагора с использованием подобных прямоугольных треугольников.Важное геометрическое обобщение теоремы Пифагора дал Евклид в «Началах», перейдя от площадей квадратов на сторонах к площадям произвольных подобных геометрических фигур[10]: сумма площадей таких фигур, построенных на катетах, будет равна площади подобной им фигуры, построенной на гипотенузе.
Главная идея этого обобщения заключается в том, что площадь подобной г
ru.wikipedia.org
Сферическая теорема Пифагора — Википедия
Материал из Википедии — свободной энциклопедии
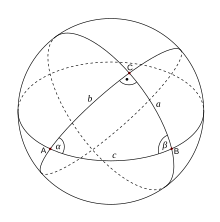 Прямоугольный сферический треугольник с гипотенузой c, катетами a и b и прямым углом C.
Прямоугольный сферический треугольник с гипотенузой c, катетами a и b и прямым углом C.Сферическая теорема Пифагора — теорема, устанавливающая соотношение между сторонами прямоугольного сферического треугольника.
Сферическая теорема Пифагора формулируется следующим образом[1]:
 | Косинус гипотенузы прямоугольного сферического треугольника равен произведению косинусов его катетов. |  |
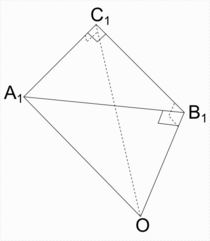 Рисунок к доказательству сферической теоремы Пифагора.
Рисунок к доказательству сферической теоремы Пифагора.Доказательство проведём с помощью трёхгранного угла[1] OA1B1C1 со сторонами (лучами) OA1, OB1, OC1 и вершиной в точке O, плоские углы A1OC1 и C1OB1 которого равны катетам b и a данного треугольника, плоский угол A1OB1 равен его гипотенузе c, двугранный угол между гранями A1OC1 и C1OB1 равен 90 градусов, а остальные два двугранных угла равны соответствующим углам сферического прямоугольного треугольника. Этот трёхгранный угол пересечен плоскостью A1B1C1, перпендикулярной лучу OB1. Тогда углы A1C1O и A1C1B1 будут прямыми.
Заметим, что
- OB1OA1=cos∠A1OB1=cosc,{\displaystyle {\frac {OB_{1}}{OA_{1}}}=\cos \angle A_{1}OB_{1}=\cos c,}
- OC1OA1=cos∠A1OC1=cosb,{\displaystyle {\frac {OC_{1}}{OA_{1}}}=\cos \angle A_{1}OC_{1}=\cos b,}
- OB1OC1=cos∠C1OB1=cosa.{\displaystyle {\frac {OB_{1}}{OC_{1}}}=\cos \angle C_{1}OB_{1}=\cos a.}
Отсюда
- cosc=OB1OA1=OB1OC1⋅OC1OA1=cosacosb.{\displaystyle \cos c={\frac {OB_{1}}{OA_{1}}}={\frac {OB_{1}}{OC_{1}}}\cdot {\frac {OC_{1}}{OA_{1}}}=\cos a\cos b.}
Что и требовалось доказать.
Если считать, что сферическая теорема косинусов уже доказана, формулу для сферической теоремы Пифагора можно сразу получить из неё, записав сферическую теорему косинусов для гипотенузы данного прямоугольного сферического треугольника и просто подставив в получившееся выражение угол 90 градусов, косинус которого равен нулю.
При радиусе сферы, стремящемся к бесконечности, сферическая теорема Пифагора переходит в теорему Пифагора планиметрии. Поэтому, поскольку радиус Земли велик, при небольших расстояниях прямоугольные треугольники на поверхности Земли (например, используемые для измерения расстояний и углов на местности) практически подчиняются теореме Пифагора планиметрии[2], тогда как для больших расстояний, сравнимых с радиусом Земли, уже необходимо применять сферическую теорему Пифагора.
С применением сферической теоремы Пифагора можно получить формулы для разности долгот и расстояния между точками земной поверхности, а, следовательно, и соответствующие формулы для расстояний и координат точек на небесной сфере.
Из сферической теоремы Пифагора следует, что в прямоугольном сферическом треугольнике количество сторон, меньших 90 градусов, нечётно, а больших — чётно[1]. Поэтому если оба катета прямоугольного сферического треугольника больше 90 градусов, то его гипотенуза меньше 90 градусов, то есть в этом случае гипотенуза короче каждого из двух катетов — положение, невозможное для прямоугольного треугольника на плоскости.
Сферическая теорема Пифагора была известна ещё Ал-Бируни, который вместе с тем не знал сферической теоремы косинусов, поэтому применил сферическую теорему Пифагора и теорему синусов для решения как минимум двух задач: определения разности долгот двух пунктов на поверхности Земли по их широтам и расстоянию между ними и определения расстояния между двумя пунктами на поверхности Земли по их широтам и долготам[3]:81.
ru.wikipedia.org
Пифагорова тройка — Википедия
 Теорема Пифагора: a2 + b2 = c2
Теорема Пифагора: a2 + b2 = c2  Анимация простейшей пифагоровой тройки: 32 + 42 = 52.
Анимация простейшей пифагоровой тройки: 32 + 42 = 52.Пифаго́рова тро́йка — упорядоченный набор из трёх натуральных чисел (x,y,z),{\displaystyle (x,\;y,\;z),} удовлетворяющих следующему однородному квадратному уравнению:
- x2+y2=z2.{\displaystyle x^{2}+y^{2}=z^{2}.}
При этом числа, образующие пифагорову тройку, называются пифагоровыми числами. Названы в честь Пифагора Самосского, хотя открыты задолго до него.
Поскольку уравнение x2+y2=z2{\displaystyle x^{2}+y^{2}=z^{2}} однородно, при умножении x{\displaystyle x}, y{\displaystyle y} и z{\displaystyle z} на одно и то же натуральное число получится другая пифагорова тройка. Пифагорова тройка (x,y,z){\displaystyle (x,y,z)} называется примитивной, если она не может быть получена таким способом из какой-то другой пифагоровой тройки, то есть если x,y,z{\displaystyle x,\;y,\;z} являются взаимно простыми числами. Другими словами, наибольший общий делитель примитивной пифагоровой тройки (x,y,z){\displaystyle (x,y,z)} равен 1.
В примитивной тройке (x,y,z){\displaystyle (x,y,z)} числа x{\displaystyle x} и y{\displaystyle y} имеют разную чётность, причём чётное делится на 4, а z{\displaystyle z} — всегда нечётно.
Любая примитивная пифагорова тройка (x,y,z){\displaystyle (x,y,z)}, где x{\displaystyle x} — нечётно, а y{\displaystyle y} — чётно, однозначно представляется в виде (m2−n2,2mn,m2+n2){\displaystyle (m^{2}-n^{2},\;2mn,\;m^{2}+n^{2})} для некоторых натуральных взаимно простых чисел m>n{\displaystyle m>n} разной чётности.
Эти числа можно вычислить по формулам:
- {m=z+x2=z+y+z−y2n=z−x2=z+y−z−y2{\displaystyle {\begin{cases}m={\sqrt {\frac {z+x}{2}}}={\frac {{\sqrt {z+y}}+{\sqrt {z-y}}}{2}}\\n={\sqrt {\frac {z-x}{2}}}={\frac {{\sqrt {z+y}}-{\sqrt {z-y}}}{2}}\end{cases}}}
Наоборот, любая такая пара чисел (m,n){\displaystyle (m,\;n)} задаёт примитивную пифагорову тройку (m2−n2,2mn,m2+n2){\displaystyle (m^{2}-n^{2},\;2mn,\;m^{2}+n^{2})}[1].
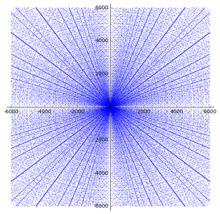 Диаграмма рассеяния катетов (a,b){\displaystyle (a,b)} пифагоровых троек с катетами, не превышающими 6000. Отрицательные значения включены для демонстрации параболических узоров
Диаграмма рассеяния катетов (a,b){\displaystyle (a,b)} пифагоровых троек с катетами, не превышающими 6000. Отрицательные значения включены для демонстрации параболических узоровИмеется 16 примитивных пифагоровых троек с z⩽100{\displaystyle z\leqslant 100}:
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
Не все тройки с z⩽100{\displaystyle z\leqslant 100} примитивны, например, (6, 8, 10) получается умножением на два тройки (3, 4, 5). Каждая из троек с небольшой гипотенузой образует хорошо различимую радиальную прямую из кратных ей троек на диаграмме рассеяния.
Примитивные тройки с 100<z⩽300{\displaystyle 100<z\leqslant 300}:
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
| (160, 231, 281) | (161, 240, 289) | (68, 285, 293) |
Возможные значения z{\displaystyle z} в пифагоровых тройках образуют последовательность (последовательность A009003 в OEIS)
- 5, 10, 13, 15, 17, 20, 25, 26, 29, 30, 34, 35, 37, 39, 40, 41, 45, 50, …
Основываясь на свойствах чисел Фибоначчи, можно образовывать из этих чисел, например, такие пифагоровы тройки:
- x=FnFn+3;y=2Fn+1Fn+2;z=Fn+12+Fn+22.{\displaystyle x=F_{n}F_{n+3};\quad y=2F_{n+1}F_{n+2};\quad z=F_{n+1}^{2}+F_{n+2}^{2}.}

Наиболее известной в развитых древних культурах была тройка (3, 4, 5), которая позволяла древним строить прямые углы. Витрувий считал эту тройку высшим достижением математики, а Платон — символом супружества, что говорит о большом значении, которое придавали древние тройке (3, 4, 5).
В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.
Вавилонские математики умели вычислять пифагоровы тройки. Вавилонская глиняная табличка, названная Plimpton 322, содержит пятнадцать пифагоровых троек (точнее пятнадцать пар чисел a,c{\displaystyle a,c}, таких что a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}). Считается, что эта табличка была создана около 1800 года до н. э.[2]
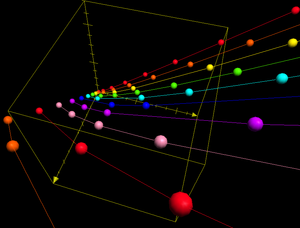 Диаграмма треугольников, полученных из формулы Евклида, показывающая часть конуса z2=x2+y2{\displaystyle z^{2}=x^{2}+y^{2}}, константы m{\displaystyle m} или n{\displaystyle n} задают след параболы на конусе
Диаграмма треугольников, полученных из формулы Евклида, показывающая часть конуса z2=x2+y2{\displaystyle z^{2}=x^{2}+y^{2}}, константы m{\displaystyle m} или n{\displaystyle n} задают след параболы на конусеФормула Евклида[3] является основным средством построения пифагоровых троек. Согласно ей для любой пары натуральных чисел m{\displaystyle m} и n{\displaystyle n} (m>n{\displaystyle m>n}) целые числа
- a=m2−n2, b=2mn, c=m2+n2{\displaystyle a=m^{2}-n^{2},\ b=2mn,\ c=m^{2}+n^{2}}
образуют пифагорову тройку. Тройки, образованные по формуле Евклида, примитивны тогда и только тогда, когда m{\displaystyle m} и n{\displaystyle n} взаимно просты и m−n{\displaystyle m-n} нечётно. Если и m{\displaystyle m}, и n{\displaystyle n} нечётны, то a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} будут чётными и тройка не примитивна. Однако деление a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} на 2 даёт примитивную тройку, если m{\displaystyle m} и n{\displaystyle n} взаимно просты[4].
Любая примитивная тройка получается из единственной пары взаимно простых чисел m{\displaystyle m} и n{\displaystyle n}, одно из которых чётно. Отсюда следует, что существует бесконечно много примитивных пифагоровых троек.
Несмотря на то, что формула Евклида генерирует все примитивные тройки, она не порождает все тройки. При добавлении дополнительного параметра k{\displaystyle k} получается формула, порождающая все пифагоровы треугольники единственным образом:
- a=k⋅(m2−n2), b=k⋅(2mn), c=k⋅(m2+n2),{\displaystyle a=k\cdot (m^{2}-n^{2}),\ b=k\cdot (2mn),\ c=k\cdot (m^{2}+n^{2}),}
где m{\displaystyle m}, n{\displaystyle n} и k{\displaystyle k} — натуральные числа, m>n{\displaystyle m>n}, m−n{\displaystyle m-n} нечётно, m{\displaystyle m} и n{\displaystyle n} взаимно просты.
То, что эти формулы образуют пифагоровы тройки, можно проверить путём подстановок в a2+b2{\displaystyle a^{2}+b^{2}} и проверки, что результат совпадает с c2{\displaystyle c^{2}}. Поскольку любую пифагорову тройку можно разделить на некоторое k{\displaystyle k}, чтобы получить примитивную тройку, любая тройка может быть образована единственным образом с использованием m{\displaystyle m} и n{\displaystyle n} для создания примитивной тройки, а затем она умножается на k{\displaystyle k}.
Со времён Евклида было найдено множество формул для генерации троек.
Доказательство формул Евклида[править | править код]
Тот факт, что числа a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c}, удовлетворяющие формуле Евклида, всегда составляют пифагоров треугольник, очевиден для положительных целых m{\displaystyle m} и n{\displaystyle n}, m>n{\displaystyle m>n}, поскольку после подстановки в формулы a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} будут положительными числами, а также из того, что выполняется
- a2+b2=(m2−n2)2+(2mn)2=(m2+n2)2=c2.{\displaystyle a^{2}+b^{2}=(m^{2}-n^{2})^{2}+(2mn)^{2}=(m^{2}+n^{2})^{2}=c^{2}.}
Обратное утверждение, что a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c} выражаются формулой Евклида для любой пифагоровой тройки, вытекает из следующего[5]. Все такие тройки можно записать в виде (a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c}), где a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}, и a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c} являются взаимно простыми, а b{\displaystyle b} и c{\displaystyle c} имеют противоположную чётность (одно из них чётно, другое нечётно). (Если c{\displaystyle c} имеет ту же самую чётность с обоими катетами, то в случае их чётности они не будут взаимно простыми, а в случае нечётности a2+b2{\displaystyle a^{2}+b^{2}} даст чётное число, и оно не может быть равно нечётному c2{\displaystyle c^{2}}.) Из a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}} мы получаем c2−a2=b2{\displaystyle c^{2}-a^{2}=b^{2}}, а следовательно, (c−a)(c+a)=b2{\displaystyle (c-a)(c+a)=b^{2}}. Тогда (c+a)/b=b/(c−a){\displaystyle (c+a)/b=b/(c-a)}. Поскольку (c+a)/b{\displaystyle (c+a)/b} является рациональным, мы представим его в виде несократимой дроби m/n{\displaystyle m/n}. Мы отсюда же получаем, что дробь (c−a)/b{\displaystyle (c-a)/b} равна n/m{\displaystyle n/m}. Решая уравнения
- cb+ab=mn, cb−ab=nm{\displaystyle {\frac {c}{b}}+{\frac {a}{b}}={\frac {m}{n}},\ {\frac {c}{b}}-{\frac {a}{b}}={\frac {n}{m}}}
относительно c/b{\displaystyle c/b} и a/b{\displaystyle a/b}, получим
- cb=m2+n22mn, ab=m2−n22mn.{\displaystyle {\frac {c}{b}}={\frac {m^{2}+n^{2}}{2mn}},\ {\frac {a}{b}}={\frac {m^{2}-n^{2}}{2mn}}.}
Поскольку c/b{\displaystyle c/b} и a/b{\displaystyle a/b} несократимы по предположению, числители и знаменатели будут равными тогда и только тогда, когда правые части каждого равенства несократимы. Как мы условились, дробь m/n{\displaystyle m/n} тоже несократима, откуда следует, что m{\displaystyle m} и n{\displaystyle n} взаимно просты. Правые части будут несократимы тогда и только тогда, когда m{\displaystyle m} и n{\displaystyle n} имеют противоположную чётность, так что числитель не делится на 2. (А m{\displaystyle m} и n{\displaystyle n} должны иметь противоположную чётность — оба не могут быть чётными ввиду несократимости, а в случае нечётности обоих чисел деление (m2+n2)/(2mn){\displaystyle (m^{2}+n^{2})/(2mn)} на 2 даст дробь, в числителе и знаменателе которой будут нечётные числа, но эта дробь равна c/b{\displaystyle c/b}, в которой числитель и знаменатель будут иметь различную чётность, что противоречит предположению.) Теперь, приравнивая числители и знаменатели, получим формулу Евклида a=m2−n2{\displaystyle a=m^{2}-n^{2}}, b=2mn{\displaystyle b=2mn}, c=m2+n2{\displaystyle c=m^{2}+n^{2}} с m{\displaystyle m} и n{\displaystyle n} взаимно простыми и имеющими различную чётность.
Более длинное, но и более общепринятое доказательство приведено в книгах Маора (Maor, 2007)[6] и Серпинского
ru.wikipedia.org
Пифагора теорема — это… Что такое Пифагора теорема?

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.
Формулировки
Теорема Пифагора: Сумма площадей квадратов, опирающихся на катеты (a и b), равна площади квадрата, построенного на гипотенузе (c).
Геометрическая формулировка:
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. |
Алгебраическая формулировка:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. |
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
- a2 + b2 = c2
Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.
Обратная теорема Пифагора:
Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c. |
Доказательства
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы [1]. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например с помощью дифференциальных уравнений).
Через подобные треугольники
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.

Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения
получаем
Что эквивалентно
Сложив, получаем
или
Доказательства методом площадей
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.
Доказательство через равнодополняемость
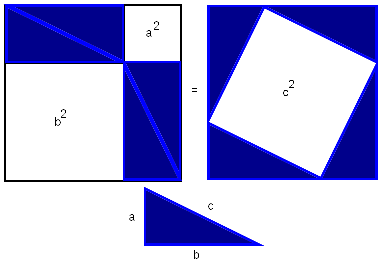
Рис.1
- Расположим четыре равных прямоугольных треугольника так, как показано на рисунке 1.
- Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
- Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и двух внутренних квадратов.
Что и требовалось доказать.
Доказательства через равносоставленность

Элегантное доказательство при помощи перестановки
Пример одного из таких доказательств указан на чертеже справа, где квадрат, построенный на гипотенузе, перестановкой преобразуется в два квадрата, построенных на катетах.
Доказательство Евклида
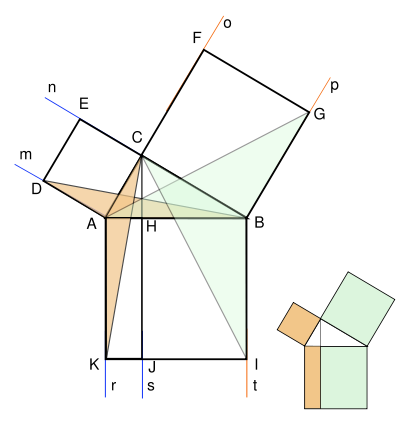
Чертеж к доказательству Евклида

Иллюстрация к доказательству Евклида
Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.
Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.
Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.
Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB=AK,AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).
Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.
Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше.
Доказательство Леонардо да Винчи

Доказательство Леонардо да Винчи
Главные элементы доказательства — симметрия и движение.
Рассмотрим чертёж, как видно из симметрии, отрезок CI рассекает квадрат ABHJ на две одинаковые части (так как треугольники ABC и JHI равны по построению). Пользуясь поворотом на 90 градусов против часовой стрелки, мы усматриваем равенство заштрихованных фигур CAJI и GDAB. Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей квадратов, построенных на катетах, и площади исходного треугольника. С другой стороны, она равна половине площади квадрата, построенного на гипотенузе, плюс площадь исходного треугольника. Последний шаг в доказательстве предоставляется читателю.
Доказательство методом бесконечно малых
Следующее доказательство при помощи дифференциальных уравнений часто приписывают известному английскому математику Харди, жившему в первой половине XX века.
Рассматривая чертёж, показанный на рисунке, и наблюдая изменение стороны a, мы можем записать следующее соотношение для бесконечно малых приращений сторон с и a (используя подобие треугольников):
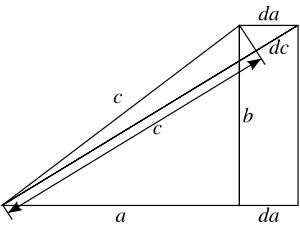
Доказательство методом бесконечно малых
Пользуясь методом разделения переменных, находим
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов
Интегрируя данное уравнение и используя начальные условия, получаем
- c2 = a2 + b2 + constant.

Таким образом, мы приходим к желаемому ответу
- c2 = a2 + b2.
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения (в данном случае катет b). Тогда для константы интегрирования получим
Вариации и обобщения
- Теорема косинусов
- В сферической геометрии, на единичной сфере, теорема Пифагора имеет вид
- cosc = cosacosb.
- В геометрии Лобачевского, на плоскости кривизны — 1, теорема Пифагора имеет вид
- Теорема де Гуа: Для треугольной пирамиды ABCD, такой, что три угла при вершине D (
 ,
,  и
и  ) — прямые, верно следующее соотношение: квадрат площади грани, противолежащей вершине D, равен сумме квадратов площадей граней, прилежащих к этому углу.
) — прямые, верно следующее соотношение: квадрат площади грани, противолежащей вершине D, равен сумме квадратов площадей граней, прилежащих к этому углу.
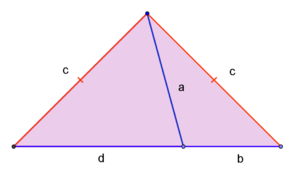
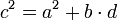
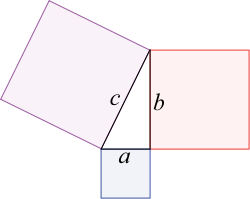
- В любом равнобедренном треугольнике верно следующее соотношение (см. рисунок внизу справа)[2]:
- Если вместо квадратов построить на катетах другие подобные фигуры, то верно следующее обобщение теоремы Пифагора: В прямоугольном треугольнике сумма площадей подобных фигур, построенных на катетах, равна площади фигуры, построенной на гипотенузе. В частности:
- Сумма площадей правильных треугольников, построенных на катетах, равна площади правильного треугольника, построенного на гипотенузе.
- Сумма площадей полукругов, построенных на катетах (как на диаметре), равна площади полукруга, построенного на гипотенузе. Этот пример используется при доказательстве свойств фигур, ограниченных дугами двух окружностей и носящих имя гиппократовых луночек.
- В случае ортогональной системы векторов
 имеет место равенство, также называемое теоремой Пифагора:
имеет место равенство, также называемое теоремой Пифагора:- Если
 — это проекции вектора на координатные оси, то эта формула совпадает с расстоянием Евклида и означает, что длина вектора есть корень квадратный из суммы квадратов его компонентов.
— это проекции вектора на координатные оси, то эта формула совпадает с расстоянием Евклида и означает, что длина вектора есть корень квадратный из суммы квадратов его компонентов. - Аналог этого равенства в случае бесконечной системы векторов носит название равенства Парсеваля.
История
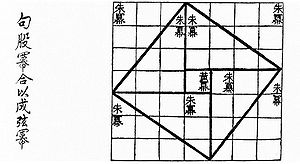
Чу-пей 500–200 до нашей эры. Слева надпись: сумма квадратов длин высоты и основания есть квадрат длины гипотенузы.
В древнекитайской книге Чу-пей говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого . Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника[3]. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой-на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод:
Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
См. также
Литература
На русском языке
- ↑ Pythagorean Proposition, by Elisha Scott Loomis
- ↑ L. Hoehn, A Neglected Pythagorean-Like Formula, Mathematical Gazette, 84 (2000), pp. 71-73
- ↑ History topic: Pythagoras’s theorem in Babylonian mathematics
На английском
Wikimedia Foundation. 2010.
dic.academic.ru
Теорема Пифагора | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Теорема Пифагора является основополагающим звеном в Евклидовой геометрии, на котором базируются большая часть всех вытекающих из теоремы Пифагора следствий и других теорем. Выведенная еще в VI веке до нашей эры, теорема связывает стороны прямоугольного треугольника простым уравнением, и имеет множество доказательств, одно из которых объединяет в себе как алгебру, так и геометрию.
Согласно теореме Пифагора, в прямоугольном треугольнике есть катеты a и b – это стороны прилегающие к прямому углу, и сумма их квадратов дает квадрат гипотенузы – третьей стороны треугольника, лежащей напротив прямого угла.

Доказать это можно, построив четыре прямоугольных треугольника так, чтобы на длинном катете каждого из них был расположен короткий катет следующего треугольника, при этом вершины углов совпадают.

Как видно из рисунка, общая фигура представляет собой квадрат со стороной c, являющей одновременно гипотенузой данных треугольников, а площадь этой фигуры равна c2, согласно формуле площади квадрата. Помимо того, что этот квадрат включает в себя четыре прямоугольных треугольника площадью  , в центре его находится еще один, маленький квадрат. Сторона маленького квадрата равна разности катетов, следовательно, его площадь будет равна квадрату этой разности.
(a-b)2=a2-2ab+b2
, в центре его находится еще один, маленький квадрат. Сторона маленького квадрата равна разности катетов, следовательно, его площадь будет равна квадрату этой разности.
(a-b)2=a2-2ab+b2
Представим площадь большого квадрата в виде суммы площадей маленького квадрата и четырех треугольников по принципу суперпозиции. 
Таким образом, площадь квадрата одновременно равна гипотенузе во второй степени и сумме катетов во вторых степенях, что и требовалось доказать. a2+b2=c2
geleot.ru
Обсуждение:Теорема Пифагора — Википедия
Уважаемые авторы статьи. Оказывается, что употребление стандартных выражений вида «Проведем прямую…», которыми наполнена эта статья, нарушает правила Википедии и необходимо писать, что-то типа «Если провести прямую, то…»! Примите участие в обсуждении поправки, устраняющей этот нонсенс. предлагаемое дополнение — Astrohist 09:26, 6 мая 2010 (UTC).
исправьте ошибку в 4 абзаце «истории»: «становиться», правильно будет «становится» 87.229.203.242 03:11, 5 января 2010 (UTC)
- Готово —Тоша 05:39, 5 января 2010 (UTC)
Уважаемый пользователь Тоша, если уж вы заменили окружности на полукруги в первой части, то надо было также заменить и круги на полу-круги во второй:
Сумма площадей полукругов, построенных на катетах (как на диаметре), равна площади круга, построенного на гипотенузе. Этот пример используется при доказательстве свойств фигур, ограниченных дугами двух окружностей и носящих имя Гиппократовых луночек.
Пожалуйста, в качестве консенсуса, воздержитесь от правок статьи в ближайшие два месяца, пока она не будет законченна. В последствии мы можем обсудить уже законченный вариант.
Я обратил внимание, Вы приложились ко всем статьям по геометрии, во многих случаях совершенно незначительно и эпизодически. Я придерживаюсь другого стиля — если делать, то до конца. Потому, пожалуйста, не надо вмешиваться в процесс. Спасибо за понимание.
FeelingOfColors 08:01, 14 февраля 2008 (UTC)
- Поспокойней, все могут ошибиться, (это википедия) —Тоша 21:22, 14 февраля 2008 (UTC)
- Совершенно с Вами согласен, я просто говорю о том, что последовательный стиль редактирования статьи будет, вероятно лучше. То есть чтобы усилия не интерферировали. Иначе приходится много времени тратить на понимание того, что же изменилось под воздействием правок другого участника. FeelingOfColors 07:48, 15 февраля 2008 (UTC)
Пока не достигнут консенсус по содержанию разделов, я внёс некоторые стилевые изменения. FeelingOfColors 07:22, 14 февраля 2008 (UTC)
Мне английская статья сильно не нравится, по-моему её не стоит переводить. —Тоша 16:34, 5 августа 2006 (UTC)
Добавить больше демонстраций, в частности доказательство Евклида, gif from France. Сделать комментарий относительно Гиппократовых луночек. FeelingOfColors 12:07, 25 декабря 2007 (UTC)
Важное обощение de Gua’s theorem, обсудить дату его появления. FeelingOfColors 12:10, 25 декабря 2007 (UTC)
Добавить обсуждение следствий из теоремы пифагора, Физика и Технология. FeelingOfColors 10:48, 27 декабря 2007 (UTC)
Уважаемый пользователь Тоша, не надо убирать английские названия философов, тем более что русская википедия оставляет желать лучшего…
Не надо убирать не законченные разделы статьи, может кто-то их дополнит видя заголовок и так далее. Статья очевидно не законченна, не надо её маскировать под законченную просто удаляя названия ещё не написанных разделов.
Последние два комментария сделаны мной. FeelingOfColors 09:11, 3 февраля 2008 (UTC)
- Английские имена не имеют смысла т.к. есть (хоть и короткая) статья на русском (оттуда можно пойти по ссылке в англ.)
- И также не нужно навязывать имена подразделов. (Надо думать прежде всего о читателях). —Тоша 05:49, 4 февраля 2008 (UTC)
Я считаю указание английских имён известных личностей, наряду с русским эквивалентом, прививает общую грамотность. Человеку не обязательно целенаправленно бороздить википедию, чтобы узнать английское написание фамилии. Тем более тут это не занимает много места и ничему не мешает. Кстати сказать, в научной литературе это обычно является правилом хорошего тона — указывать в скобках оригинальную фамилию. FeelingOfColors 15:10, 4 февраля 2008 (UTC)
- Давайте всё-таки придерживаться сложившихся стандартов (иначе придётся всё переписывать). Кроме того непонятно почему не включить ещё и греческие имена… Разумеется в статье про англичанина такое приемлемо, но не нужно дублировать везде где его фамилия появляется. —Тоша 16:27, 4 февраля 2008 (UTC)
У меня такой вопрос, неужели в китайской книге Чу-Пей так и было написано: «сумма квадратов длин высоты и основания есть квадрат длины гипотенузы»? Яна 17:24, 28 января 2010 (UTC) Яна
- Я вырезал следующее
Часто теорему Пифагора неверно называют частным случаем теоремы косинусов. В силу того, что тригонометрия органически основана на теореме Пифагора, все метрические соотношения в треугольнике вытекают именно из теоремы Пифагора, а не наоборот. Нетрудно также видеть глубокую связь между теоремой Пифагора и окружностью, общеизвестно, что треугольник вписанный в окружность и опирающийся на диаметр — прямоугольный, а значит и сумма квадратов длин катетов данного треугольника равна квадрату длины диаметра. Отсюда легко видеть метод построения окружности по заданному диаметру
.- Поная ерунда была написана…—Тоша 19:34, 7 февраля 2008 (UTC)
То есть Вы наивно считаете теорему Пифагора частным случаем теоремы косинусов? :-))))
А вообще, мне не нравится что Вы берете на себя роль редактора… Вы самолично не сильно расширили статью, тем не менее считаете позволительным для себя удалять некоторые разделы и вообще менять весь облик статьи, тем самым сводя на нет усилия других …
FeelingOfColors 09:33, 8 февраля 2008 (UTC)
Я вернул старый вариант статьи, можете творить как Вам нравится. FeelingOfColors 09:36, 8 февраля 2008 (UTC)
- Поймите, мы оба правим статью и я просто пытался сделать её лучше (для всех). Не надо противостояний, надо просто помогать друг-другу. На мой взгляд Ваши правки — очень ценны. —Тоша 14:57, 8 февраля 2008 (UTC)
- Я не согласен с тем, что Ваши правки приводят к ситуации когда лучше Всем, Вы выхолащиваете статью и делаете ее как в скучном учебнике от Бурбаки. С подобным стилем я, к сожалению, согласиться не могу. Не вижу противостояния, это элементарная дискуссия по поводу стилистики. Стоить отметить, что у Вас ушло более дня на то чтобы вернуть чертёж который Вы лично удалили, не обращая внимание на законченность абзаца. То есть получается Вы даже не удосужились прочитать свои изменения, иначе сразу бы заметили эту ошибку. Это мне не понятно. Я совершенно не против критики или изменений, я против Ваших удалений, которые Вы делаете «якобы» для всех, а на деле просто редактируете так, как Вам ЛИЧНО нравится. FeelingOfColors 08:16, 9 февраля 2008 (UTC)
- Действительно, изображение убрал по ошибке. Я разумеется не идеален, и не должен таковым быть. Мои правки объясняются в основном упрощением поиска нужной информации. Википедия это прежде всего энциклопедия и стиль должен соответствовать. —Тоша 18:41, 9 февраля 2008 (UTC)
Посмотрим как будет продвигаться обсуждение относительно стиля статьи и вообще общего метода её создания. Если верх возьмёт Ваш подход то я, пожалуй, более не буду принимать участие в её создании. FeelingOfColors 13:46, 10 февраля 2008 (UTC)
Пятый постулат (предвижу недовольства)[править код]
Я убрал замечания про пятый постулат, потому, что это общее место. То же самое можно сказать про почти все теоремы Евклидовой геометрии, и про каждый из пяти постулатов. —Тоша 18:57, 17 февраля 2008 (UTC)
Доказательство Леонардо да Винчи[править код]
Я убрал из секции ненужные слова, типа «элегантный чертёж», думаю не нужно навязывать читателю своих чуств… Плюс мат.обозначения ввёл в <math>…</math> не вижу причины ткое откатывать… —Тоша 09:11, 3 марта 2008 (UTC)
Простейшее доказательство[править код]
Чтобы понять, что такое рекурсия, сначала нужно понять, что такое рекурсия? Статья «Простейшее доказательство теоремы Пифагора» ведет на «Теорему Пифогора». 213.169.92.205 17:38, 8 апреля 2011 (UTC)
Так как сам редактировать не могу[править код]
У некоторых формул в статье перед </math> нету бэкслыша с запятой (\,), поэтому некоторые формулы по крайней мере в моем браузере отображаются мелким шрифтом. Также нужно добавить ссылку на новую статью сферическая теорема Пифагора в соответствующий абзац. 217.147.37.71 18:27, 19 октября 2011 (UTC)
- Сделано. —Illythr (Толк?) 20:25, 19 октября 2011 (UTC)
- Спасибо. 217.147.37.71 20:45, 19 октября 2011 (UTC)
- Не стоит заставлять все математические формулы переводить в png-файл, добавляя \ , \, \!, _{}, \frac{}{} и т.п. Картинки дольше грузятся и представляют проблемы при плохой связи. Вы можете изменить свои настройки (настройки ==> Отображения формул ==> Всегда генерировать PNG).—Тоша 22:30, 30 октября 2011 (UTC)
Странно, что в разделе «История» о Пифагоре не сказано ни слова. А почему тогда теорема так называется??? 🙂 Постараюсь добавить из английской статьи. —beroal 15:05, 23 октября 2011 (UTC)
Прошу лиц, обладающих полномочиями править данную статью, исправить название книги с невнятного «Чу-пей» на достоверное «Чжоу-би». Пруф: http://www.synologia.ru/a/Чжоу_би_суань_цзин 116.21.155.103 08:56, 22 февраля 2014 (UTC)Мимокитаист.
- ОК. —Illythr (Толк?) 22:17, 22 февраля 2014 (UTC)
«Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, то есть к 2000 году до н. э.». Действительно, тот текст относят к периоду Хаммурапи, но этот период расположен несколько позднее — приблизительно в 1793 — 1750 годах до н. э. 5.166.194.41 20:33, 26 мая 2014 (UTC)Андрей
Друзья, поменяйте, пожалуйста картинку! Первый, «главный» рисунок в статье — синий равнобедренный прямоугольный треугольник (частный случай). Треугольник надо бы сделать с произвольными сторонами, обозначить прямой угол, катеты, гипотенузу. И без заливки (имхо). Imial25 03:35, 12 ноября 2014 (UTC)
- Правильное замечание.
 Сделано. LGB 12:27, 12 ноября 2014 (UTC)
Сделано. LGB 12:27, 12 ноября 2014 (UTC)
Об этапах открытия теоремы[править код]
Что-то новое в истории: [1] ? РоманСузи 21:07, 11 января 2015 (UTC)
Раздел «доказательство Эвклида»[править код]
Начиная со слов «Равенство это очевидно: треугольники равны по двум сторонам» всё можно убрать, потому что эти треугольники получаются вращением друг друга вокруг точки А на 90 градусов, никакой ерунды типа «равны по двум сторонам и углу» не нужно. Кроме того чуть выше эти треугольники неправильно названы, когда речь в школе шла о равных треугольниках вершины перечисляли ровно в том порядке, в котором они переходят друг в дружку при изометрии. 91.152.91.63 08:11, 22 ноября 2015 (UTC)Анонимный доброжелатель
Раздел «Обобщение для произвольных треугольников через параллелограммы»[править код]
К предложению «Эта замена квадратов параллелограммами имеет четкое сходство с начальной теоремой Пифагора, считается, что её сформулировал Папп Александрийский в 4 г. н. э.» следует добавить (см. теорему Паппа о площадях). Там есть эта теорема. 78.132.137.69 17:37, 25 декабря 2015 (UTC)
Насколько точно число доказательств[править код]
В разделе «Доказательства» предлагается изменить «На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы» на «В научной литературе зафиксировано не менее 367 доказательств данной теоремы» (убрать «На данный момент» ВП:ИНВ и добавить «не менее»). — Albina-belenkaya 13:03, 10 января 2016 (UTC)
 Сделано Всё верно, один источник не может претендовать на полноту. — Stannic(обс)(вкл)(выкл) 00:28, 11 января 2016 (UTC)
Сделано Всё верно, один источник не может претендовать на полноту. — Stannic(обс)(вкл)(выкл) 00:28, 11 января 2016 (UTC)
заменить «треугольники» на «квадраты» (или на «подобные треугольники» (?)) и добавить «от» перед словом гипотенуза[править код]
Также может быть выражена как геометрический факт равенства площади ТРЕУГОЛЬНИКА, отложенного ? 109.87.72.194 05:25, 9 сентября 2016 (UTC) гипотенузы с суммой площадей ТРЕУГОЛЬНИКОВ, отложенных от катетов 109.87.72.194 05:25, 9 сентября 2016 (UTC)
- Да написана была бессмыслица. Обидно, что это долгое время было отпатрулировано в такой важной статье. — Алексей Копылов ✍ 🐾 15:09, 9 сентября 2016 (UTC)
ru.wikipedia.org
Теорема Пифагора | Онлайн калькулятор
Теорема Пифагора является основополагающим звеном в Евклидовой геометрии, на котором базируются большая часть всех вытекающих из теоремы Пифагора следствий и других теорем. Выведенная еще в VI веке до нашей эры, теорема связывает стороны прямоугольного треугольника простым уравнением, и имеет множество доказательств, одно из которых объединяет в себе как алгебру, так и геометрию.
Согласно теореме Пифагора, в прямоугольном треугольнике есть катеты a и b – это стороны прилегающие к прямому углу, и сумма их квадратов дает квадрат гипотенузы – третьей стороны треугольника, лежащей напротив прямого угла.
Доказать это можно, построив четыре прямоугольных треугольника так, чтобы на длинном катете каждого из них был расположен короткий катет следующего треугольника, при этом вершины углов совпадают.


Как видно из рисунка, общая фигура представляет собой квадрат со стороной c, являющей одновременно гипотенузой данных треугольников, а площадь этой фигуры равна c2, согласно формуле площади квадрата. Помимо того, что этот квадрат включает в себя четыре прямоугольных треугольника площадью  , в центре его находится еще один, маленький квадрат. Сторона маленького квадрата равна разности катетов, следовательно, его площадь будет равна квадрату этой разности. (a-b)2=a2-2ab+b2
, в центре его находится еще один, маленький квадрат. Сторона маленького квадрата равна разности катетов, следовательно, его площадь будет равна квадрату этой разности. (a-b)2=a2-2ab+b2
Представим площадь большого квадрата в виде суммы площадей маленького квадрата и четырех треугольников по принципу суперпозиции.
Таким образом, площадь квадрата одновременно равна гипотенузе во второй степени и сумме катетов во вторых степенях, что и требовалось доказать. a2+b2=c2
allcalc.ru
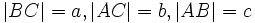
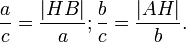
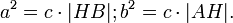
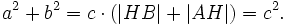
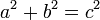
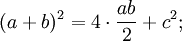
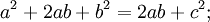
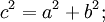
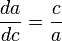
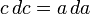
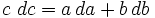
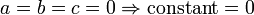
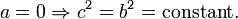
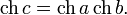
 ,
, 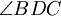 и
и 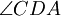 ) — прямые, верно следующее соотношение: квадрат площади грани, противолежащей вершине D, равен сумме квадратов площадей граней, прилежащих к этому углу.
) — прямые, верно следующее соотношение: квадрат площади грани, противолежащей вершине D, равен сумме квадратов площадей граней, прилежащих к этому углу.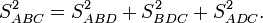
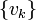 имеет место равенство, также называемое теоремой Пифагора:
имеет место равенство, также называемое теоремой Пифагора: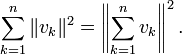
 Сделано. LGB 12:27, 12 ноября 2014 (UTC)
Сделано. LGB 12:27, 12 ноября 2014 (UTC)