Вычисление расстояния и начального азимута между двумя точками на сфере

Измерение расстояния и начального азимута между точками без проекционных преобразований

Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.

Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования

не является кратчайшим расстоянием между двумя точками.

большой круг

Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.

расстояние большого круга

На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.

Маршрут Нью-Йорк — Пекин

Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.

Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.

Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.

Существует три способа расчета сферического расстояния большого круга (подробнее).

[править] Сферическая теорема косинусов

В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением. Графическое изображение формул здесь и далее — из Википедии.

— широта и долгота двух точек в радианах

— разница координат по долготе

— угловая разница

Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).

[править] Формула гаверсинусов

Используется, чтобы избежать проблем с небольшими расстояниями.

[править] Модификация для антиподов

Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.

[править] Реализация на Avenue

На языке Avenue, используя последнюю формулу для вычисления расстояния большого круга между двумя точками, можно использовать следующий код. Точки для вычисления передаются другим скриптом, либо добавляются в начало данного в виде pnt = point.make(long, lat) (скачать скрипт):

'pnt1, pnt2 - точки между которыми вычисляются расстояния
'pi - число pi, rad - радиус сферы (Земли), num - количество знаков после запятой
pi = 3.14159265358979
rad = 6372795
num = 7

'получение координат точек в радианах
lat1 = pnt1.getY*pi/180
lat2 = pnt2.getY*pi/180
long1 = pnt1.getX*pi/180
long2 = pnt2.getX*pi/180

'косинусы и синусы широт и разниц долгот
cl1 = lat1.cos
cl2 = lat2.cos
sl1 = lat1.sin
sl2 = lat2.sin
delta = long2 - long1
cdelta = delta.cos
sdelta = delta.sin

'вычисления длины большого круга
p1 = (cl2*sdelta)^2
p2 = ((cl1*sl2) - (sl1*cl2*cdelta))^2
p3 = (p1 + p2)^0.5
p4 = sl1*sl2
p5 = cl1*cl2*cdelta
p6 = p4 + p5
p7 = p3/p6
anglerad = (p7.atan).SetFormatPrecision (num)
dist = anglerad*rad
'вычисление начального азимута
x = (cl1*sl2) - (sl1*cl2*cdelta) 
y = sdelta*cl2 
z = (-y/x).ATan.AsDegrees 
if (x < 0) then z = z+180 end 
z = -(z + 180 mod 360 - 180).AsRadians
anglerad2 = z - ((2*pi)*((z/(2*pi)).floor))
angledeg = (anglerad2*180)/pi
'возврат значений длины большого круга и начального азимута
distlist = {dist, angledeg}
return distlist

Для вызова процедуры расчета длин приведенной выше, можно также воспользоваться следующим скриптом, результатом его работы будет расчет длин между точкой testpont до всех точек активной темы вида и запись результата в поле Newdist атрибутивной таблицы этой темы:

atheme = av.getactivedoc.getactivethemes.get(0)
aftab = atheme.getftab
f_shape = aftab.findfield("Shape")

f_dist = aftab.findfield("dist")
f_ang = aftab.findfield("ang")
'testpoint - точка отсчета
testpoint = point.make(25.85, 55.15)
aftab.seteditable(true)

'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
	pnts = {}
	apoint = aftab.returnvalue(f_shape, rec)
	pnts.add(apoint.getx)
	pnts.add(testpoint.getx)
	pnts.add(apoint.gety)
	pnts.add(testpoint.gety)

	'Вызов процедуры расчета расстояний
	'"Calc-distance" - название скрипта с процедурой в проекте
	param = av.run("Calc-distance", pnts)
	aftab.setvalue(f_dist, rec, param.get(0))
	aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)

[править] Реализация на языке Python

Реализует полный вариант расчета через atan2(), более универсальнее, чем вариант для Avenue. (скачать скрипт)

import math
 
 #pi - число pi, rad - радиус сферы (Земли)
 rad = 6372795
 
 #координаты двух точек
 llat1 = 77.1539
 llong1 = -120.398
 
 llat2 = 77.1804
 llong2 = 129.55
 
 #в радианах
 lat1 = llat1*math.pi/180.
 lat2 = llat2*math.pi/180.
 long1 = llong1*math.pi/180.
 long2 = llong2*math.pi/180.
 
 #косинусы и синусы широт и разницы долгот
 cl1 = math.cos(lat1)
 cl2 = math.cos(lat2)
 sl1 = math.sin(lat1)
 sl2 = math.sin(lat2)
 delta = long2 - long1
 cdelta = math.cos(delta)
 sdelta = math.sin(delta)
 
 #вычисления длины большого круга
 y = math.sqrt(math.pow(cl2*sdelta,2)+math.pow(cl1*sl2-sl1*cl2*cdelta,2))
 x = sl1*sl2+cl1*cl2*cdelta
 ad = math.atan2(y,x)
 dist = ad*rad
 
 #вычисление начального азимута
 x = (cl1*sl2) - (sl1*cl2*cdelta)
 y = sdelta*cl2
 z = math.degrees(math.atan(-y/x))
 
 if (x < 0):
     z = z+180.
 
 z2 = (z+180.) % 360. - 180.
 z2 = - math.radians(z2)
 anglerad2 = z2 - ((2*math.pi)*math.floor((z2/(2*math.pi))) )
 angledeg = (anglerad2*180.)/math.pi
 
 print 'Distance >> %.0f' % dist, ' [meters]'
 print 'Initial bearing >> ', angledeg, '[degrees]'

[править] Реализация в Excel

Скачать пример расчета расстояния большого круга и начального азимута в Excel. Демонстрирует расчеты через закон косинусов, гаверсинус, полное уравнение и полное уравнение через atan2().

Можно также воспользоваться следующей функцией:

Public Function Distance_A_B(Lat1 As Double, Long1 As Double, Lat2 As Double, Long2 As Double)
    'определение расстояний между географическими координатами. Координаты должны быть десятичными
    'расстояние выводится в метрах

    With Application.WorksheetFunction

        Distance_A_B = .Atan2(Sin(.Pi() * Lat1 / 180) * Sin(.Pi() * Lat2 / 180) + Cos(.Pi() * Lat1 / 180) * Cos(.Pi() * Lat2 / 180) * Cos(Abs(.Pi() * Long2 / 180 - .Pi() * Long1 / 180)), _
                ((Cos(.Pi() * Lat2 / 180) * Sin(.Pi() * Long2 / 180 - .Pi() * Long1 / 180)) ^ 2 + (Cos(.Pi() * Lat1 / 180) * Sin(.Pi() * Lat2 / 180) - Sin(.Pi() * Lat1 / 180) * Cos(.Pi() * Lat2 / 180) * Cos(Abs(.Pi() * Long2 / 180 - .Pi() * Long1 / 180))) ^ 2) ^ 0.5) * 6372795

    End With

End Function

[править] Проверочный набор данных

Если все считается правильно, должны быть получены следующие результаты (координаты точек даны как широта/долгота, расстояние в метрах, начальный угол в десятичных градусах):

#	Точка 1	Точка 2	Расстояние	Угол
1	77.1539/-139.398	-77.1804/-139.55	17166029	180.077867811
2	77.1539/120.398	77.1804/129.55	225883	84.7925159033
3	77.1539/-120.398	77.1804/129.55	2332669	324.384112704

[править] Ссылки по теме

Вычисление расстояния и начального азимута между двумя точками на сфере — GIS-Lab

Измерение расстояния и начального азимута между точками без проекционных преобразований

Введение

Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.

Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.

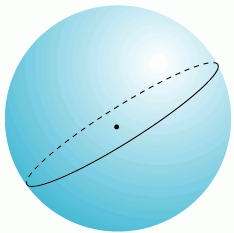
большой круг

Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.

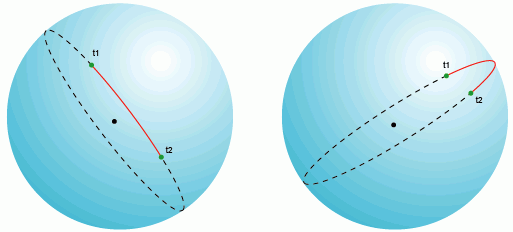
расстояние большого круга

На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.

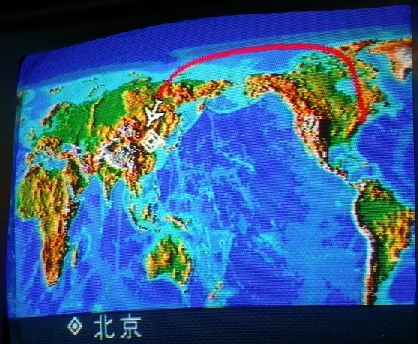
Маршрут Нью-Йорк — Пекин

Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.

Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.

Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.

Формулы

Существует три способа расчета сферического расстояния большого круга (подробнее).

Сферическая теорема косинусов

В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением. Графическое изображение формул здесь и далее — из Википедии.

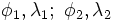— широта и долгота двух точек в радианах

— разница координат по долготе

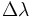
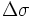— угловая разница

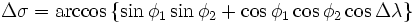
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).

Формула гаверсинусов

Используется, чтобы избежать проблем с небольшими расстояниями.

Модификация для антиподов

Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.

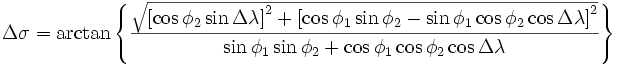
Реализация на Avenue

На языке Avenue, используя последнюю формулу для вычисления расстояния большого круга между двумя точками, можно использовать следующий код. Точки для вычисления передаются другим скриптом, либо добавляются в начало данного в виде pnt = point.make(long, lat) (скачать скрипт):

'pnt1, pnt2 - точки между которыми вычисляются расстояния
'pi - число pi, rad - радиус сферы (Земли), num - количество знаков после запятой
pi = 3.14159265358979
rad = 6372795
num = 7

'получение координат точек в радианах
lat1 = pnt1.getY*pi/180
lat2 = pnt2.getY*pi/180
long1 = pnt1.getX*pi/180
long2 = pnt2.getX*pi/180

'косинусы и синусы широт и разниц долгот
cl1 = lat1.cos
cl2 = lat2.cos
sl1 = lat1.sin
sl2 = lat2.sin
delta = long2 - long1
cdelta = delta.cos
sdelta = delta.sin

'вычисления длины большого круга
p1 = (cl2*sdelta)^2
p2 = ((cl1*sl2) - (sl1*cl2*cdelta))^2
p3 = (p1 + p2)^0.5
p4 = sl1*sl2
p5 = cl1*cl2*cdelta
p6 = p4 + p5
p7 = p3/p6
anglerad = (p7.atan).SetFormatPrecision (num)
dist = anglerad*rad
'вычисление начального азимута
x = (cl1*sl2) - (sl1*cl2*cdelta) 
y = sdelta*cl2 
z = (-y/x).ATan.AsDegrees 
if (x < 0) then z = z+180 end 
z = -(z + 180 mod 360 - 180).AsRadians
anglerad2 = z - ((2*pi)*((z/(2*pi)).floor))
angledeg = (anglerad2*180)/pi
'возврат значений длины большого круга и начального азимута
distlist = {dist, angledeg}
return distlist

Для вызова процедуры расчета длин приведенной выше, можно также воспользоваться следующим скриптом, результатом его работы будет расчет длин между точкой testpont до всех точек активной темы вида и запись результата в поле Newdist атрибутивной таблицы этой темы:

atheme = av.getactivedoc.getactivethemes.get(0)
aftab = atheme.getftab
f_shape = aftab.findfield("Shape")

f_dist = aftab.findfield("dist")
f_ang = aftab.findfield("ang")
'testpoint - точка отсчета
testpoint = point.make(25.85, 55.15)
aftab.seteditable(true)

'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
	pnts = {}
	apoint = aftab.returnvalue(f_shape, rec)
	pnts.add(apoint.getx)
	pnts.add(testpoint.getx)
	pnts.add(apoint.gety)
	pnts.add(testpoint.gety)

	'Вызов процедуры расчета расстояний
	'"Calc-distance" - название скрипта с процедурой в проекте
	param = av.run("Calc-distance", pnts)
	aftab.setvalue(f_dist, rec, param.get(0))
	aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)

Реализация на языке Python

Реализует полный вариант расчета через atan2(), более универсальнее, чем вариант для Avenue. (скачать скрипт)

import math
 
 #pi - число pi, rad - радиус сферы (Земли)
 rad = 6372795
 
 #координаты двух точек
 llat1 = 77.1539
 llong1 = -120.398
 
 llat2 = 77.1804
 llong2 = 129.55
 
 #в радианах
 lat1 = llat1*math.pi/180.
 lat2 = llat2*math.pi/180.
 long1 = llong1*math.pi/180.
 long2 = llong2*math.pi/180.
 
 #косинусы и синусы широт и разницы долгот
 cl1 = math.cos(lat1)
 cl2 = math.cos(lat2)
 sl1 = math.sin(lat1)
 sl2 = math.sin(lat2)
 delta = long2 - long1
 cdelta = math.cos(delta)
 sdelta = math.sin(delta)
 
 #вычисления длины большого круга
 y = math.sqrt(math.pow(cl2*sdelta,2)+math.pow(cl1*sl2-sl1*cl2*cdelta,2))
 x = sl1*sl2+cl1*cl2*cdelta
 ad = math.atan2(y,x)
 dist = ad*rad
 
 #вычисление начального азимута
 x = (cl1*sl2) - (sl1*cl2*cdelta)
 y = sdelta*cl2
 z = math.degrees(math.atan(-y/x))
 
 if (x < 0):
     z = z+180.
 
 z2 = (z+180.) % 360. - 180.
 z2 = - math.radians(z2)
 anglerad2 = z2 - ((2*math.pi)*math.floor((z2/(2*math.pi))) )
 angledeg = (anglerad2*180.)/math.pi
 
 print 'Distance >> %.0f' % dist, ' [meters]'
 print 'Initial bearing >> ', angledeg, '[degrees]'

Реализация в Excel

Скачать пример расчета расстояния большого круга и начального азимута в Excel. Демонстрирует расчеты через закон косинусов, гаверсинус, полное уравнение и полное уравнение через atan2().

Можно также воспользоваться следующей функцией:

Public Function Distance_A_B(Lat1 As Double, Long1 As Double, Lat2 As Double, Long2 As Double)
    'определение расстояний между географическими координатами. Координаты должны быть десятичными
    'расстояние выводится в метрах

    With Application.WorksheetFunction

        Distance_A_B = .Atan2(Sin(.Pi() * Lat1 / 180) * Sin(.Pi() * Lat2 / 180) + Cos(.Pi() * Lat1 / 180) * Cos(.Pi() * Lat2 / 180) * Cos(Abs(.Pi() * Long2 / 180 - .Pi() * Long1 / 180)), _
                ((Cos(.Pi() * Lat2 / 180) * Sin(.Pi() * Long2 / 180 - .Pi() * Long1 / 180)) ^ 2 + (Cos(.Pi() * Lat1 / 180) * Sin(.Pi() * Lat2 / 180) - Sin(.Pi() * Lat1 / 180) * Cos(.Pi() * Lat2 / 180) * Cos(Abs(.Pi() * Long2 / 180 - .Pi() * Long1 / 180))) ^ 2) ^ 0.5) * 6372795

    End With

End Function

Проверочный набор данных

Если все считается правильно, должны быть получены следующие результаты (координаты точек даны как широта/долгота, расстояние в метрах, начальный угол в десятичных градусах):

#	Точка 1	Точка 2	Расстояние	Угол
1	77.1539/-139.398	-77.1804/-139.55	17166029	180.077867811
2	77.1539/120.398	77.1804/129.55	225883	84.7925159033
3	77.1539/-120.398	77.1804/129.55	2332669	324.384112704

Ссылки по теме

Путевой угол и расстояние между двумя точками по локсодроме (линии румба).

В 16 веке фламандский географ Герхард Меркатор составил навигационную карту мира, изобразив поверхность Земли на плоскости таким образом, чтобы углы на карте не искажались. В настоящее время такой способ изображения Земли известен, как равноугольная цилиндрическая проекция Меркатора. Такая карта была очень удобна для мореплавателей, так как для того чтобы прийти из точки А в точку Б на карте Меркатора достаточно провести прямую линию между этими точками, замерить ее угол к меридиану и постоянно придерживаться этого направления, например используя секстант и полярную звезду в качестве ориентира или магнитный компас. (На самом деле с компасом не так все просто, так как он не всегда показывает на истинный север, но об этом как-нибудь в другой раз). Проекция Меркатора до сих пор широко применяется для составления навигационных карт.
Однако, еще древние мореплаватели начинали замечать, что линия румба не всегда является кратчайшим путем между двумя точками, особенно, это становилось заметно для дальних переходов. Если провести на глобусе линию, пересекающую все меридианы под одним и тем же углом, то станет понятно, отчего это происходит. Прямая линия на карте Меркатора превращается на глобусе в бесконечно закручивающуюся к полюсам спираль. Такую линию в современной науке принято называть греческим словом локсодромия, что означает «косой бег».
Следующий далее калькулятор вычисляет путевой угол и расстояние трансатлантического перехода из Лас Пальмаса (Испания) в Бриджтаун (Барбадос) по локсодромии. Полученное расстояние на десятки километров отличается от кратчайшего пути (см.Расстояние между двумя координатами).

Вычисление постоянного азимута и длины линии румба

Начальная точка, широтаНачальная точка, долготаКонечная точка, широтаКонечная точка, долготаРеференц-эллипсоид Точность вычисления

Знаков после запятой: 2

Расстояние в километрах

 

Расстояние в морских милях

 

save Сохранить share Поделиться extension Виджет

Для вычисления путевого угла используются следующие формулы:

<sup>где

Длина локсодромии вычислена по следующей формуле:</sup>

, где — широта и долгота первой точки — широта и долгота второй точки
— эксцентиситет сфероида (a — длина большой полуоси, b — длина малой полуоси)

При углах 90° или 270° для вычисления длины дуги использовалась формула: