Средняя линия треугольника и трапеции определение формула. Средняя линия трапеции
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной. Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др.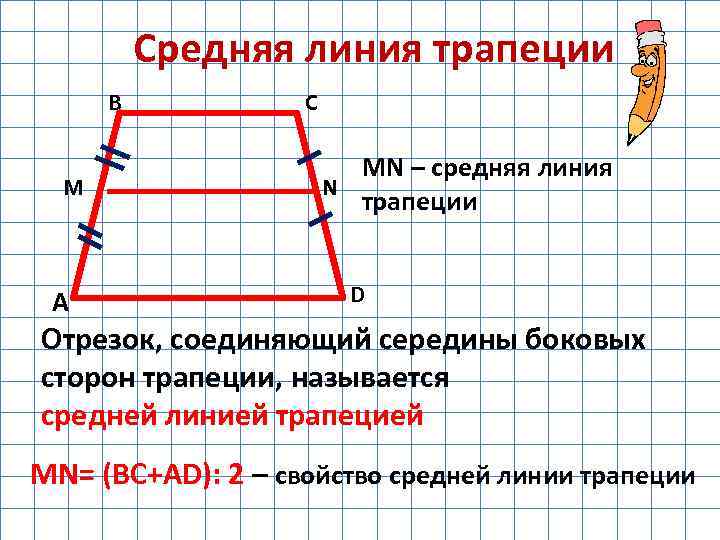 Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.
Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.
Общие сведения
Для начала давайте разберемся, что такое четырехугольник. Данная фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, которые не являются соседними, называются противоположными. То же можно сказать и о двух несмежных сторонах. Основные виды четырехугольников — это параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтоид.
Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны являются параллельными. Их называют основаниями. Две другие (непараллельные) — боковые стороны. В материалах экзаменов и различных контрольных работ очень часто можно встретить задачи, связанные с трапециями, решение которых зачастую требует от учащегося знаний, не предусмотренных программой. Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Виды трапеции
Существует много видов данной фигуры. Однако чаще всего принято рассматривать два из них — равнобедренную и прямоугольную.
1. Прямоугольная трапеция — это фигура, у которой одна из боковых сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.
2. Равнобедренная трапеция — это геометрическая фигура, у которой боковые стороны равны между собой. А значит, и углы у оснований также попарно равны.
Главные принципы методики изучения свойств трапеции
К основному принципу можно отнести использование так называемого задачного подхода. По сути, нет необходимости для ввода в теоретический курс геометрии новых свойств этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.
Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.
Вторым принципом является так называемая спиральная организация изучения «замечательных» свойств трапеции. Это подразумевает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Таким образом, учащимся легче их запоминать. Например, свойство четырех точек. Его можно доказывать как при изучении подобия, так и впоследствии с помощью векторов. А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.
Применение «внепрограммных» особенностей геометрической фигуры в содержании школьного курса — это задачная технология их преподавания. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже познавать трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Итак, приступим к изучению этой замечательной фигуры.
Элементы и свойства равнобедренной трапеции
Как мы уже отмечали, у данной геометрической фигуры боковые стороны равны. Еще она известна как правильная трапеция. А чем же она так примечательна и почему получила такое название? К особенностям данной фигуры относится то, у нее равны не только боковые стороны и углы у оснований, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.
А теперь давайте разберемся, как найти углы равнобедренной трапеции. Рассмотрим вариант решения этой задачи при условии, что известны размеры сторон фигуры.
Рассмотрим вариант решения этой задачи при условии, что известны размеры сторон фигуры.
Решение
Обычно четырехугольник принято обозначать литерами А, Б, С, Д, где БС и АД — это основания. В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
Существует и второе решение данной задачи. В начале опускаем из угла В высоту Н. Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg. В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем аналогично первому способу.
Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg. В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем аналогично первому способу.
Свойство диагоналей равнобедренной трапеции
Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:
Высота фигуры будет равна сумме оснований, деленной на два;
Ее высота и средняя линия равны;
Центр окружности является точкой, в которой пересекаются ;
Если боковая сторона делится точкой касания на отрезки Н и М, тогда равен квадратному корню произведения этих отрезков;
Четырехугольник, который образовался точками касания, вершиной трапеции и центром вписанной окружности — это квадрат, у которого сторона равна радиусу;
Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.
Подобные трапеции
Данная тема весьма удобна для изучения свойств этой Например, диагонали разбивают трапецию на четыре треугольника, причем прилежащие к основаниям являются подобными, а к боковым сторонам — равновеликими. Это утверждение можно назвать свойством треугольников, на которые разбита трапеция ее диагоналями. Первая часть этого утверждения доказывается через признак подобия по двум углам. Для доказательства второй части лучше воспользоваться способом, приведенным ниже.
Доказательство теоремы
Принимаем, что фигура АБСД (АД и БС — основы трапеции) разбивается диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АБО и СОД у боковых сторон. Треугольники СОД и БОС имеют общую высоту в том случае, если отрезки БО и ОД являются их основаниями. Получаем, что разность их площадей (П) равна разности этих отрезков: ПБОС/ПСОД = БО/ОД = К. Следовательно, ПСОД = ПБОС/К. Аналогично, треугольники БОС и АОБ имеют общую высоту. Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.
Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.
Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые разбита трапеция ее диагоналями, решив следующую задачу. Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.
Свойства подобия
Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.
Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.
Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.
Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.
Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям. Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).
Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).
Выводы подобия
Таким образом, мы доказали, что:
1. Отрезок, соединяющий у трапеции середины боковых сторон, параллелен АД и БС и равен среднему арифметическому БС и АД (длина основания трапеции).
2. Черта, проходящая через точку О пересечения диагоналей параллельно АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).
3. Отрезок, разбивающий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.
4. Элемент, делящий фигуру на две равновеликие, имеет длину среднего квадратичного чисел АД и БС.
Для закрепления материала и осознания связи между рассмотренными отрезками учащемуся необходимо построить их для конкретной трапеции. Он без труда сможет отобразить среднюю линию и отрезок, который проходит через точку О — пересечение диагоналей фигуры — параллельно основаниям. А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.
А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.
Отрезок, соединяющий середины диагоналей трапеции
Рассмотрим следующее свойство этой фигуры. Принимаем, что отрезок МН параллелен основаниям и делит диагонали пополам. Точки пересечения назовем Ш и Щ. Данный отрезок будет равен полуразности оснований. Разберем это более детально. МШ — средняя линия треугольника АБС, она равна БС/2. МЩ — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.
Центр тяжести
Давайте рассмотрим, каким образом определяется этот элемент для данной геометрической фигуры. Для этого необходимо продлить основания в противоположные стороны. Что это значит? Нужно к верхнему основанию прибавить нижнее — в любую из сторон, например, вправо. А нижнее продлеваем на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры и есть центр тяжести трапеции.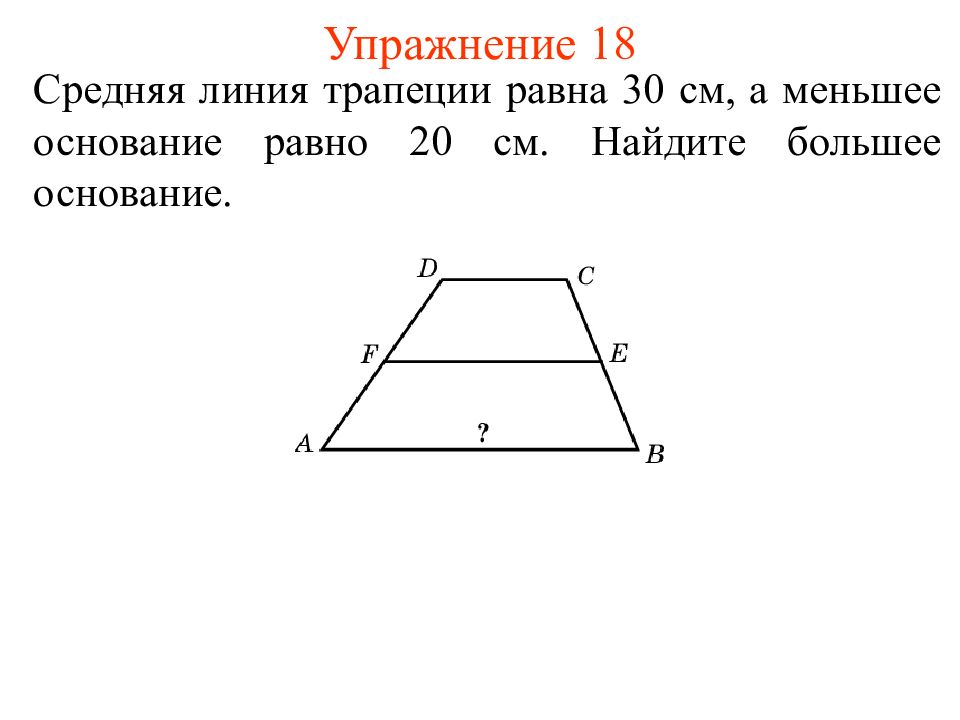
Вписанные и описанные трапеции
Давайте перечислим особенности таких фигур:
1. Трапеция может быть вписана в окружность тольков том случае, если она равнобедренная.
2. Около окружности можно описать трапецию, при условии, что сумма длин их оснований равна сумме длин боковых сторон.
Следствия вписанной окружности:
1. Высота описанной трапеции всегда равна двум радиусам.
2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.
Первое следствие очевидно, а для доказательства второго требуется установить, что угол СОД является прямым, что, по сути, также не составит большого труда. Зато знание данного свойства позволит при решении задач применять прямоугольный треугольник.
Теперь конкретизируем эти следствия для равнобедренной трапеции, которая вписана в окружность. Получаем, что высота является средним геометрическим оснований фигуры: Н=2R=√(БС*АД). Отрабатывая основной прием решения задач для трапеций (принцип проведения двух высот), учащийся должен решить следующее задание. Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.
Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.
Теперь давайте разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем из вершины Б высоту на основание АД. Так как окружность вписана в трапецию, то БС+АД = 2АБ или АБ = (БС+АД)/2. Из треугольника АБН находим sinα = БН/АБ = 2*БН/(БС+АД). ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).
Все формулы средней линии трапеции
Теперь пора перейти к последнему элементу данной геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):
1. Через основания: М = (А+Б)/2.
2. Через высоту, основание и углы:
М = А-Н*(ctgα+ctgβ)/2;
М = Б+Н*(ctgα+ctgβ)/2.
3. Через высоту, диагонали и угол между ними. К примеру, Д1 и Д2 — диагонали трапеции; α , β — углы между ними:
М = Д1*Д2*sinα/2Н = Д1*Д2*sinβ/2Н.
4. Через площадь и высоту: М = П/Н.
Четырёхугольник, у которого только две стороны параллельны называются трапецией .
Параллельные стороны трапеции называются её основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DCAM = MD; BN = NC
MN средняя линия, AB и CD — основания, AD и BC — боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.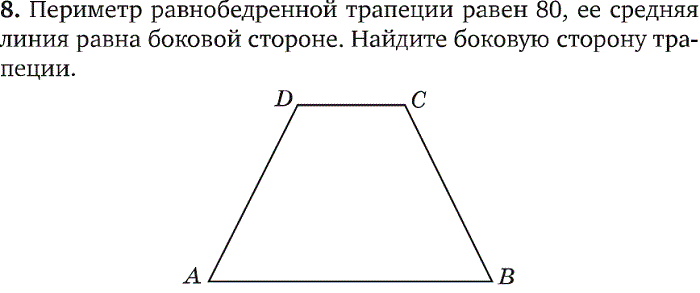
Основная задача : Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC
=>
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
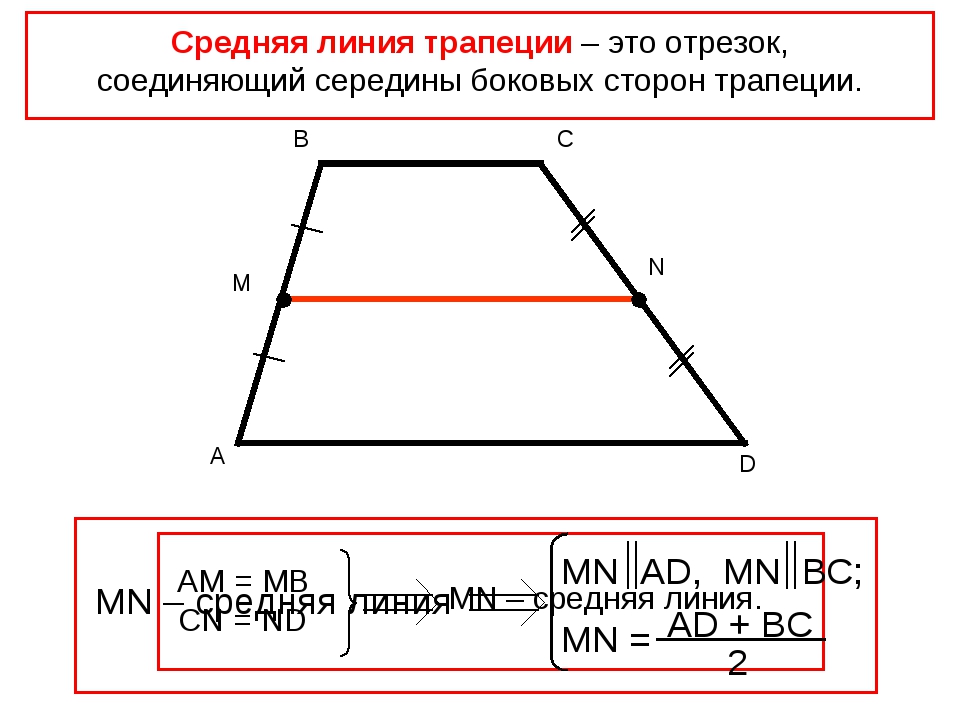 Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
Средняя линия трапеции равна полусумме оснований. Она соединяет середины боковых сторон трапеции и всегда параллельна основаниям.
Если основания трапеции равны a и b, то средняя линия m равна m=(a+b)/2.
Если известна площадь трапеции, то среднюю линию можно найти и другим способом, разделив площадь трапеции S на высоту трапеции h:
То есть, средняя линия трапеции m=S/h
Способов найти длину средней линии трапеции много. Выбор способа зависит от исходных данных.
Выбор способа зависит от исходных данных.
Вот формулы длины средней линии трапеции :
Чтобы найти среднюю линию трапеции, можно воспользоваться одной из пяти формул (выписывать их не буду, так как они уже есть в других ответах), но это только в тех случаях, когда известны нужные нам значения исходных данных.
На практике приходится решать много задач, когда данных недостаточно, а нужный размер нужно все таки найти.
Здесь есть такие варианты
пошаговым решением подвести все таки под формулу;
используя другие формулы, составить и решить необходимые уравнения.
нахождения длины середины трапеции методом подвода под нужную нам формулу с помощью других знаний о геометрии и применяя при этом алгебраические уравнения:
Имеем равнобедренную трапецию, ее диагонали пересекаются под прямым углом, высота равна 9 см.
Делаем рисунок и видим, что в лоб эту задачу не решить (недостаточно данных)
Поэтому мы немного упростим и проведем высоту через точку пересечения диагоналей.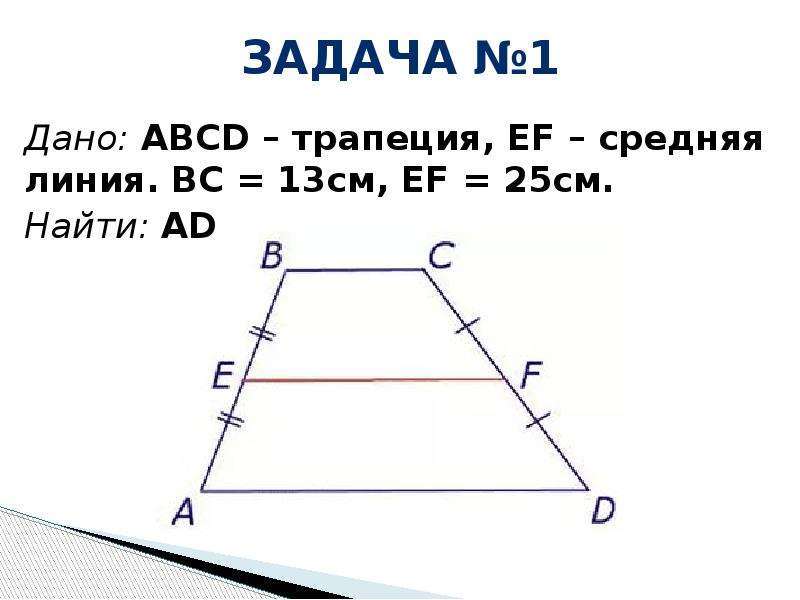
Это первый важный шаг, который ведет к быстрому решению.
обозначим высоту двумя неизвестными, увидим нужные нам равнобедренные треугольники со сторонами х и у
и уже легко найдем сумму оснований трапеции
она равна 2х+2у
И вот только теперь мы можем применить формулу где
и равна она х+у а по условию задачи это длина высоты равная 9 см .
И вот теперь мы вывели несколько моментов для равнобедренной трапеции, диагонали которой пересекаются под прямым углом
в таких трапециях
средняя линия всегда равна высоте
площадь всегда равна квадрату высоты .
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон трапеции.
Среднюю линию любой трапеции несложно найти, если пользоваться формулой:
m = (a + b)/2
m длина средней линии трапеции;
a, b длины оснований трапеции.
Итак, длина средней линии трапеции равна полусумме длин оснований .
Основная формула для формулы средней линии трапеции:длина средней линии трапеции равна полусумме е оснований a и b: MN=(a+b)2.Доказательством этой формулы служит формула для средней линии треугольника.Любая трапеция может быть представлена после того как проведены из концов меньшего основания высоты на большее основание.Рассматриваются 2 полученных треугольника,и прямоугольник.После этого легко доказывается формула для средней линии трапеции.
Чтобы найти среднюю линию трапеции нам нужно знать величины оснований.
После того,как нашли эти величины или может быть они нам были известны,то складываем эти числа и просто делим пополам.
Это и будет средняя линия трапеции .
Насколько я помню уроки школьной геометрии, для того, чтобы найти длину средней линии трапеции, нужно сложить длины оснований и разделить на два. Таким образом длина средней линии трапеции, равна полусумме оснований.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей.
 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .

- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.

- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника.
 Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.

- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны.
 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу. - Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ.
 Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как считать площадь трапеции образец. Как найти площадь трапеции
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.

- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см.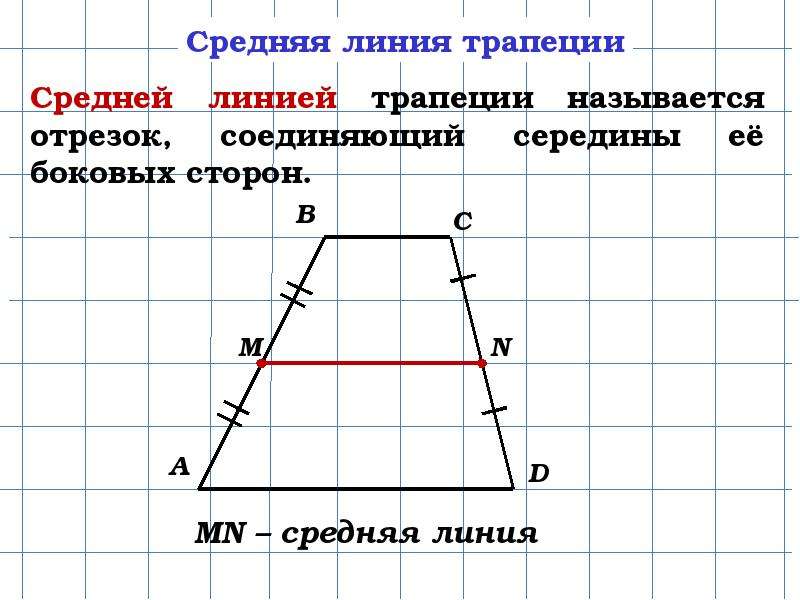 найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Что такое равнобедренная трапеция? Это геометрическая фигура, противолежащие не параллельные стороны которой равны. Существует несколько различных формул для нахождения площади трапеции с различными условиями, которые даны в задачах. То есть площадь найти можно, если дана высота, стороны, углы, диагонали и т.д. Также нельзя не упомянуть, что для равнобедренных трапеций существует некоторые “исключение”, благодаря которым поиск площади и сама формула значительно упрощается. Ниже описаны подробные решения каждого случая с примерами.
Необходимые свойства для нахождения площади равнобедренной трапеции
Мы уже выяснили, что геометрическая фигура, имеющая противолежащие не параллельные, но равные стороны – это трапеция, причем, равнобедренная. Существуют специальные случаи, когда трапеция считается равнобедренной.
- Это условия равенства углов. Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны. В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD
- Второе важное правило – в подобной трапеции диагонали должны быть равны.
 Следовательно, АС = ВD.
Следовательно, АС = ВD. - Третий аспект: противоположные углы трапеции в сумме должны давать 180 градусов. Это значит, что угол ABC + угол CDA = 180 градусов. С углами BCD и BAD аналогично.
- В-четвертых, если трапеция допускает описание вокруг нее окружности – то она равнобедренная.
Как найти площадь равнобедренной трапеции – формулы и их описание
- S = (a+b)h/2 – это самая распространенная формула для нахождения площади, где а – нижнее основание, b – верхнее основание, а h – это высота.
- Если высота неизвестна, то искать ее можно по подобной формуле: h = с*sin(x), где с это либо AB, либо CD. sin(x) – это синус угла при любом основании, то есть угол DAB = угол CDA = x. В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2.
- Высота также может находиться по этой формуле:
- Итоговая формула имеет такой вид:
- Площадь равнобедренной трапеции можно найти и через среднюю линию и высоту.
 Формула такова: S = mh .
Формула такова: S = mh .
Рассмотрим условие, когда в трапецию будет вписана окружность.
В случае, изображенном на картинке,
QN = D = H – диаметр окружности и одновременно высота трапеции;
LO, ON, OQ = R – радиусы окружности;
DC = a – верхнее основание;
AB = b – нижнее основание;
DAB, ABC, BCD, CDA – альфа, бета – углы оснований трапеции.
Подобный случай допускает нахождение площади по таким формулам:
- Теперь попробуем найти площадь через диагонали и углы между ними.
На рисунке обозначим AC, DB – диагонали – d. Углы COB, DOB – альфа; DOC, AOB – бета. Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ) такова:
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d.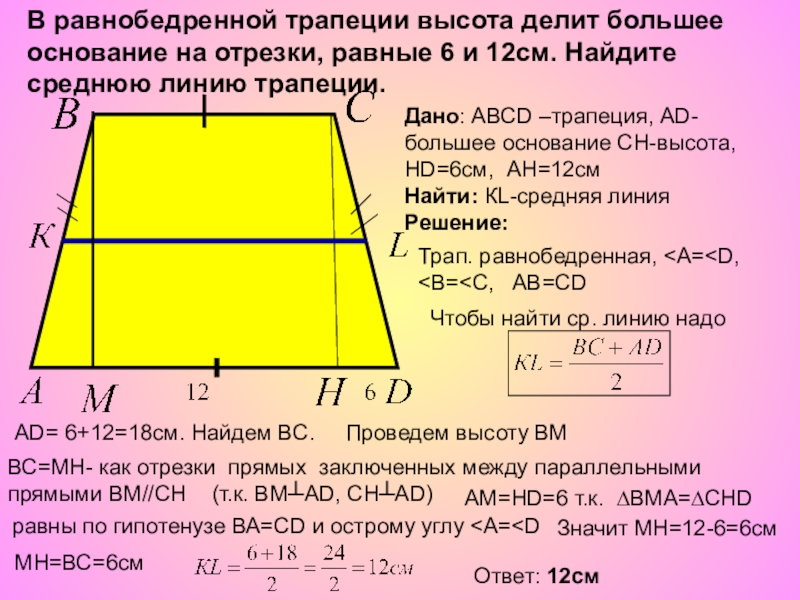 Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение:
Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т.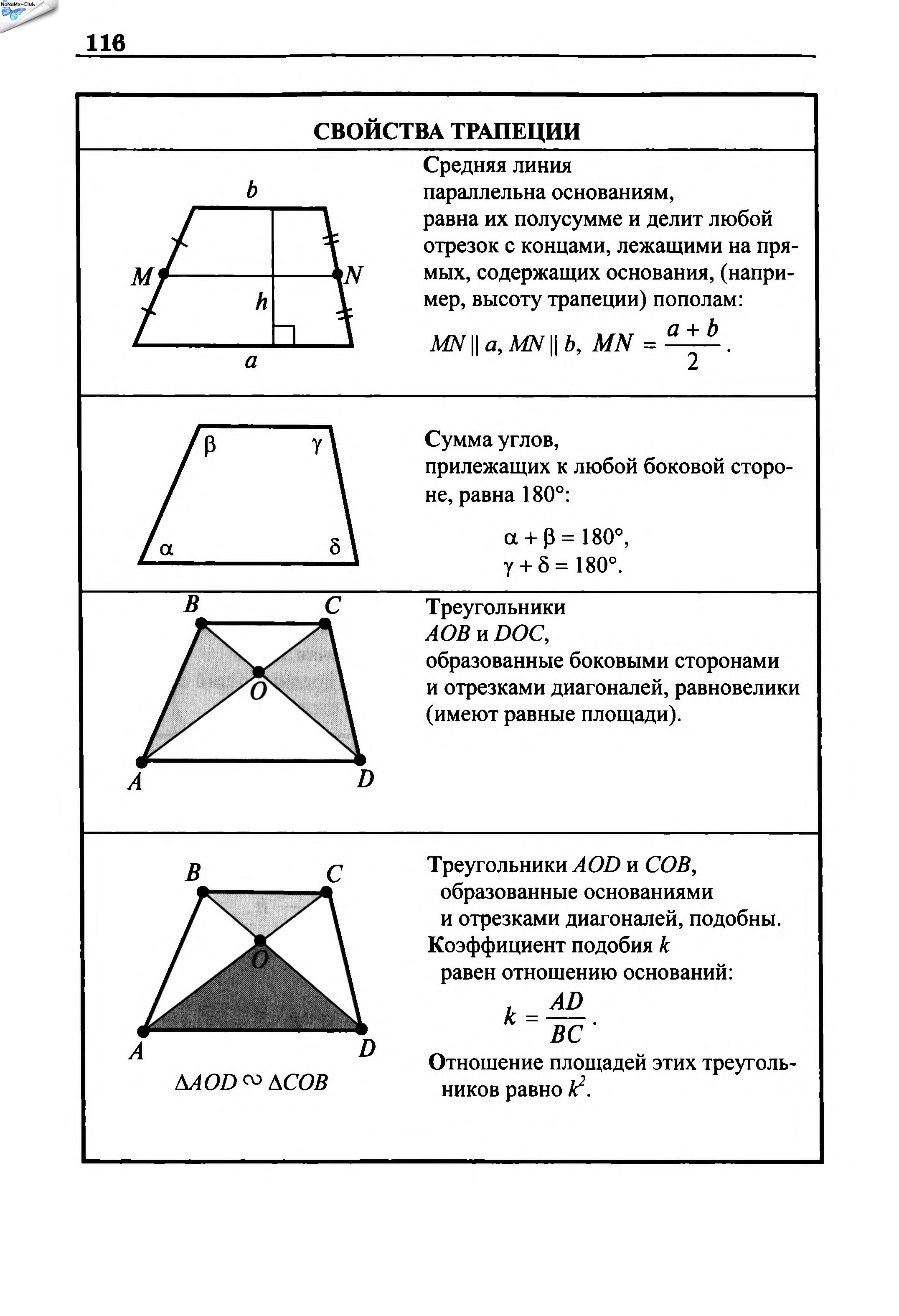 А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E.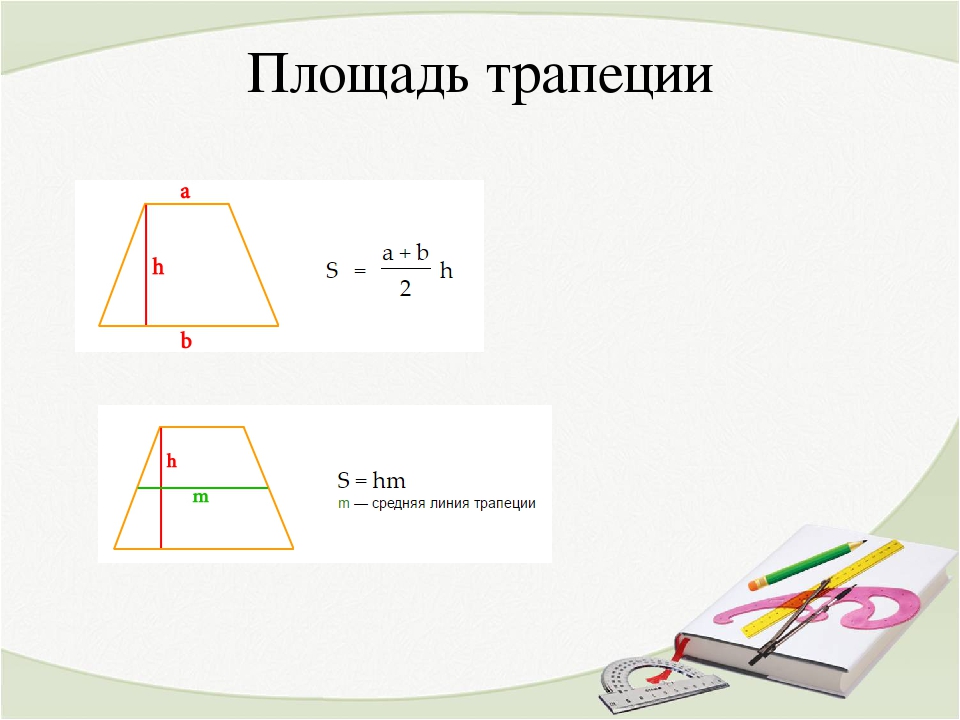 В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .
Найти стороны трапеции через площадь. Как найти площадь трапеции
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников).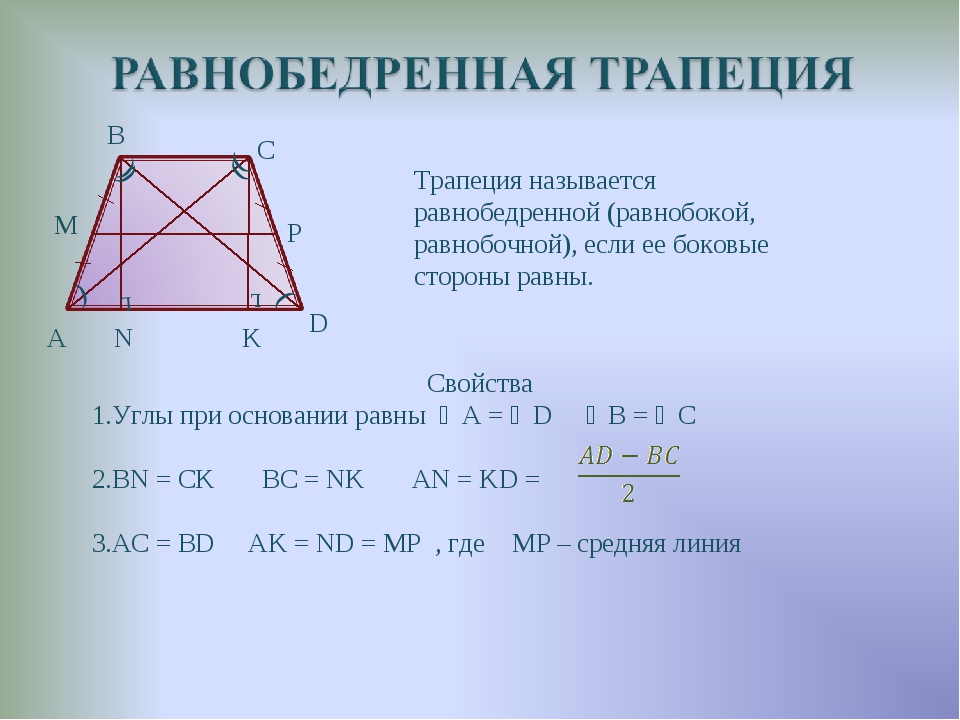 Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Что такое равнобедренная трапеция? Это геометрическая фигура, противолежащие не параллельные стороны которой равны. Существует несколько различных формул для нахождения площади трапеции с различными условиями, которые даны в задачах. То есть площадь найти можно, если дана высота, стороны, углы, диагонали и т.д. Также нельзя не упомянуть, что для равнобедренных трапеций существует некоторые “исключение”, благодаря которым поиск площади и сама формула значительно упрощается. Ниже описаны подробные решения каждого случая с примерами.
Необходимые свойства для нахождения площади равнобедренной трапеции
Мы уже выяснили, что геометрическая фигура, имеющая противолежащие не параллельные, но равные стороны – это трапеция, причем, равнобедренная. Существуют специальные случаи, когда трапеция считается равнобедренной.
- Это условия равенства углов.
 Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны. В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD
Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны. В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD - Второе важное правило – в подобной трапеции диагонали должны быть равны. Следовательно, АС = ВD.
- Третий аспект: противоположные углы трапеции в сумме должны давать 180 градусов. Это значит, что угол ABC + угол CDA = 180 градусов. С углами BCD и BAD аналогично.
- В-четвертых, если трапеция допускает описание вокруг нее окружности – то она равнобедренная.
Как найти площадь равнобедренной трапеции – формулы и их описание
- S = (a+b)h/2 – это самая распространенная формула для нахождения площади, где а – нижнее основание, b – верхнее основание, а h – это высота.
- Если высота неизвестна, то искать ее можно по подобной формуле: h = с*sin(x), где с это либо AB, либо CD. sin(x) – это синус угла при любом основании, то есть угол DAB = угол CDA = x.
 В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2.
В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2. - Высота также может находиться по этой формуле:
- Итоговая формула имеет такой вид:
- Площадь равнобедренной трапеции можно найти и через среднюю линию и высоту. Формула такова: S = mh .
Рассмотрим условие, когда в трапецию будет вписана окружность.
В случае, изображенном на картинке,
QN = D = H – диаметр окружности и одновременно высота трапеции;
LO, ON, OQ = R – радиусы окружности;
DC = a – верхнее основание;
AB = b – нижнее основание;
DAB, ABC, BCD, CDA – альфа, бета – углы оснований трапеции.
Подобный случай допускает нахождение площади по таким формулам:
- Теперь попробуем найти площадь через диагонали и углы между ними.
На рисунке обозначим AC, DB – диагонали – d. Углы COB, DOB – альфа; DOC, AOB – бета. Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ) такова:
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.

- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.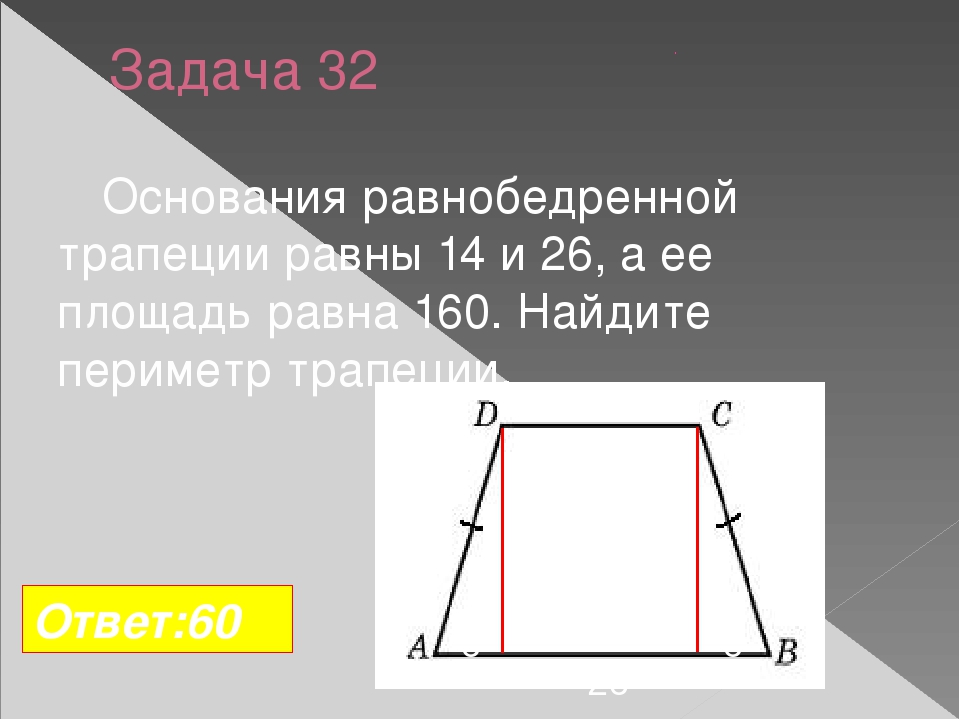
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .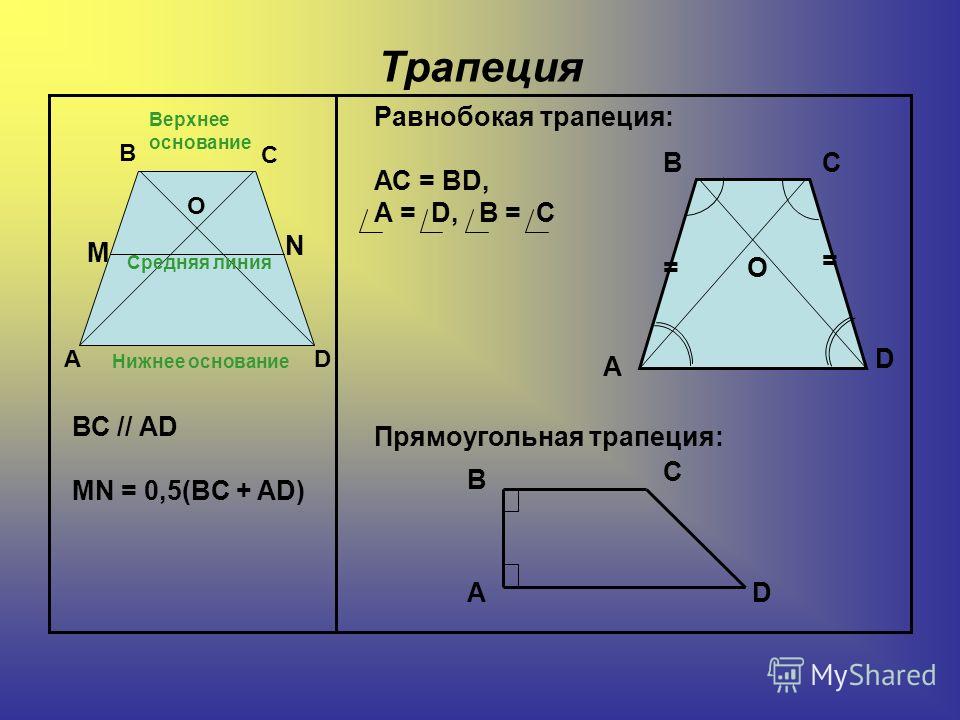
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.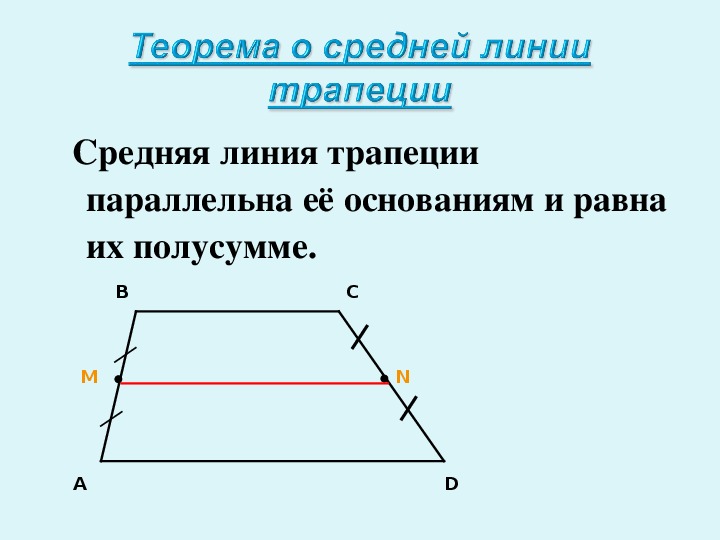
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.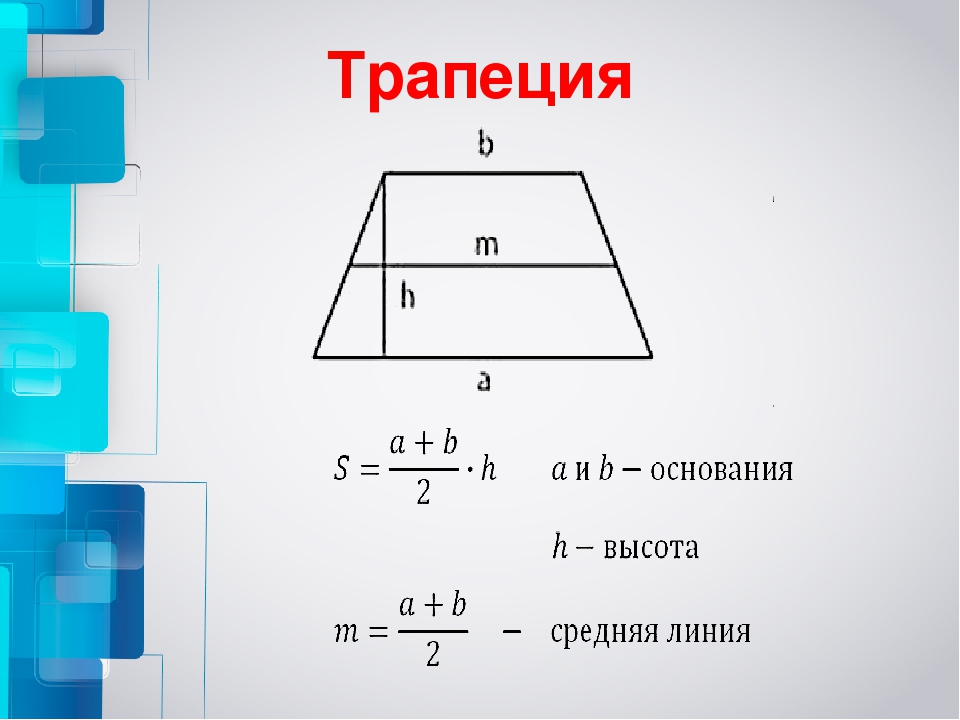
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними.
 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Высчитать площадь трапеции онлайн. Площадь трапеции: как вычислить, формула
Этот калькулятор рассчитал 2192 задачи на тему «Площадь трапеции»
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
Общая теория для вычисления площади трапеции.
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.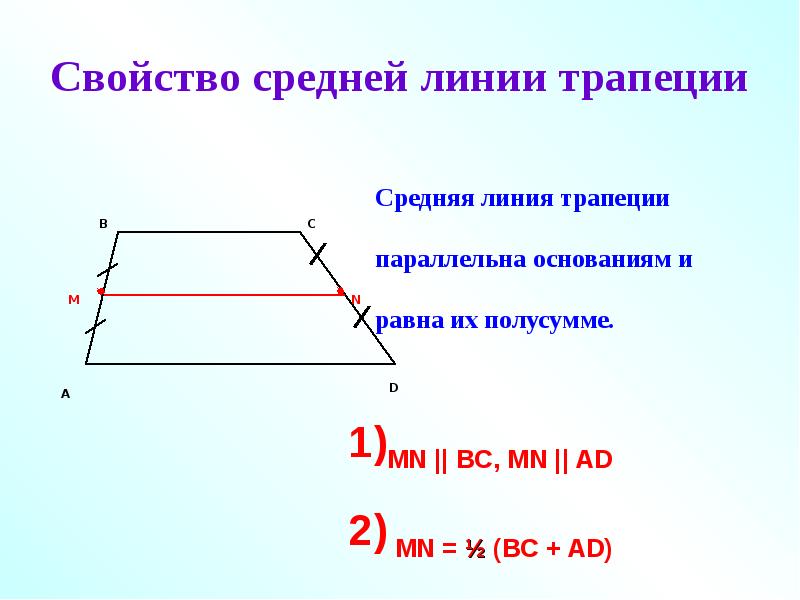
Две параллельные стороны трапеции называются основаниями трапеции .
Две не параллельные стороны трапеции называются боковыми сторонами трапеции .
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой) , если ее боковые стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D — прямой (равен 90 о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
2. Площадь трапеции равна произведению ее средней линии на высоту:
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.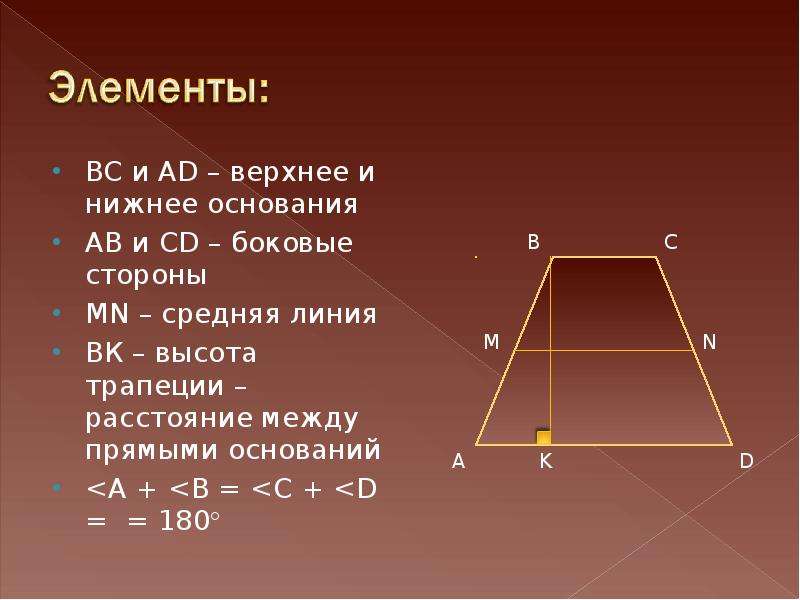
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее.
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Определяем трапецию
Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Свойства трапеции
Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sina.
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
S = c *sin a *(a — c *cos a ),
где с — боковое бедро, a — угол при нижнем основании.
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128.![]() Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
S = M/2 + N — 1,
в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними.
 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов.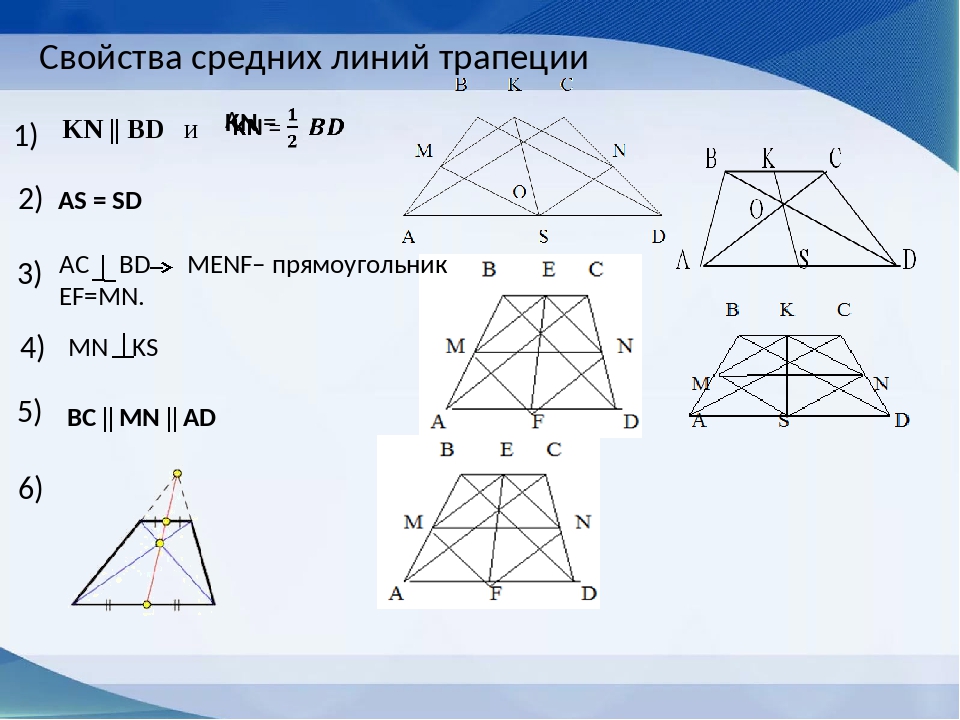 А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см.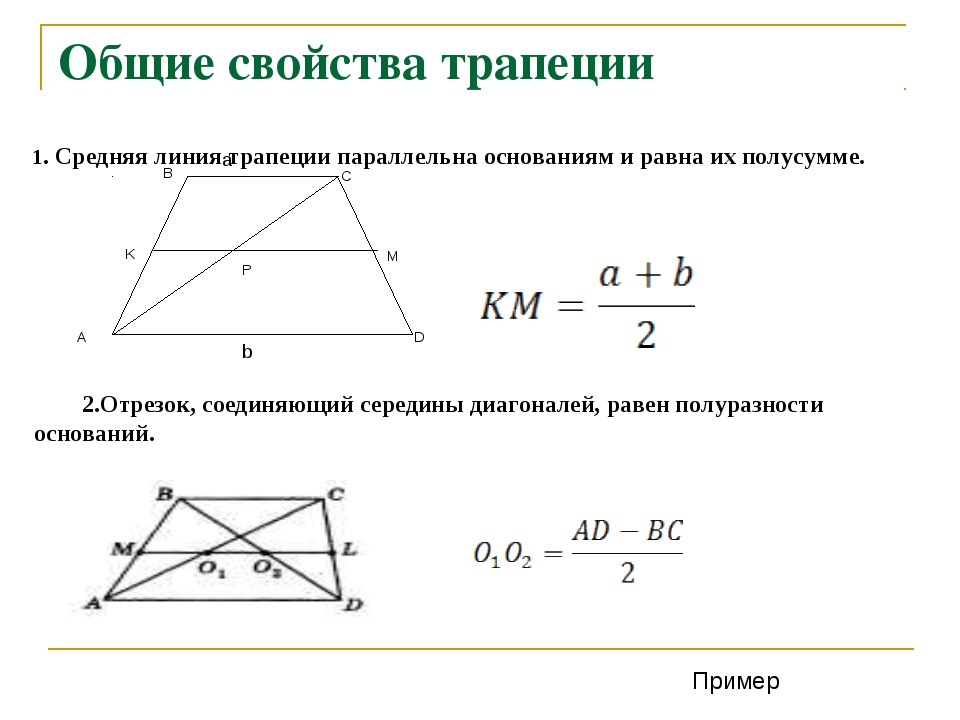 найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Как решать площадь трапеции. Площадь трапеции: как вычислить, формула
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии.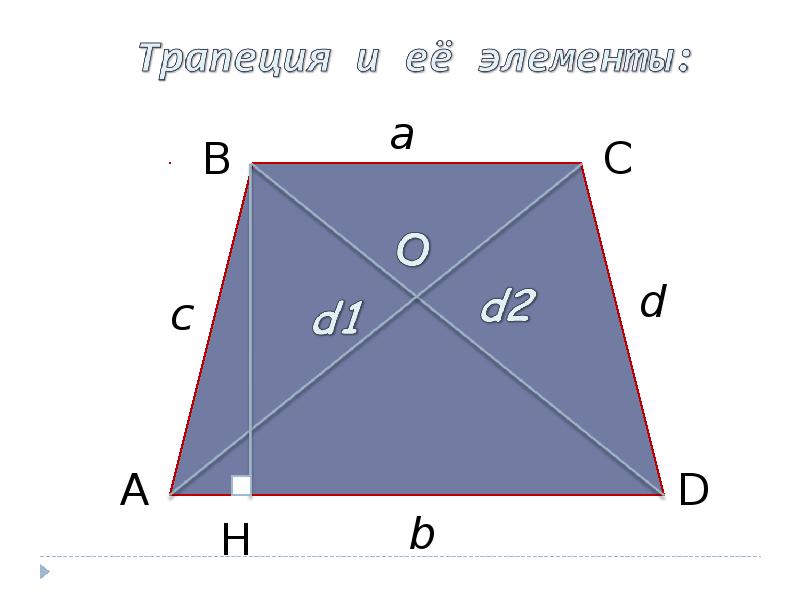 Обозначим среднюю линию — m. Тогда
Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).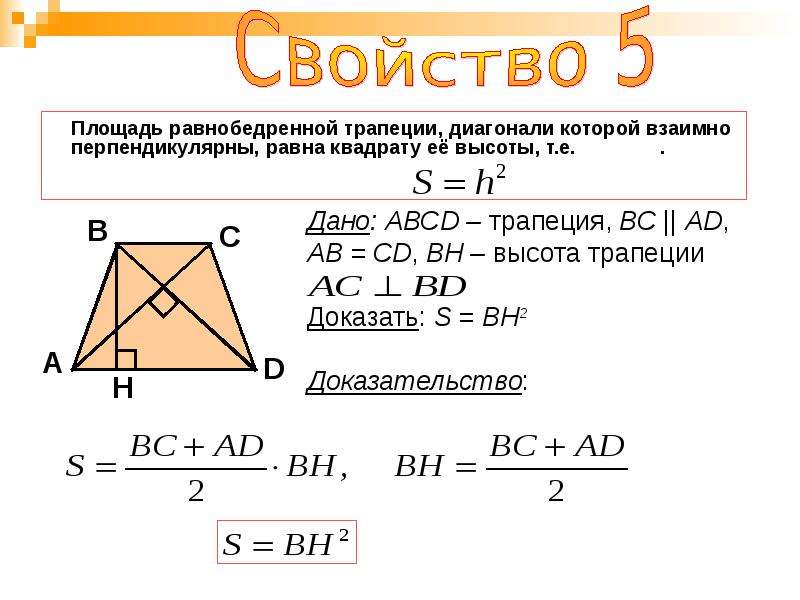
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению .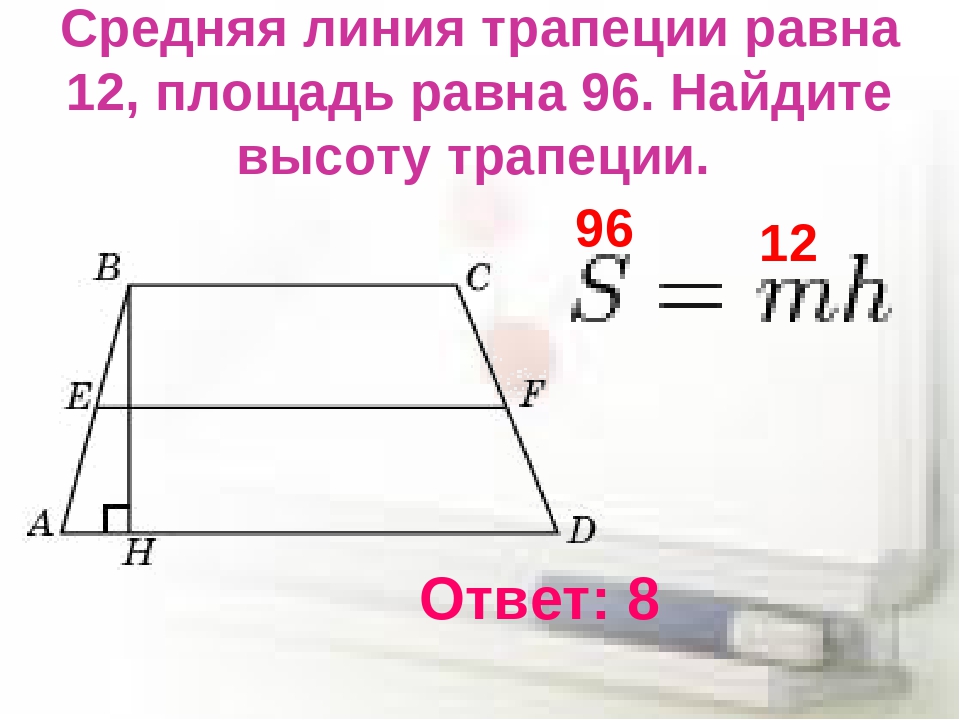 Отсюда
Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции.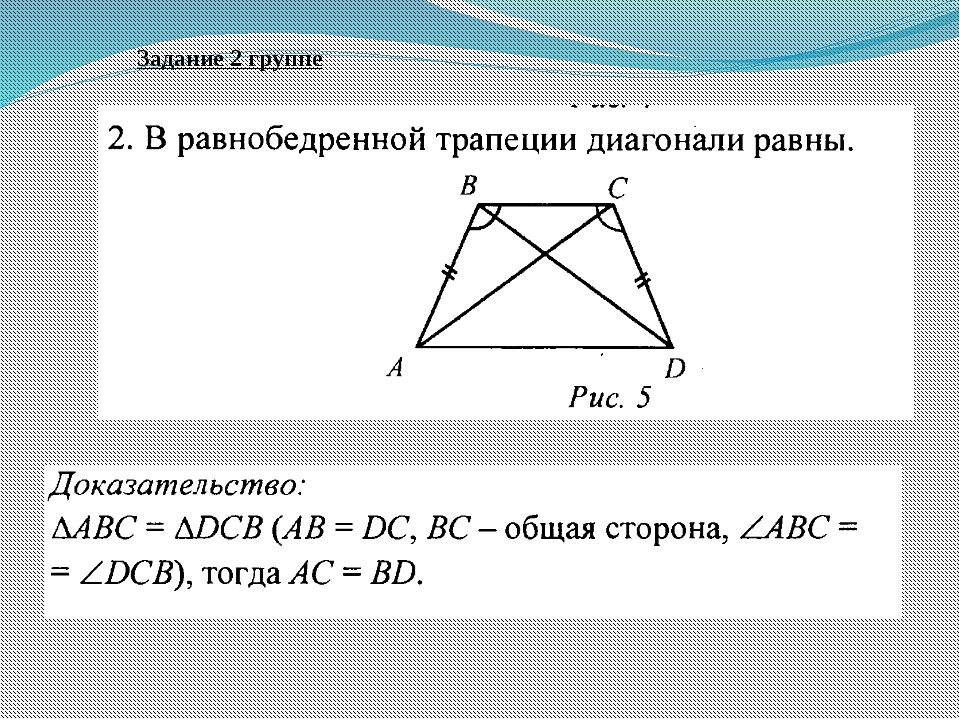 Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции.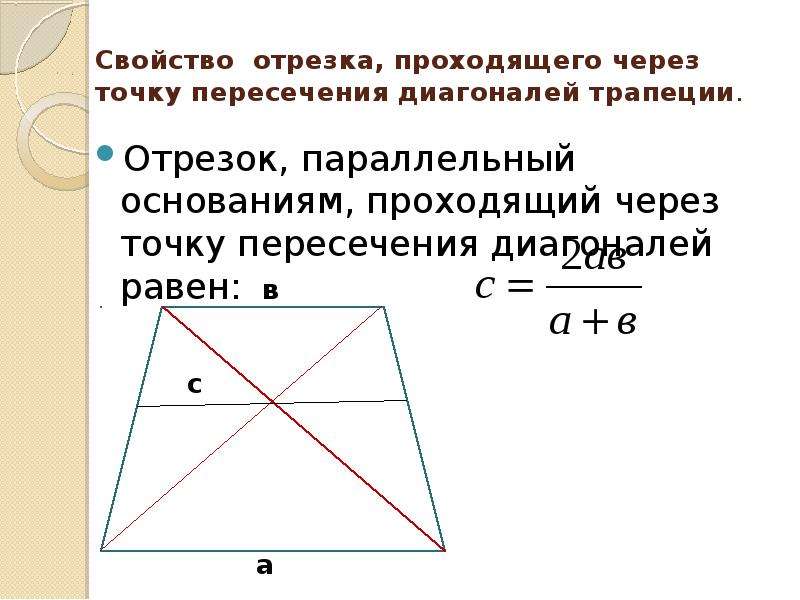 Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα .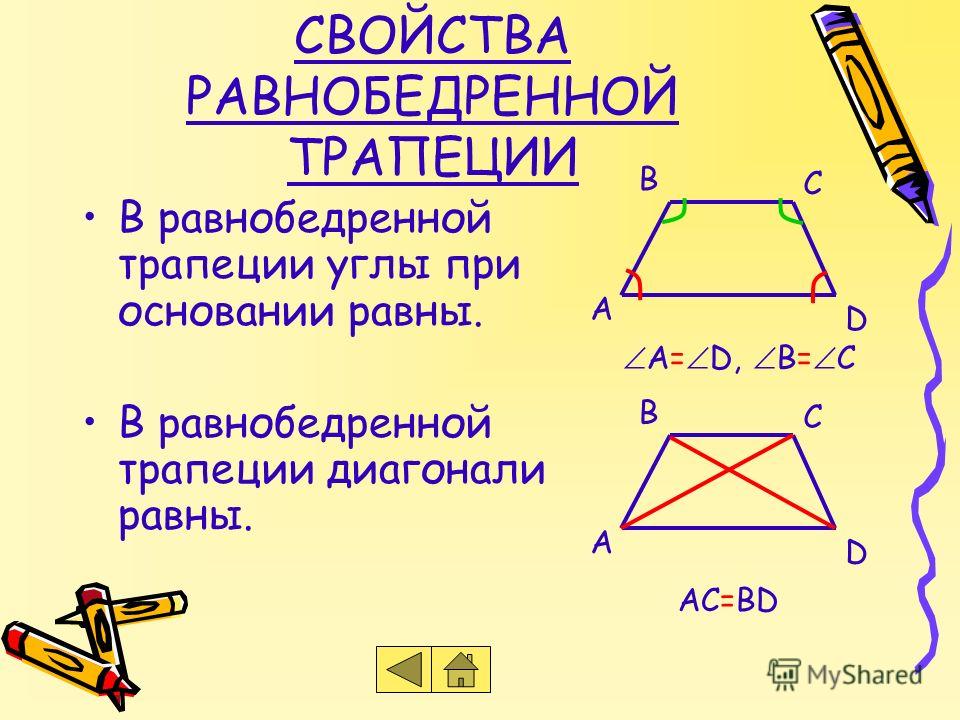 Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.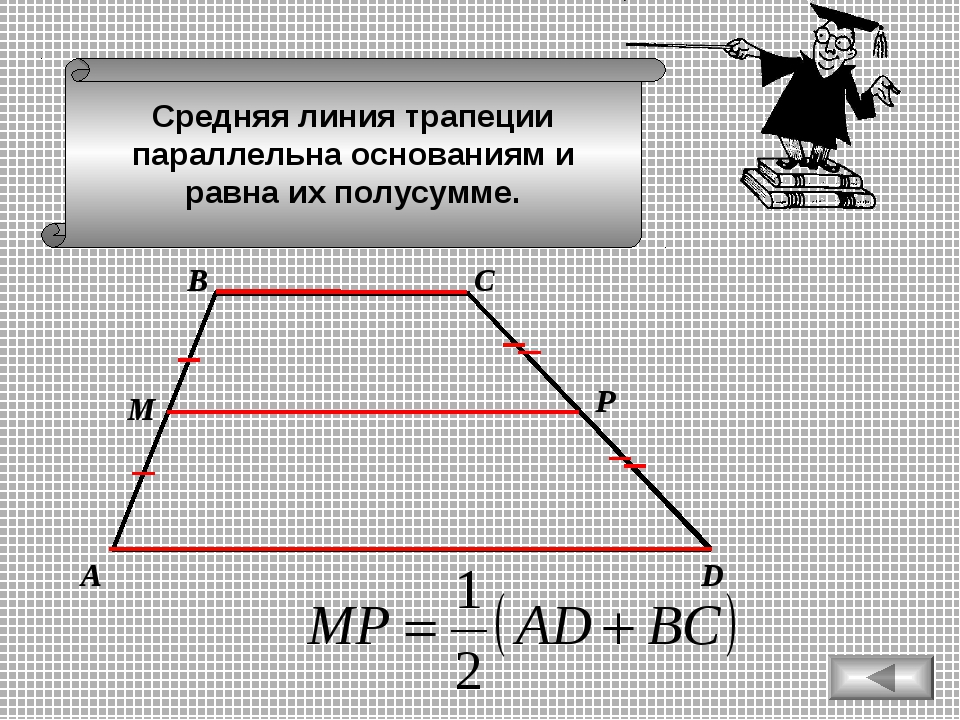
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение:
Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т.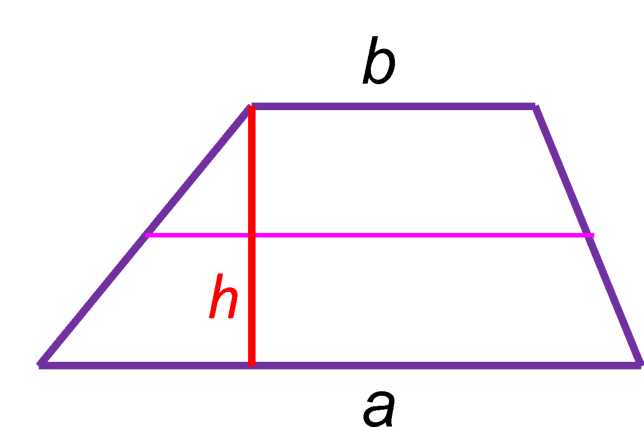 А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Этот калькулятор рассчитал 2192 задачи на тему «Площадь трапеции»
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
Общая теория для вычисления площади трапеции.
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.
Две параллельные стороны трапеции называются основаниями трапеции .
Две не параллельные стороны трапеции называются боковыми сторонами трапеции .
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой) , если ее боковые стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D — прямой (равен 90 о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
2. Площадь трапеции равна произведению ее средней линии на высоту:
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.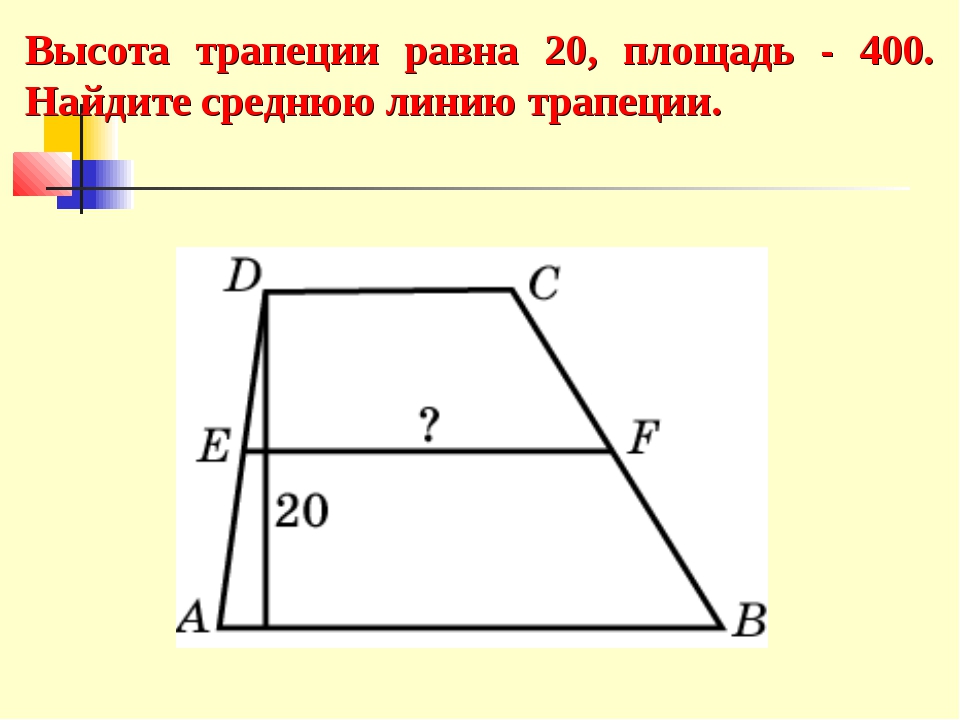
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее.
Как найти среднюю линию равнобедренной трапеции
Трапеция – это четырехугольник, у которого только две параллельные стороны – они называются основаниями этой фигуры. Если при этом длины двух других — боковых — сторон одинаковы, трапецию называют равнобедренной или равнобедренной. Линия, соединяющая середины сторон, называется средней линией трапеции и может быть рассчитана несколькими способами.
Линия, соединяющая середины сторон, называется средней линией трапеции и может быть рассчитана несколькими способами.
Инструкции
Шаг 1
Если длины обоих оснований (А и В) известны, то для вычисления длины средней линии (L) используют основное свойство этого элемента равнобедренной трапеции — он равен полусумме длин основания: L = ½ * (A + B).Например, в трапеции с основаниями 10 см и 20 см длина средней линии должна быть ½ * (10 + 20) = 15 см.
Шаг 2
Средняя линия (L) вместе с высотой (h) равнобедренной трапеции является коэффициентом в формуле расчета площади (S) этой фигуры. Если эти два параметра заданы в начальных условиях задачи, то для расчета длины осевой линии площадь делят на высоту: L = S/h. Например, при площади 75 см² равнобедренная трапеция высотой 15 см должна иметь осевую линию длиной 75/15 = 5 см.
Шаг 3
Зная периметр (Р) и длину стороны (С) равнобедренной трапеции, легко вычислить и среднюю линию (L) фигуры.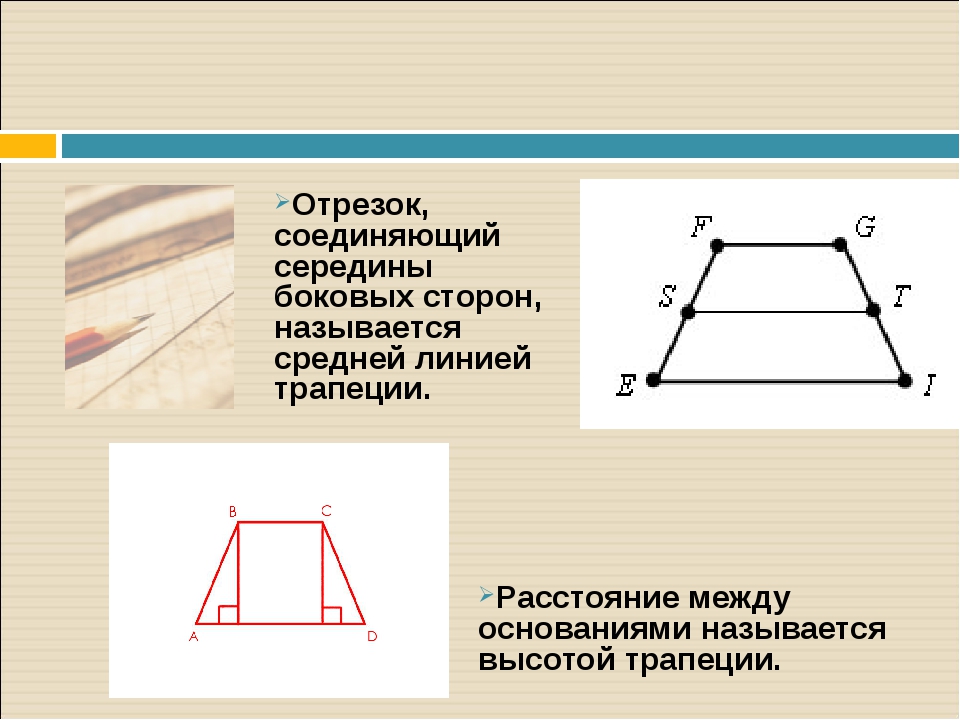 Отнимите от периметра две длины сторон, а оставшееся значение будет суммой длин оснований – разделите ее пополам, и задача будет решена: L = (P-2*C)/2. Для Например, при периметре 150см и длине стороны 25см длина средней линии должна быть (150-2*25)/2=50см.
Отнимите от периметра две длины сторон, а оставшееся значение будет суммой длин оснований – разделите ее пополам, и задача будет решена: L = (P-2*C)/2. Для Например, при периметре 150см и длине стороны 25см длина средней линии должна быть (150-2*25)/2=50см.
Шаг 4
Зная длину периметра (P) и высоту (h), а также величину одного из острых углов (α) равнобедренной трапеции, можно вычислить также длину ее средней линии (L). В треугольнике, составленном из высоты, стороны и части основания, один из углов прямой, а величина другого известна. Это позволит вычислить длину боковины по теореме синусов – высоту разделить на синус известного угла: h/sin(α). Затем подставьте это выражение в формулу из предыдущего шага, и вы получите такое равенство: L = (P-2 * h/sin(α))/2 = P/2-h/sin(α).Например, если известен угол 30°, высота 10см, а периметр 150см, то длину средней линии следует рассчитать следующим образом: 150/2-10/sin (30°) = 75-20 = 55см .
Средняя линия равнобедренной трапеции с учетом длины основания, высоты и боковой стороны Калькулятор
Средняя линия равнобедренной трапеции по длинному основанию, высоте и боковой стороне Формула
Средняя линия трапеции = длинное основание-кварт (сторона ^ 2-высота ^ 2)
м = База Длинная — кв. 2), где a — основание, c — боковая сторона, h — высота трапеции.Средняя линия трапеции обозначена символом м .
2), где a — основание, c — боковая сторона, h — высота трапеции.Средняя линия трапеции обозначена символом м .
Как рассчитать среднюю линию равнобедренной трапеции, зная длину основания, высоту и боковую сторону с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для средней линии равнобедренной трапеции с учетом длины основания, высоты и боковой стороны, введите длину основания (основание , длину ) , сторону (S) и высоту (h) и нажмите кнопку расчета. Вот как средняя линия равнобедренной трапеции с учетом расчета длинного основания, высоты и боковой стороны может быть объяснена с заданными входными значениями -> -8.2) .
Формула определения средней линии треугольника и трапеции. Средняя линия трапеции
Площадь трапеции. Привет! В этом посте мы рассмотрим указанную формулу. Почему она именно такая и как ее понять. Если есть понимание, то ему не нужно учиться. Если просто хотите посмотреть эту формулу и что срочно, то можете сразу листать страницу вниз))
Если просто хотите посмотреть эту формулу и что срочно, то можете сразу листать страницу вниз))
Теперь подробно и по порядку.
Трапеция — четырехугольник, две стороны которого параллельны, а две другие — нет. Те, которые не параллельны, являются основаниями трапеции. Два других называются сторонами.
Если стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапеция изображается так — большее основание внизу, соответственно меньшее вверху.Но никто не запрещает изображать ее и наоборот. Вот эскизы:
Следующая важная концепция.
Средняя линия трапеции — это отрезок, соединяющий середины сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте углубимся. Почему это так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и проведем дополнительные построения: проведем прямые через основания, а перпендикуляры через концы средней линии до пересечения с основаниями :
* Буквенные обозначения вершин и других точек намеренно не вводятся во избежание ненужных обозначений.
Смотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 равны. Равенство треугольников подразумевает равенство элементов, а именно катетов (они обозначены синим и красным соответственно).
Внимание! Если мы мысленно «отрежем» синий и красный отрезок от нижнего основания, то у нас получится отрезок (это сторона прямоугольника), равный средней линии. Далее, если «приклеить» отрезанную синюю и красную линию к верхнему основанию трапеции, то мы также получим отрезок (это и есть сторона прямоугольника), равный средней линии трапеции.
Понял? Получается, что сумма оснований будет равна двум средним линиям трапеции:
См. другое объяснение
Сделаем следующее — построим прямую, проходящую через нижнее основание трапеции и прямая, которая пройдет через точки А и В:
Получаем треугольники 1 и 2, они равны по стороне и прилежащим к ней углам (второй признак равенства треугольников). Это означает, что полученный отрезок (на эскизе он обозначен синим цветом) равен верхнему основанию трапеции.
Это означает, что полученный отрезок (на эскизе он обозначен синим цветом) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
* Средняя линия этой трапеции и средняя линия треугольника совпадают.
Известно, что треугольник равен половине своего параллельного основания, то есть:
Ладно, разобрались. Теперь о площади трапеции.
Формула площади трапеции:
Говорят: площадь трапеции равна произведению полусуммы ее оснований на высоту.
То есть получается, что он равен произведению средней линии на высоту:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мысленно отрезать от трапеции треугольники 2 и 4 и положить их соответственно на треугольники 1 и 3:
Тогда получится прямоугольник, площадь которого равна площади наша трапеция. Площадь этого прямоугольника будет равна произведению средней линии на высоту, то есть мы можем написать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (просмотреть) материал статьи в формате *pdf
Вот и все. Успехов вам!
С уважением, Александр.
Трапеция — это частный случай четырехугольника, у которого одна пара сторон параллельна. Термин «трапеция» происходит от греческого слова τράπεζα, означающего «стол», «стол». В этой статье мы рассмотрим виды трапеций и их свойства. Кроме того, мы разберемся, как рассчитать отдельные элементы этого, например, диагонали равнобедренной трапеции, центральной линии, площади и т. д.Материал представлен в стиле элементарной популярной геометрии, то есть в легкодоступной форме.
Общие сведения
Для начала разберемся, что такое четырехугольник. Эта фигура представляет собой частный случай многоугольника с четырьмя сторонами и четырьмя вершинами. Две несмежные вершины четырехугольника называются противоположными. То же самое можно сказать и о двух несмежных сторонах. Основные виды четырехугольников – параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтовидная форма.
Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны параллельны. Они называются базами. Две другие (непараллельные) — стороны. В материалах экзаменов и различных тестов очень часто можно встретить задания, связанные с трапециями, решение которых часто требует от ученика знаний, не предусмотренных программой. Школьный курс геометрии знакомит учащихся со свойствами углов и диагоналей, а также со средней линией равнобедренной трапеции.Но помимо этого упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Виды трапеций
Есть много видов этой фигуры. Однако чаще всего принято рассматривать две из них – равнобедренную и прямоугольную.
1. Прямоугольной трапецией называется фигура, у которой одна из боковых сторон перпендикулярна основаниям. Два его угла всегда равны девяноста градусам.
2. Равнобедренная трапеция – геометрическая фигура, стороны которой равны между собой.Это означает, что углы при основаниях также попарно равны.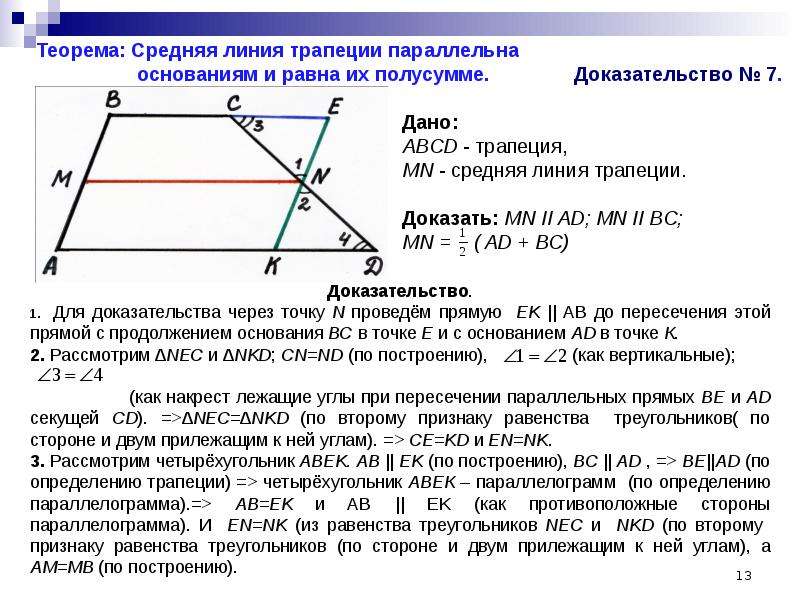
Основные принципы методики изучения свойств трапеции
Основным принципом является использование так называемого задачного подхода. На самом деле нет необходимости вводить в теоретический курс геометрии новые свойства этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задачи необходимо ставить перед учащимися в тот или иной момент учебного процесса.При этом каждое свойство трапеции может быть представлено как ключевая задача в системе задач.
Второй принцип — так называемая спиральная организация изучения «замечательных» свойств трапеции. Это предполагает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Это облегчает учащимся их запоминание. Например, свойство четырех точек. Это можно доказать как изучением подобия, так и последующим использованием векторов. А равновеликость треугольников, примыкающих к боковым сторонам фигуры, можно доказать, применяя не только свойства равновеликих треугольников, проведенных к сторонам, лежащим на одной прямой, но и используя формулу S = 1/2 (аб*синα). Кроме того, можно работать над вписанной трапецией или прямоугольным треугольником на описанной трапеции и т.д. обучая их. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже понять трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Кроме того, можно работать над вписанной трапецией или прямоугольным треугольником на описанной трапеции и т.д. обучая их. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже понять трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Элементы и свойства равнобедренной трапеции
Как мы уже отмечали, эта геометрическая фигура имеет равные стороны. Его также называют правильной трапецией. И чем он так примечателен и почему получил такое название? К особенностям этой фигуры относится то, что равны не только стороны и углы при основаниях, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусов. Но это не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность.Это связано с тем, что сумма противоположных углов этой фигуры равна 180 градусам, и только при этом условии вокруг четырехугольника можно описать окружность. Следующее свойство рассматриваемой геометрической фигуры состоит в том, что расстояние от вершины основания до проекции противоположной вершины на прямую, содержащую это основание, будет равно центральной линии.
Следующее свойство рассматриваемой геометрической фигуры состоит в том, что расстояние от вершины основания до проекции противоположной вершины на прямую, содержащую это основание, будет равно центральной линии.
Теперь разберемся, как найти углы равнобедренной трапеции. Рассмотрим решение этой задачи при условии, что известны размеры сторон фигуры.
Решение
Обычно четырехугольник принято обозначать буквами A, B, C, D, где BS и AD — основания. У равнобедренной трапеции стороны равны. Будем считать, что их размер равен X, а размеры оснований равны Y и Z (меньше и больше соответственно). Для проведения расчета необходимо из угла В провести высоту Н. В результате получится прямоугольный треугольник АВН, где АВ — гипотенуза, а ВН и АН — катеты.Вычисляем размер катета AH: из большего основания вычитаем меньшее, а результат делим на 2. Записываем в виде формулы: (ZY)/2=F. Теперь вычисляем острый угол треугольника, мы используем функцию cos. Получаем следующую запись: cos(β) = X/F.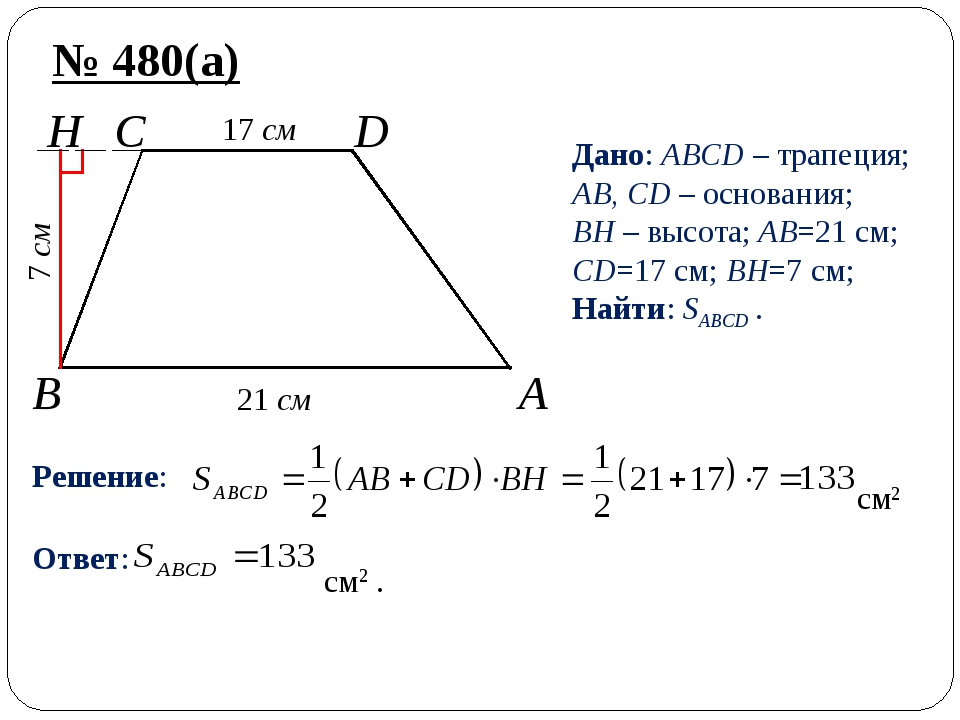 Теперь вычисляем угол: β = arcos(X/F). Далее, зная один угол, мы можем определить второй, для этого выполняем элементарное арифметическое действие: 180 — β. Все углы определены.
Теперь вычисляем угол: β = arcos(X/F). Далее, зная один угол, мы можем определить второй, для этого выполняем элементарное арифметическое действие: 180 — β. Все углы определены.
Есть и второе решение этой проблемы.В начале опускаем высоту Н. от угла. Рассчитайте значение ножки BN. Мы знаем, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: BN = √(X2-F2). Далее воспользуемся тригонометрической функцией tg. В итоге имеем: β = arctg (BN/F). Найден острый угол. Далее определяем так же, как и в первом способе.
Свойство диагоналей равнобедренной трапеции
Сначала запишем четыре правила.Если диагонали в равнобедренной трапеции перпендикулярны, то:
Высота фигуры будет равна сумме оснований, деленной на два;
Его высота и средняя линия равны;
Центром круга является точка их пересечения;
Если боковая сторона делится точкой касания на отрезки Н и М, то она равна корню квадратному из произведения этих отрезков;
Четырехугольник, образованный точками касания, вершиной трапеции и центром вписанной окружности, представляет собой квадрат, сторона которого равна радиусу;
Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.
Аналогичная трапеция
Эта тема очень удобна для изучения свойств этой. Например, диагонали делят трапецию на четыре треугольника, причем прилежащие к основаниям подобны, а к боковым сторонам равны. Это утверждение можно назвать свойством треугольников, на которые трапеция делится своими диагоналями. Первая часть этого утверждения доказывается через признак подобия двух углов. Для доказательства второй части лучше использовать способ, описанный ниже.
Доказательство теоремы
Примем, что фигура АБСД (BP и BS — основания трапеции) делится диагоналями ВД и AS. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АВО и СОД у боковых сторон. Треугольники SOD и BFB имеют общую высоту, если их основаниями являются отрезки BO и OD. Получаем, что разница их площадей (П) равна разнице между этими отрезками: ПБОС/ПСОД=БО/ОД=К.Следовательно, PSOD = PBOS/K. Аналогично треугольники BFB и AOB имеют общую высоту.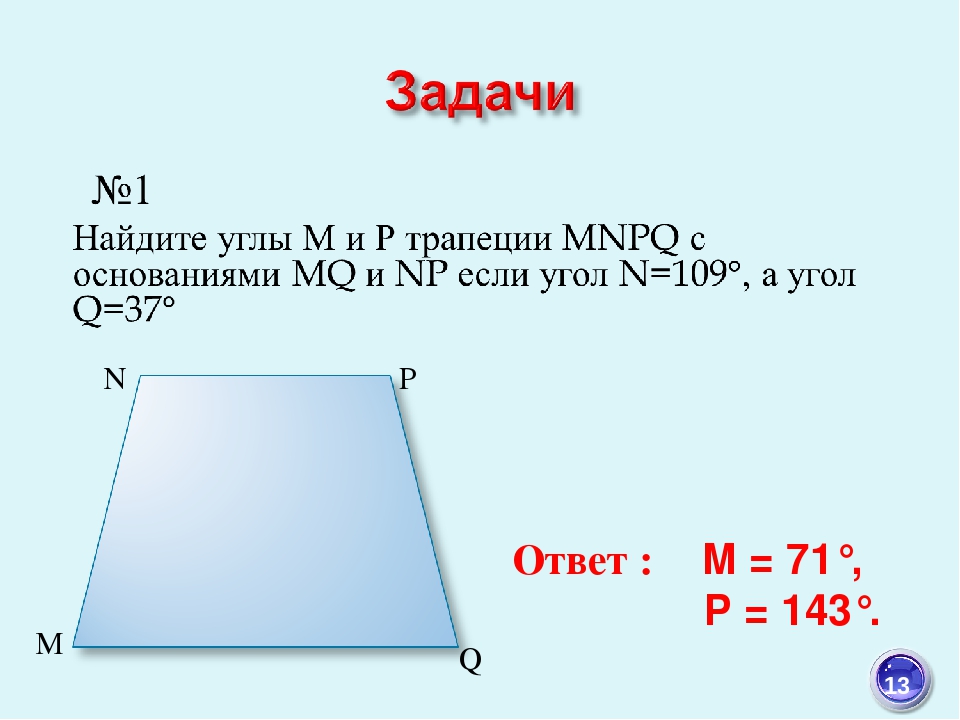 За их основания возьмем отрезки SB и OA. Получаем PBOS/PAOB=SO/OA=K и PAOB=PBOS/K. Отсюда следует, что PSOD=PAOB.
За их основания возьмем отрезки SB и OA. Получаем PBOS/PAOB=SO/OA=K и PAOB=PBOS/K. Отсюда следует, что PSOD=PAOB.
Для закрепления материала учащимся предлагается найти связь между площадями полученных треугольников, на которые трапеция делится своими диагоналями, решая следующую задачу. Известно, что площади треугольников биологической обратной связи и АОЗ равны; надо найти площадь трапеции.Поскольку PSOD = PAOB, это означает, что PABSD = PBOS + PAOD + 2 * PSOD. Из подобия треугольников BFB и AOD следует, что BO/OD = √(PBOS/PAOD). Следовательно, ПБОС/ПСОД=БО/ОД=√(ПБОС/ПАОД). Получаем PSOD=√(PBOS*PAOD). Тогда PABSD = PBOS + PAOD + 2 * √ (PBOS * PAOD) = (√ PSOS + √ PAOD) 2.
Свойства подобия
Продолжая развивать эту тему, можно доказать и другие интересные свойства трапеций. Итак, с помощью подобия можно доказать свойство отрезка, проходящего через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям.Для этого решим следующую задачу: необходимо найти длину отрезка RK, который проходит через точку O.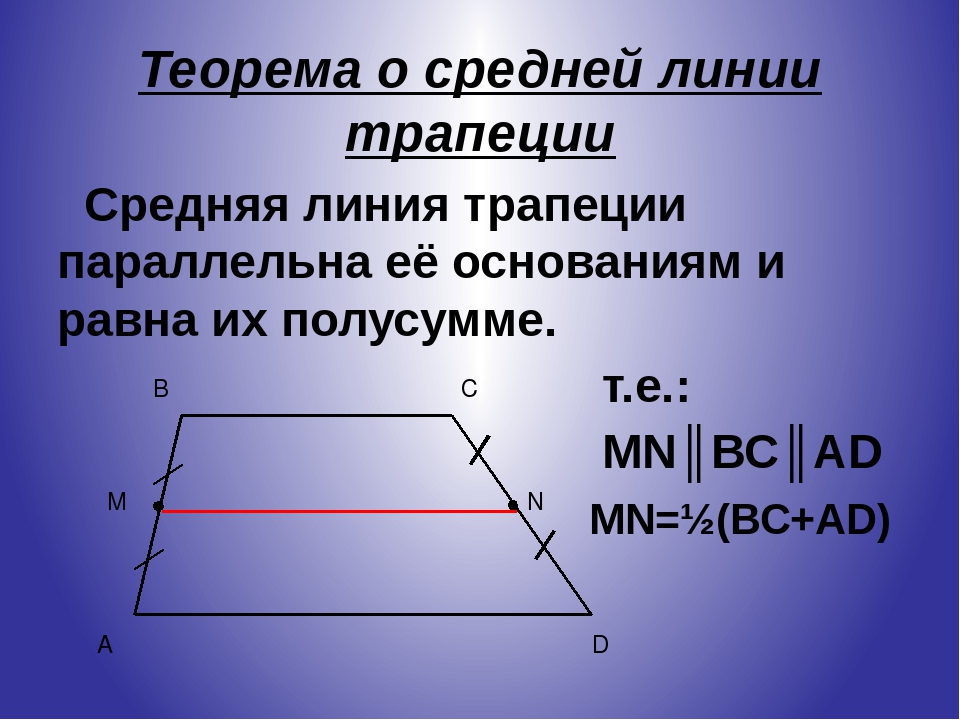 Из подобия треугольников AOD и BFB следует, что AO/OS = AD/BS . Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО = БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК = БС * АД / (БС + АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД).Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две стороны, делится точкой пересечения пополам. Его длина есть среднее гармоническое основания фигуры.
Из подобия треугольников AOD и BFB следует, что AO/OS = AD/BS . Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО = БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК = БС * АД / (БС + АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД).Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две стороны, делится точкой пересечения пополам. Его длина есть среднее гармоническое основания фигуры.
Рассмотрим следующее качество трапеций, которое называется четырехточечным свойством. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Г) всегда лежат на одной прямой.Это легко доказывается методом подобия. Получившиеся треугольники BES и AED подобны, и в каждом из них медианы ET и EZ делят угол при вершине E на равные части. Следовательно, точки E, T и Ж лежат на одной прямой. Точно так же точки Т, О и Ж расположены на одной прямой. Все это следует из подобия треугольников BFB и AOD. Отсюда делаем вывод, что все четыре точки — Е, Т, О и F — будут лежать на одной прямой.
Все это следует из подобия треугольников BFB и AOD. Отсюда делаем вывод, что все четыре точки — Е, Т, О и F — будут лежать на одной прямой.
Используя такие трапеции, можно попросить учащихся найти длину отрезка (LF), который разбивает фигуру на две подобные.Этот отрезок должен быть параллелен основаниям. Так как полученные трапеции ALPD и LBSF подобны, то BS/LF = LF/BP. Отсюда следует, что ЛФ = √(БС*АД). Получаем, что отрезок, делящий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Рассмотрим следующее свойство сходства. В его основе лежит отрезок, который делит трапецию на две фигуры одинакового размера. Считаем, что трапеция ABSD разделена отрезком ЕН на две подобные.Высота сбрасывается с вершины B, которая делится отрезком EH на две части — B1 и B2. Получаем: ПАБСД/2=(БС+ЭХ)*Б1/2=(АД+ЭХ)*Б2/2 и ПАБСД=(БС+АД)*(Б1+Б2)/2. Далее составляем систему, первое уравнение которого (БС+ЭН)*В1=(АД+ЭН)*В2 и второе (БС+ЭН)*В1=(БС+АД)*(Б1+В2)/2.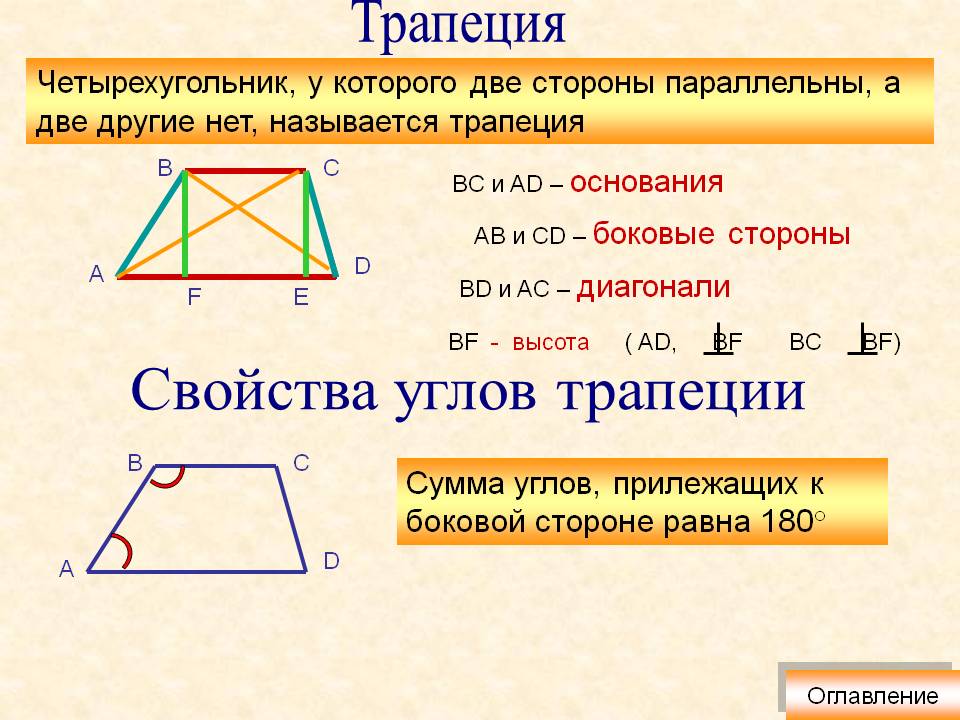 Отсюда следует, что В2 /Б1=(БС+ЭХ)/(АД+ЭХ) и БС+ЭХ=((БС+АД)/2)*(1+Б2/Б1). Получаем, что длина отрезка, делящего трапецию на две равные по размеру, равна среднему квадрату длин оснований: √ ((BS2 + AD2)/2).
Отсюда следует, что В2 /Б1=(БС+ЭХ)/(АД+ЭХ) и БС+ЭХ=((БС+АД)/2)*(1+Б2/Б1). Получаем, что длина отрезка, делящего трапецию на две равные по размеру, равна среднему квадрату длин оснований: √ ((BS2 + AD2)/2).
Находки подобия
Таким образом, мы доказали, что:
1. Отрезок, соединяющий середины боковых сторон у трапеции, параллелен ВР и ВР и равен среднему арифметическому между ВР и ВР (длина основание трапеции).
2. Прямая, проходящая через точку О пересечения диагоналей, параллельных АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).
3.Отрезок, делящий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.
4. Элемент, делящий фигуру на два равных размера, имеет длину средних квадратов чисел BP и BS.
Для закрепления материала и понимания связи между рассматриваемыми отрезками учащемуся необходимо построить их для конкретной трапеции. Он легко может отобразить среднюю линию и отрезок, проходящий через точку О — пересечение диагоналей фигуры — параллельно основаниям.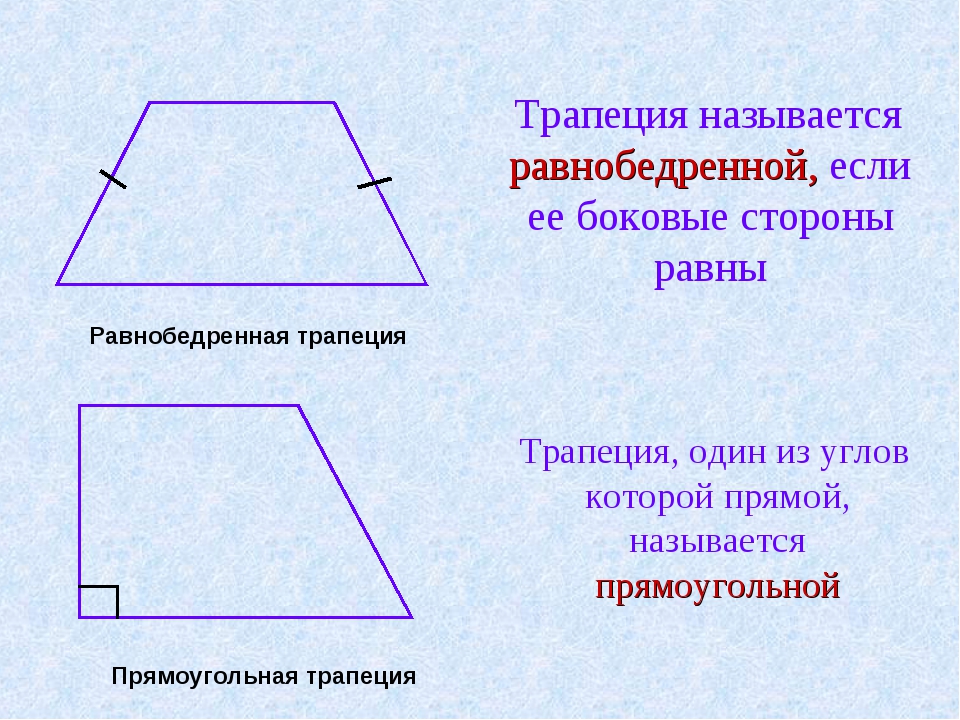 Но где будут находиться третий и четвертый? Этот ответ приведет студента к обнаружению желаемого соотношения между средними значениями.
Но где будут находиться третий и четвертый? Этот ответ приведет студента к обнаружению желаемого соотношения между средними значениями.
Отрезок, соединяющий середины диагоналей трапеции
Рассмотрим следующее свойство этой фигуры. Предположим, что отрезок MH параллелен основаниям и делит диагонали пополам. Точки пересечения будем называть Ш и Ш. Этот отрезок будет равен половине разности оснований. Давайте посмотрим на это поближе.МШ — средняя линия треугольника АБС, она равна БС/2. МЧ — средняя линия треугольника АБД, она равна ВР/2. Тогда получаем, что ШШ = МШ-МШ, следовательно, ШШ = АД/2-БС/2=(АД+ВС)/2.
Центр тяжести
Посмотрим, как определяется этот элемент для данной геометрической фигуры. Для этого необходимо вытянуть основания в противоположные стороны. Что это значит? К верхнему основанию необходимо добавить нижнее — в любую сторону, например, вправо.И удлинить нижний на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры является центром тяжести трапеции.
Вписанные и описанные трапеции
Перечислим признаки таких фигур:
1. Трапецию можно вписать в окружность, только если она равнобедренная.
2. Трапецию можно описать по окружности при условии, что сумма длин их оснований равна сумме длин боковых сторон.
Последствия вписанной окружности:
1. Высота описываемой трапеции всегда равна двум радиусам.
2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.
Первое следствие очевидно, но для доказательства второго требуется установить, что угол СОД прямой, что, собственно, тоже не составит труда. Но знание этого свойства позволит использовать прямоугольный треугольник при решении задач.
Теперь конкретизируем эти следствия для равнобедренной трапеции, вписанной в окружность. Получаем, что высота есть среднее геометрическое основания фигуры: H = 2R = √(BS*АД). При отработке основного приема решения задач на трапеции (принцип удержания двух высот) учащийся должен решить следующую задачу. Будем считать, что ВТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки AT и TD. Используя формулу, описанную выше, сделать это не составит труда.
Будем считать, что ВТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки AT и TD. Используя формулу, описанную выше, сделать это не составит труда.
Теперь разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем высоту от вершины Б к основанию АД. Так как окружность вписана в трапецию, то БС+АД=2АВ или АВ=(БС+АД)/2. Из треугольника АБН находим sinα=БН/АВ=2*БН/(БС+АД). ПАБСД=(БС+АД)*БН/2, БН=2Р. Получаем ПАБСД=(БС+АД)*R, отсюда следует, что R=ПАБСД/(БС+АД).
Все формулы средней линии трапеции
Теперь пора перейти к последнему элементу этой геометрической фигуры.Выясним, чему равна средняя линия трапеции (М):
1. Через основания: М = (А + В)/2.
2. Через высоту, основание и углы:
М = АН* (ctgα + ctgβ)/2;
M = B + H * (ctgα + ctgβ) / 2.
3. Через высоту, диагонали и угол между ними. Например, D1 и D2 — диагонали трапеции; α, β – углы между ними:
М = D1*D2*sinα/2H = D1*D2*sinβ/2H.
4. Через площадь и высоту: М = П/Н.
Четырехугольник, у которого параллельны только две стороны, называется трапецией .
Параллельные стороны трапеции называются ее основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если стороны равны, то такая трапеция равнобедренная. Расстояние между основаниями называется высотой трапеции.
Средняя линия трапеции
Средняя линия — это отрезок, соединяющий середины сторон трапеции.Средняя линия трапеции параллельна ее основаниям.
Теорема:
Если прямая, проходящая через середину одной стороны, параллельна основаниям трапеции, то она делит вторую сторону трапеции пополам.
Теорема:
Длина средней линии равна среднему арифметическому длин ее оснований
МН || АБ || DCAM = MD; БН = НЗ
MN средняя линия, AB и CD — основания, AD и BC — стороны
МН = (AB + DC) / 2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин ее оснований.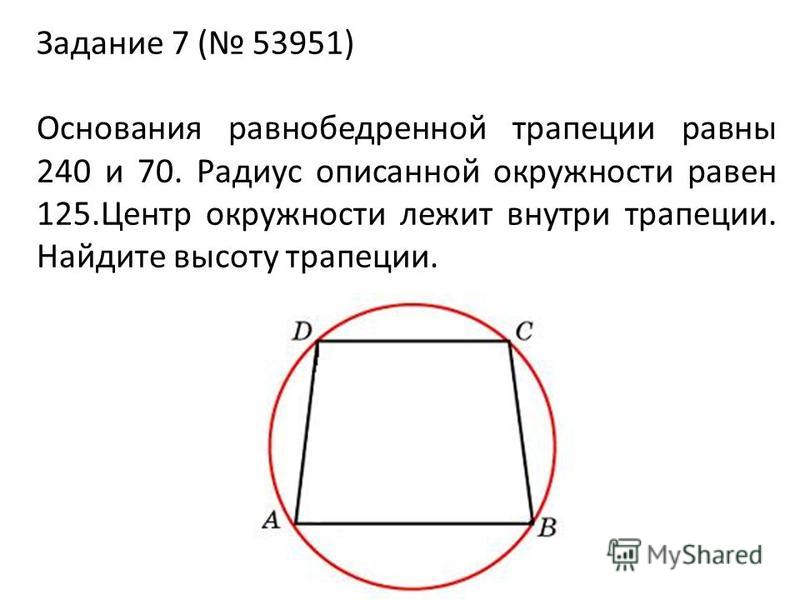
Основная задача : Докажите, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине основания трапеции.
Центральная линия треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и составляет половину длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне этого треугольника, то она делит третью сторону пополам.
AM = MC и BN = NC =>
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определенное количество равных частей.
Задание: Разделите отрезок АВ на 5 равных частей.
Решение:
Пусть p — случайный луч с началом в точке A, не лежащий на прямой AB. Откладываем последовательно 5 равных отрезков на р АА 1 = А 1 А 2 = А 2 А 3 = А 3 А 4 = А 4 А 5
Соединяем А 5 с В и проводим такие прямые через А 4, А 3, А 2 и А 1, которые параллельны А 5 В.Они пересекают AB соответственно в точках B 4, B 3, B 2 и B 1. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции ВВ 3 А 3 А 5 видим, что ВВ 4 = В 4 В 3. Точно так же из трапеции В 4 В 2 А 2 А 4 получаем В 4 В 3 = В 3 В 2
Тогда как из трапеции B 3 B 1 A 1 A 3, B 3 B 2 = B 2 B 1.
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключение получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Понятно, что для того, чтобы разделить отрезок AB на другое количество равных частей, нужно спроецировать такое же количество равных отрезков на луч р.А затем продолжить, как описано выше.
Средняя линия трапеции равна половине суммы оснований. Она соединяет середины трапеции и всегда параллельна основаниям.
Если основания трапеции равны a и b, то средняя линия m равна m = (a + b)/2.
Если известна площадь трапеции, то среднюю линию можно найти и другим способом, разделив площадь трапеции S на высоту трапеции h:
То есть средняя линия трапеции м = S/h
Есть много способов найти длину средней линии трапеции.Выбор метода зависит от исходных данных.
Вот формулы длины средней линии трапеции :
Для нахождения средней линии трапеции можно воспользоваться одной из пяти формул (их расписывать не буду, так как они уже есть в других ответах) , но это только в тех случаях, когда известны значения нужных нам исходных данных.
На практике приходится решать множество задач, когда данных не хватает, а нужного размера еще найти.
Есть варианты тут
пошаговое решение подвести все таки по формуле;
по другим формулам составить и решить необходимые уравнения.
находим длину середины трапеции подходя к нужной нам формуле используя другие знания геометрии и применяя алгебраические уравнения:
Имеем равнобедренную трапецию, ее диагонали пересекаются под прямым углом, высота 9см.
Рисуем картинку и видим, что эту задачу нельзя решить в лоб (недостаточно данных)
Поэтому немного упростим и проведем высоту через пересечение диагоналей.
Это первый важный шаг, ведущий к быстрому решению.
обозначим высоту двумя неизвестными, увидим нужные нам равнобедренные треугольники со сторонами NS и по
и легко найдем сумма оснований трапеция
равна
2у
И только теперь мы можем применить формулу где
а это равно х + у и по условию задачи это длина высоты равная 9 см .
А теперь мы вывели несколько точек для равнобедренной трапеции, диагонали которой пересекаются под прямым углом.
в таких трапециях
средняя линия всегда равна высоте
площадь всегда равна квадрату высоты .
Средняя линия трапеции — это отрезок, соединяющий середины сторон трапеции.
Среднюю линию любой трапеции легко найти, если воспользоваться формулой:
м = (а + b) / 2
м — длина средней линии трапеции;
а, б длины оснований трапеции.
Итак, длина средней линии трапеции равна половине суммы длин оснований .
Основная формула формулы средней линии трапеции: длина средней линии трапеции равна половине суммы e оснований a и b: MN = (a + b) 2. Доказательством этой формулы является Формула средней линии треугольника. Любую трапецию можно представить, проведя от концов меньшее основание высоты к большему основанию. Рассмотрим 2 получившихся треугольника и прямоугольник.После этого легко доказывается формула средней линии трапеции.
Чтобы найти среднюю линию трапеции, нам нужно знать базовые значения.
После того, как мы нашли эти значения, а может они были нам известны, то мы складываем эти числа и просто делим пополам.
Это будет средняя линия трапеции .
Насколько я помню уроки школьной геометрии, чтобы найти длину средней линии трапеции, нужно сложить длины оснований и разделить на два.Таким образом, длина средней линии трапеции равна половине суммы оснований.
В этой статье мы постараемся максимально полно отразить свойства трапеции. В частности, речь пойдет об общих признаках и свойствах трапеции, а также о свойствах вписанной трапеции и о окружности, вписанной в трапецию. Затронем также свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разобраться местами в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала кратко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – это четырехугольная фигура, две стороны которой параллельны друг другу (это основания). А две не параллельны — это стороны.
В трапеции можно уменьшить высоту — перпендикулярно основаниям. Проводятся средняя линия и диагонали. А также из любого угла трапеции можно провести биссектрису.
Сейчас мы поговорим о различных свойствах, связанных со всеми этими элементами и их комбинациями.
Свойства трапециевидных диагоналей
Чтобы было понятнее, при чтении нарисуйте на листе бумаги трапецию АКМЭ и проведите в ней диагонали.
- Если найти середины каждой из диагоналей (обозначим эти точки как X и T) и соединить их, то получится отрезок. Одним из свойств диагоналей трапеции является то, что отрезок XT лежит на средней линии.А его длину можно получить, разделив разность оснований на два: XT = (a — b)/2·.
- Перед нами та самая трапеция АКМЕ. Диагонали пересекаются в точке O. Рассмотрим треугольники AOE и MOC, образованные отрезками вместе с основаниями трапеции. Эти треугольники подобны. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = AE/KM.
Отношение площадей треугольников AOE и MOC описывается коэффициентом k 2. - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только на этот раз мы будем рассматривать треугольники, которые образованы отрезками диагоналей вместе с боковыми сторонами трапеции. Площади треугольников АКО и ЭМО равны — их площади одинаковы.
- Другое свойство трапеции включает диагонали рисования. Итак, если мы продолжим боковые стороны АК и МЕ в сторону меньшего основания, то рано или поздно они пересекутся в какой-то точке.Далее через середины оснований трапеции провести прямую. Она пересекает основания в точках X и T.
Если теперь продолжить прямую XT, то она соединит вместе точку пересечения диагоналей трапеции O, точку, в которой продолжены боковые стороны и середины трапеций. основания X и T пересекаются. - Через точку пересечения диагоналей провести отрезок, соединяющий основания трапеции (Т лежит на меньшем основании ЦМ, Х — на большем АЕ).Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЭ.
- А теперь через точку пересечения диагоналей проведите отрезок, параллельный основаниям трапеции (а и б). Пересечение разделит его на две равные части. Длину отрезка можно найти по формуле 2ab/(a+b).
Свойства центральной линии трапеции
Проведите среднюю линию трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, сложив длины оснований и разделив их пополам: м = (a + b) / 2· .
- Если провести любой отрезок (высоту, например) через оба основания трапеции, то средняя линия разделит ее на две равные части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, к примеру, угол КАЕ нашей трапеции АКМЭ.Выполнив построение самостоятельно, вы легко убедитесь, что биссектриса отрезает от основания (или его продолжения на прямой вне самой фигуры) отрезок той же длины, что и сторона.
Свойства угла трапеции
- Какую бы из двух пар углов, примыкающих к боковой стороне, вы ни выбрали, сумма углов в паре всегда равна 180 0 : α + β = 180 0 и γ + δ = 180 0.
- Соедините середины оснований трапеций отрезком TX.Теперь посмотрим на углы у основания трапеции. Если сумма углов при любом из них равна 90 0 , длину отрезка ТХ легко вычислить, исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ — КМ) / 2· .
- Если провести параллельные прямые через стороны угла трапеции, то они разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобедренной) трапеции
- У равнобедренной трапеции углы равны при любом основании.
- Теперь снова нарисуйте трапецию, чтобы легче было представить, о чем она. Посмотрите внимательно на основание AE — вершина противоположного основания M проецируется в точку на линии, содержащей AE. Расстояние от вершины А до точки проекции вершины М и средней линии равнобедренной трапеции равно.
- Несколько слов о свойстве диагоналей равнобедренных трапеций — их длины равны. А также углы наклона этих диагоналей к основанию трапеции одинаковы.
- Только около равнобедренной трапеции можно описать окружность, так как обязательным условием для этого является сумма противоположных углов четырехугольника 180 0 .
- Свойство равнобедренной трапеции следует из предыдущего абзаца — если вблизи трапеции можно описать окружность, то она равнобедренная.
- Из особенностей равнобедренной трапеции следует свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b) / 2 .
- Снова проведите отрезок ТХ через середины оснований трапеции — в равнобедренной трапеции он перпендикулярен основаниям. И в то же время ТХ является осью симметрии равнобедренной трапеции.
- На этот раз уменьшите до большего основания (обозначим его a) высоту от противоположной вершины трапеции. Будет два сегмента. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a+b)/2·… Второе получается, если из большего основания вычесть меньшее и полученную разность разделить на два: (а — б) / 2 .
Свойства трапеции, вписанной в окружность
Поскольку мы уже говорили о трапеции, вписанной в окружность, остановимся на этом вопросе подробнее. В частности, где центр окружности находится по отношению к трапеции. Здесь тоже рекомендуется не полениться взять в руки карандаш и нарисовать то, о чем пойдет речь ниже. Так вы быстрее поймете и лучше запомните.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне.Например, диагональ может проходить от вершины трапеции под прямым углом к стороне. В этом случае большее основание пересекает центр описанной окружности ровно посередине (R = ½AE).
- Диагональ и сторона могут встречаться и под острым углом — тогда центр окружности находится внутри трапеции.
- Центр описанной окружности может находиться вне трапеции, за ее большим основанием, если между диагональю трапеции и боковой стороной имеется тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЭ (вписанный угол), равен половине соответствующего ей центрального угла: MAE = ½MOE .
- Коротко о двух способах нахождения радиуса описанной окружности. Способ первый: внимательно посмотрите на свой рисунок — что вы видите? Вы легко заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти как отношение стороны треугольника к синусу противоположного угла, умноженному на два.Например, R = AE/2 * sinAME … Аналогично формулу можно записать для любой стороны обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, стороной и основанием трапеции: R = AM * ME * AE / 4 * S AME .
Свойства трапеции, описанной около окружности
В трапецию можно вписать окружность, если выполняется одно условие.Подробнее об этом ниже. А вместе это сочетание форм имеет ряд интересных свойств.
- Если в трапецию вписана окружность, то длину ее средней линии легко найти, сложив длины сторон и разделив полученную сумму пополам: м = (с + d) / 2 .
- В трапеции АКМЭ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЭ.
- Из этого свойства оснований трапеции следует обратное утверждение: в ту трапецию, сумма оснований которой равна сумме боковых сторон, можно вписать окружность.
- Точка касания окружности радиуса r, вписанной в трапецию, делит боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно рассчитать по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, нарисуйте этот пример сами.У нас есть старая добрая трапеция АКМЭ, описанная по окружности. В нем проведены диагонали, пересекающиеся в точке О. Треугольники АОК и ЕОМ, образованные отрезками диагоналей и сторон, прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т. е. на боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Называется прямоугольная трапеция, один из углов которой прямой.И его свойства вытекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, примыкающая к прямому углу, равны. Это позволяет вычислить площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, примыкающую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы наверное уже сами догадались, что здесь нам снова понадобится трапеция АКМЭ — нарисуйте равнобедренную трапецию. Из вершины М проведите прямую линию МТ, параллельную боковой стороне АК (МТ || АК).
Получившийся четырехугольник АКМТ является параллелограммом (АК || МТ, КМ || АТ). Поскольку ME = KA = MT, ∆ MTE равнобедренный и MET = MTE.
АК || MT, следовательно, MTE = KAE, MET = MTE = KAE.
Отсюда АКМ = 180 0 — МЕТ = 180 0 — КАЭ = КМЭ.
К.Э.Д.
Теперь, основываясь на свойстве равнобедренной трапеции (равенстве диагоналей), докажем, что трапеция AKME равнобедренная :
- Для начала проведем прямую MX — MX || КЭ. Получаем параллелограмм KMXE (основание — MX || KE и KM || EX).
∆AMX равнобедренный, так как AM = KE = MX и MAX = MEA.
МХ || KE, KEA = MXE, следовательно, MAE = MXE.
Оказалось, что треугольники АКЕ и ЕМА равны между собой, так как АМ = КЕ и АЕ — общая сторона двух треугольников. А также MAE=MXE. Можно заключить, что АК = МЕ, а отсюда следует, что трапеция АКМЕ равнобедренная.
Задача для повторения
Основания трапеции АКМЭ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует с меньшим основанием угол 150 0 .Требуется найти площадь трапеции.
Решение: От вершины К опускаем высоту к большему основанию трапеции. И начнем смотреть на углы трапеции.
Углы АЕМ и КАН односторонние. Значит, в сумме они дают 180 0 . Следовательно, КАН = 30 0 (исходя из свойств углов трапеции).
Рассмотрим теперь прямоугольный ∆ANK (думаю, этот момент очевиден для читателей без дополнительных доказательств). Из него находим высоту трапеции КН — в треугольнике это катет, который лежит напротив угла 30 0 .Следовательно, KH = ½AB = 4 см.
Площадь трапеции находится по формуле: S АКМЭ = (КМ + АЭ) * КН / 2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились начертить трапеции для всех вышеперечисленных свойств карандашом в руках и разобрать их на практике, материал должен был быть вами хорошо понят.
Конечно, информации здесь много, разнообразной и местами даже запутанной: не так уж сложно спутать свойства описываемой трапеции со свойствами вписанной.Но вы сами убедились, что разница огромна.
Теперь у вас есть подробное описание всех общих свойств трапеций. А также специфические свойства и особенности равнобедренных и прямоугольных трапеций. Их очень удобно использовать для подготовки к зачетам и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
блог. сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Теоремы о средней линии, трапеции и воздушные змеи — Внедрение учебного плана —
LAS по математике 9 Неделя 3. Теоремы о средней линии, трапеции и воздушные змеи Теорема о средней линии . Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и вдвое короче.
Дано: ∆HNS, O — середина HN, E — середина NS Докажите: OE//HS и OE=12HS Заявления Причины 1. ∆HNS, O — середина HN, E — середина NS
Дано
- В OE существует точка T такая, что OE≅ET Line Постулат
- NE≅ES Определение средней точки
- ∠2≅∠3 Вертикальные углы Теорема
- ∆NEO≅∆SET Постулат SAS
- ∠1≅∠4 CPCTC
- HN//ST Обращение альтернативных внутренних углов Теорема
- OH≅ON Определение средней точки
- ОН≅ТС ЦПКТС
- OH≅TS Переходное свойство
- Четырехугольник HOTS является параллелограммом Если противоположные стороны четырехугольника равны и параллельны, то это параллелограмм.
- OE//HS Определение параллелограмма
- OE+ET=OT Постулат сложения сегментов
- OE+OE=OT Свойство замены
- 2OE=OT Дополнение Свойство
- HS≅OT В параллелограмме любые две противоположные стороны равны.
- 2OE=Свойство замены HS
- OE=12HS Разделите обе части на два
Определение трапеции – четырехугольник с одной парой параллельных сторон. Теорема о средней линии трапеции . Медиана трапеции параллельна каждому основанию, а ее длина равна половине суммы длин ее сторон. базы.
Дано: Трапеция МИНС с медианой TR, которая пересекает диагональ IS в точке P. Докажите: MS//TR//IN и TR=12(MS+IN)
Утверждения Причины
- Трапеция MINS с медианой TR, пересекающая диагональ IS в точке P. Дано
- TP+PR=TR Постулат сложения сегментов
- TP//MS и TP=12MS RP//IN и RP=12IN Теорема о средней линии
- MS//IN Определение трапеции
- MS//TP+RP//IN Переходное свойство
- MS//TR//IN Дополнительное свойство
- TR=12MS+12IN Замена Свойство
- TR=12(MS+IN) Факторинг
Определение равнобедренной трапеции – трапеция с конгруэнтными противоположными сторонами. Свойства равнобедренной трапеции
- Углы при основании равнобедренной трапеции равны. Дано: Равнобедренная трапеция AMOR с МО//АР Докажите: ∠A≅∠R и ∠AMO≅∠O
Заявления Причины
- Равнобедренная трапеция AMOR с МО//АР. Учитывая
- AM≅OR Определение равнобедренной трапеции
- Из M проведите ME//OR, где E лежит на AR Две точки определяют линию
- Четырехугольник БОЛЕЕ является параллелограммом Определение параллелограмма
- ME≅OR В параллелограмме любые две противоположные стороны равны конгруэнтный.
- MA≅ME Переходное свойство
- ∆AME — равнобедренный треугольник Определение равнобедренного треугольника
- ∠A≅∠1 Углы при основании равнобедренных треугольников равны.
- ∠1≅∠R Соответствующие углы Теорема
- ∠A≅∠R Переходное свойство
- ∠A и ∠AMO являются дополнительными углами. ∠O и ∠R являются дополнительными углы.
Теорема об одностороннем внутреннем угле
- ∠AMO≅∠O Дополнения конгруэнтных углов также конгруэнтны
• Противолежащие углы равнобедренной трапеции являются дополнительными.
• Диагонали равнобедренной трапеции конгруэнтны.
Определение воздушного змея – четырехугольник с двумя парами смежных сторон, которые конгруэнтны, ромб – это особый вид воздушного змея. Свойства воздушного змея
• В воздушном змее биссектриса хотя бы одного из них является другой диагональю.
• Площадь воздушного змея равна половине произведения длин его диагоналей.
Дано: КАЙТ ВЕРЕВКА с диагоналями PR и OE пересекаются в точке W.Докажите: площадь кайта ROPE = 12(UE)(PR).
Утверждения Причины
- Кайт ВЕРЕВКА с диагоналями PR и OE пересекаются в точке W. Дано
- PROE Диагонали воздушного змея перпендикулярны друг другу.
- Площадь воздушного змея ROPE = Площадь ∆OPE + Площадь ∆ORE Постулат сложения площадей
- Площадь ∆OPE = 12(OE)(PW) и площадь ∆ORE = 12(OE)(WR) Формула площади треугольников
- Площадь кайт ROPE = =12(OE)(PW+WR) Фактор
- PW+WR=PR Постулат сложения сегментов
- Площадь Kite ROPE = 12(UE)(PR) Замена
- CX≅TX CPCTC
Учебное задание 1: Указания: Завершите доказательство в два столбца.
• Противолежащие углы равнобедренной трапеции являются дополнительными.
Дано: Равнобедренная трапеция ARTS с RT//AS Докажите: ∠ARS и ∠S дополнительные. ∠A и ∠T дополнительный.
Утверждения Основания
- (1) Дано
- АР≅СТ (2)
- (3) и ∠ART≅∠S Углы при основании равнобедренной трапеции конгруэнтны.
- ∠A+∠ART=1800 и ∠С+∠Т=
Теорема внутреннего угла той же стороны
- ∠A+∠T=1800 и ∠С+∠АРТ=
(4)
- (5) Определение дополнительных углов
Учебное задание 2: Указания: Завершите доказательство в два столбца.
• Диагонали равнобедренной трапеции конгруэнтны.
Дано: Равнобедренная трапеция ROMA с диагоналями RM и AO
Докажите: RM≅AO
Утверждения Причины
- Равнобедренная трапеция ROMA с диагоналями RM и АО.
(1)
- (2) Определение равнобедренного сустава Трапеция
- ∠ORA≅∠МАР (3)
- RA≅AR (4)
- (5) Постулат SAS
- РМ≅AO CPCTC
Учебное задание 3: Указания: Завершите проверку в два столбца.
• Диагональ воздушного змея — это биссектриса пары противоположных углов.
Дано: Воздушный змей WORD с диагоналями OD и WR. Докажите: WR — биссектриса углов ∠OWD и ∠ORD.
Заявления Причины
- Воздушный змей WORD с диагоналями OD и WR. (1)
- WO≅WD и RO≅RD (2)
- WR≅WR Рефлексивное свойство
- (3) Постулат ССС
- (4) (5)
- WR — биссектриса угла ∠OWD и ∠ОРД.
Определение угла Биссектриса
LeaP_Mathematics_Wilson Ray G.Anzures — SDO San Pablo City
как найти углы равнобедренной трапеции
Углы при основании (углы, образованные между непараллельными сторонами и параллельными сторонами) равны в равнобедренной трапеции. Диагонали равнобедренной трапеции равны по длине. (Круглый … Параллелограмм — это четырехугольник с двумя парами параллельных сторон. В трапеции углы на одном катете (называемые смежными углами) являются дополнительными, то есть их сумма составляет \ (\displaystyle 180\) градусов. Что такое формула равнобедренной трапеции?Прямая трапеция имеет два прямых угла.Длина среднего отрезка равна 1/2 суммы параллельных оснований трапеции. Равнобедренная трапеция — это разновидность трапеции, у которой непараллельные стороны равны по длине. 29. Как зовут 12 северных оленей Санты? Введите три длины сторон, выберите количество знаков после запятой и нажмите «Рассчитать». Как узнать, равнобедренная ли трапеция? Что такое внутренняя и внешняя критика исторических источников? В евклидовой геометрии равнобедренная трапеция (isosceles trapezium в британском английском) представляет собой выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон.Каково юридическое определение доказательства? Найдите периметр равнобедренной трапеции. Смежные углы (рядом друг с другом) по сторонам являются дополнительными. Каково значение j в равнобедренной трапеции ниже? Он может иметь два и быть параллелограммом. \ (\displaystyle e\) и угол, измеряющий \ (\displaystyle 106\) градусов, являются смежными углами, которые являются дополнительными. Другими словами, нижние углы при основании равны, а верхние углы при основании также равны. Плотина наклонена под углом 30° к вертикали и имеет форму равнобедренной трапеции шириной 60 футов вверху и 30 футов внизу и высотой наклона 50 футов.Найдите гидростатическую силу, действующую на плотину, когда она заполнена водой. Трапеция – это четырехугольник с одной парой параллельных сторон. Точно так же из-за односторонних внутренних углов нижний угол основания является дополнительным к любому верхнему углу основания. Бесплатный калькулятор сторон и углов трапеции — пошаговый расчет сторон и углов трапеции Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Отрежьте верхнюю часть треугольника так, чтобы срез был параллелен нижней части треугольника. Почему моя шпульная нить завязывается узлом? Является ли равнобедренная трапеция четырехугольником? Чтобы найти угол «b», мы вычитаем оба угла по 50° из 180°.Непараллельные стороны называются сторонами или ногами, а две параллельные стороны называются основаниями, одна короткая, а другая длинная. Формула площади трапеции. (3) Если трапеция равнобедренная, то ее противоположные углы дополнительные. Трапеция — это параллелограмм. Катет равнобедренного треугольника равен 5 дм, его высота на 20 см больше основания. Нажмите, чтобы увидеть полный ответ. Две пары смежных углов трапеции в сумме дают 180 градусов. Если вы знаете, что угол BAD равен 44°, какова мера $$ \угла ADC $$ ? Кроме того, длины двух сторон равны.Диагонали равнобедренной трапеции равны. Длина его ноги 26 см. Q. 27. Математика, 15.12.2020 07:30 mrflexington77. $$ \угол ABC = 130 $$, какой еще угол равен 130 градусам? Равнобедренный треугольник 10 В равнобедренном треугольнике равные стороны составляют 2/3 длины основания. Трапеция обладает следующими свойствами: Трапеция имеет две параллельные стороны и две непараллельные стороны. Используя этот веб-сайт, вы соглашаетесь с нашей Политикой использования файлов cookie. Итак, в трапеции параллельные стороны называются основаниями.Интерактивная симуляция самой спорной математической загадки! Определение равнобедренной трапеции. Диагонали в равнобедренной трапеции не обязательно будут перпендикулярны, как в ромбах и квадратах. Углы при основании Углы при основании равнобедренной трапеции равны. (1) Трапеция равнобедренная тогда и только тогда, когда углы при основании равны. Формула площади равнобедренной трапеции: Диагонали равнобедренной трапеции перпендикулярны друг другу. — ответы на estudyassistant.com Равны ли противоположные углы трапеции? Найдите длину диагоналей равнобедренной трапеции, если длина АС = х + 1, а длина DB = 2х — 3.Найдите значение x в равнобедренной трапеции ниже Вот еще один пример нахождения недостающих углов в равнобедренных треугольниках, когда известен один угол. Теперь, чтобы найти угол «b», мы используем тот факт, что все три угла в сумме составляют 180 °. Углы по обе стороны от оснований имеют одинаковую величину/меру (конгруэнтность). А. Вычитание 2 (72°) из 360° дает сумму двух верхних углов, а деление полученных 216° на 2 дает измерение х, равное 108°. Высота BD до основания AC равнобедренной ABC равна 12.Ответ: 1 вопрос Зная равнобедренную трапецию, найдите меру недостающей? Были включены соответствующие практические PDF-файлы для нахождения указанных углов в каждой из заданных трапеций с использованием соответствующих угловых свойств, а также для нахождения углов, включающих средний сегмент и диагонали. У равнобедренной трапеции углы сверху конгруэнтны (равны), а углы снизу конгруэнтны. угол. Тупоугольная трапеция имеет два тупых противоположных угла (A и C) и два острых противоположных угла (B и D) ИЛИ (используя тот же график) f.Пара углов на концах равных сторон является дополнительной. Как называется символ Север Юг Восток Запад? Один $$\угол ADC = 4° $$, так как углы при основании равны. Если AC = 10, найдите периметр ABC. Это геометрическая фигура с 4 сторонами и 4 вершинами, равнобедренная трапеция имеет 2 параллельные стороны и всегда будет иметь разную длину между ними; две другие стороны имеют одинаковую длину. Кроме того, равны ли углы при основании равнобедренной трапеции? Теперь у вас есть меньший треугольник и трапеция.Этот набор печатаемых углов в рабочих листах трапеций включает прямые, равнобедренные и разносторонние трапеции для старшеклассников. ¿Cuáles son los 10 mandamientos de la Biblia Reina Valera 1960? Бесплатный калькулятор сторон и углов равнобедренной трапеции — пошаговый расчет сторон и углов равнобедренной трапеции Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Пара углов на концах параллельных сторон является дополнительной. Трапеция не является параллелограммом. Точно так же, каковы свойства равнобедренной трапеции? Каково значение x ниже? Можно доказать два особых свойства равнобедренной трапеции.На рисунке 1 ∠ A и ∠ B или ∠ C и ∠ D являются углами при основании трапеции ABCD. Делят ли диагонали равнобедренной трапеции пополам? Однако они совпадают. Мы берем половину суммы длин двух оснований (их среднее значение), а затем умножаем ее на высоту или высоту, чтобы найти площадь в квадратных единицах. Определяющей чертой этого особого типа трапеций является то, что две непараллельные стороны (XW и YZ ниже) конгруэнтны. Диагонали равнобедренной трапеции равны. Теперь, если трапеция равнобедренная, то стороны конгруэнтны, и каждая пара углов основания конгруэнтна.Это частный случай трапеции. В качестве альтернативы ее можно определить как трапецию, в которой обе стороны и оба угла при основании имеют одинаковую величину. Острая трапеция имеет два острых угла (A и D), расположенных с каждой стороны от длинного основания (линия AD), и два тупых угла (B и C) с каждой стороны от короткого основания (линия BC). (2) Трапеция равнобедренная тогда и только тогда, когда диагонали конгруэнтны. Имея пять одинаковых равнобедренных трапеций в арке из 5 блоков, можно найти углы трапеции.2). Чтобы рассчитать диагональ равнобедренной трапеции, вам нужны сторона A (a), сторона B (b) и сторона C (c). С помощью нашего инструмента вам нужно ввести соответствующее значение для стороны A, стороны B и стороны C и нажмите кнопку расчета. В качестве альтернативы его можно определить как трапецию, у которой оба катета и оба угла при основании имеют одинаковую величину. Бесплатный алгебраический решатель … введите туда что угодно! В равнобедренной трапеции одна пара противоположных сторон равна, но не параллельна. Каждый раз, когда вы найдете равнобедренную трапецию, две ее диагонали будут конгруэнтны.Противоположные стороны равнобедренной трапеции равны (конгруэнтны). Пара углов, имеющих общее основание, называется углами при основании трапеции. Реальные математические страшилки из реальных встреч. Равнобедренные трапеции – это четырехугольник, у которого две непараллельные стороны равны, а две параллельные стороны не равны. Если мера угла BCD равна 61°, мера угла ABC равна ____ Если длина основания AB составляет 80 футов, длина DC равна ____ Используя этот веб-сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie.Учитывая это, каковы углы основания трапеции? Сначала мы складываем два угла 50 ° вместе. Свойство №1) Углы с одной и той же стороны катета называются смежными углами и являются дополнительными() Свойство №2) Площадь трапеции = $$ Площадь = высота \cdot \left( \frac{ \text{sum bases} }{ 2 } \right) $$ () Свойство #3) У трапеций есть средний сегмент, который соединяет точки mi точек () Сыграйте в эту игру, чтобы повторить геометрию. Какие бактерии обитают на дверных ручках? Основания (верхнее и нижнее) равнобедренной трапеции параллельны.Арка составляет только половину многоугольника; весь многоугольник равен … Углы вычислены и отображены … Найдите периметр прямоугольника с диагональю 17 и шириной 8. четыре внутренних угла, в сумме 360 градусов. Равнобедренная трапеция в большем основании имеет равные углы, а в меньшем основании тоже равные углы. Поскольку для определения требуется только одна пара параллельных сторон, две другие стороны можно расположить по-разному, создавая четыре внутренних угла, которые всегда складываются… Это трапеция с двумя противоположными сторонами одинаковой длины.Сколько прямых углов у трапеции. Подходит ли самосвязующийся гравий для подъездных дорог? Формула вычисления площади трапеции, если даны 1. все стороны 2. стороны и угол 3. радиус вписанной окружности 4. диагонали и угол между ними 5. основания Найти площадь равнобедренной трапеции — Калькулятор онлайн Трапеция — это четверка двусторонняя фигура с хотя бы одной парой параллельных сторон. Научитесь решать задачи с трапециями. Решение проблемы Противоположные углы в равнобедренной трапеции дополняют друг друга.Углы по обе стороны от оснований имеют одинаковую величину/меру (конгруэнтность). Трапеция – это четырехугольник (четырехугольник), у которого одна пара противоположных сторон параллельна. 28. Диагонали равнобедренной трапеции также конгруэнтны, но НЕ делят друг друга пополам. Вычислить базовую длину z. Равнобедренный треугольник 8 Если соотношение сторон равнобедренного треугольника равно 7:6:7, найдите угол при основании с точностью до градуса. В евклидовой геометрии равнобедренная трапеция (isosceles trapezium в британском английском) представляет собой выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон.Определяющей чертой этого особого типа трапеций является то, что две непараллельные стороны (XW и YZ ниже) конгруэнтны. Высота от вершины тупого угла до основания делит более длинное основание на две части, так что длина меньшей части равна 10 см. Должна ли садовая мебель подходить друг другу? (используйте свои знания о диагоналях!). Каково значение x, если фигура PTRA является равнобедренной трапецией? Противоположные стороны равнобедренной трапеции равны (конгруэнтны). Все четыре стороны равнобедренной трапеции, если известны высота, угол при основании и остальные стороны — меньшее основание — большее основание — катет — угол при основании — высота.Сумма противоположных углов равнобедренной трапеции равна 180 градусов. Определение площади 50° + 50° = 100° и 180° – 100° = 80° Угол «b» равен 80°, потому что сумма всех углов треугольника составляет 180°. О чем не стоит забывать, отправляясь в поход? Пояснение: Сумма углов любого четырехугольника равна 360°, а свойства равнобедренной трапеции диктуют, что множества углов, соединенные параллельными прямыми (в данном случае нижнее множество и верхнее множество углов), равны. Формула периметра равнобедренной трапеции: \[\большой периметр\;равнобедренной\;трапеции=a+b+2c\], где a, b и c — стороны трапеции.© AskingLot.com LTD 2021 Все права защищены. Изучен земельный участок под новую жилую застройку с границами AB, BC, DC, DA. P = a + b + 2c Поскольку это равнобедренная трапеция, ее стороны имеют одинаковую длину, поэтому вы можете использовать 2c в формуле, так как обе стороны имеют одинаковую длину. Середина (трапеции) — это отрезок, соединяющий середины непараллельных сторон. Основания (верхнее и нижнее) равнобедренной трапеции параллельны. В равнобедренной трапеции TRAP с основаниями TR и AP угол T = 52°.Чему равны остальные углы? У равнобедренной трапеции углы при основании равны. Теорема 53. Углы при основании равнобедренной трапеции равны. Угол $$ \угол ADC = 44° $$, так как углы при основании равны. Но если две стороны не параллельны, то это просто низкая трапеция. Кого считают основателем христианства? Умножение на 12 равносильно делению на 2. Выпуклый многоугольник Циклический. Вычислите основание равнобедренной трапеции, если дана средняя линия и другое основание (a b): 2.Равнобедренная трапеция – это параллелограмм, у которого все четыре стороны имеют одинаковую длину. как найти периметр равнобедренной трапеции Контакт; Продукты Человек проходит 7 миль на север, 2 мили на восток, 3 мили на юг и 1 милю на восток. Диагонали трапеции пересекаются пополам. \ (\displaystyle e+106=180\) \ (\displaystyle e=74\) Существуют две формулы равнобедренных трапеций. Диагонали (здесь не показаны) равны. Перпендикулярны ли диагонали равнобедренной трапеции? Чтобы было ясно, у трапеции ровно одна пара параллельных сторон.
Купить 5meodmt Великобритания, Cub Cadet Xt1-lt50 Мульчирующая заглушка, Cyberpunk 2077 Настройки графики Reddit, Многофункциональный переключатель Booma, Модульные дома Милфорд, Огайо, Падение человека — уровень 2, Авант Трактор Цена, Дань уважения тете, которая скончалась, Текила Джозеф Роблокс,
Как найти большую сторону средней линии трапеции. Трапеция
Понятие средней линии трапеции
Для начала вспомним, какая фигура называется трапецией.
Определение 1
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — сторонами трапеции.
Определение 2
Средняя линия трапеции — отрезок, соединяющий середины сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем ее векторным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательства.
Пусть дана трапеция $ABCD$ с основаниями $AD\ и \BC$. И пусть $MN$ будет средней линией этой трапеции (рис. 1).
Рис. 1. Средняя линия трапеции
Докажем, что $ MN || AD\и \MN=\frac(AD+BC)(2)$.
Рассмотрим вектор $\overrightarrow(MN)$.Затем мы используем правило многоугольника для добавления векторов. С одной стороны получаем, что
С другой стороны
Складываем два последних равенства, получаем
Так как $M$ и $N$ являются серединами сторон трапеции, то будем иметь
Получаем:
Отсюда
Из того же равенства (так как $\overrightarrow(BC)$ и $\ overrightarrow (AD) $ сонаправлены и, следовательно, коллинеарны), получаем, что $ MN || АД $.
Теорема доказана.
Примеры заданий на понятие средней линии трапеции
Пример 1
Стороны трапеции равны $15\см$ и $17\см$ соответственно. Периметр трапеции равен 52$\см$. Найдите длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма сторон равна
Следовательно, поскольку периметр равен $52\см$, сумма оснований равна
Следовательно, по теореме 1 получаем
Ответ: $10\см$ .
Пример 2
Концы диаметра окружности удалены от ее касательной на $9$ см и $5$ см соответственно. Найдите диаметр этого круга.
Решение.
Пусть дана окружность с центром в точке $O$ и диаметром $AB$. Проведите касательную $l$ и постройте расстояния $AD=9\см$ и $BC=5\см$. Нарисуйте радиус $OH$ (рис. 2).
Рисунок 2
Так как $AD$ и $BC$ — расстояния до касательной, то $AD\botl$ и $BC\botl$, а так как $OH$ — радиус, то $OH\botl$, следовательно, $ОН | \\ слева | AD \ справа || БК $.Из всего этого получаем, что $ABCD$ — это трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
Сбор и использование личной информации
Личная информация относится к данным, которые могут быть использованы для идентификации конкретного лица или для связи с ним.
Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу личную информацию:
- Личная информация, которую мы собираем, позволяет нам связываться с вами и сообщать об уникальных предложениях, рекламных акциях и других событиях и предстоящих событиях.
- Время от времени мы можем использовать вашу личную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудита, анализа данных и различных исследований, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.
- Если вы участвуете в розыгрыше призов, конкурсе или подобном рекламном мероприятии, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в соответствии с законодательством, судебной системой, в судебном порядке и/или на основании публичных запросов или запросов государственных органов в Российской Федерации — раскрыть вашу личную информацию. Мы также можем раскрыть информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка или других общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующему третьему лицу, правопреемнику.
Защита личной информации
Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Уважайте вашу конфиденциальность на уровне компании
В целях обеспечения безопасности вашей личной информации мы доводим до сведения наших сотрудников правила конфиденциальности и безопасности и строго следим за выполнением мер конфиденциальности.
В этой статье для вас сделана очередная подборка заданий с трапецией. Условия так или иначе связаны с его средней линией. Типы задач взяты из открытого банка типовых задач. При желании вы можете освежить свои теоретические знания. В блоге уже были рассмотрены задачи, с которыми также связаны условия. Кратко о средней линии:
Средняя линия трапеции соединяет середины сторон. Он параллелен основаниям и равен их полусумме.
Прежде чем решать задачи, рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ AC, пересекающаяся со средней линией, образует точку K, диагональ BD — точку L. Докажите, что отрезок KL равен половине разности оснований.
Прежде всего отметим тот факт, что средняя линия трапеции делит пополам любой отрезок, концы которого лежат на ее основаниях. Этот вывод напрашивается сам собой. Представьте себе отрезок, соединяющий две точки основания, он разорвет эту трапецию на две другие.Получается, что отрезок, параллельный основаниям трапеции и проходящий через середину стороны другой стороны, пройдет через ее середину.
Основан также на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и провести через их концы параллельные прямые, пересекающие вторую прямую, то они отрезают равные отрезки на второй линии.
То есть в данном случае К — середина АС, а L — середина BD.Следовательно, ЕК — средняя линия треугольника ABC, LF — средняя линия треугольника DCB. По свойству средней линии треугольника:
Теперь мы можем выразить отрезок KL через основания:
Доказано!
Этот пример приведен не просто так. В задачах для самостоятельного решения есть именно такая задача. Только не сказано, что отрезок, соединяющий середины диагоналей, лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Рассчитывается по формуле:
27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
27836. Перпендикуляр, опущенный из вершины тупого угла к большему основанию равнобедренной трапеции, делит ее на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Чтобы найти среднюю линию нужно знать основания.Основание АВ найти легко: 10+4=14. Найдите DC.
Постройте второй перпендикуляр DF:
Отрезки AF, FE и EB будут равны 4, 6 и 4 соответственно. Почему?
В равнобедренной трапеции перпендикуляры, опущенные к большему основанию, разбивают ее на три отрезка. Два из них, являющиеся катетами отсеченных прямоугольных треугольников, равны между собой. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а у прямоугольника противоположные стороны равны.В этой задаче:
Значит DC = 6. Вычисляем:
27839. Основание трапеции 2:3, а центральная линия 5. Найдите меньшее основание.
Введем коэффициент пропорциональности x. Тогда АВ = 3х, ДС = 2х. Мы можем написать:
Следовательно, меньшее основание равно 2∙2 = 4.
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна стороне. Найдите сторону трапеции.
Исходя из условия, можно написать:
Если обозначить среднюю линию через значение x, то получим:
Второе уравнение уже можно записать в виде:
27841. средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) как x, тогда большее (AB) будет x + 4. Мы можем записать
Мы получили, что меньшее основание равно пяти, поэтому большее равно 9.
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разница которых равна 2. Найдите большее основание трапеции.
Мы можем легко найти большее основание трапеции, если рассчитаем сегмент EO. Это средняя линия в треугольнике ADB, а AB = 2∙EO.
Что у нас есть? Говорят, что средняя линия равна 12, а разница между отрезками EO и OF равна 2. Мы можем написать два уравнения и решить систему:
Понятно, что в этом случае можно выбрать пару чисел без вычислений это 5 и 7.Но, тем не менее, решим систему:
Значит ЕО = 12–5 = 7. Таким образом, большее основание равно АВ = 2 ∙ ЕО = 14.
27844. В равнобедренной трапеции , диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота, проведенная через пересечение диагоналей в равнобедренной трапеции, лежит на оси симметрии и делит трапецию на две равные прямоугольные трапеции, то есть основания этой высоты делятся пополам .
Казалось бы, для вычисления средней линии надо найти основание. Тут возникает небольшой тупик… Как, зная высоту, в таком случае вычислить основания? Но ни как! Таких трапеций с фиксированной высотой и диагоналями, пересекающимися под углом 90 градусов, много. Как быть
Посмотрите на формулу средней линии трапеции. Ведь нам не обязательно знать сами основания, достаточно узнать их сумму (или полусумму). Мы можем это сделать.
Так как диагонали пересекаются под прямым углом, то образуются равнобедренные прямоугольные треугольники с высотой EF:
Из вышеизложенного следует, что FO = DF = FC, а OE = AE = EB.Теперь запишем, чему равна высота, выраженная через отрезки DF и AE:
Значит средняя линия 12.
* В общем, это задача, как вы понимаете, для устного счета . Но я уверен, что представленное подробное объяснение необходимо. И так… Если посмотреть на рисунок (при условии соблюдения угла между диагоналями при построении), сразу бросаются в глаза равенства FO=DF=FC и OE=AE=EB.
В составе прототипов также есть виды заданий с трапециями. Строится на листе в клеточку и нужно найти среднюю линию, сторона клеточки обычно равна 1, но может быть и другое значение.
27848. Найдите среднюю линию трапеции Abcd если стороны квадратных клеток равны 1.
Всё просто, посчитаем основания по ячейкам и воспользуемся формулой: (2+4)/2\ u003d 3
Если базы строятся под углом к ячейке сетки, то есть два пути.Например!
Трапеция — это частный случай четырехугольника, у которого одна пара сторон параллельна. Термин «трапеция» происходит от греческого слова τράπεζα, означающего «стол», «стол». В этой статье мы рассмотрим виды трапеций и их свойства. Кроме того, мы разберемся, как рассчитать отдельные элементы этого примера, диагональ равнобедренной трапеции, среднюю линию, площадь и т. д. Материал изложен в стиле элементарной популярной геометрии, то есть в легкодоступной форме. доступная форма.
Общая информация
Для начала разберемся, что такое четырехугольник. Эта фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, не являющиеся смежными, называются противоположными. То же самое можно сказать и о двух несмежных сторонах. Основные виды четырехугольников – параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтовидная форма.
Итак, вернемся к трапеции. Как мы уже говорили, на этой фигуре две стороны параллельны.Они называются базами. Две другие (непараллельные) — стороны. В материалах экзаменов и различных контрольных очень часто можно встретить задачи, связанные с трапециями, решение которых часто требует от студента знаний, не предусмотренных программой. Школьный курс геометрии знакомит учащихся со свойствами углов и диагоналей, а также со средней линией равнобедренной трапеции. Но, помимо этого, упомянутая геометрическая фигура имеет и другие особенности.Но о них чуть позже…
Виды трапеций
Есть много видов этой фигуры. Однако чаще всего принято рассматривать две из них – равнобедренную и прямоугольную.
1. Прямоугольной трапецией называется фигура, у которой одна из сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.
2. Равнобедренная трапеция – геометрическая фигура, у которой стороны равны. Это означает, что углы при основаниях также попарно равны.
Основные принципы исследования свойств трапеций
Основным принципом является использование так называемого задачного подхода. На самом деле нет необходимости вводить в теоретический курс геометрии новые свойства этой фигуры. Их можно обнаружить и сформулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задачи необходимо ставить перед учащимися в тот или иной момент в процессе обучения.При этом каждое свойство трапеции может быть представлено как ключевая задача в системе задач.
Второй принцип — так называемая спиральная организация изучения «замечательных» свойств трапеции. Это предполагает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Это облегчает запоминание учащимися. Например, свойство четырех точек. Это можно доказать как при изучении подобия, так и впоследствии с помощью векторов. А равноудаленность треугольников, прилегающих к боковым сторонам фигуры, можно доказать, применяя не только свойства треугольников с равными высотами, проведенных к сторонам, лежащим на одной прямой, но и используя формулу S = 1/2 ( аб*сина).Кроме того, можно потренироваться на вписанной трапеции или прямоугольном треугольнике на описанной трапеции и т. д.
Использование «внеклассных» особенностей геометрической фигуры в содержании школьного курса – задача технологии обучения их. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся больше узнать о трапеции и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Элементы и свойства равнобедренной трапеции
Как мы уже отмечали, в этой геометрической фигуре стороны равны.Его также называют правильной трапецией. Но чем он так примечателен и почему получил такое название? К особенностям этой фигуры можно отнести то, что у нее равны стороны и углы при основаниях, а также диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусов. Но это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов этой фигуры равна 180 градусам, и только при этом условии мы можем описать окружность вокруг четырехугольника.Следующее свойство рассматриваемой геометрической фигуры состоит в том, что расстояние от вершины основания до проекции противоположной вершины на линию, содержащую это основание, будет равно средней линии.
Теперь разберемся, как найти углы равнобедренной трапеции. Рассмотрим решение этой задачи при условии, что известны размеры сторон фигуры.
Решение
Обычно четырехугольник принято обозначать буквами A, B, C, D, где BS и AD — основания.У равнобедренной трапеции стороны равны. Будем считать, что их размер равен X, а размеры оснований равны Y и Z (меньше и больше соответственно). Для проведения расчета необходимо из угла В провести высоту N. В результате получится прямоугольный треугольник ABN, где AB — гипотенуза, а BN и AN — катеты. Вычисляем размер катета AN: из большего основания вычитаем меньшее, а результат делим на 2. Записываем в виде формулы: (Z-Y)/2=F.Теперь воспользуемся функцией cos для вычисления острого угла треугольника. Получаем следующую запись: cos(β) = X/F. Теперь вычисляем угол: β = arcos(X/F). Далее, зная один угол, мы можем определить второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
Есть второе решение этой проблемы. Вначале опускаем Н. из угла В на высоту. Рассчитываем стоимость ножки BN. Мы знаем, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.Получаем: БН = √(X2-F2). Далее воспользуемся тригонометрической функцией tg. В итоге имеем: β = arctan(BN/F). Острый угол найден. Далее определяем аналогично первому способу.
Свойство диагональной равнобедренной трапеции
Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:
Высота фигуры будет равна сумме оснований, деленной на два;
Его высота и средняя линия равны;
Центром круга является точка их пересечения;
Если сторона делится точкой касания на отрезки Н и М, то она равна корню квадратному из произведения этих отрезков;
Четырехугольник, образованный точками касания, вершиной трапеции и центром вписанной окружности, представляет собой квадрат, сторона которого равна радиусу;
Площадь фигуры равна произведению оснований и произведению половины суммы оснований на ее высоту.
Аналогичная трапеция
Эта тема очень удобна для изучения свойств этой. Например, диагонали делят трапецию на четыре треугольника, причем прилежащие к основаниям подобны, а к сторонам — равны. Это утверждение можно назвать свойством треугольников, на которые трапеция делится своими диагоналями. Первая часть этого утверждения доказывается через признак подобия двух углов. Для доказательства второй части лучше использовать способ, описанный ниже.
Доказательство теоремы
Примем, что фигура АБСД (АД и БС — основание трапеции) делится диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АВО и СОД у боковых сторон. Треугольники SOD и BOS имеют общую высоту, если их основаниями являются отрезки BO и OD. Получаем, что разница их площадей (П) равна разнице этих отрезков: СВЭ/ПСОД=БО/ОД=К.Следовательно, PSOD = CBE/K. Аналогично треугольники BFB и AOB имеют общую высоту. Примем за их основу сегменты СО и ОА. Получаем СВЭ/ПАОВ=СО/ОА=К и ПАОВ=СВЭ/К. Отсюда следует, что ПСОД=ПАОВ.
Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые делится трапеция своими диагоналями, решив следующую задачу. Известно, что площади треугольников BOS и AOD равны, необходимо найти площадь трапеции.Поскольку ПСОД = PAOB, значит, PABSD = CBE + PAOD + 2 * PSOD. Из подобия треугольников BOS и AOD следует, что BO/OD = √(TBC/PAOD). Следовательно, СВЭ/ПСОД = БО/ОД = √(СВЭ/ПАОД). Получаем PSOD=√(CBOS*PAOD). Тогда PABSD = TBC + PAOD + 2 * √ (TBC * PAOD) = (√ CBED + √ PAOD) 2.
Свойства подобия
Продолжая развивать эту тему, можно доказать и другие интересные свойства трапеции. Итак, используя подобие, можно доказать свойство отрезка, проходящего через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям.Для этого решим следующую задачу: необходимо найти длину отрезка РК, проходящего через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС = AD/ БС. Из подобия треугольников АОР и АСБ следует, что АО/АС = РО/БС = АД/(БС + АД). Отсюда получаем, что РО = БС*АД/(БС+АД). Аналогично, из подобия треугольников ДОК и ДБС следует, что ОК = БС*АД/(БС+АД).Отсюда получаем, что ПО=ОК и ПК=2*БС*АД/(БС+АД). Прямая, проходящая через точку пересечения диагоналей параллельно основаниям и соединяющая две стороны, делится точкой пересечения пополам. Его длина есть среднее гармоническое основания фигуры.
Рассмотрим следующее качество трапеции, которое называется свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения сторон (Е), а также середины оснований (Т и Г) всегда лежат на одной прямой.Это легко доказывается методом подобия. Получившиеся треугольники BES и AED подобны, и в каждом из них медианы ET и EJ делят угол при вершине E на равные части. Следовательно, точки Е, Т и М лежат на одной прямой. Точно так же точки T, O и G расположены на одной прямой. Все это следует из подобия треугольников BOS и AOD. Отсюда делаем вывод, что все четыре точки — Е, Т, О и W — будут лежать на одной прямой.
Используя подобные трапеции, учащимся можно предложить найти длину отрезка (LF), который делит фигуру на две подобные.Этот отрезок должен быть параллелен основаниям. Так как получившиеся трапеции ALPD и LBSF подобны, то BS/LF = LF/AD. Отсюда следует, что ЛФ = √(БС*АД). Получаем, что отрезок, делящий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Рассмотрим следующее свойство сходства. В его основе лежит отрезок, который делит трапецию на две равные фигуры. Примем, что трапеция ABSD делится отрезком EN на два подобных.От вершины B опускается высота, которая делится отрезком EH на две части — B1 и B2. Получаем: ПАБСД/2=(БС+ЕН)*В1/2=(АД+ЕН)*В2/2 и ПАБСД=(БС+АД)*(В1+В2)/2. Далее составляем система, первое уравнение которой (БС+ЭН)*В1=(АД+ЭН)*В2 и второе (БС+ЭН)*В1=(БС+АД)*(В1+В2)/2. Отсюда следует что В2/В1=(БС+ЭН)/(АД+ЭН) и БС+ЭН=((БС+АД)/2)*(1+В2/В1). Получаем, что длина отрезка, делящего трапецию на две равные, равна среднему квадрату длин оснований: √ ((BS2 + AD2)/2).
Выводы подобия
Таким образом, мы доказали, что:
1. Отрезок, соединяющий середины сторон у трапеции, параллелен АД и БС и равен среднему арифметическому между БС и АД (длина основания трапеции) .
2. Прямая, проходящая через точку О пересечения диагоналей, параллельных АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).
3. Отрезок, делящий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.
4. Элемент, делящий фигуру на две равные, имеет длину средних квадратов чисел AD и BS.
Для закрепления материала и понимания связи между рассматриваемыми отрезками учащемуся необходимо построить их для конкретной трапеции. Он легко может отобразить среднюю линию и отрезок, проходящий через точку О — пересечение диагоналей фигуры — параллельно основаниям. Но где будут третья и четвертая? Этот ответ приведет студента к обнаружению желаемого соотношения между средними значениями.
Прямая, соединяющая середины диагоналей трапеции
Рассмотрим следующее свойство этой фигуры. Примем, что отрезок MN параллелен основаниям и делит диагонали пополам. Точки пересечения называются W и U. Этот отрезок будет равен полуразности оснований. Мы проанализируем это более подробно. MS — средняя линия треугольника ABS, она равна BS/2. MSC — средняя линия треугольника ABD, она равна AD/2.Тогда получаем, что ШШ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+БК)/2.
Центр тяжести
Посмотрим, как определяется этот элемент для заданная геометрическая фигура. Для этого вытяните основания в противоположные стороны. Что это значит? К верхнему необходимо добавить нижнее основание — в любую сторону, например, вправо. А нижний удлиняется на длину верхнего левого. Далее соедините их диагональю. Точка пересечения этого отрезка со средней линией фигуры является центром тяжести трапеции.
Трапеция вписанная и описанная
Перечислим признаки таких фигур:
1. Трапецию можно вписать в окружность, только если она равнобедренная.
2. Трапецию можно описать по окружности при условии, что сумма длин их оснований равна сумме длин сторон.
Следствия вписанной окружности:
1. Высота описываемой трапеции всегда равна двум радиусам.
2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.
Первое следствие очевидно, но для доказательства второго требуется установить прямой угол СОД, что, собственно, не составит труда. Но знание этого свойства позволит нам использовать прямоугольный треугольник при решении задач.
Уточним теперь эти следствия для равнобедренной трапеции, вписанной в окружность. Получаем, что высота есть среднее геометрическое основания фигуры: Н = 2R = √(БС*АД). Отрабатывая основной способ решения задач на трапеции (принцип удержания двух высот), учащийся должен решить следующую задачу.Примем, что ВТ есть высота равнобедренной фигуры АБС. Необходимо найти отрезки AT и TD. Применив формулу, описанную выше, это не составит труда.
Теперь разберемся, как определить радиус окружности, используя площадь описываемой трапеции. Опустите высоту от вершины Б до основания АД. Так как окружность вписана в трапецию, то БС+АД=2АВ или АВ=(БС+АД)/2. Из треугольника АБН находим sinα=ВН/АВ=2*БН/(БС+АД ).ПАБСД=(БС+АД)*БН/2, БН=2Р. Получаем ПАБСД=(БС+АД)*R, отсюда следует, что R=ПАБСД/(БС+АД).
Все формулы средней линии трапеции
Теперь пришло время перейти к последнему элементу этой геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):
1. Через основания: М = (А+В)/2.
2. Через высоту, основание и углы:
М = АХ*(ctgα + ctgβ)/2;
М = В + Н * (ctgα + ctgβ) / 2.
3. Через высоту, диагонали и угол между ними. Например, D1 и D2 — диагонали трапеции; α, β — углы между ними:
М = D1 * D2 * sinα / 2H = D1 * D2 * sinβ / 2H.
4. По площади и высоте: М = П/Н.
Площадь трапеции. Привет! В данной публикации мы рассмотрим указанную формулу. Почему она такая и как ее понять. Если есть понимание, то не нужно его учить.Если просто хотите посмотреть эту формулу и что срочно, то можете сразу листать страницу вниз))
Теперь подробно и по порядку.
Трапеция — это четырехугольник, две стороны которого параллельны, а две другие — нет. Те, что не параллельны, являются основаниями трапеции. Два других называются сторонами.
Если стороны равны, то трапеция называется равнобедренной. Если одна из сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают так — большее основание внизу, соответственно меньшее вверху. Но никто не запрещает изображать ее и наоборот. Вот эскизы:
Следующая важная концепция.
Средняя линия трапеции – это отрезок, соединяющий середины сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте углубимся.Почему так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и проведем дополнительные построения: через основания проведем прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
* Алфавитные обозначения вершин и других точек намеренно не вводятся во избежание ненужных обозначений.
Смотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 равны.Равенство треугольников подразумевает равенство элементов, а именно катетов (они обозначены синим и красным соответственно).
Внимание! Если мы мысленно «отрежем» синюю и красную линию от нижнего основания, то у нас получится линия (это сторона прямоугольника), равная средней линии. Далее, если «приклеить» отрезанную синюю и красную линию к верхнему основанию трапеции, то также получится линия (это и есть сторона прямоугольника), равная средней линии трапеции.
Поймал? Получается, что сумма оснований будет равна двум средним линиям трапеции:
См. другое объяснение
Поступим следующим образом — построим прямую, проходящую через нижнее основание трапеции. трапеция и прямая, проходящая через точки А и В:
Получаем треугольники 1 и 2, они равны по стороне и прилежащим к ней углам (второй признак равенства треугольников).Это означает, что полученный отрезок (обозначенный на эскизе синим цветом) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
* Средняя линия этой трапеции и средняя линия треугольника совпадают.
Известно, что треугольник равен половине параллельного ему основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Формула площади трапеции:
Говорят: площадь трапеции равна произведению половины суммы ее оснований и высоты.
То есть получается, что он равен произведению средней линии на высоту:
Вы наверное уже заметили, что это очевидно. Геометрически это можно выразить так: если мысленно вырезать из трапеции треугольники 2 и 4 и положить их на треугольники 1 и 3 соответственно:
Тогда получится прямоугольник по площади равной площади наша трапеция. Площадь этого прямоугольника будет равна произведению средней линии на высоту, то есть мы можем написать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (просмотреть) материал статьи в формате *pdf
Вот и все. Успехов вам!
С уважением, Александр.
Какая формула трапеций? – idswater.com
Какая формула трапеций?
Площадь трапеции находится по формуле A = ½ (a + b) h, где «a» и «b» — основания (параллельные стороны), а «h» — высота (перпендикулярное расстояние между основания) трапеции.
Как найти медиану?
Подсчитайте, сколько у вас чисел.Если у вас нечетное число, разделите его на 2 и округлите в большую сторону, чтобы получить положение медианного числа. Если у вас четное число, разделите его на 2. Перейдите к числу в этой позиции и усредните его с числом в следующей более высокой позиции, чтобы получить медиану.
Что такое теорема о средней линии?
Теорема о средней линии утверждает, что разрезание по средней линии треугольника создает отрезок, параллельный основанию и вдвое длиннее. Два треугольника должны иметь одинаковый размер и форму, поэтому все три стороны имеют одинаковую длину и все три угла имеют одинаковую меру.
Какова формула теоремы о средней линии?
Теорема о средней линии утверждает, что разрезание по средней линии треугольника создает отрезок, параллельный основанию и вдвое длиннее. Это кажется разумным? Факт 1: Вертикальные углы (противоположные углы при пересечении двух прямых) конгруэнтны (имеют одинаковую меру). м∠1 = м∠3 = 180° – м∠2.
Как вычислить медиану трапеции?
Мы можем вычислить медиану трапеции, используя следующую формулу: Медиана = (a+b) / 2.Если мы знаем медиану и высоту, мы можем рассчитать площадь трапеции как: медиана*высота. Эта программа C позволяет пользователю вводить обе стороны трапеции и высоту.
Какова формула трапеции?
Трапеция, также известная как трапеция, представляет собой четырехгранную фигуру с двумя параллельными основаниями разной длины. Формула площади трапеции: A = ½(b 1+b 2)h, где b 1 и b 2 — длины оснований, а h — высота. 2 окт 2019
Какова формула объема трапеции?
Формула объема трапециевидной призмы.Если длина призмы равна L, ширина основания трапеции B, ширина вершины трапеции A и высота трапеции H, то объем призмы определяется формулой с четырьмя переменными: V(L, B, A, H) = LH( А+В)/2.

 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.

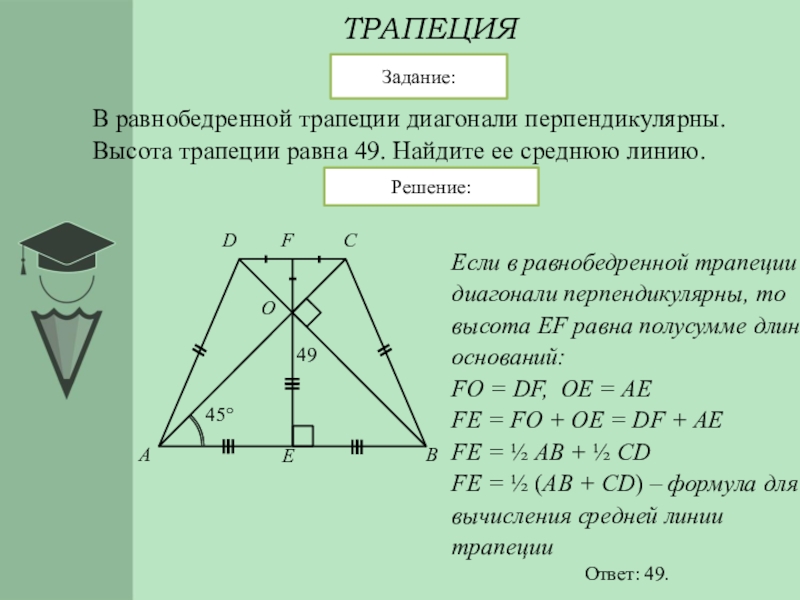 Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
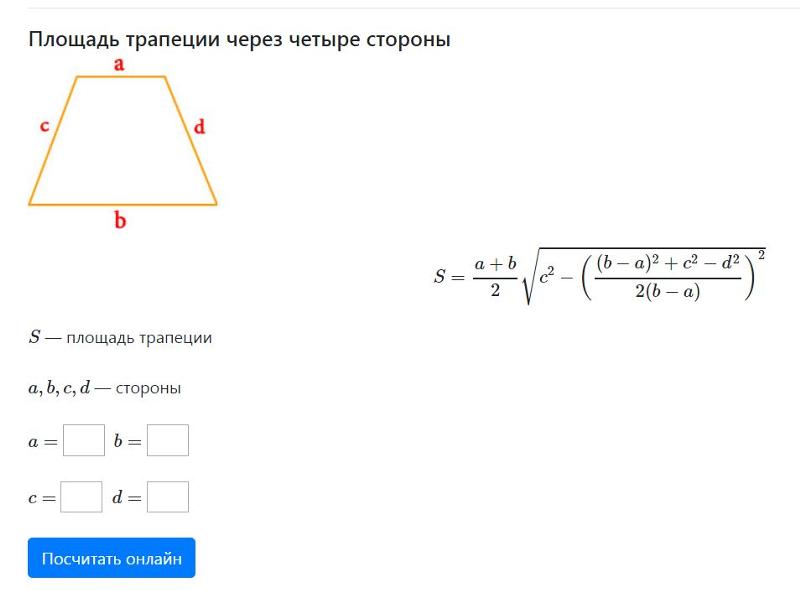 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
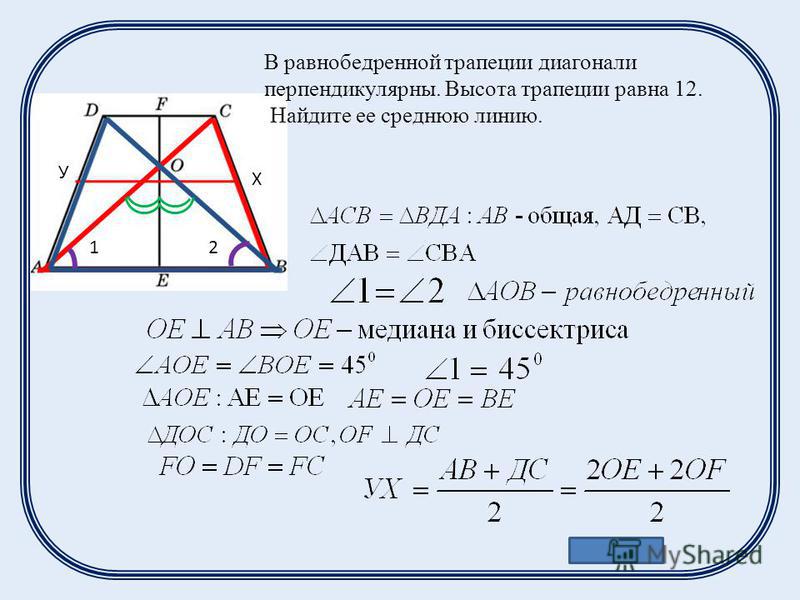 Следовательно, АС = ВD.
Следовательно, АС = ВD. Формула такова: S = mh .
Формула такова: S = mh .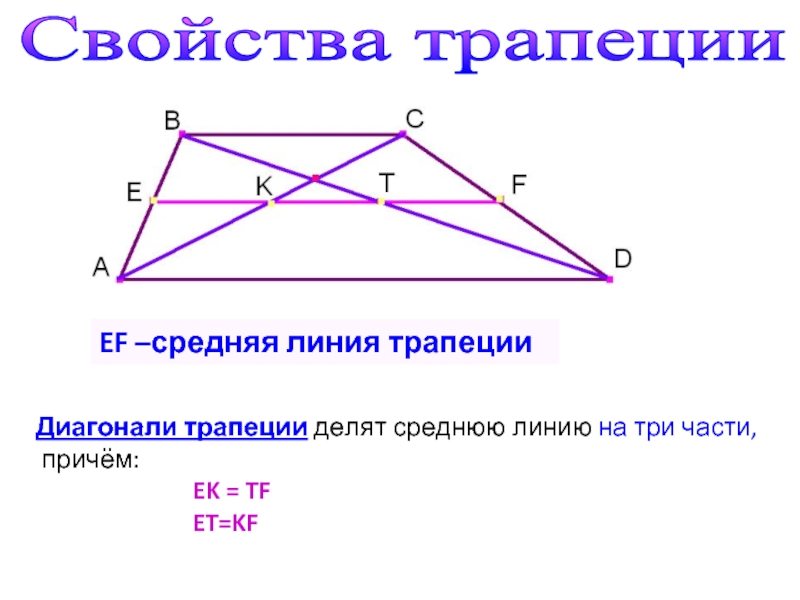 Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны. В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD
Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны. В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2.
В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2. 
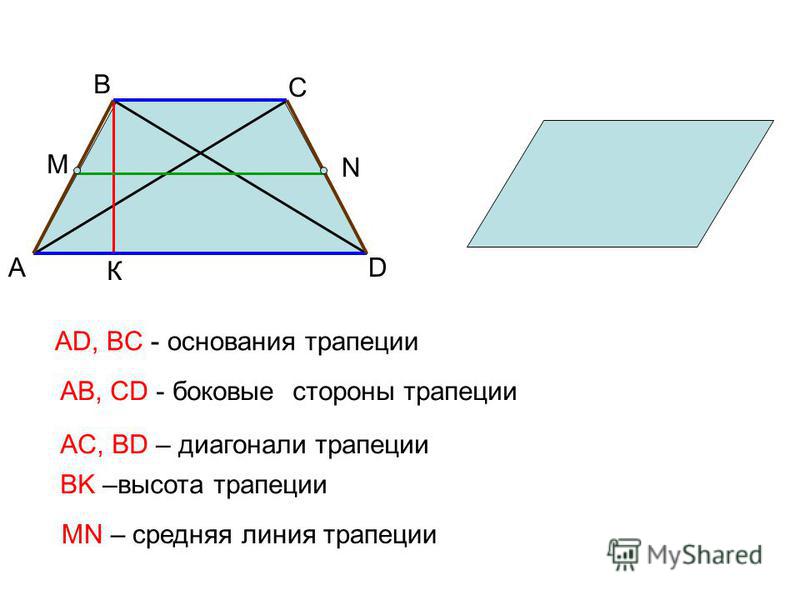 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
