Разложение многочлена на множители. Теория и примеры.

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Для чего нужно раскладывать многочлен на множители?

Чтобы облегчить себе жизнь! После того как ты сделаешь это, выражение станет намного проще и ты сможешь с ним «разобраться»! Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности. 

Прочитай эту статью и у тебя не останется вопросов по этой теме. Сначала мы разберем что означают все «сложные» слова, потом объясним все пять ВОЛШЕБНЫХ способов разложения многочлена на множители. И затем разберем на примерах как это делать.

Let’s dive right in… (Поехали!) 

– это могут быть числа, переменные, произведения чисел и переменных, а так же переменные в степени (если забыл, что такое степень, посмотри тему «Степень и ее свойства»)

Все это — одночлены. Видишь у них нет знаков «+» или «-«, как бы нет других членов… 

— это выражение, состоящее из суммы (или разности) нескольких одночленов различного вида:

Так, ну давай по порядку. Как не трудно догадаться, слово «множитель» происходит от слова «умножать».

Возьмем, например, число  , разложить его на множители означает расписать его в виде «умножения» или, как принято говорить в математике «произведения» множителей. Так   мы можем получить, умножив   на  , а  , в свою очередь, можно представить как произведение   и  .

Чтоб было более наглядно, обратимся к картинке:

На картинке мы видим пошаговое разложение на множители, те которые подчеркнуты – это множители, которые дальше разложить уже нельзя, т.е. их нельзя уже представить в виде произведения (можно конечно представить каждое из них как единица, умноженная на само число, но это нам ничего не дает).

Я обещал, что картинка все разъяснит, ну разве из нее не понятно, что,  , а  ? Вот и я говорю, что элементарно!

Иными словами,  . Тут  , еще раз   и   – это и есть множители, на которые мы раскладываем.

Это самый главный вопрос. Я уже говорил — чтобы облегчить тебе жизнь. Раскладывая многочлен на множители, ты упрощаешь выражение! Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.

А теперь «официальное» определение.

Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. При этом каждый множитель может быть как многочленом, так и одночленом. 

Потому что нет универсального способа, подходящего для всех многочленов.

Давай посмотрим на каждый из них…

Применяется если преобразование не очевидно.

Здесь, например, можно переставить второй член на другое место:

Можно преобразовать многочлен и привести к виду разности квадратов, например и применить формулу сокращенного умножения

Теорема. Если квадратное уравнение   имеет корни  , то его можно записать в виде:

 .

 

1. Вынесение общего множителя за скобки

Это один из самых элементарных способов упростить выражение. Для применения этого метода давай вспомним распределительный закон умножения относительно сложения (не пугайся этих слов, ты обязательно знаешь этот закон, просто мог забыть его название).

Закон гласит: чтобы сумму двух чисел умножить на третье число, нужно каждое слагаемое умножить на это число и полученные результаты сложить, иначе говоря,  .

Так же можно проделать и обратную операцию,  , вот именно эта обратная операция нас и интересует. Как видно из образца, общий множитель а, можно вынести за скобку.

Подобную операцию можно проделывать как с переменными, такими как   и  , например, так и с числами:  .

Да, это слишком элементарный пример, так же, как и приведенный ранее пример, с разложением числа  , ведь все знают, что числа  ,   и   делятся на  , а как быть, если вам досталось выражение посложнее:

 ?

Как узнать на что, например, делится число  , неет, с калькулятором-то любой сможет, а без него слабо? А для этого существуют признаки делимости, эти признаки действительно стоит знать, они помогут быстро понять, можно ли вынести за скобку общий множитель.

Признаки делимости

Запомнить их не так сложно, скорее всего, большинство из них и так тебе были знакомы, а что-то будет новым полезным открытием, подробнее в таблице:

Делится на	Признак делимости числа на данный делитель
2	Оканчивается одной из цифр: 0, 2, 4, 6, 8
3	Сумма цифр делится на 3
5	Последняя цифра 5 или 0
7	Разность между числом десятков и удвоенной цифрой единиц делится на семь
9	Сумма цифр делится на 9
10	Последняя цифра – ноль
11	Разность между суммой цифр, стоящих на нечетных местах, и суммой цифр, стоящих на четных местах, делится на 11

Примечание: В таблице не хватает признака делимости на 4. Если две последние цифры делятся на 4, то и всё число делится на 4. 

Ну как тебе табличка? Советую ее запомнить!

Что ж, вернемся к выражению  , может вынести за скобку   да и хватит с него? Нет, у математиков принято упрощать, так по полной, выносить ВСЕ что выносится!

И так, с игреком все понятно, а что с числовой частью выражения? Оба числа нечетные, так что на   разделить не удастся, 

Можно воспользоваться признаком делимости на  , сумма цифр  ,   и  , из которых состоит число  , равна  , а   делится на  , значит и   делится на  .

Зная это, можно смело делить в столбик, в результате деления   на   получаем   (признаки делимости пригодились!). Таким образом, число   мы можем вынести за скобку, так же, как y и в результате имеем:

 .

Чтоб удостовериться, что разложили все верно, можно проверить разложение, умножением! 

Также общий множитель можно выносить и в степенных выражениях. Вот тут, например,  , видишь общий множитель?

У всех членов этого выражения есть иксы – выносим, все делятся на   – снова выносим, смотрим что получилось:  .

 

2. Формулы сокращенного умножения

Формулы сокращенного умножения уже упоминались в теории, если ты с трудом помнишь что это, то тебе стоит освежить их в памяти «Формулы сокращенного умножения».

Ну, а если ты считаешь себя очень умным и тебе лень читать такую тучу информации, то просто читай дальше, глянь на формулы и сразу берись за примеры.

Суть этого разложения в том, что бы заметить в имеющемся перед тобой выражении какую-то определенную формулу, применить ее и получить, таким образом, произведение чего-то и чего-то, вот и все разложение. Дальше приведены формулы:

 

А теперь попробуй, разложи на множители следующие выражения, используя приведенные выше формулы:

1.  
2.  
3.  
4.  
5.  
6.  

А вот что должно было получиться:

 

1.  
2.  
3.  
4.  
5.  
6.  

Как ты успел заметить, эти формулы – весьма действенный способ разложения на множители, он подходит не всегда, но может очень пригодиться!

 

3. Группировка или метод группировки

А вот тебе еще примерчик:

 ­­

ну и что с ним делать будешь? Вроде бы и на   что-то делится и на  , а что-то на   и на  

 Но все вместе на что-то одно не разделишь, ну нет тут общего множителя, как не ищи, что, так и оставить, не раскладывая на множители?

Тут надо смекалку проявить, а имя этой смекалке – группировка!

Применяется она как раз, когда общие делители есть не у всех членов. Для группировки необходимо найти группки слагаемых, имеющих общие делители и переставить их так, чтобы из каждой группы можно было получить один и тот же множитель.

Переставлять местами конечно не обязательно, но это дает наглядность, для наглядности же можно взять отдельные части выражения в скобки, их ставить не запрещается сколько угодно, главное со знаками не напутать.

Не очень понятно все это? Объясню на примере: 

В многочлене  ­­ ставим член –   после члена –   получаем   

 группируем первые два члена вместе в отдельной скобке и так же группируем третий и четвертый члены, вынеся за скобку знак «минус», получаем:  

А теперь смотрим по отдельности на каждую из двух «кучек», на которые мы разбили выражение скобками.

Хитрость в том, чтоб разбить на такие кучки, из которых можно будет вынести максимально большой множитель, либо, как в этом примере, постараться сгруппировать члены так, чтобы после вынесения из кучек множителей за скобку у нас внутри скобок оставались одинаковые выражения.

Из обеих скобок выносим за скобки общие множители членов, из первой скобки  , а из второй  , получаем:  

Но это же не разложение!

После разложения должно остаться только умножение, а пока у нас многочлен просто поделен на две части…

НО! Этот многочлен имеет общий множитель. Это  

 за скобку и получаем финальное произведение  

Бинго! Как видишь, тут уже произведение и вне скобок нет ни сложения, ни вычитания, разложение завершено, т.к. вынести за скобки нам больше нечего.

Может показаться чудом, что после вынесения множителей за скобки у нас в скобках остались одинаковые выражения  , которые опять же мы и вынесли за скобку.

И вовсе это не чудо, дело в том, что примеры в учебниках и в ЕГЭ специально сделаны так, что большинство выражений в заданиях на упрощение или разложение на множители при правильном к ним подходе легко упрощаются и резко схлопываются как зонтик при нажатии на кнопку, вот и ищи в каждом выражении ту самую кнопку.

Что-то я отвлекся, что у нас там с упрощением? Замысловатый многочлен принял более простой вид:  .

Согласись, уже не такой громоздкий, как был?

 

4. Выделение полного квадрата.

Иногда для применения формул сокращенного умножения (повтори тему «Формулы сокращенного умножения») необходимо преобразовать имеющийся многочлен, представив одно из его слагаемых в виде суммы или разности двух членов.

В каком случае приходится это делать, узнаешь из примера: 

Многочлен   в таком виде не может быть разложен при помощи формул сокращенного умножения, поэтому его необходимо преобразовать. Возможно, поначалу тебе будет не очевидно какой член на какие разбивать, но со временем ты научишься сразу видеть формулы сокращенного умножения, даже если они не присутствуют не целиком, и будете довольно быстро определять, чего здесь не хватает до полной формулы, а пока – учись, студент, точнее школьник.

Для полной формулы квадрата разности здесь нужно   вместо  . Представим третий член   как разность  , получим:   К выражению в скобках можно применить формулу квадрата разности (не путать с разностью квадратов!!!), имеем:  , к данному выражению можно применить формулу разности квадратов (не путать с квадратом разности!!!), представив  , как  , получим:  .

Не всегда разложенное на множители выражение выглядит проще и меньше, чем было до разложения, но в таком виде оно становится более подвижным, в том плане, что можно не париться про смену знаков и прочую математическую ерунду. Ну а вот тебе для самостоятельного решения, следующие выражения нужно разложить на множители.

Примеры:

1.  
2.  
3.  
4.  
5.  

Ответы:​

 

1.  

2.  

3.  

4.  

5.  

 

 

5. Разложение квадратного трехчлена на множители

О разложении квадратного трехчлена на множители смотри далее в примерах разложения.

 

Примеры 5 методов разложения многочлена на множители

1. Вынесение общего множителя за скобки. Примеры.

Помнишь, что такое распределительный закон? Это такое правило:  

Пример:

Разложить многочлен на множители  .

Решение:

 .

Еще пример:

Разложи на множители  .

Решение:

 .

Если слагаемое целиком выносится за скобки, в скобках вместо него остается единица!

 .

 

2. Формулы сокращенного умножения. Примеры.

Чаще всего используем формулы разность квадратов, разность кубов и сумма кубов. Помнишь эти формулы? Если нет, срочно повтори тему «Формулы сокращенного умножения»!

Пример:

Разложите на множители выражение  .

Решение:

В этом выражении несложно узнать разность кубов:

 

Пример:

Разложите на множители многочлен  .

Решение:

 

 

3. Метод группировки. Примеры

 

Иногда можно поменять слагаемые местами таким образом, чтобы из каждой пары соседних слагаемых можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен превратится в произведение.

Пример:

Разложите на множители многочлен  .

 

Решение:

Сгруппируем слагаемые следующим образом:
 .

В первой группе вынесем за скобку общий множитель  , а во второй −  :
 .

Теперь общий множитель   также можно вынести за скобки:
 .

 

4. Метод выделения полного квадрата. Примеры.

Если многочлен удастся представить в виде разности квадратов двух выражений, останется только применить формулу сокращенного умножения (разность квадратов).

Пример:

Разложите на множители многочлен  .

Решение: Пример:

 

\begin{array}{*{35}{l}}
{{x}^{2}}+6{x}-7=\underbrace{{{x}^{2}}+2\cdot 3\cdot x+9}_{квадрат\ суммы\ {{\left( x+3 \right)}^{2}}}-9-7={{\left( x+3 \right)}^{2}}-16= \\
=\left( x+3+4 \right)\left( x+3-4 \right)=\left( x+7 \right)\left( x-1 \right) \\
\end{array}

 

Разложите на множители многочлен  .

Решение:

 

\begin{array}{*{35}{l}}
{{x}^{4}}-4{{x}^{2}}-1=\underbrace{{{x}^{4}}-2\cdot 2\cdot {{x}^{2}}+4}_{квадрат\ разности{{\left( {{x}^{2}}-2 \right)}^{2}}}-4-1={{\left( {{x}^{2}}-2 \right)}^{2}}-5= \\
=\left( {{x}^{2}}-2+\sqrt{5} \right)\left( {{x}^{2}}-2-\sqrt{5} \right) \\
\end{array}

 

5. Разложение квадратного трехчлена на множители. Пример.

Квадратный трехчлен – многочлен вида  , где   – неизвестное,  ,  ,   – некоторые числа, причем  .

Значения переменной  , которые обращают квадратный трехчлен в ноль, называются корнями трехчлена. Следовательно, корни трехчлена – это корни квадратного уравнения  .

Если не помнишь, как находить эти корни, читай тему «Квадратные уравнения».

Теорема. 

Если квадратное уравнение   имеет корни  , то его можно записать в виде:  .

Пример:

Разложим на множители квадратный трехчлен:  .

Сначала решим квадратное уравнение:Теперь можно записать разложение данного квадратного трехчлена на множители:

 

 

 .

 

Теперь твое мнение…

Мы расписали подробно как и для чего раскладывать многочлен на множители.

Мы привели массу примеров как это делать на практике, указали на подводные камни, дали решения…

А что скажешь ты? 

Как тебе эта статья? Ты пользуешься этими приемами? Понимаешь их суть?

Пиши в комментриях и… готовься к экзамену! 

Пока что он самый важный в твоей жизни.

Удачи.

 

 

Получить доступ к учебнику YouClever без ограничений можно кликнув по этой ссылке:

youclever.org

Формулы при разложении на множители

Рассматривая умножение многочленов, мы запомнили несколько формул, а именно: формулы для (a + b)², для (a – b)², для (a + b) (a – b), для (a + b)³ и для (a – b)³.

Если данный многочлен окажется совпадающим с одною из этих формул, то его явится возможным разложить на множители. Напр., многочлен a² – 2ab + b², мы знаем, равен (a – b)² [или (a – b) · (a – b), т. е. удалось a² – 2ab + b² разложить на 2 множителя]; также

Рассмотрим второй из этих примеров. Мы видим, что данный здесь многочлен подходит к формуле, получающейся от возведения в квадрат разности двух чисел (квадрат первого числа, минус произведение двойки на первое число и на второе, плюс квадрат второго числа): x⁶ есть квадрат первого числа, а, следовательно, само первое число есть x³, квадратом второго числа является последний член данного многочлена, т. е. 1, само второе число есть, следовательно, также 1; произведением двойки на первое число и на второе является член –2x³, ибо 2x³ = 2 · x³ · 1. Поэтому наш многочлен получился от возведения в квадрат разности чисел x³ и 1, т. е. он равен (x³ – 1)². Рассмотрим еще 4-ый пример. Мы видим, что данный многочлен a²b² – 25 можно рассматривать, как разность квадратов двух чисел, а именно квадратом первого числа служит a²b², следовательно, само первое число есть ab, квадратом второго числа является 25, почему само второе число есть 5. Поэтому наш многочлен можно рассматривать получившимся от умножения суммы двух чисел на их разность, т. е.

(ab + 5) (ab – 5).

Иногда случается, что в данном многочлене члены расположены не в том порядке, к которому мы привыкли, напр.

9a² + b² + 6ab – мысленно мы можем переставить второй и третий члены, и тогда нам станет ясным, что наш трехчлен = (3a + b)².

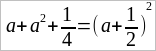… (переставим мысленно первый и второй члены).

25a⁶ + 1 – 10x³ = (5x³ – 1)² и т. п.

Рассмотрим еще многочлен

a² + 2ab + 4b².

Мы видим, что первый член его представляет собою квадрат числа a и третий член представляет собою квадрат числа 2b, но второй член не является произведением двойки на первое число и на второе, – такое бы произведение было бы равно 2 · a · 2b = 4ab. Поэтому нельзя применить к этому многочлену формулу квадрата суммы двух чисел. Если бы кто написал, что a² + 2ab + 4b² = (a + 2b)², то это было бы неверно – надо тщательно рассмотреть все члены многочлена, прежде чем применять к нему разложение на множители по формулам.

40. Соединение обоих приемов. Иногда при разложении многочленов на множители приходится комбинировать и прием вынесения общего множителя за скобки и прием применения формул. Вот примеры:

1. 2a³ – 2ab². Вынесем сначала общего множителя 2a за скобки, – получим 2a (a² – b²). Множитель a² – b², в свою очередь, разлагается по формуле на множители (a + b) и (a – b).

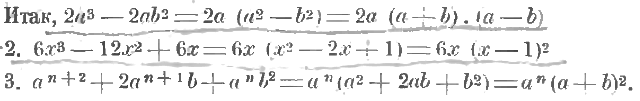
Иногда приходится применять прием разложения по формулам многократно:

1. a⁴ – b⁴ = (a² + b²) (a² – b²)

Мы видим, что первый множитель a² + b² не подходит ни к одной из знакомых формул; мало того, вспоминая особые случаи деления (п. 37), мы установим, что a² + b² (сумма квадратов двух чисел) вовсе на множители не раскладывается. Второй из полученных множителей a² – b² (разность квадратом двух чисел) разлагается на множители (a + b) и (a – b). Итак,

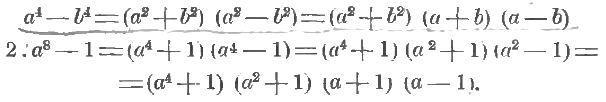
41. Применение особых случаев деления. На основании п. 37 мы можем сразу написать, что, напр.,

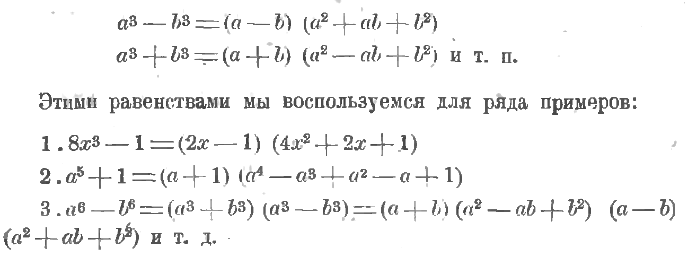
maths-public.ru

Разложение многочленов на множители в комбинации с формулами сокращённого умножения

На предыдущих уроках мы изучили два способа разложения многочлена на множители – способ вынесения общего множителя и способ группировки. Кроме того, мы изучили формулы сокращенного умножения и говорили, что их также можно использовать для разложения многочлена на множители.

Теперь для начала рассмотрим простейшие способы комбинирования вышеуказанных методов разложения.

Пример 1:

;

Теперь усложним выражение, умножив заданный многочлен на три:

;

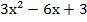Данная формула очень похожа на полный квадрат, но в таком виде свернуть ее мы не можем, но мы видим, что у всех членов есть общий множитель и можем вынести его за скобку. Получаем:

;

Итак, первая комбинация это формулы сокращенного умножения плюс вынесение общего множителя за скобки.

Пример 2:

;

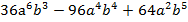Определим, что можно вынести за скобки. Для этого для начала найдем НОД:

;

Вынесем найденный общий множитель:

;

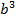Определим, какие буквенные множители можно вынести. Обе переменные a и b есть во всех членах многочлена, значит, их можно выносить. Осталось определить только, в какой степени. Для этого найдем минимальную степень каждой из переменных. Это  и . Вынесем найденную буквенную часть:

;

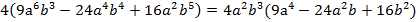Распишем полученную скобку более подробно, для этого определим, квадратами каких выражений являются первое и третье

interneturok.ru

Разложение многочлена на множители. Часть 1

Разложение многочлена на множители. Часть 1

Разложение на множители — это универсальный прием, помогающий решить сложные уравнения и неравенства. Первая мысль, которая должна прийти в голову при решении уравнений и неравенств, в которых в правой части стоит ноль — попробовать  разложить левую часть на множители.

Перечислим основные  способы разложения многочлена на множители:

• вынесение общего множителя за скобку
• использование формул сокращенного умножения
• по формуле разложения на множители квадратного трехчлена
• способ группировки
• деление многочлена на двучлен
• метод неопределенных коэффициентов

В этой статье мы остановимся подробно на первых трех способах, остальные рассмотрим в следующих статьях.

1. Вынесение общего множителя за скобку.

Чтобы вынести за скобку общий множитель надо сначала его найти. Коэффициент общего множителя равен наибольшему общему делителю всех коэффициентов.

Буквенная часть общего множителя равна произведению выражений, входящих в состав каждого слагаемого с наименьшим показателем степени.

Схема вынесения общего множителя выглядит так:

Внимание!
Количество членов в скобках равно количеству слагаемых в исходном выражении. Если одно из слагаемых совпадает с общим множителем, то при его делении на общий множитель, получаем единицу.

Пример 1.

Разложить на множители многочлен:  

Вынесем за скобки общий множитель. Для этого сначала его найдем.

1.Находим наибольший общий делитель всех коэффициентов многочлена, т.е. чисел 20, 35 и 15. Он равен 5.

2. Устанавливаем, что переменная  содержится во всех слагаемых, причем наименьший из её показателей степени равен 2. Переменная  содержится во всех слагаемых, и наименьший из её показателей степени равен 3.

Переменная  содержится только во втором слагаемом, поэтому она не входит в состав общего множителя.

Итак, общий множитель равен 

3. Выносим за скобки множитель  пользуясь схемой, приведенной выше:

 

Пример 2. Решить уравнение: 

Решение. Разложим левую часть уравнения на множители. Вынесем за скобки множитель :

Итак, получили уравнение 

Приравняем каждый множитель к нулю:

или 

Получаем  —   корень первого уравнения.

Корни квадратного уравнения  :

или 

Ответ: -1, 2, 4

 

2. Разложение на множители с помощью формул сокращенного умножения.

Если  количество слагаемых в многочлене, который мы собираемся разложить на множители меньше или равно трех, то мы пытаемся применить формулы сокращенного умножения.

1. Если многочлен представляет собой разность двух слагаемых, то пытаемся применить формулу разности квадратов:

   

или формулу разности кубов:

   

Здесь буквы и обозначают  число или алгебраическое выражение.

2. Если многочлен представляет собой сумму двух слагаемых, то, возможно, его можно разложить на множители с помощью формулы суммы кубов:

   

3. Если многочлен состоит из трех слагаемых, то пытаемся применить формулу квадрата суммы:

   

или формулу квадрата разности:

 

   

 

Или пытаемся разложить на множители по формуле разложения на множители квадратного трехчлена:

Здесь  и  — корни квадратного уравнения 

Пример 3.  Разложить на множители выражение:

Решение. Перед нами сумма двух слагаемых. Попытаемся применить формулу суммы кубов. Для этого нужно сначала каждое слагаемое представить в виде куба какого-то выражения, а затем применить формулу для суммы кубов:

Пример 4. Разложить на множители выражение:  Рещение. Перед нами разность квадратов  двух выражений. Первое выражение: , второе выражение: 

Применим формулу для разности квадратов:

Раскроем скобки и приведем подобные члены, получим:

Пример 5. Разложить на множители выражение:  Решение. Перед нами  многочлен, состоящий из трех слагаемых. Заметим, что ; ;

 Так как перед удвоенным произведением стоит знак «минус», воспользуемся формулой для квадрата разности:

Внимание!  Коэффициенты обоих членов трехчлена, которые являются квадратами одночленов, положительны.

Пример 6. Разложить на множители квадратный трехчлен 

Приготовим для разложения квадратного трехчлена готовую форму:

Впишем значения корней в готовую форму:

Внесем множитель 3 во вторую скобку:

Итак:

ege-ok.ru

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Алгебраические уравнения

      Пусть   n   – произвольное натуральное число. Рассмотрим многочлен   n   – ой степени от переменной   x  

Pn (x) = = a0 xn + a1 x n –1 + + … + an –1 x + an ,

(1)

коэффициенты которого

a0 ,  a1 , … , an –1 , an

(2)

являются любыми комплексными числами.

      Заметим, что в этом случае коэффициент   a₀   отличен от нуля, и введем следующее определение.

      Определение 1. Алгебраическим уравнением степени   n   с неизвестным   x   называют уравнение вида

      Определение 2. Корнем уравнения (3) называют вещественное или комплексное число   α ,   для которого

P_n (α) = 0 .

      Определение 3 . Число   α   называют корнем кратности   k   уравнения (3), если справедливо равенство

P_n (α) = (x – α )^k Q (x) ,

где

.

Разложение многочленов на множители в комплексной области

      Основная теорема алгебры (теорема Гаусса) утверждает, что любое алгебраическое уравнение вида (3) имеет   n   корней, при условии, что каждый корень считается столько раз, какова его кратность.

      Если

z₁ ,  z₂ , … , z_{k –1} , z_k

– полный набор корней уравнения (3), а

l₁ ,  l₂ , … , l_{k –1} , l_k

– их кратности, то, во-первых,

l₁ +  l₂ + … + l_{k –1} + l_k = n ,

а, во-вторых, справедливо равенство

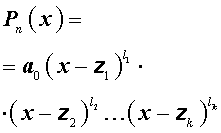(4)

      Замечание. Линейными множителями называют многочлены первой степени

x – z₁ ,  x – z₂ , … , x – z_k ,

входящие в формулу (4), а саму формулу (4) называют формулой разложения многочленов на линейные множители в комплексной области.

Разложение на множители многочленов с действительными коэффициентами

      Рассмотрим теперь многочлены степени 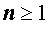  ,   все коэффициенты которых являются вещественными числами.

      Тогда справедливо следующее

      Утверждение. Если комплексное число

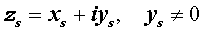
является корнем кратности   l_s   многочлена с вещественными коэффициентами, то и комплексно сопряженное число

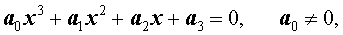
является корнем этого многочлена, причем тоже кратности   l_s .

      Из утверждения вытекает, что в разложение (4) степень каждого бинома, содержащая комплексный корень   z_s   и имеющая вид

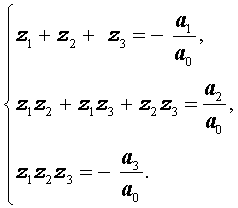(5)

входит в паре со степенью бинома, содержащей комплексно сопряженный корень     и имеющей вид

(6)

      А поскольку

то произведение каждой пары биномов (5) и (6), входящей в формулу (4), даёт степень квадратного трехчлена с вещественными коэффициентами:

      Следствие. Каждый многочлен ненулевой степени, коэффициенты которого являются вещественными числами, разлагается на множители, являющиеся многочленами с вещественными коэффициентами первой или второй степени.

      Пример. Разложить на множители многочлен четвертой степени

x⁴ + 1 .

      Решение.

Теорема (формулы) Виета

      Снова рассмотрим уравнение   n – ой степени от переменной   x  

(7)

и, немного изменив предыдущие обозначения, предположим, что

z1 ,  z2 , … , zn –1 , zn

(8)

— его корни, причем в записи (8) каждый корень взят столько раз, какова его кратность.

      Тогда из формулы (4) вытекают следующие равенства, которые называют формулами Виета для уравнения   n – ой степени:

      Формулы Виета для   n = 2   доказаны в разделе «Квадратные уравнения» нашего справочника.

      При   n = 3   уравнение (7) имеет вид

а формулы Виета записываются так:

      В случае уравнения 4-ой степени

формулы Виета записываются так:

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

www.resolventa.ru

Разложение многочленов на множители. Метод выделения полного квадрата. Комбинация методов

Тема: Разложение многочленов на множители

Урок: Разложение многочленов на множители. Метод выделения полного квадрата. Комбинация методов

Напомним основные методы разложения многочлена на множители, которые были изучены ранее:

-Метод вынесения общего множителя за скобки, то есть такого множителя, который присутствует во всех членах многочлена. Рассмотрим пример:

;

Напомним, что одночлен есть произведение степеней и чисел. В нашем примере в обоих членах есть некоторые общие, одинаковые элементы.

Итак, вынесем общий множитель за скобки:

;

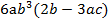Напомним, что перемножив вынесенный множитель на скобку можно проверить правильность вынесения.

-Метод группировки. Не всегда в многочлене можно вынести общий множитель. В таком случае нужно его члены разбить на группы таким образом, чтобы в каждой группе можно было вынести общий множитель и постараться разбить так, чтобы после вынесения множителей в группах появился общий множитель у всего выражения, и можно было бы продолжить разложение. Рассмотрим пример:

;

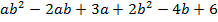Сгруппируем  первый член с четвертым, второй с пятым, и третий соответственно с шестым:

;

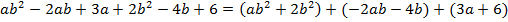Вынесем общие множители в группах:

;

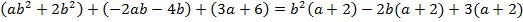У выражения появился общий множитель. Вынесем его:

;

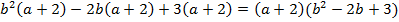— Применение формул сокращенного умножения. Рассмотрим пример:

;

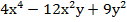Распишем выражение подробно:

;

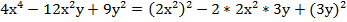Очевидно, что перед нами формула квадрата разности, так как есть сумма квадратов двух выражений и из нее вычитается их удвоенное произведение. Свернем по формуле:

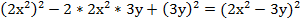
interneturok.ru

Разложение на множители, разбор основных заданий

По сути, здесь приведены основные формулы сокращенного умножения. Но формулы представлены так, что именно из суммы получено произведение. Чаще всего именно так приходится работать с формулами, будь то сокращение дробей, решение неравенств методом интервалов и т.п.

 

Основные способы разложения многочлена на множители

 

 1. Вынесение общего множителя за скобку

 

2. (формула разности квадратов)

 

3. (формула квадрата суммы/разности)

 
4. (формула суммы/разности кубов)

 

5. (формула куба суммы/разности)

 

6. Способ группировки

Например, 

7.  ,

где – корни  уравнения

 

Пример 1.
Разложить на множители: .

Решение: + показать

Пример 2.
Разложить на множители: .

Решение: + показать

Пример 3.
Разложить на множители: .

Решение: + показать

Пример 4.
Разложить на множители: .

Решение: + показать

Пример 5.
Разложить на множители: .

Решение: + показать

Пример 6.
Сократить дробь:.

Решение: + показать

Чтобы сократить дробь, следует разбить на множители числитель и\или знаменатель. Применяем способ группировки (п.6) (а также формулу “разность квадратов”, п.2) к числителю:
 

Пример 7.
Разложить на множители: .

Решение: + показать

Пример 8.
Сократить дробь:

Решение: + показать

Для полного квадрата (п.3) первым трем слагаемым числителя не хватает коэффициента 2 перед вторым слагаемым. Представим как , что, кстати, еще и поможет нам в дальнейшем выйти на разность квадратов (п.2):
 

Пример 9.
Разложить на множители: .

Решение: + показать

 

egemaximum.ru