Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра — Формулы сокращенного умножения

      Формулы сокращенного умножения включают в себя следующие группы формул:

Сумма нечетных степеней

      Группа формул «Сумма нечетных степеней» приведена в Таблице 3.

      Таблица 3. – Сумма нечетных степеней

Название формулы	Формула
Сумма кубов	x3 + y3 = (x + y) (x2 – xy + y2)
Сумма пятых степеней	x5 + y5 = (x + y) (x4 – x3y + x2y2 – xy3 + y4)
Сумма седьмых степеней	x7 + y7 = (x + y) (x6 – x5y + x4y2 – x3y3 + x2y4 – xy5 + y6)
…	…
Сумма степеней порядка  2n + 1	x2n + 1 + y2n + 1 = (x + y) (x2n – x2n – 1y + x2n – 2 y2 – …– xy2n – 1 + y2n)

Сумма кубов x3 + y3 = = (x + y) (x2 – xy + y2)

Сумма пятых степеней x5 + y5 = = (x + y) (x4 – x3y + + x2y2 – xy3 + y4)

Сумма седьмых степеней x7 + y7 = = (x + y) (x6 – x5y + + x4y2 – x3y3 + + x2y4 – xy5 + y6)

…

Сумма степеней порядка  2n + 1   x2n + 1 + y2n + 1 = = (x + y) (x2n – – x2n – 1y + + x2n – 2 y2 – – …– xy2n – 1 + y2n)

Разность нечетных степеней

      Если в формулах из Таблицы 3 заменить  y  на  – y ,  то мы получим группу формул «Разность нечетных степеней» (Таблица 4.):

      Таблица 4. – Разность нечетных степеней

Название формулы	Формула
Разность кубов	x3– y3 = (x – y) (x2 + xy + y2)
Разность пятых степеней	x5– y5 = (x – y) (x4 + x3y + x2y2 + xy3 + y4)
Разность седьмых степеней	x7– y7 = (x – y) (x6 + x5y + x4y2 + x3y3 + x2y4 + xy5 + y6)
…	…
Разность степеней порядка  2n + 1	x2n + 1– y2n + 1 = (x – y) (x2n + x2n – 1y + x2n – 2 y2 + …+ xy2n – 1 + y2n)

Разность кубов x3– y3 = = (x – y) (x2 + xy + y2)

Разность пятых степеней x5– y5 = = (x – y) (x4 + x3y + + x2y2 + xy3 + y4)

Разность седьмых степеней x7– y7 = = (x – y) (x6 + x5y + + x4y2 + x3y3 + + x2y4 + xy5 + y6)

…

Разность степеней порядка  2n + 1 x2n + 1– y2n + 1 = = (x – y) (x2n + + x2n – 1y + + x2n – 2 y2 + + …+ xy2n – 1 + y2n)

Разность четных степеней

      Группа формул «Разность четных степеней» приведена в Таблице 5.

      Таблица 5. – Разность четных степеней

Название формулы	Формула
Разность квадратов	x2– y2 = (x + y) (x – y)
Разность четвертых степеней	x4– y4 = = (x + y) (x3 – x2y + xy2 –y3) = = (x + y) (x – y) (x2 + y2)
Разность шестых степеней	x6– y6 = = (x + y) (x5 – x4y + x3y2 – x2y3 + xy4 –y5) = = (x + y) (x – y) (x2 – xy + y2) (x2 + xy + y2)
Разность восьмых степеней	x8– y8 = = (x + y) (x7 – x6y + x5y2 – x4y3 + x3y4 – x2y5 + xy6 –y7) = = (x + y) (x – y) (x2 + y2) (x4 + y4)
…	…
Разность степеней порядка  2n	x2n– y2n = (x + y) (x2n – 1 – x2n – 2 y + x2n – 3 y2 – …+ xy2n – 2 – y2n – 1) , x2n– y2n = (x – y) (x2n – 1 + x2n – 2 y + x2n – 3 y2 + …+ xy2n – 2 + y2n – 1)

Разность квадратов x2– y2 = (x + y) (x – y)

Разность четвертых степеней x4– y4 = = (x + y) (x3 – x2y + + xy2 –y3) = = (x + y) (x – y) (x2 + + y2)

Разность шестых степеней x6– y6 = = (x + y) (x5 – x4y + + x3y2 – – x2y3 + + xy4 –y5) = = (x + y) (x – y) (x2 – – xy + y2) (x2 + + xy + y2)

Разность восьмых степеней x8– y8 = = (x + y) (x7 – x6y + + x5y2 – x4y3 + + x3y4 – – x2y5 + xy6 –y7) = = (x + y) (x – y) (x2 + + y2) (x4 + y4)

…

Разность степеней порядка  2n x2n– y2n = = (x + y) (x2n – 1 – – x2n – 2 y + + x2n – 3 y2 – – …+ xy2n – 2 – – y2n – 1) * * * x2n– y2n = = (x – y) (x2n – 1 + + x2n – 2 y + + x2n – 3 y2 + + …+ xy2n – 2 + + y2n – 1)

      Замечание. Оба разложения на множители двучлена:

x²ⁿ– y²ⁿ ,

приведенные в последней строке Таблицы 5, можно продолжить и далее, по аналогии с тем, как это сделано в других строках таблицы.

      Другие формулы сокращенного умножения можно посмотреть в разделе «Формулы сокращенного умножения: степень суммы, степень разности» нашего справочника.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

www.resolventa.ru

Формулы понижения степени. Видеоурок. Алгебра 10 Класс

Тема: Преобразование тригонометрических выражений

Урок: Формулы понижения степени

На уроке выводятся формулы понижения степени для синуса и косинуса из формул двойного аргумента, также выводятся формулы понижения степени для  тангенса и котангенса с использованием формул понижения степени для синуса и косинуса. Решается несколько задач с использованием данных формул.

Дано:

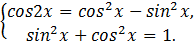
Доказать:.

Доказательство:

1) 

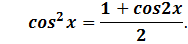
2) 

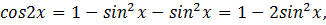
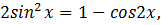
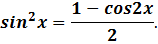
Итак, степень понижается за счет удвоения аргумента:

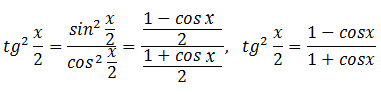
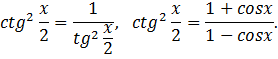
Получается,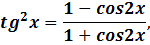

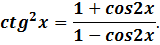
1. Доказать:

Доказательство:

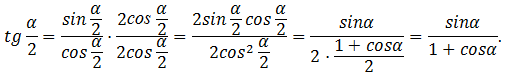
Анализ: ОДЗ не изменяется

2. Доказать:

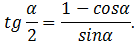
Доказательство:

Анализ: кроме 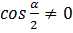 добавляется 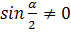, что сужает ОДЗ.

3. Дано: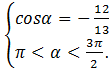

Найти:

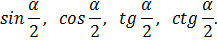
Анализ условия: Угол задан однозначно, см. рис.1.

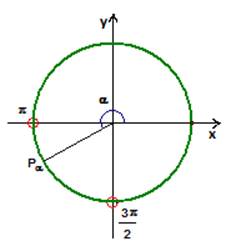
Рис. 1.

Указание: все функции половинного аргумента можно вычислять через косинус полного аргумента.

Решение:

1) 

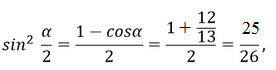
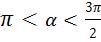, то , т.е. угол второй четверти, где синус величина положительная.

Ответ: .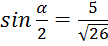

2)

Выше показали, что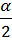

 находится во второй четверти, где его косинус величина отрицательная.

Ответ:.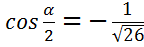

Проверка:

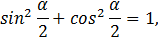
3) 

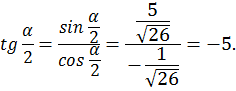
Ответ:

4) 

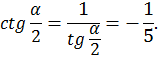
Ответ: .

4. Дано:  

Найти: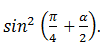 

Решение:

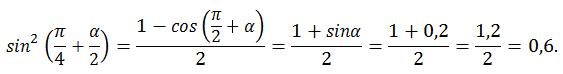
Ответ:

На уроке рассматривались формулы понижения степени и их использование при решении задач.

На следующем уроке будут рассмотрены формулы преобразования суммы тригонометрических функций в произведение.

 

Список рекомендованной литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.

8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983

 

Дополнительные веб-ресурсы

1. Интернет-портал Mathematics.ru (Источник). 

2. Портал Естественных Наук (Источник). 

3. Интернет-портал exponenta.ru (Источник). 

 

Сделай дома

№№ 21.20(а, б), 21.22(а), 21.23 (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)

interneturok.ru

Возведение в степень | Формулы с примерами

Формула возведения в степень

Степенью числа a с показателем n, называется произведение n сомножителей, каждый из которых равен a.
a — действительное число,
n — натуральное число.

Калькулятор возведения в степень онлайн

Правило возведения в степень

Степень показывает количество раз, которое некое число умножается на себя. Она обозначается малой цифрой (показателем степени) справа вверху от основного числа (основани степени).

Возведение в степень — действие нахождения степени:

Умножение числа на себя один раз называется возведением числа в квадрат.

Умножение числа на себя два раза называется возведением в куб.

Свойства возведения в степень

1. Если отрицательно число возвести в четную степень, то получим положительное число.

Пример

(-2)22 > 0; (-3)34 > 0; (-5)88 > 0.

2.Если отрицательное число возвести в нечетную степень, то получим отрицательное число.

! Возведение в степень — действие третьей ступени, его выполняют перед действиями второй ступени (умножением и делением) и первой ступени (сложением и вычитанем).

Возведение в степень примеры

1. x³ = x • x • x ;
a = x ;

2. k⁵ = k • k • k • k • k ;
a = k ;

3. 18¹ = 18 ;
a = 18;

4. 1¹⁸ = 1;
a = 1 ;

5. 0 ⁷ = 0;
a = 0;

6. 5³ = 5 • 5 • 5 = 125 ;
a = 5 ;

7. 7⁴ = 7 • 7 • 7 • 7 = 2 401 ;
a = 5 ;

formula-xyz.ru

Степенные функции y=xn и y=x1/n, n∈Z. Свойства, графики. Квадратичная функция. Свойства степеней. Свойства арифметических корней. Формулы сокращенного умножения. Примеры значения степенных функций.

Техническая информация тут Перевод единиц измерения величин Таблицы числовых значений Алфавиты, номиналы, единицы Математический справочник тут Физический справочник Химический справочник Материалы Рабочие среды Оборудование Инженерное ремесло Инженерные системы Технологии и чертежи Личная жизнь инженеров Калькуляторы Поиск на сайте DPVAПоставщики оборудованияПолезные ссылкиО проектеОбратная связьОтветы на вопросы.Оглавление

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  / / Степенные функции y=xn и y=x1/n, n∈Z. Свойства, графики. Квадратичная функция. Свойства степеней. Свойства арифметических корней. Формулы сокращенного умножения. Примеры значения степенных функций. Поделиться:    Степенные функции y=xn и y=x1/n, n∈Z. Свойства, графики. Квадратичная функция. Свойства степеней. Свойства арифметических корней. Формулы сокращенного умножения. Примеры значения степенных функций. Справочно: Действительные числа: натуральные числа, целые числа, рациональные числа, иррациональные числа. Понятия и обозначения. Примерно 6 или 7-класс (12-13 лет) Свойства функции y=xn Область определения Область значений Четность Промежутки знакопостоянства на которых: y > 0 y < 0 Промежутки монотонности: возрастания убывания Общие точки всех графиков Свойства Область определения Область значений Четность Промежутки знакопостоянства на которых: y > 0 y < 0

dpva.ru