Что такое корень уравнения

Корнем уравнения называют число, подстановка которого в уравнение вместо переменной (обычно \(x\)), дает одинаковые значения выражений справа и слева от знака равно.

Решая, например, уравнение \(2x+1=x+4\) находим ответ: \(x=3\). Если подставить тройку вместо икса, получатся одинаковые значения слева и справа: 

\(2x+1=x+4\)
\(2\cdot3+1=3+4\)
\(7=7\)

И никакое другое число, кроме тройки такого равенства нам не даст. Значит, число \(3\) – единственный корень уравнения.

Еще раз: корень – это НЕ ИКС! Икс – это переменная, а корень – это число, которое превращает уравнение в верное равенство (в примере выше – тройка). И при решении уравнений мы это неизвестное число (или числа) ищем.

Пример: Является ли \(5\) корнем уравнения \(x^{2}-2x-15=0\)?
Решение: Подставим \(5\) вместо икса:

\(5^{2}-2\cdot5-15=0\)
\(25-10-15=0\)
\(0=0\)

По обе стороны от равно — одинаковые значения (ноль), значит 5 действительно корень.

Матхак: на контрольных таким способом можно проверить верно ли вы нашли корни.

Пример: Какое из чисел \(0, \pm1, \pm2\), является корнем для \(2x^{2}+15x+22=0\)?
Решение: Проверим подстановкой каждое из чисел:

проверяем \(0\):	\(2\cdot0^{2}+15\cdot0+22=0\)
	\(0+0+22=0\)
	\(22=0\) — не сошлось, значит \(0\) не подходит
проверяем \(1\):	\(2\cdot1^{2}+15\cdot1+22=0\)
	\(2+15+22=0\)
	\(39=0\) — опять не сошлось, то есть и \(1\) не корень
проверяем \(-1\):	\(2\cdot(-1)^{2}+15\cdot(-1)+22=0\)
	\(2-15+22=0\)
	\(9=0\) — снова равенство неверное, \(-1\) тоже мимо
проверяем \(2\):	\(2\cdot2^{2}+15\cdot2+22=0\)
	\(2\cdot4+30+22=0\)
	\(60=0\) — и вновь не то, \(2\) также не подходит
проверяем \(-2\):	\(2\cdot(-2)^{2}+15\cdot(-2)+22=0\)
	\(2\cdot4-30+22=0\)
	\(0=0\) — сошлось, значит \(-2\) — корень уравнения

Очевидно, что решать уравнения перебором всех возможных значений – безумие, ведь чисел бесконечно много. Потому были разработаны специальные методы нахождения корней. Так, например, для линейных уравнений достаточно одних только равносильных преобразований, для квадратных – уже используются формулы дискриминанта и т.д. Каждому типу уравнений – свой метод.

Ответы на часто задаваемые вопросы

Вопрос: Может ли корень уравнения быть равен нулю?
Ответ: Да, конечно. Например, уравнение \(3x=0\) имеет единственный корень — ноль. Можете проверить подстановкой.

Вопрос: Когда в уравнении нет корней?
Ответ:

В уравнении может не быть корней, если нет таких значений для икса, которые сделают уравнение верным равенством. Яркий примером тут может быть уравнение \(0\cdot x=5\). Это уравнение не имеет корней, так как значение икса здесь не играет роли (из-за умножения на ноль) — все равно левая часть будет всегда равна нулю. А ноль не равен пятерке. Значит, корней нет.

Вопрос: Как составить уравнение так, чтоб корень этого уравенения был равен некоторому заданному числу (например, тройке)?
Ответ: появится позже.

Вопрос: Что значит «найдите меньший корень уравнения»?
Ответ: Это значит, что нужно решить уравнение, и в ответ указать его меньший корень. Например, уравнение \(x^2-5x-6=0\) имеет два корня: \(x_1=-1\) и \(x_2=6\). Меньший из корней: \(-1\). Вот его и надо будет записать в ответ. Если бы спрашивали про больший корень, то надо было бы записать \(6\).

Скачать статью

Урок математики на тему «Уравнение. Решение уравнений способом подбора» (2 класс)

Михайлова Галина Николаевна,

учитель начальных классов

МБОУ «СОШ № 38 имени Героя РФ Константинова Леонида Сергеевича» г. Чебоксары

Первые уроки по решению уравнений в начальных классах.

В условиях внедрения ФГОС НОО формируется активная личность, обладающая способностью эффективно решать новые жизненные проблемы. В связи с этим учителю начальной школы необходимо развивать потенциал каждого ученика, используя новые формы подачи учебной информации для усиления мыслительной деятельности и повышения активности обучения.

Решение уравнений — одна из главных тем математики начальной школы. Грамотно организованное обучение этой темы поможет учащемуся в дальнейшем успешно справляться со сложными уравнениями и задачами. Поэтому на первых уроках учитель должен показать эффективный путь решения уравнения способом подбора. Прежде всего, этот способ развивает осознанно верный подход к решению уравнения: ученик сразу ориентируется на то, что подобранное им число он должен проверить и выяснить, верное или неверное числовое равенство получится. Так, решая уравнение x + 2 = 5, ученик подставляет вместо x числа 1, 2, 3. Даже если он смог сразу дать верный ответ, то должен еще “доказать” его правильность, подставив найденное число в уравнение вместо х. В этом случае для проверки осознанности действий учащегося можно задать ему вопрос: «Почему х равен 3?». «Если вместо х подставить 3, то получится верное равенство: 3 + 2 = 5. 5 = 5». Таким образом, на первых уроках в процессе решения уравнений ученик учится целесообразно подбирать числа и выполнять самопроверку.

Урок математики во 2 классе

«Уравнение. Решение уравнений способом подбора»

Цели урока:

1) Обучающие: познакомить учащихся с новым математическим понятием «уравнение», с решением уравнения способом подбора значения неизвестного; сформировать умение правильно записывать уравнение и выполнять его проверку.

2) Развивающие: продолжить работу над развитием УУД; развить вычислительные навыки учащихся и умение решать текстовые задачи.

3) Воспитательные: воспитать чувство товарищества и взаимопомощи; повысить уровень познавательного интереса к предмету математики.

Оборудование: мультимедийная презентация к уроку, карточки с заданиями для групповой работы, учебник М. И. Моро и др. «Математика», 2 класс, 1 часть. – М.: Просвещение, 2011.

Тип урока: урок формирования новых умений.

Формирование познавательных УУД: добывать новые знания, найти и переработать необходимую информацию в учебнике, наблюдать и делать самостоятельные выводы, моделировать алгоритм решения уравнения способом подбора, учиться строить речевые высказывания и эффективно решать уравнения, выполнять рефлексию.

Формирование регулятивных УУД: определить цель деятельности на уроке с помощью учителя, совместно с ним обнаруживать и формулировать учебную проблему, выполнять самоанализ и самоконтроль результата учебной деятельности, оценивать свои знания и незнания, качество и уровень усвоения новых знаний.

Формирование коммуникативных УУД: учиться сотрудничать с учителем и с одноклассниками, работать в группе: контролировать, корректировать действия одноклассников; формулировать с достаточной полнотой и точностью несложные выводы и находить аргументы, подтверждающие вывод.

Ход урока.

I. Организационный момент.

Самоопределение к деятельности.

Эмоциональный настрой.

Долгожданный дан звонок, начинается урок!

Сегодня важная работа у нас:

Знайка — математик пришёл к нам в класс.

Решение уравнения мы с ним разберём,

Будем внимательны – всё быстро поймём.

— Ребята, сегодня нас ждут новые интересные задания (слайд 2).

Читают стихотворение вместе с учителем.

II. Постановка учебной задачи.

— Откройте тетрадь и красиво запишите число, классная работа.

— Как вы думаете, что разберём на уроке? Правильно, на уроке будем учиться решать уравнения.

— А что такое уравнение? Верно, мы ещё не знаем, что такое уравнение.

— Какие учебные задачи появились? Правильно, познакомимся с уравнениями, будем старательны и научимся решать их.

Записывают число, классная работа.

Определяют цель деятельности на уроке и формулируют учебную задачу с помощью учителя.

III. Актуализация опорных знаний и фиксация затруднений в

деятельности.

— Ребята, на уроке нам пригодится ваше умение считать быстро и правильно. Поэтому начнём урок с устного счёта. Каждое число увеличьте на 5 (слайд 3).

Молодцы!

— Ребята, вы уже знаете, что числовые равенства бывают верные и неверные. Следующее задание. Найдите и выпишите в первый столбик верные равенства, а во второй – неверные равенства:

63 – 3 = 60 10 + 4 = 12 10 + 7= 17 85 – 80 = 5

8 – 2 = 3 6 + 5 = 11 5 + 6 = 12 9 – 4 = 4

– Проверьте свою работу и оцените её (слайд 4).

— Кто нашёл у себя ошибку? В каком примере? Объясните причину ошибки. Что необходимо сделать, чтобы избежать дальнейших ошибок? А кто не ошибся? Молодцы, ребята!

Устно составляют примеры и решают их.

Самостоятельная работа.

Самопроверка и самоанализ.

IV.Усвоение нового учебного материала.

— Рассмотрите рисунок в учебнике на странице 80. Что вы видите? Какое число надо поместить в окошко, чтобы это равенство стало верным? Выберите его. Правильно, поставив число 8 в окошко, получится верное равенство.

— Дети, посмотрите внимательно на доску. Я заменю окошко буквой x — маленькой буквой латинского алфавита и запишу: x + 4 = 12. В этой записи есть знак «=». О чём говорит этот знак?

— Правильно, получилось равенство. Чем отличается это равенство от равенств, знакомых нам? Верно, в этом равенстве есть неизвестное число х, его надо найти. Это равенство называется уравнением. Подумайте и сделайте вывод: что такое уравнение? Сравним наш вывод с правилом в учебнике на стр. 80. Наш вывод точный?

— Запишите в тетрадь это уравнение. Подумайте и найдите ответ на вопрос: как его решить? Как найти значение х, при котором наше равенство будет верным? Правильно, надо подобрать подходящее число. (Подходящее число 8). Почему х равен 8? (Если вместо х подставить 8, то получится верное равенство). Правильно, запишем: x = 8. Выполним проверку. Подставим вместо х число 8, получим равенство: 8 + 4 = 12. Проверим: верное ли равенство получили? Сумма 8 и 4 равна 12. Отметим: 12 = 12. Мы нашли корень уравнения: x = 8.

— Составим алгоритм решения уравнения способом подбора:

1) выбирать число, подставить его в уравнение и

проверить, получится ли верное равенство;

2) если равенство неверное, то надо выбрать

другое число и выполнить проверку;

3) если получили верное равенство, то уравнение решено, найден корень уравнения.

Отвечают на вопросы.

Делают вывод и сравнивают его с правилом в учебнике.

Записывают уравнение в тетрадь и решают его способом подбора. Выполняют проверку.

Составляют алгоритм решения уравнения способом подбора.

V.Первичное закрепление новой темы.

— Работаем по учебнику. Выполним №1 на стр. 80. Решим уравнения по составленному алгоритму.

Решу уравнение 9 + х = 14 подбором чисел. Выберу первое число 7. Проверю: получится равенство 9 + 7 = 14. Это равенство неверное. Выберу второе число 5. Получилось верное равенство: 9 + 5 = 14. Уравнение решено: (корень уравнения) х = 5. (Устно продолжают работу.)

Поясняют, уточняют, проверяют свою работу,

контролируют, корректируют действия одноклассников

VI.Закрепление знаний. Самостоятельная групповая работа с самопроверкой по эталону.

— Ребята, помогая друг другу, выберите уравнения и решите их:

28 + а 14 – 9 = 5 x + 3 = 10 9 – х = 4

20 – х х – 8 = 12 b > 10 8 + х = 12

— Будьте внимательны. Успехов вам, дружной работы!

Групповая работа.

Самоконтроль результата групповой деятельности (

слайд 5).

VII. Физминутка.

Отдохнём, выполним гимнастику для глаз.

Выполняют гимнастику

(слайд 6).

VIII. Закрепление ранее изученного.

— К задаче №7 на стр. 81 выбираете задания любого уровня сложности:

А) Узнать, сколько времени занимает дорога на автобусе.

Б) Узнать, за сколько минут мама доедет до работы.

На оценку «4» выполнить задание А.

На оценку «5» выполнить задания А и Б.

— Проверьте свою работу.

Самостоятельно решают задачу №7 (с. 81) по уровням сложности.

Проверяют и оценивают свою работу по

слайду 7.

IX.Логическая задача.

Определите закономерность и продолжите ряд чисел: 4, 7, 11, 16, 22, …, …, … (слайд 8).

Резервное задание.

X.Рефлексия учебной деятельности.

— Ребята, чем запомнился вам сегодняшний урок? Что понравилось больше всего?

— Какие учебные задачи появились в начале урока?

— Кто выполнил все учебные задачи?

— Запомнили, что называется уравнением? Что значит решить уравнение?

— Вы молодцы!

Оценивают свою работу, собственные знания, соотносят цель и

результаты деятельности на уроке.

XI.Домашнее задание.

№ 2 (с. 80) и № 6 (с. 81).

УМК «Школа России»; 2 класс; Урок (ОНЗ) математики во 2-м классе по теме «Уравнение»

УМК «Школа России»; 2 класс; Урок (ОНЗ) математики во 2-м классе по теме «Уравнение» (открытие новых знаний)

Цели урока:

Обучающие:

• дать детям новое математическое понятие: «уравнение»;

• сформировать умение решать уравнения на основе взаимосвязи между частью и целым;

Развивающие:

• развивать вычислительные навыки, внимание, наблюдательность, память; активизировать мыслительную деятельность;

• развивать устойчивую мотивацию к процессу обучения;

• развивать интеллектуальные и коммуникативные общеучебные умения;

• развивать организационные общеучебные умения, в том числе умение исправлять собственные ошибки.

Воспитательные:

• воспитание стремления совершенствовать свою математическую речь;

• умение контролировать самого себя, находить, исправлять и оценивать самостоятельно результаты своих действий; повышение уровня познавательного интереса к предмету математики.

Тип урока: открытия нового знания.

ХОД УРОКА

1. Мотивация к учебной деятельности:

Цель:

1) создать мотивацию к учебной деятельности на уроке путём обращения к внутреннему состоянию каждого;

• Ребята! Прочтите высказывание. «Всегда, везде и всюду – хочу, могу и буду!»

• Как вы объясните смысл высказывания? ( Мы будем узнавать что-то новое.)

• Какие шаги нужно выполнить, чтобы приобрести новое знание? (Повторить необходимое. Выполнение пробного действия. Фиксация затруднения. Постановка цели. Составление плана. Фиксация нового способа. Отработка умений по применению нового способа. Рефлексия учебной деятельности.

Пожелайте друг другу удачи! В путь!

II. Актуализация знаний и фиксация затруднения в пробном действии.

Цель:

1. актуализировать правила нахождения слагаемого и суммы, решение примеров с «окошками» на основе взаимосвязи слагаемого и суммы ;

2. создание проблемной ситуации.

Ну, а сейчас мы поиграем в игру «Домик и квартира» знакомые для нас задания для того, чтобы подготовиться к изучению нового материала. Класс делится на группы и каждая группа выполняет своё задание.

Дом № 1

Выпишите и решите только выражения с окошечком.

37 — 8 + 40 = 60

10+4 * 18 25 + 30

+ 7 = 14 23 * 9 + 9

9 + 7 m – 7, при m= 10, 16.

5 + 6 * 6 + 7 12 – 8

20 + = 25 12 – 4 * 9 + 7

а + 6, если а = 10, 12. – 8 = 10

Дом № 2

Выпишите и решите только неравенства.

37 — 8 + 40 = 60

10+4 * 18 25 + 30

+ 7 = 14 23 * 9 + 9

9 + 7 m – 7, при m= 10, 16.

5 + 6 * 6 + 7 12 – 8

20 + = 25 12 – 4 * 9 + 7

а + 6, если а = 10, 12. – 8 = 10

Дом № 3

Выпишите и решите только числовые выражения.

37 — 8 + 40 = 60

10+4 * 18 25 + 30

+ 7 = 14 23 * 9 + 9

9 + 7 m – 7, при m= 10, 16.

5 + 6 * 6 + 7 12 – 8

20 + = 25 12 – 4 * 9 + 7

а + 6, если а = 10, 12. – 8 = 10

Дом № 4

Выпишите и решите только буквенные выражения.

37 — 8 + 40 = 60

10+4 * 18 25 + 30

+ 7 = 14 23 * 9 + 9

9 + 7 m – 7, при m= 10, 16.

5 + 6 * 6 + 7 12 – 8

20 + = 25 12 – 4 * 9 + 7

а + 6, если а = 10, 12. – 8 = 10

Х + 3 = 18

-Какая группа выражений является лишней? (Неравенство, а все остальные равенства)

х + 9 = 18

• Ребята! Посмотрите на эту математическую запись! Решите. (Мы не можем решить. Мы не знаем как записать.)

• Какую цель перед собой ставите?

• Узнать, как называется это выражение и учиться решать.

— Как можно назвать это выражение? (□ + 9 = 18? Это пример с «окошком»)

• А кто знает как называется такая запись: a — 6? (Это буквенное выражение)

• А теперь посмотрите на эту запись: x + 9 = 18

• Встречалась ли нам раньше такая запись?

• На что она похожа? (на выражение с «окошком», буквенное выражение и т.д.)

• Было много разных предположений.

• Кто знает, как же правильно оно называется?

• Рассмотрим более подробно это выражение.

• Что нам говорит знак «=»? (это равенство)

• Какое слово говорят ребята когда начинаются каникулы? (Ура!)

• А теперь соедините эти два слова «ура»+ «равнение»= «Уравнение»Это равенство получило специальное название – «уравнение» (учитель вывешивает карточку со словом на доске).

Уточним, что же такое «уравнение». (Это равенство, с неизвестным, которое надо найти)

• Как вы думаете, что значит, решить уравнение? (Значит найти такое число, при котором равенство будет верным. Найти неизвестный компонент.)

• Верно, это число еще называют «корень уравнения» (учитель вывешивает карточку с термином на доске).

• Какой вывод вы сделаете? (Нам удалось выяснить, что такое уравнение)

• Молодцы!

• Расскажите друг другу, что такое уравнение.

• Решим это уравнение. (Учитель записывает на доске)

х + 9 = 18, -Что неизвестно? Как найти?

х = 18- 9

х=9.

9+9=18

18=18

Ответ: х=9.

IV. Первичное закрепление во внешней речи

Цель: проговаривание в устной речи.

• Докажите, что эта запись является уравнением?

• Назовите корень уравнения.

Цель: составление алгоритма решения.

-Как мы действовали при решении уравнения?

-Составим алгоритм (план решения). Работав парах

Алгоритм решения уравнений

1.Запиши уравнение.

2.Определим неизвестный компонент.

3.Подберём правило. вывешивается на доску

4.Найдём корень уравнения.

5.Выполним проверку.

6.Запишем ответ.

V. Первичное закрепление во внешней речи.

Цель: создать условия для фиксации изученного способа действия во внешней речи.

Уравнения: 9 + х = 14

• Решаем первое уравнение (читает его). (Определяю неизвестный компонент. Выделяю «целое» и «части». Неизвестно часть. Применяю правило: чтобы найти часть, из целого вычитаю часть. Нахожу часть. Это корень уравнения. Выполняю проверку. Записываю ответ.)

VI.Самостоятельная работа с самопроверкой по эталону (алгоритму).

Проверка.

х + 3 = 18

9 + х=14

7. Рефлексия деятельности. (Итог урока).

• Выполнили ли мы сегодня задачи, которые поставили в начале урока?

• Какие открытия вы сделали?

• Что называется уравнением?

• Что значит решить уравнение?

• Кто научился решать уравнения, поднимите желтый шарик, кто ещё испытывает затруднения, поднимите синий шарик.

• Это значит, что мы продолжим находить ответы на трудные вопросы на следующих уроках математики.

• Ребята! Вы сегодня молодцы. Ваша работа заслуживает похвалы. Удалось ли нам следовать нашему девизу?

• Урок окончен, но я уверена, что на этом не закончилось ваше стремление искать и находить ответы на трудные вопросы.

VIII. Инструктаж и запись домашнего задания

с. 81 № 9; составить и решить свое уравнение

Конспект урока по теме «Уравнения и его корни»

Урок алгебры в 7 классе А

Тема: Уравнение и его корни.

Тип урока: объяснение нового материала.

Цели:

1. Образовательные. Дать ученикам понятие о уравнении и его корнях.

2. Развивающие. Продолжать формирование элементов алгоритмической культуры, развивать логическое  мышление, память, формировать грамотную математическую речь, способность к анализу и самооценке.

3. Воспитательные. Продолжить формирование коммуникабельности, толерантности, ответственности за свои суждения.

4. Предполагаемые цели ученика: вспомнить из 6 класса решение  уравнений с помощью свойств; научиться решать уравнения более сложные, чем те, способы решения которых ему известны.

Ход урока:

1.Приветствие

2.Устный счет:

а) +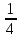

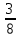
б) —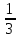

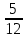
в) ·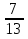

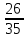
г) 7² +5

д)(-3)² +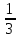

е)(-2)³ —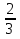

3.Изучение нового материала:

Сначала рассмотрим несколько примеров.

Пример 1.

Рассмотрим старинную задачу:

Летела стая гусей, а навстречу им летит гусь. «Здравствуйте, сто гусей!» — говорит гусь. «Нас не сто, — отвечают ему гуси. – Если бы нас было столько, сколько теперь, да ещё столько, да полстолька, да четверть столька, да ещё и ты, гусь, то тогда нас было бы сто». Сколько гусей в стае?

Обозначим буквой х число гусей в стае. По условию задачи

х+х+½х+¼х+1=100

Чтобы найти неизвестное число гусей, мы составили равенство, содержащее переменную. Дайте попробуем его решить: Перенесем слагаемое 1 в правую часть, изменив его знак на противоположный и приведем подобные слагаемые:

х+х+½х+¼х=100-1, 2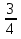х=99.

Разделим обе части уравнения на 2 :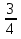

х=36.

Такие равенства называют уравнениями с одной переменной или уравнениями с одним неизвестным. Для решения задачи надо найти такие числа, которые обращают наше равенство в верное. Эти числа х называют решениями уравнения или корнями уравнения.

Определение: Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.

Решить уравнение – значит найти множество его корней. Иначе говоря, решить уравнение – значит найти все его корни или доказать, что их нет.

Решим примеры:

а) уравнение х + 1 = 6 имеет один корень – число 5.

б) постарайтесь решить уравнение (х-1)(х-5)(х-8)=0 , чтобы решить это уравнение нужно каждый множитель приравнять к нулю и найти корни:1,5 и8.Каждое из этих значений х обращает данное произведение в ноль, а при любых других значениях х ни один из множителей не равен нулю, а значит, не равно нулю и их произведение.

в)уравнение х=х+4 не имеет корней, т.к. значение его левой части меньше значения правой части при любом значении х.

г) решим уравнение 3(х+5)=3х+15 имеет бесконечно много корней, т.к. в силу распределительного свойства умножения значение его левой части равно значению правой части при любом значении х, т.е. по сути, уравнение является тождеством.

В уравнении 17-3х=2х-2 обе его части имеют смысл при любом значении х, а в уравнении 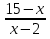= х+9 обе его части имеют смысл только тогда, когда х ≠2. Говорят, что областью определения первого уравнения (или область допустимых значение переменной) является множество всех чисел, а областью определения второго уравнения – множество всех чисел кроме 2.

Определение: Областью определения уравнения (областью допустимых значений переменной в уравнении) называется значение переменной, при которых обе части уравнения имеют смысл.

Рассмотрим пример:

а) уравнение х²-5х+6=0 и (х-2)(х-3)=0 являются равносильными, т.к. каждое из этих уравнений имеет одни и те же корни.

б)уравнения х²+х=-3 и 2х+5=2х также являются равносильными, т.к. каждое из этих уравнений корней не имеет.

в)уравнения х²-5х+6=0 и х+4=6 не являются равносильными, т.к. первое уравнение имеет два корня х=2 и х=3,второе уравнение только один корень х=2.Несмотря на то, что уравнения имеют один общий корень х=2.

В процессе решения уравнений стремятся данное уравнение заменить более простым уравнением, равносильным ему. При этом используются следующие свойства:

Из данного уравнения получается равносильное ему уравнение,

1)если перенести слагаемое из одной части уравнения в другую, изменив его знак;

2)если обе части уравнения умножить или разделить на одно и тоже отличное от нуля число.

4.Формирование умений и навыков:

№502,504(а,б,в),508(а,в)

Самостоятельная работа (на 10 минут):

1 вариант

1.Из множества 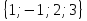выделите подмножество состоящее из корней уравнения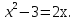

2.Укажите область определения уравнения:

.

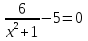3.Сколько корней имеет уравнение:

3х — 21=16 + 3х.

2 вариант

1.Из множества 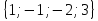выделите подмножество состоящее из корней уравнения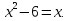

2.Укажите область определения уравнения:

.

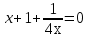3.Сколько корней имеет уравнение:

12х — 2=7х+ 1.

5.Подведение итогов.

Контрольные вопросы:

1.Что называется уравнением? Приведите примеры.

2.Что называется корнем уравнения?

3.Какие уравнения называются равносильными?

4.Сформулируте основное свойства уравнений.

Выставление оценок за урок.

6.Задание на дом

П.16, вопросы 1-3 на стр.106,№503,512(в,г),515.

Конспект урока по математике на тему «Корень уравнения»

Конспект урока

Предмет: Математика

Класс: 5

Тип урока: открытие новых знаний

Название урока: Основа, на которой все держится

Тема урока: Уравнение и его корни.

Основные понятия: уравнение, корень уравнения, решить уравнение.

Межпредметное понятие: корень

Предметное понятие: корень уравнения

Планируемый результат:

Личностные: самопознание,

самооценивание,

формирование целостного мировоззрения,

смыслообразование

Метапредметные: формирование

Регулятивных УУД: умение определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.

Коммуникативных УУД: умение оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.

Познавательных УУД: умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания; находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.

Предметные: Понимание, что такое «уравнение», «корень уравнения», «решение уравнений»

Умение решать уравнения вида а + х = b, а – х = b, х – а = b.

Ход урока.

Этапы урока

Деятельность учителя

Деятельность учащихся

Формируемые УУД

I.

Подготовитель-

ный этап

Учитель приветствует детей и читает пожелания:

Прозвенел звонок весёлый.

Вы начать урок готовы?

Будем слушать, рассуждать,

И друг другу помогать!

Улыбнёмся друг другу, пожелаем удачи. (хлопки в ладони друг другу)

— Что вам пригодится для успешной работы?

— Какое нужно настроение, чтобы урок для вас был удачным?

— Я желаю вам сохранить хорошее настроение весь урок. Я верю в вас, у вас всё получится.

— Ребята, а вы любите тайны и секреты?

— Сегодня на уроке нам предстоит научиться раскрывать что-то тайное и неизвестное. Вы готовы? Вам интересно?

— Что ж отправляемся в царство математики совершать новые открытия.

Название нашего урока «Основа, на которой все держится».

Как вы думаете, о чем это?

Включаются в учебную деятельность.

Отвечают на вопросы учителя.

Коммуникативные УУД.

Формирование обобщенного представления о межпредметном понятии

Выявление субъектного опыта

Актуализация знаний

Что изображено на рисунках?

Загадка:

Я у дуба,

Я у зуба,

Я у слов

И у цветов.

Я упрятан в темноту.

Я не вверх, а вниз расту

Что такое корень?

Запишите на рабочих листах

Давайте обратимся к толковому словарю, узнаем значение этого слова.

(Учащиеся зачитывают все значения слова корень).
= 1) Подземная часть растения, служащая, для укрепления его в почве и всасывания из нее воды и питательных веществ. Например: пустить корни.
2) Внутренняя находящаяся в теле часть волоса, зуба, ногтя. Например: покраснеть до корней волос.
3) В русском языке основная часть слова без приставок и суффиксов.
4) В математике: корень ?
Где еще вы слышали слово «корень»?
(слайд )

Обясните следующие фразы:

Корень зла

В корне неправильно

Коренная перестройка

Смотри в корень или зри в корень

Значит, корень – это основа чего – то.

Слово «корень» имеет несколько значений, оно является многозначным. Можно ли употреблять слово одно слово корень? (нет)

Обязательно корень чего — то

О каких корнях пойдет сегодня речь на нашем уроке? О корне уравнения.

Сегодня мы с вами будем работать с уравнениями, с корнями уравнений.

Сформулируйте тему нашего урока и его цель.

А что такое уравнение?

Среди записей найдите уравнения

1. 25 > 13

2. 15 + 8 = 23

3. a + b =b+ a

4. 18 + Х = 56

5. 138 – Х

6. У – 7 = 20

7. (Х+ 10) – 3 = 17

Сформулируйте, что такое уравнение?

(равенство, содержащее букву, значение которой надо найти)

Уравнение – это:

1. Равенство

2. Содержит букву

Что значит решить уравнение?

(найти значение буквы)

А что такое корень уравнения?

Запишите на рабочих листах

Отвечают на поставленные вопросы.

Осмысление собственного опыта.

Проговаривают то, что знают.

Выполняют задание устно, письменно

Предлагают разные варианты.

Осмысление собственного опыта,

Познание

нового

Слушают учителя

Формулируют цели урока с помощью учителя.

Знаково – символьные УУД

Познавательные УУД

Логические УУД (обобщения, сравнения)

Личностные УУД

Познавательные УУД

Регулятивные УУД

Личностные УУД

II Основной этап.

Формулировка определения и запись в алгоритмизированном виде

Физминутка

Работа с определением

Первичное закрепление

Что вы видите на дереве? (уравнения)

Запишите уравнения с корнем 8.

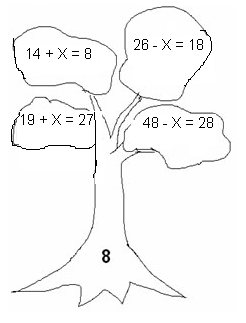
Взаимопроверка. Работа в парах. Учащиеся зачитывают свои уравнения.

Почему вы выбрали именно эти?

(при подстановке вместо буквы получалось верное числовое равенство)

Что –же такое корень уравнения?

(значение буквы, при котором уравнение превращается в верное числовое равенство)

Вывод: Корень уравнения- это

1. число (значение буквы)

2. при подстановке в уравнение получается верное числовое равенство

Давайте прочитаем определения корня уравнения в учебнике, откройте стр. 59.

Что значит решить уравнение? (найти его корни)

Какие из чисел 0, 1, 2, 3 являются корнем уравнения Х + 3 = 6

Умеете ли вы решать уравнения?

Решите уравнения

Х + 14 = 36

Х – 23 = 95

95 – Х = 23

Взаимопроверка. Работа в парах.

Назовите корни уравнения

А как вы решили 1 уравнение?

Действием вычитанием. Находим неизвестное слагаемое

Как решили 2 уравнение?

Действием сложением. Находим неизвестное уменьшаемое

Как решили 3 уравнение?

Действием вычитанием. Находим неизвестное вычитаемое

Молодцы!

Выполняют задание .

Предлагают свои варианты.

По учебнику читают

Сравнивают свой вывод с выводом в учебнике

Решают уравнения.

Познавательные УУД

Коммуникативные УУД

Логические УУД

Познавательные УУД

Логические УУД (отнесение объекта к понятию)

Предметные УУД

Проблемная ситуация, связанная с возможным количеством корней уравнений

Работа в парах

А как вы думаете, ребята, уравнения могут иметь только один корень?

Запишите и найдите корень уравнения:

а : а = 1

Сколько корней может иметь это уравнение?

Много. Вместо а можно поставить любые числа.

Какое только число нельзя подставить в это равенство (на что нельзя делить)?

= Нельзя делить на 0.

Какой вывод можно сделать?

= Вывод: уравнение может иметь несколько корней.

2) Могут ли уравнения не иметь корней? 
решите уравнение и сделайте вывод.

Уравнение: 0 ∙ х = 7

Уравнение 0 ∙ х = 7 не имеет корней.

На рабочих листах заполните таблицу и сделайте вывод.

Вывод: Уравнение может иметь разное количество корней

Работают в парах

Коммуникативные УУД

Логические УУД (умение обосновывать)

Домашнее задание

Запишите в дневники домашнее задание

П. 10, № 395 (а, в, д) – решить 3 уравнения

№ 403 (а) – решить пример в несколько действий

Рефлексия учебной деятельности

Выявление субъектного опыта

Подведем итог нашего урока

Какая была цель урока?

Что узнали на уроке?

Что общего у всех значений слова корень?

Что такое корень уравнения?

(исправьте другим цветом ваши определения в рабочих листах)

Отвечают на вопросы учителя.

рассказывают, что узнали, знают, смогли.

Делают самооценку

Личностные УУД (развитие рефлексивных способностей)

Коммуникативные УУД

Рабочий лист к уроку по теме «Уравнение и его корни»

самооценка

Корень –

Корень уравнения –

Заполните таблицу:

Сколько корней имеет каждое уравнение?

b + 40 = 60

х :х = 1

у • 0 = 1000

Уравнение имеет

.

Уравнение имеет .

Уравнение имеет .

Вставь пропущенные слова

Когда уравненье решаешь, дружок,

Ты должен найти у него ……..

Значение буквы проверить несложно,

Поставь в …………………. его осторожно.

Коль верное …………… выйдет у вас,

То …………….. значенье зовите тотчас.