Площадь трапеции | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Трапеция – это четырехугольник, у которого две стороны параллельны друг другу. Высотой трапеции называют линию, перпендикулярную основаниями, для удобства ее часто проводят из тупого угла трапеции на большее основание. Средняя линия трапеции – это линия, которая параллельна основаниям, и разделяет боковые стороны ровно пополам. Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два.
Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.
Доказательством этой формулы будет служить представление площади трапеции, как суммы площадей двух треугольников полученных при проведении диагонали.
Площади этих треугольников будут равны соответственно и (для того, чтобы нарисовать высоту во втором треугольнике, необходимо будет продлить основание b).
Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с помощью метода подстановки.
Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y.
Таким образом x+y=d-b, y=d-b-x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту и . Приравнивая, получаем a2-x2=c2-y2 или x2-y2=a2-c2.
x2-(d-b-x)2=a2-c2 — Подставляем вместо х полученное выше выражение d-b-y.
x2-d2+bd+dx-b2+bd-bx-x2+dx-bx=a2-c2 — Раскрываем скобки.

2dx-2bx=a2-c2+d2+b2-2bd — Переносим все вправо, оставляя слева только y.
2x(d-b)=a2-c2+(d-b)2 — Выносим общие множители.
Подставляем обратно y в формулу высоты .
Формула площади трапеции через стороны будет выглядеть так:
Площадь трапеции через диагонали и угол между ними считается условным делением трапеции на четыре треугольника, точно также как и площадь любого произвольного четырехугольника.
Площадь равнобедренной трапеции можно найти еще одним способом, если даны угол при основании и радиус вписанной окружности. Дело в том, что центр вписанной окружности, откуда берет свое начало радиус, находится точно в центре трапеции, таким образом, приравнивая высоту и диаметр окружности (либо удвоенный радиус). Также одно из свойств трапеции, описанной вокруг окружности – это равенство суммы оснований и суммы боковых сторон, значит, мы сможем найти среднюю линию, зная боковые стороны.
Тогда площадь трапеции равна
Площадь трапеции — формулы, примеры расчета,
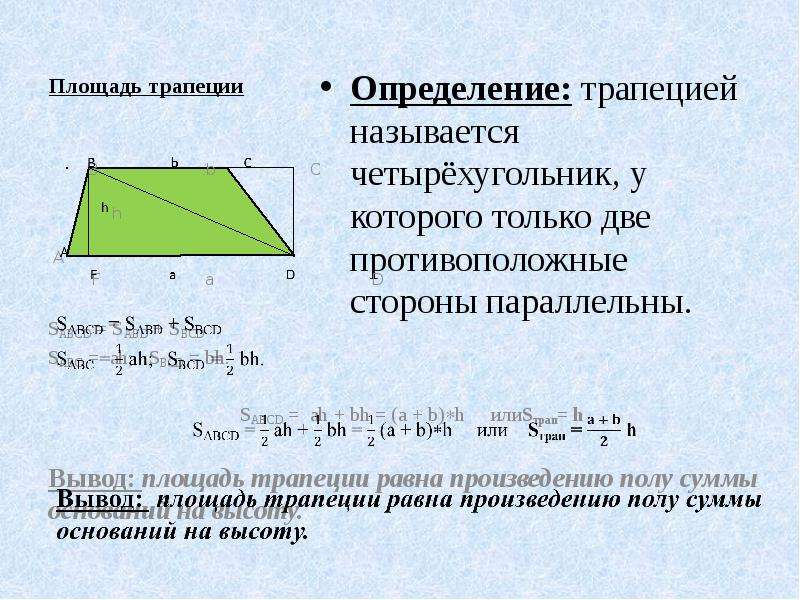
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
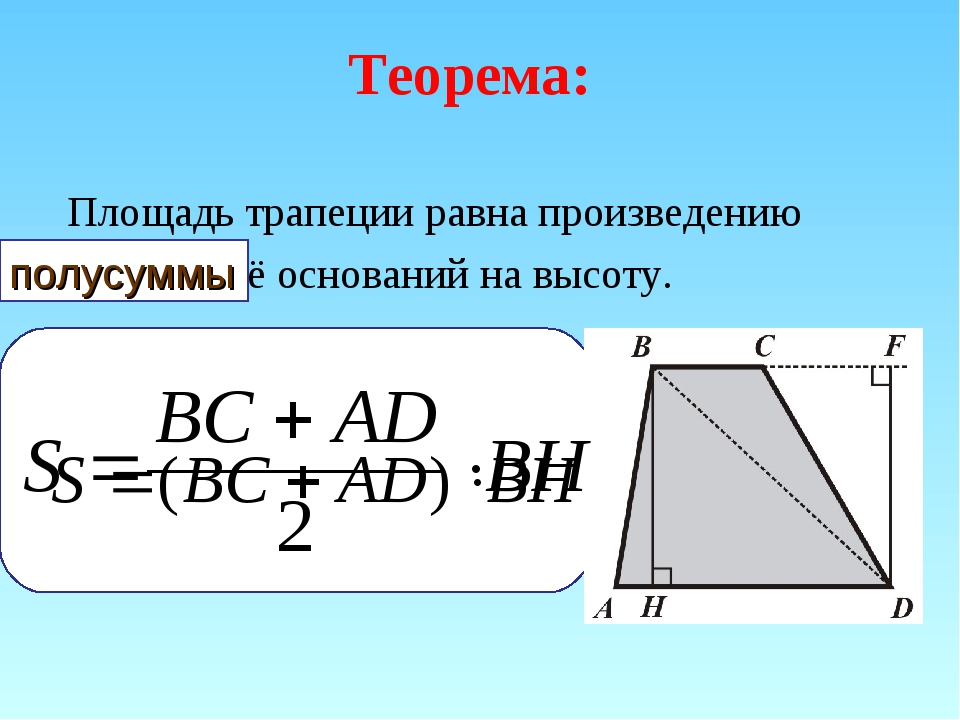
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Допустим, дана трапеция с основаниями a = 3 см, b = 7 см и боковыми сторонами c = 5 см, d = 4 см.
 найдем площадь фигуры:
найдем площадь фигуры:Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Помните, что диагонали равнобокой трапеции равны между собой!
Далее рассмотрим еще один пример расчета площади равнобедренной (равнобокой) трапеции. Формула через стороны и прилегающие к основанию углы позволит легко найти площадь фигуры.
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция. Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Площадь трапеции: как вычислить, формула. Как найти площадь трапеции: формулы и примеры
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
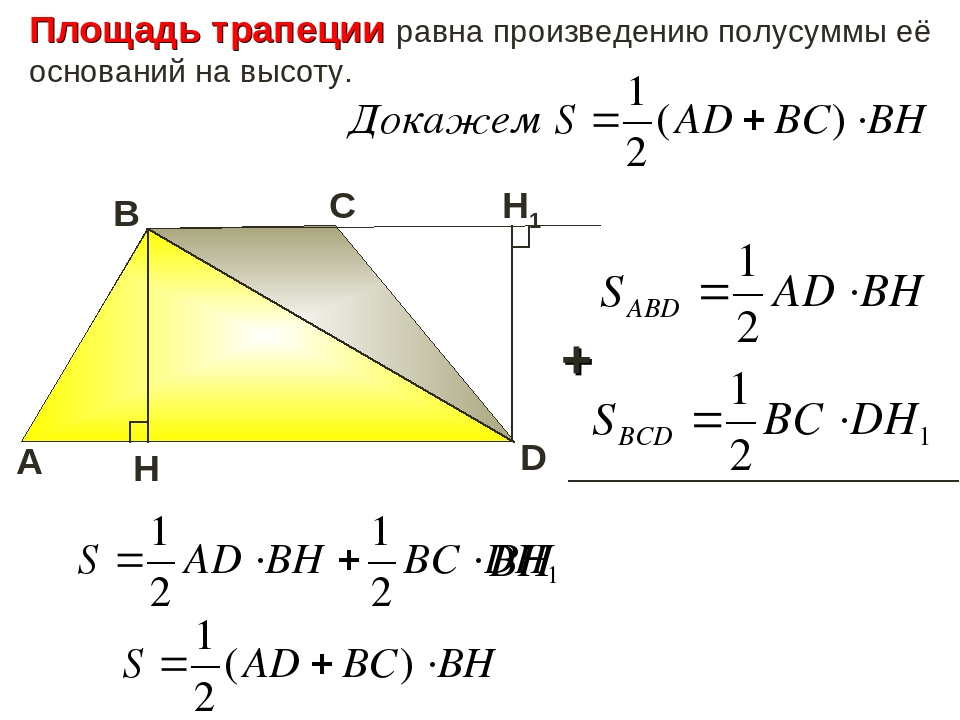
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E.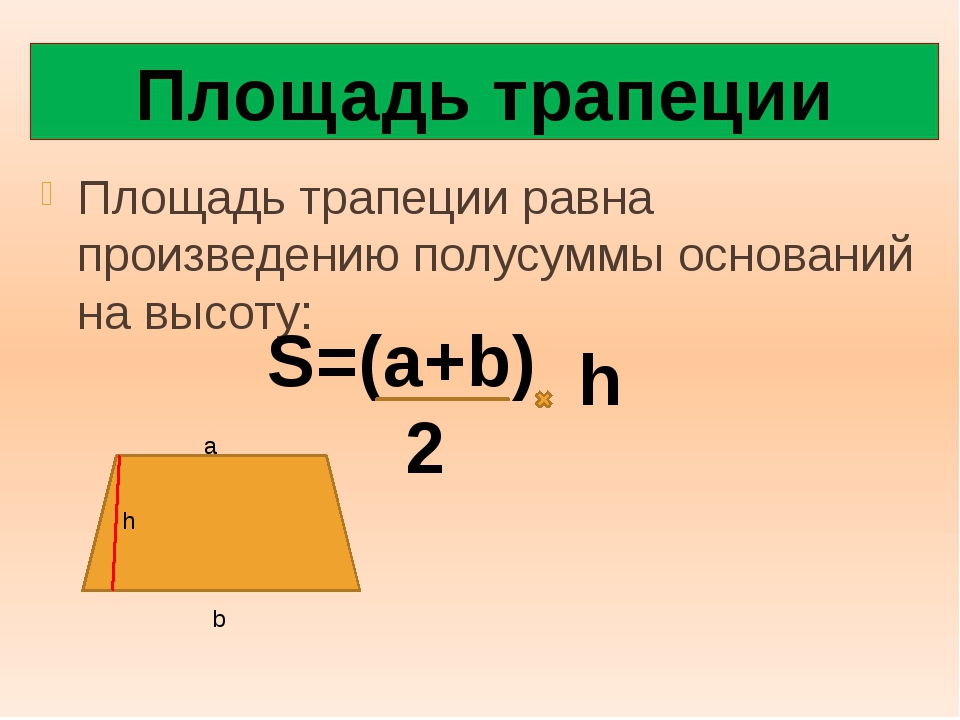
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать.
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2.
 Найти площадь трапеции (Мехмат МГУ, 1970г).
Найти площадь трапеции (Мехмат МГУ, 1970г).Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними.
 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям.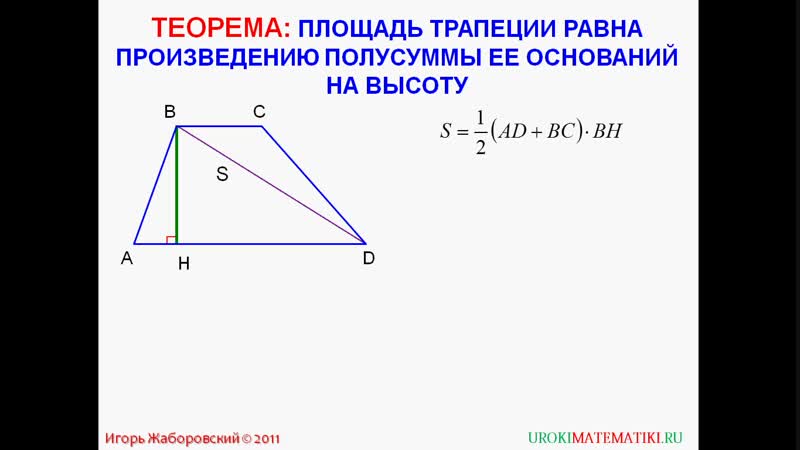 В этом случае боковая сторона по длине совпадает с высотой трапеции.
В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Определяем трапецию
Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других.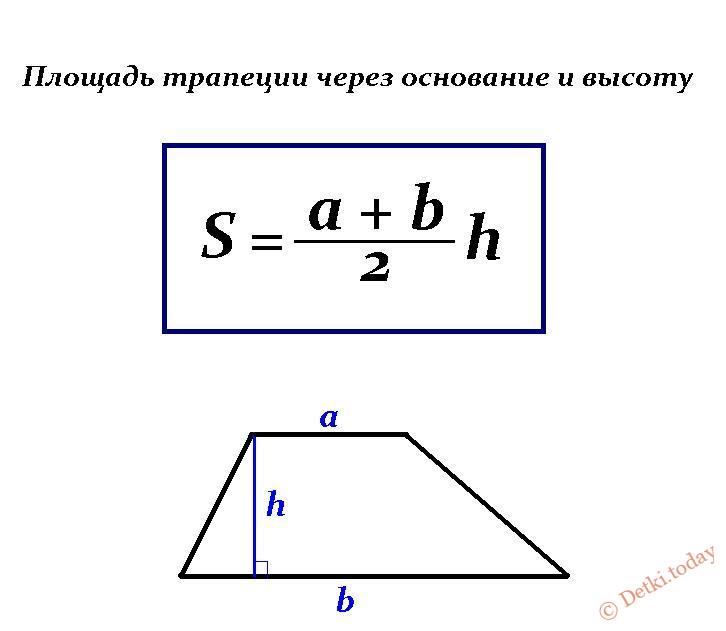 Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Свойства трапеции
Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sina.
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
S = c *sin a *(a — c *cos a ),
где с — боковое бедро, a — угол при нижнем основании.
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
S = M/2 + N — 1,
в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.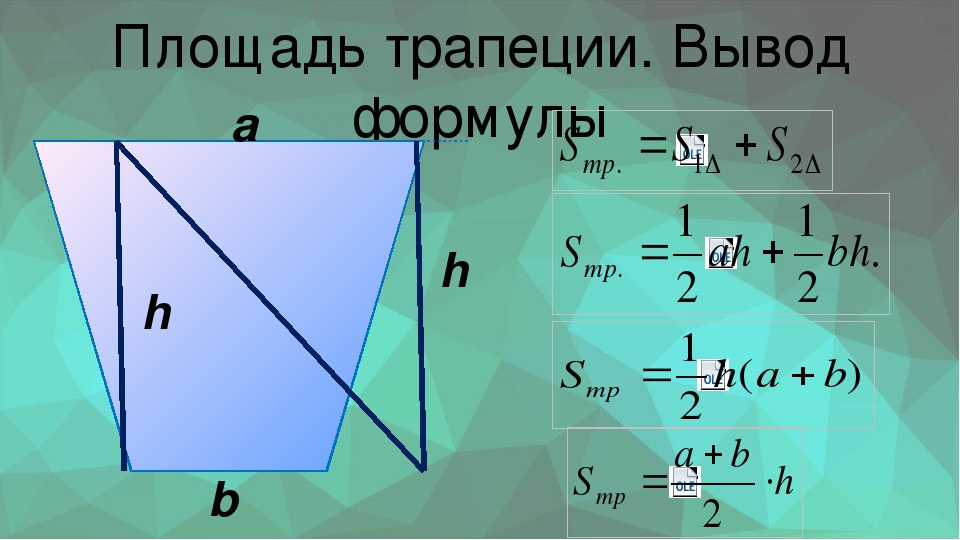
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Формула площади трапеции через угол. Все варианты того, как найти площадь трапеции
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Определяем трапецию
Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Свойства трапеции
Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sina.
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
S = c *sin a *(a — c *cos a ),
где с — боковое бедро, a — угол при нижнем основании.
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
S = M/2 + N — 1,
в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое.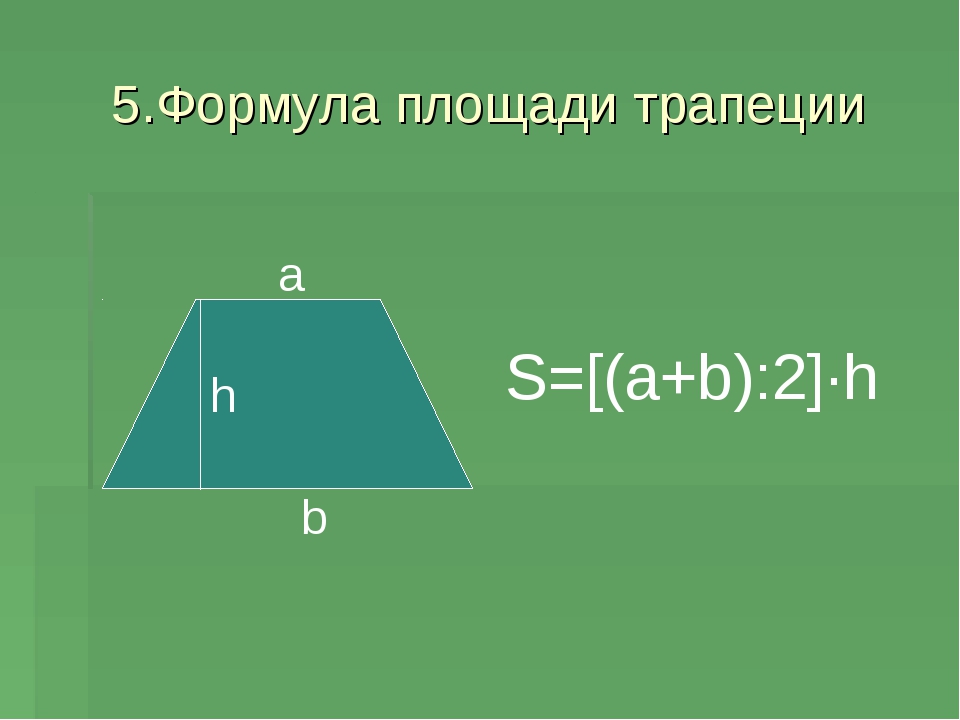 Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
Успеха вам!
С уважением, Александр.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол .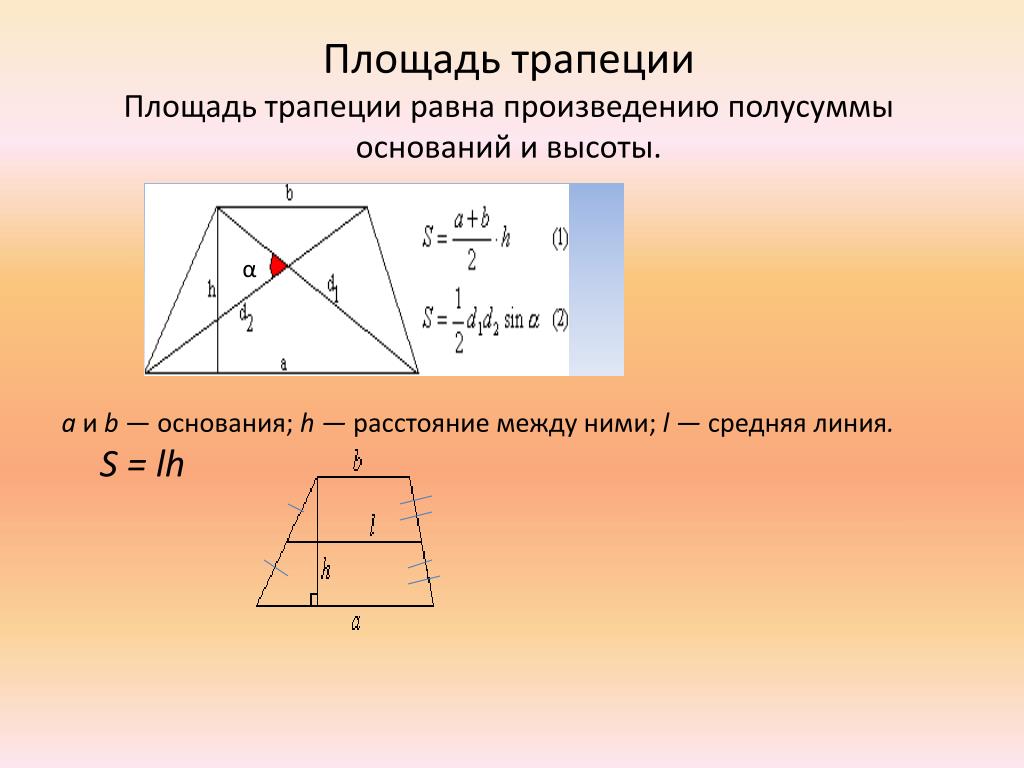 Найти площадь трапеции, если ее высота равна 6см.
Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).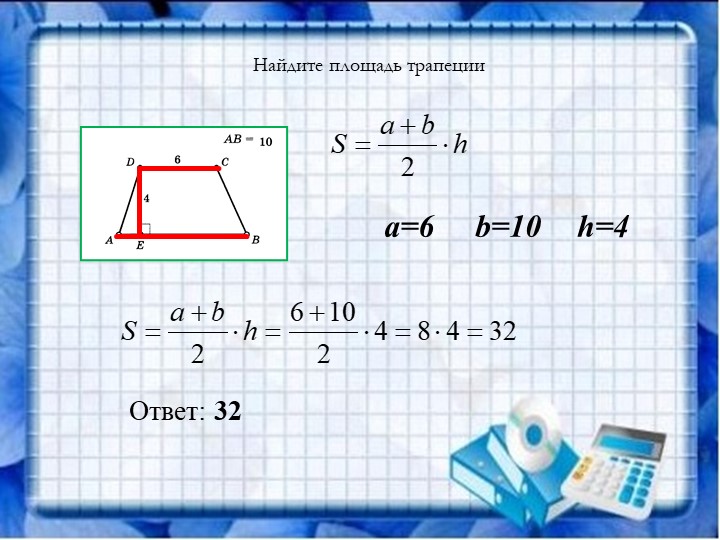
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Формула вычисления трапеции. Площадь трапеции: как вычислить, формула
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции.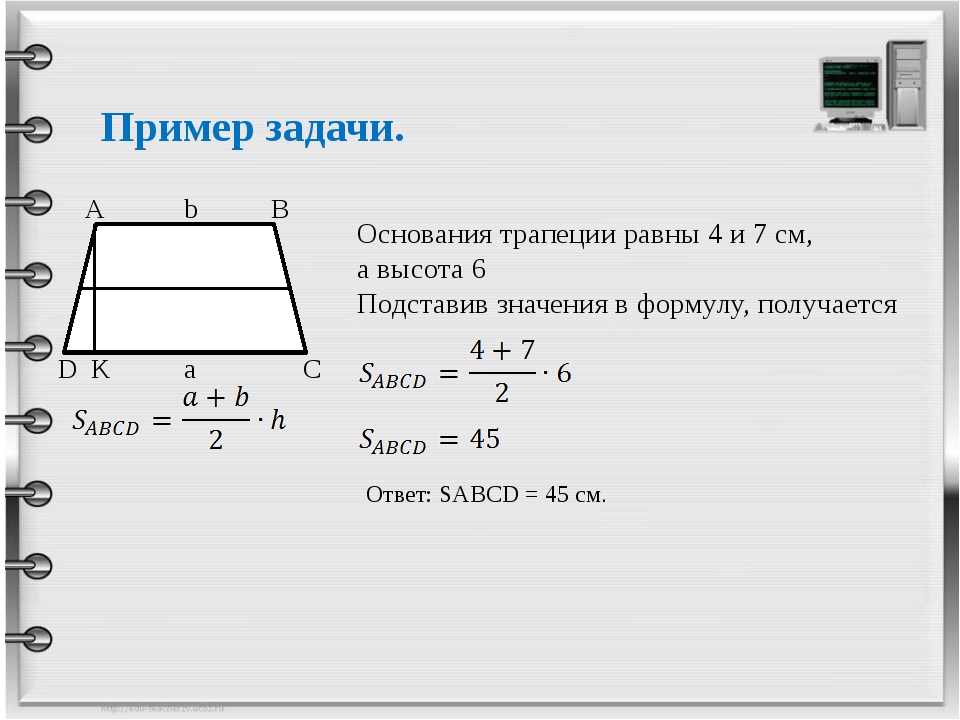 С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол .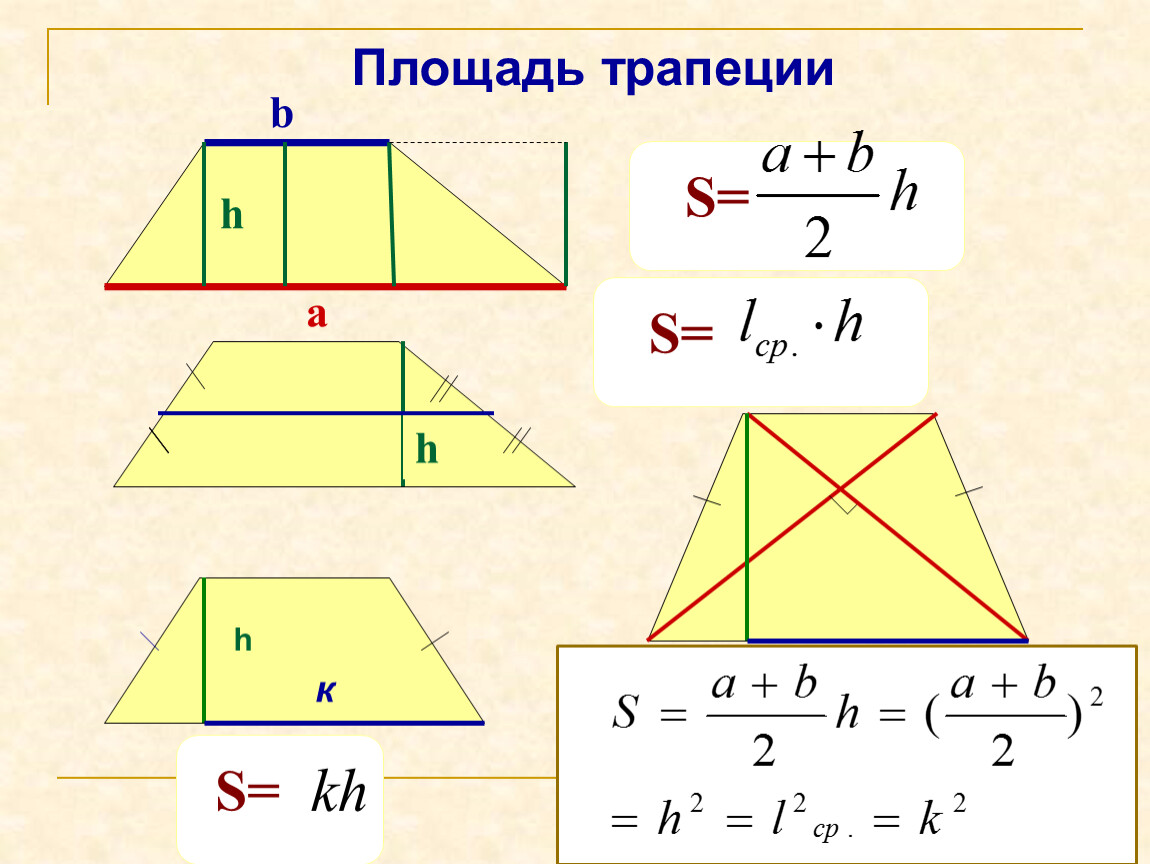 Найти площадь трапеции, если ее высота равна 6см.
Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см.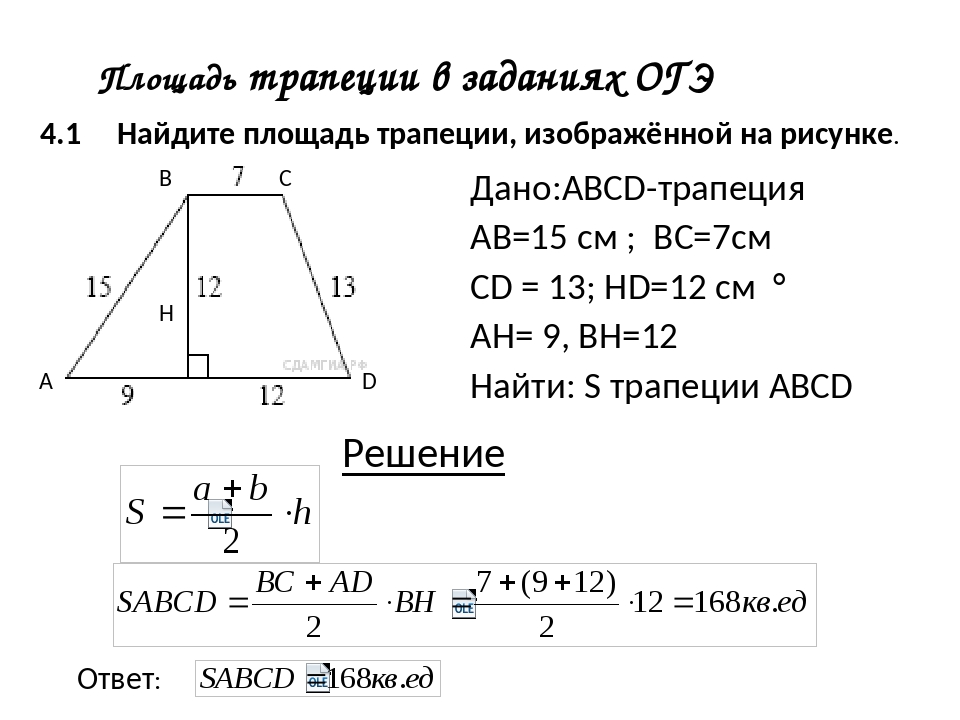 найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.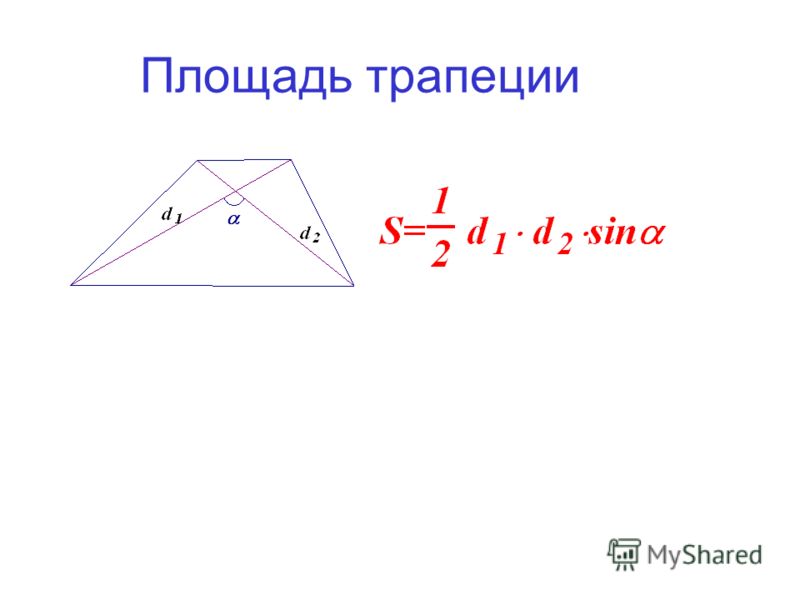
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.

- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
формула расчета равнобедренной трапеции / 01.12.2021
Если вам необходимо вычислить площадь трапеции, воспользуйтесь нашим пошаговым путеводителем. Prostobank.ua рассказывает, как узнать площадь трапеции с помощью простых расчетов.
Вычислять площадь трапеции можно не только на уроках математики, но и в повседневной жизни. Нередко бывают помещения, участки в виде трапеции. Поэтому расчет площади такой фигуры может стать актуальным нашим посетителям.
Перед вычислением площади любой геометрической фигуры, нужно понять, что это за фигура, какие ее особенности, как обозначаются стороны. Поэтому сначала определим, что является трапецией.
Что такое трапеция?
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны. Параллельные противоположные стороны называются основаниями трапеции и обозначаются латинскими буквами a и b, а две другие — боковыми сторонами.
Формула расчета площади трапеции
Площадь трапеции равна произведению полусуммы ее оснований (a, b) на высоту (h)
Sтрапеции=½* (a+b)* h
Как видно из вышеописанной формулы, посчитать площадь трапеции достаточно просто. Нужно только знать длину сторон и высоту трапеции. Если вам необходимо перевести площадь трапеции из одной единицы измерения в другую, воспользуйтесь нашим калькулятором площади.
Нужно только знать длину сторон и высоту трапеции. Если вам необходимо перевести площадь трапеции из одной единицы измерения в другую, воспользуйтесь нашим калькулятором площади.
Как найти площадь равнобедренной трапеции?
Найти площадь равнобедренной трапеции можно с помощью формулы площади обычной трапеции Sтрапеции=½* (a+b)* h
Но учитывая особенности равнобедренной трапеции (или углы при основе трапеции равны, или диагонали равны, или одинаковые углы между диагоналями и основаниями, или сумма противоположных углов равна 180), можно использовать другие формулы расчета площади.
S= √ (p−a)(p−b)(p−c)2,
где a и b – основания трапеции, с – боковые стороны (в равнобедренной трапеции боковые стороны равны), p — полупериметр трапеции: p = ½*(a+b+2c)
С помощью вышеописанных формул вы сможете измерить площадь трапеции.
Урок по геометрии на тему «Формула площади трапеции»(8 класс)
Формула площади трапеции
Тема: изучение формулы площади трапеции
Учебник: Атанасян. Геометрия 7-9. Глава VI §2 п.53
Тип урока: урок изучения нового.
Учебная задача: в совместной деятельности с учащимися открыть формулу площади трапеции, доказать её.
Диагностируемые цели:
в результате урока ученик:
воспроизводит запись формулы площади трапеции;
умеет читать её разными формулами;
выражает линейный элемент трапеции из формулы её площади;
знает прием доказательства формулы и при этом использует свойства площадей;
применяет формулу при решении простейших задач на нахождение площади трапеции.
Методы обучения:
Форма работы: фронтальная
Средства обучения: мел, доска, учебник, инструменты.
Структура урока:
мотивационно-ориентировочный этап(10 мин)
содержательный этап (30 мин)
рефлексивно-оценочный этап (5 мин)
Ход урока
I.Мотивационно — ориентировочный этап.
Актуализация:
Речь учителя: Мы с вами изучаем тему «Площадь». Площади каких фигур вы уже умеете вычислять?
Речь ученика: квадрата, треугольника, прямоугольника, параллелограмма.
Речь учителя: Хорошо, посмотрим на рисунок 1.
Записи на доске:
B C
8 SABCD-?
300
A D
20
Речь учителя: Что дано?
Речь ученика: АВ=8, АD=20, BAD=30˚.
Речь учителя: Что нужно найти?
Речь ученика: SABCD.
Речь учителя: Чему она равна?
Речь ученика: 80 см.2
Речь учителя: Молодцы. Чем пользовались при нахождении площади ABCD?
Речь ученика: формулой для вычисления площади S=ah.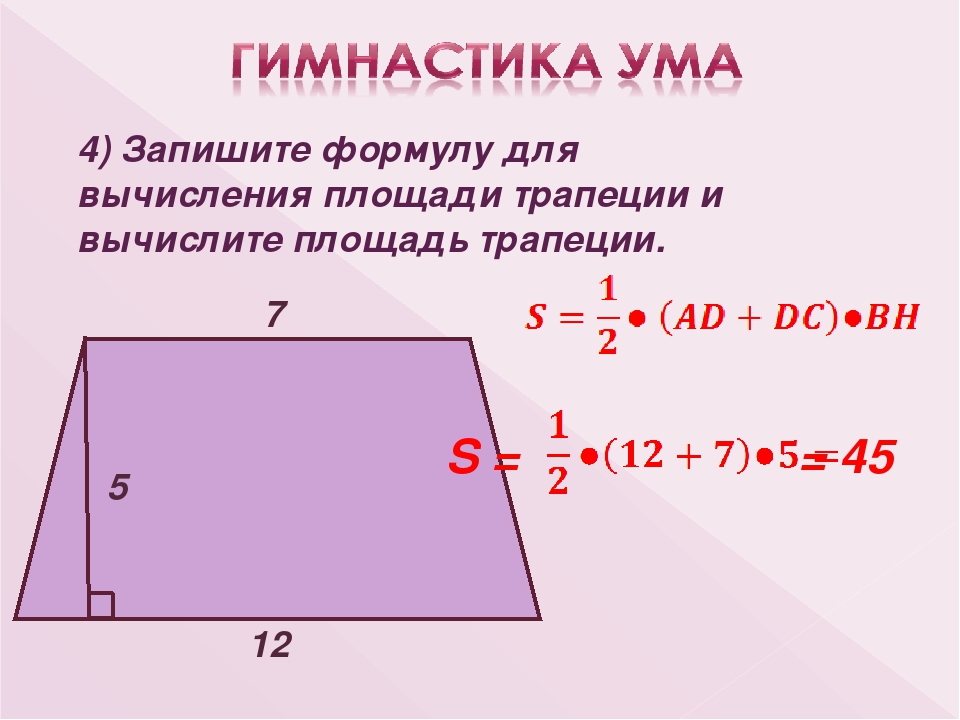
Речь учителя: а теперь посмотрим на след. рисунок:
Записи на доске:
E
A D
Выразить SABCDЕ=?
B C
Речь учителя: что изображено на рисунке?
Речь ученика: пятиугольник ABCDE.
Речь учителя: что надо сделать?
Речь ученика: найти его площадь.
Речь учителя: какие фигуры можно получить из этого пятиугольника?
Речь ученика: соединим В с Е, C c Е. Получим 3 треугольника.
Записи на доске:
E
A D
B C
Речь учителя: как тогда можно выразить SABCDЕ?
Речь ученика: SABCDЕ= SABЕ+SBCЕ+ SCDЕ
Записи на доске: SABCDЕ= SABЕ+SBCЕ+ SCDЕ
Речь учителя: выразили площадь?
Речь ученика: да
Речь учителя: чем пользовались при выражении площади пятиугольниками?
Речь ученика: тем, что площадь многоугольника равна сумме площадей многоугольников, из которых составлен данный многоугольник.
Мотивация.
Речь учителя: молодцы! Вернемся к рис.1. На продолжении стороны АD отложим DK=3 см. Найдите площадь полученного четырехугольника.
Записи на доске:
B C
8
300
A 20 D 3 K
Речь учителя: чем является ABCK?
Речь ученика: трапецией.
Речь учителя: почему это трапеция?
Речь ученика: так как ВС//АК, а АВ и СК пересекаются.
Речь учителя: что надо найти?
Речь ученика: SABCК
Речь учителя: каким способом можно вычислить площадь SABCК?
Речь ученика: как сумма площадей параллелограмма АВСD и треугол. АСК.
Речь учителя: верно. Чему равна площадь параллелограмма.
Речь ученика: 80 см2
Речь учителя: верно. А чему равна высота ВМ в параллелограмме?
Речь ученика: ВМ=4, т.к. ВМ- это катет прямоугольного треугольника АВМ, у которого АВ=8, а угол А=300 ).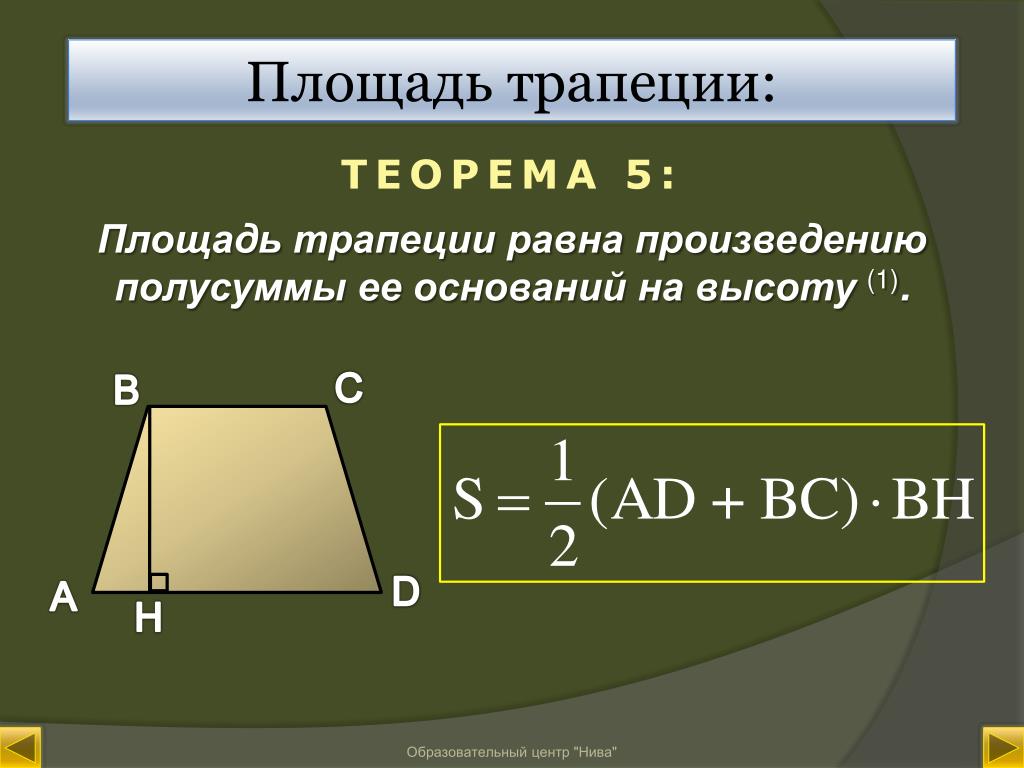
Речь учителя: как найти SDCK-?
Речь ученика: S=1/2*CH*DK=1/2*4*3
Речь учителя: Почему СH=4?
Речь ученика: так как CH=BM.
Речь учителя: итак, чему равна SABCК?
Речь ученика: SABCК= SABCD+ SDCК=80+6=86.
Записи на доске:
h= BM=CH=1/2*AB=1/2*8=4
SABCD=80
SCDК=6
SABCК= SABCD+ SDCК=80+6=86.
Речь учителя: итак, как найдена площадь трапеции?
Речь ученика: как сумма площадей треугольника и параллелограмма.
Речь учителя: всегда ли можно использовать такой способ для нахождения площади трапеции?
Речь ученика: да
Речь учителя: а всегда ли удобно?
Речь ученика: нет, так много действий.
Речь учителя: как вы думаете, можно ли найти другой способ для вычисления площади трапеции?
Речь ученика: наверное, да.
Речь учителя: как мы находим площади параллелограмма и треугольника?
Речь ученика: по формулам
Речь учителя: так, оказывается, для трапеции тоже существует формула нахождения её площади. Какую цель мы поставим перед собой на сегодняшнем уроке?
Речь ученика: вывести формулу для вычисления формулы трапеции.
Речь учителя: итак, открываем тетради и записываем тему урока: «Площадь трапеции»
Записи на доске: Площадь трапеции.
Содержательный этап
Речь учителя: как вы думаете, что нам поможет при нахождении формулы трапеции?
Речь ученика: рисунок 1.
Речь учителя: правильно. Начертим у себя в тетради трапецию ABCK по рис.1, сохраняя не только построения, но и буквенные обозначения.
Записи на доске:
B C
A D K
Речь учителя: что надо найти?
Речь ученика: формулу площади трапеции
Речь учителя: вспомним, как решали предыдущую задачу на нахождение площади трапеции
Речь ученика: мы говорили, что площадь трапеции равна сумме площадей параллелограмма и трапеции
Речь учителя: значит, что в нашей задаче нужно сделать?
Речь ученика: провести CD//АВ, ВМ, СМ.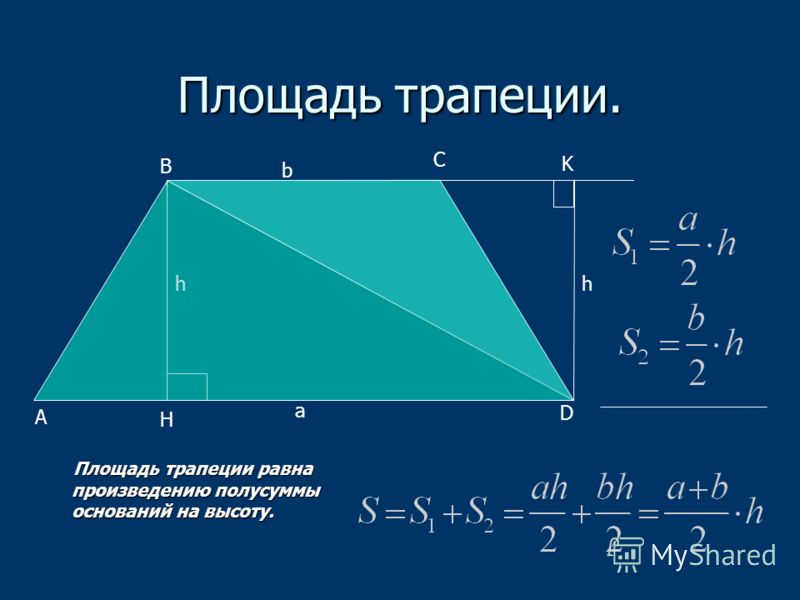
Речь учителя: как находиться площадь параллелограмма АВСD?
Речь ученика: SABCD=АD*BM.
Речь учителя: обозначим ВМ=h(высота), AD=а(основание), так как АВСD параллелограмм, то ВС=АD=а, АВ=СD. Как находится площадь треугольника СDK?
Речь ученика: SCDК=1/2*CH*DK.
Речь учителя: чему равна СН?
Речь ученика: СН=ВМ=h, так как высоты в трапеции равны.
Речь учителя: как связаны основания трапеции АК, основание параллелограмма AD и основание треугольника DK?
Речь ученика: основание трапеции состоит из основания параллелограмма и треугольника.
Речь учителя: какой вывод можно сделать о формуле площади трапеции, зная, что формула площади параллелограмма выражается через основание и высоту и треугольника выражается через основание и высоту?
Речь ученика: наверно площадь трапеции выражается через основание и высоту.
Речь учителя: обозначим нижнее основание трапеции за b, то есть АК= b. Выразим площадь трапеции.
Речь ученика: SABCК =SABCD+ SCDК
Записи на доске: SABCК =аh+1/2*(b-a)h=ah+1/2*b*h-1/2*ah=1/2*(ah+bh)=
=1/2*h(a+b).
Речь учителя: мы с вами получили формулу для вычисления формулы площади трапеции. Какие величины используются в формуле?
Речь ученика: 2 основания и высота.
Речь учителя: а что мы называем основанием трапеции?
Речь ученика: две параллельные стороны трапеции.
Речь учителя: видите, в формуле снова используются высота и основание. Значит, наше предположение было верным. Вернемся к рисунку 1. и проверим, правильно ли мы нашли формулу? Подставляем, получим:
Записи на доске: SABCК = ½*ВМ(ВС+АК)=1/2*4*(23+20)=2*43=86
Речь учителя: ответ совпал?
Речь ученика: да.
Речь учителя: удобна ли эта формула?
Речь ученика: да, помогает быстро найти площадь трапеции.
Речь учителя: кто сформулирует мне теорему?
Речь ученика: площадь трапеции равна произведению полусуммы её оснований на высоту.
Речь учителя: хорошо! А теперь запишем её разными способами, а вы мне её прочитаете.
Записи на доске:
S=1/2*h(a+b)= h/2*(a+b) =h(a+b)/2=(h*(a+b))/2.
Речь учителя: молодцы! А теперь давайте по шагам восстановим доказательство. Шаг первый?
Речь ученика: построили трапецию и провели прямую CD//АВ.
Речь учителя: шаг второй?
Речь ученика: обозначили ВМ за h, ВС и АК за а и b.
Речь учителя: третий шаг: как выразили площадь трапеции ABCК?
Речь ученика: SABCК =SABCD+ SCDК
Речь учителя: шаг четвертый…
Речь ученика: все поставили, раскрыли скобки, привели подобные и вычислили.
Записи на доске:
1.АВСК-трапеция
2.Построили CD//АВ.
3. Обозначим ВМ=h, ВС = а, АК=b.
4. SABCК =SABCD+ SCDК. SABCD=ha, SCDК= ½*h*(b-a)
5. SABCК = ha+½*h*(b-a)= ½*h(b + a)
Речь учителя: используя формулу площади трапеции какие элементы мы можем находить?
Речь ученика: высоту и основания.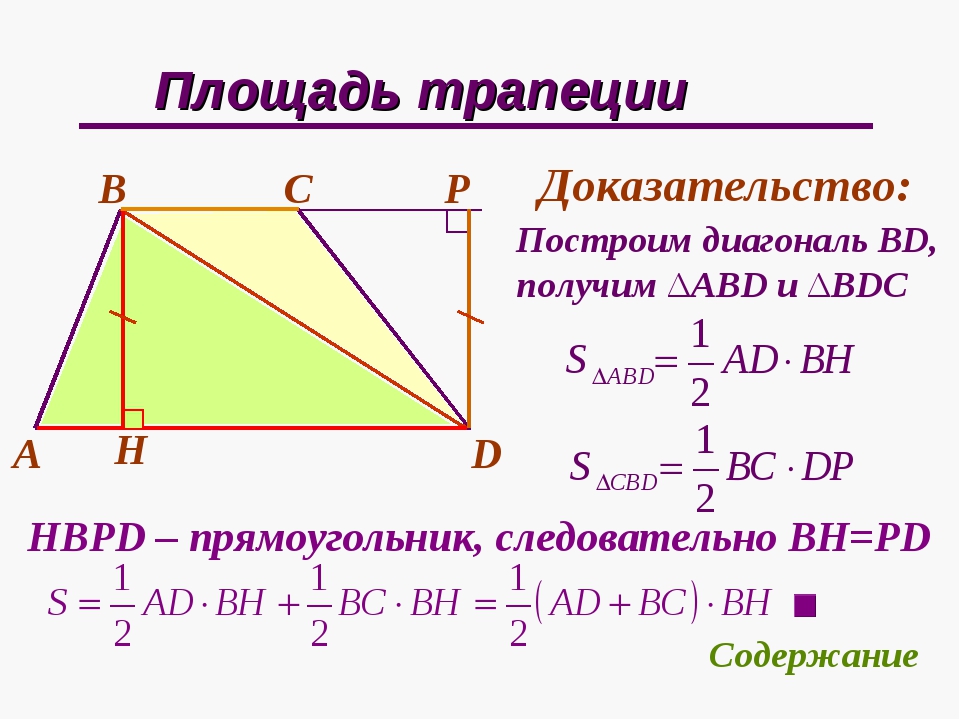
Речь учителя: а теперь задание по рядам — выразите первый ряд из этой формулы h, второй- b, третий — а.
Записи на доске:
2S=h(b + a) 2S=hb + ha 2S=hb + ha
h=2S/ (b + a) hb =2S-ha ha=2S-hb
b=2S-ha/h a=2S-hb/h
Речь учителя: а теперь посмотрим на рисунки на доске и решим след. задачи.
Записи на доске:
25
B 22 C B C O C
2
5 4A H D A D A H B D
24 27 10
SABCD-? (46) SABCD-?(130) SAOCD-?(15)
Учащиеся устно решают задачи, последнюю оформляют в тетради.
Записи на доске:
Проведем высоту ОН. Так как ∆ АОН прямоугольный, ОАН=300, то ОН=1/2АО=1/2*4=2
SAOCD=1/2*(AD+OC)*OH
ОС=НВ=1/2АD=1/2*10=5.
SAOCD=1/2*(10+5)*2=15.
Рефлексивно-оценочный этап
Речь учителя: какая задача стояла перед нами в начале урока?
Речь ученика: вывести формулу площади трапеции
Речь учителя: достигли ли мы её?
Речь ученика: да
Речь учителя: как выражается формула площади трапеции?
Речь ученика: S= ½*h(b+a)
Речь учителя: какими свойствами и формулами мы пользовались?
Речь ученика: S=S1+S2, S=ah, S=1/2(b-a)h.
Речь учителя: а что мы можем найти из формулы площади трапеции?
Речь ученика: два основания, высоту.
Речь учителя: молодцы! А теперь мы запишем домашнее задание-параграф 2, пункт.53, номера 481, 480.
Анализ увиденного урока учителя:
Данный урок был проведён 26 ноября 2010 года в 8 «а» классе, в 53 гимназии Советского района, учителем математики Гусевой Е.П.
Тема урока: «Формула площади трапеции» изучается в главе «Четырёхугольники» после изучения площади треугольника.
Дидактические единицы:
Теорема: «площадь трапеции равна произведению полусуммы её оснований на высоту».
свойства площадей.
Формулы площади параллелограмма, треугольника.
Используется метод доказательства, основанный на методе площадей . Этот урок является по типу уроком изучения нового, где даются основные теоретические сведения , необходимые для последующих занятий, на которых будет проходить отработка доказанной теоремы.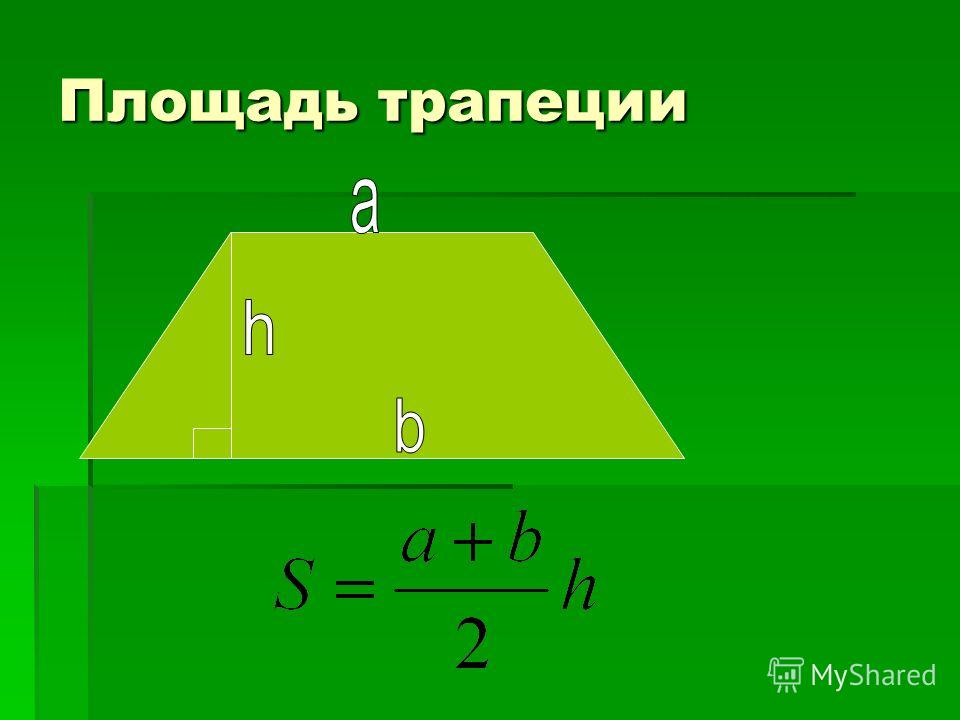 Поэтому в системе уроков по данной теме этот урок имеет важное фундаментальное значение.
Поэтому в системе уроков по данной теме этот урок имеет важное фундаментальное значение.
Далее формула нахождения площади трапеции будет часто использоваться
при решении различных задач. С термином « теорема» учащиеся знакомы
давно, метод доказательства, основанный на свойствах площадей также уже знаком ученикам при доказательстве формулы нахождения площади прямоугольника.
3)Учебная задача урока : в совместной деятельности с учащимися открыть формулу площади трапеции, доказать её. Учебная задача была сформулирована учащимися при помощи учителя на мотивационно- ориентировочном этапе.
Диагностируемые цели:
в результате урока ученик:
воспроизводит запись формулы площади трапеции;
умеет читать её разными формулами;
выражает линейный элемент трапеции из формулы её площади;
знает прием доказательства формулы и при этом использует свойства площадей;
применяет формулу при решении простейших задач на нахождение площади трапеции.

4)Тип урока: урок изучения нового.
Методы обучения: частично – поисковой, репродуктивны й.
Средства обучения: мел, доска, учебник.
Форма работы: фронтальная.
При решении каждой задачи учитель строил фигуру и писал решение на доске, таким образом, ученики могли наглядно представлять материал, изучаемый на уроке.
Структура урока
1.
Организационный момент
2.
Мотивационно-ориентировочный этап:
3.
Содержательный этап
-«открытие» теоремы, её доказательство,
-решение задач.
4.
Рефлексивно-оценочный этап.
— Подведение итогов
— Домашнее задание
Была избрана традиционная структура урока. Ребята и ранее в начале урока решали задания , чтобы включиться в учебную деятельность. На актуализации были повторены задания, которые впоследствии помогли на операционно – познавательном этапе «открыть» теорему. Домашнее задание на уроке не проверялось из – за ограниченности во времени. В качестве мотивации выступила задача, которую учащиеся могли решить одним способом, но учитель им сообщил, что можно иначе решить это задание. Впоследствии учитель, при помощи хорошо разработанной системы вопросов, помог ребятам «открыть» теорему, доказать её.
Ребята и ранее в начале урока решали задания , чтобы включиться в учебную деятельность. На актуализации были повторены задания, которые впоследствии помогли на операционно – познавательном этапе «открыть» теорему. Домашнее задание на уроке не проверялось из – за ограниченности во времени. В качестве мотивации выступила задача, которую учащиеся могли решить одним способом, но учитель им сообщил, что можно иначе решить это задание. Впоследствии учитель, при помощи хорошо разработанной системы вопросов, помог ребятам «открыть» теорему, доказать её.
Система упражнений и заданий на различных этапах урока соответствовала целям. На этапе актуализации ученики вспомнили некоторые формулы, определения, которые они изучали ранее. В мотивационном и содержательном этапах использовались задания, необходимые для достижения целей урока.
По окончании урока, учитель подвёл итоги, повторил с учениками, какие теоретические факты получены на уроке, все определения, свойства и теоремы, используемые на уроке.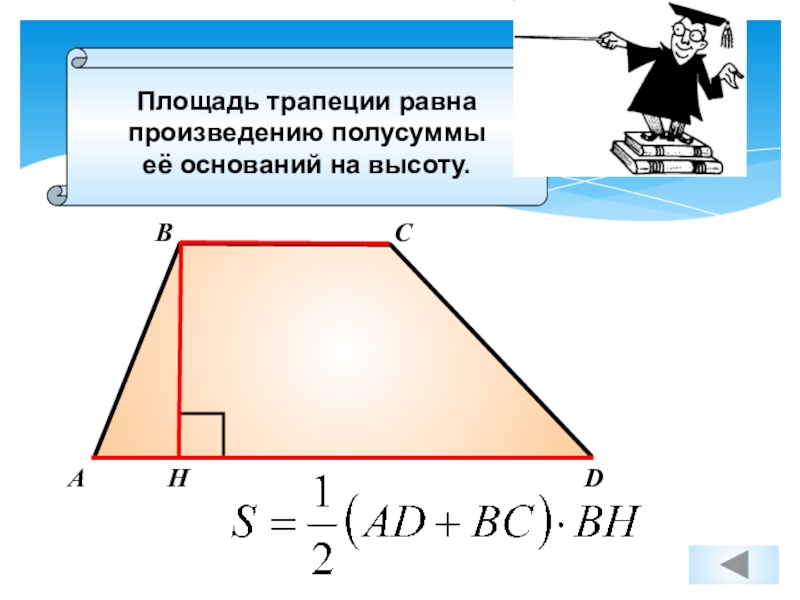 Далее Елена Павловна задала домашнее задание.
Далее Елена Павловна задала домашнее задание.
5) Урок прошел отлично. Учитель достиг всех поставленных целей, выполнил запланированный материал, ребятам было интересно работать с Еленой Павловной. Я считаю, что интересным было само доказательство теоремы. Оно отличается от доказательства в учебнике, тем самым, учитель показал своё мастерство. При повторном проведении урока на эту тему я, наверное, ничего бы не поменяла.
Мне урок очень понравился, я считаю его полностью продуманным и оцениваю я его на отлично.
Площадь трапеции — формула, примеры, определение, вывод
Часто задаваемые вопросы по Area of Trapezoid
Что такое площадь трапеции в математике?
Трапеция — это четырехугольник (многоугольник) с четырьмя сторонами, в котором одна пара противоположных сторон параллельна. Площадь трапеции — это количество единичных квадратов, которые могут в нее поместиться. Математически это выражается как A = ½ (a + b) h, где «a» и «b» — основания (параллельные стороны), а «h» — высота перпендикуляра.Он представлен в квадратных единицах.
Математически это выражается как A = ½ (a + b) h, где «a» и «b» — основания (параллельные стороны), а «h» — высота перпендикуляра.Он представлен в квадратных единицах.
Как найти площадь трапеции?
Площадь трапеции определяется по формуле A = ½ (a + b) h, где ‘a’ и ‘b’ — основания (параллельные стороны), а ‘h’ — высота (перпендикулярное расстояние между основания) трапеции.
Почему площадь трапеции ½ (a + b) h?
Рассмотрим трапецию с основанием «a» и «b» и высотой «h». Мы можем вырезать часть треугольной формы из трапеции и прикрепить ее внизу так, чтобы вся трапеция превратилась в треугольник.Тогда полученный треугольник имеет основание (a + b) и высоту h. Применяя формулу площади треугольника, площадь трапеции (или треугольника) = ½ (a + b) h. Для получения дополнительной информации, вы можете обратиться к Как получить площадь формулы трапеции? раздел этой страницы.
Как найти недостающую основу трапеции, если вы знаете местность?
Площадь трапеции с основаниями «a» и «b» и высотой «h» равна A = ½ (a + b) h. Если даны одно из оснований (скажем, ‘a’), высота и площадь, то мы просто подставим эти значения в приведенную выше формулу и решим ее для недостающего основания (a) следующим образом:
Если даны одно из оснований (скажем, ‘a’), высота и площадь, то мы просто подставим эти значения в приведенную выше формулу и решим ее для недостающего основания (a) следующим образом:
A = ½ (a + b) h
Умножение обеих сторон на 2,
2А = (а + б) ч
Делим обе стороны на h,
2А / ч = а + б
Вычитая b с обеих сторон,
а = (2А / ч) —
бКак определить высоту трапеции с учетом площади и оснований?
Площадь трапеции с основаниями «a» и «b» и высотой «h» равна A = ½ (a + b) h.Мы можем найти высоту трапеции с площадью и основаниями, решив приведенную выше формулу для h следующим образом:
A = ½ (a + b) h
Умножение обеих сторон на 2,
2А = (а + б) ч
Делим обе стороны на (a + b),
h = (2A) / (a + b).
Какова площадь равнобедренной трапеции со сторонами?
Если даны длины сторон равнобедренной трапеции, то мы разделим ее на два равных прямоугольных треугольника и прямоугольник. Мы находим площади каждой из этих фигур и складываем их, что дает площадь данной трапеции. Вы можете увидеть это подробно в Примере 2 в разделе «Решенные примеры» на этой странице.
Мы находим площади каждой из этих фигур и складываем их, что дает площадь данной трапеции. Вы можете увидеть это подробно в Примере 2 в разделе «Решенные примеры» на этой странице.
Какова площадь трапеции с координатами?
Если даны координаты вершин трапеции, то мы можем найти длины ее оснований ‘a’ и ‘b’, используя формулу расстояния. Чтобы найти высоту «h» (перпендикулярное расстояние между основаниями), мы можем использовать перпендикулярное расстояние от точки к формуле линии (для этого нам нужно найти уравнение линии для одного из оснований).2}} \).
Затем мы можем применить формулу A = ½ (a + b) h, чтобы найти площадь трапеции.
Как найти площадь равнобедренной трапеции без высоты?
Если высота трапеции не указана, а вместо нее указаны все ее стороны, то мы разделим ее на два равных прямоугольных треугольника и прямоугольник. Мы находим площади каждой из этих фигур и складываем их, что дает площадь данной трапеции. Вы можете увидеть это подробно в Примере 2 в разделе «Решенные примеры» на этой странице.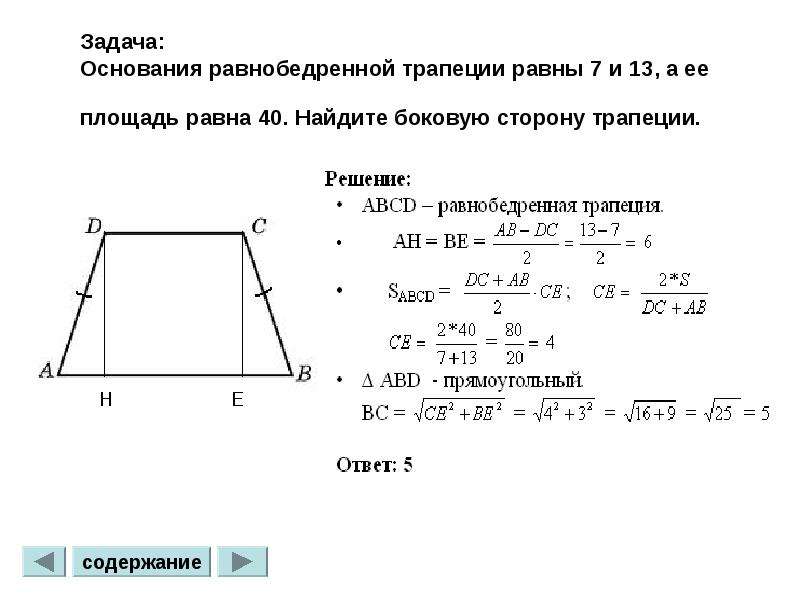
Площадь трапеции
Площадь трапеции — это пространство внутри ее периметра. Серое пространство — это область трапеции на диаграмме ниже.
Формула площади трапеции
Площадь A трапеции:
, где h — высота, а b 1 и b 2 — базовые длины.
Вывод
Дана трапеция, если мы сформируем конгруэнтную трапецию и повернем ее так, чтобы две конгруэнтные трапеции можно было соединить вместе, чтобы образовать параллелограмм, как показано конгруэнтными черными и серыми трапециями ниже.
Площадь параллелограмма A = bh. Параллелограмм, образованный двумя совпадающими трапециями, имеет основание b 1 + b 2 и высоту h. Следовательно, площадь этого параллелограмма равна: A = (b 1 + b 2 ) h. Поскольку параллелограмм состоит из двух совпадающих трапеций, деление пополам приведенной выше формулы дает нам формулу для площади одной из трапеций:
Пример:
Найдите площадь трапеции, имеющей высоту 16 и основание 18 и 35.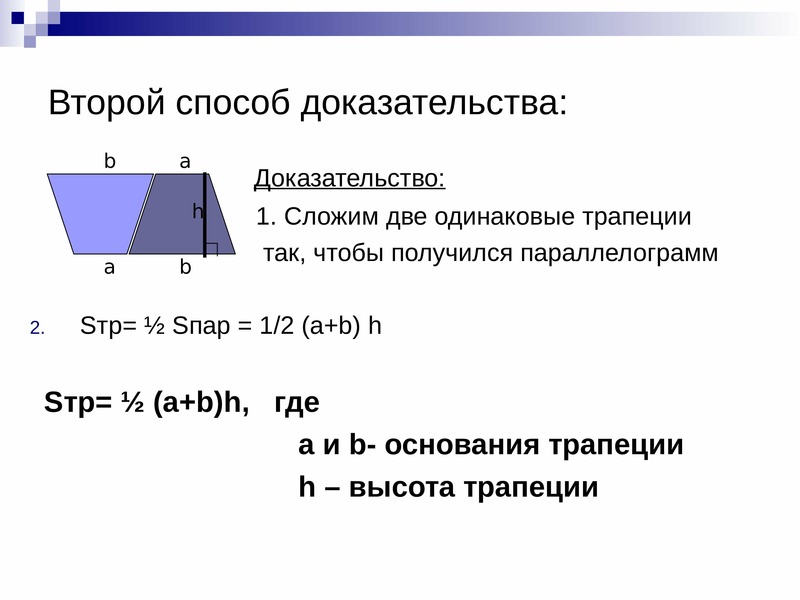
Подключаем их к формуле площади:
Использование среднего сегмента
Середина трапеции — это отрезок прямой, соединяющий середину ее ног. Средний сегмент имеет длину, равную средней длине двух его оснований, что составляет
.Площадь A трапеции с использованием длины среднего сегмента составляет:
А = hm
Вывод
Подставляем значение m в исходную формулу площади трапеции:
Нахождение местности по сетке
Другой способ найти площадь трапеции — определить, сколько единичных квадратов нужно, чтобы покрыть ее поверхность.Ниже представлен единичный квадрат со стороной 1 см.
При определении площади трапеции можно использовать сетку из единичных квадратов.
Сетка выше содержит единичные квадраты площадью 1 см 2 каждый. Трапеция слева содержит 6 полных квадратов и 4 частичных квадрата, поэтому ее площадь составляет приблизительно:
Трапеция справа содержит 7 полных квадратов и 4 частичных квадрата, поэтому ее площадь составляет приблизительно:
С помощью этого метода можно найти площадь любой формы; это не ограничивается трапециями. Однако это лишь приблизительная стоимость площади. Чем меньше используемый единичный квадрат, тем выше точность приближения. Использование сетки из квадратов размером 1 мм в 10 раз точнее, чем использование сетки из квадратов размером 1 см.
Однако это лишь приблизительная стоимость площади. Чем меньше используемый единичный квадрат, тем выше точность приближения. Использование сетки из квадратов размером 1 мм в 10 раз точнее, чем использование сетки из квадратов размером 1 см.
Как найти периметр и площадь трапеции [Видео и практика]
Привет, и добро пожаловать в это видео о поиске площади и периметра трапеции!
Что такое трапеция?
Трапеция — это четырехгранный многоугольник или «четырехугольник», у которого есть по крайней мере один набор параллельных сторон.У трапеции есть два типа сторон: ножки и основания. У трапеции две ножки и два основания.
Мы можем сказать, какие стороны являются основаниями, потому что они параллельны друг другу.
Здесь мы видим, что верх и низ параллельны из-за совпадающих стрелок на этих сторонах.
Как найти периметр трапеции
Зная длину опор и оснований, мы можем найти периметр трапеции.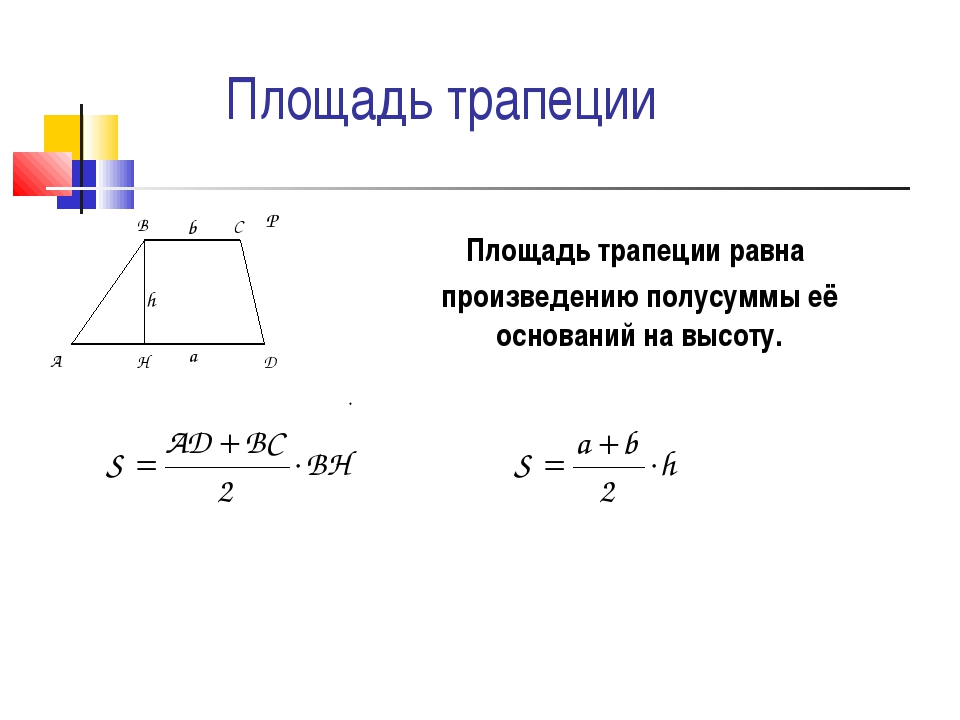 Периметр — это расстояние вокруг объекта.Например, если мы хотим построить забор вокруг двора в форме трапеции, нам нужно знать периметр двора, чтобы знать, сколько ограждения купить.
Периметр — это расстояние вокруг объекта.Например, если мы хотим построить забор вокруг двора в форме трапеции, нам нужно знать периметр двора, чтобы знать, сколько ограждения купить.
Формула периметра трапеции
Для трапеции формула периметра равна \ (P = b_1 + b_2 + l_1 + l_2 \).
Нам не нужно запоминать эту формулу, потому что, как и в случае с любым другим типом многоугольника, это просто причудливый способ сказать, что складывает все стороны вместе !
Давайте найдем периметр этой трапеции:
\ (10 + 21 + 12 + 16 = 59 м \)
Вот и все! Перейдем к области .
Как найти площадь трапеции
Вот трапеция на миллиметровой бумаге:
Помните, что площадь — это мера того, сколько квадратных единиц уместится внутри фигуры. Сколько квадратов внутри нашей трапеции?
24 полных квадрата плюс восемь половинных квадратов, что означает, что площадь трапеции составляет 28 квадратных единиц. 2 \)
2 \)
Это тот же ответ, который мы получили при подсчете!
Давайте попробуем еще одну:
Хорошо, она выглядит немного иначе, чем трапеция, которую мы только что сделали.Но мы можем сказать, что это трапеция, потому что у нее один набор из параллельных сторон . Мы можем использовать формулу, поэтому теперь нам просто нужно выяснить, какие числа куда идут. Параллельные стороны являются основаниями, поэтому мы можем установить основание 1 равным 6 сантиметрам и основание 2 равным 3 сантиметрам. Внутри трапеции нет пунктирной или цветной линии, соединяющей основания, которые явно соответствовали бы высоте, но нижняя сторона соединяет основания и перпендикулярна им, как мы можем судить по символу прямого угла.2 \)
Эта формула также работает для определения площади параллелограммов . Это потому, что все параллелограммы являются трапециями, поскольку у них есть по крайней мере один набор параллельных сторон. Фактически, у всех параллелограммов есть два набора.
Вот и все, что нужно для определения периметра и площади трапеций.
Спасибо за просмотр и удачной учебы!
Площадь трапеции — формула, примеры, решения
Студенты должны выполнять различные домашние задания по геометрии. Однако наибольшие трудности возникают у учеников средней школы, потому что они изучали только математику и алгебру, а также геометрию. Например, им нужно найти перпендикулярное расстояние, площадь поверхности или параллельные стороны трапеции. Сегодня мы поговорим конкретно о трапециях, нахождении площади и рассмотрении ее одной из важнейших теорем.
Однако наибольшие трудности возникают у учеников средней школы, потому что они изучали только математику и алгебру, а также геометрию. Например, им нужно найти перпендикулярное расстояние, площадь поверхности или параллельные стороны трапеции. Сегодня мы поговорим конкретно о трапециях, нахождении площади и рассмотрении ее одной из важнейших теорем.
Трапеция — что это за фигура?
Трапеция — это четырехугольник, у которого две параллельные стороны и две непараллельные стороны.Параллельные стороны называются основаниями трапеций, а две другие — боковыми сторонами. Высота трапеции — это расстояние между линиями, на которых лежат основания трапеции, любого общего перпендикуляра этих линий. Срединный отрезок трапеции — отрезок, соединяющий середины сторон.
Характеристики трапеции
Если в трапецию вписан круг, то сумма основ всегда совпадает с суммой сторон: a + b = c + d, а средняя линия всегда равна полусумме сторон:
Равнобедренная трапеция — это трапеция, стороны которой равны AB = CD. Тогда диагонали AC = BD и углы при основании равны:
Тогда диагонали AC = BD и углы при основании равны:
Из всех трапеций только равнобедренную трапецию можно описать окружностью, если сумма противоположных прямых углов равна 180 °. В равнобедренной трапеции расстояние от верха одного основания до выступа противоположного верха, который напрямую связан с основанием, всегда точно соответствует средней линии.
Прямоугольная трапеция — это трапеция, имеющая базовый угол 90 °.
Теорема: Площадь трапеции
Чтобы вычислить площадь произвольного многоугольника, мы делаем следующее: делим многоугольник на треугольники и находим площадь треугольника.Сумма площадей этих треугольников равна площади многоугольника. Используя эту технику, мы выводим формулу для расчета площади свободной трапеции. Условимся называть высоту трапеции перпендикуляром, проведенным из любой точки одного из оснований к прямой, содержащей другое основание. На рисунке ниже мы указали, что отрезок линии BH соответствует высоте трапеции ABCD:
На основании этого получаем теорему: «Площадь трапеции равна произведению полусуммы ее оснований на высоту. «Основываясь на формуле площади, мы можем доказать эту теорему.
«Основываясь на формуле площади, мы можем доказать эту теорему.
Дана трапеция: ABCD, AD и BC — длины оснований, BH — высота.
Докажите: площадь этой трапеции ABCD будет равна S = ½ (AD + BC) · BH.
Доказательство: начертите диагональ BD. Он делит трапецию на два треугольника ABD и BCD. Это означает, что периметр трапеции ABCD будет равен сумме площадей этих треугольников.
В треугольнике ABD: AD — основание, а BH — высота.В треугольнике BCD: BC — основание.
Нарисуем высоту ДК. Площадь S треугольника ABD = 1/2 AD · BH; площадь S треугольника BCD = 1/2 BC · DK. Поскольку BH = DK, то площадь S треугольника BCD = 1/2 BC · BH. Таким образом, площадь S трапеции ABCD = 1/2 AD · BH + 1/2 BC · BH = 1/2 (AD + BC) · BH. Что требовалось доказать.
Расчет площадей в прошлые времена
Еще 4–5 тысяч лет назад вавилоняне умели определять площадь трапеции в квадратных единицах.Древние египтяне 4000 лет назад использовали почти те же уловки, что и мы: сумму параллельных сторон делили пополам и умножали на высоту.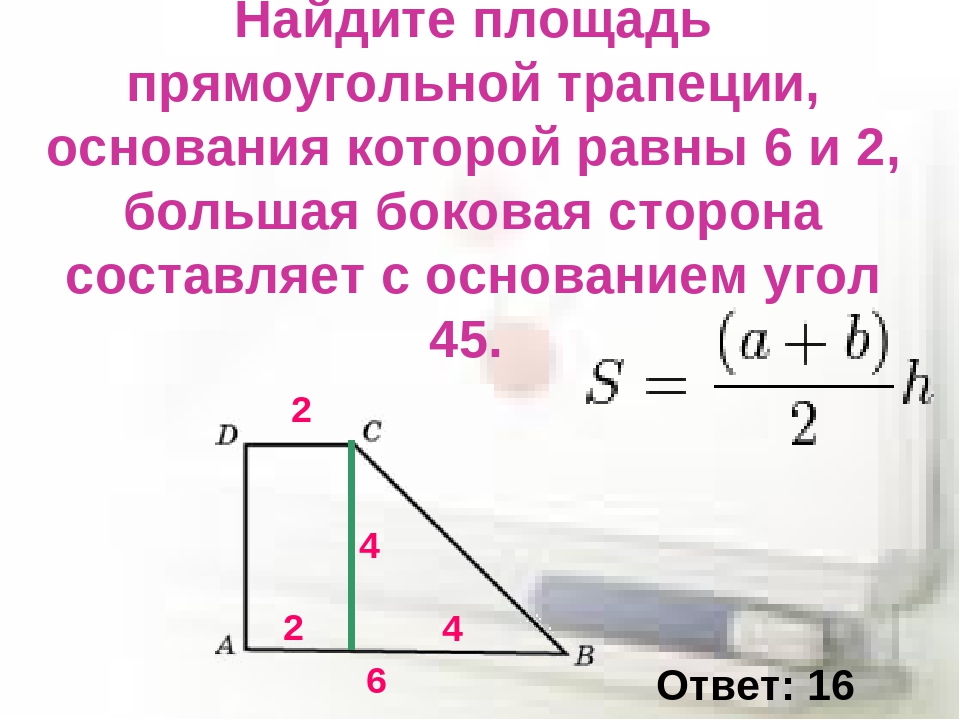
Определение площадей геометрических фигур — одна из древнейших практических задач. Люди не сразу нашли правильный подход к своему решению. Один из самых простых и доступных способов вычисления площадей открыл Евклид. При расчете площадей он использовал простую технику, называемую методом разбиения.
Расчет площадей в современном мире
Сегодня существует множество формул для расчета длин сторон, вершин, параллельных оснований и трапеции с площадью.Мы рассмотрим самые основные из них. Приведенные ниже формулы просты в использовании, но если вам сложно понять и вам нужна помощь в выполнении домашних заданий, вы всегда можете связаться с нашей службой. Опытные авторы проконсультируют вас по всем задачам, и вы значительно улучшите свою успеваемость.
Формула для вычисления площади трапеции по основанию и высоте
Дана произвольная трапеция. Чтобы найти его площадь, воспользуемся следующей формулой:
В этой формуле:
- а, б — основание трапеции;
- hh — высота трапеции.

Представьте, что нам нужно найти область трапеции с известными основаниями, численно равными 10 см и 8 см. Также всем известный рост, 6 см в длину.
Решение:
Сразу подставляем числа в имеющуюся формулу и вычисляем значение:
Ответ: 54 квадратных сантиметра.
Формула площади трапеции в основании и средней линии
Отметим, что средняя линия трапеции составляет половину суммы ее оснований.Таким образом, нахождение области через осевую линию — не что иное, как метод, аналогичный первому. Постольку:
В этой формуле:
- S = 1 ч;
- л — средняя линия трапеции;
- h — высота.
Предположим, нам нужно найти область трапеции, если известно, что средняя линия равна 5 см, а высота трапеции в два раза больше ее высоты.
Решение:
Найдите высоту трапеции:
h = 2 ⋅ 5 = 10
Площадь:
S = l ⋅ h = 5 ⋅ 10 = 50 см. кв.
кв.
Ответ: 50 кв. сантиметров
Формула площади трапеции через радиус вписанной окружности и угол
Этот футляр подходит только для равнобедренной трапеции:
В этой формуле:
- r — радиус вписанной окружности;
- α — угол между основанием и стороной.
Предположим, нам дан радиус вписанной окружности в трапецию, равный 4 см.Угол α равен 90 градусам. Нам нужно найти площадь трапеции.
Решение:
По формуле:
Ответ: 64 квадратных сантиметра.
Формула площади трапеции через диагонали и угла между ними
Существует простая формула для определения площади трапеции по диагоналям и угла между ними:
В этой формуле:
- d1, d2 — диагонали трапеции;
- α — угол между диагоналями.
Пусть две диагонали трапеции равны 20 см и 7 см. Когда они пересекаются, они образуют угол в 30 градусов. Нам нужно найти площадь трапеции.
Нам нужно найти площадь трапеции.
Решение:
- d1 = 20;
- d2 = 7;
- α = 30 °.
Площадь:
Ответ: 35 квадратных сантиметров.
Трапеции и созвездия
Трапеция встречается не только в домашних заданиях по математике.Этот рисунок можно найти при изучении созвездий. Выдающийся астеризм весеннего неба — трапеция Льва, наблюдаемая по вечерам с февраля по май. Эта фигура находится в зодиакальном созвездии Лев, образуя тело животного, и по форме напоминает трапецию.
Четыре яркие звезды созвездия α, β, γ и δ расположены на вершинах трапеции — тела льва. А голова льва образована звездами, расположенными в форме серпа.Отсюда и название — трапеция Льва.
Трапеции в экспериментальной физике Посмотреть
Союз физики и математики предполагает непрерывное движение науки вперед. В физике ученые проводят эксперименты, суть которых становится полностью ясной только после математического анализа. Многие разделы математики обязаны своим происхождением и дальнейшим развитием новым физическим экспериментам. В качестве примера рассмотрим школьные лабораторные работы по физике.
Многие разделы математики обязаны своим происхождением и дальнейшим развитием новым физическим экспериментам. В качестве примера рассмотрим школьные лабораторные работы по физике.
Постановка вопроса: Рассмотрим фигуру — произвольную трапецию ABCD.Нарисуйте две ее диагонали AC и BD, которые делят трапецию на четыре треугольника — ABO, BCO, CDO и DAO. Треугольники ABO и CDO равны:
Формулировка цели экспериментальной работы: с помощью взвешивания доказать, что массы треугольников, полученных по диагоналям и сторонам трапеции, равны.
Ход лабораторных работ:
- Учащимся необходимо взять с собой: лист бумаги, линейку, карандаш, ластик, ножницы.
- Учащиеся рисуют параллельные линии с помощью прямоугольных линеек.
- Учащимся нужно построить пять разных трапеций и нарисовать диагональ.
- Учащиеся ножницами вырезают из трапеции треугольники, которые имеют одну сторону от трапеции.
- На весах учащиеся взвешивают разрезанные треугольники ABO и CDO.

- Студенты записывают полученные результаты в таблицу и сравнивают.
Как видите, знания о трапеции пригодятся вам в физике и других науках.
Площадь трапеции — веб-формулы
Трапеция — это четырехугольник, у которого только одна пара параллельных сторон. Чтобы вычислить площадь трапеций, возьмите среднее значение оснований и умножьте на его высоту.
Площадь трапеции определяется как:
A = (a + b) ∙ h / 2
a: длина вершины
б: длина основания
h: высота
Когда a = 0, форма становится треугольником.
Пример 1:
Какова площадь трапеции с основаниями 5 см и 8 см и высотой 6 см?
Решение :
Используя формулу площади трапеции, получим:
Площадь трапеции = 0.5 × в × (а + б)
Площадь трапеции = 0,5 × 6 × (5 + 8)
Площадь трапеции = 0,5 × 6 × 13
Площадь трапеции = 39 см 2
Пример 2:
Площадь трапеции составляет 52 см 2 , а основания — 11 дюймов и 15 дюймов соответственно. Найдите его высоту.
Найдите его высоту.
Решение : Мы знаем, что площадь трапеции определяется по формуле:
Площадь трапеции = 0,5 × h × (a + b), где h — высота, выделив h из формулы, мы сможем определить ее высоту
Площадь = 0.5 × в × (а + б)
или
52 = 0,5 × (11 + 15) × в
52 = 0,5 × 26 × в
52 = 13ч
Таким образом:
h = 52/13 = 4 дюйма
Пример 3: Площадь трапеции составляет 15 см 2 , а расстояние между параллельными основаниями составляет 6 см. Если длина одного из параллельных оснований составляет 3 см, то какова длина другого параллельного основания?
Решение : Пусть a будет длиной неизвестной параллельной стороны, а b будет известным основанием.
Площадь трапеции = 0,5 × высота × (a + b) = 15 см 2
Подставляя значения получим:
(0,5) × 6 × (3 + a) = 15
Умножить каждую сторону на 2
6 х (3 + а) = 30
Разделив каждую сторону на 6, получим
3 + а = 5
а = 2 см
Следовательно, длина другой параллельной стороны составляет 2 см.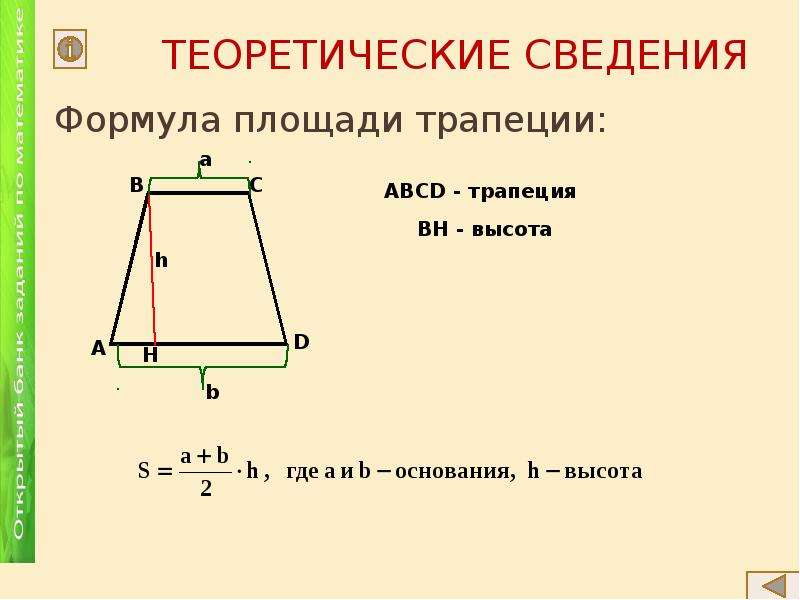
Пример 4: Какова длина параллельных сторон трапеции, если ее площадь составляет 18 см 2 , высота равна 4 см, а длина ее более короткой стороны на 5 см короче ее длинной стороны?
Решение : Пусть y будет длиной большей стороны.
Длина более короткой стороны составляет (y — 5) см, так как более короткая сторона на 5 см короче длинной стороны.
Площадь трапеции = 18 см 2
По формуле для площади трапеции имеем:
(0,5) × 4 × [y + (y — 5)] = 18
Умножаем каждую сторону на 2,
4 × (2y — 5) = 36
Разделите каждую сторону на 4,
2лет — 5 = 9
Упростив уравнение, мы получим:
2y = 14 и y = 7 см
Таким образом, длина более длинной стороны равна y = 7 см, тогда как длина более короткой стороны равна y — 5 = 7 — 5 = 2 см
Пример 5: Площадь трапеция 160 см2.Параллельные стороны 18 см и 14 см. Найдите расстояние между параллельными сторонами.
Решение :
Дано A = 160 см 2 , a = 18 см и b = 14 см.
Площадь трапеции, A = (0,5) × (a + b) × h
Подставляя известные значения, получаем:
160 = (0,5) × (18 + 14) × h
т.е. (0,5) × (18 + 14) × h = 160
0,5 × 32 × в = 160
16 × h = 160
Разделить на 16 с каждой стороны,
в = 10 см
Таким образом, расстояние между параллельными сторонами составляет 10 сантиметров.
Онлайн-калькулятор площади
| Расчет площади трапеции Зная все четыре стороны, но не высота
|
Как найти площадь и периметр трапеции
Трапеция — это четырехугольник или многоугольник с четырьмя сторонами, с одной парой параллельных сторон и одной парой непараллельных сторон. За пределами Северной Америки трапеции могут называться трапециями.
За пределами Северной Америки трапеции могут называться трапециями.
Как нам найти периметр и площадь трапеции? Прочтите примеры.
Определение периметра трапеции
Изображение создано в Desmos
Мы знаем, что многоугольник ABCD трапециевидный, потому что верхнее и нижнее основание трапеции параллельны.
Чтобы найти периметр или общую длину всех сторон трапеции, мы просто складываем длины каждой стороны. На этой трапеции ABCD мы видим, что периметр трапеции представляет собой сумму AB, BC, DC и AD:
- Длина нижнего основания DC равна 4.5.
- Длина верхнего основания AB составляет 2.
- Длина левой стороны AD равна 3.
- Длина правой стороны BC составляет 2.
Периметр этой трапеции наверху равен 2 + 2 + 4,5 + 3 = 11,5.
Определение площади трапеции
Чтобы найти площадь трапеции, воспользуемся следующей формулой:
Формула умножает высоту трапеции h на сумму двух оснований a и b , а затем делит на 2, потому что площадь трапеции всегда равна половине параллелограмма, образованного путем переворота трапеции на сам. Посмотрите на диаграмму здесь, как оранжевая трапеция — это просто синяя трапеция, перевернутая сама по себе:
Посмотрите на диаграмму здесь, как оранжевая трапеция — это просто синяя трапеция, перевернутая сама по себе:
Изображение создано в Desmos
Чтобы найти площадь параллелограмма, нам также понадобится высота. Как показано на этой диаграмме, высота параллелограмма равна высоте трапеции (оба равны 2). Высота основания параллелограмма равна сумме верхнего основания и нижнего основания трапеции, которая в данном случае составляет 2 + 4,5 = 6,5.
Попрактикуемся в использовании формулы площади трапеции.
Изображение создано в Desmos
На этой диаграмме мы видим, что высота трапеции равна BC, или 2. Это то же самое, что и правая сторона трапеции, потому что сторона, соединяющая вершины B и C, находится под прямым углом или перпендикулярна обеим сторонам. базы. ABCD известен как прямая трапеция, потому что он содержит прямой угол.
Буквы a и b в формуле обозначают основание и высоту трапеции, которые, как мы знаем, равны DC = 4,5 и AB = 2.
Если сложить все вместе, мы получим площадь трапеции:
Расчет площади и периметра трапеции
Теперь вы знаете, как рассчитать периметр трапеции — сложите все стороны и основания трапеции.
И вы знаете, как рассчитать площадь трапеции, используя формулу площади трапеции и длины основания и высоты.
Для дополнительной оценки теперь должно быть ясно, почему формула для площади работает именно так.
Домашнее задание по математике:
.
 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов: