Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь сложных геометрических фигур.
 Как вычислить площадь фигуры. Формулы площади трапеции
Как вычислить площадь фигуры. Формулы площади трапецииЕсли вы планируете сделать ремонт самостоятельно, то у вас возникнет необходимость составить смету по строительным и отделочным материалам. Для этого вам понадобится рассчитать площадь помещения, в котором вы планируете произвести ремонтные работы. Главным помощником в этом выступает специально разработанная формула. Площадь помещения, а именно ее расчет, позволит вам сэкономить немалые деньги на строительных материалах и направить высвободившиеся денежные ресурсы в более нужное русло.
Геометрическая форма комнаты
Формула расчета площади помещения напрямую зависит от ее формы. Наиболее типичными для отечественных сооружений являются прямоугольные и квадратные комнаты. Однако в ходе перепланировки стандартная форма может искажаться. Комнаты бывают:
- Прямоугольные.
- Квадратные.
- Сложной конфигурации (например, круглые).
- С нишами и выступами.
Каждая из них имеет свои особенности расчета, но, как правило, используется одна и та же формула. Площадь помещения любой формы и размера, так или иначе, поддается вычислению.
Площадь помещения любой формы и размера, так или иначе, поддается вычислению.
Помещение прямоугольной или квадратной формы
Чтобы рассчитать площадь комнаты прямоугольной или квадратной формы, достаточно вспомнить школьные уроки геометрии. Поэтому для вас не должно составить особого труда определить площадь помещения. Формула расчета имеет вид:
S комнаты=A*B, где
А — длина помещения.
В — ширина помещения.
Для измерения этих величин вам понадобится обычная рулетка. Чтобы получить наиболее точные расчёты, стоит измерить стену с обеих сторон. Если значения не сходятся, возьмите за основу среднее значение получившихся данных. Но помните, что любые расчёты имеют свои погрешности, поэтому материал стоит закупать с запасом.
Помещение со сложной конфигурацией
Если ваша комната не попадает под определение «типичной», т.е. имеет форму круга, треугольника, многоугольника, то, возможно, для расчетов вам понадобится другая формула. Площадь помещения с такой характеристикой можно попробовать условно разделить на прямоугольные элементы и произвести расчеты стандартным путем.
- Формула нахождения площади круга:
S комн.=π*R 2 , где
R — радиус помещения.
- Формула нахождения площади треугольника:
S комн.= √ (P(P — A) х (Р — В) х (Р — С)), где
Р — полупериметр треугольника.
А, В, С — длины его сторон.
Отсюда Р=А+В+С/2
Если в процессе расчета у вас возникли затруднения, то лучше не мучать себя и обратиться к профессионалам.
Площадь помещения с выступами и нишами
Зачастую стены украшают декоративными элементами в форме всевозможных ниш или выступов. Также их наличие может быть обусловлено необходимостью скрыть некоторые неэстетичные элементы вашей комнаты. Наличие выступов или ниш на вашей стене означает, что расчет следует проводить поэтапно. Т.е. сначала находится площадь ровного участка стены, а затем к нему прибавляется площадь ниши или выступа.
Площадь стены находится по формуле:
S стен = Р х С, где
Р — периметр
С — высота
Также нужно учитывать наличие окон и дверей. Их площадь необходимо отнять от получившегося значения.
Их площадь необходимо отнять от получившегося значения.
Комната с многоуровневым потолком
Многоуровневый потолок не так сильно усложняет расчеты, как это кажется на первый взгляд. Если он имеет простую конструкцию, то можно произвести расчеты по принципу нахождения площади стен, осложненных нишами и выступами.
Однако если конструкция вашего потолка имеет дуго- и волнообразные элементы, то целесообразнее определить его площадь с помощью площади пола. Для этого необходимо:
- Найти размеры всех прямых участков стен.
- Найти площадь пола.
- Перемножить длину и высоту вертикальных участков.
- Суммировать получившееся значение с площадью пола.
Пошаговая инструкция по определению общей
площади помещения
- Освободите помещение от ненужных вещей. В процессе замеров вам понадобится свободный доступ ко всем участкам вашей комнаты, поэтому нужно избавиться от всего, что может этому препятствовать.
- Визуально разделите комнату на участки правильной и неправильной формы.
 Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить.
Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить. - Сделайте произвольную схему помещения. Этот чертеж нужен для того, чтобы все данные были у вас всегда под рукой. Также он не даст вам возможности запутаться в многочисленных замерах.
- Замеры необходимо производить несколько раз. Это важное правило для исключения ошибок в подсчетах. Также если вы используете убедитесь, что луч лежит ровно на поверхности стены.
- Найдите общую площадь помещения. Формула общей площади помещения заключается в нахождении суммы всех площадей отдельных участков комнаты. Т.е. S общ.= S стен+S пола+S потолка
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали. где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Как найти площадь фигуры?
Знать и уметь рассчитывать площади различных фигур необходимо не только для решения простых геометрических задач.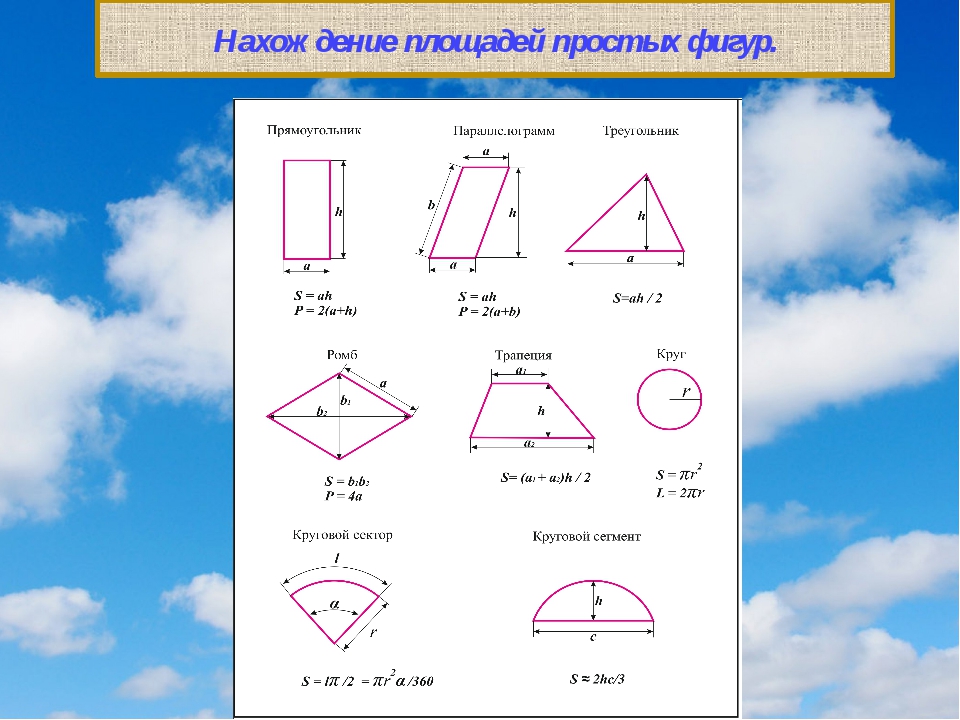 Не обойтись без этих знаний и при составлении или проверке смет на ремонт помещений, расчета количества необходимых расходных материалов. Поэтому давайте разберемся, как находить площади разных фигур.
Не обойтись без этих знаний и при составлении или проверке смет на ремонт помещений, расчета количества необходимых расходных материалов. Поэтому давайте разберемся, как находить площади разных фигур.
Часть плоскости, заключенная внутри замкнутого контура, называется площадью этой плоскости. Выражается площадь количеством заключенных в ней квадратных единиц.
Чтобы вычислить площадь основных геометрических фигур, необходимо использовать правильную формулу.
Площадь треугольника
Обозначения:
- Если известны h, a, то площадь искомого треугольника определяется как произведение длин стороны и высоты треугольника, опущенной к этой стороне, разделенное пополам: S=(a·h)/2
- Если известны a, b, c, то искомая площадь рассчитывается по формуле Герона: корень квадратный, взятый из произведения половины периметра треугольника и трех разностей половины периметра и каждой стороны треугольника: S = √(p·(p — a)·(p — b)·(p — c)).
- Если известны a, b, γ, то площадь треугольника определяется как половина произведения 2-х сторон, умноженная на значение синуса угла между этими сторонами: S=(a·b·sin γ)/2
- Если известны a, b, c, R, то искомая площадь определяется как деление произведения длин всех сторон треугольника на четыре радиуса описанной окружности: S=(a·b·c)/4R
- Если известны p, r, то искомая площадь треугольника определяется умножением половины периметра на радиус вписанной в него окружности: S=p·r
Площадь квадрата
Обозначения:
- Если известна сторона, то площадь данной фигуры определяется как квадрат длины его стороны: S=a 2
- Если известна d, то площадь квадрата определяется как половина квадрата длины его диагонали: S=d 2 /2
Площадь прямоугольника
Обозначения:
- S — определяемая площадь,
- a, b — длины сторон прямоугольника.

- Если известны a, b, то площадь данного прямоугольника определяется произведением длин двух его сторон: S=a·b
- Если длины сторон неизвестны, то площадь прямоугольника нужно разбить на треугольники. В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.
Площадь параллелограмма
Обозначения:
- S — искомая площадь,
- a, b — длины сторон,
- h — длина высоты данного параллелограмма,
- d1, d2 — длины двух диагоналей,
- α — угол, находящийся между сторонами,
- γ — угол, находящийся между диагоналями.
- Если известны a, h, то искомая площадь определяется перемножением длин стороны и высоты, опущенной на эту сторону: S=a·h
- Если известны a, b, α, то площадь параллелограмма определяется перемножением длин сторон параллелограмма и значения синуса угла между этими сторонами: S=a·b·sin α
- Если известны d 1 , d 2 , γ то площадь параллелограмма определяется как половина произведения длин диагоналей и значения синуса угла между этими диагоналями: S=(d 1 ·d 2 ·sinγ)/2
Площадь ромба
Обозначения:
- S — искомая площадь,
- a — длина стороны,
- h — длина высоты,
- α — меньший угол между двумя сторонами,
- d1, d2 — длины двух диагоналей.

- Если известны a, h, то площадь ромба определяется умножением длины стороны на длину высоты, которая опущена на эту сторону: S=a·h
- Если известны a, α, то площадь ромба определяется перемножением квадрата длины стороны на синус угла между сторонами: S=a 2 ·sin α
- Если известны d 1 и d 2 , то искомая площадь определяется как половина произведения длин диагоналей ромба: S=(d 1 ·d 2)/2
Площадь трапеции
Обозначения:
- Если известны a, b, c, d, то искомая площадь определяется по формуле: S= (a+b) /2 *√ .
- При известных a, b, h, искомая площадь определяется как произведение половины суммы оснований и высоты трапеции: S=(a+b)/2·h
Площадь выпуклого четырехугольника
Обозначения:
- Если известны d 1 , d 2 , α, то площадь выпуклого четырехугольника определяется как половина произведения диагоналей четырехугольника, умноженная на величину синуса угла между этими диагоналями: S=(d 1 · d 2 ·sin α)/2
- При известных p, r площадь выпуклого четырехугольника определяется как произведение полупериметра четырехугольника на радиус окружности, вписанной в этот четырехугольник: S=p·r
- Если известны a, b, c, d, θ, то площадь выпуклого четырехугольника определяется как корень квадратный из произведений разницы полупериметра и длины каждой стороны за минусом произведения длин всех сторон и квадрата косинуса половины суммы двух противоположных углов: S 2 = (p — a)(p — b)(p — c)(p — d) — abcd·cos 2 ((α+β)/2)
Площадь круга
Обозначения:
Если известен r, то искомая площадь определяется как произведение числа π на радиус в квадрате: S=π r 2
Если известна d, то площадь круга определяется как произведение числа π на квадрат диаметра, поделенное на четыре: S=(π·d 2)/4
Площадь сложной фигуры
Сложную можно разбить на простые геометрические фигуры. Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.
Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.
Обозначение:
- S — площадь кольца,
- R, r — радиусы внешней окружности и внутренней соответственно,
- D, d — диаметры внешней окружности и внутренней соответственно.
Для того чтобы найти площадь кольца, надо из площади большего круга отнять площадь меньшего круга. S = S1-S2 = πR 2 -πr 2 = π (R 2 -r 2).
Таким образом, если известны R и r, то площадь кольца определяется как разница квадратов радиусов внешней и внутренней окружностей, умноженная на число пи: S=π(R 2 -r 2).
Если известны D и d, то площадь кольца определяется как четверть разницы квадратов диаметров внешней и внутренней окружностей, умноженная на число пи: S= (1/4)(D 2 -d 2) π.
Площадь закрашенной фигуры
Предположим, что внутри одного квадрата (А) находится другой (Б) (меньшего размера), и нам нужно найти закрашенную полость между фигурами «А» и «Б». Скажем так, «рамку» маленького квадрата. Для этого:
Скажем так, «рамку» маленького квадрата. Для этого:
- Находим площадь фигуры «А» (вычисляется по формуле нахождения площади квадрата).
- Аналогичным образом находим площадь фигуры «Б».
- Вычитаем из площади «А» площадь «Б». И таким образом получаем площадь закрашенной фигуры.
Теперь вы знаете, как находить площади разных фигур.
Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.
Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:
2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении.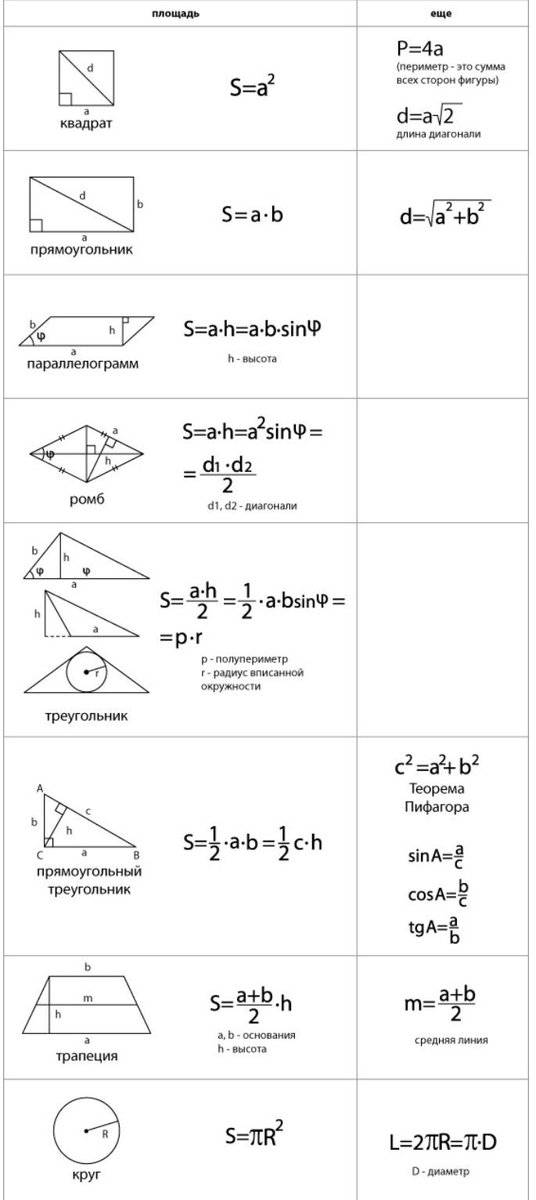 Такая формула площади прямоугольника имеет вид:
Такая формула площади прямоугольника имеет вид:
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы.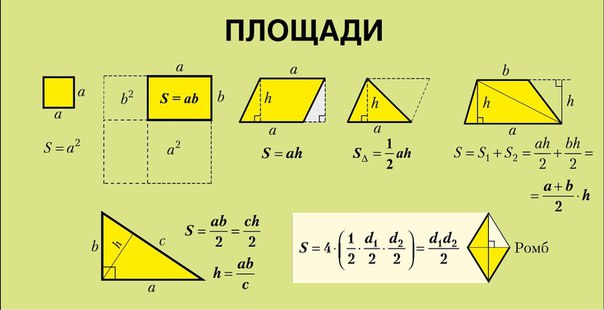 Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.
Формула Пика
Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.
Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.
В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.
Площадь искомой фигуры можно найти по формуле:
М – количество узлов на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника
*Под «узлами» имеется ввиду пересечение линий.
Найдём площадь треугольника:
Отметим узлы:
1 клетка = 1 см
M = 15 (обозначены красным)
N = 34 (обозначены синим)
Ещё пример. Найдём площадь параллелограмма:
Найдём площадь параллелограмма:
Отметим узлы:
M = 18 (обозначены красным)
N = 20 (обозначены синим)
Найдём площадь трапеции:
Отметим узлы:
M = 24 (обозначены красным)
N = 25 (обозначены синим)
Найдём площадь многоугольника:
Отметим узлы:
M = 14 (обозначены красным)
N = 43 (обозначены синим)
Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.
А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.
Теперь взгляните на следующие фигуры:
Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:
Отметим узлы:
M = 11 (обозначены красным)
N = 5 (обозначены синим)
Ответ: 9,5
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.
Рассмотрим подход оговоренный в статье «Площадь четырёхугольника. Универсальный способ».
Найдём площадь фигуры:
Опишем около неё прямоугольник:
Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:
Ответ: 4,5
В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!
Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Формулы площадей всех фигур в геометрии — примеры вычислений
Площадь — это одна из наиболее важных и неотъемлемых характеристик любой замкнутой геометрической фигуры, показывающая её размер. Она может измеряться в различных единицах: квадратных миллиметрах, сантиметрах, дециметрах, метрах и так далее. Это своеобразный аналог объёма трёхмерных фигур (шара, цилиндра, конуса и других). В геометрии разработаны формулы площадей. Их доказательством являются соответствующие теоремы. Существует общепринятое обозначение площади — буква S (от англ. square).
Формулы для треугольников
Имеется несколько формул площади треугольника. Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.
Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.
При известности всех трёх сторон — a, b, c, широко применяется формула, названная в честь Герона — математика из Древней Греции: S = √(p*(p — a)*(p — b)*(p — c)). Величина p — это половина от периметра треугольника (полупериметр). Чтобы его рассчитать, необходимо суммировать все стороны и разделить сумму на два: (a + b + c)/2.
Для ещё одной формулы требуются следующие данные:
- длина двух соприкасающихся в одной вершине сторон — a и b;
- градус угла, который образуют эти стороны.
Тогда расчёт можно произвести таким способом: S = ½ * a * b * sin γ. Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.
Значение sin γ для конкретного угла можно посмотреть в специальной таблице.
Когда два треугольника являются подобными (подобие означает, что у них равны углы и стороны пропорциональны), то отношение их площадей соответствует отношению возведённых в квадрат сторон. Такое отношение сторон для них (например, AB: A (1) B (1)) именуется коэффициентом подобия (k). Поэтому отношение площадей равняется коэффициенту подобия в квадрате.
Если в треугольнике даны все стороны, тогда, кроме формулы Герона, есть возможность воспользоваться ещё одним способом. Он основан на том, что можно вписать любой треугольник в круг. Зная такую величину, радиус ® окружности и три стороны треугольника, производится расчёт: S = (a * b * c) / 4 R.
В любой треугольник: равносторонний и разносторонний, остроугольный и тупоугольный, в силу его геометрических свойств также может быть вписана окружность. В таком случае формула нахождения площади следующая: S = p * r. Буква p обозначает ½ периметра треугольника, r — это радиус окружности.
Площадь четырёхугольников
Четырёхугольник — это одна из фигур в геометрии (многоугольник), имеющая четыре стороны, а также четыре вершины, три из которых не находятся на одной прямой. Четырёхугольник называется выпуклым, если он располагается по одну сторону относительно прямой, являющейся продолжением любой из его сторон.
К выпуклым четырёхугольникам относятся практически все известные фигуры, имеющие четыре вершины, а также четыре стороны. Основными их видами выступают: 1) ромб; 2) прямоугольник; 3) трапеция; 4) квадрат; 5) параллелограмм.
Квадрат и прямоугольник
Самый простой способ вычисления площади квадрата — умножить сторону «саму на себя», иными словами, возвести в квадрат длину любой из его сторон (S = a2 ). Такой расчёт обусловлен особым признаком квадрата — тем, что все его стороны являются абсолютно равными между собой, поэтому квадрат называется правильной фигурой.
Существует вторая, более сложная, формула площади квадрата, где осуществляется расчёт через диагональ. Диагональ — это линия, соединяющая в фигуре два угла, друг другу противоположных. Для определения площади необходимо длину диагонали возвести в квадрат и полученный результат разделить на два: S = ½ d 2.
Для прямоугольника используется формула: S = a * b, где a, b — длина двух разных, имеющих общую вершину, сторон.
Параллелограмм, ромб и трапеция
Параллелограмм представляет собой четырёхугольник, в котором имеются два противоположных друг другу тупых угла и два — острых.
Применяются три формулы площади параллелограмма:
- Умножить сторону на высоту, перпендикулярную стороне: S = a * h.
- Перемножить две, выходящих из одной вершины, стороны параллелограмма, и умножить на синус угла, образованного ими: S = a * b * sin γ.

- Перемножить диагонали фигуры, затем умножить на синус угла, образованного диагоналями, и разделить результат на два: S = ½ d (1) * d (2) * sin γ.
Ромб похож на параллелограмм с одним отличием: он является равносторонним. Поэтому для вычисления площади ромба используются похожие формулы:
Трапеция является геометрической фигурой, имеющей такие элементы: два параллельных основания — верхнее и нижнее, две боковые стороны, расположенные к нижнему основанию под острым углом. Что касается боковых сторон, то они могут быть как равными по длине (так называемая равнобедренная трапеция), так и разными.
В связи с тем, что в «составе» трапеции можно «выделить» прямоугольник и два расположенных по бокам от него треугольника, то можно определить площадь по специальной формуле Герона: S = (a + b): | a + b | * √(p — a) * (p — b) * (p — a — c) * (p — a — d).
В этой формуле имеются следующие обозначения:
- буквы a, b — это основы трапеции,
- буквы c, d — стороны,
- p — полупериметр.
Выпуклый четырёхугольник
В отношении всех иных выпуклых четырёхугольников, то есть имеющих разные по длине стороны и разные углы, разработаны свои формулы вычисления площади.
Прежде всего, можно перемножить две диагонали, а также синус образуемого ими угла, разделив общий результат на два, то есть применить формулу: S = ½ d (1) * d (2) * sin γ.
В том случае, когда внутри выпуклого четырёхугольника, так же как и внутри треугольника, может быть вписан круг, то для нахождения площади четырёхугольной фигуры, требуется определить две величины:
- r — радиус окружности;
- p — ½ периметра четырёхугольника.

После чего полупериметр умножается на радиус. Это и будет площадь четырёхугольника. Формула выглядит так: S = p * r.
Для тех случаев, когда круг может быть очерчен вокруг четырёхугольника, применяется другая формула. Для её использования все стороны фигуры должны быть известны. Они обозначаются буквами a, b, c, d. Рассчитывается половина периметра: p = (a + b + c + d)/2. Затем определяется площадь: S = √(p — a)(p — b)(p — c)(p — d).
Когда конфигурация четырёхугольника такова, что не позволяет возле него описать круг, то в связи с этим формула площади немного дополняется: S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2 γ.
Коэффициент γ представляет собой половину от суммы двух противоположных углов четырёхугольной фигуры: γ = (угол (1) + угол (2)) / 2.
Круг и эллипс
Самое распространённое и широко применяемое правило определения площади круга — это умножение радиуса окружности в квадрате на число пи: S = π * r 2.
Число пи, обозначаемое греческой буквой «π» — это математическая постоянная, которая является результатом деления длины окружности на диаметр. π — иррациональное число. Для расчётов признаётся его среднее значение, равное 3,14.
Вместо радиуса можно использовать диаметр окружности: диаметр возводится в квадрат, умножается на число π, результат делится на четыре. Формула выглядит так: S = (π * d 2) / 4.
Для того чтобы посчитать площадь такой фигуры, как эллипс, необходимо провести две оси, то есть две линии, каждая из которых разделяет эллипс на две равные части, при этом сами линии перпендикулярны друг другу (образуют прямой угол). Точка пересечения разделяет каждую из осей напополам, образуя полуоси.
Площадь эллипса вычисляется как произведение трёх величин: числа π, длины большой полуоси (а) и длины малой полуоси (b): S = π * a * b. Для удобства расчёта площадей различных фигур также можно использовать специальные онлайн-калькуляторы.
youtube.com/embed/2aFhtqYi4B4″/>
ПредыдущаяМатематикаМетод координат в геометрии — примеры решения и построения
СледующаяМатематикаСвойства и признаки диагоналей прямоугольника — формулы и примеры расчетов
Площадь параллелограмма, треугольника и трапеции — урок. Геометрия, 8 класс.
Площадь параллелограмма
Необходимо определить, что такое высота параллелограмма.
Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону. Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.
Высота \(BE\), проведённая между длинными сторонами, короче высоты \(BF\), проведённой между короткими сторонами.
Так как стороны ромба одинаковы, то высоты ромба также одинаковы: \(BE = BF\).
Площадь произвольного параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
Проведём высоты из двух вершин \(B\) и \(C\) к стороне \(AD\) .
Прямоугольные треугольники \(ABE\) и \(DCF\) равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
Параллелограмм \(ABCD\) и прямоугольник \(EBCF\) — равновеликие, так как состоят из равных фигур:
SABCD=SABE+SEBCD;SEBCF=SEBCD+SDCF.
Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
SEBCF=BE⋅BC;SABCD=BE⋅BC=BE⋅AD.
Если обозначить сторону через \(a\), высоту — через \(h\), то:
Sп−гр=a⋅h.
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
Площадь ромба
Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.
SABCD=4⋅SABO=4⋅BO⋅AO2=2⋅BO⋅AO.
Формула определения площади ромба:
Sромба=d1⋅d22.
Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.
Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали:
Sквадрата=d22.
Площадь произвольного треугольника
Так как диагональ параллелограмма делит его на два равных треугольника, то площадь треугольника равна половине площади параллелограмма.
Sтреуг=aha2, где \(h\) — высота (на рисунке — \(BE\)), проведённая к стороне \(a\) (на рисунке — \(AD\)).
Для определения площади треугольника можно использовать любую сторону и высоту, проведённую к этой стороне.
Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.
SΔ=pp−ap−bp−c;p=a+b+c2
— формула Герона, где \(a\), \(b\) и \(c\) — стороны треугольника, \(p\) — полупериметр треугольника.

Площадь прямоугольного треугольника
Так как катеты прямоугольного треугольника взаимно перпендикулярны, то один катет может быть высотой, а другой катет — стороной, к которой проведена высота. Получаем формулу:
S=a⋅b2, где \(a\) и \(b\) — катеты.
Для прямоугольного треугольника также можно применять формулы площади произвольного треугольника.
Пример:
1. вычислим площадь треугольника со сторонами \(17\) см, \(39\) см, \(44\) см.
Решение:
p=17+39+442=50;SΔ=50⋅50−17⋅50−39⋅50−44=50⋅33⋅11⋅6==25⋅2⋅3⋅11⋅11⋅2⋅3=5⋅2⋅3⋅11=330см2.
Чтобы легче было вычислить корень, необходимо не перемножать все числа, а раскладывать их на множители: a⋅a=a.
Формулу Герона можно использовать для вычисления высоты треугольника.Пример:
2. вычислим меньшую высоту треугольника, стороны которого равны \(15\) см, \(13\) см, \(4\) см.
Решение:
используем две формулы вычисления площади: SΔ=aha2 и SΔ=pp−ap−bp−c.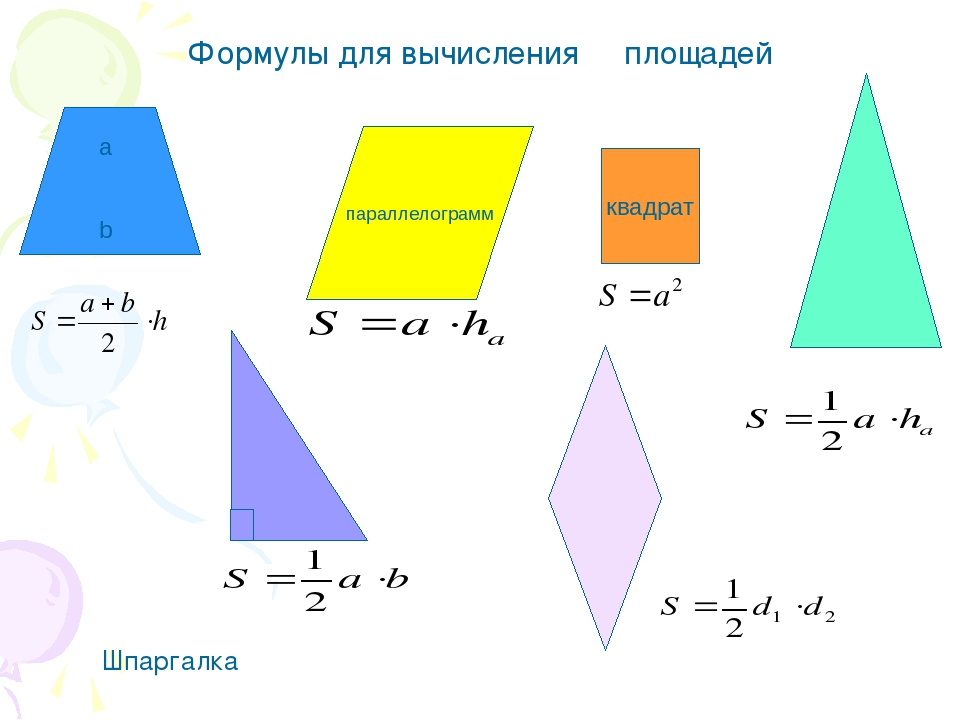
Меньшая высота в треугольнике — та, которая проведена к большей стороне, поэтому \(a =\) \(15\) см.
SΔ=pp−ap−bp−c=16⋅1⋅3⋅12=24см2.
Составляем уравнение:
15⋅h3=24⋅215⋅h=48;h=4815=3,2(см).
Иногда формула Герона используется для вычисления площади параллелограмма, если даны стороны параллелограмма и его диагональ.
Пример:
3. дан параллелограмм со сторонами \(17\) см и \(39\) см, длина диагонали равна \(44\) см. Вычислим площадь параллелограмма.
Решение:
диагональ делит параллелограмм на два равных треугольника. Используем результат, полученный в первом примере:
Sпараллелограмма=2⋅SΔ=2⋅330=660(см2).
Площадь трапеции
Трапеция имеет одну пару параллельных сторон, следовательно, имеет одну высоту — перпендикуляр, проведённый между параллельными сторонами.
Чаще всего высоту трапеции проводят из вершин или через точку пересечения диагоналей.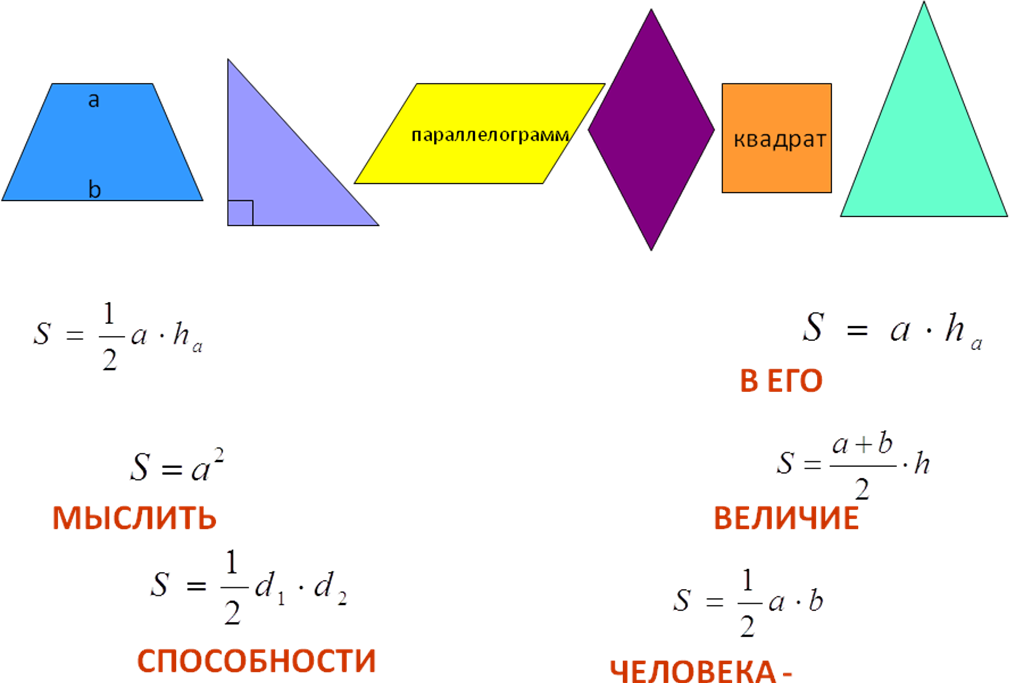
Площадь трапеции определим как сумму площадей треугольников, на которые трапецию делит диагональ.
SABCD=SABD+SDBC;SABCD=AD⋅BE2+BC⋅DF2=AD⋅BE2+BC⋅BE2==AD+BC⋅BE2.
Если обозначить параллельные стороны (основания) трапеции через \(a\) и \(b\), высоту через \(h\), то:
Sтрап=a+b2⋅h.
Обрати внимание!
Важные следствия:
1. если высоты треугольников равны, то их площади относятся как длины оснований.
2. Если основания треугольников равны, то их площади относятся как длины высот.
3. Если высоты треугольников равны и их основания равны, то они равновелики, например, медиана делит треугольник на две равновеликие части.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
S = ab,
которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник | S = ab | a и b – смежные стороны | |
Посмотреть вывод формулы | d – диагональ, | ||
S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R | R – радиус описанной окружности, | ||
| Параллелограмм | S = a ha Посмотреть вывод формулы | a – сторона, | |
S = absin φ Посмотреть вывод формулы | a и b – смежные стороны, | ||
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | ||
| Квадрат | S = a2 | a – сторона квадрата | |
| S = 4r2 | r – радиус вписанной окружности | ||
Посмотреть вывод формулы | d – диагональ квадрата | ||
S = 2R2 Получается из верхней формулы подстановкой d = 2R | R – радиус описанной окружности | ||
| Ромб | S = a ha Посмотреть вывод формулы | a – сторона, | |
S = a2 sin φ Посмотреть вывод формулы | a – сторона, | ||
Посмотреть вывод формулы | d1, d2 – диагонали | ||
S = 2ar Посмотреть вывод формулы | a – сторона, | ||
Посмотреть вывод формулы | r – радиус вписанной окружности, | ||
| Трапеция | Посмотреть вывод формулы | a и b – основания, | |
| S = m h | m – средняя линия, | ||
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | ||
Посмотреть вывод формулы | a и b – основания, | ||
| Дельтоид | S = ab sin φ | a и b – неравные стороны, | |
a и b – неравные стороны, | |||
S = (a + b) r Посмотреть вывод формулы | a и b – неравные стороны, | ||
Посмотреть вывод формулы | d1, d2 – диагонали | ||
| Произвольный выпуклый четырёхугольник | Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
| Вписанный четырёхугольник | , Посмотреть вывод формулы Брахмагупты | a, b, c, d – длины сторон четырёхугольника, Формулу называют «Формула Брахмагупты» |
| Прямоугольник | |
S = ab где | |
где Посмотреть вывод формулы | |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R | |
| Параллелограмм | |
S = a ha где Посмотреть вывод формулы | |
S = absin φ где Посмотреть вывод формулы | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
| Квадрат | |
| S = a2 где | |
| S = 4r2 где | |
где Посмотреть вывод формулы | |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R | |
| Ромб | |
S = a ha где Посмотреть вывод формулы | |
S = a2 sin φ где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
S = 2ar где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Трапеция | |
где Посмотреть вывод формулы | |
S = m h где | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Дельтоид | |
S = ab sin φ где | |
где | |
S = (a + b) r где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Произвольный выпуклый четырёхугольник | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
| Вписанный четырёхугольник | |
, где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты | |
| Прямоугольник |
S = ab где |
где Посмотреть вывод формулы |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм |
S = a ha где Посмотреть вывод формулы |
S = absin φ где Посмотреть вывод формулы |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат |
S = a2 где |
S = 4r2 где |
где Посмотреть вывод формулы |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб |
S = a ha где Посмотреть вывод формулы |
S = a2 sin φ где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
S = 2ar где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Трапеция |
где Посмотреть вывод формулы |
S = m h где |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Дельтоид |
S = ab sin φ где |
где |
S = (a + b) r где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник |
где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
Вывод формул для площадей четырехугольников
Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле
Площадь выпуклого четырёхугольника можно найти по формуле
где d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).
Рис. 1
Доказательство. В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле
S = a ha ,
где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).
Рис. 2
Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
SABCD = SAEFD = a ha ,
что и требовалось доказать.
Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле
S = ab sin φ,
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
Рис. 3
Доказательство. Поскольку
ha = b sin φ,
то, в силу утверждения 2, справедлива формула
S = a ha = ab sin φ,
что и требовалось доказать.
Утверждение 4. Площадь ромбаромба можно найти по формуле
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
Рис. 4
Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности. Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
что и требовалось доказать.
Утверждение 5. Площадь трапеции можно найти по формуле
,
где a и b – основания трапеции, а h – высотавысотавысота (рис.5).
Рис. 5
Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому
что и требовалось доказать.
Утверждение 6. Площадь трапеции трапеции можно найти по формуле
,где a и b – основания, а c и d – боковые стороны трапеции,
(рис.6).
Рис. 6
Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
Следовательно,
где
,что и требовалось доказать.
Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:
S = (a + b) r,
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Рис. 7
Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Все формулы по геометрии. Задача в3: площади фигур
Больше половины всех задач В3 из вариантов ЕГЭ — это задачи, в которых надо посчитать площадь фигуры. Чтобы решить их, надо знать формулы по геометрии — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала стоит выучить формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно же, не все формулы по геометрии есть в нашей таблице. Например, для решения задачи С4 применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
S = 5 + 7,5 = 12,5.
Ответ: 12,5.
В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
S = 25 – 5 – 5 – 4,5 = 10,5.
Ответ: 10,5.
Иногда в задании В3 надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
На этом рисунке мы видим часть круга. Площадь всего круга равна πR² = π, так как R=1. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна 2πR = 2π (так как R=1), а длина дуги данного сектора равна 2, следовательно, длина дуги в π раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в π раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в π раз меньше, чем площадь всего круга.
Ответ: 1.
И ещё примерно половина прототипов задачи В3 — это простые задачи на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по Х) и что такое ордината (координата по Y). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами. Все прототипы задачи В3 можно найти на сайте mathege.ru.
Геометрия на егэ по математике
Геометрия на ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.
Геометрия на ЕГЭ — это четыре задачи в части и В (две по планиметрии и две по стереометрии), а также задача С2 и для многих недосягаемая С4. Как же научиться их решать?
Начнем с планиметрии. Прежде всего, вам нужно выучить основные формулы геометрии.
На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части В.
Для решения задачи С4 нужна более серьезная подготовка. Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Программа по геометрии.
1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).
2. Построение треугольника: практические задания. а) Три стороны треугольника АВС равны 4, 6 и 8 сантиметров соответственно. Постройте треугольник АВС с помощью циркуля и линейки. б) В треугольнике АВС угол В равен 48 градусов, сторона АВ равна двум, ВС равна 9. Постройте треугольник АВС. в) В треугольнике АВС сторона ВС равна 5, угол В равен 26°, угол С равен 58°. Постройте треугольник АВС.
3. Три признака равенства треугольников. Неравенство треугольника.
4. Постройте с помощью циркуля и линейки: а) серединный перпендикуляр к отрезку; б) биссектрису угла.
5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.
6. Теорема о сумме углов треугольника.
7. Внешний угол треугольника.
8. Постройте в одном и том же треугольнике а) три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника. б) три биссектрисы. в) три медианы.
9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.
10. Средняя линия треугольника и ее свойства.
11. Прямоугольный треугольник. Теорема Пифагора.
12. Определения синуса, косинуса и тангенса — для острого угла прямоугольного треугольника — для произвольного угла.
13. Четырехугольники. Сумма углов четырехугольника.
14. Параллелограмм. Определение и свойства. Площадь параллелограмма.
15. Виды параллелограммов и их свойства. (ромб, прямоугольник, квадрат).
16. Трапеция. Средняя линия трапеции. Площадь трапеции.
17. Подобные треугольники. Три признака подобия треугольников.
18. Площадь треугольника. Формулы и .
19. Теоремы синусов и косинусов.
20. Чему равно отношение площадей подобных фигур.
21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)
22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)
23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.
24. Теорема о радиусе, проведенном в точку касания.
25. Центральный и вписанный углы. Связь между ними.
26. Теоремы о вписанных углах.
27. Теорема о пересекающихся хордах.
28. Теорема об отрезках длин касательных, проведенных из одной точки.
29. Теорема о секущей и касательной.
30. Дан треугольник АВС. Постройте а) окружность, вписанную в данный треугольник б) окружность, описанную вокруг данного треугольника. Где находятся центры этих окружностей?
31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).
32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?
(Программа по стереометрии будет размещена в ближайшее время.)
Отдельно — тема «Векторы». Напомним, что на ЕГЭ по математике векторы встречаются в задаче В3. Они также пригодятся вам в решении задачи С2.
Освоив теорию, можно приступать к решению сложных задач по геометрии, входящих в часть С ЕГЭ. Мы рекомендуем вам сборники: Р. К. Гордин «ЕГЭ 2012. Математика. Задача С4. Геометрия. Планиметрия» и А. Г. Корянов и А. А. Прокофьев «Пособие по решению заданий типа С4». Можно найти на сайте alexlarin.net.
Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части В, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные С4.
Решая на ЕГЭ задачи С4 по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:
«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90º. Другими словами, половина развернутого угла.
Острый угол — меньший 90º.
Тупой угол — больший 90º. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается С. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла А, обозначается а.
Угол А обозначается соответствующей греческой буквой α.
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет а, лежащий напротив угла α, называется противолежащим (по отношению к углу α). Другой катет b, который лежит на одной из сторон угла α, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
Сумма углов любого треугольника равна 180º. Значит, сумма двух острых углов прямоугольного треугольника равнa 90º.
С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла β катет а будет прилежащим.
Получаем, что cos β = sin A. Иными словами, cos (90º — А) = sin A.
Возьмем теорему Пифагора: a2 + b2 = c2.
Поделим обе части на cos2 A:
Мы получили основное тригонометрическое тождество:
Поделив обе части основного тригонометрического тождества на cos2 A, получим:
Это значит, что если нам дан тангенс острого угла α, то мы сразу можем найти его косинус.
Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна 180°.
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: a2 + b2 = с2.
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от 0 до 90°.
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике ABC угол C равен 90°, sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку А+В = 90°, sin A = cos B = 0,1.
2. В треугольнике ABC угол C равен 90°, АВ = 5, . Найдите AC.
Имеем:
Отсюда
Найдем АС по теореме Пифагора.
Задача решена.
Часто в задачах встречаются треугольники с углами 90°, 30° и 60° или с углами 90°, 45° и 45°. Основные соотношения для них запоминайте наизусть!
Для треугольника с углами 90°, 30° и 60° катет, лежащий напротив угла в 30°, равен половине гипотенузы.
Треугольник с углами 90°, 45° и 45° — равнобедренный. В нем гипотенуза в раз больше катета.
Периметр, площадь и объем
1. В периметр из многоугольник (или любая другая замкнутая кривая, например окружность) — это расстояние вокруг внешней стороны.
2. В область из простая замкнутая плоская кривая — это количество внутреннего пространства.
3. В объем из твердый 3 D shape — это количество перемещаемого им пространства.
Некоторые формулы для общих 2 -мерные плоские фигуры и 3 -мерные тела приведены ниже.Ответов один, два, или три измерения; периметр измеряется в линейные единицы , область измеряется в квадратные единицы , а также объем измеряется в кубические единицы .
| Таблица 1 . Формулы периметра | ||
Форма | Формула | Переменные |
Квадратный | п знак равно 4 s | s длина стороны квадрата. |
Прямоугольник | п знак равно 2 L + 2 W | L а также W — длины сторон прямоугольника (длина и ширина). |
Треугольник | а + б + c | а , б , а также c — длины сторон. |
п знак равно а + б + а 2 + б 2 | а а также б длины двух катетов треугольника | |
Круг | р это радиус и d это диаметр. | |
| Таблица 2. Формулы площади | ||
Форма | Формула | Переменные |
Квадратный | s длина стороны квадрата. | |
Прямоугольник | L а также W — длины сторон прямоугольника (длина и ширина). | |
Треугольник | А знак равно 1 2 б час | б а также час основание и высота |
Треугольник | А знак равно s ( s — а ) ( s — б ) ( s — c ) где s знак равно а + б + c 2 | а , б , а также c длины сторон и s полупериметр |
Параллелограмм | б длина основания и час это высота. | |
Трапеция | А знак равно б 1 + б 2 2 час | б 1 а также б 2 — длины параллельных сторон и час расстояние (высота) между параллелями. |
Круг | А знак равно π р 2 | р это радиус. |
| Таблица 3. Формулы объема | ||
Форма | Формула | Переменные |
Куб | s длина стороны. | |
Правая прямоугольная призма | L это длина, W это ширина и ЧАС это высота. | |
Призма или цилиндр | А площадь основания, час это высота. | |
Пирамида или конус | А площадь основания, час это высота. | |
Сфера | р это радиус. | |
Площадь круга, треугольника, квадрата, прямоугольника, параллелограмма, трапеции, эллипса и сектора
Площадь — это размер поверхности!
Узнайте больше о площади или воспользуйтесь калькулятором площади.
Пример: Какова площадь этого прямоугольника?
Формула:
Площадь = ш × в
ш = ширина
в = высота
Мы знаем w = 5 и h = 3 , поэтому:
Площадь = 5 × 3 = 15
Пример: Какова площадь этого круга?
Радиус = r = 3
| Площадь | = π × r 2 | |
| = π × 3 2 | ||
| = π × (3 × 3) | ||
| = 3.14159 … × 9 | ||
| = 28,27 (до 2 знаков после запятой) |
Пример: Какова площадь этого треугольника?
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Более сложный пример:
Пример: Сэм косит траву по цене 0,10 доллара за квадратный метр
Сколько зарабатывает Сэм, обрабатывая эту область:
Разобьем область на две части:
Часть А представляет собой квадрат:
Площадь A = 2 = 20 м × 20 м = 400 м 2
Часть B представляет собой треугольник.При взгляде сбоку он имеет основание 20 м и высоту 14 м.
Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2
Итак, общая площадь:
Площадь = Площадь A + Площадь B = 400 м 2 + 140 м 2 = 540 м 2
Сэм зарабатывает 0,10 доллара за квадратный метр
Сэм зарабатывает = 0,10 доллара × 540 млн 2 = 54 доллара
Нахождение неправильных фигур
Результаты обучения
- Объедините области правильных форм, чтобы найти области неправильных форм.
Итак, мы нашли область для прямоугольников, треугольников, трапеций и кругов. Неправильная фигура — это фигура, не имеющая стандартной геометрической формы. Его площадь не может быть рассчитана ни по одной из стандартных формул площади. Но некоторые неправильные фигуры состоят из двух или более стандартных геометрических фигур. Чтобы найти площадь одной из этих неправильных фигур, мы можем разбить ее на фигуры, формулы которых нам известны, а затем сложить площади фигур.
пример
Найдите площадь заштрихованной области.
Решение
Данный рисунок неправильный, но мы можем разбить его на два прямоугольника. Площадь заштрихованной области будет суммой площадей обоих прямоугольников.
Синий прямоугольник имеет ширину [латекс] 12 [/ латекс] и длину [латекс] 4 [/ латекс]. Красный прямоугольник имеет ширину [латекс] 2 [/ латекс], но его длина не указана. Правая часть рисунка — это длина красного прямоугольника плюс длина синего прямоугольника. Поскольку правая сторона синего прямоугольника имеет длину [латекс] 4 [/ латекс] единиц, длина красного прямоугольника должна быть [латекс] 6 [/ латекс] единиц.
Площадь рисунка [латекс] 60 [/ латекс] квадратных единиц.
Есть ли другой способ разбить эту фигуру на два прямоугольника? Попробуйте и убедитесь, что у вас такая же площадь.
пример
Найдите площадь заштрихованной области.
Показать решение Решение
Мы можем разбить эту неправильную фигуру на треугольник и прямоугольник. Площадь фигуры будет суммой площадей треугольника и прямоугольника.
Прямоугольник имеет длину [латекс] 8 [/ латекс] единиц и ширину [латекс] 4 [/ латекс] единиц.
Нам нужно найти основание и высоту треугольника.
Поскольку обе стороны прямоугольника [латекс] 4 [/ латекс], вертикальная сторона треугольника — [латекс] 3 [/ латекс], то есть [латекс] 7 — 4 [/ латекс].
Длина прямоугольника составляет [латекс] 8 [/ латекс], поэтому основание треугольника будет [латекс] 3 [/ латекс], то есть [латекс] 8 — 4 [/ латекс].
Теперь мы можем добавить области, чтобы найти площадь неправильной фигуры.
Площадь рисунка [латекс] 36,5 [/ латекс] квадратных единиц.
пример
Трасса средней школы имеет форму прямоугольника с полукругом (полукругом) на каждом конце. Прямоугольник имеет длину [латекс] 105 [/ латекс] метров и ширину [латекс] 68 [/ латекс] метров. Найдите область, ограниченную дорожкой. Округлите ответ до ближайшей сотой.
Показать решение Решение
Разобьем фигуру на прямоугольник и два полукруга.Площадь фигуры будет суммой площадей прямоугольника и полукругов.
Прямоугольник имеет длину [латекс] 105 [/ латекс] м и ширину [латекс] 68 [/ латекс] м. Полукруги имеют диаметр [латекс] 68 [/ латекс] м, поэтому каждый имеет радиус [латекс] 34 [/ латекс] м.
математических формул для основных фигур и трехмерных фигур
В математике (особенно в геометрии) и естественных науках вам часто нужно вычислять площадь поверхности, объем или периметр различных форм.Будь то сфера или круг, прямоугольник или куб, пирамида или треугольник, каждая форма имеет определенные формулы, которым вы должны следовать, чтобы получить правильные измерения.
Мы собираемся изучить формулы, которые понадобятся вам для определения площади поверхности и объема трехмерных фигур, а также площади и периметра двухмерных фигур. Вы можете изучить этот урок, чтобы изучить каждую формулу, а затем сохранить ее для быстрого ознакомления в следующий раз, когда она вам понадобится. Хорошая новость заключается в том, что в каждой формуле используются одни и те же базовые измерения, поэтому изучение каждого нового становится немного проще.
Площадь поверхности и объем сферы
Д. РасселТрехмерный круг известен как сфера. Чтобы вычислить площадь поверхности или объем сферы, вам необходимо знать радиус ( r ). Радиус — это расстояние от центра сферы до края, и оно всегда одинаково, независимо от того, от каких точек на краю сферы вы измеряете.
Когда у вас есть радиус, формулы довольно просто запомнить. Как и в случае с окружностью круга, вам нужно будет использовать число пи ( π ).Как правило, это бесконечное число можно округлить до 3,14 или 3,14159 (принятая дробь — 22/7).
- Площадь поверхности = 4πr 2
- Объем = 4/3 πr 3
Площадь поверхности и объем конуса
Д. РасселКонус — это пирамида с круглым основанием, имеющая наклонные стороны, которые сходятся в центральной точке. Чтобы рассчитать его площадь поверхности или объем, необходимо знать радиус основания и длину стороны.
Если вы этого не знаете, вы можете найти длину стороны ( s ), используя радиус ( r ) и высоту конуса ( h ).
После этого вы можете найти общую площадь поверхности, которая является суммой площади основания и площади стороны.
- Площадь основания: πr 2
- Площадь стороны: πrs
- Общая площадь поверхности = πr 2 + πrs
Чтобы найти объем сферы, вам нужны только радиус и высота.
Площадь поверхности и объем цилиндра
Д. РасселВы обнаружите, что с цилиндром намного легче работать, чем с конусом. Эта форма имеет круглое основание и прямые параллельные стороны. Это означает, что для определения его площади поверхности или объема вам понадобятся только радиус ( r ) и высота ( h ).
Тем не менее, вы также должны учитывать то, что есть как верх, так и низ, поэтому радиус необходимо умножить на два для площади поверхности.
- Площадь поверхности = 2πr 2 + 2πrh
- Объем = πr 2 ч
Площадь и объем прямоугольной призмы
Д. РасселПрямоугольник в трех измерениях становится прямоугольной призмой (или коробкой). Когда все стороны равны, он становится кубом. В любом случае для определения площади поверхности и объема требуются одни и те же формулы.
Для них вам нужно знать длину ( l ), высоту ( h ) и ширину ( w ).С кубом все три будут одинаковыми.
- Площадь поверхности = 2 (левый) + 2 (левый) + 2 (белый)
- Объем = л. С.
Площадь и объем пирамиды
Д. РасселС пирамидой с квадратным основанием и гранями из равносторонних треугольников работать сравнительно легко.
Вам нужно будет знать размер одной длины основания ( b ). Высота ( х ) — это расстояние от основания до центральной точки пирамиды.Сторона ( s ) — это длина одной грани пирамиды от основания до верхней точки.
- Площадь поверхности = 2bs + b 2
- Объем = 1/3 b 2 h
Другой способ вычислить это — использовать периметр ( P ) и площадь ( A ) базовой формы. Это можно использовать для пирамиды с прямоугольным, а не квадратным основанием.
- Площадь поверхности = (½ x P x s) + A
- Объем = 1/3 Ач
Площадь поверхности и объем призмы
Д.РасселПри переходе от пирамиды к равнобедренной треугольной призме необходимо также учитывать длину формы ( l ). Запомните сокращения для основания ( b ), высоты ( h ) и стороны ( s ), потому что они необходимы для этих расчетов.
- Площадь поверхности = bh + 2ls + lb
- Объем = 1/2 (бч) л
Тем не менее, призма может быть любой формы. Если вам нужно определить площадь или объем нечетной призмы, вы можете полагаться на площадь ( A ) и периметр ( P ) базовой формы.Часто в этой формуле будет использоваться высота призмы или глубина ( d ), а не длина ( l ), хотя вы можете увидеть любое сокращение.
- Площадь поверхности = 2A + Pd
- Объем = объявления
Площадь сектора круга
Д. РасселПлощадь сектора круга может быть вычислена в градусах (или радианах, как это чаще всего используется в расчетах). Для этого вам понадобятся радиус ( r ), пи ( π ) и центральный угол ( θ ).
- Площадь = θ / 2 r 2 (в радианах)
- Площадь = θ / 360 πr 2 (в градусах)
Площадь эллипса
Д. РасселЭллипс также называют овалом и по сути представляет собой удлиненный круг. Расстояния от центральной точки до стороны непостоянны, что делает формулу для определения ее площади немного сложной.
Чтобы использовать эту формулу, вы должны знать:
- Semiminor Axis ( a ): кратчайшее расстояние между центральной точкой и краем.
- Большая полуось ( b ): наибольшее расстояние между центральной точкой и краем.
Сумма этих двух точек остается постоянной. Вот почему мы можем использовать следующую формулу для вычисления площади любого эллипса.
Иногда вы можете увидеть эту формулу, записанную как r 1 (радиус 1 или малая полуось) и r 2 (радиус 2 или большая полуось), а не a и b .
Площадь и периметр треугольника
Треугольник — одна из самых простых фигур, и вычислить периметр этой трехсторонней формы довольно просто. Вам необходимо знать длины всех трех сторон ( a, b, c ), чтобы измерить полный периметр.
Чтобы узнать площадь треугольника, вам понадобится только длина основания ( b ) и высота ( h ), которая измеряется от основания до вершины треугольника. Эта формула работает для любого треугольника, независимо от того, равны ли стороны или нет.
Площадь и окружность круга
Подобно сфере, вам нужно знать радиус ( r ) круга, чтобы узнать его диаметр ( d ) и длину окружности ( c ). Имейте в виду, что круг — это эллипс, у которого одинаковое расстояние от центральной точки до каждой стороны (радиуса), поэтому не имеет значения, где на краю вы измеряете.
- Диаметр (d) = 2r
- Окружность (c) = πd или 2πr
Эти два измерения используются в формуле для вычисления площади круга.Также важно помнить, что отношение длины окружности к ее диаметру равно пи ( π ).
Площадь и периметр параллелограмма
У параллелограмма есть два набора противоположных сторон, идущих параллельно друг другу. Форма четырехугольная, поэтому у нее четыре стороны: две стороны одной длины ( a ) и две стороны другой длины ( b ).
Чтобы узнать периметр любого параллелограмма, используйте эту простую формулу:
Когда вам нужно найти площадь параллелограмма, вам понадобится высота ( х ).Это расстояние между двумя параллельными сторонами. Также требуется основание ( b ) — это длина одной из сторон.
Имейте в виду, что b в формуле площади не то же самое, что b в формуле периметра. Вы можете использовать любую из сторон, которые были объединены в пары как a и b при вычислении периметра, хотя чаще всего мы используем сторону, перпендикулярную высоте.
Площадь и периметр прямоугольника
Прямоугольник — это тоже четырехугольник.В отличие от параллелограмма, внутренние углы всегда равны 90 градусам. Кроме того, стороны, противоположные друг другу, всегда будут иметь одинаковую длину.
Чтобы использовать формулы для периметра и площади, вам необходимо измерить длину прямоугольника ( l ) и его ширину ( w ).
- Периметр = 2ч + 2Вт
- Площадь = в x ш
Площадь и периметр квадрата
Квадрат даже проще, чем прямоугольник, потому что это прямоугольник с четырьмя равными сторонами.Это означает, что вам нужно знать длину только одной стороны ( s ), чтобы найти ее периметр и площадь.
Площадь и периметр трапеции
Трапеция — это четырехугольник, который может показаться сложной задачей, но на самом деле это довольно просто. У этой формы только две стороны параллельны друг другу, хотя все четыре стороны могут иметь разную длину. Это означает, что вам нужно знать длину каждой стороны ( a, b 1 , b 2 , c ), чтобы найти периметр трапеции.
- Периметр = a + b 1 + b 2 + c
Чтобы найти площадь трапеции, вам также понадобится высота ( х ). Это расстояние между двумя параллельными сторонами.
Площадь и периметр шестиугольника
Шестигранный многоугольник с равными сторонами — это правильный шестиугольник. Длина каждой стороны равна радиусу ( r ). Хотя это может показаться сложной формой, вычисление периметра — это простой вопрос умножения радиуса на шесть сторон.
Определить площадь шестиугольника немного сложнее, и вам придется запомнить эту формулу:
Площадь и периметр восьмиугольника
Правильный восьмиугольник похож на шестиугольник, но у этого многоугольника восемь равных сторон. Чтобы найти периметр и площадь этой формы, вам понадобится длина одной стороны ( a ).
- Периметр = 8a
- Площадь = (2 + 2√2) a 2
Обнаружение формул площади — элементарная математика
Формулы площади
Учащиеся, неформально относящиеся к области как к «количеству двумерного« материала », содержащегося внутри области, могут придумать для себя большинство формул, которые их часто просят просто запомнить.Каждая формула, которую они изобретают заново, помогает укрепить их понимание (и память) о других формулах, которые они знают. (См. Также площадь поверхности.)
Площадь прямоугольников
Выбирая квадрат в качестве единицы площади, мы получаем интуитивное представление о площади прямоугольников. Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, который в 7 раз длиннее, будет иметь площадь 7 × 1.
Прямоугольник, который вдвое превышает высоту, будет иметь удвоенную площадь, поэтому площадь составляет 2 × 7 единиц площади.Мы можем сосчитать два ряда по семь квадратов. Точно так же он имеет 3 ряда по 7 квадратов (или 7 столбцов по 3 квадрата), всего 7 × 3 квадратов, поэтому его площадь составляет 21 квадратную единицу.
Количество квадратов в одном ряду — это длина прямоугольника. Количество строк — это высота прямоугольника. Таким образом, площадь равна длине × высоте.
Поскольку прямоугольник можно нарисовать под наклоном, «высота» определяется как «направление, перпендикулярное основанию», а «основание» определяется как, ну, с какой бы стороны вы его ни выбрали.
Это работает для подсчета чисел. Это работает даже для дробей. Показанный здесь синий прямоугольник измеряет половину единицы длины на пять с половиной единиц длины. Если мы выберем соответствующий квадрат в качестве единицы площади, мы увидим, что синий прямоугольник содержит пять половинных единиц площади и одну четверть единицы площади, или всего две и три четверти единицы площади. (Розовые части показывают заполнение каждой квадратной единицы площади.)
Чтобы включить все числа , мы определяем площадь прямоугольника как основание × высота (где «основание» и «высота» означают длину этих сторон, измеряется в те же единицы ).
Площадь параллелограммов
Идея
Мы можем вычислить формулу площади параллелограмма, разрезав параллелограмм и переставив части, чтобы получился прямоугольник. Поскольку параллелограмм и прямоугольник состоят из одинаковых частей, они обязательно имеют одинаковую площадь. (См. Определение площади, чтобы узнать, почему эти области одинаковы.)
Мы видим, что и имеют точно такую же длину основания (синий) и точно такую же высоту (зеленый).Поскольку основание × высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме, чтобы вычислить его площадь: основание × высота . (Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это та сторона, которую вы выбрали первой. См. Параллелограмм.)
На разрезе, показанном выше, легко увидеть, что базовая длина не изменилась.Фактически, перпендикулярный разрез можно делать где угодно по основанию.
Укрепление отверстий
Интуиция и доказательство
Это рассечение дает интуитивное понимание формулы площади параллелограмма, причина , что он должен быть таким, какой есть. Но мы не сомневались, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидаем, что получит , и результат определенно будет таким.Но внешность может быть обманчива. Что убеждает нас в том, что когда мы перемещаем этот треугольник, в результате получается прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если результат не всегда является идеальным прямоугольником, мы не можем использовать наши знания формулы площади прямоугольника, чтобы разработать формулу для параллелограмма. В старших классах учащиеся смогут доказать, что две части параллелограмма, если правильно собрать их, действительно образуют прямоугольник. В классах K-8 учащиеся по большей части должны полагаться на визуальный эксперимент и получать интуитивное ощущение.Узнайте больше о том, почему эти вскрытия работают.
Что, если мы выберем короткую сторону в качестве основания?
Мы можем выбрать любую сторону в качестве основы; «Высота» определяется как измеряемая перпендикулярно стороне, которую мы выбираем в качестве основания. Если мы возьмем за основу короткую сторону (синюю), то рассечение, показанное выше, не будет таким убедительным. Резка на такой высоте и перестановка деталей оставляет беспорядок:
В этом конкретном примере мы можем спасти беспорядок, сделав еще один разрез, но что, если бы параллелограмм был еще длиннее и тоньше?
Оказывается, любой параллелограмм , независимо от его длины и тонкости, можно разрезать таким образом, чтобы части — возможно, многие из них — могли быть преобразованы в прямоугольник.Но нужно потрудиться, чтобы показать, что это всегда можно сделать. Нам нужна другая идея.
Немного другая идея вскрытия в этом случае значительно упрощает жизнь. (Самостоятельно вы можете показать, что это работает и в исходном случае.)
- Заключите параллелограмм в прямоугольник.
- Две части прямоугольника, которые находятся на , а не на внутри параллелограмма, являются конгруэнтными треугольниками.
- Сдвиньте один из этих треугольников по направлению к другому, пока они не встретятся, образуя прямоугольник.Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше), а желтая область не изменилась (части просто перемещались), разница между ними — фиолетовыми областями — должна быть такой же. Как и раньше, мы также можем видеть, что размеры прямоугольной фиолетовой области являются основанием и высотой исходного параллелограмма.
Интуиция и доказательство, повторение: Опять же, рассечение дает существенное понимание, но требуется немного больше работы, чтобы убедиться, что два желтых треугольника, которые, безусловно, выглядят , как будто они соединяются вместе, образуя прямоугольник, на самом деле точно подходят, а не просто почти .
Почему так важно быть осторожным?
При построении других формул площади (см. Ниже) мы захотим, чтобы использовал , как найти площадь параллелограмма, и поэтому мы хотим иметь возможность полагаться на найденное нами правило. Мы, , можем быть уверены, что перестановка частей не повлияет на область: это, в конце концов, то, как мы определяем область . Но мы также должны быть уверены, что детали подходят друг к другу, как мы заявляем, что они делают, или мы не можем полагаться на сделанные нами измерения.И мы должны быть уверены, что base × height Правило не зависит от удачного выбора базы.
В большинстве учебных программ учащиеся не имеют достаточной систематической базы геометрических знаний до 8-го класса, чтобы убедительно доказать, что эти вскрытия работают. Но интуитивного понимания достаточно для объяснения и обоснования формул и хорошей основы для дальнейшего изучения геометрии.
Площадь треугольника
Знание того, как найти площадь параллелограмма, помогает нам найти площадь треугольника.
Рассечение треугольника
Мы можем разрезать треугольник на две части — одну из них треугольник, а другую — трапецию, разрезав его параллельно основанию. Если мы разрежем высоту ровно пополам с этим срезом, две части сложатся вместе, образуя параллелограмм с таким же основанием , но половиной высоты .
Итак, основание × полувысота дает площадь треугольника. Аналогичный разрез показывает полубаз × высота .Любой из них сокращается до bh .
Удвоение треугольника и уменьшение полученной площади пополам
Другой способ мышления: две копии треугольника образуют параллелограмм с тем же основанием и той же высотой , что и треугольник.
Площадь параллелограмма составляет основание × высота , но это вдвое больше площади треугольника, поэтому площадь треугольника составляет из основания × высоты , как мы видели с методом рассечения.
(Как всегда, выберите «основание» и измерьте высоту перпендикулярно этому основанию, от основания до противоположной вершины.)
Площадь трапеции
Удвоение трапеции и уменьшение полученной площади пополам
Как и в случае с треугольником, две копии трапеции можно соединить вместе, чтобы получился параллелограмм.
Высота параллелограмма равна высоте трапеции, но его основание представляет собой сумму двух оснований трапеции.Таким образом, площадь параллелограмма равна по высоте × ( base1 + base2 ). Но эта площадь составляет две трапеций, поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.
Рассечение трапеции
Мы также можем разрезать трапецию так же, как мы разрезали треугольник, с одним срезом, разрезающим ее высоту пополам. Две части соединяются вместе, образуя параллелограмм, основание которого является суммой двух оснований трапеции, но высота которого равна половине высоты трапеции.
В случае трапеции основания не могут быть выбраны произвольно. Две стороны , параллельные , являются основаниями, а высота, как всегда, представляет собой перпендикулярное расстояние от одного основания до противоположного.
Площадь этого параллелограмма равна его высоте (полувысоте трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь составляет половинной высоты × ( base1 + base2 ). Поскольку параллелограмм сделан из того же материала, что и трапеция, это тоже площадь трапеции.
В любом случае площадь трапеции составляет × по высоте × ( base1 + base2 ) .
Площадь других специальных четырехугольников
Площадь ромба
Площадь ромба можно найти, разрезав и переставив части так, чтобы получился параллелограмм. Это можно сделать несколькими способами:
- Разрежьте более короткую диагональ (a), чтобы получились два равных треугольника. Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы получился параллелограмм.Более короткая диагональ (a) становится основанием параллелограмма, а половина более длинной диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
- Другой аналогичный способ — разрезать ромб на четыре равных треугольника и переставить их в прямоугольник с более короткой диагональю в качестве основания и половиной длинной диагонали в качестве высоты.
- После разрезания ромба на два равных треугольника, мы можем вычислить площадь одного из треугольников, которая равна * основанию (a) * высоте (b) = ab.Затем умножьте на два, так как их два: 2 * ab = ab.
Зона воздушного змея
Площадь воздушного змея может быть похожа на площадь ромба. Если разрезать более длинную диагональ, получатся два равных треугольника. Если мы переставим их, мы можем сформировать параллелограмм с более длинной диагональю (b) в качестве основания и половиной более короткой диагонали (a) в качестве высоты. Итак, площадь становится b * a = ab. Более сложный подход требует немного алгебры. Разрежьте змей по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (a) в качестве основы.Таким образом, площадь первого треугольника — * волнистая, где волнистая — высота. Площадь второго треугольника равна a * (b — волнистый), где (b — волнистый) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится (a * волнистая) + (a * (b — волнистая)). Вынося за скобки a, получаем a (волнистый + b — волнистый) = ab.
Ну что вы знаете. По сути, вам нужно только знать формулу для площади параллелограмма, а затем вывести формулу для других.
Что такое область 2D-форм?
Что такое площадь 2D-фигур?
Площадь любой 2D-формы — это размер области, заключенной в нее.Есть несколько 2D-форм, таких как квадрат, прямоугольник, круг, ромб и треугольник. Цветная область в каждой форме представляет область соответствующей формы.
Единица площади называется квадратными. У разных форм есть разные формулы для расчета площади.Площадь квадрата и прямоугольника :
Площадь квадрата и прямоугольника равна произведению двух смежных сторон.
| 2D Форма | Формула площади | Пример |
| Квадрат | Площадь квадрата = Сторона × Сторона Площадь = S × S | Площадь = 4 × 4 = 16 кв.размеры в см |
| Прямоугольник | Площадь прямоугольника = длина × ширина = длина × ширина | Площадь = 8 × 3 = 24 кв. См |
Площадь треугольника :
Треугольники могут быть разных типов, например равносторонний треугольник, равнобедренный треугольник и прямоугольный треугольник, но формула для площади всех видов треугольников одинакова.
Площадь треугольника определяется по формуле: 1 ⁄ 2 × b × h, где основание (b) — длина любой стороны треугольника, а высота (h) — перпендикулярное расстояние между основанием. и верхняя вершина треугольника.
Пример:
В треугольнике ABC основание составляет 6 единиц, а высота — 4 единицы.
Итак, площадь треугольника ABC = 1 ⁄ 2 × b × h
= 1 ⁄ 2 × 6 × 4
= 12 кв. Единиц
Круг :
Площадь круга вычисляется по формуле π × r 2 , где r — радиус круга, а π — константа, значение которой равно 227 или 3.14
Пример: Площадь вышеуказанного круга = π × r 2
= 3,14 × 4 2
= 3,14 × 16
= 50,24 кв. См
Ромб :
Формула для определения площади ромба: pq / 2, где p и q — две диагонали ромба.
В ромбе ABCD площадь можно вычислить следующим образом:
Площадь ромба = 1 ⁄ 2 pq
= 1 ⁄ 2 × 3 × 5
= 7,5 кв. См
Параллелограмм :
Чтобы найти площадь параллелограмма, мы используем формулу b × h, где b обозначает основание, а h обозначает высоту. Высота — это расстояние по вертикали между основанием и верхом.
Пример:
На приведенном выше рисунке площадь параллелограмма равна b × h. Следовательно, это 6 × 4 = 24 кв. См
Интересные факты |
Что такое площадь формы?
Площадь фигур
Геометрические фигуры — это фигуры с набором точек, соединенных линиями, в результате чего получается замкнутая фигура.
Например, , треугольник, квадрат, прямоугольник и четырехугольник — это фигуры с 3 и 4 точками, соединенными линиями.Фигуры с ограниченными кривыми не имеют сторон, но имеют окружность.
Зеркала разной формы со сторонами и закруглениями.
ПлощадьПлощадь фигуры — это «пространство, заключенное внутри периметра или границы» данной фигуры. Рассчитываем площадь для разных форм по математическим формулам.
На следующих рисунках заштрихованная область обозначает область для соответствующих форм.
| Имя и форма | Недвижимость | Площадь |
Круг |
| А = πr2 π = 3.14 (постоянная) |
Треугольник |
| A = 1 ⁄ 2 × основание × высота |
Квадрат |
| A = длина стороны 2 |
Ромб |
| А = p × q |
Прямоугольник |
| A = длина × ширина |
Параллелограмм |
| A = основание × высота |
«Текстурированная» область представляет собой область формы
Единица измерения
Единицей измерения площади всегда является квадрат единицы, в которой даны длины.Результирующая единица является произведением единиц данной длины.
Возьмем для примера площадь квадрата со стороной 8 см:
Площадь = (длина стороны) 2
Площадь = 8 см × 8 см
Площадь = 64 см 2
Заявка
Область применения формулы площади — архитектура, землеустройство и картографирование. Измененная версия области для данного места полезна при разработке инструментов знаний, таких как глобусы и геофизические карты.Расчет площади для двумерной формы — это первый шаг к интерпретации объема трехмерного объекта, такого как конус, цилиндр, шар и куб.
Интересные факты
|
Сопутствующий математический словарь
. Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить.
Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить.