Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y)

Необходимо вычислить площадь фигуры, которая ограничена кривыми y=x3, y=-log2x+1 и осью абсцисс.

Решение

Нанесем все линии на график. Мы можем получить график функции y=-log2x+1 из графика y=log2x, если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у=0.

Обозначим точки пересечения линий.

Как видно из рисунка, графики функций y=x3 и y=0 пересекаются в точке (0;0). Так получается потому, что х=0 является единственным действительным корнем уравнения x3=0.

x=2 является единственным корнем уравнения -log2x+1=0, поэтому графики функций y=-log2x+1  и y=0 пересекаются в точке (2;0).

x=1 является единственным корнем уравнения x3=-log2x+1. В связи с этим графики функций y=x3 и y=-log2x+1 пересекаются в точке (1;1). Последнее утверждение может быть неочевидным, но уравнение x3=-log2x+1 не может иметь более одного корня, так как функция y=x3 является строго возрастающей, а функция y=-log2x+1 строго убывающей.

Дальнейшее решение предполагает несколько вариантов.

Вариант №1

Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x∈0; 1, а вторая ниже красной линии на отрезке x∈1;2. Это значит, что площадь будет равна S(G)=∫01x3dx+∫12(-log2x+1)dx.

Вариант №2

Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x∈0; 2, а вторая между красной и синей линиями на отрезке x∈1; 2. Это позволяет нам найти площадь следующим образом:

S(G)=∫02x3dx-∫12×3-(-log2x+1)dx

В этом случае для нахождения площади придется использовать формулу вида S(G)=∫cd(g2(y)-g1(y))dy.  Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y.

Разрешим уравнения y=x3 и -log2x+1 относительно x: 

y=x3⇒x=y3y=-log2x+1⇒log2x=1-y⇒x=21-y

Получим искомую площадь:

S(G)=∫01(21-y-y3)dy=-21-yln 2-y4401==-21-1ln 2-144—21-0ln 2-044=-1ln 2-14+2ln 2=1ln 2-14

Ответ: S(G)=1ln 2-14

1.

8. Как вычислить площадь фигуры с помощью определённого интеграла? 

Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:

Пример 10
Вычислить площадь фигуры, ограниченной линиями .

И первый важнейший этап решения состоит как раз в построении чертежа

. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.

В нашей задаче: прямая  определяет ось , прямые  параллельны оси  и парабола  симметрична относительно оси , для неё находим несколько опорных точек:

Искомую фигуру желательно штриховать:

Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл.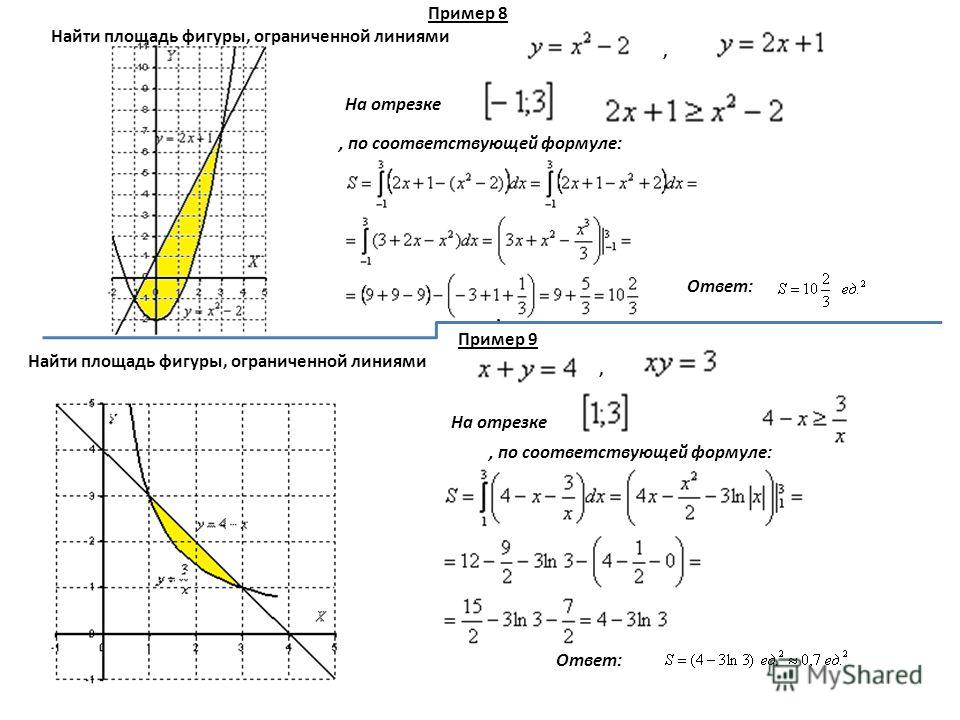 На отрезке   график функции  расположен над осью , поэтому искомая площадь:

Ответ:

После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.

И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.

Пример 11
Вычислить площадь фигуры, ограниченной линиями  и осью

Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью :

Пример 12
Вычислить площадь фигуры, ограниченной линиями ,  и координатными осями.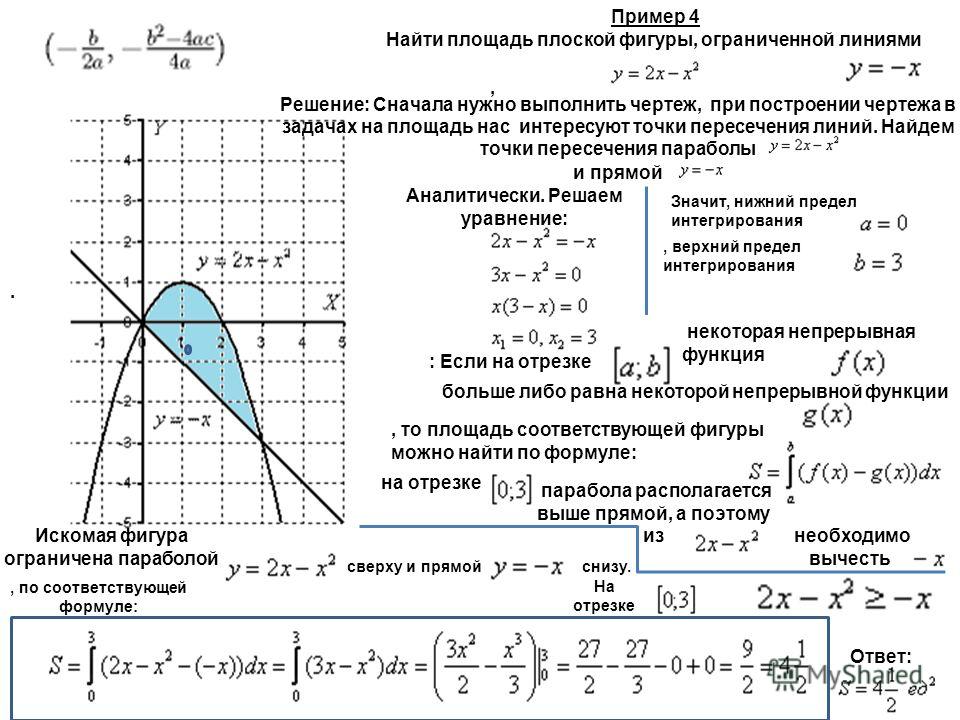

Решение: найдём несколько опорных точек для построения экспоненты:

и выполним чертёж, получая фигуру площадью около двух клеток:

Если криволинейная трапеция расположена не выше оси , то её площадь можно найти по формуле: .
В данном случае:

Ответ:  – ну что же, очень и очень похоже на правду.

На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:

Пример 13
Найти площадь плоской фигуры, ограниченной линиями , .

Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы  и прямой , поскольку здесь будут находиться пределы интегрирования.  Найти их можно двумя способами. Первый способ – аналитический.

Составим и решим уравнение:

таким образом:

Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».

С прямой  всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
 – именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:

Выполним чертеж:

А теперь рабочая формула: если на отрезке  некоторая непрерывная функция  больше либо равна непрерывной функции , то площадь фигуры, ограниченной графиками этих функций и отрезками прямых , можно найти по формуле:

Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.

В нашем примере очевидно, что на отрезке  парабола располагается выше прямой, а поэтому из  нужно вычесть

Завершение решения может выглядеть так:

На отрезке : , по соответствующей формуле:

Ответ:

Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы . Поскольку ось  задаётся уравнением , то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу  либо

А сейчас пара типовых задач для самостоятельного решения

Пример 14
Найти площадь фигур, ограниченных линиями:

а) , .

б) , ,

Решение с чертежами и краткими комментариями в конце книги

В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:

Пример 15
Вычислить площадь фигуры, ограниченной линиями

Решение: выполним бесхитростный чертёж,

хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую  можно недочертить до оси , и тогда мы вовсе не увидим нужную фигуру.

Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:

1) на отрезке  над осью  расположен график прямой ;
2) на отрезке  над осью  расположен график гиперболы .

Совершенно понятно, что площади можно (и нужно) сложить:

Ответ:

И познавательный пример для самостоятельного решения:

Пример 16
Вычислить площадь фигуры, ограниченной линиями , ,  и координатными осями.

Итак, систематизируем важные моменты этой задачи:

На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс  зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.

Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.

Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой  и прямой , где из чертежа не понятна одна из точек их пересечения.

В таких случаях следует использовать аналитический метод, составляем уравнение:

и находим его корни:
 – нижний предел интегрирования,  – верхний предел.

Во-вторых, не всегда понятен «внешний вид» линии, и функция  (Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html

После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.

Составляем определённый интеграл или несколько интегралов по формуле , все основные вариации мы разобрали выше.

Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.

Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!

1.9. Объём тела вращения

1.7. Геометрический смысл определённого интеграла

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

вычисление площади фигуры ограниченной линиями

Вы искали вычисление площади фигуры ограниченной линиями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление площади фигуры ограниченной линиями онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление площади фигуры ограниченной линиями».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вычисление площади фигуры ограниченной линиями,вычисление площади фигуры ограниченной линиями онлайн,вычислите площадь фигуры,вычислите площадь фигуры ограниченной,вычислите площадь фигуры ограниченной линиями,вычислите площадь фигуры ограниченной линиями y,вычислите площадь фигуры ограниченной линиями y 0 x 1 y x,вычислите площадь фигуры ограниченной линиями онлайн,вычислите площадь фигуры ограниченной линиями онлайн решение,вычислите площадь фигуры ограниченной линиями у 1 x y 2 x 2,вычислить онлайн площадь ограниченную линиями,вычислить площади фигур ограниченных линиями,вычислить площадь ограниченную линиями,вычислить площадь ограниченную линиями онлайн,вычислить площадь плоской фигуры ограниченной заданными кривыми онлайн,вычислить площадь плоской фигуры ограниченной линиями,вычислить площадь плоской фигуры ограниченной линиями онлайн с решением,вычислить площадь фигур ограниченных линиями онлайн,вычислить площадь фигуры,вычислить площадь фигуры ограниченной,вычислить площадь фигуры ограниченной графиками функций,вычислить площадь фигуры ограниченной графиками функций онлайн,вычислить площадь фигуры ограниченной графиками функций онлайн решение,вычислить площадь фигуры ограниченной линиями,вычислить площадь фигуры ограниченной линиями y,вычислить площадь фигуры ограниченной линиями y x 2 1 y x 1,вычислить площадь фигуры ограниченной линиями y x 2 y 2 x,вычислить площадь фигуры ограниченной линиями y x 2 y x,вычислить площадь фигуры ограниченной линиями онлайн,вычислить площадь фигуры ограниченной линиями онлайн калькулятор,вычислить площадь фигуры ограниченной линиями онлайн калькулятор с графиком,вычислить площадь фигуры ограниченной линиями онлайн калькулятор с решением,вычислить площадь фигуры ограниченной линиями онлайн подробное решение,вычислить площадь фигуры ограниченной линиями онлайн с решением калькулятор,вычислить площадь фигуры ограниченной линиями примеры решения,вычислить площадь фигуры ограниченной указанными линиями сделать чертеж,вычислить площадь фигуры онлайн,заштрихуй фигуры ограниченные двумя линиями,заштрихуй фигуры ограниченные линиями,как найти площадь фигуры ограниченной графиками функций,как найти площадь фигуры ограниченной линиями,калькулятор вычислить площадь фигуры ограниченной линиями онлайн с решением,калькулятор онлайн площадь фигуры,найдите площадь плоской фигуры ограниченной линиями,найдите площадь фигуры ограниченной линиями,найдите площадь фигуры ограниченной линиями y 5 x 2 y 1,найдите площадь фигуры ограниченной линиями y x 2 1 y 1 x,найдите площадь фигуры ограниченной линиями онлайн,найдите площадь фигуры ограниченной линиями онлайн калькулятор,найдите площадь фигуры ограниченной указанными линиями,найти площадь криволинейной трапеции ограниченной линиями онлайн,найти площадь криволинейной трапеции онлайн,найти площадь области ограниченной линиями онлайн,найти площадь ограниченной фигуры,найти площадь ограниченную линиями,найти площадь ограниченную линиями онлайн калькулятор,найти площадь плоской фигуры ограниченной линиями,найти площадь плоской фигуры ограниченной линиями онлайн,найти площадь фигуры,найти площадь фигуры ограниченной,найти площадь фигуры ограниченной графиками функций,найти площадь фигуры ограниченной кривыми,найти площадь фигуры ограниченной линиями,найти площадь фигуры ограниченной линиями онлайн,найти площадь фигуры ограниченной линиями онлайн калькулятор,найти площадь фигуры ограниченной линиями онлайн калькулятор подробно,найти площадь фигуры ограниченной линиями онлайн решение,найти площадь фигуры ограниченной линиями онлайн с подробным решением,найти площадь фигуры ограниченной линиями примеры решения,найти площадь фигуры ограниченной линиями с помощью определенного интеграла сделать иллюстрацию,найти площадь фигуры ограниченной указанными линиями,найти площадь фигуры онлайн,нахождение площади фигуры ограниченной линиями,нахождение площади фигуры ограниченной линиями онлайн,онлайн вычисление площади фигуры ограниченной линиями,онлайн вычислить площадь фигуры ограниченной графиками функций онлайн,онлайн калькулятор площадь фигуры ограниченной линиями,онлайн нахождение площади фигуры ограниченной линиями,онлайн площадь фигуры,площадь криволинейной трапеции онлайн,площадь ограниченная линиями,площадь плоской фигуры ограниченной линиями онлайн,площадь под графиком,площадь фигуры ограниченной графиками функций,площадь фигуры ограниченной линиями,площадь фигуры ограниченной линиями онлайн,площадь фигуры ограниченной линиями онлайн калькулятор,площадь фигуры онлайн,построить фигуру ограниченную линиями онлайн,сделайте чертеж и вычислите площадь фигуры ограниченной данными линиями,фигуры ограниченные двумя линиями,фигуры ограниченные линиями.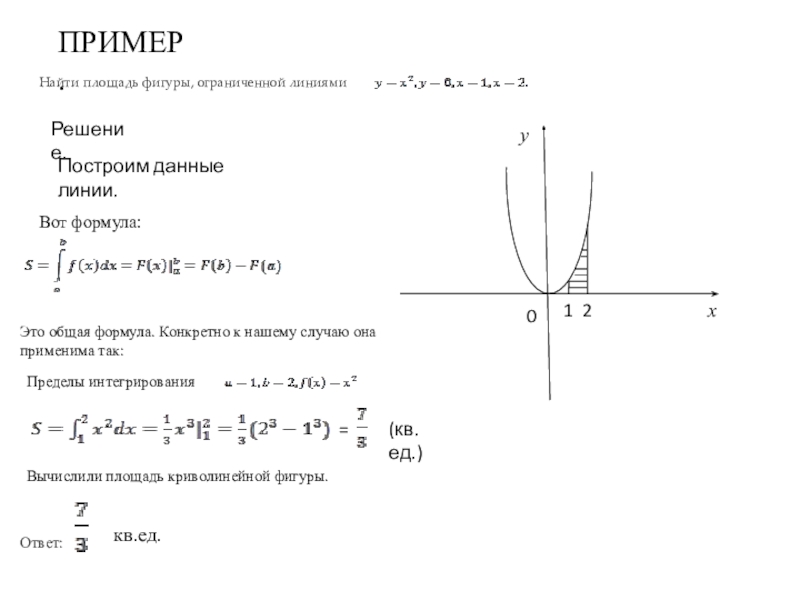 На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вычисление площади фигуры ограниченной линиями. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислите площадь фигуры).

Где можно решить любую задачу по математике, а так же вычисление площади фигуры ограниченной линиями Онлайн?

Решить задачу вычисление площади фигуры ограниченной линиями вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.

— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?

— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.

Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.

Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.

— Расскажите поподробнее?

— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.

— Система оценивания останется прежней?

— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.

Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.

— А апелляция?

— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.

— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?

— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.

— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?

— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.

— На сколько процентов будет обновлена база вопросов?

— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.

— По вашему мнению система справится с возможными хакерскими атаками, взломами?

— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.

Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.

— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?

— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.

— Сколько человек будет сидеть в одной аудитории?

— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.

— Будут ли ужесточены требования по дисциплине, запрещенным предметам?

— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.

Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.

— А наблюдатели будут присутствовать во время сдачи тестирования?

— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.

— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?

— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.

Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.

— Сколько средств выделено на проведение ЕНТ в этом году?

Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. 2}{6}\) .

---

2012-12-05 • Просмотров [ 20248 ]

Как найти площадь фигуры ограниченной линиями

Геометрический смысл определенного интеграла – площадь криволинейной трапеции. Чтобы найти площадь фигуры, ограниченной линиями, применяется одно из свойств интеграла, которое заключается в аддитивности площадей, интегрируемых на одном и том же отрезке функций.

По определению интеграла, он равен площади криволинейной трапеции, ограниченной графиком заданной функции. Когда требуется найти площадь фигуры, ограниченной линиями, речь идет о кривых, заданных на графике двумя функциями f1(x) и f2(x).

Пусть на некотором интервале [a, b] заданы две функции, которые определены и непрерывны. Причем одна из функций графике расположена выше другой. Таким образом, образуется визуальная фигура, ограниченная линиями функций и прямыми x = a, x = b.

Тогда площадь фигуры можно выразить формулой, интегрирующей разность функций на интервале [a, b]. Вычисление интеграла производится по закону Ньютона-Лейбница, согласно которому результат равен разности первообразной функции от граничных значений интервала.

Пример1.
Найти площадь фигуры, ограниченной прямыми линиями y = -1/3·x – ½, x = 1, x = 4 и параболой y = -x² + 6·x – 5.

Решение.
Постройте графики всех линий. Вы можете увидеть, что линия параболы находится выше прямой y = -1/3·x – ½. Следовательно, под знаком интеграла в данном случае должна стоять разность между уравнением параболы и заданной прямой. Интервал интегрирования, соответственно, находится между точками x = 1 и x = 4:
S = ∫(-x² + 6·x – 5 – (-1/3·x – 1/2))dx = (-x² +19/3·x – 9/2)dx на отрезке [1, 4].

Найдите первообразную для полученного подынтегрального выражения:
F(-x² + 19/3x – 9/2) = -1/3x³ + 19/6x² – 9/2x.

Подставьте значения концов отрезка:
S = (-1/3·4³ + 19/6·4² – 9/2·4) – (-1/3·1³ + 19/6·1² – 9/2·1) = 13.

Пример2.
Вычислите площадь фигуры, ограниченной линиями y = √(x + 2), y = x и прямой x = 7.

Решение.
Эта задача является более сложной по сравнению с предыдущей, поскольку в ней нет второй прямой, параллельной оси абсцисс. Это значит, что второе граничное значение интеграла неопределенно. Следовательно, его нужно найти из графика. Постройте заданные линии.

Вы увидите, то прямая линия y = x проходит диагонально относительно координатных осей. А график функции корня – это положительная половина параболы. Очевидно, что линии на графике пересекаются, поэтому точка пересечения и будет нижним пределом интегрирования.

Найдите точку пересечения, решив уравнение:
x = √(x + 2) → x² = x + 2 [x ≥ -2] → x² – x – 2 = 0.

Определите корни квадратного уравнения с помощью дискриминанта:
D = 9 → x1 = 2; x2 = -1.

Очевидно, что значение -1 не подходит, поскольку абсцисса токи пересечения – положительная величина. Следовательно, второй предел интегрирования x = 2. Функция y = x на графике выше функции y = √(x + 2), поэтому в интеграле она будет первой. (3/2)) = 59/6.

Найти площадь фигуры, ограниченной линиями

Из данной статьи вы узнаете, как найти площадь фигуры, ограниченной линиями, используя вычисления с помощью интегралов. Впервые с постановкой такой задачи мы сталкиваемся в старших классах, когда только-только пройдено изучение определенных интегралов и пора приступить к геометрической интерпретации полученных знаний на практике.

Итак, что потребуется для успешного решения задачи по поиску площади фигуры с помощью интегралов:

• Умение грамотно строить чертежи;
• Умение решать определенный интеграл с помощью известной формулы Ньютона-Лейбница;
• Умение «увидеть» более выгодный вариант решения — т.е. понять, как в том или ином случае будет удобнее проводить интегрирование? Вдоль оси икс (OX) или оси игрек (OY)?
• Ну и куда без корректных вычислений? ) Сюда входит понимание как решать тот иной тип интегралов и правильные численные вычисления.

Алгоритм решения задачи по вычислению площади фигуры, ограниченной линиями:

1. Строим чертеж. Желательно это делать на листке в клетку, с большим масштабом. Подписываем карандашом над каждым графиком название этой функции. Подпись графиков делается исключительно ради удобства дальнейших вычислений. Получив график искомой фигуры, в большинстве случаев будет видно сразу, какие пределы интегрирования будут использованы. Таким образом мы решаем задачу графическим методом. Однако бывает так, что значения пределов дробные или иррациональные. Поэтому, можно сделать дополнительные расчеты, переходим в шагу два.

2. Если явно не заданы пределы интегрирования, то находим точки пересечения графиков друг с другом, и смотрим, совпадает ли наше графическое решение с аналитическим.

3. Далее, необходимо проанализировать чертеж. В зависимости от того, как располагаются графики функций, существуют разные подходы к нахождению площади фигуры. Рассмотрим разные примеры на нахождение площади фигуры при помощи интегралов.

3. 1. Самый классический и простой вариант задачи, это когда нужно найти площадь криволинейной трапеции. Что такое криволинейная трапеция? Это плоская фигура, ограниченная осью икс ( у = 0 ), прямыми х = а, х = b и любой кривой, непрерывной на промежутке от a до b. При этом, данная фигура неотрицательна и располагается не ниже оси абсцисс. В этом случае, площадь криволинейной трапеции численно равна определенному интегралу, вычисляемого по формуле Ньютона-Лейбница:

Пример 1. Вычислить площадь фигуры, ограниченной линиями y = x2 — 3x + 3, x = 1, x = 3, y = 0.

Решение:

Какими линиями ограничена фигура? Имеем параболу y = x2 — 3x + 3, которая располагается над осью ОХ, она неотрицательна, т.к. все точки этой параболы имеют положительные значения. Далее, заданы прямые х = 1 и х = 3, которые пролегают параллельно оси ОУ, являются ограничительными линиями фигуры слева и справа. Ну и у = 0, она же ось икс, которая ограничивает фигуру снизу. Полученная фигура заштрихована, как видно из рисунка слева. В данном случае, можно сразу приступать к решению задачи. Перед нами простой пример криволинейной трапеции, которую далее решаем с помощью формулы Ньютона-Лейбница.

3.2. В предыдущем пункте 3.1 разобран случай, когда криволинейная трапеция расположена над осью икс. Теперь рассмотрим случай, когда условия задачи такие же, за исключением того, что функция пролегает под осью икс. К стандартной формуле Ньютона-Лейбница добавляется минус. Как решать подобную задачу рассмотрим далее.

Пример 2. Вычислить площадь фигуры, ограниченной линиями y = x2 + 6x + 2, x = -4, x = -1, y = 0.

Решение:

В данном примере имеем параболу y = x2 + 6x + 2, которая берет свое начало из-под оси ОХ, прямые х = -4, х = -1, у = 0. Здесь у = 0 ограничивает искомую фигуру сверху. Прямые х = -4 и х = -1 это границы, в пределах которых будет вычисляться определенный интеграл. Принцип решения задачи на поиск площади фигуры практически полностью совпадает с примером номер 1. Единственное различие в том, что заданная функция не положительная, и все также непрерывная на промежутке [-4; -1]. Что значит не положительная? Как видно из рисунка, фигура, которая заключается в рамках заданных иксов имеет исключительно «отрицательные» координаты, что нам и требуется увидеть и помнить при решении задачи. Площадь фигуры ищем по формуле Ньютона-Лейбница, только со знаком минус в начале.

 

Статья не завершена.

Нахождение площади (почти) любой закрытой области

Здравствуйте, ребята, Алекс здесь! Я подумал, что начну этот блог правильно, с одной из самых популярных (и головокружительных) задач, которые бросают моим студентам-математикам. Проблема выглядит примерно так:

Найдите площадь области, заключенную между линиями \ (y = 2x \), \ (y = 3x \) и \ (y = 2 \). Вы должны использовать исчисление, иначе вы не получите никаких кредитов!

Ух ты. Сильные слова от парня с зачетной книжкой.Хорошо, надеюсь, вы уже видели проблемы, которые запрашивают область между двумя функциями . Если нет, достаньте учебник;). Задачи с двумя функциональными областями решаются путем интеграции разницы между функциями «сверху» и «снизу», например:

Но подождите минутку! Наша проблема заключается в том, чтобы дать нам ТРИ функции, а не две. Как, во имя Бибера, мы можем применить приведенную выше формулу к области, заключенной между тремя функциями?

Расскажу как.Мы собираемся найти способ, как разложить , или разбить эту сложную проблему на несколько более мелких и простых задач. Кстати, умение разбирать проблемы — это причина, по которой вы должны заниматься расчетом по своей специальности — даже если вы никогда больше не увидите другого интеграла за всю свою жизнь. Исчисление — отличный способ научиться более общим навыкам решения проблем, математике и т. Д.

Хорошо, вернемся к нашей проблеме. Я повторю это здесь, так как я довольно много бродил с тех пор, как впервые заявил об этом:

Найдите площадь области, заключенную между линиями \ (y = 2x \), \ (y = 3x \) и \ (y = 2 \).Вы должны использовать исчисление, иначе вы не получите никаких кредитов!

Во-первых, я хочу, чтобы вы изобразили линии на одних и тех же осях. Я также хочу, чтобы вы пометили линии соответствующими уравнениями. Попробуйте сделать это самостоятельно, прежде чем смотреть на мой график. ПОДСКАЗКА: вы можете построить график любой линии, выбрав два разных значения \ (x \), подставив их в уравнение, чтобы найти соответствующие значения \ (y \), нанеся эти две точки и проведя через них прямую линию. .

Глядя на это изображение, неясно, какая функция является «верхней» функцией, а какая — «нижней».Ну, строка \ (y = 2 \) выглядит как верхняя функция, а \ (y = 2x \) выглядит как нижняя функция, но как насчет \ (y = 3x \)? Это сверху, снизу или где-то еще?

Ответ состоит в том, что \ (y = 3x \) также находится наверху.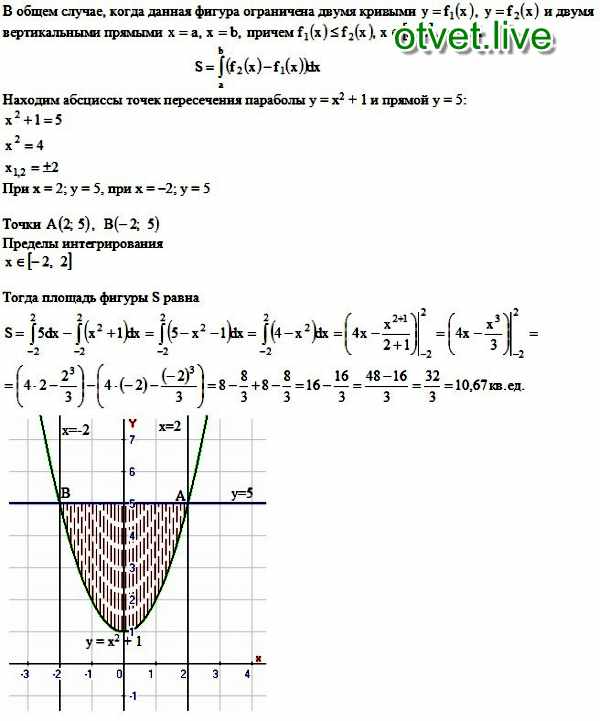 Иногда бывает. На самом деле, это зависит от того, на какую часть треугольника мы смотрим. Если мы разрежем эту область в точке пересечения \ (y = 3x \) и \ (y = 2 \), то часть, которая находится слева от разреза, будет ограничена сверху \ (y = 3x \). Часть справа от разреза ограничена сверху \ (y = 2 \).Позвольте мне показать вам, что я имею в виду:

Я нарисовал пунктирную линию, чтобы показать, где я вырезал область. Если вы посмотрите на каждую деталь по отдельности, вы увидите, что теперь каждая из них имеет различные функции «вверху» и «внизу». Это горячо. Теперь нам просто нужно использовать формулу, чтобы найти площадь каждой части, а затем сложить их вместе, чтобы получить окончательный ответ.

Хорошо, значит, кусок слева от пунктирной линии ограничен сверху \ (y = 3x \), а снизу — \ (y = 2x \). Это дает нам этот интеграл:

Фрагмент справа от пунктирной линии ограничен сверху \ (y = 2 \), а снизу — \ (y = 2x \).Это дает нам интеграл:

Отлично! Мы готовы к интеграции, верно? Держи это, партнер. Формула площади требует определенного интеграла , а это означает, что нам нужны пределы интегрирования (также известные как «границы»). Что ж, помните, что наши границы — это просто значения \ (x \), которые говорят нам, где область начинается и заканчивается. Чтобы найти их, давайте еще раз посмотрим на график:

Если посмотреть вдоль оси x, левая часть начинается с 0 и заканчивается пунктирной линией.Вы можете спросить, каково значение x у пунктирной линии? Заметьте, что он проходит через точку пересечения \ (y = 3x \) и \ (y = 2 \). Чтобы найти значение x этой точки, мы просто устанавливаем эти два уравнения равными друг другу, например:

Правая часть начинается с пунктирной линии (которая, как мы только что обнаружили, находится в \ (x = \ frac {2} {3} \)) и заканчивается цифрой 1. Почему 1? Потому что это место пересечения верхней и нижней функций , таким образом закрывая область. Мы можем показать это математически, установив уравнения верхней и нижней функций равными друг другу:

Хорошо, теперь у нас есть границы (от 0 до \ (\ frac {2} {3} \) для левой области и от \ (\ frac {2} {3} \) до 1 для правой области), мы готовы установить и решить наши определенные интегралы. Для левой части получаем:

Для правой части получаем:

Чтобы получить площадь всего региона, мы просто складываем площади отдельных частей:

Вот и все. Не так уж и плохо, правда? Как я уже сказал, эта проблема — отличный пример того, почему мы заставляем студентов, изучающих бизнес и биологию, заниматься математическим расчетом. Конечно, вам, вероятно, никогда не придется искать область ограниченного региона, когда вы обедаете с Гордоном Гекко или лечите рак, но он учит, как решать сложные проблемы, разбивая их на более простые части.b {f \ left (x \ right) dx} = F \ left (b \ right) — F \ left (a \ right), \]

, где \ (F \ left (x \ right) \) — любая первообразная от \ (f \ left (x \ right). \)

Рисунок 1.

Мы можем расширить понятие площади под кривой и рассмотреть площадь области между двумя кривыми.

Если \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) две непрерывные функции и \ (f \ left (x \ right) \ ge g \ left (x \ right) \) на отрезке \ (\ left [{a, b} \ right], \), то область между кривыми \ (y = f \ left (x \ right) \) и \ (y = g \ left (x \ right) \) в этом интервале равно

\ [A = \ int \ limits_a ^ b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx}. b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx}} = {F \ left (b \ right) — G \ left (b \ right) — F \ left (a \ right) + G \ left (a \ right),} \]

, где \ (F \ left (x \ right) \) и \ (G \ left (x \ right) \) — первообразные функций \ (f \ left (x \ right) \) и \ (g \ left (x \ right), \) соответственно.

Обратите внимание, что эта область всегда будет неотрицательной как \ (f \ left (x \ right) — g \ left (x \ right) \ ge 0 \) для всех \ (x \ in \ left [{a, b } \ right]. \)

Если есть точки пересечения, мы должны разбить интервал на несколько подинтервалов и определить, какая кривая больше на каждом подынтервале.\ prime \ left (t \ right), \) \ (y \ left (t \ right) \) здесь предполагается непрерывными на интервале \ (\ left [{a, b} \ right]. \) Кроме того то есть функция \ (x \ left (t \ right), \) должна быть монотонной на этом интервале.

Рис. 5.

Если \ (x = x \ left (t \ right), \) \ (y = y \ left (t \ right), \) \ (0 \ le t \ le T \) являются параметрическими уравнениями гладкая кусочно замкнутая кривая \ (C \), пересекаемая против часовой стрелки и ограничивающая область слева (рисунок \ (5 \)), то площадь области задается следующими интегралами:

\ [{A = — \ int \ limits_0 ^ T {y \ left (t \ right) x ^ \ prime \ left (t \ right) dt}} = {\ int \ limits_0 ^ T {x \ left (t \ right) y ^ \ prime \ left (t \ right) dt}} = {\ frac {1} {2} \ int \ limits_0 ^ T {\ left [{x \ left (t \ right) y ^ \ prime \ left (t \ right) — x ^ \ prime \ left (t \ right) y \ left (t \ right)} \ right] dt}. 2} \) на интервале \ (\ left [{1, b} \ right] \) равно \ (1? \)

Пример 3

Найдите координату точки \ (a \), которая разделяет область под корневой функцией \ (y = \ sqrt {x} \) на интервале \ (\ left [{0,4} \ right] \) на равные части.

Пример 4

Область ограничена вертикальными линиями \ (x = t \), \ (x = t + \ large {\ frac {\ pi} {2}} \ normalsize \), осью \ (x — \) и кривая \ (y = a + \ cos x, \), где \ (a \ ge 1. \). Определите значение \ (t \), при котором область имеет наибольшую площадь.{t + \ frac {\ pi} {2}}} = {a \ left ({t + \ frac {\ pi} {2}} \ right) + \ sin \ left ({t + \ frac {\ pi } {2}} \ right)} — ​​{at — \ sin t} = {\ cancel {at} + \ frac {{a \ pi}} {2} + \ sin \ left ({t + \ frac {\ pi} {2}} \ right)} — ​​{\ cancel {at} — \ sin t} = {\ frac {{a \ pi}} {2} + \ sin \ left ({t + \ frac {\ pi } {2}} \ right) — \ sin t.} \]

Использование тождества разницы синусов

\ [{\ sin \ alpha — \ sin \ beta} = {2 \ cos \ frac {{\ alpha + \ beta}} {2} \ sin \ frac {{\ alpha — \ beta}} {2}, } \]

получаем

\ [{A = \ frac {{a \ pi}} {2}} + {2 \ cos \ frac {{t + \ frac {\ pi} {2} + t}} {2} \ sin \ frac {{\ cancel {t} + \ frac {\ pi} {2} — \ cancel {t}}} {2}} = {\ frac {{a \ pi}} {2} + 2 \ cos \ left ( {t + \ frac {\ pi} {4}} \ right) \ sin \ frac {\ pi} {4}} = {\ frac {{a \ pi}} {2} + 2 \ cos \ left ({ t + \ frac {\ pi} {4}} \ right) \ cdot \ frac {{\ sqrt 2}} {2}} = {\ frac {{a \ pi}} {2} + \ sqrt 2 \ cos \ left ({t + \ frac {\ pi} {4}} \ right). } \]

Область имеет наибольшую площадь, когда \ (\ cos \ left ({t + \ large {\ frac {\ pi} {4}} \ normalsize} \ right) = -1. \)

Решая это уравнение, находим

\ [{\ cos \ left ({t + \ frac {\ pi} {4}} \ right) = — 1,} \; \; \ Rightarrow {t + \ frac {\ pi} {4} = \ pi + 2 \ pi n,} \; \; \ Rightarrow {t = \ frac {{3 \ pi}} {4} + 2 \ pi n, \, n \ in \ mathbb {Z}.} \]

Пример 5.

Найдите площадь области, заключенной между кривой \ (y = \ sqrt {x + 1} \) и прямой \ (y = x + 1. \)

Решение.0} = {\ left ({\ frac {2} {3} — 0 — 0} \ right) — \ left ({0 — \ frac {1} {2} + 1} \ right)} = {\ frac {2} {3} — \ frac {1} {2}} = {\ frac {1} {6}.} \]

Пример 6.

Найдите площадь области, заключенной между корневой кривой \ (y = \ sqrt {x} \) и прямой \ (y = kx, \), где \ (k \ gt 0. \)

Решение.

Сначала находим точки пересечения обеих кривых:

\ [{\ sqrt x = kx,} \; \; \ Rightarrow {\ sqrt x — kx = 0,} \; \; \ Rightarrow {\ sqrt x \ left ({1 — k \ sqrt x} \ right) = 0,} \; \; \ Rightarrow {{x_1} = 0, \;} \ kern0pt {{x_2} = \ frac {1} {{{k ^ 2}}}. {2 \ pi} {\ left ({3 + 4 \ cos \ theta + \ cos 2 \ theta} \ right) d \ theta}} = {\ frac {1} {4} \ left.{2 \ pi}} = {\ frac {3} {{16}} \ cdot 2 \ pi} = {\ frac {{3 \ pi}} {8}} \]

Исчисление I — площадь между кривыми

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон).Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 6-2: Площадь между кривыми

В этом разделе мы собираемся найти область между двумя кривыми.На самом деле есть два случая, которые мы собираемся рассмотреть.

В первом случае мы хотим определить область между \ (y = f \ left (x \ right) \) и \ (y = g \ left (x \ right) \) на интервале \ (\ left [{ яркий]\). Мы также будем предполагать, что \ (f \ left (x \ right) \ ge g \ left (x \ right) \). Взгляните на следующий рисунок, чтобы понять, на что мы изначально будем смотреть.

В разделе «Формулы площади и объема» главы «Дополнительно» мы вывели следующую формулу для площади в данном случае.{{\, d}} {{f \ left (y \ right) — g \ left (y \ right) \, dy}} \ label {eq: eq2} \ end {уравнение} \]

Теперь \ (\ eqref {eq: eq1} \) и \ (\ eqref {eq: eq2} \) — совершенно удобные формулы, однако иногда легко забыть, что они всегда требуют, чтобы первая функция была большей из две функции. 2} \) и \ (y = \ sqrt x \).Показать решение

Прежде всего, что мы подразумеваем под «замкнутой площадью». Это означает, что интересующая нас область должна иметь одну из двух кривых на каждой границе области. Итак, вот график двух функций с заштрихованной областью.

Обратите внимание, что мы не берем какую-либо часть области справа от точки пересечения этих двух графиков. В этой области нет границы с правой стороны, поэтому она не является частью замкнутой области.2} \) является верхней функцией, и они будут правильными для подавляющего большинства \ (x \) ‘s. Однако в данном случае это младшая из двух функций.

Пределы интегрирования для этого будут точками пересечения двух кривых. В этом случае довольно легко увидеть, что они будут пересекаться в точках \ (x = 0 \) и \ (x = 1 \), так что это пределы интегрирования.

Итак, интеграл, который нам потребуется вычислить, чтобы найти площадь, равен

. 2} \, dx}} \\ & = \ left.1 \\ & = \ frac {1} {3} \ end {align *} \]

Прежде чем перейти к следующему примеру, следует отметить несколько важных моментов.

Во-первых, почти во всех этих задачах граф требуется. Часто ограничивающую область, которая дает пределы интегрирования, трудно определить без графика.

Кроме того, без графика часто бывает сложно определить, какая из функций является верхней, а какая нижней функцией.Это особенно верно в случаях, подобных последнему примеру, где ответ на этот вопрос фактически зависел от диапазона значений \ (x \), которые мы использовали.

Наконец, в отличие от площади под кривой, которую мы рассматривали в предыдущей главе, площадь между двумя кривыми всегда будет положительной. Если мы получим отрицательное число или ноль, мы можем быть уверены, что где-то допустили ошибку, и нам нужно будет вернуться и найти ее.

Также обратите внимание, что иногда вместо того, чтобы говорить «регион, заключенный в», мы говорим «регион, ограниченный». 2}}} \), \ (y = x + 1 \), \ (x = 2 \) и ось \ (y \) -. Показать решение

В этом случае последние две части информации, \ (x = 2 \) и ось \ (y \), сообщают нам правую и левую границы области. Также напомним, что ось \ (y \) задается линией \ (x = 0 \). Вот график с заштрихованной областью.

Здесь, в отличие от первого примера, две кривые не пересекаются. Вместо этого мы полагаемся на две вертикальные линии, чтобы ограничить левую и правую стороны области, как мы отметили выше

.

Вот интеграл, который даст площадь.2} + 10 \) и \ (y = 4x + 16 \). Показать решение

В этом случае точки пересечения (которые нам в конечном итоге понадобятся) будет нелегко идентифицировать по графику, поэтому давайте продолжим и получим их сейчас. Обратите внимание, что для большинства этих проблем вы не сможете точно определить точки пересечения на графике, поэтому вам нужно будет определить их вручную. 2} — 4x — 6 & = 0 \\ 2 \ left ({x + 1} \ right) \ left ({x — 3} \ right) & = 0 \ end {align *} \]

Итак, похоже, что две кривые пересекутся в точках \ (x = — 1 \) и \ (x = 3 \).Если они нам нужны, мы можем получить значения \ (y \), соответствующие каждому из них, вставив значения обратно в любое из уравнений. Мы предоставим вам проверить, что координаты двух точек пересечения на графике равны \ (\ left ({- 1,12} \ right) \) и \ (\ left ({3,28} \ right) ) \).

Также обратите внимание, что если вы не умеете строить графики, знание точек пересечения может помочь хотя бы в начале построения графика. Вот график региона.

С помощью графика мы теперь можем идентифицировать верхнюю и нижнюю функцию, и теперь мы можем найти замкнутую область.2} + 10 \), \ (y = 4x + 16 \), \ (x = — 2 \) и \ (x = 5 \). Показать решение

Итак, функции, используемые в этой задаче, идентичны функциям из первой задачи. Разница в том, что мы расширили ограниченную область за пределы точек пересечения. Поскольку это те же функции, которые мы использовали в предыдущем примере, мы больше не будем утруждать себя поиском точек пересечения.

Вот график этого региона.

Хорошо, у нас тут небольшая проблема.Наша формула требует, чтобы одна функция всегда была верхней функцией, а другая функция всегда была нижней функцией, а здесь этого явно нет. Однако на самом деле проблема не в этом, как может показаться на первый взгляд. Есть три области, в которых одна функция всегда является верхней функцией, а другая всегда является нижней функцией. Итак, все, что нам нужно сделать, это найти площадь каждой из трех областей, что мы можем сделать, а затем сложить их все.

Вот площадь.5 \\ & = \ frac {{14}} {3} + \ frac {{64}} {3} + \ frac {{64}} {3} \\ & = \ frac {{142}} {3 } \ end {align *} \] Пример 5 Определите площадь области, заключенной в \ (y = \ sin x \), \ (y = \ cos x \), \ (x = \ frac {\ pi} {2} \) и \ ( у \) — ось. 2} — 2y — 8 \\ 0 & = \ left ({y — 4} \ right) \ left ({y + 2} \ right) \ end {align *} \]

Итак, похоже, что две кривые пересекутся в точках \ (y = — 2 \) и \ (y = 4 \), или, если нам нужны полные координаты, они будут: \ (\ left ({- 1, — 2 } \ right) \) и \ (\ left ({5,4} \ right) \).

Вот эскиз двух кривых.

Если мы не будем осторожны, у нас возникнет серьезная проблема. До сих пор мы использовали верхнюю функцию и нижнюю функцию. Для этого обратите внимание, что на самом деле есть две части региона, которые будут выполнять разные нижние функции. В диапазоне \ (\ left [{- 3, — 1} \ right] \) парабола фактически является как верхней, так и нижней функцией.

Чтобы использовать формулу, которую мы использовали до сих пор, нам нужно решить параболу для \ (y \).Это дает,

\ [y = \ pm \ sqrt {2x + 6} \]

, где «+» означает верхнюю часть параболы, а «-» — нижнюю часть. {{\, 5}} {{- x + 1 \, dx}} \\ & = \ left.{{\, d}} {{\ left (\ begin {array} {c} {\ mbox {right}} \\ {\ mbox {function}} \ end {array} \ right) — \ left (\ begin {array} {c} {\ mbox {left}} \\ {\ mbox {function}} \ end {array} \ right) \, dy}}, \ hspace {0,5 дюйма} c \ le y \ le d \ ]

, и в нашем случае у нас есть одна функция, которая всегда слева, а другая всегда справа. Так что в данном случае это определенно правильный путь. Обратите внимание, что нам нужно будет переписать уравнение линии, поскольку оно должно быть в форме \ (x = f \ left (y \ right) \), но это достаточно легко сделать.4 \\ & = 18 \ end {align *} \]

Это то же самое, что мы получили, используя первую формулу, и это было определенно проще, чем первый метод.

Итак, в этом последнем примере мы видели случай, когда мы могли использовать любую формулу для определения площади. Однако второе было определенно легче.

Студенты часто приходят в класс по математике с идеей, что единственный простой способ работать с функциями — использовать их в форме \ (y = f \ left (x \ right) \). 2} + 4y + 6 \, dy} } \\ & = \ left.3 = \ frac {{64}} {3} \ end {align *} \]

Исчисление I — Объемы вращающихся тел / Метод колец

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 6-3: Объем с кольцами

В этом разделе мы начнем смотреть на объем твердого тела вращения. Сначала мы должны определить, что такое твердое тело революции. Чтобы получить твердое тело вращения, мы начинаем с функции \ (y = f \ left (x \ right) \) на интервале \ (\ left [{a, b} \ right] \).

Затем мы вращаем эту кривую вокруг заданной оси, чтобы получить поверхность тела вращения. Для целей этого обсуждения давайте повернем кривую вокруг оси \ (x \), хотя это может быть любая вертикальная или горизонтальная ось. Выполнение этого для кривой выше дает следующую трехмерную область.{{\, d}} {{A \ left (y \ right) \, dy}} \]

, где \ (A \ left (x \ right) \) и \ (A \ left (y \ right) \) — площадь поперечного сечения твердого тела. Есть много способов получить площадь поперечного сечения, и мы увидим два (или три, в зависимости от того, как на это смотреть) в следующих двух разделах. Будем ли мы использовать \ (A \ left (x \ right) \) или \ (A \ left (y \ right) \), будет зависеть от метода и оси вращения, используемых для каждой задачи.

Один из самых простых способов получить площадь поперечного сечения — разрезать объект перпендикулярно оси вращения.2}} \ справа) \]

, где оба радиуса снова будут зависеть от заданных функций и оси вращения. Также обратите внимание, что в случае твердого диска мы можем думать о внутреннем радиусе как о нуле, и мы придем к правильной формуле для твердого диска, так что это гораздо более общая формула для использования.

Кроме того, в обоих случаях, является ли площадь функцией \ (x \) или функцией \ (y \), как мы увидим, будет зависеть от оси вращения.

Этот метод часто называют методом дисков или методом колец .2} — 4x + 5 \), \ (x = 1 \), \ (x = 4 \) и ось \ (x \) вокруг оси \ (x \) -. Показать решение

Первое, что нужно сделать, это получить эскиз ограничивающей области и твердого тела, полученный вращением области вокруг оси \ (x \). Нам не нужен идеальный набросок кривых, нам просто нужно что-то, что позволит нам почувствовать, как выглядит ограниченная область, чтобы мы могли быстро получить набросок твердого тела. Имея это в виду, мы можем отметить, что первое уравнение — это просто парабола с вершиной \ (\ left ({2,1} \ right) \) (вы помните, как получить вершину параболы справа?) И открывается вверх. и поэтому нам действительно не нужно тратить много времени на его набросок.

Вот оба этих скетча.

Хорошо, чтобы получить поперечное сечение, мы разрезаем твердое тело в любой точке \ (x \). Ниже приведены несколько эскизов, показывающих типичное поперечное сечение. На эскизе справа показан вырез объекта с типичным поперечным сечением без заглушек. Эскиз слева показывает только кривую, которую мы вращаем, а также ее зеркальное отображение в нижней части твердого тела.

В этом случае радиус — это просто расстояние от оси \ (x \) до кривой, и это не что иное, как значение функции в этом конкретном \ (x \), как показано выше.4 \\ & = \ frac {{78 \ pi}} {5} \ end {align *} \]

В приведенном выше примере объект был твердым, но более интересными являются не твердые объекты, поэтому давайте взглянем на один из них.

Пример 2 Определите объем твердого тела, полученного вращением части области, ограниченной \ (y = \ sqrt [3] {x} \) и \ (\ displaystyle y = \ frac {x} {4} \), которые лежит в первом квадранте вокруг оси ординат. Показать решение

Во-первых, давайте возьмем график ограничивающей области и график объекта.Помните, что нам нужна только часть ограничивающей области, которая находится в первом квадранте. Есть часть ограничивающей области, которая также находится в третьем квадранте, но мы не хотим этого для этой проблемы.

В связи с этой проблемой следует обратить внимание на несколько моментов. Во-первых, мы ищем только объем «стен» этого твердого тела, а не весь интерьер, как мы это делали в последнем примере.

Далее мы получим наше поперечное сечение, разрезав объект перпендикулярно оси вращения.3} \\ y & = \ frac {x} {4} \ hspace {0,65 дюйма} \ Rightarrow \ hspace {0,5 дюйма} x = 4y \ end {align *} \]

Вот пара эскизов границ стен этого объекта, а также типичное кольцо. Набросок слева включает заднюю часть объекта, чтобы дать небольшой контекст рисунку справа.

Внутренний радиус в этом случае — это расстояние от оси \ (y \) до внутренней кривой, а внешний радиус — это расстояние от оси \ (y \) до внешней кривой.2 \\ & = \ frac {{512 \ pi}} {{21}} \ end {align *} \]

Разобрав эти два примера, мы можем сделать обобщение об этом методе. Если мы вращаемся вокруг горизонтальной оси (например, оси \ (x \)), то площадь поперечного сечения будет функцией \ (x \). Аналогичным образом, если мы вращаемся вокруг вертикальной оси (например, оси \ (y \)), площадь поперечного сечения будет функцией \ (y \).

Остальные два примера в этом разделе помогут нам не слишком привыкнуть к идее постоянного вращения вокруг оси \ (x \) или \ (y \).2} — 2x \) и \ (y = x \) относительно прямой \ (y = 4 \). Показать решение

Сначала давайте нарисуем ограничивающую область и твердое тело.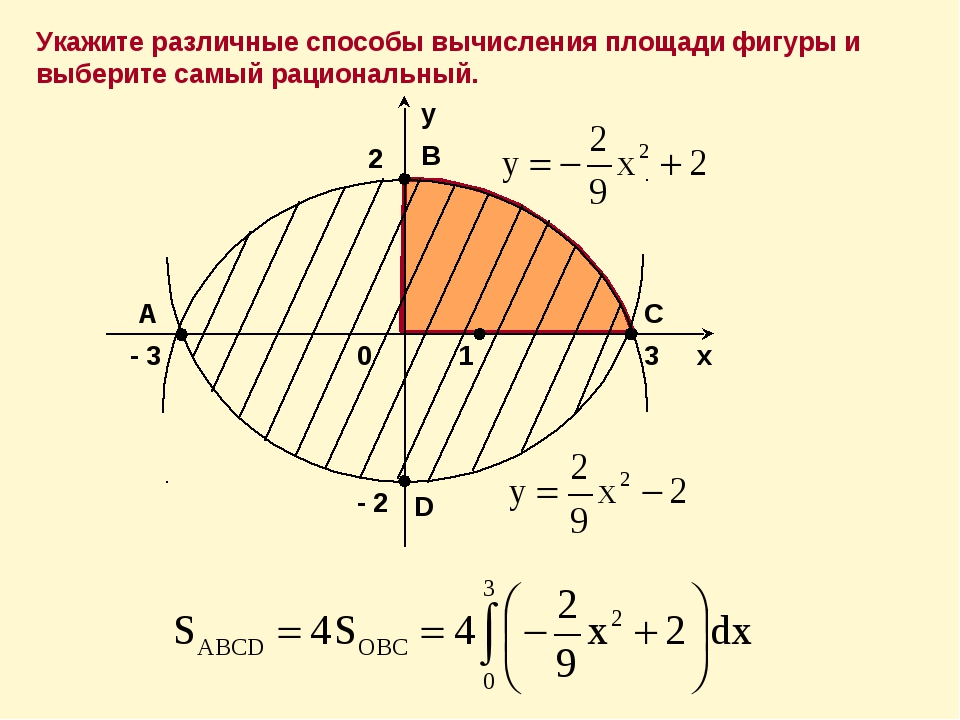

Опять же, мы будем искать объем стен этого объекта. Кроме того, поскольку мы вращаемся вокруг горизонтальной оси, мы знаем, что площадь поперечного сечения будет функцией \ (x \).

Вот пара эскизов границ стен этого объекта, а также типичное кольцо.Набросок слева включает заднюю часть объекта, чтобы дать небольшой контекст рисунку справа.

Теперь нам нужно быть осторожными при определении внутреннего и внешнего радиуса, поскольку они не будут такими простыми, как в предыдущих двух примерах.

Начнем с внутреннего радиуса, так как этот немного яснее. Во-первых, внутренний радиус НЕ \ (x \). Расстояние от оси \ (x \) до внутреннего края кольца равно \ (x \), но нам нужен радиус, и это расстояние от оси вращения до внутреннего края кольца.2} + 2x + 4 \]

Обратите внимание, что, учитывая расположение типичного кольца на рисунке выше, формула для внешнего радиуса может выглядеть не совсем правильно, но на самом деле она верна. Как показано на рисунке, внешний край кольца находится ниже оси \ (x \), и в этой точке значение функции будет отрицательным, поэтому, когда мы выполняем вычитание в формуле для внешнего радиуса, мы фактически вычитаем от отрицательного числа, которое имеет чистый эффект прибавления этого расстояния к 4 и дает правильный внешний радиус.3 \\ & = \ frac {{153 \ pi}} {5} \ end {align *} \] Пример 4 Определите объем твердого тела, полученного вращением области, ограниченной \ (y = 2 \ sqrt {x — 1} \) и \ (y = x — 1 \), вокруг линии \ (x = — 1 \) . Показать решение

Как и в предыдущих примерах, давайте сначала изобразим ограниченную область и твердое тело.

Теперь отметим, что, поскольку мы вращаемся вокруг вертикальной оси, площадь поперечного сечения будет функцией \ (y \).2}}} {4} + 1 \\ y & = x — 1 \ hspace {0,75in} \ Rightarrow \ hspace {0,5in} x = y + 1 \ end {align *} \]

Вот пара эскизов границ стен этого объекта, а также типичное кольцо. Набросок слева включает заднюю часть объекта, чтобы дать небольшой контекст рисунку справа.

Внутренний и внешний радиус для этого случая и аналогичны, и отличаются от предыдущего примера.Этот пример похож в том смысле, что радиусы — это не просто функции. В этом примере функции — это расстояния от оси \ (y \) до краев колец. Однако центр кольца находится на расстоянии 1 от оси \ (y \). Это означает, что расстояние от центра до краев — это расстояние от оси вращения до оси \ (y \) (расстояние 1), а затем от оси \ (y \) до края кольца.

Итак, радиусы — это функции плюс 1, и это то, что отличает этот пример от предыдущего.Здесь нам нужно было добавить расстояние к значению функции, тогда как в предыдущем примере нам нужно было вычесть функцию из этого расстояния. Обратите внимание, что без эскизов радиусы на этих задачах получить трудно.

Итак, в итоге мы получили следующие значения внутреннего и внешнего радиуса для этого примера. 4}}}} {{16}}} \ right) \]

Первое кольцо будет в точке \ (y = 0 \), а последнее кольцо будет в точке \ (y = 4 \), и это будут наши пределы интегрирования.4 \\ & = \ frac {{96 \ pi}} {5} \ end {align *} \]

Исчисление I — Среднее значение функции

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон).Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. 2} + 3x + 2 \) на интервале \ (\ left [{1,4} \ right] \).2} + 9c — \ frac {{87}} {2} \ end {align *} \]

Это квадратное уравнение, которое мы можем решить. Используя формулу корней квадратного уравнения, мы получаем следующие два решения:

\ [\ begin {align *} c & = \ frac {{- 3 + \ sqrt {67}}} {2} = 2,593 \\ c & = \ frac {{- 3 — \ sqrt {67}}} { 2} = — 5.593 \ end {align *} \]

Очевидно, что второе число не входит в интервал, и поэтому это не тот номер, который мы ищем. Однако первый находится в интервале, и это то число, которое нам нужно.{1}

долл. США

Ставя лимиты, получаем,

$ = (1 + 1) — \ left (\ dfrac {1} {3} + \ dfrac {1} {3} \ right)

$

$ = 2- \ dfrac {2} {3}

$

$ A = \ dfrac {4} {3}

$

1.1: Площадь между двумя кривыми

1. Последнее обновление

2. Сохранить как PDF

1. Площадь, ограниченная двумя функциями от \ (y \)
2. Приложение
3. Участники и авторства

Напомним, что площадь под кривой и над осью x может быть вычислена с помощью определенного интеграла.1 \\ & = \ big (- \ dfrac {3} {4} + \ dfrac {3} {2} \ big) — \ big (\ dfrac {3} {4} — \ dfrac {3} {2} \ big) \\ & = \ dfrac {3} {2} \ end {align *}. \]

Приложение

Пусть \ (y = f (x) \) будет функцией спроса на продукт, а \ (y = g (x) \) будет функцией предложения. Затем мы определяем точку равновесия как пересечение двух кривых. Излишек потребителя определяется площадью выше равновесного значения и ниже кривой спроса, в то время как излишек производителя определяется площадью ниже равновесного значения и выше кривой предложения.х \) и \ (у = 2х +1 \).

Авторы и авторство

.