Формулы площадей 📐 всех фигур

Площадь треугольника

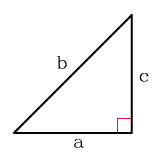
Прямоугольного

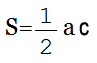
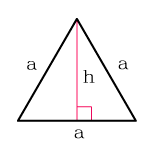
Равностороннего треугольника

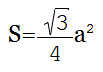
Площадь равнобедренного прямоугольного треугольника

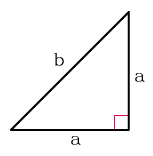
S = a²/2

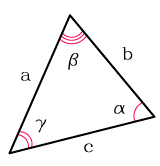
Площадь треугольника через синус

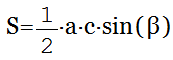
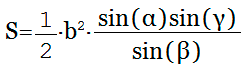
Площадь треугольника через косинус

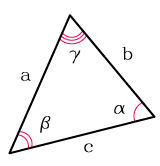Для нахождения площади треугольника нужно знать все стороны.  По теореме косинусов квадрат неизвестной стороны равен: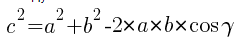
Следовательно:
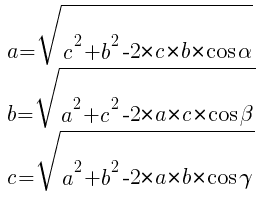
Далее используем формулу Герона:

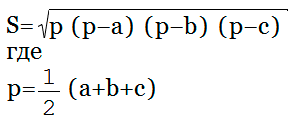
Площадь треугольника через радиус описанной окружности

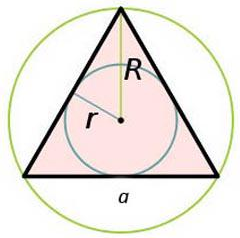
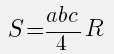
Произвольного треугольника

Формула Герона

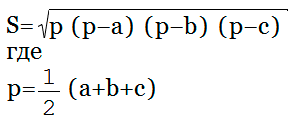
Площадь треугольника через высоту

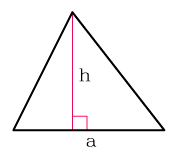
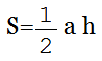
Площадь треугольника через полупериметр

Формула Герона
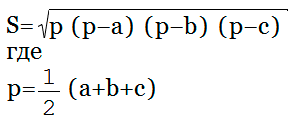
является полупериметром.

Площадь тупоугольного треугольника

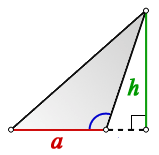
S = ah/2

Площадь треугольника через радиус вписанной окружности

S = p×r

где p — полупериметр: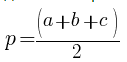

Площадь параллелограмма

Через синус

Через стороны и углы

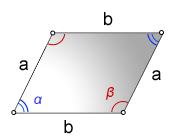
S = a×b×sin(α) =  a×b×sin(β)

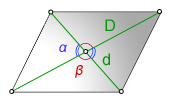
Через диагонали и угол между ними

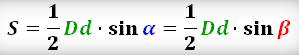
Формула площади прямоугольника

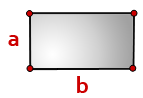
S = a×b

Площадь квадрата

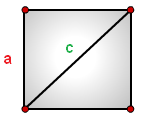
S = a²

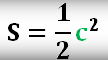
Площадь четырехугольника

Выпуклого четырехугольника

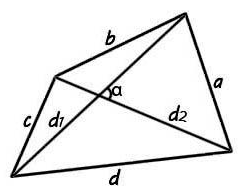
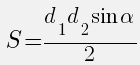
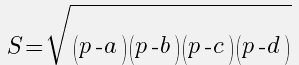
где

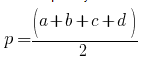
Площадь многоугольника

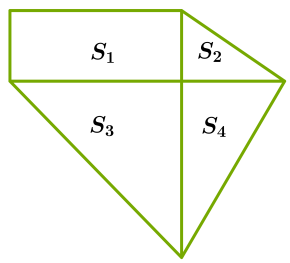
S = S

1 + S₂ + S₃ + S₄

Правильного многоугольника

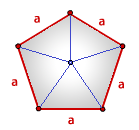
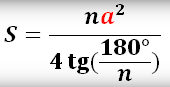
где n — количество сторон многоугольника.

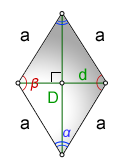
Площадь ромба

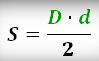
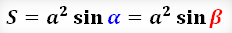
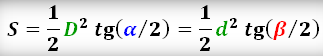
Площадь многогранника

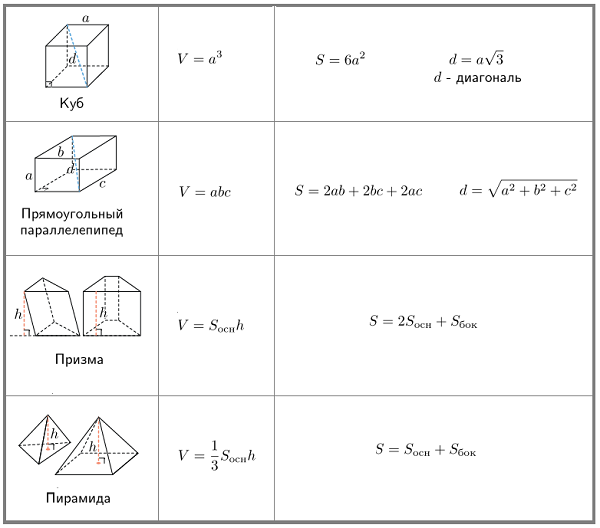
Площадь пятиугольника

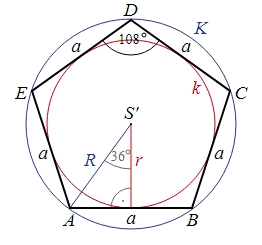
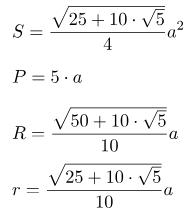
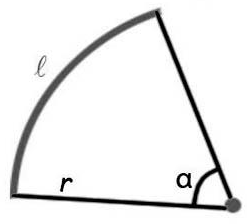
Площадь закрашенного сектора

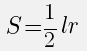
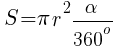
Площадь круга

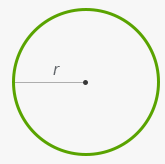
S = πr²

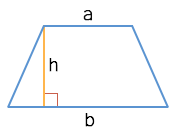
Площадь трапеции

Через основания и высоту

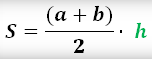
Через высоту и среднюю линию

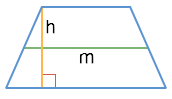
S = hm

Через четыре стороны

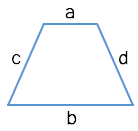
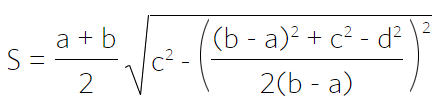
Через диагонали и угол между ними

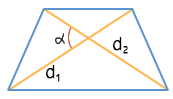
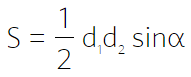
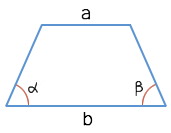
Через основания и два угла

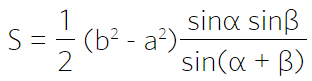
nauka.club

Площади геометрических фигур / math5school.ru

	Треугольник		Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.
	Треугольник		Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
	Треугольник		Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон.
	Треугольник		Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла.
	Треугольник		Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов.
	Треугольник		Площадь треугольника равна произведению квадрата его полупериметра на тангенсы половин всех углов треугольника.
	Прямоугольный треугольник		Площадь прямоугольного треугольника равна половине произведения его катетов.
	Равнобедренный треугольник		Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания.
	Равносторонний треугольник		Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх.
	Равносторонний треугольник		Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх.
	Треугольник		Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности.
	Треугольник		Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов.
	Треугольник		Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник).
	Треугольник		Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника.
	Прямоугольник		Площадь прямоугольника равна произведению двух соседних его сторон.
	Квадрат		Площадь квадрата равна квадрату его стороны.
	Квадрат		Площадь квадрата равна половине квадрата его диагонали.
	Параллелограмм		Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.
	Параллелограмм		Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними.
	Ромб		Площадь ромба равна произведению квадрата его стороны на синус одного из его углов.
	Ромб (дельтоид)		Площадь ромба (как и дельтоида) равна половине произведения его диагоналей.
	Трапеция		Площадь трапеции равна произведению полусуммы её оснований на высоту.
	Трапеция		Площадь трапеции равна произведению её средней линии на высоту.
	Выпуклый четырёхугольник		Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
	Вписанный четырёхугольник		Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон.
	Круг		Площадь круга равна произведению числа «пи» на квадрат радиуса.
	Круг		Площадь круга равна четверти произведения числа «пи» на квадрат диаметра.
	Круговой сектор	формулы для случаев градусной и радианной мер центральных углов	Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору.
	Круговое кольцо		Площадь кругового кольца равна произведению числа «пи» на разность квадратов внешнего и внутреннего радиусов.
	Круговое кольцо		Площадь кругового кольца равна четверти произведения числа «пи» на разность квадратов внешнего и внутреннего диаметров.
	Круговое кольцо		Площадь кругового кольца равна удвоенному произведению числа «пи», среднего радиуса кольца и его ширины.

math4school.ru

Площади фигур — формулы.

2014-07-25 | Автор: Анна

 

 

Вспоминаем формулы для вычисления площадей фигур!

Формулы площадей фигур

Треугольник общего вида. a, b, c — стороны, p — полупериметр, r — радиус вписанной окружности, R — радиус описанной окружности
Прямоугольный треугольник. a, b — катеты, с — гипотенуза, p — полупериметр, r — радиус вписанной окружности, R — радиус описанной окружности
Правильный треугольник
Прямоугольник. a,b — стороны, d — диагонали.
Квадрат.
Параллелограмм. a,b — стороны, d — диагонали, h — высота
Ромб. a — сторона, d — диагональ, h — высота
Трапеция. a,b — основания, h — высота, d — диагонали.
Круг.
Элементы круга.
Правильный n-угольник

 

 

easy-physic.ru

Формула вычисления площади для всех геометрических фигур

Стандартное обозначение площади — S

Площадь

Пусть длина стороны квадрата равна a, тогда формул квадрата:

S = a ⋅ a = a²

Прямоугльник

Пусть длины сторон прямоугольника равны a и b

S = a ⋅ b

Параллелограмм

Пусть длины сторон параллелограмма равны a и b и h_a это высота на сторону a, и h_b это высота на сторону b
Формула площади параллелограмма:

S = a ⋅ h_a = b ⋅ h_b

Трапеция

Допустим, что длины параллельных сторон трапеции имеют длину a и b и расстояние между двумя основами s h(the trapezoid altitude). Тогда формула площади:

$S = \frac{(a + b)\cdot h}{2}$

Площадь круга

$P = \pi\cdot r^2$

$\pi=3,14$

Площадь прямоугольного треугольника

$S=\frac{a \cdot b}{2}$

$S=\frac{c \cdot h_c}{2}$

Площадь треугольника — калькулятор

Стороны треугольника:

Треугольник

ABC — треугольник

длина его сторон: a, b, c и длина его высот: h_a, h_b и h_c.

S = ½(a ⋅ h_a) = ½(b ⋅ h_b) = ½(c ⋅ h_c)

S = ½(ab ⋅ sinC) = ½(ac ⋅ sinB) = ½(bc ⋅ sinA)

p = ½(a + b + c)

S = √p(p — a)(p — b)(p — c) — формула Герона

$S = R^2\sin(A) \cdot \sin(B) \cdot \sin(C) = \frac{abc}{4R}$

где R — радиус описанной окружности

---

Площадь параллелограмма(ромба)

$S = AB\cdot DE = BC \cdot DF$
$S = AB \cdot AD \sin \alpha$
$S = \frac12 AC \cdot BD \sin \gamma$

Площадь выпуклого четырехугольника

$S = \frac12 AC \cdot BD \sin \varphi $

Площадь правильного многоугольника

$S = \frac14 n\cdot a^2\cdot \text{ctg}(\frac{\pi}{n})$

n — число ребер(вершин).
$\pi=3,14159265359$

www.math10.com

Площади фигур

 

 

Формула площади треугольника

Площадь треугольника (S):

h — высота треугольника;

a — основание.

---

Площадь прямоугольного треугольника по катетам

Формула площади прямоугольного треугольника, (S):

a, b — катеты треугольника.

---

Площадь треугольника, формула Герона

Формула (Герона) площади треугольника через полупериметр (S):

a, b, c — стороны треугольника

p — полупериметр, p=(a+b+c)/2

---

Площадь равнобедренного треугольника

Площадь треугольника с двумя одинаковыми сторонами.

b — основание треугольника

a — равные стороны

h — высота

 

---

Формула площади треугольника через высоту h и основание b, (S):

 

Формула площади треугольника через, стороны a, b, (S):

 

---

Площадь равностороннего треугольника равна:

 

Формулы расчета, площади равностороннего треугольника.

a — сторона треугольника

h — высота

---

Площадь квадрата через диагональ

Как рассчитать площадь квадрата через диагональ

a — сторона квадрата

c — диагональ

---

Формула площади параллелограмма через сторону и высоту

a, b — стороны параллелограмма

H_b — высота на сторону b

H_a — высота на сторону a

---

Формула площади ромба

S = a · H

  где: H — высота ромба.

          a — сторона ромба

 

 

---

Площадь неравнобедренной трапеции :

a — нижнее основание;

b — верхнее основание;

h — высота трапеции.

---

Формула площади правильного многоугольника

a — сторона многоугольника

n — количество сторон

 

Записи по теме

Площади кругов и окружностей Формулы площадей для кругов и окружностей: площадь круга, площадь сегмента круга, площадь кольца, площадь сектора кольца. Площади поверхностей Формулы площади поверхностей объёмных фигур. Формулы для расчёта площади поверхности куба, прямоугольного параллелепипеда, правильной и усечённой пирамид, усечённого конуса.

 

 

inter-net.pro

Все формулы площади плоских фигур

Все формулы площади плоских фигур

Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

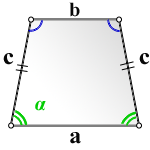
а — нижнее основание

b — верхнее основание

с — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S ):

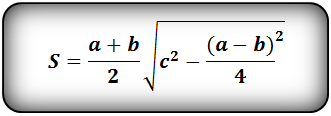
Формула площади равнобедренной трапеции через стороны и угол, (S ):

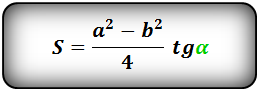
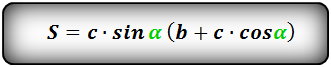
2. Формула площади равнобедренной трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α, β — углы трапеции

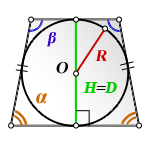
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):

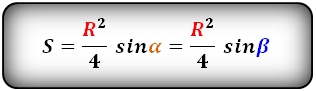
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

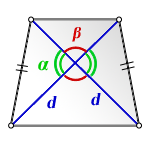
d — диагональ трапеции

α, β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

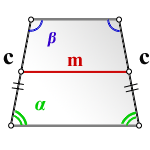
c — боковая сторона

m — средняя линия трапеции

α, β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,

(S ):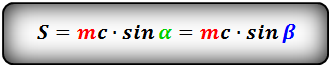

5. Формула площади равнобедренной трапеции через основания и высоту

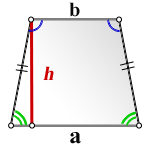
a — нижнее основание

b — верхнее основание

h — высота трапеции

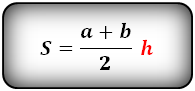
Формула площади равнобедренной трапеции через основания и высоту, (S ):

Площадь треугольника по стороне и двум углам, формула.

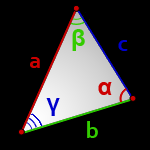
a, b, c- стороны треугольника

α, β, γ- противолежащие углы

Площадь треугольника через сторону и два угла (S):

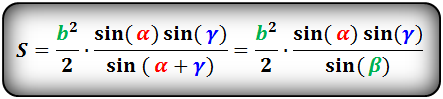
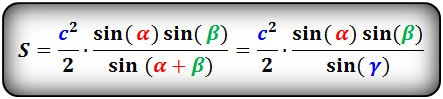
Формула площади правильного многоугольника

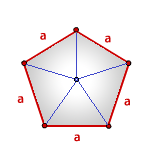
a — сторона многоугольника

n — количество сторон

Площадь правильного многоугольника, (S):

Формула (Герона) площади треугольника через полупериметр (S):

Площадь равностороннего треугольника равна:

Формулы расчета, площади равностороннего треугольника.

a — сторона треугольника

h – высота

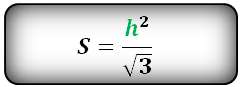
Как вычислить площадь равнобедренного треугольника ?

b — основание треугольника

a — равные стороны

h – высота

3. Формула площади трапеции через четыре стороны

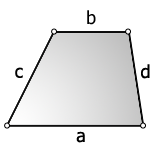
a — нижнее основание

b — верхнее основание

c , d — боковые стороны

Радиус описанной окружности трапеции по сторонам и диагонали

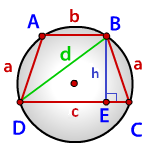
a — боковые стороны трапеции

c — нижнее основание

b — верхнее основание

d — диагональ

h — высота

p = (a+d+c)/2

Формула радиуса описанной окружности трапеции, (R)

найти радиус описанной окружности равнобедренного треугольника по сторонам

Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

a, b — стороны треугольника

Радиус описанной окружности равнобедренного треугольника (R):

Радиус вписанной окружности в шестиугольник

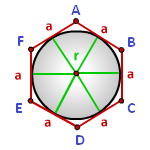
a — сторона шестиугольника

Радиус вписанной окружности в шестиугольник, (r):

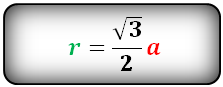
Радиус вписанной окружности в ромб

r — радиус вписанной окружности

a — сторона ромба

D, d — диагонали

h — высота ромба

Радиус вписанной окружности в равнобочную трапецию

с — нижнее основание

b — верхнее основание

a — боковые стороны

h — высота

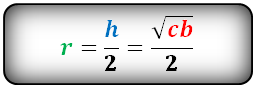
Радиус вписанной окружности в прямоугольный треугольник

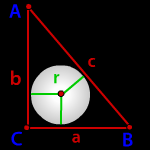
a, b — катеты треугольника

с — гипотенуза

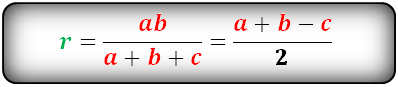
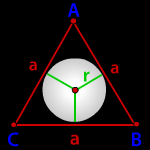
Радиус вписанной окружности в равнобедренный треугольник

a, b — стороны треугольника

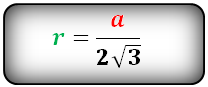
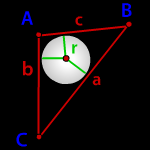
.Доказать, что площадь вписанного четырёхугольника равна

\/(р — а)(р — b) (р — с) (р — d),

где р — полупериметр и а, b, с и d — стороны четырёхугольника.

Доказать, что площадь вписанного в круг четырёхугольника равна

1/2 (ab + cb) · sin α , где а, b, с и d — стороны четырёхугольника и α — угол между сторонами а и b.

S = √[ a • ƀ • c • d] • sin ½ (α + β). — Читайте подробнее на FB.ru:

Площадь произвольного четырёхугольника (рис. 1.13) можно выразить через его стороны а, b, c и сумму пары противоположных углов:

где р – полупериметр четырёхугольника.

Площадь вписанного в окружность четырёхугольника (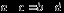) (рис. 1.14, а) вычисляется по формуле Брахмагупты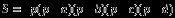

а описанного (рис. 1.14, б) () – по формуле

Если же четырёхугольник вписан и описан одновременно (рис. 1.14, в), то формула становится совсем простой:

Формула Пика

Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, — число клеток, которые целиком лежат внутри многоугольника, и — число клеток, которые имеют с внутренностью многоугольника хоть одну общую точку .

Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:

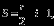
где — площадь, r – число узлов, которые лежат строго внутри многоугольника.

Эту формулу называют «формула Пика» — по имени математика, открывшего её в 1899 году.

.

studfile.net

8 класс. Геометрия. Площадь. Площадь треугольника и трапеции. — Повторение темы «Площадь». Решение задач.

Комментарии преподавателя

Повторение темы «Площадь». Решение задач

1. Повторение теоретической части главы «Площадь»

Вначале уделим внимание тому, что вспомним все основные теоремы, формулы и факты, полученные нами при изучении главы «Площадь», и акцентируем внимание на их особенностях. Затем рассмотрим сложный пример на комплексное применение нескольких из упомянутых фактов, касающихся площадей фигур.

1. Площадь квадрата равна квадрату его стороны (см. Рис. 1). .

Рис. 1. Квадрат

2. Площадь прямоугольника равна произведению его сторон (см. Рис. 2).  .

Рис. 2. Прямоугольник

          3. Площадь параллелограмма равна произведению основания на опущенную на него высоту (см. Рис. 3). .

Рис. 3. Параллелограмм

4. Площадь произвольного треугольника равна половине произведения основания на опущенную на него высоту (см. Рис. 4). .

Рис. 4. Произвольный треугольник

5. Площадь прямоугольного треугольника равна половине произведения катетов (см. Рис. 5). .

Рис. 5. Прямоугольный треугольник

6. Если у двух треугольников высоты равны (), то их площади относятся, как основания (см. Рис. 6). .

www.kursoteka.ru