Как находить высоту в равнобедренном треугольнике? Формула нахождения, свойства высоты в равнобедренном треугольнике
Образование 30 августа 2014Геометрия – это не только предмет в школе, по которому нужно получить отличную оценку. Это еще и знания, которые часто требуются в жизни. Например, при строительстве дома с высокой крышей необходимо рассчитать толщину бревен и их количество. Это несложно, если знать, как находить высоту в равнобедренном треугольнике. Архитектурные сооружения базируются на знании свойств геометрических фигур. Формы зданий зачастую визуально напоминают их. Египетские пирамиды, пакеты с молоком, художественная вышивка, северные росписи и даже пирожки – это все треугольники, окружающие человека. Как говорил Платон, весь мир базируется на треугольниках.
Равнобедренный треугольник
Чтобы было понятнее, о чем далее пойдет речь, стоит немного вспомнить азы геометрии.
Треугольник является равнобедренным, если он имеет две равных стороны. Их всегда называют боковыми. Сторона, размеры которой отличаются, получила название основания.
Основные понятия
Как и любая наука, геометрия имеет свои основные правила и понятия. Их достаточно много. Рассмотрим лишь те, без которых наша тема будет несколько непонятна.
Высота – это прямая линия, проведенная перпендикулярно к противоположной стороне.
Медиана – это отрезок, направленный из любой вершины треугольника исключительно к середине противоположной стороны.
Биссектриса угла – это луч, разделяющий угол пополам.
Биссектриса треугольника – это прямая, вернее, отрезок биссектрисы угла, соединяющий вершину с противоположной стороной.
Очень важно запомнить, что биссектриса угла – это обязательно луч, а биссектриса треугольника – это часть такого луча.
Углы при основании
Теорема гласит, что углы, расположенные при основании любого равнобедренного треугольника, всегда равны. Доказать эту теорему очень просто. Рассмотрим изображенный равнобедренный треугольник АВС, у которого АВ=ВС. Из угла АВС необходимо провести биссектрису ВД. Теперь следует рассмотреть два полученных треугольника. По условию АВ=ВС, сторона ВД у треугольников общая, а углы АВД и СВД равны, ведь ВД – биссектриса. Вспомнив первый признак равенства, можно смело заключить, что рассматриваемые треугольники равны. А следовательно, равны все соответствующие углы. И, конечно, стороны, но к этому моменту вернемся позже.
Высота равнобедренного треугольника
Основная теорема, на которой базируется решение практически всех задач, звучит так: высота в равнобедренном треугольнике является биссектрисой и медианой. Чтобы понять её практический смысл (или суть), следует сделать вспомогательное пособие. Для этого необходимо вырезать из бумаги равнобедренный треугольник. Легче всего это сделать из обычного тетрадного листка в клеточку.
Согните полученный треугольник пополам, совместив боковые стороны. Что получилось? Два равных треугольника. Теперь следует проверить догадки. Разверните полученное оригами. Прочертите линию сгиба. При помощи транспортира проверьте угол между прочерченной линией и основанием треугольника. О чем говорит угол в 90 градусов? О том, что прочерченная линия – перпендикуляр. По определению – высота. Как находить высоту в равнобедренном треугольнике, мы разобрались. Теперь займемся углами при вершине. При помощи того же транспортира проверьте углы, образованные теперь уже высотой. Они равны. Значит, высота одновременно является и биссектрисой. Вооружившись линейкой, измерьте отрезки, на которые разбивает высота основание. Они равны. Следовательно, высота в равнобедренном треугольнике делит основание пополам и является медианой.
Доказательство теоремы
Наглядное пособие ярко демонстрирует истинность теоремы. Но геометрия – наука достаточно точная, поэтому требует доказательств.
Во время рассмотрения равенства углов при основании было доказано равенство треугольников. Напомним, ВД – биссектриса, а треугольники АВД и СВД равны. Вывод был таков: соответствующие стороны треугольника и, естественно, углы равны. Значит, АД = СД. Следовательно, ВД – медиана. Осталось доказать, что ВД является высотой. Исходя из равенства рассматриваемых треугольников, получается, что угол АДВ равен углу СДВ. Но эти два угла являются смежными, и, как известно, дают в сумме 180 градусов. Следовательно, чему они равны? Конечно, 90 градусам. Таким образом, ВД – это высота в равнобедренном треугольнике, проведенная к основанию. Что и требовалось доказать.
Основные признаки
- Чтобы успешно решать задачи, следует запомнить основные признаки равнобедренных треугольников. Они как бы обратны теоремам.
- Если в ходе решения задачи обнаруживается равенство двух углов, значит, вы имеете дело с равнобедренным треугольником.
- Если удалось доказать, что медиана является одновременно и высотой треугольника, смело заключайте – треугольник равнобедренный.
- Если биссектриса является и высотой, то, опираясь на основные признаки, треугольник относят к равнобедренным.
- И, конечно, если медиана выступает и в роли высоты, то такой треугольник — равнобедренный.
Формула высоты 1
Однако для большинства задач требуется найти арифметическую величину высоты. Именно поэтому рассмотрим, как находить высоту в равнобедренном треугольнике.
Вернемся к представленной выше фигуре АВС, у которой а – боковые стороны, в — основание. ВД – высота этого треугольника, она имеет обозначение h.
Что представляет собой треугольник АВД? Так как ВД – высота, то треугольник АВД – прямоугольный, катет которого необходимо найти. Воспользовавшись формулой Пифагора, получаем:
АВ² = АД² + ВД²
Определив из выражения ВД и подставив принятые ранее обозначения, получим:
Н² = а² – (в/2)².
Необходимо извлечь корень:
Н = √а² – в²/4.
Если вынести из под знака корня ¼ , то формула будет иметь вид:
Н = ½ √4а² – в².
Так находится высота в равнобедренном треугольнике. Формула вытекает из теоремы Пифагора. Даже если забыть эту символическую запись, то, зная метод нахождения, всегда можно её вывести.
Формула высоты 2
Формула, описанная выше, является основной и чаще всего используется при решении большинства геометрических задач. Но она не единственная. Иногда в условии, вместо основания, дано значение угла. При таких данных как находить высоту в равнобедренном треугольнике? Для решения подобных задач целесообразно использовать другую формулу:
Н = а/sin α,
где Н – высота, направленная к основанию,
а – боковая сторона,
α – угол при основании.
Если в задаче дано значение угла при вершине, то высота в равнобедренном треугольнике находится следующим образом:
Н = а/cos (β/2),
где Н – высота, опущенная на основание,,
β – угол при вершине,
а – боковая сторона.
Прямоугольный равнобедренный треугольник
Очень интересным свойством обладает треугольник, вершина которого равна 90 градусам. Рассмотрим прямоугольный треугольник АВС. Как и в предыдущих случаях, ВД – высота, направленная к основанию.
Углы при основании равны. Вычислить их большого труда не составит:
α = (180 – 90)/2.
Таким образом, углы, находящиеся при основании, всегда по 45 градусов. Теперь рассмотрим треугольник АДВ. Он также является прямоугольным. Найдем угол АВД. Путем несложных вычислений получаем 45 градусов. А, следовательно, этот треугольник не только прямоугольный, но и равнобедренный. Стороны АД и ВД являются боковыми сторонами и равны между собой.
Но сторона АД в то же время является половиной стороны АС. Получается, что высота в равнобедренном треугольнике равна половине основания, а если записать в виде формулы, то получим следующее выражение:
Н = в/2.
Следует не забывать, что данная формула является исключительно частным случаем, и может быть использована только для прямоугольных равнобедренных треугольников.
Золотые треугольники
Очень интересным является золотой треугольник. В этой фигуре отношение боковой стороны к основанию равняется величине, названной числом Фидия. Угол, расположенный при вершине — 36 градусов, при основании – 72 градуса. Этим треугольником восхищались пифагорейцы. Принципы золотого треугольника положены в основу множества бессмертных шедевров. Известная всем пятиконечная звезда построена на пересечении равнобедренных треугольников. Для многих творений Леонардо да Винчи использовал принцип «золотого треугольника». Композиция «Джоконды» основана как раз на фигурах, которые создают собой правильный звездчатый пятиугольник.
Картина «Кубизм», одно из творений Пабло Пикассо, завораживает взгляд положенными в основу равнобедренными треугольниками.
Источник: fb.rumonateka.com
Все формулы для треугольника
L — биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC, разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.
L — высота=биссектриса=медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол вершины
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты= биссектрисы= медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — стороны треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам. Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a , b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам. Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).
M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом). Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
H — высота треугольника
a — сторона, основание
b. c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
*Внимательно, при подстановке в формулу, для тупого угла ( α>90), сosα, принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Есть следующие формулы для определения катета или гипотенузы
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (c, a, b):
zdesformula.ru
Как находить высоту в равнобедренном треугольнике? Формула нахождения, свойства высоты в равнобедренном треугольнике
Геометрия – это не только предмет в школе, по которому нужно получить отличную оценку. Это еще и знания, которые часто требуются в жизни. Например, при строительстве дома с высокой крышей необходимо рассчитать толщину бревен и их количество. Это несложно, если знать, как находить высоту в равнобедренном треугольнике. Архитектурные сооружения базируются на знании свойств геометрических фигур. Формы зданий зачастую визуально напоминают их. Египетские пирамиды, пакеты с молоком, художественная вышивка, северные росписи и даже пирожки – это все треугольники, окружающие человека. Как говорил Платон, весь мир базируется на треугольниках.
Равнобедренный треугольник
Чтобы было понятнее, о чем далее пойдет речь, стоит немного вспомнить азы геометрии.
Треугольник является равнобедренным, если он имеет две равных стороны. Их всегда называют боковыми. Сторона, размеры которой отличаются, получила название основания.
Основные понятия
Как и любая наука, геометрия имеет свои основные правила и понятия. Их достаточно много. Рассмотрим лишь те, без которых наша тема будет несколько непонятна.
Высота – это прямая линия, проведенная перпендикулярно к противоположной стороне.
Медиана – это отрезок, направленный из любой вершины треугольника исключительно к середине противоположной стороны.
Биссектриса угла – это луч, разделяющий угол пополам.
Биссектриса треугольника – это прямая, вернее, отрезок биссектрисы угла, соединяющий вершину с противоположной стороной.
Очень важно запомнить, что биссектриса угла – это обязательно луч, а биссектриса треугольника – это часть такого луча.
Углы при основании
Теорема гласит, что углы, расположенные при основании любого равнобедренного треугольника, всегда равны. Доказать эту теорему очень просто. Рассмотрим изображенный равнобедренный треугольник АВС, у которого АВ=ВС. Из угла АВС необходимо провести биссектрису ВД. Теперь следует рассмотреть два полученных треугольника. По условию АВ=ВС, сторона ВД у треугольников общая, а углы АВД и СВД равны, ведь ВД – биссектриса. Вспомнив первый признак равенства, можно смело заключить, что рассматриваемые треугольники равны. А следовательно, равны все соответствующие углы. И, конечно, стороны, но к этому моменту вернемся позже.
Высота равнобедренного треугольника
Основная теорема, на которой базируется решение практически всех задач, звучит так: высота в равнобедренном треугольнике является биссектрисой и медианой. Чтобы понять её практический смысл (или суть), следует сделать вспомогательное пособие. Для этого необходимо вырезать из бумаги равнобедренный треугольник. Легче всего это сделать из обычного тетрадного листка в клеточку.
Согните полученный треугольник пополам, совместив боковые стороны. Что получилось? Два равных треугольника. Теперь следует проверить догадки. Разверните полученное оригами. Прочертите линию сгиба. При помощи транспортира проверьте угол между прочерченной линией и основанием треугольника. О чем говорит угол в 90 градусов? О том, что прочерченная линия – перпендикуляр. По определению – высота. Как находить высоту в равнобедренном треугольнике, мы разобрались. Теперь займемся углами при вершине. При помощи того же транспортира проверьте углы, образованные теперь уже высотой. Они равны. Значит, высота одновременно является и биссектрисой. Вооружившись линейкой, измерьте отрезки, на которые разбивает высота основание. Они равны. Следовательно, высота в равнобедренном треугольнике делит основание пополам и является медианой.
Доказательство теоремы
Наглядное пособие ярко демонстрирует истинность теоремы. Но геометрия – наука достаточно точная, поэтому требует доказательств.
Во время рассмотрения равенства углов при основании было доказано равенство треугольников. Напомним, ВД – биссектриса, а треугольники АВД и СВД равны. Вывод был таков: соответствующие стороны треугольника и, естественно, углы равны. Значит, АД = СД. Следовательно, ВД – медиана. Осталось доказать, что ВД является высотой. Исходя из равенства рассматриваемых треугольников, получается, что угол АДВ равен углу СДВ. Но эти два угла являются смежными, и, как известно, дают в сумме 180 градусов. Следовательно, чему они равны? Конечно, 90 градусам. Таким образом, ВД – это высота в равнобедренном треугольнике, проведенная к основанию. Что и требовалось доказать.
Основные признаки
- Чтобы успешно решать задачи, следует запомнить основные признаки равнобедренных треугольников. Они как бы обратны теоремам.
- Если в ходе решения задачи обнаруживается равенство двух углов, значит, вы имеете дело с равнобедренным треугольником.
- Если удалось доказать, что медиана является одновременно и высотой треугольника, смело заключайте – треугольник равнобедренный.
- Если биссектриса является и высотой, то, опираясь на основные признаки, треугольник относят к равнобедренным.
- И, конечно, если медиана выступает и в роли высоты, то такой треугольник — равнобедренный.
Формула высоты 1
Однако для большинства задач требуется найти арифметическую величину высоты. Именно поэтому рассмотрим, как находить высоту в равнобедренном треугольнике.
Вернемся к представленной выше фигуре АВС, у которой а – боковые стороны, в — основание. ВД – высота этого треугольника, она имеет обозначение h.
Что представляет собой треугольник АВД? Так как ВД – высота, то треугольник АВД – прямоугольный, катет которого необходимо найти. Воспользовавшись формулой Пифагора, получаем:
АВ² = АД² + ВД²
Определив из выражения ВД и подставив принятые ранее обозначения, получим:
Н² = а² – (в/2)².
Необходимо извлечь корень:
Н = √а² – в²/4.
Если вынести из под знака корня ¼ , то формула будет иметь вид:
Н = ½ √4а² – в².
Так находится высота в равнобедренном треугольнике. Формула вытекает из теоремы Пифагора. Даже если забыть эту символическую запись, то, зная метод нахождения, всегда можно её вывести.
Формула высоты 2
Формула, описанная выше, является основной и чаще всего используется при решении большинства геометрических задач. Но она не единственная. Иногда в условии, вместо основания, дано значение угла. При таких данных как находить высоту в равнобедренном треугольнике? Для решения подобных задач целесообразно использовать другую формулу:
Н = а/sin α,
где Н – высота, направленная к основанию,
а – боковая сторона,
α – угол при основании.
Если в задаче дано значение угла при вершине, то высота в равнобедренном треугольнике находится следующим образом:
Н = а/cos (β/2),
где Н – высота, опущенная на основание,,
β – угол при вершине,
а – боковая сторона.
Прямоугольный равнобедренный треугольник
Очень интересным свойством обладает треугольник, вершина которого равна 90 градусам. Рассмотрим прямоугольный треугольник АВС. Как и в предыдущих случаях, ВД – высота, направленная к основанию.
Углы при основании равны. Вычислить их большого труда не составит:
α = (180 – 90)/2.
Таким образом, углы, находящиеся при основании, всегда по 45 градусов. Теперь рассмотрим треугольник АДВ. Он также является прямоугольным. Найдем угол АВД. Путем несложных вычислений получаем 45 градусов. А, следовательно, этот треугольник не только прямоугольный, но и равнобедренный. Стороны АД и ВД являются боковыми сторонами и равны между собой.
Но сторона АД в то же время является половиной стороны АС. Получается, что высота в равнобедренном треугольнике равна половине основания, а если записать в виде формулы, то получим следующее выражение:
Н = в/2.
Следует не забывать, что данная формула является исключительно частным случаем, и может быть использована только для прямоугольных равнобедренных треугольников.
Золотые треугольники
Очень интересным является золотой треугольник. В этой фигуре отношение боковой стороны к основанию равняется величине, названной числом Фидия. Угол, расположенный при вершине — 36 градусов, при основании – 72 градуса. Этим треугольником восхищались пифагорейцы. Принципы золотого треугольника положены в основу множества бессмертных шедевров. Известная всем пятиконечная звезда построена на пересечении равнобедренных треугольников. Для многих творений Леонардо да Винчи использовал принцип «золотого треугольника». Композиция «Джоконды» основана как раз на фигурах, которые создают собой правильный звездчатый пятиугольник.
Картина «Кубизм», одно из творений Пабло Пикассо, завораживает взгляд положенными в основу равнобедренными треугольниками.
autogear.ru
Все формулы высоты, медианы, биссектрисы равнобедренного треугольника
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
- Подробности
- Автор: Administrator
www-formula.ru
Высота треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Высота, проведенная в любом треугольнике, делит его на два прямоугольных треугольника, становясь смежным катетом. Сторона, на которую опущена высота, оказывается также разделенной на две пропорциональных части. Зная все три стороны, можно собрать их по теореме Пифагора, и приравняв высоту в качестве катета в двух вышеуказанных треугольниках, получить ее формулу для любого произвольного треугольника: 
С другой стороны, можно использовать сторону, прилежащую к высоте и угол α, чтобы вычислить высоту треугольника.
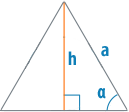
Известная его сторона будет гипотенузой в прямоугольном треугольнике, а сама высота – катетом, противолежащим углу α. Два этих измерения связывает синус угла, поэтому высота равна его произведению на сторону a: h=a sinα
Высота в прямоугольном треугольнике, опущенная из прямого угла (остальные две совпадают с катетами), получает особые свойства. Так как все три получившихся прямоугольных треугольника подобны друг другу, их стороны составляют пропорцию, которая раскладывается как квадрат высоты, равный произведению проекцию катетов на гипотенузу, или проще говоря, частей гипотенузы, на которые ее делит высота.
Из этого следует, что высота равна квадратному корню из данного произведения, а это есть не что иное как среднее пропорциональное приведенного выражения.
В равностороннем треугольнике, высота делит угол, из которого она исходит, на два одинаковых угла по 30°. Высота, оказываясь катетом, прилежащим к этому углу, внутри прямоугольного треугольника, подчиняется отношению косинуса угла α, а так как 
, а гипотенуза a, то формула высоты в равностороннем треугольнике будет выглядеть так: 
geleot.ru
Все формулы высоты треугольника
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
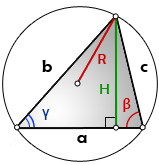H — высота треугольника
a — сторона, основание
b, c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
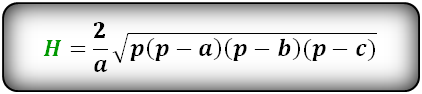
Формула длины высоты через сторону и угол, (H):
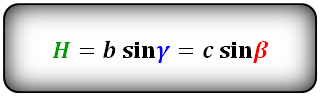
Формула длины высоты через сторону и площадь, (H):
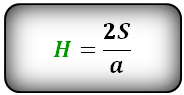
Формула длины высоты через стороны и радиус, (H):
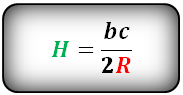
- Подробности
- Автор: Administrator
www-formula.ru